Chapter 19. Technology
|
|
|
- Dina Walters
- 5 years ago
- Views:
Transcription
1 Chpter 9 Technolog
2 Technologies A technolog is process b which inputs re converted to n output. E.g. lbor, computer, projector, electricit, nd softwre re being combined to produce this lecture.
3 Technologies Usull severl technologies will produce the sme product -- blckbord nd chlk cn be used insted of computer nd projector. Which technolog is best? How do we compre technologies?
4 Input Bundles i denotes the mount used of input i; i.e. the level of input i. An input bundle is vector of the input levels; (,,, n ). E.g. (,, 3 ) = (6, 0, 9 3).
5 Production Functions denotes the output level. The technolog s production function sttes the mimum mount of output possible from n input bundle. f(,, n )
6 Production Functions One input, one output Output Level = f() is the production function. = f( ) is the miml output level obtinble from input units. Input Level
7 Technolog Sets A production pln is n input bundle nd n output level; (,, n, ). A production pln is fesible if f(,, n ) The collection of ll fesible production plns is the technolog set.
8 Technolog Sets One input, one output Output Level = f() is the production function. = f( ) is the miml output level obtinble from input units. = f( ) is n output level tht is fesible from input units. Input Level
9 Technolog Sets The technolog set is T {(,,, ) f(,, ) nd n n 0,, 0}. n
10 Output Level Technolog Sets One input, one output The technolog set Input Level
11 Output Level Technolog Sets One input, one output Technicll inefficient plns Technicll efficient plns The technolog set Input Level
12 Technologies with Multiple Inputs Wht does technolog look like when there is more thn one input? The two input cse: Input levels re nd. Output level is. Suppose the production function is f (, ) /3 /3.
13 Technologies with Multiple Inputs E.g. the miml output level possible from the input bundle (, ) = (, 8) is 8 /3 /3 /3 /3 4. And the miml output level possible from (, ) = (8,8) is /3 /3 /3 /
14 Technologies with Multiple Output, Inputs (8,) (8,8)
15 Technologies with Multiple Inputs The output unit isoqunt is the set of ll input bundles tht ield t most the sme output level.
16 Isoqunts with Two Vrible Inputs
17 Isoqunts with Two Vrible Inputs Isoqunts cn be grphed b dding n output level is nd displing ech isoqunt t the height of the isoqunt s output level.
18 Isoqunts with Two Vrible Output, Inputs
19 Isoqunts with Two Vrible Inputs More isoqunts tell us more bout the technolog.
20 Isoqunts with Two Vrible Inputs
21 Isoqunts with Two Vrible Output, Inputs
22 Technologies with Multiple Inputs The complete collection of isoqunts is the isoqunt mp. The isoqunt mp is equivlent to the production function -- ech is the other. E.g. f (, ) /3 / 3
23 Technologies with Multiple Inputs
24 Technologies with Multiple Inputs
25 Technologies with Multiple Inputs
26 Technologies with Multiple Inputs
27 Technologies with Multiple Inputs
28 Technologies with Multiple Inputs
29 Technologies with Multiple Inputs
30 Technologies with Multiple Inputs
31 Technologies with Multiple Inputs
32 Technologies with Multiple Inputs
33 Technologies with Multiple Inputs
34 Technologies with Multiple Inputs
35 Technologies with Multiple Inputs
36 Technologies with Multiple Inputs
37 Technologies with Multiple Inputs
38 Technologies with Multiple Inputs
39 Cobb-Dougls Technologies A Cobb-Dougls production function is of the form A n n. E.g. /3 /3 with n, A, nd 3 3.
40 Cobb-Dougls Technologies All isoqunts re hperbolic, smptoting to, but never touching n is.
41 Cobb-Dougls Technologies All isoqunts re hperbolic, smptoting to, but never touching n is. "
42 Cobb-Dougls Technologies All isoqunts re hperbolic, smptoting to, but never touching n is. " '
43 Cobb-Dougls Technologies All isoqunts re hperbolic, smptoting to, but never touching n is. " ' > " '
44 Fied-Proportions Technologies A fied-proportions production function is of the form E.g. min{,,, n n }. min{, } With n, nd. Q: Fied-proportions is nlogous to wht other concept?
45 Fied-Proportions Technologies min{,} = min{, } = 4 min{, } = 8 min{, } = 4
46 Perfect-Substitutes Technologies A perfect-substitutes production function is of the form E.g. n n 3. with n, nd 3.
47 Perfect-Substitution Technologies = = = 48 All re liner nd prllel 9 8 4
48 Mrginl (Phsicl) Products f (,, n ) The mrginl product of input i is the rte-of-chnge of the output level s the level of input i chnges, holding ll other input levels fied. Tht is, MP i i
49 Mrginl (Phsicl) Products E.g. if /3 / 3 f (, ) then the mrginl product of input is obtined b the prtil derivtive of output WRT good : MP 3 /3 /3
50 Mrginl (Phsicl) Products E.g. if f(, ) / /3 3 then the mrginl product of input is MP / 3 / 3 3 nd the mrginl product of input is
51 Mrginl (Phsicl) Products E.g. if f(, ) / /3 3 then the mrginl product of input is MP / 3 / 3 3 nd the mrginl product of input is MP /3 / 3 3.
52 Mrginl (Phsicl) Products Tpicll the mrginl product of one input depends upon the mount used of other inputs. E.g. if MP 3 if = 8, /3 /3 MP nd if = 7 then then, /3 /3 4 / MP /3 7 /3 3 / 3 3.
53 Mrginl (Phsicl) Products The mrginl product of input i is diminishing if it becomes smller s the level of input i increses. Tht is, if the second derivtive of output WRT good I is negtive: 0. i i i i i MP
54 Mrginl (Phsicl) Products E.g. if /3 /3 then MP 3 /3 /3 nd MP /3 /3 3
55 so Mrginl (Phsicl) Products /3 / 3 E.g. if MP 3 /3 /3 MP nd then MP /3 /3 3 5/3 / 3 9 0
56 Mrginl (Phsicl) Products E.g. if then MP / 3 / 3 nd MP 3 3 so MP 5 / 3 / nd MP /3 4 / /3 / 3 /3 /3
57 Mrginl (Phsicl) Products E.g. if MP so nd 3 nd /3 /3 /3 / 3 MP MP MP /3 /3 5/3 / 3 9 /3 4/ 3 9 then Both mrginl products re diminishing
58 Returns-to-Scle Mrginl products describe the chnge in output level s single input level chnges. Returns-to-scle describes how the output level chnges s ll input levels chnge in direct proportion (e.g. ll input levels doubled, or hlved).
59 Returns-to-Scle If, for n input bundle (,, n ), f ( k, k,, kn) kf (,,, n then the technolog described b the production function f ehibits constnt returns-to-scle. E.g. (k = ) doubling ll input levels doubles the output level. )
60 Output Level Returns-to-Scle One input, one output = f() Constnt returns-to-scle Input Level
61 Returns-to-Scle If, for n input bundle (,, n ), f ( k, k,, kn) kf (,,, n then the technolog ehibits diminishing returns-to-scle. E.g. (k = ) doubling ll input levels less thn doubles the output level. )
62 Output Level Returns-to-Scle One input, one output f( ) f( ) f( ) = f() Decresing returns-to-scle Input Level
63 Returns-to-Scle If, for n input bundle (,, n ), f( k, k,, k ) kf(,,, ) n then the technolog ehibits incresing returns-to-scle. E.g. (k = ) doubling ll input levels more thn doubles the output level. n
64 Returns-to-Scle One input, one output Output Level f( ) Incresing returns-to-scle = f() f( ) f( ) Input Level
65 Returns-to-Scle A single technolog cn locll ehibit different returns-to-scle.
66 Output Level Returns-to-Scle One input, one output Incresing returns-to-scle = f() Decresing returns-to-scle Input Level
67 Emples of Returns-to-Scle The perfect-substitutes production function is n n Epnd ll input levels proportiontel b k. The output level becomes ( k ) ( k) n ( k n ).
68 Emples of Returns-to-Scle The perfect-substitutes production function is n n Epnd ll input levels proportiontel b k. The output level becomes ( k ) ( k ) ( k ) k( ) n n n. n
69 Emples of Returns-to-Scle. n n The perfect-substitutes production function is Epnd ll input levels proportiontel b k. The output level becomes. ) ( ) ( ) ( ) ( k k k k k n n n n The perfect-substitutes production function ehibits constnt returns-to-scle.
70 Emples of Returns-to-Scle The perfect-complements production function is }. min{,,, n n Epnd ll input levels proportiontel b k. The output level becomes min{ ( k ), ( k),, n ( k n )}
71 Emples of Returns-to-Scle The perfect-complements production function is min{,,, }. Epnd ll input levels proportiontel b k. The output level becomes min{ ( k k(min{ ),, ( k ),,,, n n n }) n ( k n n )}
72 Emples of Returns-to-Scle The perfect-complements production function is min{,,, n n Epnd ll input levels proportiontel b k. The output level becomes min{ ( k k(min{ k. ),, ( k ),,,, n n n ( k The perfect-complements production function ehibits constnt returns-to-scle. }) n )} }.
73 Emples of Returns-to-Scle The Cobb-Dougls production function is Epnd ll input levels proportiontel b k. The output level becomes n n k ( k ) ( ) ( k ). n n
74 Emples of Returns-to-Scle. n n The Cobb-Dougls production function is Epnd ll input levels proportiontel b k. The output level becomes n n n n k k k k k k ) ( ) ( ) (
75 Emples of Returns-to-Scle The Cobb-Dougls production function is. n n Epnd ll input levels proportiontel b k. The output level becomes n ( k ) ( k ) ( k ) k k k n k n n n n n
76 Emples of Returns-to-Scle. n n The Cobb-Dougls production function is Epnd ll input levels proportiontel b k. The output level becomes. ) ( ) ( ) ( k k k k k k k k n n n n n n n n
77 Emples of Returns-to-Scle The Cobb-Dougls production function is ) ( k ) n ( k n n ( k n n The Cobb-Dougls technolog s returnsto-scle is constnt if + + n =. ) k.
78 Emples of Returns-to-Scle The Cobb-Dougls production function is ( k ) ( k ) ( k ) n k n. n n n. The Cobb-Dougls technolog s returnsto-scle is constnt if + + n = incresing if + + n >
79 Emples of Returns-to-Scle The Cobb-Dougls production function is. n n n ( k ) ( k ) ( k ) n k n. The Cobb-Dougls technolog s returnsto-scle is constnt if + + n = incresing if + + n > decresing if + + n <.
80 Returns-to-Scle Q: Cn technolog ehibit incresing returns-to-scle even though ll of its mrginl products re diminishing?
81 Returns-to-Scle Q: Cn technolog ehibit incresing returns-to-scle even if ll of its mrginl products re diminishing? A: Yes. E.g. /3 /3.
82 Returns-to-Scle /3 /3 4 3 so even though ech individul eponent is <, this technolog ehibits incresing returns-to-scle.
83 Returns-to-Scle /3 /3 But 4 3 MP 3 /3 so this technolog ehibits incresing returns-to-scle. /3 diminishes s increses
84 Returns-to-Scle / / so this technolog ehibits 3 incresing returns-to-scle. 3 /3 / 3 But MP diminishes s increses nd increses. /3 /3 MP diminishes s 3
85 Returns-to-Scle So technolog cn ehibit incresing returns-to-scle even if ll of its mrginl products re diminishing. Wh?
86 Returns-to-Scle A mrginl product is the rte-ofchnge of output s one input level increses, holding ll other input levels fied. Mrginl product diminishes becuse the other input levels re fied, so the incresing input s units hve ech less nd less of other inputs with which to work.
87 Returns-to-Scle When ll input levels re incresed proportiontel, there need be no diminution of mrginl products since ech input will lws hve the sme mount of other inputs with which to work. Input productivities need not fll nd so returns-to-scle cn be constnt or incresing.
88 Technicl Rte-of-Substitution TRS = the rte t which firm substitute one input for nother without chnging its output level (nlogous to MRS).
89 Technicl Rte-of-Substitution ' '
90 Technicl Rte-of-Substitution ' The slope is the rte t which input must be given up s input s level is incresed so s not to chnge the output level. The slope of n isoqunt is its technicl rte-ofsubstitution. '
91 Technicl Rte-of-Substitution How is technicl rte-of-substitution computed?
92 Technicl Rte-of-Substitution How is technicl rte-of-substitution computed? The production function is (, A smll chnge (d, d ) in the input bundle cuses chnge to the output level of f ). d d d.
93 Technicl Rte-of-Substitution d d d. But d = 0 since there is to be no chnge to the output level, so the chnges d nd d to the input levels must stisf 0 d d.
94 Technicl Rte-of-Substitution 0 d d rerrnges to d d so. / / d d
95 Technicl Rte-of-Substitution d d / / is the rte t which input must be given up s input increses so s to keep the output level constnt. It is the slope of the isoqunt.
96 so Technicl Rte-of-Substitution; A Cobb-Dougls Emple f (, ) b b nd b b The technicl rte-of-substitution is. d d / / b b b b.
97 Technicl Rte-of-Substitution; A Cobb-Dougls Emple ; ndb 3 /3 /3 3 TRS b (/ 3) ( / 3)
98 Technicl Rte-of-Substitution; A Cobb-Dougls Emple /3 /3 ; ndb TRS TRS b (/ 3) ( / 3) 8 4 4
99 Technicl Rte-of-Substitution; 6 A Cobb-Dougls Emple / ; nd b 3 3 TRS ( / 3) b ( / 3) TRS 6 4 /3 3
100 Well-Behved Technologies A well-behved technolog is monotonic, nd conve.
101 Well-Behved Technologies - Monotonicit Monotonicit: More of n input genertes more output. monotonic not monotonic
102 Well-Behved Technologies - Conveit Conveit: If the input bundles nd both provide units of output then the miture t + (-t) provides t lest units of output, for n 0 < t <.
103 Well-Behved Technologies - Conveit ' " ' "
104 Well-Behved Technologies - Conveit ' " ' ' " ' " t ( t), t ( t) "
105 Well-Behved Technologies - Conveit ' " ' ' " ' " t ( t), t ( t) "
106 Well-Behved Technologies - ' Conveit Conveit implies tht the TRS increses (becomes less negtive) s increses. " ' "
107 Well-Behved Technologies higher output
108 The Long-Run nd the Short- Runs The long-run is the circumstnce in which firm is unrestricted in its choice of ll input levels. There re mn possible short-runs. A short-run is circumstnce in which firm is restricted in some w in its choice of t lest one input level.
109 The Long-Run nd the Short- Runs Emples of restrictions tht plce firm into short-run: temporril being unble to instll, or remove, mchiner being required b lw to meet ffirmtive ction quots hving to meet domestic content regultions.
110 The Long-Run nd the Short- Runs A useful w to think of the long-run is tht the firm cn choose s it pleses in which short-run circumstnce to be.
111 The Long-Run nd the Short- Runs Wht do short-run restrictions impl for firm s technolog? Suppose the short-run restriction is fiing the level of input. Input is thus fied input in the short-run. Input remins vrible.
112 The Long-Run nd the Short- Runs
113 The Long-Run nd the Short- Runs
114 The Long-Run nd the Short- Runs
115 The Long-Run nd the Short- Runs
116 The Long-Run nd the Short- Runs
117 The Long-Run nd the Short- Runs
118 The Long-Run nd the Short- Runs
119 The Long-Run nd the Short- Runs
120 The Long-Run nd the Short- Runs
121 The Long-Run nd the Short- Runs
122 The Long-Run nd the Short- Runs
123 The Long-Run nd the Short- Runs
124 The Long-Run nd the Short- Runs Four short-run production functions.
125 The Long-Run nd the Short- /3 /3 Runs is the long-run production function (both nd re vrible). The short-run production function when is /3 /3 /3. The short-run production function when 0 is /3 /3 /3 0 5.
126 The Long-Run nd the Short- Runs / = 3 0 / 3 / = 3 5 / 3 = / 3 / 3 = / 3 / 3 Four short-run production functions.
Technologies. Chapter Eighteen. Technologies. Input Bundles. Production Functions. Production Functions. Technology
 Technologies Chapter Eighteen Technolog A technolog is a process b which inputs are converted to an output. E.g. labor, a computer, a projector, electricit, and software are being combined to produce this
Technologies Chapter Eighteen Technolog A technolog is a process b which inputs are converted to an output. E.g. labor, a computer, a projector, electricit, and software are being combined to produce this
ARITHMETIC OPERATIONS. The real numbers have the following properties: a b c ab ac
 REVIEW OF ALGEBRA Here we review the bsic rules nd procedures of lgebr tht you need to know in order to be successful in clculus. ARITHMETIC OPERATIONS The rel numbers hve the following properties: b b
REVIEW OF ALGEBRA Here we review the bsic rules nd procedures of lgebr tht you need to know in order to be successful in clculus. ARITHMETIC OPERATIONS The rel numbers hve the following properties: b b
MAT137 Calculus! Lecture 20
 officil website http://uoft.me/mat137 MAT137 Clculus! Lecture 20 Tody: 4.6 Concvity 4.7 Asypmtotes Net: 4.8 Curve Sketching 4.5 More Optimiztion Problems MVT Applictions Emple 1 Let f () = 3 27 20. 1 Find
officil website http://uoft.me/mat137 MAT137 Clculus! Lecture 20 Tody: 4.6 Concvity 4.7 Asypmtotes Net: 4.8 Curve Sketching 4.5 More Optimiztion Problems MVT Applictions Emple 1 Let f () = 3 27 20. 1 Find
3.1 Exponential Functions and Their Graphs
 . Eponentil Functions nd Their Grphs Sllbus Objective: 9. The student will sketch the grph of eponentil, logistic, or logrithmic function. 9. The student will evlute eponentil or logrithmic epressions.
. Eponentil Functions nd Their Grphs Sllbus Objective: 9. The student will sketch the grph of eponentil, logistic, or logrithmic function. 9. The student will evlute eponentil or logrithmic epressions.
Chapter 6 Notes, Larson/Hostetler 3e
 Contents 6. Antiderivtives nd the Rules of Integrtion.......................... 6. Are nd the Definite Integrl.................................. 6.. Are............................................ 6. Reimnn
Contents 6. Antiderivtives nd the Rules of Integrtion.......................... 6. Are nd the Definite Integrl.................................. 6.. Are............................................ 6. Reimnn
Operations with Polynomials
 38 Chpter P Prerequisites P.4 Opertions with Polynomils Wht you should lern: How to identify the leding coefficients nd degrees of polynomils How to dd nd subtrct polynomils How to multiply polynomils
38 Chpter P Prerequisites P.4 Opertions with Polynomils Wht you should lern: How to identify the leding coefficients nd degrees of polynomils How to dd nd subtrct polynomils How to multiply polynomils
LINEAR ALGEBRA APPLIED
 5.5 Applictions of Inner Product Spces 5.5 Applictions of Inner Product Spces 7 Find the cross product of two vectors in R. Find the liner or qudrtic lest squres pproimtion of function. Find the nth-order
5.5 Applictions of Inner Product Spces 5.5 Applictions of Inner Product Spces 7 Find the cross product of two vectors in R. Find the liner or qudrtic lest squres pproimtion of function. Find the nth-order
AQA Further Pure 2. Hyperbolic Functions. Section 2: The inverse hyperbolic functions
 Hperbolic Functions Section : The inverse hperbolic functions Notes nd Emples These notes contin subsections on The inverse hperbolic functions Integrtion using the inverse hperbolic functions Logrithmic
Hperbolic Functions Section : The inverse hperbolic functions Notes nd Emples These notes contin subsections on The inverse hperbolic functions Integrtion using the inverse hperbolic functions Logrithmic
5.2 Exponent Properties Involving Quotients
 5. Eponent Properties Involving Quotients Lerning Objectives Use the quotient of powers property. Use the power of quotient property. Simplify epressions involving quotient properties of eponents. Use
5. Eponent Properties Involving Quotients Lerning Objectives Use the quotient of powers property. Use the power of quotient property. Simplify epressions involving quotient properties of eponents. Use
Chapter 3 Exponential and Logarithmic Functions Section 3.1
 Chpter 3 Eponentil nd Logrithmic Functions Section 3. EXPONENTIAL FUNCTIONS AND THEIR GRAPHS Eponentil Functions Eponentil functions re non-lgebric functions. The re clled trnscendentl functions. The eponentil
Chpter 3 Eponentil nd Logrithmic Functions Section 3. EXPONENTIAL FUNCTIONS AND THEIR GRAPHS Eponentil Functions Eponentil functions re non-lgebric functions. The re clled trnscendentl functions. The eponentil
Lesson 1: Quadratic Equations
 Lesson 1: Qudrtic Equtions Qudrtic Eqution: The qudrtic eqution in form is. In this section, we will review 4 methods of qudrtic equtions, nd when it is most to use ech method. 1. 3.. 4. Method 1: Fctoring
Lesson 1: Qudrtic Equtions Qudrtic Eqution: The qudrtic eqution in form is. In this section, we will review 4 methods of qudrtic equtions, nd when it is most to use ech method. 1. 3.. 4. Method 1: Fctoring
Appendix 3, Rises and runs, slopes and sums: tools from calculus
 Appendi 3, Rises nd runs, slopes nd sums: tools from clculus Sometimes we will wnt to eplore how quntity chnges s condition is vried. Clculus ws invented to do just this. We certinly do not need the full
Appendi 3, Rises nd runs, slopes nd sums: tools from clculus Sometimes we will wnt to eplore how quntity chnges s condition is vried. Clculus ws invented to do just this. We certinly do not need the full
A REVIEW OF CALCULUS CONCEPTS FOR JDEP 384H. Thomas Shores Department of Mathematics University of Nebraska Spring 2007
 A REVIEW OF CALCULUS CONCEPTS FOR JDEP 384H Thoms Shores Deprtment of Mthemtics University of Nebrsk Spring 2007 Contents Rtes of Chnge nd Derivtives 1 Dierentils 4 Are nd Integrls 5 Multivrite Clculus
A REVIEW OF CALCULUS CONCEPTS FOR JDEP 384H Thoms Shores Deprtment of Mthemtics University of Nebrsk Spring 2007 Contents Rtes of Chnge nd Derivtives 1 Dierentils 4 Are nd Integrls 5 Multivrite Clculus
BIFURCATIONS IN ONE-DIMENSIONAL DISCRETE SYSTEMS
 BIFRCATIONS IN ONE-DIMENSIONAL DISCRETE SYSTEMS FRANCESCA AICARDI In this lesson we will study the simplest dynmicl systems. We will see, however, tht even in this cse the scenrio of different possible
BIFRCATIONS IN ONE-DIMENSIONAL DISCRETE SYSTEMS FRANCESCA AICARDI In this lesson we will study the simplest dynmicl systems. We will see, however, tht even in this cse the scenrio of different possible
DERIVATIVES NOTES HARRIS MATH CAMP Introduction
 f DERIVATIVES NOTES HARRIS MATH CAMP 208. Introduction Reding: Section 2. The derivtive of function t point is the slope of the tngent line to the function t tht point. Wht does this men, nd how do we
f DERIVATIVES NOTES HARRIS MATH CAMP 208. Introduction Reding: Section 2. The derivtive of function t point is the slope of the tngent line to the function t tht point. Wht does this men, nd how do we
5.7 Improper Integrals
 458 pplictions of definite integrls 5.7 Improper Integrls In Section 5.4, we computed the work required to lift pylod of mss m from the surfce of moon of mss nd rdius R to height H bove the surfce of the
458 pplictions of definite integrls 5.7 Improper Integrls In Section 5.4, we computed the work required to lift pylod of mss m from the surfce of moon of mss nd rdius R to height H bove the surfce of the
Calculus - Activity 1 Rate of change of a function at a point.
 Nme: Clss: p 77 Mths Helper Plus Resource Set. Copright 00 Bruce A. Vughn, Techers Choice Softwre Clculus - Activit Rte of chnge of function t point. ) Strt Mths Helper Plus, then lod the file: Clculus
Nme: Clss: p 77 Mths Helper Plus Resource Set. Copright 00 Bruce A. Vughn, Techers Choice Softwre Clculus - Activit Rte of chnge of function t point. ) Strt Mths Helper Plus, then lod the file: Clculus
Math 8 Winter 2015 Applications of Integration
 Mth 8 Winter 205 Applictions of Integrtion Here re few importnt pplictions of integrtion. The pplictions you my see on n exm in this course include only the Net Chnge Theorem (which is relly just the Fundmentl
Mth 8 Winter 205 Applictions of Integrtion Here re few importnt pplictions of integrtion. The pplictions you my see on n exm in this course include only the Net Chnge Theorem (which is relly just the Fundmentl
5.3 The Fundamental Theorem of Calculus
 CHAPTER 5. THE DEFINITE INTEGRAL 35 5.3 The Funmentl Theorem of Clculus Emple. Let f(t) t +. () Fin the re of the region below f(t), bove the t-is, n between t n t. (You my wnt to look up the re formul
CHAPTER 5. THE DEFINITE INTEGRAL 35 5.3 The Funmentl Theorem of Clculus Emple. Let f(t) t +. () Fin the re of the region below f(t), bove the t-is, n between t n t. (You my wnt to look up the re formul
Lecture 6: Singular Integrals, Open Quadrature rules, and Gauss Quadrature
 Lecture notes on Vritionl nd Approximte Methods in Applied Mthemtics - A Peirce UBC Lecture 6: Singulr Integrls, Open Qudrture rules, nd Guss Qudrture (Compiled 6 August 7) In this lecture we discuss the
Lecture notes on Vritionl nd Approximte Methods in Applied Mthemtics - A Peirce UBC Lecture 6: Singulr Integrls, Open Qudrture rules, nd Guss Qudrture (Compiled 6 August 7) In this lecture we discuss the
Advanced Functions Page 1 of 3 Investigating Exponential Functions y= b x
 Advnced Functions Pge of Investigting Eponentil Functions = b Emple : Write n Eqution to Fit Dt Write n eqution to fit the dt in the tble of vlues. 0 4 4 Properties of the Eponentil Function =b () The
Advnced Functions Pge of Investigting Eponentil Functions = b Emple : Write n Eqution to Fit Dt Write n eqution to fit the dt in the tble of vlues. 0 4 4 Properties of the Eponentil Function =b () The
Properties of Integrals, Indefinite Integrals. Goals: Definition of the Definite Integral Integral Calculations using Antiderivatives
 Block #6: Properties of Integrls, Indefinite Integrls Gols: Definition of the Definite Integrl Integrl Clcultions using Antiderivtives Properties of Integrls The Indefinite Integrl 1 Riemnn Sums - 1 Riemnn
Block #6: Properties of Integrls, Indefinite Integrls Gols: Definition of the Definite Integrl Integrl Clcultions using Antiderivtives Properties of Integrls The Indefinite Integrl 1 Riemnn Sums - 1 Riemnn
13.3. The Area Bounded by a Curve. Introduction. Prerequisites. Learning Outcomes
 The Are Bounded b Curve 3.3 Introduction One of the importnt pplictions of integrtion is to find the re bounded b curve. Often such n re cn hve phsicl significnce like the work done b motor, or the distnce
The Are Bounded b Curve 3.3 Introduction One of the importnt pplictions of integrtion is to find the re bounded b curve. Often such n re cn hve phsicl significnce like the work done b motor, or the distnce
M344 - ADVANCED ENGINEERING MATHEMATICS
 M3 - ADVANCED ENGINEERING MATHEMATICS Lecture 18: Lplce s Eqution, Anltic nd Numericl Solution Our emple of n elliptic prtil differentil eqution is Lplce s eqution, lso clled the Diffusion Eqution. If
M3 - ADVANCED ENGINEERING MATHEMATICS Lecture 18: Lplce s Eqution, Anltic nd Numericl Solution Our emple of n elliptic prtil differentil eqution is Lplce s eqution, lso clled the Diffusion Eqution. If
Logarithmic Functions
 Logrithmic Functions Definition: Let > 0,. Then log is the number to which you rise to get. Logrithms re in essence eponents. Their domins re powers of the bse nd their rnges re the eponents needed to
Logrithmic Functions Definition: Let > 0,. Then log is the number to which you rise to get. Logrithms re in essence eponents. Their domins re powers of the bse nd their rnges re the eponents needed to
MATHEMATICS AND STATISTICS 1.2
 MATHEMATICS AND STATISTICS. Apply lgebric procedures in solving problems Eternlly ssessed 4 credits Electronic technology, such s clcultors or computers, re not permitted in the ssessment of this stndr
MATHEMATICS AND STATISTICS. Apply lgebric procedures in solving problems Eternlly ssessed 4 credits Electronic technology, such s clcultors or computers, re not permitted in the ssessment of this stndr
Functions and transformations
 Functions nd trnsformtions A Trnsformtions nd the prbol B The cubic function in power form C The power function (the hperbol) D The power function (the truncus) E The squre root function in power form
Functions nd trnsformtions A Trnsformtions nd the prbol B The cubic function in power form C The power function (the hperbol) D The power function (the truncus) E The squre root function in power form
Introduction to Algebra - Part 2
 Alger Module A Introduction to Alger - Prt Copright This puliction The Northern Alert Institute of Technolog 00. All Rights Reserved. LAST REVISED Oct., 008 Introduction to Alger - Prt Sttement of Prerequisite
Alger Module A Introduction to Alger - Prt Copright This puliction The Northern Alert Institute of Technolog 00. All Rights Reserved. LAST REVISED Oct., 008 Introduction to Alger - Prt Sttement of Prerequisite
Duality # Second iteration for HW problem. Recall our LP example problem we have been working on, in equality form, is given below.
 Dulity #. Second itertion for HW problem Recll our LP emple problem we hve been working on, in equlity form, is given below.,,,, 8 m F which, when written in slightly different form, is 8 F Recll tht we
Dulity #. Second itertion for HW problem Recll our LP emple problem we hve been working on, in equlity form, is given below.,,,, 8 m F which, when written in slightly different form, is 8 F Recll tht we
Topic 1 Notes Jeremy Orloff
 Topic 1 Notes Jerem Orloff 1 Introduction to differentil equtions 1.1 Gols 1. Know the definition of differentil eqution. 2. Know our first nd second most importnt equtions nd their solutions. 3. Be ble
Topic 1 Notes Jerem Orloff 1 Introduction to differentil equtions 1.1 Gols 1. Know the definition of differentil eqution. 2. Know our first nd second most importnt equtions nd their solutions. 3. Be ble
approaches as n becomes larger and larger. Since e > 1, the graph of the natural exponential function is as below
 . Eponentil nd rithmic functions.1 Eponentil Functions A function of the form f() =, > 0, 1 is clled n eponentil function. Its domin is the set of ll rel f ( 1) numbers. For n eponentil function f we hve.
. Eponentil nd rithmic functions.1 Eponentil Functions A function of the form f() =, > 0, 1 is clled n eponentil function. Its domin is the set of ll rel f ( 1) numbers. For n eponentil function f we hve.
Designing Information Devices and Systems I Discussion 8B
 Lst Updted: 2018-10-17 19:40 1 EECS 16A Fll 2018 Designing Informtion Devices nd Systems I Discussion 8B 1. Why Bother With Thévenin Anywy? () Find Thévenin eqiuvlent for the circuit shown elow. 2kΩ 5V
Lst Updted: 2018-10-17 19:40 1 EECS 16A Fll 2018 Designing Informtion Devices nd Systems I Discussion 8B 1. Why Bother With Thévenin Anywy? () Find Thévenin eqiuvlent for the circuit shown elow. 2kΩ 5V
FUNCTIONS: Grade 11. or y = ax 2 +bx + c or y = a(x- x1)(x- x2) a y
 FUNCTIONS: Grde 11 The prbol: ( p) q or = +b + c or = (- 1)(- ) The hperbol: p q The eponentil function: b p q Importnt fetures: -intercept : Let = 0 -intercept : Let = 0 Turning points (Where pplicble)
FUNCTIONS: Grde 11 The prbol: ( p) q or = +b + c or = (- 1)(- ) The hperbol: p q The eponentil function: b p q Importnt fetures: -intercept : Let = 0 -intercept : Let = 0 Turning points (Where pplicble)
Math 1431 Section M TH 4:00 PM 6:00 PM Susan Wheeler Office Hours: Wed 6:00 7:00 PM Online ***NOTE LABS ARE MON AND WED
 Mth 43 Section 4839 M TH 4: PM 6: PM Susn Wheeler swheeler@mth.uh.edu Office Hours: Wed 6: 7: PM Online ***NOTE LABS ARE MON AND WED t :3 PM to 3: pm ONLINE Approimting the re under curve given the type
Mth 43 Section 4839 M TH 4: PM 6: PM Susn Wheeler swheeler@mth.uh.edu Office Hours: Wed 6: 7: PM Online ***NOTE LABS ARE MON AND WED t :3 PM to 3: pm ONLINE Approimting the re under curve given the type
State space systems analysis (continued) Stability. A. Definitions A system is said to be Asymptotically Stable (AS) when it satisfies
 Stte spce systems nlysis (continued) Stbility A. Definitions A system is sid to be Asymptoticlly Stble (AS) when it stisfies ut () = 0, t > 0 lim xt () 0. t A system is AS if nd only if the impulse response
Stte spce systems nlysis (continued) Stbility A. Definitions A system is sid to be Asymptoticlly Stble (AS) when it stisfies ut () = 0, t > 0 lim xt () 0. t A system is AS if nd only if the impulse response
Problem set 2 The Ricardian Model
 Problem set 2 The Ricrdin Model Eercise 1 Consider world with two countries, U nd V, nd two goods, nd F. It is known tht the mount of work vilble in U is 150 nd in V is 84. The unit lbor requirements for
Problem set 2 The Ricrdin Model Eercise 1 Consider world with two countries, U nd V, nd two goods, nd F. It is known tht the mount of work vilble in U is 150 nd in V is 84. The unit lbor requirements for
The semester B examination for Algebra 2 will consist of two parts. Part 1 will be selected response. Part 2 will be short answer.
 ALGEBRA B Semester Em Review The semester B emintion for Algebr will consist of two prts. Prt will be selected response. Prt will be short nswer. Students m use clcultor. If clcultor is used to find points
ALGEBRA B Semester Em Review The semester B emintion for Algebr will consist of two prts. Prt will be selected response. Prt will be short nswer. Students m use clcultor. If clcultor is used to find points
Interpreting Integrals and the Fundamental Theorem
 Interpreting Integrls nd the Fundmentl Theorem Tody, we go further in interpreting the mening of the definite integrl. Using Units to Aid Interprettion We lredy know tht if f(t) is the rte of chnge of
Interpreting Integrls nd the Fundmentl Theorem Tody, we go further in interpreting the mening of the definite integrl. Using Units to Aid Interprettion We lredy know tht if f(t) is the rte of chnge of
The Regulated and Riemann Integrals
 Chpter 1 The Regulted nd Riemnn Integrls 1.1 Introduction We will consider severl different pproches to defining the definite integrl f(x) dx of function f(x). These definitions will ll ssign the sme vlue
Chpter 1 The Regulted nd Riemnn Integrls 1.1 Introduction We will consider severl different pproches to defining the definite integrl f(x) dx of function f(x). These definitions will ll ssign the sme vlue
MA Lesson 21 Notes
 MA 000 Lesson 1 Notes ( 5) How would person solve n eqution with vrible in n eponent, such s 9? (We cnnot re-write this eqution esil with the sme bse.) A nottion ws developed so tht equtions such s this
MA 000 Lesson 1 Notes ( 5) How would person solve n eqution with vrible in n eponent, such s 9? (We cnnot re-write this eqution esil with the sme bse.) A nottion ws developed so tht equtions such s this
Polynomial Approximations for the Natural Logarithm and Arctangent Functions. Math 230
 Polynomil Approimtions for the Nturl Logrithm nd Arctngent Functions Mth 23 You recll from first semester clculus how one cn use the derivtive to find n eqution for the tngent line to function t given
Polynomil Approimtions for the Nturl Logrithm nd Arctngent Functions Mth 23 You recll from first semester clculus how one cn use the derivtive to find n eqution for the tngent line to function t given
Identify graphs of linear inequalities on a number line.
 COMPETENCY 1.0 KNOWLEDGE OF ALGEBRA SKILL 1.1 Identify grphs of liner inequlities on number line. - When grphing first-degree eqution, solve for the vrible. The grph of this solution will be single point
COMPETENCY 1.0 KNOWLEDGE OF ALGEBRA SKILL 1.1 Identify grphs of liner inequlities on number line. - When grphing first-degree eqution, solve for the vrible. The grph of this solution will be single point
Math 1102: Calculus I (Math/Sci majors) MWF 3pm, Fulton Hall 230 Homework 2 solutions
 Mth 1102: Clculus I (Mth/Sci mjors) MWF 3pm, Fulton Hll 230 Homework 2 solutions Plese write netly, nd show ll work. Cution: An nswer with no work is wrong! Do the following problems from Chpter III: 6,
Mth 1102: Clculus I (Mth/Sci mjors) MWF 3pm, Fulton Hll 230 Homework 2 solutions Plese write netly, nd show ll work. Cution: An nswer with no work is wrong! Do the following problems from Chpter III: 6,
Sections 1.3, 7.1, and 9.2: Properties of Exponents and Radical Notation
 Sections., 7., nd 9.: Properties of Eponents nd Rdicl Nottion Let p nd q be rtionl numbers. For ll rel numbers nd b for which the epressions re rel numbers, the following properties hold. i = + p q p q
Sections., 7., nd 9.: Properties of Eponents nd Rdicl Nottion Let p nd q be rtionl numbers. For ll rel numbers nd b for which the epressions re rel numbers, the following properties hold. i = + p q p q
Math 520 Final Exam Topic Outline Sections 1 3 (Xiao/Dumas/Liaw) Spring 2008
 Mth 520 Finl Exm Topic Outline Sections 1 3 (Xio/Dums/Liw) Spring 2008 The finl exm will be held on Tuesdy, My 13, 2-5pm in 117 McMilln Wht will be covered The finl exm will cover the mteril from ll of
Mth 520 Finl Exm Topic Outline Sections 1 3 (Xio/Dums/Liw) Spring 2008 The finl exm will be held on Tuesdy, My 13, 2-5pm in 117 McMilln Wht will be covered The finl exm will cover the mteril from ll of
du = C dy = 1 dy = dy W is invertible with inverse U, so that y = W(t) is exactly the same thing as t = U(y),
 29. Differentil equtions. The conceptul bsis of llometr Did it occur to ou in Lecture 3 wh Fiboncci would even cre how rpidl rbbit popultion grows? Mbe he wnted to et the rbbits. If so, then he would be
29. Differentil equtions. The conceptul bsis of llometr Did it occur to ou in Lecture 3 wh Fiboncci would even cre how rpidl rbbit popultion grows? Mbe he wnted to et the rbbits. If so, then he would be
SESSION 2 Exponential and Logarithmic Functions. Math 30-1 R 3. (Revisit, Review and Revive)
 Mth 0-1 R (Revisit, Review nd Revive) SESSION Eponentil nd Logrithmic Functions 1 Eponentil nd Logrithmic Functions Key Concepts The Eponent Lws m n 1 n n m m n m n m mn m m m m mn m m m b n b b b Simplify
Mth 0-1 R (Revisit, Review nd Revive) SESSION Eponentil nd Logrithmic Functions 1 Eponentil nd Logrithmic Functions Key Concepts The Eponent Lws m n 1 n n m m n m n m mn m m m m mn m m m b n b b b Simplify
SUMMER KNOWHOW STUDY AND LEARNING CENTRE
 SUMMER KNOWHOW STUDY AND LEARNING CENTRE Indices & Logrithms 2 Contents Indices.2 Frctionl Indices.4 Logrithms 6 Exponentil equtions. Simplifying Surds 13 Opertions on Surds..16 Scientific Nottion..18
SUMMER KNOWHOW STUDY AND LEARNING CENTRE Indices & Logrithms 2 Contents Indices.2 Frctionl Indices.4 Logrithms 6 Exponentil equtions. Simplifying Surds 13 Opertions on Surds..16 Scientific Nottion..18
(i) b b. (ii) (iii) (vi) b. P a g e Exponential Functions 1. Properties of Exponents: Ex1. Solve the following equation
 P g e 30 4.2 Eponentil Functions 1. Properties of Eponents: (i) (iii) (iv) (v) (vi) 1 If 1, 0 1, nd 1, then E1. Solve the following eqution 4 3. 1 2 89 8(2 ) 7 Definition: The eponentil function with se
P g e 30 4.2 Eponentil Functions 1. Properties of Eponents: (i) (iii) (iv) (v) (vi) 1 If 1, 0 1, nd 1, then E1. Solve the following eqution 4 3. 1 2 89 8(2 ) 7 Definition: The eponentil function with se
1 Part II: Numerical Integration
 Mth 4 Lb 1 Prt II: Numericl Integrtion This section includes severl techniques for getting pproimte numericl vlues for definite integrls without using ntiderivtives. Mthemticll, ect nswers re preferble
Mth 4 Lb 1 Prt II: Numericl Integrtion This section includes severl techniques for getting pproimte numericl vlues for definite integrls without using ntiderivtives. Mthemticll, ect nswers re preferble
EXPONENT. Section 2.1. Do you see a pattern? Do you see a pattern? Try a) ( ) b) ( ) c) ( ) d)
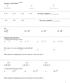 Section. EXPONENT RULES Do ou see pttern? Do ou see pttern? Tr ) ( ) b) ( ) c) ( ) d) Eponent rules strt here:. Epnd the following s bove. ) b) 7 c) d) How n 's re ou ultipling in ech proble? ) b) c) d)
Section. EXPONENT RULES Do ou see pttern? Do ou see pttern? Tr ) ( ) b) ( ) c) ( ) d) Eponent rules strt here:. Epnd the following s bove. ) b) 7 c) d) How n 's re ou ultipling in ech proble? ) b) c) d)
Chapter 14. Matrix Representations of Linear Transformations
 Chpter 4 Mtrix Representtions of Liner Trnsformtions When considering the Het Stte Evolution, we found tht we could describe this process using multipliction by mtrix. This ws nice becuse computers cn
Chpter 4 Mtrix Representtions of Liner Trnsformtions When considering the Het Stte Evolution, we found tht we could describe this process using multipliction by mtrix. This ws nice becuse computers cn
Some Methods in the Calculus of Variations
 CHAPTER 6 Some Methods in the Clculus of Vritions 6-. If we use the vried function ( α, ) α sin( ) + () Then d α cos ( ) () d Thus, the totl length of the pth is d S + d d α cos ( ) + α cos ( ) d Setting
CHAPTER 6 Some Methods in the Clculus of Vritions 6-. If we use the vried function ( α, ) α sin( ) + () Then d α cos ( ) () d Thus, the totl length of the pth is d S + d d α cos ( ) + α cos ( ) d Setting
The graphs of Rational Functions
 Lecture 4 5A: The its of Rtionl Functions s x nd s x + The grphs of Rtionl Functions The grphs of rtionl functions hve severl differences compred to power functions. One of the differences is the behvior
Lecture 4 5A: The its of Rtionl Functions s x nd s x + The grphs of Rtionl Functions The grphs of rtionl functions hve severl differences compred to power functions. One of the differences is the behvior
Before we can begin Ch. 3 on Radicals, we need to be familiar with perfect squares, cubes, etc. Try and do as many as you can without a calculator!!!
 Nme: Algebr II Honors Pre-Chpter Homework Before we cn begin Ch on Rdicls, we need to be fmilir with perfect squres, cubes, etc Try nd do s mny s you cn without clcultor!!! n The nth root of n n Be ble
Nme: Algebr II Honors Pre-Chpter Homework Before we cn begin Ch on Rdicls, we need to be fmilir with perfect squres, cubes, etc Try nd do s mny s you cn without clcultor!!! n The nth root of n n Be ble
Unit 1 Exponentials and Logarithms
 HARTFIELD PRECALCULUS UNIT 1 NOTES PAGE 1 Unit 1 Eponentils nd Logrithms (2) Eponentil Functions (3) The number e (4) Logrithms (5) Specil Logrithms (7) Chnge of Bse Formul (8) Logrithmic Functions (10)
HARTFIELD PRECALCULUS UNIT 1 NOTES PAGE 1 Unit 1 Eponentils nd Logrithms (2) Eponentil Functions (3) The number e (4) Logrithms (5) Specil Logrithms (7) Chnge of Bse Formul (8) Logrithmic Functions (10)
Lecture 14: Quadrature
 Lecture 14: Qudrture This lecture is concerned with the evlution of integrls fx)dx 1) over finite intervl [, b] The integrnd fx) is ssumed to be rel-vlues nd smooth The pproximtion of n integrl by numericl
Lecture 14: Qudrture This lecture is concerned with the evlution of integrls fx)dx 1) over finite intervl [, b] The integrnd fx) is ssumed to be rel-vlues nd smooth The pproximtion of n integrl by numericl
Calculus 2: Integration. Differentiation. Integration
 Clculus 2: Integrtion The reverse process to differentition is known s integrtion. Differentition f() f () Integrtion As it is the opposite of finding the derivtive, the function obtined b integrtion is
Clculus 2: Integrtion The reverse process to differentition is known s integrtion. Differentition f() f () Integrtion As it is the opposite of finding the derivtive, the function obtined b integrtion is
1 Online Learning and Regret Minimization
 2.997 Decision-Mking in Lrge-Scle Systems My 10 MIT, Spring 2004 Hndout #29 Lecture Note 24 1 Online Lerning nd Regret Minimiztion In this lecture, we consider the problem of sequentil decision mking in
2.997 Decision-Mking in Lrge-Scle Systems My 10 MIT, Spring 2004 Hndout #29 Lecture Note 24 1 Online Lerning nd Regret Minimiztion In this lecture, we consider the problem of sequentil decision mking in
ES.182A Topic 30 Notes Jeremy Orloff
 ES82A opic 3 Notes Jerem Orloff 3 Non-independent vribles: chin rule Recll the chin rule: If w = f, ; nd = r, t, = r, t then = + r t r t r t = + t t t r nfortuntel, sometimes there re more complicted reltions
ES82A opic 3 Notes Jerem Orloff 3 Non-independent vribles: chin rule Recll the chin rule: If w = f, ; nd = r, t, = r, t then = + r t r t r t = + t t t r nfortuntel, sometimes there re more complicted reltions
Physics 212. Faraday s Law
 Phsics 1 Lecture 17 Frd s Lw Phsics 1 Lecture 17, Slide 1 Motionl EMF Chnge Are of loop Chnge mgnetic field through loop Chnge orienttion of loop reltive to In ech cse the flu of the mgnetic field through
Phsics 1 Lecture 17 Frd s Lw Phsics 1 Lecture 17, Slide 1 Motionl EMF Chnge Are of loop Chnge mgnetic field through loop Chnge orienttion of loop reltive to In ech cse the flu of the mgnetic field through
ES.182A Topic 32 Notes Jeremy Orloff
 ES.8A Topic 3 Notes Jerem Orloff 3 Polr coordintes nd double integrls 3. Polr Coordintes (, ) = (r cos(θ), r sin(θ)) r θ Stndrd,, r, θ tringle Polr coordintes re just stndrd trigonometric reltions. In
ES.8A Topic 3 Notes Jerem Orloff 3 Polr coordintes nd double integrls 3. Polr Coordintes (, ) = (r cos(θ), r sin(θ)) r θ Stndrd,, r, θ tringle Polr coordintes re just stndrd trigonometric reltions. In
A-Level Mathematics Transition Task (compulsory for all maths students and all further maths student)
 A-Level Mthemtics Trnsition Tsk (compulsory for ll mths students nd ll further mths student) Due: st Lesson of the yer. Length: - hours work (depending on prior knowledge) This trnsition tsk provides revision
A-Level Mthemtics Trnsition Tsk (compulsory for ll mths students nd ll further mths student) Due: st Lesson of the yer. Length: - hours work (depending on prior knowledge) This trnsition tsk provides revision
Exponents and Logarithms Exam Questions
 Eponents nd Logrithms Em Questions Nme: ANSWERS Multiple Choice 1. If 4, then is equl to:. 5 b. 8 c. 16 d.. Identify the vlue of the -intercept of the function ln y.. -1 b. 0 c. d.. Which eqution is represented
Eponents nd Logrithms Em Questions Nme: ANSWERS Multiple Choice 1. If 4, then is equl to:. 5 b. 8 c. 16 d.. Identify the vlue of the -intercept of the function ln y.. -1 b. 0 c. d.. Which eqution is represented
8.6 The Hyperbola. and F 2. is a constant. P F 2. P =k The two fixed points, F 1. , are called the foci of the hyperbola. The line segments F 1
 8. The Hperol Some ships nvigte using rdio nvigtion sstem clled LORAN, which is n cronm for LOng RAnge Nvigtion. A ship receives rdio signls from pirs of trnsmitting sttions tht send signls t the sme time.
8. The Hperol Some ships nvigte using rdio nvigtion sstem clled LORAN, which is n cronm for LOng RAnge Nvigtion. A ship receives rdio signls from pirs of trnsmitting sttions tht send signls t the sme time.
Test , 8.2, 8.4 (density only), 8.5 (work only), 9.1, 9.2 and 9.3 related test 1 material and material from prior classes
 Test 2 8., 8.2, 8.4 (density only), 8.5 (work only), 9., 9.2 nd 9.3 relted test mteril nd mteril from prior clsses Locl to Globl Perspectives Anlyze smll pieces to understnd the big picture. Exmples: numericl
Test 2 8., 8.2, 8.4 (density only), 8.5 (work only), 9., 9.2 nd 9.3 relted test mteril nd mteril from prior clsses Locl to Globl Perspectives Anlyze smll pieces to understnd the big picture. Exmples: numericl
Chapter 1 Cumulative Review
 1 Chpter 1 Cumultive Review (Chpter 1) 1. Simplify 7 1 1. Evlute (0.7). 1. (Prerequisite Skill) (Prerequisite Skill). For Questions nd 4, find the vlue of ech expression.. 4 6 1 4. 19 [(6 4) 7 ] (Lesson
1 Chpter 1 Cumultive Review (Chpter 1) 1. Simplify 7 1 1. Evlute (0.7). 1. (Prerequisite Skill) (Prerequisite Skill). For Questions nd 4, find the vlue of ech expression.. 4 6 1 4. 19 [(6 4) 7 ] (Lesson
Model Solutions to Assignment 4
 Oberlin College Physics 110, Fll 2011 Model Solutions to Assignment 4 Additionl problem 56: A girl, sled, nd n ice-covered lke geometry digrm: girl shore rope sled ice free body digrms: force on girl by
Oberlin College Physics 110, Fll 2011 Model Solutions to Assignment 4 Additionl problem 56: A girl, sled, nd n ice-covered lke geometry digrm: girl shore rope sled ice free body digrms: force on girl by
Introduction. Definition of Hyperbola
 Section 10.4 Hperbols 751 10.4 HYPERBOLAS Wht ou should lern Write equtions of hperbols in stndrd form. Find smptotes of nd grph hperbols. Use properties of hperbols to solve rel-life problems. Clssif
Section 10.4 Hperbols 751 10.4 HYPERBOLAS Wht ou should lern Write equtions of hperbols in stndrd form. Find smptotes of nd grph hperbols. Use properties of hperbols to solve rel-life problems. Clssif
Review of basic calculus
 Review of bsic clculus This brief review reclls some of the most importnt concepts, definitions, nd theorems from bsic clculus. It is not intended to tech bsic clculus from scrtch. If ny of the items below
Review of bsic clculus This brief review reclls some of the most importnt concepts, definitions, nd theorems from bsic clculus. It is not intended to tech bsic clculus from scrtch. If ny of the items below
Data Structures and Algorithms CMPSC 465
 Dt Structures nd Algorithms CMPSC 465 LECTURE 10 Solving recurrences Mster theorem Adm Smith S. Rskhodnikov nd A. Smith; bsed on slides by E. Demine nd C. Leiserson Review questions Guess the solution
Dt Structures nd Algorithms CMPSC 465 LECTURE 10 Solving recurrences Mster theorem Adm Smith S. Rskhodnikov nd A. Smith; bsed on slides by E. Demine nd C. Leiserson Review questions Guess the solution
Definition of Continuity: The function f(x) is continuous at x = a if f(a) exists and lim
 Mth 9 Course Summry/Study Guide Fll, 2005 [1] Limits Definition of Limit: We sy tht L is the limit of f(x) s x pproches if f(x) gets closer nd closer to L s x gets closer nd closer to. We write lim f(x)
Mth 9 Course Summry/Study Guide Fll, 2005 [1] Limits Definition of Limit: We sy tht L is the limit of f(x) s x pproches if f(x) gets closer nd closer to L s x gets closer nd closer to. We write lim f(x)
Name Date. In Exercises 1 6, tell whether x and y show direct variation, inverse variation, or neither.
 1 Prctice A In Eercises 1 6, tell whether nd show direct vrition, inverse vrition, or neither.. 7. 6. 10. 8 6. In Eercises 7 10, tell whether nd show direct vrition, inverse vrition, or neither. 8 10 8.
1 Prctice A In Eercises 1 6, tell whether nd show direct vrition, inverse vrition, or neither.. 7. 6. 10. 8 6. In Eercises 7 10, tell whether nd show direct vrition, inverse vrition, or neither. 8 10 8.
13.3. The Area Bounded by a Curve. Introduction. Prerequisites. Learning Outcomes
 The Are Bounded b Curve 3.3 Introduction One of the importnt pplictions of integrtion is to find the re bounded b curve. Often such n re cn hve phsicl significnce like the work done b motor, or the distnce
The Are Bounded b Curve 3.3 Introduction One of the importnt pplictions of integrtion is to find the re bounded b curve. Often such n re cn hve phsicl significnce like the work done b motor, or the distnce
CHM Physical Chemistry I Chapter 1 - Supplementary Material
 CHM 3410 - Physicl Chemistry I Chpter 1 - Supplementry Mteril For review of some bsic concepts in mth, see Atkins "Mthemticl Bckground 1 (pp 59-6), nd "Mthemticl Bckground " (pp 109-111). 1. Derivtion
CHM 3410 - Physicl Chemistry I Chpter 1 - Supplementry Mteril For review of some bsic concepts in mth, see Atkins "Mthemticl Bckground 1 (pp 59-6), nd "Mthemticl Bckground " (pp 109-111). 1. Derivtion
Lecture 13 - Linking E, ϕ, and ρ
 Lecture 13 - Linking E, ϕ, nd ρ A Puzzle... Inner-Surfce Chrge Density A positive point chrge q is locted off-center inside neutrl conducting sphericl shell. We know from Guss s lw tht the totl chrge on
Lecture 13 - Linking E, ϕ, nd ρ A Puzzle... Inner-Surfce Chrge Density A positive point chrge q is locted off-center inside neutrl conducting sphericl shell. We know from Guss s lw tht the totl chrge on
Calculus in R. Chapter Di erentiation
 Chpter 3 Clculus in R 3.1 Di erentition Definition 3.1. Suppose U R is open. A function f : U! R is di erentible t x 2 U if there exists number m such tht lim y!0 pple f(x + y) f(x) my y =0. If f is di
Chpter 3 Clculus in R 3.1 Di erentition Definition 3.1. Suppose U R is open. A function f : U! R is di erentible t x 2 U if there exists number m such tht lim y!0 pple f(x + y) f(x) my y =0. If f is di
Basic Derivative Properties
 Bsic Derivtive Properties Let s strt this section by remining ourselves tht the erivtive is the slope of function Wht is the slope of constnt function? c FACT 2 Let f () =c, where c is constnt Then f 0
Bsic Derivtive Properties Let s strt this section by remining ourselves tht the erivtive is the slope of function Wht is the slope of constnt function? c FACT 2 Let f () =c, where c is constnt Then f 0
INTRODUCTION TO LINEAR ALGEBRA
 ME Applied Mthemtics for Mechnicl Engineers INTRODUCTION TO INEAR AGEBRA Mtrices nd Vectors Prof. Dr. Bülent E. Pltin Spring Sections & / ME Applied Mthemtics for Mechnicl Engineers INTRODUCTION TO INEAR
ME Applied Mthemtics for Mechnicl Engineers INTRODUCTION TO INEAR AGEBRA Mtrices nd Vectors Prof. Dr. Bülent E. Pltin Spring Sections & / ME Applied Mthemtics for Mechnicl Engineers INTRODUCTION TO INEAR
Solutions to Problems in Merzbacher, Quantum Mechanics, Third Edition. Chapter 7
 Solutions to Problems in Merzbcher, Quntum Mechnics, Third Edition Homer Reid April 5, 200 Chpter 7 Before strting on these problems I found it useful to review how the WKB pproimtion works in the first
Solutions to Problems in Merzbcher, Quntum Mechnics, Third Edition Homer Reid April 5, 200 Chpter 7 Before strting on these problems I found it useful to review how the WKB pproimtion works in the first
Quadratic Forms. Quadratic Forms
 Qudrtic Forms Recll the Simon & Blume excerpt from n erlier lecture which sid tht the min tsk of clculus is to pproximte nonliner functions with liner functions. It s ctully more ccurte to sy tht we pproximte
Qudrtic Forms Recll the Simon & Blume excerpt from n erlier lecture which sid tht the min tsk of clculus is to pproximte nonliner functions with liner functions. It s ctully more ccurte to sy tht we pproximte
Recitation 3: More Applications of the Derivative
 Mth 1c TA: Pdric Brtlett Recittion 3: More Applictions of the Derivtive Week 3 Cltech 2012 1 Rndom Question Question 1 A grph consists of the following: A set V of vertices. A set E of edges where ech
Mth 1c TA: Pdric Brtlett Recittion 3: More Applictions of the Derivtive Week 3 Cltech 2012 1 Rndom Question Question 1 A grph consists of the following: A set V of vertices. A set E of edges where ech
Homework 11. Andrew Ma November 30, sin x (1+x) (1+x)
 Homewor Andrew M November 3, 4 Problem 9 Clim: Pf: + + d = d = sin b +b + sin (+) d sin (+) d using integrtion by prts. By pplying + d = lim b sin b +b + sin (+) d. Since limits to both sides, lim b sin
Homewor Andrew M November 3, 4 Problem 9 Clim: Pf: + + d = d = sin b +b + sin (+) d sin (+) d using integrtion by prts. By pplying + d = lim b sin b +b + sin (+) d. Since limits to both sides, lim b sin
Unit #9 : Definite Integral Properties; Fundamental Theorem of Calculus
 Unit #9 : Definite Integrl Properties; Fundmentl Theorem of Clculus Gols: Identify properties of definite integrls Define odd nd even functions, nd reltionship to integrl vlues Introduce the Fundmentl
Unit #9 : Definite Integrl Properties; Fundmentl Theorem of Clculus Gols: Identify properties of definite integrls Define odd nd even functions, nd reltionship to integrl vlues Introduce the Fundmentl
ragsdale (zdr82) HW2 ditmire (58335) 1
 rgsdle (zdr82) HW2 ditmire (58335) This print-out should hve 22 questions. Multiple-choice questions my continue on the next column or pge find ll choices before nswering. 00 0.0 points A chrge of 8. µc
rgsdle (zdr82) HW2 ditmire (58335) This print-out should hve 22 questions. Multiple-choice questions my continue on the next column or pge find ll choices before nswering. 00 0.0 points A chrge of 8. µc
Consolidation Worksheet
 Cmbridge Essentils Mthemtics Core 8 NConsolidtion Worksheet N Consolidtion Worksheet Work these out. 8 b 7 + 0 c 6 + 7 5 Use the number line to help. 2 Remember + 2 2 +2 2 2 + 2 Adding negtive number is
Cmbridge Essentils Mthemtics Core 8 NConsolidtion Worksheet N Consolidtion Worksheet Work these out. 8 b 7 + 0 c 6 + 7 5 Use the number line to help. 2 Remember + 2 2 +2 2 2 + 2 Adding negtive number is
fractions Let s Learn to
 5 simple lgebric frctions corne lens pupil retin Norml vision light focused on the retin concve lens Shortsightedness (myopi) light focused in front of the retin Corrected myopi light focused on the retin
5 simple lgebric frctions corne lens pupil retin Norml vision light focused on the retin concve lens Shortsightedness (myopi) light focused in front of the retin Corrected myopi light focused on the retin
SECTION 9-4 Translation of Axes
 9-4 Trnsltion of Aes 639 Rdiotelescope For the receiving ntenn shown in the figure, the common focus F is locted 120 feet bove the verte of the prbol, nd focus F (for the hperbol) is 20 feet bove the verte.
9-4 Trnsltion of Aes 639 Rdiotelescope For the receiving ntenn shown in the figure, the common focus F is locted 120 feet bove the verte of the prbol, nd focus F (for the hperbol) is 20 feet bove the verte.
DEFINITION OF ASSOCIATIVE OR DIRECT PRODUCT AND ROTATION OF VECTORS
 3 DEFINITION OF ASSOCIATIVE OR DIRECT PRODUCT AND ROTATION OF VECTORS This chpter summrizes few properties of Cli ord Algebr nd describe its usefulness in e ecting vector rottions. 3.1 De nition of Associtive
3 DEFINITION OF ASSOCIATIVE OR DIRECT PRODUCT AND ROTATION OF VECTORS This chpter summrizes few properties of Cli ord Algebr nd describe its usefulness in e ecting vector rottions. 3.1 De nition of Associtive
Tests for the Ratio of Two Poisson Rates
 Chpter 437 Tests for the Rtio of Two Poisson Rtes Introduction The Poisson probbility lw gives the probbility distribution of the number of events occurring in specified intervl of time or spce. The Poisson
Chpter 437 Tests for the Rtio of Two Poisson Rtes Introduction The Poisson probbility lw gives the probbility distribution of the number of events occurring in specified intervl of time or spce. The Poisson
Goals: Determine how to calculate the area described by a function. Define the definite integral. Explore the relationship between the definite
 Unit #8 : The Integrl Gols: Determine how to clculte the re described by function. Define the definite integrl. Eplore the reltionship between the definite integrl nd re. Eplore wys to estimte the definite
Unit #8 : The Integrl Gols: Determine how to clculte the re described by function. Define the definite integrl. Eplore the reltionship between the definite integrl nd re. Eplore wys to estimte the definite
Consequently, the temperature must be the same at each point in the cross section at x. Let:
 HW 2 Comments: L1-3. Derive the het eqution for n inhomogeneous rod where the therml coefficients used in the derivtion of the het eqution for homogeneous rod now become functions of position x in the
HW 2 Comments: L1-3. Derive the het eqution for n inhomogeneous rod where the therml coefficients used in the derivtion of the het eqution for homogeneous rod now become functions of position x in the
How do we solve these things, especially when they get complicated? How do we know when a system has a solution, and when is it unique?
 XII. LINEAR ALGEBRA: SOLVING SYSTEMS OF EQUATIONS Tody we re going to tlk bout solving systems of liner equtions. These re problems tht give couple of equtions with couple of unknowns, like: 6 2 3 7 4
XII. LINEAR ALGEBRA: SOLVING SYSTEMS OF EQUATIONS Tody we re going to tlk bout solving systems of liner equtions. These re problems tht give couple of equtions with couple of unknowns, like: 6 2 3 7 4
DETERMINANTS. All Mathematical truths are relative and conditional. C.P. STEINMETZ
 All Mthemticl truths re reltive nd conditionl. C.P. STEINMETZ 4. Introduction DETERMINANTS In the previous chpter, we hve studied bout mtrices nd lgebr of mtrices. We hve lso lernt tht system of lgebric
All Mthemticl truths re reltive nd conditionl. C.P. STEINMETZ 4. Introduction DETERMINANTS In the previous chpter, we hve studied bout mtrices nd lgebr of mtrices. We hve lso lernt tht system of lgebric
MATHS NOTES. SUBJECT: Maths LEVEL: Higher TEACHER: Aidan Roantree. The Institute of Education Topics Covered: Powers and Logs
 MATHS NOTES The Institute of Eduction 06 SUBJECT: Mths LEVEL: Higher TEACHER: Aidn Rontree Topics Covered: Powers nd Logs About Aidn: Aidn is our senior Mths techer t the Institute, where he hs been teching
MATHS NOTES The Institute of Eduction 06 SUBJECT: Mths LEVEL: Higher TEACHER: Aidn Rontree Topics Covered: Powers nd Logs About Aidn: Aidn is our senior Mths techer t the Institute, where he hs been teching
Matrices and Determinants
 Nme Chpter 8 Mtrices nd Determinnts Section 8.1 Mtrices nd Systems of Equtions Objective: In this lesson you lerned how to use mtrices, Gussin elimintion, nd Guss-Jordn elimintion to solve systems of liner
Nme Chpter 8 Mtrices nd Determinnts Section 8.1 Mtrices nd Systems of Equtions Objective: In this lesson you lerned how to use mtrices, Gussin elimintion, nd Guss-Jordn elimintion to solve systems of liner
We will see what is meant by standard form very shortly
 THEOREM: For fesible liner progrm in its stndrd form, the optimum vlue of the objective over its nonempty fesible region is () either unbounded or (b) is chievble t lest t one extreme point of the fesible
THEOREM: For fesible liner progrm in its stndrd form, the optimum vlue of the objective over its nonempty fesible region is () either unbounded or (b) is chievble t lest t one extreme point of the fesible
( dg. ) 2 dt. + dt. dt j + dh. + dt. r(t) dt. Comparing this equation with the one listed above for the length of see that
 Arc Length of Curves in Three Dimensionl Spce If the vector function r(t) f(t) i + g(t) j + h(t) k trces out the curve C s t vries, we cn mesure distnces long C using formul nerly identicl to one tht we
Arc Length of Curves in Three Dimensionl Spce If the vector function r(t) f(t) i + g(t) j + h(t) k trces out the curve C s t vries, we cn mesure distnces long C using formul nerly identicl to one tht we
Review of Calculus, cont d
 Jim Lmbers MAT 460 Fll Semester 2009-10 Lecture 3 Notes These notes correspond to Section 1.1 in the text. Review of Clculus, cont d Riemnn Sums nd the Definite Integrl There re mny cses in which some
Jim Lmbers MAT 460 Fll Semester 2009-10 Lecture 3 Notes These notes correspond to Section 1.1 in the text. Review of Clculus, cont d Riemnn Sums nd the Definite Integrl There re mny cses in which some
