Area of left square = Area of right square c 2 + (4 Area of (a, b)-triangle) = a 2 + b 2 + (4 Area of (a, b)-triangle) c 2 = a 2 + b 2.
|
|
|
- Dennis Goodman
- 5 years ago
- Views:
Transcription
1 Worksheet
2 Proof (of Pythagoras Theorem). The proof can be shown using the two squares in Figure To draw the first square begin by drawing a general triangle with sides a and b and then extend these edges by lengths b and a respectively. Then we can complete the drawing to get the square on the left-hand side of Figure We can draw another square like the one on the right-hand side of the figure. From the figure we can see that both squares have equal area and so we can conclude that Area of left square = Area of right square c 2 + (4 Area of (a, b)-triangle) = a 2 + b 2 + (4 Area of (a, b)-triangle) c 2 = a 2 + b 2. a b a a b c b b c 2 b 2 c a a a 2 a b a b Figure 19.3 Proof of Pythagoras Theorem
3 Proof by cases Claim: For all integers n, n 2 ` 3n ` 7 is odd.
4 Proof by cases Claim: For all integers n, n 2 ` 3n ` 7 is odd. Proof (by cases). If n P Z, then either n is even or n is odd.
5 Proof by cases Claim: For all integers n, n 2 ` 3n ` 7 is odd. Proof (by cases). If n P Z, then either n is even or n is odd. If n is even, then n 2k for some k P Z.
6 Proof by cases Claim: For all integers n, n 2 ` 3n ` 7 is odd. Proof (by cases). If n P Z, then either n is even or n is odd. If n is even, then n 2k for some k P Z. Thus n 2 ` 3n ` 7 p2kq 2 ` 3p2kq ` 7 2p2k 2 ` 3k ` 3q ` 1.
7 Proof by cases Claim: For all integers n, n 2 ` 3n ` 7 is odd. Proof (by cases). If n P Z, then either n is even or n is odd. If n is even, then n 2k for some k P Z. Thus n 2 ` 3n ` 7 p2kq 2 ` 3p2kq ` 7 2p2k 2 ` 3k ` 3q ` 1. So since 2k 2 ` 3k ` 3 P Z, we have n 2 ` 3n ` 7 is odd.
8 Proof by cases Claim: For all integers n, n 2 ` 3n ` 7 is odd. Proof (by cases). If n P Z, then either n is even or n is odd. If n is even, then n 2k for some k P Z. Thus n 2 ` 3n ` 7 p2kq 2 ` 3p2kq ` 7 2p2k 2 ` 3k ` 3q ` 1. So since 2k 2 ` 3k ` 3 P Z, we have n 2 ` 3n ` 7 is odd. Similarly, if n is odd, then n 2k ` 1 for some k P Z.
9 Proof by cases Claim: For all integers n, n 2 ` 3n ` 7 is odd. Proof (by cases). If n P Z, then either n is even or n is odd. If n is even, then n 2k for some k P Z. Thus n 2 ` 3n ` 7 p2kq 2 ` 3p2kq ` 7 2p2k 2 ` 3k ` 3q ` 1. So since 2k 2 ` 3k ` 3 P Z, we have n 2 ` 3n ` 7 is odd. Similarly, if n is odd, then n 2k ` 1 for some k P Z. Thus n 2 ` 3n ` 7 p2k ` 1q 2 ` 3p2k ` 1q ` 7 2p2k 2 ` 5k ` 5q ` 1.
10 Proof by cases Claim: For all integers n, n 2 ` 3n ` 7 is odd. Proof (by cases). If n P Z, then either n is even or n is odd. If n is even, then n 2k for some k P Z. Thus n 2 ` 3n ` 7 p2kq 2 ` 3p2kq ` 7 2p2k 2 ` 3k ` 3q ` 1. So since 2k 2 ` 3k ` 3 P Z, we have n 2 ` 3n ` 7 is odd. Similarly, if n is odd, then n 2k ` 1 for some k P Z. Thus n 2 ` 3n ` 7 p2k ` 1q 2 ` 3p2k ` 1q ` 7 2p2k 2 ` 5k ` 5q ` 1. So since 2k 2 ` 5k ` 5q P Z, we have n 2 ` 3n ` 7 is odd.
11 Proof by cases Claim: For all integers n, n 2 ` 3n ` 7 is odd. Proof (by cases). If n P Z, then either n is even or n is odd. Case 1: If n is even, then n 2k for some k P Z. Thus n 2 ` 3n ` 7 p2kq 2 ` 3p2kq ` 7 2p2k 2 ` 3k ` 3q ` 1. So since 2k 2 ` 3k ` 3 P Z, we have n 2 ` 3n ` 7 is odd. Case 2: If n is odd, then n 2k ` 1 for some k P Z. Thus n 2 ` 3n ` 7 p2k ` 1q 2 ` 3p2k ` 1q ` 7 2p2k 2 ` 5k ` 5q ` 1. So since 2k 2 ` 5k ` 5q P Z, we have n 2 ` 3n ` 7 is odd.
12 Proof by cases Claim: For all integers n, n 2 ` 3n ` 7 is odd. Proof (direct).
13 Proof by cases Claim: For all integers n, n 2 ` 3n ` 7 is odd. Proof (direct). First, we note that n 2 ` 3n ` 7 npn ` 3q ` 7.
14 Proof by cases Claim: For all integers n, n 2 ` 3n ` 7 is odd. Proof (direct). First, we note that n 2 ` 3n ` 7 npn ` 3q ` 7. We have seen if a is even and b is odd, then a ` b is odd.
15 Proof by cases Claim: For all integers n, n 2 ` 3n ` 7 is odd. Proof (direct). First, we note that n 2 ` 3n ` 7 npn ` 3q ` 7. We have seen if a is even and b is odd, then a ` b is odd. So one of n or n ` 3 is even and the other is odd.
16 Proof by cases Claim: For all integers n, n 2 ` 3n ` 7 is odd. Proof (direct). First, we note that n 2 ` 3n ` 7 npn ` 3q ` 7. We have seen if a is even and b is odd, then a ` b is odd. So one of n or n ` 3 is even and the other is odd. Thus npn ` 3q is even; and hence npn ` 3q ` 7 is odd.
17 Proof by cases Claim: For all integers n, n 2 ` 3n ` 7 is odd. Proof (direct). First, we note that n 2 ` 3n ` 7 npn ` 3q ` 7. We have seen if a is even and b is odd, then a ` b is odd. So one of n or n ` 3 is even and the other is odd. Thus npn ` 3q is even; and hence npn ` 3q ` 7 is odd. Note: we kind of cheated by using previously formed machinery! We used the lemma, If a is even and b is odd, then a ` b is odd.
18 Proof by cases Claim: For all integers n, n 2 ` 3n ` 7 is odd. Proof (direct). First, we note that n 2 ` 3n ` 7 npn ` 3q ` 7. We have seen if a is even and b is odd, then a ` b is odd. So one of n or n ` 3 is even and the other is odd. Thus npn ` 3q is even; and hence npn ` 3q ` 7 is odd. Note: we kind of cheated by using previously formed machinery! We used the lemma, If a is even and b is odd, then a ` b is odd. Our first proof was called a proof by cases or proof by exhaustion. It was a little more obvious, but not as illuminating.
19 Tip: Anything with multiples or remainders lend themselves to proof by cases. Claim: For all n P Z, n 3 n is a multiple of 3.
20 Tip: Anything with multiples or remainders lend themselves to proof by cases. Claim: For all n P Z, n 3 n is a multiple of 3. Proof (by cases). Every n P Z can be written as 3n ` r for r 0, 1, or 2 (r is the remainder of n divided by 3).
21 Tip: Anything with multiples or remainders lend themselves to proof by cases. Claim: For all n P Z, n 3 n is a multiple of 3. Proof (by cases). Every n P Z can be written as 3n ` r for r 0, 1, or 2 (r is the remainder of n divided by 3). Case 1: r 0. Then... Case 2: r 1. Then... Case 3: r 2. Then... (See Example 22.3 for details.)
22 Tip: Anything with multiples or remainders lend themselves to proof by cases. Claim: For all n P Z, n 3 n is a multiple of 3. Proof (by cases). Every n P Z can be written as 3n ` r for r 0, 1, or 2 (r is the remainder of n divided by 3). Case 1: r 0. Then... Case 2: r 1. Then... Case 3: r 2. Then... (See Example 22.3 for details.) Proof (by cases, but more direct). Note that n 3 n npn ` 1qpn 1q. Then we will have our desired result by showing that one of n, n ` 1, or n 1 must be a multiple of three.
23 Tip: Anything with multiples or remainders lend themselves to proof by cases. Claim: For all n P Z, n 3 n is a multiple of 3. Proof (by cases). Every n P Z can be written as 3n ` r for r 0, 1, or 2 (r is the remainder of n divided by 3). Case 1: r 0. Then... Case 2: r 1. Then... Case 3: r 2. Then... (See Example 22.3 for details.) Proof (by cases, but more direct). Note that n 3 n npn ` 1qpn 1q. Then we will have our desired result by showing that one of n, n ` 1, or n 1 must be a multiple of three. Namely, every n P Z can be written as 3n ` r for r 0, 1, or 2.
24 Tip: Anything with multiples or remainders lend themselves to proof by cases. Claim: For all n P Z, n 3 n is a multiple of 3. Proof (by cases). Every n P Z can be written as 3n ` r for r 0, 1, or 2 (r is the remainder of n divided by 3). Case 1: r 0. Then... Case 2: r 1. Then... Case 3: r 2. Then... (See Example 22.3 for details.) Proof (by cases, but more direct). Note that n 3 n npn ` 1qpn 1q. Then we will have our desired result by showing that one of n, n ` 1, or n 1 must be a multiple of three. Namely, every n P Z can be written as 3n ` r for r 0, 1, or 2. But if n and n ` 1 are not multiples of 3, then r must be 1, so that n 1 is a multiple of 3.
25 Tip: Anything with multiples or remainders lend themselves to proof by cases. Claim: For all n P Z, n 3 n is a multiple of 3. Proof (by cases). Every n P Z can be written as 3n ` r for r 0, 1, or 2 (r is the remainder of n divided by 3). Case 1: r 0. Then... Case 2: r 1. Then... Case 3: r 2. Then... (See Example 22.3 for details.) Proof (by cases, but more direct). Note that n 3 n npn ` 1qpn 1q. Then we will have our desired result by showing that one of n, n ` 1, or n 1 must be a multiple of three. Namely, every n P Z can be written as 3n ` r for r 0, 1, or 2. But if n and n ` 1 are not multiples of 3, then r must be 1, so that n 1 is a multiple of 3. Note: Again, we cheated, this time by assuming our reader was knowledgeable enough to understand second and fourth sentences.
26 Tip: Piecewise functions lend themselves to proof by cases. Theorem (Triangle inequality). For real numbers x and y, we have x ` y ď x ` y.
27 Tip: Piecewise functions lend themselves to proof by cases. Theorem (Triangle inequality). For real numbers x and y, we have x ` y ď x ` y. Note: absolute value is secretly a piecewise function! # x x ě 0 x x x ă 0.
28 Tip: Piecewise functions lend themselves to proof by cases. Theorem (Triangle inequality). For real numbers x and y, we have x ` y ď x ` y. Note: absolute value is secretly a piecewise function! # x x ě 0 x x x ă 0. Proof (by cases). Suppose, without loss of generality, that x ě y.
29 Tip: Piecewise functions lend themselves to proof by cases. Theorem (Triangle inequality). For real numbers x and y, we have x ` y ď x ` y. Note: absolute value is secretly a piecewise function! # x x ě 0 x x x ă 0. Proof (by cases). Suppose, without loss of generality, that x ě y. Case 1: x, y ě 0. Note: The triangle inequality is an important part of the definition of a metric, i.e. a distance function. Absolute value is just one metric on R.
30 Tip: Piecewise functions lend themselves to proof by cases. Theorem (Triangle inequality). For real numbers x and y, we have x ` y ď x ` y. Note: absolute value is secretly a piecewise function! # x x ě 0 x x x ă 0. Proof (by cases). Suppose, without loss of generality, that x ě y. Case 1: x, y ě 0. Case 2: y ă 0 and x ě 0. Case 3: x, y ă 0. Note: The triangle inequality is an important part of the definition of a metric, i.e. a distance function. Absolute value is just one metric on R.
31 Tip: Piecewise functions lend themselves to proof by cases. Theorem (Triangle inequality). For real numbers x and y, we have x ` y ď x ` y. Note: absolute value is secretly a piecewise function! # x x ě 0 x x x ă 0. Proof (by cases). Suppose, without loss of generality, that x ě y. Case 1: x, y ě 0. If x, y ě 0, then x ` y ě 0. So x x y y and x ` y x ` y x ` y. Case 2: y ă 0 and x ě 0. Case 3: x, y ă 0. Note: The triangle inequality is an important part of the definition of a metric, i.e. a distance function. Absolute value is just one metric on R.
32 Tip: Piecewise functions lend themselves to proof by cases. Theorem (Triangle inequality). For real numbers x and y, we have x ` y ď x ` y. Note: absolute value is secretly a piecewise function! # x x ě 0 x x x ă 0. Proof (by cases). Suppose, without loss of generality, that x ě y. Case 1: x, y ě 0. If x, y ě 0, then x ` y ě 0. So x x y y and x ` y x ` y x ` y. Case 2: y ă 0 and x ě 0. (See Theorem 22.7) Case 3: x, y ă 0. (See Theorem 22.7) Note: The triangle inequality is an important part of the definition of a metric, i.e. a distance function. Absolute value is just one metric on R.
33 Theorem. Let X, Y and Z be points in the plane. Then, all lie on a line or all lie on a circle.
34 Theorem. Let X, Y and Z be points in the plane. Then, all lie on a line or all lie on a circle. Proof. Denote by L the perpendicular bisector between X and Y, and by M the perpendicular bisector between Y and Z. If the points all lie on a line, then they satisfy the conclusion of the theorem and we are done. If the points are not on a line, then L and M are not parallel and so must meet at a point W, say. As W is on the perpendicular bisector L it is equidistant from X and Y. Similarly it is equidistant from Y and Z. As the distance from W to X and the distance from Y and Z are the same we deduce that the three points lie on a circle centered at W of radius equal to the distance from W to X. 158 CHAPTER 22 Techniques of proof II: Proof by cases L Y M X Z W
35 Theorem. Let X, Y and Z be points in the plane. Then, all lie on a line or all lie on a circle. Tip: Or statements lend themselves to proof by cases. Tip: Extreme examples lend themselves to proof by cases.
36 You try: Outline a proof by cases for each of the following statements. 1. The square of any integer is of the form 3k or 3k ` 1 for some k P Z. 2. The cube of any integer is of the form 9k, 9k ` 1, or 9k ` 8 for some k P Z. 3. For all x, y P R, we have xy x y and ˇ ˇ x y ˇˇ ď x y. 4. For sets A and B, we have A Y B pa X Bq Y pa Bq Y pb Aq.
37 You try: Outline a proof by cases for each of the following statements. 1. The square of any integer is of the form 3k or 3k ` 1 for some k P Z. 2. The cube of any integer is of the form 9k, 9k ` 1, or 9k ` 8 for some k P Z. 3. For all x, y P R, we have xy x y and ˇ ˇ x y ˇˇ ď x y. 4. For sets A and B, we have A Y B pa X Bq Y pa Bq Y pb Aq. Tip: Unions lend themselves to proof by cases (since they re secretly or statements).
Edexcel New GCE A Level Maths workbook Circle.
Edexcel New GCE A Level Maths workbook Circle. Edited by: K V Kumaran kumarmaths.weebly.com 1 Finding the Midpoint of a Line To work out the midpoint of line we need to find the halfway point Midpoint
CBSE X Mathematics 2012 Solution (SET 1) Section B
CBSE X Mathematics 01 Solution (SET 1) Section B Q11. Find the value(s) of k so that the quadratic equation x kx + k = 0 has equal roots. Given equation is x kx k 0 For the given equation to have equal
Consider the equation different values of x we shall find the values of y and the tabulate t the values in the following table
Consider the equation y = 2 x + 3 for different values of x we shall find the values of y and the tabulate t the values in the following table x 0 1 2 1 2 y 3 5 7 1 1 When the points are plotted on the
Chapter 3: Inequalities, Lines and Circles, Introduction to Functions
QUIZ AND TEST INFORMATION: The material in this chapter is on Quiz 3 and Exam 2. You should complete at least one attempt of Quiz 3 before taking Exam 2. This material is also on the final exam and used
1. Suppose that a, b, c and d are four different integers. Explain why. (a b)(a c)(a d)(b c)(b d)(c d) a 2 + ab b = 2018.
New Zealand Mathematical Olympiad Committee Camp Selection Problems 2018 Solutions Due: 28th September 2018 1. Suppose that a, b, c and d are four different integers. Explain why must be a multiple of
COMPLEX NUMBERS LAURENT DEMONET
COMPLEX NUMBERS LAURENT DEMONET Contents Introduction: numbers 1 1. Construction of complex numbers. Conjugation 4 3. Geometric representation of complex numbers 5 3.1. The unit circle 6 3.. Modulus of
UNDERSTANDING RULER AND COMPASS CONSTRUCTIONS WITH FIELD THEORY
UNDERSTANDING RULER AND COMPASS CONSTRUCTIONS WITH FIELD THEORY ISAAC M. DAVIS Abstract. By associating a subfield of R to a set of points P 0 R 2, geometric properties of ruler and compass constructions
Math 46 Final Exam Review Packet
Math 46 Final Exam Review Packet Question 1. Perform the indicated operation. Simplify if possible. 7 x x 2 2x + 3 2 x Question 2. The sum of a number and its square is 72. Find the number. Question 3.
Give a geometric description of the set of points in space whose coordinates satisfy the given pair of equations.
1. Give a geometric description of the set of points in space whose coordinates satisfy the given pair of equations. x + y = 5, z = 4 Choose the correct description. A. The circle with center (0,0, 4)
LOCUS. Definition: The set of all points (and only those points) which satisfy the given geometrical condition(s) (or properties) is called a locus.
LOCUS Definition: The set of all points (and only those points) which satisfy the given geometrical condition(s) (or properties) is called a locus. Eg. The set of points in a plane which are at a constant
Australian Intermediate Mathematics Olympiad 2016
Australian Intermediate Mathematics Olympiad 06 Questions. Find the smallest positive integer x such that x = 5y, where y is a positive integer. [ marks]. A 3-digit number in base 7 is also a 3-digit number
Reteach Simplifying Algebraic Expressions
1-4 Simplifying Algebraic Expressions To evaluate an algebraic expression you substitute numbers for variables. Then follow the order of operations. Here is a sentence that can help you remember the order
Math Circles: Number Theory III
Math Circles: Number Theory III Centre for Education in Mathematics and Computing University of Waterloo March 9, 2011 A prime-generating polynomial The polynomial f (n) = n 2 n + 41 generates a lot of
Australian Intermediate Mathematics Olympiad 2016
A u s t r a l i a n M at h e m at i c a l O ly m p i a d C o m m i t t e e a d e p a r t m e n t o f t h e a u s t r a l i a n m at h e m at i c s t r u s t Australian Intermediate Mathematics Olympiad
Taiwan International Mathematics Competition 2012 (TAIMC 2012)
Section. (5 points each) orrect nswers: Taiwan International Mathematics ompetition 01 (TIM 01) World onference on the Mathematically Gifted Students ---- the Role of Educators and Parents Taipei, Taiwan,
or i 2 = -1 i 4 = 1 Example : ( i ),, 7 i and 0 are complex numbers. and Imaginary part of z = b or img z = b
1 A- LEVEL MATHEMATICS P 3 Complex Numbers (NOTES) 1. Given a quadratic equation : x 2 + 1 = 0 or ( x 2 = -1 ) has no solution in the set of real numbers, as there does not exist any real number whose
Try the assignment f(1) = 2; f(2) = 1; f(3) = 4; f(4) = 3;.
I. Precisely complete the following definitions: 1. A natural number n is composite whenever... See class notes for the precise definitions 2. Fix n in N. The number s(n) represents... 3. For A and B sets,
Reading Mathematical Expressions & Arithmetic Operations Expression Reads Note
Math 001 - Term 171 Reading Mathematical Expressions & Arithmetic Operations Expression Reads Note x A x belongs to A,x is in A Between an element and a set. A B A is a subset of B Between two sets. φ
Probability Generating Functions
Probability Generating Functions Andreas Klappenecker Texas A&M University 2018 by Andreas Klappenecker. All rights reserved. 1 / 27 Probability Generating Functions Definition Let X be a discrete random
Mathematical induction
Mathematical induction Notes and Examples These notes contain subsections on Proof Proof by induction Types of proof by induction Proof You have probably already met the idea of proof in your study of
Mathematics 220 Midterm Practice problems from old exams Page 1 of 8
Mathematics 220 Midterm Practice problems from old exams Page 1 of 8 1. (a) Write the converse, contrapositive and negation of the following statement: For every integer n, if n is divisible by 3 then
9.7 Extension: Writing and Graphing the Equations
www.ck12.org Chapter 9. Circles 9.7 Extension: Writing and Graphing the Equations of Circles Learning Objectives Graph a circle. Find the equation of a circle in the coordinate plane. Find the radius and
of a circle Q that can be inscribed in a corner of the square tangent to two sides of the square and to the circle inscribed in the square?
Problem 1) Suppose A, B, and C are the vertices of a right triangle with C being the vertex of the right angle, c the length of the hypotenuse, a the length of the leg opposite A, and b the length of the
Basic Math. Curriculum (358 topics additional topics)
Basic Math This course covers the topics outlined below and is available for use with integrated, interactive ebooks. You can customize the scope and sequence of this course to meet your curricular needs.
5 Find an equation of the circle in which AB is a diameter in each case. a A (1, 2) B (3, 2) b A ( 7, 2) B (1, 8) c A (1, 1) B (4, 0)
C2 CRDINATE GEMETRY Worksheet A 1 Write down an equation of the circle with the given centre and radius in each case. a centre (0, 0) radius 5 b centre (1, 3) radius 2 c centre (4, 6) radius 1 1 d centre
1997 Solutions Cayley Contest(Grade 10)
Canadian Mathematics Competition n activity of The Centre for Education in Mathematics and Computing, University of Waterloo, Waterloo, Ontario 199 Solutions Cayley Contest(Grade 10) for the wards 199
Problem 1. Solve the equation 3 x + 9 x = 27 x. Solution: 3 x + 3 2x = 3 3x. Denote: y = 3 x, then. y + y 2 = y 3. y 3 y 2 y = 0. y(y 2 y 1) = 0.
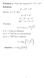Problem 1. Solve the equation 3 x + 9 x = 7 x. Solution: 3 x + 3 x = 3 3x. Denote: y = 3 x, then Therefore, y + y = y 3. y 3 y y = 0. y(y y 1) = 0. y = 0 or y = 1 ± 5. i) 3 x = 0 has no solutions, ii)
Chapter 1: Precalculus Review
: Precalculus Review Math 115 17 January 2018 Overview 1 Important Notation 2 Exponents 3 Polynomials 4 Rational Functions 5 Cartesian Coordinates 6 Lines Notation Intervals: Interval Notation (a, b) (a,
CHAPTER 8: EXPLORING R
CHAPTER 8: EXPLORING R LECTURE NOTES FOR MATH 378 (CSUSM, SPRING 2009). WAYNE AITKEN In the previous chapter we discussed the need for a complete ordered field. The field Q is not complete, so we constructed
Math 320: Real Analysis MWF 1pm, Campion Hall 302 Homework 8 Solutions Please write neatly, and in complete sentences when possible.
Math 320: Real Analysis MWF pm, Campion Hall 302 Homework 8 Solutions Please write neatly, and in complete sentences when possible. Do the following problems from the book: 4.3.5, 4.3.7, 4.3.8, 4.3.9,
BMO Round 2 Problem 3 Generalisation and Bounds
BMO 2007 2008 Round 2 Problem 3 Generalisation and Bounds Joseph Myers February 2008 1 Introduction Problem 3 (by Paul Jefferys) is: 3. Adrian has drawn a circle in the xy-plane whose radius is a positive
Fall 09/MAT 140/Worksheet 1 Name: Show all your work. 1. (6pts) Simplify and write the answer so all exponents are positive:
Fall 09/MAT 140/Worksheet 1 Name: Show all your work. 1. (6pts) Simplify and write the answer so all exponents are positive: a) (x 3 y 6 ) 3 x 4 y 5 = b) 4x 2 (3y) 2 (6x 3 y 4 ) 2 = 2. (2pts) Convert to
Mark scheme Pure Mathematics Year 1 (AS) Unit Test 2: Coordinate geometry in the (x, y) plane
Mark scheme Pure Mathematics Year 1 (AS) Unit Test : Coordinate in the (x, y) plane Q Scheme Marks AOs Pearson 1a Use of the gradient formula to begin attempt to find k. k 1 ( ) or 1 (k 4) ( k 1) (i.e.
CSC 344 Algorithms and Complexity. Proof by Mathematical Induction
CSC 344 Algorithms and Complexity Lecture #1 Review of Mathematical Induction Proof by Mathematical Induction Many results in mathematics are claimed true for every positive integer. Any of these results
THE TRIANGULAR THEOREM OF THE PRIMES : BINARY QUADRATIC FORMS AND PRIMITIVE PYTHAGOREAN TRIPLES
THE TRIANGULAR THEOREM OF THE PRIMES : BINARY QUADRATIC FORMS AND PRIMITIVE PYTHAGOREAN TRIPLES Abstract. This article reports the occurrence of binary quadratic forms in primitive Pythagorean triangles
AKU-EB May Examination 2017
Page 1 of 1 AGA KHAN UNIVERSITY EXAMINATION BOARD SECONDARY SCHOOL CERTIFICATE CLASS IX EXAMINATION APRIL/ MAY 017 Mathematics Paper I INSTRUCTIONS 1. Read each question carefully. Time: 40 minutes Marks:
Pre Algebra and Introductory Algebra
Pre Algebra and Introductory Algebra This course covers the topics outlined below and is available for use with integrated, interactive ebooks. You can customize the scope and sequence of this course to
Algebraic. techniques1
techniques Algebraic An electrician, a bank worker, a plumber and so on all have tools of their trade. Without these tools, and a good working knowledge of how to use them, it would be impossible for them
Twitter: @Owen134866 www.mathsfreeresourcelibrary.com Prior Knowledge Check 1) Find the point of intersection for each pair of lines: a) y = 4x + 7 and 5y = 2x 1 b) y = 5x 1 and 3x + 7y = 11 c) 2x 5y =
Baltic Way 2008 Gdańsk, November 8, 2008
Baltic Way 008 Gdańsk, November 8, 008 Problems and solutions Problem 1. Determine all polynomials p(x) with real coefficients such that p((x + 1) ) = (p(x) + 1) and p(0) = 0. Answer: p(x) = x. Solution:
COMPLEX NUMBERS AND QUADRATIC EQUATIONS
Chapter 5 COMPLEX NUMBERS AND QUADRATIC EQUATIONS 5. Overview We know that the square of a real number is always non-negative e.g. (4) 6 and ( 4) 6. Therefore, square root of 6 is ± 4. What about the square
chapter 1 vector geometry solutions V Consider the parallelogram shown alongside. Which of the following statements are true?
chapter vector geometry solutions V. Exercise A. For the shape shown, find a single vector which is equal to a)!!! " AB + BC AC b)! AD!!! " + DB AB c)! AC + CD AD d)! BC + CD!!! " + DA BA e) CD!!! " "
CHMMC 2015 Individual Round Problems
CHMMC 05 Individual Round Problems November, 05 Problem 0.. The following number is the product of the divisors of n. What is n? 6 3 3 Solution.. In general, the product of the divisors of n is n # of
The Riemann Roch theorem for metric graphs
The Riemann Roch theorem for metric graphs R. van Dobben de Bruyn 1 Preface These are the notes of a talk I gave at the graduate student algebraic geometry seminar at Columbia University. I present a short
The Advantage Testing Foundation Olympiad Solutions
The Advantage Testing Foundation 015 Olympiad Problem 1 Prove that every positive integer has a unique representation in the form d i i, where k is a nonnegative integer and each d i is either 1 or. (This
ZEROES OF INTEGER LINEAR RECURRENCES. 1. Introduction. 4 ( )( 2 1) n
ZEROES OF INTEGER LINEAR RECURRENCES DANIEL LITT Consider the integer linear recurrence 1. Introduction x n = x n 1 + 2x n 2 + 3x n 3 with x 0 = x 1 = x 2 = 1. For which n is x n = 0? Answer: x n is never
Circles & Interval & Set Notation.notebook. November 16, 2009 CIRCLES. OBJECTIVE Graph a Circle given the equation in standard form.
OBJECTIVE Graph a Circle given the equation in standard form. Write the equation of a circle in standard form given a graph or two points (one being the center). Students will be able to write the domain
Natural Numbers: Also called the counting numbers The set of natural numbers is represented by the symbol,.
Name Period Date: Topic: Real Numbers and Their Graphs Standard: 9-12.A.1.3 Objective: Essential Question: What is the significance of a point on a number line? Determine the relative position on the number
Prep for College Algebra
Prep for College Algebra This course covers the topics outlined below. You can customize the scope and sequence of this course to meet your curricular needs. Curriculum (219 topics + 85 additional topics)
Class IX Chapter 5 Introduction to Euclid's Geometry Maths
Class IX Chapter 5 Introduction to Euclid's Geometry Maths Exercise 5.1 Question 1: Which of the following statements are true and which are false? Give reasons for your answers. (i) Only one line can
2. Two binary operations (addition, denoted + and multiplication, denoted
Chapter 2 The Structure of R The purpose of this chapter is to explain to the reader why the set of real numbers is so special. By the end of this chapter, the reader should understand the difference between
Prep for College Algebra with Trigonometry
Prep for College Algebra with Trigonometry This course covers the topics outlined below. You can customize the scope and sequence of this course to meet your curricular needs. Curriculum (246 topics +
not to be republished NCERT REAL NUMBERS CHAPTER 1 (A) Main Concepts and Results
REAL NUMBERS CHAPTER 1 (A) Main Concepts and Results Euclid s Division Lemma : Given two positive integers a and b, there exist unique integers q and r satisfying a = bq + r, 0 r < b. Euclid s Division
Abstract The symmedian point of a triangle is known to give rise to two circles, obtained by drawing respectively parallels and antiparallels to the
bstract The symmedian point of a triangle is known to give rise to two circles, obtained by drawing respectively parallels and antiparallels to the sides of the triangle through the symmedian point. In
Unit equations in characteristic p. Peter Koymans
Unit equations in characteristic p Peter Koymans Universiteit Leiden XXX th Journées Arithmétiques Caen, France, July 2017 Introduction Let K be a number field with unit group OK. For fixed a, b, c K consider
King Fahd University of Petroleum and Minerals Prep-Year Math Program Math (001) - Term 181 Recitation (1.1)
Recitation (1.1) Question 1: Find a point on the y-axis that is equidistant from the points (5, 5) and (1, 1) Question 2: Find the distance between the points P(2 x, 7 x) and Q( 2 x, 4 x) where x 0. Question
Examples: Identify three pairs of parallel segments in the diagram. 1. AB 2. BC 3. AC. Write an equation to model this theorem based on the figure.
5.1: Midsegments of Triangles NOTE: Midsegments are also to the third side in the triangle. Example: Identify the 3 midsegments in the diagram. Examples: Identify three pairs of parallel segments in the
STEP Support Programme. STEP 2 Complex Numbers: Solutions
STEP Support Programme STEP Complex Numbers: Solutions i Rewriting the given relationship gives arg = arg arg = α. We can then draw a picture as below: The loci is therefore a section of the circle between
STEP Support Programme. Hints and Partial Solutions for Assignment 4
STEP Support Programme Hints and Partial Solutions for Assignment 4 Warm-up 1 (i) This question was asking you to prove that the angle at the centre of a circle is twice the angle at the circumference.
Outline. 1 The Role of Functions. 2 Polynomial Functions. 3 Power Functions. 4 Rational Functions. 5 Exponential & Logarithmic Functions
Outline MS11: IT Mathematics Functions Catalogue of Essential Functions John Carroll School of Mathematical Sciences Dublin City University 1 The Role of Functions 3 Power Functions 4 Rational Functions
P1 Chapter 6 :: Circles
P1 Chapter 6 :: Circles jfrost@tiffin.kingston.sch.uk www.drfrostmaths.com @DrFrostMaths Last modified: 11 th August 2017 Use of DrFrostMaths for practice Register for free at: www.drfrostmaths.com/homework
Twitter: @Owen134866 www.mathsfreeresourcelibrary.com Prior Knowledge Check 1) Simplify: a) 3x 2 5x 5 b) 5x3 y 2 15x 7 2) Factorise: a) x 2 2x 24 b) 3x 2 17x + 20 15x 2 y 3 3) Use long division to calculate:
Math Precalculus I University of Hawai i at Mānoa Spring
Math 135 - Precalculus I University of Hawai i at Mānoa Spring - 2013 Created for Math 135, Spring 2008 by Lukasz Grabarek and Michael Joyce Send comments and corrections to lukasz@math.hawaii.edu Contents
Core Mathematics 2 Coordinate Geometry
Core Mathematics 2 Coordinate Geometry Edited by: K V Kumaran Email: kvkumaran@gmail.com Core Mathematics 2 Coordinate Geometry 1 Coordinate geometry in the (x, y) plane Coordinate geometry of the circle
Algebra 1 Correlation of the ALEKS course Algebra 1 to the Washington Algebra 1 Standards
Algebra 1 Correlation of the ALEKS course Algebra 1 to the Washington Algebra 1 Standards A1.1: Core Content: Solving Problems A1.1.A: Select and justify functions and equations to model and solve problems.
The Alberta High School Mathematics Competition Solution to Part I, 2013.
The Alberta High School Mathematics Competition Solution to Part I, 201 1 Of the first 100 positive integers 1, 2,, 100, the number of those not divisible by 7 is (a) 14 (b) 15 (c) 85 (d) 86 (e) none of
Section 1.4 Circles. Objective #1: Writing the Equation of a Circle in Standard Form.
1 Section 1. Circles Objective #1: Writing the Equation of a Circle in Standard Form. We begin by giving a definition of a circle: Definition: A Circle is the set of all points that are equidistant from
Web Solutions for How to Read and Do Proofs
Web Solutions for How to Read and Do Proofs An Introduction to Mathematical Thought Processes Sixth Edition Daniel Solow Department of Operations Weatherhead School of Management Case Western Reserve University
Constructions with ruler and compass.
Constructions with ruler and compass. Semyon Alesker. 1 Introduction. Let us assume that we have a ruler and a compass. Let us also assume that we have a segment of length one. Using these tools we can
Circles in F 2 q. Jacob Haddock, Wesley Perkins, and John Pope Faculty Adviser: Dr. Jeremy Chapman
Circles in F q Jacob Haddock, Wesley Perkins, and John Pope Faculty Adviser: Dr. Jeremy Chapman Abstract. In Euclid s The Elements, a unique circle in R is determined by three noncollinear points. This
Math Precalculus I University of Hawai i at Mānoa Spring
Math 135 - Precalculus I University of Hawai i at Mānoa Spring - 2014 Created for Math 135, Spring 2008 by Lukasz Grabarek and Michael Joyce Send comments and corrections to lukasz@math.hawaii.edu Contents
CHAPTER 6 : LITERATURE REVIEW
CHAPTER 6 : LITERATURE REVIEW Chapter : LITERATURE REVIEW 77 M E A S U R I N G T H E E F F I C I E N C Y O F D E C I S I O N M A K I N G U N I T S A B S T R A C T A n o n l i n e a r ( n o n c o n v e
P E R E N C O - C H R I S T M A S P A R T Y
L E T T I C E L E T T I C E I S A F A M I L Y R U N C O M P A N Y S P A N N I N G T W O G E N E R A T I O N S A N D T H R E E D E C A D E S. B A S E D I N L O N D O N, W E H A V E T H E P E R F E C T R
Strong Mathematical Induction
Strong Mathematical Induction Lecture 23 Section 5.4 Robb T. Koether Hampden-Sydney College Mon, Feb 24, 2014 Robb T. Koether (Hampden-Sydney College) Strong Mathematical Induction Mon, Feb 24, 2014 1
Test Corrections for Unit 1 Test
MUST READ DIRECTIONS: Read the directions located on www.koltymath.weebly.com to understand how to properly do test corrections. Ask for clarification from your teacher if there are parts that you are
MATH II CCR MATH STANDARDS
RELATIONSHIPS BETWEEN QUANTITIES M.2HS.1 M.2HS.2 M.2HS.3 M.2HS.4 M.2HS.5 M.2HS.6 Explain how the definition of the meaning of rational exponents follows from extending the properties of integer exponents
Verulam School Mathematics. Year 9 Revision Material (with answers) Page 1
Verulam School Mathematics Year 9 Revision Material (with answers) Page 1 Q1. (a) Simplify a 2 a 4 Answer... (b) Simplify b 9 b 3 Answer... (c) Simplify c 5 c c 5 Answer... (Total 3 marks) Q2. (a) Expand
Unit Circle: The unit circle has radius 1 unit and is centred at the origin on the Cartesian plane. POA
The Unit Circle Unit Circle: The unit circle has radius 1 unit and is centred at the origin on the Cartesian plane THE EQUATION OF THE UNIT CIRCLE Consider any point P on the unit circle with coordinates
Show Your Work! Point values are in square brackets. There are 35 points possible. Some facts about sets are on the last page.
Formal Methods Name: Key Midterm 2, Spring, 2007 Show Your Work! Point values are in square brackets. There are 35 points possible. Some facts about sets are on the last page.. Determine whether each of
American Math Competition 10 Practice Test 10. American Mathematics Competitions. Practice 10 AMC 10 (American Mathematics Contest 10) INSTRUCTIONS
American Math Competition 0 Practice Test 0 American Mathematics Competitions Practice 0 AMC 0 (American Mathematics Contest 0) INSTRUCTIONS. This is a twenty-five question multiple choice test. Each question
For all questions, answer choice E. NOTA" means none of the above answers is correct.
For all questions, answer choice " means none of the above answers is correct. 1. The sum of the integers 1 through n can be modeled by a quadratic polynomial. What is the product of the non-zero coefficients
College Algebra with Corequisite Support: A Blended Approach
College Algebra with Corequisite Support: A Blended Approach 978-1-63545-058-3 To learn more about all our offerings Visit Knewtonalta.com Source Author(s) (Text or Video) Title(s) Link (where applicable)
CBSE Class IX Syllabus. Mathematics Class 9 Syllabus
Mathematics Class 9 Syllabus Course Structure First Term Units Unit Marks I Number System 17 II Algebra 25 III Geometry 37 IV Co-ordinate Geometry 6 V Mensuration 5 Total 90 Second Term Units Unit Marks
International Mathematical Olympiad. Preliminary Selection Contest 2017 Hong Kong. Outline of Solutions 5. 3*
International Mathematical Olympiad Preliminary Selection Contest Hong Kong Outline of Solutions Answers: 06 0000 * 6 97 7 6 8 7007 9 6 0 6 8 77 66 7 7 0 6 7 7 6 8 9 8 0 0 8 *See the remar after the solution
LAMC Beginners Circle November 10, Oleg Gleizer. Warm-up
LAMC Beginners Circle November 10, 2013 Oleg Gleizer oleg1140@gmail.com Warm-up Problem 1 Can a power of two (a number of the form 2 n ) have all the decimal digits 0, 1,..., 9 the same number of times?
(x 1, y 1 ) = (x 2, y 2 ) if and only if x 1 = x 2 and y 1 = y 2.
1. Complex numbers A complex number z is defined as an ordered pair z = (x, y), where x and y are a pair of real numbers. In usual notation, we write z = x + iy, where i is a symbol. The operations of
Integers, Fractions, Decimals and Percentages. Equations and Inequations
Integers, Fractions, Decimals and Percentages Round a whole number to a specified number of significant figures Round a decimal number to a specified number of decimal places or significant figures Perform
Mathematical Olympiad for Girls
UKMT UKMT UKMT Mathematical Olympiad for Girls Organised by the United Kingdom Mathematics Trust These are polished solutions and do not illustrate the process of failed ideas and rough work by which candidates
Homework 1. 10(b) A useful denial of the statement We will win the first game or the second one is We will lose the first two games.
Homework 1 Exercises 1.1 (f) P Q Q Q Q P (Q Q) T T F T T T F T T T F T F T F F F T T F 5(d) The proposition Horses have four legs but three quarters do not equal one dollar is of the form A C. Since A
MASTERS EXAMINATION IN MATHEMATICS SOLUTIONS
MASTERS EXAMINATION IN MATHEMATICS PURE MATHEMATICS OPTION SPRING 010 SOLUTIONS Algebra A1. Let F be a finite field. Prove that F [x] contains infinitely many prime ideals. Solution: The ring F [x] of
Plane geometry Circles: Problems with some Solutions
The University of Western ustralia SHL F MTHMTIS & STTISTIS UW MY FR YUNG MTHMTIINS Plane geometry ircles: Problems with some Solutions 1. Prove that for any triangle, the perpendicular bisectors of the
Draft Version 1 Mark scheme Further Maths Core Pure (AS/Year 1) Unit Test 1: Complex numbers 1
1 w z k k States or implies that 4 i TBC Uses the definition of argument to write 4 k π tan 1 k 4 Makes an attempt to solve for k, for example 4 + k = k is seen. M1.a Finds k = 6 (4 marks) Pearson Education
Immerse Metric Space Homework
Immerse Metric Space Homework (Exercises -2). In R n, define d(x, y) = x y +... + x n y n. Show that d is a metric that induces the usual topology. Sketch the basis elements when n = 2. Solution: Steps
College Algebra with Corequisite Support: A Compressed Approach
College Algebra with Corequisite Support: A Compressed Approach 978-1-63545-059-0 To learn more about all our offerings Visit Knewton.com Source Author(s) (Text or Video) Title(s) Link (where applicable)
Understand the difference between truncating and rounding. Calculate with roots, and with integer and fractional indices.
The assessments will cover the following content headings: 1. Number 2. Algebra 3. Ratio, and rates of change 4. Geometry and measures 5. Probability 6. Statistics Higher Year 7 Year 8 Year 9 Year 10 Year
Circles, Mixed Exercise 6
Circles, Mixed Exercise 6 a QR is the diameter of the circle so the centre, C, is the midpoint of QR ( 5) 0 Midpoint = +, + = (, 6) C(, 6) b Radius = of diameter = of QR = of ( x x ) + ( y y ) = of ( 5
Entropy and Ergodic Theory Lecture 17: Transportation and concentration
Entropy and Ergodic Theory Lecture 17: Transportation and concentration 1 Concentration in terms of metric spaces In this course, a metric probability or m.p. space is a triple px, d, µq in which px, dq
Baltic Way 2003 Riga, November 2, 2003
altic Way 2003 Riga, November 2, 2003 Problems and solutions. Let Q + be the set of positive rational numbers. Find all functions f : Q + Q + which for all x Q + fulfil () f ( x ) = f (x) (2) ( + x ) f
It was well known that each suspect told exactly one lie. Which suspect did it? a. Edward b. Derek c. Arnold d. Brian e. Charles. c. 1, d.
March, 018 018 State Math Contest 1. During a recent police investigation, Chief Inspector Stone was interviewing five local villains to try and identify who stole Mrs. Archer's cake from the fair. Below
CISC-102 Winter 2016 Lecture 11 Greatest Common Divisor
CISC-102 Winter 2016 Lecture 11 Greatest Common Divisor Consider any two integers, a,b, at least one non-zero. If we list the positive divisors in numeric order from smallest to largest, we would get two