r some or all of m, x, yz. Similarly for I yy and I zz.
|
|
|
- Marsha Chapman
- 5 years ago
- Views:
Transcription
1 Homework 10. Chapters 1, 1. Moments and products of inertia Concepts: What objects have a moment of inertia? (Section 1.1). Consider the moment of inertia S/ bu bu of an object S about a point for the unit vector û. n general, for S/ bu bu to be a positive real number, S should be a (circle all appropriate objects): Real number Matri Set of points Mass center of a rigid bod Vector Point Reference frame Fleible bod D orthogonal unit basis Particle Rigid bod Sstem of particles and bodies 10. Formulas for a particle s moments and products of inertia (Sections 1.1 and 1.). The figure shows a particle of mass m and right-handed orthogonal unit vectors n, n, n z. s position vector from a point is n + n + z n z. (m) n Epress ( s moment of inertia about for n ) in terms of r some or all of m,, z. Similarl for and. Epress ( s product of inertia about for n and n ) in z terms of some or all of m,, z. Similarl for z and z. n z Result: = ( + ) = = n = z = z = Circa 189, Gibbs invented the inertia dadic as a convenient suitcase for holding moments and products of inertia. Write s inertia dadic about in terms of n, n, n z and ij (i, j =,, z). f needed, refer to Section 1.1. = n n + n n + n n z + n n + n n Parallel ais theorem and moments of inertia (Section 1.1.). The sstem S shown to the right consists of particles 1 and, each of mass m, in a plane perpendicular to the unit vector n z. G n The shift theorem (also called the parallel ais theorem) shifts S s moment of inertia about S cm (the mass center of S) for the unit vector n z to an arbitrar point P in the plane using A n z C D F E n S/P = S/Scm + m S d where S/Scm is the sstem s moment of inertia about S cm for n z, m S is the mass of S, andd is the distance from S cm to P. Use the shift theorem to estimate the order of S s moment of inertia for the lines parallel to n z that pass through points A,, C, D, E, F, G, andh, respectivel. Note: Grid lines are equall spaced. Result: Smallest Largest Knowing each particle has mass m = 1 kg and the grid lines are spaced 1 m apart, calculate S s moment of inertia about A,, C, D, E, F, G, andh, respectivel. Result: S/A S/ (in kg m ) 8 S/C S/D S/E S/F S/G H S/H Copright c Paul Mitigu. All rights reserved. Homework 10: Moments/products of inertia
2 10. Sign conventions for products of inertia (Section 1..). There are two sign conventions ( ± ) for products of inertia which often lead to errors True/False. 10. Calculations: Product of inertia for a single particle (Section 1.). The product of inertia of a single particle about a point for the and ŷ directions is calculated b the formula = m m is the mass of is the measure of s position vector from is the ŷ measure of s position vector from For eample, if m =1kg, =m, and =m, = (1kg)(m)(m) = kgm Knowing particle has a mass of 1 kg and each tick-mark represents 1 m, calculate s product of inertia about point for each figure below. = kgm = kg m = kg m = kg m = kgm = kg m = kg m = kg m Circle the correct answer (negative, zero, or positive) for each statement about particle. When is in quadrant, is negative/zero/positive. When is in quadrant, is negative/zero/positive. When is in quadrant, is negative/zero/positive. When is in quadrant, is negative/zero/positive. When is on a quadrant boundar, is negative/zero/positive. Copright c Paul Mitigu. All rights reserved. 8 Homework 10: Moments/products of inertia
3 10. Calculations: Product of inertia for a sstem of particles (Section 1.). The product of inertia of a sstem of particles is simpl the sum of the products of inertias of each of the individual particles. For eample, the product of inertia of particles 1 and about point for the and ŷ directions is calculated b the formula = i=1 mi i i m i is the mass of particle i (i=1, ) i is the measure of i s position vector from i is the ŷ measure of i s position vector from (, ) For eample, if m 1 =1kg, 1 =m, 1 =1m, and m =kg, =m, =m, 1 ( 1, 1 ) = m m = (1kg)(m)(1m) + (kg)(m)(m) = 1 kg m Knowing each particle has a mass of 1 kg and each tick-mark represents 1 m, calculate the sstem s product of inertia about point for each figure below = kg m = kg m = kg m 1 = kg m Circle the correct answer (negative, zero, or positive) for each of the following statements. When the particles are in quadrants and, is negative/zero/positive. When the particles are in quadrants and, is negative/zero/positive. When the particles are on quadrant boundaries, is negative/zero/positive. 10. Concepts: Products of inertia of propellers (Section 1..). The following shows four uniform-densit objects. For each object, consider the product of inertia of the object for lines that pass through point and are parallel to n and n. For each object, visuall determine whether the product of inertia is negative, zero, or positive. n z n n zero negative negative zero n Guess n z n Copright c Paul Mitigu. All rights reserved. 9 Homework 10: Moments/products of inertia
4 10.8 Concepts: Products of inertia what is? (Section 1..). Product of inertia is a measure of the smmetr of mass distribution in two directions about a point. To investigate this concept, use our geometrical insights (not equations) to determine which of the following uniform-densit objects have a negative, zero, or positive product of inertia. Visuall sum the mass distribution for in quadrants and and compare that to the mass distribution in quadrants and. Complete each blank below with < or = or >. f mass distribution in quadrants + is greater than in quadrants +, > 0. f mass distribution in quadrants + is smaller than in quadrants +, < 0. f mass distribution in quadrants + is equal to quadrants +, =0. = Purchase rattleback at Eplained: Copright c Paul Mitigu. All rights reserved. 0 Homework 10: Moments/products of inertia
5 10.9 Conceptual understanding of moments and products of inertia (Sections 1.1. and 1..). bjects A,, C, D, ande are all flat planar objects with uniform densit and the same mass. The circle and semi-circle s diameter, square and rectangle s width, and thin rod s length are equal. A C D E n S denotes one of n n z A,, C, D, ore. % Consider S/, S s moment of inertia about the line passing through point and parallel to n z. Knowing moment of inertia is mass distance, use visual estimates to list the objects in ascending order of S/. ftwoobjectshavethesamevalueof S/, group them together. Result: Smallest Largest 8% Consider S/Scm, S s moment of inertia about the line passing through S cm (the mass center of S) and parallel to n z. Use visual estimates to list the objects in ascending order of S/Scm. Note: A and E have nearl equal S/Scm. The tetbook s inertia appendi helps resolve their difference. Result: Smallest D Largest (given) % Consider S/, S s product of inertia for point and unit vectors n and n. For each object, visuall determine if S/ is negative ( ), zero (0), or positive (+). A C D E Result: Assembling inertia dadics from the tetbook s inertia appendi (Sections 1.1 and 1.). Referring to the following figures and the tetbook s inertia appendi, assemble / cm ( s inertia dadic about its center of mass cm) for the unit vectors b, b,. Epress results in matri form. b b b cm b bz b b b a 1 ma a 0 b a c m(a + b ) b r b cm b b r b h = b 1 b Copright c Paul Mitigu. All rights reserved. 1 Homework 10: Moments/products of inertia
6 10.11 iomechanics: Estimating mass distribution properties of a bone (Sections 1.1 and 1.). The following figure shows a relativel thin, uniform-densit, rigid bone. Right-handed orthogonal unit vectors b, b, are fied in. Apoint o of is midwa though the bone ( r cm/o =0). Estimate and draw the location of cm ( s center of mass) on the figure. b cm Hint: Draw horizontal (parallel to b ) and vertical (parallel to b ) lines passing through o. Similarl for cm. o b 0 cm Knowingthe1kgbonefitssnuglina0cmbcmb1cmbo,visuall estimate the following values. Note: ther than 0.0 which is used times, use each of the following values once in our table Description Smbol Approimate value b measure of cm s position vector from o. cm b measure of cm s position vector from o 1. cm s moment of inertia about cm for b s moment of inertia about cm for b s moment of inertia about cm for s product of inertia about cm for b and b s product of inertia about cm for b and s product of inertia about cm for b and s moment of inertia about o for b s moment of inertia about o for b s moment of inertia about o for /cm kg cm /cm kg cm /cm kg cm /cm kg cm /cm z kg cm /cm z kg cm /o kg cm /o kg cm /o kg cm s product of inertia about o for b and b s product of inertia about o for b and /o kg cm /o z kg cm s product of inertia about o for b and /o z kg cm Hint: Start with products of inertia, then smallest moments of inertia, then largest moments of inertia. Hint: Draw an end-view of the bone to help estimate the two z. Draw a top-view to estimate the two z Dadics and dot-products with orthogonal unit vectors b, b, (Section 1.1). Non-smmetric dadic: Smmetric dadic: N = b b + b b + b bz + bz b S = b b + b b + b bz + b + bz Non-smmetric dadic Smmetric dadic N ( b + b ) = b + b S ( b + b ) = + + ( b + b ) N = + + ( b + b ) S = + + N anvector = anvector N True/False S anvector = anvector S b True/False Copright c Paul Mitigu. All rights reserved. Homework 10: Moments/products of inertia
Dynamic Celt. Context: Product of inertia affects rotational motion
 Dnamic Celt From earliest recorded histor, children have been skipping stones and spinning tops. The challenge in phsics is to provide scientific eplanations for their curious behavior. Until now, the
Dnamic Celt From earliest recorded histor, children have been skipping stones and spinning tops. The challenge in phsics is to provide scientific eplanations for their curious behavior. Until now, the
Example: Inverted pendulum on cart
 Chapter 11 Eample: Inverted pendulum on cart The figure to the right shows a rigid body attached by an frictionless pin (revolute) joint to a cart (modeled as a particle). Thecart slides on a horizontal
Chapter 11 Eample: Inverted pendulum on cart The figure to the right shows a rigid body attached by an frictionless pin (revolute) joint to a cart (modeled as a particle). Thecart slides on a horizontal
ENGI 4430 Advanced Calculus for Engineering Faculty of Engineering and Applied Science Problem Set 3 Solutions [Multiple Integration; Lines of Force]
![ENGI 4430 Advanced Calculus for Engineering Faculty of Engineering and Applied Science Problem Set 3 Solutions [Multiple Integration; Lines of Force] ENGI 4430 Advanced Calculus for Engineering Faculty of Engineering and Applied Science Problem Set 3 Solutions [Multiple Integration; Lines of Force]](/thumbs/84/89723886.jpg) ENGI 44 Advanced Calculus for Engineering Facult of Engineering and Applied Science Problem Set Solutions [Multiple Integration; Lines of Force]. Evaluate D da over the triangular region D that is bounded
ENGI 44 Advanced Calculus for Engineering Facult of Engineering and Applied Science Problem Set Solutions [Multiple Integration; Lines of Force]. Evaluate D da over the triangular region D that is bounded
1.1 The Equations of Motion
 1.1 The Equations of Motion In Book I, balance of forces and moments acting on an component was enforced in order to ensure that the component was in equilibrium. Here, allowance is made for stresses which
1.1 The Equations of Motion In Book I, balance of forces and moments acting on an component was enforced in order to ensure that the component was in equilibrium. Here, allowance is made for stresses which
Dynamics and control of mechanical systems
 JU 18/HL Dnamics and control of mechanical sstems Date Da 1 (3/5) 5/5 Da (7/5) Da 3 (9/5) Da 4 (11/5) Da 5 (14/5) Da 6 (16/5) Content Revie of the basics of mechanics. Kinematics of rigid bodies coordinate
JU 18/HL Dnamics and control of mechanical sstems Date Da 1 (3/5) 5/5 Da (7/5) Da 3 (9/5) Da 4 (11/5) Da 5 (14/5) Da 6 (16/5) Content Revie of the basics of mechanics. Kinematics of rigid bodies coordinate
2. Supports which resist forces in two directions. Fig Hinge. Rough Surface. Fig Rocker. Roller. Frictionless Surface
 4. Structural Equilibrium 4.1 ntroduction n statics, it becomes convenient to ignore the small deformation and displacement. We pretend that the materials used are rigid, having the propert or infinite
4. Structural Equilibrium 4.1 ntroduction n statics, it becomes convenient to ignore the small deformation and displacement. We pretend that the materials used are rigid, having the propert or infinite
ME 101: Engineering Mechanics
 ME 0: Engineering Mechanics Rajib Kumar Bhattacharja Department of Civil Engineering ndian nstitute of Technolog Guwahati M Block : Room No 005 : Tel: 8 www.iitg.ernet.in/rkbc Area Moments of nertia Parallel
ME 0: Engineering Mechanics Rajib Kumar Bhattacharja Department of Civil Engineering ndian nstitute of Technolog Guwahati M Block : Room No 005 : Tel: 8 www.iitg.ernet.in/rkbc Area Moments of nertia Parallel
Concepts in Newtonian mechanics
 Concepts in ewtonian mechanics For each question, fill in the blank, circle true or false, circle one (or more) of the multiple choice answers, write the definition, or complete the drawing. The percentages
Concepts in ewtonian mechanics For each question, fill in the blank, circle true or false, circle one (or more) of the multiple choice answers, write the definition, or complete the drawing. The percentages
Example: Inverted pendulum on cart
 Chapter 25 Eample: Inverted pendulum on cart The figure to the right shows a rigid body attached by an frictionless pin (revolute joint to a cart (modeled as a particle. Thecart slides on a horizontal
Chapter 25 Eample: Inverted pendulum on cart The figure to the right shows a rigid body attached by an frictionless pin (revolute joint to a cart (modeled as a particle. Thecart slides on a horizontal
The Plane Stress Problem
 . 4 The Plane Stress Problem 4 Chapter 4: THE PLANE STRESS PROBLEM 4 TABLE OF CONTENTS Page 4.. INTRODUCTION 4 3 4... Plate in Plane Stress............... 4 3 4... Mathematical Model.............. 4 4
. 4 The Plane Stress Problem 4 Chapter 4: THE PLANE STRESS PROBLEM 4 TABLE OF CONTENTS Page 4.. INTRODUCTION 4 3 4... Plate in Plane Stress............... 4 3 4... Mathematical Model.............. 4 4
1 HOMOGENEOUS TRANSFORMATIONS
 HOMOGENEOUS TRANSFORMATIONS Purpose: The purpose of this chapter is to introduce ou to the Homogeneous Transformation. This simple 4 4 transformation is used in the geometr engines of CAD sstems and in
HOMOGENEOUS TRANSFORMATIONS Purpose: The purpose of this chapter is to introduce ou to the Homogeneous Transformation. This simple 4 4 transformation is used in the geometr engines of CAD sstems and in
[4] Properties of Geometry
![[4] Properties of Geometry [4] Properties of Geometry](/thumbs/91/107196493.jpg) [4] Properties of Geometr Page 1 of 6 [4] Properties of Geometr [4.1] Center of Gravit and Centroid [4.] Composite Bodies [4.3] Moments of Inertia [4.4] Composite reas and Products of Inertia [4] Properties
[4] Properties of Geometr Page 1 of 6 [4] Properties of Geometr [4.1] Center of Gravit and Centroid [4.] Composite Bodies [4.3] Moments of Inertia [4.4] Composite reas and Products of Inertia [4] Properties
EMA 3702 Mechanics & Materials Science (Mechanics of Materials) Chapter 4 Pure Bending
 EA 3702 echanics & aterials Science (echanics of aterials) Chapter 4 Pure Bending Pure Bending Ch 2 Aial Loading & Parallel Loading: uniform normal stress and shearing stress distribution Ch 3 Torsion:
EA 3702 echanics & aterials Science (echanics of aterials) Chapter 4 Pure Bending Pure Bending Ch 2 Aial Loading & Parallel Loading: uniform normal stress and shearing stress distribution Ch 3 Torsion:
Chapter 5 Equilibrium of a Rigid Body Objectives
 Chapter 5 Equilibrium of a Rigid Bod Objectives Develop the equations of equilibrium for a rigid bod Concept of the free-bod diagram for a rigid bod Solve rigid-bod equilibrium problems using the equations
Chapter 5 Equilibrium of a Rigid Bod Objectives Develop the equations of equilibrium for a rigid bod Concept of the free-bod diagram for a rigid bod Solve rigid-bod equilibrium problems using the equations
Identifying second degree equations
 Chapter 7 Identifing second degree equations 71 The eigenvalue method In this section we appl eigenvalue methods to determine the geometrical nature of the second degree equation a 2 + 2h + b 2 + 2g +
Chapter 7 Identifing second degree equations 71 The eigenvalue method In this section we appl eigenvalue methods to determine the geometrical nature of the second degree equation a 2 + 2h + b 2 + 2g +
Distributed Forces: Moments of Inertia
 Distributed Forces: Moments of nertia Contents ntroduction Moments of nertia of an Area Moments of nertia of an Area b ntegration Polar Moments of nertia Radius of Gration of an Area Sample Problems Parallel
Distributed Forces: Moments of nertia Contents ntroduction Moments of nertia of an Area Moments of nertia of an Area b ntegration Polar Moments of nertia Radius of Gration of an Area Sample Problems Parallel
x y plane is the plane in which the stresses act, yy xy xy Figure 3.5.1: non-zero stress components acting in the x y plane
 3.5 Plane Stress This section is concerned with a special two-dimensional state of stress called plane stress. It is important for two reasons: () it arises in real components (particularl in thin components
3.5 Plane Stress This section is concerned with a special two-dimensional state of stress called plane stress. It is important for two reasons: () it arises in real components (particularl in thin components
3. TRANSLATED PARABOLAS
 3. TRANSLATED PARABOLAS The Parabola with Verte V(h, k) and Aes Parallel to the ais Consider the concave up parabola with verte V(h, k) shown below. This parabola is obtained b translating the parabola
3. TRANSLATED PARABOLAS The Parabola with Verte V(h, k) and Aes Parallel to the ais Consider the concave up parabola with verte V(h, k) shown below. This parabola is obtained b translating the parabola
STATICS. Moments of Inertia VECTOR MECHANICS FOR ENGINEERS: Seventh Edition CHAPTER. Ferdinand P. Beer
 00 The McGraw-Hill Companies, nc. All rights reserved. Seventh E CHAPTER VECTOR MECHANCS FOR ENGNEERS: 9 STATCS Ferdinand P. Beer E. Russell Johnston, Jr. Distributed Forces: Lecture Notes: J. Walt Oler
00 The McGraw-Hill Companies, nc. All rights reserved. Seventh E CHAPTER VECTOR MECHANCS FOR ENGNEERS: 9 STATCS Ferdinand P. Beer E. Russell Johnston, Jr. Distributed Forces: Lecture Notes: J. Walt Oler
KINEMATIC RELATIONS IN DEFORMATION OF SOLIDS
 Chapter 8 KINEMATIC RELATIONS IN DEFORMATION OF SOLIDS Figure 8.1: 195 196 CHAPTER 8. KINEMATIC RELATIONS IN DEFORMATION OF SOLIDS 8.1 Motivation In Chapter 3, the conservation of linear momentum for a
Chapter 8 KINEMATIC RELATIONS IN DEFORMATION OF SOLIDS Figure 8.1: 195 196 CHAPTER 8. KINEMATIC RELATIONS IN DEFORMATION OF SOLIDS 8.1 Motivation In Chapter 3, the conservation of linear momentum for a
Contents. Dynamics and control of mechanical systems. Focuses on
 Dnamics and control of mechanical sstems Date Da (/8) Da (3/8) Da 3 (5/8) Da 4 (7/8) Da 5 (9/8) Da 6 (/8) Content Review of the basics of mechanics. Kinematics of rigid bodies - coordinate transformation,
Dnamics and control of mechanical sstems Date Da (/8) Da (3/8) Da 3 (5/8) Da 4 (7/8) Da 5 (9/8) Da 6 (/8) Content Review of the basics of mechanics. Kinematics of rigid bodies - coordinate transformation,
9.2. Cartesian Components of Vectors. Introduction. Prerequisites. Learning Outcomes
 Cartesian Components of Vectors 9.2 Introduction It is useful to be able to describe vectors with reference to specific coordinate sstems, such as the Cartesian coordinate sstem. So, in this Section, we
Cartesian Components of Vectors 9.2 Introduction It is useful to be able to describe vectors with reference to specific coordinate sstems, such as the Cartesian coordinate sstem. So, in this Section, we
Functions of Several Variables
 Chapter 1 Functions of Several Variables 1.1 Introduction A real valued function of n variables is a function f : R, where the domain is a subset of R n. So: for each ( 1,,..., n ) in, the value of f is
Chapter 1 Functions of Several Variables 1.1 Introduction A real valued function of n variables is a function f : R, where the domain is a subset of R n. So: for each ( 1,,..., n ) in, the value of f is
9-1. The Function with Equation y = ax 2. Vocabulary. Graphing y = x 2. Lesson
 Chapter 9 Lesson 9-1 The Function with Equation = a BIG IDEA The graph of an quadratic function with equation = a, with a 0, is a parabola with verte at the origin. Vocabular parabola refl ection-smmetric
Chapter 9 Lesson 9-1 The Function with Equation = a BIG IDEA The graph of an quadratic function with equation = a, with a 0, is a parabola with verte at the origin. Vocabular parabola refl ection-smmetric
Research Article Equivalent Elastic Modulus of Asymmetrical Honeycomb
 International Scholarl Research Network ISRN Mechanical Engineering Volume, Article ID 57, pages doi:.5//57 Research Article Equivalent Elastic Modulus of Asmmetrical Honecomb Dai-Heng Chen and Kenichi
International Scholarl Research Network ISRN Mechanical Engineering Volume, Article ID 57, pages doi:.5//57 Research Article Equivalent Elastic Modulus of Asmmetrical Honecomb Dai-Heng Chen and Kenichi
STATICS. Moments of Inertia VECTOR MECHANICS FOR ENGINEERS: Ninth Edition CHAPTER. Ferdinand P. Beer E. Russell Johnston, Jr.
 N E 9 Distributed CHAPTER VECTOR MECHANCS FOR ENGNEERS: STATCS Ferdinand P. Beer E. Russell Johnston, Jr. Lecture Notes: J. Walt Oler Teas Tech Universit Forces: Moments of nertia Contents ntroduction
N E 9 Distributed CHAPTER VECTOR MECHANCS FOR ENGNEERS: STATCS Ferdinand P. Beer E. Russell Johnston, Jr. Lecture Notes: J. Walt Oler Teas Tech Universit Forces: Moments of nertia Contents ntroduction
CHAPTER SIXTEEN. = 4 x y + 6 x y + 3 x y + 4 x y = 17 x y = 31(0.1)(0.2) = f(x i, y i) x y = 7 x y + 10 x y + 6 x y + 8 x y = 31 x y. x = 0.
 CHAPTE SIXTEEN 6. SOLUTIONS 5 Solutions for Section 6. Eercises. Mark the values of the function on the plane, as shown in Figure 6., so that ou can guess respectivel at the smallest and largest values
CHAPTE SIXTEEN 6. SOLUTIONS 5 Solutions for Section 6. Eercises. Mark the values of the function on the plane, as shown in Figure 6., so that ou can guess respectivel at the smallest and largest values
4 The Cartesian Coordinate System- Pictures of Equations
 The Cartesian Coordinate Sstem- Pictures of Equations Concepts: The Cartesian Coordinate Sstem Graphs of Equations in Two Variables -intercepts and -intercepts Distance in Two Dimensions and the Pthagorean
The Cartesian Coordinate Sstem- Pictures of Equations Concepts: The Cartesian Coordinate Sstem Graphs of Equations in Two Variables -intercepts and -intercepts Distance in Two Dimensions and the Pthagorean
Triple Integrals in Cartesian Coordinates. Triple Integrals in Cylindrical Coordinates. Triple Integrals in Spherical Coordinates
 Chapter 3 Multiple Integral 3. Double Integrals 3. Iterated Integrals 3.3 Double Integrals in Polar Coordinates 3.4 Triple Integrals Triple Integrals in Cartesian Coordinates Triple Integrals in Clindrical
Chapter 3 Multiple Integral 3. Double Integrals 3. Iterated Integrals 3.3 Double Integrals in Polar Coordinates 3.4 Triple Integrals Triple Integrals in Cartesian Coordinates Triple Integrals in Clindrical
6 = 1 2. The right endpoints of the subintervals are then 2 5, 3, 7 2, 4, 2 9, 5, while the left endpoints are 2, 5 2, 3, 7 2, 4, 9 2.
 5 THE ITEGRAL 5. Approimating and Computing Area Preliminar Questions. What are the right and left endpoints if [, 5] is divided into si subintervals? If the interval [, 5] is divided into si subintervals,
5 THE ITEGRAL 5. Approimating and Computing Area Preliminar Questions. What are the right and left endpoints if [, 5] is divided into si subintervals? If the interval [, 5] is divided into si subintervals,
Announcements. Topics: Homework: - section 12.4 (cross/vector product) - section 12.5 (equations of lines and planes)
 Topics: Announcements - section 12.4 (cross/vector product) - section 12.5 (equations of lines and planes) Homework: ü review lecture notes thoroughl ü work on eercises from the tetbook in sections 12.4
Topics: Announcements - section 12.4 (cross/vector product) - section 12.5 (equations of lines and planes) Homework: ü review lecture notes thoroughl ü work on eercises from the tetbook in sections 12.4
Mathematics 309 Conic sections and their applicationsn. Chapter 2. Quadric figures. ai,j x i x j + b i x i + c =0. 1. Coordinate changes
 Mathematics 309 Conic sections and their applicationsn Chapter 2. Quadric figures In this chapter want to outline quickl how to decide what figure associated in 2D and 3D to quadratic equations look like.
Mathematics 309 Conic sections and their applicationsn Chapter 2. Quadric figures In this chapter want to outline quickl how to decide what figure associated in 2D and 3D to quadratic equations look like.
I xx + I yy + I zz = (y 2 + z 2 )dm + (x 2 + y 2 )dm. (x 2 + z 2 )dm + (x 2 + y 2 + z 2 )dm = 2
 9196_1_s1_p095-0987 6/8/09 1:09 PM Page 95 010 Pearson Education, Inc., Upper Saddle River, NJ. ll rights reserved. This material is protected under all copright laws as the currentl 1 1. Show that the
9196_1_s1_p095-0987 6/8/09 1:09 PM Page 95 010 Pearson Education, Inc., Upper Saddle River, NJ. ll rights reserved. This material is protected under all copright laws as the currentl 1 1. Show that the
11.4 Polar Coordinates
 11. Polar Coordinates 917 11. Polar Coordinates In Section 1.1, we introduced the Cartesian coordinates of a point in the plane as a means of assigning ordered pairs of numbers to points in the plane.
11. Polar Coordinates 917 11. Polar Coordinates In Section 1.1, we introduced the Cartesian coordinates of a point in the plane as a means of assigning ordered pairs of numbers to points in the plane.
10.4 Nonlinear Inequalities and Systems of Inequalities. OBJECTIVES 1 Graph a Nonlinear Inequality. 2 Graph a System of Nonlinear Inequalities.
 Section 0. Nonlinear Inequalities and Sstems of Inequalities 6 CONCEPT EXTENSIONS For the eercises below, see the Concept Check in this section.. Without graphing, how can ou tell that the graph of + =
Section 0. Nonlinear Inequalities and Sstems of Inequalities 6 CONCEPT EXTENSIONS For the eercises below, see the Concept Check in this section.. Without graphing, how can ou tell that the graph of + =
ENGI 4430 Multiple Integration Cartesian Double Integrals Page 3-01
 ENGI 4430 Multiple Integration Cartesian Double Integrals Page 3-01 3. Multiple Integration This chapter provides only a very brief introduction to the major topic of multiple integration. Uses of multiple
ENGI 4430 Multiple Integration Cartesian Double Integrals Page 3-01 3. Multiple Integration This chapter provides only a very brief introduction to the major topic of multiple integration. Uses of multiple
4 Strain true strain engineering strain plane strain strain transformation formulae
 4 Strain The concept of strain is introduced in this Chapter. The approimation to the true strain of the engineering strain is discussed. The practical case of two dimensional plane strain is discussed,
4 Strain The concept of strain is introduced in this Chapter. The approimation to the true strain of the engineering strain is discussed. The practical case of two dimensional plane strain is discussed,
2.1 The Rectangular Coordinate System
 . The Rectangular Coordinate Sstem In this section ou will learn to: plot points in a rectangular coordinate sstem understand basic functions of the graphing calculator graph equations b generating a table
. The Rectangular Coordinate Sstem In this section ou will learn to: plot points in a rectangular coordinate sstem understand basic functions of the graphing calculator graph equations b generating a table
c) Words: The cost of a taxicab is $2.00 for the first 1/4 of a mile and $1.00 for each additional 1/8 of a mile.
 Functions Definition: A function f, defined from a set A to a set B, is a rule that associates with each element of the set A one, and onl one, element of the set B. Eamples: a) Graphs: b) Tables: 0 50
Functions Definition: A function f, defined from a set A to a set B, is a rule that associates with each element of the set A one, and onl one, element of the set B. Eamples: a) Graphs: b) Tables: 0 50
Force Couple Systems = Replacement of a Force with an Equivalent Force and Moment (Moving a Force to Another Point)
 orce Couple Sstems = eplacement of a orce with an Equivalent orce and oment (oving a orce to Another Point) The force acting on a bod has two effects: The first one is the tendenc to push or pull the bod
orce Couple Sstems = eplacement of a orce with an Equivalent orce and oment (oving a orce to Another Point) The force acting on a bod has two effects: The first one is the tendenc to push or pull the bod
17. Find the moments of inertia I x, I y, I 0 for the lamina of. 4. D x, y 0 x a, 0 y b ; CAS. 20. D is enclosed by the cardioid r 1 cos ; x, y 3
 SCTION 2.5 TRIPL INTGRALS 69 2.4 XRCISS. lectric charge is distributed over the rectangle, 2 so that the charge densit at, is, 2 2 (measured in coulombs per square meter). Find the total charge on the
SCTION 2.5 TRIPL INTGRALS 69 2.4 XRCISS. lectric charge is distributed over the rectangle, 2 so that the charge densit at, is, 2 2 (measured in coulombs per square meter). Find the total charge on the
Vocabulary. The Pythagorean Identity. Lesson 4-3. Pythagorean Identity Theorem. Mental Math
 Lesson 4-3 Basic Basic Trigonometric Identities Identities Vocabular identit BIG IDEA If ou know cos, ou can easil fi nd cos( ), cos(90º - ), cos(180º - ), and cos(180º + ) without a calculator, and similarl
Lesson 4-3 Basic Basic Trigonometric Identities Identities Vocabular identit BIG IDEA If ou know cos, ou can easil fi nd cos( ), cos(90º - ), cos(180º - ), and cos(180º + ) without a calculator, and similarl
Complete Solutions Manual. Technical Calculus with Analytic Geometry FIFTH EDITION. Peter Kuhfittig Milwaukee School of Engineering.
 Complete Solutions Manual Technical Calculus with Analtic Geometr FIFTH EDITION Peter Kuhfittig Milwaukee School of Engineering Australia Brazil Meico Singapore United Kingdom United States 213 Cengage
Complete Solutions Manual Technical Calculus with Analtic Geometr FIFTH EDITION Peter Kuhfittig Milwaukee School of Engineering Australia Brazil Meico Singapore United Kingdom United States 213 Cengage
Graph and Write Equations of Ellipses. You graphed and wrote equations of parabolas and circles. You will graph and write equations of ellipses.
 TEKS 9.4 a.5, A.5.B, A.5.C Before Now Graph and Write Equations of Ellipses You graphed and wrote equations of parabolas and circles. You will graph and write equations of ellipses. Wh? So ou can model
TEKS 9.4 a.5, A.5.B, A.5.C Before Now Graph and Write Equations of Ellipses You graphed and wrote equations of parabolas and circles. You will graph and write equations of ellipses. Wh? So ou can model
11.1 Double Riemann Sums and Double Integrals over Rectangles
 Chapter 11 Multiple Integrals 11.1 ouble Riemann Sums and ouble Integrals over Rectangles Motivating Questions In this section, we strive to understand the ideas generated b the following important questions:
Chapter 11 Multiple Integrals 11.1 ouble Riemann Sums and ouble Integrals over Rectangles Motivating Questions In this section, we strive to understand the ideas generated b the following important questions:
BEAMS: SHEAR AND MOMENT DIAGRAMS (FORMULA)
 LETURE Third Edition BEMS: SHER ND MOMENT DGRMS (FORMUL). J. lark School of Engineering Department of ivil and Environmental Engineering 1 hapter 5.1 5. b Dr. brahim. ssakkaf SPRNG 00 ENES 0 Mechanics
LETURE Third Edition BEMS: SHER ND MOMENT DGRMS (FORMUL). J. lark School of Engineering Department of ivil and Environmental Engineering 1 hapter 5.1 5. b Dr. brahim. ssakkaf SPRNG 00 ENES 0 Mechanics
Moments of Inertia. Notation:
 RCH 1 Note Set 9. S015abn Moments of nertia Notation: b d d d h c Jo O = name for area = name for a (base) width = calculus smbol for differentiation = name for a difference = name for a depth = difference
RCH 1 Note Set 9. S015abn Moments of nertia Notation: b d d d h c Jo O = name for area = name for a (base) width = calculus smbol for differentiation = name for a difference = name for a depth = difference
f x and the x axis on an interval from x a and
 Unit 6: Chapter 8 Areas and Volumes & Density Functions Part 1: Areas To find the area bounded by a function bwe use the integral: f d b a b 0 f d f d. a b a f and the ais on an interval from a and. This
Unit 6: Chapter 8 Areas and Volumes & Density Functions Part 1: Areas To find the area bounded by a function bwe use the integral: f d b a b 0 f d f d. a b a f and the ais on an interval from a and. This
Equilibrium of Rigid Bodies
 Equilibrium of Rigid Bodies 1 2 Contents Introduction Free-Bod Diagram Reactions at Supports and Connections for a wo-dimensional Structure Equilibrium of a Rigid Bod in wo Dimensions Staticall Indeterminate
Equilibrium of Rigid Bodies 1 2 Contents Introduction Free-Bod Diagram Reactions at Supports and Connections for a wo-dimensional Structure Equilibrium of a Rigid Bod in wo Dimensions Staticall Indeterminate
Introduction to 3D Game Programming with DirectX 9.0c: A Shader Approach
 Introduction to 3D Game Programming with DirectX 90c: A Shader Approach Part I Solutions Note : Please email to frank@moon-labscom if ou find an errors Note : Use onl after ou have tried, and struggled
Introduction to 3D Game Programming with DirectX 90c: A Shader Approach Part I Solutions Note : Please email to frank@moon-labscom if ou find an errors Note : Use onl after ou have tried, and struggled
MMJ1153 COMPUTATIONAL METHOD IN SOLID MECHANICS PRELIMINARIES TO FEM
 B Course Content: A INTRODUCTION AND OVERVIEW Numerical method and Computer-Aided Engineering; Phsical problems; Mathematical models; Finite element method;. B Elements and nodes, natural coordinates,
B Course Content: A INTRODUCTION AND OVERVIEW Numerical method and Computer-Aided Engineering; Phsical problems; Mathematical models; Finite element method;. B Elements and nodes, natural coordinates,
UNCORRECTED SAMPLE PAGES. 3Quadratics. Chapter 3. Objectives
 Chapter 3 3Quadratics Objectives To recognise and sketch the graphs of quadratic polnomials. To find the ke features of the graph of a quadratic polnomial: ais intercepts, turning point and ais of smmetr.
Chapter 3 3Quadratics Objectives To recognise and sketch the graphs of quadratic polnomials. To find the ke features of the graph of a quadratic polnomial: ais intercepts, turning point and ais of smmetr.
PRINCIPLES OF MATHEMATICS 11 Chapter 2 Quadratic Functions Lesson 1 Graphs of Quadratic Functions (2.1) where a, b, and c are constants and a 0
 PRINCIPLES OF MATHEMATICS 11 Chapter Quadratic Functions Lesson 1 Graphs of Quadratic Functions (.1) Date A. QUADRATIC FUNCTIONS A quadratic function is an equation that can be written in the following
PRINCIPLES OF MATHEMATICS 11 Chapter Quadratic Functions Lesson 1 Graphs of Quadratic Functions (.1) Date A. QUADRATIC FUNCTIONS A quadratic function is an equation that can be written in the following
10 3. Determine the moment of inertia of the area about the x axis.
 10 3. Determine the moment of inertia of the area about the ais. m m 10 4. Determine the moment of inertia of the area about the ais. m m 10 3. Determine the moment of inertia of the shaded area about
10 3. Determine the moment of inertia of the area about the ais. m m 10 4. Determine the moment of inertia of the area about the ais. m m 10 3. Determine the moment of inertia of the shaded area about
Fluid Mechanics II. Newton s second law applied to a control volume
 Fluid Mechanics II Stead flow momentum equation Newton s second law applied to a control volume Fluids, either in a static or dnamic motion state, impose forces on immersed bodies and confining boundaries.
Fluid Mechanics II Stead flow momentum equation Newton s second law applied to a control volume Fluids, either in a static or dnamic motion state, impose forces on immersed bodies and confining boundaries.
10.2 The Unit Circle: Cosine and Sine
 0. The Unit Circle: Cosine and Sine 77 0. The Unit Circle: Cosine and Sine In Section 0.., we introduced circular motion and derived a formula which describes the linear velocit of an object moving on
0. The Unit Circle: Cosine and Sine 77 0. The Unit Circle: Cosine and Sine In Section 0.., we introduced circular motion and derived a formula which describes the linear velocit of an object moving on
LESSON 4.3 GRAPHING INEQUALITIES
 LESSON.3 GRAPHING INEQUALITIES LESSON.3 GRAPHING INEQUALITIES 9 OVERVIEW Here s what ou ll learn in this lesson: Linear Inequalities a. Ordered pairs as solutions of linear inequalities b. Graphing linear
LESSON.3 GRAPHING INEQUALITIES LESSON.3 GRAPHING INEQUALITIES 9 OVERVIEW Here s what ou ll learn in this lesson: Linear Inequalities a. Ordered pairs as solutions of linear inequalities b. Graphing linear
EXERCISES Chapter 15: Multiple Integrals. Evaluating Integrals in Cylindrical Coordinates
 08 Chapter 5: Multiple Integrals EXERCISES 5.6 Evaluating Integrals in Clindrical Evaluate the clindrical coordinate integrals in Eercises 6... 3. 4. 5. 6. Changing Order of Integration in Clindrical The
08 Chapter 5: Multiple Integrals EXERCISES 5.6 Evaluating Integrals in Clindrical Evaluate the clindrical coordinate integrals in Eercises 6... 3. 4. 5. 6. Changing Order of Integration in Clindrical The
Statics: Lecture Notes for Sections 10.1,10.2,10.3 1
 Chapter 10 MOMENTS of INERTIA for AREAS, RADIUS OF GYRATION Today s Objectives: Students will be able to: a) Define the moments of inertia (MoI) for an area. b) Determine the MoI for an area by integration.
Chapter 10 MOMENTS of INERTIA for AREAS, RADIUS OF GYRATION Today s Objectives: Students will be able to: a) Define the moments of inertia (MoI) for an area. b) Determine the MoI for an area by integration.
a x b x b y b z Homework 3. Chapter 4. Vector bases and rotation matrices
 Homework 3. Chapter 4. Vector bases and rotation matrices 3.1 Dynamics project rotation matrices Update your typed problem description and identifiers as necessary. Include schematics showing the bodies,
Homework 3. Chapter 4. Vector bases and rotation matrices 3.1 Dynamics project rotation matrices Update your typed problem description and identifiers as necessary. Include schematics showing the bodies,
Consider a slender rod, fixed at one end and stretched, as illustrated in Fig ; the original position of the rod is shown dotted.
 4.1 Strain If an object is placed on a table and then the table is moved, each material particle moves in space. The particles undergo a displacement. The particles have moved in space as a rigid bod.
4.1 Strain If an object is placed on a table and then the table is moved, each material particle moves in space. The particles undergo a displacement. The particles have moved in space as a rigid bod.
Physics Gravitational force. 2. Strong or color force. 3. Electroweak force
 Phsics 360 Notes on Griffths - pluses and minuses No tetbook is perfect, and Griffithsisnoeception. Themajorplusisthat it is prett readable. For minuses, see below. Much of what G sas about the del operator
Phsics 360 Notes on Griffths - pluses and minuses No tetbook is perfect, and Griffithsisnoeception. Themajorplusisthat it is prett readable. For minuses, see below. Much of what G sas about the del operator
Reteaching (continued)
 Quadratic Functions and Transformations If a, the graph is a stretch or compression of the parent function b a factor of 0 a 0. 0 0 0 0 0 a a 7 The graph is a vertical The graph is a vertical compression
Quadratic Functions and Transformations If a, the graph is a stretch or compression of the parent function b a factor of 0 a 0. 0 0 0 0 0 a a 7 The graph is a vertical The graph is a vertical compression
y=1/4 x x=4y y=x 3 x=y 1/3 Example: 3.1 (1/2, 1/8) (1/2, 1/8) Find the area in the positive quadrant bounded by y = 1 x and y = x3
 Eample: 3.1 Find the area in the positive quadrant bounded b 1 and 3 4 First find the points of intersection of the two curves: clearl the curves intersect at (, ) and at 1 4 3 1, 1 8 Select a strip at
Eample: 3.1 Find the area in the positive quadrant bounded b 1 and 3 4 First find the points of intersection of the two curves: clearl the curves intersect at (, ) and at 1 4 3 1, 1 8 Select a strip at
Mechanics Departmental Exam Last updated November 2013
 Mechanics Departmental Eam Last updated November 213 1. Two satellites are moving about each other in circular orbits under the influence of their mutual gravitational attractions. The satellites have
Mechanics Departmental Eam Last updated November 213 1. Two satellites are moving about each other in circular orbits under the influence of their mutual gravitational attractions. The satellites have
Problem 1: (3 points) Recall that the dot product of two vectors in R 3 is
 Linear Algebra, Spring 206 Homework 3 Name: Problem : (3 points) Recall that the dot product of two vectors in R 3 is a x b y = ax + by + cz, c z and this is essentially the same as the matrix multiplication
Linear Algebra, Spring 206 Homework 3 Name: Problem : (3 points) Recall that the dot product of two vectors in R 3 is a x b y = ax + by + cz, c z and this is essentially the same as the matrix multiplication
The Plane Stress Problem
 . 14 The Plane Stress Problem 14 1 Chapter 14: THE PLANE STRESS PROBLEM 14 TABLE OF CONTENTS Page 14.1. Introduction 14 3 14.1.1. Plate in Plane Stress............... 14 3 14.1.. Mathematical Model..............
. 14 The Plane Stress Problem 14 1 Chapter 14: THE PLANE STRESS PROBLEM 14 TABLE OF CONTENTS Page 14.1. Introduction 14 3 14.1.1. Plate in Plane Stress............... 14 3 14.1.. Mathematical Model..............
Chapter 18 KINETICS OF RIGID BODIES IN THREE DIMENSIONS. The two fundamental equations for the motion of a system of particles .
 hapter 18 KINETIS F RIID DIES IN THREE DIMENSINS The to fundamental equations for the motion of a sstem of particles ΣF = ma ΣM = H H provide the foundation for three dimensional analsis, just as the do
hapter 18 KINETIS F RIID DIES IN THREE DIMENSINS The to fundamental equations for the motion of a sstem of particles ΣF = ma ΣM = H H provide the foundation for three dimensional analsis, just as the do
APPLIED MECHANICS I Resultant of Concurrent Forces Consider a body acted upon by co-planar forces as shown in Fig 1.1(a).
 PPLIED MECHNICS I 1. Introduction to Mechanics Mechanics is a science that describes and predicts the conditions of rest or motion of bodies under the action of forces. It is divided into three parts 1.
PPLIED MECHNICS I 1. Introduction to Mechanics Mechanics is a science that describes and predicts the conditions of rest or motion of bodies under the action of forces. It is divided into three parts 1.
Analytic Geometry in Three Dimensions
 Analtic Geometr in Three Dimensions. The Three-Dimensional Coordinate Sstem. Vectors in Space. The Cross Product of Two Vectors. Lines and Planes in Space The three-dimensional coordinate sstem is used
Analtic Geometr in Three Dimensions. The Three-Dimensional Coordinate Sstem. Vectors in Space. The Cross Product of Two Vectors. Lines and Planes in Space The three-dimensional coordinate sstem is used
CHAPTER 2: Partial Derivatives. 2.2 Increments and Differential
 CHAPTER : Partial Derivatives.1 Definition of a Partial Derivative. Increments and Differential.3 Chain Rules.4 Local Etrema.5 Absolute Etrema 1 Chapter : Partial Derivatives.1 Definition of a Partial
CHAPTER : Partial Derivatives.1 Definition of a Partial Derivative. Increments and Differential.3 Chain Rules.4 Local Etrema.5 Absolute Etrema 1 Chapter : Partial Derivatives.1 Definition of a Partial
Attributes and Transformations of Quadratic Functions VOCABULARY. Maximum value the greatest. Minimum value the least. Parabola the set of points in a
 - Attributes and Transformations of Quadratic Functions TEKS FCUS VCABULARY TEKS ()(B) Write the equation of a parabola using given attributes, including verte, focus, directri, ais of smmetr, and direction
- Attributes and Transformations of Quadratic Functions TEKS FCUS VCABULARY TEKS ()(B) Write the equation of a parabola using given attributes, including verte, focus, directri, ais of smmetr, and direction
Are You Ready? Find Area in the Coordinate Plane
 SKILL 38 Are You Read? Find Area in the Coordinate Plane Teaching Skill 38 Objective Find the areas of figures in the coordinate plane. Review with students the definition of area. Ask: Is the definition
SKILL 38 Are You Read? Find Area in the Coordinate Plane Teaching Skill 38 Objective Find the areas of figures in the coordinate plane. Review with students the definition of area. Ask: Is the definition
5. Nonholonomic constraint Mechanics of Manipulation
 5. Nonholonomic constraint Mechanics of Manipulation Matt Mason matt.mason@cs.cmu.edu http://www.cs.cmu.edu/~mason Carnegie Mellon Lecture 5. Mechanics of Manipulation p.1 Lecture 5. Nonholonomic constraint.
5. Nonholonomic constraint Mechanics of Manipulation Matt Mason matt.mason@cs.cmu.edu http://www.cs.cmu.edu/~mason Carnegie Mellon Lecture 5. Mechanics of Manipulation p.1 Lecture 5. Nonholonomic constraint.
Math 122 Fall Solutions to Homework #5. ( ) 2 " ln x. y = x 2
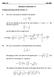 Math 1 Fall 8 Solutions to Homework #5 Problems from Pages 383-38 (Section 7.) 6. The curve in this problem is defined b the equation: = ( ) " ln and we are interested in the part of the curve between
Math 1 Fall 8 Solutions to Homework #5 Problems from Pages 383-38 (Section 7.) 6. The curve in this problem is defined b the equation: = ( ) " ln and we are interested in the part of the curve between
Chapter 9 BIAXIAL SHEARING
 9. DEFNTON Chapter 9 BAXAL SHEARNG As we have seen in the previous chapter, biaial (oblique) shearing produced b the shear forces and, appears in a bar onl accompanied b biaial bending (we ma discuss about
9. DEFNTON Chapter 9 BAXAL SHEARNG As we have seen in the previous chapter, biaial (oblique) shearing produced b the shear forces and, appears in a bar onl accompanied b biaial bending (we ma discuss about
Partial Differential Equations
 ++++++++++ Partial Differential Equations Previous ear Questions from 016 to 199 Ramanasri 017 S H O P NO- 4, 1 S T F L O O R, N E A R R A P I D F L O U R M I L L S, O L D R A J E N D E R N A G A R, N
++++++++++ Partial Differential Equations Previous ear Questions from 016 to 199 Ramanasri 017 S H O P NO- 4, 1 S T F L O O R, N E A R R A P I D F L O U R M I L L S, O L D R A J E N D E R N A G A R, N
Symmetry Arguments and the Role They Play in Using Gauss Law
 Smmetr Arguments and the Role The la in Using Gauss Law K. M. Westerberg (9/2005) Smmetr plas a ver important role in science in general, and phsics in particular. Arguments based on smmetr can often simplif
Smmetr Arguments and the Role The la in Using Gauss Law K. M. Westerberg (9/2005) Smmetr plas a ver important role in science in general, and phsics in particular. Arguments based on smmetr can often simplif
This problem set is a good representation of some of the key skills you should have when entering this course.
 Math 4 Review of Previous Material: This problem set is a good representation of some of the key skills you should have when entering this course. Based on the course work leading up to Math 4, you should
Math 4 Review of Previous Material: This problem set is a good representation of some of the key skills you should have when entering this course. Based on the course work leading up to Math 4, you should
ARCH 614 Note Set 2 S2011abn. Forces and Vectors
 orces and Vectors Notation: = name for force vectors, as is A, B, C, T and P = force component in the direction = force component in the direction h = cable sag height L = span length = name for resultant
orces and Vectors Notation: = name for force vectors, as is A, B, C, T and P = force component in the direction = force component in the direction h = cable sag height L = span length = name for resultant
CHAPTER 1 MEASUREMENTS AND VECTORS
 CHPTER 1 MESUREMENTS ND VECTORS 1 CHPTER 1 MESUREMENTS ND VECTORS 1.1 UNITS ND STNDRDS n phsical quantit must have, besides its numerical value, a standard unit. It will be meaningless to sa that the distance
CHPTER 1 MESUREMENTS ND VECTORS 1 CHPTER 1 MESUREMENTS ND VECTORS 1.1 UNITS ND STNDRDS n phsical quantit must have, besides its numerical value, a standard unit. It will be meaningless to sa that the distance
MAE 323: Chapter 4. Plane Stress and Plane Strain. The Stress Equilibrium Equation
 The Stress Equilibrium Equation As we mentioned in Chapter 2, using the Galerkin formulation and a choice of shape functions, we can derive a discretized form of most differential equations. In Structural
The Stress Equilibrium Equation As we mentioned in Chapter 2, using the Galerkin formulation and a choice of shape functions, we can derive a discretized form of most differential equations. In Structural
MAT 1275: Introduction to Mathematical Analysis. Graphs and Simplest Equations for Basic Trigonometric Functions. y=sin( x) Function
 MAT 275: Introduction to Mathematical Analsis Dr. A. Rozenblum Graphs and Simplest Equations for Basic Trigonometric Functions We consider here three basic functions: sine, cosine and tangent. For them,
MAT 275: Introduction to Mathematical Analsis Dr. A. Rozenblum Graphs and Simplest Equations for Basic Trigonometric Functions We consider here three basic functions: sine, cosine and tangent. For them,
Midterm Solutions. EE127A L. El Ghaoui 3/19/11
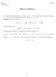 EE27A L. El Ghaoui 3/9/ Midterm Solutions. (6 points Find the projection z of the vector = (2, on the line that passes through 0 = (, 2 and with direction given by the vector u = (,. Solution: The line
EE27A L. El Ghaoui 3/9/ Midterm Solutions. (6 points Find the projection z of the vector = (2, on the line that passes through 0 = (, 2 and with direction given by the vector u = (,. Solution: The line
MATH 152 COLLEGE ALGEBRA AND TRIGONOMETRY UNIT 1 HOMEWORK ASSIGNMENTS
 0//0 MATH COLLEGE ALGEBRA AND TRIGONOMETRY UNIT HOMEWORK ASSIGNMENTS General Instructions Be sure to write out all our work, because method is as important as getting the correct answer. The answers to
0//0 MATH COLLEGE ALGEBRA AND TRIGONOMETRY UNIT HOMEWORK ASSIGNMENTS General Instructions Be sure to write out all our work, because method is as important as getting the correct answer. The answers to
EXERCISES Chapter 7: Transcendental Functions. Hyperbolic Function Values and Identities
 54 Chapter 7: ranscendental Functions EXERCISES 7.8 perbolic Function Values and Identities Each of Eercises 4 gives a value of sinh or cosh. Use the definitions and the identit cosh - sinh = to find the
54 Chapter 7: ranscendental Functions EXERCISES 7.8 perbolic Function Values and Identities Each of Eercises 4 gives a value of sinh or cosh. Use the definitions and the identit cosh - sinh = to find the
Solution 11. Kinetics of rigid body(newton s Second Law)
 Solution () urpose and Requirement Solution Kinetics of rigid bod(newton s Second Law) In rob, kinematics stud regarding acceleration of mass center should be done before Newton s second law is used to
Solution () urpose and Requirement Solution Kinetics of rigid bod(newton s Second Law) In rob, kinematics stud regarding acceleration of mass center should be done before Newton s second law is used to
Math Analysis/Honors Math Analysis Summer Assignment
 Math Analysis/Honors Math Analysis Summer Assignment To be successful in Math Analysis or Honors Math Analysis, a full understanding of the topics listed below is required prior to the school year. To
Math Analysis/Honors Math Analysis Summer Assignment To be successful in Math Analysis or Honors Math Analysis, a full understanding of the topics listed below is required prior to the school year. To
Stress and Strain ( , 3.14) MAE 316 Strength of Mechanical Components NC State University Department of Mechanical & Aerospace Engineering
 (3.8-3.1, 3.14) MAE 316 Strength of Mechanical Components NC State Universit Department of Mechanical & Aerospace Engineering 1 Introduction MAE 316 is a continuation of MAE 314 (solid mechanics) Review
(3.8-3.1, 3.14) MAE 316 Strength of Mechanical Components NC State Universit Department of Mechanical & Aerospace Engineering 1 Introduction MAE 316 is a continuation of MAE 314 (solid mechanics) Review
Exercise solutions: concepts from chapter 5
 1) Stud the oöids depicted in Figure 1a and 1b. a) Assume that the thin sections of Figure 1 lie in a principal plane of the deformation. Measure and record the lengths and orientations of the principal
1) Stud the oöids depicted in Figure 1a and 1b. a) Assume that the thin sections of Figure 1 lie in a principal plane of the deformation. Measure and record the lengths and orientations of the principal
Chapter 2 Polynomial, Power, and Rational Functions
 Section. Linear and Quadratic Functions and Modeling 6 Chapter Polnomial, Power, and Rational Functions Section. Linear and Quadratic Functions and Modeling Eploration. $000 per ear.. The equation will
Section. Linear and Quadratic Functions and Modeling 6 Chapter Polnomial, Power, and Rational Functions Section. Linear and Quadratic Functions and Modeling Eploration. $000 per ear.. The equation will
Polynomial and Rational Functions
 Polnomial and Rational Functions Figure -mm film, once the standard for capturing photographic images, has been made largel obsolete b digital photograph. (credit film : modification of work b Horia Varlan;
Polnomial and Rational Functions Figure -mm film, once the standard for capturing photographic images, has been made largel obsolete b digital photograph. (credit film : modification of work b Horia Varlan;
AB Calculus 2013 Summer Assignment. Theme 1: Linear Functions
 01 Summer Assignment Theme 1: Linear Functions 1. Write the equation for the line through the point P(, -1) that is perpendicular to the line 5y = 7. (A) + 5y = -1 (B) 5 y = 8 (C) 5 y = 1 (D) 5 + y = 7
01 Summer Assignment Theme 1: Linear Functions 1. Write the equation for the line through the point P(, -1) that is perpendicular to the line 5y = 7. (A) + 5y = -1 (B) 5 y = 8 (C) 5 y = 1 (D) 5 + y = 7
ARCH 331 Note Set 3.1 Su2016abn. Forces and Vectors
 orces and Vectors Notation: = name for force vectors, as is A, B, C, T and P = force component in the direction = force component in the direction R = name for resultant vectors R = resultant component
orces and Vectors Notation: = name for force vectors, as is A, B, C, T and P = force component in the direction = force component in the direction R = name for resultant vectors R = resultant component
1 Differential Equations for Solid Mechanics
 1 Differential Eqations for Solid Mechanics Simple problems involving homogeneos stress states have been considered so far, wherein the stress is the same throghot the component nder std. An eception to
1 Differential Eqations for Solid Mechanics Simple problems involving homogeneos stress states have been considered so far, wherein the stress is the same throghot the component nder std. An eception to
15.4 Equation of a Circle
 Name Class Date 1.4 Equation of a Circle Essential Question: How can ou write the equation of a circle if ou know its radius and the coordinates of its center? Eplore G.1.E Show the equation of a circle
Name Class Date 1.4 Equation of a Circle Essential Question: How can ou write the equation of a circle if ou know its radius and the coordinates of its center? Eplore G.1.E Show the equation of a circle
Transformation of kinematical quantities from rotating into static coordinate system
 Transformation of kinematical quantities from rotating into static coordinate sstem Dimitar G Stoanov Facult of Engineering and Pedagog in Sliven, Technical Universit of Sofia 59, Bourgasko Shaussee Blvd,
Transformation of kinematical quantities from rotating into static coordinate sstem Dimitar G Stoanov Facult of Engineering and Pedagog in Sliven, Technical Universit of Sofia 59, Bourgasko Shaussee Blvd,
Dielectric metasurfaces for complete control of phase and polarization with subwavelength spatial resolution and high transmission
 DOI:.38/NNANO.25.86 Dielectric metasurfaces for complete control of phase and polarization with subwavelength spatial resolution and high transmission Amir Arbabi, Yu Horie, Mahmood Bagheri, and Andrei
DOI:.38/NNANO.25.86 Dielectric metasurfaces for complete control of phase and polarization with subwavelength spatial resolution and high transmission Amir Arbabi, Yu Horie, Mahmood Bagheri, and Andrei
ME 141. Lecture 8: Moment of Inertia
 ME 4 Engineering Mechanics Lecture 8: Moment of nertia Ahmad Shahedi Shakil Lecturer, Dept. of Mechanical Engg, BUET E-mail: sshakil@me.buet.ac.bd, shakil679@gmail.com Website: teacher.buet.ac.bd/sshakil
ME 4 Engineering Mechanics Lecture 8: Moment of nertia Ahmad Shahedi Shakil Lecturer, Dept. of Mechanical Engg, BUET E-mail: sshakil@me.buet.ac.bd, shakil679@gmail.com Website: teacher.buet.ac.bd/sshakil
