Chapter 7 - Section 8, Morris H. DeGroot and Mark J. Schervish, Probability and Statistics, 3 rd
|
|
|
- Scott Powers
- 5 years ago
- Views:
Transcription
1 References Chapter 7 - Section 8, Mris H. DeGroot and Mark J. Schervish, Probability and Statistics, 3 rd Edition, Addison-Wesley, Boston. Chapter 5 - Section 1.3, Bernard W. Lindgren, Statistical They, 3 rd Edition, MacMillan, New Yk. Properties of the Sce Equations The expected value of the sce equations is zero. Since the probability of the entire sample space is one, we have: If(X)dX = 1 where the integral denote an n-dimensional integral over the sample space of X. Note that f(x) is a function of 2. Differentiating with respect to the vect 2 gives M[If(X)dX ]/M2 = 0 Assuming that the der of differentiation and integration may be reversed: I[Mf(X)/M2]dX = 0 (The region of integration should not be a function of 2. See Amemiya f details.) The chain rule gives Mlnf(X)/M2 = [f(x)] -1 [Mf(X)/M2] Substituting into the previous equation gives: I[Mlnf(X)/M2]f(X)dX = 0 since Mlnf(X)/M2 = MlnL(2)/M2 I[MlnL(2)/M2]f(X)dX = 0 which states E X S(2) = 0
2 The Infmation Matrix The Infmation Matrix is the variance covariance matrix of the sce. Since E X S(2) = 0, I(2) = E X {[MlnL(2)/M2][MlnL(2)/M2']} by definition. The Infmation Matrix may be expressed in terms of the Hessian matrix of lnl(2). Since the mean sce is zero, we have: I[MlnL(2)/M2]f(X)dX = 0 Differentiating with respect to 2', again assuming the der of differentiation and integration may be reversed, and applying the product rule, gives the (kxk) matrix equality I[M 2 lnl(2)/m2m2']f(x)dx + I[MlnL(2)/M2][Mf(X)/M2']dX = 0 since Mlnf(X)/M2 = [f(x)] -1 [Mf(X)/M2], I[M 2 lnl(2)/m2m2']f(x)dx + I[MlnL(2)/M2][Mlnf(X)/M2']f(X)dX = 0 I[M 2 lnl(2)/m2m2']f(x)dx + I[MlnL(2)/M2][MlnL(2)/M2']f(X)dX = 0 In terms of expectations, E X {[MlnL(2)/M2][MlnL(2)/M2']} = - E X [M 2 lnl(2)/m2m2'] Hence, we have an alternative expression f the infmation matrix. I(2) = - E X [M 2 lnl(2)/m2m2'] = - E X [H(2)]
3 The Cramer-Rao Bound The CR bound establishes a lower bound f the variance of unbiased estimats. Letting t(x) denote an arbitrary unbiased estimat of the parameter 2, we know that E X [t(x)] = 2 f any sample size n and any valid 2. In the continuous case we have It(X)f(X)dX = 2. Differentiating with respect to 2' gives This states that: It(X)[Mf(X)/M2']dX = I K It(X)[Mlnf(X)/M2']f(X)dX = I K. It(X)[MlnL(2)/M2']f(X)dX = I K. E X [t(x)s(2)'] = I K. Since the mean sce is a zero vect, the covariance matrix of any unbiased estimat and the sce is an identity matrix. Thus, the covariance matrix of the stacked vect +, +, * t(x) * is * E t I K * * S(2) * * I K I(2) * where E t denote the covariance matrix of the estimat t(x). If we denote the covariance matrix of the stacked vect by C, then Z'CZ$0 f arbitrary Z 0, since any covariance matrix is positive semi-definite. This inequality must hold f an arbitrary non-zero 2K-vect Z, including +, * W * * - I(2) -1 W * where W is an arbitrary non-zero k-vect. F this choice of Z, the inequality above reduces to
4 Z'CZ = W'[E t -I(2) -1 ]W $ 0 f W 0. That is, the difference between the covariance matrix of an unbiased estimat t(x) and the inverse of the infmation matrix is a positive semi-definite matrix. Since the diagonal elements of a positive semi-definite matrix must be non-negative, the variance of an unbiased estimat is not less than the cresponding diagonal element of the inverse of the infmation matrix. Theem ( Properties of ML Estimates ) Let X represent a random sample from a population with joint density f(x) of known fm (not necessarily nmal). Then subject to certain regularity conditions, ML estimats are consistent, asymptotically efficient, and asymptotically nmal. (Most notable among the regularity conditions, the sample space of X must not depend on 2, and the joint density must be differentiable with respect to 2. Details may be found in Econometrics, Peter Schmidt, 1976, Marcel Dekker, New Yk.)
5 Application Consider a SI sequence of Bernoulli trials. Since the observations are statistically independent, the joint density is the product of the marginal densities. f(x) = A n i=1f(x i ) The log likelihood function is thus lnl(p) = E n i=1[ X i ln(p) + (1-X i ) ln(1-p) ] and the sce equation is MlnL(p)/Mp = E n i=1[(x i /p)-(1-x i )/(1-p)] The ML estimat solves S(p$) = E n i=1[(x i /p$)-(1-x i )/(1-p$)] = 0 Multiplying both sides by p$(1-p$) gives E n i=1[x i (1-p$)-(1-X i )p$] = 0 E n i=1x i - p$ E n i=1x i -n p$ + p$ E n i=1x i = 0 E n i=1x i -n p$ = 0 Thus, p$ = [E n i=1x i /n] = &X, and the ML estimat of p is just the sample mean. We have seen that &X has mean : X and variance F 2 x/n, regardless of the underlying distribution. F the Bernoulli trial, : x = p and F 2 x = p(1-p). Consequently, E(p$) = E(&X) = p and V(p$) = V(&X) = p(1-p)/n. This implies that the ML estimat p$ is an unbiased estimat of p.
6 The Hessian matrix -- a scalar in this case -- is M 2 lnl(p)/mp 2 = -[E n i=1(x i /p 2 ) + E n i=1(1-x i )/(1-p) 2 ] Since E[E n i=1x i ]=np, the infmation matrix is E[-H(p)] = np/(p 2 ) + n(1-p)/[(1-p) 2 ] = n/p + n/(1-p) = n(1-p)/[p(1-p)] + np/[p(1-p)] = n/[p(1-p)] The CR bound f unbiased estimats of p is thus p(1-p)/n. Since p$ is an unbiased estimat of p and has variance that meets the CR bound, p$ is efficient. Application Assume that X i are iidn(:,f 2 ). That is, X~N(:,F 2 I n ). (Note that we are using the same notation to denote the scalar parameter : and the vect of common means :.) The joint density of the random vect X is f(x) = (2B) -n/2 (F 2 ) -n/2 exp[-½ (X-:)'(F 2 ) -1 (X-:)] The log-likelihood function is thus lnl($,f 2 ) = - (n/2)ln(2b) - (n/2)ln(f 2 ) - ½ (X-:)'(F 2 ) -1 (X-:) Note that : enters the log-likelihood function only through the last term. In der to find the sce equations, we will need to find the vect of partial derivatives of (X-:)'(X-:) with respect to :. This is done most easily, by recognizing that (X-:)'(X-:) = E n i=1(x i -:) 2
7 Consequently, M(X-:)'(X-:)/M: = - 2 E n i=1(x i -:) The first sce equation is thus MnL(:,F 2 )/M: = - ½ (F 2 ) -1 [- 2 E n i=1(x i -:)] = (F 2 ) -1 [E n i=1(x i -:)] and the second sce equation is MlnL(:,F 2 )/MF 2 = - (n/2)(f 2 ) -1 + ½(F 2 ) -2 [(X-:)'(X-:)] = - (n/2f 2 ) + (1/2F 4 )[(X-:)'(X-:)] The ML estimats solve S($2)=0. F this problem we have (1/F$ 2 )[E n i=1(x i -$:)] = 0 and -(n/2 F$ 2 ) + (1/2 F$ 4 )[(X-$:)'(X-$:)] = 0 The first sce equation may be solved f $: = E n i=1(x i /n) = &X Given $:, the final sce equation may solved f F$ 2 = (X-$:)'(X-$:)/n. At this point, it is convenient to find the Hessian matrix, the matrix of second partials and cross-partials of the log-likelihood function. The first diagonal element is given by M 2 lnl(:,f 2 )/M: 2 = - (n/f 2 ) The off-diagonal element is given by M 2 lnl(:,f 2 )/M:MF 2 = - (F 2 ) -2 [E n i=1(x i -:)] = - (1/F 4 )[E n i=1(x i -:)]
8 The second diagonal element is M 2 lnl(:,f 2 )/MF 4 = (n/2)(f 2 ) -2 - (F 2 ) -3 [(X-:)'(X-:)] = (n/2f 4 ) - (1/F 6 )[(X-:)'(X-:)] The Hessian matrix is thus given by +, * -(n/f 2 ) -(1/F 4 )[E n i=1(x i -:)] * * * * -(1/F 4 )[E n i=1(x i -:)] (n/2f 4 ) - (1/F 6 )[(X-:)'(X-:)] * The infmation matrix is -E X [H(2)]. Note that E(X i -:) = 0, and E[(X-:)'(X-:)] = nf 2. Thus, the infmation matrix f this problem is +, * (n/f 2 ) 0 * * * * 0 - (n/2f 4 ) + (nf 2 /F 6 ) * which reduces to +, * (n/f 2 ) 0 * * * * 0 (n/2f 4 ) * The CR bound is the inverse of the infmation matrix. Since the infmation matrix f this problem is block diagonal, the CR bound is simply +, * F 2 /n 0 * * * * 0 (2F 4 /n) * We saw earlier that $: = &X ~ N(:,F 2 /n). Since $: is unbiased f : and has variance that meets the CR bound, $: is efficient. We will see later that F$ 2 =(X-$:)'(X-$:)/n has mean [(n-1)/n]f 2 F 2, and consequently, cannot be efficient.
Chapter 6 - Sections 5 and 6, Morris H. DeGroot and Mark J. Schervish, Probability and
 References Chapter 6 - Sections 5 and 6, Morris H. DeGroot and Mark J. Schervish, Probability and Statistics, 3 rd Edition, Addison-Wesley, Boston. Chapter 5 - Section 2, Bernard W. Lindgren, Statistical
References Chapter 6 - Sections 5 and 6, Morris H. DeGroot and Mark J. Schervish, Probability and Statistics, 3 rd Edition, Addison-Wesley, Boston. Chapter 5 - Section 2, Bernard W. Lindgren, Statistical
Large Sample Properties of Estimators in the Classical Linear Regression Model
 Large Sample Properties of Estimators in the Classical Linear Regression Model 7 October 004 A. Statement of the classical linear regression model The classical linear regression model can be written in
Large Sample Properties of Estimators in the Classical Linear Regression Model 7 October 004 A. Statement of the classical linear regression model The classical linear regression model can be written in
Variations. ECE 6540, Lecture 10 Maximum Likelihood Estimation
 Variations ECE 6540, Lecture 10 Last Time BLUE (Best Linear Unbiased Estimator) Formulation Advantages Disadvantages 2 The BLUE A simplification Assume the estimator is a linear system For a single parameter
Variations ECE 6540, Lecture 10 Last Time BLUE (Best Linear Unbiased Estimator) Formulation Advantages Disadvantages 2 The BLUE A simplification Assume the estimator is a linear system For a single parameter
Introduction to Maximum Likelihood Estimation
 Introduction to Maximum Likelihood Estimation Eric Zivot July 26, 2012 The Likelihood Function Let 1 be an iid sample with pdf ( ; ) where is a ( 1) vector of parameters that characterize ( ; ) Example:
Introduction to Maximum Likelihood Estimation Eric Zivot July 26, 2012 The Likelihood Function Let 1 be an iid sample with pdf ( ; ) where is a ( 1) vector of parameters that characterize ( ; ) Example:
Final Exam. 1. (6 points) True/False. Please read the statements carefully, as no partial credit will be given.
 1. (6 points) True/False. Please read the statements carefully, as no partial credit will be given. (a) If X and Y are independent, Corr(X, Y ) = 0. (b) (c) (d) (e) A consistent estimator must be asymptotically
1. (6 points) True/False. Please read the statements carefully, as no partial credit will be given. (a) If X and Y are independent, Corr(X, Y ) = 0. (b) (c) (d) (e) A consistent estimator must be asymptotically
Maximum Likelihood (ML) Estimation
 Econometrics 2 Fall 2004 Maximum Likelihood (ML) Estimation Heino Bohn Nielsen 1of32 Outline of the Lecture (1) Introduction. (2) ML estimation defined. (3) ExampleI:Binomialtrials. (4) Example II: Linear
Econometrics 2 Fall 2004 Maximum Likelihood (ML) Estimation Heino Bohn Nielsen 1of32 Outline of the Lecture (1) Introduction. (2) ML estimation defined. (3) ExampleI:Binomialtrials. (4) Example II: Linear
Econ 583 Homework 7 Suggested Solutions: Wald, LM and LR based on GMM and MLE
 Econ 583 Homework 7 Suggested Solutions: Wald, LM and LR based on GMM and MLE Eric Zivot Winter 013 1 Wald, LR and LM statistics based on generalized method of moments estimation Let 1 be an iid sample
Econ 583 Homework 7 Suggested Solutions: Wald, LM and LR based on GMM and MLE Eric Zivot Winter 013 1 Wald, LR and LM statistics based on generalized method of moments estimation Let 1 be an iid sample
Exercises and Answers to Chapter 1
 Exercises and Answers to Chapter The continuous type of random variable X has the following density function: a x, if < x < a, f (x), otherwise. Answer the following questions. () Find a. () Obtain mean
Exercises and Answers to Chapter The continuous type of random variable X has the following density function: a x, if < x < a, f (x), otherwise. Answer the following questions. () Find a. () Obtain mean
Primer on statistics:
 Primer on statistics: MLE, Confidence Intervals, and Hypothesis Testing ryan.reece@gmail.com http://rreece.github.io/ Insight Data Science - AI Fellows Workshop Feb 16, 018 Outline 1. Maximum likelihood
Primer on statistics: MLE, Confidence Intervals, and Hypothesis Testing ryan.reece@gmail.com http://rreece.github.io/ Insight Data Science - AI Fellows Workshop Feb 16, 018 Outline 1. Maximum likelihood
Hypothesis Testing Problem. TMS-062: Lecture 5 Hypotheses Testing. Alternative Hypotheses. Test Statistic
 Hypothesis Testing Problem TMS-062: Lecture 5 Hypotheses Testing Same basic situation as befe: Data: random i. i. d. sample X 1,..., X n from a population and we wish to draw inference about unknown population
Hypothesis Testing Problem TMS-062: Lecture 5 Hypotheses Testing Same basic situation as befe: Data: random i. i. d. sample X 1,..., X n from a population and we wish to draw inference about unknown population
Parameter Estimation
 Parameter Estimation Consider a sample of observations on a random variable Y. his generates random variables: (y 1, y 2,, y ). A random sample is a sample (y 1, y 2,, y ) where the random variables y
Parameter Estimation Consider a sample of observations on a random variable Y. his generates random variables: (y 1, y 2,, y ). A random sample is a sample (y 1, y 2,, y ) where the random variables y
Finite. U-46 Curriculum Scope and Sequence. Reporting Strand Instructional Focus Standards Semester. Represent linear equations in matrices.
 Finite U-46 Curriculum Scope and Sequence Repting Strand Instructional Focus Standards Semester Represent linear equations in matrices. A.REI.8, A.REI.9 Matrices Perfm operations on matrices and use matrices
Finite U-46 Curriculum Scope and Sequence Repting Strand Instructional Focus Standards Semester Represent linear equations in matrices. A.REI.8, A.REI.9 Matrices Perfm operations on matrices and use matrices
Let X and Y denote two random variables. The joint distribution of these random
 EE385 Class Notes 9/7/0 John Stensby Chapter 3: Multiple Random Variables Let X and Y denote two random variables. The joint distribution of these random variables is defined as F XY(x,y) = [X x,y y] P.
EE385 Class Notes 9/7/0 John Stensby Chapter 3: Multiple Random Variables Let X and Y denote two random variables. The joint distribution of these random variables is defined as F XY(x,y) = [X x,y y] P.
Poisson Regression. Ryan Godwin. ECON University of Manitoba
 Poisson Regression Ryan Godwin ECON 7010 - University of Manitoba Abstract. These lecture notes introduce Maximum Likelihood Estimation (MLE) of a Poisson regression model. 1 Motivating the Poisson Regression
Poisson Regression Ryan Godwin ECON 7010 - University of Manitoba Abstract. These lecture notes introduce Maximum Likelihood Estimation (MLE) of a Poisson regression model. 1 Motivating the Poisson Regression
Linear models. Linear models are computationally convenient and remain widely used in. applied econometric research
 Linear models Linear models are computationally convenient and remain widely used in applied econometric research Our main focus in these lectures will be on single equation linear models of the form y
Linear models Linear models are computationally convenient and remain widely used in applied econometric research Our main focus in these lectures will be on single equation linear models of the form y
Tests and Their Power
 Tests and Their Power Ling Kiong Doong Department of Mathematics National University of Singapore 1. Introduction In Statistical Inference, the two main areas of study are estimation and testing of hypotheses.
Tests and Their Power Ling Kiong Doong Department of Mathematics National University of Singapore 1. Introduction In Statistical Inference, the two main areas of study are estimation and testing of hypotheses.
1. Fisher Information
 1. Fisher Information Let f(x θ) be a density function with the property that log f(x θ) is differentiable in θ throughout the open p-dimensional parameter set Θ R p ; then the score statistic (or score
1. Fisher Information Let f(x θ) be a density function with the property that log f(x θ) is differentiable in θ throughout the open p-dimensional parameter set Θ R p ; then the score statistic (or score
Economics 573 Problem Set 5 Fall 2002 Due: 4 October b. The sample mean converges in probability to the population mean.
 Economics 573 Problem Set 5 Fall 00 Due: 4 October 00 1. In random sampling from any population with E(X) = and Var(X) =, show (using Chebyshev's inequality) that sample mean converges in probability to..
Economics 573 Problem Set 5 Fall 00 Due: 4 October 00 1. In random sampling from any population with E(X) = and Var(X) =, show (using Chebyshev's inequality) that sample mean converges in probability to..
Parameter estimation and forecasting. Cristiano Porciani AIfA, Uni-Bonn
 Parameter estimation and forecasting Cristiano Porciani AIfA, Uni-Bonn Questions? C. Porciani Estimation & forecasting 2 Temperature fluctuations Variance at multipole l (angle ~180o/l) C. Porciani Estimation
Parameter estimation and forecasting Cristiano Porciani AIfA, Uni-Bonn Questions? C. Porciani Estimation & forecasting 2 Temperature fluctuations Variance at multipole l (angle ~180o/l) C. Porciani Estimation
Estimation Theory Fredrik Rusek. Chapters
 Estimation Theory Fredrik Rusek Chapters 3.5-3.10 Recap We deal with unbiased estimators of deterministic parameters Performance of an estimator is measured by the variance of the estimate (due to the
Estimation Theory Fredrik Rusek Chapters 3.5-3.10 Recap We deal with unbiased estimators of deterministic parameters Performance of an estimator is measured by the variance of the estimate (due to the
Topic 12 Overview of Estimation
 Topic 12 Overview of Estimation Classical Statistics 1 / 9 Outline Introduction Parameter Estimation Classical Statistics Densities and Likelihoods 2 / 9 Introduction In the simplest possible terms, the
Topic 12 Overview of Estimation Classical Statistics 1 / 9 Outline Introduction Parameter Estimation Classical Statistics Densities and Likelihoods 2 / 9 Introduction In the simplest possible terms, the
Econ 583 Final Exam Fall 2008
 Econ 583 Final Exam Fall 2008 Eric Zivot December 11, 2008 Exam is due at 9:00 am in my office on Friday, December 12. 1 Maximum Likelihood Estimation and Asymptotic Theory Let X 1,...,X n be iid random
Econ 583 Final Exam Fall 2008 Eric Zivot December 11, 2008 Exam is due at 9:00 am in my office on Friday, December 12. 1 Maximum Likelihood Estimation and Asymptotic Theory Let X 1,...,X n be iid random
. Find E(V ) and var(v ).
 Math 6382/6383: Probability Models and Mathematical Statistics Sample Preliminary Exam Questions 1. A person tosses a fair coin until she obtains 2 heads in a row. She then tosses a fair die the same number
Math 6382/6383: Probability Models and Mathematical Statistics Sample Preliminary Exam Questions 1. A person tosses a fair coin until she obtains 2 heads in a row. She then tosses a fair die the same number
A Few Notes on Fisher Information (WIP)
 A Few Notes on Fisher Information (WIP) David Meyer dmm@{-4-5.net,uoregon.edu} Last update: April 30, 208 Definitions There are so many interesting things about Fisher Information and its theoretical properties
A Few Notes on Fisher Information (WIP) David Meyer dmm@{-4-5.net,uoregon.edu} Last update: April 30, 208 Definitions There are so many interesting things about Fisher Information and its theoretical properties
Chapter 5 Class Notes
 Chapter 5 Class Notes Sections 5.1 and 5.2 It is quite common to measure several variables (some of which may be correlated) and to examine the corresponding joint probability distribution One example
Chapter 5 Class Notes Sections 5.1 and 5.2 It is quite common to measure several variables (some of which may be correlated) and to examine the corresponding joint probability distribution One example
Regression. Oscar García
 Regression Oscar García Regression methods are fundamental in Forest Mensuration For a more concise and general presentation, we shall first review some matrix concepts 1 Matrices An order n m matrix is
Regression Oscar García Regression methods are fundamental in Forest Mensuration For a more concise and general presentation, we shall first review some matrix concepts 1 Matrices An order n m matrix is
Least Squares Regression
 Least Squares Regression Chemical Engineering 2450 - Numerical Methods Given N data points x i, y i, i 1 N, and a function that we wish to fit to these data points, fx, we define S as the sum of the squared
Least Squares Regression Chemical Engineering 2450 - Numerical Methods Given N data points x i, y i, i 1 N, and a function that we wish to fit to these data points, fx, we define S as the sum of the squared
Minimum Error-Rate Discriminant
 Discriminants Minimum Error-Rate Discriminant In the case of zero-one loss function, the Bayes Discriminant can be further simplified: g i (x) =P (ω i x). (29) J. Corso (SUNY at Buffalo) Bayesian Decision
Discriminants Minimum Error-Rate Discriminant In the case of zero-one loss function, the Bayes Discriminant can be further simplified: g i (x) =P (ω i x). (29) J. Corso (SUNY at Buffalo) Bayesian Decision
f(x θ)dx with respect to θ. Assuming certain smoothness conditions concern differentiating under the integral the integral sign, we first obtain
 0.1. INTRODUCTION 1 0.1 Introduction R. A. Fisher, a pioneer in the development of mathematical statistics, introduced a measure of the amount of information contained in an observaton from f(x θ). Fisher
0.1. INTRODUCTION 1 0.1 Introduction R. A. Fisher, a pioneer in the development of mathematical statistics, introduced a measure of the amount of information contained in an observaton from f(x θ). Fisher
Chapter 3: Maximum Likelihood Theory
 Chapter 3: Maximum Likelihood Theory Florian Pelgrin HEC September-December, 2010 Florian Pelgrin (HEC) Maximum Likelihood Theory September-December, 2010 1 / 40 1 Introduction Example 2 Maximum likelihood
Chapter 3: Maximum Likelihood Theory Florian Pelgrin HEC September-December, 2010 Florian Pelgrin (HEC) Maximum Likelihood Theory September-December, 2010 1 / 40 1 Introduction Example 2 Maximum likelihood
Exercises Chapter 4 Statistical Hypothesis Testing
 Exercises Chapter 4 Statistical Hypothesis Testing Advanced Econometrics - HEC Lausanne Christophe Hurlin University of Orléans December 5, 013 Christophe Hurlin (University of Orléans) Advanced Econometrics
Exercises Chapter 4 Statistical Hypothesis Testing Advanced Econometrics - HEC Lausanne Christophe Hurlin University of Orléans December 5, 013 Christophe Hurlin (University of Orléans) Advanced Econometrics
Expectation Maximization (EM) Algorithm. Each has it s own probability of seeing H on any one flip. Let. p 1 = P ( H on Coin 1 )
 Expectation Maximization (EM Algorithm Motivating Example: Have two coins: Coin 1 and Coin 2 Each has it s own probability of seeing H on any one flip. Let p 1 = P ( H on Coin 1 p 2 = P ( H on Coin 2 Select
Expectation Maximization (EM Algorithm Motivating Example: Have two coins: Coin 1 and Coin 2 Each has it s own probability of seeing H on any one flip. Let p 1 = P ( H on Coin 1 p 2 = P ( H on Coin 2 Select
Mathematical statistics
 October 18 th, 2018 Lecture 16: Midterm review Countdown to mid-term exam: 7 days Week 1 Chapter 1: Probability review Week 2 Week 4 Week 7 Chapter 6: Statistics Chapter 7: Point Estimation Chapter 8:
October 18 th, 2018 Lecture 16: Midterm review Countdown to mid-term exam: 7 days Week 1 Chapter 1: Probability review Week 2 Week 4 Week 7 Chapter 6: Statistics Chapter 7: Point Estimation Chapter 8:
Estimation theory. Parametric estimation. Properties of estimators. Minimum variance estimator. Cramer-Rao bound. Maximum likelihood estimators
 Estimation theory Parametric estimation Properties of estimators Minimum variance estimator Cramer-Rao bound Maximum likelihood estimators Confidence intervals Bayesian estimation 1 Random Variables Let
Estimation theory Parametric estimation Properties of estimators Minimum variance estimator Cramer-Rao bound Maximum likelihood estimators Confidence intervals Bayesian estimation 1 Random Variables Let
Statement: With my signature I confirm that the solutions are the product of my own work. Name: Signature:.
 MATHEMATICAL STATISTICS Homework assignment Instructions Please turn in the homework with this cover page. You do not need to edit the solutions. Just make sure the handwriting is legible. You may discuss
MATHEMATICAL STATISTICS Homework assignment Instructions Please turn in the homework with this cover page. You do not need to edit the solutions. Just make sure the handwriting is legible. You may discuss
Statement: With my signature I confirm that the solutions are the product of my own work. Name: Signature:.
 MATHEMATICAL STATISTICS Take-home final examination February 1 st -February 8 th, 019 Instructions You do not need to edit the solutions Just make sure the handwriting is legible The final solutions should
MATHEMATICAL STATISTICS Take-home final examination February 1 st -February 8 th, 019 Instructions You do not need to edit the solutions Just make sure the handwriting is legible The final solutions should
The Multivariate Gaussian Distribution [DRAFT]
![The Multivariate Gaussian Distribution [DRAFT] The Multivariate Gaussian Distribution [DRAFT]](/thumbs/90/102238180.jpg) The Multivariate Gaussian Distribution DRAFT David S. Rosenberg Abstract This is a collection of a few key and standard results about multivariate Gaussian distributions. I have not included many proofs,
The Multivariate Gaussian Distribution DRAFT David S. Rosenberg Abstract This is a collection of a few key and standard results about multivariate Gaussian distributions. I have not included many proofs,
LIST OF FORMULAS FOR STK1100 AND STK1110
 LIST OF FORMULAS FOR STK1100 AND STK1110 (Version of 11. November 2015) 1. Probability Let A, B, A 1, A 2,..., B 1, B 2,... be events, that is, subsets of a sample space Ω. a) Axioms: A probability function
LIST OF FORMULAS FOR STK1100 AND STK1110 (Version of 11. November 2015) 1. Probability Let A, B, A 1, A 2,..., B 1, B 2,... be events, that is, subsets of a sample space Ω. a) Axioms: A probability function
Multiple Random Variables
 Multiple Random Variables This Version: July 30, 2015 Multiple Random Variables 2 Now we consider models with more than one r.v. These are called multivariate models For instance: height and weight An
Multiple Random Variables This Version: July 30, 2015 Multiple Random Variables 2 Now we consider models with more than one r.v. These are called multivariate models For instance: height and weight An
Notes on the Multivariate Normal and Related Topics
 Version: July 10, 2013 Notes on the Multivariate Normal and Related Topics Let me refresh your memory about the distinctions between population and sample; parameters and statistics; population distributions
Version: July 10, 2013 Notes on the Multivariate Normal and Related Topics Let me refresh your memory about the distinctions between population and sample; parameters and statistics; population distributions
Economics 620, Lecture 9: Asymptotics III: Maximum Likelihood Estimation
 Economics 620, Lecture 9: Asymptotics III: Maximum Likelihood Estimation Nicholas M. Kiefer Cornell University Professor N. M. Kiefer (Cornell University) Lecture 9: Asymptotics III(MLE) 1 / 20 Jensen
Economics 620, Lecture 9: Asymptotics III: Maximum Likelihood Estimation Nicholas M. Kiefer Cornell University Professor N. M. Kiefer (Cornell University) Lecture 9: Asymptotics III(MLE) 1 / 20 Jensen
First Year Examination Department of Statistics, University of Florida
 First Year Examination Department of Statistics, University of Florida August 19, 010, 8:00 am - 1:00 noon Instructions: 1. You have four hours to answer questions in this examination.. You must show your
First Year Examination Department of Statistics, University of Florida August 19, 010, 8:00 am - 1:00 noon Instructions: 1. You have four hours to answer questions in this examination.. You must show your
Tutorial: Statistical distance and Fisher information
 Tutorial: Statistical distance and Fisher information Pieter Kok Department of Materials, Oxford University, Parks Road, Oxford OX1 3PH, UK Statistical distance We wish to construct a space of probability
Tutorial: Statistical distance and Fisher information Pieter Kok Department of Materials, Oxford University, Parks Road, Oxford OX1 3PH, UK Statistical distance We wish to construct a space of probability
MATH4427 Notebook 2 Fall Semester 2017/2018
 MATH4427 Notebook 2 Fall Semester 2017/2018 prepared by Professor Jenny Baglivo c Copyright 2009-2018 by Jenny A. Baglivo. All Rights Reserved. 2 MATH4427 Notebook 2 3 2.1 Definitions and Examples...................................
MATH4427 Notebook 2 Fall Semester 2017/2018 prepared by Professor Jenny Baglivo c Copyright 2009-2018 by Jenny A. Baglivo. All Rights Reserved. 2 MATH4427 Notebook 2 3 2.1 Definitions and Examples...................................
Cramér-Rao Bounds for Estimation of Linear System Noise Covariances
 Journal of Mechanical Engineering and Automation (): 6- DOI: 593/jjmea Cramér-Rao Bounds for Estimation of Linear System oise Covariances Peter Matiso * Vladimír Havlena Czech echnical University in Prague
Journal of Mechanical Engineering and Automation (): 6- DOI: 593/jjmea Cramér-Rao Bounds for Estimation of Linear System oise Covariances Peter Matiso * Vladimír Havlena Czech echnical University in Prague
Inferring from data. Theory of estimators
 Inferring from data Theory of estimators 1 Estimators Estimator is any function of the data e(x) used to provide an estimate ( a measurement ) of an unknown parameter. Because estimators are functions
Inferring from data Theory of estimators 1 Estimators Estimator is any function of the data e(x) used to provide an estimate ( a measurement ) of an unknown parameter. Because estimators are functions
Random variables (discrete)
 Random variables (discrete) Saad Mneimneh 1 Introducing random variables A random variable is a mapping from the sample space to the real line. We usually denote the random variable by X, and a value that
Random variables (discrete) Saad Mneimneh 1 Introducing random variables A random variable is a mapping from the sample space to the real line. We usually denote the random variable by X, and a value that
Chapter 3. Point Estimation. 3.1 Introduction
 Chapter 3 Point Estimation Let (Ω, A, P θ ), P θ P = {P θ θ Θ}be probability space, X 1, X 2,..., X n : (Ω, A) (IR k, B k ) random variables (X, B X ) sample space γ : Θ IR k measurable function, i.e.
Chapter 3 Point Estimation Let (Ω, A, P θ ), P θ P = {P θ θ Θ}be probability space, X 1, X 2,..., X n : (Ω, A) (IR k, B k ) random variables (X, B X ) sample space γ : Θ IR k measurable function, i.e.
Econometrics I, Estimation
 Econometrics I, Estimation Department of Economics Stanford University September, 2008 Part I Parameter, Estimator, Estimate A parametric is a feature of the population. An estimator is a function of the
Econometrics I, Estimation Department of Economics Stanford University September, 2008 Part I Parameter, Estimator, Estimate A parametric is a feature of the population. An estimator is a function of the
STATISTICS SYLLABUS UNIT I
 STATISTICS SYLLABUS UNIT I (Probability Theory) Definition Classical and axiomatic approaches.laws of total and compound probability, conditional probability, Bayes Theorem. Random variable and its distribution
STATISTICS SYLLABUS UNIT I (Probability Theory) Definition Classical and axiomatic approaches.laws of total and compound probability, conditional probability, Bayes Theorem. Random variable and its distribution
Lecture Notes Part 2: Matrix Algebra
 17.874 Lecture Notes Part 2: Matrix Algebra 2. Matrix Algebra 2.1. Introduction: Design Matrices and Data Matrices Matrices are arrays of numbers. We encounter them in statistics in at least three di erent
17.874 Lecture Notes Part 2: Matrix Algebra 2. Matrix Algebra 2.1. Introduction: Design Matrices and Data Matrices Matrices are arrays of numbers. We encounter them in statistics in at least three di erent
Multivariate Distributions
 IEOR E4602: Quantitative Risk Management Spring 2016 c 2016 by Martin Haugh Multivariate Distributions We will study multivariate distributions in these notes, focusing 1 in particular on multivariate
IEOR E4602: Quantitative Risk Management Spring 2016 c 2016 by Martin Haugh Multivariate Distributions We will study multivariate distributions in these notes, focusing 1 in particular on multivariate
1. Point Estimators, Review
 AMS571 Prof. Wei Zhu 1. Point Estimators, Review Example 1. Let be a random sample from. Please find a good point estimator for Solutions. There are the typical estimators for and. Both are unbiased estimators.
AMS571 Prof. Wei Zhu 1. Point Estimators, Review Example 1. Let be a random sample from. Please find a good point estimator for Solutions. There are the typical estimators for and. Both are unbiased estimators.
TAMS39 Lecture 2 Multivariate normal distribution
 TAMS39 Lecture 2 Multivariate normal distribution Martin Singull Department of Mathematics Mathematical Statistics Linköping University, Sweden Content Lecture Random vectors Multivariate normal distribution
TAMS39 Lecture 2 Multivariate normal distribution Martin Singull Department of Mathematics Mathematical Statistics Linköping University, Sweden Content Lecture Random vectors Multivariate normal distribution
Lecture 3. Inference about multivariate normal distribution
 Lecture 3. Inference about multivariate normal distribution 3.1 Point and Interval Estimation Let X 1,..., X n be i.i.d. N p (µ, Σ). We are interested in evaluation of the maximum likelihood estimates
Lecture 3. Inference about multivariate normal distribution 3.1 Point and Interval Estimation Let X 1,..., X n be i.i.d. N p (µ, Σ). We are interested in evaluation of the maximum likelihood estimates
matrix-free Elements of Probability Theory 1 Random Variables and Distributions Contents Elements of Probability Theory 2
 Short Guides to Microeconometrics Fall 2018 Kurt Schmidheiny Unversität Basel Elements of Probability Theory 2 1 Random Variables and Distributions Contents Elements of Probability Theory matrix-free 1
Short Guides to Microeconometrics Fall 2018 Kurt Schmidheiny Unversität Basel Elements of Probability Theory 2 1 Random Variables and Distributions Contents Elements of Probability Theory matrix-free 1
2 (Statistics) Random variables
 2 (Statistics) Random variables References: DeGroot and Schervish, chapters 3, 4 and 5; Stirzaker, chapters 4, 5 and 6 We will now study the main tools use for modeling experiments with unknown outcomes
2 (Statistics) Random variables References: DeGroot and Schervish, chapters 3, 4 and 5; Stirzaker, chapters 4, 5 and 6 We will now study the main tools use for modeling experiments with unknown outcomes
On the convergence of the iterative solution of the likelihood equations
 On the convergence of the iterative solution of the likelihood equations R. Moddemeijer University of Groningen, Department of Computing Science, P.O. Box 800, NL-9700 AV Groningen, The Netherlands, e-mail:
On the convergence of the iterative solution of the likelihood equations R. Moddemeijer University of Groningen, Department of Computing Science, P.O. Box 800, NL-9700 AV Groningen, The Netherlands, e-mail:
5 Operations on Multiple Random Variables
 EE360 Random Signal analysis Chapter 5: Operations on Multiple Random Variables 5 Operations on Multiple Random Variables Expected value of a function of r.v. s Two r.v. s: ḡ = E[g(X, Y )] = g(x, y)f X,Y
EE360 Random Signal analysis Chapter 5: Operations on Multiple Random Variables 5 Operations on Multiple Random Variables Expected value of a function of r.v. s Two r.v. s: ḡ = E[g(X, Y )] = g(x, y)f X,Y
Homework 1 Due: Thursday 2/5/2015. Instructions: Turn in your homework in class on Thursday 2/5/2015
 10-704 Homework 1 Due: Thursday 2/5/2015 Instructions: Turn in your homework in class on Thursday 2/5/2015 1. Information Theory Basics and Inequalities C&T 2.47, 2.29 (a) A deck of n cards in order 1,
10-704 Homework 1 Due: Thursday 2/5/2015 Instructions: Turn in your homework in class on Thursday 2/5/2015 1. Information Theory Basics and Inequalities C&T 2.47, 2.29 (a) A deck of n cards in order 1,
V. Properties of estimators {Parts C, D & E in this file}
 A. Definitions & Desiderata. model. estimator V. Properties of estimators {Parts C, D & E in this file}. sampling errors and sampling distribution 4. unbiasedness 5. low sampling variance 6. low mean squared
A. Definitions & Desiderata. model. estimator V. Properties of estimators {Parts C, D & E in this file}. sampling errors and sampling distribution 4. unbiasedness 5. low sampling variance 6. low mean squared
STATISTICS/ECONOMETRICS PREP COURSE PROF. MASSIMO GUIDOLIN
 Massimo Guidolin Massimo.Guidolin@unibocconi.it Dept. of Finance STATISTICS/ECONOMETRICS PREP COURSE PROF. MASSIMO GUIDOLIN SECOND PART, LECTURE 2: MODES OF CONVERGENCE AND POINT ESTIMATION Lecture 2:
Massimo Guidolin Massimo.Guidolin@unibocconi.it Dept. of Finance STATISTICS/ECONOMETRICS PREP COURSE PROF. MASSIMO GUIDOLIN SECOND PART, LECTURE 2: MODES OF CONVERGENCE AND POINT ESTIMATION Lecture 2:
Example: An experiment can either result in success or failure with probability θ and (1 θ) respectively. The experiment is performed independently
 Chapter 3 Sufficient statistics and variance reduction Let X 1,X 2,...,X n be a random sample from a certain distribution with p.m/d.f fx θ. A function T X 1,X 2,...,X n = T X of these observations is
Chapter 3 Sufficient statistics and variance reduction Let X 1,X 2,...,X n be a random sample from a certain distribution with p.m/d.f fx θ. A function T X 1,X 2,...,X n = T X of these observations is
Chernoff Bounds. Theme: try to show that it is unlikely a random variable X is far away from its expectation.
 Chernoff Bounds Theme: try to show that it is unlikely a random variable X is far away from its expectation. The more you know about X, the better the bound you obtain. Markov s inequality: use E[X ] Chebyshev
Chernoff Bounds Theme: try to show that it is unlikely a random variable X is far away from its expectation. The more you know about X, the better the bound you obtain. Markov s inequality: use E[X ] Chebyshev
Notes on Random Vectors and Multivariate Normal
 MATH 590 Spring 06 Notes on Random Vectors and Multivariate Normal Properties of Random Vectors If X,, X n are random variables, then X = X,, X n ) is a random vector, with the cumulative distribution
MATH 590 Spring 06 Notes on Random Vectors and Multivariate Normal Properties of Random Vectors If X,, X n are random variables, then X = X,, X n ) is a random vector, with the cumulative distribution
MULTIVARIATE PROBABILITY DISTRIBUTIONS
 MULTIVARIATE PROBABILITY DISTRIBUTIONS. PRELIMINARIES.. Example. Consider an experiment that consists of tossing a die and a coin at the same time. We can consider a number of random variables defined
MULTIVARIATE PROBABILITY DISTRIBUTIONS. PRELIMINARIES.. Example. Consider an experiment that consists of tossing a die and a coin at the same time. We can consider a number of random variables defined
Review Quiz. 1. Prove that in a one-dimensional canonical exponential family, the complete and sufficient statistic achieves the
 Review Quiz 1. Prove that in a one-dimensional canonical exponential family, the complete and sufficient statistic achieves the Cramér Rao lower bound (CRLB). That is, if where { } and are scalars, then
Review Quiz 1. Prove that in a one-dimensional canonical exponential family, the complete and sufficient statistic achieves the Cramér Rao lower bound (CRLB). That is, if where { } and are scalars, then
Solution. (i) Find a minimal sufficient statistic for (θ, β) and give your justification. X i=1. By the factorization theorem, ( n
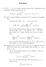 Solution 1. Let (X 1,..., X n ) be a simple random sample from a distribution with probability density function given by f(x;, β) = 1 ( ) 1 β x β, 0 x, > 0, β < 1. β (i) Find a minimal sufficient statistic
Solution 1. Let (X 1,..., X n ) be a simple random sample from a distribution with probability density function given by f(x;, β) = 1 ( ) 1 β x β, 0 x, > 0, β < 1. β (i) Find a minimal sufficient statistic
Discrete Probability Refresher
 ECE 1502 Information Theory Discrete Probability Refresher F. R. Kschischang Dept. of Electrical and Computer Engineering University of Toronto January 13, 1999 revised January 11, 2006 Probability theory
ECE 1502 Information Theory Discrete Probability Refresher F. R. Kschischang Dept. of Electrical and Computer Engineering University of Toronto January 13, 1999 revised January 11, 2006 Probability theory
1 INFO Sep 05
 Events A 1,...A n are said to be mutually independent if for all subsets S {1,..., n}, p( i S A i ) = p(a i ). (For example, flip a coin N times, then the events {A i = i th flip is heads} are mutually
Events A 1,...A n are said to be mutually independent if for all subsets S {1,..., n}, p( i S A i ) = p(a i ). (For example, flip a coin N times, then the events {A i = i th flip is heads} are mutually
STAT 730 Chapter 4: Estimation
 STAT 730 Chapter 4: Estimation Timothy Hanson Department of Statistics, University of South Carolina Stat 730: Multivariate Analysis 1 / 23 The likelihood We have iid data, at least initially. Each datum
STAT 730 Chapter 4: Estimation Timothy Hanson Department of Statistics, University of South Carolina Stat 730: Multivariate Analysis 1 / 23 The likelihood We have iid data, at least initially. Each datum
Midterm. Introduction to Machine Learning. CS 189 Spring You have 1 hour 20 minutes for the exam.
 CS 189 Spring 2013 Introduction to Machine Learning Midterm You have 1 hour 20 minutes for the exam. The exam is closed book, closed notes except your one-page crib sheet. Please use non-programmable calculators
CS 189 Spring 2013 Introduction to Machine Learning Midterm You have 1 hour 20 minutes for the exam. The exam is closed book, closed notes except your one-page crib sheet. Please use non-programmable calculators
Mathematical statistics
 October 4 th, 2018 Lecture 12: Information Where are we? Week 1 Week 2 Week 4 Week 7 Week 10 Week 14 Probability reviews Chapter 6: Statistics and Sampling Distributions Chapter 7: Point Estimation Chapter
October 4 th, 2018 Lecture 12: Information Where are we? Week 1 Week 2 Week 4 Week 7 Week 10 Week 14 Probability reviews Chapter 6: Statistics and Sampling Distributions Chapter 7: Point Estimation Chapter
(Multivariate) Gaussian (Normal) Probability Densities
 (Multivariate) Gaussian (Normal) Probability Densities Carl Edward Rasmussen, José Miguel Hernández-Lobato & Richard Turner April 20th, 2018 Rasmussen, Hernàndez-Lobato & Turner Gaussian Densities April
(Multivariate) Gaussian (Normal) Probability Densities Carl Edward Rasmussen, José Miguel Hernández-Lobato & Richard Turner April 20th, 2018 Rasmussen, Hernàndez-Lobato & Turner Gaussian Densities April
Theory of Maximum Likelihood Estimation. Konstantin Kashin
 Gov 2001 Section 5: Theory of Maximum Likelihood Estimation Konstantin Kashin February 28, 2013 Outline Introduction Likelihood Examples of MLE Variance of MLE Asymptotic Properties What is Statistical
Gov 2001 Section 5: Theory of Maximum Likelihood Estimation Konstantin Kashin February 28, 2013 Outline Introduction Likelihood Examples of MLE Variance of MLE Asymptotic Properties What is Statistical
ECE 275A Homework 6 Solutions
 ECE 275A Homework 6 Solutions. The notation used in the solutions for the concentration (hyper) ellipsoid problems is defined in the lecture supplement on concentration ellipsoids. Note that θ T Σ θ =
ECE 275A Homework 6 Solutions. The notation used in the solutions for the concentration (hyper) ellipsoid problems is defined in the lecture supplement on concentration ellipsoids. Note that θ T Σ θ =
An Introduction to Parameter Estimation
 Introduction Introduction to Econometrics An Introduction to Parameter Estimation This document combines several important econometric foundations and corresponds to other documents such as the Introduction
Introduction Introduction to Econometrics An Introduction to Parameter Estimation This document combines several important econometric foundations and corresponds to other documents such as the Introduction
The Logit Model: Estimation, Testing and Interpretation
 The Logit Model: Estimation, Testing and Interpretation Herman J. Bierens October 25, 2008 1 Introduction to maximum likelihood estimation 1.1 The likelihood function Consider a random sample Y 1,...,
The Logit Model: Estimation, Testing and Interpretation Herman J. Bierens October 25, 2008 1 Introduction to maximum likelihood estimation 1.1 The likelihood function Consider a random sample Y 1,...,
Asymptotic Statistics-III. Changliang Zou
 Asymptotic Statistics-III Changliang Zou The multivariate central limit theorem Theorem (Multivariate CLT for iid case) Let X i be iid random p-vectors with mean µ and and covariance matrix Σ. Then n (
Asymptotic Statistics-III Changliang Zou The multivariate central limit theorem Theorem (Multivariate CLT for iid case) Let X i be iid random p-vectors with mean µ and and covariance matrix Σ. Then n (
01 Probability Theory and Statistics Review
 NAVARCH/EECS 568, ROB 530 - Winter 2018 01 Probability Theory and Statistics Review Maani Ghaffari January 08, 2018 Last Time: Bayes Filters Given: Stream of observations z 1:t and action data u 1:t Sensor/measurement
NAVARCH/EECS 568, ROB 530 - Winter 2018 01 Probability Theory and Statistics Review Maani Ghaffari January 08, 2018 Last Time: Bayes Filters Given: Stream of observations z 1:t and action data u 1:t Sensor/measurement
Estimation of Parameters of the Weibull Distribution Based on Progressively Censored Data
 International Mathematical Forum, 2, 2007, no. 41, 2031-2043 Estimation of Parameters of the Weibull Distribution Based on Progressively Censored Data K. S. Sultan 1 Department of Statistics Operations
International Mathematical Forum, 2, 2007, no. 41, 2031-2043 Estimation of Parameters of the Weibull Distribution Based on Progressively Censored Data K. S. Sultan 1 Department of Statistics Operations
Efficient Monte Carlo computation of Fisher information matrix using prior information
 Efficient Monte Carlo computation of Fisher information matrix using prior information Sonjoy Das, UB James C. Spall, APL/JHU Roger Ghanem, USC SIAM Conference on Data Mining Anaheim, California, USA April
Efficient Monte Carlo computation of Fisher information matrix using prior information Sonjoy Das, UB James C. Spall, APL/JHU Roger Ghanem, USC SIAM Conference on Data Mining Anaheim, California, USA April
HIGHER ORDER CUMULANTS OF RANDOM VECTORS, DIFFERENTIAL OPERATORS, AND APPLICATIONS TO STATISTICAL INFERENCE AND TIME SERIES
 HIGHER ORDER CUMULANTS OF RANDOM VECTORS DIFFERENTIAL OPERATORS AND APPLICATIONS TO STATISTICAL INFERENCE AND TIME SERIES S RAO JAMMALAMADAKA T SUBBA RAO AND GYÖRGY TERDIK Abstract This paper provides
HIGHER ORDER CUMULANTS OF RANDOM VECTORS DIFFERENTIAL OPERATORS AND APPLICATIONS TO STATISTICAL INFERENCE AND TIME SERIES S RAO JAMMALAMADAKA T SUBBA RAO AND GYÖRGY TERDIK Abstract This paper provides
M.Sc. (F) Mathematics Model Paper - A Paper -I (Analysis and Advanced Calculus) Time allowed : 3 Hrs Max. Marks : 100
 M.Sc. (F) Mathematics Model Paper - A Paper -I (Analysis and Advanced Calculus) Time allowed : 3 Hrs Max. Marks : 100 Note : Attempt any five question in all. Select at least one from each unit. Each question
M.Sc. (F) Mathematics Model Paper - A Paper -I (Analysis and Advanced Calculus) Time allowed : 3 Hrs Max. Marks : 100 Note : Attempt any five question in all. Select at least one from each unit. Each question
Terminology Suppose we have N observations {x(n)} N 1. Estimators as Random Variables. {x(n)} N 1
 Estimation Theory Overview Properties Bias, Variance, and Mean Square Error Cramér-Rao lower bound Maximum likelihood Consistency Confidence intervals Properties of the mean estimator Properties of the
Estimation Theory Overview Properties Bias, Variance, and Mean Square Error Cramér-Rao lower bound Maximum likelihood Consistency Confidence intervals Properties of the mean estimator Properties of the
2. Matrix Algebra and Random Vectors
 2. Matrix Algebra and Random Vectors 2.1 Introduction Multivariate data can be conveniently display as array of numbers. In general, a rectangular array of numbers with, for instance, n rows and p columns
2. Matrix Algebra and Random Vectors 2.1 Introduction Multivariate data can be conveniently display as array of numbers. In general, a rectangular array of numbers with, for instance, n rows and p columns
Parametric Models: from data to models
 Parametric Models: from data to models Pradeep Ravikumar Co-instructor: Manuela Veloso Machine Learning 10-701 Jan 22, 2018 Recall: Model-based ML DATA MODEL LEARNING MODEL MODEL INFERENCE KNOWLEDGE Learning:
Parametric Models: from data to models Pradeep Ravikumar Co-instructor: Manuela Veloso Machine Learning 10-701 Jan 22, 2018 Recall: Model-based ML DATA MODEL LEARNING MODEL MODEL INFERENCE KNOWLEDGE Learning:
ECE 275A Homework 7 Solutions
 ECE 275A Homework 7 Solutions Solutions 1. For the same specification as in Homework Problem 6.11 we want to determine an estimator for θ using the Method of Moments (MOM). In general, the MOM estimator
ECE 275A Homework 7 Solutions Solutions 1. For the same specification as in Homework Problem 6.11 we want to determine an estimator for θ using the Method of Moments (MOM). In general, the MOM estimator
ENEE 621 SPRING 2016 DETECTION AND ESTIMATION THEORY THE PARAMETER ESTIMATION PROBLEM
 c 2007-2016 by Armand M. Makowski 1 ENEE 621 SPRING 2016 DETECTION AND ESTIMATION THEORY THE PARAMETER ESTIMATION PROBLEM 1 The basic setting Throughout, p, q and k are positive integers. The setup With
c 2007-2016 by Armand M. Makowski 1 ENEE 621 SPRING 2016 DETECTION AND ESTIMATION THEORY THE PARAMETER ESTIMATION PROBLEM 1 The basic setting Throughout, p, q and k are positive integers. The setup With
A Brief Review of Probability, Bayesian Statistics, and Information Theory
 A Brief Review of Probability, Bayesian Statistics, and Information Theory Brendan Frey Electrical and Computer Engineering University of Toronto frey@psi.toronto.edu http://www.psi.toronto.edu A system
A Brief Review of Probability, Bayesian Statistics, and Information Theory Brendan Frey Electrical and Computer Engineering University of Toronto frey@psi.toronto.edu http://www.psi.toronto.edu A system
Probability and Estimation. Alan Moses
 Probability and Estimation Alan Moses Random variables and probability A random variable is like a variable in algebra (e.g., y=e x ), but where at least part of the variability is taken to be stochastic.
Probability and Estimation Alan Moses Random variables and probability A random variable is like a variable in algebra (e.g., y=e x ), but where at least part of the variability is taken to be stochastic.
ELEG 5633 Detection and Estimation Minimum Variance Unbiased Estimators (MVUE)
 1 ELEG 5633 Detection and Estimation Minimum Variance Unbiased Estimators (MVUE) Jingxian Wu Department of Electrical Engineering University of Arkansas Outline Minimum Variance Unbiased Estimators (MVUE)
1 ELEG 5633 Detection and Estimation Minimum Variance Unbiased Estimators (MVUE) Jingxian Wu Department of Electrical Engineering University of Arkansas Outline Minimum Variance Unbiased Estimators (MVUE)
Introduction to Probability Theory for Graduate Economics Fall 2008
 Introduction to Probability Theory for Graduate Economics Fall 008 Yiğit Sağlam October 10, 008 CHAPTER - RANDOM VARIABLES AND EXPECTATION 1 1 Random Variables A random variable (RV) is a real-valued function
Introduction to Probability Theory for Graduate Economics Fall 008 Yiğit Sağlam October 10, 008 CHAPTER - RANDOM VARIABLES AND EXPECTATION 1 1 Random Variables A random variable (RV) is a real-valued function
APPM/MATH 4/5520 Solutions to Exam I Review Problems. f X 1,X 2. 2e x 1 x 2. = x 2
 APPM/MATH 4/5520 Solutions to Exam I Review Problems. (a) f X (x ) f X,X 2 (x,x 2 )dx 2 x 2e x x 2 dx 2 2e 2x x was below x 2, but when marginalizing out x 2, we ran it over all values from 0 to and so
APPM/MATH 4/5520 Solutions to Exam I Review Problems. (a) f X (x ) f X,X 2 (x,x 2 )dx 2 x 2e x x 2 dx 2 2e 2x x was below x 2, but when marginalizing out x 2, we ran it over all values from 0 to and so
Math 3013 Problem Set 6
 Math 3013 Problem Set 6 Problems from 31 (pgs 189-190 of text): 11,16,18 Problems from 32 (pgs 140-141 of text): 4,8,12,23,25,26 1 (Problems 3111 and 31 16 in text) Determine whether the given set is closed
Math 3013 Problem Set 6 Problems from 31 (pgs 189-190 of text): 11,16,18 Problems from 32 (pgs 140-141 of text): 4,8,12,23,25,26 1 (Problems 3111 and 31 16 in text) Determine whether the given set is closed
Quick Tour of Basic Probability Theory and Linear Algebra
 Quick Tour of and Linear Algebra Quick Tour of and Linear Algebra CS224w: Social and Information Network Analysis Fall 2011 Quick Tour of and Linear Algebra Quick Tour of and Linear Algebra Outline Definitions
Quick Tour of and Linear Algebra Quick Tour of and Linear Algebra CS224w: Social and Information Network Analysis Fall 2011 Quick Tour of and Linear Algebra Quick Tour of and Linear Algebra Outline Definitions
Probability Theory and Statistics. Peter Jochumzen
 Probability Theory and Statistics Peter Jochumzen April 18, 2016 Contents 1 Probability Theory And Statistics 3 1.1 Experiment, Outcome and Event................................ 3 1.2 Probability............................................
Probability Theory and Statistics Peter Jochumzen April 18, 2016 Contents 1 Probability Theory And Statistics 3 1.1 Experiment, Outcome and Event................................ 3 1.2 Probability............................................
A. Motivation To motivate the analysis of variance framework, we consider the following example.
 9.07 ntroduction to Statistics for Brain and Cognitive Sciences Emery N. Brown Lecture 14: Analysis of Variance. Objectives Understand analysis of variance as a special case of the linear model. Understand
9.07 ntroduction to Statistics for Brain and Cognitive Sciences Emery N. Brown Lecture 14: Analysis of Variance. Objectives Understand analysis of variance as a special case of the linear model. Understand
Partial effects in fixed effects models
 1 Partial effects in fixed effects models J.M.C. Santos Silva School of Economics, University of Surrey Gordon C.R. Kemp Department of Economics, University of Essex 22 nd London Stata Users Group Meeting
1 Partial effects in fixed effects models J.M.C. Santos Silva School of Economics, University of Surrey Gordon C.R. Kemp Department of Economics, University of Essex 22 nd London Stata Users Group Meeting
x. Figure 1: Examples of univariate Gaussian pdfs N (x; µ, σ 2 ).
 .8.6 µ =, σ = 1 µ = 1, σ = 1 / µ =, σ =.. 3 1 1 3 x Figure 1: Examples of univariate Gaussian pdfs N (x; µ, σ ). The Gaussian distribution Probably the most-important distribution in all of statistics
.8.6 µ =, σ = 1 µ = 1, σ = 1 / µ =, σ =.. 3 1 1 3 x Figure 1: Examples of univariate Gaussian pdfs N (x; µ, σ ). The Gaussian distribution Probably the most-important distribution in all of statistics
