Lecture III CONTEXT FREE LANGUAGES
|
|
|
- Vincent Pearson
- 5 years ago
- Views:
Transcription
1 1. Context Free Languages and Grammar Lecture III Page 1 Lecture III CONTEXT FREE LANGUAGES Lecture 3: Honors Theory, Spring 02. We introduce context free languages (CFL), context free grammar (CFG) and pushdown automata (PDA). The pumping lemma for context free languages is used to show various languages to be non-cfl. 1. Context Free Languages and Grammar We have seen automatas (dfa, nfa) and expressions (regular) that can describe languages. We now introduce formal grammars as another device for describing languages. The notion of grammars is motivated by natural languages. Consider the structure of very simple English sentences. The following are grammatical rules : <Sentence> --> <Noun Phrase> <Verb Phrase> <Noun Phrase> --> <Article> <Noun> <Noun> <Verb Phrase> --> <Verb> <Verb> <Noun Phrase> <Article> --> a the <Noun> --> boy girl ball dog... <Verb> --> caught saw took... Note the use of as alternatives. Thus we can generate sentences such as Girl took the ball The boy saw a girl Dog caught ball A ball saw the boy... The proof that the first sentence can be generated by the simple grammar amounts to giving a parse tree: <Sentence> / \ / \ <Noun Phrase> <Verb Phrase> / \ / \ <Noun> <Verb> <Noun Phrase> / \ / \ Girl took <Article> <Noun> the ball
2 2. Normal Form Lecture III Page 2 The grammatical rules or productions has a left-hand side and a right-hand side. Each side is a string of variables (indicated by <...>) and terminals (such as boy, girl, etc). Using the rules, we generate sentence which has only terminals. We now formalize this. Let V,Σ be disjoint alphabets. A context free grammar (CFG) is a 4-tuple G =(V,Σ,R,S) where V is the set of variables,σthesetofterminals, S V is the start symbol, andr is a finite set of rules. A rule has the form form A w where w (V Σ).Ifu, v, w Σ, define the produce relation as the binary relation on words u G v (or simply, u v) ifu = u Au, v = v wv and A w is a rule in G. Thus A is replaced by w in this produce relation. The derivation relation G (or simply ) is the reflexive, transitive closure of. Thus, u v iff there is a sequence u 0 u 1 u m (m 0) (1) such that u = u 0 and u m = v. Ifm =0thenu = v. We call (1) a derivation of u m from u 0.Thelanguage generated by G is L(G) ={w Σ : S G w} A language is context free if it is generated by some CFG. The derivation (1) is called a leftmost derivation if the variable being replaced at each step is the leftmost variable. The order of replacing these variables is somewhat artificial in a derivation. One way to remove this artificial ordering is to consider the parse tree of a derivation. This is defined in the natural was to be an oriented rooted tree in which the internal nodes are variables and the leaves are terminals. The root has the start symbol S and the children of an internal node A are labeled by the symbols on the righthand side of some production, A w. An example is the parse tree of the sentence Girl took the ball above. E.g., Let the rules of G be be given by S 0S0 1S1 ɛ. This generates the set of binary palindromes of even length. To generate all binary palindromes, add two more rules: S 0 1. Here is another example for simple arithmetic expressions: <E> --> <id> <num> (<E>) - <E> <E> <op> <E> <id> --> a b c... x y z <num> --> <dig> <dig><num> <dig> --> <op> --> + - * / 2. Normal Form
3 3. Pumping Lemma Lecture III Page 3 There are two special forms for CFG s: (i) A grammar G is in Chomsky Normal Form if every rule has the form A BC, A a where A, B, C are variables, B,C is not the start symbol, and a Σ. In addition, we allow the special rule of the form S ɛ. (ii) We say G is in Greibach Normal Form if every rule has the form A ab 1 B 2 B m, (m 0) where a ΣandB i s are variables. Every CFL can be generated by grammars in both normal forms. We give the prove for Chomsky normal form: Theorem 1 Every context-free language is generated by a CFG in Chomsky Normal Form. Proof. Starting from a CFG G, we transform G into Chomsky Normal Form in five steps: First ensure that S does not appear on the right hand side of any rule. To do this, replace all occurences of S on the RHS of any rule by a new variable S. Also, add the rule S S. Second, remove each rule of the form A ɛ and introduce, for any rule B w where A occurs in w, a new rule B w[a/ɛ] (w[a/ɛ] means we replace each occurence of A in w by ɛ). If ɛ L(G), we also add the special rule S ɛ. Third, we replace every rule of the form A u 1,...,u k (k 3) by the new rules: A u 1 A 1, A k 2 u k 1 u k,andk 3 rules of the form A i u i+1 A i+1, (i =1,...,k 3), where A 1,...,A k 2 are new variables. The degree of a rule is the length of its RHS. At this point, any remaining rules have degrees 1 or 2. Fourth, we fix rules of degree 2. For each rule of the form A bc, whereb T and C V, we replace it by A BC and B b (B is a new variable). We have a similar treatment for rules of the form A Cb or A bc. Fifth and finally, we fix rules of degree 1. If we have a derivation of the form A B and A B and B a or B CD. Then introduce the rule A a or A CD (respectively). Moreover remove all rules of the form A B. This completes the proof. Q.E.D. This is useful if we want to show that something cannot be context-free: we only have to attack grammars in this special form. As exercise, try convert the CFG example above to Chomsky Normal Form. 3. Pumping Lemma As for regular languages, we are interested to know if there are non-context free languages. Which of the following two languages are CFL? DOUBLE = {ww : w 0, 1 }. PAL = {ww R : w 0, 1 }. To show it is something is context free, we construct an appropriate CFG or PDA. What if it is not context
4 3. Pumping Lemma Lecture III Page 4 free? One basic technique is via a pumping lemma for CFL. Suitably formulated, this will be a generalization of the corresponding pumping lemma for regular languages. The idea of the pumping lemma for CFL is based on the following observation. Suppose T is a derivation tree for a word w L. Let π =(A 0,A 1,...,A n,a) be any path in T starting from the root A 0 = S (the start symbol). Here, the A i s are variables and a is a terminal. Suppose A i = A j for some 0 i<j n. Then w can be decomposed as w = uvxyz where x is the word generated by the subtree rooted at A j v (resp., y) is the word generated by the subtrees rooted at the left (resp., right) children of node in the subpath (A i,...,a j ). u (resp., z) is the word generated by the subtrees rooted at the left (resp., right) children of node in the subpath (A 0,...,A i ). This is called the uvxyz-decomposition of w ( uvxyz is pronounced eu-vitz ). This is illustrated by figure 1(a). Now we can modify the tree T in two ways: (a) We may delete the subpath (A i,...,a j 1 )andall A i A j u v x y z A i A i x u v y z u z v x y Figure 1: The uvxyz decomposition of w and two transformations of the parse tree. the associated subtrees to the left or right, and produce a derivation tree for uxz, or (b) We may duplicate the subpath (A i,...,a j 1 ) and all the associated subtrees to the left or right, and produce a derivation tree for uv 2 xy 2 z. This shows that uxz, uv 2 xy 2 z L. In fact, we can repeat (b) as many times as we like to show that uv i xy i z L. We are now ready to prove the pumping lemma. Theorem 2 (Pumping Lemma) If L is a CFL then there exists n>0 such that for all w L, w n implies that w = uvxyz such that (i) vy > 0. (ii) uv i xy i z L for all i 0. (iii) vxy n.
5 4. PDA Lecture III Page 5 Proof. Assume L is generated by a grammar G in Chomsky Normal Form. Choose n =2 m where m is the number of variables in G. If w n, then the derivation tree T (w) ofw must have height h that is at least m + 1 (this is because T (w) is a binary tree, and the last variable in any path that generates a leaf has degree 1). But in any path (A 0,A 1,...,A h 1,a)oflengthh m + 1, there are at least m + 1 variables (only the last node can be a terminal). Hence some variable is repeated, say A i = A j where 0 i<j h 1. The above uvxyz-decomposition is therefore applicable. Moreover, both (i) and (ii) are clear. To see (iii), we simply make sure that the subpath (A i,a i+1,...,a h 1 ) has length m. Q.E.D. We should note that there can be slight variations in the formulation of this lemma, but the underlying proof technique is the same. Hence, if this version of the pumping lemma is inadequate for a situation, you can sometimes use the underlying uvxyz-decomposition and argue directly. 4. PDA A pushdown automata (pda) is like an nfa except it has a linear storage structure called a pushdown store which we also call 1 a stack for brevity. The pda can read only the topmost symbol of the stack. Depending on the transition rules, may replace the topmost symbol by a new symbol or ɛ (this means the topmost symbol is popped); it may also place a new symbol on top of old topmost symbol (this pushes a new symbol). This is illustrated in figure 2. a 1 a 2 a i a n b t Top of stack a b 1 b 0 Bottom of stack Figure 2: Illustration of a push down automata For example, it is quite easy to design a pda to accept L 1 = {0 n 1 n : n 0}. Formally, a pushdown automata (pda) is a 6-tuple M =(Q, Σ, Γ,δ,q 0,F) where Σ, Γ are input and stack alphabets, q 0 Q is the start state, F Q the final states, and δ the transition function δ : Q Σ ɛ Γ ɛ 2 Q Γɛ The relation (q,b ) δ(q, a, b) (2) represents a transition rule. Similar to grammars, we can write such a rule using the arrow notation: (q, a, b q,b ). 1 A stack is sometimes reserved for a generalization of pushdown store in which the automata could go below the topmost symbol for the purposes of reading (but not changing) the store contents. Since we will not discuss such stack automata, our current terminology should not be a source of confusion.
6 4. PDA Lecture III Page 6 This rule says that if the current state is q, a is the current input symbol and b the top of stack, then we can next go to state q and replace b by b.thusδ gives rise to a finite set of such rules, and conversely from any such set there is a unique δ. We will use whichever viewpoint that is convenient. What makes the notion of a pda transition slightly confusing is that a, b, b can independently be ɛ. Our goal, as usual, is to define the language L(M) accepted by M. Towards this end, it is useful to formalize the concept of a configuration or current state of the computation of a pda. A configuration is simply an triple of the form C =(q, w, v) Q Σ Γ. Intuitively, q is the current state, w is the rest of the unread input (with w[1] the current input symbol) and v the stack contents (with v[1] the top of stack). If C =(q,w,v ) is another configuration, then the binary relation C M C (or, simply, C C ) holds if C can reach C by applying a single transition rule of M. More precisely, (2) is a transition rule of M and w = aw, a Σ ɛ v = bu, b Γ ɛ v = b u. Let denote the reflexive transitive closure of. ThusC C iff there exists a finite sequence of the form C 0 C 1 C m, m 0 (3) where C 0 = C and C m = C. We then say C derives C in m steps. We define L(M) to comprise all w Σ such that (q 0,w,ɛ) (q, ɛ, v) for some q F and v Γ. We say M accepts w. An alternative definition of acceptance is to insist that v = ɛ, inwhichcasewesaym accepts by empty store and denote the corresponding language by L ɛ (M). Nondeterminism and Example. A pda in inherently nondeterministic in this definition. The nondeterminism in the above relation C =(q, w, v) (q,w,v )=C arises in three ways: There may be several choices of (q,b ) from the set δ(q, a, b). If w ɛ then we have a choice of a = w[1] or a = ɛ. If v ɛ then we have a choice of b = v[1] or b = ɛ. To illustrate this nondeterminism, let us consider a pda to accept the language PAL = PAL 2 = {w {0, 1} : w = w R } of binary palindromes. We make a simple observation: if w PAL then w = uav for some u, v {0, 1} and a {0, 1,ɛ} and u = v R. The idea is to operate in two phases: in the first phase, we just push u into the stack. In the second phase, we verify that the rest of the input (namely v) isequal to to the stack contents (namely u R ). But how do we know when we have reached the middle of the input, namely, the position of a? We use nondeterminism! More precisely, our pda will have 4 states: start state q 0, phase 1 state q 1, phase 2 state q 2, and accept state q f. This pda is represented in the following state diagram: While nondeterminism in finite automata turns out to be inessential in some sense, the nondeterminism of pda s turns out to be essential. We can define the notion of a deterministic pda (dpda) and show that the language PAL cannot be accepted by any dpda.
7 5. PDA Characterization Lecture III Page 7 (ɛ, ɛ $) q 0 q 1 (0,ɛ 0) (1,ɛ 1) (ɛ, ɛ ɛ) (0,ɛ ɛ) (1,ɛ ɛ) q f (ɛ, $ ɛ) q 2 (0, 0 ɛ) (1, 1 ɛ) Figure 3: PDA to accept binary palindromes. Pragmatics of pda s. the form We can generalize the transition function δ slightly, by allowing transition rules of (q, a, u q,v) (4) where q, q Q, a Σ ɛ, u, v Γ. We leave it as an exercise to show that this does enlarge the class of languages accepted by pda s. In state diagrams, the rule (4) appears as a label (a, u v) of the edge from q to q. Often, a pda need to act when its stack is empty. A standard way to achieve this is to provide only one transition rule for the start state q 0,namely (q 0,ɛ,ɛ q 1, $) where $ is a special symbol that marks the bottom of the stack and q 1 some new state. 5. PDA Characterization The main result in this section is that pda and CFG are equivalent. We split the proof into two parts. Lemma 3 Every context free language is accepted by a pda. Proof. Assume G =(V,Σ,S,R) is a grammar in Chomsky Normal Form. We will construct an equivalent pda M =(Q, Σ, Γ,δ,q 0,F). Let w be generated by G using the following leftmost derivation: S u 1 u 2 u m = w. Write u i = w i A i v i where w i is a prefix of w and A i a variable. Our pda will simulate this derivation in m steps. In the ith step, M will have finished read w i and its stack contains A i v i (with A i at the top of stack). It remains to show how to proceed to the i + 1st step. M has only three states Q = {q 0,q 1,q f } and each simulation step above is performed while in state q 1. There are only two kinds of rules for A i : (a) A i a. In this case, the pda has the transition rule (q 1,a,A i q 1,ɛ). (b) A i BC. In this case, the pda has the transition rule (q 1,ɛ,A i q 1,BC). It is clear that this achieves our step by step simulation. To start off the induction, we have the transition (q 0,ɛ,ɛ S$)
8 5. PDA Characterization Lecture III Page 8 where S is the start symbol of the grammar and $ is a special symbol to indiate the bottom of stack. To terminate the simulation, we have the rule (q 1,ɛ,$ q f,ɛ) This is the only way to enter the final state q f. Q.E.D. The reverse direction is slightly harder but not much more. Lemma 4 Every language accepted by a pda is context free. Proof. Given a pda M =(Q, Σ, Γ,δ,q 0,F), we will construct a grammar G =(V,Σ,S,R). We may assume that M accepts by empty stack, namely if it ever enters a state of F,thenitsstackisempty. Infact,we can assume F = {q f }. Another simplification will be useful: each transition of M will either push a symbol or pop a symbol from the stack. That is each rule (q, a, b q,b ) satisfies either b = ɛ and b ɛ, orb ɛ and b = ɛ. Let p, q Q. Define the language L pq to comprise all words w Σ such that (p, w, ɛ) (q, ɛ, ɛ). Our grammar G will have variable A pq to generate precisely the language L pq. To do this, consider a computation path starting from configuration C p =(p, w, ɛ) and terminating in C q =(q, ɛ, ɛ). There are two cases. (A) There is configuration C r =(r, w,ɛ) such that C p + C r + C q. In this case, w = w w where w L pr and w L rq. Our grammar has the rule A pq A pr A rq for every p, q, r. Hence, inductively we could generate w and w. What is the induction hypothesis at stage n? It is that every word of length less than n in L pq can be generated by our grammer, for all p, q Q. (B) There is no such configuration C r. We know that first and last step of this path be a push action and a pop action, respectively. If the state after the push action (resp., before the pop action) is r (resp., s), then let the corresponding transition rules be (p, a, ɛ r, b), (s, a,b q, ɛ). But our grammar has, for every such pair of transitions, a rule of the form A pq aa rs a. Thus w = aw a for some w Σ. Moreover, w L rs. Again, by induction, we know that w can be generated from A rs, and hence we are done. Q.E.D. NOTES The notion of context free grammars and pda s were introduced by Chomsky (1956) and Oettinger (1961), respectively. Context free grammars is closely related to the Backus Normal Form or Backus-Naur Form formulation, described by John Bakus and Peter Naur in the late 1950 s. The dynamic programming algorithm for recognizing context free grammars (Exercise) is from T. Kasami (1965). In the 1950s, the study of formal languages led to considerable optimism in the ability of machines to understand natural languages. In particular, machine translation (MT) was thought imminent. This turns out to be misplaced optimism. As an undergraduate, my professor (M.L. Dertouzos) told us,
9 5. PDA Characterization Lecture III Page 9 When I was a graduate student, my professor told us that MT will be possible in a few years He also gave anecdotal examples of what machines produced. Machine translating the sentence The spirit is willing but the flesh is weak into Russian, and back again, produced The vodka is strong but the meat is rotten. The sentence Out of sight, out of mind was translated into Blind idiot. Considerable progress has been made today, especially in specialized domains. For instance, in the European community (EC), official documents can be automatically translated quite accurately to all the official languages of the EC. If formal languages turns out to be inadequate for natural languages, they have great impact in the design and analysis of computer languages. Exercises Exercise 5.1: Recall the example of translating The spirit is willing but the flesh is weak, etc, described in the Notes. Try to outdo these machine translations from the early days of MT. [It only goes to prove that the machine translation is too hard for machines alone.] Exercise 5.2: Extend the simplistic English grammar in the introduction to generate slightly more complex sentences. (i) Allow nouns that are either singular or plural. So you will need new variables such as <NP Singular>, <NP Plural>, etc. (ii) Introduce simple tenses (past, present, future). Exercise 5.3: Prove that every CFL can be generated by grammar in Greibach normal form. Exercise 5.4: Show that we can allow pda s with the more general rule of the form (4). Exercise 5.5: Prove or disprove that the following are context free: (i) L 1 = {w {a, b, c} :# a (w) =# b (w) or # b (w) =# c (w) or # b (w) =# c (w)}. (ii) L 2 = {w {a, b, c} :# a (w) # b (w) or # b (w) # c (w) or # b (w) # c (w)}. (iii) L 3 = {w {a, b, c} :# a (w) =# b (w) and # b (w) =# c (w) and # b (w) =# c (w)}. NOTE: # a (w) counts the number of occurences of a in w. Exercise 5.6: Let L {0}. Such a language is called a sla language (sla stands for single letter alphabet ). (i) Show a sla language that is not context free. (ii) Show that any sla language L that is context free must be regular. HINT: assume G is a Chomsky Normal Form grammar for L. Try to construct an nfa to accept L. Exercise 5.7: Let A, B Σ.Theright quotient of A by B is defined to be A/B :={w Σ :( u B)[wu A]}. (i) Show that if A is context free and B is regular, then A/B is context free. (ii) Use part (i) to show that the language {0 p 1 n : p is prime, n>p} is not context free.
10 5. PDA Characterization Lecture III Page 10 Exercise 5.8: We say that a pda M is nondeterministic if it has two distinct transition rules (q, a, b r, c) and (q,a,b r,c ) such that either (A) or (B) holds: (A) a = a, or a = ɛor a = ɛ, (B) b = b, or b = ɛor b = ɛ. If M is not nondeterministic, we say it is deterministic. Call a language strongly deterministic context free if it is accepted by some deterministic pda. (i) Show that L 1 = {0 n 1 n : n 0} is strongly deterministic context free. (ii) Show that L 2 = {0 n 1 m : m = nor m =0} is not strongly deterministic context free. Exercise 5.9: (i) Construct an efficient algorithm that, on input G, w where G =(V,T,S,R) is a grammar in Chomsky Normal Form and w a string, decide whether w L(G). HINT: Use dynamic programming. For 1 i j n, letw ij denote the substring a i a j where w = a 1,...,a n. Define V ij = {A V : A w ij }. How do you compute V ij if you know the sets V ik,v kj for all k = i,...,j? (ii) What is the worst-case complexity of your algorithm, as a function of input sizes m = G,n= w? There is an interesting low-level issue here: w and G must be suitably interpreted! Note that V,T are arbitrary alphabets, but your algorithm must accept input with a fixed alphabet (say Σ). Hence use the following convention: assume Σ contains the special symbols A, a, 0, 1 (among others), and each symbol of V is encoded as a string of the form A(0 + 1), and each symbol of T and w is encoded as a string of the form a(0 + 1). The definition of G can be taken to be the number of symbols in writing down all the rules of G plus V T. Theneachsymbolinx has length equal to its encoding as a string in L(a(0 + 1) )! Similarly, you need specify your encoding G over the fixed alphabet Σ and tell us how to determine its length G. End Exercises References
Computational Models - Lecture 4
 Computational Models - Lecture 4 Regular languages: The Myhill-Nerode Theorem Context-free Grammars Chomsky Normal Form Pumping Lemma for context free languages Non context-free languages: Examples Push
Computational Models - Lecture 4 Regular languages: The Myhill-Nerode Theorem Context-free Grammars Chomsky Normal Form Pumping Lemma for context free languages Non context-free languages: Examples Push
Introduction to Theory of Computing
 CSCI 2670, Fall 2012 Introduction to Theory of Computing Department of Computer Science University of Georgia Athens, GA 30602 Instructor: Liming Cai www.cs.uga.edu/ cai 0 Lecture Note 3 Context-Free Languages
CSCI 2670, Fall 2012 Introduction to Theory of Computing Department of Computer Science University of Georgia Athens, GA 30602 Instructor: Liming Cai www.cs.uga.edu/ cai 0 Lecture Note 3 Context-Free Languages
CISC4090: Theory of Computation
 CISC4090: Theory of Computation Chapter 2 Context-Free Languages Courtesy of Prof. Arthur G. Werschulz Fordham University Department of Computer and Information Sciences Spring, 2014 Overview In Chapter
CISC4090: Theory of Computation Chapter 2 Context-Free Languages Courtesy of Prof. Arthur G. Werschulz Fordham University Department of Computer and Information Sciences Spring, 2014 Overview In Chapter
Computational Models - Lecture 4 1
 Computational Models - Lecture 4 1 Handout Mode Iftach Haitner and Yishay Mansour. Tel Aviv University. April 3/8, 2013 1 Based on frames by Benny Chor, Tel Aviv University, modifying frames by Maurice
Computational Models - Lecture 4 1 Handout Mode Iftach Haitner and Yishay Mansour. Tel Aviv University. April 3/8, 2013 1 Based on frames by Benny Chor, Tel Aviv University, modifying frames by Maurice
Pushdown Automata. Notes on Automata and Theory of Computation. Chia-Ping Chen
 Pushdown Automata Notes on Automata and Theory of Computation Chia-Ping Chen Department of Computer Science and Engineering National Sun Yat-Sen University Kaohsiung, Taiwan ROC Pushdown Automata p. 1
Pushdown Automata Notes on Automata and Theory of Computation Chia-Ping Chen Department of Computer Science and Engineering National Sun Yat-Sen University Kaohsiung, Taiwan ROC Pushdown Automata p. 1
The View Over The Horizon
 The View Over The Horizon enumerable decidable context free regular Context-Free Grammars An example of a context free grammar, G 1 : A 0A1 A B B # Terminology: Each line is a substitution rule or production.
The View Over The Horizon enumerable decidable context free regular Context-Free Grammars An example of a context free grammar, G 1 : A 0A1 A B B # Terminology: Each line is a substitution rule or production.
Pushdown Automata. We have seen examples of context-free languages that are not regular, and hence can not be recognized by finite automata.
 Pushdown Automata We have seen examples of context-free languages that are not regular, and hence can not be recognized by finite automata. Next we consider a more powerful computation model, called a
Pushdown Automata We have seen examples of context-free languages that are not regular, and hence can not be recognized by finite automata. Next we consider a more powerful computation model, called a
Theory of Computation (II) Yijia Chen Fudan University
 Theory of Computation (II) Yijia Chen Fudan University Review A language L is a subset of strings over an alphabet Σ. Our goal is to identify those languages that can be recognized by one of the simplest
Theory of Computation (II) Yijia Chen Fudan University Review A language L is a subset of strings over an alphabet Σ. Our goal is to identify those languages that can be recognized by one of the simplest
Einführung in die Computerlinguistik
 Einführung in die Computerlinguistik Context-Free Grammars (CFG) Laura Kallmeyer Heinrich-Heine-Universität Düsseldorf Summer 2016 1 / 22 CFG (1) Example: Grammar G telescope : Productions: S NP VP NP
Einführung in die Computerlinguistik Context-Free Grammars (CFG) Laura Kallmeyer Heinrich-Heine-Universität Düsseldorf Summer 2016 1 / 22 CFG (1) Example: Grammar G telescope : Productions: S NP VP NP
Foundations of Informatics: a Bridging Course
 Foundations of Informatics: a Bridging Course Week 3: Formal Languages and Semantics Thomas Noll Lehrstuhl für Informatik 2 RWTH Aachen University noll@cs.rwth-aachen.de http://www.b-it-center.de/wob/en/view/class211_id948.html
Foundations of Informatics: a Bridging Course Week 3: Formal Languages and Semantics Thomas Noll Lehrstuhl für Informatik 2 RWTH Aachen University noll@cs.rwth-aachen.de http://www.b-it-center.de/wob/en/view/class211_id948.html
Theory of Computation (IV) Yijia Chen Fudan University
 Theory of Computation (IV) Yijia Chen Fudan University Review language regular context-free machine DFA/ NFA PDA syntax regular expression context-free grammar Pushdown automata Definition A pushdown automaton
Theory of Computation (IV) Yijia Chen Fudan University Review language regular context-free machine DFA/ NFA PDA syntax regular expression context-free grammar Pushdown automata Definition A pushdown automaton
October 6, Equivalence of Pushdown Automata with Context-Free Gramm
 Equivalence of Pushdown Automata with Context-Free Grammar October 6, 2013 Motivation Motivation CFG and PDA are equivalent in power: a CFG generates a context-free language and a PDA recognizes a context-free
Equivalence of Pushdown Automata with Context-Free Grammar October 6, 2013 Motivation Motivation CFG and PDA are equivalent in power: a CFG generates a context-free language and a PDA recognizes a context-free
FORMAL LANGUAGES, AUTOMATA AND COMPUTABILITY
 15-453 FORMAL LANGUAGES, AUTOMATA AND COMPUTABILITY REVIEW for MIDTERM 1 THURSDAY Feb 6 Midterm 1 will cover everything we have seen so far The PROBLEMS will be from Sipser, Chapters 1, 2, 3 It will be
15-453 FORMAL LANGUAGES, AUTOMATA AND COMPUTABILITY REVIEW for MIDTERM 1 THURSDAY Feb 6 Midterm 1 will cover everything we have seen so far The PROBLEMS will be from Sipser, Chapters 1, 2, 3 It will be
Lecture 17: Language Recognition
 Lecture 17: Language Recognition Finite State Automata Deterministic and Non-Deterministic Finite Automata Regular Expressions Push-Down Automata Turing Machines Modeling Computation When attempting to
Lecture 17: Language Recognition Finite State Automata Deterministic and Non-Deterministic Finite Automata Regular Expressions Push-Down Automata Turing Machines Modeling Computation When attempting to
Computational Models - Lecture 3
 Slides modified by Benny Chor, based on original slides by Maurice Herlihy, Brown University. p. 1 Computational Models - Lecture 3 Equivalence of regular expressions and regular languages (lukewarm leftover
Slides modified by Benny Chor, based on original slides by Maurice Herlihy, Brown University. p. 1 Computational Models - Lecture 3 Equivalence of regular expressions and regular languages (lukewarm leftover
Outline. CS21 Decidability and Tractability. Machine view of FA. Machine view of FA. Machine view of FA. Machine view of FA.
 Outline CS21 Decidability and Tractability Lecture 5 January 16, 219 and Languages equivalence of NPDAs and CFGs non context-free languages January 16, 219 CS21 Lecture 5 1 January 16, 219 CS21 Lecture
Outline CS21 Decidability and Tractability Lecture 5 January 16, 219 and Languages equivalence of NPDAs and CFGs non context-free languages January 16, 219 CS21 Lecture 5 1 January 16, 219 CS21 Lecture
Computational Models - Lecture 4 1
 Computational Models - Lecture 4 1 Handout Mode Iftach Haitner. Tel Aviv University. November 21, 2016 1 Based on frames by Benny Chor, Tel Aviv University, modifying frames by Maurice Herlihy, Brown University.
Computational Models - Lecture 4 1 Handout Mode Iftach Haitner. Tel Aviv University. November 21, 2016 1 Based on frames by Benny Chor, Tel Aviv University, modifying frames by Maurice Herlihy, Brown University.
What we have done so far
 What we have done so far DFAs and regular languages NFAs and their equivalence to DFAs Regular expressions. Regular expressions capture exactly regular languages: Construct a NFA from a regular expression.
What we have done so far DFAs and regular languages NFAs and their equivalence to DFAs Regular expressions. Regular expressions capture exactly regular languages: Construct a NFA from a regular expression.
CS5371 Theory of Computation. Lecture 9: Automata Theory VII (Pumping Lemma, Non-CFL, DPDA PDA)
 CS5371 Theory of Computation Lecture 9: Automata Theory VII (Pumping Lemma, Non-CFL, DPDA PDA) Objectives Introduce the Pumping Lemma for CFL Show that some languages are non- CFL Discuss the DPDA, which
CS5371 Theory of Computation Lecture 9: Automata Theory VII (Pumping Lemma, Non-CFL, DPDA PDA) Objectives Introduce the Pumping Lemma for CFL Show that some languages are non- CFL Discuss the DPDA, which
CISC 4090 Theory of Computation
 CISC 4090 Theory of Computation Context-Free Languages and Push Down Automata Professor Daniel Leeds dleeds@fordham.edu JMH 332 Languages: Regular and Beyond Regular: a b c b d e a Not-regular: c n bd
CISC 4090 Theory of Computation Context-Free Languages and Push Down Automata Professor Daniel Leeds dleeds@fordham.edu JMH 332 Languages: Regular and Beyond Regular: a b c b d e a Not-regular: c n bd
Final exam study sheet for CS3719 Turing machines and decidability.
 Final exam study sheet for CS3719 Turing machines and decidability. A Turing machine is a finite automaton with an infinite memory (tape). Formally, a Turing machine is a 6-tuple M = (Q, Σ, Γ, δ, q 0,
Final exam study sheet for CS3719 Turing machines and decidability. A Turing machine is a finite automaton with an infinite memory (tape). Formally, a Turing machine is a 6-tuple M = (Q, Σ, Γ, δ, q 0,
Context-Free Languages
 CS:4330 Theory of Computation Spring 2018 Context-Free Languages Pushdown Automata Haniel Barbosa Readings for this lecture Chapter 2 of [Sipser 1996], 3rd edition. Section 2.2. Finite automaton 1 / 13
CS:4330 Theory of Computation Spring 2018 Context-Free Languages Pushdown Automata Haniel Barbosa Readings for this lecture Chapter 2 of [Sipser 1996], 3rd edition. Section 2.2. Finite automaton 1 / 13
Cliff s notes for equivalence of CFLs and L(PDAs) LisaCFL L = L(M) for some PDA M L=L(M)forsomePDAM L = L(G) for some CFG G
 What s on our plate today? Cliff s notes for equivalence of CFLs and L(PDAs) LisaCFL L = L(M) for some PDA M L=L(M)forsomePDAM L = L(G) for some CFG G Pumping Lemma (one last time) Statement of Pumping
What s on our plate today? Cliff s notes for equivalence of CFLs and L(PDAs) LisaCFL L = L(M) for some PDA M L=L(M)forsomePDAM L = L(G) for some CFG G Pumping Lemma (one last time) Statement of Pumping
Harvard CS 121 and CSCI E-207 Lecture 10: CFLs: PDAs, Closure Properties, and Non-CFLs
 Harvard CS 121 and CSCI E-207 Lecture 10: CFLs: PDAs, Closure Properties, and Non-CFLs Harry Lewis October 8, 2013 Reading: Sipser, pp. 119-128. Pushdown Automata (review) Pushdown Automata = Finite automaton
Harvard CS 121 and CSCI E-207 Lecture 10: CFLs: PDAs, Closure Properties, and Non-CFLs Harry Lewis October 8, 2013 Reading: Sipser, pp. 119-128. Pushdown Automata (review) Pushdown Automata = Finite automaton
60-354, Theory of Computation Fall Asish Mukhopadhyay School of Computer Science University of Windsor
 60-354, Theory of Computation Fall 2013 Asish Mukhopadhyay School of Computer Science University of Windsor Pushdown Automata (PDA) PDA = ε-nfa + stack Acceptance ε-nfa enters a final state or Stack is
60-354, Theory of Computation Fall 2013 Asish Mukhopadhyay School of Computer Science University of Windsor Pushdown Automata (PDA) PDA = ε-nfa + stack Acceptance ε-nfa enters a final state or Stack is
UNIT-VI PUSHDOWN AUTOMATA
 Syllabus R09 Regulation UNIT-VI PUSHDOWN AUTOMATA The context free languages have a type of automaton that defined them. This automaton, called a pushdown automaton, is an extension of the nondeterministic
Syllabus R09 Regulation UNIT-VI PUSHDOWN AUTOMATA The context free languages have a type of automaton that defined them. This automaton, called a pushdown automaton, is an extension of the nondeterministic
COMP-330 Theory of Computation. Fall Prof. Claude Crépeau. Lec. 10 : Context-Free Grammars
 COMP-330 Theory of Computation Fall 2017 -- Prof. Claude Crépeau Lec. 10 : Context-Free Grammars COMP 330 Fall 2017: Lectures Schedule 1-2. Introduction 1.5. Some basic mathematics 2-3. Deterministic finite
COMP-330 Theory of Computation Fall 2017 -- Prof. Claude Crépeau Lec. 10 : Context-Free Grammars COMP 330 Fall 2017: Lectures Schedule 1-2. Introduction 1.5. Some basic mathematics 2-3. Deterministic finite
Computational Models - Lecture 5 1
 Computational Models - Lecture 5 1 Handout Mode Iftach Haitner and Yishay Mansour. Tel Aviv University. April 10/22, 2013 1 Based on frames by Benny Chor, Tel Aviv University, modifying frames by Maurice
Computational Models - Lecture 5 1 Handout Mode Iftach Haitner and Yishay Mansour. Tel Aviv University. April 10/22, 2013 1 Based on frames by Benny Chor, Tel Aviv University, modifying frames by Maurice
SCHEME FOR INTERNAL ASSESSMENT TEST 3
 SCHEME FOR INTERNAL ASSESSMENT TEST 3 Max Marks: 40 Subject& Code: Automata Theory & Computability (15CS54) Sem: V ISE (A & B) Note: Answer any FIVE full questions, choosing one full question from each
SCHEME FOR INTERNAL ASSESSMENT TEST 3 Max Marks: 40 Subject& Code: Automata Theory & Computability (15CS54) Sem: V ISE (A & B) Note: Answer any FIVE full questions, choosing one full question from each
THEORY OF COMPUTATION (AUBER) EXAM CRIB SHEET
 THEORY OF COMPUTATION (AUBER) EXAM CRIB SHEET Regular Languages and FA A language is a set of strings over a finite alphabet Σ. All languages are finite or countably infinite. The set of all languages
THEORY OF COMPUTATION (AUBER) EXAM CRIB SHEET Regular Languages and FA A language is a set of strings over a finite alphabet Σ. All languages are finite or countably infinite. The set of all languages
PUSHDOWN AUTOMATA (PDA)
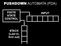 PUSHDOWN AUTOMATA (PDA) FINITE STATE CONTROL INPUT STACK (Last in, first out) input pop push ε,ε $ 0,ε 0 1,0 ε ε,$ ε 1,0 ε PDA that recognizes L = { 0 n 1 n n 0 } Definition: A (non-deterministic) PDA
PUSHDOWN AUTOMATA (PDA) FINITE STATE CONTROL INPUT STACK (Last in, first out) input pop push ε,ε $ 0,ε 0 1,0 ε ε,$ ε 1,0 ε PDA that recognizes L = { 0 n 1 n n 0 } Definition: A (non-deterministic) PDA
CISC 4090 Theory of Computation
 CISC 4090 Theory of Computation Context-Free Languages and Push Down Automata Professor Daniel Leeds dleeds@fordham.edu JMH 332 Languages: Regular and Beyond Regular: Captured by Regular Operations a b
CISC 4090 Theory of Computation Context-Free Languages and Push Down Automata Professor Daniel Leeds dleeds@fordham.edu JMH 332 Languages: Regular and Beyond Regular: Captured by Regular Operations a b
Harvard CS 121 and CSCI E-207 Lecture 10: Ambiguity, Pushdown Automata
 Harvard CS 121 and CSCI E-207 Lecture 10: Ambiguity, Pushdown Automata Salil Vadhan October 4, 2012 Reading: Sipser, 2.2. Another example of a CFG (with proof) L = {x {a, b} : x has the same # of a s and
Harvard CS 121 and CSCI E-207 Lecture 10: Ambiguity, Pushdown Automata Salil Vadhan October 4, 2012 Reading: Sipser, 2.2. Another example of a CFG (with proof) L = {x {a, b} : x has the same # of a s and
CS5371 Theory of Computation. Lecture 9: Automata Theory VII (Pumping Lemma, Non-CFL)
 CS5371 Theory of Computation Lecture 9: Automata Theory VII (Pumping Lemma, Non-CFL) Objectives Introduce Pumping Lemma for CFL Apply Pumping Lemma to show that some languages are non-cfl Pumping Lemma
CS5371 Theory of Computation Lecture 9: Automata Theory VII (Pumping Lemma, Non-CFL) Objectives Introduce Pumping Lemma for CFL Apply Pumping Lemma to show that some languages are non-cfl Pumping Lemma
Pushdown Automata (2015/11/23)
 Chapter 6 Pushdown Automata (2015/11/23) Sagrada Familia, Barcelona, Spain Outline 6.0 Introduction 6.1 Definition of PDA 6.2 The Language of a PDA 6.3 Euivalence of PDA s and CFG s 6.4 Deterministic PDA
Chapter 6 Pushdown Automata (2015/11/23) Sagrada Familia, Barcelona, Spain Outline 6.0 Introduction 6.1 Definition of PDA 6.2 The Language of a PDA 6.3 Euivalence of PDA s and CFG s 6.4 Deterministic PDA
CpSc 421 Final Exam December 15, 2006
 CpSc 421 Final Exam December 15, 2006 Do problem zero and six of problems 1 through 9. If you write down solutions for more that six problems, clearly indicate those that you want graded. Note that problems
CpSc 421 Final Exam December 15, 2006 Do problem zero and six of problems 1 through 9. If you write down solutions for more that six problems, clearly indicate those that you want graded. Note that problems
(pp ) PDAs and CFGs (Sec. 2.2)
 (pp. 117-124) PDAs and CFGs (Sec. 2.2) A language is context free iff all strings in L can be generated by some context free grammar Theorem 2.20: L is Context Free iff a PDA accepts it I.e. if L is context
(pp. 117-124) PDAs and CFGs (Sec. 2.2) A language is context free iff all strings in L can be generated by some context free grammar Theorem 2.20: L is Context Free iff a PDA accepts it I.e. if L is context
Introduction to Formal Languages, Automata and Computability p.1/42
 Introduction to Formal Languages, Automata and Computability Pushdown Automata K. Krithivasan and R. Rama Introduction to Formal Languages, Automata and Computability p.1/42 Introduction We have considered
Introduction to Formal Languages, Automata and Computability Pushdown Automata K. Krithivasan and R. Rama Introduction to Formal Languages, Automata and Computability p.1/42 Introduction We have considered
CS500 Homework #2 Solutions
 CS500 Homework #2 Solutions 1. Consider the two languages Show that L 1 is context-free but L 2 is not. L 1 = {a i b j c k d l i = j k = l} L 2 = {a i b j c k d l i = k j = l} Answer. L 1 is the concatenation
CS500 Homework #2 Solutions 1. Consider the two languages Show that L 1 is context-free but L 2 is not. L 1 = {a i b j c k d l i = j k = l} L 2 = {a i b j c k d l i = k j = l} Answer. L 1 is the concatenation
MA/CSSE 474 Theory of Computation
 MA/CSSE 474 Theory of Computation Bottom-up parsing Pumping Theorem for CFLs Recap: Going One Way Lemma: Each context-free language is accepted by some PDA. Proof (by construction): The idea: Let the stack
MA/CSSE 474 Theory of Computation Bottom-up parsing Pumping Theorem for CFLs Recap: Going One Way Lemma: Each context-free language is accepted by some PDA. Proof (by construction): The idea: Let the stack
ECS 120: Theory of Computation UC Davis Phillip Rogaway February 16, Midterm Exam
 ECS 120: Theory of Computation Handout MT UC Davis Phillip Rogaway February 16, 2012 Midterm Exam Instructions: The exam has six pages, including this cover page, printed out two-sided (no more wasted
ECS 120: Theory of Computation Handout MT UC Davis Phillip Rogaway February 16, 2012 Midterm Exam Instructions: The exam has six pages, including this cover page, printed out two-sided (no more wasted
Pushdown Automata: Introduction (2)
 Pushdown Automata: Introduction Pushdown automaton (PDA) M = (K, Σ, Γ,, s, A) where K is a set of states Σ is an input alphabet Γ is a set of stack symbols s K is the start state A K is a set of accepting
Pushdown Automata: Introduction Pushdown automaton (PDA) M = (K, Σ, Γ,, s, A) where K is a set of states Σ is an input alphabet Γ is a set of stack symbols s K is the start state A K is a set of accepting
Computational Models - Lecture 5 1
 Computational Models - Lecture 5 1 Handout Mode Iftach Haitner. Tel Aviv University. November 28, 2016 1 Based on frames by Benny Chor, Tel Aviv University, modifying frames by Maurice Herlihy, Brown University.
Computational Models - Lecture 5 1 Handout Mode Iftach Haitner. Tel Aviv University. November 28, 2016 1 Based on frames by Benny Chor, Tel Aviv University, modifying frames by Maurice Herlihy, Brown University.
Context Free Languages (CFL) Language Recognizer A device that accepts valid strings. The FA are formalized types of language recognizer.
 Context Free Languages (CFL) Language Recognizer A device that accepts valid strings. The FA are formalized types of language recognizer. Language Generator: Context free grammars are language generators,
Context Free Languages (CFL) Language Recognizer A device that accepts valid strings. The FA are formalized types of language recognizer. Language Generator: Context free grammars are language generators,
Pushdown automata. Twan van Laarhoven. Institute for Computing and Information Sciences Intelligent Systems Radboud University Nijmegen
 Pushdown automata Twan van Laarhoven Institute for Computing and Information Sciences Intelligent Systems Version: fall 2014 T. van Laarhoven Version: fall 2014 Formal Languages, Grammars and Automata
Pushdown automata Twan van Laarhoven Institute for Computing and Information Sciences Intelligent Systems Version: fall 2014 T. van Laarhoven Version: fall 2014 Formal Languages, Grammars and Automata
Context-Free Grammars and Languages. Reading: Chapter 5
 Context-Free Grammars and Languages Reading: Chapter 5 1 Context-Free Languages The class of context-free languages generalizes the class of regular languages, i.e., every regular language is a context-free
Context-Free Grammars and Languages Reading: Chapter 5 1 Context-Free Languages The class of context-free languages generalizes the class of regular languages, i.e., every regular language is a context-free
Computational Models: Class 5
 Computational Models: Class 5 Benny Chor School of Computer Science Tel Aviv University March 27, 2019 Based on slides by Maurice Herlihy, Brown University, and modifications by Iftach Haitner and Yishay
Computational Models: Class 5 Benny Chor School of Computer Science Tel Aviv University March 27, 2019 Based on slides by Maurice Herlihy, Brown University, and modifications by Iftach Haitner and Yishay
CS5371 Theory of Computation. Lecture 7: Automata Theory V (CFG, CFL, CNF)
 CS5371 Theory of Computation Lecture 7: Automata Theory V (CFG, CFL, CNF) Announcement Homework 2 will be given soon (before Tue) Due date: Oct 31 (Tue), before class Midterm: Nov 3, (Fri), first hour
CS5371 Theory of Computation Lecture 7: Automata Theory V (CFG, CFL, CNF) Announcement Homework 2 will be given soon (before Tue) Due date: Oct 31 (Tue), before class Midterm: Nov 3, (Fri), first hour
Part 4 out of 5 DFA NFA REX. Automata & languages. A primer on the Theory of Computation. Last week, we showed the equivalence of DFA, NFA and REX
 Automata & languages A primer on the Theory of Computation Laurent Vanbever www.vanbever.eu Part 4 out of 5 ETH Zürich (D-ITET) October, 12 2017 Last week, we showed the equivalence of DFA, NFA and REX
Automata & languages A primer on the Theory of Computation Laurent Vanbever www.vanbever.eu Part 4 out of 5 ETH Zürich (D-ITET) October, 12 2017 Last week, we showed the equivalence of DFA, NFA and REX
Accept or reject. Stack
 Pushdown Automata CS351 Just as a DFA was equivalent to a regular expression, we have a similar analogy for the context-free grammar. A pushdown automata (PDA) is equivalent in power to contextfree grammars.
Pushdown Automata CS351 Just as a DFA was equivalent to a regular expression, we have a similar analogy for the context-free grammar. A pushdown automata (PDA) is equivalent in power to contextfree grammars.
Automata and Computability. Solutions to Exercises
 Automata and Computability Solutions to Exercises Spring 27 Alexis Maciel Department of Computer Science Clarkson University Copyright c 27 Alexis Maciel ii Contents Preface vii Introduction 2 Finite Automata
Automata and Computability Solutions to Exercises Spring 27 Alexis Maciel Department of Computer Science Clarkson University Copyright c 27 Alexis Maciel ii Contents Preface vii Introduction 2 Finite Automata
Context-Free Languages
 CS:4330 Theory of Computation Spring 2018 Context-Free Languages Non-Context-Free Languages Haniel Barbosa Readings for this lecture Chapter 2 of [Sipser 1996], 3rd edition. Section 2.3. Proving context-freeness
CS:4330 Theory of Computation Spring 2018 Context-Free Languages Non-Context-Free Languages Haniel Barbosa Readings for this lecture Chapter 2 of [Sipser 1996], 3rd edition. Section 2.3. Proving context-freeness
Properties of Context-Free Languages
 Properties of Context-Free Languages Seungjin Choi Department of Computer Science and Engineering Pohang University of Science and Technology 77 Cheongam-ro, Nam-gu, Pohang 37673, Korea seungjin@postech.ac.kr
Properties of Context-Free Languages Seungjin Choi Department of Computer Science and Engineering Pohang University of Science and Technology 77 Cheongam-ro, Nam-gu, Pohang 37673, Korea seungjin@postech.ac.kr
Automata and Computability. Solutions to Exercises
 Automata and Computability Solutions to Exercises Fall 28 Alexis Maciel Department of Computer Science Clarkson University Copyright c 28 Alexis Maciel ii Contents Preface vii Introduction 2 Finite Automata
Automata and Computability Solutions to Exercises Fall 28 Alexis Maciel Department of Computer Science Clarkson University Copyright c 28 Alexis Maciel ii Contents Preface vii Introduction 2 Finite Automata
5 Context-Free Languages
 CA320: COMPUTABILITY AND COMPLEXITY 1 5 Context-Free Languages 5.1 Context-Free Grammars Context-Free Grammars Context-free languages are specified with a context-free grammar (CFG). Formally, a CFG G
CA320: COMPUTABILITY AND COMPLEXITY 1 5 Context-Free Languages 5.1 Context-Free Grammars Context-Free Grammars Context-free languages are specified with a context-free grammar (CFG). Formally, a CFG G
Context-Free and Noncontext-Free Languages
 Examples: Context-Free and Noncontext-Free Languages a*b* is regular. A n B n = {a n b n : n 0} is context-free but not regular. A n B n C n = {a n b n c n : n 0} is not context-free The Regular and the
Examples: Context-Free and Noncontext-Free Languages a*b* is regular. A n B n = {a n b n : n 0} is context-free but not regular. A n B n C n = {a n b n c n : n 0} is not context-free The Regular and the
Fundamentele Informatica II
 Fundamentele Informatica II Answer to selected exercises 5 John C Martin: Introduction to Languages and the Theory of Computation M.M. Bonsangue (and J. Kleijn) Fall 2011 5.1.a (q 0, ab, Z 0 ) (q 1, b,
Fundamentele Informatica II Answer to selected exercises 5 John C Martin: Introduction to Languages and the Theory of Computation M.M. Bonsangue (and J. Kleijn) Fall 2011 5.1.a (q 0, ab, Z 0 ) (q 1, b,
Pumping Lemma for CFLs
 Pumping Lemma for CFLs v y s Here we go again! Intuition: If L is CF, then some CFG G produces strings in L If some string in L is very long, it will have a very tall parse tree If a parse tree is taller
Pumping Lemma for CFLs v y s Here we go again! Intuition: If L is CF, then some CFG G produces strings in L If some string in L is very long, it will have a very tall parse tree If a parse tree is taller
3.13. PUSHDOWN AUTOMATA Pushdown Automata
 3.13. PUSHDOWN AUTOMATA 317 3.13 Pushdown Automata We have seen that the regular languages are exactly the languages accepted by DFA s or NFA s. The context-free languages are exactly the languages accepted
3.13. PUSHDOWN AUTOMATA 317 3.13 Pushdown Automata We have seen that the regular languages are exactly the languages accepted by DFA s or NFA s. The context-free languages are exactly the languages accepted
(pp ) PDAs and CFGs (Sec. 2.2)
 (pp. 117-124) PDAs and CFGs (Sec. 2.2) A language is context free iff all strings in L can be generated by some context free grammar Theorem 2.20: L is Context Free iff a PDA accepts it I.e. if L is context
(pp. 117-124) PDAs and CFGs (Sec. 2.2) A language is context free iff all strings in L can be generated by some context free grammar Theorem 2.20: L is Context Free iff a PDA accepts it I.e. if L is context
CSE 211. Pushdown Automata. CSE 211 (Theory of Computation) Atif Hasan Rahman
 CSE 211 Pushdown Automata CSE 211 (Theory of Computation) Atif Hasan Rahman Lecturer Department of Computer Science and Engineering Bangladesh University of Engineering & Technology Adapted from slides
CSE 211 Pushdown Automata CSE 211 (Theory of Computation) Atif Hasan Rahman Lecturer Department of Computer Science and Engineering Bangladesh University of Engineering & Technology Adapted from slides
Suppose h maps number and variables to ɛ, and opening parenthesis to 0 and closing parenthesis
 1 Introduction Parenthesis Matching Problem Describe the set of arithmetic expressions with correctly matched parenthesis. Arithmetic expressions with correctly matched parenthesis cannot be described
1 Introduction Parenthesis Matching Problem Describe the set of arithmetic expressions with correctly matched parenthesis. Arithmetic expressions with correctly matched parenthesis cannot be described
NPDA, CFG equivalence
 NPDA, CFG equivalence Theorem A language L is recognized by a NPDA iff L is described by a CFG. Must prove two directions: ( ) L is recognized by a NPDA implies L is described by a CFG. ( ) L is described
NPDA, CFG equivalence Theorem A language L is recognized by a NPDA iff L is described by a CFG. Must prove two directions: ( ) L is recognized by a NPDA implies L is described by a CFG. ( ) L is described
CS311 Computational Structures More about PDAs & Context-Free Languages. Lecture 9. Andrew P. Black Andrew Tolmach
 CS311 Computational Structures More about PDAs & Context-Free Languages Lecture 9 Andrew P. Black Andrew Tolmach 1 Three important results 1. Any CFG can be simulated by a PDA 2. Any PDA can be simulated
CS311 Computational Structures More about PDAs & Context-Free Languages Lecture 9 Andrew P. Black Andrew Tolmach 1 Three important results 1. Any CFG can be simulated by a PDA 2. Any PDA can be simulated
Pushdown Automata. Reading: Chapter 6
 Pushdown Automata Reading: Chapter 6 1 Pushdown Automata (PDA) Informally: A PDA is an NFA-ε with a infinite stack. Transitions are modified to accommodate stack operations. Questions: What is a stack?
Pushdown Automata Reading: Chapter 6 1 Pushdown Automata (PDA) Informally: A PDA is an NFA-ε with a infinite stack. Transitions are modified to accommodate stack operations. Questions: What is a stack?
Context-Free Languages (Pre Lecture)
 Context-Free Languages (Pre Lecture) Dr. Neil T. Dantam CSCI-561, Colorado School of Mines Fall 2017 Dantam (Mines CSCI-561) Context-Free Languages (Pre Lecture) Fall 2017 1 / 34 Outline Pumping Lemma
Context-Free Languages (Pre Lecture) Dr. Neil T. Dantam CSCI-561, Colorado School of Mines Fall 2017 Dantam (Mines CSCI-561) Context-Free Languages (Pre Lecture) Fall 2017 1 / 34 Outline Pumping Lemma
This lecture covers Chapter 6 of HMU: Pushdown Automata
 This lecture covers Chapter 6 of HMU: ushdown Automata ushdown Automata (DA) Language accepted by a DA Equivalence of CFs and the languages accepted by DAs Deterministic DAs Additional Reading: Chapter
This lecture covers Chapter 6 of HMU: ushdown Automata ushdown Automata (DA) Language accepted by a DA Equivalence of CFs and the languages accepted by DAs Deterministic DAs Additional Reading: Chapter
Theory of Computation
 Fall 2002 (YEN) Theory of Computation Midterm Exam. Name:... I.D.#:... 1. (30 pts) True or false (mark O for true ; X for false ). (Score=Max{0, Right- 1 2 Wrong}.) (1) X... If L 1 is regular and L 2 L
Fall 2002 (YEN) Theory of Computation Midterm Exam. Name:... I.D.#:... 1. (30 pts) True or false (mark O for true ; X for false ). (Score=Max{0, Right- 1 2 Wrong}.) (1) X... If L 1 is regular and L 2 L
CS481F01 Prelim 2 Solutions
 CS481F01 Prelim 2 Solutions A. Demers 7 Nov 2001 1 (30 pts = 4 pts each part + 2 free points). For this question we use the following notation: x y means x is a prefix of y m k n means m n k For each of
CS481F01 Prelim 2 Solutions A. Demers 7 Nov 2001 1 (30 pts = 4 pts each part + 2 free points). For this question we use the following notation: x y means x is a prefix of y m k n means m n k For each of
Section 1 (closed-book) Total points 30
 CS 454 Theory of Computation Fall 2011 Section 1 (closed-book) Total points 30 1. Which of the following are true? (a) a PDA can always be converted to an equivalent PDA that at each step pops or pushes
CS 454 Theory of Computation Fall 2011 Section 1 (closed-book) Total points 30 1. Which of the following are true? (a) a PDA can always be converted to an equivalent PDA that at each step pops or pushes
CPS 220 Theory of Computation
 CPS 22 Theory of Computation Review - Regular Languages RL - a simple class of languages that can be represented in two ways: 1 Machine description: Finite Automata are machines with a finite number of
CPS 22 Theory of Computation Review - Regular Languages RL - a simple class of languages that can be represented in two ways: 1 Machine description: Finite Automata are machines with a finite number of
Automata & languages. A primer on the Theory of Computation. Laurent Vanbever. ETH Zürich (D-ITET) October,
 Automata & languages A primer on the Theory of Computation Laurent Vanbever www.vanbever.eu ETH Zürich (D-ITET) October, 5 2017 Part 3 out of 5 Last week, we learned about closure and equivalence of regular
Automata & languages A primer on the Theory of Computation Laurent Vanbever www.vanbever.eu ETH Zürich (D-ITET) October, 5 2017 Part 3 out of 5 Last week, we learned about closure and equivalence of regular
Part 3 out of 5. Automata & languages. A primer on the Theory of Computation. Last week, we learned about closure and equivalence of regular languages
 Automata & languages A primer on the Theory of Computation Laurent Vanbever www.vanbever.eu Part 3 out of 5 ETH Zürich (D-ITET) October, 5 2017 Last week, we learned about closure and equivalence of regular
Automata & languages A primer on the Theory of Computation Laurent Vanbever www.vanbever.eu Part 3 out of 5 ETH Zürich (D-ITET) October, 5 2017 Last week, we learned about closure and equivalence of regular
CSE 105 THEORY OF COMPUTATION
 CSE 105 THEORY OF COMPUTATION Spring 2017 http://cseweb.ucsd.edu/classes/sp17/cse105-ab/ Review of CFG, CFL, ambiguity What is the language generated by the CFG below: G 1 = ({S,T 1,T 2 }, {0,1,2}, { S
CSE 105 THEORY OF COMPUTATION Spring 2017 http://cseweb.ucsd.edu/classes/sp17/cse105-ab/ Review of CFG, CFL, ambiguity What is the language generated by the CFG below: G 1 = ({S,T 1,T 2 }, {0,1,2}, { S
MA/CSSE 474 Theory of Computation
 MA/CSSE 474 Theory of Computation CFL Hierarchy CFL Decision Problems Your Questions? Previous class days' material Reading Assignments HW 12 or 13 problems Anything else I have included some slides online
MA/CSSE 474 Theory of Computation CFL Hierarchy CFL Decision Problems Your Questions? Previous class days' material Reading Assignments HW 12 or 13 problems Anything else I have included some slides online
cse303 ELEMENTS OF THE THEORY OF COMPUTATION Professor Anita Wasilewska
 cse303 ELEMENTS OF THE THEORY OF COMPUTATION Professor Anita Wasilewska LECTURE 6 CHAPTER 2 FINITE AUTOMATA 2. Nondeterministic Finite Automata NFA 3. Finite Automata and Regular Expressions 4. Languages
cse303 ELEMENTS OF THE THEORY OF COMPUTATION Professor Anita Wasilewska LECTURE 6 CHAPTER 2 FINITE AUTOMATA 2. Nondeterministic Finite Automata NFA 3. Finite Automata and Regular Expressions 4. Languages
Functions on languages:
 MA/CSSE 474 Final Exam Notation and Formulas page Name (turn this in with your exam) Unless specified otherwise, r,s,t,u,v,w,x,y,z are strings over alphabet Σ; while a, b, c, d are individual alphabet
MA/CSSE 474 Final Exam Notation and Formulas page Name (turn this in with your exam) Unless specified otherwise, r,s,t,u,v,w,x,y,z are strings over alphabet Σ; while a, b, c, d are individual alphabet
Pushdown Automata. Chapter 12
 Pushdown Automata Chapter 12 Recognizing Context-Free Languages We need a device similar to an FSM except that it needs more power. The insight: Precisely what it needs is a stack, which gives it an unlimited
Pushdown Automata Chapter 12 Recognizing Context-Free Languages We need a device similar to an FSM except that it needs more power. The insight: Precisely what it needs is a stack, which gives it an unlimited
Computational Models Lecture 5
 Computational Models Lecture 5 One More PDAs Example Equivalence of PDAs and CFLs Nondeterminism adds power to PDAs (not in book) Closure Properties of CFLs Algorithmic Aspects of PDAs and CFLs DFAs and
Computational Models Lecture 5 One More PDAs Example Equivalence of PDAs and CFLs Nondeterminism adds power to PDAs (not in book) Closure Properties of CFLs Algorithmic Aspects of PDAs and CFLs DFAs and
CPSC 421: Tutorial #1
 CPSC 421: Tutorial #1 October 14, 2016 Set Theory. 1. Let A be an arbitrary set, and let B = {x A : x / x}. That is, B contains all sets in A that do not contain themselves: For all y, ( ) y B if and only
CPSC 421: Tutorial #1 October 14, 2016 Set Theory. 1. Let A be an arbitrary set, and let B = {x A : x / x}. That is, B contains all sets in A that do not contain themselves: For all y, ( ) y B if and only
Theory of Computation (VI) Yijia Chen Fudan University
 Theory of Computation (VI) Yijia Chen Fudan University Review Forced handles Definition A handle h of a valid string v = xhy is a forced handle if h is the unique handle in every valid string xhŷ where
Theory of Computation (VI) Yijia Chen Fudan University Review Forced handles Definition A handle h of a valid string v = xhy is a forced handle if h is the unique handle in every valid string xhŷ where
Introduction to Turing Machines. Reading: Chapters 8 & 9
 Introduction to Turing Machines Reading: Chapters 8 & 9 1 Turing Machines (TM) Generalize the class of CFLs: Recursively Enumerable Languages Recursive Languages Context-Free Languages Regular Languages
Introduction to Turing Machines Reading: Chapters 8 & 9 1 Turing Machines (TM) Generalize the class of CFLs: Recursively Enumerable Languages Recursive Languages Context-Free Languages Regular Languages
The Pumping Lemma. for all n 0, u 1 v n u 2 L (i.e. u 1 u 2 L, u 1 vu 2 L [but we knew that anyway], u 1 vvu 2 L, u 1 vvvu 2 L, etc.
![The Pumping Lemma. for all n 0, u 1 v n u 2 L (i.e. u 1 u 2 L, u 1 vu 2 L [but we knew that anyway], u 1 vvu 2 L, u 1 vvvu 2 L, etc. The Pumping Lemma. for all n 0, u 1 v n u 2 L (i.e. u 1 u 2 L, u 1 vu 2 L [but we knew that anyway], u 1 vvu 2 L, u 1 vvvu 2 L, etc.](/thumbs/89/99844223.jpg) The Pumping Lemma For every regular language L, there is a number l 1 satisfying the pumping lemma property: All w L with w l can be expressed as a concatenation of three strings, w = u 1 vu 2, where u
The Pumping Lemma For every regular language L, there is a number l 1 satisfying the pumping lemma property: All w L with w l can be expressed as a concatenation of three strings, w = u 1 vu 2, where u
Push-down Automata = FA + Stack
 Push-down Automata = FA + Stack PDA Definition A push-down automaton M is a tuple M = (Q,, Γ, δ, q0, F) where Q is a finite set of states is the input alphabet (of terminal symbols, terminals) Γ is the
Push-down Automata = FA + Stack PDA Definition A push-down automaton M is a tuple M = (Q,, Γ, δ, q0, F) where Q is a finite set of states is the input alphabet (of terminal symbols, terminals) Γ is the
CSE 105 THEORY OF COMPUTATION
 CSE 105 THEORY OF COMPUTATION Spring 2016 http://cseweb.ucsd.edu/classes/sp16/cse105-ab/ Today's learning goals Sipser Ch 2 Define push down automata Trace the computation of a push down automaton Design
CSE 105 THEORY OF COMPUTATION Spring 2016 http://cseweb.ucsd.edu/classes/sp16/cse105-ab/ Today's learning goals Sipser Ch 2 Define push down automata Trace the computation of a push down automaton Design
DM17. Beregnelighed. Jacob Aae Mikkelsen
 DM17 Beregnelighed Jacob Aae Mikkelsen January 12, 2007 CONTENTS Contents 1 Introduction 2 1.1 Operations with languages...................... 2 2 Finite Automata 3 2.1 Regular expressions/languages....................
DM17 Beregnelighed Jacob Aae Mikkelsen January 12, 2007 CONTENTS Contents 1 Introduction 2 1.1 Operations with languages...................... 2 2 Finite Automata 3 2.1 Regular expressions/languages....................
Computability and Complexity
 Computability and Complexity Push-Down Automata CAS 705 Ryszard Janicki Department of Computing and Software McMaster University Hamilton, Ontario, Canada janicki@mcmaster.ca Ryszard Janicki Computability
Computability and Complexity Push-Down Automata CAS 705 Ryszard Janicki Department of Computing and Software McMaster University Hamilton, Ontario, Canada janicki@mcmaster.ca Ryszard Janicki Computability
Automata Theory. CS F-10 Non-Context-Free Langauges Closure Properties of Context-Free Languages. David Galles
 Automata Theory CS411-2015F-10 Non-Context-Free Langauges Closure Properties of Context-Free Languages David Galles Department of Computer Science University of San Francisco 10-0: Fun with CFGs Create
Automata Theory CS411-2015F-10 Non-Context-Free Langauges Closure Properties of Context-Free Languages David Galles Department of Computer Science University of San Francisco 10-0: Fun with CFGs Create
Please give details of your answer. A direct answer without explanation is not counted.
 Please give details of your answer. A direct answer without explanation is not counted. Your answers must be in English. Please carefully read problem statements. During the exam you are not allowed to
Please give details of your answer. A direct answer without explanation is not counted. Your answers must be in English. Please carefully read problem statements. During the exam you are not allowed to
Context Free Grammars
 Automata and Formal Languages Context Free Grammars Sipser pages 101-111 Lecture 11 Tim Sheard 1 Formal Languages 1. Context free languages provide a convenient notation for recursive description of languages.
Automata and Formal Languages Context Free Grammars Sipser pages 101-111 Lecture 11 Tim Sheard 1 Formal Languages 1. Context free languages provide a convenient notation for recursive description of languages.
DD2371 Automata Theory
 KTH CSC VT 2008 DD2371 Automata Theory Dilian Gurov Lecture Outline 1. The lecturer 2. Introduction to automata theory 3. Course syllabus 4. Course objectives 5. Course organization 6. First definitions
KTH CSC VT 2008 DD2371 Automata Theory Dilian Gurov Lecture Outline 1. The lecturer 2. Introduction to automata theory 3. Course syllabus 4. Course objectives 5. Course organization 6. First definitions
CSE 355 Test 2, Fall 2016
 CSE 355 Test 2, Fall 2016 28 October 2016, 8:35-9:25 a.m., LSA 191 Last Name SAMPLE ASU ID 1357924680 First Name(s) Ima Regrading of Midterms If you believe that your grade has not been added up correctly,
CSE 355 Test 2, Fall 2016 28 October 2016, 8:35-9:25 a.m., LSA 191 Last Name SAMPLE ASU ID 1357924680 First Name(s) Ima Regrading of Midterms If you believe that your grade has not been added up correctly,
Finite Automata Theory and Formal Languages TMV027/DIT321 LP4 2018
 Finite Automata Theory and Formal Languages TMV027/DIT321 LP4 2018 Lecture 14 Ana Bove May 14th 2018 Recap: Context-free Grammars Simplification of grammars: Elimination of ǫ-productions; Elimination of
Finite Automata Theory and Formal Languages TMV027/DIT321 LP4 2018 Lecture 14 Ana Bove May 14th 2018 Recap: Context-free Grammars Simplification of grammars: Elimination of ǫ-productions; Elimination of
Languages, regular languages, finite automata
 Notes on Computer Theory Last updated: January, 2018 Languages, regular languages, finite automata Content largely taken from Richards [1] and Sipser [2] 1 Languages An alphabet is a finite set of characters,
Notes on Computer Theory Last updated: January, 2018 Languages, regular languages, finite automata Content largely taken from Richards [1] and Sipser [2] 1 Languages An alphabet is a finite set of characters,
MTH401A Theory of Computation. Lecture 17
 MTH401A Theory of Computation Lecture 17 Chomsky Normal Form for CFG s Chomsky Normal Form for CFG s For every context free language, L, the language L {ε} has a grammar in which every production looks
MTH401A Theory of Computation Lecture 17 Chomsky Normal Form for CFG s Chomsky Normal Form for CFG s For every context free language, L, the language L {ε} has a grammar in which every production looks
Intro to Theory of Computation
 Intro to Theory of Computation LECTURE 9 Last time: Converting a PDA to a CFG Pumping Lemma for CFLs Today: Pumping Lemma for CFLs Review of CFGs/PDAs Sofya Raskhodnikova 2/9/2016 Sofya Raskhodnikova;
Intro to Theory of Computation LECTURE 9 Last time: Converting a PDA to a CFG Pumping Lemma for CFLs Today: Pumping Lemma for CFLs Review of CFGs/PDAs Sofya Raskhodnikova 2/9/2016 Sofya Raskhodnikova;
Non-context-Free Languages. CS215, Lecture 5 c
 Non-context-Free Languages CS215, Lecture 5 c 2007 1 The Pumping Lemma Theorem. (Pumping Lemma) Let be context-free. There exists a positive integer divided into five pieces, Proof for for each, and..
Non-context-Free Languages CS215, Lecture 5 c 2007 1 The Pumping Lemma Theorem. (Pumping Lemma) Let be context-free. There exists a positive integer divided into five pieces, Proof for for each, and..
Computational Models: Class 3
 Computational Models: Class 3 Benny Chor School of Computer Science Tel Aviv University November 2, 2015 Based on slides by Maurice Herlihy, Brown University, and modifications by Iftach Haitner and Yishay
Computational Models: Class 3 Benny Chor School of Computer Science Tel Aviv University November 2, 2015 Based on slides by Maurice Herlihy, Brown University, and modifications by Iftach Haitner and Yishay
CS481F01 Solutions 6 PDAS
 CS481F01 Solutions 6 PDAS A. Demers 2 November 2001 1. Give a NPDAs that recognize the following languages: (a) The set of all strings in {0, 1} that contain twice as many 1s as 0s. (answer a) We build
CS481F01 Solutions 6 PDAS A. Demers 2 November 2001 1. Give a NPDAs that recognize the following languages: (a) The set of all strings in {0, 1} that contain twice as many 1s as 0s. (answer a) We build
Context-free grammars and languages
 Context-free grammars and languages The next class of languages we will study in the course is the class of context-free languages. They are defined by the notion of a context-free grammar, or a CFG for
Context-free grammars and languages The next class of languages we will study in the course is the class of context-free languages. They are defined by the notion of a context-free grammar, or a CFG for
