Computational Models Lecture 5
|
|
|
- Jonah O’Neal’
- 5 years ago
- Views:
Transcription
1 Computational Models Lecture 5 One More PDAs Example Equivalence of PDAs and CFLs Nondeterminism adds power to PDAs (not in book) Closure Properties of CFLs Algorithmic Aspects of PDAs and CFLs DFAs and PDAs: Perspectives Sipser s book, 2.2 & 2.3 Slides modified by Benny Chor, based on original slides by Maurice Herlihy, Brown University. p.1
2 Mid-term exam on Friday, April 13. Material is first five lectures (i.e. up to and including today, and Chomsky normal form from lecture 4). Closed books (no auxiliary material). 10 multiple choice ( closed, American ) questions. Duration 1:40 hrs. Slides modified by Benny Chor, based on original slides by Maurice Herlihy, Brown University. p.2
3 Another PDA Example A palindrome is a string w satisfying w = w R. Madam I m Adam Dennis and Edna sinned Red rum, sir, is murder Able was I ere I saw Elba In girum imus nocte et consumimur igni (Latin: "we go into the circle by night, we are consumed by fire.) νιψoν ανoµηµατα µη µoναν oψιν Palindromes also appear in nature. For example as DNA restriction sites short genomic strings over {A, C, T, G}, being cut by (naturally occurring) restriction enzymes. Slides modified by Benny Chor, based on original slides by Maurice Herlihy, Brown University. p.3
4 Another PDA Example On input x, the PDA start pushing x into stack. At some point, PDA guesses that the mid point of x was reached. Pops and compares to input, letter by letter. This PDA accepts palindromes of even length over the alphabet. Again, non-determinism seems necessary. Slides modified by Benny Chor, based on original slides by Maurice Herlihy, Brown University. p.4
5 Non-Deterministm Adds Power: Proof Theorem: Let M be a PDA that accepts L = {x n y n n 0} { x n y 2n n 0 }. Then M is non-deterministic. Proof: a Suppose, by way of contradiction, that M is deterministic. Create two copies of this PDA, denoted M 1 and M 2. Two states in M 1 and M 2 are called cousins if they are copies of the same state in the original PDA. a (prf modified from jpower/courses/parsing/node38.html) Slides modified by Benny Chor, based on original slides by Maurice Herlihy, Brown University. p.5
6 Non-Deterministm Adds Power (cont.) We now modify these PDA copies to make them into one PDA, M 0, over the alphabet {x, y, z}. States of the new M 0 are those of M 1 union M 2. Start state of the new M 0 is the start state of M 1. The accepting states of the new M 0 are the accepting states of M 2. Slides modified by Benny Chor, based on original slides by Maurice Herlihy, Brown University. p.6
7 Non-Deterministm Adds Power (cont.) Modifications: Erase all x transitions of M 2. Replace every existing y transition of M 2 byanewz transition. At this point M 2 got only z transition (so x and y inputs lead immediately to rejection). Erase all x transitions out of accept states of M 1. Slides modified by Benny Chor, based on original slides by Maurice Herlihy, Brown University. p.7
8 Non-Deterministm Adds Power (cont.) The surgery is almost done, but if we don t connect the two halves of its brain, the patient will not function coherently. Replace every existing y transition leading out of accept states of M 1 byanewz transition, and redirect it to its cousin in M 2. Surgery over. Patient (a deterministic PDA) still alive. Let us now diagnose what, if anything, it can do. Slides modified by Benny Chor, based on original slides by Maurice Herlihy, Brown University. p.8
9 Non-Deterministm Adds Power (cont.) What language M 0 recognizes? Certainly if M 0 accepts a string, it must be of the form (x y) z. But surely not all strings of that form are accepted by M 0. For example, the (x y) prefix must be accepted by the original M. Otherwise there will be no switch to M 2, and no acceptance by M 0.(think why is L(M 0 )? Would this also be true for non deterministic M?) So the prefix of an accepted string is either of the form x n y n or x n y 2n. And the whole string is of the form x n y n z i or x n y 2n z j. Slides modified by Benny Chor, based on original slides by Maurice Herlihy, Brown University. p.9
10 Non-Deterministm Adds Power (cont.) What can we say about the z i part? First, i must be greater than 0 for a transition to take place. By construction, M 2 on z i imitates the actions of M on y i from the same starting point. This means that if M 0 accepts x n y n z i then M accepts x n y n+i. Which is possible if either i = n, som 0 accepts x n y n z n, n>0, or M 0 accepts x n y 2n z j,som accepts x n y 2n+j. But L contains no strings of this last form! Slides modified by Benny Chor, based on original slides by Maurice Herlihy, Brown University. p.10
11 Conclusion of Proof We just showed that the PDA M 0 accepts the language {x n y n z n n 1}. Contradiction. Contradiction? What contradiction? What the $%&# does this contradict? It contradics the fact that by the so called uvxyz pumping lemma, the language {x n y n z n n 1} is not context free, so is not accepted by a PDA. So our initial supposition that the language {x n y n } { x n y 2n} is accepted by a deterministic PDA, does not hold. While thinking about the proof, where would it fail if the original M were non-deterministic? Slides modified by Benny Chor, based on original slides by Maurice Herlihy, Brown University. p.11
12 PDA Languages vs. CFLs The set of Push-Down Automata Languages, L PDA, is the collection of all languages that are accepted by some PDA: L PDA = {L : PDAM L(M) =L}. Natural questions: L CFG L PDA? L PDA L CFG? Slides modified by Benny Chor, based on original slides by Maurice Herlihy, Brown University. p.12
13 Equivalence Theorem Theorem: A language is context free if and only if some pushdown automata accepts it. This time (unlike the regular expression vs. regular languages theorem), the proofs of both the if part and the only if part are non trivial. Slides modified by Benny Chor, based on original slides by Maurice Herlihy, Brown University. p.13
14 If Part Theorem: If a language is context free, then some pushdown automaton accepts it. Let A be a context-free language. By definition, A has a context-free grammar G generating it. On input w, the PDA P should figure out if there is a derivation of w using G. Question: How does P figure out which substitution to make? Answer: It guesses. Slides modified by Benny Chor, based on original slides by Maurice Herlihy, Brown University. p.14
15 CFL Implies PDA (cont.) Where do we keep the intermediate string? can t put it all on the stack only strings whose first letter is a variable are kept on stack Slides modified by Benny Chor, based on original slides by Maurice Herlihy, Brown University. p.15
16 CFL Implies PDA Will be more convenient to use grammar in Chomsky normal form, due to compact derivation rules. Informally, on input string w Σ : P pushes start variable S on stack keeps making substitutions when popping a terminal, P checks equality with current input string rejects if not equal when popping a variable, P pushes to top of stack a right hand side of some rule corresponding to variable (zero, one, or two symbols). if EOI reached when stack is empty, accept. Slides modified by Benny Chor, based on original slides by Maurice Herlihy, Brown University. p.16
17 CFL Implies PDA (cont.) Informal description: push S$ on stack if top of stack is variable A, non-deterministically select rule and substitute. if top of stack is terminal a, read next input and compare. If they differ, reject. if top of stack and input symbol are both $, enter accept state. (Namely accepts only if input has all been read and stack is empty!). Slides modified by Benny Chor, based on original slides by Maurice Herlihy, Brown University. p.17
18 CFL Implies PDA (cont.) Need shorthand to push strings of length 2 onto stack. For example, suppose A BC is a derivation of the CFG. Then we add a shorthand state, q e, and the two transitions (q e,c) δ(q l,a,ε), δ(q e,ε,ε)={(q l,b)} Notice that the second transition is deterministic (the first one may or may not be). Also notice order: Push C first, then B. These intermediate states are different for different derivations. Slides modified by Benny Chor, based on original slides by Maurice Herlihy, Brown University. p.18
19 CFL Implies PDA (cont.) States of P are start state q s accept state q a loop state q l q e states, needed for shorthand of right hand sides of rules Slides modified by Benny Chor, based on original slides by Maurice Herlihy, Brown University. p.19
20 Transition Function Initialize stack δ(q s,ε,ε)={q l,s$} Top of stack is variable (shorthand for two transitions) δ(q l,ε,a)={(q l,w) where A w is a rule } Top of stack is terminal δ(q l,a,a)={(q l,ε)} End of Stack and End of Input δ(q l, $, $) = {(q a,ε)} Slides modified by Benny Chor, based on original slides by Maurice Herlihy, Brown University. p.20
21 Example S AT ε A AB AA a B b T TT t Transition rules for PDA: On black/white board. Slides modified by Benny Chor, based on original slides by Maurice Herlihy, Brown University. p.21
22 Only If Part Theorem: If a PDA accepts a language, L, then L is context-free. For each pair of states p and q in P, we will have a variable A pq in the grammar G. This variable, A pq, generates all strings that take P from p with an empty stack to q with empty stack. Same string also takes p with any stack to q with same stack! Start variable is A q0,q a (assuming a single accept state q a ). Slides modified by Benny Chor, based on original slides by Maurice Herlihy, Brown University. p.22
23 PDA Implies CFL To make things easier, we slightly modify P Has single accept state q a. It empties stack before accepting. Each transition either pushes a symbol on stack, or pops a symbol from stack, but not both. Slides modified by Benny Chor, based on original slides by Maurice Herlihy, Brown University. p.23
24 PDA Implies CFL (2) Modify P to make things easier single accept state q a ε,ε ε,ε ε ε empties stack before accepting each transition pushes or pops, but not both. Slides modified by Benny Chor, based on original slides by Maurice Herlihy, Brown University. p.24
25 PDA Implies CFL (3) Modify P to make things easier single accept state q a empties stack before accepting ε,ε ε ε,ε ε ε,ε ε ε,a ε ε,ε ε ε,ε ε Slides modified by Benny Chor, based on original slides by Maurice Herlihy, Brown University. p.25
26 PDA Implies CFL (4) Modify P to make things easier single accept state q a empties stack before accepting transition either pushes or pops, but not both a,b c a,b ε c ε,ε Slides modified by Benny Chor, based on original slides by Maurice Herlihy, Brown University. p.26
27 Proof Idea Suppose string x takes P from p with empty stack to q with empty stack. First move that touches the stack must be a push, last must be a pop. In between, two possibilities: Stack is empty only at start and finish, but not in middle. Stack was also empty at some point in between. Slides modified by Benny Chor, based on original slides by Maurice Herlihy, Brown University. p.27
28 Proof Idea (2) Suppose string x takes P from p with empty stack to q with empty stack. First move that touches the stack must be a push, last must be a pop. In between, two possibilities: Stack is empty only at start and finish, but not in middle. Simulate by: A pq aa rs b, where a, b are first and last symbols in x (shorter x will be taken care of too), r follows p, and s precedes q. Stack was also empty at some point in between. Simulate by: A pq A pr A rq, r is intermediate state where P has empty stack. Slides modified by Benny Chor, based on original slides by Maurice Herlihy, Brown University. p.28
29 Details of Simulating Grammar Given PDA P =(Q, Σ, Γ,δ,q 0, {q a }), construct grammar G. Variables are {A pq p, q Q}. Start variable is A q0 q a. Rules: For p, q, r, s Q, t Γ, and a, b Σ, if(r, t) δ(p, a, ε) and (q, ε) δ(s, b, t), add rule A pq aa rs b. for every p, q, r Q, add rule A pq A pr A rq. for each p Q, add rule A pp ε. Slides modified by Benny Chor, based on original slides by Maurice Herlihy, Brown University. p.29
30 Overall Structure Should now prove Claim: A pq generates x if and only if x brings P from p with empty stack to q with empty stack. Slides modified by Benny Chor, based on original slides by Maurice Herlihy, Brown University. p.30
31 Only If Part Theorem: If a PDA accepts a language, L, then L is context-free. Proof: After constructing the grammar G, should prove it generates exactly the same language accepted by the PDA. This is done by induction on the length of any computation of P on any input string x. The induction argument is a bit lengthy and tedious, and we ll skip it. Diehards are welcome to consult pp in Sipser s book, and/or slides from fall 2003/4. Slides modified by Benny Chor, based on original slides by Maurice Herlihy, Brown University. p.31
32 CFL Closure Properties We saw that Context-Free Languages are closed under union, concatenation, and star? It is time we resolve closure with respect to complementation and intersection. Slides modified by Benny Chor, based on original slides by Maurice Herlihy, Brown University. p.32
33 CFL Closure Properties Are the context free languages context free languages closed under intersection? Suggested approach: Can we intersect two context free languages langauges to get 0 n 1 n 2 n? Slides modified by Benny Chor, based on original slides by Maurice Herlihy, Brown University. p.33
34 CFL Closure Properties Are the context free languages closed under intersection? S 1 A 1 B 1 S 2 A 2 B 2 A 1 0A A 2 0A 2 ε B 1 2B 1 ε B 2 1B L 1 =0 n 1 n 2 L 2 =0 1 n 2 n L 1 L 2 =0 n 1 n 2 n L 1 is a context free language, L 2 is a context free language, but L 1 L 2 is not a context free languages Slides modified by Benny Chor, based on original slides by Maurice Herlihy, Brown University. p.34
35 CFL Closure Properties The fact that CFLs are not closed under intersection but are closed under union implies they are not closed under complementation, as L 1 L 2 = L 1 L 2. Slides modified by Benny Chor, based on original slides by Maurice Herlihy, Brown University. p.35
36 CFL Closure Properties Can we give a simple, specific example, where L is not CFL but L is? Take L = {ww w {0, 1} }. For any y L, either y s length is odd. y s length is even, 2l, and there is an i 1 such that y i y l+i. PDA non-deterministically tries to verify one of the options. Employs stack for matching locations. Accepts only on a successful branch (voluntary home assignment: fill in the details!). Slides modified by Benny Chor, based on original slides by Maurice Herlihy, Brown University. p.36
37 CFL Closure Properties Are the context free languages context free languages closed under intersection with a regular language? That is, if L 1 is context free languages, and L 2 is regular, must L 1 L 2 be context free languages? Run PDA L 1 and DFA L 2 in parallel (just like the intersection of two regular languages). Formal details omitted (but you should be able to figure them out). Slides modified by Benny Chor, based on original slides by Maurice Herlihy, Brown University. p.37
38 CFL Closure Properties: Example Is L = {(0+1+2) : #of0 s=#of1 s=#of2 s } context free? Slides modified by Benny Chor, based on original slides by Maurice Herlihy, Brown University. p.38
39 CFL Closure Properties L {(0 1 2) : # 0 s = # 1 s = # 2 s } Is L context free? L ={0 n 1 n 2 n : n>0} which is not context free. Context free languages intersected with a regular languages are context free is regular. So L is not a context free language! Slides modified by Benny Chor, based on original slides by Maurice Herlihy, Brown University. p.39
40 Algorithmic Questions Regarding DFAs Given a regular expression, R, find the smallest DFA (minimum number of states) that accepts L(R). Initial Idea: Use the algorithm describe in class to transform R into an NFA. Then transform this NFA into a DFA, M. That s very nice, but how do we know M is minimal? It need not be! Slides modified by Benny Chor, based on original slides by Maurice Herlihy, Brown University. p.40
41 Algorithmic Questions for DFAs (2) Given a regular expression, R, find the smallest DFA that accepts L(R) (minimum number of states). We can enumerate all DFAs that are strictly smaller than M. For each such M i, test if L(M i ) = L(M) (we saw an algorithm for this). Take the smallest such M i. Algorithm is very inefficient. If smallest M has n states, algorithm will take time that is exponential in n. More efficient algorithm is known, using the Myhill-Nerode theorem. Slides modified by Benny Chor, based on original slides by Maurice Herlihy, Brown University. p.41
42 Algorithmic Questions Regarding CFGs Given a CFG, G, and a string w, does G generate w? Initial Idea: Design an algorithm that tries all derivations. Problem: If G does not generate w, we ll never stop. Slides modified by Benny Chor, based on original slides by Maurice Herlihy, Brown University. p.42
43 Algorithmic Questions for CFGs (2) Lemma: If G is in Chomsky normal form, w = n, and w is generated by G, then w has a derivation of length 2n 1 or less. We won t prove this (go ahead try it at home!). Algorithm s idea: First, convert G to Chomsky normal form. Now need only consider a finite number of derivations those of length 2n 1 or less. Slides modified by Benny Chor, based on original slides by Maurice Herlihy, Brown University. p.43
44 Algorithmic Questions for CFGs (3) Theorem: There is an algorithm (that halts on every inputs) A, that on inputs G and w, decides if G generates w. On input G, w, where G is a grammar and w a string, 1. Convert G to Chomsky normal form. 2. List all derivations with 2n 1 steps, were n = w. 3. If any generates w, accept, otherwise reject. Slides modified by Benny Chor, based on original slides by Maurice Herlihy, Brown University. p.44
45 Algorithmic Questions for CFGs (4) Theorem: There is an algorithm (that halts on every inputs) A, that on inputs G and w, decides if G generates w. Remarks: Related to problem of compiling prog. languages. Would you want to use this algorithm at work? Every theorem about CFLs is also about PDAs. Slides modified by Benny Chor, based on original slides by Maurice Herlihy, Brown University. p.45
46 Emptiness of CFGs Given a CFG, G, is L(G) =? In other words, is there any string w, such that G generate w? Theorem: There is an algorithm that solves this problem (and always halts). Possible approaches for a proof: Bad Idea: We know how to test whether w L(G) for any string w, so just try it for each w. (criticize this...) Better Idea: Can the start variable generate a string of terminals? Even Better Idea: Can a particular variable generate a string of terminals? Slides modified by Benny Chor, based on original slides by Maurice Herlihy, Brown University. p.46
47 CFG Emptiness (2) Algorithm: On input G (a CFG), 1. Mark all terminal symbols in G. 2. Repeat until no new variables become marked. 3. Mark any A where A U 1 U 2...U k and all U i have already been marked. 4. If start symbol marked, accept, else reject. Slides modified by Benny Chor, based on original slides by Maurice Herlihy, Brown University. p.47
48 CFGs Fullness Given a CFG, G, isl(g) =Σ? We just saw an algorithm to determine, given a CFG, G, if L(G) = L(G) =Σ iff L(G) =. Why not modify the algorithm so it determines emptiness of the complement? Unfortunately, CFGs are not closed under complement. Fact: There is no algorithm to solve this problem. We are not prepared to prove this remarkable fact (yet). Slides modified by Benny Chor, based on original slides by Maurice Herlihy, Brown University. p.48
49 When Are Two CFGs equivalent? Given two CFGs, G, H, is L(G) =L(H)? Hey, we did this already for equivalence of DFAs! We constructed C from A and B: ( ) L(C) = L(A) L(B) and tested whether L(C) is empty. ( ) L(A) L(B). Stop! Danger! Abyss ahead! Slides modified by Benny Chor, based on original slides by Maurice Herlihy, Brown University. p.49
50 When Are Two CFGs equivalent? This approach was fine for DFAs, but not for CFLs! The class of context-free languages is not closed under complementation or intersection. Fact: There is no algorithm to solve this problem. We are not prepared to prove this remarkable fact (yet). Slides modified by Benny Chor, based on original slides by Maurice Herlihy, Brown University. p.50
51 A Short Summary Regular Languages Finite Automata. Context Free Languages Push Down Automata. Closure properties of regular languages and of CFLs. Most algorithmic problems for finite automata are solvable. Some algorithmic problems for finite automata are not solvable. Pumping lemmata for both classes of languages. There are additional languages out there. Slides modified by Benny Chor, based on original slides by Maurice Herlihy, Brown University. p.51
52 The View Over The Horizon enumerable decidable context free regular Happy passover (& kosher for legumes eaters)! Slides modified by Benny Chor, based on original slides by Maurice Herlihy, Brown University. p.52
Computational Models: Class 5
 Computational Models: Class 5 Benny Chor School of Computer Science Tel Aviv University March 27, 2019 Based on slides by Maurice Herlihy, Brown University, and modifications by Iftach Haitner and Yishay
Computational Models: Class 5 Benny Chor School of Computer Science Tel Aviv University March 27, 2019 Based on slides by Maurice Herlihy, Brown University, and modifications by Iftach Haitner and Yishay
Computational Models - Lecture 5 1
 Computational Models - Lecture 5 1 Handout Mode Iftach Haitner and Yishay Mansour. Tel Aviv University. April 10/22, 2013 1 Based on frames by Benny Chor, Tel Aviv University, modifying frames by Maurice
Computational Models - Lecture 5 1 Handout Mode Iftach Haitner and Yishay Mansour. Tel Aviv University. April 10/22, 2013 1 Based on frames by Benny Chor, Tel Aviv University, modifying frames by Maurice
Computational Models - Lecture 4
 Computational Models - Lecture 4 Regular languages: The Myhill-Nerode Theorem Context-free Grammars Chomsky Normal Form Pumping Lemma for context free languages Non context-free languages: Examples Push
Computational Models - Lecture 4 Regular languages: The Myhill-Nerode Theorem Context-free Grammars Chomsky Normal Form Pumping Lemma for context free languages Non context-free languages: Examples Push
FORMAL LANGUAGES, AUTOMATA AND COMPUTABILITY
 15-453 FORMAL LANGUAGES, AUTOMATA AND COMPUTABILITY REVIEW for MIDTERM 1 THURSDAY Feb 6 Midterm 1 will cover everything we have seen so far The PROBLEMS will be from Sipser, Chapters 1, 2, 3 It will be
15-453 FORMAL LANGUAGES, AUTOMATA AND COMPUTABILITY REVIEW for MIDTERM 1 THURSDAY Feb 6 Midterm 1 will cover everything we have seen so far The PROBLEMS will be from Sipser, Chapters 1, 2, 3 It will be
October 6, Equivalence of Pushdown Automata with Context-Free Gramm
 Equivalence of Pushdown Automata with Context-Free Grammar October 6, 2013 Motivation Motivation CFG and PDA are equivalent in power: a CFG generates a context-free language and a PDA recognizes a context-free
Equivalence of Pushdown Automata with Context-Free Grammar October 6, 2013 Motivation Motivation CFG and PDA are equivalent in power: a CFG generates a context-free language and a PDA recognizes a context-free
(pp ) PDAs and CFGs (Sec. 2.2)
 (pp. 117-124) PDAs and CFGs (Sec. 2.2) A language is context free iff all strings in L can be generated by some context free grammar Theorem 2.20: L is Context Free iff a PDA accepts it I.e. if L is context
(pp. 117-124) PDAs and CFGs (Sec. 2.2) A language is context free iff all strings in L can be generated by some context free grammar Theorem 2.20: L is Context Free iff a PDA accepts it I.e. if L is context
What we have done so far
 What we have done so far DFAs and regular languages NFAs and their equivalence to DFAs Regular expressions. Regular expressions capture exactly regular languages: Construct a NFA from a regular expression.
What we have done so far DFAs and regular languages NFAs and their equivalence to DFAs Regular expressions. Regular expressions capture exactly regular languages: Construct a NFA from a regular expression.
Computational Models: Class 3
 Computational Models: Class 3 Benny Chor School of Computer Science Tel Aviv University November 2, 2015 Based on slides by Maurice Herlihy, Brown University, and modifications by Iftach Haitner and Yishay
Computational Models: Class 3 Benny Chor School of Computer Science Tel Aviv University November 2, 2015 Based on slides by Maurice Herlihy, Brown University, and modifications by Iftach Haitner and Yishay
CSE 105 THEORY OF COMPUTATION
 CSE 105 THEORY OF COMPUTATION Spring 2016 http://cseweb.ucsd.edu/classes/sp16/cse105-ab/ Today's learning goals Sipser Ch 2 Define push down automata Trace the computation of a push down automaton Design
CSE 105 THEORY OF COMPUTATION Spring 2016 http://cseweb.ucsd.edu/classes/sp16/cse105-ab/ Today's learning goals Sipser Ch 2 Define push down automata Trace the computation of a push down automaton Design
Harvard CS 121 and CSCI E-207 Lecture 10: CFLs: PDAs, Closure Properties, and Non-CFLs
 Harvard CS 121 and CSCI E-207 Lecture 10: CFLs: PDAs, Closure Properties, and Non-CFLs Harry Lewis October 8, 2013 Reading: Sipser, pp. 119-128. Pushdown Automata (review) Pushdown Automata = Finite automaton
Harvard CS 121 and CSCI E-207 Lecture 10: CFLs: PDAs, Closure Properties, and Non-CFLs Harry Lewis October 8, 2013 Reading: Sipser, pp. 119-128. Pushdown Automata (review) Pushdown Automata = Finite automaton
(pp ) PDAs and CFGs (Sec. 2.2)
 (pp. 117-124) PDAs and CFGs (Sec. 2.2) A language is context free iff all strings in L can be generated by some context free grammar Theorem 2.20: L is Context Free iff a PDA accepts it I.e. if L is context
(pp. 117-124) PDAs and CFGs (Sec. 2.2) A language is context free iff all strings in L can be generated by some context free grammar Theorem 2.20: L is Context Free iff a PDA accepts it I.e. if L is context
Pushdown automata. Twan van Laarhoven. Institute for Computing and Information Sciences Intelligent Systems Radboud University Nijmegen
 Pushdown automata Twan van Laarhoven Institute for Computing and Information Sciences Intelligent Systems Version: fall 2014 T. van Laarhoven Version: fall 2014 Formal Languages, Grammars and Automata
Pushdown automata Twan van Laarhoven Institute for Computing and Information Sciences Intelligent Systems Version: fall 2014 T. van Laarhoven Version: fall 2014 Formal Languages, Grammars and Automata
Computational Models - Lecture 4 1
 Computational Models - Lecture 4 1 Handout Mode Iftach Haitner and Yishay Mansour. Tel Aviv University. April 3/8, 2013 1 Based on frames by Benny Chor, Tel Aviv University, modifying frames by Maurice
Computational Models - Lecture 4 1 Handout Mode Iftach Haitner and Yishay Mansour. Tel Aviv University. April 3/8, 2013 1 Based on frames by Benny Chor, Tel Aviv University, modifying frames by Maurice
THEORY OF COMPUTATION (AUBER) EXAM CRIB SHEET
 THEORY OF COMPUTATION (AUBER) EXAM CRIB SHEET Regular Languages and FA A language is a set of strings over a finite alphabet Σ. All languages are finite or countably infinite. The set of all languages
THEORY OF COMPUTATION (AUBER) EXAM CRIB SHEET Regular Languages and FA A language is a set of strings over a finite alphabet Σ. All languages are finite or countably infinite. The set of all languages
Computational Models - Lecture 3
 Slides modified by Benny Chor, based on original slides by Maurice Herlihy, Brown University. p. 1 Computational Models - Lecture 3 Equivalence of regular expressions and regular languages (lukewarm leftover
Slides modified by Benny Chor, based on original slides by Maurice Herlihy, Brown University. p. 1 Computational Models - Lecture 3 Equivalence of regular expressions and regular languages (lukewarm leftover
Introduction to Theory of Computing
 CSCI 2670, Fall 2012 Introduction to Theory of Computing Department of Computer Science University of Georgia Athens, GA 30602 Instructor: Liming Cai www.cs.uga.edu/ cai 0 Lecture Note 3 Context-Free Languages
CSCI 2670, Fall 2012 Introduction to Theory of Computing Department of Computer Science University of Georgia Athens, GA 30602 Instructor: Liming Cai www.cs.uga.edu/ cai 0 Lecture Note 3 Context-Free Languages
CS 301. Lecture 18 Decidable languages. Stephen Checkoway. April 2, 2018
 CS 301 Lecture 18 Decidable languages Stephen Checkoway April 2, 2018 1 / 26 Decidable language Recall, a language A is decidable if there is some TM M that 1 recognizes A (i.e., L(M) = A), and 2 halts
CS 301 Lecture 18 Decidable languages Stephen Checkoway April 2, 2018 1 / 26 Decidable language Recall, a language A is decidable if there is some TM M that 1 recognizes A (i.e., L(M) = A), and 2 halts
MA/CSSE 474 Theory of Computation
 MA/CSSE 474 Theory of Computation CFL Hierarchy CFL Decision Problems Your Questions? Previous class days' material Reading Assignments HW 12 or 13 problems Anything else I have included some slides online
MA/CSSE 474 Theory of Computation CFL Hierarchy CFL Decision Problems Your Questions? Previous class days' material Reading Assignments HW 12 or 13 problems Anything else I have included some slides online
CISC4090: Theory of Computation
 CISC4090: Theory of Computation Chapter 2 Context-Free Languages Courtesy of Prof. Arthur G. Werschulz Fordham University Department of Computer and Information Sciences Spring, 2014 Overview In Chapter
CISC4090: Theory of Computation Chapter 2 Context-Free Languages Courtesy of Prof. Arthur G. Werschulz Fordham University Department of Computer and Information Sciences Spring, 2014 Overview In Chapter
Computational Models - Lecture 4 1
 Computational Models - Lecture 4 1 Handout Mode Iftach Haitner. Tel Aviv University. November 21, 2016 1 Based on frames by Benny Chor, Tel Aviv University, modifying frames by Maurice Herlihy, Brown University.
Computational Models - Lecture 4 1 Handout Mode Iftach Haitner. Tel Aviv University. November 21, 2016 1 Based on frames by Benny Chor, Tel Aviv University, modifying frames by Maurice Herlihy, Brown University.
Computational Models Lecture 2 1
 Computational Models Lecture 2 1 Handout Mode Ronitt Rubinfeld and Iftach Haitner. Tel Aviv University. March 16/18, 2015 1 Based on frames by Benny Chor, Tel Aviv University, modifying frames by Maurice
Computational Models Lecture 2 1 Handout Mode Ronitt Rubinfeld and Iftach Haitner. Tel Aviv University. March 16/18, 2015 1 Based on frames by Benny Chor, Tel Aviv University, modifying frames by Maurice
CSE 105 THEORY OF COMPUTATION
 CSE 105 THEORY OF COMPUTATION Spring 2016 http://cseweb.ucsd.edu/classes/sp16/cse105-ab/ Today's learning goals Sipser Ch 3.3, 4.1 State and use the Church-Turing thesis. Give examples of decidable problems.
CSE 105 THEORY OF COMPUTATION Spring 2016 http://cseweb.ucsd.edu/classes/sp16/cse105-ab/ Today's learning goals Sipser Ch 3.3, 4.1 State and use the Church-Turing thesis. Give examples of decidable problems.
Theory of Computation (IV) Yijia Chen Fudan University
 Theory of Computation (IV) Yijia Chen Fudan University Review language regular context-free machine DFA/ NFA PDA syntax regular expression context-free grammar Pushdown automata Definition A pushdown automaton
Theory of Computation (IV) Yijia Chen Fudan University Review language regular context-free machine DFA/ NFA PDA syntax regular expression context-free grammar Pushdown automata Definition A pushdown automaton
Pushdown Automata. Notes on Automata and Theory of Computation. Chia-Ping Chen
 Pushdown Automata Notes on Automata and Theory of Computation Chia-Ping Chen Department of Computer Science and Engineering National Sun Yat-Sen University Kaohsiung, Taiwan ROC Pushdown Automata p. 1
Pushdown Automata Notes on Automata and Theory of Computation Chia-Ping Chen Department of Computer Science and Engineering National Sun Yat-Sen University Kaohsiung, Taiwan ROC Pushdown Automata p. 1
CISC 4090: Theory of Computation Chapter 1 Regular Languages. Section 1.1: Finite Automata. What is a computer? Finite automata
 CISC 4090: Theory of Computation Chapter Regular Languages Xiaolan Zhang, adapted from slides by Prof. Werschulz Section.: Finite Automata Fordham University Department of Computer and Information Sciences
CISC 4090: Theory of Computation Chapter Regular Languages Xiaolan Zhang, adapted from slides by Prof. Werschulz Section.: Finite Automata Fordham University Department of Computer and Information Sciences
Computational Models - Lecture 5 1
 Computational Models - Lecture 5 1 Handout Mode Iftach Haitner. Tel Aviv University. November 28, 2016 1 Based on frames by Benny Chor, Tel Aviv University, modifying frames by Maurice Herlihy, Brown University.
Computational Models - Lecture 5 1 Handout Mode Iftach Haitner. Tel Aviv University. November 28, 2016 1 Based on frames by Benny Chor, Tel Aviv University, modifying frames by Maurice Herlihy, Brown University.
What languages are Turing-decidable? What languages are not Turing-decidable? Is there a language that isn t even Turingrecognizable?
 } We ll now take a look at Turing Machines at a high level and consider what types of problems can be solved algorithmically and what types can t: What languages are Turing-decidable? What languages are
} We ll now take a look at Turing Machines at a high level and consider what types of problems can be solved algorithmically and what types can t: What languages are Turing-decidable? What languages are
CSE 105 THEORY OF COMPUTATION
 CSE 105 THEORY OF COMPUTATION Spring 2017 http://cseweb.ucsd.edu/classes/sp17/cse105-ab/ Review of CFG, CFL, ambiguity What is the language generated by the CFG below: G 1 = ({S,T 1,T 2 }, {0,1,2}, { S
CSE 105 THEORY OF COMPUTATION Spring 2017 http://cseweb.ucsd.edu/classes/sp17/cse105-ab/ Review of CFG, CFL, ambiguity What is the language generated by the CFG below: G 1 = ({S,T 1,T 2 }, {0,1,2}, { S
Lecture 17: Language Recognition
 Lecture 17: Language Recognition Finite State Automata Deterministic and Non-Deterministic Finite Automata Regular Expressions Push-Down Automata Turing Machines Modeling Computation When attempting to
Lecture 17: Language Recognition Finite State Automata Deterministic and Non-Deterministic Finite Automata Regular Expressions Push-Down Automata Turing Machines Modeling Computation When attempting to
Computational Models Lecture 8 1
 Computational Models Lecture 8 1 Handout Mode Nachum Dershowitz & Yishay Mansour. Tel Aviv University. May 17 22, 2017 1 Based on frames by Benny Chor, Tel Aviv University, modifying frames by Maurice
Computational Models Lecture 8 1 Handout Mode Nachum Dershowitz & Yishay Mansour. Tel Aviv University. May 17 22, 2017 1 Based on frames by Benny Chor, Tel Aviv University, modifying frames by Maurice
Computational Models - Lecture 3 1
 Computational Models - Lecture 3 1 Handout Mode Iftach Haitner and Yishay Mansour. Tel Aviv University. March 13/18, 2013 1 Based on frames by Benny Chor, Tel Aviv University, modifying frames by Maurice
Computational Models - Lecture 3 1 Handout Mode Iftach Haitner and Yishay Mansour. Tel Aviv University. March 13/18, 2013 1 Based on frames by Benny Chor, Tel Aviv University, modifying frames by Maurice
Computational Models - Lecture 1 1
 Computational Models - Lecture 1 1 Handout Mode Ronitt Rubinfeld and Iftach Haitner. Tel Aviv University. February 29/ March 02, 2016 1 Based on frames by Benny Chor, Tel Aviv University, modifying frames
Computational Models - Lecture 1 1 Handout Mode Ronitt Rubinfeld and Iftach Haitner. Tel Aviv University. February 29/ March 02, 2016 1 Based on frames by Benny Chor, Tel Aviv University, modifying frames
CS 154, Lecture 2: Finite Automata, Closure Properties Nondeterminism,
 CS 54, Lecture 2: Finite Automata, Closure Properties Nondeterminism, Why so Many Models? Streaming Algorithms 0 42 Deterministic Finite Automata Anatomy of Deterministic Finite Automata transition: for
CS 54, Lecture 2: Finite Automata, Closure Properties Nondeterminism, Why so Many Models? Streaming Algorithms 0 42 Deterministic Finite Automata Anatomy of Deterministic Finite Automata transition: for
2.1 Solution. E T F a. E E + T T + T F + T a + T a + F a + a
 . Solution E T F a E E + T T + T F + T a + T a + F a + a E E + T E + T + T T + T + T F + T + T a + T + T a + F + T a + a + T a + a + F a + a + a E T F ( E) ( T ) ( F) (( E)) (( T )) (( F)) (( a)) . Solution
. Solution E T F a E E + T T + T F + T a + T a + F a + a E E + T E + T + T T + T + T F + T + T a + T + T a + F + T a + a + T a + a + F a + a + a E T F ( E) ( T ) ( F) (( E)) (( T )) (( F)) (( a)) . Solution
Closure Properties of Context-Free Languages. Foundations of Computer Science Theory
 Closure Properties of Context-Free Languages Foundations of Computer Science Theory Closure Properties of CFLs CFLs are closed under: Union Concatenation Kleene closure Reversal CFLs are not closed under
Closure Properties of Context-Free Languages Foundations of Computer Science Theory Closure Properties of CFLs CFLs are closed under: Union Concatenation Kleene closure Reversal CFLs are not closed under
CS 154. Finite Automata, Nondeterminism, Regular Expressions
 CS 54 Finite Automata, Nondeterminism, Regular Expressions Read string left to right The DFA accepts a string if the process ends in a double circle A DFA is a 5-tuple M = (Q, Σ, δ, q, F) Q is the set
CS 54 Finite Automata, Nondeterminism, Regular Expressions Read string left to right The DFA accepts a string if the process ends in a double circle A DFA is a 5-tuple M = (Q, Σ, δ, q, F) Q is the set
Computational Models Lecture 2 1
 Computational Models Lecture 2 1 Handout Mode Iftach Haitner. Tel Aviv University. October 30, 2017 1 Based on frames by Benny Chor, Tel Aviv University, modifying frames by Maurice Herlihy, Brown University.
Computational Models Lecture 2 1 Handout Mode Iftach Haitner. Tel Aviv University. October 30, 2017 1 Based on frames by Benny Chor, Tel Aviv University, modifying frames by Maurice Herlihy, Brown University.
Decidability (What, stuff is unsolvable?)
 University of Georgia Fall 2014 Outline Decidability Decidable Problems for Regular Languages Decidable Problems for Context Free Languages The Halting Problem Countable and Uncountable Sets Diagonalization
University of Georgia Fall 2014 Outline Decidability Decidable Problems for Regular Languages Decidable Problems for Context Free Languages The Halting Problem Countable and Uncountable Sets Diagonalization
Computational Models Lecture 8 1
 Computational Models Lecture 8 1 Handout Mode Ronitt Rubinfeld and Iftach Haitner. Tel Aviv University. May 11/13, 2015 1 Based on frames by Benny Chor, Tel Aviv University, modifying frames by Maurice
Computational Models Lecture 8 1 Handout Mode Ronitt Rubinfeld and Iftach Haitner. Tel Aviv University. May 11/13, 2015 1 Based on frames by Benny Chor, Tel Aviv University, modifying frames by Maurice
Final exam study sheet for CS3719 Turing machines and decidability.
 Final exam study sheet for CS3719 Turing machines and decidability. A Turing machine is a finite automaton with an infinite memory (tape). Formally, a Turing machine is a 6-tuple M = (Q, Σ, Γ, δ, q 0,
Final exam study sheet for CS3719 Turing machines and decidability. A Turing machine is a finite automaton with an infinite memory (tape). Formally, a Turing machine is a 6-tuple M = (Q, Σ, Γ, δ, q 0,
Introduction to the Theory of Computation. Automata 1VO + 1PS. Lecturer: Dr. Ana Sokolova.
 Introduction to the Theory of Computation Automata 1VO + 1PS Lecturer: Dr. Ana Sokolova http://cs.uni-salzburg.at/~anas/ Setup and Dates Lectures Tuesday 10:45 pm - 12:15 pm Instructions Tuesday 12:30
Introduction to the Theory of Computation Automata 1VO + 1PS Lecturer: Dr. Ana Sokolova http://cs.uni-salzburg.at/~anas/ Setup and Dates Lectures Tuesday 10:45 pm - 12:15 pm Instructions Tuesday 12:30
Computational Models Lecture 8 1
 Computational Models Lecture 8 1 Handout Mode Ronitt Rubinfeld and Iftach Haitner. Tel Aviv University. April 18/ May 2, 2016 1 Based on frames by Benny Chor, Tel Aviv University, modifying frames by Maurice
Computational Models Lecture 8 1 Handout Mode Ronitt Rubinfeld and Iftach Haitner. Tel Aviv University. April 18/ May 2, 2016 1 Based on frames by Benny Chor, Tel Aviv University, modifying frames by Maurice
Languages, regular languages, finite automata
 Notes on Computer Theory Last updated: January, 2018 Languages, regular languages, finite automata Content largely taken from Richards [1] and Sipser [2] 1 Languages An alphabet is a finite set of characters,
Notes on Computer Theory Last updated: January, 2018 Languages, regular languages, finite automata Content largely taken from Richards [1] and Sipser [2] 1 Languages An alphabet is a finite set of characters,
FORMAL LANGUAGES, AUTOMATA AND COMPUTATION
 FORMAL LANGUAGES, AUTOMATA AND COMPUTATION DECIDABILITY ( LECTURE 15) SLIDES FOR 15-453 SPRING 2011 1 / 34 TURING MACHINES-SYNOPSIS The most general model of computation Computations of a TM are described
FORMAL LANGUAGES, AUTOMATA AND COMPUTATION DECIDABILITY ( LECTURE 15) SLIDES FOR 15-453 SPRING 2011 1 / 34 TURING MACHINES-SYNOPSIS The most general model of computation Computations of a TM are described
ECS 120: Theory of Computation UC Davis Phillip Rogaway February 16, Midterm Exam
 ECS 120: Theory of Computation Handout MT UC Davis Phillip Rogaway February 16, 2012 Midterm Exam Instructions: The exam has six pages, including this cover page, printed out two-sided (no more wasted
ECS 120: Theory of Computation Handout MT UC Davis Phillip Rogaway February 16, 2012 Midterm Exam Instructions: The exam has six pages, including this cover page, printed out two-sided (no more wasted
Introduction to the Theory of Computation. Automata 1VO + 1PS. Lecturer: Dr. Ana Sokolova.
 Introduction to the Theory of Computation Automata 1VO + 1PS Lecturer: Dr. Ana Sokolova http://cs.uni-salzburg.at/~anas/ Setup and Dates Lectures and Instructions 23.10. 3.11. 17.11. 24.11. 1.12. 11.12.
Introduction to the Theory of Computation Automata 1VO + 1PS Lecturer: Dr. Ana Sokolova http://cs.uni-salzburg.at/~anas/ Setup and Dates Lectures and Instructions 23.10. 3.11. 17.11. 24.11. 1.12. 11.12.
FORMAL LANGUAGES, AUTOMATA AND COMPUTABILITY
 5-453 FORMAL LANGUAGES, AUTOMATA AND COMPUTABILITY NON-DETERMINISM and REGULAR OPERATIONS THURSDAY JAN 6 UNION THEOREM The union of two regular languages is also a regular language Regular Languages Are
5-453 FORMAL LANGUAGES, AUTOMATA AND COMPUTABILITY NON-DETERMINISM and REGULAR OPERATIONS THURSDAY JAN 6 UNION THEOREM The union of two regular languages is also a regular language Regular Languages Are
The View Over The Horizon
 The View Over The Horizon enumerable decidable context free regular Context-Free Grammars An example of a context free grammar, G 1 : A 0A1 A B B # Terminology: Each line is a substitution rule or production.
The View Over The Horizon enumerable decidable context free regular Context-Free Grammars An example of a context free grammar, G 1 : A 0A1 A B B # Terminology: Each line is a substitution rule or production.
Intro to Theory of Computation
 Intro to Theory of Computation 1/19/2016 LECTURE 3 Last time: DFAs and NFAs Operations on languages Today: Nondeterminism Equivalence of NFAs and DFAs Closure properties of regular languages Sofya Raskhodnikova
Intro to Theory of Computation 1/19/2016 LECTURE 3 Last time: DFAs and NFAs Operations on languages Today: Nondeterminism Equivalence of NFAs and DFAs Closure properties of regular languages Sofya Raskhodnikova
CSE 105 THEORY OF COMPUTATION
 CSE 105 THEORY OF COMPUTATION Spring 2016 http://cseweb.ucsd.edu/classes/sp16/cse105-ab/ Today's learning goals Sipser Ch 2 Design a PDA and a CFG for a given language Give informal description for a PDA,
CSE 105 THEORY OF COMPUTATION Spring 2016 http://cseweb.ucsd.edu/classes/sp16/cse105-ab/ Today's learning goals Sipser Ch 2 Design a PDA and a CFG for a given language Give informal description for a PDA,
Automata and Computability. Solutions to Exercises
 Automata and Computability Solutions to Exercises Spring 27 Alexis Maciel Department of Computer Science Clarkson University Copyright c 27 Alexis Maciel ii Contents Preface vii Introduction 2 Finite Automata
Automata and Computability Solutions to Exercises Spring 27 Alexis Maciel Department of Computer Science Clarkson University Copyright c 27 Alexis Maciel ii Contents Preface vii Introduction 2 Finite Automata
PUSHDOWN AUTOMATA (PDA)
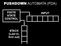 PUSHDOWN AUTOMATA (PDA) FINITE STATE CONTROL INPUT STACK (Last in, first out) input pop push ε,ε $ 0,ε 0 1,0 ε ε,$ ε 1,0 ε PDA that recognizes L = { 0 n 1 n n 0 } Definition: A (non-deterministic) PDA
PUSHDOWN AUTOMATA (PDA) FINITE STATE CONTROL INPUT STACK (Last in, first out) input pop push ε,ε $ 0,ε 0 1,0 ε ε,$ ε 1,0 ε PDA that recognizes L = { 0 n 1 n n 0 } Definition: A (non-deterministic) PDA
Foundations of Informatics: a Bridging Course
 Foundations of Informatics: a Bridging Course Week 3: Formal Languages and Semantics Thomas Noll Lehrstuhl für Informatik 2 RWTH Aachen University noll@cs.rwth-aachen.de http://www.b-it-center.de/wob/en/view/class211_id948.html
Foundations of Informatics: a Bridging Course Week 3: Formal Languages and Semantics Thomas Noll Lehrstuhl für Informatik 2 RWTH Aachen University noll@cs.rwth-aachen.de http://www.b-it-center.de/wob/en/view/class211_id948.html
Properties of Context-Free Languages. Closure Properties Decision Properties
 Properties of Context-Free Languages Closure Properties Decision Properties 1 Closure Properties of CFL s CFL s are closed under union, concatenation, and Kleene closure. Also, under reversal, homomorphisms
Properties of Context-Free Languages Closure Properties Decision Properties 1 Closure Properties of CFL s CFL s are closed under union, concatenation, and Kleene closure. Also, under reversal, homomorphisms
COM364 Automata Theory Lecture Note 2 - Nondeterminism
 COM364 Automata Theory Lecture Note 2 - Nondeterminism Kurtuluş Küllü March 2018 The FA we saw until now were deterministic FA (DFA) in the sense that for each state and input symbol there was exactly
COM364 Automata Theory Lecture Note 2 - Nondeterminism Kurtuluş Küllü March 2018 The FA we saw until now were deterministic FA (DFA) in the sense that for each state and input symbol there was exactly
CS 154, Lecture 3: DFA NFA, Regular Expressions
 CS 154, Lecture 3: DFA NFA, Regular Expressions Homework 1 is coming out Deterministic Finite Automata Computation with finite memory Non-Deterministic Finite Automata Computation with finite memory and
CS 154, Lecture 3: DFA NFA, Regular Expressions Homework 1 is coming out Deterministic Finite Automata Computation with finite memory Non-Deterministic Finite Automata Computation with finite memory and
CS481F01 Solutions 6 PDAS
 CS481F01 Solutions 6 PDAS A. Demers 2 November 2001 1. Give a NPDAs that recognize the following languages: (a) The set of all strings in {0, 1} that contain twice as many 1s as 0s. (answer a) We build
CS481F01 Solutions 6 PDAS A. Demers 2 November 2001 1. Give a NPDAs that recognize the following languages: (a) The set of all strings in {0, 1} that contain twice as many 1s as 0s. (answer a) We build
CpSc 421 Final Exam December 15, 2006
 CpSc 421 Final Exam December 15, 2006 Do problem zero and six of problems 1 through 9. If you write down solutions for more that six problems, clearly indicate those that you want graded. Note that problems
CpSc 421 Final Exam December 15, 2006 Do problem zero and six of problems 1 through 9. If you write down solutions for more that six problems, clearly indicate those that you want graded. Note that problems
Non-Deterministic Finite Automata
 Slides modified Yishay Mansour on modification by Benny Chor, based on original slides by Maurice Herlihy, Brown University. p. 8 Non-Deterministic Finite Automata 0,1 0,1 0 0,ε q q 1 q 2 3 1 q 4 an NFA
Slides modified Yishay Mansour on modification by Benny Chor, based on original slides by Maurice Herlihy, Brown University. p. 8 Non-Deterministic Finite Automata 0,1 0,1 0 0,ε q q 1 q 2 3 1 q 4 an NFA
Automata and Computability. Solutions to Exercises
 Automata and Computability Solutions to Exercises Fall 28 Alexis Maciel Department of Computer Science Clarkson University Copyright c 28 Alexis Maciel ii Contents Preface vii Introduction 2 Finite Automata
Automata and Computability Solutions to Exercises Fall 28 Alexis Maciel Department of Computer Science Clarkson University Copyright c 28 Alexis Maciel ii Contents Preface vii Introduction 2 Finite Automata
Context-Free and Noncontext-Free Languages
 Examples: Context-Free and Noncontext-Free Languages a*b* is regular. A n B n = {a n b n : n 0} is context-free but not regular. A n B n C n = {a n b n c n : n 0} is not context-free The Regular and the
Examples: Context-Free and Noncontext-Free Languages a*b* is regular. A n B n = {a n b n : n 0} is context-free but not regular. A n B n C n = {a n b n c n : n 0} is not context-free The Regular and the
DM17. Beregnelighed. Jacob Aae Mikkelsen
 DM17 Beregnelighed Jacob Aae Mikkelsen January 12, 2007 CONTENTS Contents 1 Introduction 2 1.1 Operations with languages...................... 2 2 Finite Automata 3 2.1 Regular expressions/languages....................
DM17 Beregnelighed Jacob Aae Mikkelsen January 12, 2007 CONTENTS Contents 1 Introduction 2 1.1 Operations with languages...................... 2 2 Finite Automata 3 2.1 Regular expressions/languages....................
Miscellaneous. Closure Properties Decision Properties
 Miscellaneous Closure Properties Decision Properties 1 Closure Properties of CFL s CFL s are closed under union, concatenation, and Kleene closure. Also, under reversal, homomorphisms and inverse homomorphisms.
Miscellaneous Closure Properties Decision Properties 1 Closure Properties of CFL s CFL s are closed under union, concatenation, and Kleene closure. Also, under reversal, homomorphisms and inverse homomorphisms.
NPDA, CFG equivalence
 NPDA, CFG equivalence Theorem A language L is recognized by a NPDA iff L is described by a CFG. Must prove two directions: ( ) L is recognized by a NPDA implies L is described by a CFG. ( ) L is described
NPDA, CFG equivalence Theorem A language L is recognized by a NPDA iff L is described by a CFG. Must prove two directions: ( ) L is recognized by a NPDA implies L is described by a CFG. ( ) L is described
Fooling Sets and. Lecture 5
 Fooling Sets and Introduction to Nondeterministic Finite Automata Lecture 5 Proving that a language is not regular Given a language, we saw how to prove it is regular (union, intersection, concatenation,
Fooling Sets and Introduction to Nondeterministic Finite Automata Lecture 5 Proving that a language is not regular Given a language, we saw how to prove it is regular (union, intersection, concatenation,
Pushdown Automata. Chapter 12
 Pushdown Automata Chapter 12 Recognizing Context-Free Languages We need a device similar to an FSM except that it needs more power. The insight: Precisely what it needs is a stack, which gives it an unlimited
Pushdown Automata Chapter 12 Recognizing Context-Free Languages We need a device similar to an FSM except that it needs more power. The insight: Precisely what it needs is a stack, which gives it an unlimited
HKN CS/ECE 374 Midterm 1 Review. Nathan Bleier and Mahir Morshed
 HKN CS/ECE 374 Midterm 1 Review Nathan Bleier and Mahir Morshed For the most part, all about strings! String induction (to some extent) Regular languages Regular expressions (regexps) Deterministic finite
HKN CS/ECE 374 Midterm 1 Review Nathan Bleier and Mahir Morshed For the most part, all about strings! String induction (to some extent) Regular languages Regular expressions (regexps) Deterministic finite
Theory of Computation
 Fall 2002 (YEN) Theory of Computation Midterm Exam. Name:... I.D.#:... 1. (30 pts) True or false (mark O for true ; X for false ). (Score=Max{0, Right- 1 2 Wrong}.) (1) X... If L 1 is regular and L 2 L
Fall 2002 (YEN) Theory of Computation Midterm Exam. Name:... I.D.#:... 1. (30 pts) True or false (mark O for true ; X for false ). (Score=Max{0, Right- 1 2 Wrong}.) (1) X... If L 1 is regular and L 2 L
CS 154 Introduction to Automata and Complexity Theory
 CS 154 Introduction to Automata and Complexity Theory cs154.stanford.edu 1 INSTRUCTORS & TAs Ryan Williams Cody Murray Lera Nikolaenko Sunny Rajan 2 Textbook 3 Homework / Problem Sets Homework will be
CS 154 Introduction to Automata and Complexity Theory cs154.stanford.edu 1 INSTRUCTORS & TAs Ryan Williams Cody Murray Lera Nikolaenko Sunny Rajan 2 Textbook 3 Homework / Problem Sets Homework will be
Theory of Computation (VI) Yijia Chen Fudan University
 Theory of Computation (VI) Yijia Chen Fudan University Review Forced handles Definition A handle h of a valid string v = xhy is a forced handle if h is the unique handle in every valid string xhŷ where
Theory of Computation (VI) Yijia Chen Fudan University Review Forced handles Definition A handle h of a valid string v = xhy is a forced handle if h is the unique handle in every valid string xhŷ where
Critical CS Questions
 Slides modified by Benny Chor, based on original slides by Maurice Herlihy, Brown University. p. 1 Critical CS Questions What is a computer? And What is a Computation? real computers too complex for any
Slides modified by Benny Chor, based on original slides by Maurice Herlihy, Brown University. p. 1 Critical CS Questions What is a computer? And What is a Computation? real computers too complex for any
Part 4 out of 5 DFA NFA REX. Automata & languages. A primer on the Theory of Computation. Last week, we showed the equivalence of DFA, NFA and REX
 Automata & languages A primer on the Theory of Computation Laurent Vanbever www.vanbever.eu Part 4 out of 5 ETH Zürich (D-ITET) October, 12 2017 Last week, we showed the equivalence of DFA, NFA and REX
Automata & languages A primer on the Theory of Computation Laurent Vanbever www.vanbever.eu Part 4 out of 5 ETH Zürich (D-ITET) October, 12 2017 Last week, we showed the equivalence of DFA, NFA and REX
Harvard CS 121 and CSCI E-207 Lecture 10: Ambiguity, Pushdown Automata
 Harvard CS 121 and CSCI E-207 Lecture 10: Ambiguity, Pushdown Automata Salil Vadhan October 4, 2012 Reading: Sipser, 2.2. Another example of a CFG (with proof) L = {x {a, b} : x has the same # of a s and
Harvard CS 121 and CSCI E-207 Lecture 10: Ambiguity, Pushdown Automata Salil Vadhan October 4, 2012 Reading: Sipser, 2.2. Another example of a CFG (with proof) L = {x {a, b} : x has the same # of a s and
Context-free Languages and Pushdown Automata
 Context-free Languages and Pushdown Automata Finite Automata vs CFLs E.g., {a n b n } CFLs Regular From earlier results: Languages every regular language is a CFL but there are CFLs that are not regular
Context-free Languages and Pushdown Automata Finite Automata vs CFLs E.g., {a n b n } CFLs Regular From earlier results: Languages every regular language is a CFL but there are CFLs that are not regular
Theory Bridge Exam Example Questions
 Theory Bridge Exam Example Questions Annotated version with some (sometimes rather sketchy) answers and notes. This is a collection of sample theory bridge exam questions. This is just to get some idea
Theory Bridge Exam Example Questions Annotated version with some (sometimes rather sketchy) answers and notes. This is a collection of sample theory bridge exam questions. This is just to get some idea
Clarifications from last time. This Lecture. Last Lecture. CMSC 330: Organization of Programming Languages. Finite Automata.
 CMSC 330: Organization of Programming Languages Last Lecture Languages Sets of strings Operations on languages Finite Automata Regular expressions Constants Operators Precedence CMSC 330 2 Clarifications
CMSC 330: Organization of Programming Languages Last Lecture Languages Sets of strings Operations on languages Finite Automata Regular expressions Constants Operators Precedence CMSC 330 2 Clarifications
60-354, Theory of Computation Fall Asish Mukhopadhyay School of Computer Science University of Windsor
 60-354, Theory of Computation Fall 2013 Asish Mukhopadhyay School of Computer Science University of Windsor Pushdown Automata (PDA) PDA = ε-nfa + stack Acceptance ε-nfa enters a final state or Stack is
60-354, Theory of Computation Fall 2013 Asish Mukhopadhyay School of Computer Science University of Windsor Pushdown Automata (PDA) PDA = ε-nfa + stack Acceptance ε-nfa enters a final state or Stack is
Finite Automata and Regular languages
 Finite Automata and Regular languages Huan Long Shanghai Jiao Tong University Acknowledgements Part of the slides comes from a similar course in Fudan University given by Prof. Yijia Chen. http://basics.sjtu.edu.cn/
Finite Automata and Regular languages Huan Long Shanghai Jiao Tong University Acknowledgements Part of the slides comes from a similar course in Fudan University given by Prof. Yijia Chen. http://basics.sjtu.edu.cn/
Fundamentele Informatica II
 Fundamentele Informatica II Answer to selected exercises 5 John C Martin: Introduction to Languages and the Theory of Computation M.M. Bonsangue (and J. Kleijn) Fall 2011 5.1.a (q 0, ab, Z 0 ) (q 1, b,
Fundamentele Informatica II Answer to selected exercises 5 John C Martin: Introduction to Languages and the Theory of Computation M.M. Bonsangue (and J. Kleijn) Fall 2011 5.1.a (q 0, ab, Z 0 ) (q 1, b,
Automata Theory. Lecture on Discussion Course of CS120. Runzhe SJTU ACM CLASS
 Automata Theory Lecture on Discussion Course of CS2 This Lecture is about Mathematical Models of Computation. Why Should I Care? - Ways of thinking. - Theory can drive practice. - Don t be an Instrumentalist.
Automata Theory Lecture on Discussion Course of CS2 This Lecture is about Mathematical Models of Computation. Why Should I Care? - Ways of thinking. - Theory can drive practice. - Don t be an Instrumentalist.
SCHEME FOR INTERNAL ASSESSMENT TEST 3
 SCHEME FOR INTERNAL ASSESSMENT TEST 3 Max Marks: 40 Subject& Code: Automata Theory & Computability (15CS54) Sem: V ISE (A & B) Note: Answer any FIVE full questions, choosing one full question from each
SCHEME FOR INTERNAL ASSESSMENT TEST 3 Max Marks: 40 Subject& Code: Automata Theory & Computability (15CS54) Sem: V ISE (A & B) Note: Answer any FIVE full questions, choosing one full question from each
Before We Start. The Pumping Lemma. Languages. Context Free Languages. Plan for today. Now our picture looks like. Any questions?
 Before We Start The Pumping Lemma Any questions? The Lemma & Decision/ Languages Future Exam Question What is a language? What is a class of languages? Context Free Languages Context Free Languages(CFL)
Before We Start The Pumping Lemma Any questions? The Lemma & Decision/ Languages Future Exam Question What is a language? What is a class of languages? Context Free Languages Context Free Languages(CFL)
Decidability (intro.)
 CHAPTER 4 Decidability Contents Decidable Languages decidable problems concerning regular languages decidable problems concerning context-free languages The Halting Problem The diagonalization method The
CHAPTER 4 Decidability Contents Decidable Languages decidable problems concerning regular languages decidable problems concerning context-free languages The Halting Problem The diagonalization method The
V Honors Theory of Computation
 V22.0453-001 Honors Theory of Computation Problem Set 3 Solutions Problem 1 Solution: The class of languages recognized by these machines is the exactly the class of regular languages, thus this TM variant
V22.0453-001 Honors Theory of Computation Problem Set 3 Solutions Problem 1 Solution: The class of languages recognized by these machines is the exactly the class of regular languages, thus this TM variant
Pushdown Automata (2015/11/23)
 Chapter 6 Pushdown Automata (2015/11/23) Sagrada Familia, Barcelona, Spain Outline 6.0 Introduction 6.1 Definition of PDA 6.2 The Language of a PDA 6.3 Euivalence of PDA s and CFG s 6.4 Deterministic PDA
Chapter 6 Pushdown Automata (2015/11/23) Sagrada Familia, Barcelona, Spain Outline 6.0 Introduction 6.1 Definition of PDA 6.2 The Language of a PDA 6.3 Euivalence of PDA s and CFG s 6.4 Deterministic PDA
CSE 105 THEORY OF COMPUTATION. Spring 2018 review class
 CSE 105 THEORY OF COMPUTATION Spring 2018 review class Today's learning goals Summarize key concepts, ideas, themes from CSE 105. Approach your final exam studying with confidence. Identify areas to focus
CSE 105 THEORY OF COMPUTATION Spring 2018 review class Today's learning goals Summarize key concepts, ideas, themes from CSE 105. Approach your final exam studying with confidence. Identify areas to focus
Theory of Computation
 Theory of Computation Lecture #10 Sarmad Abbasi Virtual University Sarmad Abbasi (Virtual University) Theory of Computation 1 / 43 Lecture 10: Overview Linear Bounded Automata Acceptance Problem for LBAs
Theory of Computation Lecture #10 Sarmad Abbasi Virtual University Sarmad Abbasi (Virtual University) Theory of Computation 1 / 43 Lecture 10: Overview Linear Bounded Automata Acceptance Problem for LBAs
CDM Parsing and Decidability
 CDM Parsing and Decidability 1 Parsing Klaus Sutner Carnegie Mellon Universality 65-parsing 2017/12/15 23:17 CFGs and Decidability Pushdown Automata The Recognition Problem 3 What Could Go Wrong? 4 Problem:
CDM Parsing and Decidability 1 Parsing Klaus Sutner Carnegie Mellon Universality 65-parsing 2017/12/15 23:17 CFGs and Decidability Pushdown Automata The Recognition Problem 3 What Could Go Wrong? 4 Problem:
Accept or reject. Stack
 Pushdown Automata CS351 Just as a DFA was equivalent to a regular expression, we have a similar analogy for the context-free grammar. A pushdown automata (PDA) is equivalent in power to contextfree grammars.
Pushdown Automata CS351 Just as a DFA was equivalent to a regular expression, we have a similar analogy for the context-free grammar. A pushdown automata (PDA) is equivalent in power to contextfree grammars.
Pushdown Automata. We have seen examples of context-free languages that are not regular, and hence can not be recognized by finite automata.
 Pushdown Automata We have seen examples of context-free languages that are not regular, and hence can not be recognized by finite automata. Next we consider a more powerful computation model, called a
Pushdown Automata We have seen examples of context-free languages that are not regular, and hence can not be recognized by finite automata. Next we consider a more powerful computation model, called a
Computational Models - Lecture 3 1
 Computational Models - Lecture 3 1 Handout Mode Iftach Haitner. Tel Aviv University. November 14, 2016 1 Based on frames by Benny Chor, Tel Aviv University, modifying frames by Maurice Herlihy, Brown University.
Computational Models - Lecture 3 1 Handout Mode Iftach Haitner. Tel Aviv University. November 14, 2016 1 Based on frames by Benny Chor, Tel Aviv University, modifying frames by Maurice Herlihy, Brown University.
Theory of Computation
 Thomas Zeugmann Hokkaido University Laboratory for Algorithmics http://www-alg.ist.hokudai.ac.jp/ thomas/toc/ Lecture 10: CF, PDAs and Beyond Greibach Normal Form I We want to show that all context-free
Thomas Zeugmann Hokkaido University Laboratory for Algorithmics http://www-alg.ist.hokudai.ac.jp/ thomas/toc/ Lecture 10: CF, PDAs and Beyond Greibach Normal Form I We want to show that all context-free
CS311 Computational Structures More about PDAs & Context-Free Languages. Lecture 9. Andrew P. Black Andrew Tolmach
 CS311 Computational Structures More about PDAs & Context-Free Languages Lecture 9 Andrew P. Black Andrew Tolmach 1 Three important results 1. Any CFG can be simulated by a PDA 2. Any PDA can be simulated
CS311 Computational Structures More about PDAs & Context-Free Languages Lecture 9 Andrew P. Black Andrew Tolmach 1 Three important results 1. Any CFG can be simulated by a PDA 2. Any PDA can be simulated
CS481F01 Prelim 2 Solutions
 CS481F01 Prelim 2 Solutions A. Demers 7 Nov 2001 1 (30 pts = 4 pts each part + 2 free points). For this question we use the following notation: x y means x is a prefix of y m k n means m n k For each of
CS481F01 Prelim 2 Solutions A. Demers 7 Nov 2001 1 (30 pts = 4 pts each part + 2 free points). For this question we use the following notation: x y means x is a prefix of y m k n means m n k For each of
CSC173 Workshop: 13 Sept. Notes
 CSC173 Workshop: 13 Sept. Notes Frank Ferraro Department of Computer Science University of Rochester September 14, 2010 1 Regular Languages and Equivalent Forms A language can be thought of a set L of
CSC173 Workshop: 13 Sept. Notes Frank Ferraro Department of Computer Science University of Rochester September 14, 2010 1 Regular Languages and Equivalent Forms A language can be thought of a set L of
Introduction to Turing Machines. Reading: Chapters 8 & 9
 Introduction to Turing Machines Reading: Chapters 8 & 9 1 Turing Machines (TM) Generalize the class of CFLs: Recursively Enumerable Languages Recursive Languages Context-Free Languages Regular Languages
Introduction to Turing Machines Reading: Chapters 8 & 9 1 Turing Machines (TM) Generalize the class of CFLs: Recursively Enumerable Languages Recursive Languages Context-Free Languages Regular Languages
Theory of Computation (II) Yijia Chen Fudan University
 Theory of Computation (II) Yijia Chen Fudan University Review A language L is a subset of strings over an alphabet Σ. Our goal is to identify those languages that can be recognized by one of the simplest
Theory of Computation (II) Yijia Chen Fudan University Review A language L is a subset of strings over an alphabet Σ. Our goal is to identify those languages that can be recognized by one of the simplest
CS500 Homework #2 Solutions
 CS500 Homework #2 Solutions 1. Consider the two languages Show that L 1 is context-free but L 2 is not. L 1 = {a i b j c k d l i = j k = l} L 2 = {a i b j c k d l i = k j = l} Answer. L 1 is the concatenation
CS500 Homework #2 Solutions 1. Consider the two languages Show that L 1 is context-free but L 2 is not. L 1 = {a i b j c k d l i = j k = l} L 2 = {a i b j c k d l i = k j = l} Answer. L 1 is the concatenation
Computational Models: Class 1
 Computational Models: Class 1 Benny Chor School of Computer Science Tel Aviv University October 19, 2015 Based on slides by Maurice Herlihy, Brown University, and modifications by Iftach Haitner and Yishay
Computational Models: Class 1 Benny Chor School of Computer Science Tel Aviv University October 19, 2015 Based on slides by Maurice Herlihy, Brown University, and modifications by Iftach Haitner and Yishay
CSE 355 Test 2, Fall 2016
 CSE 355 Test 2, Fall 2016 28 October 2016, 8:35-9:25 a.m., LSA 191 Last Name SAMPLE ASU ID 1357924680 First Name(s) Ima Regrading of Midterms If you believe that your grade has not been added up correctly,
CSE 355 Test 2, Fall 2016 28 October 2016, 8:35-9:25 a.m., LSA 191 Last Name SAMPLE ASU ID 1357924680 First Name(s) Ima Regrading of Midterms If you believe that your grade has not been added up correctly,
