Computability and Complexity
|
|
|
- Anabel O’Neal’
- 6 years ago
- Views:
Transcription
1 Computability and Complexity Push-Down Automata CAS 705 Ryszard Janicki Department of Computing and Software McMaster University Hamilton, Ontario, Canada Ryszard Janicki Computability and Complexity 1 / 45
2 Pushdown Automata (PDAs): A Preview a1 a2 a3 a4 a5 a6 a7 a8 an left to right, read only Q Finite Control push/pop A B C B Stack Ryszard Janicki Computability and Complexity 2 / 45
3 Pushdown Automata (PDAs): A Preview A nondeterministic pushdown automaton (NPDA) is like a nondeterministic nite automaton, except it has a stack Its input head is read-only and may only move right The stack is used in a last-in-rst-out (LIFO) fashion It can push symbols onto the top of the stack or pop them o the top of the stack In each step, the machine pops the top symbol o the stack Ryszard Janicki Computability and Complexity 3 / 45
4 Pushdown Automata (PDAs): A Preview Based on this symbol, the input symbol it is currently reading, and its current state, it can push a sequence of symbols onto the stack, move its read head one cell to the right, and enter a new state, according to the transition rules of the machine It allows also ɛ-transitions in which it can pop and push without reading the next input symbol or moving its read head Ryszard Janicki Computability and Complexity 4 / 45
5 Nondeterministic Pushdown Automaton Formal Denition A nondeterministic PDA is a 7-tuple M = (Q, Σ, Γ, δ, s 0,, F ), where Q is a nite set (the states), Σ is a nite set (the input alphabet), Γ is a nite set (the stack alphabet), δ : Q (Σ {ε}) Γ 2 Q Γ, is a function (the transition function), s 0 Q (the start state), Γ (the initial stack symbol), and F Q (the nal or accept states). Ryszard Janicki Computability and Complexity 5 / 45
6 Nondeterministic Pushdown Automaton Example (q, B 1 B 2 B k ) δ(p, a, A) means whenever the machine is in state p reading input symbol a on the input tape and A on the top of the stack then it can pop A o the stack, push B 1 B 2 B k onto the stack (B k rst and B 1 last), leave its read head where it is, and enter state q. Ryszard Janicki Computability and Complexity 6 / 45
7 Nondeterministic Pushdown Automaton Example (q, B 1 B 2 B k ) δ(p, ε, A) means whenever the machine is in state p and A on the top of the stack then it can pop A o the stack, push B 1 B 2 B k onto the stack (B k rst and B 1 last), leave its read head where it is, and enter state q. Ryszard Janicki Computability and Complexity 7 / 45
8 Congurations Denition A conguration of the machine M is an element of Q Σ Γ describing the current state, the portion of the input yet unread, and the current stack contents. A conguration gives complete information about the global state of M at some point during a computation In general, the set of congurations is innite The start conguration on input x is (s, x, ) Ryszard Janicki Computability and Complexity 8 / 45
9 Congurations The conguration might describe the following (p, baaabba, ABAC ) a b a b b a a a b b a p A B A C Stack Ryszard Janicki Computability and Complexity 9 / 45
10 Congurations The next conguration relation 1 describes how the M machine can move from one conguration to another in one step It is dened formally as follows: if (q, γ) δ(p, a, A) then y Σ, β Γ. (p, ay, Aβ) and if ((p, ɛ, A), (q, γ)) δ then y Σ, β Γ. (p, y, Aβ) 1 (q, y, γβ) M 1 (q, y, γβ) M Ryszard Janicki Computability and Complexity 10 / 45
11 Congurations Denition For C, D, E conguration of M, we dene the relations M as follows: n M and C 0 D def M C = D C n+1 D def E. C n E E 1 M M M D C M D def n 0. C n M D M is the reexive transitive closure of 1 M Ryszard Janicki Computability and Complexity 11 / 45
12 Acceptance There are two alternative denitions of acceptance in common use: by empty stack and by nal state It turns out that it doesn't matter which denition we use, since each kind of machine can simulate the other. Formally, M accepts x by nal state if (s, x, ) M (q, ε, γ) for some q F and γ Γ. Let L F (M) denote the language of all sequences accepted by M by nal state. Formally, M accepts x by empty stack if (s, x, ) M (q, ε, ε) for some q Q. Let L E (M) denote the language of all sequences accepted by M by empty stack. Ryszard Janicki Computability and Complexity 12 / 45
13 Acceptance: Example 1 Example A nondeterministic pushdown automaton that accepts the set of balanced strings of parentheses [ ] by empty stack. Q = {q}, Σ = {[, ]}, Γ = {, [}, start state = q, initial stack symbol = and δ is dened as follows: (i) δ(q, [, ) = {(q, [ )}; (ii) δ(q, [, [) = {(q, [[)}; (iii) δ(q, ], [) = {(q, ε)}; (iv) δ(q, ε, ) = {(q, ɛ)}. (v) δ(,, ) = for all other cases (usually dened by default) Ryszard Janicki Computability and Complexity 13 / 45
14 Acceptance: Example 1 A sequence of congurations leading to the acceptance of the balanced string [ [ [] ] [] ] [] Ryszard Janicki Computability and Complexity 14 / 45
15 Acceptance: Example 2 The pushdown automaton M below accepts the language L E (M) = {xcx R x {a, b} } with empty stack, where (a 1 a 2... a n ) R = a n a n 1... a 1. Ryszard Janicki Computability and Complexity 15 / 45
16 Acceptance: Example 3 The pushdown automaton M below accepts the language L E (M) = {xx R x {a, b} } with empty stack. Ryszard Janicki Computability and Complexity 16 / 45
17 Graphical Notation: meaning of a, b c We write a, b c to signify that when the automaton is reading an a from the input, it may replace the symbol b on the top of the stack with a c. Any of a, b, and c may be ε. If a is ε, the automaton may make this transition without reading any symbol from the input. If b is ε, the automaton may make this transition without reading and popping any symbol from the stack. If c is ε, the automaton does not write any symbol on the stack when going along this transition. Ryszard Janicki Computability and Complexity 17 / 45
18 Graphical Notation: Example 1 The pushdown automaton M below accepts the language L F (M) = {0 n 1 n n 0} with F = {q 1, q 4 }. Ryszard Janicki Computability and Complexity 18 / 45
19 Graphical Notation: Example 2 The pushdown automaton M below accepts the language L F (M) = {a i b j c k i, j, k 0 and i = j or i = k} with F = {q 4, q 7 }. Ryszard Janicki Computability and Complexity 19 / 45
20 From Final States To Empty Stack Theorem For every pushdown automaton M there is a pushdown automaton M such that: L F (M) = L E (M ). Proof. (sketch). We just have to pop stuck until empty when in nal state. Let M = (Q, Σ, Γ, δ, s 0,, F ). Dene M = (Q {s e, s 0 }, Σ, Γ { }, δ, s 0,, ), where 1 δ (s 0, ε, ) = {(s 0, )} 2 q Q, a Σ {ε}, Z Γ. δ (q, a, Z) = δ(q, a, Z) 3 q F, Z Γ. δ (q, ε, Z) = δ(q, ε, Z) {(s e, ε)} 4 Z Γ { }. δ (s e, ε, Z) = {(s e, ε)}. Clearly L F (M) = L E (M ). Ryszard Janicki Computability and Complexity 20 / 45
21 From Empty Stack To Final States Theorem For every pushdown automaton M there is a pushdown automaton M such that: L E (M) = L M (M ). Proof. (sketch). We just have to jump to nal state when stack is `empty'. Let M = (Q, Σ, Γ, δ, s 0,, ). Dene M = (Q {s f, s 0 }, Σ, Γ { }, δ, s 0,, {s f }), where 1 δ (s 0, ε, ) = {(s 0, )} 2 q Q, a Σ {ε}, Z Γ. δ (q, a, Z) = δ(q, a, Z) 3 q Q {s f, s 0 }. δ (q, ε, ) = {(s f, ε)}. Clearly L E (M) = L F (M ). Ryszard Janicki Computability and Complexity 21 / 45
22 Denition (Deterministic Pushdown Automata) A pushdown automaton M = (Q, Σ, Γ, δ, s 0,, F ) is deterministic if and only if 1 q Q. Z Γ. δ(q, ε) = ( a Σ. δ(q, a, Z) = ) 2 q Q. Z Γ. a Σ {ε}. δ(q, a, Z) 1. Theorem L = {ww R w {0, 1} }, (where (a 1 a 2... a n ) R = a n a n 1... a 1 ). There is no deterministic pushdown automaton M such that L F (M) = L or L E (M) = L. The language {ww R w {0, 1} } is given by the following nondeterministic pushdown automaton: Ryszard Janicki Computability and Complexity 22 / 45
23 From CF-Grammars To Pushdown Automata We will show how to convert a given CF-grammar to an equivalent nondeterministic pushdown automaton Suppose we are given a CF-grammar G = (V, T, P, σ). We wish to construct a nondeterministic pushdown automaton M such that L(M) = L(G) Without loss of generality we can that all productions of G are of the Greibach normal form where c Σ {ε} and k 0. A cb 1 B 2 B k Ryszard Janicki Computability and Complexity 23 / 45
24 From CF-Grammars To Pushdown Automata We construct from G = (V, T, P, σ) an equivalent nondeterministic pushdown automaton M with only one state that accepts by empty stack. Let M = ({q}, T, V, δ, q, σ, ), where q is the only state, T,the set of terminals of G, is the input alphabet of M, V, the set of variables of G, is the stack alphabet of M, δ is the transition function dened below, q is the start state, σ, the start symbol of G, is the initial stack symbol of M,, the null set, is the set of nal states. The transition function δ is dened as follows. For each production in P, we have A cb 1 B 2... B k (q, B 1 B 2... B k ) δ(q, c, A). Ryszard Janicki Computability and Complexity 24 / 45
25 Theorem Let G be a context-free grammar and M G be a nondeterministic pushdown automaton derived from G using the procedure from page 24. Then L(G) = L E (M G ). Example Consider the set of nonnull balanced strings of parentheses [ ] Transformation: S [B [SB [BS [SBS B ] (i) S [BS (q, BS) δ(q, [, S) (ii) S [B (q, B) δ(q, [, S) (iii) S [SB (q, SB) δ(q, [, S) (iv) S [SBS (q, SBS) δ(q, [, S) (v) B ] (q, ε) δ(q, ], B) In other words δ(q, [, S) = {(q, BS), (q, B), (q, SB), (q, SBS)}, δ(q, ], S) = {(q, ε)} and δ(,, ) = for all other cases. Ryszard Janicki Computability and Complexity 25 / 45
26 From CF-Grammars To Pushdown Automata Example (Continued) For the input x = [[[]][]], we have Ryszard Janicki Computability and Complexity 26 / 45
27 From Pushdown Automata To CF-Grammars Theorem Let L = L E (M) for some pushdown automaton M. Then L is a context-free language. Proof.(sketch). Let M = (Q, Σ, Γ, δ, s 0,, ). We construct G M = (V, T, P, σ), where V = (Q Γ Q) {σ}, (with elements of V \ {σ} written as [p, A, q]) T = Σ, P is the following set of productions: 1 σ [s 0,, q] for each q Q, 2 [s, A, q m+1 ] a[q 1, B 1, q 2 ][q 2, B 2, q 3 ]... [q m, B m, q m+1 ] for each s, q 1,..., q m+1 Q, each a Σ {ε} and A, B 1,..., B m Γ, such that (q 1, B 1 B 2... B m ) δ(s, a, A). If m = 0, the the production is [s, A, q 1 ] a. Ryszard Janicki Computability and Complexity 27 / 45
28 From Pushdown Automata To CF-Grammars Proof.(sketch) (continuation). Explanation: The intuition is that a variable [q, A, p] derive x if and only if x causes M to erase an A from its stack by some sequence of moves, beginning in q and ending in p. It may be proved that: [q, A, p] G x T (q, x, A) M (p, ε, ε). Ryszard Janicki Computability and Complexity 28 / 45
29 Example Let M = ({q 0, q 1 }, {a, b}, {X, }, δ, q 0,, ), where δ is given by: δ(q 0, a, ) = {(q 0, X )} δ(q 0, a, X ) = {(q 0, XX )} δ(q 0, b, X ) = {(q 1, ε)} δ(q 1, b, X ) = {(q 1, ε)} δ(q 1, ε, X ) = {(q 1, ε)} δ(q 1, ε, ) = {(q 1, ε)} Dene G M = (V, T, P, σ) where: V = {σ, [q 0, X, q 0 ], [q 0, X, q 1 ], [q 1, X, q 0 ], [q 1, X, q 1 ], [q 0,, q 0 ], [q 0,, q 1 ], [q 1,, q 0 ], [q 1,, q 1 ]}, T = {a, b}, and P is of the following } form: σ [q 0,, q 0 ] since σ [q σ [q 0,, q 1 ] 0,, q] for each q Q [q 0,, q 0 ] a[q 0, X, q 0 ][q 0,, q 0 ] [q 0,, q 0 ] a[q 0, X, q 1 ][q 1,, q 0 ] [q 0,, q 1 ] a[q 0, X, q 0 ][q 0,, q 1 ] [q 0,, q 1 ] a[q 0, X, q 1 ][q 1,, q 1 ] since δ(q 0, a, ) = {q 0, X )} Ryszard Janicki Computability and Complexity 29 / 45
30 Example (continued) [q 0, X, q 0 ] a[q 0, X, q 0 ][q 0, X, q 0 ] [q 0, X, q 0 ] a[q 0, X, q 1 ][q 1, X, q 0 ] since δ(q [q 0, X, q 1 ] a[q 0, X, q 0 ][q 0, X, q 1 ] 0, a, X ) = {q 0, XX )} [q 0, X, q 1 ] a[q 0, X, q 1 ][q 1, X, q 1 ] [q 0, X, q 1 ] b since δ(q 0, b, X ) = {q 1, ε)} [q 1,, q 1 ] ε since δ(q 1, ε, ) = {q 1, ε)} [q 1, X, q 1 ] ε since δ(q 1, ε, X ) = {q 1, ε)} [q 1, X, q 1 ] b since δ(q 1, b, X ) = {q 1, ε)} Some optimization: There are no productions for the variables [q 1, X, q 0 ] and [q 1,, q 0 ]. All productions from [q 0, X, q 0 ] and [q 0,, q 0 ] have [q 1, X, q 0 ] or [q 1,, q 0 ] on the right, i.e. no terminal string can be derived from [q 0, X, q 0 ] or [q 0,, q 0 ]. This means the variables [q 0, X, q 0 ], [q 0,, q 0 ], [q 1, X, q 0 ] and [q 1,, q 0 ] are useless, i.e. we can remove all productions involving these symbols. Ryszard Janicki Computability and Complexity 30 / 45
31 Example (continued) The result is: V = {σ, [q 0, X, q 1 ], [q 1, X, q 1 ], [q 0,, q 1 ], [q 1,, q 1 ]} T = {a, b} P = σ [q 0,, q 1 ] [q 0,, q 1 ] a[q 0, X, q 0 ][q 0,, q 1 ] [q 0, X, q 1 ] a[q 0, X, q 1 ][q 1, X, q 1 ] [q 0, X, q 1 ] b [q 1,, q 1 ] ε [q 1, X, q 1 ] ε [q 1, X, q 1 ] b Ryszard Janicki Computability and Complexity 31 / 45
32 Automata and CF-Lanuages Theorem The following statements are equivalent: 1 L L CF, 2 L = L E (M) for some pushdown automaton M, 3 L = L F (M) for some pushdown automaton M. Remark. We may prove the above theorem without using Greibach Normal Form. Ryszard Janicki Computability and Complexity 32 / 45
33 Theorem Let L L CF. There is a pushdown automaton M such that L = L E (M). Proof. (sketch). Let G = (V, T, P, σ) be a CG-grammar. Dene M = (Q, Σ, Γ, δ, s 0,, ) as follows: Q = {s 0, q}, Σ = T, Γ = V T, = σ, and δ is dened as follows: 1 A Γ. δ(q, ε, A) = {(q, x) A x P}, { 2 {(q, ε)} if a = X a σ. X Γ. δ(q, a, X ) = if a X { 3 {(q, σ), (q, ε)} if ε L δ(s 0, ε, σ) = {(q, σ)} if ε / L 4 δ(,, ) = for all remaining cases. One can prove that L E (M) = L(G). Ryszard Janicki Computability and Complexity 33 / 45
34 Deterministic Context-Free Languages Denition A context-free language L is called deterministic if there exists a deterministic pushdown automaton M such that L = L(M). Let L DCF denotes the class of all deterministic context-free languages. Theorem L R L DCF L CF. Proof. By the denition L DCF L CF and Theorem from page 22 states that L DCF L CF, so L DCF L CF. Every deterministic nite automaton can be transformed into deterministic pushdown automaton by adding one element stack and not using it at all. Hence L R L DCF. The language from page 13 is deterministic context free but not regular, so L R L DCF. Ryszard Janicki Computability and Complexity 34 / 45
35 Pumping Lemma for CF-Languages Lemma Let L Σ be a context-free language. Then there is a constant n, depending only on L, such that if z L and z n then there are u, v, w, x, y Σ such that z = uvwxy and 1 vx 1, 2 vwx n, 3 i 0. uv i wx i y L. Using the above Pumping Lemma, one may easily show that {a n b n c n n 0} / L CF. Ryszard Janicki Computability and Complexity 35 / 45
36 Closures Theorem Let L 1, L 2 L CF. Then 1 L 1 L 2 L CF. 2 L 1 L 2 L CF. 3 L 1 L CF. Proof. Let G i = (V i, T i, P i, σ i ) be CF-grammars such that L I = L(G i ) for i = 1, 2. We may assume that V 1 V 2 =. New grammars: 1 σ L1 L 2 σ 1 σ 2 plus P 1 P 2, 2 σ L1 L 2 σ 1 σ 2 plus P 1 P 2, 3 σ L 1 σ L 1 σ 1 ε plus P 1. Ryszard Janicki Computability and Complexity 36 / 45
37 Intersection and Subtraction Theorem If L 1, L 2 L CF, the language L 1 L 2 may not be context-free. Proof. Take L 1 = {a n b n c k n, k 0} and L 2 = {a k b n c n n, k 0}. The language L 1 L 2 = {a n b n c n n 0} / L CF. Corollary If L Σ and L L CF, the language Σ \ L may not be context-free. Ryszard Janicki Computability and Complexity 37 / 45
38 Intersection with a Regular Language Theorem Let L L CF and R L R, i.e. L is context-free and R is regular. Then L R L CF, i.e. L R is context-free. Proof. (sketch). Let M L be a pushdown automaton such that L = L(M L ), and let M R be a deterministic nite state automaton such that R = L(M R ). Let M be constructed from M)L and M R in such a way that the state part of M is a product of states of M L and M R, and the stack part is the same as for M L. Then we have L(M) = L R. Corollary L = {x # a (x) = # b (x) = # c (x)} / L CF. Proof. Suppose L is context-free. Clearly a b c is regular, so L a b c L CF. But L a b c = {a n b n c n n 0}, a contradiction. Ryszard Janicki Computability and Complexity 38 / 45
39 Decision Algorithms for CF-Languages Theorem There are algorithms to determine if a CF-language is 1 empty 2 nite 3 innite Proof. (1) The test of Lemma A for useless symbols (page 36 of Lecture Notes 4) determines if a variable generates any string of terminals. Hence: L(G) σ generates some string of terminals. (2) and (3) We may assume that a grammar is in Chomsky Normal Form (we have a algorithm for appropriate transformation). We dene a directed graph with a vertex for each variable and an edge from A to B if there is a production of the form A BC or A CB for any C. Then L(G) is nite if and only if this graph has no cycles. Otherwise it is innite. Ryszard Janicki Computability and Complexity 39 / 45
40 Membership Theorem There is an algorithm to decide if x L for each L L CF. Proof. Theorem about grammars without ε-productions gives an algorithm to decide if ε L. Let x ε. We may assume that we have a grammar G in Greibach Normal Form such that L = L(G). Let x = a 1...a n. If x L then σ G a 1 y 1 G a 1 a 2 y 2 G... G a 1...a n 1 y n 1 }{{ G a 1...a n = x. } n steps, n = x There is a nite number of derivations in G starting from σ and doing n steps. If no variable in G jas more than k productions, we have: {y σ n y y (V T ) } k n. More ecient G algorithms, as O(n 3 ) do exist. Ryszard Janicki Computability and Complexity 40 / 45
41 Undecidability of CF-Languages The concept of Undecidability will be discussed later, here we will just mention undecidable properties of CF-grammars and CF-Languages. Theorem The following properties are undecidable for CF-grammars over sets of terminals with more than one element. 1 L(G 1 ) L(G 2 ) L CF 2 Is G ambiguous? 3 L(G) L R 4 L(G 1 ) L(G 2 ) 5 L(G 1 ) = L(G 2 ) 6 For L L CF, is L inherently ambiguous? Ryszard Janicki Computability and Complexity 41 / 45
42 Context-Sensitive/Monotone Languages Lemma The language L = {a n b n c n n 1} is context-sensitive or monotone, i.e. L L CS = L M. Proof. The following two dierent monotone grammars generate L: σ aσx ay YX byc cx Xc Y bc σ aσbc abc CB BC ab ab bb bb bc bc cc cc Ryszard Janicki Computability and Complexity 42 / 45
43 Context-Sensitive/Monotone Languages - Properties Theorem L CF L CS = L M Proof. The theorem about removal of ε-productions implies L CF L CS and the lemma form page 42 gives L CF L CS. Theorem If L 1, L 2 L CS = L M then: 1 L 1 L 2 L CS 2 L 1 L 2 L CS 3 L 1 L 2 L CS 4 L 1 L CS 5 Σ \ L 1 L CS (if L 1 Σ ) Ryszard Janicki Computability and Complexity 43 / 45
44 Membership for Context-Sensitive Languages Theorem There is an algorithm to decide if x L for each L L CS. Proof. From the denition of context-sensitive grammar we immediately know if ε is in L or not. Let L = L(G) for some context-sensitive (or monotone) grammar. If x ε, then σ = x 0 x 1... x n = x, where x i (V T ) for i = 1,..., n and x i x i+1 for i = 0,..., n 1. We construct a graph whose vertices are the strings in (V T ) of length n or less. We put an arc from the vertex α to the vertex β if α β. Then paths in the graph correspond to derivations in the grammar G, and w L(G) if and only if there is a path from the vertex σ to the vertex x. Any path nding techniques can be used. Ryszard Janicki Computability and Complexity 44 / 45
45 This is the end of GRAMMARS THEORY Ryszard Janicki Computability and Complexity 45 / 45
Introduction to Formal Languages, Automata and Computability p.1/42
 Introduction to Formal Languages, Automata and Computability Pushdown Automata K. Krithivasan and R. Rama Introduction to Formal Languages, Automata and Computability p.1/42 Introduction We have considered
Introduction to Formal Languages, Automata and Computability Pushdown Automata K. Krithivasan and R. Rama Introduction to Formal Languages, Automata and Computability p.1/42 Introduction We have considered
Harvard CS 121 and CSCI E-207 Lecture 10: CFLs: PDAs, Closure Properties, and Non-CFLs
 Harvard CS 121 and CSCI E-207 Lecture 10: CFLs: PDAs, Closure Properties, and Non-CFLs Harry Lewis October 8, 2013 Reading: Sipser, pp. 119-128. Pushdown Automata (review) Pushdown Automata = Finite automaton
Harvard CS 121 and CSCI E-207 Lecture 10: CFLs: PDAs, Closure Properties, and Non-CFLs Harry Lewis October 8, 2013 Reading: Sipser, pp. 119-128. Pushdown Automata (review) Pushdown Automata = Finite automaton
Computability and Complexity
 Computability and Complexity Decidability, Undecidability and Reducibility; Codes, Algorithms and Languages CAS 705 Ryszard Janicki Department of Computing and Software McMaster University Hamilton, Ontario,
Computability and Complexity Decidability, Undecidability and Reducibility; Codes, Algorithms and Languages CAS 705 Ryszard Janicki Department of Computing and Software McMaster University Hamilton, Ontario,
Computability and Complexity
 Computability and Complexity Rewriting Systems and Chomsky Grammars CAS 705 Ryszard Janicki Department of Computing and Software McMaster University Hamilton, Ontario, Canada janicki@mcmaster.ca Ryszard
Computability and Complexity Rewriting Systems and Chomsky Grammars CAS 705 Ryszard Janicki Department of Computing and Software McMaster University Hamilton, Ontario, Canada janicki@mcmaster.ca Ryszard
Computability and Complexity
 Computability and Complexity Non-determinism, Regular Expressions CAS 705 Ryszard Janicki Department of Computing and Software McMaster University Hamilton, Ontario, Canada janicki@mcmaster.ca Ryszard
Computability and Complexity Non-determinism, Regular Expressions CAS 705 Ryszard Janicki Department of Computing and Software McMaster University Hamilton, Ontario, Canada janicki@mcmaster.ca Ryszard
Computability and Complexity
 Computability and Complexity Sequences and Automata CAS 705 Ryszard Janicki Department of Computing and Software McMaster University Hamilton, Ontario, Canada janicki@mcmaster.ca Ryszard Janicki Computability
Computability and Complexity Sequences and Automata CAS 705 Ryszard Janicki Department of Computing and Software McMaster University Hamilton, Ontario, Canada janicki@mcmaster.ca Ryszard Janicki Computability
Pushdown automata. Twan van Laarhoven. Institute for Computing and Information Sciences Intelligent Systems Radboud University Nijmegen
 Pushdown automata Twan van Laarhoven Institute for Computing and Information Sciences Intelligent Systems Version: fall 2014 T. van Laarhoven Version: fall 2014 Formal Languages, Grammars and Automata
Pushdown automata Twan van Laarhoven Institute for Computing and Information Sciences Intelligent Systems Version: fall 2014 T. van Laarhoven Version: fall 2014 Formal Languages, Grammars and Automata
Section 1 (closed-book) Total points 30
 CS 454 Theory of Computation Fall 2011 Section 1 (closed-book) Total points 30 1. Which of the following are true? (a) a PDA can always be converted to an equivalent PDA that at each step pops or pushes
CS 454 Theory of Computation Fall 2011 Section 1 (closed-book) Total points 30 1. Which of the following are true? (a) a PDA can always be converted to an equivalent PDA that at each step pops or pushes
Definition: A grammar G = (V, T, P,S) is a context free grammar (cfg) if all productions in P have the form A x where
 Recitation 11 Notes Context Free Grammars Definition: A grammar G = (V, T, P,S) is a context free grammar (cfg) if all productions in P have the form A x A V, and x (V T)*. Examples Problem 1. Given the
Recitation 11 Notes Context Free Grammars Definition: A grammar G = (V, T, P,S) is a context free grammar (cfg) if all productions in P have the form A x A V, and x (V T)*. Examples Problem 1. Given the
Pushdown Automata. We have seen examples of context-free languages that are not regular, and hence can not be recognized by finite automata.
 Pushdown Automata We have seen examples of context-free languages that are not regular, and hence can not be recognized by finite automata. Next we consider a more powerful computation model, called a
Pushdown Automata We have seen examples of context-free languages that are not regular, and hence can not be recognized by finite automata. Next we consider a more powerful computation model, called a
Pushdown Automata. Notes on Automata and Theory of Computation. Chia-Ping Chen
 Pushdown Automata Notes on Automata and Theory of Computation Chia-Ping Chen Department of Computer Science and Engineering National Sun Yat-Sen University Kaohsiung, Taiwan ROC Pushdown Automata p. 1
Pushdown Automata Notes on Automata and Theory of Computation Chia-Ping Chen Department of Computer Science and Engineering National Sun Yat-Sen University Kaohsiung, Taiwan ROC Pushdown Automata p. 1
Harvard CS 121 and CSCI E-207 Lecture 10: Ambiguity, Pushdown Automata
 Harvard CS 121 and CSCI E-207 Lecture 10: Ambiguity, Pushdown Automata Salil Vadhan October 4, 2012 Reading: Sipser, 2.2. Another example of a CFG (with proof) L = {x {a, b} : x has the same # of a s and
Harvard CS 121 and CSCI E-207 Lecture 10: Ambiguity, Pushdown Automata Salil Vadhan October 4, 2012 Reading: Sipser, 2.2. Another example of a CFG (with proof) L = {x {a, b} : x has the same # of a s and
Pushdown Automata. Pushdown Automata. Pushdown Automata. Pushdown Automata. Pushdown Automata. Pushdown Automata. The stack
 A pushdown automata (PDA) is essentially: An NFA with a stack A move of a PDA will depend upon Current state of the machine Current symbol being read in Current symbol popped off the top of the stack With
A pushdown automata (PDA) is essentially: An NFA with a stack A move of a PDA will depend upon Current state of the machine Current symbol being read in Current symbol popped off the top of the stack With
MA/CSSE 474 Theory of Computation
 MA/CSSE 474 Theory of Computation CFL Hierarchy CFL Decision Problems Your Questions? Previous class days' material Reading Assignments HW 12 or 13 problems Anything else I have included some slides online
MA/CSSE 474 Theory of Computation CFL Hierarchy CFL Decision Problems Your Questions? Previous class days' material Reading Assignments HW 12 or 13 problems Anything else I have included some slides online
Miscellaneous. Closure Properties Decision Properties
 Miscellaneous Closure Properties Decision Properties 1 Closure Properties of CFL s CFL s are closed under union, concatenation, and Kleene closure. Also, under reversal, homomorphisms and inverse homomorphisms.
Miscellaneous Closure Properties Decision Properties 1 Closure Properties of CFL s CFL s are closed under union, concatenation, and Kleene closure. Also, under reversal, homomorphisms and inverse homomorphisms.
Theory of Computation Turing Machine and Pushdown Automata
 Theory of Computation Turing Machine and Pushdown Automata 1. What is a Turing Machine? A Turing Machine is an accepting device which accepts the languages (recursively enumerable set) generated by type
Theory of Computation Turing Machine and Pushdown Automata 1. What is a Turing Machine? A Turing Machine is an accepting device which accepts the languages (recursively enumerable set) generated by type
FORMAL LANGUAGES, AUTOMATA AND COMPUTABILITY
 15-453 FORMAL LANGUAGES, AUTOMATA AND COMPUTABILITY REVIEW for MIDTERM 1 THURSDAY Feb 6 Midterm 1 will cover everything we have seen so far The PROBLEMS will be from Sipser, Chapters 1, 2, 3 It will be
15-453 FORMAL LANGUAGES, AUTOMATA AND COMPUTABILITY REVIEW for MIDTERM 1 THURSDAY Feb 6 Midterm 1 will cover everything we have seen so far The PROBLEMS will be from Sipser, Chapters 1, 2, 3 It will be
Properties of Context-Free Languages
 Properties of Context-Free Languages Seungjin Choi Department of Computer Science and Engineering Pohang University of Science and Technology 77 Cheongam-ro, Nam-gu, Pohang 37673, Korea seungjin@postech.ac.kr
Properties of Context-Free Languages Seungjin Choi Department of Computer Science and Engineering Pohang University of Science and Technology 77 Cheongam-ro, Nam-gu, Pohang 37673, Korea seungjin@postech.ac.kr
Pushdown Automata (Pre Lecture)
 Pushdown Automata (Pre Lecture) Dr. Neil T. Dantam CSCI-561, Colorado School of Mines Fall 2017 Dantam (Mines CSCI-561) Pushdown Automata (Pre Lecture) Fall 2017 1 / 41 Outline Pushdown Automata Pushdown
Pushdown Automata (Pre Lecture) Dr. Neil T. Dantam CSCI-561, Colorado School of Mines Fall 2017 Dantam (Mines CSCI-561) Pushdown Automata (Pre Lecture) Fall 2017 1 / 41 Outline Pushdown Automata Pushdown
Foundations of Informatics: a Bridging Course
 Foundations of Informatics: a Bridging Course Week 3: Formal Languages and Semantics Thomas Noll Lehrstuhl für Informatik 2 RWTH Aachen University noll@cs.rwth-aachen.de http://www.b-it-center.de/wob/en/view/class211_id948.html
Foundations of Informatics: a Bridging Course Week 3: Formal Languages and Semantics Thomas Noll Lehrstuhl für Informatik 2 RWTH Aachen University noll@cs.rwth-aachen.de http://www.b-it-center.de/wob/en/view/class211_id948.html
MTH401A Theory of Computation. Lecture 17
 MTH401A Theory of Computation Lecture 17 Chomsky Normal Form for CFG s Chomsky Normal Form for CFG s For every context free language, L, the language L {ε} has a grammar in which every production looks
MTH401A Theory of Computation Lecture 17 Chomsky Normal Form for CFG s Chomsky Normal Form for CFG s For every context free language, L, the language L {ε} has a grammar in which every production looks
This lecture covers Chapter 7 of HMU: Properties of CFLs
 This lecture covers Chapter 7 of HMU: Properties of CFLs Chomsky Normal Form Pumping Lemma for CFs Closure Properties of CFLs Decision Properties of CFLs Additional Reading: Chapter 7 of HMU. Chomsky Normal
This lecture covers Chapter 7 of HMU: Properties of CFLs Chomsky Normal Form Pumping Lemma for CFs Closure Properties of CFLs Decision Properties of CFLs Additional Reading: Chapter 7 of HMU. Chomsky Normal
NPDA, CFG equivalence
 NPDA, CFG equivalence Theorem A language L is recognized by a NPDA iff L is described by a CFG. Must prove two directions: ( ) L is recognized by a NPDA implies L is described by a CFG. ( ) L is described
NPDA, CFG equivalence Theorem A language L is recognized by a NPDA iff L is described by a CFG. Must prove two directions: ( ) L is recognized by a NPDA implies L is described by a CFG. ( ) L is described
CS311 Computational Structures More about PDAs & Context-Free Languages. Lecture 9. Andrew P. Black Andrew Tolmach
 CS311 Computational Structures More about PDAs & Context-Free Languages Lecture 9 Andrew P. Black Andrew Tolmach 1 Three important results 1. Any CFG can be simulated by a PDA 2. Any PDA can be simulated
CS311 Computational Structures More about PDAs & Context-Free Languages Lecture 9 Andrew P. Black Andrew Tolmach 1 Three important results 1. Any CFG can be simulated by a PDA 2. Any PDA can be simulated
Properties of Context-Free Languages. Closure Properties Decision Properties
 Properties of Context-Free Languages Closure Properties Decision Properties 1 Closure Properties of CFL s CFL s are closed under union, concatenation, and Kleene closure. Also, under reversal, homomorphisms
Properties of Context-Free Languages Closure Properties Decision Properties 1 Closure Properties of CFL s CFL s are closed under union, concatenation, and Kleene closure. Also, under reversal, homomorphisms
DD2371 Automata Theory
 KTH CSC VT 2008 DD2371 Automata Theory Dilian Gurov Lecture Outline 1. The lecturer 2. Introduction to automata theory 3. Course syllabus 4. Course objectives 5. Course organization 6. First definitions
KTH CSC VT 2008 DD2371 Automata Theory Dilian Gurov Lecture Outline 1. The lecturer 2. Introduction to automata theory 3. Course syllabus 4. Course objectives 5. Course organization 6. First definitions
Einführung in die Computerlinguistik
 Einführung in die Computerlinguistik Context-Free Grammars (CFG) Laura Kallmeyer Heinrich-Heine-Universität Düsseldorf Summer 2016 1 / 22 CFG (1) Example: Grammar G telescope : Productions: S NP VP NP
Einführung in die Computerlinguistik Context-Free Grammars (CFG) Laura Kallmeyer Heinrich-Heine-Universität Düsseldorf Summer 2016 1 / 22 CFG (1) Example: Grammar G telescope : Productions: S NP VP NP
Outline. CS21 Decidability and Tractability. Machine view of FA. Machine view of FA. Machine view of FA. Machine view of FA.
 Outline CS21 Decidability and Tractability Lecture 5 January 16, 219 and Languages equivalence of NPDAs and CFGs non context-free languages January 16, 219 CS21 Lecture 5 1 January 16, 219 CS21 Lecture
Outline CS21 Decidability and Tractability Lecture 5 January 16, 219 and Languages equivalence of NPDAs and CFGs non context-free languages January 16, 219 CS21 Lecture 5 1 January 16, 219 CS21 Lecture
CSE 105 THEORY OF COMPUTATION
 CSE 105 THEORY OF COMPUTATION Spring 2017 http://cseweb.ucsd.edu/classes/sp17/cse105-ab/ Review of CFG, CFL, ambiguity What is the language generated by the CFG below: G 1 = ({S,T 1,T 2 }, {0,1,2}, { S
CSE 105 THEORY OF COMPUTATION Spring 2017 http://cseweb.ucsd.edu/classes/sp17/cse105-ab/ Review of CFG, CFL, ambiguity What is the language generated by the CFG below: G 1 = ({S,T 1,T 2 }, {0,1,2}, { S
input tape head moves current state a a
 CPS 140 - Mathematical Foundations of CS Dr. S. Rodger Section: Pushdown Automata (Ch. 3.3-3.4) (handout) Pushdown Automata ADFA=(K,,,q 0,F) input tape a a b b a b tape head head moves current state 0
CPS 140 - Mathematical Foundations of CS Dr. S. Rodger Section: Pushdown Automata (Ch. 3.3-3.4) (handout) Pushdown Automata ADFA=(K,,,q 0,F) input tape a a b b a b tape head head moves current state 0
Theory of Computation (IV) Yijia Chen Fudan University
 Theory of Computation (IV) Yijia Chen Fudan University Review language regular context-free machine DFA/ NFA PDA syntax regular expression context-free grammar Pushdown automata Definition A pushdown automaton
Theory of Computation (IV) Yijia Chen Fudan University Review language regular context-free machine DFA/ NFA PDA syntax regular expression context-free grammar Pushdown automata Definition A pushdown automaton
How to Pop a Deep PDA Matters
 How to Pop a Deep PDA Matters Peter Leupold Department of Mathematics, Faculty of Science Kyoto Sangyo University Kyoto 603-8555, Japan email:leupold@cc.kyoto-su.ac.jp Abstract Deep PDA are push-down automata
How to Pop a Deep PDA Matters Peter Leupold Department of Mathematics, Faculty of Science Kyoto Sangyo University Kyoto 603-8555, Japan email:leupold@cc.kyoto-su.ac.jp Abstract Deep PDA are push-down automata
DM17. Beregnelighed. Jacob Aae Mikkelsen
 DM17 Beregnelighed Jacob Aae Mikkelsen January 12, 2007 CONTENTS Contents 1 Introduction 2 1.1 Operations with languages...................... 2 2 Finite Automata 3 2.1 Regular expressions/languages....................
DM17 Beregnelighed Jacob Aae Mikkelsen January 12, 2007 CONTENTS Contents 1 Introduction 2 1.1 Operations with languages...................... 2 2 Finite Automata 3 2.1 Regular expressions/languages....................
Context Free Languages (CFL) Language Recognizer A device that accepts valid strings. The FA are formalized types of language recognizer.
 Context Free Languages (CFL) Language Recognizer A device that accepts valid strings. The FA are formalized types of language recognizer. Language Generator: Context free grammars are language generators,
Context Free Languages (CFL) Language Recognizer A device that accepts valid strings. The FA are formalized types of language recognizer. Language Generator: Context free grammars are language generators,
Undecidable Problems and Reducibility
 University of Georgia Fall 2014 Reducibility We show a problem decidable/undecidable by reducing it to another problem. One type of reduction: mapping reduction. Definition Let A, B be languages over Σ.
University of Georgia Fall 2014 Reducibility We show a problem decidable/undecidable by reducing it to another problem. One type of reduction: mapping reduction. Definition Let A, B be languages over Σ.
CISC4090: Theory of Computation
 CISC4090: Theory of Computation Chapter 2 Context-Free Languages Courtesy of Prof. Arthur G. Werschulz Fordham University Department of Computer and Information Sciences Spring, 2014 Overview In Chapter
CISC4090: Theory of Computation Chapter 2 Context-Free Languages Courtesy of Prof. Arthur G. Werschulz Fordham University Department of Computer and Information Sciences Spring, 2014 Overview In Chapter
St.MARTIN S ENGINEERING COLLEGE Dhulapally, Secunderabad
 St.MARTIN S ENGINEERING COLLEGE Dhulapally, Secunderabad-500 014 Subject: FORMAL LANGUAGES AND AUTOMATA THEORY Class : CSE II PART A (SHORT ANSWER QUESTIONS) UNIT- I 1 Explain transition diagram, transition
St.MARTIN S ENGINEERING COLLEGE Dhulapally, Secunderabad-500 014 Subject: FORMAL LANGUAGES AND AUTOMATA THEORY Class : CSE II PART A (SHORT ANSWER QUESTIONS) UNIT- I 1 Explain transition diagram, transition
Theory of Computation - Module 3
 Theory of Computation - Module 3 Syllabus Context Free Grammar Simplification of CFG- Normal forms-chomsky Normal form and Greibach Normal formpumping lemma for Context free languages- Applications of
Theory of Computation - Module 3 Syllabus Context Free Grammar Simplification of CFG- Normal forms-chomsky Normal form and Greibach Normal formpumping lemma for Context free languages- Applications of
Non-context-Free Languages. CS215, Lecture 5 c
 Non-context-Free Languages CS215, Lecture 5 c 2007 1 The Pumping Lemma Theorem. (Pumping Lemma) Let be context-free. There exists a positive integer divided into five pieces, Proof for for each, and..
Non-context-Free Languages CS215, Lecture 5 c 2007 1 The Pumping Lemma Theorem. (Pumping Lemma) Let be context-free. There exists a positive integer divided into five pieces, Proof for for each, and..
Context Free Language Properties
 Context Free Language Properties Knowing that the context free languages are exactly those sets accepted by nondeterministic pushdown automata provides us a bit of information about them. We know that
Context Free Language Properties Knowing that the context free languages are exactly those sets accepted by nondeterministic pushdown automata provides us a bit of information about them. We know that
Introduction to Theory of Computing
 CSCI 2670, Fall 2012 Introduction to Theory of Computing Department of Computer Science University of Georgia Athens, GA 30602 Instructor: Liming Cai www.cs.uga.edu/ cai 0 Lecture Note 3 Context-Free Languages
CSCI 2670, Fall 2012 Introduction to Theory of Computing Department of Computer Science University of Georgia Athens, GA 30602 Instructor: Liming Cai www.cs.uga.edu/ cai 0 Lecture Note 3 Context-Free Languages
CS481F01 Solutions 6 PDAS
 CS481F01 Solutions 6 PDAS A. Demers 2 November 2001 1. Give a NPDAs that recognize the following languages: (a) The set of all strings in {0, 1} that contain twice as many 1s as 0s. (answer a) We build
CS481F01 Solutions 6 PDAS A. Demers 2 November 2001 1. Give a NPDAs that recognize the following languages: (a) The set of all strings in {0, 1} that contain twice as many 1s as 0s. (answer a) We build
CS21 Decidability and Tractability
 CS21 Decidability and Tractability Lecture 8 January 24, 2018 Outline Turing Machines and variants multitape TMs nondeterministic TMs Church-Turing Thesis So far several models of computation finite automata
CS21 Decidability and Tractability Lecture 8 January 24, 2018 Outline Turing Machines and variants multitape TMs nondeterministic TMs Church-Turing Thesis So far several models of computation finite automata
Pushdown Automata. Reading: Chapter 6
 Pushdown Automata Reading: Chapter 6 1 Pushdown Automata (PDA) Informally: A PDA is an NFA-ε with a infinite stack. Transitions are modified to accommodate stack operations. Questions: What is a stack?
Pushdown Automata Reading: Chapter 6 1 Pushdown Automata (PDA) Informally: A PDA is an NFA-ε with a infinite stack. Transitions are modified to accommodate stack operations. Questions: What is a stack?
THEORY OF COMPUTATION (AUBER) EXAM CRIB SHEET
 THEORY OF COMPUTATION (AUBER) EXAM CRIB SHEET Regular Languages and FA A language is a set of strings over a finite alphabet Σ. All languages are finite or countably infinite. The set of all languages
THEORY OF COMPUTATION (AUBER) EXAM CRIB SHEET Regular Languages and FA A language is a set of strings over a finite alphabet Σ. All languages are finite or countably infinite. The set of all languages
CS20a: summary (Oct 24, 2002)
 CS20a: summary (Oct 24, 2002) Context-free languages Grammars G = (V, T, P, S) Pushdown automata N-PDA = CFG D-PDA < CFG Today What languages are context-free? Pumping lemma (similar to pumping lemma for
CS20a: summary (Oct 24, 2002) Context-free languages Grammars G = (V, T, P, S) Pushdown automata N-PDA = CFG D-PDA < CFG Today What languages are context-free? Pumping lemma (similar to pumping lemma for
Before We Start. The Pumping Lemma. Languages. Context Free Languages. Plan for today. Now our picture looks like. Any questions?
 Before We Start The Pumping Lemma Any questions? The Lemma & Decision/ Languages Future Exam Question What is a language? What is a class of languages? Context Free Languages Context Free Languages(CFL)
Before We Start The Pumping Lemma Any questions? The Lemma & Decision/ Languages Future Exam Question What is a language? What is a class of languages? Context Free Languages Context Free Languages(CFL)
V Honors Theory of Computation
 V22.0453-001 Honors Theory of Computation Problem Set 3 Solutions Problem 1 Solution: The class of languages recognized by these machines is the exactly the class of regular languages, thus this TM variant
V22.0453-001 Honors Theory of Computation Problem Set 3 Solutions Problem 1 Solution: The class of languages recognized by these machines is the exactly the class of regular languages, thus this TM variant
Automata and Computability. Solutions to Exercises
 Automata and Computability Solutions to Exercises Fall 28 Alexis Maciel Department of Computer Science Clarkson University Copyright c 28 Alexis Maciel ii Contents Preface vii Introduction 2 Finite Automata
Automata and Computability Solutions to Exercises Fall 28 Alexis Maciel Department of Computer Science Clarkson University Copyright c 28 Alexis Maciel ii Contents Preface vii Introduction 2 Finite Automata
UNIT-VI PUSHDOWN AUTOMATA
 Syllabus R09 Regulation UNIT-VI PUSHDOWN AUTOMATA The context free languages have a type of automaton that defined them. This automaton, called a pushdown automaton, is an extension of the nondeterministic
Syllabus R09 Regulation UNIT-VI PUSHDOWN AUTOMATA The context free languages have a type of automaton that defined them. This automaton, called a pushdown automaton, is an extension of the nondeterministic
CPS 220 Theory of Computation Pushdown Automata (PDA)
 CPS 220 Theory of Computation Pushdown Automata (PDA) Nondeterministic Finite Automaton with some extra memory Memory is called the stack, accessed in a very restricted way: in a First-In First-Out fashion
CPS 220 Theory of Computation Pushdown Automata (PDA) Nondeterministic Finite Automaton with some extra memory Memory is called the stack, accessed in a very restricted way: in a First-In First-Out fashion
FORMAL LANGUAGES, AUTOMATA AND COMPUTATION
 FORMAL LANGUAGES, AUTOMATA AND COMPUTATION DECIDABILITY ( LECTURE 15) SLIDES FOR 15-453 SPRING 2011 1 / 34 TURING MACHINES-SYNOPSIS The most general model of computation Computations of a TM are described
FORMAL LANGUAGES, AUTOMATA AND COMPUTATION DECIDABILITY ( LECTURE 15) SLIDES FOR 15-453 SPRING 2011 1 / 34 TURING MACHINES-SYNOPSIS The most general model of computation Computations of a TM are described
October 6, Equivalence of Pushdown Automata with Context-Free Gramm
 Equivalence of Pushdown Automata with Context-Free Grammar October 6, 2013 Motivation Motivation CFG and PDA are equivalent in power: a CFG generates a context-free language and a PDA recognizes a context-free
Equivalence of Pushdown Automata with Context-Free Grammar October 6, 2013 Motivation Motivation CFG and PDA are equivalent in power: a CFG generates a context-free language and a PDA recognizes a context-free
SFWR ENG 2FA3. Solution to the Assignment #4
 SFWR ENG 2FA3. Solution to the Assignment #4 Total = 131, 100%= 115 The solutions below are often very detailed on purpose. Such level of details is not required from students solutions. Some questions
SFWR ENG 2FA3. Solution to the Assignment #4 Total = 131, 100%= 115 The solutions below are often very detailed on purpose. Such level of details is not required from students solutions. Some questions
Computational Models - Lecture 4
 Computational Models - Lecture 4 Regular languages: The Myhill-Nerode Theorem Context-free Grammars Chomsky Normal Form Pumping Lemma for context free languages Non context-free languages: Examples Push
Computational Models - Lecture 4 Regular languages: The Myhill-Nerode Theorem Context-free Grammars Chomsky Normal Form Pumping Lemma for context free languages Non context-free languages: Examples Push
1. Draw a parse tree for the following derivation: S C A C C A b b b b A b b b b B b b b b a A a a b b b b a b a a b b 2. Show on your parse tree u,
 1. Draw a parse tree for the following derivation: S C A C C A b b b b A b b b b B b b b b a A a a b b b b a b a a b b 2. Show on your parse tree u, v, x, y, z as per the pumping theorem. 3. Prove that
1. Draw a parse tree for the following derivation: S C A C C A b b b b A b b b b B b b b b a A a a b b b b a b a a b b 2. Show on your parse tree u, v, x, y, z as per the pumping theorem. 3. Prove that
Theory of Computation
 Thomas Zeugmann Hokkaido University Laboratory for Algorithmics http://www-alg.ist.hokudai.ac.jp/ thomas/toc/ Lecture 3: Finite State Automata Motivation In the previous lecture we learned how to formalize
Thomas Zeugmann Hokkaido University Laboratory for Algorithmics http://www-alg.ist.hokudai.ac.jp/ thomas/toc/ Lecture 3: Finite State Automata Motivation In the previous lecture we learned how to formalize
Automata and Computability. Solutions to Exercises
 Automata and Computability Solutions to Exercises Spring 27 Alexis Maciel Department of Computer Science Clarkson University Copyright c 27 Alexis Maciel ii Contents Preface vii Introduction 2 Finite Automata
Automata and Computability Solutions to Exercises Spring 27 Alexis Maciel Department of Computer Science Clarkson University Copyright c 27 Alexis Maciel ii Contents Preface vii Introduction 2 Finite Automata
(b) If G=({S}, {a}, {S SS}, S) find the language generated by G. [8+8] 2. Convert the following grammar to Greibach Normal Form G = ({A1, A2, A3},
![(b) If G=({S}, {a}, {S SS}, S) find the language generated by G. [8+8] 2. Convert the following grammar to Greibach Normal Form G = ({A1, A2, A3}, (b) If G=({S}, {a}, {S SS}, S) find the language generated by G. [8+8] 2. Convert the following grammar to Greibach Normal Form G = ({A1, A2, A3},](/thumbs/81/83182922.jpg) Code No: 07A50501 R07 Set No. 2 III B.Tech I Semester Examinations,MAY 2011 FORMAL LANGUAGES AND AUTOMATA THEORY Computer Science And Engineering Time: 3 hours Max Marks: 80 Answer any FIVE Questions All
Code No: 07A50501 R07 Set No. 2 III B.Tech I Semester Examinations,MAY 2011 FORMAL LANGUAGES AND AUTOMATA THEORY Computer Science And Engineering Time: 3 hours Max Marks: 80 Answer any FIVE Questions All
Computational Models - Lecture 5 1
 Computational Models - Lecture 5 1 Handout Mode Iftach Haitner and Yishay Mansour. Tel Aviv University. April 10/22, 2013 1 Based on frames by Benny Chor, Tel Aviv University, modifying frames by Maurice
Computational Models - Lecture 5 1 Handout Mode Iftach Haitner and Yishay Mansour. Tel Aviv University. April 10/22, 2013 1 Based on frames by Benny Chor, Tel Aviv University, modifying frames by Maurice
Computational Models: Class 5
 Computational Models: Class 5 Benny Chor School of Computer Science Tel Aviv University March 27, 2019 Based on slides by Maurice Herlihy, Brown University, and modifications by Iftach Haitner and Yishay
Computational Models: Class 5 Benny Chor School of Computer Science Tel Aviv University March 27, 2019 Based on slides by Maurice Herlihy, Brown University, and modifications by Iftach Haitner and Yishay
60-354, Theory of Computation Fall Asish Mukhopadhyay School of Computer Science University of Windsor
 60-354, Theory of Computation Fall 2013 Asish Mukhopadhyay School of Computer Science University of Windsor Pushdown Automata (PDA) PDA = ε-nfa + stack Acceptance ε-nfa enters a final state or Stack is
60-354, Theory of Computation Fall 2013 Asish Mukhopadhyay School of Computer Science University of Windsor Pushdown Automata (PDA) PDA = ε-nfa + stack Acceptance ε-nfa enters a final state or Stack is
Theory of Computation
 Theory of Computation Lecture #10 Sarmad Abbasi Virtual University Sarmad Abbasi (Virtual University) Theory of Computation 1 / 43 Lecture 10: Overview Linear Bounded Automata Acceptance Problem for LBAs
Theory of Computation Lecture #10 Sarmad Abbasi Virtual University Sarmad Abbasi (Virtual University) Theory of Computation 1 / 43 Lecture 10: Overview Linear Bounded Automata Acceptance Problem for LBAs
PUSHDOWN AUTOMATA (PDA)
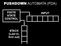 PUSHDOWN AUTOMATA (PDA) FINITE STATE CONTROL INPUT STACK (Last in, first out) input pop push ε,ε $ 0,ε 0 1,0 ε ε,$ ε 1,0 ε PDA that recognizes L = { 0 n 1 n n 0 } Definition: A (non-deterministic) PDA
PUSHDOWN AUTOMATA (PDA) FINITE STATE CONTROL INPUT STACK (Last in, first out) input pop push ε,ε $ 0,ε 0 1,0 ε ε,$ ε 1,0 ε PDA that recognizes L = { 0 n 1 n n 0 } Definition: A (non-deterministic) PDA
Chapter 6. Properties of Regular Languages
 Chapter 6 Properties of Regular Languages Regular Sets and Languages Claim(1). The family of languages accepted by FSAs consists of precisely the regular sets over a given alphabet. Every regular set is
Chapter 6 Properties of Regular Languages Regular Sets and Languages Claim(1). The family of languages accepted by FSAs consists of precisely the regular sets over a given alphabet. Every regular set is
Homework 4. Chapter 7. CS A Term 2009: Foundations of Computer Science. By Li Feng, Shweta Srivastava, and Carolina Ruiz
 CS3133 - A Term 2009: Foundations of Computer Science Prof. Carolina Ruiz Homework 4 WPI By Li Feng, Shweta Srivastava, and Carolina Ruiz Chapter 7 Problem: Chap 7.1 part a This PDA accepts the language
CS3133 - A Term 2009: Foundations of Computer Science Prof. Carolina Ruiz Homework 4 WPI By Li Feng, Shweta Srivastava, and Carolina Ruiz Chapter 7 Problem: Chap 7.1 part a This PDA accepts the language
Properties of context-free Languages
 Properties of context-free Languages We simplify CFL s. Greibach Normal Form Chomsky Normal Form We prove pumping lemma for CFL s. We study closure properties and decision properties. Some of them remain,
Properties of context-free Languages We simplify CFL s. Greibach Normal Form Chomsky Normal Form We prove pumping lemma for CFL s. We study closure properties and decision properties. Some of them remain,
CS Pushdown Automata
 Chap. 6 Pushdown Automata 6.1 Definition of Pushdown Automata Example 6.2 L ww R = {ww R w (0+1) * } Palindromes over {0, 1}. A cfg P 0 1 0P0 1P1. Consider a FA with a stack(= a Pushdown automaton; PDA).
Chap. 6 Pushdown Automata 6.1 Definition of Pushdown Automata Example 6.2 L ww R = {ww R w (0+1) * } Palindromes over {0, 1}. A cfg P 0 1 0P0 1P1. Consider a FA with a stack(= a Pushdown automaton; PDA).
Properties of Context-free Languages. Reading: Chapter 7
 Properties of Context-free Languages Reading: Chapter 7 1 Topics 1) Simplifying CFGs, Normal forms 2) Pumping lemma for CFLs 3) Closure and decision properties of CFLs 2 How to simplify CFGs? 3 Three ways
Properties of Context-free Languages Reading: Chapter 7 1 Topics 1) Simplifying CFGs, Normal forms 2) Pumping lemma for CFLs 3) Closure and decision properties of CFLs 2 How to simplify CFGs? 3 Three ways
CPS 220 Theory of Computation
 CPS 22 Theory of Computation Review - Regular Languages RL - a simple class of languages that can be represented in two ways: 1 Machine description: Finite Automata are machines with a finite number of
CPS 22 Theory of Computation Review - Regular Languages RL - a simple class of languages that can be represented in two ways: 1 Machine description: Finite Automata are machines with a finite number of
Part 4 out of 5 DFA NFA REX. Automata & languages. A primer on the Theory of Computation. Last week, we showed the equivalence of DFA, NFA and REX
 Automata & languages A primer on the Theory of Computation Laurent Vanbever www.vanbever.eu Part 4 out of 5 ETH Zürich (D-ITET) October, 12 2017 Last week, we showed the equivalence of DFA, NFA and REX
Automata & languages A primer on the Theory of Computation Laurent Vanbever www.vanbever.eu Part 4 out of 5 ETH Zürich (D-ITET) October, 12 2017 Last week, we showed the equivalence of DFA, NFA and REX
Please give details of your answer. A direct answer without explanation is not counted.
 Please give details of your answer. A direct answer without explanation is not counted. Your answers must be in English. Please carefully read problem statements. During the exam you are not allowed to
Please give details of your answer. A direct answer without explanation is not counted. Your answers must be in English. Please carefully read problem statements. During the exam you are not allowed to
Pushdown Automata (2015/11/23)
 Chapter 6 Pushdown Automata (2015/11/23) Sagrada Familia, Barcelona, Spain Outline 6.0 Introduction 6.1 Definition of PDA 6.2 The Language of a PDA 6.3 Euivalence of PDA s and CFG s 6.4 Deterministic PDA
Chapter 6 Pushdown Automata (2015/11/23) Sagrada Familia, Barcelona, Spain Outline 6.0 Introduction 6.1 Definition of PDA 6.2 The Language of a PDA 6.3 Euivalence of PDA s and CFG s 6.4 Deterministic PDA
NODIA AND COMPANY. GATE SOLVED PAPER Computer Science Engineering Theory of Computation. Copyright By NODIA & COMPANY
 No part of this publication may be reproduced or distributed in any form or any means, electronic, mechanical, photocopying, or otherwise without the prior permission of the author. GATE SOLVED PAPER Computer
No part of this publication may be reproduced or distributed in any form or any means, electronic, mechanical, photocopying, or otherwise without the prior permission of the author. GATE SOLVED PAPER Computer
Languages, regular languages, finite automata
 Notes on Computer Theory Last updated: January, 2018 Languages, regular languages, finite automata Content largely taken from Richards [1] and Sipser [2] 1 Languages An alphabet is a finite set of characters,
Notes on Computer Theory Last updated: January, 2018 Languages, regular languages, finite automata Content largely taken from Richards [1] and Sipser [2] 1 Languages An alphabet is a finite set of characters,
COMP-330 Theory of Computation. Fall Prof. Claude Crépeau. Lec. 10 : Context-Free Grammars
 COMP-330 Theory of Computation Fall 2017 -- Prof. Claude Crépeau Lec. 10 : Context-Free Grammars COMP 330 Fall 2017: Lectures Schedule 1-2. Introduction 1.5. Some basic mathematics 2-3. Deterministic finite
COMP-330 Theory of Computation Fall 2017 -- Prof. Claude Crépeau Lec. 10 : Context-Free Grammars COMP 330 Fall 2017: Lectures Schedule 1-2. Introduction 1.5. Some basic mathematics 2-3. Deterministic finite
Blackhole Pushdown Automata
 Fundamenta Informaticae XXI (2001) 1001 1020 1001 IOS Press Blackhole Pushdown Automata Erzsébet Csuhaj-Varjú Computer and Automation Research Institute, Hungarian Academy of Sciences Kende u. 13 17, 1111
Fundamenta Informaticae XXI (2001) 1001 1020 1001 IOS Press Blackhole Pushdown Automata Erzsébet Csuhaj-Varjú Computer and Automation Research Institute, Hungarian Academy of Sciences Kende u. 13 17, 1111
Fundamentele Informatica II
 Fundamentele Informatica II Answer to selected exercises 5 John C Martin: Introduction to Languages and the Theory of Computation M.M. Bonsangue (and J. Kleijn) Fall 2011 5.1.a (q 0, ab, Z 0 ) (q 1, b,
Fundamentele Informatica II Answer to selected exercises 5 John C Martin: Introduction to Languages and the Theory of Computation M.M. Bonsangue (and J. Kleijn) Fall 2011 5.1.a (q 0, ab, Z 0 ) (q 1, b,
5 Context-Free Languages
 CA320: COMPUTABILITY AND COMPLEXITY 1 5 Context-Free Languages 5.1 Context-Free Grammars Context-Free Grammars Context-free languages are specified with a context-free grammar (CFG). Formally, a CFG G
CA320: COMPUTABILITY AND COMPLEXITY 1 5 Context-Free Languages 5.1 Context-Free Grammars Context-Free Grammars Context-free languages are specified with a context-free grammar (CFG). Formally, a CFG G
CSE 105 THEORY OF COMPUTATION
 CSE 105 THEORY OF COMPUTATION Spring 2016 http://cseweb.ucsd.edu/classes/sp16/cse105-ab/ Today's learning goals Sipser Ch 2 Design a PDA and a CFG for a given language Give informal description for a PDA,
CSE 105 THEORY OF COMPUTATION Spring 2016 http://cseweb.ucsd.edu/classes/sp16/cse105-ab/ Today's learning goals Sipser Ch 2 Design a PDA and a CFG for a given language Give informal description for a PDA,
Automata Theory (2A) Young Won Lim 5/31/18
 Automata Theory (2A) Copyright (c) 2018 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2 or any later
Automata Theory (2A) Copyright (c) 2018 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2 or any later
SYLLABUS. Introduction to Finite Automata, Central Concepts of Automata Theory. CHAPTER - 3 : REGULAR EXPRESSIONS AND LANGUAGES
 Contents i SYLLABUS UNIT - I CHAPTER - 1 : AUT UTOMA OMATA Introduction to Finite Automata, Central Concepts of Automata Theory. CHAPTER - 2 : FINITE AUT UTOMA OMATA An Informal Picture of Finite Automata,
Contents i SYLLABUS UNIT - I CHAPTER - 1 : AUT UTOMA OMATA Introduction to Finite Automata, Central Concepts of Automata Theory. CHAPTER - 2 : FINITE AUT UTOMA OMATA An Informal Picture of Finite Automata,
3130CIT Theory of Computation
 GRIFFITH UNIVERSITY School of Computing and Information Technology 3130CIT Theory of Computation Final Examination, Semester 2, 2006 Details Total marks: 120 (40% of the total marks for this subject) Perusal:
GRIFFITH UNIVERSITY School of Computing and Information Technology 3130CIT Theory of Computation Final Examination, Semester 2, 2006 Details Total marks: 120 (40% of the total marks for this subject) Perusal:
Context-Free Languages
 CS:4330 Theory of Computation Spring 2018 Context-Free Languages Pushdown Automata Haniel Barbosa Readings for this lecture Chapter 2 of [Sipser 1996], 3rd edition. Section 2.2. Finite automaton 1 / 13
CS:4330 Theory of Computation Spring 2018 Context-Free Languages Pushdown Automata Haniel Barbosa Readings for this lecture Chapter 2 of [Sipser 1996], 3rd edition. Section 2.2. Finite automaton 1 / 13
ECS 120: Theory of Computation UC Davis Phillip Rogaway February 16, Midterm Exam
 ECS 120: Theory of Computation Handout MT UC Davis Phillip Rogaway February 16, 2012 Midterm Exam Instructions: The exam has six pages, including this cover page, printed out two-sided (no more wasted
ECS 120: Theory of Computation Handout MT UC Davis Phillip Rogaway February 16, 2012 Midterm Exam Instructions: The exam has six pages, including this cover page, printed out two-sided (no more wasted
C6.2 Push-Down Automata
 Theory of Computer Science April 5, 2017 C6. Context-free Languages: Push-down Automata Theory of Computer Science C6. Context-free Languages: Push-down Automata Malte Helmert University of Basel April
Theory of Computer Science April 5, 2017 C6. Context-free Languages: Push-down Automata Theory of Computer Science C6. Context-free Languages: Push-down Automata Malte Helmert University of Basel April
Discrete Mathematics and Logic II. Regular Sets
 Discrete Mathematics and Logic II. Regular Sets SFWR ENG 2FA3 Ryszard Janicki Winter 24 Acknowledgments: Material based on Automata and Computability by Dexter C. Kozen (Chapter 4). Ryszard Janicki Discrete
Discrete Mathematics and Logic II. Regular Sets SFWR ENG 2FA3 Ryszard Janicki Winter 24 Acknowledgments: Material based on Automata and Computability by Dexter C. Kozen (Chapter 4). Ryszard Janicki Discrete
(pp ) PDAs and CFGs (Sec. 2.2)
 (pp. 117-124) PDAs and CFGs (Sec. 2.2) A language is context free iff all strings in L can be generated by some context free grammar Theorem 2.20: L is Context Free iff a PDA accepts it I.e. if L is context
(pp. 117-124) PDAs and CFGs (Sec. 2.2) A language is context free iff all strings in L can be generated by some context free grammar Theorem 2.20: L is Context Free iff a PDA accepts it I.e. if L is context
cse303 ELEMENTS OF THE THEORY OF COMPUTATION Professor Anita Wasilewska
 cse303 ELEMENTS OF THE THEORY OF COMPUTATION Professor Anita Wasilewska LECTURE 11 CHAPTER 3 CONTEXT-FREE LANGUAGES 1. Context Free Grammars 2. Pushdown Automata 3. Pushdown automata and context -free
cse303 ELEMENTS OF THE THEORY OF COMPUTATION Professor Anita Wasilewska LECTURE 11 CHAPTER 3 CONTEXT-FREE LANGUAGES 1. Context Free Grammars 2. Pushdown Automata 3. Pushdown automata and context -free
CS375: Logic and Theory of Computing
 CS375: Logic and Theory of Computing Fuhua (Frank) Cheng Department of Computer Science University of Kentucky 1 Tale of Contents: Week 1: Preliminaries (set alger relations, functions) (read Chapters
CS375: Logic and Theory of Computing Fuhua (Frank) Cheng Department of Computer Science University of Kentucky 1 Tale of Contents: Week 1: Preliminaries (set alger relations, functions) (read Chapters
Theory of Computation (II) Yijia Chen Fudan University
 Theory of Computation (II) Yijia Chen Fudan University Review A language L is a subset of strings over an alphabet Σ. Our goal is to identify those languages that can be recognized by one of the simplest
Theory of Computation (II) Yijia Chen Fudan University Review A language L is a subset of strings over an alphabet Σ. Our goal is to identify those languages that can be recognized by one of the simplest
Context Sensitive Grammar
 Context Sensitive Grammar Aparna S Vijayan Department of Computer Science and Automation December 2, 2011 Aparna S Vijayan (CSA) CSG December 2, 2011 1 / 12 Contents Aparna S Vijayan (CSA) CSG December
Context Sensitive Grammar Aparna S Vijayan Department of Computer Science and Automation December 2, 2011 Aparna S Vijayan (CSA) CSG December 2, 2011 1 / 12 Contents Aparna S Vijayan (CSA) CSG December
INSTITUTE OF AERONAUTICAL ENGINEERING
 INSTITUTE OF AERONAUTICAL ENGINEERING DUNDIGAL 500 043, HYDERABAD COMPUTER SCIENCE AND ENGINEERING TUTORIAL QUESTION BANK Course Name : FORMAL LANGUAGES AND AUTOMATA THEORY Course Code : A40509 Class :
INSTITUTE OF AERONAUTICAL ENGINEERING DUNDIGAL 500 043, HYDERABAD COMPUTER SCIENCE AND ENGINEERING TUTORIAL QUESTION BANK Course Name : FORMAL LANGUAGES AND AUTOMATA THEORY Course Code : A40509 Class :
CSE 105 THEORY OF COMPUTATION
 CSE 105 THEORY OF COMPUTATION Spring 2016 http://cseweb.ucsd.edu/classes/sp16/cse105-ab/ Today's learning goals Sipser Ch 2 Define push down automata Trace the computation of a push down automaton Design
CSE 105 THEORY OF COMPUTATION Spring 2016 http://cseweb.ucsd.edu/classes/sp16/cse105-ab/ Today's learning goals Sipser Ch 2 Define push down automata Trace the computation of a push down automaton Design
Homework 5 - Solution
 DCP3122 Introduction to Formal Languages, Spring 2015 Instructor: Prof. Wen-Guey Tzeng Homework 5 - Solution 5-May-2015 Due: 18-May-2015 1. Given Σ = {a, b, c}, find an NPDA that accepts L = {a n b n+m
DCP3122 Introduction to Formal Languages, Spring 2015 Instructor: Prof. Wen-Guey Tzeng Homework 5 - Solution 5-May-2015 Due: 18-May-2015 1. Given Σ = {a, b, c}, find an NPDA that accepts L = {a n b n+m
Notes for Comp 497 (454) Week 10
 Notes for Comp 497 (454) Week 10 Today we look at the last two chapters in Part II. Cohen presents some results concerning the two categories of language we have seen so far: Regular languages (RL). Context-free
Notes for Comp 497 (454) Week 10 Today we look at the last two chapters in Part II. Cohen presents some results concerning the two categories of language we have seen so far: Regular languages (RL). Context-free
AC68 FINITE AUTOMATA & FORMULA LANGUAGES DEC 2013
 Q.2 a. Prove by mathematical induction n 4 4n 2 is divisible by 3 for n 0. Basic step: For n = 0, n 3 n = 0 which is divisible by 3. Induction hypothesis: Let p(n) = n 3 n is divisible by 3. Induction
Q.2 a. Prove by mathematical induction n 4 4n 2 is divisible by 3 for n 0. Basic step: For n = 0, n 3 n = 0 which is divisible by 3. Induction hypothesis: Let p(n) = n 3 n is divisible by 3. Induction
CSE 211. Pushdown Automata. CSE 211 (Theory of Computation) Atif Hasan Rahman
 CSE 211 Pushdown Automata CSE 211 (Theory of Computation) Atif Hasan Rahman Lecturer Department of Computer Science and Engineering Bangladesh University of Engineering & Technology Adapted from slides
CSE 211 Pushdown Automata CSE 211 (Theory of Computation) Atif Hasan Rahman Lecturer Department of Computer Science and Engineering Bangladesh University of Engineering & Technology Adapted from slides
Chap. 7 Properties of Context-free Languages
 Chap. 7 Properties of Context-free Languages 7.1 Normal Forms for Context-free Grammars Context-free grammars A where A N, (N T). 0. Chomsky Normal Form A BC or A a except S where A, B, C N, a T. 1. Eliminating
Chap. 7 Properties of Context-free Languages 7.1 Normal Forms for Context-free Grammars Context-free grammars A where A N, (N T). 0. Chomsky Normal Form A BC or A a except S where A, B, C N, a T. 1. Eliminating
Finite Automata Theory and Formal Languages TMV027/DIT321 LP4 2018
 Finite Automata Theory and Formal Languages TMV027/DIT321 LP4 2018 Lecture 14 Ana Bove May 14th 2018 Recap: Context-free Grammars Simplification of grammars: Elimination of ǫ-productions; Elimination of
Finite Automata Theory and Formal Languages TMV027/DIT321 LP4 2018 Lecture 14 Ana Bove May 14th 2018 Recap: Context-free Grammars Simplification of grammars: Elimination of ǫ-productions; Elimination of
