Computability and Complexity
|
|
|
- Clyde Gardner
- 5 years ago
- Views:
Transcription
1 Computability and Complexity Rewriting Systems and Chomsky Grammars CAS 705 Ryszard Janicki Department of Computing and Software McMaster University Hamilton, Ontario, Canada Ryszard Janicki Computability and Complexity 1 / 48
2 Rewriting Systems: Idea Another view of computation. Each program instruction also rewrite one string into another! Ryszard Janicki Computability and Complexity 2 / 48
3 Rewriting Systems Denition A rewriting system is a tuple: S = (Σ, P), where: Σ is an alphabet (nite), P Σ Σ is a set of productions (nite). A production (u, v) P is usually written as u P v or u v, if P is clear from the context. Ryszard Janicki Computability and Complexity 3 / 48
4 Most Known Rewriting Systems Thue and semi-thue systems ( 1900) Post systems ( ) Markov algorithms (early 1950) Chomsky grammars ( 1958) context-free context-sensitive monotone general Lindenmayer systems (early 1970) Ryszard Janicki Computability and Complexity 4 / 48
5 Thue and semi-thue systems Denition A rewriting system S = (Σ, P) is a semi-thue system, if the following rewriting relation (rule) is used: w 1 P w 2 u v P. w 1 = xuy w 2 = xvy A sequence w 1, w 2,..., w n such that w i P w i+1 is called a derivation. The relation = P i=0 i (reexive and transitive closure of P ) is called a derivation relation. P A semi-thue system (Σ, P) is called a Thue system if P is symmetric. Sometimes, a semi-thue system is denes as S = (Σ, P, σ), where σ Σ + plays the role of initial string. Ryszard Janicki Computability and Complexity 5 / 48
6 Basic Problems and Example Example Basic problems for rewriting systems: the word problem: let x, y Σ, is it true that x y? the characterization problem: for which x, y Σ, x y holds? Σ = {A, C, E, I, L, M, N, O, P, R, T, W } P = {EAT AT, AT EAT, ATE A, A ATE, LATER LOW, LOW LATER, PAN PILLOW, PILLOW PAN, CARP ME, ME CARP} Ryszard Janicki Computability and Complexity 6 / 48
7 Context-Free Grammars: Intuitions The original motivation for context-free grammars was a description of a natural language, in particular, English. < sentence > < noun phrase >< verb phrase > < noun phrase > < adjective >< noun phrase > < noun phrase > < noun > < noun > boy < noun > girl < adjective > little < adjective > big < sentence > < noun phrase >< verb phrase > < adjective >< noun phrase >< verb phrase > big < noun phrase >< verb phrase > big < noun >< verb phrase > big girl < verb phrase >... Ryszard Janicki Computability and Complexity 7 / 48
8 < sentence > < noun-phrase >< verb-phrase > < noun-phrase > < cmplx-noun > < cmplx-noun >< prep-phrase > < verb-phrase > < cmplx-verb > < cmplx-verb >< prep-phrase > < prep-phrase > < prep >< cmplx-noun > < cmplx-noun > < article >< noun > < cmplx-verb > < verb >< verb >< noun-phrase > < article > a the < noun > boy girl ower < verb > touches likes sees < prep > with One can easily derive: a boy sees the boy sees a ower a girl with a ower likes a boy a ower with a boy sees a girl < s > < n-p >< v-p > < cmplx-n >< v-p > < article >< n >< v-p > a < n >< v-p > a boy < v-p > a boy < cmplx-v > a boy < verb > a boy sees Ryszard Janicki Computability and Complexity 8 / 48
9 Context-Free Grammars: Example < expr > < expr > + < expr > < expr > < expr > < expr > < expr > (< expr >) < expr > a < expr > b < expr > c < expr > < expr > < expr > (< expr >) < expr > (< expr >) a (< expr > + < expr >) a (< expr > +b) a (c + b) a Ryszard Janicki Computability and Complexity 9 / 48
10 Chomsky Grammars Denition A (Chomsky) grammar is a 4-tuple: G = (V, T, P, σ), where: V is a nite set of variables (non-terminals), T is a nite set of terminals, V T =, σ V is the start symbol (axiom), P (V T ) + (V T ) is a nite set of productions. For every (x, y) P we shall rather write x y. Ryszard Janicki Computability and Complexity 10 / 48
11 Direct Derivation, Derivation and Language Denition Let G = (V, T, P, σ) be a grammar. A direct derivation is a relation (V T ) (V T ) dened as follows, for all u, w (V T ) u w def. x y P. z, v (V T ). u = zxv w = zyv. A relation = i=0 i, or u w u = w ( u 1,..., u m, m > 0. u u 1... u m w), is called a derivation. Denition Let G = (V, T, P, σ) be a grammar. The set of sequences; L(G) = {x σ x x T } is said to be the language generated by G. Ryszard Janicki Computability and Complexity 11 / 48
12 Denition (Right-Linear Grammar) A grammar G = (V, T, P, σ) is called right-linear (or regular) if every production satises: x y P = ( A, B V. z T. x = A y = zb) ( A, B V. z T. x = A y = z) Let L RL denotes the set of all languages generated by right linear grammars. Denition (Strict Right-Linear Grammar) A grammar G = (V, T, P, σ) is called right-linear (or regular) if every production satises: x y P = ( A, B V. z T {ε}. x = A y = zb) ( A, B V. z T. x = A y = z) Let L RL denotes the set of all languages generated by right linear grammars. Ryszard Janicki Computability and Complexity 12 / 48
13 Right-Linear Grammars Proposition For every right linear grammar G, there exists a strictly right linear grammar G such that L(G) = L(G ). Proof. Note that: A a 1 a 2... a k B A a 1 A 1 A 1 a 2 A 2... A k 1 a k B which ends the proof. Ryszard Janicki Computability and Complexity 13 / 48
14 Context-Free and Context-Sensitive Grammars Denition A grammar G = (V, T, P, σ) is called context-free (or CF-grammar) if every production satises: x y P = A V. x = A Let L CF denotes the set of all languages generated by context-free grammars. Denition A grammar G = (V, T, P, σ) is called context-sensitive (or CS-grammar) if and only if production satises: x ε P = x = σ x y P. # σ (y) = 0 x y y ε P = u, v, t (V T ). A V. x = uav y = utv t 1 Let L CS denotes the set of all languages generated by context-sensitive grammars. Ryszard Janicki Computability and Complexity 14 / 48
15 Monotone Grammars Denition A grammar G = (V, T, P, σ) is called monotone if and only if production satises: x ε P = x = σ x y P. # σ (y) = 0 x y y ε P = x y Let L M denotes the set of all languages generated by monotone grammars. Corollary 1 Every context-sensitive grammar is monotone. 2 Not every context-free grammar is monotone. Ryszard Janicki Computability and Complexity 15 / 48
16 Right-Linear Grammars and Automata Theorem Proof. (sketch). L RG = L R. Main idea: σ of a grammar correspond to the initial state of an automaton, and Ryszard Janicki Computability and Complexity 16 / 48
17 Regular Languages vs Context-Free Languages Theorem Every regular language is context-free but not vice versa, i.e. L R L CF. Proof. Clearly every right linear grammar is context-free, i.e. L R L R. Consider the following context-free grammar: σ ε aσb It generates the language {a n b n n 0} which is not regular. Ryszard Janicki Computability and Complexity 17 / 48
18 Special Form of Monotone Grammars Lemma For every monotone grammar G there is a monotone grammar G such that every production of G is either of the form A 1... A n B 1... B m where A i, B i are non-terminals, or A a where A is a non-terminal and a is terminal. Proof. (sketch). aabab BAaaBB in G C a ABC a C c BAC a C a BB C a a in G C b b Ryszard Janicki Computability and Complexity 18 / 48
19 Context-Free Languages vs Monotone Languages Theorem For every monotone grammar G there exists a context-free grammar G such that: L(G) = L(G ). Proof. (sketch). Recall that for the context-free grammars we have the pattern: uaw utw where t 1. The idea of the construction is the following: ABABC BCBACBAC in G ABABC C 1 BABC C 1 BABC C 1 C 2 ABC C 1 C 2 ABC C 1 C 2 C 3 BC in G C 1 C 2 C 3 BC C 1 C 2 C 3 C 4 C C 1 C 2 C 3 C 4 C C 1 C 2 C 3 C 4 C 5 C 6 C 7 C 8 Ryszard Janicki Computability and Complexity 19 / 48
20 Proof. (sketch, continuation). C 1 C 2 C 3 C 4 C C 1 C 2 C 3 C 4 C 5 C 6 C 7 C 8 C 1 C 2 C 3 C 4 C 5 C 6 C 7 C 8 BC 2 C 3 C 4 C 5 C 6 C 7 C 8 BC 2 C 3 C 4 C 5 C 6 C 7 C 8 BC C 3 C 4 C 5 C 6 C 7 C 8 in G BC C 3 C 4 C 5 C 6 C 7 C 8 BC BC 4 C 5 C 6 C 7 C 8 BCBC 4 C 5 C 6 C 7 C 8 BCBAC 5 C 6 C 7 C 8 BCBAC 5 C 6 C 7 C 8 BCBAC C 6 C 7 C 8 BCBAC C 6 C 7 C 8 BCBAC BC 7 C 8 BCBACBC 7 C 8 BCBACBAC 8 BCBACBAC 8 BCBACBAC The above construction can easily be extended to the general case. Corollary L CF = L M. Ryszard Janicki Computability and Complexity 20 / 48
21 Chomsky Hierarchy Theorem L RG = L R L CF L CS = L M L G = L TM, where L TM is the set of all languages recognized by Turing Machines. The `red' relations have not been proven yet. Ryszard Janicki Computability and Complexity 21 / 48
22 CF-Grammars: Left-Most and Right-Most Derivations Consider the following CF-grammar: E E E E + E E E (E) a b c It is a shorthand for a more formal denition: V = {E}, σ = E, T = {a, b, c, +,,, (, ), } and P = {E E E, E E + E, E E E, E (E), E a, E b, E c}. Derivation: E E E (E) E (E) c (E + E) c (E + b) c (a + b) c Left-Most Derivation: E E E (E) E (E + E) E (a + E) E (a + b) E (a + b) c Right-Most Derivation: E E E E c (E) c (E + E) c (E + b) c (a + b) c Ryszard Janicki Computability and Complexity 22 / 48
23 Derivation Tree The following left-most derivation E E E (E) E (E + E) E (a + E) E (a + b) E (a + b) c is equivalent to the below derivation tree: Ryszard Janicki Computability and Complexity 23 / 48
24 Derivations and Derivation Trees Theorem Let G = (V, T, σ, P) be a CF-grammar. Then we have: 1 σ x there is a derivation tree in G that yields x, 2 σ x σ L x, 3 σ x σ R x, where L is a left-most derivation and R is a right-most derivation. Proof. By induction on the length of x. Ryszard Janicki Computability and Complexity 24 / 48
25 Ambiguity: Intuition (1) Consider the following grammar: E E + E E E a b c It has the following two dierent left-most derivations: 1 E E E E + E E a + E E a + b E a + b c 2 E E + E a + E a + E E a + b E a + b c The derivation (1) yields to the left tree below while the derivation (2) yields to the right tree below: (a + b) c a + (b c) PROBLEM! Ryszard Janicki Computability and Complexity 25 / 48
26 Ambiguity: Example of a Fix A possible x for the grammar from previous page: σ A + σ A σ A A a b c There is only one left-most derivation of the string a + b c, namely: σ A + σ a + σ a + A σ a + b σ a + b A a + b c a + (b c) Ryszard Janicki Computability and Complexity 26 / 48
27 Ambiguity and Inherent Ambiguity Denition A grammar G is ambiguous if the exists x L(G) such that are two dierent left-most derivations yielding x. We can replace left-most derivations with right-most derivations or derivation trees. A grammar G is unambiguous if it is not ambiguous. A context-free language L is inherently ambiguous if every grammar G such that L(G) = L is ambiguous. Proposition The language L = {a n b n c m d m n 1, m 1} {a n b m c m d n n 1, m 1} is inherently ambiguous. Ryszard Janicki Computability and Complexity 27 / 48
28 Building Better Grammars An arbitrary context-free grammar may have: useless symbols ε-productions of the form A ε unit productions of the form A B Ryszard Janicki Computability and Complexity 28 / 48
29 Useless Symbols σ aab aσ BaB a A aσa Ba b B BB BBa C aσa BcB a Type A The symbol B is useless since (B x) for all x T, so we cannot get rid of B. Type B The symbol C is useless since σ x implies C is not in x, so C cannot be generated starting from σ. The order of removing useless symbols is important! Type A symbols must be erased rst. Ryszard Janicki Computability and Complexity 29 / 48
30 Erasing Useless Symbols: Example σ AB σ a A a 1 Erase type A, i.e. the variable B σ a A a 2 Erase type B, i.e. the variable A σ a 1 Erase type B, i.e. none! σ AB σ a A a 2 Erase type A, i.e. the variable B σ a A a Ryszard Janicki Computability and Complexity 30 / 48
31 ε-productions σ σaa Aa aba A Ab aa ε ab B aa b ε σ σaa Aa aba a aa σa A Ab aa ab a b B aa b a Ryszard Janicki Computability and Complexity 31 / 48
32 ε-productions: Removal Intuition Rule: ε's are replaced with consequences of their applications. σ abab acc... A ε... B ε... C AB... σ abab = σ abbb aab abb ab σ acc = σ acc ac Ryszard Janicki Computability and Complexity 32 / 48
33 Unit Productions: Removal Intuition σ aaσb aba A aab a B B ab Ba b σ aaσb aba A aab a B ab Ba b B ab Ba b Ryszard Janicki Computability and Complexity 33 / 48
34 Better Grammars We can always get rid of: useless symbols ε-productions if ε / L(G) unit productions Ryszard Janicki Computability and Complexity 34 / 48
35 Useless Symbols: Formal Denition Denition Let G = (V, T, P, σ) be a CF-grammar. A symbol α V T is useful is there is a derivation: σ uαv w for some u, v (V T ) and w T. Otherwise α is useless. There are two aspects of usefulness: some terminal must be derivable from α α must occur in some string derivable from σ Ryszard Janicki Computability and Complexity 35 / 48
36 Removing Useless Symbols of Type A Lemma (A) Let G = (V, T, P, σ) be a CF-grammar. We can construct G = (V, T, P, σ) such that L(G) = L(G ) and A V. w T. A w. Proof. 1 If A x P and w T then A V. 2 If A x 1... x n P and x i T V then A V. We can repeat (2) until all possibilities are exhausted. Then P = {A x A V A x P}. Ryszard Janicki Computability and Complexity 36 / 48
37 Removing Useless Symbols of Type B Lemma (B) Let G = (V, T, P, σ) be a CF-grammar. We can construct G = (V, T, P, σ) such that L(G) = L(G ) and α V T. x, y (V T ). σ xαy. Proof. Clearly σ V. If A V and A x 1... x n P, then x i V = x i V and x i T = x i T. We repeat it until all cases are considered. Then P = {A x A V A x P x (V T ) }. Ryszard Janicki Computability and Complexity 37 / 48
38 Removing Useless Symbols of Type A+B Theorem After Lemma A followed by Lemma B, the new gramar does not have useless symbols. Note the the order Lemma A rst and Lemma B second is important. See page 30. Ryszard Janicki Computability and Complexity 38 / 48
39 Removing ε-productions Theorem Let G = (V, T, P, σ) be a CF-grammar. There is a CF-grammar G with no useless symbols and no ε-productions such that L(G ) = L(G) \ {ε}. Proof. (sketch). We remove all useless symbols rst. Then: (a) We add a new start variable σ 0 and σ 0 σ. (b) We remove A ε and 1 each B u 1 Au 2 A... Au n is replaced by B u 1 Ãu 2 Ã... Ãu n, where à is either A or ε. All cases must be included. For example: B uavaw is replaced by B uavaw uvaw uavw uvw. 2 B A is replaces by B A ε unless B ε was previously removed We repeat (1) and (2) until all ε-productions are removed. Ryszard Janicki Computability and Complexity 39 / 48
40 Removing Unit Productions Theorem Every context-free language without ε can be dened by a CF-grammar with no useless symbols, ε-productions, or unit productions. Proof. (sketch). Let G = (V, T, P, σ) be a CF-grammar such that ε / L(G) and G has no useless symbols or ε-productions. Dene G = (V, T, P, σ) where P = {A x P x / V } {A x B x P. x / V A B}, where means G derivation in the grammar G. Note that G does not have any unit production and L(G ) = L(G). Less formally the above construction can be described as follows: We remove A B and whenever B u appears, we add A u unless it was a unit production previously removed. We repeat it until all unit productions are eliminated. Ryszard Janicki Computability and Complexity 40 / 48
41 Chomsky Normal Form Denition A CF-grammar is in Chomsky Normal Form if each production is of the form A BC or A a, where A, B, C V and a T. Theorem Every CF-language without ε can be generated by a CF-grammar in Chomsky Normal Form. Proof. (sketch). Let G be a grammar that generates a given CF-language. We may assume that G does not have any useless symbols, ε and unit productions. We replace A u 1 u 2... u k, where u i V T, by A u 1 A 1 A 1 u 2 A 2 A i are new variables A k 2 u k1 u k We replace any u T by a new variable U and add U u. Ryszard Janicki Computability and Complexity 41 / 48
42 G : σ ba ab A baa aσ a = B abb bσ b σ ba implies σ C b A, C b b σ ab implies σ C a B, C a a A baa implies A C b C AA, C AA AA A aσ implies A C a σ, A a implies A a, = B abb implies B C a C BB, C BB BB B bσ implies B C b σ, B b implies B b, G : σ C b A C a B A C b C AA C a σ a B C a C BB C b σ b C AA AA C BB BB Ryszard Janicki Computability and Complexity 42 / 48
43 Greibach Normal Form Denition A CF-grammar is in Greibach Normal Form if each production is of the form A aa 1... A n or A a, where A, A i V and a T. Theorem Every CF-language without ε can be generated by a CF-grammar in Greibach Normal Form. Ryszard Janicki Computability and Complexity 43 / 48
44 Proof. (sketch). Let L be a CF-language and G = (V, T, P, σ) be a CF-grammar such that L = L(G). Assume G is in Chomsky Normal Form and V = {A 1,..., A m }. 1 We can eectively dene a new grammar G such that L(G ) = L(G) = L, and every production of G is of the form: A i A j x and i j or A i a. Note that if L = then there exists at least one k such that there is a production: A k A k x. 2 Every A k A k x can be replaced by the productions: B k x B k xb k A k αb k, for every A k α, α A k y 3 Now we have only productions of the form (a) A i A j x, i < j (b) A i aγ, a T (c) B i γ, γ (V {B 1,..., B i 1 }) We may now replace (using a nite number of substitutions) the above productions by Greibach productions (see the example next page). Ryszard Janicki Computability and Complexity 44 / 48
45 From Chomsky to Greibach: an Example A 1 A 2 A 3 A 2 A 3 A 1 b A 3 A 1 A 2 a Step 1. We replace A 3 A 1 A 2 by A 3 A 2 A 3 A 2, and next by A 3 A 3 A 1 A 3 A 2 ba 3 A 2. Clearly A 3 2 A G 3 A 1 A 3 A 2 and A 3 2 ba G 3 A 2. Thus we now have G with P of the form: A 1 A 2 A 3 A 2 A 3 A 1 b A 3 A 3 A 1 A 3 A }{{} 2 α=a 3 γ ba 3 A 2 }{{} α a }{{} α Ryszard Janicki Computability and Complexity 45 / 48
46 Step 2: The only `troublemaker' is A 3 A 3 A 1 A 3 A 2. It has to be replaced by: B 3 A 1 A 3 A 2 B 3 A 1 A 3 A 2 B 3 A 3 ba 3 A }{{} 2 B 3 α }{{} a α Thus we now have G with P of the form: B 3 A 1 A 2 A 3 A 2 A 3 A 1 b A 3 ba 3 A 2 B 3 ab 3 ba 3 A 2 a B 3 A 1 A 3 A 2 A 1 A 3 A 2 B 3 Note that L(G ) = L(G ) = L(G) = L. For example left A 3 G right A 3 G left left A 3 A 1 A 3 A 2 G A 3 A 1 A 3 A 2 A 1 A 3 A 2 G ba 3 A 1 A 3 A 2 A 1 A 3 A 2, right right ba 3 A 2 B 3 G ba 3 A 2 A 1 A 3 A 2 B 3 ba G 3A 1 A 3 A 2 A 1 A 3 A 2. Ryszard Janicki Computability and Complexity 46 / 48
47 Step 3: A 3 is now in Greibach Form. A 2 A 3 A 1 is not, so it has to be replaced by: A 2 ba 3 A 2 B 3 A 1 ab 3 A 1 ba 3 A 2 A 2 aa 1 b. A 1 A 2 A 3 is not in Greibach Form, so A 1 ba 3 A 2 B 3 A 1 A 3 ab 3 A 1 A 3 ba 3 A 2 A 1 A 3 aa 1 A 3 ba 3. At this point only B 3 A 1 A 3 A 2 A 1 A 3 A 2 B 3 is left, so: B 3 ba 3 A 2 B 3 A 1 A 3 A 3 A 2 ba 3 A 2 B 3 A 1 A 3 A 3 A 3 A 2 B 3 ab 3 A 1 A 3 A 3 A 2 ab 3 A 1 A 3 A 3 A 2 B 3 ba 3 A 2 A 1 A 3 A 3 A 2 ba 3 A 2 A 1 A 3 A 3 A 2 B 3 aa 1 A 3 A 3 A 2 aa 1 A 3 A 3 A 2 B 3 ba 3 A 3 A 2 ba 3 A 3 A 2 B 3 Ryszard Janicki Computability and Complexity 47 / 48
48 Popular Trick Greibach Form is only problematic when the rst symbol on the right hand side of a production is a variable like A BaBACc. When the rst symbol on the right hand side of a production is a terminal, for example A bcababa, the construction of a Graibach Form is almost trivial, we just replace each terminal a which is not the rst one by a variable C a and we add a production C a a. For example A bcababa is replaced by A bc c ABC a BA and C a a, C c c. Ryszard Janicki Computability and Complexity 48 / 48
Computability and Complexity
 Computability and Complexity Push-Down Automata CAS 705 Ryszard Janicki Department of Computing and Software McMaster University Hamilton, Ontario, Canada janicki@mcmaster.ca Ryszard Janicki Computability
Computability and Complexity Push-Down Automata CAS 705 Ryszard Janicki Department of Computing and Software McMaster University Hamilton, Ontario, Canada janicki@mcmaster.ca Ryszard Janicki Computability
Theory of Computation (II) Yijia Chen Fudan University
 Theory of Computation (II) Yijia Chen Fudan University Review A language L is a subset of strings over an alphabet Σ. Our goal is to identify those languages that can be recognized by one of the simplest
Theory of Computation (II) Yijia Chen Fudan University Review A language L is a subset of strings over an alphabet Σ. Our goal is to identify those languages that can be recognized by one of the simplest
CISC4090: Theory of Computation
 CISC4090: Theory of Computation Chapter 2 Context-Free Languages Courtesy of Prof. Arthur G. Werschulz Fordham University Department of Computer and Information Sciences Spring, 2014 Overview In Chapter
CISC4090: Theory of Computation Chapter 2 Context-Free Languages Courtesy of Prof. Arthur G. Werschulz Fordham University Department of Computer and Information Sciences Spring, 2014 Overview In Chapter
Computability and Complexity
 Computability and Complexity Decidability, Undecidability and Reducibility; Codes, Algorithms and Languages CAS 705 Ryszard Janicki Department of Computing and Software McMaster University Hamilton, Ontario,
Computability and Complexity Decidability, Undecidability and Reducibility; Codes, Algorithms and Languages CAS 705 Ryszard Janicki Department of Computing and Software McMaster University Hamilton, Ontario,
Computational Models - Lecture 4
 Computational Models - Lecture 4 Regular languages: The Myhill-Nerode Theorem Context-free Grammars Chomsky Normal Form Pumping Lemma for context free languages Non context-free languages: Examples Push
Computational Models - Lecture 4 Regular languages: The Myhill-Nerode Theorem Context-free Grammars Chomsky Normal Form Pumping Lemma for context free languages Non context-free languages: Examples Push
1. (a) Explain the procedure to convert Context Free Grammar to Push Down Automata.
 Code No: R09220504 R09 Set No. 2 II B.Tech II Semester Examinations,December-January, 2011-2012 FORMAL LANGUAGES AND AUTOMATA THEORY Computer Science And Engineering Time: 3 hours Max Marks: 75 Answer
Code No: R09220504 R09 Set No. 2 II B.Tech II Semester Examinations,December-January, 2011-2012 FORMAL LANGUAGES AND AUTOMATA THEORY Computer Science And Engineering Time: 3 hours Max Marks: 75 Answer
CISC 4090 Theory of Computation
 CISC 4090 Theory of Computation Context-Free Languages and Push Down Automata Professor Daniel Leeds dleeds@fordham.edu JMH 332 Languages: Regular and Beyond Regular: a b c b d e a Not-regular: c n bd
CISC 4090 Theory of Computation Context-Free Languages and Push Down Automata Professor Daniel Leeds dleeds@fordham.edu JMH 332 Languages: Regular and Beyond Regular: a b c b d e a Not-regular: c n bd
Definition: A grammar G = (V, T, P,S) is a context free grammar (cfg) if all productions in P have the form A x where
 Recitation 11 Notes Context Free Grammars Definition: A grammar G = (V, T, P,S) is a context free grammar (cfg) if all productions in P have the form A x A V, and x (V T)*. Examples Problem 1. Given the
Recitation 11 Notes Context Free Grammars Definition: A grammar G = (V, T, P,S) is a context free grammar (cfg) if all productions in P have the form A x A V, and x (V T)*. Examples Problem 1. Given the
The View Over The Horizon
 The View Over The Horizon enumerable decidable context free regular Context-Free Grammars An example of a context free grammar, G 1 : A 0A1 A B B # Terminology: Each line is a substitution rule or production.
The View Over The Horizon enumerable decidable context free regular Context-Free Grammars An example of a context free grammar, G 1 : A 0A1 A B B # Terminology: Each line is a substitution rule or production.
Computational Models - Lecture 3
 Slides modified by Benny Chor, based on original slides by Maurice Herlihy, Brown University. p. 1 Computational Models - Lecture 3 Equivalence of regular expressions and regular languages (lukewarm leftover
Slides modified by Benny Chor, based on original slides by Maurice Herlihy, Brown University. p. 1 Computational Models - Lecture 3 Equivalence of regular expressions and regular languages (lukewarm leftover
6.8 The Post Correspondence Problem
 6.8. THE POST CORRESPONDENCE PROBLEM 423 6.8 The Post Correspondence Problem The Post correspondence problem (due to Emil Post) is another undecidable problem that turns out to be a very helpful tool for
6.8. THE POST CORRESPONDENCE PROBLEM 423 6.8 The Post Correspondence Problem The Post correspondence problem (due to Emil Post) is another undecidable problem that turns out to be a very helpful tool for
Grammars and Context-free Languages; Chomsky Hierarchy
 Regular and Context-free Languages; Chomsky Hierarchy H. Geuvers Institute for Computing and Information Sciences Version: fall 2015 H. Geuvers Version: fall 2015 Huygens College 1 / 23 Outline Regular
Regular and Context-free Languages; Chomsky Hierarchy H. Geuvers Institute for Computing and Information Sciences Version: fall 2015 H. Geuvers Version: fall 2015 Huygens College 1 / 23 Outline Regular
COMP-330 Theory of Computation. Fall Prof. Claude Crépeau. Lec. 10 : Context-Free Grammars
 COMP-330 Theory of Computation Fall 2017 -- Prof. Claude Crépeau Lec. 10 : Context-Free Grammars COMP 330 Fall 2017: Lectures Schedule 1-2. Introduction 1.5. Some basic mathematics 2-3. Deterministic finite
COMP-330 Theory of Computation Fall 2017 -- Prof. Claude Crépeau Lec. 10 : Context-Free Grammars COMP 330 Fall 2017: Lectures Schedule 1-2. Introduction 1.5. Some basic mathematics 2-3. Deterministic finite
Computability and Complexity
 Computability and Complexity Sequences and Automata CAS 705 Ryszard Janicki Department of Computing and Software McMaster University Hamilton, Ontario, Canada janicki@mcmaster.ca Ryszard Janicki Computability
Computability and Complexity Sequences and Automata CAS 705 Ryszard Janicki Department of Computing and Software McMaster University Hamilton, Ontario, Canada janicki@mcmaster.ca Ryszard Janicki Computability
Context Free Languages (CFL) Language Recognizer A device that accepts valid strings. The FA are formalized types of language recognizer.
 Context Free Languages (CFL) Language Recognizer A device that accepts valid strings. The FA are formalized types of language recognizer. Language Generator: Context free grammars are language generators,
Context Free Languages (CFL) Language Recognizer A device that accepts valid strings. The FA are formalized types of language recognizer. Language Generator: Context free grammars are language generators,
CS5371 Theory of Computation. Lecture 7: Automata Theory V (CFG, CFL, CNF)
 CS5371 Theory of Computation Lecture 7: Automata Theory V (CFG, CFL, CNF) Announcement Homework 2 will be given soon (before Tue) Due date: Oct 31 (Tue), before class Midterm: Nov 3, (Fri), first hour
CS5371 Theory of Computation Lecture 7: Automata Theory V (CFG, CFL, CNF) Announcement Homework 2 will be given soon (before Tue) Due date: Oct 31 (Tue), before class Midterm: Nov 3, (Fri), first hour
60-354, Theory of Computation Fall Asish Mukhopadhyay School of Computer Science University of Windsor
 60-354, Theory of Computation Fall 2013 Asish Mukhopadhyay School of Computer Science University of Windsor Pushdown Automata (PDA) PDA = ε-nfa + stack Acceptance ε-nfa enters a final state or Stack is
60-354, Theory of Computation Fall 2013 Asish Mukhopadhyay School of Computer Science University of Windsor Pushdown Automata (PDA) PDA = ε-nfa + stack Acceptance ε-nfa enters a final state or Stack is
Homework 4 Solutions. 2. Find context-free grammars for the language L = {a n b m c k : k n + m}. (with n 0,
 Introduction to Formal Language, Fall 2016 Due: 21-Apr-2016 (Thursday) Instructor: Prof. Wen-Guey Tzeng Homework 4 Solutions Scribe: Yi-Ruei Chen 1. Find context-free grammars for the language L = {a n
Introduction to Formal Language, Fall 2016 Due: 21-Apr-2016 (Thursday) Instructor: Prof. Wen-Guey Tzeng Homework 4 Solutions Scribe: Yi-Ruei Chen 1. Find context-free grammars for the language L = {a n
Parsing. Context-Free Grammars (CFG) Laura Kallmeyer. Winter 2017/18. Heinrich-Heine-Universität Düsseldorf 1 / 26
 Parsing Context-Free Grammars (CFG) Laura Kallmeyer Heinrich-Heine-Universität Düsseldorf Winter 2017/18 1 / 26 Table of contents 1 Context-Free Grammars 2 Simplifying CFGs Removing useless symbols Eliminating
Parsing Context-Free Grammars (CFG) Laura Kallmeyer Heinrich-Heine-Universität Düsseldorf Winter 2017/18 1 / 26 Table of contents 1 Context-Free Grammars 2 Simplifying CFGs Removing useless symbols Eliminating
Theory of Computer Science
 Theory of Computer Science C1. Formal Languages and Grammars Malte Helmert University of Basel March 14, 2016 Introduction Example: Propositional Formulas from the logic part: Definition (Syntax of Propositional
Theory of Computer Science C1. Formal Languages and Grammars Malte Helmert University of Basel March 14, 2016 Introduction Example: Propositional Formulas from the logic part: Definition (Syntax of Propositional
SFWR ENG 2FA3. Solution to the Assignment #4
 SFWR ENG 2FA3. Solution to the Assignment #4 Total = 131, 100%= 115 The solutions below are often very detailed on purpose. Such level of details is not required from students solutions. Some questions
SFWR ENG 2FA3. Solution to the Assignment #4 Total = 131, 100%= 115 The solutions below are often very detailed on purpose. Such level of details is not required from students solutions. Some questions
Computational Models - Lecture 4 1
 Computational Models - Lecture 4 1 Handout Mode Iftach Haitner. Tel Aviv University. November 21, 2016 1 Based on frames by Benny Chor, Tel Aviv University, modifying frames by Maurice Herlihy, Brown University.
Computational Models - Lecture 4 1 Handout Mode Iftach Haitner. Tel Aviv University. November 21, 2016 1 Based on frames by Benny Chor, Tel Aviv University, modifying frames by Maurice Herlihy, Brown University.
(b) If G=({S}, {a}, {S SS}, S) find the language generated by G. [8+8] 2. Convert the following grammar to Greibach Normal Form G = ({A1, A2, A3},
![(b) If G=({S}, {a}, {S SS}, S) find the language generated by G. [8+8] 2. Convert the following grammar to Greibach Normal Form G = ({A1, A2, A3}, (b) If G=({S}, {a}, {S SS}, S) find the language generated by G. [8+8] 2. Convert the following grammar to Greibach Normal Form G = ({A1, A2, A3},](/thumbs/81/83182922.jpg) Code No: 07A50501 R07 Set No. 2 III B.Tech I Semester Examinations,MAY 2011 FORMAL LANGUAGES AND AUTOMATA THEORY Computer Science And Engineering Time: 3 hours Max Marks: 80 Answer any FIVE Questions All
Code No: 07A50501 R07 Set No. 2 III B.Tech I Semester Examinations,MAY 2011 FORMAL LANGUAGES AND AUTOMATA THEORY Computer Science And Engineering Time: 3 hours Max Marks: 80 Answer any FIVE Questions All
Context-Free Grammar
 Context-Free Grammar CFGs are more powerful than regular expressions. They are more powerful in the sense that whatever can be expressed using regular expressions can be expressed using context-free grammars,
Context-Free Grammar CFGs are more powerful than regular expressions. They are more powerful in the sense that whatever can be expressed using regular expressions can be expressed using context-free grammars,
CS 373: Theory of Computation. Fall 2010
 CS 373: Theory of Computation Gul Agha Mahesh Viswanathan Fall 2010 1 1 Normal Forms for CFG Normal Forms for Grammars It is typically easier to work with a context free language if given a CFG in a normal
CS 373: Theory of Computation Gul Agha Mahesh Viswanathan Fall 2010 1 1 Normal Forms for CFG Normal Forms for Grammars It is typically easier to work with a context free language if given a CFG in a normal
Theory of Computation - Module 3
 Theory of Computation - Module 3 Syllabus Context Free Grammar Simplification of CFG- Normal forms-chomsky Normal form and Greibach Normal formpumping lemma for Context free languages- Applications of
Theory of Computation - Module 3 Syllabus Context Free Grammar Simplification of CFG- Normal forms-chomsky Normal form and Greibach Normal formpumping lemma for Context free languages- Applications of
Computability and Complexity
 Computability and Complexity Non-determinism, Regular Expressions CAS 705 Ryszard Janicki Department of Computing and Software McMaster University Hamilton, Ontario, Canada janicki@mcmaster.ca Ryszard
Computability and Complexity Non-determinism, Regular Expressions CAS 705 Ryszard Janicki Department of Computing and Software McMaster University Hamilton, Ontario, Canada janicki@mcmaster.ca Ryszard
AC68 FINITE AUTOMATA & FORMULA LANGUAGES DEC 2013
 Q.2 a. Prove by mathematical induction n 4 4n 2 is divisible by 3 for n 0. Basic step: For n = 0, n 3 n = 0 which is divisible by 3. Induction hypothesis: Let p(n) = n 3 n is divisible by 3. Induction
Q.2 a. Prove by mathematical induction n 4 4n 2 is divisible by 3 for n 0. Basic step: For n = 0, n 3 n = 0 which is divisible by 3. Induction hypothesis: Let p(n) = n 3 n is divisible by 3. Induction
FLAC Context-Free Grammars
 FLAC Context-Free Grammars Klaus Sutner Carnegie Mellon Universality Fall 2017 1 Generating Languages Properties of CFLs Generation vs. Recognition 3 Turing machines can be used to check membership in
FLAC Context-Free Grammars Klaus Sutner Carnegie Mellon Universality Fall 2017 1 Generating Languages Properties of CFLs Generation vs. Recognition 3 Turing machines can be used to check membership in
Context-Free Grammars: Normal Forms
 Context-Free Grammars: Normal Forms Seungjin Choi Department of Computer Science and Engineering Pohang University of Science and Technology 77 Cheongam-ro, Nam-gu, Pohang 37673, Korea seungjin@postech.ac.kr
Context-Free Grammars: Normal Forms Seungjin Choi Department of Computer Science and Engineering Pohang University of Science and Technology 77 Cheongam-ro, Nam-gu, Pohang 37673, Korea seungjin@postech.ac.kr
Automata Theory Final Exam Solution 08:10-10:00 am Friday, June 13, 2008
 Automata Theory Final Exam Solution 08:10-10:00 am Friday, June 13, 2008 Name: ID #: This is a Close Book examination. Only an A4 cheating sheet belonging to you is acceptable. You can write your answers
Automata Theory Final Exam Solution 08:10-10:00 am Friday, June 13, 2008 Name: ID #: This is a Close Book examination. Only an A4 cheating sheet belonging to you is acceptable. You can write your answers
FORMAL LANGUAGES, AUTOMATA AND COMPUTABILITY
 15-453 FORMAL LANGUAGES, AUTOMATA AND COMPUTABILITY REVIEW for MIDTERM 1 THURSDAY Feb 6 Midterm 1 will cover everything we have seen so far The PROBLEMS will be from Sipser, Chapters 1, 2, 3 It will be
15-453 FORMAL LANGUAGES, AUTOMATA AND COMPUTABILITY REVIEW for MIDTERM 1 THURSDAY Feb 6 Midterm 1 will cover everything we have seen so far The PROBLEMS will be from Sipser, Chapters 1, 2, 3 It will be
Context-Free Grammars and Languages. Reading: Chapter 5
 Context-Free Grammars and Languages Reading: Chapter 5 1 Context-Free Languages The class of context-free languages generalizes the class of regular languages, i.e., every regular language is a context-free
Context-Free Grammars and Languages Reading: Chapter 5 1 Context-Free Languages The class of context-free languages generalizes the class of regular languages, i.e., every regular language is a context-free
C1.1 Introduction. Theory of Computer Science. Theory of Computer Science. C1.1 Introduction. C1.2 Alphabets and Formal Languages. C1.
 Theory of Computer Science March 20, 2017 C1. Formal Languages and Grammars Theory of Computer Science C1. Formal Languages and Grammars Malte Helmert University of Basel March 20, 2017 C1.1 Introduction
Theory of Computer Science March 20, 2017 C1. Formal Languages and Grammars Theory of Computer Science C1. Formal Languages and Grammars Malte Helmert University of Basel March 20, 2017 C1.1 Introduction
Chomsky and Greibach Normal Forms
 Chomsky and Greibach Normal Forms Teodor Rus rus@cs.uiowa.edu The University of Iowa, Department of Computer Science Computation Theory p.1/25 Simplifying a CFG It is often convenient to simplify CFG One
Chomsky and Greibach Normal Forms Teodor Rus rus@cs.uiowa.edu The University of Iowa, Department of Computer Science Computation Theory p.1/25 Simplifying a CFG It is often convenient to simplify CFG One
Automata Theory CS F-08 Context-Free Grammars
 Automata Theory CS411-2015F-08 Context-Free Grammars David Galles Department of Computer Science University of San Francisco 08-0: Context-Free Grammars Set of Terminals (Σ) Set of Non-Terminals Set of
Automata Theory CS411-2015F-08 Context-Free Grammars David Galles Department of Computer Science University of San Francisco 08-0: Context-Free Grammars Set of Terminals (Σ) Set of Non-Terminals Set of
Chomsky Normal Form and TURING MACHINES. TUESDAY Feb 4
 Chomsky Normal Form and TURING MACHINES TUESDAY Feb 4 CHOMSKY NORMAL FORM A context-free grammar is in Chomsky normal form if every rule is of the form: A BC A a S ε B and C aren t start variables a is
Chomsky Normal Form and TURING MACHINES TUESDAY Feb 4 CHOMSKY NORMAL FORM A context-free grammar is in Chomsky normal form if every rule is of the form: A BC A a S ε B and C aren t start variables a is
FORMAL LANGUAGES, AUTOMATA AND COMPUTABILITY
 15-453 FORMAL LANGUAGES, AUTOMATA AND COMPUTABILITY Chomsky Normal Form and TURING MACHINES TUESDAY Feb 4 CHOMSKY NORMAL FORM A context-free grammar is in Chomsky normal form if every rule is of the form:
15-453 FORMAL LANGUAGES, AUTOMATA AND COMPUTABILITY Chomsky Normal Form and TURING MACHINES TUESDAY Feb 4 CHOMSKY NORMAL FORM A context-free grammar is in Chomsky normal form if every rule is of the form:
Solutions to Problem Set 3
 V22.0453-001 Theory of Computation October 8, 2003 TA: Nelly Fazio Solutions to Problem Set 3 Problem 1 We have seen that a grammar where all productions are of the form: A ab, A c (where A, B non-terminals,
V22.0453-001 Theory of Computation October 8, 2003 TA: Nelly Fazio Solutions to Problem Set 3 Problem 1 We have seen that a grammar where all productions are of the form: A ab, A c (where A, B non-terminals,
Finite Automata Theory and Formal Languages TMV026/TMV027/DIT321 Responsible: Ana Bove
 Finite Automata Theory and Formal Languages TMV026/TMV027/DIT321 Responsible: Ana Bove Tuesday 28 of May 2013 Total: 60 points TMV027/DIT321 registration VT13 TMV026/DIT321 registration before VT13 Exam
Finite Automata Theory and Formal Languages TMV026/TMV027/DIT321 Responsible: Ana Bove Tuesday 28 of May 2013 Total: 60 points TMV027/DIT321 registration VT13 TMV026/DIT321 registration before VT13 Exam
Discrete Mathematics and Logic II. Regular Sets
 Discrete Mathematics and Logic II. Regular Sets SFWR ENG 2FA3 Ryszard Janicki Winter 24 Acknowledgments: Material based on Automata and Computability by Dexter C. Kozen (Chapter 4). Ryszard Janicki Discrete
Discrete Mathematics and Logic II. Regular Sets SFWR ENG 2FA3 Ryszard Janicki Winter 24 Acknowledgments: Material based on Automata and Computability by Dexter C. Kozen (Chapter 4). Ryszard Janicki Discrete
TAFL 1 (ECS-403) Unit- III. 3.1 Definition of CFG (Context Free Grammar) and problems. 3.2 Derivation. 3.3 Ambiguity in Grammar
 TAFL 1 (ECS-403) Unit- III 3.1 Definition of CFG (Context Free Grammar) and problems 3.2 Derivation 3.3 Ambiguity in Grammar 3.3.1 Inherent Ambiguity 3.3.2 Ambiguous to Unambiguous CFG 3.4 Simplification
TAFL 1 (ECS-403) Unit- III 3.1 Definition of CFG (Context Free Grammar) and problems 3.2 Derivation 3.3 Ambiguity in Grammar 3.3.1 Inherent Ambiguity 3.3.2 Ambiguous to Unambiguous CFG 3.4 Simplification
Lecture 12 Simplification of Context-Free Grammars and Normal Forms
 Lecture 12 Simplification of Context-Free Grammars and Normal Forms COT 4420 Theory of Computation Chapter 6 Normal Forms for CFGs 1. Chomsky Normal Form CNF Productions of form A BC A, B, C V A a a T
Lecture 12 Simplification of Context-Free Grammars and Normal Forms COT 4420 Theory of Computation Chapter 6 Normal Forms for CFGs 1. Chomsky Normal Form CNF Productions of form A BC A, B, C V A a a T
Outline. CS21 Decidability and Tractability. Machine view of FA. Machine view of FA. Machine view of FA. Machine view of FA.
 Outline CS21 Decidability and Tractability Lecture 5 January 16, 219 and Languages equivalence of NPDAs and CFGs non context-free languages January 16, 219 CS21 Lecture 5 1 January 16, 219 CS21 Lecture
Outline CS21 Decidability and Tractability Lecture 5 January 16, 219 and Languages equivalence of NPDAs and CFGs non context-free languages January 16, 219 CS21 Lecture 5 1 January 16, 219 CS21 Lecture
MA/CSSE 474 Theory of Computation
 MA/CSSE 474 Theory of Computation CFL Hierarchy CFL Decision Problems Your Questions? Previous class days' material Reading Assignments HW 12 or 13 problems Anything else I have included some slides online
MA/CSSE 474 Theory of Computation CFL Hierarchy CFL Decision Problems Your Questions? Previous class days' material Reading Assignments HW 12 or 13 problems Anything else I have included some slides online
CS375: Logic and Theory of Computing
 CS375: Logic and Theory of Computing Fuhua (Frank) Cheng Department of Computer Science University of Kentucky 1 Table of Contents: Week 1: Preliminaries (set algebra, relations, functions) (read Chapters
CS375: Logic and Theory of Computing Fuhua (Frank) Cheng Department of Computer Science University of Kentucky 1 Table of Contents: Week 1: Preliminaries (set algebra, relations, functions) (read Chapters
CS A Term 2009: Foundations of Computer Science. Homework 2. By Li Feng, Shweta Srivastava, and Carolina Ruiz.
 CS3133 - A Term 2009: Foundations of Computer Science Prof. Carolina Ruiz Homework 2 WPI By Li Feng, Shweta Srivastava, and Carolina Ruiz Chapter 4 Problem 1: (10 Points) Exercise 4.3 Solution 1: S is
CS3133 - A Term 2009: Foundations of Computer Science Prof. Carolina Ruiz Homework 2 WPI By Li Feng, Shweta Srivastava, and Carolina Ruiz Chapter 4 Problem 1: (10 Points) Exercise 4.3 Solution 1: S is
St.MARTIN S ENGINEERING COLLEGE Dhulapally, Secunderabad
 St.MARTIN S ENGINEERING COLLEGE Dhulapally, Secunderabad-500 014 Subject: FORMAL LANGUAGES AND AUTOMATA THEORY Class : CSE II PART A (SHORT ANSWER QUESTIONS) UNIT- I 1 Explain transition diagram, transition
St.MARTIN S ENGINEERING COLLEGE Dhulapally, Secunderabad-500 014 Subject: FORMAL LANGUAGES AND AUTOMATA THEORY Class : CSE II PART A (SHORT ANSWER QUESTIONS) UNIT- I 1 Explain transition diagram, transition
PUSHDOWN AUTOMATA (PDA)
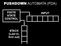 PUSHDOWN AUTOMATA (PDA) FINITE STATE CONTROL INPUT STACK (Last in, first out) input pop push ε,ε $ 0,ε 0 1,0 ε ε,$ ε 1,0 ε PDA that recognizes L = { 0 n 1 n n 0 } Definition: A (non-deterministic) PDA
PUSHDOWN AUTOMATA (PDA) FINITE STATE CONTROL INPUT STACK (Last in, first out) input pop push ε,ε $ 0,ε 0 1,0 ε ε,$ ε 1,0 ε PDA that recognizes L = { 0 n 1 n n 0 } Definition: A (non-deterministic) PDA
Finite Automata Theory and Formal Languages TMV027/DIT321 LP4 2018
 Finite Automata Theory and Formal Languages TMV027/DIT321 LP4 2018 Lecture 14 Ana Bove May 14th 2018 Recap: Context-free Grammars Simplification of grammars: Elimination of ǫ-productions; Elimination of
Finite Automata Theory and Formal Languages TMV027/DIT321 LP4 2018 Lecture 14 Ana Bove May 14th 2018 Recap: Context-free Grammars Simplification of grammars: Elimination of ǫ-productions; Elimination of
Section 1 (closed-book) Total points 30
 CS 454 Theory of Computation Fall 2011 Section 1 (closed-book) Total points 30 1. Which of the following are true? (a) a PDA can always be converted to an equivalent PDA that at each step pops or pushes
CS 454 Theory of Computation Fall 2011 Section 1 (closed-book) Total points 30 1. Which of the following are true? (a) a PDA can always be converted to an equivalent PDA that at each step pops or pushes
Computational Models - Lecture 4 1
 Computational Models - Lecture 4 1 Handout Mode Iftach Haitner and Yishay Mansour. Tel Aviv University. April 3/8, 2013 1 Based on frames by Benny Chor, Tel Aviv University, modifying frames by Maurice
Computational Models - Lecture 4 1 Handout Mode Iftach Haitner and Yishay Mansour. Tel Aviv University. April 3/8, 2013 1 Based on frames by Benny Chor, Tel Aviv University, modifying frames by Maurice
Einführung in die Computerlinguistik
 Einführung in die Computerlinguistik Context-Free Grammars (CFG) Laura Kallmeyer Heinrich-Heine-Universität Düsseldorf Summer 2016 1 / 22 CFG (1) Example: Grammar G telescope : Productions: S NP VP NP
Einführung in die Computerlinguistik Context-Free Grammars (CFG) Laura Kallmeyer Heinrich-Heine-Universität Düsseldorf Summer 2016 1 / 22 CFG (1) Example: Grammar G telescope : Productions: S NP VP NP
CISC 4090 Theory of Computation
 CISC 4090 Theory of Computation Context-Free Languages and Push Down Automata Professor Daniel Leeds dleeds@fordham.edu JMH 332 Languages: Regular and Beyond Regular: Captured by Regular Operations a b
CISC 4090 Theory of Computation Context-Free Languages and Push Down Automata Professor Daniel Leeds dleeds@fordham.edu JMH 332 Languages: Regular and Beyond Regular: Captured by Regular Operations a b
CS311 Computational Structures More about PDAs & Context-Free Languages. Lecture 9. Andrew P. Black Andrew Tolmach
 CS311 Computational Structures More about PDAs & Context-Free Languages Lecture 9 Andrew P. Black Andrew Tolmach 1 Three important results 1. Any CFG can be simulated by a PDA 2. Any PDA can be simulated
CS311 Computational Structures More about PDAs & Context-Free Languages Lecture 9 Andrew P. Black Andrew Tolmach 1 Three important results 1. Any CFG can be simulated by a PDA 2. Any PDA can be simulated
Linear conjunctive languages are closed under complement
 Linear conjunctive languages are closed under complement Alexander Okhotin okhotin@cs.queensu.ca Technical report 2002-455 Department of Computing and Information Science, Queen s University, Kingston,
Linear conjunctive languages are closed under complement Alexander Okhotin okhotin@cs.queensu.ca Technical report 2002-455 Department of Computing and Information Science, Queen s University, Kingston,
What we have done so far
 What we have done so far DFAs and regular languages NFAs and their equivalence to DFAs Regular expressions. Regular expressions capture exactly regular languages: Construct a NFA from a regular expression.
What we have done so far DFAs and regular languages NFAs and their equivalence to DFAs Regular expressions. Regular expressions capture exactly regular languages: Construct a NFA from a regular expression.
Undecidable Problems and Reducibility
 University of Georgia Fall 2014 Reducibility We show a problem decidable/undecidable by reducing it to another problem. One type of reduction: mapping reduction. Definition Let A, B be languages over Σ.
University of Georgia Fall 2014 Reducibility We show a problem decidable/undecidable by reducing it to another problem. One type of reduction: mapping reduction. Definition Let A, B be languages over Σ.
Context Free Grammars
 Automata and Formal Languages Context Free Grammars Sipser pages 101-111 Lecture 11 Tim Sheard 1 Formal Languages 1. Context free languages provide a convenient notation for recursive description of languages.
Automata and Formal Languages Context Free Grammars Sipser pages 101-111 Lecture 11 Tim Sheard 1 Formal Languages 1. Context free languages provide a convenient notation for recursive description of languages.
Theory of Computation
 Thomas Zeugmann Hokkaido University Laboratory for Algorithmics http://www-alg.ist.hokudai.ac.jp/ thomas/toc/ Lecture 3: Finite State Automata Motivation In the previous lecture we learned how to formalize
Thomas Zeugmann Hokkaido University Laboratory for Algorithmics http://www-alg.ist.hokudai.ac.jp/ thomas/toc/ Lecture 3: Finite State Automata Motivation In the previous lecture we learned how to formalize
cse303 ELEMENTS OF THE THEORY OF COMPUTATION Professor Anita Wasilewska
 cse303 ELEMENTS OF THE THEORY OF COMPUTATION Professor Anita Wasilewska LECTURE 14 SMALL REVIEW FOR FINAL SOME Y/N QUESTIONS Q1 Given Σ =, there is L over Σ Yes: = {e} and L = {e} Σ Q2 There are uncountably
cse303 ELEMENTS OF THE THEORY OF COMPUTATION Professor Anita Wasilewska LECTURE 14 SMALL REVIEW FOR FINAL SOME Y/N QUESTIONS Q1 Given Σ =, there is L over Σ Yes: = {e} and L = {e} Σ Q2 There are uncountably
Context Free Languages. Automata Theory and Formal Grammars: Lecture 6. Languages That Are Not Regular. Non-Regular Languages
 Context Free Languages Automata Theory and Formal Grammars: Lecture 6 Context Free Languages Last Time Decision procedures for FAs Minimum-state DFAs Today The Myhill-Nerode Theorem The Pumping Lemma Context-free
Context Free Languages Automata Theory and Formal Grammars: Lecture 6 Context Free Languages Last Time Decision procedures for FAs Minimum-state DFAs Today The Myhill-Nerode Theorem The Pumping Lemma Context-free
CPS 220 Theory of Computation
 CPS 22 Theory of Computation Review - Regular Languages RL - a simple class of languages that can be represented in two ways: 1 Machine description: Finite Automata are machines with a finite number of
CPS 22 Theory of Computation Review - Regular Languages RL - a simple class of languages that can be represented in two ways: 1 Machine description: Finite Automata are machines with a finite number of
Context Free Languages and Grammars
 Algorithms & Models of Computation CS/ECE 374, Fall 2017 Context Free Languages and Grammars Lecture 7 Tuesday, September 19, 2017 Sariel Har-Peled (UIUC) CS374 1 Fall 2017 1 / 36 What stack got to do
Algorithms & Models of Computation CS/ECE 374, Fall 2017 Context Free Languages and Grammars Lecture 7 Tuesday, September 19, 2017 Sariel Har-Peled (UIUC) CS374 1 Fall 2017 1 / 36 What stack got to do
Harvard CS 121 and CSCI E-207 Lecture 10: CFLs: PDAs, Closure Properties, and Non-CFLs
 Harvard CS 121 and CSCI E-207 Lecture 10: CFLs: PDAs, Closure Properties, and Non-CFLs Harry Lewis October 8, 2013 Reading: Sipser, pp. 119-128. Pushdown Automata (review) Pushdown Automata = Finite automaton
Harvard CS 121 and CSCI E-207 Lecture 10: CFLs: PDAs, Closure Properties, and Non-CFLs Harry Lewis October 8, 2013 Reading: Sipser, pp. 119-128. Pushdown Automata (review) Pushdown Automata = Finite automaton
COSE212: Programming Languages. Lecture 1 Inductive Definitions (1)
 COSE212: Programming Languages Lecture 1 Inductive Definitions (1) Hakjoo Oh 2017 Fall Hakjoo Oh COSE212 2017 Fall, Lecture 1 September 4, 2017 1 / 9 Inductive Definitions Inductive definition (induction)
COSE212: Programming Languages Lecture 1 Inductive Definitions (1) Hakjoo Oh 2017 Fall Hakjoo Oh COSE212 2017 Fall, Lecture 1 September 4, 2017 1 / 9 Inductive Definitions Inductive definition (induction)
Pushdown Automata. Reading: Chapter 6
 Pushdown Automata Reading: Chapter 6 1 Pushdown Automata (PDA) Informally: A PDA is an NFA-ε with a infinite stack. Transitions are modified to accommodate stack operations. Questions: What is a stack?
Pushdown Automata Reading: Chapter 6 1 Pushdown Automata (PDA) Informally: A PDA is an NFA-ε with a infinite stack. Transitions are modified to accommodate stack operations. Questions: What is a stack?
Power of controlled insertion and deletion
 Power of controlled insertion and deletion Lila Kari Academy of Finland and Department of Mathematics 1 University of Turku 20500 Turku Finland Abstract The paper investigates classes of languages obtained
Power of controlled insertion and deletion Lila Kari Academy of Finland and Department of Mathematics 1 University of Turku 20500 Turku Finland Abstract The paper investigates classes of languages obtained
Harvard CS 121 and CSCI E-207 Lecture 12: General Context-Free Recognition
 Harvard CS 121 and CSCI E-207 Lecture 12: General Context-Free Recognition Salil Vadhan October 11, 2012 Reading: Sipser, Section 2.3 and Section 2.1 (material on Chomsky Normal Form). Pumping Lemma for
Harvard CS 121 and CSCI E-207 Lecture 12: General Context-Free Recognition Salil Vadhan October 11, 2012 Reading: Sipser, Section 2.3 and Section 2.1 (material on Chomsky Normal Form). Pumping Lemma for
INSTITUTE OF AERONAUTICAL ENGINEERING
 INSTITUTE OF AERONAUTICAL ENGINEERING DUNDIGAL 500 043, HYDERABAD COMPUTER SCIENCE AND ENGINEERING TUTORIAL QUESTION BANK Course Name : FORMAL LANGUAGES AND AUTOMATA THEORY Course Code : A40509 Class :
INSTITUTE OF AERONAUTICAL ENGINEERING DUNDIGAL 500 043, HYDERABAD COMPUTER SCIENCE AND ENGINEERING TUTORIAL QUESTION BANK Course Name : FORMAL LANGUAGES AND AUTOMATA THEORY Course Code : A40509 Class :
Theory of Computation Turing Machine and Pushdown Automata
 Theory of Computation Turing Machine and Pushdown Automata 1. What is a Turing Machine? A Turing Machine is an accepting device which accepts the languages (recursively enumerable set) generated by type
Theory of Computation Turing Machine and Pushdown Automata 1. What is a Turing Machine? A Turing Machine is an accepting device which accepts the languages (recursively enumerable set) generated by type
CMSC 330: Organization of Programming Languages. Theory of Regular Expressions Finite Automata
 : Organization of Programming Languages Theory of Regular Expressions Finite Automata Previous Course Review {s s defined} means the set of string s such that s is chosen or defined as given s A means
: Organization of Programming Languages Theory of Regular Expressions Finite Automata Previous Course Review {s s defined} means the set of string s such that s is chosen or defined as given s A means
The Pumping Lemma for Context Free Grammars
 The Pumping Lemma for Context Free Grammars Chomsky Normal Form Chomsky Normal Form (CNF) is a simple and useful form of a CFG Every rule of a CNF grammar is in the form A BC A a Where a is any terminal
The Pumping Lemma for Context Free Grammars Chomsky Normal Form Chomsky Normal Form (CNF) is a simple and useful form of a CFG Every rule of a CNF grammar is in the form A BC A a Where a is any terminal
CS 133 : Automata Theory and Computability
 CS 133 : Automata Theory and Computability Lecture Slides 1 Regular Languages and Finite Automata Nestine Hope S. Hernandez Algorithms and Complexity Laboratory Department of Computer Science University
CS 133 : Automata Theory and Computability Lecture Slides 1 Regular Languages and Finite Automata Nestine Hope S. Hernandez Algorithms and Complexity Laboratory Department of Computer Science University
1.[3] Give an unambiguous grammar that generates the set of all regular expressions on Ó = {a,b}. Justify your construction.
![1.[3] Give an unambiguous grammar that generates the set of all regular expressions on Ó = {a,b}. Justify your construction. 1.[3] Give an unambiguous grammar that generates the set of all regular expressions on Ó = {a,b}. Justify your construction.](/thumbs/78/78529386.jpg) CAS 705. Sample solutions to the assignment 2 (many questions have more than one solutions). Total of this assignment is 135 pts. Each assignment is worth 25%. 1.[3] Give an unambiguous grammar that generates
CAS 705. Sample solutions to the assignment 2 (many questions have more than one solutions). Total of this assignment is 135 pts. Each assignment is worth 25%. 1.[3] Give an unambiguous grammar that generates
Theory of Computation
 Thomas Zeugmann Hokkaido University Laboratory for Algorithmics http://www-alg.ist.hokudai.ac.jp/ thomas/toc/ Lecture 10: CF, PDAs and Beyond Greibach Normal Form I We want to show that all context-free
Thomas Zeugmann Hokkaido University Laboratory for Algorithmics http://www-alg.ist.hokudai.ac.jp/ thomas/toc/ Lecture 10: CF, PDAs and Beyond Greibach Normal Form I We want to show that all context-free
How to Pop a Deep PDA Matters
 How to Pop a Deep PDA Matters Peter Leupold Department of Mathematics, Faculty of Science Kyoto Sangyo University Kyoto 603-8555, Japan email:leupold@cc.kyoto-su.ac.jp Abstract Deep PDA are push-down automata
How to Pop a Deep PDA Matters Peter Leupold Department of Mathematics, Faculty of Science Kyoto Sangyo University Kyoto 603-8555, Japan email:leupold@cc.kyoto-su.ac.jp Abstract Deep PDA are push-down automata
MTH401A Theory of Computation. Lecture 17
 MTH401A Theory of Computation Lecture 17 Chomsky Normal Form for CFG s Chomsky Normal Form for CFG s For every context free language, L, the language L {ε} has a grammar in which every production looks
MTH401A Theory of Computation Lecture 17 Chomsky Normal Form for CFG s Chomsky Normal Form for CFG s For every context free language, L, the language L {ε} has a grammar in which every production looks
download instant at Assume that (w R ) R = w for all strings w Σ of length n or less.
 Chapter 2 Languages 3. We prove, by induction on the length of the string, that w = (w R ) R for every string w Σ. Basis: The basis consists of the null string. In this case, (λ R ) R = (λ) R = λ as desired.
Chapter 2 Languages 3. We prove, by induction on the length of the string, that w = (w R ) R for every string w Σ. Basis: The basis consists of the null string. In this case, (λ R ) R = (λ) R = λ as desired.
Theory of Computation
 Fall 2002 (YEN) Theory of Computation Midterm Exam. Name:... I.D.#:... 1. (30 pts) True or false (mark O for true ; X for false ). (Score=Max{0, Right- 1 2 Wrong}.) (1) X... If L 1 is regular and L 2 L
Fall 2002 (YEN) Theory of Computation Midterm Exam. Name:... I.D.#:... 1. (30 pts) True or false (mark O for true ; X for false ). (Score=Max{0, Right- 1 2 Wrong}.) (1) X... If L 1 is regular and L 2 L
REGular and Context-Free Grammars
 REGular and Context-Free Grammars Nicholas Mainardi 1 Dipartimento di Elettronica e Informazione Politecnico di Milano nicholas.mainardi@polimi.it March 26, 2018 1 Partly Based on Alessandro Barenghi s
REGular and Context-Free Grammars Nicholas Mainardi 1 Dipartimento di Elettronica e Informazione Politecnico di Milano nicholas.mainardi@polimi.it March 26, 2018 1 Partly Based on Alessandro Barenghi s
Chapter 3. Regular grammars
 Chapter 3 Regular grammars 59 3.1 Introduction Other view of the concept of language: not the formalization of the notion of effective procedure, but set of words satisfying a given set of rules Origin
Chapter 3 Regular grammars 59 3.1 Introduction Other view of the concept of language: not the formalization of the notion of effective procedure, but set of words satisfying a given set of rules Origin
CSE 105 Homework 1 Due: Monday October 9, Instructions. should be on each page of the submission.
 CSE 5 Homework Due: Monday October 9, 7 Instructions Upload a single file to Gradescope for each group. should be on each page of the submission. All group members names and PIDs Your assignments in this
CSE 5 Homework Due: Monday October 9, 7 Instructions Upload a single file to Gradescope for each group. should be on each page of the submission. All group members names and PIDs Your assignments in this
Concordia University Department of Computer Science & Software Engineering
 Concordia University Department of Computer Science & Software Engineering COMP 335/4 Theoretical Computer Science Winter 2015 Assignment 3 1. In each case, what language is generated by CFG s below. Justify
Concordia University Department of Computer Science & Software Engineering COMP 335/4 Theoretical Computer Science Winter 2015 Assignment 3 1. In each case, what language is generated by CFG s below. Justify
CS 121, Section 2. Week of September 16, 2013
 CS 121, Section 2 Week of September 16, 2013 1 Concept Review 1.1 Overview In the past weeks, we have examined the finite automaton, a simple computational model with limited memory. We proved that DFAs,
CS 121, Section 2 Week of September 16, 2013 1 Concept Review 1.1 Overview In the past weeks, we have examined the finite automaton, a simple computational model with limited memory. We proved that DFAs,
Theory of Computation (Classroom Practice Booklet Solutions)
 Theory of Computation (Classroom Practice Booklet Solutions) 1. Finite Automata & Regular Sets 01. Ans: (a) & (c) Sol: (a) The reversal of a regular set is regular as the reversal of a regular expression
Theory of Computation (Classroom Practice Booklet Solutions) 1. Finite Automata & Regular Sets 01. Ans: (a) & (c) Sol: (a) The reversal of a regular set is regular as the reversal of a regular expression
CPSC 313 Introduction to Computability
 CPSC 313 Introduction to Computability Grammars in Chomsky Normal Form (Cont d) (Sipser, pages 109-111 (3 rd ed) and 107-109 (2 nd ed)) Renate Scheidler Fall 2018 Chomsky Normal Form A context-free grammar
CPSC 313 Introduction to Computability Grammars in Chomsky Normal Form (Cont d) (Sipser, pages 109-111 (3 rd ed) and 107-109 (2 nd ed)) Renate Scheidler Fall 2018 Chomsky Normal Form A context-free grammar
Formal Definition of a Finite Automaton. August 26, 2013
 August 26, 2013 Why a formal definition? A formal definition is precise: - It resolves any uncertainties about what is allowed in a finite automaton such as the number of accept states and number of transitions
August 26, 2013 Why a formal definition? A formal definition is precise: - It resolves any uncertainties about what is allowed in a finite automaton such as the number of accept states and number of transitions
UNIT II REGULAR LANGUAGES
 1 UNIT II REGULAR LANGUAGES Introduction: A regular expression is a way of describing a regular language. The various operations are closure, union and concatenation. We can also find the equivalent regular
1 UNIT II REGULAR LANGUAGES Introduction: A regular expression is a way of describing a regular language. The various operations are closure, union and concatenation. We can also find the equivalent regular
Computational Models: Class 5
 Computational Models: Class 5 Benny Chor School of Computer Science Tel Aviv University March 27, 2019 Based on slides by Maurice Herlihy, Brown University, and modifications by Iftach Haitner and Yishay
Computational Models: Class 5 Benny Chor School of Computer Science Tel Aviv University March 27, 2019 Based on slides by Maurice Herlihy, Brown University, and modifications by Iftach Haitner and Yishay
AC68 FINITE AUTOMATA & FORMULA LANGUAGES JUNE 2014
 Q.2 a. Show by using Mathematical Induction that n i= 1 i 2 n = ( n + 1) ( 2 n + 1) 6 b. Define language. Let = {0; 1} denote an alphabet. Enumerate five elements of the following languages: (i) Even binary
Q.2 a. Show by using Mathematical Induction that n i= 1 i 2 n = ( n + 1) ( 2 n + 1) 6 b. Define language. Let = {0; 1} denote an alphabet. Enumerate five elements of the following languages: (i) Even binary
Sheet 1-8 Dr. Mostafa Aref Format By : Mostafa Sayed
 Sheet -8 Dr. Mostafa Aref Format By : Mostafa Sayed 09 Introduction Assignment. For = {a, } a) Write 0 strings of the following languages i) All strings with no more than one a,,, a, a, a, a, a, a, a ii)
Sheet -8 Dr. Mostafa Aref Format By : Mostafa Sayed 09 Introduction Assignment. For = {a, } a) Write 0 strings of the following languages i) All strings with no more than one a,,, a, a, a, a, a, a, a ii)
Introduction to Formal Languages, Automata and Computability p.1/42
 Introduction to Formal Languages, Automata and Computability Pushdown Automata K. Krithivasan and R. Rama Introduction to Formal Languages, Automata and Computability p.1/42 Introduction We have considered
Introduction to Formal Languages, Automata and Computability Pushdown Automata K. Krithivasan and R. Rama Introduction to Formal Languages, Automata and Computability p.1/42 Introduction We have considered
Foundations of Informatics: a Bridging Course
 Foundations of Informatics: a Bridging Course Week 3: Formal Languages and Semantics Thomas Noll Lehrstuhl für Informatik 2 RWTH Aachen University noll@cs.rwth-aachen.de http://www.b-it-center.de/wob/en/view/class211_id948.html
Foundations of Informatics: a Bridging Course Week 3: Formal Languages and Semantics Thomas Noll Lehrstuhl für Informatik 2 RWTH Aachen University noll@cs.rwth-aachen.de http://www.b-it-center.de/wob/en/view/class211_id948.html
Author: Vivek Kulkarni ( )
 Author: Vivek Kulkarni ( vivek_kulkarni@yahoo.com ) Chapter-3: Regular Expressions Solutions for Review Questions @ Oxford University Press 2013. All rights reserved. 1 Q.1 Define the following and give
Author: Vivek Kulkarni ( vivek_kulkarni@yahoo.com ) Chapter-3: Regular Expressions Solutions for Review Questions @ Oxford University Press 2013. All rights reserved. 1 Q.1 Define the following and give
Theory Of Computation UNIT-II
 Regular Expressions and Context Free Grammars: Regular expression formalism- equivalence with finite automata-regular sets and closure properties- pumping lemma for regular languages- decision algorithms
Regular Expressions and Context Free Grammars: Regular expression formalism- equivalence with finite automata-regular sets and closure properties- pumping lemma for regular languages- decision algorithms
Suppose h maps number and variables to ɛ, and opening parenthesis to 0 and closing parenthesis
 1 Introduction Parenthesis Matching Problem Describe the set of arithmetic expressions with correctly matched parenthesis. Arithmetic expressions with correctly matched parenthesis cannot be described
1 Introduction Parenthesis Matching Problem Describe the set of arithmetic expressions with correctly matched parenthesis. Arithmetic expressions with correctly matched parenthesis cannot be described
Languages. Languages. An Example Grammar. Grammars. Suppose we have an alphabet V. Then we can write:
 Languages A language is a set (usually infinite) of strings, also known as sentences Each string consists of a sequence of symbols taken from some alphabet An alphabet, V, is a finite set of symbols, e.g.
Languages A language is a set (usually infinite) of strings, also known as sentences Each string consists of a sequence of symbols taken from some alphabet An alphabet, V, is a finite set of symbols, e.g.
Lecture Notes On THEORY OF COMPUTATION MODULE -1 UNIT - 2
 BIJU PATNAIK UNIVERSITY OF TECHNOLOGY, ODISHA Lecture Notes On THEORY OF COMPUTATION MODULE -1 UNIT - 2 Prepared by, Dr. Subhendu Kumar Rath, BPUT, Odisha. UNIT 2 Structure NON-DETERMINISTIC FINITE AUTOMATA
BIJU PATNAIK UNIVERSITY OF TECHNOLOGY, ODISHA Lecture Notes On THEORY OF COMPUTATION MODULE -1 UNIT - 2 Prepared by, Dr. Subhendu Kumar Rath, BPUT, Odisha. UNIT 2 Structure NON-DETERMINISTIC FINITE AUTOMATA
ECS 120: Theory of Computation UC Davis Phillip Rogaway February 16, Midterm Exam
 ECS 120: Theory of Computation Handout MT UC Davis Phillip Rogaway February 16, 2012 Midterm Exam Instructions: The exam has six pages, including this cover page, printed out two-sided (no more wasted
ECS 120: Theory of Computation Handout MT UC Davis Phillip Rogaway February 16, 2012 Midterm Exam Instructions: The exam has six pages, including this cover page, printed out two-sided (no more wasted
