Chapter 7 Channel Capacity and Coding

Transcription

1 Wreless Informaton Transmsson System Lab. Chapter 7 Channel Capacty and Codng Insttute of Communcatons Engneerng atonal Sun Yat-sen Unversty

2 Contents 7. Channel models and channel capacty 7.. Channel models Bnary symmetrc channel Dscrete memoryless channels Dscrete-nput, contnuous-output channel Waveform channels 7.. Channel capacty

3 Introducton In chapter 5, we demonstrate that orthogonal sgnalng waveforms allow us to make the probablty of error arbtrarly small by lettng the number of waveforms M, provded that the SR per bt γ b -.6dB. Thus, we can operate at the capacty of the addtve whte Gaussan nose channel n the lmt as the bandwdth expanson factor B e =W/R. Ths s a heavy prce to pay, because B e grows exponentally wth the block length k. Such neffcent use of channel bandwdth s hghly undesrable. 3

4 Introducton Code waveforms offer the potental for greater bandwdth effcency than orthogonal M-ary waveforms snce the bandwdth expanson factor that grows only lnearly wth k. We shall observe that, n general, coded waveforms offer performance advantages not only n power-lmted applcatons where R/W <, but also n bandwdthlmted systems where R/W >. 4

5 7.. Channel Models Bnary symmetrc channel (BSC) If the channel nose and other dsturbances cause statstcally ndependent errors n the transmtted bnary sequence wth average probablty p, then ( = X = ) = P( Y = X = ) = p ( = X = ) = P( Y = X = ) = p P Y P Y 5

6 7.. Channel Models Dscrete memoryless channels (DMC) BSC s a specal case of a more general dscrete-nput, dscrete-output channel. Output symbols from the channel encoder are q-ary symbols,.e., X={x, x,, x q- }. Output of the detector conssts of Q-ary symbols, where Q M= q. If the channel and modulaton are memoryless, we have a set of qq condtonal probabltes: P Y = y X = x P y x ( ) ( ) where =,,,Q- and j=,,,q-. Such a channel s called a dscrete memoryless channel (DMC). 6 j j

7 7.. Channel Models Dscrete memoryless channels (DMC) Input u,u,,u n Output: v,v,,v n The condtonal probablty s gven by: ( = v, Y = v,...,y = v X = u,..., X = u ) P Y = n k = ( = v X = u ) P Y k n In general, the condtonal probabltes P(y j x ) can be arranged n the matrx form P=[p j ], called probablty transton matrx. n k n Dscrete q-ary nput, Q-ary output channel 7

8 7.. Channel Models Dscrete-nput, contnuous-output channel p Dscrete nput alphabet X={x,x,,x q- }. Output of the detector s unquantzed (Q= ). The most mportant channel of ths type s the addtve whte Gaussan nose (AWG) channel, for whch Y = X + G where G s a zeor-mean Gaussan random varable wth varance σ and X=x k, k=,,,q-. ( y x ) ( ) k σ p y X = xk = e πσ ( y ), y,..., yn X = u, X = u,..., X n = un = p( y X = u ) 8 n =

9 Waveform channels 7.. Channel Models Assume that a channel has a gven bandwdth W, wth deal frequency response C( f )= wthn the bandwdth W, and the sgnal at ts output s corrupted by AWG: y(t)=x(t)+n(t). Expand y(t), x(t), and n(t) nto a complete set of orthonormal functons: y t = yf t, x t = x f t, n t = n f t. ( ) ( ) ( ) ( ) ( ) ( ) T T * * () () () () () y = y t f t dt = x t + n t f t dt = x + n T f * () t f () t j dt = δ 9 j = ( = j) ( j)

10 Waveform channels Snce y =x +n, t follows that: p ( y x ) = 7.. Channel Models e πσ ( ) y x σ, = Snce the functons {f (t)} are orthonormal, t follows that the {n } are uncorrelated. Snce they are Gaussan, they are also statstcally ndependent: p Samples of x(t) and y(t) may be taken at the yqust rate of W samples per second. Thus, n a tme nterval of length T, there are =WT samples.,,... ( y ), y,..., y x, x,..., x = p( y x ) =

11 7.. Channel Capacty Consder a DMC havng an nput alphabet X={x,x,,x q- }, an output alphabet Y={y,y,,y Q- }, and the set of transton probabltes P(y,x j ). The mutual nformaton provded about the event X=x j by the occurrence of the event Y=y s log[p(y x j )/P(y )], where ( ) ( ) ( ) ( ) q = P y P Y = y P xk P y xk k = Hence, the average mutual nformaton provded by the output Y about the nput X s: ( xj) q Q P y I( X; Y) = P( xj) P( y xj) log P y ( ) j= =

12 7.. Channel Capacty The value of I(X;Y) maxmzed over the set of nput symbol probabltes P(x j ) s a quantty that depends only on the characterstcs of the DMC through the condtonal probabltes P(y x j ). Ths quantty s called the capacty of the channel and s denoted by C: C = max I( X; Y) P( xj ) q Q = ( ) ( ) max P xj P y xj log P( xj ) ( x ) P y ( ) j= = The maxmzaton of I(X;Y) s performed under the constrants q that P x and P x =. ( ) ( ) j j j= P y j

13 7.. Channel Capacty Example 7.- BSC wth transton probabltes P( )=P( )=p. The average mutual nformaton s maxmzed when the nput probabltes P()=P()=½. The capacty of the BSC s C = p log p + p log p = where H(p) s the bnary entropy functon. ( ) ( ) H ( p) 3

14 7.. Channel Capacty Consder the dscrete-tme AWG memoryless channel descrbed by ( y x ) ( ) k σ p y X = xk = e πσ The capacty of ths channel n bts per channel use s the maxmum average mutual nformaton between the dscrete nput X={x,x,,x q- } and the output Y={,- }: where C = max ( x ) q P = p p ( y x ) P( x ) q 4 log ( y) p( y x ) P( ) = k = k x k P ( y x ) P( y) dy

15 7.. Channel Capacty Example 7.-. Consder a bnarynput AWG memoryless channel wth possble nputs X=A and X=-A. The average mutual nformaton I(X;Y) s maxmzed when the nput probabltes are P(X=A)=P(X=- A)=½. ( ) p( y) p( y A) p( y) p y A C = p( y A) log dy + p ( y A) log dy 5

16 7.. Channel Capacty It s not always the case to obtan the channel capacty by assumng that the nput symbols are equally probable. othng can be sad n general about the nput probablty assgnment that maxmzes the average mutual nformaton. It can be shown that the necessary and suffcent condtons for the set of nput probabltes {P(x j )} to maxmze I(X;Y) and to acheve capacty on a DMC are: I ( x ) ( ) j; Y = C for all j wth P x j > I x ; Y C for all j wth P x = ( ) ( ) j where C s the capacty of the channel and Q ( ) ; = ( ) P y I x j Y P y x j log P = 6 j ( x ) ( y ) j

17 7.. Channel Capacty Consder a band-lmted waveform channel wth AWG. The capacty of the channel per unt tme has been defned by Shannon (948) as C = lm max I ( X ; Y ) T p( x) T Alternatvely, we may use the samples or the coeffcents {y }, {x }, and {n } n the seres expansons of y(t), x(t), and n(t) to determne the average mutual nformaton between x =[x x x ] and y =[y y y ], where =WT, y = x + n. p ( ) ( ) ( ) ( y x ) I X ; Y = p y x p x log dx dy x y p y = = p ( y x ) p( x ) 7 log ( ) ( y x ) dydx ( y ) p p (7.-4)

18 7.. Channel Capacty where ( y x ) p( y x ) = e π The maxmum of I(X;Y) over the nput PDFs p(x ) s obtaned when the {x } are statstcally ndependent zero-mean Gaussan random varables,.e., p ( ) x σ x x = e πσ From 7.-4 σ x σ x max I( X; Y) = log + = log + px ( ) = σ x = WT log + =WT 8 x

19 7.. Channel Capacty If we put a constrant on the average power n x(t),.e., T () ( σ ) x Pav = E x t dt E x T = = T T TPav Pav σ x = = W P ( ) ( ) = + av max I X ; Y WT log p x W Dvdng both sdes by T and we can obtan the capacty of the band-lmted AWG waveform channel wth a band-lmted and average power-lmted nput: P = + av C W log W 9 =

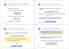
20 7.. Channel Capacty ormalzed channel capacty as a functon of SR for band-lmted AWG channel Channel capacty as a functon of bandwdth wth a fxed transmtted average power

21 7.. Channel Capacty ote that as W approaches nfnty, the capacty of the channel approaches the asymptotc value C = Pav log e = Pav ln bts/s Snce P av represents the average transmtted power and C s the rate n bts/s, t follows that P = Cε av b Hence, we have C W C log + W ε = b Consequently ε C C W W b =

22 When C/W=, ε b / = ( db). 7.. Channel Capacty When C/W, CW ε b C C exp ln ln C W W W ε b ncreases expontally as CW. When C/W C W ε b = lm C W C W = ln

23 7.. Channel Capacty The channel capacty formulas serve as upper lmts on the transmsson rate for relable communcaton over a nosy channel. osy channel codng theorem by Shannon (948) There exst channel codes (and decoders) that make t possble to acheve relable communcaton, wth as small an error probablty as desred, f the transmsson rate R<C, where C s the channel capacty. If R>C, t s not possble to make the probablty of error tend toward zero wth any code. 3