Exponential Functions" Differentiation and lintegration
|
|
|
- Gwendoline McLaughlin
- 5 years ago
- Views:
Transcription
1 5t)8 Chapter 5 Logarithmic, Exponential, and Other Transcendental Functions Section 5.4 Exponential Functions" Differentiation and lintegration l. e lnx = x = e x/ e 4. e lnx = 50 x = 84 = e 4 X=6 3. e x = x = In,~ e x = 83 e x = 83 4 x= e x = 7 ln(8. ~] ~ e x = X In 84 = - x = n84 ~ e x e x 499 = e x In 499 = x x =-ln 499 ~ 3.9 e x = X= e x = 8 3e x = 4 e x = e -x = 30 e-x = ~_ 5 ~.540 ~ e -4"~ = 5 e-4x _ 5 _ ~ x =, ln x = 0 x = e ~ X = e o x = ±e 5 ~ ± o ln(x- 3) = 4. In 4x = 4x = e l x-3=e x = 3 +e ~ e X ~ in x/-~x + =.,/-~x + x+ x e =el=e = e 6o ln(x-) = (x- ) = e = x-=e 6 = e - = x = + e 6 ~ Brooks/Cole, Cengage Learning
2 Section 5.4 Exponential Functions." Differentiation and Integration 5)9 7o y = e -~". y = e -4z x 8. y = $e 3. (a) 4" (b) Horizontal shift units to the right 9o y=ex + t4 (c) -3 A reflection in the x-axis and a vertical shrink / 3 4. (a) Vertical shift 3 units upward and a reflection in the y-axis ", y = e -x Symmetric with respect to the y-axis Horizontal asymptote: y = 0 (b) ~ ~ ~ 0 - Horizontal asymptotes: y = 0 and y = 8 l0-8 ~ 0 - Horizontal asymptote: y = 4 5. y = Ce ~ Horizontal asymptote: y = 0 Matches (c) 00 Brooks/Cole, Cengage Learning
3 56 Chapter 5 Logarithmic, Exponential, and Other Transcendental Functions 6. y = Ce -~ ~ 3. f(x) Horizontal asymptote: y = 0 Reflection in the y-axis Matches (d) g(x) 4- = ln(x + ) Vertical shift C units ~ Reflection in both the x- and y-axes Matches (a) C 8. y- l+e -ox C lim -- x~o~l + e -~ -C c lim x-~l + e -~ -0 Horizontal asymptotes: y = C and y = 0 Matches (b) 3 f(x) = e x- g(x) = l+lnx 9. f(x) : e x l lnx g(x) : ln-,/-~ = I 3 4 g - As x --~ 0% the graph off approaches the graph ofg. lim. + = e f(x) : e x/3 g(x) = lnx3 = 3nx y 34. Using the result from Exercise 33: lim + = e ~forr > O /,O0~,O00J ~ e ~ e > ( + Too,,oo6,ooo) ~ + -g + + ]~ + 7-T6 + = e ~ e>l+l+½+++ +-T6+7-~ -~4 +~ Brooks/Cole, Cengage Learning
4 Section 5.4 Exponential Functions." Differentiation and Integration (a) y : e 3x y = 3e 3x y (O) = 3 Tangent line: y - = 3(x - 0) y =3x+l y = e -3x y = _3e -3x y (O) = -3 Tangent line: y - = -3(x - 0) y = -3x (a) y = e x y = e x y (O) : Tangent line: y - = (x - 0) y = x+l (b) y = e -x y = _e -x y (o) -- Tangent line: y - = -(x - 0) S(x): f (x) : e x 40. y = e -Sx dy = _5e-SX y = -x y = e x In x 46. y = xe x y = xe x + ex() = ex(x + l) 47. y = x3e x, : x3e x + 3x~(e ~) : x~e~(x + 3): ex(x~ + 3x ~) 48. y = xe -x y = x(-e -x) + xe -x : xe- ~( - x) 49. g(t) = (e -t + e ) 3 g (,) : 3(e- + et)(e - e- ) 50. g(t) : e -3/t g,(t) = e_3/t(6t_3) = 6 t3 e3/t 5. y = ln( + e x) dy e x -- dx + e x 5. ha( l+ ex) = In(l+ ex) - In(l-e x) Y= ~,~) dy e x e x e x -- dx + e x - e x - e x 53. y - _ (ex +e_x) -~ ex + e -x 4. y = e "/~ dy e y = e -x dy = _xe-x 54. dy_dx (ex + e-x)-(ex -e-x) = (e :~ + e-:~) y ~~ e x _ e-x dy e x + e -x dx 43. y = e x-4 y = e x-4 -e x 44. f(x)= 3e l-x f (x) : 3ei-X (-x) : -6xe l-x 00 Brooks/Cole, Cengage Learning
5 5 Chapter 5 Logarithmic, Exponential, and Other Transcendental Functions -- e x 65. y = xe ~ -xe x +e x, (, e) y = xe x + xe x - xe x - e x + e x = xe x y () = e Tangent line: y - e = e(x - ) 57. y ~ ex(sin x + cos x) 58. y = ln ex = x dx e ~(cos x -sin x) + (sin x + cos x)(e*) ex( cos x) = e ~ cos x 59. F(x)= ::Xcose dt F (4 = ~os(e ~X). ± = ~os(~/ x x 60. F(x) =![ x ln(t + ) dt F (x) = ln(e x + )e ~" 6. :(x) = e -, (l, 0 f (x) =-e -x, f ()=-I Tangent line: y - = -l(x - ) 6, y = e -x+x, (, ) y=-x+ y = (x- )e -zr+xz, y () = Tangent line: y - = (x - ) y = x y= ln(e :3) = x ~, (-, 4) y = x y (-) = -4 Tangent line: y - 4 = -4(x + ) y = -4x - 4 e x + e 64. y : ~ -x (o, o) = e x _ e -x] 66. y = xe x -e x, (,0) y = xe x + e x _ e x = xe x y O) = e Tangent line: y - 0 = e(x - ) y=ex-e 67. :(x) = e -x ln x, (,0) f (x) = e-x(~;-e-xlnx = e-~(-~ - () = Tangent line: y - 0 = e-l(x - ) y = e e 68. f(x) = e ~lnx, (,0) :,(x) = :- x s () = e3 Tangent line: y - 0 = e3(x - ) y = e3(x -) 69. xe y - l Ox + 3 y = 0 xe y- : + e y : = 0 dx dx dy(xey + 3)= 0- e y dx ~ dy 0 - e y -- dx xe y ex~, + x _ y = 0 + x-ydy = 0 dx dy(xe~y - y)= -ye x, - x dx ~ dy ye "~ + x dx -- xe x* - y y (0) : 0 Tangent line: y = 0 00 Brooks/Cole, Cengage Learning
6 Section 5.4 Exponential Functions." Differentiation and Integration xe y + ye x =, (0, ) xeyy + ey + ye x + y e x = 0 At(0,): e+l+y = 0 y = -e - Tangent line: y - = (-e - )(x - 0) y : (-e-)x + l l+ln(v ) = e x-y, (,), [ y ] -~-[xy + y] = e x-y - at (, ): [y + ] = t- y y = 0 Tangent line: y - = 0(x - ) y=l f(x) = (3 + x)e -3x f (x) = (3 + x)(-3e -3x) + e -3x = (-7-6x)e -3x f"(x) = (-7-6x)(-3e -3x) - 6e -3" = 3(6x + S)e -3x 74. g(x) = ~x + ex ln x e g (x) = ~ + --x x + ex lnx g"(x) = Xe x -- e x e x ex ln x 4X 3/ X X ex(zx -) + +exlnx 4 x./ x x y = 4e -x y = _4e -x y" = 4e -x y"- y = 4e -x -4e-x = 0 y = e 3x + e -3x y = 3e 3x _ 3e-3X y" = 9e 3x + 9e -3x /,- = 9(e, _-o 77. y = ex(cosxi~x + sin x/~x) 78. y = ex(-.,4~ sin x/~x + ~ cos x/~x)+ ex(cos ~/-~x + sin w/-~x) = ex[( + x/~) cos w/-~x + ( - ~) sin ~x],"= ex[-(~ + )sin ~x+ (~- )cos ~x]+ e ;[( + ~)cos ~x+ (- ~)sin ~x~ = ex[(-, - ~) sin ~x + (- + ~) cos ~x~ -y + 3y= -e ~( + ~)cos ~x+ (- ~)sin ~x~+ 3eX[cos ~x + sin ~x~ = ex[o- )cos (,+ )sin Therefore, -y + 3y = -y" ~ y" - y + 3y = 0. y = ex(3 cos x - 4 sin x) y = ex(-6 sin x - 8cosx) + ex(3 cosx - 4sin x) = e ~(-losin x - 5 cosx) = -SeX( sin x + cos x) y" = -SEX(4 cos x - sin x) - 5e ~( sin x + cos x) = -SEX(5 cos x) = -5e x cos x y"- y = -5e xcos x - (-5eX)( sin x + cos x) = -5eX(3 cos x - 4 sin x) = -Sy Therefore, y" - y = -5y ~ y" - y + 5y = Brooks/Cole, Cengage Learning
7 54 Chapter 5 Logarithmic, Exponential, and Other Transcendental Functions ~x _ e-x f (x~ = = 0 when x = 0. f ()-" x" - ex + e-x >0 Relative minimum: (0, ) g(x) = ~l~g -(x-3)/ ",/Z g (x) = - --~z(x- 3)e_(X_3)/ g"(x) = ~(~- - )(x 4)e -(x-3)/ Relative maximum: 3, Points of inflection: t3,0.39 (,-~ze ),l _/~ ) (4, &e_,/~, (,0.4),(4,0.4 )~/;,r ) if(x) ex + e -x >0 e x _ e-x f"(x} = ~ = 0 when x = 0. Point of inflection: (0, 0) 8. g(x) = -~ e-(x-) / g (x) = - --~z(x- )e_(x_)/ g,,(~) = ~;(~- )(x -3)e -( ~-)/ ~ Relative maximum: (~ff), (,0.399) Points of inflection: -/") -/"] ll, -~ffe ), 3,-~ffe ) ~ (,0.4),(3,0.4) 83. o f(x).= xe -x f~ (X) :--X~ -x -t- xe -x = xe-*( -x) = 0when x = 0,. f"(x) = -e-x(x - x ) q- e-x( - x) = e-x(x -4x+)= 0whenx = _+ Relative minimum: (0, 0) Relative maximum: (, 4e -) x = _+~/~ Points of inflection: / ~ (3.44, 0.384),(0.586, 0.9) o 00 Brooks/Cole, Cengage Learning
8 Section 5.4 Exponential Functions." Differentiation and Integration f(x) = xe -~ f (x) = -xe -x + e -~ = e- ~(- x) = 0when x =. s"(4 : + (-e-do- x) = e-"(x-) = 0whenx =. Relative maximum: (, e -l) Point of inflection: (, e -) - (, e -I) / g(t) : + ( + t)e- g (t) : -( + t)e- g"(t) : te -t Relative maximum: (-, + e)~ (-,3.78) Point of inflection: (0, 3) A = (base)(height)= xe -x da dx _4xe_.~ + e_.~ = e-~(- x ) = 0when x - A = x/~e (a) S(c) l Oce -c c e c ce c+x = (C + X)e c ce x = f(c + x) = 0(c + ) -- Ce x --C = X C -- ec+x =CWX X 86. f(x) = - + e3x(4- x) f (x) : e3x(-)+ 3eaX(4 - x) = e 3 ~0-6x ( ) = 0whenx = f"(x) : e3x(-6) + 3e3X(0-6x) = e3x(4-8x) = 0when x = 4 3" Relative maximum: (-}, 96.94) Point of inflection: (-}, ) 00 ( ) -0,5 - ~-~J.5 o 0x x/(-e x) (C) A(X)... e" e x - (.8, 4.59) 9 0 The maximum area is 4.59 for x =.8 and f(x) =.547. x (d) c- e~-i lim c = l~ x--~. 0 + lim c = 0 x---~ oo Answers will vary. Sample answer: As x approaches 0 from the right, the height of the rectangle approaches. As x approaches ~o, the height of the rectangle approaches Brooks/Cole, Cengage Learning
9 56 Chapter 5 Logarithmic, Exponential, and Other Transcendental Functions 89 f(x) = e x s (x) : ex Let (x, y) = (x, ex)be the point on the graphwhere the tangent line passes through the origin. Equating slopes, ex _ e x - 0 x-o =- x x = 5 y = e, y = e. P int: (~, e / 9. V = 5,000e - 686t, 0 _< t _< 0 (a) (b) d.._~v = _949e_O.686 t dt When t =, -- dv~ dt dv When t = 5,- ~, dt C) 0,000 Tangent line: y- e = e(x-½ y = ex o 90 Let (Xo, Y0) be the desired point on y = e -x e - t cos 4.9t _< 0.5 (3 inches equals one-fourth foot.) Using a graphing utility or Newton s Method, you have t > 7.79 seconds. y = -e -x (Slope of tangent line) = e x (Slope of normal line) y y-e-xo = exo (x- Xo) You want (0, O) to satisfy the equation: _e-xo = -xoexo XO exo -- = 0 = XO exo Using a graphing utility or Newton s Method,the solution is x0 = (0.463, e -0"463 ) ~x h P 0, In P a) o y = h is the regression line for data (h, In P). (b) lnp = ah +b P = e ah+b = ebe ah P = Ce ah, C = e b a = and C = e = 0, So, P = 0,957.7e - ~499h (C) ~,ooo o o
10 Section 5.4 Exponential Functions." Differentiation and Integration 57 dp = (0,957.7)(_0.499)e_0.499 h (d) -~ = e - 499h For h = 5,-- = dh For h = 8, dp -- ~ dh 94. (a) Linear model: V = t Quadratic model: V = 09.5t z t ,000 Quadratic. Linear[, L 0 0 (b) The slope represents the average loss in value per year. (c) Exponential model: V = 30,58.68(0.9074) t = 30,58.68 e t (d) As t -~ 0, V --~ 0 for the exponential model. The value tends to zero (e) When t = 4, V = -07 dollars/year When t = 8, V ~ -366 dollars/year 95. f(x)= e x f(o) = f (x) = e >: f (O) = f"(x) = e,< f"(o) = Pl(x) = +l(x-o)= + x P~(x) = + l(xi O)= )(x- 0) = + x f(x) = e x/:, f(o) =, f (x) : e 4, f (O) :7 f"(x) : e 4, f"(o) = -~ P~(x) = + ½( x-o) : x 7 + Pl(O) :, : 7 = -7 0)+ 0) P~(O) P~(x) : +-~(x- ~(x- : X X = P~ (x) : 4 -x + 7 : -7 The values of f, P~, P~ and their first derivatives agree at x = 0. The values of the second derivatives off and P agree at x = n =.! = = 479,00,600 Stirlings Formula: ~,~~,, ~ 475,687,487! 98 n = 5.5! = =,307,674,368,000 Stirlings Formula: 5t ~,~,,,, ~,300,430,7,00 ~.3004 x 0 l~ The values off, P~, and P and their first derivatives agree at x = Let u = 5x, du = 5 dr. [esx(5"~ dr = e 5x + C )0. Let u = -x 4, d// = i4x3dr. le-x4(_4~t ~x _-e -~4 ~ 0. Let u = x-l, du = dr. l e x- II x-l( dr ) l_x- = -~ e dr = -~e + C 00 Brooks/Cole, Cengage Learning
11 58 Chapter 5 Logarithmic, Exponential, and Other Transcendental Functions t). Let u = - 3x, du = -3 dx. Ie,-3.~dx = _½Iel-a,(_3)dx = --~ 03. Let u = x 3,du = 3x dx. = ~x Letu = e x +l, du = e xdx. + C. Let u = e ~ +e -x,du = (e ~ - e-x) dx. (ex + e-x) C e x + e -x iex(e, + )dx = l(ex + )(ex)dx _ (e" + ) --+C ~ Letu = ~,du =~&. 4. fe x + e x + e"g Ie "/~ Let u = -- du = dx. X ~ 7 gl/x dx = e "/; + C J e x = e x +x-e -x + C ~. le-x tan(e-x) dx : -I[tan(e-X)l(-e-X) dx = In cos(e -x ) + C 6. " "~ln{e z~-~) dx =" J{x - l)dx =x-x+c l~7. Let u = + ~-x 7. ~o [~e -x dx = -+ f e-~(-)dx = [--e-~l L Jo e~ - = -~( - e-) - e e 3-x d~ = ~-e3-x~ 4 = -e -~ + = - -- k -3 e 08. Let u = + e ~, du = e ~-x dx. e x f e x ln[ l~ dx = -~al + e -----Tdx =-k ~+ ezx) +c 09. Let u = -e x,du =-e xdx. l~-~,]i- ~x dx =-(-ex) /(-e~)dx = --}( - e x)3/ + C 0. Letu = e" +e -x,du = (e x - e-x) dx. e x _ e-x I~ dx = ln(e x + e -x) + C. Letu = e x-ex,- du = (e x +e-x) dx.! e~ + ~-x dx = lne x-e-x +C e x _ e-x 9. xe-x= dx = --~I~e-~(-x)dx =, L ]o =-+Ee - -~ _ ~ - O/e) _ e - e 0. l~ xe x3/ dx =. Z fo ~x3/(x dx 3 ~-~ \ ~ _ IeX3/~ - 3 ~-~ =--~I-~4 - (e4-3e4 ) 00 Brooks/Cole, Cengage Learning,
12 Section 5.4 Exponential Fidnctions: Differentiation and Integration Let u = --, du = --~ dx. x 3 e3/x 3e3/X _Z~dx 7. Let Id = ax, dld = ax dx. (Assume a : 0.) y = Ixear dx _- --~a f ax ae (ax) dx =a l ~_eax + C _x. Let u = --., du = -x dx. 3. Let u = l+e x,du = e xdx.!o~ dx = I / + = In( + e 6) - ln 4. Let u = 5 - M, du = -e x dx. ~dx = -I 5 - e x~ 5 -- e x = -ln(5 - e) + In 4 In 4 5. Let u = sin ~x, du = ~c cos ~cx dx. l o~r/esin~x cos ~cx dx = -~!~/esin~x(zc cos ~x) dx ~k AO 6. Let u = sec x, du = sec x tan x dx. e~r/ ~. [~/~e ~ ~x sec xtan x dx = J,d~ e... X{sec xtan x)dx ~/~ = l[e~o z~-]~/~ u -~/~ =~[e-l-e -] = "~[~ - -~TJ = e ~ x _ x - _-x - -~e -~ + C ~. f (x) = [.½(e+~ + e-x)ax = ½(e x- e -x) + C, f (O) = C = 0 f(x) = [.½(e~ - e-x)dx = ½(e x + e -x) + C f(o) = + C = ~ C~ = 0 f(x) = ½(e x + e -x) 30. f (x) = sinx+e x dx =-cosx+te + C~ f (0) = - 4- ~ 4- C, = -~ ~ C = _x f (x) = -cos x + e + s(x) = l(- os + + A.~ ) dx _x =-sinx+-~ +x+c f(0) = X + C -- ~" :=~ C = 0 ~x f(x] = x - sin x + =~ 3. (a) Y (b) ffl!is Iit (0,,,I )t s I ~ l Ill! " / i / //--,-,... i i.!// " 5 "- / /,,,/./.,,,,.,....,.,...+~ Sl~l-: -7,... dy = e_xl (0,) dx y= e-xl~ dx = -4e-xl(-~ dx ) = -me -x/ + C (0,): =-4e + C =-4+ C ~ C = 5 y = -4e -x/ + 5 / 6 00 Brooks/Cole, Cengage Learning
13 5 Chapter 5 Logarithmic, Exponential, and Other Transcendental Functions ~3. (a) y = Ixe - "~ dx = l~ie- x(-o.4x) dx ~ e- :~ + C = -.5e - x + C 0.4 -~ = -.5e +C =-.5+C ~ C = I y = -.5e - x + ~ /---4 x 37o Jo.,l xe dx, n : Midpoint Rule: Trapezoidal Rule: Simpson s Rule: Graphing utility: o xe-xdx, n = Midpoint Rule:.906 Trapezoidal Rule:.87 Simpson s Rule:.880 Graphing utility: I~] e- 39(t-48)dt Graphing utility: = 47.7% = e 5 - ~ ) t dt = - -e - 3x + = -- e_o.3x : e -a _ e-b = -e -3/ + = x = ln- = -In ln x = ~ =.3 minutes 0.3 4o x(t) = Ae ~ + Be-k ; A, B, k > 0 (a) x (t) = Ake ~ - Bke -~ = 0 Ae kt = Be -kt B A t = ~ By the first Derivative Test, this is a minimum. (b) x"(t)= Ak~e ~ + Bk~e -~ k z is the constant 00 Brooks/Cole, Cengage Learning
14 Section 5.4 Exponential Functions." Differentiation and Integration 5 4. t R lnr (a) In R = t R = e t = 48.78e - 6~55t (b) 4~o - o (C) IR(t)dt =ao[448"78e- 655 dt 637. liters 43. f(x) = ex.domain is (-~o, ~)and range is (0, c~). f is continuous, increasing, one-to-one, and concave upwards on its entire domain. lime x = 0andlime x = o~. X--+--oo 44o Yes. f(x) = Ce x, C a constant. 45. (a) Log Rule: (u = e x + ) 46. (a) (b) Substitution: (u = x ) -4 - (b) When x increases without bound, Ix approaches zero, and e l/x approaches. Therefore, f(x) approaches /( + ) =.So, f(x)has a horizontal asymptote at y =. As x approaches zero from the right, Ix approaches ~o, e ~/x approaches ~o and f(x) approaches zero. As x approaches zero from the left, Ix approaches -~o, e l/x approaches zero, and f(x) approaches. The limit does not exist because the left limit does not equal the right limit. Therefore, x = 0 is a nonremovable discontinuity. 47. l~ e t dt >_ l~ l dt [e ]~ >_ e: - > x ~ e x > + xforx > The graphs of f(x) : In x and g(x) : e x are mirror images across the line y = x. 49. e -x = x ~ f(x) = x-e -x f (x) = + e -~" Xn+l-= Xn xl = X = X --_ X 3 = X --_ X 4 = X 3 y(x,,) _ f (x,) X n f(x,).~ f(x) ~ Z (~) f(x3) ~ f (x3) X n -- e-xn + e -x" Approximate the root off to be x ~ Area = 8_ =!_~e_xd x = -e-x3 ~ = -e- ~ + e~ 3 o a Let z = ca: 8-3Z -- 8z - 3 = 0 8 -z = - + z 3 (3z+l)(z-3) = 0 z = 3 ~ e ~ =3~ a=ln3 e, z = -- ~ = ~ -- impossible 3 3 ] So, a = In Brooks/Cole, Cengage Learning
15 5 Chapter 5 Logarithmic, Exponential, and Other Transcendental Functions 5. y - a > O,b > O,L > 0 al e-x] b b y tt ~ y" = Oifae -x/b = ~ b L y(b, In a], = ae -(6 ",)/b + a(/a) Therefore, the y-coordinate of the inflection point is L/. 5. f(x) - lnx x (a) f (x) - - In x x = Owhenx = e. On (0, e),f (x) > 0 ~ f is increasing. On (e, oo),f (x) < 0 ~ f is decreasing. (b) For e < A < B, youhave lna lnb -- > A B BInA > AInB In A s > In B a A B > B "4. (c) Because e < ~, from part (b) you have e y Section 5.5 Bases Other than e and Applcations. log ½ = log -3 = -3. 0g7 9 = 0g7 7/3 = o log 7 = 0 4. log,-- = log,,-og,,a = - a 5. (a) (b) 3 =8 log 8 = 3 3-~ = _. 3 log3 ~ = - 00 Brooks/Cole, Cengage Learning
1. The graph of a function f is given above. Answer the question: a. Find the value(s) of x where f is not differentiable. Ans: x = 4, x = 3, x = 2,
 1. The graph of a function f is given above. Answer the question: a. Find the value(s) of x where f is not differentiable. x = 4, x = 3, x = 2, x = 1, x = 1, x = 2, x = 3, x = 4, x = 5 b. Find the value(s)
1. The graph of a function f is given above. Answer the question: a. Find the value(s) of x where f is not differentiable. x = 4, x = 3, x = 2, x = 1, x = 1, x = 2, x = 3, x = 4, x = 5 b. Find the value(s)
Formulas that must be memorized:
 Formulas that must be memorized: Position, Velocity, Acceleration Speed is increasing when v(t) and a(t) have the same signs. Speed is decreasing when v(t) and a(t) have different signs. Section I: Limits
Formulas that must be memorized: Position, Velocity, Acceleration Speed is increasing when v(t) and a(t) have the same signs. Speed is decreasing when v(t) and a(t) have different signs. Section I: Limits
Final Examination 201-NYA-05 May 18, 2018
 . ( points) Evaluate each of the following limits. 3x x + (a) lim x x 3 8 x + sin(5x) (b) lim x sin(x) (c) lim x π/3 + sec x ( (d) x x + 5x ) (e) lim x 5 x lim x 5 + x 6. (3 points) What value of c makes
. ( points) Evaluate each of the following limits. 3x x + (a) lim x x 3 8 x + sin(5x) (b) lim x sin(x) (c) lim x π/3 + sec x ( (d) x x + 5x ) (e) lim x 5 x lim x 5 + x 6. (3 points) What value of c makes
Matrix Theory and Differential Equations Homework 2 Solutions, due 9/7/6
 Matrix Theory and Differential Equations Homework Solutions, due 9/7/6 Question 1 Consider the differential equation = x y +. Plot the slope field for the differential equation. In particular plot all
Matrix Theory and Differential Equations Homework Solutions, due 9/7/6 Question 1 Consider the differential equation = x y +. Plot the slope field for the differential equation. In particular plot all
Find the indicated derivative. 1) Find y(4) if y = 3 sin x. A) y(4) = 3 cos x B) y(4) = 3 sin x C) y(4) = - 3 cos x D) y(4) = - 3 sin x
 Assignment 5 Name Find the indicated derivative. ) Find y(4) if y = sin x. ) A) y(4) = cos x B) y(4) = sin x y(4) = - cos x y(4) = - sin x ) y = (csc x + cot x)(csc x - cot x) ) A) y = 0 B) y = y = - csc
Assignment 5 Name Find the indicated derivative. ) Find y(4) if y = sin x. ) A) y(4) = cos x B) y(4) = sin x y(4) = - cos x y(4) = - sin x ) y = (csc x + cot x)(csc x - cot x) ) A) y = 0 B) y = y = - csc
Math 222 Spring 2013 Exam 3 Review Problem Answers
 . (a) By the Chain ule, Math Spring 3 Exam 3 eview Problem Answers w s w x x s + w y y s (y xy)() + (xy x )( ) (( s + 4t) (s 3t)( s + 4t)) ((s 3t)( s + 4t) (s 3t) ) 8s 94st + 3t (b) By the Chain ule, w
. (a) By the Chain ule, Math Spring 3 Exam 3 eview Problem Answers w s w x x s + w y y s (y xy)() + (xy x )( ) (( s + 4t) (s 3t)( s + 4t)) ((s 3t)( s + 4t) (s 3t) ) 8s 94st + 3t (b) By the Chain ule, w
Math 180, Exam 2, Practice Fall 2009 Problem 1 Solution. f(x) = arcsin(2x + 1) = sin 1 (3x + 1), lnx
 Math 80, Exam, Practice Fall 009 Problem Solution. Differentiate the functions: (do not simplify) f(x) = x ln(x + ), f(x) = xe x f(x) = arcsin(x + ) = sin (3x + ), f(x) = e3x lnx Solution: For the first
Math 80, Exam, Practice Fall 009 Problem Solution. Differentiate the functions: (do not simplify) f(x) = x ln(x + ), f(x) = xe x f(x) = arcsin(x + ) = sin (3x + ), f(x) = e3x lnx Solution: For the first
a x a y = a x+y a x a = y ax y (a x ) r = a rx and log a (xy) = log a (x) + log a (y) log a ( x y ) = log a(x) log a (y) log a (x r ) = r log a (x).
 You should prepare the following topics for our final exam. () Pre-calculus. (2) Inverses. (3) Algebra of Limits. (4) Derivative Formulas and Rules. (5) Graphing Techniques. (6) Optimization (Maxima and
You should prepare the following topics for our final exam. () Pre-calculus. (2) Inverses. (3) Algebra of Limits. (4) Derivative Formulas and Rules. (5) Graphing Techniques. (6) Optimization (Maxima and
or - CHAPTER 7 Applications of Integration Section 7.1 Area of a Region Between Two Curves 1. A= ~2[0- (x :2-6x)] dr=-~2(x 2-6x) dr
![or - CHAPTER 7 Applications of Integration Section 7.1 Area of a Region Between Two Curves 1. A= ~2[0- (x :2-6x)] dr=-~2(x 2-6x) dr or - CHAPTER 7 Applications of Integration Section 7.1 Area of a Region Between Two Curves 1. A= ~2[0- (x :2-6x)] dr=-~2(x 2-6x) dr](/thumbs/89/98001178.jpg) CHAPTER 7 Applications of Integration Section 7.1 Area of a Region Between Two Curves 1. A= ~[0- (x : 6x)] dr=-~(x 6x) dr 6~ 1356 or - 6. A: ~[(x- 1) 3 -(x-1)]dx 11. [~/3 ( - see x) dx 5- - 3 - I 1 3 5
CHAPTER 7 Applications of Integration Section 7.1 Area of a Region Between Two Curves 1. A= ~[0- (x : 6x)] dr=-~(x 6x) dr 6~ 1356 or - 6. A: ~[(x- 1) 3 -(x-1)]dx 11. [~/3 ( - see x) dx 5- - 3 - I 1 3 5
Solutions to Exam 1, Math Solution. Because f(x) is one-to-one, we know the inverse function exists. Recall that (f 1 ) (a) =
 Solutions to Exam, Math 56 The function f(x) e x + x 3 + x is one-to-one (there is no need to check this) What is (f ) ( + e )? Solution Because f(x) is one-to-one, we know the inverse function exists
Solutions to Exam, Math 56 The function f(x) e x + x 3 + x is one-to-one (there is no need to check this) What is (f ) ( + e )? Solution Because f(x) is one-to-one, we know the inverse function exists
Math 2413 General Review for Calculus Last Updated 02/23/2016
 Math 243 General Review for Calculus Last Updated 02/23/206 Find the average velocity of the function over the given interval.. y = 6x 3-5x 2-8, [-8, ] Find the slope of the curve for the given value of
Math 243 General Review for Calculus Last Updated 02/23/206 Find the average velocity of the function over the given interval.. y = 6x 3-5x 2-8, [-8, ] Find the slope of the curve for the given value of
Solution: APPM 1350 Final Exam Spring 2014
 APPM 135 Final Exam Spring 214 1. (a) (5 pts. each) Find the following derivatives, f (x), for the f given: (a) f(x) = x 2 sin 1 (x 2 ) (b) f(x) = 1 1 + x 2 (c) f(x) = x ln x (d) f(x) = x x d (b) (15 pts)
APPM 135 Final Exam Spring 214 1. (a) (5 pts. each) Find the following derivatives, f (x), for the f given: (a) f(x) = x 2 sin 1 (x 2 ) (b) f(x) = 1 1 + x 2 (c) f(x) = x ln x (d) f(x) = x x d (b) (15 pts)
Section 5.5 More Integration Formula (The Substitution Method) 2 Lectures. Dr. Abdulla Eid. College of Science. MATHS 101: Calculus I
 Section 5.5 More Integration Formula (The Substitution Method) 2 Lectures College of Science MATHS : Calculus I (University of Bahrain) Integrals / 7 The Substitution Method Idea: To replace a relatively
Section 5.5 More Integration Formula (The Substitution Method) 2 Lectures College of Science MATHS : Calculus I (University of Bahrain) Integrals / 7 The Substitution Method Idea: To replace a relatively
A.P. Calculus BC Test Two Section One Multiple-Choice Calculators Allowed Time 40 minutes Number of Questions 15
 A.P. Calculus BC Test Two Section One Multiple-Choice Calculators Allowed Time 40 minutes Number of Questions 15 The scoring for this section is determined by the formula [C (0.25 I)] 1.8 where C is the
A.P. Calculus BC Test Two Section One Multiple-Choice Calculators Allowed Time 40 minutes Number of Questions 15 The scoring for this section is determined by the formula [C (0.25 I)] 1.8 where C is the
Math 106: Review for Exam II - SOLUTIONS
 Math 6: Review for Exam II - SOLUTIONS INTEGRATION TIPS Substitution: usually let u a function that s inside another function, especially if du (possibly off by a multiplying constant) is also present
Math 6: Review for Exam II - SOLUTIONS INTEGRATION TIPS Substitution: usually let u a function that s inside another function, especially if du (possibly off by a multiplying constant) is also present
S(x) Section 1.5 infinite Limits. lim f(x)=-m x --," -3 + Jkx) - x ~
 8 Chapter Limits and Their Properties Section.5 infinite Limits -. f(x)- (x-) As x approaches from the left, x - is a small negative number. So, lim f(x) : -m As x approaches from the right, x - is a small
8 Chapter Limits and Their Properties Section.5 infinite Limits -. f(x)- (x-) As x approaches from the left, x - is a small negative number. So, lim f(x) : -m As x approaches from the right, x - is a small
EXAM II CALCULUS BC SECTION I PART A Time-55 minutes Number of questions-28 A CALCULATOR MAY NOT BE USED ON THIS PART OF THE EXAMINATION
 6 EXAM II CALCULUS BC SECTION I PART A Time-55 minutes Number of questions-8 A CALCULATOR MAY NOT BE USE ON THIS PART OF THE EXAMINATION irections: Solve each of the following problems, using the available
6 EXAM II CALCULUS BC SECTION I PART A Time-55 minutes Number of questions-8 A CALCULATOR MAY NOT BE USE ON THIS PART OF THE EXAMINATION irections: Solve each of the following problems, using the available
(b) x = (d) x = (b) x = e (d) x = e4 2 ln(3) 2 x x. is. (b) 2 x, x 0. (d) x 2, x 0
 1. Solve the equation 3 4x+5 = 6 for x. ln(6)/ ln(3) 5 (a) x = 4 ln(3) ln(6)/ ln(3) 5 (c) x = 4 ln(3)/ ln(6) 5 (e) x = 4. Solve the equation e x 1 = 1 for x. (b) x = (d) x = ln(5)/ ln(3) 6 4 ln(6) 5/ ln(3)
1. Solve the equation 3 4x+5 = 6 for x. ln(6)/ ln(3) 5 (a) x = 4 ln(3) ln(6)/ ln(3) 5 (c) x = 4 ln(3)/ ln(6) 5 (e) x = 4. Solve the equation e x 1 = 1 for x. (b) x = (d) x = ln(5)/ ln(3) 6 4 ln(6) 5/ ln(3)
8.7 MacLaurin Polynomials
 8.7 maclaurin polynomials 67 8.7 MacLaurin Polynomials In this chapter you have learned to find antiderivatives of a wide variety of elementary functions, but many more such functions fail to have an antiderivative
8.7 maclaurin polynomials 67 8.7 MacLaurin Polynomials In this chapter you have learned to find antiderivatives of a wide variety of elementary functions, but many more such functions fail to have an antiderivative
Math 226 Calculus Spring 2016 Practice Exam 1. (1) (10 Points) Let the differentiable function y = f(x) have inverse function x = f 1 (y).
 Math 6 Calculus Spring 016 Practice Exam 1 1) 10 Points) Let the differentiable function y = fx) have inverse function x = f 1 y). a) Write down the formula relating the derivatives f x) and f 1 ) y).
Math 6 Calculus Spring 016 Practice Exam 1 1) 10 Points) Let the differentiable function y = fx) have inverse function x = f 1 y). a) Write down the formula relating the derivatives f x) and f 1 ) y).
Integration by Parts
 Calculus 2 Lia Vas Integration by Parts Using integration by parts one transforms an integral of a product of two functions into a simpler integral. Divide the initial function into two parts called u
Calculus 2 Lia Vas Integration by Parts Using integration by parts one transforms an integral of a product of two functions into a simpler integral. Divide the initial function into two parts called u
Final Exam Review Quesitons
 Final Exam Review Quesitons. Compute the following integrals. (a) x x 4 (x ) (x + 4) dx. The appropriate partial fraction form is which simplifies to x x 4 (x ) (x + 4) = A x + B (x ) + C x + 4 + Dx x
Final Exam Review Quesitons. Compute the following integrals. (a) x x 4 (x ) (x + 4) dx. The appropriate partial fraction form is which simplifies to x x 4 (x ) (x + 4) = A x + B (x ) + C x + 4 + Dx x
MathsGeeks. Everything You Need to Know A Level Edexcel C4. March 2014 MathsGeeks Copyright 2014 Elite Learning Limited
 Everything You Need to Know A Level Edexcel C4 March 4 Copyright 4 Elite Learning Limited Page of 4 Further Binomial Expansion: Make sure it starts with a e.g. for ( x) ( x ) then use ( + x) n + nx + n(n
Everything You Need to Know A Level Edexcel C4 March 4 Copyright 4 Elite Learning Limited Page of 4 Further Binomial Expansion: Make sure it starts with a e.g. for ( x) ( x ) then use ( + x) n + nx + n(n
CHAPTER 5 Logarithmic, Exponential, and Other Transcendental Functions
 CHAPTER 5 Logarithmic, Eponential, and Other Transcendental Functions Section 5. The Natural Logarithmic Function: Dierentiation.... Section 5. The Natural Logarithmic Function: Integration...... Section
CHAPTER 5 Logarithmic, Eponential, and Other Transcendental Functions Section 5. The Natural Logarithmic Function: Dierentiation.... Section 5. The Natural Logarithmic Function: Integration...... Section
Brief answers to assigned even numbered problems that were not to be turned in
 Brief answers to assigned even numbered problems that were not to be turned in Section 2.2 2. At point (x 0, x 2 0) on the curve the slope is 2x 0. The point-slope equation of the tangent line to the curve
Brief answers to assigned even numbered problems that were not to be turned in Section 2.2 2. At point (x 0, x 2 0) on the curve the slope is 2x 0. The point-slope equation of the tangent line to the curve
MATH 408N PRACTICE FINAL
 2/03/20 Bormashenko MATH 408N PRACTICE FINAL Show your work for all the problems. Good luck! () Let f(x) = ex e x. (a) [5 pts] State the domain and range of f(x). Name: TA session: Since e x is defined
2/03/20 Bormashenko MATH 408N PRACTICE FINAL Show your work for all the problems. Good luck! () Let f(x) = ex e x. (a) [5 pts] State the domain and range of f(x). Name: TA session: Since e x is defined
Exam VI Section I Part A - No Calculators
 No Calculators SOLUTONS-Exam V Section Part A 81 Exam V Section Part A - No Calculators 1. A p.121 Using the product rule we obtain the first and second derivatives of y = xe x. X X Y = e + xe X X x y=e+e+xe
No Calculators SOLUTONS-Exam V Section Part A 81 Exam V Section Part A - No Calculators 1. A p.121 Using the product rule we obtain the first and second derivatives of y = xe x. X X Y = e + xe X X x y=e+e+xe
Ordinary Differential Equations (ODEs)
 c01.tex 8/10/2010 22: 55 Page 1 PART A Ordinary Differential Equations (ODEs) Chap. 1 First-Order ODEs Sec. 1.1 Basic Concepts. Modeling To get a good start into this chapter and this section, quickly
c01.tex 8/10/2010 22: 55 Page 1 PART A Ordinary Differential Equations (ODEs) Chap. 1 First-Order ODEs Sec. 1.1 Basic Concepts. Modeling To get a good start into this chapter and this section, quickly
Math 106: Review for Exam II - SOLUTIONS
 Math 6: Review for Exam II - SOLUTIONS INTEGRATION TIPS Substitution: usually let u a function that s inside another function, especially if du (possibly off by a multiplying constant) is also present
Math 6: Review for Exam II - SOLUTIONS INTEGRATION TIPS Substitution: usually let u a function that s inside another function, especially if du (possibly off by a multiplying constant) is also present
Free Response Questions Compiled by Kaye Autrey for face-to-face student instruction in the AP Calculus classroom
 Free Response Questions 1969-010 Compiled by Kaye Autrey for face-to-face student instruction in the AP Calculus classroom 1 AP Calculus Free-Response Questions 1969 AB 1 Consider the following functions
Free Response Questions 1969-010 Compiled by Kaye Autrey for face-to-face student instruction in the AP Calculus classroom 1 AP Calculus Free-Response Questions 1969 AB 1 Consider the following functions
Review for the Final Exam
 Math 171 Review for the Final Exam 1 Find the limits (4 points each) (a) lim 4x 2 3; x x (b) lim ( x 2 x x 1 )x ; (c) lim( 1 1 ); x 1 ln x x 1 sin (x 2) (d) lim x 2 x 2 4 Solutions (a) The limit lim 4x
Math 171 Review for the Final Exam 1 Find the limits (4 points each) (a) lim 4x 2 3; x x (b) lim ( x 2 x x 1 )x ; (c) lim( 1 1 ); x 1 ln x x 1 sin (x 2) (d) lim x 2 x 2 4 Solutions (a) The limit lim 4x
Calculus I Announcements
 Slide 1 Calculus I Announcements Read sections 4.2,4.3,4.4,4.1 and 5.3 Do the homework from sections 4.2,4.3,4.4,4.1 and 5.3 Exam 3 is Thursday, November 12th See inside for a possible exam question. Slide
Slide 1 Calculus I Announcements Read sections 4.2,4.3,4.4,4.1 and 5.3 Do the homework from sections 4.2,4.3,4.4,4.1 and 5.3 Exam 3 is Thursday, November 12th See inside for a possible exam question. Slide
Integrated Calculus II Exam 1 Solutions 2/6/4
 Integrated Calculus II Exam Solutions /6/ Question Determine the following integrals: te t dt. We integrate by parts: u = t, du = dt, dv = e t dt, v = dv = e t dt = e t, te t dt = udv = uv vdu = te t (
Integrated Calculus II Exam Solutions /6/ Question Determine the following integrals: te t dt. We integrate by parts: u = t, du = dt, dv = e t dt, v = dv = e t dt = e t, te t dt = udv = uv vdu = te t (
Name: Instructor: 1. a b c d e. 15. a b c d e. 2. a b c d e a b c d e. 16. a b c d e a b c d e. 4. a b c d e... 5.
 Name: Instructor: Math 155, Practice Final Exam, December The Honor Code is in effect for this examination. All work is to be your own. No calculators. The exam lasts for 2 hours. Be sure that your name
Name: Instructor: Math 155, Practice Final Exam, December The Honor Code is in effect for this examination. All work is to be your own. No calculators. The exam lasts for 2 hours. Be sure that your name
M GENERAL MATHEMATICS -2- Dr. Tariq A. AlFadhel 1 Solution of the First Mid-Term Exam First semester H
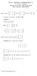 M - GENERAL MATHEMATICS -- Dr. Tariq A. AlFadhel Solution of the First Mid-Term Exam First semester 38-39 H 3 Q. Let A =, B = and C = 3 Compute (if possible) : A+B and BC A+B is impossible. ( ) BC = 3
M - GENERAL MATHEMATICS -- Dr. Tariq A. AlFadhel Solution of the First Mid-Term Exam First semester 38-39 H 3 Q. Let A =, B = and C = 3 Compute (if possible) : A+B and BC A+B is impossible. ( ) BC = 3
c) xy 3 = cos(7x +5y), y 0 = y3 + 7 sin(7x +5y) 3xy sin(7x +5y) d) xe y = sin(xy), y 0 = ey + y cos(xy) x(e y cos(xy)) e) y = x ln(3x + 5), y 0
 Some Math 35 review problems With answers 2/6/2005 The following problems are based heavily on problems written by Professor Stephen Greenfield for his Math 35 class in spring 2005. His willingness to
Some Math 35 review problems With answers 2/6/2005 The following problems are based heavily on problems written by Professor Stephen Greenfield for his Math 35 class in spring 2005. His willingness to
Solutions to Math 41 Final Exam December 10, 2012
 Solutions to Math 4 Final Exam December,. ( points) Find each of the following limits, with justification. If there is an infinite limit, then explain whether it is or. x ln(t + ) dt (a) lim x x (5 points)
Solutions to Math 4 Final Exam December,. ( points) Find each of the following limits, with justification. If there is an infinite limit, then explain whether it is or. x ln(t + ) dt (a) lim x x (5 points)
Review Problems Math115 Final Exam (Final covers Sec , )
 Review Problems Math5 Final Exam (Final covers Sec 2.-5.2, 5.4-6.5) Final Exam, Monday, Dec 2, 206, 4:0PM - 7:00PM, Budig 20 unless Mallot 200( Jocobs), Mallot 2074( Pham), Snow 20( Beaty), Lindley 7 (
Review Problems Math5 Final Exam (Final covers Sec 2.-5.2, 5.4-6.5) Final Exam, Monday, Dec 2, 206, 4:0PM - 7:00PM, Budig 20 unless Mallot 200( Jocobs), Mallot 2074( Pham), Snow 20( Beaty), Lindley 7 (
SOLUTIONS FOR PRACTICE FINAL EXAM
 SOLUTIONS FOR PRACTICE FINAL EXAM ANDREW J. BLUMBERG. Solutions () Short answer questions: (a) State the mean value theorem. Proof. The mean value theorem says that if f is continuous on (a, b) and differentiable
SOLUTIONS FOR PRACTICE FINAL EXAM ANDREW J. BLUMBERG. Solutions () Short answer questions: (a) State the mean value theorem. Proof. The mean value theorem says that if f is continuous on (a, b) and differentiable
3.4 The Chain Rule. F (x) = f (g(x))g (x) Alternate way of thinking about it: If y = f(u) and u = g(x) where both are differentiable functions, then
 3.4 The Chain Rule To find the derivative of a function that is the composition of two functions for which we already know the derivatives, we can use the Chain Rule. The Chain Rule: Suppose F (x) = f(g(x)).
3.4 The Chain Rule To find the derivative of a function that is the composition of two functions for which we already know the derivatives, we can use the Chain Rule. The Chain Rule: Suppose F (x) = f(g(x)).
Find all points where the function is discontinuous. 1) Find all vertical asymptotes of the given function. x(x - 1) 2) f(x) =
 Math 90 Final Review Find all points where the function is discontinuous. ) Find all vertical asymptotes of the given function. x(x - ) 2) f(x) = x3 + 4x Provide an appropriate response. 3) If x 3 f(x)
Math 90 Final Review Find all points where the function is discontinuous. ) Find all vertical asymptotes of the given function. x(x - ) 2) f(x) = x3 + 4x Provide an appropriate response. 3) If x 3 f(x)
MTH Calculus with Analytic Geom I TEST 1
 MTH 229-105 Calculus with Analytic Geom I TEST 1 Name Please write your solutions in a clear and precise manner. SHOW your work entirely. (1) Find the equation of a straight line perpendicular to the line
MTH 229-105 Calculus with Analytic Geom I TEST 1 Name Please write your solutions in a clear and precise manner. SHOW your work entirely. (1) Find the equation of a straight line perpendicular to the line
Spring 2015 Sample Final Exam
 Math 1151 Spring 2015 Sample Final Exam Final Exam on 4/30/14 Name (Print): Time Limit on Final: 105 Minutes Go on carmen.osu.edu to see where your final exam will be. NOTE: This exam is much longer than
Math 1151 Spring 2015 Sample Final Exam Final Exam on 4/30/14 Name (Print): Time Limit on Final: 105 Minutes Go on carmen.osu.edu to see where your final exam will be. NOTE: This exam is much longer than
Calculus I (Math 241) (In Progress)
 Calculus I (Math 241) (In Progress) The following is a collection of Calculus I (Math 241) problems. Students may expect that their final exam is comprised, more or less, of one problem from each section,
Calculus I (Math 241) (In Progress) The following is a collection of Calculus I (Math 241) problems. Students may expect that their final exam is comprised, more or less, of one problem from each section,
Limit. Chapter Introduction
 Chapter 9 Limit Limit is the foundation of calculus that it is so useful to understand more complicating chapters of calculus. Besides, Mathematics has black hole scenarios (dividing by zero, going to
Chapter 9 Limit Limit is the foundation of calculus that it is so useful to understand more complicating chapters of calculus. Besides, Mathematics has black hole scenarios (dividing by zero, going to
1 Cost, Revenue and Profit
 MATH 104 - SECTION 101 FIN AL REVIEW 1 Cost, Revenue and Profit C(x), R(x), and P(x); marginal cost MC(x), marginal revenue MR(x), and marginal profit M P(x). 1. Profit is the difference between cost and
MATH 104 - SECTION 101 FIN AL REVIEW 1 Cost, Revenue and Profit C(x), R(x), and P(x); marginal cost MC(x), marginal revenue MR(x), and marginal profit M P(x). 1. Profit is the difference between cost and
SECTION A. f(x) = ln(x). Sketch the graph of y = f(x), indicating the coordinates of any points where the graph crosses the axes.
 SECTION A 1. State the maximal domain and range of the function f(x) = ln(x). Sketch the graph of y = f(x), indicating the coordinates of any points where the graph crosses the axes. 2. By evaluating f(0),
SECTION A 1. State the maximal domain and range of the function f(x) = ln(x). Sketch the graph of y = f(x), indicating the coordinates of any points where the graph crosses the axes. 2. By evaluating f(0),
CALCULUS II MATH Dr. Hyunju Ban
 CALCULUS II MATH 2414 Dr. Hyunju Ban Introduction Syllabus Chapter 5.1 5.4 Chapters To Be Covered: Chap 5: Logarithmic, Exponential, and Other Transcendental Functions (2 week) Chap 7: Applications of
CALCULUS II MATH 2414 Dr. Hyunju Ban Introduction Syllabus Chapter 5.1 5.4 Chapters To Be Covered: Chap 5: Logarithmic, Exponential, and Other Transcendental Functions (2 week) Chap 7: Applications of
Math 131 Exam 2 Spring 2016
 Math 3 Exam Spring 06 Name: ID: 7 multiple choice questions worth 4.7 points each. hand graded questions worth 0 points each. 0. free points (so the total will be 00). Exam covers sections.7 through 3.0
Math 3 Exam Spring 06 Name: ID: 7 multiple choice questions worth 4.7 points each. hand graded questions worth 0 points each. 0. free points (so the total will be 00). Exam covers sections.7 through 3.0
Math 1310 Final Exam
 Math 1310 Final Exam December 11, 2014 NAME: INSTRUCTOR: Write neatly and show all your work in the space provided below each question. You may use the back of the exam pages if you need additional space
Math 1310 Final Exam December 11, 2014 NAME: INSTRUCTOR: Write neatly and show all your work in the space provided below each question. You may use the back of the exam pages if you need additional space
AP Calculus BC Chapter 4 AP Exam Problems. Answers
 AP Calculus BC Chapter 4 AP Exam Problems Answers. A 988 AB # 48%. D 998 AB #4 5%. E 998 BC # % 5. C 99 AB # % 6. B 998 AB #80 48% 7. C 99 AB #7 65% 8. C 998 AB # 69% 9. B 99 BC # 75% 0. C 998 BC # 80%.
AP Calculus BC Chapter 4 AP Exam Problems Answers. A 988 AB # 48%. D 998 AB #4 5%. E 998 BC # % 5. C 99 AB # % 6. B 998 AB #80 48% 7. C 99 AB #7 65% 8. C 998 AB # 69% 9. B 99 BC # 75% 0. C 998 BC # 80%.
Topics and Concepts. 1. Limits
 Topics and Concepts 1. Limits (a) Evaluating its (Know: it exists if and only if the it from the left is the same as the it from the right) (b) Infinite its (give rise to vertical asymptotes) (c) Limits
Topics and Concepts 1. Limits (a) Evaluating its (Know: it exists if and only if the it from the left is the same as the it from the right) (b) Infinite its (give rise to vertical asymptotes) (c) Limits
Calculus I Sample Exam #01
 Calculus I Sample Exam #01 1. Sketch the graph of the function and define the domain and range. 1 a) f( x) 3 b) g( x) x 1 x c) hx ( ) x x 1 5x6 d) jx ( ) x x x 3 6 . Evaluate the following. a) 5 sin 6
Calculus I Sample Exam #01 1. Sketch the graph of the function and define the domain and range. 1 a) f( x) 3 b) g( x) x 1 x c) hx ( ) x x 1 5x6 d) jx ( ) x x x 3 6 . Evaluate the following. a) 5 sin 6
Final Exam. Math 3 December 7, 2010
 Final Exam Math 3 December 7, 200 Name: On this final examination for Math 3 in Fall 200, I will work individually, neither giving nor receiving help, guided by the Dartmouth Academic Honor Principle.
Final Exam Math 3 December 7, 200 Name: On this final examination for Math 3 in Fall 200, I will work individually, neither giving nor receiving help, guided by the Dartmouth Academic Honor Principle.
Week 1: need to know. November 14, / 20
 Week 1: need to know How to find domains and ranges, operations on functions (addition, subtraction, multiplication, division, composition), behaviors of functions (even/odd/ increasing/decreasing), library
Week 1: need to know How to find domains and ranges, operations on functions (addition, subtraction, multiplication, division, composition), behaviors of functions (even/odd/ increasing/decreasing), library
CHAPTER 5 Logarithmic, Exponential, and Other Transcendental Functions
 CHAPTER 5 Logarithmic, Eponential, and Other Transcendental Functions Section 5. The Natural Logarithmic Function: Differentiation.... 9 Section 5. The Natural Logarithmic Function: Integration...... 98
CHAPTER 5 Logarithmic, Eponential, and Other Transcendental Functions Section 5. The Natural Logarithmic Function: Differentiation.... 9 Section 5. The Natural Logarithmic Function: Integration...... 98
Review Problems for the Final
 Review Problems for the Final Math -3 5 7 These problems are provided to help you study. The presence of a problem on this handout does not imply that there will be a similar problem on the test. And the
Review Problems for the Final Math -3 5 7 These problems are provided to help you study. The presence of a problem on this handout does not imply that there will be a similar problem on the test. And the
and verify that it satisfies the differential equation:
 MOTIVATION: Chapter One: Basic and Review Why study differential equations? Suppose we know how a certain quantity changes with time (for example, the temperature of coffee in a cup, the number of people
MOTIVATION: Chapter One: Basic and Review Why study differential equations? Suppose we know how a certain quantity changes with time (for example, the temperature of coffee in a cup, the number of people
Solutions: Homework 8
 Solutions: Homework 8 1 Chapter 7.1 Problem 3 This is one of those problems where we substitute in solutions and just check to see if they work or not. (a) Substituting y = e rx into the differential equation
Solutions: Homework 8 1 Chapter 7.1 Problem 3 This is one of those problems where we substitute in solutions and just check to see if they work or not. (a) Substituting y = e rx into the differential equation
Test one Review Cal 2
 Name: Class: Date: ID: A Test one Review Cal 2 Short Answer. Write the following expression as a logarithm of a single quantity. lnx 2ln x 2 ˆ 6 2. Write the following expression as a logarithm of a single
Name: Class: Date: ID: A Test one Review Cal 2 Short Answer. Write the following expression as a logarithm of a single quantity. lnx 2ln x 2 ˆ 6 2. Write the following expression as a logarithm of a single
18.01 EXERCISES. Unit 3. Integration. 3A. Differentials, indefinite integration. 3A-1 Compute the differentials df(x) of the following functions.
 8. EXERCISES Unit 3. Integration 3A. Differentials, indefinite integration 3A- Compute the differentials df(x) of the following functions. a) d(x 7 + sin ) b) d x c) d(x 8x + 6) d) d(e 3x sin x) e) Express
8. EXERCISES Unit 3. Integration 3A. Differentials, indefinite integration 3A- Compute the differentials df(x) of the following functions. a) d(x 7 + sin ) b) d x c) d(x 8x + 6) d) d(e 3x sin x) e) Express
Math 131 Final Exam Spring 2016
 Math 3 Final Exam Spring 06 Name: ID: multiple choice questions worth 5 points each. Exam is only out of 00 (so there is the possibility of getting more than 00%) Exam covers sections. through 5.4 No graphing
Math 3 Final Exam Spring 06 Name: ID: multiple choice questions worth 5 points each. Exam is only out of 00 (so there is the possibility of getting more than 00%) Exam covers sections. through 5.4 No graphing
AP Calculus Free-Response Questions 1969-present AB
 AP Calculus Free-Response Questions 1969-present AB 1969 1. Consider the following functions defined for all x: f 1 (x) = x, f (x) = xcos x, f 3 (x) = 3e x, f 4 (x) = x - x. Answer the following questions
AP Calculus Free-Response Questions 1969-present AB 1969 1. Consider the following functions defined for all x: f 1 (x) = x, f (x) = xcos x, f 3 (x) = 3e x, f 4 (x) = x - x. Answer the following questions
MATH 1241 Common Final Exam Fall 2010
 MATH 1241 Common Final Exam Fall 2010 Please print the following information: Name: Instructor: Student ID: Section/Time: The MATH 1241 Final Exam consists of three parts. You have three hours for the
MATH 1241 Common Final Exam Fall 2010 Please print the following information: Name: Instructor: Student ID: Section/Time: The MATH 1241 Final Exam consists of three parts. You have three hours for the
AP Calculus Testbank (Chapter 6) (Mr. Surowski)
 AP Calculus Testbank (Chapter 6) (Mr. Surowski) Part I. Multiple-Choice Questions 1. Suppose that f is an odd differentiable function. Then (A) f(1); (B) f (1) (C) f(1) f( 1) (D) 0 (E). 1 1 xf (x) =. The
AP Calculus Testbank (Chapter 6) (Mr. Surowski) Part I. Multiple-Choice Questions 1. Suppose that f is an odd differentiable function. Then (A) f(1); (B) f (1) (C) f(1) f( 1) (D) 0 (E). 1 1 xf (x) =. The
MATH 151, FALL SEMESTER 2011 COMMON EXAMINATION 3 - VERSION B - SOLUTIONS
 Name (print): Signature: MATH 5, FALL SEMESTER 0 COMMON EXAMINATION - VERSION B - SOLUTIONS Instructor s name: Section No: Part Multiple Choice ( questions, points each, No Calculators) Write your name,
Name (print): Signature: MATH 5, FALL SEMESTER 0 COMMON EXAMINATION - VERSION B - SOLUTIONS Instructor s name: Section No: Part Multiple Choice ( questions, points each, No Calculators) Write your name,
APPM 1350 Final Exam Fall 2017
 APPM 350 Final Exam Fall 207. (26 pts) Evaluate the following. (a) Let g(x) cos 3 (π 2x). Find g (π/3). (b) Let y ( x) x. Find y (4). (c) lim r 0 e /r ln(r) + (a) (9 pt) g (x) 3 cos 2 (π 2x)( sin(π 2x))(
APPM 350 Final Exam Fall 207. (26 pts) Evaluate the following. (a) Let g(x) cos 3 (π 2x). Find g (π/3). (b) Let y ( x) x. Find y (4). (c) lim r 0 e /r ln(r) + (a) (9 pt) g (x) 3 cos 2 (π 2x)( sin(π 2x))(
Review for the Final Exam
 Calculus Lia Vas. Integrals. Evaluate the following integrals. (a) ( x 4 x 2 ) dx (b) (2 3 x + x2 4 ) dx (c) (3x + 5) 6 dx (d) x 2 dx x 3 + (e) x 9x 2 dx (f) x dx x 2 (g) xe x2 + dx (h) 2 3x+ dx (i) x
Calculus Lia Vas. Integrals. Evaluate the following integrals. (a) ( x 4 x 2 ) dx (b) (2 3 x + x2 4 ) dx (c) (3x + 5) 6 dx (d) x 2 dx x 3 + (e) x 9x 2 dx (f) x dx x 2 (g) xe x2 + dx (h) 2 3x+ dx (i) x
Find the slope of the curve at the given point P and an equation of the tangent line at P. 1) y = x2 + 11x - 15, P(1, -3)
 Final Exam Review AP Calculus AB Find the slope of the curve at the given point P and an equation of the tangent line at P. 1) y = x2 + 11x - 15, P(1, -3) Use the graph to evaluate the limit. 2) lim x
Final Exam Review AP Calculus AB Find the slope of the curve at the given point P and an equation of the tangent line at P. 1) y = x2 + 11x - 15, P(1, -3) Use the graph to evaluate the limit. 2) lim x
MATH 2053 Calculus I Review for the Final Exam
 MATH 05 Calculus I Review for the Final Exam (x+ x) 9 x 9 1. Find the limit: lim x 0. x. Find the limit: lim x + x x (x ).. Find lim x (x 5) = L, find such that f(x) L < 0.01 whenever 0 < x
MATH 05 Calculus I Review for the Final Exam (x+ x) 9 x 9 1. Find the limit: lim x 0. x. Find the limit: lim x + x x (x ).. Find lim x (x 5) = L, find such that f(x) L < 0.01 whenever 0 < x
Old Math 220 Exams. David M. McClendon. Department of Mathematics Ferris State University
 Old Math 0 Exams David M. McClendon Department of Mathematics Ferris State University Last updated to include exams from Spring 05 Contents Contents General information about these exams 4 Exams from 0
Old Math 0 Exams David M. McClendon Department of Mathematics Ferris State University Last updated to include exams from Spring 05 Contents Contents General information about these exams 4 Exams from 0
THE USE OF A CALCULATOR, CELL PHONE, OR ANY OTHER ELECTRONIC DEVICE IS NOT PERMITTED IN THIS EXAMINATION.
 MATH 110 FINAL EXAM SPRING 2008 FORM A NAME STUDENT NUMBER INSTRUCTOR SECTION NUMBER This examination will be machine processed by the University Testing Service. Use only a number 2 pencil on your scantron.
MATH 110 FINAL EXAM SPRING 2008 FORM A NAME STUDENT NUMBER INSTRUCTOR SECTION NUMBER This examination will be machine processed by the University Testing Service. Use only a number 2 pencil on your scantron.
LSU AP Calculus Practice Test Day
 LSU AP Calculus Practice Test Day AP Calculus AB 2018 Practice Exam Section I Part A AP CALCULUS AB: PRACTICE EXAM SECTION I: PART A NO CALCULATORS ALLOWED. YOU HAVE 60 MINUTES. 1. If y = ( 1 + x 5) 3
LSU AP Calculus Practice Test Day AP Calculus AB 2018 Practice Exam Section I Part A AP CALCULUS AB: PRACTICE EXAM SECTION I: PART A NO CALCULATORS ALLOWED. YOU HAVE 60 MINUTES. 1. If y = ( 1 + x 5) 3
Lesson 3: Linear differential equations of the first order Solve each of the following differential equations by two methods.
 Lesson 3: Linear differential equations of the first der Solve each of the following differential equations by two methods. Exercise 3.1. Solution. Method 1. It is clear that y + y = 3 e dx = e x is an
Lesson 3: Linear differential equations of the first der Solve each of the following differential equations by two methods. Exercise 3.1. Solution. Method 1. It is clear that y + y = 3 e dx = e x is an
Solutions to Section 1.1
 Solutions to Section True-False Review: FALSE A derivative must involve some derivative of the function y f(x), not necessarily the first derivative TRUE The initial conditions accompanying a differential
Solutions to Section True-False Review: FALSE A derivative must involve some derivative of the function y f(x), not necessarily the first derivative TRUE The initial conditions accompanying a differential
/ =0. (c) Section P.3 Functions and Their Graphs. (c) g(-2) = 5-(-2) 2 = 5-4 = 1. (e) g(x) = 0 for x = -I, 1 and 2. 2.
 Section P,3 Functions and Their Graphs 3 Section P.3 Functions and Their Graphs. (a) Domain off." -4 < x < 4 ~ [-4, 4] Range off:-3 < y < 5 ~ [-3, 5] Domain of g: -3 < x < 3 ~ [-3, 3] Range of g: -4
Section P,3 Functions and Their Graphs 3 Section P.3 Functions and Their Graphs. (a) Domain off." -4 < x < 4 ~ [-4, 4] Range off:-3 < y < 5 ~ [-3, 5] Domain of g: -3 < x < 3 ~ [-3, 3] Range of g: -4
7.1. Calculus of inverse functions. Text Section 7.1 Exercise:
 Contents 7. Inverse functions 1 7.1. Calculus of inverse functions 2 7.2. Derivatives of exponential function 4 7.3. Logarithmic function 6 7.4. Derivatives of logarithmic functions 7 7.5. Exponential
Contents 7. Inverse functions 1 7.1. Calculus of inverse functions 2 7.2. Derivatives of exponential function 4 7.3. Logarithmic function 6 7.4. Derivatives of logarithmic functions 7 7.5. Exponential
3 Algebraic Methods. we can differentiate both sides implicitly to obtain a differential equation involving x and y:
 3 Algebraic Methods b The first appearance of the equation E Mc 2 in Einstein s handwritten notes. So far, the only general class of differential equations that we know how to solve are directly integrable
3 Algebraic Methods b The first appearance of the equation E Mc 2 in Einstein s handwritten notes. So far, the only general class of differential equations that we know how to solve are directly integrable
DRAFT - Math 101 Lecture Note - Dr. Said Algarni
 3 Differentiation Rules 3.1 The Derivative of Polynomial and Exponential Functions In this section we learn how to differentiate constant functions, power functions, polynomials, and exponential functions.
3 Differentiation Rules 3.1 The Derivative of Polynomial and Exponential Functions In this section we learn how to differentiate constant functions, power functions, polynomials, and exponential functions.
Problem Max. Possible Points Total
 MA 262 Exam 1 Fall 2011 Instructor: Raphael Hora Name: Max Possible Student ID#: 1234567890 1. No books or notes are allowed. 2. You CAN NOT USE calculators or any electronic devices. 3. Show all work
MA 262 Exam 1 Fall 2011 Instructor: Raphael Hora Name: Max Possible Student ID#: 1234567890 1. No books or notes are allowed. 2. You CAN NOT USE calculators or any electronic devices. 3. Show all work
Note: Final Exam is at 10:45 on Tuesday, 5/3/11 (This is the Final Exam time reserved for our labs). From Practice Test I
 MA Practice Final Answers in Red 4/8/ and 4/9/ Name Note: Final Exam is at :45 on Tuesday, 5// (This is the Final Exam time reserved for our labs). From Practice Test I Consider the integral 5 x dx. Sketch
MA Practice Final Answers in Red 4/8/ and 4/9/ Name Note: Final Exam is at :45 on Tuesday, 5// (This is the Final Exam time reserved for our labs). From Practice Test I Consider the integral 5 x dx. Sketch
90 Chapter 5 Logarithmic, Exponential, and Other Transcendental Functions. Name Class. (a) (b) ln x (c) (a) (b) (c) 1 x. y e (a) 0 (b) y.
 90 Chapter 5 Logarithmic, Eponential, and Other Transcendental Functions Test Form A Chapter 5 Name Class Date Section. Find the derivative: f ln. 6. Differentiate: y. ln y y y y. Find dy d if ey y. y
90 Chapter 5 Logarithmic, Eponential, and Other Transcendental Functions Test Form A Chapter 5 Name Class Date Section. Find the derivative: f ln. 6. Differentiate: y. ln y y y y. Find dy d if ey y. y
AB CALCULUS SEMESTER A REVIEW Show all work on separate paper. (b) lim. lim. (f) x a. for each of the following functions: (b) y = 3x 4 x + 2
 AB CALCULUS Page 1 of 6 NAME DATE 1. Evaluate each it: AB CALCULUS Show all work on separate paper. x 3 x 9 x 5x + 6 x 0 5x 3sin x x 7 x 3 x 3 5x (d) 5x 3 x +1 x x 4 (e) x x 9 3x 4 6x (f) h 0 sin( π 6
AB CALCULUS Page 1 of 6 NAME DATE 1. Evaluate each it: AB CALCULUS Show all work on separate paper. x 3 x 9 x 5x + 6 x 0 5x 3sin x x 7 x 3 x 3 5x (d) 5x 3 x +1 x x 4 (e) x x 9 3x 4 6x (f) h 0 sin( π 6
Calculus II. George Voutsadakis 1. LSSU Math 152. Lake Superior State University. 1 Mathematics and Computer Science
 Calculus II George Voutsadakis Mathematics and Computer Science Lake Superior State University LSSU Math 52 George Voutsadakis (LSSU) Calculus II February 205 / 88 Outline Techniques of Integration Integration
Calculus II George Voutsadakis Mathematics and Computer Science Lake Superior State University LSSU Math 52 George Voutsadakis (LSSU) Calculus II February 205 / 88 Outline Techniques of Integration Integration
Name: AK-Nummer: Ergänzungsprüfung January 29, 2016
 INSTRUCTIONS: The test has a total of 32 pages including this title page and 9 questions which are marked out of 10 points; ensure that you do not omit a page by mistake. Please write your name and AK-Nummer
INSTRUCTIONS: The test has a total of 32 pages including this title page and 9 questions which are marked out of 10 points; ensure that you do not omit a page by mistake. Please write your name and AK-Nummer
DIFFERENTIAL EQUATIONS
 Mr. Isaac Akpor Adjei (MSc. Mathematics, MSc. Biostats) isaac.adjei@gmail.com April 7, 2017 ORDINARY In many physical situation, equation arise which involve differential coefficients. For example: 1 The
Mr. Isaac Akpor Adjei (MSc. Mathematics, MSc. Biostats) isaac.adjei@gmail.com April 7, 2017 ORDINARY In many physical situation, equation arise which involve differential coefficients. For example: 1 The
Solutions to Exam 2, Math 10560
 Solutions to Exam, Math 6. Which of the following expressions gives the partial fraction decomposition of the function x + x + f(x = (x (x (x +? Solution: Notice that (x is not an irreducile factor. If
Solutions to Exam, Math 6. Which of the following expressions gives the partial fraction decomposition of the function x + x + f(x = (x (x (x +? Solution: Notice that (x is not an irreducile factor. If
AP Calculus Chapter 3 Testbank (Mr. Surowski)
 AP Calculus Chapter 3 Testbank (Mr. Surowski) Part I. Multiple-Choice Questions (5 points each; please circle the correct answer.). If f(x) = 0x 4 3 + x, then f (8) = (A) (B) 4 3 (C) 83 3 (D) 2 3 (E) 2
AP Calculus Chapter 3 Testbank (Mr. Surowski) Part I. Multiple-Choice Questions (5 points each; please circle the correct answer.). If f(x) = 0x 4 3 + x, then f (8) = (A) (B) 4 3 (C) 83 3 (D) 2 3 (E) 2
Final Exam Review Exercise Set A, Math 1551, Fall 2017
 Final Exam Review Exercise Set A, Math 1551, Fall 2017 This review set gives a list of topics that we explored throughout this course, as well as a few practice problems at the end of the document. A complete
Final Exam Review Exercise Set A, Math 1551, Fall 2017 This review set gives a list of topics that we explored throughout this course, as well as a few practice problems at the end of the document. A complete
1 Review of di erential calculus
 Review of di erential calculus This chapter presents the main elements of di erential calculus needed in probability theory. Often, students taking a course on probability theory have problems with concepts
Review of di erential calculus This chapter presents the main elements of di erential calculus needed in probability theory. Often, students taking a course on probability theory have problems with concepts
UNIT 3: DERIVATIVES STUDY GUIDE
 Calculus I UNIT 3: Derivatives REVIEW Name: Date: UNIT 3: DERIVATIVES STUDY GUIDE Section 1: Section 2: Limit Definition (Derivative as the Slope of the Tangent Line) Calculating Rates of Change (Average
Calculus I UNIT 3: Derivatives REVIEW Name: Date: UNIT 3: DERIVATIVES STUDY GUIDE Section 1: Section 2: Limit Definition (Derivative as the Slope of the Tangent Line) Calculating Rates of Change (Average
Math 21B - Homework Set 8
 Math B - Homework Set 8 Section 8.:. t cos t dt Let u t, du t dt and v sin t, dv cos t dt Let u t, du dt and v cos t, dv sin t dt t cos t dt u v v du t sin t t sin t dt [ t sin t u v ] v du [ ] t sin t
Math B - Homework Set 8 Section 8.:. t cos t dt Let u t, du t dt and v sin t, dv cos t dt Let u t, du dt and v cos t, dv sin t dt t cos t dt u v v du t sin t t sin t dt [ t sin t u v ] v du [ ] t sin t
Sample Questions Exam II, FS2009 Paulette Saab Calculators are neither needed nor allowed.
 Sample Questions Exam II, FS2009 Paulette Saab Calculators are neither needed nor allowed. Part A: (SHORT ANSWER QUESTIONS) Do the following problems. Write the answer in the space provided. Only the answers
Sample Questions Exam II, FS2009 Paulette Saab Calculators are neither needed nor allowed. Part A: (SHORT ANSWER QUESTIONS) Do the following problems. Write the answer in the space provided. Only the answers
MA1021 Calculus I B Term, Sign:
 MA1021 Calculus I B Term, 2014 Final Exam Print Name: Sign: Write up your solutions neatly and show all your work. 1. (28 pts) Compute each of the following derivatives: You do not have to simplify your
MA1021 Calculus I B Term, 2014 Final Exam Print Name: Sign: Write up your solutions neatly and show all your work. 1. (28 pts) Compute each of the following derivatives: You do not have to simplify your
F. KEEP YOUR BUBBLE SHEET COVERED AT ALL TIMES.
 UF UNIVERSITY of Department of Mathematics FLORIDA MAC 2233 Exam 2A Spring 2017 A. Sign your bubble sheet on the back at the bottom in ink. B. In pencil, write and encode in the spaces indicated: 1) Name
UF UNIVERSITY of Department of Mathematics FLORIDA MAC 2233 Exam 2A Spring 2017 A. Sign your bubble sheet on the back at the bottom in ink. B. In pencil, write and encode in the spaces indicated: 1) Name
UNIVERSITY OF SOUTHAMPTON
 UNIVERSITY OF SOUTHAMPTON MATH03W SEMESTER EXAMINATION 0/ MATHEMATICS FOR ELECTRONIC & ELECTRICAL ENGINEERING Duration: 0 min This paper has two parts, part A and part B. Answer all questions from part
UNIVERSITY OF SOUTHAMPTON MATH03W SEMESTER EXAMINATION 0/ MATHEMATICS FOR ELECTRONIC & ELECTRICAL ENGINEERING Duration: 0 min This paper has two parts, part A and part B. Answer all questions from part
Name Date Period. MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question.
 AB Fall Final Exam Review 200-20 Name Date Period MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Solve the problem. ) The position of a particle
AB Fall Final Exam Review 200-20 Name Date Period MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Solve the problem. ) The position of a particle
(e) 2 (f) 2. (c) + (d). Limits at Infinity. 2.5) 9-14,25-34,41-43,46-47,56-57, (c) (d) 2
 Math 150A. Final Review Answers, Spring 2018. Limits. 2.2) 7-10, 21-24, 28-1, 6-8, 4-44. 1. Find the values, or state they do not exist. (a) (b) 1 (c) DNE (d) 1 (e) 2 (f) 2 (g) 2 (h) 4 2. lim f(x) = 2,
Math 150A. Final Review Answers, Spring 2018. Limits. 2.2) 7-10, 21-24, 28-1, 6-8, 4-44. 1. Find the values, or state they do not exist. (a) (b) 1 (c) DNE (d) 1 (e) 2 (f) 2 (g) 2 (h) 4 2. lim f(x) = 2,
Practice Final Exam Solutions
 Important Notice: To prepare for the final exam, study past exams and practice exams, and homeworks, quizzes, and worksheets, not just this practice final. A topic not being on the practice final does
Important Notice: To prepare for the final exam, study past exams and practice exams, and homeworks, quizzes, and worksheets, not just this practice final. A topic not being on the practice final does

 J cc) c, >o,, c, =c7 $"(x\
J cc) c, >o,, c, =c7 $"(x\