1. The graph of a function f is given above. Answer the question: a. Find the value(s) of x where f is not differentiable. Ans: x = 4, x = 3, x = 2,
|
|
|
- Baldric Sherman
- 5 years ago
- Views:
Transcription
1 1. The graph of a function f is given above. Answer the question: a. Find the value(s) of x where f is not differentiable. x = 4, x = 3, x = 2, x = 1, x = 1, x = 2, x = 3, x = 4, x = 5 b. Find the value(s) of x where f is not differentiable but is continuous. x = 2, x = 3 c. Find the value(s) of x where f is not continuous, but has a limit. x = 1, x = 4 d. Find the value(s) of x where f does not have a limit. x = 4, x = 3, x = 1, x = 2, x = 5
2 2. The graph of a function f is given above. Answer the question: a. Find the value(s) of x where f is not differentiable. x = 5, x = 4, x = 3, x = 2, x = 1, x = 1, x = 2, x = 3 x = 4, x = 5 b. Find the value(s) of x where f is not differentiable but is continuous. x = 1, x = 2, x = 3, x = 4 c. Find the value(s) of x where f is not continuous, but has a limit. x = 5, x = 3, x = 1 d. Find the value(s) of x where f does not have a limit. x = 4, x = 2, x = 5
3 3. Find f (x), or, as appropriate: dx a. f(x) = 3 f (x) = 0 b. f(x) = 4x + 1 f (x) = 4 c. f(x) = 2x 2 3x + 1 f (x) = 4x 3 d. f(x) = 3x3 4 f (x) = 9 4 x2 e. f(x) = x 1 f (x) = 1 2 x f. f(x) = x x x f (x) = 5 2 x3/ x x g. f(x) = e x f (x) = e x h. f(x) = e f (x) = 0 i. f(x) = 3xe x f (x) = 3e x + 3xe x x + 1 j. y = 3x 4 dx = (3x 4)( 1 2 x ) ( x + 1)(3) (3x 4) 2 = 3x 6 x 4 (3x 4) 2 (2 x) k. y = (4x + 3) 3 dx = 3(4x + 3)2 (4) = 12(4x + 3) 2 l. y = (x 2 3x 2) 5 dx = 5(x2 3x 2) 4 (2x 3) m. f(x) = 4x 3 2x 2 + 4x + 5 f (x) = n. f(x) = e 3x 1 f (x) = 3e 3x 1 o. y = e x2 dx = 2 2xex p. y = ln x dx = 1 x q. y = ln(x 2 + 4x 1) 12x 2 4x x 3 2x 2 + 4x + 5 = 6x 2 2x + 2 4x3 2x 2 + 4x + 5
4 dx = 2x + 4 x 2 + 4x 1 r. y = ln 1 x dx = 1 x s. y = ln(ln x) dx = 1 x ln x t. y = 1 ln x dx = 1 x(ln x) 2 u. y = sin x f (x) = cos x ( ) 3π v. f(x) = sin 4 f (x) = 0 w. f(x) = 3x sin x + sin x cos x f (x) = 3 sin x + 3x cos x + cos 2 x sin 2 x x. f(x) = 3x 2 e x + 4x tan x f (x) = 6xe x + 3x 2 e x + 4x sec 2 x + 4 tan x y. f(x) = sin x cos xe x f (x) = sin x cos xe x sin 2 xe x + cos 2 xe x z. y = 3x 2 sin x cos xe x dx = 6x sin x cos xex + 3x 2 cos 2 xe x 3x 2 sin 2 xe x + 3x 2 sin x cos xe x aa. y = e 4 sin(x2 1) sin(x = 2 1) ( e4 4 cos ( x 2 1 ) 2x ) = 8xe 4 1) ( sin(x2 cos ( x 2 1 )) dx bb. y = 3ex sin x cos x 4e x dx = (cos x 4ex )(3e x cos x) (3e x sin x)( sin x 4e x ) (cos x 4e x ) 2 = (cos x 4ex )(3e x cos x) + (3e x sin x)(sin x + 4e x ) (cos x 4e x ) 2 cc. y = 9x2 e x + 4x cos x 2 sin x + xe x (2 sin x + xe x )[9(2xe x + x 2 e x ) + 4(cos x x sin x)] = dx (2 sin x + (9x2 e x x e + 4x cos x)(2 cos x + 2 x + xe x ) xe x ) 2 (2 sin x + xe x ) 2 dd. y = ex sin x x cos x 3x cos x + 4xe x dx = (3x cos x + 4xex )(e x cos x + e x sin x cos x + x sin x) (3x cos x + 4xe x ) 2 (ex sin x x cos x)[3(cos x x sin x) + 4e x + 4xe x ] (3x cos x + 4xe x ) 2 ee. f(x) = sin(3x 2 + 1) f (x) = 6x cos(3x 2 + 1) ff. f(x) = cos (sin (4x 2)) f (x) = 4 sin(sin(4x 2))(cos(4x 2)) gg. y = sin(e 3x )
5 dx = cos ( e 3x) 3e 3x hh. f(x) = sin(4x) f (x) = 4 cos 4x ii. y = sin 3 x dx = 3 sin2 x cos x jj. y = cos 4 (x 2 + 1) dx = 8x cos3 (x 2 + 1)(sin(x 2 + 1)) kk. y = e cos2 x 1 = 2 sin x cos 2 x 1 xecos dx ll. f(x) = tan 3 ( e 2x 1) f (x) = 6 tan 2 (e 2x 1 )(sec 2 (e 2x 1 ))(e 2x 1 ) mm. f(x) = cos(2x 3 4)e cos x f (x) = e cos x ( sin(2x 3 4)(6x 2 )) + cos(2x 3 4)(e cos x )( sin x) nn. f(x) = x tan(x 2 + 1)e 3x f (x) = tan(x 2 + 1)e 3x + x[sec 2 (x 2 + 1)(2x)e 3x + 3e 3x tan(x 2 + 1)] oo. f(x) = x 2 e sin x2 + e x sin(cos(3x 1)) f (x) = 2xe sin(x2) + x 2 (e sin(x2) )(cos(x 2 ))(2x)+ e x (cos(cos(3x 1)))( sin(3x 1)(3)) + sin(cos(3x 1))e x pp. y = e + 3xex2 2 e 4 sin x cos 2 x dx = (e 4 sin x cos2 x)[3xe x 2 2 (2x) + 3e x2 2 ] (e + 3xe x2 2 )[ 4 cos 3 x + 8 sin 2 x cos x] (e 4 sin x cos 2 x) 2 qq. y = tan 5 ( sec 3 ( x )) dx = 5 ( tan4 sec 3 ( x )) sec 2 ( sec 3 ( x )) 3 sec 2 ( x ) sec ( x ) tan ( x ) (2x) rr. y = arccos x dx = 1 1 x 2 ss. y = sin 5 ( e 3π+5 + 4e 3) x 2 dx = 2 sin5 ( e 3π+5 + 4e 3) x tt. y = arcsin(x 2 5x + 1) dx = 2x 5 1 (x2 5x + 1) 2 uu. y = arctan 2 (ln 3x) vv. y = dx = 2 arctan(ln(3x)) 1 x[1 + (ln(3x)) 2 ] ln(3x) sin(ln x 2 ) dx = sin(ln x2 ) 1 x ln(3x)(cos(ln(x2 )) 2 x ) (sin(ln(x 2 ))) 2 ww. y = 3e4x sin 1 (3x 2 + 1) ln x sin 5x + 3x 2 cos 2 x
6 dx = ( ) (ln x sin(5x) + 3x 2 cos 2 x)[12e 4x (sin 1 (3x 2 + 1) + 3e 4x 6x 1 (3x 2 +1) 2 (ln x sin(5x) + 3x 2 cos 2 x) 2 (3e 4x sin 1 (3x 2 + 1)) [ 1 x sin(5x) + 5 ln x cos(5x) + 3(2x cos2 x 2x 2 cos x sin x) ] (ln x sin(5x) + 3x 2 cos 2 x) 2 4. Find the equation of the line tangent to the given function f at the given point x = a: a. f(x) = 2, a = 3 y = 2 b. f(x) = 5x 1, a = 2 y = 5x 1 c. f(x) = x 2 2x + 4, a = 1 y = 3 d. f(x) = ln x, a = 3 y ln 3 = 1 (x 3) 3 e. f(x) = e 3x, a = 2 y 1 e 6 = 3 (x + 2) e6 f. f(x) = xe x ln 4x, a = 1 y (e ln 4) = (2e 1)(x 1) g. f(x) = sin x, a = π 6 y 1 2 = 3 2 ( x π ) 6 5. a. Define a function that has a left and right handed limit at a point a, but f does not have a limit at a. b. Define a function that has a limit at a point b but is undefined at b. c. Define a function that has a limit at point c, is defined at c, but is discontinuous at c. d. Define a function that is continuous at point d but is not differentiable at d. e. Define a function that is first differentiable at point p but is not second differentiable at point p. f. Draw the graph of a function which has all of the properties in a, b, c, d, e, above. There are more than one correct answer. The function defined below satisfies all conditions a through e: 3 if x 2 2 if 2 < x < 1 f(x) = sin x x if 1 x < 1 x 2 4 x 2 if 1 x < 3, x 2 5 if x = 2 3 x 4 if 3 x 5 3 (x 6) 4 if 5 < x
7 lim f(x) = 3 x 2 lim f(x) = 2 x 2 + lim f(x) Does not exist. x 2 lim x 0 f(x) = 1, f(0) is undefined. 10 lim f(x) = 4, f(2) = 5, f is discontinuous at 5. x 2 9 f is continuous at x = 4 but not differentiable at 4. f is first differentiable at x = 6 but 8 not second differentiable at 6. The graph of f is drawn below y Think About: -6 a. Given the graph of the original function f(x), how can you draw the graph of its derivative, f (x)? b. Given the graph of the derivative -7 of a function, f (x), how can you draw the graph of the original function, f(x)? Find dx a. y sin x = x cos y by implicite differentiation: -9 cos y y cos x = dx sin x + x sin y b. x 2 y + y 2 x = 5 2xy y2 = dx x 2 + 2xy c. 2y 4x sin x = e y 4 sin x + 4x cos x = dx 2 e y
8 d. ln(xy) + x y = 1 dx = y2 xy xy x 2 e. e xy + ln(x + y) = 2xy dx = 2y(x + y) yexy (x + y) 1 2x(x + y) + xe xy (x + y) Find f (x) and f (x): a. f(x) = 4 f (x) = 0 f (x) = 0 f (x) = 0 b. f(x) = 3x 2 f (x) = 6x f (x) = 6 f (x) = 0 c. f(x) = e x f (x) = e x f (x) = e x f (x) = e x d. f(x) = ln x f (x) = 1 x f (x) = 1 x 2 f (x) = 2 x 3 e. f(x) = x2 + 1 x 1 f (x) = x2 2x 1 (x 1) 2 f 4 (x) = (x 1) 3 f (x) = 12 (x 1) 4 f. f(x) = x f (x) = 1 2 x f (x) = 1 4 x 3 f (x) = 3 8 x 5 g. f(x) = x 5/4 f (x) = 5 4 x1/4 f (x) = 5 16 x 3/4 f (x) = x 7/4 h. f(x) = arccos x f 1 (x) = f x (x) = 1 x 2 (1 x 2 ) f (x) = (1 x 2 ) 3/2 3x 2 (1 x 2 ) 5/2 3/2 i. f(x) = sin x f (x) = cos x f (x) = sin x f (x) = cos x j. f(x) = e sin x f (x) = cos xe sin x f (x) = e sin x (cos 2 x sin x) f (x) = e sin x (cos 3 x 3 sin x cos x cos x) 9. Find the linearization of the given function at the given point a: a. f(x) = 2x 3, a = 2 L(x) = 2x 3, the linearization of a line is itself. b. f(x) = 2x 3, a = 4 L(x) = 2x 3, the linearization of a line is itself. c. f(x) = 2x 3, a = 10 L(x) = 2x 3, the linearization of a line is itself. d. f(x) = 4x 2 x + 3, a = 1 L(x) = 9x 1
9 e. f(x) = sin x, a = 0 L(x) = x f. f(x) = cos x, a = π ( L(x) = 2 x π ) 2 4 g. f(x) = e x, a = 0 L(x) = x + 1 h. f(x) = e x, a = 1 L(x) = e + e(x 1) i. f(x) = ln x, a = 1 L(x) = x 1 j. f(x) = ln x, a = 2 L(x) = (ln 2) + 1 (x 2) 2 k. f(x) = arctan x, a = 0 L(x) = x
Math 250 Skills Assessment Test
Math 5 Skills Assessment Test Page Math 5 Skills Assessment Test The purpose of this test is purely diagnostic (before beginning your review, it will be helpful to assess both strengths and weaknesses).
Name Date Period. MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question.
AB Fall Final Exam Review 200-20 Name Date Period MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Solve the problem. ) The position of a particle
SET 1. (1) Solve for x: (a) e 2x = 5 3x
() Solve for x: (a) e x = 5 3x SET We take natural log on both sides: ln(e x ) = ln(5 3x ) x = 3 x ln(5) Now we take log base on both sides: log ( x ) = log (3 x ln 5) x = log (3 x ) + log (ln(5)) x x
Math 180, Exam 2, Practice Fall 2009 Problem 1 Solution. f(x) = arcsin(2x + 1) = sin 1 (3x + 1), lnx
Math 80, Exam, Practice Fall 009 Problem Solution. Differentiate the functions: (do not simplify) f(x) = x ln(x + ), f(x) = xe x f(x) = arcsin(x + ) = sin (3x + ), f(x) = e3x lnx Solution: For the first
Mth Review Problems for Test 2 Stewart 8e Chapter 3. For Test #2 study these problems, the examples in your notes, and the homework.
For Test # study these problems, the examples in your notes, and the homework. Derivative Rules D [u n ] = nu n 1 du D [ln u] = du u D [log b u] = du u ln b D [e u ] = e u du D [a u ] = a u ln a du D [sin
Inverse Trigonometric Functions. September 5, 2018
Inverse Trigonometric Functions September 5, 08 / 7 Restricted Sine Function. The trigonometric function sin x is not a one-to-one functions..0 0.5 Π 6, 5Π 6, Π Π Π Π 0.5 We still want an inverse, so what
A.P. Calculus BC Test Two Section One Multiple-Choice Calculators Allowed Time 40 minutes Number of Questions 15
A.P. Calculus BC Test Two Section One Multiple-Choice Calculators Allowed Time 40 minutes Number of Questions 15 The scoring for this section is determined by the formula [C (0.25 I)] 1.8 where C is the
Week #6 - Taylor Series, Derivatives and Graphs Section 10.1
Week #6 - Taylor Series, Derivatives and Graphs Section 10.1 From Calculus, Single Variable by Hughes-Hallett, Gleason, McCallum et. al. Copyright 005 by John Wiley & Sons, Inc. This material is used by
Week 1: need to know. November 14, / 20
Week 1: need to know How to find domains and ranges, operations on functions (addition, subtraction, multiplication, division, composition), behaviors of functions (even/odd/ increasing/decreasing), library
Test one Review Cal 2
Name: Class: Date: ID: A Test one Review Cal 2 Short Answer. Write the following expression as a logarithm of a single quantity. lnx 2ln x 2 ˆ 6 2. Write the following expression as a logarithm of a single
Math 222 Spring 2013 Exam 3 Review Problem Answers
. (a) By the Chain ule, Math Spring 3 Exam 3 eview Problem Answers w s w x x s + w y y s (y xy)() + (xy x )( ) (( s + 4t) (s 3t)( s + 4t)) ((s 3t)( s + 4t) (s 3t) ) 8s 94st + 3t (b) By the Chain ule, w
Find the indicated derivative. 1) Find y(4) if y = 3 sin x. A) y(4) = 3 cos x B) y(4) = 3 sin x C) y(4) = - 3 cos x D) y(4) = - 3 sin x
Assignment 5 Name Find the indicated derivative. ) Find y(4) if y = sin x. ) A) y(4) = cos x B) y(4) = sin x y(4) = - cos x y(4) = - sin x ) y = (csc x + cot x)(csc x - cot x) ) A) y = 0 B) y = y = - csc
Inverse Trig Functions
6.6i Inverse Trigonometric Functions Inverse Sine Function Does g(x) = sin(x) have an inverse? What restriction would we need to make so that at least a piece of this function has an inverse? Given f (x)
3.4 The Chain Rule. F (x) = f (g(x))g (x) Alternate way of thinking about it: If y = f(u) and u = g(x) where both are differentiable functions, then
3.4 The Chain Rule To find the derivative of a function that is the composition of two functions for which we already know the derivatives, we can use the Chain Rule. The Chain Rule: Suppose F (x) = f(g(x)).
1 Solution to Homework 4
Solution to Homework Section. 5. The characteristic equation is r r + = (r )(r ) = 0 r = or r =. y(t) = c e t + c e t y = c e t + c e t. y(0) =, y (0) = c + c =, c + c = c =, c =. To find the maximum value
dx dx [x2 + y 2 ] = y d [tan x] + tan x = 2x + 2y = y sec 2 x + tan x dy dy = tan x dy dy = [tan x 2y] dy dx = 2x y sec2 x [1 + sin y] = sin(xy)
![dx dx [x2 + y 2 ] = y d [tan x] + tan x = 2x + 2y = y sec 2 x + tan x dy dy = tan x dy dy = [tan x 2y] dy dx = 2x y sec2 x [1 + sin y] = sin(xy)](/thumbs/75/71716329.jpg "dx dx [x2 + y 2 ] = y d [tan x] + tan x = 2x + 2y = y sec 2 x + tan x dy dy = tan x dy dy = [tan x 2y] dy dx = 2x y sec2 x [1 + sin y] = sin(xy)")
Math 7 Activit: Implicit & Logarithmic Differentiation (Solutions) Implicit Differentiation. For each of the following equations, etermine x. a. tan x = x 2 + 2 tan x] = x x x2 + 2 ] = tan x] + tan x =
Worksheets for GCSE Mathematics. Quadratics. mr-mathematics.com Maths Resources for Teachers. Algebra
Worksheets for GCSE Mathematics Quadratics mr-mathematics.com Maths Resources for Teachers Algebra Quadratics Worksheets Contents Differentiated Independent Learning Worksheets Solving x + bx + c by factorisation
Homework Problem Answers
Homework Problem Answers Integration by Parts. (x + ln(x + x. 5x tan 9x 5 ln sec 9x 9 8 (. 55 π π + 6 ln 4. 9 ln 9 (ln 6 8 8 5. (6 + 56 0/ 6. 6 x sin x +6cos x. ( + x e x 8. 4/e 9. 5 x [sin(ln x cos(ln
Final Exam 2011 Winter Term 2 Solutions
. (a Find the radius of convergence of the series: ( k k+ x k. Solution: Using the Ratio Test, we get: L = lim a k+ a k = lim ( k+ k+ x k+ ( k k+ x k = lim x = x. Note that the series converges for L
(e) 2 (f) 2. (c) + (d). Limits at Infinity. 2.5) 9-14,25-34,41-43,46-47,56-57, (c) (d) 2
Math 150A. Final Review Answers, Spring 2018. Limits. 2.2) 7-10, 21-24, 28-1, 6-8, 4-44. 1. Find the values, or state they do not exist. (a) (b) 1 (c) DNE (d) 1 (e) 2 (f) 2 (g) 2 (h) 4 2. lim f(x) = 2,
MATH 104 Practice Problems for Exam 2
. Find the area between: MATH 4 Practice Problems for Exam (a) x =, y = / + x, y = x/ Answer: ln( + ) 4 (b) y = e x, y = xe x, x = Answer: e6 4 7 4 (c) y = x and the x axis, for x 4. x Answer: ln 5. Calculate
Solutions to Exam 2, Math 10560
Solutions to Exam, Math 6. Which of the following expressions gives the partial fraction decomposition of the function x + x + f(x = (x (x (x +? Solution: Notice that (x is not an irreducile factor. If
3 Algebraic Methods. we can differentiate both sides implicitly to obtain a differential equation involving x and y:
3 Algebraic Methods b The first appearance of the equation E Mc 2 in Einstein s handwritten notes. So far, the only general class of differential equations that we know how to solve are directly integrable
Solution: APPM 1350 Final Exam Spring 2014
APPM 135 Final Exam Spring 214 1. (a) (5 pts. each) Find the following derivatives, f (x), for the f given: (a) f(x) = x 2 sin 1 (x 2 ) (b) f(x) = 1 1 + x 2 (c) f(x) = x ln x (d) f(x) = x x d (b) (15 pts)
Tangent Lines Sec. 2.1, 2.7, & 2.8 (continued)
Tangent Lines Sec. 2.1, 2.7, & 2.8 (continued) Prove this Result How Can a Derivative Not Exist? Remember that the derivative at a point (or slope of a tangent line) is a LIMIT, so it doesn t exist whenever
MATH 151, FALL SEMESTER 2011 COMMON EXAMINATION 3 - VERSION B - SOLUTIONS
Name (print): Signature: MATH 5, FALL SEMESTER 0 COMMON EXAMINATION - VERSION B - SOLUTIONS Instructor s name: Section No: Part Multiple Choice ( questions, points each, No Calculators) Write your name,
Mathematics 1052, Calculus II Exam 1, April 3rd, 2010
Mathematics 5, Calculus II Exam, April 3rd,. (8 points) If an unknown function y satisfies the equation y = x 3 x + 4 with the condition that y()=, then what is y? Solution: We must integrate y against
MATH 151, SPRING 2018
MATH 151, SPRING 2018 COMMON EXAM II - VERSIONBKEY LAST NAME(print): FIRST NAME(print): INSTRUCTOR: SECTION NUMBER: DIRECTIONS: 1. The use of a calculator, laptop or computer is prohibited. 2. TURN OFF
c) xy 3 = cos(7x +5y), y 0 = y3 + 7 sin(7x +5y) 3xy sin(7x +5y) d) xe y = sin(xy), y 0 = ey + y cos(xy) x(e y cos(xy)) e) y = x ln(3x + 5), y 0
Some Math 35 review problems With answers 2/6/2005 The following problems are based heavily on problems written by Professor Stephen Greenfield for his Math 35 class in spring 2005. His willingness to
UNIT 3: DERIVATIVES STUDY GUIDE
Calculus I UNIT 3: Derivatives REVIEW Name: Date: UNIT 3: DERIVATIVES STUDY GUIDE Section 1: Section 2: Limit Definition (Derivative as the Slope of the Tangent Line) Calculating Rates of Change (Average
DRAFT - Math 101 Lecture Note - Dr. Said Algarni
3 Differentiation Rules 3.1 The Derivative of Polynomial and Exponential Functions In this section we learn how to differentiate constant functions, power functions, polynomials, and exponential functions.
Math 147 Exam II Practice Problems
Math 147 Exam II Practice Problems This review should not be used as your sole source for preparation for the exam. You should also re-work all examples given in lecture, all homework problems, all lab
Section 3.5: Implicit Differentiation
Section 3.5: Implicit Differentiation In the previous sections, we considered the problem of finding the slopes of the tangent line to a given function y = f(x). The idea of a tangent line however is not
Unit #3 - Differentiability, Computing Derivatives, Trig Review
Unit #3 - Differentiability, Computing Derivatives, Trig Review Some problems and solutions selected or adapted from Hughes-Hallett Calculus. Derivative Interpretation and Existence 1. The cost, C (in
Solution to Review Problems for Midterm II
Solution to Review Problems for Midterm II Midterm II: Monday, October 18 in class Topics: 31-3 (except 34) 1 Use te definition of derivative f f(x+) f(x) (x) lim 0 to find te derivative of te functions
Final Exam. Math 3 December 7, 2010
Final Exam Math 3 December 7, 200 Name: On this final examination for Math 3 in Fall 200, I will work individually, neither giving nor receiving help, guided by the Dartmouth Academic Honor Principle.
MathsGeeks. Everything You Need to Know A Level Edexcel C4. March 2014 MathsGeeks Copyright 2014 Elite Learning Limited
Everything You Need to Know A Level Edexcel C4 March 4 Copyright 4 Elite Learning Limited Page of 4 Further Binomial Expansion: Make sure it starts with a e.g. for ( x) ( x ) then use ( + x) n + nx + n(n
(1) Find derivatives of the following functions: (a) y = x5 + 2x + 1. Use the quotient and product rules: ( 3 x cos(x)) 2
Calc 1: Practice Exam Solutions Name: (1) Find derivatives of the following functions: (a) y = x5 + x + 1 x cos(x) Answer: Use the quotient and product rules: y = xcos(x)(5x 4 + ) (x 5 + x + 1)( 1 x /
Math 131 Final Exam Spring 2016
Math 3 Final Exam Spring 06 Name: ID: multiple choice questions worth 5 points each. Exam is only out of 00 (so there is the possibility of getting more than 00%) Exam covers sections. through 5.4 No graphing
Multiple Choice Answers. MA 113 Calculus I Spring 2018 Exam 2 Tuesday, 6 March Question
MA 113 Calculus I Spring 2018 Exam 2 Tuesday, 6 March 2018 Name: Section: Last 4 digits of student ID #: This exam has 12 multiple choice questions (five points each) and 4 free response questions (ten
Terms of Use. Copyright Embark on the Journey
Terms of Use All rights reserved. No part of this packet may be reproduced, stored in a retrieval system, or transmitted in any form by any means - electronic, mechanical, photo-copies, recording, or otherwise
Math 251, Spring 2005: Exam #2 Preview Problems
Math 5, Spring 005: Exam # Preview Problems. Using the definition of derivative find the derivative of the following functions: a) fx) = e x e h. Use the following lim =, e x+h = e x e h.) h b) fx) = x
11.5. The Chain Rule. Introduction. Prerequisites. Learning Outcomes
The Chain Rule 11.5 Introduction In this Section we will see how to obtain the derivative of a composite function (often referred to as a function of a function ). To do this we use the chain rule. This
MA1021 Calculus I B Term, Sign:
MA1021 Calculus I B Term, 2014 Final Exam Print Name: Sign: Write up your solutions neatly and show all your work. 1. (28 pts) Compute each of the following derivatives: You do not have to simplify your
Brief answers to assigned even numbered problems that were not to be turned in
Brief answers to assigned even numbered problems that were not to be turned in Section 2.2 2. At point (x 0, x 2 0) on the curve the slope is 2x 0. The point-slope equation of the tangent line to the curve
16 Inverse Trigonometric Functions
6 Inverse Trigonometric Functions Concepts: Restricting the Domain of the Trigonometric Functions The Inverse Sine Function The Inverse Cosine Function The Inverse Tangent Function Using the Inverse Trigonometric
1d C4 Integration cot4x 1 4 1e C4 Integration trig reverse chain 1
A Assignment Nu Cover Sheet Name: Drill Current work Question Done BP Ready Topic Comment Aa C4 Integration Repeated linear factors 3 (x ) 3 (x ) + c Ab C4 Integration cos^ conversion x + sinx + c Ac C4
Practice Questions From Calculus II. 0. State the following calculus rules (these are many of the key rules from Test 1 topics).
Math 132. Practice Questions From Calculus II I. Topics Covered in Test I 0. State the following calculus rules (these are many of the key rules from Test 1 topics). (Trapezoidal Rule) b a f(x) dx (Fundamental
MATH 151 Engineering Mathematics I
MATH 151 Engineering Mathematics I Fall 2017, WEEK 14 JoungDong Kim Week 14 Section 5.4, 5.5, 6.1, Indefinite Integrals and the Net Change Theorem, The Substitution Rule, Areas Between Curves. Section
Mrs. Charnley, J303 Mrs. Zayaitz Ruhf, J305
Mrs. Charnley, J303 charnleyc@eastonsd.org Mrs. Zayaitz Ruhf, J305 zayaitzruhfm@eastonsd.org Part I. Online Quiz/Review, DUE June 30, 016 This is a quick review of some material from Pre-Calculus and other
AP Calculus Summer Prep
AP Calculus Summer Prep Topics from Algebra and Pre-Calculus (Solutions are on the Answer Key on the Last Pages) The purpose of this packet is to give you a review of basic skills. You are asked to have
Dr. Sophie Marques. MAM1020S Tutorial 8 August Divide. 1. 6x 2 + x 15 by 3x + 5. Solution: Do a long division show your work.
Dr. Sophie Marques MAM100S Tutorial 8 August 017 1. Divide 1. 6x + x 15 by 3x + 5. 6x + x 15 = (x 3)(3x + 5) + 0. 1a 4 17a 3 + 9a + 7a 6 by 3a 1a 4 17a 3 + 9a + 7a 6 = (4a 3 3a + a + 3)(3a ) + 0 3. 1a
6.1 The Inverse Sine, Cosine, and Tangent Functions Objectives
Objectives 1. Find the Exact Value of an Inverse Sine, Cosine, or Tangent Function. 2. Find an Approximate Value of an Inverse Sine Function. 3. Use Properties of Inverse Functions to Find Exact Values
Partial Derivatives for Math 229. Our puropose here is to explain how one computes partial derivatives. We will not attempt
Partial Derivatives for Math 229 Our puropose here is to explain how one computes partial derivatives. We will not attempt to explain how they arise or why one would use them; that is left to other courses
Math 106: Review for Exam II - SOLUTIONS
Math 6: Review for Exam II - SOLUTIONS INTEGRATION TIPS Substitution: usually let u a function that s inside another function, especially if du (possibly off by a multiplying constant) is also present
Math 171 Spring 2017 Final Exam. Problem Worth
Math 171 Spring 2017 Final Exam Problem 1 2 3 4 5 6 7 8 9 10 11 Worth 9 6 6 5 9 8 5 8 8 8 10 12 13 14 15 16 17 18 19 20 21 22 Total 8 5 5 6 6 8 6 6 6 6 6 150 Last Name: First Name: Student ID: Section:
Chapter 5 Notes. 5.1 Using Fundamental Identities
Chapter 5 Notes 5.1 Using Fundamental Identities 1. Simplify each expression to its lowest terms. Write the answer to part as the product of factors. (a) sin x csc x cot x ( 1+ sinσ + cosσ ) (c) 1 tanx
2. Which of the following is an equation of the line tangent to the graph of f(x) = x 4 + 2x 2 at the point where
AP Review Chapter Name: Date: Per: 1. The radius of a circle is decreasing at a constant rate of 0.1 centimeter per second. In terms of the circumference C, what is the rate of change of the area of the
Chapter 7: Techniques of Integration
Chapter 7: Techniques of Integration MATH 206-01: Calculus II Department of Mathematics University of Louisville last corrected September 14, 2013 1 / 43 Chapter 7: Techniques of Integration 7.1. Integration
MCV4U - Practice Mastery Test #9 & #10
Name: Class: Date: ID: A MCV4U - Practice Mastery Test #9 & #10 Multiple Choice Identify the choice that best completes the statement or answers the question. 1. x + 2 is a factor of i) x 3 3x 2 + 6x 8
Final Examination 201-NYA-05 May 18, 2018
. ( points) Evaluate each of the following limits. 3x x + (a) lim x x 3 8 x + sin(5x) (b) lim x sin(x) (c) lim x π/3 + sec x ( (d) x x + 5x ) (e) lim x 5 x lim x 5 + x 6. (3 points) What value of c makes
Math 106: Review for Exam II - SOLUTIONS
Math 6: Review for Exam II - SOLUTIONS INTEGRATION TIPS Substitution: usually let u a function that s inside another function, especially if du (possibly off by a multiplying constant) is also present
Homework Solutions: , plus Substitutions
Homework Solutions: 2.-2.2, plus Substitutions Section 2. I have not included any drawings/direction fields. We can see them using Maple or by hand, so we ll be focusing on getting the analytic solutions
Review Problems for Test 1
Review Problems for Test Math 6-03/06 9 9/0 007 These problems are provided to help you study The presence of a problem on this handout does not imply that there will be a similar problem on the test And
Grade: The remainder of this page has been left blank for your workings. VERSION E. Midterm E: Page 1 of 12
First Name: Student-No: Last Name: Section: Grade: The remainder of this page has been left blank for your workings. Midterm E: Page of Indefinite Integrals. 9 marks Each part is worth 3 marks. Please
Integration by Parts
Calculus 2 Lia Vas Integration by Parts Using integration by parts one transforms an integral of a product of two functions into a simpler integral. Divide the initial function into two parts called u
Hello Future Calculus Level One Student,
Hello Future Calculus Level One Student, This assignment must be completed and handed in on the first day of class. This assignment will serve as the main review for a test on this material. The test will
Chapter 3 Differentiation Rules (continued)
Chapter 3 Differentiation Rules (continued) Sec 3.5: Implicit Differentiation (continued) Implicit Differentiation What if you want to find the slope of the tangent line to a curve that is not the graph
and lim lim 6. The Squeeze Theorem
Limits (day 3) Things we ll go over today 1. Limits of the form 0 0 (continued) 2. Limits of piecewise functions 3. Limits involving absolute values 4. Limits of compositions of functions 5. Limits similar
5 t + t2 4. (ii) f(x) = ln(x 2 1). (iii) f(x) = e 2x 2e x + 3 4
Study Guide for Final Exam 1. You are supposed to be able to determine the domain of a function, looking at the conditions for its expression to be well-defined. Some examples of the conditions are: What
INVERSE FUNCTIONS DERIVATIVES. terms on one side and everything else on the other. (3) Factor out dy. for the following functions: 1.
INVERSE FUNCTIONS DERIVATIVES Recall the steps for computing y implicitly: (1) Take of both sies, treating y like a function. (2) Expan, a, subtract to get the y terms on one sie an everything else on
Chapter 22 : Electric potential
Chapter 22 : Electric potential What is electric potential? How does it relate to potential energy? How does it relate to electric field? Some simple applications What does it mean when it says 1.5 Volts
WeBWorK, Problems 2 and 3
WeBWorK, Problems 2 and 3 7 dx 2. Evaluate x ln(6x) This can be done using integration by parts or substitution. (Most can not). However, it is much more easily done using substitution. This can be written
Math 131 Exam 2 Spring 2016
Math 3 Exam Spring 06 Name: ID: 7 multiple choice questions worth 4.7 points each. hand graded questions worth 0 points each. 0. free points (so the total will be 00). Exam covers sections.7 through 3.0
Differential Equations: Homework 2
Differential Equations: Homework Alvin Lin January 08 - May 08 Section.3 Exercise The direction field for provided x 0. dx = 4x y is shown. Verify that the straight lines y = ±x are solution curves, y
MATH 162. Midterm Exam 1 - Solutions February 22, 2007
MATH 62 Midterm Exam - Solutions February 22, 27. (8 points) Evaluate the following integrals: (a) x sin(x 4 + 7) dx Solution: Let u = x 4 + 7, then du = 4x dx and x sin(x 4 + 7) dx = 4 sin(u) du = 4 [
Sec 2.2: Infinite Limits / Vertical Asymptotes Sec 2.6: Limits At Infinity / Horizontal Asymptotes
Sec 2.2: Infinite Limits / Vertical Asymptotes Sec 2.6: Limits At Infinity / Horizontal Asymptotes Sec 2.2: Infinite Limits / Vertical Asymptotes Sec 2.6: Limits At Infinity / Horizontal Asymptotes Infinite
Sec 2.2: Infinite Limits / Vertical Asymptotes Sec 2.6: Limits At Infinity / Horizontal Asymptotes
Sec 2.2: Infinite Limits / Vertical Asymptotes Sec 2.6: Limits At Infinity / Horizontal Asymptotes Sec 2.2: Infinite Limits / Vertical Asymptotes Sec 2.6: Limits At Infinity / Horizontal Asymptotes Infinite
Math 152 Take Home Test 1
Math 5 Take Home Test Due Monday 5 th October (5 points) The following test will be done at home in order to ensure that it is a fair and representative reflection of your own ability in mathematics I
2.1 The derivative. Rates of change. m sec = y f (a + h) f (a)
2.1 The derivative Rates of change 1 The slope of a secant line is m sec = y f (b) f (a) = x b a and represents the average rate of change over [a, b]. Letting b = a + h, we can express the slope of the
MATH 408N PRACTICE FINAL
05/05/2012 Bormashenko MATH 408N PRACTICE FINAL Name: TA session: Show your work for all the problems. Good luck! (1) Calculate the following limits, using whatever tools are appropriate. State which results
M GENERAL MATHEMATICS -2- Dr. Tariq A. AlFadhel 1 Solution of the First Mid-Term Exam First semester H
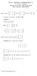M - GENERAL MATHEMATICS -- Dr. Tariq A. AlFadhel Solution of the First Mid-Term Exam First semester 38-39 H 3 Q. Let A =, B = and C = 3 Compute (if possible) : A+B and BC A+B is impossible. ( ) BC = 3
Math 180, Final Exam, Fall 2012 Problem 1 Solution
Math 80, Final Exam, Fall 0 Problem Solution. Find the derivatives of the following functions: (a) ln(ln(x)) (b) x 6 + sin(x) e x (c) tan(x ) + cot(x ) (a) We evaluate the derivative using the Chain Rule.
A A A A A A A A A A A A. a a a a a a a a a a a a a a a. Apples taste amazingly good.
Victorian Handwriting Sheet Aa A A A A A A A A A A A A Aa Aa Aa Aa Aa Aa Aa a a a a a a a a a a a a a a a Apples taste amazingly good. Apples taste amazingly good. Now make up a sentence of your own using
MA Practice Exam #2 Solutions
MA 123 - Practice Exam #2 Solutions Name: Instructions: For some of the questions, you must show all your work as indicated. No calculators, books or notes of any form are allowed. Note that the questions
Inverse Trig Functions
Inverse Trig Functions -8-006 If you restrict fx) = sinx to the interval π x π, the function increases: y = sin x - / / This implies that the function is one-to-one, an hence it has an inverse. The inverse
Find all points where the function is discontinuous. 1) Find all vertical asymptotes of the given function. x(x - 1) 2) f(x) =
Math 90 Final Review Find all points where the function is discontinuous. ) Find all vertical asymptotes of the given function. x(x - ) 2) f(x) = x3 + 4x Provide an appropriate response. 3) If x 3 f(x)
Section 4.8 Anti Derivative and Indefinite Integrals 2 Lectures. Dr. Abdulla Eid. College of Science. MATHS 101: Calculus I
Section 4.8 Anti Derivative and Indefinite Integrals 2 Lectures College of Science MATHS 101: Calculus I (University of Bahrain) 1 / 28 Indefinite Integral Given a function f, if F is a function such that
Section 3.6 The chain rule 1 Lecture. Dr. Abdulla Eid. College of Science. MATHS 101: Calculus I
Section 3.6 The chain rule 1 Lecture College of Science MATHS 101: Calculus I (University of Bahrain) Logarithmic Differentiation 1 / 23 Motivation Goal: We want to derive rules to find the derivative
A special rule, the chain rule, exists for differentiating a function of another function. This unit illustrates this rule.
The Chain Rule A special rule, the chain rule, exists for differentiating a function of another function. This unit illustrates this rule. In order to master the techniques explained here it is vital that
Math 1431 Final Exam Review
Math 1431 Final Exam Review Comprehensive exam. I recommend you study all past reviews and practice exams as well. Know all rules/formulas. Make a reservation for the final exam. If you miss it, go back
" = Y(#,$) % R(r) = 1 4& % " = Y(#,$) % R(r) = Recitation Problems: Week 4. a. 5 B, b. 6. , Ne Mg + 15 P 2+ c. 23 V,
Recitation Problems: Week 4 1. Which of the following combinations of quantum numbers are allowed for an electron in a one-electron atom: n l m l m s 2 2 1! 3 1 0 -! 5 1 2! 4-1 0! 3 2 1 0 2 0 0 -! 7 2-2!
Chapter 3: Transcendental Functions
Chapter 3: Transcendental Functions Spring 2018 Department of Mathematics Hong Kong Baptist University 1 / 32 Except for the power functions, the other basic elementary functions are also called the transcendental
Section 3.6 The chain rule 1 Lecture. Dr. Abdulla Eid. College of Science. MATHS 101: Calculus I
Section 3.6 The chain rule 1 Lecture College of Science MATHS 101: Calculus I (University of Bahrain) Logarithmic Differentiation 1 / 1 Motivation Goal: We want to derive rules to find the derivative of
1 + x 2 d dx (sec 1 x) =
Page This exam has: 8 multiple choice questions worth 4 points each. hand graded questions worth 4 points each. Important: No graphing calculators! Any non-graphing, non-differentiating, non-integrating
Solutions to Exam 1, Math Solution. Because f(x) is one-to-one, we know the inverse function exists. Recall that (f 1 ) (a) =
Solutions to Exam, Math 56 The function f(x) e x + x 3 + x is one-to-one (there is no need to check this) What is (f ) ( + e )? Solution Because f(x) is one-to-one, we know the inverse function exists
AP Calculus AB Summer Math Packet
Name Date Section AP Calculus AB Summer Math Packet This assignment is to be done at you leisure during the summer. It is meant to help you practice mathematical skills necessary to be successful in Calculus
PART A: Solve the following equations/inequalities. Give all solutions. x 3 > x + 3 x
CFHS Honors Precalculus Calculus BC Review PART A: Solve the following equations/inequalities. Give all solutions. 1. 2x 3 + 3x 2 8x = 3 2. 3 x 1 + 4 = 8 3. 1 x + 1 2 x 4 = 5 x 2 3x 4 1 4. log 2 2 + log
MATH 1241 Common Final Exam Fall 2010
MATH 1241 Common Final Exam Fall 2010 Please print the following information: Name: Instructor: Student ID: Section/Time: The MATH 1241 Final Exam consists of three parts. You have three hours for the
SANDERSON HIGH SCHOOL AP CALCULUS AB/BC SUMMER REVIEW PACKET
SANDERSON HIGH SCHOOL AP CALCULUS AB/BC SUMMER REVIEW PACKET 017-018 Name: 1. This packet is to be handed in on Monday August 8, 017.. All work must be shown on separate paper attached to the packet. 3.