On q-gamma Distributions, Marshall-Olkin q-gamma Distributions and Minification Processes
|
|
|
- Andrew Carpenter
- 5 years ago
- Views:
Transcription
1 CHAPTER 4 On q-gamma Distributions, Marshall-Olkin q-gamma Distributions and Minification Processes 4.1 Introduction Several skewed distributions such as logistic, Weibull, gamma and beta distributions have been used for modelling various random phenomena which arise in engineering, time series modelling, reliability assessment studies etc. Mathai (2005) introduced a real matrix variate probability model which cover almost all real matrix-variate densities used in multivariate statistical analysis. Through the new density introduced, a pathway is created from matrix- variate type I to matrix- variate type II beta to matrix- variate gamma to matrixvariate Gaussian densities. In this chapter we consider the scalar version of the matrixvariate gamma distribution and study the various properties. Recently several q-type distributions such as q-exponential, q-weibull, and q-logistic and various pathway models are 65
2 developed in the context of information theory, statistical mechanics, reliability modelling etc. See Wilk and Wlodarczyk (2000, 2001), Tsallis (1988),Jose and Naik (2009). Marshall and Olkin (1997) introduced a method of construction of a family of distributions by adding a new parameter to an existing distribution which resulted in added flexibility of the distribution. Alice and Jose (2003, 2004, 2005a, 2005b), conducted detailed studies of various Marshall-Olkin distributions. Ristic et al. (2007) introduced and studied the various properties of Marshall-Olkin gamma distribution. Jose, Naik and Ristic (2008) introduced Marshall-Olkin q- Weibull distribution and also developed time series models having this distribution as marginals. Different first order autoregressive (AR(1)) time series models can be developed using the Marshall-Olkin distribution which are very useful in various fields like time series modelling,reliability studies etc. Here we also extend the q-gamma distribution to obtain a more general class called Marshall-Olkin q- gamma distribution. In this chapter we give a detailed study of q-gamma distribution and its properties. The estimation of the parameters is discussed and a theorem which is useful in stressstrength analysis is established. The new distribution is found to be a better fit than the standard gamma distribution using a real data set. We introduce the Marshall-Olkin q- gamma distribution and develop AR(1) minification model and max-min process. Also the sample path properties are studied. 4.2 The q-analogue of the Gamma Distribution Mathai (2005) introduced a pathway model connecting matrix variate gamma distribution and normal densities. The following is the scalar version of the matrix-variate density introduced by Mathai (2005). When the pathway parameter q > 1: f 1 (x) = c 1 x α 1 [1 + a(q 1) x δ ] ; (4.2.1) < x <, a > 0, > 0, δ > 0, q > 1 66
3 where c 1 = ( ) δ[a(q 1)] α δ Γ q 1 ( α ) ( 2Γ Γ δ q 1 α δ ), R ( q 1 > α ), R(α) > 0 δ where R( ) denotes the real part of ( ). Since in most statistical problems the parameters are real, we will consider all parameters to be real. Note that for q < 1, writing q 1 = (1 q), the density in (4.2.1) reduces to the following form: f 2 (x) = c 2 x α 1 [1 a(1 q) x δ ] 1 q ; (4.2.2) q < 1, a > 0, > 0, δ > 0, 1 a(1 q) x δ > 0 where the normalizing constant c 2 is given by c 2 = ( ) δ(a(1 q)) α δ Γ + α q δ 2Γ ( ) ( ), R(α) > 0. α δ Γ q As q 1, f 1 (x) and f 2 (x) tend to f 3 (x), which is the generalized gamma density. f 3 (x) is given by f 3 (x) = δ(a) α δ 2Γ ( ) x α 1 exp( a x δ ); < x < ; a, α,, δ > 0. (4.2.3) α δ For different values of the parameters in (4.2.1) and (4.2.2), we get different distributions like beta type-1, beta type-2, etc. More results are available in Mathai and Haubold (2007) and Mathai and Provost (2006). Here we introduce a q-analogue of the gamma distribution as a special case of Mathai (2005), by taking δ = 1, a = 1 in f 1 (x). Then for x > 0 and for q > 1, f 1 (x) reduces to the following density which we call the q-gamma distribution: f 4 (x) = k 1 x α 1 [1 + (q 1)x)] (4.2.4) where the normalizing constant k 1 is given by 67
4 Table 4.1: The q-gamma distribution characteristics when q > 1 Characteristics Functional form p.d.f f 4 (x) = ()α Γ [1 + (q 1)x)] ΓαΓ( ; x > 0, α, > 0, α)xα 1 CDF F 4 (x) = B(x(),α, α) B(α, α) HRF h 4 (x) = ()α x α 1 [1+()x)] CHR H 4 (x) = B(α, α) B(x(),α, α) (x(),α, α) B(α, α) (x(),α, α) s th moment E(x s ) = Γ(α+s)Γ α s Γ(α)Γ( α). ()s mean value E(x) = α (α 1)() k 1 = (q 1)α Γ ( ) (4.2.5) ΓαΓ α For x > 0 and q < 1, f 2 (x) reduces to the following density function of the q-gamma distribution: where k 2 is given by f 5 (x) = k 2 x α 1 [1 (1 q)x)] 1 q (4.2.6) k 2 = ( ) (1 q) α Γ + α q ( ) (4.2.7) ΓαΓ q for 0 x 1 (1 q), α > 0. The q-gamma distributions exhibits various shapes as can be seen from the figures 4.1 and 4.2. and hence it can be applied for modelling different types of data from various fields. The graph of the hazard rate function of MO-q-G is flexible and by giving various values for the pathway parameter q we can get different shapes which makes it applicable in a variety of situations (see figure 4.3). 68
5 Table 4.2: The q-gamma distribution characteristics when q < 1 Characteristics Functional form p.d.f f 4 (x) = (1 q)α Γ 1 q +α+1 x α 1 [1 (1 q)x] 1 q CDF ΓαΓ( α) 1 q F 4 (x) = B(x(1 q),α, 1 q α) B(α, 1 q α) 1 q HRF h 4 (x) = (1 q)α x α 1 [1 (1 q)x)] CHR H 4 (x) = s th moment E(x s ) = B(α, 1 q α) B(x(1 q),α, 1 q α) B(x(1 q),α, 1 q α) B(α, 1 q α) B(x(1 q),α, 1 q α) Γ(α+s)Γ 1 q +α+1 Γ(α)Γ( +α+s+1)(1 q)6s. 1 q mean value E(x) = α +(1 q)(α+1) Figure 4.1: The q-gamma pdf for q > 1 69
6 Figure 4.2: The q-gamma pdf for q < 1 Figure 4.3: Hazard rate function for various values of q 70
7 Figure 4.4: Estimated densities of gamma and q-gamma. 4.3 Estimation (i) First we consider method of moments. Since the distribution has explicit expressions for the moments we can get the values of the parameters by equating sample and population moments. We kept = 1 and estimated the values of the parameters for the data given in Gross and Clark(1975)(Data given in chapter 3). The estimated densities are given and the graph shows that q-gamma better fits the data. The estimates were obtained as α = and q = The estimated densities are given in figure (4.4). (ii) Now we consider maximum likelihood estimation for the parameters. When q > 1 the likelihood function is L = (q 1)n α ((Γ(/(q 1)) n x α 1 Γ(α) n (Γ(/(q 1) α) n i [1 + (q 1)x i )] 71
8 log L = nα log(q 1) + n log(γ(/(q 1))) + (α 1) (log((x i ) /(q 1))) log L α log L log L q (log((1 + (q 1)x i ))) n log(γ(α)) n log(γ(beta/(q 1) α)) = n log(q 1) + (log(y)) nψ(α) + nψ(/(q 1) α) 1 = nψ(/(q 1)) q 1 1 (log(1 + (q 1)y)) q 1 n ψ(/(q 1) α) q 1 = nα q 1 n (q 1) ψ(/(q 1)) 1 2 q 1 1 (log(1 + (q 1)y)) q 1 n ψ(/(q 1) α). q 1 The function nlm in R package can be used to solve these normal equations. The case q < 1 can be considered similarly. 4.4 Application in Stress-Strength Analysis Stress-Strength analysis is concerned with the probability of failure which is the probability of stress exceeding strength. Let X represent the stress and Y represent the strength of the system. Then R = P (X < Y ) is the probability that the system will function. More details on stress-strength analysis can be found in Kotz et al. (2007). H-function is defined as follows: [ Hp,q m,n z ] (a 1,α 1 ),(a 2,α 2 ),,(a k,α k ) (b 1, 1 ),(b 2, 2 ),,(b q, q) = 1 h(s)z s ds 2πi L where h(s) = { m } { n } Γ(b j + j s) Γ(1 a j α j s) j=1 { q j=1 } { p } Γ(1 b j j s) Γ(a j + α j s) j=m+1 j=n+1 and L is a suitable path. Here a 1, a 2,..., a p ; b 1, b 2,..., b q are complex numbers and α 1, α 2,..., α p, 1, 2,..., q 72
9 are positive real numbers. The poles of Γ(b j + j s), j = 1, 2,..., m are at the points s = b j+ν j where j = 1, 2,..., m, ν = 0, 1,... and the poles of Γ(1 a j α j s), j = 1, 2,..., n are at s = 1 a k+λ α k where k = 1, 2,..., n, λ = 0, 1,.... The details of the existence conditions, various properties and applications of H-functions are available in Mathai (1993). Now we state a theorem which is useful in the context of stress-strength analysis of a multi component system subjected to a number of independent stresses X 1, X 2,..., X k, whose cumulative effect is the actual effective stress against a single strength Y. Then R = P ( k i=1 X i < Y ) is the probability that the system will function and it is called the reliability of the system. Theorem Let {X i, i = 1, 2,..., k} be i.i.d. random variables having a q- Gamma distribution function and Y be distributed as exponential distribution with parameter θ. Then P ( k i=1 X i < Y ) is an H-function. Proof: Let X 1, X 2,..., X k be continuous i.i.d. q-gamma r.v.s and let Y follow the exponential distribution with parameter θ. Let g 1 ( ) and g 2 ( ) be the probability density functions of the q-gamma distribution for q < 1 and for q > 1. Let g k ( ) and G k ( ) be the probability density function and cumulative distribution function of the random variable k i=1 X i. Let g 1( ) and g 2( ) be the corresponding Laplace transforms of the q-gamma distribution for q > 1 and for q < 1 respectively. Then P ( k X i < Y ) = θ i=1 = 0 G k (x)e θx dx {g1(θ)} k for q > 1 {g2(θ)} k for q < 1. Now for q > 1 we have to evaluate the integral I 1(α, λ, q : θ) = 0 e θx x α 1 [1 + (q 1)x)] dx. The integrand can be taken as a product of two integrable functions. Let x 1 and x 2 be two 73
10 independently distributed real scalar random variables with probability density functions f 1 (x) and f 2 (x). Consider the transformation u = x 1 x 2 and v = x 2 dx 1 dx 2 = v du dv where is the wedge product discussed in ( Mathai1997). Then the joint density of u and v is g(u, v) = vf 1 (uv)f 2 (v). Now g 1 (u) is obtained by integrating out the joint probability density function g(u, v) with respect to v. That is g 1 (u) = v vf 1(uv)f 2 (v)dv. Let f 1 (x 1 ) = c 1 e θx 1, x 1 0 and f 2 (x 2 ) = c 2 x α 1 2 [1 + (q 1)x 2 ], x2 0, α, λ > 0 where c 1 and c 2 are normalizing constants. These constants can be obtained by integrating f 1 (x) and f 2 (x) with respect to x. Thus we have g 1 (u) = c 1 c 2 Now E(x1 s 1 ) = c 1 E(x 1 s 0 2 ) = c 2 = = 0 0 c 2 (q 1) α s+1 e θuv v α 1 {1 + (q 1)v] dv. (4.4.1) x s 1 1 e θx 1 dx 1 = θ s Γ(s), R(s) > 0 x α s 2 [1 + (q 1)x 2 ] dx2 ω α s (1 + ω) dω 0 c 2 Γ(α s + 1) Γ( (q 1) α s+1 α + s 1) Γ( ), for R(1 s α ) > 0, R( 1 q 1 + s 1) > 0. α Then E(u) s 1 = E(x 1 ) s 1 E(x 2 ) 1 s θ s Γ(s)Γ(1 + α s)γ( = c 1 c α + s 1) 2 (q 1) α s+1 Γ( ), q > 1 for R(s) > 0, R(α s) > 0, R( α + s 1) > 0. Now the density of u is obtained by the inverse Mellin transform. The detailed existence conditions for Mellin and inverse Mellin transforms are available in Mathai (1993). 74
11 Thus g 1 (u) = 1 2πi = c+i c i c 1 c 2 (q 1) α+1 Γ u s E(u) s 1 1 c+i 2πi c i Γ(s)Γ(1 + α s)γ( q 1 α + s 1) ( ) θu s ds q 1 for R(s) > 0, R(α s) > 0, R( α s) > 0, q > 1. I 1(α,, q : θ) = [ 1 )H2,1 θ αγ( 1,2 (q 1) (0,α) (0,1),( q+1,α) ], q > 1. On substituting this we get, k P ( X i < Y ) = i=1 { [ q 1 α)h2,1 θ Γ( 1,2 (q 1) (0,α) (0,1),( q+1,α) ]} k, q > 1. Now for q < 1, we have to evaluate the integral I 2(α,, q : θ) = 0 e θx x α 1 [1 (1 q)x] 1 q dx. Let f 1 (x 1 ) = c 1 e θx 1, x 1 0 c 2 x α 1 2 [1 (1 q)x] 1 q for 1 (1 q)x > 0 and f 2 (x 2 ) = 0 otherwise where c 1 and c 2 are the normalizing constants. Then proceeding as in the case for q > 1, we have P ( k X i < Y ) = i=1 { [ 1 q 1)H2,1 θ Γ( 1 q + α + 1,2 (q 1) (0,α) (0,1),( αq+α,α) ]} k, q > 1. 75
12 4.5 Marshall-Olkin q-gamma Distribution Marshall and Olkin (1997) introduced a new family of survival functions which is constructed by adding a new parameter to an existing distribution. The introduction of a new parameter will result in flexibility in the distribution. Different first order autoregressive (AR(1)) time series models can be developed using the Marshall-Olkin Gamma distribution. Now we shall extend the q-gamma distributions to obtain a more general class called Marshall-Olkin q-gamma distribution using (??). Now consider the case q > 1. Substituting the q-gamma distribution function defined in F 4 (x) in (??), we get a new family of distributions called Marshall-Olkin q-gamma distribution (MO-q-G), whose distribution function and the survival function Ḡ1( )are given by G 1 (x; p, q, α, ) = B(x(q 1), α, α) pb(α, α) + (1 p)b(x(q 1), α,. (4.5.1) α) Ḡ 1 (x; p, q, α, ) = p [B(α, α) B(x(q 1), α, α)] pb(α, α) + (1 p)b(x(q 1), α,. (4.5.2) α) Then the p.d.f. corresponding to G 1 ( ) is given by g 1 (x; p, q, α, ) = p(q 1)α x α 1 [1 + (q 1)x)] B(α, α) pb(α, α) + (1 p)b(x(q 1), α,, x > 0, q > 1. α)2 Similarly when q < 1, the cdf is given by G 2 (x; p, q, α, ) = B(x(1 q), α, + 1) 1 q pb(α, + 1) + (1 p)b(x(1 q), α,. (4.5.3) + 1) 1 q 1 q 76
13 and the p.d.f. corresponding to G 2 ( ) is given by is given by g 2 (x; p, q, α, ) = p(1 q)α x α 1 [1 (1 q)x)] 1 q B(α, + 1) 1 q pb(α, + 1) + (1 p)b(x(1 q), α,, 0 < x < (1/1 q). + 1)2 1 q 1 q The hazard rate functions are given by h 1 (x) = pb(α, (q 1) α x α 1 [1 + (q 1)x)] B(α, α) α) + (1 p)u(x) (B(α, ) α) U(x) for q > 1 and h 2 (x) = pb(α, (1 q) α x α 1 [1 (1 q)x)] 1 q B(α, 1 q + 1) 1 q + 1) + (1 p)v (x) (B(α, ) + 1) V (x) 1 q where and U(x) = B(x(q 1), α, V (x) = B(x(1 q), α, q 1 α). 1 q + 1). Theorem Let {X i, i 1} be a sequence of i.i.d. random variables with common distribution function F (x) and let N be a geometric random variable independently distributed of {X i } such that P [N = n] = θ(1 θ) n 1, n = 1, 2,..., 0 < θ < 1, which is for all i 1. Let U N = min 1 i N X i. Then {U N } is distributed as MO-q-G if and only if {X i } follows q-gamma distribution. Proof: The survival function of the random variable U N is H(x) = P (U N > x) = θ [ F (x)] n (1 θ) n 1 = n=1 θ F (x) 1 (1 θ) F (x). If X i has the survival function of the q-gamma distribution given by (6.2), then U N has the survival function of the MO-q-G distribution. The converse easily follows. 77
14 4.6 AR(1)models with q-gamma Marginal Distribution Tavares(1977, 1980) introduced two stationary Markov processes with similar structural forms which had applications in hydrological applications. Lewis and McKenzie (1991) discuss various aspects of first order autoregressive minification processes. In this section we develop autoregressive minification processes of order one and order k with minification structures where MO-q-G distribution is the stationary marginal distribution. We call the process as MO-q-G AR(1) process. Now we have the following theorem. Theorem Consider an AR(1) structure given by ɛ n, w.p. p 1 X n = min(x n 1, ɛ n ), w.p. 1 p 1 0 < p 1 < 1 and {ɛ n } is a sequence of i.i.d. random variables independently distributed of X n. Then {X n } is a stationary Markovian AR(1) process with MO-q-G marginal if and only if {ɛ n } is distributed as q-gamma distribution. Proof: From the given structure it follows that F Xn (x) = p 1 Fɛn (x) + (1 p 1 ) F Xn 1 (x) F ɛn (x). Under stationary equilibrium, it reduces to F X (x) = On substituting the survival function F 1 (x) of ɛ, for q > 1, we get p 1 Fɛ (x) 1 (1 p 1 ) F ɛ (x). (4.6.1) F 1X (x) = p 1 [(α, α) (x(q 1), α, α] p 1 (α, α) + (1 p 1) (x(q 1), α, α) which resembles the survival function Ḡ1( ) of the MO-q-G distribution. Conversely, if 78
15 we take the survival function of the above form, we get the survival function of ɛ n as the q-gamma distribution under stationary equilibrium. Similar is the case when q < 1. The following theorem generalizes the results to a k th order autoregressive structure. Theorem Consider an AR(k) structure given by ɛ n, w.p. p 0 X n = min(x n 1, ɛ n ), w.p. p 1 min(x n 2, ɛ n ), w.p. p 2.. min(x n k, ɛ n ), w.p. p k where {ɛ n } is a sequence of i.i.d. random variables independently distributed of X n, 0 < p i < 1, p 1 + p p k = 1 p 0. Then the stationary marginal distribution of {X n } is MO-q-G if and only if {ɛ n } is distributed as q-gamma distribution. Proof: From the given structure the survival function is given as follows: F Xn (x) = p 0 Fɛn (x) + p 1 FXn 1 (x) F ɛn (x) + + p k FXn k (x) F ɛn (x). Under stationary equilibrium, this yields F X (x) = p 0 Fɛ (x) + p 1 FX (x) F ɛ (x) + + p k FX (x) F ɛ (x). This reduces to F X (x) = p 0 Fɛ (x) 1 (1 p 0 ) F ɛ (x). Then the theorem easily follows by similar arguments as in Theorem (4.6.1). For q > 1 and for q < 1, if we substitute the survival function of q-gama distribution we get the survival function of the MO-q-G distribution. The sample path of the minification process is given in figure
16 Figure 4.5: Sample path of MO-q-gamma process for α = 1.7, p = 0.4, q = 1.2, = The Max-min AR(1) Processes Next we introduce the model called the max-min process given by Jose et al.(2008b). The structure is given as follows. Theorem Consider an AR(1) structure given by X n = ɛ n, w.p. p 1 max(x n 1, ɛ n ), w.p. p 2 min(x n 1, ɛ n ), w.p. p 3 subject to the conditions 0 < p 1, p 2 < 1, p 2 < p 1 and p 1 + p 2 + p 3 = 1, where {ɛ n } is a sequence of i.i.d. random variables independently distributed of X n. Then {X n } is a stationary Markovian AR(1) max-min process with q-gamma stationary marginal distribution if and only if {ɛ n } follows Marshall-Olkin q-gamma distribution. 80
17 Proof: From the given structure it follows that P (X n > x) = p 1 P (ɛ n ) > x) + p 2 P (max(x n 1, ɛ n ) > x) + p 3 P (min(x n 1, ɛ n ) > x) On simplification we get, ] P (X n > x) = p 1 P (ɛ n ) > x) + p 2 [1 P (max(x n 1, ɛ n ) x) + p 3 FXn 1 (x) F ɛn (x) ] = p 1 Fɛn (x) + p 2 [1 (1 F Xn 1 (x))(1 F ɛn (x)) + p 3 FXn 1 (x) F ɛn (x). Under stationary equilibrium, F ɛ (x) = = p 1 +p 3 p 1 +p 2 FX (x) 1 (1 p 1+p 3 p 1 +p 2 ) F X (x) p FX (x) 1 (1 p ) F X (x) This has the same functional form of Marshall-Olkin survival function.substituting for F X (x) we can obtain the survival function of ɛ n. F ɛ (x) = (α, which is the required MO-q-G function. procedure as in theorem (4.6.1). p [(x(q 1), α, α] α) + (1 p ) (x(q 1), α, α) The converse can be proved using the same 81
18 4.8 Conclusions In this chapter we introduced the q- analogue of gamma distribution and studied its properties. Estimation problems are addressed. Its application in stress- strength analysis is discussed. The goodness of fit of the new distribution also tested. It is generalized using Marshall -olkin procedure and minification amd max-min model developed. References Alice, T., Jose, K.K. (2003). Marshall-Olkin Pareto Processes. Far East Journal of Theoretical Statistics, 9, Alice, T., Jose, K.K. (2004). Bivariate semi-pareto minification processes. Metrika, 59, Alice, T., Jose, K.K. (2005a). Marshall-Olkin Semi-Weibull Minification Processes. Recent Advances in Statistical Theory and Applications, I, Alice, T. and Jose, K.K. (2005b). Marshall-Olkin logistic processes.stars Int. Journal, 6, Gross,A.J.,Clark,V. (1975). Survival distributions: Reliability applications in the Biomedical Sciences. Wiley, New York. Jose, K.K. and Naik, S.R., (2009). On the q-weibull Distribution and Its Applications. Comm. Stat. Theory Methods, 38, Jose, K.K., Naik, S.R. and Ristic, M.M. (2008). Marshall-Olkin q-weibull Distribution and Max-Min Processes.Statistical Papers, doi: /s Kotz, S., Lumelskii, Y. and Pensky, M. (2007). Stress-strength Model and Its Generalizations. World Scientific Publishing, New York. Marshall, A.W., Olkin, I. (1997). A new method for adding a parameter to a family of distributions with application to the exponential and Weibull families. 82
19 Biometrika, 84, Mathai, A.M. (1993). A Handbook of Generalized Special Functions for Statistical and Physical Sciences. Oxford University Press, Oxford. Mathai, A.M. (1997). Jacobians of Matrix Transformations and Functions of Matrix Argument. World Scientific Publishing, New York. Mathai, A.M. (2005). A pathway to matrix-variate gamma and normal densities. Linear Algebra and Its Applications, 396, Mathai, A.M., and Haubold, H.J. (2007). Pathway model, superstatistics, Tsallis statistics and a generalized measure of entropy. Physica A, 375, Mathai, A.M. and Provost, S.B. (2006). On q-logistic and related distributions. IEEE Transactions on Reliability, 55(2), Ristic, M.M., Jose, K.K. and Ancy, J. (2007). A Marshall-Olkin gamma distribution and minification process, STARS: International Journal (Sciences), 1(2). Tsallis, C. (1988). Possible generalizations of Boltzmann-Gibbs statistics. Journal of Statistical Physics, 52, Wilk, G. and Wlodarczyk, Z. (2000). Interpretation of the nonextensivity parameter q in some applications of Tsallis statistics and Lévy distributions. Phys. Rev. Lett, 84, Wilk, G. and Wlodarczyk, Z. (2001). Non-exponential decays and nonextensivity. Physica A, 290, Tavares, V.L. (1977). The exact distribution of extremes of a non-gaussian process. Stochastic Processes and Their Applications, 5, Tavares, V.L. (1980). An exponential Markovian stationary process, J. Appl. Prob., 17,
Gumbel Distribution: Generalizations and Applications
 CHAPTER 3 Gumbel Distribution: Generalizations and Applications 31 Introduction Extreme Value Theory is widely used by many researchers in applied sciences when faced with modeling extreme values of certain
CHAPTER 3 Gumbel Distribution: Generalizations and Applications 31 Introduction Extreme Value Theory is widely used by many researchers in applied sciences when faced with modeling extreme values of certain
A Marshall-Olkin Gamma Distribution and Process
 CHAPTER 3 A Marshall-Olkin Gamma Distribution and Process 3.1 Introduction Gamma distribution is a widely used distribution in many fields such as lifetime data analysis, reliability, hydrology, medicine,
CHAPTER 3 A Marshall-Olkin Gamma Distribution and Process 3.1 Introduction Gamma distribution is a widely used distribution in many fields such as lifetime data analysis, reliability, hydrology, medicine,
Marshall-Olkin Univariate and Bivariate Logistic Processes
 CHAPTER 5 Marshall-Olkin Univariate and Bivariate Logistic Processes 5. Introduction The logistic distribution is the most commonly used probability model for modelling data on population growth, bioassay,
CHAPTER 5 Marshall-Olkin Univariate and Bivariate Logistic Processes 5. Introduction The logistic distribution is the most commonly used probability model for modelling data on population growth, bioassay,
A BIVARIATE MARSHALL AND OLKIN EXPONENTIAL MINIFICATION PROCESS
 Faculty of Sciences Mathematics, University of Niš, Serbia Available at: http://wwwpmfniacyu/filomat Filomat 22: (2008), 69 77 A BIVARIATE MARSHALL AND OLKIN EXPONENTIAL MINIFICATION PROCESS Miroslav M
Faculty of Sciences Mathematics, University of Niš, Serbia Available at: http://wwwpmfniacyu/filomat Filomat 22: (2008), 69 77 A BIVARIATE MARSHALL AND OLKIN EXPONENTIAL MINIFICATION PROCESS Miroslav M
Marshall-Olkin Bivariate Exponential Distribution: Generalisations and Applications
 CHAPTER 6 Marshall-Olkin Bivariate Exponential Distribution: Generalisations and Applications 6.1 Introduction Exponential distributions have been introduced as a simple model for statistical analysis
CHAPTER 6 Marshall-Olkin Bivariate Exponential Distribution: Generalisations and Applications 6.1 Introduction Exponential distributions have been introduced as a simple model for statistical analysis
Some Generalizations of Weibull Distribution and Related Processes
 Journal of Statistical Theory and Applications, Vol. 4, No. 4 (December 205), 425-434 Some Generalizations of Weibull Distribution and Related Processes K. Jayakumar Department of Statistics, University
Journal of Statistical Theory and Applications, Vol. 4, No. 4 (December 205), 425-434 Some Generalizations of Weibull Distribution and Related Processes K. Jayakumar Department of Statistics, University
The Distributions of Sums, Products and Ratios of Inverted Bivariate Beta Distribution 1
 Applied Mathematical Sciences, Vol. 2, 28, no. 48, 2377-2391 The Distributions of Sums, Products and Ratios of Inverted Bivariate Beta Distribution 1 A. S. Al-Ruzaiza and Awad El-Gohary 2 Department of
Applied Mathematical Sciences, Vol. 2, 28, no. 48, 2377-2391 The Distributions of Sums, Products and Ratios of Inverted Bivariate Beta Distribution 1 A. S. Al-Ruzaiza and Awad El-Gohary 2 Department of
Weighted Exponential Distribution and Process
 Weighted Exponential Distribution and Process Jilesh V Some generalizations of exponential distribution and related time series models Thesis. Department of Statistics, University of Calicut, 200 Chapter
Weighted Exponential Distribution and Process Jilesh V Some generalizations of exponential distribution and related time series models Thesis. Department of Statistics, University of Calicut, 200 Chapter
Pathway Extension of Weibull-Gamma Model
 Journal of Statistical Theory and Applications, Vol. 5, No. (March 26), 47-6 Pathway Extension of Weibull-Gamma Model Centre for Mathematical and Statistical Sciences Peechi Campus, KFRI, Peechi-68653,
Journal of Statistical Theory and Applications, Vol. 5, No. (March 26), 47-6 Pathway Extension of Weibull-Gamma Model Centre for Mathematical and Statistical Sciences Peechi Campus, KFRI, Peechi-68653,
MAXIMUM LQ-LIKELIHOOD ESTIMATION FOR THE PARAMETERS OF MARSHALL-OLKIN EXTENDED BURR XII DISTRIBUTION
 Available online: December 20, 2017 Commun. Fac. Sci. Univ. Ank. Ser. A1 Math. Stat. Volume 68, Number 1, Pages 17 34 (2019) DOI: 10.1501/Commua1_0000000887 ISSN 1303 5991 http://communications.science.ankara.edu.tr/index.php?series=a1
Available online: December 20, 2017 Commun. Fac. Sci. Univ. Ank. Ser. A1 Math. Stat. Volume 68, Number 1, Pages 17 34 (2019) DOI: 10.1501/Commua1_0000000887 ISSN 1303 5991 http://communications.science.ankara.edu.tr/index.php?series=a1
Research Article A q-weibull Counting Process through a Fractional Differential Operator
 International Stochastic Analysis Volume 2, Article ID 797656, 4 pages doi:.55/2/797656 Research Article A q-weibull Counting Process through a Fractional Differential Operator Kunnummal Muralidharan and
International Stochastic Analysis Volume 2, Article ID 797656, 4 pages doi:.55/2/797656 Research Article A q-weibull Counting Process through a Fractional Differential Operator Kunnummal Muralidharan and
A New Class of Positively Quadrant Dependent Bivariate Distributions with Pareto
 International Mathematical Forum, 2, 27, no. 26, 1259-1273 A New Class of Positively Quadrant Dependent Bivariate Distributions with Pareto A. S. Al-Ruzaiza and Awad El-Gohary 1 Department of Statistics
International Mathematical Forum, 2, 27, no. 26, 1259-1273 A New Class of Positively Quadrant Dependent Bivariate Distributions with Pareto A. S. Al-Ruzaiza and Awad El-Gohary 1 Department of Statistics
ON THE NORMAL MOMENT DISTRIBUTIONS
 ON THE NORMAL MOMENT DISTRIBUTIONS Akin Olosunde Department of Statistics, P.M.B. 40, University of Agriculture, Abeokuta. 00, NIGERIA. Abstract Normal moment distribution is a particular case of well
ON THE NORMAL MOMENT DISTRIBUTIONS Akin Olosunde Department of Statistics, P.M.B. 40, University of Agriculture, Abeokuta. 00, NIGERIA. Abstract Normal moment distribution is a particular case of well
Chapter 5 continued. Chapter 5 sections
 Chapter 5 sections Discrete univariate distributions: 5.2 Bernoulli and Binomial distributions Just skim 5.3 Hypergeometric distributions 5.4 Poisson distributions Just skim 5.5 Negative Binomial distributions
Chapter 5 sections Discrete univariate distributions: 5.2 Bernoulli and Binomial distributions Just skim 5.3 Hypergeometric distributions 5.4 Poisson distributions Just skim 5.5 Negative Binomial distributions
Recall that the Fourier transform (also known as characteristic function) of a random variable always exists, given by. e itx f(x)dx.
 I am going to talk about algebraic calculations of random variables: i.e. how to add, subtract, multiply, divide random variables. A main disadvantage is that complex analysis is used often, but I will
I am going to talk about algebraic calculations of random variables: i.e. how to add, subtract, multiply, divide random variables. A main disadvantage is that complex analysis is used often, but I will
Multivariate Normal-Laplace Distribution and Processes
 CHAPTER 4 Multivariate Normal-Laplace Distribution and Processes The normal-laplace distribution, which results from the convolution of independent normal and Laplace random variables is introduced by
CHAPTER 4 Multivariate Normal-Laplace Distribution and Processes The normal-laplace distribution, which results from the convolution of independent normal and Laplace random variables is introduced by
Estimation of Stress-Strength Reliability for Kumaraswamy Exponential Distribution Based on Upper Record Values
 International Journal of Contemporary Mathematical Sciences Vol. 12, 2017, no. 2, 59-71 HIKARI Ltd, www.m-hikari.com https://doi.org/10.12988/ijcms.2017.7210 Estimation of Stress-Strength Reliability for
International Journal of Contemporary Mathematical Sciences Vol. 12, 2017, no. 2, 59-71 HIKARI Ltd, www.m-hikari.com https://doi.org/10.12988/ijcms.2017.7210 Estimation of Stress-Strength Reliability for
On Generalized Entropy Measures and Non-extensive Statistical Mechanics
 First Prev Next Last On Generalized Entropy Measures and Non-extensive Statistical Mechanics A. M. MATHAI [Emeritus Professor of Mathematics and Statistics, McGill University, Canada, and Director, Centre
First Prev Next Last On Generalized Entropy Measures and Non-extensive Statistical Mechanics A. M. MATHAI [Emeritus Professor of Mathematics and Statistics, McGill University, Canada, and Director, Centre
Further results involving Marshall Olkin log logistic distribution: reliability analysis, estimation of the parameter, and applications
 DOI 1.1186/s464-16-27- RESEARCH Open Access Further results involving Marshall Olkin log logistic distribution: reliability analysis, estimation of the parameter, and applications Arwa M. Alshangiti *,
DOI 1.1186/s464-16-27- RESEARCH Open Access Further results involving Marshall Olkin log logistic distribution: reliability analysis, estimation of the parameter, and applications Arwa M. Alshangiti *,
MAS223 Statistical Inference and Modelling Exercises
 MAS223 Statistical Inference and Modelling Exercises The exercises are grouped into sections, corresponding to chapters of the lecture notes Within each section exercises are divided into warm-up questions,
MAS223 Statistical Inference and Modelling Exercises The exercises are grouped into sections, corresponding to chapters of the lecture notes Within each section exercises are divided into warm-up questions,
4. CONTINUOUS RANDOM VARIABLES
 IA Probability Lent Term 4 CONTINUOUS RANDOM VARIABLES 4 Introduction Up to now we have restricted consideration to sample spaces Ω which are finite, or countable; we will now relax that assumption We
IA Probability Lent Term 4 CONTINUOUS RANDOM VARIABLES 4 Introduction Up to now we have restricted consideration to sample spaces Ω which are finite, or countable; we will now relax that assumption We
The Inverse Weibull Inverse Exponential. Distribution with Application
 International Journal of Contemporary Mathematical Sciences Vol. 14, 2019, no. 1, 17-30 HIKARI Ltd, www.m-hikari.com https://doi.org/10.12988/ijcms.2019.913 The Inverse Weibull Inverse Exponential Distribution
International Journal of Contemporary Mathematical Sciences Vol. 14, 2019, no. 1, 17-30 HIKARI Ltd, www.m-hikari.com https://doi.org/10.12988/ijcms.2019.913 The Inverse Weibull Inverse Exponential Distribution
Probability and Distributions
 Probability and Distributions What is a statistical model? A statistical model is a set of assumptions by which the hypothetical population distribution of data is inferred. It is typically postulated
Probability and Distributions What is a statistical model? A statistical model is a set of assumptions by which the hypothetical population distribution of data is inferred. It is typically postulated
Basic concepts of probability theory
 Basic concepts of probability theory Random variable discrete/continuous random variable Transform Z transform, Laplace transform Distribution Geometric, mixed-geometric, Binomial, Poisson, exponential,
Basic concepts of probability theory Random variable discrete/continuous random variable Transform Z transform, Laplace transform Distribution Geometric, mixed-geometric, Binomial, Poisson, exponential,
Bivariate Geometric (Maximum) Generalized Exponential Distribution
 Bivariate Geometric (Maximum) Generalized Exponential Distribution Debasis Kundu 1 Abstract In this paper we propose a new five parameter bivariate distribution obtained by taking geometric maximum of
Bivariate Geometric (Maximum) Generalized Exponential Distribution Debasis Kundu 1 Abstract In this paper we propose a new five parameter bivariate distribution obtained by taking geometric maximum of
Chapter 5. Logistic Processes
 Chapter 5 Logistic Processes * 5.1 Introduction The logistic distribution is the most commonly used probability model for demographic contexts for modeling growth of populations. Oliver (1964) use it to
Chapter 5 Logistic Processes * 5.1 Introduction The logistic distribution is the most commonly used probability model for demographic contexts for modeling growth of populations. Oliver (1964) use it to
Distributions of Functions of Random Variables. 5.1 Functions of One Random Variable
 Distributions of Functions of Random Variables 5.1 Functions of One Random Variable 5.2 Transformations of Two Random Variables 5.3 Several Random Variables 5.4 The Moment-Generating Function Technique
Distributions of Functions of Random Variables 5.1 Functions of One Random Variable 5.2 Transformations of Two Random Variables 5.3 Several Random Variables 5.4 The Moment-Generating Function Technique
ABC methods for phase-type distributions with applications in insurance risk problems
 ABC methods for phase-type with applications problems Concepcion Ausin, Department of Statistics, Universidad Carlos III de Madrid Joint work with: Pedro Galeano, Universidad Carlos III de Madrid Simon
ABC methods for phase-type with applications problems Concepcion Ausin, Department of Statistics, Universidad Carlos III de Madrid Joint work with: Pedro Galeano, Universidad Carlos III de Madrid Simon
The Complementary Exponential-Geometric Distribution Based On Generalized Order Statistics
 Applied Mathematics E-Notes, 152015, 287-303 c ISSN 1607-2510 Available free at mirror sites of http://www.math.nthu.edu.tw/ amen/ The Complementary Exponential-Geometric Distribution Based On Generalized
Applied Mathematics E-Notes, 152015, 287-303 c ISSN 1607-2510 Available free at mirror sites of http://www.math.nthu.edu.tw/ amen/ The Complementary Exponential-Geometric Distribution Based On Generalized
HANDBOOK OF APPLICABLE MATHEMATICS
 HANDBOOK OF APPLICABLE MATHEMATICS Chief Editor: Walter Ledermann Volume II: Probability Emlyn Lloyd University oflancaster A Wiley-Interscience Publication JOHN WILEY & SONS Chichester - New York - Brisbane
HANDBOOK OF APPLICABLE MATHEMATICS Chief Editor: Walter Ledermann Volume II: Probability Emlyn Lloyd University oflancaster A Wiley-Interscience Publication JOHN WILEY & SONS Chichester - New York - Brisbane
Lecture 3. Probability - Part 2. Luigi Freda. ALCOR Lab DIAG University of Rome La Sapienza. October 19, 2016
 Lecture 3 Probability - Part 2 Luigi Freda ALCOR Lab DIAG University of Rome La Sapienza October 19, 2016 Luigi Freda ( La Sapienza University) Lecture 3 October 19, 2016 1 / 46 Outline 1 Common Continuous
Lecture 3 Probability - Part 2 Luigi Freda ALCOR Lab DIAG University of Rome La Sapienza October 19, 2016 Luigi Freda ( La Sapienza University) Lecture 3 October 19, 2016 1 / 46 Outline 1 Common Continuous
APPM/MATH 4/5520 Solutions to Problem Set Two. = 2 y = y 2. e 1 2 x2 1 = 1. (g 1
 APPM/MATH 4/552 Solutions to Problem Set Two. Let Y X /X 2 and let Y 2 X 2. (We can select Y 2 to be anything but when dealing with a fraction for Y, it is usually convenient to set Y 2 to be the denominator.)
APPM/MATH 4/552 Solutions to Problem Set Two. Let Y X /X 2 and let Y 2 X 2. (We can select Y 2 to be anything but when dealing with a fraction for Y, it is usually convenient to set Y 2 to be the denominator.)
Multivariate Survival Data With Censoring.
 1 Multivariate Survival Data With Censoring. Shulamith Gross and Catherine Huber-Carol Baruch College of the City University of New York, Dept of Statistics and CIS, Box 11-220, 1 Baruch way, 10010 NY.
1 Multivariate Survival Data With Censoring. Shulamith Gross and Catherine Huber-Carol Baruch College of the City University of New York, Dept of Statistics and CIS, Box 11-220, 1 Baruch way, 10010 NY.
Slash Distributions and Applications
 CHAPTER 2 Slash Distributions and Alications 2.1 Introduction The concet of slash distributions was introduced by Kafadar (1988) as a heavy tailed alternative to the normal distribution. Further literature
CHAPTER 2 Slash Distributions and Alications 2.1 Introduction The concet of slash distributions was introduced by Kafadar (1988) as a heavy tailed alternative to the normal distribution. Further literature
MARSHALL-OLKIN EXTENDED POWER FUNCTION DISTRIBUTION I. E. Okorie 1, A. C. Akpanta 2 and J. Ohakwe 3
 MARSHALL-OLKIN EXTENDED POWER FUNCTION DISTRIBUTION I. E. Okorie 1, A. C. Akpanta 2 and J. Ohakwe 3 1 School of Mathematics, University of Manchester, Manchester M13 9PL, UK 2 Department of Statistics,
MARSHALL-OLKIN EXTENDED POWER FUNCTION DISTRIBUTION I. E. Okorie 1, A. C. Akpanta 2 and J. Ohakwe 3 1 School of Mathematics, University of Manchester, Manchester M13 9PL, UK 2 Department of Statistics,
Statistics 3858 : Maximum Likelihood Estimators
 Statistics 3858 : Maximum Likelihood Estimators 1 Method of Maximum Likelihood In this method we construct the so called likelihood function, that is L(θ) = L(θ; X 1, X 2,..., X n ) = f n (X 1, X 2,...,
Statistics 3858 : Maximum Likelihood Estimators 1 Method of Maximum Likelihood In this method we construct the so called likelihood function, that is L(θ) = L(θ; X 1, X 2,..., X n ) = f n (X 1, X 2,...,
Katz Family of Distributions and Processes
 CHAPTER 7 Katz Family of Distributions and Processes 7. Introduction The Poisson distribution and the Negative binomial distribution are the most widely used discrete probability distributions for the
CHAPTER 7 Katz Family of Distributions and Processes 7. Introduction The Poisson distribution and the Negative binomial distribution are the most widely used discrete probability distributions for the
Basic concepts of probability theory
 Basic concepts of probability theory Random variable discrete/continuous random variable Transform Z transform, Laplace transform Distribution Geometric, mixed-geometric, Binomial, Poisson, exponential,
Basic concepts of probability theory Random variable discrete/continuous random variable Transform Z transform, Laplace transform Distribution Geometric, mixed-geometric, Binomial, Poisson, exponential,
COMPOSITE RELIABILITY MODELS FOR SYSTEMS WITH TWO DISTINCT KINDS OF STOCHASTIC DEPENDENCES BETWEEN THEIR COMPONENTS LIFE TIMES
 COMPOSITE RELIABILITY MODELS FOR SYSTEMS WITH TWO DISTINCT KINDS OF STOCHASTIC DEPENDENCES BETWEEN THEIR COMPONENTS LIFE TIMES Jerzy Filus Department of Mathematics and Computer Science, Oakton Community
COMPOSITE RELIABILITY MODELS FOR SYSTEMS WITH TWO DISTINCT KINDS OF STOCHASTIC DEPENDENCES BETWEEN THEIR COMPONENTS LIFE TIMES Jerzy Filus Department of Mathematics and Computer Science, Oakton Community
Random Infinite Divisibility on Z + and Generalized INAR(1) Models
 ProbStat Forum, Volume 03, July 2010, Pages 108-117 ISSN 0974-3235 Random Infinite Divisibility on Z + and Generalized INAR(1) Models Satheesh S NEELOLPALAM, S. N. Park Road Trichur - 680 004, India. ssatheesh1963@yahoo.co.in
ProbStat Forum, Volume 03, July 2010, Pages 108-117 ISSN 0974-3235 Random Infinite Divisibility on Z + and Generalized INAR(1) Models Satheesh S NEELOLPALAM, S. N. Park Road Trichur - 680 004, India. ssatheesh1963@yahoo.co.in
Products and Ratios of Two Gaussian Class Correlated Weibull Random Variables
 Products and Ratios of Two Gaussian Class Correlated Weibull Random Variables Petros S. Bithas, Nikos C. Sagias 2, Theodoros A. Tsiftsis 3, and George K. Karagiannidis 3 Electrical and Computer Engineering
Products and Ratios of Two Gaussian Class Correlated Weibull Random Variables Petros S. Bithas, Nikos C. Sagias 2, Theodoros A. Tsiftsis 3, and George K. Karagiannidis 3 Electrical and Computer Engineering
A New Method for Generating Distributions with an Application to Exponential Distribution
 A New Method for Generating Distributions with an Application to Exponential Distribution Abbas Mahdavi & Debasis Kundu Abstract Anewmethodhasbeenproposedtointroduceanextraparametertoafamilyofdistributions
A New Method for Generating Distributions with an Application to Exponential Distribution Abbas Mahdavi & Debasis Kundu Abstract Anewmethodhasbeenproposedtointroduceanextraparametertoafamilyofdistributions
Some Results on Moment of Order Statistics for the Quadratic Hazard Rate Distribution
 J. Stat. Appl. Pro. 5, No. 2, 371-376 (2016) 371 Journal of Statistics Applications & Probability An International Journal http://dx.doi.org/10.18576/jsap/050218 Some Results on Moment of Order Statistics
J. Stat. Appl. Pro. 5, No. 2, 371-376 (2016) 371 Journal of Statistics Applications & Probability An International Journal http://dx.doi.org/10.18576/jsap/050218 Some Results on Moment of Order Statistics
Estimation of P (X > Y ) for Weibull distribution based on hybrid censored samples
 Estimation of P (X > Y ) for Weibull distribution based on hybrid censored samples A. Asgharzadeh a, M. Kazemi a, D. Kundu b a Department of Statistics, Faculty of Mathematical Sciences, University of
Estimation of P (X > Y ) for Weibull distribution based on hybrid censored samples A. Asgharzadeh a, M. Kazemi a, D. Kundu b a Department of Statistics, Faculty of Mathematical Sciences, University of
On Five Parameter Beta Lomax Distribution
 ISSN 1684-840 Journal of Statistics Volume 0, 01. pp. 10-118 On Five Parameter Beta Lomax Distribution Muhammad Rajab 1, Muhammad Aleem, Tahir Nawaz and Muhammad Daniyal 4 Abstract Lomax (1954) developed
ISSN 1684-840 Journal of Statistics Volume 0, 01. pp. 10-118 On Five Parameter Beta Lomax Distribution Muhammad Rajab 1, Muhammad Aleem, Tahir Nawaz and Muhammad Daniyal 4 Abstract Lomax (1954) developed
Transmuted distributions and extrema of random number of variables
 Working Papers in Statistics No 2016:6 Department of Statistics School of Economics and Management Lund University Transmuted distributions and extrema of random number of variables TOMASZ J. KOZUBOWSKI,
Working Papers in Statistics No 2016:6 Department of Statistics School of Economics and Management Lund University Transmuted distributions and extrema of random number of variables TOMASZ J. KOZUBOWSKI,
arxiv: v1 [astro-ph] 16 Aug 2007
![arxiv: v1 [astro-ph] 16 Aug 2007 arxiv: v1 [astro-ph] 16 Aug 2007](/thumbs/91/105877678.jpg) EXTENSION OF THERMONUCLEAR FUNCTIONS THROUGH THE PATHWAY MODEL INCLUDING MAXWELL-BOLTZMANN AND TSALLIS DISTRIBUTIONS arxiv:78.2239v [astro-ph] 6 Aug 27 H.J. Haubold Office for Outer Space Affairs, United
EXTENSION OF THERMONUCLEAR FUNCTIONS THROUGH THE PATHWAY MODEL INCLUDING MAXWELL-BOLTZMANN AND TSALLIS DISTRIBUTIONS arxiv:78.2239v [astro-ph] 6 Aug 27 H.J. Haubold Office for Outer Space Affairs, United
Continuous Random Variables
 1 / 24 Continuous Random Variables Saravanan Vijayakumaran sarva@ee.iitb.ac.in Department of Electrical Engineering Indian Institute of Technology Bombay February 27, 2013 2 / 24 Continuous Random Variables
1 / 24 Continuous Random Variables Saravanan Vijayakumaran sarva@ee.iitb.ac.in Department of Electrical Engineering Indian Institute of Technology Bombay February 27, 2013 2 / 24 Continuous Random Variables
Three hours. To be supplied by the Examinations Office: Mathematical Formula Tables and Statistical Tables THE UNIVERSITY OF MANCHESTER.
 Three hours To be supplied by the Examinations Office: Mathematical Formula Tables and Statistical Tables THE UNIVERSITY OF MANCHESTER EXTREME VALUES AND FINANCIAL RISK Examiner: Answer QUESTION 1, QUESTION
Three hours To be supplied by the Examinations Office: Mathematical Formula Tables and Statistical Tables THE UNIVERSITY OF MANCHESTER EXTREME VALUES AND FINANCIAL RISK Examiner: Answer QUESTION 1, QUESTION
Two Weighted Distributions Generated by Exponential Distribution
 Journal of Mathematical Extension Vol. 9, No. 1, (2015), 1-12 ISSN: 1735-8299 URL: http://www.ijmex.com Two Weighted Distributions Generated by Exponential Distribution A. Mahdavi Vali-e-Asr University
Journal of Mathematical Extension Vol. 9, No. 1, (2015), 1-12 ISSN: 1735-8299 URL: http://www.ijmex.com Two Weighted Distributions Generated by Exponential Distribution A. Mahdavi Vali-e-Asr University
RESEARCH REPORT. Estimation of sample spacing in stochastic processes. Anders Rønn-Nielsen, Jon Sporring and Eva B.
 CENTRE FOR STOCHASTIC GEOMETRY AND ADVANCED BIOIMAGING www.csgb.dk RESEARCH REPORT 6 Anders Rønn-Nielsen, Jon Sporring and Eva B. Vedel Jensen Estimation of sample spacing in stochastic processes No. 7,
CENTRE FOR STOCHASTIC GEOMETRY AND ADVANCED BIOIMAGING www.csgb.dk RESEARCH REPORT 6 Anders Rønn-Nielsen, Jon Sporring and Eva B. Vedel Jensen Estimation of sample spacing in stochastic processes No. 7,
Chapter 3 sections. SKIP: 3.10 Markov Chains. SKIP: pages Chapter 3 - continued
 Chapter 3 sections Chapter 3 - continued 3.1 Random Variables and Discrete Distributions 3.2 Continuous Distributions 3.3 The Cumulative Distribution Function 3.4 Bivariate Distributions 3.5 Marginal Distributions
Chapter 3 sections Chapter 3 - continued 3.1 Random Variables and Discrete Distributions 3.2 Continuous Distributions 3.3 The Cumulative Distribution Function 3.4 Bivariate Distributions 3.5 Marginal Distributions
MATH c UNIVERSITY OF LEEDS Examination for the Module MATH2715 (January 2015) STATISTICAL METHODS. Time allowed: 2 hours
 MATH2750 This question paper consists of 8 printed pages, each of which is identified by the reference MATH275. All calculators must carry an approval sticker issued by the School of Mathematics. c UNIVERSITY
MATH2750 This question paper consists of 8 printed pages, each of which is identified by the reference MATH275. All calculators must carry an approval sticker issued by the School of Mathematics. c UNIVERSITY
Basic concepts of probability theory
 Basic concepts of probability theory Random variable discrete/continuous random variable Transform Z transform, Laplace transform Distribution Geometric, mixed-geometric, Binomial, Poisson, exponential,
Basic concepts of probability theory Random variable discrete/continuous random variable Transform Z transform, Laplace transform Distribution Geometric, mixed-geometric, Binomial, Poisson, exponential,
PROPERTIES AND DATA MODELLING APPLICATIONS OF THE KUMARASWAMY GENERALIZED MARSHALL-OLKIN-G FAMILY OF DISTRIBUTIONS
 Journal of Data Science 605-620, DOI: 10.6339/JDS.201807_16(3.0009 PROPERTIES AND DATA MODELLING APPLICATIONS OF THE KUMARASWAMY GENERALIZED MARSHALL-OLKIN-G FAMILY OF DISTRIBUTIONS Subrata Chakraborty
Journal of Data Science 605-620, DOI: 10.6339/JDS.201807_16(3.0009 PROPERTIES AND DATA MODELLING APPLICATIONS OF THE KUMARASWAMY GENERALIZED MARSHALL-OLKIN-G FAMILY OF DISTRIBUTIONS Subrata Chakraborty
Univariate and Bivariate Geometric Discrete Generalized Exponential Distributions
 Univariate and Bivariate Geometric Discrete Generalized Exponential Distributions Debasis Kundu 1 & Vahid Nekoukhou 2 Abstract Marshall and Olkin (1997, Biometrika, 84, 641-652) introduced a very powerful
Univariate and Bivariate Geometric Discrete Generalized Exponential Distributions Debasis Kundu 1 & Vahid Nekoukhou 2 Abstract Marshall and Olkin (1997, Biometrika, 84, 641-652) introduced a very powerful
ON THE SUM OF EXPONENTIALLY DISTRIBUTED RANDOM VARIABLES: A CONVOLUTION APPROACH
 ON THE SUM OF EXPONENTIALLY DISTRIBUTED RANDOM VARIABLES: A CONVOLUTION APPROACH Oguntunde P.E 1 ; Odetunmibi O.A 2 ;and Adejumo, A. O 3. 1,2 Department of Mathematics, Covenant University, Ota, Ogun State,
ON THE SUM OF EXPONENTIALLY DISTRIBUTED RANDOM VARIABLES: A CONVOLUTION APPROACH Oguntunde P.E 1 ; Odetunmibi O.A 2 ;and Adejumo, A. O 3. 1,2 Department of Mathematics, Covenant University, Ota, Ogun State,
Order Statistics and Distributions
 Order Statistics and Distributions 1 Some Preliminary Comments and Ideas In this section we consider a random sample X 1, X 2,..., X n common continuous distribution function F and probability density
Order Statistics and Distributions 1 Some Preliminary Comments and Ideas In this section we consider a random sample X 1, X 2,..., X n common continuous distribution function F and probability density
Lecture 17: The Exponential and Some Related Distributions
 Lecture 7: The Exponential and Some Related Distributions. Definition Definition: A continuous random variable X is said to have the exponential distribution with parameter if the density of X is e x if
Lecture 7: The Exponential and Some Related Distributions. Definition Definition: A continuous random variable X is said to have the exponential distribution with parameter if the density of X is e x if
Multivariate Distributions
 IEOR E4602: Quantitative Risk Management Spring 2016 c 2016 by Martin Haugh Multivariate Distributions We will study multivariate distributions in these notes, focusing 1 in particular on multivariate
IEOR E4602: Quantitative Risk Management Spring 2016 c 2016 by Martin Haugh Multivariate Distributions We will study multivariate distributions in these notes, focusing 1 in particular on multivariate
4. Distributions of Functions of Random Variables
 4. Distributions of Functions of Random Variables Setup: Consider as given the joint distribution of X 1,..., X n (i.e. consider as given f X1,...,X n and F X1,...,X n ) Consider k functions g 1 : R n
4. Distributions of Functions of Random Variables Setup: Consider as given the joint distribution of X 1,..., X n (i.e. consider as given f X1,...,X n and F X1,...,X n ) Consider k functions g 1 : R n
University of Lisbon, Portugal
 Development and comparative study of two near-exact approximations to the distribution of the product of an odd number of independent Beta random variables Luís M. Grilo a,, Carlos A. Coelho b, a Dep.
Development and comparative study of two near-exact approximations to the distribution of the product of an odd number of independent Beta random variables Luís M. Grilo a,, Carlos A. Coelho b, a Dep.
Parameter addition to a family of multivariate exponential and weibull distribution
 ISSN: 2455-216X Impact Factor: RJIF 5.12 www.allnationaljournal.com Volume 4; Issue 3; September 2018; Page No. 31-38 Parameter addition to a family of multivariate exponential and weibull distribution
ISSN: 2455-216X Impact Factor: RJIF 5.12 www.allnationaljournal.com Volume 4; Issue 3; September 2018; Page No. 31-38 Parameter addition to a family of multivariate exponential and weibull distribution
2 Random Variable Generation
 2 Random Variable Generation Most Monte Carlo computations require, as a starting point, a sequence of i.i.d. random variables with given marginal distribution. We describe here some of the basic methods
2 Random Variable Generation Most Monte Carlo computations require, as a starting point, a sequence of i.i.d. random variables with given marginal distribution. We describe here some of the basic methods
Generalized Laplacian Distributions and Autoregressive Processes
 CHAPTER Generalized Laplacian Distributions and Autoregressive Processes. Introduction Generalized Laplacian distribution corresponds to the distribution of differences of independently and identically
CHAPTER Generalized Laplacian Distributions and Autoregressive Processes. Introduction Generalized Laplacian distribution corresponds to the distribution of differences of independently and identically
Continuous Random Variables
 Continuous Random Variables Recall: For discrete random variables, only a finite or countably infinite number of possible values with positive probability. Often, there is interest in random variables
Continuous Random Variables Recall: For discrete random variables, only a finite or countably infinite number of possible values with positive probability. Often, there is interest in random variables
Random Variables and Their Distributions
 Chapter 3 Random Variables and Their Distributions A random variable (r.v.) is a function that assigns one and only one numerical value to each simple event in an experiment. We will denote r.vs by capital
Chapter 3 Random Variables and Their Distributions A random variable (r.v.) is a function that assigns one and only one numerical value to each simple event in an experiment. We will denote r.vs by capital
Lecture 2: Repetition of probability theory and statistics
 Algorithms for Uncertainty Quantification SS8, IN2345 Tobias Neckel Scientific Computing in Computer Science TUM Lecture 2: Repetition of probability theory and statistics Concept of Building Block: Prerequisites:
Algorithms for Uncertainty Quantification SS8, IN2345 Tobias Neckel Scientific Computing in Computer Science TUM Lecture 2: Repetition of probability theory and statistics Concept of Building Block: Prerequisites:
Bivariate Weibull-power series class of distributions
 Bivariate Weibull-power series class of distributions Saralees Nadarajah and Rasool Roozegar EM algorithm, Maximum likelihood estimation, Power series distri- Keywords: bution. Abstract We point out that
Bivariate Weibull-power series class of distributions Saralees Nadarajah and Rasool Roozegar EM algorithm, Maximum likelihood estimation, Power series distri- Keywords: bution. Abstract We point out that
Actuarial Science Exam 1/P
 Actuarial Science Exam /P Ville A. Satopää December 5, 2009 Contents Review of Algebra and Calculus 2 2 Basic Probability Concepts 3 3 Conditional Probability and Independence 4 4 Combinatorial Principles,
Actuarial Science Exam /P Ville A. Satopää December 5, 2009 Contents Review of Algebra and Calculus 2 2 Basic Probability Concepts 3 3 Conditional Probability and Independence 4 4 Combinatorial Principles,
SOLUTIONS TO MATH68181 EXTREME VALUES AND FINANCIAL RISK EXAM
 SOLUTIONS TO MATH68181 EXTREME VALUES AND FINANCIAL RISK EXAM Solutions to Question A1 a) The marginal cdfs of F X,Y (x, y) = [1 + exp( x) + exp( y) + (1 α) exp( x y)] 1 are F X (x) = F X,Y (x, ) = [1
SOLUTIONS TO MATH68181 EXTREME VALUES AND FINANCIAL RISK EXAM Solutions to Question A1 a) The marginal cdfs of F X,Y (x, y) = [1 + exp( x) + exp( y) + (1 α) exp( x y)] 1 are F X (x) = F X,Y (x, ) = [1
Product measure and Fubini s theorem
 Chapter 7 Product measure and Fubini s theorem This is based on [Billingsley, Section 18]. 1. Product spaces Suppose (Ω 1, F 1 ) and (Ω 2, F 2 ) are two probability spaces. In a product space Ω = Ω 1 Ω
Chapter 7 Product measure and Fubini s theorem This is based on [Billingsley, Section 18]. 1. Product spaces Suppose (Ω 1, F 1 ) and (Ω 2, F 2 ) are two probability spaces. In a product space Ω = Ω 1 Ω
Nonlinear Time Series Modeling
 Nonlinear Time Series Modeling Part II: Time Series Models in Finance Richard A. Davis Colorado State University (http://www.stat.colostate.edu/~rdavis/lectures) MaPhySto Workshop Copenhagen September
Nonlinear Time Series Modeling Part II: Time Series Models in Finance Richard A. Davis Colorado State University (http://www.stat.colostate.edu/~rdavis/lectures) MaPhySto Workshop Copenhagen September
Statistics 581, Problem Set 1 Solutions Wellner; 10/3/ (a) The case r = 1 of Chebychev s Inequality is known as Markov s Inequality
 Statistics 581, Problem Set 1 Solutions Wellner; 1/3/218 1. (a) The case r = 1 of Chebychev s Inequality is known as Markov s Inequality and is usually written P ( X ɛ) E( X )/ɛ for an arbitrary random
Statistics 581, Problem Set 1 Solutions Wellner; 1/3/218 1. (a) The case r = 1 of Chebychev s Inequality is known as Markov s Inequality and is usually written P ( X ɛ) E( X )/ɛ for an arbitrary random
Discriminating Between the Bivariate Generalized Exponential and Bivariate Weibull Distributions
 Discriminating Between the Bivariate Generalized Exponential and Bivariate Weibull Distributions Arabin Kumar Dey & Debasis Kundu Abstract Recently Kundu and Gupta ( Bivariate generalized exponential distribution,
Discriminating Between the Bivariate Generalized Exponential and Bivariate Weibull Distributions Arabin Kumar Dey & Debasis Kundu Abstract Recently Kundu and Gupta ( Bivariate generalized exponential distribution,
EEL 5544 Noise in Linear Systems Lecture 30. X (s) = E [ e sx] f X (x)e sx dx. Moments can be found from the Laplace transform as
![EEL 5544 Noise in Linear Systems Lecture 30. X (s) = E [ e sx] f X (x)e sx dx. Moments can be found from the Laplace transform as EEL 5544 Noise in Linear Systems Lecture 30. X (s) = E [ e sx] f X (x)e sx dx. Moments can be found from the Laplace transform as](/thumbs/85/92409620.jpg) L30-1 EEL 5544 Noise in Linear Systems Lecture 30 OTHER TRANSFORMS For a continuous, nonnegative RV X, the Laplace transform of X is X (s) = E [ e sx] = 0 f X (x)e sx dx. For a nonnegative RV, the Laplace
L30-1 EEL 5544 Noise in Linear Systems Lecture 30 OTHER TRANSFORMS For a continuous, nonnegative RV X, the Laplace transform of X is X (s) = E [ e sx] = 0 f X (x)e sx dx. For a nonnegative RV, the Laplace
Chapter 5. Chapter 5 sections
 1 / 43 sections Discrete univariate distributions: 5.2 Bernoulli and Binomial distributions Just skim 5.3 Hypergeometric distributions 5.4 Poisson distributions Just skim 5.5 Negative Binomial distributions
1 / 43 sections Discrete univariate distributions: 5.2 Bernoulli and Binomial distributions Just skim 5.3 Hypergeometric distributions 5.4 Poisson distributions Just skim 5.5 Negative Binomial distributions
ON A GENERALIZATION OF THE GUMBEL DISTRIBUTION
 ON A GENERALIZATION OF THE GUMBEL DISTRIBUTION S. Adeyemi Department of Mathematics Obafemi Awolowo University, Ile-Ife. Nigeria.0005 e-mail:shollerss00@yahoo.co.uk Abstract A simple generalization of
ON A GENERALIZATION OF THE GUMBEL DISTRIBUTION S. Adeyemi Department of Mathematics Obafemi Awolowo University, Ile-Ife. Nigeria.0005 e-mail:shollerss00@yahoo.co.uk Abstract A simple generalization of
Stat 512 Homework key 2
 Stat 51 Homework key October 4, 015 REGULAR PROBLEMS 1 Suppose continuous random variable X belongs to the family of all distributions having a linear probability density function (pdf) over the interval
Stat 51 Homework key October 4, 015 REGULAR PROBLEMS 1 Suppose continuous random variable X belongs to the family of all distributions having a linear probability density function (pdf) over the interval
EXPLICIT EXPRESSIONS FOR MOMENTS OF χ 2 ORDER STATISTICS
 Bulletin of the Institute of Mathematics Academia Sinica (New Series) Vol. 3 (28), No. 3, pp. 433-444 EXPLICIT EXPRESSIONS FOR MOMENTS OF χ 2 ORDER STATISTICS BY SARALEES NADARAJAH Abstract Explicit closed
Bulletin of the Institute of Mathematics Academia Sinica (New Series) Vol. 3 (28), No. 3, pp. 433-444 EXPLICIT EXPRESSIONS FOR MOMENTS OF χ 2 ORDER STATISTICS BY SARALEES NADARAJAH Abstract Explicit closed
On Sarhan-Balakrishnan Bivariate Distribution
 J. Stat. Appl. Pro. 1, No. 3, 163-17 (212) 163 Journal of Statistics Applications & Probability An International Journal c 212 NSP On Sarhan-Balakrishnan Bivariate Distribution D. Kundu 1, A. Sarhan 2
J. Stat. Appl. Pro. 1, No. 3, 163-17 (212) 163 Journal of Statistics Applications & Probability An International Journal c 212 NSP On Sarhan-Balakrishnan Bivariate Distribution D. Kundu 1, A. Sarhan 2
THE QUEEN S UNIVERSITY OF BELFAST
 THE QUEEN S UNIVERSITY OF BELFAST 0SOR20 Level 2 Examination Statistics and Operational Research 20 Probability and Distribution Theory Wednesday 4 August 2002 2.30 pm 5.30 pm Examiners { Professor R M
THE QUEEN S UNIVERSITY OF BELFAST 0SOR20 Level 2 Examination Statistics and Operational Research 20 Probability and Distribution Theory Wednesday 4 August 2002 2.30 pm 5.30 pm Examiners { Professor R M
Moments of the Reliability, R = P(Y<X), As a Random Variable
 International Journal of Computational Engineering Research Vol, 03 Issue, 8 Moments of the Reliability, R = P(Y
International Journal of Computational Engineering Research Vol, 03 Issue, 8 Moments of the Reliability, R = P(Y
conditional cdf, conditional pdf, total probability theorem?
 6 Multiple Random Variables 6.0 INTRODUCTION scalar vs. random variable cdf, pdf transformation of a random variable conditional cdf, conditional pdf, total probability theorem expectation of a random
6 Multiple Random Variables 6.0 INTRODUCTION scalar vs. random variable cdf, pdf transformation of a random variable conditional cdf, conditional pdf, total probability theorem expectation of a random
Statistics Masters Comprehensive Exam March 21, 2003
 Statistics Masters Comprehensive Exam March 21, 2003 Student Name: 1. Answer 8 out of 12 problems. Mark the problems you selected in the following table. 1 2 3 4 5 6 7 8 9 10 11 12 2. Write your answer
Statistics Masters Comprehensive Exam March 21, 2003 Student Name: 1. Answer 8 out of 12 problems. Mark the problems you selected in the following table. 1 2 3 4 5 6 7 8 9 10 11 12 2. Write your answer
Univariate Normal Probability Density Function
 Statistical Distributions Univariate Normal Probability Density Function A random variable, x, is normally distributed if, and only if, its probability density function has the following form: Prob(x θ,
Statistical Distributions Univariate Normal Probability Density Function A random variable, x, is normally distributed if, and only if, its probability density function has the following form: Prob(x θ,
A NOTE ON A DISTRIBUTION OF WEIGHTED SUMS OF I.I.D. RAYLEIGH RANDOM VARIABLES
 Sankhyā : The Indian Journal of Statistics 1998, Volume 6, Series A, Pt. 2, pp. 171-175 A NOTE ON A DISTRIBUTION OF WEIGHTED SUMS OF I.I.D. RAYLEIGH RANDOM VARIABLES By P. HITCZENKO North Carolina State
Sankhyā : The Indian Journal of Statistics 1998, Volume 6, Series A, Pt. 2, pp. 171-175 A NOTE ON A DISTRIBUTION OF WEIGHTED SUMS OF I.I.D. RAYLEIGH RANDOM VARIABLES By P. HITCZENKO North Carolina State
Chapter 3 sections. SKIP: 3.10 Markov Chains. SKIP: pages Chapter 3 - continued
 Chapter 3 sections 3.1 Random Variables and Discrete Distributions 3.2 Continuous Distributions 3.3 The Cumulative Distribution Function 3.4 Bivariate Distributions 3.5 Marginal Distributions 3.6 Conditional
Chapter 3 sections 3.1 Random Variables and Discrete Distributions 3.2 Continuous Distributions 3.3 The Cumulative Distribution Function 3.4 Bivariate Distributions 3.5 Marginal Distributions 3.6 Conditional
Inference on reliability in two-parameter exponential stress strength model
 Metrika DOI 10.1007/s00184-006-0074-7 Inference on reliability in two-parameter exponential stress strength model K. Krishnamoorthy Shubhabrata Mukherjee Huizhen Guo Received: 19 January 2005 Springer-Verlag
Metrika DOI 10.1007/s00184-006-0074-7 Inference on reliability in two-parameter exponential stress strength model K. Krishnamoorthy Shubhabrata Mukherjee Huizhen Guo Received: 19 January 2005 Springer-Verlag
Part IA Probability. Definitions. Based on lectures by R. Weber Notes taken by Dexter Chua. Lent 2015
 Part IA Probability Definitions Based on lectures by R. Weber Notes taken by Dexter Chua Lent 2015 These notes are not endorsed by the lecturers, and I have modified them (often significantly) after lectures.
Part IA Probability Definitions Based on lectures by R. Weber Notes taken by Dexter Chua Lent 2015 These notes are not endorsed by the lecturers, and I have modified them (often significantly) after lectures.
EXAMINATIONS OF THE ROYAL STATISTICAL SOCIETY
 EXAMINATIONS OF THE ROYAL STATISTICAL SOCIETY GRADUATE DIPLOMA, 2016 MODULE 1 : Probability distributions Time allowed: Three hours Candidates should answer FIVE questions. All questions carry equal marks.
EXAMINATIONS OF THE ROYAL STATISTICAL SOCIETY GRADUATE DIPLOMA, 2016 MODULE 1 : Probability distributions Time allowed: Three hours Candidates should answer FIVE questions. All questions carry equal marks.
Review for the previous lecture
 Lecture 1 and 13 on BST 631: Statistical Theory I Kui Zhang, 09/8/006 Review for the previous lecture Definition: Several discrete distributions, including discrete uniform, hypergeometric, Bernoulli,
Lecture 1 and 13 on BST 631: Statistical Theory I Kui Zhang, 09/8/006 Review for the previous lecture Definition: Several discrete distributions, including discrete uniform, hypergeometric, Bernoulli,
The Geometric Inverse Burr Distribution: Model, Properties and Simulation
 IOSR Journal of Mathematics (IOSR-JM) e-issn: 2278-5728, p-issn: 2319-765X. Volume 11, Issue 2 Ver. I (Mar - Apr. 2015), PP 83-93 www.iosrjournals.org The Geometric Inverse Burr Distribution: Model, Properties
IOSR Journal of Mathematics (IOSR-JM) e-issn: 2278-5728, p-issn: 2319-765X. Volume 11, Issue 2 Ver. I (Mar - Apr. 2015), PP 83-93 www.iosrjournals.org The Geometric Inverse Burr Distribution: Model, Properties
Definition 1.1 (Parametric family of distributions) A parametric distribution is a set of distribution functions, each of which is determined by speci
 Definition 1.1 (Parametric family of distributions) A parametric distribution is a set of distribution functions, each of which is determined by specifying one or more values called parameters. The number
Definition 1.1 (Parametric family of distributions) A parametric distribution is a set of distribution functions, each of which is determined by specifying one or more values called parameters. The number
Marshall-Olkin Geometric Distribution
 Chapter 4 Marshall-Olkin Geometric Distribution 4.1. Introduction Here, we consider a new famil of distributions b adding an additional parameter to geometric distribution b using the MO scheme. We call
Chapter 4 Marshall-Olkin Geometric Distribution 4.1. Introduction Here, we consider a new famil of distributions b adding an additional parameter to geometric distribution b using the MO scheme. We call
Conditional independence of blocked ordered data
 Conditional independence of blocked ordered data G. Iliopoulos 1 and N. Balakrishnan 2 Abstract In this paper, we prove that blocks of ordered data formed by some conditioning events are mutually independent.
Conditional independence of blocked ordered data G. Iliopoulos 1 and N. Balakrishnan 2 Abstract In this paper, we prove that blocks of ordered data formed by some conditioning events are mutually independent.
Ch3. Generating Random Variates with Non-Uniform Distributions
 ST4231, Semester I, 2003-2004 Ch3. Generating Random Variates with Non-Uniform Distributions This chapter mainly focuses on methods for generating non-uniform random numbers based on the built-in standard
ST4231, Semester I, 2003-2004 Ch3. Generating Random Variates with Non-Uniform Distributions This chapter mainly focuses on methods for generating non-uniform random numbers based on the built-in standard
Solution. (i) Find a minimal sufficient statistic for (θ, β) and give your justification. X i=1. By the factorization theorem, ( n
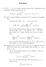 Solution 1. Let (X 1,..., X n ) be a simple random sample from a distribution with probability density function given by f(x;, β) = 1 ( ) 1 β x β, 0 x, > 0, β < 1. β (i) Find a minimal sufficient statistic
Solution 1. Let (X 1,..., X n ) be a simple random sample from a distribution with probability density function given by f(x;, β) = 1 ( ) 1 β x β, 0 x, > 0, β < 1. β (i) Find a minimal sufficient statistic
Extreme Value Analysis and Spatial Extremes
 Extreme Value Analysis and Department of Statistics Purdue University 11/07/2013 Outline Motivation 1 Motivation 2 Extreme Value Theorem and 3 Bayesian Hierarchical Models Copula Models Max-stable Models
Extreme Value Analysis and Department of Statistics Purdue University 11/07/2013 Outline Motivation 1 Motivation 2 Extreme Value Theorem and 3 Bayesian Hierarchical Models Copula Models Max-stable Models
1.1 Review of Probability Theory
 1.1 Review of Probability Theory Angela Peace Biomathemtics II MATH 5355 Spring 2017 Lecture notes follow: Allen, Linda JS. An introduction to stochastic processes with applications to biology. CRC Press,
1.1 Review of Probability Theory Angela Peace Biomathemtics II MATH 5355 Spring 2017 Lecture notes follow: Allen, Linda JS. An introduction to stochastic processes with applications to biology. CRC Press,
