P( y = 1) = 1+ e b 0+b 1 x 1 1 ( ) Activity #13: Generalized Linear Models: Logistic, Poisson Regression
|
|
|
- Maryann Melton
- 5 years ago
- Views:
Transcription
1 Activity #3: Generalized Linear Models: Logistic, Poisson Regression In every regression model we ve used thus far, our dependent variable has been a continuous variable. In this activity, we ll learn how to use the Generalized Linear Model to model binary (or ordinal) dependent variables. We ll also learn how to model a dependent variable that represents a count.. Suppose we want to predict whether an individual will develop lung cancer. It might be reasonable to model lung cancer as a function of the number of cigarettes smoked each day. Suppose we sample,000 individuals for this study. To the right, sketch a scatterplot we might expect. # of cigarettes 2. Could we fit a regression line to that scatterplot? Evaluate how well that line would model the data. Are there any problems in trying to fit a line to this data? 3. Our regular linear regression techniques won t work for binary dependent variables. Since our dependent variable can take only one of two values (0 or ), the coefficients of our line won t make much sense. We might be more interested in modeling the probability of our dependent variable. In this case, we want to predict the probability that an individual gets lung cancer based on the number of cigarettes smoked each day. Using your intuition, fit a curve that you think would best describe this relationship. Probability of lung cancer # of cigarettes The relationship between a single predictor (x) and a binary dependent variable (y) can be modeled by a logistic function: P( y = ) = ( ) + e b 0+b x
2 4. In this fictitious lung cancer example, we might find the logistic function displayed to the right. We could enter our observed data into a computer and have it find the best-fitting logistic curve (just as we fit nonlinear models in the previous activity). This method is tedious, though. Probability of lung cancer # of cigarettes ( ) = P y = + e ( b 0+b x ) Notice that logistic functions have three properties: a) They are asymptotic with respect to P(y) = 0 and P(y) =. This allows us to use logistic functions to model probabilities (since probabilities range from 0-). b) The are monotonically increasing. This can be useful if we believe higher values of our independent variable correspond with higher probabilities of the dependent variable. c) They are continuous. If fitting the logistic curve as a nonlinear model is tedious, how else can we estimate the coefficients? To answer this, we need to take a quick detour back to the concepts of probabilities and odds. A 994 study of 7,096 college students found that 3,34 identified themselves as frequent binge drinkers. Source: Henry Wechsler, Ph.D., et.al., "Health and Behavioral Consequences of Binge Drinking in College," Journal of the American Medical Association, Dec. 7, 994, p ; "The Disruptions of Campus Drunkenness," US News & World Report, Dec. 9, 994, p If the students in this study are representative of students at St. Ambrose, what s the probability that a St. Ambrose student is a binge drinker? ( ) ( ) P event 6. Recall that we define odds to be: odds of an event =. Calculate and interpret the following: P event a) The odds that a student is a binge drinker: b) The odds that a student is not a binge drinker: 2
3 7. Recall that with a logistic function, we can model the probability of an event by. ( ) We can convert this to an odds function to get: ( ) + e b 0+b x + e b 0+b x ( ) ( ) = P y = + e b 0+b x To simplify the notation, let s substitute z for the exponent and simplify: odds = + e z = + e z + e z + e z + e z + e z = + e z e z + e z + e z = + e z e z = e = ( z ez = e b 0+b x ) If we take the natural log of the odds, we get the log odds (also called the logit): ( ) = ln e b 0+b x ln odds ( ) ( ) = b 0 + b x The logit (log-odds) is simply a linear function. This means a computer can use iterative methods to fit a linear function to the log-odds. We can then transform those log-odds into odds and, finally, probabilities to interpret the model. We ll use the logistic function to model the probability of an event: ( ) + e b 0+b x To estimate the coefficients, we convert this to a logit (log-odds): ln( odds) = b 0 + b x Once we have our coefficients, we may want to convert log-odds back to odds: odds = e b 0+b x Then we may want to convert the odds back to a probability: P( y) = odds odds + = eb0+bx e b 0+b x + = ( ) + e b 0+b x Let s work through a simple example by hand. In this scenario, we ll try to see if gender predicts whether a student is more likely to be a frequent binge drinker. 3
4 8. The following table displays the results from that binge drinking study. Fill-in the table below. Frequent binge drinker Not Total Male Female Total Female Male P(binge drinker) = Odds(binge drinker) = ln(odds) = Odds ratio = 9. Suppose we code our gender variable as female = 0 and male =. We d get the following results: Female (gender = 0) Male (gender = ) ln(odds) = ln(0.205) = -.59 ln(0.294) = = b 0 + b (0) Recall that ln( odds) = b 0 + b x -.23 = b () Therefore, b 0 = Therefore, b = Our model for the ln(odds) is: Odds(binge drinker) = Odds ratio = P(binge drinker) = Relative probability = 4
5 0. We ve just gone through our first example of a logistic regression. We use logistic regression when our dependent variable is dichotomous/binary. We ll see more (real) examples of logistic regression later. For now, let s discuss the generalized linear model. When we fit a linear regression model, we re predicting the expected value of a dependent variable as a linear combination of a set of predictors. We interpret the coefficients of the model in such a way that a constant change in a predictor leads to a constant change in the dependent variable. This works when our dependent variable can, essentially, vary indefinitely in either direction. Linear models are not appropriate for many other types of dependent variables. For example, suppose we want to model the number of students attending St. Ambrose as a function of the cost of tuition. Notice that our dependent variable (number of students) represents a count that must be positive. If we fit a linear model to this data, we may predict a negative number of students at some tuition cost. This is clearly impossible. In this case, it may be better to use a linear model to predict a constant rate of student enrollment (e.g., an increase in tuition of $,000 leads to % fewer students attending). This type of model is called a log-linear model, since the logarithm of the dependent variable is predicted to vary linearly. Like we concluded on the first page of this activity, it s not appropriate to use a linear model to predict a binary dependent variable (a Bernoulli variable). A line will predict values other than the 0 or that are possible for the dependent variable. Generalized linear models handle these situations by: allowing dependent variables to have arbitrary distributions (other than normal distributions) allowing an arbitrary (link) function of the dependent variable to vary linearly with the predicted values. In the case of modeling student enrollment as a function of tuition, we may choose a Poisson model (to model counts) and a log link. In the binge drinking example, we chose a Binomial model (to model probabilities) and a logit (log-odds) link function. Generalized linear models consist of three components: ) Random component This specifies the distribution of the dependent variable (y) given values of the predictor variables. If y is a continuous variable, its probability distribution might be normal; if y is binary, the distribution might be binomial; if y represents counts, the distribution might be Poisson 2) Systematic (linear) component This represents a linear combination of the predictor variables: η i = b 0 + b x b k x k These predictor variables may be continuous, categorical, transformations of continuous variables, polynomial terms, interactions, etc. 3) Link function This links the random and systematic components by linking the expected value of y to the predictors: g E y. Some common link functions include: ( [ ]) = η i = b 0 + b x b k x k Identity link g( E[ y] ) = µ y Log link Logit link g( E[ y] ) = ln µ y g( E[ y] ) = ln µ y / µ y which is used in standard linear models. ( ) ( ( )) which is used for count data in log-linear models. which is used for binary dependent variables. 5
6 Because the link function is invertible, we can write E[ y] = g ( η i ) = g ( b 0 + b x b k x k ) With this, the generalized linear model can be thought of as a linear model for a transformation of the expected value of the dependent variable, or a nonlinear regression model for the dependent variable Scenario: A researcher is interested in how variables such as GRE scores, undergraduate GPAs, and the prestige of the undergraduate institution predict admission to graduate school. The dataset consists of 400 observations on these 4 variables. The dependent variable, admit, is binary: admit = = the student was admitted admit = 0 = the student was not admitted 46.6% of the students in the data were admitted. The rank variable represents the prestige of the undergraduate institution on a scale from -4.. Since our dependent variable is binary, we ll use logistic regression. I ll first see if GRE scores predict admission. To do this, I entered the following model into R and obtained the following estimates: Entered into R: admit.gre <- glm(admit ~ gre, data=admit, family="binomial") Output: Coefficients: Estimate Std. Error z value Pr(> z ) 95% CI (Intercept) e-06 (-4.09, -.7) gre (0.002, 0.005) Note the p-values come from a Wald Test: Write out this estimated model: ln(odds of admission) = Based on the p-value and/or confidence interval, what can we conclude about GRE scores? The mean GRE score (for the old version) was 500 with a standard deviation of 00. Given a student has a GRE score of 400, what are the odds that the student is admitted into this graduate school? Remember that the computer estimates coefficients for the log-odds. What s the probability a student with a GRE score of 400 gets admitted? 6
7 2. This time, calculate the odds of admission for a student with a GRE score of 40. Convert that to a probability. 3. Now that we know the odds of admission for scores of 400 and 40, calculate the odds ratio. How much higher are the odds of admission for a student with a score of 40? 4. The computer output shows the coefficient of GRE is Calculate the exp( ) and interpret what that coefficient represents. Below, I ve pasted output from R when I asked for odds ratios from this data. Interpret. OR 2.5 % 97.5 % (Intercept) gre We could calculate the odds and probabilities of admission for various GRE scores. Verify some of these values. GRE Odds P(admit) Below, I ve plotted the proportion of students admitted as a function of GRE scores. The red line represents our fitted logistic model. Evaluate how well the model fit the data. Proportion admitted We ll come back to this admissions example in a bit. For now, let s see another application of logistic regression. GRE score 7
8 Scenario: On January 28, 986, the space shuttle Challenger exploded and seven astronauts died because two rubber O-rings leaked. These rings had lost their resiliency because the shuttle was launched on a very cold day. Ambient temperatures were in the low 30s and the O-rings themselves were much colder, less than 20 degrees Fahrenheit. Flight Temp Damage The table to the right displays a sample of the data from 25 trial launches of the space shuttle. The O-rings from each launch were examined to see if they sustained damage () or no damage (0) from the launch. The ambient temperature at the time of the launch was also recorded.. The estimated coefficients for a logistic regression analysis are displayed below: Coefficients: Estimate Std. Error z value Pr(> z ) 95% Confidence Interval (Intercept) (-4.404, 4.478) temp (-0.99, ) Source: Tufte, E. (997). Visual and Statistical Thinking: Displays of Evidence for Making Decisions. 6. Interpret the coefficient of temperature in our model. 7. Calculate the probability of sustaining damage if the temperature were 30-degrees. Then, calculate the probability if the temperature were 60-degrees. Interpret the relative probability. 8. Based on the output pasted above or the plot to the right, evaluate how well this model fits the data. 8
9 Scenario: Approximately 2-3% of Americans have dermatophyte onychomycosis (a toenail infection). The infection is caused by a fungus and does not only disfigure the nails but can also cause physical pain and impair the ability to work. Researchers conducted a randomized, double-blind clinical trial of treatments for this toenail infection. 378 patients were randomly allocated into two oral antifungal treatments: 250 mg/day terbinafine, or 200 mg/day itraconazole. The patients were them monitored over time. The data generated from this study include: y = onycholysis (0 = none or mild; = moderate or severe) x = treatment (0 = itraconazole; = terbinafine) x 2 = month = number of months since first treatment The main research question was whether the treatments differ in their efficacy. In other words, do patients receiving one treatment experience a greater decrease in their probability of having onycholysis than those receiving the other treatment? Source: De Backer, M. et al. (998). Twelve weeks of continuous oral therapy for toenail onychomycosis caused by dermatophytes: a double-blind comparative trial of terbinafine 250 mg/day versus itraconazole 200 mg/day. Journal of the American Academy of Dermatology. 38: Before we begin, let s take a look at the proportion of patients in each treatment with toenail infections over time. Based on this plot, which treatment appears to be more effective? From this plot, how can we tell what proportion of the 378 patients even had the toenail infection? 20. I used R to estimate the coefficients of following logistic regression model: ln( odds) = b 0 + b ( Terbinafine) + b 2 ( month) + b 3 ( Terbinafine) ( month) Coefficients: Estimate Std. Error z value Pr(> z ) 95% CI (Intercept) e-07 (-0.770, ) treatmentterbinafine (-0.307, 0.305) month e-3 (-0.27, -0.24) treatmentterbinafine:month (-0.4, 0.006) OR 2.5 % 97.5 % (Intercept) treatmentterbinafine month treatmentterbinafine:month
10 2. Let s rearrange some of the terms in this model to see if we can gain a better understanding. Original model: ln( odds) = b 0 + b ( Terbinafine) + b 2 ( month) + b 3 ( Terbinafine x month) Model for itraconazole (terbinafine = 0) Model for terbinafine (terbinafine = ) ( ) = b 0 + b ( 0) + b 2 ( month) + b 3 ( 0 x month) ( ) = b 0 + b 2 ( month) ln odds ln odds ( ) = b 0 + b ( ) + b 2 ( month) + b 3 ( x month) ( ) = b 0 + b + b 2 ( month) + b 3 ( month) ( ) = ( b 0 + b ) + ( b 2 + b 3 )( month) ln odds ln odds ln odds Based on these rewritten models, which model parameters represent the increased effectiveness of terbinafine? Odds itraconazole (terbinafine = 0) Odds for terbinafine (terbinafine = ) Odds ratio 22. Sketch a graph of the odds ratio as a function of time. Try the reciprocal so you re comparing the odds of infection for terbinafine compare to the odds of infection for itraconazole. How can we interpret this graph? 23. Calculate the odds ratio comparing the effectiveness of the treatments at 0 months. What does this represent? 0
11 24. Calculate the odds ratio comparing the effectiveness of the treatments at 5 months. 25. Calculate and interpret the relative probability comparing the effectiveness of the treatments at 5 months. 26. Using R, I plotted our logistic model on top of the proportion of patients with infections at each month. Evaluate the fit of the model.
12 27. Let s go back to our graduate admissions example. We ve already investigated the extent to which GRE scores predict admissions. Let s try to incorporate more predictors into our model. Let s try a full model of: ln( odds) = b 0 + b ( GRE) + b 2 ( GPA) + b 3 ( rank) Interpret: Coefficients: Estimate Std. Error z value Pr(> z ) 95% CI (Intercept) (-6.223, -.756) gre ( 0.000, 0.004) gpa ( 0.54,.454) rank (-.296, ) rank (-2.07, ) rank (-2.370, ) OR 2.5 % 97.5 % (Intercept) gre gpa rank rank rank To see if the rank of a student s undergraduate school improves our prediction, we can conduct a test on terms 4-6 in our model. Interpret: wald.test(b = coef(admitlogit), Sigma = vcov(admitlogit), Terms = 4:6) Wald test: Chi-squared test: X2 = 20.9, df = 3, P(> X2) = We could also compare rank 2 institutions to rank 3. Interpret: wald.test(b = coef(admitlogit), Sigma = vcov(admitlogit), L = l) Wald test: Chi-squared test: X2 = 5.5, df =, P(> X2) = 0.09 Finally, we can evaluate the fit of our model. If we compare it to a null model, we get a p-value of In the assignment for this activity, you ll figure out the factors that influenced the odds of surviving the Titanic. You ll also try to develop (and test) a model to predict the retention of this year s freshman class. 2
13 Scenario: When elephants reach maturity (around the age of 4), they have to compete with all adult males for mating opportunities. Elephants get bigger as they get older and females are generally more receptive to larger males so the number of matings should increase with age. We re going to model the number of matings as a function of the age of the males. Elephant # Age # of Matings Mean = Variance = Source: gpk package: Here we have a scenario in which our dependent variable represents a count (number of matings). Counts tend to be: () discrete, (2) positive, (3) positively skewed with a high proportion of zeros. If we try to fit an ordinary least squares regression line, we ll run into problems: () the relationship between X and Y is nonlinear (2) counts tend to be heteroskedastic (3) our line will predict negative values (which cannot exist). We can use the generalized linear model to predict counts. To do so, we ll use a natural log link function: g( E [ y] ) = ln ( µ y ) = b 0 + b x This link function ensures our predicted values for y are positive and positively skewed. To see this more clearly, we can use the exponential function: e ln ( µ y) = e b 0 +b x µ y = e b 0+b x When we use this log link function, we re conducting a Poisson regression. If you took MATH 300, you might remember the Poisson distribution. We used it to calculate the probability of eating at least 5 bug parts when we eat peanut butter. We learned the Poisson distribution is like a binomial distribution with an infinite number of trials: One thing to note is that in a Poisson distribution, the mean is assumed to equal the variance. 3
14 29. Based on the scatterplot for our elephant data, it looks as though when age increases: a. the (mean) number of matings increases b. the variability (dispersion) in number of matings increases Since the dispersion increases with the mean for our count dependent variable, Poisson regression might be a good choice. We can then model: ln matings ( ) = b 0 + b ( age) Before I do that, let s fit a null model: ln( matings) = b 0 I used R to estimate the coefficients of this null model: Estimate Std. Error z value Pr(> z ) (Intercept) <2e-6 *** Null deviance: on 40 degrees of freedom AIC: ( ) = So our null model is: ln matings model. What does this number represent?. Convert this to predict the number of matings under this null 30. The deviance of is a measure of how poorly our model fits the data. If the model fits the data, then we would expect the deviance to be approximately equal to the degrees of freedom. We could also compare the deviance to a chi-squared distribution to get a sense of model fit. Based on this value, does our null model fit the data well? 3. I then had R estimate the coefficients of a model including the age predictor using an iterative process: Estimate Std. Error z value Pr(> z ) (Intercept) Age e-07 Null deviance: on 40 degrees of freedom Residual deviance: 5.02 on 39 degrees of freedom AIC: Write out this model. I then used the model to predict the average number of matings at ages 30, 3, and 45. By what amount are the matings increasing each year? What are the predicted variances in matings at each age? matings at 30 years = e (30) = matings at 3 years = e (3) = matings at 45 years = e (45) =
15 32. In general, we can interpret the parameters of a Poisson regression like this: b 0 : the mean of the Poisson distribution when our predictor equals zero b : a -unit increase in X is associated with an e b increase in the expected count of Y In our example, the b 0 parameter doesn t make sense, since age=0 is not meaningful. What does the b parameter represent in our scenario? Interpret that coefficient of We can plot our predictions (from both the null and age-based models) on top of our data. Obviously, the model with age as a predictor appears to better fit the data. We can also compare models by comparing the decrease in deviance values from our null to full models. Using R, I conducted a chi-squared test that the difference in deviance values between our two models is zero. R reported a p-value of Interpret this value. Scenario: University professors typically need to publish articles in order to earn promotions and tenure. The number of articles a professor publishes could be predicted by a number of factors. In this scenario, we ll have the following data: art = number of articles published fem = gender mar = marriage status kid5 = # of kids under age 6 phd = prestige of PhD program Professor art fem mar kid5 phd Mean = Variance = 0 man married woman single man married Source: Long (990) 34. To get a sense of our data, go ahead and predict the relationship between each predictor and our dependent variable. Explain why we shouldn t use ordinary least squares regression on this data. 5
16 35. Take a look at the mean and variance of our dependent variable. Should we conduct a Poisson regression? 36. If we were to fit a null model with no predictors, what would be the value of our b 0 coefficient? Explain. 37. Using Poisson regression, I fit a series of models. Interpret the coefficients and evaluate model fit. Coefficients: Estimate Std. Error z value Pr(> z ) (Intercept) < 2e-6 *** femwomen e-06 *** --- Null deviance: 87.4 on 94 degrees of freedom Residual deviance: on 93 degrees of freedom AIC: Exponentiated coefficients: (Intercept) femwomen Coefficients: Estimate Std. Error z value Pr(> z ) (Intercept) < 2e-6 *** femwomen e-06 *** marsingle Null deviance: 87.4 on 94 degrees of freedom Residual deviance: 794. on 92 degrees of freedom AIC: Exponentiated coefficients: (Intercept) femwomen marsingle Coefficients: Estimate Std. Error z value Pr(> z ) (Intercept) <2e-6 *** kid * --- Null deviance: 87.4 on 94 degrees of freedom Residual deviance: 83.2 on 93 degrees of freedom AIC: 3485 Exponentiated coefficients: (Intercept) kid
17 38. Finally, I fit a model with all our predictors. Interpret the coefficients and evaluate model fit. Coefficients: Estimate Std. Error z value Pr(> z ) (Intercept) e-08 *** femwomen e-07 *** marsingle * kid e-05 *** phd ** --- Null deviance: 87.4 on 94 degrees of freedom Residual deviance: on 90 degrees of freedom AIC: 3444 Exponentiated coefficients: (Intercept) femwomen marsingle kid5 phd Why does this model still not fit our data well? What could we do about this? We can use our model to make predictions: Single female with kid under the age of 6: Predicted publications =.066 Married man with no kids under the age of 6: Predicted publications = 2.57 Scenario: Suppose we want to predict the number absences for students at a high school. We have this data: math = math test score daysabs = days absent prog = type of program Student gender math daysabs prog male 63 4 academic 2 female 20 2 general Mean = Variance = 34 female 77 2 vocational Source: UCLA TISE 7
18 39. Even though the variance is much higher than the mean (even within each program type), let s try to fit a Poisson regression model with all our predictors. Coefficients: Estimate Std. Error z value Pr(> z ) (Intercept) < 2e-6 *** gendermale e-07 *** math e-3 *** progacademic e-4 *** progvocational < 2e-6 *** --- Null deviance: on 33 degrees of freedom Residual deviance: on 309 degrees of freedom AIC: Exponentiated coefficients: (Intercept) gendermale math progacademic progvocational The fit is terrible because of that over-dispersion. So what could we do about this? One thing we could do is fit a negative binomial regression model. The negative binomial model is just like the Poisson model except it includes an extra parameter to model dispersion. I fit this model using R and found: Coefficients: Estimate Std. Error z value Pr(> z ) (Intercept) < 2e-6 *** gendermale math * progacademic * progvocational e-0 *** --- (Dispersion parameter for Negative Binomial(.0473) family taken to be ) Null deviance: on 33 degrees of freedom Residual deviance: on 309 degrees of freedom AIC: Exponentiated coefficients: (Intercept) gendermale math progacademic progvocational The deviance decreased by a large amount, so this model does fit our data better. Suppose we re interested in seeing the the type of program (academic, general, vocational) predicts absences. To do so, we can fit a reduced model that does not include the program predictor. We can then test the difference in deviance between the models. I did this in R and found a p- value of Interpret. 8
19 Scenario: Suppose we want to predict the number of times an individual visits a doctor s office. Data from the U.S. National Medical Expenditure Survey (NMES) for include: ofp = number of physician office visits hosp = number of hospital stays health = self-perceived health status numchron = number of chronic conditions gender school = years of education privins = private insurance? 40. We can fit a Poisson regression model with all our predictors, but we ll have an over-dispersion problem (too many zeros in our data). We could also try other methods, such as quasi-poisson regression, zero-inflated poisson regression, or negative binomial regression. On the next page, I ve pasted output comparing the coefficients and standard errors for each model. Below that, I ve shown how many zeros each model predicts (compared to the observed number of zeros). Which model fits best? 9
20 ML-Pois Quasi-Pois NB (Intercept) hosp healthexcellent healthpoor numchron gendermale school privinsyes ML-Pois Adj-Pois Quasi-Pois NB (Intercept) hosp healthexcellent healthpoor numchron gendermale school privinsyes Obs ML-Pois NB
( ) ( ) 2. ( ) = e b 0 +b 1 x. logistic function: P( y = 1) = eb 0 +b 1 x. 1+ e b 0 +b 1 x. Linear model: cancer = b 0. + b 1 ( cigarettes) b 0 +b 1 x
 Lesson #13: Generalized Linear Models: Logistic, Poisson Regression So far, we ve fit linear models to predict continuous dependent variables. In this lesson, we ll learn how to use the Generalized Linear
Lesson #13: Generalized Linear Models: Logistic, Poisson Regression So far, we ve fit linear models to predict continuous dependent variables. In this lesson, we ll learn how to use the Generalized Linear
Class Notes: Week 8. Probit versus Logit Link Functions and Count Data
 Ronald Heck Class Notes: Week 8 1 Class Notes: Week 8 Probit versus Logit Link Functions and Count Data This week we ll take up a couple of issues. The first is working with a probit link function. While
Ronald Heck Class Notes: Week 8 1 Class Notes: Week 8 Probit versus Logit Link Functions and Count Data This week we ll take up a couple of issues. The first is working with a probit link function. While
STA 4504/5503 Sample Exam 1 Spring 2011 Categorical Data Analysis. 1. Indicate whether each of the following is true (T) or false (F).
 STA 4504/5503 Sample Exam 1 Spring 2011 Categorical Data Analysis 1. Indicate whether each of the following is true (T) or false (F). (a) (b) (c) (d) (e) In 2 2 tables, statistical independence is equivalent
STA 4504/5503 Sample Exam 1 Spring 2011 Categorical Data Analysis 1. Indicate whether each of the following is true (T) or false (F). (a) (b) (c) (d) (e) In 2 2 tables, statistical independence is equivalent
STA 4504/5503 Sample Exam 1 Spring 2011 Categorical Data Analysis. 1. Indicate whether each of the following is true (T) or false (F).
 STA 4504/5503 Sample Exam 1 Spring 2011 Categorical Data Analysis 1. Indicate whether each of the following is true (T) or false (F). (a) T In 2 2 tables, statistical independence is equivalent to a population
STA 4504/5503 Sample Exam 1 Spring 2011 Categorical Data Analysis 1. Indicate whether each of the following is true (T) or false (F). (a) T In 2 2 tables, statistical independence is equivalent to a population
Ron Heck, Fall Week 8: Introducing Generalized Linear Models: Logistic Regression 1 (Replaces prior revision dated October 20, 2011)
 Ron Heck, Fall 2011 1 EDEP 768E: Seminar in Multilevel Modeling rev. January 3, 2012 (see footnote) Week 8: Introducing Generalized Linear Models: Logistic Regression 1 (Replaces prior revision dated October
Ron Heck, Fall 2011 1 EDEP 768E: Seminar in Multilevel Modeling rev. January 3, 2012 (see footnote) Week 8: Introducing Generalized Linear Models: Logistic Regression 1 (Replaces prior revision dated October
Introducing Generalized Linear Models: Logistic Regression
 Ron Heck, Summer 2012 Seminars 1 Multilevel Regression Models and Their Applications Seminar Introducing Generalized Linear Models: Logistic Regression The generalized linear model (GLM) represents and
Ron Heck, Summer 2012 Seminars 1 Multilevel Regression Models and Their Applications Seminar Introducing Generalized Linear Models: Logistic Regression The generalized linear model (GLM) represents and
Truck prices - linear model? Truck prices - log transform of the response variable. Interpreting models with log transformation
 Background Regression so far... Lecture 23 - Sta 111 Colin Rundel June 17, 2014 At this point we have covered: Simple linear regression Relationship between numerical response and a numerical or categorical
Background Regression so far... Lecture 23 - Sta 111 Colin Rundel June 17, 2014 At this point we have covered: Simple linear regression Relationship between numerical response and a numerical or categorical
9 Generalized Linear Models
 9 Generalized Linear Models The Generalized Linear Model (GLM) is a model which has been built to include a wide range of different models you already know, e.g. ANOVA and multiple linear regression models
9 Generalized Linear Models The Generalized Linear Model (GLM) is a model which has been built to include a wide range of different models you already know, e.g. ANOVA and multiple linear regression models
Regression so far... Lecture 21 - Logistic Regression. Odds. Recap of what you should know how to do... At this point we have covered: Sta102 / BME102
 Background Regression so far... Lecture 21 - Sta102 / BME102 Colin Rundel November 18, 2014 At this point we have covered: Simple linear regression Relationship between numerical response and a numerical
Background Regression so far... Lecture 21 - Sta102 / BME102 Colin Rundel November 18, 2014 At this point we have covered: Simple linear regression Relationship between numerical response and a numerical
Binary Logistic Regression
 The coefficients of the multiple regression model are estimated using sample data with k independent variables Estimated (or predicted) value of Y Estimated intercept Estimated slope coefficients Ŷ = b
The coefficients of the multiple regression model are estimated using sample data with k independent variables Estimated (or predicted) value of Y Estimated intercept Estimated slope coefficients Ŷ = b
Let s see if we can predict whether a student returns or does not return to St. Ambrose for their second year.
 Assignment #13: GLM Scenario: Over the past few years, our first-to-second year retention rate has ranged from 77-80%. In other words, 77-80% of our first-year students come back to St. Ambrose for their
Assignment #13: GLM Scenario: Over the past few years, our first-to-second year retention rate has ranged from 77-80%. In other words, 77-80% of our first-year students come back to St. Ambrose for their
Generalized linear models
 Generalized linear models Douglas Bates November 01, 2010 Contents 1 Definition 1 2 Links 2 3 Estimating parameters 5 4 Example 6 5 Model building 8 6 Conclusions 8 7 Summary 9 1 Generalized Linear Models
Generalized linear models Douglas Bates November 01, 2010 Contents 1 Definition 1 2 Links 2 3 Estimating parameters 5 4 Example 6 5 Model building 8 6 Conclusions 8 7 Summary 9 1 Generalized Linear Models
EPSY 905: Fundamentals of Multivariate Modeling Online Lecture #7
 Introduction to Generalized Univariate Models: Models for Binary Outcomes EPSY 905: Fundamentals of Multivariate Modeling Online Lecture #7 EPSY 905: Intro to Generalized In This Lecture A short review
Introduction to Generalized Univariate Models: Models for Binary Outcomes EPSY 905: Fundamentals of Multivariate Modeling Online Lecture #7 EPSY 905: Intro to Generalized In This Lecture A short review
Lecture 14: Introduction to Poisson Regression
 Lecture 14: Introduction to Poisson Regression Ani Manichaikul amanicha@jhsph.edu 8 May 2007 1 / 52 Overview Modelling counts Contingency tables Poisson regression models 2 / 52 Modelling counts I Why
Lecture 14: Introduction to Poisson Regression Ani Manichaikul amanicha@jhsph.edu 8 May 2007 1 / 52 Overview Modelling counts Contingency tables Poisson regression models 2 / 52 Modelling counts I Why
Modelling counts. Lecture 14: Introduction to Poisson Regression. Overview
 Modelling counts I Lecture 14: Introduction to Poisson Regression Ani Manichaikul amanicha@jhsph.edu Why count data? Number of traffic accidents per day Mortality counts in a given neighborhood, per week
Modelling counts I Lecture 14: Introduction to Poisson Regression Ani Manichaikul amanicha@jhsph.edu Why count data? Number of traffic accidents per day Mortality counts in a given neighborhood, per week
Activity #12: More regression topics: LOWESS; polynomial, nonlinear, robust, quantile; ANOVA as regression
 Activity #12: More regression topics: LOWESS; polynomial, nonlinear, robust, quantile; ANOVA as regression Scenario: 31 counts (over a 30-second period) were recorded from a Geiger counter at a nuclear
Activity #12: More regression topics: LOWESS; polynomial, nonlinear, robust, quantile; ANOVA as regression Scenario: 31 counts (over a 30-second period) were recorded from a Geiger counter at a nuclear
Review: what is a linear model. Y = β 0 + β 1 X 1 + β 2 X 2 + A model of the following form:
 Outline for today What is a generalized linear model Linear predictors and link functions Example: fit a constant (the proportion) Analysis of deviance table Example: fit dose-response data using logistic
Outline for today What is a generalized linear model Linear predictors and link functions Example: fit a constant (the proportion) Analysis of deviance table Example: fit dose-response data using logistic
UNIVERSITY OF TORONTO Faculty of Arts and Science
 UNIVERSITY OF TORONTO Faculty of Arts and Science December 2013 Final Examination STA442H1F/2101HF Methods of Applied Statistics Jerry Brunner Duration - 3 hours Aids: Calculator Model(s): Any calculator
UNIVERSITY OF TORONTO Faculty of Arts and Science December 2013 Final Examination STA442H1F/2101HF Methods of Applied Statistics Jerry Brunner Duration - 3 hours Aids: Calculator Model(s): Any calculator
Hierarchical Generalized Linear Models. ERSH 8990 REMS Seminar on HLM Last Lecture!
 Hierarchical Generalized Linear Models ERSH 8990 REMS Seminar on HLM Last Lecture! Hierarchical Generalized Linear Models Introduction to generalized models Models for binary outcomes Interpreting parameter
Hierarchical Generalized Linear Models ERSH 8990 REMS Seminar on HLM Last Lecture! Hierarchical Generalized Linear Models Introduction to generalized models Models for binary outcomes Interpreting parameter
Linear Regression Models P8111
 Linear Regression Models P8111 Lecture 25 Jeff Goldsmith April 26, 2016 1 of 37 Today s Lecture Logistic regression / GLMs Model framework Interpretation Estimation 2 of 37 Linear regression Course started
Linear Regression Models P8111 Lecture 25 Jeff Goldsmith April 26, 2016 1 of 37 Today s Lecture Logistic regression / GLMs Model framework Interpretation Estimation 2 of 37 Linear regression Course started
On the Inference of the Logistic Regression Model
 On the Inference of the Logistic Regression Model 1. Model ln =(; ), i.e. = representing false. The linear form of (;) is entertained, i.e. ((;)) ((;)), where ==1 ;, with 1 representing true, 0 ;= 1+ +
On the Inference of the Logistic Regression Model 1. Model ln =(; ), i.e. = representing false. The linear form of (;) is entertained, i.e. ((;)) ((;)), where ==1 ;, with 1 representing true, 0 ;= 1+ +
Lecture 12: Effect modification, and confounding in logistic regression
 Lecture 12: Effect modification, and confounding in logistic regression Ani Manichaikul amanicha@jhsph.edu 4 May 2007 Today Categorical predictor create dummy variables just like for linear regression
Lecture 12: Effect modification, and confounding in logistic regression Ani Manichaikul amanicha@jhsph.edu 4 May 2007 Today Categorical predictor create dummy variables just like for linear regression
Generalized Linear Models for Non-Normal Data
 Generalized Linear Models for Non-Normal Data Today s Class: 3 parts of a generalized model Models for binary outcomes Complications for generalized multivariate or multilevel models SPLH 861: Lecture
Generalized Linear Models for Non-Normal Data Today s Class: 3 parts of a generalized model Models for binary outcomes Complications for generalized multivariate or multilevel models SPLH 861: Lecture
Exam Applied Statistical Regression. Good Luck!
 Dr. M. Dettling Summer 2011 Exam Applied Statistical Regression Approved: Tables: Note: Any written material, calculator (without communication facility). Attached. All tests have to be done at the 5%-level.
Dr. M. Dettling Summer 2011 Exam Applied Statistical Regression Approved: Tables: Note: Any written material, calculator (without communication facility). Attached. All tests have to be done at the 5%-level.
The Flight of the Space Shuttle Challenger
 The Flight of the Space Shuttle Challenger On January 28, 1986, the space shuttle Challenger took off on the 25 th flight in NASA s space shuttle program. Less than 2 minutes into the flight, the spacecraft
The Flight of the Space Shuttle Challenger On January 28, 1986, the space shuttle Challenger took off on the 25 th flight in NASA s space shuttle program. Less than 2 minutes into the flight, the spacecraft
Chapter 26: Comparing Counts (Chi Square)
 Chapter 6: Comparing Counts (Chi Square) We ve seen that you can turn a qualitative variable into a quantitative one (by counting the number of successes and failures), but that s a compromise it forces
Chapter 6: Comparing Counts (Chi Square) We ve seen that you can turn a qualitative variable into a quantitative one (by counting the number of successes and failures), but that s a compromise it forces
22s:152 Applied Linear Regression. RECALL: The Poisson distribution. Let Y be distributed as a Poisson random variable with the single parameter λ.
 22s:152 Applied Linear Regression Chapter 15 Section 2: Poisson Regression RECALL: The Poisson distribution Let Y be distributed as a Poisson random variable with the single parameter λ. P (Y = y) = e
22s:152 Applied Linear Regression Chapter 15 Section 2: Poisson Regression RECALL: The Poisson distribution Let Y be distributed as a Poisson random variable with the single parameter λ. P (Y = y) = e
Interactions in Logistic Regression
 Interactions in Logistic Regression > # UCBAdmissions is a 3-D table: Gender by Dept by Admit > # Same data in another format: > # One col for Yes counts, another for No counts. > Berkeley = read.table("http://www.utstat.toronto.edu/~brunner/312f12/
Interactions in Logistic Regression > # UCBAdmissions is a 3-D table: Gender by Dept by Admit > # Same data in another format: > # One col for Yes counts, another for No counts. > Berkeley = read.table("http://www.utstat.toronto.edu/~brunner/312f12/
Clinical Trials. Olli Saarela. September 18, Dalla Lana School of Public Health University of Toronto.
 Introduction to Dalla Lana School of Public Health University of Toronto olli.saarela@utoronto.ca September 18, 2014 38-1 : a review 38-2 Evidence Ideal: to advance the knowledge-base of clinical medicine,
Introduction to Dalla Lana School of Public Health University of Toronto olli.saarela@utoronto.ca September 18, 2014 38-1 : a review 38-2 Evidence Ideal: to advance the knowledge-base of clinical medicine,
Generalized linear models
 Generalized linear models Outline for today What is a generalized linear model Linear predictors and link functions Example: estimate a proportion Analysis of deviance Example: fit dose- response data
Generalized linear models Outline for today What is a generalized linear model Linear predictors and link functions Example: estimate a proportion Analysis of deviance Example: fit dose- response data
Statistics Boot Camp. Dr. Stephanie Lane Institute for Defense Analyses DATAWorks 2018
 Statistics Boot Camp Dr. Stephanie Lane Institute for Defense Analyses DATAWorks 2018 March 21, 2018 Outline of boot camp Summarizing and simplifying data Point and interval estimation Foundations of statistical
Statistics Boot Camp Dr. Stephanie Lane Institute for Defense Analyses DATAWorks 2018 March 21, 2018 Outline of boot camp Summarizing and simplifying data Point and interval estimation Foundations of statistical
Simple logistic regression
 Simple logistic regression Biometry 755 Spring 2009 Simple logistic regression p. 1/47 Model assumptions 1. The observed data are independent realizations of a binary response variable Y that follows a
Simple logistic regression Biometry 755 Spring 2009 Simple logistic regression p. 1/47 Model assumptions 1. The observed data are independent realizations of a binary response variable Y that follows a
SCHOOL OF MATHEMATICS AND STATISTICS. Linear and Generalised Linear Models
 SCHOOL OF MATHEMATICS AND STATISTICS Linear and Generalised Linear Models Autumn Semester 2017 18 2 hours Attempt all the questions. The allocation of marks is shown in brackets. RESTRICTED OPEN BOOK EXAMINATION
SCHOOL OF MATHEMATICS AND STATISTICS Linear and Generalised Linear Models Autumn Semester 2017 18 2 hours Attempt all the questions. The allocation of marks is shown in brackets. RESTRICTED OPEN BOOK EXAMINATION
Consider fitting a model using ordinary least squares (OLS) regression:
 Example 1: Mating Success of African Elephants In this study, 41 male African elephants were followed over a period of 8 years. The age of the elephant at the beginning of the study and the number of successful
Example 1: Mating Success of African Elephants In this study, 41 male African elephants were followed over a period of 8 years. The age of the elephant at the beginning of the study and the number of successful
Log-linear Models for Contingency Tables
 Log-linear Models for Contingency Tables Statistics 149 Spring 2006 Copyright 2006 by Mark E. Irwin Log-linear Models for Two-way Contingency Tables Example: Business Administration Majors and Gender A
Log-linear Models for Contingency Tables Statistics 149 Spring 2006 Copyright 2006 by Mark E. Irwin Log-linear Models for Two-way Contingency Tables Example: Business Administration Majors and Gender A
STA102 Class Notes Chapter Logistic Regression
 STA0 Class Notes Chapter 0 0. Logistic Regression We continue to study the relationship between a response variable and one or more eplanatory variables. For SLR and MLR (Chapters 8 and 9), our response
STA0 Class Notes Chapter 0 0. Logistic Regression We continue to study the relationship between a response variable and one or more eplanatory variables. For SLR and MLR (Chapters 8 and 9), our response
Investigating Models with Two or Three Categories
 Ronald H. Heck and Lynn N. Tabata 1 Investigating Models with Two or Three Categories For the past few weeks we have been working with discriminant analysis. Let s now see what the same sort of model might
Ronald H. Heck and Lynn N. Tabata 1 Investigating Models with Two or Three Categories For the past few weeks we have been working with discriminant analysis. Let s now see what the same sort of model might
Model Estimation Example
 Ronald H. Heck 1 EDEP 606: Multivariate Methods (S2013) April 7, 2013 Model Estimation Example As we have moved through the course this semester, we have encountered the concept of model estimation. Discussions
Ronald H. Heck 1 EDEP 606: Multivariate Methods (S2013) April 7, 2013 Model Estimation Example As we have moved through the course this semester, we have encountered the concept of model estimation. Discussions
An Introduction to Mplus and Path Analysis
 An Introduction to Mplus and Path Analysis PSYC 943: Fundamentals of Multivariate Modeling Lecture 10: October 30, 2013 PSYC 943: Lecture 10 Today s Lecture Path analysis starting with multivariate regression
An Introduction to Mplus and Path Analysis PSYC 943: Fundamentals of Multivariate Modeling Lecture 10: October 30, 2013 PSYC 943: Lecture 10 Today s Lecture Path analysis starting with multivariate regression
Chapter 1 Statistical Inference
 Chapter 1 Statistical Inference causal inference To infer causality, you need a randomized experiment (or a huge observational study and lots of outside information). inference to populations Generalizations
Chapter 1 Statistical Inference causal inference To infer causality, you need a randomized experiment (or a huge observational study and lots of outside information). inference to populations Generalizations
Logistic Regression. James H. Steiger. Department of Psychology and Human Development Vanderbilt University
 Logistic Regression James H. Steiger Department of Psychology and Human Development Vanderbilt University James H. Steiger (Vanderbilt University) Logistic Regression 1 / 38 Logistic Regression 1 Introduction
Logistic Regression James H. Steiger Department of Psychology and Human Development Vanderbilt University James H. Steiger (Vanderbilt University) Logistic Regression 1 / 38 Logistic Regression 1 Introduction
We d like to know the equation of the line shown (the so called best fit or regression line).
 Linear Regression in R. Example. Let s create a data frame. > exam1 = c(100,90,90,85,80,75,60) > exam2 = c(95,100,90,80,95,60,40) > students = c("asuka", "Rei", "Shinji", "Mari", "Hikari", "Toji", "Kensuke")
Linear Regression in R. Example. Let s create a data frame. > exam1 = c(100,90,90,85,80,75,60) > exam2 = c(95,100,90,80,95,60,40) > students = c("asuka", "Rei", "Shinji", "Mari", "Hikari", "Toji", "Kensuke")
Introduction to the Analysis of Tabular Data
 Introduction to the Analysis of Tabular Data Anthropological Sciences 192/292 Data Analysis in the Anthropological Sciences James Holland Jones & Ian G. Robertson March 15, 2006 1 Tabular Data Is there
Introduction to the Analysis of Tabular Data Anthropological Sciences 192/292 Data Analysis in the Anthropological Sciences James Holland Jones & Ian G. Robertson March 15, 2006 1 Tabular Data Is there
Semiparametric Generalized Linear Models
 Semiparametric Generalized Linear Models North American Stata Users Group Meeting Chicago, Illinois Paul Rathouz Department of Health Studies University of Chicago prathouz@uchicago.edu Liping Gao MS Student
Semiparametric Generalized Linear Models North American Stata Users Group Meeting Chicago, Illinois Paul Rathouz Department of Health Studies University of Chicago prathouz@uchicago.edu Liping Gao MS Student
Section IX. Introduction to Logistic Regression for binary outcomes. Poisson regression
 Section IX Introduction to Logistic Regression for binary outcomes Poisson regression 0 Sec 9 - Logistic regression In linear regression, we studied models where Y is a continuous variable. What about
Section IX Introduction to Logistic Regression for binary outcomes Poisson regression 0 Sec 9 - Logistic regression In linear regression, we studied models where Y is a continuous variable. What about
Binomial Model. Lecture 10: Introduction to Logistic Regression. Logistic Regression. Binomial Distribution. n independent trials
 Lecture : Introduction to Logistic Regression Ani Manichaikul amanicha@jhsph.edu 2 May 27 Binomial Model n independent trials (e.g., coin tosses) p = probability of success on each trial (e.g., p =! =
Lecture : Introduction to Logistic Regression Ani Manichaikul amanicha@jhsph.edu 2 May 27 Binomial Model n independent trials (e.g., coin tosses) p = probability of success on each trial (e.g., p =! =
Generalised linear models. Response variable can take a number of different formats
 Generalised linear models Response variable can take a number of different formats Structure Limitations of linear models and GLM theory GLM for count data GLM for presence \ absence data GLM for proportion
Generalised linear models Response variable can take a number of different formats Structure Limitations of linear models and GLM theory GLM for count data GLM for presence \ absence data GLM for proportion
Stat 579: Generalized Linear Models and Extensions
 Stat 579: Generalized Linear Models and Extensions Yan Lu Jan, 2018, week 3 1 / 67 Hypothesis tests Likelihood ratio tests Wald tests Score tests 2 / 67 Generalized Likelihood ratio tests Let Y = (Y 1,
Stat 579: Generalized Linear Models and Extensions Yan Lu Jan, 2018, week 3 1 / 67 Hypothesis tests Likelihood ratio tests Wald tests Score tests 2 / 67 Generalized Likelihood ratio tests Let Y = (Y 1,
Lecture 10: Introduction to Logistic Regression
 Lecture 10: Introduction to Logistic Regression Ani Manichaikul amanicha@jhsph.edu 2 May 2007 Logistic Regression Regression for a response variable that follows a binomial distribution Recall the binomial
Lecture 10: Introduction to Logistic Regression Ani Manichaikul amanicha@jhsph.edu 2 May 2007 Logistic Regression Regression for a response variable that follows a binomial distribution Recall the binomial
Chapter 14. Multiple Regression Models. Multiple Regression Models. Multiple Regression Models
 Chapter 14 Multiple Regression Models 1 Multiple Regression Models A general additive multiple regression model, which relates a dependent variable y to k predictor variables,,, is given by the model equation
Chapter 14 Multiple Regression Models 1 Multiple Regression Models A general additive multiple regression model, which relates a dependent variable y to k predictor variables,,, is given by the model equation
MODELING COUNT DATA Joseph M. Hilbe
 MODELING COUNT DATA Joseph M. Hilbe Arizona State University Count models are a subset of discrete response regression models. Count data are distributed as non-negative integers, are intrinsically heteroskedastic,
MODELING COUNT DATA Joseph M. Hilbe Arizona State University Count models are a subset of discrete response regression models. Count data are distributed as non-negative integers, are intrinsically heteroskedastic,
An Introduction to Path Analysis
 An Introduction to Path Analysis PRE 905: Multivariate Analysis Lecture 10: April 15, 2014 PRE 905: Lecture 10 Path Analysis Today s Lecture Path analysis starting with multivariate regression then arriving
An Introduction to Path Analysis PRE 905: Multivariate Analysis Lecture 10: April 15, 2014 PRE 905: Lecture 10 Path Analysis Today s Lecture Path analysis starting with multivariate regression then arriving
Chapter 6. Logistic Regression. 6.1 A linear model for the log odds
 Chapter 6 Logistic Regression In logistic regression, there is a categorical response variables, often coded 1=Yes and 0=No. Many important phenomena fit this framework. The patient survives the operation,
Chapter 6 Logistic Regression In logistic regression, there is a categorical response variables, often coded 1=Yes and 0=No. Many important phenomena fit this framework. The patient survives the operation,
Lecture 12: Interactions and Splines
 Lecture 12: Interactions and Splines Sandy Eckel seckel@jhsph.edu 12 May 2007 1 Definition Effect Modification The phenomenon in which the relationship between the primary predictor and outcome varies
Lecture 12: Interactions and Splines Sandy Eckel seckel@jhsph.edu 12 May 2007 1 Definition Effect Modification The phenomenon in which the relationship between the primary predictor and outcome varies
7/28/15. Review Homework. Overview. Lecture 6: Logistic Regression Analysis
 Lecture 6: Logistic Regression Analysis Christopher S. Hollenbeak, PhD Jane R. Schubart, PhD The Outcomes Research Toolbox Review Homework 2 Overview Logistic regression model conceptually Logistic regression
Lecture 6: Logistic Regression Analysis Christopher S. Hollenbeak, PhD Jane R. Schubart, PhD The Outcomes Research Toolbox Review Homework 2 Overview Logistic regression model conceptually Logistic regression
Parametric Modelling of Over-dispersed Count Data. Part III / MMath (Applied Statistics) 1
 Parametric Modelling of Over-dispersed Count Data Part III / MMath (Applied Statistics) 1 Introduction Poisson regression is the de facto approach for handling count data What happens then when Poisson
Parametric Modelling of Over-dispersed Count Data Part III / MMath (Applied Statistics) 1 Introduction Poisson regression is the de facto approach for handling count data What happens then when Poisson
STA 303 H1S / 1002 HS Winter 2011 Test March 7, ab 1cde 2abcde 2fghij 3
 STA 303 H1S / 1002 HS Winter 2011 Test March 7, 2011 LAST NAME: FIRST NAME: STUDENT NUMBER: ENROLLED IN: (circle one) STA 303 STA 1002 INSTRUCTIONS: Time: 90 minutes Aids allowed: calculator. Some formulae
STA 303 H1S / 1002 HS Winter 2011 Test March 7, 2011 LAST NAME: FIRST NAME: STUDENT NUMBER: ENROLLED IN: (circle one) STA 303 STA 1002 INSTRUCTIONS: Time: 90 minutes Aids allowed: calculator. Some formulae
BOOTSTRAPPING WITH MODELS FOR COUNT DATA
 Journal of Biopharmaceutical Statistics, 21: 1164 1176, 2011 Copyright Taylor & Francis Group, LLC ISSN: 1054-3406 print/1520-5711 online DOI: 10.1080/10543406.2011.607748 BOOTSTRAPPING WITH MODELS FOR
Journal of Biopharmaceutical Statistics, 21: 1164 1176, 2011 Copyright Taylor & Francis Group, LLC ISSN: 1054-3406 print/1520-5711 online DOI: 10.1080/10543406.2011.607748 BOOTSTRAPPING WITH MODELS FOR
Introduction to logistic regression
 Introduction to logistic regression Tuan V. Nguyen Professor and NHMRC Senior Research Fellow Garvan Institute of Medical Research University of New South Wales Sydney, Australia What we are going to learn
Introduction to logistic regression Tuan V. Nguyen Professor and NHMRC Senior Research Fellow Garvan Institute of Medical Research University of New South Wales Sydney, Australia What we are going to learn
Regression and Generalized Linear Models. Dr. Wolfgang Rolke Expo in Statistics C3TEC, Caguas, October 9, 2015
 Regression and Generalized Linear Models Dr. Wolfgang Rolke Expo in Statistics C3TEC, Caguas, October 9, 2015 Example: Predicting Success of UPR Students Data: information from application forms of 25495
Regression and Generalized Linear Models Dr. Wolfgang Rolke Expo in Statistics C3TEC, Caguas, October 9, 2015 Example: Predicting Success of UPR Students Data: information from application forms of 25495
A Generalized Linear Model for Binomial Response Data. Copyright c 2017 Dan Nettleton (Iowa State University) Statistics / 46
 A Generalized Linear Model for Binomial Response Data Copyright c 2017 Dan Nettleton (Iowa State University) Statistics 510 1 / 46 Now suppose that instead of a Bernoulli response, we have a binomial response
A Generalized Linear Model for Binomial Response Data Copyright c 2017 Dan Nettleton (Iowa State University) Statistics 510 1 / 46 Now suppose that instead of a Bernoulli response, we have a binomial response
McGill University. Faculty of Science. Department of Mathematics and Statistics. Statistics Part A Comprehensive Exam Methodology Paper
 Student Name: ID: McGill University Faculty of Science Department of Mathematics and Statistics Statistics Part A Comprehensive Exam Methodology Paper Date: Friday, May 13, 2016 Time: 13:00 17:00 Instructions
Student Name: ID: McGill University Faculty of Science Department of Mathematics and Statistics Statistics Part A Comprehensive Exam Methodology Paper Date: Friday, May 13, 2016 Time: 13:00 17:00 Instructions
Practice exam questions
 Practice exam questions Nathaniel Higgins nhiggins@jhu.edu, nhiggins@ers.usda.gov 1. The following question is based on the model y = β 0 + β 1 x 1 + β 2 x 2 + β 3 x 3 + u. Discuss the following two hypotheses.
Practice exam questions Nathaniel Higgins nhiggins@jhu.edu, nhiggins@ers.usda.gov 1. The following question is based on the model y = β 0 + β 1 x 1 + β 2 x 2 + β 3 x 3 + u. Discuss the following two hypotheses.
11. Generalized Linear Models: An Introduction
 Sociology 740 John Fox Lecture Notes 11. Generalized Linear Models: An Introduction Copyright 2014 by John Fox Generalized Linear Models: An Introduction 1 1. Introduction I A synthesis due to Nelder and
Sociology 740 John Fox Lecture Notes 11. Generalized Linear Models: An Introduction Copyright 2014 by John Fox Generalized Linear Models: An Introduction 1 1. Introduction I A synthesis due to Nelder and
Tento projekt je spolufinancován Evropským sociálním fondem a Státním rozpočtem ČR InoBio CZ.1.07/2.2.00/
 Tento projekt je spolufinancován Evropským sociálním fondem a Státním rozpočtem ČR InoBio CZ.1.07/2.2.00/28.0018 Statistical Analysis in Ecology using R Linear Models/GLM Ing. Daniel Volařík, Ph.D. 13.
Tento projekt je spolufinancován Evropským sociálním fondem a Státním rozpočtem ČR InoBio CZ.1.07/2.2.00/28.0018 Statistical Analysis in Ecology using R Linear Models/GLM Ing. Daniel Volařík, Ph.D. 13.
Generalized Linear Models
 York SPIDA John Fox Notes Generalized Linear Models Copyright 2010 by John Fox Generalized Linear Models 1 1. Topics I The structure of generalized linear models I Poisson and other generalized linear
York SPIDA John Fox Notes Generalized Linear Models Copyright 2010 by John Fox Generalized Linear Models 1 1. Topics I The structure of generalized linear models I Poisson and other generalized linear
Sampling Distributions: Central Limit Theorem
 Review for Exam 2 Sampling Distributions: Central Limit Theorem Conceptually, we can break up the theorem into three parts: 1. The mean (µ M ) of a population of sample means (M) is equal to the mean (µ)
Review for Exam 2 Sampling Distributions: Central Limit Theorem Conceptually, we can break up the theorem into three parts: 1. The mean (µ M ) of a population of sample means (M) is equal to the mean (µ)
REVIEW 8/2/2017 陈芳华东师大英语系
 REVIEW Hypothesis testing starts with a null hypothesis and a null distribution. We compare what we have to the null distribution, if the result is too extreme to belong to the null distribution (p
REVIEW Hypothesis testing starts with a null hypothesis and a null distribution. We compare what we have to the null distribution, if the result is too extreme to belong to the null distribution (p
Single-level Models for Binary Responses
 Single-level Models for Binary Responses Distribution of Binary Data y i response for individual i (i = 1,..., n), coded 0 or 1 Denote by r the number in the sample with y = 1 Mean and variance E(y) =
Single-level Models for Binary Responses Distribution of Binary Data y i response for individual i (i = 1,..., n), coded 0 or 1 Denote by r the number in the sample with y = 1 Mean and variance E(y) =
Logistic Regression - problem 6.14
 Logistic Regression - problem 6.14 Let x 1, x 2,, x m be given values of an input variable x and let Y 1,, Y m be independent binomial random variables whose distributions depend on the corresponding values
Logistic Regression - problem 6.14 Let x 1, x 2,, x m be given values of an input variable x and let Y 1,, Y m be independent binomial random variables whose distributions depend on the corresponding values
Generalized Linear Models
 Generalized Linear Models Advanced Methods for Data Analysis (36-402/36-608 Spring 2014 1 Generalized linear models 1.1 Introduction: two regressions So far we ve seen two canonical settings for regression.
Generalized Linear Models Advanced Methods for Data Analysis (36-402/36-608 Spring 2014 1 Generalized linear models 1.1 Introduction: two regressions So far we ve seen two canonical settings for regression.
Multinomial Logistic Regression Models
 Stat 544, Lecture 19 1 Multinomial Logistic Regression Models Polytomous responses. Logistic regression can be extended to handle responses that are polytomous, i.e. taking r>2 categories. (Note: The word
Stat 544, Lecture 19 1 Multinomial Logistic Regression Models Polytomous responses. Logistic regression can be extended to handle responses that are polytomous, i.e. taking r>2 categories. (Note: The word
Ron Heck, Fall Week 3: Notes Building a Two-Level Model
 Ron Heck, Fall 2011 1 EDEP 768E: Seminar on Multilevel Modeling rev. 9/6/2011@11:27pm Week 3: Notes Building a Two-Level Model We will build a model to explain student math achievement using student-level
Ron Heck, Fall 2011 1 EDEP 768E: Seminar on Multilevel Modeling rev. 9/6/2011@11:27pm Week 3: Notes Building a Two-Level Model We will build a model to explain student math achievement using student-level
8 Nominal and Ordinal Logistic Regression
 8 Nominal and Ordinal Logistic Regression 8.1 Introduction If the response variable is categorical, with more then two categories, then there are two options for generalized linear models. One relies on
8 Nominal and Ordinal Logistic Regression 8.1 Introduction If the response variable is categorical, with more then two categories, then there are two options for generalized linear models. One relies on
Final Exam. Name: Solution:
 Final Exam. Name: Instructions. Answer all questions on the exam. Open books, open notes, but no electronic devices. The first 13 problems are worth 5 points each. The rest are worth 1 point each. HW1.
Final Exam. Name: Instructions. Answer all questions on the exam. Open books, open notes, but no electronic devices. The first 13 problems are worth 5 points each. The rest are worth 1 point each. HW1.
Chapter 20: Logistic regression for binary response variables
 Chapter 20: Logistic regression for binary response variables In 1846, the Donner and Reed families left Illinois for California by covered wagon (87 people, 20 wagons). They attempted a new and untried
Chapter 20: Logistic regression for binary response variables In 1846, the Donner and Reed families left Illinois for California by covered wagon (87 people, 20 wagons). They attempted a new and untried
ST3241 Categorical Data Analysis I Generalized Linear Models. Introduction and Some Examples
 ST3241 Categorical Data Analysis I Generalized Linear Models Introduction and Some Examples 1 Introduction We have discussed methods for analyzing associations in two-way and three-way tables. Now we will
ST3241 Categorical Data Analysis I Generalized Linear Models Introduction and Some Examples 1 Introduction We have discussed methods for analyzing associations in two-way and three-way tables. Now we will
Sociology 593 Exam 2 Answer Key March 28, 2002
 Sociology 59 Exam Answer Key March 8, 00 I. True-False. (0 points) Indicate whether the following statements are true or false. If false, briefly explain why.. A variable is called CATHOLIC. This probably
Sociology 59 Exam Answer Key March 8, 00 I. True-False. (0 points) Indicate whether the following statements are true or false. If false, briefly explain why.. A variable is called CATHOLIC. This probably
Mixed models in R using the lme4 package Part 5: Generalized linear mixed models
 Mixed models in R using the lme4 package Part 5: Generalized linear mixed models Douglas Bates Madison January 11, 2011 Contents 1 Definition 1 2 Links 2 3 Example 7 4 Model building 9 5 Conclusions 14
Mixed models in R using the lme4 package Part 5: Generalized linear mixed models Douglas Bates Madison January 11, 2011 Contents 1 Definition 1 2 Links 2 3 Example 7 4 Model building 9 5 Conclusions 14
5. Let W follow a normal distribution with mean of μ and the variance of 1. Then, the pdf of W is
 Practice Final Exam Last Name:, First Name:. Please write LEGIBLY. Answer all questions on this exam in the space provided (you may use the back of any page if you need more space). Show all work but do
Practice Final Exam Last Name:, First Name:. Please write LEGIBLY. Answer all questions on this exam in the space provided (you may use the back of any page if you need more space). Show all work but do
Generalized linear models for binary data. A better graphical exploratory data analysis. The simple linear logistic regression model
 Stat 3302 (Spring 2017) Peter F. Craigmile Simple linear logistic regression (part 1) [Dobson and Barnett, 2008, Sections 7.1 7.3] Generalized linear models for binary data Beetles dose-response example
Stat 3302 (Spring 2017) Peter F. Craigmile Simple linear logistic regression (part 1) [Dobson and Barnett, 2008, Sections 7.1 7.3] Generalized linear models for binary data Beetles dose-response example
Regression Analysis: Exploring relationships between variables. Stat 251
 Regression Analysis: Exploring relationships between variables Stat 251 Introduction Objective of regression analysis is to explore the relationship between two (or more) variables so that information
Regression Analysis: Exploring relationships between variables Stat 251 Introduction Objective of regression analysis is to explore the relationship between two (or more) variables so that information
Introduction To Logistic Regression
 Introduction To Lecture 22 April 28, 2005 Applied Regression Analysis Lecture #22-4/28/2005 Slide 1 of 28 Today s Lecture Logistic regression. Today s Lecture Lecture #22-4/28/2005 Slide 2 of 28 Background
Introduction To Lecture 22 April 28, 2005 Applied Regression Analysis Lecture #22-4/28/2005 Slide 1 of 28 Today s Lecture Logistic regression. Today s Lecture Lecture #22-4/28/2005 Slide 2 of 28 Background
Multiple Regression: Chapter 13. July 24, 2015
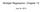 Multiple Regression: Chapter 13 July 24, 2015 Multiple Regression (MR) Response Variable: Y - only one response variable (quantitative) Several Predictor Variables: X 1, X 2, X 3,..., X p (p = # predictors)
Multiple Regression: Chapter 13 July 24, 2015 Multiple Regression (MR) Response Variable: Y - only one response variable (quantitative) Several Predictor Variables: X 1, X 2, X 3,..., X p (p = # predictors)
NATIONAL UNIVERSITY OF SINGAPORE EXAMINATION. ST3241 Categorical Data Analysis. (Semester II: ) April/May, 2011 Time Allowed : 2 Hours
 NATIONAL UNIVERSITY OF SINGAPORE EXAMINATION Categorical Data Analysis (Semester II: 2010 2011) April/May, 2011 Time Allowed : 2 Hours Matriculation No: Seat No: Grade Table Question 1 2 3 4 5 6 Full marks
NATIONAL UNIVERSITY OF SINGAPORE EXAMINATION Categorical Data Analysis (Semester II: 2010 2011) April/May, 2011 Time Allowed : 2 Hours Matriculation No: Seat No: Grade Table Question 1 2 3 4 5 6 Full marks
Mixed models in R using the lme4 package Part 7: Generalized linear mixed models
 Mixed models in R using the lme4 package Part 7: Generalized linear mixed models Douglas Bates University of Wisconsin - Madison and R Development Core Team University of
Mixed models in R using the lme4 package Part 7: Generalized linear mixed models Douglas Bates University of Wisconsin - Madison and R Development Core Team University of
Logistic Regression 21/05
 Logistic Regression 21/05 Recall that we are trying to solve a classification problem in which features x i can be continuous or discrete (coded as 0/1) and the response y is discrete (0/1). Logistic regression
Logistic Regression 21/05 Recall that we are trying to solve a classification problem in which features x i can be continuous or discrete (coded as 0/1) and the response y is discrete (0/1). Logistic regression
Chapter 22: Log-linear regression for Poisson counts
 Chapter 22: Log-linear regression for Poisson counts Exposure to ionizing radiation is recognized as a cancer risk. In the United States, EPA sets guidelines specifying upper limits on the amount of exposure
Chapter 22: Log-linear regression for Poisson counts Exposure to ionizing radiation is recognized as a cancer risk. In the United States, EPA sets guidelines specifying upper limits on the amount of exposure
Elementary Statistics Lecture 3 Association: Contingency, Correlation and Regression
 Elementary Statistics Lecture 3 Association: Contingency, Correlation and Regression Chong Ma Department of Statistics University of South Carolina chongm@email.sc.edu Chong Ma (Statistics, USC) STAT 201
Elementary Statistics Lecture 3 Association: Contingency, Correlation and Regression Chong Ma Department of Statistics University of South Carolina chongm@email.sc.edu Chong Ma (Statistics, USC) STAT 201
Lab 3: Two levels Poisson models (taken from Multilevel and Longitudinal Modeling Using Stata, p )
 Lab 3: Two levels Poisson models (taken from Multilevel and Longitudinal Modeling Using Stata, p. 376-390) BIO656 2009 Goal: To see if a major health-care reform which took place in 1997 in Germany was
Lab 3: Two levels Poisson models (taken from Multilevel and Longitudinal Modeling Using Stata, p. 376-390) BIO656 2009 Goal: To see if a major health-care reform which took place in 1997 in Germany was
Week 7 Multiple factors. Ch , Some miscellaneous parts
 Week 7 Multiple factors Ch. 18-19, Some miscellaneous parts Multiple Factors Most experiments will involve multiple factors, some of which will be nuisance variables Dealing with these factors requires
Week 7 Multiple factors Ch. 18-19, Some miscellaneous parts Multiple Factors Most experiments will involve multiple factors, some of which will be nuisance variables Dealing with these factors requires
Logistic Regressions. Stat 430
 Logistic Regressions Stat 430 Final Project Final Project is, again, team based You will decide on a project - only constraint is: you are supposed to use techniques for a solution that are related to
Logistic Regressions Stat 430 Final Project Final Project is, again, team based You will decide on a project - only constraint is: you are supposed to use techniques for a solution that are related to
UNIVERSITY OF TORONTO. Faculty of Arts and Science APRIL 2010 EXAMINATIONS STA 303 H1S / STA 1002 HS. Duration - 3 hours. Aids Allowed: Calculator
 UNIVERSITY OF TORONTO Faculty of Arts and Science APRIL 2010 EXAMINATIONS STA 303 H1S / STA 1002 HS Duration - 3 hours Aids Allowed: Calculator LAST NAME: FIRST NAME: STUDENT NUMBER: There are 27 pages
UNIVERSITY OF TORONTO Faculty of Arts and Science APRIL 2010 EXAMINATIONS STA 303 H1S / STA 1002 HS Duration - 3 hours Aids Allowed: Calculator LAST NAME: FIRST NAME: STUDENT NUMBER: There are 27 pages
ZERO INFLATED POISSON REGRESSION
 STAT 6500 ZERO INFLATED POISSON REGRESSION FINAL PROJECT DEC 6 th, 2013 SUN JEON DEPARTMENT OF SOCIOLOGY UTAH STATE UNIVERSITY POISSON REGRESSION REVIEW INTRODUCING - ZERO-INFLATED POISSON REGRESSION SAS
STAT 6500 ZERO INFLATED POISSON REGRESSION FINAL PROJECT DEC 6 th, 2013 SUN JEON DEPARTMENT OF SOCIOLOGY UTAH STATE UNIVERSITY POISSON REGRESSION REVIEW INTRODUCING - ZERO-INFLATED POISSON REGRESSION SAS
A Handbook of Statistical Analyses Using R 2nd Edition. Brian S. Everitt and Torsten Hothorn
 A Handbook of Statistical Analyses Using R 2nd Edition Brian S. Everitt and Torsten Hothorn CHAPTER 7 Logistic Regression and Generalised Linear Models: Blood Screening, Women s Role in Society, Colonic
A Handbook of Statistical Analyses Using R 2nd Edition Brian S. Everitt and Torsten Hothorn CHAPTER 7 Logistic Regression and Generalised Linear Models: Blood Screening, Women s Role in Society, Colonic
LISA Short Course Series Generalized Linear Models (GLMs) & Categorical Data Analysis (CDA) in R. Liang (Sally) Shan Nov. 4, 2014
 LISA Short Course Series Generalized Linear Models (GLMs) & Categorical Data Analysis (CDA) in R Liang (Sally) Shan Nov. 4, 2014 L Laboratory for Interdisciplinary Statistical Analysis LISA helps VT researchers
LISA Short Course Series Generalized Linear Models (GLMs) & Categorical Data Analysis (CDA) in R Liang (Sally) Shan Nov. 4, 2014 L Laboratory for Interdisciplinary Statistical Analysis LISA helps VT researchers
EXAMINATIONS OF THE ROYAL STATISTICAL SOCIETY (formerly the Examinations of the Institute of Statisticians) GRADUATE DIPLOMA, 2007
 EXAMINATIONS OF THE ROYAL STATISTICAL SOCIETY (formerly the Examinations of the Institute of Statisticians) GRADUATE DIPLOMA, 2007 Applied Statistics I Time Allowed: Three Hours Candidates should answer
EXAMINATIONS OF THE ROYAL STATISTICAL SOCIETY (formerly the Examinations of the Institute of Statisticians) GRADUATE DIPLOMA, 2007 Applied Statistics I Time Allowed: Three Hours Candidates should answer
Chapter 11. Correlation and Regression
 Chapter 11. Correlation and Regression The word correlation is used in everyday life to denote some form of association. We might say that we have noticed a correlation between foggy days and attacks of
Chapter 11. Correlation and Regression The word correlation is used in everyday life to denote some form of association. We might say that we have noticed a correlation between foggy days and attacks of
Today. HW 1: due February 4, pm. Aspects of Design CD Chapter 2. Continue with Chapter 2 of ELM. In the News:
 Today HW 1: due February 4, 11.59 pm. Aspects of Design CD Chapter 2 Continue with Chapter 2 of ELM In the News: STA 2201: Applied Statistics II January 14, 2015 1/35 Recap: data on proportions data: y
Today HW 1: due February 4, 11.59 pm. Aspects of Design CD Chapter 2 Continue with Chapter 2 of ELM In the News: STA 2201: Applied Statistics II January 14, 2015 1/35 Recap: data on proportions data: y
Announcements. J. Parman (UC-Davis) Analysis of Economic Data, Winter 2011 February 8, / 45
 Announcements Solutions to Problem Set 3 are posted Problem Set 4 is posted, It will be graded and is due a week from Friday You already know everything you need to work on Problem Set 4 Professor Miller
Announcements Solutions to Problem Set 3 are posted Problem Set 4 is posted, It will be graded and is due a week from Friday You already know everything you need to work on Problem Set 4 Professor Miller
