COPYRIGHTED MATERIAL WAVES A GENERAL DESCRIPTION CHAPTER GENERAL DEFINITIONS OF WAVES A QUALITATIVE DESCRIPTION
|
|
|
- Albert Ball
- 5 years ago
- Views:
Transcription
1 CHAPTER 1 WAVES A GENERAL DESCRIPTION Synopsis: This chapter deals with the basic definitions of waves in general and acoustic waves in particular. The objective of this chapter is to touch base with wave properties and their mathematical description. We shall start with a qualitative description and define the various types of waves. We shall examine what properties can be used to describe waves, introduce the wave equation in a homogeneous medium, learn about group and standing waves, and describe in detail spherical and cylindrical waves. Finally, we shall study the wave equation in a nonhomogeneous medium and the Born and Rytov approximations associated with its solution. (Note: It is likely that many of the items presented in this chapter are trivial or familiar to most readers. Thus, a reader who is well aquatinted with the material may hop to the next chapter.) 1.1 GENERAL DEFINITIONS OF WAVES A QUALITATIVE DESCRIPTION When a mechanical wave propagates through matter, energy is transferred from one location to another [1, ]. However, this energy is not associated with mass transfer. For example, one may consider the propagating waves formed when moving an end point of a jumping rope or when the first piece from a set of dominoes aligned in a row falls down. Clearly, energy is transferred by motion of matter, but mass is not really transferred from one location to another. The nature of the propagating wave is determined by the type of perturbation causing it to appear but also and mainly by the properties of the COPYRIGHTED MATERIAL Basics of Biomedical Ultrasound for Engineers, by Haim Azhari Copyright 010 John Wiley & Sons, Inc. 9
2 10 1 WAVES A GENERAL DESCRIPTION Figure 1.1. Schematic depiction of two possible configuration of mechanical wave propagation. (Top) The wave propagation direction is limited to only one direction. (Bottom) Although the small masses motion is horizontal, waves can propagate along the vertical direction as well. media through which it travels. For clarity, let us observe the two examples shown in Fig. 1.1 : Example 1. A cylinder filled with gas or fluid has a piston on its left side. At a certain time point the piston is pushed back and forth. Consequently, a pressure wave will propagate through the gas or fluid along the cylinder s axis. In this case the wave may be considered as one - dimensional. Example. A matrix consisting of springs and spherical masses is at rest. At a certain time point, one mass is pushed back and forth. As a result, the masses along the line of perturbation will vibrate and a mechanical wave will propagate through the matrix. However, in this case the perturbation will also be associated with deformation of springs from both sides of the moving mass. Hence, one may expect mechanical waves to propagate along directions that are perpendicular to the induced motion as well. From Example, one can conclude that several types of waves, each characterized by different properties, can be generated at the same time and even from the same perturbation. (This issue will be discussed in Chapter 4, where wave propagation in solids is analyzed.) Also, it is important to note that the motion direction of the particles constituting the medium does not have to align with the wave propagation direction. Using this fact, we can apply a preliminary division of wave types based on the relation between the wave propagation direction and the motion direction of the particles constituting the medium (see also Fig. 1. ):
3 1.1 GENERAL DEFINITIONS OF WAVES A QUALITATIVE DESCRIPTION 11 Figure 1.. Division of waves into two types based on the relation between the wave propagation direction and the motion direction of the particles constituting the medium. (Top) In a longitudinal wave the particles motion is parallel to the wave propagation direction. (Bottom) In a transverse wave the particles motion is perpendicular to the wave propagation direction. A Longitudinal Wave A wave for which the direction of displacement for the medium s particles is parallel to the direction of wave propagation A Transverse Wave A wave for which the direction of displacement for the medium s particles is perpendicular to the direction of wave propagation. This basic division is frequently used in ultrasound, but it is important to note that there are also wave types for which the direction of motion for the medium s particles is not fixed relative to the wave propagation direction. For example, in surface waves (as in sea waves) the angle between the two directions changes continuously. A second and important division is based on the wave front geometry. Using this approach we can again divide the waves into two basic types (Fig. 1.3 ): A. A Planar Wave A wave for which the wave front is located on a plane that propagates in space. B. A Circular Wave A wave that propagates symmetrically around a reference point (as a sphere or a ring), or around a reference line (as a cylinder).
4 1 1 WAVES A GENERAL DESCRIPTION Planar Wave Circular Wave Figure 1.3. Division of waves into two types based on the geometry of the wave front. (Left) A planar wave. (Right) a circular wave. Wave Source New Wave Front Figure 1.4. Schematic demonstration of the Huygens Principle implementation to an arbitrarily shaped wave source (or wave front). Each point on the wave front is assumed to emanate a spherical wave (only a few are depicted for clarity). The superposition of all these small spherical waves forms the new wave front. Of course in nature one can encounter also intermediate type of waves. For example, the acoustic beam transmitted from a disc - shaped transducer (see Chapter 8 ) has planar wave characteristics (particularly around its center). However, as the ratio between the transducer diameter and the wavelength is decreased, the wave will have more and more spherical wave characteristics. In the general case, one can use Huygens Principle to investigate the propagating wave front of an arbitrary shape. Huygens Principle states that any wave source (or wave front for that matter) can be considered as an infinite collection of spherical wave sources [3]. This is schematically demonstrated in Fig GENERAL PROPERTIES OF WAVES A QUALITATIVE DESCRIPTION 1..1 Interference and the Superposition Principle One interesting property of wave interaction is the interference phenomenon. When two waves collide, they can form constructive interference and their
5 1. GENERAL PROPERTIES OF WAVES A QUALITATIVE DESCRIPTION 13 constructive interference D 1D destructive interference Figure 1.5. (Top) Demonstration of constructive interference in a water bath (D case left ) and for strings (1D case middle ). For clarity, the 1D case is also schematically depicted on the right side. (Bottom) Demonstration of destructive interference. Reprinted with permission from PSSC Physics, 7th edition, by Haber - Schaim, Dodge, Gardner, and Shore, Kendall/Hunt Publishing Company, amplitudes seem to enhance each other or destructive interference and their amplitudes seem to attenuate each other (see Fig. 1.5 ) [4]. However, after passing through each other, each wave proceeds as though nothing has happened (if nonlinear effects are negligible). The superposition principle states that within an interference zone the net amplitude is the sum of all the interacting wave amplitudes. 1.. Reflection and Transmission of Waves When a wave passes from one material to another or when it encounters a discontinuity in the medium in which it travels, part of its energy is reflected and part of it is through - transmitted with or without a change in direction. For an acoustic wave the reflected part is usually referred to as an echo. It is worth noting that in ultrasound we distinguish between the waves reflected along a straight line to the source which are referred to as backscatter and which are scatted to other directions. The energy partition and the change in wave properties of the transmitted and scattered waves contain a lot of information that can be utilized for imaging or diagnosis (as indicated in the introduction chapter). In the one - dimensional (1D) case, when a wave passes from a spring that has certain mechanical properties to another spring that has different
6 14 1 WAVES A GENERAL DESCRIPTION Free End Fixed End From Light To Heavy From Heavy to Light TIME Figure 1.6. A demonstration of wave transmission and reflection phenomenon in springs. The arrow indicates the propagation direction of the impinging wave. Each picture indicates a new time frame. (Left column) A wave reaching a free end. (Second column) A wave reaching a fixed end. (Third column) A wave traveling in a light (low density) spring encounters a heavy (high - density) spring. (Right column) A wave traveling in a heavy (high - density) spring encounters a light (low - density) spring. Reprinted with permission from PSSC Physics, 7th edition, by Haber - Schaim, Dodge, Gardner, and Shore, Kendall/Hunt Publishing Company, properties, or when the wave reaches an end point, reflection occurs and, if possible, transmission occurs as well. In Fig. 1.6, four different scenarios of a wave propagating in a spring and encountering a discontinuity point are demonstrated (from left to right): (a) a wave reaching a free end, (b) a wave reaching a fixed end, (c) a wave traveling in a low - density spring reaching a point connecting the spring with a high - density spring, and (d) a wave traveling in a high - density spring reaching a point connecting the spring with a low - density spring. It is important to note that when the wave encounters a tough medium, such as a heavy spring or a fixed end point, the phase of its echo changes (i.e., its amplitude changes signs). Also, it is important to note that when the wave travels from a heavy spring to a light one, its amplitude is increased (energy, however, is conserved as will be explained in the next chapter). In the two - dimensional (D) case and naturally in the three dimensions (3D), one has to distinguish between circular and planar waves. In the case of a planar wave, the rule is simple: The angle of reflection from a reflector is equal to the angle of incidence. However, for a circular wave (e.g., spherical or cylindrical), things are a little bit more complicated. The reflected wave seems to emanate from a virtual source which is located on the other side of the reflector (see Fig. 1.7 ).
7 1. GENERAL PROPERTIES OF WAVES A QUALITATIVE DESCRIPTION 15 Planar Wave Reflection Spherical Wave Reflection Reflector Reflector Figure 1.7. A demonstration of the reflection phenomenon for a planar wave (left) and for a circular wave (right). Reprinted with permission from PSSC Physics, 7th edition, by Haber - Schaim, Dodge, Gardner, and Shore, Kendall/Hunt Publishing Company, Diffraction Another phenomenon that is associated with waves is diffraction. Waves that impinge upon a corner or pass through a slot in a screen bend their trajectory and propagate into zones that should have been shadowed. This phenomenon is enhanced for wavelengths that are relatively long relative to the geometry of the obstacle. Diffraction may be significant in medical ultrasound since the typical wavelengths are in the scale of a millimeter (for example, for a frequency of 1 MHz, the wavelength is about 1.5 mm in soft tissues), and so is the needed resolution. The diffraction phenomenon is demonstrated in Fig. 1.8 for clarity Standing Waves Another phenomenon that needs to be noted is the appearance of standing waves. When waves rush back and forth within a confined medium (e.g., when strong reflectors are located at each end point of the medium), the waves interfere with each other and with their reflections. Consequently, a motion pattern is formed which is spatially fixed but temporally changes its amplitude (see, for example, Fig. 1.9 ). This pattern is referred to as a standing wave, since an illusion is formed where the wave seems to stand still while its amplitude changes. This type of wave is most probably observed in string - based musical instruments. They may be noticed in vibrating strings and in resonance boxes. In medical applications, this type of wave may be significant when considering the design of instruments and particularly the design of instruments that use constant wave (CW) transmission.
8 16 1 WAVES A GENERAL DESCRIPTION λ/w = 0.1 λ/w = 0.6 w Figure 1.8. Demonstration of the diffraction phenomenon for a planar wave propagating from the bottom toward the top and passing through a slot for which width is W. The ratio between the wavelength λ and the slot width W is 0.1 for the case shown on the left and 0.6 for the case shown on the right. As can be noted, the phenomenon is much more enhanced on the right side. Reprinted with permission from PSSC Physics, 7th edition, by Haber - Schaim, Dodge, Gardner, and Shore, Kendall/Hunt Publishing Company, w Figure 1.9. A demonstration of the standing wave phenomenon. In these four pictures taken with a long exposure time, four vibration modes for a string tied at both end points are depicted. As can be noted, certain nodal points (marked by the arrows) do not move. Reprinted with permission from PSSC Physics, 7th edition, by Haber - Schaim, Dodge, Gardner, and Shore, Kendall/Hunt Publishing Company, 1991.
9 1.3 MECHANICAL ONE-DIMENSIONAL WAVES MECHANICAL ONE - DIMENSIONAL WAVES Consider the familiar entertaining device that consists of a set of pendulums made from small metal balls tied in a compact row as shown in Fig At time point t = Δ t 0 the first pendulum (marked as #0) is tilted by an angle θ 0 and is allowed to swing back. The initial potential energy of its metal ball will be converted into both kinetic and potential energy as the ball swings toward its neighbor. At time t = 0 the ball will hit the ball of pendulum #1 and the impact will transfer some of its energy. The ball of pendulum #0 will then swing slightly (if there is a gap between adjacent balls) and resume its original equilibrium position. The ball of pendulum #1 will hit the ball of pendulum # and in turn will transfer to it some of its energy and so forth. If we would take a camera and photograph the set of pendulums at time t = 0 and at time t = t 1, we would be able to notice that there are calm regions (i.e., where the balls are in their equilibrium position and the are stormy regions where the balls swing back and forth. The stormy region that was created by the initial perturbation propagates along the medium (toward its left side in the case shown in Fig ). Intuitively, we can relate this experiment to waves. Hence, we shall refer to the propagating perturbation of pendulums from their equilibrium state as a wave. Comparing our observation to the definition given in the previous sections, we shall indeed note that it suits our criteria. We have in this example a propagating mechanical energy that propagates through matter and that is not associated with mass transfer x N+1 N θ t=0 x N+1 N t=t 1 Figure A demonstration of a propagating mechanical wave in a one - dimensional medium. The perturbation from equilibrium which is induced at time t = 0 by swinging the first pendulum will propagate and eventually reach the Nth pendulum at time t = t 1.
10 18 1 WAVES A GENERAL DESCRIPTION and that stems from a perturbation induced to the medium. This perturbation, which we refer to as a wave, varies with time and space and therefore can be designated in the most general case by the term U = U( x, y, z, t) (1.1) where the function U can designate any physical property that characterizes the propagation of the propagating perturbation. In the example given above, U could express the pendulum angle relative to its equilibrium state, the metal ball velocity, or its energy, and so forth. In the one - dimensional case the wave can be represented by U = U( x, t) (1.) If we set the time to be constant and we plot U as a function of location, we shall obtain a profile of the property described by U = U (x,t = const). On the other hand, we can set the location to be a constant and plot the profile described by U = U (x = const, t ). Comparing the two obtained plots, we shall realize that the two plots characteristics are identical except for the reverse in directions and the natural change in scaling. This plot is called the wave profile (see Fig ). Amplitude Wave Profile Amplitude [X]Location Time [t] Figure A demonstration of a wave profile when plotted as a function of location for a given time point (top) or as a function of time for a given spatial location (bottom). As can be noted, the two profile characteristics are identical except for scaling and directions.
11 1.4 THE WAVE FUNCTION THE WAVE FUNCTION Generally speaking, a wave propagating along the positive direction of the X axis can be described by the general function [5] U(x, t) = U(x ct) (1.3) whereas a wave propagating along the negative direction of the X axis can be described by U (x, t) = U(x + ct) (1.4) In order to validate this statement, let us examine a function U (x, t ) = U (x ct ) representing a wave that has a profile of maximal amplitude U 0 and a single peak, such as shown for example in the following icon: U 0. At time t = 0 the peak of the wave profile is found at some point x 0, that is, U (x 0, t = 0) = U 0. Clearly, if for some other point x in time t = Δ t we can find a location for which x c Δ t = x 0, its value must be U (x c Δ t ) = U (x 0, 0) = U 0. However, since by definition we have C > 0, and time is always positive ( t > 0), it follows that the value of x which fulfills the condition x c Δ t = x 0 must continuously increase. Or in other words, the peak of the wave profile must move along the positive direction of x. This can also be demonstrated graphically by plotting the location of the wave profile peak (or any other landmark for that matter) in the plane ( x, t ). There it will move along a straight line given by x x 0 = c Δ t and whose slope is 1/ c = Δ t /(x x 0 ) as shown in Fig Similarly, it can be shown that U (x + ct ) describes a wave that propagates along the negative direction of x. Time t U(x + ct) U(x - ct) α 1 C = tan α Xo Space X Figure 1.1. Propagation of waves defined by the general function U (x + ct ) in the space time (x, t ) plane.
12 0 1 WAVES A GENERAL DESCRIPTION 1.5 THE WAVE EQUATION The wave function U (x ± ct ) described above is related to a differential equation for which it can serve as a solution. This equation is defined as the wave equation and for the one - dimensional (1D) case in a homogeneous medium is given by [5] = U 1 U X C t ( one dimension ) (1.5) We can prove this statement for the function U (x ct ). Let us define a new parameter x ct g and its corresponding derivative as u = U g. Using the chain rule, we can write the relation u = u g and also the relation x g x u = u g t g t. And since u = C t u, it is easy to see that the relation g = = u 1 u U x c t is valid. For the three - dimensional (3D) case we can use the term U = U (nˆ r ct ) to describe the wave, where nˆ is a unit vector along the wave propagation direction and r is the spatial location vector. The corresponding wave equation in this case is given by = 1 U U C t ( three dimensions ) (1.6) 1.6 HARMONIC WAVES Each wave can be represented using the Fourier transform by a series of harmonic waves. Harmonic waves are waves with a defined periodic profile (such as sine or cosine functions). These types of waves are mathematically convenient to work with and can be described (for the 1D case) by u Ae j [ ωt kx] = = A[ cos( ωt kx))+ jsin ( ωt kx)) ] (1.7) or more generally (for 3D) by
13 1.6 HARMONIC WAVES 1 u= Ae j ω t k R (1.8) where the wave temporal (also called angular) frequency is given by π ω = πf = T (1.9) and the wave spatial frequency is given by k k nˆ (1.10) where nˆ is a unit vector along the wave propagation direction and k is called the wave number. The parameter k is required for two reasons: (a) To cancel the physical dimension of the exponential term. (b) To ensure the periodicity of the function with a wavelength of λ. The value of k can be determined by studying a simple harmonic wave, for example: u= A[ cos( ωt kx+ ϕ )] (1.11) where ϕ represents the phase of the wave. Naturally, a peak of the wave profile will appear at time t = 0 wherever the following relation applies: cos( ϕ kx)= 1 (1.1) Thus, for two consecutive peak points x n and x n +1 on the wave profile at time t = 0, the following relations must apply: By subtracting the two equations, we shall obtain ϕ kxn = n π (1.13) ϕ kxn+ 1 = ( n + 1) π (1.14) k( xn+ 1 xn)= π (1.15) And since the distance between two adjacent peak points for a harmonic wave equals the wavelength λ = c /f, it follows that k = π λ (1.16)
14 1 WAVES A GENERAL DESCRIPTION It is important to note that the physical units of k are radians/length. Hence, it is actually a parameter defining spatial frequency. The full spatial frequency spectrum of a given wave can be obtained by applying the Fourier transform to the wave profile at a given time point Equivalent Presentations It is also worth noting that harmonic waves can be presented mathematically using alternative arguments. However, the physical interpretation is the same. Three exemplary presentations are given below: U = x t Acos π T + ϕ, (1.17) λ U = A cos π ( x ct)+ ϕ λ, (1.18) x U = A cos ft π + ϕ λ (1.19) 1.7 GROUP WAVES When a group of waves travel together in a medium, their amplitudes and phases interfere with each other and a pattern is formed which seems to propagate in a speed that differs from the speed of its components. In order to demonstrate this phenomenon, let us consider the simplest case where two waves having the same amplitude, but with different temporal (angular) and spatial frequencies, travel together. For example, if the first wave is given by U = Acos( k x ω t) (1.0) and the second wave that accompanies it is given by U = Acos( k x ω t) (1.1) then the pattern given in Fig is obtained. Marking the envelope of this combination, it would appear as though the envelope travels as a new wave in the medium. This pattern is called a group wave and is given mathematically for this specific example by k + k U = A 1 + x ω1 ω cos t k1 k ω1 ω cos x t (1.) High-frequency components Low-frequency components
15 1.8 WAVE VELOCITY 3.5 Group wave Amplitude [AU] Time [AU] Figure A group wave obtained by combining two sinusoidal waves of different frequencies. (The envelope is depicted by the dashed line for clarity.) As can be noted, the combined pattern is represented by a multiplication between a high - frequency - components (both spatial and temporal) wave (the carrier wave) and a low - frequency - components (modulating) wave. 1.8 WAVE VELOCITY Wave velocity is not so trivial to define. The more intuitive concept is to track the speed at which the energy carried by the wave propagates. This can be estimated by tracking a specific point of reference on the envelope of a propagating wavepacket (for a group wave). Such point of reference could be, for example, the front edge of the profile envelope or its point of maximal value. In the example given in Fig. 1.10, we can refer to the ball located on the left side of the stormy region as the front end of the wave envelope. By measuring the propagation Δ x of this landmark at time interval Δ t, the wave velocity can be estimated from c x = Δ Δ t (1.3) This type of wave propagation speed estimation by envelope amplitude tracking is called group velocity. For a group comprised of a set of harmonic waves, the group velocity c g is given by
16 4 1 WAVES A GENERAL DESCRIPTION k cg = ω ( ) k (1.4) In case of a single - frequency wave, one can track the phase propagation speed. This can be done, for example, by selecting any point of reference on the wave profile. In the case of a wavepacket (a group wave), one can track the phase of one of its high frequency components. In such a case the obtained value is defined as the phase velocity c p and is given by c p = ω ( k) k (1.5) If dispersion is negligible or not existent (such as the case for electromagnetic waves in vacuum), the angular (temporal) frequency and the wave number are linearly related, that is, ω = ck (1.6) Hence for this case the group velocity and the phase velocity are the same, that is, c g = c p. If the relation between the angular (temporal) frequency and the wave number is not linear, the speed of sound varies with the wave frequency. This case is discussed in Chapter 5 (Section 5.5 ). 1.9 STANDING WAVES (A MATHEMATICAL DESCRIPTION) As was presented in Section 1..4, the standing wave phenomenon occurs when a string (or some other type of bounded medium such as a beam or a tube) fixed on both sides vibrates. While most of the particles on the string (or medium) move periodically, there are specific points, called nodal points, that do not move (as shown in Fig. 1.9 ). This phenomenon is explained by the existence of two waves of the same amplitude and frequency propagating in the same medium toward opposite directions. Such waves can be generated by the reflections caused by the boundaries (see Fig. 1.6 ). As a result, the two waves continuously interfere with each other. For a specific length of the medium and for specific frequencies (see Chapter ), destructive interference occurs constantly at the nodal points and prevent them from moving. Let us define the wave propagating along the positive x direction as U 1, U1 = Acos( kx ω t) (1.7) and define the wave propagating along the negative x direction as U, U = Acos( kx+ ω t) (1.8)
17 1.10 SPHERICAL WAVES 5 The resulting displacements within the medium will be given by U = U 1 + U. And recalling the trigonometric relation, α β α β cosα + cosβ = cos + cos (1.9) we obtain or, in a more general form, U = U1 + U = Acos( kx) cos( t) ω (1.30) Χ( x) Θ( t) U = X( x) Θ () t (1.31) As can be noted, the combined displacement pattern is comprised of a multiplication between two functions: (i) the function Θ (t ), which depends solely on time and which modulates only the wave amplitude, and (ii) the function X (x ), which depends solely on location and exhibit a constant profile in space. And since at the nodal points we have X (x ) = 0, no displacement will occur at these points, and hence we have the resulting impression of a standing wave. (This phenomenon will be discussed again in Chapter.) 1.10 SPHERICAL WAVES In daily life we occasionally encounter waves with circular symmetry (see Fig ). Most commonly, we associate such waves with the ripples pattern formed when a pebble is thrown into a water pond. In such cases the symmetry is two-dimensional (D). However, waves with three - dimensional (3D) symmetry which propagate as a sphere in space (and are therefore referred to as spherical waves) are also very common. In fact, such waves are created from almost any noise - or stress - generating event. For example, the noise generated when two objects collide, generated by a ringing bell, or generated by an explosion can all produce spherical waves. If the source for the waves may be considered small enough relative to the wavelength, we can assume that the wave stems from a single - point source and hence may be considered as spherical. Moreover, Huygens Principle (see above) states that any wave source can be considered as an infinite collection of spherical wave sources. A spherical wave is characterized by 3D spatial symmetry around its source (in an isotropic medium). Therefore it is natural to describe this type of wave in a spherical coordinate system. Defining the function describing the wave as ϕ, the three - dimensional wave equation is given by
18 6 1 WAVES A GENERAL DESCRIPTION Imploding (+) Exploding (-) Y r q Figure Schematic depiction of a spherical wave spreading symmetrically from (or toward) a central point. 1 ϕ ϕ = c t (1.3) Rewriting the left - hand side of Eq. (1.3) in a spherical coordinate system r, θ Ψ,, we obtain [6] ϕ ϕ + θ ϕ + ϕ r r r sin r r sinθ θ θ r sinθ ψ (1.33) And since function ϕ should be symmetric relative to θ and Ψ, it follows that ϕ = ψ 0 (1.34) ϕ = 0 (1.35) θ And therefore we shall obtain = ϕ ϕ + = 1 ( rϕ) = 1 ϕ ϕ r r r r r c t (1.36) It can be easily shown that a solution to this wave equation is given by the generic function:
19 1.11 CYLINDRICAL WAVES 7 A ϕ = ± r f t r c (1.37) where the + sign designates an imploding wave (i.e., propagating toward the central point) and the sign designates an exploding wave. A is the wave amplitude, whose units are the physical units of ϕ (pressure, for example) multiplied by length. This can be shown by substitution of Eq. (1.37) into the left - hand side of Eq. (1.36) (for simplicity we shall assume that the amplitude A = 1), r ± f t ( ) = = 1 rϕ 1 c 1 ϕ = 1 ± r r r r r r c f = 1 rc f (1.38) while from Eq (1.3) we shall obtain the same term, = = 1 ϕ 1 1 f 1 1 ϕ = c t c r t c r f (1.39) It should be pointed out that f r t± c is equivalent to f (ct ± r ). But it is very important to note that unlike a planar wave, the amplitude of a spherical wave decays with the distance from the source according to 1, even when r attenuation is negligible CYLINDRICAL WAVES Cylindrical waves are those that propagate from a line source and that keep angular symmetry around the source axis. (The source could, for example, be an antenna pole.) A schematic depiction of a cylindrical wave front propagating from or toward a line of symmetry (in this case the Z axis) is shown in Fig Rewriting the left - hand side of Eq. (1.3) in a cylindrical coordinate system r, z, θ, we obtain [6] ϕ + ϕ ϕ + ϕ ϕ r r r r θ z (1.40) The symmetry around Z and θ yields
20 8 1 WAVES A GENERAL DESCRIPTION Z r θ Figure Schematic depiction of a cylindrical wave front propagating symmetrically from (or toward) a central line ( Z axis in this case). ϕ ϕ = 0, = 0 (1.41) z θ And therefore we obtain = + ϕ 1 ϕ = 1 ϕ ϕ r r r r r r r (1.4) Substituting Eq. (1.4) into Eq. (1.3), we obtain the wave equation for this type of wave: + ϕ 1 ϕ = 1 ϕ r r r C t (1.43) Multiplying both sides by r and moving all terms to the left - hand side yields r ϕ r + r ϕ r r ϕ = C t 0 (1.44) To find a solution, we shall assume that the space time relationship could be presented by two functions multiplied by each other, that is, jωt ϕ = e ψ() r (1.45)
21 1.1 THE WAVE EQUATION IN A NONHOMOGENEOUS MEDIUM 9 Thus, if follows that ϕ = ω ϕ t (1.46) And if we recall that ω C πf = ( ) ( λ f ) k = (1.47) we shall obtain r ϕ + r ϕ rk 0 r r + ϕ = (1.48) As can be noted, this equation is actually a Bessel differential equation of order zero. The solution for this equation is given by the Hankel function of the first kind and of order zero H0 1 ( kr): ϕ = H0 1 ( kr)= A J0( kr)+ B Y0 ( kr) (1.49) where J 0 (kr ) and Y 0 (kr ) are Bessel functions of the first and second types respectively, and A and B are two constants. It should be noted that this solution is a complex function. For simplicity the following approximation can be used: D ϕ ψ( ωt± kr ) (1.50) r The exact solution (absolute value) and its approximation are graphically compared in Fig The solutions were calculated for an expanding cylindrical wave propagating in water ( C = 1500 m/sec) with a frequency of 1 MHz. As can be observed, the approximated solution follows the pattern of the exact solution (particularly for large kr values); however, it has an overestimating offset (which could be partially reduced by subtracting a constant). 1.1 THE WAVE EQUATION IN A NONHOMOGENEOUS MEDIUM Thus far we have assumed that the medium in which the waves propagate is uniform. However, in the majority of cases this assumption is not true, because the body consists of many complicated structures of tissues and blood vessels.
22 30 1 WAVES A GENERAL DESCRIPTION Amplitude [AU] r [mm] Figure A graphic comparison between the absolute value of the exact solution (solid line) and the approximated solution (dashed line) for a cylindrical wave propagating with a frequency of 1 MHz in water. ( Note : In order to avoid the singularity at the axes origin, the calculated range started at r = 1 mm.) Indeed the assumption of homogeneity is practically convenient; however, in certain applications (e.g., acoustic computed tomography), inhomogeneity has to be accounted for. Inhomogeneity can stem from spatial changes in density or elastic properties; however, since these properties affect the speed of sound, we may consider the speed of sound as the significant variable. Without affecting the generality of the following discussion, we shall consider only one harmonic wave with a given frequency in the equations (the reader should bear in mind that any wave can be expanded into a series of monochromatic harmonic waves using the Fourier transform). Consequently, the changes in the speed of sound will be manifested in changes of the wavelength. This spatial variation can thus be presented by the wave number k (r ), where the vector r represents the spatial coordinates. Following the derivation presented in Kak and Slaney [7], the wave equation in a nonhomogeneous medium is given by + k( r) u( r )= 0 (1.51) where u (r ) is a function that represents the acoustic field. Using, for example, water (whose acoustic properties are close to that of soft tissues) as a reference medium, this equation can be rewritten as [ + 0 ] ( )= 0 k ur k nr ( ) 1 ] ur ( ) (1.5)
23 1.1 THE WAVE EQUATION IN A NONHOMOGENEOUS MEDIUM 31 where k 0 is the wave number for that reference medium, and n (r ) is the corresponding refractive index defined by C0 nr ( )= C( r) (1.53) where C 0 is the speed of sound in the reference medium. Commonly, in the context of soft tissues, the changes in the speed of sound are minor. Hence, we may represent the object by a function F (r ) that describes the changes as a perturbation with respect to the reference medium. Thus, the function describing the scanned object is given by F( r)= k0 n( r) 1 (1.54) The acoustic field u (r ) within the medium may be presented by two components, ur ( )= u0 ( r)+ us ( r) (1.55) where u 0 (r ) is the (transmitted) incident field, which is the solution for the homogeneous wave equation in the reference medium, [ + k0 ] u0 ( r )= 0 (1.56) and the field u S (r ) describes the scattered field. Substituting into Eq. (1.5) yields [ + k0 ] us ( r)= F( r) u( r) (1.57) This equation is called the Helmholtz equation. The object function cannot be derived explicitly from this equation; but since u 0 (r ) is assumed to be known and u S (r ) can usually be measured at defined locations around the object, we can write an implicit equation relating the measured filed u S (r ) to the object function F (r ). To obtain this relation, we can use the Green function, defined as jk0 r r e g( r r )= 4π r r (1.58) Using this function, the following integral equation can be obtained: us ( r)= g( r r ) F( r ) u( r ) dr (1.59) As noted above, this equation cannot be solved directly. However, we can try to approximate u S (r ) on the right - hand side of Eq. (1.59). There are two known approximations for the scattered field which are given in the following.
24 3 1 WAVES A GENERAL DESCRIPTION The Born Approximation The idea behind this approximation is to utilize Eq. (1.55) and substitute it into Eq. (1.59). By doing so, we obtain us ( r)= g( r r ) F( r ) u0 ( r ) dr + g( r r ) F( r ) us ( r ) dr (1.60) But since the scattered field is much weaker than the incident field (which is typically the case for soft tissues), we can omit the second term on the right - hand side of this equation and write the following approximation: us ( r) g( r r ) F( r ) u0 ( r ) dr (1.61) Defining this approximation as the first Born approximation that is, us( r) ub( r) we can go back and substitute its value again into Eq. (1.55) and obtain a better approximation for the scattered field in Eq. (1.60). This approximation is called the second Born approximation and is marked by ( u ) ( r) and is given by B ( u ) B ( r) g( r r ) F( r ) ( u0 ( r )+ ub( r )) dr (1.6) Having this approximation at hand, it doesn t take much to realize that we can further improve it by re - substitution into Eq. (1.55) and Eq. (1.60) and then repeat the procedure over and over again. The general expression ( i+ 1 for the u ) ( r) Born approximation is thus given by B u ( + 1 ) ( r) g( r r ) F( r ) u r u ( ) 0 ( )+ ( r ) dr (1.63) B i ( B i ) As noted above, this approximation is based on the assumption that the scattered field is much weaker than the incident field The Rytov Approximation With this approximation the acoustic field is represented by a complex phase that is given by while the incident field is given by ur ( )= e φ ( r ) (1.64) φ0( u ( r)= e r ) 0 (1.65) and the total field is given by
25 REFERENCES 33 φ( r)= φ0 ( r)+ φs ( r) (1.66) where φ S (r ) designates the scattered field. Following some derivations and assumptions, it can be shown that the following relation can be obtained: φ S 1 ( r ) u ( r) 0 g( r r ) F( r ) u0 ( r ) dr (1.67) The condition needed for the Rytov approximation to be valid is given by F( r) [ φ ( r) ] S (1.68) As reported in the literature (see, for example, Keller [8] ), the Rytov approximation is valid under less restrictive conditions than the Born approximation. REFERENCES 1. Filippi P, Habault D, Bergassoli A, and Lefebvre JP, Acoustics: Basic Physics, Theory, and Methods, Academic Press, New York, Rose JL, Ultrasonic Waves in Solid Media, Cambridge University Press, Cambridge, Ferwerda HA, Huygens Principle : Theory and Applications, Proceedings of an International Symposium; Studies in Mathematical Physics, Blok HP, Kuiken HK, and Ferweda HA, editors, the Hague/Scheveningen, Holland, November 19, Haber-Schaim U, Dodge JH, Gardner R, Shore EA, PSSC Physics, 7th Ed., Kendall/ Hunt Publishing Company, Dubuque, IA, Coulson CA, Waves: A Mathematical Approach to the Common Types of Wave Motion, nd edition, revised by Alan Jeffrey, Longman, London, Spiegel MR, Mathematical Handbook of Formulas and Tables, Schaum s Outline Series in Mathematics; McGraw-Hill, New York, Kak AC and Slaney M, Principles of Computerized Tomographic Imaging, IEEE Press, New York, Keller JB, Accuracy and validity of the Born and Rytov approximations, J Optical Soc Am 59 : , 1969.
26
Light as a Transverse Wave.
 Waves and Superposition (Keating Chapter 21) The ray model for light (i.e. light travels in straight lines) can be used to explain a lot of phenomena (like basic object and image formation and even aberrations)
Waves and Superposition (Keating Chapter 21) The ray model for light (i.e. light travels in straight lines) can be used to explain a lot of phenomena (like basic object and image formation and even aberrations)
Chapter 11 Vibrations and Waves
 Chapter 11 Vibrations and Waves 11-1 Simple Harmonic Motion If an object vibrates or oscillates back and forth over the same path, each cycle taking the same amount of time, the motion is called periodic.
Chapter 11 Vibrations and Waves 11-1 Simple Harmonic Motion If an object vibrates or oscillates back and forth over the same path, each cycle taking the same amount of time, the motion is called periodic.
1. Types of Waves. There are three main types of waves:
 Chapter 16 WAVES I 1. Types of Waves There are three main types of waves: https://youtu.be/kvc7obkzq9u?t=3m49s 1. Mechanical waves: These are the most familiar waves. Examples include water waves, sound
Chapter 16 WAVES I 1. Types of Waves There are three main types of waves: https://youtu.be/kvc7obkzq9u?t=3m49s 1. Mechanical waves: These are the most familiar waves. Examples include water waves, sound
Chapter 15. Mechanical Waves
 Chapter 15 Mechanical Waves A wave is any disturbance from an equilibrium condition, which travels or propagates with time from one region of space to another. A harmonic wave is a periodic wave in which
Chapter 15 Mechanical Waves A wave is any disturbance from an equilibrium condition, which travels or propagates with time from one region of space to another. A harmonic wave is a periodic wave in which
Lecture 17. Mechanical waves. Transverse waves. Sound waves. Standing Waves.
 Lecture 17 Mechanical waves. Transverse waves. Sound waves. Standing Waves. What is a wave? A wave is a traveling disturbance that transports energy but not matter. Examples: Sound waves (air moves back
Lecture 17 Mechanical waves. Transverse waves. Sound waves. Standing Waves. What is a wave? A wave is a traveling disturbance that transports energy but not matter. Examples: Sound waves (air moves back
Physics 142 Mechanical Waves Page 1. Mechanical Waves
 Physics 142 Mechanical Waves Page 1 Mechanical Waves This set of notes contains a review of wave motion in mechanics, emphasizing the mathematical formulation that will be used in our discussion of electromagnetic
Physics 142 Mechanical Waves Page 1 Mechanical Waves This set of notes contains a review of wave motion in mechanics, emphasizing the mathematical formulation that will be used in our discussion of electromagnetic
Doppler echocardiography & Magnetic Resonance Imaging. Doppler echocardiography. History: - Langevin developed sonar.
 1 Doppler echocardiography & Magnetic Resonance Imaging History: - Langevin developed sonar. - 1940s development of pulse-echo. - 1950s development of mode A and B. - 1957 development of continuous wave
1 Doppler echocardiography & Magnetic Resonance Imaging History: - Langevin developed sonar. - 1940s development of pulse-echo. - 1950s development of mode A and B. - 1957 development of continuous wave
Topic 4: Waves 4.3 Wave characteristics
 Guidance: Students will be expected to calculate the resultant of two waves or pulses both graphically and algebraically Methods of polarization will be restricted to the use of polarizing filters and
Guidance: Students will be expected to calculate the resultant of two waves or pulses both graphically and algebraically Methods of polarization will be restricted to the use of polarizing filters and
CHAPTER 11 VIBRATIONS AND WAVES
 CHAPTER 11 VIBRATIONS AND WAVES http://www.physicsclassroom.com/class/waves/u10l1a.html UNITS Simple Harmonic Motion Energy in the Simple Harmonic Oscillator The Period and Sinusoidal Nature of SHM The
CHAPTER 11 VIBRATIONS AND WAVES http://www.physicsclassroom.com/class/waves/u10l1a.html UNITS Simple Harmonic Motion Energy in the Simple Harmonic Oscillator The Period and Sinusoidal Nature of SHM The
PHYSICS. Chapter 16 Lecture FOR SCIENTISTS AND ENGINEERS A STRATEGIC APPROACH 4/E RANDALL D. KNIGHT Pearson Education, Inc.
 PHYSICS FOR SCIENTISTS AND ENGINEERS A STRATEGIC APPROACH 4/E Chapter 16 Lecture RANDALL D. KNIGHT 2017 Pearson Education, Inc. Chapter 16 Traveling Waves IN THIS CHAPTER, you will learn the basic properties
PHYSICS FOR SCIENTISTS AND ENGINEERS A STRATEGIC APPROACH 4/E Chapter 16 Lecture RANDALL D. KNIGHT 2017 Pearson Education, Inc. Chapter 16 Traveling Waves IN THIS CHAPTER, you will learn the basic properties
Chapter 16 Traveling Waves
 Chapter 16 Traveling Waves GOALS When you have mastered the contents of this chapter, you will be able to achieve the following goals: Definitions Define each of the following terms as it is used in physics,
Chapter 16 Traveling Waves GOALS When you have mastered the contents of this chapter, you will be able to achieve the following goals: Definitions Define each of the following terms as it is used in physics,
4. What is the speed (in cm s - 1 ) of the tip of the minute hand?
 Topic 4 Waves PROBLEM SET Formative Assessment NAME: TEAM: THIS IS A PRACTICE ASSESSMENT. Show formulas, substitutions, answers, and units! Topic 4.1 Oscillations A mass is attached to a horizontal spring.
Topic 4 Waves PROBLEM SET Formative Assessment NAME: TEAM: THIS IS A PRACTICE ASSESSMENT. Show formulas, substitutions, answers, and units! Topic 4.1 Oscillations A mass is attached to a horizontal spring.
PHYSICS 149: Lecture 24
 PHYSICS 149: Lecture 24 Chapter 11: Waves 11.8 Reflection and Refraction 11.10 Standing Waves Chapter 12: Sound 12.1 Sound Waves 12.4 Standing Sound Waves Lecture 24 Purdue University, Physics 149 1 ILQ
PHYSICS 149: Lecture 24 Chapter 11: Waves 11.8 Reflection and Refraction 11.10 Standing Waves Chapter 12: Sound 12.1 Sound Waves 12.4 Standing Sound Waves Lecture 24 Purdue University, Physics 149 1 ILQ
Electromagnetic fields and waves
 Electromagnetic fields and waves Maxwell s rainbow Outline Maxwell s equations Plane waves Pulses and group velocity Polarization of light Transmission and reflection at an interface Macroscopic Maxwell
Electromagnetic fields and waves Maxwell s rainbow Outline Maxwell s equations Plane waves Pulses and group velocity Polarization of light Transmission and reflection at an interface Macroscopic Maxwell
7.2.1 Seismic waves. Waves in a mass- spring system
 7..1 Seismic waves Waves in a mass- spring system Acoustic waves in a liquid or gas Seismic waves in a solid Surface waves Wavefronts, rays and geometrical attenuation Amplitude and energy Waves in a mass-
7..1 Seismic waves Waves in a mass- spring system Acoustic waves in a liquid or gas Seismic waves in a solid Surface waves Wavefronts, rays and geometrical attenuation Amplitude and energy Waves in a mass-
MATH 308 COURSE SUMMARY
 MATH 308 COURSE SUMMARY Approximately a third of the exam cover the material from the first two midterms, that is, chapter 6 and the first six sections of chapter 7. The rest of the exam will cover the
MATH 308 COURSE SUMMARY Approximately a third of the exam cover the material from the first two midterms, that is, chapter 6 and the first six sections of chapter 7. The rest of the exam will cover the
UNIVERSITY OF SOUTHAMPTON
 UNIVERSITY OF SOUTHAMPTON PHYS2023W1 SEMESTER 1 EXAMINATION 2016-2017 WAVE PHYSICS Duration: 120 MINS (2 hours) This paper contains 9 questions. Answers to Section A and Section B must be in separate answer
UNIVERSITY OF SOUTHAMPTON PHYS2023W1 SEMESTER 1 EXAMINATION 2016-2017 WAVE PHYSICS Duration: 120 MINS (2 hours) This paper contains 9 questions. Answers to Section A and Section B must be in separate answer
Waves Encountering Barriers
 Waves Encountering Barriers Reflection and Refraction: When a wave is incident on a boundary that separates two regions of different wave speed, part of the wave is reflected and part is transmitted. Figure
Waves Encountering Barriers Reflection and Refraction: When a wave is incident on a boundary that separates two regions of different wave speed, part of the wave is reflected and part is transmitted. Figure
Chapter 16: Oscillations
 Chapter 16: Oscillations Brent Royuk Phys-111 Concordia University Periodic Motion Periodic Motion is any motion that repeats itself. The Period (T) is the time it takes for one complete cycle of motion.
Chapter 16: Oscillations Brent Royuk Phys-111 Concordia University Periodic Motion Periodic Motion is any motion that repeats itself. The Period (T) is the time it takes for one complete cycle of motion.
Chapter 16 Waves in One Dimension
 Chapter 16 Waves in One Dimension Slide 16-1 Reading Quiz 16.05 f = c Slide 16-2 Reading Quiz 16.06 Slide 16-3 Reading Quiz 16.07 Heavier portion looks like a fixed end, pulse is inverted on reflection.
Chapter 16 Waves in One Dimension Slide 16-1 Reading Quiz 16.05 f = c Slide 16-2 Reading Quiz 16.06 Slide 16-3 Reading Quiz 16.07 Heavier portion looks like a fixed end, pulse is inverted on reflection.
Chapter 16: Oscillatory Motion and Waves. Simple Harmonic Motion (SHM)
 Chapter 6: Oscillatory Motion and Waves Hooke s Law (revisited) F = - k x Tthe elastic potential energy of a stretched or compressed spring is PE elastic = kx / Spring-block Note: To consider the potential
Chapter 6: Oscillatory Motion and Waves Hooke s Law (revisited) F = - k x Tthe elastic potential energy of a stretched or compressed spring is PE elastic = kx / Spring-block Note: To consider the potential
Raymond A. Serway Chris Vuille. Chapter Thirteen. Vibrations and Waves
 Raymond A. Serway Chris Vuille Chapter Thirteen Vibrations and Waves Periodic Motion and Waves Periodic motion is one of the most important kinds of physical behavior Will include a closer look at Hooke
Raymond A. Serway Chris Vuille Chapter Thirteen Vibrations and Waves Periodic Motion and Waves Periodic motion is one of the most important kinds of physical behavior Will include a closer look at Hooke
OPAC102. The Acoustic Wave Equation
 OPAC102 The Acoustic Wave Equation Acoustic waves in fluid Acoustic waves constitute one kind of pressure fluctuation that can exist in a compressible fluid. The restoring forces responsible for propagating
OPAC102 The Acoustic Wave Equation Acoustic waves in fluid Acoustic waves constitute one kind of pressure fluctuation that can exist in a compressible fluid. The restoring forces responsible for propagating
kg meter ii) Note the dimensions of ρ τ are kg 2 velocity 2 meter = 1 sec 2 We will interpret this velocity in upcoming slides.
 II. Generalizing the 1-dimensional wave equation First generalize the notation. i) "q" has meant transverse deflection of the string. Replace q Ψ, where Ψ may indicate other properties of the medium that
II. Generalizing the 1-dimensional wave equation First generalize the notation. i) "q" has meant transverse deflection of the string. Replace q Ψ, where Ψ may indicate other properties of the medium that
WAVE OPTICS GENERAL. Fig.1a The electromagnetic spectrum
 WAVE OPTICS GENERAL - The ray optics cannot explain the results of the two following experimental situations: a) When passing by small openings or illuminating small obstacles, the light bends around borders
WAVE OPTICS GENERAL - The ray optics cannot explain the results of the two following experimental situations: a) When passing by small openings or illuminating small obstacles, the light bends around borders
Exam 3 Review. Chapter 10: Elasticity and Oscillations A stress will deform a body and that body can be set into periodic oscillations.
 Exam 3 Review Chapter 10: Elasticity and Oscillations stress will deform a body and that body can be set into periodic oscillations. Elastic Deformations of Solids Elastic objects return to their original
Exam 3 Review Chapter 10: Elasticity and Oscillations stress will deform a body and that body can be set into periodic oscillations. Elastic Deformations of Solids Elastic objects return to their original
Electromagnetic Waves
 Electromagnetic Waves As the chart shows, the electromagnetic spectrum covers an extremely wide range of wavelengths and frequencies. Though the names indicate that these waves have a number of sources,
Electromagnetic Waves As the chart shows, the electromagnetic spectrum covers an extremely wide range of wavelengths and frequencies. Though the names indicate that these waves have a number of sources,
Chapter 9. Electromagnetic Waves
 Chapter 9. Electromagnetic Waves 9.1 Waves in One Dimension 9.1.1 The Wave Equation What is a "wave?" Let's start with the simple case: fixed shape, constant speed: How would you represent such a string
Chapter 9. Electromagnetic Waves 9.1 Waves in One Dimension 9.1.1 The Wave Equation What is a "wave?" Let's start with the simple case: fixed shape, constant speed: How would you represent such a string
Work. Work and Energy Examples. Energy. To move an object we must do work Work is calculated as the force applied to the object through a distance or:
 Work To move an object we must do work Work is calculated as the force applied to the object through a distance or: W F( d) Work has the units Newton meters (N m) or Joules 1 Joule = 1 N m Energy Work
Work To move an object we must do work Work is calculated as the force applied to the object through a distance or: W F( d) Work has the units Newton meters (N m) or Joules 1 Joule = 1 N m Energy Work
Section 1 Simple Harmonic Motion. The student is expected to:
 Section 1 Simple Harmonic Motion TEKS The student is expected to: 7A examine and describe oscillatory motion and wave propagation in various types of media Section 1 Simple Harmonic Motion Preview Objectives
Section 1 Simple Harmonic Motion TEKS The student is expected to: 7A examine and describe oscillatory motion and wave propagation in various types of media Section 1 Simple Harmonic Motion Preview Objectives
Chap 11. Vibration and Waves. The impressed force on an object is proportional to its displacement from it equilibrium position.
 Chap 11. Vibration and Waves Sec. 11.1 - Simple Harmonic Motion The impressed force on an object is proportional to its displacement from it equilibrium position. F x This restoring force opposes the change
Chap 11. Vibration and Waves Sec. 11.1 - Simple Harmonic Motion The impressed force on an object is proportional to its displacement from it equilibrium position. F x This restoring force opposes the change
Chapter 15 Mechanical Waves
 Chapter 15 Mechanical Waves 1 Types of Mechanical Waves This chapter and the next are about mechanical waves waves that travel within some material called a medium. Waves play an important role in how
Chapter 15 Mechanical Waves 1 Types of Mechanical Waves This chapter and the next are about mechanical waves waves that travel within some material called a medium. Waves play an important role in how
Oscillation the vibration of an object. Wave a transfer of energy without a transfer of matter
 Oscillation the vibration of an object Wave a transfer of energy without a transfer of matter Equilibrium Position position of object at rest (mean position) Displacement (x) distance in a particular direction
Oscillation the vibration of an object Wave a transfer of energy without a transfer of matter Equilibrium Position position of object at rest (mean position) Displacement (x) distance in a particular direction
Sound, acoustics Slides based on: Rossing, The science of sound, 1990, and Pulkki, Karjalainen, Communication acoutics, 2015
 Acoustics 1 Sound, acoustics Slides based on: Rossing, The science of sound, 1990, and Pulkki, Karjalainen, Communication acoutics, 2015 Contents: 1. Introduction 2. Vibrating systems 3. Waves 4. Resonance
Acoustics 1 Sound, acoustics Slides based on: Rossing, The science of sound, 1990, and Pulkki, Karjalainen, Communication acoutics, 2015 Contents: 1. Introduction 2. Vibrating systems 3. Waves 4. Resonance
(Total 1 mark) IB Questionbank Physics 1
 1. A transverse wave travels from left to right. The diagram below shows how, at a particular instant of time, the displacement of particles in the medium varies with position. Which arrow represents the
1. A transverse wave travels from left to right. The diagram below shows how, at a particular instant of time, the displacement of particles in the medium varies with position. Which arrow represents the
Basic principles of the seismic method
 Chapter 2 Basic principles of the seismic method In this chapter we introduce the basic notion of seismic waves. In the earth, seismic waves can propagate as longitudinal (P) or as shear (S) waves. For
Chapter 2 Basic principles of the seismic method In this chapter we introduce the basic notion of seismic waves. In the earth, seismic waves can propagate as longitudinal (P) or as shear (S) waves. For
Lecture 4 Notes: 06 / 30. Energy carried by a wave
 Lecture 4 Notes: 06 / 30 Energy carried by a wave We want to find the total energy (kinetic and potential) in a sine wave on a string. A small segment of a string at a fixed point x 0 behaves as a harmonic
Lecture 4 Notes: 06 / 30 Energy carried by a wave We want to find the total energy (kinetic and potential) in a sine wave on a string. A small segment of a string at a fixed point x 0 behaves as a harmonic
Physics 9e/Cutnell. correlated to the. College Board AP Physics 2 Course Objectives
 correlated to the College Board AP Physics 2 Course Objectives Big Idea 1: Objects and systems have properties such as mass and charge. Systems may have internal structure. Enduring Understanding 1.A:
correlated to the College Board AP Physics 2 Course Objectives Big Idea 1: Objects and systems have properties such as mass and charge. Systems may have internal structure. Enduring Understanding 1.A:
G r a d e 1 1 P h y s i c s ( 3 0 s ) Final Practice exam
 G r a d e 1 1 P h y s i c s ( 3 0 s ) Final Practice exam G r a d e 1 1 P h y s i c s ( 3 0 s ) Final Practice Exam Instructions The final exam will be weighted as follows: Modules 1 6 15 20% Modules
G r a d e 1 1 P h y s i c s ( 3 0 s ) Final Practice exam G r a d e 1 1 P h y s i c s ( 3 0 s ) Final Practice Exam Instructions The final exam will be weighted as follows: Modules 1 6 15 20% Modules
Course Name: AP Physics. Team Names: Jon Collins. Velocity Acceleration Displacement
 Course Name: AP Physics Team Names: Jon Collins 1 st 9 weeks Objectives Vocabulary 1. NEWTONIAN MECHANICS and lab skills: Kinematics (including vectors, vector algebra, components of vectors, coordinate
Course Name: AP Physics Team Names: Jon Collins 1 st 9 weeks Objectives Vocabulary 1. NEWTONIAN MECHANICS and lab skills: Kinematics (including vectors, vector algebra, components of vectors, coordinate
Chapter 16 Waves. Types of waves Mechanical waves. Electromagnetic waves. Matter waves
 Chapter 16 Waves Types of waves Mechanical waves exist only within a material medium. e.g. water waves, sound waves, etc. Electromagnetic waves require no material medium to exist. e.g. light, radio, microwaves,
Chapter 16 Waves Types of waves Mechanical waves exist only within a material medium. e.g. water waves, sound waves, etc. Electromagnetic waves require no material medium to exist. e.g. light, radio, microwaves,
Oscillations and Waves
 Oscillations and Waves Oscillation: Wave: Examples of oscillations: 1. mass on spring (eg. bungee jumping) 2. pendulum (eg. swing) 3. object bobbing in water (eg. buoy, boat) 4. vibrating cantilever (eg.
Oscillations and Waves Oscillation: Wave: Examples of oscillations: 1. mass on spring (eg. bungee jumping) 2. pendulum (eg. swing) 3. object bobbing in water (eg. buoy, boat) 4. vibrating cantilever (eg.
Chapter 13. Hooke s Law: F = - kx Periodic & Simple Harmonic Motion Springs & Pendula Waves Superposition. Next Week!
 Chapter 13 Hooke s Law: F = - kx Periodic & Simple Harmonic Motion Springs & Pendula Waves Superposition Next Week! Review Physics 2A: Springs, Pendula & Circular Motion Elastic Systems F = kx Small Vibrations
Chapter 13 Hooke s Law: F = - kx Periodic & Simple Harmonic Motion Springs & Pendula Waves Superposition Next Week! Review Physics 2A: Springs, Pendula & Circular Motion Elastic Systems F = kx Small Vibrations
Curriculum interpretation
 Curriculum interpretation Wave Motion and Radioactivity and Nuclear Energy YAU Wing-yee 12 April 2011 Wave Motion a. Nature and properties of waves nature of waves Point-to-note interpret wave motion in
Curriculum interpretation Wave Motion and Radioactivity and Nuclear Energy YAU Wing-yee 12 April 2011 Wave Motion a. Nature and properties of waves nature of waves Point-to-note interpret wave motion in
A second look at waves
 A second loo at waves ravelling waves A first loo at Amplitude Modulation (AM) Stationary and reflected waves Lossy waves: dispersion & evanescence I thin this is the MOS IMPORAN of my eight lectures,
A second loo at waves ravelling waves A first loo at Amplitude Modulation (AM) Stationary and reflected waves Lossy waves: dispersion & evanescence I thin this is the MOS IMPORAN of my eight lectures,
Chapter 16 Waves in One Dimension
 Lecture Outline Chapter 16 Waves in One Dimension Slide 16-1 Chapter 16: Waves in One Dimension Chapter Goal: To study the kinematic and dynamics of wave motion, i.e., the transport of energy through a
Lecture Outline Chapter 16 Waves in One Dimension Slide 16-1 Chapter 16: Waves in One Dimension Chapter Goal: To study the kinematic and dynamics of wave motion, i.e., the transport of energy through a
Lab 1: Damped, Driven Harmonic Oscillator
 1 Introduction Lab 1: Damped, Driven Harmonic Oscillator The purpose of this experiment is to study the resonant properties of a driven, damped harmonic oscillator. This type of motion is characteristic
1 Introduction Lab 1: Damped, Driven Harmonic Oscillator The purpose of this experiment is to study the resonant properties of a driven, damped harmonic oscillator. This type of motion is characteristic
NYS STANDARD/KEY IDEA/PERFORMANCE INDICATOR 5.1 a-e. 5.1a Measured quantities can be classified as either vector or scalar.
 INDICATOR 5.1 a-e September Unit 1 Units and Scientific Notation SI System of Units Unit Conversion Scientific Notation Significant Figures Graphical Analysis Unit Kinematics Scalar vs. vector Displacement/dis
INDICATOR 5.1 a-e September Unit 1 Units and Scientific Notation SI System of Units Unit Conversion Scientific Notation Significant Figures Graphical Analysis Unit Kinematics Scalar vs. vector Displacement/dis
Week 7: Interference
 Week 7: Interference Superposition: Till now we have mostly discusssed single waves. While discussing group velocity we did talk briefly about superposing more than one wave. We will now focus on superposition
Week 7: Interference Superposition: Till now we have mostly discusssed single waves. While discussing group velocity we did talk briefly about superposing more than one wave. We will now focus on superposition
UNIT 1 MODULE 2: OSCILLATIONS AND WAVES GENERAL OBJECTIVES EXPLANATORY NOTES SPECIFIC OBJECTIVES. On completion of this Module, students should:
 MODULE 2: OSCILLATIONS AND WAVES GENERAL OBJECTIVES On completion of this Module, students should: 1. understand the different types of oscillatory motion; 2. appreciate the properties common to all 3.
MODULE 2: OSCILLATIONS AND WAVES GENERAL OBJECTIVES On completion of this Module, students should: 1. understand the different types of oscillatory motion; 2. appreciate the properties common to all 3.
Lab 1: damped, driven harmonic oscillator
 Lab 1: damped, driven harmonic oscillator 1 Introduction The purpose of this experiment is to study the resonant properties of a driven, damped harmonic oscillator. This type of motion is characteristic
Lab 1: damped, driven harmonic oscillator 1 Introduction The purpose of this experiment is to study the resonant properties of a driven, damped harmonic oscillator. This type of motion is characteristic
Oscillatory Motion and Wave Motion
 Oscillatory Motion and Wave Motion Oscillatory Motion Simple Harmonic Motion Wave Motion Waves Motion of an Object Attached to a Spring The Pendulum Transverse and Longitudinal Waves Sinusoidal Wave Function
Oscillatory Motion and Wave Motion Oscillatory Motion Simple Harmonic Motion Wave Motion Waves Motion of an Object Attached to a Spring The Pendulum Transverse and Longitudinal Waves Sinusoidal Wave Function
SOUND. Representative Sample Physics: Sound. 1. Periodic Motion of Particles PLANCESS CONCEPTS
 Representative Sample Physics: Sound SOUND 1. Periodic Motion of Particles Before we move on to study the nature and transmission of sound, we need to understand the different types of vibratory or oscillatory
Representative Sample Physics: Sound SOUND 1. Periodic Motion of Particles Before we move on to study the nature and transmission of sound, we need to understand the different types of vibratory or oscillatory
Physics General Physics. Lecture 25 Waves. Fall 2016 Semester Prof. Matthew Jones
 Physics 22000 General Physics Lecture 25 Waves Fall 2016 Semester Prof. Matthew Jones 1 Final Exam 2 3 Mechanical Waves Waves and wave fronts: 4 Wave Motion 5 Two Kinds of Waves 6 Reflection of Waves When
Physics 22000 General Physics Lecture 25 Waves Fall 2016 Semester Prof. Matthew Jones 1 Final Exam 2 3 Mechanical Waves Waves and wave fronts: 4 Wave Motion 5 Two Kinds of Waves 6 Reflection of Waves When
Outline. Hook s law. Mass spring system Simple harmonic motion Travelling waves Waves in string Sound waves
 Outline Hook s law. Mass spring system Simple harmonic motion Travelling waves Waves in string Sound waves Hooke s Law Force is directly proportional to the displacement of the object from the equilibrium
Outline Hook s law. Mass spring system Simple harmonic motion Travelling waves Waves in string Sound waves Hooke s Law Force is directly proportional to the displacement of the object from the equilibrium
Short Wire Antennas: A Simplified Approach Part I: Scaling Arguments. Dan Dobkin version 1.0 July 8, 2005
 Short Wire Antennas: A Simplified Approach Part I: Scaling Arguments Dan Dobkin version 1.0 July 8, 2005 0. Introduction: How does a wire dipole antenna work? How do we find the resistance and the reactance?
Short Wire Antennas: A Simplified Approach Part I: Scaling Arguments Dan Dobkin version 1.0 July 8, 2005 0. Introduction: How does a wire dipole antenna work? How do we find the resistance and the reactance?
CMPT 889: Lecture 8 Digital Waveguides
 CMPT 889: Lecture 8 Digital Waveguides Tamara Smyth, tamaras@cs.sfu.ca School of Computing Science, Simon Fraser University February 10, 2012 1 Motion for a Wave For the string, we are interested in the
CMPT 889: Lecture 8 Digital Waveguides Tamara Smyth, tamaras@cs.sfu.ca School of Computing Science, Simon Fraser University February 10, 2012 1 Motion for a Wave For the string, we are interested in the
Experiment 8. Fresnel Coefficients. 8.1 Introduction. References
 Experiment 8 Fresnel Coefficients References Optics by Eugene Hecht, Chapter 4 Introduction to Modern Optics by Grant Fowles, Chapter 2 Principles of Optics by Max Born and Emil Wolf, Chapter 1 Optical
Experiment 8 Fresnel Coefficients References Optics by Eugene Hecht, Chapter 4 Introduction to Modern Optics by Grant Fowles, Chapter 2 Principles of Optics by Max Born and Emil Wolf, Chapter 1 Optical
Lecture notes 5: Diffraction
 Lecture notes 5: Diffraction Let us now consider how light reacts to being confined to a given aperture. The resolution of an aperture is restricted due to the wave nature of light: as light passes through
Lecture notes 5: Diffraction Let us now consider how light reacts to being confined to a given aperture. The resolution of an aperture is restricted due to the wave nature of light: as light passes through
1 Pushing your Friend on a Swing
 Massachusetts Institute of Technology MITES 017 Physics III Lecture 05: Driven Oscillations In these notes, we derive the properties of both an undamped and damped harmonic oscillator under the influence
Massachusetts Institute of Technology MITES 017 Physics III Lecture 05: Driven Oscillations In these notes, we derive the properties of both an undamped and damped harmonic oscillator under the influence
A beam of coherent monochromatic light from a distant galaxy is used in an optics experiment on Earth.
 Waves_P2 [152 marks] A beam of coherent monochromatic light from a distant galaxy is used in an optics experiment on Earth. The beam is incident normally on a double slit. The distance between the slits
Waves_P2 [152 marks] A beam of coherent monochromatic light from a distant galaxy is used in an optics experiment on Earth. The beam is incident normally on a double slit. The distance between the slits
Chapter 33: ELECTROMAGNETIC WAVES 559
 Chapter 33: ELECTROMAGNETIC WAVES 1 Select the correct statement: A ultraviolet light has a longer wavelength than infrared B blue light has a higher frequency than x rays C radio waves have higher frequency
Chapter 33: ELECTROMAGNETIC WAVES 1 Select the correct statement: A ultraviolet light has a longer wavelength than infrared B blue light has a higher frequency than x rays C radio waves have higher frequency
Lectures on Certain Problems in the Theory of Oscillations
 Lectures on Certain Problems in the Theory of Oscillations L. I. Mandel shtam May 5, 1944 Abstract [By the translator] This lecture covers the problems of energy velocity and its relation to group velocity.
Lectures on Certain Problems in the Theory of Oscillations L. I. Mandel shtam May 5, 1944 Abstract [By the translator] This lecture covers the problems of energy velocity and its relation to group velocity.
Physics 41: Waves, Optics, Thermo
 Physics 41: Waves, Optics, Thermo Particles & Waves Localized in Space: LOCAL Have Mass & Momentum No Superposition: Two particles cannot occupy the same space at the same time! Particles have energy.
Physics 41: Waves, Optics, Thermo Particles & Waves Localized in Space: LOCAL Have Mass & Momentum No Superposition: Two particles cannot occupy the same space at the same time! Particles have energy.
f 1/ T T 1/ f Formulas Fs kx m T s 2 k l T p 2 g v f
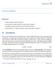
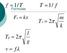 f 1/T Formulas T 1/ f Fs kx Ts 2 m k Tp 2 l g v f What do the following all have in common? Swing, pendulum, vibrating string They all exhibit forms of periodic motion. Periodic Motion: When a vibration
f 1/T Formulas T 1/ f Fs kx Ts 2 m k Tp 2 l g v f What do the following all have in common? Swing, pendulum, vibrating string They all exhibit forms of periodic motion. Periodic Motion: When a vibration
P5 Revision Questions
 P5 Revision Questions Part 2 Question 1 How can microwaves be used to communicate? Answer 1 Sent from transmitter, received and amplified by satellite in space, re-transmitted back to earth and picked
P5 Revision Questions Part 2 Question 1 How can microwaves be used to communicate? Answer 1 Sent from transmitter, received and amplified by satellite in space, re-transmitted back to earth and picked
No Lecture on Wed. But, there is a lecture on Thursday, at your normal recitation time, so please be sure to come!
 Announcements Quiz 6 tomorrow Driscoll Auditorium Covers: Chapter 15 (lecture and homework, look at Questions, Checkpoint, and Summary) Chapter 16 (Lecture material covered, associated Checkpoints and
Announcements Quiz 6 tomorrow Driscoll Auditorium Covers: Chapter 15 (lecture and homework, look at Questions, Checkpoint, and Summary) Chapter 16 (Lecture material covered, associated Checkpoints and
Exam tomorrow on Chapter 15, 16, and 17 (Oscilla;ons and Waves 1 &2)
 Exam tomorrow on Chapter 15, 16, and 17 (Oscilla;ons and Waves 1 &2) What to study: Quiz 6 Homework problems for Chapters 15 & 16 Material indicated in the following review slides Other Specific things:
Exam tomorrow on Chapter 15, 16, and 17 (Oscilla;ons and Waves 1 &2) What to study: Quiz 6 Homework problems for Chapters 15 & 16 Material indicated in the following review slides Other Specific things:
The Basic Properties of Surface Waves
 The Basic Properties of Surface Waves Lapo Boschi lapo@erdw.ethz.ch April 24, 202 Love and Rayleigh Waves Whenever an elastic medium is bounded by a free surface, coherent waves arise that travel along
The Basic Properties of Surface Waves Lapo Boschi lapo@erdw.ethz.ch April 24, 202 Love and Rayleigh Waves Whenever an elastic medium is bounded by a free surface, coherent waves arise that travel along
Topic 4 &11 Review Waves & Oscillations
 Name: Date: Topic 4 &11 Review Waves & Oscillations 1. A source produces water waves of frequency 10 Hz. The graph shows the variation with horizontal position of the vertical displacement of the surface
Name: Date: Topic 4 &11 Review Waves & Oscillations 1. A source produces water waves of frequency 10 Hz. The graph shows the variation with horizontal position of the vertical displacement of the surface
General Physics I. Lecture 14: Sinusoidal Waves. Prof. WAN, Xin ( 万歆 )
 General Physics I Lecture 14: Sinusoidal Waves Prof. WAN, Xin ( 万歆 ) xinwan@zju.edu.cn http://zimp.zju.edu.cn/~xinwan/ Motivation When analyzing a linear medium that is, one in which the restoring force
General Physics I Lecture 14: Sinusoidal Waves Prof. WAN, Xin ( 万歆 ) xinwan@zju.edu.cn http://zimp.zju.edu.cn/~xinwan/ Motivation When analyzing a linear medium that is, one in which the restoring force
Lecture 9: Waves in Classical Physics
 PHYS419 Lecture 9 Waves in Classical Physics 1 Lecture 9: Waves in Classical Physics If I say the word wave in no particular context, the image which most probably springs to your mind is one of a roughly
PHYS419 Lecture 9 Waves in Classical Physics 1 Lecture 9: Waves in Classical Physics If I say the word wave in no particular context, the image which most probably springs to your mind is one of a roughly
Mathematical Models of Fluids
 SOUND WAVES Mathematical Models of Fluids Fluids molecules roam and collide no springs Collisions cause pressure in fluid (Units: Pascal Pa = N/m 2 ) 2 mathematical models for fluid motion: 1) Bulk properties
SOUND WAVES Mathematical Models of Fluids Fluids molecules roam and collide no springs Collisions cause pressure in fluid (Units: Pascal Pa = N/m 2 ) 2 mathematical models for fluid motion: 1) Bulk properties
1 2 Models, Theories, and Laws 1.5 Distinguish between models, theories, and laws 2.1 State the origin of significant figures in measurement
 Textbook Correlation Textbook Correlation Physics 1115/2015 Chapter 1 Introduction, Measurement, Estimating 1.1 Describe thoughts of Aristotle vs. Galileo in describing motion 1 1 Nature of Science 1.2
Textbook Correlation Textbook Correlation Physics 1115/2015 Chapter 1 Introduction, Measurement, Estimating 1.1 Describe thoughts of Aristotle vs. Galileo in describing motion 1 1 Nature of Science 1.2
2 u 1-D: 3-D: x + 2 u
 c 2013 C.S. Casari - Politecnico di Milano - Introduction to Nanoscience 2013-14 Onde 1 1 Waves 1.1 wave propagation 1.1.1 field Field: a physical quantity (measurable, at least in principle) function
c 2013 C.S. Casari - Politecnico di Milano - Introduction to Nanoscience 2013-14 Onde 1 1 Waves 1.1 wave propagation 1.1.1 field Field: a physical quantity (measurable, at least in principle) function
Larbert High School. Quanta and Waves. Homework Exercises ADVANCED HIGHER PHYSICS
 Larbert High School ADVANCED HIGHER PHYSICS Quanta and Waves Homework Exercises 3.1 3.6 3.1 Intro to Quantum Theory HW 1. (a) Explain what is meant by term black body. (1) (b) State two observations that
Larbert High School ADVANCED HIGHER PHYSICS Quanta and Waves Homework Exercises 3.1 3.6 3.1 Intro to Quantum Theory HW 1. (a) Explain what is meant by term black body. (1) (b) State two observations that
01 Harmonic Oscillations
 Utah State University DigitalCommons@USU Foundations of Wave Phenomena Library Digital Monographs 8-2014 01 Harmonic Oscillations Charles G. Torre Department of Physics, Utah State University, Charles.Torre@usu.edu
Utah State University DigitalCommons@USU Foundations of Wave Phenomena Library Digital Monographs 8-2014 01 Harmonic Oscillations Charles G. Torre Department of Physics, Utah State University, Charles.Torre@usu.edu
16 SUPERPOSITION & STANDING WAVES
 Chapter 6 SUPERPOSITION & STANDING WAVES 6. Superposition of waves Principle of superposition: When two or more waves overlap, the resultant wave is the algebraic sum of the individual waves. Illustration:
Chapter 6 SUPERPOSITION & STANDING WAVES 6. Superposition of waves Principle of superposition: When two or more waves overlap, the resultant wave is the algebraic sum of the individual waves. Illustration:
FIBER OPTICS. Prof. R.K. Shevgaonkar. Department of Electrical Engineering. Indian Institute of Technology, Bombay. Lecture: 07
 FIBER OPTICS Prof. R.K. Shevgaonkar Department of Electrical Engineering Indian Institute of Technology, Bombay Lecture: 07 Analysis of Wave-Model of Light Fiber Optics, Prof. R.K. Shevgaonkar, Dept. of
FIBER OPTICS Prof. R.K. Shevgaonkar Department of Electrical Engineering Indian Institute of Technology, Bombay Lecture: 07 Analysis of Wave-Model of Light Fiber Optics, Prof. R.K. Shevgaonkar, Dept. of
in Electromagnetics Numerical Method Introduction to Electromagnetics I Lecturer: Charusluk Viphavakit, PhD
 2141418 Numerical Method in Electromagnetics Introduction to Electromagnetics I Lecturer: Charusluk Viphavakit, PhD ISE, Chulalongkorn University, 2 nd /2018 Email: charusluk.v@chula.ac.th Website: Light
2141418 Numerical Method in Electromagnetics Introduction to Electromagnetics I Lecturer: Charusluk Viphavakit, PhD ISE, Chulalongkorn University, 2 nd /2018 Email: charusluk.v@chula.ac.th Website: Light
Physical and Biological Properties of Agricultural Products Acoustic, Electrical and Optical Properties and Biochemical Property
 Physical and Biological Properties of Agricultural Products Acoustic, Electrical and Optical Properties and Biochemical Property 1. Acoustic and Vibrational Properties 1.1 Acoustics and Vibration Engineering
Physical and Biological Properties of Agricultural Products Acoustic, Electrical and Optical Properties and Biochemical Property 1. Acoustic and Vibrational Properties 1.1 Acoustics and Vibration Engineering
Physics 101 Lecture 18 Vibrations, SHM, Waves (II)
 Physics 101 Lecture 18 Vibrations, SHM, Waves (II) Reminder: simple harmonic motion is the result if we have a restoring force that is linear with the displacement: F = -k x What would happen if you could
Physics 101 Lecture 18 Vibrations, SHM, Waves (II) Reminder: simple harmonic motion is the result if we have a restoring force that is linear with the displacement: F = -k x What would happen if you could
Physics 142 Wave Optics 1 Page 1. Wave Optics 1. For every complex problem there is one solution that is simple, neat, and wrong. H.L.
 Physics 142 Wave Optics 1 Page 1 Wave Optics 1 For every complex problem there is one solution that is simple, neat, and wrong. H.L. Mencken Interference and diffraction of waves The essential characteristic
Physics 142 Wave Optics 1 Page 1 Wave Optics 1 For every complex problem there is one solution that is simple, neat, and wrong. H.L. Mencken Interference and diffraction of waves The essential characteristic
Waves Review Checklist Pulses 5.1.1A Explain the relationship between the period of a pendulum and the factors involved in building one
 5.1.1 Oscillating Systems Waves Review Checklist 5.1.2 Pulses 5.1.1A Explain the relationship between the period of a pendulum and the factors involved in building one Four pendulums are built as shown
5.1.1 Oscillating Systems Waves Review Checklist 5.1.2 Pulses 5.1.1A Explain the relationship between the period of a pendulum and the factors involved in building one Four pendulums are built as shown
x(t+ δt) - x(t) = slope δt t+δt
 Techniques of Physics Worksheet 2 Classical Vibrations and Waves Introduction You will have encountered many different examples of wave phenomena in your courses and should be familiar with most of the
Techniques of Physics Worksheet 2 Classical Vibrations and Waves Introduction You will have encountered many different examples of wave phenomena in your courses and should be familiar with most of the
SIMPLE HARMONIC MOTION AND WAVES
 Simple Harmonic Motion (SHM) SIMPLE HARMONIC MOTION AND WAVES - Periodic motion any type of motion that repeats itself in a regular cycle. Ex: a pendulum swinging, a mass bobbing up and down on a spring.
Simple Harmonic Motion (SHM) SIMPLE HARMONIC MOTION AND WAVES - Periodic motion any type of motion that repeats itself in a regular cycle. Ex: a pendulum swinging, a mass bobbing up and down on a spring.
General Physics (PHY 2130)
 General Physics (PHY 2130) Lecture XII Sound sound waves Doppler effect Standing waves Light Reflection and refraction Lightning Review Last lecture: 1. Vibration and waves Hooke s law Potential energy
General Physics (PHY 2130) Lecture XII Sound sound waves Doppler effect Standing waves Light Reflection and refraction Lightning Review Last lecture: 1. Vibration and waves Hooke s law Potential energy
Section 1 Simple Harmonic Motion. Chapter 11. Preview. Objectives Hooke s Law Sample Problem Simple Harmonic Motion The Simple Pendulum
 Section 1 Simple Harmonic Motion Preview Objectives Hooke s Law Sample Problem Simple Harmonic Motion The Simple Pendulum Section 1 Simple Harmonic Motion Objectives Identify the conditions of simple harmonic
Section 1 Simple Harmonic Motion Preview Objectives Hooke s Law Sample Problem Simple Harmonic Motion The Simple Pendulum Section 1 Simple Harmonic Motion Objectives Identify the conditions of simple harmonic
Notes on Huygens Principle 2000 Lawrence Rees
 Notes on Huygens Principle 2000 Lawrence Rees In the 17 th Century, Christiaan Huygens (1629 1695) proposed what we now know as Huygens Principle. We often invoke Huygens Principle as one of the fundamental
Notes on Huygens Principle 2000 Lawrence Rees In the 17 th Century, Christiaan Huygens (1629 1695) proposed what we now know as Huygens Principle. We often invoke Huygens Principle as one of the fundamental
Vibrations and Waves Physics Year 1. Handout 1: Course Details
 Vibrations and Waves Jan-Feb 2011 Handout 1: Course Details Office Hours Vibrations and Waves Physics Year 1 Handout 1: Course Details Dr Carl Paterson (Blackett 621, carl.paterson@imperial.ac.uk Office
Vibrations and Waves Jan-Feb 2011 Handout 1: Course Details Office Hours Vibrations and Waves Physics Year 1 Handout 1: Course Details Dr Carl Paterson (Blackett 621, carl.paterson@imperial.ac.uk Office
General Physics (PHY 2130)
 General Physics (PHY 2130) Lecture XII Sound sound waves Doppler effect Standing waves Light Reflection and refraction http://www.physics.wayne.edu/~apetrov/phy2130/ Lightning Review Last lecture: 1. Vibration
General Physics (PHY 2130) Lecture XII Sound sound waves Doppler effect Standing waves Light Reflection and refraction http://www.physics.wayne.edu/~apetrov/phy2130/ Lightning Review Last lecture: 1. Vibration
Mass on a Horizontal Spring
 Course- B.Sc. Applied Physical Science (Computer Science) Year- IInd, Sem- IVth Subject Physics Paper- XIVth, Electromagnetic Theory Lecture No. 22, Simple Harmonic Motion Introduction Hello friends in
Course- B.Sc. Applied Physical Science (Computer Science) Year- IInd, Sem- IVth Subject Physics Paper- XIVth, Electromagnetic Theory Lecture No. 22, Simple Harmonic Motion Introduction Hello friends in
Chapter 16 Lectures. Oscillatory Motion and Waves
 Chapter 16 Lectures January-06-18 5:48 PM Oscillatory Motion and Waves Oscillations are back-and-forth motions. Sometimes the word vibration is used in place of oscillation; for our purposes, we can consider
Chapter 16 Lectures January-06-18 5:48 PM Oscillatory Motion and Waves Oscillations are back-and-forth motions. Sometimes the word vibration is used in place of oscillation; for our purposes, we can consider
Chapter 9. Reflection, Refraction and Polarization
 Reflection, Refraction and Polarization Introduction When you solved Problem 5.2 using the standing-wave approach, you found a rather curious behavior as the wave propagates and meets the boundary. A new
Reflection, Refraction and Polarization Introduction When you solved Problem 5.2 using the standing-wave approach, you found a rather curious behavior as the wave propagates and meets the boundary. A new
Music 206: Digital Waveguides
 Music 206: Digital Waveguides Tamara Smyth, trsmyth@ucsd.edu Department of Music, University of California, San Diego (UCSD) January 22, 2016 1 Motion for a Wave The 1-dimensional digital waveguide model
Music 206: Digital Waveguides Tamara Smyth, trsmyth@ucsd.edu Department of Music, University of California, San Diego (UCSD) January 22, 2016 1 Motion for a Wave The 1-dimensional digital waveguide model
single uniform density, but has a step change in density at x = 0, with the string essentially y(x, t) =A sin(!t k 1 x), (5.1)
 Chapter 5 Waves II 5.1 Reflection & Transmission of waves et us now consider what happens to a wave travelling along a string which no longer has a single uniform density, but has a step change in density
Chapter 5 Waves II 5.1 Reflection & Transmission of waves et us now consider what happens to a wave travelling along a string which no longer has a single uniform density, but has a step change in density
Electromagnetic Waves
 Electromagnetic Waves Maxwell s equations predict the propagation of electromagnetic energy away from time-varying sources (current and charge) in the form of waves. Consider a linear, homogeneous, isotropic
Electromagnetic Waves Maxwell s equations predict the propagation of electromagnetic energy away from time-varying sources (current and charge) in the form of waves. Consider a linear, homogeneous, isotropic
PEAT SEISMOLOGY Lecture 9: Anisotropy, attenuation and anelasticity
 PEAT8002 - SEISMOLOGY Lecture 9: Anisotropy, attenuation and anelasticity Nick Rawlinson Research School of Earth Sciences Australian National University Anisotropy Introduction Most of the theoretical
PEAT8002 - SEISMOLOGY Lecture 9: Anisotropy, attenuation and anelasticity Nick Rawlinson Research School of Earth Sciences Australian National University Anisotropy Introduction Most of the theoretical
= k, (2) p = h λ. x o = f1/2 o a. +vt (4)
 Traveling Functions, Traveling Waves, and the Uncertainty Principle R.M. Suter Department of Physics, Carnegie Mellon University Experimental observations have indicated that all quanta have a wave-like
Traveling Functions, Traveling Waves, and the Uncertainty Principle R.M. Suter Department of Physics, Carnegie Mellon University Experimental observations have indicated that all quanta have a wave-like
AP Waves/Optics ~ Learning Guide
 AP Waves/Optics ~ Learning Guide Name: Instructions: Using a pencil, answer the following questions. The guide is marked based on effort, completeness, thoughtfulness, and neatness (not accuracy). Do your
AP Waves/Optics ~ Learning Guide Name: Instructions: Using a pencil, answer the following questions. The guide is marked based on effort, completeness, thoughtfulness, and neatness (not accuracy). Do your
