7.2.1 Seismic waves. Waves in a mass- spring system
|
|
|
- Hubert Cameron
- 5 years ago
- Views:
Transcription
1 7..1 Seismic waves Waves in a mass- spring system Acoustic waves in a liquid or gas Seismic waves in a solid Surface waves Wavefronts, rays and geometrical attenuation Amplitude and energy Waves in a mass- spring system A simple physical model that is useful for describing the motion of a sound wave in a gas or fluid is shown in the following cartoon. The density of the medium is represented by the distributed masses, and the compressibility is represented by the distributed springs. The masses and springs should be envisioned as lying in a frictionless track which confines any motion to the x coordinate direction. F In this thought experiment the first mass is displaced to the right by an external impulsive force F. The mass accelerates to the right, compressing the spring and transmitting the force to the second mass. Meanwhile the external force is removed and the compressed first spring returns the first x
2 mass towards its initial position while acting on the second mass to transmit the forces to the right essentially initiating a continuous sequence of mass displacements along the chain of masses. Examined in time, any individual mass would be observed to undergo a short oscillatory movement in the x direction as the disturbance moved along the chain. A snapshot in time would show a chain of compressions and extensions of the springs as in the above cartoon. Successive snapshots in time of the whole chain would show the disturbance progressing from left to right as a wave. A particular state of, say, compression, called a point of constant phase of the wave, propagates to the right with the phase velocity, V ph. Acoustic waves in a liquid or gas A quantitative analysis of this phenomenon in a liquid illustrates the relationship between the wave and the density and compressibility of the liquid or gas. Consider two planes at x and x + dx perpendicular to the x axis with a uniform force applied in the x direction on the plane at x. A small patch on these planes has area A. The volume A dx is an element of the medium. x x + dx F dx+( u/ x) dx dx x + u x+dx+( u/ x)dx
3 The force applied to the plane at x causes its displacement to x + u which in turn causes the second plane to be displaced by a different amount given by the rate of change of the displacement with x, times the separation of the planes or ( u/ x )dx. The strain, the change in dimension in the x direction normalized by the unstressed dimension in x, is then simply u/ x. The stress at x is P, which is the force per unit area or F/A. The force also varies with x so we may write the stress at x + dx as P +( P/ x) dx. Hooke s law relates the stress and strain through the elastic constant of the medium, in this case through the bulk modulus K. So writing the stress at x in terms of K and the above strain we find that: P = K strain = K ( u/ x) P changes with x and so at x = x + dx, P = P + ( P/ x) dx = P + / x (K ( u/ x) dx = P + K ( u/ x ) dx So there can be an unbalanced force, A K( u/ x ) dx, acting on the element dx which causes it to accelerate. By Newton s Law this force must equal the mass of the element times its resulting acceleration, so A K ( u/ x ) dx = ρ A dx u/ t where ρ is the density of the medium. So, finally, we have an equation of motion for the element, u/ x -ρ/k u/ t = 0 Since we normally deal with oscillatory or quasi-harmonic disturbances we can explore the behavior of solutions to this equation by assuming that the solution in time is sinusoidal and that the time dependence is given by e iωt,
4 where ω is the angular frequency in radians/sec (equal to πf, where f is the frequency in cycles per second or Hertz). With this solution in t the equation of motion becomes: u/ x +ω ρ/k u = 0 or, with ω ρ/k = k u/ x +k u = 0 The solution for the displacement u is, u(x,t) = u 0 e iωt e ±ikx = u 0 e i(ωt±kx) This solution is basically the definition of a propagating wave. At a fixed position in x, a particular element of the medium oscillates back and forth in the x direction about a rest position (corresponding to the in-line oscillation of a particular mass in the above mass-spring analog). At a fixed time the displacements are distributed sinusoidally along x just as the spring distortions were distributed in the mass-spring analog. Another way to visualize the solution is to imagine the movement of a molecule or particle in the liquid. The particle movement would be back and forth along the x-axis, an oscillatory movement in the direction of propagation. At this microscopic level the masses in the mass-spring analog are like particles in the liquid. The derivation for compressive-extensional waves in a thin rod is identical except that the bulk modulus is replaced by Young s modulus, E. The exponent ωt ± kz is called the phase and we can easily see what is required to stay at a point in x and t where the phase is constant. When ωt ± kz = C, z/ t = ±ω/k which is the velocity of the phase point, the phase velocity V ph. The plus sign is for a wave traveling in the plus x direction, the minus sign for one traveling in the opposite direction.
5 Substituting for k, the phase velocity is given by: V ph = (K/ρ) 1/ The phase velocity is equal to the square root of the ratio of the bulk modulus to the density. Denser fluids thus have lower velocity than lighter fluids. Gases follow the same formula. The table below lists some densities and compressibilities and the derived velocities for some common liquids and air. The distance at a given time between two successive points of equal phase on the wave is the wavelength, λ, and the time between two successive points of equal displacement at a given position on the x axis is the period, T, of the wave. The velocity, frequency, period and wavelength are all related as can be seen in the following figure. u 0 T= π/ω = 1/f t u 0 λ= π/k = V ph /f x
6 Seismic waves in a solid The derivation of the equation of motion for an element in a solid is basically the same as that outlined above but it is much more complicated to the fact that the restoring elastic forces include shear as well as compression. The detailed analysis, done very well for example in Telford et al., shows that there exists a compressional wave with particle motion in the direction of wave propagation and also a shear wave with particle motion in the plane perpendicular to the direction of propagation. The velocities of these waves are given in terms of the bulk and shear modulii, K,µ and density, ρ, viz.: µ = K + 4 V 3 P and ρ V S = µ ρ It is clear from these expressions that the P-wave velocity is always larger than the S-wave velocity and that the S-wave is not viable in a medium with no shear strength. Why the shear modulus is involved in the P-wave velocity is not intuitively obvious. The above derivation for the wave motion in a fluid is based on the fact that the bulk modulus K relates the volumetric strain to a hydrostatic pressure field. Although not depicted in the cross section the volume element is deformed equally in each coordinate direction the moving pressure field does not change the shape of the element. In a solid the pressure disturbance is not hydrostatic and the shape of the element changes under deformation. It is the difference in deformation in different directions that brings the shear modulus into play in the resulting equations of motion.
7 The particle velocity in a shear wave can be in any direction in the plane perpendicular to the propagation direction and it has become conventional to describe a shear wave by a component whose particle movement is in the horizontal direction, the S H wave and a component whose particle motion is in a vertical plane, the S V wave. Any S-wave propagating in any direction can always be represented by a superposition of S H and S V waves. The elastic constants are all interrelated and a consequence that is very useful in the study of soils and rocks is that Poisson s ratio (ν) can be determined from the P and S wave velocities via the following equation; VP VS = ( ν ) 1 1 ν and so, ν = V V P S ( V V ) Poisson s ratio is theoretically bounded between 0 and 0.5 and for most rocks lies around 0.5, so typically V P /V S is about 1.7. The values of P wave velocities in representative crustal rocks are shown in the following Figure: P S
8 Surface waves On the surface between a solid or liquid and air the deformation of an element is unconstrained in the direction normal to the surface. This changes the equation of motion for elements or particles adjacent to the surface and gives rise to another wave type commonly called the surface wave. Water waves are familiar and are readily seen as having a much lower velocity than a sound wave propagating through the bulk of the medium. Further a particle moves up and down vertically as well as in the direction of the wave. In detail a particle traces an ellipse with a prograde rotation as shown in the sketch below. The surface wave on an isotropic half -space is known as a Rayleigh wave and it is similar in form to the surface wave on a liquid half-space except that the particle motion is retrograde. Rayleigh waves carry a large
9 amount of energy away from surface sources and are the noticeable, or felt, ground motion when one is standing near a seismic source. In exploration seismology Rayleigh wave are known as ground roll. Surface wave on fluid prograde particle motion Propagation direction x x Surface wave on solid retrograde particle motion The velocity of a Rayleigh wave, V R, is tied to the S-wave velocity and Poisson s ratio (and hence to V P ) through the solution to the following equation (White, 1983) = S R P R S R V V V V V V The two plots below are taken from Mavko et al., 1998.
10 They show that for typical values of Poisson s ratio the Rayleigh wave velocity varies only from 0.91 to 0.93 V S. The amplitude of the particle displacement for surface waves decreases exponentially beneath the surface and the exponent is proportional to the frequency as well as the elastic constants and density of the medium. Since it is observed that velocity generally increases with depth, Rayleigh waves of high frequency penetrate to shallow depth and have low velocity whereas Rayleigh waves of low frequency penetrate to greater depth and have high velocity. The change in velocity with frequency is known as dispersion. For a typical surface source of Rayleigh waves the initiating disturbance has a broad frequency spectrum so the observed surface motion at some distance from the source is spread out in time, with low frequencies coming first and high frequencies coming later. Measured Rayleigh wave dispersion can be used to invert for the vertical velocity profile. Finally, where the shear wave velocity increases with depth from the surface, Love showed that a horizontally polarized surface wave could exist. This wave, now called a Love wave, is also dispersive, and measurements of
11 it s dispersion can also be inverted to find the distribution of shear wave velocity with depth. Love waves require a distinct shear component in the source stress field so they are not a strong component of the disturbance propagated from the explosive or surface impact sources used in seismic exploration. They can be, and are, generated by special horizontal shear sources. For many shallow earthquakes they may be the dominant surface wave. This is a major factor used in discriminating between underground nuclear explosions and shallow earthquakes. Wavefronts, rays and geometrical attenuation Until now we have concentrated on the physics of stress-strain fields and their propagation in homogeneous solids and liquids. The fields arising from actual natural or artificial sources and what happens to such waves when they encounter inhomogeneities in density or elastic modulii is the real subject of interest. These are the properties that we wish to extract from measurements of the waves that have propagated into the earth. To begin, an assumption is made that a point source is responsible for the resulting seismic wave. In the case of an explosive source it is assumed that an impulse of radially directed compressive force is created at a point. Similarly a hammer hitting a small steel plate on the surface is considered a point source of vertical compressive force. Such simple concepts immediately run into practical limitations (what if the ground surrounding the explosive is itself inhomogeneous, or the charge is close to the free surface? The stress field of the steel plate is not hemispherical and there is, in practice a strong component of shear stress along the edges of the plate.).
12 P Source function t O Ray Wave front t 1 t 1 Considering the ideal compressive source at point O on a homogeneous half-space, the resulting seismic P-wave propagates such that all the points of constant phase lie on a hemisphere centered at O. The surface of all points of the same phase is called a wave front although the inferred meaning is that the phase in question is associated with some identifiable first arrival of the wave. A more rigorous definition is that the wave front is the surface of all equal travel times from the source. A cross section of such a hemispherical spreading wave is shown in the following cartoon for two successive time steps, t 1 and t 1. The wave in this cartoon is really a wavelet, the impulsive short wave train generated by the first compression of the source region, its subsequent recovery and perhaps a few highly damped oscillations. (The source deformation is large, not infinitesimal, and non-linear. Energy is dissipated in irreversible deformation (damage) to the surroundings, and the pulse dies quickly as suggested by the cartoon source function ).
13 For convenience is describing wave propagation, the vector perpendicular to a wave front is defined as a ray. The ray in the cartoon is directed along a radius from the source, but this is not always the case. Rays are useful for describing what happens to waves when they pass through an interface and we will use them later to describe reflecting and refracting waves in layered media. A numerical simulation of a seismic P-wave propagating away from a point source is shown in the following movie. In the movie the amplitude of the wavelet is contoured and color-coded. The high amplitude values are in red and the low amplitude in blue in this plot. The zero of the wavelet is the color of the undistorted background half-space. The time traces of geophones located in a well in the right hand side of the section are shown in the graph on the right of the figure. This is the fundamental form of the traces recorded in the vertical seismic profiling (VSP) method that we will return to later in the course.
14 Click here to start the movie Amplitude and energy The energy imparted to the wave is proportional to the square of the amplitude of the resulting propagated wavelet. Barring actual non-elastic losses in the medium, the energy is conserved but is spread over the hemispherical shell that contains the wavelet. The energy in a volume element of this shell at radius r is roughly the total energy of the disturbance, E 0, divided by the area of the hemisphere, /3πr. The energy in the wavelet thus falls off, or attenuates, as 1/r. The energy in the wavelet is proportional to the square of the amplitude of the wavelet, so the amplitude of the spherically spreading wave falls off as 1/r. The second wave front at
15 t 1 in the above cartoon is twice as far from the source as the first and so the amplitude of the wavelet is reduced by half. This is called the geometric attenuation and it is separate from any other attenuation due to loss mechanisms in the medium. Surface waves spread in circular patterns from a point source (think water waves spreading from the impact point of a stone) and in this case the energy decays as 1/r from the source and the amplitude consequently falls as 1/ r. At very large distances from the source, the curvature of the wave front becomes small and in some situations it is possible to neglect the curvature and assume that the wave front is a plane. Such a wave is then known as a plane wave.
ERTH2020 Introduction to Geophysics The Seismic Method. 1. Basic Concepts in Seismology. 1.1 Seismic Wave Types
 ERTH2020 Introduction to Geophysics The Seismic Method 1. Basic Concepts in Seismology 1.1 Seismic Wave Types Existence of different wave types The existence of different seismic wave types can be understood
ERTH2020 Introduction to Geophysics The Seismic Method 1. Basic Concepts in Seismology 1.1 Seismic Wave Types Existence of different wave types The existence of different seismic wave types can be understood
Summary PHY101 ( 2 ) T / Hanadi Al Harbi
 الكمية Physical Quantity القانون Low التعريف Definition الوحدة SI Unit Linear Momentum P = mθ be equal to the mass of an object times its velocity. Kg. m/s vector quantity Stress F \ A the external force
الكمية Physical Quantity القانون Low التعريف Definition الوحدة SI Unit Linear Momentum P = mθ be equal to the mass of an object times its velocity. Kg. m/s vector quantity Stress F \ A the external force
Oscillatory Motion and Wave Motion
 Oscillatory Motion and Wave Motion Oscillatory Motion Simple Harmonic Motion Wave Motion Waves Motion of an Object Attached to a Spring The Pendulum Transverse and Longitudinal Waves Sinusoidal Wave Function
Oscillatory Motion and Wave Motion Oscillatory Motion Simple Harmonic Motion Wave Motion Waves Motion of an Object Attached to a Spring The Pendulum Transverse and Longitudinal Waves Sinusoidal Wave Function
2.1 Introduction to waves
 Seismic waves 2.1 Introduction to waves A wave: is a periodic disturbance transmits energy through a material no permanent deformation Seismic waves: transmit elastic strain energy (stretching, tearing,
Seismic waves 2.1 Introduction to waves A wave: is a periodic disturbance transmits energy through a material no permanent deformation Seismic waves: transmit elastic strain energy (stretching, tearing,
Physical and Biological Properties of Agricultural Products Acoustic, Electrical and Optical Properties and Biochemical Property
 Physical and Biological Properties of Agricultural Products Acoustic, Electrical and Optical Properties and Biochemical Property 1. Acoustic and Vibrational Properties 1.1 Acoustics and Vibration Engineering
Physical and Biological Properties of Agricultural Products Acoustic, Electrical and Optical Properties and Biochemical Property 1. Acoustic and Vibrational Properties 1.1 Acoustics and Vibration Engineering
PEAT SEISMOLOGY Lecture 9: Anisotropy, attenuation and anelasticity
 PEAT8002 - SEISMOLOGY Lecture 9: Anisotropy, attenuation and anelasticity Nick Rawlinson Research School of Earth Sciences Australian National University Anisotropy Introduction Most of the theoretical
PEAT8002 - SEISMOLOGY Lecture 9: Anisotropy, attenuation and anelasticity Nick Rawlinson Research School of Earth Sciences Australian National University Anisotropy Introduction Most of the theoretical
Basic principles of the seismic method
 Chapter 2 Basic principles of the seismic method In this chapter we introduce the basic notion of seismic waves. In the earth, seismic waves can propagate as longitudinal (P) or as shear (S) waves. For
Chapter 2 Basic principles of the seismic method In this chapter we introduce the basic notion of seismic waves. In the earth, seismic waves can propagate as longitudinal (P) or as shear (S) waves. For
Global geophysics and wave propagation
 Global geophysics and wave propagation Reading: Fowler p76 83 Remote sensing Geophysical methods Seismology Gravity and bathymetry Magnetics Heat flow Seismology: Directly samples the physical properties
Global geophysics and wave propagation Reading: Fowler p76 83 Remote sensing Geophysical methods Seismology Gravity and bathymetry Magnetics Heat flow Seismology: Directly samples the physical properties
Surface Waves and Free Oscillations. Surface Waves and Free Oscillations
 Surface waves in in an an elastic half spaces: Rayleigh waves -Potentials - Free surface boundary conditions - Solutions propagating along the surface, decaying with depth - Lamb s problem Surface waves
Surface waves in in an an elastic half spaces: Rayleigh waves -Potentials - Free surface boundary conditions - Solutions propagating along the surface, decaying with depth - Lamb s problem Surface waves
Chapter 11. Vibrations and Waves
 Chapter 11 Vibrations and Waves Driven Harmonic Motion and Resonance RESONANCE Resonance is the condition in which a time-dependent force can transmit large amounts of energy to an oscillating object,
Chapter 11 Vibrations and Waves Driven Harmonic Motion and Resonance RESONANCE Resonance is the condition in which a time-dependent force can transmit large amounts of energy to an oscillating object,
Chapter 11 Vibrations and Waves
 Chapter 11 Vibrations and Waves 11-1 Simple Harmonic Motion If an object vibrates or oscillates back and forth over the same path, each cycle taking the same amount of time, the motion is called periodic.
Chapter 11 Vibrations and Waves 11-1 Simple Harmonic Motion If an object vibrates or oscillates back and forth over the same path, each cycle taking the same amount of time, the motion is called periodic.
Exam 3 Review. Chapter 10: Elasticity and Oscillations A stress will deform a body and that body can be set into periodic oscillations.
 Exam 3 Review Chapter 10: Elasticity and Oscillations stress will deform a body and that body can be set into periodic oscillations. Elastic Deformations of Solids Elastic objects return to their original
Exam 3 Review Chapter 10: Elasticity and Oscillations stress will deform a body and that body can be set into periodic oscillations. Elastic Deformations of Solids Elastic objects return to their original
LECTURE 5 - Wave Equation Hrvoje Tkalčić " 2 # & 2 #
 LECTURE 5 - Wave Equation Hrvoje Tkalčić " 2 # "t = ( $ + 2µ ) & 2 # 2 % " 2 (& ' u r ) = µ "t 2 % & 2 (& ' u r ) *** N.B. The material presented in these lectures is from the principal textbooks, other
LECTURE 5 - Wave Equation Hrvoje Tkalčić " 2 # "t = ( $ + 2µ ) & 2 # 2 % " 2 (& ' u r ) = µ "t 2 % & 2 (& ' u r ) *** N.B. The material presented in these lectures is from the principal textbooks, other
Lecture 17. Mechanical waves. Transverse waves. Sound waves. Standing Waves.
 Lecture 17 Mechanical waves. Transverse waves. Sound waves. Standing Waves. What is a wave? A wave is a traveling disturbance that transports energy but not matter. Examples: Sound waves (air moves back
Lecture 17 Mechanical waves. Transverse waves. Sound waves. Standing Waves. What is a wave? A wave is a traveling disturbance that transports energy but not matter. Examples: Sound waves (air moves back
Longitudinal Waves. waves in which the particle or oscillator motion is in the same direction as the wave propagation
 Longitudinal Waves waves in which the particle or oscillator motion is in the same direction as the wave propagation Longitudinal waves propagate as sound waves in all phases of matter, plasmas, gases,
Longitudinal Waves waves in which the particle or oscillator motion is in the same direction as the wave propagation Longitudinal waves propagate as sound waves in all phases of matter, plasmas, gases,
Borehole Geophysics. Acoustic logging measurements
 Acoustic logging measurements - Review of basic physics background - Concept of P- and S-wave measurements and logging tools - Tube waves - Seismic imaging - Synthetic seismograms - Field application examples
Acoustic logging measurements - Review of basic physics background - Concept of P- and S-wave measurements and logging tools - Tube waves - Seismic imaging - Synthetic seismograms - Field application examples
Outline. Hook s law. Mass spring system Simple harmonic motion Travelling waves Waves in string Sound waves
 Outline Hook s law. Mass spring system Simple harmonic motion Travelling waves Waves in string Sound waves Hooke s Law Force is directly proportional to the displacement of the object from the equilibrium
Outline Hook s law. Mass spring system Simple harmonic motion Travelling waves Waves in string Sound waves Hooke s Law Force is directly proportional to the displacement of the object from the equilibrium
SURFACE WAVE MODELLING USING SEISMIC GROUND RESPONSE ANALYSIS
 43 SURFACE WAVE MODELLING USING SEISMIC GROUND RESPONSE ANALYSIS E John MARSH And Tam J LARKIN SUMMARY This paper presents a study of surface wave characteristics using a two dimensional nonlinear seismic
43 SURFACE WAVE MODELLING USING SEISMIC GROUND RESPONSE ANALYSIS E John MARSH And Tam J LARKIN SUMMARY This paper presents a study of surface wave characteristics using a two dimensional nonlinear seismic
Producing a Sound Wave. Chapter 14. Using a Tuning Fork to Produce a Sound Wave. Using a Tuning Fork, cont.
 Producing a Sound Wave Chapter 14 Sound Sound waves are longitudinal waves traveling through a medium A tuning fork can be used as an example of producing a sound wave Using a Tuning Fork to Produce a
Producing a Sound Wave Chapter 14 Sound Sound waves are longitudinal waves traveling through a medium A tuning fork can be used as an example of producing a sound wave Using a Tuning Fork to Produce a
Geology 229 Engineering Geology. Lecture 5. Engineering Properties of Rocks (West, Ch. 6)
 Geology 229 Engineering Geology Lecture 5 Engineering Properties of Rocks (West, Ch. 6) Common mechanic properties: Density; Elastic properties: - elastic modulii Outline of this Lecture 1. Uniaxial rock
Geology 229 Engineering Geology Lecture 5 Engineering Properties of Rocks (West, Ch. 6) Common mechanic properties: Density; Elastic properties: - elastic modulii Outline of this Lecture 1. Uniaxial rock
Lecture 4 Notes: 06 / 30. Energy carried by a wave
 Lecture 4 Notes: 06 / 30 Energy carried by a wave We want to find the total energy (kinetic and potential) in a sine wave on a string. A small segment of a string at a fixed point x 0 behaves as a harmonic
Lecture 4 Notes: 06 / 30 Energy carried by a wave We want to find the total energy (kinetic and potential) in a sine wave on a string. A small segment of a string at a fixed point x 0 behaves as a harmonic
CHAPTER 11 VIBRATIONS AND WAVES
 CHAPTER 11 VIBRATIONS AND WAVES http://www.physicsclassroom.com/class/waves/u10l1a.html UNITS Simple Harmonic Motion Energy in the Simple Harmonic Oscillator The Period and Sinusoidal Nature of SHM The
CHAPTER 11 VIBRATIONS AND WAVES http://www.physicsclassroom.com/class/waves/u10l1a.html UNITS Simple Harmonic Motion Energy in the Simple Harmonic Oscillator The Period and Sinusoidal Nature of SHM The
Sound Propagation through Media. Nachiketa Tiwari Indian Institute of Technology Kanpur
 Sound Propagation through Media Nachiketa Tiwari Indian Institute of Technology Kanpur LECTURE-13 WAVE PROPAGATION IN SOLIDS Longitudinal Vibrations In Thin Plates Unlike 3-D solids, thin plates have surfaces
Sound Propagation through Media Nachiketa Tiwari Indian Institute of Technology Kanpur LECTURE-13 WAVE PROPAGATION IN SOLIDS Longitudinal Vibrations In Thin Plates Unlike 3-D solids, thin plates have surfaces
Multi-station Seismograph Network
 Multi-station Seismograph Network Background page to accompany the animations on the website: IRIS Animations Introduction One seismic station can give information about how far away the earthquake occurred,
Multi-station Seismograph Network Background page to accompany the animations on the website: IRIS Animations Introduction One seismic station can give information about how far away the earthquake occurred,
NDT&E Methods: UT. VJ Technologies CAVITY INSPECTION. Nondestructive Testing & Evaluation TPU Lecture Course 2015/16.
 CAVITY INSPECTION NDT&E Methods: UT VJ Technologies NDT&E Methods: UT 6. NDT&E: Introduction to Methods 6.1. Ultrasonic Testing: Basics of Elasto-Dynamics 6.2. Principles of Measurement 6.3. The Pulse-Echo
CAVITY INSPECTION NDT&E Methods: UT VJ Technologies NDT&E Methods: UT 6. NDT&E: Introduction to Methods 6.1. Ultrasonic Testing: Basics of Elasto-Dynamics 6.2. Principles of Measurement 6.3. The Pulse-Echo
Chapter 13. Hooke s Law: F = - kx Periodic & Simple Harmonic Motion Springs & Pendula Waves Superposition. Next Week!
 Chapter 13 Hooke s Law: F = - kx Periodic & Simple Harmonic Motion Springs & Pendula Waves Superposition Next Week! Review Physics 2A: Springs, Pendula & Circular Motion Elastic Systems F = kx Small Vibrations
Chapter 13 Hooke s Law: F = - kx Periodic & Simple Harmonic Motion Springs & Pendula Waves Superposition Next Week! Review Physics 2A: Springs, Pendula & Circular Motion Elastic Systems F = kx Small Vibrations
Section 1 Simple Harmonic Motion. The student is expected to:
 Section 1 Simple Harmonic Motion TEKS The student is expected to: 7A examine and describe oscillatory motion and wave propagation in various types of media Section 1 Simple Harmonic Motion Preview Objectives
Section 1 Simple Harmonic Motion TEKS The student is expected to: 7A examine and describe oscillatory motion and wave propagation in various types of media Section 1 Simple Harmonic Motion Preview Objectives
OPAC102. The Acoustic Wave Equation
 OPAC102 The Acoustic Wave Equation Acoustic waves in fluid Acoustic waves constitute one kind of pressure fluctuation that can exist in a compressible fluid. The restoring forces responsible for propagating
OPAC102 The Acoustic Wave Equation Acoustic waves in fluid Acoustic waves constitute one kind of pressure fluctuation that can exist in a compressible fluid. The restoring forces responsible for propagating
Physics 207 Lecture 28
 Goals: Lecture 28 Chapter 20 Employ the wae model Visualize wae motion Analyze functions of two ariables Know the properties of sinusoidal waes, including waelength, wae number, phase, and frequency. Work
Goals: Lecture 28 Chapter 20 Employ the wae model Visualize wae motion Analyze functions of two ariables Know the properties of sinusoidal waes, including waelength, wae number, phase, and frequency. Work
Exam tomorrow on Chapter 15, 16, and 17 (Oscilla;ons and Waves 1 &2)
 Exam tomorrow on Chapter 15, 16, and 17 (Oscilla;ons and Waves 1 &2) What to study: Quiz 6 Homework problems for Chapters 15 & 16 Material indicated in the following review slides Other Specific things:
Exam tomorrow on Chapter 15, 16, and 17 (Oscilla;ons and Waves 1 &2) What to study: Quiz 6 Homework problems for Chapters 15 & 16 Material indicated in the following review slides Other Specific things:
Oscillations and Waves
 Oscillations and Waves Oscillation: Wave: Examples of oscillations: 1. mass on spring (eg. bungee jumping) 2. pendulum (eg. swing) 3. object bobbing in water (eg. buoy, boat) 4. vibrating cantilever (eg.
Oscillations and Waves Oscillation: Wave: Examples of oscillations: 1. mass on spring (eg. bungee jumping) 2. pendulum (eg. swing) 3. object bobbing in water (eg. buoy, boat) 4. vibrating cantilever (eg.
Macroscopic theory Rock as 'elastic continuum'
 Elasticity and Seismic Waves Macroscopic theory Rock as 'elastic continuum' Elastic body is deformed in response to stress Two types of deformation: Change in volume and shape Equations of motion Wave
Elasticity and Seismic Waves Macroscopic theory Rock as 'elastic continuum' Elastic body is deformed in response to stress Two types of deformation: Change in volume and shape Equations of motion Wave
UNIVERSITY OF MALTA G.F. ABELA JUNIOR COLLEGE
 UNIVERSITY OF MALTA G.F. ABELA JUNIOR COLLEGE FIRST YEAR END-OF-YEAR EXAMINATION SUBJECT: PHYSICS DATE: JUNE 2010 LEVEL: INTERMEDIATE TIME: 09.00h to 12.00h Show ALL working Write units where appropriate
UNIVERSITY OF MALTA G.F. ABELA JUNIOR COLLEGE FIRST YEAR END-OF-YEAR EXAMINATION SUBJECT: PHYSICS DATE: JUNE 2010 LEVEL: INTERMEDIATE TIME: 09.00h to 12.00h Show ALL working Write units where appropriate
Schedule for the remainder of class
 Schedule for the remainder of class 04/25 (today): Regular class - Sound and the Doppler Effect 04/27: Cover any remaining new material, then Problem Solving/Review (ALL chapters) 04/29: Problem Solving/Review
Schedule for the remainder of class 04/25 (today): Regular class - Sound and the Doppler Effect 04/27: Cover any remaining new material, then Problem Solving/Review (ALL chapters) 04/29: Problem Solving/Review
Nicholas J. Giordano. Chapter 13 Sound
 Nicholas J. Giordano www.cengage.com/physics/giordano Chapter 13 Sound Sound Sounds waves are an important example of wave motion Sound is central to hearing, speech, music and many other daily activities
Nicholas J. Giordano www.cengage.com/physics/giordano Chapter 13 Sound Sound Sounds waves are an important example of wave motion Sound is central to hearing, speech, music and many other daily activities
Chapter 16 Waves in One Dimension
 Chapter 16 Waves in One Dimension Slide 16-1 Reading Quiz 16.05 f = c Slide 16-2 Reading Quiz 16.06 Slide 16-3 Reading Quiz 16.07 Heavier portion looks like a fixed end, pulse is inverted on reflection.
Chapter 16 Waves in One Dimension Slide 16-1 Reading Quiz 16.05 f = c Slide 16-2 Reading Quiz 16.06 Slide 16-3 Reading Quiz 16.07 Heavier portion looks like a fixed end, pulse is inverted on reflection.
Chapter 16: Oscillatory Motion and Waves. Simple Harmonic Motion (SHM)
 Chapter 6: Oscillatory Motion and Waves Hooke s Law (revisited) F = - k x Tthe elastic potential energy of a stretched or compressed spring is PE elastic = kx / Spring-block Note: To consider the potential
Chapter 6: Oscillatory Motion and Waves Hooke s Law (revisited) F = - k x Tthe elastic potential energy of a stretched or compressed spring is PE elastic = kx / Spring-block Note: To consider the potential
PREMED COURSE, 14/08/2015 OSCILLATIONS
 PREMED COURSE, 14/08/2015 OSCILLATIONS PERIODIC MOTIONS Mechanical Metronom Laser Optical Bunjee jumping Electrical Astronomical Pulsar Biological ECG AC 50 Hz Another biological exampe PERIODIC MOTIONS
PREMED COURSE, 14/08/2015 OSCILLATIONS PERIODIC MOTIONS Mechanical Metronom Laser Optical Bunjee jumping Electrical Astronomical Pulsar Biological ECG AC 50 Hz Another biological exampe PERIODIC MOTIONS
Oscillation the vibration of an object. Wave a transfer of energy without a transfer of matter
 Oscillation the vibration of an object Wave a transfer of energy without a transfer of matter Equilibrium Position position of object at rest (mean position) Displacement (x) distance in a particular direction
Oscillation the vibration of an object Wave a transfer of energy without a transfer of matter Equilibrium Position position of object at rest (mean position) Displacement (x) distance in a particular direction
Physics in Faculty of
 Why we study Physics in Faculty of Engineering? Dimensional analysis Scalars and vector analysis Rotational of a rigid body about a fixed axis Rotational kinematics 1. Dimensional analysis The ward dimension
Why we study Physics in Faculty of Engineering? Dimensional analysis Scalars and vector analysis Rotational of a rigid body about a fixed axis Rotational kinematics 1. Dimensional analysis The ward dimension
(Total 1 mark) IB Questionbank Physics 1
 1. A transverse wave travels from left to right. The diagram below shows how, at a particular instant of time, the displacement of particles in the medium varies with position. Which arrow represents the
1. A transverse wave travels from left to right. The diagram below shows how, at a particular instant of time, the displacement of particles in the medium varies with position. Which arrow represents the
Class XI Physics Syllabus One Paper Three Hours Max Marks: 70
 Class XI Physics Syllabus 2013 One Paper Three Hours Max Marks: 70 Class XI Weightage Unit I Physical World & Measurement 03 Unit II Kinematics 10 Unit III Laws of Motion 10 Unit IV Work, Energy & Power
Class XI Physics Syllabus 2013 One Paper Three Hours Max Marks: 70 Class XI Weightage Unit I Physical World & Measurement 03 Unit II Kinematics 10 Unit III Laws of Motion 10 Unit IV Work, Energy & Power
Topic 4 &11 Review Waves & Oscillations
 Name: Date: Topic 4 &11 Review Waves & Oscillations 1. A source produces water waves of frequency 10 Hz. The graph shows the variation with horizontal position of the vertical displacement of the surface
Name: Date: Topic 4 &11 Review Waves & Oscillations 1. A source produces water waves of frequency 10 Hz. The graph shows the variation with horizontal position of the vertical displacement of the surface
Oscillations. Oscillations and Simple Harmonic Motion
 Oscillations AP Physics C Oscillations and Simple Harmonic Motion 1 Equilibrium and Oscillations A marble that is free to roll inside a spherical bowl has an equilibrium position at the bottom of the bowl
Oscillations AP Physics C Oscillations and Simple Harmonic Motion 1 Equilibrium and Oscillations A marble that is free to roll inside a spherical bowl has an equilibrium position at the bottom of the bowl
PHYSICS. Course Structure. Unit Topics Marks. Physical World and Measurement. 1 Physical World. 2 Units and Measurements.
 PHYSICS Course Structure Unit Topics Marks I Physical World and Measurement 1 Physical World 2 Units and Measurements II Kinematics 3 Motion in a Straight Line 23 4 Motion in a Plane III Laws of Motion
PHYSICS Course Structure Unit Topics Marks I Physical World and Measurement 1 Physical World 2 Units and Measurements II Kinematics 3 Motion in a Straight Line 23 4 Motion in a Plane III Laws of Motion
9 MECHANICAL PROPERTIES OF SOLIDS
 9 MECHANICAL PROPERTIES OF SOLIDS Deforming force Deforming force is the force which changes the shape or size of a body. Restoring force Restoring force is the internal force developed inside the body
9 MECHANICAL PROPERTIES OF SOLIDS Deforming force Deforming force is the force which changes the shape or size of a body. Restoring force Restoring force is the internal force developed inside the body
Phys101 Lectures 28, 29. Wave Motion
 Phys101 Lectures 8, 9 Wave Motion Key points: Types of Waves: Transverse and Longitudinal Mathematical Representation of a Traveling Wave The Principle of Superposition Standing Waves; Resonance Ref: 11-7,8,9,10,11,16,1,13,16.
Phys101 Lectures 8, 9 Wave Motion Key points: Types of Waves: Transverse and Longitudinal Mathematical Representation of a Traveling Wave The Principle of Superposition Standing Waves; Resonance Ref: 11-7,8,9,10,11,16,1,13,16.
Chapter 11: Elasticity and Periodic Motion
 Chapter 11 Lecture Chapter 11: Elasticity and Periodic Motion Goals for Chapter 11 To study stress, strain, and elastic deformation. To define elasticity and plasticity. To follow periodic motion to a
Chapter 11 Lecture Chapter 11: Elasticity and Periodic Motion Goals for Chapter 11 To study stress, strain, and elastic deformation. To define elasticity and plasticity. To follow periodic motion to a
16 WAVES. Introduction. Chapter Outline
 Chapter 16 Waves 795 16 WAVES Figure 16.1 From the world of renewable energy sources comes the electric power-generating buoy. Although there are many versions, this one converts the up-and-down motion,
Chapter 16 Waves 795 16 WAVES Figure 16.1 From the world of renewable energy sources comes the electric power-generating buoy. Although there are many versions, this one converts the up-and-down motion,
PHYSICS. Chapter 16 Lecture FOR SCIENTISTS AND ENGINEERS A STRATEGIC APPROACH 4/E RANDALL D. KNIGHT Pearson Education, Inc.
 PHYSICS FOR SCIENTISTS AND ENGINEERS A STRATEGIC APPROACH 4/E Chapter 16 Lecture RANDALL D. KNIGHT 2017 Pearson Education, Inc. Chapter 16 Traveling Waves IN THIS CHAPTER, you will learn the basic properties
PHYSICS FOR SCIENTISTS AND ENGINEERS A STRATEGIC APPROACH 4/E Chapter 16 Lecture RANDALL D. KNIGHT 2017 Pearson Education, Inc. Chapter 16 Traveling Waves IN THIS CHAPTER, you will learn the basic properties
Electromagnetic fields and waves
 Electromagnetic fields and waves Maxwell s rainbow Outline Maxwell s equations Plane waves Pulses and group velocity Polarization of light Transmission and reflection at an interface Macroscopic Maxwell
Electromagnetic fields and waves Maxwell s rainbow Outline Maxwell s equations Plane waves Pulses and group velocity Polarization of light Transmission and reflection at an interface Macroscopic Maxwell
Waves Encountering Barriers
 Waves Encountering Barriers Reflection and Refraction: When a wave is incident on a boundary that separates two regions of different wave speed, part of the wave is reflected and part is transmitted. Figure
Waves Encountering Barriers Reflection and Refraction: When a wave is incident on a boundary that separates two regions of different wave speed, part of the wave is reflected and part is transmitted. Figure
Raymond A. Serway Chris Vuille. Chapter Thirteen. Vibrations and Waves
 Raymond A. Serway Chris Vuille Chapter Thirteen Vibrations and Waves Periodic Motion and Waves Periodic motion is one of the most important kinds of physical behavior Will include a closer look at Hooke
Raymond A. Serway Chris Vuille Chapter Thirteen Vibrations and Waves Periodic Motion and Waves Periodic motion is one of the most important kinds of physical behavior Will include a closer look at Hooke
SURFACE WAVE DISPERSION PRACTICAL (Keith Priestley)
 SURFACE WAVE DISPERSION PRACTICAL (Keith Priestley) This practical deals with surface waves, which are usually the largest amplitude arrivals on the seismogram. The velocity at which surface waves propagate
SURFACE WAVE DISPERSION PRACTICAL (Keith Priestley) This practical deals with surface waves, which are usually the largest amplitude arrivals on the seismogram. The velocity at which surface waves propagate
Page # Physics 103: Lecture 26 Sound. Lecture 26, Preflight 2. Lecture 26, Preflight 1. Producing a Sound Wave. Sound from a Tuning Fork
 Physics 103: Lecture 6 Sound Producing a Sound Wave Sound waves are longitudinal waves traveling through a medium A tuning fork can be used as an example of producing a sound wave A tuning fork will produce
Physics 103: Lecture 6 Sound Producing a Sound Wave Sound waves are longitudinal waves traveling through a medium A tuning fork can be used as an example of producing a sound wave A tuning fork will produce
Chapter 14 Oscillations. Copyright 2009 Pearson Education, Inc.
 Chapter 14 Oscillations 14-1 Oscillations of a Spring If an object vibrates or oscillates back and forth over the same path, each cycle taking the same amount of time, the motion is called periodic. The
Chapter 14 Oscillations 14-1 Oscillations of a Spring If an object vibrates or oscillates back and forth over the same path, each cycle taking the same amount of time, the motion is called periodic. The
SURFACE WAVES & DISPERSION
 SEISMOLOGY Master Degree Programme in Physics - UNITS Physics of the Earth and of the Environment SURFACE WAVES & DISPERSION FABIO ROMANELLI Department of Mathematics & Geosciences University of Trieste
SEISMOLOGY Master Degree Programme in Physics - UNITS Physics of the Earth and of the Environment SURFACE WAVES & DISPERSION FABIO ROMANELLI Department of Mathematics & Geosciences University of Trieste
Geophysical Site Investigation (Seismic methods) Amit Prashant Indian Institute of Technology Gandhinagar
 Geophysical Site Investigation (Seismic methods) Amit Prashant Indian Institute of Technology Gandhinagar Short Course on Geotechnical Aspects of Earthquake Engineering 04 08 March, 2013 Seismic Waves
Geophysical Site Investigation (Seismic methods) Amit Prashant Indian Institute of Technology Gandhinagar Short Course on Geotechnical Aspects of Earthquake Engineering 04 08 March, 2013 Seismic Waves
On the study of elastic wave scattering and Rayleigh wave velocity measurement of concrete with steel bar
 NDT&E International 33 (2000) 401 407 www.elsevier.com/locate/ndteint On the study of elastic wave scattering and Rayleigh wave velocity measurement of concrete with steel bar T.-T. Wu*, J.-H. Sun, J.-H.
NDT&E International 33 (2000) 401 407 www.elsevier.com/locate/ndteint On the study of elastic wave scattering and Rayleigh wave velocity measurement of concrete with steel bar T.-T. Wu*, J.-H. Sun, J.-H.
CENTER FOR INFRASTRUCTURE ENGINEERING STUDIES
 1 CENTER FOR INFRASTRUCTURE ENGINEERING STUDIES Acquisition of an Engineering Seismograph By Dr. Neil Anderson UTC RE116 University Transportation Center Program at The University of Missouri-Rolla 2 Disclaimer
1 CENTER FOR INFRASTRUCTURE ENGINEERING STUDIES Acquisition of an Engineering Seismograph By Dr. Neil Anderson UTC RE116 University Transportation Center Program at The University of Missouri-Rolla 2 Disclaimer
Receiver. Johana Brokešová Charles University in Prague
 Propagation of seismic waves - theoretical background Receiver Johana Brokešová Charles University in Prague Seismic waves = waves in elastic continuum a model of the medium through which the waves propagate
Propagation of seismic waves - theoretical background Receiver Johana Brokešová Charles University in Prague Seismic waves = waves in elastic continuum a model of the medium through which the waves propagate
Chapter 14 Oscillations
 Chapter 14 Oscillations If an object vibrates or oscillates back and forth over the same path, each cycle taking the same amount of time, the motion is called periodic. The mass and spring system is a
Chapter 14 Oscillations If an object vibrates or oscillates back and forth over the same path, each cycle taking the same amount of time, the motion is called periodic. The mass and spring system is a
Course Name: AP Physics. Team Names: Jon Collins. Velocity Acceleration Displacement
 Course Name: AP Physics Team Names: Jon Collins 1 st 9 weeks Objectives Vocabulary 1. NEWTONIAN MECHANICS and lab skills: Kinematics (including vectors, vector algebra, components of vectors, coordinate
Course Name: AP Physics Team Names: Jon Collins 1 st 9 weeks Objectives Vocabulary 1. NEWTONIAN MECHANICS and lab skills: Kinematics (including vectors, vector algebra, components of vectors, coordinate
Mass on a Horizontal Spring
 Course- B.Sc. Applied Physical Science (Computer Science) Year- IInd, Sem- IVth Subject Physics Paper- XIVth, Electromagnetic Theory Lecture No. 22, Simple Harmonic Motion Introduction Hello friends in
Course- B.Sc. Applied Physical Science (Computer Science) Year- IInd, Sem- IVth Subject Physics Paper- XIVth, Electromagnetic Theory Lecture No. 22, Simple Harmonic Motion Introduction Hello friends in
Homework #4 Reminder Due Wed. 10/6
 Homework #4 Reminder Chap. 6 Concept: 36 Problems 14, 18 Chap. 8 Concept: 8, 12, 30, 34 Problems 2, 10 Due Wed. 10/6 Chapter 8: Wave Motion A wave is a sort of motion But unlike motion of particles A propagating
Homework #4 Reminder Chap. 6 Concept: 36 Problems 14, 18 Chap. 8 Concept: 8, 12, 30, 34 Problems 2, 10 Due Wed. 10/6 Chapter 8: Wave Motion A wave is a sort of motion But unlike motion of particles A propagating
Sound Waves. Sound waves are longitudinal waves traveling through a medium Sound waves are produced from vibrating objects.
 Sound Waves Sound waves are longitudinal waves traveling through a medium Sound waves are produced from vibrating objects Introduction Sound Waves: Molecular View When sound travels through a medium, there
Sound Waves Sound waves are longitudinal waves traveling through a medium Sound waves are produced from vibrating objects Introduction Sound Waves: Molecular View When sound travels through a medium, there
Physics 41: Waves, Optics, Thermo
 Physics 41: Waves, Optics, Thermo Particles & Waves Localized in Space: LOCAL Have Mass & Momentum No Superposition: Two particles cannot occupy the same space at the same time! Particles have energy.
Physics 41: Waves, Optics, Thermo Particles & Waves Localized in Space: LOCAL Have Mass & Momentum No Superposition: Two particles cannot occupy the same space at the same time! Particles have energy.
Chapter 16 Traveling Waves
 Chapter 16 Traveling Waves GOALS When you have mastered the contents of this chapter, you will be able to achieve the following goals: Definitions Define each of the following terms as it is used in physics,
Chapter 16 Traveling Waves GOALS When you have mastered the contents of this chapter, you will be able to achieve the following goals: Definitions Define each of the following terms as it is used in physics,
DIVIDED SYLLABUS ( ) - CLASS XI PHYSICS (CODE 042) COURSE STRUCTURE APRIL
 DIVIDED SYLLABUS (2015-16 ) - CLASS XI PHYSICS (CODE 042) COURSE STRUCTURE APRIL Unit I: Physical World and Measurement Physics Need for measurement: Units of measurement; systems of units; SI units, fundamental
DIVIDED SYLLABUS (2015-16 ) - CLASS XI PHYSICS (CODE 042) COURSE STRUCTURE APRIL Unit I: Physical World and Measurement Physics Need for measurement: Units of measurement; systems of units; SI units, fundamental
Lecture 18. In other words, if you double the stress, you double the resulting strain.
 Lecture 18 Stress and Strain and Springs Simple Harmonic Motion Cutnell+Johnson: 10.1-10.4,10.7-10.8 Stress and Strain and Springs So far we ve dealt with rigid objects. A rigid object doesn t change shape
Lecture 18 Stress and Strain and Springs Simple Harmonic Motion Cutnell+Johnson: 10.1-10.4,10.7-10.8 Stress and Strain and Springs So far we ve dealt with rigid objects. A rigid object doesn t change shape
CHAPTER 4 TEST REVIEW
 IB PHYSICS Name: Period: Date: # Marks: 74 Raw Score: IB Curve: DEVIL PHYSICS BADDEST CLASS ON CAMPUS CHAPTER 4 TEST REVIEW 1. In which of the following regions of the electromagnetic spectrum is radiation
IB PHYSICS Name: Period: Date: # Marks: 74 Raw Score: IB Curve: DEVIL PHYSICS BADDEST CLASS ON CAMPUS CHAPTER 4 TEST REVIEW 1. In which of the following regions of the electromagnetic spectrum is radiation
PEAT SEISMOLOGY Lecture 12: Earthquake source mechanisms and radiation patterns II
 PEAT8002 - SEISMOLOGY Lecture 12: Earthquake source mechanisms and radiation patterns II Nick Rawlinson Research School of Earth Sciences Australian National University Waveform modelling P-wave first-motions
PEAT8002 - SEISMOLOGY Lecture 12: Earthquake source mechanisms and radiation patterns II Nick Rawlinson Research School of Earth Sciences Australian National University Waveform modelling P-wave first-motions
SIMPLE HARMONIC MOTION AND WAVES
 Simple Harmonic Motion (SHM) SIMPLE HARMONIC MOTION AND WAVES - Periodic motion any type of motion that repeats itself in a regular cycle. Ex: a pendulum swinging, a mass bobbing up and down on a spring.
Simple Harmonic Motion (SHM) SIMPLE HARMONIC MOTION AND WAVES - Periodic motion any type of motion that repeats itself in a regular cycle. Ex: a pendulum swinging, a mass bobbing up and down on a spring.
4. What is the speed (in cm s - 1 ) of the tip of the minute hand?
 Topic 4 Waves PROBLEM SET Formative Assessment NAME: TEAM: THIS IS A PRACTICE ASSESSMENT. Show formulas, substitutions, answers, and units! Topic 4.1 Oscillations A mass is attached to a horizontal spring.
Topic 4 Waves PROBLEM SET Formative Assessment NAME: TEAM: THIS IS A PRACTICE ASSESSMENT. Show formulas, substitutions, answers, and units! Topic 4.1 Oscillations A mass is attached to a horizontal spring.
(Total 1 mark) IB Questionbank Physics 1
 1. A transverse wave travels from left to right. The diagram below shows how, at a particular instant of time, the displacement of particles in the medium varies with position. Which arrow represents the
1. A transverse wave travels from left to right. The diagram below shows how, at a particular instant of time, the displacement of particles in the medium varies with position. Which arrow represents the
Wave Motions and Sound
 EA Notes (Scen 101), Tillery Chapter 5 Wave Motions and Sound Introduction Microscopic molecular vibrations determine temperature (last Chapt.). Macroscopic vibrations of objects set up what we call Sound
EA Notes (Scen 101), Tillery Chapter 5 Wave Motions and Sound Introduction Microscopic molecular vibrations determine temperature (last Chapt.). Macroscopic vibrations of objects set up what we call Sound
Global Seismology Chapter 4
 Global Seismology Chapter 4 Earthquake: an event of ground shaking usually caused by the rupturing of a fault within the Earth. Who studies Earthquakes? Seismologists waves Geophysicists Mechanics Geodesy
Global Seismology Chapter 4 Earthquake: an event of ground shaking usually caused by the rupturing of a fault within the Earth. Who studies Earthquakes? Seismologists waves Geophysicists Mechanics Geodesy
Chapter 8: Wave Motion. Homework #4 Reminder. But what moves? Wave properties. Waves can reflect. Waves can pass through each other
 Homework #4 Reminder Chap. 6 Concept: 36 Problems 14, 18 Chap. 8 Concept: 8, 12, 30, 34 Problems 2, 10 Chapter 8: Wave Motion A wave is a sort of motion But unlike motion of particles A propagating disturbance
Homework #4 Reminder Chap. 6 Concept: 36 Problems 14, 18 Chap. 8 Concept: 8, 12, 30, 34 Problems 2, 10 Chapter 8: Wave Motion A wave is a sort of motion But unlike motion of particles A propagating disturbance
21. Earthquakes I (p ; 306)
 21. Earthquakes I (p. 296-303; 306) How many people have been killed by earthquakes in the last 4,000 years? How many people have been killed by earthquakes in the past century? What two recent earthquakes
21. Earthquakes I (p. 296-303; 306) How many people have been killed by earthquakes in the last 4,000 years? How many people have been killed by earthquakes in the past century? What two recent earthquakes
Section 1 Simple Harmonic Motion. Chapter 11. Preview. Objectives Hooke s Law Sample Problem Simple Harmonic Motion The Simple Pendulum
 Section 1 Simple Harmonic Motion Preview Objectives Hooke s Law Sample Problem Simple Harmonic Motion The Simple Pendulum Section 1 Simple Harmonic Motion Objectives Identify the conditions of simple harmonic
Section 1 Simple Harmonic Motion Preview Objectives Hooke s Law Sample Problem Simple Harmonic Motion The Simple Pendulum Section 1 Simple Harmonic Motion Objectives Identify the conditions of simple harmonic
The velocity (v) of the transverse wave in the string is given by the relation: Time taken by the disturbance to reach the other end, t =
 Question 15.1: A string of mass 2.50 kg is under a tension of 200 N. The length of the stretched string is 20.0 m. If the transverse jerk is struck at one end of the string, how long does the disturbance
Question 15.1: A string of mass 2.50 kg is under a tension of 200 N. The length of the stretched string is 20.0 m. If the transverse jerk is struck at one end of the string, how long does the disturbance
Wave Equation in One Dimension: Vibrating Strings and Pressure Waves
 BENG 1: Mathematical Methods in Bioengineering Lecture 19 Wave Equation in One Dimension: Vibrating Strings and Pressure Waves References Haberman APDE, Ch. 4 and Ch. 1. http://en.wikipedia.org/wiki/wave_equation
BENG 1: Mathematical Methods in Bioengineering Lecture 19 Wave Equation in One Dimension: Vibrating Strings and Pressure Waves References Haberman APDE, Ch. 4 and Ch. 1. http://en.wikipedia.org/wiki/wave_equation
Waves PY1054. Special Topics in Physics. Coláiste na hollscoile Corcaigh, Éire University College Cork, Ireland. ROINN NA FISICE Department of Physics
 Waves Special Topics in Physics 1 Waves Types of Waves: - longitudinal - transverse Longitudinal: Compression waves, e.g. sound Surface: Transverse: Attributes: Ocean Waves. Light, string etc. Speed, wavelength,
Waves Special Topics in Physics 1 Waves Types of Waves: - longitudinal - transverse Longitudinal: Compression waves, e.g. sound Surface: Transverse: Attributes: Ocean Waves. Light, string etc. Speed, wavelength,
Corso di Laurea in Fisica - UNITS ISTITUZIONI DI FISICA PER IL SISTEMA TERRA. Wave propagation FABIO ROMANELLI
 Corso di Laurea in Fisica - UNITS ISTITUZIONI DI FISICA PER IL SISTEMA TERRA Wave propagation FABIO ROMANELLI Department of Mathematics & Geosciences University of Trieste romanel@units.it http://moodle2.units.it/course/view.php?id=887
Corso di Laurea in Fisica - UNITS ISTITUZIONI DI FISICA PER IL SISTEMA TERRA Wave propagation FABIO ROMANELLI Department of Mathematics & Geosciences University of Trieste romanel@units.it http://moodle2.units.it/course/view.php?id=887
Game Physics. Game and Media Technology Master Program - Utrecht University. Dr. Nicolas Pronost
 Game and Media Technology Master Program - Utrecht University Dr. Nicolas Pronost Soft body physics Soft bodies In reality, objects are not purely rigid for some it is a good approximation but if you hit
Game and Media Technology Master Program - Utrecht University Dr. Nicolas Pronost Soft body physics Soft bodies In reality, objects are not purely rigid for some it is a good approximation but if you hit
Hydrogeophysics - Seismics
 Hydrogeophysics - Seismics Matthias Zillmer EOST-ULP p. 1 Table of contents SH polarized shear waves: Seismic source Case study: porosity of an aquifer Seismic velocities for porous media: The Frenkel-Biot-Gassmann
Hydrogeophysics - Seismics Matthias Zillmer EOST-ULP p. 1 Table of contents SH polarized shear waves: Seismic source Case study: porosity of an aquifer Seismic velocities for porous media: The Frenkel-Biot-Gassmann
Seismic Waves. 1. Seismic Deformation
 Types of Waves 1. Seismic Deformation Seismic Waves When an earthquake fault ruptures, it causes two types of deformation: static; and dynamic. Static deformation is the permanent displacement of the ground
Types of Waves 1. Seismic Deformation Seismic Waves When an earthquake fault ruptures, it causes two types of deformation: static; and dynamic. Static deformation is the permanent displacement of the ground
DOWN-HOLE SEISMIC SURVEY AND VERTICAL ELECTRIC SOUNDINGS RABASKA PROJECT, LÉVIS, QUÉBEC. Presented to :
 DOWN-HOLE SEISMIC SURVEY AND VERTICAL ELECTRIC SOUNDINGS RABASKA PROJECT, LÉVIS, QUÉBEC Presented to : TERRATECH 455, René-Lévesque Blvd. West Montreal, Québec HZ 1Z3 Presented by : GEOPHYSICS GPR INTERNATIONAL
DOWN-HOLE SEISMIC SURVEY AND VERTICAL ELECTRIC SOUNDINGS RABASKA PROJECT, LÉVIS, QUÉBEC Presented to : TERRATECH 455, René-Lévesque Blvd. West Montreal, Québec HZ 1Z3 Presented by : GEOPHYSICS GPR INTERNATIONAL
Chap 11. Vibration and Waves. The impressed force on an object is proportional to its displacement from it equilibrium position.
 Chap 11. Vibration and Waves Sec. 11.1 - Simple Harmonic Motion The impressed force on an object is proportional to its displacement from it equilibrium position. F x This restoring force opposes the change
Chap 11. Vibration and Waves Sec. 11.1 - Simple Harmonic Motion The impressed force on an object is proportional to its displacement from it equilibrium position. F x This restoring force opposes the change
LECTURE 19: Simple harmonic oscillators
 Lectures Page 1 Select LEARNING OBJECTIVES: LECTURE 19: Simple harmonic oscillators Be able to identify the features of a system that oscillates - i.e. systems with a restoring force and a potential energy
Lectures Page 1 Select LEARNING OBJECTIVES: LECTURE 19: Simple harmonic oscillators Be able to identify the features of a system that oscillates - i.e. systems with a restoring force and a potential energy
Introduction to Engineering Seismology Lecture 6
 Lecture 6: Theory of wave propagation; Seismic waves, body and surface waves. Topics How seismic waves are produced? Wave and its Properties Wave Propagation Types of Seismic Waves Compressional or P-Waves
Lecture 6: Theory of wave propagation; Seismic waves, body and surface waves. Topics How seismic waves are produced? Wave and its Properties Wave Propagation Types of Seismic Waves Compressional or P-Waves
202 Index. failure, 26 field equation, 122 force, 1
 Index acceleration, 12, 161 admissible function, 155 admissible stress, 32 Airy's stress function, 122, 124 d'alembert's principle, 165, 167, 177 amplitude, 171 analogy, 76 anisotropic material, 20 aperiodic
Index acceleration, 12, 161 admissible function, 155 admissible stress, 32 Airy's stress function, 122, 124 d'alembert's principle, 165, 167, 177 amplitude, 171 analogy, 76 anisotropic material, 20 aperiodic
Chapter 16 Waves in One Dimension
 Lecture Outline Chapter 16 Waves in One Dimension Slide 16-1 Chapter 16: Waves in One Dimension Chapter Goal: To study the kinematic and dynamics of wave motion, i.e., the transport of energy through a
Lecture Outline Chapter 16 Waves in One Dimension Slide 16-1 Chapter 16: Waves in One Dimension Chapter Goal: To study the kinematic and dynamics of wave motion, i.e., the transport of energy through a
1. For a simple harmonic motion governed by Hooke s Law, F = kx, if T is the period then the quantity T/2π is equal to
 1. For a simple harmonic motion governed by Hooke s Law, F = kx, if T is the period then the quantity T/2π is equal to (a) m (b) (c) m k k k m (d) k m (e) the angular frequency ω 2. If the mass of a simple
1. For a simple harmonic motion governed by Hooke s Law, F = kx, if T is the period then the quantity T/2π is equal to (a) m (b) (c) m k k k m (d) k m (e) the angular frequency ω 2. If the mass of a simple
Earthquakes.
 Earthquakes http://quake.usgs.gov/recenteqs/latestfault.htm An earthquake is a sudden motion or shaking of the Earth's crust, caused by the abrupt release of stored energy in the rocks beneath the surface.
Earthquakes http://quake.usgs.gov/recenteqs/latestfault.htm An earthquake is a sudden motion or shaking of the Earth's crust, caused by the abrupt release of stored energy in the rocks beneath the surface.
f 1/ T T 1/ f Formulas Fs kx m T s 2 k l T p 2 g v f
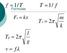 f 1/T Formulas T 1/ f Fs kx Ts 2 m k Tp 2 l g v f What do the following all have in common? Swing, pendulum, vibrating string They all exhibit forms of periodic motion. Periodic Motion: When a vibration
f 1/T Formulas T 1/ f Fs kx Ts 2 m k Tp 2 l g v f What do the following all have in common? Swing, pendulum, vibrating string They all exhibit forms of periodic motion. Periodic Motion: When a vibration
(Total 1 mark) IB Questionbank Physics 1
 1. A transverse wave travels from left to right. The diagram below shows how, at a particular instant of time, the displacement of particles in the medium varies with position. Which arrow represents the
1. A transverse wave travels from left to right. The diagram below shows how, at a particular instant of time, the displacement of particles in the medium varies with position. Which arrow represents the
Chapter 14 Oscillations
 Chapter 14 Oscillations Chapter Goal: To understand systems that oscillate with simple harmonic motion. Slide 14-2 Chapter 14 Preview Slide 14-3 Chapter 14 Preview Slide 14-4 Chapter 14 Preview Slide 14-5
Chapter 14 Oscillations Chapter Goal: To understand systems that oscillate with simple harmonic motion. Slide 14-2 Chapter 14 Preview Slide 14-3 Chapter 14 Preview Slide 14-4 Chapter 14 Preview Slide 14-5
What does the speed of a wave depend on?
 Today s experiment Goal answer the question What does the speed of a wave depend on? Materials: Wave on a String PHeT Simulation (link in schedule) and Wave Machine Write a CER in pairs. Think about the
Today s experiment Goal answer the question What does the speed of a wave depend on? Materials: Wave on a String PHeT Simulation (link in schedule) and Wave Machine Write a CER in pairs. Think about the
Chapter 13, Vibrations and Waves. 1. A large spring requires a force of 150 N to compress it only m. What is the spring constant of the spring?
 CHAPTER 13 1. A large spring requires a force of 150 N to compress it only 0.010 m. What is the spring constant of the spring? a. 125 000 N/m b. 15 000 N/m c. 15 N/m d. 1.5 N/m 2. A 0.20-kg object is attached
CHAPTER 13 1. A large spring requires a force of 150 N to compress it only 0.010 m. What is the spring constant of the spring? a. 125 000 N/m b. 15 000 N/m c. 15 N/m d. 1.5 N/m 2. A 0.20-kg object is attached
