AN INTRODUCTION TO FULLY AND PARTIALLY ACCELERATED LIFE TESTING MODELS
|
|
|
- Mary Briggs
- 5 years ago
- Views:
Transcription
1 CHAPTER 1 AN INTRODUCTION TO FULLY AND PARTIALLY ACCELERATED LIFE TESTING MODELS 1.1 INTRODUCTION The term reliability refers to failure free or fault free performance of a unit during a given period of time under specified design and environmental conditions. Quantitatively it is the probability that the unit will perform satisfactorily at least for a specified period of time without a major breakdown. The unit may refer to a component, equipment, subsystem or system. Today s manufacturers have to develop and deliver highly reliable products in order to satisfy the sophisticated needs of customers and withstand stiff global competition. The evaluation of reliabilities of these products within time and cost constraints is of great challenge to the reliability engineers. Accelerating the life test helps in meeting this challenge. Introduced by Chernoff (1962), and Bessler, Chernoff and Marshall (1962), acceleration of life test is widely undertaken to provide information quickly about the life distribution of a product. In order to shorten the testing period and save cost of testing, all or some of the test units are subject to a more severe environment (increased or decreased stress levels) than the normal operating environment so that failures can be induced in a short period of test time. The test 1
2 data so obtained at accelerated conditions are extrapolated by means of an appropriate model to estimate the characteristics of life distribution at design condition. The optimal test plan under accelerated conditions determines the number of test units at each stress level, test duration, and other experimental variables and thus helps in obtaining accurate reliability estimates. The accuracy of reliability estimates so obtained has a direct impact on the subsequent decisions on system configuration, warranties, and preventive maintenance schedules. Acceleration of life test is applied in materials, products and degradation mechanisms such as insulation life, conductive particle-filled adhesives that have been widely used for flex-to-rigid board interconnections in calculators, multi-layer ceramic capacitors and power capacitors. Life test under accelerated environmental conditions may be fully accelerated or partially accelerated. In fully accelerated life testing all the test units are run at accelerated condition, while in partially accelerated life testing they are run at both normal and accelerated conditions. The term fully accelerated life test has been coined by Bhattacharya and Soejoeti (1989), and the term partially accelerated life test is due to Degroot and Goel (1979). 1.2 TYPES OF STRESS LOADINGS Stress under accelerated condition can be applied using constant-stress, stepstress, progressive-stress, cyclic-stress, random-stress, or combinations of such loadings. The choice of a stress loading depends on how the product or unit is used in service and other practical and theoretical limitations (Nelson (1980), Elsayed (1996)). 2
3 1.2.1 Constant-Stress Loading The constant-stress scheme comprises multiple sub-samples tested at different but fixed stress levels until a pre-specified time or upon the occurrence of a fixed number of failures Step-Stress Loading In step-stress loading, test units are subject to successively higher levels of stress during some pre-specified amount of time, or until the occurrence of fixed number of failures Progressive-Stress Loading In a progressive-stress loading, the stress level is increased continually either until the censoring time or up to the maximum stress level which is maintained until the censoring time. A ramp-stress test results when stress is increased linearly. In particular, a ramp test with two linearly increasing stresses is a simple ramp test. Ramp tests are used for example in fatigue testing (Prot (1948)), capacitors (Endicott, Hatch, and Schmer (1965), Starr and Endicott (1961)), insulation (Goba (1969), Solomon, Klein and Albert (1976)), and integrated circuits (Chan (1990)) Cyclic-Stress Loading In cyclic-stress testing, the stress level is changed according to a fixed pattern. For many products, the frequency and length of a cycle affect the lifetime of a product, so they are included in the model as stress variable. Common examples of such stress are thermal cycling, and sinusoidal vibration. 3
4 1.2.5 Random-Stress Loading In random-stress testing the level of stress changes at random and has a probabilistic distribution. This type of test is often used for vibration stresses Combined Stress Loading Stress in accelerated condition can be applied using combination of stress loadings described in The traditional constant-stress and step-stress testing assume instantaneous changes in the stress levels. However, from a practical point of view, it is desirable to increase the stress at some finite rate, because a sudden jump in stress level may cause a stress (thermal) shock or undesirable failure modes which may not appear under the normal use condition. In addition, it may be impossible for some test units to jump instantaneously from a lower stress level to a higher level. This has necessitated the use of modified constant-stress testing and modified step-stress testing in each of which stress from one level to another higher level is increased at a finite rate. In both the cases two or more stress levels higher than the normal stress level are employed. Between any two stress levels, the stress is increased at the same rate. Modified constant-stress loading and modified step-stress loading can also be referred to as ramp-constant-stress loading and ramp-stepstress loading, respectively. See for example Elsayed (2003), Park and Yum (1998), Gao, Hu, Shi and Qin (2008), Shi (2011). Figures depict different forms of stress loadings. 4
5 Figure 1.1: Constant-stress loading Stress Time Figure 1.2: Step-stress loading 5
6 Figure 1.3: Progressive-stress loading Figure 1.4: Cyclic-stress loading 6
7 Figure 1.5: Random-stress loading Stress Time Figure 1.6: Modified step-stress loading 7
8 Stress Time Figure 1.7: Modified constant-stress loading 1.3 TYPES OF STRESSES The type of applied stress depends on the intended operating conditions of the product and the potential cause of failure. See for example, Nelson (1990) and Elsayed (2003) Mechanical Stresses The most commonly used acceleration test for mechanical components is fatigue stress. When components are subject to elevated temperature then creep testing (which combines both temperature and load) is applied. Shock and vibration testing is suitable for bearings, shock absorbers, tires and circuit boards in airplanes and automobiles Electrical Stresses These include power cycling, electric field, current density, and electro migration. 8
9 1.3.3 Environmental Stresses Temperature and thermal cycling are commonly used for most products. It is important to use appropriate stress levels that do not induce different failure mechanisms than those under normal conditions. Other environmental stresses include humidity, ultraviolet light, sulphur dioxide, salt and fine particles, and alpha and gamma rays Usage Rate Acceleration This is appropriate for products that do not operate continuously under normal conditions, so the only alternative to accelerate the life is to run the product more - at a higher usage rate. There are two ways of doing such compressed time testing, namely, faster and reduced off time. In the former the analyst operates the product faster than at normal conditions. For example, rolling bearings run at about three times their normal speed. The latter is done on products that are off most of the time in actual use. Such products can be accelerated by running them a greater fraction of time. For example, in most homes, a major appliance (say, washer or dryer) runs an hour or two a day; on test it runs 24 hours a day. 1.4 A PRODUCT S LIFE DISTRIBUTION A life distribution represents scatter in product s life. The use of a correct life distribution model, especially in the presence of a limited data-as typically occurs with modern devices, having high reliability, helps in preventing the choice of unnecessary and expensive planned replacements. Significant errors in the extrapolation of accelerated life testing results could occur if the assumed model does not provide a good approximation of the actual failure mechanism. 9
10 1.4.1 Basic Concepts Let T be a non-negative random variable representing the lifetime of an item with life distribution F( t ), satisfying F0 ( ) = 0. Definition 1.1: The life distribution denoted by F( t ) is the probability that the item fails before time t, and is given by F( t) = P[ T t ], F( 0) = 0. (1.1) Definition 1.2: The reliability of an item is defined as the probability that it will perform satisfactorily for a specified period of time without a major failure, and is given by F( t) = P[ T > t] = 1 F( t ). (1.2) It is also known as survival function, survival distribution, and survival probability. Definition 1.3: Let f() be the pdf of F(), then the failure rate function denoted by h( t ) is defined as f( t) h() t, F() t for t such that F( t) > 0. = (1.3) h( t ) is a measure of the rate at which failures in the total population occur at time t. It is also known as conditional failure rate function, or the hazard rate function. It can be easily seen from (1.3) that 10
11 t F() t = exp h(u)du,0 t <, (1.4) 0 which is an alternative form of reliability and signifies that one can find F( t ) from h( t ). Definition 1.4: The 100p th percentile (or p th quantile) of a distribution F() is the age ξ p by which a proportion p of the population fails. It is the solution of ( p ) p= F ξ. (1.5) It is also called the 100p percent point or p fractile. The 50% point is called the median, and is usually used as a typical life. The characteristic life is the time at which 63.2% of the units will fail. Definition 1.5: The mean life time of a unit is defined as ( ) E T = F(t)dt. (1.6) Some Life Distribution Models of Relevance under Accelerated Conditions Some of the life distribution models depicted by a product subject to accelerated conditions are briefly described below (Nelson (1990): Exponential Distribution The population fraction failing by age t is t/ θ F(t) = 1 e ; t 0, (1.7) where θ> 0 is the mean time to failure and the pdf is 11
12 1 t/ θ f(t) = e ;t 0. (1.8) θ The 100p th percentile is ξ p = θ ln (1 p), (1.9) where the base of log is e. The failure rate is 1 h(t) = =λ; t 0. (1.10) θ Only the exponential distribution has a constant failure rate, a key characteristic. In other words for this distribution only, an old unit and a new unit have the same chance of failing over a future time interval Normal Distribution The population fraction failing by age t is t x μ F(t) = exp dx; < t <, 2 2 σ σ π (1.11) where μ is the population mean and may have any value, σ is the population standard deviation and must be positive. The pdf is t μ f(t) = exp ; < t <. 2 2 σ (1.12) σ π The pdf is symmetric about the mean (median) μ, and σ determines the spread. The range of t is from to. Life must, of course, be positive. Thus the distribution fraction below zero must be small for this distribution to be a satisfactory approximation in practice. The 100p th percentile is 12
13 ξ p =μ+ z pσ, (1.13) where z p is the 100p th standard normal percentile and the median (50 th percentile) of the normal distribution is ξ p =μ, since z0.50 = 0. The failure rate function of normal distribution increases without limit. Thus, it may describe products with wear out failure Lognormal Distribution The population fraction failing by age t is ln t μ { σ } F(t) =Φ ;t > 0; σ> 0, (1.14) where μ is called the log mean and may have any value from to, σ is called the log standard deviation and must be positive, Φ ( ) denotes the standardized normal distribution function, and the base of log is e. The pdf is ( ln t ) 2 1 μ f(t) = exp ;t> 0. 2 tσ 2π 2σ The 100p th percentile is p { p } (1.15) ξ = exp μ+ z σ, (1.16) where z p is the 100p th standard normal percentile and the median (50 th percentile) of the normal distribution is ξ 0.50 = anti log [ μ ], since z0.50 = 0. The failure rate function is given as ln at { } ( ln at) 2 1 exp 2 tσ 2π 2σ h(t) = ;u > 0, (1.17) 1 Φ σ 13
14 μ where a = e. The failure rate function of lognormal distribution has a property seldom seen in products. It is zero at time zero, increases to a maximum, and then decreases to zero with increasing age. Nonetheless, over most of its range and especially over the lower tail, the lognormal distribution fits life data of many products. Often one uses only the lower tail in applications Weibull Distribution The population fraction failing by age t is β t F(t) = 1 exp ; t > 0, (1.18) α where β is the shape parameter and α is the scale parameter, and are positive. The pdf is β 1 β β t t f(t) = exp ;t> 0. α α α The 100p th percentile is ( ) 1/ β (1.19) ξ p =α ln 1 p, (1.20) where the base of log is e. The 63.2 th percentile of the distribution is always equal to the characteristic life of the distribution, i.e. ξ0.632 α. and the failure rate function is given by β 1 β t h(t) = ; t > 0. (1.21) α α With a simply increasing or decreasing failure rate, the Weibull distribution flexibly describes failure rate. 14
15 Extreme Value Distribution The extreme value distribution is used to analyze Weibull data. The natural log of time to failure for a Weibull distribution has an extreme value distribution. The population fraction failing by age t is t μ { σ } F(t) = 1 exp exp ; < t <, (1.22) where μ is the location parameter and may have any value from to, and σ is the scale parameter and is positive. The pdf is μ { } 1 t μ t f (t) = exp exp exp ; < t <. σ σ σ The 100p th percentile is ( ) (1.23) ξ p = ln ln 1 p. (1.24) The 63.2 th percentile of the distribution is equal to the location parameter of the distribution, i.e. ξ0.632 μ. The failure rate function is 1 t μ h(t) = exp ; < t <. σ σ (1.25) Logistic Distribution The Logistic distribution has a shape very close to that of a normal distribution but has heavier tails than the normal. The population fraction failing by age t is 1 F(t) = ; < t <, (1.26) t μ 1+ exp{ σ } 15
16 and pdf is { σ } t μ { } 2 σ 1 exp t μ σ f(t) = ; < t <, 1+ exp (1.27) where μ is the location parameter and may have any value from to, and σ is the scale parameter and is positive. The range of t is from to. Thus the distribution fraction below zero must be small, for this distribution to be a satisfactory approximation in practice as the lifetime of a unit cannot be negative. The 100p th percentile is 1 p ln. p ξ p =μ σ The median (50 th percentile) of the logistic distribution is ξ 0.50 =μ. (1.28) The failure rate function is given by 1 h(t) = ; < t <. (1.29) σ t μ 1+ exp{ σ } Unlike normal distribution which has failure rate function increasing without limit, i.e., increasing failure rate, the h(t) for logistic distribution lies between 0 and 1/σ Log-Logistic Distribution The log-logistic life distribution has been found appropriate for high reliability components. The population fraction failing by age t is 16
17 1 F(t) = 1 ; t > 0, α t 1+ ( λ ) and the pdf is t ( ) t ( ) α 1 α f(t) = λ λ ;t > 0, α 2 1+ λ where λ is the scale parameter and α is the shape parameter, and are positive. The 100p th percentile is ξ p =λ p 1 p 1/ α. The median (50 th percentile) of the logistic distribution is ξ 0.50 =λ. The failure rate function is given by t ( ) t ( ) α 1 α h(t) = λ λ ; t > 0 α 1+ λ (1.30) (1.31) (1.32) (1.33) which is always decreasing with time if α 1 first increasing, then decreasing with time if α> 1. The latter property has been observed for insulating material Truncated Logistic Distribution The logistic distribution described above can be used for modeling lifetime data only when the distribution fraction below zero is small, else it can result in modeling negative times-to-failure. This has necessitated the use of truncated logistic distribution truncated at point zero for modeling lifetime data. The failure 17
18 rate of truncated logistic distribution is increasing and more realistically bounded below and above by non-zero finite quantity. The cdf, pdf, reliability function, and hazard function, respectively, of the truncated logistic distribution, respectively, are F(t) =, t, 0,, A t σ> <μ< (1.34) μ μ 1+ exp{ } 1+ exp{ } σ σ t μ { σ } t μ { } 2 σ t μ { σ } t μ { σ } exp f(t) =,t, σ> 0, <μ<, Aσ 1+ exp (Mood, Graybill and Boes (1974)) (1.35) exp R(t) =,t, σ> 0, <μ<, and (1.36) A 1+ exp 1 h(t) =, t, 0,, t μ 1 exp{ } σ> <μ< (1.37) σ + σ where μ and σ are the location and scale parameters, respectively. The hazard function (1.37) is an increasing function of t, and is bounded by 1 σ 1+ exp μ { σ}, and 1 σ. The 100p th percentile is 1 1 ξ p =μ σ ln Ap + 1, μ 1 exp + { } σ (1.38) 18
19 where the ln has natural base Burr Type-XII Distribution The Burr type-xii distribution has a non-monotone hazard function which can accommodate many shapes of hazard function. The pdf and cdf, respectively, of the Burr type-xii distribution, are (k+ 1) c1 c kc t t g(t) = 1 +,t 0, α α α k c t G(t) = 1 1 +,t 0. α (1.39) (1.40) The Burr type-xii distribution is uni-modal, and its mode is 1 c c 1 T mod e =α ck + 1 if c> 1. The pdf is L-shaped if c 1. The reliability function and hazard function, respectively, are k c t R(t) = 1 +,t 0, α (1.41) 1 c1 c kc t t h(t) = 1 +,t 0. (1.42) α α α The Weibull life distribution tends to the Burr type-xii distribution as k, such that 1/c α= k (see Appendix A.1). The exponential life distribution also tends to the Burr type-xii distribution as k, such that 1/c α= k, and c= 1 (see Appendix A.2), and the log-logistic distribution is a particular case of this distribution as for k = 1, the distribution reduces to the log-logistic distribution. 19
20 Abd-Elfattah, Hassan and Nassr (2008), Lewis (1981), Soliman (2005), Tadikamalla (1980) have discussed the statistical and probabilistic properties of the Burr type-xii distribution, and its relationship to other distributions used in reliability analysis. This distribution has been found appropriate for life testing experiments under accelerated conditions. As an example of a product lifetime distribution in which the Burr distribution is more appropriate, Nelson (1982, pg. 105) has given data on times to breakdown of an insulating fluid between electrodes at a voltage of 34 KV (minutes). Zimmer, Keats and Wang (1998) have shown that the Burr type- XII model is acceptable for these data. Cook and Jhonson (1986) have used the Burr model to obtain better fits to a uranium survey data set. See also Lai and Xie (2006), Murthy, Xie, and Jiang (2003) for reference. 1.5 FULLY ACCELERATED LIFE TEST (ALT) MODEL In fully accelerated life testing, all the test units are run at accelerated conditions. The term fully accelerated life test has been coined by Bhattacharya and Soejoeti (1989). The fully accelerated life test is widely referred to as an accelerated life test (ALT) in the literature. A fully ALT model or simply an ALT model consists of a) a life distribution that represents the scatter in product life, and b) relationship between life and stress. After having specified an appropriate life distribution (see 1.4.2) a model that describes a life characteristic of the distribution such as mean life, quantile life is formulated. The life characteristic can be any reliability measure such as mean life, quantile life etc., and is expressed as a function of stress. Some of the 20
21 common stress-life relationships describing life characteristic as a function of stress are described below briefly: Stress-Life Relationship Arrhenius Relationship Arrhenius model is used when the damaging mechanism is temperature sensitive (especially for integrating circuits, light emitting diodes, dielectrics, semiconductors, battery cells, insulating tapes, lubricant, grease, plastic, incandescent bulb filaments). The Arrhenius equation relates the rate of a chemical reaction R to temperature T. This relationship can be written as E R = Aexp, (1.43) k T where E is the activation energy of the reaction, usually in electron-volts, k is Boltzmann s constant, x10-5 electron-volts per 0 C, T is the absolute Kelvin temperature, and A is a constant, that is, characteristic of the product failure mechanism, and test conditions. The Arrhenius life relationship is based on the idea that failure occurs after there has been a critical amount C of chemical reaction. The product is assumed to fail when some critical amount of the chemical has reacted, i.e., C = R (time to failure). Equivalently, (time to failure) = C / R. 21
22 This suggests that nominal time, ψ to failure is inversely proportional to the rate, (1.43). This yields the Arrhenius life relationship E ψ= Aexp, (1.44) k T where A is a constant that depends on product geometry, specimen size, fabrication, test method, and other factors. ψ represents a quantifiable life measure, such as mean life, characteristic life, median life etc. The natural log of (1.44) is the linear function of the inverse of T, i.e., γ ln ψ 1 ( ) γ T = 0 +, (1.45) T where γ 0 and γ 1 are characteristic of the product and test method; they are estimated from data. Thus the log of nominal life is a linear function of inverse absolute temperature Inverse Power Law Relationship It is used for analyzing data for which the accelerated stress is non-thermal in nature. It is frequently used as an accelerating stress for products such as capacitors, transformers, and insulators. Suppose that the accelerating stress variable V is positive. The inverse power law relationship between nominal life ψ of a product and V is A ψ( V) = γ, (1.46) 1 V where A and γ 1 are parameters characteristic of the product, specimen geometry and fabrication, the test method, etc.. 22
23 Equivalent forms are γ1 A ψ( V) =, V and γ1 V ψ( ) = A 0 V, V where V0 is a specified (standard) level of stress. The natural log of (1.46) is [ ψ ] = γ0 + γ1 [ ] ln ( V) ln( V ). (1.47) Thus, the natural log of typical life, ln [ ψ ], is a linear function of the transformed stress x = ln[ V ] with γ 0 = ln(a) Eyring Relationship It was formulated from quantum mechanics principles and is most often used when thermal stress (temperature) is the acceleration variable. However the Eyring relationship is also often used for stress variables other than temperature, such as humidity. The Eyring relationship for nominal life ψ as a function of absolute temperature T is A B ψ ( T ) = exp, T k T (1.48) where A and B are constants of the product and test method, and k is Boltzmann s constant. For the small range of absolute temperature in most applications, (A/T) is essentially constant, and (1.48) is close to the Arrhenius relationship (1.43). 23
24 Temperature-Humidity Relationship It is a two-stress relationship and is used for predicting the life at use conditions when temperature and humidity are the accelerated stresses in a test. The model is given by φ υ ψ ( UT, ) = Aexp +, (1.49) T U where A, φ, and υ are constants of the product and test method, T is temperature (in absolute units) and U is the relative humidity Temperature-Non-Thermal Relationship It is another two-stress model. It is used for analyzing the data for which the temperature and non-thermal are accelerated stresses. The model is given by ψ ( UT, ) = C, n U exp B { υ } (1.50) where B, C and n are constants of the product and test method, T is temperature (in absolute units) and U is the non thermal stress, for example, voltage Multivariable Relationship In most practical applications however, life is a function of more than one or two variables (stress types). In addition, there are many applications where the life of a product as a function of stress and of some engineering variable other than stress is sought. A multivariable relationship is therefore needed in order to analyze such data. 24
25 Such a relationship is the general log-linear relationship, which describes a life characteristic as a function of n stresses. Mathematically, the model is given by, n ln ( x 1, x 2,, xn) = exp β 0 + β1x i, (1.51) i= 1 where β 0 and β 1 are unknown parameters, and x,x 1 2,,xn are stress levels. Remark 1.1: A great variety of other stress relationships, for example, exponential relationship, exponential-power relationship, quadratic and polynomial relationship, and relationships involving more than one accelerating variables exist in the literature (Nelson ( 1990)) Constant-Stress ALT Models When the stress is constant, the stress level applied to a sample of units does not vary with time. Each unit is tested under the same accelerated stress, say, temperature for a fixed duration of time. For example, ten units are tested at 310K for 100 hours, ten different units are tested at 320K for 100 hours and ten different units are tested at 330K for 100 hours. Example 1.1: Arrhenius-Weibull Model At absolute temperature T, using (1.18) and (1.45), the population fraction failing by age t is β t F(t, T ) = 1 exp ( ) α T β γ 1 exp t exp 1 = γ 0, (1.52) T 25
26 where the shape parameter β is a constant independent of temperature. Example 1.2: Power-Weibull Model At stress level V, using (1.18) and (1.46) with A = e 0, the population fraction failing by age t is β t F(t, V) = 1 exp α( ) V = V γ γ β 1 exp t e 0 1. (1.53) Remark 1.2: Similarly Arrhenius-exponential, Arrhenius-Lognormal, Powerexponential, Power-Lognormal, and other models with different life distributions and stress-life relationships have been developed (Nelson (1990)). γ ALT Models under Varying Stress In some areas of reliability testing, stress on individual units is varied during the test. The primary motivation for using varying stress models is to turn up the stress on the surviving units in order to force all or most of the units to fail more quickly than with constant-stress model. When the stress is time-dependent, the stress applied to a sample of units varies with time. Time-dependent stresses can be applied in a variety of ways. For example, if temperature is the stress type, each unit may be tested at 310K for 10 hours then increased to 320K for 10 hours then increased to 330K for 10 hours over the duration of the test. Alternatively, the units may be placed in a test chamber where the temperature starts at 310K and increases by five degrees every ten minutes until the temperature reaches 330K. 26
27 Some common types of time-dependent stress profiles include step-stress, rampstress and various profiles in which the application of the stress is a continuous function of time (see Nelson (1990), Miller and Nelson (1983)). Some models are described below: Step-Stress ALT Model To model a data from step-stress test, the life distribution under step-stressing needs to be related to the distribution under a constant-stress. Such a model known as Cumulative Exposure Model is described below: Cumulative Exposure Model Assumptions: The model assumes that the remaining life of units depends only on the current cumulative fraction failed and current stress-regardless of how the fraction got accumulated. Moreover, if held at the current stress, survivors will fail according to the cdf for that stress but starting at the previously accumulated fraction failed. Mathematical Formulation: Let F(t) 0 be the cdf of time to failure under a particular step-stress pattern. Suppose that for a particular pattern, step i runs at stress s i, starts at time t i-1, and runs to time t i (t 0 = 0). The cdf of time to failure for units run at constant-stress s i is denoted by F(t). i The population cumulative fraction of specimens failing in Step 1 is F(t) 0 = F(t),0 1 t t. 1 (1.54) Step 2 has an equivalent start time l 1, which would have produced the same population cumulative fraction failing, i.e., l 1 is the solution of F(l) = F(t). (1.55) The population cumulative fraction of specimens failing in Step 2 by total time t is 27
28 F(t) 0 = F(t 2 t1+ l),t 1 1 t t 2. (1.56) Similarly, Step 3 has the equivalent start time l 2 and l 2 is the solution of F(l 3 2) = F(t 2 2 t1+ l). 1 (1.57) Similarly, for Step 3, F(t) 0 = F(t 3 t2 + l 2),t2 t t. 3 (1.58) In general, Step i has the equivalent start time l i 1 that is the solution of F(l ) = F (t t + l ), (1.59) i i 1 i 1 i 1 i 2 i 2 and F(t) = F(t t + l ),t t t. (1.60) 0 i i 1 i 1 i 1 i Thus, F(t) 0 for the step-stress pattern is made up of segments of the cdfs F() 1, F() 2, etc. A different step-stress pattern would have different F(t) 0 distribution. Figure 1.8 depicts the cumulative exposure model for a failure mode. Figure 1.8a depicts a step-stress pattern with four steps. Figure 1.8b shows the four cumulative distributions for the constant stresses (s 1,s 2,s 3,s 4). The resulting cumulative distribution for life under the step-stress pattern is shown in Figure 1.8c. 28
29 Figure 1.8 Step-stress profile and the corresponding life distributions S 4 Stress s S 3 S 2 S 1 0 t 1 t 2 t 3 t 4 Time t Figure 1.8a l 1 Figure 1.8b 29
30 l 1 Figure 1.8c Example 1.3: Power-Weibull Step-Stress Model γ 0 Using (1.18) and (1.46) with A = V 1 the cdf for the fraction of units failing by time t for the constant-stress s i is γ 1 F(t) i i 1 exp V = t V0 β Then, for step 1, (1.54) becomes γ β 1 V1 0 = 1 V0 F(t) 1 exp t,0 t t. The equivalent time l 1 at l 2 is given by (1.55) as (1.61) (1.62) 30
31 p V1 l1 = t 1. V0 For step 2 (1.63) p β 2 F(t) 0 1 exp V = (t t1 l) + 1,t1 t t 2. V0 Similarly, for step 3, V2 l 2 = (t2 t1+ l 1), V3 p p β 3 F(t) 0 1 exp V = (t t2 l 2) +,t2 t t. 3 V0 In general, for step i, Vi 1 l i 1= (ti 1 ti 2+ l i 2), Vi p β i F(t) 0 1 exp V = (t ti 1 l i 1) +,ti 1 t t. i V0 Thus, F(t) 0 consists of segments of Weibull distributions. p (1.64) (1.65) (1.66) (1.67) (1.68) Progressive-Stress ALT Model When the stress mode depends on V (t) is a function of time, and the life distribution for a failure V (t) only through a scale parameter θ( V ), then the cumulative exposure ε for the failure mode is given by 31
32 t du ε (t) =, θ( V (u)) 0 and the population fraction failed by time t under 0 V (t) (1.69) F (t, V (t)) = G( ε(t)), (1.70) where G(.) is the assumed cumulative distribution with the scale parameter set equal to one. This is a generalized formulation of the cumulative damage model, where stress can be any function of time, for example, a ramp-stress, a monotonically increasing stress, sinusoidal, etc. When V (t) = kt, where k is the rate of increase of stress, we have ramp-stress model. Example 1.4: Power-Weibull Ramp-Stress Model γ 0 Using (1.18) and (1.46) with A = V 1 and V (t) = kt, the cumulative exposure (1.69) at time t is t du ε (t) =, α( V (u)) where 0 γ (1.71) V0 α ( V(t)) = V γ γ 1 γ k t ε (t) = (1.72) V γ + 1 The population fraction failed by time t under V (t) is 32
33 0 β { [ ] } F (t, V(t)) = 1 exp ε(t) (using (1.70)) γ β 1 γ 1+ 1 k t = 1 exp (using ( 1.72)) γ V This is a Weibull distribution with shape and scale parameters β= ( γ + 1) β and 1 γ 1 γ V0 α= 1 + ( 1), respectively. k 1.6 PARTIALLY ACCELERATED LIFE TEST (PALT) MODEL In partially accelerated life testing the test units are run at both normal and accelerated conditions. The term partially accelerated life test is due to Degroot and Goel (1979). The fully ALT models discussed in Section 1.5 are based on a stress-life relationship. If such a relationship is not known or cannot be assumed to be known the accelerated data cannot be extrapolated to use condition, and PALT is then the reasonable scheme to extrapolate accelerated data to use condition. A PALT model consists of a life distribution and an acceleration factor. The acceleration factor provides a quantitative estimate of the relationship between the test condition and the field condition and is a necessary relationship to properly design and execute an accelerated test. Definition 1.6: An acceleration factor is defined as the ratio of a reliability measure, say mean life, at use condition to that at accelerated condition. The two PALT models existing in the literature are step-stress PALT and constantstress PALT. 33
34 1.6.1 Constant-Stress PALT Models The constant-stress PALT runs each item at either use or accelerated condition only. n π items randomly chosen among n test items are allocated to use condition, and the n(1 π ) remaining items to accelerated condition, where π denotes the proportion of items allocated at use condition. Each test item is run until a prespecified time or upon the occurrence of a fixed number of failures. To describe the model for this constant-stress PALT, let T denote the lifetime of a test item tested at use condition and Y denotes the lifetime of a test item at accelerated condition, then Y =α T, where α is the acceleration factor. The lifetimes T and Y are mutually independent. Example 1.5: Let T follow exponential distribution with hazard rate λ, then the pdf of T is λt λe,(t, λ ) > 0, and that of Y is 1 1 λα y λα e,(y, λ ) > Step-Stress PALT Models The step-stress PALT permits the test to be changed from use to accelerated condition at a predetermined time. Let the lifetime of an item under use condition be denoted by the random variable T with life distribution F(t; θ ). Here the value of the parameter θ is unknown and is to be estimated. Suppose the item has not failed by some time τ, then it is switched to the higher level of stress and the test is continued until the item fails. It is assumed that the effect of this switch is to multiply the remaining lifetime of the item by unknown acceleration factor α ( > 0). In general, α will be a function of the higher stress levels that are chosen. If only one higher stress is used, then α is 34
35 regarded as a constant. Furthermore, since the effect of switching to the higher stress level will typically be to shorten the life of the test item, usually α will be less than one. To describe the model for this step-stress PALT, let Y denote the total lifetime of a test item. Then, Y is defined by the relation T,T τ Y = (1.73) τ+α (T τ ),T >τ Since switching to the higher stress level can be regarded as tampering with the ordinary life test, Y is called a tampered random variable, τ is called the tampering point or stress change point, and α is called the tampering coefficient or acceleration factor. See for example, Degroot and Goel (1979). Example 1.6: Let lifetime of an item at use condition be exponential with hazard rate λ, then the pdf of the total lifetime Y can be written in the form λy λ < τ e,0 y 1 1 λ( τ+α (y τ)) g y(y) = λα e, y>τ 0,otherwise. (1.74) 1.7 DATA ANALYSIS Traditional Life Data Analysis involves analyzing times-to-failure data (of a product, system or component) obtained under normal operating conditions in order to quantify the life characteristics of the product, component or system. See for example Epstein and Sobel (1953), Barlow and Proschan (1975), Bandyopadhyay and Basu (1990a, 1990b), Basu and Ebrahimi (1984a, 1984b, 1985a, 1985b), Basu, Ebrahimi and Klefsjo (1983), Basu and Habibullah (1987), Deshpande (1992, 1983), 35
36 Deshpande and Kochar (1983a, 1983b), Deshpande, Kochar and Singh (1986), Deshpande and Purohit (2006), Hollander and Proschan ((1975), (1980), (1984)), Kanwar Sen and Jain (1990, 1991a, 1991b, 1991c), Kanwar Sen and Srivastava (1995, 1998a, 1998b, 1999, 2000, 2001a, 2001b,2001c, 2003) However, modern products are designed to operate without failures for years, decades or longer. Thus, few units will fail in a test of practical length at normal use conditions. For example, the design and construction of communication satellites may allow only eight months for testing components that are expected to be in service for years. For such applications accelerated life testing is used. The analysis of test data under accelerated condition depends on the type of data. Specifically, analysis relies on life and stress data or time-to-failure data at a specific stress level. Since obtaining exact life (failure age) of each test item may be time consuming and costly, so modern practice couple accelerated tests with censoring. Two types of censoring schemes considered in this work are described below: Type-I Censoring It involves running each test unit a pre-specified time unless it fails sooner. The censoring time is fixed, and the number of failures is random. The data set obtained is known as type-i censored data or time-censored data Type-II Censoring It involves simultaneous testing of the test units until a pre-specified number of them failed. The common censoring time is random, and the number of failures is fixed. The data set obtained is known as type-ii censored data or failure-censored data. 36
37 Some specific data analysis methods in ALT are estimates, confidence intervals, and hypothesis tests. There are several methods of estimation for fitting an accelerated life testing model to the data. Applicable methods include maximum likelihood estimation, linear estimation based on order statistics, and graphical estimation. Ordinary least squares estimation does not apply to censored data. These methods are compared by Hahn and Nelson (1974). ML estimation is preferred for the reasons outlined by Meeker and Nelson (1974a, 1974b). Confidence intervals are essential. By their width, confidence intervals for parameters indicate the uncertainty in estimates. Hypothesis tests indicate whether observed differences are statistically significant. Goodness of fit is employed to determine how well the observed sample data fits some proposed models. Probability plot is the most commonly used graphical goodness of fit test (see Grosh (1989)). Mann, Schafer and Singpurwalla (1974) and Lawless (1982) have provided general theory and applications of lifetime data analysis. 1.8 OPTIMUM TEST PLAN A detailed test plan is usually designed before conducting a test under accelerated condition. A test plan is used to decide on the appropriate stress levels, appropriate stress change times, optimum number of test units to be allocated at different stress levels, and optimum duration of the test. It is therefore not only important but imperative to have a test plan that helps in accurately estimating reliability measures at operating conditions without waste of time, effort and money. The optimal test plans are considered as minimizing or maximizing the selected objective functions that are purely based on the Fisher information matrix. The 37
38 Fisher information is a way of measuring the amount of information that an observable random variable X carries about an unknown parameter θ upon which the likelihood function L( θ ) depends. The likelihood function is the joint probability of the data, the Xs, conditional on the value of θ, or a function of θ. Fisher information is the negative of the expectation of the second derivative of the log of L( θ ) with respect to θ. Thus for k parameters θ 1, θ 2,, θ k, the true Fisher information matrix F is L L L E 2 E E θ1 θ1 θ2 θ1 θk L L L E E E F 2 = θ2 θ1 θ2 θ2 θ k, L L L E E E 2 θk θ1 θk θ 2 θk where L L( θ, θ,, θ ). 1 2 k An optimum test plan can be obtained using variance optimality, D- optimality or A-optimality criterion (see for example, Gouno, Sen, and Balakrishnan (2004), Balakrishnan and Han (2009)). These optimality criteria are briefly described below: Variance Optimality The Variance optimality criterion is based on minimizing the asymptotic (large sample) variance of the ML estimators of the mean or of a quantile life at a 38
39 specified design stress. It is assumed that the high test stress, x H, has been specified. Example 1.7: For a constant-stress test, the optimum plan the low test stress x L and the proportion of test unit allocated at the lower stress is found by minimizing the asymptotic variance of the maximum likelihood estimator of a stated mean or quantile life at design stress. Example 1.8: For a simple time step-stress test, the variance is minimized by the optimum choice of the stress change time of x L. Example 1.9: For a ramp-stress test, the optimum plan low stress rate and the proportion of test units allocated at low stress rate is found by minimizing the asymptotic variance of the maximum likelihood estimator of a stated mean or quantile life at design stress. The higher stress rate is assumed to be given because of technical consideration D-Optimality The D-optimality criterion is based on the determinant of the Fisher information matrix which is the same as the reciprocal of the asymptotic variance-covariance matrix. The volume of the asymptotic joint confidence region of parameters, say, ( αβ, ) is proportional to the square root of the determinant of the inverse of the Fisher information matrix, is inversely proportional to 11/2 F, at a fixed confidence level. In other words, it 1/2 F. Consequently, a smaller value of the determinant would correspond to a higher (joint) precision of the estimators of 2 αβ,. Thus, the D-optimality criterion is the one which maximizes the F /n. 39
40 Example 1.10: For a simple step-stress test, the D-optimal stress change time of x L is the one which maximizes the A-Optimality 2 F /n. The A-optimality criterion is also known as trace criterion. It is based on the sum of the diagonal entries of Fisher's information matrix. Thus, the A-optimality criterion is the one which maximizes trace (F) / n. Example 1.11: For a simple step-stress test, the A-optimal stress change time of 2 x L is the one which maximizes the objective function defined by F /n. 1.9 SENSITIVITY ANALYSIS The use of an optimum test plan requires information about the design parameters. Incorrect choice of these gives a poor estimate of the mean or quantile life at design stress. The sensitivity analysis identifies the sensitive parameters which need to be estimated with special care for the purpose of minimizing the risk of obtaining erroneous solutions. If a small change in any parameter value does not result in relatively large change in the optimum plan, then the proposed test plan is robust, and the initial values have a small effect on optimal values REVIEW WORK Several life test models under fully and partially accelerated environmental conditions have been devised in the literature keeping in view the physical behavior of the material subject to the elevated stress level under various life distribution models and different types of censoring schemes. A fully ALT model 40
41 is commonly referred to as an ALT model in the literature. A brief description of these models follows: Constant-Stress ALT Models In the literature, much research has been focused on the design of constant-stress ALT models. Chernoff (1962) has developed locally optimum ALT plan for the exponential distribution to estimate the failure rate at a specified design stress. He has assumed two forms for the failure rate, viz., a quadratic function, and an exponential function of stress. He has given results for both simultaneous testing of a sample of units until a pre-specified time (allowing for time-censoring), and for successive testing in which units are tested one at a time until they fail. For the simple linear regression model, Gaylor and Sweeny (1965) have summarized the literature. Little and Jebe (1969) have considered least squares estimation of the mean of a normal distribution at a design stress. The mean is a simple linear regression function of a stress, and the standard deviation is a constant. They have given the optimum plans for successive testing with complete data. Mann (1972) has considered linear estimation with order statistics to estimate a percentile of an extreme value (or Weibull) distribution at a design stress. The percentile is a multiple linear regression function of a number of stresses, and the scale parameter is a constant. The optimum plans for type-ii censored data have also been obtained. Herzberg and Cox (1972) briefly survey key papers on the optimum design for multiple linear regression models, and Chernoff (1972) has surveyed the optimal design in experiments. Nelson and Kielpinski (1975, 1976) have considered ML estimation of the median of a normal (or lognormal) distribution at a design stress. The (log) median is a simple linear regression function of a stress, 41
42 and the (log) standard deviation is a constant. They have given the optimum plans, and best standard plans for simultaneous testing with type-i censored data. Meeker and Nelson (1978) have considered ML estimation of a percentile of an extreme value (or Weibull) distribution at a design stress. The percentile is a simple linear regression function of a stress, and the scale parameter is a constant. They have given the optimum plans for simultaneous testing with type-i censored data. Yang (1994) has formulated a constrained nonlinear programme to obtain an optimal test plan. The objective function to be minimized consists of a weighted sum of the standardized asymptotic variance, the product of the test duration at the lowest stress level, and the sum of test duration. The solution for four stress levels has been presented. A similar approach has been used by Yang and Jin (1994) with three stress levels, where the middle stress is the average of the low and high stresses. Bai and Yun (1996) considered estimation problem of the lifetime distribution and optimal design of constant-stress ALT plans for products of unequal size. ML estimators of parameters of Weibull distribution are obtained, and their properties are studied. Tang (1999) has imposed constraints that limit the probability of having probability plots with best-fit lines crossing at the lower tails. In this way, the stress levels, and their corresponding sample allocations are best suited to infer whether the shape parameters are indeed different at different stress levels. Motivated by the fact that the mid stress level is meant for validating the assumed stress-life model, Tang, Tan, and Ong (2002) have considered the test plans in which the mid stress level will have the least influence on the slope of the stress-life relationship plot. Although these plans are more robust, variances of the estimates at design stress for these compromised plans may be much higher than those under the two stress level optimum plans. Tang and Yang (2002) have proposed a graphical approach for planning multiple constant-stress levels ALT so 42
43 that the uncertainty involved for some estimate of interest is not worse than that of a statistical optimum plan by margin determined by the experimenter before the test. Kim and Bai (2002) proposed a method for estimating the lifetime distribution in constant-stress ALT. The authors used a mixture of two distributions to describe these failure modes. Tang and Xu (2005) have considered a multiple objective framework for planning ALT. Watkins and John (2008) considered the problem of constant-stress ALT based on type-ii censoring data using Weibull distribution for estimating the MLEs of model parameters. Liu and Tang (2009) proposed a sequential constant-stress ALT scheme and its Bayesian inference. Most of the work has been summarized in Nelson (1990), Meeker and Escobar (1998) Step-Stress ALT Models Regarding ALT using time-varying stress loadings, step-stress ALT plans have been the main focus. Nelson (1980) obtained the ML estimators for the parameters of the Weibull distribution under the inverse power law using the break down time data of an electrical insulation. Miller and Nelson (1983) have obtained the optimum simple step-stress ALT plans for the case where tests units have exponentially distributed life, and are observed continuously until all test units are run to fail. Bai, Kim, and Lee (1989) have extended the results of Miller and Nelson (1983) to the case where prescribed censoring time is involved. Bai and Chun (1991) have obtained optimum simple step-stress accelerated life-tests with competing causes of failure. Bai and Kim (1993) have presented an optimal simple step-stress ALT for the Weibull distribution under type-i censoring. A log-linear relationship, and the 43
44 cumulative exposure model have been assumed, and nomographs have been used to find the optimal plan. Madi (1993) generalizes from the simple (2-step) stepstress setting to the multiple (k-step, k 2) step-stress setting and get the MLEs of the parameters for the multiple step-stress setting when the initial life distribution belongs to a two-parameter Weibull family. Tang, Sun, Goh, and Ong (1996) have analyzed data from a step-stress ALT using linear cumulative exposure model, and 3-parameter Weibull distribution. Khamis and Higgins (1996) have obtained the optimal three-step, step-stress test using exponential distribution. Khamis (1997) has developed an optimum design for the multiple-step, multiple-stress exponential model. Khamis and Higgins (1998) have proposed an optimum design for the multiple-step, multiple-stress model using an alternative to the Weibull cumulative exposure model which is based on a time transformation of the exponential cumulative exposure model. They have called this model Khamis- Higgins model. They have also used the proposed model to obtain an optimum design, and study inferential problem for two-step ALT with known shape parameter (Khamis and Higgins (1999)). Watkins (2001) has considered simple step-stress models with type-ii censored exponential data. Yeo and Tang (1999), Tang (2003) have derived a simple step-stress accelerated life testing for an optimum hold time under low stress, and an optimum low stress level by taking the target acceleration factor into consideration. These studies were based on the assumption that the failure time follows exponential distribution because of its simplicity. Bai and Chung (1998) have provided the optimal designs of simple step-stress ALTs for lognormal lifetime distributions. Xiong (1998) has presented the inferences of parameters in the simple step-stress model in accelerated life testing with type-ii censored exponential data. Xiong and Milliken (1999) have 44
Optimum Test Plan for 3-Step, Step-Stress Accelerated Life Tests
 International Journal of Performability Engineering, Vol., No., January 24, pp.3-4. RAMS Consultants Printed in India Optimum Test Plan for 3-Step, Step-Stress Accelerated Life Tests N. CHANDRA *, MASHROOR
International Journal of Performability Engineering, Vol., No., January 24, pp.3-4. RAMS Consultants Printed in India Optimum Test Plan for 3-Step, Step-Stress Accelerated Life Tests N. CHANDRA *, MASHROOR
Constant Stress Partially Accelerated Life Test Design for Inverted Weibull Distribution with Type-I Censoring
 Algorithms Research 013, (): 43-49 DOI: 10.593/j.algorithms.01300.0 Constant Stress Partially Accelerated Life Test Design for Mustafa Kamal *, Shazia Zarrin, Arif-Ul-Islam Department of Statistics & Operations
Algorithms Research 013, (): 43-49 DOI: 10.593/j.algorithms.01300.0 Constant Stress Partially Accelerated Life Test Design for Mustafa Kamal *, Shazia Zarrin, Arif-Ul-Islam Department of Statistics & Operations
Step-Stress Models and Associated Inference
 Department of Mathematics & Statistics Indian Institute of Technology Kanpur August 19, 2014 Outline Accelerated Life Test 1 Accelerated Life Test 2 3 4 5 6 7 Outline Accelerated Life Test 1 Accelerated
Department of Mathematics & Statistics Indian Institute of Technology Kanpur August 19, 2014 Outline Accelerated Life Test 1 Accelerated Life Test 2 3 4 5 6 7 Outline Accelerated Life Test 1 Accelerated
10 Introduction to Reliability
 0 Introduction to Reliability 10 Introduction to Reliability The following notes are based on Volume 6: How to Analyze Reliability Data, by Wayne Nelson (1993), ASQC Press. When considering the reliability
0 Introduction to Reliability 10 Introduction to Reliability The following notes are based on Volume 6: How to Analyze Reliability Data, by Wayne Nelson (1993), ASQC Press. When considering the reliability
STATISTICAL INFERENCE IN ACCELERATED LIFE TESTING WITH GEOMETRIC PROCESS MODEL. A Thesis. Presented to the. Faculty of. San Diego State University
 STATISTICAL INFERENCE IN ACCELERATED LIFE TESTING WITH GEOMETRIC PROCESS MODEL A Thesis Presented to the Faculty of San Diego State University In Partial Fulfillment of the Requirements for the Degree
STATISTICAL INFERENCE IN ACCELERATED LIFE TESTING WITH GEOMETRIC PROCESS MODEL A Thesis Presented to the Faculty of San Diego State University In Partial Fulfillment of the Requirements for the Degree
Unit 20: Planning Accelerated Life Tests
 Unit 20: Planning Accelerated Life Tests Ramón V. León Notes largely based on Statistical Methods for Reliability Data by W.Q. Meeker and L. A. Escobar, Wiley, 1998 and on their class notes. 11/13/2004
Unit 20: Planning Accelerated Life Tests Ramón V. León Notes largely based on Statistical Methods for Reliability Data by W.Q. Meeker and L. A. Escobar, Wiley, 1998 and on their class notes. 11/13/2004
A Tool for Evaluating Time-Varying-Stress Accelerated Life Test Plans with Log-Location- Scale Distributions
 Statistics Preprints Statistics 6-2010 A Tool for Evaluating Time-Varying-Stress Accelerated Life Test Plans with Log-Location- Scale Distributions Yili Hong Virginia Tech Haiming Ma Iowa State University,
Statistics Preprints Statistics 6-2010 A Tool for Evaluating Time-Varying-Stress Accelerated Life Test Plans with Log-Location- Scale Distributions Yili Hong Virginia Tech Haiming Ma Iowa State University,
OPTIMAL DESIGN AND EQUIVALENCY OF ACCELERATED LIFE TESTING PLANS
 OPTIMAL DESIGN AND EQUIVALENCY OF ACCELERATED LIFE TESTING PLANS by YADA ZHU A dissertation submitted to the Graduate School-New Brunswick Rutgers, The State University of New Jersey In partial fulfillment
OPTIMAL DESIGN AND EQUIVALENCY OF ACCELERATED LIFE TESTING PLANS by YADA ZHU A dissertation submitted to the Graduate School-New Brunswick Rutgers, The State University of New Jersey In partial fulfillment
Time-varying failure rate for system reliability analysis in large-scale railway risk assessment simulation
 Time-varying failure rate for system reliability analysis in large-scale railway risk assessment simulation H. Zhang, E. Cutright & T. Giras Center of Rail Safety-Critical Excellence, University of Virginia,
Time-varying failure rate for system reliability analysis in large-scale railway risk assessment simulation H. Zhang, E. Cutright & T. Giras Center of Rail Safety-Critical Excellence, University of Virginia,
OPTIMUM DESIGN ON STEP-STRESS LIFE TESTING
 Libraries Conference on Applied Statistics in Agriculture 1998-10th Annual Conference Proceedings OPTIMUM DESIGN ON STEP-STRESS LIFE TESTING C. Xiong Follow this and additional works at: http://newprairiepress.org/agstatconference
Libraries Conference on Applied Statistics in Agriculture 1998-10th Annual Conference Proceedings OPTIMUM DESIGN ON STEP-STRESS LIFE TESTING C. Xiong Follow this and additional works at: http://newprairiepress.org/agstatconference
Temperature and Humidity Acceleration Factors on MLV Lifetime
 Temperature and Humidity Acceleration Factors on MLV Lifetime With and Without DC Bias Greg Caswell Introduction This white paper assesses the temperature and humidity acceleration factors both with and
Temperature and Humidity Acceleration Factors on MLV Lifetime With and Without DC Bias Greg Caswell Introduction This white paper assesses the temperature and humidity acceleration factors both with and
INFERENCE FOR A GAMMA STEP-STRESS MODEL UNDER CENSORING
 INFERENCE FOR A GAMMA STEP-STRESS MODEL UNDER CENSORING INFERENCE FOR A GAMMA STEP-STRESS MODEL UNDER CENSORING BY LAILA ALKHALFAN, M.Sc. McMaster University a thesis submitted to the school of graduate
INFERENCE FOR A GAMMA STEP-STRESS MODEL UNDER CENSORING INFERENCE FOR A GAMMA STEP-STRESS MODEL UNDER CENSORING BY LAILA ALKHALFAN, M.Sc. McMaster University a thesis submitted to the school of graduate
Data: Singly right censored observations from a temperatureaccelerated
 Chapter 19 Analyzing Accelerated Life Test Data William Q Meeker and Luis A Escobar Iowa State University and Louisiana State University Copyright 1998-2008 W Q Meeker and L A Escobar Based on the authors
Chapter 19 Analyzing Accelerated Life Test Data William Q Meeker and Luis A Escobar Iowa State University and Louisiana State University Copyright 1998-2008 W Q Meeker and L A Escobar Based on the authors
Statistical Inference on Constant Stress Accelerated Life Tests Under Generalized Gamma Lifetime Distributions
 Int. Statistical Inst.: Proc. 58th World Statistical Congress, 2011, Dublin (Session CPS040) p.4828 Statistical Inference on Constant Stress Accelerated Life Tests Under Generalized Gamma Lifetime Distributions
Int. Statistical Inst.: Proc. 58th World Statistical Congress, 2011, Dublin (Session CPS040) p.4828 Statistical Inference on Constant Stress Accelerated Life Tests Under Generalized Gamma Lifetime Distributions
Optimum Times for Step-Stress Cumulative Exposure Model Using Log-Logistic Distribution with Known Scale Parameter
 AUSTRIAN JOURNAL OF STATISTICS Volume 38 (2009, Number 1, 59 66 Optimum Times for Step-Stress Cumulative Exposure Model Using Log-Logistic Distribution with Known Scale Parameter Abedel-Qader Al-Masri
AUSTRIAN JOURNAL OF STATISTICS Volume 38 (2009, Number 1, 59 66 Optimum Times for Step-Stress Cumulative Exposure Model Using Log-Logistic Distribution with Known Scale Parameter Abedel-Qader Al-Masri
Chapter 17. Failure-Time Regression Analysis. William Q. Meeker and Luis A. Escobar Iowa State University and Louisiana State University
 Chapter 17 Failure-Time Regression Analysis William Q. Meeker and Luis A. Escobar Iowa State University and Louisiana State University Copyright 1998-2008 W. Q. Meeker and L. A. Escobar. Based on the authors
Chapter 17 Failure-Time Regression Analysis William Q. Meeker and Luis A. Escobar Iowa State University and Louisiana State University Copyright 1998-2008 W. Q. Meeker and L. A. Escobar. Based on the authors
Bilevel-Programming Based Time-Censored Ramp-Stress ALTSP with Warranty Cost
 International Journal of Performability Engineering Vol., No.3, May, 24, pp.28-29. RAMS Consultants Printed in India Bilevel-Programming Based Time-Censored Ramp-Stress ALTSP with Warranty Cost PREETI
International Journal of Performability Engineering Vol., No.3, May, 24, pp.28-29. RAMS Consultants Printed in India Bilevel-Programming Based Time-Censored Ramp-Stress ALTSP with Warranty Cost PREETI
Comparative Distributions of Hazard Modeling Analysis
 Comparative s of Hazard Modeling Analysis Rana Abdul Wajid Professor and Director Center for Statistics Lahore School of Economics Lahore E-mail: drrana@lse.edu.pk M. Shuaib Khan Department of Statistics
Comparative s of Hazard Modeling Analysis Rana Abdul Wajid Professor and Director Center for Statistics Lahore School of Economics Lahore E-mail: drrana@lse.edu.pk M. Shuaib Khan Department of Statistics
Bayesian Analysis for Step-Stress Accelerated Life Testing using Weibull Proportional Hazard Model
 Noname manuscript No. (will be inserted by the editor) Bayesian Analysis for Step-Stress Accelerated Life Testing using Weibull Proportional Hazard Model Naijun Sha Rong Pan Received: date / Accepted:
Noname manuscript No. (will be inserted by the editor) Bayesian Analysis for Step-Stress Accelerated Life Testing using Weibull Proportional Hazard Model Naijun Sha Rong Pan Received: date / Accepted:
Chapter 18. Accelerated Test Models. William Q. Meeker and Luis A. Escobar Iowa State University and Louisiana State University
 Chapter 18 Accelerated Test Models William Q. Meeker and Luis A. Escobar Iowa State University and Louisiana State University Copyright 1998-2008 W. Q. Meeker and L. A. Escobar. Based on the authors text
Chapter 18 Accelerated Test Models William Q. Meeker and Luis A. Escobar Iowa State University and Louisiana State University Copyright 1998-2008 W. Q. Meeker and L. A. Escobar. Based on the authors text
Bayesian Analysis of Simple Step-stress Model under Weibull Lifetimes
 Bayesian Analysis of Simple Step-stress Model under Weibull Lifetimes A. Ganguly 1, D. Kundu 2,3, S. Mitra 2 Abstract Step-stress model is becoming quite popular in recent times for analyzing lifetime
Bayesian Analysis of Simple Step-stress Model under Weibull Lifetimes A. Ganguly 1, D. Kundu 2,3, S. Mitra 2 Abstract Step-stress model is becoming quite popular in recent times for analyzing lifetime
Design of Repetitive Acceptance Sampling Plan for Truncated Life Test using Inverse Weibull Distribution
 Design of Repetitive Acceptance Sampling Plan for Truncated Life Test using Inverse Weibull Distribution Navjeet Singh 1, Navyodh Singh 2, Harpreet Kaur 3 1 Department of Mathematics, Sant Baba Bhag Singh
Design of Repetitive Acceptance Sampling Plan for Truncated Life Test using Inverse Weibull Distribution Navjeet Singh 1, Navyodh Singh 2, Harpreet Kaur 3 1 Department of Mathematics, Sant Baba Bhag Singh
Reliability analysis under constant-stress partially accelerated life tests using hybrid censored data from Weibull distribution
 Hacettepe Journal of Mathematics and Statistics Volume 45 (1) (2016), 181 193 Reliability analysis under constant-stress partially accelerated life tests using hybrid censored data from Weibull distribution
Hacettepe Journal of Mathematics and Statistics Volume 45 (1) (2016), 181 193 Reliability analysis under constant-stress partially accelerated life tests using hybrid censored data from Weibull distribution
STEP STRESS TESTS AND SOME EXACT INFERENTIAL RESULTS N. BALAKRISHNAN. McMaster University Hamilton, Ontario, Canada. p.
 p. 1/6 STEP STRESS TESTS AND SOME EXACT INFERENTIAL RESULTS N. BALAKRISHNAN bala@mcmaster.ca McMaster University Hamilton, Ontario, Canada p. 2/6 In collaboration with Debasis Kundu, IIT, Kapur, India
p. 1/6 STEP STRESS TESTS AND SOME EXACT INFERENTIAL RESULTS N. BALAKRISHNAN bala@mcmaster.ca McMaster University Hamilton, Ontario, Canada p. 2/6 In collaboration with Debasis Kundu, IIT, Kapur, India
Accelerated Life Test Principles and Applications in Power Solutions
 Accelerated Life Test Principles and Applications in Power Solutions Created by Michael Shover, Ph.D., Advanced Energy Industries, Inc. Abstract This paper discusses using an Accelerated Life Test (ALT)
Accelerated Life Test Principles and Applications in Power Solutions Created by Michael Shover, Ph.D., Advanced Energy Industries, Inc. Abstract This paper discusses using an Accelerated Life Test (ALT)
Arrhenius Plot. Sample StatFolio: arrhenius.sgp
 Summary The procedure is designed to plot data from an accelerated life test in which failure times have been recorded and percentiles estimated at a number of different temperatures. The percentiles P
Summary The procedure is designed to plot data from an accelerated life test in which failure times have been recorded and percentiles estimated at a number of different temperatures. The percentiles P
Bivariate Degradation Modeling Based on Gamma Process
 Bivariate Degradation Modeling Based on Gamma Process Jinglun Zhou Zhengqiang Pan Member IAENG and Quan Sun Abstract Many highly reliable products have two or more performance characteristics (PCs). The
Bivariate Degradation Modeling Based on Gamma Process Jinglun Zhou Zhengqiang Pan Member IAENG and Quan Sun Abstract Many highly reliable products have two or more performance characteristics (PCs). The
Bayesian Methods for Accelerated Destructive Degradation Test Planning
 Statistics Preprints Statistics 11-2010 Bayesian Methods for Accelerated Destructive Degradation Test Planning Ying Shi Iowa State University William Q. Meeker Iowa State University, wqmeeker@iastate.edu
Statistics Preprints Statistics 11-2010 Bayesian Methods for Accelerated Destructive Degradation Test Planning Ying Shi Iowa State University William Q. Meeker Iowa State University, wqmeeker@iastate.edu
(QALT): Data Analysis and Test Design
 (QALT): Data Analysis and Test Design Huairui(Harry) Guo, Ph.D, CRE, CQE Thanasis Gerokostopoulos, CRE, CQE ASTR 2013, Oct. 9-11, San Diego, CA Qualitative vs. Quantitative ALT (Accelerated Life Tests)
(QALT): Data Analysis and Test Design Huairui(Harry) Guo, Ph.D, CRE, CQE Thanasis Gerokostopoulos, CRE, CQE ASTR 2013, Oct. 9-11, San Diego, CA Qualitative vs. Quantitative ALT (Accelerated Life Tests)
Accelerated Testing Obtaining Reliability Information Quickly
 Accelerated Testing Background Accelerated Testing Obtaining Reliability Information Quickly William Q. Meeker Department of Statistics and Center for Nondestructive Evaluation Iowa State University Ames,
Accelerated Testing Background Accelerated Testing Obtaining Reliability Information Quickly William Q. Meeker Department of Statistics and Center for Nondestructive Evaluation Iowa State University Ames,
Parameters Estimation for a Linear Exponential Distribution Based on Grouped Data
 International Mathematical Forum, 3, 2008, no. 33, 1643-1654 Parameters Estimation for a Linear Exponential Distribution Based on Grouped Data A. Al-khedhairi Department of Statistics and O.R. Faculty
International Mathematical Forum, 3, 2008, no. 33, 1643-1654 Parameters Estimation for a Linear Exponential Distribution Based on Grouped Data A. Al-khedhairi Department of Statistics and O.R. Faculty
Reliability Analysis of Tampered Failure Rate Load-Sharing k-out-of-n:g Systems
 Reliability Analysis of Tampered Failure Rate Load-Sharing k-out-of-n:g Systems Suprasad V. Amari Relex Software Corporation 540 Pellis Road Greensburg, PA 15601 USA Krishna B. Misra RAMS Consultants 71
Reliability Analysis of Tampered Failure Rate Load-Sharing k-out-of-n:g Systems Suprasad V. Amari Relex Software Corporation 540 Pellis Road Greensburg, PA 15601 USA Krishna B. Misra RAMS Consultants 71
Reliability Engineering I
 Happiness is taking the reliability final exam. Reliability Engineering I ENM/MSC 565 Review for the Final Exam Vital Statistics What R&M concepts covered in the course When Monday April 29 from 4:30 6:00
Happiness is taking the reliability final exam. Reliability Engineering I ENM/MSC 565 Review for the Final Exam Vital Statistics What R&M concepts covered in the course When Monday April 29 from 4:30 6:00
Estimation and Confidence Intervals for Parameters of a Cumulative Damage Model
 United States Department of Agriculture Forest Service Forest Products Laboratory Research Paper FPL-RP-484 Estimation and Confidence Intervals for Parameters of a Cumulative Damage Model Carol L. Link
United States Department of Agriculture Forest Service Forest Products Laboratory Research Paper FPL-RP-484 Estimation and Confidence Intervals for Parameters of a Cumulative Damage Model Carol L. Link
Accelerated Destructive Degradation Test Planning
 Accelerated Destructive Degradation Test Planning Ying Shi Dept. of Statistics Iowa State University Ames, IA 50011 yshi@iastate.edu Luis A. Escobar Dept. of Experimental Statistics Louisiana State University
Accelerated Destructive Degradation Test Planning Ying Shi Dept. of Statistics Iowa State University Ames, IA 50011 yshi@iastate.edu Luis A. Escobar Dept. of Experimental Statistics Louisiana State University
Estimation of the Bivariate Generalized. Lomax Distribution Parameters. Based on Censored Samples
 Int. J. Contemp. Math. Sciences, Vol. 9, 2014, no. 6, 257-267 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/10.12988/ijcms.2014.4329 Estimation of the Bivariate Generalized Lomax Distribution Parameters
Int. J. Contemp. Math. Sciences, Vol. 9, 2014, no. 6, 257-267 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/10.12988/ijcms.2014.4329 Estimation of the Bivariate Generalized Lomax Distribution Parameters
Exact Inference for the Two-Parameter Exponential Distribution Under Type-II Hybrid Censoring
 Exact Inference for the Two-Parameter Exponential Distribution Under Type-II Hybrid Censoring A. Ganguly, S. Mitra, D. Samanta, D. Kundu,2 Abstract Epstein [9] introduced the Type-I hybrid censoring scheme
Exact Inference for the Two-Parameter Exponential Distribution Under Type-II Hybrid Censoring A. Ganguly, S. Mitra, D. Samanta, D. Kundu,2 Abstract Epstein [9] introduced the Type-I hybrid censoring scheme
Chapter 15. System Reliability Concepts and Methods. William Q. Meeker and Luis A. Escobar Iowa State University and Louisiana State University
 Chapter 15 System Reliability Concepts and Methods William Q. Meeker and Luis A. Escobar Iowa State University and Louisiana State University Copyright 1998-2008 W. Q. Meeker and L. A. Escobar. Based on
Chapter 15 System Reliability Concepts and Methods William Q. Meeker and Luis A. Escobar Iowa State University and Louisiana State University Copyright 1998-2008 W. Q. Meeker and L. A. Escobar. Based on
Basics of Uncertainty Analysis
 Basics of Uncertainty Analysis Chapter Six Basics of Uncertainty Analysis 6.1 Introduction As shown in Fig. 6.1, analysis models are used to predict the performances or behaviors of a product under design.
Basics of Uncertainty Analysis Chapter Six Basics of Uncertainty Analysis 6.1 Introduction As shown in Fig. 6.1, analysis models are used to predict the performances or behaviors of a product under design.
Bayesian Estimation for the Generalized Logistic Distribution Type-II Censored Accelerated Life Testing
 Int. J. Contemp. Math. Sciences, Vol. 8, 2013, no. 20, 969-986 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/10.12988/ijcms.2013.39111 Bayesian Estimation for the Generalized Logistic Distribution Type-II
Int. J. Contemp. Math. Sciences, Vol. 8, 2013, no. 20, 969-986 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/10.12988/ijcms.2013.39111 Bayesian Estimation for the Generalized Logistic Distribution Type-II
ACCELERATED DESTRUCTIVE DEGRADATION TEST PLANNING. Presented by Luis A. Escobar Experimental Statistics LSU, Baton Rouge LA 70803
 ACCELERATED DESTRUCTIVE DEGRADATION TEST PLANNING Presented by Luis A. Escobar Experimental Statistics LSU, Baton Rouge LA 70803 This is jointly work with Ying Shi and William Q. Meeker both from Iowa
ACCELERATED DESTRUCTIVE DEGRADATION TEST PLANNING Presented by Luis A. Escobar Experimental Statistics LSU, Baton Rouge LA 70803 This is jointly work with Ying Shi and William Q. Meeker both from Iowa
Bayesian Life Test Planning for the Weibull Distribution with Given Shape Parameter
 Statistics Preprints Statistics 10-8-2002 Bayesian Life Test Planning for the Weibull Distribution with Given Shape Parameter Yao Zhang Iowa State University William Q. Meeker Iowa State University, wqmeeker@iastate.edu
Statistics Preprints Statistics 10-8-2002 Bayesian Life Test Planning for the Weibull Distribution with Given Shape Parameter Yao Zhang Iowa State University William Q. Meeker Iowa State University, wqmeeker@iastate.edu
Notes largely based on Statistical Methods for Reliability Data by W.Q. Meeker and L. A. Escobar, Wiley, 1998 and on their class notes.
 Unit 2: Models, Censoring, and Likelihood for Failure-Time Data Notes largely based on Statistical Methods for Reliability Data by W.Q. Meeker and L. A. Escobar, Wiley, 1998 and on their class notes. Ramón
Unit 2: Models, Censoring, and Likelihood for Failure-Time Data Notes largely based on Statistical Methods for Reliability Data by W.Q. Meeker and L. A. Escobar, Wiley, 1998 and on their class notes. Ramón
Lifetime prediction and confidence bounds in accelerated degradation testing for lognormal response distributions with an Arrhenius rate relationship
 Scholars' Mine Doctoral Dissertations Student Research & Creative Works Spring 01 Lifetime prediction and confidence bounds in accelerated degradation testing for lognormal response distributions with
Scholars' Mine Doctoral Dissertations Student Research & Creative Works Spring 01 Lifetime prediction and confidence bounds in accelerated degradation testing for lognormal response distributions with
A General Bayes Weibull Inference Model for Accelerated Life Testing
 A General Bayes Weibull Inference Model for Accelerated Life Testing J. René Van Dorp & Thomas A. Mazzuchi The George Washington University, Washington D.C., USA Submitted to: European Safety and Reliability
A General Bayes Weibull Inference Model for Accelerated Life Testing J. René Van Dorp & Thomas A. Mazzuchi The George Washington University, Washington D.C., USA Submitted to: European Safety and Reliability
On the Application of Design of Experiments to Accelerated Life Testing
 Linköping Studies in Science and Technology. Thesis No. 323 On the Application of Design of Experiments to Accelerated Life Testing Mohsen Hakim - Mashhadi # LiU-Tek-Lic-1992: 15 Division of Quality Technology
Linköping Studies in Science and Technology. Thesis No. 323 On the Application of Design of Experiments to Accelerated Life Testing Mohsen Hakim - Mashhadi # LiU-Tek-Lic-1992: 15 Division of Quality Technology
Optimum Hybrid Censoring Scheme using Cost Function Approach
 Optimum Hybrid Censoring Scheme using Cost Function Approach Ritwik Bhattacharya 1, Biswabrata Pradhan 1, Anup Dewanji 2 1 SQC and OR Unit, Indian Statistical Institute, 203, B. T. Road, Kolkata, PIN-
Optimum Hybrid Censoring Scheme using Cost Function Approach Ritwik Bhattacharya 1, Biswabrata Pradhan 1, Anup Dewanji 2 1 SQC and OR Unit, Indian Statistical Institute, 203, B. T. Road, Kolkata, PIN-
Weibull Reliability Analysis
 Weibull Reliability Analysis = http://www.rt.cs.boeing.com/mea/stat/reliability.html Fritz Scholz (425-865-3623, 7L-22) Boeing Phantom Works Mathematics &Computing Technology Weibull Reliability Analysis
Weibull Reliability Analysis = http://www.rt.cs.boeing.com/mea/stat/reliability.html Fritz Scholz (425-865-3623, 7L-22) Boeing Phantom Works Mathematics &Computing Technology Weibull Reliability Analysis
Unit 10: Planning Life Tests
 Unit 10: Planning Life Tests Ramón V. León Notes largely based on Statistical Methods for Reliability Data by W.Q. Meeker and L. A. Escobar, Wiley, 1998 and on their class notes. 11/2/2004 Unit 10 - Stat
Unit 10: Planning Life Tests Ramón V. León Notes largely based on Statistical Methods for Reliability Data by W.Q. Meeker and L. A. Escobar, Wiley, 1998 and on their class notes. 11/2/2004 Unit 10 - Stat
Point and Interval Estimation for Gaussian Distribution, Based on Progressively Type-II Censored Samples
 90 IEEE TRANSACTIONS ON RELIABILITY, VOL. 52, NO. 1, MARCH 2003 Point and Interval Estimation for Gaussian Distribution, Based on Progressively Type-II Censored Samples N. Balakrishnan, N. Kannan, C. T.
90 IEEE TRANSACTIONS ON RELIABILITY, VOL. 52, NO. 1, MARCH 2003 Point and Interval Estimation for Gaussian Distribution, Based on Progressively Type-II Censored Samples N. Balakrishnan, N. Kannan, C. T.
Introduction to Reliability Theory (part 2)
 Introduction to Reliability Theory (part 2) Frank Coolen UTOPIAE Training School II, Durham University 3 July 2018 (UTOPIAE) Introduction to Reliability Theory 1 / 21 Outline Statistical issues Software
Introduction to Reliability Theory (part 2) Frank Coolen UTOPIAE Training School II, Durham University 3 July 2018 (UTOPIAE) Introduction to Reliability Theory 1 / 21 Outline Statistical issues Software
Semiconductor Reliability
 Semiconductor Reliability. Semiconductor Device Failure Region Below figure shows the time-dependent change in the semiconductor device failure rate. Discussions on failure rate change in time often classify
Semiconductor Reliability. Semiconductor Device Failure Region Below figure shows the time-dependent change in the semiconductor device failure rate. Discussions on failure rate change in time often classify
Chapter 5. System Reliability and Reliability Prediction.
 Chapter 5. System Reliability and Reliability Prediction. Problems & Solutions. Problem 1. Estimate the individual part failure rate given a base failure rate of 0.0333 failure/hour, a quality factor of
Chapter 5. System Reliability and Reliability Prediction. Problems & Solutions. Problem 1. Estimate the individual part failure rate given a base failure rate of 0.0333 failure/hour, a quality factor of
Failure rate in the continuous sense. Figure. Exponential failure density functions [f(t)] 1
![Failure rate in the continuous sense. Figure. Exponential failure density functions [f(t)] 1 Failure rate in the continuous sense. Figure. Exponential failure density functions [f(t)] 1](/thumbs/73/68618961.jpg) Failure rate (Updated and Adapted from Notes by Dr. A.K. Nema) Part 1: Failure rate is the frequency with which an engineered system or component fails, expressed for example in failures per hour. It is
Failure rate (Updated and Adapted from Notes by Dr. A.K. Nema) Part 1: Failure rate is the frequency with which an engineered system or component fails, expressed for example in failures per hour. It is
IoT Network Quality/Reliability
 IoT Network Quality/Reliability IEEE PHM June 19, 2017 Byung K. Yi, Dr. of Sci. Executive V.P. & CTO, InterDigital Communications, Inc Louis Kerofsky, PhD. Director of Partner Development InterDigital
IoT Network Quality/Reliability IEEE PHM June 19, 2017 Byung K. Yi, Dr. of Sci. Executive V.P. & CTO, InterDigital Communications, Inc Louis Kerofsky, PhD. Director of Partner Development InterDigital
INVERTED KUMARASWAMY DISTRIBUTION: PROPERTIES AND ESTIMATION
 Pak. J. Statist. 2017 Vol. 33(1), 37-61 INVERTED KUMARASWAMY DISTRIBUTION: PROPERTIES AND ESTIMATION A. M. Abd AL-Fattah, A.A. EL-Helbawy G.R. AL-Dayian Statistics Department, Faculty of Commerce, AL-Azhar
Pak. J. Statist. 2017 Vol. 33(1), 37-61 INVERTED KUMARASWAMY DISTRIBUTION: PROPERTIES AND ESTIMATION A. M. Abd AL-Fattah, A.A. EL-Helbawy G.R. AL-Dayian Statistics Department, Faculty of Commerce, AL-Azhar
Using Accelerated Life Tests Results to Predict Product Field Reliability
 Statistics Preprints Statistics 6-2008 Using Accelerated Life Tests Results to Predict Product Field Reliability William Q. Meeker Iowa State University, wqmeeker@iastate.edu Luis A. Escobar Louisiana
Statistics Preprints Statistics 6-2008 Using Accelerated Life Tests Results to Predict Product Field Reliability William Q. Meeker Iowa State University, wqmeeker@iastate.edu Luis A. Escobar Louisiana
Key Words: survival analysis; bathtub hazard; accelerated failure time (AFT) regression; power-law distribution.
 POWER-LAW ADJUSTED SURVIVAL MODELS William J. Reed Department of Mathematics & Statistics University of Victoria PO Box 3060 STN CSC Victoria, B.C. Canada V8W 3R4 reed@math.uvic.ca Key Words: survival
POWER-LAW ADJUSTED SURVIVAL MODELS William J. Reed Department of Mathematics & Statistics University of Victoria PO Box 3060 STN CSC Victoria, B.C. Canada V8W 3R4 reed@math.uvic.ca Key Words: survival
ON THE FAILURE RATE ESTIMATION OF THE INVERSE GAUSSIAN DISTRIBUTION
 ON THE FAILURE RATE ESTIMATION OF THE INVERSE GAUSSIAN DISTRIBUTION ZHENLINYANGandRONNIET.C.LEE Department of Statistics and Applied Probability, National University of Singapore, 3 Science Drive 2, Singapore
ON THE FAILURE RATE ESTIMATION OF THE INVERSE GAUSSIAN DISTRIBUTION ZHENLINYANGandRONNIET.C.LEE Department of Statistics and Applied Probability, National University of Singapore, 3 Science Drive 2, Singapore
Analysis of Type-II Progressively Hybrid Censored Data
 Analysis of Type-II Progressively Hybrid Censored Data Debasis Kundu & Avijit Joarder Abstract The mixture of Type-I and Type-II censoring schemes, called the hybrid censoring scheme is quite common in
Analysis of Type-II Progressively Hybrid Censored Data Debasis Kundu & Avijit Joarder Abstract The mixture of Type-I and Type-II censoring schemes, called the hybrid censoring scheme is quite common in
Engineering Risk Benefit Analysis
 Engineering Risk Benefit Analysis 1.155, 2.943, 3.577, 6.938, 10.816, 13.621, 16.862, 22.82, ESD.72, ESD.721 RPRA 3. Probability Distributions in RPRA George E. Apostolakis Massachusetts Institute of Technology
Engineering Risk Benefit Analysis 1.155, 2.943, 3.577, 6.938, 10.816, 13.621, 16.862, 22.82, ESD.72, ESD.721 RPRA 3. Probability Distributions in RPRA George E. Apostolakis Massachusetts Institute of Technology
On the Comparison of Fisher Information of the Weibull and GE Distributions
 On the Comparison of Fisher Information of the Weibull and GE Distributions Rameshwar D. Gupta Debasis Kundu Abstract In this paper we consider the Fisher information matrices of the generalized exponential
On the Comparison of Fisher Information of the Weibull and GE Distributions Rameshwar D. Gupta Debasis Kundu Abstract In this paper we consider the Fisher information matrices of the generalized exponential
Bayesian Life Test Planning for the Log-Location- Scale Family of Distributions
 Statistics Preprints Statistics 3-14 Bayesian Life Test Planning for the Log-Location- Scale Family of Distributions Yili Hong Virginia Tech Caleb King Virginia Tech Yao Zhang Pfizer Global Research and
Statistics Preprints Statistics 3-14 Bayesian Life Test Planning for the Log-Location- Scale Family of Distributions Yili Hong Virginia Tech Caleb King Virginia Tech Yao Zhang Pfizer Global Research and
A Reliability Sampling Plan to ensure Percentiles through Weibull Poisson Distribution
 Volume 117 No. 13 2017, 155-163 ISSN: 1311-8080 (printed version); ISSN: 1314-3395 (on-line version) url: http://www.ijpam.eu ijpam.eu A Reliability Sampling Plan to ensure Percentiles through Weibull
Volume 117 No. 13 2017, 155-163 ISSN: 1311-8080 (printed version); ISSN: 1314-3395 (on-line version) url: http://www.ijpam.eu ijpam.eu A Reliability Sampling Plan to ensure Percentiles through Weibull
Statistics for Engineers Lecture 4 Reliability and Lifetime Distributions
 Statistics for Engineers Lecture 4 Reliability and Lifetime Distributions Chong Ma Department of Statistics University of South Carolina chongm@email.sc.edu February 15, 2017 Chong Ma (Statistics, USC)
Statistics for Engineers Lecture 4 Reliability and Lifetime Distributions Chong Ma Department of Statistics University of South Carolina chongm@email.sc.edu February 15, 2017 Chong Ma (Statistics, USC)
Prediction for Two-Phase Degradation. A thesis presented to. the faculty of. In partial fulfillment. of the requirements for the degree
 Bayesian Degradation Analysis Considering Competing Risks and Residual-Life Prediction for Two-Phase Degradation A thesis presented to the faculty of the Russ College of Engineering and Technology of Ohio
Bayesian Degradation Analysis Considering Competing Risks and Residual-Life Prediction for Two-Phase Degradation A thesis presented to the faculty of the Russ College of Engineering and Technology of Ohio
Statistical Inference and Methods
 Department of Mathematics Imperial College London d.stephens@imperial.ac.uk http://stats.ma.ic.ac.uk/ das01/ 31st January 2006 Part VI Session 6: Filtering and Time to Event Data Session 6: Filtering and
Department of Mathematics Imperial College London d.stephens@imperial.ac.uk http://stats.ma.ic.ac.uk/ das01/ 31st January 2006 Part VI Session 6: Filtering and Time to Event Data Session 6: Filtering and
Accelerated life testing in the presence of dependent competing causes of failure
 isid/ms/25/5 April 21, 25 http://www.isid.ac.in/ statmath/eprints Accelerated life testing in the presence of dependent competing causes of failure Isha Dewan S. B. Kulathinal Indian Statistical Institute,
isid/ms/25/5 April 21, 25 http://www.isid.ac.in/ statmath/eprints Accelerated life testing in the presence of dependent competing causes of failure Isha Dewan S. B. Kulathinal Indian Statistical Institute,
STAT 6350 Analysis of Lifetime Data. Probability Plotting
 STAT 6350 Analysis of Lifetime Data Probability Plotting Purpose of Probability Plots Probability plots are an important tool for analyzing data and have been particular popular in the analysis of life
STAT 6350 Analysis of Lifetime Data Probability Plotting Purpose of Probability Plots Probability plots are an important tool for analyzing data and have been particular popular in the analysis of life
Objective Experiments Glossary of Statistical Terms
 Objective Experiments Glossary of Statistical Terms This glossary is intended to provide friendly definitions for terms used commonly in engineering and science. It is not intended to be absolutely precise.
Objective Experiments Glossary of Statistical Terms This glossary is intended to provide friendly definitions for terms used commonly in engineering and science. It is not intended to be absolutely precise.
Modified Norris Landzberg Model and Optimum Design of Temperature Cycling ALT
 UDC 539.4 Modified Norris Landzberg Model and Optimum Design of Temperature Cycling ALT F. Q. Sun, a,b,1 J. C. Liu, a,b Z. Q. Cao, b X. Y. Li, a,b and T. M. Jiang b a Science and Technology on Reliability
UDC 539.4 Modified Norris Landzberg Model and Optimum Design of Temperature Cycling ALT F. Q. Sun, a,b,1 J. C. Liu, a,b Z. Q. Cao, b X. Y. Li, a,b and T. M. Jiang b a Science and Technology on Reliability
STAT 6350 Analysis of Lifetime Data. Failure-time Regression Analysis
 STAT 6350 Analysis of Lifetime Data Failure-time Regression Analysis Explanatory Variables for Failure Times Usually explanatory variables explain/predict why some units fail quickly and some units survive
STAT 6350 Analysis of Lifetime Data Failure-time Regression Analysis Explanatory Variables for Failure Times Usually explanatory variables explain/predict why some units fail quickly and some units survive
n =10,220 observations. Smaller samples analyzed here to illustrate sample size effect.
 Chapter 7 Parametric Likelihood Fitting Concepts: Chapter 7 Parametric Likelihood Fitting Concepts: Objectives Show how to compute a likelihood for a parametric model using discrete data. Show how to compute
Chapter 7 Parametric Likelihood Fitting Concepts: Chapter 7 Parametric Likelihood Fitting Concepts: Objectives Show how to compute a likelihood for a parametric model using discrete data. Show how to compute
Exponentiated Rayleigh Distribution: A Bayes Study Using MCMC Approach Based on Unified Hybrid Censored Data
 Exponentiated Rayleigh Distribution: A Bayes Study Using MCMC Approach Based on Unified Hybrid Censored Data ABSTRACT M. G. M. Ghazal 1, H. M. Hasaballah 2 1 Mathematics Department, Faculty of Science,
Exponentiated Rayleigh Distribution: A Bayes Study Using MCMC Approach Based on Unified Hybrid Censored Data ABSTRACT M. G. M. Ghazal 1, H. M. Hasaballah 2 1 Mathematics Department, Faculty of Science,
Copula Regression RAHUL A. PARSA DRAKE UNIVERSITY & STUART A. KLUGMAN SOCIETY OF ACTUARIES CASUALTY ACTUARIAL SOCIETY MAY 18,2011
 Copula Regression RAHUL A. PARSA DRAKE UNIVERSITY & STUART A. KLUGMAN SOCIETY OF ACTUARIES CASUALTY ACTUARIAL SOCIETY MAY 18,2011 Outline Ordinary Least Squares (OLS) Regression Generalized Linear Models
Copula Regression RAHUL A. PARSA DRAKE UNIVERSITY & STUART A. KLUGMAN SOCIETY OF ACTUARIES CASUALTY ACTUARIAL SOCIETY MAY 18,2011 Outline Ordinary Least Squares (OLS) Regression Generalized Linear Models
p-birnbaum SAUNDERS DISTRIBUTION: APPLICATIONS TO RELIABILITY AND ELECTRONIC BANKING HABITS
 p-birnbaum SAUNDERS DISTRIBUTION: APPLICATIONS TO RELIABILITY AND ELECTRONIC BANKING 1 V.M.Chacko, Mariya Jeeja P V and 3 Deepa Paul 1, Department of Statistics St.Thomas College, Thrissur Kerala-681 e-mail:chackovm@gmail.com
p-birnbaum SAUNDERS DISTRIBUTION: APPLICATIONS TO RELIABILITY AND ELECTRONIC BANKING 1 V.M.Chacko, Mariya Jeeja P V and 3 Deepa Paul 1, Department of Statistics St.Thomas College, Thrissur Kerala-681 e-mail:chackovm@gmail.com
Multistate Modeling and Applications
 Multistate Modeling and Applications Yang Yang Department of Statistics University of Michigan, Ann Arbor IBM Research Graduate Student Workshop: Statistics for a Smarter Planet Yang Yang (UM, Ann Arbor)
Multistate Modeling and Applications Yang Yang Department of Statistics University of Michigan, Ann Arbor IBM Research Graduate Student Workshop: Statistics for a Smarter Planet Yang Yang (UM, Ann Arbor)
Strategic Allocation of Test Units in an Accelerated Degradation Test Plan
 Strategic Allocation of Test Units in an Accelerated Degradation Test Plan Zhi-Sheng YE, Qingpei HU, and Dan YU Department of Industrial and Systems Engineering, National University of Singapore Academy
Strategic Allocation of Test Units in an Accelerated Degradation Test Plan Zhi-Sheng YE, Qingpei HU, and Dan YU Department of Industrial and Systems Engineering, National University of Singapore Academy
The Relationship Between Confidence Intervals for Failure Probabilities and Life Time Quantiles
 Statistics Preprints Statistics 2008 The Relationship Between Confidence Intervals for Failure Probabilities and Life Time Quantiles Yili Hong Iowa State University, yili_hong@hotmail.com William Q. Meeker
Statistics Preprints Statistics 2008 The Relationship Between Confidence Intervals for Failure Probabilities and Life Time Quantiles Yili Hong Iowa State University, yili_hong@hotmail.com William Q. Meeker
Estimation of Quantiles
 9 Estimation of Quantiles The notion of quantiles was introduced in Section 3.2: recall that a quantile x α for an r.v. X is a constant such that P(X x α )=1 α. (9.1) In this chapter we examine quantiles
9 Estimation of Quantiles The notion of quantiles was introduced in Section 3.2: recall that a quantile x α for an r.v. X is a constant such that P(X x α )=1 α. (9.1) In this chapter we examine quantiles
Hybrid Censoring; An Introduction 2
 Hybrid Censoring; An Introduction 2 Debasis Kundu Department of Mathematics & Statistics Indian Institute of Technology Kanpur 23-rd November, 2010 2 This is a joint work with N. Balakrishnan Debasis Kundu
Hybrid Censoring; An Introduction 2 Debasis Kundu Department of Mathematics & Statistics Indian Institute of Technology Kanpur 23-rd November, 2010 2 This is a joint work with N. Balakrishnan Debasis Kundu
Simultaneous Prediction Intervals for the (Log)- Location-Scale Family of Distributions
 Statistics Preprints Statistics 10-2014 Simultaneous Prediction Intervals for the (Log)- Location-Scale Family of Distributions Yimeng Xie Virginia Tech Yili Hong Virginia Tech Luis A. Escobar Louisiana
Statistics Preprints Statistics 10-2014 Simultaneous Prediction Intervals for the (Log)- Location-Scale Family of Distributions Yimeng Xie Virginia Tech Yili Hong Virginia Tech Luis A. Escobar Louisiana
Statistical Methods for Reliability Data from Designed Experiments
 Statistical Methods for Reliability Data from Designed Experiments Laura J. Freeman Dissertation submitted to the Faculty of the Virginia Polytechnic Institute and State University in partial fulfillment
Statistical Methods for Reliability Data from Designed Experiments Laura J. Freeman Dissertation submitted to the Faculty of the Virginia Polytechnic Institute and State University in partial fulfillment
Accelerated Destructive Degradation Tests: Data, Models, and Analysis
 Statistics Preprints Statistics 03 Accelerated Destructive Degradation Tests: Data, Models, and Analysis Luis A. Escobar Louisiana State University William Q. Meeker Iowa State University, wqmeeker@iastate.edu
Statistics Preprints Statistics 03 Accelerated Destructive Degradation Tests: Data, Models, and Analysis Luis A. Escobar Louisiana State University William Q. Meeker Iowa State University, wqmeeker@iastate.edu
Warranty Prediction Based on Auxiliary Use-rate Information
 Statistics Preprints Statistics 2009 Warranty Prediction Based on Auxiliary Use-rate Information Yili Hong Virginia Polytechnic Institute and State University William Q. Meeker Iowa State University, wqmeeker@iastate.edu
Statistics Preprints Statistics 2009 Warranty Prediction Based on Auxiliary Use-rate Information Yili Hong Virginia Polytechnic Institute and State University William Q. Meeker Iowa State University, wqmeeker@iastate.edu
Reliability prediction based on complicated data and dynamic data
 Graduate Theses and Dissertations Graduate College 2009 Reliability prediction based on complicated data and dynamic data Yili Hong Iowa State University Follow this and additional works at: http://lib.dr.iastate.edu/etd
Graduate Theses and Dissertations Graduate College 2009 Reliability prediction based on complicated data and dynamic data Yili Hong Iowa State University Follow this and additional works at: http://lib.dr.iastate.edu/etd
Noninformative Priors for the Ratio of the Scale Parameters in the Inverted Exponential Distributions
 Communications for Statistical Applications and Methods 03, Vol. 0, No. 5, 387 394 DOI: http://dx.doi.org/0.535/csam.03.0.5.387 Noninformative Priors for the Ratio of the Scale Parameters in the Inverted
Communications for Statistical Applications and Methods 03, Vol. 0, No. 5, 387 394 DOI: http://dx.doi.org/0.535/csam.03.0.5.387 Noninformative Priors for the Ratio of the Scale Parameters in the Inverted
Hazard Function, Failure Rate, and A Rule of Thumb for Calculating Empirical Hazard Function of Continuous-Time Failure Data
 Hazard Function, Failure Rate, and A Rule of Thumb for Calculating Empirical Hazard Function of Continuous-Time Failure Data Feng-feng Li,2, Gang Xie,2, Yong Sun,2, Lin Ma,2 CRC for Infrastructure and
Hazard Function, Failure Rate, and A Rule of Thumb for Calculating Empirical Hazard Function of Continuous-Time Failure Data Feng-feng Li,2, Gang Xie,2, Yong Sun,2, Lin Ma,2 CRC for Infrastructure and
A general Bayes weibull inference model for accelerated life testing
 A general Bayes weibull inference model for accelerated life testing J. René Van Dorp, Thomas A. Mazzuchi* Depratmenty of Engineering Management and Systems Engineering The George Washington University,
A general Bayes weibull inference model for accelerated life testing J. René Van Dorp, Thomas A. Mazzuchi* Depratmenty of Engineering Management and Systems Engineering The George Washington University,
Estimation in an Exponentiated Half Logistic Distribution under Progressively Type-II Censoring
 Communications of the Korean Statistical Society 2011, Vol. 18, No. 5, 657 666 DOI: http://dx.doi.org/10.5351/ckss.2011.18.5.657 Estimation in an Exponentiated Half Logistic Distribution under Progressively
Communications of the Korean Statistical Society 2011, Vol. 18, No. 5, 657 666 DOI: http://dx.doi.org/10.5351/ckss.2011.18.5.657 Estimation in an Exponentiated Half Logistic Distribution under Progressively
Statistical Prediction Based on Censored Life Data. Luis A. Escobar Department of Experimental Statistics Louisiana State University.
 Statistical Prediction Based on Censored Life Data Overview Luis A. Escobar Department of Experimental Statistics Louisiana State University and William Q. Meeker Department of Statistics Iowa State University
Statistical Prediction Based on Censored Life Data Overview Luis A. Escobar Department of Experimental Statistics Louisiana State University and William Q. Meeker Department of Statistics Iowa State University
Structural Reliability
 Structural Reliability Thuong Van DANG May 28, 2018 1 / 41 2 / 41 Introduction to Structural Reliability Concept of Limit State and Reliability Review of Probability Theory First Order Second Moment Method
Structural Reliability Thuong Van DANG May 28, 2018 1 / 41 2 / 41 Introduction to Structural Reliability Concept of Limit State and Reliability Review of Probability Theory First Order Second Moment Method
Chapter 2. 1 From Equation 2.10: P(A 1 F) ˆ P(A 1)P(F A 1 ) S i P(F A i )P(A i ) The denominator is
 Chapter 2 1 From Equation 2.10: P(A 1 F) ˆ P(A 1)P(F A 1 ) S i P(F A i )P(A i ) The denominator is 0:3 0:0001 0:01 0:005 0:001 0:002 0:0002 0:04 ˆ 0:00009 P(A 1 F) ˆ 0:0001 0:3 ˆ 0:133: 0:00009 Similarly
Chapter 2 1 From Equation 2.10: P(A 1 F) ˆ P(A 1)P(F A 1 ) S i P(F A i )P(A i ) The denominator is 0:3 0:0001 0:01 0:005 0:001 0:002 0:0002 0:04 ˆ 0:00009 P(A 1 F) ˆ 0:0001 0:3 ˆ 0:133: 0:00009 Similarly
Key Words: Lifetime Data Analysis (LDA), Probability Density Function (PDF), Goodness of fit methods, Chi-square method.
 Reliability prediction based on lifetime data analysis methodology: The pump case study Abstract: The business case aims to demonstrate the lifetime data analysis methodology application from the historical
Reliability prediction based on lifetime data analysis methodology: The pump case study Abstract: The business case aims to demonstrate the lifetime data analysis methodology application from the historical
Inference on reliability in two-parameter exponential stress strength model
 Metrika DOI 10.1007/s00184-006-0074-7 Inference on reliability in two-parameter exponential stress strength model K. Krishnamoorthy Shubhabrata Mukherjee Huizhen Guo Received: 19 January 2005 Springer-Verlag
Metrika DOI 10.1007/s00184-006-0074-7 Inference on reliability in two-parameter exponential stress strength model K. Krishnamoorthy Shubhabrata Mukherjee Huizhen Guo Received: 19 January 2005 Springer-Verlag
Survival Distributions, Hazard Functions, Cumulative Hazards
 BIO 244: Unit 1 Survival Distributions, Hazard Functions, Cumulative Hazards 1.1 Definitions: The goals of this unit are to introduce notation, discuss ways of probabilistically describing the distribution
BIO 244: Unit 1 Survival Distributions, Hazard Functions, Cumulative Hazards 1.1 Definitions: The goals of this unit are to introduce notation, discuss ways of probabilistically describing the distribution
A Time Truncated Two Stage Group Acceptance Sampling Plan For Compound Rayleigh Distribution
 International Journal of Mathematics And its Applications Volume 4, Issue 3 A (2016), 73 80. ISSN: 2347-1557 Available Online: http://ijmaa.in/ International Journal 2347-1557 of Mathematics Applications
International Journal of Mathematics And its Applications Volume 4, Issue 3 A (2016), 73 80. ISSN: 2347-1557 Available Online: http://ijmaa.in/ International Journal 2347-1557 of Mathematics Applications
Weibull Reliability Analysis
 Weibull Reliability Analysis = http://www.rt.cs.boeing.com/mea/stat/scholz/ http://www.rt.cs.boeing.com/mea/stat/reliability.html http://www.rt.cs.boeing.com/mea/stat/scholz/weibull.html Fritz Scholz (425-865-3623,
Weibull Reliability Analysis = http://www.rt.cs.boeing.com/mea/stat/scholz/ http://www.rt.cs.boeing.com/mea/stat/reliability.html http://www.rt.cs.boeing.com/mea/stat/scholz/weibull.html Fritz Scholz (425-865-3623,
Experimental Designs for Planning Efficient Accelerated Life Tests
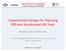 Experimental Designs for Planning Efficient Accelerated Life Tests Kangwon Seo and Rong Pan School of Compu@ng, Informa@cs, and Decision Systems Engineering Arizona State University ASTR 2015, Sep 9-11,
Experimental Designs for Planning Efficient Accelerated Life Tests Kangwon Seo and Rong Pan School of Compu@ng, Informa@cs, and Decision Systems Engineering Arizona State University ASTR 2015, Sep 9-11,
ECMA st Edition / June Test Method for the Estimation of the Archival Lifetime of Optical Media
 ECMA-379 1 st Edition / June 2007 Test Method for the Estimation of the Archival Lifetime of Optical Media COPYRIGHT PROTECTED DOCUMENT Ecma International 2007 Standard ECMA-379 1 st Edition / June 2007
ECMA-379 1 st Edition / June 2007 Test Method for the Estimation of the Archival Lifetime of Optical Media COPYRIGHT PROTECTED DOCUMENT Ecma International 2007 Standard ECMA-379 1 st Edition / June 2007
