MOMENTS OF NONIDENTICAL ORDER STATISTICS FROM BURR XII DISTRIBUTION WITH GAMMA AND NORMAL OUTLIERS
|
|
|
- Dale Leslie Perry
- 5 years ago
- Views:
Transcription
1 Journa of Matheat and Statt, 9 (): 5-6, 3 ISSN Sene Puaton do:.3844/p Puhed Onne 9 () 3 ( MOMENTS OF NONIDENTIAL ORDER STATISTIS FROM BURR XII DISTRIBUTION WITH GAMMA AND NORMAL OUTLIERS Jaoo, A.A. and Z.A. A-Saary Departent of Statt, Gr oege of Sene-Kng, Adu-Azz Unverty, Jeddah, Saud Araa Reeved --9, Reved 3--9; Aepted 3-4- ABSTRAT There are oe dtruton wth no pe oed for for dtruton funton uh a the Nora and Gaa dtruton. Th w e the proe f we want to fnd oent of nondenta order tatt n the preene of Gaa and Nora outer oervaton. We ued the dea of approxatng Nora and Gaa dtruton wth Burr type XII dtruton. We get nge oent for order tatt fro ape of ndependent nondentay dtruted Burr XII rando varae that ontan p-outer fro Nora or Gaa dtruton. Approxatng thee dtruton wth Burr XII dtruton and then we opared the reut y prevou ethod. Keyword: Approxaton, Nondenta Order Statt, Burr XII Dtruton, Nora Dtruton, PERMINANTS, Gaa Dtruton. INTRODUTION In th hapter we ued the dea of approxatng Nora and Gaa dtruton wth Burr XII to get There are no pe oed for ext for the nge oent for order tatt fro ape of nora dtruton funton and the gaa dtruton ndependent nondentay dtruted Burr XII rando funton o that approxaton to G (x) ut e ued to varae that ontan p-outer fro nora or Gaa fnd oent of the rth denta order tatt. An dtruton. approxatng thee dtruton wth Burr approah of otanng oe approxaton to the nora XII dtruton and then we opared the reut y thoe dtruton wa preented y Burr (94). Burr (967; ung the Baraat and Adeader (4). 973), Burr reauated the vaue of hape paraeter Barnett and Lew (994) have defned an outer n for Burr XII dtruton. Thee vaue gve a oer a et of data to e an oervaton or uet of approxaton to the nora dtruton. Another oervaton whh appear to e nontent wth the approah aed on approxatng gaa dtruton reander of the et of data. They ao dere evera wth the Burr fay dtruton ha een preented y ode for outer; ee (Mohref and Sutan, 7). Tadaaa and Raerg (975) and Wheeer (975), Denty funton and ont denty funton of order who approxate Gaa wth two paraeter wth Burr tatt arng fro a ape of a nge outer have wth two paraeter. Tadaaa (977) ued the een gven y Shu (978) and Hartey and Davd (978). generazed four paraeter B-dtruton to One ay ao refer to Vaughan and Venae (97) for approxate gaa dtruton and put a tae for ore genera expreon of dtruton of order eeted ntegra vaue of hape paraeter and other tatt ung peranent expreon. Arnod and paraeter whh Burr XII dtruton funton Baarhnan (989) have otaned the denty funton approxate to the exat Gaa dtruton funton. of X when the ape of ze n ontan undentfed orrepondng Author: Jaoo, A.A., Departent of Statt, Gr oege of Sene- Kng Adu-Azz Unverty, Jeddah, Saud Araa Sene Puaton 5
2 Jaoo, A.A. and Z.A. A-Saary /Journa of Matheat and Statt 9 (): 5-6, 3 nge outer. They ao otaned the ont denty funton of X and X :n, r< n. Baarhnan and Baauraanan (995) ha derved oe reurrene reaton atfed y the nge and produt oent of order tatt fro the rght trunated exponenta dtruton. Ao he ha dedued the reurrene reaton for the utpe outer ode (wth ppage of oervaton), ee ao Baarhnan (994). hd et a. () have derved oe reurrene reaton for the nge and produt oent of order tatt fro n ndependent and non-dentay dtruted Loax and the rght-trunated Loax rando varae. We aue X, X,,X p are ndependent wth proaty denty funton f (x) whe X n -p+,,x n are ndependent were are fro oe odfed veron of f (x) whh a g(x) n whh the hape paraeter have een hfted n vaue. Fnay, oe pea ae are dedued. The proaty denty funton of the rth order tatt X, under the utpe outer ode an e wrtten a, ee hd (996) Equaton : f [ ] p (x) = n ( np, r) = ax (, rp) f (x){f(x)} {G(x)} Sene Puaton r { F(x)} { G(x)} + np p r+ + n ( np,r) = ax (, rp) g(x){f(x)} {G(x)} r np p r+ { F(x)} { G(x)}, r n, p =,,, n, < x< Where Equaton : =! (r - -)!(n - p - -)!(p - r + +) (n - p)!p! () () (n - p)!p! =! (r - -)!(n - p - )!(p - r + ) Settng p = n () we otan the orrepondng pdf n ae of the nge outer gven y Shu (978). In th tudy, we onder the ae when the varae X, X,, X n-p are ndependent oervaton fro Burr XII wth four paraeter dtruton wth denty Equaton 3: 5 ρ xa ρ f(x) = ( + ) xa, a x, ρ >, >, > (3) and X n-p+,, X n are fro the ae dtruton wth denty Equaton 4: τ x a g(x) = ( + ) τ x a, a x, τ>, >,> (4) The orrepondng uuatve dtruton funton F (x) and G(x) are gven a Equaton 5 and 6: ρ x a F(x ) = ( + ), x a, ρ>, >, > -τ (5) x -a G( x )=- (+ ), (6) a x,τ>, >, > The reaton etween f (x) and F (x) gven y Equaton 7: ρ x a f ( x ) = [F( x )] x a f ( x ) (7) Sary, the reaton etween g(x) and G(x) Equaton 8: τ x a g (x ) = [G (x )] x a g (x ) (8) In the foowng eton, we ue (3) and (4) to derve the nge and produt oent of order tatt fro Burr XII dtruton under the utpe outer ode. Th tuaton nown a a utpe outer ode wth
3 Jaoo, A.A. and Z.A. A-Saary /Journa of Matheat and Statt 9 (): 5-6, 3 ppage of p oervaton; Barnett and Lewe (994). Th pef utpe outer ode wa ntrodued y Launer and B (979)... Snge Moent We derve the th oent of the r th order tatt under utpe outer ode (wth a ppage of p oervaton). Let () [p]; ( r n) denote the th nge oent of order tatt n the preene of p-outer oervaton fro BurrXII dtruton The foowng theore gve an expt for of () [p]. Theore For r n, p =,,, n and =,, the nge ( ) oent gven y Equaton 9: [p] n ( n p, r ) ( ) r : n [ p ] = ρ = ax (, r p ) r r + ( ) = = a β ( φ +, + ) = + τ n ( n p, r ) = ax (, r p ) r r + = ( ) = a β ( φ +, + ) = where, =, Equaton : φ = ρ(n p + ) + τ(p r ) +, (n p)!p! =! (r )!(n p )!(p r + + ) (n p)!p! =! (r )!(n p )!(p r + ) Proof Startng fro (), we have Equaton : ( ) r :n [ p ] = x f [ p ]( x ) dx = n ( np,r ) = ax (, rp) np p r+ + { F( x )} { G ( x )} dx + n ( np, r) = ax (, r p ) np p r+ { F( x )} { G ( x )} x f ( x ){F( x )} {G ( x )} r x g ( x ){F( x )} {G ( x )} r dx () (9) () Ung the reaton Equaton : [ F( x )] = ρ x a x a f (x )( + ) τ x a [G ( x )] g (x ) = x a ( + ) ( ) We get Equaton 3 and 4: n (n p, r) = ax (, r p) a [p] = x f (x ){F(x )} {G (x )} r { F(x )} np ρ x a x a f ( x ) ( + ) p r + + { G ( x )} dx n ( np, r ) = ax (, r p ) a + x τ x a [G ( x )] x a (+ ) {F( x )} {G (x )} r np p r + { F(x )} { G ( x )} dx ( ) ρ [p] = n ( np, r ) = ax (, r p) x a + a x (x a ) ( ) {F( x )} {G (x )} r np p r + + { F( x )} { G ( x )} dx τ + n ( np,r ) = ax (, r p ) x a + a x (x a ) ( ) r np {F( x )} {G (x )} p r + + { G (x )} dx Now y wrtng: { F( x )} () (3) (4) Sene Puaton 53
4 Jaoo, A.A. and Z.A. A-Saary /Journa of Matheat and Statt 9 (): 5-6, 3 F (x) = - (-F (x)) and G (x) = -(-G (x)) n (4) and expand we get Equaton 5: ( ) ρ [p] = n ( np, r ) = ax (, r p) x a + a x (x a ) ( ) r r ( ) + = = { F(x )} n p + p r { G ( x )} dx n ( n p, r ) τ + = ax (, rp ) a n p + p r { G ( x )} dx x a x (x a ) ( + ) r r ( ) + = { F(x )} a = We now that Equaton 6-8: = ρ r r ( ) + = τ x a x a F(x ) = ( + ) G ( x ) = ( + ) n ( n p, r ) ( ) ρ [p] = = ax (, rp) x ( x a ) [ ρ(n p + ) + τ x a (p r+ + + ) + ] ( + ) dx τ + n ( np, r) = ax (, r p ) x (x a ) a = r r ( ) + = [ ρ(n p + ) + τ x a (p r+ + + ) + ] ( + ) dx Le: (5) (6) x a x a y = + = y y x a y y = x a = y y y x = + a y y dx = dy y y at x = a y=, at x = y= n ( np,r ) ( ) [p] = ax (, r p) = ρ r r ( ) = = y ( ) a + y [ ρ(n p + ) y + τ ( p r ) + ] + τ n ( np,r ) = ax (, r p ) r = = y Let: ( p r ) + ] dy r ( ) y ( ) a + y [ ρ(n p + ) + τ y ( ) + a y dy = y = a = y n ( np, r) ( ) [p] = ρ = ax (, r p) + + (7) Sene Puaton 54
5 Jaoo, A.A. and Z.A. A-Saary /Journa of Matheat and Statt 9 (): 5-6, 3 r r ( ) = [ ρ(n p + ) + a ( y) = τ ( p r ) + ] y dy n ( np,r ) + τ = ax (, r p ) r r ( ) = = a [ ρ(n p + ) + y ( ) y = τ ( p r ) + ] Sene Puaton dy + + Let Φ = ρ(n-p-+)+τ(p-r+++)+ Equaton 9: Φ ( ) y y dy = β Φ, + n ( np, r) ( ) [p] = ρ = ax (, rp) r r + ( ) = = a β( φ +, + ) = n ( np, r) r +τ = ax (, r p) = = r + ( ) a β( φ +, + ) Rear (8) (9) If we put a =, = n (9) and onder = we get oent of order tatt fro Burr XII dtruton wth two paraeter n the preene of outer oervaton a Equaton : 55 n ( np, r ) ( ) r :n [p] = ρ = ax (, r p) r r = = + ( ) β( φ, + ) +τ n ( np,r ) r = ax (, r p ) = = r β φ + + ( ) (, ) 4 Spea ae () We dedue oe pea ae fro the nge oent gven n (9) and () a foow: Settng p =, we get the nge oent of order tatt when x, x,,x n have Burr dtruton a Equaton and : r r ( ) ρ n! [] = (r )!(n r )! = a ( ) = () β( φ +, + ) Φ = ρ(n r + + ) + r r ( ) ρn! [] = (r )!(n r )! = β φ + + Φ = ρ(n r + + ) + ( ) (, ) () If we put p = n, we have the ae reaton aove ut wth paraeter τ If we put p =, we have the reaton for nge outer Exape () Let X, X ~Barr XII wth =.39533, ρ = 3, a =.3445, = and X 3 ~Gaa(β =, α = ). Fnd :3. Souton A nge outer n th ape that X 3 ~Gaa(β =, α = ).
6 Jaoo, A.A. and Z.A. A-Saary /Journa of Matheat and Statt 9 (): 5-6, 3 Tae. Reut of Tadaaa (977) for the paraeter ρ, a,,,, σ when α nteger and β = α a σ * * Nora E Fg. Burr dtruton wth ( = , τ = ) Fg. Nora dtruton wth ( =.64477, σ =.699) Sene Puaton 56
7 Jaoo, A.A. and Z.A. A-Saary /Journa of Matheat and Statt 9 (): 5-6, 3 But we now that Tadaaa (977) approxate Gaa dtruton β =, α = wth Burr XII wth four paraeter a =.39533, ρ = , a =.3445, = Tae and Fg. and. So when X 3 ~Gaa (β =, α = ) X 3 ~ Burr IIX wth paraeter ( =.39533, ρ = , a =.3445, = ). Now ung Equaton 9: n (, ) ( ) :3 [] = 3 ( ) r r ( ) = =.3445 = = ax (, ) + β( φ +, + ) n (,) ( ) = ax (, ) r r = = = ( ) β( φ +, + ) ( ) Φ = 3( 3 + ) ( ) + = 3( ) + ( )(++)+ ( ) :3 ( ) [] = r r ( ) = = n (, ) = ax (, ) = β( φ +, + ) ( ) r r ( ) = = n (,) = ax (, ) = β( φ +, + ) ( ) + :3 [] 3 ( ) ( ) = = = =.3445 ( β φ + =, + ) ( ) ( ) = = = = β( φ +, + ) ( ).3445 :3 [] = 3 ( ) = β ( 6 + ( ) , + ) β + = ( ) ( 6 ( ) +, + ) Fro (): = = = = ( ).3445 :3 [] = 6 ( ) = β ( 6 + ( ) , + ) β + = ( ) ( 6 ( ) +, + ) If = :.3445 :3[] = 6 ( ) = β ( 6 + ( ) , + ) ( ) Sene Puaton 57
8 Jaoo, A.A. and Z.A. A-Saary /Journa of Matheat and Statt 9 (): 5-6, 3 Tae. The expeted vaue and the varane n the preene of utpe outer fro Burr XII wth four paraeter when =, n = 5, =.39533, ρ = 3, a =.3445, = , τ = p r r:5 [p] Varane p r r:5 [p] Varane p r r:5 [p] Varane β ( 6 + ( ) = +, + ) = More reut an e een n Tae for n = 5, r =,,,5 and p =,,. Tae gven eow dpay the vaue of the nge oent of order tatt n (.9) when = ; n = 5; τ = ; α =.3445; = and = Exape () Let X,X ~Barr XII wth = , ρ = 5 and X 3 ~Nora (.64477,.699). Fnd :3 Souton A nge outer n th ape that X 3 ~Nora (.64477,.699). But we now that Burr (94) approxate the nora dtruton wth Burr XII wth two paraeter a = and ρ = fro whh the ore aurate vaue of, σ, α 3 and α 4 an e otaned a =.64477, σ =.699, α 3 =., α 4 =.. So when X 3 ~ Nora ( =.64477, σ =.699) X 3 ~ Burr ( = ), τ = Now ung Equaton : n (, ) r-- ( ) :3 = ax (, -) = = [] = r-- + (-) β Φ- -, + n (,) r (-) = ax (, ) = = β Φ- -, r-- ( ) ( )( ) ( ) ( )( ) Φ = = ( ) :3 = = = = [] (-) β Φ- -, = = = (-) β Φ- -, + ( ) :3 [] = 5 () β 5() ()+ - -, ()β 5() ()+ - -, Fro (): = = = = ( ) [] = β :3 5() () +, β 5() () +, If = : ( ) :3 ( ) [] = β , =.553 Sene Puaton 58
9 Jaoo, A.A. and Z.A. A-Saary /Journa of Matheat and Statt 9 (): 5-6, 3 Tae 3. The expeted vaue and the varane n the preene of utpe outer fro Burr XII wth two paraeter when =, n = 5, = and ρ = 3, τ = p r r:3 [p] Varane p r r:3 [p] Varane p r r:3 [p] Varane More reut an e een n Tae 3 for n = 5, r =,,,5 and p =,,... Moent of Order Statt fro Burr XII wth Four Paraeter Ung Theore of Baraat and Adeader (4) Let X, X,, X n e ndependent nondentay dtruted r.v,.. The th oent of a order ( ) tatt, for r n and =,, gven y (Baraat and Adeader, 4) Equaton 3: = n ( ) (n r+ ) ( ) I ( ) (3) nr = n r+ I ( ) = Where Equaton 4: < < < n x G ( x )dx, =,,,n t t= (4) G (x) = -F (x), wth (, I,, n ) a perutaton of (,,, n ) for whh < < n. We onder the ae when the varae X, X,, X n-p are ndependent oervaton fro Burr XII wth four paraeter dtruton wth denty Equaton 5: ρ x a ρ f (x ) = ( + ) x a, a x, ρ >, >, > (5) The orrepondng uuatve dtruton funton F (x) gven a: x a ρ F(x ) = ( + ), x a, ρ>, >, > Ung (4) n (): I ( ) = < < < n x a t = ρ t x ( + ) dx a x a Suttutng y = : x = y+ a dx = dy at x = a y y =, at x = y = The aove Equaton redue to: I ( ) = = < < < n t t = ( y+ a ) (+ y ) dy < < < n a ( y) ( y ) + = ρ t = t < < < n dy ( y) ρ a ρ t (+ y ) dy = t = Upon ung: α ( y) (+ y ) dy = β ( α, ) where, β (a, ) the reguar eta funton: Sene Puaton 59
10 Jaoo, A.A. and Z.A. A-Saary /Journa of Matheat and Statt 9 (): 5-6, 3 Tae 4. The expeted vaue and the varane n the preene of utpe outer ung Baraat and Adeader (4) and ethod fro Burr XII wth four paraeter when =, n=5, =.39533, ρ = 3, a =.3445, = , τ = p r r:3 [p] Varane p r r:3 [p] Varane p r r:3 [p] Varane I ( ) = < < < n a β ( ρ, ) t = t = n ( ) (n r + ) = ( ) nr = n r + < < < n a (, ) t β ρ = t = If = : n (n r + ) = ( ) nr = n r+ Exape t < < < n t = β ( ρ, ) Let X,X ~Barr XII wth =.39533, ρ = 3, a =.3445, = and X 3 ~ Gaa (β =, α = ). Fnd :3. Souton X 3 ~ Gaa (β =, α = ) X 3 ~Burr IIX wth paraeter ( =.39533, ρ = , a =.3445, = ): :3 3 = ( ) = 3 < < < 3 3 β ρ, t t= = < < < β ρ, t t= = (, ) β ρ + ρ + ρ = β ( , ) =.5563 More reut an e een n Tae 4 for r =,,,5 and p =,,.. ONLUSION We an fnd oent of order tatt fro ndependent and nondentay dtruted rando varae for any dtruton wth no pe oed fro ung approxatng dea wth Burr XII or any other dtruton. 3. REFRENES Arnod, B.. and N. Baarhnan, 989. Reaton, Bound and Approxaton for Order Statt. t Edn., Sprnger-Verga, New Yor, ISBN-: , pp: 73. Baarhnan, N. and K. Baauraanan, 995. Order tatt fro non-denta power funton rando varae. oun. Stat. Theor. Meth., 4: DOI:.8/ Baarhnan, N., 994. Order tatt fro nondenta exponenta rando varae and oe appaton. oput. Stat. Data Ana., 8: DOI:.6/ (94)97-4 Baraat, H. and Y. Adeader, 4. oputng the oent of order tatt fro nondenta rando varae. Stat. Meth. App., 3: 5-6. DOI:.7/ Sene Puaton 6
11 Jaoo, A.A. and Z.A. A-Saary /Journa of Matheat and Statt 9 (): 5-6, 3 Barnett, V. and T. Lew, 994. Outer n Statta Data. 3rd Edn., Wey and Son, hheter, ISBN- : , pp: 584. Burr, I.W., 94. uuatve frequeny funton. Anna Math. Stat., 3: 5-3. Burr, I.W., 967. A uefu approxaton to the nora dtruton funton, wth appaton to uaton. Tehnoetr, 9: DOI:.8/ Burr, I.W., 973. Paraeter for a genera yte of dtruton to ath a grd of á3 and á4. oun. Stat, : -. hd, A, 996. Advane n tatta nferene and outer reated ue. Ph.D. The, MMater Unverty. hd, A., N. Baarhnan and M. Mohref,. Order tatt fro non-denta rght-trunated Loax rando varae wth appaton. Stat. Paper, 4: Hartey, H.O. and H.A. Davd, 978. ontruton to Survey Sapng and Apped Statt. t Edn., Aade Pre, San Frano, ISBN-: 4758, pp: 38. Launer,.A. and T.D. B, 979. Infuene of Seeted Envronenta Fator on the Atvty of a Propetve Fh Toxant, -(Dgeranyano)- Ethano, n Laoratory Tet. t Edn., Departent of the Interor, Wahngton, pp: 4. Mohref, M.E. and K.S. Sutan, 7. Moent of order tatt fro Rayegh dtruton n the preene of outer oervaton. Departent of Matheat, A-Azhar Unverty, Shu, V.S., 978. Rout Etaton of a Loaton Paraeter n the Preene of Outer. t Edn., Iowa, A, pp: 37. Tadaaa, P.R. and J.S. Raerg, 975. An approxate ethod for generatng gaa and other varae. J. Stat. oput. Su., 3: Tadaaa, P.R., 977. An approxaton to the oent and the perente of gaa order tatt. Sanhya: IJS, 39: Vaughan, R.J. and W.N. Venae, 97. Peranent expreon for order tatt dente. J. Roya Stat. So., 34: Wheeer, D.J., 975. An approxaton for uaton of gaa dtruton. J. Stat. oput. Su., 3: 5-3. DOI:.8/ Sene Puaton 6
International Conference on Electromechanical Control Technology and Transportation (ICECTT 2015)
 Internatona Conferene on Eetroehana Contro Tehnoogy and Tranportaton (ICECTT ) Mode Anay of Car Fve Degree of Freedo Vbraton Syte Baed on Energy Deoupng Method XU Boa BAO Jadngb* WU Janwe4 WANG Hanhao
Internatona Conferene on Eetroehana Contro Tehnoogy and Tranportaton (ICECTT ) Mode Anay of Car Fve Degree of Freedo Vbraton Syte Baed on Energy Deoupng Method XU Boa BAO Jadngb* WU Janwe4 WANG Hanhao
Inverse Kinematics From Position to Angles
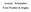 Invere Knemat From Poton to Ange Invere Knemat Gven a dered poton P & orentaton R o the end-eetor Y,, z, O, A, T z q,, n Fnd the jont varabe whh an brng the robot to the dered onguraton. Sovabt 0 Gven
Invere Knemat From Poton to Ange Invere Knemat Gven a dered poton P & orentaton R o the end-eetor Y,, z, O, A, T z q,, n Fnd the jont varabe whh an brng the robot to the dered onguraton. Sovabt 0 Gven
The calculation of ternary vapor-liquid system equilibrium by using P-R equation of state
 The alulaton of ternary vapor-lqud syste equlbru by usng P-R equaton of state Y Lu, Janzhong Yn *, Rune Lu, Wenhua Sh and We We Shool of Cheal Engneerng, Dalan Unversty of Tehnology, Dalan 11601, P.R.Chna
The alulaton of ternary vapor-lqud syste equlbru by usng P-R equaton of state Y Lu, Janzhong Yn *, Rune Lu, Wenhua Sh and We We Shool of Cheal Engneerng, Dalan Unversty of Tehnology, Dalan 11601, P.R.Chna
WEYL MANIFOLDS WITH SEMI-SYMMETRIC CONNECTION. Füsun Ünal 1 and Aynur Uysal 2. Turkey.
 Mateatca and Coputatona Appcaton, Vo. 0, No. 3, pp. 35-358, 005. Aocaton for centfc eearc WEYL MANIFOLD WITH EMI-YMMETIC CONNECTION Füun Üna and Aynur Uya Marara Unverty, Facuty of cence and Letter, Departent
Mateatca and Coputatona Appcaton, Vo. 0, No. 3, pp. 35-358, 005. Aocaton for centfc eearc WEYL MANIFOLD WITH EMI-YMMETIC CONNECTION Füun Üna and Aynur Uya Marara Unverty, Facuty of cence and Letter, Departent
Einstein Summation Convention
 Ensten Suaton Conventon Ths s a ethod to wrte equaton nvovng severa suatons n a uncuttered for Exape:. δ where δ or 0 Suaton runs over to snce we are denson No ndces appear ore than two tes n the equaton
Ensten Suaton Conventon Ths s a ethod to wrte equaton nvovng severa suatons n a uncuttered for Exape:. δ where δ or 0 Suaton runs over to snce we are denson No ndces appear ore than two tes n the equaton
Module 3: Element Properties Lecture 5: Solid Elements
 Modue : Eement Propertes eture 5: Sod Eements There re two s fmes of three-dmenson eements smr to two-dmenson se. Etenson of trngur eements w produe tetrhedrons n three dmensons. Smr retngur preeppeds
Modue : Eement Propertes eture 5: Sod Eements There re two s fmes of three-dmenson eements smr to two-dmenson se. Etenson of trngur eements w produe tetrhedrons n three dmensons. Smr retngur preeppeds
Journal of Engineering and Applied Sciences. Ultraspherical Integration Method for Solving Beam Bending Boundary Value Problem
 Journal of Engneerng and Appled Senes Volue: Edton: Year: 4 Pages: 7 4 Ultraspheral Integraton Method for Solvng Bea Bendng Boundary Value Proble M El-Kady Matheats Departent Faulty of Sene Helwan UnverstyEgypt
Journal of Engneerng and Appled Senes Volue: Edton: Year: 4 Pages: 7 4 Ultraspheral Integraton Method for Solvng Bea Bendng Boundary Value Proble M El-Kady Matheats Departent Faulty of Sene Helwan UnverstyEgypt
and decompose in cycles of length two
 Permutaton of Proceedng of the Natona Conference On Undergraduate Reearch (NCUR) 006 Domncan Unverty of Caforna San Rafae, Caforna Apr - 4, 007 that are gven by bnoma and decompoe n cyce of ength two Yeena
Permutaton of Proceedng of the Natona Conference On Undergraduate Reearch (NCUR) 006 Domncan Unverty of Caforna San Rafae, Caforna Apr - 4, 007 that are gven by bnoma and decompoe n cyce of ength two Yeena
Hyun-Woo Jin* and Min-Young Lee**
 JOURNAL OF THE CHUNGCHEONG MATHEMATICAL SOCIETY Volue 27, No. 2, May 214 http://dx.doi.org/1.1443/jcs.214.27.2.157 CHARACTERIZATIONS OF THE GAMMA DISTRIBUTION BY INDEPENDENCE PROPERTY OF RANDOM VARIABLES
JOURNAL OF THE CHUNGCHEONG MATHEMATICAL SOCIETY Volue 27, No. 2, May 214 http://dx.doi.org/1.1443/jcs.214.27.2.157 CHARACTERIZATIONS OF THE GAMMA DISTRIBUTION BY INDEPENDENCE PROPERTY OF RANDOM VARIABLES
Wave Particle Dualism for Both Matter and Wave and Non-Einsteinian View of Relativity
 Talukder and Aad: Wave Partle Dual for Bot Matter and Wave and Non-Entenan Vew of Relatvty (8-91) Wave Partle Dual for Bot Matter and Wave and Non-Entenan Vew of Relatvty M.O.G. Talukder 1, Mufq Aad 1
Talukder and Aad: Wave Partle Dual for Bot Matter and Wave and Non-Entenan Vew of Relatvty (8-91) Wave Partle Dual for Bot Matter and Wave and Non-Entenan Vew of Relatvty M.O.G. Talukder 1, Mufq Aad 1
k p theory for bulk semiconductors
 p theory for bu seconductors The attce perodc ndependent partce wave equaton s gven by p + V r + V p + δ H rψ ( r ) = εψ ( r ) (A) 4c In Eq. (A) V ( r ) s the effectve attce perodc potenta caused by the
p theory for bu seconductors The attce perodc ndependent partce wave equaton s gven by p + V r + V p + δ H rψ ( r ) = εψ ( r ) (A) 4c In Eq. (A) V ( r ) s the effectve attce perodc potenta caused by the
BINOMIAL COEFFICIENT HARMONIC SUM IDENTITIES ASSOCIATED TO SUPERCONGRUENCES
 #A37 INTEGERS (20) BINOMIAL COEFFICIENT HARMONIC SUM IDENTITIES ASSOCIATED TO SUPERCONGRUENCES Derot McCarthy Departet of Matheatics, Texas A&M Uiversity, Texas ccarthy@athtauedu Received: /3/, Accepted:
#A37 INTEGERS (20) BINOMIAL COEFFICIENT HARMONIC SUM IDENTITIES ASSOCIATED TO SUPERCONGRUENCES Derot McCarthy Departet of Matheatics, Texas A&M Uiversity, Texas ccarthy@athtauedu Received: /3/, Accepted:
Chapter 5: Root Locus
 Chater 5: Root Locu ey condton for Plottng Root Locu g n G Gven oen-loo tranfer functon G Charactertc equaton n g,,.., n Magntude Condton and Arguent Condton 5-3 Rule for Plottng Root Locu 5.3. Rule Rule
Chater 5: Root Locu ey condton for Plottng Root Locu g n G Gven oen-loo tranfer functon G Charactertc equaton n g,,.., n Magntude Condton and Arguent Condton 5-3 Rule for Plottng Root Locu 5.3. Rule Rule
XII.3 The EM (Expectation-Maximization) Algorithm
 XII.3 The EM (Expectaton-Maxzaton) Algorth Toshnor Munaata 3/7/06 The EM algorth s a technque to deal wth varous types of ncoplete data or hdden varables. It can be appled to a wde range of learnng probles
XII.3 The EM (Expectaton-Maxzaton) Algorth Toshnor Munaata 3/7/06 The EM algorth s a technque to deal wth varous types of ncoplete data or hdden varables. It can be appled to a wde range of learnng probles
SELECTED PROOFS. DeMorgan s formulas: The first one is clear from Venn diagram, or the following truth table:
 SELECTED PROOFS DeMorgan s formulas: The frst one s clear from Venn dagram, or the followng truth table: A B A B A B Ā B Ā B T T T F F F F T F T F F T F F T T F T F F F F F T T T T The second one can be
SELECTED PROOFS DeMorgan s formulas: The frst one s clear from Venn dagram, or the followng truth table: A B A B A B Ā B Ā B T T T F F F F T F T F F T F F T T F T F F F F F T T T T The second one can be
Cyclic Codes BCH Codes
 Cycc Codes BCH Codes Gaos Feds GF m A Gaos fed of m eements can be obtaned usng the symbos 0,, á, and the eements beng 0,, á, á, á 3 m,... so that fed F* s cosed under mutpcaton wth m eements. The operator
Cycc Codes BCH Codes Gaos Feds GF m A Gaos fed of m eements can be obtaned usng the symbos 0,, á, and the eements beng 0,, á, á, á 3 m,... so that fed F* s cosed under mutpcaton wth m eements. The operator
Differentiating Gaussian Processes
 Dfferentatng Gaussan Processes Andrew McHutchon Aprl 17, 013 1 Frst Order Dervatve of the Posteror Mean The posteror mean of a GP s gven by, f = x, X KX, X 1 y x, X α 1 Only the x, X term depends on the
Dfferentatng Gaussan Processes Andrew McHutchon Aprl 17, 013 1 Frst Order Dervatve of the Posteror Mean The posteror mean of a GP s gven by, f = x, X KX, X 1 y x, X α 1 Only the x, X term depends on the
LECTURE 21 Mohr s Method for Calculation of General Displacements. 1 The Reciprocal Theorem
 V. DEMENKO MECHANICS OF MATERIALS 05 LECTURE Mohr s Method for Cacuaton of Genera Dspacements The Recproca Theorem The recproca theorem s one of the genera theorems of strength of materas. It foows drect
V. DEMENKO MECHANICS OF MATERIALS 05 LECTURE Mohr s Method for Cacuaton of Genera Dspacements The Recproca Theorem The recproca theorem s one of the genera theorems of strength of materas. It foows drect
Jacobians: Velocities and Static Force.
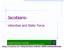 Jaoban: Veote and Stat Fore mrkabr Unerty o ehnoogy Computer Engneerng Inormaton ehnoogy Department http://e.aut.a.r/~hry/eture/robot-4/robot4.htm Derentaton o poton etor Derate o a etor: V Q d dt Q m
Jaoban: Veote and Stat Fore mrkabr Unerty o ehnoogy Computer Engneerng Inormaton ehnoogy Department http://e.aut.a.r/~hry/eture/robot-4/robot4.htm Derentaton o poton etor Derate o a etor: V Q d dt Q m
arxiv: v2 [math.co] 3 Sep 2017
![arxiv: v2 [math.co] 3 Sep 2017 arxiv: v2 [math.co] 3 Sep 2017](/thumbs/76/73623234.jpg) On the Approxate Asyptotc Statstcal Independence of the Peranents of 0- Matrces arxv:705.0868v2 ath.co 3 Sep 207 Paul Federbush Departent of Matheatcs Unversty of Mchgan Ann Arbor, MI, 4809-043 Septeber
On the Approxate Asyptotc Statstcal Independence of the Peranents of 0- Matrces arxv:705.0868v2 ath.co 3 Sep 207 Paul Federbush Departent of Matheatcs Unversty of Mchgan Ann Arbor, MI, 4809-043 Septeber
Least Squares Fitting of Data
 Least Squares Fttng of Data Davd Eberly Geoetrc Tools, LLC http://www.geoetrctools.co/ Copyrght c 1998-2015. All Rghts Reserved. Created: July 15, 1999 Last Modfed: January 5, 2015 Contents 1 Lnear Fttng
Least Squares Fttng of Data Davd Eberly Geoetrc Tools, LLC http://www.geoetrctools.co/ Copyrght c 1998-2015. All Rghts Reserved. Created: July 15, 1999 Last Modfed: January 5, 2015 Contents 1 Lnear Fttng
Quick Visit to Bernoulli Land
 Although we have een the Bernoull equaton and een t derved before, th next note how t dervaton for an uncopreble & nvcd flow. The dervaton follow that of Kuethe &Chow ot cloely (I lke t better than Anderon).
Although we have een the Bernoull equaton and een t derved before, th next note how t dervaton for an uncopreble & nvcd flow. The dervaton follow that of Kuethe &Chow ot cloely (I lke t better than Anderon).
ON DUALITY FOR NONSMOOTH LIPSCHITZ OPTIMIZATION PROBLEMS
 Yugoslav Journal of Oeratons Researh Vol 9 (2009), Nuber, 4-47 DOI: 0.2298/YUJOR09004P ON DUALITY FOR NONSMOOTH LIPSCHITZ OPTIMIZATION PROBLEMS Vasle PREDA Unversty of Buharest, Buharest reda@f.unbu.ro
Yugoslav Journal of Oeratons Researh Vol 9 (2009), Nuber, 4-47 DOI: 0.2298/YUJOR09004P ON DUALITY FOR NONSMOOTH LIPSCHITZ OPTIMIZATION PROBLEMS Vasle PREDA Unversty of Buharest, Buharest reda@f.unbu.ro
Some Results on the Counterfeit Coins Problem. Li An-Ping. Beijing , P.R.China Abstract
 Some Results on the Counterfet Cons Problem L An-Png Bejng 100085, P.R.Chna apl0001@sna.om Abstrat We wll present some results on the ounterfet ons problem n the ase of mult-sets. Keywords: ombnatoral
Some Results on the Counterfet Cons Problem L An-Png Bejng 100085, P.R.Chna apl0001@sna.om Abstrat We wll present some results on the ounterfet ons problem n the ase of mult-sets. Keywords: ombnatoral
Amelioration of Verdegay s Approach for Fuzzy Linear Programs with Stochastic Parameters
 ` Iranan Journal of Manageent Stude (IJMS) http://.ut.a.r/ Vol. 11, No. 1, Wnter 2018 Prnt ISSN: 2008-7055 pp. 71-89 Onlne ISSN: 235-375 DOI: 10.22059/.2018.23617.672722 Aeloraton of Verdegay Approah for
` Iranan Journal of Manageent Stude (IJMS) http://.ut.a.r/ Vol. 11, No. 1, Wnter 2018 Prnt ISSN: 2008-7055 pp. 71-89 Onlne ISSN: 235-375 DOI: 10.22059/.2018.23617.672722 Aeloraton of Verdegay Approah for
Xiangwen Li. March 8th and March 13th, 2001
 CS49I Approxaton Algorths The Vertex-Cover Proble Lecture Notes Xangwen L March 8th and March 3th, 00 Absolute Approxaton Gven an optzaton proble P, an algorth A s an approxaton algorth for P f, for an
CS49I Approxaton Algorths The Vertex-Cover Proble Lecture Notes Xangwen L March 8th and March 3th, 00 Absolute Approxaton Gven an optzaton proble P, an algorth A s an approxaton algorth for P f, for an
ROOT-LOCUS ANALYSIS. Lecture 11: Root Locus Plot. Consider a general feedback control system with a variable gain K. Y ( s ) ( ) K
 ROOT-LOCUS ANALYSIS Coder a geeral feedback cotrol yte wth a varable ga. R( Y( G( + H( Root-Locu a plot of the loc of the pole of the cloed-loop trafer fucto whe oe of the yte paraeter ( vared. Root locu
ROOT-LOCUS ANALYSIS Coder a geeral feedback cotrol yte wth a varable ga. R( Y( G( + H( Root-Locu a plot of the loc of the pole of the cloed-loop trafer fucto whe oe of the yte paraeter ( vared. Root locu
Exact Inference: Introduction. Exact Inference: Introduction. Exact Inference: Introduction. Exact Inference: Introduction.
 Exat nferene: ntroduton Exat nferene: ntroduton Usng a ayesan network to ompute probabltes s alled nferene n general nferene nvolves queres of the form: E=e E = The evdene varables = The query varables
Exat nferene: ntroduton Exat nferene: ntroduton Usng a ayesan network to ompute probabltes s alled nferene n general nferene nvolves queres of the form: E=e E = The evdene varables = The query varables
A study of the behaviour of earth electrodes connected together in resonant earthed neutral systems
 Safety and Seurty nneern 93 A tudy of the ehavour of earth eletrode onneted toether n reonant earthed neutral ytem A. Campoa & G. Zzzo Department of letral nneern, Unverty of Palermo, taly Atrat nde uran
Safety and Seurty nneern 93 A tudy of the ehavour of earth eletrode onneted toether n reonant earthed neutral ytem A. Campoa & G. Zzzo Department of letral nneern, Unverty of Palermo, taly Atrat nde uran
Homework 9 for BST 631: Statistical Theory I Problems, 11/02/2006
 Due Tme: 5:00PM Thursda, on /09/006 Problem (8 ponts) Book problem 45 Let U = X + and V = X, then the jont pmf of ( UV, ) s θ λ θ e λ e f( u, ) = ( = 0, ; u =, +, )! ( u )! Then f( u, ) u θ λ f ( x x+
Due Tme: 5:00PM Thursda, on /09/006 Problem (8 ponts) Book problem 45 Let U = X + and V = X, then the jont pmf of ( UV, ) s θ λ θ e λ e f( u, ) = ( = 0, ; u =, +, )! ( u )! Then f( u, ) u θ λ f ( x x+
The Role of Generalized Matrix Inverses in Markov Chains
 The Role of Generalized Matrix Inverses in Markov Chains Jeffrey J Hunter Professor Eeritus of Statistics, Massey University, Professor of Matheatical Sciences, AUT University, New Zealand ANZAPW 2013,
The Role of Generalized Matrix Inverses in Markov Chains Jeffrey J Hunter Professor Eeritus of Statistics, Massey University, Professor of Matheatical Sciences, AUT University, New Zealand ANZAPW 2013,
Introduction To Robotics (Kinematics, Dynamics, and Design)
 ntroducton To obotcs Kneatcs, Dynacs, and Desgn SESSON # 6: l Meghdar, Professor School of Mechancal Engneerng Sharf Unersty of Technology Tehran, N 365-9567 Hoepage: http://eghdar.sharf.edu So far we
ntroducton To obotcs Kneatcs, Dynacs, and Desgn SESSON # 6: l Meghdar, Professor School of Mechancal Engneerng Sharf Unersty of Technology Tehran, N 365-9567 Hoepage: http://eghdar.sharf.edu So far we
Boundary Value Problems. Lecture Objectives. Ch. 27
 Boundar Vaue Probes Ch. 7 Lecture Obectves o understand the dfference between an nta vaue and boundar vaue ODE o be abe to understand when and how to app the shootng ethod and FD ethod. o understand what
Boundar Vaue Probes Ch. 7 Lecture Obectves o understand the dfference between an nta vaue and boundar vaue ODE o be abe to understand when and how to app the shootng ethod and FD ethod. o understand what
Improvements on Waring s Problem
 Improvement on Warng Problem L An-Png Bejng, PR Chna apl@nacom Abtract By a new recurve algorthm for the auxlary equaton, n th paper, we wll gve ome mprovement for Warng problem Keyword: Warng Problem,
Improvement on Warng Problem L An-Png Bejng, PR Chna apl@nacom Abtract By a new recurve algorthm for the auxlary equaton, n th paper, we wll gve ome mprovement for Warng problem Keyword: Warng Problem,
e a = 12.4 i a = 13.5i h a = xi + yj 3 a Let r a = 25cos(20) i + 25sin(20) j b = 15cos(55) i + 15sin(55) j
 Vetors MC Qld-3 49 Chapter 3 Vetors Exerse 3A Revew of vetors a d e f e a x + y omponent: x a os(θ 6 os(80 + 39 6 os(9.4 omponent: y a sn(θ 6 sn(9 0. a.4 0. f a x + y omponent: x a os(θ 5 os( 5 3.6 omponent:
Vetors MC Qld-3 49 Chapter 3 Vetors Exerse 3A Revew of vetors a d e f e a x + y omponent: x a os(θ 6 os(80 + 39 6 os(9.4 omponent: y a sn(θ 6 sn(9 0. a.4 0. f a x + y omponent: x a os(θ 5 os( 5 3.6 omponent:
Strong Markov property: Same assertion holds for stopping times τ.
 Brownan moton Let X ={X t : t R + } be a real-valued stochastc process: a famlty of real random varables all defned on the same probablty space. Defne F t = nformaton avalable by observng the process up
Brownan moton Let X ={X t : t R + } be a real-valued stochastc process: a famlty of real random varables all defned on the same probablty space. Defne F t = nformaton avalable by observng the process up
IX Mechanics of Rigid Bodies: Planar Motion
 X Mechancs of Rd Bodes: Panar Moton Center of Mass of a Rd Bod Rotaton of a Rd Bod About a Fed As Moent of nerta Penduu, A Genera heore Concernn Anuar Moentu puse and Coson nvovn Rd Bodes. Rd bod: dea
X Mechancs of Rd Bodes: Panar Moton Center of Mass of a Rd Bod Rotaton of a Rd Bod About a Fed As Moent of nerta Penduu, A Genera heore Concernn Anuar Moentu puse and Coson nvovn Rd Bodes. Rd bod: dea
BULLETIN OF MATHEMATICS AND STATISTICS RESEARCH
 Vol.6.Iue..8 (July-Set.) KY PUBLICATIONS BULLETIN OF MATHEMATICS AND STATISTICS RESEARCH A Peer Revewed Internatonal Reearch Journal htt:www.bor.co Eal:edtorbor@gal.co RESEARCH ARTICLE A GENERALISED NEGATIVE
Vol.6.Iue..8 (July-Set.) KY PUBLICATIONS BULLETIN OF MATHEMATICS AND STATISTICS RESEARCH A Peer Revewed Internatonal Reearch Journal htt:www.bor.co Eal:edtorbor@gal.co RESEARCH ARTICLE A GENERALISED NEGATIVE
Multiple Random Variables
 Multiple Random Variables This Version: July 30, 2015 Multiple Random Variables 2 Now we consider models with more than one r.v. These are called multivariate models For instance: height and weight An
Multiple Random Variables This Version: July 30, 2015 Multiple Random Variables 2 Now we consider models with more than one r.v. These are called multivariate models For instance: height and weight An
Chapter 12. Ordinary Differential Equation Boundary Value (BV) Problems
 Chapter. Ordnar Dfferental Equaton Boundar Value (BV) Problems In ths chapter we wll learn how to solve ODE boundar value problem. BV ODE s usuall gven wth x beng the ndependent space varable. p( x) q(
Chapter. Ordnar Dfferental Equaton Boundar Value (BV) Problems In ths chapter we wll learn how to solve ODE boundar value problem. BV ODE s usuall gven wth x beng the ndependent space varable. p( x) q(
PhysicsAndMathsTutor.com
 PhscsAndMathsTutor.com phscsandmathstutor.com June 005 5. The random varable X has probablt functon k, = 1,, 3, P( X = ) = k ( + 1), = 4, 5, where k s a constant. (a) Fnd the value of k. (b) Fnd the eact
PhscsAndMathsTutor.com phscsandmathstutor.com June 005 5. The random varable X has probablt functon k, = 1,, 3, P( X = ) = k ( + 1), = 4, 5, where k s a constant. (a) Fnd the value of k. (b) Fnd the eact
UNIT 7. THE FUNDAMENTAL EQUATIONS OF HYPERSURFACE THEORY
 UNIT 7. THE FUNDAMENTAL EQUATIONS OF HYPERSURFACE THEORY ================================================================================================================================================================================================================================================
UNIT 7. THE FUNDAMENTAL EQUATIONS OF HYPERSURFACE THEORY ================================================================================================================================================================================================================================================
The 7 th Balkan Conference on Operational Research BACOR 05 Constanta, May 2005, Romania
 The 7 th alan onerence on Oeratonal Reearch AOR 5 ontanta, May 5, Roana THE ESTIMATIO OF THE GRAPH OX DIMESIO OF A LASS OF FRATALS ALIA ÃRULESU Ovdu Unverty, ontanta, Roana Abtract Fractal denon are the
The 7 th alan onerence on Oeratonal Reearch AOR 5 ontanta, May 5, Roana THE ESTIMATIO OF THE GRAPH OX DIMESIO OF A LASS OF FRATALS ALIA ÃRULESU Ovdu Unverty, ontanta, Roana Abtract Fractal denon are the
The Multivariate Normal Distribution. In this case according to our theorem
 The Multivariate Normal Distribution Defn: Z R 1 N(0, 1) iff f Z (z) = 1 2π e z2 /2. Defn: Z R p MV N p (0, I) if and only if Z = (Z 1,..., Z p ) T with the Z i independent and each Z i N(0, 1). In this
The Multivariate Normal Distribution Defn: Z R 1 N(0, 1) iff f Z (z) = 1 2π e z2 /2. Defn: Z R p MV N p (0, I) if and only if Z = (Z 1,..., Z p ) T with the Z i independent and each Z i N(0, 1). In this
On the Calderón-Zygmund lemma for Sobolev functions
 arxv:0810.5029v1 [ath.ca] 28 Oct 2008 On the Calderón-Zygund lea for Sobolev functons Pascal Auscher october 16, 2008 Abstract We correct an naccuracy n the proof of a result n [Aus1]. 2000 MSC: 42B20,
arxv:0810.5029v1 [ath.ca] 28 Oct 2008 On the Calderón-Zygund lea for Sobolev functons Pascal Auscher october 16, 2008 Abstract We correct an naccuracy n the proof of a result n [Aus1]. 2000 MSC: 42B20,
Comments on Detecting Outliers in Gamma Distribution by M. Jabbari Nooghabi et al. (2010)
 Comments on Detectng Outlers n Gamma Dstrbuton by M. Jabbar Nooghab et al. (21) M. Magdalena Lucn Alejandro C. Frery September 17, 215 arxv:159.55v1 [stat.co] 16 Sep 215 Ths note shows that the results
Comments on Detectng Outlers n Gamma Dstrbuton by M. Jabbar Nooghab et al. (21) M. Magdalena Lucn Alejandro C. Frery September 17, 215 arxv:159.55v1 [stat.co] 16 Sep 215 Ths note shows that the results
Improvements on Waring s Problem
 Imrovement on Warng Problem L An-Png Bejng 85, PR Chna al@nacom Abtract By a new recurve algorthm for the auxlary equaton, n th aer, we wll gve ome mrovement for Warng roblem Keyword: Warng Problem, Hardy-Lttlewood
Imrovement on Warng Problem L An-Png Bejng 85, PR Chna al@nacom Abtract By a new recurve algorthm for the auxlary equaton, n th aer, we wll gve ome mrovement for Warng roblem Keyword: Warng Problem, Hardy-Lttlewood
BAYESIAN CURVE FITTING USING PIECEWISE POLYNOMIALS. Dariusz Biskup
 BAYESIAN CURVE FITTING USING PIECEWISE POLYNOMIALS Darusz Bskup 1. Introducton The paper presents a nonparaetrc procedure for estaton of an unknown functon f n the regresson odel y = f x + ε = N. (1) (
BAYESIAN CURVE FITTING USING PIECEWISE POLYNOMIALS Darusz Bskup 1. Introducton The paper presents a nonparaetrc procedure for estaton of an unknown functon f n the regresson odel y = f x + ε = N. (1) (
On the Use of High-Order Moment Matching to Approximate the Generalized-K Distribution by a Gamma Distribution
 On the Ue of High-Order Moent Matching to Approxiate the Generalized- Ditribution by a Gaa Ditribution Saad Al-Ahadi Departent of Syte & Coputer Engineering Carleton Univerity Ottawa Canada aahadi@ce.carleton.ca
On the Ue of High-Order Moent Matching to Approxiate the Generalized- Ditribution by a Gaa Ditribution Saad Al-Ahadi Departent of Syte & Coputer Engineering Carleton Univerity Ottawa Canada aahadi@ce.carleton.ca
Comparing Bayesian Methods for Estimating Parameters of Noisy Sinusoids. static 1 sinusoidal model which is a superposition of m sinusoids: (1)
 Iue 4, Volue 7, 3 3 Coparng Bayean Method for Etatng Paraeter of oy Snuod Durun Ütündağ Departent of Matheat, Faulty of Sene and Art, Marara Unverty, Itanbul, Turkey dutundag@arara.edu.tr Mehet Cevr Departent
Iue 4, Volue 7, 3 3 Coparng Bayean Method for Etatng Paraeter of oy Snuod Durun Ütündağ Departent of Matheat, Faulty of Sene and Art, Marara Unverty, Itanbul, Turkey dutundag@arara.edu.tr Mehet Cevr Departent
Moments of the product and ratio of two correlated chi-square variables
 Stat Papers 009 50:581 59 DOI 10.1007/s0036-007-0105-0 REGULAR ARTICLE Moents of the product and ratio of two correlated chi-square variables Anwar H. Joarder Received: June 006 / Revised: 8 October 007
Stat Papers 009 50:581 59 DOI 10.1007/s0036-007-0105-0 REGULAR ARTICLE Moents of the product and ratio of two correlated chi-square variables Anwar H. Joarder Received: June 006 / Revised: 8 October 007
The Distribution of the Covariance Matrix for a Subset of Elliptical Distributions with Extension to Two Kurtosis Parameters
 journal of ultivariate analysis 58, 96106 (1996) article no. 0041 The Distribution of the Covariance Matrix for a Subset of Elliptical Distributions with Extension to Two Kurtosis Paraeters H. S. Steyn
journal of ultivariate analysis 58, 96106 (1996) article no. 0041 The Distribution of the Covariance Matrix for a Subset of Elliptical Distributions with Extension to Two Kurtosis Paraeters H. S. Steyn
arxiv: v1 [math.nt] 13 Jan 2009
![arxiv: v1 [math.nt] 13 Jan 2009 arxiv: v1 [math.nt] 13 Jan 2009](/thumbs/93/113128572.jpg) NOTE ON THE GENERALIZATION OF THE HIGHER ORDER -GENOCCHI NUMBERS AND -EULER NUMBERS arxiv:09011697v1 [athnt] 13 Jan 2009 TAEKYUN KIM, YOUNG-HEE KIM, AND KYUNG-WON HWANG Abstract Cangu-Ozden-Sisek[1] constructed
NOTE ON THE GENERALIZATION OF THE HIGHER ORDER -GENOCCHI NUMBERS AND -EULER NUMBERS arxiv:09011697v1 [athnt] 13 Jan 2009 TAEKYUN KIM, YOUNG-HEE KIM, AND KYUNG-WON HWANG Abstract Cangu-Ozden-Sisek[1] constructed
Denote the function derivatives f(x) in given points. x a b. Using relationships (1.2), polynomials (1.1) are written in the form
 SET OF METHODS FO SOUTION THE AUHY POBEM FO STIFF SYSTEMS OF ODINAY DIFFEENTIA EUATIONS AF atypov and YuV Nulchev Insttute of Theoretcal and Appled Mechancs SB AS 639 Novosbrs ussa Introducton A constructon
SET OF METHODS FO SOUTION THE AUHY POBEM FO STIFF SYSTEMS OF ODINAY DIFFEENTIA EUATIONS AF atypov and YuV Nulchev Insttute of Theoretcal and Appled Mechancs SB AS 639 Novosbrs ussa Introducton A constructon
Chapter 6: Dynamic Simulation Environment
 Chapter 6: Dnac Suaton Envronent Prevous neatc and dnac anass has deonstrated the snguart-free worspace and the hgh force-bearng characterstcs of the Wrst. Ths chapter copetes the dnac ode of the Carpa
Chapter 6: Dnac Suaton Envronent Prevous neatc and dnac anass has deonstrated the snguart-free worspace and the hgh force-bearng characterstcs of the Wrst. Ths chapter copetes the dnac ode of the Carpa
GEE ESTIMATORS IN MIXTURE MODEL WITH VARYING CONCENTRATIONS
 ACTA UIVERSITATIS LODZIESIS FOLIA OECOOMICA 3(3142015 http://dx.doi.org/10.18778/0208-6018.314.03 Olesii Doronin *, Rostislav Maiboroda ** GEE ESTIMATORS I MIXTURE MODEL WITH VARYIG COCETRATIOS Abstract.
ACTA UIVERSITATIS LODZIESIS FOLIA OECOOMICA 3(3142015 http://dx.doi.org/10.18778/0208-6018.314.03 Olesii Doronin *, Rostislav Maiboroda ** GEE ESTIMATORS I MIXTURE MODEL WITH VARYIG COCETRATIOS Abstract.
{ In general, we are presented with a quadratic function of a random vector X
 Quadratc VAR odel Mchael Carter à Prelnares Introducton Suppose we wsh to quantfy the value-at-rsk of a Japanese etals tradng fr that has exposure to forward and opton postons n platnu. Soe of the postons
Quadratc VAR odel Mchael Carter à Prelnares Introducton Suppose we wsh to quantfy the value-at-rsk of a Japanese etals tradng fr that has exposure to forward and opton postons n platnu. Soe of the postons
System in Weibull Distribution
 Internatonal Matheatcal Foru 4 9 no. 9 94-95 Relablty Equvalence Factors of a Seres-Parallel Syste n Webull Dstrbuton M. A. El-Dacese Matheatcs Departent Faculty of Scence Tanta Unversty Tanta Egypt eldacese@yahoo.co
Internatonal Matheatcal Foru 4 9 no. 9 94-95 Relablty Equvalence Factors of a Seres-Parallel Syste n Webull Dstrbuton M. A. El-Dacese Matheatcs Departent Faculty of Scence Tanta Unversty Tanta Egypt eldacese@yahoo.co
STUDY ON SOLIDIFICATION PROPERTIES OF ICE STORAGE IN A FLAT AND RECTANGULAR CAPSULE
 Internationa Journa on Arcitectura cience, Voue 3, Nuer 4, p.35-39, TUDY ON OLIDIFICATION PROPERTIE OF ICE TORAGE IN A FLAT AND RECTANGULAR CAPULE G.Y. Fang Departent of Pyic, Nanjing Univerity, Nanjing
Internationa Journa on Arcitectura cience, Voue 3, Nuer 4, p.35-39, TUDY ON OLIDIFICATION PROPERTIE OF ICE TORAGE IN A FLAT AND RECTANGULAR CAPULE G.Y. Fang Departent of Pyic, Nanjing Univerity, Nanjing
Homework Notes Week 7
 Homework Notes Week 7 Math 4 Sprng 4 #4 (a Complete the proof n example 5 that s an nner product (the Frobenus nner product on M n n (F In the example propertes (a and (d have already been verfed so we
Homework Notes Week 7 Math 4 Sprng 4 #4 (a Complete the proof n example 5 that s an nner product (the Frobenus nner product on M n n (F In the example propertes (a and (d have already been verfed so we
4.1 Expected value of a discrete random variable. Suppose we shall win $i if the die lands on i. What is our ideal average winnings per toss?
 Chapter 4 Mathematical Expectation 4.1 Expected value of a discrete random variable Examples: (a) Given 1, 2, 3, 4, 5, 6. What is the average? (b) Toss an unbalanced die 1 times. Lands on 1 2 3 4 5 6 Probab..1.3.1.2.2.1
Chapter 4 Mathematical Expectation 4.1 Expected value of a discrete random variable Examples: (a) Given 1, 2, 3, 4, 5, 6. What is the average? (b) Toss an unbalanced die 1 times. Lands on 1 2 3 4 5 6 Probab..1.3.1.2.2.1
Congruences involving Bernoulli and Euler numbers Zhi-Hong Sun
 The aer will aear in Journal of Nuber Theory. Congruences involving Bernoulli Euler nubers Zhi-Hong Sun Deartent of Matheatics, Huaiyin Teachers College, Huaian, Jiangsu 300, PR China Received January
The aer will aear in Journal of Nuber Theory. Congruences involving Bernoulli Euler nubers Zhi-Hong Sun Deartent of Matheatics, Huaiyin Teachers College, Huaian, Jiangsu 300, PR China Received January
MULTIPOLE FIELDS. Multipoles, 2 l poles. Monopoles, dipoles, quadrupoles, octupoles... Electric Dipole R 1 R 2. P(r,θ,φ) e r
 MULTIPOLE FIELDS Mutpoes poes. Monopoes dpoes quadupoes octupoes... 4 8 6 Eectc Dpoe +q O θ e R R P(θφ) -q e The potenta at the fed pont P(θφ) s ( θϕ )= q R R Bo E. Seneus : Now R = ( e) = + cosθ R = (
MULTIPOLE FIELDS Mutpoes poes. Monopoes dpoes quadupoes octupoes... 4 8 6 Eectc Dpoe +q O θ e R R P(θφ) -q e The potenta at the fed pont P(θφ) s ( θϕ )= q R R Bo E. Seneus : Now R = ( e) = + cosθ R = (
CANKAYA UNIVERSITY FACULTY OF ENGINEERING AND ARCHITECTURE MECHANICAL ENGINEERING DEPARTMENT ME 212 THERMODYNAMICS II CHAPTER 11 EXAMPLES SOLUTION
 CANKAYA UNIVESIY FACULY OF ENGINEEING AND ACHIECUE MECHANICAL ENGINEEING DEPAMEN ME HEMODYNAMICS II CHAPE EXAMPLES SOLUION ) he reure wthn a. m tank hould not exeed 0 ar. Chek the reure wthn the tank f
CANKAYA UNIVESIY FACULY OF ENGINEEING AND ACHIECUE MECHANICAL ENGINEEING DEPAMEN ME HEMODYNAMICS II CHAPE EXAMPLES SOLUION ) he reure wthn a. m tank hould not exeed 0 ar. Chek the reure wthn the tank f
Expected Value and Variance
 MATH 38 Expected Value and Varance Dr. Neal, WKU We now shall dscuss how to fnd the average and standard devaton of a random varable X. Expected Value Defnton. The expected value (or average value, or
MATH 38 Expected Value and Varance Dr. Neal, WKU We now shall dscuss how to fnd the average and standard devaton of a random varable X. Expected Value Defnton. The expected value (or average value, or
GENERALIZED LEGENDRE POLYNOMIALS AND RELATED SUPERCONGRUENCES
 J. Nuber Theory 0, o., 9-9. GENERALIZED LEGENDRE POLYNOMIALS AND RELATED SUPERCONGRUENCES Zhi-Hog Su School of Matheatical Scieces, Huaiyi Noral Uiversity, Huaia, Jiagsu 00, PR Chia Eail: zhihogsu@yahoo.co
J. Nuber Theory 0, o., 9-9. GENERALIZED LEGENDRE POLYNOMIALS AND RELATED SUPERCONGRUENCES Zhi-Hog Su School of Matheatical Scieces, Huaiyi Noral Uiversity, Huaia, Jiagsu 00, PR Chia Eail: zhihogsu@yahoo.co
Analysis of Variance and Design of Experiments-II
 Anly of Vrne Degn of Experment-II MODULE VI LECTURE - 8 SPLIT-PLOT AND STRIP-PLOT DESIGNS Dr Shlbh Deprtment of Mthemt & Sttt Indn Inttute of Tehnology Knpur Tretment ontrt: Mn effet The uefulne of hvng
Anly of Vrne Degn of Experment-II MODULE VI LECTURE - 8 SPLIT-PLOT AND STRIP-PLOT DESIGNS Dr Shlbh Deprtment of Mthemt & Sttt Indn Inttute of Tehnology Knpur Tretment ontrt: Mn effet The uefulne of hvng
Lecture 5: Moment generating functions
 Lecture 5: Moment generating functions Definition 2.3.6. The moment generating function (mgf) of a random variable X is { x e tx f M X (t) = E(e tx X (x) if X has a pmf ) = etx f X (x)dx if X has a pdf
Lecture 5: Moment generating functions Definition 2.3.6. The moment generating function (mgf) of a random variable X is { x e tx f M X (t) = E(e tx X (x) if X has a pmf ) = etx f X (x)dx if X has a pdf
Exam-style practice: A Level
 Exa-tye practce: A Leve a Let X dete the dtrbut ae ad X dete the dtrbut eae The dee the rad varabe Y X X j j The expected vaue Y : E( Y) EX X j j EX EX j j EX E X 7 The varace : Var( Y) VarX VarX j j Var(
Exa-tye practce: A Leve a Let X dete the dtrbut ae ad X dete the dtrbut eae The dee the rad varabe Y X X j j The expected vaue Y : E( Y) EX X j j EX EX j j EX E X 7 The varace : Var( Y) VarX VarX j j Var(
Estimating Parameters for a Gaussian pdf
 Pattern Recognition and achine Learning Jaes L. Crowley ENSIAG 3 IS First Seester 00/0 Lesson 5 7 Noveber 00 Contents Estiating Paraeters for a Gaussian pdf Notation... The Pattern Recognition Proble...3
Pattern Recognition and achine Learning Jaes L. Crowley ENSIAG 3 IS First Seester 00/0 Lesson 5 7 Noveber 00 Contents Estiating Paraeters for a Gaussian pdf Notation... The Pattern Recognition Proble...3
Randić Energy and Randić Estrada Index of a Graph
 EUROPEAN JOURNAL OF PURE AND APPLIED MATHEMATICS Vol. 5, No., 202, 88-96 ISSN 307-5543 www.ejpam.com SPECIAL ISSUE FOR THE INTERNATIONAL CONFERENCE ON APPLIED ANALYSIS AND ALGEBRA 29 JUNE -02JULY 20, ISTANBUL
EUROPEAN JOURNAL OF PURE AND APPLIED MATHEMATICS Vol. 5, No., 202, 88-96 ISSN 307-5543 www.ejpam.com SPECIAL ISSUE FOR THE INTERNATIONAL CONFERENCE ON APPLIED ANALYSIS AND ALGEBRA 29 JUNE -02JULY 20, ISTANBUL
8 Waves in Uniform Magnetized Media
 8 Wave n Unform Magnetzed Meda 81 Suceptblte The frt order current can be wrtten j = j = q d 3 p v f 1 ( r, p, t) = ɛ 0 χ E For Maxwellan dtrbuton Y n (λ) = f 0 (v, v ) = 1 πvth exp (v V ) v th 1 πv th
8 Wave n Unform Magnetzed Meda 81 Suceptblte The frt order current can be wrtten j = j = q d 3 p v f 1 ( r, p, t) = ɛ 0 χ E For Maxwellan dtrbuton Y n (λ) = f 0 (v, v ) = 1 πvth exp (v V ) v th 1 πv th
Modelli Clamfim Equazione del Calore Lezione ottobre 2014
 CLAMFIM Bologna Modell 1 @ Clamfm Equazone del Calore Lezone 17 15 ottobre 2014 professor Danele Rtell danele.rtell@unbo.t 1/24? Convoluton The convoluton of two functons g(t) and f(t) s the functon (g
CLAMFIM Bologna Modell 1 @ Clamfm Equazone del Calore Lezone 17 15 ottobre 2014 professor Danele Rtell danele.rtell@unbo.t 1/24? Convoluton The convoluton of two functons g(t) and f(t) s the functon (g
Lecture 21: Numerical methods for pricing American type derivatives
 Lecture 21: Numercal methods for prcng Amercan type dervatves Xaoguang Wang STAT 598W Aprl 10th, 2014 (STAT 598W) Lecture 21 1 / 26 Outlne 1 Fnte Dfference Method Explct Method Penalty Method (STAT 598W)
Lecture 21: Numercal methods for prcng Amercan type dervatves Xaoguang Wang STAT 598W Aprl 10th, 2014 (STAT 598W) Lecture 21 1 / 26 Outlne 1 Fnte Dfference Method Explct Method Penalty Method (STAT 598W)
REVIEW OF MAIN CONCEPTS AND FORMULAS A B = Ā B. Pr(A B C) = Pr(A) Pr(A B C) =Pr(A) Pr(B A) Pr(C A B)
 REVIEW OF MAIN CONCEPTS AND FORMULAS Boolean algebra of events (subsets of a sample space) DeMorgan s formula: A B = Ā B A B = Ā B The notion of conditional probability, and of mutual independence of two
REVIEW OF MAIN CONCEPTS AND FORMULAS Boolean algebra of events (subsets of a sample space) DeMorgan s formula: A B = Ā B A B = Ā B The notion of conditional probability, and of mutual independence of two
P (x). all other X j =x j. If X is a continuous random vector (see p.172), then the marginal distributions of X i are: f(x)dx 1 dx n
 JOINT DENSITIES - RANDOM VECTORS - REVIEW Joint densities describe probability distributions of a random vector X: an n-dimensional vector of random variables, ie, X = (X 1,, X n ), where all X is are
JOINT DENSITIES - RANDOM VECTORS - REVIEW Joint densities describe probability distributions of a random vector X: an n-dimensional vector of random variables, ie, X = (X 1,, X n ), where all X is are
Physics 1501 Lecture 19
 Physcs 1501 ectue 19 Physcs 1501: ectue 19 Today s Agenda Announceents HW#7: due Oct. 1 Mdte 1: aveage 45 % Topcs otatonal Kneatcs otatonal Enegy Moents of Ineta Physcs 1501: ectue 19, Pg 1 Suay (wth copason
Physcs 1501 ectue 19 Physcs 1501: ectue 19 Today s Agenda Announceents HW#7: due Oct. 1 Mdte 1: aveage 45 % Topcs otatonal Kneatcs otatonal Enegy Moents of Ineta Physcs 1501: ectue 19, Pg 1 Suay (wth copason
MARKOV CHAIN AND HIDDEN MARKOV MODEL
 MARKOV CHAIN AND HIDDEN MARKOV MODEL JIAN ZHANG JIANZHAN@STAT.PURDUE.EDU Markov chan and hdden Markov mode are probaby the smpest modes whch can be used to mode sequenta data,.e. data sampes whch are not
MARKOV CHAIN AND HIDDEN MARKOV MODEL JIAN ZHANG JIANZHAN@STAT.PURDUE.EDU Markov chan and hdden Markov mode are probaby the smpest modes whch can be used to mode sequenta data,.e. data sampes whch are not
Power Series and Analytic Function
 Dr Mansoor Alshehri King Saud University MATH204-Differential Equations Center of Excellence in Learning and Teaching 1 / 21 Some Reviews of Power Series Differentiation and Integration of a Power Series
Dr Mansoor Alshehri King Saud University MATH204-Differential Equations Center of Excellence in Learning and Teaching 1 / 21 Some Reviews of Power Series Differentiation and Integration of a Power Series
Friction parameters identification and compensation of LuGre model base on genetic algorithms
 Internatonal Sympoum on Computer & Informat (ISCI 015) Frton parameter dentfaton and ompenaton of LuGre model bae on genet algorthm Yuqn Wen a, Mng Chu b and Hanxu Sun Shool of Automaton, Bejng Unverty
Internatonal Sympoum on Computer & Informat (ISCI 015) Frton parameter dentfaton and ompenaton of LuGre model bae on genet algorthm Yuqn Wen a, Mng Chu b and Hanxu Sun Shool of Automaton, Bejng Unverty
Solutions for Homework #9
 Solutons for Hoewor #9 PROBEM. (P. 3 on page 379 n the note) Consder a sprng ounted rgd bar of total ass and length, to whch an addtonal ass s luped at the rghtost end. he syste has no dapng. Fnd the natural
Solutons for Hoewor #9 PROBEM. (P. 3 on page 379 n the note) Consder a sprng ounted rgd bar of total ass and length, to whch an addtonal ass s luped at the rghtost end. he syste has no dapng. Fnd the natural
A finite difference method for heat equation in the unbounded domain
 Internatona Conerence on Advanced ectronc Scence and Technoogy (AST 6) A nte derence method or heat equaton n the unbounded doman a Quan Zheng and Xn Zhao Coege o Scence North Chna nversty o Technoogy
Internatona Conerence on Advanced ectronc Scence and Technoogy (AST 6) A nte derence method or heat equaton n the unbounded doman a Quan Zheng and Xn Zhao Coege o Scence North Chna nversty o Technoogy
= m 1. sin π( ai z ) )
 EXACT COVERING SYSTEMS AND THE GAUSS-LEGENDRE MULTIPLICATION FORMULA FOR THE GAMMA FUNCTION John Beeee Unversty of Alaska Anchorage July 0 199 The Gauss-Legendre ultplcaton forula for the gaa functon s
EXACT COVERING SYSTEMS AND THE GAUSS-LEGENDRE MULTIPLICATION FORMULA FOR THE GAMMA FUNCTION John Beeee Unversty of Alaska Anchorage July 0 199 The Gauss-Legendre ultplcaton forula for the gaa functon s
Slobodan Lakić. Communicated by R. Van Keer
 Serdca Math. J. 21 (1995), 335-344 AN ITERATIVE METHOD FOR THE MATRIX PRINCIPAL n-th ROOT Slobodan Lakć Councated by R. Van Keer In ths paper we gve an teratve ethod to copute the prncpal n-th root and
Serdca Math. J. 21 (1995), 335-344 AN ITERATIVE METHOD FOR THE MATRIX PRINCIPAL n-th ROOT Slobodan Lakć Councated by R. Van Keer In ths paper we gve an teratve ethod to copute the prncpal n-th root and
First Year Examination Department of Statistics, University of Florida
 Frst Year Examnaton Department of Statstcs, Unversty of Florda May 7, 010, 8:00 am - 1:00 noon Instructons: 1. You have four hours to answer questons n ths examnaton.. You must show your work to receve
Frst Year Examnaton Department of Statstcs, Unversty of Florda May 7, 010, 8:00 am - 1:00 noon Instructons: 1. You have four hours to answer questons n ths examnaton.. You must show your work to receve
Statistics Parameters
 Saplig Ditributio & Cofidece Iterval Etiator Statitical Iferece Etiatio Tetig Hypothei Statitic Ued to Etiate Populatio Paraeter Statitic Saple Mea, Saple Variace, Saple Proportio, Paraeter populatio ea
Saplig Ditributio & Cofidece Iterval Etiator Statitical Iferece Etiatio Tetig Hypothei Statitic Ued to Etiate Populatio Paraeter Statitic Saple Mea, Saple Variace, Saple Proportio, Paraeter populatio ea
Several generation methods of multinomial distributed random number Tian Lei 1, a,linxihe 1,b,Zhigang Zhang 1,c
 Internatonal Conference on Appled Scence and Engneerng Innovaton (ASEI 205) Several generaton ethods of ultnoal dstrbuted rando nuber Tan Le, a,lnhe,b,zhgang Zhang,c School of Matheatcs and Physcs, USTB,
Internatonal Conference on Appled Scence and Engneerng Innovaton (ASEI 205) Several generaton ethods of ultnoal dstrbuted rando nuber Tan Le, a,lnhe,b,zhgang Zhang,c School of Matheatcs and Physcs, USTB,
16.584: Random (Stochastic) Processes
 1 16.584: Random (Stochastic) Processes X(t): X : RV : Continuous function of the independent variable t (time, space etc.) Random process : Collection of X(t, ζ) : Indexed on another independent variable
1 16.584: Random (Stochastic) Processes X(t): X : RV : Continuous function of the independent variable t (time, space etc.) Random process : Collection of X(t, ζ) : Indexed on another independent variable
New upper bound for the B-spline basis condition number II. K. Scherer. Institut fur Angewandte Mathematik, Universitat Bonn, Bonn, Germany.
 New upper bound for the B-spline basis condition nuber II. A proof of de Boor's 2 -conjecture K. Scherer Institut fur Angewandte Matheati, Universitat Bonn, 535 Bonn, Gerany and A. Yu. Shadrin Coputing
New upper bound for the B-spline basis condition nuber II. A proof of de Boor's 2 -conjecture K. Scherer Institut fur Angewandte Matheati, Universitat Bonn, 535 Bonn, Gerany and A. Yu. Shadrin Coputing
Integration - Past Edexcel Exam Questions
 Integration - Past Edexcel Exam Questions 1. (a) Given that y = 5x 2 + 7x + 3, find i. - ii. - (b) ( 1 + 3 ) x 1 x dx. [4] 2. Question 2b - January 2005 2. The gradient of the curve C is given by The point
Integration - Past Edexcel Exam Questions 1. (a) Given that y = 5x 2 + 7x + 3, find i. - ii. - (b) ( 1 + 3 ) x 1 x dx. [4] 2. Question 2b - January 2005 2. The gradient of the curve C is given by The point
NONDIFFERENTIABLE MATHEMATICAL PROGRAMS. OPTIMALITY AND HIGHER-ORDER DUALITY RESULTS
 HE PUBLISHING HOUSE PROCEEDINGS OF HE ROMANIAN ACADEMY, See A, OF HE ROMANIAN ACADEMY Volue 9, Nube 3/8,. NONDIFFERENIABLE MAHEMAICAL PROGRAMS. OPIMALIY AND HIGHER-ORDER DUALIY RESULS Vale PREDA Uvety
HE PUBLISHING HOUSE PROCEEDINGS OF HE ROMANIAN ACADEMY, See A, OF HE ROMANIAN ACADEMY Volue 9, Nube 3/8,. NONDIFFERENIABLE MAHEMAICAL PROGRAMS. OPIMALIY AND HIGHER-ORDER DUALIY RESULS Vale PREDA Uvety
Mathematical Statistics 1 Math A 6330
 Mathematical Statistics 1 Math A 6330 Chapter 2 Transformations and Expectations Mohamed I. Riffi Department of Mathematics Islamic University of Gaza September 14, 2015 Outline 1 Distributions of Functions
Mathematical Statistics 1 Math A 6330 Chapter 2 Transformations and Expectations Mohamed I. Riffi Department of Mathematics Islamic University of Gaza September 14, 2015 Outline 1 Distributions of Functions
4r 2 12r + 9 = 0. r = 24 ± y = e 3x. y = xe 3x. r 2 6r + 25 = 0. y(0) = c 1 = 3 y (0) = 3c 1 + 4c 2 = c 2 = 1
 Mathematics MATB44, Assignment 2 Solutions to Selected Problems Question. Solve 4y 2y + 9y = 0 Soln: The characteristic equation is The solutions are (repeated root) So the solutions are and Question 2
Mathematics MATB44, Assignment 2 Solutions to Selected Problems Question. Solve 4y 2y + 9y = 0 Soln: The characteristic equation is The solutions are (repeated root) So the solutions are and Question 2
University of Southern California School Of Engineering Department Of Electrical Engineering
 Unverty f Suthern afrna Sch Of Enneern Deartent Of Eectrca Enneern EE 48: ewrk nent # fa, Due 9/7/ ha Fure : The redrawn cnfuratn f "F P." t b t a Gven the fure, ne can wrte the fwn equatn: λ t t { λ }
Unverty f Suthern afrna Sch Of Enneern Deartent Of Eectrca Enneern EE 48: ewrk nent # fa, Due 9/7/ ha Fure : The redrawn cnfuratn f "F P." t b t a Gven the fure, ne can wrte the fwn equatn: λ t t { λ }
CS Lecture 13. More Maximum Likelihood
 CS 6347 Lecture 13 More Maxiu Likelihood Recap Last tie: Introduction to axiu likelihood estiation MLE for Bayesian networks Optial CPTs correspond to epirical counts Today: MLE for CRFs 2 Maxiu Likelihood
CS 6347 Lecture 13 More Maxiu Likelihood Recap Last tie: Introduction to axiu likelihood estiation MLE for Bayesian networks Optial CPTs correspond to epirical counts Today: MLE for CRFs 2 Maxiu Likelihood
A A Non-Constructible Equilibrium 1
 A A Non-Contructbe Equbrum 1 The eampe depct a eparabe contet wth three payer and one prze of common vaue 1 (o v ( ) =1 c ( )). I contruct an equbrum (C, G, G) of the contet, n whch payer 1 bet-repone
A A Non-Contructbe Equbrum 1 The eampe depct a eparabe contet wth three payer and one prze of common vaue 1 (o v ( ) =1 c ( )). I contruct an equbrum (C, G, G) of the contet, n whch payer 1 bet-repone
Controller Design for Networked Control Systems in Multiple-packet Transmission with Random Delays
 Appled Mehans and Materals Onlne: 03-0- ISSN: 66-748, Vols. 78-80, pp 60-604 do:0.408/www.sentf.net/amm.78-80.60 03 rans eh Publatons, Swtzerland H Controller Desgn for Networed Control Systems n Multple-paet
Appled Mehans and Materals Onlne: 03-0- ISSN: 66-748, Vols. 78-80, pp 60-604 do:0.408/www.sentf.net/amm.78-80.60 03 rans eh Publatons, Swtzerland H Controller Desgn for Networed Control Systems n Multple-paet
Collapsing to Sample and Remainder Means. Ed Stanek. In order to collapse the expanded random variables to weighted sample and remainder
 Collapg to Saple ad Reader Mea Ed Staek Collapg to Saple ad Reader Average order to collape the expaded rado varable to weghted aple ad reader average, we pre-ultpled by ( M C C ( ( M C ( M M M ( M M M,
Collapg to Saple ad Reader Mea Ed Staek Collapg to Saple ad Reader Average order to collape the expaded rado varable to weghted aple ad reader average, we pre-ultpled by ( M C C ( ( M C ( M M M ( M M M,
Research on Complex Networks Control Based on Fuzzy Integral Sliding Theory
 Advanced Scence and Technoogy Letters Vo.83 (ISA 205), pp.60-65 http://dx.do.org/0.4257/ast.205.83.2 Research on Compex etworks Contro Based on Fuzzy Integra Sdng Theory Dongsheng Yang, Bngqng L, 2, He
Advanced Scence and Technoogy Letters Vo.83 (ISA 205), pp.60-65 http://dx.do.org/0.4257/ast.205.83.2 Research on Compex etworks Contro Based on Fuzzy Integra Sdng Theory Dongsheng Yang, Bngqng L, 2, He
8. INVERSE Z-TRANSFORM
 8. INVERSE Z-TRANSFORM The proce by whch Z-trnform of tme ere, nmely X(), returned to the tme domn clled the nvere Z-trnform. The nvere Z-trnform defned by: Computer tudy Z X M-fle trn.m ued to fnd nvere
8. INVERSE Z-TRANSFORM The proce by whch Z-trnform of tme ere, nmely X(), returned to the tme domn clled the nvere Z-trnform. The nvere Z-trnform defned by: Computer tudy Z X M-fle trn.m ued to fnd nvere
