I WAVES (ENGEL & REID, 13.2, 13.3 AND 12.6)
|
|
|
- Natalie Gibson
- 5 years ago
- Views:
Transcription
1 I WAVES (ENGEL & REID, 13., 13.3 AND 1.6) I.1 Introduction A significant part of the lecture From Quantum to Matter is devoted to developing the basic concepts of quantum mechanics. This is not possible without a clear understanding of classical waves. This is the purpose of these additional lecture notes. Fig. I.1: Circular wave produced by the impact of a water drop on a pond. A typical example of a circular wave at the surface of a pond is shown in Fig. I.1. Although this example triggers naturally an association with a wave it involves also the complex phenomena near the place where the drop felt in the water that is not describable as a wave. To introduce the concept of a wave we consider thus a much simpler example: that of a propagating disturbance along a stretched rope. It is characterized by a wavelength λ and a propagation velocity V. We use here a capital V instead of v to avoid confusions with the frequency ν. For an observer at a fixed place along the x-axis the rope is moving up and down with a frequency ν. V x Fig.I.: Sinusoidal disturbance along a stretched rope propagating at a velocity V. 1
2 (, ) u = u x t x Fig. I.3: For an observer sitting at a fixed position in space the rope moves up and down at a certain frequency ν. If the top picture corresponds to time t = 0, then the bottom picture corresponds to t =T/ where T is the period of the oscillation. x o It takes a certain time T for the fixed observer to see locally the rope to go up, pass through a maximum deflection, move down, pass through a minimum and to come back to the original position. This time T is called the period of an oscillation. During the time T the wave has moved by exactly one wavelength λ. We have therefore the fundamental relation λν = V ( I.1 The displacement u=u(x,t) of the rope can mathematically be described with
3 u = u πx πt, ( I. λ T ( x t) = Asin In this form λ and T are readily identifiable as λ wavelength [m] ( I.3 T period [s] ( I.4 For an observer at position x 0 the displacement varies sinusoidaly with a period T π xo π t u = u( xo, t) = Asin λ T ( I.5 The following physical quantities are introduced for a more elegant notation 1 ν = T k π λ = 1 frequency [s or Hz] 1 / wavenumber [m ] ω πν = 1 angular frequency [s ] ( I.6 The displacement u u( x, t) = can then be written as (, ) sin( ω ) u = u x t = A kx t ( I.7 Consider now a characteristic point with a given value for u. For example the red dot in Fig. I.3, which corresponds to the top of the wave, moves with the velocity V determined by the condition that top ( top ω ) constant u = u kx t = kx ωt = constant ( I.8 and thus dx top V = ω dt = k ( I.9 3
4 For reasons that will become clear later, the velocity V k ω = is called the phase velocity. So far we have claimed without demonstration that the disturbance of a stretched rope could be described by a sinusoidal expression as in Eq.I.. In the next section we show that such an expression is a solution of the so-called wave equation. I. The wave equation for a rope The string is pulled on both ends by a force F. The mass of the string per meter is called the specific mass ρ. A blow-up of the string is shown below F u( x + x, t) u( x, t) Fig. I.4: Detail of the disturbance of a stretched rope. The force F used to stretch the rope is indicated by red arrows. The displacement at position x is uxt (, ) and at position x+ x it is u u( x x, t) = +. Both displacements are strongly exagerated for clarity. In reality they are much smaller than the length of the rope. Note that we do not assume that uxt (, ) is a sine function of x and t. A string element of length x has a mass m = ρ x. The total force (broad green arrow) along the u-direction acting on the rope element between x and x+ x is 4
5 du du F = F F ( I.10 dx dx x+ x x As, by definition, in the limit x 0 du du = ( I.11 x du dx x+ x dx x dx we obtain that du du d u = + x ( I.1 dx dx dx and consequently x+ x x x du F = F x ( I.13 dx From Newton s law we know, however, that Force=mass acceleration. For the rope element this implies that du F = ρ x ( I.14 dt Equating Eqs.I13 and 14 we obtain Fdu du = ( I.15 ρ dx dt d u INTERMEZZO: At this point we must be very careful with our notation.. When we write we mean dx d u in fact a derivative with respect to x at constant t and when we write we mean in fact a derivative with dt respect to t at constant x To make this clear we use the notation and For a function depending on two variables, for example u = u( x, t) we mean that and u( x, t = ) u( x, t = ) = partial derivative with respect to x while t is kept constant = partial derivative with respect to t while x is kept constant with this notation convention, Eq.I.15 can be re-written as F ρ = 5
6 In fact, as explained in the intermezzo, we should have written F ρ Since [ F ] [ ρ ] = N m = = kg/m s has the dimension of a velocity squared we write ( I.16 V = ( I.17 This equation is called the wave equation. It is a partial differential equation. All solutions of this equation are called waves. We discuss now some interesting features. I..1 A special solution You can for example check that u = u( x, t) = Asin( kx ωt) is indeed a solution of Eq.I.19 since = Aω cos( kx ωt) = Aω sin( kx ωt) = Ak cos( kx ω t) and thus = Ak sin( kx ωt) Aω sin( kx ωt) = V ( Ak )sin( kx ωt) ω = V k ω =± Vk u = u( x, t) = Asin[ k( x± V t)] ( I.18 The + sign corresponds to a wave moving to the left while the sign corresponds to a wave moving to the right. The relation ω = Vk can also be written as 6
7 π ω = πν = V λν = V ( I.19 λ in words (wavelength) (frequency) = (phase velocity) I.. Another special solution Similarly to what is done in I.. you could check that u = u( x, t) = Acos( kx ωt) is also solution. This is left as an exercise I..3 Complex notation for waves We can simplify our lives by using complex functions. Instead of checking first that a sine-function is a solution of the wave equation, and, subsequently that a cosine-function is also a solution, we could do both at once by using uxt (, ) i( kx ωt) = Ae ( I.0 Remember that by definition e iα = cosα + isinα ( I.1 Using Eq.I.0 in Eq.I.17 we obtain = i( kx t) A( ω iω) e = A( iω)( iω) e = Aik ( ) e = Aik ( )( ik) e k ω i( kx ωt) i( kx ωt) i( kx ωt) ( I. from which follows again that ω = V k ω =± Vk I..4 General solution Not only sine- and cosine-functions are solutions of the wave equation. In fact all functions of the form uxt (, ) = g( x V t) + g( x+ V t) ( I.3 1 7
8 where g 1 and g are arbitrary functions, are solutions. Simply substitute this expression into Eq.I.17. I..5 Power and intensity The total force F acting on the string element of length x is given by (see Fig. I.4) F = F x ( I.4 For u= Asin( kx ωt) this means F = FAk xsin( kx ωt) = Fk x u x t (, ) ( I.5 In other words the force in proportional to the displacement u. It is a restoring force that wants to bring the string element back to its original position on the x-axis. Since Force displacement u ( I.6 A A work (force) du ( I.7 o The energy of the string element of length x is thus E = 1 Fk A x ( I.8 and the energy in one wavelength λ is 1 E = Fk A λ ( I.9 Since it takes a time t = T for one wavelength to pass by an observer one defines the power P carried by a wave as E 1 λ P = Fk A ( I.30 T T However, we know that λ = λν = V. Thus T 8
9 1 P = Fk A V ( I.31 or P 1 A V = ρω ( I.3 F since ω = kv and V =. Here it is important that you remember that power is ρ proportional to the square of the amplitude. The intensity I is defined as power/m. I..6 Beating of two waves So far we have only considered a wave with one frequency. What happens if we add two waves of similar wave numbers and frequencies? To be specific we consider [( k+ k) x ( ω+ ω) t] i[ ( k k) x ( ω ω) t] i uxt (, ) = e + e ( I.33 with k k and ω ω. Rearranging terms we have ( ) uxt (, ) = e e + e ikx ( ωt) i( x k t ω) i( x k t ω) [ ω] = ikx ( ωt) e cos x k t (I.34 Since k << k and ω << ω we obtain a wave with wavenumber k and angular frequency ω slowly modulated in amplitude as shown in Fig. I.5. Fig. I.5: The sum of two sinusoidal waves with slightly different frequencies leads to a single wave with modulated amplitude. This effect is called beating. 9
10 I..7 Phase velocity and group velocity The simple example treated in the previous section is very useful to illustrate the difference between phase velocity and group velocity. For this we ask the following question: what is the velocity at which the maximum (red point in Fig. I.5) of the modulated wave is moving? To answer this question we only need to consider the cosine term in Eq.I.35 [ ω] ( ) (, ) ikx ωt uxt e cos x k t = ( I.35 and to request that it stays constant. Then [ x k t ω] constant = ( I.36 implies that it moves with the velocity V g ω = ( I.37 k This is called the group velocity, as it originates from the interaction of a group (here only ) of waves. The group velocity is fundamentally different from the phase velocity V ω = ( I.38 k Assume now that we add many waves with ω=ω 1, ω, ω 3,... and k = k 1, k, k 3,.. then the result still remains that the amplitude modulation moves with a velocity V g =dω/dk if all the ω i (and k i ) are close to each other. The notion of group velocity will play an essential role the description of a particle in quantum mechanics. It will also play a crucial role in discussing metals, semiconductors and insulators. I.3 Fourier generator With many frequencies and wave numbers it is e.g. possible to construct a wave of any shape. This part of mathematics is called Fourier analysis. A useful applet for the synthesis of periodic functions can be found at In the figures below the black dot correspond to the keys of an virtual piano. Each one corresponds to a given frequency. The intensity is given by the position of the black dot. A high position means a large intensity. The examples shown in Fig. I.6 illustrate nicely 10
11 uxt (, ) x amplitude frequency f Fig. I.6: Fourier synthesis of periodic functions. (top panel): with two periodic functions with similar frequencies one obtains an amplitude modulated wave; (middle panel): with 11 frequencies with amplitudes distributed like a Gaussian function one obtains also a modulation. However, now the resulting periodic function has a very small amplitude over a substantial interval of the x -axis. (bottom panel): this effect is even more apparent when a wider range of frequencies is used. 11
12 the fact that the spread in space x of a wave decreases when the spread in frequencies ν increases and vice versa. Very roughly one expects from these examples that x ν = constant ( I.39 We shall see that this property has far reaching consequences in quantum physics. It is in fact at the basis of the so-called uncertainty principle of Heisenberg. I.4 Waves in D and 3D So far we have only considered waves in 1D. From your daily experience you know that waves can also propagate in more than one dimension. Think for example of the waves on a lake or of sound waves, or of the radio waves used in your mobile phones. All these waves are described by a wave equation of the same form as that derived for the stretched rope, i.e. they are of the form V = ( I.40 For sound in 3D we have V ρ ρ ρ ρ + + = y z ( I.41 where v is the velocity of sound and ρ the density of the medium (for example air) in which sound is propagating. A typical solution of this partial differential equation is ρ( x, yzt,, ) = Asin( kx+ ky+ kz ωt) ( I which is more elegantly written as ρ( x, yzt,, ) = Asin( kr ωt) ( I.43 where r = ( x, yz, ) and k = ( k1, k, k3) is the wave vector. Furthermore, instead of using sine and cosine functions it is more advantageous to switch to a complex notation. 1
13 One writes then ρ( xyzt,,, ) = Ae i( k r ωt) ( I.44 For electromagnetic waves in 3D we have similarly c E E E E + + = y z ( I.45 where c is the velocity of light and E is the electric field associated with the electromagnetic wave. The same equation applies to the magnetic field B associated with the electromagnetic wave. The fact that 3 partial derivatives appear in these equations is due to the x, y, and z dependence of the medium density for sound and of the electromagnetic field for the case of radio waves. I.5 Interference effects in D and 3D We shall restrict ourselves to waves in D since visualisation of waves in 3D is difficult. A nice applet for D waves can be found in We present here some examples. Fig. I.7: Circular wave produced by a pulsating point source. The intensity of the colours indicates the amplitude of the wave. This picture is somewhat similar to that shown in Fig. I.1. 13
14 I.5.1 Interference between two sources of same frequency Consider now two sources pulsating in phase at the same frequency. A phenomenon somewhat similar to that leading to the appearance of nodes in Fig. I.5 is observed: there are lines of zero amplitude. Along these lines, which have the shape of hyperboles, the waves produced by each source interfere destructively. In between, the two separate waves interact constructively and the amplitude is maximum. Fig. I.8: Interference pattern obtained with two point sources pulsating in phase. I.5. Diffraction by one slit We consider in Fig. I.9 and Fig. I.10 what happens with a plane wave coming from the top of the figures when it passes through a slit. When the slit is much larger that the wavelength the wave passes essentially undisturbed through the slit. There are only disturbances on the edges of the wave. The situation is quite different when the width of the slit is comparable to the wavelength. then the slit acts essentially like a point source. Fig. I.9: Plane wave passing through a wide slit 14
15 Fig. I.10: Diffraction of a plane wave by a narrow slit. I.5.3 Diffraction by two narrow slits From the pattern shown in Fig. I.10 one expects that two narrow slits will act as two point sources. Since these two point sources are excited by the same plane wave they are in phase and their effect should comparable to that shown in Fig. I.8. This is indeed what is observed. Fig. I.11: Diffraction pattern of a plane wave when it passes two narrow slits. I.6 Summary In these additional lecture notes I gave all the ingredients necessary to describe the propagation of classical waves. The basic characteristics of a wave such as wavelength, frequency, wave number, wave vector, angular frequency, intensity and power have been defined. The wave equation has been derived for the case of a stretched rope and the wave equations for sound and electromagnetic waves in 3D have been indicated. Furthermore you have seen that localized waves can be generated by adding several waves: the localisation is strongest when the spread in frequency is largest. Finally, you can explore with two applets the propagation of D waves through obstacles such as slits. You are now ready for the lecture From Quantum to Matter! 15
Wave Phenomena Physics 15c
 Wave Phenomena Physics 5c Lecture Fourier Analysis (H&L Sections 3. 4) (Georgi Chapter ) What We Did Last ime Studied reflection of mechanical waves Similar to reflection of electromagnetic waves Mechanical
Wave Phenomena Physics 5c Lecture Fourier Analysis (H&L Sections 3. 4) (Georgi Chapter ) What We Did Last ime Studied reflection of mechanical waves Similar to reflection of electromagnetic waves Mechanical
Chapter 15. Mechanical Waves
 Chapter 15 Mechanical Waves A wave is any disturbance from an equilibrium condition, which travels or propagates with time from one region of space to another. A harmonic wave is a periodic wave in which
Chapter 15 Mechanical Waves A wave is any disturbance from an equilibrium condition, which travels or propagates with time from one region of space to another. A harmonic wave is a periodic wave in which
General Physics I. Lecture 14: Sinusoidal Waves. Prof. WAN, Xin ( 万歆 )
 General Physics I Lecture 14: Sinusoidal Waves Prof. WAN, Xin ( 万歆 ) xinwan@zju.edu.cn http://zimp.zju.edu.cn/~xinwan/ Motivation When analyzing a linear medium that is, one in which the restoring force
General Physics I Lecture 14: Sinusoidal Waves Prof. WAN, Xin ( 万歆 ) xinwan@zju.edu.cn http://zimp.zju.edu.cn/~xinwan/ Motivation When analyzing a linear medium that is, one in which the restoring force
Chapter 16 - Waves. I m surfing the giant life wave. -William Shatner. David J. Starling Penn State Hazleton PHYS 213. Chapter 16 - Waves
 I m surfing the giant life wave. -William Shatner David J. Starling Penn State Hazleton PHYS 213 There are three main types of waves in physics: (a) Mechanical waves: described by Newton s laws and propagate
I m surfing the giant life wave. -William Shatner David J. Starling Penn State Hazleton PHYS 213 There are three main types of waves in physics: (a) Mechanical waves: described by Newton s laws and propagate
Light as a Transverse Wave.
 Waves and Superposition (Keating Chapter 21) The ray model for light (i.e. light travels in straight lines) can be used to explain a lot of phenomena (like basic object and image formation and even aberrations)
Waves and Superposition (Keating Chapter 21) The ray model for light (i.e. light travels in straight lines) can be used to explain a lot of phenomena (like basic object and image formation and even aberrations)
Lecture 17. Mechanical waves. Transverse waves. Sound waves. Standing Waves.
 Lecture 17 Mechanical waves. Transverse waves. Sound waves. Standing Waves. What is a wave? A wave is a traveling disturbance that transports energy but not matter. Examples: Sound waves (air moves back
Lecture 17 Mechanical waves. Transverse waves. Sound waves. Standing Waves. What is a wave? A wave is a traveling disturbance that transports energy but not matter. Examples: Sound waves (air moves back
Chapter 16 Mechanical Waves
 Chapter 6 Mechanical Waves A wave is a disturbance that travels, or propagates, without the transport of matter. Examples: sound/ultrasonic wave, EM waves, and earthquake wave. Mechanical waves, such as
Chapter 6 Mechanical Waves A wave is a disturbance that travels, or propagates, without the transport of matter. Examples: sound/ultrasonic wave, EM waves, and earthquake wave. Mechanical waves, such as
Important because SHM is a good model to describe vibrations of a guitar string, vibrations of atoms in molecules, etc.
 Simple Harmonic Motion Oscillatory motion under a restoring force proportional to the amount of displacement from equilibrium A restoring force is a force that tries to move the system back to equilibrium
Simple Harmonic Motion Oscillatory motion under a restoring force proportional to the amount of displacement from equilibrium A restoring force is a force that tries to move the system back to equilibrium
Exam 3 Review. Chapter 10: Elasticity and Oscillations A stress will deform a body and that body can be set into periodic oscillations.
 Exam 3 Review Chapter 10: Elasticity and Oscillations stress will deform a body and that body can be set into periodic oscillations. Elastic Deformations of Solids Elastic objects return to their original
Exam 3 Review Chapter 10: Elasticity and Oscillations stress will deform a body and that body can be set into periodic oscillations. Elastic Deformations of Solids Elastic objects return to their original
1. Types of Waves. There are three main types of waves:
 Chapter 16 WAVES I 1. Types of Waves There are three main types of waves: https://youtu.be/kvc7obkzq9u?t=3m49s 1. Mechanical waves: These are the most familiar waves. Examples include water waves, sound
Chapter 16 WAVES I 1. Types of Waves There are three main types of waves: https://youtu.be/kvc7obkzq9u?t=3m49s 1. Mechanical waves: These are the most familiar waves. Examples include water waves, sound
= k, (2) p = h λ. x o = f1/2 o a. +vt (4)
 Traveling Functions, Traveling Waves, and the Uncertainty Principle R.M. Suter Department of Physics, Carnegie Mellon University Experimental observations have indicated that all quanta have a wave-like
Traveling Functions, Traveling Waves, and the Uncertainty Principle R.M. Suter Department of Physics, Carnegie Mellon University Experimental observations have indicated that all quanta have a wave-like
Module 8: Sinusoidal Waves Lecture 8: Sinusoidal Waves
 Module 8: Sinusoidal Waves Lecture 8: Sinusoidal Waves We shift our attention to oscillations that propagate in space as time evolves. This is referred to as a wave. The sinusoidal wave a(,t) = A cos(ωt
Module 8: Sinusoidal Waves Lecture 8: Sinusoidal Waves We shift our attention to oscillations that propagate in space as time evolves. This is referred to as a wave. The sinusoidal wave a(,t) = A cos(ωt
Wave Phenomena Physics 15c. Lecture 10 Fourier Transform
 Wave Phenomena Physics 15c Lecture 10 Fourier ransform What We Did Last ime Reflection of mechanical waves Similar to reflection of electromagnetic waves Mechanical impedance is defined by For transverse/longitudinal
Wave Phenomena Physics 15c Lecture 10 Fourier ransform What We Did Last ime Reflection of mechanical waves Similar to reflection of electromagnetic waves Mechanical impedance is defined by For transverse/longitudinal
in Electromagnetics Numerical Method Introduction to Electromagnetics I Lecturer: Charusluk Viphavakit, PhD
 2141418 Numerical Method in Electromagnetics Introduction to Electromagnetics I Lecturer: Charusluk Viphavakit, PhD ISE, Chulalongkorn University, 2 nd /2018 Email: charusluk.v@chula.ac.th Website: Light
2141418 Numerical Method in Electromagnetics Introduction to Electromagnetics I Lecturer: Charusluk Viphavakit, PhD ISE, Chulalongkorn University, 2 nd /2018 Email: charusluk.v@chula.ac.th Website: Light
Chapter 16 Waves in One Dimension
 Chapter 16 Waves in One Dimension Slide 16-1 Reading Quiz 16.05 f = c Slide 16-2 Reading Quiz 16.06 Slide 16-3 Reading Quiz 16.07 Heavier portion looks like a fixed end, pulse is inverted on reflection.
Chapter 16 Waves in One Dimension Slide 16-1 Reading Quiz 16.05 f = c Slide 16-2 Reading Quiz 16.06 Slide 16-3 Reading Quiz 16.07 Heavier portion looks like a fixed end, pulse is inverted on reflection.
Oscillation the vibration of an object. Wave a transfer of energy without a transfer of matter
 Oscillation the vibration of an object Wave a transfer of energy without a transfer of matter Equilibrium Position position of object at rest (mean position) Displacement (x) distance in a particular direction
Oscillation the vibration of an object Wave a transfer of energy without a transfer of matter Equilibrium Position position of object at rest (mean position) Displacement (x) distance in a particular direction
Chapter 15 Mechanical Waves
 Chapter 15 Mechanical Waves 1 Types of Mechanical Waves This chapter and the next are about mechanical waves waves that travel within some material called a medium. Waves play an important role in how
Chapter 15 Mechanical Waves 1 Types of Mechanical Waves This chapter and the next are about mechanical waves waves that travel within some material called a medium. Waves play an important role in how
Chapter 16: Oscillations
 Chapter 16: Oscillations Brent Royuk Phys-111 Concordia University Periodic Motion Periodic Motion is any motion that repeats itself. The Period (T) is the time it takes for one complete cycle of motion.
Chapter 16: Oscillations Brent Royuk Phys-111 Concordia University Periodic Motion Periodic Motion is any motion that repeats itself. The Period (T) is the time it takes for one complete cycle of motion.
Phys101 Lectures 28, 29. Wave Motion
 Phys101 Lectures 8, 9 Wave Motion Key points: Types of Waves: Transverse and Longitudinal Mathematical Representation of a Traveling Wave The Principle of Superposition Standing Waves; Resonance Ref: 11-7,8,9,10,11,16,1,13,16.
Phys101 Lectures 8, 9 Wave Motion Key points: Types of Waves: Transverse and Longitudinal Mathematical Representation of a Traveling Wave The Principle of Superposition Standing Waves; Resonance Ref: 11-7,8,9,10,11,16,1,13,16.
Waves 2006 Physics 23. Armen Kocharian Lecture 3: Sep
 Waves 2006 Physics 23 Armen Kocharian Lecture 3: Sep 12. 2006 Last Time What is a wave? A "disturbance" that moves through space. Mechanical waves through a medium. Transverse vs. Longitudinal e.g., string
Waves 2006 Physics 23 Armen Kocharian Lecture 3: Sep 12. 2006 Last Time What is a wave? A "disturbance" that moves through space. Mechanical waves through a medium. Transverse vs. Longitudinal e.g., string
Waves Part 1: Travelling Waves
 Waves Part 1: Travelling Waves Last modified: 15/05/2018 Links Contents Travelling Waves Harmonic Waves Wavelength Period & Frequency Summary Example 1 Example 2 Example 3 Example 4 Transverse & Longitudinal
Waves Part 1: Travelling Waves Last modified: 15/05/2018 Links Contents Travelling Waves Harmonic Waves Wavelength Period & Frequency Summary Example 1 Example 2 Example 3 Example 4 Transverse & Longitudinal
Mechanical Waves. 3: Mechanical Waves (Chapter 16) Waves: Space and Time
 3: Mechanical Waves (Chapter 6) Phys3, A Dr. Robert MacDonald Mechanical Waves A mechanical wave is a travelling disturbance in a medium (like water, string, earth, Slinky, etc). Move some part of the
3: Mechanical Waves (Chapter 6) Phys3, A Dr. Robert MacDonald Mechanical Waves A mechanical wave is a travelling disturbance in a medium (like water, string, earth, Slinky, etc). Move some part of the
Superposition and Standing Waves
 Physics 1051 Lecture 9 Superposition and Standing Waves Lecture 09 - Contents 14.5 Standing Waves in Air Columns 14.6 Beats: Interference in Time 14.7 Non-sinusoidal Waves Trivia Questions 1 How many wavelengths
Physics 1051 Lecture 9 Superposition and Standing Waves Lecture 09 - Contents 14.5 Standing Waves in Air Columns 14.6 Beats: Interference in Time 14.7 Non-sinusoidal Waves Trivia Questions 1 How many wavelengths
One-Dimensional Wave Propagation (without distortion or attenuation)
 Phsics 306: Waves Lecture 1 1//008 Phsics 306 Spring, 008 Waves and Optics Sllabus To get a good grade: Stud hard Come to class Email: satapal@phsics.gmu.edu Surve of waves One-Dimensional Wave Propagation
Phsics 306: Waves Lecture 1 1//008 Phsics 306 Spring, 008 Waves and Optics Sllabus To get a good grade: Stud hard Come to class Email: satapal@phsics.gmu.edu Surve of waves One-Dimensional Wave Propagation
The maximum value of the acceleration occurs when sin=1 with magnitude
 SOLUTIONS 1231 T1 Q1. SHM Vibrating Strip (a)(i) For SHM, y = Asin(ωt + φ ) for amplitude A and angular frequency ω. Set φ = 0. (ii) The velocity is given by v = dy dx = ωa cosωt The maximum speed vm occurs
SOLUTIONS 1231 T1 Q1. SHM Vibrating Strip (a)(i) For SHM, y = Asin(ωt + φ ) for amplitude A and angular frequency ω. Set φ = 0. (ii) The velocity is given by v = dy dx = ωa cosωt The maximum speed vm occurs
Honors Differential Equations
 MIT OpenCourseWare http://ocw.mit.edu 18.034 Honors Differential Equations Spring 009 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. LECTURE 7. MECHANICAL
MIT OpenCourseWare http://ocw.mit.edu 18.034 Honors Differential Equations Spring 009 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. LECTURE 7. MECHANICAL
Oscillations. Oscillations and Simple Harmonic Motion
 Oscillations AP Physics C Oscillations and Simple Harmonic Motion 1 Equilibrium and Oscillations A marble that is free to roll inside a spherical bowl has an equilibrium position at the bottom of the bowl
Oscillations AP Physics C Oscillations and Simple Harmonic Motion 1 Equilibrium and Oscillations A marble that is free to roll inside a spherical bowl has an equilibrium position at the bottom of the bowl
16 SUPERPOSITION & STANDING WAVES
 Chapter 6 SUPERPOSITION & STANDING WAVES 6. Superposition of waves Principle of superposition: When two or more waves overlap, the resultant wave is the algebraic sum of the individual waves. Illustration:
Chapter 6 SUPERPOSITION & STANDING WAVES 6. Superposition of waves Principle of superposition: When two or more waves overlap, the resultant wave is the algebraic sum of the individual waves. Illustration:
Larbert High School. Quanta and Waves. Homework Exercises ADVANCED HIGHER PHYSICS
 Larbert High School ADVANCED HIGHER PHYSICS Quanta and Waves Homework Exercises 3.1 3.6 3.1 Intro to Quantum Theory HW 1. (a) Explain what is meant by term black body. (1) (b) State two observations that
Larbert High School ADVANCED HIGHER PHYSICS Quanta and Waves Homework Exercises 3.1 3.6 3.1 Intro to Quantum Theory HW 1. (a) Explain what is meant by term black body. (1) (b) State two observations that
Maxwell s equations and EM waves. From previous Lecture Time dependent fields and Faraday s Law
 Maxwell s equations and EM waves This Lecture More on Motional EMF and Faraday s law Displacement currents Maxwell s equations EM Waves From previous Lecture Time dependent fields and Faraday s Law 1 Radar
Maxwell s equations and EM waves This Lecture More on Motional EMF and Faraday s law Displacement currents Maxwell s equations EM Waves From previous Lecture Time dependent fields and Faraday s Law 1 Radar
Double Spring Harmonic Oscillator Lab
 Dylan Humenik and Benjamin Daily Double Spring Harmonic Oscillator Lab Objectives: -Experimentally determine harmonic equations for a double spring system using various methods Part 1 Determining k of
Dylan Humenik and Benjamin Daily Double Spring Harmonic Oscillator Lab Objectives: -Experimentally determine harmonic equations for a double spring system using various methods Part 1 Determining k of
PHYSICS 149: Lecture 24
 PHYSICS 149: Lecture 24 Chapter 11: Waves 11.8 Reflection and Refraction 11.10 Standing Waves Chapter 12: Sound 12.1 Sound Waves 12.4 Standing Sound Waves Lecture 24 Purdue University, Physics 149 1 ILQ
PHYSICS 149: Lecture 24 Chapter 11: Waves 11.8 Reflection and Refraction 11.10 Standing Waves Chapter 12: Sound 12.1 Sound Waves 12.4 Standing Sound Waves Lecture 24 Purdue University, Physics 149 1 ILQ
2 The Failure of Classical Mechanics and Wave-Particle Duality
 2 The Failure of Classical Mechanics and Wave-Particle Duality This lecture is more qualitative than the rest of the class. Very roughly speaking, in Classical Mechanics, one can describe motion in terms
2 The Failure of Classical Mechanics and Wave-Particle Duality This lecture is more qualitative than the rest of the class. Very roughly speaking, in Classical Mechanics, one can describe motion in terms
Physics 1C. Lecture 13B
 Physics 1C Lecture 13B Speed of Sound! Example values (m/s): Description of a Sound Wave! A sound wave may be considered either a displacement wave or a pressure wave! The displacement of a small element
Physics 1C Lecture 13B Speed of Sound! Example values (m/s): Description of a Sound Wave! A sound wave may be considered either a displacement wave or a pressure wave! The displacement of a small element
Electrodynamics HW Problems 06 EM Waves
 Electrodynamics HW Problems 06 EM Waves 1. Energy in a wave on a string 2. Traveling wave on a string 3. Standing wave 4. Spherical traveling wave 5. Traveling EM wave 6. 3- D electromagnetic plane wave
Electrodynamics HW Problems 06 EM Waves 1. Energy in a wave on a string 2. Traveling wave on a string 3. Standing wave 4. Spherical traveling wave 5. Traveling EM wave 6. 3- D electromagnetic plane wave
α(t) = ω 2 θ (t) κ I ω = g L L g T = 2π mgh rot com I rot
 α(t) = ω 2 θ (t) ω = κ I ω = g L T = 2π L g ω = mgh rot com I rot T = 2π I rot mgh rot com Chapter 16: Waves Mechanical Waves Waves and particles Vibration = waves - Sound - medium vibrates - Surface ocean
α(t) = ω 2 θ (t) ω = κ I ω = g L T = 2π L g ω = mgh rot com I rot T = 2π I rot mgh rot com Chapter 16: Waves Mechanical Waves Waves and particles Vibration = waves - Sound - medium vibrates - Surface ocean
kg meter ii) Note the dimensions of ρ τ are kg 2 velocity 2 meter = 1 sec 2 We will interpret this velocity in upcoming slides.
 II. Generalizing the 1-dimensional wave equation First generalize the notation. i) "q" has meant transverse deflection of the string. Replace q Ψ, where Ψ may indicate other properties of the medium that
II. Generalizing the 1-dimensional wave equation First generalize the notation. i) "q" has meant transverse deflection of the string. Replace q Ψ, where Ψ may indicate other properties of the medium that
Selected Topics in Physics a lecture course for 1st year students by W.B. von Schlippe Spring Semester 2007
 Selected Topics in Physics a lecture course for st year students by W.B. von Schlippe Spring Semester 7 Lecture : Oscillations simple harmonic oscillations; coupled oscillations; beats; damped oscillations;
Selected Topics in Physics a lecture course for st year students by W.B. von Schlippe Spring Semester 7 Lecture : Oscillations simple harmonic oscillations; coupled oscillations; beats; damped oscillations;
Electromagnetic Waves
 Electromagnetic Waves As the chart shows, the electromagnetic spectrum covers an extremely wide range of wavelengths and frequencies. Though the names indicate that these waves have a number of sources,
Electromagnetic Waves As the chart shows, the electromagnetic spectrum covers an extremely wide range of wavelengths and frequencies. Though the names indicate that these waves have a number of sources,
2 u 1-D: 3-D: x + 2 u
 c 2013 C.S. Casari - Politecnico di Milano - Introduction to Nanoscience 2013-14 Onde 1 1 Waves 1.1 wave propagation 1.1.1 field Field: a physical quantity (measurable, at least in principle) function
c 2013 C.S. Casari - Politecnico di Milano - Introduction to Nanoscience 2013-14 Onde 1 1 Waves 1.1 wave propagation 1.1.1 field Field: a physical quantity (measurable, at least in principle) function
Lecture 11: Introduction to diffraction of light
 Lecture 11: Introduction to diffraction of light Diffraction of waves in everyday life and applications Diffraction in everyday life Diffraction in applications Spectroscopy: physics, chemistry, medicine,
Lecture 11: Introduction to diffraction of light Diffraction of waves in everyday life and applications Diffraction in everyday life Diffraction in applications Spectroscopy: physics, chemistry, medicine,
Differential Equations
 Electricity and Magnetism I (P331) M. R. Shepherd October 14, 2008 Differential Equations The purpose of this note is to provide some supplementary background on differential equations. The problems discussed
Electricity and Magnetism I (P331) M. R. Shepherd October 14, 2008 Differential Equations The purpose of this note is to provide some supplementary background on differential equations. The problems discussed
PHY 103: Standing Waves and Harmonics. Segev BenZvi Department of Physics and Astronomy University of Rochester
 PHY 103: Standing Waves and Harmonics Segev BenZvi Department of Physics and Astronomy University of Rochester Sounds of the Universe NASA/JPL, September 2016 2 Properties of Waves Wavelength: λ, length
PHY 103: Standing Waves and Harmonics Segev BenZvi Department of Physics and Astronomy University of Rochester Sounds of the Universe NASA/JPL, September 2016 2 Properties of Waves Wavelength: λ, length
Chapter 16: Oscillatory Motion and Waves. Simple Harmonic Motion (SHM)
 Chapter 6: Oscillatory Motion and Waves Hooke s Law (revisited) F = - k x Tthe elastic potential energy of a stretched or compressed spring is PE elastic = kx / Spring-block Note: To consider the potential
Chapter 6: Oscillatory Motion and Waves Hooke s Law (revisited) F = - k x Tthe elastic potential energy of a stretched or compressed spring is PE elastic = kx / Spring-block Note: To consider the potential
What is a wave? Waves
 What is a wave? Waves Waves What is a wave? A wave is a disturbance that carries energy from one place to another. Classifying waves 1. Mechanical Waves - e.g., water waves, sound waves, and waves on strings.
What is a wave? Waves Waves What is a wave? A wave is a disturbance that carries energy from one place to another. Classifying waves 1. Mechanical Waves - e.g., water waves, sound waves, and waves on strings.
Lecture 9: Introduction to Diffraction of Light
 Lecture 9: Introduction to Diffraction of Light Lecture aims to explain: 1. Diffraction of waves in everyday life and applications 2. Interference of two one dimensional electromagnetic waves 3. Typical
Lecture 9: Introduction to Diffraction of Light Lecture aims to explain: 1. Diffraction of waves in everyday life and applications 2. Interference of two one dimensional electromagnetic waves 3. Typical
David J. Starling Penn State Hazleton PHYS 214
 All the fifty years of conscious brooding have brought me no closer to answer the question, What are light quanta? Of course today every rascal thinks he knows the answer, but he is deluding himself. -Albert
All the fifty years of conscious brooding have brought me no closer to answer the question, What are light quanta? Of course today every rascal thinks he knows the answer, but he is deluding himself. -Albert
Chapter 13 Lecture. Essential University Physics Richard Wolfson 2 nd Edition. Oscillatory Motion Pearson Education, Inc.
 Chapter 13 Lecture Essential University Physics Richard Wolfson nd Edition Oscillatory Motion Slide 13-1 In this lecture you ll learn To describe the conditions under which oscillatory motion occurs To
Chapter 13 Lecture Essential University Physics Richard Wolfson nd Edition Oscillatory Motion Slide 13-1 In this lecture you ll learn To describe the conditions under which oscillatory motion occurs To
Rapid Review of Early Quantum Mechanics
 Rapid Review of Early Quantum Mechanics 8/9/07 (Note: This is stuff you already know from an undergraduate Modern Physics course. We re going through it quickly just to remind you: more details are to
Rapid Review of Early Quantum Mechanics 8/9/07 (Note: This is stuff you already know from an undergraduate Modern Physics course. We re going through it quickly just to remind you: more details are to
Physics 1C. Lecture 12C
 Physics 1C Lecture 12C Simple Pendulum The simple pendulum is another example of simple harmonic motion. Making a quick force diagram of the situation, we find:! The tension in the string cancels out with
Physics 1C Lecture 12C Simple Pendulum The simple pendulum is another example of simple harmonic motion. Making a quick force diagram of the situation, we find:! The tension in the string cancels out with
Section 1 Simple Harmonic Motion. The student is expected to:
 Section 1 Simple Harmonic Motion TEKS The student is expected to: 7A examine and describe oscillatory motion and wave propagation in various types of media Section 1 Simple Harmonic Motion Preview Objectives
Section 1 Simple Harmonic Motion TEKS The student is expected to: 7A examine and describe oscillatory motion and wave propagation in various types of media Section 1 Simple Harmonic Motion Preview Objectives
Wave Phenomena Physics 15c. Masahiro Morii
 Wave Phenomena Physics 15c Masahiro Morii Teaching Staff! Masahiro Morii gives the lectures.! Tuesday and Thursday @ 1:00 :30.! Thomas Hayes supervises the lab.! 3 hours/week. Date & time to be decided.!
Wave Phenomena Physics 15c Masahiro Morii Teaching Staff! Masahiro Morii gives the lectures.! Tuesday and Thursday @ 1:00 :30.! Thomas Hayes supervises the lab.! 3 hours/week. Date & time to be decided.!
Mass on a Horizontal Spring
 Course- B.Sc. Applied Physical Science (Computer Science) Year- IInd, Sem- IVth Subject Physics Paper- XIVth, Electromagnetic Theory Lecture No. 22, Simple Harmonic Motion Introduction Hello friends in
Course- B.Sc. Applied Physical Science (Computer Science) Year- IInd, Sem- IVth Subject Physics Paper- XIVth, Electromagnetic Theory Lecture No. 22, Simple Harmonic Motion Introduction Hello friends in
1 f. result from periodic disturbance same period (frequency) as source Longitudinal or Transverse Waves Characterized by
 result from periodic disturbance same period (frequency) as source Longitudinal or Transverse Waves Characterized by amplitude (how far do the bits move from their equilibrium positions? Amplitude of MEDIUM)
result from periodic disturbance same period (frequency) as source Longitudinal or Transverse Waves Characterized by amplitude (how far do the bits move from their equilibrium positions? Amplitude of MEDIUM)
CHM 532 Notes on Wavefunctions and the Schrödinger Equation
 CHM 532 Notes on Wavefunctions and the Schrödinger Equation In class we have discussed a thought experiment 1 that contrasts the behavior of classical particles, classical waves and quantum particles.
CHM 532 Notes on Wavefunctions and the Schrödinger Equation In class we have discussed a thought experiment 1 that contrasts the behavior of classical particles, classical waves and quantum particles.
Physics 121H Fall Homework #15 23-November-2015 Due Date : 2-December-2015
 Reading : Chapters 16 and 17 Note: Reminder: Physics 121H Fall 2015 Homework #15 23-November-2015 Due Date : 2-December-2015 This is a two-week homework assignment that will be worth 2 homework grades
Reading : Chapters 16 and 17 Note: Reminder: Physics 121H Fall 2015 Homework #15 23-November-2015 Due Date : 2-December-2015 This is a two-week homework assignment that will be worth 2 homework grades
CHAPTER 11 VIBRATIONS AND WAVES
 CHAPTER 11 VIBRATIONS AND WAVES http://www.physicsclassroom.com/class/waves/u10l1a.html UNITS Simple Harmonic Motion Energy in the Simple Harmonic Oscillator The Period and Sinusoidal Nature of SHM The
CHAPTER 11 VIBRATIONS AND WAVES http://www.physicsclassroom.com/class/waves/u10l1a.html UNITS Simple Harmonic Motion Energy in the Simple Harmonic Oscillator The Period and Sinusoidal Nature of SHM The
WAVE OPTICS GENERAL. Fig.1a The electromagnetic spectrum
 WAVE OPTICS GENERAL - The ray optics cannot explain the results of the two following experimental situations: a) When passing by small openings or illuminating small obstacles, the light bends around borders
WAVE OPTICS GENERAL - The ray optics cannot explain the results of the two following experimental situations: a) When passing by small openings or illuminating small obstacles, the light bends around borders
Wave Motion: v=λf [m/s=m 1/s] Example 1: A person on a pier observes a set of incoming waves that have a sinusoidal form with a distance of 1.
![Wave Motion: v=λf [m/s=m 1/s] Example 1: A person on a pier observes a set of incoming waves that have a sinusoidal form with a distance of 1. Wave Motion: v=λf [m/s=m 1/s] Example 1: A person on a pier observes a set of incoming waves that have a sinusoidal form with a distance of 1.](/thumbs/89/99797096.jpg) Wave Motion: v=λf [m/s=m 1/s] Example 1: A person on a pier observes a set of incoming waves that have a sinusoidal form with a distance of 1.6 m between the crests. If a wave laps against the pier every
Wave Motion: v=λf [m/s=m 1/s] Example 1: A person on a pier observes a set of incoming waves that have a sinusoidal form with a distance of 1.6 m between the crests. If a wave laps against the pier every
Class Average = 71. Counts Scores
 30 Class Average = 71 25 20 Counts 15 10 5 0 0 20 10 30 40 50 60 70 80 90 100 Scores Chapter 12 Mechanical Waves and Sound To describe mechanical waves. To study superposition, standing waves, and interference.
30 Class Average = 71 25 20 Counts 15 10 5 0 0 20 10 30 40 50 60 70 80 90 100 Scores Chapter 12 Mechanical Waves and Sound To describe mechanical waves. To study superposition, standing waves, and interference.
GBS765 Electron microscopy
 GBS765 Electron microscopy Lecture 1 Waves and Fourier transforms 10/14/14 9:05 AM Some fundamental concepts: Periodicity! If there is some a, for a function f(x), such that f(x) = f(x + na) then function
GBS765 Electron microscopy Lecture 1 Waves and Fourier transforms 10/14/14 9:05 AM Some fundamental concepts: Periodicity! If there is some a, for a function f(x), such that f(x) = f(x + na) then function
Physics 101 Lecture 18 Vibrations, SHM, Waves (II)
 Physics 101 Lecture 18 Vibrations, SHM, Waves (II) Reminder: simple harmonic motion is the result if we have a restoring force that is linear with the displacement: F = -k x What would happen if you could
Physics 101 Lecture 18 Vibrations, SHM, Waves (II) Reminder: simple harmonic motion is the result if we have a restoring force that is linear with the displacement: F = -k x What would happen if you could
Physics I : Oscillations and Waves Prof. S. Bharadwaj Department of Physics and Meteorology Indian Institute of Technology, Kharagpur
 Physics I : Oscillations and Waves Prof. S. Bharadwaj Department of Physics and Meteorology Indian Institute of Technology, Kharagpur Lecture - 21 Diffraction-II Good morning. In the last class, we had
Physics I : Oscillations and Waves Prof. S. Bharadwaj Department of Physics and Meteorology Indian Institute of Technology, Kharagpur Lecture - 21 Diffraction-II Good morning. In the last class, we had
Lecture 9: Waves in Classical Physics
 PHYS419 Lecture 9 Waves in Classical Physics 1 Lecture 9: Waves in Classical Physics If I say the word wave in no particular context, the image which most probably springs to your mind is one of a roughly
PHYS419 Lecture 9 Waves in Classical Physics 1 Lecture 9: Waves in Classical Physics If I say the word wave in no particular context, the image which most probably springs to your mind is one of a roughly
Matter Waves. Chapter 5
 Matter Waves Chapter 5 De Broglie pilot waves Electromagnetic waves are associated with quanta - particles called photons. Turning this fact on its head, Louis de Broglie guessed : Matter particles have
Matter Waves Chapter 5 De Broglie pilot waves Electromagnetic waves are associated with quanta - particles called photons. Turning this fact on its head, Louis de Broglie guessed : Matter particles have
Basics of Radiation Fields
 Basics of Radiation Fields Initial questions: How could you estimate the distance to a radio source in our galaxy if you don t have a parallax? We are now going to shift gears a bit. In order to understand
Basics of Radiation Fields Initial questions: How could you estimate the distance to a radio source in our galaxy if you don t have a parallax? We are now going to shift gears a bit. In order to understand
Transverse wave - the disturbance is perpendicular to the propagation direction (e.g., wave on a string)
 1 Part 5: Waves 5.1: Harmonic Waves Wave a disturbance in a medium that propagates Transverse wave - the disturbance is perpendicular to the propagation direction (e.g., wave on a string) Longitudinal
1 Part 5: Waves 5.1: Harmonic Waves Wave a disturbance in a medium that propagates Transverse wave - the disturbance is perpendicular to the propagation direction (e.g., wave on a string) Longitudinal
THE PHYSICS OF WAVES CHAPTER 1. Problem 1.1 Show that Ψ(x, t) = (x vt) 2. is a traveling wave.
 CHAPTER 1 THE PHYSICS OF WAVES Problem 1.1 Show that Ψ(x, t) = (x vt) is a traveling wave. Show thatψ(x, t) is a wave by substitutioninto Equation 1.1. Proceed as in Example 1.1. On line version uses Ψ(x,
CHAPTER 1 THE PHYSICS OF WAVES Problem 1.1 Show that Ψ(x, t) = (x vt) is a traveling wave. Show thatψ(x, t) is a wave by substitutioninto Equation 1.1. Proceed as in Example 1.1. On line version uses Ψ(x,
single uniform density, but has a step change in density at x = 0, with the string essentially y(x, t) =A sin(!t k 1 x), (5.1)
 Chapter 5 Waves II 5.1 Reflection & Transmission of waves et us now consider what happens to a wave travelling along a string which no longer has a single uniform density, but has a step change in density
Chapter 5 Waves II 5.1 Reflection & Transmission of waves et us now consider what happens to a wave travelling along a string which no longer has a single uniform density, but has a step change in density
Physics 142 Mechanical Waves Page 1. Mechanical Waves
 Physics 142 Mechanical Waves Page 1 Mechanical Waves This set of notes contains a review of wave motion in mechanics, emphasizing the mathematical formulation that will be used in our discussion of electromagnetic
Physics 142 Mechanical Waves Page 1 Mechanical Waves This set of notes contains a review of wave motion in mechanics, emphasizing the mathematical formulation that will be used in our discussion of electromagnetic
Lecture 1. Rejish Nath. Optics, IDC202
 Lecture 1. Rejish Nath Optics, IDC202 Contents 1. Waves: The wave equation 2. Harmonic Waves 3. Plane waves 4. Spherical Waves Literature: 1. Optics, (Eugene Hecht and A. R. Ganesan) 2. Optical Physics,
Lecture 1. Rejish Nath Optics, IDC202 Contents 1. Waves: The wave equation 2. Harmonic Waves 3. Plane waves 4. Spherical Waves Literature: 1. Optics, (Eugene Hecht and A. R. Ganesan) 2. Optical Physics,
Notes on Fourier Series and Integrals Fourier Series
 Notes on Fourier Series and Integrals Fourier Series et f(x) be a piecewise linear function on [, ] (This means that f(x) may possess a finite number of finite discontinuities on the interval). Then f(x)
Notes on Fourier Series and Integrals Fourier Series et f(x) be a piecewise linear function on [, ] (This means that f(x) may possess a finite number of finite discontinuities on the interval). Then f(x)
Section 1 Simple Harmonic Motion. Chapter 11. Preview. Objectives Hooke s Law Sample Problem Simple Harmonic Motion The Simple Pendulum
 Section 1 Simple Harmonic Motion Preview Objectives Hooke s Law Sample Problem Simple Harmonic Motion The Simple Pendulum Section 1 Simple Harmonic Motion Objectives Identify the conditions of simple harmonic
Section 1 Simple Harmonic Motion Preview Objectives Hooke s Law Sample Problem Simple Harmonic Motion The Simple Pendulum Section 1 Simple Harmonic Motion Objectives Identify the conditions of simple harmonic
Content of the course 3NAB0 (see study guide)
 Content of the course 3NAB0 (see study guide) 17 November diagnostic test! Week 1 : 14 November Week 2 : 21 November Introduction, units (Ch1), Circuits (Ch25,26) Heat (Ch17), Kinematics (Ch2 3) Week 3:
Content of the course 3NAB0 (see study guide) 17 November diagnostic test! Week 1 : 14 November Week 2 : 21 November Introduction, units (Ch1), Circuits (Ch25,26) Heat (Ch17), Kinematics (Ch2 3) Week 3:
f 1/ T T 1/ f Formulas Fs kx m T s 2 k l T p 2 g v f
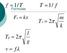 f 1/T Formulas T 1/ f Fs kx Ts 2 m k Tp 2 l g v f What do the following all have in common? Swing, pendulum, vibrating string They all exhibit forms of periodic motion. Periodic Motion: When a vibration
f 1/T Formulas T 1/ f Fs kx Ts 2 m k Tp 2 l g v f What do the following all have in common? Swing, pendulum, vibrating string They all exhibit forms of periodic motion. Periodic Motion: When a vibration
Chapter 16 Waves in One Dimension
 Lecture Outline Chapter 16 Waves in One Dimension Slide 16-1 Chapter 16: Waves in One Dimension Chapter Goal: To study the kinematic and dynamics of wave motion, i.e., the transport of energy through a
Lecture Outline Chapter 16 Waves in One Dimension Slide 16-1 Chapter 16: Waves in One Dimension Chapter Goal: To study the kinematic and dynamics of wave motion, i.e., the transport of energy through a
Lecture 30. Chapter 21 Examine two wave superposition (-ωt and +ωt) Examine two wave superposition (-ω 1 t and -ω 2 t)
 To do : Lecture 30 Chapter 21 Examine two wave superposition (-ωt and +ωt) Examine two wave superposition (-ω 1 t and -ω 2 t) Review for final (Location: CHEM 1351, 7:45 am ) Tomorrow: Review session,
To do : Lecture 30 Chapter 21 Examine two wave superposition (-ωt and +ωt) Examine two wave superposition (-ω 1 t and -ω 2 t) Review for final (Location: CHEM 1351, 7:45 am ) Tomorrow: Review session,
BASIC WAVE CONCEPTS. Reading: Main 9.0, 9.1, 9.3 GEM 9.1.1, Giancoli?
 1 BASIC WAVE CONCEPTS Reading: Main 9.0, 9.1, 9.3 GEM 9.1.1, 9.1.2 Giancoli? REVIEW SINGLE OSCILLATOR: The oscillation functions you re used to describe how one quantity (position, charge, electric field,
1 BASIC WAVE CONCEPTS Reading: Main 9.0, 9.1, 9.3 GEM 9.1.1, 9.1.2 Giancoli? REVIEW SINGLE OSCILLATOR: The oscillation functions you re used to describe how one quantity (position, charge, electric field,
No Lecture on Wed. But, there is a lecture on Thursday, at your normal recitation time, so please be sure to come!
 Announcements Quiz 6 tomorrow Driscoll Auditorium Covers: Chapter 15 (lecture and homework, look at Questions, Checkpoint, and Summary) Chapter 16 (Lecture material covered, associated Checkpoints and
Announcements Quiz 6 tomorrow Driscoll Auditorium Covers: Chapter 15 (lecture and homework, look at Questions, Checkpoint, and Summary) Chapter 16 (Lecture material covered, associated Checkpoints and
Standing Waves If the same type of waves move through a common region and their frequencies, f, are the same then so are their wavelengths, λ.
 Standing Waves I the same type o waves move through a common region and their requencies,, are the same then so are their wavelengths,. This ollows rom: v=. Since the waves move through a common region,
Standing Waves I the same type o waves move through a common region and their requencies,, are the same then so are their wavelengths,. This ollows rom: v=. Since the waves move through a common region,
Chapter 9: Waves, incl. e & m waves, light
 Chapter 9: Waves, incl. e & m waves, light Review of interference Light Electromagnetic waves/radiation in general Solar radiation Global warming as an important application INTERFERENCE: absolutely crucial,
Chapter 9: Waves, incl. e & m waves, light Review of interference Light Electromagnetic waves/radiation in general Solar radiation Global warming as an important application INTERFERENCE: absolutely crucial,
x(t+ δt) - x(t) = slope δt t+δt
 Techniques of Physics Worksheet 2 Classical Vibrations and Waves Introduction You will have encountered many different examples of wave phenomena in your courses and should be familiar with most of the
Techniques of Physics Worksheet 2 Classical Vibrations and Waves Introduction You will have encountered many different examples of wave phenomena in your courses and should be familiar with most of the
The velocity (v) of the transverse wave in the string is given by the relation: Time taken by the disturbance to reach the other end, t =
 Question 15.1: A string of mass 2.50 kg is under a tension of 200 N. The length of the stretched string is 20.0 m. If the transverse jerk is struck at one end of the string, how long does the disturbance
Question 15.1: A string of mass 2.50 kg is under a tension of 200 N. The length of the stretched string is 20.0 m. If the transverse jerk is struck at one end of the string, how long does the disturbance
Vibrations and waves: revision. Martin Dove Queen Mary University of London
 Vibrations and waves: revision Martin Dove Queen Mary University of London Form of the examination Part A = 50%, 10 short questions, no options Part B = 50%, Answer questions from a choice of 4 Total exam
Vibrations and waves: revision Martin Dove Queen Mary University of London Form of the examination Part A = 50%, 10 short questions, no options Part B = 50%, Answer questions from a choice of 4 Total exam
Wave Phenomena Physics 15c. Lecture 11 Dispersion
 Wave Phenomena Physics 15c Lecture 11 Dispersion What We Did Last Time Defined Fourier transform f (t) = F(ω)e iωt dω F(ω) = 1 2π f(t) and F(w) represent a function in time and frequency domains Analyzed
Wave Phenomena Physics 15c Lecture 11 Dispersion What We Did Last Time Defined Fourier transform f (t) = F(ω)e iωt dω F(ω) = 1 2π f(t) and F(w) represent a function in time and frequency domains Analyzed
Chapter One Introduction to Oscillations
 Chapter One Introduction to Oscillations This chapter discusses simple oscillations. This chapter also discusses simple functions to model oscillations like the sine and cosine functions. Part One Sine
Chapter One Introduction to Oscillations This chapter discusses simple oscillations. This chapter also discusses simple functions to model oscillations like the sine and cosine functions. Part One Sine
PREMED COURSE, 14/08/2015 OSCILLATIONS
 PREMED COURSE, 14/08/2015 OSCILLATIONS PERIODIC MOTIONS Mechanical Metronom Laser Optical Bunjee jumping Electrical Astronomical Pulsar Biological ECG AC 50 Hz Another biological exampe PERIODIC MOTIONS
PREMED COURSE, 14/08/2015 OSCILLATIONS PERIODIC MOTIONS Mechanical Metronom Laser Optical Bunjee jumping Electrical Astronomical Pulsar Biological ECG AC 50 Hz Another biological exampe PERIODIC MOTIONS
Re-radiation: Scattering. Electric fields are not blocked by matter: how can E decrease?
 Re-radiation: Scattering lectric fields are not blocked by matter: how can decrease? Cardboard Why there is no light going through a cardboard? lectric fields are not blocked by matter lectrons and nucleus
Re-radiation: Scattering lectric fields are not blocked by matter: how can decrease? Cardboard Why there is no light going through a cardboard? lectric fields are not blocked by matter lectrons and nucleus
THE WAVE EQUATION. F = T (x, t) j + T (x + x, t) j = T (sin(θ(x, t)) + sin(θ(x + x, t)))
 THE WAVE EQUATION The aim is to derive a mathematical model that describes small vibrations of a tightly stretched flexible string for the one-dimensional case, or of a tightly stretched membrane for the
THE WAVE EQUATION The aim is to derive a mathematical model that describes small vibrations of a tightly stretched flexible string for the one-dimensional case, or of a tightly stretched membrane for the
Chapter 16 Waves. Types of waves Mechanical waves. Electromagnetic waves. Matter waves
 Chapter 16 Waves Types of waves Mechanical waves exist only within a material medium. e.g. water waves, sound waves, etc. Electromagnetic waves require no material medium to exist. e.g. light, radio, microwaves,
Chapter 16 Waves Types of waves Mechanical waves exist only within a material medium. e.g. water waves, sound waves, etc. Electromagnetic waves require no material medium to exist. e.g. light, radio, microwaves,
16 WAVES. Introduction. Chapter Outline
 Chapter 16 Waves 795 16 WAVES Figure 16.1 From the world of renewable energy sources comes the electric power-generating buoy. Although there are many versions, this one converts the up-and-down motion,
Chapter 16 Waves 795 16 WAVES Figure 16.1 From the world of renewable energy sources comes the electric power-generating buoy. Although there are many versions, this one converts the up-and-down motion,
Physics 41: Waves, Optics, Thermo
 Physics 41: Waves, Optics, Thermo Particles & Waves Localized in Space: LOCAL Have Mass & Momentum No Superposition: Two particles cannot occupy the same space at the same time! Particles have energy.
Physics 41: Waves, Optics, Thermo Particles & Waves Localized in Space: LOCAL Have Mass & Momentum No Superposition: Two particles cannot occupy the same space at the same time! Particles have energy.
Traveling Harmonic Waves
 Traveling Harmonic Waves 6 January 2016 PHYC 1290 Department of Physics and Atmospheric Science Functional Form for Traveling Waves We can show that traveling waves whose shape does not change with time
Traveling Harmonic Waves 6 January 2016 PHYC 1290 Department of Physics and Atmospheric Science Functional Form for Traveling Waves We can show that traveling waves whose shape does not change with time
Chapter 14. PowerPoint Lectures for University Physics, Thirteenth Edition Hugh D. Young and Roger A. Freedman. Lectures by Wayne Anderson
 Chapter 14 Periodic Motion PowerPoint Lectures for University Physics, Thirteenth Edition Hugh D. Young and Roger A. Freedman Lectures by Wayne Anderson Exam 3 results Class Average - 57 (Approximate grade
Chapter 14 Periodic Motion PowerPoint Lectures for University Physics, Thirteenth Edition Hugh D. Young and Roger A. Freedman Lectures by Wayne Anderson Exam 3 results Class Average - 57 (Approximate grade
Physics 106a/196a Problem Set 7 Due Dec 2, 2005
 Physics 06a/96a Problem Set 7 Due Dec, 005 Version 3, Nov 7, 005 In this set we finish up the SHO and study coupled oscillations/normal modes and waves. Problems,, and 3 are for 06a students only, 4, 5,
Physics 06a/96a Problem Set 7 Due Dec, 005 Version 3, Nov 7, 005 In this set we finish up the SHO and study coupled oscillations/normal modes and waves. Problems,, and 3 are for 06a students only, 4, 5,
Waves and the Schroedinger Equation
 Waves and the Schroedinger Equation 5 april 010 1 The Wave Equation We have seen from previous discussions that the wave-particle duality of matter requires we describe entities through some wave-form
Waves and the Schroedinger Equation 5 april 010 1 The Wave Equation We have seen from previous discussions that the wave-particle duality of matter requires we describe entities through some wave-form
CHAPTER 15 Wave Motion. 1. The speed of the wave is
 CHAPTER 15 Wave Motion 1. The speed of the wave is v = fλ = λ/t = (9.0 m)/(4.0 s) = 2.3 m/s. 7. We find the tension from the speed of the wave: v = [F T /(m/l)] 1/2 ; (4.8 m)/(0.85 s) = {F T /[(0.40 kg)/(4.8
CHAPTER 15 Wave Motion 1. The speed of the wave is v = fλ = λ/t = (9.0 m)/(4.0 s) = 2.3 m/s. 7. We find the tension from the speed of the wave: v = [F T /(m/l)] 1/2 ; (4.8 m)/(0.85 s) = {F T /[(0.40 kg)/(4.8
7.2.1 Seismic waves. Waves in a mass- spring system
 7..1 Seismic waves Waves in a mass- spring system Acoustic waves in a liquid or gas Seismic waves in a solid Surface waves Wavefronts, rays and geometrical attenuation Amplitude and energy Waves in a mass-
7..1 Seismic waves Waves in a mass- spring system Acoustic waves in a liquid or gas Seismic waves in a solid Surface waves Wavefronts, rays and geometrical attenuation Amplitude and energy Waves in a mass-
Lecture 2: Interference
 Lecture 2: Interference l S 1 d S 2 Lecture 2, p.1 Today Interference of sound waves Two-slit interference Lecture 2, p.2 Review: Wave Summary The formula y x,t Acos kx t describes a harmonic plane wave
Lecture 2: Interference l S 1 d S 2 Lecture 2, p.1 Today Interference of sound waves Two-slit interference Lecture 2, p.2 Review: Wave Summary The formula y x,t Acos kx t describes a harmonic plane wave
Vibrations and Waves Physics Year 1. Handout 1: Course Details
 Vibrations and Waves Jan-Feb 2011 Handout 1: Course Details Office Hours Vibrations and Waves Physics Year 1 Handout 1: Course Details Dr Carl Paterson (Blackett 621, carl.paterson@imperial.ac.uk Office
Vibrations and Waves Jan-Feb 2011 Handout 1: Course Details Office Hours Vibrations and Waves Physics Year 1 Handout 1: Course Details Dr Carl Paterson (Blackett 621, carl.paterson@imperial.ac.uk Office
