Power law violation of the area law in quantum spin chains
|
|
|
- Allan McCarthy
- 5 years ago
- Views:
Transcription
1 Power law violation of the area law in quantum spin chains and Peter W. Shor Northeastern / M.I.T. QIP, Sydney, Jan. 2015
2 Quantifying entanglement: SVD (Schmidt Decomposition, aka SVD) Suppose ψ AB is the pure state of a composite system, AB. Then there exists orthonormal states Φ α A for A and orthonormal states θ α B for B ψ AB = λ α Φ α A θ B α α where λ α s satisfy α λ α 2 = 1 known as Schmidt numbers. The number of non-zero Schmidt numbers is called the Schmidt rank, χ, of the state (a quantification of entanglement).
3 Quantifying entanglement: Entropy Another measure of entanglement is entanglement entropy. Recall we had ψ AB = λ α Φ α A θ B α α where λ α s satisfy α λ α 2 = 1. The entanglement entropy is: S λ α 2 log λ α 2 α where λ α 2 = p α are the probabilities.
4 Area laws Area Laws nomena, one thinks less of very detailed properties, b rather interested in the scaling of the entanglement ent when the distinguished region grows in size. In fact, for q tum chains, this scaling of entanglement as genuine qua correlations a priori very different from the scaling of point correlation functions reflects to a large extent the ical behavior of the quantum many-body system, and sh some relationship to conformal charges. At first sight one might be tempted to think that the ent of a distinguished region I, will always possess an exten character. Such a behavior is referred to as a volume sc and is observed for thermal states. Intriguingly, for ty FIG. 1 A lattice L with a distinguished set I L (shaded area). Vertices depict the of I with surface area s(i) ground states, however, this is not at all what one encoun Instead, one typically finds an area law, or an area law a small (often logarithmic) correction: This means that i distinguishes a region, the scaling of the entropy is m of the region I, the state will not be pure in general and will have a non-vanishing von-neumann entropy S( I). 1 linear in the boundary area of the region. The entangle entropy is then said to fulfill an area law. It is the purpo In contrast to thermal states this entropy does not originate this article to review studies on area laws and the scalin from a lack of knowledge about the microstate of the system. Even at zero temperature we will encounter a non-zero The main four motivations to approach this que the entanglement entropy in a non-technical manner. entropy! This entropy arises because of a very fundamental (known to the authors) are as follows: property of quantum mechanics: Entanglement. This quite intriguing trait of quantum mechanics gives rise to correlations The holographic principle and black hole entr even in situations where the randomness cannot be traced back The historical motivation to study the entangleme to a mere lack of knowledge. The mentioned quantity, the entropy of a subregion is called entanglement entropy or geomet- hole physics: It has been suggested in the seminal geometric entropy stems from considerations of b ric entropy and, in quantum information, entropy of entanglement, which represents an operationally defined entanglement for a discrete version of a massless free scalar fie of refs. 23,207 that the area law of the geometric ent measure for pure states (for recent reviews see refs. 125,186 ). then numerically found for an imaginary sphere in In the context of quantum field theory, questions of scaling Ramis of entanglement Movassagh entropies in themovassagh size of I have some andtra- Shor: arxiv: holes, 118 in particular[quant-ph] the Bekenstein-Hawking dial symmetry could be related to the physics of b ent Picture from Eisert, Cramer, Plenio, Rev. Mod. Phys. 82 (2010) Area law: Suppose you have a Hamiltonian with only local interactions, and a quantum system is in the ground state of the Hamiltonian. Then the entropy of entanglement between two subsystems of a quantum system is proportional to the area of the boundary between them.
5 Area law and implications for simulability 1D gapped local systems obey an area law. [M.B. Hastings (2007)] This makes them easy to simulate on a classical comuter. Matrix Product States, DMRG, PEP, etc. work very well for 1D systems with an area law.
6 higher dimensions It is believed that higher-dimensional gapped systems obey an area law (open). For critical systems, it is believed the area law contains an extra log factor. In D spatial dimensions one expects: S L D 1 : Gapped S L D 1 log(l) : Critical
7 Phase transitions For 1-dimensional spin chains at critical points, the continuous limit is generally a conformal field theory: Entropy of entanglement: O(log n), Spectral gap: O(1/n).
8 Basic idea that started our research Simulating 1D spin chains with local Hamiltonians is BQP-complete. (Gottesman, Irani). 1D spin chains with low entanglement are classically simulable. Therefore: there must be 1D spin chains with high entanglement.
9 arxiv: Movassagh, Farhi, Goldstone, Nagaj, Osborne, Shor (2010) We investigated spin chains with qudits of dimenision d, interaction is a projection dimension r. The ground state is frustration-free but entangled when d r d 2 /4. we could compute the Schmidt ranks, We could not obtain definitive results on the spectral gap or the entanglement entropy.
10 arxiv: Irani (2010) There are Hamiltonians whose ground states have: spectral gap O(1/n c ), entanglement entropy O(n), complicated Hamiltonians, high-dimensional spins.
11 Bravyi et al 2012 Bravyi, Caha, Movassagh, Nagaj, Shor (2012) There are Hamiltonians whose ground states have spectral gap O(1/n c ), have entanglement entropy O(log n), are frustration free, have spins of dimension 3.
12 New result Movassagh, Shor (2014) There are Hamiltonians whose ground states have spectral gap O(1/n c ), c 2 have entanglement entropy O( n), are frustration free, have spins of dimension 2s + 1, s > 1.
13 Another new result Movassagh, Shor (2014) There are Hamiltonians whose ground states numerically have spectral gap O(1/n c ), c 2 have entanglement entropy O( n), are unique, are not frustration free, have spins of dimension 2s + 1, s > 1. These properties do not depend on the boundary conditions.
14 Summary of the new result The Motzkin state, M 2n,s is the unique ground state of the local Hamiltonian Entanglement entropy violates the area law: S (n) = c 1 (s)log 2 (s) n log(n) + c 2 (s) χ = sn+1 1 s 1. The gap upper bound: O ( n 2). Brownian excursion and universality of Brownian motion. The gap lower bound: Ω((n c ), c 1. Fractional matching and statistics of random walks
15 States: d = 2s + 1 s = 1 l 1 ( 0 0 d = 3 r 1 )
16 States s = 1 l 1 ( 0 0 d = 3 r 1 )
17 s 1 s = 2 l 1 l 2 0 r 1 r 2 ( [ 0 ) ] d = 5
18 Ground states
19 How to quantify entanglement Entanglement of Motzkin States is due to the mutual information between halves Motzkin walk A B ( ) ( 0 ( ( 0 ) ) )
20 How to quantify entanglement Entanglement of Motzkin States is due to the mutual information between halves Motzkin walk m A B ( ) ( 0 ( ( 0 ) ) )
21 More than one type of parenthesis e.g., s = 2 Suppose there are two types ( and { to match { } ( 0 { ( 0 ) } )
22 More than one type of parenthesis e.g., s = 2 Entanglement of Colored Motzkin States is due to the mutual information between halves Motzkin walk { } ( 0 { ( 0 ) } )
23 Subtlety for s > 1 Suppose there are two types ( and { to match ( 0 { 0 } ) O.K.
24 Matching that does NOT work Suppose there are two types ( and { to match ( 0 { 0 ) } Not O.K.! ( 0 { 0 } ) O.K.
25 The ground state s = 1 e.g., 2n = {2,4} M 2n,s = 1 M2n p th Motzkin walk p M 2 = 1 { 00 + lr } 2 M 4 = 1 { lr + 0l0r + l00r + 0l0r 9 + l0r0 + lr00 + lrlr + llrr }
26 The ground state s 1 e.g., 2n = 2 M 2n,s = 1 M2n p th s-colored Motzkin walk M 2,s p { 00 + s k=1 l k r k }
27 Entanglement: Schmidt rank χ p n,m,s = M2 n,m,s, N n,s N n,s n m=0 s m M 2 n,m,s, (1) Geometric sum on m gives χ = sn+1 1 s 1 and entanglement entropy is S ({p n,m,s }) = n m=0 s m p n,m,s log 2 p n,m,s. (2)
28 Combinatorial factors M n,m,s : number of walks starting at zero ending at height m with s total colors M n,m,s = m + 1 ( n + 1 i 0 M n,m,i,s i 0 n + 1 i + m + 1 i n 2i m ) s i
29 Quantifying entanglement, area laws and simulability Location of the Saddle # M n,m,i,s, n = 90 and s = i Saddle point: Mn,m,s,i +1 Mn,m,s,i = 1, m 0 Mn,m+1,s,i Mn,m,s,i = 1.
30 Saddle point approximation Turning the sum into an integral (carefully) and performing saddle point integration m = α n : M n,m,s S 2log(s) σ ( 1 s 2 πσn 3/2 σ 2σ π s s. ) n+1 ) αs α n/2 exp( α2 4σ n logn + γ log(2πσ),.
31 Underlying Hamiltonian implements local moves H = { s k=1 r k 1 r k + s k=1 } 2n 1 l k 2n l k + Π j,j+1 projects onto the span of ( k,= 1,,s) 1 ] [0l k l k ] [0r k r k ] [00 l k r k 2 j=1 : 0l k l k 0 : 0r k r k 0 : 00 l k r k Π cross = l k r i r i l k. k i Π j,j+1,
32 Meaning of terms in Hamiltonian The terms 1 ] [0l k l k ] [0r k r k ] [00 l k r k 2 : 0l k l k 0 : 0r k r k 0 : 00 l k r k enforce an equal superposition of all walks which can be reached by switching l k and 0 switching r k and 0, replacing l k r k by 00.
33 Meaning of terms in Hamiltonian The cross terms Π cross = l k r i r i l k. k i ensure that the types of parentheses match. The boundary terms { s k=1 r k 1 r k + ensure that the walk is balanced. s k=1 l k 2n l k }
34 Gap Upper-Bound We show that the gap is O(n 2 ).
35 Gap: Upper bound I We want any state φ such that φ H φ = O ( n 2), φ ground H φ < 1 2. Then φ = α g φ g + α 1 φ 1 + α 2 φ and φ H φ = α 2 1 φ 1 H φ 1 + α 2 2 φ 2 H φ 2 + α 2 3 φ 3 H φ (1 α 2 g ) φ 1 H φ 1
36 Gap: Upper bound II φ = 1 M2n e p { 2πiθ ( Area of p th )} Motzkin walk p th Motzkin walk M 2n φ = 1 M 2n e p { 2πiθ ( Area of p th )} Motzkin walk
37 Gap: Upper bound II φ = 1 M2n e p { 2πiθ ( Area of p th )} Motzkin walk p th Motzkin walk M 2n φ = 1 M 2n e p { 2πiθ ( Area of p th )} Motzkin walk lim 2n φ F A (θ) n 0 f A (x)e 2πixθ dx.
38 Gap: Upper bound III f A (x) F A(θ) x f A (x) = 2 6 x 2 j=1 ( v 2/3 j e v j U 5 6, 4 ) 3 ;v j θ x [0, ) v j = 2 a j 3 /27x 2 where a j are the zeros of the Airy function.
39 Gap Lower-Bound Θ(n c ), for some constant c. We use the same techniques as in Bravyi, Caha, Movassagh, Nagaj, Shor. the projection lemma relating Motzkin walks and Dyck walks, proving rapid mixing with the canonical paths method, fractional matchings.
40 This Hamiltonian isn t completely satisfactory requires boundary conditions to have unique ground state. Without the boundary conditions, there would be ( ) n+2 2 ground states, each coming from a superposition of unbalanced walks: ( 0 ( ( ) 0 ) () How can we eliminate these ground states without boundary conditions? We add an energy penalty for l and r i.e., for ( and ).
41 Hamiltonian with extermal magnetic field. How can we prove anything about these states? The argument that the gap is at most O(n 2 ) still holds. Only have to worry about the gap in two cases: Unbalanced walks Superposition of balanced walks with positive coefficients.
42 Hamiltonian with extermal magnetic field. The gap for unbalanced walks: Let ε be the energy penalty for l k, r k. We can use perturbation theory (backed up with numerics) to show that these ground states have an increased energy of around cε 2 /n.
43 Hamiltonian with extermal magnetic field. The gap for states in the balanced subspace. There is a polynomial gap in the balanced subspace in the Hamiltonian without an energy penalty. It appears from numerics (on chains of relatively small length) that the gap in this case is Numerics seem to show that the gap in the balanced subspace with an energy penalty is also Θ(n 2 ).
44 Open problems Is there a continuum limit for these Hamiltonians? Can we rigorously prove the results with an external magnetic field? Are there frustration-free Hamiltonians with unique ground states which violate the area law by large factors?
45 Lastly... Thank you
The computational difficulty of finding MPS ground states
 The computational difficulty of finding MPS ground states Norbert Schuch 1, Ignacio Cirac 1, and Frank Verstraete 2 1 Max-Planck-Institute for Quantum Optics, Garching, Germany 2 University of Vienna,
The computational difficulty of finding MPS ground states Norbert Schuch 1, Ignacio Cirac 1, and Frank Verstraete 2 1 Max-Planck-Institute for Quantum Optics, Garching, Germany 2 University of Vienna,
arxiv: v2 [cond-mat.stat-mech] 15 Mar 2017
![arxiv: v2 [cond-mat.stat-mech] 15 Mar 2017 arxiv: v2 [cond-mat.stat-mech] 15 Mar 2017](/thumbs/82/86166745.jpg) Entropy, gap and a multi-parameter deformation of the Fredkin spin chain Zhao Zhang and Israel Klich arxiv:1702.03581v2 [cond-mat.stat-mech] 15 Mar 2017 Department of Physics, University of Virginia, Charlottesville,
Entropy, gap and a multi-parameter deformation of the Fredkin spin chain Zhao Zhang and Israel Klich arxiv:1702.03581v2 [cond-mat.stat-mech] 15 Mar 2017 Department of Physics, University of Virginia, Charlottesville,
Semigroup Quantum Spin Chains
 Semigroup Quantum Spin Chains Pramod Padmanabhan Center for Physics of Complex Systems Institute for Basic Science, Korea 12th July, 2018 Based on work done with D. Texeira, D. Trancanelli ; F. Sugino
Semigroup Quantum Spin Chains Pramod Padmanabhan Center for Physics of Complex Systems Institute for Basic Science, Korea 12th July, 2018 Based on work done with D. Texeira, D. Trancanelli ; F. Sugino
The density matrix renormalization group and tensor network methods
 The density matrix renormalization group and tensor network methods Outline Steve White Exploiting the low entanglement of ground states Matrix product states and DMRG 1D 2D Tensor network states Some
The density matrix renormalization group and tensor network methods Outline Steve White Exploiting the low entanglement of ground states Matrix product states and DMRG 1D 2D Tensor network states Some
4 Matrix product states
 Physics 3b Lecture 5 Caltech, 05//7 4 Matrix product states Matrix product state (MPS) is a highly useful tool in the study of interacting quantum systems in one dimension, both analytically and numerically.
Physics 3b Lecture 5 Caltech, 05//7 4 Matrix product states Matrix product state (MPS) is a highly useful tool in the study of interacting quantum systems in one dimension, both analytically and numerically.
Quantum Hamiltonian Complexity. Itai Arad
 1 18 / Quantum Hamiltonian Complexity Itai Arad Centre of Quantum Technologies National University of Singapore QIP 2015 2 18 / Quantum Hamiltonian Complexity condensed matter physics QHC complexity theory
1 18 / Quantum Hamiltonian Complexity Itai Arad Centre of Quantum Technologies National University of Singapore QIP 2015 2 18 / Quantum Hamiltonian Complexity condensed matter physics QHC complexity theory
Efficient time evolution of one-dimensional quantum systems
 Efficient time evolution of one-dimensional quantum systems Frank Pollmann Max-Planck-Institut für komplexer Systeme, Dresden, Germany Sep. 5, 2012 Hsinchu Problems we will address... Finding ground states
Efficient time evolution of one-dimensional quantum systems Frank Pollmann Max-Planck-Institut für komplexer Systeme, Dresden, Germany Sep. 5, 2012 Hsinchu Problems we will address... Finding ground states
Simulating Quantum Systems through Matrix Product States. Laura Foini SISSA Journal Club
 Simulating Quantum Systems through Matrix Product States Laura Foini SISSA Journal Club 15-04-2010 Motivations Theoretical interest in Matrix Product States Wide spectrum of their numerical applications
Simulating Quantum Systems through Matrix Product States Laura Foini SISSA Journal Club 15-04-2010 Motivations Theoretical interest in Matrix Product States Wide spectrum of their numerical applications
3 Symmetry Protected Topological Phase
 Physics 3b Lecture 16 Caltech, 05/30/18 3 Symmetry Protected Topological Phase 3.1 Breakdown of noninteracting SPT phases with interaction Building on our previous discussion of the Majorana chain and
Physics 3b Lecture 16 Caltech, 05/30/18 3 Symmetry Protected Topological Phase 3.1 Breakdown of noninteracting SPT phases with interaction Building on our previous discussion of the Majorana chain and
Black Holes, Holography, and Quantum Information
 Black Holes, Holography, and Quantum Information Daniel Harlow Massachusetts Institute of Technology August 31, 2017 1 Black Holes Black holes are the most extreme objects we see in nature! Classically
Black Holes, Holography, and Quantum Information Daniel Harlow Massachusetts Institute of Technology August 31, 2017 1 Black Holes Black holes are the most extreme objects we see in nature! Classically
An Inverse Mass Expansion for Entanglement Entropy. Free Massive Scalar Field Theory
 in Free Massive Scalar Field Theory NCSR Demokritos National Technical University of Athens based on arxiv:1711.02618 [hep-th] in collaboration with Dimitris Katsinis March 28 2018 Entanglement and Entanglement
in Free Massive Scalar Field Theory NCSR Demokritos National Technical University of Athens based on arxiv:1711.02618 [hep-th] in collaboration with Dimitris Katsinis March 28 2018 Entanglement and Entanglement
Quantum Many Body Systems and Tensor Networks
 Quantum Many Body Systems and Tensor Networks Aditya Jain International Institute of Information Technology, Hyderabad aditya.jain@research.iiit.ac.in July 30, 2015 Aditya Jain (IIIT-H) Quantum Hamiltonian
Quantum Many Body Systems and Tensor Networks Aditya Jain International Institute of Information Technology, Hyderabad aditya.jain@research.iiit.ac.in July 30, 2015 Aditya Jain (IIIT-H) Quantum Hamiltonian
04. Five Principles of Quantum Mechanics
 04. Five Principles of Quantum Mechanics () States are represented by vectors of length. A physical system is represented by a linear vector space (the space of all its possible states). () Properties
04. Five Principles of Quantum Mechanics () States are represented by vectors of length. A physical system is represented by a linear vector space (the space of all its possible states). () Properties
Ground State Entanglement in One Dimensional Translationally Invariant Quantum Systems
 Ground State Entanglement in One Dimensional Translationally Invariant Quantum Systems Sandy Irani Computer Science Department University of California, Irvine, USA (Dated: October 2, 2009) Abstract We
Ground State Entanglement in One Dimensional Translationally Invariant Quantum Systems Sandy Irani Computer Science Department University of California, Irvine, USA (Dated: October 2, 2009) Abstract We
Isotropic Entanglement
 Isotropic Entanglement Ramis Movassagh 1 and Alan Edelman 1 1 Department of Mathematics, M.I.T. QIP, January 2011 Acknowledgments Peter W. Shor Jerey Goldstone X-G Wen, Patrick Lee, Peter Young, Mehran
Isotropic Entanglement Ramis Movassagh 1 and Alan Edelman 1 1 Department of Mathematics, M.I.T. QIP, January 2011 Acknowledgments Peter W. Shor Jerey Goldstone X-G Wen, Patrick Lee, Peter Young, Mehran
Tensor network simulations of strongly correlated quantum systems
 CENTRE FOR QUANTUM TECHNOLOGIES NATIONAL UNIVERSITY OF SINGAPORE AND CLARENDON LABORATORY UNIVERSITY OF OXFORD Tensor network simulations of strongly correlated quantum systems Stephen Clark LXXT[[[GSQPEFS\EGYOEGXMZMXMIWUYERXYQGSYVWI
CENTRE FOR QUANTUM TECHNOLOGIES NATIONAL UNIVERSITY OF SINGAPORE AND CLARENDON LABORATORY UNIVERSITY OF OXFORD Tensor network simulations of strongly correlated quantum systems Stephen Clark LXXT[[[GSQPEFS\EGYOEGXMZMXMIWUYERXYQGSYVWI
Nullity of Measurement-induced Nonlocality. Yu Guo
 Jul. 18-22, 2011, at Taiyuan. Nullity of Measurement-induced Nonlocality Yu Guo (Joint work with Pro. Jinchuan Hou) 1 1 27 Department of Mathematics Shanxi Datong University Datong, China guoyu3@yahoo.com.cn
Jul. 18-22, 2011, at Taiyuan. Nullity of Measurement-induced Nonlocality Yu Guo (Joint work with Pro. Jinchuan Hou) 1 1 27 Department of Mathematics Shanxi Datong University Datong, China guoyu3@yahoo.com.cn
arxiv: v1 [quant-ph] 7 Jan 2013
![arxiv: v1 [quant-ph] 7 Jan 2013 arxiv: v1 [quant-ph] 7 Jan 2013](/thumbs/92/108595133.jpg) An area law and sub-exponential algorithm for D systems Itai Arad, Alexei Kitaev 2, Zeph Landau 3, Umesh Vazirani 4 Abstract arxiv:30.62v [quant-ph] 7 Jan 203 We give a new proof for the area law for general
An area law and sub-exponential algorithm for D systems Itai Arad, Alexei Kitaev 2, Zeph Landau 3, Umesh Vazirani 4 Abstract arxiv:30.62v [quant-ph] 7 Jan 203 We give a new proof for the area law for general
Fradkin, Fredkin or Fridkin?
 Workshop@IIP, Natal (2018/6/19) 1/30 Fradkin, Fredkin or Fridkin? Hosho Katsura (Department of Physics, UTokyo) Collaborators: Masafumi Udagawa (UTokyo Topcon), Vladimir Korepin, Olof Salberger (Stony
Workshop@IIP, Natal (2018/6/19) 1/30 Fradkin, Fredkin or Fridkin? Hosho Katsura (Department of Physics, UTokyo) Collaborators: Masafumi Udagawa (UTokyo Topcon), Vladimir Korepin, Olof Salberger (Stony
Algebraic Theory of Entanglement
 Algebraic Theory of (arxiv: 1205.2882) 1 (in collaboration with T.R. Govindarajan, A. Queiroz and A.F. Reyes-Lega) 1 Physics Department, Syracuse University, Syracuse, N.Y. and The Institute of Mathematical
Algebraic Theory of (arxiv: 1205.2882) 1 (in collaboration with T.R. Govindarajan, A. Queiroz and A.F. Reyes-Lega) 1 Physics Department, Syracuse University, Syracuse, N.Y. and The Institute of Mathematical
Entanglement, quantum critical phenomena and efficient simulation of quantum dynamics
 Entanglement, quantum critical phenomena and efficient simulation of quantum dynamics Simons Conference on Reversible and Quantum Computation Stony Brook, May 28-31 2003 Guifre Vidal Institute for Quantum
Entanglement, quantum critical phenomena and efficient simulation of quantum dynamics Simons Conference on Reversible and Quantum Computation Stony Brook, May 28-31 2003 Guifre Vidal Institute for Quantum
Mutual Information in Conformal Field Theories in Higher Dimensions
 Mutual Information in Conformal Field Theories in Higher Dimensions John Cardy University of Oxford Conference on Mathematical Statistical Physics Kyoto 2013 arxiv:1304.7985; J. Phys. : Math. Theor. 46
Mutual Information in Conformal Field Theories in Higher Dimensions John Cardy University of Oxford Conference on Mathematical Statistical Physics Kyoto 2013 arxiv:1304.7985; J. Phys. : Math. Theor. 46
Quantum algorithms based on span programs
 Quantum algorithms based on span programs Ben Reichardt IQC, U Waterloo [arxiv:0904.2759] Model: Complexity measure: Quantum algorithms Black-box query complexity Span programs Witness size [KW 93] [RŠ
Quantum algorithms based on span programs Ben Reichardt IQC, U Waterloo [arxiv:0904.2759] Model: Complexity measure: Quantum algorithms Black-box query complexity Span programs Witness size [KW 93] [RŠ
arxiv: v1 [hep-th] 26 Sep 2017
![arxiv: v1 [hep-th] 26 Sep 2017 arxiv: v1 [hep-th] 26 Sep 2017](/thumbs/93/113646333.jpg) Eigenstate entanglement in the Sachdev-Ye-Kitaev model arxiv:709.0960v [hep-th] 6 Sep 07 Yichen Huang ( 黄溢辰 ) Institute for Quantum Information and Matter, California Institute of Technology Pasadena,
Eigenstate entanglement in the Sachdev-Ye-Kitaev model arxiv:709.0960v [hep-th] 6 Sep 07 Yichen Huang ( 黄溢辰 ) Institute for Quantum Information and Matter, California Institute of Technology Pasadena,
Matrix Product States
 Matrix Product States Ian McCulloch University of Queensland Centre for Engineered Quantum Systems 28 August 2017 Hilbert space (Hilbert) space is big. Really big. You just won t believe how vastly, hugely,
Matrix Product States Ian McCulloch University of Queensland Centre for Engineered Quantum Systems 28 August 2017 Hilbert space (Hilbert) space is big. Really big. You just won t believe how vastly, hugely,
Frustration and Area law
 Frustration and Area law When the frustration goes odd S. M. Giampaolo Institut Ruder Bošković, Zagreb, Croatia Workshop: Exactly Solvable Quantum Chains Natal 18-29 June 2018 Coauthors F. Franchini Institut
Frustration and Area law When the frustration goes odd S. M. Giampaolo Institut Ruder Bošković, Zagreb, Croatia Workshop: Exactly Solvable Quantum Chains Natal 18-29 June 2018 Coauthors F. Franchini Institut
Lecture 21: Quantum communication complexity
 CPSC 519/619: Quantum Computation John Watrous, University of Calgary Lecture 21: Quantum communication complexity April 6, 2006 In this lecture we will discuss how quantum information can allow for a
CPSC 519/619: Quantum Computation John Watrous, University of Calgary Lecture 21: Quantum communication complexity April 6, 2006 In this lecture we will discuss how quantum information can allow for a
SPACETIME FROM ENTANGLEMENT - journal club notes -
 SPACETIME FROM ENTANGLEMENT - journal club notes - Chris Heinrich 1 Outline 1. Introduction Big picture: Want a quantum theory of gravity Best understanding of quantum gravity so far arises through AdS/CFT
SPACETIME FROM ENTANGLEMENT - journal club notes - Chris Heinrich 1 Outline 1. Introduction Big picture: Want a quantum theory of gravity Best understanding of quantum gravity so far arises through AdS/CFT
Quantum Simulation. 9 December Scott Crawford Justin Bonnar
 Quantum Simulation 9 December 2008 Scott Crawford Justin Bonnar Quantum Simulation Studies the efficient classical simulation of quantum circuits Understanding what is (and is not) efficiently simulable
Quantum Simulation 9 December 2008 Scott Crawford Justin Bonnar Quantum Simulation Studies the efficient classical simulation of quantum circuits Understanding what is (and is not) efficiently simulable
17 Entanglement and Tensor Network States
 17 Entanglement and Tensor Network States Jens Eisert Freie Universität Berlin Dahlem Center for Complex Quantum Systems Contents 1 Correlations and entanglement in quantum many-body systems 2 1.1 Quantum
17 Entanglement and Tensor Network States Jens Eisert Freie Universität Berlin Dahlem Center for Complex Quantum Systems Contents 1 Correlations and entanglement in quantum many-body systems 2 1.1 Quantum
Thermal pure quantum state
 Thermal pure quantum state Sho Sugiura ( 杉浦祥 ) Institute for Solid State Physics, Univ. Tokyo Collaborator: Akira Shimizu (Univ. Tokyo) SS and A.Shimizu, PRL 108, 240401 (2012) SS and A.Shimizu, PRL 111,
Thermal pure quantum state Sho Sugiura ( 杉浦祥 ) Institute for Solid State Physics, Univ. Tokyo Collaborator: Akira Shimizu (Univ. Tokyo) SS and A.Shimizu, PRL 108, 240401 (2012) SS and A.Shimizu, PRL 111,
arxiv: v1 [quant-ph] 12 May 2016
![arxiv: v1 [quant-ph] 12 May 2016 arxiv: v1 [quant-ph] 12 May 2016](/thumbs/79/80238817.jpg) Fredkin Spin Chain Olof Salberger and Vladimir Korepin arxiv:1605.0384v1 [quant-ph] 1 May 016 May 13, 016 Abstract We introduce a new model of interacting spin 1/. It describes interaction of three nearest
Fredkin Spin Chain Olof Salberger and Vladimir Korepin arxiv:1605.0384v1 [quant-ph] 1 May 016 May 13, 016 Abstract We introduce a new model of interacting spin 1/. It describes interaction of three nearest
Quantum Information Types
 qitd181 Quantum Information Types Robert B. Griffiths Version of 6 February 2012 References: R. B. Griffiths, Types of Quantum Information, Phys. Rev. A 76 (2007) 062320; arxiv:0707.3752 Contents 1 Introduction
qitd181 Quantum Information Types Robert B. Griffiths Version of 6 February 2012 References: R. B. Griffiths, Types of Quantum Information, Phys. Rev. A 76 (2007) 062320; arxiv:0707.3752 Contents 1 Introduction
Journal Club: Brief Introduction to Tensor Network
 Journal Club: Brief Introduction to Tensor Network Wei-Han Hsiao a a The University of Chicago E-mail: weihanhsiao@uchicago.edu Abstract: This note summarizes the talk given on March 8th 2016 which was
Journal Club: Brief Introduction to Tensor Network Wei-Han Hsiao a a The University of Chicago E-mail: weihanhsiao@uchicago.edu Abstract: This note summarizes the talk given on March 8th 2016 which was
Shared Purity of Multipartite Quantum States
 Shared Purity of Multipartite Quantum States Anindya Biswas Harish-Chandra Research Institute December 3, 2013 Anindya Biswas (HRI) Shared Purity December 3, 2013 1 / 38 Outline of the talk 1 Motivation
Shared Purity of Multipartite Quantum States Anindya Biswas Harish-Chandra Research Institute December 3, 2013 Anindya Biswas (HRI) Shared Purity December 3, 2013 1 / 38 Outline of the talk 1 Motivation
21 Holographic Entanglement Entropy
 21 Holographic Entanglement Entropy 21.1 The formula We now turn to entanglement entropy in CFTs with a semiclassical holographic dual. That is, we assume the CFT has a large number of degrees of freedom
21 Holographic Entanglement Entropy 21.1 The formula We now turn to entanglement entropy in CFTs with a semiclassical holographic dual. That is, we assume the CFT has a large number of degrees of freedom
arxiv: v2 [quant-ph] 31 Oct 2013
![arxiv: v2 [quant-ph] 31 Oct 2013 arxiv: v2 [quant-ph] 31 Oct 2013](/thumbs/93/112286981.jpg) Quantum Criticality with the Multi-scale Entanglement Renormalization Ansatz arxiv:1109.5334v2 [quant-ph] 31 Oct 2013 G. Evenbly 1 and G. Vidal 2 1 The University of Queensland, Brisbane, Queensland 4072,
Quantum Criticality with the Multi-scale Entanglement Renormalization Ansatz arxiv:1109.5334v2 [quant-ph] 31 Oct 2013 G. Evenbly 1 and G. Vidal 2 1 The University of Queensland, Brisbane, Queensland 4072,
31st Jerusalem Winter School in Theoretical Physics: Problem Set 2
 31st Jerusalem Winter School in Theoretical Physics: Problem Set Contents Frank Verstraete: Quantum Information and Quantum Matter : 3 : Solution to Problem 9 7 Daniel Harlow: Black Holes and Quantum Information
31st Jerusalem Winter School in Theoretical Physics: Problem Set Contents Frank Verstraete: Quantum Information and Quantum Matter : 3 : Solution to Problem 9 7 Daniel Harlow: Black Holes and Quantum Information
Tensor network simulation of QED on infinite lattices: learning from (1 + 1)d, and prospects for (2 + 1)d
 Tensor network simulation of QED on infinite lattices: learning from (1 + 1)d, and prospects for (2 + 1)d Román Orús University of Mainz (Germany) K. Zapp, RO, Phys. Rev. D 95, 114508 (2017) Goal of this
Tensor network simulation of QED on infinite lattices: learning from (1 + 1)d, and prospects for (2 + 1)d Román Orús University of Mainz (Germany) K. Zapp, RO, Phys. Rev. D 95, 114508 (2017) Goal of this
Principles of Quantum Mechanics Pt. 2
 Principles of Quantum Mechanics Pt. 2 PHYS 500 - Southern Illinois University February 9, 2017 PHYS 500 - Southern Illinois University Principles of Quantum Mechanics Pt. 2 February 9, 2017 1 / 13 The
Principles of Quantum Mechanics Pt. 2 PHYS 500 - Southern Illinois University February 9, 2017 PHYS 500 - Southern Illinois University Principles of Quantum Mechanics Pt. 2 February 9, 2017 1 / 13 The
arxiv: v1 [cond-mat.str-el] 7 Aug 2011
![arxiv: v1 [cond-mat.str-el] 7 Aug 2011 arxiv: v1 [cond-mat.str-el] 7 Aug 2011](/thumbs/72/67542281.jpg) Topological Geometric Entanglement of Blocks Román Orús 1, 2 and Tzu-Chieh Wei 3, 4 1 School of Mathematics and Physics, The University of Queensland, QLD 4072, Australia 2 Max-Planck-Institut für Quantenoptik,
Topological Geometric Entanglement of Blocks Román Orús 1, 2 and Tzu-Chieh Wei 3, 4 1 School of Mathematics and Physics, The University of Queensland, QLD 4072, Australia 2 Max-Planck-Institut für Quantenoptik,
Density Matrices. Chapter Introduction
 Chapter 15 Density Matrices 15.1 Introduction Density matrices are employed in quantum mechanics to give a partial description of a quantum system, one from which certain details have been omitted. For
Chapter 15 Density Matrices 15.1 Introduction Density matrices are employed in quantum mechanics to give a partial description of a quantum system, one from which certain details have been omitted. For
Entanglement in Many-Body Fermion Systems
 Entanglement in Many-Body Fermion Systems Michelle Storms 1, 2 1 Department of Physics, University of California Davis, CA 95616, USA 2 Department of Physics and Astronomy, Ohio Wesleyan University, Delaware,
Entanglement in Many-Body Fermion Systems Michelle Storms 1, 2 1 Department of Physics, University of California Davis, CA 95616, USA 2 Department of Physics and Astronomy, Ohio Wesleyan University, Delaware,
Entanglement in Valence-Bond-Solid States on Symmetric Graphs
 Entanglement in Valence-Bond-Solid States on Symmetric Graphs Shu Tanaka A, Hosho Katsura B, Naoki Kawashima C Anatol N. Kirillov D, and Vladimir E. Korepin E A. Kinki University B. Gakushuin University
Entanglement in Valence-Bond-Solid States on Symmetric Graphs Shu Tanaka A, Hosho Katsura B, Naoki Kawashima C Anatol N. Kirillov D, and Vladimir E. Korepin E A. Kinki University B. Gakushuin University
Simulation of Quantum Many-Body Systems
 Numerical Quantum Simulation of Matteo Rizzi - KOMET 7 - JGU Mainz Vorstellung der Arbeitsgruppen WS 15-16 recent developments in control of quantum objects (e.g., cold atoms, trapped ions) General Framework
Numerical Quantum Simulation of Matteo Rizzi - KOMET 7 - JGU Mainz Vorstellung der Arbeitsgruppen WS 15-16 recent developments in control of quantum objects (e.g., cold atoms, trapped ions) General Framework
1. Griffiths Suppose two spin-1/2 particles are known to be in the singlet configuration.
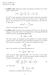 Physics 443 HW #7 Due March 12, 2008 1. Griffiths 4.50. Suppose two spin-1/2 particles are known to be in the singlet configuration. ( 00 = 1 2 ( + 1 2 1 2 1 2 +1 2 ) Let S a (1) be the component of the
Physics 443 HW #7 Due March 12, 2008 1. Griffiths 4.50. Suppose two spin-1/2 particles are known to be in the singlet configuration. ( 00 = 1 2 ( + 1 2 1 2 1 2 +1 2 ) Let S a (1) be the component of the
arxiv:quant-ph/ v2 24 Dec 2003
 Quantum Entanglement in Heisenberg Antiferromagnets V. Subrahmanyam Department of Physics, Indian Institute of Technology, Kanpur, India. arxiv:quant-ph/0309004 v2 24 Dec 2003 Entanglement sharing among
Quantum Entanglement in Heisenberg Antiferromagnets V. Subrahmanyam Department of Physics, Indian Institute of Technology, Kanpur, India. arxiv:quant-ph/0309004 v2 24 Dec 2003 Entanglement sharing among
Quantum Entanglement- Fundamental Aspects
 Quantum Entanglement- Fundamental Aspects Debasis Sarkar Department of Applied Mathematics, University of Calcutta, 92, A.P.C. Road, Kolkata- 700009, India Abstract Entanglement is one of the most useful
Quantum Entanglement- Fundamental Aspects Debasis Sarkar Department of Applied Mathematics, University of Calcutta, 92, A.P.C. Road, Kolkata- 700009, India Abstract Entanglement is one of the most useful
Consistent Histories. Chapter Chain Operators and Weights
 Chapter 10 Consistent Histories 10.1 Chain Operators and Weights The previous chapter showed how the Born rule can be used to assign probabilities to a sample space of histories based upon an initial state
Chapter 10 Consistent Histories 10.1 Chain Operators and Weights The previous chapter showed how the Born rule can be used to assign probabilities to a sample space of histories based upon an initial state
arxiv: v1 [quant-ph] 6 Jun 2011
![arxiv: v1 [quant-ph] 6 Jun 2011 arxiv: v1 [quant-ph] 6 Jun 2011](/thumbs/93/112286933.jpg) Tensor network states and geometry G. Evenbly 1, G. Vidal 1,2 1 School of Mathematics and Physics, the University of Queensland, Brisbane 4072, Australia 2 Perimeter Institute for Theoretical Physics,
Tensor network states and geometry G. Evenbly 1, G. Vidal 1,2 1 School of Mathematics and Physics, the University of Queensland, Brisbane 4072, Australia 2 Perimeter Institute for Theoretical Physics,
Entanglement entropy and gauge fields
 Entanglement entropy and gauge fields H. C., M.Huerta and A. Rosabal (2012) H. C., M. Huerta (2014) H. C., M. Huerta, in preparation Puzzling results Lattice calculations with extended lattice (Buividovich-Polikarpov,
Entanglement entropy and gauge fields H. C., M.Huerta and A. Rosabal (2012) H. C., M. Huerta (2014) H. C., M. Huerta, in preparation Puzzling results Lattice calculations with extended lattice (Buividovich-Polikarpov,
FRG Workshop in Cambridge MA, May
 FRG Workshop in Cambridge MA, May 18-19 2011 Programme Wednesday May 18 09:00 09:10 (welcoming) 09:10 09:50 Bachmann 09:55 10:35 Sims 10:55 11:35 Borovyk 11:40 12:20 Bravyi 14:10 14:50 Datta 14:55 15:35
FRG Workshop in Cambridge MA, May 18-19 2011 Programme Wednesday May 18 09:00 09:10 (welcoming) 09:10 09:50 Bachmann 09:55 10:35 Sims 10:55 11:35 Borovyk 11:40 12:20 Bravyi 14:10 14:50 Datta 14:55 15:35
Decoherence and the Classical Limit
 Chapter 26 Decoherence and the Classical Limit 26.1 Introduction Classical mechanics deals with objects which have a precise location and move in a deterministic way as a function of time. By contrast,
Chapter 26 Decoherence and the Classical Limit 26.1 Introduction Classical mechanics deals with objects which have a precise location and move in a deterministic way as a function of time. By contrast,
Entanglement in Quantum Field Theory
 Entanglement in Quantum Field Theory John Cardy University of Oxford DAMTP, December 2013 Outline Quantum entanglement in general and its quantification Path integral approach Entanglement entropy in 1+1-dimensional
Entanglement in Quantum Field Theory John Cardy University of Oxford DAMTP, December 2013 Outline Quantum entanglement in general and its quantification Path integral approach Entanglement entropy in 1+1-dimensional
Entanglement Entropy of Quantum Spin Chains:
 : Infinitely Degenerate Ground States Olalla A. Castro-Alvaredo School of Engineering and Mathematical Sciences Centre for Mathematical Science City University London 8th Bologna Workshop on CFT and Integrable
: Infinitely Degenerate Ground States Olalla A. Castro-Alvaredo School of Engineering and Mathematical Sciences Centre for Mathematical Science City University London 8th Bologna Workshop on CFT and Integrable
Ensembles and incomplete information
 p. 1/32 Ensembles and incomplete information So far in this course, we have described quantum systems by states that are normalized vectors in a complex Hilbert space. This works so long as (a) the system
p. 1/32 Ensembles and incomplete information So far in this course, we have described quantum systems by states that are normalized vectors in a complex Hilbert space. This works so long as (a) the system
Entanglement spectra in the NRG
 PRB 84, 125130 (2011) Entanglement spectra in the NRG Andreas Weichselbaum Ludwig Maximilians Universität, München Arnold Sommerfeld Center (ASC) Acknowledgement Jan von Delft (LMU) Theo Costi (Jülich)
PRB 84, 125130 (2011) Entanglement spectra in the NRG Andreas Weichselbaum Ludwig Maximilians Universität, München Arnold Sommerfeld Center (ASC) Acknowledgement Jan von Delft (LMU) Theo Costi (Jülich)
Chapter 5. Density matrix formalism
 Chapter 5 Density matrix formalism In chap we formulated quantum mechanics for isolated systems. In practice systems interect with their environnement and we need a description that takes this feature
Chapter 5 Density matrix formalism In chap we formulated quantum mechanics for isolated systems. In practice systems interect with their environnement and we need a description that takes this feature
Fredkin model. Vladimir Korepin January 12th. Stony Brook University
 Fredkin model Vladimir Korepin Stony Brook University 2018 January 12th Introduction Spin chains are important for high energy theory: N. Nekrasov, S. Sahatashvill. arxiv:0908.4052 K. Costello, E. Witten,
Fredkin model Vladimir Korepin Stony Brook University 2018 January 12th Introduction Spin chains are important for high energy theory: N. Nekrasov, S. Sahatashvill. arxiv:0908.4052 K. Costello, E. Witten,
Scaling analysis of snapshot spectra in the world-line quantum Monte Carlo for the transverse-field Ising chain
 TNSAA 2018-2019 Dec. 3-6, 2018, Kobe, Japan Scaling analysis of snapshot spectra in the world-line quantum Monte Carlo for the transverse-field Ising chain Kouichi Seki, Kouichi Okunishi Niigata University,
TNSAA 2018-2019 Dec. 3-6, 2018, Kobe, Japan Scaling analysis of snapshot spectra in the world-line quantum Monte Carlo for the transverse-field Ising chain Kouichi Seki, Kouichi Okunishi Niigata University,
Entanglement spectrum and Matrix Product States
 Entanglement spectrum and Matrix Product States Frank Verstraete J. Haegeman, D. Draxler, B. Pirvu, V. Stojevic, V. Zauner, I. Pizorn I. Cirac (MPQ), T. Osborne (Hannover), N. Schuch (Aachen) Outline Valence
Entanglement spectrum and Matrix Product States Frank Verstraete J. Haegeman, D. Draxler, B. Pirvu, V. Stojevic, V. Zauner, I. Pizorn I. Cirac (MPQ), T. Osborne (Hannover), N. Schuch (Aachen) Outline Valence
Lecture 3: Tensor Product Ansatz
 Lecture 3: Tensor Product nsatz Graduate Lectures Dr Gunnar Möller Cavendish Laboratory, University of Cambridge slide credits: Philippe Corboz (ETH / msterdam) January 2014 Cavendish Laboratory Part I:
Lecture 3: Tensor Product nsatz Graduate Lectures Dr Gunnar Möller Cavendish Laboratory, University of Cambridge slide credits: Philippe Corboz (ETH / msterdam) January 2014 Cavendish Laboratory Part I:
ENTANGLEMENT OF N DISTINGUISHABLE PARTICLES
 STUDIES IN LOGIC, GRAMMAR AND RHETORIC 27(40) 2012 Tomasz Bigaj ENTANGLEMENT OF N DISTINGUISHABLE PARTICLES Abstract. In their 2002 article, Ghirardi, Marinatto and Weber proposed a formal analysis of
STUDIES IN LOGIC, GRAMMAR AND RHETORIC 27(40) 2012 Tomasz Bigaj ENTANGLEMENT OF N DISTINGUISHABLE PARTICLES Abstract. In their 2002 article, Ghirardi, Marinatto and Weber proposed a formal analysis of
Physics 221A Fall 1996 Notes 12 Orbital Angular Momentum and Spherical Harmonics
 Physics 221A Fall 1996 Notes 12 Orbital Angular Momentum and Spherical Harmonics We now consider the spatial degrees of freedom of a particle moving in 3-dimensional space, which of course is an important
Physics 221A Fall 1996 Notes 12 Orbital Angular Momentum and Spherical Harmonics We now consider the spatial degrees of freedom of a particle moving in 3-dimensional space, which of course is an important
Entanglement: concept, measures and open problems
 Entanglement: concept, measures and open problems Division of Mathematical Physics Lund University June 2013 Project in Quantum information. Supervisor: Peter Samuelsson Outline 1 Motivation for study
Entanglement: concept, measures and open problems Division of Mathematical Physics Lund University June 2013 Project in Quantum information. Supervisor: Peter Samuelsson Outline 1 Motivation for study
FQXI 2014: Foundations of Probability and Information
 FQXI 2014: Foundations of Probability and Information CONTINGENT or DERIVABLE To what degree are the Laws of Physics dictated yet arbitrary (i.e. must be discovered)? and to what degree are Laws of Physics
FQXI 2014: Foundations of Probability and Information CONTINGENT or DERIVABLE To what degree are the Laws of Physics dictated yet arbitrary (i.e. must be discovered)? and to what degree are Laws of Physics
Lecture 2: November 9
 Semidefinite programming and computational aspects of entanglement IHP Fall 017 Lecturer: Aram Harrow Lecture : November 9 Scribe: Anand (Notes available at http://webmitedu/aram/www/teaching/sdphtml)
Semidefinite programming and computational aspects of entanglement IHP Fall 017 Lecturer: Aram Harrow Lecture : November 9 Scribe: Anand (Notes available at http://webmitedu/aram/www/teaching/sdphtml)
Stability of local observables
 Stability of local observables in closed and open quantum systems Angelo Lucia anlucia@ucm.es Universidad Complutense de Madrid NSF/CBMS Conference Quantum Spin Systems UAB, June 20, 2014 A. Lucia (UCM)
Stability of local observables in closed and open quantum systems Angelo Lucia anlucia@ucm.es Universidad Complutense de Madrid NSF/CBMS Conference Quantum Spin Systems UAB, June 20, 2014 A. Lucia (UCM)
Linear Algebra and Dirac Notation, Pt. 3
 Linear Algebra and Dirac Notation, Pt. 3 PHYS 500 - Southern Illinois University February 1, 2017 PHYS 500 - Southern Illinois University Linear Algebra and Dirac Notation, Pt. 3 February 1, 2017 1 / 16
Linear Algebra and Dirac Notation, Pt. 3 PHYS 500 - Southern Illinois University February 1, 2017 PHYS 500 - Southern Illinois University Linear Algebra and Dirac Notation, Pt. 3 February 1, 2017 1 / 16
Entropy in Classical and Quantum Information Theory
 Entropy in Classical and Quantum Information Theory William Fedus Physics Department, University of California, San Diego. Entropy is a central concept in both classical and quantum information theory,
Entropy in Classical and Quantum Information Theory William Fedus Physics Department, University of California, San Diego. Entropy is a central concept in both classical and quantum information theory,
Many-body entanglement witness
 Many-body entanglement witness Jeongwan Haah, MIT 21 January 2015 Coogee, Australia arxiv:1407.2926 Quiz Energy Entanglement Charge Invariant Momentum Total spin Rest Mass Complexity Class Many-body Entanglement
Many-body entanglement witness Jeongwan Haah, MIT 21 January 2015 Coogee, Australia arxiv:1407.2926 Quiz Energy Entanglement Charge Invariant Momentum Total spin Rest Mass Complexity Class Many-body Entanglement
Realizing non-abelian statistics in quantum loop models
 Realizing non-abelian statistics in quantum loop models Paul Fendley Experimental and theoretical successes have made us take a close look at quantum physics in two spatial dimensions. We have now found
Realizing non-abelian statistics in quantum loop models Paul Fendley Experimental and theoretical successes have made us take a close look at quantum physics in two spatial dimensions. We have now found
On preparing ground states of gapped Hamiltonians: An efficient Quantum Lovász Local Lemma
 On preparing ground states of gapped Hamiltonians: An efficient Quantum Lovász Local Lemma András Gilyén QuSoft, CWI, Amsterdam, Netherlands Joint work with: Or Sattath Hebrew University and MIT 1 / 20
On preparing ground states of gapped Hamiltonians: An efficient Quantum Lovász Local Lemma András Gilyén QuSoft, CWI, Amsterdam, Netherlands Joint work with: Or Sattath Hebrew University and MIT 1 / 20
Applied Linear Algebra in Geoscience Using MATLAB
 Applied Linear Algebra in Geoscience Using MATLAB Contents Getting Started Creating Arrays Mathematical Operations with Arrays Using Script Files and Managing Data Two-Dimensional Plots Programming in
Applied Linear Algebra in Geoscience Using MATLAB Contents Getting Started Creating Arrays Mathematical Operations with Arrays Using Script Files and Managing Data Two-Dimensional Plots Programming in
Quantum wires, orthogonal polynomials and Diophantine approximation
 Quantum wires, orthogonal polynomials and Diophantine approximation Introduction Quantum Mechanics (QM) is a linear theory Main idea behind Quantum Information (QI): use the superposition principle of
Quantum wires, orthogonal polynomials and Diophantine approximation Introduction Quantum Mechanics (QM) is a linear theory Main idea behind Quantum Information (QI): use the superposition principle of
Introduction to Quantum Information Hermann Kampermann
 Introduction to Quantum Information Hermann Kampermann Heinrich-Heine-Universität Düsseldorf Theoretische Physik III Summer school Bleubeuren July 014 Contents 1 Quantum Mechanics...........................
Introduction to Quantum Information Hermann Kampermann Heinrich-Heine-Universität Düsseldorf Theoretische Physik III Summer school Bleubeuren July 014 Contents 1 Quantum Mechanics...........................
Nonlocal Effects in Quantum Gravity
 Nonlocal Effects in Quantum Gravity Suvrat Raju International Centre for Theoretical Sciences 29th Meeting of the IAGRG IIT Guwahati 20 May 2017 Collaborators Based on work with 1 Kyriakos Papadodimas
Nonlocal Effects in Quantum Gravity Suvrat Raju International Centre for Theoretical Sciences 29th Meeting of the IAGRG IIT Guwahati 20 May 2017 Collaborators Based on work with 1 Kyriakos Papadodimas
Spin liquids in frustrated magnets
 May 20, 2010 Contents 1 Frustration 2 3 4 Exotic excitations 5 Frustration The presence of competing forces that cannot be simultaneously satisfied. Heisenberg-Hamiltonian H = 1 J ij S i S j 2 ij The ground
May 20, 2010 Contents 1 Frustration 2 3 4 Exotic excitations 5 Frustration The presence of competing forces that cannot be simultaneously satisfied. Heisenberg-Hamiltonian H = 1 J ij S i S j 2 ij The ground
Rigorous RG Algorithms and Area Laws for Low Energy Eigenstates in 1D
 Commun. Math. Phys. 356, 65 105 (2017) Digital Object Identifier (DOI) 10.1007/s00220-017-2973-z Communications in Mathematical Physics Rigorous RG Algorithms and Area Laws for Low Energy Eigenstates in
Commun. Math. Phys. 356, 65 105 (2017) Digital Object Identifier (DOI) 10.1007/s00220-017-2973-z Communications in Mathematical Physics Rigorous RG Algorithms and Area Laws for Low Energy Eigenstates in
arxiv: v2 [quant-ph] 20 Jun 2017
![arxiv: v2 [quant-ph] 20 Jun 2017 arxiv: v2 [quant-ph] 20 Jun 2017](/thumbs/90/102014096.jpg) Rigorous RG algorithms and area laws for low energy eigenstates in 1D Itai Arad Zeph Landau Umesh Vazirani Thomas Vidick arxiv:1602.08828v2 [quant-ph] 20 Jun 2017 Abstract One of the central challenges
Rigorous RG algorithms and area laws for low energy eigenstates in 1D Itai Arad Zeph Landau Umesh Vazirani Thomas Vidick arxiv:1602.08828v2 [quant-ph] 20 Jun 2017 Abstract One of the central challenges
Entanglement Entropy in Extended Quantum Systems
 Entanglement Entropy in Extended Quantum Systems John Cardy University of Oxford STATPHYS 23 Genoa Outline A. Universal properties of entanglement entropy near quantum critical points B. Behaviour of entanglement
Entanglement Entropy in Extended Quantum Systems John Cardy University of Oxford STATPHYS 23 Genoa Outline A. Universal properties of entanglement entropy near quantum critical points B. Behaviour of entanglement
Markovian Marginals. Isaac H. Kim. Oct. 9, arxiv: IBM T.J. Watson Research Center
 Markovian Marginals Isaac H. Kim IBM T.J. Watson Research Center Oct. 9, 2016 arxiv:1609.08579 Marginal Problem Consider a physical system I. Given { I 0}, istherea 0 such that I = I 8I? If yes, the marginals
Markovian Marginals Isaac H. Kim IBM T.J. Watson Research Center Oct. 9, 2016 arxiv:1609.08579 Marginal Problem Consider a physical system I. Given { I 0}, istherea 0 such that I = I 8I? If yes, the marginals
Propagation bounds for quantum dynamics and applications 1
 1 Quantum Systems, Chennai, August 14-18, 2010 Propagation bounds for quantum dynamics and applications 1 Bruno Nachtergaele (UC Davis) based on joint work with Eman Hamza, Spyridon Michalakis, Yoshiko
1 Quantum Systems, Chennai, August 14-18, 2010 Propagation bounds for quantum dynamics and applications 1 Bruno Nachtergaele (UC Davis) based on joint work with Eman Hamza, Spyridon Michalakis, Yoshiko
Mathematics Department Stanford University Math 61CM/DM Inner products
 Mathematics Department Stanford University Math 61CM/DM Inner products Recall the definition of an inner product space; see Appendix A.8 of the textbook. Definition 1 An inner product space V is a vector
Mathematics Department Stanford University Math 61CM/DM Inner products Recall the definition of an inner product space; see Appendix A.8 of the textbook. Definition 1 An inner product space V is a vector
Entanglement spectrum of the 2D Bose-Hubbard model
 of the D Bose-Hubbard model V. Alba,M. Haque, A. Läuchli 3 Ludwig-Maximilians Universität, München Max Planck Institute for the Physics of Complex Systems, Dresden 3 University of Innsbruck, Innsbruck
of the D Bose-Hubbard model V. Alba,M. Haque, A. Läuchli 3 Ludwig-Maximilians Universität, München Max Planck Institute for the Physics of Complex Systems, Dresden 3 University of Innsbruck, Innsbruck
Entanglement in Topological Phases
 Entanglement in Topological Phases Dylan Liu August 31, 2012 Abstract In this report, the research conducted on entanglement in topological phases is detailed and summarized. This includes background developed
Entanglement in Topological Phases Dylan Liu August 31, 2012 Abstract In this report, the research conducted on entanglement in topological phases is detailed and summarized. This includes background developed
(r) 2.0 E N 1.0
 The Numerical Renormalization Group Ralf Bulla Institut für Theoretische Physik Universität zu Köln 4.0 3.0 Q=0, S=1/2 Q=1, S=0 Q=1, S=1 E N 2.0 1.0 Contents 1. introduction to basic rg concepts 2. introduction
The Numerical Renormalization Group Ralf Bulla Institut für Theoretische Physik Universität zu Köln 4.0 3.0 Q=0, S=1/2 Q=1, S=0 Q=1, S=1 E N 2.0 1.0 Contents 1. introduction to basic rg concepts 2. introduction
Quantum Metropolis Sampling. K. Temme, K. Vollbrecht, T. Osborne, D. Poulin, F. Verstraete arxiv:
 Quantum Metropolis Sampling K. Temme, K. Vollbrecht, T. Osborne, D. Poulin, F. Verstraete arxiv: 09110365 Quantum Simulation Principal use of quantum computers: quantum simulation Quantum Chemistry Determination
Quantum Metropolis Sampling K. Temme, K. Vollbrecht, T. Osborne, D. Poulin, F. Verstraete arxiv: 09110365 Quantum Simulation Principal use of quantum computers: quantum simulation Quantum Chemistry Determination
Lecture Notes 1: Vector spaces
 Optimization-based data analysis Fall 2017 Lecture Notes 1: Vector spaces In this chapter we review certain basic concepts of linear algebra, highlighting their application to signal processing. 1 Vector
Optimization-based data analysis Fall 2017 Lecture Notes 1: Vector spaces In this chapter we review certain basic concepts of linear algebra, highlighting their application to signal processing. 1 Vector
Time Evolving Block Decimation Algorithm
 Time Evolving Block Decimation Algorithm Application to bosons on a lattice Jakub Zakrzewski Marian Smoluchowski Institute of Physics and Mark Kac Complex Systems Research Center, Jagiellonian University,
Time Evolving Block Decimation Algorithm Application to bosons on a lattice Jakub Zakrzewski Marian Smoluchowski Institute of Physics and Mark Kac Complex Systems Research Center, Jagiellonian University,
It from Qubit Summer School
 It from Qubit Summer School July 27 th, 2016 Tensor Networks Guifre Vidal NSERC Wednesday 27 th 9AM ecture Tensor Networks 2:30PM Problem session 5PM Focus ecture MARKUS HAURU MERA: a tensor network for
It from Qubit Summer School July 27 th, 2016 Tensor Networks Guifre Vidal NSERC Wednesday 27 th 9AM ecture Tensor Networks 2:30PM Problem session 5PM Focus ecture MARKUS HAURU MERA: a tensor network for
Max-Planck-Institut für Mathematik in den Naturwissenschaften Leipzig
 Max-Planck-Institut für Mathematik in den Naturwissenschaften Leipzig Coherence of Assistance and Regularized Coherence of Assistance by Ming-Jing Zhao, Teng Ma, and Shao-Ming Fei Preprint no.: 14 2018
Max-Planck-Institut für Mathematik in den Naturwissenschaften Leipzig Coherence of Assistance and Regularized Coherence of Assistance by Ming-Jing Zhao, Teng Ma, and Shao-Ming Fei Preprint no.: 14 2018
Physics 221A Fall 2017 Notes 27 The Variational Method
 Copyright c 2018 by Robert G. Littlejohn Physics 221A Fall 2017 Notes 27 The Variational Method 1. Introduction Very few realistic problems in quantum mechanics are exactly solvable, so approximation methods
Copyright c 2018 by Robert G. Littlejohn Physics 221A Fall 2017 Notes 27 The Variational Method 1. Introduction Very few realistic problems in quantum mechanics are exactly solvable, so approximation methods
Spekkens Toy Model, Finite Field Quantum Mechanics, and the Role of Linearity arxiv: v1 [quant-ph] 15 Mar 2019
![Spekkens Toy Model, Finite Field Quantum Mechanics, and the Role of Linearity arxiv: v1 [quant-ph] 15 Mar 2019 Spekkens Toy Model, Finite Field Quantum Mechanics, and the Role of Linearity arxiv: v1 [quant-ph] 15 Mar 2019](/thumbs/94/121785856.jpg) Spekkens Toy Model, Finite Field Quantum Mechanics, and the Role of Linearity arxiv:903.06337v [quant-ph] 5 Mar 209 Lay Nam Chang, Djordje Minic, and Tatsu Takeuchi Department of Physics, Virginia Tech,
Spekkens Toy Model, Finite Field Quantum Mechanics, and the Role of Linearity arxiv:903.06337v [quant-ph] 5 Mar 209 Lay Nam Chang, Djordje Minic, and Tatsu Takeuchi Department of Physics, Virginia Tech,
Under what conditions do quantum systems thermalize?
 Under what conditions do quantum systems thermalize? 1 / 9 Under what conditions do quantum systems thermalize? New insights from quantum information theory Christian Gogolin, Arnau Riera, Markus Müller,
Under what conditions do quantum systems thermalize? 1 / 9 Under what conditions do quantum systems thermalize? New insights from quantum information theory Christian Gogolin, Arnau Riera, Markus Müller,
Inner product spaces. Layers of structure:
 Inner product spaces Layers of structure: vector space normed linear space inner product space The abstract definition of an inner product, which we will see very shortly, is simple (and by itself is pretty
Inner product spaces Layers of structure: vector space normed linear space inner product space The abstract definition of an inner product, which we will see very shortly, is simple (and by itself is pretty
Logical operators of quantum codes
 Logical operators of quantum codes Mark M. Wilde* Electronic Systems Division, Science Applications International Corporation, 4001 North Fairfax Drive, Arlington, Virginia 22203, USA Received 30 March
Logical operators of quantum codes Mark M. Wilde* Electronic Systems Division, Science Applications International Corporation, 4001 North Fairfax Drive, Arlington, Virginia 22203, USA Received 30 March
Simulation of Quantum Many-Body Systems
 Numerical Quantum Simulation of Matteo Rizzi - KOMET 337 - JGU Mainz Vorstellung der Arbeitsgruppen WS 14-15 QMBS: An interdisciplinary topic entanglement structure of relevant states anyons for q-memory
Numerical Quantum Simulation of Matteo Rizzi - KOMET 337 - JGU Mainz Vorstellung der Arbeitsgruppen WS 14-15 QMBS: An interdisciplinary topic entanglement structure of relevant states anyons for q-memory
Conformal Blocks, Entanglement Entropy & Heavy States
 Conformal Blocks, Entanglement Entropy & Heavy States Pinaki Banerjee The Institute of Mathematical Sciences, Chennai April 25, 2016 arxiv : 1601.06794 Higher-point conformal blocks & entanglement entropy
Conformal Blocks, Entanglement Entropy & Heavy States Pinaki Banerjee The Institute of Mathematical Sciences, Chennai April 25, 2016 arxiv : 1601.06794 Higher-point conformal blocks & entanglement entropy
Page 404. Lecture 22: Simple Harmonic Oscillator: Energy Basis Date Given: 2008/11/19 Date Revised: 2008/11/19
 Page 404 Lecture : Simple Harmonic Oscillator: Energy Basis Date Given: 008/11/19 Date Revised: 008/11/19 Coordinate Basis Section 6. The One-Dimensional Simple Harmonic Oscillator: Coordinate Basis Page
Page 404 Lecture : Simple Harmonic Oscillator: Energy Basis Date Given: 008/11/19 Date Revised: 008/11/19 Coordinate Basis Section 6. The One-Dimensional Simple Harmonic Oscillator: Coordinate Basis Page
