MS327. Diagnostic Quiz. Are you ready for MS327? Copyright c 2017 The Open University 1.4
|
|
|
- Angelica Little
- 5 years ago
- Views:
Transcription
1 Faculty of Science, Technology, Engineering and Mathematics MS327 Deterministic and stochastic dynamics MS327 Diagnostic Quiz Are you ready for MS327? This diagnostic quiz is designed to help you decide if you are ready to study Deterministic and stochastic dynamics (MS327). This document also contains some advice on preparatory work that you may find useful before starting MS327 (see below and page 7). The better prepared you are for MS327 the more time you will have to enjoy the mathematics, and the greater your chance of success. The topics which are included in this quiz are those that we expect you to be familiar with before you start the module. If you have previously studied Mathematical methods, models and modelling (MST20) or Mathematical methods (MST224) then you should be familiar with most of the topics covered in the quiz. We suggest that you try this quiz first without looking at any books, and only look at a book when you are stuck. You will not necessarily remember everything; for instance, for the calculus questions you may need to look up a set of rules for differentiation or integration or use the table of standard derivatives or integrals provided on page 2. This is perfectly all right, as such tables are provided in the Handbook for MS327. You need to check that you are able to use them though. If you can complete the quiz with only the occasional need to look at other material, then you should be well prepared for MS327. If you find some topics that you remember having met before but need to do some more work on, then you should consider the suggestions for refreshing your knowledge on page 7. Try the questions now, and then see the notes on page 7 of this document to see if you are ready for MS327. (The answers to the questions begin on page 8.) Do contact your Student Support Team via StudentHome if you have any queries about MS327, or your readiness to study it. Copyright c 207 The Open University.4
2 Tables of standard derivatives and integrals Function Derivative Function Integral a 0 x a e ax ln(ax) sin(ax) cos(ax) tan(ax) cot(ax) sec(ax) cosec(ax) arcsin(ax) arccos(ax) arctan(ax) arccot(ax) arcsec(ax) arccosec(ax) ax a ae ax x a cos(ax) a sin(ax) asec 2 (ax) acosec 2 (ax) a sec(ax) tan(ax) acosec(ax) cot(ax) a a 2 x 2 a a 2 x 2 a +a 2 x 2 a +a 2 x 2 a ax a 2 x 2 a ax a 2 x 2 a x a (a ) ax+b ax e ax a eax x a+ a+ a ln ax+b ln(ax) x(ln(ax) ) sin(ax) cos(ax) tan(ax) cot(ax) sec(ax) cosec(ax) sec 2 (ax) x 2 +a 2 x 2 a 2 a cos(ax) a sin(ax) a ln cos(ax) a ln sin(ax) a ln sec(ax)+tan(ax) a ln cosec(ax) cot(ax) a tan(ax) cosec 2 (ax) a cot(ax) ( x ) x 2 +a 2 a arctan a (x a)(x b) a b ln a x x b ln(x+ ( x x 2 +a 2 ) or arcsinh a) a 2 x 2 ln x+ ( x x 2 a 2 or arccosh a) ( x arcsin a) page 2 of 6
3 Diagnostic quiz questions Differentiation Question Differentiate the following functions with respect to x. (a) f(x) = x2 +2x 3x+4 Question 2 (b) f(x) = sin(3x 2 +2) Find the second derivative with respect to x of f(x) = 3x 4 +2sin3x. Question 3 Find and classify the stationary points of y = x 3 +3x 2 24x+0. 2 Integration Question 4 Calculate the following integrals. 2 ( (a) x ) dx (b) x 2 (x 2 +5) 0 dx (c) x xcos3xdx 3 Ordinary differential equations Question 5 Find the particular solution of the differential equation y > 0, which satisfies y() = 5 2. dy dx = xy x 2 +, where Question 6 Find the general solution of the differential equation dy dx + 2y x = x. Question 7 Find the particular solution of the differential equation d 2 y dx 2 2dy +5y = 5x+8 dx that satisfies y(0) = 4 and dy (0) = 9. dx page 3 of 6
4 4 Partial differentiation Question 8 Find the second-order partial derivatives of the function u(x,y) = cos(4x+3y), and confirm that Question 9 2 u x y = 2 u y x. Use the Chain Rule to find du dt, where u(x,y) = ln( x 2 y 4) and x = cos2t, y = sint. 5 Matrices Question Let A = 2 0, B = 3 ( ) 3 and C = 4 2 ( ) Calculate each of the following, or state why the calculation is not possible. (a) AB (b) BA (c) 2A+3B (d) 2B+C Question Calculate the determinants of the following matrices. ( ) (a) (b) Question 2 Find the eigenvalues and eigenvectors of the matrix ( ) 8. 5 Question Find the eigenvalue of the matrix that corresponds to the eigenvector. 3 page 4 of 6
5 6 Vector algebra and calculus Question 4 If a = 3i+2j 5k and b = 2i j k, find (a) a+b, a+b, a b, and a b, (b) the angle between a and b, to the nearest degree. Question 5 If φ(x,y,z) = x 2 y +2xz, find φ (also known as gradφ) at the point (2, 2,3). Question 6 If F = x 2 yi 2xzj+2yzk, find F (also known as divf) and F (also known as curlf) at the point (,2, ). 7 Multiple integration Question 7 Evaluate the surface integral S xyda, where S is the region of the plane z = 0 bounded by the curve y = x 2 and by the line y = x. Question 8 Evaluate the volume integral B ( x 2 y +2xz 2) dv, where B is the interior of the cube with faces in the planes x = 0, y = 0, z = 0, x =, y = and z =. 8 Mechanics Question 9 The acceleration of particle of mass 5kg is given by a = 3sin6ti+3cos6tj+4k. At t = 0 the velocity, v(0) = i and the position, r(0) = j+k. (a) Find the magnitude of the force acting on the particle. (b) Find the position of the particle at any time t. page 5 of 6
6 Question 20 A particle connected to a spring moves in a straight line. The position of the particle along the line, x, is given by d 2 x 4x = 0. dt2 Initially, x(0) = 3 and x (0) = 0. (a) What is the speed of the particle as it passes the point x = 0 for the first time? (b) What is the period of the motion? 9 Complex numbers Question 2 If w = 2+i and z = 3 4i find, in Cartesian form (a) wz (b) w/z Question 22 Express w = +i and z = 3 i in complex exponential form (re iθ ), and hence express the following also in complex exponential form. (a) wz (b) w/z 0 Fourier series Question 23 Find a Fourier series for the function f(x) = +x for < x <. page 6 of 6
7 What can I do to prepare for MS327? Now that you have finished the quiz, how did you get on? The information below should help you to decide what, if anything, you should do next. Most of this quiz was unfamiliar to me. I don t think I have met any of the topics before. You should consider taking MST20 or MST224 before MS327. Contact your Student Support Team to discuss this. Some of these topics are familiar to me, but not all of them. If you have met less than 75% of these topics then you should consider taking MST20 or MST224 before MS327. Contact your Student Support Team to discuss this. If you have taken MST224, then the material in Section 8 might be new to you. If so, you might like to review some of the resources suggested below. I have met all these topics before, but I am a bit rusty on some, and had to look up how to do a few of them. You will benefit from doing some revision before starting MS327 see below for possible sources of help. I can do all these questions. You are probably well prepared for MS327, but do brush up on any topics you need to further enhance your confidence. If you have any queries contact your Student Support Team via StudentHome. What resources are there to help me prepare for MS327? If you have studied MST20, its predecessor MST209, or MST224, then you could use parts of these to revise for MS327. If you need to brush up some of the more basic topics like algebra, trigonometry and calculus, then you may find revising material from Essential mathematics (MST24) and Essential mathematics 2 (MST25) (or their predecessors MST2 and MS22) helpful. Alternatively, such material is often covered by standard A-level textbooks. If you have studied MST224 rather than MST20 then you might not have met mechanics before (Section 8 of the diagnostic quiz). You might like to review some material on this, such as the MST20 Bridging material available at mcs-notes2.open.ac.uk/webresources/maths.nsf/a/odm8/$file/mst20bridging.pdf, or an A-level mechanics textbook. The mathcentre web-site ( includes several teach-yourself books, summary sheets, revision booklets, online exercises and video tutorials on a range of mathematical skills. page 7 of 6
8 Diagnostic quiz solutions Solution (a) f (x) = (3x+4)(2x+2) 3(x2 +2x ) (3x+4) 2 (b) f (x) = 6xcos(3x 2 +2) = 3x2 +8x+ (3x+4) 2 Solution 2 f (x) = 2x 3 +6cos3x, so, f (x) = 36x 2 8sin3x. Solution 3 The stationary points occur when dy dx = 0, that is, when 3x2 +6x 24 = 0. This can be written 3(x 2)(x+4) = 0, so the stationary points are x = 2 and x = 4. At x = 2, y = 8 and at x = 4, y = 90. The second derivative, d2 y dx 2 = 6x+6. At x = 2, d2 y > 0, so (2, 8) is a minimum. dx2 At x = 4, d2 y < 0, so ( 4,90) is a maximum. dx2 Solution 4 2 ( (a) x ) dx = x (b) [ ] 2 3 x3 +2lnx = ln2 3 = ln2. x 2 (x 3 +5) 0 dx = 33 (x3 +5) +c, where c is an arbitrary constant. (Using the substitution u = x 3 +5.) (c) Integrating by parts gives xcos3xdx = x 3 sin3x 3 sin3xdx = 3 xsin3x+ 9 cos3x+c where c is an arbitrary constant. page 8 of 6
9 Solution 5 The differential equation is of first order, and the right-hand side can be written as f(x)g(y), for some functions f(x) and g(y). So the equation can be solved using separation of variables. Rearrange the equation so that all the terms involving y are on the left-hand side, and all those involving x are on the right: Integrating both sides gives hence, dy y dx = x x 2 +. y dy = x x 2 + dx lny = 2 ln(x2 +)+c, where c is an arbitrary constant. So y = exp ( 2 ln(x2 +)+c ) = A x 2 +,where A = e c. Since y = 5 2 when x =, we have 5 2 = A 2, so A = 5 and hence y = 5 x 2 +. Solution 6 The equation is of the form dy +g(x)y = f(x) so can be solved using the dx integrating factor method. The integrating factor is p(x) = exp ( g(x)dx ), which in this case is ( ) 2 p(x) = exp x dx = exp(2lnx) = x 2. (x So, x 2 y = 2 x ) dx = x 3 dx = x4 +c, where c is an arbitrary 4 constant. Hence y = x2 4 + c x 2. Solution 7 First solve the associated homogeneous equation The auxiliary equation is λ 2 2λ+5 = 0, d 2 y dx 2 2dy +5y = 0. dx The solutions are, λ = 2± 4 20 = 2±4i = ±2i. 2 2 Hence the complementary function is y c = e x (Acos(2x)+Bsin(2x)), where A and B are arbitrary constants. Returning to the inhomogeneous equation, d2 y dx 2 2dy +5y = 5x+8, dx the form of the right-hand side suggests a trial solution of the form y p = ax+b. So, dy p dx = a and d2 y p dx 2 = 0. page 9 of 6
10 Substituting into the inhomogeneous equation gives 0 2a+5(ax+b) = 5x+8 which can be written 5ax+(5b 2a) = 5x+8. Comparing coefficients gives 5a = 5 and 5b 2a = 8. So, a = and b = 2. The particular integral is y p = x+2. The general solution is y = y c +y p, that is, y = e x (Acos(2x)+Bsin(2x))+x+2. When x = 0, y = 4, so 4 = A+2, and A = 2. The derivative of the general solution is (using the Product Rule) dy dx = ex ((A+2B)cos(2x)+(B 2A)sin(2x))+. When x = 0, dy/dx = 9, so 9 = A+2B + = 2B +3 and so B = 3. The particular solution required is y = e x (2cos(2x)+3sin(2x))+x+2. Solution 8 u = sin(4x+3y) 4 = 4sin(4x+3y) x u y = sin(4x+3y) 3 = 3sin(4x+3y) 2 u x 2 = ( 4sin(4x+3y)) = 4cos(4x+3y) 4 = 6cos(4x+3y) x 2 u x y = ( 3sin(4x+3y)) = 3cos(4x+3y) 4 = 2cos(4x+3y) x 2 u y 2 = ( 3sin(4x+3y)) = 3cos(4x+3y) 3 = 9cos(4x+3y) y 2 u y x = ( 4sin(4x+3y)) = 4cos(4x+3y) 3 = 2cos(4x+3y) y Comparison of Solution 9 The Chain Rule gives We know, So, 2 u y x with 2 u x y confirms that 2 u x y = 2 u y x. u x = x 2 2x = 2 x, du dt = u dx x dt + u dy y dt. dx dt = 2sin2t, du dt = 2 x ( 2sin2t)+ 4 4cost cost = y y Now substitute for x and y in terms of t: 4sin2t. x u y = y 4 4y3 = 4 y, du dt = 4cost sint 4sin2t cos2t = 4cott 4tan2t. dy dt = cost. page 0 of 6
11 Solution (a) AB = (b) BA cannot be calculated, since B is 2 2 and A is 3 2. (c) 2A+3B cannot be calculated, since A is 3 2 and B is 2 2. ( ) 7 7 (d) 2B+C = 0 4 Solution (a) = = (b) = = 4(4 0) (3 2) = 25 Solution 2 The characteristic equation is given by λ 8 5 λ = 0, that is ( λ)( 5 λ)+8 = 0 or λ 2 +4λ+3 = 0. This can be factorised as (λ+)(λ+3) = 0, hence the eigenvalues are and 3. ( ) x The eigenvectors x = associated with the eigenvalue λ are found by y solving ( )( ) λ 8 x = 0. 5 λ y For λ = this gives 2x+8y = 0 x 4y = 0. ( )( ) 2 8 x = 0 which can be written as 4 y ( ) 4 These are satisfied when x = 4y, so an eigenvector is. ( )( ) 4 8 x For λ = 3 the equation gives = 0 which can be 2 y written as 4x+8y = 0 x 2y = 0. These are satisfied when x = 2y, so an eigenvector is ( ) 2. page of 6
12 Solution 3 Multiplying the matrix by the given eigenvector gives = 2 = The product is 2 times the eigenvector, so the corresponding eigenvalue is 2. Solution 4 (a) a+b = (3i+2j 5k)+(2i j k) = 5i+j 6k. a+b = 5i+j 6k = ( 6) 2 = = 62. a b = ( )+( 5) ( ) = = 9. i j k a b = = (2 ( ) ( 5) ( ))i (3 ( ) ( 5) 2)j+(3 ( ) 2 2)k = 7i 7j 7k = 7(i+j+k). (b) The cosine of the angle θ between a and b can be calculated using cosθ = a b a b. a = ( 5) 2 = 38 and b = 2 2 +( ) 2 +( ) 2 = 6. 9 So, cosθ = = ( ) 3 3 Hence, θ = arccos = 53 (to the nearest degree). 2 9 Solution 5 The scalar field is φ(x,y,z) = x 2 y +2xz. The partial derivatives are φ φ = 2xy +2z, x y = x2, and φ z = 2x. So, φ = gradφ = φ φ φ i+ j+ x y z k = (2xy +2z)i+x2 j+2xk. At the point (2, 2,3), φ = gradφ = (2 2 ( 2)+2 3)i+2 2 j+2 2k = 2i+4j+4k. page 2 of 6
13 Solution 6 If F = F i+f 2 j+f 3 k, then F = divf = F x + F 2 y + F 3 z i j k and F = curlf = / x / y / z = F F 2 F 3 ) i ( F3 y F 2 z ( F3 x F z ) ( F2 j + x F ) k. y Here, F = x 2 yi 2xzj+2yzk, so, F = divf = 2xy 0+2y = 2y(x+) i j k and F = curlf = / x / y / z x 2 y 2xz 2yz = (2z +2x)i 0j+( 2z x 2 )k = 2(x+z)i (x 2 +2z)k. At (,2, ), F = divf = 2 2(+) = 8 and F = curlf = 2( )i ( 2)k = k. Solution 7 y 2 y = x First sketch the region of integration, S: 0 S 0 x Note that y = x and y = x 2 intersect where x = 0 and x =, giving the minimum and maximum values of x for the region S. In Cartesian coordinates we can write xyda = xydydx, in which we integrate with respect to y first, and then respect to x, and hence divide the region of integration into strips as shown in the diagram above. Using the diagram to identify the limits of x and y we obtain xyda = y=x Now, xydy = x [ ( y=x 2 2 y2] y=x = x y=x 2 2 x2 ) 2 x4 = 2 (x3 x 5 ), x= and hence xyda = 2 (x3 x 5 )dx = [ S x=0 2 4 x4 ] 6 x6 = 0 2 S S S x= ( y=x x=0 ( 4 ) = ) xydy dx. y=x 2 page 3 of 6
14 Solution 8 z First sketch the region of integration, B: In Cartesian coordinates, B x ( x 2 y +2xz 2) dv = B y ( x 2 y +2xz 2) dxdydz. Since the boundaries of the volume of integration are coordinate planes, we have ( x 2 y +2xz 2) ( )dv = x 2 y +2xz 2) dxdydz B = = = = = [ 3 x3 y +x 2 z 2 ( ) 0 3 y +z2 dydz [ ] y= 6 y2 +z 2 y dz y=0 ( ) 6 +z2 dz [ 6 z + 3 z3 ] z= z=0 ] x= x=0 dydz dz = = 2. page 4 of 6
15 Solution 9 (a) The force, F, is given by Newton s second law: F = ma, where m is the mass of the particle. So, F = 5(3sin6ti+3cos6tj+4k) = 5sin6ti+5cos6tj+20k.. Hence, the magnitude of the force, F = 225sin 2 6t+225cos 2 6t+400 = = 625 = 25. (b) The velocity, v, is given by v = adt = (3sin6ti+3cos6tj+4k) dt = 2 cos6ti+ 2 sin6tj+4tk+c, where c is an arbitrary vector constant. Since v(0) = i, we have 2 i+c = i, so c = 3 2 i and v = ( 3 2 ) 2 cos6t i+ 2 sin6tj+4tk. The position, r, is given by (( 3 r = vdt = 2 ) 2 cos6t i+ ) 2 sin6tj+4tk dt ( 3 = 2 t ) 2 sin6t i 2 cos6tj+2t2 k+d, where d is an arbitrary vector constant. Since r(0) = j+k, we have 3 j+d = j+k, so d = j+k and 2 2 ( 3 r = 2 t ) ( 3 2 sin6t i+ 2 ) 2 cos6t j+ ( +2t 2) k. Solution 20 (a) The solution of the differential equation is for arbitrary constants A and B. x = Acos2t+Bsin2t, When t = 0, x = 3, so 3 = A and x = 3cos2t+Bsin2t.. Hence x (t) = 6sin2t+2Bcos2t, and since x (0) = 0, then 2B = 0 and so B = 0. So the motion is given by x = 3cos2t. The particle is at x = 0 when 3cos2t = 0, that is cos2t = 0. The first solution for t > 0 is 2t = π/2, that is t = π/4. We know x (t) = 6sin2t, so at t = π/4: x (t) = 6sin π 2 = 6. So the speed of the particle as it crosses x = 0 for the first time is 6. (b) The angular frequency, ω = 4 = 2. So the period is given by T = 2π ω = 2π 2 = π. page 5 of 6
16 Solution 2 (a) w +2z (2+i)(3 4i) = 6 8i+3i 4i 2 = 6 5i+4 = 0 5i. (b) w z = 2+i. This can be expressed in Cartesian form by rationalising 3 4i the denominator. 2+i 3 4i = 2+i 3 4i 3+4i 3+4i = 6+8i+3i+4i2 9 6i 2 = 2+i = i. Solution 22 Since w = +i then w = = 2 and arg(w) = arctan(/) = π/4, so w has complex exponential form w = 2e iπ/4. Likewise z = 3 i so z = = 2 and arg(z) = arctan( / 3) = π/6, so z has complex exponential form z = 2e iπ/6. (a) wz = 2e iπ/4 2e iπ/6 = 2 3/2 e iπ/2 2e iπ/4 (b) w/z = 2e iπ/6 = e 5iπ/2. 2 Solution 23 The Fourier series for a function f(x) over L < x < L is given by where a n = L F(x) = a ( a n cos nπx L +b nsin nπx ) L L L n= f(x)cos nπx L dx, and b n = L f(x)sin nπx L L L dx. Here, f(x) = +x and L =, so a 0 = a n = b n = (+x)dx = ] [x+ x2 = + ( ) = 2 2 [ (+x)cosnπxdx = (+x) ] ( nπ sinnπx ) nπ sinnπx dx = 0+ n 2 π 2 [cosnπx] = n 2 (cosnπ cos( nπ)) = 0 π2 [ (+x)sinnπxdx = (+x) ] ( nπ cosnπx + ) nπ cosnπx dx = 2 nπ cosnπ + n 2 π 2 [sinnπx] = 2 nπ cosnπ + 2 n 2 (sinnπ sin( nπ)) = π2 nπ cosnπ = 2 nπ ( )n Hence, the Fourier series is F(x) = n= 2 nπ ( )n sin nπx L. page 6 of 6
M373 Optimization. Diagnostic Quiz
 Faculty of Science, Technology, Engineering and Mathematics M373 Optimization M373 Optimization Diagnostic Quiz Contents Are you ready for M373? 1 Table of standard derivatives 2 Diagnostic quiz questions
Faculty of Science, Technology, Engineering and Mathematics M373 Optimization M373 Optimization Diagnostic Quiz Contents Are you ready for M373? 1 Table of standard derivatives 2 Diagnostic quiz questions
M208 Diagnostic quiz. Am I ready to start M208? Copyright c 2015 The Open University WEB
 Mathematics, Computing and Technology M08 Pure Mathematics M08 Diagnostic quiz Am I ready to start M08? The diagnostic quiz below is designed to help you to answer this question. This document also contains
Mathematics, Computing and Technology M08 Pure Mathematics M08 Diagnostic quiz Am I ready to start M08? The diagnostic quiz below is designed to help you to answer this question. This document also contains
Diagnostic quiz for M303: Further Pure Mathematics
 Diagnostic quiz for M303: Further Pure Mathematics Am I ready to start M303? M303, Further pure mathematics is a fascinating third level module, that builds on topics introduced in our second level module
Diagnostic quiz for M303: Further Pure Mathematics Am I ready to start M303? M303, Further pure mathematics is a fascinating third level module, that builds on topics introduced in our second level module
Mathematics Revision Questions for the University of Bristol School of Physics
 Mathematics Revision Questions for the University of Bristol School of Physics You will not be surprised to find you have to use a lot of maths in your stu of physics at university! You need to be completely
Mathematics Revision Questions for the University of Bristol School of Physics You will not be surprised to find you have to use a lot of maths in your stu of physics at university! You need to be completely
Diagnostic quiz for M337 Complex analysis
 Diagnostic quiz for M337 Complex analysis The aim of this diagnostic quiz is to help you assess how well prepared you are for M337, and to identify topics that you should revise or study before beginning
Diagnostic quiz for M337 Complex analysis The aim of this diagnostic quiz is to help you assess how well prepared you are for M337, and to identify topics that you should revise or study before beginning
MST326 Revision Booklet
 Mathematics and Computing/Science/Technology MST36 Mathematical methods and fluid mechanics MST36 RB MST36 Revision Booklet Contents Introduction Ordinary differential equations 3. Separation of variables
Mathematics and Computing/Science/Technology MST36 Mathematical methods and fluid mechanics MST36 RB MST36 Revision Booklet Contents Introduction Ordinary differential equations 3. Separation of variables
UNIVERSITY OF SOUTHAMPTON. A foreign language dictionary (paper version) is permitted provided it contains no notes, additions or annotations.
 UNIVERSITY OF SOUTHAMPTON MATH055W SEMESTER EXAMINATION 03/4 MATHEMATICS FOR ELECTRONIC & ELECTRICAL ENGINEERING Duration: 0 min Solutions Only University approved calculators may be used. A foreign language
UNIVERSITY OF SOUTHAMPTON MATH055W SEMESTER EXAMINATION 03/4 MATHEMATICS FOR ELECTRONIC & ELECTRICAL ENGINEERING Duration: 0 min Solutions Only University approved calculators may be used. A foreign language
DEPARTMENT OF MATHEMATICS
 DEPARTMENT OF MATHEMATICS A2 level Mathematics Core 3 course workbook 2015-2016 Name: Welcome to Core 3 (C3) Mathematics. We hope that you will use this workbook to give you an organised set of notes for
DEPARTMENT OF MATHEMATICS A2 level Mathematics Core 3 course workbook 2015-2016 Name: Welcome to Core 3 (C3) Mathematics. We hope that you will use this workbook to give you an organised set of notes for
Homework Solutions: , plus Substitutions
 Homework Solutions: 2.-2.2, plus Substitutions Section 2. I have not included any drawings/direction fields. We can see them using Maple or by hand, so we ll be focusing on getting the analytic solutions
Homework Solutions: 2.-2.2, plus Substitutions Section 2. I have not included any drawings/direction fields. We can see them using Maple or by hand, so we ll be focusing on getting the analytic solutions
Week beginning Videos Page
 1 M Week beginning Videos Page June/July C3 Algebraic Fractions 3 June/July C3 Algebraic Division 4 June/July C3 Reciprocal Trig Functions 5 June/July C3 Pythagorean Identities 6 June/July C3 Trig Consolidation
1 M Week beginning Videos Page June/July C3 Algebraic Fractions 3 June/July C3 Algebraic Division 4 June/July C3 Reciprocal Trig Functions 5 June/July C3 Pythagorean Identities 6 June/July C3 Trig Consolidation
4 Partial Differentiation
 4 Partial Differentiation Many equations in engineering, physics and mathematics tie together more than two variables. For example Ohm s Law (V = IR) and the equation for an ideal gas, PV = nrt, which
4 Partial Differentiation Many equations in engineering, physics and mathematics tie together more than two variables. For example Ohm s Law (V = IR) and the equation for an ideal gas, PV = nrt, which
Math 23b Practice Final Summer 2011
 Math 2b Practice Final Summer 211 1. (1 points) Sketch or describe the region of integration for 1 x y and interchange the order to dy dx dz. f(x, y, z) dz dy dx Solution. 1 1 x z z f(x, y, z) dy dx dz
Math 2b Practice Final Summer 211 1. (1 points) Sketch or describe the region of integration for 1 x y and interchange the order to dy dx dz. f(x, y, z) dz dy dx Solution. 1 1 x z z f(x, y, z) dy dx dz
THE NATIONAL UNIVERSITY OF IRELAND, CORK COLÁISTE NA hollscoile, CORCAIGH UNIVERSITY COLLEGE, CORK. Summer Examination 2009.
 OLLSCOIL NA héireann, CORCAIGH THE NATIONAL UNIVERSITY OF IRELAND, CORK COLÁISTE NA hollscoile, CORCAIGH UNIVERSITY COLLEGE, CORK Summer Examination 2009 First Engineering MA008 Calculus and Linear Algebra
OLLSCOIL NA héireann, CORCAIGH THE NATIONAL UNIVERSITY OF IRELAND, CORK COLÁISTE NA hollscoile, CORCAIGH UNIVERSITY COLLEGE, CORK Summer Examination 2009 First Engineering MA008 Calculus and Linear Algebra
Essential Mathematics 2 Introduction to the calculus
 Essential Mathematics Introduction to the calculus As you will alrea know, the calculus may be broadly separated into two major parts. The first part the Differential Calculus is concerned with finding
Essential Mathematics Introduction to the calculus As you will alrea know, the calculus may be broadly separated into two major parts. The first part the Differential Calculus is concerned with finding
MathsGeeks. Everything You Need to Know A Level Edexcel C4. March 2014 MathsGeeks Copyright 2014 Elite Learning Limited
 Everything You Need to Know A Level Edexcel C4 March 4 Copyright 4 Elite Learning Limited Page of 4 Further Binomial Expansion: Make sure it starts with a e.g. for ( x) ( x ) then use ( + x) n + nx + n(n
Everything You Need to Know A Level Edexcel C4 March 4 Copyright 4 Elite Learning Limited Page of 4 Further Binomial Expansion: Make sure it starts with a e.g. for ( x) ( x ) then use ( + x) n + nx + n(n
Review of Differentiation and Integration for Ordinary Differential Equations
 Schreyer Fall 208 Review of Differentiation an Integration for Orinary Differential Equations In this course you will be expecte to be able to ifferentiate an integrate quickly an accurately. Many stuents
Schreyer Fall 208 Review of Differentiation an Integration for Orinary Differential Equations In this course you will be expecte to be able to ifferentiate an integrate quickly an accurately. Many stuents
Ma 221 Final Exam Solutions 5/14/13
 Ma 221 Final Exam Solutions 5/14/13 1. Solve (a) (8 pts) Solution: The equation is separable. dy dx exy y 1 y0 0 y 1e y dy e x dx y 1e y dy e x dx ye y e y dy e x dx ye y e y e y e x c The last step comes
Ma 221 Final Exam Solutions 5/14/13 1. Solve (a) (8 pts) Solution: The equation is separable. dy dx exy y 1 y0 0 y 1e y dy e x dx y 1e y dy e x dx ye y e y dy e x dx ye y e y e y e x c The last step comes
0 3 x < x < 5. By continuing in this fashion, and drawing a graph, it can be seen that T = 2.
 04 Section 10. y (π) = c = 0, and thus λ = 0 is an eigenvalue, with y 0 (x) = 1 as the eigenfunction. For λ > 0 we again have y(x) = c 1 sin λ x + c cos λ x, so y (0) = λ c 1 = 0 and y () = -c λ sin λ
04 Section 10. y (π) = c = 0, and thus λ = 0 is an eigenvalue, with y 0 (x) = 1 as the eigenfunction. For λ > 0 we again have y(x) = c 1 sin λ x + c cos λ x, so y (0) = λ c 1 = 0 and y () = -c λ sin λ
Practice Problems: Integration by Parts
 Practice Problems: Integration by Parts Answers. (a) Neither term will get simpler through differentiation, so let s try some choice for u and dv, and see how it works out (we can always go back and try
Practice Problems: Integration by Parts Answers. (a) Neither term will get simpler through differentiation, so let s try some choice for u and dv, and see how it works out (we can always go back and try
Integration 1/10. Integration. Student Guidance Centre Learning Development Service
 Integration / Integration Student Guidance Centre Learning Development Service lds@qub.ac.uk Integration / Contents Introduction. Indefinite Integration....................... Definite Integration.......................
Integration / Integration Student Guidance Centre Learning Development Service lds@qub.ac.uk Integration / Contents Introduction. Indefinite Integration....................... Definite Integration.......................
ADDITIONAL MATHEMATICS
 ADDITIONAL MATHEMATICS GCE Ordinary Level (Syllabus 4018) CONTENTS Page NOTES 1 GCE ORDINARY LEVEL ADDITIONAL MATHEMATICS 4018 2 MATHEMATICAL NOTATION 7 4018 ADDITIONAL MATHEMATICS O LEVEL (2009) NOTES
ADDITIONAL MATHEMATICS GCE Ordinary Level (Syllabus 4018) CONTENTS Page NOTES 1 GCE ORDINARY LEVEL ADDITIONAL MATHEMATICS 4018 2 MATHEMATICAL NOTATION 7 4018 ADDITIONAL MATHEMATICS O LEVEL (2009) NOTES
UNIVERSITY OF CAMBRIDGE Faculty of Mathematics MATHEMATICS WORKBOOK
 UNIVERSITY OF CAMBRIDGE Faculty of Mathematics MATHEMATICS WORKBOOK August, 07 Introduction The Mathematical Tripos is designed to be accessible to students who are familiar with the the core A-level syllabus
UNIVERSITY OF CAMBRIDGE Faculty of Mathematics MATHEMATICS WORKBOOK August, 07 Introduction The Mathematical Tripos is designed to be accessible to students who are familiar with the the core A-level syllabus
A Level Maths summer preparation work
 A Level Maths summer preparation work Welcome to A Level Maths! We hope you are looking forward to two years of challenging and rewarding learning. You must make sure that you are prepared to study A Level
A Level Maths summer preparation work Welcome to A Level Maths! We hope you are looking forward to two years of challenging and rewarding learning. You must make sure that you are prepared to study A Level
MATHEMATICS FOR ENGINEERING DIFFERENTIATION TUTORIAL 2 ADVANCED DIFFERENTIATION
 MATHEMATICS FOR ENGINEERING DIFFERENTIATION TUTORIAL ADVANCED DIFFERENTIATION CONTENTS Function of a Function Differentiation of a Sum Differentiation of a Proct Differentiation of a Quotient Turning Points
MATHEMATICS FOR ENGINEERING DIFFERENTIATION TUTORIAL ADVANCED DIFFERENTIATION CONTENTS Function of a Function Differentiation of a Sum Differentiation of a Proct Differentiation of a Quotient Turning Points
Grade: The remainder of this page has been left blank for your workings. VERSION D. Midterm D: Page 1 of 12
 First Name: Student-No: Last Name: Section: Grade: The remainder of this page has been left blank for your workings. Midterm D: Page of 2 Indefinite Integrals. 9 marks Each part is worth marks. Please
First Name: Student-No: Last Name: Section: Grade: The remainder of this page has been left blank for your workings. Midterm D: Page of 2 Indefinite Integrals. 9 marks Each part is worth marks. Please
Example. Evaluate. 3x 2 4 x dx.
 3x 2 4 x 3 + 4 dx. Solution: We need a new technique to integrate this function. Notice that if we let u x 3 + 4, and we compute the differential du of u, we get: du 3x 2 dx Going back to our integral,
3x 2 4 x 3 + 4 dx. Solution: We need a new technique to integrate this function. Notice that if we let u x 3 + 4, and we compute the differential du of u, we get: du 3x 2 dx Going back to our integral,
Math 1552: Integral Calculus Final Exam Study Guide, Spring 2018
 Math 55: Integral Calculus Final Exam Study Guide, Spring 08 PART : Concept Review (Note: concepts may be tested on the exam in the form of true/false or short-answer questions.). Complete each statement
Math 55: Integral Calculus Final Exam Study Guide, Spring 08 PART : Concept Review (Note: concepts may be tested on the exam in the form of true/false or short-answer questions.). Complete each statement
Introduction and preliminaries
 Chapter Introduction and preliminaries Partial differential equations What is a partial differential equation? ODEs Ordinary Differential Equations) have one variable x). PDEs Partial Differential Equations)
Chapter Introduction and preliminaries Partial differential equations What is a partial differential equation? ODEs Ordinary Differential Equations) have one variable x). PDEs Partial Differential Equations)
Core 3 (A2) Practice Examination Questions
 Core 3 (A) Practice Examination Questions Trigonometry Mr A Slack Trigonometric Identities and Equations I know what secant; cosecant and cotangent graphs look like and can identify appropriate restricted
Core 3 (A) Practice Examination Questions Trigonometry Mr A Slack Trigonometric Identities and Equations I know what secant; cosecant and cotangent graphs look like and can identify appropriate restricted
Ch 4 Differentiation
 Ch 1 Partial fractions Ch 6 Integration Ch 2 Coordinate geometry C4 Ch 5 Vectors Ch 3 The binomial expansion Ch 4 Differentiation Chapter 1 Partial fractions We can add (or take away) two fractions only
Ch 1 Partial fractions Ch 6 Integration Ch 2 Coordinate geometry C4 Ch 5 Vectors Ch 3 The binomial expansion Ch 4 Differentiation Chapter 1 Partial fractions We can add (or take away) two fractions only
Polytechnic Institute of NYU MA 2132 Final Practice Answers Fall 2012
 Polytechnic Institute of NYU MA Final Practice Answers Fall Studying from past or sample exams is NOT recommended. If you do, it should be only AFTER you know how to do all of the homework and worksheet
Polytechnic Institute of NYU MA Final Practice Answers Fall Studying from past or sample exams is NOT recommended. If you do, it should be only AFTER you know how to do all of the homework and worksheet
a x a y = a x+y a x a = y ax y (a x ) r = a rx and log a (xy) = log a (x) + log a (y) log a ( x y ) = log a(x) log a (y) log a (x r ) = r log a (x).
 You should prepare the following topics for our final exam. () Pre-calculus. (2) Inverses. (3) Algebra of Limits. (4) Derivative Formulas and Rules. (5) Graphing Techniques. (6) Optimization (Maxima and
You should prepare the following topics for our final exam. () Pre-calculus. (2) Inverses. (3) Algebra of Limits. (4) Derivative Formulas and Rules. (5) Graphing Techniques. (6) Optimization (Maxima and
3.4 Conic sections. Such type of curves are called conics, because they arise from different slices through a cone
 3.4 Conic sections Next we consider the objects resulting from ax 2 + bxy + cy 2 + + ey + f = 0. Such type of curves are called conics, because they arise from different slices through a cone Circles belong
3.4 Conic sections Next we consider the objects resulting from ax 2 + bxy + cy 2 + + ey + f = 0. Such type of curves are called conics, because they arise from different slices through a cone Circles belong
Consider an ideal pendulum as shown below. l θ is the angular acceleration θ is the angular velocity
 1 Second Order Ordinary Differential Equations 1.1 The harmonic oscillator Consider an ideal pendulum as shown below. θ l Fr mg l θ is the angular acceleration θ is the angular velocity A point mass m
1 Second Order Ordinary Differential Equations 1.1 The harmonic oscillator Consider an ideal pendulum as shown below. θ l Fr mg l θ is the angular acceleration θ is the angular velocity A point mass m
P1 Calculus II. Partial Differentiation & Multiple Integration. Prof David Murray. dwm/courses/1pd
 P1 2017 1 / 39 P1 Calculus II Partial Differentiation & Multiple Integration Prof David Murray david.murray@eng.ox.ac.uk www.robots.ox.ac.uk/ dwm/courses/1pd 4 lectures, MT 2017 P1 2017 2 / 39 Motivation
P1 2017 1 / 39 P1 Calculus II Partial Differentiation & Multiple Integration Prof David Murray david.murray@eng.ox.ac.uk www.robots.ox.ac.uk/ dwm/courses/1pd 4 lectures, MT 2017 P1 2017 2 / 39 Motivation
x n cos 2x dx. dx = nx n 1 and v = 1 2 sin(2x). Andreas Fring (City University London) AS1051 Lecture Autumn / 36
 We saw in Example 5.4. that we sometimes need to apply integration by parts several times in the course of a single calculation. Example 5.4.4: For n let S n = x n cos x dx. Find an expression for S n
We saw in Example 5.4. that we sometimes need to apply integration by parts several times in the course of a single calculation. Example 5.4.4: For n let S n = x n cos x dx. Find an expression for S n
Differentiation by taking logarithms
 Differentiation by taking logarithms In this unit we look at how we can use logarithms to simplify certain functions before we differentiate them. In order to master the techniques explained here it is
Differentiation by taking logarithms In this unit we look at how we can use logarithms to simplify certain functions before we differentiate them. In order to master the techniques explained here it is
Review for Ma 221 Final Exam
 Review for Ma 22 Final Exam The Ma 22 Final Exam from December 995.a) Solve the initial value problem 2xcosy 3x2 y dx x 3 x 2 sin y y dy 0 y 0 2 The equation is first order, for which we have techniques
Review for Ma 22 Final Exam The Ma 22 Final Exam from December 995.a) Solve the initial value problem 2xcosy 3x2 y dx x 3 x 2 sin y y dy 0 y 0 2 The equation is first order, for which we have techniques
Ordinary Differential Equations (ODEs)
 c01.tex 8/10/2010 22: 55 Page 1 PART A Ordinary Differential Equations (ODEs) Chap. 1 First-Order ODEs Sec. 1.1 Basic Concepts. Modeling To get a good start into this chapter and this section, quickly
c01.tex 8/10/2010 22: 55 Page 1 PART A Ordinary Differential Equations (ODEs) Chap. 1 First-Order ODEs Sec. 1.1 Basic Concepts. Modeling To get a good start into this chapter and this section, quickly
No calculators, cell phones or any other electronic devices can be used on this exam. Clear your desk of everything excepts pens, pencils and erasers.
 Name: Section: Recitation Instructor: READ THE FOLLOWING INSTRUCTIONS. Do not open your exam until told to do so. No calculators, cell phones or any other electronic devices can be used on this exam. Clear
Name: Section: Recitation Instructor: READ THE FOLLOWING INSTRUCTIONS. Do not open your exam until told to do so. No calculators, cell phones or any other electronic devices can be used on this exam. Clear
M GENERAL MATHEMATICS -2- Dr. Tariq A. AlFadhel 1 Solution of the First Mid-Term Exam First semester H
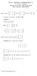 M - GENERAL MATHEMATICS -- Dr. Tariq A. AlFadhel Solution of the First Mid-Term Exam First semester 38-39 H 3 Q. Let A =, B = and C = 3 Compute (if possible) : A+B and BC A+B is impossible. ( ) BC = 3
M - GENERAL MATHEMATICS -- Dr. Tariq A. AlFadhel Solution of the First Mid-Term Exam First semester 38-39 H 3 Q. Let A =, B = and C = 3 Compute (if possible) : A+B and BC A+B is impossible. ( ) BC = 3
Without fully opening the exam, check that you have pages 1 through 12.
 Name: Section: Recitation Instructor: INSTRUCTIONS Fill in your name, etc. on this first page. Without fully opening the exam, check that you have pages 1 through 12. Show all your work on the standard
Name: Section: Recitation Instructor: INSTRUCTIONS Fill in your name, etc. on this first page. Without fully opening the exam, check that you have pages 1 through 12. Show all your work on the standard
Brushing up on Basic skills. Calculus AB (*problems for BC)
 Brushing up on Basic skills To get you ready for Calculus AB (*problems for BC) Name: Directions: Use a pencil and the space provided next to each question to show all work. The purpose of this packet
Brushing up on Basic skills To get you ready for Calculus AB (*problems for BC) Name: Directions: Use a pencil and the space provided next to each question to show all work. The purpose of this packet
( ) - 4(x -3) ( ) 3 (2x -3) - (2x +12) ( x -1) 2 x -1) 2 (3x -1) - 2(x -1) Section 1: Algebra Review. Welcome to AP Calculus!
 Welcome to AP Calculus! Successful Calculus students must have a strong foundation in algebra and trigonometry. The following packet was designed to help you review your algebra skills in preparation for
Welcome to AP Calculus! Successful Calculus students must have a strong foundation in algebra and trigonometry. The following packet was designed to help you review your algebra skills in preparation for
Time: 1 hour 30 minutes
 Paper Reference(s) 6666/0 Edexcel GCE Core Mathematics C4 Silver Level S5 Time: hour 0 minutes Materials required for examination papers Mathematical Formulae (Green) Items included with question Nil Candidates
Paper Reference(s) 6666/0 Edexcel GCE Core Mathematics C4 Silver Level S5 Time: hour 0 minutes Materials required for examination papers Mathematical Formulae (Green) Items included with question Nil Candidates
Math 4B Notes. Written by Victoria Kala SH 6432u Office Hours: T 12:45 1:45pm Last updated 7/24/2016
 Math 4B Notes Written by Victoria Kala vtkala@math.ucsb.edu SH 6432u Office Hours: T 2:45 :45pm Last updated 7/24/206 Classification of Differential Equations The order of a differential equation is the
Math 4B Notes Written by Victoria Kala vtkala@math.ucsb.edu SH 6432u Office Hours: T 2:45 :45pm Last updated 7/24/206 Classification of Differential Equations The order of a differential equation is the
Exam Question 10: Differential Equations. June 19, Applied Mathematics: Lecture 6. Brendan Williamson. Introduction.
 Exam Question 10: June 19, 2016 In this lecture we will study differential equations, which pertains to Q. 10 of the Higher Level paper. It s arguably more theoretical than other topics on the syllabus,
Exam Question 10: June 19, 2016 In this lecture we will study differential equations, which pertains to Q. 10 of the Higher Level paper. It s arguably more theoretical than other topics on the syllabus,
Lecture 5: Integrals and Applications
 Lecture 5: Integrals and Applications Lejla Batina Institute for Computing and Information Sciences Digital Security Version: spring 2012 Lejla Batina Version: spring 2012 Wiskunde 1 1 / 21 Outline The
Lecture 5: Integrals and Applications Lejla Batina Institute for Computing and Information Sciences Digital Security Version: spring 2012 Lejla Batina Version: spring 2012 Wiskunde 1 1 / 21 Outline The
Mathematics 1 Lecture Notes Chapter 1 Algebra Review
 Mathematics 1 Lecture Notes Chapter 1 Algebra Review c Trinity College 1 A note to the students from the lecturer: This course will be moving rather quickly, and it will be in your own best interests to
Mathematics 1 Lecture Notes Chapter 1 Algebra Review c Trinity College 1 A note to the students from the lecturer: This course will be moving rather quickly, and it will be in your own best interests to
MAT 132 Midterm 1 Spring 2017
 MAT Midterm Spring 7 Name: ID: Problem 5 6 7 8 Total ( pts) ( pts) ( pts) ( pts) ( pts) ( pts) (5 pts) (5 pts) ( pts) Score Instructions: () Fill in your name and Stony Brook ID number at the top of this
MAT Midterm Spring 7 Name: ID: Problem 5 6 7 8 Total ( pts) ( pts) ( pts) ( pts) ( pts) ( pts) (5 pts) (5 pts) ( pts) Score Instructions: () Fill in your name and Stony Brook ID number at the top of this
Math Reading assignment for Chapter 1: Study Sections 1.1 and 1.2.
 Math 3350 1 Chapter 1 Reading assignment for Chapter 1: Study Sections 1.1 and 1.2. 1.1 Material for Section 1.1 An Ordinary Differential Equation (ODE) is a relation between an independent variable x
Math 3350 1 Chapter 1 Reading assignment for Chapter 1: Study Sections 1.1 and 1.2. 1.1 Material for Section 1.1 An Ordinary Differential Equation (ODE) is a relation between an independent variable x
ADDITIONAL MATHEMATICS
 ADDITIONAL MATHEMATICS GCE Ordinary Level (06) (Syllabus 4047) CONTENTS Page INTRODUCTION AIMS ASSESSMENT OBJECTIVES SCHEME OF ASSESSMENT 3 USE OF CALCULATORS 3 SUBJECT CONTENT 4 MATHEMATICAL FORMULAE
ADDITIONAL MATHEMATICS GCE Ordinary Level (06) (Syllabus 4047) CONTENTS Page INTRODUCTION AIMS ASSESSMENT OBJECTIVES SCHEME OF ASSESSMENT 3 USE OF CALCULATORS 3 SUBJECT CONTENT 4 MATHEMATICAL FORMULAE
Mathematics Extension 1
 009 HIGHER SCHOOL CERTIFICATE EXAMINATION Mathematics Extension General Instructions Reading time 5 minutes Working time hours Write using black or blue pen Board-approved calculators may be used A table
009 HIGHER SCHOOL CERTIFICATE EXAMINATION Mathematics Extension General Instructions Reading time 5 minutes Working time hours Write using black or blue pen Board-approved calculators may be used A table
Differentiation by taking logarithms
 Differentiation by taking logarithms mc-ty-difftakelogs-2009-1 In this unit we look at how we can use logarithms to simplify certain functions before we differentiate them. In order to master the techniques
Differentiation by taking logarithms mc-ty-difftakelogs-2009-1 In this unit we look at how we can use logarithms to simplify certain functions before we differentiate them. In order to master the techniques
Access to Science, Engineering and Agriculture: Mathematics 2 MATH00040 Chapter 4 Solutions
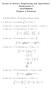 Access to Science, Engineering and Agriculture: Mathematics MATH4 Chapter 4 Solutions In all these solutions, c will represent an arbitrary constant.. (a) Since f(x) 5 is a constant, 5dx 5x] 5. (b) Since
Access to Science, Engineering and Agriculture: Mathematics MATH4 Chapter 4 Solutions In all these solutions, c will represent an arbitrary constant.. (a) Since f(x) 5 is a constant, 5dx 5x] 5. (b) Since
13 Implicit Differentiation
 - 13 Implicit Differentiation This sections highlights the difference between explicit and implicit expressions, and focuses on the differentiation of the latter, which can be a very useful tool in mathematics.
- 13 Implicit Differentiation This sections highlights the difference between explicit and implicit expressions, and focuses on the differentiation of the latter, which can be a very useful tool in mathematics.
YEAR 13 - Mathematics Pure (C3) Term 1 plan
 Week Topic YEAR 13 - Mathematics Pure (C3) Term 1 plan 2016-2017 1-2 Algebra and functions Simplification of rational expressions including factorising and cancelling. Definition of a function. Domain
Week Topic YEAR 13 - Mathematics Pure (C3) Term 1 plan 2016-2017 1-2 Algebra and functions Simplification of rational expressions including factorising and cancelling. Definition of a function. Domain
Partial Derivatives for Math 229. Our puropose here is to explain how one computes partial derivatives. We will not attempt
 Partial Derivatives for Math 229 Our puropose here is to explain how one computes partial derivatives. We will not attempt to explain how they arise or why one would use them; that is left to other courses
Partial Derivatives for Math 229 Our puropose here is to explain how one computes partial derivatives. We will not attempt to explain how they arise or why one would use them; that is left to other courses
Some suggested repetition for the course MAA508
 Some suggested repetition for the course MAA58 Linus Carlsson, Karl Lundengård, Johan Richter July, 14 Contents Introduction 1 1 Basic algebra and trigonometry Univariate calculus 5 3 Linear algebra 8
Some suggested repetition for the course MAA58 Linus Carlsson, Karl Lundengård, Johan Richter July, 14 Contents Introduction 1 1 Basic algebra and trigonometry Univariate calculus 5 3 Linear algebra 8
Final Exam 2011 Winter Term 2 Solutions
 . (a Find the radius of convergence of the series: ( k k+ x k. Solution: Using the Ratio Test, we get: L = lim a k+ a k = lim ( k+ k+ x k+ ( k k+ x k = lim x = x. Note that the series converges for L
. (a Find the radius of convergence of the series: ( k k+ x k. Solution: Using the Ratio Test, we get: L = lim a k+ a k = lim ( k+ k+ x k+ ( k k+ x k = lim x = x. Note that the series converges for L
c) xy 3 = cos(7x +5y), y 0 = y3 + 7 sin(7x +5y) 3xy sin(7x +5y) d) xe y = sin(xy), y 0 = ey + y cos(xy) x(e y cos(xy)) e) y = x ln(3x + 5), y 0
 Some Math 35 review problems With answers 2/6/2005 The following problems are based heavily on problems written by Professor Stephen Greenfield for his Math 35 class in spring 2005. His willingness to
Some Math 35 review problems With answers 2/6/2005 The following problems are based heavily on problems written by Professor Stephen Greenfield for his Math 35 class in spring 2005. His willingness to
Solutions to old Exam 3 problems
 Solutions to old Exam 3 problems Hi students! I am putting this version of my review for the Final exam review here on the web site, place and time to be announced. Enjoy!! Best, Bill Meeks PS. There are
Solutions to old Exam 3 problems Hi students! I am putting this version of my review for the Final exam review here on the web site, place and time to be announced. Enjoy!! Best, Bill Meeks PS. There are
1 Arithmetic calculations (calculator is not allowed)
 1 ARITHMETIC CALCULATIONS (CALCULATOR IS NOT ALLOWED) 1 Arithmetic calculations (calculator is not allowed) 1.1 Check the result Problem 1.1. Problem 1.2. Problem 1.3. Problem 1.4. 78 5 6 + 24 3 4 99 1
1 ARITHMETIC CALCULATIONS (CALCULATOR IS NOT ALLOWED) 1 Arithmetic calculations (calculator is not allowed) 1.1 Check the result Problem 1.1. Problem 1.2. Problem 1.3. Problem 1.4. 78 5 6 + 24 3 4 99 1
Regression and Nonlinear Axes
 Introduction to Chemical Engineering Calculations Lecture 2. What is regression analysis? A technique for modeling and analyzing the relationship between 2 or more variables. Usually, 1 variable is designated
Introduction to Chemical Engineering Calculations Lecture 2. What is regression analysis? A technique for modeling and analyzing the relationship between 2 or more variables. Usually, 1 variable is designated
Section 3.5: Implicit Differentiation
 Section 3.5: Implicit Differentiation In the previous sections, we considered the problem of finding the slopes of the tangent line to a given function y = f(x). The idea of a tangent line however is not
Section 3.5: Implicit Differentiation In the previous sections, we considered the problem of finding the slopes of the tangent line to a given function y = f(x). The idea of a tangent line however is not
4 Differential Equations
 Advanced Calculus Chapter 4 Differential Equations 65 4 Differential Equations 4.1 Terminology Let U R n, and let y : U R. A differential equation in y is an equation involving y and its (partial) derivatives.
Advanced Calculus Chapter 4 Differential Equations 65 4 Differential Equations 4.1 Terminology Let U R n, and let y : U R. A differential equation in y is an equation involving y and its (partial) derivatives.
MATH 250 TOPIC 13 INTEGRATION. 13B. Constant, Sum, and Difference Rules
 Math 5 Integration Topic 3 Page MATH 5 TOPIC 3 INTEGRATION 3A. Integration of Common Functions Practice Problems 3B. Constant, Sum, and Difference Rules Practice Problems 3C. Substitution Practice Problems
Math 5 Integration Topic 3 Page MATH 5 TOPIC 3 INTEGRATION 3A. Integration of Common Functions Practice Problems 3B. Constant, Sum, and Difference Rules Practice Problems 3C. Substitution Practice Problems
Chapter 3. Integration. 3.1 Indefinite Integration
 Chapter 3 Integration 3. Indefinite Integration Integration is the reverse of differentiation. Consider a function f(x) and suppose that there exists another function F (x) such that df f(x). (3.) For
Chapter 3 Integration 3. Indefinite Integration Integration is the reverse of differentiation. Consider a function f(x) and suppose that there exists another function F (x) such that df f(x). (3.) For
Limit. Chapter Introduction
 Chapter 9 Limit Limit is the foundation of calculus that it is so useful to understand more complicating chapters of calculus. Besides, Mathematics has black hole scenarios (dividing by zero, going to
Chapter 9 Limit Limit is the foundation of calculus that it is so useful to understand more complicating chapters of calculus. Besides, Mathematics has black hole scenarios (dividing by zero, going to
Higher-order ordinary differential equations
 Higher-order ordinary differential equations 1 A linear ODE of general order n has the form a n (x) dn y dx n +a n 1(x) dn 1 y dx n 1 + +a 1(x) dy dx +a 0(x)y = f(x). If f(x) = 0 then the equation is called
Higher-order ordinary differential equations 1 A linear ODE of general order n has the form a n (x) dn y dx n +a n 1(x) dn 1 y dx n 1 + +a 1(x) dy dx +a 0(x)y = f(x). If f(x) = 0 then the equation is called
1MA1 Introduction to the Maths Course
 1MA1/-1 1MA1 Introduction to the Maths Course Preamble Throughout your time as an engineering student at Oxford you will receive lectures and tuition in the range of applied mathematical tools that today
1MA1/-1 1MA1 Introduction to the Maths Course Preamble Throughout your time as an engineering student at Oxford you will receive lectures and tuition in the range of applied mathematical tools that today
Page Points Score Total: 210. No more than 200 points may be earned on the exam.
 Name: PID: Section: Recitation Instructor: DO NOT WRITE BELOW THIS LINE. GO ON TO THE NEXT PAGE. Page Points Score 3 18 4 18 5 18 6 18 7 18 8 18 9 18 10 21 11 21 12 21 13 21 Total: 210 No more than 200
Name: PID: Section: Recitation Instructor: DO NOT WRITE BELOW THIS LINE. GO ON TO THE NEXT PAGE. Page Points Score 3 18 4 18 5 18 6 18 7 18 8 18 9 18 10 21 11 21 12 21 13 21 Total: 210 No more than 200
MATH20411 PDEs and Vector Calculus B
 MATH2411 PDEs and Vector Calculus B Dr Stefan Güttel Acknowledgement The lecture notes and other course materials are based on notes provided by Dr Catherine Powell. SECTION 1: Introctory Material MATH2411
MATH2411 PDEs and Vector Calculus B Dr Stefan Güttel Acknowledgement The lecture notes and other course materials are based on notes provided by Dr Catherine Powell. SECTION 1: Introctory Material MATH2411
Lecture 4: Integrals and applications
 Lecture 4: Integrals and applications Lejla Batina Institute for Computing and Information Sciences Digital Security Version: autumn 2013 Lejla Batina Version: autumn 2013 Calculus en Kansrekenen 1 / 18
Lecture 4: Integrals and applications Lejla Batina Institute for Computing and Information Sciences Digital Security Version: autumn 2013 Lejla Batina Version: autumn 2013 Calculus en Kansrekenen 1 / 18
Multiple Integrals and Vector Calculus (Oxford Physics) Synopsis and Problem Sets; Hilary 2015
 Multiple Integrals and Vector Calculus (Oxford Physics) Ramin Golestanian Synopsis and Problem Sets; Hilary 215 The outline of the material, which will be covered in 14 lectures, is as follows: 1. Introduction
Multiple Integrals and Vector Calculus (Oxford Physics) Ramin Golestanian Synopsis and Problem Sets; Hilary 215 The outline of the material, which will be covered in 14 lectures, is as follows: 1. Introduction
Advanced Mathematics Support Programme Edexcel Year 2 Core Pure Suggested Scheme of Work ( )
 Edexcel Year 2 Core Pure Suggested Scheme of Work (2018-2019) This template shows how Integral Resources and AMSP FM videos can be used to support Further Mathematics students and teachers. This template
Edexcel Year 2 Core Pure Suggested Scheme of Work (2018-2019) This template shows how Integral Resources and AMSP FM videos can be used to support Further Mathematics students and teachers. This template
6 Second Order Linear Differential Equations
 6 Second Order Linear Differential Equations A differential equation for an unknown function y = f(x) that depends on a variable x is any equation that ties together functions of x with y and its derivatives.
6 Second Order Linear Differential Equations A differential equation for an unknown function y = f(x) that depends on a variable x is any equation that ties together functions of x with y and its derivatives.
MATH 391 Test 1 Fall, (1) (12 points each)compute the general solution of each of the following differential equations: = 4x 2y.
 MATH 391 Test 1 Fall, 2018 (1) (12 points each)compute the general solution of each of the following differential equations: (a) (b) x dy dx + xy = x2 + y. (x + y) dy dx = 4x 2y. (c) yy + (y ) 2 = 0 (y
MATH 391 Test 1 Fall, 2018 (1) (12 points each)compute the general solution of each of the following differential equations: (a) (b) x dy dx + xy = x2 + y. (x + y) dy dx = 4x 2y. (c) yy + (y ) 2 = 0 (y
Coordinate systems and vectors in three spatial dimensions
 PHYS2796 Introduction to Modern Physics (Spring 2015) Notes on Mathematics Prerequisites Jim Napolitano, Department of Physics, Temple University January 7, 2015 This is a brief summary of material on
PHYS2796 Introduction to Modern Physics (Spring 2015) Notes on Mathematics Prerequisites Jim Napolitano, Department of Physics, Temple University January 7, 2015 This is a brief summary of material on
7.1 Integration by Parts (...or, undoing the product rule.)
 7.1 1 7.1 Integration by Parts (...or, undoing the product rule.) Integration by Parts Recall the differential form of the chain rule. If u and v are differentiable functions. Then (1) d(uv) = du v +u
7.1 1 7.1 Integration by Parts (...or, undoing the product rule.) Integration by Parts Recall the differential form of the chain rule. If u and v are differentiable functions. Then (1) d(uv) = du v +u
Without fully opening the exam, check that you have pages 1 through 12.
 MTH 34 Solutions to Exam April 9th, 8 Name: Section: Recitation Instructor: INSTRUTIONS Fill in your name, etc. on this first page. Without fully opening the exam, check that you have pages through. Show
MTH 34 Solutions to Exam April 9th, 8 Name: Section: Recitation Instructor: INSTRUTIONS Fill in your name, etc. on this first page. Without fully opening the exam, check that you have pages through. Show
22. Periodic Functions and Fourier Series
 November 29, 2010 22-1 22. Periodic Functions and Fourier Series 1 Periodic Functions A real-valued function f(x) of a real variable is called periodic of period T > 0 if f(x + T ) = f(x) for all x R.
November 29, 2010 22-1 22. Periodic Functions and Fourier Series 1 Periodic Functions A real-valued function f(x) of a real variable is called periodic of period T > 0 if f(x + T ) = f(x) for all x R.
Core A-level mathematics reproduced from the QCA s Subject criteria for Mathematics document
 Core A-level mathematics reproduced from the QCA s Subject criteria for Mathematics document Background knowledge: (a) The arithmetic of integers (including HCFs and LCMs), of fractions, and of real numbers.
Core A-level mathematics reproduced from the QCA s Subject criteria for Mathematics document Background knowledge: (a) The arithmetic of integers (including HCFs and LCMs), of fractions, and of real numbers.
Topic Learning Outcomes Suggested Teaching Activities Resources On-Line Resources
 UNIT 3 Trigonometry and Vectors (P1) Recommended Prior Knowledge. Students will need an understanding and proficiency in the algebraic techniques from either O Level Mathematics or IGCSE Mathematics. Context.
UNIT 3 Trigonometry and Vectors (P1) Recommended Prior Knowledge. Students will need an understanding and proficiency in the algebraic techniques from either O Level Mathematics or IGCSE Mathematics. Context.
Basic Algebra. CAPS Mathematics
 Basic Algebra CAPS Mathematics 1 Outcomes for this TOPIC In this TOPIC you will: Revise factorization. LESSON 1. Revise simplification of algebraic fractions. LESSON. Discuss when trinomials can be factorized.
Basic Algebra CAPS Mathematics 1 Outcomes for this TOPIC In this TOPIC you will: Revise factorization. LESSON 1. Revise simplification of algebraic fractions. LESSON. Discuss when trinomials can be factorized.
CALCULUS AB SUMMER ASSIGNMENT
 CALCULUS AB SUMMER ASSIGNMENT Dear Prospective Calculus Students, Welcome to AP Calculus. This is a rigorous, yet rewarding, math course. Most of the students who have taken Calculus in the past are amazed
CALCULUS AB SUMMER ASSIGNMENT Dear Prospective Calculus Students, Welcome to AP Calculus. This is a rigorous, yet rewarding, math course. Most of the students who have taken Calculus in the past are amazed
Mathematics DAPTO HIGH SCHOOL HSC Preliminary Course FINAL EXAMINATION. General Instructions
 DAPTO HIGH SCHOOL 2009 HSC Preliminary Course FINAL EXAMINATION Mathematics General Instructions o Reading Time 5 minutes o Working Time 2 hours Total marks (80) o Write using a blue or black pen o Board
DAPTO HIGH SCHOOL 2009 HSC Preliminary Course FINAL EXAMINATION Mathematics General Instructions o Reading Time 5 minutes o Working Time 2 hours Total marks (80) o Write using a blue or black pen o Board
Without fully opening the exam, check that you have pages 1 through 12.
 MTH 34 Solutions to Exam November 9, 8 Name: Section: Recitation Instructor: INSTRUCTIONS Fill in your name, etc. on this first page. Without fully opening the exam, check that you have pages through.
MTH 34 Solutions to Exam November 9, 8 Name: Section: Recitation Instructor: INSTRUCTIONS Fill in your name, etc. on this first page. Without fully opening the exam, check that you have pages through.
3 Algebraic Methods. we can differentiate both sides implicitly to obtain a differential equation involving x and y:
 3 Algebraic Methods b The first appearance of the equation E Mc 2 in Einstein s handwritten notes. So far, the only general class of differential equations that we know how to solve are directly integrable
3 Algebraic Methods b The first appearance of the equation E Mc 2 in Einstein s handwritten notes. So far, the only general class of differential equations that we know how to solve are directly integrable
CALCULUS PROBLEMS Courtesy of Prof. Julia Yeomans. Michaelmas Term
 CALCULUS PROBLEMS Courtesy of Prof. Julia Yeomans Michaelmas Term The problems are in 5 sections. The first 4, A Differentiation, B Integration, C Series and limits, and D Partial differentiation follow
CALCULUS PROBLEMS Courtesy of Prof. Julia Yeomans Michaelmas Term The problems are in 5 sections. The first 4, A Differentiation, B Integration, C Series and limits, and D Partial differentiation follow
A-Level Maths Induction Summer Work
 A-Level Maths Induction Summer Work Name:. (Show workings for every question in this booklet) This booklet contains GCSE Algebra skills that you will need in order to successfully complete the A-Level
A-Level Maths Induction Summer Work Name:. (Show workings for every question in this booklet) This booklet contains GCSE Algebra skills that you will need in order to successfully complete the A-Level
Integration by parts Integration by parts is a direct reversal of the product rule. By integrating both sides, we get:
 Integration by parts Integration by parts is a direct reversal of the proct rule. By integrating both sides, we get: u dv dx x n sin mx dx (make u = x n ) dx = uv v dx dx When to use integration by parts
Integration by parts Integration by parts is a direct reversal of the proct rule. By integrating both sides, we get: u dv dx x n sin mx dx (make u = x n ) dx = uv v dx dx When to use integration by parts
Table of Contents. Module 1
 Table of Contents Module Order of operations 6 Signed Numbers Factorization of Integers 7 Further Signed Numbers 3 Fractions 8 Power Laws 4 Fractions and Decimals 9 Introduction to Algebra 5 Percentages
Table of Contents Module Order of operations 6 Signed Numbers Factorization of Integers 7 Further Signed Numbers 3 Fractions 8 Power Laws 4 Fractions and Decimals 9 Introduction to Algebra 5 Percentages
CONTENTS CHECK LIST ACCURACY FRACTIONS INDICES SURDS RATIONALISING THE DENOMINATOR SUBSTITUTION
 CONTENTS CHECK LIST - - ACCURACY - 4 - FRACTIONS - 6 - INDICES - 9 - SURDS - - RATIONALISING THE DENOMINATOR - 4 - SUBSTITUTION - 5 - REMOVING BRACKETS - 7 - FACTORISING - 8 - COMMON FACTORS - 8 - DIFFERENCE
CONTENTS CHECK LIST - - ACCURACY - 4 - FRACTIONS - 6 - INDICES - 9 - SURDS - - RATIONALISING THE DENOMINATOR - 4 - SUBSTITUTION - 5 - REMOVING BRACKETS - 7 - FACTORISING - 8 - COMMON FACTORS - 8 - DIFFERENCE
Review for the Final Exam
 Math 171 Review for the Final Exam 1 Find the limits (4 points each) (a) lim 4x 2 3; x x (b) lim ( x 2 x x 1 )x ; (c) lim( 1 1 ); x 1 ln x x 1 sin (x 2) (d) lim x 2 x 2 4 Solutions (a) The limit lim 4x
Math 171 Review for the Final Exam 1 Find the limits (4 points each) (a) lim 4x 2 3; x x (b) lim ( x 2 x x 1 )x ; (c) lim( 1 1 ); x 1 ln x x 1 sin (x 2) (d) lim x 2 x 2 4 Solutions (a) The limit lim 4x
2009 A-level Maths Tutor All Rights Reserved
 2 This book is under copyright to A-level Maths Tutor. However, it may be distributed freely provided it is not sold for profit. Contents the derivative formula 3 tangents & normals 7 maxima & minima 10
2 This book is under copyright to A-level Maths Tutor. However, it may be distributed freely provided it is not sold for profit. Contents the derivative formula 3 tangents & normals 7 maxima & minima 10
C3 Revision Questions. (using questions from January 2006, January 2007, January 2008 and January 2009)
 C3 Revision Questions (using questions from January 2006, January 2007, January 2008 and January 2009) 1 2 1. f(x) = 1 3 x 2 + 3, x 2. 2 ( x 2) (a) 2 x x 1 Show that f(x) =, x 2. 2 ( x 2) (4) (b) Show
C3 Revision Questions (using questions from January 2006, January 2007, January 2008 and January 2009) 1 2 1. f(x) = 1 3 x 2 + 3, x 2. 2 ( x 2) (a) 2 x x 1 Show that f(x) =, x 2. 2 ( x 2) (4) (b) Show
What students need to know for CALCULUS (Regular, AB and BC) Students expecting to take Calculus should demonstrate the ability to:
 What students need to know for CALCULUS (Regular, AB and BC) Students expecting to take Calculus should demonstrate the ability to: General: keep an organized notebook take good notes complete homework
What students need to know for CALCULUS (Regular, AB and BC) Students expecting to take Calculus should demonstrate the ability to: General: keep an organized notebook take good notes complete homework
OPTI 511R, Spring 2018 Problem Set 1 Prof. R.J. Jones
 OPTI 511R, Spring 2018 Problem Set 1 Prof. R.J. Jones Due in class Thursday, Jan 18, 2018 Math Refresher The first 11 questions are just to get you to review some very basic mathematical concepts needed
OPTI 511R, Spring 2018 Problem Set 1 Prof. R.J. Jones Due in class Thursday, Jan 18, 2018 Math Refresher The first 11 questions are just to get you to review some very basic mathematical concepts needed
Summary: Primer on Integral Calculus:
 Physics 2460 Electricity and Magnetism I, Fall 2006, Primer on Integration: Part I 1 Summary: Primer on Integral Calculus: Part I 1. Integrating over a single variable: Area under a curve Properties of
Physics 2460 Electricity and Magnetism I, Fall 2006, Primer on Integration: Part I 1 Summary: Primer on Integral Calculus: Part I 1. Integrating over a single variable: Area under a curve Properties of
