Access to Science, Engineering and Agriculture: Mathematics 2 MATH00040 Chapter 4 Solutions
|
|
|
- Buck Dickerson
- 5 years ago
- Views:
Transcription
1 Access to Science, Engineering and Agriculture: Mathematics MATH4 Chapter 4 Solutions In all these solutions, c will represent an arbitrary constant.. (a) Since f(x) 5 is a constant, 5dx 5x] 5. (b) Since f(x) πcos(e) is a constant, πcos(e)dx πcos(e)x+c. (c) Since f(x) x is of the form f(x) x n with n, x x + dx + ] x ]. (d) Since f(x) x 9 is of the form f(x) x n with n 9, x 9 dx 9/+ x9 + +c x +c. (e) Since f(x) x 5 is of the form f(x) x n with n 5, x 5 dx 5+ x 5+ ] ] 4 x ( 4 ) (f) Since f(x) x cos() is of the form f(x) x n with n cos(), x cos() dx cos()+ xcos()+ +c. (g) Since f(x) e 4x is of the form f(x) e ax with a 4, e 4x dx ] 4 e4x 4 e4() 4 e 4 (e8 ).
2 (h) Since f(x) e x is of the form f(x) e ax with a, e x dx / e x +c e x +c. (i) Since f(x) e 6x is of the form f(x) e ax with a 6, e 6x dx 6 e 6x ] ] 6 e 6x 6 e ( 6 ) e 6() 6 ( e 6 ). (j) Since f(x) e πx is of the form f(x) e ax with a π, e πx dx π eπx +c. (k) x dx ln(x)] ln() ln() ln() ln(). (l) Since f(x) sin(x) is of the form f(x) sin(ax) with a, sin(x)dx cos(x)+c. (m) Since f(x) sin( x) is of the form f(x) sin(ax) with a, π sin( x) dx cos( x) ]π cos( x) π ) cos ( ]π cos( π) cos() () (). cos( ()) (n) Since f(x) sin(ex) is of the form f(x) sin(ax) with a e, sin(ex)dx e cos(ex)+c.
3 (o) Since f(x) cos(x) is of the form f(x) cos(ax) with a, π π ]π cos(x)dx sin(x) π ( sin π ) sin(( π)) sin(π) sin( π) () (). (p) Since f(x) cos( πx) is of the form f(x) cos(ax) with a π, cos( πx)dx π sin( πx)+c π sin( πx)+c.. (a) We will first use the sum and multiple rules to find the corresponding definite integral. +x x +x 4x 4 dx dx+ xdx+ x dx+ x dx+ 4x 4 dx dx+ xdx x dx+ x dx 4 x 4 dx ( ) ( ) ( ) ( ) x+ x x + 4 x4 4 5 x5 +c x+ x x + 4 x4 4 5 x5 +c. Note that in your assignment or exam solutions you don t need to give as much detail as this. I am just setting out everything carefully until you get used to the ideas involved. +x x +x 4x 4 dx x+ x x + 4 x4 4 ] 5 x5 + ( ) ( )+ 4 (4 ) 4 5 (5 ) + () () + 4 ()4 45 ] ()
4 (b) Using the sum and multiple rules, x +sin4xdx x dx+ sin4xdx x dx+ sin4xdx x dx+ sin4xdx ln(x)+ ( 4 ) cos(4x) +c ln(x) cos(4x)+c. (c) We will first use the sum and multiple rules to find the corresponding definite integral. ( ) ( ) e x cos x dx e x dx+ cos x dx ( ) e x dx cos dx π e x cos x ( ( / e ) x / sin ( ) 6e x 4sin x. ( ) ( x dx 6e x 4sin x ( ) 6e π 4sin π )] π 6e π 4() 6() 4()] 6e π. ( x )) +c 6e () 4sin (d) Using the sum and multiple rules, 4cos( x) e x dx 4cos( x)dx+ e x dx 4 cos( x) dx e x dx ( ) ( 4 sin( x) / e )+c x 4 sin( x)+ e x +c. (e) We will first use the sum and multiple rules to find the corresponding definite ( )] () 4
5 integral. x +e cos()x dx x dx+ e cos()x dx x dx+ e cos()x dx ( ) x + cos() ecos()x +c x + cos() ecos()x +c. x +e cos()x dx x + ] cos() ecos()x ( )+ cos() ecos()() cos() ( e cos() e cos()) 6. (f) Using the sum and multiple rules, sin(x) sin(x)+cos(x) cos(x)dx sin(x)dx+ sin(x)dx+ cos(x)dx+ sin(x)dx sin(x)dx+ ( ) cos(x) ( ) cos(x) cos(x)+ cos(x)+ sin(x) sin(x)+c ( ) + ] cos() ecos()( ) cos(x) dx cos(x)dx cos(x) dx ( ) ( ) + sin(x) sin(x) +c (g) We will first use the sum rule to find the corresponding definite integral. e +e x 4dx e 4dx+ e x dx (e 4)x+ ex +c. Note that we didn t need the multiple rule here and also note that we could deal with e 4 all at once since e 4 is a constant. e +e x 4dx (e 4)x+ ] ex (e 4)()+ e() (e 4)()+ ] e() (e 4)+ e6 + e 8. ( e 6 e ) 5
6 (h) Using the sum and multiple rules, x +4x 4 +5x 5 +x dx x dx+ 4x 4 dx+ x dx+4 ( + x + x x5 5 4 x 4 +x+c. 5x 5 dx+ x dx x 4 dx+5 x 5 dx+ dx ) ( ) x4+ +5 ( 5+ x 5+ ) +x+c For the remainder of the questions we will still need the sum and multiple rules but I will not mention them explicitly.. (a) Here we use integration by substitution. Let u x+5, so that du dx. Then dx du du/dx du du. Also, when x, u 5 and when x, u 6. 6 ] 6 (x+5) 9 dx u 9 du 5 u (6 5 ). (b) Here we use integration by substitution. Let u x 5, so that du dx x. Then dx du du/dx du x. x (x 5) 5 dx x u 5 du x u5 du ( ) 6 u6 +c 8 u6 +c ( x 5 )6 +c. 8 (c) Here we use integration by substitution. Let u cos(x), so that du sin(x). Note we chose u cos(x) rather dx than u sin(x) since this ensures the sin(x) in the numerator cancels. This is part of the skill you will have to learn when performing integration; what 6
7 works and what doesn t. Then dx du du/dx du sin(x). Also, when x, u and when x π 4, u. π 4 sin(x) cos(x) dx sin(x) u u du du sin(x) ln(u)] ( ln ) ( ln()) ( ) ln + ( ) ln() ln(). (d) Here we use integration by substitution. Let u sin(x), so that du dx cos(x). Then dx du du/dx du cos(x). cos(x) cos(x) sin(x) dx u (e) Here we use integration by substitution. Let u du, so that x dx x. Then dx du du/dx du /x x du. Also, when x, u and when x, u. du cos(x) du ln(u)+c ln(sin(x))+c. u x e x dx e u ] x eu ( x )du e u du e ( e ) e e e e. 7
8 (f) Here we use integration by substitution. Let u x 4 x +x x, so that du dx 4x x +x. Then dx du du/dx du 4x x +x. x 9x +6x x x 4 x +x x dx 9x +6x u u du ln(u)+c ln(x 4 x +x x)+c. (g) Here we use integration by substitution. Let u x, so that du dx x. Then dx du du/dx du x. Also, when x, u and when x, u. x x dx x u du x u du ( u u ] )] ( du 4x x +x ) +. (h) Here we use integration by substitution. Let u x x, so that du dx 4x +4x. Then dx du du/dx du 4x +4x. 8
9 (x +x )sin (x ) x dx 4 sin(u)du (i) Here we use integration by substitution. Let u x +4, so that du dx x. Then dx du du/dx du x. Also, when x, u 4 and when x, u 5. (x +x )sin(u) du 4x +4x 4 ( cos(u))+c 4 cos ( x x )+c. x 5 x +4 dx x du 4 u x 5 du 4 u u ( u ] ) ] 5 (j) Here we use integration by substitution. Let u x +, so that du dx x. Then dx du du/dx du x. x ( x + ) dx x u du x u du ( ) 5 u5 +c 5 u5 +c ( x + )5. 5 (k) Here we use integration by substitution. Let u cos(x), so that du dx sin(x). 9 4
10 Then dx du du/dx du sin(x). Also, when x, u and when x π, u. π sin(x)e cos(x) dx sin(x)e u e u du e u ] e ( e ) +e e. du sin(x) (l) Here we use integration by substitution. Let u x 4, so that du dx 4x. Then dx du du/dx du 4x. x cos ( x 4) dx x cos(u) du 4x 4 cos(u)du 4 sin(u)+c 4 sin( x 4) +c. (m) Here we use integration by substitution. Let x sin(u), so that dx du cos(u). Then dx dx du cos(u)du. du Also, when x, u and when x, u π. x dx π π π π π sin (u)cos(u)du cos (u)cos(u)du cos(u) cos(u)du cos (u)du + cos(u)du
11 ( )]π sin(u) u+ u+ ]π 4 sin(u) π 4 + ( 4 sin(π) π 4 + (+) π sin() ) We don t cover this in MATH4 but the equation of a circle of radius one centred at the origin is x +y and on solving this for y we obtain y ± x. So what we have actually calculated here is the area inside this circle that lies in the first quadrant. The area inside a circle of radius r is πr π π and we have found a quarter of this area, that is π 4. Note in addition that if we replace x with r x and the upper limit with r then we can actually derive the formula πr for the area inside a circle. See if you can decide what the substitution should be in this case and then derive the formula. 4. (a) Here we use integration by parts. Let f(x) x and g (x) e x, so that f (x) and g(x) ex., using the integration by parts formula, xe x dx x ex ex dx xex ex dx xex ( ) ex +c (b) Here we use integration by parts. xex 4 ex +c Let f(x) 5x and g (x) cos(x), so that f (x) 5 and g(x) sin(x)., using the integration by parts formula, π ( )] π xcos(x)dx 5x sin(x) ] π 5 π xsin(x) π 5 sin(x)dx 5 sin(x)dx 5 (π)sin(π) 5 5 ()sin(()) ] π cos(x) 5 4 cos(π) 5 4 cos(()) ( cos(x) )] π
12 (c) Here we use integration by parts. Let f(x) ln(x) and g (x) x, so that f (x) x and g(x) x., using the integration by parts formula, ( ) ( ) xln(x)dx ln(x) x x x dx x ln(x) xdx (d) Here we use integration by parts. x ln(x) 4 x +c. Let f(x) ln(x) and g (x) x 4 +, so that f (x) x and g(x) 5 x5 +x., using the integration by parts formula, ( x 4 + ) ( )] ( ) ln(x)dx ln(x) 5 x5 +x x 5 x5 +x dx ( ) ] 5 x5 +x ln(x) 5 x4 +dx ( ) ( ) ] 5 5 +() ln() 5 5 +() ln() 5 x5 +x ( ) ( ) 5 +6 ln() 5 + ln() ( ) ( )] 5 5 +() 5 5 +() ln() 5 76 ] ln() 6 5. (e) Here we will have to integration by parts twice. First we let f(x) x and g (x) sin(x), so that f (x) x and g(x) cos(x)., using the integration by parts formula, x sin(x)dx x ( cos(x)) x( cos(x)) dx x cos(x)+ x cos(x) dx. () We will now find x cos(x) dx by integrating by parts again. So let f(x) x and g (x) cos(x), so that f (x) and g(x) sin(x). Then, using the integration by parts formula, xcos(x)dx xsin(x) sinxdx xsin(x) ( cos(x))+c xsin(x)+cos(x)+c. ()
13 If we now substitute () into (), we finally obtain x sin(x)dx x cos(x)+xsin(x)+cos(x)+c. (f) Again here we will have to integrate by parts twice. We will first find the associated definite integral x e x dx. Let f(x) x and g (x) e x, so that f (x) x and g(x) e x., using the integration by parts formula, x e x dx x e x xe x dx () We will now find xe x dx by integrating by parts again. Let f(x) x and g (x) e x, so that f (x) and g(x) e x., using the integration by parts formula, xe x dx xe x e x dx xe x e x. (4) If we now substitute (4) into (), we see that x e x dx x e x (xe x e x )+c x e x xe x +e x +c. x e x dx x e x xe x +e x] e ()e +e e ()e +e ] e e+e +] e. 5. (a) Here we use partial fractions. Since x 4 (x )(x+), we let x+ x 4 A x + B x+, (5) where A and B are constants we have to find. Multiplying both sides of (5) by x 4 we obtain x+ A(x+)+B(x ). (6) If we let x in (6), we obtain 4 4B, so that B. If we let x in (6), we obtain 8 4A, so that A. x+ x 4 dx x + x+ dx ln(x )+ln(x+)+c. Note that if you can t spot the integrals, then you can use the substitutions u x and u x+ for the two terms, respectively. Similar substitutions will work in all the examples below but I won t explicitly mention them.
14 (b) Again we use partial fractions. Since x +9x+ (x+4)(x+5), we let x +9x+ A x+4 + B x+5, (7) where A and B are constants we have to find. Multiplying both sides of (7) by x +9x+ we obtain A(x+5)+B(x+4). (8) If we let x 5 in (8), we obtain B, so that B. If we let x 4 in (8), we obtain A, so that A. x +9x+ dx (c) Again we use partial fractions. Since x +4x x(x+4), we let x+4 + x+5 dx ln(x+4)+ln(x+5)] ln(5)+ln(6) ( ln(4)+ln(5)) ln(6) ln(5)+ln(4) x 8 x +4x A x + B x+4, (9) where A and B are constants we have to find. Multiplying both sides of (9) by x +4x we obtain x 8 A(x+4)+Bx. () If we let x 4 in (), we obtain 4 4B, so that B. If we let x in (), we obtain 8 4A, so that A. x 8 x +4x dxx x + x+4 dx ln(x)+ln(x+4)+c ln(x+4) ln(x)+c. (d) Again we use partial fractions. Since (x )(x+) (x)(x+)(x+), we let x +4x (x )(x+) A x + B x+ + C x+, () where A, B and C are constants we have to find. Multiplying both sides of () by (x )(x+) we obtain x +4x A(x+)(x+)+B(x)(x+)+C(x)(x+). () 4
15 If we let x in (), we obtain C, so that C. If we let x in (), we obtain B, so that B. If we let x in (), we obtain 6 6A, so that A. x +4x (x )(x+) dx x + x+ + x+ dx ln(x)+ln(x+)+ln(x+)] ln()+ln(4)+ln(5) (ln()+ln()+ln(4)) ln()+ln(5) ln(). (e) Again we use partial fractions. Ths time we have a repeated root, so we let x (x ) A (x ) + B x, () where A and B are constants we have to find. Multiplying both sides of () by (x ) we obtain x A+B(x ) x Bx+(A B). Comparing the coefficients of x we obtain B and comparing the constant terms we obtain A B. Since B, this means that A as well. x (x ) dx (x ) + x dx x +ln(x )+c ln(x ) x +c. Note the substitution u x will also work for the term here. (x ) (f) Again we use partial fractions. Ths time we have a quadratic term in the denominator which doesn t factorise, so we let x +6x+4 (x +x+)(x+) Ax+B x +x+ + C x+, (4) where A, B and C are constants we have to find. Multiplying both sides of (4) by (x +x+)(x+) we obtain x +6x+4 (Ax+B)(x+)+C(x +x+) x +6x+4 Ax +Ax+Bx+B +Cx +Cx+C x +6x+4 (A+C)x +(A+B +C)+B +C. (5) Comparing coefficients of powers of x in (5), we get the simultaneous equations A+C, A+B +C 6 and B +C 4. 5
16 Subtracting the third of these from the second yields A. Then substituting A in to the first gives C and finally substitution C into the third gives B. Note if you can spot these manipuations, you can always do a formal row reduction. x +6x+4 (x +x+)(x+) dx x+ x +x+ + x+ dx ln ( x +x+ ) +ln(x+) ] ln(5)+ln() (ln()+ln()) ln(5). Note that if you can t spot the integral of the use the substitution u x +x+. x+ term then you can x +x+ 6. (a) The graph of f(x) x 7 lies below the x-axis between x and x and above the x-axis between x and x. Thus the required area is ] ] x 7 dx+ x 7 dx 8 x8 + 8 x8 ( 8 ) ( ) ()8 + 8 (8 ) (b) Thegraphoff(x) cos(x)lies belowthex-axis between the pointsx π and x π 6 and above the x-axis between the points π and. Thus the 6 required area is π 6 π cos(x)dx+ (. π 6 ] π 6 cos(x) dx ] sin(x) + sin(x) π π 6 ( sin π ) ) ( sin( π) + sin() ( sin π ) ) ( () ) ( () + () ) () (c) The graph of f(x) e x lies above the x-axis everyhere. Thus the required area is ] e x dx ex e e (e e ). 6
17 (d) Since f() and the graph of f(x) x x x + only crosses the x-axis at x between the points x and x, it follows that the graph of f(x) x x x + lies below the x-axis between the points x and x and above the x-axis between the points x and x (since f() > it is above the x-axis at x ). the required area is x x x+dx+ 4 x4 x x +x 4 +. x x x+dx ] ( x4 x x +x )] + b 7. In all these questions we will use the formula V π f(x) dx. a (a) The volume is (b) The volume is (c) The volume is π π π π (x ) dx π ] x 4 dx π 5 x5 5 π. ( ) π sin(x) dx π sin(x) dx π cos(x)] π π cos(π) ( cos())] π( () ()) π. ( ) e x dx π e x dx π ] e x ( π e ( )) e ( π ( e )) π ( ) e. ] ( 4 + )] 7
18 (d) The volume is π π π sin (x)dx π + cos(x)dx π x+ ] π 4 sin(x) ( π π + (+ 4 sin(π) 4 )) sin() ( π ) π + (+) π. 8
Math 181, Exam 1, Study Guide 2 Problem 1 Solution. =[17ln 5 +3(5)] [17 ln 1 +3(1)] =17ln = 17ln5+12
![Math 181, Exam 1, Study Guide 2 Problem 1 Solution. =[17ln 5 +3(5)] [17 ln 1 +3(1)] =17ln = 17ln5+12 Math 181, Exam 1, Study Guide 2 Problem 1 Solution. =[17ln 5 +3(5)] [17 ln 1 +3(1)] =17ln = 17ln5+12](/thumbs/83/87603917.jpg) Math 8, Exam, Study Guide Problem Solution. Compute the definite integral: 5 ( ) 7 x +3 dx Solution: UsingtheFundamentalTheoremofCalculusPartI,thevalueof the integral is: 5 ( ) 7 [ ] 5 x +3 dx = 7 ln x
Math 8, Exam, Study Guide Problem Solution. Compute the definite integral: 5 ( ) 7 x +3 dx Solution: UsingtheFundamentalTheoremofCalculusPartI,thevalueof the integral is: 5 ( ) 7 [ ] 5 x +3 dx = 7 ln x
Integration 1/10. Integration. Student Guidance Centre Learning Development Service
 Integration / Integration Student Guidance Centre Learning Development Service lds@qub.ac.uk Integration / Contents Introduction. Indefinite Integration....................... Definite Integration.......................
Integration / Integration Student Guidance Centre Learning Development Service lds@qub.ac.uk Integration / Contents Introduction. Indefinite Integration....................... Definite Integration.......................
Section 5.5 More Integration Formula (The Substitution Method) 2 Lectures. Dr. Abdulla Eid. College of Science. MATHS 101: Calculus I
 Section 5.5 More Integration Formula (The Substitution Method) 2 Lectures College of Science MATHS : Calculus I (University of Bahrain) Integrals / 7 The Substitution Method Idea: To replace a relatively
Section 5.5 More Integration Formula (The Substitution Method) 2 Lectures College of Science MATHS : Calculus I (University of Bahrain) Integrals / 7 The Substitution Method Idea: To replace a relatively
Final Exam Review Quesitons
 Final Exam Review Quesitons. Compute the following integrals. (a) x x 4 (x ) (x + 4) dx. The appropriate partial fraction form is which simplifies to x x 4 (x ) (x + 4) = A x + B (x ) + C x + 4 + Dx x
Final Exam Review Quesitons. Compute the following integrals. (a) x x 4 (x ) (x + 4) dx. The appropriate partial fraction form is which simplifies to x x 4 (x ) (x + 4) = A x + B (x ) + C x + 4 + Dx x
Grade: The remainder of this page has been left blank for your workings. VERSION D. Midterm D: Page 1 of 12
 First Name: Student-No: Last Name: Section: Grade: The remainder of this page has been left blank for your workings. Midterm D: Page of 2 Indefinite Integrals. 9 marks Each part is worth marks. Please
First Name: Student-No: Last Name: Section: Grade: The remainder of this page has been left blank for your workings. Midterm D: Page of 2 Indefinite Integrals. 9 marks Each part is worth marks. Please
MATH 250 TOPIC 13 INTEGRATION. 13B. Constant, Sum, and Difference Rules
 Math 5 Integration Topic 3 Page MATH 5 TOPIC 3 INTEGRATION 3A. Integration of Common Functions Practice Problems 3B. Constant, Sum, and Difference Rules Practice Problems 3C. Substitution Practice Problems
Math 5 Integration Topic 3 Page MATH 5 TOPIC 3 INTEGRATION 3A. Integration of Common Functions Practice Problems 3B. Constant, Sum, and Difference Rules Practice Problems 3C. Substitution Practice Problems
7.1 Integration by Parts (...or, undoing the product rule.)
 7.1 1 7.1 Integration by Parts (...or, undoing the product rule.) Integration by Parts Recall the differential form of the chain rule. If u and v are differentiable functions. Then (1) d(uv) = du v +u
7.1 1 7.1 Integration by Parts (...or, undoing the product rule.) Integration by Parts Recall the differential form of the chain rule. If u and v are differentiable functions. Then (1) d(uv) = du v +u
Techniques of Integration
 0 Techniques of Integration ½¼º½ ÈÓÛ Ö Ó Ò Ò Ó Ò Functions consisting of products of the sine and cosine can be integrated by using substitution and trigonometric identities. These can sometimes be tedious,
0 Techniques of Integration ½¼º½ ÈÓÛ Ö Ó Ò Ò Ó Ò Functions consisting of products of the sine and cosine can be integrated by using substitution and trigonometric identities. These can sometimes be tedious,
MAT 132 Midterm 1 Spring 2017
 MAT Midterm Spring 7 Name: ID: Problem 5 6 7 8 Total ( pts) ( pts) ( pts) ( pts) ( pts) ( pts) (5 pts) (5 pts) ( pts) Score Instructions: () Fill in your name and Stony Brook ID number at the top of this
MAT Midterm Spring 7 Name: ID: Problem 5 6 7 8 Total ( pts) ( pts) ( pts) ( pts) ( pts) ( pts) (5 pts) (5 pts) ( pts) Score Instructions: () Fill in your name and Stony Brook ID number at the top of this
Math 250 Skills Assessment Test
 Math 5 Skills Assessment Test Page Math 5 Skills Assessment Test The purpose of this test is purely diagnostic (before beginning your review, it will be helpful to assess both strengths and weaknesses).
Math 5 Skills Assessment Test Page Math 5 Skills Assessment Test The purpose of this test is purely diagnostic (before beginning your review, it will be helpful to assess both strengths and weaknesses).
Grade: The remainder of this page has been left blank for your workings. VERSION E. Midterm E: Page 1 of 12
 First Name: Student-No: Last Name: Section: Grade: The remainder of this page has been left blank for your workings. Midterm E: Page of Indefinite Integrals. 9 marks Each part is worth 3 marks. Please
First Name: Student-No: Last Name: Section: Grade: The remainder of this page has been left blank for your workings. Midterm E: Page of Indefinite Integrals. 9 marks Each part is worth 3 marks. Please
Techniques of Integration
 8 Techniques of Integration Over the next few sections we examine some techniques that are frequently successful when seeking antiderivatives of functions. Sometimes this is a simple problem, since it
8 Techniques of Integration Over the next few sections we examine some techniques that are frequently successful when seeking antiderivatives of functions. Sometimes this is a simple problem, since it
Math 226 Calculus Spring 2016 Exam 2V1
 Math 6 Calculus Spring 6 Exam V () (35 Points) Evaluate the following integrals. (a) (7 Points) tan 5 (x) sec 3 (x) dx (b) (8 Points) cos 4 (x) dx Math 6 Calculus Spring 6 Exam V () (Continued) Evaluate
Math 6 Calculus Spring 6 Exam V () (35 Points) Evaluate the following integrals. (a) (7 Points) tan 5 (x) sec 3 (x) dx (b) (8 Points) cos 4 (x) dx Math 6 Calculus Spring 6 Exam V () (Continued) Evaluate
Solutions to Tutorial Sheet 12 Topics: Integration by Substitution + Integration by the Method of Partial Fractions + Applications to Geometry
 The University of Sydney School of Mathematics and Statistics Solutions to Tutorial Sheet Topics: Integration by Substitution + Integration by the Method of Partial Fractions + Applications to Geometry
The University of Sydney School of Mathematics and Statistics Solutions to Tutorial Sheet Topics: Integration by Substitution + Integration by the Method of Partial Fractions + Applications to Geometry
Chapter 7 Notes, Stewart 7e. 7.1 Integration by Parts Trigonometric Integrals Evaluating sin m xcos n (x)dx...
 Contents 7.1 Integration by Parts........................................ 2 7.2 Trigonometric Integrals...................................... 8 7.2.1 Evaluating sin m xcos n (x)dx..............................
Contents 7.1 Integration by Parts........................................ 2 7.2 Trigonometric Integrals...................................... 8 7.2.1 Evaluating sin m xcos n (x)dx..............................
Math 180, Final Exam, Fall 2012 Problem 1 Solution
 Math 80, Final Exam, Fall 0 Problem Solution. Find the derivatives of the following functions: (a) ln(ln(x)) (b) x 6 + sin(x) e x (c) tan(x ) + cot(x ) (a) We evaluate the derivative using the Chain Rule.
Math 80, Final Exam, Fall 0 Problem Solution. Find the derivatives of the following functions: (a) ln(ln(x)) (b) x 6 + sin(x) e x (c) tan(x ) + cot(x ) (a) We evaluate the derivative using the Chain Rule.
If y = f (u) is a differentiable function of u and u = g(x) is a differentiable function of x then dy dx = dy. du du. If y = f (u) then y = f (u) u
 Section 3 4B The Chain Rule If y = f (u) is a differentiable function of u and u = g(x) is a differentiable function of x then dy dx = dy du du dx or If y = f (u) then f (u) u The Chain Rule with the Power
Section 3 4B The Chain Rule If y = f (u) is a differentiable function of u and u = g(x) is a differentiable function of x then dy dx = dy du du dx or If y = f (u) then f (u) u The Chain Rule with the Power
Change of Variables: Indefinite Integrals
 Change of Variables: Indefinite Integrals Mathematics 11: Lecture 39 Dan Sloughter Furman University November 29, 2007 Dan Sloughter (Furman University) Change of Variables: Indefinite Integrals November
Change of Variables: Indefinite Integrals Mathematics 11: Lecture 39 Dan Sloughter Furman University November 29, 2007 Dan Sloughter (Furman University) Change of Variables: Indefinite Integrals November
If y = f (u) is a differentiable function of u and u = g(x) is a differentiable function of x then dy dx = dy. du du. If y = f (u) then y = f (u) u
 Section 3 4B Lecture The Chain Rule If y = f (u) is a differentiable function of u and u = g(x) is a differentiable function of x then dy dx = dy du du dx or If y = f (u) then y = f (u) u The Chain Rule
Section 3 4B Lecture The Chain Rule If y = f (u) is a differentiable function of u and u = g(x) is a differentiable function of x then dy dx = dy du du dx or If y = f (u) then y = f (u) u The Chain Rule
Integration by parts Integration by parts is a direct reversal of the product rule. By integrating both sides, we get:
 Integration by parts Integration by parts is a direct reversal of the proct rule. By integrating both sides, we get: u dv dx x n sin mx dx (make u = x n ) dx = uv v dx dx When to use integration by parts
Integration by parts Integration by parts is a direct reversal of the proct rule. By integrating both sides, we get: u dv dx x n sin mx dx (make u = x n ) dx = uv v dx dx When to use integration by parts
2.4 THE CHAIN RULE THE CHAIN RULE
 1 2.4 THE CHAIN RULE The Chain Rule is the most important and most used of the differentiation patterns. It enables us to differentiate composites of functions such as y = sin( x 2 ). It is a powerful
1 2.4 THE CHAIN RULE The Chain Rule is the most important and most used of the differentiation patterns. It enables us to differentiate composites of functions such as y = sin( x 2 ). It is a powerful
4. Theory of the Integral
 4. Theory of the Integral 4.1 Antidifferentiation 4.2 The Definite Integral 4.3 Riemann Sums 4.4 The Fundamental Theorem of Calculus 4.5 Fundamental Integration Rules 4.6 U-Substitutions 4.1 Antidifferentiation
4. Theory of the Integral 4.1 Antidifferentiation 4.2 The Definite Integral 4.3 Riemann Sums 4.4 The Fundamental Theorem of Calculus 4.5 Fundamental Integration Rules 4.6 U-Substitutions 4.1 Antidifferentiation
MathsGeeks. Everything You Need to Know A Level Edexcel C4. March 2014 MathsGeeks Copyright 2014 Elite Learning Limited
 Everything You Need to Know A Level Edexcel C4 March 4 Copyright 4 Elite Learning Limited Page of 4 Further Binomial Expansion: Make sure it starts with a e.g. for ( x) ( x ) then use ( + x) n + nx + n(n
Everything You Need to Know A Level Edexcel C4 March 4 Copyright 4 Elite Learning Limited Page of 4 Further Binomial Expansion: Make sure it starts with a e.g. for ( x) ( x ) then use ( + x) n + nx + n(n
Math Final Exam Review
 Math - Final Exam Review. Find dx x + 6x +. Name: Solution: We complete the square to see if this function has a nice form. Note we have: x + 6x + (x + + dx x + 6x + dx (x + + Note that this looks a lot
Math - Final Exam Review. Find dx x + 6x +. Name: Solution: We complete the square to see if this function has a nice form. Note we have: x + 6x + (x + + dx x + 6x + dx (x + + Note that this looks a lot
Note: Final Exam is at 10:45 on Tuesday, 5/3/11 (This is the Final Exam time reserved for our labs). From Practice Test I
 MA Practice Final Answers in Red 4/8/ and 4/9/ Name Note: Final Exam is at :45 on Tuesday, 5// (This is the Final Exam time reserved for our labs). From Practice Test I Consider the integral 5 x dx. Sketch
MA Practice Final Answers in Red 4/8/ and 4/9/ Name Note: Final Exam is at :45 on Tuesday, 5// (This is the Final Exam time reserved for our labs). From Practice Test I Consider the integral 5 x dx. Sketch
Practice Exam I. Summer Term I Kostadinov. MA124 Calculus II Boston University
 student: Practice Exam I Problem 1: Find the derivative of the functions T 1 (x), T 2 (x), T 3 (x). State the reason of your answers. a) T 1 (x) = x 2t dt 2 b) T 2 (x) = e x ln(t2 )dt c) T 3 (x) = x 2
student: Practice Exam I Problem 1: Find the derivative of the functions T 1 (x), T 2 (x), T 3 (x). State the reason of your answers. a) T 1 (x) = x 2t dt 2 b) T 2 (x) = e x ln(t2 )dt c) T 3 (x) = x 2
Example. Evaluate. 3x 2 4 x dx.
 3x 2 4 x 3 + 4 dx. Solution: We need a new technique to integrate this function. Notice that if we let u x 3 + 4, and we compute the differential du of u, we get: du 3x 2 dx Going back to our integral,
3x 2 4 x 3 + 4 dx. Solution: We need a new technique to integrate this function. Notice that if we let u x 3 + 4, and we compute the differential du of u, we get: du 3x 2 dx Going back to our integral,
Techniques of Integration
 0 Techniques of Integration ½¼º½ ÈÓÛ Ö Ó Ò Ò Ó Ò Functions consisting of products of the sine and cosine can be integrated by using substitution and trigonometric identities. These can sometimes be tedious,
0 Techniques of Integration ½¼º½ ÈÓÛ Ö Ó Ò Ò Ó Ò Functions consisting of products of the sine and cosine can be integrated by using substitution and trigonometric identities. These can sometimes be tedious,
Solutions to Exam 2, Math 10560
 Solutions to Exam, Math 6. Which of the following expressions gives the partial fraction decomposition of the function x + x + f(x = (x (x (x +? Solution: Notice that (x is not an irreducile factor. If
Solutions to Exam, Math 6. Which of the following expressions gives the partial fraction decomposition of the function x + x + f(x = (x (x (x +? Solution: Notice that (x is not an irreducile factor. If
APPENDIX : PARTIAL FRACTIONS
 APPENDIX : PARTIAL FRACTIONS Appendix : Partial Fractions Given the expression x 2 and asked to find its integral, x + you can use work from Section. to give x 2 =ln( x 2) ln( x + )+c x + = ln k x 2 x+
APPENDIX : PARTIAL FRACTIONS Appendix : Partial Fractions Given the expression x 2 and asked to find its integral, x + you can use work from Section. to give x 2 =ln( x 2) ln( x + )+c x + = ln k x 2 x+
The goal of today is to determine what u-substitution to use for trigonometric integrals. The most common substitutions are the following:
 Trigonometric Integrals The goal of today is to determine what u-substitution to use for trigonometric integrals. The most common substitutions are the following: Substitution u sinx u cosx u tanx u secx
Trigonometric Integrals The goal of today is to determine what u-substitution to use for trigonometric integrals. The most common substitutions are the following: Substitution u sinx u cosx u tanx u secx
Assignment # 8, Math 370, Fall 2018 SOLUTIONS:
 Assignment # 8, Math 370, Fall 018 SOLUTIONS: Problem 1: Solve the equations (a) y y = 3x + x 4, (i) y(0) = 1, y (0) = 1, y (0) = 1. Characteristic equation: α 3 α = 0 so α 1, = 0 and α 3 =. y c = C 1
Assignment # 8, Math 370, Fall 018 SOLUTIONS: Problem 1: Solve the equations (a) y y = 3x + x 4, (i) y(0) = 1, y (0) = 1, y (0) = 1. Characteristic equation: α 3 α = 0 so α 1, = 0 and α 3 =. y c = C 1
Practice Problems: Integration by Parts
 Practice Problems: Integration by Parts Answers. (a) Neither term will get simpler through differentiation, so let s try some choice for u and dv, and see how it works out (we can always go back and try
Practice Problems: Integration by Parts Answers. (a) Neither term will get simpler through differentiation, so let s try some choice for u and dv, and see how it works out (we can always go back and try
M GENERAL MATHEMATICS -2- Dr. Tariq A. AlFadhel 1 Solution of the First Mid-Term Exam First semester H
 M 4 - GENERAL MATHEMATICS -- Dr. Tariq A. AlFadhel Solution of the First Mid-Term Exam First semester 435-436 H Q. Let A ( ) 4 and B 3 3 Compute (if possible) : AB and BA ( ) 4 AB 3 3 ( ) ( ) ++ 4+4+ 4
M 4 - GENERAL MATHEMATICS -- Dr. Tariq A. AlFadhel Solution of the First Mid-Term Exam First semester 435-436 H Q. Let A ( ) 4 and B 3 3 Compute (if possible) : AB and BA ( ) 4 AB 3 3 ( ) ( ) ++ 4+4+ 4
REVERSE CHAIN RULE CALCULUS 7. Dr Adrian Jannetta MIMA CMath FRAS INU0115/515 (MATHS 2) Reverse Chain Rule 1/12 Adrian Jannetta
 REVERSE CHAIN RULE CALCULUS 7 INU05/55 (MATHS 2) Dr Adrian Jannetta MIMA CMath FRAS Reverse Chain Rule /2 Adrian Jannetta Reversing the chain rule In differentiation the chain rule is used to get the derivative
REVERSE CHAIN RULE CALCULUS 7 INU05/55 (MATHS 2) Dr Adrian Jannetta MIMA CMath FRAS Reverse Chain Rule /2 Adrian Jannetta Reversing the chain rule In differentiation the chain rule is used to get the derivative
HOMEWORK SOLUTIONS MATH 1910 Sections 8.2, 8.3, 8.5 Fall 2016
 HOMEWORK SOLUTIONS MATH 191 Sections 8., 8., 8.5 Fall 16 Problem 8..19 Evaluate using methods similar to those that apply to integral tan m xsec n x. cot x SOLUTION. Using the reduction formula for cot
HOMEWORK SOLUTIONS MATH 191 Sections 8., 8., 8.5 Fall 16 Problem 8..19 Evaluate using methods similar to those that apply to integral tan m xsec n x. cot x SOLUTION. Using the reduction formula for cot
Calculus II - Fall 2013
 Calculus II - Fall Midterm Exam II, November, In the following problems you are required to show all your work and provide the necessary explanations everywhere to get full credit.. Find the area between
Calculus II - Fall Midterm Exam II, November, In the following problems you are required to show all your work and provide the necessary explanations everywhere to get full credit.. Find the area between
SOLUTIONS FOR PRACTICE FINAL EXAM
 SOLUTIONS FOR PRACTICE FINAL EXAM ANDREW J. BLUMBERG. Solutions () Short answer questions: (a) State the mean value theorem. Proof. The mean value theorem says that if f is continuous on (a, b) and differentiable
SOLUTIONS FOR PRACTICE FINAL EXAM ANDREW J. BLUMBERG. Solutions () Short answer questions: (a) State the mean value theorem. Proof. The mean value theorem says that if f is continuous on (a, b) and differentiable
Integration by Parts
 Calculus 2 Lia Vas Integration by Parts Using integration by parts one transforms an integral of a product of two functions into a simpler integral. Divide the initial function into two parts called u
Calculus 2 Lia Vas Integration by Parts Using integration by parts one transforms an integral of a product of two functions into a simpler integral. Divide the initial function into two parts called u
Math 106 Fall 2014 Exam 2.1 October 31, ln(x) x 3 dx = 1. 2 x 2 ln(x) + = 1 2 x 2 ln(x) + 1. = 1 2 x 2 ln(x) 1 4 x 2 + C
 Math 6 Fall 4 Exam. October 3, 4. The following questions have to do with the integral (a) Evaluate dx. Use integration by parts (x 3 dx = ) ( dx = ) x3 x dx = x x () dx = x + x x dx = x + x 3 dx dx =
Math 6 Fall 4 Exam. October 3, 4. The following questions have to do with the integral (a) Evaluate dx. Use integration by parts (x 3 dx = ) ( dx = ) x3 x dx = x x () dx = x + x x dx = x + x 3 dx dx =
Calculus II. George Voutsadakis 1. LSSU Math 152. Lake Superior State University. 1 Mathematics and Computer Science
 Calculus II George Voutsadakis Mathematics and Computer Science Lake Superior State University LSSU Math 52 George Voutsadakis (LSSU) Calculus II February 205 / 88 Outline Techniques of Integration Integration
Calculus II George Voutsadakis Mathematics and Computer Science Lake Superior State University LSSU Math 52 George Voutsadakis (LSSU) Calculus II February 205 / 88 Outline Techniques of Integration Integration
Math 142, Final Exam, Fall 2006, Solutions
 Math 4, Final Exam, Fall 6, Solutions There are problems. Each problem is worth points. SHOW your wor. Mae your wor be coherent and clear. Write in complete sentences whenever this is possible. CIRCLE
Math 4, Final Exam, Fall 6, Solutions There are problems. Each problem is worth points. SHOW your wor. Mae your wor be coherent and clear. Write in complete sentences whenever this is possible. CIRCLE
Math 42: Fall 2015 Midterm 2 November 3, 2015
 Math 4: Fall 5 Midterm November 3, 5 NAME: Solutions Time: 8 minutes For each problem, you should write down all of your work carefully and legibly to receive full credit When asked to justify your answer,
Math 4: Fall 5 Midterm November 3, 5 NAME: Solutions Time: 8 minutes For each problem, you should write down all of your work carefully and legibly to receive full credit When asked to justify your answer,
Differentiation Review, Part 1 (Part 2 follows; there are answers at the end of each part.)
 Differentiation Review 1 Name Differentiation Review, Part 1 (Part 2 follows; there are answers at the end of each part.) Derivatives Review: Summary of Rules Each derivative rule is summarized for you
Differentiation Review 1 Name Differentiation Review, Part 1 (Part 2 follows; there are answers at the end of each part.) Derivatives Review: Summary of Rules Each derivative rule is summarized for you
Math 226 Calculus Spring 2016 Practice Exam 1. (1) (10 Points) Let the differentiable function y = f(x) have inverse function x = f 1 (y).
 Math 6 Calculus Spring 016 Practice Exam 1 1) 10 Points) Let the differentiable function y = fx) have inverse function x = f 1 y). a) Write down the formula relating the derivatives f x) and f 1 ) y).
Math 6 Calculus Spring 016 Practice Exam 1 1) 10 Points) Let the differentiable function y = fx) have inverse function x = f 1 y). a) Write down the formula relating the derivatives f x) and f 1 ) y).
Solutions to Math 41 Final Exam December 10, 2012
 Solutions to Math 4 Final Exam December,. ( points) Find each of the following limits, with justification. If there is an infinite limit, then explain whether it is or. x ln(t + ) dt (a) lim x x (5 points)
Solutions to Math 4 Final Exam December,. ( points) Find each of the following limits, with justification. If there is an infinite limit, then explain whether it is or. x ln(t + ) dt (a) lim x x (5 points)
Chapter 6. Techniques of Integration. 6.1 Differential notation
 Chapter 6 Techniques of Integration In this chapter, we expand our repertoire for antiderivatives beyond the elementary functions discussed so far. A review of the table of elementary antiderivatives (found
Chapter 6 Techniques of Integration In this chapter, we expand our repertoire for antiderivatives beyond the elementary functions discussed so far. A review of the table of elementary antiderivatives (found
Integrated Calculus II Exam 1 Solutions 2/6/4
 Integrated Calculus II Exam Solutions /6/ Question Determine the following integrals: te t dt. We integrate by parts: u = t, du = dt, dv = e t dt, v = dv = e t dt = e t, te t dt = udv = uv vdu = te t (
Integrated Calculus II Exam Solutions /6/ Question Determine the following integrals: te t dt. We integrate by parts: u = t, du = dt, dv = e t dt, v = dv = e t dt = e t, te t dt = udv = uv vdu = te t (
Math 106: Review for Exam II - SOLUTIONS
 Math 6: Review for Exam II - SOLUTIONS INTEGRATION TIPS Substitution: usually let u a function that s inside another function, especially if du (possibly off by a multiplying constant) is also present
Math 6: Review for Exam II - SOLUTIONS INTEGRATION TIPS Substitution: usually let u a function that s inside another function, especially if du (possibly off by a multiplying constant) is also present
Assignment 6 Solution. Please do not copy and paste my answer. You will get similar questions but with different numbers!
 Assignment 6 Solution Please do not copy and paste my answer. You will get similar questions but with different numbers! This question tests you the following points: Integration by Parts: Let u = x, dv
Assignment 6 Solution Please do not copy and paste my answer. You will get similar questions but with different numbers! This question tests you the following points: Integration by Parts: Let u = x, dv
Ma 530 Power Series II
 Ma 530 Power Series II Please note that there is material on power series at Visual Calculus. Some of this material was used as part of the presentation of the topics that follow. Operations on Power Series
Ma 530 Power Series II Please note that there is material on power series at Visual Calculus. Some of this material was used as part of the presentation of the topics that follow. Operations on Power Series
b n x n + b n 1 x n b 1 x + b 0
 Math Partial Fractions Stewart 7.4 Integrating basic rational functions. For a function f(x), we have examined several algebraic methods for finding its indefinite integral (antiderivative) F (x) = f(x)
Math Partial Fractions Stewart 7.4 Integrating basic rational functions. For a function f(x), we have examined several algebraic methods for finding its indefinite integral (antiderivative) F (x) = f(x)
Solutions to Exam 1, Math Solution. Because f(x) is one-to-one, we know the inverse function exists. Recall that (f 1 ) (a) =
 Solutions to Exam, Math 56 The function f(x) e x + x 3 + x is one-to-one (there is no need to check this) What is (f ) ( + e )? Solution Because f(x) is one-to-one, we know the inverse function exists
Solutions to Exam, Math 56 The function f(x) e x + x 3 + x is one-to-one (there is no need to check this) What is (f ) ( + e )? Solution Because f(x) is one-to-one, we know the inverse function exists
Chapter 6. Techniques of Integration. 6.1 Differential notation
 Chapter 6 Techniques of Integration In this chapter, we expand our repertoire for antiderivatives beyond the elementary functions discussed so far. A review of the table of elementary antiderivatives (found
Chapter 6 Techniques of Integration In this chapter, we expand our repertoire for antiderivatives beyond the elementary functions discussed so far. A review of the table of elementary antiderivatives (found
The Substitution Rule
 The Sbstittion Rle Kiryl Tsishchanka THEOREM The Fndamental Theorem Of Calcls, Part II): If f is continos on [a,b], then where F is any antiderivative of f, that is F f. b a ] b fx)dx Fb) Fa) Fx) a NOTATION:
The Sbstittion Rle Kiryl Tsishchanka THEOREM The Fndamental Theorem Of Calcls, Part II): If f is continos on [a,b], then where F is any antiderivative of f, that is F f. b a ] b fx)dx Fb) Fa) Fx) a NOTATION:
MATH 162. Midterm Exam 1 - Solutions February 22, 2007
 MATH 62 Midterm Exam - Solutions February 22, 27. (8 points) Evaluate the following integrals: (a) x sin(x 4 + 7) dx Solution: Let u = x 4 + 7, then du = 4x dx and x sin(x 4 + 7) dx = 4 sin(u) du = 4 [
MATH 62 Midterm Exam - Solutions February 22, 27. (8 points) Evaluate the following integrals: (a) x sin(x 4 + 7) dx Solution: Let u = x 4 + 7, then du = 4x dx and x sin(x 4 + 7) dx = 4 sin(u) du = 4 [
Solution: As x approaches 3, (x 2) approaches 1, so ln(x 2) approaches ln(1) = 0. Therefore we have a limit of the form 0/0 and can apply the.
 MATH, solutions to practice problems for the final eam. Compute the it: a) 3 e / Answer: e /3. b) 3 ln( 3) Answer:. c) 3 ln( ) 3 Solution: As approaches 3, ( ) approaches, so ln( ) approaches ln() =. Therefore
MATH, solutions to practice problems for the final eam. Compute the it: a) 3 e / Answer: e /3. b) 3 ln( 3) Answer:. c) 3 ln( ) 3 Solution: As approaches 3, ( ) approaches, so ln( ) approaches ln() =. Therefore
Chapter 3. Integration. 3.1 Indefinite Integration
 Chapter 3 Integration 3. Indefinite Integration Integration is the reverse of differentiation. Consider a function f(x) and suppose that there exists another function F (x) such that df f(x). (3.) For
Chapter 3 Integration 3. Indefinite Integration Integration is the reverse of differentiation. Consider a function f(x) and suppose that there exists another function F (x) such that df f(x). (3.) For
Section 4.4. Using the Fundamental Theorem. Difference Equations to Differential Equations
 Difference Equations to Differential Equations Section 4.4 Using the Fundamental Theorem As we saw in Section 4.3, using the Fundamental Theorem of Integral Calculus reduces the problem of evaluating a
Difference Equations to Differential Equations Section 4.4 Using the Fundamental Theorem As we saw in Section 4.3, using the Fundamental Theorem of Integral Calculus reduces the problem of evaluating a
Math 10C - Fall Final Exam
 Math 1C - Fall 217 - Final Exam Problem 1. Consider the function f(x, y) = 1 x 2 (y 1) 2. (i) Draw the level curve through the point P (1, 2). Find the gradient of f at the point P and draw the gradient
Math 1C - Fall 217 - Final Exam Problem 1. Consider the function f(x, y) = 1 x 2 (y 1) 2. (i) Draw the level curve through the point P (1, 2). Find the gradient of f at the point P and draw the gradient
The 2014 Integration Bee Solutions and comments. Mike Hirschhorn. u 4 du = 1 5 u5 +C = 1 5 (x3 1) 5 +C cosx dx = 1 2 x 1 2 sinx+c.
 The Integration Bee Solutions and comments Qualifying Round Mike Hirschhorn. x x dx u du 5 u5 +C 5 x 5 +C.. 5 x ] x dx 5 x.. sin x dx cosx dx x sinx+c.. a +x dx a tan x +C. a 5. x x+ dx 7 x+ dx x 7 log
The Integration Bee Solutions and comments Qualifying Round Mike Hirschhorn. x x dx u du 5 u5 +C 5 x 5 +C.. 5 x ] x dx 5 x.. sin x dx cosx dx x sinx+c.. a +x dx a tan x +C. a 5. x x+ dx 7 x+ dx x 7 log
Review Problems for the Final
 Review Problems for the Final Math -3 5 7 These problems are provided to help you study. The presence of a problem on this handout does not imply that there will be a similar problem on the test. And the
Review Problems for the Final Math -3 5 7 These problems are provided to help you study. The presence of a problem on this handout does not imply that there will be a similar problem on the test. And the
Math 131 Final Exam Spring 2016
 Math 3 Final Exam Spring 06 Name: ID: multiple choice questions worth 5 points each. Exam is only out of 00 (so there is the possibility of getting more than 00%) Exam covers sections. through 5.4 No graphing
Math 3 Final Exam Spring 06 Name: ID: multiple choice questions worth 5 points each. Exam is only out of 00 (so there is the possibility of getting more than 00%) Exam covers sections. through 5.4 No graphing
Examples. 1. (Solution) (a) Suppose f is an increasing function, and let A(x) = x
 Math 31A Final Exam Practice Problems Austin Christian December 1, 15 Here are some practice problems for the final. You ll notice that these problems all come from material since the last exam. You are,
Math 31A Final Exam Practice Problems Austin Christian December 1, 15 Here are some practice problems for the final. You ll notice that these problems all come from material since the last exam. You are,
CALCULUS ASSESSMENT REVIEW
 CALCULUS ASSESSMENT REVIEW DEPARTMENT OF MATHEMATICS CHRISTOPHER NEWPORT UNIVERSITY 1. Introduction and Topics The purpose of these notes is to give an idea of what to expect on the Calculus Readiness
CALCULUS ASSESSMENT REVIEW DEPARTMENT OF MATHEMATICS CHRISTOPHER NEWPORT UNIVERSITY 1. Introduction and Topics The purpose of these notes is to give an idea of what to expect on the Calculus Readiness
Classroom Voting Questions: Calculus II
 Classroom Voting Questions: Calculus II Section 5.1: How Do We Measure Distance Traveled? 1. True or False The left-sum always underestimates the area under the curve. 2. True or False Averaging the left
Classroom Voting Questions: Calculus II Section 5.1: How Do We Measure Distance Traveled? 1. True or False The left-sum always underestimates the area under the curve. 2. True or False Averaging the left
Math 180, Exam 2, Practice Fall 2009 Problem 1 Solution. f(x) = arcsin(2x + 1) = sin 1 (3x + 1), lnx
 Math 80, Exam, Practice Fall 009 Problem Solution. Differentiate the functions: (do not simplify) f(x) = x ln(x + ), f(x) = xe x f(x) = arcsin(x + ) = sin (3x + ), f(x) = e3x lnx Solution: For the first
Math 80, Exam, Practice Fall 009 Problem Solution. Differentiate the functions: (do not simplify) f(x) = x ln(x + ), f(x) = xe x f(x) = arcsin(x + ) = sin (3x + ), f(x) = e3x lnx Solution: For the first
MATH 151, FALL SEMESTER 2011 COMMON EXAMINATION 3 - VERSION B - SOLUTIONS
 Name (print): Signature: MATH 5, FALL SEMESTER 0 COMMON EXAMINATION - VERSION B - SOLUTIONS Instructor s name: Section No: Part Multiple Choice ( questions, points each, No Calculators) Write your name,
Name (print): Signature: MATH 5, FALL SEMESTER 0 COMMON EXAMINATION - VERSION B - SOLUTIONS Instructor s name: Section No: Part Multiple Choice ( questions, points each, No Calculators) Write your name,
1.4 Techniques of Integration
 .4 Techniques of Integration Recall the following strategy for evaluating definite integrals, which arose from the Fundamental Theorem of Calculus (see Section.3). To calculate b a f(x) dx. Find a function
.4 Techniques of Integration Recall the following strategy for evaluating definite integrals, which arose from the Fundamental Theorem of Calculus (see Section.3). To calculate b a f(x) dx. Find a function
Exam 3 Solutions. Multiple Choice Questions
 MA 4 Exam 3 Solutions Fall 26 Exam 3 Solutions Multiple Choice Questions. The average value of the function f (x) = x + sin(x) on the interval [, 2π] is: A. 2π 2 2π B. π 2π 2 + 2π 4π 2 2π 4π 2 + 2π 2.
MA 4 Exam 3 Solutions Fall 26 Exam 3 Solutions Multiple Choice Questions. The average value of the function f (x) = x + sin(x) on the interval [, 2π] is: A. 2π 2 2π B. π 2π 2 + 2π 4π 2 2π 4π 2 + 2π 2.
Math 152 Take Home Test 1
 Math 5 Take Home Test Due Monday 5 th October (5 points) The following test will be done at home in order to ensure that it is a fair and representative reflection of your own ability in mathematics I
Math 5 Take Home Test Due Monday 5 th October (5 points) The following test will be done at home in order to ensure that it is a fair and representative reflection of your own ability in mathematics I
Math Reading assignment for Chapter 1: Study Sections 1.1 and 1.2.
 Math 3350 1 Chapter 1 Reading assignment for Chapter 1: Study Sections 1.1 and 1.2. 1.1 Material for Section 1.1 An Ordinary Differential Equation (ODE) is a relation between an independent variable x
Math 3350 1 Chapter 1 Reading assignment for Chapter 1: Study Sections 1.1 and 1.2. 1.1 Material for Section 1.1 An Ordinary Differential Equation (ODE) is a relation between an independent variable x
M GENERAL MATHEMATICS -2- Dr. Tariq A. AlFadhel 1 Solution of the First Mid-Term Exam First semester H
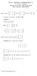 M - GENERAL MATHEMATICS -- Dr. Tariq A. AlFadhel Solution of the First Mid-Term Exam First semester 38-39 H 3 Q. Let A =, B = and C = 3 Compute (if possible) : A+B and BC A+B is impossible. ( ) BC = 3
M - GENERAL MATHEMATICS -- Dr. Tariq A. AlFadhel Solution of the First Mid-Term Exam First semester 38-39 H 3 Q. Let A =, B = and C = 3 Compute (if possible) : A+B and BC A+B is impossible. ( ) BC = 3
Chapter 13: Integrals
 Chapter : Integrals Chapter Overview: The Integral Calculus is essentially comprised of two operations. Interspersed throughout the chapters of this book has been the first of these operations the derivative.
Chapter : Integrals Chapter Overview: The Integral Calculus is essentially comprised of two operations. Interspersed throughout the chapters of this book has been the first of these operations the derivative.
5.5. The Substitution Rule
 INTEGRALS 5 INTEGRALS 5.5 The Substitution Rule In this section, we will learn: To substitute a new variable in place of an existing expression in a function, making integration easier. INTRODUCTION Due
INTEGRALS 5 INTEGRALS 5.5 The Substitution Rule In this section, we will learn: To substitute a new variable in place of an existing expression in a function, making integration easier. INTRODUCTION Due
y = x 3 and y = 2x 2 x. 2x 2 x = x 3 x 3 2x 2 + x = 0 x(x 2 2x + 1) = 0 x(x 1) 2 = 0 x = 0 and x = (x 3 (2x 2 x)) dx
 Millersville University Name Answer Key Mathematics Department MATH 2, Calculus II, Final Examination May 4, 2, 8:AM-:AM Please answer the following questions. Your answers will be evaluated on their correctness,
Millersville University Name Answer Key Mathematics Department MATH 2, Calculus II, Final Examination May 4, 2, 8:AM-:AM Please answer the following questions. Your answers will be evaluated on their correctness,
MATH 151 Engineering Mathematics I
 MATH 151 Engineering Mathematics I Fall 2017, WEEK 14 JoungDong Kim Week 14 Section 5.4, 5.5, 6.1, Indefinite Integrals and the Net Change Theorem, The Substitution Rule, Areas Between Curves. Section
MATH 151 Engineering Mathematics I Fall 2017, WEEK 14 JoungDong Kim Week 14 Section 5.4, 5.5, 6.1, Indefinite Integrals and the Net Change Theorem, The Substitution Rule, Areas Between Curves. Section
Math 181, Exam 2, Study Guide 2 Problem 1 Solution. 1 + dx. 1 + (cos x)2 dx. 1 + cos2 xdx. = π ( 1 + cos π 2
 Math 8, Exam, Study Guide Problem Solution. Use the trapezoid rule with n to estimate the arc-length of the curve y sin x between x and x π. Solution: The arclength is: L b a π π + ( ) dy + (cos x) + cos
Math 8, Exam, Study Guide Problem Solution. Use the trapezoid rule with n to estimate the arc-length of the curve y sin x between x and x π. Solution: The arclength is: L b a π π + ( ) dy + (cos x) + cos
THE NATIONAL UNIVERSITY OF IRELAND, CORK COLÁISTE NA hollscoile, CORCAIGH UNIVERSITY COLLEGE, CORK. Summer Examination 2009.
 OLLSCOIL NA héireann, CORCAIGH THE NATIONAL UNIVERSITY OF IRELAND, CORK COLÁISTE NA hollscoile, CORCAIGH UNIVERSITY COLLEGE, CORK Summer Examination 2009 First Engineering MA008 Calculus and Linear Algebra
OLLSCOIL NA héireann, CORCAIGH THE NATIONAL UNIVERSITY OF IRELAND, CORK COLÁISTE NA hollscoile, CORCAIGH UNIVERSITY COLLEGE, CORK Summer Examination 2009 First Engineering MA008 Calculus and Linear Algebra
t 2 + 2t dt = (t + 1) dt + 1 = arctan t x + 6 x(x 3)(x + 2) = A x +
 MATH 06 0 Practice Exam #. (0 points) Evaluate the following integrals: (a) (0 points). t +t+7 This is an irreducible quadratic; its denominator can thus be rephrased via completion of the square as a
MATH 06 0 Practice Exam #. (0 points) Evaluate the following integrals: (a) (0 points). t +t+7 This is an irreducible quadratic; its denominator can thus be rephrased via completion of the square as a
Spring 2015, MA 252, Calculus II, Final Exam Preview Solutions
 Spring 5, MA 5, Calculus II, Final Exam Preview Solutions I will put the following formulas on the front of the final exam, to speed up certain problems. You do not need to put them on your index card,
Spring 5, MA 5, Calculus II, Final Exam Preview Solutions I will put the following formulas on the front of the final exam, to speed up certain problems. You do not need to put them on your index card,
Final Exam SOLUTIONS MAT 131 Fall 2011
 1. Compute the following its. (a) Final Exam SOLUTIONS MAT 131 Fall 11 x + 1 x 1 x 1 The numerator is always positive, whereas the denominator is negative for numbers slightly smaller than 1. Also, as
1. Compute the following its. (a) Final Exam SOLUTIONS MAT 131 Fall 11 x + 1 x 1 x 1 The numerator is always positive, whereas the denominator is negative for numbers slightly smaller than 1. Also, as
MATH 1A - FINAL EXAM DELUXE - SOLUTIONS. x x x x x 2. = lim = 1 =0. 2) Then ln(y) = x 2 ln(x) 3) ln(x)
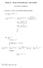 MATH A - FINAL EXAM DELUXE - SOLUTIONS PEYAM RYAN TABRIZIAN. ( points, 5 points each) Find the following limits (a) lim x x2 + x ( ) x lim x2 + x x2 + x 2 + + x x x x2 + + x x 2 + x 2 x x2 + + x x x2 +
MATH A - FINAL EXAM DELUXE - SOLUTIONS PEYAM RYAN TABRIZIAN. ( points, 5 points each) Find the following limits (a) lim x x2 + x ( ) x lim x2 + x x2 + x 2 + + x x x x2 + + x x 2 + x 2 x x2 + + x x x2 +
Math 106: Review for Exam II - SOLUTIONS
 Math 6: Review for Exam II - SOLUTIONS INTEGRATION TIPS Substitution: usually let u a function that s inside another function, especially if du (possibly off by a multiplying constant) is also present
Math 6: Review for Exam II - SOLUTIONS INTEGRATION TIPS Substitution: usually let u a function that s inside another function, especially if du (possibly off by a multiplying constant) is also present
Old Math 220 Exams. David M. McClendon. Department of Mathematics Ferris State University
 Old Math 0 Exams David M. McClendon Department of Mathematics Ferris State University Last updated to include exams from Spring 05 Contents Contents General information about these exams 4 Exams from 0
Old Math 0 Exams David M. McClendon Department of Mathematics Ferris State University Last updated to include exams from Spring 05 Contents Contents General information about these exams 4 Exams from 0
Chapter 2: Differentiation
 Chapter 2: Differentiation Spring 2018 Department of Mathematics Hong Kong Baptist University 1 / 82 2.1 Tangent Lines and Their Slopes This section deals with the problem of finding a straight line L
Chapter 2: Differentiation Spring 2018 Department of Mathematics Hong Kong Baptist University 1 / 82 2.1 Tangent Lines and Their Slopes This section deals with the problem of finding a straight line L
MATH 152 Spring 2018 COMMON EXAM I - VERSION A
 MATH 52 Spring 28 COMMON EXAM I - VERSION A LAST NAME: FIRST NAME: INSTRUCTOR: SECTION NUMBER: UIN: DIRECTIONS:. The use of a calculator, laptop or cell phone is prohibited. 2. TURN OFF cell phones and
MATH 52 Spring 28 COMMON EXAM I - VERSION A LAST NAME: FIRST NAME: INSTRUCTOR: SECTION NUMBER: UIN: DIRECTIONS:. The use of a calculator, laptop or cell phone is prohibited. 2. TURN OFF cell phones and
Math 111 lecture for Friday, Week 10
 Math lecture for Friday, Week Finding antiderivatives mean reversing the operation of taking derivatives. Today we ll consider reversing the chain rule and the product rule. Substitution technique. Recall
Math lecture for Friday, Week Finding antiderivatives mean reversing the operation of taking derivatives. Today we ll consider reversing the chain rule and the product rule. Substitution technique. Recall
Solutions to Final Review Sheet. The Math 5a final exam will be Tuesday, May 1 from 9:15 am 12:15 p.m.
 Math 5a Solutions to Final Review Sheet The Math 5a final exam will be Tuesday, May 1 from 9:15 am 1:15 p.m. Location: Gerstenzang 1 The final exam is cumulative (i.e., it will cover all the material we
Math 5a Solutions to Final Review Sheet The Math 5a final exam will be Tuesday, May 1 from 9:15 am 1:15 p.m. Location: Gerstenzang 1 The final exam is cumulative (i.e., it will cover all the material we
Final exam (practice) UCLA: Math 31B, Spring 2017
 Instructor: Noah White Date: Final exam (practice) UCLA: Math 3B, Spring 207 This exam has 8 questions, for a total of 80 points. Please print your working and answers neatly. Write your solutions in the
Instructor: Noah White Date: Final exam (practice) UCLA: Math 3B, Spring 207 This exam has 8 questions, for a total of 80 points. Please print your working and answers neatly. Write your solutions in the
The Product Rule state that if f and g are differentiable functions, then
 Chpter 6 Techniques of Integrtion 6. Integrtion by Prts Every differentition rule hs corresponding integrtion rule. For instnce, the Substitution Rule for integrtion corresponds to the Chin Rule for differentition.
Chpter 6 Techniques of Integrtion 6. Integrtion by Prts Every differentition rule hs corresponding integrtion rule. For instnce, the Substitution Rule for integrtion corresponds to the Chin Rule for differentition.
Integration of Rational Functions by Partial Fractions
 Title Integration of Rational Functions by MATH 1700 MATH 1700 1 / 11 Readings Readings Readings: Section 7.4 MATH 1700 2 / 11 Rational functions A rational function is one of the form where P and Q are
Title Integration of Rational Functions by MATH 1700 MATH 1700 1 / 11 Readings Readings Readings: Section 7.4 MATH 1700 2 / 11 Rational functions A rational function is one of the form where P and Q are
AB 1: Find lim. x a.
 AB 1: Find lim x a f ( x) AB 1 Answer: Step 1: Find f ( a). If you get a zero in the denominator, Step 2: Factor numerator and denominator of f ( x). Do any cancellations and go back to Step 1. If you
AB 1: Find lim x a f ( x) AB 1 Answer: Step 1: Find f ( a). If you get a zero in the denominator, Step 2: Factor numerator and denominator of f ( x). Do any cancellations and go back to Step 1. If you
Integration by Substitution
 Integration by Substitution Dr. Philippe B. Laval Kennesaw State University Abstract This handout contains material on a very important integration method called integration by substitution. Substitution
Integration by Substitution Dr. Philippe B. Laval Kennesaw State University Abstract This handout contains material on a very important integration method called integration by substitution. Substitution
Math 1552: Integral Calculus Final Exam Study Guide, Spring 2018
 Math 55: Integral Calculus Final Exam Study Guide, Spring 08 PART : Concept Review (Note: concepts may be tested on the exam in the form of true/false or short-answer questions.). Complete each statement
Math 55: Integral Calculus Final Exam Study Guide, Spring 08 PART : Concept Review (Note: concepts may be tested on the exam in the form of true/false or short-answer questions.). Complete each statement
a k 0, then k + 1 = 2 lim 1 + 1
 Math 7 - Midterm - Form A - Page From the desk of C. Davis Buenger. https://people.math.osu.edu/buenger.8/ Problem a) [3 pts] If lim a k = then a k converges. False: The divergence test states that if
Math 7 - Midterm - Form A - Page From the desk of C. Davis Buenger. https://people.math.osu.edu/buenger.8/ Problem a) [3 pts] If lim a k = then a k converges. False: The divergence test states that if
2t t dt.. So the distance is (t2 +6) 3/2
 Math 8, Solutions to Review for the Final Exam Question : The distance is 5 t t + dt To work that out, integrate by parts with u t +, so that t dt du The integral is t t + dt u du u 3/ (t +) 3/ So the
Math 8, Solutions to Review for the Final Exam Question : The distance is 5 t t + dt To work that out, integrate by parts with u t +, so that t dt du The integral is t t + dt u du u 3/ (t +) 3/ So the
Chapter 3. Reading assignment: In this chapter we will cover Sections dx 1 + a 0(x)y(x) = g(x). (1)
 Chapter 3 3 Introduction Reading assignment: In this chapter we will cover Sections 3.1 3.6. 3.1 Theory of Linear Equations Recall that an nth order Linear ODE is an equation that can be written in the
Chapter 3 3 Introduction Reading assignment: In this chapter we will cover Sections 3.1 3.6. 3.1 Theory of Linear Equations Recall that an nth order Linear ODE is an equation that can be written in the
Review of Differentiation and Integration for Ordinary Differential Equations
 Schreyer Fall 208 Review of Differentiation an Integration for Orinary Differential Equations In this course you will be expecte to be able to ifferentiate an integrate quickly an accurately. Many stuents
Schreyer Fall 208 Review of Differentiation an Integration for Orinary Differential Equations In this course you will be expecte to be able to ifferentiate an integrate quickly an accurately. Many stuents
Integration by Substitution
 November 22, 2013 Introduction 7x 2 cos(3x 3 )dx =? 2xe x2 +5 dx =? Chain rule The chain rule: d dx (f (g(x))) = f (g(x)) g (x). Use the chain rule to find f (x) and then write the corresponding anti-differentiation
November 22, 2013 Introduction 7x 2 cos(3x 3 )dx =? 2xe x2 +5 dx =? Chain rule The chain rule: d dx (f (g(x))) = f (g(x)) g (x). Use the chain rule to find f (x) and then write the corresponding anti-differentiation
