Assignment # 8, Math 370, Fall 2018 SOLUTIONS:
|
|
|
- Bertha Harmon
- 5 years ago
- Views:
Transcription
1 Assignment # 8, Math 370, Fall 018 SOLUTIONS: Problem 1: Solve the equations (a) y y = 3x + x 4, (i) y(0) = 1, y (0) = 1, y (0) = 1. Characteristic equation: α 3 α = 0 so α 1, = 0 and α 3 =. y c = C 1 + C x + C 3 e x. Particular solution of non-homogeneous equation: normally we would look for y p in the form y p = Ax + Bx + C. Since 0 is a double root of the characteristic equation (0 corresponds to constant and polynomial solutions of homogeneous equation) we have to multiply y p by x. We take Then y p = Ax 4 + Bx 3 + Cx. y p = 4Ax 3 + 3Bx + Cx, y p = 1Ax + 6Bx + C, y p = 4Ax + 6B. We substitute and obtain which gives 4Ax + 6B 4Ax 1Bx 4C = 3x + x 4, 4A = 3 4A 1B = 1 6B 4C = 4, which gives A = 1, B = 8 1, C = 1. The general solution is 3 y = C 1 + C x + C 3 e x 1 8 x4 1 3 x3 + 1 x. IVP: y(0) = 1 gives 1 = C 1 + C 3. y = C + C 3 e x 1 x3 x + x, so y (0) = 1 gives 1 = C + C 3. y = 4C 3 e x 3 x x + 1, so y (0) = 1 gives 1 = 4C The system of equations gives C 3 = 0 and C 1 = C = 1. The solution of IVP is y = 1 + x 1 8 x4 1 3 x3 + 1 x. (b) y 3y y = 4xe x, (i) y(0) = 1, y (0) = 1, y (0) = 1. Characteristic equation: α 3 3α = 0 so α 1, = 1 and α 3 =. y c = C 1 e x + C xe x + C 3 e x.
2 Particular solution of non-homogeneous equation: normally we would look for y p in the form y p = (Ax + B)e x. Since 1 is not a root of the characteristic equation (1 corresponds to solutions e x of homogeneous equation) we leave y p as it is. We take Then y p = (Ax + B)e x. y p = Aex +(Ax+B)e x = (Ax+A+B)e x, y p = (A)ex +(Ax+A+B)e x = (Ax+A+B)e x, We substitute and obtain which gives y p = (Ax + 3A + B)e x. e x (Ax + 3A + B 3Ax 3A 3B Ax B) = e x ( 4x), 4A = 4 4B = 0, which gives A = 1, B = 0. The general solution is y = C 1 e x + C xe x + C 3 e x + xe x. IVP: y(0) = 1 gives 1 = C 1 + C 3. y = C 1 e x C xe x +C e x +C 3 e x +xe x +e x, so y (0) = 1 gives 1 = C 1 +C +C y = C 1 e x + C xe x C e x C e x + 4C 3 e x + xe x + e x, so y (0) = 1 gives 1 = C 1 C + 4C 3 +. We have to solve C 1 + C 3 = 1 C 1 + C + C 3 = 0 C 1 C + 4C 3 = 1 The system of equations gives C 3 = 0 and C 1 = C = 1. The solution of IVP is y = e x + xe x + xe x. (c) y + 6y + 13y = e 3x cos x, (i) y(0) = 1, y (0) = 1. Characteristic equation: α + 6α + 13 = 0, = 36 5 = 16 so α 1, = 3 ± i. y c = C 1 e 3x cos(x) + C e 3x sin(x). Particular solution of non-homogeneous equation: normally we would look for y p in the form y p = (A cos x+b sin x)e 3x. Since 3 ±i is not a root of the characteristic equation ( 3 ±i corresponds to solutions e 3x cosx of homogeneous equation) we leave y p as it is. We take y p = (A cosx + B sinx)e 3x.
3 Then y p = e 3x ( 3A cos x 3B sinx A sinx + B cos x) = e 3x (( 3A + B)cosx + ( 3B A)sinx). y p = e 3x ((9A 3B)cos x + (9B + 3A)sinx + (3A B)sinx + ( 3B A)cosx) = e 3x ((8A 6B)cos x + (8B + 6A)sinx). We substitute and obtain e 3x ((8A 6B 18A + 6B + 13A)cos x + (8B + 6A 18B 6A + 13B)sin x) = e 3x cos x, which gives 3A = 1 3B = 0, which gives A = 1/3, B = 0. The general solution is y = C 1 e 3x cos(x)+c e 3x sin(x)+ 1 3 e 3x cosx = e 3x ( C 1 cos(x) + C sin(x) cos x ). IVP: y(0) = 1 gives 1 = C y = e 3x (( 3C 1 + C )cos(x) + ( 3C C 1 )sin(x) cosx + sinx), so y (0) = 1 gives 1 = 3C 1 + C 1. These give C 1 = /3 and C =. The solution of IVP is ( y = e 3x 3 cos(x) + sin(x) + 1 ) 3 cosx. Problem : Solve the equation y + 9y = 9e 3x + 18sin(3x) 9cos(3x), y(0) = 1, y (0) = 1, y (0) = 1. Characteristic equation: α 3 + 9α = 0 so α 1, = ±3i and α 3 = 0. y c = C 1 + C cos(3x) + C 3 sin(3x). Particular solution of non-homogeneous equation: we will do this in two steps, first for RHS 9e 3x and then for RHS 18sin(3x) 9cos(3x). (i) normally we would look for y p in the form y p = Ae 3x. Since 3 is not a root of the characteristic equation (3 corresponds to solutions e 3x of homogeneous equation) we leave y p as it is. We take Then y p = Ae 3x. y p = 3Ae 3x, y p = 9Ae 3x, y p = 7Ae 3x.
4 We substitute and obtain (7A + 7A)e 3x = 9e 3x, which gives A = 1/6. This part of particular solution is y p = 1 6 e3x. (ii) normally we would look for y p in the form y p = A cos(3x) + B sin(3x). Since ±3i is a single root of the characteristic equation we need to multiply this y p by x. We take Then y p = Ax cos(3x) + Bx sin(3x). y p = A cos(3x)+b sin(3x) 3Ax sin(3x)+3bx cos(3x) = (A+3Bx)cos(3x)+(B 3Ax)sin(3x), y p = 3B cos(3x) 3A sin(3x) 3(A + 3Bx)sin(3x) + 3(B 3Ax)cos(3x) = (6B 9Ax)cos(3x) + ( 6A 9Bx)sin(3x), y p = 9A cos(3x) 9B sin(3x) 3(6B 9Ax)sin(3x) + 3( 6A 9Bx)cos(3x) = ( 7A 7Bx)cos(3x) + ( 7B + 7Ax)sin(3x). We substitute and obtain ( 7A 7Bx)cos(3x) + ( 7B + 7Ax)sin(3x) + 9(A + 3Bx)cos(3x) + 9(B 3Ax)sin(3x) The terms with x on the LHS cancel and we have 18A = 9 18B = 18, which gives A = 1 The general solution is and B = 1. This part of particular solution is y p = 1 x cos(3x) x sin(3x). y = C 1 + C cos(3x) + C 3 sin(3x) 1 6 e3x + 1 x cos(3x) x sin(3x). IVP: y(0) = 1 gives 1 = C 1 + C 1 6. = 18sin(3x) 9cos(3x). y = 3C sin(3x) + 3C 3 cos(3x) 1 e3x + 1 cos(3x) 3 x sin(3x) sin(3x) 3x cos(3x), so y (0) = 1 gives 1 = 3C y = 9C cos(3x) 9C 3 sin(3x) 3 e3x 3sin(3x) 9 x cos(3x) 6cos(3x) + 9x sin(3x), so y (0) = 1 gives 1 = 9C 3 6. We have to solve C 1 + C = 7 6 3C 3 = 1 9C = 17
5 The system of equations gives C 3 = 1, C 3 1 = 19 and C 9 = 17. The solution of IVP is 18 y = cos(3x) sin(3x) 1 6 e3x + 1 x cos(3x) x sin(3x)x. Problem 3: Consider a general linear non-homogeneous DE with constant coefficients a n y (n) + a n 1 y (n 1) + + a 1 y + a 0 y = g(x). Below, You are given the roots of characteristic equation and the RHS g(x). Write the form of the particular solution y p You would use to find it by the Method of Undefined Coefficients. DO NOT SOLVE. (a) roots:,, 1 ; g(x) = x e x + xe x ; For g 1 (x) = x e x, standard is y p = (Ax + Bx + C)e x. Since α = corresponding to such y p is a double root of characteristic equation we have to multiply it by x. We use y p = x (Ax + Bx + C)e x. For g (x) = xe x, standard is y p = (Ax + B)e x. Since α = 1 corresponding to such y p is a single root of characteristic equation we have to multiply it by x. We use y p = x(ax + B)e x. (b) roots: 4, 0, + i, i; g(x) = x + sin(x) + x cos x; For g 1 (x) = x, standard is y p = (Ax + Bx + C). Since α = 0 corresponding to such y p is a single root of characteristic equation we have to multiply it by x. We use y p = x(ax + Bx + C). For g (x) = sin(x), standard is y p = A sin(x)+b cos(x). Since α = ±i corresponding to such y p is not a root of characteristic equation we keep it as it is. We use y p = A sin(x) + B cos(x). For g 3 (x) = x cos x, standard is y p = (Ax +Bx +C)sinx +(Ex +Fx + G)cos x. Since α = ±i corresponding to such y p is not a root of characteristic equation we keep it as it is. We use y p = (Ax + Bx + C)sinx + (Ex + Fx + G)cos x. (c) roots:, + 3i, 3i; g(x) = sin(3x)e x + cos(x)e x ; For g 1 (x) = sin(3x)e x, standard is y p = (A cos(3x) + B sin(3x))e x. Since α = ± 3i corresponding to such y p is a single root of characteristic equation we have to
6 multiply it by x. We use y p = x(a cos(3x) + B sin(3x))e x. For g (x) = cos(x)e x, standard is y p = (A cos x+b sinx)e x. Since α = ±i corresponding to such y p is not a root of characteristic equation we keep it as it is. We use y p = (A cosx + B sinx)e x. Problem 4: Solve equation: (a) y + 3y + y = e x + e x, y(0) = 0, y (0) = 0. Characteristic equation: α + 3α + = 0 so α 1 = 1 and α =. y c = C 1 e x + C e x. We will use the Method of Variation of Parameters: Since the equation is in standard form we do not have to standardize it. Let y 1 = e x and y = e x. Then, y 1 = e x and y = e x. We get the system of equations C 1y 1 + C y = 0 C 1y 1 + C y Adding both equation we obtain Then, or = e x +e x C 1e x + C e x = 0 C 1e x C e x C e x = e x + e x or C = ex + e x. = e x +e x C 1 = C e x = 1 + e x. We have C = ex + e xdx = ex = t, e x dx = dt} = 1 + t dt = ln( + t) = ln( + ex ) + D. 1 C 1 = + e xdx = ex = t, e x 1 dx = dt} = t( + t) dt = 1 ( 1 t 1 ) dt + t = 1 ( ) t ln + D 1 = 1 ( ) e x + t ln + D + e x 1 = 1 x ln( + ex ) + D 1. We obtain the general solution y = ( 1 x 1 ln( + ex ) + D 1 )e x + ( ln( + e x ) + D )e x. IVP: y(0) = 0 gives 0 = 1 ln3 + D 1 ln3 + D.
7 We have e x y = ( 1 1 ( 1 + e x)e x x 1 ln( + ex ) + D 1 )e x + ( ex ( ln( + e x ) + D + e x)e x )e x, so y (0) = 0 gives 0 = ln3 D 3. We have D 1 + D = 3 ln3 D 1 D = 5 ln3, which gives D 1 = 1 ln3 and D = ln3. The solution of IVP is y = ( 1 x 1 ln( + ex ) + 1 ln3)e x + ( ln( + e x ) + ln3)e x. (b) y + 4y = 4 sin(x), y(π/4) = 0, y (π/4) = 0. Characteristic equation: α + 4 = 0 so α 1, = ±i. y c = C 1 cos(x) + C sin(x). We will use the Method of Variation of Parameters: Since the equation is in standard form we do not have to standardize it. Let y 1 = cos(x) and y = sin(x). Then, y 1 = sin(x) and y = cos(x). We get the system of equations C 1y 1 + C y = 0 C 1y 1 + C y = 4 sin(x) or C 1 cos(x) + C sin(x) = 0 C 1 sin(x) + C cos(x) = 4 sin(x) We divide second equation by and multiply by sin(x). The first we multiply by cos(x). We add them and obtain Then from the first equation C 1 = sin(x) sin(x) = 4sin x cosx sin(x) = 4cos x. C = C 1 cos(x) sin(x) = 4cos x cos(x) sin x cosx = cos(x) sinx. We integrate C 1 = 4sinx + D 1.
8 cos(x) cos C = sin x dx = x sin x sin x 1 t = t = cos x, dt = sinxdx} = 1 t dt = ( = 1 ( 1 1 t t = 4cos x + ln(1 cos x) ln(1 + cos x) + D. The general solution is cos x 1 dx = sin x sinxdx ( t 1 t 1 1 t )) dt = 4t + ln(1 t) ln(1 + t) + D ) dt = y = ( 4sinx + D 1 )cos(x) + (4cos x + ln(1 cos x) ln(1 + cos x) + D )sin(x). IVP: y(π/4) = 0 gives 0 = + ln(1 /) ln(1 + /) + D so D = ln(1 /) + ln(1 + /) = ( + ) + ln. We have y = ( 4cos x)cos(x) ( 4sin x + D 1 )sin(x) y (π/4) = 0 gives so sinx + ( 4sin x + (1 cos x) + sin x (1 + cosx) )sin(x) + (4cos x + ln(1 cos x) ln(1 + cos x) + D )cos(x). 0 = ( + D 1 ) + ( + D 1 =. / / (1 /) + (1 + /) ), The solution of the IVP is ( y = 4sin x + ( ) cos(x)+ 4cos x + ln(1 cos x) ln(1 + cosx) ( + )) + ln sin(x).
Review for Ma 221 Final Exam
 Review for Ma 22 Final Exam The Ma 22 Final Exam from December 995.a) Solve the initial value problem 2xcosy 3x2 y dx x 3 x 2 sin y y dy 0 y 0 2 The equation is first order, for which we have techniques
Review for Ma 22 Final Exam The Ma 22 Final Exam from December 995.a) Solve the initial value problem 2xcosy 3x2 y dx x 3 x 2 sin y y dy 0 y 0 2 The equation is first order, for which we have techniques
Section 5.5 More Integration Formula (The Substitution Method) 2 Lectures. Dr. Abdulla Eid. College of Science. MATHS 101: Calculus I
 Section 5.5 More Integration Formula (The Substitution Method) 2 Lectures College of Science MATHS : Calculus I (University of Bahrain) Integrals / 7 The Substitution Method Idea: To replace a relatively
Section 5.5 More Integration Formula (The Substitution Method) 2 Lectures College of Science MATHS : Calculus I (University of Bahrain) Integrals / 7 The Substitution Method Idea: To replace a relatively
Math 2Z03 - Tutorial # 6. Oct. 26th, 27th, 28th, 2015
 Math 2Z03 - Tutorial # 6 Oct. 26th, 27th, 28th, 2015 Tutorial Info: Tutorial Website: http://ms.mcmaster.ca/ dedieula/2z03.html Office Hours: Mondays 3pm - 5pm (in the Math Help Centre) Tutorial #6: 3.4
Math 2Z03 - Tutorial # 6 Oct. 26th, 27th, 28th, 2015 Tutorial Info: Tutorial Website: http://ms.mcmaster.ca/ dedieula/2z03.html Office Hours: Mondays 3pm - 5pm (in the Math Help Centre) Tutorial #6: 3.4
Ma 221. The material below was covered during the lecture given last Wed. (1/29/14). Homogeneous Linear Equations with Constant Coefficients
 Ma 1 The material below was covered during the lecture given last Wed. (1/9/1). Homogeneous Linear Equations with Constant Coefficients We shall now discuss the problem of solving the homogeneous equation
Ma 1 The material below was covered during the lecture given last Wed. (1/9/1). Homogeneous Linear Equations with Constant Coefficients We shall now discuss the problem of solving the homogeneous equation
Polytechnic Institute of NYU MA 2132 Final Practice Answers Fall 2012
 Polytechnic Institute of NYU MA Final Practice Answers Fall Studying from past or sample exams is NOT recommended. If you do, it should be only AFTER you know how to do all of the homework and worksheet
Polytechnic Institute of NYU MA Final Practice Answers Fall Studying from past or sample exams is NOT recommended. If you do, it should be only AFTER you know how to do all of the homework and worksheet
Mathematics 104 Fall Term 2006 Solutions to Final Exam. sin(ln t) dt = e x sin(x) dx.
 Mathematics 14 Fall Term 26 Solutions to Final Exam 1. Evaluate sin(ln t) dt. Solution. We first make the substitution t = e x, for which dt = e x. This gives sin(ln t) dt = e x sin(x). To evaluate the
Mathematics 14 Fall Term 26 Solutions to Final Exam 1. Evaluate sin(ln t) dt. Solution. We first make the substitution t = e x, for which dt = e x. This gives sin(ln t) dt = e x sin(x). To evaluate the
Introduction to Differential Equations Math 286 X1 Fall 2009 Homework 2 Solutions
 Introuction to Differential Equations Math 286 X1 Fall 2009 Homewk 2 Solutions 1. Solve each of the following ifferential equations: (a) y + 3xy = 0 (b) y + 3y = 3x (c) y t = cos(t)y () x 2 y x y = 3 Solution:
Introuction to Differential Equations Math 286 X1 Fall 2009 Homewk 2 Solutions 1. Solve each of the following ifferential equations: (a) y + 3xy = 0 (b) y + 3y = 3x (c) y t = cos(t)y () x 2 y x y = 3 Solution:
Math 201 Solutions to Assignment 1. 2ydy = x 2 dx. y = C 1 3 x3
 Math 201 Solutions to Assignment 1 1. Solve the initial value problem: x 2 dx + 2y = 0, y(0) = 2. x 2 dx + 2y = 0, y(0) = 2 2y = x 2 dx y 2 = 1 3 x3 + C y = C 1 3 x3 Notice that y is not defined for some
Math 201 Solutions to Assignment 1 1. Solve the initial value problem: x 2 dx + 2y = 0, y(0) = 2. x 2 dx + 2y = 0, y(0) = 2 2y = x 2 dx y 2 = 1 3 x3 + C y = C 1 3 x3 Notice that y is not defined for some
Integration by Substitution
 November 22, 2013 Introduction 7x 2 cos(3x 3 )dx =? 2xe x2 +5 dx =? Chain rule The chain rule: d dx (f (g(x))) = f (g(x)) g (x). Use the chain rule to find f (x) and then write the corresponding anti-differentiation
November 22, 2013 Introduction 7x 2 cos(3x 3 )dx =? 2xe x2 +5 dx =? Chain rule The chain rule: d dx (f (g(x))) = f (g(x)) g (x). Use the chain rule to find f (x) and then write the corresponding anti-differentiation
Section 5.6. Integration By Parts. MATH 126 (Section 5.6) Integration By Parts The University of Kansas 1 / 10
 Section 5.6 Integration By Parts MATH 126 (Section 5.6) Integration By Parts The University of Kansas 1 / 10 Integration By Parts Manipulating the Product Rule d dx (f (x) g(x)) = f (x) g (x) + f (x) g(x)
Section 5.6 Integration By Parts MATH 126 (Section 5.6) Integration By Parts The University of Kansas 1 / 10 Integration By Parts Manipulating the Product Rule d dx (f (x) g(x)) = f (x) g (x) + f (x) g(x)
Math 115 Practice for Exam 3
 Math 115 Practice for Exam 3 Generated November 17, 2017 Name: SOLUTIONS Instructor: Section Number: 1. This exam has 6 questions. Note that the problems are not of equal difficulty, so you may want to
Math 115 Practice for Exam 3 Generated November 17, 2017 Name: SOLUTIONS Instructor: Section Number: 1. This exam has 6 questions. Note that the problems are not of equal difficulty, so you may want to
Formulas that must be memorized:
 Formulas that must be memorized: Position, Velocity, Acceleration Speed is increasing when v(t) and a(t) have the same signs. Speed is decreasing when v(t) and a(t) have different signs. Section I: Limits
Formulas that must be memorized: Position, Velocity, Acceleration Speed is increasing when v(t) and a(t) have the same signs. Speed is decreasing when v(t) and a(t) have different signs. Section I: Limits
June 2011 PURDUE UNIVERSITY Study Guide for the Credit Exam in (MA 262) Linear Algebra and Differential Equations
 June 20 PURDUE UNIVERSITY Study Guide for the Credit Exam in (MA 262) Linear Algebra and Differential Equations The topics covered in this exam can be found in An introduction to differential equations
June 20 PURDUE UNIVERSITY Study Guide for the Credit Exam in (MA 262) Linear Algebra and Differential Equations The topics covered in this exam can be found in An introduction to differential equations
Math 135-2, Homework 1
 Mth 35-, Homework Solutions Problem 7. Find the generl solution of ech of the following equtions: ) 6y 8y + y q) y + 4y + 5y r) y + 4y 5y ) 6y 8y +y y e rx y re rx y r e rx 6r e rx 8re rx +e rx 6r 8r +)e
Mth 35-, Homework Solutions Problem 7. Find the generl solution of ech of the following equtions: ) 6y 8y + y q) y + 4y + 5y r) y + 4y 5y ) 6y 8y +y y e rx y re rx y r e rx 6r e rx 8re rx +e rx 6r 8r +)e
Access to Science, Engineering and Agriculture: Mathematics 2 MATH00040 Chapter 4 Solutions
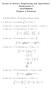 Access to Science, Engineering and Agriculture: Mathematics MATH4 Chapter 4 Solutions In all these solutions, c will represent an arbitrary constant.. (a) Since f(x) 5 is a constant, 5dx 5x] 5. (b) Since
Access to Science, Engineering and Agriculture: Mathematics MATH4 Chapter 4 Solutions In all these solutions, c will represent an arbitrary constant.. (a) Since f(x) 5 is a constant, 5dx 5x] 5. (b) Since
Practice Problems: Integration by Parts
 Practice Problems: Integration by Parts Answers. (a) Neither term will get simpler through differentiation, so let s try some choice for u and dv, and see how it works out (we can always go back and try
Practice Problems: Integration by Parts Answers. (a) Neither term will get simpler through differentiation, so let s try some choice for u and dv, and see how it works out (we can always go back and try
Solutions to Exam 1, Math Solution. Because f(x) is one-to-one, we know the inverse function exists. Recall that (f 1 ) (a) =
 Solutions to Exam, Math 56 The function f(x) e x + x 3 + x is one-to-one (there is no need to check this) What is (f ) ( + e )? Solution Because f(x) is one-to-one, we know the inverse function exists
Solutions to Exam, Math 56 The function f(x) e x + x 3 + x is one-to-one (there is no need to check this) What is (f ) ( + e )? Solution Because f(x) is one-to-one, we know the inverse function exists
Assignment # 7, Math 370, Fall 2018 SOLUTIONS: y = e x. y = e 3x + 4xe 3x. y = e x cosx.
 Assignment # 7, Math 370, Fall 2018 SOLUTIONS: Problem 1: Solve the equations (a) y 8y + 7y = 0, (i) y(0) = 1, y (0) = 1. Characteristic equation: α 2 8α+7 = 0, = 64 28 = 36 so α 1,2 = (8 ±6)/2 and α 1
Assignment # 7, Math 370, Fall 2018 SOLUTIONS: Problem 1: Solve the equations (a) y 8y + 7y = 0, (i) y(0) = 1, y (0) = 1. Characteristic equation: α 2 8α+7 = 0, = 64 28 = 36 so α 1,2 = (8 ±6)/2 and α 1
Math 106 Fall 2014 Exam 2.1 October 31, ln(x) x 3 dx = 1. 2 x 2 ln(x) + = 1 2 x 2 ln(x) + 1. = 1 2 x 2 ln(x) 1 4 x 2 + C
 Math 6 Fall 4 Exam. October 3, 4. The following questions have to do with the integral (a) Evaluate dx. Use integration by parts (x 3 dx = ) ( dx = ) x3 x dx = x x () dx = x + x x dx = x + x 3 dx dx =
Math 6 Fall 4 Exam. October 3, 4. The following questions have to do with the integral (a) Evaluate dx. Use integration by parts (x 3 dx = ) ( dx = ) x3 x dx = x x () dx = x + x x dx = x + x 3 dx dx =
Math 115 HW #10 Solutions
 Math 11 HW #10 Solutions 1. Suppose y 1 (t and y 2 (t are both solutions of the differential equation P (ty + Q(ty + R(ty = 0. Show that, for any constants C 1 and C 2, the function C 1 y 1 (t + C 2 y
Math 11 HW #10 Solutions 1. Suppose y 1 (t and y 2 (t are both solutions of the differential equation P (ty + Q(ty + R(ty = 0. Show that, for any constants C 1 and C 2, the function C 1 y 1 (t + C 2 y
Grade: The remainder of this page has been left blank for your workings. VERSION D. Midterm D: Page 1 of 12
 First Name: Student-No: Last Name: Section: Grade: The remainder of this page has been left blank for your workings. Midterm D: Page of 2 Indefinite Integrals. 9 marks Each part is worth marks. Please
First Name: Student-No: Last Name: Section: Grade: The remainder of this page has been left blank for your workings. Midterm D: Page of 2 Indefinite Integrals. 9 marks Each part is worth marks. Please
Section 10.7 Taylor series
 Section 10.7 Taylor series 1. Common Maclaurin series 2. s and approximations with Taylor polynomials 3. Multiplication and division of power series Math 126 Enhanced 10.7 Taylor Series The University
Section 10.7 Taylor series 1. Common Maclaurin series 2. s and approximations with Taylor polynomials 3. Multiplication and division of power series Math 126 Enhanced 10.7 Taylor Series The University
DIFFERENTIAL EQUATIONS
 DIFFERENTIAL EQUATIONS 1. Basic Terminology A differential equation is an equation that contains an unknown function together with one or more of its derivatives. 1 Examples: 1. y = 2x + cos x 2. dy dt
DIFFERENTIAL EQUATIONS 1. Basic Terminology A differential equation is an equation that contains an unknown function together with one or more of its derivatives. 1 Examples: 1. y = 2x + cos x 2. dy dt
Ordinary Differential Equations
 Ordinary Differential Equations (MA102 Mathematics II) Shyamashree Upadhyay IIT Guwahati Shyamashree Upadhyay ( IIT Guwahati ) Ordinary Differential Equations 1 / 15 Method of Undetermined Coefficients
Ordinary Differential Equations (MA102 Mathematics II) Shyamashree Upadhyay IIT Guwahati Shyamashree Upadhyay ( IIT Guwahati ) Ordinary Differential Equations 1 / 15 Method of Undetermined Coefficients
y = x 3 and y = 2x 2 x. 2x 2 x = x 3 x 3 2x 2 + x = 0 x(x 2 2x + 1) = 0 x(x 1) 2 = 0 x = 0 and x = (x 3 (2x 2 x)) dx
 Millersville University Name Answer Key Mathematics Department MATH 2, Calculus II, Final Examination May 4, 2, 8:AM-:AM Please answer the following questions. Your answers will be evaluated on their correctness,
Millersville University Name Answer Key Mathematics Department MATH 2, Calculus II, Final Examination May 4, 2, 8:AM-:AM Please answer the following questions. Your answers will be evaluated on their correctness,
Chapter 3. Reading assignment: In this chapter we will cover Sections dx 1 + a 0(x)y(x) = g(x). (1)
 Chapter 3 3 Introduction Reading assignment: In this chapter we will cover Sections 3.1 3.6. 3.1 Theory of Linear Equations Recall that an nth order Linear ODE is an equation that can be written in the
Chapter 3 3 Introduction Reading assignment: In this chapter we will cover Sections 3.1 3.6. 3.1 Theory of Linear Equations Recall that an nth order Linear ODE is an equation that can be written in the
Nonhomogeneous Linear Differential Equations with Constant Coefficients - (3.4) Method of Undetermined Coefficients
 Nonhomogeneous Linear Differential Equations with Constant Coefficients - (3.4) Method of Undetermined Coefficients Consider an nth-order nonhomogeneous linear differential equation with constant coefficients:
Nonhomogeneous Linear Differential Equations with Constant Coefficients - (3.4) Method of Undetermined Coefficients Consider an nth-order nonhomogeneous linear differential equation with constant coefficients:
Math 201 Lecture 08 Undetermined Coefficients
 Math 201 Lecture 08 Undetermined Coefficients Jan. 25, 2012 Many examples here are taken from the textbook. The first number in () refers to the problem number in the UA Custom edition, the second number
Math 201 Lecture 08 Undetermined Coefficients Jan. 25, 2012 Many examples here are taken from the textbook. The first number in () refers to the problem number in the UA Custom edition, the second number
Math 131 Final Exam Spring 2016
 Math 3 Final Exam Spring 06 Name: ID: multiple choice questions worth 5 points each. Exam is only out of 00 (so there is the possibility of getting more than 00%) Exam covers sections. through 5.4 No graphing
Math 3 Final Exam Spring 06 Name: ID: multiple choice questions worth 5 points each. Exam is only out of 00 (so there is the possibility of getting more than 00%) Exam covers sections. through 5.4 No graphing
Ma 530. Special Methods for First Order Equations. Separation of Variables. Consider the equation. M x,y N x,y y 0
 Ma 530 Consider the equation Special Methods for First Order Equations Mx, Nx, 0 1 This equation is first order and first degree. The functions Mx, and Nx, are given. Often we write this as Mx, Nx,d 0
Ma 530 Consider the equation Special Methods for First Order Equations Mx, Nx, 0 1 This equation is first order and first degree. The functions Mx, and Nx, are given. Often we write this as Mx, Nx,d 0
Math 2142 Homework 5 Part 1 Solutions
 Math 2142 Homework 5 Part 1 Solutions Problem 1. For the following homogeneous second order differential equations, give the general solution and the particular solution satisfying the given initial conditions.
Math 2142 Homework 5 Part 1 Solutions Problem 1. For the following homogeneous second order differential equations, give the general solution and the particular solution satisfying the given initial conditions.
The Area bounded by Two Functions
 The Area bounded by Two Functions The graph below shows 2 functions f(x) and g(x) that are continuous between x = a and x = b and f(x) g(x). The area shaded in green is the area between the 2 curves. We
The Area bounded by Two Functions The graph below shows 2 functions f(x) and g(x) that are continuous between x = a and x = b and f(x) g(x). The area shaded in green is the area between the 2 curves. We
FLAP M6.1 Introducing differential equations COPYRIGHT 1998 THE OPEN UNIVERSITY S570 V1.1
 F1 (a) This equation is of first order and of first degree. It is a linear equation, since the dependent variable y and its derivative only appear raised to the first power, and there are no products of
F1 (a) This equation is of first order and of first degree. It is a linear equation, since the dependent variable y and its derivative only appear raised to the first power, and there are no products of
QC-1.2-FUNCTIONS I. REAL AND COMPLEX FUNCTIONS. Dr. A. Dayalan ; QC-1.2-FUNCTIONS 1
 Dr. A. Dayalan ; QC-1.2-FUNCTIONS 1 QUANTUM CHEMISTRY Dr. A. DAYALAN, Former Professor & Head, Dept. of Chemistry, LOYOLA COLLEGE (Autonomous), Chennai-34 QC-1.2-FUNCTIONS I. REAL AND COMPLEX FUNCTIONS.
Dr. A. Dayalan ; QC-1.2-FUNCTIONS 1 QUANTUM CHEMISTRY Dr. A. DAYALAN, Former Professor & Head, Dept. of Chemistry, LOYOLA COLLEGE (Autonomous), Chennai-34 QC-1.2-FUNCTIONS I. REAL AND COMPLEX FUNCTIONS.
4. Theory of the Integral
 4. Theory of the Integral 4.1 Antidifferentiation 4.2 The Definite Integral 4.3 Riemann Sums 4.4 The Fundamental Theorem of Calculus 4.5 Fundamental Integration Rules 4.6 U-Substitutions 4.1 Antidifferentiation
4. Theory of the Integral 4.1 Antidifferentiation 4.2 The Definite Integral 4.3 Riemann Sums 4.4 The Fundamental Theorem of Calculus 4.5 Fundamental Integration Rules 4.6 U-Substitutions 4.1 Antidifferentiation
DIFFERENTIAL EQUATIONS
 DIFFERENTIAL EQUATIONS Basic Terminology A differential equation is an equation that contains an unknown function together with one or more of its derivatives. 1 Examples: 1. y = 2x + cos x 2. dy dt =
DIFFERENTIAL EQUATIONS Basic Terminology A differential equation is an equation that contains an unknown function together with one or more of its derivatives. 1 Examples: 1. y = 2x + cos x 2. dy dt =
Integration by Parts
 Calculus 2 Lia Vas Integration by Parts Using integration by parts one transforms an integral of a product of two functions into a simpler integral. Divide the initial function into two parts called u
Calculus 2 Lia Vas Integration by Parts Using integration by parts one transforms an integral of a product of two functions into a simpler integral. Divide the initial function into two parts called u
REVERSE CHAIN RULE CALCULUS 7. Dr Adrian Jannetta MIMA CMath FRAS INU0115/515 (MATHS 2) Reverse Chain Rule 1/12 Adrian Jannetta
 REVERSE CHAIN RULE CALCULUS 7 INU05/55 (MATHS 2) Dr Adrian Jannetta MIMA CMath FRAS Reverse Chain Rule /2 Adrian Jannetta Reversing the chain rule In differentiation the chain rule is used to get the derivative
REVERSE CHAIN RULE CALCULUS 7 INU05/55 (MATHS 2) Dr Adrian Jannetta MIMA CMath FRAS Reverse Chain Rule /2 Adrian Jannetta Reversing the chain rule In differentiation the chain rule is used to get the derivative
Indefinite Integration
 Indefinite Integration 1 An antiderivative of a function y = f(x) defined on some interval (a, b) is called any function F(x) whose derivative at any point of this interval is equal to f(x): F'(x) = f(x)
Indefinite Integration 1 An antiderivative of a function y = f(x) defined on some interval (a, b) is called any function F(x) whose derivative at any point of this interval is equal to f(x): F'(x) = f(x)
M GENERAL MATHEMATICS -2- Dr. Tariq A. AlFadhel 1 Solution of the First Mid-Term Exam First semester H
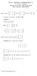 M - GENERAL MATHEMATICS -- Dr. Tariq A. AlFadhel Solution of the First Mid-Term Exam First semester 38-39 H 3 Q. Let A =, B = and C = 3 Compute (if possible) : A+B and BC A+B is impossible. ( ) BC = 3
M - GENERAL MATHEMATICS -- Dr. Tariq A. AlFadhel Solution of the First Mid-Term Exam First semester 38-39 H 3 Q. Let A =, B = and C = 3 Compute (if possible) : A+B and BC A+B is impossible. ( ) BC = 3
2.3 Linear Equations 69
 2.3 Linear Equations 69 2.3 Linear Equations An equation y = fx,y) is called first-order linear or a linear equation provided it can be rewritten in the special form 1) y + px)y = rx) for some functions
2.3 Linear Equations 69 2.3 Linear Equations An equation y = fx,y) is called first-order linear or a linear equation provided it can be rewritten in the special form 1) y + px)y = rx) for some functions
Math 226 Calculus Spring 2016 Exam 2V1
 Math 6 Calculus Spring 6 Exam V () (35 Points) Evaluate the following integrals. (a) (7 Points) tan 5 (x) sec 3 (x) dx (b) (8 Points) cos 4 (x) dx Math 6 Calculus Spring 6 Exam V () (Continued) Evaluate
Math 6 Calculus Spring 6 Exam V () (35 Points) Evaluate the following integrals. (a) (7 Points) tan 5 (x) sec 3 (x) dx (b) (8 Points) cos 4 (x) dx Math 6 Calculus Spring 6 Exam V () (Continued) Evaluate
0.1 Problems to solve
 0.1 Problems to solve Homework Set No. NEEP 547 Due September 0, 013 DLH Nonlinear Eqs. reducible to first order: 1. 5pts) Find the general solution to the differential equation: y = [ 1 + y ) ] 3/. 5pts)
0.1 Problems to solve Homework Set No. NEEP 547 Due September 0, 013 DLH Nonlinear Eqs. reducible to first order: 1. 5pts) Find the general solution to the differential equation: y = [ 1 + y ) ] 3/. 5pts)
(e) 2 (f) 2. (c) + (d). Limits at Infinity. 2.5) 9-14,25-34,41-43,46-47,56-57, (c) (d) 2
 Math 150A. Final Review Answers, Spring 2018. Limits. 2.2) 7-10, 21-24, 28-1, 6-8, 4-44. 1. Find the values, or state they do not exist. (a) (b) 1 (c) DNE (d) 1 (e) 2 (f) 2 (g) 2 (h) 4 2. lim f(x) = 2,
Math 150A. Final Review Answers, Spring 2018. Limits. 2.2) 7-10, 21-24, 28-1, 6-8, 4-44. 1. Find the values, or state they do not exist. (a) (b) 1 (c) DNE (d) 1 (e) 2 (f) 2 (g) 2 (h) 4 2. lim f(x) = 2,
Theory of Higher-Order Linear Differential Equations
 Chapter 6 Theory of Higher-Order Linear Differential Equations 6.1 Basic Theory A linear differential equation of order n has the form a n (x)y (n) (x) + a n 1 (x)y (n 1) (x) + + a 0 (x)y(x) = b(x), (6.1.1)
Chapter 6 Theory of Higher-Order Linear Differential Equations 6.1 Basic Theory A linear differential equation of order n has the form a n (x)y (n) (x) + a n 1 (x)y (n 1) (x) + + a 0 (x)y(x) = b(x), (6.1.1)
π π π π Trigonometry Homework Booklet 1. Convert 5.3 radians to degrees. A B C D Determine the period of 15
 Trigonometry Homework Booklet 1. Convert 5.3 radians to degrees. A. 0.09 B. 0.18 C. 151.83 D. 303.67. Determine the period of y = 6cos x + 8. 15 15 A. B. C. 15 D. 30 15 3. Determine the exact value of
Trigonometry Homework Booklet 1. Convert 5.3 radians to degrees. A. 0.09 B. 0.18 C. 151.83 D. 303.67. Determine the period of y = 6cos x + 8. 15 15 A. B. C. 15 D. 30 15 3. Determine the exact value of
McGill University Math 325A: Differential Equations LECTURE 12: SOLUTIONS FOR EQUATIONS WITH CONSTANTS COEFFICIENTS (II)
 McGill University Math 325A: Differential Equations LECTURE 12: SOLUTIONS FOR EQUATIONS WITH CONSTANTS COEFFICIENTS (II) HIGHER ORDER DIFFERENTIAL EQUATIONS (IV) 1 Introduction (Text: pp. 338-367, Chap.
McGill University Math 325A: Differential Equations LECTURE 12: SOLUTIONS FOR EQUATIONS WITH CONSTANTS COEFFICIENTS (II) HIGHER ORDER DIFFERENTIAL EQUATIONS (IV) 1 Introduction (Text: pp. 338-367, Chap.
Differential Equations DIRECT INTEGRATION. Graham S McDonald
 Differential Equations DIRECT INTEGRATION Graham S McDonald A Tutorial Module introducing ordinary differential equations and the method of direct integration Table of contents Begin Tutorial c 2004 g.s.mcdonald@salford.ac.uk
Differential Equations DIRECT INTEGRATION Graham S McDonald A Tutorial Module introducing ordinary differential equations and the method of direct integration Table of contents Begin Tutorial c 2004 g.s.mcdonald@salford.ac.uk
8.7 Taylor s Inequality Math 2300 Section 005 Calculus II. f(x) = ln(1 + x) f(0) = 0
 8.7 Taylor s Inequality Math 00 Section 005 Calculus II Name: ANSWER KEY Taylor s Inequality: If f (n+) is continuous and f (n+) < M between the center a and some point x, then f(x) T n (x) M x a n+ (n
8.7 Taylor s Inequality Math 00 Section 005 Calculus II Name: ANSWER KEY Taylor s Inequality: If f (n+) is continuous and f (n+) < M between the center a and some point x, then f(x) T n (x) M x a n+ (n
MATH 151, FALL SEMESTER 2011 COMMON EXAMINATION 3 - VERSION B - SOLUTIONS
 Name (print): Signature: MATH 5, FALL SEMESTER 0 COMMON EXAMINATION - VERSION B - SOLUTIONS Instructor s name: Section No: Part Multiple Choice ( questions, points each, No Calculators) Write your name,
Name (print): Signature: MATH 5, FALL SEMESTER 0 COMMON EXAMINATION - VERSION B - SOLUTIONS Instructor s name: Section No: Part Multiple Choice ( questions, points each, No Calculators) Write your name,
Mar 10, Calculus with Algebra and Trigonometry II Lecture 14Undoing the Marproduct 10, 2015 rule: integration 1 / 18
 Calculus with Algebra and Trigonometry II Lecture 14 Undoing the product rule: integration by parts Mar 10, 2015 Calculus with Algebra and Trigonometry II Lecture 14Undoing the Marproduct 10, 2015 rule:
Calculus with Algebra and Trigonometry II Lecture 14 Undoing the product rule: integration by parts Mar 10, 2015 Calculus with Algebra and Trigonometry II Lecture 14Undoing the Marproduct 10, 2015 rule:
Math 106: Review for Exam II - SOLUTIONS
 Math 6: Review for Exam II - SOLUTIONS INTEGRATION TIPS Substitution: usually let u a function that s inside another function, especially if du (possibly off by a multiplying constant) is also present
Math 6: Review for Exam II - SOLUTIONS INTEGRATION TIPS Substitution: usually let u a function that s inside another function, especially if du (possibly off by a multiplying constant) is also present
DRAFT - Math 102 Lecture Note - Dr. Said Algarni
 Math02 - Term72 - Guides and Exercises - DRAFT 7 Techniques of Integration A summery for the most important integrals that we have learned so far: 7. Integration by Parts The Product Rule states that if
Math02 - Term72 - Guides and Exercises - DRAFT 7 Techniques of Integration A summery for the most important integrals that we have learned so far: 7. Integration by Parts The Product Rule states that if
x 3y 2z = 6 1.2) 2x 4y 3z = 8 3x + 6y + 8z = 5 x + 3y 2z + 5t = 4 1.5) 2x + 8y z + 9t = 9 3x + 5y 12z + 17t = 7
 Linear Algebra and its Applications-Lab 1 1) Use Gaussian elimination to solve the following systems x 1 + x 2 2x 3 + 4x 4 = 5 1.1) 2x 1 + 2x 2 3x 3 + x 4 = 3 3x 1 + 3x 2 4x 3 2x 4 = 1 x + y + 2z = 4 1.4)
Linear Algebra and its Applications-Lab 1 1) Use Gaussian elimination to solve the following systems x 1 + x 2 2x 3 + 4x 4 = 5 1.1) 2x 1 + 2x 2 3x 3 + x 4 = 3 3x 1 + 3x 2 4x 3 2x 4 = 1 x + y + 2z = 4 1.4)
Integration of Rational Functions by Partial Fractions
 Title Integration of Rational Functions by MATH 1700 MATH 1700 1 / 11 Readings Readings Readings: Section 7.4 MATH 1700 2 / 11 Rational functions A rational function is one of the form where P and Q are
Title Integration of Rational Functions by MATH 1700 MATH 1700 1 / 11 Readings Readings Readings: Section 7.4 MATH 1700 2 / 11 Rational functions A rational function is one of the form where P and Q are
Review For the Final: Problem 1 Find the general solutions of the following DEs. a) x 2 y xy y 2 = 0 solution: = 0 : homogeneous equation.
 Review For the Final: Problem 1 Find the general solutions of the following DEs. a) x 2 y xy y 2 = 0 solution: y y x y2 = 0 : homogeneous equation. x2 v = y dy, y = vx, and x v + x dv dx = v + v2. dx =
Review For the Final: Problem 1 Find the general solutions of the following DEs. a) x 2 y xy y 2 = 0 solution: y y x y2 = 0 : homogeneous equation. x2 v = y dy, y = vx, and x v + x dv dx = v + v2. dx =
Math 4B Notes. Written by Victoria Kala SH 6432u Office Hours: T 12:45 1:45pm Last updated 7/24/2016
 Math 4B Notes Written by Victoria Kala vtkala@math.ucsb.edu SH 6432u Office Hours: T 2:45 :45pm Last updated 7/24/206 Classification of Differential Equations The order of a differential equation is the
Math 4B Notes Written by Victoria Kala vtkala@math.ucsb.edu SH 6432u Office Hours: T 2:45 :45pm Last updated 7/24/206 Classification of Differential Equations The order of a differential equation is the
Math 106: Review for Exam II - SOLUTIONS
 Math 6: Review for Exam II - SOLUTIONS INTEGRATION TIPS Substitution: usually let u a function that s inside another function, especially if du (possibly off by a multiplying constant) is also present
Math 6: Review for Exam II - SOLUTIONS INTEGRATION TIPS Substitution: usually let u a function that s inside another function, especially if du (possibly off by a multiplying constant) is also present
Integration of Rational Functions by Partial Fractions
 Title Integration of Rational Functions by Partial Fractions MATH 1700 December 6, 2016 MATH 1700 Partial Fractions December 6, 2016 1 / 11 Readings Readings Readings: Section 7.4 MATH 1700 Partial Fractions
Title Integration of Rational Functions by Partial Fractions MATH 1700 December 6, 2016 MATH 1700 Partial Fractions December 6, 2016 1 / 11 Readings Readings Readings: Section 7.4 MATH 1700 Partial Fractions
APPENDIX : PARTIAL FRACTIONS
 APPENDIX : PARTIAL FRACTIONS Appendix : Partial Fractions Given the expression x 2 and asked to find its integral, x + you can use work from Section. to give x 2 =ln( x 2) ln( x + )+c x + = ln k x 2 x+
APPENDIX : PARTIAL FRACTIONS Appendix : Partial Fractions Given the expression x 2 and asked to find its integral, x + you can use work from Section. to give x 2 =ln( x 2) ln( x + )+c x + = ln k x 2 x+
Math 1431 Final Exam Review
 Math 1431 Final Exam Review Comprehensive exam. I recommend you study all past reviews and practice exams as well. Know all rules/formulas. Make a reservation for the final exam. If you miss it, go back
Math 1431 Final Exam Review Comprehensive exam. I recommend you study all past reviews and practice exams as well. Know all rules/formulas. Make a reservation for the final exam. If you miss it, go back
6 Second Order Linear Differential Equations
 6 Second Order Linear Differential Equations A differential equation for an unknown function y = f(x) that depends on a variable x is any equation that ties together functions of x with y and its derivatives.
6 Second Order Linear Differential Equations A differential equation for an unknown function y = f(x) that depends on a variable x is any equation that ties together functions of x with y and its derivatives.
Math 113 (Calculus 2) Exam 4
 Math 3 (Calculus ) Exam 4 November 0 November, 009 Sections 0, 3 7 Name Student ID Section Instructor In some cases a series may be seen to converge or diverge for more than one reason. For such problems
Math 3 (Calculus ) Exam 4 November 0 November, 009 Sections 0, 3 7 Name Student ID Section Instructor In some cases a series may be seen to converge or diverge for more than one reason. For such problems
Equations of Ellipse Conics HSC Maths Extension 2
 Equations of Ellipse HSC Maths Extension 1 Question 1 Find the equation of the ellipse whose foci on the y-axis, centre 0,0, a, b. Question Find the equation of the ellipse whose foci 4,0, b. Question
Equations of Ellipse HSC Maths Extension 1 Question 1 Find the equation of the ellipse whose foci on the y-axis, centre 0,0, a, b. Question Find the equation of the ellipse whose foci 4,0, b. Question
Homework #6 Solutions
 Problems Section.1: 6, 4, 40, 46 Section.:, 8, 10, 14, 18, 4, 0 Homework #6 Solutions.1.6. Determine whether the functions f (x) = cos x + sin x and g(x) = cos x sin x are linearly dependent or linearly
Problems Section.1: 6, 4, 40, 46 Section.:, 8, 10, 14, 18, 4, 0 Homework #6 Solutions.1.6. Determine whether the functions f (x) = cos x + sin x and g(x) = cos x sin x are linearly dependent or linearly
Mathematics 3 Differential Calculus
 Differential Calculus 3-1a A derivative function defines the slope described by the original function. Example 1 (FEIM): Given: y(x) = 3x 3 2x 2 + 7. What is the slope of the function y(x) at x = 4? y
Differential Calculus 3-1a A derivative function defines the slope described by the original function. Example 1 (FEIM): Given: y(x) = 3x 3 2x 2 + 7. What is the slope of the function y(x) at x = 4? y
MS 2001: Test 1 B Solutions
 MS 2001: Test 1 B Solutions Name: Student Number: Answer all questions. Marks may be lost if necessary work is not clearly shown. Remarks by me in italics and would not be required in a test - J.P. Question
MS 2001: Test 1 B Solutions Name: Student Number: Answer all questions. Marks may be lost if necessary work is not clearly shown. Remarks by me in italics and would not be required in a test - J.P. Question
DIFFERENTIAL EQUATIONS
 DIFFERENTIAL EQUATIONS 1. Basic Terminology A differential equation is an equation that contains an unknown function together with one or more of its derivatives. 1 Examples: 1. y = 2x + cos x 2. dy dt
DIFFERENTIAL EQUATIONS 1. Basic Terminology A differential equation is an equation that contains an unknown function together with one or more of its derivatives. 1 Examples: 1. y = 2x + cos x 2. dy dt
1.4 Techniques of Integration
 .4 Techniques of Integration Recall the following strategy for evaluating definite integrals, which arose from the Fundamental Theorem of Calculus (see Section.3). To calculate b a f(x) dx. Find a function
.4 Techniques of Integration Recall the following strategy for evaluating definite integrals, which arose from the Fundamental Theorem of Calculus (see Section.3). To calculate b a f(x) dx. Find a function
Puzzle 1 Puzzle 2 Puzzle 3 Puzzle 4 Puzzle 5 /10 /10 /10 /10 /10
 MATH-65 Puzzle Collection 6 Nov 8 :pm-:pm Name:... 3 :pm Wumaier :pm Njus 5 :pm Wumaier 6 :pm Njus 7 :pm Wumaier 8 :pm Njus This puzzle collection is closed book and closed notes. NO calculators are allowed
MATH-65 Puzzle Collection 6 Nov 8 :pm-:pm Name:... 3 :pm Wumaier :pm Njus 5 :pm Wumaier 6 :pm Njus 7 :pm Wumaier 8 :pm Njus This puzzle collection is closed book and closed notes. NO calculators are allowed
Infinite series, improper integrals, and Taylor series
 Chapter Infinite series, improper integrals, and Taylor series. Determine which of the following sequences converge or diverge (a) {e n } (b) {2 n } (c) {ne 2n } (d) { 2 n } (e) {n } (f) {ln(n)} 2.2 Which
Chapter Infinite series, improper integrals, and Taylor series. Determine which of the following sequences converge or diverge (a) {e n } (b) {2 n } (c) {ne 2n } (d) { 2 n } (e) {n } (f) {ln(n)} 2.2 Which
Math 152 Take Home Test 1
 Math 5 Take Home Test Due Monday 5 th October (5 points) The following test will be done at home in order to ensure that it is a fair and representative reflection of your own ability in mathematics I
Math 5 Take Home Test Due Monday 5 th October (5 points) The following test will be done at home in order to ensure that it is a fair and representative reflection of your own ability in mathematics I
Lecture : The Indefinite Integral MTH 124
 Up to this point we have investigated the definite integral of a function over an interval. In particular we have done the following. Approximated integrals using left and right Riemann sums. Defined the
Up to this point we have investigated the definite integral of a function over an interval. In particular we have done the following. Approximated integrals using left and right Riemann sums. Defined the
5.4 Variation of Parameters
 202 5.4 Variation of Parameters The method of variation of parameters applies to solve (1) a(x)y + b(x)y + c(x)y = f(x). Continuity of a, b, c and f is assumed, plus a(x) 0. The method is important because
202 5.4 Variation of Parameters The method of variation of parameters applies to solve (1) a(x)y + b(x)y + c(x)y = f(x). Continuity of a, b, c and f is assumed, plus a(x) 0. The method is important because
Math Assignment 5
 Math 2280 - Assignment 5 Dylan Zwick Fall 2013 Section 3.4-1, 5, 18, 21 Section 3.5-1, 11, 23, 28, 35, 47, 56 Section 3.6-1, 2, 9, 17, 24 1 Section 3.4 - Mechanical Vibrations 3.4.1 - Determine the period
Math 2280 - Assignment 5 Dylan Zwick Fall 2013 Section 3.4-1, 5, 18, 21 Section 3.5-1, 11, 23, 28, 35, 47, 56 Section 3.6-1, 2, 9, 17, 24 1 Section 3.4 - Mechanical Vibrations 3.4.1 - Determine the period
State Precalculus/Trigonometry Contest 2008
 State Precalculus/Trigonometry Contest 008 Select the best answer for each of the following questions and mark it on the answer sheet provided. Be sure to read all the answer choices before making your
State Precalculus/Trigonometry Contest 008 Select the best answer for each of the following questions and mark it on the answer sheet provided. Be sure to read all the answer choices before making your
dx n a 1(x) dy
 HIGHER ORDER DIFFERENTIAL EQUATIONS Theory of linear equations Initial-value and boundary-value problem nth-order initial value problem is Solve: a n (x) dn y dx n + a n 1(x) dn 1 y dx n 1 +... + a 1(x)
HIGHER ORDER DIFFERENTIAL EQUATIONS Theory of linear equations Initial-value and boundary-value problem nth-order initial value problem is Solve: a n (x) dn y dx n + a n 1(x) dn 1 y dx n 1 +... + a 1(x)
Section 3.4. Second Order Nonhomogeneous. The corresponding homogeneous equation. is called the reduced equation of (N).
 Section 3.4. Second Order Nonhomogeneous Equations y + p(x)y + q(x)y = f(x) (N) The corresponding homogeneous equation y + p(x)y + q(x)y = 0 (H) is called the reduced equation of (N). 1 General Results
Section 3.4. Second Order Nonhomogeneous Equations y + p(x)y + q(x)y = f(x) (N) The corresponding homogeneous equation y + p(x)y + q(x)y = 0 (H) is called the reduced equation of (N). 1 General Results
CHALLENGE! (0) = 5. Construct a polynomial with the following behavior at x = 0:
 TAYLOR SERIES Construct a polynomial with the following behavior at x = 0: CHALLENGE! P( x) = a + ax+ ax + ax + ax 2 3 4 0 1 2 3 4 P(0) = 1 P (0) = 2 P (0) = 3 P (0) = 4 P (4) (0) = 5 Sounds hard right?
TAYLOR SERIES Construct a polynomial with the following behavior at x = 0: CHALLENGE! P( x) = a + ax+ ax + ax + ax 2 3 4 0 1 2 3 4 P(0) = 1 P (0) = 2 P (0) = 3 P (0) = 4 P (4) (0) = 5 Sounds hard right?
Ma 221 Final Exam Solutions 5/14/13
 Ma 221 Final Exam Solutions 5/14/13 1. Solve (a) (8 pts) Solution: The equation is separable. dy dx exy y 1 y0 0 y 1e y dy e x dx y 1e y dy e x dx ye y e y dy e x dx ye y e y e y e x c The last step comes
Ma 221 Final Exam Solutions 5/14/13 1. Solve (a) (8 pts) Solution: The equation is separable. dy dx exy y 1 y0 0 y 1e y dy e x dx y 1e y dy e x dx ye y e y dy e x dx ye y e y e y e x c The last step comes
Grade: The remainder of this page has been left blank for your workings. VERSION E. Midterm E: Page 1 of 12
 First Name: Student-No: Last Name: Section: Grade: The remainder of this page has been left blank for your workings. Midterm E: Page of Indefinite Integrals. 9 marks Each part is worth 3 marks. Please
First Name: Student-No: Last Name: Section: Grade: The remainder of this page has been left blank for your workings. Midterm E: Page of Indefinite Integrals. 9 marks Each part is worth 3 marks. Please
For more information visit
 If the integrand is a derivative of a known function, then the corresponding indefinite integral can be directly evaluated. If the integrand is not a derivative of a known function, the integral may be
If the integrand is a derivative of a known function, then the corresponding indefinite integral can be directly evaluated. If the integrand is not a derivative of a known function, the integral may be
2.12: Derivatives of Exp/Log (cont d) and 2.15: Antiderivatives and Initial Value Problems
 2.12: Derivatives of Exp/Log (cont d) and 2.15: Antiderivatives and Initial Value Problems Mathematics 3 Lecture 14 Dartmouth College February 03, 2010 Derivatives of the Exponential and Logarithmic Functions
2.12: Derivatives of Exp/Log (cont d) and 2.15: Antiderivatives and Initial Value Problems Mathematics 3 Lecture 14 Dartmouth College February 03, 2010 Derivatives of the Exponential and Logarithmic Functions
and lim lim 6. The Squeeze Theorem
 Limits (day 3) Things we ll go over today 1. Limits of the form 0 0 (continued) 2. Limits of piecewise functions 3. Limits involving absolute values 4. Limits of compositions of functions 5. Limits similar
Limits (day 3) Things we ll go over today 1. Limits of the form 0 0 (continued) 2. Limits of piecewise functions 3. Limits involving absolute values 4. Limits of compositions of functions 5. Limits similar
Section 3.4. Second Order Nonhomogeneous. The corresponding homogeneous equation. is called the reduced equation of (N).
 Section 3.4. Second Order Nonhomogeneous Equations y + p(x)y + q(x)y = f(x) (N) The corresponding homogeneous equation y + p(x)y + q(x)y = 0 (H) is called the reduced equation of (N). 1 General Results
Section 3.4. Second Order Nonhomogeneous Equations y + p(x)y + q(x)y = f(x) (N) The corresponding homogeneous equation y + p(x)y + q(x)y = 0 (H) is called the reduced equation of (N). 1 General Results
JUST THE MATHS UNIT NUMBER INTEGRATION 1 (Elementary indefinite integrals) A.J.Hobson
 JUST THE MATHS UNIT NUMBER 2. INTEGRATION (Elementary indefinite integrals) by A.J.Hobson 2.. The definition of an integral 2..2 Elementary techniques of integration 2..3 Exercises 2..4 Answers to exercises
JUST THE MATHS UNIT NUMBER 2. INTEGRATION (Elementary indefinite integrals) by A.J.Hobson 2.. The definition of an integral 2..2 Elementary techniques of integration 2..3 Exercises 2..4 Answers to exercises
Form A. 1. Which of the following is a second-order, linear, homogenous differential equation? 2
 Form A Math 4 Common Part of Final Exam December 6, 996 INSTRUCTIONS: Please enter your NAME, ID NUMBER, FORM designation, and INDEX NUMBER on your op scan sheet. The index number should be written in
Form A Math 4 Common Part of Final Exam December 6, 996 INSTRUCTIONS: Please enter your NAME, ID NUMBER, FORM designation, and INDEX NUMBER on your op scan sheet. The index number should be written in
If y = f (u) is a differentiable function of u and u = g(x) is a differentiable function of x then dy dx = dy. du du. If y = f (u) then y = f (u) u
 Section 3 4B The Chain Rule If y = f (u) is a differentiable function of u and u = g(x) is a differentiable function of x then dy dx = dy du du dx or If y = f (u) then f (u) u The Chain Rule with the Power
Section 3 4B The Chain Rule If y = f (u) is a differentiable function of u and u = g(x) is a differentiable function of x then dy dx = dy du du dx or If y = f (u) then f (u) u The Chain Rule with the Power
Section 3.4. Second Order Nonhomogeneous. The corresponding homogeneous equation. is called the reduced equation of (N).
 Section 3.4. Second Order Nonhomogeneous Equations y + p(x)y + q(x)y = f(x) (N) The corresponding homogeneous equation y + p(x)y + q(x)y = 0 (H) is called the reduced equation of (N). 1 General Results
Section 3.4. Second Order Nonhomogeneous Equations y + p(x)y + q(x)y = f(x) (N) The corresponding homogeneous equation y + p(x)y + q(x)y = 0 (H) is called the reduced equation of (N). 1 General Results
Math 217 Practice Exam 1. Page Which of the following differential equations is exact?
 Page 1 1. Which of the following differential equations is exact? (a) (3x x 3 )dx + (3x 3x 2 ) d = 0 (b) sin(x) dx + cos(x) d = 0 (c) x 2 x 2 = 0 (d) (1 + e x ) + (2 + xe x ) d = 0 CORRECT dx (e) e x dx
Page 1 1. Which of the following differential equations is exact? (a) (3x x 3 )dx + (3x 3x 2 ) d = 0 (b) sin(x) dx + cos(x) d = 0 (c) x 2 x 2 = 0 (d) (1 + e x ) + (2 + xe x ) d = 0 CORRECT dx (e) e x dx
First Order Differential Equations f ( x,
 Chapter d dx First Order Differential Equations f ( x, ).1 Linear Equations; Method of Integrating Factors Usuall the general first order linear equations has the form p( t ) g ( t ) (1) where pt () and
Chapter d dx First Order Differential Equations f ( x, ).1 Linear Equations; Method of Integrating Factors Usuall the general first order linear equations has the form p( t ) g ( t ) (1) where pt () and
17.2 Nonhomogeneous Linear Equations. 27 September 2007
 17.2 Nonhomogeneous Linear Equations 27 September 2007 Nonhomogeneous Linear Equations The differential equation to be studied is of the form ay (x) + by (x) + cy(x) = G(x) (1) where a 0, b, c are given
17.2 Nonhomogeneous Linear Equations 27 September 2007 Nonhomogeneous Linear Equations The differential equation to be studied is of the form ay (x) + by (x) + cy(x) = G(x) (1) where a 0, b, c are given
7.1 Integration by Parts (...or, undoing the product rule.)
 7.1 1 7.1 Integration by Parts (...or, undoing the product rule.) Integration by Parts Recall the differential form of the chain rule. If u and v are differentiable functions. Then (1) d(uv) = du v +u
7.1 1 7.1 Integration by Parts (...or, undoing the product rule.) Integration by Parts Recall the differential form of the chain rule. If u and v are differentiable functions. Then (1) d(uv) = du v +u
MATH 1231 MATHEMATICS 1B CALCULUS. Section 5: - Power Series and Taylor Series.
 MATH 1231 MATHEMATICS 1B CALCULUS. Section 5: - Power Series and Taylor Series. The objective of this section is to become familiar with the theory and application of power series and Taylor series. By
MATH 1231 MATHEMATICS 1B CALCULUS. Section 5: - Power Series and Taylor Series. The objective of this section is to become familiar with the theory and application of power series and Taylor series. By
If y = f (u) is a differentiable function of u and u = g(x) is a differentiable function of x then dy dx = dy. du du. If y = f (u) then y = f (u) u
 Section 3 4B Lecture The Chain Rule If y = f (u) is a differentiable function of u and u = g(x) is a differentiable function of x then dy dx = dy du du dx or If y = f (u) then y = f (u) u The Chain Rule
Section 3 4B Lecture The Chain Rule If y = f (u) is a differentiable function of u and u = g(x) is a differentiable function of x then dy dx = dy du du dx or If y = f (u) then y = f (u) u The Chain Rule
2003 Mathematics. Advanced Higher. Finalised Marking Instructions
 2003 Mathematics Advanced Higher Finalised Marking Instructions 2003 Mathematics Advanced Higher Section A Finalised Marking Instructions Advanced Higher 2003: Section A Solutions and marks A. (a) Given
2003 Mathematics Advanced Higher Finalised Marking Instructions 2003 Mathematics Advanced Higher Section A Finalised Marking Instructions Advanced Higher 2003: Section A Solutions and marks A. (a) Given
Chapter 13: General Solutions to Homogeneous Linear Differential Equations
 Worked Solutions 1 Chapter 13: General Solutions to Homogeneous Linear Differential Equations 13.2 a. Verifying that {y 1, y 2 } is a fundamental solution set: We have y 1 (x) = cos(2x) y 1 (x) = 2 sin(2x)
Worked Solutions 1 Chapter 13: General Solutions to Homogeneous Linear Differential Equations 13.2 a. Verifying that {y 1, y 2 } is a fundamental solution set: We have y 1 (x) = cos(2x) y 1 (x) = 2 sin(2x)
MA 262, Fall 2017, Final Version 01(Green)
 INSTRUCTIONS MA 262, Fall 2017, Final Version 01(Green) (1) Switch off your phone upon entering the exam room. (2) Do not open the exam booklet until you are instructed to do so. (3) Before you open the
INSTRUCTIONS MA 262, Fall 2017, Final Version 01(Green) (1) Switch off your phone upon entering the exam room. (2) Do not open the exam booklet until you are instructed to do so. (3) Before you open the
C3 Revision Questions. (using questions from January 2006, January 2007, January 2008 and January 2009)
 C3 Revision Questions (using questions from January 2006, January 2007, January 2008 and January 2009) 1 2 1. f(x) = 1 3 x 2 + 3, x 2. 2 ( x 2) (a) 2 x x 1 Show that f(x) =, x 2. 2 ( x 2) (4) (b) Show
C3 Revision Questions (using questions from January 2006, January 2007, January 2008 and January 2009) 1 2 1. f(x) = 1 3 x 2 + 3, x 2. 2 ( x 2) (a) 2 x x 1 Show that f(x) =, x 2. 2 ( x 2) (4) (b) Show
1 Solution to Homework 4
 Solution to Homework Section. 5. The characteristic equation is r r + = (r )(r ) = 0 r = or r =. y(t) = c e t + c e t y = c e t + c e t. y(0) =, y (0) = c + c =, c + c = c =, c =. To find the maximum value
Solution to Homework Section. 5. The characteristic equation is r r + = (r )(r ) = 0 r = or r =. y(t) = c e t + c e t y = c e t + c e t. y(0) =, y (0) = c + c =, c + c = c =, c =. To find the maximum value
