where p oo is a reference level constant pressure (often 10 5 Pa). Since θ is conserved for adiabatic motions, a prognostic temperature equation is:
|
|
|
- Sheila Sullivan
- 5 years ago
- Views:
Transcription
1 1 Appendix C Useful Equations Purposes: Provide foundation equations and sketch some derivations. These equations are used as starting places for discussions in various parts of the book. C.1. Thermodynamic equations Thermodynamics is important in understanding the general circulation. Several key equations are diagnostic. The ideal gas law (C.1) often used to relate mass and temperature variables: p = ρ RT (C.1) Temperature is not conserved when moving adiabatically while undergoing compression or expansion, but a related variable, potential temperature, θ is conserved. Poisson s equation (C.) relates the two: RC / P p θ T oo = (C.) p where p oo is a reference level constant pressure (often 10 5 Pa). Since θ is conserved for adiabatic motions, a prognostic temperature equation is: d θ = θ = D θ = D θ (C.3) J dt C T T p where D J contains all the diabatic heating with units J s -1 kg -1 and D T is a corresponding heating rate with units K/s. The first law of thermodynamics relates how heat exchanges, including work done on or by the environment, in order to conserve energy. An increment of such work per unit mass, dw could be written: dw = p dα This dw can enter a meteorological problem as the change in temperature due to moving a mass (air parcel) vertically (and adiabatically) so that the mass is compressed or expanded. An increment in the non-adiabatic heating could be written as D T. It can be written several ways (e.g. Wallace and Hobbs, 006). One form, uses (C.1), (C.) and (C.3): d T d p d θ D ds ln ln ln J o Cp R = Cp = dt dt dt T dt dt dp Cp α = DJ dt dt T (C.4) where S o is entropy per unit mass (Holton, 004) and from (C.4) d S o =C p dln(θ). A related quantity, the enthalpy (S a =C p T) measures the heat added to raise the temperature of a mass from 0 K to T. One major source of diabatic heating occurs when moisture has a net change of state. The amount of moisture available for a given temperature is related by the Clausius-Clapeyron equation:
2 des L = (C.5) dt Tαv where e s is the saturation vapor pressure, and α v is the specific volume for water vapor. (C.5) assumes that the specific volume for liquid water is much less than for vapor (Tsonis, 007). Assuming that water vapor behaves like an ideal gas and employing Dalton s law of partial pressures, (C.5) can be rearranged as: des LdT = (C.6) es RT v (C.6) shows that e s is a nonlinear function of temperature. Assuming L is independent of T (L varies by ~10% over 73K T 373K) and integrating (C.6) from a reference temperature T o to T obtains (James, 1994): L 1 1 es( T) = es( To) exp (C.7) Rv To T The dependence is approximately exponential. For T>T o the saturation vapor pressure increases as T increases. Alternatively, (Tsonis, 007) for T o =73K: 5417 es ( T) = 6.11exp in hpa T (C.8) Diabatic heating from net changes in the state of water can be included in a conserved temperature quantity, equivalent potential temperature, θ e Lw d θe = θexp (C.9) CT p where w d is the mixing ratio (i.e. the saturation mixing ratio with respect to liquid water at the dewpoint temperature) and the specific heat of dry air (C p ) is assumed much larger than the specific heat from the fraction of water vapor present. Note that. From the LHS of (C.4) one can relate the heating rate to the dry static energy (DSE) as: ddse dct ( p +Φ) = DJ (C.10) dt dt where Φ is the geopotential. The DSE is the internal plus gravitational potential energy. Similarly, inspired by (C.9) with wd q one can define a moist static energy (MSE) equation from (C.4), where MSE is conserved if the only diabatic processes are moist diabatic processes (so-called psuedoadiabatic processes). dmse d( CpT +Φ+ Lq) = DNM (C.11) dt dt where D NM is diabatic heating from non-moisture sources (such as radiation and conduction) and q is the specific humidity. A balance of forces between gravity and vertical pressure gradient force leads to an expression relating pressure variation with elevation. The resultant hydrostatic balance (C.13) follows from ignoring vertical accelerations and is a good approximation for large scale motions and is useful when converting between height and pressure coordinates.
3 3 p = ρ g (C.1) z Other forms of hydrostatic balance, in pressure and isentropic coordinates can be deduced from the PGCF terms in (C.4) and (C.5) below. Substituting (C.1) into (C.1) and rearranging obtains a variation on hydrostatic balance: p / p = ( RT / g ) z z / H. Assuming a vertically-averaged temperature, this variation can be easily integrated to obtain an approximate formula wherein pressure is an exponential function of elevation: p = pooexp( z / H). H has units of length, is an e-folding scale, and is called the scale height. A similar procedure can eliminate pressure to obtain an exponential function for density variation with elevation. Combining (C.1) and (C.1) yields the hypsometric equation relating the thickness ΔZ between pressure surfaces p t and p b and the temperature of that layer R pb Z = Zt Zb = Td ln p g (C.13) pt where a constant acceleration of gravity, g was assumed. Combining (C.1) and the definition of DSE (C.10) obtains the dry adiabatic lapse rate of temperature: Γ dt g d dz = C (C.14) p A moist adiabatic lapse rate, Γ m can be derived (Tsonis, 007) from the first law of thermodynamics (C.4) and using hydrostatic balance (C.1). Lw 1+ dt g RT Γm = (C.15) dz Cp Lw 1+ CpRT v Γ m Γ d since the term inside the brackets is less than one. C.. Equations of motion and continuity The equations of motion and continuity are used in several different coordinate frames depending upon the problem being examined. The equations of motion, or momentum equations (per unit mass) include a total derivative. The vector curl operation also appears in the momentum equations. The equation for mass continuity, or continuity equation uses a divergence operator. These three operators differ with coordinate frame and so the general forms of the operators are discussed first, drawing inspiration from Haltiner and Williams (1980). da A d d A v1 A v A v3 A = + V A= (C.16) dt t t m1 x1 m x m3 x3 where A is a scalar. The three dimensional velocity vector V =(v 1, v,v 3 ) while the m i is a map factor in the direction x i. A curl operator is defined as: i mg 3 3 mg j mg 1 1 mg 3 3 k mg mg 1 1 G = + + (C.17) m m 3 x x 3 mm 1 3 x 3 x 1 mm 1 x 1 x
4 4 where G =(G 1, G,G 3 ) is a vector. The divergence of G is: 1 mmg 3 1 mmg 1 3 mmg 1 3 G = + + (C.18) mm 1 m 3 x 1 x x 3 Two commonly-used horizontal coordinate frames are Cartesian and spherical coordinates. The map factors for those systems are: ( x, x) = ( xy, ) Cartesian Coordinates 1 ( m, m, m ) = (1,1,1) Cartesian Coordinates 1 3 ( n, n, n ) = (0, 0, 0) Cartesian Coordinates 1 3 ( v, v) = ( uv, ) Cartesian Coordinates 1 (C.19) ( x, x ) = ( lϕ, ) Spherical Coordinates 1 ( m, m, m ) = ( rcos ϕ, r,1) Spherical Coordinates 1 3 ( n, n, n ) = (1,1,1) Spherical Coordinates 1 3 dl dϕ ( v1, v) = ( rcos ϕ, r ) Spherical Coordinates dt dt (C.0) where n 1, n, and n 3 are used below. In general, the wind components are: dx1 dx dx3 ( v1, v, v3) = m1, m, m3 dt dt dt (C.1) Several choices are commonly-used for the vertical coordinate, x 3 and the choice affects the definitions of the vertical derivatives and velocity component v 3. Specifically: x v 3 3 = z = w ( n n n n ) Height Coordinates Height Coordinates,,, = ( r,1,1,1) Height Coordinates o t z v h = p 1 p F 1 p PGCF = + = + g r z z r z x v 3 3 = p = ω ( n n n n ) Height Coordinates Height Coordinates Pressure Coordinates Pressure Coordinates 1 1 o, t, z, v = 1,1,, Pressure Coordinates rg rg h = F Pressure Coordinates F PGCF = g 1 + r Pressure Coordinates p (C.) (C.3)
5 5 x3 = θ θ Coordinates v3 = θ θ Coordinates z z ( no, nt, nz, nv) = 1,,1, θ θ θ Coordinates (C.4) h= CT p +F θ Coordinates θ h CT p θ CT p PGCF = = ( C pt +F) z θ θ z θ θ θ Coordinates where the h and n o values are used in the equations below. The quantity h in potential temperature ( theta ) coordinates is generally referred to as the Montgomery Stream function and it is obviously related to the DSE. The so-called primitive equations of motion actually result from several assumptions applied to the Navier-Stokes equations, along with additional thermodynamic relations to have sufficient independent equations to match the number of dependent variables. Derivations can be found in several books, e.g. Vallis (006). The primitive equations include momentum equations which equate the acceleration of the wind components to operant body and surface forces. For large scale atmospheric flows gravity is the only body force while pressure gradient and friction (including diffusion) are surface forces. Apparent forces, like the Coriolis terms arise from a coordinate frame of reference rotating with respect to a fixed point on the Earth s surface. (The Coriolis is sometimes thought of as a body force.) Even the primitive equations form has three primary traditional assumptions: 1) thin atmosphere (use a constant distance, r in (C.0) instead of the distance from the point in the atmosphere to the center of the earth), ) ignore small metric terms (uw/r and uw/r), 3) ignore Coriolis terms involving the vertical component of the wind. Momentum is altered following the motion of an air parcel by body and surface forces and for the atmosphere can be written in vector form as: d dv 1 d d d d d = p F Ω V + F (C.5) dt ρ where the geopotential is defined to include both the gravitational geopotential and the centrifugal acceleration (due to the Earth s rotation). It is understood that (C.5) is an equation for momentum per unit mass. Examining (C.5) it is clear that the pressure gradient term using height coordinates will not have a contribution from the Φ term except for gravity in the vertical component equation. And, in pressure coordinates the p term vanishes except for the vertical component equation. For some other coordinate, like θ both terms are present. The component momentum equations are: dv1 1 h n1 = + Ω+ v1( vsinϕ nnv 3 v 3cosϕ) + F1 (C.6) dt nom1 x1 m1
6 6 dv 1 h n1 nn v = Ω+ v1v1sinϕ vv 3+ F (C.7) dt nom x m1 m dnt v3 1 p x3 1 F x3 n nz = + Ω v1cos ϕ + ( v1 + v ) + F3 dt ρm3 x3 z m3 x3 z m (C.8) n = PGCF + Ω v1cos ϕ + ( v1 + v ) + F3 m The hydrostatic equation (C.1) is easily seen by retaining only the pressure gradient and gravity forces in (C.8) which are contained in the term labeled PGCF defined in (C.). PGCF reveals the hydrostatic relation in p and θ coordinates in (C.3) and (C.4), respectively. The continuity equation is: d p d d ln + V = 0 (C.9) dt x 3 It is obvious from (C.9) and (C.3) that the continuity equation has a very simple form in pressure coordinates: V = 0 (C.30) Following Vallis (006) (C.5) can be expressed using three dimensional vorticity 1 ζ = V and kinetic energy, ( ) V V V 1 = no h+ g ( Ω ζ ) V ( V V) (C.31) t where g =(0,0,g) is the gravity vector and F is the friction vector.using just the vertical component of the vorticity, ζ the horizontal momentum equations can be written VH v3 V d d d d d H + = n h f k V V V t m x 3 3 where V H vorticity is inside the curly brackets. 1 { ζ } ( ) o H H H H (C.3) = (v 1, v, 0) and f (=Ωsinφ) is the Coriolis parameter and the absolute C.3. Two simplifications Two simplifications of these equations are noteworthy for this book: the shallow water system and the quasi-geostrophic system. Either by formally integrating in the vertical or by considering only density and velocity fields that are independent of the vertical coordinate, one may obtain the shallow water equations (SWE) system of equations. Hydrostatic balance (C.1) is assumed so the pressure gradient force is independent of elevation. Considering (C.6), (C.7), and (C.9), constant density leads to linear pressure change with height and scaling eliminates some smaller Coriolis terms. The SWE simplify to: dv 1 h = no + fv + F 1 dt x1 dv h = no fv1+ F dt x (C.33) (C.34)
7 7 dh h V 0 dt + d d = (C.35) where tilda overbars indicate vertical average velocity and friction while h is specifically the thickness of the fluid layer. Vertical variation may be created by applying the SW system to multiple layers. Topography and variable layer top allow h to vary in the horizontal. These equations have several advantages: they contain a wide variety of wave types found in the atmosphere and they have a simple and intuitive expression for potential vorticity. Another system of interest is the quasi-geostrophic (QG) system. The derivation proceeds as follows. The momentum and thermodynamic equations, an example of the latter being (C.3), are nondimensionalized, typically using scales relevant to midlatitude frontal cyclones. Nondimensional weights are expressed in terms of the Rossby number (R o ) and different orders of the small R o. The lowest order is geostrophic winds and a hydrostatic static state for the horizontally mean mass and temperature fields. Geostrophic winds balance the pressure gradient and largest Coriolis terms (usually assuming a constant value for f): 1 h vg1 = (C.36) no fo x 1 h vg = (C.37) no fo x1 where the subscript g indicates these are geostrophic balance winds and f o is a specified constant value of f. A thermal wind relation can be derived by eliminating h from (C.36) and (C.37) while using the hydrostatic and ideal gas relations. Generally, a vertical shear in the horizontal wind will be proportional to a horizontal temperature gradient normal to the wind direction. For example, in pressure coordinates (Holton, 004) Vg R = k p T (C.38) ln p f In Cartesian geometry, component form: ug R T = (C.39) p pf y p vg R T = p pf x (C.40) p where p subscript means the derivative is on a surface holding p constant. The QG system is the next higher order in the small R o number expansion. For latitudes other than the deep tropics, and for large scale motions above the planetary boundary layer the geostrophic component of the wind is generally much larger than the remaining non-geostrophic ( ageostrophic ) part of the total wind. The small parameter expansion (e.g. Grotjahn, 1979) results in ageostrophic winds substituting for the advecting winds in a total derivative and for the advected quantity in the horizontal equations of motion. Hydrostatic balance applies to perturbations from the zonal mean mass fields. Hence,
8 8 d v v d d v v v v v g g1 g1 g1 g1 g1 g g1 = + Vg vg1 = + + = fvag + F1 dt t t m1 x1 m x d v v d d v v v v v g g g g g g g g = + Vg vg = + + = fvag1+ F dt t t m1 x1 m x (C.41) (C.4) where the subscript ag indicates the ageostrophic wind. Vertical motion is small relative to horizontal motions, even after accounting for the smaller vertical to horizontal scales aspect ratio. Vertical motion does not appear explicitly except through the divergence of those ageostrophic winds. Vertical motion is missing from (C.41) and (C.4) due to strong static stability, but must be included in a temperature tendency equation, for example: d θ θ d d θ θ v θ v θ v θ θ g s g g 3 s s = + Vg θ + v3 = = θ = Q dt t x3 t m1 x1 m x m3 x3 Ts (C.43) where the s subscripts refer to the horizontally uniform static state. Hydrostatic balance and (lower order) continuity equation complete the QG system. C.3. Potential vorticity relations A primary diagnostic is potential vorticity. It takes different mathematical forms in different vertical coordinates and systems of equations. The form in Cartesian geometry of the SWE is particularly simple and intuitive. Forming a vorticity equation from y derivative of (C.33) and an x derivative of (C.34) while using (C.19) and (C.) yields the inviscid form: d ( g ζ g + f ) ζ g d d v g f = + Vg ζ g + = dt t m x (C.44) ζg vg ζg v g ( ζ g + f ) 1 v1 1 v + + = fo + t m1 x1 m x m1 x1 m x Combining this equation with (C.35) to eliminate the divergence yields: dqswe d ζ g + f = 0 (C.45) dt dt h The quantity inside the parentheses is the SWE potential vorticity, P SWE. The QG potential vorticity can be formed in an analogous way. Forming a vorticity equation from y derivative of (C.41) and an x derivative of (C.4) while using (C.19) and (C.3) yields the inviscid form of the vorticity equation in Cartesian, pressure coordinates: ( ζ ) dg g + f ζ g d d f = + Vg ζ g + vg = dt t x ( ζ g ) (C.46) ζg ζ + f g u 1 v ω + ug + vg = fo + = fo t x1 x x m y p Clearly this is in a similar form as (C.44) though the QG vorticity equation has vertical variation. A Cartesian, pressure coordinates form of (C.43) will have ω multiplying the static state static stability term. Eliminating ω from (C.43) and (C.46) yields:
9 9 dq QG d 1 fo p Φ Φ+ f + 0 dt dt f ln o p θ = (C.47) s p RT s p where the quantity inside the brackets is the QG potential vorticity in this coordinate system (Holton, 004). As with (C.45) this potential vorticity equation reveals a powerful constraint that the potential vorticity must be conserved following the flow (for frictionless, adiabatic motion). A height coordinate form (e.g. Vallis, 006) is: dqqg d 1 fo ρ p p+ f + 0 = (C.48) dt dt fo ρ z N z where N is the Brunt-Väisälä frequency. The potential vorticity in isentropic coordinates also has a simple form. Combining (C.1) and (C.) and using Kelvin s circulation theorem to a small loop on an isentropic surface recovers both the absolute vorticity and the area of that loop (Holton, 004). For adiabatic motion a parcel s area on an isentropic surface swells or shrinks as adjacent isentropic surfaces approach or recede. For adiabatic motion: dqe d g + = dt dt p θ ( ζ g f ) 0 (C.49) Similar to (C.45) the term inside the curly brackets is always positive and inversely related to the spacing between θ surfaces. As the θ surfaces stretch apart, the absolute vorticity must decrease in magnitude to compensate, and vice versa. C.4. Other useful relations The area of a region on a sphere is a double integral of the area increment over the specified longitude λ and latitude φ ranges. The area increment is the longitude increment: r cosφ dλ multiplying the latitude increment: r dφ. Hence, when the full ranges of λ and φ are used, that double integral equals 4πr. Hence: 1 1 p/ p area of whole sphere = 4p r = r cos ϕdldϕ, ϕ l p / 0 area of region = r cosϕdldϕ ϕ l (C.50)
1/18/2011. Conservation of Momentum Conservation of Mass Conservation of Energy Scaling Analysis ESS227 Prof. Jin-Yi Yu
 Lecture 2: Basic Conservation Laws Conservation Law of Momentum Newton s 2 nd Law of Momentum = absolute velocity viewed in an inertial system = rate of change of Ua following the motion in an inertial
Lecture 2: Basic Conservation Laws Conservation Law of Momentum Newton s 2 nd Law of Momentum = absolute velocity viewed in an inertial system = rate of change of Ua following the motion in an inertial
Chapter 2. Quasi-Geostrophic Theory: Formulation (review) ε =U f o L <<1, β = 2Ω cosθ o R. 2.1 Introduction
 Chapter 2. Quasi-Geostrophic Theory: Formulation (review) 2.1 Introduction For most of the course we will be concerned with instabilities that an be analyzed by the quasi-geostrophic equations. These are
Chapter 2. Quasi-Geostrophic Theory: Formulation (review) 2.1 Introduction For most of the course we will be concerned with instabilities that an be analyzed by the quasi-geostrophic equations. These are
Conservation of Mass Conservation of Energy Scaling Analysis. ESS227 Prof. Jin-Yi Yu
 Lecture 2: Basic Conservation Laws Conservation of Momentum Conservation of Mass Conservation of Energy Scaling Analysis Conservation Law of Momentum Newton s 2 nd Law of Momentum = absolute velocity viewed
Lecture 2: Basic Conservation Laws Conservation of Momentum Conservation of Mass Conservation of Energy Scaling Analysis Conservation Law of Momentum Newton s 2 nd Law of Momentum = absolute velocity viewed
ρ x + fv f 'w + F x ρ y fu + F y Fundamental Equation in z coordinate p = ρrt or pα = RT Du uv tanφ Dv Dt + u2 tanφ + vw a a = 1 p Dw Dt u2 + v 2
 Fundamental Equation in z coordinate p = ρrt or pα = RT Du uv tanφ + uw Dt a a = 1 p ρ x + fv f 'w + F x Dv Dt + u2 tanφ + vw a a = 1 p ρ y fu + F y Dw Dt u2 + v 2 = 1 p a ρ z g + f 'u + F z Dρ Dt + ρ
Fundamental Equation in z coordinate p = ρrt or pα = RT Du uv tanφ + uw Dt a a = 1 p ρ x + fv f 'w + F x Dv Dt + u2 tanφ + vw a a = 1 p ρ y fu + F y Dw Dt u2 + v 2 = 1 p a ρ z g + f 'u + F z Dρ Dt + ρ
2. Conservation laws and basic equations
 2. Conservation laws and basic equations Equatorial region is mapped well by cylindrical (Mercator) projection: eastward, northward, upward (local Cartesian) coordinates:,, velocity vector:,,,, material
2. Conservation laws and basic equations Equatorial region is mapped well by cylindrical (Mercator) projection: eastward, northward, upward (local Cartesian) coordinates:,, velocity vector:,,,, material
t tendency advection convergence twisting baroclinicity
 RELATIVE VORTICITY EQUATION Newton s law in a rotating frame in z-coordinate (frictionless): U + U U = 2Ω U Φ α p U + U U 2 + ( U) U = 2Ω U Φ α p Applying to both sides, and noting ω U and using identities
RELATIVE VORTICITY EQUATION Newton s law in a rotating frame in z-coordinate (frictionless): U + U U = 2Ω U Φ α p U + U U 2 + ( U) U = 2Ω U Φ α p Applying to both sides, and noting ω U and using identities
EATS Notes 1. Some course material will be online at
 EATS 3040-2015 Notes 1 14 Aug 2015 Some course material will be online at http://www.yorku.ca/pat/esse3040/ HH = Holton and Hakim. An Introduction to Dynamic Meteorology, 5th Edition. Most of the images
EATS 3040-2015 Notes 1 14 Aug 2015 Some course material will be online at http://www.yorku.ca/pat/esse3040/ HH = Holton and Hakim. An Introduction to Dynamic Meteorology, 5th Edition. Most of the images
Circulation and Vorticity
 Circulation and Vorticity Example: Rotation in the atmosphere water vapor satellite animation Circulation a macroscopic measure of rotation for a finite area of a fluid Vorticity a microscopic measure
Circulation and Vorticity Example: Rotation in the atmosphere water vapor satellite animation Circulation a macroscopic measure of rotation for a finite area of a fluid Vorticity a microscopic measure
Chapter 1. Governing Equations of GFD. 1.1 Mass continuity
 Chapter 1 Governing Equations of GFD The fluid dynamical governing equations consist of an equation for mass continuity, one for the momentum budget, and one or more additional equations to account for
Chapter 1 Governing Equations of GFD The fluid dynamical governing equations consist of an equation for mass continuity, one for the momentum budget, and one or more additional equations to account for
APPENDIX B. The primitive equations
 APPENDIX B The primitive equations The physical and mathematical basis of all methods of dynamical atmospheric prediction lies in the principles of conservation of momentum, mass, and energy. Applied to
APPENDIX B The primitive equations The physical and mathematical basis of all methods of dynamical atmospheric prediction lies in the principles of conservation of momentum, mass, and energy. Applied to
Chapter 2. The continuous equations
 Chapter. The continuous equations Fig. 1.: Schematic of a forecast with slowly varying weather-related variations and superimposed high frequency Lamb waves. Note that even though the forecast of the slow
Chapter. The continuous equations Fig. 1.: Schematic of a forecast with slowly varying weather-related variations and superimposed high frequency Lamb waves. Note that even though the forecast of the slow
2 Equations of Motion
 2 Equations of Motion system. In this section, we will derive the six full equations of motion in a non-rotating, Cartesian coordinate 2.1 Six equations of motion (non-rotating, Cartesian coordinates)
2 Equations of Motion system. In this section, we will derive the six full equations of motion in a non-rotating, Cartesian coordinate 2.1 Six equations of motion (non-rotating, Cartesian coordinates)
Atmospheric dynamics and meteorology
 Atmospheric dynamics and meteorology B. Legras, http://www.lmd.ens.fr/legras III Frontogenesis (pre requisite: quasi-geostrophic equation, baroclinic instability in the Eady and Phillips models ) Recommended
Atmospheric dynamics and meteorology B. Legras, http://www.lmd.ens.fr/legras III Frontogenesis (pre requisite: quasi-geostrophic equation, baroclinic instability in the Eady and Phillips models ) Recommended
Chapter 9. Geostrophy, Quasi-Geostrophy and the Potential Vorticity Equation
 Chapter 9 Geostrophy, Quasi-Geostrophy and the Potential Vorticity Equation 9.1 Geostrophy and scaling. We examined in the last chapter some consequences of the dynamical balances for low frequency, nearly
Chapter 9 Geostrophy, Quasi-Geostrophy and the Potential Vorticity Equation 9.1 Geostrophy and scaling. We examined in the last chapter some consequences of the dynamical balances for low frequency, nearly
2.5 Shallow water equations, quasigeostrophic filtering, and filtering of inertia-gravity waves
 Chapter. The continuous equations φ=gh Φ=gH φ s =gh s Fig..5: Schematic of the shallow water model, a hydrostatic, incompressible fluid with a rigid bottom h s (x,y), a free surface h(x,y,t), and horizontal
Chapter. The continuous equations φ=gh Φ=gH φ s =gh s Fig..5: Schematic of the shallow water model, a hydrostatic, incompressible fluid with a rigid bottom h s (x,y), a free surface h(x,y,t), and horizontal
Atmospheric Dynamics: lecture 2
 Atmospheric Dynamics: lecture 2 Topics Some aspects of advection and the Coriolis-effect (1.7) Composition of the atmosphere (figure 1.6) Equation of state (1.8&1.9) Water vapour in the atmosphere (1.10)
Atmospheric Dynamics: lecture 2 Topics Some aspects of advection and the Coriolis-effect (1.7) Composition of the atmosphere (figure 1.6) Equation of state (1.8&1.9) Water vapour in the atmosphere (1.10)
+ ω = 0, (1) (b) In geometric height coordinates in the rotating frame of the Earth, momentum balance for an inviscid fluid is given by
 Problem Sheet 1: Due Thurs 3rd Feb 1. Primitive equations in different coordinate systems (a) Using Lagrangian considerations and starting from an infinitesimal mass element in cartesian coordinates (x,y,z)
Problem Sheet 1: Due Thurs 3rd Feb 1. Primitive equations in different coordinate systems (a) Using Lagrangian considerations and starting from an infinitesimal mass element in cartesian coordinates (x,y,z)
Meteorology 6150 Cloud System Modeling
 Meteorology 6150 Cloud System Modeling Steve Krueger Spring 2009 1 Fundamental Equations 1.1 The Basic Equations 1.1.1 Equation of motion The movement of air in the atmosphere is governed by Newton s Second
Meteorology 6150 Cloud System Modeling Steve Krueger Spring 2009 1 Fundamental Equations 1.1 The Basic Equations 1.1.1 Equation of motion The movement of air in the atmosphere is governed by Newton s Second
Chapter 5. Shallow Water Equations. 5.1 Derivation of shallow water equations
 Chapter 5 Shallow Water Equations So far we have concentrated on the dynamics of small-scale disturbances in the atmosphere and ocean with relatively simple background flows. In these analyses we have
Chapter 5 Shallow Water Equations So far we have concentrated on the dynamics of small-scale disturbances in the atmosphere and ocean with relatively simple background flows. In these analyses we have
ESCI 485 Air/Sea Interaction Lesson 1 Stresses and Fluxes Dr. DeCaria
 ESCI 485 Air/Sea Interaction Lesson 1 Stresses and Fluxes Dr DeCaria References: An Introduction to Dynamic Meteorology, Holton MOMENTUM EQUATIONS The momentum equations governing the ocean or atmosphere
ESCI 485 Air/Sea Interaction Lesson 1 Stresses and Fluxes Dr DeCaria References: An Introduction to Dynamic Meteorology, Holton MOMENTUM EQUATIONS The momentum equations governing the ocean or atmosphere
The Shallow Water Equations
 If you have not already done so, you are strongly encouraged to read the companion file on the non-divergent barotropic vorticity equation, before proceeding to this shallow water case. We do not repeat
If you have not already done so, you are strongly encouraged to read the companion file on the non-divergent barotropic vorticity equation, before proceeding to this shallow water case. We do not repeat
Today s Lecture: Atmosphere finish primitive equations, mostly thermodynamics
 Today s Lecture: Atmosphere finish primitive equations, mostly thermodynamics Reference Peixoto and Oort, Sec. 3.1, 3.2, 3.4, 3.5 (but skip the discussion of oceans until next week); Ch. 10 Thermodynamic
Today s Lecture: Atmosphere finish primitive equations, mostly thermodynamics Reference Peixoto and Oort, Sec. 3.1, 3.2, 3.4, 3.5 (but skip the discussion of oceans until next week); Ch. 10 Thermodynamic
( ) (9.1.1) Chapter 9. Geostrophy, Quasi-Geostrophy and the Potential Vorticity Equation. 9.1 Geostrophy and scaling.
 Chapter 9 Geostrophy, Quasi-Geostrophy and the Potential Vorticity Equation 9.1 Geostrophy and scaling. We examined in the last chapter some consequences of the dynamical balances for low frequency, nearly
Chapter 9 Geostrophy, Quasi-Geostrophy and the Potential Vorticity Equation 9.1 Geostrophy and scaling. We examined in the last chapter some consequences of the dynamical balances for low frequency, nearly
Chapter 5. Sound Waves and Vortices. 5.1 Sound waves
 Chapter 5 Sound Waves and Vortices In this chapter we explore a set of characteristic solutions to the uid equations with the goal of familiarizing the reader with typical behaviors in uid dynamics. Sound
Chapter 5 Sound Waves and Vortices In this chapter we explore a set of characteristic solutions to the uid equations with the goal of familiarizing the reader with typical behaviors in uid dynamics. Sound
Thermodynamics Review [?] Entropy & thermodynamic potentials Hydrostatic equilibrium & buoyancy Stability [dry & moist adiabatic]
![Thermodynamics Review [?] Entropy & thermodynamic potentials Hydrostatic equilibrium & buoyancy Stability [dry & moist adiabatic] Thermodynamics Review [?] Entropy & thermodynamic potentials Hydrostatic equilibrium & buoyancy Stability [dry & moist adiabatic]](/thumbs/81/83694823.jpg) Thermodynamics Review [?] Entropy & thermodynamic potentials Hydrostatic equilibrium & buoyancy Stability [dry & moist adiabatic] Entropy 1. (Thermodynamics) a thermodynamic quantity that changes in a
Thermodynamics Review [?] Entropy & thermodynamic potentials Hydrostatic equilibrium & buoyancy Stability [dry & moist adiabatic] Entropy 1. (Thermodynamics) a thermodynamic quantity that changes in a
Quasi-equilibrium Theory of Small Perturbations to Radiative- Convective Equilibrium States
 Quasi-equilibrium Theory of Small Perturbations to Radiative- Convective Equilibrium States See CalTech 2005 paper on course web site Free troposphere assumed to have moist adiabatic lapse rate (s* does
Quasi-equilibrium Theory of Small Perturbations to Radiative- Convective Equilibrium States See CalTech 2005 paper on course web site Free troposphere assumed to have moist adiabatic lapse rate (s* does
BALANCED FLOW: EXAMPLES (PHH lecture 3) Potential Vorticity in the real atmosphere. Potential temperature θ. Rossby Ertel potential vorticity
 BALANCED FLOW: EXAMPLES (PHH lecture 3) Potential Vorticity in the real atmosphere Need to introduce a new measure of the buoyancy Potential temperature θ In a compressible fluid, the relevant measure
BALANCED FLOW: EXAMPLES (PHH lecture 3) Potential Vorticity in the real atmosphere Need to introduce a new measure of the buoyancy Potential temperature θ In a compressible fluid, the relevant measure
( u,v). For simplicity, the density is considered to be a constant, denoted by ρ 0
 ! Revised Friday, April 19, 2013! 1 Inertial Stability and Instability David Randall Introduction Inertial stability and instability are relevant to the atmosphere and ocean, and also in other contexts
! Revised Friday, April 19, 2013! 1 Inertial Stability and Instability David Randall Introduction Inertial stability and instability are relevant to the atmosphere and ocean, and also in other contexts
d v 2 v = d v d t i n where "in" and "rot" denote the inertial (absolute) and rotating frames. Equation of motion F =
 Governing equations of fluid dynamics under the influence of Earth rotation (Navier-Stokes Equations in rotating frame) Recap: From kinematic consideration, d v i n d t i n = d v rot d t r o t 2 v rot
Governing equations of fluid dynamics under the influence of Earth rotation (Navier-Stokes Equations in rotating frame) Recap: From kinematic consideration, d v i n d t i n = d v rot d t r o t 2 v rot
Chapter 7: Circulation and Vorticity
 Chapter 7: Circulation and Vorticity Circulation C = u ds Integration is performed in a counterclockwise direction C is positive for counterclockwise flow!!! Kelvin s Circulation Theorem The rate of change
Chapter 7: Circulation and Vorticity Circulation C = u ds Integration is performed in a counterclockwise direction C is positive for counterclockwise flow!!! Kelvin s Circulation Theorem The rate of change
1. The vertical structure of the atmosphere. Temperature profile.
 Lecture 4. The structure of the atmosphere. Air in motion. Objectives: 1. The vertical structure of the atmosphere. Temperature profile. 2. Temperature in the lower atmosphere: dry adiabatic lapse rate.
Lecture 4. The structure of the atmosphere. Air in motion. Objectives: 1. The vertical structure of the atmosphere. Temperature profile. 2. Temperature in the lower atmosphere: dry adiabatic lapse rate.
V (r,t) = i ˆ u( x, y,z,t) + ˆ j v( x, y,z,t) + k ˆ w( x, y, z,t)
 IV. DIFFERENTIAL RELATIONS FOR A FLUID PARTICLE This chapter presents the development and application of the basic differential equations of fluid motion. Simplifications in the general equations and common
IV. DIFFERENTIAL RELATIONS FOR A FLUID PARTICLE This chapter presents the development and application of the basic differential equations of fluid motion. Simplifications in the general equations and common
PV Thinking. What is PV thinking?
 PV Thinking CH 06 What is PV thinking? Two main approaches to solving fluid flow problems:. We can integrate the momentum, continuity and thermodynamic equations (the primitive equations) directly.. In
PV Thinking CH 06 What is PV thinking? Two main approaches to solving fluid flow problems:. We can integrate the momentum, continuity and thermodynamic equations (the primitive equations) directly.. In
Chapter 4: Fundamental Forces
 Chapter 4: Fundamental Forces Newton s Second Law: F=ma In atmospheric science it is typical to consider the force per unit mass acting on the atmosphere: Force mass = a In order to understand atmospheric
Chapter 4: Fundamental Forces Newton s Second Law: F=ma In atmospheric science it is typical to consider the force per unit mass acting on the atmosphere: Force mass = a In order to understand atmospheric
Needs work : define boundary conditions and fluxes before, change slides Useful definitions and conservation equations
 Needs work : define boundary conditions and fluxes before, change slides 1-2-3 Useful definitions and conservation equations Turbulent Kinetic energy The fluxes are crucial to define our boundary conditions,
Needs work : define boundary conditions and fluxes before, change slides 1-2-3 Useful definitions and conservation equations Turbulent Kinetic energy The fluxes are crucial to define our boundary conditions,
EAS372 Open Book Final Exam 11 April, 2013
 EAS372 Open Book Final Exam 11 April, 2013 Professor: J.D. Wilson Time available: 2 hours Value: 30% Please check the Terminology, Equations and Data section before beginning your responses. Answer all
EAS372 Open Book Final Exam 11 April, 2013 Professor: J.D. Wilson Time available: 2 hours Value: 30% Please check the Terminology, Equations and Data section before beginning your responses. Answer all
The Equations of Motion in a Rotating Coordinate System. Chapter 3
 The Equations of Motion in a Rotating Coordinate System Chapter 3 Since the earth is rotating about its axis and since it is convenient to adopt a frame of reference fixed in the earth, we need to study
The Equations of Motion in a Rotating Coordinate System Chapter 3 Since the earth is rotating about its axis and since it is convenient to adopt a frame of reference fixed in the earth, we need to study
CHAPTER 7 SEVERAL FORMS OF THE EQUATIONS OF MOTION
 CHAPTER 7 SEVERAL FORMS OF THE EQUATIONS OF MOTION 7.1 THE NAVIER-STOKES EQUATIONS Under the assumption of a Newtonian stress-rate-of-strain constitutive equation and a linear, thermally conductive medium,
CHAPTER 7 SEVERAL FORMS OF THE EQUATIONS OF MOTION 7.1 THE NAVIER-STOKES EQUATIONS Under the assumption of a Newtonian stress-rate-of-strain constitutive equation and a linear, thermally conductive medium,
Control Volume. Dynamics and Kinematics. Basic Conservation Laws. Lecture 1: Introduction and Review 1/24/2017
 Lecture 1: Introduction and Review Dynamics and Kinematics Kinematics: The term kinematics means motion. Kinematics is the study of motion without regard for the cause. Dynamics: On the other hand, dynamics
Lecture 1: Introduction and Review Dynamics and Kinematics Kinematics: The term kinematics means motion. Kinematics is the study of motion without regard for the cause. Dynamics: On the other hand, dynamics
Lecture 1: Introduction and Review
 Lecture 1: Introduction and Review Review of fundamental mathematical tools Fundamental and apparent forces Dynamics and Kinematics Kinematics: The term kinematics means motion. Kinematics is the study
Lecture 1: Introduction and Review Review of fundamental mathematical tools Fundamental and apparent forces Dynamics and Kinematics Kinematics: The term kinematics means motion. Kinematics is the study
Isentropic Analysis. Much of this presentation is due to Jim Moore, SLU
 Isentropic Analysis Much of this presentation is due to Jim Moore, SLU Utility of Isentropic Analysis Diagnose and visualize vertical motion - through advection of pressure and system-relative flow Depict
Isentropic Analysis Much of this presentation is due to Jim Moore, SLU Utility of Isentropic Analysis Diagnose and visualize vertical motion - through advection of pressure and system-relative flow Depict
Chapter 3. Stability theory for zonal flows :formulation
 Chapter 3. Stability theory for zonal flows :formulation 3.1 Introduction Although flows in the atmosphere and ocean are never strictly zonal major currents are nearly so and the simplifications springing
Chapter 3. Stability theory for zonal flows :formulation 3.1 Introduction Although flows in the atmosphere and ocean are never strictly zonal major currents are nearly so and the simplifications springing
Lecture 1. Equations of motion - Newton s second law in three dimensions. Pressure gradient + force force
 Lecture 3 Lecture 1 Basic dynamics Equations of motion - Newton s second law in three dimensions Acceleration = Pressure Coriolis + gravity + friction gradient + force force This set of equations is the
Lecture 3 Lecture 1 Basic dynamics Equations of motion - Newton s second law in three dimensions Acceleration = Pressure Coriolis + gravity + friction gradient + force force This set of equations is the
Goal: Use understanding of physically-relevant scales to reduce the complexity of the governing equations
 Scale analysis relevant to the tropics [large-scale synoptic systems]* Goal: Use understanding of physically-relevant scales to reduce the complexity of the governing equations *Reminder: Midlatitude scale
Scale analysis relevant to the tropics [large-scale synoptic systems]* Goal: Use understanding of physically-relevant scales to reduce the complexity of the governing equations *Reminder: Midlatitude scale
Thermodynamic Energy Equation
 Thermodynamic Energy Equation The temperature tendency is = u T x v T y w T z + dt dt (1) where dt/dt is the individual derivative of temperature. This temperature change experienced by the air parcel
Thermodynamic Energy Equation The temperature tendency is = u T x v T y w T z + dt dt (1) where dt/dt is the individual derivative of temperature. This temperature change experienced by the air parcel
Radiative equilibrium Some thermodynamics review Radiative-convective equilibrium. Goal: Develop a 1D description of the [tropical] atmosphere
![Radiative equilibrium Some thermodynamics review Radiative-convective equilibrium. Goal: Develop a 1D description of the [tropical] atmosphere Radiative equilibrium Some thermodynamics review Radiative-convective equilibrium. Goal: Develop a 1D description of the [tropical] atmosphere](/thumbs/72/66535634.jpg) Radiative equilibrium Some thermodynamics review Radiative-convective equilibrium Goal: Develop a 1D description of the [tropical] atmosphere Vertical temperature profile Total atmospheric mass: ~5.15x10
Radiative equilibrium Some thermodynamics review Radiative-convective equilibrium Goal: Develop a 1D description of the [tropical] atmosphere Vertical temperature profile Total atmospheric mass: ~5.15x10
Parcel Model. Atmospheric Sciences September 30, 2012
 Parcel Model Atmospheric Sciences 6150 September 30, 2012 1 Governing Equations for Precipitating Convection For precipitating convection, we have the following set of equations for potential temperature,
Parcel Model Atmospheric Sciences 6150 September 30, 2012 1 Governing Equations for Precipitating Convection For precipitating convection, we have the following set of equations for potential temperature,
Parcel Model. Meteorology September 3, 2008
 Parcel Model Meteorology 5210 September 3, 2008 1 Governing Equations for Precipitating Convection For precipitating convection, we have the following set of equations for potential temperature, θ, mixing
Parcel Model Meteorology 5210 September 3, 2008 1 Governing Equations for Precipitating Convection For precipitating convection, we have the following set of equations for potential temperature, θ, mixing
Class exercises Chapter 3. Elementary Applications of the Basic Equations
 Class exercises Chapter 3. Elementary Applications of the Basic Equations Section 3.1 Basic Equations in Isobaric Coordinates 3.1 For some (in fact many) applications we assume that the change of the Coriolis
Class exercises Chapter 3. Elementary Applications of the Basic Equations Section 3.1 Basic Equations in Isobaric Coordinates 3.1 For some (in fact many) applications we assume that the change of the Coriolis
1/3/2011. This course discusses the physical laws that govern atmosphere/ocean motions.
 Lecture 1: Introduction and Review Dynamics and Kinematics Kinematics: The term kinematics means motion. Kinematics is the study of motion without regard for the cause. Dynamics: On the other hand, dynamics
Lecture 1: Introduction and Review Dynamics and Kinematics Kinematics: The term kinematics means motion. Kinematics is the study of motion without regard for the cause. Dynamics: On the other hand, dynamics
Dynamic Meteorology - Introduction
 Dynamic Meteorology - Introduction Atmospheric dynamics the study of atmospheric motions that are associated with weather and climate We will consider the atmosphere to be a continuous fluid medium, or
Dynamic Meteorology - Introduction Atmospheric dynamics the study of atmospheric motions that are associated with weather and climate We will consider the atmosphere to be a continuous fluid medium, or
Buoyancy and Coriolis forces
 Chapter 2 Buoyancy and Coriolis forces In this chapter we address several topics that we need to understand before starting on our study of geophysical uid dynamics. 2.1 Hydrostatic approximation Consider
Chapter 2 Buoyancy and Coriolis forces In this chapter we address several topics that we need to understand before starting on our study of geophysical uid dynamics. 2.1 Hydrostatic approximation Consider
Dynamics and Kinematics
 Geophysics Fluid Dynamics () Syllabus Course Time Lectures: Tu, Th 09:30-10:50 Discussion: 3315 Croul Hall Text Book J. R. Holton, "An introduction to Dynamic Meteorology", Academic Press (Ch. 1, 2, 3,
Geophysics Fluid Dynamics () Syllabus Course Time Lectures: Tu, Th 09:30-10:50 Discussion: 3315 Croul Hall Text Book J. R. Holton, "An introduction to Dynamic Meteorology", Academic Press (Ch. 1, 2, 3,
Geophysics Fluid Dynamics (ESS228)
 Geophysics Fluid Dynamics (ESS228) Course Time Lectures: Tu, Th 09:30-10:50 Discussion: 3315 Croul Hall Text Book J. R. Holton, "An introduction to Dynamic Meteorology", Academic Press (Ch. 1, 2, 3, 4,
Geophysics Fluid Dynamics (ESS228) Course Time Lectures: Tu, Th 09:30-10:50 Discussion: 3315 Croul Hall Text Book J. R. Holton, "An introduction to Dynamic Meteorology", Academic Press (Ch. 1, 2, 3, 4,
Vorticity in natural coordinates
 Vorticity in natural coordinates (see Holton pg 95, section 4.2.) Let s consider the vertical vorticity component only, i.e. ζ kˆ ω, we have ω u dl kˆ ω lim --- lim ----------------- curve is in xy plane
Vorticity in natural coordinates (see Holton pg 95, section 4.2.) Let s consider the vertical vorticity component only, i.e. ζ kˆ ω, we have ω u dl kˆ ω lim --- lim ----------------- curve is in xy plane
Dynamics Rotating Tank
 Institute for Atmospheric and Climate Science - IACETH Atmospheric Physics Lab Work Dynamics Rotating Tank Large scale flows on different latitudes of the rotating Earth Abstract The large scale atmospheric
Institute for Atmospheric and Climate Science - IACETH Atmospheric Physics Lab Work Dynamics Rotating Tank Large scale flows on different latitudes of the rotating Earth Abstract The large scale atmospheric
References: Parcel Theory. Vertical Force Balance. ESCI Cloud Physics and Precipitation Processes Lesson 3 - Stability and Buoyancy Dr.
 References: ESCI 340 - Cloud Physics and Precipitation Processes Lesson 3 - Stability and Buoyancy Dr. DeCaria Glossary of Meteorology, 2nd ed., American Meteorological Society A Short Course in Cloud
References: ESCI 340 - Cloud Physics and Precipitation Processes Lesson 3 - Stability and Buoyancy Dr. DeCaria Glossary of Meteorology, 2nd ed., American Meteorological Society A Short Course in Cloud
Dynamic Meteorology 1
 Dynamic Meteorology 1 Lecture 14 Sahraei Department of Physics, Razi University http://www.razi.ac.ir/sahraei Buys-Ballot rule (Northern Hemisphere) If the wind blows into your back, the Low will be to
Dynamic Meteorology 1 Lecture 14 Sahraei Department of Physics, Razi University http://www.razi.ac.ir/sahraei Buys-Ballot rule (Northern Hemisphere) If the wind blows into your back, the Low will be to
Fluid dynamics and moist thermodynamics
 Chapter 1 Fluid dynamics and moist thermodynamics In this chapter we review the equations that represent the physical laws governing atmospheric motion. Rigorous derivations of the equations may be found
Chapter 1 Fluid dynamics and moist thermodynamics In this chapter we review the equations that represent the physical laws governing atmospheric motion. Rigorous derivations of the equations may be found
1 Introduction to Governing Equations 2 1a Methodology... 2
 Contents 1 Introduction to Governing Equations 2 1a Methodology............................ 2 2 Equation of State 2 2a Mean and Turbulent Parts...................... 3 2b Reynolds Averaging.........................
Contents 1 Introduction to Governing Equations 2 1a Methodology............................ 2 2 Equation of State 2 2a Mean and Turbulent Parts...................... 3 2b Reynolds Averaging.........................
The dynamics of high and low pressure systems
 The dynamics of high and low pressure systems Newton s second law for a parcel of air in an inertial coordinate system (a coordinate system in which the coordinate axes do not change direction and are
The dynamics of high and low pressure systems Newton s second law for a parcel of air in an inertial coordinate system (a coordinate system in which the coordinate axes do not change direction and are
By convention, C > 0 for counterclockwise flow, hence the contour must be counterclockwise.
 Chapter 4 4.1 The Circulation Theorem Circulation is a measure of rotation. It is calculated for a closed contour by taking the line integral of the velocity component tangent to the contour evaluated
Chapter 4 4.1 The Circulation Theorem Circulation is a measure of rotation. It is calculated for a closed contour by taking the line integral of the velocity component tangent to the contour evaluated
Section 2: Lecture 1 Integral Form of the Conservation Equations for Compressible Flow
 Section 2: Lecture 1 Integral Form of the Conservation Equations for Compressible Flow Anderson: Chapter 2 pp. 41-54 1 Equation of State: Section 1 Review p = R g T " > R g = R u M w - R u = 8314.4126
Section 2: Lecture 1 Integral Form of the Conservation Equations for Compressible Flow Anderson: Chapter 2 pp. 41-54 1 Equation of State: Section 1 Review p = R g T " > R g = R u M w - R u = 8314.4126
Measurement of Rotation. Circulation. Example. Lecture 4: Circulation and Vorticity 1/31/2017
 Lecture 4: Circulation and Vorticity Measurement of Rotation Circulation Bjerknes Circulation Theorem Vorticity Potential Vorticity Conservation of Potential Vorticity Circulation and vorticity are the
Lecture 4: Circulation and Vorticity Measurement of Rotation Circulation Bjerknes Circulation Theorem Vorticity Potential Vorticity Conservation of Potential Vorticity Circulation and vorticity are the
NWP Equations (Adapted from UCAR/COMET Online Modules)
 NWP Equations (Adapted from UCAR/COMET Online Modules) Certain physical laws of motion and conservation of energy (for example, Newton's Second Law of Motion and the First Law of Thermodynamics) govern
NWP Equations (Adapted from UCAR/COMET Online Modules) Certain physical laws of motion and conservation of energy (for example, Newton's Second Law of Motion and the First Law of Thermodynamics) govern
EAS372 Open Book Final Exam 11 April, 2013
 EAS372 Open Book Final Exam 11 April, 2013 Professor: J.D. Wilson Time available: 2 hours Value: 30% Please check the Terminology, Equations and Data section before beginning your responses. Answer all
EAS372 Open Book Final Exam 11 April, 2013 Professor: J.D. Wilson Time available: 2 hours Value: 30% Please check the Terminology, Equations and Data section before beginning your responses. Answer all
Adiabatic expansion Isothermal compression Adiabatic compression
 Tropical Cyclones: Steady State Physics 1 Energy Production 2 Carnot Theorem: Maximum efficiency results from a pa rticular energy e cycle: Isothermal expansion Adiabatic expansion Isothermal compression
Tropical Cyclones: Steady State Physics 1 Energy Production 2 Carnot Theorem: Maximum efficiency results from a pa rticular energy e cycle: Isothermal expansion Adiabatic expansion Isothermal compression
6 Two-layer shallow water theory.
 6 Two-layer shallow water theory. Wewillnowgoontolookatashallowwatersystemthathastwolayersofdifferent density. This is the next level of complexity and a simple starting point for understanding the behaviour
6 Two-layer shallow water theory. Wewillnowgoontolookatashallowwatersystemthathastwolayersofdifferent density. This is the next level of complexity and a simple starting point for understanding the behaviour
Geostrophic and Quasi-Geostrophic Balances
 Geostrophic and Quasi-Geostrophic Balances Qiyu Xiao June 19, 2018 1 Introduction Understanding how the atmosphere and ocean behave is important to our everyday lives. Techniques such as weather forecasting
Geostrophic and Quasi-Geostrophic Balances Qiyu Xiao June 19, 2018 1 Introduction Understanding how the atmosphere and ocean behave is important to our everyday lives. Techniques such as weather forecasting
Eliassen-Palm Theory
 Eliassen-Palm Theory David Painemal MPO611 April 2007 I. Introduction The separation of the flow into its zonal average and the deviations therefrom has been a dominant paradigm for analyses of the general
Eliassen-Palm Theory David Painemal MPO611 April 2007 I. Introduction The separation of the flow into its zonal average and the deviations therefrom has been a dominant paradigm for analyses of the general
( ) = 1005 J kg 1 K 1 ;
 Problem Set 3 1. A parcel of water is added to the ocean surface that is denser (heavier) than any of the waters in the ocean. Suppose the parcel sinks to the ocean bottom; estimate the change in temperature
Problem Set 3 1. A parcel of water is added to the ocean surface that is denser (heavier) than any of the waters in the ocean. Suppose the parcel sinks to the ocean bottom; estimate the change in temperature
Governing Equations and Scaling in the Tropics
 Governing Equations and Scaling in the Tropics M 1 ( ) e R ε er Tropical v Midlatitude Meteorology Why is the general circulation and synoptic weather systems in the tropics different to the those in the
Governing Equations and Scaling in the Tropics M 1 ( ) e R ε er Tropical v Midlatitude Meteorology Why is the general circulation and synoptic weather systems in the tropics different to the those in the
The Hydrostatic Approximation. - Euler Equations in Spherical Coordinates. - The Approximation and the Equations
 OUTLINE: The Hydrostatic Approximation - Euler Equations in Spherical Coordinates - The Approximation and the Equations - Critique of Hydrostatic Approximation Inertial Instability - The Phenomenon - The
OUTLINE: The Hydrostatic Approximation - Euler Equations in Spherical Coordinates - The Approximation and the Equations - Critique of Hydrostatic Approximation Inertial Instability - The Phenomenon - The
Generalizing the Boussinesq Approximation to Stratified Compressible Flow
 Generalizing the Boussinesq Approximation to Stratified Compressible Flow Dale R. Durran a Akio Arakawa b a University of Washington, Seattle, USA b University of California, Los Angeles, USA Abstract
Generalizing the Boussinesq Approximation to Stratified Compressible Flow Dale R. Durran a Akio Arakawa b a University of Washington, Seattle, USA b University of California, Los Angeles, USA Abstract
Mathematical Concepts & Notation
 Mathematical Concepts & Notation Appendix A: Notation x, δx: a small change in x t : the partial derivative with respect to t holding the other variables fixed d : the time derivative of a quantity that
Mathematical Concepts & Notation Appendix A: Notation x, δx: a small change in x t : the partial derivative with respect to t holding the other variables fixed d : the time derivative of a quantity that
Lecture 10a: The Hadley Cell
 Lecture 10a: The Hadley Cell Geoff Vallis; notes by Jim Thomas and Geoff J. Stanley June 27 In this short lecture we take a look at the general circulation of the atmosphere, and in particular the Hadley
Lecture 10a: The Hadley Cell Geoff Vallis; notes by Jim Thomas and Geoff J. Stanley June 27 In this short lecture we take a look at the general circulation of the atmosphere, and in particular the Hadley
Models of ocean circulation are all based on the equations of motion.
 Equations of motion Models of ocean circulation are all based on the equations of motion. Only in simple cases the equations of motion can be solved analytically, usually they must be solved numerically.
Equations of motion Models of ocean circulation are all based on the equations of motion. Only in simple cases the equations of motion can be solved analytically, usually they must be solved numerically.
Gravity Waves. Lecture 5: Waves in Atmosphere. Waves in the Atmosphere and Oceans. Internal Gravity (Buoyancy) Waves 2/9/2017
 Lecture 5: Waves in Atmosphere Perturbation Method Properties of Wave Shallow Water Model Gravity Waves Rossby Waves Waves in the Atmosphere and Oceans Restoring Force Conservation of potential temperature
Lecture 5: Waves in Atmosphere Perturbation Method Properties of Wave Shallow Water Model Gravity Waves Rossby Waves Waves in the Atmosphere and Oceans Restoring Force Conservation of potential temperature
4. The rules of the game
 ! Revised Friday, November 14, 2014! 1 4. The rules of the game Introduction This chapter gives a quick review of concepts to be used later. Topics covered including the conservation principles for momentum,
! Revised Friday, November 14, 2014! 1 4. The rules of the game Introduction This chapter gives a quick review of concepts to be used later. Topics covered including the conservation principles for momentum,
Part 4. Atmospheric Dynamics
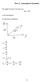 Part 4. Atmospheric Dynamics We apply Newton s Second Law: ma =Σ F i to the atmosphere. In Cartesian coordinates dx u = dt dy v = dt dz w = dt 1 ai = F m i i du dv dw a = ; ay = ; az = x dt dt dt 78 Coordinate
Part 4. Atmospheric Dynamics We apply Newton s Second Law: ma =Σ F i to the atmosphere. In Cartesian coordinates dx u = dt dy v = dt dz w = dt 1 ai = F m i i du dv dw a = ; ay = ; az = x dt dt dt 78 Coordinate
Model description of AGCM5 of GFD-Dennou-Club edition. SWAMP project, GFD-Dennou-Club
 Model description of AGCM5 of GFD-Dennou-Club edition SWAMP project, GFD-Dennou-Club Mar 01, 2006 AGCM5 of the GFD-DENNOU CLUB edition is a three-dimensional primitive system on a sphere (Swamp Project,
Model description of AGCM5 of GFD-Dennou-Club edition SWAMP project, GFD-Dennou-Club Mar 01, 2006 AGCM5 of the GFD-DENNOU CLUB edition is a three-dimensional primitive system on a sphere (Swamp Project,
Continuum Mechanics Lecture 5 Ideal fluids
 Continuum Mechanics Lecture 5 Ideal fluids Prof. http://www.itp.uzh.ch/~teyssier Outline - Helmholtz decomposition - Divergence and curl theorem - Kelvin s circulation theorem - The vorticity equation
Continuum Mechanics Lecture 5 Ideal fluids Prof. http://www.itp.uzh.ch/~teyssier Outline - Helmholtz decomposition - Divergence and curl theorem - Kelvin s circulation theorem - The vorticity equation
Quick Recapitulation of Fluid Mechanics
 Quick Recapitulation of Fluid Mechanics Amey Joshi 07-Feb-018 1 Equations of ideal fluids onsider a volume element of a fluid of density ρ. If there are no sources or sinks in, the mass in it will change
Quick Recapitulation of Fluid Mechanics Amey Joshi 07-Feb-018 1 Equations of ideal fluids onsider a volume element of a fluid of density ρ. If there are no sources or sinks in, the mass in it will change
Introduction to Isentropic Coordinates:! a new view of mean meridional & eddy circulations" Cristiana Stan
 Introduction to Isentropic Coordinates:! a new view of mean meridional & eddy circulations" Cristiana Stan School and Conference on the General Circulation of the Atmosphere and Oceans: a Modern Perspective!
Introduction to Isentropic Coordinates:! a new view of mean meridional & eddy circulations" Cristiana Stan School and Conference on the General Circulation of the Atmosphere and Oceans: a Modern Perspective!
Chapter 5. Fundamentals of Atmospheric Modeling
 Overhead Slides for Chapter 5 of Fundamentals of Atmospheric Modeling by Mark Z. Jacobson Department of Civil & Environmental Engineering Stanford University Stanford, CA 94305-4020 January 30, 2002 Altitude
Overhead Slides for Chapter 5 of Fundamentals of Atmospheric Modeling by Mark Z. Jacobson Department of Civil & Environmental Engineering Stanford University Stanford, CA 94305-4020 January 30, 2002 Altitude
Model equations for planetary and synoptic scale atmospheric motions associated with different background stratification
 Model equations for planetary and synoptic scale atmospheric motions associated with different background stratification Stamen Dolaptchiev & Rupert Klein Potsdam Institute for Climate Impact Research
Model equations for planetary and synoptic scale atmospheric motions associated with different background stratification Stamen Dolaptchiev & Rupert Klein Potsdam Institute for Climate Impact Research
df dz = dp dt Essentially, this is just a statement of the first law in one of the forms we derived earlier (expressed here in W m 3 ) dq p dt dp
 A problem with using entropy as a variable is that it is not a particularly intuitive concept. The mechanics of using entropy for evaluating system evolution is well developed, but it sometimes feels a
A problem with using entropy as a variable is that it is not a particularly intuitive concept. The mechanics of using entropy for evaluating system evolution is well developed, but it sometimes feels a
Isentropic flows and monsoonal circulations
 Isentropic flows and monsoonal circulations Olivier Pauluis (NYU) Monsoons- Past, Present and future May 20th, 2015 Caltech, Pasadena Outline Introduction Global monsoon in isentropic coordinates Dry ventilation
Isentropic flows and monsoonal circulations Olivier Pauluis (NYU) Monsoons- Past, Present and future May 20th, 2015 Caltech, Pasadena Outline Introduction Global monsoon in isentropic coordinates Dry ventilation
The dynamics of a simple troposphere-stratosphere model
 The dynamics of a simple troposphere-stratosphere model by Jessica Duin under supervision of Prof. Dr. A. Doelman, UvA Dr. W.T.M. Verkley, KNMI August 31, 25 Universiteit van Amsterdam Korteweg-de vries
The dynamics of a simple troposphere-stratosphere model by Jessica Duin under supervision of Prof. Dr. A. Doelman, UvA Dr. W.T.M. Verkley, KNMI August 31, 25 Universiteit van Amsterdam Korteweg-de vries
8 Mechanisms for tropical rainfall responses to equatorial
 8 Mechanisms for tropical rainfall responses to equatorial heating More reading: 1. Hamouda, M. and Kucharski, F. (2019) Ekman pumping Mechanism driving Precipitation anomalies in Response to Equatorial
8 Mechanisms for tropical rainfall responses to equatorial heating More reading: 1. Hamouda, M. and Kucharski, F. (2019) Ekman pumping Mechanism driving Precipitation anomalies in Response to Equatorial
Quasi-geostrophic system
 Quasi-eostrophic system (or, why we love elliptic equations for QGPV) Charney s QG the motion of lare-scale atmospheric disturbances is overned by Laws of conservation of potential temperature and potential
Quasi-eostrophic system (or, why we love elliptic equations for QGPV) Charney s QG the motion of lare-scale atmospheric disturbances is overned by Laws of conservation of potential temperature and potential
ESCI 343 Atmospheric Dynamics II Lesson 11 - Rossby Waves
 ESCI 343 Atmospheric Dynamics II Lesson 11 - Rossby Waves Reference: An Introduction to Dynamic Meteorology (4 rd edition), J.R. Holton Atmosphere-Ocean Dynamics, A.E. Gill Fundamentals of Atmospheric
ESCI 343 Atmospheric Dynamics II Lesson 11 - Rossby Waves Reference: An Introduction to Dynamic Meteorology (4 rd edition), J.R. Holton Atmosphere-Ocean Dynamics, A.E. Gill Fundamentals of Atmospheric
Reynolds Averaging. We separate the dynamical fields into slowly varying mean fields and rapidly varying turbulent components.
 Reynolds Averaging Reynolds Averaging We separate the dynamical fields into sloly varying mean fields and rapidly varying turbulent components. Reynolds Averaging We separate the dynamical fields into
Reynolds Averaging Reynolds Averaging We separate the dynamical fields into sloly varying mean fields and rapidly varying turbulent components. Reynolds Averaging We separate the dynamical fields into
Dynamic Meteorology: lecture 2
 Dynamic Meteorology: lecture 2 Sections 1.3-1.5 and Box 1.5 Potential temperature Radiatively determined temperature (boxes 1.1-1.4) Buoyancy (-oscillations) and static instability, Brunt-Vaisala frequency
Dynamic Meteorology: lecture 2 Sections 1.3-1.5 and Box 1.5 Potential temperature Radiatively determined temperature (boxes 1.1-1.4) Buoyancy (-oscillations) and static instability, Brunt-Vaisala frequency
The Tropical Atmosphere: Hurricane Incubator
 The Tropical Atmosphere: Hurricane Incubator Images from journals published by the American Meteorological Society are copyright AMS and used with permission. A One-Dimensional Description of the Tropical
The Tropical Atmosphere: Hurricane Incubator Images from journals published by the American Meteorological Society are copyright AMS and used with permission. A One-Dimensional Description of the Tropical
ESCI 342 Atmospheric Dynamics I Lesson 12 Vorticity
 ESCI 34 tmospheric Dynamics I Lesson 1 Vorticity Reference: n Introduction to Dynamic Meteorology (4 rd edition), Holton n Informal Introduction to Theoretical Fluid Mechanics, Lighthill Reading: Martin,
ESCI 34 tmospheric Dynamics I Lesson 1 Vorticity Reference: n Introduction to Dynamic Meteorology (4 rd edition), Holton n Informal Introduction to Theoretical Fluid Mechanics, Lighthill Reading: Martin,
On the effect of forward shear and reversed shear baroclinic flows for polar low developments. Thor Erik Nordeng Norwegian Meteorological Institute
 On the effect of forward shear and reversed shear baroclinic flows for polar low developments Thor Erik Nordeng Norwegian Meteorological Institute Outline Baroclinic growth a) Normal mode solution b) Initial
On the effect of forward shear and reversed shear baroclinic flows for polar low developments Thor Erik Nordeng Norwegian Meteorological Institute Outline Baroclinic growth a) Normal mode solution b) Initial
The General Circulation of the Atmosphere: A Numerical Experiment
 The General Circulation of the Atmosphere: A Numerical Experiment Norman A. Phillips (1956) Presentation by Lukas Strebel and Fabian Thüring Goal of the Model Numerically predict the mean state of the
The General Circulation of the Atmosphere: A Numerical Experiment Norman A. Phillips (1956) Presentation by Lukas Strebel and Fabian Thüring Goal of the Model Numerically predict the mean state of the
Hurricanes are intense vortical (rotational) storms that develop over the tropical oceans in regions of very warm surface water.
 Hurricanes: Observations and Dynamics Houze Section 10.1. Holton Section 9.7. Emanuel, K. A., 1988: Toward a general theory of hurricanes. American Scientist, 76, 371-379 (web link). http://ww2010.atmos.uiuc.edu/(gh)/guides/mtr/hurr/home.rxml
Hurricanes: Observations and Dynamics Houze Section 10.1. Holton Section 9.7. Emanuel, K. A., 1988: Toward a general theory of hurricanes. American Scientist, 76, 371-379 (web link). http://ww2010.atmos.uiuc.edu/(gh)/guides/mtr/hurr/home.rxml
Atmospheric Thermodynamics
 Atmospheric Thermodynamics Atmospheric Composition What is the composition of the Earth s atmosphere? Gaseous Constituents of the Earth s atmosphere (dry air) Constituent Molecular Weight Fractional Concentration
Atmospheric Thermodynamics Atmospheric Composition What is the composition of the Earth s atmosphere? Gaseous Constituents of the Earth s atmosphere (dry air) Constituent Molecular Weight Fractional Concentration
