ESCI 485 Air/Sea Interaction Lesson 1 Stresses and Fluxes Dr. DeCaria
|
|
|
- Cuthbert Williamson
- 6 years ago
- Views:
Transcription
1 ESCI 485 Air/Sea Interaction Lesson 1 Stresses and Fluxes Dr DeCaria References: An Introduction to Dynamic Meteorology, Holton MOMENTUM EQUATIONS The momentum equations governing the ocean or atmosphere are u 1 p + V u = + fv + Fx ρ v 1 p + V v = fu + Fy ρ w 1 p + V w = g + Fz ρ z The terms F x, F y, and F z represent dissipative effects due to molecular effects (viscosity), and are often simply referred to as friction The Boussinesq approximation ο Let density and pressure be represented by a base or reference state plus a perturbation, so that p = p ( z) + p ρ = ρ ( z) + ρ If we also assume that the base state is in hydrostatic balance, and assume that p can be ignored everywhere except where it is multiplied by gravity, we get the Boussinesq approximation momentum equations where and is called the buoyancy u 1 p + V u = + fv + Fx ρ v 1 p + V v = fu + Fy ρ w 1 p + V w = + b + Fz ρ z ρ b g ρ The Boussinesq approximation is valid only if compressibility effects are small
2 ο In the atmosphere this means the Boussinesq approximation can only be reasonably applied over relatively shallow layers, such as the planetary boundary layer ο In the ocean the Boussinesq approximation can often be applied over the entire depth, since water is far less compressible than air TURBULENCE Meteorological and oceanographic variables fluctuate rapidly around some base value Standard weather observations record averaged wind speed and direction, not instantaneous speed and direction ο In the US the standard wind speed is a two-minute average for synoptic observations The rapidly fluctuating part is the turbulence We are also mainly interested in the time-averaged effects of the turbulence, not its instantaneous effects In order to isolate the time-averaged effects of turbulence from the mean values of the variables themselves, we perform Reynolds averaging REYNOLDS AVERAGING First decompose all of the dependent variables into mean and perturbation quantities u = u + u v = v + v w = w + w p = p + p ρ = ρ + ρ ο The mean quantities, symbolized with the over-bar symbol ( ) are time averaged quantities given by t+ τ 1 F = F( x, y, z, t ) dt τ where τ is the averaging interval 2 t
3 ο The mean quantities are not necessarily constant in time or space ο The perturbation quantities are symbolized with a prime ( ) After decomposing the dependent variables into mean and perturbation quantities we again time average the equations The rules for the time-averaging operator: ο The sum of two means is the mean of the sum: A + B = A + B ο The mean of a mean is just the mean (very Zen-like): A = A ο The mean of a single perturbation is zero: A = ο The mean of the product of two means is just the product of the two means: AB = AB ο The mean of the product containing a single perturbation is zero: A B = ο The mean of the product of two perturbations is NOT zero: A B Example of Reynolds averaging the total derivative ( u + u ) + u = u + u z ( u + u ) ( u + u ) + ( v + v ) ( u + u ) + ( w + w ) ( u + u ) which, when applying or rules for averaging, becomes u u u u u u u + u + v + w + u + v + w z z For an incompressible fluid it turns out that u u w u + v + w = z z ( u u ) + ( v u ) + ( w u ) so that the total derivative in the u-momentum equation is u u u u + u + v + w + u u + v u + w u z z 3
4 The Reynolds averaged momentum equations are where Du 1 p = + f v u u + v u + w u Dt ρ x y z Dv 1 p = f u u v + v v + w v Dt ρ x y z Dw 1 p ρ = g u w + v w + w w Dt ρ z ρ z D Dt + u + v + w z The over-barred terms are turbulent momentum fluxes In most applications we can usually ignore these terms because they are small compared to the other terms in the equations However, in the atmospheric and oceanic boundary layers the turbulent momentum fluxes are important The thermodynamic energy equation for the atmosphere is DT Dt + g c p 4 w = J where J is the heating rate due to diabatic processes (latent heat release, radiation, etc) ο The Reynolds averaged thermodynamic energy equation is DT g + w + u T + v T + w T = J Dt c z p ο The over-barred terms are turbulent heat fluxes The conservation equation for water vapor is Dρ v Dt = P L, where ρ v is the absolute humidity (mass of water vapor per volume of air), P represents processes which produce water vapor (eg, evaporation and sublimation), and L represents loss processes (eg, condensation and deposition) ο The Reynolds averaged equation for water vapor is Dρv + u ρ v + v ρ v + w ρ v = P L Dt z
5 ο The overbarred terms are turbulent moisture fluxes ο Moisture flux is sometimes called latent heat flux, because as the moisture condenses it releases heat For air/sea interaction we are most concerned with the vertical fluxes (those with the w ) We will usually ignore the horizontal fluxes MORE ON FLUXES A dynamic flux is defined as the flow of a quantity per unit area per unit time A kinematic flux is defined as the dynamic flux divided by the density To show that a term like w u is a kinematic momentum flux, we look at the units ο w u has units of m 2 /s 2 ο Kinematic momentum flux has units of ( momentum) ( area)( time)( density) ( kg m / s) 2 m = = ( m )( s)( kg m ) s REYNOLDS STRESSES A stress is a force per unit area ο Stresses can either be normal or tangential ο Stress has same units as pressure The turbulent momentum fluxes are also known as Reynolds stresses, because their effects on the shape of a volume of fluid are identical to that from a viscous stress The relation between the momentum flux and Reynolds stress is τ ρ = u w R and so the Reynolds averaged momentum equations can be written as Du 1 p 1 τ R = + f v + Dt ρ ρ z That the Reynolds stress terms act to deform a cube of fluid is illustrated for westerly flow (u > ) as follows: 5
6 ο For westerly flow u w is usually negative, signifying a downward transport of positive momentum ο If u w decreases with height (larger magnitude, but more negative) there is more positive momentum put into the top of the cube than is removed from it at the bottom (see diagram) and the cube will deform just as if it were under a stress ο Also, since there is a net increase in momentum over the cube, the cube will accelerate This is consistent with the equation Du = u w > Dt z FLUXES AND AIR/SEA INTERACTION The atmosphere interacts with the surface of the Earth The effects of this interaction are to exchange momentum, heat, and moisture This exchange is quantified in terms of the fluxes of momentum, moisture, and heat 6
7 Thus, understanding the vertical fluxes of heat, moisture, and momentum is key to understanding air-sea interaction 7
1 Introduction to Governing Equations 2 1a Methodology... 2
 Contents 1 Introduction to Governing Equations 2 1a Methodology............................ 2 2 Equation of State 2 2a Mean and Turbulent Parts...................... 3 2b Reynolds Averaging.........................
Contents 1 Introduction to Governing Equations 2 1a Methodology............................ 2 2 Equation of State 2 2a Mean and Turbulent Parts...................... 3 2b Reynolds Averaging.........................
Meteorology 6150 Cloud System Modeling
 Meteorology 6150 Cloud System Modeling Steve Krueger Spring 2009 1 Fundamental Equations 1.1 The Basic Equations 1.1.1 Equation of motion The movement of air in the atmosphere is governed by Newton s Second
Meteorology 6150 Cloud System Modeling Steve Krueger Spring 2009 1 Fundamental Equations 1.1 The Basic Equations 1.1.1 Equation of motion The movement of air in the atmosphere is governed by Newton s Second
ESCI 485 Air/sea Interaction Lesson 2 Turbulence Dr. DeCaria
 ESCI 485 Air/sea Interaction Lesson Turbulence Dr. DeCaria References: Air-sea Interaction: Laws and Mechanisms, Csanady An Introduction to Dynamic Meteorology ( rd edition), J.R. Holton An Introduction
ESCI 485 Air/sea Interaction Lesson Turbulence Dr. DeCaria References: Air-sea Interaction: Laws and Mechanisms, Csanady An Introduction to Dynamic Meteorology ( rd edition), J.R. Holton An Introduction
Needs work : define boundary conditions and fluxes before, change slides Useful definitions and conservation equations
 Needs work : define boundary conditions and fluxes before, change slides 1-2-3 Useful definitions and conservation equations Turbulent Kinetic energy The fluxes are crucial to define our boundary conditions,
Needs work : define boundary conditions and fluxes before, change slides 1-2-3 Useful definitions and conservation equations Turbulent Kinetic energy The fluxes are crucial to define our boundary conditions,
Lecture 3. Turbulent fluxes and TKE budgets (Garratt, Ch 2)
 Lecture 3. Turbulent fluxes and TKE budgets (Garratt, Ch 2) The ABL, though turbulent, is not homogeneous, and a critical role of turbulence is transport and mixing of air properties, especially in the
Lecture 3. Turbulent fluxes and TKE budgets (Garratt, Ch 2) The ABL, though turbulent, is not homogeneous, and a critical role of turbulence is transport and mixing of air properties, especially in the
Reynolds Averaging. We separate the dynamical fields into slowly varying mean fields and rapidly varying turbulent components.
 Reynolds Averaging Reynolds Averaging We separate the dynamical fields into sloly varying mean fields and rapidly varying turbulent components. Reynolds Averaging We separate the dynamical fields into
Reynolds Averaging Reynolds Averaging We separate the dynamical fields into sloly varying mean fields and rapidly varying turbulent components. Reynolds Averaging We separate the dynamical fields into
ρ x + fv f 'w + F x ρ y fu + F y Fundamental Equation in z coordinate p = ρrt or pα = RT Du uv tanφ Dv Dt + u2 tanφ + vw a a = 1 p Dw Dt u2 + v 2
 Fundamental Equation in z coordinate p = ρrt or pα = RT Du uv tanφ + uw Dt a a = 1 p ρ x + fv f 'w + F x Dv Dt + u2 tanφ + vw a a = 1 p ρ y fu + F y Dw Dt u2 + v 2 = 1 p a ρ z g + f 'u + F z Dρ Dt + ρ
Fundamental Equation in z coordinate p = ρrt or pα = RT Du uv tanφ + uw Dt a a = 1 p ρ x + fv f 'w + F x Dv Dt + u2 tanφ + vw a a = 1 p ρ y fu + F y Dw Dt u2 + v 2 = 1 p a ρ z g + f 'u + F z Dρ Dt + ρ
Non-Newtonian fluids is the fluids in which shear stress is not directly proportional to deformation rate, such as toothpaste,
 CHAPTER1: Basic Definitions, Zeroth, First, and Second Laws of Thermodynamics 1.1. Definitions What does thermodynamic mean? It is a Greeks word which means a motion of the heat. Water is a liquid substance
CHAPTER1: Basic Definitions, Zeroth, First, and Second Laws of Thermodynamics 1.1. Definitions What does thermodynamic mean? It is a Greeks word which means a motion of the heat. Water is a liquid substance
1/18/2011. Conservation of Momentum Conservation of Mass Conservation of Energy Scaling Analysis ESS227 Prof. Jin-Yi Yu
 Lecture 2: Basic Conservation Laws Conservation Law of Momentum Newton s 2 nd Law of Momentum = absolute velocity viewed in an inertial system = rate of change of Ua following the motion in an inertial
Lecture 2: Basic Conservation Laws Conservation Law of Momentum Newton s 2 nd Law of Momentum = absolute velocity viewed in an inertial system = rate of change of Ua following the motion in an inertial
Chapter 1. Governing Equations of GFD. 1.1 Mass continuity
 Chapter 1 Governing Equations of GFD The fluid dynamical governing equations consist of an equation for mass continuity, one for the momentum budget, and one or more additional equations to account for
Chapter 1 Governing Equations of GFD The fluid dynamical governing equations consist of an equation for mass continuity, one for the momentum budget, and one or more additional equations to account for
centrifugal acceleration, whose magnitude is r cos, is zero at the poles and maximum at the equator. This distribution of the centrifugal acceleration
 Lecture 10. Equations of Motion Centripetal Acceleration, Gravitation and Gravity The centripetal acceleration of a body located on the Earth's surface at a distance from the center is the force (per unit
Lecture 10. Equations of Motion Centripetal Acceleration, Gravitation and Gravity The centripetal acceleration of a body located on the Earth's surface at a distance from the center is the force (per unit
Rational derivation of the Boussinesq approximation
 Rational derivation of the Boussinesq approximation Kiyoshi Maruyama Department of Earth and Ocean Sciences, National Defense Academy, Yokosuka, Kanagawa 239-8686, Japan February 22, 2019 Abstract This
Rational derivation of the Boussinesq approximation Kiyoshi Maruyama Department of Earth and Ocean Sciences, National Defense Academy, Yokosuka, Kanagawa 239-8686, Japan February 22, 2019 Abstract This
Conservation of Mass Conservation of Energy Scaling Analysis. ESS227 Prof. Jin-Yi Yu
 Lecture 2: Basic Conservation Laws Conservation of Momentum Conservation of Mass Conservation of Energy Scaling Analysis Conservation Law of Momentum Newton s 2 nd Law of Momentum = absolute velocity viewed
Lecture 2: Basic Conservation Laws Conservation of Momentum Conservation of Mass Conservation of Energy Scaling Analysis Conservation Law of Momentum Newton s 2 nd Law of Momentum = absolute velocity viewed
NWP Equations (Adapted from UCAR/COMET Online Modules)
 NWP Equations (Adapted from UCAR/COMET Online Modules) Certain physical laws of motion and conservation of energy (for example, Newton's Second Law of Motion and the First Law of Thermodynamics) govern
NWP Equations (Adapted from UCAR/COMET Online Modules) Certain physical laws of motion and conservation of energy (for example, Newton's Second Law of Motion and the First Law of Thermodynamics) govern
5. General Circulation Models
 5. General Circulation Models I. 3-D Climate Models (General Circulation Models) To include the full three-dimensional aspect of climate, including the calculation of the dynamical transports, requires
5. General Circulation Models I. 3-D Climate Models (General Circulation Models) To include the full three-dimensional aspect of climate, including the calculation of the dynamical transports, requires
 Convective Fluxes: Sensible and Latent Heat Convective Fluxes Convective fluxes require Vertical gradient of temperature / water AND Turbulence ( mixing ) Vertical gradient, but no turbulence: only very
Convective Fluxes: Sensible and Latent Heat Convective Fluxes Convective fluxes require Vertical gradient of temperature / water AND Turbulence ( mixing ) Vertical gradient, but no turbulence: only very
Fluid Dynamics Exercises and questions for the course
 Fluid Dynamics Exercises and questions for the course January 15, 2014 A two dimensional flow field characterised by the following velocity components in polar coordinates is called a free vortex: u r
Fluid Dynamics Exercises and questions for the course January 15, 2014 A two dimensional flow field characterised by the following velocity components in polar coordinates is called a free vortex: u r
The atmospheric boundary layer: Where the atmosphere meets the surface. The atmospheric boundary layer:
 The atmospheric boundary layer: Utrecht Summer School on Physics of the Climate System Carleen Tijm-Reijmer IMAU The atmospheric boundary layer: Where the atmosphere meets the surface Photo: Mark Wolvenne:
The atmospheric boundary layer: Utrecht Summer School on Physics of the Climate System Carleen Tijm-Reijmer IMAU The atmospheric boundary layer: Where the atmosphere meets the surface Photo: Mark Wolvenne:
g (z) = 1 (1 + z/a) = 1
 1.4.2 Gravitational Force g is the gravitational force. It always points towards the center of mass, and it is proportional to the inverse square of the distance above the center of mass: g (z) = GM (a
1.4.2 Gravitational Force g is the gravitational force. It always points towards the center of mass, and it is proportional to the inverse square of the distance above the center of mass: g (z) = GM (a
1. The vertical structure of the atmosphere. Temperature profile.
 Lecture 4. The structure of the atmosphere. Air in motion. Objectives: 1. The vertical structure of the atmosphere. Temperature profile. 2. Temperature in the lower atmosphere: dry adiabatic lapse rate.
Lecture 4. The structure of the atmosphere. Air in motion. Objectives: 1. The vertical structure of the atmosphere. Temperature profile. 2. Temperature in the lower atmosphere: dry adiabatic lapse rate.
2 Equations of Motion
 2 Equations of Motion system. In this section, we will derive the six full equations of motion in a non-rotating, Cartesian coordinate 2.1 Six equations of motion (non-rotating, Cartesian coordinates)
2 Equations of Motion system. In this section, we will derive the six full equations of motion in a non-rotating, Cartesian coordinate 2.1 Six equations of motion (non-rotating, Cartesian coordinates)
Chapter (3) TURBULENCE KINETIC ENERGY
 Chapter (3) TURBULENCE KINETIC ENERGY 3.1 The TKE budget Derivation : The definition of TKE presented is TKE/m= e = 0.5 ( u 2 + v 2 + w 2 ). we recognize immediately that TKE/m is nothing more than the
Chapter (3) TURBULENCE KINETIC ENERGY 3.1 The TKE budget Derivation : The definition of TKE presented is TKE/m= e = 0.5 ( u 2 + v 2 + w 2 ). we recognize immediately that TKE/m is nothing more than the
Scale analysis of the vertical equation of motion:
 Scale analysis of the vertical equation of motion: As we did with the hz eqns, we do for the vertical to estimate the order of magnitude of Dw/ we take the largest of the terms, Dw -- W/T h UW/L W 2 /H
Scale analysis of the vertical equation of motion: As we did with the hz eqns, we do for the vertical to estimate the order of magnitude of Dw/ we take the largest of the terms, Dw -- W/T h UW/L W 2 /H
Parcel Model. Atmospheric Sciences September 30, 2012
 Parcel Model Atmospheric Sciences 6150 September 30, 2012 1 Governing Equations for Precipitating Convection For precipitating convection, we have the following set of equations for potential temperature,
Parcel Model Atmospheric Sciences 6150 September 30, 2012 1 Governing Equations for Precipitating Convection For precipitating convection, we have the following set of equations for potential temperature,
Dynamics Rotating Tank
 Institute for Atmospheric and Climate Science - IACETH Atmospheric Physics Lab Work Dynamics Rotating Tank Large scale flows on different latitudes of the rotating Earth Abstract The large scale atmospheric
Institute for Atmospheric and Climate Science - IACETH Atmospheric Physics Lab Work Dynamics Rotating Tank Large scale flows on different latitudes of the rotating Earth Abstract The large scale atmospheric
The Behaviour of the Atmosphere
 3 The Behaviour of the Atmosphere Learning Goals After studying this chapter, students should be able to: apply the ideal gas law and the concept of hydrostatic balance to the atmosphere (pp. 49 54); apply
3 The Behaviour of the Atmosphere Learning Goals After studying this chapter, students should be able to: apply the ideal gas law and the concept of hydrostatic balance to the atmosphere (pp. 49 54); apply
g (z) = 1 (1 + z/a) = 1 1 ( km/10 4 km) 2
 1.4.2 Gravitational Force g is the gravitational force. It always points towards the center of mass, and it is proportional to the inverse square of the distance above the center of mass: g (z) = GM (a
1.4.2 Gravitational Force g is the gravitational force. It always points towards the center of mass, and it is proportional to the inverse square of the distance above the center of mass: g (z) = GM (a
Dynamic Meteorology - Introduction
 Dynamic Meteorology - Introduction Atmospheric dynamics the study of atmospheric motions that are associated with weather and climate We will consider the atmosphere to be a continuous fluid medium, or
Dynamic Meteorology - Introduction Atmospheric dynamics the study of atmospheric motions that are associated with weather and climate We will consider the atmosphere to be a continuous fluid medium, or
Goal: Use understanding of physically-relevant scales to reduce the complexity of the governing equations
 Scale analysis relevant to the tropics [large-scale synoptic systems]* Goal: Use understanding of physically-relevant scales to reduce the complexity of the governing equations *Reminder: Midlatitude scale
Scale analysis relevant to the tropics [large-scale synoptic systems]* Goal: Use understanding of physically-relevant scales to reduce the complexity of the governing equations *Reminder: Midlatitude scale
Fluid Mechanics. du dy
 FLUID MECHANICS Technical English - I 1 th week Fluid Mechanics FLUID STATICS FLUID DYNAMICS Fluid Statics or Hydrostatics is the study of fluids at rest. The main equation required for this is Newton's
FLUID MECHANICS Technical English - I 1 th week Fluid Mechanics FLUID STATICS FLUID DYNAMICS Fluid Statics or Hydrostatics is the study of fluids at rest. The main equation required for this is Newton's
ATS 421/521. Climate Modeling. Spring 2015
 ATS 421/521 Climate Modeling Spring 2015 Lecture 9 Hadley Circulation (Held and Hou, 1980) General Circulation Models (tetbook chapter 3.2.3; course notes chapter 5.3) The Primitive Equations (tetbook
ATS 421/521 Climate Modeling Spring 2015 Lecture 9 Hadley Circulation (Held and Hou, 1980) General Circulation Models (tetbook chapter 3.2.3; course notes chapter 5.3) The Primitive Equations (tetbook
1. Introduction, fluid properties (1.1, 2.8, 4.1, and handouts)
 1. Introduction, fluid properties (1.1, 2.8, 4.1, and handouts) Introduction, general information Course overview Fluids as a continuum Density Compressibility Viscosity Exercises: A1 Fluid mechanics Fluid
1. Introduction, fluid properties (1.1, 2.8, 4.1, and handouts) Introduction, general information Course overview Fluids as a continuum Density Compressibility Viscosity Exercises: A1 Fluid mechanics Fluid
Eddy viscosity. AdOc 4060/5060 Spring 2013 Chris Jenkins. Turbulence (video 1hr):
 AdOc 4060/5060 Spring 2013 Chris Jenkins Eddy viscosity Turbulence (video 1hr): http://cosee.umaine.edu/programs/webinars/turbulence/?cfid=8452711&cftoken=36780601 Part B Surface wind stress Wind stress
AdOc 4060/5060 Spring 2013 Chris Jenkins Eddy viscosity Turbulence (video 1hr): http://cosee.umaine.edu/programs/webinars/turbulence/?cfid=8452711&cftoken=36780601 Part B Surface wind stress Wind stress
On side wall labeled A: we can express the pressure in a Taylor s series expansion: x 2. + higher order terms,
 Chapter 1 Notes A Note About Coordinates We nearly always use a coordinate system in this class where the vertical, ˆk, is normal to the Earth s surface and the x-direction, î, points to the east and the
Chapter 1 Notes A Note About Coordinates We nearly always use a coordinate system in this class where the vertical, ˆk, is normal to the Earth s surface and the x-direction, î, points to the east and the
Chapter 4 Water Vapor
 Chapter 4 Water Vapor Chapter overview: Phases of water Vapor pressure at saturation Moisture variables o Mixing ratio, specific humidity, relative humidity, dew point temperature o Absolute vs. relative
Chapter 4 Water Vapor Chapter overview: Phases of water Vapor pressure at saturation Moisture variables o Mixing ratio, specific humidity, relative humidity, dew point temperature o Absolute vs. relative
Fundamentals of Fluid Dynamics: Elementary Viscous Flow
 Fundamentals of Fluid Dynamics: Elementary Viscous Flow Introductory Course on Multiphysics Modelling TOMASZ G. ZIELIŃSKI bluebox.ippt.pan.pl/ tzielins/ Institute of Fundamental Technological Research
Fundamentals of Fluid Dynamics: Elementary Viscous Flow Introductory Course on Multiphysics Modelling TOMASZ G. ZIELIŃSKI bluebox.ippt.pan.pl/ tzielins/ Institute of Fundamental Technological Research
OCN/ATM/ESS 587. The wind-driven ocean circulation. Friction and stress. The Ekman layer, top and bottom. Ekman pumping, Ekman suction
 OCN/ATM/ESS 587 The wind-driven ocean circulation. Friction and stress The Ekman layer, top and bottom Ekman pumping, Ekman suction Westward intensification The wind-driven ocean. The major ocean gyres
OCN/ATM/ESS 587 The wind-driven ocean circulation. Friction and stress The Ekman layer, top and bottom Ekman pumping, Ekman suction Westward intensification The wind-driven ocean. The major ocean gyres
Atmospheric Processes
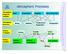 Atmospheric Processes Atmospheric prognostic variables Wind Temperature Humidity Cloud Water/Ice Atmospheric processes Mixing Radiation Condensation/ Evaporation Precipitation Surface exchanges Friction
Atmospheric Processes Atmospheric prognostic variables Wind Temperature Humidity Cloud Water/Ice Atmospheric processes Mixing Radiation Condensation/ Evaporation Precipitation Surface exchanges Friction
ESS Turbulence and Diffusion in the Atmospheric Boundary-Layer : Winter 2017: Notes 1
 ESS5203.03 - Turbulence and Diffusion in the Atmospheric Boundary-Layer : Winter 2017: Notes 1 Text: J.R.Garratt, The Atmospheric Boundary Layer, 1994. Cambridge Also some material from J.C. Kaimal and
ESS5203.03 - Turbulence and Diffusion in the Atmospheric Boundary-Layer : Winter 2017: Notes 1 Text: J.R.Garratt, The Atmospheric Boundary Layer, 1994. Cambridge Also some material from J.C. Kaimal and
ESCI 343 Atmospheric Dynamics II Lesson 11 - Rossby Waves
 ESCI 343 Atmospheric Dynamics II Lesson 11 - Rossby Waves Reference: An Introduction to Dynamic Meteorology (4 rd edition), J.R. Holton Atmosphere-Ocean Dynamics, A.E. Gill Fundamentals of Atmospheric
ESCI 343 Atmospheric Dynamics II Lesson 11 - Rossby Waves Reference: An Introduction to Dynamic Meteorology (4 rd edition), J.R. Holton Atmosphere-Ocean Dynamics, A.E. Gill Fundamentals of Atmospheric
The Equations of Motion in a Rotating Coordinate System. Chapter 3
 The Equations of Motion in a Rotating Coordinate System Chapter 3 Since the earth is rotating about its axis and since it is convenient to adopt a frame of reference fixed in the earth, we need to study
The Equations of Motion in a Rotating Coordinate System Chapter 3 Since the earth is rotating about its axis and since it is convenient to adopt a frame of reference fixed in the earth, we need to study
6.2 Governing Equations for Natural Convection
 6. Governing Equations for Natural Convection 6..1 Generalized Governing Equations The governing equations for natural convection are special cases of the generalized governing equations that were discussed
6. Governing Equations for Natural Convection 6..1 Generalized Governing Equations The governing equations for natural convection are special cases of the generalized governing equations that were discussed
Today s Lecture: Atmosphere finish primitive equations, mostly thermodynamics
 Today s Lecture: Atmosphere finish primitive equations, mostly thermodynamics Reference Peixoto and Oort, Sec. 3.1, 3.2, 3.4, 3.5 (but skip the discussion of oceans until next week); Ch. 10 Thermodynamic
Today s Lecture: Atmosphere finish primitive equations, mostly thermodynamics Reference Peixoto and Oort, Sec. 3.1, 3.2, 3.4, 3.5 (but skip the discussion of oceans until next week); Ch. 10 Thermodynamic
Dynamics and Kinematics
 Geophysics Fluid Dynamics () Syllabus Course Time Lectures: Tu, Th 09:30-10:50 Discussion: 3315 Croul Hall Text Book J. R. Holton, "An introduction to Dynamic Meteorology", Academic Press (Ch. 1, 2, 3,
Geophysics Fluid Dynamics () Syllabus Course Time Lectures: Tu, Th 09:30-10:50 Discussion: 3315 Croul Hall Text Book J. R. Holton, "An introduction to Dynamic Meteorology", Academic Press (Ch. 1, 2, 3,
Differential relations for fluid flow
 Differential relations for fluid flow In this approach, we apply basic conservation laws to an infinitesimally small control volume. The differential approach provides point by point details of a flow
Differential relations for fluid flow In this approach, we apply basic conservation laws to an infinitesimally small control volume. The differential approach provides point by point details of a flow
Geophysics Fluid Dynamics (ESS228)
 Geophysics Fluid Dynamics (ESS228) Course Time Lectures: Tu, Th 09:30-10:50 Discussion: 3315 Croul Hall Text Book J. R. Holton, "An introduction to Dynamic Meteorology", Academic Press (Ch. 1, 2, 3, 4,
Geophysics Fluid Dynamics (ESS228) Course Time Lectures: Tu, Th 09:30-10:50 Discussion: 3315 Croul Hall Text Book J. R. Holton, "An introduction to Dynamic Meteorology", Academic Press (Ch. 1, 2, 3, 4,
Models of ocean circulation are all based on the equations of motion.
 Equations of motion Models of ocean circulation are all based on the equations of motion. Only in simple cases the equations of motion can be solved analytically, usually they must be solved numerically.
Equations of motion Models of ocean circulation are all based on the equations of motion. Only in simple cases the equations of motion can be solved analytically, usually they must be solved numerically.
Where does Bernoulli's Equation come from?
 Where does Bernoulli's Equation come from? Introduction By now, you have seen the following equation many times, using it to solve simple fluid problems. P ρ + v + gz = constant (along a streamline) This
Where does Bernoulli's Equation come from? Introduction By now, you have seen the following equation many times, using it to solve simple fluid problems. P ρ + v + gz = constant (along a streamline) This
Numerical Heat and Mass Transfer
 Master Degree in Mechanical Engineering Numerical Heat and Mass Transfer 15-Convective Heat Transfer Fausto Arpino f.arpino@unicas.it Introduction In conduction problems the convection entered the analysis
Master Degree in Mechanical Engineering Numerical Heat and Mass Transfer 15-Convective Heat Transfer Fausto Arpino f.arpino@unicas.it Introduction In conduction problems the convection entered the analysis
Parcel Model. Meteorology September 3, 2008
 Parcel Model Meteorology 5210 September 3, 2008 1 Governing Equations for Precipitating Convection For precipitating convection, we have the following set of equations for potential temperature, θ, mixing
Parcel Model Meteorology 5210 September 3, 2008 1 Governing Equations for Precipitating Convection For precipitating convection, we have the following set of equations for potential temperature, θ, mixing
ESCI 485 Air/sea Interaction Lesson 5 Oceanic Boundary Layer
 ESCI 485 Air/sea Interaction Lesson 5 Oceanic Boundar Laer References: Descriptive Phsical Oceanograph, Pickard and Emer Introductor Dnamical Oceanograph, Pond and Pickard Principles of Ocean Phsics, Apel
ESCI 485 Air/sea Interaction Lesson 5 Oceanic Boundar Laer References: Descriptive Phsical Oceanograph, Pickard and Emer Introductor Dnamical Oceanograph, Pond and Pickard Principles of Ocean Phsics, Apel
The dynamics of high and low pressure systems
 The dynamics of high and low pressure systems Newton s second law for a parcel of air in an inertial coordinate system (a coordinate system in which the coordinate axes do not change direction and are
The dynamics of high and low pressure systems Newton s second law for a parcel of air in an inertial coordinate system (a coordinate system in which the coordinate axes do not change direction and are
On the validation study devoted to stratified atmospheric flow over an isolated hill
 On the validation study devoted to stratified atmospheric flow over an isolated hill Sládek I. 2/, Kozel K. 1/, Jaňour Z. 2/ 1/ U1211, Faculty of Mechanical Engineering, Czech Technical University in Prague.
On the validation study devoted to stratified atmospheric flow over an isolated hill Sládek I. 2/, Kozel K. 1/, Jaňour Z. 2/ 1/ U1211, Faculty of Mechanical Engineering, Czech Technical University in Prague.
Eliassen-Palm Theory
 Eliassen-Palm Theory David Painemal MPO611 April 2007 I. Introduction The separation of the flow into its zonal average and the deviations therefrom has been a dominant paradigm for analyses of the general
Eliassen-Palm Theory David Painemal MPO611 April 2007 I. Introduction The separation of the flow into its zonal average and the deviations therefrom has been a dominant paradigm for analyses of the general
150A Review Session 2/13/2014 Fluid Statics. Pressure acts in all directions, normal to the surrounding surfaces
 Fluid Statics Pressure acts in all directions, normal to the surrounding surfaces or Whenever a pressure difference is the driving force, use gauge pressure o Bernoulli equation o Momentum balance with
Fluid Statics Pressure acts in all directions, normal to the surrounding surfaces or Whenever a pressure difference is the driving force, use gauge pressure o Bernoulli equation o Momentum balance with
Chapter 2. Quasi-Geostrophic Theory: Formulation (review) ε =U f o L <<1, β = 2Ω cosθ o R. 2.1 Introduction
 Chapter 2. Quasi-Geostrophic Theory: Formulation (review) 2.1 Introduction For most of the course we will be concerned with instabilities that an be analyzed by the quasi-geostrophic equations. These are
Chapter 2. Quasi-Geostrophic Theory: Formulation (review) 2.1 Introduction For most of the course we will be concerned with instabilities that an be analyzed by the quasi-geostrophic equations. These are
( ) = 1005 J kg 1 K 1 ;
 Problem Set 3 1. A parcel of water is added to the ocean surface that is denser (heavier) than any of the waters in the ocean. Suppose the parcel sinks to the ocean bottom; estimate the change in temperature
Problem Set 3 1. A parcel of water is added to the ocean surface that is denser (heavier) than any of the waters in the ocean. Suppose the parcel sinks to the ocean bottom; estimate the change in temperature
Model description of AGCM5 of GFD-Dennou-Club edition. SWAMP project, GFD-Dennou-Club
 Model description of AGCM5 of GFD-Dennou-Club edition SWAMP project, GFD-Dennou-Club Mar 01, 2006 AGCM5 of the GFD-DENNOU CLUB edition is a three-dimensional primitive system on a sphere (Swamp Project,
Model description of AGCM5 of GFD-Dennou-Club edition SWAMP project, GFD-Dennou-Club Mar 01, 2006 AGCM5 of the GFD-DENNOU CLUB edition is a three-dimensional primitive system on a sphere (Swamp Project,
wavelength (nm)
 Blackbody radiation Everything with a temperature above absolute zero emits electromagnetic radiation. This phenomenon is called blackbody radiation. The intensity and the peak wavelength of the radiation
Blackbody radiation Everything with a temperature above absolute zero emits electromagnetic radiation. This phenomenon is called blackbody radiation. The intensity and the peak wavelength of the radiation
AE/ME 339. Computational Fluid Dynamics (CFD) K. M. Isaac. Momentum equation. Computational Fluid Dynamics (AE/ME 339) MAEEM Dept.
 AE/ME 339 Computational Fluid Dynamics (CFD) 9//005 Topic7_NS_ F0 1 Momentum equation 9//005 Topic7_NS_ F0 1 Consider the moving fluid element model shown in Figure.b Basis is Newton s nd Law which says
AE/ME 339 Computational Fluid Dynamics (CFD) 9//005 Topic7_NS_ F0 1 Momentum equation 9//005 Topic7_NS_ F0 1 Consider the moving fluid element model shown in Figure.b Basis is Newton s nd Law which says
Introduction to Atmospheric Circulation
 Introduction to Atmospheric Circulation Start rotating table Start heated bottle experiment Scientific Practice Observe nature Develop a model*/hypothesis for what is happening Carry out experiments Make
Introduction to Atmospheric Circulation Start rotating table Start heated bottle experiment Scientific Practice Observe nature Develop a model*/hypothesis for what is happening Carry out experiments Make
1/27/2010. With this method, all filed variables are separated into. from the basic state: Assumptions 1: : the basic state variables must
 Lecture 5: Waves in Atmosphere Perturbation Method With this method, all filed variables are separated into two parts: (a) a basic state part and (b) a deviation from the basic state: Perturbation Method
Lecture 5: Waves in Atmosphere Perturbation Method With this method, all filed variables are separated into two parts: (a) a basic state part and (b) a deviation from the basic state: Perturbation Method
Monday 7 October 2013, Class #15
 Monday 7 October 2013, Class #15 Concepts for Today (Basics for Thermodynamics) Weather versus climate Lapse Rate (Adiabatic Lapse Rate) Ideal Gas Law Adiabatic Processes Potential Temperature Hydrostatic
Monday 7 October 2013, Class #15 Concepts for Today (Basics for Thermodynamics) Weather versus climate Lapse Rate (Adiabatic Lapse Rate) Ideal Gas Law Adiabatic Processes Potential Temperature Hydrostatic
Some remarks on climate modeling
 Some remarks on climate modeling A. Gettelman & J. J. Hack National Center for Atmospheric Research Boulder, Colorado USA Selected overheads by Doug Nychka Outline Hierarchy of atmospheric modeling strategies
Some remarks on climate modeling A. Gettelman & J. J. Hack National Center for Atmospheric Research Boulder, Colorado USA Selected overheads by Doug Nychka Outline Hierarchy of atmospheric modeling strategies
Theory of linear gravity waves April 1987
 April 1987 By Tim Palmer European Centre for Medium-Range Weather Forecasts Table of contents 1. Simple properties of internal gravity waves 2. Gravity-wave drag REFERENCES 1. SIMPLE PROPERTIES OF INTERNAL
April 1987 By Tim Palmer European Centre for Medium-Range Weather Forecasts Table of contents 1. Simple properties of internal gravity waves 2. Gravity-wave drag REFERENCES 1. SIMPLE PROPERTIES OF INTERNAL
2. Conservation laws and basic equations
 2. Conservation laws and basic equations Equatorial region is mapped well by cylindrical (Mercator) projection: eastward, northward, upward (local Cartesian) coordinates:,, velocity vector:,,,, material
2. Conservation laws and basic equations Equatorial region is mapped well by cylindrical (Mercator) projection: eastward, northward, upward (local Cartesian) coordinates:,, velocity vector:,,,, material
Boundary Layer Meteorology. Chapter 2
 Boundary Layer Meteorology Chapter 2 Contents Some mathematical tools: Statistics The turbulence spectrum Energy cascade, The spectral gap Mean and turbulent parts of the flow Some basic statistical methods
Boundary Layer Meteorology Chapter 2 Contents Some mathematical tools: Statistics The turbulence spectrum Energy cascade, The spectral gap Mean and turbulent parts of the flow Some basic statistical methods
Physical Oceanography, MSCI 3001 Oceanographic Processes, MSCI Dr. Katrin Meissner Week 5.
 Physical Oceanography, MSCI 3001 Oceanographic Processes, MSCI 5004 Dr. Katrin Meissner k.meissner@unsw.e.au Week 5 Ocean Dynamics Transport of Volume, Heat & Salt Flux: Amount of heat, salt or volume
Physical Oceanography, MSCI 3001 Oceanographic Processes, MSCI 5004 Dr. Katrin Meissner k.meissner@unsw.e.au Week 5 Ocean Dynamics Transport of Volume, Heat & Salt Flux: Amount of heat, salt or volume
Fundamentals of Weather and Climate
 Fundamentals of Weather and Climate ROBIN McILVEEN Environmental Science Division Institute of Environmental and Biological Sciences Lancaster University CHAPMAN & HALL London Glasgow Weinheim New York
Fundamentals of Weather and Climate ROBIN McILVEEN Environmental Science Division Institute of Environmental and Biological Sciences Lancaster University CHAPMAN & HALL London Glasgow Weinheim New York
Dynamic Meteorology (lecture 13, 2016)
 Dynamic Meteorology (lecture 13, 2016) Topics Chapter 3, lecture notes: High frequency waves (no rota;on) Boussinesq approxima4on Normal mode analysis of the stability of hydrosta4c balance Buoyancy waves
Dynamic Meteorology (lecture 13, 2016) Topics Chapter 3, lecture notes: High frequency waves (no rota;on) Boussinesq approxima4on Normal mode analysis of the stability of hydrosta4c balance Buoyancy waves
The Navier-Stokes Equations
 s University of New Hampshire February 22, 202 and equations describe the non-relativistic time evolution of mass and momentum in fluid substances. mass density field: ρ = ρ(t, x, y, z) velocity field:
s University of New Hampshire February 22, 202 and equations describe the non-relativistic time evolution of mass and momentum in fluid substances. mass density field: ρ = ρ(t, x, y, z) velocity field:
Fluid Mechanics Abdusselam Altunkaynak
 Fluid Mechanics Abdusselam Altunkaynak 1. Unit systems 1.1 Introduction Natural events are independent on units. The unit to be used in a certain variable is related to the advantage that we get from it.
Fluid Mechanics Abdusselam Altunkaynak 1. Unit systems 1.1 Introduction Natural events are independent on units. The unit to be used in a certain variable is related to the advantage that we get from it.
The Shallow Water Equations
 The Shallow Water Equations Clint Dawson and Christopher M. Mirabito Institute for Computational Engineering and Sciences University of Texas at Austin clint@ices.utexas.edu September 29, 2008 The Shallow
The Shallow Water Equations Clint Dawson and Christopher M. Mirabito Institute for Computational Engineering and Sciences University of Texas at Austin clint@ices.utexas.edu September 29, 2008 The Shallow
Summary of Dimensionless Numbers of Fluid Mechanics and Heat Transfer
 1. Nusselt number Summary of Dimensionless Numbers of Fluid Mechanics and Heat Transfer Average Nusselt number: convective heat transfer Nu L = conductive heat transfer = hl where L is the characteristic
1. Nusselt number Summary of Dimensionless Numbers of Fluid Mechanics and Heat Transfer Average Nusselt number: convective heat transfer Nu L = conductive heat transfer = hl where L is the characteristic
ATM 298, Spring 2013 Lecture 2 The Equa;ons of Fluid Mo;on April 3, Paul A. Ullrich (HH 251)
 ATM 298, Spring 2013 Lecture 2 The Equa;ons of Fluid Mo;on April 3, 2013 Paul A. Ullrich (HH 251) paullrich@ucdavis.edu Global Atmospheric Modeling Global atmospheric models were originally constructed
ATM 298, Spring 2013 Lecture 2 The Equa;ons of Fluid Mo;on April 3, 2013 Paul A. Ullrich (HH 251) paullrich@ucdavis.edu Global Atmospheric Modeling Global atmospheric models were originally constructed
Improved Fields of Satellite-Derived Ocean Surface Turbulent Fluxes of Energy and Moisture
 Improved Fields of Satellite-Derived Ocean Surface Turbulent Fluxes of Energy and Moisture First year report on NASA grant NNX09AJ49G PI: Mark A. Bourassa Co-Is: Carol Anne Clayson, Shawn Smith, and Gary
Improved Fields of Satellite-Derived Ocean Surface Turbulent Fluxes of Energy and Moisture First year report on NASA grant NNX09AJ49G PI: Mark A. Bourassa Co-Is: Carol Anne Clayson, Shawn Smith, and Gary
z g + F w (2.56) p(x, y, z, t) = p(z) + p (x, y, z, t) (2.120) ρ(x, y, z, t) = ρ(z) + ρ (x, y, z, t), (2.121)
 = + dw dt = 1 ρ p z g + F w (.56) Let us describe the total pressure p and density ρ as the sum of a horizontally homogeneous base state pressure and density, and a deviation from this base state, that
= + dw dt = 1 ρ p z g + F w (.56) Let us describe the total pressure p and density ρ as the sum of a horizontally homogeneous base state pressure and density, and a deviation from this base state, that
Principles of Convection
 Principles of Convection Point Conduction & convection are similar both require the presence of a material medium. But convection requires the presence of fluid motion. Heat transfer through the: Solid
Principles of Convection Point Conduction & convection are similar both require the presence of a material medium. But convection requires the presence of fluid motion. Heat transfer through the: Solid
Atmospheric Dynamics: lecture 2
 Atmospheric Dynamics: lecture 2 Topics Some aspects of advection and the Coriolis-effect (1.7) Composition of the atmosphere (figure 1.6) Equation of state (1.8&1.9) Water vapour in the atmosphere (1.10)
Atmospheric Dynamics: lecture 2 Topics Some aspects of advection and the Coriolis-effect (1.7) Composition of the atmosphere (figure 1.6) Equation of state (1.8&1.9) Water vapour in the atmosphere (1.10)
Atmospheric Sciences 321. Science of Climate. Lecture 13: Surface Energy Balance Chapter 4
 Atmospheric Sciences 321 Science of Climate Lecture 13: Surface Energy Balance Chapter 4 Community Business Check the assignments HW #4 due Wednesday Quiz #2 Wednesday Mid Term is Wednesday May 6 Practice
Atmospheric Sciences 321 Science of Climate Lecture 13: Surface Energy Balance Chapter 4 Community Business Check the assignments HW #4 due Wednesday Quiz #2 Wednesday Mid Term is Wednesday May 6 Practice
ES265 Order of Magnitude Phys & Chem Convection
 ES265 Order of Magnitude Phys & Chem Convection Convection deals with moving fluids in which there are spatial variations in temperature or chemical concentration. In forced convection, these variations
ES265 Order of Magnitude Phys & Chem Convection Convection deals with moving fluids in which there are spatial variations in temperature or chemical concentration. In forced convection, these variations
Quick Recapitulation of Fluid Mechanics
 Quick Recapitulation of Fluid Mechanics Amey Joshi 07-Feb-018 1 Equations of ideal fluids onsider a volume element of a fluid of density ρ. If there are no sources or sinks in, the mass in it will change
Quick Recapitulation of Fluid Mechanics Amey Joshi 07-Feb-018 1 Equations of ideal fluids onsider a volume element of a fluid of density ρ. If there are no sources or sinks in, the mass in it will change
Governing Equations and Scaling in the Tropics
 Governing Equations and Scaling in the Tropics M 1 ( ) e R ε er Tropical v Midlatitude Meteorology Why is the general circulation and synoptic weather systems in the tropics different to the those in the
Governing Equations and Scaling in the Tropics M 1 ( ) e R ε er Tropical v Midlatitude Meteorology Why is the general circulation and synoptic weather systems in the tropics different to the those in the
Lecture 2. Lecture 1. Forces on a rotating planet. We will describe the atmosphere and ocean in terms of their:
 Lecture 2 Lecture 1 Forces on a rotating planet We will describe the atmosphere and ocean in terms of their: velocity u = (u,v,w) pressure P density ρ temperature T salinity S up For convenience, we will
Lecture 2 Lecture 1 Forces on a rotating planet We will describe the atmosphere and ocean in terms of their: velocity u = (u,v,w) pressure P density ρ temperature T salinity S up For convenience, we will
Synoptic Meteorology I: Skew-T Diagrams and Thermodynamic Properties
 Synoptic Meteorology I: Skew-T Diagrams and Thermodynamic Properties For Further Reading Most information contained within these lecture notes is drawn from Chapters 1, 2, 4, and 6 of The Use of the Skew
Synoptic Meteorology I: Skew-T Diagrams and Thermodynamic Properties For Further Reading Most information contained within these lecture notes is drawn from Chapters 1, 2, 4, and 6 of The Use of the Skew
meters, we can re-arrange this expression to give
 Turbulence When the Reynolds number becomes sufficiently large, the non-linear term (u ) u in the momentum equation inevitably becomes comparable to other important terms and the flow becomes more complicated.
Turbulence When the Reynolds number becomes sufficiently large, the non-linear term (u ) u in the momentum equation inevitably becomes comparable to other important terms and the flow becomes more complicated.
BAE 820 Physical Principles of Environmental Systems
 BAE 820 Physical Principles of Environmental Systems Stokes' law and Reynold number Dr. Zifei Liu The motion of a particle in a fluid environment, such as air or water m dv =F(t) - F dt d - 1 4 2 3 πr3
BAE 820 Physical Principles of Environmental Systems Stokes' law and Reynold number Dr. Zifei Liu The motion of a particle in a fluid environment, such as air or water m dv =F(t) - F dt d - 1 4 2 3 πr3
of Friction in Fluids Dept. of Earth & Clim. Sci., SFSU
 Summary. Shear is the gradient of velocity in a direction normal to the velocity. In the presence of shear, collisions among molecules in random motion tend to transfer momentum down-shear (from faster
Summary. Shear is the gradient of velocity in a direction normal to the velocity. In the presence of shear, collisions among molecules in random motion tend to transfer momentum down-shear (from faster
Hydrostatic Equation and Thermal Wind. Meteorology 411 Iowa State University Week 5 Bill Gallus
 Hydrostatic Equation and Thermal Wind Meteorology 411 Iowa State University Week 5 Bill Gallus Hydrostatic Equation In the atmosphere, vertical accelerations (dw/dt) are normally fairly small, and we can
Hydrostatic Equation and Thermal Wind Meteorology 411 Iowa State University Week 5 Bill Gallus Hydrostatic Equation In the atmosphere, vertical accelerations (dw/dt) are normally fairly small, and we can
Introduction to Atmospheric Circulation
 Introduction to Atmospheric Circulation Start rotating table Cloud Fraction Dice Results from http://eos.atmos.washington.edu/erbe/ from http://eos.atmos.washington.edu/erbe/ from http://eos.atmos.washington.edu/erbe/
Introduction to Atmospheric Circulation Start rotating table Cloud Fraction Dice Results from http://eos.atmos.washington.edu/erbe/ from http://eos.atmos.washington.edu/erbe/ from http://eos.atmos.washington.edu/erbe/
Chapter 4: Fundamental Forces
 Chapter 4: Fundamental Forces Newton s Second Law: F=ma In atmospheric science it is typical to consider the force per unit mass acting on the atmosphere: Force mass = a In order to understand atmospheric
Chapter 4: Fundamental Forces Newton s Second Law: F=ma In atmospheric science it is typical to consider the force per unit mass acting on the atmosphere: Force mass = a In order to understand atmospheric
ESCI 485 Air/sea Interaction Lesson 3 The Surface Layer
 ESCI 485 Air/sea Interaction Lesson 3 he Surface Layer References: Air-sea Interaction: Laws and Mechanisms, Csanady Structure of the Atmospheric Boundary Layer, Sorbjan HE PLANEARY BOUNDARY LAYER he atmospheric
ESCI 485 Air/sea Interaction Lesson 3 he Surface Layer References: Air-sea Interaction: Laws and Mechanisms, Csanady Structure of the Atmospheric Boundary Layer, Sorbjan HE PLANEARY BOUNDARY LAYER he atmospheric
Fluid Mechanics II Viscosity and shear stresses
 Fluid Mechanics II Viscosity and shear stresses Shear stresses in a Newtonian fluid A fluid at rest can not resist shearing forces. Under the action of such forces it deforms continuously, however small
Fluid Mechanics II Viscosity and shear stresses Shear stresses in a Newtonian fluid A fluid at rest can not resist shearing forces. Under the action of such forces it deforms continuously, however small
CHAPTER 8 ENTROPY GENERATION AND TRANSPORT
 CHAPTER 8 ENTROPY GENERATION AND TRANSPORT 8.1 CONVECTIVE FORM OF THE GIBBS EQUATION In this chapter we will address two questions. 1) How is Gibbs equation related to the energy conservation equation?
CHAPTER 8 ENTROPY GENERATION AND TRANSPORT 8.1 CONVECTIVE FORM OF THE GIBBS EQUATION In this chapter we will address two questions. 1) How is Gibbs equation related to the energy conservation equation?
10 Shallow Water Models
 10 Shallow Water Models So far, we have studied the effects due to rotation and stratification in isolation. We then looked at the effects of rotation in a barotropic model, but what about if we add stratification
10 Shallow Water Models So far, we have studied the effects due to rotation and stratification in isolation. We then looked at the effects of rotation in a barotropic model, but what about if we add stratification
Computational Fluid Dynamics 2
 Seite 1 Introduction Computational Fluid Dynamics 11.07.2016 Computational Fluid Dynamics 2 Turbulence effects and Particle transport Martin Pietsch Computational Biomechanics Summer Term 2016 Seite 2
Seite 1 Introduction Computational Fluid Dynamics 11.07.2016 Computational Fluid Dynamics 2 Turbulence effects and Particle transport Martin Pietsch Computational Biomechanics Summer Term 2016 Seite 2
FLUID MECHANICS PROF. DR. METİN GÜNER COMPILER
 FLUID MECHANICS PROF. DR. METİN GÜNER COMPILER ANKARA UNIVERSITY FACULTY OF AGRICULTURE DEPARTMENT OF AGRICULTURAL MACHINERY AND TECHNOLOGIES ENGINEERING 1 5. FLOW IN PIPES 5.1.3. Pressure and Shear Stress
FLUID MECHANICS PROF. DR. METİN GÜNER COMPILER ANKARA UNIVERSITY FACULTY OF AGRICULTURE DEPARTMENT OF AGRICULTURAL MACHINERY AND TECHNOLOGIES ENGINEERING 1 5. FLOW IN PIPES 5.1.3. Pressure and Shear Stress
References: Parcel Theory. Vertical Force Balance. ESCI Cloud Physics and Precipitation Processes Lesson 3 - Stability and Buoyancy Dr.
 References: ESCI 340 - Cloud Physics and Precipitation Processes Lesson 3 - Stability and Buoyancy Dr. DeCaria Glossary of Meteorology, 2nd ed., American Meteorological Society A Short Course in Cloud
References: ESCI 340 - Cloud Physics and Precipitation Processes Lesson 3 - Stability and Buoyancy Dr. DeCaria Glossary of Meteorology, 2nd ed., American Meteorological Society A Short Course in Cloud
6. Laminar and turbulent boundary layers
 6. Laminar and turbulent boundary layers John Richard Thome 8 avril 2008 John Richard Thome (LTCM - SGM - EPFL) Heat transfer - Convection 8 avril 2008 1 / 34 6.1 Some introductory ideas Figure 6.1 A boundary
6. Laminar and turbulent boundary layers John Richard Thome 8 avril 2008 John Richard Thome (LTCM - SGM - EPFL) Heat transfer - Convection 8 avril 2008 1 / 34 6.1 Some introductory ideas Figure 6.1 A boundary
BALANCED FLOW: EXAMPLES (PHH lecture 3) Potential Vorticity in the real atmosphere. Potential temperature θ. Rossby Ertel potential vorticity
 BALANCED FLOW: EXAMPLES (PHH lecture 3) Potential Vorticity in the real atmosphere Need to introduce a new measure of the buoyancy Potential temperature θ In a compressible fluid, the relevant measure
BALANCED FLOW: EXAMPLES (PHH lecture 3) Potential Vorticity in the real atmosphere Need to introduce a new measure of the buoyancy Potential temperature θ In a compressible fluid, the relevant measure
