2.5 Shallow water equations, quasigeostrophic filtering, and filtering of inertia-gravity waves
|
|
|
- Rolf O’Brien’
- 6 years ago
- Views:
Transcription
1 Chapter. The continuous equations φ=gh Φ=gH φ s =gh s Fig..5: Schematic of the shallow water model, a hydrostatic, incompressible fluid with a rigid bottom h s (x,y), a free surface h(x,y,t), and horizontal scales L much larger than the mean vertical scale H..5 Shallow water equations, quasigeostrophic filtering, and filtering of inertia-gravity waves The shallow water equations (SWE, fig..5), are valid for an incompressible hydrostatic motion of a fluid with a free surface h(x,y,t). Shallow means that the vertical depth is much smaller than the typical horizontal depth, which justifies the hydrostatic approximation. These equations are appropriate for representing a shallow mass of water (e.g., shallow sea, river flow, storm surges). They are also a prototype of the primitive equations based on the hydrostatic approximation and are frequently used to test numerical schemes. ch-5-swe-filteringcreated on August 3, :19 AM 1
2 The SWE horizontal momentum equations are dv dt = " fkxv " #! (5.1) d! where = +." dt! t v, v = vh = ui + vk, and! = gh. The continuity equation is d(! "! s ) = "(! "! s )#. v, (5.a) dt which can also be written as "! = #.[(! $! s ) v ]. " t (5.b) Here! = gh ( x, y) and h s is the bottom topography. s s Exercise.5.1: derive the SWE from the Primitive Equations (PE) assuming: hydrostatic, incompressible motion, and that the horizontal velocity is uniform in height. Is the vertical velocity uniform in height as well? ch-5-swe-filteringcreated on August 3, :19 AM
3 We derive the equation of conservation of potential vorticity: expanding the total derivative of the momentum equation, and making use of the useful relationship v v v k v where! = k. "xv H H." H = "( H / ) +! x H we obtain "! + v. #! +! #. v = $ f #. v $ v. # f (5.) " t df or (since. dt = v!f ) d( f +!) = "( f +!)#.v (5.3) dt which indicates that the absolute vorticity of a parcel of water increases proportionally to its convergence (or vertical stretching). Eliminating the divergence from (5.4) and (5.a), we obtain d dt $ f +! ' & % " # " ) s ( = 0 (5.4) The potential vorticity is the absolute vorticity divided by the depth of the fluid: q = $ f +! ' & % " # " s ( ) (5.5) A parcel moving around conserves its potential vorticity! ch-5-swe-filteringcreated on August 3, :19 AM 3
4 The conservation of potential vorticity is an extremely powerful dynamical constraint. In a multilevel primitive equations model, the isentropic potential vorticity (absolute vorticity divided by the distance between two surfaces of constant potential temperature) is also individually conserved:!p! + "!! d $ f +! ' dt % & "p / "# ( ) = 0 Or, as the size of the parcel goes to zero, d dt $ ( f +!) "# ' % & "p ( ) = 0 If the initial potential vorticity distribution is accurately represented in a numerical model, and the model is able to transport potential vorticity accurately, then the forecast will also be accurate. Note that IPV can change with time if there is heating or friction because heating changes! and friction changes the vorticity. ch-5-swe-filteringcreated on August 3, :19 AM 4
5 Frequency Dispersion Relationship in SWE: We now consider small perturbations on a flat bottom and a mean height! = gh = const., on a constant f-plane. " v ' " t and = # fkxv '# $! ' (5.6) "! ' " t = #$%. ' v (5.7) (note that (5.6) and (5.7) are the same equations as in the case 5 of horizontal sound (Lamb) waves, with gh = c s =! RT o, g" = p' # ) 0 Assume solutions of the form (u',v',! ')e i(kx"#t ) and get!(! " f " #k ) = 0 (5.8) with three solutions for ν: " = f +!k (5.9) the frequency of inertia-gravity waves, analogous to the inertia-lamb wave, and ν=0, the geostrophic mode. As we saw with the primitive equations, this is a geostrophic, non-divergent steady-state solution!!t kx"# = 0, v =, ".v = 0. f ch-5-swe-filteringcreated on August 3, :19 AM 5
6 Following Arakawa (1997), we compare the FDR of IGW in the SWE with the FDR of a 3-dimensional isothermal equation using the hydrostatic approximation:! = f + c s k for Lamb waves, and! = f + N k n + 1 4H for inertia-gravity waves. We see that the SWE FDR " = f +!k is analogous to internal inertia-gravity waves for an isothermal hydrostatic atmosphere (eq.3.6) if we define an equivalent depth such that! = gh : eq h eq N / g d ln! 0 / dz = = 1 1 n + n + 4H 4H 0 0 (5.10) and is analogous to the (external) inertia Lamb waves if we define the equivalent depth as h c g H eq = s / =! 0 (5.11) So, the SWE can be used as a toy model of the primitive equations with the inertia-lamb wave and inertial-internal gravity waves by choosing the equivalent depth! = gheq appropriately. ch-5-swe-filteringcreated on August 3, :19 AM 6
7 .5.1 Quasigeostrophic scaling for the SWE If we want to filter the inertia-gravity waves (IGW), as Charney did in the first successful numerical weather forecasting experiment (Chapter 1), we can develop a quasigeostrophic version of the SWE. Do it first on an f-plane f = f 0 Assume that the atmosphere is in quasi-geostrophic balance: v = v + v = v + v ' g ag g! where we assume that the typical size of the ageostrophic wind is much smaller (order! = U / fl, the Rossby number) than the geostrophic wind! v ' << v g, and that the same is true for their time derivatives " v ' " v! << " t " t The geostrophic wind is given by 1 v g = k x"! f. (5.1) g. ch-5-swe-filteringcreated on August 3, :19 AM 7
8 Plugging these into the perturbation equations (5.6) and (5.7) we obtain # v g # v ' +! = $% " $ fkxv g $! fkxv ' = $! fkxv ' (5.13) # t # t In this equation, the dominant terms (pressure gradient and Coriolis force on the geostrophic flow) cancel each other (geostrophic balance), so that the smaller effect of the Coriolis force acting on the ageostrophic flow is left to balance the time derivative. #! = $%&. v g $ " %&. v ' = $ " %&. v ' (5.14) # t Here the geostrophic wind is non-divergent, so that the time derivative of the pressure is given by the divergence of the smaller ageostrophic wind. From (5.13) and (5.14)we can conclude that! v g! t and "! " t are of order ε i.e., the geostrophic flow changes slowly (it is almost stationary compared with other types of motion), ch-5-swe-filteringcreated on August 3, :19 AM 8
9 and that ε.! v " vag " v ' g =!, which is smaller than " t " t! t, is of order With quasi-geostrophic scaling we neglect terms of O(ε ) and we obtain the linearized QG SWE: " v g = #$! # fkxv = # fkxv ag " t!. v = #%$. vag " t a b v = 1/ f kx$! c g (5.15) Note that in (5.15) there is only one independent time derivative because of the geostrophic relationship (we lost the other two time derivatives when we neglected! vag the term ).! t Physically, this means that we only allow divergent motion to exist as required to maintain the quasi-geostrophic balance, and eliminate the degrees of freedom necessary for the propagation of gravity waves. We can rewrite (5.15) as ch-5-swe-filteringcreated on August 3, :19 AM 9
10 " ug "! = # + fv = fvag " t " x a " vg "! = # + fu = # fuag " t " y b "! $ " u " v % $ " uag " vag % = #& ' + ( = & ' + ( " t ) " x " y * ) " x " y * 1 "! 1 "! ug = # ; vg = f " y f " x d c (5.16) We can compute the equation for the geostrophic vorticity evolution from (5.16) by taking the x-derivative of b minus the y-derivative of a: %! # % u % v $ = & f0 ' + ( & " v % t ) % x % y * (5.17) where the last term in (5.17) appears if we are on a betaplane: f = f0 +! y. Then we can eliminate the (ageostrophic) divergence between (5.17) and (5.16)c and obtain the linear quasigeostrophic potential vorticity equation on a beta-plane: $ (! " ) # $ % = % " $ t f & f $ x 0 0 (5.18) or, since " = # f 0!, ch-5-swe-filteringcreated on August 3, :19 AM 10
11 ! #!t (" f $ # 0 % ) = $ & f 0!#!x (5.19) Note that there is a single independent variable (! ) so that there is a single solution for the frequency. If we neglect the! -term (i.e., assume an f-plane) and allow for plane wavetype solutions " = Fe, the only solution of the FDR in i( kx#! t) (5.19) is ν=0, the geostrophic mode. This confirms that by eliminating the time derivative of the ageostrophic (divergent) wind wave solution. v ag, we have eliminated the inertia-gravity If we assume a beta-plane, i.e. keep the! term in (5.19), the quasi-geostrophic FDR becomes " = k #! k 0 / + f $ (5.0) These are Rossby waves, the essential weather waves. As shown in table.1, have rather large amplitudes (up to 50 hpa). The ageostrophic flow associated with these waves is responsible for the upward motion that produces precipitation ahead of the troughs. In a multilevel model, the FDR (5.0) can be used with the equivalent depths (5.10), (5.11) applied to the baroclinic (internal) and barotropic Rossby waves respectively. ch-5-swe-filteringcreated on August 3, :19 AM 11
12 With these definitions, we can say that the waves in the atmosphere are analogous to the SWE waves. However because the h eq appears as a separation constant in the definition of the normal modes of the atmosphere, the equivalent depth depends on the vertical wavenumber, and on the type of wave considered (Lamb or IGW). The QG Potential Vorticity equation (PVE) for nonlinear # % % % $# &!! $ " %! SWE is ( + ug + vg )( ' ) = ' (5.1) + % t % x % y,+ f * f 0, 0 % x using similar scaling arguments. If we add a basic flow ug ( total) = U + ug ; vg ( total) = vg, it becomes "!!t + (U + u )! g!x + v g # $! % " ( )!y & ' f * ) % $ # 0 + ' & = *, f 0!)!x.5. Inertia-gravity waves in the presence of a basic flow As we just saw, the SWE are a simple version of the primitive equations, which are widely used to understand numerical and dynamical processes in primitive equations. As we noted in Chapter 1, filtered quasi-geostrophic models have been substituted by PE models for NWP, because the quasi-geostrophic filtering is not an accurate approximation (it assumes that the Rossby number is much smaller than 1). Recall that quasi-geostrophic filtering was introduced by Charney et al (1950) in order to eliminate the problem of gravity waves, which requires a small time step, and whose high frequencies produced a huge time derivative in ch-5-swe-filteringcreated on August 3, :19 AM 1
13 Richardson's computation, masking the time derivative of the actual weather signal. An alternative way to deal with the presence of fast gravity waves without resorting to quasi-geostrophic filtering is the use of semi-implicit time schemes (to be discussed in Chapter 3). Consider small perturbations in the SWE including a basic flow U in the x-direction. Then the total linearized time d derivative becomes dt =! t +U!!! x In that case, when we assume solutions of the form Ae i( kx t )!", d dt = i(!" + ku ). Therefore the FDR remains the same except that! is replaced by! " ku. The FDR for small perturbations in the SWE with a basic flow U is therefore (! " ku )[(! " ku ) " f " # k ] = 0 (5.) As noted before, it has three solutions, the quasi-geostrophic flow (which is steady state, except for the uniform translation with speed U), and two solutions for the inertia-gravity waves, modified by the basic flow translation: (! G " ku ) = 0 (Geostrophic mode) and [(! IGW " ku ) " f " # k ] = 0 (inertia gravity waves, modified by the basic flow U) The phase speed of the IGW is given by ch-5-swe-filteringcreated on August 3, :19 AM 13
14 c IGW! IGW f = = U ± + " (5.3) k k Finally, we note that for the Lamb wave (as well as for the external GW), the phase speed of the IGW is dominated by the term! " g. 10km " 300 m / sec. As we will see in section 3..5, it is possible to avoid using costly small time steps by means of a semi-implicit time scheme. An implicit time scheme has no constraint on the time step. Therefore, in a semi-implicit scheme, the terms that give rise to the fast gravity waves, namely the horizontal divergence and the horizontal pressure gradient are written implicitly, while the rest of the SWE terms can be written explicitly. The terms generating the GW are underlined in the nonlinear SWE: " u " u " u "! + u + v = # + fv " t " x " y " x " v " v " v "! + u + v = # # fu " t " x " y " y "! "! "! " u " v " u " v + u + v = #$[ + ]# (! # $ )[ + ] " t " x " y " x " y " x " y (5.4) ch-5-swe-filteringcreated on August 3, :19 AM 14
Chapter 2. The continuous equations
 Chapter. The continuous equations Fig. 1.: Schematic of a forecast with slowly varying weather-related variations and superimposed high frequency Lamb waves. Note that even though the forecast of the slow
Chapter. The continuous equations Fig. 1.: Schematic of a forecast with slowly varying weather-related variations and superimposed high frequency Lamb waves. Note that even though the forecast of the slow
A few examples Shallow water equation derivation and solutions. Goal: Develop the mathematical foundation of tropical waves
 A few examples Shallow water equation derivation and solutions Goal: Develop the mathematical foundation of tropical waves Previously: MCS Hovmoller Propagating w/ wave velocity From Chen et al (1996)
A few examples Shallow water equation derivation and solutions Goal: Develop the mathematical foundation of tropical waves Previously: MCS Hovmoller Propagating w/ wave velocity From Chen et al (1996)
1/27/2010. With this method, all filed variables are separated into. from the basic state: Assumptions 1: : the basic state variables must
 Lecture 5: Waves in Atmosphere Perturbation Method With this method, all filed variables are separated into two parts: (a) a basic state part and (b) a deviation from the basic state: Perturbation Method
Lecture 5: Waves in Atmosphere Perturbation Method With this method, all filed variables are separated into two parts: (a) a basic state part and (b) a deviation from the basic state: Perturbation Method
6 Two-layer shallow water theory.
 6 Two-layer shallow water theory. Wewillnowgoontolookatashallowwatersystemthathastwolayersofdifferent density. This is the next level of complexity and a simple starting point for understanding the behaviour
6 Two-layer shallow water theory. Wewillnowgoontolookatashallowwatersystemthathastwolayersofdifferent density. This is the next level of complexity and a simple starting point for understanding the behaviour
196 7 atmospheric oscillations:
 196 7 atmospheric oscillations: 7.4 INTERNAL GRAVITY (BUOYANCY) WAVES We now consider the nature of gravity wave propagation in the atmosphere. Atmospheric gravity waves can only exist when the atmosphere
196 7 atmospheric oscillations: 7.4 INTERNAL GRAVITY (BUOYANCY) WAVES We now consider the nature of gravity wave propagation in the atmosphere. Atmospheric gravity waves can only exist when the atmosphere
Goals of this Chapter
 Waves in the Atmosphere and Oceans Restoring Force Conservation of potential temperature in the presence of positive static stability internal gravity waves Conservation of potential vorticity in the presence
Waves in the Atmosphere and Oceans Restoring Force Conservation of potential temperature in the presence of positive static stability internal gravity waves Conservation of potential vorticity in the presence
10 Shallow Water Models
 10 Shallow Water Models So far, we have studied the effects due to rotation and stratification in isolation. We then looked at the effects of rotation in a barotropic model, but what about if we add stratification
10 Shallow Water Models So far, we have studied the effects due to rotation and stratification in isolation. We then looked at the effects of rotation in a barotropic model, but what about if we add stratification
) 2 ψ +β ψ. x = 0. (71) ν = uk βk/k 2, (74) c x u = β/k 2. (75)
 3 Rossby Waves 3.1 Free Barotropic Rossby Waves The dispersion relation for free barotropic Rossby waves can be derived by linearizing the barotropic vortiticy equation in the form (21). This equation
3 Rossby Waves 3.1 Free Barotropic Rossby Waves The dispersion relation for free barotropic Rossby waves can be derived by linearizing the barotropic vortiticy equation in the form (21). This equation
Circulation and Vorticity
 Circulation and Vorticity Example: Rotation in the atmosphere water vapor satellite animation Circulation a macroscopic measure of rotation for a finite area of a fluid Vorticity a microscopic measure
Circulation and Vorticity Example: Rotation in the atmosphere water vapor satellite animation Circulation a macroscopic measure of rotation for a finite area of a fluid Vorticity a microscopic measure
ρ x + fv f 'w + F x ρ y fu + F y Fundamental Equation in z coordinate p = ρrt or pα = RT Du uv tanφ Dv Dt + u2 tanφ + vw a a = 1 p Dw Dt u2 + v 2
 Fundamental Equation in z coordinate p = ρrt or pα = RT Du uv tanφ + uw Dt a a = 1 p ρ x + fv f 'w + F x Dv Dt + u2 tanφ + vw a a = 1 p ρ y fu + F y Dw Dt u2 + v 2 = 1 p a ρ z g + f 'u + F z Dρ Dt + ρ
Fundamental Equation in z coordinate p = ρrt or pα = RT Du uv tanφ + uw Dt a a = 1 p ρ x + fv f 'w + F x Dv Dt + u2 tanφ + vw a a = 1 p ρ y fu + F y Dw Dt u2 + v 2 = 1 p a ρ z g + f 'u + F z Dρ Dt + ρ
= vorticity dilution + tilting horizontal vortices + microscopic solenoid
 4.4 Vorticity Eq 4.4.1 Cartesian Coordinates Because ζ = ˆk V, gives D(ζ + f) x minus [v momentum eq. in Cartesian Coordinates] y [u momentum eq. in Cartesian Coordinates] = vorticity dilution + tilting
4.4 Vorticity Eq 4.4.1 Cartesian Coordinates Because ζ = ˆk V, gives D(ζ + f) x minus [v momentum eq. in Cartesian Coordinates] y [u momentum eq. in Cartesian Coordinates] = vorticity dilution + tilting
Contents. Parti Fundamentals. 1. Introduction. 2. The Coriolis Force. Preface Preface of the First Edition
 Foreword Preface Preface of the First Edition xiii xv xvii Parti Fundamentals 1. Introduction 1.1 Objective 3 1.2 Importance of Geophysical Fluid Dynamics 4 1.3 Distinguishing Attributes of Geophysical
Foreword Preface Preface of the First Edition xiii xv xvii Parti Fundamentals 1. Introduction 1.1 Objective 3 1.2 Importance of Geophysical Fluid Dynamics 4 1.3 Distinguishing Attributes of Geophysical
Geostrophic and Quasi-Geostrophic Balances
 Geostrophic and Quasi-Geostrophic Balances Qiyu Xiao June 19, 2018 1 Introduction Understanding how the atmosphere and ocean behave is important to our everyday lives. Techniques such as weather forecasting
Geostrophic and Quasi-Geostrophic Balances Qiyu Xiao June 19, 2018 1 Introduction Understanding how the atmosphere and ocean behave is important to our everyday lives. Techniques such as weather forecasting
Chapter 2. Quasi-Geostrophic Theory: Formulation (review) ε =U f o L <<1, β = 2Ω cosθ o R. 2.1 Introduction
 Chapter 2. Quasi-Geostrophic Theory: Formulation (review) 2.1 Introduction For most of the course we will be concerned with instabilities that an be analyzed by the quasi-geostrophic equations. These are
Chapter 2. Quasi-Geostrophic Theory: Formulation (review) 2.1 Introduction For most of the course we will be concerned with instabilities that an be analyzed by the quasi-geostrophic equations. These are
M.Sc. in Meteorology. Numerical Weather Prediction Prof Peter Lynch
 M.Sc. in Meteorology UCD Numerical Weather Prediction Prof Peter Lynch Meteorology & Climate Centre School of Mathematical Sciences University College Dublin Second Semester, 2005 2006. In this section
M.Sc. in Meteorology UCD Numerical Weather Prediction Prof Peter Lynch Meteorology & Climate Centre School of Mathematical Sciences University College Dublin Second Semester, 2005 2006. In this section
Gravity Waves. Lecture 5: Waves in Atmosphere. Waves in the Atmosphere and Oceans. Internal Gravity (Buoyancy) Waves 2/9/2017
 Lecture 5: Waves in Atmosphere Perturbation Method Properties of Wave Shallow Water Model Gravity Waves Rossby Waves Waves in the Atmosphere and Oceans Restoring Force Conservation of potential temperature
Lecture 5: Waves in Atmosphere Perturbation Method Properties of Wave Shallow Water Model Gravity Waves Rossby Waves Waves in the Atmosphere and Oceans Restoring Force Conservation of potential temperature
Chapter 5. Shallow Water Equations. 5.1 Derivation of shallow water equations
 Chapter 5 Shallow Water Equations So far we have concentrated on the dynamics of small-scale disturbances in the atmosphere and ocean with relatively simple background flows. In these analyses we have
Chapter 5 Shallow Water Equations So far we have concentrated on the dynamics of small-scale disturbances in the atmosphere and ocean with relatively simple background flows. In these analyses we have
v t + fu = 1 p y w t = 1 p z g u x + v y + w
 1 For each of the waves that we will be talking about we need to know the governing equators for the waves. The linear equations of motion are used for many types of waves, ignoring the advective terms,
1 For each of the waves that we will be talking about we need to know the governing equators for the waves. The linear equations of motion are used for many types of waves, ignoring the advective terms,
Chapter 9. Geostrophy, Quasi-Geostrophy and the Potential Vorticity Equation
 Chapter 9 Geostrophy, Quasi-Geostrophy and the Potential Vorticity Equation 9.1 Geostrophy and scaling. We examined in the last chapter some consequences of the dynamical balances for low frequency, nearly
Chapter 9 Geostrophy, Quasi-Geostrophy and the Potential Vorticity Equation 9.1 Geostrophy and scaling. We examined in the last chapter some consequences of the dynamical balances for low frequency, nearly
An Optimal Control Problem Formulation for. the Atmospheric Large-Scale Wave Dynamics
 pplied Mathematical Sciences, Vol. 9, 5, no. 8, 875-884 HIKRI Ltd, www.m-hikari.com http://dx.doi.org/.988/ams.5.448 n Optimal Control Problem Formulation for the tmospheric Large-Scale Wave Dynamics Sergei
pplied Mathematical Sciences, Vol. 9, 5, no. 8, 875-884 HIKRI Ltd, www.m-hikari.com http://dx.doi.org/.988/ams.5.448 n Optimal Control Problem Formulation for the tmospheric Large-Scale Wave Dynamics Sergei
Eliassen-Palm Theory
 Eliassen-Palm Theory David Painemal MPO611 April 2007 I. Introduction The separation of the flow into its zonal average and the deviations therefrom has been a dominant paradigm for analyses of the general
Eliassen-Palm Theory David Painemal MPO611 April 2007 I. Introduction The separation of the flow into its zonal average and the deviations therefrom has been a dominant paradigm for analyses of the general
Atmospheric dynamics and meteorology
 Atmospheric dynamics and meteorology B. Legras, http://www.lmd.ens.fr/legras III Frontogenesis (pre requisite: quasi-geostrophic equation, baroclinic instability in the Eady and Phillips models ) Recommended
Atmospheric dynamics and meteorology B. Legras, http://www.lmd.ens.fr/legras III Frontogenesis (pre requisite: quasi-geostrophic equation, baroclinic instability in the Eady and Phillips models ) Recommended
Chapter 1. Governing Equations of GFD. 1.1 Mass continuity
 Chapter 1 Governing Equations of GFD The fluid dynamical governing equations consist of an equation for mass continuity, one for the momentum budget, and one or more additional equations to account for
Chapter 1 Governing Equations of GFD The fluid dynamical governing equations consist of an equation for mass continuity, one for the momentum budget, and one or more additional equations to account for
ESCI 343 Atmospheric Dynamics II Lesson 11 - Rossby Waves
 ESCI 343 Atmospheric Dynamics II Lesson 11 - Rossby Waves Reference: An Introduction to Dynamic Meteorology (4 rd edition), J.R. Holton Atmosphere-Ocean Dynamics, A.E. Gill Fundamentals of Atmospheric
ESCI 343 Atmospheric Dynamics II Lesson 11 - Rossby Waves Reference: An Introduction to Dynamic Meteorology (4 rd edition), J.R. Holton Atmosphere-Ocean Dynamics, A.E. Gill Fundamentals of Atmospheric
Baroclinic wave. Atmospheric Dynamics: lecture 14 18/12/15. Topics. Chapter 9: Baroclinic waves and cyclogenesis. What is a baroclinic wave?
 Atmospheric Dynamics: lecture 14 (http://www.staff.science.uu.nl/~delde102/) Topics Chapter 9: Baroclinic waves and cyclogenesis What is a baroclinic wave? Quasi-geostrophic equations Omega equation Original
Atmospheric Dynamics: lecture 14 (http://www.staff.science.uu.nl/~delde102/) Topics Chapter 9: Baroclinic waves and cyclogenesis What is a baroclinic wave? Quasi-geostrophic equations Omega equation Original
The Shallow Water Equations
 If you have not already done so, you are strongly encouraged to read the companion file on the non-divergent barotropic vorticity equation, before proceeding to this shallow water case. We do not repeat
If you have not already done so, you are strongly encouraged to read the companion file on the non-divergent barotropic vorticity equation, before proceeding to this shallow water case. We do not repeat
where p oo is a reference level constant pressure (often 10 5 Pa). Since θ is conserved for adiabatic motions, a prognostic temperature equation is:
 1 Appendix C Useful Equations Purposes: Provide foundation equations and sketch some derivations. These equations are used as starting places for discussions in various parts of the book. C.1. Thermodynamic
1 Appendix C Useful Equations Purposes: Provide foundation equations and sketch some derivations. These equations are used as starting places for discussions in various parts of the book. C.1. Thermodynamic
Lecture #2 Planetary Wave Models. Charles McLandress (Banff Summer School 7-13 May 2005)
 Lecture #2 Planetary Wave Models Charles McLandress (Banff Summer School 7-13 May 2005) 1 Outline of Lecture 1. Observational motivation 2. Forced planetary waves in the stratosphere 3. Traveling planetary
Lecture #2 Planetary Wave Models Charles McLandress (Banff Summer School 7-13 May 2005) 1 Outline of Lecture 1. Observational motivation 2. Forced planetary waves in the stratosphere 3. Traveling planetary
Atmospheric Dynamics: lecture 11
 Atmospheric Dynamics: lecture 11 (http://www.staff.science.uu.nl/~delde102/) Chapter 9 Baroclinic waves and cyclogenesis What is a baroclinic wave? Quasi-geostrophic equations Omega equation Original articles:
Atmospheric Dynamics: lecture 11 (http://www.staff.science.uu.nl/~delde102/) Chapter 9 Baroclinic waves and cyclogenesis What is a baroclinic wave? Quasi-geostrophic equations Omega equation Original articles:
( ) = 1005 J kg 1 K 1 ;
 Problem Set 3 1. A parcel of water is added to the ocean surface that is denser (heavier) than any of the waters in the ocean. Suppose the parcel sinks to the ocean bottom; estimate the change in temperature
Problem Set 3 1. A parcel of water is added to the ocean surface that is denser (heavier) than any of the waters in the ocean. Suppose the parcel sinks to the ocean bottom; estimate the change in temperature
GFD I: Midterm Exam Solutions
 GFD I: Midterm Exam Solutions Parker MacCready /6/0 (a) [ points] The initial condition is not in geostrophic balance, because it has a velocity field but no surface height changes. (b) [ points] We may
GFD I: Midterm Exam Solutions Parker MacCready /6/0 (a) [ points] The initial condition is not in geostrophic balance, because it has a velocity field but no surface height changes. (b) [ points] We may
Note that Rossby waves are tranverse waves, that is the particles move perpendicular to the direction of propagation. f up, down (clockwise)
 Ocean 423 Rossby waves 1 Rossby waves: Restoring force is the north-south gradient of background potential vorticity (f/h). That gradient can be due to either the variation in f with latitude, or to a
Ocean 423 Rossby waves 1 Rossby waves: Restoring force is the north-south gradient of background potential vorticity (f/h). That gradient can be due to either the variation in f with latitude, or to a
EAS372 Open Book Final Exam 11 April, 2013
 EAS372 Open Book Final Exam 11 April, 2013 Professor: J.D. Wilson Time available: 2 hours Value: 30% Please check the Terminology, Equations and Data section before beginning your responses. Answer all
EAS372 Open Book Final Exam 11 April, 2013 Professor: J.D. Wilson Time available: 2 hours Value: 30% Please check the Terminology, Equations and Data section before beginning your responses. Answer all
Using simplified vorticity equation,* by assumption 1 above: *Metr 430 handout on Circulation and Vorticity. Equations (4) and (5) on that handout
 Rossby Wave Equation A. Assumptions 1. Non-divergence 2. Initially, zonal flow, or nearly zonal flow in which u>>v>>w. 3. Initial westerly wind is geostrophic and does not vary along the x-axis and equations
Rossby Wave Equation A. Assumptions 1. Non-divergence 2. Initially, zonal flow, or nearly zonal flow in which u>>v>>w. 3. Initial westerly wind is geostrophic and does not vary along the x-axis and equations
1/18/2011. Conservation of Momentum Conservation of Mass Conservation of Energy Scaling Analysis ESS227 Prof. Jin-Yi Yu
 Lecture 2: Basic Conservation Laws Conservation Law of Momentum Newton s 2 nd Law of Momentum = absolute velocity viewed in an inertial system = rate of change of Ua following the motion in an inertial
Lecture 2: Basic Conservation Laws Conservation Law of Momentum Newton s 2 nd Law of Momentum = absolute velocity viewed in an inertial system = rate of change of Ua following the motion in an inertial
Chapter 3. Stability theory for zonal flows :formulation
 Chapter 3. Stability theory for zonal flows :formulation 3.1 Introduction Although flows in the atmosphere and ocean are never strictly zonal major currents are nearly so and the simplifications springing
Chapter 3. Stability theory for zonal flows :formulation 3.1 Introduction Although flows in the atmosphere and ocean are never strictly zonal major currents are nearly so and the simplifications springing
( ) (9.1.1) Chapter 9. Geostrophy, Quasi-Geostrophy and the Potential Vorticity Equation. 9.1 Geostrophy and scaling.
 Chapter 9 Geostrophy, Quasi-Geostrophy and the Potential Vorticity Equation 9.1 Geostrophy and scaling. We examined in the last chapter some consequences of the dynamical balances for low frequency, nearly
Chapter 9 Geostrophy, Quasi-Geostrophy and the Potential Vorticity Equation 9.1 Geostrophy and scaling. We examined in the last chapter some consequences of the dynamical balances for low frequency, nearly
The Euler Equation of Gas-Dynamics
 The Euler Equation of Gas-Dynamics A. Mignone October 24, 217 In this lecture we study some properties of the Euler equations of gasdynamics, + (u) = ( ) u + u u + p = a p + u p + γp u = where, p and u
The Euler Equation of Gas-Dynamics A. Mignone October 24, 217 In this lecture we study some properties of the Euler equations of gasdynamics, + (u) = ( ) u + u u + p = a p + u p + γp u = where, p and u
+ ω = 0, (1) (b) In geometric height coordinates in the rotating frame of the Earth, momentum balance for an inviscid fluid is given by
 Problem Sheet 1: Due Thurs 3rd Feb 1. Primitive equations in different coordinate systems (a) Using Lagrangian considerations and starting from an infinitesimal mass element in cartesian coordinates (x,y,z)
Problem Sheet 1: Due Thurs 3rd Feb 1. Primitive equations in different coordinate systems (a) Using Lagrangian considerations and starting from an infinitesimal mass element in cartesian coordinates (x,y,z)
Symmetric Instability and Rossby Waves
 Chapter 8 Symmetric Instability and Rossby Waves We are now in a position to begin investigating more complex disturbances in a rotating, stratified environment. Most of the disturbances of interest are
Chapter 8 Symmetric Instability and Rossby Waves We are now in a position to begin investigating more complex disturbances in a rotating, stratified environment. Most of the disturbances of interest are
Dynamic Meteorology (lecture 9, 2014)
 Dynamic Meteorology (lecture 9, 2014) Topics Assessment criteria High frequency waves (no rota5on) Boussinesq approxima/on Normal model analysis of the stability of hydrosta/c balance Buoyancy waves and
Dynamic Meteorology (lecture 9, 2014) Topics Assessment criteria High frequency waves (no rota5on) Boussinesq approxima/on Normal model analysis of the stability of hydrosta/c balance Buoyancy waves and
The dynamics of a simple troposphere-stratosphere model
 The dynamics of a simple troposphere-stratosphere model by Jessica Duin under supervision of Prof. Dr. A. Doelman, UvA Dr. W.T.M. Verkley, KNMI August 31, 25 Universiteit van Amsterdam Korteweg-de vries
The dynamics of a simple troposphere-stratosphere model by Jessica Duin under supervision of Prof. Dr. A. Doelman, UvA Dr. W.T.M. Verkley, KNMI August 31, 25 Universiteit van Amsterdam Korteweg-de vries
Nonlinear Balance on an Equatorial Beta Plane
 Nonlinear Balance on an Equatorial Beta Plane David J. Raymond Physics Department and Geophysical Research Center New Mexico Tech Socorro, NM 87801 April 26, 2009 Summary Extension of the nonlinear balance
Nonlinear Balance on an Equatorial Beta Plane David J. Raymond Physics Department and Geophysical Research Center New Mexico Tech Socorro, NM 87801 April 26, 2009 Summary Extension of the nonlinear balance
2.6 Primitive equations and vertical coordinates
 Chater 2. The continuous equations 2.6 Primitive equations and vertical coordinates As Charney (1951) foresaw, most NWP modelers went back to using the rimitive equations, with the hydrostatic aroximation,
Chater 2. The continuous equations 2.6 Primitive equations and vertical coordinates As Charney (1951) foresaw, most NWP modelers went back to using the rimitive equations, with the hydrostatic aroximation,
Dust devils, water spouts, tornados
 Balanced flow Things we know Primitive equations are very comprehensive, but there may be a number of vast simplifications that may be relevant (e.g., geostrophic balance). Seems that there are things
Balanced flow Things we know Primitive equations are very comprehensive, but there may be a number of vast simplifications that may be relevant (e.g., geostrophic balance). Seems that there are things
Balanced Flow Geostrophic, Inertial, Gradient, and Cyclostrophic Flow
 Balanced Flow Geostrophic, Inertial, Gradient, and Cyclostrophic Flow The types of atmospheric flows describe here have the following characteristics: 1) Steady state (meaning that the flows do not change
Balanced Flow Geostrophic, Inertial, Gradient, and Cyclostrophic Flow The types of atmospheric flows describe here have the following characteristics: 1) Steady state (meaning that the flows do not change
d v 2 v = d v d t i n where "in" and "rot" denote the inertial (absolute) and rotating frames. Equation of motion F =
 Governing equations of fluid dynamics under the influence of Earth rotation (Navier-Stokes Equations in rotating frame) Recap: From kinematic consideration, d v i n d t i n = d v rot d t r o t 2 v rot
Governing equations of fluid dynamics under the influence of Earth rotation (Navier-Stokes Equations in rotating frame) Recap: From kinematic consideration, d v i n d t i n = d v rot d t r o t 2 v rot
EAS372 Open Book Final Exam 11 April, 2013
 EAS372 Open Book Final Exam 11 April, 2013 Professor: J.D. Wilson Time available: 2 hours Value: 30% Please check the Terminology, Equations and Data section before beginning your responses. Answer all
EAS372 Open Book Final Exam 11 April, 2013 Professor: J.D. Wilson Time available: 2 hours Value: 30% Please check the Terminology, Equations and Data section before beginning your responses. Answer all
ICON-IAP: A non-hydrostatic global. Almut Gassmann IAP Kühlungsborn, Germany. model designed for energetic consistency
 ICON-IAP: A non-hydrostatic global Almut Gassmann IAP Kühlungsborn, Germany model designed for energetic consistency ICON-IAP is a model on a Voronoi mesh: The divergence lives on Voronoi cells (mostly
ICON-IAP: A non-hydrostatic global Almut Gassmann IAP Kühlungsborn, Germany model designed for energetic consistency ICON-IAP is a model on a Voronoi mesh: The divergence lives on Voronoi cells (mostly
Conservation of Mass Conservation of Energy Scaling Analysis. ESS227 Prof. Jin-Yi Yu
 Lecture 2: Basic Conservation Laws Conservation of Momentum Conservation of Mass Conservation of Energy Scaling Analysis Conservation Law of Momentum Newton s 2 nd Law of Momentum = absolute velocity viewed
Lecture 2: Basic Conservation Laws Conservation of Momentum Conservation of Mass Conservation of Energy Scaling Analysis Conservation Law of Momentum Newton s 2 nd Law of Momentum = absolute velocity viewed
PAPER 333 FLUID DYNAMICS OF CLIMATE
 MATHEMATICAL TRIPOS Part III Wednesday, 1 June, 2016 1:30 pm to 4:30 pm Draft 21 June, 2016 PAPER 333 FLUID DYNAMICS OF CLIMATE Attempt no more than THREE questions. There are FOUR questions in total.
MATHEMATICAL TRIPOS Part III Wednesday, 1 June, 2016 1:30 pm to 4:30 pm Draft 21 June, 2016 PAPER 333 FLUID DYNAMICS OF CLIMATE Attempt no more than THREE questions. There are FOUR questions in total.
By convention, C > 0 for counterclockwise flow, hence the contour must be counterclockwise.
 Chapter 4 4.1 The Circulation Theorem Circulation is a measure of rotation. It is calculated for a closed contour by taking the line integral of the velocity component tangent to the contour evaluated
Chapter 4 4.1 The Circulation Theorem Circulation is a measure of rotation. It is calculated for a closed contour by taking the line integral of the velocity component tangent to the contour evaluated
Dynamics Rotating Tank
 Institute for Atmospheric and Climate Science - IACETH Atmospheric Physics Lab Work Dynamics Rotating Tank Large scale flows on different latitudes of the rotating Earth Abstract The large scale atmospheric
Institute for Atmospheric and Climate Science - IACETH Atmospheric Physics Lab Work Dynamics Rotating Tank Large scale flows on different latitudes of the rotating Earth Abstract The large scale atmospheric
Quasi-equilibrium Theory of Small Perturbations to Radiative- Convective Equilibrium States
 Quasi-equilibrium Theory of Small Perturbations to Radiative- Convective Equilibrium States See CalTech 2005 paper on course web site Free troposphere assumed to have moist adiabatic lapse rate (s* does
Quasi-equilibrium Theory of Small Perturbations to Radiative- Convective Equilibrium States See CalTech 2005 paper on course web site Free troposphere assumed to have moist adiabatic lapse rate (s* does
BALANCED FLOW: EXAMPLES (PHH lecture 3) Potential Vorticity in the real atmosphere. Potential temperature θ. Rossby Ertel potential vorticity
 BALANCED FLOW: EXAMPLES (PHH lecture 3) Potential Vorticity in the real atmosphere Need to introduce a new measure of the buoyancy Potential temperature θ In a compressible fluid, the relevant measure
BALANCED FLOW: EXAMPLES (PHH lecture 3) Potential Vorticity in the real atmosphere Need to introduce a new measure of the buoyancy Potential temperature θ In a compressible fluid, the relevant measure
Class exercises Chapter 3. Elementary Applications of the Basic Equations
 Class exercises Chapter 3. Elementary Applications of the Basic Equations Section 3.1 Basic Equations in Isobaric Coordinates 3.1 For some (in fact many) applications we assume that the change of the Coriolis
Class exercises Chapter 3. Elementary Applications of the Basic Equations Section 3.1 Basic Equations in Isobaric Coordinates 3.1 For some (in fact many) applications we assume that the change of the Coriolis
Prototype Instabilities
 Prototype Instabilities David Randall Introduction Broadly speaking, a growing atmospheric disturbance can draw its kinetic energy from two possible sources: the kinetic and available potential energies
Prototype Instabilities David Randall Introduction Broadly speaking, a growing atmospheric disturbance can draw its kinetic energy from two possible sources: the kinetic and available potential energies
1/18/2011. From the hydrostatic equation, it is clear that a single. pressure and height in each vertical column of the atmosphere.
 Lecture 3: Applications of Basic Equations Pressure as Vertical Coordinate From the hydrostatic equation, it is clear that a single valued monotonic relationship exists between pressure and height in each
Lecture 3: Applications of Basic Equations Pressure as Vertical Coordinate From the hydrostatic equation, it is clear that a single valued monotonic relationship exists between pressure and height in each
ROSSBY WAVE PROPAGATION
 ROSSBY WAVE PROPAGATION (PHH lecture 4) The presence of a gradient of PV (or q.-g. p.v.) allows slow wave motions generally called Rossby waves These waves arise through the Rossby restoration mechanism,
ROSSBY WAVE PROPAGATION (PHH lecture 4) The presence of a gradient of PV (or q.-g. p.v.) allows slow wave motions generally called Rossby waves These waves arise through the Rossby restoration mechanism,
7 Balanced Motion. 7.1 Return of the...scale analysis for hydrostatic balance! CSU ATS601 Fall 2015
 7 Balanced Motion We previously discussed the concept of balance earlier, in the context of hydrostatic balance. Recall that the balanced condition means no accelerations (balance of forces). That is,
7 Balanced Motion We previously discussed the concept of balance earlier, in the context of hydrostatic balance. Recall that the balanced condition means no accelerations (balance of forces). That is,
Quasi-geostrophic ocean models
 Quasi-geostrophic ocean models March 19, 2002 1 Introduction The starting point for theoretical and numerical study of the three dimensional large-scale circulation of the atmosphere and ocean is a vorticity
Quasi-geostrophic ocean models March 19, 2002 1 Introduction The starting point for theoretical and numerical study of the three dimensional large-scale circulation of the atmosphere and ocean is a vorticity
Large-scale atmospheric circulation, semi-geostrophic motion and Lagrangian particle methods
 Large-scale atmospheric circulation, semi-geostrophic motion and Lagrangian particle methods Colin Cotter (Imperial College London) & Sebastian Reich (Universität Potsdam) Outline 1. Hydrostatic and semi-geostrophic
Large-scale atmospheric circulation, semi-geostrophic motion and Lagrangian particle methods Colin Cotter (Imperial College London) & Sebastian Reich (Universität Potsdam) Outline 1. Hydrostatic and semi-geostrophic
On the effect of forward shear and reversed shear baroclinic flows for polar low developments. Thor Erik Nordeng Norwegian Meteorological Institute
 On the effect of forward shear and reversed shear baroclinic flows for polar low developments Thor Erik Nordeng Norwegian Meteorological Institute Outline Baroclinic growth a) Normal mode solution b) Initial
On the effect of forward shear and reversed shear baroclinic flows for polar low developments Thor Erik Nordeng Norwegian Meteorological Institute Outline Baroclinic growth a) Normal mode solution b) Initial
Fundamentals of Atmospheric Modelling
 M.Sc. in Computational Science Fundamentals of Atmospheric Modelling Peter Lynch, Met Éireann Mathematical Computation Laboratory (Opp. Room 30) Dept. of Maths. Physics, UCD, Belfield. January April, 2004.
M.Sc. in Computational Science Fundamentals of Atmospheric Modelling Peter Lynch, Met Éireann Mathematical Computation Laboratory (Opp. Room 30) Dept. of Maths. Physics, UCD, Belfield. January April, 2004.
( ) where the phase! is given by! = kx + mz!"t. We also know
 GFD I, Final Exam Solutions 3/7/1 Parker MacCready 1.(a) The expression for the pressure perturbation is found from the vertical momentum equation: Z-MOM w t! 1! p' z b which may be rearranged to give:
GFD I, Final Exam Solutions 3/7/1 Parker MacCready 1.(a) The expression for the pressure perturbation is found from the vertical momentum equation: Z-MOM w t! 1! p' z b which may be rearranged to give:
Dynamic Meteorology (lecture 13, 2016)
 Dynamic Meteorology (lecture 13, 2016) Topics Chapter 3, lecture notes: High frequency waves (no rota;on) Boussinesq approxima4on Normal mode analysis of the stability of hydrosta4c balance Buoyancy waves
Dynamic Meteorology (lecture 13, 2016) Topics Chapter 3, lecture notes: High frequency waves (no rota;on) Boussinesq approxima4on Normal mode analysis of the stability of hydrosta4c balance Buoyancy waves
Transformed Eulerian Mean
 Chapter 15 Transformed Eulerian Mean In the last few lectures we introduced some fundamental ideas on 1) the properties of turbulent flows in rotating stratified environments, like the ocean and the atmosphere,
Chapter 15 Transformed Eulerian Mean In the last few lectures we introduced some fundamental ideas on 1) the properties of turbulent flows in rotating stratified environments, like the ocean and the atmosphere,
Understanding inertial instability on the f-plane with complete Coriolis force
 Understanding inertial instability on the f-plane with complete Coriolis force Abstract Vladimir Zeitlin Laboratory of Dynamical Meteorology, University P. and M. Curie and Ecole Normale Supérieure, Paris,
Understanding inertial instability on the f-plane with complete Coriolis force Abstract Vladimir Zeitlin Laboratory of Dynamical Meteorology, University P. and M. Curie and Ecole Normale Supérieure, Paris,
Quasi-geostrophic system
 Quasi-eostrophic system (or, why we love elliptic equations for QGPV) Charney s QG the motion of lare-scale atmospheric disturbances is overned by Laws of conservation of potential temperature and potential
Quasi-eostrophic system (or, why we love elliptic equations for QGPV) Charney s QG the motion of lare-scale atmospheric disturbances is overned by Laws of conservation of potential temperature and potential
9 Rossby Waves. 9.1 Non-divergent barotropic vorticity equation. CSU ATS601 Fall (Holton Chapter 7, Vallis Chapter 5)
 9 Rossby Waves (Holton Chapter 7, Vallis Chapter 5) 9.1 Non-divergent barotropic vorticity equation We are now at a point that we can discuss our first fundamental application of the equations of motion:
9 Rossby Waves (Holton Chapter 7, Vallis Chapter 5) 9.1 Non-divergent barotropic vorticity equation We are now at a point that we can discuss our first fundamental application of the equations of motion:
t tendency advection convergence twisting baroclinicity
 RELATIVE VORTICITY EQUATION Newton s law in a rotating frame in z-coordinate (frictionless): U + U U = 2Ω U Φ α p U + U U 2 + ( U) U = 2Ω U Φ α p Applying to both sides, and noting ω U and using identities
RELATIVE VORTICITY EQUATION Newton s law in a rotating frame in z-coordinate (frictionless): U + U U = 2Ω U Φ α p U + U U 2 + ( U) U = 2Ω U Φ α p Applying to both sides, and noting ω U and using identities
2 Equations of Motion
 2 Equations of Motion system. In this section, we will derive the six full equations of motion in a non-rotating, Cartesian coordinate 2.1 Six equations of motion (non-rotating, Cartesian coordinates)
2 Equations of Motion system. In this section, we will derive the six full equations of motion in a non-rotating, Cartesian coordinate 2.1 Six equations of motion (non-rotating, Cartesian coordinates)
NWP Equations (Adapted from UCAR/COMET Online Modules)
 NWP Equations (Adapted from UCAR/COMET Online Modules) Certain physical laws of motion and conservation of energy (for example, Newton's Second Law of Motion and the First Law of Thermodynamics) govern
NWP Equations (Adapted from UCAR/COMET Online Modules) Certain physical laws of motion and conservation of energy (for example, Newton's Second Law of Motion and the First Law of Thermodynamics) govern
Atmospheric Fronts. The material in this section is based largely on. Lectures on Dynamical Meteorology by Roger Smith.
 Atmospheric Fronts The material in this section is based largely on Lectures on Dynamical Meteorology by Roger Smith. Atmospheric Fronts 2 Atmospheric Fronts A front is the sloping interfacial region of
Atmospheric Fronts The material in this section is based largely on Lectures on Dynamical Meteorology by Roger Smith. Atmospheric Fronts 2 Atmospheric Fronts A front is the sloping interfacial region of
Asymmetric inertial instability
 Asymmetric inertial instability V. Zeitlin Institut Universitaire de France 2 Laboratory of Dynamical Meteorology, University P. and M. Curie, Paris, France UCL, December 2 Instabilities of jets Motivations,
Asymmetric inertial instability V. Zeitlin Institut Universitaire de France 2 Laboratory of Dynamical Meteorology, University P. and M. Curie, Paris, France UCL, December 2 Instabilities of jets Motivations,
Theory of linear gravity waves April 1987
 April 1987 By Tim Palmer European Centre for Medium-Range Weather Forecasts Table of contents 1. Simple properties of internal gravity waves 2. Gravity-wave drag REFERENCES 1. SIMPLE PROPERTIES OF INTERNAL
April 1987 By Tim Palmer European Centre for Medium-Range Weather Forecasts Table of contents 1. Simple properties of internal gravity waves 2. Gravity-wave drag REFERENCES 1. SIMPLE PROPERTIES OF INTERNAL
Part 4. Atmospheric Dynamics
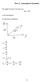 Part 4. Atmospheric Dynamics We apply Newton s Second Law: ma =Σ F i to the atmosphere. In Cartesian coordinates dx u = dt dy v = dt dz w = dt 1 ai = F m i i du dv dw a = ; ay = ; az = x dt dt dt 78 Coordinate
Part 4. Atmospheric Dynamics We apply Newton s Second Law: ma =Σ F i to the atmosphere. In Cartesian coordinates dx u = dt dy v = dt dz w = dt 1 ai = F m i i du dv dw a = ; ay = ; az = x dt dt dt 78 Coordinate
ESS Turbulence and Diffusion in the Atmospheric Boundary-Layer : Winter 2017: Notes 1
 ESS5203.03 - Turbulence and Diffusion in the Atmospheric Boundary-Layer : Winter 2017: Notes 1 Text: J.R.Garratt, The Atmospheric Boundary Layer, 1994. Cambridge Also some material from J.C. Kaimal and
ESS5203.03 - Turbulence and Diffusion in the Atmospheric Boundary-Layer : Winter 2017: Notes 1 Text: J.R.Garratt, The Atmospheric Boundary Layer, 1994. Cambridge Also some material from J.C. Kaimal and
EART164: PLANETARY ATMOSPHERES
 EART164: PLANETARY ATMOSPHERES Francis Nimmo Last Week Radiative Transfer Black body radiation, Planck function, Wien s law Absorption, emission, opacity, optical depth Intensity, flux Radiative diffusion,
EART164: PLANETARY ATMOSPHERES Francis Nimmo Last Week Radiative Transfer Black body radiation, Planck function, Wien s law Absorption, emission, opacity, optical depth Intensity, flux Radiative diffusion,
Introduction to Isentropic Coordinates: a new view of mean meridional & eddy circulations. Cristiana Stan
 Introduction to Isentropic Coordinates: a new view of mean meridional & eddy circulations Cristiana Stan School and Conference on the General Circulation of the Atmosphere and Oceans: a Modern Perspective
Introduction to Isentropic Coordinates: a new view of mean meridional & eddy circulations Cristiana Stan School and Conference on the General Circulation of the Atmosphere and Oceans: a Modern Perspective
Model equations for planetary and synoptic scale atmospheric motions associated with different background stratification
 Model equations for planetary and synoptic scale atmospheric motions associated with different background stratification Stamen Dolaptchiev & Rupert Klein Potsdam Institute for Climate Impact Research
Model equations for planetary and synoptic scale atmospheric motions associated with different background stratification Stamen Dolaptchiev & Rupert Klein Potsdam Institute for Climate Impact Research
INTERNAL GRAVITY WAVES
 INTERNAL GRAVITY WAVES B. R. Sutherland Departments of Physics and of Earth&Atmospheric Sciences University of Alberta Contents Preface List of Tables vii xi 1 Stratified Fluids and Waves 1 1.1 Introduction
INTERNAL GRAVITY WAVES B. R. Sutherland Departments of Physics and of Earth&Atmospheric Sciences University of Alberta Contents Preface List of Tables vii xi 1 Stratified Fluids and Waves 1 1.1 Introduction
Dynamics and Kinematics
 Geophysics Fluid Dynamics () Syllabus Course Time Lectures: Tu, Th 09:30-10:50 Discussion: 3315 Croul Hall Text Book J. R. Holton, "An introduction to Dynamic Meteorology", Academic Press (Ch. 1, 2, 3,
Geophysics Fluid Dynamics () Syllabus Course Time Lectures: Tu, Th 09:30-10:50 Discussion: 3315 Croul Hall Text Book J. R. Holton, "An introduction to Dynamic Meteorology", Academic Press (Ch. 1, 2, 3,
Geophysics Fluid Dynamics (ESS228)
 Geophysics Fluid Dynamics (ESS228) Course Time Lectures: Tu, Th 09:30-10:50 Discussion: 3315 Croul Hall Text Book J. R. Holton, "An introduction to Dynamic Meteorology", Academic Press (Ch. 1, 2, 3, 4,
Geophysics Fluid Dynamics (ESS228) Course Time Lectures: Tu, Th 09:30-10:50 Discussion: 3315 Croul Hall Text Book J. R. Holton, "An introduction to Dynamic Meteorology", Academic Press (Ch. 1, 2, 3, 4,
Modeling Large-Scale Atmospheric and Oceanic Flows 2
 Modeling Large-Scale Atmospheric and Oceanic Flows V. Zeitlin known s of the Laboratoire de Météorologie Dynamique, Univ. P. and M. Curie, Paris Mathematics of the Oceans, Fields Institute, Toronto, 3
Modeling Large-Scale Atmospheric and Oceanic Flows V. Zeitlin known s of the Laboratoire de Météorologie Dynamique, Univ. P. and M. Curie, Paris Mathematics of the Oceans, Fields Institute, Toronto, 3
SIO 210: Dynamics VI (Potential vorticity) L. Talley Fall, 2014 (Section 2: including some derivations) (this lecture was not given in 2015)
 SIO 210: Dynamics VI (Potential vorticity) L. Talley Fall, 2014 (Section 2: including some derivations) (this lecture was not given in 2015) Variation of Coriolis with latitude: β Vorticity Potential vorticity
SIO 210: Dynamics VI (Potential vorticity) L. Talley Fall, 2014 (Section 2: including some derivations) (this lecture was not given in 2015) Variation of Coriolis with latitude: β Vorticity Potential vorticity
Chapter 13 Instability on non-parallel flow Introduction and formulation
 Chapter 13 Instability on non-parallel flow. 13.1 Introduction and formulation We have concentrated our discussion on the instabilities of parallel, zonal flows. There is the largest amount of literature
Chapter 13 Instability on non-parallel flow. 13.1 Introduction and formulation We have concentrated our discussion on the instabilities of parallel, zonal flows. There is the largest amount of literature
Dynamics of the Atmosphere. Large-scale flow with rotation and stratification
 12.810 Dynamics of the Atmosphere Large-scale flow with rotation and stratification Visualization of meandering jet stream Upper level winds from June 10th to July 8th 1988 from MERRA Red shows faster
12.810 Dynamics of the Atmosphere Large-scale flow with rotation and stratification Visualization of meandering jet stream Upper level winds from June 10th to July 8th 1988 from MERRA Red shows faster
The general circulation: midlatitude storms
 The general circulation: midlatitude storms Motivation for this class Provide understanding basic motions of the atmosphere: Ability to diagnose individual weather systems, and predict how they will change
The general circulation: midlatitude storms Motivation for this class Provide understanding basic motions of the atmosphere: Ability to diagnose individual weather systems, and predict how they will change
Stability of meridionally-flowing grounded abyssal currents in the ocean
 Advances in Fluid Mechanics VII 93 Stability of meridionally-flowing grounded abyssal currents in the ocean G. E. Swaters Applied Mathematics Institute, Department of Mathematical & Statistical Sciences
Advances in Fluid Mechanics VII 93 Stability of meridionally-flowing grounded abyssal currents in the ocean G. E. Swaters Applied Mathematics Institute, Department of Mathematical & Statistical Sciences
Fixed Rossby Waves: Quasigeostrophic Explanations and Conservation of Potential Vorticity
 Fixed Rossby Waves: Quasigeostrophic Explanations and Conservation of Potential Vorticity 1. Observed Planetary Wave Patterns After upper air observations became routine, it became easy to produce contour
Fixed Rossby Waves: Quasigeostrophic Explanations and Conservation of Potential Vorticity 1. Observed Planetary Wave Patterns After upper air observations became routine, it became easy to produce contour
2 Transport of heat, momentum and potential vorticity
 Transport of heat, momentum and potential vorticity. Conventional mean momentum equation We ll write the inviscid equation of onal motion (we ll here be using log-pressure coordinates with = H ln p=p,
Transport of heat, momentum and potential vorticity. Conventional mean momentum equation We ll write the inviscid equation of onal motion (we ll here be using log-pressure coordinates with = H ln p=p,
Dynamic Meteorology - Introduction
 Dynamic Meteorology - Introduction Atmospheric dynamics the study of atmospheric motions that are associated with weather and climate We will consider the atmosphere to be a continuous fluid medium, or
Dynamic Meteorology - Introduction Atmospheric dynamics the study of atmospheric motions that are associated with weather and climate We will consider the atmosphere to be a continuous fluid medium, or
Lecture 25: Ocean circulation: inferences from geostrophic and thermal wind balance
 Lecture 25: Ocean circulation: inferences from geostrophic and thermal wind balance November 5, 2003 Today we are going to study vertical sections through the ocean and discuss what we can learn about
Lecture 25: Ocean circulation: inferences from geostrophic and thermal wind balance November 5, 2003 Today we are going to study vertical sections through the ocean and discuss what we can learn about
Introduction to Mesoscale Meteorology
 Introduction to Mesoscale Meteorology Overview Scale Definitions Synoptic Synoptic derived from Greek synoptikos meaning general view of the whole. Also has grown to imply at the same time or simultaneous.
Introduction to Mesoscale Meteorology Overview Scale Definitions Synoptic Synoptic derived from Greek synoptikos meaning general view of the whole. Also has grown to imply at the same time or simultaneous.
Vorticity and Potential Vorticity
 Chapter 4 Vorticity and Potential Vorticity In this chapter we explore a way of solving the shallow water equations for motions with characteristic time scales longer than the rotation period of the earth.
Chapter 4 Vorticity and Potential Vorticity In this chapter we explore a way of solving the shallow water equations for motions with characteristic time scales longer than the rotation period of the earth.
SAMPLE CHAPTERS UNESCO EOLSS WAVES IN THE OCEANS. Wolfgang Fennel Institut für Ostseeforschung Warnemünde (IOW) an der Universität Rostock,Germany
 WAVES IN THE OCEANS Wolfgang Fennel Institut für Ostseeforschung Warnemünde (IOW) an der Universität Rostock,Germany Keywords: Wind waves, dispersion, internal waves, inertial oscillations, inertial waves,
WAVES IN THE OCEANS Wolfgang Fennel Institut für Ostseeforschung Warnemünde (IOW) an der Universität Rostock,Germany Keywords: Wind waves, dispersion, internal waves, inertial oscillations, inertial waves,
A Hamiltonian Numerical Scheme for Large Scale Geophysical Fluid Systems
 A Hamiltonian Numerical Scheme for Large Scale Geophysical Fluid Systems Bob Peeters Joint work with Onno Bokhove & Jason Frank TW, University of Twente, Enschede CWI, Amsterdam PhD-TW colloquium, 9th
A Hamiltonian Numerical Scheme for Large Scale Geophysical Fluid Systems Bob Peeters Joint work with Onno Bokhove & Jason Frank TW, University of Twente, Enschede CWI, Amsterdam PhD-TW colloquium, 9th
Chapter 1. Introduction
 Chapter 1. Introduction In this class, we will examine atmospheric phenomena that occurs at the mesoscale, including some boundary layer processes, convective storms, and hurricanes. We will emphasize
Chapter 1. Introduction In this class, we will examine atmospheric phenomena that occurs at the mesoscale, including some boundary layer processes, convective storms, and hurricanes. We will emphasize
Influence of Gravity Waves on the Atmospheric Climate
 Influence of Gravity Waves on the Atmospheric Climate François Lott, LMD/CNRS, Ecole Normale Supérieure, Paris flott@lmd.ens.fr 1)Dynamical impact of mountains on atmospheric flows 2)Representations of
Influence of Gravity Waves on the Atmospheric Climate François Lott, LMD/CNRS, Ecole Normale Supérieure, Paris flott@lmd.ens.fr 1)Dynamical impact of mountains on atmospheric flows 2)Representations of
