Safet Penjić, mr sc Filozofski fakultet u Zenici
|
|
|
- Winifred Simon
- 5 years ago
- Views:
Transcription
1 Safe Penjć, mr sc Flozofs faule u Zenc Uloga speralnh projeora u rješavanju ssema homogenh dferencjalnh jednačna sa onsannm oefcjenma jedna zanmljva prmjena u bologj Sažea Za podprosore, prosora ažemo da su omplemenarn adgod = + Y = {0} u om slučaju za ažemo da je drena suma od, ovo označavamo sa =. Ovo je evvalenno sa vrdnjom da za sva v posoje jednsven veor x y av da v= x+ y. Za prozvoljan aav v možemo defnsa operaor P sa Pv = x ovo je jednsven lnearn operaor sa osobnom Pv = x ( v= x+ y, x y ) oj je pozna pod menom projeor na paralelno sa. U ovom radu posmara ćemo speralne projeore sors njhove osobne za rješavanje ssema dferencjalnh jednačna obla y'= Ay čje rješenje reba zadovoljava ncjaln uslov y(0) = c, razmara ćemo slučaj samo ada je marca ssema A djagonablna. Da b smo došl do odgovarajućeg rješenja prvo smo uvel defncju funcje na djagonablnm marcama. Poslje oga je prezenrana jedna njhova zanmljva prmjena - prmjena od dfuzje (šrenja) ćelja u medcn bologj. Na raju rada je prezenran MaLab od funcje oja daje rješenje ssema dferencjalnh jednačna ada nam je daa marcu ssema A, dmenzja 3 3 marca olona daog uslova c. Ključne rječ: speraln projeor, djagonablna marca, ssem homogenh lnearnh dferencjalnh jednačna Role of specral projecors n solvng sysems of homogeneous lnear dfferenal equaons wh consan coeffcens and one neresng applcaon n bology Absrac Subspaces, of a space are sad o be complemenary whenever = + and Y ={ 0}, n whch case s sad o be he drec sum of and, and hs s denoed by wrng =. Ths s equvalen o sayng ha for each v here s unque vecors x and y such ha v= x+ y. For arbrary such v we can defne operaor P by Pv = x, and hs operaor s unque lnear operaor wh propery Pv = x ( v= x+ y, x and y ) and s called he projecor ono along. In hs paper we wll consder specral projecors and we wll use her properes o solve a sysems of frs-order lnear dfferenal equaons, whch can be wre n marx form as y'= Ay wh gven nal value y(0) = c, and we wll examne only case when marx A of gven sysem s dagonalzable. For hese purpose we had frs defned funcons of dagonalzable marces. Afer ha we have presened one neresng applcaon - an applcaon o dffuson of cells n medcne and bology.
2 In he end of paper we gve MaLab code of funcon whch solves sysems of frs-order lnear dfferenal equaons when we have marx of sysem A of form 3 3 and marxcolumn of nal value c. Keywords: specral projecors, dagonalzable marx, sysems of homogeneous lnear dfferenal equaons 0 Osnovne defncje rezula Defnšmo oznae oje ćemo ors u nasavu esa prsjemo se neh osnovnh defncja eorema z Lnearne algebre. Za n n marcu A, salare veore x = n 0 oj zadovoljavaju jednaos Ax= x, zovemo redom, svojsvene vrjednos svojsven veor marce A, blo oj aav par (, x ) nazvamo svojsven par marce A. Sup svh razlčh svojsvenh vrjednos ćemo označava sa σ ( A ). Za dvje n n marce A B ažemo da su slčne adgod posoj nesngularna marca P ava da je P AP = B. Prozvod P AP se nazva ransformacja slčnos na A. Za vadranu marcu A ažemo da je djagonablna adgod je A slčna djagonalnoj marc. Popun sup svojsvenh veora marce A, oja je obla n n, je blo oj sup od n lnearno nezavsnh svojsvenh veora marce A. Algebarsa všesruos svojsvene vrjednos je broj pua u ojoj se ona ponov ao orjen araersčnog polnoma. Algebarsu všesruos od ćemo označava sa algmul A ( ). Geomerjsa všesruos svojsvene vrjednos je dm er( A I ). Geomerjsu všesruos od ćemo označava sa geomul A ( ). Tvrdnj (a.)-(a.5) su poznae od ranje (z Lnearne algebre) a zaneresranog čaoca možemo upu na [] (l [5] l [3]). (a.) σ( A ) A I je sngularna marca de( A I ) = 0 (a.) { x= 0 x er( A I )} je sup svh svojsvenh veora prdruženh. Prosor E = er( A I ) se nazva svojsven prosor marce A. (a.3) Marca A, obla n n, je djagonablna ao samo ao A posjeduje popun sup svojsvenh veora. (a.4) Marca A obla n n sa razlčh svojsvenh vrjednos σ( A ) = {,,..., } je djagonablna ao samo ao posoje marce { G, G,... G } ave da A= G+ G G () gdje marce G maju sljedeće osobne () G je projeor na er( A I) paralelno sa m( A I). () GG 0 gdje je = j. () G+ G G = I. Razvoj () je pozna pod menom speralna deompozcja marce A, a marce G se nazvaju speraln projeor prdružen marc A. (a.5) Marca A, obla n n, je djagonablna ao samo ao je algmul ( )= geomul ( ) A A.
3 Funcje defnsane na djagonablnm marcama Ša b za vadranu marcu A značlo da napšemo sna, e A, lna slčno. Navan prsup b mogao b da jednosavno prmjenmo danu funcju na sva elemen marce A ao da a? a sn a sn a sn =. a a sn a sn a Al radeć ovao n jedna osobna od marčnh funcja se neće polop sa njhovm salarnm olegama. Na prmjer, ao je sn x+ cos x= za sve salare x, voljel b da naša defncja od sna cosa ao rezula dadne analogn marčn dene sn A+ cos A= I za sve vadrane marce A. Jasno je da prsup po vrjednosma () neće ma ove osobne. Drug načn da defnšemo marčnu funcju oja će ma se osobne ao njhove salarne olege je da orsmo razvoje funcja u besonačne redove. Na prmjer, posmarajmo esponencjalnu funcju 3 z z z z e = = + z !! 3! =0 Formalno zamjenjvanje salarnog argumena z sa vadranom marcom A ( z 0 = je zamjenjeno sa A 0 = I) ao rezula daje besonačan red marca 3 A A A e = I+ A (3)! 3! oj se nazva marčn esponencjal. Iao ovaj prsup ma rezula da marčne funcje maju se osobne ao njhove salarne olege, vela mana ovavog prsupa je da sva pu moramo razmšlja o onvergencj, sva pu se suobljavamo sa problemom opsa elemenaa pomoću lmesa. Međum, ao je A djagonablna marca, ada je A= PDP = P dag(,..., n ) P, A = PD P = P dag(,..., n ) P gdje je dag(,..., n ) =, pa je n e = A = PD P A = P D P = Pdag( e,..., e ) P. =0! =0! =0! Drugm rječma, ne moramo ors besonačan red (3) da defnšemo e A. Umjeso oga, D defnšemo e = dag( e, e,..., e n ) savmo A D = = (,,..., ). e e dag e e e n P P P P Ova deja se može poopš na blo oju funcju f( z ) oja je defnsana na svojsvenm vrjednosma djagonablne marce A= PDP defnšuć f ( D ) da bude f ( D ) = dag( f ( ), f ( ),..., f ( )) savljajuć n f ( A) = Pf ( DP ) = Pdag( f ( ), f ( ),..., f ( n )) P. Puno vše o funcjama defnranm na djagonablnm marcama možee proča u [] na srancama Ovdje samo još sumrajmo vrdnje oje ćemo ors u nasavu esa: 3 ()
4 Nea je A= PDP djagonablna marca gdje su svojsvene vrjednos u D= dag( I, I,..., I ) gruprane po ponavljanju. Za funcju f( z ) oja ma onačnu vrjednos za sva σ( A ) defnšmo gdje su f ( ) I f ( )... 0 f( )= f( ) = I A P DP P P f ( ) I = f( ) G + f( ) G f( ) G, (4) G -ev -e speralne projecje oje se mogu zračuna na ne od sljedećh načna: () G je projeor na er( A I ) paralelno sa m( A I ); Τ Τ () G = XY gdje olone marce X formraju bazu za er( A I ), do su Y Τ Y Τ Y dobjen z marce P = gdje je P= ( X Τ Y X... X ) ; () PP = I= G + G G ; (v) G= ( A ji ), gdje je π = ( j). π Prmjena lnearne algebre u rješavanju ssema dferencjalnh jednačna Sad razmaramo ao rješ ssem lnearnh dferencjalnh jednačna prvog reda sa onsannm oefcjenma uz da ncjaln uslov oršenjem svojsvenh vrjednos svojsvenh veora. Za onsane a j, clj nam je da rješmo sljedeć ssem po nepoznam funcjama y (). y = ay + a y a nyn; y (0) = c, y = ay + a y anyn; y(0) = c, (5) y = a y + a y a y ; y (0) = c. n n n nn n n n α Kao je salarn esponen y ()= e cjednsveno rješenje jedne dferencjalne jednačne obla y ()= α y () sa ncjalnm uslovom y(0) = c, sasvm je prrodno da poušamo sors marčn esponen na popuno s načn da rješmo ssem dferencjalnh jednačna. Započe ćemo ao šo ćemo napsa ssem (5) u marčnom oblu y'= Ay, y(0) = c gdje je 4
5 y ( ) a a... a n c y ( ) a a... a c y A c y ( ) a a... a c n =, =, =. n n n nn n Ao je marca A djagonablna sa σ( A ) = {,,..., } ada (4) garanuje da je A e = e G + e G +... e G. Sljedeće jednaos se zvode z osobna marca A () = ( = )( = ) 5 G oje smo navel u (a.4). de / d = e G = G e G = A e A () Ae = e A A (zbog slčnh argumenaa). A A A A 0 () e e = e e == I e (zbog slčnh argumenaa). A A Osobna ( ) znad de / d = A e nam osgurava da je funcja y= A e A c jedno od rješenja ssema y'= Ay sa ncjalnm uslovom y(0) = c. Da b vdjel da je y= e A c jedno rješenje, preposavmo da je v () neo drugo rješenje ao da je v'= Av sa v(0) = c. Dferencrajuć e A v dob ćemo A de [ v] = A A e Av+ e v '= 0, d pa je e A A 0 v onsana za sve. Za =0 mamo e v =0= e v(0) = Ic= c, me e A v= c za sve. Množeć obe srane ove jednaos sa e A A A 0 orseć osobnu ( ) znad e e == I e možemo zaljuč da je v= e A c. Tme smo dobl da je y= e A c jednsveno rješenje ssema dferencjalnh jednačna y'= Ay sa ncjalnm uslovom y(0) = c. Na raju prmjemo da je v= Gc er ( A I ) svojsven veor prdružen svojsvenoj vrjednos, ao da je rješenje za y'= Ay, y(0) = c u svar y= e v + e v e v ovo rješenje je popuno određeno svojsvenm parovma (, v ). Može se doaza da se y aođer može zraz u oblu blo ojeg popunog supa nezavsnh svojsvenh veora. U sljedećoj eorem sumrajmo prehodnu prču. (.0) Teorema (rješenje ssema dferencjalnh jednačna) Ao je A marca obla n n oja je djagonablna sa σ( A ) = {,,..., } ada jednsveno rješenje ssema dferencjalnh jednačna y'= Ay oje zadovoljava uslov y(0) = c je dano sa gdje je A y= e c= e v + e v e v v svojsven veor v = Gc, a G je - speraln projeor. (.0) Problem Rješ ssem dferencjalnh jednačna x =3x y+ z y = x+ 5y z z = x y+ 3z ao da rješenja zadovoljavaju ncjalne uslov x (0) =, y (0) = z (0) = 3.
6 Rješenje: Da ssem možemo napsa u oblu x'= Ax, x(0) = b gdje je x 3 x= y, A= 5, b =. z 3 3 Lagano računanje nam daje svojsvene vrjednos marce A, σ( A ) = { = 6, = 3, 3 = }. Koršenjem formule G= ( A ji ), π za računanje speralnh projeora, gdje je π = ( ), mamo π = ( )( ) = 3 4 = ; 3 π =( )( )=( 3)= 3; 3 π = ( )( ) = ( 4) ( ) = 4 ; j 0 /6 /3 /6 G= ( A 3 I)( A I )= 3 = /3 /3 /3, 0 /6 /3 /6 3 /3 /3 /3 G = ( A 6 I)( A I ) = 3 = /3 /3 /3, /3 /3 /3 3 0 / 0 / G3= ( A 6 I)( A 3 I )= = / 0 / Lagana provjera nam poazuje da je G+ G =, = = + G3 I G G j 0 za j ao A= G + G + G 3 3 pa su dobvene marce G, G G 3 zasa speraln projeor prdružen marc A. Sad zračunajmo veore v= Gb, v= G b v3= G3b : Možemo zaljuč da je 0 v= 0, v=, v 3= 0. 0 x e e 3 ()= y 3 ()=e 3 z ()=e + e rješenje daog ssema dferencjalnh jednačna oje zadovoljava dae ncjalne uslove. 6
7 (.03) Problem Rješ ssem dferencjalnh jednačna x =x y+ z y = x+ y z z = x z+ z ao da rješenja zadovoljavaju uslov x (0) =, y (0) = 3 z (0) = 4. Rješenje: Da ssem možemo napsa u oblu x'= Ax, x(0) = b gdje je x x= y, A=, b = 3. z 4 Svojsvene vrjednos marce A su σ( A ) = { = 3, =, 3 = }. Uz pomoć formule G= ( A ji ), π za računanje speralnh projeora, gdje je π = ( ), dobjamo π = ( )( ) = ; 3 π = ( )( ) = ; 3 π = ( )( ) = ; j 0 G= ( A I)( A I )= 0 0 0, 0 G = ( A 3 I)( A I ) =, G3= ( A 3 I)( A I ) = Lagana provjera nam poazuje da je G+ G =, = = + G3 I G G j 0 za j ao A= G + G + G 3 3 pa su dobvene marce G, G G 3 zasa speraln projeor prdružen marc A. Sad zračunajmo veore v= Gb, v= G b v3= G3b : Možemo zaljuč da je 0 v= 0, v=, v 3=. 7
8 x e + e 3 ()= y e + e ()= 3 z ()= e + e + e rješenje daog ssema dferencjalnh jednačna oje zadovoljava dae ncjalne uslove. 3 Prmjena od dfuzje Važna ema u medcn bologj uljučuje panje ao droga l hemjs sasav uču na pomjeranje jedne ćelje na drugu u smslu šrenja roz zdove ćelje. Posmarajmo dvje ćelje, ao šo je prazano na Fgur, gdje su obe zguble do neog svog sasava. Jednčna olčna sasava je ubačena u prvu ćelju u vremenu =0, ao vrjeme prolaz, njezn sasav se šr prema sljedećm preposavama. FIGURA Šrenje zdova jedne ćelja u odnosu na drugu. U svaom renuu vremena omjer (olčna po seund) šrenja jedne ćelje prema drugoj je proporconalna oncenracj (olčna po jednčnoj zapremn) smjese ćelj oja preda do svog sasava - recmo omjer šrenja ćelje prema ćelj je α pua oncenracja u ćelj, a omjer šrenja ćelje prema ćelj je β pua oncenracja u ćelj. Preposavmo da je αβ, >0. (3.0) Problem Odred oncenracju smjese svae od ćelja u blo ojem renuu vremena,, posmarajuć duž vremens perod, odred oncenracju sablnog sanja. Rješenje: Ao u = u() označava oncenracju sasava u ćelj u renuu, ada vrdnja u gornjoj preposavc se može preves na sljedeć načn: du = omjer oj ulaz omjer oj zlaz = βu αu, gdje u(0) =, d du = omjer oj ulaz omjer oj zlaz = αu βu, gdje u(0) = 0. d U marčnm oznaama ovaj ssem je u'= Au, u(0) = c, gdje α β u A=, u=, c =. α β u 0 Karaersčna jednačna za A je + ( α+ β ) =0, ao da su svojsvene vrjednos 8
9 marce A =0 = ( α β) +. Prmjemo da se svojsvene vrjednos ne ponavljaju, pa je marca A djagonablna. Korseć funcju aže da je f( z)= e z, speralna reprezenacja (4) nam + + A e = f( A)= f( ) G f( ) G = e G e G. Speraln projeor G G se mogu zračuna po formul G= ( A ji ), gdje je π π = ( ), gdje ćemo dob da je j A I β β A α β G= = G = =, α + β α α α + β α β pa je ( ) α β β β ( α β) α β A + + e = G+ e G = + e α + β α α α β Sad mamo β β ( ) α β A ()= e = e α + u c + β, α + β α α α β 0 z čega sljed β α ( α+ β) α ( α+ β) u( ) = + e u( ) = ( e ). α + β α + β α + β Posmarajuć duž perod, oncenracja u ćelj će se sablzra u smslu da β α lmu()= lmu()=. α + β α + β 4 MaLab od Kod funcje oja ao ulazne vrjednos ma marcu ssema A, olona marcu ncjalnog uslova b je: funcon [rjesenje] = rjes_ssem(a,b) % MaLab od funcje oja daje rješenje % ssema dferencjalnh jednačna ada nam % je daa marcu ssema $A$, dmenzja % $3\mes 3$ marca olona daog uslova $c$ I=[ 0 0; 0 0; 0 0 ]; syms x; a=[ ]; ara_pol=de(a-x*i); % zvadmo oefcjene z araersčnog polnma [oefcjen,]=coeffs(ara_pol); % dodajmo oefcjene u veor a for =:numel(oefcjen) a()=oefcjen(); end % odredmo nule araersčnog polnoma orjen=roos(a); lambda=(orjen()); 9
10 lambda=(orjen()); lambda3=(orjen(3)); % zaoružmo svojsvene vrjednos na 4 decmalna mjesa lambda=round(lambda*000)/000; lambda=round(lambda*000)/000; lambda3=round(lambda3*000)/000; % zračunajmo p_, p_ p_3 p_=(lambda-lambda)*(lambda-lambda3); p_=(lambda-lambda)*(lambda-lambda3); p_3=(lambda3-lambda)*(lambda3-lambda); % zračunajmo G, G G3 G=sym(/p_)*(A-lambda*I)*(A-lambda3*I); G=sym(/p_)*(A-lambda*I)*(A-lambda3*I); G3=sym(/p_3)*(A-lambda*I)*(A-lambda*I); % zračunajmo veore v, v, v3 v=g*b; v=g*b; v3=g3*b; % spšmo rješenje dferencjalne jednačne syms ; dsp('rješenje daog ssema u marčnom oblu je'); rjesenje=exp(lambda*)*v+exp(lambda*)*v+exp(lambda3*)*v3; prey(rjesenje) end Pažljv čalac će prmje da da MaLab od ne provjerava da l je unesena marca djagonablna. Naravno funcja bez og djela rad dovoljno dobro a umeanje og djela oda osavljamo ao zanmljvu vježbu. Leraura [] J. L. Massey: "Appled Dgal Informaon Theory II", blješe sa predavanja, srpa oja je oršena na predavanjma oje je držao prof. dr James L. Massey od 98 do 997 na ETF-u u Crhu, snuo sa hp:// sr. -59 [] C. D. Meyer: "Marx analyss and appled lnear algebra", SIAM, 000., sr [3] L. Mrsy: "An nroducon o lnear algebra", Oxford Unversy Press, 955., sr [4] P. J. Olver C. Shaban: "Appled lnear algebra", Pearson Prence Hall, 006., sr [5] V. Perć: "Algebra I (prsen modul, lnearna algebra)", Svjelos, 987., sr [6] V. V. Prasolov: "Problems and heorems n Lnear Algebra", Amercan Mahemacal Socey, 000., sr 97-0
Density Matrix Description of NMR BCMB/CHEM 8190
 Densy Marx Descrpon of NMR BCMBCHEM 89 Operaors n Marx Noaon Alernae approach o second order specra: ask abou x magnezaon nsead of energes and ranson probables. If we say wh one bass se, properes vary
Densy Marx Descrpon of NMR BCMBCHEM 89 Operaors n Marx Noaon Alernae approach o second order specra: ask abou x magnezaon nsead of energes and ranson probables. If we say wh one bass se, properes vary
Solution in semi infinite diffusion couples (error function analysis)
 Soluon n sem nfne dffuson couples (error funcon analyss) Le us consder now he sem nfne dffuson couple of wo blocks wh concenraon of and I means ha, n a A- bnary sysem, s bondng beween wo blocks made of
Soluon n sem nfne dffuson couples (error funcon analyss) Le us consder now he sem nfne dffuson couple of wo blocks wh concenraon of and I means ha, n a A- bnary sysem, s bondng beween wo blocks made of
Density Matrix Description of NMR BCMB/CHEM 8190
 Densy Marx Descrpon of NMR BCMBCHEM 89 Operaors n Marx Noaon If we say wh one bass se, properes vary only because of changes n he coeffcens weghng each bass se funcon x = h< Ix > - hs s how we calculae
Densy Marx Descrpon of NMR BCMBCHEM 89 Operaors n Marx Noaon If we say wh one bass se, properes vary only because of changes n he coeffcens weghng each bass se funcon x = h< Ix > - hs s how we calculae
HEAT CONDUCTION PROBLEM IN A TWO-LAYERED HOLLOW CYLINDER BY USING THE GREEN S FUNCTION METHOD
 Journal of Appled Mahemacs and Compuaonal Mechancs 3, (), 45-5 HEAT CONDUCTION PROBLEM IN A TWO-LAYERED HOLLOW CYLINDER BY USING THE GREEN S FUNCTION METHOD Sansław Kukla, Urszula Sedlecka Insue of Mahemacs,
Journal of Appled Mahemacs and Compuaonal Mechancs 3, (), 45-5 HEAT CONDUCTION PROBLEM IN A TWO-LAYERED HOLLOW CYLINDER BY USING THE GREEN S FUNCTION METHOD Sansław Kukla, Urszula Sedlecka Insue of Mahemacs,
Relative controllability of nonlinear systems with delays in control
 Relave conrollably o nonlnear sysems wh delays n conrol Jerzy Klamka Insue o Conrol Engneerng, Slesan Techncal Unversy, 44- Glwce, Poland. phone/ax : 48 32 37227, {jklamka}@a.polsl.glwce.pl Keywor: Conrollably.
Relave conrollably o nonlnear sysems wh delays n conrol Jerzy Klamka Insue o Conrol Engneerng, Slesan Techncal Unversy, 44- Glwce, Poland. phone/ax : 48 32 37227, {jklamka}@a.polsl.glwce.pl Keywor: Conrollably.
Approximate Analytic Solution of (2+1) - Dimensional Zakharov-Kuznetsov(Zk) Equations Using Homotopy
 Arcle Inernaonal Journal of Modern Mahemacal Scences, 4, (): - Inernaonal Journal of Modern Mahemacal Scences Journal homepage: www.modernscenfcpress.com/journals/jmms.aspx ISSN: 66-86X Florda, USA Approxmae
Arcle Inernaonal Journal of Modern Mahemacal Scences, 4, (): - Inernaonal Journal of Modern Mahemacal Scences Journal homepage: www.modernscenfcpress.com/journals/jmms.aspx ISSN: 66-86X Florda, USA Approxmae
Notes on the stability of dynamic systems and the use of Eigen Values.
 Noes on he sabl of dnamc ssems and he use of Egen Values. Source: Macro II course noes, Dr. Davd Bessler s Tme Seres course noes, zarads (999) Ineremporal Macroeconomcs chaper 4 & Techncal ppend, and Hamlon
Noes on he sabl of dnamc ssems and he use of Egen Values. Source: Macro II course noes, Dr. Davd Bessler s Tme Seres course noes, zarads (999) Ineremporal Macroeconomcs chaper 4 & Techncal ppend, and Hamlon
Existence and Uniqueness Results for Random Impulsive Integro-Differential Equation
 Global Journal of Pure and Appled Mahemacs. ISSN 973-768 Volume 4, Number 6 (8), pp. 89-87 Research Inda Publcaons hp://www.rpublcaon.com Exsence and Unqueness Resuls for Random Impulsve Inegro-Dfferenal
Global Journal of Pure and Appled Mahemacs. ISSN 973-768 Volume 4, Number 6 (8), pp. 89-87 Research Inda Publcaons hp://www.rpublcaon.com Exsence and Unqueness Resuls for Random Impulsve Inegro-Dfferenal
Comparison of Differences between Power Means 1
 In. Journal of Mah. Analyss, Vol. 7, 203, no., 5-55 Comparson of Dfferences beween Power Means Chang-An Tan, Guanghua Sh and Fe Zuo College of Mahemacs and Informaon Scence Henan Normal Unversy, 453007,
In. Journal of Mah. Analyss, Vol. 7, 203, no., 5-55 Comparson of Dfferences beween Power Means Chang-An Tan, Guanghua Sh and Fe Zuo College of Mahemacs and Informaon Scence Henan Normal Unversy, 453007,
John Geweke a and Gianni Amisano b a Departments of Economics and Statistics, University of Iowa, USA b European Central Bank, Frankfurt, Germany
 Herarchcal Markov Normal Mxure models wh Applcaons o Fnancal Asse Reurns Appendx: Proofs of Theorems and Condonal Poseror Dsrbuons John Geweke a and Gann Amsano b a Deparmens of Economcs and Sascs, Unversy
Herarchcal Markov Normal Mxure models wh Applcaons o Fnancal Asse Reurns Appendx: Proofs of Theorems and Condonal Poseror Dsrbuons John Geweke a and Gann Amsano b a Deparmens of Economcs and Sascs, Unversy
On One Analytic Method of. Constructing Program Controls
 Appled Mahemacal Scences, Vol. 9, 05, no. 8, 409-407 HIKARI Ld, www.m-hkar.com hp://dx.do.org/0.988/ams.05.54349 On One Analyc Mehod of Consrucng Program Conrols A. N. Kvko, S. V. Chsyakov and Yu. E. Balyna
Appled Mahemacal Scences, Vol. 9, 05, no. 8, 409-407 HIKARI Ld, www.m-hkar.com hp://dx.do.org/0.988/ams.05.54349 On One Analyc Mehod of Consrucng Program Conrols A. N. Kvko, S. V. Chsyakov and Yu. E. Balyna
CS434a/541a: Pattern Recognition Prof. Olga Veksler. Lecture 4
 CS434a/54a: Paern Recognon Prof. Olga Veksler Lecure 4 Oulne Normal Random Varable Properes Dscrmnan funcons Why Normal Random Varables? Analycally racable Works well when observaon comes form a corruped
CS434a/54a: Paern Recognon Prof. Olga Veksler Lecure 4 Oulne Normal Random Varable Properes Dscrmnan funcons Why Normal Random Varables? Analycally racable Works well when observaon comes form a corruped
Ordinary Differential Equations in Neuroscience with Matlab examples. Aim 1- Gain understanding of how to set up and solve ODE s
 Ordnary Dfferenal Equaons n Neuroscence wh Malab eamples. Am - Gan undersandng of how o se up and solve ODE s Am Undersand how o se up an solve a smple eample of he Hebb rule n D Our goal a end of class
Ordnary Dfferenal Equaons n Neuroscence wh Malab eamples. Am - Gan undersandng of how o se up and solve ODE s Am Undersand how o se up an solve a smple eample of he Hebb rule n D Our goal a end of class
J i-1 i. J i i+1. Numerical integration of the diffusion equation (I) Finite difference method. Spatial Discretization. Internal nodes.
 umercal negraon of he dffuson equaon (I) Fne dfference mehod. Spaal screaon. Inernal nodes. R L V For hermal conducon le s dscree he spaal doman no small fne spans, =,,: Balance of parcles for an nernal
umercal negraon of he dffuson equaon (I) Fne dfference mehod. Spaal screaon. Inernal nodes. R L V For hermal conducon le s dscree he spaal doman no small fne spans, =,,: Balance of parcles for an nernal
Mechanics Physics 151
 Mechancs Physcs 5 Lecure 0 Canoncal Transformaons (Chaper 9) Wha We Dd Las Tme Hamlon s Prncple n he Hamlonan formalsm Dervaon was smple δi δ Addonal end-pon consrans pq H( q, p, ) d 0 δ q ( ) δq ( ) δ
Mechancs Physcs 5 Lecure 0 Canoncal Transformaons (Chaper 9) Wha We Dd Las Tme Hamlon s Prncple n he Hamlonan formalsm Dervaon was smple δi δ Addonal end-pon consrans pq H( q, p, ) d 0 δ q ( ) δq ( ) δ
Online Appendix for. Strategic safety stocks in supply chains with evolving forecasts
 Onlne Appendx for Sraegc safey socs n supply chans wh evolvng forecass Tor Schoenmeyr Sephen C. Graves Opsolar, Inc. 332 Hunwood Avenue Hayward, CA 94544 A. P. Sloan School of Managemen Massachuses Insue
Onlne Appendx for Sraegc safey socs n supply chans wh evolvng forecass Tor Schoenmeyr Sephen C. Graves Opsolar, Inc. 332 Hunwood Avenue Hayward, CA 94544 A. P. Sloan School of Managemen Massachuses Insue
GENERATING CERTAIN QUINTIC IRREDUCIBLE POLYNOMIALS OVER FINITE FIELDS. Youngwoo Ahn and Kitae Kim
 Korean J. Mah. 19 (2011), No. 3, pp. 263 272 GENERATING CERTAIN QUINTIC IRREDUCIBLE POLYNOMIALS OVER FINITE FIELDS Youngwoo Ahn and Kae Km Absrac. In he paper [1], an explc correspondence beween ceran
Korean J. Mah. 19 (2011), No. 3, pp. 263 272 GENERATING CERTAIN QUINTIC IRREDUCIBLE POLYNOMIALS OVER FINITE FIELDS Youngwoo Ahn and Kae Km Absrac. In he paper [1], an explc correspondence beween ceran
M. Y. Adamu Mathematical Sciences Programme, AbubakarTafawaBalewa University, Bauchi, Nigeria
 IOSR Journal of Mahemacs (IOSR-JM e-issn: 78-578, p-issn: 9-765X. Volume 0, Issue 4 Ver. IV (Jul-Aug. 04, PP 40-44 Mulple SolonSoluons for a (+-dmensonalhroa-sasuma shallow waer wave equaon UsngPanlevé-Bӓclund
IOSR Journal of Mahemacs (IOSR-JM e-issn: 78-578, p-issn: 9-765X. Volume 0, Issue 4 Ver. IV (Jul-Aug. 04, PP 40-44 Mulple SolonSoluons for a (+-dmensonalhroa-sasuma shallow waer wave equaon UsngPanlevé-Bӓclund
Normal Random Variable and its discriminant functions
 Noral Rando Varable and s dscrnan funcons Oulne Noral Rando Varable Properes Dscrnan funcons Why Noral Rando Varables? Analycally racable Works well when observaon coes for a corruped snle prooype 3 The
Noral Rando Varable and s dscrnan funcons Oulne Noral Rando Varable Properes Dscrnan funcons Why Noral Rando Varables? Analycally racable Works well when observaon coes for a corruped snle prooype 3 The
2/20/2013. EE 101 Midterm 2 Review
 //3 EE Mderm eew //3 Volage-mplfer Model The npu ressance s he equalen ressance see when lookng no he npu ermnals of he amplfer. o s he oupu ressance. I causes he oupu olage o decrease as he load ressance
//3 EE Mderm eew //3 Volage-mplfer Model The npu ressance s he equalen ressance see when lookng no he npu ermnals of he amplfer. o s he oupu ressance. I causes he oupu olage o decrease as he load ressance
Response of MDOF systems
 Response of MDOF syses Degree of freedo DOF: he nu nuber of ndependen coordnaes requred o deerne copleely he posons of all pars of a syse a any nsan of e. wo DOF syses hree DOF syses he noral ode analyss
Response of MDOF syses Degree of freedo DOF: he nu nuber of ndependen coordnaes requred o deerne copleely he posons of all pars of a syse a any nsan of e. wo DOF syses hree DOF syses he noral ode analyss
Volatility Interpolation
 Volaly Inerpolaon Prelmnary Verson March 00 Jesper Andreasen and Bran Huge Danse Mares, Copenhagen wan.daddy@danseban.com brno@danseban.com Elecronc copy avalable a: hp://ssrn.com/absrac=69497 Inro Local
Volaly Inerpolaon Prelmnary Verson March 00 Jesper Andreasen and Bran Huge Danse Mares, Copenhagen wan.daddy@danseban.com brno@danseban.com Elecronc copy avalable a: hp://ssrn.com/absrac=69497 Inro Local
Transcription: Messenger RNA, mrna, is produced and transported to Ribosomes
 Quanave Cenral Dogma I Reference hp//book.bonumbers.org Inaon ranscrpon RNA polymerase and ranscrpon Facor (F) s bnds o promoer regon of DNA ranscrpon Meenger RNA, mrna, s produced and ranspored o Rbosomes
Quanave Cenral Dogma I Reference hp//book.bonumbers.org Inaon ranscrpon RNA polymerase and ranscrpon Facor (F) s bnds o promoer regon of DNA ranscrpon Meenger RNA, mrna, s produced and ranspored o Rbosomes
Chapter 6: AC Circuits
 Chaper 6: AC Crcus Chaper 6: Oulne Phasors and he AC Seady Sae AC Crcus A sable, lnear crcu operang n he seady sae wh snusodal excaon (.e., snusodal seady sae. Complee response forced response naural response.
Chaper 6: AC Crcus Chaper 6: Oulne Phasors and he AC Seady Sae AC Crcus A sable, lnear crcu operang n he seady sae wh snusodal excaon (.e., snusodal seady sae. Complee response forced response naural response.
Electromagnetic waves in vacuum.
 leromagne waves n vauum. The dsovery of dsplaemen urrens enals a peular lass of soluons of Maxwell equaons: ravellng waves of eler and magne felds n vauum. In he absene of urrens and harges, he equaons
leromagne waves n vauum. The dsovery of dsplaemen urrens enals a peular lass of soluons of Maxwell equaons: ravellng waves of eler and magne felds n vauum. In he absene of urrens and harges, he equaons
V.Abramov - FURTHER ANALYSIS OF CONFIDENCE INTERVALS FOR LARGE CLIENT/SERVER COMPUTER NETWORKS
 R&RATA # Vol.) 8, March FURTHER AALYSIS OF COFIDECE ITERVALS FOR LARGE CLIET/SERVER COMPUTER ETWORKS Vyacheslav Abramov School of Mahemacal Scences, Monash Unversy, Buldng 8, Level 4, Clayon Campus, Wellngon
R&RATA # Vol.) 8, March FURTHER AALYSIS OF COFIDECE ITERVALS FOR LARGE CLIET/SERVER COMPUTER ETWORKS Vyacheslav Abramov School of Mahemacal Scences, Monash Unversy, Buldng 8, Level 4, Clayon Campus, Wellngon
THE POLYNOMIAL TENSOR INTERPOLATION
 Pease ce hs arce as: Grzegorz Berna, Ana Ceo, The oynoma ensor neroaon, Scenfc Research of he Insue of Mahemacs and Comuer Scence, 28, oume 7, Issue, ages 5-. The webse: h://www.amcm.cz./ Scenfc Research
Pease ce hs arce as: Grzegorz Berna, Ana Ceo, The oynoma ensor neroaon, Scenfc Research of he Insue of Mahemacs and Comuer Scence, 28, oume 7, Issue, ages 5-. The webse: h://www.amcm.cz./ Scenfc Research
Advanced Machine Learning & Perception
 Advanced Machne Learnng & Percepon Insrucor: Tony Jebara SVM Feaure & Kernel Selecon SVM Eensons Feaure Selecon (Flerng and Wrappng) SVM Feaure Selecon SVM Kernel Selecon SVM Eensons Classfcaon Feaure/Kernel
Advanced Machne Learnng & Percepon Insrucor: Tony Jebara SVM Feaure & Kernel Selecon SVM Eensons Feaure Selecon (Flerng and Wrappng) SVM Feaure Selecon SVM Kernel Selecon SVM Eensons Classfcaon Feaure/Kernel
Robust and Accurate Cancer Classification with Gene Expression Profiling
 Robus and Accurae Cancer Classfcaon wh Gene Expresson Proflng (Compuaonal ysems Bology, 2005) Auhor: Hafeng L, Keshu Zhang, ao Jang Oulne Background LDA (lnear dscrmnan analyss) and small sample sze problem
Robus and Accurae Cancer Classfcaon wh Gene Expresson Proflng (Compuaonal ysems Bology, 2005) Auhor: Hafeng L, Keshu Zhang, ao Jang Oulne Background LDA (lnear dscrmnan analyss) and small sample sze problem
Li An-Ping. Beijing , P.R.China
 A New Type of Cpher: DICING_csb L An-Png Bejng 100085, P.R.Chna apl0001@sna.com Absrac: In hs paper, we wll propose a new ype of cpher named DICING_csb, whch s derved from our prevous sream cpher DICING.
A New Type of Cpher: DICING_csb L An-Png Bejng 100085, P.R.Chna apl0001@sna.com Absrac: In hs paper, we wll propose a new ype of cpher named DICING_csb, whch s derved from our prevous sream cpher DICING.
Existence of Time Periodic Solutions for the Ginzburg-Landau Equations. model of superconductivity
 Journal of Mahemacal Analyss and Applcaons 3, 3944 999 Arcle ID jmaa.999.683, avalable onlne a hp:www.dealbrary.com on Exsence of me Perodc Soluons for he Gnzburg-Landau Equaons of Superconducvy Bxang
Journal of Mahemacal Analyss and Applcaons 3, 3944 999 Arcle ID jmaa.999.683, avalable onlne a hp:www.dealbrary.com on Exsence of me Perodc Soluons for he Gnzburg-Landau Equaons of Superconducvy Bxang
Dynamic Team Decision Theory. EECS 558 Project Shrutivandana Sharma and David Shuman December 10, 2005
 Dynamc Team Decson Theory EECS 558 Proec Shruvandana Sharma and Davd Shuman December 0, 005 Oulne Inroducon o Team Decson Theory Decomposon of he Dynamc Team Decson Problem Equvalence of Sac and Dynamc
Dynamc Team Decson Theory EECS 558 Proec Shruvandana Sharma and Davd Shuman December 0, 005 Oulne Inroducon o Team Decson Theory Decomposon of he Dynamc Team Decson Problem Equvalence of Sac and Dynamc
UNIVERSITAT AUTÒNOMA DE BARCELONA MARCH 2017 EXAMINATION
 INTERNATIONAL TRADE T. J. KEHOE UNIVERSITAT AUTÒNOMA DE BARCELONA MARCH 27 EXAMINATION Please answer wo of he hree quesons. You can consul class noes, workng papers, and arcles whle you are workng on he
INTERNATIONAL TRADE T. J. KEHOE UNIVERSITAT AUTÒNOMA DE BARCELONA MARCH 27 EXAMINATION Please answer wo of he hree quesons. You can consul class noes, workng papers, and arcles whle you are workng on he
How about the more general "linear" scalar functions of scalars (i.e., a 1st degree polynomial of the following form with a constant term )?
 lmcd Lnear ransformaon of a vecor he deas presened here are que general hey go beyond he radonal mar-vecor ype seen n lnear algebra Furhermore, hey do no deal wh bass and are equally vald for any se of
lmcd Lnear ransformaon of a vecor he deas presened here are que general hey go beyond he radonal mar-vecor ype seen n lnear algebra Furhermore, hey do no deal wh bass and are equally vald for any se of
. The geometric multiplicity is dim[ker( λi. number of linearly independent eigenvectors associated with this eigenvalue.
 Lnear Algebra Lecure # Noes We connue wh he dscusson of egenvalues, egenvecors, and dagonalzably of marces We wan o know, n parcular wha condons wll assure ha a marx can be dagonalzed and wha he obsrucons
Lnear Algebra Lecure # Noes We connue wh he dscusson of egenvalues, egenvecors, and dagonalzably of marces We wan o know, n parcular wha condons wll assure ha a marx can be dagonalzed and wha he obsrucons
(,,, ) (,,, ). In addition, there are three other consumers, -2, -1, and 0. Consumer -2 has the utility function
 MACROECONOMIC THEORY T J KEHOE ECON 87 SPRING 5 PROBLEM SET # Conder an overlappng generaon economy le ha n queon 5 on problem e n whch conumer lve for perod The uly funcon of he conumer born n perod,
MACROECONOMIC THEORY T J KEHOE ECON 87 SPRING 5 PROBLEM SET # Conder an overlappng generaon economy le ha n queon 5 on problem e n whch conumer lve for perod The uly funcon of he conumer born n perod,
Scattering at an Interface: Oblique Incidence
 Course Insrucor Dr. Raymond C. Rumpf Offce: A 337 Phone: (915) 747 6958 E Mal: rcrumpf@uep.edu EE 4347 Appled Elecromagnecs Topc 3g Scaerng a an Inerface: Oblque Incdence Scaerng These Oblque noes may
Course Insrucor Dr. Raymond C. Rumpf Offce: A 337 Phone: (915) 747 6958 E Mal: rcrumpf@uep.edu EE 4347 Appled Elecromagnecs Topc 3g Scaerng a an Inerface: Oblque Incdence Scaerng These Oblque noes may
Perron Vectors of an Irreducible Nonnegative Interval Matrix
 Perron Vectors of an Irreducble Nonnegatve Interval Matrx Jr Rohn August 4 2005 Abstract As s well known an rreducble nonnegatve matrx possesses a unquely determned Perron vector. As the man result of
Perron Vectors of an Irreducble Nonnegatve Interval Matrx Jr Rohn August 4 2005 Abstract As s well known an rreducble nonnegatve matrx possesses a unquely determned Perron vector. As the man result of
A NEW TECHNIQUE FOR SOLVING THE 1-D BURGERS EQUATION
 S19 A NEW TECHNIQUE FOR SOLVING THE 1-D BURGERS EQUATION by Xaojun YANG a,b, Yugu YANG a*, Carlo CATTANI c, and Mngzheng ZHU b a Sae Key Laboraory for Geomechancs and Deep Underground Engneerng, Chna Unversy
S19 A NEW TECHNIQUE FOR SOLVING THE 1-D BURGERS EQUATION by Xaojun YANG a,b, Yugu YANG a*, Carlo CATTANI c, and Mngzheng ZHU b a Sae Key Laboraory for Geomechancs and Deep Underground Engneerng, Chna Unversy
SOME NOISELESS CODING THEOREMS OF INACCURACY MEASURE OF ORDER α AND TYPE β
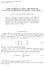 SARAJEVO JOURNAL OF MATHEMATICS Vol.3 (15) (2007), 137 143 SOME NOISELESS CODING THEOREMS OF INACCURACY MEASURE OF ORDER α AND TYPE β M. A. K. BAIG AND RAYEES AHMAD DAR Absrac. In hs paper, we propose
SARAJEVO JOURNAL OF MATHEMATICS Vol.3 (15) (2007), 137 143 SOME NOISELESS CODING THEOREMS OF INACCURACY MEASURE OF ORDER α AND TYPE β M. A. K. BAIG AND RAYEES AHMAD DAR Absrac. In hs paper, we propose
. The geometric multiplicity is dim[ker( λi. A )], i.e. the number of linearly independent eigenvectors associated with this eigenvalue.
![. The geometric multiplicity is dim[ker( λi. A )], i.e. the number of linearly independent eigenvectors associated with this eigenvalue. . The geometric multiplicity is dim[ker( λi. A )], i.e. the number of linearly independent eigenvectors associated with this eigenvalue.](/thumbs/78/77822798.jpg) Mah E-b Lecure #0 Noes We connue wh he dscusson of egenvalues, egenvecors, and dagonalzably of marces We wan o know, n parcular wha condons wll assure ha a marx can be dagonalzed and wha he obsrucons are
Mah E-b Lecure #0 Noes We connue wh he dscusson of egenvalues, egenvecors, and dagonalzably of marces We wan o know, n parcular wha condons wll assure ha a marx can be dagonalzed and wha he obsrucons are
( t) Outline of program: BGC1: Survival and event history analysis Oslo, March-May Recapitulation. The additive regression model
 BGC1: Survval and even hsory analyss Oslo, March-May 212 Monday May 7h and Tuesday May 8h The addve regresson model Ørnulf Borgan Deparmen of Mahemacs Unversy of Oslo Oulne of program: Recapulaon Counng
BGC1: Survval and even hsory analyss Oslo, March-May 212 Monday May 7h and Tuesday May 8h The addve regresson model Ørnulf Borgan Deparmen of Mahemacs Unversy of Oslo Oulne of program: Recapulaon Counng
In the complete model, these slopes are ANALYSIS OF VARIANCE FOR THE COMPLETE TWO-WAY MODEL. (! i+1 -! i ) + [(!") i+1,q - [(!
 ANALYSIS OF VARIANCE FOR THE COMPLETE TWO-WAY MODEL The frs hng o es n wo-way ANOVA: Is here neracon? "No neracon" means: The man effecs model would f. Ths n urn means: In he neracon plo (wh A on he horzonal
ANALYSIS OF VARIANCE FOR THE COMPLETE TWO-WAY MODEL The frs hng o es n wo-way ANOVA: Is here neracon? "No neracon" means: The man effecs model would f. Ths n urn means: In he neracon plo (wh A on he horzonal
Let s treat the problem of the response of a system to an applied external force. Again,
 Page 33 QUANTUM LNEAR RESPONSE FUNCTON Le s rea he problem of he response of a sysem o an appled exernal force. Agan, H() H f () A H + V () Exernal agen acng on nernal varable Hamlonan for equlbrum sysem
Page 33 QUANTUM LNEAR RESPONSE FUNCTON Le s rea he problem of he response of a sysem o an appled exernal force. Agan, H() H f () A H + V () Exernal agen acng on nernal varable Hamlonan for equlbrum sysem
Projektovanje paralelnih algoritama II
 Projektovanje paralelnih algoritama II Primeri paralelnih algoritama, I deo Paralelni algoritmi za množenje matrica 1 Algoritmi za množenje matrica Ovde su data tri paralelna algoritma: Direktan algoritam
Projektovanje paralelnih algoritama II Primeri paralelnih algoritama, I deo Paralelni algoritmi za množenje matrica 1 Algoritmi za množenje matrica Ovde su data tri paralelna algoritma: Direktan algoritam
T h e C S E T I P r o j e c t
 T h e P r o j e c t T H E P R O J E C T T A B L E O F C O N T E N T S A r t i c l e P a g e C o m p r e h e n s i v e A s s es s m e n t o f t h e U F O / E T I P h e n o m e n o n M a y 1 9 9 1 1 E T
T h e P r o j e c t T H E P R O J E C T T A B L E O F C O N T E N T S A r t i c l e P a g e C o m p r e h e n s i v e A s s es s m e n t o f t h e U F O / E T I P h e n o m e n o n M a y 1 9 9 1 1 E T
Pendulum Dynamics. = Ft tangential direction (2) radial direction (1)
 Pendulum Dynams Consder a smple pendulum wh a massless arm of lengh L and a pon mass, m, a he end of he arm. Assumng ha he fron n he sysem s proporonal o he negave of he angenal veloy, Newon s seond law
Pendulum Dynams Consder a smple pendulum wh a massless arm of lengh L and a pon mass, m, a he end of he arm. Assumng ha he fron n he sysem s proporonal o he negave of he angenal veloy, Newon s seond law
Observer Design for Nonlinear Systems using Linear Approximations
 Observer Desgn for Nonlnear Ssems sng Lnear Appromaons C. Navarro Hernandez, S.P. Banks and M. Aldeen Deparmen of Aomac Conrol and Ssems Engneerng, Unvers of Sheffeld, Mappn Sree, Sheffeld S 3JD. e-mal:
Observer Desgn for Nonlnear Ssems sng Lnear Appromaons C. Navarro Hernandez, S.P. Banks and M. Aldeen Deparmen of Aomac Conrol and Ssems Engneerng, Unvers of Sheffeld, Mappn Sree, Sheffeld S 3JD. e-mal:
( ) [ ] MAP Decision Rule
![( ) [ ] MAP Decision Rule ( ) [ ] MAP Decision Rule](/thumbs/82/84970741.jpg) Announcemens Bayes Decson Theory wh Normal Dsrbuons HW0 due oday HW o be assgned soon Proec descrpon posed Bomercs CSE 90 Lecure 4 CSE90, Sprng 04 CSE90, Sprng 04 Key Probables 4 ω class label X feaure
Announcemens Bayes Decson Theory wh Normal Dsrbuons HW0 due oday HW o be assgned soon Proec descrpon posed Bomercs CSE 90 Lecure 4 CSE90, Sprng 04 CSE90, Sprng 04 Key Probables 4 ω class label X feaure
A L A BA M A L A W R E V IE W
 A L A BA M A L A W R E V IE W Volume 52 Fall 2000 Number 1 B E F O R E D I S A B I L I T Y C I V I L R I G HT S : C I V I L W A R P E N S I O N S A N D TH E P O L I T I C S O F D I S A B I L I T Y I N
A L A BA M A L A W R E V IE W Volume 52 Fall 2000 Number 1 B E F O R E D I S A B I L I T Y C I V I L R I G HT S : C I V I L W A R P E N S I O N S A N D TH E P O L I T I C S O F D I S A B I L I T Y I N
10. A.C CIRCUITS. Theoretically current grows to maximum value after infinite time. But practically it grows to maximum after 5τ. Decay of current :
 . A. IUITS Synopss : GOWTH OF UNT IN IUIT : d. When swch S s closed a =; = d. A me, curren = e 3. The consan / has dmensons of me and s called he nducve me consan ( τ ) of he crcu. 4. = τ; =.63, n one
. A. IUITS Synopss : GOWTH OF UNT IN IUIT : d. When swch S s closed a =; = d. A me, curren = e 3. The consan / has dmensons of me and s called he nducve me consan ( τ ) of he crcu. 4. = τ; =.63, n one
Appendix H: Rarefaction and extrapolation of Hill numbers for incidence data
 Anne Chao Ncholas J Goell C seh lzabeh L ander K Ma Rober K Colwell and Aaron M llson 03 Rarefacon and erapolaon wh ll numbers: a framewor for samplng and esmaon n speces dversy sudes cology Monographs
Anne Chao Ncholas J Goell C seh lzabeh L ander K Ma Rober K Colwell and Aaron M llson 03 Rarefacon and erapolaon wh ll numbers: a framewor for samplng and esmaon n speces dversy sudes cology Monographs
[ ] 2. [ ]3 + (Δx i + Δx i 1 ) / 2. Δx i-1 Δx i Δx i+1. TPG4160 Reservoir Simulation 2018 Lecture note 3. page 1 of 5
![[ ] 2. [ ]3 + (Δx i + Δx i 1 ) / 2. Δx i-1 Δx i Δx i+1. TPG4160 Reservoir Simulation 2018 Lecture note 3. page 1 of 5 [ ] 2. [ ]3 + (Δx i + Δx i 1 ) / 2. Δx i-1 Δx i Δx i+1. TPG4160 Reservoir Simulation 2018 Lecture note 3. page 1 of 5](/thumbs/85/92299540.jpg) TPG460 Reservor Smulaon 08 page of 5 DISCRETIZATIO OF THE FOW EQUATIOS As we already have seen, fne dfference appromaons of he paral dervaves appearng n he flow equaons may be obaned from Taylor seres
TPG460 Reservor Smulaon 08 page of 5 DISCRETIZATIO OF THE FOW EQUATIOS As we already have seen, fne dfference appromaons of he paral dervaves appearng n he flow equaons may be obaned from Taylor seres
THE PREDICTION OF COMPETITIVE ENVIRONMENT IN BUSINESS
 THE PREICTION OF COMPETITIVE ENVIRONMENT IN BUSINESS INTROUCTION The wo dmensonal paral dfferenal equaons of second order can be used for he smulaon of compeve envronmen n busness The arcle presens he
THE PREICTION OF COMPETITIVE ENVIRONMENT IN BUSINESS INTROUCTION The wo dmensonal paral dfferenal equaons of second order can be used for he smulaon of compeve envronmen n busness The arcle presens he
Digital Integrated CircuitDesign
 Dgal Inegraed CrcuDesgn Lecure 6 BJT Inverer Swchng Tmes µ s 01. 1 3 4 6 2 Adb Abrshamfar EE Deparmen IUST Cnens BJT Inverer Cuff Regn ( 1 ) Acve Regn ( 1 2 ) Sauran Regn ( 3 4 ) Acve Regn ( 4 ) Recvery
Dgal Inegraed CrcuDesgn Lecure 6 BJT Inverer Swchng Tmes µ s 01. 1 3 4 6 2 Adb Abrshamfar EE Deparmen IUST Cnens BJT Inverer Cuff Regn ( 1 ) Acve Regn ( 1 2 ) Sauran Regn ( 3 4 ) Acve Regn ( 4 ) Recvery
Method of upper lower solutions for nonlinear system of fractional differential equations and applications
 Malaya Journal of Maemak, Vol. 6, No. 3, 467-472, 218 hps://do.org/1.26637/mjm63/1 Mehod of upper lower soluons for nonlnear sysem of fraconal dfferenal equaons and applcaons D.B. Dhagude1 *, N.B. Jadhav2
Malaya Journal of Maemak, Vol. 6, No. 3, 467-472, 218 hps://do.org/1.26637/mjm63/1 Mehod of upper lower soluons for nonlnear sysem of fraconal dfferenal equaons and applcaons D.B. Dhagude1 *, N.B. Jadhav2
Generalized double sinh-gordon equation: Symmetry reductions, exact solutions and conservation laws
 IJS (05) 9A: 89-96 Iranan Journal of Scence & echnology hp://ss.shrazu.ac.r Generalzed double snh-gordon equaon: Symmery reducons eac soluons and conservaon laws G. Magalawe B. Muaeea and C. M. Khalque
IJS (05) 9A: 89-96 Iranan Journal of Scence & echnology hp://ss.shrazu.ac.r Generalzed double snh-gordon equaon: Symmery reducons eac soluons and conservaon laws G. Magalawe B. Muaeea and C. M. Khalque
by Lauren DeDieu Advisor: George Chen
 b Laren DeDe Advsor: George Chen Are one of he mos powerfl mehods o nmercall solve me dependen paral dfferenal eqaons PDE wh some knd of snglar shock waves & blow-p problems. Fed nmber of mesh pons Moves
b Laren DeDe Advsor: George Chen Are one of he mos powerfl mehods o nmercall solve me dependen paral dfferenal eqaons PDE wh some knd of snglar shock waves & blow-p problems. Fed nmber of mesh pons Moves
P a g e 3 6 of R e p o r t P B 4 / 0 9
 P a g e 3 6 of R e p o r t P B 4 / 0 9 p r o t e c t h um a n h e a l t h a n d p r o p e r t y fr om t h e d a n g e rs i n h e r e n t i n m i n i n g o p e r a t i o n s s u c h a s a q u a r r y. J
P a g e 3 6 of R e p o r t P B 4 / 0 9 p r o t e c t h um a n h e a l t h a n d p r o p e r t y fr om t h e d a n g e rs i n h e r e n t i n m i n i n g o p e r a t i o n s s u c h a s a q u a r r y. J
CH.3. COMPATIBILITY EQUATIONS. Continuum Mechanics Course (MMC) - ETSECCPB - UPC
 CH.3. COMPATIBILITY EQUATIONS Connuum Mechancs Course (MMC) - ETSECCPB - UPC Overvew Compably Condons Compably Equaons of a Poenal Vecor Feld Compably Condons for Infnesmal Srans Inegraon of he Infnesmal
CH.3. COMPATIBILITY EQUATIONS Connuum Mechancs Course (MMC) - ETSECCPB - UPC Overvew Compably Condons Compably Equaons of a Poenal Vecor Feld Compably Condons for Infnesmal Srans Inegraon of he Infnesmal
Motion in Two Dimensions
 Phys 1 Chaper 4 Moon n Two Dmensons adzyubenko@csub.edu hp://www.csub.edu/~adzyubenko 005, 014 A. Dzyubenko 004 Brooks/Cole 1 Dsplacemen as a Vecor The poson of an objec s descrbed by s poson ecor, r The
Phys 1 Chaper 4 Moon n Two Dmensons adzyubenko@csub.edu hp://www.csub.edu/~adzyubenko 005, 014 A. Dzyubenko 004 Brooks/Cole 1 Dsplacemen as a Vecor The poson of an objec s descrbed by s poson ecor, r The
Linear Response Theory: The connection between QFT and experiments
 Phys540.nb 39 3 Lnear Response Theory: The connecon beween QFT and expermens 3.1. Basc conceps and deas Q: ow do we measure he conducvy of a meal? A: we frs nroduce a weak elecrc feld E, and hen measure
Phys540.nb 39 3 Lnear Response Theory: The connecon beween QFT and expermens 3.1. Basc conceps and deas Q: ow do we measure he conducvy of a meal? A: we frs nroduce a weak elecrc feld E, and hen measure
Born Oppenheimer Approximation and Beyond
 L Born Oppenhemer Approxmaon and Beyond aro Barba A*dex Char Professor maro.barba@unv amu.fr Ax arselle Unversé, nsu de Chme Radcalare LGHT AD Adabac x dabac x nonadabac LGHT AD From Gree dabaos: o be
L Born Oppenhemer Approxmaon and Beyond aro Barba A*dex Char Professor maro.barba@unv amu.fr Ax arselle Unversé, nsu de Chme Radcalare LGHT AD Adabac x dabac x nonadabac LGHT AD From Gree dabaos: o be
Lecture 2 M/G/1 queues. M/G/1-queue
 Lecure M/G/ queues M/G/-queue Posson arrval process Arbrary servce me dsrbuon Sngle server To deermne he sae of he sysem a me, we mus now The number of cusomers n he sysems N() Tme ha he cusomer currenly
Lecure M/G/ queues M/G/-queue Posson arrval process Arbrary servce me dsrbuon Sngle server To deermne he sae of he sysem a me, we mus now The number of cusomers n he sysems N() Tme ha he cusomer currenly
( ) () we define the interaction representation by the unitary transformation () = ()
 Hgher Order Perurbaon Theory Mchael Fowler 3/7/6 The neracon Represenaon Recall ha n he frs par of hs course sequence, we dscussed he chrödnger and Hesenberg represenaons of quanum mechancs here n he chrödnger
Hgher Order Perurbaon Theory Mchael Fowler 3/7/6 The neracon Represenaon Recall ha n he frs par of hs course sequence, we dscussed he chrödnger and Hesenberg represenaons of quanum mechancs here n he chrödnger
TEORIJA SKUPOVA Zadaci
 TEORIJA SKUPOVA Zadai LOGIKA 1 I. godina 1. Zapišite simbolima: ( x nije element skupa S (b) d je član skupa S () F je podskup slupa S (d) Skup S sadrži skup R 2. Neka je S { x;2x 6} = = i neka je b =
TEORIJA SKUPOVA Zadai LOGIKA 1 I. godina 1. Zapišite simbolima: ( x nije element skupa S (b) d je član skupa S () F je podskup slupa S (d) Skup S sadrži skup R 2. Neka je S { x;2x 6} = = i neka je b =
A Deterministic Algorithm for Summarizing Asynchronous Streams over a Sliding Window
 A Deermnsc Algorhm for Summarzng Asynchronous Sreams over a Sldng ndow Cosas Busch Rensselaer Polyechnc Insue Srkana Trhapura Iowa Sae Unversy Oulne of Talk Inroducon Algorhm Analyss Tme C Daa sream: 3
A Deermnsc Algorhm for Summarzng Asynchronous Sreams over a Sldng ndow Cosas Busch Rensselaer Polyechnc Insue Srkana Trhapura Iowa Sae Unversy Oulne of Talk Inroducon Algorhm Analyss Tme C Daa sream: 3
P a g e 5 1 of R e p o r t P B 4 / 0 9
 P a g e 5 1 of R e p o r t P B 4 / 0 9 J A R T a l s o c o n c l u d e d t h a t a l t h o u g h t h e i n t e n t o f N e l s o n s r e h a b i l i t a t i o n p l a n i s t o e n h a n c e c o n n e
P a g e 5 1 of R e p o r t P B 4 / 0 9 J A R T a l s o c o n c l u d e d t h a t a l t h o u g h t h e i n t e n t o f N e l s o n s r e h a b i l i t a t i o n p l a n i s t o e n h a n c e c o n n e
3. OVERVIEW OF NUMERICAL METHODS
 3 OVERVIEW OF NUMERICAL METHODS 3 Inroducory remarks Ths chaper summarzes hose numercal echnques whose knowledge s ndspensable for he undersandng of he dfferen dscree elemen mehods: he Newon-Raphson-mehod,
3 OVERVIEW OF NUMERICAL METHODS 3 Inroducory remarks Ths chaper summarzes hose numercal echnques whose knowledge s ndspensable for he undersandng of he dfferen dscree elemen mehods: he Newon-Raphson-mehod,
MATH 5630: Discrete Time-Space Model Hung Phan, UMass Lowell March 1, 2018
 MATH 5630: Dscrete Tme-Space Model Hung Phan, UMass Lowell March, 08 Newton s Law of Coolng Consder the coolng of a well strred coffee so that the temperature does not depend on space Newton s law of collng
MATH 5630: Dscrete Tme-Space Model Hung Phan, UMass Lowell March, 08 Newton s Law of Coolng Consder the coolng of a well strred coffee so that the temperature does not depend on space Newton s law of collng
Cubic Bezier Homotopy Function for Solving Exponential Equations
 Penerb Journal of Advanced Research n Compung and Applcaons ISSN (onlne: 46-97 Vol. 4, No.. Pages -8, 6 omoopy Funcon for Solvng Eponenal Equaons S. S. Raml *,,. Mohamad Nor,a, N. S. Saharzan,b and M.
Penerb Journal of Advanced Research n Compung and Applcaons ISSN (onlne: 46-97 Vol. 4, No.. Pages -8, 6 omoopy Funcon for Solvng Eponenal Equaons S. S. Raml *,,. Mohamad Nor,a, N. S. Saharzan,b and M.
FTCS Solution to the Heat Equation
 FTCS Soluon o he Hea Equaon ME 448/548 Noes Gerald Reckenwald Porland Sae Unversy Deparmen of Mechancal Engneerng gerry@pdxedu ME 448/548: FTCS Soluon o he Hea Equaon Overvew Use he forward fne d erence
FTCS Soluon o he Hea Equaon ME 448/548 Noes Gerald Reckenwald Porland Sae Unversy Deparmen of Mechancal Engneerng gerry@pdxedu ME 448/548: FTCS Soluon o he Hea Equaon Overvew Use he forward fne d erence
Track Properities of Normal Chain
 In. J. Conemp. Mah. Scences, Vol. 8, 213, no. 4, 163-171 HIKARI Ld, www.m-har.com rac Propes of Normal Chan L Chen School of Mahemacs and Sascs, Zhengzhou Normal Unversy Zhengzhou Cy, Hennan Provnce, 4544,
In. J. Conemp. Mah. Scences, Vol. 8, 213, no. 4, 163-171 HIKARI Ld, www.m-har.com rac Propes of Normal Chan L Chen School of Mahemacs and Sascs, Zhengzhou Normal Unversy Zhengzhou Cy, Hennan Provnce, 4544,
Implementation of Quantized State Systems in MATLAB/Simulink
 SNE T ECHNICAL N OTE Implemenaon of Quanzed Sae Sysems n MATLAB/Smulnk Parck Grabher, Mahas Rößler 2*, Bernhard Henzl 3 Ins. of Analyss and Scenfc Compung, Venna Unversy of Technology, Wedner Haupsraße
SNE T ECHNICAL N OTE Implemenaon of Quanzed Sae Sysems n MATLAB/Smulnk Parck Grabher, Mahas Rößler 2*, Bernhard Henzl 3 Ins. of Analyss and Scenfc Compung, Venna Unversy of Technology, Wedner Haupsraße
Control Systems. Mathematical Modeling of Control Systems.
 Conrol Syem Mahemacal Modelng of Conrol Syem chbum@eoulech.ac.kr Oulne Mahemacal model and model ype. Tranfer funcon model Syem pole and zero Chbum Lee -Seoulech Conrol Syem Mahemacal Model Model are key
Conrol Syem Mahemacal Modelng of Conrol Syem chbum@eoulech.ac.kr Oulne Mahemacal model and model ype. Tranfer funcon model Syem pole and zero Chbum Lee -Seoulech Conrol Syem Mahemacal Model Model are key
Mechanics Physics 151
 Mechancs Physcs 5 Lecure 9 Hamlonan Equaons of Moon (Chaper 8) Wha We Dd Las Tme Consruced Hamlonan formalsm H ( q, p, ) = q p L( q, q, ) H p = q H q = p H = L Equvalen o Lagrangan formalsm Smpler, bu
Mechancs Physcs 5 Lecure 9 Hamlonan Equaons of Moon (Chaper 8) Wha We Dd Las Tme Consruced Hamlonan formalsm H ( q, p, ) = q p L( q, q, ) H p = q H q = p H = L Equvalen o Lagrangan formalsm Smpler, bu
Panel Data Regression Models
 Panel Daa Regresson Models Wha s Panel Daa? () Mulple dmensoned Dmensons, e.g., cross-secon and me node-o-node (c) Pongsa Pornchawseskul, Faculy of Economcs, Chulalongkorn Unversy (c) Pongsa Pornchawseskul,
Panel Daa Regresson Models Wha s Panel Daa? () Mulple dmensoned Dmensons, e.g., cross-secon and me node-o-node (c) Pongsa Pornchawseskul, Faculy of Economcs, Chulalongkorn Unversy (c) Pongsa Pornchawseskul,
Transient Response in Electric Circuits
 Transen esponse n Elecrc rcus The elemen equaon for he branch of he fgure when he source s gven by a generc funcon of me, s v () r d r ds = r Mrs d d r (')d' () V The crcu s descrbed by he opology equaons
Transen esponse n Elecrc rcus The elemen equaon for he branch of he fgure when he source s gven by a generc funcon of me, s v () r d r ds = r Mrs d d r (')d' () V The crcu s descrbed by he opology equaons
û s L u t 0 s a ; i.e., û s 0
 Te Hille-Yosida Teorem We ave seen a wen e absrac IVP is uniquely solvable en e soluion operaor defines a semigroup of bounded operaors. We ave no ye discussed e condiions under wic e IVP is uniquely solvable.
Te Hille-Yosida Teorem We ave seen a wen e absrac IVP is uniquely solvable en e soluion operaor defines a semigroup of bounded operaors. We ave no ye discussed e condiions under wic e IVP is uniquely solvable.
NATIONAL UNIVERSITY OF SINGAPORE PC5202 ADVANCED STATISTICAL MECHANICS. (Semester II: AY ) Time Allowed: 2 Hours
 NATONAL UNVERSTY OF SNGAPORE PC5 ADVANCED STATSTCAL MECHANCS (Semeser : AY 1-13) Tme Allowed: Hours NSTRUCTONS TO CANDDATES 1. Ths examnaon paper conans 5 quesons and comprses 4 prned pages.. Answer all
NATONAL UNVERSTY OF SNGAPORE PC5 ADVANCED STATSTCAL MECHANCS (Semeser : AY 1-13) Tme Allowed: Hours NSTRUCTONS TO CANDDATES 1. Ths examnaon paper conans 5 quesons and comprses 4 prned pages.. Answer all
Mechanics Physics 151
 Mechancs Physcs 5 Lecure 9 Hamlonan Equaons of Moon (Chaper 8) Wha We Dd Las Tme Consruced Hamlonan formalsm Hqp (,,) = qp Lqq (,,) H p = q H q = p H L = Equvalen o Lagrangan formalsm Smpler, bu wce as
Mechancs Physcs 5 Lecure 9 Hamlonan Equaons of Moon (Chaper 8) Wha We Dd Las Tme Consruced Hamlonan formalsm Hqp (,,) = qp Lqq (,,) H p = q H q = p H L = Equvalen o Lagrangan formalsm Smpler, bu wce as
Fall 2010 Graduate Course on Dynamic Learning
 Fall 200 Graduae Course on Dynamc Learnng Chaper 4: Parcle Flers Sepember 27, 200 Byoung-Tak Zhang School of Compuer Scence and Engneerng & Cognve Scence and Bran Scence Programs Seoul aonal Unversy hp://b.snu.ac.kr/~bzhang/
Fall 200 Graduae Course on Dynamc Learnng Chaper 4: Parcle Flers Sepember 27, 200 Byoung-Tak Zhang School of Compuer Scence and Engneerng & Cognve Scence and Bran Scence Programs Seoul aonal Unversy hp://b.snu.ac.kr/~bzhang/
January Examinations 2012
 Page of 5 EC79 January Examnaons No. of Pages: 5 No. of Quesons: 8 Subjec ECONOMICS (POSTGRADUATE) Tle of Paper EC79 QUANTITATIVE METHODS FOR BUSINESS AND FINANCE Tme Allowed Two Hours ( hours) Insrucons
Page of 5 EC79 January Examnaons No. of Pages: 5 No. of Quesons: 8 Subjec ECONOMICS (POSTGRADUATE) Tle of Paper EC79 QUANTITATIVE METHODS FOR BUSINESS AND FINANCE Tme Allowed Two Hours ( hours) Insrucons
Automorphic Inversion and Circular Quartics in Isotropic Plane
 Original scientific paper Accepted 0. 11. 008. EMA JURKIN Automorphic Inversion and Circular Quartics in Isotropic Plane Automorphic Inversion and Circular Quartics in Isotropic Plane ABSTRACT In this
Original scientific paper Accepted 0. 11. 008. EMA JURKIN Automorphic Inversion and Circular Quartics in Isotropic Plane Automorphic Inversion and Circular Quartics in Isotropic Plane ABSTRACT In this
OP = OO' + Ut + Vn + Wb. Material We Will Cover Today. Computer Vision Lecture 3. Multi-view Geometry I. Amnon Shashua
 Comuer Vson 27 Lecure 3 Mul-vew Geomer I Amnon Shashua Maeral We Wll Cover oa he srucure of 3D->2D rojecon mar omograh Marces A rmer on rojecve geomer of he lane Eolar Geomer an Funamenal Mar ebrew Unvers
Comuer Vson 27 Lecure 3 Mul-vew Geomer I Amnon Shashua Maeral We Wll Cover oa he srucure of 3D->2D rojecon mar omograh Marces A rmer on rojecve geomer of he lane Eolar Geomer an Funamenal Mar ebrew Unvers
On elements with index of the form 2 a 3 b in a parametric family of biquadratic elds
 On elemens wh ndex of he form a 3 b n a paramerc famly of bquadrac elds Bora JadrevĆ Absrac In hs paper we gve some resuls abou prmve negral elemens p(c p n he famly of bcyclc bquadrac elds L c = Q ) c;
On elemens wh ndex of he form a 3 b n a paramerc famly of bquadrac elds Bora JadrevĆ Absrac In hs paper we gve some resuls abou prmve negral elemens p(c p n he famly of bcyclc bquadrac elds L c = Q ) c;
c- : r - C ' ',. A a \ V
 HS PAGE DECLASSFED AW EO 2958 c C \ V A A a HS PAGE DECLASSFED AW EO 2958 HS PAGE DECLASSFED AW EO 2958 = N! [! D!! * J!! [ c 9 c 6 j C v C! ( «! Y y Y ^ L! J ( ) J! J ~ n + ~ L a Y C + J " J 7 = [ " S!
HS PAGE DECLASSFED AW EO 2958 c C \ V A A a HS PAGE DECLASSFED AW EO 2958 HS PAGE DECLASSFED AW EO 2958 = N! [! D!! * J!! [ c 9 c 6 j C v C! ( «! Y y Y ^ L! J ( ) J! J ~ n + ~ L a Y C + J " J 7 = [ " S!
14. Poisson Processes
 4. Posso Processes I Lecure 4 we roduced Posso arrvals as he lmg behavor of Bomal radom varables. Refer o Posso approxmao of Bomal radom varables. From he dscusso here see 4-6-4-8 Lecure 4 " arrvals occur
4. Posso Processes I Lecure 4 we roduced Posso arrvals as he lmg behavor of Bomal radom varables. Refer o Posso approxmao of Bomal radom varables. From he dscusso here see 4-6-4-8 Lecure 4 " arrvals occur
n α j x j = 0 j=1 has a nontrivial solution. Here A is the n k matrix whose jth column is the vector for all t j=0
 MODULE 2 Topcs: Lnear ndependence, bass and dmenson We have seen that f n a set of vectors one vector s a lnear combnaton of the remanng vectors n the set then the span of the set s unchanged f that vector
MODULE 2 Topcs: Lnear ndependence, bass and dmenson We have seen that f n a set of vectors one vector s a lnear combnaton of the remanng vectors n the set then the span of the set s unchanged f that vector
Scilab Textbook Companion for Linear Algebra and Its Applications by D. C. Lay 1
 Scilab Textbook Companion for Linear Algebra and Its Applications by D. C. Lay 1 Created by Animesh Biyani B.Tech (Pursuing) Electrical Engineering National Institute Of Technology, Karnataka College Teacher
Scilab Textbook Companion for Linear Algebra and Its Applications by D. C. Lay 1 Created by Animesh Biyani B.Tech (Pursuing) Electrical Engineering National Institute Of Technology, Karnataka College Teacher
Online Supplement for Dynamic Multi-Technology. Production-Inventory Problem with Emissions Trading
 Onlne Supplemen for Dynamc Mul-Technology Producon-Invenory Problem wh Emssons Tradng by We Zhang Zhongsheng Hua Yu Xa and Baofeng Huo Proof of Lemma For any ( qr ) Θ s easy o verfy ha he lnear programmng
Onlne Supplemen for Dynamc Mul-Technology Producon-Invenory Problem wh Emssons Tradng by We Zhang Zhongsheng Hua Yu Xa and Baofeng Huo Proof of Lemma For any ( qr ) Θ s easy o verfy ha he lnear programmng
Comb Filters. Comb Filters
 The smple flers dscussed so far are characered eher by a sngle passband and/or a sngle sopband There are applcaons where flers wh mulple passbands and sopbands are requred Thecomb fler s an example of
The smple flers dscussed so far are characered eher by a sngle passband and/or a sngle sopband There are applcaons where flers wh mulple passbands and sopbands are requred Thecomb fler s an example of
ZANIMLJIV NAČIN IZRAČUNAVANJA NEKIH GRANIČNIH VRIJEDNOSTI FUNKCIJA. Šefket Arslanagić, Sarajevo, BiH
 MAT-KOL (Banja Luka) XXIII ()(7), -7 http://wwwimviblorg/dmbl/dmblhtm DOI: 75/МК7A ISSN 5-6969 (o) ISSN 986-588 (o) ZANIMLJIV NAČIN IZRAČUNAVANJA NEKIH GRANIČNIH VRIJEDNOSTI FUNKCIJA Šefket Arslanagić,
MAT-KOL (Banja Luka) XXIII ()(7), -7 http://wwwimviblorg/dmbl/dmblhtm DOI: 75/МК7A ISSN 5-6969 (o) ISSN 986-588 (o) ZANIMLJIV NAČIN IZRAČUNAVANJA NEKIH GRANIČNIH VRIJEDNOSTI FUNKCIJA Šefket Arslanagić,
DEEP UNFOLDING FOR MULTICHANNEL SOURCE SEPARATION SUPPLEMENTARY MATERIAL
 DEEP UNFOLDING FOR MULTICHANNEL SOURCE SEPARATION SUPPLEMENTARY MATERIAL Sco Wsdom, John Hershey 2, Jonahan Le Roux 2, and Shnj Waanabe 2 Deparmen o Elecrcal Engneerng, Unversy o Washngon, Seale, WA, USA
DEEP UNFOLDING FOR MULTICHANNEL SOURCE SEPARATION SUPPLEMENTARY MATERIAL Sco Wsdom, John Hershey 2, Jonahan Le Roux 2, and Shnj Waanabe 2 Deparmen o Elecrcal Engneerng, Unversy o Washngon, Seale, WA, USA
Part II CONTINUOUS TIME STOCHASTIC PROCESSES
 Par II CONTINUOUS TIME STOCHASTIC PROCESSES 4 Chaper 4 For an advanced analyss of he properes of he Wener process, see: Revus D and Yor M: Connuous marngales and Brownan Moon Karazas I and Shreve S E:
Par II CONTINUOUS TIME STOCHASTIC PROCESSES 4 Chaper 4 For an advanced analyss of he properes of he Wener process, see: Revus D and Yor M: Connuous marngales and Brownan Moon Karazas I and Shreve S E:
Sampling Procedure of the Sum of two Binary Markov Process Realizations
 Samplng Procedure of he Sum of wo Bnary Markov Process Realzaons YURY GORITSKIY Dep. of Mahemacal Modelng of Moscow Power Insue (Techncal Unversy), Moscow, RUSSIA, E-mal: gorsky@yandex.ru VLADIMIR KAZAKOV
Samplng Procedure of he Sum of wo Bnary Markov Process Realzaons YURY GORITSKIY Dep. of Mahemacal Modelng of Moscow Power Insue (Techncal Unversy), Moscow, RUSSIA, E-mal: gorsky@yandex.ru VLADIMIR KAZAKOV
COMPUTER SCIENCE 349A SAMPLE EXAM QUESTIONS WITH SOLUTIONS PARTS 1, 2
 COMPUTE SCIENCE 49A SAMPLE EXAM QUESTIONS WITH SOLUTIONS PATS, PAT.. a Dene he erm ll-ondoned problem. b Gve an eample o a polynomal ha has ll-ondoned zeros.. Consder evaluaon o anh, where e e anh. e e
COMPUTE SCIENCE 49A SAMPLE EXAM QUESTIONS WITH SOLUTIONS PATS, PAT.. a Dene he erm ll-ondoned problem. b Gve an eample o a polynomal ha has ll-ondoned zeros.. Consder evaluaon o anh, where e e anh. e e
OH BOY! Story. N a r r a t iv e a n d o bj e c t s th ea t e r Fo r a l l a g e s, fr o m th e a ge of 9
 OH BOY! O h Boy!, was or igin a lly cr eat ed in F r en ch an d was a m a jor s u cc ess on t h e Fr en ch st a ge f or young au di enc es. It h a s b een s een by ap pr ox i ma t ely 175,000 sp ect at
OH BOY! O h Boy!, was or igin a lly cr eat ed in F r en ch an d was a m a jor s u cc ess on t h e Fr en ch st a ge f or young au di enc es. It h a s b een s een by ap pr ox i ma t ely 175,000 sp ect at
ABSTRACT KEYWORDS. Bonus-malus systems, frequency component, severity component. 1. INTRODUCTION
 EERAIED BU-MAU YTEM ITH A FREQUECY AD A EVERITY CMET A IDIVIDUA BAI I AUTMBIE IURACE* BY RAHIM MAHMUDVAD AD HEI HAAI ABTRACT Frangos and Vronos (2001) proposed an opmal bonus-malus sysems wh a frequency
EERAIED BU-MAU YTEM ITH A FREQUECY AD A EVERITY CMET A IDIVIDUA BAI I AUTMBIE IURACE* BY RAHIM MAHMUDVAD AD HEI HAAI ABTRACT Frangos and Vronos (2001) proposed an opmal bonus-malus sysems wh a frequency
Bandlimited channel. Intersymbol interference (ISI) This non-ideal communication channel is also called dispersive channel
 Inersymol nererence ISI ISI s a sgnal-dependen orm o nererence ha arses ecause o devaons n he requency response o a channel rom he deal channel. Example: Bandlmed channel Tme Doman Bandlmed channel Frequency
Inersymol nererence ISI ISI s a sgnal-dependen orm o nererence ha arses ecause o devaons n he requency response o a channel rom he deal channel. Example: Bandlmed channel Tme Doman Bandlmed channel Frequency
