On use of Mixed Quadrature Rule for Numerical Integration over a Triangular Domain
|
|
|
- Arline Carpenter
- 5 years ago
- Views:
Transcription
1 International Journal of Pure and Applied Mathematical Sciences. ISSN Volume 9, Number 2 (26), pp Research India Publications On use of Mixed Quadrature Rule for Numerical Integration over a Triangular Domain Dwiti Krushna Behera and Rajani Ballav Dash Department of Mathematics Ravenshaw University, Cuttack-7533, Odisha, India. dwiti78@gmail.com, rajani_bdash@rediffmail.com Abstract In this paper, we introduce a mixed quadrature of Fejer s second rule and Gaussian rule for numerical integration over the standard triangular surface: {(x, y) x, y, x + y } in the Cartesian two-dimensional (x, y) space. Mathematical transformation from (x, y) space to (ξ, η) space maps the standard triangle in (x, y) space to a standard 2-square in (ξ, η) space: {(ξ, η) ξ, η }. The relative efficiencies of this rule have been numerically verified on test integrals. Asymptotic error estimate of this rule has been determined. Keywords: Fejer s second quadrature rule, Gaussian rule, mixed quadrature rule, finite element Method(FEM), extended numerical integration. 2 Mathematics Subject Classification: 65D3, 65D32 I. INTRODUCTION The integration theory extends from real line to the plane and three dimensional spaces by the introduction of multiple integrals. In practice, most of integrals those can t be evaluated either analytically or through the evaluation process are very lengthy and tedious. In probabilistic estimation, the finite element method(fem) is also a well known method for evaluating of integrals over arbitrary-shaped domain Ω. The triangular and tetrahedral elements are very widely used in FEM. Also, FEM are used in calculation of mass shell, fluid and mass flows across a surface, electric charge distribution over a surface, plate bending, heat conduction over a plate and
2 92 Dwiti Krushna Behera and Rajani Ballav Dash similar problems in other areas of engineering which are very difficult to analyze using analytic techniques but these problems can be solved by using FEM. The basic problem of integration of an arbitrary function of two variables over the surface of a triangle was first introduced by Hammer et. al. [] and Hammer and Stroud [2, 3]. In connection of FEM, the triangular elements provide a tremendous results. Cowper [4] provided a table of Gaussian quadrature formula for symmetrically placed integration points. Lyness and Jespersen [5] made an elaborate study of symmetric quadrature rules by formulating the problem in polar coordinates. Lannoy [6] discussed the numerical error in integration rule [4]. Laurie [7] derived 7-point integration rule and discussed the numerical error in integrating some functions. Laursen and Gellert [8] gave a detailed table of symmetric integration formulae and suggested some new higher-order formulae of precision up to degree. Lether [9], Hillion[2] and Lague and Baldur [3] considered the product formulae derivable from one-dimensional Gaussian quadrature rules. Reddy [4 ], and Reddy and Shippy [8]derived 3-, 4-, 6 and 7-point formulae which give improved accuracy. The formulation of mixed quadrature rules was first coined by R. N. Das and G. Pradhan [9]. Many author s [2-2, 24] have produced different mixed quadrature rules. Very recently D. K. Behera et. al. [2-2] formed a mixed quadrature rule blending Fejer s second rule and Gaussian rule for evaluating integrals of both real and analytic functions, which leads a excellent result. In this paper, we get motivation for successfully forming a mixed quadrature rule of Fejer s second rule and Gaussian rule over a triangular domain. The mixed quadrature rule over a triangular domain so found has been tested and compared with its constituent rules by computing numerically three tested integrals. II. FORMULATION OF INTEGRALS OVER A TRIANGULAR AREA The finite-element method for two-dimensional problems with triangular elements requires the numerical integration of shape functions on a triangle. Since an affine transformation makes it possible to transform any triangle into the two-dimensional standard triangle T with co-ordinates (, ), (, ) and (, ) in Cartesian frame, we have to consider just the numerical integration on T. The numerical integration of an arbitrary function f over the triangle T is given by I = T f(x, y) x y dxdy = dx f(x, y)dy = dy f(x, y)dx. (2.) It is now required to find the value of the integral by a quadrature formula: N I= m= C m f(x m, y m ). (2.2) Where C m are the weights associated with specific points (x m, y m ) and N is the number of pivotal points related to the required precision.
3 On use of Mixed Quadrature Rule for Numerical Integration over a Triangular Domain 93 The double integral over the triangle surface of equation (2.) can be transformed to the standard square {(u, v) u, v } by substitution x = u and y = ( u)v We have I = Where J(u, v) = x f(x, y) dydx = f(x(u, v), y(u, v)) x y u x u y v v = u. J dudv. (2.3) From equation (2.3), we have I = f(u, ( u)v)( u)dudv. (2.4) The integral I of equation (2.4) can be transformed further into an integral over the standard 2-square: {(ξ, η) ξ, η } by substitution u = +ξ Then clearly the determinant of the Jacobian and the differential area are (u, v) = u v u v = (ξ, η ) ξ η η ξ 2 () = 2 4 (u, v) 2, v = +η 2. (2.5) dudv = dξdη = dξdη (2.6) (ξ, η ) 4 Now on using equations (2.5) and (2.6) in equation(2.4) we have I = x f(x, y) dydx = f(u, ( u)v)( u) dudv = f ( +ξ, ( ξ)(+η) 2 4 ) ( ξ ) dξdη (2.7) 8 Equation(2.7) represents an integral over the surface of standard 2-square: {(ξ, η) ξ, η }. Efficiently quadrature coefficients are readily obtained [25]. From equation(2.7), we can write: I = f(x(ξ, η), y(ξ, η)) n n ( ξ 8 ) dξdη. I = ( ξ i i= j= w i w j f(x(ξ i, η j ), y(ξ i, η j ) ). (2.8) 8 ) Where ξ i, η j are Gaussian points in the ξ, η directions respectively, and w i, w j are the corresponding weights.
4 94 Dwiti Krushna Behera and Rajani Ballav Dash We can write equation(2.8) as: N=n n I = k= C k f(x k, y k ). (2.9) Where C k, x k, y k are obtained from the relation C k = ( ξ i 8 ) w iw j x k = +ξ i 2 y k = ( ξ i )(+η j) 4 } Where k =,2,, n i =,2,, n j =,2,, n (2.) The weighting coefficients C k and sampling points (x k, y k ) of various orders can now be easily computed by formulae (2.9) and (2.). We have tabulated a sample of these weight coefficients and sampling points in Table-. III. MIXED QUADRATURE OF FEJER S 2 ND RULE AND GAUSS- LEGENDRE RULE IN ONE VARIABLE The mixed quadrature (I mix ) of Fejer s 2 nd rule and Gauss-Legendre rule in one variable developed by D. K. Behera et.al.[2] is given below: I mix = f(x)dx 225 [ 896f ( 3 2 ) 375f ( 3 5 ) + 52f ( 2 ) + 64f() + 52f ( 2 ) 375f ( 3 ) + 896f ( 3 ) 5 2 ] (3.) Where w = , w 2 = , w 3 = , w 4 = , w 5 = , w 6 = , w 7 = Applying the mixed rule(3.) to double integral we have I mix = f(x(ξ, η), y(ξ, η)) ( ξ 8 ) dξdη I mix k= C k f(x ij, y ij ) = k= C k f(x k, y k ) (3.2) Where C k = C ij = ( ξ i 8 ) w iw j x k = x ij and y k = y ij } (3.3)
5 On use of Mixed Quadrature Rule for Numerical Integration over a Triangular Domain 95 The weighting coefficients C k and sampling points (x k, y k ) of various orders can be easily computed using the equation (2.). NUMERICAL VERIFICATIONS Integrals Exact Value Approximate Values Error y I = (x + y) 2dxdy y I 2 = (x + y) 2dxdy x I 3 = e y2 cos(xy)dxdy V. CONCLUSIONS From the numerical verification we conclude that the mixed quadratute rule used in this paper gives better result than those obtained in the previous papers [6, 22, 24 ] on integration of real functions over triangles. REFERENCES [] P. C. Hammer, O. J. Marlowe and A. H. Stroud, Numerical integration over simplexes and cones, Math Tables other Aids Computation,, 3-36 (956). [2] P. C. Hammer and A. H. Stroud, Numerical integration over simplexes, Math Tables other Aids Computation,, (956). [3] P. C. Hammer and A. H. Stroud, Numerical evaluation of multiple integrals, Math Tables other Aids Computation, 2, (958). [4] G. R. Cowper, Gaussian quadrature formulas for triangles, Int. Num. Meth. Engg., 7, (973). [5] J. N. Lyness and D. Jespersen, Moderate degree symmetric quadrature rules for the triangle, J. Inst. Math. Applic., 5, 9-32 (975). [6] F. G. Lannoy, Triangular Finite Elements and Numerical Integration, Computer Struct, 7, 63 (977). [7] D. P. Laurie, Automatic numerical integration over a triangle, CSIR Spec. Rep. WISK 273, National Institute for Mathematical Sciences, Pretoria (977).
6 96 Dwiti Krushna Behera and Rajani Ballav Dash [8] M. E. Laursen and M. Gellert, Some criteria for numerically integrated matrices and quadrature formulas for triangles, Int. J. Num. Meth. Engg, 2, (978). [9] F. G. Lether, Computation of double integrals over a triangle, J. Comp. Applic. Math., 2, (976). [] J. Stoer and R.Bulirsch, Introduction to Numerical Analysis, 3 rd ed.(springer International Edition). [] Kendall E. Atkinson, An Introduction to numerical Analysis, 2 nd ed.(john Wiley). [2] P. Hillion, Numerical integration on a triangle, Int. J. Num. Meth. Engg.,, (977). [3] G. Lague and R. Baldur, Extended numerical integration method for triangular surfaces, Int. J. Num. Meth. Engg.,, (977). [4] C. T. Reddy, Improved three point integration schemes for triangular finite elements, Int. J. Num. Meth. Engg., 2, (978). [5] H. T. Rathod and M. S. Karim, An Explicit Integration Scheme based on Recursion for Curved Triangular Finite Elements, Computer Struct, 8, 43-76(22). [6] H. T. Rathod et. al., Gauss-Legendre Quadrature over Triangles, J. Indian Inst. Sci., 84, 83 88(24). [7] H. T. Rathod and M. S. Karim, An explicit integration scheme based on recursion for curved triangular finite elements, Computers Struct., 8, 43-76(22). [8] C. T. Reddy and D. J. Shippy, Alternative integration formulae for triangular finite elements, Int. J. Num. Meth. Engg., 7, 33-39(98). [9] R. N. Das and G. Pradhan, A mixed quadrature rule for approximate evalution of real definite integrals, Int. J. Math. Educ. Sci. and Technology, 27(2), (996). [2] D. K. Behera, A. K. Sethi and R. B. Dash, An Open type Mixed Quadrature Rule using Fejer and Gaussian Quadrature Rules, American International Journal of Research in Science, Technology, Engineering & Mathematics, 9(3), (25). [2] D. K. Behera and R. B. Dash, A Mixed Quadrature Rule for Numerical Integration of Analytic Functions by using Fejer and Gaussian Quadrature Rules, Bulletin of Pure and Applied Sciences, 34E(2), 6-67 (25). [22] K. T. Shivaram, Generalised Gaussian Quadrature over a triangle, American Journal of Engineering Research, 2(9), (23. [23] F. Hussain and M. S. Karim, Accurate Evalution Schemes for Triangular Domain Integrals, IOSR Journal of Mechanical and Civil Engineering, 2(6), 38-5(22). [24] S. R. Jena and R. B. Dash, Mixed Quadrature of real definite Integral over triangles, Pacific-Asian Journal of Mathematics, 3(-2), 9-24(29). [25] M. Abramowicz and I. A. Stegum(eds), Handbook of Mathematical Functions, Dover (964).
Short Communication. Gauss Legendre quadrature over a triangle
 J. Indian Inst. Sci., Sept. Oct. 4, 4, 3 Indian Institute of Science. Short Communication Gauss Legendre quadrature over a triangle H. T. RATHOD *, K. V. NAGARAJA, B. VENKATESUDU 3 AND N. L. RAMESH 4 Department
J. Indian Inst. Sci., Sept. Oct. 4, 4, 3 Indian Institute of Science. Short Communication Gauss Legendre quadrature over a triangle H. T. RATHOD *, K. V. NAGARAJA, B. VENKATESUDU 3 AND N. L. RAMESH 4 Department
Gauss Legendre quadrature over a parabolic region
 Gauss Legendre quadrature over a parabolic region K. T. Shivaram Department of Mathematics, Dayananda sagar college of Engineering, Bangalore, India Abstract In this paper, we introduce a Gauss Legendre
Gauss Legendre quadrature over a parabolic region K. T. Shivaram Department of Mathematics, Dayananda sagar college of Engineering, Bangalore, India Abstract In this paper, we introduce a Gauss Legendre
Numerical Evaluation of Integrals with weight function x k Using Gauss Legendre Quadrature Rules
 IOSR Journal of Mathematics (IOSR-JM) e-issn: 2278-728, p-issn: 29-76X. Volume, Issue Ver. V (May - Jun. 2), PP 9-6 www.iosrjournals.org Numerical Evaluation of Integrals with weight function k Using Gauss
IOSR Journal of Mathematics (IOSR-JM) e-issn: 2278-728, p-issn: 29-76X. Volume, Issue Ver. V (May - Jun. 2), PP 9-6 www.iosrjournals.org Numerical Evaluation of Integrals with weight function k Using Gauss
CHAPTER 4 NUMERICAL INTEGRATION METHODS TO EVALUATE TRIPLE INTEGRALS USING GENERALIZED GAUSSIAN QUADRATURE
 CHAPTER 4 NUMERICAL INTEGRATION METHODS TO EVALUATE TRIPLE INTEGRALS USING GENERALIZED GAUSSIAN QUADRATURE 4.1 Introduction Many applications in science and engineering require the solution of three dimensional
CHAPTER 4 NUMERICAL INTEGRATION METHODS TO EVALUATE TRIPLE INTEGRALS USING GENERALIZED GAUSSIAN QUADRATURE 4.1 Introduction Many applications in science and engineering require the solution of three dimensional
Numerical Integration exact integration is not needed to achieve the optimal convergence rate of nite element solutions ([, 9, 11], and Chapter 7). In
![Numerical Integration exact integration is not needed to achieve the optimal convergence rate of nite element solutions ([, 9, 11], and Chapter 7). In Numerical Integration exact integration is not needed to achieve the optimal convergence rate of nite element solutions ([, 9, 11], and Chapter 7). In](/thumbs/80/80480766.jpg) Chapter 6 Numerical Integration 6.1 Introduction After transformation to a canonical element,typical integrals in the element stiness or mass matrices (cf. (5.5.8)) have the forms Q = T ( )N s Nt det(j
Chapter 6 Numerical Integration 6.1 Introduction After transformation to a canonical element,typical integrals in the element stiness or mass matrices (cf. (5.5.8)) have the forms Q = T ( )N s Nt det(j
An Accurate Quadrature for the Numerical Integration of Polynomial Functions
 International Journal of Applied Mathematics and Theoretical Physics 2018; 4(1: 1-7 http://www.sciencepublishinggroup.com/j/ijamtp doi: 10.11648/j.ijamtp.20180401.11 ISSN: 2575-5919 (Print; ISSN: 2575-5927
International Journal of Applied Mathematics and Theoretical Physics 2018; 4(1: 1-7 http://www.sciencepublishinggroup.com/j/ijamtp doi: 10.11648/j.ijamtp.20180401.11 ISSN: 2575-5919 (Print; ISSN: 2575-5927
Chapter 10 INTEGRATION METHODS Introduction Unit Coordinate Integration
 Chapter 0 INTEGRATION METHODS 0. Introduction The finite element analysis techniques are always based on an integral formulation. At the very minimum it will always be necessary to integrate at least an
Chapter 0 INTEGRATION METHODS 0. Introduction The finite element analysis techniques are always based on an integral formulation. At the very minimum it will always be necessary to integrate at least an
Romberg Integration and Gaussian Quadrature
 Romberg Integration and Gaussian Quadrature P. Sam Johnson October 17, 014 P. Sam Johnson (NITK) Romberg Integration and Gaussian Quadrature October 17, 014 1 / 19 Overview We discuss two methods for integration.
Romberg Integration and Gaussian Quadrature P. Sam Johnson October 17, 014 P. Sam Johnson (NITK) Romberg Integration and Gaussian Quadrature October 17, 014 1 / 19 Overview We discuss two methods for integration.
MATH 52 FINAL EXAM DECEMBER 7, 2009
 MATH 52 FINAL EXAM DECEMBER 7, 2009 THIS IS A CLOSED BOOK, CLOSED NOTES EXAM. NO CALCULATORS OR OTHER ELECTRONIC DEVICES ARE PERMITTED. IF YOU NEED EXTRA SPACE, PLEASE USE THE BACK OF THE PREVIOUS PROB-
MATH 52 FINAL EXAM DECEMBER 7, 2009 THIS IS A CLOSED BOOK, CLOSED NOTES EXAM. NO CALCULATORS OR OTHER ELECTRONIC DEVICES ARE PERMITTED. IF YOU NEED EXTRA SPACE, PLEASE USE THE BACK OF THE PREVIOUS PROB-
16.2 Iterated Integrals
 6.2 Iterated Integrals So far: We have defined what we mean by a double integral. We have estimated the value of a double integral from contour diagrams and from tables of values. We have interpreted the
6.2 Iterated Integrals So far: We have defined what we mean by a double integral. We have estimated the value of a double integral from contour diagrams and from tables of values. We have interpreted the
xm y n dx dy so that similar expressions could be used to evaluate the volume integrals.
 Chapter Integration methods. Introduction The finite element analysis techniques are always based on an integral formulation. At the very minimum it will always be necessary to integrate at least an element
Chapter Integration methods. Introduction The finite element analysis techniques are always based on an integral formulation. At the very minimum it will always be necessary to integrate at least an element
4.4 Change of Variable in Integrals: The Jacobian
 4.4. CHANGE OF VAIABLE IN INTEGALS: THE JACOBIAN 4 4.4 Change of Variable in Integrals: The Jacobian In this section, we generalize to multiple integrals the substitution technique used with definite integrals.
4.4. CHANGE OF VAIABLE IN INTEGALS: THE JACOBIAN 4 4.4 Change of Variable in Integrals: The Jacobian In this section, we generalize to multiple integrals the substitution technique used with definite integrals.
Oct : Lecture 15: Surface Integrals and Some Related Theorems
 90 MIT 3.016 Fall 2005 c W.C Carter Lecture 15 Oct. 21 2005: Lecture 15: Surface Integrals and Some Related Theorems Reading: Kreyszig Sections: 9.4 pp:485 90), 9.5 pp:491 495) 9.6 pp:496 505) 9.7 pp:505
90 MIT 3.016 Fall 2005 c W.C Carter Lecture 15 Oct. 21 2005: Lecture 15: Surface Integrals and Some Related Theorems Reading: Kreyszig Sections: 9.4 pp:485 90), 9.5 pp:491 495) 9.6 pp:496 505) 9.7 pp:505
3. Numerical integration
 3. Numerical integration... 3. One-dimensional quadratures... 3. Two- and three-dimensional quadratures... 3.3 Exact Integrals for Straight Sided Triangles... 5 3.4 Reduced and Selected Integration...
3. Numerical integration... 3. One-dimensional quadratures... 3. Two- and three-dimensional quadratures... 3.3 Exact Integrals for Straight Sided Triangles... 5 3.4 Reduced and Selected Integration...
Instructions: No books. No notes. Non-graphing calculators only. You are encouraged, although not required, to show your work.
 Exam 3 Math 850-007 Fall 04 Odenthal Name: Instructions: No books. No notes. Non-graphing calculators only. You are encouraged, although not required, to show your work.. Evaluate the iterated integral
Exam 3 Math 850-007 Fall 04 Odenthal Name: Instructions: No books. No notes. Non-graphing calculators only. You are encouraged, although not required, to show your work.. Evaluate the iterated integral
A MODIFIED DECOUPLED SCALED BOUNDARY-FINITE ELEMENT METHOD FOR MODELING 2D IN-PLANE-MOTION TRANSIENT ELASTODYNAMIC PROBLEMS IN SEMI-INFINITE MEDIA
 8 th GRACM International Congress on Computational Mechanics Volos, 2 July 5 July 205 A MODIFIED DECOUPLED SCALED BOUNDARY-FINITE ELEMENT METHOD FOR MODELING 2D IN-PLANE-MOTION TRANSIENT ELASTODYNAMIC
8 th GRACM International Congress on Computational Mechanics Volos, 2 July 5 July 205 A MODIFIED DECOUPLED SCALED BOUNDARY-FINITE ELEMENT METHOD FOR MODELING 2D IN-PLANE-MOTION TRANSIENT ELASTODYNAMIC
ME 1401 FINITE ELEMENT ANALYSIS UNIT I PART -A. 2. Why polynomial type of interpolation functions is mostly used in FEM?
 SHRI ANGALAMMAN COLLEGE OF ENGINEERING AND TECHNOLOGY (An ISO 9001:2008 Certified Institution) SIRUGANOOR, TIRUCHIRAPPALLI 621 105 Department of Mechanical Engineering ME 1401 FINITE ELEMENT ANALYSIS 1.
SHRI ANGALAMMAN COLLEGE OF ENGINEERING AND TECHNOLOGY (An ISO 9001:2008 Certified Institution) SIRUGANOOR, TIRUCHIRAPPALLI 621 105 Department of Mechanical Engineering ME 1401 FINITE ELEMENT ANALYSIS 1.
Vector Calculus. Dr. D. Sukumar
 Vector Calculus Dr. D. Sukumar Space co-ordinates Change of variable Cartesian co-ordinates < x < Cartesian co-ordinates < x < < y < Cartesian co-ordinates < x < < y < < z < Cylindrical Cylindrical Cylindrical
Vector Calculus Dr. D. Sukumar Space co-ordinates Change of variable Cartesian co-ordinates < x < Cartesian co-ordinates < x < < y < Cartesian co-ordinates < x < < y < < z < Cylindrical Cylindrical Cylindrical
MA2501 Numerical Methods Spring 2015
 Norwegian University of Science and Technology Department of Mathematics MA5 Numerical Methods Spring 5 Solutions to exercise set 9 Find approximate values of the following integrals using the adaptive
Norwegian University of Science and Technology Department of Mathematics MA5 Numerical Methods Spring 5 Solutions to exercise set 9 Find approximate values of the following integrals using the adaptive
4. Be able to set up and solve an integral using a change of variables. 5. Might be useful to remember the transformation formula for rotations.
 Change of variables What to know. Be able to find the image of a transformation 2. Be able to invert a transformation 3. Be able to find the Jacobian of a transformation 4. Be able to set up and solve
Change of variables What to know. Be able to find the image of a transformation 2. Be able to invert a transformation 3. Be able to find the Jacobian of a transformation 4. Be able to set up and solve
Numerical integration formulas of degree two
 Applied Numerical Mathematics 58 (2008) 1515 1520 www.elsevier.com/locate/apnum Numerical integration formulas of degree two ongbin Xiu epartment of Mathematics, Purdue University, West Lafayette, IN 47907,
Applied Numerical Mathematics 58 (2008) 1515 1520 www.elsevier.com/locate/apnum Numerical integration formulas of degree two ongbin Xiu epartment of Mathematics, Purdue University, West Lafayette, IN 47907,
Solution of Fuzzy System of Linear Equations with Polynomial Parametric Form
 Available at http://pvamu.edu/aam Appl. Appl. Math. ISSN: 1932-9466 Vol. 7, Issue 2 (December 2012), pp. 648-657 Applications and Applied Mathematics: An International Journal (AAM) Solution of Fuzzy System
Available at http://pvamu.edu/aam Appl. Appl. Math. ISSN: 1932-9466 Vol. 7, Issue 2 (December 2012), pp. 648-657 Applications and Applied Mathematics: An International Journal (AAM) Solution of Fuzzy System
Math 340 Final Exam December 16, 2006
 Math 34 Final Exam December 6, 6. () Suppose A 3 4. a) Find the row-reduced echelon form of A. 3 4 so the row reduced echelon form is b) What is rank(a)? 3 4 4 The rank is two since there are two pivots.
Math 34 Final Exam December 6, 6. () Suppose A 3 4. a) Find the row-reduced echelon form of A. 3 4 so the row reduced echelon form is b) What is rank(a)? 3 4 4 The rank is two since there are two pivots.
f dr. (6.1) f(x i, y i, z i ) r i. (6.2) N i=1
 hapter 6 Integrals In this chapter we will look at integrals in more detail. We will look at integrals along a curve, and multi-dimensional integrals in 2 or more dimensions. In physics we use these integrals
hapter 6 Integrals In this chapter we will look at integrals in more detail. We will look at integrals along a curve, and multi-dimensional integrals in 2 or more dimensions. In physics we use these integrals
ANALYTICAL MATHEMATICS FOR APPLICATIONS 2018 LECTURE NOTES 3
 ANALYTICAL MATHEMATICS FOR APPLICATIONS 2018 LECTURE NOTES 3 ISSUED 24 FEBRUARY 2018 1 Gaussian elimination Let A be an (m n)-matrix Consider the following row operations on A (1) Swap the positions any
ANALYTICAL MATHEMATICS FOR APPLICATIONS 2018 LECTURE NOTES 3 ISSUED 24 FEBRUARY 2018 1 Gaussian elimination Let A be an (m n)-matrix Consider the following row operations on A (1) Swap the positions any
 Code No: RT41033 R13 Set No. 1 IV B.Tech I Semester Regular Examinations, November - 2016 FINITE ELEMENT METHODS (Common to Mechanical Engineering, Aeronautical Engineering and Automobile Engineering)
Code No: RT41033 R13 Set No. 1 IV B.Tech I Semester Regular Examinations, November - 2016 FINITE ELEMENT METHODS (Common to Mechanical Engineering, Aeronautical Engineering and Automobile Engineering)
Math 67. Rumbos Fall Solutions to Review Problems for Final Exam. (a) Use the triangle inequality to derive the inequality
 Math 67. umbos Fall 8 Solutions to eview Problems for Final Exam. In this problem, u and v denote vectors in n. (a) Use the triangle inequality to derive the inequality Solution: Write v u v u for all
Math 67. umbos Fall 8 Solutions to eview Problems for Final Exam. In this problem, u and v denote vectors in n. (a) Use the triangle inequality to derive the inequality Solution: Write v u v u for all
Math 425 Notes 9. We state a rough version of the fundamental theorem of calculus. Almost all calculations involving integrals lead back to this.
 Multiple Integrals: efintion Math 425 Notes 9 We state a rough version of the fundamental theorem of calculus. Almost all calculations involving integrals lead back to this. efinition 1. Let f : R R and
Multiple Integrals: efintion Math 425 Notes 9 We state a rough version of the fundamental theorem of calculus. Almost all calculations involving integrals lead back to this. efinition 1. Let f : R R and
JEPPIAAR ENGINEERING COLLEGE
 JEPPIAAR ENGINEERING COLLEGE Jeppiaar Nagar, Rajiv Gandhi Salai 600 119 DEPARTMENT OFMECHANICAL ENGINEERING QUESTION BANK VI SEMESTER ME6603 FINITE ELEMENT ANALYSIS Regulation 013 SUBJECT YEAR /SEM: III
JEPPIAAR ENGINEERING COLLEGE Jeppiaar Nagar, Rajiv Gandhi Salai 600 119 DEPARTMENT OFMECHANICAL ENGINEERING QUESTION BANK VI SEMESTER ME6603 FINITE ELEMENT ANALYSIS Regulation 013 SUBJECT YEAR /SEM: III
Math 127C, Spring 2006 Final Exam Solutions. x 2 ), g(y 1, y 2 ) = ( y 1 y 2, y1 2 + y2) 2. (g f) (0) = g (f(0))f (0).
 Math 27C, Spring 26 Final Exam Solutions. Define f : R 2 R 2 and g : R 2 R 2 by f(x, x 2 (sin x 2 x, e x x 2, g(y, y 2 ( y y 2, y 2 + y2 2. Use the chain rule to compute the matrix of (g f (,. By the chain
Math 27C, Spring 26 Final Exam Solutions. Define f : R 2 R 2 and g : R 2 R 2 by f(x, x 2 (sin x 2 x, e x x 2, g(y, y 2 ( y y 2, y 2 + y2 2. Use the chain rule to compute the matrix of (g f (,. By the chain
MATH2111 Higher Several Variable Calculus Integration
 MATH2 Higher Several Variable Calculus Integration Dr. Jonathan Kress School of Mathematics and Statistics University of New South Wales Semester, 26 [updated: April 3, 26] JM Kress (UNSW Maths & Stats)
MATH2 Higher Several Variable Calculus Integration Dr. Jonathan Kress School of Mathematics and Statistics University of New South Wales Semester, 26 [updated: April 3, 26] JM Kress (UNSW Maths & Stats)
The Discontinuous Galerkin Method for Hyperbolic Problems
 Chapter 2 The Discontinuous Galerkin Method for Hyperbolic Problems In this chapter we shall specify the types of problems we consider, introduce most of our notation, and recall some theory on the DG
Chapter 2 The Discontinuous Galerkin Method for Hyperbolic Problems In this chapter we shall specify the types of problems we consider, introduce most of our notation, and recall some theory on the DG
Reflections and Rotations in R 3
 Reflections and Rotations in R 3 P. J. Ryan May 29, 21 Rotations as Compositions of Reflections Recall that the reflection in the hyperplane H through the origin in R n is given by f(x) = x 2 ξ, x ξ (1)
Reflections and Rotations in R 3 P. J. Ryan May 29, 21 Rotations as Compositions of Reflections Recall that the reflection in the hyperplane H through the origin in R n is given by f(x) = x 2 ξ, x ξ (1)
Sixth Order Newton-Type Method For Solving System Of Nonlinear Equations And Its Applications
 Applied Mathematics E-Notes, 17(017), 1-30 c ISSN 1607-510 Available free at mirror sites of http://www.math.nthu.edu.tw/ amen/ Sixth Order Newton-Type Method For Solving System Of Nonlinear Equations
Applied Mathematics E-Notes, 17(017), 1-30 c ISSN 1607-510 Available free at mirror sites of http://www.math.nthu.edu.tw/ amen/ Sixth Order Newton-Type Method For Solving System Of Nonlinear Equations
MULTIVARIABLE INTEGRATION
 MULTIVARIABLE INTEGRATION (PLANE & CYLINDRICAL POLAR COORDINATES) PLANE POLAR COORDINATES Question 1 The finite region on the x-y plane satisfies 1 x + y 4, y 0. Find, in terms of π, the value of I. I
MULTIVARIABLE INTEGRATION (PLANE & CYLINDRICAL POLAR COORDINATES) PLANE POLAR COORDINATES Question 1 The finite region on the x-y plane satisfies 1 x + y 4, y 0. Find, in terms of π, the value of I. I
LINEAR SECOND-ORDER EQUATIONS
 LINEAR SECON-ORER EQUATIONS Classification In two independent variables x and y, the general form is Au xx + 2Bu xy + Cu yy + u x + Eu y + Fu + G = 0. The coefficients are continuous functions of (x, y)
LINEAR SECON-ORER EQUATIONS Classification In two independent variables x and y, the general form is Au xx + 2Bu xy + Cu yy + u x + Eu y + Fu + G = 0. The coefficients are continuous functions of (x, y)
BACKGROUNDS. Two Models of Deformable Body. Distinct Element Method (DEM)
 BACKGROUNDS Two Models of Deformable Body continuum rigid-body spring deformation expressed in terms of field variables assembly of rigid-bodies connected by spring Distinct Element Method (DEM) simple
BACKGROUNDS Two Models of Deformable Body continuum rigid-body spring deformation expressed in terms of field variables assembly of rigid-bodies connected by spring Distinct Element Method (DEM) simple
1MA6 Partial Differentiation and Multiple Integrals: I
 1MA6/1 1MA6 Partial Differentiation and Multiple Integrals: I Dr D W Murray Michaelmas Term 1994 1. Total differential. (a) State the conditions for the expression P (x, y)dx+q(x, y)dy to be the perfect
1MA6/1 1MA6 Partial Differentiation and Multiple Integrals: I Dr D W Murray Michaelmas Term 1994 1. Total differential. (a) State the conditions for the expression P (x, y)dx+q(x, y)dy to be the perfect
Near Field Asymptotic Formulation for Dendritic Growth Due to Buoyancy
 Advances in Theoretical and Applied Mathematics. ISSN 973-4554 Volume 11 Number 4 16 pp. 437 44 Research India Publications http://www.ripublication.com/atam.htm Near Field Asymptotic Formulation for Dendritic
Advances in Theoretical and Applied Mathematics. ISSN 973-4554 Volume 11 Number 4 16 pp. 437 44 Research India Publications http://www.ripublication.com/atam.htm Near Field Asymptotic Formulation for Dendritic
Math 172 Problem Set 5 Solutions
 Math 172 Problem Set 5 Solutions 2.4 Let E = {(t, x : < x b, x t b}. To prove integrability of g, first observe that b b b f(t b b g(x dx = dt t dx f(t t dtdx. x Next note that f(t/t χ E is a measurable
Math 172 Problem Set 5 Solutions 2.4 Let E = {(t, x : < x b, x t b}. To prove integrability of g, first observe that b b b f(t b b g(x dx = dt t dx f(t t dtdx. x Next note that f(t/t χ E is a measurable
MATH 280 Multivariate Calculus Fall Integrating a vector field over a surface
 MATH 280 Multivariate Calculus Fall 2011 Definition Integrating a vector field over a surface We are given a vector field F in space and an oriented surface in the domain of F as shown in the figure below
MATH 280 Multivariate Calculus Fall 2011 Definition Integrating a vector field over a surface We are given a vector field F in space and an oriented surface in the domain of F as shown in the figure below
is a surface above the xy-plane over R.
 Chapter 13 Multiple Integration Section 13.1Double Integrals over ectangular egions ecall the Definite Integral from Chapter 5 b a n * lim i f x dx f x x n i 1 b If f x 0 then f xdx is the area under the
Chapter 13 Multiple Integration Section 13.1Double Integrals over ectangular egions ecall the Definite Integral from Chapter 5 b a n * lim i f x dx f x x n i 1 b If f x 0 then f xdx is the area under the
LEAST-SQUARES FINITE ELEMENT MODELS
 LEAST-SQUARES FINITE ELEMENT MODELS General idea of the least-squares formulation applied to an abstract boundary-value problem Works of our group Application to Poisson s equation Application to flows
LEAST-SQUARES FINITE ELEMENT MODELS General idea of the least-squares formulation applied to an abstract boundary-value problem Works of our group Application to Poisson s equation Application to flows
Spectra of Multiplication Operators as a Numerical Tool. B. Vioreanu and V. Rokhlin Technical Report YALEU/DCS/TR-1443 March 3, 2011
 We introduce a numerical procedure for the construction of interpolation and quadrature formulae on bounded convex regions in the plane. The construction is based on the behavior of spectra of certain
We introduce a numerical procedure for the construction of interpolation and quadrature formulae on bounded convex regions in the plane. The construction is based on the behavior of spectra of certain
Section 6.6 Gaussian Quadrature
 Section 6.6 Gaussian Quadrature Key Terms: Method of undetermined coefficients Nonlinear systems Gaussian quadrature Error Legendre polynomials Inner product Adapted from http://pathfinder.scar.utoronto.ca/~dyer/csca57/book_p/node44.html
Section 6.6 Gaussian Quadrature Key Terms: Method of undetermined coefficients Nonlinear systems Gaussian quadrature Error Legendre polynomials Inner product Adapted from http://pathfinder.scar.utoronto.ca/~dyer/csca57/book_p/node44.html
[2] (a) Develop and describe the piecewise linear Galerkin finite element approximation of,
![[2] (a) Develop and describe the piecewise linear Galerkin finite element approximation of, [2] (a) Develop and describe the piecewise linear Galerkin finite element approximation of,](/thumbs/88/117157910.jpg) 269 C, Vese Practice problems [1] Write the differential equation u + u = f(x, y), (x, y) Ω u = 1 (x, y) Ω 1 n + u = x (x, y) Ω 2, Ω = {(x, y) x 2 + y 2 < 1}, Ω 1 = {(x, y) x 2 + y 2 = 1, x 0}, Ω 2 = {(x,
269 C, Vese Practice problems [1] Write the differential equation u + u = f(x, y), (x, y) Ω u = 1 (x, y) Ω 1 n + u = x (x, y) Ω 2, Ω = {(x, y) x 2 + y 2 < 1}, Ω 1 = {(x, y) x 2 + y 2 = 1, x 0}, Ω 2 = {(x,
Four Point Gauss Quadrature Runge Kuta Method Of Order 8 For Ordinary Differential Equations
 International journal of scientific and technical research in engineering (IJSTRE) www.ijstre.com Volume Issue ǁ July 206. Four Point Gauss Quadrature Runge Kuta Method Of Order 8 For Ordinary Differential
International journal of scientific and technical research in engineering (IJSTRE) www.ijstre.com Volume Issue ǁ July 206. Four Point Gauss Quadrature Runge Kuta Method Of Order 8 For Ordinary Differential
Solution of First Order Initial Value Problem by Sixth Order Predictor Corrector Method
 Global Journal of Pure and Applied Mathematics. ISSN 0973-1768 Volume 13, Number 6 (2017), pp. 2277 2290 Research India Publications http://www.ripublication.com/gjpam.htm Solution of First Order Initial
Global Journal of Pure and Applied Mathematics. ISSN 0973-1768 Volume 13, Number 6 (2017), pp. 2277 2290 Research India Publications http://www.ripublication.com/gjpam.htm Solution of First Order Initial
Orthogonal Polynomials, Quadratures & Sparse-Grid Methods for Probability Integrals
 1/31 Orthogonal Polynomials, Quadratures & Sparse-Grid Methods for Probability Integrals Dr. Abebe Geletu May, 2010 Technische Universität Ilmenau, Institut für Automatisierungs- und Systemtechnik Fachgebiet
1/31 Orthogonal Polynomials, Quadratures & Sparse-Grid Methods for Probability Integrals Dr. Abebe Geletu May, 2010 Technische Universität Ilmenau, Institut für Automatisierungs- und Systemtechnik Fachgebiet
Conservation Laws & Applications
 Rocky Mountain Mathematics Consortium Summer School Conservation Laws & Applications Lecture V: Discontinuous Galerkin Methods James A. Rossmanith Department of Mathematics University of Wisconsin Madison
Rocky Mountain Mathematics Consortium Summer School Conservation Laws & Applications Lecture V: Discontinuous Galerkin Methods James A. Rossmanith Department of Mathematics University of Wisconsin Madison
MATH 317 Fall 2016 Assignment 5
 MATH 37 Fall 26 Assignment 5 6.3, 6.4. ( 6.3) etermine whether F(x, y) e x sin y îı + e x cos y ĵj is a conservative vector field. If it is, find a function f such that F f. enote F (P, Q). We have Q x
MATH 37 Fall 26 Assignment 5 6.3, 6.4. ( 6.3) etermine whether F(x, y) e x sin y îı + e x cos y ĵj is a conservative vector field. If it is, find a function f such that F f. enote F (P, Q). We have Q x
Transactions on Modelling and Simulation vol 12, 1996 WIT Press, ISSN X
 Simplifying integration for logarithmic singularities R.N.L. Smith Department ofapplied Mathematics & OR, Cranfield University, RMCS, Shrivenham, Swindon, Wiltshire SN6 SLA, UK Introduction Any implementation
Simplifying integration for logarithmic singularities R.N.L. Smith Department ofapplied Mathematics & OR, Cranfield University, RMCS, Shrivenham, Swindon, Wiltshire SN6 SLA, UK Introduction Any implementation
Applications of Gauss-Radau and Gauss-Lobatto Numerical Integrations Over a Four Node Quadrilateral Finite Element
 Avaiable online at www.banglaol.info angladesh J. Sci. Ind. Res. (), 77-86, 008 ANGLADESH JOURNAL OF SCIENTIFIC AND INDUSTRIAL RESEARCH CSIR E-mail: bsir07gmail.com Abstract Applications of Gauss-Radau
Avaiable online at www.banglaol.info angladesh J. Sci. Ind. Res. (), 77-86, 008 ANGLADESH JOURNAL OF SCIENTIFIC AND INDUSTRIAL RESEARCH CSIR E-mail: bsir07gmail.com Abstract Applications of Gauss-Radau
Quarter-Sweep Gauss-Seidel Method for Solving First Order Linear Fredholm Integro-differential Equations
 MATEMATIKA, 2011, Volume 27, Number 2, 199 208 c Department of Mathematical Sciences, UTM Quarter-Sweep Gauss-Seidel Method for Solving First Order Linear Fredholm Integro-differential Equations 1 E. Aruchunan
MATEMATIKA, 2011, Volume 27, Number 2, 199 208 c Department of Mathematical Sciences, UTM Quarter-Sweep Gauss-Seidel Method for Solving First Order Linear Fredholm Integro-differential Equations 1 E. Aruchunan
An Approximate Solution for Volterra Integral Equations of the Second Kind in Space with Weight Function
 International Journal of Mathematical Analysis Vol. 11 17 no. 18 849-861 HIKARI Ltd www.m-hikari.com https://doi.org/1.1988/ijma.17.771 An Approximate Solution for Volterra Integral Equations of the Second
International Journal of Mathematical Analysis Vol. 11 17 no. 18 849-861 HIKARI Ltd www.m-hikari.com https://doi.org/1.1988/ijma.17.771 An Approximate Solution for Volterra Integral Equations of the Second
Numerical solution of system of linear integral equations via improvement of block-pulse functions
 Journal of Mathematical Modeling Vol. 4, No., 16, pp. 133-159 JMM Numerical solution of system of linear integral equations via improvement of block-pulse functions Farshid Mirzaee Faculty of Mathematical
Journal of Mathematical Modeling Vol. 4, No., 16, pp. 133-159 JMM Numerical solution of system of linear integral equations via improvement of block-pulse functions Farshid Mirzaee Faculty of Mathematical
Kernel Density Estimation
 EECS 598: Statistical Learning Theory, Winter 2014 Topic 19 Kernel Density Estimation Lecturer: Clayton Scott Scribe: Yun Wei, Yanzhen Deng Disclaimer: These notes have not been subjected to the usual
EECS 598: Statistical Learning Theory, Winter 2014 Topic 19 Kernel Density Estimation Lecturer: Clayton Scott Scribe: Yun Wei, Yanzhen Deng Disclaimer: These notes have not been subjected to the usual
ƒ f(x)dx ~ X) ^i,nf(%i,n) -1 *=1 are the zeros of P«(#) and where the num
 ZEROS OF THE HERMITE POLYNOMIALS AND WEIGHTS FOR GAUSS' MECHANICAL QUADRATURE FORMULA ROBERT E. GREENWOOD AND J. J. MILLER In the numerical integration of a function ƒ (x) it is very desirable to choose
ZEROS OF THE HERMITE POLYNOMIALS AND WEIGHTS FOR GAUSS' MECHANICAL QUADRATURE FORMULA ROBERT E. GREENWOOD AND J. J. MILLER In the numerical integration of a function ƒ (x) it is very desirable to choose
CONVERGENCE THEORY. G. ALLAIRE CMAP, Ecole Polytechnique. 1. Maximum principle. 2. Oscillating test function. 3. Two-scale convergence
 1 CONVERGENCE THEOR G. ALLAIRE CMAP, Ecole Polytechnique 1. Maximum principle 2. Oscillating test function 3. Two-scale convergence 4. Application to homogenization 5. General theory H-convergence) 6.
1 CONVERGENCE THEOR G. ALLAIRE CMAP, Ecole Polytechnique 1. Maximum principle 2. Oscillating test function 3. Two-scale convergence 4. Application to homogenization 5. General theory H-convergence) 6.
Math 265H: Calculus III Practice Midterm II: Fall 2014
 Name: Section #: Math 65H: alculus III Practice Midterm II: Fall 14 Instructions: This exam has 7 problems. The number of points awarded for each question is indicated in the problem. Answer each question
Name: Section #: Math 65H: alculus III Practice Midterm II: Fall 14 Instructions: This exam has 7 problems. The number of points awarded for each question is indicated in the problem. Answer each question
Scientific Computing: Numerical Integration
 Scientific Computing: Numerical Integration Aleksandar Donev Courant Institute, NYU 1 donev@courant.nyu.edu 1 Course MATH-GA.2043 or CSCI-GA.2112, Fall 2015 Nov 5th, 2015 A. Donev (Courant Institute) Lecture
Scientific Computing: Numerical Integration Aleksandar Donev Courant Institute, NYU 1 donev@courant.nyu.edu 1 Course MATH-GA.2043 or CSCI-GA.2112, Fall 2015 Nov 5th, 2015 A. Donev (Courant Institute) Lecture
PHYS-4007/5007: Computational Physics Course Lecture Notes Appendix G
 PHYS-4007/5007: Computational Physics Course Lecture Notes Appendix G Dr. Donald G. Luttermoser East Tennessee State University Version 7.0 Abstract These class notes are designed for use of the instructor
PHYS-4007/5007: Computational Physics Course Lecture Notes Appendix G Dr. Donald G. Luttermoser East Tennessee State University Version 7.0 Abstract These class notes are designed for use of the instructor
QMUL, School of Physics and Astronomy Date: 18/01/2019
 QMUL, School of Physics and stronomy Date: 8//9 PHY Mathematical Techniques Solutions for Exercise Class Script : Coordinate Systems and Double Integrals. Calculate the integral: where the region is defined
QMUL, School of Physics and stronomy Date: 8//9 PHY Mathematical Techniques Solutions for Exercise Class Script : Coordinate Systems and Double Integrals. Calculate the integral: where the region is defined
Department of Structural, Faculty of Civil Engineering, Architecture and Urban Design, State University of Campinas, Brazil
 Blucher Mechanical Engineering Proceedings May 2014, vol. 1, num. 1 www.proceedings.blucher.com.br/evento/10wccm A SIMPLIFIED FORMULATION FOR STRESS AND TRACTION BOUNDARY IN- TEGRAL EQUATIONS USING THE
Blucher Mechanical Engineering Proceedings May 2014, vol. 1, num. 1 www.proceedings.blucher.com.br/evento/10wccm A SIMPLIFIED FORMULATION FOR STRESS AND TRACTION BOUNDARY IN- TEGRAL EQUATIONS USING THE
Integration. Topic: Trapezoidal Rule. Major: General Engineering. Author: Autar Kaw, Charlie Barker.
 Integration Topic: Trapezoidal Rule Major: General Engineering Author: Autar Kaw, Charlie Barker 1 What is Integration Integration: The process of measuring the area under a function plotted on a graph.
Integration Topic: Trapezoidal Rule Major: General Engineering Author: Autar Kaw, Charlie Barker 1 What is Integration Integration: The process of measuring the area under a function plotted on a graph.
APPENDIX 2.1 LINE AND SURFACE INTEGRALS
 2 APPENDIX 2. LINE AND URFACE INTEGRAL Consider a path connecting points (a) and (b) as shown in Fig. A.2.. Assume that a vector field A(r) exists in the space in which the path is situated. Then the line
2 APPENDIX 2. LINE AND URFACE INTEGRAL Consider a path connecting points (a) and (b) as shown in Fig. A.2.. Assume that a vector field A(r) exists in the space in which the path is situated. Then the line
Integration using Gaussian Quadrature
 Integration using Gaussian Quadrature Tutorials November 25, 2017 Department of Aeronautics, Imperial College London, UK Scientific Computing and Imaging Institute, University of Utah, USA 2 Chapter 1
Integration using Gaussian Quadrature Tutorials November 25, 2017 Department of Aeronautics, Imperial College London, UK Scientific Computing and Imaging Institute, University of Utah, USA 2 Chapter 1
A note on multivariate Gauss-Hermite quadrature
 A note on multivariate Gauss-Hermite quadrature Peter Jäckel 1th May 5 1 Introduction Gaussian quadratures are an ingenious way to approximate the integral of an unknown function f(x) over a specified
A note on multivariate Gauss-Hermite quadrature Peter Jäckel 1th May 5 1 Introduction Gaussian quadratures are an ingenious way to approximate the integral of an unknown function f(x) over a specified
Asymptotic Waveform Evaluation(AWE) Technique for Frequency Domain Electromagnetic Analysis
 NASA Technical Memorandum 110292 Asymptotic Waveform Evaluation(AWE Technique for Frequency Domain Electromagnetic Analysis C. R. Cockrell and F.B. Beck NASA Langley Research Center, Hampton, Virginia
NASA Technical Memorandum 110292 Asymptotic Waveform Evaluation(AWE Technique for Frequency Domain Electromagnetic Analysis C. R. Cockrell and F.B. Beck NASA Langley Research Center, Hampton, Virginia
Section 4.5. Integration and Expectation
 4.5. Integration and Expectation 1 Section 4.5. Integration and Expectation Note. In this section we consider integrals of scalar valued functions of a vector and matrix valued functions of a scalar. We
4.5. Integration and Expectation 1 Section 4.5. Integration and Expectation Note. In this section we consider integrals of scalar valued functions of a vector and matrix valued functions of a scalar. We
MULTIVARIABLE INTEGRATION
 MULTIVARIABLE INTEGRATION (SPHERICAL POLAR COORDINATES) Question 1 a) Determine with the aid of a diagram an expression for the volume element in r, θ, ϕ. spherical polar coordinates, ( ) [You may not
MULTIVARIABLE INTEGRATION (SPHERICAL POLAR COORDINATES) Question 1 a) Determine with the aid of a diagram an expression for the volume element in r, θ, ϕ. spherical polar coordinates, ( ) [You may not
1. The Debye scattering formula in n = 3 dimensions
 Available online at http://scik.org J. Math. Comput. Sci. (01), No. 4, 1086-1090 ISSN: 197-5307 THE DEBYE SCATTERING FORMULA IN n DIMENSIONS THOMAS WIEDER https://sites.google.com/site/twieder1stcenturyad/
Available online at http://scik.org J. Math. Comput. Sci. (01), No. 4, 1086-1090 ISSN: 197-5307 THE DEBYE SCATTERING FORMULA IN n DIMENSIONS THOMAS WIEDER https://sites.google.com/site/twieder1stcenturyad/
CIV-E1060 Engineering Computation and Simulation Examination, December 12, 2017 / Niiranen
 CIV-E16 Engineering Computation and Simulation Examination, December 12, 217 / Niiranen This examination consists of 3 problems rated by the standard scale 1...6. Problem 1 Let us consider a long and tall
CIV-E16 Engineering Computation and Simulation Examination, December 12, 217 / Niiranen This examination consists of 3 problems rated by the standard scale 1...6. Problem 1 Let us consider a long and tall
Concepts. 3.1 Numerical Analysis. Chapter Numerical Analysis Scheme
 Chapter 3 Concepts The objective of this work is to create a framework to implement multi-disciplinary finite element applications. Before starting, it is necessary to explain some basic concepts of the
Chapter 3 Concepts The objective of this work is to create a framework to implement multi-disciplinary finite element applications. Before starting, it is necessary to explain some basic concepts of the
Chapter Two: Numerical Methods for Elliptic PDEs. 1 Finite Difference Methods for Elliptic PDEs
 Chapter Two: Numerical Methods for Elliptic PDEs Finite Difference Methods for Elliptic PDEs.. Finite difference scheme. We consider a simple example u := subject to Dirichlet boundary conditions ( ) u
Chapter Two: Numerical Methods for Elliptic PDEs Finite Difference Methods for Elliptic PDEs.. Finite difference scheme. We consider a simple example u := subject to Dirichlet boundary conditions ( ) u
Matrix construction: Singular integral contributions
 Matrix construction: Singular integral contributions Seminar Boundary Element Methods for Wave Scattering Sophie Haug ETH Zurich November 2010 Outline 1 General concepts in singular integral computation
Matrix construction: Singular integral contributions Seminar Boundary Element Methods for Wave Scattering Sophie Haug ETH Zurich November 2010 Outline 1 General concepts in singular integral computation
Estimates of the error in Gauss-Legendre quadrature for double integrals
 Estimates of the error in Gauss-Legendre quadrature for double integrals Author Elliott, David, Johnston, Peter, Johnston, Barbara Published 211 Journal Title Journal of Computational and Applied Mathematics
Estimates of the error in Gauss-Legendre quadrature for double integrals Author Elliott, David, Johnston, Peter, Johnston, Barbara Published 211 Journal Title Journal of Computational and Applied Mathematics
Figure 25:Differentials of surface.
 2.5. Change of variables and Jacobians In the previous example we saw that, once we have identified the type of coordinates which is best to use for solving a particular problem, the next step is to do
2.5. Change of variables and Jacobians In the previous example we saw that, once we have identified the type of coordinates which is best to use for solving a particular problem, the next step is to do
Wavelets For Computer Graphics
 {f g} := f(x) g(x) dx A collection of linearly independent functions Ψ j spanning W j are called wavelets. i J(x) := 6 x +2 x + x + x Ψ j (x) := Ψ j (2 j x i) i =,..., 2 j Res. Avge. Detail Coef 4 [9 7
{f g} := f(x) g(x) dx A collection of linearly independent functions Ψ j spanning W j are called wavelets. i J(x) := 6 x +2 x + x + x Ψ j (x) := Ψ j (2 j x i) i =,..., 2 j Res. Avge. Detail Coef 4 [9 7
ON `-TH ORDER GAP BALANCING NUMBERS
 #A56 INTEGERS 18 (018) ON `-TH ORDER GAP BALANCING NUMBERS S. S. Rout Institute of Mathematics and Applications, Bhubaneswar, Odisha, India lbs.sudhansu@gmail.com; sudhansu@iomaorissa.ac.in R. Thangadurai
#A56 INTEGERS 18 (018) ON `-TH ORDER GAP BALANCING NUMBERS S. S. Rout Institute of Mathematics and Applications, Bhubaneswar, Odisha, India lbs.sudhansu@gmail.com; sudhansu@iomaorissa.ac.in R. Thangadurai
Engg. Math. II (Unit-IV) Numerical Analysis
 Dr. Satish Shukla of 33 Engg. Math. II (Unit-IV) Numerical Analysis Syllabus. Interpolation and Curve Fitting: Introduction to Interpolation; Calculus of Finite Differences; Finite Difference and Divided
Dr. Satish Shukla of 33 Engg. Math. II (Unit-IV) Numerical Analysis Syllabus. Interpolation and Curve Fitting: Introduction to Interpolation; Calculus of Finite Differences; Finite Difference and Divided
Use partial integration with respect to y to compute the inner integral (treating x as a constant.)
 Math 54 ~ Multiple Integration 4. Iterated Integrals and Area in the Plane Iterated Integrals f ( x, y) dydx = f ( x, y) dy dx b g ( x) b g ( x) a g ( x) a g ( x) Use partial integration with respect to
Math 54 ~ Multiple Integration 4. Iterated Integrals and Area in the Plane Iterated Integrals f ( x, y) dydx = f ( x, y) dy dx b g ( x) b g ( x) a g ( x) a g ( x) Use partial integration with respect to
Multiple Integrals. Introduction and Double Integrals Over Rectangular Regions. Philippe B. Laval KSU. Today
 Multiple Integrals Introduction and Double Integrals Over Rectangular Regions Philippe B. Laval KSU Today Philippe B. Laval (KSU) Double Integrals Today 1 / 21 Introduction In this section we define multiple
Multiple Integrals Introduction and Double Integrals Over Rectangular Regions Philippe B. Laval KSU Today Philippe B. Laval (KSU) Double Integrals Today 1 / 21 Introduction In this section we define multiple
3 2 6 Solve the initial value problem u ( t) 3. a- If A has eigenvalues λ =, λ = 1 and corresponding eigenvectors 1
 Math Problem a- If A has eigenvalues λ =, λ = 1 and corresponding eigenvectors 1 3 6 Solve the initial value problem u ( t) = Au( t) with u (0) =. 3 1 u 1 =, u 1 3 = b- True or false and why 1. if A is
Math Problem a- If A has eigenvalues λ =, λ = 1 and corresponding eigenvectors 1 3 6 Solve the initial value problem u ( t) = Au( t) with u (0) =. 3 1 u 1 =, u 1 3 = b- True or false and why 1. if A is
TUTORIAL QUESTION BANK
 St.MARTIN S ENGINEERING COLLEGE Dhulapally, Secunderabad-500 014 Subject: FINITE ELEMENT METHODS Class : MECH III TUTORIAL QUESTION BANK UNIT - I 1 Using variational approach (potential energy), describe
St.MARTIN S ENGINEERING COLLEGE Dhulapally, Secunderabad-500 014 Subject: FINITE ELEMENT METHODS Class : MECH III TUTORIAL QUESTION BANK UNIT - I 1 Using variational approach (potential energy), describe
Multiple Integrals. Chapter 4. Section 7. Department of Mathematics, Kookmin Univerisity. Numerical Methods.
 4.7.1 Multiple Integrals Chapter 4 Section 7 4.7.2 Double Integral R f ( x, y) da 4.7.3 Double Integral Apply Simpson s rule twice R [ a, b] [ c, d] a x, x,..., x b, c y, y,..., y d 0 1 n 0 1 h ( b a)
4.7.1 Multiple Integrals Chapter 4 Section 7 4.7.2 Double Integral R f ( x, y) da 4.7.3 Double Integral Apply Simpson s rule twice R [ a, b] [ c, d] a x, x,..., x b, c y, y,..., y d 0 1 n 0 1 h ( b a)
Math 115 ( ) Yum-Tong Siu 1. Euler-Lagrange Equations for Many Functions and Variables and High-Order Derivatives
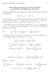 Math 115 006-007 Yum-Tong Siu 1 Euler-Lagrange Equations for Many Functions and Variables and High-Order Derivatives The Case of High-Order Derivatives. The context is to find the extremal for the functional
Math 115 006-007 Yum-Tong Siu 1 Euler-Lagrange Equations for Many Functions and Variables and High-Order Derivatives The Case of High-Order Derivatives. The context is to find the extremal for the functional
Multiple Integrals. Introduction and Double Integrals Over Rectangular Regions. Philippe B. Laval. Spring 2012 KSU
 Multiple Integrals Introduction and Double Integrals Over Rectangular Regions Philippe B Laval KSU Spring 2012 Philippe B Laval (KSU) Multiple Integrals Spring 2012 1 / 21 Introduction In this section
Multiple Integrals Introduction and Double Integrals Over Rectangular Regions Philippe B Laval KSU Spring 2012 Philippe B Laval (KSU) Multiple Integrals Spring 2012 1 / 21 Introduction In this section
BHAR AT HID AS AN ENGIN E ERI N G C O L L E G E NATTR A MPA LL I
 BHAR AT HID AS AN ENGIN E ERI N G C O L L E G E NATTR A MPA LL I 635 8 54. Third Year M E C H A NICAL VI S E M ES TER QUE S T I ON B ANK Subject: ME 6 603 FIN I T E E LE ME N T A N A L YSIS UNI T - I INTRODUCTION
BHAR AT HID AS AN ENGIN E ERI N G C O L L E G E NATTR A MPA LL I 635 8 54. Third Year M E C H A NICAL VI S E M ES TER QUE S T I ON B ANK Subject: ME 6 603 FIN I T E E LE ME N T A N A L YSIS UNI T - I INTRODUCTION
ARITHMETIC PROGRESSION OF SQUARES AND SOLVABILITY OF THE DIOPHANTINE EQUATION 8x = y 2
 International Conference in Number Theory and Applications 01 Department of Mathematics, Faculty of Science, Kasetsart University Speaker: G. K. Panda 1 ARITHMETIC PROGRESSION OF SQUARES AND SOLVABILITY
International Conference in Number Theory and Applications 01 Department of Mathematics, Faculty of Science, Kasetsart University Speaker: G. K. Panda 1 ARITHMETIC PROGRESSION OF SQUARES AND SOLVABILITY
ONE - DIMENSIONAL INTEGRATION
 Chapter 4 ONE - DIMENSIONA INTEGRATION 4. Introduction Since the finite element method is based on integral relations it is logical to expect that one should strive to carry out the integrations as efficiently
Chapter 4 ONE - DIMENSIONA INTEGRATION 4. Introduction Since the finite element method is based on integral relations it is logical to expect that one should strive to carry out the integrations as efficiently
Symmetric Gauss Legendre quadrature formulas for composite numerical integration over a triangular surface
 Applied Mathematics ad Computatio 1 (27) 65 76 www.elsevier.com/locate/amc Symmetric Gauss Legedre quadrature ormulas or composite umerical itegratio over a triagular surace H.. Rathod a, *, K.V. Nagaraja
Applied Mathematics ad Computatio 1 (27) 65 76 www.elsevier.com/locate/amc Symmetric Gauss Legedre quadrature ormulas or composite umerical itegratio over a triagular surace H.. Rathod a, *, K.V. Nagaraja
A High Order Conservative Semi-Lagrangian Discontinuous Galerkin Method for Two-Dimensional Transport Simulations
 Motivation Numerical methods Numerical tests Conclusions A High Order Conservative Semi-Lagrangian Discontinuous Galerkin Method for Two-Dimensional Transport Simulations Xiaofeng Cai Department of Mathematics
Motivation Numerical methods Numerical tests Conclusions A High Order Conservative Semi-Lagrangian Discontinuous Galerkin Method for Two-Dimensional Transport Simulations Xiaofeng Cai Department of Mathematics
NEW ITERATIVE METHODS BASED ON SPLINE FUNCTIONS FOR SOLVING NONLINEAR EQUATIONS
 Bulletin of Mathematical Analysis and Applications ISSN: 181-191, URL: http://www.bmathaa.org Volume 3 Issue 4(011, Pages 31-37. NEW ITERATIVE METHODS BASED ON SPLINE FUNCTIONS FOR SOLVING NONLINEAR EQUATIONS
Bulletin of Mathematical Analysis and Applications ISSN: 181-191, URL: http://www.bmathaa.org Volume 3 Issue 4(011, Pages 31-37. NEW ITERATIVE METHODS BASED ON SPLINE FUNCTIONS FOR SOLVING NONLINEAR EQUATIONS
Verified Calculation of the Nodes and Weights for Gaussian Quadrature Formulas
 Interval Computations No 4, 1993 Verified Calculation of the Nodes and Weights for Gaussian Quadrature Formulas Ulrike Storck Using Gaussian Quadrature for the verified calculation of an integral assumes
Interval Computations No 4, 1993 Verified Calculation of the Nodes and Weights for Gaussian Quadrature Formulas Ulrike Storck Using Gaussian Quadrature for the verified calculation of an integral assumes
Note: Each problem is worth 14 points except numbers 5 and 6 which are 15 points. = 3 2
 Math Prelim II Solutions Spring Note: Each problem is worth points except numbers 5 and 6 which are 5 points. x. Compute x da where is the region in the second quadrant between the + y circles x + y and
Math Prelim II Solutions Spring Note: Each problem is worth points except numbers 5 and 6 which are 5 points. x. Compute x da where is the region in the second quadrant between the + y circles x + y and
INTERNATIONAL JOURNAL OF PURE AND APPLIED RESEARCH IN ENGINEERING AND TECHNOLOGY
 INTERNATIONAL JOURNAL OF PURE AND APPLIED RESEARCH IN ENGINEERING AND TECHNOLOGY A PATH FOR HORIZING YOUR INNOVATIVE WORK SPECIAL ISSUE FOR INTERNATIONAL LEVEL CONFERENCE "ADVANCES IN SCIENCE, TECHNOLOGY
INTERNATIONAL JOURNAL OF PURE AND APPLIED RESEARCH IN ENGINEERING AND TECHNOLOGY A PATH FOR HORIZING YOUR INNOVATIVE WORK SPECIAL ISSUE FOR INTERNATIONAL LEVEL CONFERENCE "ADVANCES IN SCIENCE, TECHNOLOGY
LECTURE 16 GAUSS QUADRATURE In general for Newton-Cotes (equispaced interpolation points/ data points/ integration points/ nodes).
 CE 025 - Lecture 6 LECTURE 6 GAUSS QUADRATURE In general for ewton-cotes (equispaced interpolation points/ data points/ integration points/ nodes). x E x S fx dx hw' o f o + w' f + + w' f + E 84 f 0 f
CE 025 - Lecture 6 LECTURE 6 GAUSS QUADRATURE In general for ewton-cotes (equispaced interpolation points/ data points/ integration points/ nodes). x E x S fx dx hw' o f o + w' f + + w' f + E 84 f 0 f
Dynamic Analysis of Laminated Composite Plate Structure with Square Cut-Out under Hygrothermal Load
 Dynamic Analysis of Laminated Composite Plate Structure with Square Cut-Out under Hygrothermal Load Arun Mukherjee 1, Dr. Sreyashi Das (nee Pal) 2 and Dr. A. Guha Niyogi 3 1 PG student, 2 Asst. Professor,
Dynamic Analysis of Laminated Composite Plate Structure with Square Cut-Out under Hygrothermal Load Arun Mukherjee 1, Dr. Sreyashi Das (nee Pal) 2 and Dr. A. Guha Niyogi 3 1 PG student, 2 Asst. Professor,
Transverse Vibration Analysis of an Arbitrarily-shaped Membrane by the Weak-form Quadrature Element Method
 COMPUTATIOAL MECHAICS ISCM7, July 3-August, 7, Being, China 7 Tsinghua University Press & Springer Transverse Vibration Analysis of an Arbitrarily-shaped Membrane by the Weak-form Quadrature Element Method
COMPUTATIOAL MECHAICS ISCM7, July 3-August, 7, Being, China 7 Tsinghua University Press & Springer Transverse Vibration Analysis of an Arbitrarily-shaped Membrane by the Weak-form Quadrature Element Method
