Short Communication. Gauss Legendre quadrature over a triangle
|
|
|
- Norman Malone
- 6 years ago
- Views:
Transcription
1 J. Indian Inst. Sci., Sept. Oct. 4, 4, 3 Indian Institute of Science. Short Communication Gauss Legendre quadrature over a triangle H. T. RATHOD *, K. V. NAGARAJA, B. VENKATESUDU 3 AND N. L. RAMESH 4 Department of Mathematics, Central College Campus, Bangalore University, Bangalore 560, India. Department of Mathematics, Amrita Institute of Technology and Science, Bangalore 5637, India. 3 Department of Mathematics, The Oxford College of Engineering, Bangalore 566, India. 4 Department of Mathematics, M. S. Ramaiah Institute of Technology (MSRIT), Bangalore 566, India. s: htrathod@yahoo.com; nagarajaitec3@yahoo.com; 3 venkateshoxford3@yahoo.com; 4 nlramesh607@yahoo.com; Phones: ; ; ; Received on November 7, 3; Revised on April 06, 4. Abstract This paper presents a Gauss Legendre quadrature method for numerical integration over the standard triangular surface: {(x, y) 0 x, y, x + y } in the Cartesian two-dimensional (x, y) space. Mathematical transformation from (x, y) space to (ξ, η) space map the standard triangle in (x, y) space to a standard -square in (ξ, η) space: {(ξ, η) ξ, η }. This overcomes the difficulties associated with the derivation of new weight coefficients and sampling points and yields results which are accurate and reliable. Results obtained with new formulae are compared with the existing formulae. Keywords: Finite-element method, numerical integration, Gauss Legendre quadrature, triangular elements, standard -square, extended numerical integration.. Introduction In recent years, the finite-element method (FEM) has become a very powerful tool for the approximate solution of boundary-value problems governing diverse physical phenomena. Its use in industry and research is extensive and without it many practical problems in science and engineering would be incapable of solution. The triangular elements with either straight or curved sides are very widely used in finite-element analysis. The versatility of these triangular elements can be enhanced further by improved numerical integration schemes. In FEM, various integrals are to be determined numerically in the evaluation of the stiffness matrix, mass matrix, body force vector, etc. The basic problem of integrating an arbitrary function of two variables over the surface of triangle was first given by Hammer et al. [] and Hammer and Stroud [, 3]. With the advent of the finite-element method, the triangular elements proved to be versatile. There has been considerable interest in the area of numerical integration schemes over triangles. Cowper [4] provided a table of Gaussian quadrature formulae for symmetrically placed integration points. *Author for correspondence.
2 4 H. T. RATHOD et al. Lyness and Jespersen [5] made an elaborate study of symmetric quadrature rules by formulating the problem in polar coordinates. Lannoy [6] discussed the symmetric 4-point integration rule [4]. Laurie [7] derived a 7-point integration rule and discussed the numerical error in integrating some functions. Laursen and Gellert [] gave a detailed table of symmetric integration formulae and suggested some new higher-order formulae of precision up to degree 0. Lether [9], Hillion [0] and Lague and Baldur [] considered the product formulae derivable from one-dimensional Gaussian quadrature rules. Reddy [], and Reddy and Shippy [3] derived 3-, 4-, 6- and 7-point formulae which give improved accuracy. However, Lague and Baldur have not listed the explicit weighting coefficients and sampling points for numerical applications. The present work aims to provide this information in a systematic manner for future reference. There is a great need for higher-order quadrature rules over the triangular surface [4]. A similar suggestion was also made by Lague and Baldur [].. Formulation of integrals over a triangular area The finite-element method for two-dimensional problems with triangular elements requires the numerical integration of shape functions on a triangle. Since an affine transformation makes it possible to transform any triangle into the two-dimensional standard triangle T with coordinates (0,0), (0,), (,0) in Cartesian frame, we have to consider just the numerical integration on T. The integral of an arbitrary function, f, over the surface of a triangle T is given by = dx f( x, y) dy = dy f( x, y) dx. () I = f( x, y) dxdy T x y It is now required to find the value of the integral by a quadrature formula: N I = cmf( xm, ym) () m= where c m are the weights associated with specific points (x m, y m ) and N is the number of pivotal points related to the required precision. One such accurate method known to the present authors is based on 3 integration points [4]. It is not likely that this technique will be extended further to give greater accuracy which may be demanded in future. The other method is the approximation of I by product formulae [0] which is of type () based on the roots and weights of Gauss Legendre and Gauss Jacobi polynomials. The precision of these formulae is limited to polynomials of degree seven; this is because the weights and roots of Jacobi polynomials are not tabulated in standard texts for sufficiently higher degree polynomials. The product formulae proposed in this paper and in the work of Lague and Baldur [] are based only on the roots and weights of Gauss Legendre polynomials. The integral I of eqn () can be transformed into an integral over the surface of the square: {(u, v) 0 u, v } by the substitution: x = u, y = ( u)v. (3) Then the determinant of the Jacobian and the differential area are: ( xy, ) x y x y = = () ( u) 0 ( v) = u ( uv, ) u v v u
3 GAUSS LEGENDRE QUADRATURE OVER A TRIANGLE 5 and dx dy = ( xy, ) dudv = ( ududv ). ( uv, ) (4) Then, on using eqns (3) and (4) in eqn (), we have x f( x, y) dydx= f( u,( uv ))( u) dudv. (5) The integral I of eqn (5) can be transformed further into an integral over the standard - square: {(ξ, η) ξ, η } by the substitution u = ( + ξ)/, v = ( + η)/, (6) then clearly the determinant of the Jacobian and the differential area are: ( uv, ) = u v u v = (/)(/) (0) (0) =/4 ( ξη, ) ξ η η ξ dudv = ( uv, ) d ξ d η = dξdη. (7) ( ξη, ) 4 Now, on using eqns (6) and (7) in eqn (5), we have: x I = f( x, y) dydx= f( u,( uv ))( u) dudv + ξ ( ξ)( + η) ξ = f, dξdη. 4 () Equation () represents an integral over the surface of a standard -square: {(ξ, η) ξ, η }. Efficient quadrature coefficients are readily available in the literature so that any desired accuracy can be readily obtained [5]. From eqn (), we can write: I = ξ f( x( ξη, ), y( ξη, )) dξdη, I = n n ξi ww i j f( x( ξi, ηj), y( ξi, ηj)), (9) i= j= where ξ i, η i are Gaussian points in the ξ, η directions, respectively, and w i and w j are the corresponding weights. We can rewrite eqn (9) as: I = N= n n ck f( xk, yk) (0) k=
4 6 H. T. RATHOD et al. Table I Gauss points and weighting coefficients over a triangle x i y i c i n = n = where c k, x k and y k can be obtained from the relations: c ( ξi ) = ww, k i j x k ( +ξi ) =, y k ( ξi )( + ηj) = 4 (k =,,, n), (i, j =,, 3,.., n). () The weighting coefficients c k and sampling points (x k, y k ) of various orders can now be easily computed by formula of eqns (0) and (). We have tabulated a sample of these weight coefficients and sampling points for n =, 3 (Table I). 3. Some numerical results We consider some typical integrals with known exact values [3]. y I = ( x+ y) dxdy = 0.4; y I = ( x+ y) dxdy = ; y I3 = ( x + y ) dxdy = ; π y I4 = sin( x+ ydxdy ) =.0;
5 GAUSS LEGENDRE QUADRATURE OVER A TRIANGLE 7 Table II Numerical results of double integration n I I I 3 I 4 I y x+ y I5 e dxdy = = These integrals were evaluated using the integration schemes derived in the present paper and it is found that excellent convergence occurs to the exact values. The calculations give very accurate results and are reliable as proved by Lague and Baldur []. The results are summarized in Table II. 4. Conclusions We have derived various orders of extended numerical integration rules based on classical Gauss Legendre quadrature over a triangle (Table I). This is made possible by transforming the triangular surface: 0 x, y, x + y to a standard -square; ξ, η. Over the -square, the Gauss Legendre quadrature rule of all orders is applicable. It may be noted that a lot of mathematical effort is needed to derive the numerical integration rules over the triangular surface and the integration formulae available at this moment in the literature are confined to a precision of degree up to ten. With the proposed method, this restriction is removed and one can now obtain numerical integration rules of very high degree as the derivations proposed here rely on the standard Gauss Legendre quadrature rules. This is essential as the demand for higher-order integration rules in the finite-element method is increasing. References. P. C. Hammer, O. J. Marlowe and A. H. Stroud, Numerical integration over simplexes and cones, Math. Tables Other Aids Computation, 0, (956).. P. C. Hammer and A. H. Stroud, Numerical integration over simplexes, Math. Tables Other Aids Computation, 0, (956). 3. P. C. Hammer and A. H. Stroud, Numerical evaluation of multiple integrals, Math. Tables Other Aids Computation,, 7 0 (95). 4. G. R. Cowper, Gaussian quadrature formulas for triangles, Int. J. Num. Meth. Engng, 7, (973). 5. J. N. Lyness and D. Jespersen, Moderate degree symmetric quadrature rules for the triangle, J. Inst. Math. Applic., 5, 9 3 (975). 6. F. G. Lannoy, Triangular finite elements and numerical integration, Computers Struct., 7, 63 (977).
6 H. T. RATHOD et al. 7. D. P. Laurie, Automatic numerical integration over a triangle, CSIR Spec. Rep. WISK 73, National Institute for Mathematical Sciences, Pretoria (977).. M. E. Laursen and M. Gellert, Some criteria for numerically integrated matrices and quadrature formulas for triangles, Int. J. Num. Meth. Engng,, (97). 9. F. G. Lether, Computation of double integrals over a triangle, J. Comp. Applic. Math.,, 9 4 (976). 0. P. Hillion, Numerical integration on a triangle, Int. J. Num. Meth. Engng,, (977).. G. Lague and R. Baldur, Extended numerical integration method for triangular surfaces, Int. J. Num. Meth. Engng,, 3 39 (977).. C. T. Reddy, Improved three point integration schemes for triangular finite elements, Int. J. Num. Meth. Engng,, (97). 3. C. T. Reddy and D. J. Shippy, Alternative integration formulae for triangular finite elements, Int. J. Num. Meth. Engng, 7, (9). 4. H. T. Rathod and M. S. Karim, An explicit integration scheme based on recursion for curved triangular finite elements, Computers Struct., 0, (). 5. M. Abramowicz and I. A. Stegun (eds), Handbook of mathematical functions, Dover (964). Printed and published by Dr S. Venkadesan, Executive Editor, Journal of the Indian Institute of Science, Bangalore 56; Printed at Ravi Graphics, Bangalore 5644.
On use of Mixed Quadrature Rule for Numerical Integration over a Triangular Domain
 International Journal of Pure and Applied Mathematical Sciences. ISSN 972-9828 Volume 9, Number 2 (26), pp. 9-96 Research India Publications http://www.ripublication.com On use of Mixed Quadrature Rule
International Journal of Pure and Applied Mathematical Sciences. ISSN 972-9828 Volume 9, Number 2 (26), pp. 9-96 Research India Publications http://www.ripublication.com On use of Mixed Quadrature Rule
Gauss Legendre quadrature over a parabolic region
 Gauss Legendre quadrature over a parabolic region K. T. Shivaram Department of Mathematics, Dayananda sagar college of Engineering, Bangalore, India Abstract In this paper, we introduce a Gauss Legendre
Gauss Legendre quadrature over a parabolic region K. T. Shivaram Department of Mathematics, Dayananda sagar college of Engineering, Bangalore, India Abstract In this paper, we introduce a Gauss Legendre
CHAPTER 4 NUMERICAL INTEGRATION METHODS TO EVALUATE TRIPLE INTEGRALS USING GENERALIZED GAUSSIAN QUADRATURE
 CHAPTER 4 NUMERICAL INTEGRATION METHODS TO EVALUATE TRIPLE INTEGRALS USING GENERALIZED GAUSSIAN QUADRATURE 4.1 Introduction Many applications in science and engineering require the solution of three dimensional
CHAPTER 4 NUMERICAL INTEGRATION METHODS TO EVALUATE TRIPLE INTEGRALS USING GENERALIZED GAUSSIAN QUADRATURE 4.1 Introduction Many applications in science and engineering require the solution of three dimensional
Numerical Evaluation of Integrals with weight function x k Using Gauss Legendre Quadrature Rules
 IOSR Journal of Mathematics (IOSR-JM) e-issn: 2278-728, p-issn: 29-76X. Volume, Issue Ver. V (May - Jun. 2), PP 9-6 www.iosrjournals.org Numerical Evaluation of Integrals with weight function k Using Gauss
IOSR Journal of Mathematics (IOSR-JM) e-issn: 2278-728, p-issn: 29-76X. Volume, Issue Ver. V (May - Jun. 2), PP 9-6 www.iosrjournals.org Numerical Evaluation of Integrals with weight function k Using Gauss
An Accurate Quadrature for the Numerical Integration of Polynomial Functions
 International Journal of Applied Mathematics and Theoretical Physics 2018; 4(1: 1-7 http://www.sciencepublishinggroup.com/j/ijamtp doi: 10.11648/j.ijamtp.20180401.11 ISSN: 2575-5919 (Print; ISSN: 2575-5927
International Journal of Applied Mathematics and Theoretical Physics 2018; 4(1: 1-7 http://www.sciencepublishinggroup.com/j/ijamtp doi: 10.11648/j.ijamtp.20180401.11 ISSN: 2575-5919 (Print; ISSN: 2575-5927
4.4 Change of Variable in Integrals: The Jacobian
 4.4. CHANGE OF VAIABLE IN INTEGALS: THE JACOBIAN 4 4.4 Change of Variable in Integrals: The Jacobian In this section, we generalize to multiple integrals the substitution technique used with definite integrals.
4.4. CHANGE OF VAIABLE IN INTEGALS: THE JACOBIAN 4 4.4 Change of Variable in Integrals: The Jacobian In this section, we generalize to multiple integrals the substitution technique used with definite integrals.
Numerical Integration exact integration is not needed to achieve the optimal convergence rate of nite element solutions ([, 9, 11], and Chapter 7). In
![Numerical Integration exact integration is not needed to achieve the optimal convergence rate of nite element solutions ([, 9, 11], and Chapter 7). In Numerical Integration exact integration is not needed to achieve the optimal convergence rate of nite element solutions ([, 9, 11], and Chapter 7). In](/thumbs/80/80480766.jpg) Chapter 6 Numerical Integration 6.1 Introduction After transformation to a canonical element,typical integrals in the element stiness or mass matrices (cf. (5.5.8)) have the forms Q = T ( )N s Nt det(j
Chapter 6 Numerical Integration 6.1 Introduction After transformation to a canonical element,typical integrals in the element stiness or mass matrices (cf. (5.5.8)) have the forms Q = T ( )N s Nt det(j
Chapter 10 INTEGRATION METHODS Introduction Unit Coordinate Integration
 Chapter 0 INTEGRATION METHODS 0. Introduction The finite element analysis techniques are always based on an integral formulation. At the very minimum it will always be necessary to integrate at least an
Chapter 0 INTEGRATION METHODS 0. Introduction The finite element analysis techniques are always based on an integral formulation. At the very minimum it will always be necessary to integrate at least an
Vector Calculus. Dr. D. Sukumar
 Vector Calculus Dr. D. Sukumar Space co-ordinates Change of variable Cartesian co-ordinates < x < Cartesian co-ordinates < x < < y < Cartesian co-ordinates < x < < y < < z < Cylindrical Cylindrical Cylindrical
Vector Calculus Dr. D. Sukumar Space co-ordinates Change of variable Cartesian co-ordinates < x < Cartesian co-ordinates < x < < y < Cartesian co-ordinates < x < < y < < z < Cylindrical Cylindrical Cylindrical
MULTIVARIABLE INTEGRATION
 MULTIVARIABLE INTEGRATION (PLANE & CYLINDRICAL POLAR COORDINATES) PLANE POLAR COORDINATES Question 1 The finite region on the x-y plane satisfies 1 x + y 4, y 0. Find, in terms of π, the value of I. I
MULTIVARIABLE INTEGRATION (PLANE & CYLINDRICAL POLAR COORDINATES) PLANE POLAR COORDINATES Question 1 The finite region on the x-y plane satisfies 1 x + y 4, y 0. Find, in terms of π, the value of I. I
xm y n dx dy so that similar expressions could be used to evaluate the volume integrals.
 Chapter Integration methods. Introduction The finite element analysis techniques are always based on an integral formulation. At the very minimum it will always be necessary to integrate at least an element
Chapter Integration methods. Introduction The finite element analysis techniques are always based on an integral formulation. At the very minimum it will always be necessary to integrate at least an element
Applications of Gauss-Radau and Gauss-Lobatto Numerical Integrations Over a Four Node Quadrilateral Finite Element
 Avaiable online at www.banglaol.info angladesh J. Sci. Ind. Res. (), 77-86, 008 ANGLADESH JOURNAL OF SCIENTIFIC AND INDUSTRIAL RESEARCH CSIR E-mail: bsir07gmail.com Abstract Applications of Gauss-Radau
Avaiable online at www.banglaol.info angladesh J. Sci. Ind. Res. (), 77-86, 008 ANGLADESH JOURNAL OF SCIENTIFIC AND INDUSTRIAL RESEARCH CSIR E-mail: bsir07gmail.com Abstract Applications of Gauss-Radau
Romberg Integration and Gaussian Quadrature
 Romberg Integration and Gaussian Quadrature P. Sam Johnson October 17, 014 P. Sam Johnson (NITK) Romberg Integration and Gaussian Quadrature October 17, 014 1 / 19 Overview We discuss two methods for integration.
Romberg Integration and Gaussian Quadrature P. Sam Johnson October 17, 014 P. Sam Johnson (NITK) Romberg Integration and Gaussian Quadrature October 17, 014 1 / 19 Overview We discuss two methods for integration.
MATH 52 FINAL EXAM DECEMBER 7, 2009
 MATH 52 FINAL EXAM DECEMBER 7, 2009 THIS IS A CLOSED BOOK, CLOSED NOTES EXAM. NO CALCULATORS OR OTHER ELECTRONIC DEVICES ARE PERMITTED. IF YOU NEED EXTRA SPACE, PLEASE USE THE BACK OF THE PREVIOUS PROB-
MATH 52 FINAL EXAM DECEMBER 7, 2009 THIS IS A CLOSED BOOK, CLOSED NOTES EXAM. NO CALCULATORS OR OTHER ELECTRONIC DEVICES ARE PERMITTED. IF YOU NEED EXTRA SPACE, PLEASE USE THE BACK OF THE PREVIOUS PROB-
Module 6: Implicit Runge-Kutta Methods Lecture 17: Derivation of Implicit Runge-Kutta Methods(Contd.) The Lecture Contains:
 The Lecture Contains: We continue with the details about the derivation of the two stage implicit Runge- Kutta methods. A brief description of semi-explicit Runge-Kutta methods is also given. Finally,
The Lecture Contains: We continue with the details about the derivation of the two stage implicit Runge- Kutta methods. A brief description of semi-explicit Runge-Kutta methods is also given. Finally,
 Code No: RT41033 R13 Set No. 1 IV B.Tech I Semester Regular Examinations, November - 2016 FINITE ELEMENT METHODS (Common to Mechanical Engineering, Aeronautical Engineering and Automobile Engineering)
Code No: RT41033 R13 Set No. 1 IV B.Tech I Semester Regular Examinations, November - 2016 FINITE ELEMENT METHODS (Common to Mechanical Engineering, Aeronautical Engineering and Automobile Engineering)
Integration using Gaussian Quadrature
 Integration using Gaussian Quadrature Tutorials November 25, 2017 Department of Aeronautics, Imperial College London, UK Scientific Computing and Imaging Institute, University of Utah, USA 2 Chapter 1
Integration using Gaussian Quadrature Tutorials November 25, 2017 Department of Aeronautics, Imperial College London, UK Scientific Computing and Imaging Institute, University of Utah, USA 2 Chapter 1
Transactions on Modelling and Simulation vol 12, 1996 WIT Press, ISSN X
 Simplifying integration for logarithmic singularities R.N.L. Smith Department ofapplied Mathematics & OR, Cranfield University, RMCS, Shrivenham, Swindon, Wiltshire SN6 SLA, UK Introduction Any implementation
Simplifying integration for logarithmic singularities R.N.L. Smith Department ofapplied Mathematics & OR, Cranfield University, RMCS, Shrivenham, Swindon, Wiltshire SN6 SLA, UK Introduction Any implementation
Transverse Vibration Analysis of an Arbitrarily-shaped Membrane by the Weak-form Quadrature Element Method
 COMPUTATIOAL MECHAICS ISCM7, July 3-August, 7, Being, China 7 Tsinghua University Press & Springer Transverse Vibration Analysis of an Arbitrarily-shaped Membrane by the Weak-form Quadrature Element Method
COMPUTATIOAL MECHAICS ISCM7, July 3-August, 7, Being, China 7 Tsinghua University Press & Springer Transverse Vibration Analysis of an Arbitrarily-shaped Membrane by the Weak-form Quadrature Element Method
Chapter Two: Numerical Methods for Elliptic PDEs. 1 Finite Difference Methods for Elliptic PDEs
 Chapter Two: Numerical Methods for Elliptic PDEs Finite Difference Methods for Elliptic PDEs.. Finite difference scheme. We consider a simple example u := subject to Dirichlet boundary conditions ( ) u
Chapter Two: Numerical Methods for Elliptic PDEs Finite Difference Methods for Elliptic PDEs.. Finite difference scheme. We consider a simple example u := subject to Dirichlet boundary conditions ( ) u
Numerical integration formulas of degree two
 Applied Numerical Mathematics 58 (2008) 1515 1520 www.elsevier.com/locate/apnum Numerical integration formulas of degree two ongbin Xiu epartment of Mathematics, Purdue University, West Lafayette, IN 47907,
Applied Numerical Mathematics 58 (2008) 1515 1520 www.elsevier.com/locate/apnum Numerical integration formulas of degree two ongbin Xiu epartment of Mathematics, Purdue University, West Lafayette, IN 47907,
ONE - DIMENSIONAL INTEGRATION
 Chapter 4 ONE - DIMENSIONA INTEGRATION 4. Introduction Since the finite element method is based on integral relations it is logical to expect that one should strive to carry out the integrations as efficiently
Chapter 4 ONE - DIMENSIONA INTEGRATION 4. Introduction Since the finite element method is based on integral relations it is logical to expect that one should strive to carry out the integrations as efficiently
Finite Element Method-Part II Isoparametric FE Formulation and some numerical examples Lecture 29 Smart and Micro Systems
 Finite Element Method-Part II Isoparametric FE Formulation and some numerical examples Lecture 29 Smart and Micro Systems Introduction Till now we dealt only with finite elements having straight edges.
Finite Element Method-Part II Isoparametric FE Formulation and some numerical examples Lecture 29 Smart and Micro Systems Introduction Till now we dealt only with finite elements having straight edges.
ME 1401 FINITE ELEMENT ANALYSIS UNIT I PART -A. 2. Why polynomial type of interpolation functions is mostly used in FEM?
 SHRI ANGALAMMAN COLLEGE OF ENGINEERING AND TECHNOLOGY (An ISO 9001:2008 Certified Institution) SIRUGANOOR, TIRUCHIRAPPALLI 621 105 Department of Mechanical Engineering ME 1401 FINITE ELEMENT ANALYSIS 1.
SHRI ANGALAMMAN COLLEGE OF ENGINEERING AND TECHNOLOGY (An ISO 9001:2008 Certified Institution) SIRUGANOOR, TIRUCHIRAPPALLI 621 105 Department of Mechanical Engineering ME 1401 FINITE ELEMENT ANALYSIS 1.
Use partial integration with respect to y to compute the inner integral (treating x as a constant.)
 Math 54 ~ Multiple Integration 4. Iterated Integrals and Area in the Plane Iterated Integrals f ( x, y) dydx = f ( x, y) dy dx b g ( x) b g ( x) a g ( x) a g ( x) Use partial integration with respect to
Math 54 ~ Multiple Integration 4. Iterated Integrals and Area in the Plane Iterated Integrals f ( x, y) dydx = f ( x, y) dy dx b g ( x) b g ( x) a g ( x) a g ( x) Use partial integration with respect to
f dr. (6.1) f(x i, y i, z i ) r i. (6.2) N i=1
 hapter 6 Integrals In this chapter we will look at integrals in more detail. We will look at integrals along a curve, and multi-dimensional integrals in 2 or more dimensions. In physics we use these integrals
hapter 6 Integrals In this chapter we will look at integrals in more detail. We will look at integrals along a curve, and multi-dimensional integrals in 2 or more dimensions. In physics we use these integrals
Today s class. Linear Algebraic Equations LU Decomposition. Numerical Methods, Fall 2011 Lecture 8. Prof. Jinbo Bi CSE, UConn
 Today s class Linear Algebraic Equations LU Decomposition 1 Linear Algebraic Equations Gaussian Elimination works well for solving linear systems of the form: AX = B What if you have to solve the linear
Today s class Linear Algebraic Equations LU Decomposition 1 Linear Algebraic Equations Gaussian Elimination works well for solving linear systems of the form: AX = B What if you have to solve the linear
Multi Variable Calculus
 Multi Variable Calculus Joshua Wilde, revised by Isabel Tecu, Takeshi Suzuki and María José Boccardi August 3, 03 Functions from R n to R m So far we have looked at functions that map one number to another
Multi Variable Calculus Joshua Wilde, revised by Isabel Tecu, Takeshi Suzuki and María José Boccardi August 3, 03 Functions from R n to R m So far we have looked at functions that map one number to another
3. Numerical integration
 3. Numerical integration... 3. One-dimensional quadratures... 3. Two- and three-dimensional quadratures... 3.3 Exact Integrals for Straight Sided Triangles... 5 3.4 Reduced and Selected Integration...
3. Numerical integration... 3. One-dimensional quadratures... 3. Two- and three-dimensional quadratures... 3.3 Exact Integrals for Straight Sided Triangles... 5 3.4 Reduced and Selected Integration...
Multiple Integrals. Chapter 4. Section 7. Department of Mathematics, Kookmin Univerisity. Numerical Methods.
 4.7.1 Multiple Integrals Chapter 4 Section 7 4.7.2 Double Integral R f ( x, y) da 4.7.3 Double Integral Apply Simpson s rule twice R [ a, b] [ c, d] a x, x,..., x b, c y, y,..., y d 0 1 n 0 1 h ( b a)
4.7.1 Multiple Integrals Chapter 4 Section 7 4.7.2 Double Integral R f ( x, y) da 4.7.3 Double Integral Apply Simpson s rule twice R [ a, b] [ c, d] a x, x,..., x b, c y, y,..., y d 0 1 n 0 1 h ( b a)
Symmetric Gauss Legendre quadrature formulas for composite numerical integration over a triangular surface
 Applied Mathematics ad Computatio 1 (27) 65 76 www.elsevier.com/locate/amc Symmetric Gauss Legedre quadrature ormulas or composite umerical itegratio over a triagular surace H.. Rathod a, *, K.V. Nagaraja
Applied Mathematics ad Computatio 1 (27) 65 76 www.elsevier.com/locate/amc Symmetric Gauss Legedre quadrature ormulas or composite umerical itegratio over a triagular surace H.. Rathod a, *, K.V. Nagaraja
Instructions: No books. No notes. Non-graphing calculators only. You are encouraged, although not required, to show your work.
 Exam 3 Math 850-007 Fall 04 Odenthal Name: Instructions: No books. No notes. Non-graphing calculators only. You are encouraged, although not required, to show your work.. Evaluate the iterated integral
Exam 3 Math 850-007 Fall 04 Odenthal Name: Instructions: No books. No notes. Non-graphing calculators only. You are encouraged, although not required, to show your work.. Evaluate the iterated integral
PHYS-4007/5007: Computational Physics Course Lecture Notes Appendix G
 PHYS-4007/5007: Computational Physics Course Lecture Notes Appendix G Dr. Donald G. Luttermoser East Tennessee State University Version 7.0 Abstract These class notes are designed for use of the instructor
PHYS-4007/5007: Computational Physics Course Lecture Notes Appendix G Dr. Donald G. Luttermoser East Tennessee State University Version 7.0 Abstract These class notes are designed for use of the instructor
Math 265H: Calculus III Practice Midterm II: Fall 2014
 Name: Section #: Math 65H: alculus III Practice Midterm II: Fall 14 Instructions: This exam has 7 problems. The number of points awarded for each question is indicated in the problem. Answer each question
Name: Section #: Math 65H: alculus III Practice Midterm II: Fall 14 Instructions: This exam has 7 problems. The number of points awarded for each question is indicated in the problem. Answer each question
COMPUTATION OF BESSEL AND AIRY FUNCTIONS AND OF RELATED GAUSSIAN QUADRATURE FORMULAE
 BIT 6-85//41-11 $16., Vol. 4, No. 1, pp. 11 118 c Swets & Zeitlinger COMPUTATION OF BESSEL AND AIRY FUNCTIONS AND OF RELATED GAUSSIAN QUADRATURE FORMULAE WALTER GAUTSCHI Department of Computer Sciences,
BIT 6-85//41-11 $16., Vol. 4, No. 1, pp. 11 118 c Swets & Zeitlinger COMPUTATION OF BESSEL AND AIRY FUNCTIONS AND OF RELATED GAUSSIAN QUADRATURE FORMULAE WALTER GAUTSCHI Department of Computer Sciences,
Lecture 21: Isoparametric Formulation of Plane Elements.
 6.6. Rectangular Plane Stress/Strain Element. he CS element uses a triangular shape. he 3 nodes of the CS element allow us to employ linear multivariate approximations to the u and v displacements. he
6.6. Rectangular Plane Stress/Strain Element. he CS element uses a triangular shape. he 3 nodes of the CS element allow us to employ linear multivariate approximations to the u and v displacements. he
The Discontinuous Galerkin Method for Hyperbolic Problems
 Chapter 2 The Discontinuous Galerkin Method for Hyperbolic Problems In this chapter we shall specify the types of problems we consider, introduce most of our notation, and recall some theory on the DG
Chapter 2 The Discontinuous Galerkin Method for Hyperbolic Problems In this chapter we shall specify the types of problems we consider, introduce most of our notation, and recall some theory on the DG
Math 127C, Spring 2006 Final Exam Solutions. x 2 ), g(y 1, y 2 ) = ( y 1 y 2, y1 2 + y2) 2. (g f) (0) = g (f(0))f (0).
 Math 27C, Spring 26 Final Exam Solutions. Define f : R 2 R 2 and g : R 2 R 2 by f(x, x 2 (sin x 2 x, e x x 2, g(y, y 2 ( y y 2, y 2 + y2 2. Use the chain rule to compute the matrix of (g f (,. By the chain
Math 27C, Spring 26 Final Exam Solutions. Define f : R 2 R 2 and g : R 2 R 2 by f(x, x 2 (sin x 2 x, e x x 2, g(y, y 2 ( y y 2, y 2 + y2 2. Use the chain rule to compute the matrix of (g f (,. By the chain
Substitutions in Multiple Integrals
 Substitutions in Multiple Integrals P. Sam Johnson April 10, 2017 P. Sam Johnson (NIT Karnataka) Substitutions in Multiple Integrals April 10, 2017 1 / 23 Overview In the lecture, we discuss how to evaluate
Substitutions in Multiple Integrals P. Sam Johnson April 10, 2017 P. Sam Johnson (NIT Karnataka) Substitutions in Multiple Integrals April 10, 2017 1 / 23 Overview In the lecture, we discuss how to evaluate
Oct : Lecture 15: Surface Integrals and Some Related Theorems
 90 MIT 3.016 Fall 2005 c W.C Carter Lecture 15 Oct. 21 2005: Lecture 15: Surface Integrals and Some Related Theorems Reading: Kreyszig Sections: 9.4 pp:485 90), 9.5 pp:491 495) 9.6 pp:496 505) 9.7 pp:505
90 MIT 3.016 Fall 2005 c W.C Carter Lecture 15 Oct. 21 2005: Lecture 15: Surface Integrals and Some Related Theorems Reading: Kreyszig Sections: 9.4 pp:485 90), 9.5 pp:491 495) 9.6 pp:496 505) 9.7 pp:505
1 4 (1 cos(4θ))dθ = θ 4 sin(4θ)
 M48M Final Exam Solutions, December 9, 5 ) A polar curve Let C be the portion of the cloverleaf curve r = sin(θ) that lies in the first quadrant a) Draw a rough sketch of C This looks like one quarter
M48M Final Exam Solutions, December 9, 5 ) A polar curve Let C be the portion of the cloverleaf curve r = sin(θ) that lies in the first quadrant a) Draw a rough sketch of C This looks like one quarter
Lecture Notes in Mathematics. Arkansas Tech University Department of Mathematics. The Basics of Linear Algebra
 Lecture Notes in Mathematics Arkansas Tech University Department of Mathematics The Basics of Linear Algebra Marcel B. Finan c All Rights Reserved Last Updated November 30, 2015 2 Preface Linear algebra
Lecture Notes in Mathematics Arkansas Tech University Department of Mathematics The Basics of Linear Algebra Marcel B. Finan c All Rights Reserved Last Updated November 30, 2015 2 Preface Linear algebra
Numerical Analysis. A Comprehensive Introduction. H. R. Schwarz University of Zürich Switzerland. with a contribution by
 Numerical Analysis A Comprehensive Introduction H. R. Schwarz University of Zürich Switzerland with a contribution by J. Waldvogel Swiss Federal Institute of Technology, Zürich JOHN WILEY & SONS Chichester
Numerical Analysis A Comprehensive Introduction H. R. Schwarz University of Zürich Switzerland with a contribution by J. Waldvogel Swiss Federal Institute of Technology, Zürich JOHN WILEY & SONS Chichester
is a surface above the xy-plane over R.
 Chapter 13 Multiple Integration Section 13.1Double Integrals over ectangular egions ecall the Definite Integral from Chapter 5 b a n * lim i f x dx f x x n i 1 b If f x 0 then f xdx is the area under the
Chapter 13 Multiple Integration Section 13.1Double Integrals over ectangular egions ecall the Definite Integral from Chapter 5 b a n * lim i f x dx f x x n i 1 b If f x 0 then f xdx is the area under the
A NEW STABILIZED ONE POINT INTEGRATED SHEAR ELASTIC PLATE ELEMENT
 European Congress on Computational Methods in Applied Sciences and Engineering ECCOMAS 2004 P. Neittaanmäki, T. Rossi, K. Majava, and O. Pironneau (eds.) R. Owen and M. Mikkola (assoc. eds.) Jyväskylä,
European Congress on Computational Methods in Applied Sciences and Engineering ECCOMAS 2004 P. Neittaanmäki, T. Rossi, K. Majava, and O. Pironneau (eds.) R. Owen and M. Mikkola (assoc. eds.) Jyväskylä,
A MODIFIED DECOUPLED SCALED BOUNDARY-FINITE ELEMENT METHOD FOR MODELING 2D IN-PLANE-MOTION TRANSIENT ELASTODYNAMIC PROBLEMS IN SEMI-INFINITE MEDIA
 8 th GRACM International Congress on Computational Mechanics Volos, 2 July 5 July 205 A MODIFIED DECOUPLED SCALED BOUNDARY-FINITE ELEMENT METHOD FOR MODELING 2D IN-PLANE-MOTION TRANSIENT ELASTODYNAMIC
8 th GRACM International Congress on Computational Mechanics Volos, 2 July 5 July 205 A MODIFIED DECOUPLED SCALED BOUNDARY-FINITE ELEMENT METHOD FOR MODELING 2D IN-PLANE-MOTION TRANSIENT ELASTODYNAMIC
Math 175 Common Exam 2A Spring 2018
 Math 175 Common Exam 2A Spring 2018 Part I: Short Form The first seven (7) pages are short answer. You don t need to show work. Partial credit will be rare and small. 1. (8 points) Suppose f(x) is a function
Math 175 Common Exam 2A Spring 2018 Part I: Short Form The first seven (7) pages are short answer. You don t need to show work. Partial credit will be rare and small. 1. (8 points) Suppose f(x) is a function
16.2 Iterated Integrals
 6.2 Iterated Integrals So far: We have defined what we mean by a double integral. We have estimated the value of a double integral from contour diagrams and from tables of values. We have interpreted the
6.2 Iterated Integrals So far: We have defined what we mean by a double integral. We have estimated the value of a double integral from contour diagrams and from tables of values. We have interpreted the
CIV-E1060 Engineering Computation and Simulation Examination, December 12, 2017 / Niiranen
 CIV-E16 Engineering Computation and Simulation Examination, December 12, 217 / Niiranen This examination consists of 3 problems rated by the standard scale 1...6. Problem 1 Let us consider a long and tall
CIV-E16 Engineering Computation and Simulation Examination, December 12, 217 / Niiranen This examination consists of 3 problems rated by the standard scale 1...6. Problem 1 Let us consider a long and tall
MA2501 Numerical Methods Spring 2015
 Norwegian University of Science and Technology Department of Mathematics MA5 Numerical Methods Spring 5 Solutions to exercise set 9 Find approximate values of the following integrals using the adaptive
Norwegian University of Science and Technology Department of Mathematics MA5 Numerical Methods Spring 5 Solutions to exercise set 9 Find approximate values of the following integrals using the adaptive
Section 6.6 Gaussian Quadrature
 Section 6.6 Gaussian Quadrature Key Terms: Method of undetermined coefficients Nonlinear systems Gaussian quadrature Error Legendre polynomials Inner product Adapted from http://pathfinder.scar.utoronto.ca/~dyer/csca57/book_p/node44.html
Section 6.6 Gaussian Quadrature Key Terms: Method of undetermined coefficients Nonlinear systems Gaussian quadrature Error Legendre polynomials Inner product Adapted from http://pathfinder.scar.utoronto.ca/~dyer/csca57/book_p/node44.html
Vibration of Thin Beams by PIM and RPIM methods. *B. Kanber¹, and O. M. Tufik 1
 APCOM & ISCM -4 th December, 23, Singapore Vibration of Thin Beams by PIM and RPIM methods *B. Kanber¹, and O. M. Tufik Mechanical Engineering Department, University of Gaziantep, Turkey. *Corresponding
APCOM & ISCM -4 th December, 23, Singapore Vibration of Thin Beams by PIM and RPIM methods *B. Kanber¹, and O. M. Tufik Mechanical Engineering Department, University of Gaziantep, Turkey. *Corresponding
Chapter 4: Linear Equations
 Chapter 4: Linear Equations Daniel Chan UNSW Semester 1 2018 Daniel Chan (UNSW) Chapter 4: Linear Equations Semester 1 2018 1 / 42 An Ancient Chinese Problem The following maths problem was taken from
Chapter 4: Linear Equations Daniel Chan UNSW Semester 1 2018 Daniel Chan (UNSW) Chapter 4: Linear Equations Semester 1 2018 1 / 42 An Ancient Chinese Problem The following maths problem was taken from
Note: Each problem is worth 14 points except numbers 5 and 6 which are 15 points. = 3 2
 Math Prelim II Solutions Spring Note: Each problem is worth points except numbers 5 and 6 which are 5 points. x. Compute x da where is the region in the second quadrant between the + y circles x + y and
Math Prelim II Solutions Spring Note: Each problem is worth points except numbers 5 and 6 which are 5 points. x. Compute x da where is the region in the second quadrant between the + y circles x + y and
Homework 6 Solutions
 Homeork 6 Solutions Igor Yanovsky (Math 151B TA) Section 114, Problem 1: For the boundary-value problem y (y ) y + log x, 1 x, y(1) 0, y() log, (1) rite the nonlinear system and formulas for Neton s method
Homeork 6 Solutions Igor Yanovsky (Math 151B TA) Section 114, Problem 1: For the boundary-value problem y (y ) y + log x, 1 x, y(1) 0, y() log, (1) rite the nonlinear system and formulas for Neton s method
Math 151. Rumbos Spring Solutions to Review Problems for Exam 2
 Math 5. Rumbos Spring 22 Solutions to Review Problems for Exam 2. Let X and Y be independent Normal(, ) random variables. Put Z = Y X. Compute the distribution functions (z) and (z). Solution: Since X,
Math 5. Rumbos Spring 22 Solutions to Review Problems for Exam 2. Let X and Y be independent Normal(, ) random variables. Put Z = Y X. Compute the distribution functions (z) and (z). Solution: Since X,
A GLOBAL COLLOCATION METHOD FOR TWO-DIMENSIONAL RECTANGULAR DOMAINS
 JOURNAL OF MECHANICS OF MATERIALS AND STRUCTURES Vol., No., A GLOBAL COLLOCATION METHOD FOR TWO-DIMENSIONAL RECTANGULAR DOMAINS CHRISTOPHER G. PROVATIDIS This paper proposes the use of a global collocation
JOURNAL OF MECHANICS OF MATERIALS AND STRUCTURES Vol., No., A GLOBAL COLLOCATION METHOD FOR TWO-DIMENSIONAL RECTANGULAR DOMAINS CHRISTOPHER G. PROVATIDIS This paper proposes the use of a global collocation
Math 23b Practice Final Summer 2011
 Math 2b Practice Final Summer 211 1. (1 points) Sketch or describe the region of integration for 1 x y and interchange the order to dy dx dz. f(x, y, z) dz dy dx Solution. 1 1 x z z f(x, y, z) dy dx dz
Math 2b Practice Final Summer 211 1. (1 points) Sketch or describe the region of integration for 1 x y and interchange the order to dy dx dz. f(x, y, z) dz dy dx Solution. 1 1 x z z f(x, y, z) dy dx dz
18.01 Single Variable Calculus Fall 2006
 MIT OpenCourseWare http://ocw.mit.edu 18.01 Single Variable Calculus Fall 2006 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. Exam 4 Review 1. Trig substitution
MIT OpenCourseWare http://ocw.mit.edu 18.01 Single Variable Calculus Fall 2006 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. Exam 4 Review 1. Trig substitution
JEPPIAAR ENGINEERING COLLEGE
 JEPPIAAR ENGINEERING COLLEGE Jeppiaar Nagar, Rajiv Gandhi Salai 600 119 DEPARTMENT OFMECHANICAL ENGINEERING QUESTION BANK VI SEMESTER ME6603 FINITE ELEMENT ANALYSIS Regulation 013 SUBJECT YEAR /SEM: III
JEPPIAAR ENGINEERING COLLEGE Jeppiaar Nagar, Rajiv Gandhi Salai 600 119 DEPARTMENT OFMECHANICAL ENGINEERING QUESTION BANK VI SEMESTER ME6603 FINITE ELEMENT ANALYSIS Regulation 013 SUBJECT YEAR /SEM: III
NUMERICAL COMPUTATION IN SCIENCE AND ENGINEERING
 NUMERICAL COMPUTATION IN SCIENCE AND ENGINEERING C. Pozrikidis University of California, San Diego New York Oxford OXFORD UNIVERSITY PRESS 1998 CONTENTS Preface ix Pseudocode Language Commands xi 1 Numerical
NUMERICAL COMPUTATION IN SCIENCE AND ENGINEERING C. Pozrikidis University of California, San Diego New York Oxford OXFORD UNIVERSITY PRESS 1998 CONTENTS Preface ix Pseudocode Language Commands xi 1 Numerical
Multiple Integrals. Introduction and Double Integrals Over Rectangular Regions. Philippe B. Laval. Spring 2012 KSU
 Multiple Integrals Introduction and Double Integrals Over Rectangular Regions Philippe B Laval KSU Spring 2012 Philippe B Laval (KSU) Multiple Integrals Spring 2012 1 / 21 Introduction In this section
Multiple Integrals Introduction and Double Integrals Over Rectangular Regions Philippe B Laval KSU Spring 2012 Philippe B Laval (KSU) Multiple Integrals Spring 2012 1 / 21 Introduction In this section
COURSE Numerical integration of functions (continuation) 3.3. The Romberg s iterative generation method
 COURSE 7 3. Numerical integration of functions (continuation) 3.3. The Romberg s iterative generation method The presence of derivatives in the remainder difficulties in applicability to practical problems
COURSE 7 3. Numerical integration of functions (continuation) 3.3. The Romberg s iterative generation method The presence of derivatives in the remainder difficulties in applicability to practical problems
Figure 25:Differentials of surface.
 2.5. Change of variables and Jacobians In the previous example we saw that, once we have identified the type of coordinates which is best to use for solving a particular problem, the next step is to do
2.5. Change of variables and Jacobians In the previous example we saw that, once we have identified the type of coordinates which is best to use for solving a particular problem, the next step is to do
(a) 0 (b) 1/4 (c) 1/3 (d) 1/2 (e) 2/3 (f) 3/4 (g) 1 (h) 4/3
 Math 114 Practice Problems for Test 3 omments: 0. urface integrals, tokes Theorem and Gauss Theorem used to be in the Math40 syllabus until last year, so we will look at some of the questions from those
Math 114 Practice Problems for Test 3 omments: 0. urface integrals, tokes Theorem and Gauss Theorem used to be in the Math40 syllabus until last year, so we will look at some of the questions from those
Numerical Integration over Pyramids
 Numerical Integration over Pyramids Chuan Miao Chen, Michal řížek, Liping Liu Corresponding Author: Dr. Liping Liu Department of Mathematical Sciences Lakehead University Thunder Bay, ON Canada P7B 5E1
Numerical Integration over Pyramids Chuan Miao Chen, Michal řížek, Liping Liu Corresponding Author: Dr. Liping Liu Department of Mathematical Sciences Lakehead University Thunder Bay, ON Canada P7B 5E1
FINAL REVIEW Answers and hints Math 311 Fall 2017
 FINAL RVIW Answers and hints Math 3 Fall 7. Let R be a Jordan region and let f : R be integrable. Prove that the graph of f, as a subset of R 3, has zero volume. Let R be a rectangle with R. Since f is
FINAL RVIW Answers and hints Math 3 Fall 7. Let R be a Jordan region and let f : R be integrable. Prove that the graph of f, as a subset of R 3, has zero volume. Let R be a rectangle with R. Since f is
42. Change of Variables: The Jacobian
 . Change of Variables: The Jacobian It is common to change the variable(s) of integration, the main goal being to rewrite a complicated integrand into a simpler equivalent form. However, in doing so, the
. Change of Variables: The Jacobian It is common to change the variable(s) of integration, the main goal being to rewrite a complicated integrand into a simpler equivalent form. However, in doing so, the
QMUL, School of Physics and Astronomy Date: 18/01/2019
 QMUL, School of Physics and stronomy Date: 8//9 PHY Mathematical Techniques Solutions for Exercise Class Script : Coordinate Systems and Double Integrals. Calculate the integral: where the region is defined
QMUL, School of Physics and stronomy Date: 8//9 PHY Mathematical Techniques Solutions for Exercise Class Script : Coordinate Systems and Double Integrals. Calculate the integral: where the region is defined
Efficient hp-finite elements
 Efficient hp-finite elements Ammon Washburn July 31, 2015 Abstract Ways to make an hp-finite element method efficient are presented. Standard FEMs and hp-fems with their various strengths and weaknesses
Efficient hp-finite elements Ammon Washburn July 31, 2015 Abstract Ways to make an hp-finite element method efficient are presented. Standard FEMs and hp-fems with their various strengths and weaknesses
The multidimensional moment-constrained maximum entropy problem: A BFGS algorithm with constraint scaling
 The multidimensional moment-constrained maximum entropy problem: A BFGS algorithm with constraint scaling Rafail V. Abramov Department of Mathematics, Statistics and Computer Science University of Illinois
The multidimensional moment-constrained maximum entropy problem: A BFGS algorithm with constraint scaling Rafail V. Abramov Department of Mathematics, Statistics and Computer Science University of Illinois
EFFICIENT SHAPE OPTIMIZATION USING POLYNOMIAL CHAOS EXPANSION AND LOCAL SENSITIVITIES
 9 th ASCE Specialty Conference on Probabilistic Mechanics and Structural Reliability EFFICIENT SHAPE OPTIMIZATION USING POLYNOMIAL CHAOS EXPANSION AND LOCAL SENSITIVITIES Nam H. Kim and Haoyu Wang University
9 th ASCE Specialty Conference on Probabilistic Mechanics and Structural Reliability EFFICIENT SHAPE OPTIMIZATION USING POLYNOMIAL CHAOS EXPANSION AND LOCAL SENSITIVITIES Nam H. Kim and Haoyu Wang University
Formation of H-atom in 2s excited state of proton-lithium and proton-sodium scattering
 PRAMANA c Indian Academy of Sciences Vol. 70, No. 4 journal of April 008 physics pp. 753 758 Formation of H-atom in s excited state of proton-lithium and proton-sodium scattering Y N TIWARI Department
PRAMANA c Indian Academy of Sciences Vol. 70, No. 4 journal of April 008 physics pp. 753 758 Formation of H-atom in s excited state of proton-lithium and proton-sodium scattering Y N TIWARI Department
International Journal of Scientific & Engineering Research, Volume 4, Issue 10, October ISSN
 International Journal of Scientific & Engineering Research, Volume 4, Issue 0, October-203 956 Optimum Design for Minimum Mass Configuration Of Stepped Cantilever Compound Columns With Constraint On Axial
International Journal of Scientific & Engineering Research, Volume 4, Issue 0, October-203 956 Optimum Design for Minimum Mass Configuration Of Stepped Cantilever Compound Columns With Constraint On Axial
School of the Art Institute of Chicago. Calculus. Frank Timmes. flash.uchicago.edu/~fxt/class_pages/class_calc.
 School of the Art Institute of Chicago Calculus Frank Timmes ftimmes@artic.edu flash.uchicago.edu/~fxt/class_pages/class_calc.shtml Syllabus 1 Aug 29 Pre-calculus 2 Sept 05 Rates and areas 3 Sept 12 Trapezoids
School of the Art Institute of Chicago Calculus Frank Timmes ftimmes@artic.edu flash.uchicago.edu/~fxt/class_pages/class_calc.shtml Syllabus 1 Aug 29 Pre-calculus 2 Sept 05 Rates and areas 3 Sept 12 Trapezoids
Ch. 03 Numerical Quadrature. Andrea Mignone Physics Department, University of Torino AA
 Ch. 03 Numerical Quadrature Andrea Mignone Physics Department, University of Torino AA 2017-2018 Numerical Quadrature In numerical analysis quadrature refers to the computation of definite integrals. y
Ch. 03 Numerical Quadrature Andrea Mignone Physics Department, University of Torino AA 2017-2018 Numerical Quadrature In numerical analysis quadrature refers to the computation of definite integrals. y
Integration. Topic: Trapezoidal Rule. Major: General Engineering. Author: Autar Kaw, Charlie Barker.
 Integration Topic: Trapezoidal Rule Major: General Engineering Author: Autar Kaw, Charlie Barker 1 What is Integration Integration: The process of measuring the area under a function plotted on a graph.
Integration Topic: Trapezoidal Rule Major: General Engineering Author: Autar Kaw, Charlie Barker 1 What is Integration Integration: The process of measuring the area under a function plotted on a graph.
AM205: Assignment 3 (due 5 PM, October 20)
 AM25: Assignment 3 (due 5 PM, October 2) For this assignment, first complete problems 1, 2, 3, and 4, and then complete either problem 5 (on theory) or problem 6 (on an application). If you submit answers
AM25: Assignment 3 (due 5 PM, October 2) For this assignment, first complete problems 1, 2, 3, and 4, and then complete either problem 5 (on theory) or problem 6 (on an application). If you submit answers
Solution of First Order Initial Value Problem by Sixth Order Predictor Corrector Method
 Global Journal of Pure and Applied Mathematics. ISSN 0973-1768 Volume 13, Number 6 (2017), pp. 2277 2290 Research India Publications http://www.ripublication.com/gjpam.htm Solution of First Order Initial
Global Journal of Pure and Applied Mathematics. ISSN 0973-1768 Volume 13, Number 6 (2017), pp. 2277 2290 Research India Publications http://www.ripublication.com/gjpam.htm Solution of First Order Initial
A note on multivariate Gauss-Hermite quadrature
 A note on multivariate Gauss-Hermite quadrature Peter Jäckel 1th May 5 1 Introduction Gaussian quadratures are an ingenious way to approximate the integral of an unknown function f(x) over a specified
A note on multivariate Gauss-Hermite quadrature Peter Jäckel 1th May 5 1 Introduction Gaussian quadratures are an ingenious way to approximate the integral of an unknown function f(x) over a specified
Construction of `Wachspress type' rational basis functions over rectangles
 Proc. Indian Acad. Sci. (Math. Sci.), Vol. 110, No. 1, February 2000, pp. 69±77. # Printed in India Construction of `Wachspress type' rational basis functions over rectangles P L POWAR and S S RANA Department
Proc. Indian Acad. Sci. (Math. Sci.), Vol. 110, No. 1, February 2000, pp. 69±77. # Printed in India Construction of `Wachspress type' rational basis functions over rectangles P L POWAR and S S RANA Department
The Evaluation Of early Singular Integrals In The Direct Regularized Boundary Element Method
 The Evaluation Of early Singular Integrals In The Direct Regularized Boundary Element Method * School of Science Shandong university of technology Zhangzhou Road #, Zibo, Shandong, 55049 China Zhengbin60@6.com
The Evaluation Of early Singular Integrals In The Direct Regularized Boundary Element Method * School of Science Shandong university of technology Zhangzhou Road #, Zibo, Shandong, 55049 China Zhengbin60@6.com
A Legendre Computational Matrix Method for Solving High-Order Fractional Differential Equations
 Mathematics A Legendre Computational Matrix Method for Solving High-Order Fractional Differential Equations Mohamed Meabed KHADER * and Ahmed Saied HENDY Department of Mathematics, Faculty of Science,
Mathematics A Legendre Computational Matrix Method for Solving High-Order Fractional Differential Equations Mohamed Meabed KHADER * and Ahmed Saied HENDY Department of Mathematics, Faculty of Science,
Research Computing with Python, Lecture 7, Numerical Integration and Solving Ordinary Differential Equations
 Research Computing with Python, Lecture 7, Numerical Integration and Solving Ordinary Differential Equations Ramses van Zon SciNet HPC Consortium November 25, 2014 Ramses van Zon (SciNet HPC Consortium)Research
Research Computing with Python, Lecture 7, Numerical Integration and Solving Ordinary Differential Equations Ramses van Zon SciNet HPC Consortium November 25, 2014 Ramses van Zon (SciNet HPC Consortium)Research
Numerical solution of system of linear integral equations via improvement of block-pulse functions
 Journal of Mathematical Modeling Vol. 4, No., 16, pp. 133-159 JMM Numerical solution of system of linear integral equations via improvement of block-pulse functions Farshid Mirzaee Faculty of Mathematical
Journal of Mathematical Modeling Vol. 4, No., 16, pp. 133-159 JMM Numerical solution of system of linear integral equations via improvement of block-pulse functions Farshid Mirzaee Faculty of Mathematical
Solving Partial Differential Equations Numerically. Miklós Bergou with: Gary Miller, David Cardoze, Todd Phillips, Mark Olah
 Solving Partial Dierential Equations Numerically Miklós Bergou with: Gary Miller, David Cardoze, Todd Phillips, Mark Olah Overview What are partial dierential equations? How do we solve them? (Example)
Solving Partial Dierential Equations Numerically Miklós Bergou with: Gary Miller, David Cardoze, Todd Phillips, Mark Olah Overview What are partial dierential equations? How do we solve them? (Example)
Matrix construction: Singular integral contributions
 Matrix construction: Singular integral contributions Seminar Boundary Element Methods for Wave Scattering Sophie Haug ETH Zurich November 2010 Outline 1 General concepts in singular integral computation
Matrix construction: Singular integral contributions Seminar Boundary Element Methods for Wave Scattering Sophie Haug ETH Zurich November 2010 Outline 1 General concepts in singular integral computation
1 Number Systems and Errors 1
 Contents 1 Number Systems and Errors 1 1.1 Introduction................................ 1 1.2 Number Representation and Base of Numbers............. 1 1.2.1 Normalized Floating-point Representation...........
Contents 1 Number Systems and Errors 1 1.1 Introduction................................ 1 1.2 Number Representation and Base of Numbers............. 1 1.2.1 Normalized Floating-point Representation...........
APPM/MATH Problem Set 6 Solutions
 APPM/MATH 460 Problem Set 6 Solutions This assignment is due by 4pm on Wednesday, November 6th You may either turn it in to me in class or in the box outside my office door (ECOT ) Minimal credit will
APPM/MATH 460 Problem Set 6 Solutions This assignment is due by 4pm on Wednesday, November 6th You may either turn it in to me in class or in the box outside my office door (ECOT ) Minimal credit will
Numerical Solutions of Laplacian Problems over L-Shaped Domains and Calculations of the Generalized Stress Intensity Factors
 WCCM V Fifth World Congress on Computational Mechanics July 7-2, 2002, Vienna, Austria Eds.: H.A. Mang, F.G. Rammerstorfer, J. Eberhardsteiner Numerical Solutions of Laplacian Problems over L-Shaped Domains
WCCM V Fifth World Congress on Computational Mechanics July 7-2, 2002, Vienna, Austria Eds.: H.A. Mang, F.G. Rammerstorfer, J. Eberhardsteiner Numerical Solutions of Laplacian Problems over L-Shaped Domains
Local discontinuous Galerkin methods for elliptic problems
 COMMUNICATIONS IN NUMERICAL METHODS IN ENGINEERING Commun. Numer. Meth. Engng 2002; 18:69 75 [Version: 2000/03/22 v1.0] Local discontinuous Galerkin methods for elliptic problems P. Castillo 1 B. Cockburn
COMMUNICATIONS IN NUMERICAL METHODS IN ENGINEERING Commun. Numer. Meth. Engng 2002; 18:69 75 [Version: 2000/03/22 v1.0] Local discontinuous Galerkin methods for elliptic problems P. Castillo 1 B. Cockburn
Math 115 ( ) Yum-Tong Siu 1. Euler-Lagrange Equations for Many Functions and Variables and High-Order Derivatives
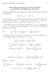 Math 115 006-007 Yum-Tong Siu 1 Euler-Lagrange Equations for Many Functions and Variables and High-Order Derivatives The Case of High-Order Derivatives. The context is to find the extremal for the functional
Math 115 006-007 Yum-Tong Siu 1 Euler-Lagrange Equations for Many Functions and Variables and High-Order Derivatives The Case of High-Order Derivatives. The context is to find the extremal for the functional
Math 265 (Butler) Practice Midterm III B (Solutions)
 Math 265 (Butler) Practice Midterm III B (Solutions). Set up (but do not evaluate) an integral for the surface area of the surface f(x, y) x 2 y y over the region x, y 4. We have that the surface are is
Math 265 (Butler) Practice Midterm III B (Solutions). Set up (but do not evaluate) an integral for the surface area of the surface f(x, y) x 2 y y over the region x, y 4. We have that the surface are is
Section 4.5. Integration and Expectation
 4.5. Integration and Expectation 1 Section 4.5. Integration and Expectation Note. In this section we consider integrals of scalar valued functions of a vector and matrix valued functions of a scalar. We
4.5. Integration and Expectation 1 Section 4.5. Integration and Expectation Note. In this section we consider integrals of scalar valued functions of a vector and matrix valued functions of a scalar. We
A Hybrid Method for the Wave Equation. beilina
 A Hybrid Method for the Wave Equation http://www.math.unibas.ch/ beilina 1 The mathematical model The model problem is the wave equation 2 u t 2 = (a 2 u) + f, x Ω R 3, t > 0, (1) u(x, 0) = 0, x Ω, (2)
A Hybrid Method for the Wave Equation http://www.math.unibas.ch/ beilina 1 The mathematical model The model problem is the wave equation 2 u t 2 = (a 2 u) + f, x Ω R 3, t > 0, (1) u(x, 0) = 0, x Ω, (2)
Department of Mathematics California State University, Los Angeles Master s Degree Comprehensive Examination in. NUMERICAL ANALYSIS Spring 2015
 Department of Mathematics California State University, Los Angeles Master s Degree Comprehensive Examination in NUMERICAL ANALYSIS Spring 2015 Instructions: Do exactly two problems from Part A AND two
Department of Mathematics California State University, Los Angeles Master s Degree Comprehensive Examination in NUMERICAL ANALYSIS Spring 2015 Instructions: Do exactly two problems from Part A AND two
LECTURE NOTES ELEMENTARY NUMERICAL METHODS. Eusebius Doedel
 LECTURE NOTES on ELEMENTARY NUMERICAL METHODS Eusebius Doedel TABLE OF CONTENTS Vector and Matrix Norms 1 Banach Lemma 20 The Numerical Solution of Linear Systems 25 Gauss Elimination 25 Operation Count
LECTURE NOTES on ELEMENTARY NUMERICAL METHODS Eusebius Doedel TABLE OF CONTENTS Vector and Matrix Norms 1 Banach Lemma 20 The Numerical Solution of Linear Systems 25 Gauss Elimination 25 Operation Count
Math221: HW# 7 solutions
 Math22: HW# 7 solutions Andy Royston November 7, 25.3.3 let x = e u. Then ln x = u, x2 = e 2u, and dx = e 2u du. Furthermore, when x =, u, and when x =, u =. Hence x 2 ln x) 3 dx = e 2u u 3 e u du) = e
Math22: HW# 7 solutions Andy Royston November 7, 25.3.3 let x = e u. Then ln x = u, x2 = e 2u, and dx = e 2u du. Furthermore, when x =, u, and when x =, u =. Hence x 2 ln x) 3 dx = e 2u u 3 e u du) = e
ETNA Kent State University
 Electronic Transactions on Numerical Analysis. Volume 39, pp. 1-11, 1. Copyright 1,. ISSN 168-9613. ETNA TRIGONOMETRIC GAUSSIAN QUADRATURE ON SUBINTERVALS OF THE PERIOD GASPARE DA FIES AND MARCO VIANELLO
Electronic Transactions on Numerical Analysis. Volume 39, pp. 1-11, 1. Copyright 1,. ISSN 168-9613. ETNA TRIGONOMETRIC GAUSSIAN QUADRATURE ON SUBINTERVALS OF THE PERIOD GASPARE DA FIES AND MARCO VIANELLO
Sixth Order Newton-Type Method For Solving System Of Nonlinear Equations And Its Applications
 Applied Mathematics E-Notes, 17(017), 1-30 c ISSN 1607-510 Available free at mirror sites of http://www.math.nthu.edu.tw/ amen/ Sixth Order Newton-Type Method For Solving System Of Nonlinear Equations
Applied Mathematics E-Notes, 17(017), 1-30 c ISSN 1607-510 Available free at mirror sites of http://www.math.nthu.edu.tw/ amen/ Sixth Order Newton-Type Method For Solving System Of Nonlinear Equations
