An almost Anti-Windup scheme for plants with magnitude, rate and curvature saturation
|
|
|
- Jesse Mitchell
- 5 years ago
- Views:
Transcription
1 2 Ameian ontol onfeene Maiott Watefont, Baltimoe, MD, USA June 3-July 2, 2 F4.5 An almot Anti-Winup heme fo plant with magnitue, ate an uvatue atuation Fulvio Foni, Segio Galeani, Lua Zaaian Abtat We ae the anti-winup augmentation poblem fo plant with atuation on the magnitue, ate an uvatue of the ontol input. To thi aim, given an unontaine loe-loop, we geneate a lightly moifie titly pope ontolle fo whih the eivative of the ontol ignal ae available an we olve the anti-winup poblem fo thi moifie ontol heme (namely, an almot anti-winup fo the oiginal loe-loop). Bae on thi almot appoah, we eviit an exiting Moel Reovey anti-winup olution fo ate an magnitue atuate plant an then we exten the eult to the ae of ate, magnitue an uvatue atuation, by poviing a Moel Reovey olution to thi aitional poblem. An example illutate the peuliaitie an the effetivene of the popoe olution. I. INTRODUTION Plant input atuation in othewie linea ontol ytem ha been long tuie ine the 95. In patiula the oalle anti-winup appoah aoe in thoe ealy yea a a poible epone to the nee of not aifiing the mall ignal behavio to obtain a atifatoy lage ignal behavio. While the anti-winup appoah ha been hitoially aoiate with magnitue only atuation (ee fo a uvey of ome ealy anti-winup metho an 6, 7 fo a eent uvey an a eent tutoial on thi topi), ine the late 99 quite a bit of attention ha been evote to extening the available eult to the ae whee the plant input i not only ubjet to magnitue but alo to ate atuation. Thi ontext i epeially elevant in a numbe of appliation, inluing flight ontol, ontol of Tokamak plama with upeonuting oil an many othe whee the equet to the atuato i not allowe to hange too fat (ee, e.g., 3, 9, 3, 4). Anti-winup appoahe fo magnitueate atuate plant have been given in 2 an 8 whee a plant-oe an a tati ompenation heme, epetively, ae popoe an in 6 (futhe extene in 5), whee a tati olution i given. A non-ontutive plantoe olution to the poblem wa alo given in, but key tabilizing feebak nee to be eigne fo the peial plant une onieation in that heme. Thee feebak ae not alway eay to etemine. Finally, the o-alle efeene goveno (o omman-goveno) appoahe whih ely on eeing hoizon optimal ontol iea (ee, e.g., 2, 8, 5) an be fomulate by inopoating ate atuation in the ontol eign poblem. Reently, in 4, we have haateize two Moel Reovey Anti-winup olution fo plant with ate an magnitue atuation, builing upon the peliminay eult of 7 (fo the fit appoah) an 2 (fo the eon one). In thi pape we takle a genealize poblem a ompae to the magniue an ate ae by not only impoing that the Wok uppote in pat by ENEA-Euatom an MIUR une PRIN pojet. All the autho ae with the Dipatimento i Infomatia, Sitemi e Pouzione, Univeity of Rome, To Vegata, 33 Rome, Italy foni galeani zak@ip.unioma2.it zeo (magnitue) an fit (ate) oe time eivative of the plant input nee to be boune, but alo impoing that it eon oe eivative (that we all uvatue) i boune by uitable ontant. Thi equiement genealize the magnitueate atuation equiement in impoing a plant ontol input that i vey egula beaue it oen t allow fo pike of any kin on the plant input afte ompenation. The anti-winup ahitetue that we aopt to takle the magnitueateuvatue atuaiton poblem equie the availability of the fit an eon time eivative of the ontolle output. Thi paallel the olution given in 4 whee the fit time eivative wa equie. While in 4 tit popene of the ontolle allowe fo that equiement, hee it i uneaonable that the elative egee of the ontolle i two an we iu a poible appoah to moify a linea ontol ytem to inue an abitaily mall hange in it tanfe funtion an make thoe eivative available in the moifie ontolle. A imila appoah an be aopte in the ae of a nonlinea ontolle, wheea lineaity of the plant i a key popety fo ou ontution to apply. Then, the heme popoe to geneate the moifie ontolle an alo be ue to ae anti-winup fo magnitueate only atuation with nontitly pope ontolle applying the appoah of 4 to the moifie loe-loop ytem. In all ae, the anti-winup poblem that we ae an be een a an almot anti-winup olution fo the oiginal ontol ytem, inee the moifie loe-loop that we intoue will be almot the ame a the oiginal one up to a etain fequeny of opeation. The pape i oganize a follow. In Setion II we iu how to moify an unontaine loe-loop to obtain in expliit fom N eivative of the plant input. In Setion III we illutate the almot anti-winup olution on plant with ate an magnitue atuation an in Setion IV we apply it to plant with uvatue, ate an magnitue atuation. An example i given to illutate the popoe appoahe. All poof ae omitte ue to lak of pae. II. MODIFIED LOSED-LOOPS FOR AHIEVING STRITLY PROPER ONTROLLERS The pupoe of thi etion i to how how, given a plantontolle pai (poibly, both non titly pope) an a poitive intege N, it i poible to eplae the ontolle by a titly pope one uh that the oiginal an the moifie loe loop ae abitaily loe to eah othe (in a ene to be peifie late), an moeove the output of the moifie ontolle i N time iffeentiable an it N eivative an be mae available a aitional output of the moifie ontolle. A. The oiginal loe loop W onie the following linea plant P ẋ = Ax B u u B y = y x u D y z = z x D zu u D z, () //$26. 2 AA 6769
2 whee x R n i the plant tate, u R m i the plant ontol input, y R q i the meauement output, z i the pefomane output an i a itubane input. Following the tana anti-winup appoah, we aume that a ontolle ha been aleay eigne fo plant (). We make vey few aumption on the tutue of the ontolle,, that an be eibe by the following equation: ẋ = A x B u u B y = x D u u D whee x i the ontolle tate, u i it meauement input an i an extenal efeene ignal. To guaantee exitene an uniquene of olution, we aume that loe-loop between plant () an ontolle (2) i well behave in the abene of atuation, namely with the following unontaine inteonnetion: (2) u = y, u = y. (3) Aumption : The loe-loop betwen plant () an ontolle (2) via the inteonnetion (3) i well poe an aymptotially table. Note that Aumption implie that plant () i tabilizable fom u. In the following, W will enote the oiginal loe loop ytem of (), (2) inteonnete by (3) having tanfe matix W. B. The moifie loe loop Ŵ. In oe to ahieve the availability of the fit N eivative of the ontolle output, we want to eplae the oiginal ontolle by a new ontolle whih i eentially the aae of an a filte F (ue to ompute the appoximate eivative of the ontol ignal y ) with tanfe matix F() = F () F () F N () T I I N I T = ( τ) N, (4) whee τ > i uffiiently mall an the oeffiient α,..., α N ae obtaine by witing p() = N α N N α α with p() = (τ ) N ; it i eay to ee that a τ, the output of F get loe an loe to the input of F an to it fit N eivative. While intuition ugget that, povie that τ > i uffiiently mall, the moifie loe loop will emain table an the loe loop epone with eplae by will be abitaily loe to the oiginal one, it will be hown that fo ou plan to wok it i neeay to exeie ome aitional ae. u Fig.. Let filte F be eibe by y F y, The tutue of the moifie ontolle. ẋ f = A f x f B f u f y f = f x f y (N )f = (N )f x f y Nf = Nf x D Nf u f y (5) whee A f = m(n ) m I m(n ) m(n ) α I α I α N 2 I α N I (6a) B f = I, (6b) f = τ N I, (6) (N )f = τ N I, (6) Nf = τ N α I α I α N I, (6e) D Nf = τ N I an efine by impoing the inteonnetion (ee Fig. ) (6f) u f = y, u = u y y f, y = y f. (7) Fom (2), (5), (6) an (7) the ontolle i eibe by ẋ = A x B u u B y = x y (i) = i x, i =,...,N, = N x D Nu u D N, y (N) whee y (i), i =,...,N i the i th eivative of the main ontolle output y. We will enote by y, the veto T. By efining M = (I D u ) an M = (I D u ), A,B u,b,,d u,d an be haateize a follow. A B u M B u M f A = B f (ID u M ) A f B f D u M f f B B u B = u M B M B f D u M B f D M y ()...y (n) an (note that = ) i = if, i =,...,N, N = D Nf M Nf D Nf MD u f (9) D Nu D N = D Nf MD u D Nf MD () The moifie loe loop ytem Ŵ, with tanfe matix Ŵ, i given by (), (2) an (5) inteonnete by (7) an (8) u = y, u = y ; () equivalently, Ŵ i given by (), (8) inteonnete by (). Looking at the efinition of u in (7) (ee alo Fig. ), it i lea that i not jut the aae of an F, but ontain two iet feethough tem ating with oppoing ign. The aim of uh tem (whih ae abent if =, i.e. if the plant ha no iet feethough fom u to y) an be bette unetoo looking at Fig. 2: eentially, the at the output of F (the ubytem of F having tanfe matix F ()) ha the ole of emoving the iet feethough tem fom P, o that F peeive that it i onnete to a titly pope ytem. Then, the at the output of ha the ole of guaanteeing that the oiginal loe loop (befoe the inetion of F ) i not moifie. The motivation fo thi ouble tanfomation i given in the following emak. Remak : ontol folkloe ay that intouing a uffiiently mall time ontant in a table loe loop oe not impai tability. Howeve, it may be ueful to eall that uh a tatement i tue une the aumption that the loe loop whee the time ontant i inete oe not ontain an 677
3 u Fig. 2. y y, F y = ũ u = ỹ P y = u Loop moifiation to enue that F ee a titly pope ytem. algebai loop 9, Se. 4.7; hene, ou inteet in enuing the onition =. The following example an be ueful in oe to laify thi point. onie a tati plant P with = 2 an a tati ontolle with D u =, whih ontitute a wellpoe, table loe loop. Intouing the filte F () = (τ) the loe loop pole ae the oot of the polynomial 2 (τ) 2 2 = τ 2 2 2τ, whih ha one poitive oot fo any hoie of τ >. Though in the above example both P an ae tati, it i eay to poue imila example whee eithe P o (o both) have a nontivial tate. Notie alo that, if, the folkloe tatement an till hol, but the aitional aumption that i uffiiently mall i neee (thi fat an be poven, even fo nonlinea ytem, by a taightfowa moifiation of the poof of 9, Popoition 4.7.2). Remak 2: The tability pat of the following popoition an be genealize to nonlinea ontolle. In patiula, 9, Popoition 4.7.2, Se. 4.7 an be ue to how that une the aumption that = an fo uffiiently mall τ >, the (loal) aymptoti tability of the loe loop ytem i peeve (an, in the linea ae, thi woul be enough to eue alo global exponential tability). The ame poof an be lightly moifie to how that the ame eult till hol povie that the feethough tem (poibly epening on x) i unifomly boune by a uffiiently mall ontant. On the othe han, genealizing the pefomane pat of the popoition i muh le taightfowa. The following Popoition ompae the loe loop epone of W an Ŵ, by howing that it i alway poible to hooe the filte F uh that the iffeene W := W Ŵ between W an Ŵ i abitaily mall up to an abitay lage fequeny. Popoition : Let Aumption hol. Fo all ε >, ω (, ) thee exit τ > uh that if τ (,τ ) then ) Ŵ i well poe an aymptotially table; 2) σ( W (jω)) < ε, fo all ω, ω): 3) moeove, σ( W (jω)) < ǫ fo all ω, ) if η Ŵ Q u D zu D =, D zu D u D y =. (2) y F µ u P u P y Fig. 3. Relation among Ŵ, Q, F an ; Ŵ eue to W when =. z y z 677 Remak 3: The alulation in the poof of the theoem how that, in geneal, a mimath will alway be intoue by filte F ; howeve, they alo laify that it i alway poible to guaantee that uh egaation will be malle than an abitay mall amount up to an abitay high fequeny, povie that τ > i hoen uffiiently mall. Howeve, the ame alulation how that, unle D zu D D u D y =, the pefomane output will be eteioate by the peene of the filte at uffiiently high fequenie, whee W (jω) D zu D D u D y inepenently fom the filte paamete τ. Example : onie the example in 2, oniting in an exponentially table plant ontolle by an integal ation plu tabilize. Fo thi example, the moifie loe loop ytem (), (2), (5), (7) oepon to A y Bu = A B u = D u (3) an the filte F ha tanfe funtion F () = τ 2 2 (4) 2τ Figue 4 ummaize the iffeene among the moifie loe loop ytem, fo eveal value of τ, an the oiginal loe loop ytem. Although the tep epone of the moifie loe loop ytem ae quite imila to the tep epone of the oiginal loe loop ytem, Boe iagam of figue 4 haateize the iffeene between them. Amplitue tep epone.4 Oiginal l Moifie l, τ=.4.2 Moifie l, τ=.2 Moifie l, τ=. Moifie l, τ= Time (e) Magnitue (B) Phae (eg) boe iagam Fequeny (a/e) Fig. 4. Example : tep epone an boe iagam of the oiginal loe loop an of the moifie loe loop, fo eveal τ. III. ALMOST ANTI-WINDUP WITH MAGNITUDE AND RATE SATURATION We ae in thi etion the poblem aiing when wanting to enue that the plant input u neve exee ome peibe magnitue boun M = (M,...,M m ) an ate boun R = (R,...,R m ). In othe wo the ontol peifiation i that the plant input u i iffeentiable almot eveywhee an that it value i boune between ±M (omponentwie) while it eivative (whih i efine almot eveywhee) i limite between ±R (omponentwie). To implify the expoition, efine at M ( ) a the eentalize ymmeti atuation funtion with boun
4 ±M an at R ( ) a the eentalize ymmeti atuation funtion with boun ±R. In 4, two moel eovey anti-winup olution have been popoe fo thi poblem. We eviit hee the eon olution peente thee, whih aume the availability of the ontolle output eivative an onite in the inetion of a filte oniting in a opy of the plant plu n u exta tate. In 4 that olution wa given fo titly pope ontolle o that the eivative of the ontolle output wa available in expliit fom. With the moifie loe-loop of Setion II, thi i alway poible. In patiula, to takle the atemagnitue atuation ae we ue a eon oe filte in (5), o that it two output y (t) an y () (t) oepon to the moifie ontolle output an it eivative, epetively, at time t. Then the anti-winup olution onit in augmenting the moifie plant-ontolle pai (), (8) with the following filte: ẋ aw = Ax aw B u (u y ) δ = at R (y () v ) y aw = y x aw (u y ) z aw = z x aw D zu (u y ), (5) whee v i a tabilizing ignal futhe iue below an whee the following inteonnetion i ue: u = y y aw, u = at M (δ ). (6) A blok iagam epeentation of the oeponing antiwinup olution (), (8), (5), (6) i epeente in Figue 5 an will be alle anti-winup loe loop though thi etion. Fig. 5. y aw- y () y AW v Rate Satuation δ aw Magnitue Satuation δ u P y Moel eovey anti-winup with ate an magnitue atuation. When inteonneting the anti-winup ompenato (5), (6) to the moifie plant-ontolle pai (), (8), the loeloop appea into a ueful aae fom whih an be appeiate in the ooinate (x l,x,x aw,δ aw ) := (x x aw,x,x aw,δ y ). In patiula, if one make the following linea eletion of v : x v = K aw aw δ y, (7) afte ome eivation, the following tutue i obtaine: ẋ l = Ax l B u y B y l = y x l y D y z l = z x l D zu y D z (8a) ẋ = A x B u u B y = x D u u D The eletion (7) i linea fo impliity of expoition but in geneal nonlinea eletion oul lea to impove tability egion an/o pefomane. - ẋ aw = Ax aw B u (at M (δ aw y ) y ) xaw ) δ aw = at R (K aw δ aw y () y () (8b) z aw = z x aw D zu (at M (δ aw y ) y ), whee y l = y y aw an whee z aw = z z l quantifie the mimath between the atual pefomane output z of the anti-winup loe-loop ytem (), (8), (5), (6) an the eiable pefomane output of the moifie loe-loop ytem (), (8), (), whih ha been hown in the peviou etion to be loe (in a uitable ene) to the pefomane output of the oiginal loe-loop (), (2), (3). Fo the anti-winup loe-loop (), (8), (5), (6), bae on the eult in 4 an on the hange of ooinate in (8), it poible to pove the following tatement, whih illutate the eiable popetie inue by the anti-winup olution. Theoem : Given the anti-winup loe-loop (), (8), (5), (6), if x aw () = an δ () = y (), then the plant input u neve exee the ate an magnitue atuation boun. Moeove, if the eletion (7) of the ignal v guaantee loal (epetively, global) aymptoti tability of the ubytem (8b), then the following hol: ) Given any epone of the moifie loe-loop (), (8), () uh that y (t) = at M (y (t)) an y () (t) = at R (y () (t)) fo all t, then z(t) z l (t) =, fo all t, namely the epone of the anti-winup loe-loop oinie with the epone of the moifie loeloop; 2) The oigin of the anti-winup loe-loop i loally (epetively, globally) aymptotially table. Note that not muh i onveye by Theoem about the omain of attation of the ytem in the ae when v only loally tabilize the ynami (8b). A qualitative tatement i that the lage the tability egion of (8b), the lage efeene an itubane will till enue onvegene of the anti-winup loe-loop. In 4 ome eipe fo the eign of K aw in (7) wee given, in aition to aitional L 2 popetie of thi heme. In thi pape, in light of the genealization aie out in the next etion, we fou on the iffeent apet lite in Theoem an we ely on the fat that any K aw tabilizing the ynami ( ) ẋaw A Bu xaw = δ aw I K aw δ, (9) aw inue loal aymptoti tability of (8b). Inee (9) oepon to (8b) when y, y () an v ae uffiiently mall not to ativate the atuation nonlineatitie. Bae on the above eult, in ou example we will ue LQR gain fo v eigne bae on the linea ynami (9). Nevethele iffeent eletion fo K aw in (7), an of v in geneal, aime at inuing lage tability egion an exteme pefomane fom a nonlinea viewpoint in (8b) ontitute a vey inteeting poblem to takle an we ega it a futue wok. In 4, Remak 5, a fix with no guaantee of effetivene wa given to ae the ae whee the ontolle wa not titly pope. In thi fix, fo whih no tability guaantee wee given, the ontol output wa appoximately iffeentiate by a filte of the type τ, with a uffiiently mall τ. In light of the iuion of the peviou etion, thi fix an be inappliable if thee i an algebai loop between plant an ontolle, while an effetive olution an be alway obtaine by ontuting the moifie loe-loop of Setion II-B. In the following example, the anti-winup olution iue hee i illutate on the ame ae tuy ue in
5 IV. ALMOST ANTI-WINDUP WITH MAGNITUDE, RATE AND URVATURE SATURATION In thi etion, the olution given in Setion III fo the ae with magnitue an ate i extene to the moe geneal poblem aiing when in aition to equiing plant input that ae boune in magnitue an ate by, epetively, ±M an ±R, bounene of thei uvatue by anothe et of boun = (,..., m ) i alo equie. Moe peifially, the equiement on the plant input i extene hee to the fat that the plant input i twie iffeentiable almot eveywhee an that it value i between ±M, it fit eivative i between ±R an it eon eivative i between ± at all time. Simila to the peviou etion efine at ( ) a the eentalize ymmeti atuation with boun ±. Genealizing the appoah of Setion III fo atemagnitue atuation, we tat fom an oiginal loe-loop ytem (), (2), (3) an ontut the moifie loe-loop ytem (), (8), (), whee the filte F i elete with two intenal tate o that, in aition to the ontolle output y, it fit eivative y () an it eon eivative y (2) ae alo available at the output of the ontolle (8). Then the following anti-winup ompenato i eigne to augment the moifie plant-ontolle pai (), (8) ẋ aw = Ax aw B u (u y ) (2a) δ = at (y (2) v ) (2b) δ = at R(δ) R(δ (δ ) ) (2) y aw = y x aw (u y ) (2) z aw = z x aw D zu (u y ), (2e) whee, given α,α R m, the funtion at α α( ) in (2) enote the non-ymmeti eentalize atuation funtion with uppe omponentwie boun α, an lowe omponentwie boun α, an, given =... m T, the ith element of the boun R( ) an R( ) ae efine a ( R i () = min R i, ) 2 i (M i at Mi ( i )) ( R i () = max R i, ) (2) 2 i (M i at Mi ( i )) The antiwinup ompenato (2) i inteonnete to the moifie loe loop a follow: u = y y aw, u = δ. (22) One again, the ignal v in (2) i a tabilizing ignal to be efine late. A blok iagam epeentation of thi anti-winup olution i epeente in Figue 6. y (2) y y () v yaw - uvatue Satuation AW - δ δaw, δaw, Rate Satuation R(δ) - δ = u Fig. 6. Moel eovey anti-winup with uvatue, ate an magnitue atuation. P y When inteonneting the anti-winup ompenato (2), (22) to the moifie plant-ontolle pai (), (8), the loeloop appea again into a ueful aae fom, paallel to (8), whih an be appeiate in the ooinate (x l,x,x aw,δ aw,,δ aw, ) := (x x aw,x,x aw,δ y,δ y () ). In patiula, if one make the following linea eletion 2 of v : v = K aw x T aw (δ y ) T (δ y () ) T T, (23) afte ome eivation, the following tutue i obtaine: ẋ l = Ax l B u y B y l = y x l y D y z l = z x l D zu y D z (24a) ẋ = A x B u u B y = x D u u D ẋ aw = Ax aw B u δ aw, ( ) δ aw, = at R(δaw,y) R(δ aw,y ) δ aw, y () y () ( xaw ) (24b) δ aw, = at K δ aw aw, y (2) δ y (2) aw, z aw = z x aw D zu δ aw, whee y l = y y aw an whee z aw = z z l quantifie the mimath between the atual pefomane output z of the anti-winup loe-loop ytem (), (8), (2), (22) an the eiable pefomane output of the moifie loe-loop ytem (), (8), (), whih ha been hown in the peviou etion to be loe (in a uitable ene) to the pefomane output of the oiginal loe-loop (), (2), (3). Fo the anti-winup loe-loop (), (8), (2), (22), bae on the hange of ooinate in (24), it poible to pove the following tatement, whih illutate the eiable popetie inue by the anti-winup olution, an genealize the eult in Theoem. Theoem 2: Given the anti-winup loe-loop (), (8), (2), (22), if δ () M,M then the plant input u neve exee the uvatue, ate an magnitue atuation boun. Moeove, if δ () = at M (y ()), δ () = at R (y () ()), x aw () = an if the eletion (7) of the ignal v guaantee loal (epetively, global) aymptoti tability of the ubytem (8b), then the following hol: ) Given any epone of the moifie loe-loop (), (8), () uh that y (t) = at M (y (t)) an y () (t) = at R (y () (t)) an y (2) (t) = at (y (2) (t)) fo all t, then z(t) z l (t) =, fo all t, namely the epone of the anti-winup loe-loop oinie with the epone of the moifie loe-loop; 2) The oigin of the anti-winup loe-loop i loally (epetively, globally) aymptotially table. Remak 4: A key tep in the poof of Theoem 2 onit in howing that a ignal y epeting all the magnitue, ate an uvatue boun at all time mut atually epet tite boun on the ate, whih ae magnitue epenent an oepon to (2). Hene, in oe to olve the poblem with uvatue boun, ometime it i neeay to pefom an antiipatoy ation an to moify the ontolle output when it i till titly inie all the thee limit (on magnitue, ate an uvatue), beaue othewie a violation woul inevitably ou at futue time. Thi featue 2 The eletion (23) i linea fo impliity of expoition but in geneal nonlinea eletion oul lea to impove tability egion an/o pefomane. 6773
6 i aially iffeent fom what i foun in the ae with jut magnitue an/o ate ontaint. Note alo that if R i > 2 M i i fo ome i, then the min an max funtion in (2) will alway etun the eon agument, namely the ate ontaint will neve be ative. Paalleling the iuion afte Theoem, note that any K aw tabilizing the ynami ( A Bu = I ẋ aw δ aw, δ aw, I ) xaw K aw δ aw,, (25) δ aw, inue loal aymptoti tability of (24b). Inee (25) oepon to (24b) when y, y (), y (2) an v ae uffiiently mall not to ativate the atuation nonlineaitie. Bae on the above eult, in ou example we will ue LQR gain fo v eigne bae on the linea ynami (25). Nevethele iffeent eletion fo K aw in (23), an of v in geneal, aime at inuing lage tability egion an exteme pefomane fom a nonlinea viewpoint in (24b) ontitute an open eeah poblem. V. SIMULATION EXAMPLE The hot-peio longituinal ynami of the VISTA/MATV F-6 at Mah.2 an altitue feet (oeponing to a ynami peue value of 4.8pf) at a tim angle of attak of 28 egee i eibe loally by a eon oe plant a in () with two tate oeponing to the angle of attak an the pith ate, epetively, an two input oeponing to the eviation of the elevato efletion an of the pith thut vetoing fom the tim onition (ee 7 fo etail). A in 7, the ontolle i nonlinea an oepon to a aiy haine alloation of the input, iven by a efeene ignal fo the angle of attak. We eign the anti-winup ompenato by following the appoah of Setion III, with v a in (7) an whee K aw i an LQR gain fo (9) etemine uing weight Q = I, R = I an tate matix A B u I I intea of A B u, o that the eal pat of the eigenvalue of the loe loop ytem i foe to be le than : K aw = Then, we eign the anti-winup ompenato by following the appoah of Setion IV, with v a in (23) an whee K aw i an LQR gain fo (25) etemine uing weight Q = I, R = I an tate matix A Bu I I I intea of I A Bu I o that the eal pat of the eigenvalue of the loe loop ytem i foe to be le than : K aw = Figue 7 how a ompaion among the epone of the (i) unontaine (ii) magnitue an ate anti-winup an (iii) magnitue, ate an uvatue anti-winup loe loop ytem. VI. ONLUSIONS In thi pape we popoe a olution to the moel eovey anti-winup augmentation poblem fo plant with magnitue, ate an uvatue atuation boun. The popoe ontution ae illutate on eveal imulation example Angle of attak Refeene Unontaine Boun on magnitue an ate Boun on magnitue, ate an uvatue 5 5 Fit input Seon input 5 5 Fig. 7. Repone of (i) unontaine (ii) magnitue an ate anti-winup an (iii) magnitue, ate an uvatue anti-winup loe loop ytem. M =.3665,.8727, R =.2967,.7854, =.5236, REFERENES. Babu, R. Reginatto, A.R. Teel, an L. Zaaian. Anti-winup fo exponentially untable linea ytem with input limite in magnitue an ate. In Ameian ontol onfeene, page , hiago (IL), USA, June 2. 2 A. Bempoa, A. aavola, an E. Moa. Nonlinea ontol of ontaine linea ytem via peitive efeene management. IEEE Tan. Aut. ont., 42(3):34 349, Mah Shifin A. Sween eek aue of Gipen ah. Aviation Week an Spae Tehnology, 39:78 79, F. Foni, S. Galeani, an L. Zaaian. Moel eovey anti-winup fo plant with ate an magnitue atuation. In Euopean ontol onfeene, page , Buapet (Hungay), Augut S. Galeani, S. Onoi, A.R. Teel, an L. Zaaian. Futhe eult on tati linea anti-winup eign fo ontol ytem ubjet to magnitue an ate atuation. In onfeene on Deiion an ontol, page , San Diego (A), USA, Deembe S. Galeani, S. Onoi, A.R. Teel, an L. Zaaian. A magnitue an ate atuation moel an it ue in the olution of a tati anti-winup poblem. Sytem an ontol Lette, 57(): 9, S. Galeani, S. Tabouieh, M.. Tune, an L. Zaaian. A tutoial on moen anti-winup eign. Euopean Jounal of ontol, 5(3-4):48 44, E.G. Gilbet, I. Kolmanovky, an K.T. Tan. Diete-time efeene goveno an the nonlinea ontol of ytem with tate an ontol ontaint. Intenat. J. Robut Nonlinea ontol, 5(5):487 54, A. Iioi. Nonlinea ontol Sytem. Spinge, thi eition, 995. M.V. Kothae, P.J. ampo, M. Moai, an N. Nett. A unifie famewok fo the tuy of anti-winup eign. Automatia, 3(2): , 994. J.. Lozie. A teay-tate appoah to the theoy of atuable evo ytem. IRE Tanation on Automati ontol, :9 39, May E.F. Mule an M.V. Kothae. Synthei of tabilizing anti-winup ontolle uing pieewie quaati Lyapunov funtion. In Poeeing of the Ameian ontol onfeene, page , hiago (IL), June 2. 3 A. Pionti an M. Walke. Speial iue on ontol of tokamak plama (vol ). IEEE ontol Sytem Magazine, 25(5), A. Pionti an M. Walke. Speial iue on ontol of tokamak plama (vol 2). IEEE ontol Sytem Magazine, 26(2), J.S. Shamma. Anti-winup via ontaine egulation with obeve. Sytem an ontol Lette, 4: , 2. 6 S. Tabouieh an M. Tune. Anti-winup eign: an oveview of ome eent avane an open poblem. ontol Theoy & Appliation, IET, 3(): 9, A.R. Teel an J.B. Buffington. Anti-winup fo an F-6 aiy hain ontol alloato. In Po. of AIAA GN onfeene, page , New Olean (LA), USA, Augut N. Waa an M. Saeki. Synthei of a tati anti-winup ompenato fo ytem with magnitue an ate limite atuato. Po. of Symp. on RoonD, :3 36, 2. 9 Y. Wang, S. Yeung, an R.M. Muay. Bifuation ontol of otating tall with atuato magnitue an ate limit: Pat II ontol ynthei an ompaion with expeiment. Automatia, 38:6 625, F. Wu an M. Soto. Extene anti-winup ontol heme fo lti an lft ytem with atuato atuation. Int. J. Robut an Nonlinea ontol, 4:255 28, L. Zaaian. Dynami alloation fo input-eunant ontol ytem. Automatia, 45:43 438, 29.
Proceedings of Clima 2007 WellBeing Indoors
 Poeeing of Clima 2007 WellBeing Inoo Deivation an analyi of the outoo Wet Bulb Globe Tempeatue inex (WBGT) with a human themal engineeing appoah Pat 2. Popetie of the WBGT fomula fo outoo onition with
Poeeing of Clima 2007 WellBeing Inoo Deivation an analyi of the outoo Wet Bulb Globe Tempeatue inex (WBGT) with a human themal engineeing appoah Pat 2. Popetie of the WBGT fomula fo outoo onition with
Then the number of elements of S of weight n is exactly the number of compositions of n into k parts.
 Geneating Function In a geneal combinatoial poblem, we have a univee S of object, and we want to count the numbe of object with a cetain popety. Fo example, if S i the et of all gaph, we might want to
Geneating Function In a geneal combinatoial poblem, we have a univee S of object, and we want to count the numbe of object with a cetain popety. Fo example, if S i the et of all gaph, we might want to
Chapter 19 Webassign Help Problems
 Chapte 9 Webaign Help Poblem 4 5 6 7 8 9 0 Poblem 4: The pictue fo thi poblem i a bit mileading. They eally jut give you the pictue fo Pat b. So let fix that. Hee i the pictue fo Pat (a): Pat (a) imply
Chapte 9 Webaign Help Poblem 4 5 6 7 8 9 0 Poblem 4: The pictue fo thi poblem i a bit mileading. They eally jut give you the pictue fo Pat b. So let fix that. Hee i the pictue fo Pat (a): Pat (a) imply
A Crash Course in (2 2) Matrices
 A Cash Couse in ( ) Matices Seveal weeks woth of matix algeba in an hou (Relax, we will only stuy the simplest case, that of matices) Review topics: What is a matix (pl matices)? A matix is a ectangula
A Cash Couse in ( ) Matices Seveal weeks woth of matix algeba in an hou (Relax, we will only stuy the simplest case, that of matices) Review topics: What is a matix (pl matices)? A matix is a ectangula
Minimum Energy Forced Dynamic Position Control of PMSM Drives
 3 IASME/WSEAS Int. Conf. on Enegy & Envionment, Univeity of Cambige, UK, Febuay 3-5, 8 Minimum Enegy Foe Dynami Poition Contol of PMSM Dive STEPHEN J. DODDS, GUNARATNAM SOORIYAKUMAR, ROY PERRYMAN Shool
3 IASME/WSEAS Int. Conf. on Enegy & Envionment, Univeity of Cambige, UK, Febuay 3-5, 8 Minimum Enegy Foe Dynami Poition Contol of PMSM Dive STEPHEN J. DODDS, GUNARATNAM SOORIYAKUMAR, ROY PERRYMAN Shool
Gravity. David Barwacz 7778 Thornapple Bayou SE, Grand Rapids, MI David Barwacz 12/03/2003
 avity David Bawacz 7778 Thonapple Bayou, and Rapid, MI 495 David Bawacz /3/3 http://membe.titon.net/daveb Uing the concept dicued in the peceding pape ( http://membe.titon.net/daveb ), I will now deive
avity David Bawacz 7778 Thonapple Bayou, and Rapid, MI 495 David Bawacz /3/3 http://membe.titon.net/daveb Uing the concept dicued in the peceding pape ( http://membe.titon.net/daveb ), I will now deive
Symmetry of Lagrangians of holonomic systems in terms of quasi-coordinates
 Vol 18 No 8, Augut 009 c 009 Chin. Phy. Soc. 1674-1056/009/1808/3145-05 Chinee Phyic B an IOP Publihing Lt Symmety of Lagangian of holonomic ytem in tem of quai-cooinate Wu Hui-Bin an Mei Feng-Xiang School
Vol 18 No 8, Augut 009 c 009 Chin. Phy. Soc. 1674-1056/009/1808/3145-05 Chinee Phyic B an IOP Publihing Lt Symmety of Lagangian of holonomic ytem in tem of quai-cooinate Wu Hui-Bin an Mei Feng-Xiang School
Circular Motion Problem Solving
 iula Motion Poblem Soling Aeleation o a hange in eloity i aued by a net foe: Newton nd Law An objet aeleate when eithe the magnitude o the dietion of the eloity hange We aw in the lat unit that an objet
iula Motion Poblem Soling Aeleation o a hange in eloity i aued by a net foe: Newton nd Law An objet aeleate when eithe the magnitude o the dietion of the eloity hange We aw in the lat unit that an objet
Fall 2004/05 Solutions to Assignment 5: The Stationary Phase Method Provided by Mustafa Sabri Kilic. I(x) = e ixt e it5 /5 dt (1) Z J(λ) =
 8.35 Fall 24/5 Solution to Aignment 5: The Stationay Phae Method Povided by Mutafa Sabi Kilic. Find the leading tem fo each of the integal below fo λ >>. (a) R eiλt3 dt (b) R e iλt2 dt (c) R eiλ co t dt
8.35 Fall 24/5 Solution to Aignment 5: The Stationay Phae Method Povided by Mutafa Sabi Kilic. Find the leading tem fo each of the integal below fo λ >>. (a) R eiλt3 dt (b) R e iλt2 dt (c) R eiλ co t dt
Lag-Lead Compensator Design
 Lag-Lead Compenator Deign ELEC 3 Spring 08 Lag or Lead Struture A bai ompenator onit of a gain, one real pole and one real zero Two type: phae-lead and phae-lag Phae-lead: provide poitive phae hift and
Lag-Lead Compenator Deign ELEC 3 Spring 08 Lag or Lead Struture A bai ompenator onit of a gain, one real pole and one real zero Two type: phae-lead and phae-lag Phae-lead: provide poitive phae hift and
User s Guide NBC 2005, Structural Commentaries (Part 4 of Division B)
 Ue Guide NBC 2005, Stutual Commentaie (Pat 4 of Diviion B) Eata Iued by the Canadian Commiion on Building and Fie Code The table that follow lit eata that apply to the Ue Guide NBC 2005, Stutual Commentaie
Ue Guide NBC 2005, Stutual Commentaie (Pat 4 of Diviion B) Eata Iued by the Canadian Commiion on Building and Fie Code The table that follow lit eata that apply to the Ue Guide NBC 2005, Stutual Commentaie
ANALYSIS AND TEMPERATURES CONTROL IN A TUBULAR CHEMICAL REACTOR
 PHYSCON 9 Catania Italy Septembe Septembe 9 NLYSIS ND TEMPERTURES CONTROL IN TUBULR CHEMICL RECTOR Pet Dotál Vladimí Bobál and Jiří Vojtěšek Depatment of Poe Contol Faulty of pplied Infomati Toma Bata
PHYSCON 9 Catania Italy Septembe Septembe 9 NLYSIS ND TEMPERTURES CONTROL IN TUBULR CHEMICL RECTOR Pet Dotál Vladimí Bobál and Jiří Vojtěšek Depatment of Poe Contol Faulty of pplied Infomati Toma Bata
Supplementary Information for On characterizing protein spatial clusters with correlation approaches
 Supplementay Infomation fo On chaacteizing potein spatial clustes with coelation appoaches A. Shivananan, J. Unnikishnan, A. Raenovic Supplementay Notes Contents Deivation of expessions fo p = a t................................
Supplementay Infomation fo On chaacteizing potein spatial clustes with coelation appoaches A. Shivananan, J. Unnikishnan, A. Raenovic Supplementay Notes Contents Deivation of expessions fo p = a t................................
Adaptive LQ Cascade Control of a Tubular Chemical Reactor
 MATEC Web of Confeene 7, () DOI:./ mateonf/ 7 CSCC Adaptive LQ Caade Contol of a Tubula Chemial Reato Dotal Pet, Vladimí obal and Jii Vojteek Toma ata Univeity in Zlin, Faulty of Applied Infomati, Nad
MATEC Web of Confeene 7, () DOI:./ mateonf/ 7 CSCC Adaptive LQ Caade Contol of a Tubula Chemial Reato Dotal Pet, Vladimí obal and Jii Vojteek Toma ata Univeity in Zlin, Faulty of Applied Infomati, Nad
PH126 Exam I Solutions
 PH6 Exam I Solutions q Q Q q. Fou positively chage boies, two with chage Q an two with chage q, ae connecte by fou unstetchable stings of equal length. In the absence of extenal foces they assume the equilibium
PH6 Exam I Solutions q Q Q q. Fou positively chage boies, two with chage Q an two with chage q, ae connecte by fou unstetchable stings of equal length. In the absence of extenal foces they assume the equilibium
International Journal of Automation and Computing. International Journal of Automation and Computing 00(0), Mouth 20, range of pages
 Intenational Jounal of Automation and Computing Page of 0 0 0 0 Intenational Jounal of Automation and Computing 00(0 Mh 0 ange of page Joint Reoue Alloation in Coopeative Multi-Caie DF Sytem Chao-ping
Intenational Jounal of Automation and Computing Page of 0 0 0 0 Intenational Jounal of Automation and Computing 00(0 Mh 0 ange of page Joint Reoue Alloation in Coopeative Multi-Caie DF Sytem Chao-ping
Quantum Mechanics I - Session 5
 Quantum Mechanics I - Session 5 Apil 7, 015 1 Commuting opeatos - an example Remine: You saw in class that Â, ˆB ae commuting opeatos iff they have a complete set of commuting obsevables. In aition you
Quantum Mechanics I - Session 5 Apil 7, 015 1 Commuting opeatos - an example Remine: You saw in class that Â, ˆB ae commuting opeatos iff they have a complete set of commuting obsevables. In aition you
Inference for A One Way Factorial Experiment. By Ed Stanek and Elaine Puleo
 Infeence fo A One Way Factoial Expeiment By Ed Stanek and Elaine Puleo. Intoduction We develop etimating equation fo Facto Level mean in a completely andomized one way factoial expeiment. Thi development
Infeence fo A One Way Factoial Expeiment By Ed Stanek and Elaine Puleo. Intoduction We develop etimating equation fo Facto Level mean in a completely andomized one way factoial expeiment. Thi development
Ch. 3: Inverse Kinematics Ch. 4: Velocity Kinematics. The Interventional Centre
 Ch. : Invee Kinemati Ch. : Velity Kinemati The Inteventinal Cente eap: kinemati eupling Apppiate f ytem that have an am a wit Suh that the wit jint ae ae aligne at a pint F uh ytem, we an plit the invee
Ch. : Invee Kinemati Ch. : Velity Kinemati The Inteventinal Cente eap: kinemati eupling Apppiate f ytem that have an am a wit Suh that the wit jint ae ae aligne at a pint F uh ytem, we an plit the invee
On the quadratic support of strongly convex functions
 Int. J. Nonlinea Anal. Appl. 7 2016 No. 1, 15-20 ISSN: 2008-6822 electonic http://dx.doi.og/10.22075/ijnaa.2015.273 On the quadatic uppot of tongly convex function S. Abbazadeh a,b,, M. Ehaghi Godji a
Int. J. Nonlinea Anal. Appl. 7 2016 No. 1, 15-20 ISSN: 2008-6822 electonic http://dx.doi.og/10.22075/ijnaa.2015.273 On the quadatic uppot of tongly convex function S. Abbazadeh a,b,, M. Ehaghi Godji a
SIMPLE LOW-ORDER AND INTEGRAL-ACTION CONTROLLER SYNTHESIS FOR MIMO SYSTEMS WITH TIME DELAYS
 Appl. Comput. Math., V.10, N.2, 2011, pp.242-249 SIMPLE LOW-ORDER AND INTEGRAL-ACTION CONTROLLER SYNTHESIS FOR MIMO SYSTEMS WITH TIME DELAYS A.N. GÜNDEŞ1, A.N. METE 2 Abtact. A imple finite-dimenional
Appl. Comput. Math., V.10, N.2, 2011, pp.242-249 SIMPLE LOW-ORDER AND INTEGRAL-ACTION CONTROLLER SYNTHESIS FOR MIMO SYSTEMS WITH TIME DELAYS A.N. GÜNDEŞ1, A.N. METE 2 Abtact. A imple finite-dimenional
Passivity-Based Control of Saturated Induction Motors
 Passivity-Base Contol of Satuate Inuction otos Levent U. Gökee, embe, IEEE, awan A. Simaan, Fellow, IEEE, an Chales W. Bice, Senio embe, IEEE Depatment of Electical Engineeing Univesity of South Caolina
Passivity-Base Contol of Satuate Inuction otos Levent U. Gökee, embe, IEEE, awan A. Simaan, Fellow, IEEE, an Chales W. Bice, Senio embe, IEEE Depatment of Electical Engineeing Univesity of South Caolina
Development of Model Reduction using Stability Equation and Cauer Continued Fraction Method
 Intenational Jounal of Electical and Compute Engineeing. ISSN 0974-90 Volume 5, Numbe (03), pp. -7 Intenational Reeach Publication Houe http://www.iphoue.com Development of Model Reduction uing Stability
Intenational Jounal of Electical and Compute Engineeing. ISSN 0974-90 Volume 5, Numbe (03), pp. -7 Intenational Reeach Publication Houe http://www.iphoue.com Development of Model Reduction uing Stability
Chapter 6 Control Systems Design by Root-Locus Method. Lag-Lead Compensation. Lag lead Compensation Techniques Based on the Root-Locus Approach.
 hapter 6 ontrol Sytem Deign by Root-Lou Method Lag-Lead ompenation Lag lead ompenation ehnique Baed on the Root-Lou Approah. γ β K, ( γ >, β > ) In deigning lag lead ompenator, we onider two ae where γ
hapter 6 ontrol Sytem Deign by Root-Lou Method Lag-Lead ompenation Lag lead ompenation ehnique Baed on the Root-Lou Approah. γ β K, ( γ >, β > ) In deigning lag lead ompenator, we onider two ae where γ
Multivariable Control Systems
 Multivaiable Contol Sytem Ali Kaimpou Aociate ofeo Fedowi Univeity of Mahhad Refeence ae appeaed in the lat lide. Stability of Multivaiable Feedback Contol Sytem Topic to be coveed include: Well - oedne
Multivaiable Contol Sytem Ali Kaimpou Aociate ofeo Fedowi Univeity of Mahhad Refeence ae appeaed in the lat lide. Stability of Multivaiable Feedback Contol Sytem Topic to be coveed include: Well - oedne
THE SOLAR SYSTEM. We begin with an inertial system and locate the planet and the sun with respect to it. Then. F m. Then
 THE SOLAR SYSTEM We now want to apply what we have learned to the olar ytem. Hitorially thi wa the great teting ground for mehani and provided ome of it greatet triumph, uh a the diovery of the outer planet.
THE SOLAR SYSTEM We now want to apply what we have learned to the olar ytem. Hitorially thi wa the great teting ground for mehani and provided ome of it greatet triumph, uh a the diovery of the outer planet.
Several new identities involving Euler and Bernoulli polynomials
 Bull. Math. Soc. Sci. Math. Roumanie Tome 9107 No. 1, 016, 101 108 Seveal new identitie involving Eule and Benoulli polynomial by Wang Xiaoying and Zhang Wenpeng Abtact The main pupoe of thi pape i uing
Bull. Math. Soc. Sci. Math. Roumanie Tome 9107 No. 1, 016, 101 108 Seveal new identitie involving Eule and Benoulli polynomial by Wang Xiaoying and Zhang Wenpeng Abtact The main pupoe of thi pape i uing
CHAPTER 3 DIODES. NTUEE Electronics L. H. Lu 3-1
 CHAPER 3 OE Chapte Outline 3.1 he eal ioe 3.2 eminal Chaacteistics of Junction ioes 3.3 Moeling the ioe Fowa Chaacteistics 3.4 Opeation in the Reese Beakown Region ene ioes 3.5 Rectifie Cicuits 3.6 Limiting
CHAPER 3 OE Chapte Outline 3.1 he eal ioe 3.2 eminal Chaacteistics of Junction ioes 3.3 Moeling the ioe Fowa Chaacteistics 3.4 Opeation in the Reese Beakown Region ene ioes 3.5 Rectifie Cicuits 3.6 Limiting
Solutions Practice Test PHYS 211 Exam 2
 Solution Pactice Tet PHYS 11 Exam 1A We can plit thi poblem up into two pat, each one dealing with a epaate axi. Fo both the x- and y- axe, we have two foce (one given, one unknown) and we get the following
Solution Pactice Tet PHYS 11 Exam 1A We can plit thi poblem up into two pat, each one dealing with a epaate axi. Fo both the x- and y- axe, we have two foce (one given, one unknown) and we get the following
FORMATION FLYING IMPULSIVE CONTROL USING MEAN ORBITAL SPEED
 (Pepint) AAS XX-XXX FORMATION FLYING IMPULSIVE CONTROL USING MEAN ORBITAL SPEED Sunghoon Mok, * Yoonhyuk Choi, an Hyohoong Bang INTRODUCTION In this poeeing, an impulsive ontol metho fo satellite fomation
(Pepint) AAS XX-XXX FORMATION FLYING IMPULSIVE CONTROL USING MEAN ORBITAL SPEED Sunghoon Mok, * Yoonhyuk Choi, an Hyohoong Bang INTRODUCTION In this poeeing, an impulsive ontol metho fo satellite fomation
( )( )( ) ( ) + ( ) ( ) ( )
 3.7. Moel: The magnetic fiel is that of a moving chage paticle. Please efe to Figue Ex3.7. Solve: Using the iot-savat law, 7 19 7 ( ) + ( ) qvsinθ 1 T m/a 1.6 1 C. 1 m/s sin135 1. 1 m 1. 1 m 15 = = = 1.13
3.7. Moel: The magnetic fiel is that of a moving chage paticle. Please efe to Figue Ex3.7. Solve: Using the iot-savat law, 7 19 7 ( ) + ( ) qvsinθ 1 T m/a 1.6 1 C. 1 m/s sin135 1. 1 m 1. 1 m 15 = = = 1.13
Electric Potential and Gauss s Law, Configuration Energy Challenge Problem Solutions
 Poblem 1: Electic Potential an Gauss s Law, Configuation Enegy Challenge Poblem Solutions Consie a vey long o, aius an chage to a unifom linea chage ensity λ a) Calculate the electic fiel eveywhee outsie
Poblem 1: Electic Potential an Gauss s Law, Configuation Enegy Challenge Poblem Solutions Consie a vey long o, aius an chage to a unifom linea chage ensity λ a) Calculate the electic fiel eveywhee outsie
Homework Set 3 Physics 319 Classical Mechanics
 Homewok Set 3 Phsics 319 lassical Mechanics Poblem 5.13 a) To fin the equilibium position (whee thee is no foce) set the eivative of the potential to zeo U 1 R U0 R U 0 at R R b) If R is much smalle than
Homewok Set 3 Phsics 319 lassical Mechanics Poblem 5.13 a) To fin the equilibium position (whee thee is no foce) set the eivative of the potential to zeo U 1 R U0 R U 0 at R R b) If R is much smalle than
Accounting for magnetic saturation in induction machines modelling
 Accounting fo magnetic atuation in inuction machine moelling Hami Ouai, Foua Gii, Luc Duga To cite thi veion: Hami Ouai, Foua Gii, Luc Duga. Accounting fo magnetic atuation in inuction machine moelling.
Accounting fo magnetic atuation in inuction machine moelling Hami Ouai, Foua Gii, Luc Duga To cite thi veion: Hami Ouai, Foua Gii, Luc Duga. Accounting fo magnetic atuation in inuction machine moelling.
FUZZY INVENTORY MODEL FOR DETERIORATION ITEMS THROUGH JUST IN TIME WITH SHORTAGES ALLOWED
 Inian J.i.e. : 6-7 IN: 976-76 Pint IN: 5- Online FUZZY INVENTOY MODEL FO DETEIOTION ITEM THOUGH JUT IN TIME WITH HOTGE LLOWED J. JYNTHI a ND M. MGTHM b a Depatment of Mathemati Peiya Maniammai Univeity
Inian J.i.e. : 6-7 IN: 976-76 Pint IN: 5- Online FUZZY INVENTOY MODEL FO DETEIOTION ITEM THOUGH JUT IN TIME WITH HOTGE LLOWED J. JYNTHI a ND M. MGTHM b a Depatment of Mathemati Peiya Maniammai Univeity
Solution to HW 3, Ma 1a Fall 2016
 Solution to HW 3, Ma a Fall 206 Section 2. Execise 2: Let C be a subset of the eal numbes consisting of those eal numbes x having the popety that evey digit in the decimal expansion of x is, 3, 5, o 7.
Solution to HW 3, Ma a Fall 206 Section 2. Execise 2: Let C be a subset of the eal numbes consisting of those eal numbes x having the popety that evey digit in the decimal expansion of x is, 3, 5, o 7.
Ultrasonic Measurement Models for Imaging with Phased Arrays
 Ultaoni Meauement Model fo Imaging with Phaed Aay Lete W. Shme J. ab Bady J. Engle ab Alexande Sedov and Xiongbing Li d a Cente fo NDE Iowa State Univeity Ame IA 50011 USA b Dept. of Aeopae Eng. Iowa State
Ultaoni Meauement Model fo Imaging with Phaed Aay Lete W. Shme J. ab Bady J. Engle ab Alexande Sedov and Xiongbing Li d a Cente fo NDE Iowa State Univeity Ame IA 50011 USA b Dept. of Aeopae Eng. Iowa State
Multiple Criteria Secretary Problem: A New Approach
 J. Stat. Appl. Po. 3, o., 9-38 (04 9 Jounal of Statistics Applications & Pobability An Intenational Jounal http://dx.doi.og/0.785/jsap/0303 Multiple Citeia Secetay Poblem: A ew Appoach Alaka Padhye, and
J. Stat. Appl. Po. 3, o., 9-38 (04 9 Jounal of Statistics Applications & Pobability An Intenational Jounal http://dx.doi.og/0.785/jsap/0303 Multiple Citeia Secetay Poblem: A ew Appoach Alaka Padhye, and
ASTR 3740 Relativity & Cosmology Spring Answers to Problem Set 4.
 ASTR 3740 Relativity & Comology Sping 019. Anwe to Poblem Set 4. 1. Tajectoie of paticle in the Schwazchild geomety The equation of motion fo a maive paticle feely falling in the Schwazchild geomety ae
ASTR 3740 Relativity & Comology Sping 019. Anwe to Poblem Set 4. 1. Tajectoie of paticle in the Schwazchild geomety The equation of motion fo a maive paticle feely falling in the Schwazchild geomety ae
Chapter 4. Simulations. 4.1 Introduction
 Chapter 4 Simulation 4.1 Introdution In the previou hapter, a methodology ha been developed that will be ued to perform the ontrol needed for atuator haraterization. A tudy uing thi methodology allowed
Chapter 4 Simulation 4.1 Introdution In the previou hapter, a methodology ha been developed that will be ued to perform the ontrol needed for atuator haraterization. A tudy uing thi methodology allowed
Near-Optimal Relay Station Placement for Power Minimization in WiMAX Networks
 Nea-Optimal elay Station lacement fo owe Minimization in WiMAX Netwok Dejun Yang, Xi Fang an Guoliang Xue Abtact In the IEEE 80.16j tana, the elay tation ha been intouce to inceae the coveage an the thoughput
Nea-Optimal elay Station lacement fo owe Minimization in WiMAX Netwok Dejun Yang, Xi Fang an Guoliang Xue Abtact In the IEEE 80.16j tana, the elay tation ha been intouce to inceae the coveage an the thoughput
Simulation of Spatially Correlated Large-Scale Parameters and Obtaining Model Parameters from Measurements
 Simulation of Spatially Coelated Lage-Scale Paamete and Obtaining Model Paamete fom PER ZETTERBERG Stockholm Septembe 8 TRITA EE 8:49 Simulation of Spatially Coelated Lage-Scale Paamete and Obtaining Model
Simulation of Spatially Coelated Lage-Scale Paamete and Obtaining Model Paamete fom PER ZETTERBERG Stockholm Septembe 8 TRITA EE 8:49 Simulation of Spatially Coelated Lage-Scale Paamete and Obtaining Model
Chapter 3: Theory of Modular Arithmetic 38
 Chapte 3: Theoy of Modula Aithmetic 38 Section D Chinese Remainde Theoem By the end of this section you will be able to pove the Chinese Remainde Theoem apply this theoem to solve simultaneous linea conguences
Chapte 3: Theoy of Modula Aithmetic 38 Section D Chinese Remainde Theoem By the end of this section you will be able to pove the Chinese Remainde Theoem apply this theoem to solve simultaneous linea conguences
Non-Ideal Gas Behavior P.V.T Relationships for Liquid and Solid:
 hemodynamis Non-Ideal Gas Behavio.. Relationships fo Liquid and Solid: An equation of state may be solved fo any one of the thee quantities, o as a funtion of the othe two. If is onsideed a funtion of
hemodynamis Non-Ideal Gas Behavio.. Relationships fo Liquid and Solid: An equation of state may be solved fo any one of the thee quantities, o as a funtion of the othe two. If is onsideed a funtion of
SCHAUDER ESTIMATES FOR ELLIPTIC AND PARABOLIC EQUATIONS. Xu-Jia Wang The Australian National University
 SCHAUDER ESTIMATES FOR ELLIPTIC AND PARABOLIC EQUATIONS Xu-Jia Wang The Austalian National Univesity Intouction The Schaue estimate fo the Laplace equation was taitionally built upon the Newton potential
SCHAUDER ESTIMATES FOR ELLIPTIC AND PARABOLIC EQUATIONS Xu-Jia Wang The Austalian National Univesity Intouction The Schaue estimate fo the Laplace equation was taitionally built upon the Newton potential
RE 11.e Mon. Review for Final (1-11) HW11: Pr s 39, 57, 64, 74, 78 Sat. 9 a.m. Final Exam (Ch. 1-11)
 Mon. Tue. We. ab i..4-.6, (.) ngula Momentum Pincile & Toque.7 -.9, (.) Motion With & Without Toque Rotation Coue Eval.0 Quantization, Quiz RE.c EP RE. RE.e Mon. Review fo inal (-) HW: P 9, 57, 64, 74,
Mon. Tue. We. ab i..4-.6, (.) ngula Momentum Pincile & Toque.7 -.9, (.) Motion With & Without Toque Rotation Coue Eval.0 Quantization, Quiz RE.c EP RE. RE.e Mon. Review fo inal (-) HW: P 9, 57, 64, 74,
Topic 4a Introduction to Root Finding & Bracketing Methods
 /8/18 Couse Instucto D. Raymond C. Rumpf Office: A 337 Phone: (915) 747 6958 E Mail: cumpf@utep.edu Topic 4a Intoduction to Root Finding & Backeting Methods EE 4386/531 Computational Methods in EE Outline
/8/18 Couse Instucto D. Raymond C. Rumpf Office: A 337 Phone: (915) 747 6958 E Mail: cumpf@utep.edu Topic 4a Intoduction to Root Finding & Backeting Methods EE 4386/531 Computational Methods in EE Outline
Exceptional regular singular points of second-order ODEs. 1. Solving second-order ODEs
 (May 14, 2011 Exceptional egula singula points of second-ode ODEs Paul Gaett gaett@math.umn.edu http://www.math.umn.edu/ gaett/ 1. Solving second-ode ODEs 2. Examples 3. Convegence Fobenius method fo solving
(May 14, 2011 Exceptional egula singula points of second-ode ODEs Paul Gaett gaett@math.umn.edu http://www.math.umn.edu/ gaett/ 1. Solving second-ode ODEs 2. Examples 3. Convegence Fobenius method fo solving
LINEAR AND NONLINEAR ANALYSES OF A WIND-TUNNEL BALANCE
 LINEAR AND NONLINEAR ANALYSES O A WIND-TUNNEL INTRODUCTION BALANCE R. Kakehabadi and R. D. Rhew NASA LaRC, Hampton, VA The NASA Langley Reseach Cente (LaRC) has been designing stain-gauge balances fo utilization
LINEAR AND NONLINEAR ANALYSES O A WIND-TUNNEL INTRODUCTION BALANCE R. Kakehabadi and R. D. Rhew NASA LaRC, Hampton, VA The NASA Langley Reseach Cente (LaRC) has been designing stain-gauge balances fo utilization
TP A.4 Post-impact cue ball trajectory for any cut angle, speed, and spin
 technical poof TP A.4 Pot-impact cue ball tajectoy fo any cut anle, peed, and pin uppotin: The Illutated Pinciple of Pool and Billiad http://billiad.colotate.edu by Daid G. Alciatoe, PhD, PE ("D. Dae")
technical poof TP A.4 Pot-impact cue ball tajectoy fo any cut anle, peed, and pin uppotin: The Illutated Pinciple of Pool and Billiad http://billiad.colotate.edu by Daid G. Alciatoe, PhD, PE ("D. Dae")
On Secure Network Coding with Unequal Link Capacities and Restricted Wiretapping Sets
 010 IEEE Infomation Theoy Wokhop - ITW 010 Dublin On Secue Netwok Coing with Unequal Link Capacitie an Reticte Wietapping Set Tao Cui an Tacey Ho Depatment of Electical Engineeing Califonia Intitute of
010 IEEE Infomation Theoy Wokhop - ITW 010 Dublin On Secue Netwok Coing with Unequal Link Capacitie an Reticte Wietapping Set Tao Cui an Tacey Ho Depatment of Electical Engineeing Califonia Intitute of
Improved Research on the Transformer-Inductor Simulation Model of Magnetics
 Jounal of Eletoni Reeah and Appliation OPEN Impoved Reeah on the Tanfome-Induto Simulation Model of Magneti Jiang Liyuan, Liu Baoyuan, Zhang Li Beijing Jiaotong Univeity Haibin College, Hebei 0600, China
Jounal of Eletoni Reeah and Appliation OPEN Impoved Reeah on the Tanfome-Induto Simulation Model of Magneti Jiang Liyuan, Liu Baoyuan, Zhang Li Beijing Jiaotong Univeity Haibin College, Hebei 0600, China
Lecture 8 - Gauss s Law
 Lectue 8 - Gauss s Law A Puzzle... Example Calculate the potential enegy, pe ion, fo an infinite 1D ionic cystal with sepaation a; that is, a ow of equally spaced chages of magnitude e and altenating sign.
Lectue 8 - Gauss s Law A Puzzle... Example Calculate the potential enegy, pe ion, fo an infinite 1D ionic cystal with sepaation a; that is, a ow of equally spaced chages of magnitude e and altenating sign.
Expression of the radiative heat exchange for the human body and its application to modifying the original WBGT for outdoor environment
 Poceeing of Clima 27 WellBeing Inoo Expeion of the aiative heat exchange fo the human boy an it application to moifying the oiginal WBGT fo outoo envionment Kouhei Kuwabaa, Katunoi Nagano, Tohu Mochia
Poceeing of Clima 27 WellBeing Inoo Expeion of the aiative heat exchange fo the human boy an it application to moifying the oiginal WBGT fo outoo envionment Kouhei Kuwabaa, Katunoi Nagano, Tohu Mochia
10/04/18. P [P(x)] 1 negl(n).
![10/04/18. P [P(x)] 1 negl(n). 10/04/18. P [P(x)] 1 negl(n).](/thumbs/92/110495316.jpg) Mastemath, Sping 208 Into to Lattice lgs & Cypto Lectue 0 0/04/8 Lectues: D. Dadush, L. Ducas Scibe: K. de Boe Intoduction In this lectue, we will teat two main pats. Duing the fist pat we continue the
Mastemath, Sping 208 Into to Lattice lgs & Cypto Lectue 0 0/04/8 Lectues: D. Dadush, L. Ducas Scibe: K. de Boe Intoduction In this lectue, we will teat two main pats. Duing the fist pat we continue the
Conjugate Gradient (CG) Method
 Optimization II Conugate Gaient CG Metho Anothe metho oes not equie explicit secon eivatives, an oes not even stoe appoximation to Hessian matix CG geneates sequence of conugate seach iections, implicitly
Optimization II Conugate Gaient CG Metho Anothe metho oes not equie explicit secon eivatives, an oes not even stoe appoximation to Hessian matix CG geneates sequence of conugate seach iections, implicitly
A Novel Discrete-Time Predictive Current Control for PMSM
 A Novel Dicete-Time Peictive Cuent Contol fo SM Jung-Won Sun, Jin-Woo Lee, Jin-Ho Suh, Young-Jin Lee, an Kwon-Soon Lee Depatment of Electical Engineeing, Dong-A Univeity 840, Haan-ong, Saha-gu, Buan, 604-714,
A Novel Dicete-Time Peictive Cuent Contol fo SM Jung-Won Sun, Jin-Woo Lee, Jin-Ho Suh, Young-Jin Lee, an Kwon-Soon Lee Depatment of Electical Engineeing, Dong-A Univeity 840, Haan-ong, Saha-gu, Buan, 604-714,
Numerical approximation to ζ(2n+1)
 Illinois Wesleyan Univesity Fom the SelectedWoks of Tian-Xiao He 6 Numeical appoximation to ζ(n+1) Tian-Xiao He, Illinois Wesleyan Univesity Michael J. Dancs Available at: https://woks.bepess.com/tian_xiao_he/6/
Illinois Wesleyan Univesity Fom the SelectedWoks of Tian-Xiao He 6 Numeical appoximation to ζ(n+1) Tian-Xiao He, Illinois Wesleyan Univesity Michael J. Dancs Available at: https://woks.bepess.com/tian_xiao_he/6/
arxiv: v1 [math.oc] 2 Mar 2009
![arxiv: v1 [math.oc] 2 Mar 2009 arxiv: v1 [math.oc] 2 Mar 2009](/thumbs/96/127246563.jpg) HOMOGENEOUS APPROXIMATION RECURSIVE OBSERVER DESIGN AND OUTPUT FEEDBACK VINCENT ANDRIEU, LAURENT PRALY, AND ALESSANDRO ASTOLFI axiv:09030298v [mathoc] 2 Ma 2009 Abstact We intouce two new tools that can
HOMOGENEOUS APPROXIMATION RECURSIVE OBSERVER DESIGN AND OUTPUT FEEDBACK VINCENT ANDRIEU, LAURENT PRALY, AND ALESSANDRO ASTOLFI axiv:09030298v [mathoc] 2 Ma 2009 Abstact We intouce two new tools that can
Chapter 4. Sampling of Continuous-Time Signals
 Chapte 4 Sampling of Continuous-Time Signals 1 Intodution Disete-time signals most ommonly ou as epesentations of sampled ontinuous-time signals. Unde easonable onstaints, a ontinuous-time signal an be
Chapte 4 Sampling of Continuous-Time Signals 1 Intodution Disete-time signals most ommonly ou as epesentations of sampled ontinuous-time signals. Unde easonable onstaints, a ontinuous-time signal an be
Theorem 2: Proof: Note 1: Proof: Note 2:
 A New 3-Dimenional Polynomial Intepolation Method: An Algoithmic Appoach Amitava Chattejee* and Rupak Bhattachayya** A new 3-dimenional intepolation method i intoduced in thi pape. Coeponding to the method
A New 3-Dimenional Polynomial Intepolation Method: An Algoithmic Appoach Amitava Chattejee* and Rupak Bhattachayya** A new 3-dimenional intepolation method i intoduced in thi pape. Coeponding to the method
Chapter 5 Linear Equations: Basic Theory and Practice
 Chapte 5 inea Equations: Basic Theoy and actice In this chapte and the next, we ae inteested in the linea algebaic equation AX = b, (5-1) whee A is an m n matix, X is an n 1 vecto to be solved fo, and
Chapte 5 inea Equations: Basic Theoy and actice In this chapte and the next, we ae inteested in the linea algebaic equation AX = b, (5-1) whee A is an m n matix, X is an n 1 vecto to be solved fo, and
Central Coverage Bayes Prediction Intervals for the Generalized Pareto Distribution
 Statistics Reseach Lettes Vol. Iss., Novembe Cental Coveage Bayes Pediction Intevals fo the Genealized Paeto Distibution Gyan Pakash Depatment of Community Medicine S. N. Medical College, Aga, U. P., India
Statistics Reseach Lettes Vol. Iss., Novembe Cental Coveage Bayes Pediction Intevals fo the Genealized Paeto Distibution Gyan Pakash Depatment of Community Medicine S. N. Medical College, Aga, U. P., India
Determining the Best Linear Unbiased Predictor of PSU Means with the Data. included with the Random Variables. Ed Stanek
 Detemining te Bet Linea Unbiaed Pedicto of PSU ean wit te Data included wit te andom Vaiable Ed Stanek Intoduction We develop te equation fo te bet linea unbiaed pedicto of PSU mean in a two tage andom
Detemining te Bet Linea Unbiaed Pedicto of PSU ean wit te Data included wit te andom Vaiable Ed Stanek Intoduction We develop te equation fo te bet linea unbiaed pedicto of PSU mean in a two tage andom
Failure Probability of 2-within-Consecutive-(2, 2)-out-of-(n, m): F System for Special Values of m
 Jounal of Mathematics and Statistics 5 (): 0-4, 009 ISSN 549-3644 009 Science Publications Failue Pobability of -within-consecutive-(, )-out-of-(n, m): F System fo Special Values of m E.M.E.. Sayed Depatment
Jounal of Mathematics and Statistics 5 (): 0-4, 009 ISSN 549-3644 009 Science Publications Failue Pobability of -within-consecutive-(, )-out-of-(n, m): F System fo Special Values of m E.M.E.. Sayed Depatment
New On-Line Algorithms for the Page Replication Problem. Susanne Albers y Hisashi Koga z. Abstract
 New On-Line Algoithm fo the Page Replication Poblem Suanne Albe y Hiahi Koga z Abtact We peent impoved competitive on-line algoithm fo the page eplication poblem and concentate on impotant netwok topologie
New On-Line Algoithm fo the Page Replication Poblem Suanne Albe y Hiahi Koga z Abtact We peent impoved competitive on-line algoithm fo the page eplication poblem and concentate on impotant netwok topologie
This lecture. Transformations in 2D. Where are we at? Why do we need transformations?
 Thi lectue Tanfomation in 2D Thoma Sheme Richa (Hao) Zhang Geomet baic Affine pace an affine tanfomation Ue of homogeneou cooinate Concatenation of tanfomation Intouction to Compute Gaphic CMT 36 Lectue
Thi lectue Tanfomation in 2D Thoma Sheme Richa (Hao) Zhang Geomet baic Affine pace an affine tanfomation Ue of homogeneou cooinate Concatenation of tanfomation Intouction to Compute Gaphic CMT 36 Lectue
15. SIMPLE MHD EQUILIBRIA
 15. SIMPLE MHD EQUILIBRIA In this Section we will examine some simple examples of MHD equilibium configuations. These will all be in cylinical geomety. They fom the basis fo moe the complicate equilibium
15. SIMPLE MHD EQUILIBRIA In this Section we will examine some simple examples of MHD equilibium configuations. These will all be in cylinical geomety. They fom the basis fo moe the complicate equilibium
TRAVELING WAVES. Chapter Simple Wave Motion. Waves in which the disturbance is parallel to the direction of propagation are called the
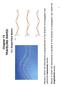 Chapte 15 RAVELING WAVES 15.1 Simple Wave Motion Wave in which the ditubance i pependicula to the diection of popagation ae called the tanvee wave. Wave in which the ditubance i paallel to the diection
Chapte 15 RAVELING WAVES 15.1 Simple Wave Motion Wave in which the ditubance i pependicula to the diection of popagation ae called the tanvee wave. Wave in which the ditubance i paallel to the diection
EM Boundary Value Problems
 EM Bounday Value Poblems 10/ 9 11/ By Ilekta chistidi & Lee, Seung-Hyun A. Geneal Desciption : Maxwell Equations & Loentz Foce We want to find the equations of motion of chaged paticles. The way to do
EM Bounday Value Poblems 10/ 9 11/ By Ilekta chistidi & Lee, Seung-Hyun A. Geneal Desciption : Maxwell Equations & Loentz Foce We want to find the equations of motion of chaged paticles. The way to do
Passive Pressure on Retaining Wall supporting c-φ Backfill using Horizontal Slices Method
 Cloud Publication Intenational Jounal of Advanced Civil Engineeing and Achitectue Reeach 2013, Volume 2, Iue 1, pp. 42-52, Aticle ID Tech-106 Reeach Aticle Open Acce Paive Peue on Retaining Wall uppoting
Cloud Publication Intenational Jounal of Advanced Civil Engineeing and Achitectue Reeach 2013, Volume 2, Iue 1, pp. 42-52, Aticle ID Tech-106 Reeach Aticle Open Acce Paive Peue on Retaining Wall uppoting
A Bijective Approach to the Permutational Power of a Priority Queue
 A Bijective Appoach to the Pemutational Powe of a Pioity Queue Ia M. Gessel Kuang-Yeh Wang Depatment of Mathematics Bandeis Univesity Waltham, MA 02254-9110 Abstact A pioity queue tansfoms an input pemutation
A Bijective Appoach to the Pemutational Powe of a Pioity Queue Ia M. Gessel Kuang-Yeh Wang Depatment of Mathematics Bandeis Univesity Waltham, MA 02254-9110 Abstact A pioity queue tansfoms an input pemutation
Precision Spectrophotometry
 Peciion Spectophotomety Pupoe The pinciple of peciion pectophotomety ae illutated in thi expeiment by the detemination of chomium (III). ppaatu Spectophotomete (B&L Spec 20 D) Cuvette (minimum 2) Pipet:
Peciion Spectophotomety Pupoe The pinciple of peciion pectophotomety ae illutated in thi expeiment by the detemination of chomium (III). ppaatu Spectophotomete (B&L Spec 20 D) Cuvette (minimum 2) Pipet:
Tutorial 5 Drive dynamics & control
 UNIVERSITY OF NEW SOUTH WALES Electic Dive Sytem School o Electical Engineeing & Telecommunication ELEC463 Electic Dive Sytem Tutoial 5 Dive dynamic & contol. The ollowing paamete ae known o two high peomance
UNIVERSITY OF NEW SOUTH WALES Electic Dive Sytem School o Electical Engineeing & Telecommunication ELEC463 Electic Dive Sytem Tutoial 5 Dive dynamic & contol. The ollowing paamete ae known o two high peomance
On the integration of the equations of hydrodynamics
 Uebe die Integation de hydodynamischen Gleichungen J f eine u angew Math 56 (859) -0 On the integation of the equations of hydodynamics (By A Clebsch at Calsuhe) Tanslated by D H Delphenich In a pevious
Uebe die Integation de hydodynamischen Gleichungen J f eine u angew Math 56 (859) -0 On the integation of the equations of hydodynamics (By A Clebsch at Calsuhe) Tanslated by D H Delphenich In a pevious
Localization of Eigenvalues in Small Specified Regions of Complex Plane by State Feedback Matrix
 Jounal of Sciences, Islamic Republic of Ian (): - () Univesity of Tehan, ISSN - http://sciencesutaci Localization of Eigenvalues in Small Specified Regions of Complex Plane by State Feedback Matix H Ahsani
Jounal of Sciences, Islamic Republic of Ian (): - () Univesity of Tehan, ISSN - http://sciencesutaci Localization of Eigenvalues in Small Specified Regions of Complex Plane by State Feedback Matix H Ahsani
Equilibria of a cylindrical plasma
 // Miscellaneous Execises Cylinical equilibia Equilibia of a cylinical plasma Consie a infinitely long cyline of plasma with a stong axial magnetic fiel (a geat fusion evice) Plasma pessue will cause the
// Miscellaneous Execises Cylinical equilibia Equilibia of a cylinical plasma Consie a infinitely long cyline of plasma with a stong axial magnetic fiel (a geat fusion evice) Plasma pessue will cause the
ON THE TWO-BODY PROBLEM IN QUANTUM MECHANICS
 ON THE TWO-BODY PROBLEM IN QUANTUM MECHANICS L. MICU Hoia Hulubei National Institute fo Physics and Nuclea Engineeing, P.O. Box MG-6, RO-0775 Buchaest-Maguele, Romania, E-mail: lmicu@theoy.nipne.o (Received
ON THE TWO-BODY PROBLEM IN QUANTUM MECHANICS L. MICU Hoia Hulubei National Institute fo Physics and Nuclea Engineeing, P.O. Box MG-6, RO-0775 Buchaest-Maguele, Romania, E-mail: lmicu@theoy.nipne.o (Received
V V The circumflex (^) tells us this is a unit vector
 Vecto Vecto have Diection and Magnitude Mike ailey mjb@c.oegontate.edu Magnitude: V V V V x y z vecto.pptx Vecto Can lo e Defined a the oitional Diffeence etween Two oint 3 Unit Vecto have a Magnitude
Vecto Vecto have Diection and Magnitude Mike ailey mjb@c.oegontate.edu Magnitude: V V V V x y z vecto.pptx Vecto Can lo e Defined a the oitional Diffeence etween Two oint 3 Unit Vecto have a Magnitude
A THREE CRITICAL POINTS THEOREM AND ITS APPLICATIONS TO THE ORDINARY DIRICHLET PROBLEM
 A THREE CRITICAL POINTS THEOREM AND ITS APPLICATIONS TO THE ORDINARY DIRICHLET PROBLEM DIEGO AVERNA AND GABRIELE BONANNO Abstact. The aim of this pape is twofold. On one hand we establish a thee citical
A THREE CRITICAL POINTS THEOREM AND ITS APPLICATIONS TO THE ORDINARY DIRICHLET PROBLEM DIEGO AVERNA AND GABRIELE BONANNO Abstact. The aim of this pape is twofold. On one hand we establish a thee citical
AE 423 Space Technology I Chapter 2 Satellite Dynamics
 AE 43 Space Technology I Chapte Satellite Dynamic.1 Intoduction In thi chapte we eview ome dynamic elevant to atellite dynamic and we etablih ome of the baic popetie of atellite dynamic.. Dynamic of a
AE 43 Space Technology I Chapte Satellite Dynamic.1 Intoduction In thi chapte we eview ome dynamic elevant to atellite dynamic and we etablih ome of the baic popetie of atellite dynamic.. Dynamic of a
Internal Model Control
 Internal Model Control Part o a et o leture note on Introdution to Robut Control by Ming T. Tham 2002 The Internal Model Prinile The Internal Model Control hiloohy relie on the Internal Model Prinile,
Internal Model Control Part o a et o leture note on Introdution to Robut Control by Ming T. Tham 2002 The Internal Model Prinile The Internal Model Control hiloohy relie on the Internal Model Prinile,
Photographing a time interval
 Potogaping a time inteval Benad Rotenstein and Ioan Damian Politennia Univesity of imisoaa Depatment of Pysis imisoaa Romania benad_otenstein@yaoo.om ijdamian@yaoo.om Abstat A metod of measuing time intevals
Potogaping a time inteval Benad Rotenstein and Ioan Damian Politennia Univesity of imisoaa Depatment of Pysis imisoaa Romania benad_otenstein@yaoo.om ijdamian@yaoo.om Abstat A metod of measuing time intevals
NOTE. Some New Bounds for Cover-Free Families
 Jounal of Combinatoial Theoy, Seies A 90, 224234 (2000) doi:10.1006jcta.1999.3036, available online at http:.idealibay.com on NOTE Some Ne Bounds fo Cove-Fee Families D. R. Stinson 1 and R. Wei Depatment
Jounal of Combinatoial Theoy, Seies A 90, 224234 (2000) doi:10.1006jcta.1999.3036, available online at http:.idealibay.com on NOTE Some Ne Bounds fo Cove-Fee Families D. R. Stinson 1 and R. Wei Depatment
22.615, MHD Theory of Fusion Systems Prof. Freidberg Lecture 18
 .65, MHD Theoy of Fuion Sytem Pof. Feidbeg Lectue 8. Deive δw fo geneal cew pinch. Deive Suydam citeion Scew Pinch Equilibia μ p + + ( ) = μ J = μ J= Stability ( ) m k ξ=ξ e ι +ι ξ=ξ e +ξ e +ξ e =ξ +ξ
.65, MHD Theoy of Fuion Sytem Pof. Feidbeg Lectue 8. Deive δw fo geneal cew pinch. Deive Suydam citeion Scew Pinch Equilibia μ p + + ( ) = μ J = μ J= Stability ( ) m k ξ=ξ e ι +ι ξ=ξ e +ξ e +ξ e =ξ +ξ
SOME GENERAL NUMERICAL RADIUS INEQUALITIES FOR THE OFF-DIAGONAL PARTS OF 2 2 OPERATOR MATRICES
 italian jounal of pue and applied mathematics n. 35 015 (433 44) 433 SOME GENERAL NUMERICAL RADIUS INEQUALITIES FOR THE OFF-DIAGONAL PARTS OF OPERATOR MATRICES Watheq Bani-Domi Depatment of Mathematics
italian jounal of pue and applied mathematics n. 35 015 (433 44) 433 SOME GENERAL NUMERICAL RADIUS INEQUALITIES FOR THE OFF-DIAGONAL PARTS OF OPERATOR MATRICES Watheq Bani-Domi Depatment of Mathematics
PID CONTROL. Presentation kindly provided by Dr Andy Clegg. Advanced Control Technology Consortium (ACTC)
 PID CONTROL Preentation kindly provided by Dr Andy Clegg Advaned Control Tehnology Conortium (ACTC) Preentation Overview Introdution PID parameteriation and truture Effet of PID term Proportional, Integral
PID CONTROL Preentation kindly provided by Dr Andy Clegg Advaned Control Tehnology Conortium (ACTC) Preentation Overview Introdution PID parameteriation and truture Effet of PID term Proportional, Integral
How can you find the dimensions of a square or a circle when you are given its area? When you multiply a number by itself, you square the number.
 7. Finding Squae Root How can you find the dimenion of a quae o a cicle when you ae given it aea? When you multiply a numbe by itelf, you quae the numbe. Symbol fo quaing i the exponent. = = 6 quaed i
7. Finding Squae Root How can you find the dimenion of a quae o a cicle when you ae given it aea? When you multiply a numbe by itelf, you quae the numbe. Symbol fo quaing i the exponent. = = 6 quaed i
Math 301: The Erdős-Stone-Simonovitz Theorem and Extremal Numbers for Bipartite Graphs
 Math 30: The Edős-Stone-Simonovitz Theoem and Extemal Numbes fo Bipatite Gaphs May Radcliffe The Edős-Stone-Simonovitz Theoem Recall, in class we poved Tuán s Gaph Theoem, namely Theoem Tuán s Theoem Let
Math 30: The Edős-Stone-Simonovitz Theoem and Extemal Numbes fo Bipatite Gaphs May Radcliffe The Edős-Stone-Simonovitz Theoem Recall, in class we poved Tuán s Gaph Theoem, namely Theoem Tuán s Theoem Let
A Fundamental Tradeoff between Computation and Communication in Distributed Computing
 1 A Fundamental Tadeoff between Computation and Communication in Ditibuted Computing Songze Li, Student embe, IEEE, ohammad Ali addah-ali, embe, IEEE, Qian Yu, Student embe, IEEE, and A. Salman Avetimeh,
1 A Fundamental Tadeoff between Computation and Communication in Ditibuted Computing Songze Li, Student embe, IEEE, ohammad Ali addah-ali, embe, IEEE, Qian Yu, Student embe, IEEE, and A. Salman Avetimeh,
CHAPTER 2 DERIVATION OF STATE EQUATIONS AND PARAMETER DETERMINATION OF AN IPM MACHINE. 2.1 Derivation of Machine Equations
 1 CHAPTER DERIVATION OF STATE EQUATIONS AND PARAMETER DETERMINATION OF AN IPM MACHINE 1 Deivation of Machine Equations A moel of a phase PM machine is shown in Figue 1 Both the abc an the q axes ae shown
1 CHAPTER DERIVATION OF STATE EQUATIONS AND PARAMETER DETERMINATION OF AN IPM MACHINE 1 Deivation of Machine Equations A moel of a phase PM machine is shown in Figue 1 Both the abc an the q axes ae shown
Physics 2A Chapter 10 - Moment of Inertia Fall 2018
 Physics Chapte 0 - oment of netia Fall 08 The moment of inetia of a otating object is a measue of its otational inetia in the same way that the mass of an object is a measue of its inetia fo linea motion.
Physics Chapte 0 - oment of netia Fall 08 The moment of inetia of a otating object is a measue of its otational inetia in the same way that the mass of an object is a measue of its inetia fo linea motion.
Boise State University Department of Electrical and Computer Engineering ECE470 Electric Machines
 Boie State Univeity Depatment of Electical and Compute Engineeing ECE470 Electic Machine Deivation of the Pe-Phae Steady-State Equivalent Cicuit of a hee-phae Induction Machine Nomenclatue θ: oto haft
Boie State Univeity Depatment of Electical and Compute Engineeing ECE470 Electic Machine Deivation of the Pe-Phae Steady-State Equivalent Cicuit of a hee-phae Induction Machine Nomenclatue θ: oto haft
Second Order Fuzzy S-Hausdorff Spaces
 Inten J Fuzzy Mathematical Achive Vol 1, 013, 41-48 ISSN: 30-34 (P), 30-350 (online) Publihed on 9 Febuay 013 wwweeachmathciog Intenational Jounal o Second Ode Fuzzy S-Haudo Space AKalaichelvi Depatment
Inten J Fuzzy Mathematical Achive Vol 1, 013, 41-48 ISSN: 30-34 (P), 30-350 (online) Publihed on 9 Febuay 013 wwweeachmathciog Intenational Jounal o Second Ode Fuzzy S-Haudo Space AKalaichelvi Depatment
8.022 (E&M) Lecture 13. What we learned about magnetism so far
 8.0 (E&M) Letue 13 Topis: B s ole in Mawell s equations Veto potential Biot-Savat law and its appliations What we leaned about magnetism so fa Magneti Field B Epeiments: uents in s geneate foes on hages
8.0 (E&M) Letue 13 Topis: B s ole in Mawell s equations Veto potential Biot-Savat law and its appliations What we leaned about magnetism so fa Magneti Field B Epeiments: uents in s geneate foes on hages
COMPARING MORE THAN TWO POPULATION MEANS: AN ANALYSIS OF VARIANCE
 COMPARING MORE THAN TWO POPULATION MEANS: AN ANALYSIS OF VARIANCE To see how the piniple behind the analysis of vaiane method woks, let us onside the following simple expeiment. The means ( 1 and ) of
COMPARING MORE THAN TWO POPULATION MEANS: AN ANALYSIS OF VARIANCE To see how the piniple behind the analysis of vaiane method woks, let us onside the following simple expeiment. The means ( 1 and ) of
How to Obtain Desirable Transfer Functions in MIMO Systems Under Internal Stability Using Open and Closed Loop Control
 How to Obtain Desiable ansfe Functions in MIMO Sstems Unde Intenal Stabilit Using Open and losed Loop ontol echnical Repot of the ISIS Goup at the Univesit of Note Dame ISIS-03-006 June, 03 Panos J. Antsaklis
How to Obtain Desiable ansfe Functions in MIMO Sstems Unde Intenal Stabilit Using Open and losed Loop ontol echnical Repot of the ISIS Goup at the Univesit of Note Dame ISIS-03-006 June, 03 Panos J. Antsaklis
Estimates on Invariant Tori near an Elliptic Equilibrium Point of a Hamiltonian System
 jounal of diffeential equation 131, 277303 (1996) aticle no. 0165 Etimate on Invaiant Toi nea an Elliptic Equilibium Point of a Hamiltonian Sytem Amadeu Delham* Depatament de Matema tica Aplicada I, Univeitat
jounal of diffeential equation 131, 277303 (1996) aticle no. 0165 Etimate on Invaiant Toi nea an Elliptic Equilibium Point of a Hamiltonian Sytem Amadeu Delham* Depatament de Matema tica Aplicada I, Univeitat
A Fuzzy Production Inventory System. with Deterioration
 Alie Matematial Sienes, Vol. 5,, no. 5, - A Fuzzy Poution Inventoy System wit Deteioation A. Nagoo Gani PG & Resea Deatment of Matematis Jamal Moame College (Autonomous Tiuiaalli-, Tamilnau, Inia ganijm@yaoo.o.in
Alie Matematial Sienes, Vol. 5,, no. 5, - A Fuzzy Poution Inventoy System wit Deteioation A. Nagoo Gani PG & Resea Deatment of Matematis Jamal Moame College (Autonomous Tiuiaalli-, Tamilnau, Inia ganijm@yaoo.o.in
Experiment 1 Electric field and electric potential
 Expeiment 1 Eleti field and eleti potential Pupose Map eleti equipotential lines and eleti field lines fo two-dimensional hage onfiguations. Equipment Thee sheets of ondutive papes with ondutive-ink eletodes,
Expeiment 1 Eleti field and eleti potential Pupose Map eleti equipotential lines and eleti field lines fo two-dimensional hage onfiguations. Equipment Thee sheets of ondutive papes with ondutive-ink eletodes,
