Preliminary chapter: Review of previous coursework. Objectives
|
|
|
- Ginger Harrell
- 5 years ago
- Views:
Transcription
1 Preliminary chapter: Review of previous coursework Objectives By the end of this chapter the student should be able to recall, from Books 1 and 2 of New General Mathematics, the facts and methods that relate to the following themes: Number and numeration Basic operations Algebraic processes Mensuration and geometry Everyday statistics. Teaching and learning materials Teacher: Addition and multiplication wall charts; number square; metre rule, measuring tape, Students: Mathematics set To make the best use of Book 3 of New General Mathematics, readers should be familiar with the contents of Books 1 and 2. This chapter contains those themes and topics from Books 1 and 2 that are necessary to understand Book 3. Number and numeration For most purposes, we write numbers using the decimal place value system (Fig. P1). The symbols 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 are called digits. hundreds tens units decimal point tenths hundredths thousandths Fig. P1 We use the words thousand, million, billion, trillion for large numbers: 1 thousand million billion trillion Similarly we use thousandth, millionth and billionth, for decimal fractions: 1 thousandth millionth billionth When writing large and small numbers, group the digits in threes from the decimal point, for example: and is a whole number that divides exactly into another whole number, is a factor of is a multiple of 7. A prime number has only two factors, itself and 1. 1 is not a prime number. 2, 3, 5, 7, 11, 13, 17 are prime numbers. They continue without end. The prime factors of a number are those factors which are prime. For example, 2 and 5 are the prime factors of can be written as a product of prime factors: either = 40 or, in index form, = 40. The numbers 18, 24 and 30 all have 3 as a factor. 3 is a common factor of the numbers. The highest common factor (HCF) is the largest of the common factors of a given set of numbers. For example, 2, 3 and 6 are the common factors of 18, 24 and 30; 6 is the HCF. The number 48 is a multiple of 4 and a multiple of is a common multiple of 4and 6. The lowest common multiple (LCM) is the smallest of the common multiples of a given set of numbers. For example, 12 is the LCM of 4 and 6. In a fraction, one number (the numerator) is divided by another number (the denominator). 2 Section 1: Additional material
2 The fraction 5 means 5 8 (Fig. P2) numerator dividing line denominator Fig. P2 Fractions are used to describe parts of quantities (Fig. P3). Fig. P3 The fractions 5 8, 10 16, and 15 represent the same 24 amount; they are equivalent fractions. 5_ is the 8 simplest form of 10 16, and Basic operations To add or subtract fractions, change them to equivalent fractions with a common denominator. For example: = = = = 8 16 = 1 2 To multiply fractions, multiply numerator by numerator and denominator by denominator. Then write your answer in the simplest form. For example: = 6 20 = 3 10 To divide by a fraction, multiply by the reciprocal of the fraction. For example: = = = = x% is short for x % means To change a fraction to an equivalent percentage, multiply the fraction by 100. For example, = = 30%. To change a fraction to a decimal, divide the numerator by the denominator. Then multiply the quotient by 100. For example: = 62.5 When adding or subtracting decimals, write the numbers in a column with the decimal points exactly under one another. For example, add 2.29, and 4.3, then subtract the result from To multiply decimals, first ignore the decimal points and multiply the numbers as if they were whole numbers. Then re-insert the decimal point so that the answer has as many digits after the point as there are in the question. For example: There are four digits after the decimal points in the question, so, replace the decimal point: To divide by decimals, change the division so that the divisor becomes a whole number. For example: = = = 80 Numbers may be positive or negative. Positive and negative numbers are called directed numbers. Directed numbers can be shown on a number line (Fig. P4). An integer is any positive or negative whole number as shown in Fig. P Fig. P4 The following examples show how to add, subtract, multiply and divide directed numbers. Section 1: Additional material 3
3 Addition (-8) + (-3) = -11 (-8) + (+3) = -5 Subtraction (-9) - (+4) = -13 (-9) - (-4) = -5 Multiplication (-2) (-7) = +14 (-2) (+7) = -14 Division (+6) (+3) = +2 (+6) (-3) = -2 (+8) + (-3) = +5 (+8) + (+3) = +11 (+9) - (+4) = +5 (+9) - (-4) = +13 (+2) (-7) = -14 (+2) (+7) = +14 (-6) (+3) = -2 (-6) (-3) = +2 An integer is any positive or negative whole number as shown in Fig. P4. The number is is in standard form. The first part of the product is a number between 1 and 10. The second part is a power of 10. When rounding off numbers, the digits 1, 2, 3, 4 are round down and the digits 5, 6, 7, 8, 9 are round up. You must also pay attention to what you are being asked to round off to. For example: Round off 425 to the nearest is the significant figure, so round the tens column up: 430 Round off 425 to the nearest is the significant figure, so round the hundreds column down: 400 When rounding off decimals, the same rules apply. For example: Round off to 2 decimal places. 3 is the significant figure, so round the hundredths column down: 7.28 Round off to 1 decimal place. 8 is the significant figure, so round the tenths column up: 7.3 Round off to the nearest whole figure. 2 is the significant figure, so round down to the nearest unit: 7 The everyday system of numeration uses ten digits and is called a base ten, or denary, system. The base two, or binary, system of numeration uses only two digits, 0 and 1. To convert between bases ten and two, express the given numbers in powers of two: 43 ten = = = = two two = = = 22 ten Use the following identities when adding, subtracting and multiplying binary numbers: Addition: = = = = 10 Multiplication: 0 0 = = = = 1 Detailed coverage of number and numeration is given in NGM SB 1, Chapters 1, 2, 3, 4, 9, 12, 23, 24; and NGM SB 2, Chapters 1, 2, 4, 5, 8, 9, 15. Review Test 1: Number and numeration, and Basic operations teacher. 1 Express each of the following as a product of factors. Hence find their square roots. a c b d Express the following in standard form. a c 5 b d Round off the following to i 1 s.f., ii 2 s.f., iii 3 s.f. a b c d Round off the following to i 1 d.p., ii 2 d.p., iii 3 d.p. a c b d Section 1: Additional material
4 5 Simplify the following. a (-6) (+3) b 22 (-2) c d (-15) 4(-3) 6 A college has 778 students. The average mass of a student is approximately 52 kg. Estimate, to 1 significant figure, the total mass in tonnes of all the students in the college. 7 Divide the following quantities in the given ratios. a N=1 500 in the ratio 1 : 2 b 400 mm in the ratio 4 : 1 c 44 oranges in the ratio 7 : 4 8 Find the discount price if: a 10% is given on a cost price of N=500 b 25% is given on a cost price of N= Use tables to find: a b c d Round off the following to the nearest i whole number, ii tenth, iii hundredth. a b Review Test 2: Number and numeration, and Basic operations work. If they do not understand why some of their answers are incorrect, they may ask a friend or teacher. 1 Express each of the following as a product of factors. Hence find their square roots. a c b d Express the following in standard form. a c 04 b d Round off the following to i 1 s.f., ii 2 s.f., iii 3 s.f. a c b d Round off the following to i 1 d.p., ii 2 d.p., iii 3 d.p. a c b d Simplify the following. a (-72) (-9) c 65-5 b d (-80) (-8) 6 A typist can type about 33 words per minute. Estimate, to 1 significant figure, how long it will take her to type a letter that is 682 words long. 7 Divide the following quantities in the given ratios. a N=300 in the ratio 5 : 1 b 90 ml in the ratio 2 : 3 c 60 eggs in the ratio 5 : 7 8 Find the discount price if: a 5% is given on a cost price of N=2 000 b 20% is given on a cost price of N= Use tables to find: a 572 b c 8005 d Round off the following to the nearest i whole number, ii tenth, iii hundredth. a b Algebraic processes 3y 2-2x + 7x is an example of an algebraic expression. The letters x and y stand for numbers. 3y 2, 2x and 7x are the terms of the expression. 3y 2 is short for 3 y y. 3 is the coefficient of y 2. Algebraic terms may be simplified by combining like terms. Thus 3y 2-2x + 7x = 3y 2 + 5x since 2x and 7x are like terms (i.e. both terms in x). 3(5x + 2) = 11x is an algebraic sentence containing an equals sign; it is an equation in x. x is the unknown of the equation. To solve an equation means to find the value of the unknown that makes the equation true. Use the balance method to solve equations. Section 1: Additional material 5
5 For example, 3(5x + 2) = 11x Clear brackets. 15x + 6 = 11x Subtract 11 from both sides. 15x - 11x + 6 = 11x - 11x Minus 6 from both sides. 4x = -6 Divide both sides by 4. 4x = -6 Simplify. x = = = In general, when solving equations, clear brackets and fractions, use equal additions and/ or subtractions to collect unknown terms on one side of the equals sign and known terms on the other, where necessary divide or multiply both sides of the equation by the same number to find the unknown. An inequality is an algebraic sentence which contains an inequality sign: < less than is less than or equal to > is greater than is greater than or equal to Inequalities are solved in much the same way as equations. However, when both sides of an inequality are multiplied or divided by a negative number, the inequality sign is reversed. For example -3a < 12 Divide both sides by -3 and reverse the inequality. a > -2 A graph of an algebraic sentence is a picture representing the meaning of the sentence. Graphs of equations and inequalities in one variable can be shown on the number line (Fig. P5). Fig. P x = x > 1 For graphs connecting two variables, draw two axes at right angles to each other to give a Cartesian plane. The horizontal x-axis and the vertical y-axis cross at their zero-point, the origin of the plane. Fig. P6 is the graph of the equation y = 2x y x A y = 2x 3 Fig. P6 To draw a straight-line graph, plot at least three points which satisfy the given equation. See the table of values in Fig. P6. At point A in Fig. P6, x = 2 and y = 1. The coordinates of A are (2, 1). The order of the coordinates is important: give the x-coordinate first, and the y-coordinate second. We can use straight-line graphs to represent any two connected variables: for example, cost and quantity, distance and time, temperature and time. Straight-line graphs can also show conversions between currencies or between marks and percentages. Factorise or expand algebraic expressions using the basic rules of arithmetic. See the following examples: Expansion 3(a + 2) = 3a + 6b (5-8x)x = 5x - 8x 2 (a + b)(c + d) = c(a + b) + d(a + b) = ac + bc + ad + bd (3x + 2)(x - 4) = 3x 2 + 2x - 12x - 8 = 3x 2-10x - 8 (a - 5b) 2 = a 2-10ab + 25b 2 Factorisation 5y + 10y 2 = 5y(1 + 2y) 4x bx - 6b = 4(x - 2) + 3b(x - 2) = (x - 2)(4 + 3b) 6 Section 1: Additional material
6 The following laws of indices are true for all values of a, b and x. x a x b = x a+b x a x b = x a-b x 0 = 1 x-a = 1 Detailed coverage of algebraic processes is given in NGM Book 1, Chapters 5, 7, 10, 15, 19; and NGM Book 2, Chapters 5, 7, 11, 12, 13, 14, 22, 23. Review Test 3: Algebraic processes teacher. Then try Test 4. 1 State the additive inverse of: a -5 b +14 c -514 d State the multiplicative inverse of: a +7 c +34 b d Remove brackets and simplify. a 7(a - b) - 8(a - 2b) b y(y - 3) - 6(y - 3) 4 Expand the following. a (6 - x)(3 + y) b (5x - y)(x + 3y) 5 State the HCF of the following. a 10x 2 and 15x 2 b 24ax 2 and 3a 2 x 6 State the LCM of the following. a pq and qr b 3a 2 and 8ab 7 Factorise the following. a 2a 2-9ab b -18pq - 12p 8 Solve the following. a 51 = 3 + 8x b 6x + 1 = 26-2x 9 Which symbol, < or >, goes in the box to make the statement true? a b Solve the following. a 2x = 10 b 27 = 4x c x x - 23 Review Test 4: Algebraic processes teacher. 1 State the additive inverse of: a +3 b -7 c +118 d State the multiplicative inverse of: a 4 b Remove brackets and simplify. a x(x + 4) - 5(x - 2) b a(a + b) - b(a + b) c -9 d Expand the following. a (x + 6) (y - 9) b (x - 2)(3x + 7) 5 State the HCF of the following. a 18xy and 6xy b 12xy 2 and 3xy 6 State the LCM of the following. a 3a and 4b b 18xy and 6xy 7 Factorise the following. a 3ab + 6ac b -5xy + 15y 8 Solve the following. a 10g - 7 = 47 b 4x - 6 = 5x Which symbol, < or >, goes in the box to make the statement true? a b Solve the following. a 2x < 10 b -7 = 4x c x + 4 = 10x - 23 Geometry and mensuration Fig. P7 gives sketches and names of some common solids. Section 1: Additional material 7
7 Fig. P9 lists the angles and their names. acute angle (between 0 and 90 ) right angle (90 ) straight angle (180 ) obtuse angle (between 90 and 180 ) Fig. P7 All solids have faces; most solids have edges and vertices (Fig. P8). Fig. P9 reflex angles (between 180 and 360 ) Use a protractor to measure and construct angles. Figure P10 shows some properties of angles formed when straight lines meet. Fig. P8 Table P1 gives the formulae for the surface area and volume of common solids. The net of a solid is the plane shape that can be folded to make the solid. Cube edge s Cuboid Length l, breadth b, width w 8 Section 1: Additional material Surface area Volume Prism Height h, base area A Sphere Radius r Cylinder Base radius r, height h Cone Base radius r, height h, slant height l An angle is a measure of rotation or turning. 1 revolution = 360 degrees (1 rev = 360 ) The names of angles change with their size. m p a e y x s d r b a n Alternate angles are equal. x = y and m = n Fig. P10 c b q c The sum of the angles on a straight line is 180. a + b + c = 180 Vertically opposite angles are equal. p = q and r = s The sum of the angles at a point is 360. a + b + c + d = 360 a Corresponding angles are equal. a = b and p = q p b q
8 In Fig. P11, α is the angle of elevation of the top of the flagpole from the girl and β is the angle of depression of the girl from the boy. Fig. P15 shows the names and properties of some common quadrilaterals. square rectangle Fig. P11 Directions are taken from the points of the compass as indicated in Fig. P12. N W SW NW Fig. P12 S NE SE E A 3-figure bearing is a direction given as the number of degrees from north measured in a clockwise direction. See Fig. P13. N A 53 Fig. P13 B The bearing of B from A is 053. X Y N 205 The bearing of X from Y is 205. Fig. P14 shows the names and properties of some common triangles. Fig. P15 parallelogram trapezium rhombus kite Fig. P16 gives the names of lines and regions in a circle. chord centre Fig. P16 radius diameter arc circumference segment semi-circle sector A polygon is a plane shape with three or more straight sides. A regular polygon has all its sides of equal length and all its angles of equal size. Fig. P17 gives the names of some common regular polygons. equilateral triangle square regular pentagon scalene right-angled obtuse-angled 60 Fig. P14 isosceles equilateral Fig. P17 regular hexagon regular octagon Section 1: Additional material 9
9 The sum of the angles of an n-sided polygon is (n - 2) 180. In particular, the sum of the angles of a triangle is 180 and the sum of the angles of a quadrilateral is 360. To solve a triangle means to calculate the sizes of its sides and angles. Use Pythagoras rule to solve right-angled triangles. A c B Fig. P18 a b C In Fig. P18, triangle ABC is right-angled at B. Side AC is the hypotenuse. Pythagoras' rule: b 2 = a 2 + c 2 Table P2 contains formulae for the perimeter and area of plane shapes. Square Side s Rectangle Length l, breadth b Triangle Base b, height h Parallelogram Base b, height h perimeter area Fig. P19 parallel lines (ruler and set square) Detailed coverage of geometry and mensuration is given in NGM Book 1, Chapters 6, 8, 11, 13, 14, 16, 20, 21; and NGM Book 2, Chapters 3, 6, 16, 17, 19, 20, 24. Review Test 5 Mensuration and geometry teacher. Then try Test 6. 1 One of the angles of a parallelogram is 119. What are the sizes of its other three angles? 2 How many lines of symmetry does a kite have? 3 Find the values of m, n, p, q, s, in Figure P m 100 n Trapezium Height h, parallels of length a and b Circle Radius r s s q p The SI system of units is given in the tables in the students book. Use a ruler and set square to construct parallel lines (Fig. P19). s Fig. P Section 1: Additional material
10 4 Which one of the following is a Pythagorean triple? a 3, 8, 9 b 4, 10, 11 c 5, 12, 13 5 Calculate to 2 s.f. the length of a diagonal of a 30 mm by 20 mm rectangle. 6 Copy and complete the following table of cylinders. Use the value 3 for π. Cylinder Radius Height Curved surface area A 8 cm 6 cm B 5.5 cm 16 cm C 11 cm 196 cm 2 Volume D 4 cm 336 cm 3 7 In Fig. P21, BC is horizontal. A Cone Slant height Angle of sector A 10 cm 150 B 4 cm 240 Curved surface area Base radius Height C 5 cm 18 cm D 4 cm 10 cm Volume Review Test 6 Mensuration and geometry teacher. 1 One of the angles of a rhombus is 42. What are the sizes of its other three angles? 2 How many lines of bilateral symmetry does a square have? 3 Find the values of p, q, r, s, t, x in Fig. P23. r B C 44 Fig. P21 Measure: a the angle of elevation of A from B b the angle of depression of C from A. 64 p q s In Fig. P22, state the bearings of A, B, C and D from the centre. North D x 80 A Fig. P23 2x 2x x 71 t C Fig. P22 B 9 Copy and complete the following table of cones. Complete only the unshaded spaces. Use the value 3 for π. 4 Which one of the following is a Pythagorean triple? a 2, 3, 4 b 3, 4, 5 c 5, 12, 13 5 Calculate to 2 s.f. the length of the longest straight line that can be drawn on a rectangular chalkboard that measures 1.2 m by 3.0 m. Section 1: Additional material 11
11 6 Copy and complete the following table of cylinders. Use the value 3 for π. Cylinder Radius Height Curved Volume surface area A 4 cm 10 cm B 4.5 cm 12 cm C 7 cm 126 cm 2 D 5 cm 300 cm 3 7 In Fig. P24, QR is horizontal. Measure: P Everyday statistics Information in numerical form is called statistics. Statistical data may be given in rank order (i.e. in order of size) like these marks out of 5: 0, 1, 1, 2, 2, 2, 3, 3, 5 Data may also be given in a frequency table (Table P3). Mark Frequency The frequency is the number of times each piece of data occurs. We also use graphs to show statistics. Figure P26 shows the above data in a pictogram, a bar chart and a pie chart. Fig. P24 Q R a the angle of elevation of P from Q b the angle of depression of R from P. barchart 8 In Fig. P25, state the bearings of the following from O. Y North 25 O V 0 marks 1 mark 2 marks 3 marks 4 marks 5marks pictogram 0 5 pie chart X Fig. P25 W a V b W c X d Y 9 Copy and complete the following table of cones. Complete only the unshaded spaces. Use the value 3 for π. Cone Slant height Angle of sector A 8 cm 210 B 5 cm 135 Curved surface area Base radius Height C 7 cm 20 cm D 3.5 cm 12 cm Volume Probability is a measure of the likelihood of a required event happening. Probability = number of required events number of possible events If an event must happen, probability = 1. If an event cannot happen, probability = 0. The probability of something happening is a fraction whose value lies between 0 and 1. If the probability of something happening is x, then the probability of it not happening is 1 - x. Detailed coverage of statistics is given in NGM Book 1, Chapters 17, 18, 22; and NGM Book 2, Chapters 18, Section 1: Additional material
12 Review Test 7: Everyday statistics teacher. 1 For each set of numbers, calculate the mean. a 12, 14, 1 c 1, 8, 6, 8, 7 b 9, 10, 14 d 7, 7, 3, 2, 11 2 Find the mode, median and mean of each set of numbers. a 7, 7, 9, 12, 15 b 0, 1, 4, 4, 5, 5, 5, 6, 6, 7 c 10, 8, 5, 12, 8, 11 d 5, 3, 9, 5, 10, 6, 4, 7, 5 3 Table P4 shows the results of a survey of vehicles on a city road in one hour. Cars Lorries Buses Others Total Number Table P4 a How many vehicles altogether? b What is the probability that the next vehicle is a car? c What is the probability that the next vehicle is not a car? d What is the probability that the next vehicle is not a car, a lorry or a bus? Review Test 8: Everyday statistics teacher. 1 For each set of numbers, calculate the mean. a 18, 6, 8, 12 b 3, 11, 6, 8 c 2, 9, 0, 6, 7, 0 d 9, 10, 12, 13, 16, 18 2 Find the mode, median and mean of each set of numbers. a 4, 5, 5, 7, 8, 10 b 4, 8, 11, 11, 12, 12, 12 c 3, 1, 17, 1, 8, 12 d 4, 3, 1, 4, 1, 0, 2, 4, 2, 3, 4, 2 3 A school enters candidates for the JSC examination. Table P5 shows the results for the years Candidates entered Number gaining JSC Table P During the four years: a How many candidates were entered for the JSC? b How many candidates gained a JSC? c What is the school s success rate as a percentage? d What is the approximate probability (as a decimal to 1 s.f.) of a student at this school getting a JSC? Section 1: Additional material 13
Section 1: Additional material
 Section 1: Additional material Section 1 provides you with optional chapters that you can use with your class. Preliminary chapters are intended for use as revision and to reinforce foundation knowledge
Section 1: Additional material Section 1 provides you with optional chapters that you can use with your class. Preliminary chapters are intended for use as revision and to reinforce foundation knowledge
NEW GENERAL MATHEMATICS for Junior Secondary Schools
 NEW GENERAL MATHEMATICS for Junior Secondary Schools JSS Teacher s Guide 3 2013 NERDC Curriculum ZI Chima, GU Garba, AO Kalejaiye, MF Macrae Pearson Education Limited Edinburgh Gate Harlow Essex CM20 2JE
NEW GENERAL MATHEMATICS for Junior Secondary Schools JSS Teacher s Guide 3 2013 NERDC Curriculum ZI Chima, GU Garba, AO Kalejaiye, MF Macrae Pearson Education Limited Edinburgh Gate Harlow Essex CM20 2JE
Year 9 Mastery Statements for Assessment 1. Topic Mastery Statements - I can Essential Knowledge - I know
 Year 9 Mastery Statements for Assessment 1 Topic Mastery Statements - I can Essential Knowledge - I know Whole Numbers and Decimals Measures, perimeter area and volume Expressions and formulae Indices
Year 9 Mastery Statements for Assessment 1 Topic Mastery Statements - I can Essential Knowledge - I know Whole Numbers and Decimals Measures, perimeter area and volume Expressions and formulae Indices
California 5 th Grade Standards / Excel Math Correlation by Lesson Number
 (Activity) L1 L2 L3 Excel Math Objective Recognizing numbers less than a million given in words or place value; recognizing addition and subtraction fact families; subtracting 2 threedigit numbers with
(Activity) L1 L2 L3 Excel Math Objective Recognizing numbers less than a million given in words or place value; recognizing addition and subtraction fact families; subtracting 2 threedigit numbers with
Integer (positive or negative whole numbers or zero) arithmetic
 Integer (positive or negative whole numbers or zero) arithmetic The number line helps to visualize the process. The exercises below include the answers but see if you agree with them and if not try to
Integer (positive or negative whole numbers or zero) arithmetic The number line helps to visualize the process. The exercises below include the answers but see if you agree with them and if not try to
02)
 GRE / GMATmath,! abscissa, scalene, intercept, markup, such that, break even. abscissa. (4, 2) 4abscissa, 2ordinate absolute value acre add adjacent angles altitude ; angle () acute angle (90 ) right angle
GRE / GMATmath,! abscissa, scalene, intercept, markup, such that, break even. abscissa. (4, 2) 4abscissa, 2ordinate absolute value acre add adjacent angles altitude ; angle () acute angle (90 ) right angle
Wednesday, 24 May Warm-Up Session. Non-Calculator Paper
 Wednesday, 24 May 2017 Warm-Up Session Non-Calculator Paper Non-Calculator Paper 80 marks in 90 minutes IF YOU FINISH EARLY CHECK EVERYTHING! You have made a silly mistake somewhere. Redo some questions
Wednesday, 24 May 2017 Warm-Up Session Non-Calculator Paper Non-Calculator Paper 80 marks in 90 minutes IF YOU FINISH EARLY CHECK EVERYTHING! You have made a silly mistake somewhere. Redo some questions
Grade Demonstrate mastery of the multiplication tables for numbers between 1 and 10 and of the corresponding division facts.
 Unit 1 Number Theory 1 a B Find the prime factorization of numbers (Lesson 1.9) 5.1.6 Describe and identify prime and composite numbers. ISTEP+ T1 Pt 1 #11-14 1b BD Rename numbers written in exponential
Unit 1 Number Theory 1 a B Find the prime factorization of numbers (Lesson 1.9) 5.1.6 Describe and identify prime and composite numbers. ISTEP+ T1 Pt 1 #11-14 1b BD Rename numbers written in exponential
Basic Math. Curriculum (358 topics additional topics)
 Basic Math This course covers the topics outlined below and is available for use with integrated, interactive ebooks. You can customize the scope and sequence of this course to meet your curricular needs.
Basic Math This course covers the topics outlined below and is available for use with integrated, interactive ebooks. You can customize the scope and sequence of this course to meet your curricular needs.
Odd numbers 4 2 = 4 X 4 = 16
 Even numbers Square numbers 2, 4, 6, 8, 10, 12, 1 2 = 1 x 1 = 1 2 divides exactly into every even number. 2 2 = 2 x 2 = 4 3 2 = 3 x 3 = 9 Odd numbers 4 2 = 4 X 4 = 16 5 2 = 5 X 5 = 25 1, 3, 5, 7, 11, 6
Even numbers Square numbers 2, 4, 6, 8, 10, 12, 1 2 = 1 x 1 = 1 2 divides exactly into every even number. 2 2 = 2 x 2 = 4 3 2 = 3 x 3 = 9 Odd numbers 4 2 = 4 X 4 = 16 5 2 = 5 X 5 = 25 1, 3, 5, 7, 11, 6
Year 1 - What I Should Know by Heart
 Year 1 - What I Should Know by Heart Count in 1 s forward and backwards from 0 to 150, beginning from any number. Count in multiples of 2, 5 and 10 up to 100. Recognise odd and even numbers. Know 1 st,
Year 1 - What I Should Know by Heart Count in 1 s forward and backwards from 0 to 150, beginning from any number. Count in multiples of 2, 5 and 10 up to 100. Recognise odd and even numbers. Know 1 st,
BRADFIELD COLLEGE. IGCSE Mathematics. Revision Guide. Bradfield College Maths Department. 1 P age
 BRADFIELD COLLEGE IGCSE Mathematics Revision Guide Bradfield College Maths Department 2010 1 P age Contents Introduction to the Revision Guide... 3 Aims... 3 How to use the guide... 3 Using the different
BRADFIELD COLLEGE IGCSE Mathematics Revision Guide Bradfield College Maths Department 2010 1 P age Contents Introduction to the Revision Guide... 3 Aims... 3 How to use the guide... 3 Using the different
Glossary 13, 14, 15 24, 26, dimensional (2-D) balance. bar line chart. 3-dimensional (3-D) capacity. Celsius. commutative.
 5 Glossary 2-dimensional (2-D) B circle right-angled equilateral isosceles square balance Things are balanced when both sides have equal value, e.g. 3 + 4 = 2 + 5 and 1000 g = 1 kg. 3-dimensional (3-D)
5 Glossary 2-dimensional (2-D) B circle right-angled equilateral isosceles square balance Things are balanced when both sides have equal value, e.g. 3 + 4 = 2 + 5 and 1000 g = 1 kg. 3-dimensional (3-D)
The Grade Descriptors below are used to assess work and student progress in Mathematics from Year 7 to
 Jersey College for Girls Assessment criteria for KS3 and KS4 Mathematics In Mathematics, students are required to become familiar, confident and competent with a range of content and procedures described
Jersey College for Girls Assessment criteria for KS3 and KS4 Mathematics In Mathematics, students are required to become familiar, confident and competent with a range of content and procedures described
Pre Algebra. Curriculum (634 topics)
 Pre Algebra This course covers the topics shown below. Students navigate learning paths based on their level of readiness. Institutional users may customize the scope and sequence to meet curricular needs.
Pre Algebra This course covers the topics shown below. Students navigate learning paths based on their level of readiness. Institutional users may customize the scope and sequence to meet curricular needs.
Pre Algebra and Introductory Algebra
 Pre Algebra and Introductory Algebra This course covers the topics outlined below and is available for use with integrated, interactive ebooks. You can customize the scope and sequence of this course to
Pre Algebra and Introductory Algebra This course covers the topics outlined below and is available for use with integrated, interactive ebooks. You can customize the scope and sequence of this course to
Destination Math. Scope & Sequence. Grades K 12 solutions
 Destination Math Scope & Sequence Grades K 12 solutions Table of Contents Destination Math Mastering Skills & Concepts I: Pre-Primary Mathematics, Grades K-1... 3 Destination Math Mastering Skills & Concepts
Destination Math Scope & Sequence Grades K 12 solutions Table of Contents Destination Math Mastering Skills & Concepts I: Pre-Primary Mathematics, Grades K-1... 3 Destination Math Mastering Skills & Concepts
Key Stage 3 Subject: Maths Foundation Year: Year 7 Year 8 Year 9 Topic/Module: Geometry
 Subject: Foundation Topic/Module: Geometry Time Geometry 1 234 Metric Units Angles/Polygons Bearings Transformations watch Clips N21 N7 N7 N7 N7 N7, R2, 112 112 G10, 46 G16, 122 G14 G13, G17, 45, 121 G23
Subject: Foundation Topic/Module: Geometry Time Geometry 1 234 Metric Units Angles/Polygons Bearings Transformations watch Clips N21 N7 N7 N7 N7 N7, R2, 112 112 G10, 46 G16, 122 G14 G13, G17, 45, 121 G23
NUMERACY TOOLKIT TOOLKIT NUMERACY
 NUMERACY TOOLKIT TOOLKIT NUMERACY Addition Calculating methods Example 534 + 2678 Place the digits in the correct place value columns with the numbers under each other. Th H T U Begin adding in the units
NUMERACY TOOLKIT TOOLKIT NUMERACY Addition Calculating methods Example 534 + 2678 Place the digits in the correct place value columns with the numbers under each other. Th H T U Begin adding in the units
2. P = { 0,2,4,6} and { 1,2,4,5} find P Q. A. { 0,6} B. { 2,4} C. {0, 2,4} D. { 0,2,6}
 SECTION A. 1. Express 24 as a product of prime factors. A. 2 2 x 3 3 B. 2 x 3 C. 2 2 x 3 D. 2 3 x 3 2. P = { 0,2,4,6} and { 1,2,4,5} find P Q. A. { 0,6} B. { 2,4} C. {0, 2,4} D. { 0,2,6} 3. Two sets which
SECTION A. 1. Express 24 as a product of prime factors. A. 2 2 x 3 3 B. 2 x 3 C. 2 2 x 3 D. 2 3 x 3 2. P = { 0,2,4,6} and { 1,2,4,5} find P Q. A. { 0,6} B. { 2,4} C. {0, 2,4} D. { 0,2,6} 3. Two sets which
High School Preparation for Algebra 1
 High School Preparation for Algebra 1 This course covers the topics shown below. Students navigate learning paths based on their level of readiness. Institutional users may customize the scope and sequence
High School Preparation for Algebra 1 This course covers the topics shown below. Students navigate learning paths based on their level of readiness. Institutional users may customize the scope and sequence
Course Readiness and Skills Review Handbook (Topics 1-10, 17) (240 topics, due. on 09/11/2015) Course Readiness (55 topics)
 Course Name: Gr. 8 Fall 2015 Course Code: C6HNH-TEK9E ALEKS Course: Middle School Math Course 3 Instructor: Mr. Fernando Course Dates: Begin: 08/31/2015 End: 06/17/2016 Course Content: 642 Topics (637
Course Name: Gr. 8 Fall 2015 Course Code: C6HNH-TEK9E ALEKS Course: Middle School Math Course 3 Instructor: Mr. Fernando Course Dates: Begin: 08/31/2015 End: 06/17/2016 Course Content: 642 Topics (637
QUESTION 1 50 FOR JSS 3
 QUESTION 1 5 FOR JSS 3 1. The knowledge of probability is necessary for the following reasons except A. In predicting B. In deciding C. In selecting D. In drawing table E. In forecasting. Factorise 7a
QUESTION 1 5 FOR JSS 3 1. The knowledge of probability is necessary for the following reasons except A. In predicting B. In deciding C. In selecting D. In drawing table E. In forecasting. Factorise 7a
Prep for the CSU ELM
 Prep for the CSU ELM This course covers the topics shown below. Students navigate learning paths based on their level of readiness. Institutional users may customize the scope and sequence to meet curricular
Prep for the CSU ELM This course covers the topics shown below. Students navigate learning paths based on their level of readiness. Institutional users may customize the scope and sequence to meet curricular
Mathematics KSHSSA Key Stage 3 Grade Descriptors
 Developing Fluency, reasoning Mathematically and Problem Solving consolidate their numerical and mathematical capability from develop their mathematical knowledge, in part through key stage 2 and extend
Developing Fluency, reasoning Mathematically and Problem Solving consolidate their numerical and mathematical capability from develop their mathematical knowledge, in part through key stage 2 and extend
California 3 rd Grade Standards / Excel Math Correlation by Lesson Number
 California 3 rd Grade Standards / Lesson (Activity) L1 L2 L3 L4 L5 L6 L7 L8 Excel Math Lesson Objective Learning about the tens place and the ones place; adding and subtracting two-digit numbers; learning
California 3 rd Grade Standards / Lesson (Activity) L1 L2 L3 L4 L5 L6 L7 L8 Excel Math Lesson Objective Learning about the tens place and the ones place; adding and subtracting two-digit numbers; learning
QUESTION 1 50 FOR JSS 1
 QUESTION 1 5 FOR JSS 1 1. The LCM of, 3 and 4 is A. 14 B. 1 C. 1 D. 16. Estimate 578.6998 to 3 decimal places. A. 578.7 B. 578.79 C. 578.8 D. 579. 3. Express 111 two as a number in base ten. A. 15 B. 18
QUESTION 1 5 FOR JSS 1 1. The LCM of, 3 and 4 is A. 14 B. 1 C. 1 D. 16. Estimate 578.6998 to 3 decimal places. A. 578.7 B. 578.79 C. 578.8 D. 579. 3. Express 111 two as a number in base ten. A. 15 B. 18
Fifth Grade Mathematics Mathematics Course Outline
 Crossings Christian School Academic Guide Middle School Division Grades 5-8 Fifth Grade Mathematics Place Value, Adding, Subtracting, Multiplying, and Dividing s will read and write whole numbers and decimals.
Crossings Christian School Academic Guide Middle School Division Grades 5-8 Fifth Grade Mathematics Place Value, Adding, Subtracting, Multiplying, and Dividing s will read and write whole numbers and decimals.
St. Ann s Academy - Mathematics
 St. Ann s Academy - Mathematics Students at St. Ann s Academy will be able to reason abstractly and quantitatively. Students will define, explain, and understand different types of word problems (simple
St. Ann s Academy - Mathematics Students at St. Ann s Academy will be able to reason abstractly and quantitatively. Students will define, explain, and understand different types of word problems (simple
Calculating methods. Addition. Multiplication. Th H T U Th H T U = Example
 1 Addition Calculating methods Example 534 + 2678 Place the digits in the correct place value columns with the numbers under each other. Th H T U Begin adding in the units column. 5 3 4 + 12 16 17 8 4+8
1 Addition Calculating methods Example 534 + 2678 Place the digits in the correct place value columns with the numbers under each other. Th H T U Begin adding in the units column. 5 3 4 + 12 16 17 8 4+8
Circle Theorems. Angles at the circumference are equal. The angle in a semi-circle is x The angle at the centre. Cyclic Quadrilateral
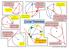 The angle in a semi-circle is 90 0 Angles at the circumference are equal. A B They must come from the same arc. Look out for a diameter. 2x Cyclic Quadrilateral Opposite angles add up to 180 0 A They must
The angle in a semi-circle is 90 0 Angles at the circumference are equal. A B They must come from the same arc. Look out for a diameter. 2x Cyclic Quadrilateral Opposite angles add up to 180 0 A They must
Foundations of High School Math
 Foundations of High School Math This course covers the topics shown below. Students navigate learning paths based on their level of readiness. Institutional users may customize the scope and sequence to
Foundations of High School Math This course covers the topics shown below. Students navigate learning paths based on their level of readiness. Institutional users may customize the scope and sequence to
CDS-I 2019 Elementary Mathematics (Set-C)
 1 CDS-I 019 Elementary Mathematics (Set-C) Direction: Consider the following for the next three (03) items : A cube is inscribed in a sphere. A right circular cylinder is within the cube touching all the
1 CDS-I 019 Elementary Mathematics (Set-C) Direction: Consider the following for the next three (03) items : A cube is inscribed in a sphere. A right circular cylinder is within the cube touching all the
Destination Math California Intervention
 Destination Math California Intervention correlated to the California Intervention 4 7 s McDougal Littell Riverdeep STANDARDS MAPS for a Mathematics Intervention Program (Grades 4-7) The standards maps
Destination Math California Intervention correlated to the California Intervention 4 7 s McDougal Littell Riverdeep STANDARDS MAPS for a Mathematics Intervention Program (Grades 4-7) The standards maps
CAMBRIDGE IGCSE MATHS EXAMINATION BOARD COVERAGE
 CAMBRIDGE IGCSE MATHS EXAMINATION BOARD COVERAGE TIER TOPIC HEADING SUB HEADING Both Number Integers Ordering numbers Both Number Integers Rounding numbers Both Number Integers Adding and subtracting whole
CAMBRIDGE IGCSE MATHS EXAMINATION BOARD COVERAGE TIER TOPIC HEADING SUB HEADING Both Number Integers Ordering numbers Both Number Integers Rounding numbers Both Number Integers Adding and subtracting whole
Harbor Creek School District
 Numeration Unit of Study Big Ideas Algebraic Concepts How do I match a story or equation to different symbols? How do I determine a missing symbol in an equation? How does understanding place value help
Numeration Unit of Study Big Ideas Algebraic Concepts How do I match a story or equation to different symbols? How do I determine a missing symbol in an equation? How does understanding place value help
PRE-ALGEBRA SUMMARY WHOLE NUMBERS
 PRE-ALGEBRA SUMMARY WHOLE NUMBERS Introduction to Whole Numbers and Place Value Digits Digits are the basic symbols of the system 0,,,, 4,, 6, 7, 8, and 9 are digits Place Value The value of a digit in
PRE-ALGEBRA SUMMARY WHOLE NUMBERS Introduction to Whole Numbers and Place Value Digits Digits are the basic symbols of the system 0,,,, 4,, 6, 7, 8, and 9 are digits Place Value The value of a digit in
Teachers' Guide for GCSE Mathematics Numeracy and GCSE Mathematics
 Teachers' Guide for GCSE Mathematics Numeracy and GCSE Mathematics Annotated specification of content Assessment objectives New content Vocabulary of finance Summary of new content topics Notes on new
Teachers' Guide for GCSE Mathematics Numeracy and GCSE Mathematics Annotated specification of content Assessment objectives New content Vocabulary of finance Summary of new content topics Notes on new
Alaska Mathematics Standards Vocabulary Word List Grade 4
 1 add addend additive comparison area area model common factor common multiple compatible numbers compose composite number counting number decompose difference digit divide dividend divisible divisor equal
1 add addend additive comparison area area model common factor common multiple compatible numbers compose composite number counting number decompose difference digit divide dividend divisible divisor equal
Kindergarten Grade 1 Grade 2
 Kindergarten Grade 1 Grade 2 NK.1 Say the whole number sequence by 1s starting anywhere from 0 to 10 and from 10 to 0. N1.1 Say the number sequence, 0 to 100, by: 1s forward and backward between any two
Kindergarten Grade 1 Grade 2 NK.1 Say the whole number sequence by 1s starting anywhere from 0 to 10 and from 10 to 0. N1.1 Say the number sequence, 0 to 100, by: 1s forward and backward between any two
Pre Algebra. Curriculum (634 topics additional topics)
 Pre Algebra This course covers the topics shown below. Students navigate learning paths based on their level of readiness. Institutional users may customize the scope and sequence to meet curricular needs.
Pre Algebra This course covers the topics shown below. Students navigate learning paths based on their level of readiness. Institutional users may customize the scope and sequence to meet curricular needs.
WITH MATH INTERMEDIATE/MIDDLE (IM) GRADE 5
 May 06 VIRGINIA MATHEMATICS STANDARDS OF LEARNING CORRELATED TO MOVING WITH MATH INTERMEDIATE/MIDDLE (IM) GRADE 5 NUMBER AND NUMBER SENSE 5.1 The student will a. read, write, and identify the place values
May 06 VIRGINIA MATHEMATICS STANDARDS OF LEARNING CORRELATED TO MOVING WITH MATH INTERMEDIATE/MIDDLE (IM) GRADE 5 NUMBER AND NUMBER SENSE 5.1 The student will a. read, write, and identify the place values
Key competencies (student abilities)
 Year 9 Mathematics Cambridge IGCSE Mathematics is accepted by universities and employers as proof of mathematical knowledge and understanding. Successful Cambridge IGCSE Mathematics candidates gain lifelong
Year 9 Mathematics Cambridge IGCSE Mathematics is accepted by universities and employers as proof of mathematical knowledge and understanding. Successful Cambridge IGCSE Mathematics candidates gain lifelong
6th Grade Mathematics
 Standard 1: Number & Operation and use numbers and use numbers 27-31% and use numbers 6.M.1.1.1 Compare magnitudes and relative magnitudes of positive rational numbers, including whole numbers through
Standard 1: Number & Operation and use numbers and use numbers 27-31% and use numbers 6.M.1.1.1 Compare magnitudes and relative magnitudes of positive rational numbers, including whole numbers through
Middle School Math Course 3
 Middle School Math Course 3 This course covers the topics shown below. Students navigate learning paths based on their level of readiness. Institutional users may customize the scope and sequence to meet
Middle School Math Course 3 This course covers the topics shown below. Students navigate learning paths based on their level of readiness. Institutional users may customize the scope and sequence to meet
VISHAL BHARTI PUBLIC SCHOOL SUBJECT-MATHEMATICS CLASS-VI ASSIGNMENT-4 REVISION (SEPTEMBER)
 I) Chapter - Knowing Our Numbers VISHAL BHARTI PUBLIC SCHOOL SUBJECT-MATHEMATICS CLASS-VI ASSIGNMENT-4 REVISION (SEPTEMBER) Q1 Write the Roman numeral for (a) 384 (b) 999 Q2 Write the number name of 74532601
I) Chapter - Knowing Our Numbers VISHAL BHARTI PUBLIC SCHOOL SUBJECT-MATHEMATICS CLASS-VI ASSIGNMENT-4 REVISION (SEPTEMBER) Q1 Write the Roman numeral for (a) 384 (b) 999 Q2 Write the number name of 74532601
OBJECTIVE TEST. Answer all questions C. N3, D. N3, Simplify Express the square root of in 4
 . In a particular year, the exchange rate of Naira (N) varies directly with the Dollar ($). If N is equivalent to $8, find the Naira equivalent of $6. A. N8976 B. N049 C. N40. D. N.7. If log = x, log =
. In a particular year, the exchange rate of Naira (N) varies directly with the Dollar ($). If N is equivalent to $8, find the Naira equivalent of $6. A. N8976 B. N049 C. N40. D. N.7. If log = x, log =
Analysis of California Mathematics standards to Common Core standards Grade 4
 Analysis of California Mathematics standards to Common Core standards Grade 4 Strand CA Math Standard Domain Common Core Standard (CCS) Alignment Comments in Reference to CCS Strand Number Sense CA Math
Analysis of California Mathematics standards to Common Core standards Grade 4 Strand CA Math Standard Domain Common Core Standard (CCS) Alignment Comments in Reference to CCS Strand Number Sense CA Math
Math Prep for College Physics
 Math Prep for College Physics This course covers the topics outlined below. You can customize the scope and sequence of this course to meet your curricular needs. Curriculum (190 topics + 52 additional
Math Prep for College Physics This course covers the topics outlined below. You can customize the scope and sequence of this course to meet your curricular needs. Curriculum (190 topics + 52 additional
Granite School District Parent Guides Utah Core State Standards for Mathematics Grades K-6
 Granite School District Parent Guides Grades K-6 GSD Parents Guide for Kindergarten The addresses Standards for Mathematical Practice and Standards for Mathematical Content. The standards stress not only
Granite School District Parent Guides Grades K-6 GSD Parents Guide for Kindergarten The addresses Standards for Mathematical Practice and Standards for Mathematical Content. The standards stress not only
Middle School Math Course 2
 Middle School Math Course 2 This course covers the topics shown below. Students navigate learning paths based on their level of readiness. Institutional users may customize the scope and sequence to meet
Middle School Math Course 2 This course covers the topics shown below. Students navigate learning paths based on their level of readiness. Institutional users may customize the scope and sequence to meet
Baldragon Academy National 4 Maths Checklist
 Baldragon Academy National 4 Maths Checklist Contents: Page Numeracy Number..2 Measure.4 Statistics...6 Expressions and Formulae Algebra..8 Geometry.....9 Statistics..11 Relationships Linear Equations
Baldragon Academy National 4 Maths Checklist Contents: Page Numeracy Number..2 Measure.4 Statistics...6 Expressions and Formulae Algebra..8 Geometry.....9 Statistics..11 Relationships Linear Equations
A. 180 B. 108 C. 360 D. 540
 Part I - Multiple Choice - Circle your answer: 1. Find the area of the shaded sector. Q O 8 P A. 2 π B. 4 π C. 8 π D. 16 π 2. An octagon has sides. A. five B. six C. eight D. ten 3. The sum of the interior
Part I - Multiple Choice - Circle your answer: 1. Find the area of the shaded sector. Q O 8 P A. 2 π B. 4 π C. 8 π D. 16 π 2. An octagon has sides. A. five B. six C. eight D. ten 3. The sum of the interior
Year 8 Autumn Term Topics Covered Calculations Ratio, Proportion and Compound Measures Manipulating Algebraic Expressions Fractions
 Year 8 Autumn Term Topics Covered Note: grades given are our own internal 'Sprowston' grades used as a guide for the purpose of tracking students' progress Calculations Grade 2 Multiply and divide integers
Year 8 Autumn Term Topics Covered Note: grades given are our own internal 'Sprowston' grades used as a guide for the purpose of tracking students' progress Calculations Grade 2 Multiply and divide integers
Scope and Sequence: National Curriculum Mathematics from Haese Mathematics (7 10A)
 Scope and Sequence: National Curriculum Mathematics from Haese Mathematics (7 10A) Updated 06/05/16 http://www.haesemathematics.com.au/ Note: Exercises in red text indicate material in the 10A textbook
Scope and Sequence: National Curriculum Mathematics from Haese Mathematics (7 10A) Updated 06/05/16 http://www.haesemathematics.com.au/ Note: Exercises in red text indicate material in the 10A textbook
Solve problems involving proportions Describe the effect of scale factor
 Strand: Ratios and Proportional Relationships (RP) 7th Grade Topic: Describe relationships of similar polygons Solve problems involving proportions Describe the effect of scale factor Compare or contrast
Strand: Ratios and Proportional Relationships (RP) 7th Grade Topic: Describe relationships of similar polygons Solve problems involving proportions Describe the effect of scale factor Compare or contrast
Strand 1: Statistics and Probability
 Strand 1: Statistics and Probability Topic 1.1 Counting Listing outcomes of experiments in a systematic way, such as in a table, using sample spaces, tree diagrams. 1.2 C oncepts of The probability of
Strand 1: Statistics and Probability Topic 1.1 Counting Listing outcomes of experiments in a systematic way, such as in a table, using sample spaces, tree diagrams. 1.2 C oncepts of The probability of
Check boxes of Edited Copy of Sp Topics (was 145 for pilot) Beginning Algebra, 3rd Ed. [open all close all] Course Readiness and
![Check boxes of Edited Copy of Sp Topics (was 145 for pilot) Beginning Algebra, 3rd Ed. [open all close all] Course Readiness and Check boxes of Edited Copy of Sp Topics (was 145 for pilot) Beginning Algebra, 3rd Ed. [open all close all] Course Readiness and](/thumbs/81/82758218.jpg) Check boxes of Edited Copy of 10021 Sp 11 152 Topics (was 145 for pilot) Beginning Algebra, 3rd Ed. [open all close all] Course Readiness and Additional Topics Appendix Course Readiness Multiplication
Check boxes of Edited Copy of 10021 Sp 11 152 Topics (was 145 for pilot) Beginning Algebra, 3rd Ed. [open all close all] Course Readiness and Additional Topics Appendix Course Readiness Multiplication
The UCL Academy Mathematics Department Achieving a grade 5 at GCSE Maths
 The UCL Academy Mathematics Department Achieving a grade 5 at GCSE Maths This document lists all the skills that are the minimum requirement to score a grade 5 or higher on the topics you learned up to
The UCL Academy Mathematics Department Achieving a grade 5 at GCSE Maths This document lists all the skills that are the minimum requirement to score a grade 5 or higher on the topics you learned up to
FOUNDATION MATHS REVISION CHECKLIST (Grades 5 1)
 FOUNDATION MATHS REVISION CHECKLIST 2017+ (s 5 1) Geometry and Measures Arc lengths and sectors 5 Derive triangle results 5 Enlargements and negative SF 5 Loci 5 Pythagoras 5 Similarity and Congruence
FOUNDATION MATHS REVISION CHECKLIST 2017+ (s 5 1) Geometry and Measures Arc lengths and sectors 5 Derive triangle results 5 Enlargements and negative SF 5 Loci 5 Pythagoras 5 Similarity and Congruence
2 year GCSE Scheme of Work
 2 year GCSE Scheme of Work Year 10 Pupils follow the 2 year Pearsons/Edexcel Scheme of Work FOUNDATION ROUTE HIGHER ROUTE YEAR 4 YEAR 5 YEAR 4 YEAR 5 GCSE (9-1) Foundation GCSE (9-1) Foundation GCSE (9-1)
2 year GCSE Scheme of Work Year 10 Pupils follow the 2 year Pearsons/Edexcel Scheme of Work FOUNDATION ROUTE HIGHER ROUTE YEAR 4 YEAR 5 YEAR 4 YEAR 5 GCSE (9-1) Foundation GCSE (9-1) Foundation GCSE (9-1)
grasp of the subject while attaining their examination objectives.
 PREFACE SUCCESS IN MATHEMATICS is designed with the purpose of assisting students in their preparation for important school and state examinations. Students requiring revision of the concepts covered in
PREFACE SUCCESS IN MATHEMATICS is designed with the purpose of assisting students in their preparation for important school and state examinations. Students requiring revision of the concepts covered in
Academic Vocabulary CONTENT BUILDER FOR THE PLC MATH GRADE 4
 Academic Vocabulary CONTENT BUILDER FOR THE PLC MATH GRADE 4 Representing and Comparing Whole Numbers and Decimals 4.2 Number and operations. The student applies mathematical process standards to represent,
Academic Vocabulary CONTENT BUILDER FOR THE PLC MATH GRADE 4 Representing and Comparing Whole Numbers and Decimals 4.2 Number and operations. The student applies mathematical process standards to represent,
WEST AFRICAN SENIOR SCHOOL CERTIFICATE EXAMINATION MATHEMATICS (CORE)/GENERAL MATHEMATICS
 PREAMBLE For all papers which involve mathematical calculations, mathematical and statistical tables published for WAEC should be used in the examination room. However, the use of nonprogrammable, silent
PREAMBLE For all papers which involve mathematical calculations, mathematical and statistical tables published for WAEC should be used in the examination room. However, the use of nonprogrammable, silent
END-OF-YEAR-EXAMINATIONS. Time allowed: 2 hours
 END-OF-YEAR-EXAMINATIONS Instructions to candidates YEAR 3 MATHEMATICS MATHEMATICS A - IGCSE Book 1 Time allowed: hours In the boxes below write your name, surname and form. Answer the questions in the
END-OF-YEAR-EXAMINATIONS Instructions to candidates YEAR 3 MATHEMATICS MATHEMATICS A - IGCSE Book 1 Time allowed: hours In the boxes below write your name, surname and form. Answer the questions in the
Spring Lake Middle School- Accelerated Math 7 Curriculum Map Updated: January 2018
 Domain Standard Learning Targets Resources Ratios and Proportional Relationships 7.RP.1 Compute unit rates associated with ratios of fractions, including ratios of lengths, areas and other quantities measured
Domain Standard Learning Targets Resources Ratios and Proportional Relationships 7.RP.1 Compute unit rates associated with ratios of fractions, including ratios of lengths, areas and other quantities measured
Paper 3 Unseen Topics
 Paper 3 Unseen Topics This is a collection of questions based on the topics that are so far UNSEEN or are usually more prominent Make sure you revise all topics as it is very likely topics from Paper 1
Paper 3 Unseen Topics This is a collection of questions based on the topics that are so far UNSEEN or are usually more prominent Make sure you revise all topics as it is very likely topics from Paper 1
Math Maps & Unit CCRS Priorities K10 SBCSC
 ISTEP+ Instructional and Assessment Guidance Math Maps & Unit CCRS Priorities 2016-2017 K10 SBCSC Prioritizing Instruction In an effort to empower teachers and focus on college and career readiness, the
ISTEP+ Instructional and Assessment Guidance Math Maps & Unit CCRS Priorities 2016-2017 K10 SBCSC Prioritizing Instruction In an effort to empower teachers and focus on college and career readiness, the
Glossary. Glossary 981. Hawkes Learning Systems. All rights reserved.
 A Glossary Absolute value The distance a number is from 0 on a number line Acute angle An angle whose measure is between 0 and 90 Addends The numbers being added in an addition problem Addition principle
A Glossary Absolute value The distance a number is from 0 on a number line Acute angle An angle whose measure is between 0 and 90 Addends The numbers being added in an addition problem Addition principle
Home NAME:... FORM:... MATHS TOOLKIT Year 6
 NAME:... FORM:... MATHS TOOLKIT 017 018 Year 6 Click on the topic of choice Contents Number... 4 Revision of Four Operations... 4 Multiplication and Division of Decimals... 5 Long Multiplication... 7 Long
NAME:... FORM:... MATHS TOOLKIT 017 018 Year 6 Click on the topic of choice Contents Number... 4 Revision of Four Operations... 4 Multiplication and Division of Decimals... 5 Long Multiplication... 7 Long
Math Glossary. Version September 1, Next release: On or before September 30, for the latest version.
 Math Glossary Version 0.1.1 September 1, 2003 Next release: On or before September 30, 2003. E-mail edu@ezlink.com for the latest version. Copyright 2003 by Brad Jolly All Rights Reserved Types of Numbers
Math Glossary Version 0.1.1 September 1, 2003 Next release: On or before September 30, 2003. E-mail edu@ezlink.com for the latest version. Copyright 2003 by Brad Jolly All Rights Reserved Types of Numbers
9-12 Mathematics Vertical Alignment ( )
 Algebra I Algebra II Geometry Pre- Calculus U1: translate between words and algebra -add and subtract real numbers -multiply and divide real numbers -evaluate containing exponents -evaluate containing
Algebra I Algebra II Geometry Pre- Calculus U1: translate between words and algebra -add and subtract real numbers -multiply and divide real numbers -evaluate containing exponents -evaluate containing
Appendix (5) The first period ( ) The second period ( ) The third period ( )
 Appendix (5) The mathematical content Analysis of mathematics curriculum for the first grade in light of the standards of content among the sub-periods of development. Standards / Periods The first period
Appendix (5) The mathematical content Analysis of mathematics curriculum for the first grade in light of the standards of content among the sub-periods of development. Standards / Periods The first period
MATHS DEPARTMENT SYNA INTERNATIONAL SCHOOL CLASS V 3 X 1 = 3 3 X 2 = 6 3 X 3 = 9 3 X 4 = 12 3 X 5 = 15 3 X 6 = 18 3 X 7 = 21 3 X 8 = 24 3 X 9 = 27
 LEARNING PAPERS FOR CLASS V TABLE 2 X 1 = 2 2 X 2 = 4 2 X 3 = 6 2 X 4 = 8 2 X 5 = 10 2 X 6 = 12 2 X 7 = 14 2 X 8 = 16 2 X 9 = 18 2 X 10 = 20 3 X 1 = 3 3 X 2 = 6 3 X 3 = 9 3 X 4 = 12 3 X 5 = 15 3 X 6 =
LEARNING PAPERS FOR CLASS V TABLE 2 X 1 = 2 2 X 2 = 4 2 X 3 = 6 2 X 4 = 8 2 X 5 = 10 2 X 6 = 12 2 X 7 = 14 2 X 8 = 16 2 X 9 = 18 2 X 10 = 20 3 X 1 = 3 3 X 2 = 6 3 X 3 = 9 3 X 4 = 12 3 X 5 = 15 3 X 6 =
MOEMS What Every Young Mathlete Should Know
 MOEMS What Every Young Mathlete Should Know 2018-2019 I. VOCABULARY AND LANGUAGE The following explains, defines, or lists some of the words that may be used in Olympiad problems. To be accepted, an answer
MOEMS What Every Young Mathlete Should Know 2018-2019 I. VOCABULARY AND LANGUAGE The following explains, defines, or lists some of the words that may be used in Olympiad problems. To be accepted, an answer
The booklet highlights some salient points for each topic in the CSEC Mathematics syllabus. At least one basic illustration/example accompanies each
 CSEC Mathematics 1 The booklet highlights some salient points for each topic in the CSEC Mathematics syllabus. At least one basic illustration/example accompanies each salient point. The booklet is meant
CSEC Mathematics 1 The booklet highlights some salient points for each topic in the CSEC Mathematics syllabus. At least one basic illustration/example accompanies each salient point. The booklet is meant
ANNUAL NATIONAL ASSESSMENT 2014 ASSESSMENT GUIDELINES MATHEMATICS GRADE 9
 INTRODUCTION The 2014 cycle of Annual National Assessment (ANA 2014) will be administered in all public and designated 1 independent schools from 16 to 19 September 2014. During this period all learners
INTRODUCTION The 2014 cycle of Annual National Assessment (ANA 2014) will be administered in all public and designated 1 independent schools from 16 to 19 September 2014. During this period all learners
Mathematics. GCSE subject content and assessment objectives
 Mathematics GCSE subject content and assessment objectives Contents Introduction 3 Subject aims and learning outcomes 3 Subject content 4 Scope of study 4 Number 4 Algebra 6 Ratio, proportion and rates
Mathematics GCSE subject content and assessment objectives Contents Introduction 3 Subject aims and learning outcomes 3 Subject content 4 Scope of study 4 Number 4 Algebra 6 Ratio, proportion and rates
MATHEMATICAL SUBJECTS Mathematics should be visualised as the vehicle for aiding a student to think, reason, analyse and articulate logically.
 MATHEMATICAL SUBJECTS Mathematics should be visualised as the vehicle for aiding a student to think, reason, analyse and articulate logically. Apart from being treated as a subject of its own, Mathematics
MATHEMATICAL SUBJECTS Mathematics should be visualised as the vehicle for aiding a student to think, reason, analyse and articulate logically. Apart from being treated as a subject of its own, Mathematics
GM1.1 Answers. Reasons given for answers are examples only. In most cases there are valid alternatives. 1 a x = 45 ; alternate angles are equal.
 Cambridge Essentials Mathematics Extension 8 GM1.1 Answers GM1.1 Answers Reasons given for answers are examples only. In most cases there are valid alternatives. 1 a x = 45 ; alternate angles are equal.
Cambridge Essentials Mathematics Extension 8 GM1.1 Answers GM1.1 Answers Reasons given for answers are examples only. In most cases there are valid alternatives. 1 a x = 45 ; alternate angles are equal.
Dawood Public School Course Outline Math Class IV
 Dawood Public School Course Outline 2017-18 Math Class IV MONTHS CONTENTS DURATION Place value + Comparing and Ordering Rounding off to the nearest 10 s and 100 s AUGUST Divisibility rule Multiplication
Dawood Public School Course Outline 2017-18 Math Class IV MONTHS CONTENTS DURATION Place value + Comparing and Ordering Rounding off to the nearest 10 s and 100 s AUGUST Divisibility rule Multiplication
MATHEMATICS COMMON CORE LEARNING TARGETS KINDERGARTEN
 KINDERGARTEN Counting and Cardinality K n o w n u m b e r n a m e s a n d t h e c o u n t s e q u e n c e Count to 100 by ones. Count to 100 by tens. Count starting at a number other than 1. Write numbers
KINDERGARTEN Counting and Cardinality K n o w n u m b e r n a m e s a n d t h e c o u n t s e q u e n c e Count to 100 by ones. Count to 100 by tens. Count starting at a number other than 1. Write numbers
Mapping Common Core State Standard Clusters and. Ohio Grade Level Indicator. Grade 6 Mathematics
 Mapping Common Core State Clusters and Ohio s Grade Level Indicators: Grade 6 Mathematics Ratios and Proportional Relationships: Understand ratio concepts and use ratio reasoning to solve problems. 1.
Mapping Common Core State Clusters and Ohio s Grade Level Indicators: Grade 6 Mathematics Ratios and Proportional Relationships: Understand ratio concepts and use ratio reasoning to solve problems. 1.
PYP Mathematics Continuum
 Counting from One By Imaging to Advanced Counting (-) Y E+ 0- K N O W L E D G E Read,Write, and Count Whole numbers up to 00, forwards and backwards in s, s, 5 s, and 0 s Recall How many tens in a two-digit
Counting from One By Imaging to Advanced Counting (-) Y E+ 0- K N O W L E D G E Read,Write, and Count Whole numbers up to 00, forwards and backwards in s, s, 5 s, and 0 s Recall How many tens in a two-digit
MATHEMATICS ( CANDIDATES WITH PRACTICALS/INTERNAL ASSESSMENT ) ( CANDIDATES WITHOUT PRACTICALS/INTERNAL ASSESSMENT )
 Total No. of Printed Pages 6 X/5/M 0 5 MATHEMATICS ( CANDIDATES WITH PRACTICALS/INTERNAL ASSESSMENT ) Full Marks : 80 Pass Marks : 4 ( CANDIDATES WITHOUT PRACTICALS/INTERNAL ASSESSMENT ) Full Marks : 00
Total No. of Printed Pages 6 X/5/M 0 5 MATHEMATICS ( CANDIDATES WITH PRACTICALS/INTERNAL ASSESSMENT ) Full Marks : 80 Pass Marks : 4 ( CANDIDATES WITHOUT PRACTICALS/INTERNAL ASSESSMENT ) Full Marks : 00
Algebra Readiness. Curriculum (445 topics additional topics)
 Algebra Readiness This course covers the topics shown below; new topics have been highlighted. Students navigate learning paths based on their level of readiness. Institutional users may customize the
Algebra Readiness This course covers the topics shown below; new topics have been highlighted. Students navigate learning paths based on their level of readiness. Institutional users may customize the
Integrated Mathematics II
 Integrated Mathematics II This course covers the topics shown below. Students navigate learning paths based on their level of readiness. Institutional users may customize the scope and sequence to meet
Integrated Mathematics II This course covers the topics shown below. Students navigate learning paths based on their level of readiness. Institutional users may customize the scope and sequence to meet
Ganado Unified School District (Math/6 Grade)
 5-4 5-5 5-6 6-1 6-2 6-3 6-4 7-1 7-3 7-4 7-5 7-6 8-1 8-2 8-3 8-4 9-1 9-2 9-3 9-4 6.NS.A.1 Interpret and compute quotients of fractions, and solve word problems involving division of fractions by fractions,
5-4 5-5 5-6 6-1 6-2 6-3 6-4 7-1 7-3 7-4 7-5 7-6 8-1 8-2 8-3 8-4 9-1 9-2 9-3 9-4 6.NS.A.1 Interpret and compute quotients of fractions, and solve word problems involving division of fractions by fractions,
GTPS Curriculum 6 th Grade Math. Topic: Topic 1- Numeration
 9 days / September Compute fluently with multi-digit numbers and find common factors and multiples. 6.NS.3 Fluently add, subtract, multiply, and divide multi-digit decimals using the standard algorithm
9 days / September Compute fluently with multi-digit numbers and find common factors and multiples. 6.NS.3 Fluently add, subtract, multiply, and divide multi-digit decimals using the standard algorithm
4R & 4A Math Pacing Guides
 GRADING PERIOD: 1st Nine Weeks Getting to Know You - Community Building 4.14- Data a. Collect data, using observations, surveys, measurement, polls, or questionnaires. b. Organize data into a chart or
GRADING PERIOD: 1st Nine Weeks Getting to Know You - Community Building 4.14- Data a. Collect data, using observations, surveys, measurement, polls, or questionnaires. b. Organize data into a chart or
Course Readiness and Skills Review Handbook (83 topics) Course Readiness (21 topics) Course Name: Algebra Course Code: UY6JA-RATXM
 Course Name: Algebra 1 2014-15 Course Code: UY6JA-RATXM ALEKS Course: Algebra 1A Instructor: Ms. Dalton Course Dates: Begin: 11/18/2014 End: 06/18/2015 Course Content: 335 Topics (334 goal + 1 prerequisite)
Course Name: Algebra 1 2014-15 Course Code: UY6JA-RATXM ALEKS Course: Algebra 1A Instructor: Ms. Dalton Course Dates: Begin: 11/18/2014 End: 06/18/2015 Course Content: 335 Topics (334 goal + 1 prerequisite)
Paper Reference. Mathematics A Paper 5 (Non Calculator) Higher Tier Tuesday 8 June 2004 Afternoon Time: 2 hours
 Centre No. Paper Reference Surname Initial(s) Candidate No. 5505 05 Signature Paper Reference(s) 5505/05 Edexcel GCSE Mathematics A 1387 Paper 5 (Non Calculator) Higher Tier Tuesday 8 June 2004 Afternoon
Centre No. Paper Reference Surname Initial(s) Candidate No. 5505 05 Signature Paper Reference(s) 5505/05 Edexcel GCSE Mathematics A 1387 Paper 5 (Non Calculator) Higher Tier Tuesday 8 June 2004 Afternoon
Arithmetic with Whole Numbers and Money Variables and Evaluation (page 6)
 LESSON Name 1 Arithmetic with Whole Numbers and Money Variables and Evaluation (page 6) Counting numbers or natural numbers are the numbers we use to count: {1, 2, 3, 4, 5, ) Whole numbers are the counting
LESSON Name 1 Arithmetic with Whole Numbers and Money Variables and Evaluation (page 6) Counting numbers or natural numbers are the numbers we use to count: {1, 2, 3, 4, 5, ) Whole numbers are the counting
12 CSEC Maths Answer Key
 1 CSEC Maths Answer Key 1 Computation No. Answers Further explanations 1 D In order to write a number in standard form it must be written in the form A 10 ±n, where 1 A < 10. B 3 B 4 D Therefore, to write
1 CSEC Maths Answer Key 1 Computation No. Answers Further explanations 1 D In order to write a number in standard form it must be written in the form A 10 ±n, where 1 A < 10. B 3 B 4 D Therefore, to write
Glossary. Glossary Hawkes Learning Systems. All rights reserved.
 A Glossary Absolute value The distance a number is from 0 on a number line Acute angle An angle whose measure is between 0 and 90 Acute triangle A triangle in which all three angles are acute Addends The
A Glossary Absolute value The distance a number is from 0 on a number line Acute angle An angle whose measure is between 0 and 90 Acute triangle A triangle in which all three angles are acute Addends The
Part 1 - Pre-Algebra Summary Page 1 of 22 1/19/12
 Part 1 - Pre-Algebra Summary Page 1 of 1/19/1 Table of Contents 1. Numbers... 1.1. NAMES FOR NUMBERS... 1.. PLACE VALUES... 3 1.3. INEQUALITIES... 4 1.4. ROUNDING... 4 1.5. DIVISIBILITY TESTS... 5 1.6.
Part 1 - Pre-Algebra Summary Page 1 of 1/19/1 Table of Contents 1. Numbers... 1.1. NAMES FOR NUMBERS... 1.. PLACE VALUES... 3 1.3. INEQUALITIES... 4 1.4. ROUNDING... 4 1.5. DIVISIBILITY TESTS... 5 1.6.
Alberta Mathematics Kindergarten to Grade 12 Scope and Sequence 2017
 Alberta Mathematics Kindergarten to Grade 12 Scope and Sequence 2017 Alberta Mathematics Kindergarten to Grade 12 Scope and Sequence ISBN 978-1-4601-3484-9 Questions or concerns regarding this document
Alberta Mathematics Kindergarten to Grade 12 Scope and Sequence 2017 Alberta Mathematics Kindergarten to Grade 12 Scope and Sequence ISBN 978-1-4601-3484-9 Questions or concerns regarding this document
JAMAICA_7th Grade Math Table of Content with Listing of Activities
 JAMAICA_7th Grade Math Table of Content with Listing of Activities 0. GSAT Review Number System: Comprehensive Review Algebra: Comprehensive Review Geometry: Comprehensive Review Mensuration: Comprehensive
JAMAICA_7th Grade Math Table of Content with Listing of Activities 0. GSAT Review Number System: Comprehensive Review Algebra: Comprehensive Review Geometry: Comprehensive Review Mensuration: Comprehensive
MATHEMATICS SYLLABUS SECONDARY 4th YEAR
 European Schools Office of the Secretary-General Pedagogical Development Unit Ref.:010-D-591-en- Orig.: EN MATHEMATICS SYLLABUS SECONDARY 4th YEAR 6 period/week course APPROVED BY THE JOINT TEACHING COMMITTEE
European Schools Office of the Secretary-General Pedagogical Development Unit Ref.:010-D-591-en- Orig.: EN MATHEMATICS SYLLABUS SECONDARY 4th YEAR 6 period/week course APPROVED BY THE JOINT TEACHING COMMITTEE
English 5 th Grade A-L Vocabulary Cards and Word Walls Revised: 11/18/14
 English 5 th Grade A-L Vocabulary Cards and Word Walls Revised: 11/18/14 Important Notes for Teachers: The vocabulary cards in this file match the Common Core, the math curriculum adopted by the Utah State
English 5 th Grade A-L Vocabulary Cards and Word Walls Revised: 11/18/14 Important Notes for Teachers: The vocabulary cards in this file match the Common Core, the math curriculum adopted by the Utah State
