The Spotted Owls 5 " 5. = 5 " œ!þ")45 Ð'!% leave nest, 30% of those succeed) + 5 " œ!þ("= 5!Þ*%+ 5 ( adults live about 20 yrs)
|
|
|
- Mervyn Harrington
- 5 years ago
- Views:
Transcription
1 The Spotted Owls Be sure to read the example at the introduction to Chapter in the textbook. It gives more general background information for this example. The example leads to a dynamical system which we can understand better using complex eigenvalues. The life cycle of the spotted owl is divided into 3 stages in this model: j s a juvenile subadult" adult The model, as described, assumes there is an approximately 1:1 ratio between male and female owls and counts only the females. There is a stage matrix E that relates the number of owls in each group to the number a year later. The matrix, with entries based on field data, is so that Ô 4 " Ô!! Þ$$ Ô 4 = " œ Þ")!! = Õ+ Õ! Þ(" Þ*% Õ+ " B " œ E B Ú4 œ number of juvenile spotted owls at year where Û= œ number of subadult spotted owls at year Ü+ œ number of adult spotted owls at year 4 " œ!þ$$+ = " œ!þ")4 Ð'!% leave nest, 30% of those succeed) + " œ!þ("=!þ*%+ ( adults live about 20 yrs) From Matlab, the eigenvectors are the ß@ ß@ " # $ of the matrix T œ Ô!Þ!)%)!Þ'(')3!Þ!)%)!Þ'(')3!Þ$"(&!Þ&*#)!Þ!""%3!Þ&*#)!Þ!""%3!Þ!&)" Õ!Þ%"'(!Þ!*('3!Þ%"'(!Þ!*('3!Þ*%'& and the corresponding eigenvalues are - " œ ! # œ $ œ!þ*)$'
2 Of course, a nonzero multiple of an is still an eigenvector with the same eigenvalue, because a multiple is in the same eigenspace itself. Therefore Ô!Þ$"(& Ô $"(& 10000*!Þ!&)" œ &)" is also an eigenvector with eigenvalue - $ Õ!Þ*%'& To get rid of some decimals, we will use this rescaled vector as a replacement for the eigenvector in column 3 of the matrix T. Ô $"(& 1) If the owl population begins (say) as B! $ œ &)" ß then the populations in successive years are and in general, B" œ EB! œ - $ B! B# œ EÐB" Ñ œ EÐEB! Ñ œ EÐ-$ B! Ñ œ -$ EÐB! Ñ œ -$ # B! B œ EÐB Ñ œ EÐEÐEB Ñ œ EE # ÐB Ñ œ EÐ-$ # B Ñ œ -$ # EB œ -$ $ B ã B œ EÐB Ñ œ E ÐB Ñ œ ÞÞÞ œ - B $ #!!!!! "! $! Ð!Þ*)$'Ñ Ô $"(&! &)" Ä Ô 8! 8 Õ! as Ô $"(& Therefore: for an initial owl population B! œ &)", the model predicts that the population will eventually die out. 2) Suppose the owl population begins at B!. Since we are thinking of B! as a population vector, we assume its entries are nonnegative real numbers Ðbut from a purely mathematical point of view, all the following calculations work even if B! has negative or any complex entriesñ. T has $ distinct eigenvalues, and the corresponding ß@ # ß@ $ are a basis for $. Note that we could also check that these vectors are a basis by confirming (via Matlab) that T is invertible. Ô $"(& B! œ -"-"@" -# -#@# -$ Ð!Þ*)$'Ñ &)" In this expression the weights -3 might be any complex numbers Þ But B! is a real vector (it was a given population vector) so whatever the - 3 's are, the imaginary parts of all the entries will cancel out to produce the real vector B! Þ
3 And, since E is a real matrix, B œ EB ß B œ EB ß... are also all real. "! # " Just as in the first example, multiplying 8 times by E leads to the equation B œ Ð!Þ*)$'Ñ " " " # # # $ Ô $"(& &)" È # # Recall that if -= +,3 is any complex number, then l-l œ +, is the distance from - to the origin in the complex plane. In the case of the eigenvalue -, l- l œ ÈÐ!Þ!#")Ñ# Ð!Þ#!&*Ñ#!Þ#!(" "Þ " " Therefore as 8 Ä, l-" l œ l-" l Ð!Þ#!("Ñ Ä!. That is, -" gets closer and closer to the the origin: - 8 " Ä! Similarly, as 8 Ä, l- l œ l- l Ð!Þ#!("Ñ Ä!ß so - Ä!. # # # So B 8 is a sum of three terms each of which tends to! as 8 Ä. So once again we conclude again that B 8 Ä! : for the given stage matrix E, the spotted owl population will eventually die out; it doesn't matter what the initial population B! is. In this dynamical system with the given matrix E, the origin! is called a universal attractor that is, B 8 Ä! for every choice of initial population vector B!. More informally, no matter where the system starts, the origin attracts the B 8 's as the dynamical system progresses. As the textbook states, the most crucial number in the model is the 0.18 in the original matrix E À the percentage of juvenile owls who (by finding a territory of their own and a mate) manage to pass into the subadult stage. Their success depends, in part, on how much good territory is available for the owls. If the success rate 0.18 for juveniles passing into the subadult stage is improved to (say)!! Þ$$!Þ&!, then the matrix for the dynamical system becomes Ô Þ&!! Þ Õ! Þ(" Þ*% The eigenvalues and corresponding Ðlinearly independent Ñ eigenvectors turn out to be Ô!Þ#!*!!Þ%$(!3 - " œ 0.!&$% 0. " œ!þ&*%)!þ%"#)3 Õ!Þ%(""!Þ"$)%3 Ô!Þ#!*!!Þ%$(!3 -# œ -" œ 0.!&$% 0. # œ!þ&*%)!þ%"#)3 Õ!Þ%(""!Þ"$)%3
4 - $ œ "Þ!%'* Ô $ œ "%#" If we write the initial population vector as a linear combination of these, B! B œ Ð"Þ!%'*Ñ! " " " # # # $ 8 Ô #*(' "%#" (*) Then B œ Ð"Þ!%'*Ñ " " " # # # $ Ô #*(' "%#" 8 8 As before, l- l and l- l are " so - and - Ä! as 8 Ä, " # " # 8 8 so - - Ä! Þ Therefore, when 8 is large " " " # # # #*(' B 8 - Ð"Þ!%'*Ñ Ô 8 $ "%#" ( exp growth*** ) (**) This means that if B! was chosen so that - $ Á 0, the population continues to grow. ( Of course, at some time the population would become so large that the model would break down Þ For example, there will eventually not be enough good territory available to maintain the 0% success rate for owls passing from the juvenile to the subadult stage.) Assume that there's enough territory and other resources to allow 8 to become big enough that the approximation in Ð Ñ is a fair statement. From that time on (until the model breaks down): i) each new population vector B 8 " is approximately "Þ!%'* times the preceding population vector: a growth rate of about %Þ(%/year. (***- $ controls long term growth) ii) the population vector remains, each year, (approximately) a constant multiple Ô #*(' of "%#". This means the population of juveniles, subadults and adults each stabilize at a fixed % of the total owl population: for example, the juveniles at #*(' Ð#*(' "%#" *%%"Ñ "!! #"Þ&% of the population.
5 To take a specific B! À suppose the matrix given above (with the 0% juvenile --> subadult rate) is accurate for a forested region with no spotted owls and that a population consisting Ô! entirely of "!!! adult owls is introduced: so B! œ! Õ" 000 In that case, from Matlab, the coefficients -" ß-# ß-$ that work in Ð Ñ, rounded to % places, are -" œ #Þ$%*% "Þ)("$3 -# œ #Þ$%*% "Þ)("$3 -$ œ!þ!!!* Some sample calculations give ( rounded to the nearest owl) Ô $$! Ô %"$ Ô %$$ B& œ "&' B"! œ "*) B"" œ #!( Õ"!%% Õ"$"$ Õ"$(% Å Å (Approximately what % growth?) The moral is that the eigenvalues and basic eigenvectors control the long term behavior of the system.
6 Another Example Suppose we have a linear dynamical system B " œ EB where E (for simplicity) is # # and where E is diagonalizable, with eigenvalues -" ß -# corresponding to eigenbasis ß@ # Þ! " " # # "! " " # # " " " # # # We can write the initial vector B œ so B œ EB œ - E@ - E@ œ - - # # B# œ EB " œ -"-" E@ " -# -# E@ # œ -"-"@" -# -#@# ã " " B œ EB œ œ - - E@ - - E@ œ - - " " " " # # # " " " # # # We can consider what happens depending on the size of the eigenvalues. To illustrate with one case: when - " and l- l " " # Write B! œ ã B œ "- #- " " # # If - œ! À Then B œ and B Ä! " #-# # If - Á 0 À Since - Ä! as Ä, we get that, for large, " # # # B - " " B - œ - B " " " " " " So, for large, B will grow approximately by a factor of -" each time so -" controls the long term growth rate of the system. Example: Predator and prey: owl and wood rat population in a forest (see Example 1, p. 302 in the textbook) S œ number of owls ß V œ number of rats (measured in rat-units = 1000's) Model: S " œ Þ&S Þ%V V œ :S "Þ"V " B S " Þ& Þ% S Þ& Þ% œ œ œ B V : "Þ" V : "Þ" " "
7 1) For : œ!þ#!&, the eigenvalues are approximately.7106 and What happens? 2) For : œ!þ08ß the eigenvalues are approximately - œ and - œ.92, with " # Þ&*%' Þ*)*# corresponding œ œ Þ)!%! Þ"%'$ Þ So, for large B œ ( since - # Ä!) " " # # " " B œ S - Ð"Þ!%!)Ñ Þ&*%' V " Þ)!%! ( The value of the constant - ", of course, is determined by the initial population B!.) This says that for large, the ratio of owls to rats œ O V -" Ð"Þ!%!)Ñ ÐÞ&*%'Ñ - Ð"Þ!%!)ÑÐÞ)!%!Ñ " œ Þ&*%' Þ)!%! Þ(% $ % Ð3 owls / 4000 rats) S+1 S Also, Ð"Þ!%!)Ñ so for large Ðand as long as the model V V +1 holds up Ñ both populations grow at a rate of about 4.08%/month. = Rats Slope 4/3 rather than 3/4 here, only because I used the horizontal axis á for the owl-axis. Owls
Example: A Markov Process
 Example: A Markov Process Divide the greater metro region into three parts: city such as St. Louis), suburbs to include such areas as Clayton, University City, Richmond Heights, Maplewood, Kirkwood,...)
Example: A Markov Process Divide the greater metro region into three parts: city such as St. Louis), suburbs to include such areas as Clayton, University City, Richmond Heights, Maplewood, Kirkwood,...)
Here are proofs for some of the results about diagonalization that were presented without proof in class.
 Suppose E is an 8 8 matrix. In what follows, terms like eigenvectors, eigenvalues, and eigenspaces all refer to the matrix E. Here are proofs for some of the results about diagonalization that were presented
Suppose E is an 8 8 matrix. In what follows, terms like eigenvectors, eigenvalues, and eigenspaces all refer to the matrix E. Here are proofs for some of the results about diagonalization that were presented
Introduction to Diagonalization
 Introduction to Diagonalization For a square matrix E, a process called diagonalization can sometimes give us more insight into how the transformation B ÈE B works. The insight has a strong geometric flavor,
Introduction to Diagonalization For a square matrix E, a process called diagonalization can sometimes give us more insight into how the transformation B ÈE B works. The insight has a strong geometric flavor,
Systems of Equations 1. Systems of Linear Equations
 Lecture 1 Systems of Equations 1. Systems of Linear Equations [We will see examples of how linear equations arise here, and how they are solved:] Example 1: In a lab experiment, a researcher wants to provide
Lecture 1 Systems of Equations 1. Systems of Linear Equations [We will see examples of how linear equations arise here, and how they are solved:] Example 1: In a lab experiment, a researcher wants to provide
: œ Ö: =? À =ß> real numbers. œ the previous plane with each point translated by : Ðfor example,! is translated to :)
 â SpanÖ?ß@ œ Ö =? > @ À =ß> real numbers : SpanÖ?ß@ œ Ö: =? > @ À =ß> real numbers œ the previous plane with each point translated by : Ðfor example, is translated to :) á In general: Adding a vector :
â SpanÖ?ß@ œ Ö =? > @ À =ß> real numbers : SpanÖ?ß@ œ Ö: =? > @ À =ß> real numbers œ the previous plane with each point translated by : Ðfor example, is translated to :) á In general: Adding a vector :
B œ c " " ã B œ c 8 8. such that substituting these values for the B 3 's will make all the equations true
 System of Linear Equations variables Ð unknowns Ñ B" ß B# ß ÞÞÞ ß B8 Æ Æ Æ + B + B ÞÞÞ + B œ, "" " "# # "8 8 " + B + B ÞÞÞ + B œ, #" " ## # #8 8 # ã + B + B ÞÞÞ + B œ, 3" " 3# # 38 8 3 ã + 7" B" + 7# B#
System of Linear Equations variables Ð unknowns Ñ B" ß B# ß ÞÞÞ ß B8 Æ Æ Æ + B + B ÞÞÞ + B œ, "" " "# # "8 8 " + B + B ÞÞÞ + B œ, #" " ## # #8 8 # ã + B + B ÞÞÞ + B œ, 3" " 3# # 38 8 3 ã + 7" B" + 7# B#
solve EB œ,, we can row reduce the augmented matrix
 Motivation To PY Decomposition: Factoring E œ P Y solve EB œ,, we can row reduce the augmented matrix Ò + + ÞÞÞ+ ÞÞÞ + l, Ó µ ÞÞÞ µ Ò- - ÞÞÞ- ÞÞÞ-. Ó " # 3 8 " # 3 8 we get to Ò-" -# ÞÞÞ -3 ÞÞÞ-8Ó in an
Motivation To PY Decomposition: Factoring E œ P Y solve EB œ,, we can row reduce the augmented matrix Ò + + ÞÞÞ+ ÞÞÞ + l, Ó µ ÞÞÞ µ Ò- - ÞÞÞ- ÞÞÞ-. Ó " # 3 8 " # 3 8 we get to Ò-" -# ÞÞÞ -3 ÞÞÞ-8Ó in an
solve EB œ,, we can row reduce the augmented matrix
 PY Decomposition: Factoring E œ P Y Motivation To solve EB œ,, we can row reduce the augmented matrix Ò + + ÞÞÞ+ ÞÞÞ + l, Ó µ ÞÞÞ µ Ò- - ÞÞÞ- ÞÞÞ-. Ó " # 3 8 " # 3 8 When we get to Ò-" -# ÞÞÞ -3 ÞÞÞ-8Ó
PY Decomposition: Factoring E œ P Y Motivation To solve EB œ,, we can row reduce the augmented matrix Ò + + ÞÞÞ+ ÞÞÞ + l, Ó µ ÞÞÞ µ Ò- - ÞÞÞ- ÞÞÞ-. Ó " # 3 8 " # 3 8 When we get to Ò-" -# ÞÞÞ -3 ÞÞÞ-8Ó
Linear Algebra. Rekha Santhanam. April 3, Johns Hopkins Univ. Rekha Santhanam (Johns Hopkins Univ.) Linear Algebra April 3, / 7
 Linear Algebra Rekha Santhanam Johns Hopkins Univ. April 3, 2009 Rekha Santhanam (Johns Hopkins Univ.) Linear Algebra April 3, 2009 1 / 7 Dynamical Systems Denote owl and wood rat populations at time k
Linear Algebra Rekha Santhanam Johns Hopkins Univ. April 3, 2009 Rekha Santhanam (Johns Hopkins Univ.) Linear Algebra April 3, 2009 1 / 7 Dynamical Systems Denote owl and wood rat populations at time k
TOTAL DIFFERENTIALS. In Section B-4, we observed that.c is a pretty good approximation for? C, which is the increment of
 TOTAL DIFFERENTIALS The differential was introduced in Section -4. Recall that the differential of a function œ0ðñis w. œ 0 ÐÑ.Þ Here. is the differential with respect to the independent variable and is
TOTAL DIFFERENTIALS The differential was introduced in Section -4. Recall that the differential of a function œ0ðñis w. œ 0 ÐÑ.Þ Here. is the differential with respect to the independent variable and is
The Leontief Open Economy Production Model
 The Leontief Open Economy Production Model We will look at the idea for Leontief's model of an open economy a term which we will explain below. It starts by looking very similar to an example of a closed
The Leontief Open Economy Production Model We will look at the idea for Leontief's model of an open economy a term which we will explain below. It starts by looking very similar to an example of a closed
ACT455H1S - TEST 2 - MARCH 25, 2008
 ACT455H1S - TEST 2 - MARCH 25, 2008 Write name and student number on each page. Write your solution for each question in the space provided. For the multiple decrement questions, it is always assumed that
ACT455H1S - TEST 2 - MARCH 25, 2008 Write name and student number on each page. Write your solution for each question in the space provided. For the multiple decrement questions, it is always assumed that
Æ Å not every column in E is a pivot column (so EB œ! has at least one free variable) Æ Å E has linearly dependent columns
 ßÞÞÞß @ is linearly independent if B" @" B# @# ÞÞÞ B: @: œ! has only the trivial solution EB œ! has only the trivial solution Ðwhere E œ Ò@ @ ÞÞÞ@ ÓÑ every column in E is a pivot column E has linearly
ßÞÞÞß @ is linearly independent if B" @" B# @# ÞÞÞ B: @: œ! has only the trivial solution EB œ! has only the trivial solution Ðwhere E œ Ò@ @ ÞÞÞ@ ÓÑ every column in E is a pivot column E has linearly
The Leontief Open Economy Production Model
 The Leontief Open Economy Production Model We will look at the idea for Leontief's model of an open economy a term which we will explain below. It starts by looking very similar to an example of a closed
The Leontief Open Economy Production Model We will look at the idea for Leontief's model of an open economy a term which we will explain below. It starts by looking very similar to an example of a closed
5 Eigenvalues and. Eigenvectors. Dynamical Systems and Spotted Owls
 5 Eigenvalues and Eigenvectors INTROUCTORY EXAMPLE ynamical Systems and Spotted Owls In 99, the northern spotted owl became the center of a nationwide controversy over the use and misuse of the majestic
5 Eigenvalues and Eigenvectors INTROUCTORY EXAMPLE ynamical Systems and Spotted Owls In 99, the northern spotted owl became the center of a nationwide controversy over the use and misuse of the majestic
ICS 6N Computational Linear Algebra Eigenvalues and Eigenvectors
 ICS 6N Computational Linear Algebra Eigenvalues and Eigenvectors Xiaohui Xie University of California, Irvine xhx@uci.edu Xiaohui Xie (UCI) ICS 6N 1 / 34 The powers of matrix Consider the following dynamic
ICS 6N Computational Linear Algebra Eigenvalues and Eigenvectors Xiaohui Xie University of California, Irvine xhx@uci.edu Xiaohui Xie (UCI) ICS 6N 1 / 34 The powers of matrix Consider the following dynamic
PART I. Multiple choice. 1. Find the slope of the line shown here. 2. Find the slope of the line with equation $ÐB CÑœ(B &.
 Math 1301 - College Algebra Final Exam Review Sheet Version X This review, while fairly comprehensive, should not be the only material used to study for the final exam. It should not be considered a preview
Math 1301 - College Algebra Final Exam Review Sheet Version X This review, while fairly comprehensive, should not be the only material used to study for the final exam. It should not be considered a preview
SIMULATION - PROBLEM SET 1
 SIMULATION - PROBLEM SET 1 " if! Ÿ B Ÿ 1. The random variable X has probability density function 0ÐBÑ œ " $ if Ÿ B Ÿ.! otherwise Using the inverse transform method of simulation, find the random observation
SIMULATION - PROBLEM SET 1 " if! Ÿ B Ÿ 1. The random variable X has probability density function 0ÐBÑ œ " $ if Ÿ B Ÿ.! otherwise Using the inverse transform method of simulation, find the random observation
8œ! This theorem is justified by repeating the process developed for a Taylor polynomial an infinite number of times.
 Taylor and Maclaurin Series We can use the same process we used to find a Taylor or Maclaurin polynomial to find a power series for a particular function as long as the function has infinitely many derivatives.
Taylor and Maclaurin Series We can use the same process we used to find a Taylor or Maclaurin polynomial to find a power series for a particular function as long as the function has infinitely many derivatives.
You may have a simple scientific calculator to assist with arithmetic, but no graphing calculators are allowed on this exam.
 Math 131 Exam 3 Solutions You may have a simple scientific calculator to assist ith arithmetic, but no graphing calculators are alloed on this exam. Part I consists of 14 multiple choice questions (orth
Math 131 Exam 3 Solutions You may have a simple scientific calculator to assist ith arithmetic, but no graphing calculators are alloed on this exam. Part I consists of 14 multiple choice questions (orth
Inner Product Spaces
 Inner Product Spaces In 8 X, we defined an inner product? @? @?@ ÞÞÞ? 8@ 8. Another notation sometimes used is? @? ß@. The inner product in 8 has several important properties ( see Theorem, p. 33) that
Inner Product Spaces In 8 X, we defined an inner product? @? @?@ ÞÞÞ? 8@ 8. Another notation sometimes used is? @? ß@. The inner product in 8 has several important properties ( see Theorem, p. 33) that
Implicit in the definition of orthogonal arrays is a projection propertyþ
 Projection properties Implicit in the definition of orthogonal arrays is a projection propertyþ factor screening effect ( factor) sparsity A design is said to be of projectivity : if in every subset of
Projection properties Implicit in the definition of orthogonal arrays is a projection propertyþ factor screening effect ( factor) sparsity A design is said to be of projectivity : if in every subset of
Recall : Eigenvalues and Eigenvectors
 Recall : Eigenvalues and Eigenvectors Let A be an n n matrix. If a nonzero vector x in R n satisfies Ax λx for a scalar λ, then : The scalar λ is called an eigenvalue of A. The vector x is called an eigenvector
Recall : Eigenvalues and Eigenvectors Let A be an n n matrix. If a nonzero vector x in R n satisfies Ax λx for a scalar λ, then : The scalar λ is called an eigenvalue of A. The vector x is called an eigenvector
Math 21b Final Exam Thursday, May 15, 2003 Solutions
 Math 2b Final Exam Thursday, May 5, 2003 Solutions. (20 points) True or False. No justification is necessary, simply circle T or F for each statement. T F (a) If W is a subspace of R n and x is not in
Math 2b Final Exam Thursday, May 5, 2003 Solutions. (20 points) True or False. No justification is necessary, simply circle T or F for each statement. T F (a) If W is a subspace of R n and x is not in
Stage-Matrix or Leslie Population Models
 spring, 206 math 204 day 40: stage matrix models Stage-Matrix or Leslie Population Models Rather than model an entire population as a whole Stage-matrix models divide the population into various classes
spring, 206 math 204 day 40: stage matrix models Stage-Matrix or Leslie Population Models Rather than model an entire population as a whole Stage-matrix models divide the population into various classes
Practice problems for Exam 3 A =
 Practice problems for Exam 3. Let A = 2 (a) Determine whether A is diagonalizable. If so, find a matrix S such that S AS is diagonal. If not, explain why not. (b) What are the eigenvalues of A? Is A diagonalizable?
Practice problems for Exam 3. Let A = 2 (a) Determine whether A is diagonalizable. If so, find a matrix S such that S AS is diagonal. If not, explain why not. (b) What are the eigenvalues of A? Is A diagonalizable?
T i t l e o f t h e w o r k : L a M a r e a Y o k o h a m a. A r t i s t : M a r i a n o P e n s o t t i ( P l a y w r i g h t, D i r e c t o r )
 v e r. E N G O u t l i n e T i t l e o f t h e w o r k : L a M a r e a Y o k o h a m a A r t i s t : M a r i a n o P e n s o t t i ( P l a y w r i g h t, D i r e c t o r ) C o n t e n t s : T h i s w o
v e r. E N G O u t l i n e T i t l e o f t h e w o r k : L a M a r e a Y o k o h a m a A r t i s t : M a r i a n o P e n s o t t i ( P l a y w r i g h t, D i r e c t o r ) C o n t e n t s : T h i s w o
Definition Suppose M is a collection (set) of sets. M is called inductive if
 Definition Suppose M is a collection (set) of sets. M is called inductive if a) g M, and b) if B Mß then B MÞ Then we ask: are there any inductive sets? Informally, it certainly looks like there are. For
Definition Suppose M is a collection (set) of sets. M is called inductive if a) g M, and b) if B Mß then B MÞ Then we ask: are there any inductive sets? Informally, it certainly looks like there are. For
Math 131 Exam 4 (Final Exam) F04M
 Math 3 Exam 4 (Final Exam) F04M3.4. Name ID Number The exam consists of 8 multiple choice questions (5 points each) and 0 true/false questions ( point each), for a total of 00 points. Mark the correct
Math 3 Exam 4 (Final Exam) F04M3.4. Name ID Number The exam consists of 8 multiple choice questions (5 points each) and 0 true/false questions ( point each), for a total of 00 points. Mark the correct
Applications of eigenvalues/eigenvectors
 Example 1. Applications of eigenvalues/eigenvectors Predator-Prey models. Foxes and Rabbits share a large forest, with the foxes eating rabbits and rabbits eating the abundant vegetation. The sizes of
Example 1. Applications of eigenvalues/eigenvectors Predator-Prey models. Foxes and Rabbits share a large forest, with the foxes eating rabbits and rabbits eating the abundant vegetation. The sizes of
MAT2342 : Introduction to Linear Algebra Mike Newman, 5 October assignment 1
 [/8 MAT4 : Introduction to Linear Algebra Mike Newman, 5 October 07 assignment You must show your work. You may use software or solvers of some sort to check calculation of eigenvalues, but you should
[/8 MAT4 : Introduction to Linear Algebra Mike Newman, 5 October 07 assignment You must show your work. You may use software or solvers of some sort to check calculation of eigenvalues, but you should
Proofs Involving Quantifiers. Proof Let B be an arbitrary member Proof Somehow show that there is a value
 Proofs Involving Quantifiers For a given universe Y : Theorem ÐaBÑ T ÐBÑ Theorem ÐbBÑ T ÐBÑ Proof Let B be an arbitrary member Proof Somehow show that there is a value of Y. Call it B œ +, say Þ ÐYou can
Proofs Involving Quantifiers For a given universe Y : Theorem ÐaBÑ T ÐBÑ Theorem ÐbBÑ T ÐBÑ Proof Let B be an arbitrary member Proof Somehow show that there is a value of Y. Call it B œ +, say Þ ÐYou can
and let s calculate the image of some vectors under the transformation T.
 Chapter 5 Eigenvalues and Eigenvectors 5. Eigenvalues and Eigenvectors Let T : R n R n be a linear transformation. Then T can be represented by a matrix (the standard matrix), and we can write T ( v) =
Chapter 5 Eigenvalues and Eigenvectors 5. Eigenvalues and Eigenvectors Let T : R n R n be a linear transformation. Then T can be represented by a matrix (the standard matrix), and we can write T ( v) =
2 Project Suggestions from the department
 2 Project Suggestions from the department Dr. R. Anderson Continued Fractions Description: See Dr. Anderson for a description of this project. Dr. R. Anderson Stock Prices and Options Description: See
2 Project Suggestions from the department Dr. R. Anderson Continued Fractions Description: See Dr. Anderson for a description of this project. Dr. R. Anderson Stock Prices and Options Description: See
Math 3191 Applied Linear Algebra
 Math 9 Applied Linear Algebra Lecture 9: Diagonalization Stephen Billups University of Colorado at Denver Math 9Applied Linear Algebra p./9 Section. Diagonalization The goal here is to develop a useful
Math 9 Applied Linear Algebra Lecture 9: Diagonalization Stephen Billups University of Colorado at Denver Math 9Applied Linear Algebra p./9 Section. Diagonalization The goal here is to develop a useful
Inner Product Spaces. Another notation sometimes used is X.?
 Inner Product Spaces X In 8 we have an inner product? @? @?@ ÞÞÞ? 8@ 8Þ Another notation sometimes used is X? ß@? @? @? @ ÞÞÞ? @ 8 8 The inner product in?@ ß in 8 has several essential properties ( see
Inner Product Spaces X In 8 we have an inner product? @? @?@ ÞÞÞ? 8@ 8Þ Another notation sometimes used is X? ß@? @? @? @ ÞÞÞ? @ 8 8 The inner product in?@ ß in 8 has several essential properties ( see
18.06 Problem Set 8 - Solutions Due Wednesday, 14 November 2007 at 4 pm in
 806 Problem Set 8 - Solutions Due Wednesday, 4 November 2007 at 4 pm in 2-06 08 03 Problem : 205+5+5+5 Consider the matrix A 02 07 a Check that A is a positive Markov matrix, and find its steady state
806 Problem Set 8 - Solutions Due Wednesday, 4 November 2007 at 4 pm in 2-06 08 03 Problem : 205+5+5+5 Consider the matrix A 02 07 a Check that A is a positive Markov matrix, and find its steady state
Solutions: 6.2 FE 1: If f is linear what is f( Solution: ) = FE 6: The fuction g : R 2 R 2 is linear Since = what is g( Solution:
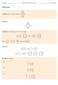 Solutions: 6 FE : If f is linear what is f(? f( 6 FE 6: The fuction g : R R is linear ( 5 ( g( g( Since ( 5 ( + ( what is g( (? 5g ( + g( ( ( + ( 5 8 5 + 5 ( g( g(5 6 FE 9: Multiply: (a (b (c [ ] ( [ ]
Solutions: 6 FE : If f is linear what is f(? f( 6 FE 6: The fuction g : R R is linear ( 5 ( g( g( Since ( 5 ( + ( what is g( (? 5g ( + g( ( ( + ( 5 8 5 + 5 ( g( g(5 6 FE 9: Multiply: (a (b (c [ ] ( [ ]
4.3 Laplace Transform in Linear System Analysis
 4.3 Laplace Transform in Linear System Analysis The main goal in analysis of any dynamic system is to find its response to a given input. The system response in general has two components: zero-state response
4.3 Laplace Transform in Linear System Analysis The main goal in analysis of any dynamic system is to find its response to a given input. The system response in general has two components: zero-state response
LA PRISE DE CALAIS. çoys, çoys, har - dis. çoys, dis. tons, mantz, tons, Gas. c est. à ce. C est à ce. coup, c est à ce
 > ƒ? @ Z [ \ _ ' µ `. l 1 2 3 z Æ Ñ 6 = Ð l sl (~131 1606) rn % & +, l r s s, r 7 nr ss r r s s s, r s, r! " # $ s s ( ) r * s, / 0 s, r 4 r r 9;: < 10 r mnz, rz, r ns, 1 s ; j;k ns, q r s { } ~ l r mnz,
> ƒ? @ Z [ \ _ ' µ `. l 1 2 3 z Æ Ñ 6 = Ð l sl (~131 1606) rn % & +, l r s s, r 7 nr ss r r s s s, r s, r! " # $ s s ( ) r * s, / 0 s, r 4 r r 9;: < 10 r mnz, rz, r ns, 1 s ; j;k ns, q r s { } ~ l r mnz,
DIAGONALIZATION. In order to see the implications of this definition, let us consider the following example Example 1. Consider the matrix
 DIAGONALIZATION Definition We say that a matrix A of size n n is diagonalizable if there is a basis of R n consisting of eigenvectors of A ie if there are n linearly independent vectors v v n such that
DIAGONALIZATION Definition We say that a matrix A of size n n is diagonalizable if there is a basis of R n consisting of eigenvectors of A ie if there are n linearly independent vectors v v n such that
Chapter 5. Eigenvalues and Eigenvectors
 Chapter 5 Eigenvalues and Eigenvectors Section 5. Eigenvectors and Eigenvalues Motivation: Difference equations A Biology Question How to predict a population of rabbits with given dynamics:. half of the
Chapter 5 Eigenvalues and Eigenvectors Section 5. Eigenvectors and Eigenvalues Motivation: Difference equations A Biology Question How to predict a population of rabbits with given dynamics:. half of the
Lecture 15, 16: Diagonalization
 Lecture 15, 16: Diagonalization Motivation: Eigenvalues and Eigenvectors are easy to compute for diagonal matrices. Hence, we would like (if possible) to convert matrix A into a diagonal matrix. Suppose
Lecture 15, 16: Diagonalization Motivation: Eigenvalues and Eigenvectors are easy to compute for diagonal matrices. Hence, we would like (if possible) to convert matrix A into a diagonal matrix. Suppose
MATH 1120 (LINEAR ALGEBRA 1), FINAL EXAM FALL 2011 SOLUTIONS TO PRACTICE VERSION
 MATH (LINEAR ALGEBRA ) FINAL EXAM FALL SOLUTIONS TO PRACTICE VERSION Problem (a) For each matrix below (i) find a basis for its column space (ii) find a basis for its row space (iii) determine whether
MATH (LINEAR ALGEBRA ) FINAL EXAM FALL SOLUTIONS TO PRACTICE VERSION Problem (a) For each matrix below (i) find a basis for its column space (ii) find a basis for its row space (iii) determine whether
Remark By definition, an eigenvector must be a nonzero vector, but eigenvalue could be zero.
 Sec 6 Eigenvalues and Eigenvectors Definition An eigenvector of an n n matrix A is a nonzero vector x such that A x λ x for some scalar λ A scalar λ is called an eigenvalue of A if there is a nontrivial
Sec 6 Eigenvalues and Eigenvectors Definition An eigenvector of an n n matrix A is a nonzero vector x such that A x λ x for some scalar λ A scalar λ is called an eigenvalue of A if there is a nontrivial
MATH 1301 (College Algebra) - Final Exam Review
 MATH 1301 (College Algebra) - Final Exam Review This review is comprehensive but should not be the only material used to study for the final exam. It should not be considered a preview of the final exam.
MATH 1301 (College Algebra) - Final Exam Review This review is comprehensive but should not be the only material used to study for the final exam. It should not be considered a preview of the final exam.
Problems for M 11/2: A =
 Math 30 Lesieutre Problem set # November 0 Problems for M /: 4 Let B be the basis given by b b Find the B-matrix for the transformation T : R R given by x Ax where 3 4 A (This just means the matrix for
Math 30 Lesieutre Problem set # November 0 Problems for M /: 4 Let B be the basis given by b b Find the B-matrix for the transformation T : R R given by x Ax where 3 4 A (This just means the matrix for
Suggestions - Problem Set (a) Show the discriminant condition (1) takes the form. ln ln, # # R R
 Suggetion - Problem Set 3 4.2 (a) Show the dicriminant condition (1) take the form x D Ð.. Ñ. D.. D. ln ln, a deired. We then replace the quantitie. 3ß D3 by their etimate to get the proper form for thi
Suggetion - Problem Set 3 4.2 (a) Show the dicriminant condition (1) take the form x D Ð.. Ñ. D.. D. ln ln, a deired. We then replace the quantitie. 3ß D3 by their etimate to get the proper form for thi
LINEAR ALGEBRA 1, 2012-I PARTIAL EXAM 3 SOLUTIONS TO PRACTICE PROBLEMS
 LINEAR ALGEBRA, -I PARTIAL EXAM SOLUTIONS TO PRACTICE PROBLEMS Problem (a) For each of the two matrices below, (i) determine whether it is diagonalizable, (ii) determine whether it is orthogonally diagonalizable,
LINEAR ALGEBRA, -I PARTIAL EXAM SOLUTIONS TO PRACTICE PROBLEMS Problem (a) For each of the two matrices below, (i) determine whether it is diagonalizable, (ii) determine whether it is orthogonally diagonalizable,
Eigenvalues, Eigenvectors, and Diagonalization
 Math 240 TA: Shuyi Weng Winter 207 February 23, 207 Eigenvalues, Eigenvectors, and Diagonalization The concepts of eigenvalues, eigenvectors, and diagonalization are best studied with examples. We will
Math 240 TA: Shuyi Weng Winter 207 February 23, 207 Eigenvalues, Eigenvectors, and Diagonalization The concepts of eigenvalues, eigenvectors, and diagonalization are best studied with examples. We will
An Introduction to Optimal Control Applied to Disease Models
 An Introduction to Optimal Control Applied to Disease Models Suzanne Lenhart University of Tennessee, Knoxville Departments of Mathematics Lecture1 p.1/37 Example Number of cancer cells at time (exponential
An Introduction to Optimal Control Applied to Disease Models Suzanne Lenhart University of Tennessee, Knoxville Departments of Mathematics Lecture1 p.1/37 Example Number of cancer cells at time (exponential
Lesson 6.6 Radical Equations
 Lesson 6.6 Radical Equations Activity 1 Radical Equations 1. a. To solve a radical equation, we: (1) isolate the radical, then () square both sides. Be careful when squaring a binomial! For example, #
Lesson 6.6 Radical Equations Activity 1 Radical Equations 1. a. To solve a radical equation, we: (1) isolate the radical, then () square both sides. Be careful when squaring a binomial! For example, #
1. Classify each number. Choose all correct answers. b. È # : (i) natural number (ii) integer (iii) rational number (iv) real number
 Review for Placement Test To ypass Math 1301 College Algebra Department of Computer and Mathematical Sciences University of Houston-Downtown Revised: Fall 2009 PLEASE READ THE FOLLOWING CAREFULLY: 1. The
Review for Placement Test To ypass Math 1301 College Algebra Department of Computer and Mathematical Sciences University of Houston-Downtown Revised: Fall 2009 PLEASE READ THE FOLLOWING CAREFULLY: 1. The
MAT 1302B Mathematical Methods II
 MAT 1302B Mathematical Methods II Alistair Savage Mathematics and Statistics University of Ottawa Winter 2015 Lecture 19 Alistair Savage (uottawa) MAT 1302B Mathematical Methods II Winter 2015 Lecture
MAT 1302B Mathematical Methods II Alistair Savage Mathematics and Statistics University of Ottawa Winter 2015 Lecture 19 Alistair Savage (uottawa) MAT 1302B Mathematical Methods II Winter 2015 Lecture
Framework for functional tree simulation applied to 'golden delicious' apple trees
 Purdue University Purdue e-pubs Open Access Theses Theses and Dissertations Spring 2015 Framework for functional tree simulation applied to 'golden delicious' apple trees Marek Fiser Purdue University
Purdue University Purdue e-pubs Open Access Theses Theses and Dissertations Spring 2015 Framework for functional tree simulation applied to 'golden delicious' apple trees Marek Fiser Purdue University
Elementary Linear Algebra Review for Exam 3 Exam is Friday, December 11th from 1:15-3:15
 Elementary Linear Algebra Review for Exam 3 Exam is Friday, December th from :5-3:5 The exam will cover sections: 6., 6.2, 7. 7.4, and the class notes on dynamical systems. You absolutely must be able
Elementary Linear Algebra Review for Exam 3 Exam is Friday, December th from :5-3:5 The exam will cover sections: 6., 6.2, 7. 7.4, and the class notes on dynamical systems. You absolutely must be able
(the matrix with b 1 and b 2 as columns). If x is a vector in R 2, then its coordinate vector [x] B relative to B satisfies the formula.
![(the matrix with b 1 and b 2 as columns). If x is a vector in R 2, then its coordinate vector [x] B relative to B satisfies the formula. (the matrix with b 1 and b 2 as columns). If x is a vector in R 2, then its coordinate vector [x] B relative to B satisfies the formula.](/thumbs/94/120601442.jpg) 4 Diagonalization 4 Change of basis Let B (b,b ) be an ordered basis for R and let B b b (the matrix with b and b as columns) If x is a vector in R, then its coordinate vector x B relative to B satisfies
4 Diagonalization 4 Change of basis Let B (b,b ) be an ordered basis for R and let B b b (the matrix with b and b as columns) If x is a vector in R, then its coordinate vector x B relative to B satisfies
B-9= B.Bà B 68 B.Bß B/.Bß B=38 B.B >+8 ab b.bß ' 68aB b.bà
 8.1 Integration y Parts.@ a.? a Consider. a? a @ a œ? a @ a Þ....@ a..? a We can write this as? a œ a? a @ a@ a Þ... If we integrate oth sides, we otain.@ a a.?. œ a? a @ a..? a @ a. or...? a.@ œ? a @
8.1 Integration y Parts.@ a.? a Consider. a? a @ a œ? a @ a Þ....@ a..? a We can write this as? a œ a? a @ a@ a Þ... If we integrate oth sides, we otain.@ a a.?. œ a? a @ a..? a @ a. or...? a.@ œ? a @
Name Solutions Linear Algebra; Test 3. Throughout the test simplify all answers except where stated otherwise.
 Name Solutions Linear Algebra; Test 3 Throughout the test simplify all answers except where stated otherwise. 1) Find the following: (10 points) ( ) Or note that so the rows are linearly independent, so
Name Solutions Linear Algebra; Test 3 Throughout the test simplify all answers except where stated otherwise. 1) Find the following: (10 points) ( ) Or note that so the rows are linearly independent, so
MAT1302F Mathematical Methods II Lecture 19
 MAT302F Mathematical Methods II Lecture 9 Aaron Christie 2 April 205 Eigenvectors, Eigenvalues, and Diagonalization Now that the basic theory of eigenvalues and eigenvectors is in place most importantly
MAT302F Mathematical Methods II Lecture 9 Aaron Christie 2 April 205 Eigenvectors, Eigenvalues, and Diagonalization Now that the basic theory of eigenvalues and eigenvectors is in place most importantly
Analyzing Autonomous DEs: Spotted Owls
 Analyzing Autonomous DEs: Spotted Owls A group of biologists are making predictions about the spotted owl population in a forest in the Pacific Northwest. The autonomous differential equation the scientist
Analyzing Autonomous DEs: Spotted Owls A group of biologists are making predictions about the spotted owl population in a forest in the Pacific Northwest. The autonomous differential equation the scientist
Lecture 12: Diagonalization
 Lecture : Diagonalization A square matrix D is called diagonal if all but diagonal entries are zero: a a D a n 5 n n. () Diagonal matrices are the simplest matrices that are basically equivalent to vectors
Lecture : Diagonalization A square matrix D is called diagonal if all but diagonal entries are zero: a a D a n 5 n n. () Diagonal matrices are the simplest matrices that are basically equivalent to vectors
Section 1.3 Functions and Their Graphs 19
 23. 0 1 2 24. 0 1 2 y 0 1 0 y 1 0 0 Section 1.3 Functions and Their Graphs 19 3, Ÿ 1, 0 25. y œ 26. y œ œ 2, 1 œ, 0 Ÿ " 27. (a) Line through a!ß! band a"ß " b: y œ Line through a"ß " band aß! b: y œ 2,
23. 0 1 2 24. 0 1 2 y 0 1 0 y 1 0 0 Section 1.3 Functions and Their Graphs 19 3, Ÿ 1, 0 25. y œ 26. y œ œ 2, 1 œ, 0 Ÿ " 27. (a) Line through a!ß! band a"ß " b: y œ Line through a"ß " band aß! b: y œ 2,
= main diagonal, in the order in which their corresponding eigenvectors appear as columns of E.
 3.3 Diagonalization Let A = 4. Then and are eigenvectors of A, with corresponding eigenvalues 2 and 6 respectively (check). This means 4 = 2, 4 = 6. 2 2 2 2 Thus 4 = 2 2 6 2 = 2 6 4 2 We have 4 = 2 0 0
3.3 Diagonalization Let A = 4. Then and are eigenvectors of A, with corresponding eigenvalues 2 and 6 respectively (check). This means 4 = 2, 4 = 6. 2 2 2 2 Thus 4 = 2 2 6 2 = 2 6 4 2 We have 4 = 2 0 0
Math 12: Discrete Dynamical Systems Homework
 Math 12: Discrete Dynamical Systems Homework Department of Mathematics, Harvey Mudd College Several of these problems will require computational software to help build our insight about discrete dynamical
Math 12: Discrete Dynamical Systems Homework Department of Mathematics, Harvey Mudd College Several of these problems will require computational software to help build our insight about discrete dynamical
Exam 2 Practice Problems
 ST 312 Exam 2 Practice Problems MATERIAL COVERED ON EXAM 2 Reiland Lecture Handouts Corresponding textbook chapters 6: Infererence for the Difference Between Means Chapters 22, 23 7: Scatterplots, Correlation,
ST 312 Exam 2 Practice Problems MATERIAL COVERED ON EXAM 2 Reiland Lecture Handouts Corresponding textbook chapters 6: Infererence for the Difference Between Means Chapters 22, 23 7: Scatterplots, Correlation,
Page 1 College Algebra : Computing Lab 1 /5 Due 1/18/18
 Page 1 College Algebra : Computing Lab 1 /5 Name Due 1/18/18 Using your calculator evaluate the following for B œ % and C œ. 1. ( œ 2. Ð (Ñ œ 3. $ÐBCÑC &B$C B œ 4. C C B Š B " " œ Winplot is a free general-purpose
Page 1 College Algebra : Computing Lab 1 /5 Name Due 1/18/18 Using your calculator evaluate the following for B œ % and C œ. 1. ( œ 2. Ð (Ñ œ 3. $ÐBCÑC &B$C B œ 4. C C B Š B " " œ Winplot is a free general-purpose
Remark 1 By definition, an eigenvector must be a nonzero vector, but eigenvalue could be zero.
 Sec 5 Eigenvectors and Eigenvalues In this chapter, vector means column vector Definition An eigenvector of an n n matrix A is a nonzero vector x such that A x λ x for some scalar λ A scalar λ is called
Sec 5 Eigenvectors and Eigenvalues In this chapter, vector means column vector Definition An eigenvector of an n n matrix A is a nonzero vector x such that A x λ x for some scalar λ A scalar λ is called
[Disclaimer: This is not a complete list of everything you need to know, just some of the topics that gave people difficulty.]
![[Disclaimer: This is not a complete list of everything you need to know, just some of the topics that gave people difficulty.] [Disclaimer: This is not a complete list of everything you need to know, just some of the topics that gave people difficulty.]](/thumbs/82/86615903.jpg) Math 43 Review Notes [Disclaimer: This is not a complete list of everything you need to know, just some of the topics that gave people difficulty Dot Product If v (v, v, v 3 and w (w, w, w 3, then the
Math 43 Review Notes [Disclaimer: This is not a complete list of everything you need to know, just some of the topics that gave people difficulty Dot Product If v (v, v, v 3 and w (w, w, w 3, then the
STAT 2122 Homework # 3 Solutions Fall 2018 Instr. Sonin
 STAT 2122 Homeork Solutions Fall 2018 Instr. Sonin Due Friday, October 5 NAME (25 + 5 points) Sho all ork on problems! (4) 1. In the... Lotto, you may pick six different numbers from the set Ö"ß ß $ß ÞÞÞß
STAT 2122 Homeork Solutions Fall 2018 Instr. Sonin Due Friday, October 5 NAME (25 + 5 points) Sho all ork on problems! (4) 1. In the... Lotto, you may pick six different numbers from the set Ö"ß ß $ß ÞÞÞß
Section 1.1 Algorithms. Key terms: Algorithm definition. Example from Trapezoidal Rule Outline of corresponding algorithm Absolute Error
 Section 1.1 Algorithms Key terms: Algorithm definition Example from Trapezoidal Rule Outline of corresponding algorithm Absolute Error Approximating square roots Iterative method Diagram of a general iterative
Section 1.1 Algorithms Key terms: Algorithm definition Example from Trapezoidal Rule Outline of corresponding algorithm Absolute Error Approximating square roots Iterative method Diagram of a general iterative
 NOVEMBER 2005 EXAM NOVEMBER 2005 CAS COURSE 3 EXAM SOLUTIONS 1. Maximum likelihood estimation: The log of the density is 68 0ÐBÑ œ 68 ) Ð) "Ñ 68 B. The loglikelihood function is & j œ 68 0ÐB Ñ œ & 68 )
NOVEMBER 2005 EXAM NOVEMBER 2005 CAS COURSE 3 EXAM SOLUTIONS 1. Maximum likelihood estimation: The log of the density is 68 0ÐBÑ œ 68 ) Ð) "Ñ 68 B. The loglikelihood function is & j œ 68 0ÐB Ñ œ & 68 )
Homework sheet 4: EIGENVALUES AND EIGENVECTORS. DIAGONALIZATION (with solutions) Year ? Why or why not? 6 9
 Bachelor in Statistics and Business Universidad Carlos III de Madrid Mathematical Methods II María Barbero Liñán Homework sheet 4: EIGENVALUES AND EIGENVECTORS DIAGONALIZATION (with solutions) Year - Is
Bachelor in Statistics and Business Universidad Carlos III de Madrid Mathematical Methods II María Barbero Liñán Homework sheet 4: EIGENVALUES AND EIGENVECTORS DIAGONALIZATION (with solutions) Year - Is
Gene expression experiments. Infinite Dimensional Vector Spaces. 1. Motivation: Statistical machine learning and reproducing kernel Hilbert Spaces
 MA 751 Part 3 Gene expression experiments Infinite Dimensional Vector Spaces 1. Motivation: Statistical machine learning and reproducing kernel Hilbert Spaces Gene expression experiments Question: Gene
MA 751 Part 3 Gene expression experiments Infinite Dimensional Vector Spaces 1. Motivation: Statistical machine learning and reproducing kernel Hilbert Spaces Gene expression experiments Question: Gene
PROBLEM SET. Problems on Eigenvalues and Diagonalization. Math 3351, Fall Oct. 20, 2010 ANSWERS
 PROBLEM SET Problems on Eigenvalues and Diagonalization Math 335, Fall 2 Oct. 2, 2 ANSWERS i Problem. In each part, find the characteristic polynomial of the matrix and the eigenvalues of the matrix by
PROBLEM SET Problems on Eigenvalues and Diagonalization Math 335, Fall 2 Oct. 2, 2 ANSWERS i Problem. In each part, find the characteristic polynomial of the matrix and the eigenvalues of the matrix by
Chapter 7: Symmetric Matrices and Quadratic Forms
 Chapter 7: Symmetric Matrices and Quadratic Forms (Last Updated: December, 06) These notes are derived primarily from Linear Algebra and its applications by David Lay (4ed). A few theorems have been moved
Chapter 7: Symmetric Matrices and Quadratic Forms (Last Updated: December, 06) These notes are derived primarily from Linear Algebra and its applications by David Lay (4ed). A few theorems have been moved
Study Guide for Linear Algebra Exam 2
 Study Guide for Linear Algebra Exam 2 Term Vector Space Definition A Vector Space is a nonempty set V of objects, on which are defined two operations, called addition and multiplication by scalars (real
Study Guide for Linear Algebra Exam 2 Term Vector Space Definition A Vector Space is a nonempty set V of objects, on which are defined two operations, called addition and multiplication by scalars (real
80 min. 65 points in total. The raw score will be normalized according to the course policy to count into the final score.
 This is a closed book, closed notes exam You need to justify every one of your answers unless you are asked not to do so Completely correct answers given without justification will receive little credit
This is a closed book, closed notes exam You need to justify every one of your answers unless you are asked not to do so Completely correct answers given without justification will receive little credit
M340L Final Exam Solutions May 13, 1995
 M340L Final Exam Solutions May 13, 1995 Name: Problem 1: Find all solutions (if any) to the system of equations. Express your answer in vector parametric form. The matrix in other words, x 1 + 2x 3 + 3x
M340L Final Exam Solutions May 13, 1995 Name: Problem 1: Find all solutions (if any) to the system of equations. Express your answer in vector parametric form. The matrix in other words, x 1 + 2x 3 + 3x
Infinite Dimensional Vector Spaces. 1. Motivation: Statistical machine learning and reproducing kernel Hilbert Spaces
 MA 751 Part 3 Infinite Dimensional Vector Spaces 1. Motivation: Statistical machine learning and reproducing kernel Hilbert Spaces Microarray experiment: Question: Gene expression - when is the DNA in
MA 751 Part 3 Infinite Dimensional Vector Spaces 1. Motivation: Statistical machine learning and reproducing kernel Hilbert Spaces Microarray experiment: Question: Gene expression - when is the DNA in
Jordan normal form notes (version date: 11/21/07)
 Jordan normal form notes (version date: /2/7) If A has an eigenbasis {u,, u n }, ie a basis made up of eigenvectors, so that Au j = λ j u j, then A is diagonal with respect to that basis To see this, let
Jordan normal form notes (version date: /2/7) If A has an eigenbasis {u,, u n }, ie a basis made up of eigenvectors, so that Au j = λ j u j, then A is diagonal with respect to that basis To see this, let
Linear Algebra Practice Problems
 Math 7, Professor Ramras Linear Algebra Practice Problems () Consider the following system of linear equations in the variables x, y, and z, in which the constants a and b are real numbers. x y + z = a
Math 7, Professor Ramras Linear Algebra Practice Problems () Consider the following system of linear equations in the variables x, y, and z, in which the constants a and b are real numbers. x y + z = a
0.1 Eigenvalues and Eigenvectors
 0.. EIGENVALUES AND EIGENVECTORS MATH 22AL Computer LAB for Linear Algebra Eigenvalues and Eigenvectors Dr. Daddel Please save your MATLAB Session (diary)as LAB9.text and submit. 0. Eigenvalues and Eigenvectors
0.. EIGENVALUES AND EIGENVECTORS MATH 22AL Computer LAB for Linear Algebra Eigenvalues and Eigenvectors Dr. Daddel Please save your MATLAB Session (diary)as LAB9.text and submit. 0. Eigenvalues and Eigenvectors
Part I consists of 14 multiple choice questions (worth 5 points each) and 5 true/false question (worth 1 point each), for a total of 75 points.
 Math 131 Exam 1 Solutions Part I consists of 14 multiple choice questions (orth 5 points each) and 5 true/false question (orth 1 point each), for a total of 75 points. 1. The folloing table gives the number
Math 131 Exam 1 Solutions Part I consists of 14 multiple choice questions (orth 5 points each) and 5 true/false question (orth 1 point each), for a total of 75 points. 1. The folloing table gives the number
City Suburbs. : population distribution after m years
 Section 5.3 Diagonalization of Matrices Definition Example: stochastic matrix To City Suburbs From City Suburbs.85.03 = A.15.97 City.15.85 Suburbs.97.03 probability matrix of a sample person s residence
Section 5.3 Diagonalization of Matrices Definition Example: stochastic matrix To City Suburbs From City Suburbs.85.03 = A.15.97 City.15.85 Suburbs.97.03 probability matrix of a sample person s residence
 ! " # $! % & '! , ) ( + - (. ) ( ) * + / 0 1 2 3 0 / 4 5 / 6 0 ; 8 7 < = 7 > 8 7 8 9 : Œ Š ž P P h ˆ Š ˆ Œ ˆ Š ˆ Ž Ž Ý Ü Ý Ü Ý Ž Ý ê ç è ± ¹ ¼ ¹ ä ± ¹ w ç ¹ è ¼ è Œ ¹ ± ¹ è ¹ è ä ç w ¹ ã ¼ ¹ ä ¹ ¼ ¹ ±
! " # $! % & '! , ) ( + - (. ) ( ) * + / 0 1 2 3 0 / 4 5 / 6 0 ; 8 7 < = 7 > 8 7 8 9 : Œ Š ž P P h ˆ Š ˆ Œ ˆ Š ˆ Ž Ž Ý Ü Ý Ü Ý Ž Ý ê ç è ± ¹ ¼ ¹ ä ± ¹ w ç ¹ è ¼ è Œ ¹ ± ¹ è ¹ è ä ç w ¹ ã ¼ ¹ ä ¹ ¼ ¹ ±
ETIKA V PROFESII PSYCHOLÓGA
 P r a ž s k á v y s o k á š k o l a p s y c h o s o c i á l n í c h s t u d i í ETIKA V PROFESII PSYCHOLÓGA N a t á l i a S l o b o d n í k o v á v e d ú c i p r á c e : P h D r. M a r t i n S t r o u
P r a ž s k á v y s o k á š k o l a p s y c h o s o c i á l n í c h s t u d i í ETIKA V PROFESII PSYCHOLÓGA N a t á l i a S l o b o d n í k o v á v e d ú c i p r á c e : P h D r. M a r t i n S t r o u
Relations. Relations occur all the time in mathematics. For example, there are many relations between # and % À
 Relations Relations occur all the time in mathematics. For example, there are many relations between and % À Ÿ% % Á% l% Ÿ,, Á ß and l are examples of relations which might or might not hold between two
Relations Relations occur all the time in mathematics. For example, there are many relations between and % À Ÿ% % Á% l% Ÿ,, Á ß and l are examples of relations which might or might not hold between two
Diagonalization. Hung-yi Lee
 Diagonalization Hung-yi Lee Review If Av = λv (v is a vector, λ is a scalar) v is an eigenvector of A excluding zero vector λ is an eigenvalue of A that corresponds to v Eigenvectors corresponding to λ
Diagonalization Hung-yi Lee Review If Av = λv (v is a vector, λ is a scalar) v is an eigenvector of A excluding zero vector λ is an eigenvalue of A that corresponds to v Eigenvectors corresponding to λ
Eigenvalues and Eigenvectors
 Eigenvalues and Eigenvectors MAT 67L, Laboratory III Contents Instructions (1) Read this document. (2) The questions labeled Experiments are not graded, and should not be turned in. They are designed for
Eigenvalues and Eigenvectors MAT 67L, Laboratory III Contents Instructions (1) Read this document. (2) The questions labeled Experiments are not graded, and should not be turned in. They are designed for
What is A + B? What is A B? What is AB? What is BA? What is A 2? and B = QUESTION 2. What is the reduced row echelon matrix of A =
 STUDENT S COMPANIONS IN BASIC MATH: THE ELEVENTH Matrix Reloaded by Block Buster Presumably you know the first part of matrix story, including its basic operations (addition and multiplication) and row
STUDENT S COMPANIONS IN BASIC MATH: THE ELEVENTH Matrix Reloaded by Block Buster Presumably you know the first part of matrix story, including its basic operations (addition and multiplication) and row
Diagonalization of Matrices
 LECTURE 4 Diagonalization of Matrices Recall that a diagonal matrix is a square n n matrix with non-zero entries only along the diagonal from the upper left to the lower right (the main diagonal) Diagonal
LECTURE 4 Diagonalization of Matrices Recall that a diagonal matrix is a square n n matrix with non-zero entries only along the diagonal from the upper left to the lower right (the main diagonal) Diagonal
Eigenvalues for Triangular Matrices. ENGI 7825: Linear Algebra Review Finding Eigenvalues and Diagonalization
 Eigenvalues for Triangular Matrices ENGI 78: Linear Algebra Review Finding Eigenvalues and Diagonalization Adapted from Notes Developed by Martin Scharlemann The eigenvalues for a triangular matrix are
Eigenvalues for Triangular Matrices ENGI 78: Linear Algebra Review Finding Eigenvalues and Diagonalization Adapted from Notes Developed by Martin Scharlemann The eigenvalues for a triangular matrix are
Lab 2 Iterative methods and eigenvalue problems. Introduction. Iterative solution of the soap film problem. Beräkningsvetenskap II/NV2, HT (6)
 Beräkningsvetenskap II/NV2, HT 2008 1 (6) Institutionen för informationsteknologi Teknisk databehandling Besöksadress: MIC hus 2, Polacksbacken Lägerhyddsvägen 2 Postadress: Box 337 751 05 Uppsala Telefon:
Beräkningsvetenskap II/NV2, HT 2008 1 (6) Institutionen för informationsteknologi Teknisk databehandling Besöksadress: MIC hus 2, Polacksbacken Lägerhyddsvägen 2 Postadress: Box 337 751 05 Uppsala Telefon:
Systems of Linear ODEs
 P a g e 1 Systems of Linear ODEs Systems of ordinary differential equations can be solved in much the same way as discrete dynamical systems if the differential equations are linear. We will focus here
P a g e 1 Systems of Linear ODEs Systems of ordinary differential equations can be solved in much the same way as discrete dynamical systems if the differential equations are linear. We will focus here
Draft. Lecture 14 Eigenvalue Problems. MATH 562 Numerical Analysis II. Songting Luo. Department of Mathematics Iowa State University
 Lecture 14 Eigenvalue Problems Songting Luo Department of Mathematics Iowa State University MATH 562 Numerical Analysis II Songting Luo ( Department of Mathematics Iowa State University[0.5in] MATH562
Lecture 14 Eigenvalue Problems Songting Luo Department of Mathematics Iowa State University MATH 562 Numerical Analysis II Songting Luo ( Department of Mathematics Iowa State University[0.5in] MATH562
A. Incorrect! Check your algebra when you solved for volume. B. Incorrect! Check your algebra when you solved for volume.
 AP Chemistry - Problem Drill 03: Basic Math for Chemistry No. 1 of 10 1. Unlike math problems, chemistry calculations have two key elements to consider in any number units and significant figures. Solve
AP Chemistry - Problem Drill 03: Basic Math for Chemistry No. 1 of 10 1. Unlike math problems, chemistry calculations have two key elements to consider in any number units and significant figures. Solve
Eigenvalues and Eigenvectors, More Direction Fields and Systems of ODEs
 Eigenvalues and Eigenvectors, More Direction Fields and Systems of ODEs First let us speak a bit about eigenvalues. Defn. An eigenvalue λ of an nxn matrix A means a scalar (perhaps a complex number) such
Eigenvalues and Eigenvectors, More Direction Fields and Systems of ODEs First let us speak a bit about eigenvalues. Defn. An eigenvalue λ of an nxn matrix A means a scalar (perhaps a complex number) such
among children that are administered the Salk vaccine
 Final Review problems (solutions available): 6.9, 6.12, 6.20, 6.27, 6.29, 6.33, 6.73 Final Review problems (solutions not available yet): 10.18, 10.34, 10.35, 10.46 Chapter 10 Categorical Data In this
Final Review problems (solutions available): 6.9, 6.12, 6.20, 6.27, 6.29, 6.33, 6.73 Final Review problems (solutions not available yet): 10.18, 10.34, 10.35, 10.46 Chapter 10 Categorical Data In this
Math 205, Summer I, Week 4b:
 Math 205, Summer I, 2016 Week 4b: Chapter 5, Sections 6, 7 and 8 (5.5 is NOT on the syllabus) 5.6 Eigenvalues and Eigenvectors 5.7 Eigenspaces, nondefective matrices 5.8 Diagonalization [*** See next slide
Math 205, Summer I, 2016 Week 4b: Chapter 5, Sections 6, 7 and 8 (5.5 is NOT on the syllabus) 5.6 Eigenvalues and Eigenvectors 5.7 Eigenspaces, nondefective matrices 5.8 Diagonalization [*** See next slide
