A generalization of the Leibniz rule for derivatives
|
|
|
- Ralph Warren
- 6 years ago
- Views:
Transcription
1 A geeralizatio of the Leibiz rule for erivatives R. DYBOWSKI School of Computig, Uiversity of East Loo, Docklas Campus, Loo E16 RD I will shamelessly tell you what my bottom lie is. It is placig balls ito boxes.... Gia-Carlo Rota (Iiscrete Thoughts) 1 Itrouctio It is commo kowlege that the first erivative of the prouct f(x)g(x) is give by f (x)g(x) + f(x)g (x), a that the seco erivative is f (x)g(x) + f (x)g (x) + f(x)g (x). We look at the more geeral case; amely, the -th erivative of a prouct of m fuctios f 1 (x) f m (x). Accorig to the Leibiz rule [e.g., 1, p. 534], the -th erivative of a prouct of two fuctios is give by f(x)g(x) = ( ) f (r) (x)g ( r) (x), (1) r r=0 where f () (x) eotes the -th erivative of fuctio f(x), with f (0) (x) = f(x), but what is the geeral form whe we have m fuctios: f 1(x) f m (x)? We will aswer this questio by usig the combiatorial tool of balls i boxes. Balls a boxes There are m ways of allocatig labele balls to m empty boxes. Each possibility will be referre to as a allocatio. The occupacy vector (α 1,..., α m ) eotes a allocatio havig α i balls (α i 0) i the i-th box. The umber of ways of allocatig α 1 labele balls i the 1st box, α labele balls i the box,..., α m labele balls i the m-th box is give by the multiomial coefficiet ( ) = α 1,..., α m! α 1! α m!, where α α m = ; thus, ( ) of the m possible allocatios have the occupacy vector (α 1,...,α m ). 1
2 Let b 1 b b m represet a allocatio of b 1 + b + + b m labele balls i m boxes, where b i is the set of labele balls i the i-th box. The occupatio vector correspoig to this allocatio is ( b 1, b,..., b m ). For example, {a, b} {c} is a allocatio base o three boxes (the seco box beig empty), a its correspoig occupacy vector is (, 0, 1). Let L 1 b 1 b m represet the set of allocatios resultig from the m possible ways of allocatig oe labele ball, say x, to the boxes of b 1 b m : For example, L 1 b 1 b m = b 1 {x} b m,..., b 1 b m {x}. () L 1 {a, b} {c} = { {a, b, x} {c}, {a, b} {x} {c}, {a, b} {c, x} }. We will exte the applicatio of L 1 to a set of γ allocatios {u 1,...,u γ }: For example, L 1 {u 1,..., v γ } = L 1 u 1 L 1 u γ. L 1{ {a}, {a} } = L 1 {a} L 1 {a} = { {a, b}, {a} {b} } { {b} {a}, {a, b} }. We ca use the L 1 operator to create the the set of all possible allocatios of labele balls i m boxes i a systematic, step-wise maer. Iitially, the m boxes are empty: m. The m possible ways of allocatig a labele ball to m is the set L 1 m. Aig a seco labele ball to the elemets of L 1 m i every possible way correspos to L 1 (L 1 m), but this is equal to the set of all possible ways of allocatig two labele balls to m (See Figure 1): Cotiuig i this maer, we obtai L m = L 1 (L 1 m). L m = L 1 (L 1 ( L 1 m )). (3) }{{} {a} {a} {a, b} {a} {b} {b} {a} {a, b} Figure 1: Formatio of possible elemets of L from allocatio via possible elemets of L 1.
3 .1 Multisets of occupacy vectors Let L 1 (α 1,..., α m ) eote the set (possibly multiset) of occupacy vectors resultig from firstly performig L 1 o a allocatio with occupacy vector (α 1,...,α m ) a the replacig each resultig allocatio with its correspoig occupacy vector. Put aother way, if a set of labele balls b i is such that b i = α i the L 1 (α 1,...,α m ) = L 1 ( b 1,..., b m ) For example from () a (4), we have = Γ(L 1 b 1 b m ). L 1 (0, 0, 0, 0) = {(1, 0, 0, 0), (0, 1, 0, 0), (0, 0, 1, 0), (0, 0, 0, 1)}. Aalogous to the case with L 1, we will exte the applicatio of L 1 to a multiset of γ occupacy vectors {v 1,...,v γ }: This ca be rewritte as L 1 {v 1,...,v γ } = L 1 v 1 L 1 v γ. γ L 1 {v i } = (4) γ L 1 v i, (5) where eotes the aitive uio operator of multisets []. The operator L 1 ca be geeralize to L ; amely, L (α 1,..., α m ) is the multiset of occupacy vectors resultig from performig L o a allocatio with occupacy vector (α 1,..., α m ) a the replacig each resultig allocatio with its correspoig occupacy vector: Theorem 1 L (α 1,..., α m ) = L ( b 1,..., b m ) L 1 (α 1,..., α m ) = where δ ij is the Kroecker elta: δ ij = = Γ(L b 1 b m ). m (α 1 + δ 1j,...,α m + δ mj ), j=1 { 1 if i = j, 0 otherwise. Proof. Let b i be ay set of labele balls such that b i = α i, the L 1 (α 1,..., α m ) = Γ(L 1 b 1 b m ) from (4) = Γ{ b 1 {x} b m,..., b 1 b m {x} } from () = {Γ b 1 {x} b m,..., Γ b 1 b m {x} } from (5) = {( b 1 + 1,..., b m ),..., ( b 1,..., b m + 1)} = {(α 1 + 1,...,α m ),..., (α 1,...,α m + 1)} m = (α 1 + δ 1j,...,α m + δ mj ). j=1 (6) 3
4 A importat relatioship exists betwee L 1 a L 1, as show by the followig lemma. Lemma 1. If u is a allocatio the ΓL 1u = L 1 Γu. Proof. Let u = b 1 b m the L 1u = { b 1 {x} b m,..., b 1 b m {x} } ; therefore, ΓL 1 u = {( b 1 + 1,..., b m ),..., ( b 1,..., b m + 1)}. However, Γu = ( b 1,..., b m ); therefore, L 1 Γu = {( b 1 + 1,..., b m ),..., ( b 1,..., b m + 1)}. The ext lemma extes Lemma 1 so that sets of allocatios ca be iclue. Lemma. If S is a set of allocatios the ΓL 1 S = L 1ΓS. Proof. Let S = {u 1,..., u γ } the L 1 S = L 1 {u 1,...,u γ } = γ L 1 u i from (5); therefore, ΓL 1S = Γ γ L 1u i = γ ΓL 1u i. Now, ΓS = {Γu 1,..., Γu γ }; therefore, L 1 ΓS = L 1 {Γu 1,...,Γu γ } = γ L 1Γu i = γ ΓL 1 u i from Lemma 1. Lemma allows a versio of (3) for L to be establishe. Theorem L (0,..., 0) m = L 1 L 1 L }{{ 1 (0,..., 0) } m. Proof. L (0,...,0) m = ΓL m from (4) = ΓL 1 L 1 m from (3) = L 1 ΓL 1 L 1 m from Lemma = = L 1 L 1 Γ m from Lemma = L 1 L 1 (0,...,0) m From Theorem 1, Theorem a (5), we ow have the followig system (System 1) that geerates the elemets of the multiset L (0,...,0) m : L (0,...,0) m = L 1 L 1 L 1 (0,...,0) }{{} m System 1 where L 1 (α 1,...,α m ) = m j=1 (α 1 + δ 1j,...,α m + δ mj ) a L γ 1 {v i} = γ L 1v i, v i eotig a occupacy vector. This geeratio of elemets is illustrate i Figure. 4
5 (0, 0) (1, 0) (0, 1) (, 0) (1, 1) (1, 1) (0, ) Figure : Formatio of the elemets of multiset L (0, 0) from occupacy vector (0, 0) via the elemets of L 1 (0, 0). 3 Beyo the Leibiz rule I orer to see more clearly the lik betwee the -th erivative of f 1 (x) f m (x) a L (0,...,0) m, we will use a special otatio. The prouct f (α1) 1 (x) f m (αm) (x) will be writte as the erivative-orer tuple α 1,...,α m ; for example, the erivatio f(a) 1 (x)f (b) (x) = f(a+1) ca be writte more succictly as 1 (x)f (b) (x) + f(a) 1 (x)f (b+1) (x) a, b = a + 1, b + a, b + 1. Furthermore, usig this otatio, the -th erivative of f 1 (x) f m (x) ca be reefie as 0,..., 0 m = 0,..., 0 m. (7) }{{ } The sum rule of ifferetial calculus ca be writte as γ w i = where w j is a erivative-orer tuple. Lemma 3. α 1,...,α m = where δ ij is the Kroecker elta. γ w i, (8) m α 1 + δ 1j,..., α m + δ mj, j=1 Proof. α 1,...,α m = α 1 + 1, α,...,α m + α 1, α + 1,...,α m + + α 1, α,..., α m
6 Gatherig together (7), (8) a Lemma 3, we obtai the followig system (System ) that geerates the terms of 0,..., 0 m (See Figure 3): 0,...,0 m = 0,...,0 m }{{ } System where α 1,..., α m = m j=1 α 1 + δ 1j,...,α m + δ mj, a γ w i = γ w i, w i eotig a erivative-orer tuple. Lemma 4. There are ( ) allocatio vectors i L (0,...,0) m equal to (α 1,...,α m ). Proof. L (0,..., 0) m = ΓL m, a, as previously state early i Sectio, ( ) of the m possible allocatios i L m have occupacy vector (α 1,..., α m ). We ow have i place the material require to prove the mai goal of this paper; amely, the -th erivative of f 1 (x) f m (x). Theorem 3 0,..., 0 m = α 1+ +α m= α i 0 ( ) α α 1,..., α 1,...,α m m Proof. By ispectio, it is clear that System 1 a System are isomorphous, with L a ; therefore, sice ( ) of the elemets i multiset ( ) L (0,...,0) m are equal to (α 1,..., α m ) (Lemma 4), it follows that of the terms i series 0,..., 0 m are equal to α 1,..., α m. Theorem 3 ca be rewritte as f 1(x) f m (x) = α 1+ +α m= α i 0 ( 0, 0 ) f α1 α 1,..., α 1 (x) fαm m (x). m 1, 0 0, 1, 0 1, 1 1, 1 0, Figure 3: Formatio of the terms of 0, 0 from erivative-orer tuple 0, 0 via the terms of 0, 0. Compare with Figure. 6
7 Refereces [1] W. Kapla. Avace Calculus. Aiso-Wesley, Reaig, MA, 4th eitio, [] W.D. Blizar. Multiset theory. Notre Dame Joural of Formal Logic, 30(1):36 66,
Commutativity in Permutation Groups
 Commutativity i Permutatio Groups Richard Wito, PhD Abstract I the group Sym(S) of permutatios o a oempty set S, fixed poits ad trasiet poits are defied Prelimiary results o fixed ad trasiet poits are
Commutativity i Permutatio Groups Richard Wito, PhD Abstract I the group Sym(S) of permutatios o a oempty set S, fixed poits ad trasiet poits are defied Prelimiary results o fixed ad trasiet poits are
arxiv: v1 [math.co] 23 Mar 2016
![arxiv: v1 [math.co] 23 Mar 2016 arxiv: v1 [math.co] 23 Mar 2016](/thumbs/92/108877827.jpg) The umber of direct-sum decompositios of a fiite vector space arxiv:603.0769v [math.co] 23 Mar 206 David Ellerma Uiversity of Califoria at Riverside August 3, 208 Abstract The theory of q-aalogs develops
The umber of direct-sum decompositios of a fiite vector space arxiv:603.0769v [math.co] 23 Mar 206 David Ellerma Uiversity of Califoria at Riverside August 3, 208 Abstract The theory of q-aalogs develops
62. Power series Definition 16. (Power series) Given a sequence {c n }, the series. c n x n = c 0 + c 1 x + c 2 x 2 + c 3 x 3 +
 62. Power series Defiitio 16. (Power series) Give a sequece {c }, the series c x = c 0 + c 1 x + c 2 x 2 + c 3 x 3 + is called a power series i the variable x. The umbers c are called the coefficiets of
62. Power series Defiitio 16. (Power series) Give a sequece {c }, the series c x = c 0 + c 1 x + c 2 x 2 + c 3 x 3 + is called a power series i the variable x. The umbers c are called the coefficiets of
Infinite Sequences and Series
 Chapter 6 Ifiite Sequeces ad Series 6.1 Ifiite Sequeces 6.1.1 Elemetary Cocepts Simply speakig, a sequece is a ordered list of umbers writte: {a 1, a 2, a 3,...a, a +1,...} where the elemets a i represet
Chapter 6 Ifiite Sequeces ad Series 6.1 Ifiite Sequeces 6.1.1 Elemetary Cocepts Simply speakig, a sequece is a ordered list of umbers writte: {a 1, a 2, a 3,...a, a +1,...} where the elemets a i represet
Matrix Operators and Functions Thereof
 Mathematics Notes Note 97 31 May 27 Matrix Operators a Fuctios Thereof Carl E. Baum Uiversity of New Mexico Departmet of Electrical a Computer Egieerig Albuquerque New Mexico 87131 Abstract This paper
Mathematics Notes Note 97 31 May 27 Matrix Operators a Fuctios Thereof Carl E. Baum Uiversity of New Mexico Departmet of Electrical a Computer Egieerig Albuquerque New Mexico 87131 Abstract This paper
6.451 Principles of Digital Communication II Wednesday, March 9, 2005 MIT, Spring 2005 Handout #12. Problem Set 5 Solutions
 6.51 Priciples of Digital Commuicatio II Weesay, March 9, 2005 MIT, Sprig 2005 Haout #12 Problem Set 5 Solutios Problem 5.1 (Eucliea ivisio algorithm). (a) For the set F[x] of polyomials over ay fiel F,
6.51 Priciples of Digital Commuicatio II Weesay, March 9, 2005 MIT, Sprig 2005 Haout #12 Problem Set 5 Solutios Problem 5.1 (Eucliea ivisio algorithm). (a) For the set F[x] of polyomials over ay fiel F,
The picture in figure 1.1 helps us to see that the area represents the distance traveled. Figure 1: Area represents distance travelled
 1 Lecture : Area Area ad distace traveled Approximatig area by rectagles Summatio The area uder a parabola 1.1 Area ad distace Suppose we have the followig iformatio about the velocity of a particle, how
1 Lecture : Area Area ad distace traveled Approximatig area by rectagles Summatio The area uder a parabola 1.1 Area ad distace Suppose we have the followig iformatio about the velocity of a particle, how
Chapter 7 COMBINATIONS AND PERMUTATIONS. where we have the specific formula for the binomial coefficients:
 Chapter 7 COMBINATIONS AND PERMUTATIONS We have see i the previous chapter that (a + b) ca be writte as 0 a % a & b%þ% a & b %þ% b where we have the specific formula for the biomial coefficiets: '!!(&)!
Chapter 7 COMBINATIONS AND PERMUTATIONS We have see i the previous chapter that (a + b) ca be writte as 0 a % a & b%þ% a & b %þ% b where we have the specific formula for the biomial coefficiets: '!!(&)!
Definition 2 (Eigenvalue Expansion). We say a d-regular graph is a λ eigenvalue expander if
 Expaer Graphs Graph Theory (Fall 011) Rutgers Uiversity Swastik Kopparty Throughout these otes G is a -regular graph 1 The Spectrum Let A G be the ajacecy matrix of G Let λ 1 λ λ be the eigevalues of A
Expaer Graphs Graph Theory (Fall 011) Rutgers Uiversity Swastik Kopparty Throughout these otes G is a -regular graph 1 The Spectrum Let A G be the ajacecy matrix of G Let λ 1 λ λ be the eigevalues of A
A GENERALIZATION OF THE SYMMETRY BETWEEN COMPLETE AND ELEMENTARY SYMMETRIC FUNCTIONS. Mircea Merca
 Idia J Pure Appl Math 45): 75-89 February 204 c Idia Natioal Sciece Academy A GENERALIZATION OF THE SYMMETRY BETWEEN COMPLETE AND ELEMENTARY SYMMETRIC FUNCTIONS Mircea Merca Departmet of Mathematics Uiversity
Idia J Pure Appl Math 45): 75-89 February 204 c Idia Natioal Sciece Academy A GENERALIZATION OF THE SYMMETRY BETWEEN COMPLETE AND ELEMENTARY SYMMETRIC FUNCTIONS Mircea Merca Departmet of Mathematics Uiversity
CSE 1400 Applied Discrete Mathematics Number Theory and Proofs
 CSE 1400 Applied Discrete Mathematics Number Theory ad Proofs Departmet of Computer Scieces College of Egieerig Florida Tech Sprig 01 Problems for Number Theory Backgroud Number theory is the brach of
CSE 1400 Applied Discrete Mathematics Number Theory ad Proofs Departmet of Computer Scieces College of Egieerig Florida Tech Sprig 01 Problems for Number Theory Backgroud Number theory is the brach of
Sparsification using Regular and Weighted. Graphs
 Sparsificatio usig Regular a Weighte 1 Graphs Aly El Gamal ECE Departmet a Cooriate Sciece Laboratory Uiversity of Illiois at Urbaa-Champaig Abstract We review the state of the art results o spectral approximatio
Sparsificatio usig Regular a Weighte 1 Graphs Aly El Gamal ECE Departmet a Cooriate Sciece Laboratory Uiversity of Illiois at Urbaa-Champaig Abstract We review the state of the art results o spectral approximatio
Math 155 (Lecture 3)
 Math 55 (Lecture 3) September 8, I this lecture, we ll cosider the aswer to oe of the most basic coutig problems i combiatorics Questio How may ways are there to choose a -elemet subset of the set {,,,
Math 55 (Lecture 3) September 8, I this lecture, we ll cosider the aswer to oe of the most basic coutig problems i combiatorics Questio How may ways are there to choose a -elemet subset of the set {,,,
TRACES OF HADAMARD AND KRONECKER PRODUCTS OF MATRICES. 1. Introduction
 Math Appl 6 2017, 143 150 DOI: 1013164/ma201709 TRACES OF HADAMARD AND KRONECKER PRODUCTS OF MATRICES PANKAJ KUMAR DAS ad LALIT K VASHISHT Abstract We preset some iequality/equality for traces of Hadamard
Math Appl 6 2017, 143 150 DOI: 1013164/ma201709 TRACES OF HADAMARD AND KRONECKER PRODUCTS OF MATRICES PANKAJ KUMAR DAS ad LALIT K VASHISHT Abstract We preset some iequality/equality for traces of Hadamard
11.1 Arithmetic Sequences and Series
 11.1 Arithmetic Sequeces ad Series A itroductio 1, 4, 7, 10, 13 9, 1, 7, 15 6., 6.6, 7, 7.4 ππ+, 3, π+ 6 Arithmetic Sequeces ADD To get ext term 35 1 7. 3π + 9, 4, 8, 16, 3 9, 3, 1, 1/ 3 1,1/ 4,1/16,1/
11.1 Arithmetic Sequeces ad Series A itroductio 1, 4, 7, 10, 13 9, 1, 7, 15 6., 6.6, 7, 7.4 ππ+, 3, π+ 6 Arithmetic Sequeces ADD To get ext term 35 1 7. 3π + 9, 4, 8, 16, 3 9, 3, 1, 1/ 3 1,1/ 4,1/16,1/
NEW FAST CONVERGENT SEQUENCES OF EULER-MASCHERONI TYPE
 UPB Sci Bull, Series A, Vol 79, Iss, 207 ISSN 22-7027 NEW FAST CONVERGENT SEQUENCES OF EULER-MASCHERONI TYPE Gabriel Bercu We itroduce two ew sequeces of Euler-Mascheroi type which have fast covergece
UPB Sci Bull, Series A, Vol 79, Iss, 207 ISSN 22-7027 NEW FAST CONVERGENT SEQUENCES OF EULER-MASCHERONI TYPE Gabriel Bercu We itroduce two ew sequeces of Euler-Mascheroi type which have fast covergece
3. Z Transform. Recall that the Fourier transform (FT) of a DT signal xn [ ] is ( ) [ ] = In order for the FT to exist in the finite magnitude sense,
![3. Z Transform. Recall that the Fourier transform (FT) of a DT signal xn [ ] is ( ) [ ] = In order for the FT to exist in the finite magnitude sense, 3. Z Transform. Recall that the Fourier transform (FT) of a DT signal xn [ ] is ( ) [ ] = In order for the FT to exist in the finite magnitude sense,](/thumbs/82/85448051.jpg) 3. Z Trasform Referece: Etire Chapter 3 of text. Recall that the Fourier trasform (FT) of a DT sigal x [ ] is ω ( ) [ ] X e = j jω k = xe I order for the FT to exist i the fiite magitude sese, S = x [
3. Z Trasform Referece: Etire Chapter 3 of text. Recall that the Fourier trasform (FT) of a DT sigal x [ ] is ω ( ) [ ] X e = j jω k = xe I order for the FT to exist i the fiite magitude sese, S = x [
arxiv: v4 [math.co] 5 May 2011
![arxiv: v4 [math.co] 5 May 2011 arxiv: v4 [math.co] 5 May 2011](/thumbs/90/102209301.jpg) A PROBLEM OF ENUMERATION OF TWO-COLOR BRACELETS WITH SEVERAL VARIATIONS arxiv:07101370v4 [mathco] 5 May 011 VLADIMIR SHEVELEV Abstract We cosier the problem of eumeratio of icogruet two-color bracelets
A PROBLEM OF ENUMERATION OF TWO-COLOR BRACELETS WITH SEVERAL VARIATIONS arxiv:07101370v4 [mathco] 5 May 011 VLADIMIR SHEVELEV Abstract We cosier the problem of eumeratio of icogruet two-color bracelets
k=1 s k (x) (3) and that the corresponding infinite series may also converge; moreover, if it converges, then it defines a function S through its sum
 0. L Hôpital s rule You alreay kow from Lecture 0 that ay sequece {s k } iuces a sequece of fiite sums {S } through S = s k, a that if s k 0 as k the {S } may coverge to the it k= S = s s s 3 s 4 = s k.
0. L Hôpital s rule You alreay kow from Lecture 0 that ay sequece {s k } iuces a sequece of fiite sums {S } through S = s k, a that if s k 0 as k the {S } may coverge to the it k= S = s s s 3 s 4 = s k.
Worksheet on Generating Functions
 Worksheet o Geeratig Fuctios October 26, 205 This worksheet is adapted from otes/exercises by Nat Thiem. Derivatives of Geeratig Fuctios. If the sequece a 0, a, a 2,... has ordiary geeratig fuctio A(x,
Worksheet o Geeratig Fuctios October 26, 205 This worksheet is adapted from otes/exercises by Nat Thiem. Derivatives of Geeratig Fuctios. If the sequece a 0, a, a 2,... has ordiary geeratig fuctio A(x,
Weighted Gcd-Sum Functions
 1 3 47 6 3 11 Joural of Iteger Sequeces, Vol. 14 (011), Article 11.7.7 Weighte Gc-Sum Fuctios László Tóth 1 Departmet of Mathematics Uiversity of Pécs Ifjúság u. 6 764 Pécs Hugary a Istitute of Mathematics,
1 3 47 6 3 11 Joural of Iteger Sequeces, Vol. 14 (011), Article 11.7.7 Weighte Gc-Sum Fuctios László Tóth 1 Departmet of Mathematics Uiversity of Pécs Ifjúság u. 6 764 Pécs Hugary a Istitute of Mathematics,
Week 5-6: The Binomial Coefficients
 Wee 5-6: The Biomial Coefficiets March 6, 2018 1 Pascal Formula Theorem 11 (Pascal s Formula For itegers ad such that 1, ( ( ( 1 1 + 1 The umbers ( 2 ( 1 2 ( 2 are triagle umbers, that is, The petago umbers
Wee 5-6: The Biomial Coefficiets March 6, 2018 1 Pascal Formula Theorem 11 (Pascal s Formula For itegers ad such that 1, ( ( ( 1 1 + 1 The umbers ( 2 ( 1 2 ( 2 are triagle umbers, that is, The petago umbers
6 Integers Modulo n. integer k can be written as k = qn + r, with q,r, 0 r b. So any integer.
 6 Itegers Modulo I Example 2.3(e), we have defied the cogruece of two itegers a,b with respect to a modulus. Let us recall that a b (mod ) meas a b. We have proved that cogruece is a equivalece relatio
6 Itegers Modulo I Example 2.3(e), we have defied the cogruece of two itegers a,b with respect to a modulus. Let us recall that a b (mod ) meas a b. We have proved that cogruece is a equivalece relatio
Orthogonal Function Solution of Differential Equations
 Royal Holloway Uiversity of Loo Departet of Physics Orthogoal Fuctio Solutio of Differetial Equatios trouctio A give oriary ifferetial equatio will have solutios i ters of its ow fuctios Thus, for eaple,
Royal Holloway Uiversity of Loo Departet of Physics Orthogoal Fuctio Solutio of Differetial Equatios trouctio A give oriary ifferetial equatio will have solutios i ters of its ow fuctios Thus, for eaple,
Course : Algebraic Combinatorics
 Course 18.312: Algebraic Combiatorics Lecture Notes # 18-19 Addedum by Gregg Musier March 18th - 20th, 2009 The followig material ca be foud i a umber of sources, icludig Sectios 7.3 7.5, 7.7, 7.10 7.11,
Course 18.312: Algebraic Combiatorics Lecture Notes # 18-19 Addedum by Gregg Musier March 18th - 20th, 2009 The followig material ca be foud i a umber of sources, icludig Sectios 7.3 7.5, 7.7, 7.10 7.11,
A Mean Paradox. John Konvalina, Jack Heidel, and Jim Rogers. Department of Mathematics University of Nebraska at Omaha Omaha, NE USA
 A Mea Paradox by Joh Kovalia, Jac Heidel, ad Jim Rogers Departmet of Mathematics Uiversity of Nebrasa at Omaha Omaha, NE 6882-243 USA Phoe: (42) 554-2836 Fax: (42) 554-2975 E-mail: joho@uomaha.edu A Mea
A Mea Paradox by Joh Kovalia, Jac Heidel, ad Jim Rogers Departmet of Mathematics Uiversity of Nebrasa at Omaha Omaha, NE 6882-243 USA Phoe: (42) 554-2836 Fax: (42) 554-2975 E-mail: joho@uomaha.edu A Mea
The structure of Fourier series
 The structure of Fourier series Valery P Dmitriyev Lomoosov Uiversity, Russia Date: February 3, 2011) Fourier series is costructe basig o the iea to moel the elemetary oscillatio 1, +1) by the expoetial
The structure of Fourier series Valery P Dmitriyev Lomoosov Uiversity, Russia Date: February 3, 2011) Fourier series is costructe basig o the iea to moel the elemetary oscillatio 1, +1) by the expoetial
THE NUMBER OF IRREDUCIBLE POLYNOMIALS AND LYNDON WORDS WITH GIVEN TRACE
 SIM J. DISCRETE MTH. Vol. 14, No. 2, pp. 240 245 c 2001 Society for Iustrial a pplie Mathematics THE NUMBER OF IRREDUCIBLE POLYNOMILS ND LYNDON WORDS WITH GIVEN TRCE F. RUSKEY, C. R. MIERS, ND J. SWD bstract.
SIM J. DISCRETE MTH. Vol. 14, No. 2, pp. 240 245 c 2001 Society for Iustrial a pplie Mathematics THE NUMBER OF IRREDUCIBLE POLYNOMILS ND LYNDON WORDS WITH GIVEN TRCE F. RUSKEY, C. R. MIERS, ND J. SWD bstract.
= n which will be written with general term a n Represent this sequence by listing its function values in order:
 Sectio 9.: Sequeces a Series (Sums) Remier:, 2, 3,, k 2, k, k, k +, k + 2, The ellipsis ots iicate the sequece is oeig, has ifiitely may terms. I. SEQUENCES Defiitio (page 706): A sequece is a fuctio whose
Sectio 9.: Sequeces a Series (Sums) Remier:, 2, 3,, k 2, k, k, k +, k + 2, The ellipsis ots iicate the sequece is oeig, has ifiitely may terms. I. SEQUENCES Defiitio (page 706): A sequece is a fuctio whose
Math 475, Problem Set #12: Answers
 Math 475, Problem Set #12: Aswers A. Chapter 8, problem 12, parts (b) ad (d). (b) S # (, 2) = 2 2, sice, from amog the 2 ways of puttig elemets ito 2 distiguishable boxes, exactly 2 of them result i oe
Math 475, Problem Set #12: Aswers A. Chapter 8, problem 12, parts (b) ad (d). (b) S # (, 2) = 2 2, sice, from amog the 2 ways of puttig elemets ito 2 distiguishable boxes, exactly 2 of them result i oe
Topic 1 2: Sequences and Series. A sequence is an ordered list of numbers, e.g. 1, 2, 4, 8, 16, or
 Topic : Sequeces ad Series A sequece is a ordered list of umbers, e.g.,,, 8, 6, or,,,.... A series is a sum of the terms of a sequece, e.g. + + + 8 + 6 + or... Sigma Notatio b The otatio f ( k) is shorthad
Topic : Sequeces ad Series A sequece is a ordered list of umbers, e.g.,,, 8, 6, or,,,.... A series is a sum of the terms of a sequece, e.g. + + + 8 + 6 + or... Sigma Notatio b The otatio f ( k) is shorthad
Dedicated to the memory of Lev Meshalkin.
 A Meshalki Theorem for Projective Geometries Matthias Beck ad Thomas Zaslavsky 2 Departmet of Mathematical Scieces State Uiversity of New York at Bighamto Bighamto, NY, U.S.A. 3902-6000 matthias@math.bighamto.edu
A Meshalki Theorem for Projective Geometries Matthias Beck ad Thomas Zaslavsky 2 Departmet of Mathematical Scieces State Uiversity of New York at Bighamto Bighamto, NY, U.S.A. 3902-6000 matthias@math.bighamto.edu
Bertrand s Postulate
 Bertrad s Postulate Lola Thompso Ross Program July 3, 2009 Lola Thompso (Ross Program Bertrad s Postulate July 3, 2009 1 / 33 Bertrad s Postulate I ve said it oce ad I ll say it agai: There s always a
Bertrad s Postulate Lola Thompso Ross Program July 3, 2009 Lola Thompso (Ross Program Bertrad s Postulate July 3, 2009 1 / 33 Bertrad s Postulate I ve said it oce ad I ll say it agai: There s always a
Composite Hermite and Anti-Hermite Polynomials
 Avaces i Pure Mathematics 5 5 87-87 Publishe Olie December 5 i SciRes. http://www.scirp.org/joural/apm http://.oi.org/.436/apm.5.5476 Composite Hermite a Ati-Hermite Polyomials Joseph Akeyo Omolo Departmet
Avaces i Pure Mathematics 5 5 87-87 Publishe Olie December 5 i SciRes. http://www.scirp.org/joural/apm http://.oi.org/.436/apm.5.5476 Composite Hermite a Ati-Hermite Polyomials Joseph Akeyo Omolo Departmet
Math 113 Exam 3 Practice
 Math Exam Practice Exam will cover.-.9. This sheet has three sectios. The first sectio will remid you about techiques ad formulas that you should kow. The secod gives a umber of practice questios for you
Math Exam Practice Exam will cover.-.9. This sheet has three sectios. The first sectio will remid you about techiques ad formulas that you should kow. The secod gives a umber of practice questios for you
Estimation for Complete Data
 Estimatio for Complete Data complete data: there is o loss of iformatio durig study. complete idividual complete data= grouped data A complete idividual data is the oe i which the complete iformatio of
Estimatio for Complete Data complete data: there is o loss of iformatio durig study. complete idividual complete data= grouped data A complete idividual data is the oe i which the complete iformatio of
Research Article Sums of Products of Cauchy Numbers, Including Poly-Cauchy Numbers
 Hiawi Publishig Corporatio Joural of Discrete Matheatics Volue 2013, Article ID 373927, 10 pages http://.oi.org/10.1155/2013/373927 Research Article Sus of Proucts of Cauchy Nubers, Icluig Poly-Cauchy
Hiawi Publishig Corporatio Joural of Discrete Matheatics Volue 2013, Article ID 373927, 10 pages http://.oi.org/10.1155/2013/373927 Research Article Sus of Proucts of Cauchy Nubers, Icluig Poly-Cauchy
Inhomogeneous Poisson process
 Chapter 22 Ihomogeeous Poisso process We coclue our stuy of Poisso processes with the case of o-statioary rates. Let us cosier a arrival rate, λ(t), that with time, but oe that is still Markovia. That
Chapter 22 Ihomogeeous Poisso process We coclue our stuy of Poisso processes with the case of o-statioary rates. Let us cosier a arrival rate, λ(t), that with time, but oe that is still Markovia. That
New method for evaluating integrals involving orthogonal polynomials: Laguerre polynomial and Bessel function example
 New metho for evaluatig itegrals ivolvig orthogoal polyomials: Laguerre polyomial a Bessel fuctio eample A. D. Alhaiari Shura Coucil, Riyah, Saui Arabia AND Physics Departmet, Kig Fah Uiversity of Petroleum
New metho for evaluatig itegrals ivolvig orthogoal polyomials: Laguerre polyomial a Bessel fuctio eample A. D. Alhaiari Shura Coucil, Riyah, Saui Arabia AND Physics Departmet, Kig Fah Uiversity of Petroleum
Taylor Series (BC Only)
 Studet Study Sessio Taylor Series (BC Oly) Taylor series provide a way to fid a polyomial look-alike to a o-polyomial fuctio. This is doe by a specific formula show below (which should be memorized): Taylor
Studet Study Sessio Taylor Series (BC Oly) Taylor series provide a way to fid a polyomial look-alike to a o-polyomial fuctio. This is doe by a specific formula show below (which should be memorized): Taylor
1 Approximating Integrals using Taylor Polynomials
 Seughee Ye Ma 8: Week 7 Nov Week 7 Summary This week, we will lear how we ca approximate itegrals usig Taylor series ad umerical methods. Topics Page Approximatig Itegrals usig Taylor Polyomials. Defiitios................................................
Seughee Ye Ma 8: Week 7 Nov Week 7 Summary This week, we will lear how we ca approximate itegrals usig Taylor series ad umerical methods. Topics Page Approximatig Itegrals usig Taylor Polyomials. Defiitios................................................
The multiplicative structure of finite field and a construction of LRC
 IERG6120 Codig for Distributed Storage Systems Lecture 8-06/10/2016 The multiplicative structure of fiite field ad a costructio of LRC Lecturer: Keeth Shum Scribe: Zhouyi Hu Notatios: We use the otatio
IERG6120 Codig for Distributed Storage Systems Lecture 8-06/10/2016 The multiplicative structure of fiite field ad a costructio of LRC Lecturer: Keeth Shum Scribe: Zhouyi Hu Notatios: We use the otatio
Representing Functions as Power Series. 3 n ...
 Math Fall 7 Lab Represetig Fuctios as Power Series I. Itrouctio I sectio.8 we leare the series c c c c c... () is calle a power series. It is a uctio o whose omai is the set o all or which it coverges.
Math Fall 7 Lab Represetig Fuctios as Power Series I. Itrouctio I sectio.8 we leare the series c c c c c... () is calle a power series. It is a uctio o whose omai is the set o all or which it coverges.
1. n! = n. tion. For example, (n+1)! working with factorials. = (n+1) n (n 1) 2 1
 Biomial Coefficiets ad Permutatios Mii-lecture The followig pages discuss a few special iteger coutig fuctios You may have see some of these before i a basic probability class or elsewhere, but perhaps
Biomial Coefficiets ad Permutatios Mii-lecture The followig pages discuss a few special iteger coutig fuctios You may have see some of these before i a basic probability class or elsewhere, but perhaps
3.3 Rules for Differentiation Calculus. Drum Roll please [In a Deep Announcer Voice] And now the moment YOU VE ALL been waiting for
![3.3 Rules for Differentiation Calculus. Drum Roll please [In a Deep Announcer Voice] And now the moment YOU VE ALL been waiting for 3.3 Rules for Differentiation Calculus. Drum Roll please [In a Deep Announcer Voice] And now the moment YOU VE ALL been waiting for](/thumbs/90/104334191.jpg) . Rules or Dieretiatio Calculus. RULES FOR DIFFERENTIATION Drum Roll please [I a Deep Aoucer Voice] A ow the momet YOU VE ALL bee waitig or Rule #1 Derivative o a Costat Fuctio I c is a costat value, the
. Rules or Dieretiatio Calculus. RULES FOR DIFFERENTIATION Drum Roll please [I a Deep Aoucer Voice] A ow the momet YOU VE ALL bee waitig or Rule #1 Derivative o a Costat Fuctio I c is a costat value, the
Lecture Notes for Analysis Class
 Lecture Notes for Aalysis Class Topological Spaces A topology for a set X is a collectio T of subsets of X such that: (a) X ad the empty set are i T (b) Uios of elemets of T are i T (c) Fiite itersectios
Lecture Notes for Aalysis Class Topological Spaces A topology for a set X is a collectio T of subsets of X such that: (a) X ad the empty set are i T (b) Uios of elemets of T are i T (c) Fiite itersectios
Enumerative & Asymptotic Combinatorics
 C50 Eumerative & Asymptotic Combiatorics Stirlig ad Lagrage Sprig 2003 This sectio of the otes cotais proofs of Stirlig s formula ad the Lagrage Iversio Formula. Stirlig s formula Theorem 1 (Stirlig s
C50 Eumerative & Asymptotic Combiatorics Stirlig ad Lagrage Sprig 2003 This sectio of the otes cotais proofs of Stirlig s formula ad the Lagrage Iversio Formula. Stirlig s formula Theorem 1 (Stirlig s
A Remark on Relationship between Pell Triangle and Zeckendorf Triangle
 Iteratioal Joural of Pure a Applie Mathematics Volume 9 No. 5 8 3357-3364 ISSN: 34-3395 (o-lie versio) url: http://www.acapubl.eu/hub/ http://www.acapubl.eu/hub/ A Remark o Relatioship betwee Pell Triagle
Iteratioal Joural of Pure a Applie Mathematics Volume 9 No. 5 8 3357-3364 ISSN: 34-3395 (o-lie versio) url: http://www.acapubl.eu/hub/ http://www.acapubl.eu/hub/ A Remark o Relatioship betwee Pell Triagle
NUMERICAL METHODS FOR SOLVING EQUATIONS
 Mathematics Revisio Guides Numerical Methods for Solvig Equatios Page 1 of 11 M.K. HOME TUITION Mathematics Revisio Guides Level: GCSE Higher Tier NUMERICAL METHODS FOR SOLVING EQUATIONS Versio:. Date:
Mathematics Revisio Guides Numerical Methods for Solvig Equatios Page 1 of 11 M.K. HOME TUITION Mathematics Revisio Guides Level: GCSE Higher Tier NUMERICAL METHODS FOR SOLVING EQUATIONS Versio:. Date:
SOME TRIBONACCI IDENTITIES
 Mathematics Today Vol.7(Dec-011) 1-9 ISSN 0976-38 Abstract: SOME TRIBONACCI IDENTITIES Shah Devbhadra V. Sir P.T.Sarvajaik College of Sciece, Athwalies, Surat 395001. e-mail : drdvshah@yahoo.com The sequece
Mathematics Today Vol.7(Dec-011) 1-9 ISSN 0976-38 Abstract: SOME TRIBONACCI IDENTITIES Shah Devbhadra V. Sir P.T.Sarvajaik College of Sciece, Athwalies, Surat 395001. e-mail : drdvshah@yahoo.com The sequece
Hoggatt and King [lo] defined a complete sequence of natural numbers
![Hoggatt and King [lo] defined a complete sequence of natural numbers Hoggatt and King [lo] defined a complete sequence of natural numbers](/thumbs/96/128001016.jpg) REPRESENTATIONS OF N AS A SUM OF DISTINCT ELEMENTS FROM SPECIAL SEQUENCES DAVID A. KLARNER, Uiversity of Alberta, Edmoto, Caada 1. INTRODUCTION Let a, I deote a sequece of atural umbers which satisfies
REPRESENTATIONS OF N AS A SUM OF DISTINCT ELEMENTS FROM SPECIAL SEQUENCES DAVID A. KLARNER, Uiversity of Alberta, Edmoto, Caada 1. INTRODUCTION Let a, I deote a sequece of atural umbers which satisfies
Some remarks for codes and lattices over imaginary quadratic
 Some remarks for codes ad lattices over imagiary quadratic fields Toy Shaska Oaklad Uiversity, Rochester, MI, USA. Caleb Shor Wester New Eglad Uiversity, Sprigfield, MA, USA. shaska@oaklad.edu Abstract
Some remarks for codes ad lattices over imagiary quadratic fields Toy Shaska Oaklad Uiversity, Rochester, MI, USA. Caleb Shor Wester New Eglad Uiversity, Sprigfield, MA, USA. shaska@oaklad.edu Abstract
Math 2784 (or 2794W) University of Connecticut
 ORDERS OF GROWTH PAT SMITH Math 2784 (or 2794W) Uiversity of Coecticut Date: Mar. 2, 22. ORDERS OF GROWTH. Itroductio Gaiig a ituitive feel for the relative growth of fuctios is importat if you really
ORDERS OF GROWTH PAT SMITH Math 2784 (or 2794W) Uiversity of Coecticut Date: Mar. 2, 22. ORDERS OF GROWTH. Itroductio Gaiig a ituitive feel for the relative growth of fuctios is importat if you really
Lecture #3. Math tools covered today
 Toay s Program:. Review of previous lecture. QM free particle a particle i a bo. 3. Priciple of spectral ecompositio. 4. Fourth Postulate Math tools covere toay Lecture #3. Lear how to solve separable
Toay s Program:. Review of previous lecture. QM free particle a particle i a bo. 3. Priciple of spectral ecompositio. 4. Fourth Postulate Math tools covere toay Lecture #3. Lear how to solve separable
2.4 - Sequences and Series
 2.4 - Sequeces ad Series Sequeces A sequece is a ordered list of elemets. Defiitio 1 A sequece is a fuctio from a subset of the set of itegers (usually either the set 80, 1, 2, 3,... < or the set 81, 2,
2.4 - Sequeces ad Series Sequeces A sequece is a ordered list of elemets. Defiitio 1 A sequece is a fuctio from a subset of the set of itegers (usually either the set 80, 1, 2, 3,... < or the set 81, 2,
1.3 Convergence Theorems of Fourier Series. k k k k. N N k 1. With this in mind, we state (without proof) the convergence of Fourier series.
 .3 Covergece Theorems of Fourier Series I this sectio, we preset the covergece of Fourier series. A ifiite sum is, by defiitio, a limit of partial sums, that is, a cos( kx) b si( kx) lim a cos( kx) b si(
.3 Covergece Theorems of Fourier Series I this sectio, we preset the covergece of Fourier series. A ifiite sum is, by defiitio, a limit of partial sums, that is, a cos( kx) b si( kx) lim a cos( kx) b si(
Mechatronics II Laboratory Exercise 5 Second Order Response
 Mechatroics II Laboratory Exercise 5 Seco Orer Respose Theoretical Backgrou Seco orer ifferetial equatios approximate the yamic respose of may systems. The respose of a geeric seco orer system ca be see
Mechatroics II Laboratory Exercise 5 Seco Orer Respose Theoretical Backgrou Seco orer ifferetial equatios approximate the yamic respose of may systems. The respose of a geeric seco orer system ca be see
How to Maximize a Function without Really Trying
 How to Maximize a Fuctio without Really Tryig MARK FLANAGAN School of Electrical, Electroic ad Commuicatios Egieerig Uiversity College Dubli We will prove a famous elemetary iequality called The Rearragemet
How to Maximize a Fuctio without Really Tryig MARK FLANAGAN School of Electrical, Electroic ad Commuicatios Egieerig Uiversity College Dubli We will prove a famous elemetary iequality called The Rearragemet
8. Applications To Linear Differential Equations
 8. Applicatios To Liear Differetial Equatios 8.. Itroductio 8.. Review Of Results Cocerig Liear Differetial Equatios Of First Ad Secod Orders 8.3. Eercises 8.4. Liear Differetial Equatios Of Order N 8.5.
8. Applicatios To Liear Differetial Equatios 8.. Itroductio 8.. Review Of Results Cocerig Liear Differetial Equatios Of First Ad Secod Orders 8.3. Eercises 8.4. Liear Differetial Equatios Of Order N 8.5.
Lecture 23 Rearrangement Inequality
 Lecture 23 Rearragemet Iequality Holde Lee 6/4/ The Iequalities We start with a example Suppose there are four boxes cotaiig $0, $20, $50 ad $00 bills, respectively You may take 2 bills from oe box, 3
Lecture 23 Rearragemet Iequality Holde Lee 6/4/ The Iequalities We start with a example Suppose there are four boxes cotaiig $0, $20, $50 ad $00 bills, respectively You may take 2 bills from oe box, 3
Recursive Algorithm for Generating Partitions of an Integer. 1 Preliminary
 Recursive Algorithm for Geeratig Partitios of a Iteger Sug-Hyuk Cha Computer Sciece Departmet, Pace Uiversity 1 Pace Plaza, New York, NY 10038 USA scha@pace.edu Abstract. This article first reviews the
Recursive Algorithm for Geeratig Partitios of a Iteger Sug-Hyuk Cha Computer Sciece Departmet, Pace Uiversity 1 Pace Plaza, New York, NY 10038 USA scha@pace.edu Abstract. This article first reviews the
Bernoulli, Ramanujan, Toeplitz e le matrici triangolari
 Due Giori di Algebra Lieare Numerica www.dima.uige.it/ dibeede/gg/home.html Geova, 6 7 Febbraio Beroulli, Ramauja, Toeplitz e le matrici triagolari Carmie Di Fiore, Fracesco Tudisco, Paolo Zellii Speaker:
Due Giori di Algebra Lieare Numerica www.dima.uige.it/ dibeede/gg/home.html Geova, 6 7 Febbraio Beroulli, Ramauja, Toeplitz e le matrici triagolari Carmie Di Fiore, Fracesco Tudisco, Paolo Zellii Speaker:
Sequences, Mathematical Induction, and Recursion. CSE 2353 Discrete Computational Structures Spring 2018
 CSE 353 Discrete Computatioal Structures Sprig 08 Sequeces, Mathematical Iductio, ad Recursio (Chapter 5, Epp) Note: some course slides adopted from publisher-provided material Overview May mathematical
CSE 353 Discrete Computatioal Structures Sprig 08 Sequeces, Mathematical Iductio, ad Recursio (Chapter 5, Epp) Note: some course slides adopted from publisher-provided material Overview May mathematical
SECTION 1.5 : SUMMATION NOTATION + WORK WITH SEQUENCES
 SECTION 1.5 : SUMMATION NOTATION + WORK WITH SEQUENCES Read Sectio 1.5 (pages 5 9) Overview I Sectio 1.5 we lear to work with summatio otatio ad formulas. We will also itroduce a brief overview of sequeces,
SECTION 1.5 : SUMMATION NOTATION + WORK WITH SEQUENCES Read Sectio 1.5 (pages 5 9) Overview I Sectio 1.5 we lear to work with summatio otatio ad formulas. We will also itroduce a brief overview of sequeces,
Product measures, Tonelli s and Fubini s theorems For use in MAT3400/4400, autumn 2014 Nadia S. Larsen. Version of 13 October 2014.
 Product measures, Toelli s ad Fubii s theorems For use i MAT3400/4400, autum 2014 Nadia S. Larse Versio of 13 October 2014. 1. Costructio of the product measure The purpose of these otes is to preset the
Product measures, Toelli s ad Fubii s theorems For use i MAT3400/4400, autum 2014 Nadia S. Larse Versio of 13 October 2014. 1. Costructio of the product measure The purpose of these otes is to preset the
An enumeration of flags in finite vector spaces
 A eumeratio of flags i fiite vector spaces C Rya Viroot Departmet of Mathematics College of William ad Mary P O Box 8795 Williamsburg VA 23187 viroot@mathwmedu Submitted: Feb 2 2012; Accepted: Ju 27 2012;
A eumeratio of flags i fiite vector spaces C Rya Viroot Departmet of Mathematics College of William ad Mary P O Box 8795 Williamsburg VA 23187 viroot@mathwmedu Submitted: Feb 2 2012; Accepted: Ju 27 2012;
Lecture 4: Grassmannians, Finite and Affine Morphisms
 18.725 Algebraic Geometry I Lecture 4 Lecture 4: Grassmaias, Fiite ad Affie Morphisms Remarks o last time 1. Last time, we proved the Noether ormalizatio lemma: If A is a fiitely geerated k-algebra, the,
18.725 Algebraic Geometry I Lecture 4 Lecture 4: Grassmaias, Fiite ad Affie Morphisms Remarks o last time 1. Last time, we proved the Noether ormalizatio lemma: If A is a fiitely geerated k-algebra, the,
( a) ( ) 1 ( ) 2 ( ) ( ) 3 3 ( ) =!
 .8,.9: Taylor ad Maclauri Series.8. Although we were able to fid power series represetatios for a limited group of fuctios i the previous sectio, it is ot immediately obvious whether ay give fuctio has
.8,.9: Taylor ad Maclauri Series.8. Although we were able to fid power series represetatios for a limited group of fuctios i the previous sectio, it is ot immediately obvious whether ay give fuctio has
De la Vallée Poussin Summability, the Combinatorial Sum 2n 1
 J o u r a l of Mathematics ad Applicatios JMA No 40, pp 5-20 (2017 De la Vallée Poussi Summability, the Combiatorial Sum 1 ( 2 ad the de la Vallée Poussi Meas Expasio Ziad S. Ali Abstract: I this paper
J o u r a l of Mathematics ad Applicatios JMA No 40, pp 5-20 (2017 De la Vallée Poussi Summability, the Combiatorial Sum 1 ( 2 ad the de la Vallée Poussi Meas Expasio Ziad S. Ali Abstract: I this paper
1 Generating functions for balls in boxes
 Math 566 Fall 05 Some otes o geeratig fuctios Give a sequece a 0, a, a,..., a,..., a geeratig fuctio some way of represetig the sequece as a fuctio. There are may ways to do this, with the most commo ways
Math 566 Fall 05 Some otes o geeratig fuctios Give a sequece a 0, a, a,..., a,..., a geeratig fuctio some way of represetig the sequece as a fuctio. There are may ways to do this, with the most commo ways
SOME RELATIONS ON HERMITE MATRIX POLYNOMIALS. Levent Kargin and Veli Kurt
 Mathematical ad Computatioal Applicatios, Vol. 18, No. 3, pp. 33-39, 013 SOME RELATIONS ON HERMITE MATRIX POLYNOMIALS Levet Kargi ad Veli Kurt Departmet of Mathematics, Faculty Sciece, Uiversity of Adeiz
Mathematical ad Computatioal Applicatios, Vol. 18, No. 3, pp. 33-39, 013 SOME RELATIONS ON HERMITE MATRIX POLYNOMIALS Levet Kargi ad Veli Kurt Departmet of Mathematics, Faculty Sciece, Uiversity of Adeiz
A 2nTH ORDER LINEAR DIFFERENCE EQUATION
 A 2TH ORDER LINEAR DIFFERENCE EQUATION Doug Aderso Departmet of Mathematics ad Computer Sciece, Cocordia College Moorhead, MN 56562, USA ABSTRACT: We give a formulatio of geeralized zeros ad (, )-discojugacy
A 2TH ORDER LINEAR DIFFERENCE EQUATION Doug Aderso Departmet of Mathematics ad Computer Sciece, Cocordia College Moorhead, MN 56562, USA ABSTRACT: We give a formulatio of geeralized zeros ad (, )-discojugacy
The Random Walk For Dummies
 The Radom Walk For Dummies Richard A Mote Abstract We look at the priciples goverig the oe-dimesioal discrete radom walk First we review five basic cocepts of probability theory The we cosider the Beroulli
The Radom Walk For Dummies Richard A Mote Abstract We look at the priciples goverig the oe-dimesioal discrete radom walk First we review five basic cocepts of probability theory The we cosider the Beroulli
MAT1026 Calculus II Basic Convergence Tests for Series
 MAT026 Calculus II Basic Covergece Tests for Series Egi MERMUT 202.03.08 Dokuz Eylül Uiversity Faculty of Sciece Departmet of Mathematics İzmir/TURKEY Cotets Mootoe Covergece Theorem 2 2 Series of Real
MAT026 Calculus II Basic Covergece Tests for Series Egi MERMUT 202.03.08 Dokuz Eylül Uiversity Faculty of Sciece Departmet of Mathematics İzmir/TURKEY Cotets Mootoe Covergece Theorem 2 2 Series of Real
Section 7 Fundamentals of Sequences and Series
 ectio Fudametals of equeces ad eries. Defiitio ad examples of sequeces A sequece ca be thought of as a ifiite list of umbers. 0, -, -0, -, -0...,,,,,,. (iii),,,,... Defiitio: A sequece is a fuctio which
ectio Fudametals of equeces ad eries. Defiitio ad examples of sequeces A sequece ca be thought of as a ifiite list of umbers. 0, -, -0, -, -0...,,,,,,. (iii),,,,... Defiitio: A sequece is a fuctio which
Similarity Solutions to Unsteady Pseudoplastic. Flow Near a Moving Wall
 Iteratioal Mathematical Forum, Vol. 9, 04, o. 3, 465-475 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/0.988/imf.04.48 Similarity Solutios to Usteady Pseudoplastic Flow Near a Movig Wall W. Robi Egieerig
Iteratioal Mathematical Forum, Vol. 9, 04, o. 3, 465-475 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/0.988/imf.04.48 Similarity Solutios to Usteady Pseudoplastic Flow Near a Movig Wall W. Robi Egieerig
Math 120 Answers for Homework 23
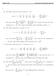 Math 0 Aswers for Homewor. (a) The Taylor series for cos(x) aroud a 0 is cos(x) x! + x4 4! x6 6! + x8 8! x0 0! + ( ) ()! x ( ) π ( ) ad so the series ()! ()! (π) is just the series for cos(x) evaluated
Math 0 Aswers for Homewor. (a) The Taylor series for cos(x) aroud a 0 is cos(x) x! + x4 4! x6 6! + x8 8! x0 0! + ( ) ()! x ( ) π ( ) ad so the series ()! ()! (π) is just the series for cos(x) evaluated
Axioms of Measure Theory
 MATH 532 Axioms of Measure Theory Dr. Neal, WKU I. The Space Throughout the course, we shall let X deote a geeric o-empty set. I geeral, we shall ot assume that ay algebraic structure exists o X so that
MATH 532 Axioms of Measure Theory Dr. Neal, WKU I. The Space Throughout the course, we shall let X deote a geeric o-empty set. I geeral, we shall ot assume that ay algebraic structure exists o X so that
(average number of points per unit length). Note that Equation (9B1) does not depend on the
 EE603 Class Notes 9/25/203 Joh Stesby Appeix 9-B: Raom Poisso Poits As iscusse i Chapter, let (t,t 2 ) eote the umber of Poisso raom poits i the iterval (t, t 2 ]. The quatity (t, t 2 ) is a o-egative-iteger-value
EE603 Class Notes 9/25/203 Joh Stesby Appeix 9-B: Raom Poisso Poits As iscusse i Chapter, let (t,t 2 ) eote the umber of Poisso raom poits i the iterval (t, t 2 ]. The quatity (t, t 2 ) is a o-egative-iteger-value
FLOOR AND ROOF FUNCTION ANALOGS OF THE BELL NUMBERS. H. W. Gould Department of Mathematics, West Virginia University, Morgantown, WV 26506, USA
 INTEGERS: ELECTRONIC JOURNAL OF COMBINATORIAL NUMBER THEORY 7 (2007), #A58 FLOOR AND ROOF FUNCTION ANALOGS OF THE BELL NUMBERS H. W. Gould Departmet of Mathematics, West Virgiia Uiversity, Morgatow, WV
INTEGERS: ELECTRONIC JOURNAL OF COMBINATORIAL NUMBER THEORY 7 (2007), #A58 FLOOR AND ROOF FUNCTION ANALOGS OF THE BELL NUMBERS H. W. Gould Departmet of Mathematics, West Virgiia Uiversity, Morgatow, WV
Structural Functionality as a Fundamental Property of Boolean Algebra and Base for Its Real-Valued Realizations
 Structural Fuctioality as a Fudametal Property of Boolea Algebra ad Base for Its Real-Valued Realizatios Draga G. Radojević Uiversity of Belgrade, Istitute Mihajlo Pupi, Belgrade draga.radojevic@pupi.rs
Structural Fuctioality as a Fudametal Property of Boolea Algebra ad Base for Its Real-Valued Realizatios Draga G. Radojević Uiversity of Belgrade, Istitute Mihajlo Pupi, Belgrade draga.radojevic@pupi.rs
Most text will write ordinary derivatives using either Leibniz notation 2 3. y + 5y= e and y y. xx tt t
 Itroductio to Differetial Equatios Defiitios ad Termiolog Differetial Equatio: A equatio cotaiig the derivatives of oe or more depedet variables, with respect to oe or more idepedet variables, is said
Itroductio to Differetial Equatios Defiitios ad Termiolog Differetial Equatio: A equatio cotaiig the derivatives of oe or more depedet variables, with respect to oe or more idepedet variables, is said
ON POINTWISE BINOMIAL APPROXIMATION
 Iteratioal Joural of Pure ad Applied Mathematics Volume 71 No. 1 2011, 57-66 ON POINTWISE BINOMIAL APPROXIMATION BY w-functions K. Teerapabolar 1, P. Wogkasem 2 Departmet of Mathematics Faculty of Sciece
Iteratioal Joural of Pure ad Applied Mathematics Volume 71 No. 1 2011, 57-66 ON POINTWISE BINOMIAL APPROXIMATION BY w-functions K. Teerapabolar 1, P. Wogkasem 2 Departmet of Mathematics Faculty of Sciece
Discrete-Time Systems, LTI Systems, and Discrete-Time Convolution
 EEL5: Discrete-Time Sigals ad Systems. Itroductio I this set of otes, we begi our mathematical treatmet of discrete-time s. As show i Figure, a discrete-time operates or trasforms some iput sequece x [
EEL5: Discrete-Time Sigals ad Systems. Itroductio I this set of otes, we begi our mathematical treatmet of discrete-time s. As show i Figure, a discrete-time operates or trasforms some iput sequece x [
IT is well known that Brouwer s fixed point theorem can
 IAENG Iteratioal Joural of Applied Mathematics, 4:, IJAM_4 0 Costructive Proof of Brouwer s Fixed Poit Theorem for Sequetially Locally No-costat ad Uiformly Sequetially Cotiuous Fuctios Yasuhito Taaka,
IAENG Iteratioal Joural of Applied Mathematics, 4:, IJAM_4 0 Costructive Proof of Brouwer s Fixed Poit Theorem for Sequetially Locally No-costat ad Uiformly Sequetially Cotiuous Fuctios Yasuhito Taaka,
Generating Functions. 1 Operations on generating functions
 Geeratig Fuctios The geeratig fuctio for a sequece a 0, a,..., a,... is defied to be the power series fx a x. 0 We say that a 0, a,... is the sequece geerated by fx ad a is the coefficiet of x. Example
Geeratig Fuctios The geeratig fuctio for a sequece a 0, a,..., a,... is defied to be the power series fx a x. 0 We say that a 0, a,... is the sequece geerated by fx ad a is the coefficiet of x. Example
LONG SNAKES IN POWERS OF THE COMPLETE GRAPH WITH AN ODD NUMBER OF VERTICES
 J Lodo Math Soc (2 50, (1994, 465 476 LONG SNAKES IN POWERS OF THE COMPLETE GRAPH WITH AN ODD NUMBER OF VERTICES Jerzy Wojciechowski Abstract I [5] Abbott ad Katchalski ask if there exists a costat c >
J Lodo Math Soc (2 50, (1994, 465 476 LONG SNAKES IN POWERS OF THE COMPLETE GRAPH WITH AN ODD NUMBER OF VERTICES Jerzy Wojciechowski Abstract I [5] Abbott ad Katchalski ask if there exists a costat c >
CALCULATION OF FIBONACCI VECTORS
 CALCULATION OF FIBONACCI VECTORS Stuart D. Aderso Departmet of Physics, Ithaca College 953 Daby Road, Ithaca NY 14850, USA email: saderso@ithaca.edu ad Dai Novak Departmet of Mathematics, Ithaca College
CALCULATION OF FIBONACCI VECTORS Stuart D. Aderso Departmet of Physics, Ithaca College 953 Daby Road, Ithaca NY 14850, USA email: saderso@ithaca.edu ad Dai Novak Departmet of Mathematics, Ithaca College
ACCELERATING CONVERGENCE OF SERIES
 ACCELERATIG COVERGECE OF SERIES KEITH CORAD. Itroductio A ifiite series is the limit of its partial sums. However, it may take a large umber of terms to get eve a few correct digits for the series from
ACCELERATIG COVERGECE OF SERIES KEITH CORAD. Itroductio A ifiite series is the limit of its partial sums. However, it may take a large umber of terms to get eve a few correct digits for the series from
A symmetrical Eulerian identity
 Joural of Combiatorics Volume 17, Number 1, 29 38, 2010 A symmetrical Euleria idetity Fa Chug, Ro Graham ad Do Kuth We give three proofs for the followig symmetrical idetity ivolvig biomial coefficiets
Joural of Combiatorics Volume 17, Number 1, 29 38, 2010 A symmetrical Euleria idetity Fa Chug, Ro Graham ad Do Kuth We give three proofs for the followig symmetrical idetity ivolvig biomial coefficiets
P. Z. Chinn Department of Mathematics, Humboldt State University, Arcata, CA
 RISES, LEVELS, DROPS AND + SIGNS IN COMPOSITIONS: EXTENSIONS OF A PAPER BY ALLADI AND HOGGATT S. Heubach Departmet of Mathematics, Califoria State Uiversity Los Ageles 55 State Uiversity Drive, Los Ageles,
RISES, LEVELS, DROPS AND + SIGNS IN COMPOSITIONS: EXTENSIONS OF A PAPER BY ALLADI AND HOGGATT S. Heubach Departmet of Mathematics, Califoria State Uiversity Los Ageles 55 State Uiversity Drive, Los Ageles,
Parallel Vector Algorithms David A. Padua
 Parallel Vector Algorithms 1 of 32 Itroductio Next, we study several algorithms where parallelism ca be easily expressed i terms of array operatios. We will use Fortra 90 to represet these algorithms.
Parallel Vector Algorithms 1 of 32 Itroductio Next, we study several algorithms where parallelism ca be easily expressed i terms of array operatios. We will use Fortra 90 to represet these algorithms.
Optimally Sparse SVMs
 A. Proof of Lemma 3. We here prove a lower boud o the umber of support vectors to achieve geeralizatio bouds of the form which we cosider. Importatly, this result holds ot oly for liear classifiers, but
A. Proof of Lemma 3. We here prove a lower boud o the umber of support vectors to achieve geeralizatio bouds of the form which we cosider. Importatly, this result holds ot oly for liear classifiers, but
Problem Cosider the curve give parametrically as x = si t ad y = + cos t for» t» ß: (a) Describe the path this traverses: Where does it start (whe t =
 Mathematics Summer Wilso Fial Exam August 8, ANSWERS Problem 1 (a) Fid the solutio to y +x y = e x x that satisfies y() = 5 : This is already i the form we used for a first order liear differetial equatio,
Mathematics Summer Wilso Fial Exam August 8, ANSWERS Problem 1 (a) Fid the solutio to y +x y = e x x that satisfies y() = 5 : This is already i the form we used for a first order liear differetial equatio,
3.2 Properties of Division 3.3 Zeros of Polynomials 3.4 Complex and Rational Zeros of Polynomials
 Math 60 www.timetodare.com 3. Properties of Divisio 3.3 Zeros of Polyomials 3.4 Complex ad Ratioal Zeros of Polyomials I these sectios we will study polyomials algebraically. Most of our work will be cocered
Math 60 www.timetodare.com 3. Properties of Divisio 3.3 Zeros of Polyomials 3.4 Complex ad Ratioal Zeros of Polyomials I these sectios we will study polyomials algebraically. Most of our work will be cocered
[ 11 ] z of degree 2 as both degree 2 each. The degree of a polynomial in n variables is the maximum of the degrees of its terms.
![[ 11 ] z of degree 2 as both degree 2 each. The degree of a polynomial in n variables is the maximum of the degrees of its terms. [ 11 ] z of degree 2 as both degree 2 each. The degree of a polynomial in n variables is the maximum of the degrees of its terms.](/thumbs/82/84777652.jpg) [ 11 ] 1 1.1 Polyomial Fuctios 1 Algebra Ay fuctio f ( x) ax a1x... a1x a0 is a polyomial fuctio if ai ( i 0,1,,,..., ) is a costat which belogs to the set of real umbers ad the idices,, 1,...,1 are atural
[ 11 ] 1 1.1 Polyomial Fuctios 1 Algebra Ay fuctio f ( x) ax a1x... a1x a0 is a polyomial fuctio if ai ( i 0,1,,,..., ) is a costat which belogs to the set of real umbers ad the idices,, 1,...,1 are atural
Sequences of Definite Integrals, Factorials and Double Factorials
 47 6 Joural of Iteger Sequeces, Vol. 8 (5), Article 5.4.6 Sequeces of Defiite Itegrals, Factorials ad Double Factorials Thierry Daa-Picard Departmet of Applied Mathematics Jerusalem College of Techology
47 6 Joural of Iteger Sequeces, Vol. 8 (5), Article 5.4.6 Sequeces of Defiite Itegrals, Factorials ad Double Factorials Thierry Daa-Picard Departmet of Applied Mathematics Jerusalem College of Techology
arxiv: v1 [math.nt] 10 Dec 2014
![arxiv: v1 [math.nt] 10 Dec 2014 arxiv: v1 [math.nt] 10 Dec 2014](/thumbs/82/85433827.jpg) A DIGITAL BINOMIAL THEOREM HIEU D. NGUYEN arxiv:42.38v [math.nt] 0 Dec 204 Abstract. We preset a triagle of coectios betwee the Sierpisi triagle, the sum-of-digits fuctio, ad the Biomial Theorem via a
A DIGITAL BINOMIAL THEOREM HIEU D. NGUYEN arxiv:42.38v [math.nt] 0 Dec 204 Abstract. We preset a triagle of coectios betwee the Sierpisi triagle, the sum-of-digits fuctio, ad the Biomial Theorem via a
If a subset E of R contains no open interval, is it of zero measure? For instance, is the set of irrationals in [0, 1] is of measure zero?
![If a subset E of R contains no open interval, is it of zero measure? For instance, is the set of irrationals in [0, 1] is of measure zero? If a subset E of R contains no open interval, is it of zero measure? For instance, is the set of irrationals in [0, 1] is of measure zero?](/thumbs/89/99848926.jpg) 2 Lebesgue Measure I Chapter 1 we defied the cocept of a set of measure zero, ad we have observed that every coutable set is of measure zero. Here are some atural questios: If a subset E of R cotais a
2 Lebesgue Measure I Chapter 1 we defied the cocept of a set of measure zero, ad we have observed that every coutable set is of measure zero. Here are some atural questios: If a subset E of R cotais a
You may work in pairs or purely individually for this assignment.
 CS 04 Problem Solvig i Computer Sciece OOC Assigmet 6: Recurreces You may work i pairs or purely idividually for this assigmet. Prepare your aswers to the followig questios i a plai ASCII text file or
CS 04 Problem Solvig i Computer Sciece OOC Assigmet 6: Recurreces You may work i pairs or purely idividually for this assigmet. Prepare your aswers to the followig questios i a plai ASCII text file or
