arxiv:quant-ph/ v3 3 Mar 2003
|
|
|
- Grace Benson
- 6 years ago
- Views:
Transcription
1 An Arbitrary Two-qubit Computation In 3 Elementary Gates arxiv:quant-ph/11v3 3 Mar 3 Stephen S. Bullock and Igor L. Markov stephnsb@umich.edu imarkov@eecs.umich.edu February 1, 8 Abstract Quantum circuits currently constitute a dominant model for quantum computation [14]. Our work addresses the problem of constructing quantum circuits to implement an arbitrary given quantum computation, in the special case of two qubits. We pursue circuits without ancilla qubits and as small a number of elementary quantum gates [1, 15] as possible. Our lower bound for worst-case optimal two-qubit circuits calls for at least 17 gates: 15 one-qubit rotations and CNOTs. To this end, we constructively prove a worst-case upper bound of 3 elementary gates, of which at most 4 (CNOTs entail multi-qubit interactions. Our analysis shows that synthesis algorithms suggested in previous work, although more general, entail much larger quantum circuits than ours in the special case of two qubits. One such algorithm [5] has a worst case of 61 gates of which 18 may be CNOTs. Our techniques rely on the KAK decomposition from Lie theory as well as the polar and spectral (symmetric Shur matrix decompositions from numerical analysis and operator theory. They are related to the canonical decomposition of a two-qubit gate with respect to the magic basis of phase-shifted Bell states [1, 13]. We further extend this decomposition in terms of elementary gates for quantum computation. Contents 1 Introduction Notation and Background 3.1 Quantum circuits and elementary gates for quantum computation Circuits for diagonal unitaries Matrix Decompositions and Prior Work Quantum circuit synthesis via the QR decomposition Other matrix decompositions: SVD, polar, symmetric Shur (spectral and KAK The Entangler Gate SU( SU( = SO(4 via the magic basis Definition and properties of E An Arbitrary Two-qubit Computation in 3 Elementary Gates or Less Decomposition algorithm The overall gate decomposition and gate counts Examples Gate Counts Versus Degrees of Freedom: Lower and Upper Bounds 16 7 Conclusions and On-going Work 18 Partially supported by the University of Michigan Mathematics department VIGRE summer stipend and the DARPA QuIST program. The views and conclusions contained herein are those of the authors and should not be interpreted as necessarily representing official policies of endorsements, either expressed or implied, of respective funding institutions. 1
2 1 Introduction Quantum computations can be described by unitary matrices [14]. In order to effect a quantum computation on a quantum computer, one must decompose such a matrix into a quantum circuit, which consists of elementary quantum gates [1] connected by Kronecker (tensor and matrix products. Those connections are often represented using quantum circuit schematics. In some cases circuit decompositions require temporarily increasing the dimension of the underlying Hilbert space, which is represented by temporary storage lines. Since there is always a multitude of valid circuit decompositions, one typically prefers those with fewer gates. Algorithms for classical logic circuit synthesis [8] read a Boolean function and output a circuit that implements the function using gates from a given gate library. By analogy, we can talk about quantum circuit synthesis. In this work we only discuss purely classical algorithms for such synthesis problems. Even at this early stage of quantum computing, it seems clear that algorithms for circuit synthesis are going to be as important in quantum computing as they are in classical Electronic Design Automation, where commercial circuit synthesis tools are necessary for the design of cellular phones, game consoles and networking chips. If a Boolean function is given by its truth table, then a two-level circuit, linear in the size of the truth table, can be constructed immediately. Thus, it is the optimization of the circuit structure that makes classical circuit synthesis interesting. Given a unitary matrix, it is not nearly as easy to find a quantum circuit that implements it. Generic algorithms for this problem are known [16, 5], but in some cases produce very large circuits even when small circuits are possible. We hope that additional optimizations are possible. Importantly, the work in [16] suggests that generic circuit decompositions can be found by means of solving a series of specialized synthesis problems, e.g., the synthesis of circuits consisting of NOT, CNOT and TOFFOLI gates as well as phase-shift circuits. Such specialized synthesis problems are addressed by other researchers [1, 15, 17]. A recent work [1] on time-optimal control of spin systems presents a holistic view of circuit-related optimizations, which is based on the Lie group theory. However, their approach is not as detailed as previously published circuit synthesis algorithms, and comparisons in terms of gate counts are not straightforward. Our work can be compared to the GQC quantum compiler [7, 3] available online. 1 That program inputs a 4 4 unitary U and returns a canonical decomposition which is not, in a strict sense, a circuit in terms of elementary gates. It also returns a circuit that computes CNOT using U and one-qubit gates. When U is used only once, this easily yields a circuit decomposition of U in terms of elementary gates. However, it appears that not all input matrices can be processed successfully. Our work pursues generic circuit decompositions [1, 5] of two-qubit quantum computations up to global phase. While some authors consider arbitrary one-qubit gates elementary, we recall that they can be decomposed, up to phase, into a product of one-parametric rotations according to Equation 3. Therefore we only view the necessary one-parametric rotations as elementary. Some of our results (constructive upper bounds in terms of such elementary gates can be reformulated in terms of coarser elementary gates. We also observe that the standard choice of elementary logic gates in classical computing (AND-OR-NOT was suggested in the XIX th century by Boole for abstract reasons rather than based on specific technologies. Today the AND gate is by far not the simplest to implement in CMOS-based integrated circuits. This fact is addressed by commercial circuit synthesis tools by decoupling library-less logic synthesis from technology-mapping [8]. The former uses an abstract gate library, such as AND-OR-NOT and emphasizes the scalability of synthesis algorithms that capture the global structure of the given computation. The latter step maps logic circuits to a technology-specific gate library, often supplied by a semiconductor manufacturer, and is based on local optimizations. Technology-specific libraries may contain composite multi-input gates with optimized layouts such as the AOI gate (AND/OR/INVERTER. To this end, our algorithms are analogous to library-less logic synthesis. 1 We point out that the term compiler in classical computing means translator from a high-level description to a register-transfer level (RTL description, e.g., machine codes. The task of producing circuits with given function is commonly referred to as circuit synthesis. In this context, digital circuits are called logic circuits. 1 3 As of March 3, the quantum compiler [7] fails on exp i The authors are working on a bugfix and expect that the problem lies in the code rather than the method.
3 Gate library. We consider the following library of elementary one- and two-qubit gates: ( cosθ/ sin θ/ R y (θ = for all θ < π; sin θ/ cosθ/ ( e iα/ R z (α = e iα/ for all α < π; The CNOT gate, conditioned on either line. A given gate may, in principle, be applied to different lines. We do not restrict to which lines the above gates may be applied. Note that the gate library we use generates U(4 up to global phase [5]. In order to find gate decompositions, we use the Lie-group techniques from [1]. The resulting procedure is often superior to previously published generic algorithms [16, 5] in terms of the size of synthesized circuits. Theorem 1.1 Up to global phase, any two qubit computation may be realized exactly by at most twenty-three elementary gates, of which at most four are CNOTs. No ancilla qubits are required. We do not know whether this result is optimal, but show that at least seventeen elementary gates are required. The remaining part of the paper is organized as follows. Section covers the necessary background on quantum circuits and elementary gates for quantum computation [1]. Relevant matrix decompositions and prior work on circuit synthesis are described in Section 3, including a related algorithm to decompose unitary matrices into elementary gates [5]. Section 4 introduces the magic basis from [13], as well as the associated entangler and disentangler gates. In Section 5, we present a generic decomposition of an arbitrary two-qubit quantum computation into 3 elementary gates or less using the KAK decomposition from Lie theory. We also give several examples. Lower bounds are discussed in Section 6, followed by conclusions and ongoing work in Section 7. Notation and Background GL( k = {M ( k k -matrices det(m }. For M GL( n, we consider its adjoint matrix M, produced from the transpose M t by conjugating each matrix element. M is called Hermitian (synonym: self-adjoint iff M = M. Hermitian matrices generalize symmetric real-valued matrices. Quantum states and quantum circuits are governed by the laws of quantum mechanics: k-qubit states are k - dimensional vectors, i.e., complex linear combinations of -1 bit-strings of length k. A quantum computation acting on k qubits (k inputs and k outputs is modelled by a unitary k k -matrix [14]. We denote such matrices by U( k = {M ( k k -matrices MM = 1}. O( k represents those matrices from U( k with real entries. SU( k and SO( k are the respective subsets with determinant one. Below, we will consider two generic elements of SU(: A = αe 11 + ( βe 1 + βe 1 + ᾱe and B = γe 11 +( δe 1 + δe 1 + γe with 1 = α + β = γ + δ. Such a parameterization of SU( can be verified directly. We largely ignore the effects of quantum measurement that is typically performed after a quantum circuit is applied, but we use the fact that any measurement is invariant under a global phase change. In mathematical terms, this means that any computation in U( k can be represented in normalized form by a matrix from SU( k..1 Quantum circuits and elementary gates for quantum computation In our work, we only discuss combinational quantum circuits, which are directed acyclic graphs where every vertex represents a gate. An output of a gate can be connected to exactly one input of another gate or one circuit output. A similar restriction applies to gate inputs (see examples of quantum circuits in Figures 1 and. Following [1, 15], we attempt to express arbitrary computations using as small numbers of elementary gates as possible. In order to write matrix elements of particular gates, we order the elements of the computational basis lexicographically [14]. The computation implemented by several gates acting independently on different qubits can be described by the Kronecker (tensor product of their matrices. In the usual computational basis 3
4 , 1, 1, 11 ordered in the dictionary order, the matrix in U(4 representing A B (for A and B defined above will then be ( αb βb (A B = (1 βb ᾱb Composition of multiple quantum computations is described by the matrix product. However, as most circuit diagrams are read left-to-right, the order in respective matrix expressions is reversed. For example, the expression (A B(C D corresponds to a two-qubit circuit where C acts on the top line and D on the bottom line, followed by A acting on the top line and B on the bottom line. Since the two lines do not interact, the same computation is performed by AC acting on the top line and BD acting on the bottom line independently, i.e., (A B(C D = (AC BD. Sometimes this identity allows one to simplify quantum circuits and reduce their gate counts. We distinguish two versions of the CNOT gate, topcnot and botcnot conditioned on the top and bottom lines respectively: (i botcnot exchanges 1 11, i.e. CNOT controlled by the top line, and (ii topcnot exchanges Those gates can be represented by matrices: topcnot = botcnot = ( An arbitrary one-qubit quantum computation can be implemented, up to phase, by three elementary gates. This is due to [1, Lemma 4.1], which decomposes an arbitrary unitary into ( e iδ U = e iδ ( e iα/ e iα/ ( cosθ/ sinθ/ sinθ/ cosθ/ ( e iβ/ e iβ/ (3 To recover the non-δ parameters, we divide U by its determinant. The resulting matrix Ũ has δ =, and ( ( Ũ t 1 e Ũ = iβ sinθ cosθ 1 cosθ e iβ sinθ (4 We routinely ignore global phase because it does not affect the result of quantum measurement, which is the last step in quantum algorithms. A particular one-qubit computation, the Hadamard gate H, can be implemented, up to global phase, using two elementary gates as follows: H = ( = ( i i ( i i ( Similarly, the NOT gate (also known as Pauli-X requires two elementary gates, up to a global phase: ( ( ( ( 1 i 1 i X =NOT = =. (6 1 i 1 i. Circuits for diagonal unitaries For a diagonal matrix D U(4, we have D = diag(z 1,z,z 3,z 4 with z i z i = 1,i = The coordinates or their product can be normalized by choosing the global phase. In contrast, the quantity z 1 z 1 z 1 3 z 4 is invariant. Proposition.1 i A diagonal matrix D = diag(z 1,z,z 3,z 4 in U(4 may be written as a tensor product of diagonal elements of U( iff z 1 z 1 z 1 3 z 4 = 1. ii Any gate which is diagonal when written in the computation basis may be implemented up to phase in five elementary gates or less. (5 4
5 W R z R z Figure 1: Any 4 4 diagonal unitary D = diag(z 1,z,z 3,z 4 may be decomposed into up to five elementary gates. We set e iφ = z 1 z 1 z 1 3 z 4 and define W = diag(e iφ/4,e iφ/4. The two one-qubit unitaries on the right are diagonal. Since the inverse of a diagonal matrix is also diagonal, the form of this circuit can be reversed for any given matrix. Proof: i The forward implication follows from diag(η 1,η diag(η 3,η 4 = diag(η 1 η 3,η 1 η 4,η η 3,η η 4. For the reverse implication, rewrite that as diag(e iθ 1,e iθ diag(e iθ 3,e iθ 4 = diag(e i(θ 1+θ 3,e i(θ 1+θ 4,e i(θ +θ 3,e i(θ +θ 4 If we are given the four diagonal entries z 1...z 4 and wish to find θ, this can be achieved by taking logarithms of z k and solving the resulting linear system in terms of θ 1,...,θ 4. The matrix of this 4 4 system is degenerate and has rank 3. However, the constraint z 1 z 1 z 1 3 z 4 = 1 ensures that the system has a unique solution. ii Consider the computation of Figure 1. For a fixed D = diag(z 1,z,z 3,z 4, put e iφ = z 1 z 1 z 1 3 z 4. Now note the leftmost three gates enact e iφ/4 1 e iφ/4 1 1 e iφ/4 11 e iφ/4 Thus by Equation 7 and part one of the present proposition, the difference between D and the leftmost three gates is a pair of single elementary gates which are diagonal elements of U(1 U(1 on each line. (7 3 Matrix Decompositions and Prior Work As shown above, quantum circuits can be modelled by matrix formulas that decompose the overall computation (one large unitary matrix into matrix products and tensor products of elementary gates (smaller unitary matrices. This suggests the use of matrix decomposition theorems from numerical analysis and Lie theory. Below, we revisit only decompositions relevant to our work: SVD, polar, symmetric Shur (spectral, QR [1] and KAK [11]. Additionally, (i a block- version of the SVD called the CS decomposition [1, pp.77-79] was used for circuit synthesis in [16], and (ii the LU decomposition [1] was used to analyze CNOT-based circuits in []. Most of those decompositions can be computed with existing softare LAPACK, downloadable from Quantum circuit synthesis via the QR decomposition The unitary matrix of a quantum computation can be analogized with the truth table of a classical logic circuit. Logic minimization aside, it is trivial to come up with a classical AND-OR-NOT circuit implementing a given truth table. Each line of the truth table is implemented using AND and NOT gates, then all lines are connected by OR gates. The algorithm proposed in [5] solves a quantum version of this task. 3 The algorithm relies on the theorem from numerical analysis, saying that an arbitrary matrix can be decomposed into a product of a unitary matrix Q and an upper triangular matrix R, not necessarily square [1]. We 3 We note that the work in [5] to a large extent relies on results in [1]. 5
6 are going to apply this theorem to unitary matrices, which makes R diagonal. The canonical algorithm for QRdecomposition is similar to the classical triangulation by row subtractions in that it zeroes out matrix elements one by one. Since elementary row operations are typically not unitary, one instead applies a specially calculated element of U( to a pair of rows so as to zero out a particular matrix element. Such matrices are known as Givens rotations and can be viewed as gates (not yet elementary in a quantum circuit for Q. This suggests that we find a decomposition for the remaining diagonal component R. Circuits for diagonal matrices are not explicitly addressed in [5], but are the subject of the work in [9]. The -qubit case addressed in the previous subsection is sufficient for further developments below. Since each Givens rotation is a non-trivial two-qubit matrix, it should be further decomposed into elementary gates. In the generic case, the algorithm from [5] entails one Givens rotation to nullify each matrix entry below the diagonal. Thus, a generic 4 4 unitary representing a -qubit computation will decompose into six Givens rotations, each uniquely determined. The first rotation (G 3,4 in [5] is between the states 1 and 11 whose indices corresponds to the last two rows of the matrix. This rotation can be thought of as a generic 1-qubit rotation on the second qubit, controlled by the first qubit. The work in [1, 5] shows that such a controlled rotationtopc V can be implemented using eight elementary gates from the same gate library that we use. Namely, decompose V according to Equation 3 and use the parameters δ, α, θ and β to define matrices ( e iα/ A = e iα/ ( cos( θ/4 sin( θ/4 B = sin( θ/4 cos( θ/4 ( cos(θ/4 sin(θ/4 sin(θ/4 cos(θ/4 ( e i(α β/4 C = e i(α β/4 ( 1 D = e iδ ( e i(α+β/4 e i(α+β/4 One can verify that ABC = I and ATBTC = V/det(V = Ṽ. Therefore topc V = (D 1 (1 A topcnot (1 B topcnot (1 C. This decomposition is illustrated in Figure 3 and implies 8 elementary gates because A and B require two each. The next Givens rotation (G,3 is between states 1 and 1. It is not a controlled one-qubit rotation and thus more difficult to implement. The remaining Givens rotations are between and 1 (G 1,, 1 and 11 (G 3,4, 1 and 1 (G,3 as well as 1 and 11 (G 3,4. Four out of six are one-qubit rotations controlled by the top line the most significant qubit. To perform accurate gate counts in the -qubit case, we first observe that an arbitrary -qubit diagonal matrix can be implemented in five gates via Proposition.1. Of those five two are CNOTs. The remaining effort is to count gates in the six Givens rotations. Following [1, 5], let topc-v be any V U( controlled on the top line and acting on the second. Then viewing a 4 4 matrix as block-, we obtain ( ( 1 V topc-v = and (X 1 topc-v (X 1 = (1 V 1 Observe that topc-v implements G 3,4 and, according to Figure 3, costs eight gates, of which two are CNOTs. As shown in Equation 6, inverters cost two elementary gates each. Therefore the rotation G 1,, implemented as above, costs twelve gates. (8 (9 (1 (11 6
7 With being a two-column-high zero vector, the rotation G,3 can be implemented as 1 t botcnot topc (XVX botcnot = V t 1 (13 The computationtopc (XVX considered astopc Ṽ takes eight elementary gates, and thus G,3 can be implemented in ten elementary gates, of which four are CNOTs. In the generic case, the algorithm from [5] is going to use three G 3,4 Givens rotations totalling 4 elementary gates of which 6 are CNOTs, two G,3 Givens rotations totalling elementary gates of which 8 are CNOTs and one G 1, Givens rotation which counts for 1 elementary gates including CNOTs. Additionally, we use 5 elementary gates (of which are CNOTs to implement the diagonal R via Proposition.1. Thus, 61 gates will be required in the generic (worst case, and 18 of those will be CNOTs. 3. Other matrix decompositions: SVD, polar, symmetric Shur (spectral and KAK Golub and Van Loan [1, p. 73] define the Singular-Value Decomposition (SVD for complex matrices as follows: Definition 3.1 If M C m n, then there exist unitary matrices U C m m and V C n n such that U MV = diag(σ 1,...,σ p R m n p = min{m,n} where the σ i are singular values and σ 1 σ... σ p. For real-valued M, U and V must be orthogonal. In this work we are only interested in the case m = n, moreover, n is typically a power of two. Definition 3. The polar decomposition of M is M = PZ, where Z is unitary and P is Hermitian. This can be derived from the SVD as follows [1, p. 149]. If M = U V, then M = (U U (UV = PZ. This decomposition is analogous to the factorization of complex numbers z = e iarg(z z and intuitively similar to writing any complex n n matrix as a sum of a Hermitian and skew-hermitian matrices, in terms of matrix elements: m i j = (m i j +m ji /+(m i j m ji /. Skew-Hermitian matrices exponentiate to unitaries, and Hermitian matrices exponentiate to Hermitian. However, in general exp(xy exp(xexp(y unless XY = Y X, and polar decompositions cannot be computed by exponentiation. On the positive side, given an explicit M, P can be computed as MM, and a possible P can be found via matrix squareroot. In our work, we need a more refined version of the polar decomposition known from Lie theory [11]. The term unitary polar in the following definition is ours. Definition 3.3 The unitary polar decomposition of M U(n is M = PZ, where Z SO(n and P = P t. Since Z and M are unitary, so is P, demanding P 1 = P. Definition 3.4 The symmetric Shur decomposition [1, p. 393], also known as the spectral theorem to operator theorists, states that M = O O t where M is a real-valued symmetric n n-matrix, is diagonal and O SO(n. For a complex-valued Hermitian M, the matrix O will have to be in SU(n. The symmetric Shur (spectral decomposition can be interpreted as choosing a basis in which M is diagonal. Since such a basis must consist of eigenvectors, the columns of O list eigenvectors of M in the initial basis and lists eigenvalues in the corresponding order. Proposition 3.5 The following mild two-step generalization of the spectral theorem holds: 1. A,B, symmetric real n n matrices with AB = BA, O SO(n such that OAO t and OBO t are diagonal; 7
8 . P U(n with P = P t, O SO(n such that P = O O t, where is diagonal with norm-one entries. Proof: 1. It suffices to construct a basis which is simultaneously a basis of eigenvectors for both A and B. Thus, say V λ is the λ eigenspace of B. For v V λ, B(Av = A(Bv = λav, i.e. v Av preserves the eigenspace. Now find eigenvectors for A restricted to V λ, which remains symmetric.. Consider the real and imaginary parts of P = A+iB. Now 1 = PP = P P = (A+iB(A ib = (A + B + i(ba AB. Since the imaginary part of 1 is, we conclude that AB = BA. The result follows from part 1. The unitary polar decomposition and Proposition 3.5 can be combined to produce the following variant of the SV D for unitary matrices. Suppose U = PZ by the unitary polar decomposition. Apply Proposition 3.5 to P and write U = PZ = O (O t Z = V W where V,W O(n. Now multiply the first column of V and the first entry of by det(v, and then multiply the first row of W and the first entry of by det(w. Thus we obtain V,W SO(n. Definition 3.6 The normalized unitary KAK decomposition of M U(n is M = V W, where V,W SO(n and U(n is diagonal. A related claim in terms of matrix groups is U(n = KAK, where K = O(n and A is the group of diagonal unitary matrices of determinant one. The term Lie theory, in its modern use, refers to the mathematical theory of continuous matrix groups. Rather than study individual matrices, as is common in numerical analysis, Lie theory studies collective behavior of various types of matrices and often extends constructions from the group GL(n to its continuous subgroups such as O(n and U(n. The KAK decomposition is a far-reaching generalization of the SVD and dates back to the origins of Lie theory in the 19s. Knapp [11, p.58] attributes it to Cartan [4]. The KAK decomposition of a reductive Lie group G entails G = KAK where K is a maximal proper compact subgroup and A is a torus. A torus is a connected Abelian group closed in G, and always a product of copies of the multiplicative group (, and U(1. The SVD decomposition can be seen as a special case with G = GL(n,C, K = U(n and the torus being the group of n n diagonal matrices with positive real entries. In our work, we use another special case of the KAK decomposition with G = U(n, K = O(n and the torus being the group of n n diagonal unitary matrices. Section 4.1 shows a surprising interpretation of O(4 in terms of one-qubit gates. 4 The Entangler Gate The entangler gate maps the computational basis into the magic basis, which we introduce below. Together with its inverse the disentangler the entangler gate is useful for breaking down arbitrary two-qubit computations into elementary gates. With such uses in mind, we implement the entangler and disentangler by elementary gates. 4.1 SU( SU( = SO(4 via the magic basis The magic basis [13] provides an elegant way of thinking about tensor products of one-qubit gates. 4 4 Stated in terms of the Lie algebra of U(4, this involves the isomorphism u( u( = o(4 [11, p. 37]. 8
9 S H Figure : Implementing E by elementary gates. Here S = diag(1, i counts as one elementary gate and the Hadamard gate H counts as two. Definition 4.1 The magic basis of phase shifted Bell states is given by m1 = ( + 11 / m = (i i 11 / m3 = (i 1 +i 1 / m4 = ( 1 1 / (14 Note that each is maximally entangled, and the Arabic numbers are indices rather than energy states. Via a startling and omitted direct computation, the matrix coefficients of A B (in the notation of Equation 1 with respect to the magic basis will all be real. Hence A B is orthogonal. For example, (A 1 m1 = (α + β 1 β 1 +ᾱ 11 / = Reα m1 + Imα m Imβ m3 Reβ m4. (15 Since changing basis does not change determinant, these computations assert a (U(4-inner Lie-group isomorphism between SU( SU( and SO(4. Importantly, both are known to be connected [11, p. 68]. Theorem 4. (from [13] The magic basis realizes the low dimensional isomorphism between SU( SU( and SO(4. Specifically, for V U(4 written with matrix coefficients relative to the magic basis of Equation 14, [V SO(4 U(4] [(V : C[, 1 ] C[, 1 ] C = A B for A,B SU(] (16 Cf. Equation 1 for the matrix for A B in the computational basis. Proof: Continuing as in Equation 15, consider all (A 1 mi and (1 B mj to show that SU( SU( maps into SO(4. Now note SU( is three dimensional since α + β = 1, so SU( SU( is six dimensional. As SO(4 has real dimensions, this shows that the map defined above is onto the identity component. 4. Definition and properties of E Definition 4.3 The entangler gate E is the two qubit gate which maps the computational basis into the magic basis: m1, 1 m, 1 m3, and 11 m4. The inverse gate E is called the disentangler. In terms of the computational basis, E has the following matrix: 1 i E = i 1 i 1 (17 1 i 9
10 Now recall generally that for g GL(n, a linear map L with matrix A subordinate to some basis {v 1,...v n } may also be expressed in terms of the basis {gv 1,...gv n } via the conjugation map A gag 1. In particular, E is also given by the matrix above in the magic basis, and likewise E, and likewise any matrix commuting with E. The typical use of E is the following Corollary of Theorem 4.. Corollary 4.4 Suppose V SO(4, that is V U(4 with det(v = 1 and all real entries. Then via the change of basis remark of the last paragraph, EVE is a tensor product of one-line gates of the form of Equation 1. One finds that E can be realized up to global phase by seven elementary gates, as shown in Figure. This is most easily verified by multiplying the appropriate 4 4 matrices. In particular, Equation writes topcnot and botcnot as permutation matrices. With that in mind, one can explicitly verify that E =botcnot topcnot botcnot 1 1 i i botcnot (18 Note that the circuit diagram in Figure travels right to left, so gate matrices are multiplied in reverse. S = diag(1,i is an elementary gate up to global phase e iπ/4, and the Hadamard gate H can be implemented, up to global phase, using two elementary gates as shown in Equation 5. In summary, E requires four CNOT gates and three one-qubit rotations. Similarly, E may be implemented in seven elementary gates by writing the inverse of each gate of Figure in reverse order. 5 An Arbitrary Two-qubit Computation in 3 Elementary Gates or Less In order to implement an arbitrary two-qubit computation with elementary gates, we first compute the normalized unitary KAK decomposition U = K 1 AK of its unitary matrix U. According to the magic isomorphism from Section 4.1, if we view K 1 and K in the basis of Bell states, they decompose into tensor products of generic one-qubit computations, each requiring up to three one-qubit elementary gates. However, we then must view the remaining diagonal matrix in the same basis as well. The remaining part is of the form E E for diagonal and, as shown below, can be implemented in 11 gates due to its pattern of zero entries. 5.1 Decomposition algorithm The matrix decomposition implied by Theorem 1.1 is derived below, and gate counts are in the next subsection. Proposition 5.1 Let U be the matrix for any two-qubit computation in the computational basis, so that EUE represents U in the magic basis. Then U = (U 1 U botcnot topc U 3 (1 U 4 botcnot (U 5 U 6 (19 where U 1...U 6 are one-qubit gates on each line andtopc U 3 is controlled by the top line. Proof: We are going to use the canonical decomposition of U(4, which is a combination of the KAK decomposition of U(4 and the magic isomorphism of Section 4.1. The proof extends an algorithmic version of the canonical decomposition towards elementary gates for quantum computation [1] in the spirit of [5]. 1
11 In the algorithm below, steps 1-4 compute the normalized unitary KAK decomposition (see Definition 3.6 of a given -qubit quantum computation U. Step 5 applies the magic isomorphism of Section 4.1 to separate four generic one-qubit gates. Step 6 implements the remaining computation. 1. First, compute P for E UE = PK 1 the unitary polar decomposition P = P t, K 1 SO(4. To do so, note P = PP t = PK 1 K t 1 Pt = E UEE t U t Ē.. Now apply Proposition 3.5 to P. This produces P = K DK 1 for K O(4, D diagonal. Furthermore, choose K SO(4, so that EK E is a tensor product via Corollary Choose squareroots entrywise on the diagonal to form D, being careful to choose the signs of each root so that in the product det D = detu. This is in fact possible, since detp = (detu. Having so chosen D, compute P = K DK One can now compute K 1 = P 1 E UE = PE UE. As detp = detu, in fact K 1 SO(4. 5. Thus E UE = PK 1 = K D(K 1 K 1, whence U = (EK E (E DE (EK 1 K 1E upon conversion back to the computational basis. Using Corollary 4.4, we define U 1,U,U 5 and U 6 by U 1 U = EK E and U 5 U 6 = EK 1 K 1E ( Both expressions may now be broken into explicit tensor products of elements of U(1. 6. What remains is to describe the implementation of E DE. For this, label D = diag(a,b,c,d with complex entries from U(1. Then E DE = 1 a+b a b c+d c d c d c+d a b a+b (1 Multiplying by a botcnot on the left flips rows two and four, while multiplying on the right flips columns two and four. Thus, E ( DE U4 =botcnot B botcnot ( for some U 4,B U(. Choose U 3 so that U 3 = BU 1 4. Then the block-diagonal matrix U 4 B may be implemented via U 4 B = (1 BU 1 4 (1 U 4 = (topc U 3 (1 U 4. Note that this algorithm has several unspecified degrees of freedom that may affect gate counts for specific -qubit computations. Arbitrary choices can be made in ordering eigenvectors in step and choosing a squareroot of a complex diagonal matrix in step 3. 11
12 V = D A B C Figure 3: The implementation of a controlled-v gate [5, Figure 7]. The gates A,B,C and D are computed ibid. for a given V. Here, C and D require one elementary gate each, while A and B require two each Figure 4: The decomposition of a generic -qubit quantum computation into up to 3 gates. Four generic onequbit rotations are marked with 3 because they require up to three elementary gates. Computations requiring two or one elementary gates are marked similarly. 5. The overall gate decomposition and gate counts Proposition 5.1 decomposes an arbitrary two-qubit unitary into U = (U 1 U botcnot topc U 3 (1 U 4 botcnot (U 5 U 6 where U 1,...,U 6 are one-qubit gates. The immediate gate count yields: three elementary rotations for each of five one-qubit gates U 1,U,U 3,U 5 and U 6, two botcnot gates, eight elementary gates to implement thetopc U 4 gate, according to [5, Figure 7]. The total gate count of 5 can be further reduced, given the structure of the topc V circuit in Figure 3. Indeed, that circuit can be written symbolically astopc U 3 = (1 C topcnot (1 B topcnot (D A. C and D are elementary gates up to phase, but A and B require up to two elementary gates [5]. Since topc U 3 is next to (1 U 4 in Proposition 5.1, we can reduce (D A (1 U 4 to (D U 7 where U 7 = AU 4. By merging the computation A with the generic one-qubit computation U 4 that may require up to three elementary gates, one reduces the overall circuit by two elementary gates. The overall circuit decomposition can be described algebraically as follows: U = (U 1 U botcnot (D U 7 topcnot (1 B topcnot (1 C botcnot (U 5 U 6 (3 It is illustrated in Figure 4, where gate counts are shown as well. Our circuit decomposition requires at most four CNOTs, while other gates are elementary one-qubit rotations. Such a small number of non-one-qubit gates may be desired in practical implementations where multi-qubit interactions are more difficult to implement. It is understood that Figure 4 and our gate counts refer to the worst case. Specific computations may require only some of those gates. In particular, the next section shows three examples that all require fewer gates than in the worst case. In those examples, our algorithm is able to capture the structure of the given quantum computation. Unlike previously known circuit synthesis algorithms, ours can always implement A B without using CNOT gates. 1
13 5.3 Examples Several examples below follow the algorithm from Theorem 1.1. The order of eigenvectors and the choices of squareroots aimed at improving gate counts, but this search was not exhaustive. Example 5. Let H H be the two dimensional Hadamard gate. Following our algorithm, E (H HE SO(4, so that P = 1 and we may choose D = P = 1 and K = 1. Then K 1 = K 1 K 1 = E (H HE, and the algorithm implements H H in four elementary one-qubit gates. The CNOTs cancel. Similar comments apply to any A B. Example 5.3 Let f : Z/Z Z/Z be the flip map, i.e. f(n = n+1. The Deutsch algorithm as described, e.g., in [14, p. 3], calls for a black-box gate U f with U f x y = x y+ f(x, so that here U f swaps 1. Thus, U f is easily implemented as U f = (X 1 topcnot (X 1 in five gates. Below, we decompose U f using our algorithm. First, we find the Hermitian part of the unitary polar decomposition of E U f E. 1 E U f EE t U t f Ē = PPt = P = 1 1 (4 1 Now we must choose a basis of eigenvectors so as to diagonalize P. Since P has both ±1 as double eigenvalues, there are uncountably many ways to do this. Simplifying things slightly, choose 1 1 K = so that U 1 U = EK E = 1 1 ( (5 Now the ordering of the column vectors of K forces the diagonal D = diag( 1,1, 1,1 with P = K DK 1. We choose D = (i,1,i,1, being careful to ensure det D = detu f = 1. 5 Now putting P = K DK 1, define K 1 = PE U f E. Then the one-line unitaries on the far side of the circuit may be computed as K 1E = e iπ/4 1 EK 1 i 1 1 i 1 i i 1 i 1 1 i 1 i i 1 = eiπ/4 1 ( i 1 i 1 1 ( 1 i i 1 (6 To implement the latter in elementary matrices, one computes that ( i 1 i 1 while for the second factor similarly ( 1 i i 1 ( e iπ/4 = e iπ/4 ( e iπ/4 = e iπ/4 ( ( ( e iπ/4 e iπ/4 ( e iπ/4 e iπ/4 (7 (8 5 Failing to do so will cause detk 1 1 eventually, at which point EK 1 K 1E is not a tensor product of one-qubit computations. 13
14 X X = U 5 U 6 U 4 U 1 Figure 5: Diagrams for the U f black box for Deutsch s algorithm, where f : Z/Z Z/Z is f(x = x+1. The typical implementation is shown at left, counting for +1+ = 5 gates and one CNOT. One result of the current algorithm is shown at right. Here, U 1 = R y ( π, U 4 = e iπ/4 R z ( π/r y (πr z (π/, U 5 = ir y (πr z ( π/, and U 6 = R z ( π/r y (πr z (π/. Thus this instance of the algorithm produces 1 gates with two CNOTs. Finally, in this example the conditioned element is not required to implement E DE. Indeed, botcnot E 1 i DE botcnot = e iπ/4 i 1 1 i = e iπ/4 1 1 ( 1 i i 1 i 1 (9 Thus, no conditioned gate is required within E DE. Moreover, as we recently described the decomposition of the complex conjugate, we see the 1 U 4 factor above counts for three gates. Hence, our algorithm in this instance produces a decomposition with 11 rather than 5 gates. It holds two CNOTs rather than one CNOT. Example 5.4 One case of the algorithm also produces a 14-gate decomposition of the quantum Fourier transform F, in contrast to the usual 1-gate implementation. It has four rather than five two-qubit elementary gates (CNOTs. Specifically, we write, as,..., 3. Then the discrete Fourier transform F is given by j F 1 3 k=( jk k so that F = 1 1 i 1 i (3 1 i 1 i Thus, the square of the Hermitian part of E F E is E F EE t F t Ē = PP t = P = e iπ/4 e iπ/4 e iπ/4 e 3iπ/4 e 3iπ/4 e iπ/4 e iπ/4 e iπ/4 (31 Now we must diagonalize P. As the eigenvalues are 1 with multiplicity two and i with multiplicity two, there are infinitely many possible eigen-bases of C 4. Choosing one such for the columns of K with determinant 1, say 1 1 ( K = so that U 1 U = EK E 1 1 = 1 ( Now the ordering of the column vectors of K forces the diagonal D = diag(i,i,1, 1 with P = K DK 1. The next step is to choose D so that det D = detef E = detf = i. Our choice is D = diag(e iπ/4,e iπ/4,1, 1. 14
15 H S H = U 5 U 6 U 3 U 1 Figure 6: Shown are circuits for the Fourier transform: standard (left and produced by our algorithm (right. U 1 = R y (3π, U 3 = e iπ/4 X, U 5 = T H = e 3π/8 R z (π/4 πr y (π, and U 6 = T = ( 1e iπ/8 R z (π/4. Counting the conditioned U 3 as seven gates, we get = 14 gates total. Then P = K DK 1, so that K 1 = PE F E is complicated 6. On the other hand, e iπ/4 e iπ/4 K 1 K 1 = e iπ/4 e iπ/4 (33 Thus, with some more matrix computations one computes that on the other side U 5 U 6 = EK 1 K 1E = [diag(1,e iπ/4 H] diag(e iπ/4, 1 (34 Note the first tensor factor would be more commonly referred to as T H = e iπ/8 R z (π/4( ir z ( πr y (π = e 3π/8 R z (π/4 πr y (π. On the other hand, more commonly U 6 = T = ( 1e iπ/8 R z (π/4, so that U 5 U 6 counts for + 1 = 3 gates. This concludes the derivation of the outside one-line unitaries. Finally, we implement E DE. The spacing of the zeroes in E DE causes botcnot E DE botcnot to be block diagonal, specifically (in blocks botcnot E DE botcnot = ( diag(e iπ/4,e iπ/4 X (35 Thus U 4 = diag(e iπ/4,e iπ/4 which is = 1 up to phase and does not cost any gates. For U 3, ( ( ( e iπ/4 e 3iπ/4 1 i X = e 3iπ/4 1 1 i (36 Thus, in the notation from the Section (and from [1, 5], δ = 3π/4, α =, θ = π, and β = π. Therefore the conditioned e 3iπ/4 X may be realized in 7 gates. As the unitaries U 1,U = 1,U 5 and U 6 (see Figure 6(b together require 5 gates, we have 14 gates total, of which are botcnots and are topcnots. Compare the above to the standardf =botcnot topcnot botcnot(1 H (botc S (H 1 illustrated in Figure 6(a. The conditioned S can be implemented in 5 gates as shown in Figure 3. Thus, the standard circuit for the two-qubit Fourier transform has 1 elementary gates. While this circuit has two gates fewer than the circuit produced by our algorithm, it contains 5 rather than 4 CNOT gates. Since multi-qubit interactions are relatively expensive in many quantum implementation technologies, the choice between the two circuits may depend on specific technology parameters and implementation objectives. 6 Moreover, we had to carefully choose det D = detf to ensure detk 1 = 1. Otherwise detk 1 K 1 1 so that EK 1 K 1E U( U(. 15
16 6 Gate Counts Versus Degrees of Freedom: Lower and Upper Bounds We have constructively shown in the previous section that any two-qubit quantum computation can be implemented in 3 elementary gates or less, of which at most 4 are CNOTs and remaining gates are one-qubit rotations. As we do not know if this result can be improved, we show that at least 17 elementary gates are required. Theorem 6.1 There exists a two-qubit computation such that any circuit implementing it in terms of elementary gates consists of at least 17 gates. In particular, 15 one-qubit rotations are required and two CNOTs. Proof: First, recall that two-qubit quantum computations can be represented by 4 4-unitary matrices, and such matrices can be normalized to have determinant one because quantum measurement is not affected by global phase. Also recall that we use two types of elementary gates: (1 one-qubit rotations with one real parameter each, and ( CNOTs which operate on two qubits and are fully specified (no parameters. Let us now consider the set Q C of quantum computations that can be performed by some given two-qubit circuit C with fixed topology, where the parameters of one-qubit rotations are allowed to vary. Fixed circuit topology means that [the graph of] connections between elementary gates cannot be changed. Since the overall unitary matrix can be expressed in terms of products and tensor products of the matrices of elementary gates, each matrix element is an infinitely differentiable function of the parameters of one-qubit rotations (more precisely, it is an algebraic function of sin and cos of those parameters. In other words, the set Q C is parameterized by one-qubit rotations and has the local structure of a differentiable manifold, whose topological dimension in GL(4 is the number of one-qubit rotations in C with variable parameters. The topological dimension is roughly-speaking the number of degrees of freedom. Since every computation can be implemented by a limited number of elementary gates, the set of possible circuit topologies is finite. The set of all implementable quantum computations is a union of sets Q C over the finite set of possible circuit topologies. Its topological dimension is the maximum of topological dimensions of Q C, i.e., the maximum number of one-qubit rotations with varying parameters, allowed in one circuit. On the other hand, Q C = SU(4. We compute its topological dimension as follows. First, we point out that the matrix logarithm (which is infinitely differentiable maps U(4 one-to-one onto the set of skew-symmetric Hermitian matrices: UU = 1 log(u+log(u = log(u+(log(u =. Furthermore, 4 4 skew-hermitian matrices have 4 independent reals on the diagonal and are otherwise completely determined by their 6 complex upper-diagonal elements. Thus, the set of skew-hermitian matrices has topological dimension 16, and the same is true about U(4. Subtracting 1 for global phase, we see that 15 one-qubit rotations are needed to implement some two-qubit computations. A randomly chosen computation is such with probability 1, i.e., almost always rather than always. If no CNOT gates are used in a given two-qubit circuit, the two lines never interact, and the two independent one-qubit computations can be implemented in 3 elementary rotations each. Therefore, two-qubit computations implementable without CNOTs have only 6 degrees of freedom. Similarly, if only one CNOT is allowed, then only 4 3= 1 rotations can be placed on two lines to the left and to the right of the CNOT to avoid gate reductions. This proves that at least CNOT gates are necessary to implement any two-qubit computation requiring 15 rotations. 16
17 Figure 7: The overall structure entailed by our circuit decomposition. Four generic one-qubit rotations are marked with 3 because they are worth up to three elementary gates. Two Hadamard gates are marked with because they are worth two elementary gates. Constant gates are in bold. Given the lower bound in Theorem 6.1, the 19 non-constant one-qubit rotations in Figure 4 seem redundant as only 15 rotations are required for dimension reasons. To this end, we offer another generic gate decomposition for arbitrary -qubit computations that entails no more than 15 non-constant one-qubit rotations, at the price of some constant rotations and significantly more CNOT gates than used by our main decomposition in Figure 4. Recall from Proposition 5.1 that an arbitrary two-qubit unitary can be decomposed into U = (U 1 U (EDE (U 3 U 4 where U 1,...,U 4 are one-qubit gates and D is a diagonal unitary. In this context, we use circuit decompositions for E, E and D given in Sections and 4. The matrix D is controlled by 3 real parameters (4 diagonal unitaries modulo global phase. It is implemented in Figure 1 using 3 one-qubit rotations and CNOTs. The entangler E and disentangler E are fixed matrices and require no parameters. The implementation of E in Figure requires 3 constant rotations and 4 CNOTs. Adding up gate counts, we see that U 1,...,U 4 may require up to 1 elementary gates alltogether. D counts for 5, while E and E count for 7 each, for a total of 31. However, upon inspection of the Figures 1 and, one notes that the circuit EDE has two canceling botcnot gates. Moreover, since the inverse of D is, too, a diagonal unitary matrix, we can flip the asymmetric circuit for D in Figure 1. This allows us to merge a constant rotations from E with a variable rotation from D. The resulting circuit decomposition is illustrated in Figure 7 and requires up to 8 elementary gates total, of which 15 are variable one-qubit rotations, 5 are constant rotations and 8 are CNOTs. The slight asymmetry in Figure 7 is explained by the asymmetric circuit for D in Figure 1. The following is a summary of our upper and lower bounds for worst-case optimal -qubit circuits: (a an upper bound of 3 elementary gates; (b a lower bound of 17 elementary gates. (c an upper bound of 4 CNOT gates; (d a lower bound of CNOT gates; (e an upper bound of 19 one-qubit rotations; (f an upper bound of 15 variable elementary rotations; (g a lower bound of 15 variable elementary rotations; In our on-going work we show that three CNOT gates are necessary and that the resulting lower bound of 18 elementary gates is tight. The implied decomposition contains at most 15 elementary rotations. 17
18 7 Conclusions and On-going Work It is a well-known result that any one-qubit computation can be implemented using three rotations or less [1]. Our work answers a similar question about arbitrary two-qubit computations assuming that CNOT gates can be used in addition to single-qubit rotations, without ancilla qubits. First, we show a lower bound that calls for at least seventeen elementary gates: fifteen rotations and two CNOTs. We then constructively prove that twenty three elementary gates suffice to implement an arbitrary two-qubit computation. At most four of those are CNOTs and the rest are single-qubit gates. In comparison, a previously known construction [1, 5] implies sixty-one gates of which eighteen are CNOTs. While this construction is more general than ours, for two-qubit computations, our algorithm generates far fewer gates in the worst (generic case. The savings in the number of multi-qubit gates (CNOTs are particularly dramatic. In terms of techniques for the synthesis of quantum circuits, our work emphasizes the following general ideas: changing the computational basis to maximally-entangled states by applying specially-designed gates with the purpose of recognizing quantum computations implementable with one-qubit gates only; systematic use of matrix decompositions from numerical analysis and Lie theory: polar, spectral and KAK; focus on matrix decompositions that are intrinsic to unitary matrices, e.g., KAK of U(4, and include multiple non-trivial unitary factors; incremental reduction of existing quantum circuits by local optimization; exploiting degrees of freedom in circuit synthesis may be useful to expose additional reductions. Specifically, we formalize the canonical decomposition of two-qubit computations [13, 1] as an instance of the KAK decomposition from Lie theory [11] for U(4 with K = O(4 and A diagonal. We propose an algorithm to compute the KAK components and observe that elements of O(4 can be interpreted in the magic basis as pairs of one-qubit unitaries. Therefore, we change basis for all related matrices and further decompose them into elementary gates for quantum computation. In our on-going work, with additional techniques, we are able to improve the lower bound to 18 elementary gates and show that it is tight. We are also attempting to extend these ideas to three qubits or more. Two obstacles arise immediately: Entanglement for three qubits is far more complicated than it is for two qubits [6]. In particular, no known magic basis makes local unitaries tractable, and there are distinct notions of maximally-entangled states. The use of the KAK decomposition does not automatically generalize beyond two qubits because K U( n must be a sufficiently large subgroup, in the sense that U( n /K must be a Riemannian symmetric space [11, 1]. Although both O(4 and U( U( are large subgroups of U(4, the set of local unitary gates n i=1 U( is not large enough in U(n for n 3. In particular, one does not expect a decomposition of the type U 1 = U DU 3 for U 1 U(8, D diagonal, and U, U 3 U( U( U(. With little hope for a direct matrix decomposition involving local unitaries, it remains possible, in principle, to construct a multi-step recursive decomposition. A related example is available in [16]. 18
C/CS/Phys 191 Quantum Gates and Universality 9/22/05 Fall 2005 Lecture 8. a b b d. w. Therefore, U preserves norms and angles (up to sign).
 C/CS/Phys 191 Quantum Gates and Universality 9//05 Fall 005 Lecture 8 1 Readings Benenti, Casati, and Strini: Classical circuits and computation Ch.1.,.6 Quantum Gates Ch. 3.-3.4 Universality Ch. 3.5-3.6
C/CS/Phys 191 Quantum Gates and Universality 9//05 Fall 005 Lecture 8 1 Readings Benenti, Casati, and Strini: Classical circuits and computation Ch.1.,.6 Quantum Gates Ch. 3.-3.4 Universality Ch. 3.5-3.6
1 Readings. 2 Unitary Operators. C/CS/Phys C191 Unitaries and Quantum Gates 9/22/09 Fall 2009 Lecture 8
 C/CS/Phys C191 Unitaries and Quantum Gates 9//09 Fall 009 Lecture 8 1 Readings Benenti, Casati, and Strini: Classical circuits and computation Ch.1.,.6 Quantum Gates Ch. 3.-3.4 Kaye et al: Ch. 1.1-1.5,
C/CS/Phys C191 Unitaries and Quantum Gates 9//09 Fall 009 Lecture 8 1 Readings Benenti, Casati, and Strini: Classical circuits and computation Ch.1.,.6 Quantum Gates Ch. 3.-3.4 Kaye et al: Ch. 1.1-1.5,
Introduction to Group Theory
 Chapter 10 Introduction to Group Theory Since symmetries described by groups play such an important role in modern physics, we will take a little time to introduce the basic structure (as seen by a physicist)
Chapter 10 Introduction to Group Theory Since symmetries described by groups play such an important role in modern physics, we will take a little time to introduce the basic structure (as seen by a physicist)
. Here we are using the standard inner-product over C k to define orthogonality. Recall that the inner-product of two vectors φ = i α i.
 CS 94- Hilbert Spaces, Tensor Products, Quantum Gates, Bell States 1//07 Spring 007 Lecture 01 Hilbert Spaces Consider a discrete quantum system that has k distinguishable states (eg k distinct energy
CS 94- Hilbert Spaces, Tensor Products, Quantum Gates, Bell States 1//07 Spring 007 Lecture 01 Hilbert Spaces Consider a discrete quantum system that has k distinguishable states (eg k distinct energy
Lecture 3: Hilbert spaces, tensor products
 CS903: Quantum computation and Information theory (Special Topics In TCS) Lecture 3: Hilbert spaces, tensor products This lecture will formalize many of the notions introduced informally in the second
CS903: Quantum computation and Information theory (Special Topics In TCS) Lecture 3: Hilbert spaces, tensor products This lecture will formalize many of the notions introduced informally in the second
Quantum Circuits for Incompletely Specified Two-Qubit Operators
 Quantum Circuits for Incompletely Specified Two-Qubit Operators arxiv:quant-ph/0401162v4 6 Jan 2005 Vivek V. Shende Igor L. Markov Department of Electrical Engineering and Computer Science The University
Quantum Circuits for Incompletely Specified Two-Qubit Operators arxiv:quant-ph/0401162v4 6 Jan 2005 Vivek V. Shende Igor L. Markov Department of Electrical Engineering and Computer Science The University
Basic Concepts of Group Theory
 Chapter 1 Basic Concepts of Group Theory The theory of groups and vector spaces has many important applications in a number of branches of modern theoretical physics. These include the formal theory of
Chapter 1 Basic Concepts of Group Theory The theory of groups and vector spaces has many important applications in a number of branches of modern theoretical physics. These include the formal theory of
Introduction to Quantum Computing
 Introduction to Quantum Computing Part I Emma Strubell http://cs.umaine.edu/~ema/quantum_tutorial.pdf April 12, 2011 Overview Outline What is quantum computing? Background Caveats Fundamental differences
Introduction to Quantum Computing Part I Emma Strubell http://cs.umaine.edu/~ema/quantum_tutorial.pdf April 12, 2011 Overview Outline What is quantum computing? Background Caveats Fundamental differences
5.6. PSEUDOINVERSES 101. A H w.
 5.6. PSEUDOINVERSES 0 Corollary 5.6.4. If A is a matrix such that A H A is invertible, then the least-squares solution to Av = w is v = A H A ) A H w. The matrix A H A ) A H is the left inverse of A and
5.6. PSEUDOINVERSES 0 Corollary 5.6.4. If A is a matrix such that A H A is invertible, then the least-squares solution to Av = w is v = A H A ) A H w. The matrix A H A ) A H is the left inverse of A and
MATRICES ARE SIMILAR TO TRIANGULAR MATRICES
 MATRICES ARE SIMILAR TO TRIANGULAR MATRICES 1 Complex matrices Recall that the complex numbers are given by a + ib where a and b are real and i is the imaginary unity, ie, i 2 = 1 In what we describe below,
MATRICES ARE SIMILAR TO TRIANGULAR MATRICES 1 Complex matrices Recall that the complex numbers are given by a + ib where a and b are real and i is the imaginary unity, ie, i 2 = 1 In what we describe below,
October 25, 2013 INNER PRODUCT SPACES
 October 25, 2013 INNER PRODUCT SPACES RODICA D. COSTIN Contents 1. Inner product 2 1.1. Inner product 2 1.2. Inner product spaces 4 2. Orthogonal bases 5 2.1. Existence of an orthogonal basis 7 2.2. Orthogonal
October 25, 2013 INNER PRODUCT SPACES RODICA D. COSTIN Contents 1. Inner product 2 1.1. Inner product 2 1.2. Inner product spaces 4 2. Orthogonal bases 5 2.1. Existence of an orthogonal basis 7 2.2. Orthogonal
Quantum Information & Quantum Computing
 Math 478, Phys 478, CS4803, February 9, 006 1 Georgia Tech Math, Physics & Computing Math 478, Phys 478, CS4803 Quantum Information & Quantum Computing Problems Set 1 Due February 9, 006 Part I : 1. Read
Math 478, Phys 478, CS4803, February 9, 006 1 Georgia Tech Math, Physics & Computing Math 478, Phys 478, CS4803 Quantum Information & Quantum Computing Problems Set 1 Due February 9, 006 Part I : 1. Read
Lecture 10: A (Brief) Introduction to Group Theory (See Chapter 3.13 in Boas, 3rd Edition)
 Lecture 0: A (Brief) Introduction to Group heory (See Chapter 3.3 in Boas, 3rd Edition) Having gained some new experience with matrices, which provide us with representations of groups, and because symmetries
Lecture 0: A (Brief) Introduction to Group heory (See Chapter 3.3 in Boas, 3rd Edition) Having gained some new experience with matrices, which provide us with representations of groups, and because symmetries
APPENDIX A. Background Mathematics. A.1 Linear Algebra. Vector algebra. Let x denote the n-dimensional column vector with components x 1 x 2.
 APPENDIX A Background Mathematics A. Linear Algebra A.. Vector algebra Let x denote the n-dimensional column vector with components 0 x x 2 B C @. A x n Definition 6 (scalar product). The scalar product
APPENDIX A Background Mathematics A. Linear Algebra A.. Vector algebra Let x denote the n-dimensional column vector with components 0 x x 2 B C @. A x n Definition 6 (scalar product). The scalar product
Matrix Factorization and Analysis
 Chapter 7 Matrix Factorization and Analysis Matrix factorizations are an important part of the practice and analysis of signal processing. They are at the heart of many signal-processing algorithms. Their
Chapter 7 Matrix Factorization and Analysis Matrix factorizations are an important part of the practice and analysis of signal processing. They are at the heart of many signal-processing algorithms. Their
Hilbert Space, Entanglement, Quantum Gates, Bell States, Superdense Coding.
 CS 94- Bell States Bell Inequalities 9//04 Fall 004 Lecture Hilbert Space Entanglement Quantum Gates Bell States Superdense Coding 1 One qubit: Recall that the state of a single qubit can be written as
CS 94- Bell States Bell Inequalities 9//04 Fall 004 Lecture Hilbert Space Entanglement Quantum Gates Bell States Superdense Coding 1 One qubit: Recall that the state of a single qubit can be written as
Quantum algorithms (CO 781, Winter 2008) Prof. Andrew Childs, University of Waterloo LECTURE 1: Quantum circuits and the abelian QFT
 Quantum algorithms (CO 78, Winter 008) Prof. Andrew Childs, University of Waterloo LECTURE : Quantum circuits and the abelian QFT This is a course on quantum algorithms. It is intended for graduate students
Quantum algorithms (CO 78, Winter 008) Prof. Andrew Childs, University of Waterloo LECTURE : Quantum circuits and the abelian QFT This is a course on quantum algorithms. It is intended for graduate students
4.2. ORTHOGONALITY 161
 4.2. ORTHOGONALITY 161 Definition 4.2.9 An affine space (E, E ) is a Euclidean affine space iff its underlying vector space E is a Euclidean vector space. Given any two points a, b E, we define the distance
4.2. ORTHOGONALITY 161 Definition 4.2.9 An affine space (E, E ) is a Euclidean affine space iff its underlying vector space E is a Euclidean vector space. Given any two points a, b E, we define the distance
Algebra I Fall 2007
 MIT OpenCourseWare http://ocw.mit.edu 18.701 Algebra I Fall 007 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. 18.701 007 Geometry of the Special Unitary
MIT OpenCourseWare http://ocw.mit.edu 18.701 Algebra I Fall 007 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. 18.701 007 Geometry of the Special Unitary
The Solovay-Kitaev theorem
 The Solovay-Kitaev theorem Maris Ozols December 10, 009 1 Introduction There are several accounts of the Solovay-Kitaev theorem available [K97, NC00, KSV0, DN05]. I chose to base my report on [NC00], since
The Solovay-Kitaev theorem Maris Ozols December 10, 009 1 Introduction There are several accounts of the Solovay-Kitaev theorem available [K97, NC00, KSV0, DN05]. I chose to base my report on [NC00], since
Clifford Algebras and Spin Groups
 Clifford Algebras and Spin Groups Math G4344, Spring 2012 We ll now turn from the general theory to examine a specific class class of groups: the orthogonal groups. Recall that O(n, R) is the group of
Clifford Algebras and Spin Groups Math G4344, Spring 2012 We ll now turn from the general theory to examine a specific class class of groups: the orthogonal groups. Recall that O(n, R) is the group of
Quantum Computing Lecture 2. Review of Linear Algebra
 Quantum Computing Lecture 2 Review of Linear Algebra Maris Ozols Linear algebra States of a quantum system form a vector space and their transformations are described by linear operators Vector spaces
Quantum Computing Lecture 2 Review of Linear Algebra Maris Ozols Linear algebra States of a quantum system form a vector space and their transformations are described by linear operators Vector spaces
Ph 219b/CS 219b. Exercises Due: Wednesday 20 November 2013
 1 h 219b/CS 219b Exercises Due: Wednesday 20 November 2013 3.1 Universal quantum gates I In this exercise and the two that follow, we will establish that several simple sets of gates are universal for
1 h 219b/CS 219b Exercises Due: Wednesday 20 November 2013 3.1 Universal quantum gates I In this exercise and the two that follow, we will establish that several simple sets of gates are universal for
LECTURE 25-26: CARTAN S THEOREM OF MAXIMAL TORI. 1. Maximal Tori
 LECTURE 25-26: CARTAN S THEOREM OF MAXIMAL TORI 1. Maximal Tori By a torus we mean a compact connected abelian Lie group, so a torus is a Lie group that is isomorphic to T n = R n /Z n. Definition 1.1.
LECTURE 25-26: CARTAN S THEOREM OF MAXIMAL TORI 1. Maximal Tori By a torus we mean a compact connected abelian Lie group, so a torus is a Lie group that is isomorphic to T n = R n /Z n. Definition 1.1.
Lecture 2: From Classical to Quantum Model of Computation
 CS 880: Quantum Information Processing 9/7/10 Lecture : From Classical to Quantum Model of Computation Instructor: Dieter van Melkebeek Scribe: Tyson Williams Last class we introduced two models for deterministic
CS 880: Quantum Information Processing 9/7/10 Lecture : From Classical to Quantum Model of Computation Instructor: Dieter van Melkebeek Scribe: Tyson Williams Last class we introduced two models for deterministic
Elementary linear algebra
 Chapter 1 Elementary linear algebra 1.1 Vector spaces Vector spaces owe their importance to the fact that so many models arising in the solutions of specific problems turn out to be vector spaces. The
Chapter 1 Elementary linear algebra 1.1 Vector spaces Vector spaces owe their importance to the fact that so many models arising in the solutions of specific problems turn out to be vector spaces. The
Symmetries, Groups, and Conservation Laws
 Chapter Symmetries, Groups, and Conservation Laws The dynamical properties and interactions of a system of particles and fields are derived from the principle of least action, where the action is a 4-dimensional
Chapter Symmetries, Groups, and Conservation Laws The dynamical properties and interactions of a system of particles and fields are derived from the principle of least action, where the action is a 4-dimensional
Decomposition of Quantum Gates
 Decomposition of Quantum Gates With Applications to Quantum Computing Dean Katsaros, Eric Berry, Diane C. Pelejo, Chi-Kwong Li College of William and Mary January 12, 215 Motivation Current Conclusions
Decomposition of Quantum Gates With Applications to Quantum Computing Dean Katsaros, Eric Berry, Diane C. Pelejo, Chi-Kwong Li College of William and Mary January 12, 215 Motivation Current Conclusions
Chapter 2 The Group U(1) and its Representations
 Chapter 2 The Group U(1) and its Representations The simplest example of a Lie group is the group of rotations of the plane, with elements parametrized by a single number, the angle of rotation θ. It is
Chapter 2 The Group U(1) and its Representations The simplest example of a Lie group is the group of rotations of the plane, with elements parametrized by a single number, the angle of rotation θ. It is
Linear Algebra: Matrix Eigenvalue Problems
 CHAPTER8 Linear Algebra: Matrix Eigenvalue Problems Chapter 8 p1 A matrix eigenvalue problem considers the vector equation (1) Ax = λx. 8.0 Linear Algebra: Matrix Eigenvalue Problems Here A is a given
CHAPTER8 Linear Algebra: Matrix Eigenvalue Problems Chapter 8 p1 A matrix eigenvalue problem considers the vector equation (1) Ax = λx. 8.0 Linear Algebra: Matrix Eigenvalue Problems Here A is a given
Optimal Realizations of Controlled Unitary Gates
 Optimal Realizations of Controlled nitary Gates Guang Song and Andreas Klappenecker Department of Computer Science Texas A&M niversity College Station, TX 77843-3112 {gsong,klappi}@cs.tamu.edu Abstract
Optimal Realizations of Controlled nitary Gates Guang Song and Andreas Klappenecker Department of Computer Science Texas A&M niversity College Station, TX 77843-3112 {gsong,klappi}@cs.tamu.edu Abstract
Symmetries, Fields and Particles. Examples 1.
 Symmetries, Fields and Particles. Examples 1. 1. O(n) consists of n n real matrices M satisfying M T M = I. Check that O(n) is a group. U(n) consists of n n complex matrices U satisfying U U = I. Check
Symmetries, Fields and Particles. Examples 1. 1. O(n) consists of n n real matrices M satisfying M T M = I. Check that O(n) is a group. U(n) consists of n n complex matrices U satisfying U U = I. Check
Linear Algebra and Dirac Notation, Pt. 3
 Linear Algebra and Dirac Notation, Pt. 3 PHYS 500 - Southern Illinois University February 1, 2017 PHYS 500 - Southern Illinois University Linear Algebra and Dirac Notation, Pt. 3 February 1, 2017 1 / 16
Linear Algebra and Dirac Notation, Pt. 3 PHYS 500 - Southern Illinois University February 1, 2017 PHYS 500 - Southern Illinois University Linear Algebra and Dirac Notation, Pt. 3 February 1, 2017 1 / 16
Linear Algebra March 16, 2019
 Linear Algebra March 16, 2019 2 Contents 0.1 Notation................................ 4 1 Systems of linear equations, and matrices 5 1.1 Systems of linear equations..................... 5 1.2 Augmented
Linear Algebra March 16, 2019 2 Contents 0.1 Notation................................ 4 1 Systems of linear equations, and matrices 5 1.1 Systems of linear equations..................... 5 1.2 Augmented
Symmetries, Fields and Particles 2013 Solutions
 Symmetries, Fields and Particles 013 Solutions Yichen Shi Easter 014 1. (a) Define the groups SU() and SO(3), and find their Lie algebras. Show that these Lie algebras, including their bracket structure,
Symmetries, Fields and Particles 013 Solutions Yichen Shi Easter 014 1. (a) Define the groups SU() and SO(3), and find their Lie algebras. Show that these Lie algebras, including their bracket structure,
Mathematical Methods wk 2: Linear Operators
 John Magorrian, magog@thphysoxacuk These are work-in-progress notes for the second-year course on mathematical methods The most up-to-date version is available from http://www-thphysphysicsoxacuk/people/johnmagorrian/mm
John Magorrian, magog@thphysoxacuk These are work-in-progress notes for the second-year course on mathematical methods The most up-to-date version is available from http://www-thphysphysicsoxacuk/people/johnmagorrian/mm
Quantum Field Theory III
 Quantum Field Theory III Prof. Erick Weinberg January 19, 2011 1 Lecture 1 1.1 Structure We will start with a bit of group theory, and we will talk about spontaneous symmetry broken. Then we will talk
Quantum Field Theory III Prof. Erick Weinberg January 19, 2011 1 Lecture 1 1.1 Structure We will start with a bit of group theory, and we will talk about spontaneous symmetry broken. Then we will talk
QLang: Qubit Language
 QLang: Qubit Language Christopher Campbell Clément Canonne Sankalpa Khadka Winnie Narang Jonathan Wong September 24, 24 Introduction In 965, Gordon Moore predicted that the number of transistors in integrated
QLang: Qubit Language Christopher Campbell Clément Canonne Sankalpa Khadka Winnie Narang Jonathan Wong September 24, 24 Introduction In 965, Gordon Moore predicted that the number of transistors in integrated
GROUP THEORY PRIMER. New terms: so(2n), so(2n+1), symplectic algebra sp(2n)
 GROUP THEORY PRIMER New terms: so(2n), so(2n+1), symplectic algebra sp(2n) 1. Some examples of semi-simple Lie algebras In the previous chapter, we developed the idea of understanding semi-simple Lie algebras
GROUP THEORY PRIMER New terms: so(2n), so(2n+1), symplectic algebra sp(2n) 1. Some examples of semi-simple Lie algebras In the previous chapter, we developed the idea of understanding semi-simple Lie algebras
THE EULER CHARACTERISTIC OF A LIE GROUP
 THE EULER CHARACTERISTIC OF A LIE GROUP JAY TAYLOR 1 Examples of Lie Groups The following is adapted from [2] We begin with the basic definition and some core examples Definition A Lie group is a smooth
THE EULER CHARACTERISTIC OF A LIE GROUP JAY TAYLOR 1 Examples of Lie Groups The following is adapted from [2] We begin with the basic definition and some core examples Definition A Lie group is a smooth
Queens College, CUNY, Department of Computer Science Numerical Methods CSCI 361 / 761 Spring 2018 Instructor: Dr. Sateesh Mane.
 Queens College, CUNY, Department of Computer Science Numerical Methods CSCI 361 / 761 Spring 2018 Instructor: Dr. Sateesh Mane c Sateesh R. Mane 2018 8 Lecture 8 8.1 Matrices July 22, 2018 We shall study
Queens College, CUNY, Department of Computer Science Numerical Methods CSCI 361 / 761 Spring 2018 Instructor: Dr. Sateesh Mane c Sateesh R. Mane 2018 8 Lecture 8 8.1 Matrices July 22, 2018 We shall study
Chapter 10. Quantum algorithms
 Chapter 10. Quantum algorithms Complex numbers: a quick review Definition: C = { a + b i : a, b R } where i = 1. Polar form of z = a + b i is z = re iθ, where r = z = a 2 + b 2 and θ = tan 1 y x Alternatively,
Chapter 10. Quantum algorithms Complex numbers: a quick review Definition: C = { a + b i : a, b R } where i = 1. Polar form of z = a + b i is z = re iθ, where r = z = a 2 + b 2 and θ = tan 1 y x Alternatively,
The Framework of Quantum Mechanics
 The Framework of Quantum Mechanics We now use the mathematical formalism covered in the last lecture to describe the theory of quantum mechanics. In the first section we outline four axioms that lie at
The Framework of Quantum Mechanics We now use the mathematical formalism covered in the last lecture to describe the theory of quantum mechanics. In the first section we outline four axioms that lie at
j=1 x j p, if 1 p <, x i ξ : x i < ξ} 0 as p.
 LINEAR ALGEBRA Fall 203 The final exam Almost all of the problems solved Exercise Let (V, ) be a normed vector space. Prove x y x y for all x, y V. Everybody knows how to do this! Exercise 2 If V is a
LINEAR ALGEBRA Fall 203 The final exam Almost all of the problems solved Exercise Let (V, ) be a normed vector space. Prove x y x y for all x, y V. Everybody knows how to do this! Exercise 2 If V is a
Unitary Dynamics and Quantum Circuits
 qitd323 Unitary Dynamics and Quantum Circuits Robert B. Griffiths Version of 20 January 2014 Contents 1 Unitary Dynamics 1 1.1 Time development operator T.................................... 1 1.2 Particular
qitd323 Unitary Dynamics and Quantum Circuits Robert B. Griffiths Version of 20 January 2014 Contents 1 Unitary Dynamics 1 1.1 Time development operator T.................................... 1 1.2 Particular
Representation theory and quantum mechanics tutorial Spin and the hydrogen atom
 Representation theory and quantum mechanics tutorial Spin and the hydrogen atom Justin Campbell August 3, 2017 1 Representations of SU 2 and SO 3 (R) 1.1 The following observation is long overdue. Proposition
Representation theory and quantum mechanics tutorial Spin and the hydrogen atom Justin Campbell August 3, 2017 1 Representations of SU 2 and SO 3 (R) 1.1 The following observation is long overdue. Proposition
Diagonalization by a unitary similarity transformation
 Physics 116A Winter 2011 Diagonalization by a unitary similarity transformation In these notes, we will always assume that the vector space V is a complex n-dimensional space 1 Introduction A semi-simple
Physics 116A Winter 2011 Diagonalization by a unitary similarity transformation In these notes, we will always assume that the vector space V is a complex n-dimensional space 1 Introduction A semi-simple
Lecture notes on Quantum Computing. Chapter 1 Mathematical Background
 Lecture notes on Quantum Computing Chapter 1 Mathematical Background Vector states of a quantum system with n physical states are represented by unique vectors in C n, the set of n 1 column vectors 1 For
Lecture notes on Quantum Computing Chapter 1 Mathematical Background Vector states of a quantum system with n physical states are represented by unique vectors in C n, the set of n 1 column vectors 1 For
Spectral Theorem for Self-adjoint Linear Operators
 Notes for the undergraduate lecture by David Adams. (These are the notes I would write if I was teaching a course on this topic. I have included more material than I will cover in the 45 minute lecture;
Notes for the undergraduate lecture by David Adams. (These are the notes I would write if I was teaching a course on this topic. I have included more material than I will cover in the 45 minute lecture;
The Classification of Clifford Gates over Qubits
 The Classification of Clifford Gates over Qubits Daniel Grier, Luke Schaeffer MIT Introduction Section 1 Introduction Classification Introduction Idea Study universality by finding non-universal gate sets.
The Classification of Clifford Gates over Qubits Daniel Grier, Luke Schaeffer MIT Introduction Section 1 Introduction Classification Introduction Idea Study universality by finding non-universal gate sets.
ROTATIONS OF THE RIEMANN SPHERE
 ROTATIONS OF THE RIEMANN SPHERE A rotation of the sphere S is a map r = r p,α described by spinning the sphere (actually, spinning the ambient space R 3 ) about the line through the origin and the point
ROTATIONS OF THE RIEMANN SPHERE A rotation of the sphere S is a map r = r p,α described by spinning the sphere (actually, spinning the ambient space R 3 ) about the line through the origin and the point
Simple Lie algebras. Classification and representations. Roots and weights
 Chapter 3 Simple Lie algebras. Classification and representations. Roots and weights 3.1 Cartan subalgebra. Roots. Canonical form of the algebra We consider a semi-simple (i.e. with no abelian ideal) Lie
Chapter 3 Simple Lie algebras. Classification and representations. Roots and weights 3.1 Cartan subalgebra. Roots. Canonical form of the algebra We consider a semi-simple (i.e. with no abelian ideal) Lie
Physics 557 Lecture 5
 Physics 557 Lecture 5 Group heory: Since symmetries and the use of group theory is so much a part of recent progress in particle physics we will take a small detour to introduce the basic structure (as
Physics 557 Lecture 5 Group heory: Since symmetries and the use of group theory is so much a part of recent progress in particle physics we will take a small detour to introduce the basic structure (as
Math 350 Fall 2011 Notes about inner product spaces. In this notes we state and prove some important properties of inner product spaces.
 Math 350 Fall 2011 Notes about inner product spaces In this notes we state and prove some important properties of inner product spaces. First, recall the dot product on R n : if x, y R n, say x = (x 1,...,
Math 350 Fall 2011 Notes about inner product spaces In this notes we state and prove some important properties of inner product spaces. First, recall the dot product on R n : if x, y R n, say x = (x 1,...,
Lecture 2: Introduction to Quantum Mechanics
 CMSC 49: Introduction to Quantum Computation Fall 5, Virginia Commonwealth University Sevag Gharibian Lecture : Introduction to Quantum Mechanics...the paradox is only a conflict between reality and your
CMSC 49: Introduction to Quantum Computation Fall 5, Virginia Commonwealth University Sevag Gharibian Lecture : Introduction to Quantum Mechanics...the paradox is only a conflict between reality and your
CS168: The Modern Algorithmic Toolbox Lecture #8: How PCA Works
 CS68: The Modern Algorithmic Toolbox Lecture #8: How PCA Works Tim Roughgarden & Gregory Valiant April 20, 206 Introduction Last lecture introduced the idea of principal components analysis (PCA). The
CS68: The Modern Algorithmic Toolbox Lecture #8: How PCA Works Tim Roughgarden & Gregory Valiant April 20, 206 Introduction Last lecture introduced the idea of principal components analysis (PCA). The
Complex numbers: a quick review. Chapter 10. Quantum algorithms. Definition: where i = 1. Polar form of z = a + b i is z = re iθ, where
 Chapter 0 Quantum algorithms Complex numbers: a quick review / 4 / 4 Definition: C = { a + b i : a, b R } where i = Polar form of z = a + b i is z = re iθ, where r = z = a + b and θ = tan y x Alternatively,
Chapter 0 Quantum algorithms Complex numbers: a quick review / 4 / 4 Definition: C = { a + b i : a, b R } where i = Polar form of z = a + b i is z = re iθ, where r = z = a + b and θ = tan y x Alternatively,
Part III Symmetries, Fields and Particles
 Part III Symmetries, Fields and Particles Theorems Based on lectures by N. Dorey Notes taken by Dexter Chua Michaelmas 2016 These notes are not endorsed by the lecturers, and I have modified them (often
Part III Symmetries, Fields and Particles Theorems Based on lectures by N. Dorey Notes taken by Dexter Chua Michaelmas 2016 These notes are not endorsed by the lecturers, and I have modified them (often
Linear Algebra. Min Yan
 Linear Algebra Min Yan January 2, 2018 2 Contents 1 Vector Space 7 1.1 Definition................................. 7 1.1.1 Axioms of Vector Space..................... 7 1.1.2 Consequence of Axiom......................
Linear Algebra Min Yan January 2, 2018 2 Contents 1 Vector Space 7 1.1 Definition................................. 7 1.1.1 Axioms of Vector Space..................... 7 1.1.2 Consequence of Axiom......................
Eigenvectors and Hermitian Operators
 7 71 Eigenvalues and Eigenvectors Basic Definitions Let L be a linear operator on some given vector space V A scalar λ and a nonzero vector v are referred to, respectively, as an eigenvalue and corresponding
7 71 Eigenvalues and Eigenvectors Basic Definitions Let L be a linear operator on some given vector space V A scalar λ and a nonzero vector v are referred to, respectively, as an eigenvalue and corresponding
Review of Matrices and Block Structures
 CHAPTER 2 Review of Matrices and Block Structures Numerical linear algebra lies at the heart of modern scientific computing and computational science. Today it is not uncommon to perform numerical computations
CHAPTER 2 Review of Matrices and Block Structures Numerical linear algebra lies at the heart of modern scientific computing and computational science. Today it is not uncommon to perform numerical computations
Quantum Information & Quantum Computing
 Math 478, Phys 478, CS4803, September 18, 007 1 Georgia Tech Math, Physics & Computing Math 478, Phys 478, CS4803 Quantum Information & Quantum Computing Homework # Due September 18, 007 1. Read carefully
Math 478, Phys 478, CS4803, September 18, 007 1 Georgia Tech Math, Physics & Computing Math 478, Phys 478, CS4803 Quantum Information & Quantum Computing Homework # Due September 18, 007 1. Read carefully
Problem set 2. Math 212b February 8, 2001 due Feb. 27
 Problem set 2 Math 212b February 8, 2001 due Feb. 27 Contents 1 The L 2 Euler operator 1 2 Symplectic vector spaces. 2 2.1 Special kinds of subspaces....................... 3 2.2 Normal forms..............................
Problem set 2 Math 212b February 8, 2001 due Feb. 27 Contents 1 The L 2 Euler operator 1 2 Symplectic vector spaces. 2 2.1 Special kinds of subspaces....................... 3 2.2 Normal forms..............................
Real symmetric matrices/1. 1 Eigenvalues and eigenvectors
 Real symmetric matrices 1 Eigenvalues and eigenvectors We use the convention that vectors are row vectors and matrices act on the right. Let A be a square matrix with entries in a field F; suppose that
Real symmetric matrices 1 Eigenvalues and eigenvectors We use the convention that vectors are row vectors and matrices act on the right. Let A be a square matrix with entries in a field F; suppose that
Elementary Linear Algebra
 Matrices J MUSCAT Elementary Linear Algebra Matrices Definition Dr J Muscat 2002 A matrix is a rectangular array of numbers, arranged in rows and columns a a 2 a 3 a n a 2 a 22 a 23 a 2n A = a m a mn We
Matrices J MUSCAT Elementary Linear Algebra Matrices Definition Dr J Muscat 2002 A matrix is a rectangular array of numbers, arranged in rows and columns a a 2 a 3 a n a 2 a 22 a 23 a 2n A = a m a mn We
QR FACTORIZATIONS USING A RESTRICTED SET OF ROTATIONS
 QR FACTORIZATIONS USING A RESTRICTED SET OF ROTATIONS DIANNE P. O LEARY AND STEPHEN S. BULLOCK Dedicated to Alan George on the occasion of his 60th birthday Abstract. Any matrix A of dimension m n (m n)
QR FACTORIZATIONS USING A RESTRICTED SET OF ROTATIONS DIANNE P. O LEARY AND STEPHEN S. BULLOCK Dedicated to Alan George on the occasion of his 60th birthday Abstract. Any matrix A of dimension m n (m n)
Compute the Fourier transform on the first register to get x {0,1} n x 0.
 CS 94 Recursive Fourier Sampling, Simon s Algorithm /5/009 Spring 009 Lecture 3 1 Review Recall that we can write any classical circuit x f(x) as a reversible circuit R f. We can view R f as a unitary
CS 94 Recursive Fourier Sampling, Simon s Algorithm /5/009 Spring 009 Lecture 3 1 Review Recall that we can write any classical circuit x f(x) as a reversible circuit R f. We can view R f as a unitary
Topological Data Analysis - Spring 2018
 Topological Data Analysis - Spring 2018 Simplicial Homology Slightly rearranged, but mostly copy-pasted from Harer s and Edelsbrunner s Computational Topology, Verovsek s class notes. Gunnar Carlsson s
Topological Data Analysis - Spring 2018 Simplicial Homology Slightly rearranged, but mostly copy-pasted from Harer s and Edelsbrunner s Computational Topology, Verovsek s class notes. Gunnar Carlsson s
ELEMENTARY LINEAR ALGEBRA
 ELEMENTARY LINEAR ALGEBRA K R MATTHEWS DEPARTMENT OF MATHEMATICS UNIVERSITY OF QUEENSLAND First Printing, 99 Chapter LINEAR EQUATIONS Introduction to linear equations A linear equation in n unknowns x,
ELEMENTARY LINEAR ALGEBRA K R MATTHEWS DEPARTMENT OF MATHEMATICS UNIVERSITY OF QUEENSLAND First Printing, 99 Chapter LINEAR EQUATIONS Introduction to linear equations A linear equation in n unknowns x,
Matrix Lie groups. and their Lie algebras. Mahmood Alaghmandan. A project in fulfillment of the requirement for the Lie algebra course
 Matrix Lie groups and their Lie algebras Mahmood Alaghmandan A project in fulfillment of the requirement for the Lie algebra course Department of Mathematics and Statistics University of Saskatchewan March
Matrix Lie groups and their Lie algebras Mahmood Alaghmandan A project in fulfillment of the requirement for the Lie algebra course Department of Mathematics and Statistics University of Saskatchewan March
REPRESENTATION THEORY WEEK 7
 REPRESENTATION THEORY WEEK 7 1. Characters of L k and S n A character of an irreducible representation of L k is a polynomial function constant on every conjugacy class. Since the set of diagonalizable
REPRESENTATION THEORY WEEK 7 1. Characters of L k and S n A character of an irreducible representation of L k is a polynomial function constant on every conjugacy class. Since the set of diagonalizable
C/CS/Phys C191 Quantum Gates, Universality and Solovay-Kitaev 9/25/07 Fall 2007 Lecture 9
 C/CS/Phys C191 Quantum Gates, Universality and Solovay-Kitaev 9/25/07 Fall 2007 Lecture 9 1 Readings Benenti, Casati, and Strini: Quantum Gates Ch. 3.2-3.4 Universality Ch. 3.5-3.6 2 Quantum Gates Continuing
C/CS/Phys C191 Quantum Gates, Universality and Solovay-Kitaev 9/25/07 Fall 2007 Lecture 9 1 Readings Benenti, Casati, and Strini: Quantum Gates Ch. 3.2-3.4 Universality Ch. 3.5-3.6 2 Quantum Gates Continuing
Topological quantum computation with anyons
 p. 1/6 Topological quantum computation with anyons Éric Oliver Paquette (Oxford) p. 2/6 Outline: 0. Quantum computation 1. Anyons 2. Modular tensor categories in a nutshell 3. Topological quantum computation
p. 1/6 Topological quantum computation with anyons Éric Oliver Paquette (Oxford) p. 2/6 Outline: 0. Quantum computation 1. Anyons 2. Modular tensor categories in a nutshell 3. Topological quantum computation
Linear Algebra Review
 Chapter 1 Linear Algebra Review It is assumed that you have had a course in linear algebra, and are familiar with matrix multiplication, eigenvectors, etc. I will review some of these terms here, but quite
Chapter 1 Linear Algebra Review It is assumed that you have had a course in linear algebra, and are familiar with matrix multiplication, eigenvectors, etc. I will review some of these terms here, but quite
MAT 445/ INTRODUCTION TO REPRESENTATION THEORY
 MAT 445/1196 - INTRODUCTION TO REPRESENTATION THEORY CHAPTER 1 Representation Theory of Groups - Algebraic Foundations 1.1 Basic definitions, Schur s Lemma 1.2 Tensor products 1.3 Unitary representations
MAT 445/1196 - INTRODUCTION TO REPRESENTATION THEORY CHAPTER 1 Representation Theory of Groups - Algebraic Foundations 1.1 Basic definitions, Schur s Lemma 1.2 Tensor products 1.3 Unitary representations
Particles I, Tutorial notes Sessions I-III: Roots & Weights
 Particles I, Tutorial notes Sessions I-III: Roots & Weights Kfir Blum June, 008 Comments/corrections regarding these notes will be appreciated. My Email address is: kf ir.blum@weizmann.ac.il Contents 1
Particles I, Tutorial notes Sessions I-III: Roots & Weights Kfir Blum June, 008 Comments/corrections regarding these notes will be appreciated. My Email address is: kf ir.blum@weizmann.ac.il Contents 1
Incompatibility Paradoxes
 Chapter 22 Incompatibility Paradoxes 22.1 Simultaneous Values There is never any difficulty in supposing that a classical mechanical system possesses, at a particular instant of time, precise values of
Chapter 22 Incompatibility Paradoxes 22.1 Simultaneous Values There is never any difficulty in supposing that a classical mechanical system possesses, at a particular instant of time, precise values of
Symmetric and anti symmetric matrices
 Symmetric and anti symmetric matrices In linear algebra, a symmetric matrix is a square matrix that is equal to its transpose. Formally, matrix A is symmetric if. A = A Because equal matrices have equal
Symmetric and anti symmetric matrices In linear algebra, a symmetric matrix is a square matrix that is equal to its transpose. Formally, matrix A is symmetric if. A = A Because equal matrices have equal
CLASSICAL GROUPS DAVID VOGAN
 CLASSICAL GROUPS DAVID VOGAN 1. Orthogonal groups These notes are about classical groups. That term is used in various ways by various people; I ll try to say a little about that as I go along. Basically
CLASSICAL GROUPS DAVID VOGAN 1. Orthogonal groups These notes are about classical groups. That term is used in various ways by various people; I ll try to say a little about that as I go along. Basically
Notation. For any Lie group G, we set G 0 to be the connected component of the identity.
 Notation. For any Lie group G, we set G 0 to be the connected component of the identity. Problem 1 Prove that GL(n, R) is homotopic to O(n, R). (Hint: Gram-Schmidt Orthogonalization.) Here is a sequence
Notation. For any Lie group G, we set G 0 to be the connected component of the identity. Problem 1 Prove that GL(n, R) is homotopic to O(n, R). (Hint: Gram-Schmidt Orthogonalization.) Here is a sequence
Linear Algebra. Workbook
 Linear Algebra Workbook Paul Yiu Department of Mathematics Florida Atlantic University Last Update: November 21 Student: Fall 2011 Checklist Name: A B C D E F F G H I J 1 2 3 4 5 6 7 8 9 10 xxx xxx xxx
Linear Algebra Workbook Paul Yiu Department of Mathematics Florida Atlantic University Last Update: November 21 Student: Fall 2011 Checklist Name: A B C D E F F G H I J 1 2 3 4 5 6 7 8 9 10 xxx xxx xxx
Background on Chevalley Groups Constructed from a Root System
 Background on Chevalley Groups Constructed from a Root System Paul Tokorcheck Department of Mathematics University of California, Santa Cruz 10 October 2011 Abstract In 1955, Claude Chevalley described
Background on Chevalley Groups Constructed from a Root System Paul Tokorcheck Department of Mathematics University of California, Santa Cruz 10 October 2011 Abstract In 1955, Claude Chevalley described
Symmetries, Fields and Particles 2013 Solutions
 Symmetries, Fields and Particles 03 Solutions Yichen Shi July 9, 04. a Define the groups SU and SO3, and find their Lie algebras. Show that these Lie algebras, including their bracket structure, are isomorphic.
Symmetries, Fields and Particles 03 Solutions Yichen Shi July 9, 04. a Define the groups SU and SO3, and find their Lie algebras. Show that these Lie algebras, including their bracket structure, are isomorphic.
14 Singular Value Decomposition
 14 Singular Value Decomposition For any high-dimensional data analysis, one s first thought should often be: can I use an SVD? The singular value decomposition is an invaluable analysis tool for dealing
14 Singular Value Decomposition For any high-dimensional data analysis, one s first thought should often be: can I use an SVD? The singular value decomposition is an invaluable analysis tool for dealing
Lecture 3: Constructing a Quantum Model
 CS 880: Quantum Information Processing 9/9/010 Lecture 3: Constructing a Quantum Model Instructor: Dieter van Melkebeek Scribe: Brian Nixon This lecture focuses on quantum computation by contrasting it
CS 880: Quantum Information Processing 9/9/010 Lecture 3: Constructing a Quantum Model Instructor: Dieter van Melkebeek Scribe: Brian Nixon This lecture focuses on quantum computation by contrasting it
IRREDUCIBLE REPRESENTATIONS OF SEMISIMPLE LIE ALGEBRAS. Contents
 IRREDUCIBLE REPRESENTATIONS OF SEMISIMPLE LIE ALGEBRAS NEEL PATEL Abstract. The goal of this paper is to study the irreducible representations of semisimple Lie algebras. We will begin by considering two
IRREDUCIBLE REPRESENTATIONS OF SEMISIMPLE LIE ALGEBRAS NEEL PATEL Abstract. The goal of this paper is to study the irreducible representations of semisimple Lie algebras. We will begin by considering two
Symmetric Spaces Toolkit
 Symmetric Spaces Toolkit SFB/TR12 Langeoog, Nov. 1st 7th 2007 H. Sebert, S. Mandt Contents 1 Lie Groups and Lie Algebras 2 1.1 Matrix Lie Groups........................ 2 1.2 Lie Group Homomorphisms...................
Symmetric Spaces Toolkit SFB/TR12 Langeoog, Nov. 1st 7th 2007 H. Sebert, S. Mandt Contents 1 Lie Groups and Lie Algebras 2 1.1 Matrix Lie Groups........................ 2 1.2 Lie Group Homomorphisms...................
Is Quantum Search Practical?
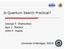 DARPA Is Quantum Search Practical? George F. Viamontes Igor L. Markov John P. Hayes University of Michigan, EECS Outline Motivation Background Quantum search Practical Requirements Quantum search versus
DARPA Is Quantum Search Practical? George F. Viamontes Igor L. Markov John P. Hayes University of Michigan, EECS Outline Motivation Background Quantum search Practical Requirements Quantum search versus
Mic ael Flohr Representation theory of semi-simple Lie algebras: Example su(3) 6. and 20. June 2003
 Handout V for the course GROUP THEORY IN PHYSICS Mic ael Flohr Representation theory of semi-simple Lie algebras: Example su(3) 6. and 20. June 2003 GENERALIZING THE HIGHEST WEIGHT PROCEDURE FROM su(2)
Handout V for the course GROUP THEORY IN PHYSICS Mic ael Flohr Representation theory of semi-simple Lie algebras: Example su(3) 6. and 20. June 2003 GENERALIZING THE HIGHEST WEIGHT PROCEDURE FROM su(2)
Fulton and Harris, Representation Theory, Graduate texts in Mathematics,
 Week 14: Group theory primer 1 Useful Reading material Fulton and Harris, Representation Theory, Graduate texts in Mathematics, Springer 1 SU(N) Most of the analysis we are going to do is for SU(N). So
Week 14: Group theory primer 1 Useful Reading material Fulton and Harris, Representation Theory, Graduate texts in Mathematics, Springer 1 SU(N) Most of the analysis we are going to do is for SU(N). So
Lecture 4: Postulates of quantum mechanics
 Lecture 4: Postulates of quantum mechanics Rajat Mittal IIT Kanpur The postulates of quantum mechanics provide us the mathematical formalism over which the physical theory is developed. For people studying
Lecture 4: Postulates of quantum mechanics Rajat Mittal IIT Kanpur The postulates of quantum mechanics provide us the mathematical formalism over which the physical theory is developed. For people studying
Linear Algebra. The analysis of many models in the social sciences reduces to the study of systems of equations.
 POLI 7 - Mathematical and Statistical Foundations Prof S Saiegh Fall Lecture Notes - Class 4 October 4, Linear Algebra The analysis of many models in the social sciences reduces to the study of systems
POLI 7 - Mathematical and Statistical Foundations Prof S Saiegh Fall Lecture Notes - Class 4 October 4, Linear Algebra The analysis of many models in the social sciences reduces to the study of systems
Foundations of Matrix Analysis
 1 Foundations of Matrix Analysis In this chapter we recall the basic elements of linear algebra which will be employed in the remainder of the text For most of the proofs as well as for the details, the
1 Foundations of Matrix Analysis In this chapter we recall the basic elements of linear algebra which will be employed in the remainder of the text For most of the proofs as well as for the details, the
A PRIMER ON SESQUILINEAR FORMS
 A PRIMER ON SESQUILINEAR FORMS BRIAN OSSERMAN This is an alternative presentation of most of the material from 8., 8.2, 8.3, 8.4, 8.5 and 8.8 of Artin s book. Any terminology (such as sesquilinear form
A PRIMER ON SESQUILINEAR FORMS BRIAN OSSERMAN This is an alternative presentation of most of the material from 8., 8.2, 8.3, 8.4, 8.5 and 8.8 of Artin s book. Any terminology (such as sesquilinear form
The Spectral Theorem for normal linear maps
 MAT067 University of California, Davis Winter 2007 The Spectral Theorem for normal linear maps Isaiah Lankham, Bruno Nachtergaele, Anne Schilling (March 14, 2007) In this section we come back to the question
MAT067 University of California, Davis Winter 2007 The Spectral Theorem for normal linear maps Isaiah Lankham, Bruno Nachtergaele, Anne Schilling (March 14, 2007) In this section we come back to the question
Geometry of the Special Unitary Group
 Geometry of the Special Unitary Group The elements of SU 2 are the unitary 2 2 matrices with determinant 1. It is not hard to see that they have the form a 1) ) b, b ā with āa+bb = 1. This is the transpose
Geometry of the Special Unitary Group The elements of SU 2 are the unitary 2 2 matrices with determinant 1. It is not hard to see that they have the form a 1) ) b, b ā with āa+bb = 1. This is the transpose
(1) A frac = b : a, b A, b 0. We can define addition and multiplication of fractions as we normally would. a b + c d
 The Algebraic Method 0.1. Integral Domains. Emmy Noether and others quickly realized that the classical algebraic number theory of Dedekind could be abstracted completely. In particular, rings of integers
The Algebraic Method 0.1. Integral Domains. Emmy Noether and others quickly realized that the classical algebraic number theory of Dedekind could be abstracted completely. In particular, rings of integers
Introduction to Quantum Algorithms Part I: Quantum Gates and Simon s Algorithm
 Part I: Quantum Gates and Simon s Algorithm Martin Rötteler NEC Laboratories America, Inc. 4 Independence Way, Suite 00 Princeton, NJ 08540, U.S.A. International Summer School on Quantum Information, Max-Planck-Institut
Part I: Quantum Gates and Simon s Algorithm Martin Rötteler NEC Laboratories America, Inc. 4 Independence Way, Suite 00 Princeton, NJ 08540, U.S.A. International Summer School on Quantum Information, Max-Planck-Institut
A Brief Outline of Math 355
 A Brief Outline of Math 355 Lecture 1 The geometry of linear equations; elimination with matrices A system of m linear equations with n unknowns can be thought of geometrically as m hyperplanes intersecting
A Brief Outline of Math 355 Lecture 1 The geometry of linear equations; elimination with matrices A system of m linear equations with n unknowns can be thought of geometrically as m hyperplanes intersecting
Group theory - QMII 2017
 Group theory - QMII 7 Daniel Aloni References. Lecture notes - Gilad Perez. Lie algebra in particle physics - H. Georgi. Google... Motivation As a warm up let us motivate the need for Group theory in physics.
Group theory - QMII 7 Daniel Aloni References. Lecture notes - Gilad Perez. Lie algebra in particle physics - H. Georgi. Google... Motivation As a warm up let us motivate the need for Group theory in physics.
