Nearly Weighted Risk Minimal Unbiased Estimation
|
|
|
- Wesley Brooks
- 6 years ago
- Views:
Transcription
1 Nearly Weighted Risk Minimal Unbiased Estimation Ulrich K. Müller and Yulong Wang Economics Department Princeton University July 2017 Abstract Consider a non-standard parametric estimation problem, such as the estimation of the AR(1) coefficient close to the unit root. We develop a numerical algorithm that determines an estimator that is nearly (mean or median) unbiased, and among all such estimators, comes close to minimizing a weighted average risk criterion. We demonstrate the usefulness of our generic approach by also applying it to estimation in a predictive regression, estimation of the degree of time variation, and long-range quantile point forecasts for an AR(1) process with coefficient close to unity. JEL classification: C13, C22 Keywords: Mean bias, median bias, local-to-unity, nearly non-invertible MA(1) The authors thank seminar participants at Harvard/MIT, Princeton, University of Kansas and University of Pennsylvania for helpful comments and suggestions. Müller gratefully acknowledges financial support by the NSF via grant SES
2 1 Introduction Much recent work in econometrics concerns inference in non-standard problems, that is problems that don t reduce to a Gaussian shift experiment, even asymptotically. Prominent examples include inference under weak identification (cf. Andrews, Moreira and Stock (2006, 2008)), in models involving local-to-unity time series (Elliott, Rothenberg, and Stock (1996), Jansson and Moreira (2006), Mikusheva (2007)), and in moment inequality models. The focus of this recent work is the derivation of hypothesis tests and confidence sets, and in many instances, optimal or nearly optimal procedures have been identified. In comparison, the systematic derivation of attractive point estimators has received less attention. In this paper we seek to make progress by deriving estimators that come close to minimizing a weighted average risk (WAR) criterion, under the constraint of having uniformly low bias. Our general framework allows for a wide range of loss functions and bias constraints, such as mean or median unbiasedness. The basic approach is to finitely discretize the bias constraint. For instance, one might impose zero or small bias only under distinct parameter values. Under this discretization, the derivation of a WAR minimizing unbiased estimator reduces to a Lagrangian problem with non-negative Lagrange multipliers. The Lagrangian can be written as an integral over the data, since both the objective and the constraints can be written as expectations. Thus, for given multipliers, the best estimator simply minimizes the integrand for all realizations of the data, and so is usually straightforward to determine. Furthermore, it follows from standard duality theory that the value of the Lagrangian, evaluated at arbitrary non-negative multipliers, provides a lower bound on the WAR of any estimator that satisfies the constraints. This lower bound holds a fortiori in the non-discretized version of the problem, since the discretization amounts to a relaxation of the uniform unbiasedness constraint. We use numerical techniques to obtain approximately optimal Lagrange multipliers, and use them for two conceptually distinct purposes. On the one hand, close to optimal Lagrange multipliers imply a large, and thus particularly informative lower bound on the WAR of any nearly unbiased estimator. On the other hand, close to optimal Lagrange multipliers yield an estimator that is nearly unbiased in the discrete problem. Thus, with a fine enough discretization and some smoothness of the problem, this estimator also has uniformly small bias. Combining these two usages then allows us to conclude that we have in fact identified a nearly WAR minimizing estimator among all estimators that have uniformly small bias. 1
3 It is not possible to finely discretize a problem involving an unbounded parameter space. At the same time, many non-standard problems become approximately standard in the unbounded part of the parameter space. For instance, a large concentration parameter in a weak instrument problem, or a large local-to-unity parameter in a time series problem, induce nearly standard behavior of test statistics and estimators. We thus suggest switching to a suitable nearly unbiased estimator in this standard part of the parameter space in a way that ensures overall attractive properties. These elements discretization of the original problem, analytical lower bound on risk, numerical approximation, switching are analogous to Elliott, Müller and Watson s (2015) approach to the determination of nearly weighted average power maximizing tests in the presence of nuisance parameters. Our contribution here is the transfer of the same ideas to estimation problems. There are two noteworthy special cases that have no counterpart in hypothesis testing. First, under squared loss and a mean bias constraint, the Lagrangian minimizing estimator is linear in the Lagrange multipliers. WAR then becomes a positive definite quadratic form in the multipliers, and the constraints are a linear function of the multipliers. The numerical determination of the multipliers thus reduces to a positive definite quadratic programming problem, which is readily solved even for large by well-known and widely implemented algorithms. 1 Second, under a median unbiasedness constraint and in absence of any nuisance parameters, it is usually straightforward to numerically determine an exactly median unbiased estimator by inverting the median function of a suitable statistic, even in a non-standard problem. This approach was prominently applied in econometrics in Andrews (1993) and Stock and Watson (1998), for instance. However, the median inversion of different statistics typically yields different median unbiased estimators. Our approach here can be used to determine the right statistic to invert under a given WAR criterion: Median inverting a nearly WAR minimizing nearly median unbiased estimator typically yields an exactly median unbiased nearly WAR minimizing estimator, as the median function of the nearly median unbiased estimator is close to the identity function. In addition, invariance considerations are more involved and potentially more powerful in 1 In this special case, and with a weighting function that puts all mass at one parameter value, the Lagrangian bound on WAR reduces to a Barankin (1946)-type bound on the MSE of an unbiased or biased estimator, as discussed by McAulay and Hofstetter (1971), Glave (1972) and Albuquerque (1973). 2
4 an estimation problem compared to a hypothesis testing problem, since it sometimes makes sense to impose invariance (or equivariance) with respect to the parameter of interest. We suitably extend the theory of invariant estimators in Chapter 3 of Lehmann and Casella (1998) in Section 4 below. We demonstrate our approach in four time series estimation problems. In all of them, we consider an asymptotic version of the problem. First, we consider mean and median unbiased estimation of the local-to-unity AR(1) parameter with known and unknown mean, and with different assumptions on the initial condition. The analysis of the bias in the AR(1) model has spawned a very large literature (see, among others, Hurvicz (1950), Marriott and Pope (1954), Kendall (1954), White (1961), Phillips (1977, 1978), Sawa (1978), Tanaka (1983, 1984), Shaman and Stine (1988), Yu (2012)), with numerous suggestions of alternative estimators with less bias (see, for instance, Quenouille (1956), Orcutt and Winokur (1969), Andrews (1993), Andrews and Chen (1994), Park and Fuller (1995), MacKinnon and Smith (1998), Cheang and Reinsel (2000), Roy and Fuller (2001), Crump (2008), Phillips and Han (2008), Han, Phillips, and Sul (2011) and Phillips (2012)). With the exception of the conditional optimality of Crump s (2008) median unbiased estimator in a model with asymptotically negligible initial condition, none of these papers make an optimality claim, and we are not aware of a previously suggested estimator with uniformly nearly vanishing mean bias. Second, we consider a nearly non-invertible MA(1) model. The parameter estimator here suffers from the so-called pile-up problem, that is the MA(1) root is estimated to be exactly unity with positive probability. Stock and Watson (1998) derive an exactly median unbiased estimator by median inverting the Nyblom (1989) statistic in the context of estimating the degree of parameter time variation. We derive an alternative, nearly WAR minimizing median unbiased estimator under absolute value loss and find it to have very substantially lower risk under moderate and large amounts of time variation. Third, we derive nearly WAR minimizing mean and median unbiased estimators of the regression coefficient in the so-called predictive regression problem, that is with a weakly exogenous local-to-unity regressor. This contributes to previous analyses and estimator suggestions by Mankiw and Shapiro (1986), Stambaugh (1986, 1999), Cavanagh, Elliott, and Stock (1995), Jansson and Moreira (2006), Kothari and Shanken (1997), Amihud and Hurvich (2004), Eliasz (2005) and Chen and Deo (2009). Finally, we use our framework to derive nearly quantile unbiased long-range forecasts from 3
5 a local-to-unity AR(1) process with unknown mean. The unbiased property here means that in repeated applications of the forecast rule for the quantile, the future value realizes to be smaller than the forecast with probability, under all parameter values. See Phillips (1979), Stock (1996), Kemp (1999), Gospodinov (2002), Turner (2004) and Elliott (2006) for related studies of forecasts in a local-to-unity AR(1). In these applications, the unbiasedness constraint may be motivated in a variety of ways. A first motivation may simply stem from the definition of unbiasedness. For instance, the average of individual unbiased AR(1) estimators in a panel with many individuals but a common value of the autoregressive coefficients takes on values close to the true parameter by construction. Also, regulatory or other institutional constraints might make it highly desirable that, in repeated quantile forecasts, the realized value takes on values smaller than the forecast 100% of the time. A second potential motivation relies on unbiasedness as a device to discipline estimators. As is well known, minimizing weighted risk without any side constraint leads to the Bayes estimator that, for each data draw minimizes posterior expected loss, with a prior proportional to the weight function. The weight function then has an enormous influence on the resulting estimator; for example, a degenerate weight with all mass on one parameter value leads to an estimator that entirely ignores the data. In contrast, imposing unbiasedness limits the influence of the weight function on the resulting estimator. For instance, in the Gaussian shift experiment, imposing mean unbiasedness yields the MLE as the unique non-randomized estimator, so the MLE is weighted risk minimizing among all unbiased estimators, for any weight function. Correspondingly, in some of our applications, we find that the weight function plays a very limited role, with the risk of the nearly unbiased risk minimizing estimator with all weight on one parameter value only slightly below the risk of the nearly unbiased estimator under a more diffuse weighting function. Finally, one may simply point to the long tradition of evaluating competing estimators by their bias. For instance, the large literature on the estimation of AR(1) parameter, as partially reviewed above, focusses heavily on the mean or median bias. Under this revealed preference it makes sense to take a systematic approach to the derivation of estimators that perform nearly optimally under this criterion. In the AR(1) and predictive regression problems, despite numerous suggestions for alternative estimators, no mean unbiased estimator is known, so our approach comes close to solving these classic time series problems. For some applications, median unbiased estimators were previously derived, but it was not known 4
6 whether there exists alternative median unbiased estimators with much less risk. In the problem of median unbiased estimation of the AR(1) coefficient with known mean, we find that the suggestion of Andrews (1993) is essentially optimal. In contrast, in the problem of estimating a nearly non-invertible MA(1) root our systematic approach yields a median unbiased estimator that outperforms a previously suggested and commonly employed estimator by a substantial margin. The remainder of the paper is organized as follows. Section 2 sets up the problem, derives the lower bound on WAR, and discusses the numerical implementation. Section 3 considers the two special cases of mean unbiased estimation under squared loss, and of median unbiased estimation without nuisance parameters. Section 4 extends the framework to invariant estimators. Throughout Sections 2-4, we use the problem of estimating the AR(1) coefficient under local-to-unity asymptotics as our running example. In Section 5, we provide details on the three additional examples mentioned above. Section 6 concludes. 2 Estimation, Bias and Risk 2.1 Set-Up and Notation We observe the random element inthesamplespacex. The density of relative to some -finite measure is,where Θ is the parameter space. We are interested in estimating = () with estimators : X 7. For scalar estimation problems, R, but our set-up allows for more general estimands. Estimation errors lead to losses as measured by the function : Θ 7 [0 ) (so that (()) is the loss incurred by the estimate () ifthetrueparameteris). The risk of the estimator is given by its expected loss, ( ) = [(())] = R (()) ()(). Beyond the estimator s risk, we are also concerned about its bias. For some function : Θ 7, the bias of is defined as ( ) = [(())]. For instance, for the mean bias, ( ) = (), sothat( ) = [()] (), and for the median bias of a scalar parameter of interest, ( ) =1[ ()] 1,sothat( ) = 2 [() ()] 1. 2 We are interested in deriving estimators that minimize risk subject to an unbiasedness constraint. In many problems of interest, a uniformly risk minimizing might not exist, even under the bias constraint. To make further progress, we thus measure the quality of estimators by their weighted average risk ( ) = R ( ) () for some given non- 5
7 negative finite measure with support in Θ. In this notation, the weighted risk minimal unbiased estimator solves the program min ( ) s.t. (1) ( ) =0 Θ. (2) More generally, one might also be interested in deriving estimators that are only approximately unbiased, that is solutions to (1) subject to ( ) Θ (3) for some 0. Allowing the bounds on ( ) to depend on does not yield greater generality, as they can be subsumed in the definition of the function. For instance, a restriction on the relative mean bias to be no more than 5% is achieved by setting ( ) = ( ())() and =005. An estimator is called risk unbiased if 0 [(() 0 )] 0 [(())] for any 0 Θ. As discussed in Chapter 3 of Lehmann and Casella (1998), risk unbiasedness is a potentially attractive property as it ensures that under 0, the estimate () is at least as close to the true value 0 in expectation as measured by as it is to any other value of. Itisstraightforward to show that under squared loss (())=(() ()) 2 a risk unbiased estimator is necessarily mean unbiased, and under absolute value loss (())= () (), itis necessarily median unbiased. From this perspective, squared loss and mean unbiased constraints, and absolute value loss and median unbiased constraints, form natural pairs, and we report results for these pairings in our examples. The following development, however, does not depend on any assumptions about the relationship between loss function and bias constraint, and other pairings of loss function and constraints might be more attractive in specific applications. In many examples, the risk of good estimators is far from constant, as the information in about () varies with. This makes risk comparisons and the weighting function more difficult to interpret. Similarly, also the mean bias of an estimator is naturally gauged relative to its sampling variability. To address this issue, we introduce a normalization function () that roughly corresponds to the root mean squared error of a good estimator at The normalized risk ( ) is then given by ( ) = [(() ) 2 ]() 2 and ( ) = [ () () ]() under squared and absolute value loss, respectively, 6
8 and the normalized mean bias is ( ) =( [()] ())(). The weighted average normalized risk with weighting function, R ( ) (), then reduces to ( ) above with () = ()() 2 and () = ()() in the squared loss and absolute value loss case, respectively, and ( ) =( ) with ( ) =( ())(). The median bias, of course, is readily interpretable without any normalization. Running Example: Consider an autoregressive process of order 1, = 1 +, = 1,where N (0 1) and 0 =0. Under local-to-unity asymptotics, = = 1, this model converges to the limit experiment (in the sense of LeCam) of observing, where is an Ornstein-Uhlenbeck process () = () + () with (0) = 0 and a standard Wiener process. The random element takes on values in the set of cadlag functions on the unit interval X, and the Radon-Nikodym derivative of relative to Wiener measure is Z 1 () =exp[ 1 2 ((1)2 1) () 2 ] (4) The aim is to estimate R in a way that (nearly) minimizes weighted risk under a mean or median bias constraint. More generally, suppose that = 1 + with 0 = ( 12 ), P 12 [ ] =1 ( ), and =1. Then for any consistent estimator ˆ 2 of the long run variance 2 of { }, ( ) = 12ˆ 1 [ ] ( ). Thus, for any -almost surely continuous estimator : X R in the limiting problem, ( 12ˆ 1 [ ] ) has the same asymptotic distribution as () by the continuous mapping theorem. Therefore, if () is (nearly) median unbiased for, then( ) is asymptotically (nearly) median unbiased. For a (nearly) mean unbiased estimator (), one could put constraints on { } that ensure uniform integrability of ( ), so that again [( )] [()] for all. Alternatively, one might define asymptotic mean bias and asymptotic risk as the sequential limits lim lim [1[ ( ) ](( ) ())] lim lim [1[(( )) ](( ))] respectively. With these definitions, the bias and (weighted average) risk of ( ) converges to the bias and weighted average risk of by construction, as long as is -almost surely continuous with finite mean and risk relative to (4). The usual OLS estimator for (which is also equal to the MLE) is () = 1 2 ((1)2 1) R 1 0 ()2. AsdemonstratedbyPhillips(1987) and Chan and Wei (1987), for large, 7 0
9 Figure 1: Normalized Mean Bias and Mean Squared Error of OLS Estimator in Local-to- Unity AR(1) (2) 12 ( () ) N (0 1) as, yielding the approximation () N ( 2). We thus use the normalization function () = (the offset of 10 ensures that () 0 even as =0). 2 We initially focus on estimating under squared loss and a mean bias constraint for 0; we return to the problem of median unbiased estimation in Section 3.2 below. Figure 1 depicts the normalized mean bias and the normalized mean squared error of as a function of. Asiswellknown,thebiasof is quite substantial: even under fairly strong mean reversion of, say, =60, the bias is approximately on fifth of the root mean squared error of the estimator. N 2.2 A Lower Bound on Weighted Risk of Unbiased Estimators In general, it will be difficult to analytically solve (1) subject to (3). Both X and are typically uncountable, so we are faced with an optimization problem in a function space. Moreover, it is usually difficult to obtain analytical closed-form expressions for the integrals defining ( ) and ( ), so one must rely on approximation techniques, such as Monte Carlo simulation. For these reasons, it seems natural to resort to numerical techniques to obtain an approximate solution. 2 For a given normalized weighting function,different values for the offset amount to different effective weighting functions. 8
10 There are potentially many ways of approaching this numerical problem. For instance, onemightpositsomesieve-typespacefor, and numerically determine the (now finitedimensional) parameter that provides the relatively best approximate solution. But to make this operational, one must choose some dimension of the sieve space, and it unclear how much better of a solution one might have been able to find in a different or more highly-dimensional sieve space. It would therefore be useful to have a lower bound on the weighted risk ( ) that holds for all estimators that satisfy (3). If an approximate solution ˆ is found that also satisfies (3) and whose weighted risk (ˆ ) is close to the bound, then we know that we have found the nearly best solution overall. To derive such a bound, we relax the constraint (3) by replacing it by a finite number of constraints: Let =1 be probability distributions on Θ and define the weighted average bias ( ) of the estimator as ( ) = R ( )(). Then any estimator that satisfies (3) clearly also satisfies ( ) for all =1 (5) A special case of (5) has equaltoapointmassat,sothat(5)amountstoimposing(3) at the finite number of parameter values 1. Now consider the Lagrangian for the problem (1) subject to (5), ( ) =( )+ X (( ) )+ =1 X ( ( ) ) (6) =1 where =( 1 ) and =( ). Bywriting( ) and ( ) in terms of their defining integrals and by assuming that we can change the order of integration, we obtain Z Ã Z X Z ( ) = ()(()) ()+ ( ()(()) () ) (7) + =1 X =1 Z (! ()(()) () ) () Let be the estimator such that for a given, () minimizes the integrand on the right hand side of (7) for each. Since minimizing the integrand at each point is sufficient to minimize the integral, necessarily minimizes over. 9
11 This argument requires that the change of the order of integration in (7) is justified. By Fubini s Theorem, this is always the case for ( ) (since is non-negative), and also for ( ) if is bounded (as is always the case for the median bias, and for the mean bias if is bounded). Under squared loss and mean bias constraints, and unbounded, itsuffices that there exists some estimator with uniformly bounded mean squared error. Standard Duality Theory for optimization implies the following Lemma. Lemma 1 Suppose satisfies (5), and for arbitrary 0 (that is, each element in is non-negative), minimizes ( ) over. Then( ) ( ). Proof. For any, ( ) ( ) by definition of,soinparticular,( ) ( ). Furthermore, ( ) ( ) since 0 and satisfies (5). Combining these inequalities yields the result. Note that the bound on ( ) in Lemma 1 does not require an exact solution to the discretized problem (1) subject to (5). Any 0 implies a valid bound ( ), although some choices for yield better (i.e., larger) bounds than others. Since (5) is implied by (3), these bounds hold a fortiori for any estimator satisfying the uniform unbiasedness constraint (3). Running Example: Suppose =1, putsunitmassat 0 =0and 1 puts point mass at 1 0. With square loss ( ) =( ) 2, normalized mean bias constraint ( ) =( )(), =0and 1 =0, () minimizes Z Z ()(()) () 1 ()(()) () = 0 () (() 0) 2 ( 0 ) () () 1 ( 1 ) This is solved by () = ( 0 ) 2 1 ()( 0 ()( 1 )). For 1 =3and 1 =15, a numerical calculation yields ( )= ( 0 )=048 and ( 1 )= ( 1 )=006 so that ( )=039. We can conclude from Lemma 1 that no estimator that is unbiased for all R can have risk ( ) = ( 0 ) smaller than 039, and the same holds also for all estimators that are unbiased only at 1. Moreover, this lower risk bound also holds for all estimators whose normalized bias is smaller than 0.06 uniformly in R, andmore generally for all estimators whose normalized mean bias is smaller than 0.06 in absolute value only at 1. N If 0 is such that satisfies (5) and the complementarity slackness conditions (( ) ) =0and ( ( ) ) =0hold, then (6) implies ( )=( ), so that by an application of Lemma 1, ( ) is the best lower bound. 10
12 2.3 Numerical Approach Solving the program (1) subject to (5) thus yields the largest, and thus most informative boundonweightedrisk( ). In addition, solutions to this program also plausibly satisfy a slightly more relaxed version of original non-discretized constraint (3). The reason is that if the bias ( ) does not vary greatly in, and the distributions are sufficiently dense in Θ, then any estimator that satisfies(5)cannotviolate(3)byverymuch. This suggests the following strategy to obtain a nearly weighted risk minimizing nearly unbiased estimator, that is, for given 0 and 0, an estimator ˆ that (i) satisfies (3) with = ; (ii) has weighted risk (ˆ ) (1 + )( ) for any estimator satisfying (3) with =. 1. Discretize Θ by point masses or other distributions, =1. 2. Obtain approximately optimal Lagrange multipliers ˆ for the problem (1) subject to (5) for =, and associated value = (ˆ ˆ ). 3. Obtain an approximate solution (ˆ ˆ ) to the problem min 0 (1 + ) (8) and ( ), =1 (9) and check whether ˆ satisfies (3). If it doesn t, go back to Step 1 and use a finer discretization. If it does, ˆ = ˆ has the desired properties by an application of Lemma 1. Importantly, neither nor ˆ have to be exact solutions to their respective programs ˆ to be able to conclude that ˆ is indeed a nearly weighted risk minimizing nearly unbiased estimator as defined above, that is, it satisfies the uniform near unbiasedness property (3) (and not only the discretized unbiasedness property (5)), and its WAR is no more than a multiple (1 + ) larger than the WAR of any such estimator. The solution ˆ totheprobleminstep3hasthesameformas,thatisˆ minimizes a weighted average of the integrand in (7), but now is the ratio of the Lagrange multipliers corresponding to the constraints (9) and the Lagrange multiplier corresponding to the constraint (8). These constraints are always feasible, since = satisfies (9) with = ˆ (at least if ˆ is the exact solution), and (ˆ )= (1 + ). The additional slack 11
13 provided by is used to tighten the constraints on (ˆ ) to potentially obtain a ˆ satisfying (3). A finer discretization implies additional constraints in (5) and thus (weakly) increases the value of. At the same time, a finer discretization also adds additional constraints on the bias function of ˆ, making it more plausible that it satisfies the uniform constraint (3). We suggest using simple fixed point iterations to obtain approximate solutions in Steps 2 and 3, similar to EMW s approach to numerically approximate an approximately least favorable distribution. See Appendix B for details. Once the Lagrange multipliers underlying ˆ are determined, ˆ () for given data is simply the minimizer of the integrand on the righthandsideof(7). Weprovidecorresponding tables and matlab code for all examples in this paper under umueller. An important class of non-standard estimation problems are limit experiments that arise from the localization of an underlying parameter Ψ around problematic parameter values Ψ Ψ, such as the local-to-unity asymptotics for the AR(1) estimation problem in the running example. Other examples include weak instrument asymptotics (where the limit is taken for values of the concentration parameter local-to-zero), or local-to-binding moment conditions in moment inequality models. In these models, standard estimators, such as, say, (bias corrected) maximum likelihood estimators, are typically asymptotically unbiased and efficient for values of Ψ. Moreover, this good behavior of standard estimators typically also arises, at least approximately, under local asymptotics with localization parameter as () for some appropriate function : Θ 7 R. For instance, as already mentioned in Section 2.1, Phillips (1987) and Chan and Wei (1987) show that the OLS estimator for the AR(1) coefficient = is approximately normal under local-to-unity asymptotics = = 1 as () =. This can be made precise by limit of experiment arguments, as discussed in Section 4.1 of EMW. Intuitively, the boundary of the localized parameter space Θ typically continuously connects to the unproblematic part of the parameter space Ψ\Ψ of the underlying parameter. It then makes sense to focus the numerical strategy on the truly problematic part of the local parameter space, where the standard estimator is substantially biased or inefficient. As in EMW, consider a partition of the parameter space Θ into two regions Θ = Θ Θ. For large enough, Θ = { : () } is the (typically unbounded) standard region where is approximately unbiased and efficient, and Θ = Θ\Θ is the problematic nonstandard region. Correspondingly, consider estimators ˆ that are of the following switching 12
14 form ˆ() =() ()+(1 ()) () (10) where () =1[ˆ() ] for some estimator ˆ() of (). By choosing a large enough cut-off, we can ensure that is only applied to realizations of that stem from the relatively unproblematic part of the parameter space Θ with high probability. The numerical problem then becomes the determination of the estimator : X 7 that leads to overall appealing bias and efficiency properties of ˆ in (10) for any Θ. As discussed in EMW, an additional advantage of this switching approach is that the weighting function can then focus on Θ and the seam part of Θ where (()) is not close to zero or one. The good efficiency properties of ˆ on the remaining part of Θ are simply inherited by the good properties of. Incorporating this switching approach in the numerical strategy above is straightforward: For given, the problem in Step 3 now has constrained to be of the form (10), that is for all that lead to () =1, ˆ () = (), and the numerical challenge is only to determine a suitable = ˆ. By not imposing the form (10) in Step 2, we still obtain a bound on weighted risk that is valid for any estimator satisfying ( ) for all Θ (that is, without imposing the functional form (10)). Of course, for a given switching rule, it might be that no nearly minimal weighted risk unbiased estimator of the form (10) exists, because is not unbiased or efficient enough relative to the weighting,soonemighttry instead with larger values for and. Running Example: Taking the local-to-unity limit of Marriott and Pope s (1954) mean bias expansion [ˆ ] = 2 + ( 1 ) for the AR(1) OLS estimator ˆ in a model without intercept suggests () = () 2 as a good candidate for. And indeed, it can be inferred from Figure 1 that the normalized mean bias of is smaller than 001 for =20. Furthermore, setting ˆ() = () and =40,wefind that (ˆ() ) 01% for all, so draws from the problematic part of the parameter space are only very rarely subject to the switching. It is now an empirical matter whether imposing the switching to in this fashion is costly in terms of risk, and this can be evaluated with the algorithm above by setting the upper bound of the support of to, say, 80, so that the weighted average risk criterion incorporates parameter values where switching to occurs with high probability ( (ˆ() ) 99% for 70). N 13
15 3 Two Special Cases 3.1 MeanUnbiasedEstimationunderQuadraticLoss Consider the special case of quadratic loss ( ) =( ()) 2 and normalized mean bias constraint ( ) =( ())() (we focus on a scalar estimand for expositional ease, but the following discussion straightforwardly extends to vector valued ). Then the integrand in (7) becomes a quadratic function of (), and the minimizing value () is () = R ()() () P R () =1 () () R (11) () () a linear function of = 1 2 ( ). Plugging this back into the objective and constraints yields Z R ( ) = () 0 () Ω +, Ω = () R () () () R (), () () Z ÃR () ( ) = Ω 0 (), = () R ()() () Z! () R () () () () () () where Z µz = () 2 () () [R ()() ()] R 2 () () () and Ω is the th column of the matrix Ω. Note that Ω is symmetric and positive semi-definite. In fact, Ω is positive definite as long as R () () () cannot be written as a linear combination of R () () (), 6= almost surely. Thus, minimizing ( ) subject to (5) becomes a (semi)-definite quadratic programming problem, which is readily solved by well-known algorithms. In the special case of =0, the solution is = Ω 1,where =( 1 ) 0. Step 3 of the algorithm generally becomes a quadratically constrained quadratic program, but since is scalar, it can easily be solved by conditioning on, witha line search as outer-loop. This remains true also if is restricted to be of the switching form (10), where is of the form (11), and ( ) and ( ) contain additional constants that arise from expectations over draws with () =1. Either way, it is computationally trivial to implement the strategy described in Section 2.3 under mean square risk and a mean bias constraint, even for a very fine discretization. 14
16 Figure 2: Mean Bias and MSE in Local-to-Unity AR(1) with Known Mean Running Example: We set uniform on [0 80], = =001, and restrict ˆ to be of the switching form (10) with ˆ = and =40as described at the end of the last section. With equal to point masses at { }, the algorithm successfully identifies a nearly weighted risk minimizing estimator ˆ that is uniformly nearly unbiased for 0. The remaining bias in ˆ is very small: with the normalized mean squared error of ˆ close to one, =001 implies that about 10,000 Monte Carlo draws are necessary for the largest bias of ˆ to be approximately of the same magnitude as the Monte Carlo standard error of its estimate. Figure 2 plots the normalized bias and risk of the nearly weighted risk minimizing unbiased estimator ˆ. As a point of reference, we also report the normalized bias and risk of the OLS estimator (replicated from Figure 1), and of the WAR minimizing estimator without any constraints. By construction, the unconstrained WAR minimizing estimator (which equals the posterior mean of under a prior proportional to )hasthesmallest possible average normalized risk on [0 80]. As can be seen from Figure 2, however, this comes at the cost of a large mean bias. The thick line plots a lower bound on the risk envelope for nearly unbiased estimators: For each, we set the weighting function equal to a point mass at that, andthenreport the lower bound on risk at among all estimator whose averaged normalized bias is no larger than =001 in absolute value for all (that is, for each, we perform Step 2 of the algorithm in Section 2.3, with equal to a point mass at ). The risk of ˆ is 15
17 seen to be approximately 10% larger than this lower bound on the envelope. This implies that our choice of a uniform normalized weighting function on [0 80] has a fairly limited influence: no other weighting function can lead to a nearly unbiased estimator with substantially less risk, for any In fact, to the extent that 10% is considered small, one could call ˆ approximately uniformly minimum variance unbiased. N 3.2 Median Unbiased Estimation Without Nuisance Parameters Suppose () =, that is there are no nuisance parameters, and Θ R. Let be an estimator taking on values in R, andlet () be its median function, ( () ()) = 12 for all Θ. If () is one-to-one on Θ with inverse 1 : R 7 Θ, then the estimator () = 1 ( ()) is exactly median unbiased by construction (cf. Lehmann (1959)). In general, different estimators yield different median unbiased estimators 1 ( ()), which raises the question how should be chosen for to have low risk. Running Example: Stock (1991) and Andrews (1993) construct median unbiased estimators for the largest autoregressive root based on the OLS estimator. Their results allow for the possibility that there exists another median unbiased estimator with much smaller risk. N A good candidate for is a nearly weighted risk minimizing nearly median unbiased estimator ˆ. A small median bias of ˆ typically also yields monotonicity of ˆ, soif = (ˆ ) 12 at the boundary points of Θ (if there are any), then ˆ has an inverse 1,and ˆ ˆ () = 1 (ˆ()) is exactly median unbiased. Furthermore, if ˆ is already nearly median ˆ unbiased, then 1 : R 7 Θ is close to the identity transformation, so that (ˆ ˆ ) is close to the nearly minimal risk (ˆ ). This suggests the following modified strategy to numerically identify an exactly median unbiased estimator ˆ whose weighted risk (ˆ ) is within (1 + ) of the risk of any other exactly median unbiased estimator. 1. Discretize Θ by the distributions, =1. 2. Obtain approximately optimal Lagrange multipliers ˆ for the problem (1) subject to (5) for =0, and associated value = (ˆ ˆ ). Choose and ˆ to ensure that = ) 12 for any boundary points of Θ. If still does not have an inverse, (ˆ ˆ go back to Step 1 and use a finer discretization. 16
18 3. Compute (ˆ ) for the exactly median unbiased estimator ˆ () = ˆˆ (ˆ ()). 1 If (ˆ ) (1 + ), gobacktostep1anduseafiner discretization. Otherwise, ˆ = ˆ has the desired properties. For the same reasons as discussed in Section 2.3, it can make sense to restrict the estimator of Step 2 of the switching form (10). For unbounded Θ, it is not possible to numerically compute exactly, but if the problem becomes well approximated by a standard problem ˆ with standard unbiased estimator as (), then setting the inverse median function to be the identity for very large ˆ() leads to numerically negligible median biases. Running Example: As discussed in Section 2.1, we combine the median unbiased constraint on 0 with absolute value loss. We make largely similar choices as in the derivation of nearly mean unbiased estimators: the normalized weighting function is uniform on [0 80], with risk now normalized as ( ) = [ () ](), where () = Phillips (1974, 1975) provides Edgeworth expansions of ˆ,which implies that ˆ (1 1 ) has a median bias of order ( 1 ) for 1. Takingthelimit as 1 suggests that the median bias of () = () 1 should be small for moderate and large, and a numerical analysis shows that this is indeed the case. We set =001, and impose switching to when () =40. Under a median bias constraint and absolute value loss, using point masses for leads to a discontinuous integrand in the Lagrangian (7) for given. In order to ensure a smooth estimator, it makes sense to instead choose the distributions in a way that any mixture of the s has a continuous density. To this end we set the Lebesgue density of, =1 proportional to the th third-order basis spline on the =51knots { } (with not-a-knot end conditions). We only compute 1 for 100 and set it equal to the identity function ˆˆ otherwise;themedianbiasofˆ for 100 is numerically indistinguishable from zero with a Monte Carlo standard error of the median bias estimate of approximately 0.2%. Figure 3 reports the median bias and normalized risk of ˆ, the OLS estimator,the OLS-based median unbiased estimator () = 1 ( ()), and the estimator that minimizes weighted risk relative to without any median unbiased constraints. The risk of ˆ is indistinguishable from the risk of. Consequently, this analysis reveals to be (also) nearly weighted risk minimal unbiased in this problem. N 17
19 Figure 3: Median and Absolute Loss in Local-to-Unity AR(1) with Known Mean 4 Invariance In this section, we consider estimation problems that have some natural invariance (or equivariance) structure, so that it makes sense to impose the corresponding invariance also on estimators. We show that the problem of identifying a (nearly) minimal risk unbiased invariant estimator becomes equivalent to the problem of identifying an unrestricted (nearly) minimal risk unbiased estimator in a related problem with a sample and parameter space generated by maximal invariants. Imposing invariance then reduces the dimension of the effective parameter space, which facilitates numerical solutions. Consider a group of transformations on the sample space : X 7 X,where denotes a group action. We write 2 1 for the composite action (( 1 ) 2 )= ( 2 1 ) for all 1 2, and we denote the inverse of action by,thatis( ) = for all and X. Assume that the elements in are distinct in the sense that ( 1 )=( 2 ) for some X implies 1 = 2. Now suppose the problem is invariant in the sense that there exists a corresponding group : Θ 7 Θ on the parameter space, and the distribution of ( ) under is (), for all and (cf. Definition 2.1 of Chapter 3 in Lehmann and Casella (1998)). Let () and () for : X 7 X and : Θ 7 Θ be maximal invariants of these two groups. Assume that and select a specific point on orbit induced by and, thatis () =( () ) for all X and () =( () ) for all Θ for some functions 18
20 : X 7 and : Θ 7 (as discussed on page in Lehmann and Casella (1998)). Then by definition of a maximal invariant, (()) = (), ( ()) = (), andwe have the decomposition = (()()) (12) = ( () ()) (13) By Theorem of Lehmann and Romano (2005), the distribution of () only depends on (). The following Lemma provides a slight generalization, which we require below. The proof is in Appendix A. Lemma 2 The joint distribution of (() ( () )) under only depends on through (). Suppose further that the estimand () is compatible with the invariance structure in the sense that ( 1 )=( 2 ) implies ( ( 1 )) = ( ( 2 )) for all 1 2 Θ and. As discussed in Chapter 3 of Lehmann and Casella (1998), this induces a group ˆ : 7 satisfying ( ( )) = ˆ(()) for all Θ and, and it is natural for the loss function and constraints to correspondingly satisfy ( ) = (ˆ( ) ( )) for all, Θ and (14) ( ) = (ˆ( ) ( )) for all, Θ and (15) Any loss function ( ) that depends on only through the parameter of interest, ( ) = ( ()) for some function : 7, such as quadratic loss or absolute value loss, automatically satisfies (14). Similarly, constraints of the form ( ) = ( ()) such as those arising from mean or median unbiased constraints, satisfy (15). With these notions of invariance in place, it makes sense to impose that estimators conform to this structure and satisfy (( )) = ˆ(()) for all and. (16) Equations (12) and (16) imply that any invariant estimator satisfies () =ˆ((())()) for all. (17) It is useful to think about the right-hand side of (17) as inducing the invariance property: Any function : (X ) defines an invariant estimator () via () = 19
21 ˆ( (())()). Given that any invariant estimator satisfies (17), the set of all invariant estimators can therefore be generated by considering all (unconstrained),andsetting () =ˆ( (())()). Running Example: Consider estimation of the AR(1) coefficient after observing = +,and = 1 +,where N (0 1) and 0 =0. Under local-to-unity asymptotics =1 for 0 and = = 12 for R, thelimiting problem involves the observation on the space of continuous functions on the unit interval, where () = + () and () = R 0 ( ) () is an Ornstein-Uhlenbeck process with (0) = 0. This observation is indexed by = ( ), and the parameter of interest is = (). The problem is invariant to transformations ( ) = + with = R, and corresponding group (( ))=( + ). One choice for maximal invariants is () = ( (0)) and (( )) = (( ) ) = ( 0). The Lemma asserts that () = (0) and ( () )=( (0)) have a joint distribution that only depends on through. The induced group ˆ is given by ˆ( ) = for all. Under (14), the loss must not depend on the location parameter. Invariant estimators are numerically invariant to translation shifts of, and can all be written in the form () =ˆ( ( (0))(0)) = ( (0)) for some function that maps paths on the unit interval with (0) = 0 to. N Now under these assumptions, we can write the risk of any invariant estimator as ( ) = [(())] and similarly = [ (()) ( () ) ] (by (12) and (14) with = () ) = ()[ (()) ( ()() ) ] (by Lemma 2) = ()[ ()[ (()) ( ()() ) ()]] ( ) = [(())] = () [ () [ (()) ( ()() ) ()]] Now set = () Θ = (Θ) ( )= = (Θ ), = () X = (X ) and ( ) = [ ( ) ( () ) = ] (18) (( ) ) = [ ( ) ( () ) = ]. (19) 20
22 Then the starred problem has exactly the same structure as the problem considered in Sections 2 and 3, and the same solution techniques can be applied to identify a nearly weighted average risk minimal estimator ˆ : X 7 (with the weighting function a nonnegative measure on Θ ). This solution is then extended to the domain of the original sample space X via ˆ() =ˆ(ˆ (())()) from (17), and the near optimality of ˆ implies the corresponding near optimality of ˆ in the class of all invariant estimators. Running Example: Since = (),and ( ) does not affect (), (( ) ( () )) = (( ) ) and (( ) ( () )) = (( ) ). Thus the starred problem amounts to estimating from the observation = () = (0) (whose distribution does not depend on ). Since is equal to the Ornstein-Uhlenbeck process with (0) = 0, the starred problem is exactly what was previously solved in the running example. So in particular, the solutions ˆ and ˆ, analyzed in Figures 2 and 3, now applied to,arealso (nearly) weighted risk minimizing unbiased translation invariant estimators in the problem of observing = +. Adifferent problem arises, however, in the empirically more relevant case with the initial condition drawn from the stationary distribution. With = + = 1 +, N (0 1) and 0 N (0 (1 2 ) 1 ) independent of { } for 1 (and zero otherwise), the limiting problem under =1 and = = 12 asymptotics is the observation of the process () = + (), where () = 2 + () and N (0 1) is independent of for 0 (and = otherwise). For 0, the density of = (0) is then given by (cf. Elliott (1999)) r " Z 2 1 ( )= 2+ exp 1 2 ( (1) 2 1) () 2 ( R # () + (1)) (20) Analogous to the discussion below (4), this asymptotic problem can be motivated more generally under suitable assumptions about the underlying processes The algorithms discussed in Section 3 can now be applied to determine nearly WAR minimizing invariant unbiased estimators in the problem of observing with density (20). We use the normalization function ( )= 2 +20,andmakethesamechoicesfor and on as in the problem with zero initial condition. Taking the local-to-unity limit of the approximately mean unbiased Orcutt and Winokur (1969) estimator of in a regression that includes a constant suggests 4 to be nearly mean unbiased for large where now ( )= 1 2 ( (1) 2 1) R 1 0 () 2 with () = () R 1 0 (). Similarly, Phillips 21
23 Figure 4: Mean Bias and MSE in Local-to-Unity AR(1) with Unknown Mean (1975) results suggest 3 to be nearly median unbiased. We switch to these estimators if ( ) =60,set =001 and =001 for the nearly median unbiased estimator, and =002 for the mean unbiased estimator. Figures 4 and 5 show the normalized bias and risk of the resulting nearly weighted risk minimizing unbiased invariant estimators. We also plot the performance of the analogous set of comparisons as in Figures 2 and 3. The mean and median bias of the OLS estimator is now even larger, and the (nearly) unbiased estimators have substantially lower normalized risk. The nearly WAR minimizing mean unbiased estimator still has risk only about 10% above the (lower bound) on the envelope. In contrast to the case considered in Figure 3, the WAR minimizing median unbiased estimator now has perceptibly lower risk than the OLS based median unbiased estimator for small, but the gains are still fairly moderate. Figure 6 compares the performance of the nearly mean unbiased estimator with some previously suggested alternative estimators: The local-to-unity limit 4 of the analytically bias corrected estimator by Orcutt and Winokur (1969), the weighted symmetric estimator analyzed by Pantula, Gonzalez-Farias, and Fuller (1994) and Park and Fuller (1995), and the MLE ( )=argmax 0 ( ) based on the maximal invariant likelihood (20) (called restricted MLE by Cheang and Reinsel (2000)). In contrast to ˆ, all of these previously suggested estimators have non-negligible mean biases for values of close to zero, with the smallest mean bias at =0of nearly a third of the root mean squared error. N 22
24 Figure 5: Median and Absolute Loss in Local-to-Unity AR(1) with Unknown Mean Figure 6: Mean Bias and MSE in Local-to-Unity AR(1) with Unknown Mean 23
25 5 Further Applications 5.1 Degree of Parameter Time Variation Consider the canonical local level model in the sense of Harvey (1989), = + X +, ( ) N (0 2 ) (21) =1 with only observed. The parameter of interest is, the degree of time variation of the local mean + P =1 Under = 12 and = 1 asymptotics, we have the functional convergence of the partial sums b c X () = 12 () = + =1 Z 0 () + () (22) with and two independent standard Wiener processes. The limit problem is the estimation of from the observation, whose distribution depends on =( ) [0 ) R This problem is invariant to transformations ( ) = + with = R, and corresponding group (( ))=( + ). One choice for maximal invariants is () =( (1)) and (( )) = (( ) ) =( 0). The results of Section 4 imply that all invariant estimators can be written as functions of = (), sothat Z µ Z 1 () = () + () () + (1) (23) 0 which does not depend on any nuisance parameters. The distribution (23) arises more generally as the limit of the suitably scaled partial sum process of the scores, evaluated at the maximum likelihood estimator, of well-behaved time series models with a time varying parameter; see Stock and Watson (1998), Elliott and Müller (2006a) and Müller and Petalas (2010). Lemma 2 and Theorem 3 of Elliott and Müller (2006a) imply that the density of with respect to the measure of a Brownian Bridge () (1) is given by ( )= r 2 exp 1 2 where () = () R 0 ( ) (). (1) 2 2R 1 0 () ³ (1) + R () ³ + (1) + R 1 0 () 2
26 As discussed by Stock (1994), the local level model (21) is intimately linked to the MA(1) model = +. Under small time variation asymptotics =, is nearly noninvertible with local-to-unity MA(1) coefficient =1 + ( 1 ). Both () = () (1) and the first differences { } =2 form small sample maximal invariants to translations of,sothattheycontainthesameinformation. Thissuggests that is also the limit problem (in the sense of LeCam) of a stationary Gaussian local-tounity MA(1) model without a constant, and it follows from the development in Elliott and Müller (2006a) that this is indeed the case. It has long been recognized that the maximum likelihood estimator of the MA(1) coefficient exhibits non-gaussian limit behavior under non-invertibility; see Stock (1994) for a historical account and references. In particular, the MLE ˆ suffers from the so-called pile-up problem (ˆ =1 =1) 0 and Sargan and Bhargava (1983) derive the limiting probability to be The full limiting distribution of the MLE does not seem to have been previously derived. The above noted equivalence leads us to conjecture that under =1 asymptotics, (1 ˆ) ( ) = argmax ( ) (24) A numerical calculation based on (23) confirms that under =0, ( ( )=0)=0657, but we leave a formal proof of the convergence in (24) to future research. In any event, with ( ( )=0) 12 under =0,itisnotpossibletobasea median unbiased estimator of [0 ) on ( ), as the median function is not one-to-one for small values of. Stock and Watson (1998) base their exactly median unbiased estimator on the Nyblom (1989) statistic R 1 0 () 2 We employ the algorithm discussed in Section 3.2 to derive an alternative median unbiased estimator that comes close to minimizing weighted average risk under absolute value loss. Taking the local-to-unity limit of Tanaka s (1984) expansions suggests ( ) = ( )+1 to be approximately median unbiased and normal with variance 2 for large. We thus consider risk normalized by ( )= +6 (the offset 6 ensures that normalized risk is well defined also for =0). We impose switching to whenever ( ) =10, set to be uniform on [0 30], choose the Lebesgue density of to be proportional to the th basis spline on the knots { }, and set the inverse median function 1 to the ˆˆ identity for arguments larger than 50 (the median bias of for 50 is indistinguishable from zero with a Monte Carlo standard error of approximately 0.2%). With =001, the 25
Long-Run Covariability
 Long-Run Covariability Ulrich K. Müller and Mark W. Watson Princeton University October 2016 Motivation Study the long-run covariability/relationship between economic variables great ratios, long-run Phillips
Long-Run Covariability Ulrich K. Müller and Mark W. Watson Princeton University October 2016 Motivation Study the long-run covariability/relationship between economic variables great ratios, long-run Phillips
Bias-Correction in Vector Autoregressive Models: A Simulation Study
 Econometrics 2014, 2, 45-71; doi:10.3390/econometrics2010045 OPEN ACCESS econometrics ISSN 2225-1146 www.mdpi.com/journal/econometrics Article Bias-Correction in Vector Autoregressive Models: A Simulation
Econometrics 2014, 2, 45-71; doi:10.3390/econometrics2010045 OPEN ACCESS econometrics ISSN 2225-1146 www.mdpi.com/journal/econometrics Article Bias-Correction in Vector Autoregressive Models: A Simulation
Nearly Optimal Tests when a Nuisance Parameter is Present Under the Null Hypothesis
 Nearly Optimal Tests when a Nuisance Parameter is Present Under the Null Hypothesis Graham Elliott UCSD Ulrich K. Müller Princeton University Mark W. Watson Princeton University and NBER January 2012 (Revised
Nearly Optimal Tests when a Nuisance Parameter is Present Under the Null Hypothesis Graham Elliott UCSD Ulrich K. Müller Princeton University Mark W. Watson Princeton University and NBER January 2012 (Revised
The Restricted Likelihood Ratio Test at the Boundary in Autoregressive Series
 The Restricted Likelihood Ratio Test at the Boundary in Autoregressive Series Willa W. Chen Rohit S. Deo July 6, 009 Abstract. The restricted likelihood ratio test, RLRT, for the autoregressive coefficient
The Restricted Likelihood Ratio Test at the Boundary in Autoregressive Series Willa W. Chen Rohit S. Deo July 6, 009 Abstract. The restricted likelihood ratio test, RLRT, for the autoregressive coefficient
Hypothesis Testing. 1 Definitions of test statistics. CB: chapter 8; section 10.3
 Hypothesis Testing CB: chapter 8; section 0.3 Hypothesis: statement about an unknown population parameter Examples: The average age of males in Sweden is 7. (statement about population mean) The lowest
Hypothesis Testing CB: chapter 8; section 0.3 Hypothesis: statement about an unknown population parameter Examples: The average age of males in Sweden is 7. (statement about population mean) The lowest
Steven Cook University of Wales Swansea. Abstract
 On the finite sample power of modified Dickey Fuller tests: The role of the initial condition Steven Cook University of Wales Swansea Abstract The relationship between the initial condition of time series
On the finite sample power of modified Dickey Fuller tests: The role of the initial condition Steven Cook University of Wales Swansea Abstract The relationship between the initial condition of time series
Efficiency Tradeoffs in Estimating the Linear Trend Plus Noise Model. Abstract
 Efficiency radeoffs in Estimating the Linear rend Plus Noise Model Barry Falk Department of Economics, Iowa State University Anindya Roy University of Maryland Baltimore County Abstract his paper presents
Efficiency radeoffs in Estimating the Linear rend Plus Noise Model Barry Falk Department of Economics, Iowa State University Anindya Roy University of Maryland Baltimore County Abstract his paper presents
Introduction to Maximum Likelihood Estimation
 Introduction to Maximum Likelihood Estimation Eric Zivot July 26, 2012 The Likelihood Function Let 1 be an iid sample with pdf ( ; ) where is a ( 1) vector of parameters that characterize ( ; ) Example:
Introduction to Maximum Likelihood Estimation Eric Zivot July 26, 2012 The Likelihood Function Let 1 be an iid sample with pdf ( ; ) where is a ( 1) vector of parameters that characterize ( ; ) Example:
A General Overview of Parametric Estimation and Inference Techniques.
 A General Overview of Parametric Estimation and Inference Techniques. Moulinath Banerjee University of Michigan September 11, 2012 The object of statistical inference is to glean information about an underlying
A General Overview of Parametric Estimation and Inference Techniques. Moulinath Banerjee University of Michigan September 11, 2012 The object of statistical inference is to glean information about an underlying
Economics Division University of Southampton Southampton SO17 1BJ, UK. Title Overlapping Sub-sampling and invariance to initial conditions
 Economics Division University of Southampton Southampton SO17 1BJ, UK Discussion Papers in Economics and Econometrics Title Overlapping Sub-sampling and invariance to initial conditions By Maria Kyriacou
Economics Division University of Southampton Southampton SO17 1BJ, UK Discussion Papers in Economics and Econometrics Title Overlapping Sub-sampling and invariance to initial conditions By Maria Kyriacou
Averaging Estimators for Regressions with a Possible Structural Break
 Averaging Estimators for Regressions with a Possible Structural Break Bruce E. Hansen University of Wisconsin y www.ssc.wisc.edu/~bhansen September 2007 Preliminary Abstract This paper investigates selection
Averaging Estimators for Regressions with a Possible Structural Break Bruce E. Hansen University of Wisconsin y www.ssc.wisc.edu/~bhansen September 2007 Preliminary Abstract This paper investigates selection
HAC Corrections for Strongly Autocorrelated Time Series
 HAC Corrections for Strongly Autocorrelated Time Series Ulrich K. Müller Princeton University Department of Economics Princeton, NJ, 08544 December 2012 Abstract Applied work routinely relies on heteroskedasticity
HAC Corrections for Strongly Autocorrelated Time Series Ulrich K. Müller Princeton University Department of Economics Princeton, NJ, 08544 December 2012 Abstract Applied work routinely relies on heteroskedasticity
Time Series Analysis. James D. Hamilton PRINCETON UNIVERSITY PRESS PRINCETON, NEW JERSEY
 Time Series Analysis James D. Hamilton PRINCETON UNIVERSITY PRESS PRINCETON, NEW JERSEY & Contents PREFACE xiii 1 1.1. 1.2. Difference Equations First-Order Difference Equations 1 /?th-order Difference
Time Series Analysis James D. Hamilton PRINCETON UNIVERSITY PRESS PRINCETON, NEW JERSEY & Contents PREFACE xiii 1 1.1. 1.2. Difference Equations First-Order Difference Equations 1 /?th-order Difference
Statistical inference
 Statistical inference Contents 1. Main definitions 2. Estimation 3. Testing L. Trapani MSc Induction - Statistical inference 1 1 Introduction: definition and preliminary theory In this chapter, we shall
Statistical inference Contents 1. Main definitions 2. Estimation 3. Testing L. Trapani MSc Induction - Statistical inference 1 1 Introduction: definition and preliminary theory In this chapter, we shall
Nearly Optimal Tests when a Nuisance Parameter is Present Under the Null Hypothesis
 Nearly Optimal Tests when a Nuisance Parameter is Present Under the Null Hypothesis Graham Elliott UCSD Ulrich K. Müller Princeton University January 2012 Mark W. Watson Princeton University and NBER Abstract
Nearly Optimal Tests when a Nuisance Parameter is Present Under the Null Hypothesis Graham Elliott UCSD Ulrich K. Müller Princeton University January 2012 Mark W. Watson Princeton University and NBER Abstract
What s New in Econometrics. Lecture 13
 What s New in Econometrics Lecture 13 Weak Instruments and Many Instruments Guido Imbens NBER Summer Institute, 2007 Outline 1. Introduction 2. Motivation 3. Weak Instruments 4. Many Weak) Instruments
What s New in Econometrics Lecture 13 Weak Instruments and Many Instruments Guido Imbens NBER Summer Institute, 2007 Outline 1. Introduction 2. Motivation 3. Weak Instruments 4. Many Weak) Instruments
Time Series Analysis. James D. Hamilton PRINCETON UNIVERSITY PRESS PRINCETON, NEW JERSEY
 Time Series Analysis James D. Hamilton PRINCETON UNIVERSITY PRESS PRINCETON, NEW JERSEY PREFACE xiii 1 Difference Equations 1.1. First-Order Difference Equations 1 1.2. pth-order Difference Equations 7
Time Series Analysis James D. Hamilton PRINCETON UNIVERSITY PRESS PRINCETON, NEW JERSEY PREFACE xiii 1 Difference Equations 1.1. First-Order Difference Equations 1 1.2. pth-order Difference Equations 7
Inference with few assumptions: Wasserman s example
 Inference with few assumptions: Wasserman s example Christopher A. Sims Princeton University sims@princeton.edu October 27, 2007 Types of assumption-free inference A simple procedure or set of statistics
Inference with few assumptions: Wasserman s example Christopher A. Sims Princeton University sims@princeton.edu October 27, 2007 Types of assumption-free inference A simple procedure or set of statistics
Testing Statistical Hypotheses
 E.L. Lehmann Joseph P. Romano Testing Statistical Hypotheses Third Edition 4y Springer Preface vii I Small-Sample Theory 1 1 The General Decision Problem 3 1.1 Statistical Inference and Statistical Decisions
E.L. Lehmann Joseph P. Romano Testing Statistical Hypotheses Third Edition 4y Springer Preface vii I Small-Sample Theory 1 1 The General Decision Problem 3 1.1 Statistical Inference and Statistical Decisions
Nearly Optimal Tests when a Nuisance Parameter is Present Under the Null Hypothesis
 Nearly Optimal Tests when a Nuisance Parameter is Present Under the Null Hypothesis Graham Elliott UCSD Ulrich K. Müller Princeton University Mark W. Watson Princeton University and NBER January 22 (Revised
Nearly Optimal Tests when a Nuisance Parameter is Present Under the Null Hypothesis Graham Elliott UCSD Ulrich K. Müller Princeton University Mark W. Watson Princeton University and NBER January 22 (Revised
Lasso Maximum Likelihood Estimation of Parametric Models with Singular Information Matrices
 Article Lasso Maximum Likelihood Estimation of Parametric Models with Singular Information Matrices Fei Jin 1,2 and Lung-fei Lee 3, * 1 School of Economics, Shanghai University of Finance and Economics,
Article Lasso Maximum Likelihood Estimation of Parametric Models with Singular Information Matrices Fei Jin 1,2 and Lung-fei Lee 3, * 1 School of Economics, Shanghai University of Finance and Economics,
Location Properties of Point Estimators in Linear Instrumental Variables and Related Models
 Location Properties of Point Estimators in Linear Instrumental Variables and Related Models Keisuke Hirano Department of Economics University of Arizona hirano@u.arizona.edu Jack R. Porter Department of
Location Properties of Point Estimators in Linear Instrumental Variables and Related Models Keisuke Hirano Department of Economics University of Arizona hirano@u.arizona.edu Jack R. Porter Department of
Comment on HAC Corrections for Strongly Autocorrelated Time Series by Ulrich K. Müller
 Comment on HAC Corrections for Strongly Autocorrelated ime Series by Ulrich K. Müller Yixiao Sun Department of Economics, UC San Diego May 2, 24 On the Nearly-optimal est Müller applies the theory of optimal
Comment on HAC Corrections for Strongly Autocorrelated ime Series by Ulrich K. Müller Yixiao Sun Department of Economics, UC San Diego May 2, 24 On the Nearly-optimal est Müller applies the theory of optimal
Testing for a Trend with Persistent Errors
 Testing for a Trend with Persistent Errors Graham Elliott UCSD August 2017 Abstract We develop new tests for the coe cient on a time trend in a regression of a variable on a constant and time trend where
Testing for a Trend with Persistent Errors Graham Elliott UCSD August 2017 Abstract We develop new tests for the coe cient on a time trend in a regression of a variable on a constant and time trend where
Testing Overidentifying Restrictions with Many Instruments and Heteroskedasticity
 Testing Overidentifying Restrictions with Many Instruments and Heteroskedasticity John C. Chao, Department of Economics, University of Maryland, chao@econ.umd.edu. Jerry A. Hausman, Department of Economics,
Testing Overidentifying Restrictions with Many Instruments and Heteroskedasticity John C. Chao, Department of Economics, University of Maryland, chao@econ.umd.edu. Jerry A. Hausman, Department of Economics,
Wooldridge, Introductory Econometrics, 4th ed. Appendix C: Fundamentals of mathematical statistics
 Wooldridge, Introductory Econometrics, 4th ed. Appendix C: Fundamentals of mathematical statistics A short review of the principles of mathematical statistics (or, what you should have learned in EC 151).
Wooldridge, Introductory Econometrics, 4th ed. Appendix C: Fundamentals of mathematical statistics A short review of the principles of mathematical statistics (or, what you should have learned in EC 151).
IV Estimation and its Limitations: Weak Instruments and Weakly Endogeneous Regressors
 IV Estimation and its Limitations: Weak Instruments and Weakly Endogeneous Regressors Laura Mayoral, IAE, Barcelona GSE and University of Gothenburg U. of Gothenburg, May 2015 Roadmap Testing for deviations
IV Estimation and its Limitations: Weak Instruments and Weakly Endogeneous Regressors Laura Mayoral, IAE, Barcelona GSE and University of Gothenburg U. of Gothenburg, May 2015 Roadmap Testing for deviations
A Primer on Asymptotics
 A Primer on Asymptotics Eric Zivot Department of Economics University of Washington September 30, 2003 Revised: October 7, 2009 Introduction The two main concepts in asymptotic theory covered in these
A Primer on Asymptotics Eric Zivot Department of Economics University of Washington September 30, 2003 Revised: October 7, 2009 Introduction The two main concepts in asymptotic theory covered in these
In-fill Asymptotic Theory for Structural Break Point in Autoregression: A Unified Theory
 In-fill Asymptotic Theory for Structural Break Point in Autoregression: A Unified Theory Liang Jiang Singapore Management University Xiaohu Wang The Chinese University of Hong Kong Jun Yu Singapore Management
In-fill Asymptotic Theory for Structural Break Point in Autoregression: A Unified Theory Liang Jiang Singapore Management University Xiaohu Wang The Chinese University of Hong Kong Jun Yu Singapore Management
Econometrics. Week 4. Fall Institute of Economic Studies Faculty of Social Sciences Charles University in Prague
 Econometrics Week 4 Institute of Economic Studies Faculty of Social Sciences Charles University in Prague Fall 2012 1 / 23 Recommended Reading For the today Serial correlation and heteroskedasticity in
Econometrics Week 4 Institute of Economic Studies Faculty of Social Sciences Charles University in Prague Fall 2012 1 / 23 Recommended Reading For the today Serial correlation and heteroskedasticity in
6 Pattern Mixture Models
 6 Pattern Mixture Models A common theme underlying the methods we have discussed so far is that interest focuses on making inference on parameters in a parametric or semiparametric model for the full data
6 Pattern Mixture Models A common theme underlying the methods we have discussed so far is that interest focuses on making inference on parameters in a parametric or semiparametric model for the full data
1 Procedures robust to weak instruments
 Comment on Weak instrument robust tests in GMM and the new Keynesian Phillips curve By Anna Mikusheva We are witnessing a growing awareness among applied researchers about the possibility of having weak
Comment on Weak instrument robust tests in GMM and the new Keynesian Phillips curve By Anna Mikusheva We are witnessing a growing awareness among applied researchers about the possibility of having weak
Introduction to Machine Learning. Lecture 2
 Introduction to Machine Learning Lecturer: Eran Halperin Lecture 2 Fall Semester Scribe: Yishay Mansour Some of the material was not presented in class (and is marked with a side line) and is given for
Introduction to Machine Learning Lecturer: Eran Halperin Lecture 2 Fall Semester Scribe: Yishay Mansour Some of the material was not presented in class (and is marked with a side line) and is given for
Comparing Forecast Accuracy of Different Models for Prices of Metal Commodities
 Comparing Forecast Accuracy of Different Models for Prices of Metal Commodities João Victor Issler (FGV) and Claudia F. Rodrigues (VALE) August, 2012 J.V. Issler and C.F. Rodrigues () Forecast Models for
Comparing Forecast Accuracy of Different Models for Prices of Metal Commodities João Victor Issler (FGV) and Claudia F. Rodrigues (VALE) August, 2012 J.V. Issler and C.F. Rodrigues () Forecast Models for
Testing Statistical Hypotheses
 E.L. Lehmann Joseph P. Romano, 02LEu1 ttd ~Lt~S Testing Statistical Hypotheses Third Edition With 6 Illustrations ~Springer 2 The Probability Background 28 2.1 Probability and Measure 28 2.2 Integration.........
E.L. Lehmann Joseph P. Romano, 02LEu1 ttd ~Lt~S Testing Statistical Hypotheses Third Edition With 6 Illustrations ~Springer 2 The Probability Background 28 2.1 Probability and Measure 28 2.2 Integration.........
LECTURE 5 NOTES. n t. t Γ(a)Γ(b) pt+a 1 (1 p) n t+b 1. The marginal density of t is. Γ(t + a)γ(n t + b) Γ(n + a + b)
 LECTURE 5 NOTES 1. Bayesian point estimators. In the conventional (frequentist) approach to statistical inference, the parameter θ Θ is considered a fixed quantity. In the Bayesian approach, it is considered
LECTURE 5 NOTES 1. Bayesian point estimators. In the conventional (frequentist) approach to statistical inference, the parameter θ Θ is considered a fixed quantity. In the Bayesian approach, it is considered
Stat 5101 Lecture Notes
 Stat 5101 Lecture Notes Charles J. Geyer Copyright 1998, 1999, 2000, 2001 by Charles J. Geyer May 7, 2001 ii Stat 5101 (Geyer) Course Notes Contents 1 Random Variables and Change of Variables 1 1.1 Random
Stat 5101 Lecture Notes Charles J. Geyer Copyright 1998, 1999, 2000, 2001 by Charles J. Geyer May 7, 2001 ii Stat 5101 (Geyer) Course Notes Contents 1 Random Variables and Change of Variables 1 1.1 Random
Instrumental Variable Estimation with Heteroskedasticity and Many Instruments
 Instrumental Variable Estimation with Heteroskedasticity and Many Instruments Jerry A. Hausman Department of Economics M.I.T. Tiemen Woutersen Department of Economics University of Arizona Norman Swanson
Instrumental Variable Estimation with Heteroskedasticity and Many Instruments Jerry A. Hausman Department of Economics M.I.T. Tiemen Woutersen Department of Economics University of Arizona Norman Swanson
Economics 583: Econometric Theory I A Primer on Asymptotics
 Economics 583: Econometric Theory I A Primer on Asymptotics Eric Zivot January 14, 2013 The two main concepts in asymptotic theory that we will use are Consistency Asymptotic Normality Intuition consistency:
Economics 583: Econometric Theory I A Primer on Asymptotics Eric Zivot January 14, 2013 The two main concepts in asymptotic theory that we will use are Consistency Asymptotic Normality Intuition consistency:
Estimation of Dynamic Regression Models
 University of Pavia 2007 Estimation of Dynamic Regression Models Eduardo Rossi University of Pavia Factorization of the density DGP: D t (x t χ t 1, d t ; Ψ) x t represent all the variables in the economy.
University of Pavia 2007 Estimation of Dynamic Regression Models Eduardo Rossi University of Pavia Factorization of the density DGP: D t (x t χ t 1, d t ; Ψ) x t represent all the variables in the economy.
Estimation, Inference, and Hypothesis Testing
 Chapter 2 Estimation, Inference, and Hypothesis Testing Note: The primary reference for these notes is Ch. 7 and 8 of Casella & Berger 2. This text may be challenging if new to this topic and Ch. 7 of
Chapter 2 Estimation, Inference, and Hypothesis Testing Note: The primary reference for these notes is Ch. 7 and 8 of Casella & Berger 2. This text may be challenging if new to this topic and Ch. 7 of
Refining the Central Limit Theorem Approximation via Extreme Value Theory
 Refining the Central Limit Theorem Approximation via Extreme Value Theory Ulrich K. Müller Economics Department Princeton University February 2018 Abstract We suggest approximating the distribution of
Refining the Central Limit Theorem Approximation via Extreme Value Theory Ulrich K. Müller Economics Department Princeton University February 2018 Abstract We suggest approximating the distribution of
Spring 2017 Econ 574 Roger Koenker. Lecture 14 GEE-GMM
 University of Illinois Department of Economics Spring 2017 Econ 574 Roger Koenker Lecture 14 GEE-GMM Throughout the course we have emphasized methods of estimation and inference based on the principle
University of Illinois Department of Economics Spring 2017 Econ 574 Roger Koenker Lecture 14 GEE-GMM Throughout the course we have emphasized methods of estimation and inference based on the principle
Least Squares Bias in Time Series with Moderate. Deviations from a Unit Root
 Least Squares Bias in ime Series with Moderate Deviations from a Unit Root Marian Z. Stoykov University of Essex March 7 Abstract his paper derives the approximate bias of the least squares estimator of
Least Squares Bias in ime Series with Moderate Deviations from a Unit Root Marian Z. Stoykov University of Essex March 7 Abstract his paper derives the approximate bias of the least squares estimator of
Statistics - Lecture One. Outline. Charlotte Wickham 1. Basic ideas about estimation
 Statistics - Lecture One Charlotte Wickham wickham@stat.berkeley.edu http://www.stat.berkeley.edu/~wickham/ Outline 1. Basic ideas about estimation 2. Method of Moments 3. Maximum Likelihood 4. Confidence
Statistics - Lecture One Charlotte Wickham wickham@stat.berkeley.edu http://www.stat.berkeley.edu/~wickham/ Outline 1. Basic ideas about estimation 2. Method of Moments 3. Maximum Likelihood 4. Confidence
A Test of Cointegration Rank Based Title Component Analysis.
 A Test of Cointegration Rank Based Title Component Analysis Author(s) Chigira, Hiroaki Citation Issue 2006-01 Date Type Technical Report Text Version publisher URL http://hdl.handle.net/10086/13683 Right
A Test of Cointegration Rank Based Title Component Analysis Author(s) Chigira, Hiroaki Citation Issue 2006-01 Date Type Technical Report Text Version publisher URL http://hdl.handle.net/10086/13683 Right
Current Version: December, 1999 FULLY MODIFIED OLS FOR HETEROGENEOUS COINTEGRATED PANELS * Peter Pedroni. Indiana University
 Current Version: December, 999 FULLY MODIFIED OLS FOR HEEROGENEOUS COINEGRAED PANELS * Peter Pedroni Indiana University mailing address: Economics, Indiana University Bloomington, IN 47405 (82) 855-7925
Current Version: December, 999 FULLY MODIFIED OLS FOR HEEROGENEOUS COINEGRAED PANELS * Peter Pedroni Indiana University mailing address: Economics, Indiana University Bloomington, IN 47405 (82) 855-7925
New Methods for Inference in Long-Horizon Regressions
 JOURNAL OF FINANCIAL AND QUANTITATIVE ANALYSIS Vol. 46, No. 3, June 2011, pp. 815 839 COPYRIGHT 2011, MICHAEL G. FOSTER SCHOOL OF BUSINESS, UNIVERSITY OF WASHINGTON, SEATTLE, WA 98195 doi:10.1017/s0022109011000135
JOURNAL OF FINANCIAL AND QUANTITATIVE ANALYSIS Vol. 46, No. 3, June 2011, pp. 815 839 COPYRIGHT 2011, MICHAEL G. FOSTER SCHOOL OF BUSINESS, UNIVERSITY OF WASHINGTON, SEATTLE, WA 98195 doi:10.1017/s0022109011000135
Review of Classical Least Squares. James L. Powell Department of Economics University of California, Berkeley
 Review of Classical Least Squares James L. Powell Department of Economics University of California, Berkeley The Classical Linear Model The object of least squares regression methods is to model and estimate
Review of Classical Least Squares James L. Powell Department of Economics University of California, Berkeley The Classical Linear Model The object of least squares regression methods is to model and estimate
A CONDITIONAL LIKELIHOOD RATIO TEST FOR STRUCTURAL MODELS. By Marcelo J. Moreira 1
 Econometrica, Vol. 71, No. 4 (July, 2003), 1027 1048 A CONDITIONAL LIKELIHOOD RATIO TEST FOR STRUCTURAL MODELS By Marcelo J. Moreira 1 This paper develops a general method for constructing exactly similar
Econometrica, Vol. 71, No. 4 (July, 2003), 1027 1048 A CONDITIONAL LIKELIHOOD RATIO TEST FOR STRUCTURAL MODELS By Marcelo J. Moreira 1 This paper develops a general method for constructing exactly similar
Darmstadt Discussion Papers in Economics
 Darmstadt Discussion Papers in Economics The Effect of Linear Time Trends on Cointegration Testing in Single Equations Uwe Hassler Nr. 111 Arbeitspapiere des Instituts für Volkswirtschaftslehre Technische
Darmstadt Discussion Papers in Economics The Effect of Linear Time Trends on Cointegration Testing in Single Equations Uwe Hassler Nr. 111 Arbeitspapiere des Instituts für Volkswirtschaftslehre Technische
Predictive Regressions: A Reduced-Bias. Estimation Method
 Predictive Regressions: A Reduced-Bias Estimation Method Yakov Amihud 1 Clifford M. Hurvich 2 November 28, 2003 1 Ira Leon Rennert Professor of Finance, Stern School of Business, New York University, New
Predictive Regressions: A Reduced-Bias Estimation Method Yakov Amihud 1 Clifford M. Hurvich 2 November 28, 2003 1 Ira Leon Rennert Professor of Finance, Stern School of Business, New York University, New
A Bayesian perspective on GMM and IV
 A Bayesian perspective on GMM and IV Christopher A. Sims Princeton University sims@princeton.edu November 26, 2013 What is a Bayesian perspective? A Bayesian perspective on scientific reporting views all
A Bayesian perspective on GMM and IV Christopher A. Sims Princeton University sims@princeton.edu November 26, 2013 What is a Bayesian perspective? A Bayesian perspective on scientific reporting views all
A TIME SERIES PARADOX: UNIT ROOT TESTS PERFORM POORLY WHEN DATA ARE COINTEGRATED
 A TIME SERIES PARADOX: UNIT ROOT TESTS PERFORM POORLY WHEN DATA ARE COINTEGRATED by W. Robert Reed Department of Economics and Finance University of Canterbury, New Zealand Email: bob.reed@canterbury.ac.nz
A TIME SERIES PARADOX: UNIT ROOT TESTS PERFORM POORLY WHEN DATA ARE COINTEGRATED by W. Robert Reed Department of Economics and Finance University of Canterbury, New Zealand Email: bob.reed@canterbury.ac.nz
Bayesian Inference in GLMs. Frequentists typically base inferences on MLEs, asymptotic confidence
 Bayesian Inference in GLMs Frequentists typically base inferences on MLEs, asymptotic confidence limits, and log-likelihood ratio tests Bayesians base inferences on the posterior distribution of the unknowns
Bayesian Inference in GLMs Frequentists typically base inferences on MLEs, asymptotic confidence limits, and log-likelihood ratio tests Bayesians base inferences on the posterior distribution of the unknowns
Ch. 5 Hypothesis Testing
 Ch. 5 Hypothesis Testing The current framework of hypothesis testing is largely due to the work of Neyman and Pearson in the late 1920s, early 30s, complementing Fisher s work on estimation. As in estimation,
Ch. 5 Hypothesis Testing The current framework of hypothesis testing is largely due to the work of Neyman and Pearson in the late 1920s, early 30s, complementing Fisher s work on estimation. As in estimation,
Cross-fitting and fast remainder rates for semiparametric estimation
 Cross-fitting and fast remainder rates for semiparametric estimation Whitney K. Newey James M. Robins The Institute for Fiscal Studies Department of Economics, UCL cemmap working paper CWP41/17 Cross-Fitting
Cross-fitting and fast remainder rates for semiparametric estimation Whitney K. Newey James M. Robins The Institute for Fiscal Studies Department of Economics, UCL cemmap working paper CWP41/17 Cross-Fitting
Using all observations when forecasting under structural breaks
 Using all observations when forecasting under structural breaks Stanislav Anatolyev New Economic School Victor Kitov Moscow State University December 2007 Abstract We extend the idea of the trade-off window
Using all observations when forecasting under structural breaks Stanislav Anatolyev New Economic School Victor Kitov Moscow State University December 2007 Abstract We extend the idea of the trade-off window
AN EMPIRICAL LIKELIHOOD RATIO TEST FOR NORMALITY
 Econometrics Working Paper EWP0401 ISSN 1485-6441 Department of Economics AN EMPIRICAL LIKELIHOOD RATIO TEST FOR NORMALITY Lauren Bin Dong & David E. A. Giles Department of Economics, University of Victoria
Econometrics Working Paper EWP0401 ISSN 1485-6441 Department of Economics AN EMPIRICAL LIKELIHOOD RATIO TEST FOR NORMALITY Lauren Bin Dong & David E. A. Giles Department of Economics, University of Victoria
Fall, 2007 Nonlinear Econometrics. Theory: Consistency for Extremum Estimators. Modeling: Probit, Logit, and Other Links.
 14.385 Fall, 2007 Nonlinear Econometrics Lecture 2. Theory: Consistency for Extremum Estimators Modeling: Probit, Logit, and Other Links. 1 Example: Binary Choice Models. The latent outcome is defined
14.385 Fall, 2007 Nonlinear Econometrics Lecture 2. Theory: Consistency for Extremum Estimators Modeling: Probit, Logit, and Other Links. 1 Example: Binary Choice Models. The latent outcome is defined
A Shape Constrained Estimator of Bidding Function of First-Price Sealed-Bid Auctions
 A Shape Constrained Estimator of Bidding Function of First-Price Sealed-Bid Auctions Yu Yvette Zhang Abstract This paper is concerned with economic analysis of first-price sealed-bid auctions with risk
A Shape Constrained Estimator of Bidding Function of First-Price Sealed-Bid Auctions Yu Yvette Zhang Abstract This paper is concerned with economic analysis of first-price sealed-bid auctions with risk
Financial Econometrics
 Financial Econometrics Estimation and Inference Gerald P. Dwyer Trinity College, Dublin January 2013 Who am I? Visiting Professor and BB&T Scholar at Clemson University Federal Reserve Bank of Atlanta
Financial Econometrics Estimation and Inference Gerald P. Dwyer Trinity College, Dublin January 2013 Who am I? Visiting Professor and BB&T Scholar at Clemson University Federal Reserve Bank of Atlanta
Lecture 11 Weak IV. Econ 715
 Lecture 11 Weak IV Instrument exogeneity and instrument relevance are two crucial requirements in empirical analysis using GMM. It now appears that in many applications of GMM and IV regressions, instruments
Lecture 11 Weak IV Instrument exogeneity and instrument relevance are two crucial requirements in empirical analysis using GMM. It now appears that in many applications of GMM and IV regressions, instruments
Testing for Anomalous Periods in Time Series Data. Graham Elliott
 Testing for Anomalous Periods in Time Series Data Graham Elliott 1 Introduction The Motivating Problem There are reasons to expect that for a time series model that an anomalous period might occur where
Testing for Anomalous Periods in Time Series Data Graham Elliott 1 Introduction The Motivating Problem There are reasons to expect that for a time series model that an anomalous period might occur where
Bayesian Inference for DSGE Models. Lawrence J. Christiano
 Bayesian Inference for DSGE Models Lawrence J. Christiano Outline State space-observer form. convenient for model estimation and many other things. Bayesian inference Bayes rule. Monte Carlo integation.
Bayesian Inference for DSGE Models Lawrence J. Christiano Outline State space-observer form. convenient for model estimation and many other things. Bayesian inference Bayes rule. Monte Carlo integation.
The Role of "Leads" in the Dynamic Title of Cointegrating Regression Models. Author(s) Hayakawa, Kazuhiko; Kurozumi, Eiji
 he Role of "Leads" in the Dynamic itle of Cointegrating Regression Models Author(s) Hayakawa, Kazuhiko; Kurozumi, Eiji Citation Issue 2006-12 Date ype echnical Report ext Version publisher URL http://hdl.handle.net/10086/13599
he Role of "Leads" in the Dynamic itle of Cointegrating Regression Models Author(s) Hayakawa, Kazuhiko; Kurozumi, Eiji Citation Issue 2006-12 Date ype echnical Report ext Version publisher URL http://hdl.handle.net/10086/13599
Supplement to Quantile-Based Nonparametric Inference for First-Price Auctions
 Supplement to Quantile-Based Nonparametric Inference for First-Price Auctions Vadim Marmer University of British Columbia Artyom Shneyerov CIRANO, CIREQ, and Concordia University August 30, 2010 Abstract
Supplement to Quantile-Based Nonparametric Inference for First-Price Auctions Vadim Marmer University of British Columbia Artyom Shneyerov CIRANO, CIREQ, and Concordia University August 30, 2010 Abstract
Discrepancy-Based Model Selection Criteria Using Cross Validation
 33 Discrepancy-Based Model Selection Criteria Using Cross Validation Joseph E. Cavanaugh, Simon L. Davies, and Andrew A. Neath Department of Biostatistics, The University of Iowa Pfizer Global Research
33 Discrepancy-Based Model Selection Criteria Using Cross Validation Joseph E. Cavanaugh, Simon L. Davies, and Andrew A. Neath Department of Biostatistics, The University of Iowa Pfizer Global Research
Bayesian Inference for DSGE Models. Lawrence J. Christiano
 Bayesian Inference for DSGE Models Lawrence J. Christiano Outline State space-observer form. convenient for model estimation and many other things. Bayesian inference Bayes rule. Monte Carlo integation.
Bayesian Inference for DSGE Models Lawrence J. Christiano Outline State space-observer form. convenient for model estimation and many other things. Bayesian inference Bayes rule. Monte Carlo integation.
SIMILAR-ON-THE-BOUNDARY TESTS FOR MOMENT INEQUALITIES EXIST, BUT HAVE POOR POWER. Donald W. K. Andrews. August 2011
 SIMILAR-ON-THE-BOUNDARY TESTS FOR MOMENT INEQUALITIES EXIST, BUT HAVE POOR POWER By Donald W. K. Andrews August 2011 COWLES FOUNDATION DISCUSSION PAPER NO. 1815 COWLES FOUNDATION FOR RESEARCH IN ECONOMICS
SIMILAR-ON-THE-BOUNDARY TESTS FOR MOMENT INEQUALITIES EXIST, BUT HAVE POOR POWER By Donald W. K. Andrews August 2011 COWLES FOUNDATION DISCUSSION PAPER NO. 1815 COWLES FOUNDATION FOR RESEARCH IN ECONOMICS
If we want to analyze experimental or simulated data we might encounter the following tasks:
 Chapter 1 Introduction If we want to analyze experimental or simulated data we might encounter the following tasks: Characterization of the source of the signal and diagnosis Studying dependencies Prediction
Chapter 1 Introduction If we want to analyze experimental or simulated data we might encounter the following tasks: Characterization of the source of the signal and diagnosis Studying dependencies Prediction
Predictive Regressions: A Reduced-Bias. Estimation Method
 Predictive Regressions: A Reduced-Bias Estimation Method Yakov Amihud 1 Clifford M. Hurvich 2 May 4, 2004 1 Ira Leon Rennert Professor of Finance, Stern School of Business, New York University, New York
Predictive Regressions: A Reduced-Bias Estimation Method Yakov Amihud 1 Clifford M. Hurvich 2 May 4, 2004 1 Ira Leon Rennert Professor of Finance, Stern School of Business, New York University, New York
Introduction to the Mathematical and Statistical Foundations of Econometrics Herman J. Bierens Pennsylvania State University
 Introduction to the Mathematical and Statistical Foundations of Econometrics 1 Herman J. Bierens Pennsylvania State University November 13, 2003 Revised: March 15, 2004 2 Contents Preface Chapter 1: Probability
Introduction to the Mathematical and Statistical Foundations of Econometrics 1 Herman J. Bierens Pennsylvania State University November 13, 2003 Revised: March 15, 2004 2 Contents Preface Chapter 1: Probability
Cointegrated VARIMA models: specification and. simulation
 Cointegrated VARIMA models: specification and simulation José L. Gallego and Carlos Díaz Universidad de Cantabria. Abstract In this note we show how specify cointegrated vector autoregressive-moving average
Cointegrated VARIMA models: specification and simulation José L. Gallego and Carlos Díaz Universidad de Cantabria. Abstract In this note we show how specify cointegrated vector autoregressive-moving average
Notes on Asymptotic Theory: Convergence in Probability and Distribution Introduction to Econometric Theory Econ. 770
 Notes on Asymptotic Theory: Convergence in Probability and Distribution Introduction to Econometric Theory Econ. 770 Jonathan B. Hill Dept. of Economics University of North Carolina - Chapel Hill November
Notes on Asymptotic Theory: Convergence in Probability and Distribution Introduction to Econometric Theory Econ. 770 Jonathan B. Hill Dept. of Economics University of North Carolina - Chapel Hill November
FREQUENTIST BEHAVIOR OF FORMAL BAYESIAN INFERENCE
 FREQUENTIST BEHAVIOR OF FORMAL BAYESIAN INFERENCE Donald A. Pierce Oregon State Univ (Emeritus), RERF Hiroshima (Retired), Oregon Health Sciences Univ (Adjunct) Ruggero Bellio Univ of Udine For Perugia
FREQUENTIST BEHAVIOR OF FORMAL BAYESIAN INFERENCE Donald A. Pierce Oregon State Univ (Emeritus), RERF Hiroshima (Retired), Oregon Health Sciences Univ (Adjunct) Ruggero Bellio Univ of Udine For Perugia
Bayesian Methods for Machine Learning
 Bayesian Methods for Machine Learning CS 584: Big Data Analytics Material adapted from Radford Neal s tutorial (http://ftp.cs.utoronto.ca/pub/radford/bayes-tut.pdf), Zoubin Ghahramni (http://hunch.net/~coms-4771/zoubin_ghahramani_bayesian_learning.pdf),
Bayesian Methods for Machine Learning CS 584: Big Data Analytics Material adapted from Radford Neal s tutorial (http://ftp.cs.utoronto.ca/pub/radford/bayes-tut.pdf), Zoubin Ghahramni (http://hunch.net/~coms-4771/zoubin_ghahramani_bayesian_learning.pdf),
Let us first identify some classes of hypotheses. simple versus simple. H 0 : θ = θ 0 versus H 1 : θ = θ 1. (1) one-sided
 Let us first identify some classes of hypotheses. simple versus simple H 0 : θ = θ 0 versus H 1 : θ = θ 1. (1) one-sided H 0 : θ θ 0 versus H 1 : θ > θ 0. (2) two-sided; null on extremes H 0 : θ θ 1 or
Let us first identify some classes of hypotheses. simple versus simple H 0 : θ = θ 0 versus H 1 : θ = θ 1. (1) one-sided H 0 : θ θ 0 versus H 1 : θ > θ 0. (2) two-sided; null on extremes H 0 : θ θ 1 or
Hypothesis Testing. Part I. James J. Heckman University of Chicago. Econ 312 This draft, April 20, 2006
 Hypothesis Testing Part I James J. Heckman University of Chicago Econ 312 This draft, April 20, 2006 1 1 A Brief Review of Hypothesis Testing and Its Uses values and pure significance tests (R.A. Fisher)
Hypothesis Testing Part I James J. Heckman University of Chicago Econ 312 This draft, April 20, 2006 1 1 A Brief Review of Hypothesis Testing and Its Uses values and pure significance tests (R.A. Fisher)
Transparent Structural Estimation. Matthew Gentzkow Fisher-Schultz Lecture (from work w/ Isaiah Andrews & Jesse M. Shapiro)
 Transparent Structural Estimation Matthew Gentzkow Fisher-Schultz Lecture (from work w/ Isaiah Andrews & Jesse M. Shapiro) 1 A hallmark of contemporary applied microeconomics is a conceptual framework
Transparent Structural Estimation Matthew Gentzkow Fisher-Schultz Lecture (from work w/ Isaiah Andrews & Jesse M. Shapiro) 1 A hallmark of contemporary applied microeconomics is a conceptual framework
Testing Restrictions and Comparing Models
 Econ. 513, Time Series Econometrics Fall 00 Chris Sims Testing Restrictions and Comparing Models 1. THE PROBLEM We consider here the problem of comparing two parametric models for the data X, defined by
Econ. 513, Time Series Econometrics Fall 00 Chris Sims Testing Restrictions and Comparing Models 1. THE PROBLEM We consider here the problem of comparing two parametric models for the data X, defined by
G. S. Maddala Kajal Lahiri. WILEY A John Wiley and Sons, Ltd., Publication
 G. S. Maddala Kajal Lahiri WILEY A John Wiley and Sons, Ltd., Publication TEMT Foreword Preface to the Fourth Edition xvii xix Part I Introduction and the Linear Regression Model 1 CHAPTER 1 What is Econometrics?
G. S. Maddala Kajal Lahiri WILEY A John Wiley and Sons, Ltd., Publication TEMT Foreword Preface to the Fourth Edition xvii xix Part I Introduction and the Linear Regression Model 1 CHAPTER 1 What is Econometrics?
The Bayesian Approach to Multi-equation Econometric Model Estimation
 Journal of Statistical and Econometric Methods, vol.3, no.1, 2014, 85-96 ISSN: 2241-0384 (print), 2241-0376 (online) Scienpress Ltd, 2014 The Bayesian Approach to Multi-equation Econometric Model Estimation
Journal of Statistical and Econometric Methods, vol.3, no.1, 2014, 85-96 ISSN: 2241-0384 (print), 2241-0376 (online) Scienpress Ltd, 2014 The Bayesian Approach to Multi-equation Econometric Model Estimation
Bias Correction and Out of Sample Forecast Accuracy
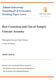 Auburn University Department of Economics Working Paper Series Bias Correction and Out of Sample Forecast Accuracy Hyeongwoo Kim and Nazif Durmaz Auburn University AUWP 2010 02 This paper can be downloaded
Auburn University Department of Economics Working Paper Series Bias Correction and Out of Sample Forecast Accuracy Hyeongwoo Kim and Nazif Durmaz Auburn University AUWP 2010 02 This paper can be downloaded
Econ 623 Econometrics II Topic 2: Stationary Time Series
 1 Introduction Econ 623 Econometrics II Topic 2: Stationary Time Series In the regression model we can model the error term as an autoregression AR(1) process. That is, we can use the past value of the
1 Introduction Econ 623 Econometrics II Topic 2: Stationary Time Series In the regression model we can model the error term as an autoregression AR(1) process. That is, we can use the past value of the
The Generalized Cochrane-Orcutt Transformation Estimation For Spurious and Fractional Spurious Regressions
 The Generalized Cochrane-Orcutt Transformation Estimation For Spurious and Fractional Spurious Regressions Shin-Huei Wang and Cheng Hsiao Jan 31, 2010 Abstract This paper proposes a highly consistent estimation,
The Generalized Cochrane-Orcutt Transformation Estimation For Spurious and Fractional Spurious Regressions Shin-Huei Wang and Cheng Hsiao Jan 31, 2010 Abstract This paper proposes a highly consistent estimation,
Econometrics I, Estimation
 Econometrics I, Estimation Department of Economics Stanford University September, 2008 Part I Parameter, Estimator, Estimate A parametric is a feature of the population. An estimator is a function of the
Econometrics I, Estimation Department of Economics Stanford University September, 2008 Part I Parameter, Estimator, Estimate A parametric is a feature of the population. An estimator is a function of the
The Bootstrap: Theory and Applications. Biing-Shen Kuo National Chengchi University
 The Bootstrap: Theory and Applications Biing-Shen Kuo National Chengchi University Motivation: Poor Asymptotic Approximation Most of statistical inference relies on asymptotic theory. Motivation: Poor
The Bootstrap: Theory and Applications Biing-Shen Kuo National Chengchi University Motivation: Poor Asymptotic Approximation Most of statistical inference relies on asymptotic theory. Motivation: Poor
Measuring nuisance parameter effects in Bayesian inference
 Measuring nuisance parameter effects in Bayesian inference Alastair Young Imperial College London WHOA-PSI-2017 1 / 31 Acknowledgements: Tom DiCiccio, Cornell University; Daniel Garcia Rasines, Imperial
Measuring nuisance parameter effects in Bayesian inference Alastair Young Imperial College London WHOA-PSI-2017 1 / 31 Acknowledgements: Tom DiCiccio, Cornell University; Daniel Garcia Rasines, Imperial
Time Series and Forecasting Lecture 4 NonLinear Time Series
 Time Series and Forecasting Lecture 4 NonLinear Time Series Bruce E. Hansen Summer School in Economics and Econometrics University of Crete July 23-27, 2012 Bruce Hansen (University of Wisconsin) Foundations
Time Series and Forecasting Lecture 4 NonLinear Time Series Bruce E. Hansen Summer School in Economics and Econometrics University of Crete July 23-27, 2012 Bruce Hansen (University of Wisconsin) Foundations
ECE531 Lecture 10b: Maximum Likelihood Estimation
 ECE531 Lecture 10b: Maximum Likelihood Estimation D. Richard Brown III Worcester Polytechnic Institute 05-Apr-2011 Worcester Polytechnic Institute D. Richard Brown III 05-Apr-2011 1 / 23 Introduction So
ECE531 Lecture 10b: Maximum Likelihood Estimation D. Richard Brown III Worcester Polytechnic Institute 05-Apr-2011 Worcester Polytechnic Institute D. Richard Brown III 05-Apr-2011 1 / 23 Introduction So
A Rothschild-Stiglitz approach to Bayesian persuasion
 A Rothschild-Stiglitz approach to Bayesian persuasion Matthew Gentzkow and Emir Kamenica Stanford University and University of Chicago December 2015 Abstract Rothschild and Stiglitz (1970) represent random
A Rothschild-Stiglitz approach to Bayesian persuasion Matthew Gentzkow and Emir Kamenica Stanford University and University of Chicago December 2015 Abstract Rothschild and Stiglitz (1970) represent random
PATTERN RECOGNITION AND MACHINE LEARNING CHAPTER 2: PROBABILITY DISTRIBUTIONS
 PATTERN RECOGNITION AND MACHINE LEARNING CHAPTER 2: PROBABILITY DISTRIBUTIONS Parametric Distributions Basic building blocks: Need to determine given Representation: or? Recall Curve Fitting Binary Variables
PATTERN RECOGNITION AND MACHINE LEARNING CHAPTER 2: PROBABILITY DISTRIBUTIONS Parametric Distributions Basic building blocks: Need to determine given Representation: or? Recall Curve Fitting Binary Variables
Multiscale Adaptive Inference on Conditional Moment Inequalities
 Multiscale Adaptive Inference on Conditional Moment Inequalities Timothy B. Armstrong 1 Hock Peng Chan 2 1 Yale University 2 National University of Singapore June 2013 Conditional moment inequality models
Multiscale Adaptive Inference on Conditional Moment Inequalities Timothy B. Armstrong 1 Hock Peng Chan 2 1 Yale University 2 National University of Singapore June 2013 Conditional moment inequality models
Fall 2017 STAT 532 Homework Peter Hoff. 1. Let P be a probability measure on a collection of sets A.
 1. Let P be a probability measure on a collection of sets A. (a) For each n N, let H n be a set in A such that H n H n+1. Show that P (H n ) monotonically converges to P ( k=1 H k) as n. (b) For each n
1. Let P be a probability measure on a collection of sets A. (a) For each n N, let H n be a set in A such that H n H n+1. Show that P (H n ) monotonically converges to P ( k=1 H k) as n. (b) For each n
Discussion of Bootstrap prediction intervals for linear, nonlinear, and nonparametric autoregressions, by Li Pan and Dimitris Politis
 Discussion of Bootstrap prediction intervals for linear, nonlinear, and nonparametric autoregressions, by Li Pan and Dimitris Politis Sílvia Gonçalves and Benoit Perron Département de sciences économiques,
Discussion of Bootstrap prediction intervals for linear, nonlinear, and nonparametric autoregressions, by Li Pan and Dimitris Politis Sílvia Gonçalves and Benoit Perron Département de sciences économiques,
arxiv: v1 [stat.me] 6 Nov 2013
![arxiv: v1 [stat.me] 6 Nov 2013 arxiv: v1 [stat.me] 6 Nov 2013](/thumbs/94/119478802.jpg) Electronic Journal of Statistics Vol. 0 (0000) ISSN: 1935-7524 DOI: 10.1214/154957804100000000 A Generalized Savage-Dickey Ratio Ewan Cameron e-mail: dr.ewan.cameron@gmail.com url: astrostatistics.wordpress.com
Electronic Journal of Statistics Vol. 0 (0000) ISSN: 1935-7524 DOI: 10.1214/154957804100000000 A Generalized Savage-Dickey Ratio Ewan Cameron e-mail: dr.ewan.cameron@gmail.com url: astrostatistics.wordpress.com
INFERENCE APPROACHES FOR INSTRUMENTAL VARIABLE QUANTILE REGRESSION. 1. Introduction
 INFERENCE APPROACHES FOR INSTRUMENTAL VARIABLE QUANTILE REGRESSION VICTOR CHERNOZHUKOV CHRISTIAN HANSEN MICHAEL JANSSON Abstract. We consider asymptotic and finite-sample confidence bounds in instrumental
INFERENCE APPROACHES FOR INSTRUMENTAL VARIABLE QUANTILE REGRESSION VICTOR CHERNOZHUKOV CHRISTIAN HANSEN MICHAEL JANSSON Abstract. We consider asymptotic and finite-sample confidence bounds in instrumental
σ(a) = a N (x; 0, 1 2 ) dx. σ(a) = Φ(a) =
 Until now we have always worked with likelihoods and prior distributions that were conjugate to each other, allowing the computation of the posterior distribution to be done in closed form. Unfortunately,
Until now we have always worked with likelihoods and prior distributions that were conjugate to each other, allowing the computation of the posterior distribution to be done in closed form. Unfortunately,
On the Correlations of Trend-Cycle Errors
 On the Correlations of Trend-Cycle Errors Tatsuma Wada Wayne State University This version: December 19, 11 Abstract This note provides explanations for an unexpected result, namely, the estimated parameter
On the Correlations of Trend-Cycle Errors Tatsuma Wada Wayne State University This version: December 19, 11 Abstract This note provides explanations for an unexpected result, namely, the estimated parameter
