Math 131. Related Rates Larson Section 2.6
|
|
|
- Brook Harrell
- 6 years ago
- Views:
Transcription
1 Math 131. Related Rates Larson Section 2.6 There are many natural situations when there are related variables that are changing with respect to time. For example, a spherical balloon is being inflated with air. The volume and radius are related by the volume equation V = 4 3 πr3, and both the volume and radius are changing with respect to time. The volume and radius are typically implicit functions of t since we may not know their explicit expressions. Then we can implicitly differentiate this volume equation with respect to time (the right side will require the chain rule); this will allow us to determine how the rates of change and are related: d [V ] = d [ ] 4 3 πr3 = d [ 4 3 πr3 ] = 4πr2 Example 1. (a) A spherical balloon is being inflated with air so that its radius is increasing at a constant rate of 2 centimiters per second. Find the rate of change of the volume when the radius is 10 centimeters. (b) Another spherical balloon is being inflated at a constant rate of 100 cubic centimeters per second. Find the rate at which the radius is increasing when the radius is 5 centimeters. Solution: (a) From the above, we know that = 2cm/s so when r = 10 cm, we find = 4πr2 = 4π(10cm)2 2 cm s = 4πr2 and the problem gives us that = 800π cm3 s (b) For this part, we also use when r = 5 cm, we have = 4πr2 and we are given that = 100 cm 3 /s. Then 100 = 4π(5 2 ) and so = π = 1 cm π s In a typical related rates problem you will: identify the given quantities and relevant quantities that are changing and label them with variables; write an equation that relates the variables; use the chain rule to implicitly differentiate both sides of the equation with respect to t; use the information given to solve for the required rate of change.
2 The remainder of these notes present several classic examples of related rates problems. Example 2. A stone opped into a still pond sends out a circular ripple whose radius increases at a constant rate of 3.2 feet per second. (a) How rapidly is the area enclosed by the ripple increasing when the radius is 3 feet? (b) How rapidly is the area enclosed by the ripple increasing at the end of 6.2 seconds? Solution: The relevant quantiies are the area of the circle which we call A and the radius of the circle which we call r. These quantities are related by the geometric formula A = πr 2. Then differentiating this with respect to t yields change of the area of the circle, and With this, we can answer both (a) and (b). = 2πr where is the rate of is the rate of change of the radius of the circle. (a) When r = 3 we have = 2 π = 19.2π ft2 /s (b) When t = 6.2 seconds we have r = feet (since it started at 0 and increased at a rate of 3.2 feet per second for 6.2 seconds so r = (3.2)(6.2) = 19.84) and thus = 2 π = π ft2 /s Example 3. A man 6 feet tall walks at a rate of 5 feet per second away from a light that is 15 feet above the ground (see the figure below). At what rate is the tip of his shadow moving when he is 10 feet from the base of the light? Solution: Let the man be x feet from the base of the lamp post and let his shadow be s feet long. Then s 6 = x + s Then 15 1 ds 6 = 1 dx ds 15
3 and so 1 ds = 1 dx and so ds = 2 dx and we know dx = 5. Thus the length of his shadow is changing at 10 feet per second, and the tip of his shadow is moving away from the lamp 3 post at a rate of 25 feet per second. 3 Example 4. An airplane flies at an altitude of 5 miles toward a point directly over an observer (see the figure below). The speed of the plane is 600 miles per hour. Find the rates at which the angle of elevation θ is changing when the angle is (i) θ = 30, and (ii) θ = 60. Express answer in radians per minute. Solution: Let x represent the length of the base of the triangle in the figure. cot θ = x ; differentiating with respect to t yields 5 Then we know dx csc 2 θ dθ = 1 5 dx = 10 miles per minute because the jet is traveling 600 miles per hour. Thus (i) When θ = 30, sin θ = 1/2 and so dθ = 1 5 sin2 θ dx radians per minute. dθ = ( 10) = (ii) When θ = 60, sin θ = 3/2 and so radians per minute. dθ = 1 5 ( 3) 2 ( 10) = Example 5. A ladder 15 feet long is leaning against the wall of a house (see the figure below). The base of the ladder is pulled away from the wall at a rate of 2 feet per second. How fast
4 is the top of the ladder moving down the wall when its base is 4 feet from the wall? See the diagram below where L = 15 and x = 2 Solution: Let b be the distance of the base of the ladder from the house, and let h be the height of the top of the ladder above the ground. Then the Pythagorean theorem implies b 2 + h 2 = 225. Differentiating both sides with respect to time yields and then dh = b h db. 2b db + 2hdh = 0 and so 2hdh = 2bdb When b = 4, we use the relation b 2 + h 2 = 225 to find h 2 = 225 and so We now plug this into h 2 = = 209 or h = 209 dh = b h db = Thus top of the ladder is moving down the wall at approximately feet per second Example 6. Gravel is being dumped from a conveyor belt at a rate of 10 cubic feet per minute. It forms a pile in the shape of a right circular cone whose base diameter and height are equal. How fast is the height of the pile increasing when the pile is 11 feet high? Recall that the volume of a right circular cone with height h and radius of the base r is given by V = π 3 r2 h. Solution: In this case r = h since the height and diameter are equal. Therefore V = π 2 12 h3. Then = 3πh2 12 dh = π 4 h2 dh Solving for dh we have dh = 4 = 40 πh 2 121π when the height is 11 feet. feet per minute
5 Example 7. A boat is pulled into a dock by means of a rope attached to a pulley on the dock. The rope is attached to the front of the boat, which is 11 feet below the level of the pulley. If the rope is pulled through the pulley at a rate of 12 ft/min, at what rate will the boat be approaching the dock when 107 ft of rope is out? Solution: Let x be the horizontal distance of the front of the boat from the dock and let r be the length of rope that is out. Then by the pythagorean theorem x 2 = r 2. Differentiating this equation with respect to t we find 2x dx = 2r and so dx = r x From the information given in the question, we know = 12 ft/min (the negative is because the rope is being pulled in). We are asked to find dx when r = 107 feet. With this information, from the pythagorean equation above, we know and therefore, x = dx = 107 ( 12) ft/min ft/min The negative sign indicates that the boat is approaching the dock. Thus, the boat is approaching the dock at a rate of approximately feet per minute. Example 8. The altitude (i.e., height) of a triangle is increasing at a rate of 4 cm/minute while the area of the triangle is increasing at a rate of 4.5 square cm/minute. At what rate is the base of the triangle changing when the altitude is 7.2 centimeters and the area is 67 square centimeters. Express answer to four decimal places Solution: The area of a triangle is given by A = 1 bh where b is the base and h is the 2 height. Differentiating both sides of this equation with respect to t yields = 1 2 ( h db + bdh We wish to find db, and so solving the above equation for it, we have db = 1 ( 2 ) h bdh )
6 Using the quantities dh obtain = 4, = 4.5, h = 7.2 and b = 2A/h = db = 1 ((2)(4.5) ( )(4)) cm/min , we Example 9. A baseball diamond has the shape of a square with sides 90 feet long (see figure). A player runs from second base to third base at a speed of 25 feet per second is 20 feet from third base. At what rate is the player s distance from home plate changing? Solution: Let s represent the distance of the runner to home plate and let x represent the distance of the runner to 3rd base. Then x = s 2. We differentiate implicitly to find 2x dx = 2s ds and so ds = x s dx. We know that x = 20 and so s = = = 10 85, and we know dx/ = 25. Therefore, ds = ( 25) = = The distance between the runner and home plate is decreasing at approximately 5.4 feet per second. Example 10. An airplane flies at an altitude of 5 miles toward a point directly over an observer (see the figure below). The ground speed of the plane is 460 miles per hour. Find the rate at which the distance between the observer and plane is changing when the angle of elevation θ = 70. Round answer to the nearest tenth of a mile per hour.
7 Solution: With reference to the diagram above, the distance between the observer and the plane is the hypotenuse of the triangle, we will lable that side h, and we will label the adjacent side x, we know dx = 460 miles per hour and by the Pythagorean theorem, x = h 2. So we differentiate this equation implicitly to find d dx [x2 + 25] = d dx [h2 ] 2x dx = 2hdh and so dh = x dx h. When θ = 70, we have x = 5 cot(70 ) and h = 5 csc(70 ) therefore dh = 5 cot(70 ) 5 csc(70 ) ( 460) = 460 cos(70 ) miles per hour This means the distance between the jet and observer is decreasing at a rate of miles per hour. Example 11. Suppose the edges of a cube are increasing at a rate of 5 centimeters per minute. (a) How fast is the volume changing when each edge is 8 centimeters? (b) How fast is the volume changing when each edge is 11 centimeters? Solution: First, the volume of a cube is given by V = x 3 where each side has length x units. Differentiating this implicitly with respect to time yields = 3x2 dx (a) Given x = 8 and dx = 5, we have = 3(8)2 (5) = 960 cm3 min (b) Given x = 11 and dx = 5, we have = 3(11)2 (5) = 1815 cm3 min
8 Example 12. An airplane fflying at an altitude of 6 miles passes directly over a radar station. When the airplane is 13 miles from the radar station (s = 13), the radar detects that the distance s is changing at a rate of 250 miles per hour. What is the speed of the airplane. (Round answer to nearest mile per hour). Solution: Using the Pythagorean theorem we note x = s 2, we are given s and ds and we look to find dx. Then differentiating this implicitly with respect to t, we find and so dx = s ds x. d [x2 + 36] = d [s2 ] 2x dx = 2sds When s = 13, we find that x = = 133, and we were given ds = 250 miles per hour. Therefore, dx = miles per hour 133 That is the plane is travelling approximately 282 miles per hour.
Days 3 & 4 Notes: Related Rates
 AP Calculus Unit 4 Applications of the Derivative Part 1 Days 3 & 4 Notes: Related Rates Implicitly differentiate the following formulas with respect to time. State what each rate in the differential equation
AP Calculus Unit 4 Applications of the Derivative Part 1 Days 3 & 4 Notes: Related Rates Implicitly differentiate the following formulas with respect to time. State what each rate in the differential equation
Chapter 3.4 Practice Problems
 EXPECTED SKILLS: Chapter.4 Practice Problems Be able to solve related rates problems. It may be helpful to remember the following strategy:. Read the problem carefully. 2. Draw a diagram, if possible,
EXPECTED SKILLS: Chapter.4 Practice Problems Be able to solve related rates problems. It may be helpful to remember the following strategy:. Read the problem carefully. 2. Draw a diagram, if possible,
Math 2413 t2rsu14. Name: 06/06/ Find the derivative of the following function using the limiting process.
 Name: 06/06/014 Math 413 trsu14 1. Find the derivative of the following function using the limiting process. f( x) = 4x + 5x. Find the derivative of the following function using the limiting process. f(
Name: 06/06/014 Math 413 trsu14 1. Find the derivative of the following function using the limiting process. f( x) = 4x + 5x. Find the derivative of the following function using the limiting process. f(
Math 1131Q Section 10
 Math 1131Q Section 10 Section 3.9 and 3.10 Oct 19, 2010 Find the derivative of ln 3 5 e 2 ln 3 5 e 2 = ln 3 + ln 5/2 + ln e 2 = 3 ln + ( 5 ) ln + 2 2 (ln 3 5 e 2 ) = 3 + 5 2 + 2 Find the derivative of
Math 1131Q Section 10 Section 3.9 and 3.10 Oct 19, 2010 Find the derivative of ln 3 5 e 2 ln 3 5 e 2 = ln 3 + ln 5/2 + ln e 2 = 3 ln + ( 5 ) ln + 2 2 (ln 3 5 e 2 ) = 3 + 5 2 + 2 Find the derivative of
MAC 2311 Review
 Name: Class: Date: MAC 2311 Review 2.6-2.9 Numeric Response 1. Calculate y. xy 4 +x 2 y =2x +3y 2. Calculate y. cos xy =x 6 y 3. The position function of a particle is given by s =t 3 10.5t 2 2t,t 0 When
Name: Class: Date: MAC 2311 Review 2.6-2.9 Numeric Response 1. Calculate y. xy 4 +x 2 y =2x +3y 2. Calculate y. cos xy =x 6 y 3. The position function of a particle is given by s =t 3 10.5t 2 2t,t 0 When
4.1 Implicit Differentiation
 4.1 Implicit Differentiation Learning Objectives A student will be able to: Find the derivative of variety of functions by using the technique of implicit differentiation. Consider the equation We want
4.1 Implicit Differentiation Learning Objectives A student will be able to: Find the derivative of variety of functions by using the technique of implicit differentiation. Consider the equation We want
Related Rates. 2. List the relevant quantities in the problem and assign them appropriate variables. Then write down all the information given.
 Calculus 1 Lia Vas Related Rates The most important reason for a non-mathematics major to learn mathematics is to be able to apply it to problems from other disciplines or real life. In this section, we
Calculus 1 Lia Vas Related Rates The most important reason for a non-mathematics major to learn mathematics is to be able to apply it to problems from other disciplines or real life. In this section, we
Implicit Differentiation
 Implicit Differentiation Much of our algebraic study of mathematics has dealt with functions. In pre-calculus, we talked about two different types of equations that relate x and y explicit and implicit.
Implicit Differentiation Much of our algebraic study of mathematics has dealt with functions. In pre-calculus, we talked about two different types of equations that relate x and y explicit and implicit.
V = π 3 r2 h. dv dt = π [ r 2dh dt r2. dv 3 dt +2rhdr dt
 9 Related Rates Related rates is the phrase used to describe the situation when two or more related variables are changing with respect to time. The rate of change, as mentioned earlier, is another expression
9 Related Rates Related rates is the phrase used to describe the situation when two or more related variables are changing with respect to time. The rate of change, as mentioned earlier, is another expression
Math 103 Selected Homework Solutions, Section 3.9
 Math 103 Selected Homework Solutions, Section 3.9 9. Let s be the distance from the base of the light pole to the top of the man s shadow, and the distance from the light pole to the man. 15 s 6 s We know:
Math 103 Selected Homework Solutions, Section 3.9 9. Let s be the distance from the base of the light pole to the top of the man s shadow, and the distance from the light pole to the man. 15 s 6 s We know:
Implicit Differentiation
 Week 6. Implicit Differentiation Let s say we want to differentiate the equation of a circle: y 2 + x 2 =9 Using the techniques we know so far, we need to write the equation as a function of one variable
Week 6. Implicit Differentiation Let s say we want to differentiate the equation of a circle: y 2 + x 2 =9 Using the techniques we know so far, we need to write the equation as a function of one variable
6.2 Related Rates Name: Notes
 Calculus Write your questions and thoughts here! 6.2 Related Rates Name: Notes Guidelines to solving related rate problems 1. Draw a picture. 2. Make a list of all known and unknown rates and quantities.
Calculus Write your questions and thoughts here! 6.2 Related Rates Name: Notes Guidelines to solving related rate problems 1. Draw a picture. 2. Make a list of all known and unknown rates and quantities.
Math 241 Homework 6 Solutions
 Math 241 Homework 6 s Section 3.7 (Pages 161-163) Problem 2. Suppose that the radius r and surface area S = 4πr 2 of a sphere are differentiable functions of t. Write an equation that relates ds/ to /.
Math 241 Homework 6 s Section 3.7 (Pages 161-163) Problem 2. Suppose that the radius r and surface area S = 4πr 2 of a sphere are differentiable functions of t. Write an equation that relates ds/ to /.
MATH1910Chapter2TestReview
 Class: Date: MATH1910Chapter2TestReview Multiple Choice Identify the choice that best completes the statement or answers the question. 1. Find the slope m of the line tangent to the graph of the function
Class: Date: MATH1910Chapter2TestReview Multiple Choice Identify the choice that best completes the statement or answers the question. 1. Find the slope m of the line tangent to the graph of the function
AP Calculus Related Rates Worksheet
 AP Calculus Related Rates Worksheet 1. A small balloon is released at a point 150 feet from an observer, who is on level ground. If the balloon goes straight up at a rate of 8 feet per second, how fast
AP Calculus Related Rates Worksheet 1. A small balloon is released at a point 150 feet from an observer, who is on level ground. If the balloon goes straight up at a rate of 8 feet per second, how fast
AP Calculus AB Chapter 4 Packet Implicit Differentiation. 4.5: Implicit Functions
 4.5: Implicit Functions We can employ implicit differentiation when an equation that defines a function is so complicated that we cannot use an explicit rule to find the derivative. EXAMPLE 1: Find dy
4.5: Implicit Functions We can employ implicit differentiation when an equation that defines a function is so complicated that we cannot use an explicit rule to find the derivative. EXAMPLE 1: Find dy
AP Calculus AB Semester 1 Practice Final
 Class: Date: AP Calculus AB Semester 1 Practice Final Multiple Choice Identify the choice that best completes the statement or answers the question. 1. Find the limit (if it exists). lim x x + 4 x a. 6
Class: Date: AP Calculus AB Semester 1 Practice Final Multiple Choice Identify the choice that best completes the statement or answers the question. 1. Find the limit (if it exists). lim x x + 4 x a. 6
a right triangle), we see that x 200 or equivalently x = 200 tan θ. The rate at which the ray of light moves along the shore is
 Example 1: A revolving beacon in a lighthouse makes one revolution every 15 seconds. The beacon is 00 ft from the nearest point P on a straight shoreline. Find the rate at which a ray from the light moves
Example 1: A revolving beacon in a lighthouse makes one revolution every 15 seconds. The beacon is 00 ft from the nearest point P on a straight shoreline. Find the rate at which a ray from the light moves
p144 Section 2.6: Related Rates Find a related rate Use related rates to solve real life problems
 1 2 p144 Section 2.6: Related Rates Find a related rate Use related rates to solve real life problems Finding Related Rates We have used the chain rule to find dy/dx implicitly, but you can also use the
1 2 p144 Section 2.6: Related Rates Find a related rate Use related rates to solve real life problems Finding Related Rates We have used the chain rule to find dy/dx implicitly, but you can also use the
p144 Section 2.6: Related Rates Find a related rate Use related rates to solve real life problems
 p144 Section 2.6: Related Rates Find a related rate Use related rates to solve real life problems Finding Related Rates We have used the chain rule to find dy/dx implicitly, but you can also use the chain
p144 Section 2.6: Related Rates Find a related rate Use related rates to solve real life problems Finding Related Rates We have used the chain rule to find dy/dx implicitly, but you can also use the chain
Solve for an unknown rate of change using related rates of change.
 Objectives: Solve for an unknown rate of change using related rates of change. 1. Draw a diagram. 2. Label your diagram, including units. If a quantity in the diagram is not changing, label it with a number.
Objectives: Solve for an unknown rate of change using related rates of change. 1. Draw a diagram. 2. Label your diagram, including units. If a quantity in the diagram is not changing, label it with a number.
MCV4U1 Worksheet 4.7. dh / dt if neither r nor h is constant?
 MCV4U1 Worksheet 4.7 This worksheet serves as an additional exercise to complement the lesson and the examples given. Worksheets may take more than one day to complete. If you are stuck, read again the
MCV4U1 Worksheet 4.7 This worksheet serves as an additional exercise to complement the lesson and the examples given. Worksheets may take more than one day to complete. If you are stuck, read again the
Chapter 3.5: Related Rates
 Expected Skills: Chapter.5: Related Rates Be able to solve related rates problems. It may be helpful to remember the following strategy:. Read the problem carefully. 2. Draw a diagram, if possible, representing
Expected Skills: Chapter.5: Related Rates Be able to solve related rates problems. It may be helpful to remember the following strategy:. Read the problem carefully. 2. Draw a diagram, if possible, representing
4.6 Related Rates Notes RELATED RATES PROBLEMS --- IT S AS EASY AS 1 2-3!
 4.6 Related Rates Notes RELATED RATES PROBLEMS --- IT S AS EASY AS 1 2-3! 1) Draw a picture. Label all variables and constant values. Identify the given rate of change, the rate to be found, and when to
4.6 Related Rates Notes RELATED RATES PROBLEMS --- IT S AS EASY AS 1 2-3! 1) Draw a picture. Label all variables and constant values. Identify the given rate of change, the rate to be found, and when to
Guidelines for implicit differentiation
 Guidelines for implicit differentiation Given an equation with x s and y s scattered, to differentiate we use implicit differentiation. Some informal guidelines to differentiate an equation containing
Guidelines for implicit differentiation Given an equation with x s and y s scattered, to differentiate we use implicit differentiation. Some informal guidelines to differentiate an equation containing
Section 4.1: Related Rates
 1 Section 4.1: Related Rates Practice HW from Stewart Textbook (not to hand in) p. 67 # 1-19 odd, 3, 5, 9 In a related rates problem, we want to compute the rate of change of one quantity in terms of the
1 Section 4.1: Related Rates Practice HW from Stewart Textbook (not to hand in) p. 67 # 1-19 odd, 3, 5, 9 In a related rates problem, we want to compute the rate of change of one quantity in terms of the
DIFFERENTIATION RULES
 3 DIFFERENTIATION RULES DIFFERENTIATION RULES If we are pumping air into a balloon, both the volume and the radius of the balloon are increasing and their rates of increase are related to each other. However,
3 DIFFERENTIATION RULES DIFFERENTIATION RULES If we are pumping air into a balloon, both the volume and the radius of the balloon are increasing and their rates of increase are related to each other. However,
Section MWF 12 1pm SR 117
 Math 1431 Section 12485 MWF 12 1pm SR 117 Dr. Melahat Almus almus@math.uh.edu http://www.math.uh.edu/~almus COURSE WEBSITE: http://www.math.uh.edu/~almus/1431_sp16.html Visit my website regularly for announcements
Math 1431 Section 12485 MWF 12 1pm SR 117 Dr. Melahat Almus almus@math.uh.edu http://www.math.uh.edu/~almus COURSE WEBSITE: http://www.math.uh.edu/~almus/1431_sp16.html Visit my website regularly for announcements
Stewart - Calculus 8e Chapter 2 Form A. 1. Differentiate. 2. Find the limit. 3. Differentiate.
 Stewart - Calculus 8e Chapter 2 Form A Multivariable Calculus 8th Edition Stewart TEST BANK Full clear download at: https://testbankreal.com/download/multivariable-calculus-8th-editionstewart-test-bank/
Stewart - Calculus 8e Chapter 2 Form A Multivariable Calculus 8th Edition Stewart TEST BANK Full clear download at: https://testbankreal.com/download/multivariable-calculus-8th-editionstewart-test-bank/
Related Rates Problems. of h.
 Basic Related Rates Problems 1. If V is the volume of a cube and x the length of an edge. Express dv What is dv in terms of dx. when x is 5 and dx = 2? 2. If V is the volume of a sphere and r is the radius.
Basic Related Rates Problems 1. If V is the volume of a cube and x the length of an edge. Express dv What is dv in terms of dx. when x is 5 and dx = 2? 2. If V is the volume of a sphere and r is the radius.
Section 3.8 Related Rates
 Section 3.8 Related Rates Read and re-read the problem until you understand it. Draw and label a picture which gives the relevant information (if possible). Introduce notation. Assign a symbol to every
Section 3.8 Related Rates Read and re-read the problem until you understand it. Draw and label a picture which gives the relevant information (if possible). Introduce notation. Assign a symbol to every
A = 1 2 ab da dt = 1 da. We can find how fast the area is growing at 3 seconds by plugging everything into that differentiated equation: da
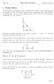 1 Related Rates In most related rates problems, we have an equation that relates a bunch of quantities that are changing over time. For example, suppose we have a right triangle whose base and height are
1 Related Rates In most related rates problems, we have an equation that relates a bunch of quantities that are changing over time. For example, suppose we have a right triangle whose base and height are
AP Calculus AB Chapter 2 Test Review #1
 AP Calculus AB Chapter Test Review # Open-Ended Practice Problems:. Nicole just loves drinking chocolate milk out of her special cone cup which has a radius of inches and a height of 8 inches. Nicole pours
AP Calculus AB Chapter Test Review # Open-Ended Practice Problems:. Nicole just loves drinking chocolate milk out of her special cone cup which has a radius of inches and a height of 8 inches. Nicole pours
Trigonometry Test 3 Practice Chapters 5 and 6 NON-CALCULATOR PORTION
 NON-CALCULATOR PORTION Find four solutions to each of the following; write your answer in 1. 2. 3. 4. 5. 6. radians: Find the value of each of the following: 7. ( ) 8. 9. ( ) 10. 11. 12. 13. ( ) Find four
NON-CALCULATOR PORTION Find four solutions to each of the following; write your answer in 1. 2. 3. 4. 5. 6. radians: Find the value of each of the following: 7. ( ) 8. 9. ( ) 10. 11. 12. 13. ( ) Find four
Calculus I - Lecture 14 - Related Rates
 Calculus I - Lecture 14 - Related Rates Lecture Notes: http://www.math.ksu.edu/ gerald/math220d/ Course Syllabus: http://www.math.ksu.edu/math220/spring-2014/indexs14.html Gerald Hoehn (based on notes
Calculus I - Lecture 14 - Related Rates Lecture Notes: http://www.math.ksu.edu/ gerald/math220d/ Course Syllabus: http://www.math.ksu.edu/math220/spring-2014/indexs14.html Gerald Hoehn (based on notes
Chapter 2: Differentiation 1. Find the slope of the tangent line to the graph of the function below at the given point.
 Chapter : Differentiation 1. Find the slope of the tangent line to the graph of the function below at the given point. f( ) 10, (, ) 10 1 E) none of the above. Find the slope of the tangent line to the
Chapter : Differentiation 1. Find the slope of the tangent line to the graph of the function below at the given point. f( ) 10, (, ) 10 1 E) none of the above. Find the slope of the tangent line to the
4.1 & 4.2 Student Notes Using the First and Second Derivatives. for all x in D, where D is the domain of f. The number f()
 4.1 & 4. Student Notes Using the First and Second Derivatives Definition A function f has an absolute maximum (or global maximum) at c if f ( c) f ( x) for all x in D, where D is the domain of f. The number
4.1 & 4. Student Notes Using the First and Second Derivatives Definition A function f has an absolute maximum (or global maximum) at c if f ( c) f ( x) for all x in D, where D is the domain of f. The number
m2413c2 the limiting process. 4. Use the alternative form of the derivative to find the derivative of the function at. a. b. c. d. e.
 m2413c2 Multiple Choice Identify the choice that best completes the statement or answers the question 1 Find the derivative of the following function using the limiting process 2 Find the derivative of
m2413c2 Multiple Choice Identify the choice that best completes the statement or answers the question 1 Find the derivative of the following function using the limiting process 2 Find the derivative of
Use a calculator to find the value of the expression in radian measure rounded to 2 decimal places. 1 8) cos-1 6
 Math 180 - chapter 7 and 8.1-8. - New Edition - Spring 09 Name Find the value of the expression. 1) sin-1 0.5 ) tan-1-1 ) cos-1 (- ) 4) sin-1 Find the exact value of the expression. 5) sin [sin-1 (0.7)]
Math 180 - chapter 7 and 8.1-8. - New Edition - Spring 09 Name Find the value of the expression. 1) sin-1 0.5 ) tan-1-1 ) cos-1 (- ) 4) sin-1 Find the exact value of the expression. 5) sin [sin-1 (0.7)]
Find the length of an arc that subtends a central angle of 45 in a circle of radius 8 m. Round your answer to 3 decimal places.
 Chapter 6 Practice Test Find the radian measure of the angle with the given degree measure. (Round your answer to three decimal places.) 80 Find the degree measure of the angle with the given radian measure:
Chapter 6 Practice Test Find the radian measure of the angle with the given degree measure. (Round your answer to three decimal places.) 80 Find the degree measure of the angle with the given radian measure:
Calculus 437 Semester 1 Review Chapters 1, 2, and 3 January 2016
 Name: Class: Date: Calculus 437 Semester 1 Review Chapters 1, 2, and 3 January 2016 Short Answer 1. Decide whether the following problem can be solved using precalculus, or whether calculus is required.
Name: Class: Date: Calculus 437 Semester 1 Review Chapters 1, 2, and 3 January 2016 Short Answer 1. Decide whether the following problem can be solved using precalculus, or whether calculus is required.
Chapter 8: Radical Functions
 Chapter 8: Radical Functions Chapter 8 Overview: Types and Traits of Radical Functions Vocabulary:. Radical (Irrational) Function an epression whose general equation contains a root of a variable and possibly
Chapter 8: Radical Functions Chapter 8 Overview: Types and Traits of Radical Functions Vocabulary:. Radical (Irrational) Function an epression whose general equation contains a root of a variable and possibly
All work must be shown in this course for full credit. Unsupported answers may receive NO credit.
 AP Calculus.5 Worksheet All work must be shown in this course for full credit. Unsupported answers may receive NO credit. 1. Consider the function y = sin x. a) Find the equation of the tangent line when
AP Calculus.5 Worksheet All work must be shown in this course for full credit. Unsupported answers may receive NO credit. 1. Consider the function y = sin x. a) Find the equation of the tangent line when
Trigonometry (Ch. 4) Test Review - CALCULATOR ALLOWED
 Name: Class: Date: ID: A Trigonometry (Ch. 4) Test Review - CALCULATOR ALLOWED 1. A guy wire runs from the ground to a cell tower. The wire is attached to the cell tower a = 190 feet above the ground.
Name: Class: Date: ID: A Trigonometry (Ch. 4) Test Review - CALCULATOR ALLOWED 1. A guy wire runs from the ground to a cell tower. The wire is attached to the cell tower a = 190 feet above the ground.
Implicit Differentiation and Related Rates
 Math 3A Discussion Notes Week 5 October 7 and October 9, 05 Because of the mierm, we re a little behind lecture, but this week s topics will help prepare you for the quiz. Implicit Differentiation and
Math 3A Discussion Notes Week 5 October 7 and October 9, 05 Because of the mierm, we re a little behind lecture, but this week s topics will help prepare you for the quiz. Implicit Differentiation and
dy dx dx dx as a BC Calculus 1 The Chain Rule is notation for a which says that we have the
 2.4 2.6 BC Calculus 1 The Chain Rule dy is notation for a which says that we have the for an expression set equal to (the dependent variable), where the variable is x. This is read dee why, dee or the
2.4 2.6 BC Calculus 1 The Chain Rule dy is notation for a which says that we have the for an expression set equal to (the dependent variable), where the variable is x. This is read dee why, dee or the
( f + g ) (3) = ( fg ) (3) = g(x) = x 7 cos x. s = 200t 10t 2. sin x cos x cos2x. lim. f (x) = 7 x 5. y = 1+ 4sin x, (0,1) f (x) = x 2 g(x)
 Stewart - Calculus ET 6e Chapter Form A 1. If f ( ) =, g() =, f () =, g () = 6, find the following numbers. ( f + g ) () = ( fg ) () = ( f / g) () = f f g ( ) =. Find the points on the curve y = + 1 +
Stewart - Calculus ET 6e Chapter Form A 1. If f ( ) =, g() =, f () =, g () = 6, find the following numbers. ( f + g ) () = ( fg ) () = ( f / g) () = f f g ( ) =. Find the points on the curve y = + 1 +
MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. C) dc. D) dr dt = 2πdC dt
 MAC 3 Chapter Review Materials (Part III) Topics Include Related Rates, Differentials, and Linear Approximations MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers
MAC 3 Chapter Review Materials (Part III) Topics Include Related Rates, Differentials, and Linear Approximations MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers
Related Rates. MATH 151 Calculus for Management. J. Robert Buchanan. Department of Mathematics. J. Robert Buchanan Related Rates
 Related Rates MATH 151 Calculus for Management J. Robert Buchanan Department of Mathematics 2014 Related Rates Problems Another common application of the derivative involved situations in which two or
Related Rates MATH 151 Calculus for Management J. Robert Buchanan Department of Mathematics 2014 Related Rates Problems Another common application of the derivative involved situations in which two or
(a) At what rate is the circumference of the circle changing when the radius is 10 inches? =2inches per minute and we want to find. c =2 r.
 3.11 Related Rates Problem 1 The radius of a circle is increasing at a rate of 2 inches per minute. (a) At what rate is the circumference of the circle changing when the radius is 10 inches? We know: dr
3.11 Related Rates Problem 1 The radius of a circle is increasing at a rate of 2 inches per minute. (a) At what rate is the circumference of the circle changing when the radius is 10 inches? We know: dr
with dt. with 2. If x = u, find an equation relating du dt
 MATH 2250 Royal Section 3.10: Related Rates EXPANDED VERSION In this section, we consider two (or more) dependent variables that depend on a third variable (the independent variable). Usually, the independent
MATH 2250 Royal Section 3.10: Related Rates EXPANDED VERSION In this section, we consider two (or more) dependent variables that depend on a third variable (the independent variable). Usually, the independent
WW Prob Lib1 Math course-section, semester year
 Young-Seon Lee WW Prob Lib Math course-section, semester year WeBWorK assignment due /4/03 at :00 PM..( pt) Give the rational number whose decimal form is: 0 7333333 Answer:.( pt) Solve the following inequality:
Young-Seon Lee WW Prob Lib Math course-section, semester year WeBWorK assignment due /4/03 at :00 PM..( pt) Give the rational number whose decimal form is: 0 7333333 Answer:.( pt) Solve the following inequality:
Math 147 Exam II Practice Problems
 Math 147 Exam II Practice Problems This review should not be used as your sole source for preparation for the exam. You should also re-work all examples given in lecture, all homework problems, all lab
Math 147 Exam II Practice Problems This review should not be used as your sole source for preparation for the exam. You should also re-work all examples given in lecture, all homework problems, all lab
2018 Midterm Review Trigonometry: Midterm Review A Missive from the Math Department Trigonometry Work Problems Study For Understanding Read Actively
 Summer . Fill in the blank to correctl complete the sentence..4 written in degrees and minutes is..4 written in degrees and minutes is.. Find the complement and the supplement of the given angle. The complement
Summer . Fill in the blank to correctl complete the sentence..4 written in degrees and minutes is..4 written in degrees and minutes is.. Find the complement and the supplement of the given angle. The complement
Derivatives and Rates of Change
 Sec.1 Derivatives and Rates of Change A. Slope of Secant Functions rise Recall: Slope = m = = run Slope of the Secant Line to a Function: Examples: y y = y1. From this we are able to derive: x x x1 m y
Sec.1 Derivatives and Rates of Change A. Slope of Secant Functions rise Recall: Slope = m = = run Slope of the Secant Line to a Function: Examples: y y = y1. From this we are able to derive: x x x1 m y
AP Calculus AB Semester 2 Practice Final
 lass: ate: I: P alculus Semester Practice Final Multiple hoice Identify the choice that best completes the statement or answers the question. Find the constants a and b such that the function f( x) = Ï
lass: ate: I: P alculus Semester Practice Final Multiple hoice Identify the choice that best completes the statement or answers the question. Find the constants a and b such that the function f( x) = Ï
APPLICATIONS OF DERIVATIVES
 ALICATIONS OF DERIVATIVES 6 INTRODUCTION Derivatives have a wide range of applications in engineering, sciences, social sciences, economics and in many other disciplines In this chapter, we shall learn
ALICATIONS OF DERIVATIVES 6 INTRODUCTION Derivatives have a wide range of applications in engineering, sciences, social sciences, economics and in many other disciplines In this chapter, we shall learn
MATH 130 FINAL REVIEW
 MATH 130 FINAL REVIEW Problems 1 5 refer to triangle ABC, with C=90º. Solve for the missing information. 1. A = 40, c = 36m. B = 53 30', b = 75mm 3. a = 91 ft, b = 85 ft 4. B = 1, c = 4. ft 5. A = 66 54',
MATH 130 FINAL REVIEW Problems 1 5 refer to triangle ABC, with C=90º. Solve for the missing information. 1. A = 40, c = 36m. B = 53 30', b = 75mm 3. a = 91 ft, b = 85 ft 4. B = 1, c = 4. ft 5. A = 66 54',
Apply & Practice 3.5 Set 1: P #3-18 (mult. of 3); 19 #21 write explicit #27-33 (mult. of 3) point #39-40 eqn tang line from graph
 Ch 0 Homework Complete Solutions V Part : S. Stirling Calculus: Earl Transcendental Functions, 4e Larson WATCH for the product rule and the chain rule. If the order that our terms are in differ from the
Ch 0 Homework Complete Solutions V Part : S. Stirling Calculus: Earl Transcendental Functions, 4e Larson WATCH for the product rule and the chain rule. If the order that our terms are in differ from the
College Calculus Final Review
 College Calculus Final Review Multiple Choice Identify the choice that best completes the statement or answers the question. 1. Determine the following limit. (Hint: Use the graph to calculate the limit.)
College Calculus Final Review Multiple Choice Identify the choice that best completes the statement or answers the question. 1. Determine the following limit. (Hint: Use the graph to calculate the limit.)
2.6 Related Rates. The Derivative as a Rate of Change. = ft related rates 175
 2.6 related rates 175 2.6 Related Rates Throughout the next several tions we ll look at a variety of applications of derivatives. Probably no single application will be of interest or use to everyone,
2.6 related rates 175 2.6 Related Rates Throughout the next several tions we ll look at a variety of applications of derivatives. Probably no single application will be of interest or use to everyone,
Skills Practice Skills Practice for Lesson 3.1
 Skills Practice Skills Practice for Lesson.1 Name Date Get Radical or (Be)! Radicals and the Pythagorean Theorem Vocabulary Write the term that best completes each statement. 1. An expression that includes
Skills Practice Skills Practice for Lesson.1 Name Date Get Radical or (Be)! Radicals and the Pythagorean Theorem Vocabulary Write the term that best completes each statement. 1. An expression that includes
Trigonometry Final Exam Review
 Name Period Trigonometry Final Exam Review 2014-2015 CHAPTER 2 RIGHT TRIANGLES 8 1. Given sin θ = and θ terminates in quadrant III, find the following: 17 a) cos θ b) tan θ c) sec θ d) csc θ 2. Use a calculator
Name Period Trigonometry Final Exam Review 2014-2015 CHAPTER 2 RIGHT TRIANGLES 8 1. Given sin θ = and θ terminates in quadrant III, find the following: 17 a) cos θ b) tan θ c) sec θ d) csc θ 2. Use a calculator
CALCULUS I: FIU FINAL EXAM PROBLEM COLLECTION: VERSION WITHOUT ANSWERS
 CALCULUS I: FIU FINAL EXAM PROBLEM COLLECTION: VERSION WITHOUT ANSWERS FIU MATHEMATICS FACULTY NOVEMBER 2017 Contents 1. Limits and Continuity 1 2. Derivatives 4 3. Local Linear Approximation and differentials
CALCULUS I: FIU FINAL EXAM PROBLEM COLLECTION: VERSION WITHOUT ANSWERS FIU MATHEMATICS FACULTY NOVEMBER 2017 Contents 1. Limits and Continuity 1 2. Derivatives 4 3. Local Linear Approximation and differentials
UNIT 2 SIMPLE APPLICATION OF DIFFERENTIAL CALCULUS
 Calculus UNIT 2 SIMPLE APPLICATION OF DIFFERENTIAL CALCULUS Structure 2.0 Introduction 2.1 Objectives 2.2 Rate of Change of Quantities 2.3 Increasing and Decreasing Function 2.4 Maima and Minima of Functions
Calculus UNIT 2 SIMPLE APPLICATION OF DIFFERENTIAL CALCULUS Structure 2.0 Introduction 2.1 Objectives 2.2 Rate of Change of Quantities 2.3 Increasing and Decreasing Function 2.4 Maima and Minima of Functions
Problems to practice for FINAL. 1. Below is the graph of a function ( ) At which of the marked values ( and ) is: (a) ( ) greatest = (b) ( ) least
 Problems to practice for FINAL. Below is the graph of a function () At which of the marked values ( and ) is: (a) () greatest = (b) () least = (c) () the greatest = (d) () the least = (e) () = = (f) ()
Problems to practice for FINAL. Below is the graph of a function () At which of the marked values ( and ) is: (a) () greatest = (b) () least = (c) () the greatest = (d) () the least = (e) () = = (f) ()
Science One Math. October 18, 2018
 Science One Math October 18, 2018 Today A few more examples of related rates problems A general discussion about mathematical modelling A simple growth model Related Rates Problems Problems where two or
Science One Math October 18, 2018 Today A few more examples of related rates problems A general discussion about mathematical modelling A simple growth model Related Rates Problems Problems where two or
Radicals and Pythagorean Theorem Date: Per:
 Math 2 Unit 7 Worksheet 1 Name: Radicals and Pythagorean Theorem Date: Per: [1-12] Simplify each radical expression. 1. 75 2. 24. 7 2 4. 10 12 5. 2 6 6. 2 15 20 7. 11 2 8. 9 2 9. 2 2 10. 5 2 11. 7 5 2
Math 2 Unit 7 Worksheet 1 Name: Radicals and Pythagorean Theorem Date: Per: [1-12] Simplify each radical expression. 1. 75 2. 24. 7 2 4. 10 12 5. 2 6 6. 2 15 20 7. 11 2 8. 9 2 9. 2 2 10. 5 2 11. 7 5 2
Log1 Contest Round 2 Theta Geometry
 008 009 Log Contest Round Theta Geometry Name: Leave answers in terms of π. Non-integer rational numbers should be given as a reduced fraction. Units are not needed. 4 points each What is the perimeter
008 009 Log Contest Round Theta Geometry Name: Leave answers in terms of π. Non-integer rational numbers should be given as a reduced fraction. Units are not needed. 4 points each What is the perimeter
Chapter 1: Trigonometric Functions 1. Find (a) the complement and (b) the supplement of 61. Show all work and / or support your answer.
 Trig Exam Review F07 O Brien Trigonometry Exam Review: Chapters,, To adequately prepare for the exam, try to work these review problems using only the trigonometry knowledge which you have internalized
Trig Exam Review F07 O Brien Trigonometry Exam Review: Chapters,, To adequately prepare for the exam, try to work these review problems using only the trigonometry knowledge which you have internalized
CHAPTER 3: DERIVATIVES
 (Exercises for Section 3.1: Derivatives, Tangent Lines, and Rates of Change) E.3.1 CHAPTER 3: DERIVATIVES SECTION 3.1: DERIVATIVES, TANGENT LINES, and RATES OF CHANGE In these Exercises, use a version
(Exercises for Section 3.1: Derivatives, Tangent Lines, and Rates of Change) E.3.1 CHAPTER 3: DERIVATIVES SECTION 3.1: DERIVATIVES, TANGENT LINES, and RATES OF CHANGE In these Exercises, use a version
2.7 Implicit Differentiation and Related Rates Math 125
 .7 IMPLICIT DIFFERENTIATION AND RELATED RATES Implicit and Explicit Functions Suppose your boss says, I have had it with your incompetence. You ve screwed up everything we ve ever given you to do! The
.7 IMPLICIT DIFFERENTIATION AND RELATED RATES Implicit and Explicit Functions Suppose your boss says, I have had it with your incompetence. You ve screwed up everything we ve ever given you to do! The
Math 2250, Spring 2017, Practice Sheet for Exam 2
 Math 2250, Spring 2017, Practice Sheet for Exam 2 (1) Find the derivative of the function f(x) = xx (x 2 4) 5 (x 1) 3 e xp x + e x (2) Solve for dy dx x 2 4y 2 =sin(xy) (3) Solve for dx dt given that e
Math 2250, Spring 2017, Practice Sheet for Exam 2 (1) Find the derivative of the function f(x) = xx (x 2 4) 5 (x 1) 3 e xp x + e x (2) Solve for dy dx x 2 4y 2 =sin(xy) (3) Solve for dx dt given that e
Old Math 120 Exams. David M. McClendon. Department of Mathematics Ferris State University
 Old Math 10 Exams David M. McClendon Department of Mathematics Ferris State University 1 Contents Contents Contents 1 General comments on these exams 3 Exams from Fall 016 4.1 Fall 016 Exam 1...............................
Old Math 10 Exams David M. McClendon Department of Mathematics Ferris State University 1 Contents Contents Contents 1 General comments on these exams 3 Exams from Fall 016 4.1 Fall 016 Exam 1...............................
Practice Test - Chapter 4
 Find the value of x. Round to the nearest tenth, if necessary. 1. An acute angle measure and the length of the hypotenuse are given, so the sine function can be used to find the length of the side opposite.
Find the value of x. Round to the nearest tenth, if necessary. 1. An acute angle measure and the length of the hypotenuse are given, so the sine function can be used to find the length of the side opposite.
APPLICATIONS OF DERIVATIVES UNIT PROBLEM SETS
 APPLICATIONS OF DERIVATIVES UNIT PROBLEM SETS PROBLEM SET #1 Related Rates ***Calculators Allowed*** 1. An oil tanker spills oil that spreads in a circular pattern whose radius increases at the rate of
APPLICATIONS OF DERIVATIVES UNIT PROBLEM SETS PROBLEM SET #1 Related Rates ***Calculators Allowed*** 1. An oil tanker spills oil that spreads in a circular pattern whose radius increases at the rate of
Implicit Differentiation and Related Rates
 Math 31A Discussion Session Week 5 Notes February 2 and 4, 2016 This week we re going to learn how to find tangent lines to curves which aren t necessarily graphs of functions, using an approach called
Math 31A Discussion Session Week 5 Notes February 2 and 4, 2016 This week we re going to learn how to find tangent lines to curves which aren t necessarily graphs of functions, using an approach called
MATH 135 Calculus 1 Solutions/Answers for Exam 3 Practice Problems November 18, 2016
 MATH 35 Calculus Solutions/Answers for Exam 3 Practice Problems November 8, 206 I. Find the indicated derivative(s) and simplify. (A) ( y = ln(x) x 7 4 ) x Solution: By the product rule and the derivative
MATH 35 Calculus Solutions/Answers for Exam 3 Practice Problems November 8, 206 I. Find the indicated derivative(s) and simplify. (A) ( y = ln(x) x 7 4 ) x Solution: By the product rule and the derivative
A = 1 2 ab da dt = 1 da. We can find how fast the area is growing at 3 seconds by plugging everything into that differentiated equation: da
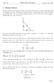 1 Related Rates In most related rates problems, we have an equation that relates a bunch of quantities that are changing over time. For example, suppose we have a right triangle whose base and height are
1 Related Rates In most related rates problems, we have an equation that relates a bunch of quantities that are changing over time. For example, suppose we have a right triangle whose base and height are
The volume of a sphere and the radius of the same sphere are related by the formula:
 Related Rates Today is a day in which we explore the behavior of derivatives rather than trying to get new formulas for derivatives. Example Let s ask the following question: Suppose that you are filling
Related Rates Today is a day in which we explore the behavior of derivatives rather than trying to get new formulas for derivatives. Example Let s ask the following question: Suppose that you are filling
AP Calculus. Applications of Derivatives. Table of Contents
 AP Calculus 2015 11 03 www.njctl.org Table of Contents click on the topic to go to that section Related Rates Linear Motion Linear Approximation & Differentials L'Hopital's Rule Horizontal Tangents 1 Related
AP Calculus 2015 11 03 www.njctl.org Table of Contents click on the topic to go to that section Related Rates Linear Motion Linear Approximation & Differentials L'Hopital's Rule Horizontal Tangents 1 Related
3.8 Exponential Growth and Decay
 3.8 Exponential Growth and Decay Suppose the rate of change of y with respect to t is proportional to y itself. So there is some constant k such that dy dt = ky The only solution to this equation is an
3.8 Exponential Growth and Decay Suppose the rate of change of y with respect to t is proportional to y itself. So there is some constant k such that dy dt = ky The only solution to this equation is an
Related Rates In each related rate problem there can be variations in the details. The problems, however, have the same general structure.
 Lab 6 Math 111 Spring 019 Related Rates In each related rate problem there can be variations in the details. The problems, however, have the same general structure. I. Relating Quantities: Independent
Lab 6 Math 111 Spring 019 Related Rates In each related rate problem there can be variations in the details. The problems, however, have the same general structure. I. Relating Quantities: Independent
1 The Derivative and Differrentiability
 1 The Derivative and Differrentiability 1.1 Derivatives and rate of change Exercise 1 Find the equation of the tangent line to f (x) = x 2 at the point (1, 1). Exercise 2 Suppose that a ball is dropped
1 The Derivative and Differrentiability 1.1 Derivatives and rate of change Exercise 1 Find the equation of the tangent line to f (x) = x 2 at the point (1, 1). Exercise 2 Suppose that a ball is dropped
Ch6prac 1.Find the degree measure of the angle with the given radian measure. (Round your answer to the nearest whole number.) -2
 Ch6prac 1.Find the degree measure of the angle with the given radian measure. (Round your answer to the nearest whole number.) -2 2. Find the degree measure of the angle with the given radian measure.
Ch6prac 1.Find the degree measure of the angle with the given radian measure. (Round your answer to the nearest whole number.) -2 2. Find the degree measure of the angle with the given radian measure.
Find the perimeter of the figure named and shown. Express the perimeter in the same unit of measure that appears on the given side or sides.
 Mth101 Chapter 8 HW Name Find the perimeter of the figure named and shown. Express the perimeter in the same unit of measure that appears on the given side or sides. 1) 1) Rectangle 6 in. 12 in. 12 in.
Mth101 Chapter 8 HW Name Find the perimeter of the figure named and shown. Express the perimeter in the same unit of measure that appears on the given side or sides. 1) 1) Rectangle 6 in. 12 in. 12 in.
CALCULUS I: FIU FINAL EXAM PROBLEM COLLECTION: VERSION WITH ANSWERS
 CALCULUS I: FIU FINAL EXAM PROBLEM COLLECTION: VERSION WITH ANSWERS FIU MATHEMATICS FACULTY NOVEMBER 2017 Contents 1. Limits and Continuity 1 2. Derivatives 4 3. Local Linear Approximation and differentials
CALCULUS I: FIU FINAL EXAM PROBLEM COLLECTION: VERSION WITH ANSWERS FIU MATHEMATICS FACULTY NOVEMBER 2017 Contents 1. Limits and Continuity 1 2. Derivatives 4 3. Local Linear Approximation and differentials
Using the distance formula Using formulas to solve unknowns. Pythagorean Theorem. Finding Legs of Right Triangles
 Math 154 Chapter 9.6: Applications of Radical Equations Objectives: Finding legs of right triangles Finding hypotenuse of right triangles Solve application problems involving right triangles Pythagorean
Math 154 Chapter 9.6: Applications of Radical Equations Objectives: Finding legs of right triangles Finding hypotenuse of right triangles Solve application problems involving right triangles Pythagorean
Solution: It could be discontinuous, or have a vertical tangent like y = x 1/3, or have a corner like y = x.
 1. Name three different reasons that a function can fail to be differentiable at a point. Give an example for each reason, and explain why your examples are valid. It could be discontinuous, or have a
1. Name three different reasons that a function can fail to be differentiable at a point. Give an example for each reason, and explain why your examples are valid. It could be discontinuous, or have a
MCB4UW Handout 4.11 Related Rates of Change
 MCB4UW Handout 4. Related Rate of Change. Water flow into a rectangular pool whoe dimenion are m long, 8 m wide, and 0 m deep. If water i entering the pool at the rate of cubic metre per econd (hint: thi
MCB4UW Handout 4. Related Rate of Change. Water flow into a rectangular pool whoe dimenion are m long, 8 m wide, and 0 m deep. If water i entering the pool at the rate of cubic metre per econd (hint: thi
DRAFT - Math 101 Lecture Note - Dr. Said Algarni
 3 Differentiation Rules 3.1 The Derivative of Polynomial and Exponential Functions In this section we learn how to differentiate constant functions, power functions, polynomials, and exponential functions.
3 Differentiation Rules 3.1 The Derivative of Polynomial and Exponential Functions In this section we learn how to differentiate constant functions, power functions, polynomials, and exponential functions.
MIDTERM 2 REVIEW: ADDITIONAL PROBLEMS. 1 2 x + 1. y = + 1 = x 1/ = 1. y = 1 2 x 3/2 = 1. into this equation would have then given. y 1.
 MIDTERM 2 REVIEW: ADDITIONAL PROBLEMS ) If x + y =, find y. IMPLICIT DIFFERENTIATION Solution. Taking the derivative (with respect to x) of both sides of the given equation, we find that 2 x + 2 y y =
MIDTERM 2 REVIEW: ADDITIONAL PROBLEMS ) If x + y =, find y. IMPLICIT DIFFERENTIATION Solution. Taking the derivative (with respect to x) of both sides of the given equation, we find that 2 x + 2 y y =
Due: Wed Oct :30 AM MDT. Question Instructions Make sure you have easy access to all three of these documents.
 Related Rates II: Guided (10862409) Due: Wed Oct 4 2017 07:30 AM MDT Question 1 2 3 4 5 6 Instructions Make sure you have easy access to all three of these documents. Today's Notes and Learning Goals Tips
Related Rates II: Guided (10862409) Due: Wed Oct 4 2017 07:30 AM MDT Question 1 2 3 4 5 6 Instructions Make sure you have easy access to all three of these documents. Today's Notes and Learning Goals Tips
Circle - Circumference
 Name : Score : Circle - Circumference Example : Circumference of a circle = 2πr or πd 8.53 m Diameter (d) = 8.53 m πd = 3.14 x 8.53 26.78 m Find the circumference of each circle. Round the answer to two
Name : Score : Circle - Circumference Example : Circumference of a circle = 2πr or πd 8.53 m Diameter (d) = 8.53 m πd = 3.14 x 8.53 26.78 m Find the circumference of each circle. Round the answer to two
Trigonometric ratios:
 0 Trigonometric ratios: The six trigonometric ratios of A are: Sine Cosine Tangent sin A = opposite leg hypotenuse adjacent leg cos A = hypotenuse tan A = opposite adjacent leg leg and their inverses:
0 Trigonometric ratios: The six trigonometric ratios of A are: Sine Cosine Tangent sin A = opposite leg hypotenuse adjacent leg cos A = hypotenuse tan A = opposite adjacent leg leg and their inverses:
MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. 6 C) - 12 (6x - 7)3
 Part B- Pre-Test 2 for Cal (2.4, 2.5, 2.6) Test 2 will be on Oct 4th, chapter 2 (except 2.6) Name MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question.
Part B- Pre-Test 2 for Cal (2.4, 2.5, 2.6) Test 2 will be on Oct 4th, chapter 2 (except 2.6) Name MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question.
WeBWorK demonstration assignment
 WeBWorK demonstration assignment The main purpose of this WeBWorK set is to familiarize yourself with WeBWorK. Here are some hints on how to use WeBWorK effectively: After first logging into WeBWorK change
WeBWorK demonstration assignment The main purpose of this WeBWorK set is to familiarize yourself with WeBWorK. Here are some hints on how to use WeBWorK effectively: After first logging into WeBWorK change
Final Exam Review / AP Calculus AB
 Chapter : Final Eam Review / AP Calculus AB Use the graph to find each limit. 1) lim f(), lim f(), and lim π - π + π f 5 4 1 y - - -1 - - -4-5 ) lim f(), - lim f(), and + lim f 8 6 4 y -4 - - -1-1 4 5-4
Chapter : Final Eam Review / AP Calculus AB Use the graph to find each limit. 1) lim f(), lim f(), and lim π - π + π f 5 4 1 y - - -1 - - -4-5 ) lim f(), - lim f(), and + lim f 8 6 4 y -4 - - -1-1 4 5-4
Unit 3 Right Triangle Trigonometry - Classwork
 Unit 3 Right Triangle Trigonometry - Classwork We have spent time learning the definitions of trig functions and finding the trig functions of both quadrant and special angles. But what about other angles?
Unit 3 Right Triangle Trigonometry - Classwork We have spent time learning the definitions of trig functions and finding the trig functions of both quadrant and special angles. But what about other angles?
(x) = f 0 (f 1 (x)) to check your answers, and then to calculate the derivatives of the other inverse trig functions: sin(arccos(x)
 Reviewing the worksheet On the worksheet, you learne how to compute the erivatives of inverse functions, such as ln(x), arcsin(x), etc. You use implicit i erentiation to calculate the erivatives. x arcsin(x)=
Reviewing the worksheet On the worksheet, you learne how to compute the erivatives of inverse functions, such as ln(x), arcsin(x), etc. You use implicit i erentiation to calculate the erivatives. x arcsin(x)=
