Interval Data Classification under Partial Information: A Chance-constraint Approach
|
|
|
- Marshall Martin
- 6 years ago
- Views:
Transcription
1 Interval Data Classification under Partial Information: A Chance-constraint Approach Sahely Bhadra J. Saketha Nath Aharon Ben-Tal Chiranjib Bhattacharyya PAKDD 2009 J. Saketha Nath (PAKDD 09) Conference Seminar 1 / 15
2 Data Uncertainty Real-world data fraught with uncertainties, noise. Measurement errors, non-zero least counts etc. Inherent heterogenity: Bio-medical data e.g. Micro-array, cancer diagnostic data. Computational/Respresentational convinience. J. Saketha Nath (PAKDD 09) Conference Seminar 2 / 15
3 Data Uncertainty Real-world data fraught with uncertainties, noise. Measurement errors, non-zero least counts etc. Inherent heterogenity: Bio-medical data e.g. Micro-array, cancer diagnostic data. Computational/Respresentational convinience. Many datasets provide partial information regarding noise. e.g., Wisconsin breast cancer datasets (support, mean, std. err.) Micro-array datasets (replicates) J. Saketha Nath (PAKDD 09) Conference Seminar 2 / 15
4 Data Uncertainty Real-world data fraught with uncertainties, noise. Measurement errors, non-zero least counts etc. Inherent heterogenity: Bio-medical data e.g. Micro-array, cancer diagnostic data. Computational/Respresentational convinience. Many datasets provide partial information regarding noise. e.g., Wisconsin breast cancer datasets (support, mean, std. err.) Micro-array datasets (replicates) Classifiers accounting for uncertainty generalize better. J. Saketha Nath (PAKDD 09) Conference Seminar 2 / 15
5 Problem Definition Problem: Assume partial information regarding uncertainties given: bounding intervals (i.e. support) and means of uncertain eg. Make no distributional assumptions. Construct classifier that generalizes well. J. Saketha Nath (PAKDD 09) Conference Seminar 3 / 15
6 Existing Methodology [Laurent El Ghaoui et.al., 2003]: Utilize support alone; neglect statistical information True datapoint lies somewhere in bounding hyper-rectangle Construct regular SVM J. Saketha Nath (PAKDD 09) Conference Seminar 4 / 15
7 Existing Methodology [Laurent El Ghaoui et.al., 2003]: Utilize support alone; neglect statistical information True datapoint lies somewhere in bounding hyper-rectangle Construct regular SVM SVM Formulation: 1 min w,b,ξ 2 w C i ξ i i s.t. y i (w x i b) 1 ξ i, ξ i 0 J. Saketha Nath (PAKDD 09) Conference Seminar 4 / 15
8 Existing Methodology [Laurent El Ghaoui et.al., 2003]: Utilize support alone; neglect statistical information True datapoint lies somewhere in bounding hyper-rectangle Construct regular SVM IC-BH Formulation: 1 min w,b,ξ 2 w C i ξ i i s.t. y i (w x i b) 1 ξ i, ξ i 0, x i R i J. Saketha Nath (PAKDD 09) Conference Seminar 4 / 15
9 Limitations of Existing Methodologies Neglect useful statistical information regarding uncertainty Overly-conservative uncertainty modeling leads to less margin Poor generalization J. Saketha Nath (PAKDD 09) Conference Seminar 5 / 15
10 Limitations of Existing Methodologies Neglect useful statistical information regarding uncertainty Overly-conservative uncertainty modeling leads to less margin Poor generalization Proposed Methodology: Use both support and statistical information Employ Chance-Constraint Program (CCP) approaches Relax CCP using Bernstein bounding schemes Not overly-conservative better margin and generalization Leads to convex Second Order Cone Program (SOCP) J. Saketha Nath (PAKDD 09) Conference Seminar 5 / 15
11 Proposed Formulation SVM: 1 min w,b,ξ 2 w C i ξ i i s.t. y i (w x i b) 1 ξ i, ξ i 0 J. Saketha Nath (PAKDD 09) Conference Seminar 6 / 15
12 Proposed Formulation SVM: 1 min w,b,ξ 2 w C i ξ i i s.t. y i (w X i b) 1 ξ i, ξ i 0 J. Saketha Nath (PAKDD 09) Conference Seminar 6 / 15
13 Proposed Formulation Chance-Constrained Program: 1 min w,b,ξ 2 w C i ξ i i s.t. Prob { y i (w X i b) 1 ξ i } ǫ, ξi 0 J. Saketha Nath (PAKDD 09) Conference Seminar 6 / 15
14 Proposed Formulation Chance-Constrained Program: 1 min w,b,ξ 2 w C i ξ i i s.t. Prob { y i (w X i b) 1 ξ i } ǫ, ξi 0 Assumptions: X i R i. E[X i ] are known. X ij, j = 1,...,n are independent random variables. J. Saketha Nath (PAKDD 09) Conference Seminar 6 / 15
15 Convex Relaxation Comments: In general, difficult to solve such CCPs. Construct an efficient relaxation: Employ Bernstein schemes to upper bound probability Constrain the upper-bound to be less than ǫ J. Saketha Nath (PAKDD 09) Conference Seminar 7 / 15
16 Convex Relaxation Comments: In general, difficult to solve such CCPs. Construct an efficient relaxation: Employ Bernstein schemes to upper bound probability Constrain the upper-bound to be less than ǫ Key Question: } Prob {y i (w X i b) 1 ξ i? J. Saketha Nath (PAKDD 09) Conference Seminar 7 / 15
17 Convex Relaxation Comments: In general, difficult to solve such CCPs. Construct an efficient relaxation: Employ Bernstein schemes to upper bound probability Constrain the upper-bound to be less than ǫ Key Question: } Prob {y i (w X i b) 1 ξ i? ǫ J. Saketha Nath (PAKDD 09) Conference Seminar 7 / 15
18 Convex Relaxation Comments: In general, difficult to solve such CCPs. Construct an efficient relaxation: Employ Bernstein schemes to upper bound probability Constrain the upper-bound to be less than ǫ Key Question: Prob u ij X ij + u i0 0? j J. Saketha Nath (PAKDD 09) Conference Seminar 7 / 15
19 Bernstein Bounding Markov Bounding: Prob (X 0)? J. Saketha Nath (PAKDD 09) Conference Seminar 8 / 15
20 Bernstein Bounding Markov Bounding: E X [1 X 0 ]? J. Saketha Nath (PAKDD 09) Conference Seminar 8 / 15
21 Bernstein Bounding Markov Bounding: E X [1 X 0 ] E[exp {αx}] α 0 J. Saketha Nath (PAKDD 09) Conference Seminar 8 / 15
22 Bernstein Bounding Markov Bounding: E X [1 X 0 ] E[exp {αx}] α 0 = E exp α u ij X ij + u i0 j = exp {u i0 } Π j E[exp {αu ij X ij }] J. Saketha Nath (PAKDD 09) Conference Seminar 8 / 15
23 Bernstein Bounding Markov Bounding: E X [1 X 0 ] E[exp {αx}] α 0 = E exp α u ij X ij + u i0 j = exp {u i0 } Π j E[exp {αu ij X ij }] J. Saketha Nath (PAKDD 09) Conference Seminar 8 / 15
24 Bernstein Bounding Markov Bounding: E X [1 X 0 ] E[exp {αx}] α 0 = E exp α u ij X ij + u i0 j = exp {u i0 } Π j E[exp {αu ij X ij }] Bounding Expectation: Given X R, E[X], tightly bound: E[exp {tx}], t R J. Saketha Nath (PAKDD 09) Conference Seminar 8 / 15
25 Bernstein Bounding Contd. Known Result: { } µij t + σ(ˆµ ij ) 2 lij 2 E[exp{tX ij }] exp t 2 2 t R (1) J. Saketha Nath (PAKDD 09) Conference Seminar 9 / 15
26 Bernstein Bounding Contd. Known Result: { } µij t + σ(ˆµ ij ) 2 lij 2 E[exp{tX ij }] exp t 2 2 t R (1) Analogous with Gaussian mgf Variance term varies with relative position of mean! J. Saketha Nath (PAKDD 09) Conference Seminar 9 / 15
27 Bernstein Bounding Contd. Known Result: { } µij t + σ(ˆµ ij ) 2 lij 2 E[exp{tX ij }] exp t 2 2 t R (1) Analogous with Gaussian mgf Variance term varies with relative position of mean! Proof Sketch: Support (a X b), mean are known. exp{tx} b X X a b a exp{ta} + b a exp{tb} Taking expectations on both sides leads to: { } a + b E[exp {tx}] exp 2 t + h(lt), h(z) log (cosh(z) + ˆµ sinh(z)) { } exp µt + σ (ˆµ)2 l 2 t 2 2 institution-logo J. Saketha Nath (PAKDD 09) Conference Seminar 9 / 15
28 Main Result A Convex Formulation IC-MBH Formulation: min w,b,z i,ξ i w C i ξ i s.t. y i (w µ i b) + z i ˆµ i 1 ξ i + z i 1 + κ Σ i (y i L i w + z i ) 2 J. Saketha Nath (PAKDD 09) Conference Seminar 10 / 15
29 Geometric Interpretation x 2 axis x axis 1 Figure: Figure showing bounding hyper-rectangle and uncertainty sets for different positions of mean. Mean and boundary of uncertainty set marked with same color. J. Saketha Nath (PAKDD 09) Conference Seminar 11 / 15 institution-logo
30 Classification of Uncertain Datapoints Labeling: Support y pr = sign(w m i b) Mean y pr = sign(w µ i b) Replicates y pr is majority label of replicates J. Saketha Nath (PAKDD 09) Conference Seminar 12 / 15
31 Classification of Uncertain Datapoints Labeling: Support y pr = sign(w m i b) Mean y pr = sign(w µ i b) Replicates y pr is majority label of replicates Error Measures: Nominal Error Calculate ǫ opt from Bernstein bounding 1 if y i y pr i OptErr i = ǫ opt if y i = y pr i and R(a i,b i ) cuts opt. hyp. 0 else (2) J. Saketha Nath (PAKDD 09) Conference Seminar 12 / 15
32 Numerical Experiments Table: Table comparing NomErr (NE) and OptErr (OE) obtained with IC-M, IC-R, IC-BH and IC-MBH. Data IC-M IC-R IC-BH IC-MBH NE OE NE OE NE OE NE OE 10 U β A-F A-S A-T F-S F-T S-T WDBC J. Saketha Nath (PAKDD 09) Conference Seminar 13 / 15
33 Conclusions Novel methodology for interval-valued data classification under partial information. Employs support as well as statistical information Idea pose the problem as CCP and relax using Bernstein bounds Bernstein bounds lead to less conservative noise modeling Better classification margin and generalization ability Empirical results show 50% decrease in generalization error Exploitation of Bernstein bounding techniques in learning has a promise. J. Saketha Nath (PAKDD 09) Conference Seminar 14 / 15
34 THANK YOU J. Saketha Nath (PAKDD 09) Conference Seminar 15 / 15
Second Order Cone Programming, Missing or Uncertain Data, and Sparse SVMs
Second Order Cone Programming, Missing or Uncertain Data, and Sparse SVMs Ammon Washburn University of Arizona September 25, 2015 1 / 28 Introduction We will begin with basic Support Vector Machines (SVMs)
A Second order Cone Programming Formulation for Classifying Missing Data
A Second order Cone Programming Formulation for Classifying Missing Data Chiranjib Bhattacharyya Department of Computer Science and Automation Indian Institute of Science Bangalore, 560 012, India chiru@csa.iisc.ernet.in
Short Course Robust Optimization and Machine Learning. Lecture 6: Robust Optimization in Machine Learning
Short Course Robust Optimization and Machine Machine Lecture 6: Robust Optimization in Machine Laurent El Ghaoui EECS and IEOR Departments UC Berkeley Spring seminar TRANSP-OR, Zinal, Jan. 16-19, 2012
Kernel Learning for Multi-modal Recognition Tasks
Kernel Learning for Multi-modal Recognition Tasks J. Saketha Nath CSE, IIT-B IBM Workshop J. Saketha Nath (IIT-B) IBM Workshop 23-Sep-09 1 / 15 Multi-modal Learning Tasks Multiple views or descriptions
Support Vector Machines for Classification and Regression. 1 Linearly Separable Data: Hard Margin SVMs
E0 270 Machine Learning Lecture 5 (Jan 22, 203) Support Vector Machines for Classification and Regression Lecturer: Shivani Agarwal Disclaimer: These notes are a brief summary of the topics covered in
Robustness and Regularization: An Optimization Perspective
Robustness and Regularization: An Optimization Perspective Laurent El Ghaoui (EECS/IEOR, UC Berkeley) with help from Brian Gawalt, Onureena Banerjee Neyman Seminar, Statistics Department, UC Berkeley September
Support Vector Machines for Classification and Regression
CIS 520: Machine Learning Oct 04, 207 Support Vector Machines for Classification and Regression Lecturer: Shivani Agarwal Disclaimer: These notes are designed to be a supplement to the lecture. They may
Introduction to Support Vector Machines
Introduction to Support Vector Machines Shivani Agarwal Support Vector Machines (SVMs) Algorithm for learning linear classifiers Motivated by idea of maximizing margin Efficient extension to non-linear
Non-Bayesian Classifiers Part II: Linear Discriminants and Support Vector Machines
Non-Bayesian Classifiers Part II: Linear Discriminants and Support Vector Machines Selim Aksoy Department of Computer Engineering Bilkent University saksoy@cs.bilkent.edu.tr CS 551, Fall 2018 CS 551, Fall
EE 227A: Convex Optimization and Applications April 24, 2008
EE 227A: Convex Optimization and Applications April 24, 2008 Lecture 24: Robust Optimization: Chance Constraints Lecturer: Laurent El Ghaoui Reading assignment: Chapter 2 of the book on Robust Optimization
Support Vector Machine (SVM) & Kernel CE-717: Machine Learning Sharif University of Technology. M. Soleymani Fall 2012
Support Vector Machine (SVM) & Kernel CE-717: Machine Learning Sharif University of Technology M. Soleymani Fall 2012 Linear classifier Which classifier? x 2 x 1 2 Linear classifier Margin concept x 2
Estimation and Optimization: Gaps and Bridges. MURI Meeting June 20, Laurent El Ghaoui. UC Berkeley EECS
MURI Meeting June 20, 2001 Estimation and Optimization: Gaps and Bridges Laurent El Ghaoui EECS UC Berkeley 1 goals currently, estimation (of model parameters) and optimization (of decision variables)
Support Vector Machines. CAP 5610: Machine Learning Instructor: Guo-Jun QI
Support Vector Machines CAP 5610: Machine Learning Instructor: Guo-Jun QI 1 Linear Classifier Naive Bayes Assume each attribute is drawn from Gaussian distribution with the same variance Generative model:
Interval Data Classification under Partial Information: A Chance-Constraint Approach
Interval Data Classfcaton under Partal Informaton: A Chance-Constrant Approach Sahely Bhadra 1, J. Saketha Nath 2, Aharon Ben-Tal 2, and Chranjb Bhattacharyya 1 1 Dept. of Computer Scence and Automaton,
Does Unlabeled Data Help?
Does Unlabeled Data Help? Worst-case Analysis of the Sample Complexity of Semi-supervised Learning. Ben-David, Lu and Pal; COLT, 2008. Presentation by Ashish Rastogi Courant Machine Learning Seminar. Outline
Support Vector Machine via Nonlinear Rescaling Method
Manuscript Click here to download Manuscript: svm-nrm_3.tex Support Vector Machine via Nonlinear Rescaling Method Roman Polyak Department of SEOR and Department of Mathematical Sciences George Mason University
A GENERAL FORMULATION FOR SUPPORT VECTOR MACHINES. Wei Chu, S. Sathiya Keerthi, Chong Jin Ong
A GENERAL FORMULATION FOR SUPPORT VECTOR MACHINES Wei Chu, S. Sathiya Keerthi, Chong Jin Ong Control Division, Department of Mechanical Engineering, National University of Singapore 0 Kent Ridge Crescent,
Convex Optimization in Classification Problems
New Trends in Optimization and Computational Algorithms December 9 13, 2001 Convex Optimization in Classification Problems Laurent El Ghaoui Department of EECS, UC Berkeley elghaoui@eecs.berkeley.edu 1
Linear & nonlinear classifiers
Linear & nonlinear classifiers Machine Learning Hamid Beigy Sharif University of Technology Fall 1396 Hamid Beigy (Sharif University of Technology) Linear & nonlinear classifiers Fall 1396 1 / 44 Table
Data Mining. Linear & nonlinear classifiers. Hamid Beigy. Sharif University of Technology. Fall 1396
Data Mining Linear & nonlinear classifiers Hamid Beigy Sharif University of Technology Fall 1396 Hamid Beigy (Sharif University of Technology) Data Mining Fall 1396 1 / 31 Table of contents 1 Introduction
Appendix A. Numeric example of Dimick Staiger Estimator and comparison between Dimick-Staiger Estimator and Hierarchical Poisson Estimator
Appendix A. Numeric example of Dimick Staiger Estimator and comparison between Dimick-Staiger Estimator and Hierarchical Poisson Estimator As described in the manuscript, the Dimick-Staiger (DS) estimator
Support Vector Machines and Bayes Regression
Statistical Techniques in Robotics (16-831, F11) Lecture #14 (Monday ctober 31th) Support Vector Machines and Bayes Regression Lecturer: Drew Bagnell Scribe: Carl Doersch 1 1 Linear SVMs We begin by considering
Robust Novelty Detection with Single Class MPM
Robust Novelty Detection with Single Class MPM Gert R.G. Lanckriet EECS, U.C. Berkeley gert@eecs.berkeley.edu Laurent El Ghaoui EECS, U.C. Berkeley elghaoui@eecs.berkeley.edu Michael I. Jordan Computer
Jeff Howbert Introduction to Machine Learning Winter
Classification / Regression Support Vector Machines Jeff Howbert Introduction to Machine Learning Winter 2012 1 Topics SVM classifiers for linearly separable classes SVM classifiers for non-linearly separable
Stephen Scott.
1 / 35 (Adapted from Ethem Alpaydin and Tom Mitchell) sscott@cse.unl.edu In Homework 1, you are (supposedly) 1 Choosing a data set 2 Extracting a test set of size > 30 3 Building a tree on the training
Support'Vector'Machines. Machine(Learning(Spring(2018 March(5(2018 Kasthuri Kannan
Support'Vector'Machines Machine(Learning(Spring(2018 March(5(2018 Kasthuri Kannan kasthuri.kannan@nyumc.org Overview Support Vector Machines for Classification Linear Discrimination Nonlinear Discrimination
Support Vector Machines. Introduction to Data Mining, 2 nd Edition by Tan, Steinbach, Karpatne, Kumar
Data Mining Support Vector Machines Introduction to Data Mining, 2 nd Edition by Tan, Steinbach, Karpatne, Kumar 02/03/2018 Introduction to Data Mining 1 Support Vector Machines Find a linear hyperplane
Robust Inverse Covariance Estimation under Noisy Measurements
.. Robust Inverse Covariance Estimation under Noisy Measurements Jun-Kun Wang, Shou-De Lin Intel-NTU, National Taiwan University ICML 2014 1 / 30 . Table of contents Introduction.1 Introduction.2 Related
A Randomized Algorithm for Large Scale Support Vector Learning
A Randomized Algorithm for Large Scale Support Vector Learning Krishnan S. Department of Computer Science and Automation Indian Institute of Science Bangalore-12 rishi@csa.iisc.ernet.in Chiranjib Bhattacharyya
A Randomized Algorithm for Large Scale Support Vector Learning
A Randomized Algorithm for Large Scale Support Vector Learning Krishnan S. Department of Computer Science and Automation, Indian Institute of Science, Bangalore-12 rishi@csa.iisc.ernet.in Chiranjib Bhattacharyya
Machine Learning 1. Linear Classifiers. Marius Kloft. Humboldt University of Berlin Summer Term Machine Learning 1 Linear Classifiers 1
Machine Learning 1 Linear Classifiers Marius Kloft Humboldt University of Berlin Summer Term 2014 Machine Learning 1 Linear Classifiers 1 Recap Past lectures: Machine Learning 1 Linear Classifiers 2 Recap
A short introduction to supervised learning, with applications to cancer pathway analysis Dr. Christina Leslie
A short introduction to supervised learning, with applications to cancer pathway analysis Dr. Christina Leslie Computational Biology Program Memorial Sloan-Kettering Cancer Center http://cbio.mskcc.org/leslielab
Linear & nonlinear classifiers
Linear & nonlinear classifiers Machine Learning Hamid Beigy Sharif University of Technology Fall 1394 Hamid Beigy (Sharif University of Technology) Linear & nonlinear classifiers Fall 1394 1 / 34 Table
COS 511: Theoretical Machine Learning. Lecturer: Rob Schapire Lecture # 12 Scribe: Indraneel Mukherjee March 12, 2008
COS 511: Theoretical Machine Learning Lecturer: Rob Schapire Lecture # 12 Scribe: Indraneel Mukherjee March 12, 2008 In the previous lecture, e ere introduced to the SVM algorithm and its basic motivation
Machine Learning. Support Vector Machines. Fabio Vandin November 20, 2017
Machine Learning Support Vector Machines Fabio Vandin November 20, 2017 1 Classification and Margin Consider a classification problem with two classes: instance set X = R d label set Y = { 1, 1}. Training
Support Vector Machine & Its Applications
Support Vector Machine & Its Applications A portion (1/3) of the slides are taken from Prof. Andrew Moore s SVM tutorial at http://www.cs.cmu.edu/~awm/tutorials Mingyue Tan The University of British Columbia
Modifying A Linear Support Vector Machine for Microarray Data Classification
Modifying A Linear Support Vector Machine for Microarray Data Classification Prof. Rosemary A. Renaut Dr. Hongbin Guo & Wang Juh Chen Department of Mathematics and Statistics, Arizona State University
Robust Kernel-Based Regression
Robust Kernel-Based Regression Budi Santosa Department of Industrial Engineering Sepuluh Nopember Institute of Technology Kampus ITS Surabaya Surabaya 60111,Indonesia Theodore B. Trafalis School of Industrial
Predicting the Probability of Correct Classification
Predicting the Probability of Correct Classification Gregory Z. Grudic Department of Computer Science University of Colorado, Boulder grudic@cs.colorado.edu Abstract We propose a formulation for binary
Lecture Notes on Support Vector Machine
Lecture Notes on Support Vector Machine Feng Li fli@sdu.edu.cn Shandong University, China 1 Hyperplane and Margin In a n-dimensional space, a hyper plane is defined by ω T x + b = 0 (1) where ω R n is
Support Vector Machine (SVM) and Kernel Methods
Support Vector Machine (SVM) and Kernel Methods CE-717: Machine Learning Sharif University of Technology Fall 2014 Soleymani Outline Margin concept Hard-Margin SVM Soft-Margin SVM Dual Problems of Hard-Margin
Support Vector Machine (SVM) and Kernel Methods
Support Vector Machine (SVM) and Kernel Methods CE-717: Machine Learning Sharif University of Technology Fall 2015 Soleymani Outline Margin concept Hard-Margin SVM Soft-Margin SVM Dual Problems of Hard-Margin
Practical Robust Optimization - an introduction -
Practical Robust Optimization - an introduction - Dick den Hertog Tilburg University, Tilburg, The Netherlands NGB/LNMB Seminar Back to school, learn about the latest developments in Operations Research
Introduction. Chapter 1
Chapter 1 Introduction In this book we will be concerned with supervised learning, which is the problem of learning input-output mappings from empirical data (the training dataset). Depending on the characteristics
Qualifying Exam in Machine Learning
Qualifying Exam in Machine Learning October 20, 2009 Instructions: Answer two out of the three questions in Part 1. In addition, answer two out of three questions in two additional parts (choose two parts
Support vector machines
Support vector machines Guillaume Obozinski Ecole des Ponts - ParisTech SOCN course 2014 SVM, kernel methods and multiclass 1/23 Outline 1 Constrained optimization, Lagrangian duality and KKT 2 Support
Optimization Tools in an Uncertain Environment
Optimization Tools in an Uncertain Environment Michael C. Ferris University of Wisconsin, Madison Uncertainty Workshop, Chicago: July 21, 2008 Michael Ferris (University of Wisconsin) Stochastic optimization
Lecture 7: Kernels for Classification and Regression
Lecture 7: Kernels for Classification and Regression CS 194-10, Fall 2011 Laurent El Ghaoui EECS Department UC Berkeley September 15, 2011 Outline Outline A linear regression problem Linear auto-regressive
Linear smoother. ŷ = S y. where s ij = s ij (x) e.g. s ij = diag(l i (x))
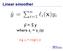Linear smoother ŷ = S y where s ij = s ij (x) e.g. s ij = diag(l i (x)) 2 Online Learning: LMS and Perceptrons Partially adapted from slides by Ryan Gabbard and Mitch Marcus (and lots original slides by
CSC 411 Lecture 17: Support Vector Machine
CSC 411 Lecture 17: Support Vector Machine Ethan Fetaya, James Lucas and Emad Andrews University of Toronto CSC411 Lec17 1 / 1 Today Max-margin classification SVM Hard SVM Duality Soft SVM CSC411 Lec17
Semidefinite and Second Order Cone Programming Seminar Fall 2012 Project: Robust Optimization and its Application of Robust Portfolio Optimization
Semidefinite and Second Order Cone Programming Seminar Fall 2012 Project: Robust Optimization and its Application of Robust Portfolio Optimization Instructor: Farid Alizadeh Author: Ai Kagawa 12/12/2012
CSE 151 Machine Learning. Instructor: Kamalika Chaudhuri
CSE 151 Machine Learning Instructor: Kamalika Chaudhuri Linear Classification Given labeled data: (xi, feature vector yi) label i=1,..,n where y is 1 or 1, find a hyperplane to separate from Linear Classification
NEW ROBUST UNSUPERVISED SUPPORT VECTOR MACHINES
J Syst Sci Complex () 24: 466 476 NEW ROBUST UNSUPERVISED SUPPORT VECTOR MACHINES Kun ZHAO Mingyu ZHANG Naiyang DENG DOI:.7/s424--82-8 Received: March 8 / Revised: 5 February 9 c The Editorial Office of
CS 484 Data Mining. Classification 7. Some slides are from Professor Padhraic Smyth at UC Irvine
CS 484 Data Mining Classification 7 Some slides are from Professor Padhraic Smyth at UC Irvine Bayesian Belief networks Conditional independence assumption of Naïve Bayes classifier is too strong. Allows
Stochastic Optimization with Variance Reduction for Infinite Datasets with Finite Sum Structure
Stochastic Optimization with Variance Reduction for Infinite Datasets with Finite Sum Structure Alberto Bietti Julien Mairal Inria Grenoble (Thoth) March 21, 2017 Alberto Bietti Stochastic MISO March 21,
Plan. Lecture: What is Chemoinformatics and Drug Design? Description of Support Vector Machine (SVM) and its used in Chemoinformatics.
Plan Lecture: What is Chemoinformatics and Drug Design? Description of Support Vector Machine (SVM) and its used in Chemoinformatics. Exercise: Example and exercise with herg potassium channel: Use of
Machine Learning And Applications: Supervised Learning-SVM
Machine Learning And Applications: Supervised Learning-SVM Raphaël Bournhonesque École Normale Supérieure de Lyon, Lyon, France raphael.bournhonesque@ens-lyon.fr 1 Supervised vs unsupervised learning Machine
Linear vs Non-linear classifier. CS789: Machine Learning and Neural Network. Introduction
Linear vs Non-linear classifier CS789: Machine Learning and Neural Network Support Vector Machine Jakramate Bootkrajang Department of Computer Science Chiang Mai University Linear classifier is in the
Classifier Complexity and Support Vector Classifiers
Classifier Complexity and Support Vector Classifiers Feature 2 6 4 2 0 2 4 6 8 RBF kernel 10 10 8 6 4 2 0 2 4 6 Feature 1 David M.J. Tax Pattern Recognition Laboratory Delft University of Technology D.M.J.Tax@tudelft.nl
CSE 546 Final Exam, Autumn 2013
CSE 546 Final Exam, Autumn 0. Personal info: Name: Student ID: E-mail address:. There should be 5 numbered pages in this exam (including this cover sheet).. You can use any material you brought: any book,
CS340 Machine learning Lecture 5 Learning theory cont'd. Some slides are borrowed from Stuart Russell and Thorsten Joachims
CS340 Machine learning Lecture 5 Learning theory cont'd Some slides are borrowed from Stuart Russell and Thorsten Joachims Inductive learning Simplest form: learn a function from examples f is the target
Contents Lecture 4. Lecture 4 Linear Discriminant Analysis. Summary of Lecture 3 (II/II) Summary of Lecture 3 (I/II)
Contents Lecture Lecture Linear Discriminant Analysis Fredrik Lindsten Division of Systems and Control Department of Information Technology Uppsala University Email: fredriklindsten@ituuse Summary of lecture
Machine Learning. Lecture 6: Support Vector Machine. Feng Li.
Machine Learning Lecture 6: Support Vector Machine Feng Li fli@sdu.edu.cn https://funglee.github.io School of Computer Science and Technology Shandong University Fall 2018 Warm Up 2 / 80 Warm Up (Contd.)
Chapter 6 Classification and Prediction (2)
Chapter 6 Classification and Prediction (2) Outline Classification and Prediction Decision Tree Naïve Bayes Classifier Support Vector Machines (SVM) K-nearest Neighbors Accuracy and Error Measures Feature
Statistical Learning Reading Assignments
Statistical Learning Reading Assignments S. Gong et al. Dynamic Vision: From Images to Face Recognition, Imperial College Press, 2001 (Chapt. 3, hard copy). T. Evgeniou, M. Pontil, and T. Poggio, "Statistical
Applications of Robust Optimization in Signal Processing: Beamforming and Power Control Fall 2012
Applications of Robust Optimization in Signal Processing: Beamforg and Power Control Fall 2012 Instructor: Farid Alizadeh Scribe: Shunqiao Sun 12/09/2012 1 Overview In this presentation, we study the applications
Support Vector Machines.
Support Vector Machines www.cs.wisc.edu/~dpage 1 Goals for the lecture you should understand the following concepts the margin slack variables the linear support vector machine nonlinear SVMs the kernel
Outline. Basic concepts: SVM and kernels SVM primal/dual problems. Chih-Jen Lin (National Taiwan Univ.) 1 / 22
Outline Basic concepts: SVM and kernels SVM primal/dual problems Chih-Jen Lin (National Taiwan Univ.) 1 / 22 Outline Basic concepts: SVM and kernels Basic concepts: SVM and kernels SVM primal/dual problems
SUPPORT VECTOR MACHINE
SUPPORT VECTOR MACHINE Mainly based on https://nlp.stanford.edu/ir-book/pdf/15svm.pdf 1 Overview SVM is a huge topic Integration of MMDS, IIR, and Andrew Moore s slides here Our foci: Geometric intuition
Linear Classification and SVM. Dr. Xin Zhang
Linear Classification and SVM Dr. Xin Zhang Email: eexinzhang@scut.edu.cn What is linear classification? Classification is intrinsically non-linear It puts non-identical things in the same class, so a
Support vector machines Lecture 4
Support vector machines Lecture 4 David Sontag New York University Slides adapted from Luke Zettlemoyer, Vibhav Gogate, and Carlos Guestrin Q: What does the Perceptron mistake bound tell us? Theorem: The
Mehryar Mohri Foundations of Machine Learning Courant Institute of Mathematical Sciences Homework assignment 3 April 5, 2013 Due: April 19, 2013
Mehryar Mohri Foundations of Machine Learning Courant Institute of Mathematical Sciences Homework assignment 3 April 5, 2013 Due: April 19, 2013 A. Kernels 1. Let X be a finite set. Show that the kernel
CS6375: Machine Learning Gautam Kunapuli. Support Vector Machines
Gautam Kunapuli Example: Text Categorization Example: Develop a model to classify news stories into various categories based on their content. sports politics Use the bag-of-words representation for this
Linear Support Vector Machine. Classification. Linear SVM. Huiping Cao. Huiping Cao, Slide 1/26
Huiping Cao, Slide 1/26 Classification Linear SVM Huiping Cao linear hyperplane (decision boundary) that will separate the data Huiping Cao, Slide 2/26 Support Vector Machines rt Vector Find a linear Machines
Statistical Learning Theory and the C-Loss cost function
Statistical Learning Theory and the C-Loss cost function Jose Principe, Ph.D. Distinguished Professor ECE, BME Computational NeuroEngineering Laboratory and principe@cnel.ufl.edu Statistical Learning Theory
Robust Optimization for Risk Control in Enterprise-wide Optimization
Robust Optimization for Risk Control in Enterprise-wide Optimization Juan Pablo Vielma Department of Industrial Engineering University of Pittsburgh EWO Seminar, 011 Pittsburgh, PA Uncertainty in Optimization
Computational Learning Theory. Definitions
Computational Learning Theory Computational learning theory is interested in theoretical analyses of the following issues. What is needed to learn effectively? Sample complexity. How many examples? Computational
Stochastic Subgradient Methods
Stochastic Subgradient Methods Stephen Boyd and Almir Mutapcic Notes for EE364b, Stanford University, Winter 26-7 April 13, 28 1 Noisy unbiased subgradient Suppose f : R n R is a convex function. We say
Neural networks and optimization
Neural networks and optimization Nicolas Le Roux INRIA 8 Nov 2011 Nicolas Le Roux (INRIA) Neural networks and optimization 8 Nov 2011 1 / 80 1 Introduction 2 Linear classifier 3 Convolutional neural networks
The definitions and notation are those introduced in the lectures slides. R Ex D [h
Mehryar Mohri Foundations of Machine Learning Courant Institute of Mathematical Sciences Homework assignment 2 October 04, 2016 Due: October 18, 2016 A. Rademacher complexity The definitions and notation
Foundations of Machine Learning
Introduction to ML Mehryar Mohri Courant Institute and Google Research mohri@cims.nyu.edu page 1 Logistics Prerequisites: basics in linear algebra, probability, and analysis of algorithms. Workload: about
Convex relaxations of chance constrained optimization problems
Convex relaxations of chance constrained optimization problems Shabbir Ahmed School of Industrial & Systems Engineering, Georgia Institute of Technology, 765 Ferst Drive, Atlanta, GA 30332. May 12, 2011
Introduction to Gaussian Processes
Introduction to Gaussian Processes Iain Murray murray@cs.toronto.edu CSC255, Introduction to Machine Learning, Fall 28 Dept. Computer Science, University of Toronto The problem Learn scalar function of
Generalization, Overfitting, and Model Selection
Generalization, Overfitting, and Model Selection Sample Complexity Results for Supervised Classification Maria-Florina (Nina) Balcan 10/03/2016 Two Core Aspects of Machine Learning Algorithm Design. How
CSCI5654 (Linear Programming, Fall 2013) Lectures Lectures 10,11 Slide# 1
CSCI5654 (Linear Programming, Fall 2013) Lectures 10-12 Lectures 10,11 Slide# 1 Today s Lecture 1. Introduction to norms: L 1,L 2,L. 2. Casting absolute value and max operators. 3. Norm minimization problems.
Efficient Methods for Robust Classification Under Uncertainty in Kernel Matrices
Journal of Machine Learning Research 13 (2012) 2923-2954 Submitted 5/11; Revised 2/12; Published 10/12 Efficient Methods for Robust Classification Under Uncertainty in Kernel Matrices Aharon Ben-Tal William
Unsupervised Classification via Convex Absolute Value Inequalities
Unsupervised Classification via Convex Absolute Value Inequalities Olvi Mangasarian University of Wisconsin - Madison University of California - San Diego January 17, 2017 Summary Classify completely unlabeled
1. Kernel ridge regression In contrast to ordinary least squares which has a cost function. m (θ T x (i) y (i) ) 2, J(θ) = 1 2.
CS229 Problem Set #2 Solutions 1 CS 229, Public Course Problem Set #2 Solutions: Theory Kernels, SVMs, and 1. Kernel ridge regression In contrast to ordinary least squares which has a cost function J(θ)
i=1 cosn (x 2 i y2 i ) over RN R N. cos y sin x
Mehryar Mohri Foundations of Machine Learning Courant Institute of Mathematical Sciences Homework assignment 3 November 16, 017 Due: Dec 01, 017 A. Kernels Show that the following kernels K are PDS: 1.
Efficient Maximum Margin Clustering
Dept. Automation, Tsinghua Univ. MLA, Nov. 8, 2008 Nanjing, China Outline 1 2 3 4 5 Outline 1 2 3 4 5 Support Vector Machine Given X = {x 1,, x n }, y = (y 1,..., y n ) { 1, +1} n, SVM finds a hyperplane
6.867 Machine Learning
6.867 Machine Learning Problem Set 2 Due date: Wednesday October 6 Please address all questions and comments about this problem set to 6867-staff@csail.mit.edu. You will need to use MATLAB for some of
Automated Segmentation of Low Light Level Imagery using Poisson MAP- MRF Labelling
Automated Segmentation of Low Light Level Imagery using Poisson MAP- MRF Labelling Abstract An automated unsupervised technique, based upon a Bayesian framework, for the segmentation of low light level
SVM and Kernel machine
SVM and Kernel machine Stéphane Canu stephane.canu@litislab.eu Escuela de Ciencias Informáticas 20 July 3, 20 Road map Linear SVM Linear classification The margin Linear SVM: the problem Optimization in
Clustering K-means. Machine Learning CSE546. Sham Kakade University of Washington. November 15, Review: PCA Start: unsupervised learning
Clustering K-means Machine Learning CSE546 Sham Kakade University of Washington November 15, 2016 1 Announcements: Project Milestones due date passed. HW3 due on Monday It ll be collaborative HW2 grades
Distributionally Robust Discrete Optimization with Entropic Value-at-Risk
Distributionally Robust Discrete Optimization with Entropic Value-at-Risk Daniel Zhuoyu Long Department of SEEM, The Chinese University of Hong Kong, zylong@se.cuhk.edu.hk Jin Qi NUS Business School, National
Support Vector Machines
EE 17/7AT: Optimization Models in Engineering Section 11/1 - April 014 Support Vector Machines Lecturer: Arturo Fernandez Scribe: Arturo Fernandez 1 Support Vector Machines Revisited 1.1 Strictly) Separable
Support Vector Machines, Kernel SVM
Support Vector Machines, Kernel SVM Professor Ameet Talwalkar Professor Ameet Talwalkar CS260 Machine Learning Algorithms February 27, 2017 1 / 40 Outline 1 Administration 2 Review of last lecture 3 SVM
Distributionally Robust Stochastic Optimization with Wasserstein Distance
Distributionally Robust Stochastic Optimization with Wasserstein Distance Rui Gao DOS Seminar, Oct 2016 Joint work with Anton Kleywegt School of Industrial and Systems Engineering Georgia Tech What is
Convex optimization COMS 4771
Convex optimization COMS 4771 1. Recap: learning via optimization Soft-margin SVMs Soft-margin SVM optimization problem defined by training data: w R d λ 2 w 2 2 + 1 n n [ ] 1 y ix T i w. + 1 / 15 Soft-margin
Statistical Machine Learning from Data
Samy Bengio Statistical Machine Learning from Data 1 Statistical Machine Learning from Data Ensembles Samy Bengio IDIAP Research Institute, Martigny, Switzerland, and Ecole Polytechnique Fédérale de Lausanne