NOTES WEEK 11 DAY 2 SCOT ADAMS
|
|
|
- Raymond Murphy
- 6 years ago
- Views:
Transcription
1 NOTES WEEK 11 DAY 2 SCOT ADAMS In Proposition 0.1 below, Bp0, δq is just the open interval p δ, δq and Bp0, x q is just the closed interval r x, x s. PROPOSITION 0.1. Let g : R R and let δ ą 0. Assume that Bp0, δq Ď domrg 1 s. Let x P Bp0, δq. Then there exists t P Bp0, x q such that rgpxqs rgp0qs rg 1 ptqsx. Proof. Unassigned exercise. (Hint: Use the Mean Value Theorem.) NOTE: We need to use B instead of B because, in Proposition 0.1, we allow the possibilty that x 0. NOTE: If we replace there exists t P Bp0, x q by the stronger there exists t P rx0, xys, then Proposition 0.1 would remain true and would be a slightly better result. However, we choose the formulation above, because it s easily stated and generalizes to higher dimensions, see Theorem 0.5 below. DEFINITION 0.2. For all m P N and for all i P t0,..., mu, we define λ m i : R m Ñ R m by λ m i pxq px 1,..., x i, 0,..., 0q, and we define ρ m i : R m Ñ R m by ρ m i pxq p0,..., 0, x m i`1,..., x m q. P R m, [ λ m mpxq ρ m mpxq x s and r λ m 0 pxq ρ m 0 pxq 0 m s. DEFINITION 0.3. For all m P N, for all i P t0,..., mu, for any set S, for all f : R m S, we define L i f : f λ m i : R m S and R i f : f ρ m i : R m S. Note: For all x P R m, both pl m fqpxq pr m fqpxq fpxq and pl 0 fqpxq pr 0 fqpxq fp0 m q. It follows both that L m f R m f f and that L 0 f R 0 f C fp0mq R m C f 0 m P CpR m, R n q. DEFINITION 0.4. For all m P N, for all i P t1,..., mu, for any vector space S, for all f : R m S, we define L i f : pl ifq pl i 1 fq and R i f : pr ifq pr i 1 fq. Date: April 6, 2017 Printout date: April 7,
2 2 SCOT ADAMS Note: For all x P R n, we have rfpxqs rfp0 m qs rpl mfqpxqs ` ` rpl 1 fqpxqs. Throughout this lecture, we will use to denote the L 8 norm on all Euclidean spaces. So, for all m P N, for all x P R m, we have x maxt x 1,..., x m u; consequently, for all i P t1,..., mu, we have x i ď x. For all m P N, for all x P R m, for all r ą 0, we define the open L 8 ball Bpx, rq : B px, rq ty P R m s.t. y x ă ru and the closed L 8 ball Bpx, rq : B px, rq ty P R m s.t. y x ď ru. We now get our first Multi-Variable Mean Value Theorem, which we ll call MVMVT1: THEOREM 0.5. Let m P N, f : R m R, i P t1,..., mu, δ ą 0. Assume that Bp0 m, δq Ď domrb i fs. Let x P Bp0 m, δq. Then there exists c P Bp0 m, x q such that pl i fqpxq rpb ifqpcqsx i. Proof. Define α : R Ñ R m by αptq px 1,..., x i 1, t, 0,..., 0q. Since x P Bp0 m, δq, it follows that x ă δ. Then, for all j P t1,..., mu, we have x i ď x ă δ. P Bp0, δq, αptq maxt x 1,..., x i 1, t, 0u ă δ. That is, α pbp0, δqq Ď Bp0 m, δq. Define g : f α : R R. Then, for all t P R, it follows from the definitions of g 1 ptq and pb i fqpαptqq, that g 1 ptq pb i fqpαptqq. Then g 1 pb i fq α. So, since α pbp0, δqq Ď Bp0 m, δq Ď domrb i fs, we get Bp0, δq Ď domrg 1 s. As x i ă δ, we get x i P p δ, δq Bp0, δq. By Proposition 0.1 (with x replaced by x i ), choose t P Bp0, x i q such that rgpx i qs rgp0qs rg 1 ptqsx i. Since t P Bp0, x i q, we get t ď x i. Then t ď x i ď x, so t P Bp0, x q. Then αptq P α pbp0, x qq Ď Bp0 m, x q. Let c : αptq. Then c P Bp0 m, x q, and we wish to prove: pl i fqpxq rpb ifqpcqsx i. We have gpx i q fpαpx i qq fpx 1,..., x i 1, x i, 0,..., 0q pl i fqpxq. Also gp0q fpαpx i qq fpx 1,..., x i 1, 0, 0,..., 0q pl i 1 fqpxq. Then pl i fqpxq rpl ifqpxqs rpl i 1 fqpxqs rgpx i qs rgp0qs rg 1 ptqsx i rpb i fqpαptqqsx i,
3 NOTES WEEK 11 DAY 2 3 DEFINITION 0.6. For all m, n P N, for all k P N 0, we define Om,npkq : OR m,r npkq and O m,npkq : O R m,r npkq. We sometimes omit the commas, and write O mn and Omn. We now get our second Multi-Variable Mean Value Theorem, which we ll call MVMVT2: THEOREM 0.7. Let m P N, f : R m R, i P t1,..., mu, k P N 0. Assume that B i f P Om1pkq. Then L i f P O m1pk ` 1q. Proof. Since B i f P Om1pkq, choose δ ą 0 such that Bp0 m, δq P domrb i fs. Combining Theorem 0.5 with the Axiom of Choice, we choose a function c : Bp0 m, δq Ñ R m such that, for all x P Bp0 m, δq, we have both cpxq P Bp0 m, x q and pl i fqpxq rpb ifqpcpxqqsx i. For all x P Bp0 m, δq, since cpxq P Bp0 m, x q, we see that cpxq ď x. Then c P O mm p1q. Then pb i fq c P rom1pkqs ro mm p1qs Ď Om1pkq. Let P SBFpR, Rq be ordinary multiplication of real numbers, defined by a b ab. Let P P LpR m, Rq be the ith standard projection, defined by P pxq x i. Then P P LpR m, Rq Ď O m1 p1q. For all x P Bp0 m, δq, we have pl i fqpxq rpb ifqpcpxqqsx i rpb i fqpcpxqqsrp pxqs rpb i fqpcpxqqs rp pxqs rppb i fq cqpxqs rp pxqs prpb i fq cs P qpxq. Then L i f rpb ifq cs P. Recall: pb i fq c P Om1pkq. Then L i f P ro m1pkqs ro m1 p1qs Ď Om1pk ` 1q, We now get our third Multi-Variable Mean Value Theorem, which we ll call MVMVT3: THEOREM 0.8. Let m P N, f : R m R, i P t1,..., mu, k P N 0. Assume that B i f P O m1 pkq. Then L i f P O m1pk ` 1q. To prove this, capitalize all the Os appearing in the preceding proof:
4 4 SCOT ADAMS Proof. Since B i f P O m1 pkq, choose δ ą 0 such that Bp0 m, δq P domrb i fs. Combining Theorem 0.5 with the Axiom of Choice, we choose a function c : Bp0 m, δq Ñ R m such that, for all x P Bp0 m, δq, we have both cpxq P Bp0 m, x q and pl i fqpxq rpb ifqpcpxqqsx i. For all x P Bp0 m, δq, since cpxq P Bp0 m, x q, we see that cpxq ď x. Then c P O mm p1q. Then pb i fq c P ro m1 pkqs ro mm p1qs Ď O m1 pkq. Let P SBFpR, Rq be ordinary multiplication of real numbers, defined by a b ab. Let P P LpR m, Rq be the ith standard projection, defined by P pxq x i. Then P P LpR m, Rq Ď O m1 p1q. For all x P Bp0 m, δq, we have pl i fqpxq rpb ifqpcpxqqsx i rpb i fqpcpxqqsrp pxqs rpb i fqpcpxqqs rp pxqs rppb i fq cqpxqs rp pxqs prpb i fq cs P qpxq. Then L i f rpb ifq cs P. Recall: pb i fq c P O m1 pkq. Then L i f P ro m1pkqs ro m1 p1qs Ď O m1 pk ` 1q, REMARK 0.9. Let m, n P N and let g : R m R n and let k P N 0. Define J : t1,..., nu. Then (i) r g P Omnpkq s ô P J, g j P Om1pkq s. (ii) r g P O mn pkq s ô P J, g j P O m1 pkq s, and Proof. Unassigned HW. We can improve Theorem 0.7 and Theorem 0.8, by upgrading the target from R to R n. We call the results MVMVT2 and MVMVT3. WARNING: Because of the spiral path t ÞÑ p cos t, sin t, t q : R Ñ R 3, Theorem 0.5 does not upgrade, even when m 1 and i 1. Let s upgrade MVMVT2 to MVMVT2 : THEOREM Let m, n P N, f : R m R n, i P t1,..., mu, k P N 0. Assume that B i f P Omnpkq. Then L i f P O mnpk ` 1q.
5 NOTES WEEK 11 DAY 2 5 Proof. Let J : t1,..., nu. By (i) of Remark 0.9, we wish to show, for all j P J, that pl i fq j P Om1pk ` 1q. Let j P J be given. We wish to show that pl i fq j P Om1pk ` 1q. Unassigned HW: Show pl i fq j L i pf jq and pb i fq j B i pf j q. Since B i f P Omnpkq, by (i) of Remark 0.9, we have pb i fq j P Om1pkq. Then B i pf j q pb i fq j P Om1pkq. Then, by Theorem 0.7, it follows that L i pf jq P Om1pk`1q. Then pl i fq j L i pf j q P Om1pk`1q, Now, let s upgrade MVMVT3 to MVMVT3 : THEOREM Let m, n P N, f : R m R n, i P t1,..., mu, k P N 0. Assume that B i f P O mn pkq. Then L i f P O mnpk ` 1q. We capitalize Os and change (i) to (ii): Proof. Let J : t1,..., nu. By (ii) of Remark 0.9, we wish to show, for all j P J, that pl i fq j P O m1 pk ` 1q. Let j P J be given. We wish to show that pl i fq j P O m1 pk ` 1q. Unassigned HW: Show pl i fq j L i pf jq and pb i fq j B i pf j q. Since B i f P O mn pkq, by (ii) of Remark 0.9, we have pb i fq j P O m1 pkq. Then B i pf j q pb i fq j P O m1 pkq. Then, by Theorem 0.7, it follows that L i pf jq P O m1 pk ` 1q. Then pl i fq j L i pf j q P O m1 pk ` 1q. DEFINITION For all m, n P N, we define 0 m,n : 0 R m,r n. We sometimes omit the commas, and write 0 mn. Note: 0 mn C 0n R m. Thus, for all x P R m, we have 0 mn pxq 0 n. For functions f and g, we will use the notation g Ě f to mean that g is an extension of f, i.e., that both ( domrgs Ě domrfs ) and Next, MVMVT4: P domrfs, gpxq fpxq q. THEOREM Let m, n P N, f : R m R n, k P N 0. Let I : t1,..., mu Assume, for all i P I, that B i f P Omnpkq. Assume that fp0 m q 0 n. Then f P Omnpk ` 1q. Proof. For all x P R n, rfpxqs rfp0 m qs rpl mfqpxqs` `rpl 1 fqpxqs. So, since fp0 m q 0 n, we conclude that f Ě pl mfq ` ` pl 1 fq. By Theorem 0.10, we see, for all i P I, that L i f P O mnpk`1q. Therefore f Ě pl mfq ` ` pl 1 fq P Omnpk ` 1q, and so f P Omnpk ` 1q.
6 6 SCOT ADAMS LEMMA Let V and W be finite dimensional vector spaces, let f, g : V W, let p P V and let q P W. Assume, for all x P V, that we have gpxq rfpp ` xqs q. Then all of the following hold: P V, pdgqpxq pdfqpp ` xq, (ii) p f is defined near p q ñ p g is defined near 0 V q (iii) p f is continuous at p q ñ p g is continuous 0 V q. and Proof. We leave (ii) and (iii) as unassigned HW and prove only (i). Let x P V be given. We wish to prove that pdgqpxq pdfqpp ` xq, i.e., that D x g D p`x f. It suffices to show: LINS x rgs LINS p`x rfs. For any φ : V W, we have LINS x rφs LINS 0V rφ T x s. Then both LINS x rgs LINS 0V rgx T s and LINS p`x rfs LINS 0V rfp`xs. T We therefore wish to show: LINS 0V rgx T s LINS 0V rfp`xs. T It suffices to show: gx T fp`x. T We wish to show, for all h P V, that gx T phq fp`xphq. T Let h P V be given. We wish to prove: gx T phq fp`xphq. T We have g T x phq rgpx ` hqs rgpxqs rpfpp ` x ` hqq qs rpfpp ` xqq qs rfpp ` x ` hqs rfpp ` xqs f T p`xphq, LEMMA Let m, n P N, let f, g : R m R n, let p P R m and let q P R n. P R m, gpxq rfpp ` xqs q. P R P t1,..., mu, pb i gqpxq pb i fqpp ` xq. Proof. Unassigned HW. THEOREM Let m, n P N, f : R m R n, k P N 0 and p P R m. Let I : t1,..., mu. Assume, for all i P I, that B i f is defined near p and continuous at p. Then p P dlinrfs. Proof. Let g : f T p. For all x P R n, we have gpxq rfpp ` xqs rfppqs. Then gp0 m q 0 n. Also, by (i) of Lemma 0.14, we see, for all x P R n, that pdgqpxq pdfqpp ` xq. Then pdgqp0 m q pdfqppq. Also, we have: [ ( 0 m P domrdgs ) iff ( p P domrdfs ) ]. Equivalently, we have: [ ( 0 m P dlinrgs ) iff ( p P dlinrfs ) ]. We wish to prove: 0 m P dlinrgs. Recall: For all x P R n, we have gpxq rfpp ` xqs rfppqs. Then, by Lemma 0.15, for all x P R n, for all i P I, pb i gqpxq pb i fqpp ` xq. By asumption, for all i P I, B i f is defined near p and continuous at p.
7 NOTES WEEK 11 DAY 2 7 Then, for all i P I, by (ii) and (iii) of Lemma 0.14 (with V replaced by R m, W by R n, f by B i f, g by B i g and q by 0 m ), we see that B i g is defined near 0 m and continuous at 0 m. For all i P I, let w i : pb i gqp0 m q. Define L P LpR m, R n q by Lpxq x 1 w 1 ` ` x m w m. Then Lp0 m q 0 n. Let h : g L. Then hp0 m q 0 n 0 n 0 n. Because L P LpR m, R n q, it follows that dlinrls R m. Then 0 m P R m dlinrls. We therefore have: [ ( 0 m P dlinrgs ) iff ( 0 m P dlinrhs ) ]. It therefore suffices to show that 0 m P dlinrhs. That is, we wish to prove that 0 m P domrdhs. It suffices to show that pdhqp0 m q 0 mn, i.e., that h T 0 m P Omnp1q. Since hp0 m q 0 n, it follows that h T 0 m h. So we wish to prove: h P Omnp1q. Then, by Theorem 0.13, it suffices to P I, B i h P Omn. Let i P I be given. We wish to prove: B i h P Omn. From the definition of L, we see, for all x P R m, that pb i Lqpxq w i. Then, for all x P R m, we have pb i hqpxq rpb i gqpxqs w i. Therefore pb i hqp0 m q w i w i 0 n. It remains to show that B i h is defined near 0 m and continuous at 0 m. Recall that B i g is defined near 0 m and continuous at 0 m, Therefore, by (i) and (ii) of Lemma 0.14 (with V replaced by R m, W by R n, f by B i f, g by B i g, p by 0 m and q by w i ), we conclude that B i h is defined near 0 m and continuous at 0 m,
Homework for MATH 4604 (Advanced Calculus II) Spring 2017
 Homework for MATH 4604 (Advanced Calculus II) Spring 2017 Homework 14: Due on Tuesday 2 May 55. Let m, n P N, A P R mˆn and v P R n. Show: L A pvq 2 ď A 2 v 2. 56. Let n P N and let A P R nˆn. Let I n
Homework for MATH 4604 (Advanced Calculus II) Spring 2017 Homework 14: Due on Tuesday 2 May 55. Let m, n P N, A P R mˆn and v P R n. Show: L A pvq 2 ď A 2 v 2. 56. Let n P N and let A P R nˆn. Let I n
NOTES WEEK 14 DAY 2 SCOT ADAMS
 NOTES WEEK 14 DAY 2 SCOT ADAMS For this lecture, we fix the following: Let n P N, let W : R n, let : 2 P N pr n q and let I : id R n : R n Ñ R n be the identity map, defined by Ipxq x. For any h : W W,
NOTES WEEK 14 DAY 2 SCOT ADAMS For this lecture, we fix the following: Let n P N, let W : R n, let : 2 P N pr n q and let I : id R n : R n Ñ R n be the identity map, defined by Ipxq x. For any h : W W,
NOTES WEEK 10 DAY 2. Unassigned HW: Let V and W be finite dimensional vector spaces and let x P V. Show, for all f, g : V W, that
 NOTES WEEK 10 DAY 2 SCOT ADAMS Unassigned HW: Let V and W be finite dimensional vector spaces and let x P V. Show, for all f, g : V W, that D x pf ` gq pd x fq ` pd x gq. Also, show, for all c P R, for
NOTES WEEK 10 DAY 2 SCOT ADAMS Unassigned HW: Let V and W be finite dimensional vector spaces and let x P V. Show, for all f, g : V W, that D x pf ` gq pd x fq ` pd x gq. Also, show, for all c P R, for
NOTES WEEK 14 DAY 2 SCOT ADAMS
 NOTES WEEK 14 DAY 2 SCOT ADAMS We igligt tat it s possible to ave two topological spaces and a continuous bijection from te one to te oter wose inverse is not continuous: Let I : r0, 2πq and let C : tpx,
NOTES WEEK 14 DAY 2 SCOT ADAMS We igligt tat it s possible to ave two topological spaces and a continuous bijection from te one to te oter wose inverse is not continuous: Let I : r0, 2πq and let C : tpx,
NOTES WEEK 15 DAY 1 SCOT ADAMS
 NOTES WEEK 15 DAY 1 SCOT ADAMS We fix some notation for the entire class today: Let n P N, W : R n, : 2 P N pw q, W : LpW, W q, I : id W P W, z : 0 W 0 n. Note that W LpR n, R n q. Recall, for all T P
NOTES WEEK 15 DAY 1 SCOT ADAMS We fix some notation for the entire class today: Let n P N, W : R n, : 2 P N pw q, W : LpW, W q, I : id W P W, z : 0 W 0 n. Note that W LpR n, R n q. Recall, for all T P
NOTES WEEK 13 DAY 2 SCOT ADAMS
 NOTES WEEK 13 DAY 2 SCOT ADAMS Recall: Let px, dq be a metric space. Then, for all S Ď X, we have p S is sequentially compact q ñ p S is closed and bounded q. DEFINITION 0.1. Let px, dq be a metric space.
NOTES WEEK 13 DAY 2 SCOT ADAMS Recall: Let px, dq be a metric space. Then, for all S Ď X, we have p S is sequentially compact q ñ p S is closed and bounded q. DEFINITION 0.1. Let px, dq be a metric space.
DS-GA 3001: PROBLEM SESSION 2 SOLUTIONS VLADIMIR KOBZAR
 DS-GA 3: PROBLEM SESSION SOLUTIONS VLADIMIR KOBZAR Note: In this discussion we allude to the fact the dimension of a vector space is given by the number of basis vectors. We will shortly establish this
DS-GA 3: PROBLEM SESSION SOLUTIONS VLADIMIR KOBZAR Note: In this discussion we allude to the fact the dimension of a vector space is given by the number of basis vectors. We will shortly establish this
NOTES WEEK 02 DAY 1. THEOREM 0.3. Let A, B and C be sets. Then
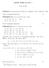 NOTES WEEK 02 DAY 1 SCOT ADAMS LEMMA 0.1. @propositions P, Q, R, rp or pq&rqs rp p or Qq&pP or Rqs. THEOREM 0.2. Let A and B be sets. Then (i) A X B B X A, and (ii) A Y B B Y A THEOREM 0.3. Let A, B and
NOTES WEEK 02 DAY 1 SCOT ADAMS LEMMA 0.1. @propositions P, Q, R, rp or pq&rqs rp p or Qq&pP or Rqs. THEOREM 0.2. Let A and B be sets. Then (i) A X B B X A, and (ii) A Y B B Y A THEOREM 0.3. Let A, B and
REAL ANALYSIS II TAKE HOME EXAM. T. Tao s Lecture Notes Set 5
 REAL ANALYSIS II TAKE HOME EXAM CİHAN BAHRAN T. Tao s Lecture Notes Set 5 1. Suppose that te 1, e 2, e 3,... u is a countable orthonormal system in a complex Hilbert space H, and c 1, c 2,... is a sequence
REAL ANALYSIS II TAKE HOME EXAM CİHAN BAHRAN T. Tao s Lecture Notes Set 5 1. Suppose that te 1, e 2, e 3,... u is a countable orthonormal system in a complex Hilbert space H, and c 1, c 2,... is a sequence
Approximation of Weighted Local Mean Operators
 Approximation of Weighted Local ean Operators Jianzhong Wang Department of athematics and Statistics Sam Houston State University Huntsville, TX 7734 Abstract Recently, weighted local mean operators are
Approximation of Weighted Local ean Operators Jianzhong Wang Department of athematics and Statistics Sam Houston State University Huntsville, TX 7734 Abstract Recently, weighted local mean operators are
Singular integral operators and the Riesz transform
 Singular integral operators and the Riesz transform Jordan Bell jordan.bell@gmail.com Department of Mathematics, University of Toronto November 17, 017 1 Calderón-Zygmund kernels Let ω n 1 be the measure
Singular integral operators and the Riesz transform Jordan Bell jordan.bell@gmail.com Department of Mathematics, University of Toronto November 17, 017 1 Calderón-Zygmund kernels Let ω n 1 be the measure
Fourier transforms. Up to now, we ve been expressing functions on finite intervals (usually the interval 0 x L or L x L) as Fourier series: a n cos L
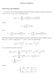 ourier transforms Motivation and definition Up to now, we ve been expressing functions on finite intervals (usually the interval 0 x or x ) as ourier series: fpxq a 0 8 nπx a n cos n b n sin nπx where
ourier transforms Motivation and definition Up to now, we ve been expressing functions on finite intervals (usually the interval 0 x or x ) as ourier series: fpxq a 0 8 nπx a n cos n b n sin nπx where
NOTES WEEK 01 DAY 1 SCOT ADAMS
 NOTES WEEK 01 DAY 1 SCOT ADAMS Question: What is Mathematics? Answer: The study of absolute truth. Question: Why is it so hard to teach and to learn? Answer: One must learn to play a variety of games called
NOTES WEEK 01 DAY 1 SCOT ADAMS Question: What is Mathematics? Answer: The study of absolute truth. Question: Why is it so hard to teach and to learn? Answer: One must learn to play a variety of games called
Lecture 2: Period Three Implies Chaos
 Dynamical Systems Instructor: Padraic Bartlett Lecture 2: Period Three Implies Chaos Week 3 Mathcamp 2014 We ended our last class by proving the following result (whose name I found while doing some research
Dynamical Systems Instructor: Padraic Bartlett Lecture 2: Period Three Implies Chaos Week 3 Mathcamp 2014 We ended our last class by proving the following result (whose name I found while doing some research
DS-GA 1002: PREREQUISITES REVIEW SOLUTIONS VLADIMIR KOBZAR
 DS-GA 2: PEEQUISIES EVIEW SOLUIONS VLADIMI KOBZA he following is a selection of questions (drawn from Mr. Bernstein s notes) for reviewing the prerequisites for DS-GA 2. Questions from Ch, 8, 9 and 2 of
DS-GA 2: PEEQUISIES EVIEW SOLUIONS VLADIMI KOBZA he following is a selection of questions (drawn from Mr. Bernstein s notes) for reviewing the prerequisites for DS-GA 2. Questions from Ch, 8, 9 and 2 of
NOTES WEEK 15 DAY 2 SCOT ADAMS
 NOTES WEEK 15 DAY 2 SCOT ADAMS We will need the Fà di Bruno result, proved erlier. It sttes: Let X nd Y nd Z be finite dimensionl vector spces, let f : X Y nd g : Y Z. Let p P X nd let k P N 0. Assume
NOTES WEEK 15 DAY 2 SCOT ADAMS We will need the Fà di Bruno result, proved erlier. It sttes: Let X nd Y nd Z be finite dimensionl vector spces, let f : X Y nd g : Y Z. Let p P X nd let k P N 0. Assume
MTH132 Exam 2 Solutions Covers: Page Total. Max
 Name: PID: A Section #: Instructor: Page 3 4 5 6 7 8 Total Score Max 30 18 4 14 150 Instructions 1. You will be given exactly 90 minutes for this exam.. No calculators, phones, or any electronic devices.
Name: PID: A Section #: Instructor: Page 3 4 5 6 7 8 Total Score Max 30 18 4 14 150 Instructions 1. You will be given exactly 90 minutes for this exam.. No calculators, phones, or any electronic devices.
NOTES WEEK 04 DAY 1 SCOT ADAMS
 NOTES WEEK 0 DAY 1 SCOT ADAMS DEFINITION 01 Let m, n P N, B P BpR m, R n q Let e 1,, e m be the standard basis of R m Let f 1,, f n be the standard basis of R n Then we define rbs P R nˆm by rbs ji Bpe
NOTES WEEK 0 DAY 1 SCOT ADAMS DEFINITION 01 Let m, n P N, B P BpR m, R n q Let e 1,, e m be the standard basis of R m Let f 1,, f n be the standard basis of R n Then we define rbs P R nˆm by rbs ji Bpe
Mathematische Methoden der Unsicherheitsquantifizierung
 Mathematische Methoden der Unsicherheitsquantifizierung Oliver Ernst Professur Numerische Mathematik Sommersemester 2014 Contents 1 Introduction 1.1 What is Uncertainty Quantification? 1.2 A Case Study:
Mathematische Methoden der Unsicherheitsquantifizierung Oliver Ernst Professur Numerische Mathematik Sommersemester 2014 Contents 1 Introduction 1.1 What is Uncertainty Quantification? 1.2 A Case Study:
NONLINEAR EVOLUTION EQUATIONS SHORT NOTES WEEK #1
 NONLNEA EVOLUTON EQUATONS SHOT NOTES WEEK #. Free Schrödinger Equation Let Bx 2 `...`Bx 2 n denote the Laplacian on d with d ě. The initial-value problem for the free Schrödinger equation (in d space dimensions)
NONLNEA EVOLUTON EQUATONS SHOT NOTES WEEK #. Free Schrödinger Equation Let Bx 2 `...`Bx 2 n denote the Laplacian on d with d ě. The initial-value problem for the free Schrödinger equation (in d space dimensions)
Variational inequality formulation of chance-constrained games
 Variational inequality formulation of chance-constrained games Joint work with Vikas Singh from IIT Delhi Université Paris Sud XI Computational Management Science Conference Bergamo, Italy May, 2017 Outline
Variational inequality formulation of chance-constrained games Joint work with Vikas Singh from IIT Delhi Université Paris Sud XI Computational Management Science Conference Bergamo, Italy May, 2017 Outline
NOTES ON SOME EXERCISES OF LECTURE 5, MODULE 2
 NOTES ON SOME EXERCISES OF LECTURE 5, MODULE 2 MARCO VITTURI Contents 1. Solution to exercise 5-2 1 2. Solution to exercise 5-3 2 3. Solution to exercise 5-7 4 4. Solution to exercise 5-8 6 5. Solution
NOTES ON SOME EXERCISES OF LECTURE 5, MODULE 2 MARCO VITTURI Contents 1. Solution to exercise 5-2 1 2. Solution to exercise 5-3 2 3. Solution to exercise 5-7 4 4. Solution to exercise 5-8 6 5. Solution
Erdinç Dündar, Celal Çakan
 DEMONSTRATIO MATHEMATICA Vol. XLVII No 3 2014 Erdinç Dündar, Celal Çakan ROUGH I-CONVERGENCE Abstract. In this work, using the concept of I-convergence and using the concept of rough convergence, we introduced
DEMONSTRATIO MATHEMATICA Vol. XLVII No 3 2014 Erdinç Dündar, Celal Çakan ROUGH I-CONVERGENCE Abstract. In this work, using the concept of I-convergence and using the concept of rough convergence, we introduced
MATH 360 Final Exam Thursday, December 14, a n 2. a n 1 1
 MATH 36 Final Exam Thursday, December 4, 27 Name. The sequence ta n u is defined by a and a n (a) Prove that lim a n exists by showing that ta n u is bounded and monotonic and invoking an appropriate result.
MATH 36 Final Exam Thursday, December 4, 27 Name. The sequence ta n u is defined by a and a n (a) Prove that lim a n exists by showing that ta n u is bounded and monotonic and invoking an appropriate result.
Lecture 16 Methods for System of Linear Equations (Linear Systems) Songting Luo. Department of Mathematics Iowa State University
 Lecture 16 Methods for System of Linear Equations (Linear Systems) Songting Luo Department of Mathematics Iowa State University MATH 481 Numerical Methods for Differential Equations Songting Luo ( Department
Lecture 16 Methods for System of Linear Equations (Linear Systems) Songting Luo Department of Mathematics Iowa State University MATH 481 Numerical Methods for Differential Equations Songting Luo ( Department
MATH 360 Exam 2 Wednesday, November 8, 2017.» b
 MATH 36 Exam Wedesday, November 8, 7 Name. Let f : ra, bs Ñ R be a cotiuous fuctio, ad suppose that for every cotiuous fuctio g : ra, bs Ñ R, Prove that fpxq for all x P ra, bs.» b a fpxqgpxq dx. We ca,
MATH 36 Exam Wedesday, November 8, 7 Name. Let f : ra, bs Ñ R be a cotiuous fuctio, ad suppose that for every cotiuous fuctio g : ra, bs Ñ R, Prove that fpxq for all x P ra, bs.» b a fpxqgpxq dx. We ca,
Eco 610 Mathematical Economics I Notes M. Jerison 8/24/14
 Eco 610 Mathematical Economics I Notes M. Jerison 8/24/14 1. Introduction Economists analyze qualitative relations (e.g., who is whose boss, or which ownership pattern is more efficient) and quantitative
Eco 610 Mathematical Economics I Notes M. Jerison 8/24/14 1. Introduction Economists analyze qualitative relations (e.g., who is whose boss, or which ownership pattern is more efficient) and quantitative
Mathematical Finance
 ETH Zürich, HS 2017 Prof. Josef Teichmann Matti Kiiski Mathematical Finance Solution sheet 14 Solution 14.1 Denote by Z pz t q tpr0,t s the density process process of Q with respect to P. (a) The second
ETH Zürich, HS 2017 Prof. Josef Teichmann Matti Kiiski Mathematical Finance Solution sheet 14 Solution 14.1 Denote by Z pz t q tpr0,t s the density process process of Q with respect to P. (a) The second
Tempered Distributions
 Tempered Distributions Lionel Fiske and Cairn Overturf May 9, 26 In the classical study of partial differential equations one requires a solution to be differentiable. While intuitively this requirement
Tempered Distributions Lionel Fiske and Cairn Overturf May 9, 26 In the classical study of partial differential equations one requires a solution to be differentiable. While intuitively this requirement
Definition 6.1. A metric space (X, d) is complete if every Cauchy sequence tends to a limit in X.
 Chapter 6 Completeness Lecture 18 Recall from Definition 2.22 that a Cauchy sequence in (X, d) is a sequence whose terms get closer and closer together, without any limit being specified. In the Euclidean
Chapter 6 Completeness Lecture 18 Recall from Definition 2.22 that a Cauchy sequence in (X, d) is a sequence whose terms get closer and closer together, without any limit being specified. In the Euclidean
MAT 128A - Practice Midterm Exam
 MAT 8A - Practice Midterm Exam Karry Wong October 3, 08 Problem (True or False) Given that f : r, s Ñ R is a continuous function, and that ta n u are its Chebyshev coefficients. Also, for N P N, p N pxq
MAT 8A - Practice Midterm Exam Karry Wong October 3, 08 Problem (True or False) Given that f : r, s Ñ R is a continuous function, and that ta n u are its Chebyshev coefficients. Also, for N P N, p N pxq
Existence of weak adiabatic limit in almost all models of perturbative QFT
 Existence of weak adiabatic limit in almost all models of perturbative QFT Paweł Duch Jagiellonian University, Cracow, Poland LQP 40 Foundations and Constructive Aspects of Quantum Field Theory, 23.06.2017
Existence of weak adiabatic limit in almost all models of perturbative QFT Paweł Duch Jagiellonian University, Cracow, Poland LQP 40 Foundations and Constructive Aspects of Quantum Field Theory, 23.06.2017
Local behaviour of Galois representations
 Local behaviour of Galois representations Devika Sharma Weizmann Institute of Science, Israel 23rd June, 2017 Devika Sharma (Weizmann) 23rd June, 2017 1 / 14 The question Let p be a prime. Let f ř 8 ně1
Local behaviour of Galois representations Devika Sharma Weizmann Institute of Science, Israel 23rd June, 2017 Devika Sharma (Weizmann) 23rd June, 2017 1 / 14 The question Let p be a prime. Let f ř 8 ně1
Approximation in the Zygmund Class
 Approximation in the Zygmund Class Odí Soler i Gibert Joint work with Artur Nicolau Universitat Autònoma de Barcelona New Developments in Complex Analysis and Function Theory, 02 July 2018 Approximation
Approximation in the Zygmund Class Odí Soler i Gibert Joint work with Artur Nicolau Universitat Autònoma de Barcelona New Developments in Complex Analysis and Function Theory, 02 July 2018 Approximation
Electronic Companion Dynamic Pricing of Perishable Assets under Competition
 1 Electronic Companion Dynamic Pricing of Perishable Assets under Competition Guillermo Gallego IEOR Department, Columbia University, New York, NY 10027 gmg2@columbia.edu Ming Hu Rotman School of Management,
1 Electronic Companion Dynamic Pricing of Perishable Assets under Competition Guillermo Gallego IEOR Department, Columbia University, New York, NY 10027 gmg2@columbia.edu Ming Hu Rotman School of Management,
PRINCIPLES OF ANALYSIS - LECTURE NOTES
 PRINCIPLES OF ANALYSIS - LECTURE NOTES PETER A. PERRY 1. Constructions of Z, Q, R Beginning with the natural numbers N t1, 2, 3,...u we can use set theory to construct, successively, Z, Q, and R. We ll
PRINCIPLES OF ANALYSIS - LECTURE NOTES PETER A. PERRY 1. Constructions of Z, Q, R Beginning with the natural numbers N t1, 2, 3,...u we can use set theory to construct, successively, Z, Q, and R. We ll
The Kpπ,1q-property for marked curves over finite fields
 The Kpπ,1q-property for marked curves over finite fields Philippe Lebacque and Alexander Schmidt arxiv:1401.1979v2 [math.nt] 24 Mar 2015 Abstract We investigate the Kpπ,1q-property for p of smooth, marked
The Kpπ,1q-property for marked curves over finite fields Philippe Lebacque and Alexander Schmidt arxiv:1401.1979v2 [math.nt] 24 Mar 2015 Abstract We investigate the Kpπ,1q-property for p of smooth, marked
q-de Rham cohomology via Λ-rings
 q-de Rham cohomology via Λ-rings J.P.Pridham arxiv:1608.07142 1 / 21 q-analogues (Gauss) rns q : qn 1 q 1 1 q... qn 1 rns q! : rns q... r2s q r1s q, ¹ n 1 i 0 n 1 ¹ i 0 p1 p1 n k q : rns q! rn ksq!rksq!
q-de Rham cohomology via Λ-rings J.P.Pridham arxiv:1608.07142 1 / 21 q-analogues (Gauss) rns q : qn 1 q 1 1 q... qn 1 rns q! : rns q... r2s q r1s q, ¹ n 1 i 0 n 1 ¹ i 0 p1 p1 n k q : rns q! rn ksq!rksq!
BOUNDS FOR HIGHER TOPOLOGICAL COMPLEXITY OF REAL PROJECTIVE SPACE IMPLIED BY BP
 BOUNDS FOR HIGHER TOPOLOGICAL COMPLEXITY OF REAL PROJECTIVE SPACE IMPLIED BY BP DONALD M. DAVIS Abstract. We use Brown-Peterson cohomology to obtain lower bounds for the higher topological complexity,
BOUNDS FOR HIGHER TOPOLOGICAL COMPLEXITY OF REAL PROJECTIVE SPACE IMPLIED BY BP DONALD M. DAVIS Abstract. We use Brown-Peterson cohomology to obtain lower bounds for the higher topological complexity,
PALINDROMIC WIDTH OF WREATH PRODUCTS, METABELIAN GROUPS, AND MAX-N SOLVABLE GROUPS
 PALINDROMIC WIDTH OF WREATH PRODUCTS, METABELIAN GROUPS, AND MAX-N SOLVABLE GROUPS T. R. RILEY AND A. W. SALE Abstract. A group has finite palindromic width if there exists n such that every element can
PALINDROMIC WIDTH OF WREATH PRODUCTS, METABELIAN GROUPS, AND MAX-N SOLVABLE GROUPS T. R. RILEY AND A. W. SALE Abstract. A group has finite palindromic width if there exists n such that every element can
Draft. Chapter 2 Approximation and Interpolation. MATH 561 Numerical Analysis. Songting Luo. Department of Mathematics Iowa State University
 Chapter 2 Approximation and Interpolation Songting Luo Department of Mathematics Iowa State University MATH 561 Numerical Analysis Songting Luo ( Department of Mathematics Iowa State University[0.5in]
Chapter 2 Approximation and Interpolation Songting Luo Department of Mathematics Iowa State University MATH 561 Numerical Analysis Songting Luo ( Department of Mathematics Iowa State University[0.5in]
Lecture 19 - Covariance, Conditioning
 THEORY OF PROBABILITY VLADIMIR KOBZAR Review. Lecture 9 - Covariance, Conditioning Proposition. (Ross, 6.3.2) If X,..., X n are independent normal RVs with respective parameters µ i, σi 2 for i,..., n,
THEORY OF PROBABILITY VLADIMIR KOBZAR Review. Lecture 9 - Covariance, Conditioning Proposition. (Ross, 6.3.2) If X,..., X n are independent normal RVs with respective parameters µ i, σi 2 for i,..., n,
LECTURE 16: UNITARY REPRESENTATIONS LECTURE BY SHEELA DEVADAS STANFORD NUMBER THEORY LEARNING SEMINAR FEBRUARY 14, 2018 NOTES BY DAN DORE
 LECTURE 16: UNITARY REPRESENTATIONS LECTURE BY SHEELA DEVADAS STANFORD NUMBER THEORY LEARNING SEMINAR FEBRUARY 14, 2018 NOTES BY DAN DORE Let F be a local field with valuation ring O F, and G F the group
LECTURE 16: UNITARY REPRESENTATIONS LECTURE BY SHEELA DEVADAS STANFORD NUMBER THEORY LEARNING SEMINAR FEBRUARY 14, 2018 NOTES BY DAN DORE Let F be a local field with valuation ring O F, and G F the group
Probability Generating Functions
 Probability Generating Functions Andreas Klappenecker Texas A&M University 2018 by Andreas Klappenecker. All rights reserved. 1 / 27 Probability Generating Functions Definition Let X be a discrete random
Probability Generating Functions Andreas Klappenecker Texas A&M University 2018 by Andreas Klappenecker. All rights reserved. 1 / 27 Probability Generating Functions Definition Let X be a discrete random
Introduction to Numerical Analysis
 Introduction to Numerical Analysis Lecture Notes for SI 507 Authors: S. Baskar and S. Sivaji Ganesh Department of Mathematics Indian Institute of Technology Bombay Powai, Mumbai 400 076. Contents 1 Mathematical
Introduction to Numerical Analysis Lecture Notes for SI 507 Authors: S. Baskar and S. Sivaji Ganesh Department of Mathematics Indian Institute of Technology Bombay Powai, Mumbai 400 076. Contents 1 Mathematical
Valuations on Sobolev Spaces
 Valuations on Sobolev Spaces Monika Ludwig Abstract All affinely covariant convex-body-valued valuations on the Sobolev space W 1,1 pr n q are completely classified. It is shown that there is a unique
Valuations on Sobolev Spaces Monika Ludwig Abstract All affinely covariant convex-body-valued valuations on the Sobolev space W 1,1 pr n q are completely classified. It is shown that there is a unique
Dynamic Asymptotic Dimension: relation to dynamics, topology, coarse geometry, and C -algebras
 Dynamic Asymptotic Dimension: relation to dynamics, topology, coarse geometry, and C -algebras Erik Guentner, Rufus Willett, and Guoliang Yu October 23, 2015 Abstract We introduce dynamic asymptotic dimension,
Dynamic Asymptotic Dimension: relation to dynamics, topology, coarse geometry, and C -algebras Erik Guentner, Rufus Willett, and Guoliang Yu October 23, 2015 Abstract We introduce dynamic asymptotic dimension,
T i t l e o f t h e w o r k : L a M a r e a Y o k o h a m a. A r t i s t : M a r i a n o P e n s o t t i ( P l a y w r i g h t, D i r e c t o r )
 v e r. E N G O u t l i n e T i t l e o f t h e w o r k : L a M a r e a Y o k o h a m a A r t i s t : M a r i a n o P e n s o t t i ( P l a y w r i g h t, D i r e c t o r ) C o n t e n t s : T h i s w o
v e r. E N G O u t l i n e T i t l e o f t h e w o r k : L a M a r e a Y o k o h a m a A r t i s t : M a r i a n o P e n s o t t i ( P l a y w r i g h t, D i r e c t o r ) C o n t e n t s : T h i s w o
Intrinsic Four-Point Properties
 Intrinsic Four-Point Properties Edward Andalafte, Raymond Freese, Brody Dylan Johnson and Rebecca Lelko Abstract. Many characterizations of euclidean spaces (real inner product spaces) among metric spaces
Intrinsic Four-Point Properties Edward Andalafte, Raymond Freese, Brody Dylan Johnson and Rebecca Lelko Abstract. Many characterizations of euclidean spaces (real inner product spaces) among metric spaces
J. M. ALMIRA, L. SZÉKELYHIDI
 MONTEL TYPE THEOREMS FOR EXPONENTIAL POLYNOMIALS arxiv:1408.2692v1 [math.ca] 12 Aug 2014 J. M. ALMIRA, L. SZÉKELYHIDI Abstract. In this paper we characterize local exponential monomials and polynomials
MONTEL TYPE THEOREMS FOR EXPONENTIAL POLYNOMIALS arxiv:1408.2692v1 [math.ca] 12 Aug 2014 J. M. ALMIRA, L. SZÉKELYHIDI Abstract. In this paper we characterize local exponential monomials and polynomials
Some Concepts of Uniform Exponential Dichotomy for Skew-Evolution Semiflows in Banach Spaces
 Theory and Applications of Mathematics & Computer Science 6 (1) (2016) 69 76 Some Concepts of Uniform Exponential Dichotomy for Skew-Evolution Semiflows in Banach Spaces Diana Borlea a, a Department of
Theory and Applications of Mathematics & Computer Science 6 (1) (2016) 69 76 Some Concepts of Uniform Exponential Dichotomy for Skew-Evolution Semiflows in Banach Spaces Diana Borlea a, a Department of
APPROXIMATE HOMOMORPHISMS BETWEEN THE BOOLEAN CUBE AND GROUPS OF PRIME ORDER
 APPROXIMATE HOMOMORPHISMS BETWEEN THE BOOLEAN CUBE AND GROUPS OF PRIME ORDER TOM SANDERS The purpose of this note is to highlight a question raised by Shachar Lovett [Lov], and to offer some motivation
APPROXIMATE HOMOMORPHISMS BETWEEN THE BOOLEAN CUBE AND GROUPS OF PRIME ORDER TOM SANDERS The purpose of this note is to highlight a question raised by Shachar Lovett [Lov], and to offer some motivation
For example, p12q p2x 1 x 2 ` 5x 2 x 2 3 q 2x 2 x 1 ` 5x 1 x 2 3. (a) Let p 12x 5 1x 7 2x 4 18x 6 2x 3 ` 11x 1 x 2 x 3 x 4,
 SOLUTIONS Math A4900 Homework 5 10/4/2017 1. (DF 2.2.12(a)-(d)+) Symmetric polynomials. The group S n acts on the set tx 1, x 2,..., x n u by σ x i x σpiq. That action extends to a function S n ˆ A Ñ A,
SOLUTIONS Math A4900 Homework 5 10/4/2017 1. (DF 2.2.12(a)-(d)+) Symmetric polynomials. The group S n acts on the set tx 1, x 2,..., x n u by σ x i x σpiq. That action extends to a function S n ˆ A Ñ A,
Random Variables. Andreas Klappenecker. Texas A&M University
 Random Variables Andreas Klappenecker Texas A&M University 1 / 29 What is a Random Variable? Random variables are functions that associate a numerical value to each outcome of an experiment. For instance,
Random Variables Andreas Klappenecker Texas A&M University 1 / 29 What is a Random Variable? Random variables are functions that associate a numerical value to each outcome of an experiment. For instance,
Short Notes in Mathematics Fundamental concepts every student of Mathematics should know
 Short Notes in Mathematics Fundamental concepts every student of Mathematics should know Markus J. Pflaum October 9, 2018 Contents Titlepage 1 1 Foundations 2 Set theory........................................
Short Notes in Mathematics Fundamental concepts every student of Mathematics should know Markus J. Pflaum October 9, 2018 Contents Titlepage 1 1 Foundations 2 Set theory........................................
Introduction to computability Tutorial 7
 Introduction to computability Tutorial 7 Context free languages and Turing machines November 6 th 2014 Context-free languages 1. Show that the following languages are not context-free: a) L ta i b j a
Introduction to computability Tutorial 7 Context free languages and Turing machines November 6 th 2014 Context-free languages 1. Show that the following languages are not context-free: a) L ta i b j a
8 Further theory of function limits and continuity
 8 Further theory of function limits and continuity 8.1 Algebra of limits and sandwich theorem for real-valued function limits The following results give versions of the algebra of limits and sandwich theorem
8 Further theory of function limits and continuity 8.1 Algebra of limits and sandwich theorem for real-valued function limits The following results give versions of the algebra of limits and sandwich theorem
Minimizing the Number of Function Evaluations to Estimate Sobol Indices Using Quasi-Monte Carlo
 Minimizing the Number of Function Evaluations to Estimate Sobol Indices Using Quasi-Monte Carlo Lluís Antoni Jiménez Rugama Joint work with: Fred J Hickernell (IIT), Clémentine Prieur (Univ Grenoble),
Minimizing the Number of Function Evaluations to Estimate Sobol Indices Using Quasi-Monte Carlo Lluís Antoni Jiménez Rugama Joint work with: Fred J Hickernell (IIT), Clémentine Prieur (Univ Grenoble),
1. Examples. We did most of the following in class in passing. Now compile all that data.
 SOLUTIONS Math A4900 Homework 12 11/22/2017 1. Examples. We did most of the following in class in passing. Now compile all that data. (a) Favorite examples: Let R tr, Z, Z{3Z, Z{6Z, M 2 prq, Rrxs, Zrxs,
SOLUTIONS Math A4900 Homework 12 11/22/2017 1. Examples. We did most of the following in class in passing. Now compile all that data. (a) Favorite examples: Let R tr, Z, Z{3Z, Z{6Z, M 2 prq, Rrxs, Zrxs,
Extensive Form Abstract Economies and Generalized Perfect Recall
 Extensive Form Abstract Economies and Generalized Perfect Recall Nicholas Butler Princeton University July 30, 2015 Nicholas Butler (Princeton) EFAE and Generalized Perfect Recall July 30, 2015 1 / 1 Motivation
Extensive Form Abstract Economies and Generalized Perfect Recall Nicholas Butler Princeton University July 30, 2015 Nicholas Butler (Princeton) EFAE and Generalized Perfect Recall July 30, 2015 1 / 1 Motivation
NOTES FOR BEILINSON-DRINFELD SEMINAR - EVEN SHORTER VERSION. Contents 1. Overview Steenrod s construction
 NOTES FOR BEILINSON-DRINFELD SEMINAR - EVEN SHORTER VERSION GUS LONERGAN Abstract. We use Steenrod s construction to prove that the quantum Coulomb branch is a Frobenius-constant quantization. Contents
NOTES FOR BEILINSON-DRINFELD SEMINAR - EVEN SHORTER VERSION GUS LONERGAN Abstract. We use Steenrod s construction to prove that the quantum Coulomb branch is a Frobenius-constant quantization. Contents
SOLUTIONS Math B4900 Homework 9 4/18/2018
 SOLUTIONS Math B4900 Homework 9 4/18/2018 1. Show that if G is a finite group and F is a field, then any simple F G-modules is finitedimensional. [This is not a consequence of Maschke s theorem; it s just
SOLUTIONS Math B4900 Homework 9 4/18/2018 1. Show that if G is a finite group and F is a field, then any simple F G-modules is finitedimensional. [This is not a consequence of Maschke s theorem; it s just
b. Induction (LfP 50 3)
 b. Induction (LfP 50 3) b.i. The principle of mathematical induction The principle of mathematical induction is a property of natural numbers. b.i.1. Natural numbers The natural numbers are the non-negative
b. Induction (LfP 50 3) b.i. The principle of mathematical induction The principle of mathematical induction is a property of natural numbers. b.i.1. Natural numbers The natural numbers are the non-negative
PALINDROMIC WIDTH OF WREATH PRODUCTS, METABELIAN GROUPS, AND MAX-N SOLVABLE GROUPS
 PALINDROMIC WIDTH OF WREATH PRODUCTS, METABELIAN GROUPS, AND MAX-N SOLVABLE GROUPS T. R. RILEY AND A. W. SALE Abstract. A group has finite palindromic width if there exists n such that every element can
PALINDROMIC WIDTH OF WREATH PRODUCTS, METABELIAN GROUPS, AND MAX-N SOLVABLE GROUPS T. R. RILEY AND A. W. SALE Abstract. A group has finite palindromic width if there exists n such that every element can
ADVANCE TOPICS IN ANALYSIS - REAL. 8 September September 2011
 ADVANCE TOPICS IN ANALYSIS - REAL NOTES COMPILED BY KATO LA Introductions 8 September 011 15 September 011 Nested Interval Theorem: If A 1 ra 1, b 1 s, A ra, b s,, A n ra n, b n s, and A 1 Ě A Ě Ě A n
ADVANCE TOPICS IN ANALYSIS - REAL NOTES COMPILED BY KATO LA Introductions 8 September 011 15 September 011 Nested Interval Theorem: If A 1 ra 1, b 1 s, A ra, b s,, A n ra n, b n s, and A 1 Ě A Ě Ě A n
Mariusz Jurkiewicz, Bogdan Przeradzki EXISTENCE OF SOLUTIONS FOR HIGHER ORDER BVP WITH PARAMETERS VIA CRITICAL POINT THEORY
 DEMONSTRATIO MATHEMATICA Vol. XLVIII No 1 215 Mariusz Jurkiewicz, Bogdan Przeradzki EXISTENCE OF SOLUTIONS FOR HIGHER ORDER BVP WITH PARAMETERS VIA CRITICAL POINT THEORY Communicated by E. Zadrzyńska Abstract.
DEMONSTRATIO MATHEMATICA Vol. XLVIII No 1 215 Mariusz Jurkiewicz, Bogdan Przeradzki EXISTENCE OF SOLUTIONS FOR HIGHER ORDER BVP WITH PARAMETERS VIA CRITICAL POINT THEORY Communicated by E. Zadrzyńska Abstract.
MATH 387 ASSIGNMENT 2
 MATH 387 ASSIGMET 2 SAMPLE SOLUTIOS BY IBRAHIM AL BALUSHI Problem 4 A matrix A ra ik s P R nˆn is called symmetric if a ik a ki for all i, k, and is called positive definite if x T Ax ě 0 for all x P R
MATH 387 ASSIGMET 2 SAMPLE SOLUTIOS BY IBRAHIM AL BALUSHI Problem 4 A matrix A ra ik s P R nˆn is called symmetric if a ik a ki for all i, k, and is called positive definite if x T Ax ě 0 for all x P R
MATH 551 HOMEWORK II SOLUTIONS. Graded problems: 1,3,4,6,7. Solutions to ungraded problems abridged. Let D d
 MATH 551 HOMEWORK II SOLUTIONS Graded problems: 1,3,4,6,7. Solutions to ungraded problems abridged. Let D d dx and xf, gy ş b fpxqgpxqdx. Integration by parts is then expressed as a xdf, gy fg b a xf,
MATH 551 HOMEWORK II SOLUTIONS Graded problems: 1,3,4,6,7. Solutions to ungraded problems abridged. Let D d dx and xf, gy ş b fpxqgpxqdx. Integration by parts is then expressed as a xdf, gy fg b a xf,
Interpolation Theory and Applications to the Boundedness of Operators in Analysis
 Master Thesis Master Advanced Mathematics Interpolation Theory and Applications to the Boundedness of Operators in Analysis Author: Jordi Lendínez Capdevila Supervisor: Department: Dr F Javier Soria de
Master Thesis Master Advanced Mathematics Interpolation Theory and Applications to the Boundedness of Operators in Analysis Author: Jordi Lendínez Capdevila Supervisor: Department: Dr F Javier Soria de
Selected Math 553 Homework Solutions
 Selected Math 553 Homework Solutions HW6, 1. Let α and β be rational numbers, with α 1/2, and let m > 0 be an integer such that α 2 mβ 2 = 1 δ where 0 δ < 1. Set ǫ:= 1 if α 0 and 1 if α < 0. Show that
Selected Math 553 Homework Solutions HW6, 1. Let α and β be rational numbers, with α 1/2, and let m > 0 be an integer such that α 2 mβ 2 = 1 δ where 0 δ < 1. Set ǫ:= 1 if α 0 and 1 if α < 0. Show that
Entropy and Ergodic Theory Notes 21: The entropy rate of a stationary process
 Entropy and Ergodic Theory Notes 21: The entropy rate of a stationary process 1 Sources with memory In information theory, a stationary stochastic processes pξ n q npz taking values in some finite alphabet
Entropy and Ergodic Theory Notes 21: The entropy rate of a stationary process 1 Sources with memory In information theory, a stationary stochastic processes pξ n q npz taking values in some finite alphabet
Fourier transforms. Up to now, we ve been expressing functions on finite intervals (usually the interval 0 x L or L x L) as Fourier series: a n cos L
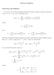 ourier trnsforms Motivtion nd definition Up to now, we ve been expressing functions on finite intervls (usully the intervl 0 x or x ) s ourier series: fpxq 0 8 nπx n cos n b n sin nπx where 0» fpxq dx
ourier trnsforms Motivtion nd definition Up to now, we ve been expressing functions on finite intervls (usully the intervl 0 x or x ) s ourier series: fpxq 0 8 nπx n cos n b n sin nπx where 0» fpxq dx
arxiv: v1 [math.ca] 4 Apr 2017
![arxiv: v1 [math.ca] 4 Apr 2017 arxiv: v1 [math.ca] 4 Apr 2017](/thumbs/88/115044967.jpg) ON LOCALIZATION OF SCHRÖDINGER MEANS PER SJÖLIN Abstract. Localization properties for Schrödinger means are studied in dimension higher than one. arxiv:704.00927v [math.ca] 4 Apr 207. Introduction Let
ON LOCALIZATION OF SCHRÖDINGER MEANS PER SJÖLIN Abstract. Localization properties for Schrödinger means are studied in dimension higher than one. arxiv:704.00927v [math.ca] 4 Apr 207. Introduction Let
FURSTENBERG S THEOREM ON PRODUCTS OF I.I.D. 2 ˆ 2 MATRICES
 FURSTENBERG S THEOREM ON PRODUCTS OF I.I.D. 2 ˆ 2 MATRICES JAIRO BOCHI Abstract. This is a revised version of some notes written ą 0 years ago. I thank Anthony Quas for pointing to a gap in the previous
FURSTENBERG S THEOREM ON PRODUCTS OF I.I.D. 2 ˆ 2 MATRICES JAIRO BOCHI Abstract. This is a revised version of some notes written ą 0 years ago. I thank Anthony Quas for pointing to a gap in the previous
Sobolev-Type Extremal Polynomials
 Soolev-Type Extremal Polyomials (case of the sigular measures) Ael Díaz-Gozález Joi with Héctor Pijeira-Carera ULL 2016 Soolev-Type Extremal Polyomials adiazgo@math.uc3m.es 1 / 18 Moic extremal polyomials
Soolev-Type Extremal Polyomials (case of the sigular measures) Ael Díaz-Gozález Joi with Héctor Pijeira-Carera ULL 2016 Soolev-Type Extremal Polyomials adiazgo@math.uc3m.es 1 / 18 Moic extremal polyomials
STK-IN4300 Statistical Learning Methods in Data Science
 Outline of the lecture STK-IN4300 Statistical Learning Methods in Data Science Riccardo De Bin debin@math.uio.no AdaBoost Introduction algorithm Statistical Boosting Boosting as a forward stagewise additive
Outline of the lecture STK-IN4300 Statistical Learning Methods in Data Science Riccardo De Bin debin@math.uio.no AdaBoost Introduction algorithm Statistical Boosting Boosting as a forward stagewise additive
An Introduction to Analysis of Boolean functions
 An Introduction to Analysis of Boolean functions Mohammad Bavarian Massachusetts Institute of Technology 1 Introduction The focus of much of harmonic analysis is the study of functions, and operators on
An Introduction to Analysis of Boolean functions Mohammad Bavarian Massachusetts Institute of Technology 1 Introduction The focus of much of harmonic analysis is the study of functions, and operators on
Automata theory and its applications
 Automata theory and its applications Lecture 12-14: Automata over ranked finite trees Zhilin Wu State Key Laboratory of Computer Science, Institute of Software, Chinese Academy of Sciences January 16,
Automata theory and its applications Lecture 12-14: Automata over ranked finite trees Zhilin Wu State Key Laboratory of Computer Science, Institute of Software, Chinese Academy of Sciences January 16,
arxiv: v2 [cs.lg] 31 Oct 2018
![arxiv: v2 [cs.lg] 31 Oct 2018 arxiv: v2 [cs.lg] 31 Oct 2018](/thumbs/96/127998133.jpg) SOME NEGATIVE RESULTS FOR SINGLE LAYER AND MULTILAYER FEEDFORWARD NEURAL NETWORKS arxiv:1810.10032v2 [cs.lg] 31 Oct 2018 J. M. ALMIRA, P. E. LOPEZ-DE-TERUEL, D. J. ROMERO-LÓPEZ Abstract. We prove, for
SOME NEGATIVE RESULTS FOR SINGLE LAYER AND MULTILAYER FEEDFORWARD NEURAL NETWORKS arxiv:1810.10032v2 [cs.lg] 31 Oct 2018 J. M. ALMIRA, P. E. LOPEZ-DE-TERUEL, D. J. ROMERO-LÓPEZ Abstract. We prove, for
ETIKA V PROFESII PSYCHOLÓGA
 P r a ž s k á v y s o k á š k o l a p s y c h o s o c i á l n í c h s t u d i í ETIKA V PROFESII PSYCHOLÓGA N a t á l i a S l o b o d n í k o v á v e d ú c i p r á c e : P h D r. M a r t i n S t r o u
P r a ž s k á v y s o k á š k o l a p s y c h o s o c i á l n í c h s t u d i í ETIKA V PROFESII PSYCHOLÓGA N a t á l i a S l o b o d n í k o v á v e d ú c i p r á c e : P h D r. M a r t i n S t r o u
Warmup Recall, a group H is cyclic if H can be generated by a single element. In other words, there is some element x P H for which Multiplicative
 Warmup Recall, a group H is cyclic if H can be generated by a single element. In other words, there is some element x P H for which Multiplicative notation: H tx l l P Zu xxy, Additive notation: H tlx
Warmup Recall, a group H is cyclic if H can be generated by a single element. In other words, there is some element x P H for which Multiplicative notation: H tx l l P Zu xxy, Additive notation: H tlx
arxiv: v2 [math.ca] 13 May 2015
![arxiv: v2 [math.ca] 13 May 2015 arxiv: v2 [math.ca] 13 May 2015](/thumbs/88/114667751.jpg) ON THE CLOSURE OF TRANSLATION-DILATION INVARIANT LINEAR SPACES OF POLYNOMIALS arxiv:1505.02370v2 [math.ca] 13 May 2015 J. M. ALMIRA AND L. SZÉKELYHIDI Abstract. Assume that a linear space of real polynomials
ON THE CLOSURE OF TRANSLATION-DILATION INVARIANT LINEAR SPACES OF POLYNOMIALS arxiv:1505.02370v2 [math.ca] 13 May 2015 J. M. ALMIRA AND L. SZÉKELYHIDI Abstract. Assume that a linear space of real polynomials
MATH 260 Homework assignment 8 March 21, px 2yq dy. (c) Where C is the part of the line y x, parametrized any way you like.
 MATH 26 Homework assignment 8 March 2, 23. Evaluate the line integral x 2 y dx px 2yq dy (a) Where is the part of the parabola y x 2 from p, q to p, q, parametrized as x t, y t 2 for t. (b) Where is the
MATH 26 Homework assignment 8 March 2, 23. Evaluate the line integral x 2 y dx px 2yq dy (a) Where is the part of the parabola y x 2 from p, q to p, q, parametrized as x t, y t 2 for t. (b) Where is the
CS 173 Lecture 7: Arithmetic (II)
 CS 173 Lecture 7: Arithmetic (II) José Meseguer University of Illinois at Urbana-Champaign 1 The Fundamental Theorem of Arithmetic (Part II) Fundamental Theorem of Arithmetic (Part II). Every natural number
CS 173 Lecture 7: Arithmetic (II) José Meseguer University of Illinois at Urbana-Champaign 1 The Fundamental Theorem of Arithmetic (Part II) Fundamental Theorem of Arithmetic (Part II). Every natural number
Lecture 15: Quadratic approximation and the second variation formula
 Lecture 15: Quadratic approximation and the second variation formula Symmetric ilinear forms and inner products (15.1) The associated self-adjoint operator. Let V e a finite dimensional real vector space
Lecture 15: Quadratic approximation and the second variation formula Symmetric ilinear forms and inner products (15.1) The associated self-adjoint operator. Let V e a finite dimensional real vector space
Expected Utility. Tommaso Denti. February 7, 2015
 Expected Utility Tommaso Denti February 7, 2015 In class some of you asked about the relation between the continuity axiom and the topology on the set of lotteries. The purpose of Herstein and Milnor (1953):
Expected Utility Tommaso Denti February 7, 2015 In class some of you asked about the relation between the continuity axiom and the topology on the set of lotteries. The purpose of Herstein and Milnor (1953):
Entropy and Ergodic Theory Lecture 7: Rate-distortion theory
 Entropy and Ergodic Theory Lecture 7: Rate-distortion theory 1 Coupling source coding to channel coding Let rσ, ps be a memoryless source and let ra, θ, Bs be a DMC. Here are the two coding problems we
Entropy and Ergodic Theory Lecture 7: Rate-distortion theory 1 Coupling source coding to channel coding Let rσ, ps be a memoryless source and let ra, θ, Bs be a DMC. Here are the two coding problems we
Immerse Metric Space Homework
 Immerse Metric Space Homework (Exercises -2). In R n, define d(x, y) = x y +... + x n y n. Show that d is a metric that induces the usual topology. Sketch the basis elements when n = 2. Solution: Steps
Immerse Metric Space Homework (Exercises -2). In R n, define d(x, y) = x y +... + x n y n. Show that d is a metric that induces the usual topology. Sketch the basis elements when n = 2. Solution: Steps
L E C T U R E 2 1 : P R O P E RT I E S O F M AT R I X T R A N S F O R M AT I O N S I I. Wednesday, November 30
 L E C T U R E 2 1 : P R O P E RT I E S O F M AT R I X T R A N S F O R M AT I O N S I I Wednesday, November 30 1 the range of a linear transformation Let s begin by defining the range of a linear transformation.
L E C T U R E 2 1 : P R O P E RT I E S O F M AT R I X T R A N S F O R M AT I O N S I I Wednesday, November 30 1 the range of a linear transformation Let s begin by defining the range of a linear transformation.
Reliable Error Estimation for Quasi-Monte Carlo Methods
 Reliable Error Estimation for Quasi-Monte Carlo Methods Department of Applied Mathematics, Joint work with Fred J. Hickernell July 8, 2014 Outline 1 Motivation Reasons Problem 2 New approach Set-up of
Reliable Error Estimation for Quasi-Monte Carlo Methods Department of Applied Mathematics, Joint work with Fred J. Hickernell July 8, 2014 Outline 1 Motivation Reasons Problem 2 New approach Set-up of
AFFINE AND PROJECTIVE GEOMETRY, E. Rosado & S.L. Rueda CHAPTER II: AFFINE AND EUCLIDEAN GEOMETRY
 CHAPTER II: AFFINE AND EUCLIDEAN GEOMETRY 2. AFFINE TRANSFORMATIONS 2.1 Definition and first properties Definition Let (A, V, φ) and (A, V, φ ) be two real affine spaces. We will say that a map f : A A
CHAPTER II: AFFINE AND EUCLIDEAN GEOMETRY 2. AFFINE TRANSFORMATIONS 2.1 Definition and first properties Definition Let (A, V, φ) and (A, V, φ ) be two real affine spaces. We will say that a map f : A A
. L( )WE WEEKLY JOURNAL.
 ) Y R G V V VV ) V R R F RP : x 2 F VV V Ṅ : V \ \ : P R : G V Y F P 35 RP 8 G V : % \ V X Q V < \ V P R V \ V< R VRG : Y ) P [ < _ & V V 6 :: V } V x V V & x 2 ) 3 RR & 8 \ R < Y q GR : XR < R V R % 7
) Y R G V V VV ) V R R F RP : x 2 F VV V Ṅ : V \ \ : P R : G V Y F P 35 RP 8 G V : % \ V X Q V < \ V P R V \ V< R VRG : Y ) P [ < _ & V V 6 :: V } V x V V & x 2 ) 3 RR & 8 \ R < Y q GR : XR < R V R % 7
Lecture 24 Properties of deals
 Lecture 24 Properties of deals Aside: Representation theory of finite groups Let G be a finite group, and let R C, R, or Q (any commutative ring). Aside: Representation theory of finite groups Let G be
Lecture 24 Properties of deals Aside: Representation theory of finite groups Let G be a finite group, and let R C, R, or Q (any commutative ring). Aside: Representation theory of finite groups Let G be
Entropy and Ergodic Theory Lecture 19: The ergodic theorems
 Entropy and Ergodic Theory Lecture 19: The ergodic theorems 1 Some history: the ergodic hypothesis Ergodic theory takes its name from the ergodic hypothesis. This is an old idea of Boltzmann in statistical
Entropy and Ergodic Theory Lecture 19: The ergodic theorems 1 Some history: the ergodic hypothesis Ergodic theory takes its name from the ergodic hypothesis. This is an old idea of Boltzmann in statistical
MATH 260 Class notes/questions January 10, 2013
 MATH 26 Class notes/questions January, 2 Linear transformations Last semester, you studied vector spaces (linear spaces) their bases, dimension, the ideas of linear dependence and linear independence Now
MATH 26 Class notes/questions January, 2 Linear transformations Last semester, you studied vector spaces (linear spaces) their bases, dimension, the ideas of linear dependence and linear independence Now
Area of left square = Area of right square c 2 + (4 Area of (a, b)-triangle) = a 2 + b 2 + (4 Area of (a, b)-triangle) c 2 = a 2 + b 2.
 Worksheet Proof (of Pythagoras Theorem). The proof can be shown using the two squares in Figure 19.3. To draw the first square begin by drawing a general triangle with sides a and b and then extend these
Worksheet Proof (of Pythagoras Theorem). The proof can be shown using the two squares in Figure 19.3. To draw the first square begin by drawing a general triangle with sides a and b and then extend these
Asymptotic Analysis 1: Limits and Asymptotic Equality
 Asymptotic Analysis 1: Limits and Asymptotic Equality Andreas Klappenecker and Hyunyoung Lee Texas A&M University 1 / 15 Motivation In asymptotic analysis, our goal is to compare a function f pnq with
Asymptotic Analysis 1: Limits and Asymptotic Equality Andreas Klappenecker and Hyunyoung Lee Texas A&M University 1 / 15 Motivation In asymptotic analysis, our goal is to compare a function f pnq with
Baire category theorem and nowhere differentiable continuous functions
 Baire category theorem and nowhere differentiable continuous functions Takako Nemoto JAIST third CORE meeting 26 January 2018 Abstract In constructive mathematics, Baire Category Theorem has at least the
Baire category theorem and nowhere differentiable continuous functions Takako Nemoto JAIST third CORE meeting 26 January 2018 Abstract In constructive mathematics, Baire Category Theorem has at least the
Computational Statistics and Optimisation. Joseph Salmon Télécom Paristech, Institut Mines-Télécom
 Computational Statistics and Optimisation Joseph Salmon http://josephsalmon.eu Télécom Paristech, Institut Mines-Télécom Plan Duality gap and stopping criterion Back to gradient descent analysis Forward-backward
Computational Statistics and Optimisation Joseph Salmon http://josephsalmon.eu Télécom Paristech, Institut Mines-Télécom Plan Duality gap and stopping criterion Back to gradient descent analysis Forward-backward
Parallel Recursion: Powerlists. Greg Plaxton Theory in Programming Practice, Fall 2005 Department of Computer Science University of Texas at Austin
 Parallel Recursion: Powerlists Greg Plaxton Theory in Programming Practice, Fall 2005 Department of Computer Science University of Texas at Austin Overview Definition of a powerlist Basic operations on
Parallel Recursion: Powerlists Greg Plaxton Theory in Programming Practice, Fall 2005 Department of Computer Science University of Texas at Austin Overview Definition of a powerlist Basic operations on
