Homework for MATH 4604 (Advanced Calculus II) Spring 2017
|
|
|
- Elisabeth Howard
- 6 years ago
- Views:
Transcription
1 Homework for MATH 4604 (Advanced Calculus II) Spring 2017 Homework 14: Due on Tuesday 2 May 55. Let m, n P N, A P R mˆn and v P R n. Show: L A pvq 2 ď A 2 v Let n P N and let A P R nˆn. Let I n denote the n ˆ n identity matrix. Assume that I n A 2 ď 1{2. Show that A is invertible. 57. Let m, n P N and let g : R m R n. Assume 0 m P dom rdgs. Assume gp0 m q 0 n. Assume, for all j P t1,..., mu, pb j gqp0 m q 0 n. Show that g P Omnp1q. Homework 13: Due on Tuesday 25 April 50. Let V and W be finite dimensional vector spaces. Show (1) QpV, W q Ď O V W p2q, and (2) rqpv, W qs X rov W p2qs t0 V W u. 51. Let m P N, q P R, v P R m, S P R mˆm sym. Define C P CpR m, Rq and L P LpR m, Rq and Q P QpR m, Rq by Cpxq q and Lpxq px H v V q 11 and Qpxq ppx H Sx V q 11 q{p2!q. Let f : C ` L ` Q P P ď2 pr m, Rq. Let I : t1,..., mu. Show (1) fp0 m q q, P I, pb i fqp0 m q v i and j P I, pb i B j fqp0 m q S ij. 52. Let f : R R and δ ą 0. Let I : p δ, δq. Assume that f 1 is defined on I, i.e., that I Ď dom rf 1 s. Show that there exists c : I Ñ I such that c P Op1q and such that, for all x P I, we have rfpxqs rfp0qs rf 1 pcpxqqsx. 53. Let f : R R, g : R 2 R. P R, fptq gpt, 0q. P R, f 1 ptq pb 1 gqpt, 0q. 54. Let f : R 2 R. Assume 0 2 P dom rd 2 fs. Show p R f P O21p2q. Hint: Show: for all x, y P R, pr f px, yq fpx, yq pfp0 2 qq ` ppb 1 fqp0 2 qqx ` ppb 2 fqp0 2 qqy ` r 1{p2!q s r ppb 1 B 1 fqp0 2 qqx 2 ` 2ppB 1 B 2 fqp0 2 qqxy ` ppb 2 B 2 fqp0 2 qqy 2 s.
2 Then show: at 0 2, 0 p R f B 1 p p R f q B 2 p p R f q B 1 B 1 p p R f q B 1 B 2 p p R f q B 2 B 2 p p R f q. Homework 12: Due on Tuesday 18 April 47. Let m P N and let W be a finite dimensional vector space. Let f : R m W. Let p P R m and let i P t1,..., mu. Show: pb i fqpp ` q B i pfpp ` qq. 48. Let V, W and X be finite dimensional vector spaces and let p P V. Let f : V W, g : V X. Show that D p ppf, gqq pd p f, D p gq. 49. Let m, n P N, let f : R m R n, let k P N 0 and let p P R m. Assume, for all i P t1,..., mu, that B i f is both defined near p and bounded near p. Show both of the following: (1) f T p P O mn p1q and (2) f is continuous at p. Hint: For (1), simply capitalize all the Os appearing in the proof of the corresponding result about O proved during class. For (2), combine (1) with O mn p1q Ď Omn to see that fp T P Omn. Homework 11: Due on Tuesday 11 April 44. Let V, W and X be vector spaces, let f : V W, g : W X and let p P dom rg fs. Show that pg fq T p pg T fppq q pf T p q. Hint: Given v P V. We wish to show: pg fq T p pvq pg T fppq qppf T p qpvqq. To keep the notation from getting messy, I suggest defining q : fppq and w : f T p pvq. Then compare pg fq T p pvq rgpfpp ` vqqs rgpfppqqs with pg T fppq qppf T p qpvqq g T q pwq rgpq ` wqs rgpqqs. 45. Let U and V be finite dimensional vector spaces, let f : U V and let p P dctrfs. Assume dom rfs is a nbd of p in U. Show f T p P OUV. Note: f T p rfpp ` qs rf C p s. Unassigned HW: Let U and V be finite dimensional vector spaces, let f : U V and let p P dlinrfs. Show that fp T P O UV p1q. Note: Paige showed us, in class, how to do the Unassigned HW above.
3 46. Let U, V, W and X be vector spaces, let P BpV, W, Xq and let m, n P N 0. Show: rp m pu, V qs rp n pu, W qs Ď rp m`n pu, Xqs. Hint: Given P P P m pu, V q and Q P P n pu, W q. We wish to show: P Q P P m`n pu, Xq. We wish to show DH P SM m`n pu, Xq such P U, Hpu,..., uq pp Qqpuq. Choose F P SM m pu, V q such P U, F pu,..., uq P puq. Choose G P SM n pu, W q such P U, Gpu,..., uq Qpuq. Define H 0 P M m`n pu,..., U, Xq by H 0 pt 1,..., t m, u 1,..., u n q rf pt 1,..., t m qs rgpu 1,..., u n qs. Let H : SymrH 0 s. Homework 10: Due on Tuesday 4 April 38. Let X be a topological space, let W be a finite dimensional vector space, let φ : X W, let x P X and let } } P N pw q. Show: r lim φ 0 W s ñ r lim }φ} 0 s. x x 39. Let W be a finite dimensional vector space and let ε P ORW p1q. εphq Show that lim hñ0 h 0 ε W, i.e., show that lim 0 W. 0 id R 40. Let V and W be finite dimensional vector spaces, let f : V W and let x P dlinrfs. Show: x P dctrfs, i.e., show: f is continuous at x. Hint: Let L : D x f and let R : fx T L. Then L P LpV, W q and R P OV W p1q. It follows that L and R are both continuous at 0 V. So, since fx T L ` R, we see that fx T is continuous at 0 V. Use this to show that f is continuous at x. 41. Let P N prq be the absolute value function. Show: 0 R dlinr s. 42. Let V be a finite dimensional vector space, let f : V R and let x P dlinrfs. Assume that D x f 0 V R. Show that f does not have a local semi-max at x. That is, show, for any nbd U in V of x, that there exists y P U such that fpyq ą fpxq.
4 Hint: Let U be given, and we seek y. Let L : D x f and let R : f T x L. Then L P LpV, Rq and R P OV Rp1q. Show that you can choose v P V such that Lpvq ą 0. Show that you can choose h ą 0 small enough so that all that of the following works. Let y : x ` hv. Then y P U, and we wish to show: fpyq ą fpxq. We have Rphvq ă h rlpvqs{100. Then f T x phvq h rlpvqs ` rrphvqs ą 99 h rlpvqs { 100 ą 0. Then rfpyqs rfpxqs f T x phvq ą 0, so fpyq ą fpxq, as desired. 43. Let V and W be finite dimensional vector spaces, C P CpV, W q. Let X : LpV, W q. Show DC 0 V X. That is, P V, D u C 0 X. Note: 0 X 0 V W. Homework 9: Due on Tuesday 28 March 34. Let V and W be finite dimensional vector spaces. Prove that P 1 pv, W q Ď O V W p1q. 35. Let V and W be finite dimensional vector spaces. Prove that rp 1 pv, W qs X rov W p1qs t0 V W u. 36. Let f : R R. Assume that f 1 P Op3q and that fp0q 0. Show that f P Op4q. Hint: Using the Choice MVT, show that there exists c P Op1q such that, for all x «0, we have fpxq rf 1 pcpxqqs x. 37. Define f : R Ñ R by fpxq x 3. Show that rd 2 fs 11 f 1 p2q. Homework 8: Due on Tuesday 21 March 31. Let V and W be finite dimensional vector spaces. Let P N pv q, ε : V W, p ą 0. Assume 0 V P dom rεs and εp0 V q 0 W. Show: ˆ ε p ε P OV W ppq q ô P Oˆ p V W. 32. Let V and W be finite dimensional vector spaces. Let P N pv q, α : V W, p ą 0. Assume 0 V P dom rαs and αp0 V q 0 W. Show: ˆ α p α P O V W ppq q ô P Oˆ p V W. 33. Let V and W be finite dimensional vector spaces. Prove that poˆ V R q poˆ V W q Ď Oˆ V W.
5 Homework 7: Due on Tuesday 7 March 26. Let R, S and T be sets. Let f : R Ñ S and let g : S Ñ T. Let U Ď T. Show: f pg puqq pg fq puq. 27. Let S and T be sets. Let f : S ĂÑą T. Let U Ď S. Show: f puq pf 1 q puq. 28. Let S and T be sets. Let f : S ĂÑ T. Let U Ď S. Show: f pf puqq U. 29. Let S and T be sets. Let f : S Ñą T. Let U Ď T. Show: f pf puqq U. 30. Let V be a vector space, P N pv q, C ą 0. Let x P V, r ą 0. Show: B px, rq B C px, Crq. Homework 6: Due on Tuesday 28 February 22. Let V be a vector space and let P SBF ě0 pv q. Show P P V, cx c x, and 0 V Let S be a set, let n P N, let V be a vector space and let f : S n Ñ V. Let g : Symrfs : S n Ñ V. Show both (i) g is symmetric, i.e., for all x 1,..., x n P S, for all σ P Σ n, we have gpx 1,..., x n q gpx σ1,..., x σn q, and (ii) the diagonal restrictions of f and g are the equal to one another, i.e., for all x P S, we have gpx, x,..., xq fpx, x,..., xq. 24. Let V be a vector space. Show: rp 2 pv qsrp 3 pv qs Ď P 5 pv q. Hint: Given fpvq Bpv, vq and gpvq T pv, v, vq, we wish to show that rfpvqsrgpvqs Qpv, v, v, v, vq. (You need to set up all the quantifications.) We know that rfpvqsrgpvqs rbpv, vqsrt pv, v, vqs. Let Let Q : SymrQ 0 s. Q 0 pv, w, x, y, zq rbpv, wqs rt px, y, zqs. 25. Let V, W be vector spaces. Show: rp 2 pw qs rp 3 pv, W qs Ď P 6 pv q.
6 Hint: Given gpwq Bpw, wq and fpvq T pv, v, vq, we wish to show that gpfpvqq Spv, v, v, v, v, vq. (You need to set up all the quantifications.) We know that gpfpvqq BpT pv, v, vq, T pv, v, vqq. Let Let S : SymrS 0 s. S 0 pu, v, w, x, y, zq Bp T pu, v, wq, T px, y, zq q. Homework 5: Due on Tuesday 21 February 18. For all p P p0, 8s, define B p : tx P R 2 s.t. x p ď 1u. Then, for all p P p0, 8q, we have B p tps, tq P R 2 s.t. s p ` t p ď 1u. Also, B 8 tps, tq P R 2 s.t. maxt s, t u ď 1u. Graph B 1{2, B 1, B 2, B 3, B 4, B Show, for all x P R 2, that x 1 ě x 2 ě x 8 ě x 1 {100. That is, show, for all s, t P R, that s ` t ě? s 2 ` t 2 ě maxt s, t u ě p s ` t q{ Find the largest C ą 0 such P R 2, x 8 ě C x 1. That is, find the largest C ą 0 such t P R, maxt s, t u ě Cp s ` t q. 21. Let a, b, c P R. Assume a ě 0. Assume, for all x P R, that ax 2 ` 2bx ` c ě 0. Show (i) pa 0q ñ pb 0q, (ii) ac b 2 ě 0. and Hint for (ii): Replacing x :Ñ b{a in the assumption, we see that ap b{aq 2 ` 2bp b{aq ` c ě 0. Homework 4: Due on Tuesday 14 February 13. Let m, n P N, L P LpR m, R n q, v P R m. Show that plpvqq V rls v V. (Note: We have Lpvq P R n, so plpvqq V P R nˆ1. Also, rls P R nˆm. Also, v P R m, so v V P R mˆ1.) 14. Let m, n P N. Show that the two maps L ÞÑ rls : LpR m, R n q Ñ R nˆm and A ÞÑ L A : R nˆm Ñ LpR m, R n q are inverses.
7 15. Let m, n P N, let u P R m, let v P R n and let A P R nˆm. Show that B A pu, vq pv H A u V q Let m, n P N. Show that the two maps B ÞÑ rbs : BpR m, R n q Ñ R nˆm and A ÞÑ B A : R nˆm Ñ BpR m, R n q are inverses. 17. Let n P N. Show: P SBFpR n q, rbs P Rsym nˆn P R nˆn sym, B A P SBFpR n q. and Homework 3: Due on Tuesday 7 February 8. Let X be a topological space, let f : R X and let a, b P R. Show that lim f pa ` q lim f. b a`b 9. Let X and Y be topological spaces. Let f, g : X Y. Assume that f Ď g; that is, assume, for all x P dom rfs, that both x P dom rgs and fpxq gpxq. Let a P LP X pdom rfsq. Assume Y is Hausdorff. Show that lim a f lim a g. 10. Let X and Y be topological spaces, φ : X Y, p P X and q P Y. Assume that φ Ñ q near p. Define ψ : pdom rφsq Y tpu Ñ Y by # φpxq, if x p; ψpxq q, if x p. Show that ψ : X Ñ Y is continuous at p. 11. Define r : Rzt0u Ñ R by rpxq 1{x. Show, for all x P Rzt0u, that r 1 pxq 1 x Let f, g : R R. Let a P LP R pdom rf{gsq. Show that pf{gq 1 paq rgpaqsrf 1 paqs rfpaqsrg 1 paqs rgpaqs 2. Hint: Define r : Rzt0u Ñ R by rpxq 1{x. Then f{g f pr gq. Homework 2: Due on Tuesday 31 January
8 4. Let f : R R, I Ď ddrfs. Assume that I is an interval. Let S : f 1 piq. Assume that S ě 0. Show that f is semi-increasing on I. That is, show, for all a, b P I, that r p a ă b q ñ p fpaq ď fpbq q s. 5. Let f : R R, I Ď ddrfs. Assume that I is an interval. Let S : f 1 piq. Assume that S ă 0. Show that f is strictly decreasing on I. That is, show, for all a, b P I, that r p a ă b q ñ p fpaq ą fpbq q s. 6. Let δ ą 0. Let U : p δ, δq. Define β : U Ñ R by βphq maxt0, hu. Show that β Ñ 0 near 0 in R. 7. Show that O O Ď O. That is, P P O, αε P O. Homework 1: Due on Tuesday 24 January 1. Let g : R R and let L P R. Assume g is defined near ă 0. Assume g ď 0 near ă 0. Assume g Ñ L near 0. Show L ď Let m, b P R. Define f : R Ñ R by fpxq mx ` b. Show f 1 C m R. 3. Let f : R R and let a P ddrfs. Assume f is defined near a in R. Assume f has a local semi-max at a in R. Show f 1 paq 0.
NOTES WEEK 11 DAY 2 SCOT ADAMS
 NOTES WEEK 11 DAY 2 SCOT ADAMS In Proposition 0.1 below, Bp0, δq is just the open interval p δ, δq and Bp0, x q is just the closed interval r x, x s. PROPOSITION 0.1. Let g : R R and let δ ą 0. Assume
NOTES WEEK 11 DAY 2 SCOT ADAMS In Proposition 0.1 below, Bp0, δq is just the open interval p δ, δq and Bp0, x q is just the closed interval r x, x s. PROPOSITION 0.1. Let g : R R and let δ ą 0. Assume
NOTES WEEK 04 DAY 1 SCOT ADAMS
 NOTES WEEK 0 DAY 1 SCOT ADAMS DEFINITION 01 Let m, n P N, B P BpR m, R n q Let e 1,, e m be the standard basis of R m Let f 1,, f n be the standard basis of R n Then we define rbs P R nˆm by rbs ji Bpe
NOTES WEEK 0 DAY 1 SCOT ADAMS DEFINITION 01 Let m, n P N, B P BpR m, R n q Let e 1,, e m be the standard basis of R m Let f 1,, f n be the standard basis of R n Then we define rbs P R nˆm by rbs ji Bpe
NOTES WEEK 15 DAY 1 SCOT ADAMS
 NOTES WEEK 15 DAY 1 SCOT ADAMS We fix some notation for the entire class today: Let n P N, W : R n, : 2 P N pw q, W : LpW, W q, I : id W P W, z : 0 W 0 n. Note that W LpR n, R n q. Recall, for all T P
NOTES WEEK 15 DAY 1 SCOT ADAMS We fix some notation for the entire class today: Let n P N, W : R n, : 2 P N pw q, W : LpW, W q, I : id W P W, z : 0 W 0 n. Note that W LpR n, R n q. Recall, for all T P
NOTES WEEK 10 DAY 2. Unassigned HW: Let V and W be finite dimensional vector spaces and let x P V. Show, for all f, g : V W, that
 NOTES WEEK 10 DAY 2 SCOT ADAMS Unassigned HW: Let V and W be finite dimensional vector spaces and let x P V. Show, for all f, g : V W, that D x pf ` gq pd x fq ` pd x gq. Also, show, for all c P R, for
NOTES WEEK 10 DAY 2 SCOT ADAMS Unassigned HW: Let V and W be finite dimensional vector spaces and let x P V. Show, for all f, g : V W, that D x pf ` gq pd x fq ` pd x gq. Also, show, for all c P R, for
NOTES WEEK 14 DAY 2 SCOT ADAMS
 NOTES WEEK 14 DAY 2 SCOT ADAMS For this lecture, we fix the following: Let n P N, let W : R n, let : 2 P N pr n q and let I : id R n : R n Ñ R n be the identity map, defined by Ipxq x. For any h : W W,
NOTES WEEK 14 DAY 2 SCOT ADAMS For this lecture, we fix the following: Let n P N, let W : R n, let : 2 P N pr n q and let I : id R n : R n Ñ R n be the identity map, defined by Ipxq x. For any h : W W,
DS-GA 1002: PREREQUISITES REVIEW SOLUTIONS VLADIMIR KOBZAR
 DS-GA 2: PEEQUISIES EVIEW SOLUIONS VLADIMI KOBZA he following is a selection of questions (drawn from Mr. Bernstein s notes) for reviewing the prerequisites for DS-GA 2. Questions from Ch, 8, 9 and 2 of
DS-GA 2: PEEQUISIES EVIEW SOLUIONS VLADIMI KOBZA he following is a selection of questions (drawn from Mr. Bernstein s notes) for reviewing the prerequisites for DS-GA 2. Questions from Ch, 8, 9 and 2 of
Singular integral operators and the Riesz transform
 Singular integral operators and the Riesz transform Jordan Bell jordan.bell@gmail.com Department of Mathematics, University of Toronto November 17, 017 1 Calderón-Zygmund kernels Let ω n 1 be the measure
Singular integral operators and the Riesz transform Jordan Bell jordan.bell@gmail.com Department of Mathematics, University of Toronto November 17, 017 1 Calderón-Zygmund kernels Let ω n 1 be the measure
NOTES WEEK 02 DAY 1. THEOREM 0.3. Let A, B and C be sets. Then
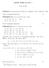 NOTES WEEK 02 DAY 1 SCOT ADAMS LEMMA 0.1. @propositions P, Q, R, rp or pq&rqs rp p or Qq&pP or Rqs. THEOREM 0.2. Let A and B be sets. Then (i) A X B B X A, and (ii) A Y B B Y A THEOREM 0.3. Let A, B and
NOTES WEEK 02 DAY 1 SCOT ADAMS LEMMA 0.1. @propositions P, Q, R, rp or pq&rqs rp p or Qq&pP or Rqs. THEOREM 0.2. Let A and B be sets. Then (i) A X B B X A, and (ii) A Y B B Y A THEOREM 0.3. Let A, B and
DS-GA 3001: PROBLEM SESSION 2 SOLUTIONS VLADIMIR KOBZAR
 DS-GA 3: PROBLEM SESSION SOLUTIONS VLADIMIR KOBZAR Note: In this discussion we allude to the fact the dimension of a vector space is given by the number of basis vectors. We will shortly establish this
DS-GA 3: PROBLEM SESSION SOLUTIONS VLADIMIR KOBZAR Note: In this discussion we allude to the fact the dimension of a vector space is given by the number of basis vectors. We will shortly establish this
MATH 360 Final Exam Thursday, December 14, a n 2. a n 1 1
 MATH 36 Final Exam Thursday, December 4, 27 Name. The sequence ta n u is defined by a and a n (a) Prove that lim a n exists by showing that ta n u is bounded and monotonic and invoking an appropriate result.
MATH 36 Final Exam Thursday, December 4, 27 Name. The sequence ta n u is defined by a and a n (a) Prove that lim a n exists by showing that ta n u is bounded and monotonic and invoking an appropriate result.
NOTES WEEK 14 DAY 2 SCOT ADAMS
 NOTES WEEK 14 DAY 2 SCOT ADAMS We igligt tat it s possible to ave two topological spaces and a continuous bijection from te one to te oter wose inverse is not continuous: Let I : r0, 2πq and let C : tpx,
NOTES WEEK 14 DAY 2 SCOT ADAMS We igligt tat it s possible to ave two topological spaces and a continuous bijection from te one to te oter wose inverse is not continuous: Let I : r0, 2πq and let C : tpx,
S. K. Mohanta, Srikanta Mohanta SOME FIXED POINT RESULTS FOR MAPPINGS IN G-METRIC SPACES
 DEMONSTRATIO MATHEMATICA Vol. XLVII No 1 2014 S. K. Mohanta Srikanta Mohanta SOME FIXED POINT RESULTS FOR MAPPINGS IN G-METRIC SPACES Abstract. We prove a common fixed point theorem for a pair of self
DEMONSTRATIO MATHEMATICA Vol. XLVII No 1 2014 S. K. Mohanta Srikanta Mohanta SOME FIXED POINT RESULTS FOR MAPPINGS IN G-METRIC SPACES Abstract. We prove a common fixed point theorem for a pair of self
Approximation of Weighted Local Mean Operators
 Approximation of Weighted Local ean Operators Jianzhong Wang Department of athematics and Statistics Sam Houston State University Huntsville, TX 7734 Abstract Recently, weighted local mean operators are
Approximation of Weighted Local ean Operators Jianzhong Wang Department of athematics and Statistics Sam Houston State University Huntsville, TX 7734 Abstract Recently, weighted local mean operators are
Lecture 16 Methods for System of Linear Equations (Linear Systems) Songting Luo. Department of Mathematics Iowa State University
 Lecture 16 Methods for System of Linear Equations (Linear Systems) Songting Luo Department of Mathematics Iowa State University MATH 481 Numerical Methods for Differential Equations Songting Luo ( Department
Lecture 16 Methods for System of Linear Equations (Linear Systems) Songting Luo Department of Mathematics Iowa State University MATH 481 Numerical Methods for Differential Equations Songting Luo ( Department
REAL ANALYSIS II TAKE HOME EXAM. T. Tao s Lecture Notes Set 5
 REAL ANALYSIS II TAKE HOME EXAM CİHAN BAHRAN T. Tao s Lecture Notes Set 5 1. Suppose that te 1, e 2, e 3,... u is a countable orthonormal system in a complex Hilbert space H, and c 1, c 2,... is a sequence
REAL ANALYSIS II TAKE HOME EXAM CİHAN BAHRAN T. Tao s Lecture Notes Set 5 1. Suppose that te 1, e 2, e 3,... u is a countable orthonormal system in a complex Hilbert space H, and c 1, c 2,... is a sequence
PROBABILITY 2018 HANDOUT 2: GAUSSIAN DISTRIBUTION
 PROAILITY 218 HANDOUT 2: GAUSSIAN DISTRIUTION GIOVANNI PISTONE Contents 1. Standard Gaussian Distribution 1 2. Positive Definite Matrices 5 3. General Gaussian Distribution 6 4. Independence of Jointly
PROAILITY 218 HANDOUT 2: GAUSSIAN DISTRIUTION GIOVANNI PISTONE Contents 1. Standard Gaussian Distribution 1 2. Positive Definite Matrices 5 3. General Gaussian Distribution 6 4. Independence of Jointly
Short Notes in Mathematics Fundamental concepts every student of Mathematics should know
 Short Notes in Mathematics Fundamental concepts every student of Mathematics should know Markus J. Pflaum October 9, 2018 Contents Titlepage 1 1 Foundations 2 Set theory........................................
Short Notes in Mathematics Fundamental concepts every student of Mathematics should know Markus J. Pflaum October 9, 2018 Contents Titlepage 1 1 Foundations 2 Set theory........................................
MATH 387 ASSIGNMENT 2
 MATH 387 ASSIGMET 2 SAMPLE SOLUTIOS BY IBRAHIM AL BALUSHI Problem 4 A matrix A ra ik s P R nˆn is called symmetric if a ik a ki for all i, k, and is called positive definite if x T Ax ě 0 for all x P R
MATH 387 ASSIGMET 2 SAMPLE SOLUTIOS BY IBRAHIM AL BALUSHI Problem 4 A matrix A ra ik s P R nˆn is called symmetric if a ik a ki for all i, k, and is called positive definite if x T Ax ě 0 for all x P R
FURSTENBERG S THEOREM ON PRODUCTS OF I.I.D. 2 ˆ 2 MATRICES
 FURSTENBERG S THEOREM ON PRODUCTS OF I.I.D. 2 ˆ 2 MATRICES JAIRO BOCHI Abstract. This is a revised version of some notes written ą 0 years ago. I thank Anthony Quas for pointing to a gap in the previous
FURSTENBERG S THEOREM ON PRODUCTS OF I.I.D. 2 ˆ 2 MATRICES JAIRO BOCHI Abstract. This is a revised version of some notes written ą 0 years ago. I thank Anthony Quas for pointing to a gap in the previous
MATH 260 Class notes/questions January 10, 2013
 MATH 26 Class notes/questions January, 2 Linear transformations Last semester, you studied vector spaces (linear spaces) their bases, dimension, the ideas of linear dependence and linear independence Now
MATH 26 Class notes/questions January, 2 Linear transformations Last semester, you studied vector spaces (linear spaces) their bases, dimension, the ideas of linear dependence and linear independence Now
Introduction to Numerical Analysis
 Introduction to Numerical Analysis Lecture Notes for SI 507 Authors: S. Baskar and S. Sivaji Ganesh Department of Mathematics Indian Institute of Technology Bombay Powai, Mumbai 400 076. Contents 1 Mathematical
Introduction to Numerical Analysis Lecture Notes for SI 507 Authors: S. Baskar and S. Sivaji Ganesh Department of Mathematics Indian Institute of Technology Bombay Powai, Mumbai 400 076. Contents 1 Mathematical
NOTES WEEK 15 DAY 2 SCOT ADAMS
 NOTES WEEK 15 DAY 2 SCOT ADAMS We will need the Fà di Bruno result, proved erlier. It sttes: Let X nd Y nd Z be finite dimensionl vector spces, let f : X Y nd g : Y Z. Let p P X nd let k P N 0. Assume
NOTES WEEK 15 DAY 2 SCOT ADAMS We will need the Fà di Bruno result, proved erlier. It sttes: Let X nd Y nd Z be finite dimensionl vector spces, let f : X Y nd g : Y Z. Let p P X nd let k P N 0. Assume
Mathematische Methoden der Unsicherheitsquantifizierung
 Mathematische Methoden der Unsicherheitsquantifizierung Oliver Ernst Professur Numerische Mathematik Sommersemester 2014 Contents 1 Introduction 1.1 What is Uncertainty Quantification? 1.2 A Case Study:
Mathematische Methoden der Unsicherheitsquantifizierung Oliver Ernst Professur Numerische Mathematik Sommersemester 2014 Contents 1 Introduction 1.1 What is Uncertainty Quantification? 1.2 A Case Study:
Markov Chains. Andreas Klappenecker by Andreas Klappenecker. All rights reserved. Texas A&M University
 Markov Chains Andreas Klappenecker Texas A&M University 208 by Andreas Klappenecker. All rights reserved. / 58 Stochastic Processes A stochastic process X tx ptq: t P T u is a collection of random variables.
Markov Chains Andreas Klappenecker Texas A&M University 208 by Andreas Klappenecker. All rights reserved. / 58 Stochastic Processes A stochastic process X tx ptq: t P T u is a collection of random variables.
ADVANCE TOPICS IN ANALYSIS - REAL. 8 September September 2011
 ADVANCE TOPICS IN ANALYSIS - REAL NOTES COMPILED BY KATO LA Introductions 8 September 011 15 September 011 Nested Interval Theorem: If A 1 ra 1, b 1 s, A ra, b s,, A n ra n, b n s, and A 1 Ě A Ě Ě A n
ADVANCE TOPICS IN ANALYSIS - REAL NOTES COMPILED BY KATO LA Introductions 8 September 011 15 September 011 Nested Interval Theorem: If A 1 ra 1, b 1 s, A ra, b s,, A n ra n, b n s, and A 1 Ě A Ě Ě A n
arxiv: v2 [math.ca] 13 May 2015
![arxiv: v2 [math.ca] 13 May 2015 arxiv: v2 [math.ca] 13 May 2015](/thumbs/88/114667751.jpg) ON THE CLOSURE OF TRANSLATION-DILATION INVARIANT LINEAR SPACES OF POLYNOMIALS arxiv:1505.02370v2 [math.ca] 13 May 2015 J. M. ALMIRA AND L. SZÉKELYHIDI Abstract. Assume that a linear space of real polynomials
ON THE CLOSURE OF TRANSLATION-DILATION INVARIANT LINEAR SPACES OF POLYNOMIALS arxiv:1505.02370v2 [math.ca] 13 May 2015 J. M. ALMIRA AND L. SZÉKELYHIDI Abstract. Assume that a linear space of real polynomials
Degeneration of Bethe subalgebras in the Yangian
 Degeneration of Bethe subalgebras in the Yangian National Research University Higher School of Economics Faculty of Mathematics Moscow, Russia Washington, 2018 Yangian for gl n Let V C n, Rpuq 1 P u 1
Degeneration of Bethe subalgebras in the Yangian National Research University Higher School of Economics Faculty of Mathematics Moscow, Russia Washington, 2018 Yangian for gl n Let V C n, Rpuq 1 P u 1
NOTES WEEK 01 DAY 1 SCOT ADAMS
 NOTES WEEK 01 DAY 1 SCOT ADAMS Question: What is Mathematics? Answer: The study of absolute truth. Question: Why is it so hard to teach and to learn? Answer: One must learn to play a variety of games called
NOTES WEEK 01 DAY 1 SCOT ADAMS Question: What is Mathematics? Answer: The study of absolute truth. Question: Why is it so hard to teach and to learn? Answer: One must learn to play a variety of games called
Tempered Distributions
 Tempered Distributions Lionel Fiske and Cairn Overturf May 9, 26 In the classical study of partial differential equations one requires a solution to be differentiable. While intuitively this requirement
Tempered Distributions Lionel Fiske and Cairn Overturf May 9, 26 In the classical study of partial differential equations one requires a solution to be differentiable. While intuitively this requirement
Zhidong Pan DERIVABLE MAPS AND GENERALIZED DERIVATIONS ON NEST AND STANDARD ALGEBRAS
 DEMONSTRATIO MATHEMATICA Vol. 49 No 3 2016 Zhidong Pan DERIVABLE MAPS AND GENERALIZED DERIVATIONS ON NEST AND STANDARD ALGEBRAS Communicated by E. Weber Abstract. For an algebra A, an A-bimodule M, and
DEMONSTRATIO MATHEMATICA Vol. 49 No 3 2016 Zhidong Pan DERIVABLE MAPS AND GENERALIZED DERIVATIONS ON NEST AND STANDARD ALGEBRAS Communicated by E. Weber Abstract. For an algebra A, an A-bimodule M, and
APPROXIMATE HOMOMORPHISMS BETWEEN THE BOOLEAN CUBE AND GROUPS OF PRIME ORDER
 APPROXIMATE HOMOMORPHISMS BETWEEN THE BOOLEAN CUBE AND GROUPS OF PRIME ORDER TOM SANDERS The purpose of this note is to highlight a question raised by Shachar Lovett [Lov], and to offer some motivation
APPROXIMATE HOMOMORPHISMS BETWEEN THE BOOLEAN CUBE AND GROUPS OF PRIME ORDER TOM SANDERS The purpose of this note is to highlight a question raised by Shachar Lovett [Lov], and to offer some motivation
K. P. R. Rao, K. R. K. Rao UNIQUE COMMON FIXED POINT THEOREMS FOR PAIRS OF HYBRID MAPS UNDER A NEW CONDITION IN PARTIAL METRIC SPACES
 DEMONSTRATIO MATHEMATICA Vol. XLVII No 3 204 K. P. R. Rao, K. R. K. Rao UNIQUE COMMON FIXED POINT THEOREMS FOR PAIRS OF HYBRID MAPS UNDER A NEW CONDITION IN PARTIAL METRIC SPACES Abstract. In this paper,
DEMONSTRATIO MATHEMATICA Vol. XLVII No 3 204 K. P. R. Rao, K. R. K. Rao UNIQUE COMMON FIXED POINT THEOREMS FOR PAIRS OF HYBRID MAPS UNDER A NEW CONDITION IN PARTIAL METRIC SPACES Abstract. In this paper,
NOTES WEEK 13 DAY 2 SCOT ADAMS
 NOTES WEEK 13 DAY 2 SCOT ADAMS Recall: Let px, dq be a metric space. Then, for all S Ď X, we have p S is sequentially compact q ñ p S is closed and bounded q. DEFINITION 0.1. Let px, dq be a metric space.
NOTES WEEK 13 DAY 2 SCOT ADAMS Recall: Let px, dq be a metric space. Then, for all S Ď X, we have p S is sequentially compact q ñ p S is closed and bounded q. DEFINITION 0.1. Let px, dq be a metric space.
MATH 360 Exam 2 Wednesday, November 8, 2017.» b
 MATH 36 Exam Wedesday, November 8, 7 Name. Let f : ra, bs Ñ R be a cotiuous fuctio, ad suppose that for every cotiuous fuctio g : ra, bs Ñ R, Prove that fpxq for all x P ra, bs.» b a fpxqgpxq dx. We ca,
MATH 36 Exam Wedesday, November 8, 7 Name. Let f : ra, bs Ñ R be a cotiuous fuctio, ad suppose that for every cotiuous fuctio g : ra, bs Ñ R, Prove that fpxq for all x P ra, bs.» b a fpxqgpxq dx. We ca,
Ground States are generically a periodic orbit
 Gonzalo Contreras CIMAT Guanajuato, Mexico Ergodic Optimization and related topics USP, Sao Paulo December 11, 2013 Expanding map X compact metric space. T : X Ñ X an expanding map i.e. T P C 0, Dd P Z`,
Gonzalo Contreras CIMAT Guanajuato, Mexico Ergodic Optimization and related topics USP, Sao Paulo December 11, 2013 Expanding map X compact metric space. T : X Ñ X an expanding map i.e. T P C 0, Dd P Z`,
MATH 260 Homework 2 solutions. 7. (a) Compute the dimension of the intersection of the following two planes in R 3 : x 2y z 0, 3x 3y z 0.
 MATH 6 Homework solutions Problems from Dr Kazdan s collection 7 (a) Compute the dimension of the intersection of the following two planes in R 3 : x y z, 3x 3y z (b) A map L: R 3 R is defined by the matrix
MATH 6 Homework solutions Problems from Dr Kazdan s collection 7 (a) Compute the dimension of the intersection of the following two planes in R 3 : x y z, 3x 3y z (b) A map L: R 3 R is defined by the matrix
Fourier transforms. Up to now, we ve been expressing functions on finite intervals (usually the interval 0 x L or L x L) as Fourier series: a n cos L
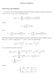 ourier transforms Motivation and definition Up to now, we ve been expressing functions on finite intervals (usually the interval 0 x or x ) as ourier series: fpxq a 0 8 nπx a n cos n b n sin nπx where
ourier transforms Motivation and definition Up to now, we ve been expressing functions on finite intervals (usually the interval 0 x or x ) as ourier series: fpxq a 0 8 nπx a n cos n b n sin nπx where
Mathematical Finance
 ETH Zürich, HS 2017 Prof. Josef Teichmann Matti Kiiski Mathematical Finance Solution sheet 14 Solution 14.1 Denote by Z pz t q tpr0,t s the density process process of Q with respect to P. (a) The second
ETH Zürich, HS 2017 Prof. Josef Teichmann Matti Kiiski Mathematical Finance Solution sheet 14 Solution 14.1 Denote by Z pz t q tpr0,t s the density process process of Q with respect to P. (a) The second
MTH132 Exam 2 Solutions Covers: Page Total. Max
 Name: PID: A Section #: Instructor: Page 3 4 5 6 7 8 Total Score Max 30 18 4 14 150 Instructions 1. You will be given exactly 90 minutes for this exam.. No calculators, phones, or any electronic devices.
Name: PID: A Section #: Instructor: Page 3 4 5 6 7 8 Total Score Max 30 18 4 14 150 Instructions 1. You will be given exactly 90 minutes for this exam.. No calculators, phones, or any electronic devices.
Introduction to Applied Algebraic Topology
 Introduction to Applied Algebraic Topology Tom Needham Last Updated: December 10, 2017 These are lecture notes for the course MATH 4570 at the Ohio State University. They are a work in progress and certainly
Introduction to Applied Algebraic Topology Tom Needham Last Updated: December 10, 2017 These are lecture notes for the course MATH 4570 at the Ohio State University. They are a work in progress and certainly
Singular Value Decomposition and its. SVD and its Applications in Computer Vision
 Singular Value Decomposition and its Applications in Computer Vision Subhashis Banerjee Department of Computer Science and Engineering IIT Delhi October 24, 2013 Overview Linear algebra basics Singular
Singular Value Decomposition and its Applications in Computer Vision Subhashis Banerjee Department of Computer Science and Engineering IIT Delhi October 24, 2013 Overview Linear algebra basics Singular
1. Examples. We did most of the following in class in passing. Now compile all that data.
 SOLUTIONS Math A4900 Homework 12 11/22/2017 1. Examples. We did most of the following in class in passing. Now compile all that data. (a) Favorite examples: Let R tr, Z, Z{3Z, Z{6Z, M 2 prq, Rrxs, Zrxs,
SOLUTIONS Math A4900 Homework 12 11/22/2017 1. Examples. We did most of the following in class in passing. Now compile all that data. (a) Favorite examples: Let R tr, Z, Z{3Z, Z{6Z, M 2 prq, Rrxs, Zrxs,
NOTES FOR BEILINSON-DRINFELD SEMINAR - EVEN SHORTER VERSION. Contents 1. Overview Steenrod s construction
 NOTES FOR BEILINSON-DRINFELD SEMINAR - EVEN SHORTER VERSION GUS LONERGAN Abstract. We use Steenrod s construction to prove that the quantum Coulomb branch is a Frobenius-constant quantization. Contents
NOTES FOR BEILINSON-DRINFELD SEMINAR - EVEN SHORTER VERSION GUS LONERGAN Abstract. We use Steenrod s construction to prove that the quantum Coulomb branch is a Frobenius-constant quantization. Contents
Integration and Fourier Theory. Lecture 14
 Integration and Fourier Theory Lecture 4 Morten Grud Rasmussen March 5, 03 Trigonometric Series Denote the unit circle in the complex plane by T tx P C x u ( T for torus ). Note that R Q t ÞÑ e it P T
Integration and Fourier Theory Lecture 4 Morten Grud Rasmussen March 5, 03 Trigonometric Series Denote the unit circle in the complex plane by T tx P C x u ( T for torus ). Note that R Q t ÞÑ e it P T
Armstrong Topology Solutions. George Blikas Gregory Grant David Hong Grant Baker Kristy Ong
 Armstrong Topology Solutions George Blikas Gregory Grant David Hong Grant Baker Kristy Ong April 2016 Contents 0 Preliminaries 7 0.1 Definitions............................... 7 0.1.1 Functions...........................
Armstrong Topology Solutions George Blikas Gregory Grant David Hong Grant Baker Kristy Ong April 2016 Contents 0 Preliminaries 7 0.1 Definitions............................... 7 0.1.1 Functions...........................
q-de Rham cohomology via Λ-rings
 q-de Rham cohomology via Λ-rings J.P.Pridham arxiv:1608.07142 1 / 21 q-analogues (Gauss) rns q : qn 1 q 1 1 q... qn 1 rns q! : rns q... r2s q r1s q, ¹ n 1 i 0 n 1 ¹ i 0 p1 p1 n k q : rns q! rn ksq!rksq!
q-de Rham cohomology via Λ-rings J.P.Pridham arxiv:1608.07142 1 / 21 q-analogues (Gauss) rns q : qn 1 q 1 1 q... qn 1 rns q! : rns q... r2s q r1s q, ¹ n 1 i 0 n 1 ¹ i 0 p1 p1 n k q : rns q! rn ksq!rksq!
Homework for MATH 4603 (Advanced Calculus I) Fall Homework 13: Due on Tuesday 15 December. Homework 12: Due on Tuesday 8 December
 Homework for MATH 4603 (Advanced Calculus I) Fall 2015 Homework 13: Due on Tuesday 15 December 49. Let D R, f : D R and S D. Let a S (acc S). Assume that f is differentiable at a. Let g := f S. Show that
Homework for MATH 4603 (Advanced Calculus I) Fall 2015 Homework 13: Due on Tuesday 15 December 49. Let D R, f : D R and S D. Let a S (acc S). Assume that f is differentiable at a. Let g := f S. Show that
Extensive Form Abstract Economies and Generalized Perfect Recall
 Extensive Form Abstract Economies and Generalized Perfect Recall Nicholas Butler Princeton University July 30, 2015 Nicholas Butler (Princeton) EFAE and Generalized Perfect Recall July 30, 2015 1 / 1 Motivation
Extensive Form Abstract Economies and Generalized Perfect Recall Nicholas Butler Princeton University July 30, 2015 Nicholas Butler (Princeton) EFAE and Generalized Perfect Recall July 30, 2015 1 / 1 Motivation
On the existence of non-oscillatory phase functions for second order ordinary differential equations in the high-frequency regime
 We observe that solutions of a large class of highly oscillatory second order linear ordinary differential equations can be approximated using nonoscillatory phase functions. In addition, we describe numerical
We observe that solutions of a large class of highly oscillatory second order linear ordinary differential equations can be approximated using nonoscillatory phase functions. In addition, we describe numerical
On the classification of toroidal circle planes
 On the classification of toroidal circle planes A thesis submitted in partial fulfilment of the requirements for the Degree of Doctor of Philosophy in the subject of Mathematics by Duy Quan Ho under the
On the classification of toroidal circle planes A thesis submitted in partial fulfilment of the requirements for the Degree of Doctor of Philosophy in the subject of Mathematics by Duy Quan Ho under the
Mathematical Quantum Theory
 Mathematical Quantum Theory Marcello Porta Eberhard Karls Universität Tübingen, Department of Mathematics, Auf der Morgenstelle 10, 72076 Tübingen, Germany January 7, 2019 Abstract These are the lecture
Mathematical Quantum Theory Marcello Porta Eberhard Karls Universität Tübingen, Department of Mathematics, Auf der Morgenstelle 10, 72076 Tübingen, Germany January 7, 2019 Abstract These are the lecture
L E C T U R E 2 1 : P R O P E RT I E S O F M AT R I X T R A N S F O R M AT I O N S I I. Wednesday, November 30
 L E C T U R E 2 1 : P R O P E RT I E S O F M AT R I X T R A N S F O R M AT I O N S I I Wednesday, November 30 1 the range of a linear transformation Let s begin by defining the range of a linear transformation.
L E C T U R E 2 1 : P R O P E RT I E S O F M AT R I X T R A N S F O R M AT I O N S I I Wednesday, November 30 1 the range of a linear transformation Let s begin by defining the range of a linear transformation.
For example, p12q p2x 1 x 2 ` 5x 2 x 2 3 q 2x 2 x 1 ` 5x 1 x 2 3. (a) Let p 12x 5 1x 7 2x 4 18x 6 2x 3 ` 11x 1 x 2 x 3 x 4,
 SOLUTIONS Math A4900 Homework 5 10/4/2017 1. (DF 2.2.12(a)-(d)+) Symmetric polynomials. The group S n acts on the set tx 1, x 2,..., x n u by σ x i x σpiq. That action extends to a function S n ˆ A Ñ A,
SOLUTIONS Math A4900 Homework 5 10/4/2017 1. (DF 2.2.12(a)-(d)+) Symmetric polynomials. The group S n acts on the set tx 1, x 2,..., x n u by σ x i x σpiq. That action extends to a function S n ˆ A Ñ A,
Solutions of exercise sheet 3
 Topology D-MATH, FS 2013 Damen Calaque Solutons o exercse sheet 3 1. (a) Let U Ă Y be open. Snce s contnuous, 1 puq s open n X. Then p A q 1 puq 1 puq X A s open n the subspace topology on A. (b) I s contnuous,
Topology D-MATH, FS 2013 Damen Calaque Solutons o exercse sheet 3 1. (a) Let U Ă Y be open. Snce s contnuous, 1 puq s open n X. Then p A q 1 puq 1 puq X A s open n the subspace topology on A. (b) I s contnuous,
C*-algebras - a case study
 - a case study Definition Suppose that H is a Hilbert space. A C -algebra is an operator-norm closed -subalgebra of BpHq. are closed under ultraproducts and subalgebras so they should be captured by continous
- a case study Definition Suppose that H is a Hilbert space. A C -algebra is an operator-norm closed -subalgebra of BpHq. are closed under ultraproducts and subalgebras so they should be captured by continous
MTH 505: Number Theory Spring 2017
 MTH 505: Number Theory Spring 017 Homework 4 Drew Armstrong 4.1. (Squares Mod 4). We say that an element ras n P Z{nZ is square if there exists an element rxs n P Z{nZ such that ras n prxs n q rx s n.
MTH 505: Number Theory Spring 017 Homework 4 Drew Armstrong 4.1. (Squares Mod 4). We say that an element ras n P Z{nZ is square if there exists an element rxs n P Z{nZ such that ras n prxs n q rx s n.
Eco 610 Mathematical Economics I Notes M. Jerison 8/24/14
 Eco 610 Mathematical Economics I Notes M. Jerison 8/24/14 1. Introduction Economists analyze qualitative relations (e.g., who is whose boss, or which ownership pattern is more efficient) and quantitative
Eco 610 Mathematical Economics I Notes M. Jerison 8/24/14 1. Introduction Economists analyze qualitative relations (e.g., who is whose boss, or which ownership pattern is more efficient) and quantitative
Dr. Marques Sophie Algebra 1 Spring Semester 2017 Problem Set 9
 Dr. Marques Sophie Algebra Spring Semester 207 Office 59 marques@cims.nyu.edu Problem Set 9 Exercise 0 : Prove that every group of order G 28 must contain a normal subgroup of order 7. (Why should it contain
Dr. Marques Sophie Algebra Spring Semester 207 Office 59 marques@cims.nyu.edu Problem Set 9 Exercise 0 : Prove that every group of order G 28 must contain a normal subgroup of order 7. (Why should it contain
Self-intersections of the Riemann zeta function on the critical line
 Self-intersections of the Riemann zeta function on the critical line William Bans Department of Mathematics University of Missouri Columbia, MO 65211, USA Victor Castillo-Garate Department of Mathematics
Self-intersections of the Riemann zeta function on the critical line William Bans Department of Mathematics University of Missouri Columbia, MO 65211, USA Victor Castillo-Garate Department of Mathematics
Automata theory and its applications
 Automata theory and its applications Lecture 12-14: Automata over ranked finite trees Zhilin Wu State Key Laboratory of Computer Science, Institute of Software, Chinese Academy of Sciences January 16,
Automata theory and its applications Lecture 12-14: Automata over ranked finite trees Zhilin Wu State Key Laboratory of Computer Science, Institute of Software, Chinese Academy of Sciences January 16,
Approximation in the Zygmund Class
 Approximation in the Zygmund Class Odí Soler i Gibert Joint work with Artur Nicolau Universitat Autònoma de Barcelona New Developments in Complex Analysis and Function Theory, 02 July 2018 Approximation
Approximation in the Zygmund Class Odí Soler i Gibert Joint work with Artur Nicolau Universitat Autònoma de Barcelona New Developments in Complex Analysis and Function Theory, 02 July 2018 Approximation
Sobolev-Type Extremal Polynomials
 Soolev-Type Extremal Polyomials (case of the sigular measures) Ael Díaz-Gozález Joi with Héctor Pijeira-Carera ULL 2016 Soolev-Type Extremal Polyomials adiazgo@math.uc3m.es 1 / 18 Moic extremal polyomials
Soolev-Type Extremal Polyomials (case of the sigular measures) Ael Díaz-Gozález Joi with Héctor Pijeira-Carera ULL 2016 Soolev-Type Extremal Polyomials adiazgo@math.uc3m.es 1 / 18 Moic extremal polyomials
RAMSEY PARTIAL ORDERS FROM ACYCLIC GRAPHS
 RAMSEY PARTIAL ORDERS FROM ACYCLIC GRAPHS JAROSLAV NEŠETŘIL AND VOJTĚCH RÖDL Abstract. We prove that finite partial orders with a linear extension form a Ramsey class. Our proof is based on the fact that
RAMSEY PARTIAL ORDERS FROM ACYCLIC GRAPHS JAROSLAV NEŠETŘIL AND VOJTĚCH RÖDL Abstract. We prove that finite partial orders with a linear extension form a Ramsey class. Our proof is based on the fact that
Roots and Coefficients Polynomials Preliminary Maths Extension 1
 Preliminary Maths Extension Question If, and are the roots of x 5x x 0, find the following. (d) (e) Question If p, q and r are the roots of x x x 4 0, evaluate the following. pq r pq qr rp p q q r r p
Preliminary Maths Extension Question If, and are the roots of x 5x x 0, find the following. (d) (e) Question If p, q and r are the roots of x x x 4 0, evaluate the following. pq r pq qr rp p q q r r p
Midterm Review. Name: Class: Date: ID: A. Short Answer. 1. For each graph, write the equation of a radical function of the form y = a b(x h) + k.
 Name: Class: Date: ID: A Midterm Review Short Answer 1. For each graph, write the equation of a radical function of the form y = a b(x h) + k. a) b) c) 2. Determine the domain and range of each function.
Name: Class: Date: ID: A Midterm Review Short Answer 1. For each graph, write the equation of a radical function of the form y = a b(x h) + k. a) b) c) 2. Determine the domain and range of each function.
Entropy and Ergodic Theory Lecture 27: Sinai s factor theorem
 Entropy and Ergodic Theory Lecture 27: Sinai s factor theorem What is special about Bernoulli shifts? Our main result in Lecture 26 is weak containment with retention of entropy. If ra Z, µs and rb Z,
Entropy and Ergodic Theory Lecture 27: Sinai s factor theorem What is special about Bernoulli shifts? Our main result in Lecture 26 is weak containment with retention of entropy. If ra Z, µs and rb Z,
Electronic Companion Dynamic Pricing of Perishable Assets under Competition
 1 Electronic Companion Dynamic Pricing of Perishable Assets under Competition Guillermo Gallego IEOR Department, Columbia University, New York, NY 10027 gmg2@columbia.edu Ming Hu Rotman School of Management,
1 Electronic Companion Dynamic Pricing of Perishable Assets under Competition Guillermo Gallego IEOR Department, Columbia University, New York, NY 10027 gmg2@columbia.edu Ming Hu Rotman School of Management,
NOTES ON SOME EXERCISES OF LECTURE 5, MODULE 2
 NOTES ON SOME EXERCISES OF LECTURE 5, MODULE 2 MARCO VITTURI Contents 1. Solution to exercise 5-2 1 2. Solution to exercise 5-3 2 3. Solution to exercise 5-7 4 4. Solution to exercise 5-8 6 5. Solution
NOTES ON SOME EXERCISES OF LECTURE 5, MODULE 2 MARCO VITTURI Contents 1. Solution to exercise 5-2 1 2. Solution to exercise 5-3 2 3. Solution to exercise 5-7 4 4. Solution to exercise 5-8 6 5. Solution
Some multilinear algebra
 Some multilinear algera Multilinear forms Let V e a finite dimensional R-vector space, dim V n. For k P N 0, we denote y T k V the vector space of k-linear forms Then T 1 V V and, y convention, T 0 V R.
Some multilinear algera Multilinear forms Let V e a finite dimensional R-vector space, dim V n. For k P N 0, we denote y T k V the vector space of k-linear forms Then T 1 V V and, y convention, T 0 V R.
PALINDROMIC WIDTH OF WREATH PRODUCTS, METABELIAN GROUPS, AND MAX-N SOLVABLE GROUPS
 PALINDROMIC WIDTH OF WREATH PRODUCTS, METABELIAN GROUPS, AND MAX-N SOLVABLE GROUPS T. R. RILEY AND A. W. SALE Abstract. A group has finite palindromic width if there exists n such that every element can
PALINDROMIC WIDTH OF WREATH PRODUCTS, METABELIAN GROUPS, AND MAX-N SOLVABLE GROUPS T. R. RILEY AND A. W. SALE Abstract. A group has finite palindromic width if there exists n such that every element can
On homorphisms between products of median algebras
 On homorphisms between products of median algebras Miguel Couceiro, Stephan Foldes, Gerasimos Meletiou To cite this version: Miguel Couceiro, Stephan Foldes, Gerasimos Meletiou. On homorphisms between
On homorphisms between products of median algebras Miguel Couceiro, Stephan Foldes, Gerasimos Meletiou To cite this version: Miguel Couceiro, Stephan Foldes, Gerasimos Meletiou. On homorphisms between
Flag Varieties. Matthew Goroff November 2, 2016
 Flag Varieties Matthew Goroff November 2, 2016 1. Grassmannian Variety Definition 1.1: Let V be a k-vector space of dimension n. The Grassmannian Grpr, V q is the set of r-dimensional subspaces of V. It
Flag Varieties Matthew Goroff November 2, 2016 1. Grassmannian Variety Definition 1.1: Let V be a k-vector space of dimension n. The Grassmannian Grpr, V q is the set of r-dimensional subspaces of V. It
Algebraic Groups. Anand Sawant Ludwig-Maximilians Universität, München. Summer Semester Version: July 8, 2016
 Algebraic Groups Anand Sawant Ludwig-Maximilians Universität, München Summer Semester 2016 Version: July 8, 2016 Note: This file will be constantly updated till the end of the semester. Contents 1 Affine
Algebraic Groups Anand Sawant Ludwig-Maximilians Universität, München Summer Semester 2016 Version: July 8, 2016 Note: This file will be constantly updated till the end of the semester. Contents 1 Affine
TOPOLOGY NOTES KLINT QINAMI
 TOPOLOGY NOTES KLINT QINAMI Preamble. The following is a collection of exercises relating to point-set topology and preliminary algebraic topology, together with my proofs of those exercises. Use at your
TOPOLOGY NOTES KLINT QINAMI Preamble. The following is a collection of exercises relating to point-set topology and preliminary algebraic topology, together with my proofs of those exercises. Use at your
MAT 128A - Practice Midterm Exam
 MAT 8A - Practice Midterm Exam Karry Wong October 3, 08 Problem (True or False) Given that f : r, s Ñ R is a continuous function, and that ta n u are its Chebyshev coefficients. Also, for N P N, p N pxq
MAT 8A - Practice Midterm Exam Karry Wong October 3, 08 Problem (True or False) Given that f : r, s Ñ R is a continuous function, and that ta n u are its Chebyshev coefficients. Also, for N P N, p N pxq
Lecture 17 Methods for System of Linear Equations: Part 2. Songting Luo. Department of Mathematics Iowa State University
 Lecture 17 Methods for System of Linear Equations: Part 2 Songting Luo Department of Mathematics Iowa State University MATH 481 Numerical Methods for Differential Equations Songting Luo ( Department of
Lecture 17 Methods for System of Linear Equations: Part 2 Songting Luo Department of Mathematics Iowa State University MATH 481 Numerical Methods for Differential Equations Songting Luo ( Department of
Gap probabilities in tiling models and Painlevé equations
 Gap probabilities in tiling models and Painlevé equations Alisa Knizel Columbia University Painlevé Equations and Applications: A Workshop in Memory of A. A. Kapaev August 26, 2017 1 / 17 Tiling model
Gap probabilities in tiling models and Painlevé equations Alisa Knizel Columbia University Painlevé Equations and Applications: A Workshop in Memory of A. A. Kapaev August 26, 2017 1 / 17 Tiling model
NONLINEAR EVOLUTION EQUATIONS SHORT NOTES WEEK #1
 NONLNEA EVOLUTON EQUATONS SHOT NOTES WEEK #. Free Schrödinger Equation Let Bx 2 `...`Bx 2 n denote the Laplacian on d with d ě. The initial-value problem for the free Schrödinger equation (in d space dimensions)
NONLNEA EVOLUTON EQUATONS SHOT NOTES WEEK #. Free Schrödinger Equation Let Bx 2 `...`Bx 2 n denote the Laplacian on d with d ě. The initial-value problem for the free Schrödinger equation (in d space dimensions)
A revealed preference test for weakly separable preferences
 A revealed preference test for weakly separable preferences John K.-H. Quah April 19, 2012 Abstract: Consider a finite data set of price vectors and consumption bundles; under what conditions will be there
A revealed preference test for weakly separable preferences John K.-H. Quah April 19, 2012 Abstract: Consider a finite data set of price vectors and consumption bundles; under what conditions will be there
Separation Logic 2/4. Chapter 7. Preservation of independent state. The frame rule. The Frame Rule. Arthur Charguéraud.
 Separation Logic 2/4 Arthur Charguéraud Chapter 7 The Frame Rule Febuary 8th, 2017 1 / 75 2 / 75 Preservation of independent state The frame rule We have: tr ÞÑ 2u pincr rq tλ. r ÞÑ 3u Principle: a triple
Separation Logic 2/4 Arthur Charguéraud Chapter 7 The Frame Rule Febuary 8th, 2017 1 / 75 2 / 75 Preservation of independent state The frame rule We have: tr ÞÑ 2u pincr rq tλ. r ÞÑ 3u Principle: a triple
A GENERALIZATION OF FULTON S CONJECTURE FOR AN EMBEDDED SUBGROUP
 A GENERALIZATION OF FULTON S CONJECTURE FOR AN EMBEDDED SUBGROUP JOSHUA KIERS Abstract. In this paper we extend a result on the relationship between intersection theory of general flag varieties and invariant
A GENERALIZATION OF FULTON S CONJECTURE FOR AN EMBEDDED SUBGROUP JOSHUA KIERS Abstract. In this paper we extend a result on the relationship between intersection theory of general flag varieties and invariant
Entropy and Ergodic Theory Notes 22: The Kolmogorov Sinai entropy of a measure-preserving system
 Entropy and Ergodic Theory Notes 22: The Kolmogorov Sinai entropy of a measure-preserving system 1 Joinings and channels 1.1 Joinings Definition 1. If px, µ, T q and py, ν, Sq are MPSs, then a joining
Entropy and Ergodic Theory Notes 22: The Kolmogorov Sinai entropy of a measure-preserving system 1 Joinings and channels 1.1 Joinings Definition 1. If px, µ, T q and py, ν, Sq are MPSs, then a joining
Jeff Connor IDEAL CONVERGENCE GENERATED BY DOUBLE SUMMABILITY METHODS
 DEMONSTRATIO MATHEMATICA Vol. 49 No 1 2016 Jeff Connor IDEAL CONVERGENCE GENERATED BY DOUBLE SUMMABILITY METHODS Communicated by J. Wesołowski Abstract. The main result of this note is that if I is an
DEMONSTRATIO MATHEMATICA Vol. 49 No 1 2016 Jeff Connor IDEAL CONVERGENCE GENERATED BY DOUBLE SUMMABILITY METHODS Communicated by J. Wesołowski Abstract. The main result of this note is that if I is an
arxiv: v3 [math.oc] 5 May 2017
![arxiv: v3 [math.oc] 5 May 2017 arxiv: v3 [math.oc] 5 May 2017](/thumbs/72/66282101.jpg) QUADRATIC GROWTH CONDITIONS FOR CONVEX MATRIX OPTIMIZATION PROBLEMS ASSOCIATED WITH SPECTRAL FUNCTIONS YING CUI, CHAO DING :, AND XINYUAN ZHAO ; arxiv:1702.03262v3 [math.oc] 5 May 2017 Abstract. In this
QUADRATIC GROWTH CONDITIONS FOR CONVEX MATRIX OPTIMIZATION PROBLEMS ASSOCIATED WITH SPECTRAL FUNCTIONS YING CUI, CHAO DING :, AND XINYUAN ZHAO ; arxiv:1702.03262v3 [math.oc] 5 May 2017 Abstract. In this
SPARSE RECOVERY VIA BASIS PURSUIT
 SPARSE RECOVERY VIA BASIS PURSUIT A thesis submitted to the Kent State University Honors College in partial fulfillment of the requirements for University Honors by Zachary M. Emrich May, 2015 Thesis
SPARSE RECOVERY VIA BASIS PURSUIT A thesis submitted to the Kent State University Honors College in partial fulfillment of the requirements for University Honors by Zachary M. Emrich May, 2015 Thesis
Draft. Chapter 2 Approximation and Interpolation. MATH 561 Numerical Analysis. Songting Luo. Department of Mathematics Iowa State University
 Chapter 2 Approximation and Interpolation Songting Luo Department of Mathematics Iowa State University MATH 561 Numerical Analysis Songting Luo ( Department of Mathematics Iowa State University[0.5in]
Chapter 2 Approximation and Interpolation Songting Luo Department of Mathematics Iowa State University MATH 561 Numerical Analysis Songting Luo ( Department of Mathematics Iowa State University[0.5in]
arxiv: v2 [math.ap] 30 Jan 2018
![arxiv: v2 [math.ap] 30 Jan 2018 arxiv: v2 [math.ap] 30 Jan 2018](/thumbs/76/73369021.jpg) Accepted Partial differential systems with nonlocal nonlinearities: Generation and solutions Margaret Beck Anastasia Doikou Simon J.A. Malham Ioannis Stylianidis arxiv:179.9253v2 [math.ap] 3 Jan 218 3th
Accepted Partial differential systems with nonlocal nonlinearities: Generation and solutions Margaret Beck Anastasia Doikou Simon J.A. Malham Ioannis Stylianidis arxiv:179.9253v2 [math.ap] 3 Jan 218 3th
arxiv: v2 [cs.lg] 31 Oct 2018
![arxiv: v2 [cs.lg] 31 Oct 2018 arxiv: v2 [cs.lg] 31 Oct 2018](/thumbs/96/127998133.jpg) SOME NEGATIVE RESULTS FOR SINGLE LAYER AND MULTILAYER FEEDFORWARD NEURAL NETWORKS arxiv:1810.10032v2 [cs.lg] 31 Oct 2018 J. M. ALMIRA, P. E. LOPEZ-DE-TERUEL, D. J. ROMERO-LÓPEZ Abstract. We prove, for
SOME NEGATIVE RESULTS FOR SINGLE LAYER AND MULTILAYER FEEDFORWARD NEURAL NETWORKS arxiv:1810.10032v2 [cs.lg] 31 Oct 2018 J. M. ALMIRA, P. E. LOPEZ-DE-TERUEL, D. J. ROMERO-LÓPEZ Abstract. We prove, for
Problem Set #7. Exercise 1 : In GLpn, Cq and SLpn, Cq define the subgroups of scalar matrices
 Dr. Marques Sophie Algebra Spring Semester 207 Office 59 marques@cims.nyu.edu Problem Set #7 In the following, denotes a isomorphism of groups. Exercise 0 : Let G be a finite abelian group with G n, we
Dr. Marques Sophie Algebra Spring Semester 207 Office 59 marques@cims.nyu.edu Problem Set #7 In the following, denotes a isomorphism of groups. Exercise 0 : Let G be a finite abelian group with G n, we
A note on causality in Banach spaces.
 A note on causality in Banach spaces. arxiv:1306.3851v3 [math.fa] 9 Mar 2014 Marcus Waurick Institut für Analysis, Fachrichtung Mathematik Technische Universität Dresden Germany marcus.waurick@tu-dresden.de
A note on causality in Banach spaces. arxiv:1306.3851v3 [math.fa] 9 Mar 2014 Marcus Waurick Institut für Analysis, Fachrichtung Mathematik Technische Universität Dresden Germany marcus.waurick@tu-dresden.de
MATH 551 HOMEWORK II SOLUTIONS. Graded problems: 1,3,4,6,7. Solutions to ungraded problems abridged. Let D d
 MATH 551 HOMEWORK II SOLUTIONS Graded problems: 1,3,4,6,7. Solutions to ungraded problems abridged. Let D d dx and xf, gy ş b fpxqgpxqdx. Integration by parts is then expressed as a xdf, gy fg b a xf,
MATH 551 HOMEWORK II SOLUTIONS Graded problems: 1,3,4,6,7. Solutions to ungraded problems abridged. Let D d dx and xf, gy ş b fpxqgpxqdx. Integration by parts is then expressed as a xdf, gy fg b a xf,
arxiv: v4 [math.ap] 14 Apr 2016
![arxiv: v4 [math.ap] 14 Apr 2016 arxiv: v4 [math.ap] 14 Apr 2016](/thumbs/76/73571665.jpg) SOME OBSEVATIONS ON THE GEEN FUNCTION FO THE BALL IN THE FACTIONAL LAPLACE FAMEWOK arxiv:5.6468v4 [math.ap] 4 Apr 6 CLAUDIA BUCU Claudia Bucur Dipartimento di Matematica Federigo Enriques Università degli
SOME OBSEVATIONS ON THE GEEN FUNCTION FO THE BALL IN THE FACTIONAL LAPLACE FAMEWOK arxiv:5.6468v4 [math.ap] 4 Apr 6 CLAUDIA BUCU Claudia Bucur Dipartimento di Matematica Federigo Enriques Università degli
Focus rules for segments. Focus and defocus rules for concatenation. Mlength with a while loop. Mlength with a while loop.
 The function nth-cell Separation Logic Part 2 Returns the i-th cell of a list: Arthur Charguéraud February 2015 let rec nth_cell (i:int) (p: a cell) = if i = 0 then p else nth_cell (i-1) (p.tl) Why is
The function nth-cell Separation Logic Part 2 Returns the i-th cell of a list: Arthur Charguéraud February 2015 let rec nth_cell (i:int) (p: a cell) = if i = 0 then p else nth_cell (i-1) (p.tl) Why is
PRINCIPLES OF ANALYSIS - LECTURE NOTES
 PRINCIPLES OF ANALYSIS - LECTURE NOTES PETER A. PERRY 1. Constructions of Z, Q, R Beginning with the natural numbers N t1, 2, 3,...u we can use set theory to construct, successively, Z, Q, and R. We ll
PRINCIPLES OF ANALYSIS - LECTURE NOTES PETER A. PERRY 1. Constructions of Z, Q, R Beginning with the natural numbers N t1, 2, 3,...u we can use set theory to construct, successively, Z, Q, and R. We ll
Very quick introduction to the conformal group and cft
 CHAPTER 1 Very quick introduction to the conformal group and cft The world of Conformal field theory is big and, like many theories in physics, it can be studied in many ways which may seem very confusing
CHAPTER 1 Very quick introduction to the conformal group and cft The world of Conformal field theory is big and, like many theories in physics, it can be studied in many ways which may seem very confusing
M e t ir c S p a c es
 A G M A A q D q O I q 4 78 q q G q 3 q v- q A G q M A G M 3 5 4 A D O I A 4 78 / 3 v D OI A G M 3 4 78 / 3 54 D D v M q D M 3 v A G M 3 v M 3 5 A 4 M W q x - - - v Z M * A D q q q v W q q q q D q q W q
A G M A A q D q O I q 4 78 q q G q 3 q v- q A G q M A G M 3 5 4 A D O I A 4 78 / 3 v D OI A G M 3 4 78 / 3 54 D D v M q D M 3 v A G M 3 v M 3 5 A 4 M W q x - - - v Z M * A D q q q v W q q q q D q q W q
EXAM. Exam #3. Math 2360, Spring April 24, 2001 ANSWERS
 EXAM Exam #3 Math 2360, Spring 200 April 24, 200 ANSWERS i 40 pts Problem In this problem, we will work in the vectorspace P 3 = { ax 2 + bx + c a, b, c R }, the space of polynomials of degree less than
EXAM Exam #3 Math 2360, Spring 200 April 24, 200 ANSWERS i 40 pts Problem In this problem, we will work in the vectorspace P 3 = { ax 2 + bx + c a, b, c R }, the space of polynomials of degree less than
L E C T U R E 1 2 : R N A N D V E C T O R S PA C E S. Monday, October 3
 L E C T U R E 1 2 : R N A N D V E C T O R S PA C E S Monday, October 3 In the last few lectures we considered various properties of matrices in order to better understand the coefficient matrices of our
L E C T U R E 1 2 : R N A N D V E C T O R S PA C E S Monday, October 3 In the last few lectures we considered various properties of matrices in order to better understand the coefficient matrices of our
Expected Scott-Suppes Utility Representation
 Expected Scott-Suppes Utility Representation Nuh Aygün Dalkıran Oral Ersoy Dokumacı Tarık Kara February 7, 2018 1 / 51 1 Introduction Motivation 2 Preliminaries Semiorders Uncertainty Continuity Independence
Expected Scott-Suppes Utility Representation Nuh Aygün Dalkıran Oral Ersoy Dokumacı Tarık Kara February 7, 2018 1 / 51 1 Introduction Motivation 2 Preliminaries Semiorders Uncertainty Continuity Independence
Adam Najdecki, Józef Tabor CONDITIONALLY APPROXIMATELY CONVEX FUNCTIONS
 DEMONSTRATIO MATHEMATICA Vol. 49 No 06 Adam Najdecki, Józef Tabor CONDITIONALLY APPROXIMATELY CONVEX FUNCTIONS Communicated by A. Fryszkowski Abstract. Let X be a real normed space, V be a subset of X
DEMONSTRATIO MATHEMATICA Vol. 49 No 06 Adam Najdecki, Józef Tabor CONDITIONALLY APPROXIMATELY CONVEX FUNCTIONS Communicated by A. Fryszkowski Abstract. Let X be a real normed space, V be a subset of X
