On the existence of non-oscillatory phase functions for second order ordinary differential equations in the high-frequency regime
|
|
|
- Amie Walsh
- 5 years ago
- Views:
Transcription
1 We observe that solutions of a large class of highly oscillatory second order linear ordinary differential equations can be approximated using nonoscillatory phase functions. In addition, we describe numerical experiments which illustrate computational implications of this fact. For example, many special functions of interest such as the Bessel functions J ν and Y ν can be evaluated accurately using a number of operations which is Opq in the order ν. The present paper is devoted to the development of an analytical apparatus. Numerical aspects of this work will be reported at a later date. On the existence of non-oscillatory phase functions for second order ordinary differential equations in the high-frequency regime Z. Heitman ;, J. Bremer, V. Rokhlin ; a, Technical Report YALEU/DCS/TR-493 August 4, 04 This author s work was supported in part under ONR N , ONR N This author s work was supported in part by a fellowship from the Alfred P. Sloan foundation a This author s work was supported in part under ONR N , ONR N , AFOSR FA Department of Mathematics, University of California, Davis, CA 9566 ; Dept. of Mathematics, Yale University, New Haven CT 065 Approved for public release: distribution is unlimited. Keywords: Kummer s Equation, WKB Approximation, Phase Functions
2 . Introduction Given a differential equation y ptq ` λ qptqyptq 0 for all 0 ď t ď, () where λ is a real number and q : r0, s Ñ R is smooth and strictly positive, a sufficiently smooth α : r0, s Ñ R is a phase function for () if the pair of functions u, v defined by the formulas uptq cospαptqq α ptq { () and vptq sinpαptqq α ptq { (3) form a basis in the space of solutions of (). Phase functions have been extensively studied: they were first introduced in [9], play a key role in the theory of global transformations of ordinary differential equations [3, 0], and are an important element in the theory of special functions [6, 6,, ]. Despite this long history, an important property of phase functions appears to have been overlooked. Specifically, that when the function q is nonoscillatory, solutions of the equation () can be accurately represented using a nonoscillatory phase function. This is somewhat surprising since α is a phase function for () if and only if it satisfies the third order nonlinear ordinary differential equation pα ptqq λ qptq α 3 ptq α ptq ` 3 ˆα ptq for all 0 ď t ď. (4) 4 α ptq The equation (4) was introduced in [9], and and we will refer to it as Kummer s equation. The form of (4) and the appearance of λ in it suggests that its solutions will be oscillatory and most of them are. However, Bessel s equation y ptq ` ˆ λ {4 t yptq 0 for all 0 ă t ă 8 (5) furnishes a nontrivial example of an equation which admits a nonoscillatory phase function regardless of the value of λ. If we define u, v by the formulas c πt uptq J λptq (6) and c πt vptq Y λptq, (7) where J λ and Y λ denote the Bessel functions of the first and second kinds of order λ, and let α be defined by the relations (),(3), then α ptq πt Jλ ptq ` Y (8) λ ptq. It can be easily verified that (8) is a strictly negative, monotonically decreasing function of t
3 on p0, 8q. That this nonoscillatory phase function for Bessel s equation exists is the basis of several methods for the evaluation of Bessel functions of large orders and for the computation of their zeros [6, 8, 5]. The general situation is not quite so favorable: there need not exist a nonoscillatory function α such that () and (3) are exact solutions of (). However, assuming that q is nonoscillatory and λ is sufficiently large, there exists a nonoscillatory function α such that (), (3) approximate solutions of () with spectral accuracy (i.e., the approximation errors decay exponentially with λ). To see that this claim is plausible, we apply Newton s method for the solution of nonlinear equations to Kummer s equation (4). In doing so, it will be convenient to move the setting of our analysis from the interval r0, s to the real line so that we can use the Fourier transform to quantity the notion of nonoscillatory. Suppose that the extension of q to the real line is smooth and strictly positive, and that the Fourier transform of logpqq is smooth and decays rapidly. Letting pα ptqq λ expprptqq (9) in (4) yields the logarithm form of Kummer s equation: r ptq 4 pr ptqq ` 4λ pexpprptqq qptqq 0 for all t P R. (0) We use tr n u to denote the sequence of Newton iterates for the equation (0) obtained from the initial guess r 0 ptq logpqptqq. () The function r 0 corresponds to the first order WKB approximations for (). That is to say that if we insert the associated phase function ż t ż ˆ t α 0 ptq λ exp r a 0puq du λ qpuqdu () into (),(3), then and 0 ˆ uptq q {4 ptq cos λ ˆ vptq q {4 ptq sin λ ż t 0 ż t 0 0 a qpuq du (3) a qpuq du. (4) For each n ě 0, r n` is obtained from r n by solving the linearized equation h ptq r nptqh ptq ` 4λ exp pr n ptqq hptq f n ptq for all t P R, (5) where f n ptq r nptq ` 4 pr nptqq 4λ pexp pr n ptqq qptqq, (6) and letting r n` ptq r n ptq ` hptq. (7) 3
4 By introducing the change of variables xptq ż t 0 ˆrn puq exp du (8) into (5), we transform it into the inhomogeneous Helmholtz equation where h pxq ` 4λ hpxq g n pxq for all x P R, (9) g n pxq exp p r n pxqq f n pxq. (0) Suppose that pg n decays rapidly (when n 0, this is a consequence of our assumption that logpqq has a rapidly decaying Fourier transform) and let h be the solution of (9) whose Fourier transform is xh pξq pg npξq 4λ ξ. () Since x h pξq is singular when ξ λ, h will necessarily have a component which oscillates at frequency λ. However, according to (), the L 8 prq norm of that component is In fact, by rearranging () as pg n pλq 4λ. () xh pξq ˆ pgn pξq 4λ λ ξ ` pg npξq λ ` ξ and decomposing each of the terms on the right-hand side of (3) as pg n pξq λ ξ ˆ pgn pξq pg n p λq exp p pλ ξq q 4λ λ ξ we obtain where h 0 is defined by the formula ph 0 pξq ˆ pgn pξq pg n p λq exp p pλ ` ξq q 4λ λ ` ξ and h is defined by the formula ph pξq 4λ ` pg n p λq exp p pλ ξq q λ ξ (3), (4) h pxq h 0 pxq ` h pxq, (5) ` pg npξq pg n pλq exp p pλ ξq q, (6) λ ξ ˆ pg n p λq exp p pλ ` ξq q ` pg n pλq exp p pλ ξq q λ ` ξ λ ξ. (7) Since the factor in the denominator in (6) has been canceled and both pg n and the Gaussian function are smooth and rapidly decaying, h0 p is also smooth and rapidly decaying. Meanwhile, a straightforward calculation shows that the Fourier transform of is x i erf exppλixq (8) exp p pλ ξq q, (9) λ ξ 4
5 so that (7) implies that h pxq ˆ pg n p λq x 4λ i erf exppλixq pg n pλq x i erf expp λixq. (30) Since g n is real-valued, pg n pλq pg n p λq. Inserting this into (30) yields h pxq pgpλq x 4λ erf sin pλxq, (3) which makes it clear that the L 8 prq norm of h is p4λq pg n pλq. In (5), the solution of (9) is decomposed as the sum of a nonoscillatory function h 0 and a highly oscillatory function h of small magnitude. However, the solution of (5) is actually given by the function h pxptqq h 0 pxptqq ` h pxptqq (3) obtained by reversing the change of variables (8). But since xptq is nonoscillatory and the Fourier transform of h 0 pxq decays rapidly, we expect that the composition h 0 pxptqq will also have a rapidly decaying Fourier transform. The L 8 prq norm of h pxptqq is, of course, the same as that of h pxq. So the solution of the linearized equation (5) can be written as the sum of a nonoscillatory function h 0 pxptqq and a highly oscillatory function h pxptqq of negligible magnitude. If, in each iteration of the Newton procedure, we approximate the solution of (5) by constructing h pxptqq and discarding the oscillatory term h ptpxqq of small magnitude, then it is plausible that we will arrive at an approximate solution rptq of the logarithm form of Kummer s equation which is nonoscillatory, assuming the Fourier transform of r 0 ptq logpqptqq decays rapidly enough and λ is sufficiently large. Most of the remainder of this paper is devoted to developing a rigorous argument to replace the preceding heuristic discussion. In Section, we summarize a number of well-known mathematical facts to be used throughout this article. In Section 3, we reformulate Kummer s equation as a nonlinear integral equation. Once that is accomplished, we are in a position to state the principal result of the paper and discuss its implications; this is done in Section 4. The proof of this principal result is contained in Sections 5, 6, 7 and 8. Section 9 contains an elementary proof of a relevant error estimate for second order differential equations of the form (). In Section 0, we present the results of numerical experiments concerning the evaluation of special functions. The details of our numerical algorithm will be reported at a later date. We conclude with a few brief remarks in Section.. Preliminaries.. Modified Bessel functions The modified Bessel function K ν ptq of the first kind of order ν is defined for t P R and ν P C by the formula K ν ptq ż 8 0 exp p t cosh ptqq coshpνtq dt. (33) 5
6 The following bound on the ratio of K ν` to K ν can be found in [4]. Theorem. Suppose that t ą 0 and ν ą 0 are real numbers. Then K ν` ptq K ν ptq ă ν `?ν ` t t ď ν t `. (34).. The binomial theorem A proof of the following can be found in [3], as well as many other sources. Theorem. Suppose that r is a real number, and that y is a real number such that y ă. Then 8ÿ p ` yq r Γpr ` q Γpk ` qγpr k ` q yk. (35) k 0.3. The Lambert W function The Lambert W function or product logarithm is the multiple-valued inverse of the function fpzq z exppzq. (36) We follow [5] in using W 0 to denote the branch of W which is real-valued and greater than or equal to on the interval r {e, 8q and W to refer to the branch which is real-valued and less than or equal to on r {e, 0q. We will make use of the following elementary facts concerning W 0 and W (all of which can be found in [5] and its references). Theorem 3. Suppose that y ě {e is a real number. Then x exppxq ď y if and only if x ď W 0 pyq. (37) Theorem 4. Suppose that 0 ă y ď {e is a real number. Then x expp xq ď y if and only if x ě W p yq. (38) Theorem 5. Suppose that 0 ď x ď is a real number. Then x ď W 0pxq ď x. (39) Theorem 6. Suppose that x ą exppq is a real number. Then ˆ logpxq ď W ď logpxq. (40) x 6
7 .4. Fréchet derivatives and the contraction mapping principle Given Banach spaces X, Y and a mapping f : X Ñ Y between them, we say that f is Fréchet differentiable at x P X if there exists a bounded linear operator X Ñ Y, denoted by fx, such that }fpx ` hq fpxq fx rhs} lim 0. (4) hñ0 }h} Theorem 7. Suppose that X and Y are a Banach spaces and that f : X Ñ Y is Fréchet differentiable at every point of X. Suppose also that D is a convex subset of X, and that there exists a real number M ą 0 such that for all x P D. Then for all x and y in D. }f x} ď M (4) }fpxq fpyq} ď M}x y} (43) Suppose that f : X Ñ X is a mapping of the Banach space X into itself. We say that f is contractive on a subset D of X if there exists a real number 0 ă α ă such that }fpxq fpyq} ď α}x y} (44) for all x, y P D. Moreover, we say that tx n u 8 n 0 is a sequence of fixed point iterates for f if x n` fpx n q for all n ě 0. Theorem 7 is often used to show that a mapping is contractive so that the following result can be applied. Theorem 8. (The Contraction Mapping Principle) Suppose that D is a closed subset of a Banach space X. Suppose also that f : X Ñ X is contractive on D and f pdq Ă D. Then the equation x fpxq (45) has a unique solution σ P D. Moreover, any sequence of fixed point iterates for the function f which contains an element in D converges to σ. A discussion of Fréchet derivatives and proofs of Theorems 7 and 8 can be found, for instance, in [8]..5. Gronwall s inequality The following well-known inequality can be found in, for instance, []. Theorem 9. Suppose that f and g are continuous functions on the interval ra, bs such that fptq ě 0 and gptq ě 0 for all a ď t ď b. (46) Suppose further that there exists a real number C ą 0 such that fptq ď C ` ż t s fpsqgpsq ds for all a ď t ď b. (47) 7
8 Then ˆż t fptq ď C exp gpsq ds a for all a ď t ď b. (48).6. Schwarzian derivatives The Schwarzian derivative of a smooth function f : R Ñ R is tf, tu f 3 ptq f ptq 3 ˆf ptq. (49) f ptq If the function xptq is a diffeomorphism of the real line (that is, a smooth, invertible mapping R Ñ R), then the Schwarzian derivative of xptq can be related to the Schwarzian derivative of its inverse tpxq; in particular, ˆdx tx, tu tt, xu. (50) dt The identity (50) can be found, for instance, in Section.3 of []. 3. Integral equation formulation In this section, we reformulate Kummer s equation pα ptqq λ qptq α 3 ptq α ptq ` 3 4 ˆα ptq α ptq as a nonlinear integral equation. As in the introduction, we assume that the function q has been extended to the real line and we seek a function α which satisfies (5) on the real line. By letting (5) pα ptqq λ expprptqq (5) in (5), we obtain the equation r ptq 4 pr ptqq ` 4λ pexpprptqq qptqq 0 for all t P R. (53) We next take r to be of the form rptq logpqptqq ` δptq, (54) which results in δ ptq q ptq qptq δ ptq 4 pδ ptqq ` 4λ qptq pexppδptqq q qptqpptq, for all t P R, (55) where p is defined by the formula pptq qptq 5 4 ˆq ptq q ptq. (56) qptq qptq Note that the function p appears in the standard error analysis of WKB approximations (see, for instance, []). Expanding the exponential in a power series and rearranging terms yields 8
9 the equation δ ptq q ptq qptq δ ptq`4λ qptqδptq 4 pδ ptqq `4λ qptq Applying the change of variables transforms (57) into δ pxq ` 4λ δpxq 4 pδ pxqq ` 4λ xptq ż t 0 pδpxqq pδptqq ` pδptqq3 3! ` qptqpptq. (57) a qpuq du (58) ` pδpxqq3 3! ` ppxq for all x P R. (59) At first glance, the relationship between the function ppxq appearing in (59) and the coefficient qptq in the ordinary differential equation () is complex. However, the function pptq defined via (56) is related to the Schwarzian derivative (see Section.6) of the function xptq defined in (58) via the formula pptq tx, tu qptq It follows from (60) and Formula (50) in Section.6 that ˆ dt tx, tu. (60) dx ppxq tt, xu. (6) That is to say: p, when viewed as a function of x, is simply twice the Schwarzian derivative of t with respect to x. It is also notable that the part of (59) which is linear in δ is a constant coefficient Helmholtz equation. This suggests that we form an integral equation for (59) using a Green s function for the Helmholtz equation. To that end, we define the integral operator T for functions f P L prq via the formula T rf s pxq 4λ ż 8 8 sin pλ x y q fpyq dy (6) The following theorem summarizes the relevant properties of the operator T. Theorem 0. Suppose that λ ą 0 is a real number, and that the operator T is defined as in (6). Suppose also that f P L prq X C prq. Then:. T rf s pxq is an element of C prq;. T rf s pxq is a solution of the ordinary differential equation y pxq ` 4λ ypxq fpxq for all x P R; and 3. the Fourier transform of T rf s pxq is the principal value of pfpξq 4λ ξ pfpξq 4λ λ ξ ` pfpξq. λ ` ξ 9
10 Proof. We observe that T rf s pxq 4λ ż x 8 4λ sinpλxq ` 4λ cospλxq ż 8 sin pλ px yqq fpyq dy ` sin pλpy xqq fpyq dy 4λ x ż x cospλyqfpyq dy ż x 4λ cospλxq sinpλyqfpyq dy 8 ż 8 x sinpλyqfpyq dy 4λ sinpλxq 8 ż 8 x cospλyqfpyq dy for all x P R. We differentiate both sides of (63) with respect to x, apply the Lebesgue dominated convergence theorem to each integral (this is permissible since the sine and cosine functions are bounded and f P L prq) and combine terms in order to conclude that T rf s is differentiable everywhere and d dx T rf s pxq ż 8 8 (63) cos pλ x y q signpx yqfpyq dy (64) for all x P R. In the same fashion, we conclude that ˆ ż d 8 T rf s pxq fpxq λ sin pλ x y q fpyq dy (65) dx for all x P R. Since f is continuous by assumption and the second term appearing on the right-hand side in (65) is a continuous function of x by the Lebesgue dominated convergence theorem, we see from (65) that T rf s is twice continuously differentiable. By combining (65) and (6), we conclude that T rf s is a solution of the ordinary differential equation 8 We now define the function g through the formula y pxq ` 4λ ypxq fpxq for all x P R. (66) pgpξq 4λ ˆ λ ξ ` λ ` ξ. (67) It is well known that the Fourier transform of the principal value of {x is the function iπ signpxq; (68) see, for instance, [7] or [7]. It follows readily that the inverse Fourier transform of the principal value of (69) λ ξ is exp p λixq signpxq. (70) i From this and (67), we conclude that gpxq 4λ ˆ exp p λixq signpxq exp pλixq signpxq i i sin pλ x q. 4λ (7) 0
11 In particular, T rf s is the convolution of f with g. As a consequence, {T rf spξq pgpξq fpξq p pfpξq 4λ λ ξ ` pfpξq, (7) λ ` ξ which is the third and final conclusion of the theorem. In light of Theorem 0, it is clear that introducing the representation into (59) yields the nonlinear integral equation δpxq T rσ s pxq (73) σpxq S rt rσ ss pxq ` ppxq for all x P R, (74) where S is the operator defined for functions f P C prq by the formula S rf s pxq pf pxqq 4λ pfpxqq ` pfpxqq3 ` pfpxqq4 `. (75) 4! 3! 4! The following theorem is immediately apparent from the procedure used to transform Kummer s equation (5) into the nonlinear integral equation (74). Theorem. Suppose that λ ą 0 is a real number, that q : R Ñ R is an infinitely differentiable, strictly positive function, that xptq is defined by (58), and that ppxq is defined via (6). Suppose also that σ P L prq X C prq is a solution of the integral equation (74), that δ is defined via the formula δpxq T rσ s pxq 4λ 0 ż 8 8 sin pλ x y q σpyq dy, (76) and that the function α is defined by the formula ż t a ˆδpxpuqq αptq λ qpuq exp du. (77) Then:. δpxq is a twice continuously differentiable solution of (59);. δpxptqq is a twice continuously differentiable solution of of (57); 3. αptq is three times continuously differentiable solution of (5); and 4. αptq is a phase function for the ordinary differential equation y ptq ` λ qptqyptq 0 for all 0 ď t ď. (78) 4. Overview and statement of the principal result The composition operator S T appearing in (74) does not map any Lebesgue space L p prq or Hölder space C k,α prq to itself, which complicates the analysis of (74). Moreover, the integral defining T rσ s only exists if either σ P L prq or pσp λq 0. Even if both of these conditions are satisfied, it is not necessarily the case that S rt rσ ss ` p will satisfy either condition. This casts doubts on whether (74) is solvable for arbitrary p.
12 We avoid a detailed discussion of which spaces and in what sense (74) admits solutions and instead show that, under mild conditions on p and λ, there exists a function p b which approximates p and such that the equation σpxq S rt rσ ss pxq ` p b pxq for all x P R (79) admits a solution. Moreover, we prove that if p is nonoscillatory then the solution of (79) is also nonoscillatory and }p p b } 8 decays exponentially in λ. The next theorem, which is the principal result of this article, makes these statements precise. Its proof is given in Sections 5, 6, 7 and 8. Theorem. Suppose that q P C 8 prq is a strictly positive, and that xptq is defined by the formula ż t a xptq qpuq du. (80) Suppose also that ppxq is defined via the formula 0 ppxq tt, xu; (8) that is, ppxq is twice the Schwarzian derivative of the variable t with respect to the variable x defined via (80). Suppose furthermore that there exist real numbers λ ą 0, Γ ą 0 and a ą 0 such that " * λ ě 6 max a, Γ (8) and ppξq ď Γ exp p a ξ q for all ξ P R. (83) Then there exist functions p b P C 8 prq and σ b P L prq X C 8 prq such that σ b is a solution of (79), ˆ pσ b pξq ď Γ exp 5 6 a ξ for all ξ P R, (84) and }p p b } 8 ă 4Γ ˆ 5a exp 5 6 aλ. (85) According to Theorem, if σ is a solution of the integral equation (74), then the function α defined by (77) is a phase function for the differential equation (). We define α b in analogy with (77) using the solution σ b of the modified equation (79). That is, we let δ b be the function defined by the formula and then define α b via δ b pxq T rσ b s pxq 4λ α b ptq λ ż t 0 ż 8 8 sinpλ x y qσ b pyq dy, (86) a ˆδb pxpuqq qpuq exp du. (87) Obviously, α b is not a phase function for the equation (). However, if we define q b : R Ñ R by the formula 5 ˆq b ptq q b ptq p b ptq, (88) q b ptq 4 q b ptq q b ptq
13 then Theorem implies that α b is a phase function for the differential equation y ptq ` λ q b ptqyptq 0 for all 0 ď t ď. (89) Since }q q b } 8 is bounded in terms of }p p b } 8 and the solutions of (89) closely approximate those of () when }q q b } 8 is small, the function α b can be used to approximation solutions of () when }p p b } 8 is small. Theorem 3, which appears below, gives a relevant error estimate. Given ɛ ą 0, it specifies a bound on }p p b } 8 which ensures that solutions of (89) approximate those of () to relative precision ɛ. Its proof appears in Section 9. Defintion. We say that α is an ɛ-approximate phase function for the ordinary differential equation () if there exists a basis of solutions tru, rvu of () such that and where u, v are defined by and uptq ruptq ď ɛ sup ruptq for all 0 ď t ď (90) 0ďtď vptq rvptq ď ɛ sup rvptq for all 0 ď t ď, (9) 0ďtď uptq sinpαptqq α ptq { (9) vptq cospαptqq. (93) α { ptq Theorem 3. Suppose that q P C 8 prq is strictly positive, that the function p is defined by the formula (56), and that there exist real numbers 0 ă η ă η such that and η ď qptq ď η for all 0 ď t ď, (94) q ptq ˇ qptq ˇ ď η for all 0 ď t ď, (95) pptq ď η for all 0 ď t ď. (96) Suppose also that λ ą 0, ɛ ą 0 are real numbers such that η 3{4 0 ă ɛ ă λ exp, (97) 4 and that k is the real number defined by ˆη k 0 η ` 8η ` 0 η η `. (98) Suppose furthermore that p b : R Ñ R is an infinitely differentiable function such that }p p b } 8 ď η exp p kq exp η3{4 ɛ. (99) λ 4 3
14 Then there exists a function q b : r0, s Ñ R such that (88) holds and any phase function for (89) is an ɛ-approximate phase function for (). By combining Theorems, and 3 we obtain the following. Corollary. Suppose that q, xptq, p, η, η, λ, ɛ, k, Γ, a and η are as in the hypotheses of Theorem and 3. Suppose that, in addition, λ ě 6 ˆ k ` η3{4 Γ 5a 4 ` log. (00) η a ɛ Then there exists a function σ b P L prq X C 8 prq such that ˆ pσ b pξq ď Γ exp 5 6 a ξ for all ξ P R (0) and the function α b ptq defined by α b ptq λ ż t 0 a ˆδb pxpuqq qpuq exp du, (0) where δ b is the function defined through the formula δ b pxq ż sinpλ x y qσ b pyq dy, (03) 4λ is an ɛ-approximate phase function for the ordinary differential equation (). Remark. The hypothesis (00) can be replaced with the weaker condition λ ą 6 5a W 5 η a exp p kq exp η3{4 ɛ, (04) 88 Γ 4 where W denotes the branch of the Lambert W function which is real-valued and less than on the interval r {e, 0q (see Section.3). The proof of Theorem is divided amongst Sections 5, 6, 7 and 8. The principal difficulty lies in constructing a function p b which approximates p and for which (79) admits a solution. We accomplish this by introducing a modified integral equation σpxq S rt b rσ ss pxq ` ppxq, (05) where T b is a band-limited version of T. That is, T b rf s is defined via the formula prq bump function. This modified integral equation is introduced in Sec- where bpξq is a Cc 8 tion 5. {T b rf spξq { T rf spξqbpξq, (06) In Section 6, we show that under mild conditions on p and λ, (05) admits a solution σ. The argument proceeds by applying the Fourier transform to (05) and using the contraction mapping principle to show that the resulting equation admits a solution. In Section 7, we estimate the Fourier transform of the solution σ of (05) under the assumption that p is exponentially decaying. We show that pσ is also exponentially decaying, albeit at a slightly slower rate. 4
15 In Section 8, we define a band-limited version σ b of the solution σ of (05) via the formula pσ b pξq pσpξqbpξq. (07) By combining the observation that T b rσ s T rσ b s with (05), we obtain σpxq S rt rσ b ss pxq ` ppxq. (08) We then define p b by the formula p b pxq ppxq ` σ b pxq σpxq (09) and rearrange (08) as σ b pxq S rt rσ b ss pxq ` p b pxq. (0) The decay estimate on pσ is then used to bound }p p b } 8 }σ σ b } 8 ď }pσ pσ b }. 5. Band-limited integral equation In this section, we introduce a band-limited version of the operator T and use it to form an alternative to the integral equation (74). Let bpξq be any infinitely differentiable function such that. bpξq for all ξ ď λ,. 0 ď bpξq ď for all λ ď ξ ď? λ, and 3. bpξq 0 for all ξ ě? λ. We define T b rf s for functions f P L prq via the formula {T b rf spξq fpξq p bpξq () 4λ ξ We will refer to T b as the band-limited version of the operator T and and we call the nonlinear integral equation σpxq S rt b rσ ss pxq ` ppxq for all x P R () obtained by replacing T with T b in (74) the band-limited version of (74). Since T b is a Fourier multiplier, it is convenient to analyze () in the Fourier domain rather than the space domain. We now introduce notation which will allow us to write down the equation obtained by applying the Fourier transform to both sides of (). We let W b and Ă W b be the linear operators defined for f P L prq via the formulas and bpξq W b rf s pξq fpξq (3) 4λ ξ ĂW b rf s pξq fpξq bpξqiξ 4λ ξ, (4) where bpξq is the function used to define the operator T b. 5
16 For functions f P L prq, it is standard to denote the Fourier transform of the function exppfpxqq by exp rfs; that is, exp rfs pξq δpξq ` fpξq ` f fpξq ` f f fpξq `. (5)! 3! In (5), δ defers to the delta distribution and f f f denotes repeated convolution of the function f with itself. The Fourier transform of exppf pxqq never appears in this paper; however, we will encounter the Fourier transforms of the functions and exppf pxqq (6) exppfpxqq fpxq. (7) So, in analogy with the definition (5), we define exp rfs for f P L prq by the formula exp rfs pξq fpξq ` f fpξq ` f f fpξq `, (8)! 3! and we define exp rfs for f P L prq via the formula exp rfs pξq f fpξq ` f f fpξq `. (9)! 3! That is, exp rfs is obtained by truncating the leading term of exp rfs and exp rfs is obtained by truncated the first two leading terms of exp rfs. Finally, we define functions ψpξq and vpξq using the formulas and ψpξq pσpξq (0) vpξq ppξq. () Applying the Fourier transform to both sides of () results in the nonlinear equation where R rfs is defined for f P L prq by the formula ψpξq R rψs pξq, () R rfs pξq 4 Ă W b rf s ĂW b rf s pξq 4λ exp rw b rf s s pξq ` vpξq. (3) 6. Existence of solutions of the band-limited equation. In this section, we give conditions under which the sequence tψ n u 8 n 0 of fixed point iterates for () obtained by using the function v defined by () as an initial approximation converges. More explicitly, ψ 0 is defined by the formula and for each integer n ě 0, ψ n` is obtained from ψ n via ψ 0 pξq vpξq, (4) ψ n` pξq R rψ n s pξq. (5) 6
17 Theorem 4. Suppose that λ ą 0 is a real number, and that v P L prq such that }v} ď λ 8. (6) Theen the sequence tψ n u 8 n 0 defined by (4) and (5) converges in L prq norm to a function ψ which satisfies the equation () for almost all ξ P R. Proof. We observe that the Fréchet derivative (see Section.4) of R at f is the linear operator R f : L prq Ñ L prq given by the formula Rf W rhs pξq Ă b rf s ĂW b rhs pξq 4λ exp rw b rf ss W b rhs pξq. (7) From formulas (3) and (4) and the definition of bpξq we see that and }W b rf s} ď }f} λ (8) W Ă b rf s ď }f}? (9) λ for all f P L prq. From (7), (8) and (9) we conclude that R f rhs ď W Ă b rf s Wb Ă rhs ` 4λ }W b rf s} exp p}w b rf s} q }W b rhs ď }f} }h} ` 4λ }f} }h} ˆ}f} 4λ λ λ exp λ ˆ}f} ď 4λ ` }f} ˆ}f} exp }h} λ λ (30) for all f and h in L prq. Similarly, by combining (3), (8) and (9) we conclude that }R rf s} ď W 4 Ă b rf s ` 4λ }W b rf s} exp p}w b rf s} q ` }v} (3) ď }f} 8λ ` }f} ˆ}f} exp ` }v} λ λ whenever f P L prq. Now we set r λ {9 and let B denote the closed ball of radius r centered at 0 in L prq. Since ˆ 9 ă W 0, (3) 8 where W 0 denotes the branch of the Lambert W function which is real-valued and greater than or equal to on the interval r {e, 8q (see Section.3), we conclude that r r λ exp ă λ 4. (33) According to Theorem 5 of Section.3 and (3), it also the case that r λ ă 8. (34) 7
18 We combine (33), (34) with (30) to conclude that R f rhs r ď 4λ ` r r ˆ λ exp }h} λ ă 3 ` }h} ă 4 }h} (35) for all h P L prq and f P B. In other words, the L prq Ñ L prq operator norm of the linear operator Rf is bounded by { whenever f is in the ball B. Similarly, we insert (33), (34) and (6) into (3) to conclude that }R rf s} ď r 8λ ` r r λ exp ` r ˆ λ r ď r 8λ ` r r λ exp ` λ ˆ ď r 64 ` 4 ` for all f P B. ď r (36) Together with Theorem 7 of Section.4, formula (35) implies that the operator R is a contraction on the ball B while (36) says that it maps the ball B into itself. We now apply the contraction mapping theorem (Theorem 8 in Section.4) to conclude that any sequence of fixed point iterates for () which originates in B will converge to a solution of (). Since tψ n u is such a sequence, we are done. If ψ is a solution of () then the function σ defined by the formula σpxq ż 8 8 exppixξqψpξq dξ (37) is clearly a solution of the band-limited integral equation (). Note that because ψ P L prq, the integral in (37) is well-defined and σ is an element of the space C 0 prq of continuous functions which vanish at infinity. We record this observation as follows: Theorem 5. Suppose that λ ą 0 is a real number. Suppose also that p P L prq such that p P L prq and }p} ă λ 8. (38) Then there exists a function σ P C 0 prq which is a solution of the integral equation (). Remark. Since σ is not necessarily in L prq, the integral ż 8 need not exist. Nor is the existence of the improper integral 8 ż R lim RÑ8 R expp ixξqσpxq dx (39) expp ixξqσpxq dx (40) guaranteed. However, when viewed as a tempered distribution, the Fourier transform of σ exists and 8
19 is ψ; that is to say, for all functions f P SpRq. ż 8 8 ψpxqf pxq dx ż 8 8 σpxq p fpxq dx (4) In the next section we will prove that under additional assumptions on v, ψ lies in L prq. This implies that σ P L prq and ensures the convergence of the improper Riemann integrals (40). 7. Fourier estimate In this section, we derive a pointwise estimate on the solution ψ of Equation () under additional assumptions on the function v. Lemma. Suppose that a and C are real numbers such that Suppose also that f P L prq, and that Then 0 ď C ă a. (4) f pξq ď C expp a ξ q for all ξ P R. (43) ˆ ˆ exp rfs pξq ď C ` a ξ C C expp a ξ q exp exp π a πa π ξ where exp is the operator defined in (9). Proof. Let for all ξ P R, (44) gpξq C expp a ξ q (45) and for each integer m ą 0, denote by g m the m-fold convolution product of the function g. That is to say that g is defined via the formula g pξq gpξq (46) and for each integer m ą 0, g m` is defined in terms of g m by the formula g m` pξq g m gpξq. (47) We observe that for each integer m ą 0 and all ξ P R, g m pξq? m { ˆC ξ K m { pa ξ q ac, (48) π Γpmq where K ν denotes the modified Bessel function of the second kind of order ν (see Section.). By repeatedly applying Theorem of Section., we conclude that for all integers m ą 0 and all real t, K m { ptq ď K { ptq K { ptq m ź j ˆ t `j ` t m Γ ` `t m Γ `. `t (49) 9
20 We insert the identity c π K { ptq expp tq (50) t into (48) in order to conclude that for all integers m ą 0 and all real numbers t ą 0,? ˆ { m π t K m { ptq ď expp tq Γ ` `t m Γ `. (5) `t By combining (5) and (48) we conclude that ˆ m C Γ `a ξ ` m g m pξq ď C expp a ξ q (5) πa ΓpmqΓ `a ξ for all integers m ą 0 and all ξ 0. Moreover, the limit as ξ Ñ 0 of each side of (5) is finite and the two limits are equal, so (5) in fact holds for all ξ P R. We sum (5) over m, 3,... in order to conclude that 8ÿ ˆ m C Γ `a ξ ` m exp rgs pξq ď C expp a ξ q πa m Γpm ` qγpmqγ `a ξ C expp a ξ q for all ξ P R. Now we observe that Γpm ` q ď Inserting (54) into (53) yields 8ÿ m m ˆ exp rgs pξq ď C expp a ξ q ˆ m C Γ `a ξ πa 8ÿ m ` m Γpm ` qγpm ` qγ `a ξ (53) for all m 0,,,.... (54) ˆ C m Γ `a ξ πa Γpm ` qγ ` m (55) `a ξ for all ξ P R. Now we apply the binomial theorem (Theorem of Section.), which is justified since C ă a, to conclude that ˆ exp rgs pξq ď C expp a ξ q C `a ξ πa for all ξ P R. We observe that and C expp a ξ q exp ` a ξ log C πa (56) exppxq ď x exppxq for all x ě 0, (57) ˆ ď log ď x for all 0 ď x ď x π. (58) 0
21 By combining (57) and (58) with (56) we conclude that exp rgs pξq ď C expp a ξ q ` a ξ log exp C πa ˆ ď C ` a ξ C expp a ξ q exp exp π a πa for all ξ P R. Owing to (43), ` a ξ ˆ C π ξ log C πa (59) exp rfs pξq ď exp rgs pξq for all ξ P R. (60) By combining this observation with (59), we obtain (44), which completes the proof. Remark 3. Kummer s confluent hypergeometric function Mpa, b, zq is defined by the series where paq n is the Pochhammer symbol Mpa, b, zq ` az b ` paq z pbq! ` paq 3z 3 pbq 3 3! `, (6) paq n Γpa ` nq Γpaq apa ` qpa ` q... pa ` n q. (6) By comparing the definition of Mpa, b, zq with (53), we conclude that ˆ ˆ ` a ξ exp rfs pξq ď C expp a ξ q M,, C πa provided for all ξ P R (63) f pξq ď C expp a ξ q for all ξ P R. (64) The weaker bound (44) is sufficient for our immediate purposes, but formula (63) might serve as a basis for improved estimates on solutions of Kummer s equation. The following lemma is a special case of Formula (48). Lemma. Suppose that C ě 0 and a ą 0 are real numbers, and that f P L prq such that Then fpξq ď C exp p a ξ q for all ξ P R. (65) ˆ ` a ξ f fpξq ď C expp a ξ q a We will also make use of the following elementary observation. for all ξ P R. (66) Lemma 3. Suppose that a ą 0 is a real number. Then expp a ξ q ξ ď a exppq for all ξ P R. (67) We combine Lemmas and with (8) and (9) in order to obtain the following key estimate.
22 Theorem 6. Suppose that Γ ą 0, λ ą 0, a ą 0 and C ě 0 are real numbers such that Suppose also that f P L prq such that and that v P L prq such that 0 ď C ă aλ. (68) fpξq ď C expp a ξ q for all ξ ď? λ, (69) Suppose further that R is the operator defined via (3). Then ˆC ˆ ` a ξ ˆ R rf s pξq ď expp a ξ q λ a 8 ` ˆ π exp for all ξ P R. Proof. We define the operator R via the formula and R by the formula where W b and Ă W b are defined as in Section 5. Then for all ξ P R. We observe that ˇ ˇĂW b rf s pξqˇ ď vpξq ď Γ expp a ξ q for all ξ P R. (70) C 4πλ a ˆ C exp 4πλ ξ ` Γ (7) R rfs pξq 4 Ă W b rf s ĂW b rf s pξq (7) R rfs pξq 4λ exp rw b rf ss pξq, (73) R rf s pξq R rfs pξq ` R rfs pξq ` vpξq (74) By combining Lemma with (75) we obtain ˆ R rfs pξq ď C ` a ξ 8λ expp a ξ q a Now we observe that C? λ expp a ξ q for all ξ P R. (75) for all ξ P R. (76) W b rf s pξq ď C expp a ξ q for all ξ P R. (77) λ Combining Lemma with (77) yields ˆ ˆ ˆ R rfs pξq ď C ` a ξ C C πλ expp a ξ q exp exp a 4πλ a 4πλ ξ (78) for all ξ P R. Note that (68) ensures that the hypothesis (4) in Lemma is satisfied. We combine (76) with (78) and (70) in order to obtain (7), and by so doing we complete the proof. Remark 4. Note that Theorem 6 only requires that fpξq satisfy a bound on the interval r?λ,? λs and not on the entire real line. In the next theorem, we use Theorem 6 to bound the solution of () under an assumption on the decay of v.
23 Theorem 7. Suppose that λ ą 0, a ą 0 and Γ ě 0 are real numbers such that " λ ě 6 max Γ, *. (79) a Suppose also that v P L prq such that vpξq ď Γ expp a ξ q for all ξ P R. (80) Then there exists a solution of ψpξq of equation () such that ˆ ˆ ψpξq ď Γ exp a ξ for all ξ P R. (8) λ Proof. Due to (79) and (80), }v} ď λ 8. (8) It follows from Theorem 4 and (8) that a solution ψpξq of () is obtained as the limit of the sequence of fixed point iterates tψ n pξqu defined by the formula and the recurrence ψ 0 pξq vpξq (83) ψ n` pξq R rψ n s pξq. (84) We now derive pointwise estimates on the iterates ψ n pξq in order to establish (8). Let tβ k u 8 k 0 be the sequence of real numbers be generated by the recurrence relation with the initial value β k` β k λ ` Γ (85) β 0 Γ. (86) It can be established by induction that (79) implies that this sequence is bounded above by Γ and monotonically increasing, and hence β k converges to a real number β such that 0 ď β ď Γ. Now suppose that n ě 0 is an integer, and that ψ n pξq ď β n expp a ξ q for all ξ ď? λ. (87) When n 0, this is simply the assumption (80). The function ψ n` pξq is obtained from ψ n pξq via the formula We combine Theorem 6 with (88) and (87) to conclude that ˆβ ψ n` pξq ď expp a ξ q n ˆ ` a ξ ˆ λ a 8 ` ˆ π exp βn 4πλ a ψ n` pξq R rψ s pξq. (88) exp ˆ βn 4πλ ξ ` Γ (89) for all ξ P R. The application of Theorem 6 is justified: the hypothesis (68) is satisfied since β n ď Γ ď λ a (90) 3
24 for all integers n ě 0. We restrict ξ to the interval r?λ,? λs in (89) and use the fact that aλ ă 6, (9) which is a consequence of (79), in order to conclude that? ˆβ ψ n` pξq ď expp a ξ q n ˆ ` a λ ˆ λ a 8 ` ˆ ˆ π exp βn βn? exp λ 4πλ a 4πλ ˆβ ď expp a ξ q n ˆ λ 6 `? ˆ 8 ` ˆ ˆ π exp βn βn exp 4πλ? ` Γ πλ for all ξ ď? λ. Now we combine (9) with the inequality β n λ ď Γ λ ă 3 and the observation that ˆ 6 `? ˆ 8 ` ˆ ˆ π exp exp 7π 6? ď π in order to conclude that ˆβ ψ n` pξq ď expp a ξ q n λ ď expp a ξ q ˆβ n λ ` Γ β n` expp a ξ q ˆ 6 `? ˆ 8 ` ˆ ˆ π exp exp 7π 6? ` Γ π for all ξ ď? λ. We conclude by induction that (87) holds for all integers n ě 0. ` Γ (9) (93) (94) (95) The sequence tψ n pξqu converges to ψpξq in L prq norm (and hence a subsequence of ψ n pξq converges to ψpξq pointwise almost everywhere) and (87) holds for all integers n ě 0. Moreover, for all integers n ě 0, β n` ď Γ. From these observations we conclude that ψpξq ď Γ expp a ξ q (96) for almost all ξ ď? λ. We also observe that ψpξq is a fixed point of the operator R, so that for all ξ P R. Clearly, ψpξq R rψ s pξq (97) R rfs pξq R rgs pξq (98) for all ξ P R if fpξq gpξq for almost all ξ ď? λ, so (96) in fact holds for all ξ ď? λ. We now apply Theorem 6 to the function ψpξq (which is justified since Γ ă λ a) to conclude that ˆ4Γ ˆ ` a ξ ˆ ψpξq ď expp a ξ q λ a 8 ` ˆ ˆ Γ Γ π exp exp 4πλ a 4πλ ξ ` Γ (99) for all ξ P R. Note the distinction between (87) and (99) is that the former only holds for all ξ in the interval r?λ,? λs, while the later holds for all ξ on the real line. It follows from (79) that λa ă 6 and Γ λ ă 6. (00) 4
25 We insert these bounds into (99) in order to conclude that ˆ ˆ ` a ξ ˆ ψpξq ď Γ expp a ξ q 3λ a 8 ` ˆ ˆ π exp exp 7π πλ ξ ` for all ξ P R. Now we observe that which, when combined with (0), yields ˆˆ ψpξq ď Γ expp a ξ q 9 ` ξ 3λ (0) ˆ π exp ă 7π 6, (0) ˆ 8 ` 6 exp By rearranging the right-hand side of (03) as ˆ Γ expp a ξ q 7 ` ˆ 56 exp πλ ξ ˆ ˆ Γ exp a ˆ ξ exp λ λ ξ ˆ 7 ` ˆ 56 exp πλ ξ ` ξ λ ` ξ 9λ exp and applying Lemma 3, we arrive at the inequality ˆ ˆ ψpξq ď Γ exp a ˆ ξ λ 7 ` 56 ` from which (8) follows immediately. ˆ πλ ξ ` for all ξ P R. (03) ` ξ λ ` ξ ˆ 9λ exp πλ ξ ` exppq ` ˆ πλ ξ ` 4 33 exppq ` for all ξ P R, Suppose that ψ P L prq is a solution of (). Then the function σ defined by the formula σpxq ż 8 8 (04) exppixξqψpξq dξ (05) is a solution of the integral equation (). However, the Fourier transform of (05) might only be defined in the sense of tempered distributions and not as a Lebesgue or improper Riemann integral. If, however, we assume the function p appearing in () is an element of L prq and impose the hypotheses of Theorem 8 on the Fourier transform of p, then ψ P L prq, from which we conclude that σ is also an element of L prq. In this event, there is no difficulty in defining the Fourier transform of σ. We record these observations in the following theorem. Theorem 8. Suppose that there exist real numbers λ ą 0, Γ ą 0 and a ą 0 such that " λ ą 6 max Γ, *. (06) a Suppose also that p P L prq such that and ppξq ď Γ exp p a ξ q for all ξ P R. (07) Then there exists a solution σpxq of the integral equation () such that ˆ ˆ pσpξq ď Γ exp a ξ for all ξ P R (08) λ 5
26 Remark 5. The bound (08) implies that pσ decays faster than any polynomial, from which we conclude that σ is infinitely differentiable. 8. Approximate solution of the original equation We would like to insert the solution σ of () into the original equation (74). However, we have no guarantee that σ is in L prq, nor do we expect that pσp λq 0. As a consequence, the integrals defining T rσ s might not exist. To remedy this problem, we define a band-limited version σ b of σ by the formula pσ b pξq pσpξqbpξq, (09) where bpξq is the function used to define the operator T b. We observe that there is no difficulty in applying T to σ b since Moreover, T b rσ s T rσ b s, so that Rearranging (), we obtain where p b pxq is defined the formula pσ b p λq 0. (0) σpxq S rt rσ b ss pxq ` ppxq for all x P R. () σ b pxq S rt rσ b ss pxq ` p b pxq for all x P R, () p b pxq ppxq ` σ b pxq σpxq. (3) Using (08) and (3), we conclude that under the hypotheses of Theorem 8, }p p b } 8 ď } pσ b pσ} ż ď Γ exp ď ξ ěλ 4Γ a exp λ ď 4Γ 5a exp ˆ ˆ a λ ˆ ˆ a λ ˆ 5 6 aλ. λ ξ dξ (4) Together Theorem 8 and (4) imply Theorem. 9. Backwards error estimate In this section, we prove Theorem 3. Although both p and p b are defined on the real line, we are only concerned with solutions of () on the interval r0, s, and so we only require estimates there. Accordingly, throughout this section we use } } 8 to denote the L 8 pr0, sq norm. 6
27 We omit the proof of the following lemma, which is somewhat long and technical but entirely elementary (it can be established with the techniques found in ordinary differential equation textbooks; see, for instance, Chapter of [4]). Lemma 4. Suppose that q : R Ñ R is infinitely differentiable and strictly positive, that pptq is defined by (56), and that there exist real numbers η ą 0 and η ą 0 such that and Let η ď qptq ď η for all 0 ď t ď, (5) pptq, q ptq ď η for all 0 ď t ď. (6) ˆη k 0 η and suppose also that ɛ ą 0 is a real number such that ` 8η ` 0 η η ` (7) ɛ ă η. (8) Suppose furthermore that p b : r0, s Ñ R is an infinitely differential function such that }p p b } 8 ď ɛ expp kq. (9) Then there exists an infinitely differentiable function q b : r0, s Ñ R such that 5 ˆq b ptq q b ptq p b ptq for all 0 ď t ď (0) q b ptq 4 q b ptq q b ptq and }q q b } 8 ď ɛ. () We derive a bound on the change in solutions of the ordinary differential equation () when the coefficient qptq is perturbed. Lemma 5. Suppose that λ ą 0, ɛ ą 0, η ą 0 and η ą 0 are real numbers. Suppose also that q : r0, s Ñ R is a continuously differentiable function such that that pptq is defined by the formula (56), and that η ď qptq ď η for all 0 ď t ď, () pptq ď η for all 0 ď t ď. (3) Suppose furthermore that q b : r0, s Ñ R is a continuously differentiable function such that qptq q b ptq ď η λ exp η3{4 ɛ for all 0 ď t ď. (4) 4 If zptq is a solution of the ordinary differential equation z ptq ` λ qptqzptq 0 for all 0 ď t ď (5) and z 0 ptq is the unique solution of the ordinary differential equation z 0ptq ` λ q b ptqz 0 ptq 0 for all 0 ď t ď (6) 7
28 such that z 0 p0q zp0q and z 0p0q z p0q, then }z z 0 } 8 ď ɛ}z} 8. (7) Proof. We start by observing that the function ψptq z 0 ptq zptq is the unique solution of the initial value problem # ψ ptq ` λ qptqψptq λ fptq for all 0 ď t ď ψp0q ψ (8) p0q 0, where fptq pqptq q 0 ptqq pψptq ` zptqq. (9) We now apply the well-known Liouville-Green transformation to (8) in two steps. First, we introduce the function φptq pqptqq {4 ψptq, (30) which is the solution of the initial value problem $ & φ ptq q ptq qptq φ ptq ` λ qptqφptq pqptqq {4 λ fptq qptqpptqφptq for all 0 ď t ď 4 % φp0q φ p0q 0. Next we introduce the change of variables xptq ż t 0 (3) a qpuq du, (3) which transforms (3) into $ & φ pxq ` λ φpxq pqpxqq 3{4 λ fpxq 4 ppxqφpxq for all 0 ď x ď x % φp0q φ p0q 0, where 0 x ż 0 (33) a qpuq du. (34) We now use the Green s function for the initial value problem (33) obtained from the Liouville- Green transform to conclude that for all 0 ď x ď x, ż x ˆ sinpλpx yqq φpxq pqpyqq 3{4 λ fpyq λ 4 ppyqφpyq dy. (35) By inserting (9) into (35) and we obtain the inequality ˆ ż λ x φpxq ď }q q b } 8 ` η φpyq dy ` λ }q q b } 8 }z} 8 for all 0 ď x ď x. (36) η 4 0 We apply Gronwall s inequality (Theorem 9 in Section.5) to (36) in order to conclude that φpxq ď λ ˆˆ λ }q q b } 8 }z} 8 exp }q q b } 8 ` η x for all 0 ď x ď x. (37) η 4 η 3{4 η 3{4 8
29 Combing (30), (37) and the observation that ż a { x qpuq du ď η (38) yields the inequality for all 0 ď t ď. Now if and only if φptq ď λ η }q q b } 8 exp λ η }q q b } 8 exp 0 ˆ λ }q q b } 8 η { η 3{4 exp }z} 8 (39) η 4 ˆ λ }q q b } 8 η { exp η λ η { }q q b } 8 ă W 0 ɛη { exp η η3{4 4 η 3{4 ă ɛ (40) 4, (4) where W 0 is the branch of the Lambert W function which is real-valued and greater than on the interval r {e, 8q (see Section.3). According to Theorem 5, λ η { }q q b } 8 ă ɛη { exp η3{4, (4) η 4 implies (4). We algebraically simplify (4) in order to conclude that }q q b } 8 ă η λ exp η3{4 ɛ (43) 4 implies (39). By combining Lemmas 4 and 5 we obtain Theorem Numerical experiments In this section, we describe numerical experiments which, inter alia, illustrate one of the important consequences of the existence of nonoscillatory phase functions. Namely, that a large class of special functions can be evaluated to high accuracy using a number of operations which does not grow with order. Although the proof of Theorem suggests a numerical procedure for the construction of nonoscillatory phase functions, we utilize a different procedure here. It has the advantage that the coefficient q in the ordinary differential equation () need not be extended outside of the interval on which the nonoscillatory phase function is constructed. A paper describing this work is in preparation. The code we used for these calculations was written in Fortran and compiled with the Intel Fortran Compiler version..3. All calculations were carried out in double precision arithmetic on a desktop computer equipped with an Intel Xeon X5690 CPU running at 3.47 GHz. 9
30 0.. A nonoscillatory solution of the logarithm form of Kummer s equation. In this experiment, we illustrate Theorem in Section 4. We first construct a nonoscillatory solution r of the logarithm form of Kummer s equation r ptq 4 pr ptqq ` 4λ pexpprptqq qptqq 0 (44) on the interval r, s, where λ =,000 and q is the function r, s Ñ R defined by the formula qptq ˆ 3 ` ` 0t ` t3 cosp5tq. (45) Then we compute the 500 leading Chebyshev coefficients of q and r. We display the results of this experiment in Figures and. Figure contains plots of the functions q and r, while Figure contains a plot of the base-0 logarithms of the absolute values of the leading Chebyshev coefficients of q and r. We observe that, consistent with Theorem, the Chebyshev coefficients of both r and q decay exponentially, although those of r decay at a slightly slower rate. 0.. Evaluation of Legendre polynomials. In this experiment, we compare the cost of evaluating Legendre polynomials of large order using the standard recurrence relation with the cost of doing so with a nonoscillatory phase function. For any integer n ě 0, the Legendre polynomial P n pxq of order n is a solution of the second order differential equation p t qy ptq ty ptq ` npn ` qyptq 0. (46) Equation (46) can be put into the standard form ˆ ` n ψ nt n pt q ptq ` ψptq 0 (47) p t q by introducing the transformation ψptq? t yptq. (48) Legendre polynomials satisfy the well-known three term recurrence relation pn ` qp n` ptq pn ` qtp n ptq np n ptq. (49) See, for instance, [] for a discussion of the these and other properties of Legendre polynomials. For each of 9 values of n, we proceed as follows. We sample 000 random points t, t,..., t 000 (50) from the uniform distribution on the interval p, q. Then we evaluate the Legendre polynomial of order n using the recurrence relation (49) at each of the points t, t,..., t 000. Next, we construct a nonoscillatory phase function for the ordinary differential equation (47) and 30
31 use it evaluate the Legendre polynomial of order n at each of the points t, t,..., t 000. Finally, for each integer j,..., 000, we compute the error in the approximation of P n pt j q obtained from the nonoscillatory phase function by comparing it to the value obtained using the recurrence relation (we regard the recurrence relation as giving the more accurate approximation). The results of this experiment are shown in Table. There, each row correponds to value of n. That value is listed n, as is the time required to compute each phase function for that value of n, the average time required to evaluate the Legendre polynomial of order n using the recurrence relation, the average cost of evaluating the Legendre polynomial of order n with the nonoscillatory phase function, and the largest of the absolute errors in the approximations of the quantities obtained via the phase function method. P n pt q, P n pt q,..., P n pt 000 q This experiment reveals that, as expected, the cost of evaluating P n ptq using the recurrence relation (49) grows as Opnq while the cost of doing so with nonoscillatory phase function is independet of order. However, it also exposes a limitation of phase functions. The values of P n ptq are obtained in part by evaluating sine and cosine of a phase function whose magnitude is on the order of n. This imposes limitations on the accuracy of the method due to the well-known difficulties in evaluating periodic functions of large arguments. Figure 3 contains a plot of the nonoscillatory phase function for the equation (47) when n,000, Evaluation of Bessel functions. In this experiment, we compare the cost of evaluating Bessel functions of integer order via the standard recurrence relation with that of doing so using a nonoscillatory phase function. We will denote by J ν the Bessel function of the first kind of order ν. It is a solution of the second order differential equation t y ptq ` ty ptq ` pt ν qyptq 0, (5) which can be brought into the standard form ˆ ψ ptq ` λ {4 ψptq 0 (5) t via the transformation ψptq? t yptq. (53) An inspection of (5) reveals that J ν is nonoscillatory on the interval ˆ 0, 4ν? (54) 3
Singular integral operators and the Riesz transform
 Singular integral operators and the Riesz transform Jordan Bell jordan.bell@gmail.com Department of Mathematics, University of Toronto November 17, 017 1 Calderón-Zygmund kernels Let ω n 1 be the measure
Singular integral operators and the Riesz transform Jordan Bell jordan.bell@gmail.com Department of Mathematics, University of Toronto November 17, 017 1 Calderón-Zygmund kernels Let ω n 1 be the measure
On the asymptotics of Bessel functions in the Fresnel regime
 We introduce a version of the asymptotic expansions for Bessel functions J ν (z), Y ν (z) that is valid whenever z > ν (which is deep in the Fresnel regime), as opposed to the standard expansions that
We introduce a version of the asymptotic expansions for Bessel functions J ν (z), Y ν (z) that is valid whenever z > ν (which is deep in the Fresnel regime), as opposed to the standard expansions that
Tempered Distributions
 Tempered Distributions Lionel Fiske and Cairn Overturf May 9, 26 In the classical study of partial differential equations one requires a solution to be differentiable. While intuitively this requirement
Tempered Distributions Lionel Fiske and Cairn Overturf May 9, 26 In the classical study of partial differential equations one requires a solution to be differentiable. While intuitively this requirement
DS-GA 1002: PREREQUISITES REVIEW SOLUTIONS VLADIMIR KOBZAR
 DS-GA 2: PEEQUISIES EVIEW SOLUIONS VLADIMI KOBZA he following is a selection of questions (drawn from Mr. Bernstein s notes) for reviewing the prerequisites for DS-GA 2. Questions from Ch, 8, 9 and 2 of
DS-GA 2: PEEQUISIES EVIEW SOLUIONS VLADIMI KOBZA he following is a selection of questions (drawn from Mr. Bernstein s notes) for reviewing the prerequisites for DS-GA 2. Questions from Ch, 8, 9 and 2 of
Introduction to Differential Equations
 Introduction to Differential Equations J. M. Veal, Ph. D. version 13.08.30 Contents 1 Introduction to Differential Equations 2 1.1 Definitions and Terminology.................... 2 1.2 Initial-Value Problems.......................
Introduction to Differential Equations J. M. Veal, Ph. D. version 13.08.30 Contents 1 Introduction to Differential Equations 2 1.1 Definitions and Terminology.................... 2 1.2 Initial-Value Problems.......................
On the asymptotics of Bessel functions in the Fresnel regime
 On the asymptotics of Bessel functions in the Fresnel regime Zhu Heitman b, James Bremer c, Vladimir Rokhlin b, Bogdan Vioreanu a a Department of Mathematics, University of Michigan b Department of Computer
On the asymptotics of Bessel functions in the Fresnel regime Zhu Heitman b, James Bremer c, Vladimir Rokhlin b, Bogdan Vioreanu a a Department of Mathematics, University of Michigan b Department of Computer
arxiv: v1 [math.ca] 4 Apr 2017
![arxiv: v1 [math.ca] 4 Apr 2017 arxiv: v1 [math.ca] 4 Apr 2017](/thumbs/88/115044967.jpg) ON LOCALIZATION OF SCHRÖDINGER MEANS PER SJÖLIN Abstract. Localization properties for Schrödinger means are studied in dimension higher than one. arxiv:704.00927v [math.ca] 4 Apr 207. Introduction Let
ON LOCALIZATION OF SCHRÖDINGER MEANS PER SJÖLIN Abstract. Localization properties for Schrödinger means are studied in dimension higher than one. arxiv:704.00927v [math.ca] 4 Apr 207. Introduction Let
Tools from Lebesgue integration
 Tools from Lebesgue integration E.P. van den Ban Fall 2005 Introduction In these notes we describe some of the basic tools from the theory of Lebesgue integration. Definitions and results will be given
Tools from Lebesgue integration E.P. van den Ban Fall 2005 Introduction In these notes we describe some of the basic tools from the theory of Lebesgue integration. Definitions and results will be given
NONLINEAR EVOLUTION EQUATIONS SHORT NOTES WEEK #1
 NONLNEA EVOLUTON EQUATONS SHOT NOTES WEEK #. Free Schrödinger Equation Let Bx 2 `...`Bx 2 n denote the Laplacian on d with d ě. The initial-value problem for the free Schrödinger equation (in d space dimensions)
NONLNEA EVOLUTON EQUATONS SHOT NOTES WEEK #. Free Schrödinger Equation Let Bx 2 `...`Bx 2 n denote the Laplacian on d with d ě. The initial-value problem for the free Schrödinger equation (in d space dimensions)
REAL ANALYSIS II TAKE HOME EXAM. T. Tao s Lecture Notes Set 5
 REAL ANALYSIS II TAKE HOME EXAM CİHAN BAHRAN T. Tao s Lecture Notes Set 5 1. Suppose that te 1, e 2, e 3,... u is a countable orthonormal system in a complex Hilbert space H, and c 1, c 2,... is a sequence
REAL ANALYSIS II TAKE HOME EXAM CİHAN BAHRAN T. Tao s Lecture Notes Set 5 1. Suppose that te 1, e 2, e 3,... u is a countable orthonormal system in a complex Hilbert space H, and c 1, c 2,... is a sequence
The Laplace Transform
 C H A P T E R 6 The Laplace Transform Many practical engineering problems involve mechanical or electrical systems acted on by discontinuous or impulsive forcing terms. For such problems the methods described
C H A P T E R 6 The Laplace Transform Many practical engineering problems involve mechanical or electrical systems acted on by discontinuous or impulsive forcing terms. For such problems the methods described
A Bowl of Kernels. By Nuriye Atasever, Cesar Alvarado, and Patrick Doherty. December 03, 2013
 December 03, 203 Introduction When we studied Fourier series we improved convergence by convolving with the Fejer and Poisson kernels on T. The analogous Fejer and Poisson kernels on the real line help
December 03, 203 Introduction When we studied Fourier series we improved convergence by convolving with the Fejer and Poisson kernels on T. The analogous Fejer and Poisson kernels on the real line help
NOTES WEEK 15 DAY 1 SCOT ADAMS
 NOTES WEEK 15 DAY 1 SCOT ADAMS We fix some notation for the entire class today: Let n P N, W : R n, : 2 P N pw q, W : LpW, W q, I : id W P W, z : 0 W 0 n. Note that W LpR n, R n q. Recall, for all T P
NOTES WEEK 15 DAY 1 SCOT ADAMS We fix some notation for the entire class today: Let n P N, W : R n, : 2 P N pw q, W : LpW, W q, I : id W P W, z : 0 W 0 n. Note that W LpR n, R n q. Recall, for all T P
Mathematics 324 Riemann Zeta Function August 5, 2005
 Mathematics 324 Riemann Zeta Function August 5, 25 In this note we give an introduction to the Riemann zeta function, which connects the ideas of real analysis with the arithmetic of the integers. Define
Mathematics 324 Riemann Zeta Function August 5, 25 In this note we give an introduction to the Riemann zeta function, which connects the ideas of real analysis with the arithmetic of the integers. Define
Integration and Fourier Theory. Lecture 14
 Integration and Fourier Theory Lecture 4 Morten Grud Rasmussen March 5, 03 Trigonometric Series Denote the unit circle in the complex plane by T tx P C x u ( T for torus ). Note that R Q t ÞÑ e it P T
Integration and Fourier Theory Lecture 4 Morten Grud Rasmussen March 5, 03 Trigonometric Series Denote the unit circle in the complex plane by T tx P C x u ( T for torus ). Note that R Q t ÞÑ e it P T
arxiv: v2 [math.ca] 13 May 2015
![arxiv: v2 [math.ca] 13 May 2015 arxiv: v2 [math.ca] 13 May 2015](/thumbs/88/114667751.jpg) ON THE CLOSURE OF TRANSLATION-DILATION INVARIANT LINEAR SPACES OF POLYNOMIALS arxiv:1505.02370v2 [math.ca] 13 May 2015 J. M. ALMIRA AND L. SZÉKELYHIDI Abstract. Assume that a linear space of real polynomials
ON THE CLOSURE OF TRANSLATION-DILATION INVARIANT LINEAR SPACES OF POLYNOMIALS arxiv:1505.02370v2 [math.ca] 13 May 2015 J. M. ALMIRA AND L. SZÉKELYHIDI Abstract. Assume that a linear space of real polynomials
MAT 128A - Practice Midterm Exam
 MAT 8A - Practice Midterm Exam Karry Wong October 3, 08 Problem (True or False) Given that f : r, s Ñ R is a continuous function, and that ta n u are its Chebyshev coefficients. Also, for N P N, p N pxq
MAT 8A - Practice Midterm Exam Karry Wong October 3, 08 Problem (True or False) Given that f : r, s Ñ R is a continuous function, and that ta n u are its Chebyshev coefficients. Also, for N P N, p N pxq
On the asymptotics of Bessel functions in the Fresnel regime
 On the asymptotics of Bessel functions in the Fresnel regime Zhu Heitman a, James Bremer b, Vladimir Rokhlin a, Bogdan Vioreanu c a Department of Computer Science, Yale University b Department of Mathematics,
On the asymptotics of Bessel functions in the Fresnel regime Zhu Heitman a, James Bremer b, Vladimir Rokhlin a, Bogdan Vioreanu c a Department of Computer Science, Yale University b Department of Mathematics,
Introduction to Numerical Analysis
 Introduction to Numerical Analysis Lecture Notes for SI 507 Authors: S. Baskar and S. Sivaji Ganesh Department of Mathematics Indian Institute of Technology Bombay Powai, Mumbai 400 076. Contents 1 Mathematical
Introduction to Numerical Analysis Lecture Notes for SI 507 Authors: S. Baskar and S. Sivaji Ganesh Department of Mathematics Indian Institute of Technology Bombay Powai, Mumbai 400 076. Contents 1 Mathematical
Mariusz Jurkiewicz, Bogdan Przeradzki EXISTENCE OF SOLUTIONS FOR HIGHER ORDER BVP WITH PARAMETERS VIA CRITICAL POINT THEORY
 DEMONSTRATIO MATHEMATICA Vol. XLVIII No 1 215 Mariusz Jurkiewicz, Bogdan Przeradzki EXISTENCE OF SOLUTIONS FOR HIGHER ORDER BVP WITH PARAMETERS VIA CRITICAL POINT THEORY Communicated by E. Zadrzyńska Abstract.
DEMONSTRATIO MATHEMATICA Vol. XLVIII No 1 215 Mariusz Jurkiewicz, Bogdan Przeradzki EXISTENCE OF SOLUTIONS FOR HIGHER ORDER BVP WITH PARAMETERS VIA CRITICAL POINT THEORY Communicated by E. Zadrzyńska Abstract.
Fast algorithms for Jacobi expansions via nonoscillatory phase functions
 Fast algorithms for Jacobi expansions via nonoscillatory phase functions James Bremer a, Haizhao Yang b a Department of Mathematics, University of California, Davis b Department of Mathematics, National
Fast algorithms for Jacobi expansions via nonoscillatory phase functions James Bremer a, Haizhao Yang b a Department of Mathematics, University of California, Davis b Department of Mathematics, National
1.5 Approximate Identities
 38 1 The Fourier Transform on L 1 (R) which are dense subspaces of L p (R). On these domains, P : D P L p (R) and M : D M L p (R). Show, however, that P and M are unbounded even when restricted to these
38 1 The Fourier Transform on L 1 (R) which are dense subspaces of L p (R). On these domains, P : D P L p (R) and M : D M L p (R). Show, however, that P and M are unbounded even when restricted to these
An algorithm for the rapid numerical evaluation of Bessel functions of real orders and arguments
 An algorithm for the rapid numerical evaluation of Bessel functions of real orders and arguments James Bremer a a Department of Mathematics, University of California, Davis Abstract We describe a method
An algorithm for the rapid numerical evaluation of Bessel functions of real orders and arguments James Bremer a a Department of Mathematics, University of California, Davis Abstract We describe a method
Self-Concordant Barrier Functions for Convex Optimization
 Appendix F Self-Concordant Barrier Functions for Convex Optimization F.1 Introduction In this Appendix we present a framework for developing polynomial-time algorithms for the solution of convex optimization
Appendix F Self-Concordant Barrier Functions for Convex Optimization F.1 Introduction In this Appendix we present a framework for developing polynomial-time algorithms for the solution of convex optimization
Almost Conservation Laws for KdV and Cubic NLS. UROP Final Paper, Summer 2018
 Almost Conservation Laws for KdV and Cubic NLS UROP Final Paper, Summer 2018 Zixuan Xu Mentor: Ricardo Grande Izquierdo Project suggested by: Gigliola Staffilani Abstract In this paper, we explore the
Almost Conservation Laws for KdV and Cubic NLS UROP Final Paper, Summer 2018 Zixuan Xu Mentor: Ricardo Grande Izquierdo Project suggested by: Gigliola Staffilani Abstract In this paper, we explore the
Non-asymptotic Analysis of Bandlimited Functions. Andrei Osipov Research Report YALEU/DCS/TR-1449 Yale University January 12, 2012
 Prolate spheroidal wave functions PSWFs play an important role in various areas, from physics e.g. wave phenomena, fluid dynamics to engineering e.g. signal processing, filter design. Even though the significance
Prolate spheroidal wave functions PSWFs play an important role in various areas, from physics e.g. wave phenomena, fluid dynamics to engineering e.g. signal processing, filter design. Even though the significance
Mathematical Finance
 ETH Zürich, HS 2017 Prof. Josef Teichmann Matti Kiiski Mathematical Finance Solution sheet 14 Solution 14.1 Denote by Z pz t q tpr0,t s the density process process of Q with respect to P. (a) The second
ETH Zürich, HS 2017 Prof. Josef Teichmann Matti Kiiski Mathematical Finance Solution sheet 14 Solution 14.1 Denote by Z pz t q tpr0,t s the density process process of Q with respect to P. (a) The second
MATH 260 Homework assignment 8 March 21, px 2yq dy. (c) Where C is the part of the line y x, parametrized any way you like.
 MATH 26 Homework assignment 8 March 2, 23. Evaluate the line integral x 2 y dx px 2yq dy (a) Where is the part of the parabola y x 2 from p, q to p, q, parametrized as x t, y t 2 for t. (b) Where is the
MATH 26 Homework assignment 8 March 2, 23. Evaluate the line integral x 2 y dx px 2yq dy (a) Where is the part of the parabola y x 2 from p, q to p, q, parametrized as x t, y t 2 for t. (b) Where is the
Outline of Fourier Series: Math 201B
 Outline of Fourier Series: Math 201B February 24, 2011 1 Functions and convolutions 1.1 Periodic functions Periodic functions. Let = R/(2πZ) denote the circle, or onedimensional torus. A function f : C
Outline of Fourier Series: Math 201B February 24, 2011 1 Functions and convolutions 1.1 Periodic functions Periodic functions. Let = R/(2πZ) denote the circle, or onedimensional torus. A function f : C
be the set of complex valued 2π-periodic functions f on R such that
 . Fourier series. Definition.. Given a real number P, we say a complex valued function f on R is P -periodic if f(x + P ) f(x) for all x R. We let be the set of complex valued -periodic functions f on
. Fourier series. Definition.. Given a real number P, we say a complex valued function f on R is P -periodic if f(x + P ) f(x) for all x R. We let be the set of complex valued -periodic functions f on
C*-algebras - a case study
 - a case study Definition Suppose that H is a Hilbert space. A C -algebra is an operator-norm closed -subalgebra of BpHq. are closed under ultraproducts and subalgebras so they should be captured by continous
- a case study Definition Suppose that H is a Hilbert space. A C -algebra is an operator-norm closed -subalgebra of BpHq. are closed under ultraproducts and subalgebras so they should be captured by continous
THE INVERSE FUNCTION THEOREM
 THE INVERSE FUNCTION THEOREM W. PATRICK HOOPER The implicit function theorem is the following result: Theorem 1. Let f be a C 1 function from a neighborhood of a point a R n into R n. Suppose A = Df(a)
THE INVERSE FUNCTION THEOREM W. PATRICK HOOPER The implicit function theorem is the following result: Theorem 1. Let f be a C 1 function from a neighborhood of a point a R n into R n. Suppose A = Df(a)
An introduction to Mathematical Theory of Control
 An introduction to Mathematical Theory of Control Vasile Staicu University of Aveiro UNICA, May 2018 Vasile Staicu (University of Aveiro) An introduction to Mathematical Theory of Control UNICA, May 2018
An introduction to Mathematical Theory of Control Vasile Staicu University of Aveiro UNICA, May 2018 Vasile Staicu (University of Aveiro) An introduction to Mathematical Theory of Control UNICA, May 2018
Research Statement. James Bremer Department of Mathematics, University of California, Davis
 Research Statement James Bremer Department of Mathematics, University of California, Davis Email: bremer@math.ucdavis.edu Webpage: https.math.ucdavis.edu/ bremer I work in the field of numerical analysis,
Research Statement James Bremer Department of Mathematics, University of California, Davis Email: bremer@math.ucdavis.edu Webpage: https.math.ucdavis.edu/ bremer I work in the field of numerical analysis,
CHAPTER 6. Differentiation
 CHPTER 6 Differentiation The generalization from elementary calculus of differentiation in measure theory is less obvious than that of integration, and the methods of treating it are somewhat involved.
CHPTER 6 Differentiation The generalization from elementary calculus of differentiation in measure theory is less obvious than that of integration, and the methods of treating it are somewhat involved.
An improved convergence theorem for the Newton method under relaxed continuity assumptions
 An improved convergence theorem for the Newton method under relaxed continuity assumptions Andrei Dubin ITEP, 117218, BCheremushinsaya 25, Moscow, Russia Abstract In the framewor of the majorization technique,
An improved convergence theorem for the Newton method under relaxed continuity assumptions Andrei Dubin ITEP, 117218, BCheremushinsaya 25, Moscow, Russia Abstract In the framewor of the majorization technique,
Introductions to ExpIntegralEi
 Introductions to ExpIntegralEi Introduction to the exponential integrals General The exponential-type integrals have a long history. After the early developments of differential calculus, mathematicians
Introductions to ExpIntegralEi Introduction to the exponential integrals General The exponential-type integrals have a long history. After the early developments of differential calculus, mathematicians
Lecture 4: Numerical solution of ordinary differential equations
 Lecture 4: Numerical solution of ordinary differential equations Department of Mathematics, ETH Zürich General explicit one-step method: Consistency; Stability; Convergence. High-order methods: Taylor
Lecture 4: Numerical solution of ordinary differential equations Department of Mathematics, ETH Zürich General explicit one-step method: Consistency; Stability; Convergence. High-order methods: Taylor
Lecture 15: Quadratic approximation and the second variation formula
 Lecture 15: Quadratic approximation and the second variation formula Symmetric ilinear forms and inner products (15.1) The associated self-adjoint operator. Let V e a finite dimensional real vector space
Lecture 15: Quadratic approximation and the second variation formula Symmetric ilinear forms and inner products (15.1) The associated self-adjoint operator. Let V e a finite dimensional real vector space
We denote the space of distributions on Ω by D ( Ω) 2.
 Sep. 1 0, 008 Distributions Distributions are generalized functions. Some familiarity with the theory of distributions helps understanding of various function spaces which play important roles in the study
Sep. 1 0, 008 Distributions Distributions are generalized functions. Some familiarity with the theory of distributions helps understanding of various function spaces which play important roles in the study
ADVANCE TOPICS IN ANALYSIS - REAL. 8 September September 2011
 ADVANCE TOPICS IN ANALYSIS - REAL NOTES COMPILED BY KATO LA Introductions 8 September 011 15 September 011 Nested Interval Theorem: If A 1 ra 1, b 1 s, A ra, b s,, A n ra n, b n s, and A 1 Ě A Ě Ě A n
ADVANCE TOPICS IN ANALYSIS - REAL NOTES COMPILED BY KATO LA Introductions 8 September 011 15 September 011 Nested Interval Theorem: If A 1 ra 1, b 1 s, A ra, b s,, A n ra n, b n s, and A 1 Ě A Ě Ě A n
Contents. 2 Sequences and Series Approximation by Rational Numbers Sequences Basics on Sequences...
 Contents 1 Real Numbers: The Basics... 1 1.1 Notation... 1 1.2 Natural Numbers... 4 1.3 Integers... 5 1.4 Fractions and Rational Numbers... 10 1.4.1 Introduction... 10 1.4.2 Powers and Radicals of Rational
Contents 1 Real Numbers: The Basics... 1 1.1 Notation... 1 1.2 Natural Numbers... 4 1.3 Integers... 5 1.4 Fractions and Rational Numbers... 10 1.4.1 Introduction... 10 1.4.2 Powers and Radicals of Rational
Homework for MATH 4604 (Advanced Calculus II) Spring 2017
 Homework for MATH 4604 (Advanced Calculus II) Spring 2017 Homework 14: Due on Tuesday 2 May 55. Let m, n P N, A P R mˆn and v P R n. Show: L A pvq 2 ď A 2 v 2. 56. Let n P N and let A P R nˆn. Let I n
Homework for MATH 4604 (Advanced Calculus II) Spring 2017 Homework 14: Due on Tuesday 2 May 55. Let m, n P N, A P R mˆn and v P R n. Show: L A pvq 2 ď A 2 v 2. 56. Let n P N and let A P R nˆn. Let I n
SPRING 2006 PRELIMINARY EXAMINATION SOLUTIONS
 SPRING 006 PRELIMINARY EXAMINATION SOLUTIONS 1A. Let G be the subgroup of the free abelian group Z 4 consisting of all integer vectors (x, y, z, w) such that x + 3y + 5z + 7w = 0. (a) Determine a linearly
SPRING 006 PRELIMINARY EXAMINATION SOLUTIONS 1A. Let G be the subgroup of the free abelian group Z 4 consisting of all integer vectors (x, y, z, w) such that x + 3y + 5z + 7w = 0. (a) Determine a linearly
MATH 360 Final Exam Thursday, December 14, a n 2. a n 1 1
 MATH 36 Final Exam Thursday, December 4, 27 Name. The sequence ta n u is defined by a and a n (a) Prove that lim a n exists by showing that ta n u is bounded and monotonic and invoking an appropriate result.
MATH 36 Final Exam Thursday, December 4, 27 Name. The sequence ta n u is defined by a and a n (a) Prove that lim a n exists by showing that ta n u is bounded and monotonic and invoking an appropriate result.
MATH 220: MIDTERM OCTOBER 29, 2015
 MATH 22: MIDTERM OCTOBER 29, 25 This is a closed book, closed notes, no electronic devices exam. There are 5 problems. Solve Problems -3 and one of Problems 4 and 5. Write your solutions to problems and
MATH 22: MIDTERM OCTOBER 29, 25 This is a closed book, closed notes, no electronic devices exam. There are 5 problems. Solve Problems -3 and one of Problems 4 and 5. Write your solutions to problems and
Inner Product Spaces An inner product on a complex linear space X is a function x y from X X C such that. (1) (2) (3) x x > 0 for x 0.
 Inner Product Spaces An inner product on a complex linear space X is a function x y from X X C such that (1) () () (4) x 1 + x y = x 1 y + x y y x = x y x αy = α x y x x > 0 for x 0 Consequently, (5) (6)
Inner Product Spaces An inner product on a complex linear space X is a function x y from X X C such that (1) () () (4) x 1 + x y = x 1 y + x y y x = x y x αy = α x y x x > 0 for x 0 Consequently, (5) (6)
6 Lecture 6: More constructions with Huber rings
 6 Lecture 6: More constructions with Huber rings 6.1 Introduction Recall from Definition 5.2.4 that a Huber ring is a commutative topological ring A equipped with an open subring A 0, such that the subspace
6 Lecture 6: More constructions with Huber rings 6.1 Introduction Recall from Definition 5.2.4 that a Huber ring is a commutative topological ring A equipped with an open subring A 0, such that the subspace
LECTURE NOTES ELEMENTARY NUMERICAL METHODS. Eusebius Doedel
 LECTURE NOTES on ELEMENTARY NUMERICAL METHODS Eusebius Doedel TABLE OF CONTENTS Vector and Matrix Norms 1 Banach Lemma 20 The Numerical Solution of Linear Systems 25 Gauss Elimination 25 Operation Count
LECTURE NOTES on ELEMENTARY NUMERICAL METHODS Eusebius Doedel TABLE OF CONTENTS Vector and Matrix Norms 1 Banach Lemma 20 The Numerical Solution of Linear Systems 25 Gauss Elimination 25 Operation Count
A LOWER BOUND ON BLOWUP RATES FOR THE 3D INCOMPRESSIBLE EULER EQUATION AND A SINGLE EXPONENTIAL BEALE-KATO-MAJDA ESTIMATE. 1.
 A LOWER BOUND ON BLOWUP RATES FOR THE 3D INCOMPRESSIBLE EULER EQUATION AND A SINGLE EXPONENTIAL BEALE-KATO-MAJDA ESTIMATE THOMAS CHEN AND NATAŠA PAVLOVIĆ Abstract. We prove a Beale-Kato-Majda criterion
A LOWER BOUND ON BLOWUP RATES FOR THE 3D INCOMPRESSIBLE EULER EQUATION AND A SINGLE EXPONENTIAL BEALE-KATO-MAJDA ESTIMATE THOMAS CHEN AND NATAŠA PAVLOVIĆ Abstract. We prove a Beale-Kato-Majda criterion
Euler Equations: local existence
 Euler Equations: local existence Mat 529, Lesson 2. 1 Active scalars formulation We start with a lemma. Lemma 1. Assume that w is a magnetization variable, i.e. t w + u w + ( u) w = 0. If u = Pw then u
Euler Equations: local existence Mat 529, Lesson 2. 1 Active scalars formulation We start with a lemma. Lemma 1. Assume that w is a magnetization variable, i.e. t w + u w + ( u) w = 0. If u = Pw then u
PART IV Spectral Methods
 PART IV Spectral Methods Additional References: R. Peyret, Spectral methods for incompressible viscous flow, Springer (2002), B. Mercier, An introduction to the numerical analysis of spectral methods,
PART IV Spectral Methods Additional References: R. Peyret, Spectral methods for incompressible viscous flow, Springer (2002), B. Mercier, An introduction to the numerical analysis of spectral methods,
Finite-dimensional spaces. C n is the space of n-tuples x = (x 1,..., x n ) of complex numbers. It is a Hilbert space with the inner product
 Chapter 4 Hilbert Spaces 4.1 Inner Product Spaces Inner Product Space. A complex vector space E is called an inner product space (or a pre-hilbert space, or a unitary space) if there is a mapping (, )
Chapter 4 Hilbert Spaces 4.1 Inner Product Spaces Inner Product Space. A complex vector space E is called an inner product space (or a pre-hilbert space, or a unitary space) if there is a mapping (, )
Asymptotic Analysis 1: Limits and Asymptotic Equality
 Asymptotic Analysis 1: Limits and Asymptotic Equality Andreas Klappenecker and Hyunyoung Lee Texas A&M University 1 / 15 Motivation In asymptotic analysis, our goal is to compare a function f pnq with
Asymptotic Analysis 1: Limits and Asymptotic Equality Andreas Klappenecker and Hyunyoung Lee Texas A&M University 1 / 15 Motivation In asymptotic analysis, our goal is to compare a function f pnq with
Scattered Data Interpolation with Polynomial Precision and Conditionally Positive Definite Functions
 Chapter 3 Scattered Data Interpolation with Polynomial Precision and Conditionally Positive Definite Functions 3.1 Scattered Data Interpolation with Polynomial Precision Sometimes the assumption on the
Chapter 3 Scattered Data Interpolation with Polynomial Precision and Conditionally Positive Definite Functions 3.1 Scattered Data Interpolation with Polynomial Precision Sometimes the assumption on the
Uniqueness theorem for p-biharmonic equations
 Electronic Journal of Differential Equations, Vol. 2222, No. 53, pp. 1 17. ISSN: 172-6691. URL: http://ejde.math.swt.edu or http://ejde.math.unt.edu ftp ejde.math.swt.edu login: ftp Uniqueness theorem
Electronic Journal of Differential Equations, Vol. 2222, No. 53, pp. 1 17. ISSN: 172-6691. URL: http://ejde.math.swt.edu or http://ejde.math.unt.edu ftp ejde.math.swt.edu login: ftp Uniqueness theorem
NOTES WEEK 14 DAY 2 SCOT ADAMS
 NOTES WEEK 14 DAY 2 SCOT ADAMS For this lecture, we fix the following: Let n P N, let W : R n, let : 2 P N pr n q and let I : id R n : R n Ñ R n be the identity map, defined by Ipxq x. For any h : W W,
NOTES WEEK 14 DAY 2 SCOT ADAMS For this lecture, we fix the following: Let n P N, let W : R n, let : 2 P N pr n q and let I : id R n : R n Ñ R n be the identity map, defined by Ipxq x. For any h : W W,
Considering our result for the sum and product of analytic functions, this means that for (a 0, a 1,..., a N ) C N+1, the polynomial.
 Lecture 3 Usual complex functions MATH-GA 245.00 Complex Variables Polynomials. Construction f : z z is analytic on all of C since its real and imaginary parts satisfy the Cauchy-Riemann relations and
Lecture 3 Usual complex functions MATH-GA 245.00 Complex Variables Polynomials. Construction f : z z is analytic on all of C since its real and imaginary parts satisfy the Cauchy-Riemann relations and
Vector Spaces. Vector space, ν, over the field of complex numbers, C, is a set of elements a, b,..., satisfying the following axioms.
 Vector Spaces Vector space, ν, over the field of complex numbers, C, is a set of elements a, b,..., satisfying the following axioms. For each two vectors a, b ν there exists a summation procedure: a +
Vector Spaces Vector space, ν, over the field of complex numbers, C, is a set of elements a, b,..., satisfying the following axioms. For each two vectors a, b ν there exists a summation procedure: a +
A COUNTEREXAMPLE TO AN ENDPOINT BILINEAR STRICHARTZ INEQUALITY TERENCE TAO. t L x (R R2 ) f L 2 x (R2 )
 Electronic Journal of Differential Equations, Vol. 2006(2006), No. 5, pp. 6. ISSN: 072-669. URL: http://ejde.math.txstate.edu or http://ejde.math.unt.edu ftp ejde.math.txstate.edu (login: ftp) A COUNTEREXAMPLE
Electronic Journal of Differential Equations, Vol. 2006(2006), No. 5, pp. 6. ISSN: 072-669. URL: http://ejde.math.txstate.edu or http://ejde.math.unt.edu ftp ejde.math.txstate.edu (login: ftp) A COUNTEREXAMPLE
DOUBLE SERIES AND PRODUCTS OF SERIES
 DOUBLE SERIES AND PRODUCTS OF SERIES KENT MERRYFIELD. Various ways to add up a doubly-indexed series: Let be a sequence of numbers depending on the two variables j and k. I will assume that 0 j < and 0
DOUBLE SERIES AND PRODUCTS OF SERIES KENT MERRYFIELD. Various ways to add up a doubly-indexed series: Let be a sequence of numbers depending on the two variables j and k. I will assume that 0 j < and 0
Probability and Measure
 Part II Year 2018 2017 2016 2015 2014 2013 2012 2011 2010 2009 2008 2007 2006 2005 2018 84 Paper 4, Section II 26J Let (X, A) be a measurable space. Let T : X X be a measurable map, and µ a probability
Part II Year 2018 2017 2016 2015 2014 2013 2012 2011 2010 2009 2008 2007 2006 2005 2018 84 Paper 4, Section II 26J Let (X, A) be a measurable space. Let T : X X be a measurable map, and µ a probability
Higher-order ordinary differential equations
 Higher-order ordinary differential equations 1 A linear ODE of general order n has the form a n (x) dn y dx n +a n 1(x) dn 1 y dx n 1 + +a 1(x) dy dx +a 0(x)y = f(x). If f(x) = 0 then the equation is called
Higher-order ordinary differential equations 1 A linear ODE of general order n has the form a n (x) dn y dx n +a n 1(x) dn 1 y dx n 1 + +a 1(x) dy dx +a 0(x)y = f(x). If f(x) = 0 then the equation is called
Approximation of Weighted Local Mean Operators
 Approximation of Weighted Local ean Operators Jianzhong Wang Department of athematics and Statistics Sam Houston State University Huntsville, TX 7734 Abstract Recently, weighted local mean operators are
Approximation of Weighted Local ean Operators Jianzhong Wang Department of athematics and Statistics Sam Houston State University Huntsville, TX 7734 Abstract Recently, weighted local mean operators are
Sobolev Spaces. Chapter 10
 Chapter 1 Sobolev Spaces We now define spaces H 1,p (R n ), known as Sobolev spaces. For u to belong to H 1,p (R n ), we require that u L p (R n ) and that u have weak derivatives of first order in L p
Chapter 1 Sobolev Spaces We now define spaces H 1,p (R n ), known as Sobolev spaces. For u to belong to H 1,p (R n ), we require that u L p (R n ) and that u have weak derivatives of first order in L p
at time t, in dimension d. The index i varies in a countable set I. We call configuration the family, denoted generically by Φ: U (x i (t) x j (t))
 Notations In this chapter we investigate infinite systems of interacting particles subject to Newtonian dynamics Each particle is characterized by its position an velocity x i t, v i t R d R d at time
Notations In this chapter we investigate infinite systems of interacting particles subject to Newtonian dynamics Each particle is characterized by its position an velocity x i t, v i t R d R d at time
Entropy and Ergodic Theory Notes 22: The Kolmogorov Sinai entropy of a measure-preserving system
 Entropy and Ergodic Theory Notes 22: The Kolmogorov Sinai entropy of a measure-preserving system 1 Joinings and channels 1.1 Joinings Definition 1. If px, µ, T q and py, ν, Sq are MPSs, then a joining
Entropy and Ergodic Theory Notes 22: The Kolmogorov Sinai entropy of a measure-preserving system 1 Joinings and channels 1.1 Joinings Definition 1. If px, µ, T q and py, ν, Sq are MPSs, then a joining
Continued fractions for complex numbers and values of binary quadratic forms
 arxiv:110.3754v1 [math.nt] 18 Feb 011 Continued fractions for complex numbers and values of binary quadratic forms S.G. Dani and Arnaldo Nogueira February 1, 011 Abstract We describe various properties
arxiv:110.3754v1 [math.nt] 18 Feb 011 Continued fractions for complex numbers and values of binary quadratic forms S.G. Dani and Arnaldo Nogueira February 1, 011 Abstract We describe various properties
arxiv: v4 [math.ap] 14 Apr 2016
![arxiv: v4 [math.ap] 14 Apr 2016 arxiv: v4 [math.ap] 14 Apr 2016](/thumbs/76/73571665.jpg) SOME OBSEVATIONS ON THE GEEN FUNCTION FO THE BALL IN THE FACTIONAL LAPLACE FAMEWOK arxiv:5.6468v4 [math.ap] 4 Apr 6 CLAUDIA BUCU Claudia Bucur Dipartimento di Matematica Federigo Enriques Università degli
SOME OBSEVATIONS ON THE GEEN FUNCTION FO THE BALL IN THE FACTIONAL LAPLACE FAMEWOK arxiv:5.6468v4 [math.ap] 4 Apr 6 CLAUDIA BUCU Claudia Bucur Dipartimento di Matematica Federigo Enriques Università degli
# 1 χ ramified χ unramified
 LECTURE 14: LOCAL UNCTIONAL EQUATION LECTURE BY ASI ZAMAN STANORD NUMBER THEORY LEARNING SEMINAR JANUARY 31, 018 NOTES BY DAN DORE AND ASI ZAMAN Let be a local field. We fix ψ P p, ψ 1, such that ψ p d
LECTURE 14: LOCAL UNCTIONAL EQUATION LECTURE BY ASI ZAMAN STANORD NUMBER THEORY LEARNING SEMINAR JANUARY 31, 018 NOTES BY DAN DORE AND ASI ZAMAN Let be a local field. We fix ψ P p, ψ 1, such that ψ p d
Sobolev spaces. May 18
 Sobolev spaces May 18 2015 1 Weak derivatives The purpose of these notes is to give a very basic introduction to Sobolev spaces. More extensive treatments can e.g. be found in the classical references
Sobolev spaces May 18 2015 1 Weak derivatives The purpose of these notes is to give a very basic introduction to Sobolev spaces. More extensive treatments can e.g. be found in the classical references
Introduction to Real Analysis Alternative Chapter 1
 Christopher Heil Introduction to Real Analysis Alternative Chapter 1 A Primer on Norms and Banach Spaces Last Updated: March 10, 2018 c 2018 by Christopher Heil Chapter 1 A Primer on Norms and Banach Spaces
Christopher Heil Introduction to Real Analysis Alternative Chapter 1 A Primer on Norms and Banach Spaces Last Updated: March 10, 2018 c 2018 by Christopher Heil Chapter 1 A Primer on Norms and Banach Spaces
d 1 µ 2 Θ = 0. (4.1) consider first the case of m = 0 where there is no azimuthal dependence on the angle φ.
 4 Legendre Functions In order to investigate the solutions of Legendre s differential equation d ( µ ) dθ ] ] + l(l + ) m dµ dµ µ Θ = 0. (4.) consider first the case of m = 0 where there is no azimuthal
4 Legendre Functions In order to investigate the solutions of Legendre s differential equation d ( µ ) dθ ] ] + l(l + ) m dµ dµ µ Θ = 0. (4.) consider first the case of m = 0 where there is no azimuthal
Some Thoughts on Guaranteed Function Approximation Satisfying Relative Error
 Some Thoughts on Guaranteed Function Approximation Satisfying Relative Error Fred J. Hickernell Department of Applied Mathematics, Illinois Institute of Technology hickernell@iit.edu mypages.iit.edu/~hickernell
Some Thoughts on Guaranteed Function Approximation Satisfying Relative Error Fred J. Hickernell Department of Applied Mathematics, Illinois Institute of Technology hickernell@iit.edu mypages.iit.edu/~hickernell
Chapter 1. Preliminaries. The purpose of this chapter is to provide some basic background information. Linear Space. Hilbert Space.
 Chapter 1 Preliminaries The purpose of this chapter is to provide some basic background information. Linear Space Hilbert Space Basic Principles 1 2 Preliminaries Linear Space The notion of linear space
Chapter 1 Preliminaries The purpose of this chapter is to provide some basic background information. Linear Space Hilbert Space Basic Principles 1 2 Preliminaries Linear Space The notion of linear space
Putzer s Algorithm. Norman Lebovitz. September 8, 2016
 Putzer s Algorithm Norman Lebovitz September 8, 2016 1 Putzer s algorithm The differential equation dx = Ax, (1) dt where A is an n n matrix of constants, possesses the fundamental matrix solution exp(at),
Putzer s Algorithm Norman Lebovitz September 8, 2016 1 Putzer s algorithm The differential equation dx = Ax, (1) dt where A is an n n matrix of constants, possesses the fundamental matrix solution exp(at),
Convex Optimization Notes
 Convex Optimization Notes Jonathan Siegel January 2017 1 Convex Analysis This section is devoted to the study of convex functions f : B R {+ } and convex sets U B, for B a Banach space. The case of B =
Convex Optimization Notes Jonathan Siegel January 2017 1 Convex Analysis This section is devoted to the study of convex functions f : B R {+ } and convex sets U B, for B a Banach space. The case of B =
Topics in Fourier analysis - Lecture 2.
 Topics in Fourier analysis - Lecture 2. Akos Magyar 1 Infinite Fourier series. In this section we develop the basic theory of Fourier series of periodic functions of one variable, but only to the extent
Topics in Fourier analysis - Lecture 2. Akos Magyar 1 Infinite Fourier series. In this section we develop the basic theory of Fourier series of periodic functions of one variable, but only to the extent
Let R be the line parameterized by x. Let f be a complex function on R that is integrable. The Fourier transform ˆf = F f is. e ikx f(x) dx. (1.
 Chapter 1 Fourier transforms 1.1 Introduction Let R be the line parameterized by x. Let f be a complex function on R that is integrable. The Fourier transform ˆf = F f is ˆf(k) = e ikx f(x) dx. (1.1) It
Chapter 1 Fourier transforms 1.1 Introduction Let R be the line parameterized by x. Let f be a complex function on R that is integrable. The Fourier transform ˆf = F f is ˆf(k) = e ikx f(x) dx. (1.1) It
MATH 205C: STATIONARY PHASE LEMMA
 MATH 205C: STATIONARY PHASE LEMMA For ω, consider an integral of the form I(ω) = e iωf(x) u(x) dx, where u Cc (R n ) complex valued, with support in a compact set K, and f C (R n ) real valued. Thus, I(ω)
MATH 205C: STATIONARY PHASE LEMMA For ω, consider an integral of the form I(ω) = e iωf(x) u(x) dx, where u Cc (R n ) complex valued, with support in a compact set K, and f C (R n ) real valued. Thus, I(ω)
Fourier transform, assorted stuff...
 Fourier transform, assorted stuff... M. Carlsson October 9, 2013 1 An example from control theory To get an idea of where real applications are, lets begin with an example from control theory. Example
Fourier transform, assorted stuff... M. Carlsson October 9, 2013 1 An example from control theory To get an idea of where real applications are, lets begin with an example from control theory. Example
MATH 260 Class notes/questions January 10, 2013
 MATH 26 Class notes/questions January, 2 Linear transformations Last semester, you studied vector spaces (linear spaces) their bases, dimension, the ideas of linear dependence and linear independence Now
MATH 26 Class notes/questions January, 2 Linear transformations Last semester, you studied vector spaces (linear spaces) their bases, dimension, the ideas of linear dependence and linear independence Now
Sequences and Series of Functions
 Chapter 13 Sequences and Series of Functions These notes are based on the notes A Teacher s Guide to Calculus by Dr. Louis Talman. The treatment of power series that we find in most of today s elementary
Chapter 13 Sequences and Series of Functions These notes are based on the notes A Teacher s Guide to Calculus by Dr. Louis Talman. The treatment of power series that we find in most of today s elementary
Chapter One. The Calderón-Zygmund Theory I: Ellipticity
 Chapter One The Calderón-Zygmund Theory I: Ellipticity Our story begins with a classical situation: convolution with homogeneous, Calderón- Zygmund ( kernels on R n. Let S n 1 R n denote the unit sphere
Chapter One The Calderón-Zygmund Theory I: Ellipticity Our story begins with a classical situation: convolution with homogeneous, Calderón- Zygmund ( kernels on R n. Let S n 1 R n denote the unit sphere
Fourier Series. 1. Review of Linear Algebra
 Fourier Series In this section we give a short introduction to Fourier Analysis. If you are interested in Fourier analysis and would like to know more detail, I highly recommend the following book: Fourier
Fourier Series In this section we give a short introduction to Fourier Analysis. If you are interested in Fourier analysis and would like to know more detail, I highly recommend the following book: Fourier
Interpolation Theory and Applications to the Boundedness of Operators in Analysis
 Master Thesis Master Advanced Mathematics Interpolation Theory and Applications to the Boundedness of Operators in Analysis Author: Jordi Lendínez Capdevila Supervisor: Department: Dr F Javier Soria de
Master Thesis Master Advanced Mathematics Interpolation Theory and Applications to the Boundedness of Operators in Analysis Author: Jordi Lendínez Capdevila Supervisor: Department: Dr F Javier Soria de
Harmonic Analysis Homework 5
 Harmonic Analysis Homework 5 Bruno Poggi Department of Mathematics, University of Minnesota November 4, 6 Notation Throughout, B, r is the ball of radius r with center in the understood metric space usually
Harmonic Analysis Homework 5 Bruno Poggi Department of Mathematics, University of Minnesota November 4, 6 Notation Throughout, B, r is the ball of radius r with center in the understood metric space usually
DS-GA 3001: PROBLEM SESSION 2 SOLUTIONS VLADIMIR KOBZAR
 DS-GA 3: PROBLEM SESSION SOLUTIONS VLADIMIR KOBZAR Note: In this discussion we allude to the fact the dimension of a vector space is given by the number of basis vectors. We will shortly establish this
DS-GA 3: PROBLEM SESSION SOLUTIONS VLADIMIR KOBZAR Note: In this discussion we allude to the fact the dimension of a vector space is given by the number of basis vectors. We will shortly establish this
Fourier transforms. Up to now, we ve been expressing functions on finite intervals (usually the interval 0 x L or L x L) as Fourier series: a n cos L
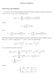 ourier transforms Motivation and definition Up to now, we ve been expressing functions on finite intervals (usually the interval 0 x or x ) as ourier series: fpxq a 0 8 nπx a n cos n b n sin nπx where
ourier transforms Motivation and definition Up to now, we ve been expressing functions on finite intervals (usually the interval 0 x or x ) as ourier series: fpxq a 0 8 nπx a n cos n b n sin nπx where
Folland: Real Analysis, Chapter 8 Sébastien Picard
 Folland: Real Analysis, Chapter 8 Sébastien Picard Problem 8.3 Let η(t) = e /t for t >, η(t) = for t. a. For k N and t >, η (k) (t) = P k (/t)e /t where P k is a polynomial of degree 2k. b. η (k) () exists
Folland: Real Analysis, Chapter 8 Sébastien Picard Problem 8.3 Let η(t) = e /t for t >, η(t) = for t. a. For k N and t >, η (k) (t) = P k (/t)e /t where P k is a polynomial of degree 2k. b. η (k) () exists
Ground States are generically a periodic orbit
 Gonzalo Contreras CIMAT Guanajuato, Mexico Ergodic Optimization and related topics USP, Sao Paulo December 11, 2013 Expanding map X compact metric space. T : X Ñ X an expanding map i.e. T P C 0, Dd P Z`,
Gonzalo Contreras CIMAT Guanajuato, Mexico Ergodic Optimization and related topics USP, Sao Paulo December 11, 2013 Expanding map X compact metric space. T : X Ñ X an expanding map i.e. T P C 0, Dd P Z`,
Riemann integral and volume are generalized to unbounded functions and sets. is an admissible set, and its volume is a Riemann integral, 1l E,
 Tel Aviv University, 26 Analysis-III 9 9 Improper integral 9a Introduction....................... 9 9b Positive integrands................... 9c Special functions gamma and beta......... 4 9d Change of
Tel Aviv University, 26 Analysis-III 9 9 Improper integral 9a Introduction....................... 9 9b Positive integrands................... 9c Special functions gamma and beta......... 4 9d Change of
Mathematical Methods for Physics and Engineering
 Mathematical Methods for Physics and Engineering Lecture notes for PDEs Sergei V. Shabanov Department of Mathematics, University of Florida, Gainesville, FL 32611 USA CHAPTER 1 The integration theory
Mathematical Methods for Physics and Engineering Lecture notes for PDEs Sergei V. Shabanov Department of Mathematics, University of Florida, Gainesville, FL 32611 USA CHAPTER 1 The integration theory
Abstract. 2. We construct several transcendental numbers.
 Abstract. We prove Liouville s Theorem for the order of approximation by rationals of real algebraic numbers. 2. We construct several transcendental numbers. 3. We define Poissonian Behaviour, and study
Abstract. We prove Liouville s Theorem for the order of approximation by rationals of real algebraic numbers. 2. We construct several transcendental numbers. 3. We define Poissonian Behaviour, and study
Vectors in Function Spaces
 Jim Lambers MAT 66 Spring Semester 15-16 Lecture 18 Notes These notes correspond to Section 6.3 in the text. Vectors in Function Spaces We begin with some necessary terminology. A vector space V, also
Jim Lambers MAT 66 Spring Semester 15-16 Lecture 18 Notes These notes correspond to Section 6.3 in the text. Vectors in Function Spaces We begin with some necessary terminology. A vector space V, also
1 Continuity Classes C m (Ω)
 0.1 Norms 0.1 Norms A norm on a linear space X is a function : X R with the properties: Positive Definite: x 0 x X (nonnegative) x = 0 x = 0 (strictly positive) λx = λ x x X, λ C(homogeneous) x + y x +
0.1 Norms 0.1 Norms A norm on a linear space X is a function : X R with the properties: Positive Definite: x 0 x X (nonnegative) x = 0 x = 0 (strictly positive) λx = λ x x X, λ C(homogeneous) x + y x +
An introduction to some aspects of functional analysis
 An introduction to some aspects of functional analysis Stephen Semmes Rice University Abstract These informal notes deal with some very basic objects in functional analysis, including norms and seminorms
An introduction to some aspects of functional analysis Stephen Semmes Rice University Abstract These informal notes deal with some very basic objects in functional analysis, including norms and seminorms
An Introduction to Complex Analysis and Geometry John P. D Angelo, Pure and Applied Undergraduate Texts Volume 12, American Mathematical Society, 2010
 An Introduction to Complex Analysis and Geometry John P. D Angelo, Pure and Applied Undergraduate Texts Volume 12, American Mathematical Society, 2010 John P. D Angelo, Univ. of Illinois, Urbana IL 61801.
An Introduction to Complex Analysis and Geometry John P. D Angelo, Pure and Applied Undergraduate Texts Volume 12, American Mathematical Society, 2010 John P. D Angelo, Univ. of Illinois, Urbana IL 61801.
Spectra of Multiplication Operators as a Numerical Tool. B. Vioreanu and V. Rokhlin Technical Report YALEU/DCS/TR-1443 March 3, 2011
 We introduce a numerical procedure for the construction of interpolation and quadrature formulae on bounded convex regions in the plane. The construction is based on the behavior of spectra of certain
We introduce a numerical procedure for the construction of interpolation and quadrature formulae on bounded convex regions in the plane. The construction is based on the behavior of spectra of certain
FURSTENBERG S THEOREM ON PRODUCTS OF I.I.D. 2 ˆ 2 MATRICES
 FURSTENBERG S THEOREM ON PRODUCTS OF I.I.D. 2 ˆ 2 MATRICES JAIRO BOCHI Abstract. This is a revised version of some notes written ą 0 years ago. I thank Anthony Quas for pointing to a gap in the previous
FURSTENBERG S THEOREM ON PRODUCTS OF I.I.D. 2 ˆ 2 MATRICES JAIRO BOCHI Abstract. This is a revised version of some notes written ą 0 years ago. I thank Anthony Quas for pointing to a gap in the previous
