8.8 Applications of Taylor Polynomials
|
|
|
- Rosalind Horn
- 6 years ago
- Views:
Transcription
1 8.8 Applications of Taylor Polynomials Mark Woodard Furman U Spring 2008 Mark Woodard (Furman U) 8.8 Applications of Taylor Polynomials Spring / 14
2 Outline 1 Point estimation 2 Estimation on an interval Mark Woodard (Furman U) 8.8 Applications of Taylor Polynomials Spring / 14
3 Point estimation Recall Mark Woodard (Furman U) 8.8 Applications of Taylor Polynomials Spring / 14
4 Point estimation Recall Recall that f (x) = T N (x) + R N (x), where T N is the Taylor polynomial of order N centered at a point a and R N is the remainder. Mark Woodard (Furman U) 8.8 Applications of Taylor Polynomials Spring / 14
5 Point estimation Recall Recall that f (x) = T N (x) + R N (x), where T N is the Taylor polynomial of order N centered at a point a and R N is the remainder. The polynomial T N (x) approximates f (x); the error in the approximation is f (x) T N (x) = R N (x) = f (N+1) (z) (N + 1)! x a N+1, where z is a number between a and x. Mark Woodard (Furman U) 8.8 Applications of Taylor Polynomials Spring / 14
6 Point estimation Recall Recall that f (x) = T N (x) + R N (x), where T N is the Taylor polynomial of order N centered at a point a and R N is the remainder. The polynomial T N (x) approximates f (x); the error in the approximation is f (x) T N (x) = R N (x) = f (N+1) (z) (N + 1)! x a N+1, where z is a number between a and x. If M is a number bounding f (N+1) (z), then f (x) T N (x) M (N + 1)! x a N+1. Mark Woodard (Furman U) 8.8 Applications of Taylor Polynomials Spring / 14
7 Point estimation Problem Use a Taylor polynomial of order 2 centered at a = 4 to estimate 4.1. Use the remainder to bound the error in this approximation. Mark Woodard (Furman U) 8.8 Applications of Taylor Polynomials Spring / 14
8 Point estimation Mark Woodard (Furman U) 8.8 Applications of Taylor Polynomials Spring / 14
9 Point estimation Let f (x) = x. We will construct T 2 for f and a = 4. Mark Woodard (Furman U) 8.8 Applications of Taylor Polynomials Spring / 14
10 Point estimation Let f (x) = x. We will construct T 2 for f and a = 4. It is not hard to show that T 2 (x) = 2 + (1/4)(x 4) (1/64)(x 4) 2. Thus 4.1 T2 (4.1) = = Mark Woodard (Furman U) 8.8 Applications of Taylor Polynomials Spring / 14
11 Point estimation Let f (x) = x. We will construct T 2 for f and a = 4. It is not hard to show that T 2 (x) = 2 + (1/4)(x 4) (1/64)(x 4) 2. Thus 4.1 T2 (4.1) = = The error in the approximation is analyzed on the next slide. Mark Woodard (Furman U) 8.8 Applications of Taylor Polynomials Spring / 14
12 Point estimation (Continued) Mark Woodard (Furman U) 8.8 Applications of Taylor Polynomials Spring / 14
13 Point estimation (Continued) To bound the error we need to first bound f (3) (z) for 4 < z < 4.1. But f (3) (z) = 3 8z 5/2 4 < z < 4.1 Mark Woodard (Furman U) 8.8 Applications of Taylor Polynomials Spring / 14
14 Point estimation (Continued) To bound the error we need to first bound f (3) (z) for 4 < z < 4.1. But f (3) (z) = 3 8z 5/2 4 < z < 4.1 Since f (3) (z) is decreasing on the interval (4, 4.1) is bounded by its value at the left-endpoint. Thus f (3) (z) = 3 8z 5/ /2 = Mark Woodard (Furman U) 8.8 Applications of Taylor Polynomials Spring / 14
15 Point estimation (Continued) To bound the error we need to first bound f (3) (z) for 4 < z < 4.1. But f (3) (z) = 3 8z 5/2 4 < z < 4.1 Since f (3) (z) is decreasing on the interval (4, 4.1) is bounded by its value at the left-endpoint. Thus f (3) (z) = 3 8z 5/ /2 = Finally, the error in the approximation is 4.1 T 2 (4.1) (3/256).1 3 < ! Mark Woodard (Furman U) 8.8 Applications of Taylor Polynomials Spring / 14
16 Point estimation Mark Woodard (Furman U) 8.8 Applications of Taylor Polynomials Spring / 14
17 Point estimation Here is an alternative method to estimate 4.1 using the binomial theorem. Mark Woodard (Furman U) 8.8 Applications of Taylor Polynomials Spring / 14
18 Point estimation Here is an alternative method to estimate 4.1 using the binomial theorem. Observe that ( ) 1/2 ( ) 1/2 4 + x = (x/4) = 2 (x/2) n = n n=0 n=0 2 4 n ( 1/2 n ) x n. Mark Woodard (Furman U) 8.8 Applications of Taylor Polynomials Spring / 14
19 Point estimation Here is an alternative method to estimate 4.1 using the binomial theorem. Observe that ( ) 1/2 ( ) 1/2 4 + x = (x/4) = 2 (x/2) n = n n=0 n=0 2 4 n ( 1/2 n ) x n. Thus 4.1 = n=0 2 4 n ( 1/2 n ) (.1) n Mark Woodard (Furman U) 8.8 Applications of Taylor Polynomials Spring / 14
20 Point estimation Here is an alternative method to estimate 4.1 using the binomial theorem. Observe that ( ) 1/2 ( ) 1/2 4 + x = (x/4) = 2 (x/2) n = n Thus 4.1 = n=0 n=0 2 4 n ( 1/2 n ) (.1) n n=0 2 4 n ( 1/2 n ) x n. After the first two terms, the series strictly alternates; thus, if we sum the first three terms, we can use the absolute value of the fourth term to bound error. This is shown on the next slide. Mark Woodard (Furman U) 8.8 Applications of Taylor Polynomials Spring / 14
21 Point estimation Mark Woodard (Furman U) 8.8 Applications of Taylor Polynomials Spring / 14
22 Point estimation The sum of the first three terms of this series gives , which is identical to before. Mark Woodard (Furman U) 8.8 Applications of Taylor Polynomials Spring / 14
23 Point estimation The sum of the first three terms of this series gives , which is identical to before. The error is not exceeding ( 2 1/ ) (.1) n = (.1) Mark Woodard (Furman U) 8.8 Applications of Taylor Polynomials Spring / 14
24 Point estimation The sum of the first three terms of this series gives , which is identical to before. The error is not exceeding ( 2 1/ ) (.1) n = (.1) This method is faster, but it is not as robust; we will not always have an alternating series. Mark Woodard (Furman U) 8.8 Applications of Taylor Polynomials Spring / 14
25 Estimation on an interval Remark Mark Woodard (Furman U) 8.8 Applications of Taylor Polynomials Spring / 14
26 Estimation on an interval Remark Often it is not enough to approximate a function f by a Taylor polynomial at a single point. In certain applications we need to approximate f by a Taylor polynomial across an interval. Mark Woodard (Furman U) 8.8 Applications of Taylor Polynomials Spring / 14
27 Estimation on an interval Remark Often it is not enough to approximate a function f by a Taylor polynomial at a single point. In certain applications we need to approximate f by a Taylor polynomial across an interval. The corresponding estimate of the error in the approximation must hold throughout the interval. In other words we must bound f (x) T N (x) simultaneously for all x in an interval. Mark Woodard (Furman U) 8.8 Applications of Taylor Polynomials Spring / 14
28 Estimation on an interval Remark Often it is not enough to approximate a function f by a Taylor polynomial at a single point. In certain applications we need to approximate f by a Taylor polynomial across an interval. The corresponding estimate of the error in the approximation must hold throughout the interval. In other words we must bound f (x) T N (x) simultaneously for all x in an interval. The problem Approximate the function f (x) by the Taylor polynomial T N (x) centered at a. How accurate is this approximation when x I, where I is an interval containing a? Mark Woodard (Furman U) 8.8 Applications of Taylor Polynomials Spring / 14
29 Estimation on an interval The method Mark Woodard (Furman U) 8.8 Applications of Taylor Polynomials Spring / 14
30 Estimation on an interval The method For each x I, there exists a number z between a and x such that f (x) T N (x) = R N (x) = f (N+1) (z) (N + 1)! x a N+1. Mark Woodard (Furman U) 8.8 Applications of Taylor Polynomials Spring / 14
31 Estimation on an interval The method For each x I, there exists a number z between a and x such that f (x) T N (x) = R N (x) = f (N+1) (z) (N + 1)! x a N+1. We can bound the error by obtaining two bounds: (1) Find the largest possible value of f (N+1) (z) where z is allowed to range over the entire interval I ; (2) Find the largest possible value of x a where x is allowed to range over the entire interval I. Let us call the first bound M (for maximum ) and the second bound ρ (for radius ). Mark Woodard (Furman U) 8.8 Applications of Taylor Polynomials Spring / 14
32 Estimation on an interval The method For each x I, there exists a number z between a and x such that f (x) T N (x) = R N (x) = f (N+1) (z) (N + 1)! x a N+1. We can bound the error by obtaining two bounds: (1) Find the largest possible value of f (N+1) (z) where z is allowed to range over the entire interval I ; (2) Find the largest possible value of x a where x is allowed to range over the entire interval I. Let us call the first bound M (for maximum ) and the second bound ρ (for radius ). Then f (x) T N (x) M (N + 1)! ρn+1 for all x I. Mark Woodard (Furman U) 8.8 Applications of Taylor Polynomials Spring / 14
33 Estimation on an interval Problem Approximate f (x) = sin(x) by a Taylor polynomial of order 6 centered at a = 0. Estimate the error in this approximation when x [.5,.5]. Mark Woodard (Furman U) 8.8 Applications of Taylor Polynomials Spring / 14
34 Estimation on an interval Mark Woodard (Furman U) 8.8 Applications of Taylor Polynomials Spring / 14
35 Estimation on an interval We can easily show that T 6 (x) = x x 3 /6 + x 5 /120. Mark Woodard (Furman U) 8.8 Applications of Taylor Polynomials Spring / 14
36 Estimation on an interval We can easily show that T 6 (x) = x x 3 /6 + x 5 /120. Note that f (7) (x) = sin(x). Thus we should choose M to be the maximum value of sin(x) on [.5,.5]. We will settle for M = 1 (which is typical in working with sines and cosines). Mark Woodard (Furman U) 8.8 Applications of Taylor Polynomials Spring / 14
37 Estimation on an interval We can easily show that T 6 (x) = x x 3 /6 + x 5 /120. Note that f (7) (x) = sin(x). Thus we should choose M to be the maximum value of sin(x) on [.5,.5]. We will settle for M = 1 (which is typical in working with sines and cosines). Next, the value of ρ is the maximum value of x a = x as x ranges over [.5,.5]. Clearly ρ =.5. Mark Woodard (Furman U) 8.8 Applications of Taylor Polynomials Spring / 14
38 Estimation on an interval We can easily show that T 6 (x) = x x 3 /6 + x 5 /120. Note that f (7) (x) = sin(x). Thus we should choose M to be the maximum value of sin(x) on [.5,.5]. We will settle for M = 1 (which is typical in working with sines and cosines). Next, the value of ρ is the maximum value of x a = x as x ranges over [.5,.5]. Clearly ρ =.5. Thus we have for all x [.5,.5]. sin(x) T 6 (x) 1 7! (.5) Mark Woodard (Furman U) 8.8 Applications of Taylor Polynomials Spring / 14
39 Estimation on an interval Problem Approximate f (x) = x by a Taylor polynomial of order 3 centered at a = 9. Estimate the error in this approximation when x [7.5, 9.5]. Mark Woodard (Furman U) 8.8 Applications of Taylor Polynomials Spring / 14
40 Estimation on an interval Mark Woodard (Furman U) 8.8 Applications of Taylor Polynomials Spring / 14
41 Estimation on an interval It can be shown that T 3 (x) = (x 9) 108 (x 9) (x 9)3. Mark Woodard (Furman U) 8.8 Applications of Taylor Polynomials Spring / 14
42 Estimation on an interval It can be shown that T 3 (x) = (x 9) 108 (x 9) (x 9)3. To find M, we maximize the absolute value of f (4) across the interval. But f (4) (x) = 15, for 7.5 x 9.5. Since this 16 x 7/2 function is decreasing across the interval, the maximum is achieved at the left endpoint, x = 7.5. Thus M = 15 16(7.5) 7/ Mark Woodard (Furman U) 8.8 Applications of Taylor Polynomials Spring / 14
43 Estimation on an interval It can be shown that T 3 (x) = (x 9) 108 (x 9) (x 9)3. To find M, we maximize the absolute value of f (4) across the interval. But f (4) (x) = 15, for 7.5 x 9.5. Since this 16 x 7/2 function is decreasing across the interval, the maximum is achieved at the left endpoint, x = 7.5. Thus M = 15 16(7.5) 7/ To find ρ, we need to maximize x 9 on the interval [7.5, 9.5]; thus, ρ = 1.5. Mark Woodard (Furman U) 8.8 Applications of Taylor Polynomials Spring / 14
44 Estimation on an interval It can be shown that T 3 (x) = (x 9) 108 (x 9) (x 9)3. To find M, we maximize the absolute value of f (4) across the interval. But f (4) (x) = 15, for 7.5 x 9.5. Since this 16 x 7/2 function is decreasing across the interval, the maximum is achieved at the left endpoint, x = 7.5. Thus M = 15 16(7.5) 7/ To find ρ, we need to maximize x 9 on the interval [7.5, 9.5]; thus, ρ = 1.5. Thus f (x) T 3 (x) 1 4! (1.5) Mark Woodard (Furman U) 8.8 Applications of Taylor Polynomials Spring / 14
5.8 Indeterminate forms and L Hôpital s rule
5.8 Indeterminate forms and L Hôpital s rule Mark Woodard Furman U Fall 2009 Mark Woodard (Furman U) 5.8 Indeterminate forms and L Hôpital s rule Fall 2009 1 / 11 Outline 1 The forms 0/0 and / 2 Examples
Power Series Solutions We use power series to solve second order differential equations
Objectives Power Series Solutions We use power series to solve second order differential equations We use power series expansions to find solutions to second order, linear, variable coefficient equations
8.7 Taylor s Inequality Math 2300 Section 005 Calculus II. f(x) = ln(1 + x) f(0) = 0
8.7 Taylor s Inequality Math 00 Section 005 Calculus II Name: ANSWER KEY Taylor s Inequality: If f (n+) is continuous and f (n+) < M between the center a and some point x, then f(x) T n (x) M x a n+ (n
Review: Power series define functions. Functions define power series. Taylor series of a function. Taylor polynomials of a function.
Taylor Series (Sect. 10.8) Review: Power series define functions. Functions define power series. Taylor series of a function. Taylor polynomials of a function. Review: Power series define functions Remarks:
Analysis II: Basic knowledge of real analysis: Part V, Power Series, Differentiation, and Taylor Series
.... Analysis II: Basic knowledge of real analysis: Part V, Power Series, Differentiation, and Taylor Series Kenichi Maruno Department of Mathematics, The University of Texas - Pan American March 4, 20
Properties of a Taylor Polynomial
3.4.4: Still Better Approximations: Taylor Polynomials Properties of a Taylor Polynomial Constant: f (x) f (a) Linear: f (x) f (a) + f (a)(x a) Quadratic: f (x) f (a) + f (a)(x a) + 1 2 f (a)(x a) 2 3.4.4:
Taylor Series and Maclaurin Series
Taylor Series and Maclaurin Series Definition (Taylor Series) Suppose the function f is infinitely di erentiable at a. The Taylor series of f about a (or at a or centered at a) isthepowerseries f (n) (a)
Examples of the Fourier Theorem (Sect. 10.3). The Fourier Theorem: Continuous case.
s of the Fourier Theorem (Sect. 1.3. The Fourier Theorem: Continuous case. : Using the Fourier Theorem. The Fourier Theorem: Piecewise continuous case. : Using the Fourier Theorem. The Fourier Theorem:
11.10a Taylor and Maclaurin Series
11.10a 1 11.10a Taylor and Maclaurin Series Let y = f(x) be a differentiable function at x = a. In first semester calculus we saw that (1) f(x) f(a)+f (a)(x a), for all x near a The right-hand side of
Infinite Series. Copyright Cengage Learning. All rights reserved.
Infinite Series Copyright Cengage Learning. All rights reserved. Taylor and Maclaurin Series Copyright Cengage Learning. All rights reserved. Objectives Find a Taylor or Maclaurin series for a function.
This practice exam is intended to help you prepare for the final exam for MTH 142 Calculus II.
MTH 142 Practice Exam Chapters 9-11 Calculus II With Analytic Geometry Fall 2011 - University of Rhode Island This practice exam is intended to help you prepare for the final exam for MTH 142 Calculus
Section Example Determine the Maclaurin series of f (x) = e x and its the interval of convergence.
Example Determine the Maclaurin series of f (x) = e x and its the interval of convergence. Example Determine the Maclaurin series of f (x) = e x and its the interval of convergence. f n (0)x n Recall from
Differentiating Series of Functions
Differentiating Series of Functions James K. Peterson Department of Biological Sciences and Department of Mathematical Sciences Clemson University October 30, 017 Outline 1 Differentiating Series Differentiating
Math 113 (Calculus 2) Exam 4
Math 3 (Calculus ) Exam 4 November 0 November, 009 Sections 0, 3 7 Name Student ID Section Instructor In some cases a series may be seen to converge or diverge for more than one reason. For such problems
JUST THE MATHS UNIT NUMBER DIFFERENTIATION APPLICATIONS 5 (Maclaurin s and Taylor s series) A.J.Hobson
JUST THE MATHS UNIT NUMBER.5 DIFFERENTIATION APPLICATIONS 5 (Maclaurin s and Taylor s series) by A.J.Hobson.5. Maclaurin s series.5. Standard series.5.3 Taylor s series.5.4 Exercises.5.5 Answers to exercises
6.3 Partial Fractions
6.3 Partial Fractions Mark Woodard Furman U Fall 2009 Mark Woodard (Furman U) 6.3 Partial Fractions Fall 2009 1 / 11 Outline 1 The method illustrated 2 Terminology 3 Factoring Polynomials 4 Partial fraction
8.5 Taylor Polynomials and Taylor Series
8.5. TAYLOR POLYNOMIALS AND TAYLOR SERIES 50 8.5 Taylor Polynomials and Taylor Series Motivating Questions In this section, we strive to understand the ideas generated by the following important questions:
7.4* General logarithmic and exponential functions
7.4* General logarithmic and exponential functions Mark Woodard Furman U Fall 2010 Mark Woodard (Furman U) 7.4* General logarithmic and exponential functions Fall 2010 1 / 9 Outline 1 General exponential
Sequences and Series
Sequences and Series What do you think of when you read the title of our next unit? In case your answers are leading us off track, let's review the following IB problems. 1 November 2013 HL 2 3 November
Chapter 11. Taylor Series. Josef Leydold Mathematical Methods WS 2018/19 11 Taylor Series 1 / 27
Chapter 11 Taylor Series Josef Leydold Mathematical Methods WS 2018/19 11 Taylor Series 1 / 27 First-Order Approximation We want to approximate function f by some simple function. Best possible approximation
TAYLOR AND MACLAURIN SERIES
TAYLOR AND MACLAURIN SERIES. Introduction Last time, we were able to represent a certain restricted class of functions as power series. This leads us to the question: can we represent more general functions
8.8. Applications of Taylor Polynomials. Infinite Sequences and Series 8
8.8 Applications of Taylor Polynomials Infinite Sequences and Series 8 Applications of Taylor Polynomials In this section we explore two types of applications of Taylor polynomials. First we look at how
Math Numerical Analysis
Math 541 - Numerical Analysis Joseph M. Mahaffy, jmahaffy@mail.sdsu.edu Department of Mathematics and Statistics Dynamical Systems Group Computational Sciences Research Center San Diego State University
Taylor and Maclaurin Series
Taylor and Maclaurin Series MATH 211, Calculus II J. Robert Buchanan Department of Mathematics Spring 2018 Background We have seen that some power series converge. When they do, we can think of them as
Math 0230 Calculus 2 Lectures
Math 00 Calculus Lectures Chapter 8 Series Numeration of sections corresponds to the text James Stewart, Essential Calculus, Early Transcendentals, Second edition. Section 8. Sequences A sequence is a
Math 651 Introduction to Numerical Analysis I Fall SOLUTIONS: Homework Set 1
ath 651 Introduction to Numerical Analysis I Fall 2010 SOLUTIONS: Homework Set 1 1. Consider the polynomial f(x) = x 2 x 2. (a) Find P 1 (x), P 2 (x) and P 3 (x) for f(x) about x 0 = 0. What is the relation
Taylor Series. Math114. March 1, Department of Mathematics, University of Kentucky. Math114 Lecture 18 1/ 13
Taylor Series Math114 Department of Mathematics, University of Kentucky March 1, 2017 Math114 Lecture 18 1/ 13 Given a function, can we find a power series representation? Math114 Lecture 18 2/ 13 Given
MATLAB Laboratory 10/14/10 Lecture. Taylor Polynomials
MATLAB Laboratory 10/14/10 Lecture Taylor Polynomials Lisa A. Oberbroeckling Loyola University Maryland loberbroeckling@loyola.edu L. Oberbroeckling (Loyola University) MATLAB 10/14/10 Lecture 1 / 7 Taylor/Maclaurin
MAT137 Calculus! Lecture 45
official website http://uoft.me/mat137 MAT137 Calculus! Lecture 45 Today: Taylor Polynomials Taylor Series Next: Taylor Series Power Series Definition (Power Series) A power series is a series of the form
Lecture 1 Notes: 06 / 27. The first part of this class will primarily cover oscillating systems (harmonic oscillators and waves).
Lecture 1 Notes: 06 / 27 The first part of this class will primarily cover oscillating systems (harmonic oscillators and waves). These systems are very common in nature - a system displaced from equilibrium
MATH 1231 MATHEMATICS 1B Calculus Section 4.4: Taylor & Power series.
MATH 1231 MATHEMATICS 1B 2010. For use in Dr Chris Tisdell s lectures. Calculus Section 4.4: Taylor & Power series. 1. What is a Taylor series? 2. Convergence of Taylor series 3. Common Maclaurin series
Section 5.2 Series Solution Near Ordinary Point
DE Section 5.2 Series Solution Near Ordinary Point Page 1 of 5 Section 5.2 Series Solution Near Ordinary Point We are interested in second order homogeneous linear differential equations with variable
Chapter 4 Sequences and Series
Chapter 4 Sequences and Series 4.1 Sequence Review Sequence: a set of elements (numbers or letters or a combination of both). The elements of the set all follow the same rule (logical progression). The
Lecture 5: Function Approximation: Taylor Series
1 / 10 Lecture 5: Function Approximation: Taylor Series MAR514 Geoffrey Cowles Department of Fisheries Oceanography School for Marine Science and Technology University of Massachusetts-Dartmouth Better
Numerical Differentiation & Integration. Numerical Differentiation II
Numerical Differentiation & Integration Numerical Differentiation II Numerical Analysis (9th Edition) R L Burden & J D Faires Beamer Presentation Slides prepared by John Carroll Dublin City University
1 + lim. n n+1. f(x) = x + 1, x 1. and we check that f is increasing, instead. Using the quotient rule, we easily find that. 1 (x + 1) 1 x (x + 1) 2 =
Chapter 5 Sequences and series 5. Sequences Definition 5. (Sequence). A sequence is a function which is defined on the set N of natural numbers. Since such a function is uniquely determined by its values
3.2 Conditional Probability and Independence
3.2 Conditional Probability and Independence Mark R. Woodard Furman U 2010 Mark R. Woodard (Furman U) 3.2 Conditional Probability and Independence 2010 1 / 6 Outline 1 Conditional Probability 2 Independence
Review of Power Series
Review of Power Series MATH 365 Ordinary Differential Equations J. Robert Buchanan Department of Mathematics Fall 2018 Introduction In addition to the techniques we have studied so far, we may use power
Power Series in Differential Equations
Power Series in Differential Equations Prof. Doug Hundley Whitman College April 18, 2014 Last time: Review of Power Series (5.1) The series a n (x x 0 ) n can converge either: Last time: Review of Power
Taylor and Maclaurin Series. Copyright Cengage Learning. All rights reserved.
11.10 Taylor and Maclaurin Series Copyright Cengage Learning. All rights reserved. We start by supposing that f is any function that can be represented by a power series f(x)= c 0 +c 1 (x a)+c 2 (x a)
Section Taylor and Maclaurin Series
Section.0 Taylor and Maclaurin Series Ruipeng Shen Feb 5 Taylor and Maclaurin Series Main Goal: How to find a power series representation for a smooth function us assume that a smooth function has a power
Lab 15 Taylor Polynomials
Name Student ID # Instructor Lab Period Date Due Lab 15 Taylor Polynomials Objectives 1. To develop an understanding for error bound, error term, and interval of convergence. 2. To visualize the convergence
Let s Get Series(ous)
Department of Mathematics, Computer Science, and Statistics Bloomsburg University Bloomsburg, Pennsylvania 785 Let s Get Series(ous) Summary Presenting infinite series can be (used to be) a tedious and
Taylor Series and Numerical Approximations
Taylor Series and Numerical Approximations Hilary Weller h.weller@reading.ac.uk August 7, 05 An introduction to the concept of a Taylor series and how these are used in numerical analysis to find numerical
Chapter 8: Taylor s theorem and L Hospital s rule
Chapter 8: Taylor s theorem and L Hospital s rule Theorem: [Inverse Mapping Theorem] Suppose that a < b and f : [a, b] R. Given that f (x) > 0 for all x (a, b) then f 1 is differentiable on (f(a), f(b))
SUMMATION TECHNIQUES
SUMMATION TECHNIQUES MATH 53, SECTION 55 (VIPUL NAIK) Corresponding material in the book: Scattered around, but the most cutting-edge parts are in Sections 2.8 and 2.9. What students should definitely
Study # 1 11, 15, 19
Goals: 1. Recognize Taylor Series. 2. Recognize the Maclaurin Series. 3. Derive Taylor series and Maclaurin series representations for known functions. Study 11.10 # 1 11, 15, 19 f (n) (c)(x c) n f(c)+
Power series and Taylor series
Power series and Taylor series D. DeTurck University of Pennsylvania March 29, 2018 D. DeTurck Math 104 002 2018A: Series 1 / 42 Series First... a review of what we have done so far: 1 We examined series
Math 106: Review for Final Exam, Part II - SOLUTIONS. (x x 0 ) 2 = !
Math 06: Review for Final Exam, Part II - SOLUTIONS. Use a second-degree Taylor polynomial to estimate 8. We choose f(x) x and x 0 7 because 7 is the perfect cube closest to 8. f(x) x /3 f(7) 3 f (x) 3
MAT 1339-S14 Class 4
MAT 9-S4 Class 4 July 4, 204 Contents Curve Sketching. Concavity and the Second Derivative Test.................4 Simple Rational Functions........................ 2.5 Putting It All Together.........................
MATHia Unit MATHia Workspace Overview TEKS
1 Function Overview Searching for Patterns Exploring and Analyzing Patterns Comparing Familiar Function Representations Students watch a video about a well-known mathematician creating an expression for
Ma 530 Power Series II
Ma 530 Power Series II Please note that there is material on power series at Visual Calculus. Some of this material was used as part of the presentation of the topics that follow. Operations on Power Series
9.5. Polynomial and Rational Inequalities. Objectives. Solve quadratic inequalities. Solve polynomial inequalities of degree 3 or greater.
Chapter 9 Section 5 9.5 Polynomial and Rational Inequalities Objectives 1 3 Solve quadratic inequalities. Solve polynomial inequalities of degree 3 or greater. Solve rational inequalities. Objective 1
The Furman University Wylie Mathematics Tournament
The Furman University Wylie Mathematics Tournament Senior Examination 15 February 2003 Please provide the following information: Name School Code 1. Do not open this test booklet until instructed. Instructions
MA2501 Numerical Methods Spring 2015
Norwegian University of Science and Technology Department of Mathematics MA2501 Numerical Methods Spring 2015 Solutions to exercise set 7 1 Cf. Cheney and Kincaid, Exercise 4.1.9 Consider the data points
ISSUED BY KENDRIYA VIDYALAYA - DOWNLOADED FROM Chapter - 2. (Polynomials)
Chapter - 2 (Polynomials) Key Concepts Constants : A symbol having a fixed numerical value is called a constant. Example : 7, 3, -2, 3/7, etc. are all constants. Variables : A symbol which may be assigned
Section 5.8. Taylor Series
Difference Equations to Differential Equations Section 5.8 Taylor Series In this section we will put together much of the work of Sections 5.-5.7 in the context of a discussion of Taylor series. We begin
Lecture 8: Optimization
Lecture 8: Optimization This lecture describes methods for the optimization of a real-valued function f(x) on a bounded real interval [a, b]. We will describe methods for determining the maximum of f(x)
10.1 Sequences. Example: A sequence is a function f(n) whose domain is a subset of the integers. Notation: *Note: n = 0 vs. n = 1.
10.1 Sequences Example: A sequence is a function f(n) whose domain is a subset of the integers. Notation: *Note: n = 0 vs. n = 1 Examples: EX1: Find a formula for the general term a n of the sequence,
Math 113: Quiz 6 Solutions, Fall 2015 Chapter 9
Math 3: Quiz 6 Solutions, Fall 05 Chapter 9 Keep in mind that more than one test will wor for a given problem. I chose one that wored. In addition, the statement lim a LR b means that L Hôpital s rule
Single Variable Calculus, Early Transcendentals
Single Variable Calculus, Early Transcendentals 978-1-63545-100-9 To learn more about all our offerings Visit Knewtonalta.com Source Author(s) (Text or Video) Title(s) Link (where applicable) OpenStax
Chapter 9: Infinite Series Part 2
Name: Date: Period: AP Calc BC Mr. Mellina/Ms. Lombardi Chapter 9: Infinite Series Part 2 Topics: 9.5 Alternating Series Remainder 9.7 Taylor Polynomials and Approximations 9.8 Power Series 9.9 Representation
Math 115 HW #5 Solutions
Math 5 HW #5 Solutions From 29 4 Find the power series representation for the function and determine the interval of convergence Answer: Using the geometric series formula, f(x) = 3 x 4 3 x 4 = 3(x 4 )
MATH 1231 MATHEMATICS 1B CALCULUS. Section 5: - Power Series and Taylor Series.
MATH 1231 MATHEMATICS 1B CALCULUS. Section 5: - Power Series and Taylor Series. The objective of this section is to become familiar with the theory and application of power series and Taylor series. By
1. Find the domain of the following functions. Write your answer using interval notation. (9 pts.)
MATH- Sample Eam Spring 7. Find the domain of the following functions. Write your answer using interval notation. (9 pts.) a. 9 f ( ) b. g ( ) 9 8 8. Write the equation of the circle in standard form given
19. TAYLOR SERIES AND TECHNIQUES
19. TAYLOR SERIES AND TECHNIQUES Taylor polynomials can be generated for a given function through a certain linear combination of its derivatives. The idea is that we can approximate a function by a polynomial,
Candidates are expected to have available a calculator. Only division by (x + a) or (x a) will be required.
Revision Checklist Unit C2: Core Mathematics 2 Unit description Algebra and functions; coordinate geometry in the (x, y) plane; sequences and series; trigonometry; exponentials and logarithms; differentiation;
Math 112 Rahman. Week Taylor Series Suppose the function f has the following power series:
Math Rahman Week 0.8-0.0 Taylor Series Suppose the function f has the following power series: fx) c 0 + c x a) + c x a) + c 3 x a) 3 + c n x a) n. ) Can we figure out what the coefficients are? Yes, yes
Advanced Calculus Math 127B, Winter 2005 Solutions: Final. nx2 1 + n 2 x, g n(x) = n2 x
. Define f n, g n : [, ] R by f n (x) = Advanced Calculus Math 27B, Winter 25 Solutions: Final nx2 + n 2 x, g n(x) = n2 x 2 + n 2 x. 2 Show that the sequences (f n ), (g n ) converge pointwise on [, ],
PRINT. 4. Be sure to write your name, section and version letter of the exam on the Scantron form.
PRINT LAST NAME INSTRUCTOR: UIN: FIRST NAME SECTION NUMBER: SEAT NUMBER: Directions. The use of all electronic devices is prohibited. 2. In Part (Problems -2), mark the correct choice on your Scantron
The First Derivative and Second Derivative Test
The First Derivative and Second Derivative Test James K. Peterson Department of Biological Sciences and Department of Mathematical Sciences Clemson University April 9, 2018 Outline 1 Extremal Values 2
Math Review for Exam Answer each of the following questions as either True or False. Circle the correct answer.
Math 22 - Review for Exam 3. Answer each of the following questions as either True or False. Circle the correct answer. (a) True/False: If a n > 0 and a n 0, the series a n converges. Soln: False: Let
The First Derivative and Second Derivative Test
The First Derivative and Second Derivative Test James K. Peterson Department of Biological Sciences and Department of Mathematical Sciences Clemson University November 8, 2017 Outline Extremal Values The
TAYLOR POLYNOMIALS DARYL DEFORD
TAYLOR POLYNOMIALS DARYL DEFORD 1. Introduction We have seen in class that Taylor polynomials provide us with a valuable tool for approximating many different types of functions. However, in order to really
EOC Assessment Outline
EOC Assessment Outline Course Name: Advanced Topics in Math Course Number: 1298310 Test 50 MAFS.912.F-BF.1.2 Write arithmetic and geometric sequences both recursively and with an explicit formula, use
INFINITE SEQUENCES AND SERIES
11 INFINITE SEQUENCES AND SERIES INFINITE SEQUENCES AND SERIES In section 11.9, we were able to find power series representations for a certain restricted class of functions. INFINITE SEQUENCES AND SERIES
Solutions to Math 1b Midterm II
Solutions to Math b Midterm II Tuesday, pril 8, 006. (6 points) Suppose that the power series a n(x + ) n converges if x = 7 and diverges if x = 7. ecide which of the following series must converge, must
Physics 6303 Lecture 11 September 24, LAST TIME: Cylindrical coordinates, spherical coordinates, and Legendre s equation
Physics 6303 Lecture September 24, 208 LAST TIME: Cylindrical coordinates, spherical coordinates, and Legendre s equation, l l l l l l. Consider problems that are no axisymmetric; i.e., the potential depends
INFINITE SEQUENCES AND SERIES
11 INFINITE SEQUENCES AND SERIES INFINITE SEQUENCES AND SERIES 11.11 Applications of Taylor Polynomials In this section, we will learn about: Two types of applications of Taylor polynomials. APPLICATIONS
(c) Find the equation of the degree 3 polynomial that has the same y-value, slope, curvature, and third derivative as ln(x + 1) at x = 0.
Chapter 7 Challenge problems Example. (a) Find the equation of the tangent line for ln(x + ) at x = 0. (b) Find the equation of the parabola that is tangent to ln(x + ) at x = 0 (i.e. the parabola has
(b) Prove that the following function does not tend to a limit as x tends. is continuous at 1. [6] you use. (i) f(x) = x 4 4x+7, I = [1,2]
![(b) Prove that the following function does not tend to a limit as x tends. is continuous at 1. [6] you use. (i) f(x) = x 4 4x+7, I = [1,2]](/thumbs/96/129243602.jpg "(b) Prove that the following function does not tend to a limit as x tends. is continuous at 1. [6] you use. (i) f(x) = x 4 4x+7, I = [1,2]")
TMA M208 06 Cut-off date 28 April 2014 (Analysis Block B) Question 1 (Unit AB1) 25 marks This question tests your understanding of limits, the ε δ definition of continuity and uniform continuity, and your
Problems for Putnam Training
Problems for Putnam Training 1 Number theory Problem 1.1. Prove that for each positive integer n, the number is not prime. 10 1010n + 10 10n + 10 n 1 Problem 1.2. Show that for any positive integer n,
Calculus II Study Guide Fall 2015 Instructor: Barry McQuarrie Page 1 of 8
Calculus II Study Guide Fall 205 Instructor: Barry McQuarrie Page of 8 You should be expanding this study guide as you see fit with details and worked examples. With this extra layer of detail you will
New York City College of Technology, CUNY Mathematics Department. MAT 1575 Final Exam Review Problems. 3x (a) x 2 (x 3 +1) 3 dx (b) dx.
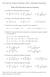New York City College of Technology, CUNY Mathematics Department MAT 575 Final Exam eview Problems. Evaluate the following definite integrals: x x (a) x (x +) dx (b) dx 0 0 x + 9 (c) 0 x + dx. Evaluate
Tangent Lines Sec. 2.1, 2.7, & 2.8 (continued)
Tangent Lines Sec. 2.1, 2.7, & 2.8 (continued) Prove this Result How Can a Derivative Not Exist? Remember that the derivative at a point (or slope of a tangent line) is a LIMIT, so it doesn t exist whenever
Lecture 32: Taylor Series and McLaurin series We saw last day that some functions are equal to a power series on part of their domain.
Lecture 32: Taylor Series and McLaurin series We saw last day that some functions are equal to a power series on part of their domain. For example f(x) = 1 1 x = 1 + x + x2 + x 3 + = ln(1 + x) = x x2 2
2t t dt.. So the distance is (t2 +6) 3/2
Math 8, Solutions to Review for the Final Exam Question : The distance is 5 t t + dt To work that out, integrate by parts with u t +, so that t dt du The integral is t t + dt u du u 3/ (t +) 3/ So the
Suppose that f is continuous on [a, b] and differentiable on (a, b). Then
![Suppose that f is continuous on [a, b] and differentiable on (a, b). Then](/thumbs/74/71325034.jpg "Suppose that f is continuous on [a, b] and differentiable on (a, b). Then")
Lectures 1/18 Derivatives and Graphs When we have a picture of the graph of a function f(x), we can make a picture of the derivative f (x) using the slopes of the tangents to the graph of f. In this section
Name Period. Date: Topic: 9-2 Circles. Standard: G-GPE.1. Objective:
Name Period Date: Topic: 9-2 Circles Essential Question: If the coefficients of the x 2 and y 2 terms in the equation for a circle were different, how would that change the shape of the graph of the equation?
Topic Outline for Algebra 2 & and Trigonometry One Year Program
Topic Outline for Algebra 2 & and Trigonometry One Year Program Algebra 2 & and Trigonometry - N - Semester 1 1. Rational Expressions 17 Days A. Factoring A2.A.7 B. Rationals A2.N.3 A2.A.17 A2.A.16 A2.A.23
Week #6 - Taylor Series, Derivatives and Graphs Section 10.1
Week #6 - Taylor Series, Derivatives and Graphs Section 10.1 From Calculus, Single Variable by Hughes-Hallett, Gleason, McCallum et. al. Copyright 005 by John Wiley & Sons, Inc. This material is used by
n=1 ( 2 3 )n (a n ) converges by direct comparison to
. (a) n = a n converges, so we know that a n =. Therefore, for n large enough we know that a n
MATH141: Calculus II Exam #4 review solutions 7/20/2017 Page 1
MATH4: Calculus II Exam #4 review solutions 7/0/07 Page. The limaçon r = + sin θ came up on Quiz. Find the area inside the loop of it. Solution. The loop is the section of the graph in between its two
MA 1: PROBLEM SET NO. 7 SOLUTIONS
MA 1: PROBLEM SET NO. 7 SOLUTIONS 1. (1) Obtain the number r = 15 3 as an approimation to the nonzero root of the equation 2 = sin() by using the cubic Taylor polynomial approimation to sin(). Proof. The
Units. Year 1. Unit 1: Course Overview
Mathematics HL Units All Pamoja courses are written by experienced subject matter experts and integrate the principles of TOK and the approaches to learning of the IB learner profile. This course has been
MATH 163 HOMEWORK Week 13, due Monday April 26 TOPICS. c n (x a) n then c n = f(n) (a) n!
MATH 63 HOMEWORK Week 3, due Monday April 6 TOPICS 4. Taylor series Reading:.0, pages 770-77 Taylor series. If a function f(x) has a power series representation f(x) = c n (x a) n then c n = f(n) (a) ()
c) xy 3 = cos(7x +5y), y 0 = y3 + 7 sin(7x +5y) 3xy sin(7x +5y) d) xe y = sin(xy), y 0 = ey + y cos(xy) x(e y cos(xy)) e) y = x ln(3x + 5), y 0
Some Math 35 review problems With answers 2/6/2005 The following problems are based heavily on problems written by Professor Stephen Greenfield for his Math 35 class in spring 2005. His willingness to
Without fully opening the exam, check that you have pages 1 through 13.
MTH 33 Solutions to Exam November th, 08 Name: Section: Recitation Instructor: INSTRUCTIONS Fill in your name, etc. on this first page. Without fully opening the exam, check that you have pages through
Warm Up Lesson Presentation Lesson Quiz. Holt McDougal Algebra 2
Warm Up Lesson Presentation Lesson Quiz Algebra 2 Warm Up Factor each expression. 1. 3x 6y 2. a 2 b 2 3(x 2y) (a + b)(a b) Find each product. 3. (x 1)(x + 3) 4. (a + 1)(a 2 + 1) x 2 + 2x 3 a 3 + a 2 +
Increasing and decreasing intervals *
OpenStax-CNX module: m15474 1 Increasing and decreasing intervals * Sunil Kumar Singh This work is produced by OpenStax-CNX and licensed under the Creative Commons Attribution License 2.0 A function is