PSS Is Secure against Random Fault Attacks
|
|
|
- Carmella Beasley
- 6 years ago
- Views:
Transcription
1 PSS Is Secure against Random Fault Attacks Jean-Sébastien Coron and Avradip Mandal University of Luxembourg Abstract. A fault attack consists in inducing hardware malfunctions in order to recover secrets from electronic devices. One of the most famous fault attack is Bellcore s attack against RSA with CRT; it consists in inducing a fault modulo p but not modulo q at signature generation step; then by taking a gcd the attacker can recover the factorization of N = pq. The Bellcore attack applies to any encoding function that is deterministic, for example FDH. Recently, the attack was extended to randomized encodings based on the iso/iec signature standard. Extending the attack to other randomized encodings remains an open problem. In this paper, we show that the Bellcore attack cannot be applied to the PSS encoding; namely we show that PSS is provably secure against random fault attacks in the random oracle model, assuming that inverting RSA is hard. Keywords: Probabilistic Signature Scheme, Provable Security, Fault Attacks, Bellcore Attack. 1 Introduction rsa [14] is still the most widely used signature scheme in practical applications. To sign a message m with rsa, the signer first applies an encoding function μ to m, and then computes the signature σ = μ(m) d mod N. The signature is verified by checking that σ e = μ(m) mod N. For efficiency reasons RSA signatures are often computed using the Chinese Remainder Theorem (crt); in this case the signature is first computed modulo p and q separately: σ p = m d mod p, σ q = m d mod q and then σ p and σ q are combined by CRT to form the signature σ. Boneh, DeMillo and Lipton showed that rsa signatures computed with CRT can be vulnerable to fault attacks [3]. If the attacker can induce a fault when σ q is computed while keeping the computation of σ p correct, one obtains: σ p = m d mod p, σ q m d mod q and the resulting faulty signature σ satisfies σ e = m mod p, σ e m mod q. M. Matsui (Ed.): ASIACRYPT 2009, LNCS 5912, pp , c International Association for Cryptologic Research 2009
2 654 J.-S. Coron and A. Mandal Therefore, given one faulty signature σ, the attacker can recover the factorization of N by computing gcd(σ e m mod N,N) =p. This attack actually applies to any deterministic rsa encoding, e.g. Full Domain Hash (fdh) [2]withσ = H(m) d mod N. More generally, the attack applies to any probabilistic scheme where the random used to generate the signature is sent along with the signature, e.g. as in the Probabilistic Full Domain Hash (pfdh) encoding [6] where the signature is σ r with σ = H(m r) d mod N. In that case, given the faulty value of σ and knowing r, the attacker can still factor N by computing gcd(σ e H(m r) modn,n) =p. However, if the random r is not given to the attacker along with the signature σ then the Bellcore attack is thwarted. This is the case for signatures of the form σ = μ(m, r) d mod N where the random r is only recovered when verifying the signature, as in pss [2]. To recover r one needs a correct signature; from a faulty signature, the attacker cannot retrieve r nor infer μ(m, r) inorderto compute gcd(σ e μ(m, r) modn,n) =p, unless r is short enough to be guessed by exhaustive search. Note that obtaining another correct signature for m would not help the attacker since with high probability a different random r would be used to generate this signature. Recently, it was shown how to extend Bellcore s attack to a large class of randomized rsa encoding schemes [7]. The extended attack was illustrated with the iso/iec standard [11]. iso/iec is originally a deterministic encoding scheme but often used in combination with message randomization, as in the emv standard [8]. The iso/iec encoded message has the form μ(m) =6A 16 m[1] H(m) BC 16 where m = m[1] m[2] is split into two parts. The authors of [7] showed that if the randomness introduced into m[1] is not too large (e.g. less than 160 bits for a 2048-bit rsa modulus), then a single faulty signature allows to factor N as in the original Bellcore attack. The attack is based on Coppersmith s technique for finding small roots of polynomial equations [5], which is based on the LLL algorithm [12]. However, extending the attack to other randomized RSA signatures remains an open problem. In particular, it is natural to ask whether the Bellcore attack could apply to PSS [2], the most popular RSA-based signature scheme. In this paper, we show that the Bellcore attack cannot be extended to PSS; namely we show that PSS is provably secure against random fault attacks in the random oracle model, assuming that inverting RSA is hard. More precisely, we consider an extended model of security in which the attacker, in addition to the regular signing oracle, has access to a faulty signature oracle; that is, the attacker can request faulty signatures either modulo p or modulo q. For a faulty signature modulo q, the signer first generates the correct value modulo p: σ p = μ(m, r) d mod p but generates a random σ q modulo q. With CRT the signer then computes σ such that σ = σ p mod p and σ = σ q mod q, and returns the faulty signature
3 PSS Is Secure against Random Fault Attacks 655 σ to the adversary. Our result is that PSS is still secure under this extended notion of security, in the random oracle model, assuming that inverting RSA is hard. 2 Security Model We recall the definition of a signature scheme. Definition 1 (signature scheme). Asignaturescheme(Gen, Sign, Verify) is defined as follows: -Thekey generation algorithm Gen is a probabilistic algorithm which given 1 k, outputs a pair of matching public and private keys, (pk, sk). -Thesigning algorithm Sign takes the message M to be signed, the public key pk and the private key sk, andreturnsasignaturex = Sign sk (M). Thesigning algorithm may be probabilistic. - The verification algorithm Verify takes a message M, a candidate signature x and pk. ItreturnsabitVerify pk (M,x ), equal to one if the signature is accepted, and zero otherwise. We require that if x Sign sk (M), then Verify pk (M,x) =1. In the existential unforgeability under an adaptive chosen message attack scenario, the forger can dynamically obtain signatures of messages of his choice and attempts to output a valid forgery. A valid forgery is a message/signature pair (M,x) such that Verify pk (M,x) = 1 whereas the signature of M was never requested by the forger. In the following, we consider an extended model of security in which the attacker, in addition to the regular signing oracle, has access to a faulty signature oracle; that is, the attacker can request faulty signatures either modulo p or modulo q. For a faulty signature modulo q, the signer first generates the correct value modulo p: σ p = μ(m, r) d mod p and generates a random σ q modulo q. With CRT the signer then computes σ such that σ = σ p mod p and σ = σ q mod q, and returns the faulty signature σ to the adversary. This is actually equivalent to first computing a correct signature σ: σ = μ(m, r) d mod N and then generating a random u modulo q and computing the faulty signature: σ = σ + u p mod N Formally, we consider the following scenario between a challenger and an attacker. Our scenario applies to any RSA based signature scheme in which a signature σ is computed as σ = μ(m, r) d mod N for some (randomized) encoding function μ(m, r).
4 656 J.-S. Coron and A. Mandal Setup: the challenger generates an RSA modulus N = p q, a public exponent e such that gcd(e, φ(n)) = 1 and a private exponent d such that e d =1 mod φ(n). The challenger sends (N,e) to the adversary. Queries: the adversary can make regular signature queries to the challenger. In this case, given a message m, the challenger generates a random r and output the (correct) signature: σ = μ(m, r) d mod N Additionally, the attacker can make faulty signature queries. For every such query, the attacker specifies whether the fault should be modulo p or modulo q. For a faulty signature modulo q, the challenger first generates a random r and computes the correct signature: σ = μ(m, r) d mod N Then the challenger generates a random u modulo q, and computes: σ = σ + u p mod N and sends σ to the attacker. The challenger proceeds similarly if a faulty signature modulo p is requested. Forgery: eventually the attacker must output a forgery, that is a message signature pair (m, x) such that Verify pk (m, x) = 1 whereas the signature of m was never requested by the forger, neither as a regular signature query nor in a faulty signature query. This completes the description of the attack scenario. As usual, we say that a signature scheme is (t, ε)-secure if no adversary running in time t can output a forgery with probability better than ε. The PSS scheme was proven secure in the random oracle model [1], and our security proof with faulty signatures is also in the random oracle model. It is well known that a security proof in the random oracle model does not necessarily imply that a scheme is secure in the real world (see [4]). Although it is always better to have a security proof in the standard model, we think that it is still better to have a proof in the random oracle model than no proof at all. 2.1 Why Random Faults? In our security model we have assumed that when a faulty signature σ is obtained, it has the uniform distribution modulo p (or modulo q). This could be seen as a very strong assumption; namely in practice the faults might have a completely non-random distribution. Consider for example a fault attack inducing the values of the registers to be set to zero. This gives σ p = 0 and recovering p is then straightforward: simply compute gcd(σ,n)=p. Topreventfromthis attack we could assume that when a fault occurs the value σ p still has enough min-entropy. In the following we argue that 1) the random fault assumption is almost unavoidable if we want to obtain a security proof and 2) such assumption might actually be reasonable in practice.
5 PSS Is Secure against Random Fault Attacks 657 Assume that a fault gives a random σ p mod p but with the k most significant bits set to 0, for some small integer k. That is, the attacker can obtain a list of faulty signatures σ i such that the corresponding σ i,p = σ i mod p satisfy: 0 σ i,p < p 2 k (1) for all 1 i n, wheren is the number of faulty signatures. We show how to recover p, using an attack similar to [13]. With LLL [12], the attacker computes a short vector (u 1,...,u n ) such that: This implies: n u i σ i =0 i=1 n u i σ i,p =0 i=1 modn modp Since from (1) the σ i,p are small modulo p, iftheu i s are small enough, then the equality will hold not only modulo p but also over Z: n u i σ i,p =0 i=1 This gives a vector (u 1,...,u n ) that is orthogonal in Z to the unknown vector (σ 1,p,...σ n,p). It is shown in [13] that by generating sufficiently many such vectors, one can recover the unknown vector (σ 1,p,...σ n,p ) and eventually p. Note that this attack applies to any RSA-based signature scheme with CRT, not only to PSS. This attack shows it is not enough for σ p to have min-entropy, as only a few bits of entropy loss compared to the uniform distribution enable to recover p. Therefore, if we want to obtain a security proof, it seems necessary to assume that σ p is uniformly distributed modulo p. Actually the random fault assumption might be reasonable in practice. Namely to prevent probing attacks, the data being transmitted in the memory bus inside the micro-processor is usually encrypted. Therefore, the content of a register after a fault attack could still be some encrypted value, so it can be reasonable to model this register value as uniformly random. 3 PSS Is Secure against Random Fault Attacks 3.1 The PSS Scheme We recall the definition of the PSS scheme [2]. The scheme uses three hash functions h : {0, 1} {0, 1} k1, g 1 : {0, 1} k1 {0, 1} k0 and g 2 : {0, 1} k1 {0, 1} k k0 k1 1,wherek, k 0 and k 1 are parameters. Key Generation: generate a k-bit RSA modulus N = pq, and a random exponent e Z φ(n). Generate d such that e d =1 modφ(n). The public-key is (N,e); the private key is (N,d).
6 658 J.-S. Coron and A. Mandal m r g 1(ω) h g 1 0 ω r g 2(ω) g 2 Fig. 1. PSS: the components of the image y =0 ω r g 2(ω) are darkened. The signature of m is y d mod N. Signature generation: given a message m, do the following: 1. r {0, 1} k0 2. ω h(m r) 3. r g 1 (ω) r 4. y 0 ω r g 2 (ω) 5. Return σ = y d mod N Signature Verification: given a message m and a signature σ, do the following: 1. Let y = σ e mod N 2. Parse y as 0 ω r γ. If the parsing fails return r r g 1 (ω) 4. If h(m r) =ω and g 2 (ω) =γ return else return Security Proof We first give an intuition of the proof. We denote by μ(m, r) the PSS encoding scheme, that is μ(m, r) =0 ω r g 2 (ω) whereω = h(m r) andr = g 1 (ω) r. We receive as input a challenge (N,e,η) and we must output η d mod N. In the original PSS security proof [2], when receiving a signature query, the simulator generates a random α modulo N such that α e mod N can be written as 0 ω s t. The simulator generates a random r of k 0 bits. Then it lets h(m, r) =ω, g 1 (ω) = s r and g 2 (ω) =t. Therefore we have that μ(m, r) =(α e mod N). The simulator can then return α as a signature for m. When receiving a hash query for h(m, r), the simulator generates a random α modulo N such that η α e canbewrittenas 0 ω s t; it then proceeds as previously. In this case we have μ(m, r) = (η α e mod N). Therefore a forgery for μ(m, r) enables to compute η d mod N. One can see that if there is no collision on the randoms r used for signature generation, and no collision on the values ω, then the simulation is perfect. Then
7 PSS Is Secure against Random Fault Attacks 659 given a forgery σ for some message m, with high probability we have that μ(m,r )=(η α e mod N) forsomeknownα. Therefore from σ = μ(m,r ) d mod N one can compute η d mod N as required and solve the RSA challenge. In our extended model of security, we must additionally simulate a faulty signature oracle. To do this, one could first generate as previously a random α modulo N such that α e mod N canbewrittenas0 ω s t. Thesimulator generates a random r of k 0 bits. Then it lets h(m,r) =ω, g 1 (ω) =s r and g 2 (ω) =t, so that again μ(m, r) =(α e mod N). Then instead of returning the correct signature α, the simulator could generate a random u modulo q, and output the faulty signature: α = α + u p mod N (2) Obviously our simulator cannot do this, because it does not know the prime factors p and q. Instead we show that the distribution of α is statistically close to uniform in Z N ; therefore, the simulator can simply return a random α Z N. Since RSA is a permutation, instead of considering the distribution of α,one can consider the distribution of y = α e mod N. From(2)wehave: y = y + v p mod N where v is uniformly distributed modulo q and y is uniformly distributed in [0, 2 k 1 [. The following lemma shows that the distribution of y is statistically close to uniform in Z N. Lemma 1. Let N = pq be a k-bit modulus where p and q are k/2-bit, and let y be a random integer such that 0 y<2 k 1.Letv be a random integer modulo q. Then the distribution of y = y + v p mod N is ɛ-statistically close to uniform modulo N, withɛ = 4 2 k/2 Proof. We consider a fixed a Z N and we provide an estimate of Pr[y = a]. For this we consider the solutions of the equation: a y + v p mod N (3) We have that for every v [0,q), there exists a unique y [0,N[ which satisfies the above relation. However we are only interested in the y s in the range [0, 2 k 1 [. We have that for each i [1,q], the pair: (v = q i, y = a + ip mod N) is a solution of (3) iff a + ip mod N<2 k 1 (4) Depending on the choice of a, there are actually either 2k 1 2k 1 p or p +1 many i values which satisfy relation (4). Hence there are 2k 1 2k 1 p or p +1 many solutions to congruence (3) such that y<2 k 1.Sincey and v are random integers in the range [0, 2 k 1 )and[0,q) respectively, this gives: 2 k 1 1 p 2 k 1 1 ( ) 2 k 1 q Pr[y = a] +1 p 1 2 k 1 1 q
8 660 J.-S. Coron and A. Mandal We write 2k 1 p = c, whichgivesp c<2k 1 <p c + p. We obtain: Pr[y = a] c 2 k 1 q = 1 N pc 2 k 1 = 1 ( ) N 1 2k 1 pc 2 k 1 > 1 ( N 1 p ) 2 k 1 (as 2 k 1 <pc+ p) > 1 ( N 1 2p ) (as 2 k 1 > N N 2 ) ( = 1 2 ) 1 q N Similarly, we have: Pr[y = a] ( 1+ 2 ) 1 q N This gives: ( 1 2 ) 1 ( q N Pr[y = a] 1+ 2 ) 1 q N for all a [0,N). This implies that the distribution of y is 4 -statistically 2 k/2 close to uniform modulo N as q>2 k/2 1. Lemma 1 shows that it is sufficient for our simulator to return a random α modulo N as the faulty signature. In other words, instead of first generating a random y [0, 2 k 1 ), then a random v modulo q, theny = y + v p and finally α = y d mod N, the simulator can simply output a random α modulo N, and such output will be statistically indistinguishable from a faulty signature. However to this faulty signature α corresponds a correct signature α such that: α = α u p mod N where u is randomly distributed modulo q. Equivalently letting y = α e mod N there exists a corresponding value y with: y = y v p mod N (5) where v is randomly distributed modulo q such that y can be written as: y =0 ω s t = μ(m, r) This implicitly defines h(m, r) =ω, g 1 (ω) =s r and g 2 (ω) =t for the simulation of random oracles h, g 1 and g 2. Since our simulator does not know p, it cannot compute y in equation (5) and therefore our simulator does not known the corresponding values of ω, s and t; therefore our simulator cannot answer the corresponding h queries, g 1 queries and g 2 queries if such queries are made by the attacker. Intuitively for h-queries it is sufficient that the set of r values is exponentially large; for this the parameter k 0 must be large enough. For g 1 and g 2 queries we must show
9 PSS Is Secure against Random Fault Attacks 661 that the adversary has a negligible probability of querying ω. This is shown in the following lemma: we show that given a faulty signature α (or equivalently y = α e mod N) the distribution of ω has enough variability, if the parameter k 1 is sufficiently large. This implies that ω does not need to be computed, and therefore the factorization of N is not needed for our simulation. Lemma 2. Let N = pq be a k-bit modulus where p and q are k/2-bit, and let y be a random integer such that 0 y<2 k 1.Letv be a random integer modulo q, andlety = y + v p mod N. Writey =0 ω x where ω is k 1 -bit and x is k k 1 1 bits. Given y, for any ω of k 1 -bit we have: Proof. We have that: Pr[ω = ω y ] 8 2 min(k1,k/2) Pr[ω = ω y ]= #(y, v) pairs, s.t. y = y + v p mod N and y =0 ω x #(y, v) pairs, s.t. y = y + v p mod N and 0 y<2 k 1 Forafixedv, thevaluey mod N gets fixed by the relation y = y+v p mod N. Moreover at least q 2 of the possible v values give y mod N in the desired range between 0 and 2 k 1. Hence the denominator of the above fraction can be lower bounded by q 2. We have that for a fixed y,thevalueofy is fixed modulo p; hence for a fixed ω with y =0 ω x, thevalueofxis also fixed modulo p. Asx is k k 1 1- bit, over Z there can be at most 2k k 1 1 p many possible x values. Hence the numerator of the above fraction can be upper bounded by 2k k 1 1 p. Hence we have, Pr[ω = ω y ] 2 k k 1 1 p q 2 < 2 k k k/ k/2 2 = 2k k k/2 1 2 k 3 < 8 2 min(k1,k/2) Formally, we obtain the following theorem: Theorem 1. Assume that no algorithm can invert RSA in time t with probability better than ε. Then the signature scheme PSS[k 0,k 1 ] is (t, q h,q g,q s,q fs,ε) secure, where t(k) =t (k) [q s (k)+q g (k)+q h (k)+1] k 0 Θ(k 3 ) ε(k) =ε (k)+(q s + q fs +1) (q s + q fs + q h ) 2 k0 +8 q g q fs 2 min(k1,k/2) +(q h + q s + q fs ) (q h + q g + q s + q fs +1) 2 k1 + q h q fs 2 k0 +4 q fs 2 k/2 Here the attacker can make at most q h,q g,q s,q fs number of h queries, g queries, signature queries and fault signature queries respectively.
10 662 J.-S. Coron and A. Mandal Proof. We use a simulator which behaves in exactly same way as in original PSS security proof [2], in addition it answers fault queries with a uniformly random integer modulo N. Now if the attacker is successful against our simulator then we break the RSA challenge (N,e,η) as in the original paper. We must show that any attacker which is successful against the original attack scenario will be successful against our simulator. For that, we use a sequence of games. We start with Game 0, which is exactly the attack scenario, which requires to know the factorization of N. Then we progressively modify the game, so that eventually knowledge of the factorization of N is not needed anymore. We denote by S i the event that the attacker succeeds in Game i. Game 0 : this is the attack scenario. We answer signature queries as specified in the signature generation algorithm, using the private exponent d. Wesimulate the faulty signature queries by first generating a correct signature σ and then computing σ = σ + u p mod N for a random u modulo q. In the following for simplicity we only consider faulty signatures modulo q; faulty signatures modulo p are simulated in exactly the same way. Game 1 : we abort if there is a collision for ω at Step 2 of the signature generation algorithm, or if the random r used during signature generation has already appeared before. We call this event A 1. More precisely event A 1 happens if one of the following is true: The random r used in a signature oracle or faulty signature oracle query collides with either 1) the r used in a previous signature oracle or faulty signature oracle query or 2) the r used in a previous h oracle query. The h function output in a signature oracle or faulty signature oracle query collides with either 1) the h function outputs in previous signature oracle or faulty signature oracle queries or 2) with a previous h oracle query output or 3) a previous g oracle query input. The h oracle query output collides with either 1) a h function output in previous signature oracle or faulty signature oracle query or 2) a previous h oracle query output or 3) a previous g oracle query input. We obtain: Pr[A 1 ] (q s +q fs ) (q s +q fs +q h ) 2 k0 +(q h +q s +q fs ) (q h +q g +q s +q fs ) 2 k1 and: Pr[S 1 ] Pr[S 0 ] Pr[A 1 ] Game 2 : we construct a similar simulator as in the original PSS security proof [2]; however to deal with faulty signature queries we continue to use the factorization of N. The simulator receives as input a challenge η and must output η d mod N. When receiving a signature query, the simulator generates a random α modulo N such that α e mod N can be written as 0 ω s t. The simulator generates a random r of k 0 bits. Then it lets h(m, r) =ω, g 1 (ω) =s r and g 2 (ω) =t.
11 PSS Is Secure against Random Fault Attacks 663 When receiving a hash query for h(m, r), the challenger generates a random α modulo N such that η α e mod N canbewrittenas0 ω s t; it then defines h(m, r) =ω, g 1 (ω) =s r and g 2 (ω) =t as previously. The queries to g 1 and g 2 are simulated by returning a random value for every new input. To simulate the faulty signature oracle, one first generates as above a random α modulo N such that α e mod N canbewrittenas0 ω s t. Thesimulator generates a random r of k 0 bits. Then it lets h(m, r) =ω, g 1 (ω) =s r and g 2 (ω) =t. Then instead of returning α, thesimulatorgenerates a random u modulo q, and outputs: α = α + u p mod N (6) In Game 2 we abort as in Game 1, and additionally in the following case: while generating a random α modulo N such that α e mod N can be written as 0 ω s t during signature or faulty signature queries (and similarly for h(m, r) queries), we stop after trying k times. This adds (q h + q s + q fs ) 2 k0 in the error term: Pr[S 2 ] Pr[S 1 ] (q h + q s + q fs ) 2 k0 Game 3 : we abort if the attacker makes a query for g(ω) whereω wasusedina faulty signature for message m and random r, while the attacker has not made aquerytoh(m, r) before. We define this event as A 3.Asallthequeryanswers are simulated independently, from Lemma 2 this gives: Pr[S 3 ] Pr[S 2 ] Pr[A 3 ] q g q fs 8 2 min(k1,k/2) Game 4 : we abort if the attacker makes a query for h(m, r) wherer was used to generate a faulty signature with ω, while the attacker has not made a query before to g(ω). In this case the attacker s view is independent from r, which gives: Pr[S 4 ] Pr[S 3 ] q h q fs 2 k0 Game 5 : we abort if the attacker makes a query for h(m, r) wherer was used to generate a faulty signature, or if the attacker makes a query for g(ω)whereω was used in a faulty signature. Game 5 is the same as Game 4 since for a faulty signature m with random r and ω, either the attacker starts with a h(m, r) queryorit starts with a g(ω) query. Pr[S 5 ]=Pr[S 4 ] Game 6 : we change the way the faulty signature oracle is simulated. Instead of first generating α and then α as in equation (6), we first generate a uniformly random α and then a random u modulo q such that α e mod N can be written as 0 ω s t. From Lemma 1 we have: Pr[S 6 ] Pr[S 5 ] q fs 4 2 k/2 Game 7 : since we do not answer the queries for h(m, r) where r was used to generate a faulty signature, and the queries for g(ω) whereω wasusedina
12 664 J.-S. Coron and A. Mandal faulty signature, we do not need to compute ω. Therefore, we do not need to compute a random u modulo q such that α e mod N canbewrittenas0 ω s t. Therefore we do not need to know the factorization of N anymore, and we have: Pr[S 7 ]=Pr[S 6 ] Finally, if the adversary outputs a forgery with probability at least ε in Game 0, then the adversary must output a forgery with probability at least ε Pr[S 7 ] Pr[S 0 ] in Game 7. As in the original PSS security proof, from this forgery we can solve the RSA challenge with probability at least: ε = ε Pr[S 7 ] Pr[S 0 ] 2 k1 Combining the previous inequalities, we get (6). 4 PSS-R Is Secure against Fault Attacks In PSS-R or PSS with message recovery the goal is to save bandwidth such that the message is recoverable from the signature; hence it is not necessary to send the message separately. 4.1 The PSS-R Scheme We recall the definition of the PSS-R scheme [2]. The scheme uses three hash functions h : {0, 1} {0, 1} k1, g 1 : {0, 1} k1 {0, 1} k0 and g 2 : {0, 1} k1 {0, 1} k k0 k1 1,wherek, k 0 and k 1 are the parameters. Key Generation: generate a k-bit RSA modulus N = pq, and a random exponent e Z φ(n). Generate d such that e d =1 modφ(n). The public-key is (N,e); the private key is (N,d). Signature generation: given a message m, do the following: 1. r {0, 1} k0 2. ω h(m r) 3. r g 1 (ω) r 4. m g 2 (ω) m 5. y 0 ω r m 6. Return σ = y d mod N Message Recovery: given a signature σ, do the following: 1. Let y = σ e mod N 2. Parse y as 0 ω r m. If the parsing fails return Reject. 3. r r g 1 (ω) 4. m m g 2 (ω) 5. If h(m r) =ω return m. 6. else return Reject.
13 PSS Is Secure against Random Fault Attacks 665 m r g 1(ω) h g 1 0 ω r M g 2 g 2(ω) Fig. 2. PSS-R: Components of image y =0 ω r M are darkened. The signature of M is y d mod N. 4.2 Security Proof Theorem 2. Assume that no algorithm can invert RSA in time t with probability better than ε. Then the signature scheme PSS-R[k 0,k 1 ] is (t, q h,q g,q s,q fs,ε) secure, where: t(k) =t (k) [q s (k)+q g (k)+q h (k)+1] k 0 Θ(k 3 ) ε(k) =ε (k)+(q s + q fs +1) (q s + q fs + q h ) 2 k0 +8 q g q fs 2 min(k1,k/2) +(q h + q s + q fs ) (q h + q g + q s + q fs +1) 2 k1 + q h q fs 2 k0 +4 q fs 2 k/2 Here the attacker can make at most q h,q g,q s,q fs number of h queries, g queries, signature queries and fault signature queries respectively. Proof. The proof of this theorem is very similar to that of Theorem 1 and hence is omitted. 5 Conclusion We obtain from the previous theorems that unless the attacker is making more fault oracle queries than hash oracle queries, one gets the same security bound as in the original PSS proof without fault oracle. We note that in practice fault queries are usually more expensive than hash queries, since those hash queries can be made offline when a concrete hash function is used. In [6] a better security bound was given for PSS (without fault oracle). It was shown that the random size k 0 could be taken as small as log 2 q s,whereq s is
14 666 J.-S. Coron and A. Mandal the maximum number of signature queries; with q s =2 30 this gives k 0 =30bits. However with a fault oracle one cannot take such a small k 0, since in this case the random r could be recovered by exhaustive search and the Bellcore attack would still apply. In summary. any parameters chosen according to the bounds in the original PSS paper [2] give the same level of security against fault attacks. One can take k = 1024, k 0 = k 1 = 128 as in [2]. References 1. Bellare, M., Rogaway, P.: Random oracles are practical: a paradigm for designing efficient protocols. In: Proceedings of the First Annual Conference on Computer and Communications Security. ACM, New York (1993) 2. Bellare, M., Rogaway, P.: The Exact security of digital signatures: How to sign with rsa and Rabin. In: Maurer, U.M. (ed.) EUROCRYPT LNCS, vol. 1070, pp Springer, Heidelberg (1996) 3. Boneh, D., DeMillo, R.A., Lipton, R.J.: On the importance of checking cryptographic protocols for faults. Journal of Cryptology, Springer-Verlag 14(2), (2001) 4. Canetti, R., Goldreich, O., Halevi, S.: The random oracle methodology, revisited. In: STOC ACM, New York (1998) 5. Coppersmith, D.: Small solutions to polynomial equations, and low exponent vulnerabilities. Journal of Cryptology 10(4), (1997) 6. Coron, J.S.: Optimal security proofs for pss and other signature schemes. In: Knudsen, L.R. (ed.) EUROCRYPT LNCS, vol. 2332, pp Springer, Heidelberg (2002) 7. Coron, J.-S., Joux, A., Kizhvatov, I., Naccache, D., Paillier, P.: Fault Attacks on Randomized RSA Signatures with Partially Unknown Messages. In: CHES 2009, pp (2009), 8. emvintegrated circuit card specifications for payment systems, Book 2. Security and Key Management. Version 4.2 (June 2008), 9. Goldwasser, S., Micali, S., Rivest, R.: A digital signature scheme secure against adaptive chosen-message attacks. SIAM Journal of computing 17(2), (1988) 10. IEEE P1363a, Standard Specifications For Public Key Cryptography: Additional Techniques, ISO/IEC :2002 Information technology Security techniques Digital signature schemes giving message recovery Part 2: Integer factorization based mechanisms (2002) 12. Lenstra, A., Lenstra Jr., H., Lovász, L.: Factoring polynomials with rational coefficients. Mathematische Annalen 261, (1982) 13. Nguyên, P.Q., Stern, J.: Cryptanalysis of a fast public key cryptosystem presented at SAC 97. In: Tavares, S., Meijer, H. (eds.) SAC LNCS, vol. 1556, p Springer, Heidelberg (1999) 14. Rivest, R., Shamir, A., Adleman, L.: A method for obtaining digital signatures and public key cryptosystems. CACM 21 (1978)
From Fixed-Length to Arbitrary-Length RSA Encoding Schemes Revisited
 From Fixed-Length to Arbitrary-Length RSA Encoding Schemes Revisited Julien Cathalo 1, Jean-Sébastien Coron 2, and David Naccache 2,3 1 UCL Crypto Group Place du Levant 3, Louvain-la-Neuve, B-1348, Belgium
From Fixed-Length to Arbitrary-Length RSA Encoding Schemes Revisited Julien Cathalo 1, Jean-Sébastien Coron 2, and David Naccache 2,3 1 UCL Crypto Group Place du Levant 3, Louvain-la-Neuve, B-1348, Belgium
Fault Attacks Against emv Signatures
 Fault Attacks Against emv Signatures Jean-Sébastien Coron 1, David Naccache 2, and Mehdi Tibouchi 2 1 Université du Luxembourg 6, rue Richard Coudenhove-Kalergi l-1359 Luxembourg, Luxembourg {jean-sebastien.coron,
Fault Attacks Against emv Signatures Jean-Sébastien Coron 1, David Naccache 2, and Mehdi Tibouchi 2 1 Université du Luxembourg 6, rue Richard Coudenhove-Kalergi l-1359 Luxembourg, Luxembourg {jean-sebastien.coron,
Lecture 16 Chiu Yuen Koo Nikolai Yakovenko. 1 Digital Signature Schemes. CMSC 858K Advanced Topics in Cryptography March 18, 2004
 CMSC 858K Advanced Topics in Cryptography March 18, 2004 Lecturer: Jonathan Katz Lecture 16 Scribe(s): Chiu Yuen Koo Nikolai Yakovenko Jeffrey Blank 1 Digital Signature Schemes In this lecture, we introduce
CMSC 858K Advanced Topics in Cryptography March 18, 2004 Lecturer: Jonathan Katz Lecture 16 Scribe(s): Chiu Yuen Koo Nikolai Yakovenko Jeffrey Blank 1 Digital Signature Schemes In this lecture, we introduce
From Fixed-Length Messages to Arbitrary-Length Messages Practical RSA Signature Padding Schemes
 From Fixed-Length Messages to Arbitrary-Length Messages Practical RSA Signature Padding Schemes [Published in D. Naccache, Ed., Topics in Cryptology CT-RSA 2001, vol. 2020 of Lecture Notes in Computer
From Fixed-Length Messages to Arbitrary-Length Messages Practical RSA Signature Padding Schemes [Published in D. Naccache, Ed., Topics in Cryptology CT-RSA 2001, vol. 2020 of Lecture Notes in Computer
Lattice-Based Fault Attacks on RSA Signatures
 Lattice-Based Fault Attacks on RSA Signatures Mehdi Tibouchi École normale supérieure Workshop on Applied Cryptography, Singapore, 2010-12-03 Gist of this talk Review a classical attack on RSA signatures
Lattice-Based Fault Attacks on RSA Signatures Mehdi Tibouchi École normale supérieure Workshop on Applied Cryptography, Singapore, 2010-12-03 Gist of this talk Review a classical attack on RSA signatures
Algorithmic Number Theory and Public-key Cryptography
 Algorithmic Number Theory and Public-key Cryptography Course 3 University of Luxembourg March 22, 2018 The RSA algorithm The RSA algorithm is the most widely-used public-key encryption algorithm Invented
Algorithmic Number Theory and Public-key Cryptography Course 3 University of Luxembourg March 22, 2018 The RSA algorithm The RSA algorithm is the most widely-used public-key encryption algorithm Invented
Cryptography. Course 1: Remainder: RSA. Jean-Sébastien Coron. September 21, Université du Luxembourg
 Course 1: Remainder: RSA Université du Luxembourg September 21, 2010 Public-key encryption Public-key encryption: two keys. One key is made public and used to encrypt. The other key is kept private and
Course 1: Remainder: RSA Université du Luxembourg September 21, 2010 Public-key encryption Public-key encryption: two keys. One key is made public and used to encrypt. The other key is kept private and
Partial Key Exposure: Generalized Framework to Attack RSA
 Partial Key Exposure: Generalized Framework to Attack RSA Cryptology Research Group Indian Statistical Institute, Kolkata 12 December 2011 Outline of the Talk 1 RSA - A brief overview 2 Partial Key Exposure
Partial Key Exposure: Generalized Framework to Attack RSA Cryptology Research Group Indian Statistical Institute, Kolkata 12 December 2011 Outline of the Talk 1 RSA - A brief overview 2 Partial Key Exposure
Transitive Signatures Based on Non-adaptive Standard Signatures
 Transitive Signatures Based on Non-adaptive Standard Signatures Zhou Sujing Nanyang Technological University, Singapore, zhousujing@pmail.ntu.edu.sg Abstract. Transitive signature, motivated by signing
Transitive Signatures Based on Non-adaptive Standard Signatures Zhou Sujing Nanyang Technological University, Singapore, zhousujing@pmail.ntu.edu.sg Abstract. Transitive signature, motivated by signing
Computing the RSA Secret Key is Deterministic Polynomial Time Equivalent to Factoring
 Computing the RSA Secret Key is Deterministic Polynomial Time Equivalent to Factoring Alexander May Faculty of Computer Science, Electrical Engineering and Mathematics University of Paderborn 33102 Paderborn,
Computing the RSA Secret Key is Deterministic Polynomial Time Equivalent to Factoring Alexander May Faculty of Computer Science, Electrical Engineering and Mathematics University of Paderborn 33102 Paderborn,
Strongly Unforgeable Signatures Based on Computational Diffie-Hellman
 Strongly Unforgeable Signatures Based on Computational Diffie-Hellman Dan Boneh 1, Emily Shen 1, and Brent Waters 2 1 Computer Science Department, Stanford University, Stanford, CA {dabo,emily}@cs.stanford.edu
Strongly Unforgeable Signatures Based on Computational Diffie-Hellman Dan Boneh 1, Emily Shen 1, and Brent Waters 2 1 Computer Science Department, Stanford University, Stanford, CA {dabo,emily}@cs.stanford.edu
Comparing With RSA. 1 ucl Crypto Group
 Comparing With RSA Julien Cathalo 1, David Naccache 2, and Jean-Jacques Quisquater 1 1 ucl Crypto Group Place du Levant 3, Louvain-la-Neuve, b-1348, Belgium julien.cathalo@uclouvain.be, jean-jacques.quisquater@uclouvain.be
Comparing With RSA Julien Cathalo 1, David Naccache 2, and Jean-Jacques Quisquater 1 1 ucl Crypto Group Place du Levant 3, Louvain-la-Neuve, b-1348, Belgium julien.cathalo@uclouvain.be, jean-jacques.quisquater@uclouvain.be
Solving Systems of Modular Equations in One Variable: How Many RSA-Encrypted Messages Does Eve Need to Know?
 Solving Systems of Modular Equations in One Variable: How Many RSA-Encrypted Messages Does Eve Need to Know? Alexander May, Maike Ritzenhofen Faculty of Mathematics Ruhr-Universität Bochum, 44780 Bochum,
Solving Systems of Modular Equations in One Variable: How Many RSA-Encrypted Messages Does Eve Need to Know? Alexander May, Maike Ritzenhofen Faculty of Mathematics Ruhr-Universität Bochum, 44780 Bochum,
Digital Signature Schemes and the Random Oracle Model. A. Hülsing
 Digital Signature Schemes and the Random Oracle Model A. Hülsing Today s goal Review provable security of in use signature schemes. (PKCS #1 v2.x) PAGE 1 Digital Signature Source: http://hari-cio-8a.blog.ugm.ac.id/files/2013/03/dsa.jpg
Digital Signature Schemes and the Random Oracle Model A. Hülsing Today s goal Review provable security of in use signature schemes. (PKCS #1 v2.x) PAGE 1 Digital Signature Source: http://hari-cio-8a.blog.ugm.ac.id/files/2013/03/dsa.jpg
Deterministic Polynomial Time Equivalence of Computing the RSA Secret Key and Factoring
 Deterministic Polynomial Time Equivalence of Computing the RSA Secret Key and Factoring Jean-Sébastien Coron and Alexander May Gemplus Card International 34 rue Guynemer, 92447 Issy-les-Moulineaux, France
Deterministic Polynomial Time Equivalence of Computing the RSA Secret Key and Factoring Jean-Sébastien Coron and Alexander May Gemplus Card International 34 rue Guynemer, 92447 Issy-les-Moulineaux, France
Public Key Cryptography
 Public Key Cryptography Ali El Kaafarani 1 Mathematical Institute 2 PQShield Ltd. 1 of 44 Outline 1 Public Key Encryption: security notions 2 RSA Encryption Scheme 2 of 44 Course main reference 3 of 44
Public Key Cryptography Ali El Kaafarani 1 Mathematical Institute 2 PQShield Ltd. 1 of 44 Outline 1 Public Key Encryption: security notions 2 RSA Encryption Scheme 2 of 44 Course main reference 3 of 44
Outline. Provable Security in the Computational Model. III Signatures. Public-Key Encryption. Outline. David Pointcheval.
 Provable Security in the Computational Model III Signatures David Pointcheval Ecole normale supérieure, CNRS & INRI Public-Key Encryption Signatures 2 dvanced Security for Signature dvanced Security Notions
Provable Security in the Computational Model III Signatures David Pointcheval Ecole normale supérieure, CNRS & INRI Public-Key Encryption Signatures 2 dvanced Security for Signature dvanced Security Notions
Protecting RSA Against Fault Attacks: The Embedding Method
 Published in L. Breveglieri et al., Eds, Fault Diagnosis and Tolerance in Cryptography (FDTC 2009), IEEE Computer Society, pp. 41 45, 2009. Protecting RSA Against Fault Attacks: The Embedding Method Marc
Published in L. Breveglieri et al., Eds, Fault Diagnosis and Tolerance in Cryptography (FDTC 2009), IEEE Computer Society, pp. 41 45, 2009. Protecting RSA Against Fault Attacks: The Embedding Method Marc
1 What are Physical Attacks. 2 Physical Attacks on RSA. Today:
 Today: Introduction to the class. Examples of concrete physical attacks on RSA A computational approach to cryptography Pseudorandomness 1 What are Physical Attacks Tampering/Leakage attacks Issue of how
Today: Introduction to the class. Examples of concrete physical attacks on RSA A computational approach to cryptography Pseudorandomness 1 What are Physical Attacks Tampering/Leakage attacks Issue of how
1 Number Theory Basics
 ECS 289M (Franklin), Winter 2010, Crypto Review 1 Number Theory Basics This section has some basic facts about number theory, mostly taken (or adapted) from Dan Boneh s number theory fact sheets for his
ECS 289M (Franklin), Winter 2010, Crypto Review 1 Number Theory Basics This section has some basic facts about number theory, mostly taken (or adapted) from Dan Boneh s number theory fact sheets for his
Lecture 15 & 16: Trapdoor Permutations, RSA, Signatures
 CS 7810 Graduate Cryptography October 30, 2017 Lecture 15 & 16: Trapdoor Permutations, RSA, Signatures Lecturer: Daniel Wichs Scribe: Willy Quach & Giorgos Zirdelis 1 Topic Covered. Trapdoor Permutations.
CS 7810 Graduate Cryptography October 30, 2017 Lecture 15 & 16: Trapdoor Permutations, RSA, Signatures Lecturer: Daniel Wichs Scribe: Willy Quach & Giorgos Zirdelis 1 Topic Covered. Trapdoor Permutations.
Design Validations for Discrete Logarithm Based Signature Schemes
 Proceedings of the 2000 International Workshop on Practice and Theory in Public Key Cryptography (PKC 2000) (18 20 january 2000, Melbourne, Australia) H. Imai and Y. Zheng Eds. Springer-Verlag, LNCS 1751,
Proceedings of the 2000 International Workshop on Practice and Theory in Public Key Cryptography (PKC 2000) (18 20 january 2000, Melbourne, Australia) H. Imai and Y. Zheng Eds. Springer-Verlag, LNCS 1751,
Cryptanalysis of a Zero-Knowledge Identification Protocol of Eurocrypt 95
 Cryptanalysis of a Zero-Knowledge Identification Protocol of Eurocrypt 95 Jean-Sébastien Coron and David Naccache Gemplus Card International 34 rue Guynemer, 92447 Issy-les-Moulineaux, France {jean-sebastien.coron,
Cryptanalysis of a Zero-Knowledge Identification Protocol of Eurocrypt 95 Jean-Sébastien Coron and David Naccache Gemplus Card International 34 rue Guynemer, 92447 Issy-les-Moulineaux, France {jean-sebastien.coron,
Digital Signatures from Challenge-Divided Σ-Protocols
 Digital Signatures from Challenge-Divided Σ-Protocols Andrew C. Yao Yunlei Zhao Abstract Digital signature is one of the basic primitives in cryptography. A common paradigm of obtaining signatures, known
Digital Signatures from Challenge-Divided Σ-Protocols Andrew C. Yao Yunlei Zhao Abstract Digital signature is one of the basic primitives in cryptography. A common paradigm of obtaining signatures, known
Practical Fault Countermeasures for Chinese Remaindering Based RSA
 Practical Fault Countermeasures for Chinese Remaindering Based RSA (Extended Abstract) Mathieu Ciet 1 and Marc Joye 2, 1 Gemplus R&D, Advanced Research and Security Centre La Vigie, ZI Athélia IV, Av.
Practical Fault Countermeasures for Chinese Remaindering Based RSA (Extended Abstract) Mathieu Ciet 1 and Marc Joye 2, 1 Gemplus R&D, Advanced Research and Security Centre La Vigie, ZI Athélia IV, Av.
John Hancock enters the 21th century Digital signature schemes. Table of contents
 John Hancock enters the 21th century Digital signature schemes Foundations of Cryptography Computer Science Department Wellesley College Fall 2016 Table of contents From last time: Good news and bad There
John Hancock enters the 21th century Digital signature schemes Foundations of Cryptography Computer Science Department Wellesley College Fall 2016 Table of contents From last time: Good news and bad There
New attacks on RSA with Moduli N = p r q
 New attacks on RSA with Moduli N = p r q Abderrahmane Nitaj 1 and Tajjeeddine Rachidi 2 1 Laboratoire de Mathématiques Nicolas Oresme Université de Caen Basse Normandie, France abderrahmane.nitaj@unicaen.fr
New attacks on RSA with Moduli N = p r q Abderrahmane Nitaj 1 and Tajjeeddine Rachidi 2 1 Laboratoire de Mathématiques Nicolas Oresme Université de Caen Basse Normandie, France abderrahmane.nitaj@unicaen.fr
Secure and Practical Identity-Based Encryption
 Secure and Practical Identity-Based Encryption David Naccache Groupe de Cyptographie, Deṕartement d Informatique École Normale Supérieure 45 rue d Ulm, 75005 Paris, France david.nacache@ens.fr Abstract.
Secure and Practical Identity-Based Encryption David Naccache Groupe de Cyptographie, Deṕartement d Informatique École Normale Supérieure 45 rue d Ulm, 75005 Paris, France david.nacache@ens.fr Abstract.
Fault Attacks on RSA Signatures with Partially Unknown Messages
 Fault Attacks on RSA Signatures with Partially Unknown Messages Jean-Sébastien Coron 1, Antoine Joux 2, Ilya Kizhvatov 1, David Naccache 3, and Pascal Paillier 4 1 Université du Luxembourg 6, rue Richard
Fault Attacks on RSA Signatures with Partially Unknown Messages Jean-Sébastien Coron 1, Antoine Joux 2, Ilya Kizhvatov 1, David Naccache 3, and Pascal Paillier 4 1 Université du Luxembourg 6, rue Richard
Efficient Identity-Based Encryption Without Random Oracles
 Efficient Identity-Based Encryption Without Random Oracles Brent Waters Abstract We present the first efficient Identity-Based Encryption (IBE) scheme that is fully secure without random oracles. We first
Efficient Identity-Based Encryption Without Random Oracles Brent Waters Abstract We present the first efficient Identity-Based Encryption (IBE) scheme that is fully secure without random oracles. We first
Katz, Lindell Introduction to Modern Cryptrography
 Katz, Lindell Introduction to Modern Cryptrography Slides Chapter 12 Markus Bläser, Saarland University Digital signature schemes Goal: integrity of messages Signer signs a message using a private key
Katz, Lindell Introduction to Modern Cryptrography Slides Chapter 12 Markus Bläser, Saarland University Digital signature schemes Goal: integrity of messages Signer signs a message using a private key
II. Digital signatures
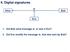 II. Digital signatures Alice m Bob Eve 1. Did Bob send message m, or was it Eve? 2. Did Eve modify the message m, that was sent by Bob? 1 Digital signatures Digital signature - are equivalent of handwritten
II. Digital signatures Alice m Bob Eve 1. Did Bob send message m, or was it Eve? 2. Did Eve modify the message m, that was sent by Bob? 1 Digital signatures Digital signature - are equivalent of handwritten
RSA and Rabin Signatures Signcryption
 T-79.5502 Advanced Course in Cryptology RSA and Rabin Signatures Signcryption Alessandro Tortelli 26-04-06 Overview Introduction Probabilistic Signature Scheme PSS PSS with message recovery Signcryption
T-79.5502 Advanced Course in Cryptology RSA and Rabin Signatures Signcryption Alessandro Tortelli 26-04-06 Overview Introduction Probabilistic Signature Scheme PSS PSS with message recovery Signcryption
Breaking Plain ElGamal and Plain RSA Encryption
 Breaking Plain ElGamal and Plain RSA Encryption (Extended Abstract) Dan Boneh Antoine Joux Phong Nguyen dabo@cs.stanford.edu joux@ens.fr pnguyen@ens.fr Abstract We present a simple attack on both plain
Breaking Plain ElGamal and Plain RSA Encryption (Extended Abstract) Dan Boneh Antoine Joux Phong Nguyen dabo@cs.stanford.edu joux@ens.fr pnguyen@ens.fr Abstract We present a simple attack on both plain
Secure Hash-and-Sign Signatures Without the Random Oracle
 Secure Hash-and-Sign Signatures Without the Random Oracle Rosario Gennaro, Shai Halevi, and Tal Rabin IBM T.J.Watson Research Center, PO Box 704, Yorktown Heights, NY 10598, USA {rosario,shaih,talr}@watson.ibm.com
Secure Hash-and-Sign Signatures Without the Random Oracle Rosario Gennaro, Shai Halevi, and Tal Rabin IBM T.J.Watson Research Center, PO Box 704, Yorktown Heights, NY 10598, USA {rosario,shaih,talr}@watson.ibm.com
f (x) f (x) easy easy
 A General Construction of IND-CCA2 Secure Public Key Encryption? Eike Kiltz 1 and John Malone-Lee 2 1 Lehrstuhl Mathematik & Informatik, Fakultat fur Mathematik, Ruhr-Universitat Bochum, Germany. URL:
A General Construction of IND-CCA2 Secure Public Key Encryption? Eike Kiltz 1 and John Malone-Lee 2 1 Lehrstuhl Mathematik & Informatik, Fakultat fur Mathematik, Ruhr-Universitat Bochum, Germany. URL:
Digital Signatures. Adam O Neill based on
 Digital Signatures Adam O Neill based on http://cseweb.ucsd.edu/~mihir/cse207/ Signing by hand COSMO ALICE ALICE Pay Bob $100 Cosmo Alice Alice Bank =? no Don t yes pay Bob Signing electronically SIGFILE
Digital Signatures Adam O Neill based on http://cseweb.ucsd.edu/~mihir/cse207/ Signing by hand COSMO ALICE ALICE Pay Bob $100 Cosmo Alice Alice Bank =? no Don t yes pay Bob Signing electronically SIGFILE
The Gap-Problems: a New Class of Problems for the Security of Cryptographic Schemes
 Proceedings of the 2001 International Workshop on Practice and Theory in Public Key Cryptography (PKC 2001) (13 15 february 2001, Cheju Islands, South Korea) K. Kim Ed. Springer-Verlag, LNCS 1992, pages
Proceedings of the 2001 International Workshop on Practice and Theory in Public Key Cryptography (PKC 2001) (13 15 february 2001, Cheju Islands, South Korea) K. Kim Ed. Springer-Verlag, LNCS 1992, pages
Evaluation Report on the ESIGN signature scheme
 Evaluation Report on the ESIGN signature scheme Jacques Stern 1 Introduction This document is an evaluation of the ESIGN signature scheme. Our work is based on the analysis of various documents [12, 13,
Evaluation Report on the ESIGN signature scheme Jacques Stern 1 Introduction This document is an evaluation of the ESIGN signature scheme. Our work is based on the analysis of various documents [12, 13,
Lecture 10 - MAC s continued, hash & MAC
 Lecture 10 - MAC s continued, hash & MAC Boaz Barak March 3, 2010 Reading: Boneh-Shoup chapters 7,8 The field GF(2 n ). A field F is a set with a multiplication ( ) and addition operations that satisfy
Lecture 10 - MAC s continued, hash & MAC Boaz Barak March 3, 2010 Reading: Boneh-Shoup chapters 7,8 The field GF(2 n ). A field F is a set with a multiplication ( ) and addition operations that satisfy
Short Unique Signatures from RSA with a Tight Security Reduction (in the Random Oracle Model)
 Short Unique Signatures from RSA with a Tight Security Reduction (in the Random Oracle Model) Hovav Shacham UC San Diego and UT Austin Abstract. A signature scheme is unique if for every public key and
Short Unique Signatures from RSA with a Tight Security Reduction (in the Random Oracle Model) Hovav Shacham UC San Diego and UT Austin Abstract. A signature scheme is unique if for every public key and
Cryptanalysis of a Fast Public Key Cryptosystem Presented at SAC 97
 Cryptanalysis of a Fast Public Key Cryptosystem Presented at SAC 97 Phong Nguyen and Jacques Stern École Normale Supérieure, Laboratoire d Informatique 45, rue d Ulm, F 75230 Paris Cedex 05 {Phong.Nguyen,Jacques.Stern}@ens.fr
Cryptanalysis of a Fast Public Key Cryptosystem Presented at SAC 97 Phong Nguyen and Jacques Stern École Normale Supérieure, Laboratoire d Informatique 45, rue d Ulm, F 75230 Paris Cedex 05 {Phong.Nguyen,Jacques.Stern}@ens.fr
Digital signature schemes
 Digital signature schemes Martin Stanek Department of Computer Science Comenius University stanek@dcs.fmph.uniba.sk Cryptology 1 (2017/18) Content Introduction digital signature scheme security of digital
Digital signature schemes Martin Stanek Department of Computer Science Comenius University stanek@dcs.fmph.uniba.sk Cryptology 1 (2017/18) Content Introduction digital signature scheme security of digital
Optimal Security Reductions for Unique Signatures: Bypassing Impossibilities with A Counterexample
 Optimal Security Reductions for Unique Signatures: Bypassing Impossibilities with A Counterexample Fuchun Guo 1, Rongmao Chen 2, Willy Susilo 1, Jianchang Lai 1, Guomin Yang 1, and Yi Mu 1 1 Institute
Optimal Security Reductions for Unique Signatures: Bypassing Impossibilities with A Counterexample Fuchun Guo 1, Rongmao Chen 2, Willy Susilo 1, Jianchang Lai 1, Guomin Yang 1, and Yi Mu 1 1 Institute
A New Attack on RSA with Two or Three Decryption Exponents
 A New Attack on RSA with Two or Three Decryption Exponents Abderrahmane Nitaj Laboratoire de Mathématiques Nicolas Oresme Université de Caen, France nitaj@math.unicaen.fr http://www.math.unicaen.fr/~nitaj
A New Attack on RSA with Two or Three Decryption Exponents Abderrahmane Nitaj Laboratoire de Mathématiques Nicolas Oresme Université de Caen, France nitaj@math.unicaen.fr http://www.math.unicaen.fr/~nitaj
Foundations of Cryptography
 - 111 - Foundations of Cryptography Notes of lecture No. 10B & 11 (given on June 11 & 18, 1989) taken by Sergio Rajsbaum Summary In this lecture we define unforgeable digital signatures and present such
- 111 - Foundations of Cryptography Notes of lecture No. 10B & 11 (given on June 11 & 18, 1989) taken by Sergio Rajsbaum Summary In this lecture we define unforgeable digital signatures and present such
A new attack on RSA with a composed decryption exponent
 A new attack on RSA with a composed decryption exponent Abderrahmane Nitaj and Mohamed Ould Douh,2 Laboratoire de Mathématiques Nicolas Oresme Université de Caen, Basse Normandie, France abderrahmane.nitaj@unicaen.fr
A new attack on RSA with a composed decryption exponent Abderrahmane Nitaj and Mohamed Ould Douh,2 Laboratoire de Mathématiques Nicolas Oresme Université de Caen, Basse Normandie, France abderrahmane.nitaj@unicaen.fr
New Approach for Selectively Convertible Undeniable Signature Schemes
 New Approach for Selectively Convertible Undeniable Signature Schemes Kaoru Kurosawa 1 and Tsuyoshi Takagi 2 1 Ibaraki University, Japan, kurosawa@mx.ibaraki.ac.jp 2 Future University-Hakodate, Japan,
New Approach for Selectively Convertible Undeniable Signature Schemes Kaoru Kurosawa 1 and Tsuyoshi Takagi 2 1 Ibaraki University, Japan, kurosawa@mx.ibaraki.ac.jp 2 Future University-Hakodate, Japan,
Cramer-Damgård Signatures Revisited: Efficient Flat-Tree Signatures Based on Factoring
 Cramer-Damgård Signatures Revisited: Efficient Flat-Tree Signatures Based on Factoring Dario Catalano 1 and Rosario Gennaro 2 1 CNRS - École normale supérieure, Laboratoire d informatique 45 rue d Ulm,
Cramer-Damgård Signatures Revisited: Efficient Flat-Tree Signatures Based on Factoring Dario Catalano 1 and Rosario Gennaro 2 1 CNRS - École normale supérieure, Laboratoire d informatique 45 rue d Ulm,
Semantic Security of RSA. Semantic Security
 Semantic Security of RSA Murat Kantarcioglu Semantic Security As before our goal is to come up with a public key system that protects against more than total break We want our system to be secure against
Semantic Security of RSA Murat Kantarcioglu Semantic Security As before our goal is to come up with a public key system that protects against more than total break We want our system to be secure against
A NEW ATTACK ON RSA WITH A COMPOSED DECRYPTION EXPONENT
 A NEW ATTACK ON RSA WITH A COMPOSED DECRYPTION EXPONENT Abderrahmane Nitaj 1 and Mohamed Ould Douh 1,2 1 Laboratoire de Mathématiques Nicolas Oresme, Université de Caen, Basse Normandie, France Université
A NEW ATTACK ON RSA WITH A COMPOSED DECRYPTION EXPONENT Abderrahmane Nitaj 1 and Mohamed Ould Douh 1,2 1 Laboratoire de Mathématiques Nicolas Oresme, Université de Caen, Basse Normandie, France Université
5 Public-Key Encryption: Rabin, Blum-Goldwasser, RSA
 Leo Reyzin. Notes for BU CAS CS 538. 1 5 Public-Key Encryption: Rabin, Blum-Goldwasser, RSA 5.1 Public Key vs. Symmetric Encryption In the encryption we ve been doing so far, the sender and the recipient
Leo Reyzin. Notes for BU CAS CS 538. 1 5 Public-Key Encryption: Rabin, Blum-Goldwasser, RSA 5.1 Public Key vs. Symmetric Encryption In the encryption we ve been doing so far, the sender and the recipient
The Random Oracle Model and the Ideal Cipher Model are Equivalent
 The Random Oracle Model and the Ideal Cipher Model are Equivalent Jean-Sébastien Coron 1, Jacques Patarin 2, and Yannick Seurin 2,3 1 University of Luxembourg 2 University of Versailles 3 Orange Labs Abstract.
The Random Oracle Model and the Ideal Cipher Model are Equivalent Jean-Sébastien Coron 1, Jacques Patarin 2, and Yannick Seurin 2,3 1 University of Luxembourg 2 University of Versailles 3 Orange Labs Abstract.
On Deterministic Polynomial-Time Equivalence of Computing the CRT-RSA Secret Keys and Factoring
 On Deterministic Polynomial-Time Equivalence of Computing the CRT-RSA Secret Keys and Factoring Subhamoy Maitra and Santanu Sarkar Applied Statistics Unit, Indian Statistical Institute, 203 B T Road, Kolkata
On Deterministic Polynomial-Time Equivalence of Computing the CRT-RSA Secret Keys and Factoring Subhamoy Maitra and Santanu Sarkar Applied Statistics Unit, Indian Statistical Institute, 203 B T Road, Kolkata
Uninstantiability of Full-Domain Hash
 Uninstantiability of based on On the Generic Insecurity of, Crypto 05, joint work with Y.Dodis and R.Oliveira Krzysztof Pietrzak CWI Amsterdam June 3, 2008 Why talk about this old stuff? Why talk about
Uninstantiability of based on On the Generic Insecurity of, Crypto 05, joint work with Y.Dodis and R.Oliveira Krzysztof Pietrzak CWI Amsterdam June 3, 2008 Why talk about this old stuff? Why talk about
one eciently recover the entire key? There is no known method for doing so. Furthermore, the common belief is that no such ecient algorithm exists. Th
 Exposing an RSA Private Key Given a Small Fraction of its Bits Dan Boneh Glenn Durfee y Yair Frankel dabo@cs.stanford.edu gdurf@cs.stanford.edu yfrankel@cs.columbia.edu Stanford University Stanford University
Exposing an RSA Private Key Given a Small Fraction of its Bits Dan Boneh Glenn Durfee y Yair Frankel dabo@cs.stanford.edu gdurf@cs.stanford.edu yfrankel@cs.columbia.edu Stanford University Stanford University
A Domain Extender for the Ideal Cipher
 A Domain Extender for the Ideal Cipher Jean-Sébastien Coron 2, Yevgeniy Dodis 1, Avradip Mandal 2, and Yannick Seurin 3,4 1 New York University 2 University of Luxembourg 3 University of Versailles 4 Orange
A Domain Extender for the Ideal Cipher Jean-Sébastien Coron 2, Yevgeniy Dodis 1, Avradip Mandal 2, and Yannick Seurin 3,4 1 New York University 2 University of Luxembourg 3 University of Versailles 4 Orange
Cryptanalysis of RSA Signatures with Fixed-Pattern Padding
 Cryptanalysis of RSA Signatures with Fixed-Pattern Padding [Published in J. Kilian Ed., Advances in Cryptology CRYPTO 2001, vol. 2139 of Lecture Notes in Computer Science, pp. 433 439, Springer-Verlag,
Cryptanalysis of RSA Signatures with Fixed-Pattern Padding [Published in J. Kilian Ed., Advances in Cryptology CRYPTO 2001, vol. 2139 of Lecture Notes in Computer Science, pp. 433 439, Springer-Verlag,
Introduction to Modern Cryptography. Benny Chor
 Introduction to Modern Cryptography Benny Chor RSA Public Key Encryption Factoring Algorithms Lecture 7 Tel-Aviv University Revised March 1st, 2008 Reminder: The Prime Number Theorem Let π(x) denote the
Introduction to Modern Cryptography Benny Chor RSA Public Key Encryption Factoring Algorithms Lecture 7 Tel-Aviv University Revised March 1st, 2008 Reminder: The Prime Number Theorem Let π(x) denote the
Public-Key Encryption: ElGamal, RSA, Rabin
 Public-Key Encryption: ElGamal, RSA, Rabin Introduction to Modern Cryptography Benny Applebaum Tel-Aviv University Fall Semester, 2011 12 Public-Key Encryption Syntax Encryption algorithm: E. Decryption
Public-Key Encryption: ElGamal, RSA, Rabin Introduction to Modern Cryptography Benny Applebaum Tel-Aviv University Fall Semester, 2011 12 Public-Key Encryption Syntax Encryption algorithm: E. Decryption
Deterministic Polynomial Time Equivalence between Factoring and Key-Recovery Attack on Takagi s RSA
 Deterministic Polynomial Time Equivalence between Factoring and Key-Recovery Attack on Takagi s RSA Noboru Kunihiro 1 and Kaoru Kurosawa 2 1 The University of Electro-Communications, Japan kunihiro@iceuecacjp
Deterministic Polynomial Time Equivalence between Factoring and Key-Recovery Attack on Takagi s RSA Noboru Kunihiro 1 and Kaoru Kurosawa 2 1 The University of Electro-Communications, Japan kunihiro@iceuecacjp
Lecture 1: Introduction to Public key cryptography
 Lecture 1: Introduction to Public key cryptography Thomas Johansson T. Johansson (Lund University) 1 / 44 Key distribution Symmetric key cryptography: Alice and Bob share a common secret key. Some means
Lecture 1: Introduction to Public key cryptography Thomas Johansson T. Johansson (Lund University) 1 / 44 Key distribution Symmetric key cryptography: Alice and Bob share a common secret key. Some means
Lecture 18: Message Authentication Codes & Digital Signa
 Lecture 18: Message Authentication Codes & Digital Signatures MACs and Signatures Both are used to assert that a message has indeed been generated by a party MAC is the private-key version and Signatures
Lecture 18: Message Authentication Codes & Digital Signatures MACs and Signatures Both are used to assert that a message has indeed been generated by a party MAC is the private-key version and Signatures
Lecture 4 Chiu Yuen Koo Nikolai Yakovenko. 1 Summary. 2 Hybrid Encryption. CMSC 858K Advanced Topics in Cryptography February 5, 2004
 CMSC 858K Advanced Topics in Cryptography February 5, 2004 Lecturer: Jonathan Katz Lecture 4 Scribe(s): Chiu Yuen Koo Nikolai Yakovenko Jeffrey Blank 1 Summary The focus of this lecture is efficient public-key
CMSC 858K Advanced Topics in Cryptography February 5, 2004 Lecturer: Jonathan Katz Lecture 4 Scribe(s): Chiu Yuen Koo Nikolai Yakovenko Jeffrey Blank 1 Summary The focus of this lecture is efficient public-key
ENEE 457: Computer Systems Security 10/3/16. Lecture 9 RSA Encryption and Diffie-Helmann Key Exchange
 ENEE 457: Computer Systems Security 10/3/16 Lecture 9 RSA Encryption and Diffie-Helmann Key Exchange Charalampos (Babis) Papamanthou Department of Electrical and Computer Engineering University of Maryland,
ENEE 457: Computer Systems Security 10/3/16 Lecture 9 RSA Encryption and Diffie-Helmann Key Exchange Charalampos (Babis) Papamanthou Department of Electrical and Computer Engineering University of Maryland,
Seifert s RSA Fault Attack: Simplified Analysis and Generalizations
 Seifert s RSA Fault Attack: Simplified Analysis and Generalizations James A. Muir School of Computer Science Carleton University jamuir@scs.carleton.ca 15 December 2005 21:11:36 EST Abstract Seifert recently
Seifert s RSA Fault Attack: Simplified Analysis and Generalizations James A. Muir School of Computer Science Carleton University jamuir@scs.carleton.ca 15 December 2005 21:11:36 EST Abstract Seifert recently
Flaws in Applying Proof Methodologies to Signature Schemes
 Flaws in Applying Proof Methodologies to Signature Schemes Jacques Stern 1,, David Pointcheval 1, John Malone-Lee 2, and Nigel P. Smart 2 1 Dépt d Informatique, ENS CNRS, 45 rue d Ulm, 75230 Paris Cedex
Flaws in Applying Proof Methodologies to Signature Schemes Jacques Stern 1,, David Pointcheval 1, John Malone-Lee 2, and Nigel P. Smart 2 1 Dépt d Informatique, ENS CNRS, 45 rue d Ulm, 75230 Paris Cedex
10 Concrete candidates for public key crypto
 10 Concrete candidates for public key crypto In the previous lecture we talked about public key cryptography and saw the Diffie Hellman system and the DSA signature scheme. In this lecture, we will see
10 Concrete candidates for public key crypto In the previous lecture we talked about public key cryptography and saw the Diffie Hellman system and the DSA signature scheme. In this lecture, we will see
5199/IOC5063 Theory of Cryptology, 2014 Fall
 5199/IOC5063 Theory of Cryptology, 2014 Fall Homework 2 Reference Solution 1. This is about the RSA common modulus problem. Consider that two users A and B use the same modulus n = 146171 for the RSA encryption.
5199/IOC5063 Theory of Cryptology, 2014 Fall Homework 2 Reference Solution 1. This is about the RSA common modulus problem. Consider that two users A and B use the same modulus n = 146171 for the RSA encryption.
SIS-based Signatures
 Lattices and Homomorphic Encryption, Spring 2013 Instructors: Shai Halevi, Tal Malkin February 26, 2013 Basics We will use the following parameters: n, the security parameter. =poly(n). m 2n log s 2 n
Lattices and Homomorphic Encryption, Spring 2013 Instructors: Shai Halevi, Tal Malkin February 26, 2013 Basics We will use the following parameters: n, the security parameter. =poly(n). m 2n log s 2 n
Lecture 14 More on Digital Signatures and Variants. COSC-260 Codes and Ciphers Adam O Neill Adapted from
 Lecture 14 More on Digital Signatures and Variants COSC-260 Codes and Ciphers Adam O Neill Adapted from http://cseweb.ucsd.edu/~mihir/cse107/ Setting the Stage We will cover in more depth some issues for
Lecture 14 More on Digital Signatures and Variants COSC-260 Codes and Ciphers Adam O Neill Adapted from http://cseweb.ucsd.edu/~mihir/cse107/ Setting the Stage We will cover in more depth some issues for
ECS 189A Final Cryptography Spring 2011
 ECS 127: Cryptography Handout F UC Davis Phillip Rogaway June 9, 2011 ECS 189A Final Cryptography Spring 2011 Hints for success: Good luck on the exam. I don t think it s all that hard (I do believe I
ECS 127: Cryptography Handout F UC Davis Phillip Rogaway June 9, 2011 ECS 189A Final Cryptography Spring 2011 Hints for success: Good luck on the exam. I don t think it s all that hard (I do believe I
A Strong Identity Based Key-Insulated Cryptosystem
 A Strong Identity Based Key-Insulated Cryptosystem Jin Li 1, Fangguo Zhang 2,3, and Yanming Wang 1,4 1 School of Mathematics and Computational Science, Sun Yat-sen University, Guangzhou, 510275, P.R.China
A Strong Identity Based Key-Insulated Cryptosystem Jin Li 1, Fangguo Zhang 2,3, and Yanming Wang 1,4 1 School of Mathematics and Computational Science, Sun Yat-sen University, Guangzhou, 510275, P.R.China
Security Proofs for Signature Schemes. Ecole Normale Superieure. 45, rue d'ulm Paris Cedex 05
 Security Proofs for Signature Schemes David Pointcheval David.Pointcheval@ens.fr Jacques Stern Jacques.Stern@ens.fr Ecole Normale Superieure Laboratoire d'informatique 45, rue d'ulm 75230 Paris Cedex 05
Security Proofs for Signature Schemes David Pointcheval David.Pointcheval@ens.fr Jacques Stern Jacques.Stern@ens.fr Ecole Normale Superieure Laboratoire d'informatique 45, rue d'ulm 75230 Paris Cedex 05
An Efficient ID-based Digital Signature with Message Recovery Based on Pairing
 An Efficient ID-based Digital Signature with Message Recovery Based on Pairing Raylin Tso, Chunxiang Gu, Takeshi Okamoto, and Eiji Okamoto Department of Risk Engineering Graduate School of Systems and
An Efficient ID-based Digital Signature with Message Recovery Based on Pairing Raylin Tso, Chunxiang Gu, Takeshi Okamoto, and Eiji Okamoto Department of Risk Engineering Graduate School of Systems and
Short and Stateless Signatures from the RSA Assumption
 Short and Stateless Signatures from the RSA Assumption Susan Hohenberger 1, and Brent Waters 2, 1 Johns Hopkins University, susan@cs.jhu.edu 2 University of Texas at Austin, bwaters@cs.utexas.edu Abstract.
Short and Stateless Signatures from the RSA Assumption Susan Hohenberger 1, and Brent Waters 2, 1 Johns Hopkins University, susan@cs.jhu.edu 2 University of Texas at Austin, bwaters@cs.utexas.edu Abstract.
Lecture 22. We first consider some constructions of standard commitment schemes. 2.1 Constructions Based on One-Way (Trapdoor) Permutations
 CMSC 858K Advanced Topics in Cryptography April 20, 2004 Lecturer: Jonathan Katz Lecture 22 Scribe(s): agaraj Anthapadmanabhan, Ji Sun Shin 1 Introduction to These otes In the previous lectures, we saw
CMSC 858K Advanced Topics in Cryptography April 20, 2004 Lecturer: Jonathan Katz Lecture 22 Scribe(s): agaraj Anthapadmanabhan, Ji Sun Shin 1 Introduction to These otes In the previous lectures, we saw
CPSC 467: Cryptography and Computer Security
 CPSC 467: Cryptography and Computer Security Michael J. Fischer Lecture 11 October 7, 2015 CPSC 467, Lecture 11 1/37 Digital Signature Algorithms Signatures from commutative cryptosystems Signatures from
CPSC 467: Cryptography and Computer Security Michael J. Fischer Lecture 11 October 7, 2015 CPSC 467, Lecture 11 1/37 Digital Signature Algorithms Signatures from commutative cryptosystems Signatures from
An Introduction to Probabilistic Encryption
 Osječki matematički list 6(2006), 37 44 37 An Introduction to Probabilistic Encryption Georg J. Fuchsbauer Abstract. An introduction to probabilistic encryption is given, presenting the first probabilistic
Osječki matematički list 6(2006), 37 44 37 An Introduction to Probabilistic Encryption Georg J. Fuchsbauer Abstract. An introduction to probabilistic encryption is given, presenting the first probabilistic
Lecture 18 - Secret Sharing, Visual Cryptography, Distributed Signatures
 Lecture 18 - Secret Sharing, Visual Cryptography, Distributed Signatures Boaz Barak November 27, 2007 Quick review of homework 7 Existence of a CPA-secure public key encryption scheme such that oracle
Lecture 18 - Secret Sharing, Visual Cryptography, Distributed Signatures Boaz Barak November 27, 2007 Quick review of homework 7 Existence of a CPA-secure public key encryption scheme such that oracle
Computers and Mathematics with Applications
 Computers and Mathematics with Applications 61 (2011) 1261 1265 Contents lists available at ScienceDirect Computers and Mathematics with Applications journal homepage: wwwelseviercom/locate/camwa Cryptanalysis
Computers and Mathematics with Applications 61 (2011) 1261 1265 Contents lists available at ScienceDirect Computers and Mathematics with Applications journal homepage: wwwelseviercom/locate/camwa Cryptanalysis
Provable Security for Public-Key Schemes. Outline. I Basics. Secrecy of Communications. Outline. David Pointcheval
 Provable Security for Public-Key Schemes I Basics David Pointcheval Ecole normale supérieure, CNRS & INRIA IACR-SEAMS School Cryptographie: Foundations and New Directions November 2016 Hanoi Vietnam Introduction
Provable Security for Public-Key Schemes I Basics David Pointcheval Ecole normale supérieure, CNRS & INRIA IACR-SEAMS School Cryptographie: Foundations and New Directions November 2016 Hanoi Vietnam Introduction
Exercise Sheet Cryptography 1, 2011
 Cryptography 1 http://www.cs.ut.ee/~unruh/crypto1-11/ Exercise Sheet Cryptography 1, 2011 Exercise 1 DES The Data Encryption Standard (DES) is a very famous and widely used block cipher. It maps 64-bit
Cryptography 1 http://www.cs.ut.ee/~unruh/crypto1-11/ Exercise Sheet Cryptography 1, 2011 Exercise 1 DES The Data Encryption Standard (DES) is a very famous and widely used block cipher. It maps 64-bit
1 Cryptographic hash functions
 CSCI 5440: Cryptography Lecture 6 The Chinese University of Hong Kong 23 February 2011 1 Cryptographic hash functions Last time we saw a construction of message authentication codes (MACs) for fixed-length
CSCI 5440: Cryptography Lecture 6 The Chinese University of Hong Kong 23 February 2011 1 Cryptographic hash functions Last time we saw a construction of message authentication codes (MACs) for fixed-length
Why One Should Also Secure RSA Public Key Elements
 Why One Should Also Secure RSA Public Key Elements [Published in L. Goubin and M. Matsui, Eds., Cryptographic Hardware and Embedded Systems CHES 2006, vol. 4249 of Lecture Notes in Computer Science, pp.
Why One Should Also Secure RSA Public Key Elements [Published in L. Goubin and M. Matsui, Eds., Cryptographic Hardware and Embedded Systems CHES 2006, vol. 4249 of Lecture Notes in Computer Science, pp.
Chosen-Ciphertext Secure RSA-type Cryptosystems
 Published in J. Pieprzyk and F. Zhang, Eds, Provable Security (ProvSec 2009), vol 5848 of Lecture Notes in Computer Science, pp. 32 46, Springer, 2009. Chosen-Ciphertext Secure RSA-type Cryptosystems Benoît
Published in J. Pieprzyk and F. Zhang, Eds, Provable Security (ProvSec 2009), vol 5848 of Lecture Notes in Computer Science, pp. 32 46, Springer, 2009. Chosen-Ciphertext Secure RSA-type Cryptosystems Benoît
RSA OAEP is Secure under the RSA Assumption
 RSA OAEP is Secure under the RSA Assumption Eiichiro Fujisaki 1, Tatsuaki Okamoto 1, David Pointcheval 2, and Jacques Stern 2 1 NTT Labs, 1-1 Hikarino-oka, Yokosuka-shi, 239-0847 Japan. E-mail: {fujisaki,okamoto}@isl.ntt.co.jp.
RSA OAEP is Secure under the RSA Assumption Eiichiro Fujisaki 1, Tatsuaki Okamoto 1, David Pointcheval 2, and Jacques Stern 2 1 NTT Labs, 1-1 Hikarino-oka, Yokosuka-shi, 239-0847 Japan. E-mail: {fujisaki,okamoto}@isl.ntt.co.jp.
Optimal Security Proofs for Full Domain Hash, Revisited
 Optimal Security Proofs for Full Domain Hash, Revisited Saqib A. Kakvi 1 and Eike Kiltz 1 Faculty of Mathematics, Horst Görtz Institute for IT Security Ruhr University Bochum {saqib.kakvi,eike.kiltz}@rub.de
Optimal Security Proofs for Full Domain Hash, Revisited Saqib A. Kakvi 1 and Eike Kiltz 1 Faculty of Mathematics, Horst Görtz Institute for IT Security Ruhr University Bochum {saqib.kakvi,eike.kiltz}@rub.de
Chosen-Ciphertext Security without Redundancy
 This is the full version of the extended abstract which appears in Advances in Cryptology Proceedings of Asiacrypt 03 (30 november 4 december 2003, Taiwan) C. S. Laih Ed. Springer-Verlag, LNCS 2894, pages
This is the full version of the extended abstract which appears in Advances in Cryptology Proceedings of Asiacrypt 03 (30 november 4 december 2003, Taiwan) C. S. Laih Ed. Springer-Verlag, LNCS 2894, pages
Blind Signature Protocol Based on Difficulty of. Simultaneous Solving Two Difficult Problems
 Applied Mathematical Sciences, Vol. 6, 202, no. 39, 6903-690 Blind Signature Protocol Based on Difficulty of Simultaneous Solving Two Difficult Problems N. H. Minh, D. V. Binh 2, N. T. Giang 3 and N. A.
Applied Mathematical Sciences, Vol. 6, 202, no. 39, 6903-690 Blind Signature Protocol Based on Difficulty of Simultaneous Solving Two Difficult Problems N. H. Minh, D. V. Binh 2, N. T. Giang 3 and N. A.
The Random Oracle Paradigm. Mike Reiter. Random oracle is a formalism to model such uses of hash functions that abound in practical cryptography
 1 The Random Oracle Paradigm Mike Reiter Based on Random Oracles are Practical: A Paradigm for Designing Efficient Protocols by M. Bellare and P. Rogaway Random Oracles 2 Random oracle is a formalism to
1 The Random Oracle Paradigm Mike Reiter Based on Random Oracles are Practical: A Paradigm for Designing Efficient Protocols by M. Bellare and P. Rogaway Random Oracles 2 Random oracle is a formalism to
Short Signature Scheme From Bilinear Pairings
 Sedat Akleylek, Barış Bülent Kırlar, Ömer Sever, and Zaliha Yüce Institute of Applied Mathematics, Middle East Technical University, Ankara, Turkey {akleylek,kirlar}@metu.edu.tr,severomer@yahoo.com,zyuce@stm.com.tr
Sedat Akleylek, Barış Bülent Kırlar, Ömer Sever, and Zaliha Yüce Institute of Applied Mathematics, Middle East Technical University, Ankara, Turkey {akleylek,kirlar}@metu.edu.tr,severomer@yahoo.com,zyuce@stm.com.tr
On the Big Gap Between p and q in DSA
 On the Big Gap Between p and in DSA Zhengjun Cao Department of Mathematics, Shanghai University, Shanghai, China, 200444. caozhj@shu.edu.cn Abstract We introduce a message attack against DSA and show that
On the Big Gap Between p and in DSA Zhengjun Cao Department of Mathematics, Shanghai University, Shanghai, China, 200444. caozhj@shu.edu.cn Abstract We introduce a message attack against DSA and show that
Chapter 8 Public-key Cryptography and Digital Signatures
 Chapter 8 Public-key Cryptography and Digital Signatures v 1. Introduction to Public-key Cryptography 2. Example of Public-key Algorithm: Diffie- Hellman Key Exchange Scheme 3. RSA Encryption and Digital
Chapter 8 Public-key Cryptography and Digital Signatures v 1. Introduction to Public-key Cryptography 2. Example of Public-key Algorithm: Diffie- Hellman Key Exchange Scheme 3. RSA Encryption and Digital
From Unpredictability to Indistinguishability: A Simple. Construction of Pseudo-Random Functions from MACs. Preliminary Version.
 From Unpredictability to Indistinguishability: A Simple Construction of Pseudo-Random Functions from MACs Preliminary Version Moni Naor Omer Reingold y Abstract This paper studies the relationship between
From Unpredictability to Indistinguishability: A Simple Construction of Pseudo-Random Functions from MACs Preliminary Version Moni Naor Omer Reingold y Abstract This paper studies the relationship between
1 Recommended Reading 1. 2 Public Key/Private Key Cryptography Overview RSA Algorithm... 2
 Contents 1 Recommended Reading 1 2 Public Key/Private Key Cryptography 1 2.1 Overview............................................. 1 2.2 RSA Algorithm.......................................... 2 3 A Number
Contents 1 Recommended Reading 1 2 Public Key/Private Key Cryptography 1 2.1 Overview............................................. 1 2.2 RSA Algorithm.......................................... 2 3 A Number
On the Security of EPOC and TSH-ESIGN
 On the Security of EPOC and TSH-ESIGN Tatsuaki Okamoto Tetsutaro Kobayashi NTT Laboratories 1-1 Hikarinooka, Yokosuka-shi, 239-0847 Japan Email: {okamoto, kotetsu }@isl.ntt.co.jp Abstract We submitted
On the Security of EPOC and TSH-ESIGN Tatsuaki Okamoto Tetsutaro Kobayashi NTT Laboratories 1-1 Hikarinooka, Yokosuka-shi, 239-0847 Japan Email: {okamoto, kotetsu }@isl.ntt.co.jp Abstract We submitted
Schnorr Signature. Schnorr Signature. October 31, 2012
 . October 31, 2012 Table of contents Salient Features Preliminaries Security Proofs Random Oracle Heuristic PKS and its Security Models Hardness Assumption The Construction Oracle Replay Attack Security
. October 31, 2012 Table of contents Salient Features Preliminaries Security Proofs Random Oracle Heuristic PKS and its Security Models Hardness Assumption The Construction Oracle Replay Attack Security
Chosen Ciphertext Security with Optimal Ciphertext Overhead
 Chosen Ciphertext Security with Optimal Ciphertext Overhead Masayuki Abe 1, Eike Kiltz 2 and Tatsuaki Okamoto 1 1 NTT Information Sharing Platform Laboratories, NTT Corporation, Japan 2 CWI Amsterdam,
Chosen Ciphertext Security with Optimal Ciphertext Overhead Masayuki Abe 1, Eike Kiltz 2 and Tatsuaki Okamoto 1 1 NTT Information Sharing Platform Laboratories, NTT Corporation, Japan 2 CWI Amsterdam,
Threshold RSA for Dynamic and Ad-Hoc Groups
 Threshold RSA for Dynamic and Ad-Hoc Groups Rosario Gennaro, Shai Halevi, Hugo Krawczyk, Tal Rabin IBM T.J.Watson Research Center Hawthorne, NY USA Abstract. We consider the use of threshold signatures
Threshold RSA for Dynamic and Ad-Hoc Groups Rosario Gennaro, Shai Halevi, Hugo Krawczyk, Tal Rabin IBM T.J.Watson Research Center Hawthorne, NY USA Abstract. We consider the use of threshold signatures
