1 Number Theory Basics
|
|
|
- Lydia Bridges
- 5 years ago
- Views:
Transcription
1 ECS 289M (Franklin), Winter 2010, Crypto Review 1 Number Theory Basics This section has some basic facts about number theory, mostly taken (or adapted) from Dan Boneh s number theory fact sheets for his course on cryptography and computer security at Stanford (CS255). 1.1 Arithmetic Modulo Primes For a prime p let Z p = {0, 1,...p 1}. Elements of Z p can be added modulo p and multiplied modulo p. Fermat s theorem: g p 1 = 1 mod p, for any g 0 mod p. Invertible elements: The inverse of x Z p is an element a satisfying a x = 1 mod p. The inverse of x modulo p is denoted by x 1. All elements x Z p except for x = 0 are invertible. Let Z p be the set of invertible elements in Z p, that is, Z p = {1, 2,..., p 1}. Structure of Zp : Z p is a cyclic group. That is, there exists g Z p such that Zp = {1, g, g 2 mod p, g 3 mod p,..., g p 2 mod p}. Such a g is called a generator of Zp. Not every element of Z p is a generator. Order of Group Element: The order of g Z p (denoted ord p (g)) is the smallest positive integer a such that g a = 1 mod p. Lagrange s Theorem: ord p (g) divides p 1, for all g Z p. Computational Considerations: For our cryptographic applications, we are dealing with primes p on the order of 300 digits long (1024 bits). Since p is huge, it cannot be stored in a single register. Elements of Z p are stored in 32-bit or 64-bit long buckets (depending on the processor s chip size). Adding two elements x, y Z p can be done in linear time in the length of p. Multiplying two elements x, y Z p can be done in quadratic time in the length of p. If p is n bits long, more clever (and practical) algorithms work in time O(n 1.7 ) (rather than O(n 2 )). Inverting an element x Z p can be done in quadratic time in the length of p. Elements of Z p can be efficiently inverted using Euclid s algorithm. If gcd(x, p) = 1 then using Euclid s algorithm it is possible to efficiently construct two integers a, b Z such that ax + bp = 1. Reducing this relation modulo p leads to ax = 1 mod p. Hence a = x 1 mod p. Using the repeated squaring algorithm, x r mod p can be computed in time (log 2 r)o(n 2 ) where p is n bits long. Note that this algorithm for modular exponentiation takes linear time in the length of r. 1
2 Discrete Log Problem: Let p be a 1024-bit prime, and let g be a generator of Z p. Given x Z p, find an r such that x = g r mod p. This problem is believed to be hard. Computational Diffie-Hellman Problem: Let p be a 1024-bit prime, and let g be a generator of Z p. Given x, y Z p where x = gr1 and y = g r2, find z = g r1r2. This problem is believed to be hard. Decision Diffie-Hellman Problem: Let p be a 1024-bit prime, and let g be a generator of Zp. Given an instance of the Computational Diffie-Hellman Problem x, y Zp, and given z which is either the solution to the Computational Diffie-Hellman problem (with probability 1/2) or a random element of Zp (with probability 1/2), try to distinguish which is the case. This problem is not hard. Large Prime Order Subgroup: The Discrete Log, Computational Diffie- Hellman, and Decision Diffie-Hellman problems are believed to be hard when the order of g is a large prime factor of p 1. Note that g is not a generator of Zp in this case (in fact, we say that g generates a large prime order subgroup of Zp). 1.2 Arithmetic Modulo Composites Unless otherwise stated, we assume N is the product of two primes of roughly equal size. For a composite N let Z N = {0, 1, 2,..., N 1}. Elements of Z N can be added and multiplied modulo N. Invertible Elements: The inverse of x Z N is an element y Z N such that x y = 1 mod N. An element x Z N has an inverse if and only if x and N are relatively prime (that is, gcd(x, N) = 1). Let ZN denote the set of invertible elements in Z N. Euler s Phi Function: Let φ(n) denote the number of elements in Z N. When N = pq is the product of two primes, φ(n) = (p 1)(q 1). Euler s Theorem: For any a Z N we have that aφ(n) = 1 mod N. Chinese Remainder Theorem (special case): Let p, q be distinct primes and let N = pq. Given r 1 Z p and r 2 Z q there exists a unique element s Z N such that s = r 1 mod p and s = r 2 mod q. Furthermore, s can be computed efficiently. Structure of Z N : The CRT implies that each element s Z N can be viewed as a pair (s 1, s 2 ) where s 1 = s mod p and s 2 = s mod q. The uniqueness guarantee shows that each pair (s 1, s 2 ) Z p Z q corresponds to one element of Z N. The CRT also shows that an element s Z N is invertible if and only if s mod p is invertible in Z p and s mod q is invertible in Z q. This yields an alternative explanation for why φ(n) = (p 1)(q 1) when N is the product of two distinct primes. 2
3 Computational Considerations: For our cryptographic applications, we are dealing with integers N on the order of 300 digits long (1024 bits). All of the observations about computing in Z p for prime p carry over without change to the setting of computing in Z N. Here is one computational trick that is unique to the setting of Z N for composite N. If the factorization p, q of N is known, then the repeated squaring algorithm for modular exponentiation (mod N) can be speeded up by about a factor of four, by exploiting the Chinese Remainder Theorem (details omitted). RSA Problem: Let e be relatively prime to φ(n). Given N and e, and given y = x e mod N for some x ZN, find x. This is believed to be hard if the factorization of N is unknown, but becomes easy if the factorization of N is known. RSA Trapdoor: Given the factorization p, q of N, it is easy to compute φ(n) = (p 1)(q 1), and then it is easy to compute d = e 1 mod φ(n), and then it is easy to compute y d mod N, which is equal to x (by Euler s Theorem). The factorization p, q (or the value d) is called a trapdoor for the RSA problem. 2 Secret Sharing Basics This section has some basic facts about secret sharing schemes, mostly taken (or adapted) from CRC Handbook of Applied Cryptography (Chapt 12, pp ), Menezes et al. (eds), (t,t) Threshold Secret Sharing: Let S be a secret integer, 0 S m 1. Here is a way to divide S into t shares, such that all of them are required in order to recover it: Choose t 1 independent random numbers S i, 0 S i m 1, 1 i t 1. Compute S t = S t 1 i=1 S i mod m. The secret is recovered as S = t i=1 S i mod m. Note that modulo m operations may be replaced by exclusive-or, using data values S and S i of fixed bit-length log 2 (m). Shamir s (t, n) Threshold Secret Sharing: Let S be a secret integer 0 S m 1. Here is a way to divide S into n shares, such that any t of them are necessary and sufficient to recover it. Let p be an arbitrary prime number greater than m 1 and n. Sharing Phase: Select t 1 random, independent coefficients a 1,..., a t 1, 0 a j p 1. Let f(x) be the following polynomial of degree t 1 over Z p : f(x) = S + t 1 j=1 a jx j. Compute S i = (i, f(i) mod p), 1 i n. Reconstruction Phase: Any subset of t or more shares can be combined to recover the secret. The shares provide t distinct points of the form (i, f(i) mod p), allowing computation of the coefficients a j, 0 j t 1 of f(x) over Z p by Lagrange interpolation (see below). The secret is recovered by noting f(0) = a 0 = S. Lagrange Interpolation: The coefficients of an unknown polynomial f(x) of degree at most t 1, defined by distinct points (x i, y i ), 1 i t, are 3
4 given by the Lagrange interpolation formulae: f(x) = t i=1 y i 1 j t,j i (x x j )/(x i x j ). Since f(0) = a 0 = S, the shared secret may be expressed as S = t i=1 c iy i mod p, where c i = 1 j t,j i x j(x j x i ) 1 mod p. Note that the c i values are non-secret constants, which for a fixed subset of t shares may be pre-computed. 3 Cryptographic Primitives Basics This section has some basic information about cryptographic primitives, mostly taken (or adapted) from Introduction to Modern Cryptography, Katz and Lindell, Chapman & Hall/CRC, One-Way Primitives negligible: A function f is negligible if for every polynomial p(.) there exists an N such that for all integers n > N it holds that f(n) < 1/p(n). We typically denote an arbitrary negligible function by negl. One-Way Function: A function f : {0, 1} {0, 1} is one-way if the following two conditions hold: 1. (Easy to compute:) There exists a polynomial-time algorithm M f computing f; that is, M f (x) = f(x) for all x. 2. (Hard to invert:) For every probabilistic polynomial-time algorithm A, there exists a negligible function negl such that the the following inverting experiment succeeds with probability at most negl(n): Choose input x {0, 1} n ; Compute y = f(x); Give 1 n and y as input to A; The experiment succeeds if A outputs any x such that f(x ) = y. One-Way Function Family: The above definition of one-way function is very convenient in that it considers a single function over an infinite domain and range. However, most candidate one-way functions that we know of do not fit naturally into this framework. Rather, there is typically an algorithm that generates some parameters I which define some function f I ; the requirement is essentially that f I should be one-way with all but negligible probability over choice of I. Exponentiation Modulo a Prime: Let p be any prime, and let g be a generator of Z p. Let f p,g (x) = g x mod p, for x Z p. This family of functions is believed to be one-way (which is closely related to the belief that the Discrete Log problem is hard over Z p when p is a sufficiently large prime). In fact, this is believd to be a family of one-way permutations, since every f p,g is a one-to-one mapping on Z p. SHA: The SHA family includes cryptographically strong hash functions that seem hard to invert in practice. They fall outside of the asymptotic security framework developed here, since the output lengths are fixed. 4
5 3.2 Pseudorandom Primitives Pseudorandom generator: Let l(.) be a polynomial and let G be a deterministic polynomial-time algorithm such that for any input s {0, 1} n, algorithm G outputs a string of length l(n). We say that G is a pseudorandom generator if the following two conditions hold: 1. (expansion) For every n it holds that l(n) > n. 2. (pseudorandom) For all probabilistic polynomial-time distinguishers D, there exists a negligible function negl such that P r[d(r) = 1] P r[d(g(s)) = 1] negl(n), where r is chosen uniformly at random from {0, 1} l(n), the seed s is chosen uniformly at random from {0, 1} n, and the probabilities are taken over the random coins used by D and the choice of r and s. Pseudorandom function: A keyed function F is a two-input function F : {0, 1} {0, 1} {0, 1}, where the first input is called the key and denoted k, and the second input is just called the input. In general, the key k will be chosen and then fixed, and we will then be interested in the single-input function F k : {0, 1} {0, 1} defined by F k (x) = F(k, x). For simplicity, we will generally assume that F is length-preserving meaning that the key, input, and output lengths of F are all the same. That is, we assume that the function F is only defined when the key k and the input x have the same length, in which case F k (x) = x = k. Let F : {0, 1} {0, 1} be an efficiently computable, length-preserving, keyed function. We say that F is a pseudorandom function if for all probabilistic polynomial-time distinguishers D, there exists a negligible function negl such that Pr[D F k(.) (1 n ) = 1] Pr[D f(.) (1 n ) = 1] negl(n), where k is chosen uniformly at random from {0, 1} n, and where f is chosen uniformly at random from the set of functions mapping n-bit strings to n-bit strings. [Note that the definition of pseudorandom function] gives D oracle access to the function in question (either F k or f. D is allowed to query the oracle at any point x {0, 1} n, in response to which the oracle returns the value of the function evaluated at x. 3.3 Symmetric Key Primitives Message Authentication Codes: A message authentication code (or MAC) is a tuple of probabilistic polynomial-time algorithms (Gen, Mac, Vrfy) such that: 1. The key generation algorithm Gen takes as input the security parameter 1 n and outputs a key k with k n. 2. The tag-generation algorithm Mac takes as input a key k and a message m {0, 1}, and outputs a tag t. Since this algorithm may be randomized, we write this as t Mac k (m). 5
6 3. The verification algorithm Vrfy takes as input a key k, a message m, and a tag t. It outputs a bit b, with b = 1 meaning valid and b = 0 meaning invalid. We assume without loss of generallity that Vrfy is deterministic and so write this as b := Vrfy k (m, t). 4. (Consistency) For every n, every key k output by Gen(1 n ), and every m {0, 1}, it holds that Vrfy k (m, Mac k (m)) = 1. Security for Message Authentication Codes: A message authentication code (Gen, Mac, Vrfy) is existentially unforgeable under an adaptive chosenmessage attack, or just secure, if for all probabilistic polynomial-time adversaries A, there exists a negligible function negl such that the following forgery experiment succeeds with probability at most negl(n): 1. A random key k s generated by running Gen(1 n ). 2. The adversary A is given input 1 n and oracle access to Mac k (.). The adversary eventually outputs a pair (m, t). Let Q denote the set of all queries that A asked to its oracle. 3. The experiment succeeds if Vrfy k (m, t) = 1 and m Q. Private Key Encryption: A private key encryption scheme (sometimes called symmetric key or secret key or shared key in the literature), is a tuple of probabilistic polynomial-time algorithms (Gen, Enc, Dec) such that: 1. The key generation algorithm Gen takes as input the security parameter 1 n and outputs a key k; we write this as k Gen(1 n ) (thus emphasizing the fact that Gen is a randomized algorithm). We will assume without loss of generality that any key k output by Gen(1 n ) satisfies k n. 2. The encryption algorithm Enc takes as input a key k and a plaintext message m {0, 1}, and outputs a ciphertext c. Since Enc may be randomized, we write this as c Enc k (m). 3. The decryption algorithm Dec takes as input a key k and a ciphertext c and outputs a message m. We assume that Dec is deterministic, and so write this as m := Dec k (c). 4. (Consistency) For every n, every key k output by Gen(1 n ), and every m {0, 1}, it holds that Dec k (Enc k (m)) = m. CPA-Security for Private Key Encryption: A private key encryption scheme (Gen, Enc, Dec) has indistinguishable encryptions in the presence of a chosen-plaintext attack (or is CPA-secure) if for all probabilistic polynomialtime adversaries A there exists a negligible function negl such that the following distinguishing experiment succeeds with probability at most 1/2 + negl(n): 1. A key k is generated by running Gen(1 n ). 2. The adversary A is given input 1 n and oracle access to Enc k (.), and outputs a pair of messages m 0, m 1 of the same length. 6
7 3. A random bit b {0, 1} is chosen, and then a ciphertext c Enc k (m b ) is computed and given to A. We call c the challenge ciphertext. 4. The adversary A continues to have oracle access to Enc k (.), and outputs a bit b. 5. The experiment succeeds if b = b. CPA-Secure Private Key Encryption from PRF: If F is a pseudorandom function, then the following private key encryption scheme can be proven to be CPA-secure: Gen(1 n ) outputs a random n-bit key; Enc(k, m) chooses a random n-bit value r and outputs ciphertext (r, F k (r) m); Dec(k, (r, s)) outputs m = F k (r) s. CCA-Security for Private Key Encryption: A stronger security notion for private key encryption is indistinguishability of encryptions in the presence of a chosen-ciphertext attack (or CCA-security). The definition is the same as for CPA-security, except that the adversary A gets oracle access to both Enc k (.) and Dec k (.) in steps 2 and 4 of the distinguishability experiment (although forbidden from using the decryption oracle in step 4 to decrypt the challenge ciphertext itself). CCA-Secure Private Key Encryption from MAC: If (Gen E, Enc, Dec) is a CPA-secure encryption, and if (Gen M, Mac, V rfy) is a secure MAC, then the following private key encryption scheme can be proven to be CCA-secure: Gen (1 n ) runs Gen E (1 n ) and Gen M (1 n ) to get encryption key k 1 and MAC key k 2 ; Enc (k 1, k 2, m) computes c Enc k1 (m) and t MAC k2 (c) and outputs the ciphertext (c, t); Dec (k 1, k 2, c, t) outputs Dec k1 (c) if V rfy k2 (c, t) = 1 and otherwise outputs (reserved null element in the message space). 3.4 Public Key Primitives Key Exchange Protocol: Alice and Bob begin by holding the security parameter 1 n ; they then choose (independent) random coins and run the key exchange protocol. At the end of the protocol, Alice and Bob output keys k A, k B {0, 1} n, respectively. The basic correctness requirement is that it should always hold that k A = k B (i.e., for all choices of random coins by Alice and Bob). Since we only deal with protocols that satisfy this requirement, we will speak simply of the key k = k A = k B generated by an honest execution of the protocol. Passive Security for Key Exchange: A key exchange protocol is secure in the presence of an eavesdropper if for every probabilistic polynomial-time adversary A there exists a negligible function negl such that the following distinguishing experiment succeeds with probability at most negl(n): 1. Two parties holding 1 n execute the key exchange protocol. This execution results in a transcript trans containing all the messages sent by the parties, and the key k that is output by each of the parties. 7
8 2. A random bit b {0, 1} is chosen. If b = 0 then choose ˆk {0, 1} n uniformly at random, and if b = 1 set ˆk := k. 3. A is given trans and ˆk, and outputs bit b. 4. The experiment succeeds if b = b. Diffie-Hellman Key Exchange: The Diffie-Hellman Key Exchange protocol is secure in the presence of an eavesdropper, under the assumption that the (Large Prime-Order Subgroup) Decision Diffie-Hellman problem is hard. Alice and Bob agree on an element g Zp of order q, for suitably large primes p, q (where q is a divisor of p 1). Alice chooses a random α Zp and sends y = g α mod p. Bob chooses a random β Zp and sends z = gβ mod p. Alice computes k A = z α mod p. Bob computes K B = y β mod p. Public Key Encryption Scheme: A public key encryption scheme is a tuple of probabilistic polynomial-time algorithms (Gen, Enc, Dec) such that: 1. The key generation algorithm Gen takes as input the security parameter 1 n and outputs a pair of keys (pk, sk). We refer to the first of these as the public key and the second as the private key. We assume for convenience that pk and sk each have length at least n, and that n can be determined from pk, sk. 2. The encryption algorithm Enc takes as input a public key pk and a message m from some underlying plaintext space (that may depend on pk). It outputs a ciphertext c, and we write this as c Enc pk (m). 3. The decryption algorithm Dec takes as input a private key sk and a ciphertext c, and ouutputs a message m or a special symbol denoting failure. We assume without loss of generality that Dec is deterministic, and write this as m := Dec sk (c). 4. (Consistency) There exists a negligible function negl such that for every n, every (pk, sk) output by Gen(1 n ), and every message m in the appropriate underlying plaintext space, it holds that Pr[Dec sk (Enc pk (m)) m] negl(n). CPA Security for Public Key Encryption: A public key encryption scheme (Gen, Enc, Dec) has indistinguishable encryptions under a chosen-plaintext attack ( CPA-secure ; sometimes called IND-CPA-secure in the literature) if for all probabilistic polynomial-time adversaries A there exists a negligible function negl such that the following distinguishing experiment succeeds with probability at most negl(n): a. Gen(1 n ) is run to obtain keys (pk, sk). b. Adversary A is given pk as well as oracle access to Enc pk (.). The adversary outputs a pair of messages m 0, m 1 of the same length. (These messages must be in the plaintext space associated with pk.) c. A random bit b {0, 1} is chosen, and then a ciphertext c Enc pk (m b ) is computed and given to A. We call c the challenge ciphertext. 8
9 d. A continues to have access to Enc pk (.), and outputs bit b. e. The distinguishing experiment succeeds if b = b. ElGamal Public Key Encryption: The ElGamal public key encryption scheme is CPA-secure, under the assumption that the (Large Prime-Order Subgroup) Decision Diffie-Hellman Problem is hard. The keys are pk = (g, g x mod p), sk = x R Z q, where p is a large prime, q is a large prime factor of p 1, and ord p (g) = q. To encrypt a message M (in the subgroup generated by g) under public key (g, y), choose a random r Z p and compute the ciphertext (g r mod p, My r mod p). To decrypt ciphertext (u, v) with secret key x, compute M = v(u 1 ) x mod p. CCA Security for Public Key Encryption: A public key encryption scheme (Gen, Enc, Dec) has indistinguishable encryptions under a chosen-ciphertext attack ( CCA-secure ; sometimes called IND-CCA2-secure in the literature) if for all probabilistic polynomial-time adversaries A there exists a negligible function negl such that the following distinguishing experiment succeeds with probability at most negl(n): a. Gen(1 n ) is run to obtain keys (pk, sk). b. Adversary A is given pk as well as oracle access to Dec sk (.). The adversary outputs a pair of messages m 0, m 1 of the same length. (These messages must be in the plaintext space associated with pk.) c. A random bit b {0, 1} is chosen, and then a ciphertext c Enc pk (m b ) is computed and given to A. We call c the challenge ciphertext. d. A continues to interact with Dec sk (.), but may not request decryption of c itself. Finally, A outputs bit b. e. The distinguishing experiment succeeds if b = b. Homomorphic Publc Key Encryption: A public key encryption scheme is homomorphic if there is an easy way to combine ciphertexts to perform some arithmetic operation on the underlying encrypted values. For example, the ElGamal public key encryption scheme is multiplicatively homomorphic : If (u 1, v 1 ) and (u 2, v 2 ) are ElGamal encryptions of M 1 and M 2 (under the same public key), then (u 1 u 2 mod p, v 1 v 2 mod p) is an ElGamal encyrption of M 1 M 2 mod p. Digital Signature Scheme: A signature scheme is a tuple of three probabilistic polynomial-time algorithms (Gen, Sign, Vrfy) satisfying the following: 1. The key generation algorithm Gen takes as input a security parameter 1 n and outputs a pair of keys (pk, sk). These are called the public key and the private key respectively. We assume for convenience that pk and sk each have length at least n, and that n can be determined from pk, sk. 9
10 2. The signing algorithm Sign takes as input a private key sk and a message m {0, 1}. It outputs a signature σ, denoted as σ Sign sk (m). 3. The deterministic verification algorithm Vrfy takes as input a public key pk, a message m, and a signature σ. It outputs a bit b, with b = 1 meaning valid and b = 0 meaning invalid. We write this as b := Vrfy pk (m, σ). 4. (Consistency) For every n, every (pk, sk) output by Gen(1 n ), and every m {0, 1}, it holds that Vrfy pk (m, Sign sk (m)) = 1. Signature Scheme Security: A signature scheme (Gen, Sign, Vrfy) is existentially unforgeable under an adaptive chosen-message attack if for all probabilistic polynomial-time adversaries A, there exists a negligible function negl such that the following forging experiment succeeds with probability at most negl(n): 1. Gen(1 n ) is run to obtain keys (pk, sk). 2. Adversary A is given pk and oracle access to Sign sk (.). (This oracle returns a signature Sign sk (m) for any message m of the adversary s choice.) The adversary then outputs (m, σ). Let Q denote the set of messages whose signatures were requested by A during its execution. 3. The forging experiment succeeds if Vrfy pk (m, σ) = 1 and m Q. 10
1 Basic Number Theory
 ECS 228 (Franklin), Winter 2013, Crypto Review 1 Basic Number Theory This section has some basic facts about number theory, mostly taken (or adapted) from Dan Boneh s number theory fact sheets for his
ECS 228 (Franklin), Winter 2013, Crypto Review 1 Basic Number Theory This section has some basic facts about number theory, mostly taken (or adapted) from Dan Boneh s number theory fact sheets for his
Chapter 11 : Private-Key Encryption
 COMP547 Claude Crépeau INTRODUCTION TO MODERN CRYPTOGRAPHY _ Second Edition _ Jonathan Katz Yehuda Lindell Chapter 11 : Private-Key Encryption 1 Chapter 11 Public-Key Encryption Apologies: all numbering
COMP547 Claude Crépeau INTRODUCTION TO MODERN CRYPTOGRAPHY _ Second Edition _ Jonathan Katz Yehuda Lindell Chapter 11 : Private-Key Encryption 1 Chapter 11 Public-Key Encryption Apologies: all numbering
ECS 189A Final Cryptography Spring 2011
 ECS 127: Cryptography Handout F UC Davis Phillip Rogaway June 9, 2011 ECS 189A Final Cryptography Spring 2011 Hints for success: Good luck on the exam. I don t think it s all that hard (I do believe I
ECS 127: Cryptography Handout F UC Davis Phillip Rogaway June 9, 2011 ECS 189A Final Cryptography Spring 2011 Hints for success: Good luck on the exam. I don t think it s all that hard (I do believe I
Katz, Lindell Introduction to Modern Cryptrography
 Katz, Lindell Introduction to Modern Cryptrography Slides Chapter 12 Markus Bläser, Saarland University Digital signature schemes Goal: integrity of messages Signer signs a message using a private key
Katz, Lindell Introduction to Modern Cryptrography Slides Chapter 12 Markus Bläser, Saarland University Digital signature schemes Goal: integrity of messages Signer signs a message using a private key
Public Key Cryptography
 Public Key Cryptography Ali El Kaafarani 1 Mathematical Institute 2 PQShield Ltd. 1 of 44 Outline 1 Public Key Encryption: security notions 2 RSA Encryption Scheme 2 of 44 Course main reference 3 of 44
Public Key Cryptography Ali El Kaafarani 1 Mathematical Institute 2 PQShield Ltd. 1 of 44 Outline 1 Public Key Encryption: security notions 2 RSA Encryption Scheme 2 of 44 Course main reference 3 of 44
Lecture 1: Introduction to Public key cryptography
 Lecture 1: Introduction to Public key cryptography Thomas Johansson T. Johansson (Lund University) 1 / 44 Key distribution Symmetric key cryptography: Alice and Bob share a common secret key. Some means
Lecture 1: Introduction to Public key cryptography Thomas Johansson T. Johansson (Lund University) 1 / 44 Key distribution Symmetric key cryptography: Alice and Bob share a common secret key. Some means
1 What are Physical Attacks. 2 Physical Attacks on RSA. Today:
 Today: Introduction to the class. Examples of concrete physical attacks on RSA A computational approach to cryptography Pseudorandomness 1 What are Physical Attacks Tampering/Leakage attacks Issue of how
Today: Introduction to the class. Examples of concrete physical attacks on RSA A computational approach to cryptography Pseudorandomness 1 What are Physical Attacks Tampering/Leakage attacks Issue of how
Block Ciphers/Pseudorandom Permutations
 Block Ciphers/Pseudorandom Permutations Definition: Pseudorandom Permutation is exactly the same as a Pseudorandom Function, except for every key k, F k must be a permutation and it must be indistinguishable
Block Ciphers/Pseudorandom Permutations Definition: Pseudorandom Permutation is exactly the same as a Pseudorandom Function, except for every key k, F k must be a permutation and it must be indistinguishable
Introduction to Cybersecurity Cryptography (Part 4)
 Introduction to Cybersecurity Cryptography (Part 4) Review of Last Lecture Blockciphers Review of DES Attacks on Blockciphers Advanced Encryption Standard (AES) Modes of Operation MACs and Hashes Message
Introduction to Cybersecurity Cryptography (Part 4) Review of Last Lecture Blockciphers Review of DES Attacks on Blockciphers Advanced Encryption Standard (AES) Modes of Operation MACs and Hashes Message
Introduction to Cryptography. Lecture 8
 Introduction to Cryptography Lecture 8 Benny Pinkas page 1 1 Groups we will use Multiplication modulo a prime number p (G, ) = ({1,2,,p-1}, ) E.g., Z 7* = ( {1,2,3,4,5,6}, ) Z p * Z N * Multiplication
Introduction to Cryptography Lecture 8 Benny Pinkas page 1 1 Groups we will use Multiplication modulo a prime number p (G, ) = ({1,2,,p-1}, ) E.g., Z 7* = ( {1,2,3,4,5,6}, ) Z p * Z N * Multiplication
CS 4770: Cryptography. CS 6750: Cryptography and Communication Security. Alina Oprea Associate Professor, CCIS Northeastern University
 CS 4770: Cryptography CS 6750: Cryptography and Communication Security Alina Oprea Associate Professor, CCIS Northeastern University March 26 2017 Outline RSA encryption in practice Transform RSA trapdoor
CS 4770: Cryptography CS 6750: Cryptography and Communication Security Alina Oprea Associate Professor, CCIS Northeastern University March 26 2017 Outline RSA encryption in practice Transform RSA trapdoor
Introduction to Cybersecurity Cryptography (Part 4)
 Introduction to Cybersecurity Cryptography (Part 4) Review of Last Lecture Blockciphers Review of DES Attacks on Blockciphers Advanced Encryption Standard (AES) Modes of Operation MACs and Hashes Message
Introduction to Cybersecurity Cryptography (Part 4) Review of Last Lecture Blockciphers Review of DES Attacks on Blockciphers Advanced Encryption Standard (AES) Modes of Operation MACs and Hashes Message
Public Key Cryptography
 Public Key Cryptography Introduction Public Key Cryptography Unlike symmetric key, there is no need for Alice and Bob to share a common secret Alice can convey her public key to Bob in a public communication:
Public Key Cryptography Introduction Public Key Cryptography Unlike symmetric key, there is no need for Alice and Bob to share a common secret Alice can convey her public key to Bob in a public communication:
Chapter 8 Public-key Cryptography and Digital Signatures
 Chapter 8 Public-key Cryptography and Digital Signatures v 1. Introduction to Public-key Cryptography 2. Example of Public-key Algorithm: Diffie- Hellman Key Exchange Scheme 3. RSA Encryption and Digital
Chapter 8 Public-key Cryptography and Digital Signatures v 1. Introduction to Public-key Cryptography 2. Example of Public-key Algorithm: Diffie- Hellman Key Exchange Scheme 3. RSA Encryption and Digital
Lecture 17 - Diffie-Hellman key exchange, pairing, Identity-Based Encryption and Forward Security
 Lecture 17 - Diffie-Hellman key exchange, pairing, Identity-Based Encryption and Forward Security Boaz Barak November 21, 2007 Cyclic groups and discrete log A group G is cyclic if there exists a generator
Lecture 17 - Diffie-Hellman key exchange, pairing, Identity-Based Encryption and Forward Security Boaz Barak November 21, 2007 Cyclic groups and discrete log A group G is cyclic if there exists a generator
Lecture 15 & 16: Trapdoor Permutations, RSA, Signatures
 CS 7810 Graduate Cryptography October 30, 2017 Lecture 15 & 16: Trapdoor Permutations, RSA, Signatures Lecturer: Daniel Wichs Scribe: Willy Quach & Giorgos Zirdelis 1 Topic Covered. Trapdoor Permutations.
CS 7810 Graduate Cryptography October 30, 2017 Lecture 15 & 16: Trapdoor Permutations, RSA, Signatures Lecturer: Daniel Wichs Scribe: Willy Quach & Giorgos Zirdelis 1 Topic Covered. Trapdoor Permutations.
CPA-Security. Definition: A private-key encryption scheme
 CPA-Security The CPA Indistinguishability Experiment PrivK cpa A,Π n : 1. A key k is generated by running Gen 1 n. 2. The adversary A is given input 1 n and oracle access to Enc k, and outputs a pair of
CPA-Security The CPA Indistinguishability Experiment PrivK cpa A,Π n : 1. A key k is generated by running Gen 1 n. 2. The adversary A is given input 1 n and oracle access to Enc k, and outputs a pair of
Lecture Notes, Week 6
 YALE UNIVERSITY DEPARTMENT OF COMPUTER SCIENCE CPSC 467b: Cryptography and Computer Security Week 6 (rev. 3) Professor M. J. Fischer February 15 & 17, 2005 1 RSA Security Lecture Notes, Week 6 Several
YALE UNIVERSITY DEPARTMENT OF COMPUTER SCIENCE CPSC 467b: Cryptography and Computer Security Week 6 (rev. 3) Professor M. J. Fischer February 15 & 17, 2005 1 RSA Security Lecture Notes, Week 6 Several
10 Concrete candidates for public key crypto
 10 Concrete candidates for public key crypto In the previous lecture we talked about public key cryptography and saw the Diffie Hellman system and the DSA signature scheme. In this lecture, we will see
10 Concrete candidates for public key crypto In the previous lecture we talked about public key cryptography and saw the Diffie Hellman system and the DSA signature scheme. In this lecture, we will see
Cryptography IV: Asymmetric Ciphers
 Cryptography IV: Asymmetric Ciphers Computer Security Lecture 7 David Aspinall School of Informatics University of Edinburgh 31st January 2011 Outline Background RSA Diffie-Hellman ElGamal Summary Outline
Cryptography IV: Asymmetric Ciphers Computer Security Lecture 7 David Aspinall School of Informatics University of Edinburgh 31st January 2011 Outline Background RSA Diffie-Hellman ElGamal Summary Outline
Lecture 16 Chiu Yuen Koo Nikolai Yakovenko. 1 Digital Signature Schemes. CMSC 858K Advanced Topics in Cryptography March 18, 2004
 CMSC 858K Advanced Topics in Cryptography March 18, 2004 Lecturer: Jonathan Katz Lecture 16 Scribe(s): Chiu Yuen Koo Nikolai Yakovenko Jeffrey Blank 1 Digital Signature Schemes In this lecture, we introduce
CMSC 858K Advanced Topics in Cryptography March 18, 2004 Lecturer: Jonathan Katz Lecture 16 Scribe(s): Chiu Yuen Koo Nikolai Yakovenko Jeffrey Blank 1 Digital Signature Schemes In this lecture, we introduce
Technische Universität München (I7) Winter 2013/14 Dr. M. Luttenberger / M. Schlund SOLUTION. Cryptography Endterm
 Technische Universität München (I7) Winter 2013/14 Dr. M. Luttenberger / M. Schlund SOLUTION Cryptography Endterm Exercise 1 One Liners 1.5P each = 12P For each of the following statements, state if it
Technische Universität München (I7) Winter 2013/14 Dr. M. Luttenberger / M. Schlund SOLUTION Cryptography Endterm Exercise 1 One Liners 1.5P each = 12P For each of the following statements, state if it
Public-Key Encryption: ElGamal, RSA, Rabin
 Public-Key Encryption: ElGamal, RSA, Rabin Introduction to Modern Cryptography Benny Applebaum Tel-Aviv University Fall Semester, 2011 12 Public-Key Encryption Syntax Encryption algorithm: E. Decryption
Public-Key Encryption: ElGamal, RSA, Rabin Introduction to Modern Cryptography Benny Applebaum Tel-Aviv University Fall Semester, 2011 12 Public-Key Encryption Syntax Encryption algorithm: E. Decryption
CPSC 467b: Cryptography and Computer Security
 CPSC 467b: Cryptography and Computer Security Michael J. Fischer Lecture 11 February 21, 2013 CPSC 467b, Lecture 11 1/27 Discrete Logarithm Diffie-Hellman Key Exchange ElGamal Key Agreement Primitive Roots
CPSC 467b: Cryptography and Computer Security Michael J. Fischer Lecture 11 February 21, 2013 CPSC 467b, Lecture 11 1/27 Discrete Logarithm Diffie-Hellman Key Exchange ElGamal Key Agreement Primitive Roots
ENEE 457: Computer Systems Security 10/3/16. Lecture 9 RSA Encryption and Diffie-Helmann Key Exchange
 ENEE 457: Computer Systems Security 10/3/16 Lecture 9 RSA Encryption and Diffie-Helmann Key Exchange Charalampos (Babis) Papamanthou Department of Electrical and Computer Engineering University of Maryland,
ENEE 457: Computer Systems Security 10/3/16 Lecture 9 RSA Encryption and Diffie-Helmann Key Exchange Charalampos (Babis) Papamanthou Department of Electrical and Computer Engineering University of Maryland,
Lecture 11: Key Agreement
 Introduction to Cryptography 02/22/2018 Lecture 11: Key Agreement Instructor: Vipul Goyal Scribe: Francisco Maturana 1 Hardness Assumptions In order to prove the security of cryptographic primitives, we
Introduction to Cryptography 02/22/2018 Lecture 11: Key Agreement Instructor: Vipul Goyal Scribe: Francisco Maturana 1 Hardness Assumptions In order to prove the security of cryptographic primitives, we
Introduction to Cybersecurity Cryptography (Part 5)
 Introduction to Cybersecurity Cryptography (Part 5) Prof. Dr. Michael Backes 13.01.2017 February 17 th Special Lecture! 45 Minutes Your Choice 1. Automotive Security 2. Smartphone Security 3. Side Channel
Introduction to Cybersecurity Cryptography (Part 5) Prof. Dr. Michael Backes 13.01.2017 February 17 th Special Lecture! 45 Minutes Your Choice 1. Automotive Security 2. Smartphone Security 3. Side Channel
Block ciphers And modes of operation. Table of contents
 Block ciphers And modes of operation Foundations of Cryptography Computer Science Department Wellesley College Table of contents Introduction Pseudorandom permutations Block Ciphers Modes of Operation
Block ciphers And modes of operation Foundations of Cryptography Computer Science Department Wellesley College Table of contents Introduction Pseudorandom permutations Block Ciphers Modes of Operation
An Introduction to Probabilistic Encryption
 Osječki matematički list 6(2006), 37 44 37 An Introduction to Probabilistic Encryption Georg J. Fuchsbauer Abstract. An introduction to probabilistic encryption is given, presenting the first probabilistic
Osječki matematički list 6(2006), 37 44 37 An Introduction to Probabilistic Encryption Georg J. Fuchsbauer Abstract. An introduction to probabilistic encryption is given, presenting the first probabilistic
Lecture 19: Public-key Cryptography (Diffie-Hellman Key Exchange & ElGamal Encryption) Public-key Cryptography
 Lecture 19: (Diffie-Hellman Key Exchange & ElGamal Encryption) Recall In private-key cryptography the secret-key sk is always established ahead of time The secrecy of the private-key cryptography relies
Lecture 19: (Diffie-Hellman Key Exchange & ElGamal Encryption) Recall In private-key cryptography the secret-key sk is always established ahead of time The secrecy of the private-key cryptography relies
CHALMERS GÖTEBORGS UNIVERSITET. TDA352 (Chalmers) - DIT250 (GU) 11 April 2017, 8:30-12:30
 CHALMERS GÖTEBORGS UNIVERSITET CRYPTOGRAPHY TDA35 (Chalmers) - DIT50 (GU) 11 April 017, 8:30-1:30 No extra material is allowed during the exam except for pens and a simple calculator (not smartphones).
CHALMERS GÖTEBORGS UNIVERSITET CRYPTOGRAPHY TDA35 (Chalmers) - DIT50 (GU) 11 April 017, 8:30-1:30 No extra material is allowed during the exam except for pens and a simple calculator (not smartphones).
TECHNISCHE UNIVERSITEIT EINDHOVEN Faculty of Mathematics and Computer Science Exam Cryptology, Friday 25 January 2019
 Faculty of Mathematics and Computer Science Exam Cryptology, Friday 25 January 2019 Name : TU/e student number : Exercise 1 2 3 4 5 total points Notes: Please hand in all sheets at the end of the exam.
Faculty of Mathematics and Computer Science Exam Cryptology, Friday 25 January 2019 Name : TU/e student number : Exercise 1 2 3 4 5 total points Notes: Please hand in all sheets at the end of the exam.
Constructing secure MACs Message authentication in action. Table of contents
 Constructing secure MACs Message authentication in action Foundations of Cryptography Computer Science Department Wellesley College Fall 2016 Table of contents From last time Recall the definition of message
Constructing secure MACs Message authentication in action Foundations of Cryptography Computer Science Department Wellesley College Fall 2016 Table of contents From last time Recall the definition of message
Question: Total Points: Score:
 University of California, Irvine COMPSCI 134: Elements of Cryptography and Computer and Network Security Midterm Exam (Fall 2016) Duration: 90 minutes November 2, 2016, 7pm-8:30pm Name (First, Last): Please
University of California, Irvine COMPSCI 134: Elements of Cryptography and Computer and Network Security Midterm Exam (Fall 2016) Duration: 90 minutes November 2, 2016, 7pm-8:30pm Name (First, Last): Please
Question 2.1. Show that. is non-negligible. 2. Since. is non-negligible so is μ n +
 Homework #2 Question 2.1 Show that 1 p n + μ n is non-negligible 1. μ n + 1 p n > 1 p n 2. Since 1 p n is non-negligible so is μ n + 1 p n Question 2.1 Show that 1 p n - μ n is non-negligible 1. μ n O(
Homework #2 Question 2.1 Show that 1 p n + μ n is non-negligible 1. μ n + 1 p n > 1 p n 2. Since 1 p n is non-negligible so is μ n + 1 p n Question 2.1 Show that 1 p n - μ n is non-negligible 1. μ n O(
Definition: For a positive integer n, if 0<a<n and gcd(a,n)=1, a is relatively prime to n. Ahmet Burak Can Hacettepe University
 Number Theory, Public Key Cryptography, RSA Ahmet Burak Can Hacettepe University abc@hacettepe.edu.tr The Euler Phi Function For a positive integer n, if 0
Number Theory, Public Key Cryptography, RSA Ahmet Burak Can Hacettepe University abc@hacettepe.edu.tr The Euler Phi Function For a positive integer n, if 0
Public-Key Cryptosystems CHAPTER 4
 Public-Key Cryptosystems CHAPTER 4 Introduction How to distribute the cryptographic keys? Naïve Solution Naïve Solution Give every user P i a separate random key K ij to communicate with every P j. Disadvantage:
Public-Key Cryptosystems CHAPTER 4 Introduction How to distribute the cryptographic keys? Naïve Solution Naïve Solution Give every user P i a separate random key K ij to communicate with every P j. Disadvantage:
Computational security & Private key encryption
 Computational security & Private key encryption Emma Arfelt Stud. BSc. Software Development Frederik Madsen Stud. MSc. Software Development March 2017 Recap Perfect Secrecy Perfect indistinguishability
Computational security & Private key encryption Emma Arfelt Stud. BSc. Software Development Frederik Madsen Stud. MSc. Software Development March 2017 Recap Perfect Secrecy Perfect indistinguishability
Lecture 4 Chiu Yuen Koo Nikolai Yakovenko. 1 Summary. 2 Hybrid Encryption. CMSC 858K Advanced Topics in Cryptography February 5, 2004
 CMSC 858K Advanced Topics in Cryptography February 5, 2004 Lecturer: Jonathan Katz Lecture 4 Scribe(s): Chiu Yuen Koo Nikolai Yakovenko Jeffrey Blank 1 Summary The focus of this lecture is efficient public-key
CMSC 858K Advanced Topics in Cryptography February 5, 2004 Lecturer: Jonathan Katz Lecture 4 Scribe(s): Chiu Yuen Koo Nikolai Yakovenko Jeffrey Blank 1 Summary The focus of this lecture is efficient public-key
Outline. The Game-based Methodology for Computational Security Proofs. Public-Key Cryptography. Outline. Introduction Provable Security
 The Game-based Methodology for Computational s David Pointcheval Ecole normale supérieure, CNRS & INRIA Computational and Symbolic Proofs of Security Atagawa Heights Japan April 6th, 2009 1/39 2/39 Public-Key
The Game-based Methodology for Computational s David Pointcheval Ecole normale supérieure, CNRS & INRIA Computational and Symbolic Proofs of Security Atagawa Heights Japan April 6th, 2009 1/39 2/39 Public-Key
Mathematics of Cryptography
 UNIT - III Mathematics of Cryptography Part III: Primes and Related Congruence Equations 1 Objectives To introduce prime numbers and their applications in cryptography. To discuss some primality test algorithms
UNIT - III Mathematics of Cryptography Part III: Primes and Related Congruence Equations 1 Objectives To introduce prime numbers and their applications in cryptography. To discuss some primality test algorithms
TECHNISCHE UNIVERSITEIT EINDHOVEN Faculty of Mathematics and Computer Science Exam Cryptology, Tuesday 30 October 2018
 Faculty of Mathematics and Computer Science Exam Cryptology, Tuesday 30 October 2018 Name : TU/e student number : Exercise 1 2 3 4 5 total points Notes: Please hand in all sheets at the end of the exam.
Faculty of Mathematics and Computer Science Exam Cryptology, Tuesday 30 October 2018 Name : TU/e student number : Exercise 1 2 3 4 5 total points Notes: Please hand in all sheets at the end of the exam.
Practice Final Exam Winter 2017, CS 485/585 Crypto March 14, 2017
 Practice Final Exam Name: Winter 2017, CS 485/585 Crypto March 14, 2017 Portland State University Prof. Fang Song Instructions This exam contains 7 pages (including this cover page) and 5 questions. Total
Practice Final Exam Name: Winter 2017, CS 485/585 Crypto March 14, 2017 Portland State University Prof. Fang Song Instructions This exam contains 7 pages (including this cover page) and 5 questions. Total
MATH 158 FINAL EXAM 20 DECEMBER 2016
 MATH 158 FINAL EXAM 20 DECEMBER 2016 Name : The exam is double-sided. Make sure to read both sides of each page. The time limit is three hours. No calculators are permitted. You are permitted one page
MATH 158 FINAL EXAM 20 DECEMBER 2016 Name : The exam is double-sided. Make sure to read both sides of each page. The time limit is three hours. No calculators are permitted. You are permitted one page
Lecture V : Public Key Cryptography
 Lecture V : Public Key Cryptography Internet Security: Principles & Practices John K. Zao, PhD (Harvard) SMIEEE Amir Rezapoor Computer Science Department, National Chiao Tung University 2 Outline Functional
Lecture V : Public Key Cryptography Internet Security: Principles & Practices John K. Zao, PhD (Harvard) SMIEEE Amir Rezapoor Computer Science Department, National Chiao Tung University 2 Outline Functional
Lemma 1.2. (1) If p is prime, then ϕ(p) = p 1. (2) If p q are two primes, then ϕ(pq) = (p 1)(q 1).
 1 Background 1.1 The group of units MAT 3343, APPLIED ALGEBRA, FALL 2003 Handout 3: The RSA Cryptosystem Peter Selinger Let (R, +, ) be a ring. Then R forms an abelian group under addition. R does not
1 Background 1.1 The group of units MAT 3343, APPLIED ALGEBRA, FALL 2003 Handout 3: The RSA Cryptosystem Peter Selinger Let (R, +, ) be a ring. Then R forms an abelian group under addition. R does not
Public Key Cryptography
 Public Key Cryptography Ali El Kaafarani Mathematical Institute Oxford University 1 of 74 Outline 1 Complexity measures 2 Algebra and Number Theory Background 3 Public Key Encryption: security notions
Public Key Cryptography Ali El Kaafarani Mathematical Institute Oxford University 1 of 74 Outline 1 Complexity measures 2 Algebra and Number Theory Background 3 Public Key Encryption: security notions
Algorithmic Number Theory and Public-key Cryptography
 Algorithmic Number Theory and Public-key Cryptography Course 3 University of Luxembourg March 22, 2018 The RSA algorithm The RSA algorithm is the most widely-used public-key encryption algorithm Invented
Algorithmic Number Theory and Public-key Cryptography Course 3 University of Luxembourg March 22, 2018 The RSA algorithm The RSA algorithm is the most widely-used public-key encryption algorithm Invented
Modern symmetric-key Encryption
 Modern symmetric-key Encryption Citation I would like to thank Claude Crepeau for allowing me to use his slide from his crypto course to mount my course. Some of these slides are taken directly from his
Modern symmetric-key Encryption Citation I would like to thank Claude Crepeau for allowing me to use his slide from his crypto course to mount my course. Some of these slides are taken directly from his
CPSC 467: Cryptography and Computer Security
 CPSC 467: Cryptography and Computer Security Michael J. Fischer Lecture 11 October 7, 2015 CPSC 467, Lecture 11 1/37 Digital Signature Algorithms Signatures from commutative cryptosystems Signatures from
CPSC 467: Cryptography and Computer Security Michael J. Fischer Lecture 11 October 7, 2015 CPSC 467, Lecture 11 1/37 Digital Signature Algorithms Signatures from commutative cryptosystems Signatures from
Cryptography CS 555. Topic 22: Number Theory/Public Key-Cryptography
 Cryptography CS 555 Topic 22: Number Theory/Public Key-Cryptography 1 Exam Recap 2 Exam Recap Highest Average Score on Question Question 4: (Feistel Network with round function f(x) = 0 n ) Tougher Questions
Cryptography CS 555 Topic 22: Number Theory/Public Key-Cryptography 1 Exam Recap 2 Exam Recap Highest Average Score on Question Question 4: (Feistel Network with round function f(x) = 0 n ) Tougher Questions
10 Public Key Cryptography : RSA
 10 Public Key Cryptography : RSA 10.1 Introduction The idea behind a public-key system is that it might be possible to find a cryptosystem where it is computationally infeasible to determine d K even if
10 Public Key Cryptography : RSA 10.1 Introduction The idea behind a public-key system is that it might be possible to find a cryptosystem where it is computationally infeasible to determine d K even if
John Hancock enters the 21th century Digital signature schemes. Table of contents
 John Hancock enters the 21th century Digital signature schemes Foundations of Cryptography Computer Science Department Wellesley College Fall 2016 Table of contents From last time: Good news and bad There
John Hancock enters the 21th century Digital signature schemes Foundations of Cryptography Computer Science Department Wellesley College Fall 2016 Table of contents From last time: Good news and bad There
Pseudo-random Number Generation. Qiuliang Tang
 Pseudo-random Number Generation Qiuliang Tang Random Numbers in Cryptography The keystream in the one-time pad The secret key in the DES encryption The prime numbers p, q in the RSA encryption The private
Pseudo-random Number Generation Qiuliang Tang Random Numbers in Cryptography The keystream in the one-time pad The secret key in the DES encryption The prime numbers p, q in the RSA encryption The private
Notes for Lecture A can repeat step 3 as many times as it wishes. We will charge A one unit of time for every time it repeats step 3.
 COS 533: Advanced Cryptography Lecture 2 (September 18, 2017) Lecturer: Mark Zhandry Princeton University Scribe: Mark Zhandry Notes for Lecture 2 1 Last Time Last time, we defined formally what an encryption
COS 533: Advanced Cryptography Lecture 2 (September 18, 2017) Lecturer: Mark Zhandry Princeton University Scribe: Mark Zhandry Notes for Lecture 2 1 Last Time Last time, we defined formally what an encryption
II. Digital signatures
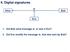 II. Digital signatures Alice m Bob Eve 1. Did Bob send message m, or was it Eve? 2. Did Eve modify the message m, that was sent by Bob? 1 Digital signatures Digital signature - are equivalent of handwritten
II. Digital signatures Alice m Bob Eve 1. Did Bob send message m, or was it Eve? 2. Did Eve modify the message m, that was sent by Bob? 1 Digital signatures Digital signature - are equivalent of handwritten
Lecture 28: Public-key Cryptography. Public-key Cryptography
 Lecture 28: Recall In private-key cryptography the secret-key sk is always established ahead of time The secrecy of the private-key cryptography relies on the fact that the adversary does not have access
Lecture 28: Recall In private-key cryptography the secret-key sk is always established ahead of time The secrecy of the private-key cryptography relies on the fact that the adversary does not have access
Lecture 18: Message Authentication Codes & Digital Signa
 Lecture 18: Message Authentication Codes & Digital Signatures MACs and Signatures Both are used to assert that a message has indeed been generated by a party MAC is the private-key version and Signatures
Lecture 18: Message Authentication Codes & Digital Signatures MACs and Signatures Both are used to assert that a message has indeed been generated by a party MAC is the private-key version and Signatures
El Gamal A DDH based encryption scheme. Table of contents
 El Gamal A DDH based encryption scheme Foundations of Cryptography Computer Science Department Wellesley College Fall 2016 Table of contents Introduction El Gamal Practical Issues The El Gamal encryption
El Gamal A DDH based encryption scheme Foundations of Cryptography Computer Science Department Wellesley College Fall 2016 Table of contents Introduction El Gamal Practical Issues The El Gamal encryption
Public Key Cryptography
 Public Key Cryptography Spotlight on Science J. Robert Buchanan Department of Mathematics 2011 What is Cryptography? cryptography: study of methods for sending messages in a form that only be understood
Public Key Cryptography Spotlight on Science J. Robert Buchanan Department of Mathematics 2011 What is Cryptography? cryptography: study of methods for sending messages in a form that only be understood
Notes for Lecture Decision Diffie Hellman and Quadratic Residues
 U.C. Berkeley CS276: Cryptography Handout N19 Luca Trevisan March 31, 2009 Notes for Lecture 19 Scribed by Cynthia Sturton, posted May 1, 2009 Summary Today we continue to discuss number-theoretic constructions
U.C. Berkeley CS276: Cryptography Handout N19 Luca Trevisan March 31, 2009 Notes for Lecture 19 Scribed by Cynthia Sturton, posted May 1, 2009 Summary Today we continue to discuss number-theoretic constructions
Chapter 4 Asymmetric Cryptography
 Chapter 4 Asymmetric Cryptography Introduction Encryption: RSA Key Exchange: Diffie-Hellman [NetSec/SysSec], WS 2008/2009 4.1 Asymmetric Cryptography General idea: Use two different keys -K and +K for
Chapter 4 Asymmetric Cryptography Introduction Encryption: RSA Key Exchange: Diffie-Hellman [NetSec/SysSec], WS 2008/2009 4.1 Asymmetric Cryptography General idea: Use two different keys -K and +K for
Asymmetric Cryptography
 Asymmetric Cryptography Chapter 4 Asymmetric Cryptography Introduction Encryption: RSA Key Exchange: Diffie-Hellman General idea: Use two different keys -K and +K for encryption and decryption Given a
Asymmetric Cryptography Chapter 4 Asymmetric Cryptography Introduction Encryption: RSA Key Exchange: Diffie-Hellman General idea: Use two different keys -K and +K for encryption and decryption Given a
Asymmetric Encryption
 -3 s s Encryption Comp Sci 3600 Outline -3 s s 1-3 2 3 4 5 s s Outline -3 s s 1-3 2 3 4 5 s s Function Using Bitwise XOR -3 s s Key Properties for -3 s s The most important property of a hash function
-3 s s Encryption Comp Sci 3600 Outline -3 s s 1-3 2 3 4 5 s s Outline -3 s s 1-3 2 3 4 5 s s Function Using Bitwise XOR -3 s s Key Properties for -3 s s The most important property of a hash function
5199/IOC5063 Theory of Cryptology, 2014 Fall
 5199/IOC5063 Theory of Cryptology, 2014 Fall Homework 2 Reference Solution 1. This is about the RSA common modulus problem. Consider that two users A and B use the same modulus n = 146171 for the RSA encryption.
5199/IOC5063 Theory of Cryptology, 2014 Fall Homework 2 Reference Solution 1. This is about the RSA common modulus problem. Consider that two users A and B use the same modulus n = 146171 for the RSA encryption.
Lecture 17: Constructions of Public-Key Encryption
 COM S 687 Introduction to Cryptography October 24, 2006 Lecture 17: Constructions of Public-Key Encryption Instructor: Rafael Pass Scribe: Muthu 1 Secure Public-Key Encryption In the previous lecture,
COM S 687 Introduction to Cryptography October 24, 2006 Lecture 17: Constructions of Public-Key Encryption Instructor: Rafael Pass Scribe: Muthu 1 Secure Public-Key Encryption In the previous lecture,
Lecture 18 - Secret Sharing, Visual Cryptography, Distributed Signatures
 Lecture 18 - Secret Sharing, Visual Cryptography, Distributed Signatures Boaz Barak November 27, 2007 Quick review of homework 7 Existence of a CPA-secure public key encryption scheme such that oracle
Lecture 18 - Secret Sharing, Visual Cryptography, Distributed Signatures Boaz Barak November 27, 2007 Quick review of homework 7 Existence of a CPA-secure public key encryption scheme such that oracle
Lecture 5, CPA Secure Encryption from PRFs
 CS 4501-6501 Topics in Cryptography 16 Feb 2018 Lecture 5, CPA Secure Encryption from PRFs Lecturer: Mohammad Mahmoody Scribe: J. Fu, D. Anderson, W. Chao, and Y. Yu 1 Review Ralling: CPA Security and
CS 4501-6501 Topics in Cryptography 16 Feb 2018 Lecture 5, CPA Secure Encryption from PRFs Lecturer: Mohammad Mahmoody Scribe: J. Fu, D. Anderson, W. Chao, and Y. Yu 1 Review Ralling: CPA Security and
Practice Exam Winter 2018, CS 485/585 Crypto March 14, 2018
 Practice Exam Name: Winter 2018, CS 485/585 Crypto March 14, 2018 Portland State University Prof. Fang Song Instructions This exam contains 8 pages (including this cover page) and 5 questions. Total of
Practice Exam Name: Winter 2018, CS 485/585 Crypto March 14, 2018 Portland State University Prof. Fang Song Instructions This exam contains 8 pages (including this cover page) and 5 questions. Total of
Introduction to Elliptic Curve Cryptography
 Indian Statistical Institute Kolkata May 19, 2017 ElGamal Public Key Cryptosystem, 1984 Key Generation: 1 Choose a suitable large prime p 2 Choose a generator g of the cyclic group IZ p 3 Choose a cyclic
Indian Statistical Institute Kolkata May 19, 2017 ElGamal Public Key Cryptosystem, 1984 Key Generation: 1 Choose a suitable large prime p 2 Choose a generator g of the cyclic group IZ p 3 Choose a cyclic
Topics in Cryptography. Lecture 5: Basic Number Theory
 Topics in Cryptography Lecture 5: Basic Number Theory Benny Pinkas page 1 1 Classical symmetric ciphers Alice and Bob share a private key k. System is secure as long as k is secret. Major problem: generating
Topics in Cryptography Lecture 5: Basic Number Theory Benny Pinkas page 1 1 Classical symmetric ciphers Alice and Bob share a private key k. System is secure as long as k is secret. Major problem: generating
Provable Security for Public-Key Schemes. Outline. I Basics. Secrecy of Communications. Outline. David Pointcheval
 Provable Security for Public-Key Schemes I Basics David Pointcheval Ecole normale supérieure, CNRS & INRIA IACR-SEAMS School Cryptographie: Foundations and New Directions November 2016 Hanoi Vietnam Introduction
Provable Security for Public-Key Schemes I Basics David Pointcheval Ecole normale supérieure, CNRS & INRIA IACR-SEAMS School Cryptographie: Foundations and New Directions November 2016 Hanoi Vietnam Introduction
Post-quantum security models for authenticated encryption
 Post-quantum security models for authenticated encryption Vladimir Soukharev David R. Cheriton School of Computer Science February 24, 2016 Introduction Bellare and Namprempre in 2008, have shown that
Post-quantum security models for authenticated encryption Vladimir Soukharev David R. Cheriton School of Computer Science February 24, 2016 Introduction Bellare and Namprempre in 2008, have shown that
Scribe for Lecture #5
 CSA E0 235: Cryptography 28 January 2016 Scribe for Lecture #5 Instructor: Dr. Arpita Patra Submitted by: Nidhi Rathi 1 Pseudo-randomness and PRG s We saw that computational security introduces two relaxations
CSA E0 235: Cryptography 28 January 2016 Scribe for Lecture #5 Instructor: Dr. Arpita Patra Submitted by: Nidhi Rathi 1 Pseudo-randomness and PRG s We saw that computational security introduces two relaxations
ASYMMETRIC ENCRYPTION
 ASYMMETRIC ENCRYPTION 1 / 1 Recommended Book Steven Levy. Crypto. Penguin books. 2001. A non-technical account of the history of public-key cryptography and the colorful characters involved. 2 / 1 Recall
ASYMMETRIC ENCRYPTION 1 / 1 Recommended Book Steven Levy. Crypto. Penguin books. 2001. A non-technical account of the history of public-key cryptography and the colorful characters involved. 2 / 1 Recall
Instructor: Daniele Venturi. Master Degree in Data Science Sapienza University of Rome Academic Year
 Data Privacy and Security Instructor: Daniele Venturi Master Degree in Data Science Sapienza University of Rome Academic Year 2017-2018 Interlude: Number Theory Cubum autem in duos cubos, aut quadratoquadratum
Data Privacy and Security Instructor: Daniele Venturi Master Degree in Data Science Sapienza University of Rome Academic Year 2017-2018 Interlude: Number Theory Cubum autem in duos cubos, aut quadratoquadratum
Introduction to Modern Cryptography. Benny Chor
 Introduction to Modern Cryptography Benny Chor RSA: Review and Properties Factoring Algorithms Trapdoor One Way Functions PKC Based on Discrete Logs (Elgamal) Signature Schemes Lecture 8 Tel-Aviv University
Introduction to Modern Cryptography Benny Chor RSA: Review and Properties Factoring Algorithms Trapdoor One Way Functions PKC Based on Discrete Logs (Elgamal) Signature Schemes Lecture 8 Tel-Aviv University
Security Issues in Cloud Computing Modern Cryptography II Asymmetric Cryptography
 Security Issues in Cloud Computing Modern Cryptography II Asymmetric Cryptography Peter Schwabe October 21 and 28, 2011 So far we assumed that Alice and Bob both have some key, which nobody else has. How
Security Issues in Cloud Computing Modern Cryptography II Asymmetric Cryptography Peter Schwabe October 21 and 28, 2011 So far we assumed that Alice and Bob both have some key, which nobody else has. How
Digital Signatures. p1.
 Digital Signatures p1. Digital Signatures Digital signature is the same as MAC except that the tag (signature) is produced using the secret key of a public-key cryptosystem. Message m MAC k (m) Message
Digital Signatures p1. Digital Signatures Digital signature is the same as MAC except that the tag (signature) is produced using the secret key of a public-key cryptosystem. Message m MAC k (m) Message
14 Diffie-Hellman Key Agreement
 14 Diffie-Hellman Key Agreement 14.1 Cyclic Groups Definition 14.1 Example Let д Z n. Define д n = {д i % n i Z}, the set of all powers of д reduced mod n. Then д is called a generator of д n, and д n
14 Diffie-Hellman Key Agreement 14.1 Cyclic Groups Definition 14.1 Example Let д Z n. Define д n = {д i % n i Z}, the set of all powers of д reduced mod n. Then д is called a generator of д n, and д n
Week : Public Key Cryptosystem and Digital Signatures
 Week 10-11 : Public Key Cryptosystem and Digital Signatures 1. Public Key Encryptions RSA, ElGamal, 2 RSA- PKC(1/3) 1st public key cryptosystem R.L.Rivest, A.Shamir, L.Adleman, A Method for Obtaining Digital
Week 10-11 : Public Key Cryptosystem and Digital Signatures 1. Public Key Encryptions RSA, ElGamal, 2 RSA- PKC(1/3) 1st public key cryptosystem R.L.Rivest, A.Shamir, L.Adleman, A Method for Obtaining Digital
Intro to Public Key Cryptography Diffie & Hellman Key Exchange
 Introduction to Modern Cryptography Lecture 5 Number Theory: 1. Quadratic residues. 2. The discrete log problem. Intro to Public Key Cryptography Diffie & Hellman Key Exchange Course Summary - Math Part
Introduction to Modern Cryptography Lecture 5 Number Theory: 1. Quadratic residues. 2. The discrete log problem. Intro to Public Key Cryptography Diffie & Hellman Key Exchange Course Summary - Math Part
Public Key Algorithms
 Public Key Algorithms Raj Jain Washington University in Saint Louis Saint Louis, MO 63130 Jain@cse.wustl.edu Audio/Video recordings of this lecture are available at: http://www.cse.wustl.edu/~jain/cse571-09/
Public Key Algorithms Raj Jain Washington University in Saint Louis Saint Louis, MO 63130 Jain@cse.wustl.edu Audio/Video recordings of this lecture are available at: http://www.cse.wustl.edu/~jain/cse571-09/
Winter 2011 Josh Benaloh Brian LaMacchia
 Winter 2011 Josh Benaloh Brian LaMacchia Fun with Public-Key Tonight we ll Introduce some basic tools of public-key crypto Combine the tools to create more powerful tools Lay the ground work for substantial
Winter 2011 Josh Benaloh Brian LaMacchia Fun with Public-Key Tonight we ll Introduce some basic tools of public-key crypto Combine the tools to create more powerful tools Lay the ground work for substantial
Practice Assignment 2 Discussion 24/02/ /02/2018
 German University in Cairo Faculty of MET (CSEN 1001 Computer and Network Security Course) Dr. Amr El Mougy 1 RSA 1.1 RSA Encryption Practice Assignment 2 Discussion 24/02/2018-29/02/2018 Perform encryption
German University in Cairo Faculty of MET (CSEN 1001 Computer and Network Security Course) Dr. Amr El Mougy 1 RSA 1.1 RSA Encryption Practice Assignment 2 Discussion 24/02/2018-29/02/2018 Perform encryption
8.1 Principles of Public-Key Cryptosystems
 Public-key cryptography is a radical departure from all that has gone before. Right up to modern times all cryptographic systems have been based on the elementary tools of substitution and permutation.
Public-key cryptography is a radical departure from all that has gone before. Right up to modern times all cryptographic systems have been based on the elementary tools of substitution and permutation.
CIS 551 / TCOM 401 Computer and Network Security
 CIS 551 / TCOM 401 Computer and Network Security Spring 2008 Lecture 15 3/20/08 CIS/TCOM 551 1 Announcements Project 3 available on the web. Get the handout in class today. Project 3 is due April 4th It
CIS 551 / TCOM 401 Computer and Network Security Spring 2008 Lecture 15 3/20/08 CIS/TCOM 551 1 Announcements Project 3 available on the web. Get the handout in class today. Project 3 is due April 4th It
Cryptography. Course 1: Remainder: RSA. Jean-Sébastien Coron. September 21, Université du Luxembourg
 Course 1: Remainder: RSA Université du Luxembourg September 21, 2010 Public-key encryption Public-key encryption: two keys. One key is made public and used to encrypt. The other key is kept private and
Course 1: Remainder: RSA Université du Luxembourg September 21, 2010 Public-key encryption Public-key encryption: two keys. One key is made public and used to encrypt. The other key is kept private and
Notes for Lecture 17
 U.C. Berkeley CS276: Cryptography Handout N17 Luca Trevisan March 17, 2009 Notes for Lecture 17 Scribed by Matt Finifter, posted April 8, 2009 Summary Today we begin to talk about public-key cryptography,
U.C. Berkeley CS276: Cryptography Handout N17 Luca Trevisan March 17, 2009 Notes for Lecture 17 Scribed by Matt Finifter, posted April 8, 2009 Summary Today we begin to talk about public-key cryptography,
Cryptography and Security Final Exam
 Cryptography and Security Final Exam Serge Vaudenay 17.1.2017 duration: 3h no documents allowed, except one 2-sided sheet of handwritten notes a pocket calculator is allowed communication devices are not
Cryptography and Security Final Exam Serge Vaudenay 17.1.2017 duration: 3h no documents allowed, except one 2-sided sheet of handwritten notes a pocket calculator is allowed communication devices are not
Lecture 9 Julie Staub Avi Dalal Abheek Anand Gelareh Taban. 1 Introduction. 2 Background. CMSC 858K Advanced Topics in Cryptography February 24, 2004
 CMSC 858K Advanced Topics in Cryptography February 24, 2004 Lecturer: Jonathan Katz Lecture 9 Scribe(s): Julie Staub Avi Dalal Abheek Anand Gelareh Taban 1 Introduction In previous lectures, we constructed
CMSC 858K Advanced Topics in Cryptography February 24, 2004 Lecturer: Jonathan Katz Lecture 9 Scribe(s): Julie Staub Avi Dalal Abheek Anand Gelareh Taban 1 Introduction In previous lectures, we constructed
b = 10 a, is the logarithm of b to the base 10. Changing the base to e we obtain natural logarithms, so a = ln b means that b = e a.
 INTRODUCTION TO CRYPTOGRAPHY 5. Discrete Logarithms Recall the classical logarithm for real numbers: If we write b = 10 a, then a = log 10 b is the logarithm of b to the base 10. Changing the base to e
INTRODUCTION TO CRYPTOGRAPHY 5. Discrete Logarithms Recall the classical logarithm for real numbers: If we write b = 10 a, then a = log 10 b is the logarithm of b to the base 10. Changing the base to e
Course 2BA1: Trinity 2006 Section 9: Introduction to Number Theory and Cryptography
 Course 2BA1: Trinity 2006 Section 9: Introduction to Number Theory and Cryptography David R. Wilkins Copyright c David R. Wilkins 2006 Contents 9 Introduction to Number Theory and Cryptography 1 9.1 Subgroups
Course 2BA1: Trinity 2006 Section 9: Introduction to Number Theory and Cryptography David R. Wilkins Copyright c David R. Wilkins 2006 Contents 9 Introduction to Number Theory and Cryptography 1 9.1 Subgroups
RSA RSA public key cryptosystem
 RSA 1 RSA As we have seen, the security of most cipher systems rests on the users keeping secret a special key, for anyone possessing the key can encrypt and/or decrypt the messages sent between them.
RSA 1 RSA As we have seen, the security of most cipher systems rests on the users keeping secret a special key, for anyone possessing the key can encrypt and/or decrypt the messages sent between them.
Number Theory: Applications. Number Theory Applications. Hash Functions II. Hash Functions III. Pseudorandom Numbers
 Number Theory: Applications Number Theory Applications Computer Science & Engineering 235: Discrete Mathematics Christopher M. Bourke cbourke@cse.unl.edu Results from Number Theory have many applications
Number Theory: Applications Number Theory Applications Computer Science & Engineering 235: Discrete Mathematics Christopher M. Bourke cbourke@cse.unl.edu Results from Number Theory have many applications
Public-Key Cryptography. Lecture 9 Public-Key Encryption Diffie-Hellman Key-Exchange
 Public-Key Cryptography Lecture 9 Public-Key Encryption Diffie-Hellman Key-Exchange Shared/Symmetric-Key Encryption (a.k.a. private-key encryption) SKE: Syntax KeyGen outputs K K E scheme E Syntax a.k.a.
Public-Key Cryptography Lecture 9 Public-Key Encryption Diffie-Hellman Key-Exchange Shared/Symmetric-Key Encryption (a.k.a. private-key encryption) SKE: Syntax KeyGen outputs K K E scheme E Syntax a.k.a.
Modern Cryptography Lecture 4
 Modern Cryptography Lecture 4 Pseudorandom Functions Block-Ciphers Modes of Operation Chosen-Ciphertext Security 1 October 30th, 2018 2 Webpage Page for first part, Homeworks, Slides http://pub.ist.ac.at/crypto/moderncrypto18.html
Modern Cryptography Lecture 4 Pseudorandom Functions Block-Ciphers Modes of Operation Chosen-Ciphertext Security 1 October 30th, 2018 2 Webpage Page for first part, Homeworks, Slides http://pub.ist.ac.at/crypto/moderncrypto18.html
G Advanced Cryptography April 10th, Lecture 11
 G.30-001 Advanced Cryptography April 10th, 007 Lecturer: Victor Shoup Lecture 11 Scribe: Kristiyan Haralambiev We continue the discussion of public key encryption. Last time, we studied Hash Proof Systems
G.30-001 Advanced Cryptography April 10th, 007 Lecturer: Victor Shoup Lecture 11 Scribe: Kristiyan Haralambiev We continue the discussion of public key encryption. Last time, we studied Hash Proof Systems
during transmission safeguard information Cryptography: used to CRYPTOGRAPHY BACKGROUND OF THE MATHEMATICAL
 THE MATHEMATICAL BACKGROUND OF CRYPTOGRAPHY Cryptography: used to safeguard information during transmission (e.g., credit card number for internet shopping) as opposed to Coding Theory: used to transmit
THE MATHEMATICAL BACKGROUND OF CRYPTOGRAPHY Cryptography: used to safeguard information during transmission (e.g., credit card number for internet shopping) as opposed to Coding Theory: used to transmit
Winter 2008 Introduction to Modern Cryptography Benny Chor and Rani Hod. Assignment #2
 0368.3049.01 Winter 2008 Introduction to Modern Cryptography Benny Chor and Rani Hod Assignment #2 Published Sunday, February 17, 2008 and very slightly revised Feb. 18. Due Tues., March 4, in Rani Hod
0368.3049.01 Winter 2008 Introduction to Modern Cryptography Benny Chor and Rani Hod Assignment #2 Published Sunday, February 17, 2008 and very slightly revised Feb. 18. Due Tues., March 4, in Rani Hod
