Hand Out: Analysis of Algorithms. September 8, Bud Mishra. In general, there can be several algorithms to solve a problem; and one is faced
|
|
|
- Valentine Lyons
- 6 years ago
- Views:
Transcription
1 Had Out Aalysis of Algorithms September 8, 998 Bud Mishra c Mishra, February 9, 986 Itroductio I geeral, there ca be several algorithms to solve a problem; ad oe is faced with the problem of choosig a algorithm for use Oe way to dieretiate betwee two competig algorithms is to assig a complexity measure to the algorithms Havig doe this, oe may choose the algorithm with the lowest complexity There are two kids of complexity measures Static A complexity measure is static, if it does ot deped o the iput values A example of such a measure is the program legth This measure is relevat oly if the algorithm is to be used oce or oly a few times Dyamic A complexity measure is dyamic, if it varies with the iput values Some examples of such a measure are ruig time or storage space complexity of a algorithm as a fuctio of the iput values This measure is relevat, whe the algorithm is to be ru several times o `large' iput values I most practical applicatios, the dyamic complexity measure is sigificat, sice all productio softwares are assumed to ru a large umber of times, ad the cost of producig ad maitaiig the software (which deped o static complexities) are amortized rather fast We shall use ruig time as our complexity measure, sice almost all the algorithms we cosider have a space boud that is a liear fuctio of the iput size Furthermore, while aalyzig ruig times, we will igore costat factors, ad will cocetrate oly o the orders of growth There are two reasos for doig so This allows us to igore details of the machie model, (such as, the hardware of the machie, the istructio sets of the computer, the memory structure of the computer, the quality of code geerated by the compiler, etc) thus givig us a machie-idepedet complexity measure
2 For large eough problem sizes the relative eciecies of two algorithms deped o the ruig times as a asymptotic fuctio of iput size, idepedet of costat factors We shall geerally measure the ruig time, T (), as a fuctio of the worst-case iput data of size ; that is, T () is the maximum, over all iputs of size, of the ruig time o that iput The worst-case aalysis provides a performace guaratee, but may be overly pessimistic, if the worst-case iputs occur seldom A alterative is a average-case aalysis we measure the ruig time, T avg (), as the average, over all possible iputs of size, of the ruig time o that iput However, such a aalysis is frequetly mathematically itractable Furthermore, we must take care that our probability distributio is realistic which may be much harder to accomplish Faced with these problems, algorithm-desigers have suggested other averagecase complexity measures; but these measures have ot achieved wide-spread acceptace, ad requires mathematics, outside the scope of this class Hece, we shall restrict ourselves to worst-case complexity aalysis, ad occasioally, try to do the average-case aalysis Big Omicro, Big Omega, Big Theta We talk about the orders of growth of the fuctio T () usig the fuctios O() (kow as big-omicro or more popularly, big-oh), () (big-omega) ad () (big-theta) They are deed as follows O(f()), if there are two positive costats C ad 0 such that T () C f(); for all 0 (f()), if there are two positive costats C ad 0 that T () C f(); for all 0 such Some dee this dieretly (f(), if there is a positive costat C such that T () C f() iitely ofte (for iitely may values of ) This is a weaker deitio, ad seems more useful for lower-boud proofs but, for all practical purposes, the stroger deitio works pretty well
3 (f()), if there are three positive costats C, C 0 ad 0 such that C f() T () C 0 f(); for all 0 3 Algebra o O May of the rules of algebra work with O-otatios, but some do't Here, the mai problem is that, i the expressio O(f()), `=' is a oe-way equality (ie, it does ot have the symmetry property of the equality) For istace + = O( ) but ot O( ) = + (Why ot?) So how do you maipulate expressios with O's? Very carefully Here are some of the simple operatios you ca do with the O-otatio f() = O(f()); c O(f()) = O(f()); c is a costat; O(f()) + O(f()) = O(f()); O(O(f()) = O(f()); O(f(()) O(g()) = O(f() g()); O(f() g()) = f() O(g()) Usig these, we ca derive may other useful relatios Let T () = O(f()) be the ruig time of the program P, ad T () = O(g()), the ruig time of P The followig program P procedure P (N); begi P (N); P (N) ed has ruig time T ()+T () It is easy to show that f() = O(max(f(); g())) ad g() = O(max(f(); g())) Usig the above idetities(?), we see that T () + T () = O(f()) + O(g()) = O(O(max(f(); g()))) + O(O(max(f(); g()))) = O(max(f(); g())) + O(max(f(); g())) = O(max(f(); g())) 3
4 4 Aalysis of Algorithms ad Recurrece Relatios I geeral, we are iterested i aalyzig algorithms that is made of a set of a mutually recursive algorithms No-recursive algorithms are usually easy to aalyze, ad require very little mathematical sophisticatio I what follows, we will cocetrate o self-recursive algorithms, sice these illustrate all the mai ideas, ad geeralizatio to mutually recursive algorithms is straightforward Let us write self-recursive algorithm i the followig schematic form procedure P (N); begi Statemet ; P (N ); Statemet ; P (N ); Statemet 3; Statemet l; P (N l ); Statemet (l + ); ed A geeral program may be trasformed ito this form after resolvig ifthe-else's ad urollig while-loop's Hece, l itself ca be fuctio of Size(N) Such schemas are somewhat simplistic, but ot overly restrictive Let Size(N) =, Size(N ) =,, Size(N l ) = l Assume that the time spet by Statemet, Statemet,, Statemet (l+) is bouded from above by f() The we ca write the complexity of the algorithm as follows T () lx i= T ( i ) + f() Such a iequality is called a recurrece relatio What we preset here are, i fact, techiques to solve recurrece equatios 4
5 of the form lx i= T ( i ) + f() Uder a rather mild assumptio, you ca show that replacig the iequality by a equality does ot create ay problem (This will be a home work problem) 5 Solvig the Recurrece Equatios The subject of solvig recurrece equatios (also called dierece equatios) arise i may other areas too combiatorics, probability theory, discretetime cotrol theory, ecoomics to ame a few There are several powerful mathematical techiques available to solve these such as, summig factors, geeratig fuctios, z-trasformatios, operator methods, etc But most of these techiques are beyod our scope We develop oly a few techiques though simple, they are suciet for our purpose 5 Guess-Work The idea is to guess a solutio, ad the verify the guess by a mathematical iductio over the iteger This method requires you to kow the solutio i order to get the solutio, ad does ot work Use it oly whe you have o other way of solvig the equatio try several guesses; if you are lucky, oe of them will work Example 5 Cosider the followig recurrece equatio ( c ; if = ; T ( ) + c ; if > () Suppose we guess that c lg +c, the by mathematical iductio over all positive itegers, we ca show the validity of our guess Hece O( lg ) It is left as a exercise for you to do the steps of the iductive proof 5
6 5 Expasio Aother way to solve a recurrece relatio is to repeatedly expad the terms as may times as possible Whe this process stops, we will be left with a sum cosistig of fuctios of f() ad lower values of T () I may cases the summatio ca be evaluated to obtai a close form solutio This method is rather messy, ad proe to error avoid it, i all but a few simple cases Example 5 Cosider the followig recurrece equatio ( c ; if = ; T ( ) + c ; if > () First rearrage the recursive part as c + T Expadig the recursive deitio of T ( ) shows that c + Multiplyig ad cacelig yields c + T 4 c + c + 4 T 4 Applyig the recursive deitio of T ( ) to above shows that 4 c + c + c + 8 T 8 This process of expasio ad cacellatio ca be iterated lg times to yield X 4 lg i= 3 c 5 + T () = c lg + c 6
7 53 Recursio Tree Aother way to solve the recurrece equatio of the form T (0 ); if = 0 ; T ( ) + T ( ) + + T ( l ) + f(); if > 0, (3) is by expadig the terms of it i a tree like maer The tree correspodig to this expasio is called a recursio tree, ad is deed as follows The recursio tree for the equatio 3 at the value is a sigle ode with the value T ( 0 ), if = 0 ; otherwise, a ode with the value f() ad l sos such that the i th so is the root of a recursio tree of the equatio 3 at i It is easy to see that T () is just the sum of values at the odes Example 53 Cosider the followig recurrece equatio ( c ; if = ; T ( ) + c ; if > (4) The recursio tree for the equatio 4 is as show below C C C C C C depth = lg + Figure Recursio Tree You may prove the followig facts about the above recursio tree 7
8 The tree has a depth of lg + The sum of values at all the iteral odes at level i (0 i < lg ) is c Thus X j=iteral ode value(j) = c lg The tree has leaves The value of each leaf ode is c X j=leaf ode value(j) = c Hece X j=ode value(j) = c lg + c 54 Telescopig The idea of telescopig or summig factors is rather simple, ad is developed step-by-step i this ad the ext sectio We start out by showig how to solve recurrece equatios of very simple form usig this techique But this techique, whe combied with the trasformatio techiques of the ext sectio, is quite powerful ad hadles almost all equatios Please try to master this techique by tryig to solve several recurrece equatios this is the ocial techique for this course Cosider the recurrece equatio ; if = 0; T ( ) + ; if (5) We ca write dow the above equatio as follows T () T ( ) = T ( ) T ( ) = T () T (0) = T () T (0) = The simplicatio is obtaied by cacelig T (i) of the curret lie by the T (i) of the ext lie Thus whe we added up all the equatios most of the 8
9 terms caceled out We say the sum telescopes Note that the al aswer is + T (0) = + Fidig the solutio above was almost trivial Sometimes however we have to use a little trickery to make the sum of successive equatios telescope Suppose that our recurrece is a 0 T (0) = c 0 ; a b T ( ) + c ; if (6) where a, b ad c are give If we try to add to successive copies of this equatio, for example, a T () b T ( ) = c a T ( ) b T ( ) = c the the T ( ) terms do ot cacel sice b is ot equal to a Note however that we could multiply the equatios by some factor which would make the T ( ) terms cacel ad the sum will telescope Let us multiply the th equatio by some (so far uspecied) factor f to obtai f a T () f b T ( ) = f c f a T ( ) f b T ( ) = f c I order to guaratee that the T ( ) terms cacel we require that or f b = f a f = f a By urollig the above equatio we get f = f a Fixig f 0 =, we get b b! a a = f b b Q = = f a i=0 i 0 Q b i= i f 0 = ; Q i=0 f = a i Q ; if (7) i= b i 9
10 f is called the summig factor for the equatio 6 Let us write Sice this yields R() = f a T () f a f b T ( ) + f c = f a T ( ) + f c ; Now the telescopy will work Hece ad simplifyig, R(0) = c 0 ; R() = R( ) + c f ; if R() R( ) = c f R( ) R( ) = c f R() R(0) = c f R() R(0) = P j= c jf j R() = f a 4 c0 + 4 c0 + f a Q! b i= i Q 4 a c0 + i=0 i X j= X j= X j= c j f j 3 5 c j f j 3 5 ; Q j c j Q j i= b i i=0 a i Example 54 Cosider the followig recurrece equatio 3 5 (8) ; if = 0; T ( ) + ; if (9) This is same as T (0) = ; T () T ( ) = ; if 0
11 This is a example of 6 with By 7 we may choose a = ; b = f 0 = ; f = ; if Multiplyig by f ( ) gives the ew equatio Usig telescopy we get T (0) = ; T () T () = ; if Hece T () T ( ) = T ( ) T ( ) = T () = T () T (0) = ( + ) 55 Rage ad Domai Trasformatios Now, we examie how to trasform a sequece so that the trasformed sequece becomes more recogizable more familiar The fuctio T maps the iteger i its domai to a real T () i its rage We call a trasformatio o the values of the sequece T () a rage trasformatio ad a trasformatio o the idices a domai trasformatio We illustrate the ideas usig examples Domai Trasformatio Example 55 Cosider the followig recurrece equatio ( c ; if = ; T ( ) + c ; if > (0)
12 Let us use the followig domai trasformatio rst = k ; (k = lg ) hece S(k) = T ( k ) The above equatio becomes c ; if k = 0; S(k) = S(k ) + c k ; if k Now we ca use telescopig to get the followig solutio S(k) = T ( k ) = k (c k + c ) Back-substitutig for k ad lg for k, we coclude that Rage Trasformatio (c lg + c ) Example 56 Cosider the followig (pseudo-o-liear) recurrece equatio ; if = 0; () 3 (T ( )) ; if Let us use the followig rage trasformatio rst S() = log 3 T (); 3 S() = T () We may rewrite the recurrece as 0; if = 0; S() = S( ) + ; if Usig multiplier f =, we get Usig telescopy, we get Hece, Hece, S() S(0) 0 = S(0) = 0 0 S() S( ) = X = i i= (=) (=)+ (=) S() = 3 S() = 3 =
13 6 Examples 6 Example Divide-ad-Coquer A importat class of recurrece equatios results from algorithms based o the `divide-ad-coquer' paradigm; such algorithms cosist of three steps divide Break the problem of size ito a smaller subproblems each of size, usig o more tha g() time b recur Recursively solve each of the a subproblems usig a T ( b ) time 3 marry Combie the solutios to the subproblems to get a solutio to the origial problem, usig o more tha h() time The recurrece equatio is of the form a + f(); where f() = g() + h() () b Use the followig domai-trasformatio rst = b m (m = log b ) The above equatio becomes T (b m ) = a T (b m ) + f(b m ) Usig the multiplyig factor f m = ( a m ) we get Usig telescopy T (b m ) a m = T (bm ) a m + f(bm ) a m T (b m ) a m T (bm ) = f (bm ) a m a m T (b m ) T (bm ) = f (bm ) a m a m a m T (b) T () = f (b) a a T (b m ) a m T () = P m i= 3 f (b i ) a i
14 Hece T (b m ) = a m "T () + mx i= # f(b i ) a i assumptio f is a multiplicative fuctio; that is, f has the followig property f(m ) = f(m) f() Example of a multiplicative fuctio is f() = c Hece f(b i ) = (f(b)) Rewrite the previous fuctio as T (b m ) = a m 4 T () + m X i= f(b) a! i 3 5 Let The a m "T () + = mx i= There are three cases to cosider f(b) a! # i = a m T () + m case a > f(b); that is, < The a m O() = O (a m ) = O a log b = O a log b case a = f(b); that is, = The a m O(m) = O (a m m) = O a log b log b case3 a < f(b); that is, > The a m O ( m ) = O (f(b) m ) = O = O log b a log b f(b) log b = O log b f (b) 4
15 6 Example Radomized Divide-ad-Coquer Let us cosider a radomized algorithm (ie algorithm ivolvig coitosses), also based o the `divide-ad-coquer' paradigm; such a algorithm cosists of three steps radom-divide Break the problem of size ito smaller subproblems as follows rst choose a umber i ( i ) with probability ; let the rst subproblem be the oe cosistig of the rst i elemets, ad the secod, cosistig of the remaiig i elemets The divisio step takes o more tha g() amout of time recur Recursively solve each of the subproblems usig T avg (i) + T avg ( i) time 3 marry Combie the solutios to the subproblems to get a solutio to the origial problem, usig o more tha h() time Let us assume that g() + h() = c Hece the recurrece equatio will be T avg () = X i= This ca be rewritte as T avg () = = = = [T avg(i) + T avg ( i)] + c P P P i= (T avg (i) + T avg ( i)) + c T i= avg(i) + P T i= avg( i) + c P i= T avg(i) + c T i= avg(i) + P T j= avg(j) + c Or ( ) T avg () = Substitutig + for, we get T avg ( + ) = X i= X i=! T avg (i) + c ( ) (3)! T avg (i) + c ( + ) (4) 5
16 Subtractig equatio 3 from equatio 4, T avg ( + ) ( ) T avg () = T avg () + c Simplifyig the above equatio T avg ( + ) = ( + ) T avg () + c Or T avg ( + ) + Usig telescopy we get T avg() = c + T avg(+) Tavg() + T avg() Tavg( ) = c + = c T avg() Tavg() = c T avg(+) + T () = c Hece Or, T avg ( + ) = ( + ) [T avg () + c (H + )] T avg () = [T avg () + c (H )] o The approximate size of the th harmoic umber H is a well-kow quatity H = l + + O Here = is Euler's costat Hece T avg () = h c l + + O ( ) + T avg () c = ( l )c lg + (c( ) + T avg ()) + c O( ) = 39c lg + [T avg () 085c] + c O( ) = O( lg ) i 6
17 7 Ed Notes These otes are about years old I origially wrote them for the master's level graduate course i algorithms ad had derived these otes from my earlier otes from graduate school, a survey paper by Leuker ad ideas due to Moier, Betley ad Saxe Clearly, there are some ew iterestig ideas that have evolved i the iterveig years The readers are urged to cosult these more up-to-date results 7
4.3 Growth Rates of Solutions to Recurrences
 4.3. GROWTH RATES OF SOLUTIONS TO RECURRENCES 81 4.3 Growth Rates of Solutios to Recurreces 4.3.1 Divide ad Coquer Algorithms Oe of the most basic ad powerful algorithmic techiques is divide ad coquer.
4.3. GROWTH RATES OF SOLUTIONS TO RECURRENCES 81 4.3 Growth Rates of Solutios to Recurreces 4.3.1 Divide ad Coquer Algorithms Oe of the most basic ad powerful algorithmic techiques is divide ad coquer.
CS 270 Algorithms. Oliver Kullmann. Growth of Functions. Divide-and- Conquer Min-Max- Problem. Tutorial. Reading from CLRS for week 2
 Geeral remarks Week 2 1 Divide ad First we cosider a importat tool for the aalysis of algorithms: Big-Oh. The we itroduce a importat algorithmic paradigm:. We coclude by presetig ad aalysig two examples.
Geeral remarks Week 2 1 Divide ad First we cosider a importat tool for the aalysis of algorithms: Big-Oh. The we itroduce a importat algorithmic paradigm:. We coclude by presetig ad aalysig two examples.
This Lecture. Divide and Conquer. Merge Sort: Algorithm. Merge Sort Algorithm. MergeSort (Example) - 1. MergeSort (Example) - 2
 This Lecture Divide-ad-coquer techique for algorithm desig. Example the merge sort. Writig ad solvig recurreces Divide ad Coquer Divide-ad-coquer method for algorithm desig: Divide: If the iput size is
This Lecture Divide-ad-coquer techique for algorithm desig. Example the merge sort. Writig ad solvig recurreces Divide ad Coquer Divide-ad-coquer method for algorithm desig: Divide: If the iput size is
Classification of problem & problem solving strategies. classification of time complexities (linear, logarithmic etc)
 Classificatio of problem & problem solvig strategies classificatio of time complexities (liear, arithmic etc) Problem subdivisio Divide ad Coquer strategy. Asymptotic otatios, lower boud ad upper boud:
Classificatio of problem & problem solvig strategies classificatio of time complexities (liear, arithmic etc) Problem subdivisio Divide ad Coquer strategy. Asymptotic otatios, lower boud ad upper boud:
CSI 5163 (95.573) ALGORITHM ANALYSIS AND DESIGN
 CSI 5163 (95.573) ALGORITHM ANALYSIS AND DESIGN CSI 5163 (95.5703) ALGORITHM ANALYSIS AND DESIGN (3 cr.) (T) Topics of curret iterest i the desig ad aalysis of computer algorithms for graphtheoretical
CSI 5163 (95.573) ALGORITHM ANALYSIS AND DESIGN CSI 5163 (95.5703) ALGORITHM ANALYSIS AND DESIGN (3 cr.) (T) Topics of curret iterest i the desig ad aalysis of computer algorithms for graphtheoretical
Math 155 (Lecture 3)
 Math 55 (Lecture 3) September 8, I this lecture, we ll cosider the aswer to oe of the most basic coutig problems i combiatorics Questio How may ways are there to choose a -elemet subset of the set {,,,
Math 55 (Lecture 3) September 8, I this lecture, we ll cosider the aswer to oe of the most basic coutig problems i combiatorics Questio How may ways are there to choose a -elemet subset of the set {,,,
Recurrence Relations
 Recurrece Relatios Aalysis of recursive algorithms, such as: it factorial (it ) { if (==0) retur ; else retur ( * factorial(-)); } Let t be the umber of multiplicatios eeded to calculate factorial(). The
Recurrece Relatios Aalysis of recursive algorithms, such as: it factorial (it ) { if (==0) retur ; else retur ( * factorial(-)); } Let t be the umber of multiplicatios eeded to calculate factorial(). The
Infinite Sequences and Series
 Chapter 6 Ifiite Sequeces ad Series 6.1 Ifiite Sequeces 6.1.1 Elemetary Cocepts Simply speakig, a sequece is a ordered list of umbers writte: {a 1, a 2, a 3,...a, a +1,...} where the elemets a i represet
Chapter 6 Ifiite Sequeces ad Series 6.1 Ifiite Sequeces 6.1.1 Elemetary Cocepts Simply speakig, a sequece is a ordered list of umbers writte: {a 1, a 2, a 3,...a, a +1,...} where the elemets a i represet
Average-Case Analysis of QuickSort
 Average-Case Aalysis of QuickSort Comp 363 Fall Semester 003 October 3, 003 The purpose of this documet is to itroduce the idea of usig recurrece relatios to do average-case aalysis. The average-case ruig
Average-Case Aalysis of QuickSort Comp 363 Fall Semester 003 October 3, 003 The purpose of this documet is to itroduce the idea of usig recurrece relatios to do average-case aalysis. The average-case ruig
Data Structures and Algorithm. Xiaoqing Zheng
 Data Structures ad Algorithm Xiaoqig Zheg zhegxq@fudaeduc What are algorithms? A sequece of computatioal steps that trasform the iput ito the output Sortig problem: Iput: A sequece of umbers
Data Structures ad Algorithm Xiaoqig Zheg zhegxq@fudaeduc What are algorithms? A sequece of computatioal steps that trasform the iput ito the output Sortig problem: Iput: A sequece of umbers
An Introduction to Randomized Algorithms
 A Itroductio to Radomized Algorithms The focus of this lecture is to study a radomized algorithm for quick sort, aalyze it usig probabilistic recurrece relatios, ad also provide more geeral tools for aalysis
A Itroductio to Radomized Algorithms The focus of this lecture is to study a radomized algorithm for quick sort, aalyze it usig probabilistic recurrece relatios, ad also provide more geeral tools for aalysis
Recursive Algorithms. Recurrences. Recursive Algorithms Analysis
 Recursive Algorithms Recurreces Computer Sciece & Egieerig 35: Discrete Mathematics Christopher M Bourke cbourke@cseuledu A recursive algorithm is oe i which objects are defied i terms of other objects
Recursive Algorithms Recurreces Computer Sciece & Egieerig 35: Discrete Mathematics Christopher M Bourke cbourke@cseuledu A recursive algorithm is oe i which objects are defied i terms of other objects
Algorithm Analysis. Chapter 3
 Data Structures Dr Ahmed Rafat Abas Computer Sciece Dept, Faculty of Computer ad Iformatio, Zagazig Uiversity arabas@zu.edu.eg http://www.arsaliem.faculty.zu.edu.eg/ Algorithm Aalysis Chapter 3 3. Itroductio
Data Structures Dr Ahmed Rafat Abas Computer Sciece Dept, Faculty of Computer ad Iformatio, Zagazig Uiversity arabas@zu.edu.eg http://www.arsaliem.faculty.zu.edu.eg/ Algorithm Aalysis Chapter 3 3. Itroductio
Test One (Answer Key)
 CS395/Ma395 (Sprig 2005) Test Oe Name: Page 1 Test Oe (Aswer Key) CS395/Ma395: Aalysis of Algorithms This is a closed book, closed otes, 70 miute examiatio. It is worth 100 poits. There are twelve (12)
CS395/Ma395 (Sprig 2005) Test Oe Name: Page 1 Test Oe (Aswer Key) CS395/Ma395: Aalysis of Algorithms This is a closed book, closed otes, 70 miute examiatio. It is worth 100 poits. There are twelve (12)
Ch3. Asymptotic Notation
 Ch. Asymptotic Notatio copyright 006 Preview of Chapters Chapter How to aalyze the space ad time complexities of program Chapter Review asymptotic otatios such as O, Ω, Θ, o for simplifyig the aalysis
Ch. Asymptotic Notatio copyright 006 Preview of Chapters Chapter How to aalyze the space ad time complexities of program Chapter Review asymptotic otatios such as O, Ω, Θ, o for simplifyig the aalysis
Sequences, Mathematical Induction, and Recursion. CSE 2353 Discrete Computational Structures Spring 2018
 CSE 353 Discrete Computatioal Structures Sprig 08 Sequeces, Mathematical Iductio, ad Recursio (Chapter 5, Epp) Note: some course slides adopted from publisher-provided material Overview May mathematical
CSE 353 Discrete Computatioal Structures Sprig 08 Sequeces, Mathematical Iductio, ad Recursio (Chapter 5, Epp) Note: some course slides adopted from publisher-provided material Overview May mathematical
CS583 Lecture 02. Jana Kosecka. some materials here are based on E. Demaine, D. Luebke slides
 CS583 Lecture 02 Jaa Kosecka some materials here are based o E. Demaie, D. Luebke slides Previously Sample algorithms Exact ruig time, pseudo-code Approximate ruig time Worst case aalysis Best case aalysis
CS583 Lecture 02 Jaa Kosecka some materials here are based o E. Demaie, D. Luebke slides Previously Sample algorithms Exact ruig time, pseudo-code Approximate ruig time Worst case aalysis Best case aalysis
Algorithms and Data Structures Lecture IV
 Algorithms ad Data Structures Lecture IV Simoas Šalteis Aalborg Uiversity simas@cs.auc.dk September 5, 00 1 This Lecture Aalyzig the ruig time of recursive algorithms (such as divide-ad-coquer) Writig
Algorithms ad Data Structures Lecture IV Simoas Šalteis Aalborg Uiversity simas@cs.auc.dk September 5, 00 1 This Lecture Aalyzig the ruig time of recursive algorithms (such as divide-ad-coquer) Writig
A recurrence equation is just a recursive function definition. It defines a function at one input in terms of its value on smaller inputs.
 CS23 Algorithms Hadout #6 Prof Ly Turbak September 8, 200 Wellesley College RECURRENCES This hadout summarizes highlights of CLRS Chapter 4 ad Appedix A (CLR Chapters 3 & 4) Two-Step Strategy for Aalyzig
CS23 Algorithms Hadout #6 Prof Ly Turbak September 8, 200 Wellesley College RECURRENCES This hadout summarizes highlights of CLRS Chapter 4 ad Appedix A (CLR Chapters 3 & 4) Two-Step Strategy for Aalyzig
CS / MCS 401 Homework 3 grader solutions
 CS / MCS 401 Homework 3 grader solutios assigmet due July 6, 016 writte by Jāis Lazovskis maximum poits: 33 Some questios from CLRS. Questios marked with a asterisk were ot graded. 1 Use the defiitio of
CS / MCS 401 Homework 3 grader solutios assigmet due July 6, 016 writte by Jāis Lazovskis maximum poits: 33 Some questios from CLRS. Questios marked with a asterisk were ot graded. 1 Use the defiitio of
Analysis of Algorithms. Introduction. Contents
 Itroductio The focus of this module is mathematical aspects of algorithms. Our mai focus is aalysis of algorithms, which meas evaluatig efficiecy of algorithms by aalytical ad mathematical methods. We
Itroductio The focus of this module is mathematical aspects of algorithms. Our mai focus is aalysis of algorithms, which meas evaluatig efficiecy of algorithms by aalytical ad mathematical methods. We
Mathematics review for CSCI 303 Spring Department of Computer Science College of William & Mary Robert Michael Lewis
 Mathematics review for CSCI 303 Sprig 019 Departmet of Computer Sciece College of William & Mary Robert Michael Lewis Copyright 018 019 Robert Michael Lewis Versio geerated: 13 : 00 Jauary 17, 019 Cotets
Mathematics review for CSCI 303 Sprig 019 Departmet of Computer Sciece College of William & Mary Robert Michael Lewis Copyright 018 019 Robert Michael Lewis Versio geerated: 13 : 00 Jauary 17, 019 Cotets
OPTIMAL ALGORITHMS -- SUPPLEMENTAL NOTES
 OPTIMAL ALGORITHMS -- SUPPLEMENTAL NOTES Peter M. Maurer Why Hashig is θ(). As i biary search, hashig assumes that keys are stored i a array which is idexed by a iteger. However, hashig attempts to bypass
OPTIMAL ALGORITHMS -- SUPPLEMENTAL NOTES Peter M. Maurer Why Hashig is θ(). As i biary search, hashig assumes that keys are stored i a array which is idexed by a iteger. However, hashig attempts to bypass
SNAP Centre Workshop. Basic Algebraic Manipulation
 SNAP Cetre Workshop Basic Algebraic Maipulatio 8 Simplifyig Algebraic Expressios Whe a expressio is writte i the most compact maer possible, it is cosidered to be simplified. Not Simplified: x(x + 4x)
SNAP Cetre Workshop Basic Algebraic Maipulatio 8 Simplifyig Algebraic Expressios Whe a expressio is writte i the most compact maer possible, it is cosidered to be simplified. Not Simplified: x(x + 4x)
Math 113 Exam 3 Practice
 Math Exam Practice Exam will cover.-.9. This sheet has three sectios. The first sectio will remid you about techiques ad formulas that you should kow. The secod gives a umber of practice questios for you
Math Exam Practice Exam will cover.-.9. This sheet has three sectios. The first sectio will remid you about techiques ad formulas that you should kow. The secod gives a umber of practice questios for you
CHAPTER 10 INFINITE SEQUENCES AND SERIES
 CHAPTER 10 INFINITE SEQUENCES AND SERIES 10.1 Sequeces 10.2 Ifiite Series 10.3 The Itegral Tests 10.4 Compariso Tests 10.5 The Ratio ad Root Tests 10.6 Alteratig Series: Absolute ad Coditioal Covergece
CHAPTER 10 INFINITE SEQUENCES AND SERIES 10.1 Sequeces 10.2 Ifiite Series 10.3 The Itegral Tests 10.4 Compariso Tests 10.5 The Ratio ad Root Tests 10.6 Alteratig Series: Absolute ad Coditioal Covergece
Assignment 5: Solutions
 McGill Uiversity Departmet of Mathematics ad Statistics MATH 54 Aalysis, Fall 05 Assigmet 5: Solutios. Let y be a ubouded sequece of positive umbers satisfyig y + > y for all N. Let x be aother sequece
McGill Uiversity Departmet of Mathematics ad Statistics MATH 54 Aalysis, Fall 05 Assigmet 5: Solutios. Let y be a ubouded sequece of positive umbers satisfyig y + > y for all N. Let x be aother sequece
SOME TRIBONACCI IDENTITIES
 Mathematics Today Vol.7(Dec-011) 1-9 ISSN 0976-38 Abstract: SOME TRIBONACCI IDENTITIES Shah Devbhadra V. Sir P.T.Sarvajaik College of Sciece, Athwalies, Surat 395001. e-mail : drdvshah@yahoo.com The sequece
Mathematics Today Vol.7(Dec-011) 1-9 ISSN 0976-38 Abstract: SOME TRIBONACCI IDENTITIES Shah Devbhadra V. Sir P.T.Sarvajaik College of Sciece, Athwalies, Surat 395001. e-mail : drdvshah@yahoo.com The sequece
SECTION 1.5 : SUMMATION NOTATION + WORK WITH SEQUENCES
 SECTION 1.5 : SUMMATION NOTATION + WORK WITH SEQUENCES Read Sectio 1.5 (pages 5 9) Overview I Sectio 1.5 we lear to work with summatio otatio ad formulas. We will also itroduce a brief overview of sequeces,
SECTION 1.5 : SUMMATION NOTATION + WORK WITH SEQUENCES Read Sectio 1.5 (pages 5 9) Overview I Sectio 1.5 we lear to work with summatio otatio ad formulas. We will also itroduce a brief overview of sequeces,
CS 332: Algorithms. Linear-Time Sorting. Order statistics. Slide credit: David Luebke (Virginia)
 1 CS 332: Algorithms Liear-Time Sortig. Order statistics. Slide credit: David Luebke (Virgiia) Quicksort: Partitio I Words Partitio(A, p, r): Select a elemet to act as the pivot (which?) Grow two regios,
1 CS 332: Algorithms Liear-Time Sortig. Order statistics. Slide credit: David Luebke (Virgiia) Quicksort: Partitio I Words Partitio(A, p, r): Select a elemet to act as the pivot (which?) Grow two regios,
Lecture 3: Asymptotic Analysis + Recurrences
 Lecture 3: Asymptotic Aalysis + Recurreces Data Structures ad Algorithms CSE 373 SU 18 BEN JONES 1 Warmup Write a model ad fid Big-O for (it i = 0; i < ; i++) { for (it j = 0; j < i; j++) { System.out.pritl(
Lecture 3: Asymptotic Aalysis + Recurreces Data Structures ad Algorithms CSE 373 SU 18 BEN JONES 1 Warmup Write a model ad fid Big-O for (it i = 0; i < ; i++) { for (it j = 0; j < i; j++) { System.out.pritl(
Optimally Sparse SVMs
 A. Proof of Lemma 3. We here prove a lower boud o the umber of support vectors to achieve geeralizatio bouds of the form which we cosider. Importatly, this result holds ot oly for liear classifiers, but
A. Proof of Lemma 3. We here prove a lower boud o the umber of support vectors to achieve geeralizatio bouds of the form which we cosider. Importatly, this result holds ot oly for liear classifiers, but
Model of Computation and Runtime Analysis
 Model of Computatio ad Rutime Aalysis Model of Computatio Model of Computatio Specifies Set of operatios Cost of operatios (ot ecessarily time) Examples Turig Machie Radom Access Machie (RAM) PRAM Map
Model of Computatio ad Rutime Aalysis Model of Computatio Model of Computatio Specifies Set of operatios Cost of operatios (ot ecessarily time) Examples Turig Machie Radom Access Machie (RAM) PRAM Map
Examples: data compression, path-finding, game-playing, scheduling, bin packing
 Algorithms - Basic Cocepts Algorithms so what is a algorithm, ayway? The dictioary defiitio: A algorithm is a well-defied computatioal procedure that takes iput ad produces output. This class will deal
Algorithms - Basic Cocepts Algorithms so what is a algorithm, ayway? The dictioary defiitio: A algorithm is a well-defied computatioal procedure that takes iput ad produces output. This class will deal
Design and Analysis of ALGORITHM (Topic 2)
 DR. Gatot F. Hertoo, MSc. Desig ad Aalysis of ALGORITHM (Topic 2) Algorithms + Data Structures = Programs Lessos Leared 1 Our Machie Model: Assumptios Geeric Radom Access Machie (RAM) Executes operatios
DR. Gatot F. Hertoo, MSc. Desig ad Aalysis of ALGORITHM (Topic 2) Algorithms + Data Structures = Programs Lessos Leared 1 Our Machie Model: Assumptios Geeric Radom Access Machie (RAM) Executes operatios
CS 332: Algorithms. Quicksort
 CS 33: Aorithms Quicsort David Luebe //03 Homewor Assiged today, due ext Wedesday Will be o web page shortly after class Go over ow David Luebe //03 Review: Quicsort Sorts i place Sorts O( ) i the average
CS 33: Aorithms Quicsort David Luebe //03 Homewor Assiged today, due ext Wedesday Will be o web page shortly after class Go over ow David Luebe //03 Review: Quicsort Sorts i place Sorts O( ) i the average
Model of Computation and Runtime Analysis
 Model of Computatio ad Rutime Aalysis Model of Computatio Model of Computatio Specifies Set of operatios Cost of operatios (ot ecessarily time) Examples Turig Machie Radom Access Machie (RAM) PRAM Map
Model of Computatio ad Rutime Aalysis Model of Computatio Model of Computatio Specifies Set of operatios Cost of operatios (ot ecessarily time) Examples Turig Machie Radom Access Machie (RAM) PRAM Map
6.3 Testing Series With Positive Terms
 6.3. TESTING SERIES WITH POSITIVE TERMS 307 6.3 Testig Series With Positive Terms 6.3. Review of what is kow up to ow I theory, testig a series a i for covergece amouts to fidig the i= sequece of partial
6.3. TESTING SERIES WITH POSITIVE TERMS 307 6.3 Testig Series With Positive Terms 6.3. Review of what is kow up to ow I theory, testig a series a i for covergece amouts to fidig the i= sequece of partial
1 Generating functions for balls in boxes
 Math 566 Fall 05 Some otes o geeratig fuctios Give a sequece a 0, a, a,..., a,..., a geeratig fuctio some way of represetig the sequece as a fuctio. There are may ways to do this, with the most commo ways
Math 566 Fall 05 Some otes o geeratig fuctios Give a sequece a 0, a, a,..., a,..., a geeratig fuctio some way of represetig the sequece as a fuctio. There are may ways to do this, with the most commo ways
NUMERICAL METHODS FOR SOLVING EQUATIONS
 Mathematics Revisio Guides Numerical Methods for Solvig Equatios Page 1 of 11 M.K. HOME TUITION Mathematics Revisio Guides Level: GCSE Higher Tier NUMERICAL METHODS FOR SOLVING EQUATIONS Versio:. Date:
Mathematics Revisio Guides Numerical Methods for Solvig Equatios Page 1 of 11 M.K. HOME TUITION Mathematics Revisio Guides Level: GCSE Higher Tier NUMERICAL METHODS FOR SOLVING EQUATIONS Versio:. Date:
CIS 121 Data Structures and Algorithms with Java Spring Code Snippets and Recurrences Monday, February 4/Tuesday, February 5
 CIS 11 Data Structures ad Algorithms with Java Sprig 019 Code Sippets ad Recurreces Moday, February 4/Tuesday, February 5 Learig Goals Practice provig asymptotic bouds with code sippets Practice solvig
CIS 11 Data Structures ad Algorithms with Java Sprig 019 Code Sippets ad Recurreces Moday, February 4/Tuesday, February 5 Learig Goals Practice provig asymptotic bouds with code sippets Practice solvig
CALCULUS BASIC SUMMER REVIEW
 CALCULUS BASIC SUMMER REVIEW NAME rise y y y Slope of a o vertical lie: m ru Poit Slope Equatio: y y m( ) The slope is m ad a poit o your lie is, ). ( y Slope-Itercept Equatio: y m b slope= m y-itercept=
CALCULUS BASIC SUMMER REVIEW NAME rise y y y Slope of a o vertical lie: m ru Poit Slope Equatio: y y m( ) The slope is m ad a poit o your lie is, ). ( y Slope-Itercept Equatio: y m b slope= m y-itercept=
Sums, products and sequences
 Sums, products ad sequeces How to write log sums, e.g., 1+2+ (-1)+ cocisely? i=1 Sum otatio ( sum from 1 to ): i 3 = 1 + 2 + + If =3, i=1 i = 1+2+3=6. The ame ii does ot matter. Could use aother letter
Sums, products ad sequeces How to write log sums, e.g., 1+2+ (-1)+ cocisely? i=1 Sum otatio ( sum from 1 to ): i 3 = 1 + 2 + + If =3, i=1 i = 1+2+3=6. The ame ii does ot matter. Could use aother letter
Discrete-Time Systems, LTI Systems, and Discrete-Time Convolution
 EEL5: Discrete-Time Sigals ad Systems. Itroductio I this set of otes, we begi our mathematical treatmet of discrete-time s. As show i Figure, a discrete-time operates or trasforms some iput sequece x [
EEL5: Discrete-Time Sigals ad Systems. Itroductio I this set of otes, we begi our mathematical treatmet of discrete-time s. As show i Figure, a discrete-time operates or trasforms some iput sequece x [
CSE Introduction to Parallel Processing. Chapter 3. Parallel Algorithm Complexity
 Dr. Izadi CSE-40533 Itroductio to Parallel Processig Chapter 3 Parallel Algorithm Complexity Review algorithm complexity ad various complexity classes Itroduce the otios of time ad time-cost optimality
Dr. Izadi CSE-40533 Itroductio to Parallel Processig Chapter 3 Parallel Algorithm Complexity Review algorithm complexity ad various complexity classes Itroduce the otios of time ad time-cost optimality
CSI 2101 Discrete Structures Winter Homework Assignment #4 (100 points, weight 5%) Due: Thursday, April 5, at 1:00pm (in lecture)
 CSI 101 Discrete Structures Witer 01 Prof. Lucia Moura Uiversity of Ottawa Homework Assigmet #4 (100 poits, weight %) Due: Thursday, April, at 1:00pm (i lecture) Program verificatio, Recurrece Relatios
CSI 101 Discrete Structures Witer 01 Prof. Lucia Moura Uiversity of Ottawa Homework Assigmet #4 (100 poits, weight %) Due: Thursday, April, at 1:00pm (i lecture) Program verificatio, Recurrece Relatios
Discrete Mathematics for CS Spring 2007 Luca Trevisan Lecture 22
 CS 70 Discrete Mathematics for CS Sprig 2007 Luca Trevisa Lecture 22 Aother Importat Distributio The Geometric Distributio Questio: A biased coi with Heads probability p is tossed repeatedly util the first
CS 70 Discrete Mathematics for CS Sprig 2007 Luca Trevisa Lecture 22 Aother Importat Distributio The Geometric Distributio Questio: A biased coi with Heads probability p is tossed repeatedly util the first
Once we have a sequence of numbers, the next thing to do is to sum them up. Given a sequence (a n ) n=1
 . Ifiite Series Oce we have a sequece of umbers, the ext thig to do is to sum them up. Give a sequece a be a sequece: ca we give a sesible meaig to the followig expressio? a = a a a a While summig ifiitely
. Ifiite Series Oce we have a sequece of umbers, the ext thig to do is to sum them up. Give a sequece a be a sequece: ca we give a sesible meaig to the followig expressio? a = a a a a While summig ifiitely
Chapter 6. Advanced Counting Techniques
 Chapter 6 Advaced Coutig Techiques 6.: Recurrece Relatios Defiitio: A recurrece relatio for the sequece {a } is a equatio expressig a i terms of oe or more of the previous terms of the sequece: a,a2,a3,,a
Chapter 6 Advaced Coutig Techiques 6.: Recurrece Relatios Defiitio: A recurrece relatio for the sequece {a } is a equatio expressig a i terms of oe or more of the previous terms of the sequece: a,a2,a3,,a
6 Integers Modulo n. integer k can be written as k = qn + r, with q,r, 0 r b. So any integer.
 6 Itegers Modulo I Example 2.3(e), we have defied the cogruece of two itegers a,b with respect to a modulus. Let us recall that a b (mod ) meas a b. We have proved that cogruece is a equivalece relatio
6 Itegers Modulo I Example 2.3(e), we have defied the cogruece of two itegers a,b with respect to a modulus. Let us recall that a b (mod ) meas a b. We have proved that cogruece is a equivalece relatio
Advanced Course of Algorithm Design and Analysis
 Differet complexity measures Advaced Course of Algorithm Desig ad Aalysis Asymptotic complexity Big-Oh otatio Properties of O otatio Aalysis of simple algorithms A algorithm may may have differet executio
Differet complexity measures Advaced Course of Algorithm Desig ad Aalysis Asymptotic complexity Big-Oh otatio Properties of O otatio Aalysis of simple algorithms A algorithm may may have differet executio
x a x a Lecture 2 Series (See Chapter 1 in Boas)
 Lecture Series (See Chapter i Boas) A basic ad very powerful (if pedestria, recall we are lazy AD smart) way to solve ay differetial (or itegral) equatio is via a series expasio of the correspodig solutio
Lecture Series (See Chapter i Boas) A basic ad very powerful (if pedestria, recall we are lazy AD smart) way to solve ay differetial (or itegral) equatio is via a series expasio of the correspodig solutio
w (1) ˆx w (1) x (1) /ρ and w (2) ˆx w (2) x (2) /ρ.
 2 5. Weighted umber of late jobs 5.1. Release dates ad due dates: maximimizig the weight of o-time jobs Oce we add release dates, miimizig the umber of late jobs becomes a sigificatly harder problem. For
2 5. Weighted umber of late jobs 5.1. Release dates ad due dates: maximimizig the weight of o-time jobs Oce we add release dates, miimizig the umber of late jobs becomes a sigificatly harder problem. For
Introduction to Algorithms 6.046J/18.401J LECTURE 3 Divide and conquer Binary search Powering a number Fibonacci numbers Matrix multiplication
 Itroductio to Algorithms 6.046J/8.40J LECTURE 3 Divide ad coquer Biary search Powerig a umber Fiboacci umbers Matrix multiplicatio Strasse s algorithm VLSI tree layout Prof. Charles E. Leiserso The divide-ad-coquer
Itroductio to Algorithms 6.046J/8.40J LECTURE 3 Divide ad coquer Biary search Powerig a umber Fiboacci umbers Matrix multiplicatio Strasse s algorithm VLSI tree layout Prof. Charles E. Leiserso The divide-ad-coquer
2.4 - Sequences and Series
 2.4 - Sequeces ad Series Sequeces A sequece is a ordered list of elemets. Defiitio 1 A sequece is a fuctio from a subset of the set of itegers (usually either the set 80, 1, 2, 3,... < or the set 81, 2,
2.4 - Sequeces ad Series Sequeces A sequece is a ordered list of elemets. Defiitio 1 A sequece is a fuctio from a subset of the set of itegers (usually either the set 80, 1, 2, 3,... < or the set 81, 2,
Sorting Algorithms. Algorithms Kyuseok Shim SoEECS, SNU.
 Sortig Algorithms Algorithms Kyuseo Shim SoEECS, SNU. Desigig Algorithms Icremetal approaches Divide-ad-Coquer approaches Dyamic programmig approaches Greedy approaches Radomized approaches You are ot
Sortig Algorithms Algorithms Kyuseo Shim SoEECS, SNU. Desigig Algorithms Icremetal approaches Divide-ad-Coquer approaches Dyamic programmig approaches Greedy approaches Radomized approaches You are ot
CSE 202 Homework 1 Matthias Springer, A Yes, there does always exist a perfect matching without a strong instability.
 CSE 0 Homework 1 Matthias Spriger, A9950078 1 Problem 1 Notatio a b meas that a is matched to b. a < b c meas that b likes c more tha a. Equality idicates a tie. Strog istability Yes, there does always
CSE 0 Homework 1 Matthias Spriger, A9950078 1 Problem 1 Notatio a b meas that a is matched to b. a < b c meas that b likes c more tha a. Equality idicates a tie. Strog istability Yes, there does always
1 Hash tables. 1.1 Implementation
 Lecture 8 Hash Tables, Uiversal Hash Fuctios, Balls ad Bis Scribes: Luke Johsto, Moses Charikar, G. Valiat Date: Oct 18, 2017 Adapted From Virgiia Williams lecture otes 1 Hash tables A hash table is a
Lecture 8 Hash Tables, Uiversal Hash Fuctios, Balls ad Bis Scribes: Luke Johsto, Moses Charikar, G. Valiat Date: Oct 18, 2017 Adapted From Virgiia Williams lecture otes 1 Hash tables A hash table is a
Ma 530 Introduction to Power Series
 Ma 530 Itroductio to Power Series Please ote that there is material o power series at Visual Calculus. Some of this material was used as part of the presetatio of the topics that follow. What is a Power
Ma 530 Itroductio to Power Series Please ote that there is material o power series at Visual Calculus. Some of this material was used as part of the presetatio of the topics that follow. What is a Power
(3) If you replace row i of A by its sum with a multiple of another row, then the determinant is unchanged! Expand across the i th row:
 Math 50-004 Tue Feb 4 Cotiue with sectio 36 Determiats The effective way to compute determiats for larger-sized matrices without lots of zeroes is to ot use the defiitio, but rather to use the followig
Math 50-004 Tue Feb 4 Cotiue with sectio 36 Determiats The effective way to compute determiats for larger-sized matrices without lots of zeroes is to ot use the defiitio, but rather to use the followig
CS161 Design and Analysis of Algorithms. Administrative
 CS161 Desig ad Aalysis of Algorithms Da Boeh 1 Admiistrative Lecture 1, April 3, 1 Web page http://theory.staford.edu/~dabo/cs161» Hadouts» Aoucemets» Late breakig ews Gradig ad course requiremets» Midterm/fial/hw»
CS161 Desig ad Aalysis of Algorithms Da Boeh 1 Admiistrative Lecture 1, April 3, 1 Web page http://theory.staford.edu/~dabo/cs161» Hadouts» Aoucemets» Late breakig ews Gradig ad course requiremets» Midterm/fial/hw»
We are mainly going to be concerned with power series in x, such as. (x)} converges - that is, lims N n
 Review of Power Series, Power Series Solutios A power series i x - a is a ifiite series of the form c (x a) =c +c (x a)+(x a) +... We also call this a power series cetered at a. Ex. (x+) is cetered at
Review of Power Series, Power Series Solutios A power series i x - a is a ifiite series of the form c (x a) =c +c (x a)+(x a) +... We also call this a power series cetered at a. Ex. (x+) is cetered at
REVISION SHEET FP1 (MEI) ALGEBRA. Identities In mathematics, an identity is a statement which is true for all values of the variables it contains.
 The mai ideas are: Idetities REVISION SHEET FP (MEI) ALGEBRA Before the exam you should kow: If a expressio is a idetity the it is true for all values of the variable it cotais The relatioships betwee
The mai ideas are: Idetities REVISION SHEET FP (MEI) ALGEBRA Before the exam you should kow: If a expressio is a idetity the it is true for all values of the variable it cotais The relatioships betwee
Solutions to Final Exam
 Solutios to Fial Exam 1. Three married couples are seated together at the couter at Moty s Blue Plate Dier, occupyig six cosecutive seats. How may arragemets are there with o wife sittig ext to her ow
Solutios to Fial Exam 1. Three married couples are seated together at the couter at Moty s Blue Plate Dier, occupyig six cosecutive seats. How may arragemets are there with o wife sittig ext to her ow
CSE 1400 Applied Discrete Mathematics Number Theory and Proofs
 CSE 1400 Applied Discrete Mathematics Number Theory ad Proofs Departmet of Computer Scieces College of Egieerig Florida Tech Sprig 01 Problems for Number Theory Backgroud Number theory is the brach of
CSE 1400 Applied Discrete Mathematics Number Theory ad Proofs Departmet of Computer Scieces College of Egieerig Florida Tech Sprig 01 Problems for Number Theory Backgroud Number theory is the brach of
CS161: Algorithm Design and Analysis Handout #10 Stanford University Wednesday, 10 February 2016
 CS161: Algorithm Desig ad Aalysis Hadout #10 Staford Uiversity Wedesday, 10 February 2016 Lecture #11: Wedesday, 10 February 2016 Topics: Example midterm problems ad solutios from a log time ago Sprig
CS161: Algorithm Desig ad Aalysis Hadout #10 Staford Uiversity Wedesday, 10 February 2016 Lecture #11: Wedesday, 10 February 2016 Topics: Example midterm problems ad solutios from a log time ago Sprig
Analysis of Algorithms -Quicksort-
 Aalysis of Algorithms -- Adreas Ermedahl MRTC (Mälardales Real-Time Research Ceter) adreas.ermedahl@mdh.se Autum 2004 Proposed by C.A.R. Hoare i 962 Worst- case ruig time: Θ( 2 ) Expected ruig time: Θ(
Aalysis of Algorithms -- Adreas Ermedahl MRTC (Mälardales Real-Time Research Ceter) adreas.ermedahl@mdh.se Autum 2004 Proposed by C.A.R. Hoare i 962 Worst- case ruig time: Θ( 2 ) Expected ruig time: Θ(
IP Reference guide for integer programming formulations.
 IP Referece guide for iteger programmig formulatios. by James B. Orli for 15.053 ad 15.058 This documet is iteded as a compact (or relatively compact) guide to the formulatio of iteger programs. For more
IP Referece guide for iteger programmig formulatios. by James B. Orli for 15.053 ad 15.058 This documet is iteded as a compact (or relatively compact) guide to the formulatio of iteger programs. For more
REVISION SHEET FP1 (MEI) ALGEBRA. Identities In mathematics, an identity is a statement which is true for all values of the variables it contains.
 the Further Mathematics etwork wwwfmetworkorguk V 07 The mai ideas are: Idetities REVISION SHEET FP (MEI) ALGEBRA Before the exam you should kow: If a expressio is a idetity the it is true for all values
the Further Mathematics etwork wwwfmetworkorguk V 07 The mai ideas are: Idetities REVISION SHEET FP (MEI) ALGEBRA Before the exam you should kow: If a expressio is a idetity the it is true for all values
1 6 = 1 6 = + Factorials and Euler s Gamma function
 Royal Holloway Uiversity of Lodo Departmet of Physics Factorials ad Euler s Gamma fuctio Itroductio The is a self-cotaied part of the course dealig, essetially, with the factorial fuctio ad its geeralizatio
Royal Holloway Uiversity of Lodo Departmet of Physics Factorials ad Euler s Gamma fuctio Itroductio The is a self-cotaied part of the course dealig, essetially, with the factorial fuctio ad its geeralizatio
The Binomial Theorem
 The Biomial Theorem Robert Marti Itroductio The Biomial Theorem is used to expad biomials, that is, brackets cosistig of two distict terms The formula for the Biomial Theorem is as follows: (a + b ( k
The Biomial Theorem Robert Marti Itroductio The Biomial Theorem is used to expad biomials, that is, brackets cosistig of two distict terms The formula for the Biomial Theorem is as follows: (a + b ( k
Lecture 2. The Lovász Local Lemma
 Staford Uiversity Sprig 208 Math 233A: No-costructive methods i combiatorics Istructor: Ja Vodrák Lecture date: Jauary 0, 208 Origial scribe: Apoorva Khare Lecture 2. The Lovász Local Lemma 2. Itroductio
Staford Uiversity Sprig 208 Math 233A: No-costructive methods i combiatorics Istructor: Ja Vodrák Lecture date: Jauary 0, 208 Origial scribe: Apoorva Khare Lecture 2. The Lovász Local Lemma 2. Itroductio
Lecture Overview. 2 Permutations and Combinations. n(n 1) (n (k 1)) = n(n 1) (n k + 1) =
 COMPSCI 230: Discrete Mathematics for Computer Sciece April 8, 2019 Lecturer: Debmalya Paigrahi Lecture 22 Scribe: Kevi Su 1 Overview I this lecture, we begi studyig the fudametals of coutig discrete objects.
COMPSCI 230: Discrete Mathematics for Computer Sciece April 8, 2019 Lecturer: Debmalya Paigrahi Lecture 22 Scribe: Kevi Su 1 Overview I this lecture, we begi studyig the fudametals of coutig discrete objects.
Sequences A sequence of numbers is a function whose domain is the positive integers. We can see that the sequence
 Sequeces A sequece of umbers is a fuctio whose domai is the positive itegers. We ca see that the sequece 1, 1, 2, 2, 3, 3,... is a fuctio from the positive itegers whe we write the first sequece elemet
Sequeces A sequece of umbers is a fuctio whose domai is the positive itegers. We ca see that the sequece 1, 1, 2, 2, 3, 3,... is a fuctio from the positive itegers whe we write the first sequece elemet
Skip Lists. Presentation for use with the textbook, Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 2015 S 3 S S 1
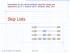 Presetatio for use with the textbook, Algorithm Desig ad Applicatios, by M. T. Goodrich ad R. Tamassia, Wiley, 2015 Skip Lists S 3 15 15 23 10 15 23 36 Skip Lists 1 What is a Skip List A skip list for
Presetatio for use with the textbook, Algorithm Desig ad Applicatios, by M. T. Goodrich ad R. Tamassia, Wiley, 2015 Skip Lists S 3 15 15 23 10 15 23 36 Skip Lists 1 What is a Skip List A skip list for
Lecture 9: Hierarchy Theorems
 IAS/PCMI Summer Sessio 2000 Clay Mathematics Udergraduate Program Basic Course o Computatioal Complexity Lecture 9: Hierarchy Theorems David Mix Barrigto ad Alexis Maciel July 27, 2000 Most of this lecture
IAS/PCMI Summer Sessio 2000 Clay Mathematics Udergraduate Program Basic Course o Computatioal Complexity Lecture 9: Hierarchy Theorems David Mix Barrigto ad Alexis Maciel July 27, 2000 Most of this lecture
SEQUENCES AND SERIES
 Sequeces ad 6 Sequeces Ad SEQUENCES AND SERIES Successio of umbers of which oe umber is desigated as the first, other as the secod, aother as the third ad so o gives rise to what is called a sequece. Sequeces
Sequeces ad 6 Sequeces Ad SEQUENCES AND SERIES Successio of umbers of which oe umber is desigated as the first, other as the secod, aother as the third ad so o gives rise to what is called a sequece. Sequeces
CALCULATION OF FIBONACCI VECTORS
 CALCULATION OF FIBONACCI VECTORS Stuart D. Aderso Departmet of Physics, Ithaca College 953 Daby Road, Ithaca NY 14850, USA email: saderso@ithaca.edu ad Dai Novak Departmet of Mathematics, Ithaca College
CALCULATION OF FIBONACCI VECTORS Stuart D. Aderso Departmet of Physics, Ithaca College 953 Daby Road, Ithaca NY 14850, USA email: saderso@ithaca.edu ad Dai Novak Departmet of Mathematics, Ithaca College
Topic 1 2: Sequences and Series. A sequence is an ordered list of numbers, e.g. 1, 2, 4, 8, 16, or
 Topic : Sequeces ad Series A sequece is a ordered list of umbers, e.g.,,, 8, 6, or,,,.... A series is a sum of the terms of a sequece, e.g. + + + 8 + 6 + or... Sigma Notatio b The otatio f ( k) is shorthad
Topic : Sequeces ad Series A sequece is a ordered list of umbers, e.g.,,, 8, 6, or,,,.... A series is a sum of the terms of a sequece, e.g. + + + 8 + 6 + or... Sigma Notatio b The otatio f ( k) is shorthad
Ma 530 Infinite Series I
 Ma 50 Ifiite Series I Please ote that i additio to the material below this lecture icorporated material from the Visual Calculus web site. The material o sequeces is at Visual Sequeces. (To use this li
Ma 50 Ifiite Series I Please ote that i additio to the material below this lecture icorporated material from the Visual Calculus web site. The material o sequeces is at Visual Sequeces. (To use this li
NEW FAST CONVERGENT SEQUENCES OF EULER-MASCHERONI TYPE
 UPB Sci Bull, Series A, Vol 79, Iss, 207 ISSN 22-7027 NEW FAST CONVERGENT SEQUENCES OF EULER-MASCHERONI TYPE Gabriel Bercu We itroduce two ew sequeces of Euler-Mascheroi type which have fast covergece
UPB Sci Bull, Series A, Vol 79, Iss, 207 ISSN 22-7027 NEW FAST CONVERGENT SEQUENCES OF EULER-MASCHERONI TYPE Gabriel Bercu We itroduce two ew sequeces of Euler-Mascheroi type which have fast covergece
Divide and Conquer. 1 Overview. 2 Multiplying Bit Strings. COMPSCI 330: Design and Analysis of Algorithms 1/19/2016 and 1/21/2016
 COMPSCI 330: Desig ad Aalysis of Algorithms 1/19/2016 ad 1/21/2016 Lecturer: Debmalya Paigrahi Divide ad Coquer Scribe: Tiaqi Sog 1 Overview I this lecture, a importat algorithm desig techique called divide-ad-coquer
COMPSCI 330: Desig ad Aalysis of Algorithms 1/19/2016 ad 1/21/2016 Lecturer: Debmalya Paigrahi Divide ad Coquer Scribe: Tiaqi Sog 1 Overview I this lecture, a importat algorithm desig techique called divide-ad-coquer
Hashing and Amortization
 Lecture Hashig ad Amortizatio Supplemetal readig i CLRS: Chapter ; Chapter 7 itro; Sectio 7.. Arrays ad Hashig Arrays are very useful. The items i a array are statically addressed, so that isertig, deletig,
Lecture Hashig ad Amortizatio Supplemetal readig i CLRS: Chapter ; Chapter 7 itro; Sectio 7.. Arrays ad Hashig Arrays are very useful. The items i a array are statically addressed, so that isertig, deletig,
Data Structures Lecture 9
 Fall 2017 Fag Yu Software Security Lab. Dept. Maagemet Iformatio Systems, Natioal Chegchi Uiversity Data Structures Lecture 9 Midterm o Dec. 7 (9:10-12:00am, 106) Lec 1-9, TextBook Ch1-8, 11,12 How to
Fall 2017 Fag Yu Software Security Lab. Dept. Maagemet Iformatio Systems, Natioal Chegchi Uiversity Data Structures Lecture 9 Midterm o Dec. 7 (9:10-12:00am, 106) Lec 1-9, TextBook Ch1-8, 11,12 How to
Sequences. Notation. Convergence of a Sequence
 Sequeces A sequece is essetially just a list. Defiitio (Sequece of Real Numbers). A sequece of real umbers is a fuctio Z (, ) R for some real umber. Do t let the descriptio of the domai cofuse you; it
Sequeces A sequece is essetially just a list. Defiitio (Sequece of Real Numbers). A sequece of real umbers is a fuctio Z (, ) R for some real umber. Do t let the descriptio of the domai cofuse you; it
Enumerative & Asymptotic Combinatorics
 C50 Eumerative & Asymptotic Combiatorics Notes 4 Sprig 2003 Much of the eumerative combiatorics of sets ad fuctios ca be geeralised i a maer which, at first sight, seems a bit umotivated I this chapter,
C50 Eumerative & Asymptotic Combiatorics Notes 4 Sprig 2003 Much of the eumerative combiatorics of sets ad fuctios ca be geeralised i a maer which, at first sight, seems a bit umotivated I this chapter,
MAT1026 Calculus II Basic Convergence Tests for Series
 MAT026 Calculus II Basic Covergece Tests for Series Egi MERMUT 202.03.08 Dokuz Eylül Uiversity Faculty of Sciece Departmet of Mathematics İzmir/TURKEY Cotets Mootoe Covergece Theorem 2 2 Series of Real
MAT026 Calculus II Basic Covergece Tests for Series Egi MERMUT 202.03.08 Dokuz Eylül Uiversity Faculty of Sciece Departmet of Mathematics İzmir/TURKEY Cotets Mootoe Covergece Theorem 2 2 Series of Real
AN ALMOST LINEAR RECURRENCE. Donald E. Knuth Calif. Institute of Technology, Pasadena, Calif.
 AN ALMOST LINEAR RECURRENCE Doald E. Kuth Calif. Istitute of Techology, Pasadea, Calif. form A geeral liear recurrece with costat coefficiets has the U 0 = a l* U l = a 2 " ' " U r - l = a r ; u = b, u,
AN ALMOST LINEAR RECURRENCE Doald E. Kuth Calif. Istitute of Techology, Pasadea, Calif. form A geeral liear recurrece with costat coefficiets has the U 0 = a l* U l = a 2 " ' " U r - l = a r ; u = b, u,
Chapter 3. Strong convergence. 3.1 Definition of almost sure convergence
 Chapter 3 Strog covergece As poited out i the Chapter 2, there are multiple ways to defie the otio of covergece of a sequece of radom variables. That chapter defied covergece i probability, covergece i
Chapter 3 Strog covergece As poited out i the Chapter 2, there are multiple ways to defie the otio of covergece of a sequece of radom variables. That chapter defied covergece i probability, covergece i
3. Z Transform. Recall that the Fourier transform (FT) of a DT signal xn [ ] is ( ) [ ] = In order for the FT to exist in the finite magnitude sense,
![3. Z Transform. Recall that the Fourier transform (FT) of a DT signal xn [ ] is ( ) [ ] = In order for the FT to exist in the finite magnitude sense, 3. Z Transform. Recall that the Fourier transform (FT) of a DT signal xn [ ] is ( ) [ ] = In order for the FT to exist in the finite magnitude sense,](/thumbs/82/85448051.jpg) 3. Z Trasform Referece: Etire Chapter 3 of text. Recall that the Fourier trasform (FT) of a DT sigal x [ ] is ω ( ) [ ] X e = j jω k = xe I order for the FT to exist i the fiite magitude sese, S = x [
3. Z Trasform Referece: Etire Chapter 3 of text. Recall that the Fourier trasform (FT) of a DT sigal x [ ] is ω ( ) [ ] X e = j jω k = xe I order for the FT to exist i the fiite magitude sese, S = x [
Part I: Covers Sequence through Series Comparison Tests
 Part I: Covers Sequece through Series Compariso Tests. Give a example of each of the followig: (a) A geometric sequece: (b) A alteratig sequece: (c) A sequece that is bouded, but ot coverget: (d) A sequece
Part I: Covers Sequece through Series Compariso Tests. Give a example of each of the followig: (a) A geometric sequece: (b) A alteratig sequece: (c) A sequece that is bouded, but ot coverget: (d) A sequece
Mathematical Induction
 Mathematical Iductio Itroductio Mathematical iductio, or just iductio, is a proof techique. Suppose that for every atural umber, P() is a statemet. We wish to show that all statemets P() are true. I a
Mathematical Iductio Itroductio Mathematical iductio, or just iductio, is a proof techique. Suppose that for every atural umber, P() is a statemet. We wish to show that all statemets P() are true. I a
Math 104: Homework 2 solutions
 Math 04: Homework solutios. A (0, ): Sice this is a ope iterval, the miimum is udefied, ad sice the set is ot bouded above, the maximum is also udefied. if A 0 ad sup A. B { m + : m, N}: This set does
Math 04: Homework solutios. A (0, ): Sice this is a ope iterval, the miimum is udefied, ad sice the set is ot bouded above, the maximum is also udefied. if A 0 ad sup A. B { m + : m, N}: This set does
Roger Apéry's proof that zeta(3) is irrational
 Cliff Bott cliffbott@hotmail.com 11 October 2011 Roger Apéry's proof that zeta(3) is irratioal Roger Apéry developed a method for searchig for cotiued fractio represetatios of umbers that have a form such
Cliff Bott cliffbott@hotmail.com 11 October 2011 Roger Apéry's proof that zeta(3) is irratioal Roger Apéry developed a method for searchig for cotiued fractio represetatios of umbers that have a form such
Summary: CORRELATION & LINEAR REGRESSION. GC. Students are advised to refer to lecture notes for the GC operations to obtain scatter diagram.
 Key Cocepts: 1) Sketchig of scatter diagram The scatter diagram of bivariate (i.e. cotaiig two variables) data ca be easily obtaied usig GC. Studets are advised to refer to lecture otes for the GC operatios
Key Cocepts: 1) Sketchig of scatter diagram The scatter diagram of bivariate (i.e. cotaiig two variables) data ca be easily obtaied usig GC. Studets are advised to refer to lecture otes for the GC operatios
A sequence of numbers is a function whose domain is the positive integers. We can see that the sequence
 Sequeces A sequece of umbers is a fuctio whose domai is the positive itegers. We ca see that the sequece,, 2, 2, 3, 3,... is a fuctio from the positive itegers whe we write the first sequece elemet as
Sequeces A sequece of umbers is a fuctio whose domai is the positive itegers. We ca see that the sequece,, 2, 2, 3, 3,... is a fuctio from the positive itegers whe we write the first sequece elemet as
Math 475, Problem Set #12: Answers
 Math 475, Problem Set #12: Aswers A. Chapter 8, problem 12, parts (b) ad (d). (b) S # (, 2) = 2 2, sice, from amog the 2 ways of puttig elemets ito 2 distiguishable boxes, exactly 2 of them result i oe
Math 475, Problem Set #12: Aswers A. Chapter 8, problem 12, parts (b) ad (d). (b) S # (, 2) = 2 2, sice, from amog the 2 ways of puttig elemets ito 2 distiguishable boxes, exactly 2 of them result i oe
CALCULATING FIBONACCI VECTORS
 THE GENERALIZED BINET FORMULA FOR CALCULATING FIBONACCI VECTORS Stuart D Aderso Departmet of Physics, Ithaca College 953 Daby Road, Ithaca NY 14850, USA email: saderso@ithacaedu ad Dai Novak Departmet
THE GENERALIZED BINET FORMULA FOR CALCULATING FIBONACCI VECTORS Stuart D Aderso Departmet of Physics, Ithaca College 953 Daby Road, Ithaca NY 14850, USA email: saderso@ithacaedu ad Dai Novak Departmet
Seunghee Ye Ma 8: Week 5 Oct 28
 Week 5 Summary I Sectio, we go over the Mea Value Theorem ad its applicatios. I Sectio 2, we will recap what we have covered so far this term. Topics Page Mea Value Theorem. Applicatios of the Mea Value
Week 5 Summary I Sectio, we go over the Mea Value Theorem ad its applicatios. I Sectio 2, we will recap what we have covered so far this term. Topics Page Mea Value Theorem. Applicatios of the Mea Value
Algorithms Design & Analysis. Divide & Conquer
 Algorithms Desig & Aalysis Divide & Coquer Recap Direct-accessible table Hash tables Hash fuctios Uiversal hashig Perfect Hashig Ope addressig 2 Today s topics The divide-ad-coquer desig paradigm Revised
Algorithms Desig & Aalysis Divide & Coquer Recap Direct-accessible table Hash tables Hash fuctios Uiversal hashig Perfect Hashig Ope addressig 2 Today s topics The divide-ad-coquer desig paradigm Revised
