CSIR NET - MATHEMATICAL SCIENCE
|
|
|
- Cody Morris
- 6 years ago
- Views:
Transcription
1 CSIR NET - MATHEMATICAL SCIENCE SAMPLE THEORY SEQUENCES, SERIES AND LIMIT POINTS OF SEQUENCES SEQUENCES LIMITS : INFERIOR & SUPERIOR ALGEBRA OF SEQUENCES SEQUENCE TESTS FOURIER SERIES SOME PROBLEMS For IIT-JAM, JNU, GATE, NET, NIMCET ad Other Etrace Exams -C-8, Sheea Chowdhary Road, Tawadi, Kota (Raj.) Te No Web Site E-mai-vmcasses@yahoo.com Phoe: Mobie: 997, , Website: E-Mai: vmcasses@yahoo.com /ifo@vmcasses.com Address: -C-8, Sheea Chowdhary Road, SFS, TALWANDI, KOTA, RAJASTHAN, 345 Page
2 SEQUENCE A seqece i a set S is a fctio whose domai is the set N of atra mbers ad whose rage is a sbset of S. A seqece whose rage is a sbset of R is caed a rea seqece. S S S + S S series Seqece Boded Seqece: A seqece is said to be boded if ad oy if its rage is boded. Ths a seqece S is boded if there exists k S K, N S [ k,k] The.. b (Sremm) ad the g..b (ifimm) of the rage of a boded seqece may be referred as its g..b ad..b resectivey. Limits iferior ad Serior: From the defiitio of imit i Sectio.4, it foows that the imitig behavior of ay seqece {a } of rea mbers, deeds oy o sets of the form {a : m}, i.e., {a m, a m +, a m +,... }. I this regard we make the foowig defiitio. Defiitio: Let {a } be a seqece of rea mbers (ot ecessariy boded). We defie im if a s if {a, a +, a +,... } Phoe: Mobie: 997, , Website: E-Mai: vmcasses@yahoo.com /ifo@vmcasses.com Address: -C-8, Sheea Chowdhary Road, SFS, TALWANDI, KOTA, RAJASTHAN, 345 Page
3 Ad im s a if s {a, a +, a +,... } As the imit iferior ad imit serior resectivey of the seqece {a }. We sha deote imit iferior ad imit serior of {a } by im a resectivey. im a ad im We sha se the foowig otatios for the seqece {a }, for each N Ad Therefore, we have A if {a, a +, a +,... }, A s {a, a +, a +,... }. im a s A a or simy by im a ad Ad im a if A Now {a +, a +,....} {a, a +, a +,....}, Therefore by takig ifimm ad sremm resectivey, it foows that A This is tre for each N. + A Ad A + A T he above ieqaities show that the associated seqeces { A } ad { A } mootoicay icrease ad decrease resectivey with. Remark: It shod be oted that both imits iferior ad serior exist iqey (fiite or ifiite) for a rea seqeces. Theorem: If {a } is ay seqece, the im ( a ) im, ad im ( a ) im a. Let b a, N the we have Ad so B if {b, b +,....} s {a, a +,....} A im ( a ) im b s( B,B,... ) Phoe: Mobie: 997, , Website: E-Mai: vmcasses@yahoo.com /ifo@vmcasses.com Address: -C-8, Sheea Chowdhary Road, SFS, TALWANDI, KOTA, RAJASTHAN, 345 Page 3
4 s{ A, A,... } if { A,A,... } if A im a. Aso, im a im ( (a )) im ( a ). Theorem: If {a } is ay seqece, the im a if ad oy if {a } is ot boded beow, Ad Let im a + if ad oy if {a } is ot boded above. A if {a, a +,....}, Ad By defiitio we have A s {a, a +,....}, N im a s { A, A,... } A, N if {a, a +,... }, N {a } is ot boded beow: The roof for imit serior is simiar. Coroary: If {a } is ay seqece, the ad (i) < im a + iff {a } is boded beow. (ii) im a < + iff {a } is boded above. For boded seqeces, we have the foowig sef criteria for imits iferior ad serior resectivey. Limit oits of a seqece: Phoe: Mobie: 997, , Website: E-Mai: vmcasses@yahoo.com /ifo@vmcasses.com Address: -C-8, Sheea Chowdhary Road, SFS, TALWANDI, KOTA, RAJASTHAN, 345 Page 4
5 A mber ξ is said to be a imit oit of a seqece S if give ay bd of ξ, S beogs to the same for a ifiite mber of vaes of. Now {S + S +, S +3,...} {S, S +, S +,...}, therefore by takig ifimm ad sremm resectivey, if foows that A + A ad A + A for each N Remark: Both imits iferior ad serior exist iqey (fiite or ifiite) for a rea seqece. Theorem: If {S } is ay seqece, the if S im S S S If {S } is ay seqece, the { } im S ims Ad { } im S ims Some Imortat Proerties of Agebra of seqeces. If {a } is a boded seqece sch that a > for a N, the (i) im,if ima > a ima (ii) im,if ima > a im a 5. If {a } ad {b } are boded seqece, a, b > for a N, the a ima (i) im,if im b > b im b a ima (ii) im,if im b > b im b SOME IMPORTANT SEQUENCE TESTS. Cachy s root test Let Σ be +ve term series ad im { } Phoe: Mobie: 997, , Website: E-Mai: vmcasses@yahoo.com /ifo@vmcasses.com Address: -C-8, Sheea Chowdhary Road, SFS, TALWANDI, KOTA, RAJASTHAN, 345 Page 5
6 The the series is (i) Cgt if < (ii) Dgt if > (iii) No firm decisio is ossibe if. Raabe s test Let Σ be a +ve term series ad im + the the series is (i) Cgt if > (ii) Dgt if < (iii) No firm decisio is ossibe if 3. Logarithmic Test: If Σ is +ve terms series sch that im og + The the series (i) cgt if > (ii) dgt if < 4. Absote coverget A series Σ is said to be absotey cgt if the ositive term series Σ formed by the mode of the terms of the series is coverget. 5. Coditioa coverget A series is said to be coditioay coverget if it is coverget withot beig absotey coverget. Theorem: Every absote coverget series is coverget. Phoe: Mobie: 997, , Website: E-Mai: vmcasses@yahoo.com /ifo@vmcasses.com Address: -C-8, Sheea Chowdhary Road, SFS, TALWANDI, KOTA, RAJASTHAN, 345 Page 6
7 Note. (i) If Σ i s cgt withot beig absotey cgt. I.e. if Σ is coditioay cgt the each of the +ve term series Σg() ad Σh() diverges to ifiity which foows from g( ) + h ( ) (ii) It shod be oted that three are o comariso tests for the cgt of coditioay cgt series. Ateratig series A series whose terms are ateratey +ve ad ve is caed a ateratig series. 6. Leibitz s test Let be a seqece sch that N (i) (ii) + (iii) im The ateratig series () () + (3) (4) ( ) + ()... is cgt. 7. Abe s Test If a is a ositive, mootoic decreasig fctio ad if Σ is coverget series, the the series Σ a is aso coverget. Uiform covergece Poit wise Cov ergece of Seqece of Fctios Defiitio: A seqece of fctios {f } defied o [a, b] is said to be oit-wise coverget to a fctio f o [a, b], if to each > to each x [a, b], there exists a ositive iteger m (deedig o ε ad the oit x) sch that f (x) f(x) < ε > m ad x [a,b]. Phoe: Mobie: 997, , Website: E-Mai: vmcasses@yahoo.com /ifo@vmcasses.com Address: -C-8, Sheea Chowdhary Road, SFS, TALWANDI, KOTA, RAJASTHAN, 345 Page 7
8 The fctio f is caed the oit-wise imit of the seqece {f }. We write ( ) ( ) FOURIER SERIES a f(x) + + Where ( < x < π) α a cosx b six π π a ( ) π f x dx π cosx dx a f ( x) Ad b f ( x) π π Ad for ( π < x < π ) π π a ( ) π f x dx a f ( x) π six dx π cosx dx π π six dx Ad b f ( x) π π im f x f x. Where f(x) is a odd fctio; a ad a where f(x) is a eve fctio; b. Forier series i the iterva ( < x < ) is f(x) a πx πx + a cos + b si f x dx Where a ( ) πx f x cos dx a ( ) Ad b ( ) πx f x si dx I the iterva ( < x < ) Phoe: Mobie: 997, , Website: E-Mai: vmcasses@yahoo.com /ifo@vmcasses.com Address: -C-8, Sheea Chowdhary Road, SFS, TALWANDI, KOTA, RAJASTHAN, 345 Page 8
9 + + πx f(x) dx, a f x cos dx a ( ) + πx Ad b f(x)si dx Note: Whe f(x) is a odd fctio, a ad a whe f(x) is a eve fctio, b. Haf-Rage series ( < x < π) A fctio f(x) defied i the iterva < x < π has two distict haf-rage series. (i) The haf-rage cosie series is f(x) a + a cos x π Where a f ( x) dx π ad a ( ) (ii) The haf rage sie series is, f(x) Σb si x Where b ( ) π f x si x dx. π π f x cos x dx Haf-Rage Series ( < x < ) A fctio f (x) defied i the iterva ( < x < ) ad havig two distict haf-rage series. (i) The haf rage cosie series is, f(x) a Where a ( ) πx +Σ a cos f x dx Ad a f ( x) cos πx dx (ii) The haf-rage sie series is, f(x) Σb si πx Phoe: Mobie: 997, , Website: E-Mai: vmcasses@yahoo.com /ifo@vmcasses.com Address: -C-8, Sheea Chowdhary Road, SFS, TALWANDI, KOTA, RAJASTHAN, 345 Page 9
10 Where b ( ) x f x si π dx Comex form of Forier series f(x) + m c e m imx π i mx Where c m f ( x) e + π π π c ( ) π f x dx ad dx C -m +π π π ( ) imx f x e dx. Parseva s Idetity For Forier series, f(x) The Parseva s idetity is a πx πx + a cos + b si, x < < f x dx a b a ( ) ( ) FOURIER INTEGRAL The Forier series of eriodic fctio f (x) o the iterva (, + ) is give by Where a The f (x) a + πx a b cos πx f (x) dx f (t)cos πt dt f (t)si πt dt + b + si πx f(t) dt...() Phoe: Mobie: 997, , Website: E-Mai: vmcasses@yahoo.com /ifo@vmcasses.com Address: -C-8, Sheea Chowdhary Road, SFS, TALWANDI, KOTA, RAJASTHAN, 345 Page
11 f(x) + d f (t )cos(x π This is a form of Forier Itegra. t)dt SOME PROBLEMS. The set of a ositive vaes of a for which the series ta coverges, is a (), 3 (), 3 (3), 3 (4), 3. Match the foowig Series (X) Domai of Covergece (Y) A. x (i) [, ] 3 + x (ii) [ e, + e] B. ( ) + C. ( ) + ( x ) (iii) [, ] D. ( + )! x (iv) [, ] A B C D () (iv) (iii) (ii) (i) () (iv) (iii) (i) (ii) (3) (iii) (iv) (i) (ii) (4) (i) (ii) (iv) (iii) 3. The series is () Coverget, if diverget, if < () Coverget, if > ad diverget, if Phoe: Mobie: 997, , Website: E-Mai: vmcasses@yahoo.com /ifo@vmcasses.com Address: -C-8, Sheea Chowdhary Road, SFS, TALWANDI, KOTA, RAJASTHAN, 345 Page
12 (3) Coverget, if ad diverget, if > (4) Coverget, if < ad diverget, if 4. For the imroer itegra x x α e dx which oe of the foowig is tre () if α <, coverget ad if α, diverget () if α >, Coverget ad if α <, diverget (3) if α >, coverget ad if α <, diverget (4) If α >, diverget ad if α <, coverget 5. Let A R ad Let f f f be fctios o A to R ad Let c be a cster oit of A if L k Lim f k for k,..., The Lim [f(x)] x c c () L () L k k N (3) L (4) x c ANSWER KEY: -. (4),. (), 3. (), 4. (3), 5. (3). (4) Use the foow ig rests: () Let Σa & Σb be two ositive term series (i) If (ii) If a Lt, b a Lt b () The series series beig a fiite o zero costat, the Σa & Σb both coverge or diverge together. & Σβν χονϖεργεσ, the Σa aso coverges. coverges if > & diverges if. We comare the give series with the a a a ta Lt Lt a a ta Phoe: Mobie: 997, , Website: E-Mai: vmcasses@yahoo.com /ifo@vmcasses.com Address: -C-8, Sheea Chowdhary Road, SFS, TALWANDI, KOTA, RAJASTHAN, 345 Page
13 Lt a For this imit to be zero or some other fiite mber 3 i.e. 3 & for the series to be coverget, a > a a > 3 a > 3 a, 3 As. is (D). () (i) x 3 a ;a ( + ) a R im im + a + So the domai of a is [, ] For x the give ower series is Which is coverget. For x the give ower series is Which is coverget, by eibitz s test. As. is (iv) (ii) ( ) + x + a + 3 R im im a + + The iterva of covergece [, ] Phoe: Mobie: 997, , Website: E-Mai: vmcasses@yahoo.com /ifo@vmcasses.com Address: -C-8, Sheea Chowdhary Road, SFS, TALWANDI, KOTA, RAJASTHAN, 345 Page 3
14 for x, the series becomes +... Which is coverget by Leibitz s test 3 5 For x the series becomes Which is agai coverget Hece the exact iterva of covergecy is [, ]. As. is (iii) a (iii) R im im a + Sice the give ower series is abot the oit x the iterva of covergece is + < x < + < x < ( ) + for x +, the give series which is coverget by eibitz s test. Hece the exact iterva of covergece is [, ]. As. is (i) (iv) ( + )! x The give ower series is abot the oit x ( + ) ( + ) + a! R im im a! + + im im + e As. is (ii) The iterva of covergece is [ e, + e], 3. () Negectig the first term ad + ( ) ( )( + ) ( ) ( + ) Phoe: Mobie: 997, , Website: E-Mai: vmcasses@yahoo.com /ifo@vmcasses.com Address: -C-8, Sheea Chowdhary Road, SFS, TALWANDI, KOTA, RAJASTHAN, 345 Page 4
15 or, im + + im + Ratio test fais. og + og + + og + og im og im From Logarithmic test. The series is coverget, if >, i.e., > The series is diverget, if <, i.e., < Phoe: Mobie: 997, , Website: E-Mai: vmcasses@yahoo.com /ifo@vmcasses.com Address: -C-8, Sheea Chowdhary Road, SFS, TALWANDI, KOTA, RAJASTHAN, 345 Page 5
16 The test fais, if i.e., Now og or, og or, og + og 3 4 og + 7 og (3) or, 3 og 7 og im Hece by higher ogarithmic test the give series is diverget, if. Hece the give series is coverget whe > ad diverget whe. The correct aswer is (). α x x e dx, Wheα >, the give itegra is a roer itegra ad hece it is coverget. Whe α <, the itegrad becomes ifiite at x. Now µ α x µ +α x im x.x e im x e x x if µ + α,i.e., µ α We the have < µ < whe < α < ad µ > where α <. It foows byµ -test that the itegra is coverget whe < α < ad diverget whe α <. Ad we have roved above that the itegra is coverget whe α >. Coseqety the give itegra is coverget if α > ad diverget if α <. Phoe: Mobie: 997, , Website: E-Mai: vmcasses@yahoo.com /ifo@vmcasses.com Address: -C-8, Sheea Chowdhary Road, SFS, TALWANDI, KOTA, RAJASTHAN, 345 Page 6
17 5. (3) if L k im fk x c the it foows from a by kow rest which is caed a Idctio armet that L + L + + L im f( + f + + f ), x c ad L L L im(f f f ). I articar, we dedce that if L im x c f ad N, the L im (f(x)). x c Phoe: Mobie: 997, , Website: E-Mai: vmcasses@yahoo.com /ifo@vmcasses.com Address: -C-8, Sheea Chowdhary Road, SFS, TALWANDI, KOTA, RAJASTHAN, 345 Page 7
MATHEMATICS I COMMON TO ALL BRANCHES
 MATHEMATCS COMMON TO ALL BRANCHES UNT Seqeces ad Series. Defiitios,. Geeral Proerties of Series,. Comariso Test,.4 tegral Test,.5 D Alembert s Ratio Test,.6 Raabe s Test,.7 Logarithmic Test,.8 Cachy s
MATHEMATCS COMMON TO ALL BRANCHES UNT Seqeces ad Series. Defiitios,. Geeral Proerties of Series,. Comariso Test,.4 tegral Test,.5 D Alembert s Ratio Test,.6 Raabe s Test,.7 Logarithmic Test,.8 Cachy s
and the sum of its first n terms be denoted by. Convergence: An infinite series is said to be convergent if, a definite unique number., finite.
 INFINITE SERIES Seqece: If a set of real mbers a seqece deoted by * + * Or * + * occr accordig to some defiite rle, the it is called + if is fiite + if is ifiite Series: is called a series ad is deoted
INFINITE SERIES Seqece: If a set of real mbers a seqece deoted by * + * Or * + * occr accordig to some defiite rle, the it is called + if is fiite + if is ifiite Series: is called a series ad is deoted
Sequences. A Sequence is a list of numbers written in order.
 Sequeces A Sequece is a list of umbers writte i order. {a, a 2, a 3,... } The sequece may be ifiite. The th term of the sequece is the th umber o the list. O the list above a = st term, a 2 = 2 d term,
Sequeces A Sequece is a list of umbers writte i order. {a, a 2, a 3,... } The sequece may be ifiite. The th term of the sequece is the th umber o the list. O the list above a = st term, a 2 = 2 d term,
Fourier Series and their Applications
 Fourier Series ad their Applicatios The fuctios, cos x, si x, cos x, si x, are orthogoal over (, ). m cos mx cos xdx = m = m = = cos mx si xdx = for all m, { m si mx si xdx = m = I fact the fuctios satisfy
Fourier Series ad their Applicatios The fuctios, cos x, si x, cos x, si x, are orthogoal over (, ). m cos mx cos xdx = m = m = = cos mx si xdx = for all m, { m si mx si xdx = m = I fact the fuctios satisfy
Solutions to Practice Midterms. Practice Midterm 1
 Solutios to Practice Midterms Practice Midterm. a False. Couterexample: a =, b = b False. Couterexample: a =, b = c False. Couterexample: c = Y cos. = cos. + 5 = 0 sice both its exist. + 5 cos π. 5 + 5
Solutios to Practice Midterms Practice Midterm. a False. Couterexample: a =, b = b False. Couterexample: a =, b = c False. Couterexample: c = Y cos. = cos. + 5 = 0 sice both its exist. + 5 cos π. 5 + 5
Are the following series absolutely convergent? n=1. n 3. n=1 n. ( 1) n. n=1 n=1
 Absolute covergece Defiitio A series P a is called absolutely coverget if the series of absolute values P a is coverget. If the terms of the series a are positive, absolute covergece is the same as covergece.
Absolute covergece Defiitio A series P a is called absolutely coverget if the series of absolute values P a is coverget. If the terms of the series a are positive, absolute covergece is the same as covergece.
SUMMARY OF SEQUENCES AND SERIES
 SUMMARY OF SEQUENCES AND SERIES Importat Defiitios, Results ad Theorems for Sequeces ad Series Defiitio. A sequece {a } has a limit L ad we write lim a = L if for every ɛ > 0, there is a correspodig iteger
SUMMARY OF SEQUENCES AND SERIES Importat Defiitios, Results ad Theorems for Sequeces ad Series Defiitio. A sequece {a } has a limit L ad we write lim a = L if for every ɛ > 0, there is a correspodig iteger
Chapter 6 Infinite Series
 Chapter 6 Ifiite Series I the previous chapter we cosidered itegrals which were improper i the sese that the iterval of itegratio was ubouded. I this chapter we are goig to discuss a topic which is somewhat
Chapter 6 Ifiite Series I the previous chapter we cosidered itegrals which were improper i the sese that the iterval of itegratio was ubouded. I this chapter we are goig to discuss a topic which is somewhat
PLEASE MARK YOUR ANSWERS WITH AN X, not a circle! 1. (a) (b) (c) (d) (e) 3. (a) (b) (c) (d) (e) 5. (a) (b) (c) (d) (e) 7. (a) (b) (c) (d) (e)
 Math 0560, Exam 3 November 6, 07 The Hoor Code is i effect for this examiatio. All work is to be your ow. No calculators. The exam lasts for hour ad 5 mi. Be sure that your ame is o every page i case pages
Math 0560, Exam 3 November 6, 07 The Hoor Code is i effect for this examiatio. All work is to be your ow. No calculators. The exam lasts for hour ad 5 mi. Be sure that your ame is o every page i case pages
Proposition 2.1. There are an infinite number of primes of the form p = 4n 1. Proof. Suppose there are only a finite number of such primes, say
 Chater 2 Euclid s Theorem Theorem 2.. There are a ifiity of rimes. This is sometimes called Euclid s Secod Theorem, what we have called Euclid s Lemma beig kow as Euclid s First Theorem. Proof. Suose to
Chater 2 Euclid s Theorem Theorem 2.. There are a ifiity of rimes. This is sometimes called Euclid s Secod Theorem, what we have called Euclid s Lemma beig kow as Euclid s First Theorem. Proof. Suose to
M17 MAT25-21 HOMEWORK 5 SOLUTIONS
 M17 MAT5-1 HOMEWORK 5 SOLUTIONS 1. To Had I Cauchy Codesatio Test. Exercise 1: Applicatio of the Cauchy Codesatio Test Use the Cauchy Codesatio Test to prove that 1 diverges. Solutio 1. Give the series
M17 MAT5-1 HOMEWORK 5 SOLUTIONS 1. To Had I Cauchy Codesatio Test. Exercise 1: Applicatio of the Cauchy Codesatio Test Use the Cauchy Codesatio Test to prove that 1 diverges. Solutio 1. Give the series
62. Power series Definition 16. (Power series) Given a sequence {c n }, the series. c n x n = c 0 + c 1 x + c 2 x 2 + c 3 x 3 +
 62. Power series Defiitio 16. (Power series) Give a sequece {c }, the series c x = c 0 + c 1 x + c 2 x 2 + c 3 x 3 + is called a power series i the variable x. The umbers c are called the coefficiets of
62. Power series Defiitio 16. (Power series) Give a sequece {c }, the series c x = c 0 + c 1 x + c 2 x 2 + c 3 x 3 + is called a power series i the variable x. The umbers c are called the coefficiets of
SCORE. Exam 2. MA 114 Exam 2 Fall 2016
 MA 4 Exam Fall 06 Exam Name: Sectio ad/or TA: Do ot remove this aswer page you will retur the whole exam. You will be allowed two hours to complete this test. No books or otes may be used. You may use
MA 4 Exam Fall 06 Exam Name: Sectio ad/or TA: Do ot remove this aswer page you will retur the whole exam. You will be allowed two hours to complete this test. No books or otes may be used. You may use
Math 106 Fall 2014 Exam 3.1 December 10, 2014
 Math 06 Fall 0 Exam 3 December 0, 0 Determie if the series is coverget or diverget by makig a compariso DCT or LCT) with a suitable b Fill i the blaks with your aswer For Coverget or Diverget write Coverget
Math 06 Fall 0 Exam 3 December 0, 0 Determie if the series is coverget or diverget by makig a compariso DCT or LCT) with a suitable b Fill i the blaks with your aswer For Coverget or Diverget write Coverget
Solutions to Final Exam Review Problems
 . Let f(x) 4+x. Solutios to Fial Exam Review Problems Math 5C, Witer 2007 (a) Fid the Maclauri series for f(x), ad compute its radius of covergece. Solutio. f(x) 4( ( x/4)) ( x/4) ( ) 4 4 + x. Sice the
. Let f(x) 4+x. Solutios to Fial Exam Review Problems Math 5C, Witer 2007 (a) Fid the Maclauri series for f(x), ad compute its radius of covergece. Solutio. f(x) 4( ( x/4)) ( x/4) ( ) 4 4 + x. Sice the
2.4.2 A Theorem About Absolutely Convergent Series
 0 Versio of August 27, 200 CHAPTER 2. INFINITE SERIES Add these two series: + 3 2 + 5 + 7 4 + 9 + 6 +... = 3 l 2. (2.20) 2 Sice the reciprocal of each iteger occurs exactly oce i the last series, we would
0 Versio of August 27, 200 CHAPTER 2. INFINITE SERIES Add these two series: + 3 2 + 5 + 7 4 + 9 + 6 +... = 3 l 2. (2.20) 2 Sice the reciprocal of each iteger occurs exactly oce i the last series, we would
Math 132, Fall 2009 Exam 2: Solutions
 Math 3, Fall 009 Exam : Solutios () a) ( poits) Determie for which positive real umbers p, is the followig improper itegral coverget, ad for which it is diverget. Evaluate the itegral for each value of
Math 3, Fall 009 Exam : Solutios () a) ( poits) Determie for which positive real umbers p, is the followig improper itegral coverget, ad for which it is diverget. Evaluate the itegral for each value of
Math 106 Fall 2014 Exam 3.2 December 10, 2014
 Math 06 Fall 04 Exam 3 December 0, 04 Determie if the series is coverget or diverget by makig a compariso (DCT or LCT) with a suitable b Fill i the blaks with your aswer For Coverget or Diverget write
Math 06 Fall 04 Exam 3 December 0, 04 Determie if the series is coverget or diverget by makig a compariso (DCT or LCT) with a suitable b Fill i the blaks with your aswer For Coverget or Diverget write
n=1 a n is the sequence (s n ) n 1 n=1 a n converges to s. We write a n = s, n=1 n=1 a n
 Series. Defiitios ad first properties A series is a ifiite sum a + a + a +..., deoted i short by a. The sequece of partial sums of the series a is the sequece s ) defied by s = a k = a +... + a,. k= Defiitio
Series. Defiitios ad first properties A series is a ifiite sum a + a + a +..., deoted i short by a. The sequece of partial sums of the series a is the sequece s ) defied by s = a k = a +... + a,. k= Defiitio
10.1 Sequences. n term. We will deal a. a n or a n n. ( 1) n ( 1) n 1 2 ( 1) a =, 0 0,,,,, ln n. n an 2. n term.
 0. Sequeces A sequece is a list of umbers writte i a defiite order: a, a,, a, a is called the first term, a is the secod term, ad i geeral eclusively with ifiite sequeces ad so each term Notatio: the sequece
0. Sequeces A sequece is a list of umbers writte i a defiite order: a, a,, a, a is called the first term, a is the secod term, ad i geeral eclusively with ifiite sequeces ad so each term Notatio: the sequece
MATH4822E FOURIER ANALYSIS AND ITS APPLICATIONS
 MATH48E FOURIER ANALYSIS AND ITS APPLICATIONS 7.. Cesàro summability. 7. Summability methods Arithmetic meas. The followig idea is due to the Italia geometer Eresto Cesàro (859-96). He shows that eve if
MATH48E FOURIER ANALYSIS AND ITS APPLICATIONS 7.. Cesàro summability. 7. Summability methods Arithmetic meas. The followig idea is due to the Italia geometer Eresto Cesàro (859-96). He shows that eve if
Topics in Fourier Analysis-I 1
 Topics i Fourier Aaysis-I 1 M.T.Nair Departmet of Mathematics, IIT Madras Cotets 1 Fourier Series 1.1 Motivatio through heat equatio.............................. 1. Fourier Series of -Periodic fuctios...........................
Topics i Fourier Aaysis-I 1 M.T.Nair Departmet of Mathematics, IIT Madras Cotets 1 Fourier Series 1.1 Motivatio through heat equatio.............................. 1. Fourier Series of -Periodic fuctios...........................
MAT2400 Assignment 2 - Solutions
 MAT24 Assigmet 2 - Soltios Notatio: For ay fctio f of oe real variable, f(a + ) deotes the limit of f() whe teds to a from above (if it eists); i.e., f(a + ) = lim t a + f(t). Similarly, f(a ) deotes the
MAT24 Assigmet 2 - Soltios Notatio: For ay fctio f of oe real variable, f(a + ) deotes the limit of f() whe teds to a from above (if it eists); i.e., f(a + ) = lim t a + f(t). Similarly, f(a ) deotes the
Please do NOT write in this box. Multiple Choice. Total
 Istructor: Math 0560, Worksheet Alteratig Series Jauary, 3000 For realistic exam practice solve these problems without lookig at your book ad without usig a calculator. Multiple choice questios should
Istructor: Math 0560, Worksheet Alteratig Series Jauary, 3000 For realistic exam practice solve these problems without lookig at your book ad without usig a calculator. Multiple choice questios should
The Interval of Convergence for a Power Series Examples
 The Iterval of Covergece for a Power Series Examples To review the process: How to Test a Power Series for Covergece. Fid the iterval where the series coverges absolutely. We have to use the Ratio or Root
The Iterval of Covergece for a Power Series Examples To review the process: How to Test a Power Series for Covergece. Fid the iterval where the series coverges absolutely. We have to use the Ratio or Root
A) is empty. B) is a finite set. C) can be a countably infinite set. D) can be an uncountable set.
 M.A./M.Sc. (Mathematics) Etrace Examiatio 016-17 Max Time: hours Max Marks: 150 Istructios: There are 50 questios. Every questio has four choices of which exactly oe is correct. For correct aswer, 3 marks
M.A./M.Sc. (Mathematics) Etrace Examiatio 016-17 Max Time: hours Max Marks: 150 Istructios: There are 50 questios. Every questio has four choices of which exactly oe is correct. For correct aswer, 3 marks
Topics. Homework Problems. MATH 301 Introduction to Analysis Chapter Four Sequences. 1. Definition of convergence of sequences.
 MATH 301 Itroductio to Aalysis Chapter Four Sequeces Topics 1. Defiitio of covergece of sequeces. 2. Fidig ad provig the limit of sequeces. 3. Bouded covergece theorem: Theorem 4.1.8. 4. Theorems 4.1.13
MATH 301 Itroductio to Aalysis Chapter Four Sequeces Topics 1. Defiitio of covergece of sequeces. 2. Fidig ad provig the limit of sequeces. 3. Bouded covergece theorem: Theorem 4.1.8. 4. Theorems 4.1.13
INFINITE SEQUENCES AND SERIES
 INFINITE SEQUENCES AND SERIES INFINITE SEQUENCES AND SERIES I geeral, it is difficult to fid the exact sum of a series. We were able to accomplish this for geometric series ad the series /[(+)]. This is
INFINITE SEQUENCES AND SERIES INFINITE SEQUENCES AND SERIES I geeral, it is difficult to fid the exact sum of a series. We were able to accomplish this for geometric series ad the series /[(+)]. This is
CHAPTER 1 SEQUENCES AND INFINITE SERIES
 CHAPTER SEQUENCES AND INFINITE SERIES SEQUENCES AND INFINITE SERIES (0 meetigs) Sequeces ad limit of a sequece Mootoic ad bouded sequece Ifiite series of costat terms Ifiite series of positive terms Alteratig
CHAPTER SEQUENCES AND INFINITE SERIES SEQUENCES AND INFINITE SERIES (0 meetigs) Sequeces ad limit of a sequece Mootoic ad bouded sequece Ifiite series of costat terms Ifiite series of positive terms Alteratig
d) If the sequence of partial sums converges to a limit L, we say that the series converges and its
 Ifiite Series. Defiitios & covergece Defiitio... Let {a } be a sequece of real umbers. a) A expressio of the form a + a +... + a +... is called a ifiite series. b) The umber a is called as the th term
Ifiite Series. Defiitios & covergece Defiitio... Let {a } be a sequece of real umbers. a) A expressio of the form a + a +... + a +... is called a ifiite series. b) The umber a is called as the th term
MAT1026 Calculus II Basic Convergence Tests for Series
 MAT026 Calculus II Basic Covergece Tests for Series Egi MERMUT 202.03.08 Dokuz Eylül Uiversity Faculty of Sciece Departmet of Mathematics İzmir/TURKEY Cotets Mootoe Covergece Theorem 2 2 Series of Real
MAT026 Calculus II Basic Covergece Tests for Series Egi MERMUT 202.03.08 Dokuz Eylül Uiversity Faculty of Sciece Departmet of Mathematics İzmir/TURKEY Cotets Mootoe Covergece Theorem 2 2 Series of Real
n 3 ln n n ln n is convergent by p-series for p = 2 > 1. n2 Therefore we can apply Limit Comparison Test to determine lutely convergent.
 06 微甲 0-04 06-0 班期中考解答和評分標準. ( poits) Determie whether the series is absolutely coverget, coditioally coverget, or diverget. Please state the tests which you use. (a) ( poits) (b) ( poits) (c) ( poits)
06 微甲 0-04 06-0 班期中考解答和評分標準. ( poits) Determie whether the series is absolutely coverget, coditioally coverget, or diverget. Please state the tests which you use. (a) ( poits) (b) ( poits) (c) ( poits)
Infinite Sequences and Series
 Chapter 6 Ifiite Sequeces ad Series 6.1 Ifiite Sequeces 6.1.1 Elemetary Cocepts Simply speakig, a sequece is a ordered list of umbers writte: {a 1, a 2, a 3,...a, a +1,...} where the elemets a i represet
Chapter 6 Ifiite Sequeces ad Series 6.1 Ifiite Sequeces 6.1.1 Elemetary Cocepts Simply speakig, a sequece is a ordered list of umbers writte: {a 1, a 2, a 3,...a, a +1,...} where the elemets a i represet
THE INTEGRAL TEST AND ESTIMATES OF SUMS
 THE INTEGRAL TEST AND ESTIMATES OF SUMS. Itroductio Determiig the exact sum of a series is i geeral ot a easy task. I the case of the geometric series ad the telescoig series it was ossible to fid a simle
THE INTEGRAL TEST AND ESTIMATES OF SUMS. Itroductio Determiig the exact sum of a series is i geeral ot a easy task. I the case of the geometric series ad the telescoig series it was ossible to fid a simle
2 n = n=1 a n is convergent and we let. i=1
 Lecture 3 : Series So far our defiitio of a sum of umbers applies oly to addig a fiite set of umbers. We ca exted this to a defiitio of a sum of a ifiite set of umbers i much the same way as we exteded
Lecture 3 : Series So far our defiitio of a sum of umbers applies oly to addig a fiite set of umbers. We ca exted this to a defiitio of a sum of a ifiite set of umbers i much the same way as we exteded
INFINITE SEQUENCES AND SERIES
 11 INFINITE SEQUENCES AND SERIES INFINITE SEQUENCES AND SERIES 11.4 The Compariso Tests I this sectio, we will lear: How to fid the value of a series by comparig it with a kow series. COMPARISON TESTS
11 INFINITE SEQUENCES AND SERIES INFINITE SEQUENCES AND SERIES 11.4 The Compariso Tests I this sectio, we will lear: How to fid the value of a series by comparig it with a kow series. COMPARISON TESTS
1 Lecture 2: Sequence, Series and power series (8/14/2012)
 Summer Jump-Start Program for Aalysis, 202 Sog-Yig Li Lecture 2: Sequece, Series ad power series (8/4/202). More o sequeces Example.. Let {x } ad {y } be two bouded sequeces. Show lim sup (x + y ) lim
Summer Jump-Start Program for Aalysis, 202 Sog-Yig Li Lecture 2: Sequece, Series ad power series (8/4/202). More o sequeces Example.. Let {x } ad {y } be two bouded sequeces. Show lim sup (x + y ) lim
19 Fourier Series and Practical Harmonic Analysis
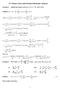 9 Fourier Series ad Practica Harmoic Aaysis Eampe : Obtai the Fourier series of f ( ) e a i. a Soutio: Let f ( ) acos bsi sih a a a a a a e a a where a f ( ) d e d e e a a e a f ( ) cos d e cos d ( a cos
9 Fourier Series ad Practica Harmoic Aaysis Eampe : Obtai the Fourier series of f ( ) e a i. a Soutio: Let f ( ) acos bsi sih a a a a a a e a a where a f ( ) d e d e e a a e a f ( ) cos d e cos d ( a cos
P-SERIES AND INTEGRAL TEST
 P-SERIES AND INTEGRAL TEST Sectio 9.3 Calcls BC AP/Dal, Revised 08 viet.dag@hmbleisd.et /4/08 0:8 PM 9.3: p-series ad Itegral Test SUMMARY OF TESTS FOR SERIES Lookig at the first few terms of the seqece
P-SERIES AND INTEGRAL TEST Sectio 9.3 Calcls BC AP/Dal, Revised 08 viet.dag@hmbleisd.et /4/08 0:8 PM 9.3: p-series ad Itegral Test SUMMARY OF TESTS FOR SERIES Lookig at the first few terms of the seqece
SOLUTIONS TO EXAM 3. Solution: Note that this defines two convergent geometric series with respective radii r 1 = 2/5 < 1 and r 2 = 1/5 < 1.
 SOLUTIONS TO EXAM 3 Problem Fid the sum of the followig series 2 + ( ) 5 5 2 5 3 25 2 2 This series diverges Solutio: Note that this defies two coverget geometric series with respective radii r 2/5 < ad
SOLUTIONS TO EXAM 3 Problem Fid the sum of the followig series 2 + ( ) 5 5 2 5 3 25 2 2 This series diverges Solutio: Note that this defies two coverget geometric series with respective radii r 2/5 < ad
sin(n) + 2 cos(2n) n 3/2 3 sin(n) 2cos(2n) n 3/2 a n =
 60. Ratio ad root tests 60.1. Absolutely coverget series. Defiitio 13. (Absolute covergece) A series a is called absolutely coverget if the series of absolute values a is coverget. The absolute covergece
60. Ratio ad root tests 60.1. Absolutely coverget series. Defiitio 13. (Absolute covergece) A series a is called absolutely coverget if the series of absolute values a is coverget. The absolute covergece
7 Sequences of real numbers
 40 7 Sequeces of real umbers 7. Defiitios ad examples Defiitio 7... A sequece of real umbers is a real fuctio whose domai is the set N of atural umbers. Let s : N R be a sequece. The the values of s are
40 7 Sequeces of real umbers 7. Defiitios ad examples Defiitio 7... A sequece of real umbers is a real fuctio whose domai is the set N of atural umbers. Let s : N R be a sequece. The the values of s are
Quiz No. 1. ln n n. 1. Define: an infinite sequence A function whose domain is N 2. Define: a convergent sequence A sequence that has a limit
 Quiz No.. Defie: a ifiite sequece A fuctio whose domai is N 2. Defie: a coverget sequece A sequece that has a limit 3. Is this sequece coverget? Why or why ot? l Yes, it is coverget sice L=0 by LHR. INFINITE
Quiz No.. Defie: a ifiite sequece A fuctio whose domai is N 2. Defie: a coverget sequece A sequece that has a limit 3. Is this sequece coverget? Why or why ot? l Yes, it is coverget sice L=0 by LHR. INFINITE
1. C only. 3. none of them. 4. B only. 5. B and C. 6. all of them. 7. A and C. 8. A and B correct
 M408D (54690/54695/54700), Midterm # Solutios Note: Solutios to the multile-choice questios for each sectio are listed below. Due to radomizatio betwee sectios, exlaatios to a versio of each of the multile-choice
M408D (54690/54695/54700), Midterm # Solutios Note: Solutios to the multile-choice questios for each sectio are listed below. Due to radomizatio betwee sectios, exlaatios to a versio of each of the multile-choice
MATH 312 Midterm I(Spring 2015)
 MATH 3 Midterm I(Sprig 05) Istructor: Xiaowei Wag Feb 3rd, :30pm-3:50pm, 05 Problem (0 poits). Test for covergece:.. 3.. p, p 0. (coverges for p < ad diverges for p by ratio test.). ( coverges, sice (log
MATH 3 Midterm I(Sprig 05) Istructor: Xiaowei Wag Feb 3rd, :30pm-3:50pm, 05 Problem (0 poits). Test for covergece:.. 3.. p, p 0. (coverges for p < ad diverges for p by ratio test.). ( coverges, sice (log
CHAPTER 4 FOURIER SERIES
 CHAPTER 4 FOURIER SERIES CONTENTS PAGE 4. Periodic Fuctio 4. Eve ad Odd Fuctio 3 4.3 Fourier Series for Periodic Fuctio 9 4.4 Fourier Series for Haf Rage Epasios 4.5 Approimate Sum of the Ifiite Series
CHAPTER 4 FOURIER SERIES CONTENTS PAGE 4. Periodic Fuctio 4. Eve ad Odd Fuctio 3 4.3 Fourier Series for Periodic Fuctio 9 4.4 Fourier Series for Haf Rage Epasios 4.5 Approimate Sum of the Ifiite Series
Section 5.5. Infinite Series: The Ratio Test
 Differece Equatios to Differetial Equatios Sectio 5.5 Ifiite Series: The Ratio Test I the last sectio we saw that we could demostrate the covergece of a series a, where a 0 for all, by showig that a approaches
Differece Equatios to Differetial Equatios Sectio 5.5 Ifiite Series: The Ratio Test I the last sectio we saw that we could demostrate the covergece of a series a, where a 0 for all, by showig that a approaches
(A sequence also can be thought of as the list of function values attained for a function f :ℵ X, where f (n) = x n for n 1.) x 1 x N +k x N +4 x 3
 MATH 337 Sequeces Dr. Neal, WKU Let X be a metric space with distace fuctio d. We shall defie the geeral cocept of sequece ad limit i a metric space, the apply the results i particular to some special
MATH 337 Sequeces Dr. Neal, WKU Let X be a metric space with distace fuctio d. We shall defie the geeral cocept of sequece ad limit i a metric space, the apply the results i particular to some special
MATH301 Real Analysis (2008 Fall) Tutorial Note #7. k=1 f k (x) converges pointwise to S(x) on E if and
 MATH01 Real Aalysis (2008 Fall) Tutorial Note #7 Sequece ad Series of fuctio 1: Poitwise Covergece ad Uiform Covergece Part I: Poitwise Covergece Defiitio of poitwise covergece: A sequece of fuctios f
MATH01 Real Aalysis (2008 Fall) Tutorial Note #7 Sequece ad Series of fuctio 1: Poitwise Covergece ad Uiform Covergece Part I: Poitwise Covergece Defiitio of poitwise covergece: A sequece of fuctios f
SCORE. Exam 2. MA 114 Exam 2 Fall 2016
 Exam 2 Name: Sectio ad/or TA: Do ot remove this aswer page you will retur the whole exam. You will be allowed two hours to complete this test. No books or otes may be used. You may use a graphig calculator
Exam 2 Name: Sectio ad/or TA: Do ot remove this aswer page you will retur the whole exam. You will be allowed two hours to complete this test. No books or otes may be used. You may use a graphig calculator
6.3 Testing Series With Positive Terms
 6.3. TESTING SERIES WITH POSITIVE TERMS 307 6.3 Testig Series With Positive Terms 6.3. Review of what is kow up to ow I theory, testig a series a i for covergece amouts to fidig the i= sequece of partial
6.3. TESTING SERIES WITH POSITIVE TERMS 307 6.3 Testig Series With Positive Terms 6.3. Review of what is kow up to ow I theory, testig a series a i for covergece amouts to fidig the i= sequece of partial
MA131 - Analysis 1. Workbook 9 Series III
 MA3 - Aalysis Workbook 9 Series III Autum 004 Cotets 4.4 Series with Positive ad Negative Terms.............. 4.5 Alteratig Series.......................... 4.6 Geeral Series.............................
MA3 - Aalysis Workbook 9 Series III Autum 004 Cotets 4.4 Series with Positive ad Negative Terms.............. 4.5 Alteratig Series.......................... 4.6 Geeral Series.............................
MTH 142 Exam 3 Spr 2011 Practice Problem Solutions 1
 MTH 42 Exam 3 Spr 20 Practice Problem Solutios No calculators will be permitted at the exam. 3. A pig-pog ball is lauched straight up, rises to a height of 5 feet, the falls back to the lauch poit ad bouces
MTH 42 Exam 3 Spr 20 Practice Problem Solutios No calculators will be permitted at the exam. 3. A pig-pog ball is lauched straight up, rises to a height of 5 feet, the falls back to the lauch poit ad bouces
Sequences and Series of Functions
 Chapter 6 Sequeces ad Series of Fuctios 6.1. Covergece of a Sequece of Fuctios Poitwise Covergece. Defiitio 6.1. Let, for each N, fuctio f : A R be defied. If, for each x A, the sequece (f (x)) coverges
Chapter 6 Sequeces ad Series of Fuctios 6.1. Covergece of a Sequece of Fuctios Poitwise Covergece. Defiitio 6.1. Let, for each N, fuctio f : A R be defied. If, for each x A, the sequece (f (x)) coverges
Sequences, Series, and All That
 Chapter Te Sequeces, Series, ad All That. Itroductio Suppose we wat to compute a approximatio of the umber e by usig the Taylor polyomial p for f ( x) = e x at a =. This polyomial is easily see to be 3
Chapter Te Sequeces, Series, ad All That. Itroductio Suppose we wat to compute a approximatio of the umber e by usig the Taylor polyomial p for f ( x) = e x at a =. This polyomial is easily see to be 3
5.6 Absolute Convergence and The Ratio and Root Tests
 5.6 Absolute Covergece ad The Ratio ad Root Tests Bria E. Veitch 5.6 Absolute Covergece ad The Ratio ad Root Tests Recall from our previous sectio that diverged but ( ) coverged. Both of these sequeces
5.6 Absolute Covergece ad The Ratio ad Root Tests Bria E. Veitch 5.6 Absolute Covergece ad The Ratio ad Root Tests Recall from our previous sectio that diverged but ( ) coverged. Both of these sequeces
Convergence of random variables. (telegram style notes) P.J.C. Spreij
 Covergece of radom variables (telegram style otes).j.c. Spreij this versio: September 6, 2005 Itroductio As we kow, radom variables are by defiitio measurable fuctios o some uderlyig measurable space
Covergece of radom variables (telegram style otes).j.c. Spreij this versio: September 6, 2005 Itroductio As we kow, radom variables are by defiitio measurable fuctios o some uderlyig measurable space
Council for Innovative Research
 ABSTRACT ON ABEL CONVERGENT SERIES OF FUNCTIONS ERDAL GÜL AND MEHMET ALBAYRAK Yildiz Techical Uiversity, Departmet of Mathematics, 34210 Eseler, Istabul egul34@gmail.com mehmetalbayrak12@gmail.com I this
ABSTRACT ON ABEL CONVERGENT SERIES OF FUNCTIONS ERDAL GÜL AND MEHMET ALBAYRAK Yildiz Techical Uiversity, Departmet of Mathematics, 34210 Eseler, Istabul egul34@gmail.com mehmetalbayrak12@gmail.com I this
Series III. Chapter Alternating Series
 Chapter 9 Series III With the exceptio of the Null Sequece Test, all the tests for series covergece ad divergece that we have cosidered so far have dealt oly with series of oegative terms. Series with
Chapter 9 Series III With the exceptio of the Null Sequece Test, all the tests for series covergece ad divergece that we have cosidered so far have dealt oly with series of oegative terms. Series with
Sequence A sequence is a function whose domain of definition is the set of natural numbers.
 Chapter Sequeces Course Title: Real Aalysis Course Code: MTH3 Course istructor: Dr Atiq ur Rehma Class: MSc-I Course URL: wwwmathcityorg/atiq/fa8-mth3 Sequeces form a importat compoet of Mathematical Aalysis
Chapter Sequeces Course Title: Real Aalysis Course Code: MTH3 Course istructor: Dr Atiq ur Rehma Class: MSc-I Course URL: wwwmathcityorg/atiq/fa8-mth3 Sequeces form a importat compoet of Mathematical Aalysis
JANE PROFESSOR WW Prob Lib1 Summer 2000
 JANE PROFESSOR WW Prob Lib Summer 000 Sample WeBWorK problems. WeBWorK assigmet Series6CompTests due /6/06 at :00 AM..( pt) Test each of the followig series for covergece by either the Compariso Test or
JANE PROFESSOR WW Prob Lib Summer 000 Sample WeBWorK problems. WeBWorK assigmet Series6CompTests due /6/06 at :00 AM..( pt) Test each of the followig series for covergece by either the Compariso Test or
Read carefully the instructions on the answer book and make sure that the particulars required are entered on each answer book.
 THE UNIVERSITY OF WARWICK FIRST YEAR EXAMINATION: Jauary 2009 Aalysis I Time Allowed:.5 hours Read carefully the istructios o the aswer book ad make sure that the particulars required are etered o each
THE UNIVERSITY OF WARWICK FIRST YEAR EXAMINATION: Jauary 2009 Aalysis I Time Allowed:.5 hours Read carefully the istructios o the aswer book ad make sure that the particulars required are etered o each
ENGI Series Page 6-01
 ENGI 3425 6 Series Page 6-01 6. Series Cotets: 6.01 Sequeces; geeral term, limits, covergece 6.02 Series; summatio otatio, covergece, divergece test 6.03 Stadard Series; telescopig series, geometric series,
ENGI 3425 6 Series Page 6-01 6. Series Cotets: 6.01 Sequeces; geeral term, limits, covergece 6.02 Series; summatio otatio, covergece, divergece test 6.03 Stadard Series; telescopig series, geometric series,
s = and t = with C ij = A i B j F. (i) Note that cs = M and so ca i µ(a i ) I E (cs) = = c a i µ(a i ) = ci E (s). (ii) Note that s + t = M and so
 3 From the otes we see that the parts of Theorem 4. that cocer us are: Let s ad t be two simple o-egative F-measurable fuctios o X, F, µ ad E, F F. The i I E cs ci E s for all c R, ii I E s + t I E s +
3 From the otes we see that the parts of Theorem 4. that cocer us are: Let s ad t be two simple o-egative F-measurable fuctios o X, F, µ ad E, F F. The i I E cs ci E s for all c R, ii I E s + t I E s +
Math 113, Calculus II Winter 2007 Final Exam Solutions
 Math, Calculus II Witer 7 Fial Exam Solutios (5 poits) Use the limit defiitio of the defiite itegral ad the sum formulas to compute x x + dx The check your aswer usig the Evaluatio Theorem Solutio: I this
Math, Calculus II Witer 7 Fial Exam Solutios (5 poits) Use the limit defiitio of the defiite itegral ad the sum formulas to compute x x + dx The check your aswer usig the Evaluatio Theorem Solutio: I this
Solutions to Math 347 Practice Problems for the final
 Solutios to Math 347 Practice Problems for the fial 1) True or False: a) There exist itegers x,y such that 50x + 76y = 6. True: the gcd of 50 ad 76 is, ad 6 is a multiple of. b) The ifiimum of a set is
Solutios to Math 347 Practice Problems for the fial 1) True or False: a) There exist itegers x,y such that 50x + 76y = 6. True: the gcd of 50 ad 76 is, ad 6 is a multiple of. b) The ifiimum of a set is
On Arithmetic Means of Sequences Generated by a Periodic Function
 Caad Math Bll Vol 4 () 1999 pp 184 189 O Arithmetic Meas of Seqeces Geerated by a Periodic Fctio Giovai Fiorito Abstract I this paper we prove the covergece of arithmetic meas of seqeces geerated by a
Caad Math Bll Vol 4 () 1999 pp 184 189 O Arithmetic Meas of Seqeces Geerated by a Periodic Fctio Giovai Fiorito Abstract I this paper we prove the covergece of arithmetic meas of seqeces geerated by a
n n 2 n n + 1 +
 Istructor: Marius Ioescu 1. Let a =. (5pts) (a) Prove that for every ε > 0 there is N 1 such that a +1 a < ε if N. Solutio: Let ε > 0. The a +1 a < ε is equivalet with + 1 < ε. Simplifyig, this iequality
Istructor: Marius Ioescu 1. Let a =. (5pts) (a) Prove that for every ε > 0 there is N 1 such that a +1 a < ε if N. Solutio: Let ε > 0. The a +1 a < ε is equivalet with + 1 < ε. Simplifyig, this iequality
Final Solutions. 1. (25pts) Define the following terms. Be as precise as you can.
 Mathematics H104 A. Ogus Fall, 004 Fial Solutios 1. (5ts) Defie the followig terms. Be as recise as you ca. (a) (3ts) A ucoutable set. A ucoutable set is a set which ca ot be ut ito bijectio with a fiite
Mathematics H104 A. Ogus Fall, 004 Fial Solutios 1. (5ts) Defie the followig terms. Be as recise as you ca. (a) (3ts) A ucoutable set. A ucoutable set is a set which ca ot be ut ito bijectio with a fiite
Section 7 Fundamentals of Sequences and Series
 ectio Fudametals of equeces ad eries. Defiitio ad examples of sequeces A sequece ca be thought of as a ifiite list of umbers. 0, -, -0, -, -0...,,,,,,. (iii),,,,... Defiitio: A sequece is a fuctio which
ectio Fudametals of equeces ad eries. Defiitio ad examples of sequeces A sequece ca be thought of as a ifiite list of umbers. 0, -, -0, -, -0...,,,,,,. (iii),,,,... Defiitio: A sequece is a fuctio which
Math 113 Exam 3 Practice
 Math Exam Practice Exam 4 will cover.-., 0. ad 0.. Note that eve though. was tested i exam, questios from that sectios may also be o this exam. For practice problems o., refer to the last review. This
Math Exam Practice Exam 4 will cover.-., 0. ad 0.. Note that eve though. was tested i exam, questios from that sectios may also be o this exam. For practice problems o., refer to the last review. This
MA541 : Real Analysis. Tutorial and Practice Problems - 1 Hints and Solutions
 MA54 : Real Aalysis Tutorial ad Practice Problems - Hits ad Solutios. Suppose that S is a oempty subset of real umbers that is bouded (i.e. bouded above as well as below). Prove that if S sup S. What ca
MA54 : Real Aalysis Tutorial ad Practice Problems - Hits ad Solutios. Suppose that S is a oempty subset of real umbers that is bouded (i.e. bouded above as well as below). Prove that if S sup S. What ca
radians A function f ( x ) is called periodic if it is defined for all real x and if there is some positive number P such that:
 Fourier Series. Graph of y Asix ad y Acos x Amplitude A ; period 36 radias. Harmoics y y six is the first harmoic y y six is the th harmoics 3. Periodic fuctio A fuctio f ( x ) is called periodic if it
Fourier Series. Graph of y Asix ad y Acos x Amplitude A ; period 36 radias. Harmoics y y six is the first harmoic y y six is the th harmoics 3. Periodic fuctio A fuctio f ( x ) is called periodic if it
9.3 The INTEGRAL TEST; p-series
 Lecture 9.3 & 9.4 Math 0B Nguye of 6 Istructor s Versio 9.3 The INTEGRAL TEST; p-series I this ad the followig sectio, you will study several covergece tests that apply to series with positive terms. Note
Lecture 9.3 & 9.4 Math 0B Nguye of 6 Istructor s Versio 9.3 The INTEGRAL TEST; p-series I this ad the followig sectio, you will study several covergece tests that apply to series with positive terms. Note
Lecture Chapter 6: Convergence of Random Sequences
 ECE5: Aalysis of Radom Sigals Fall 6 Lecture Chapter 6: Covergece of Radom Sequeces Dr Salim El Rouayheb Scribe: Abhay Ashutosh Doel, Qibo Zhag, Peiwe Tia, Pegzhe Wag, Lu Liu Radom sequece Defiitio A ifiite
ECE5: Aalysis of Radom Sigals Fall 6 Lecture Chapter 6: Covergece of Radom Sequeces Dr Salim El Rouayheb Scribe: Abhay Ashutosh Doel, Qibo Zhag, Peiwe Tia, Pegzhe Wag, Lu Liu Radom sequece Defiitio A ifiite
NATIONAL UNIVERSITY OF SINGAPORE FACULTY OF SCIENCE SEMESTER 1 EXAMINATION ADVANCED CALCULUS II. November 2003 Time allowed :
 NATIONAL UNIVERSITY OF SINGAPORE FACULTY OF SCIENCE SEMESTER EXAMINATION 003-004 MA08 ADVANCED CALCULUS II November 003 Time allowed : hours INSTRUCTIONS TO CANDIDATES This examiatio paper cosists of TWO
NATIONAL UNIVERSITY OF SINGAPORE FACULTY OF SCIENCE SEMESTER EXAMINATION 003-004 MA08 ADVANCED CALCULUS II November 003 Time allowed : hours INSTRUCTIONS TO CANDIDATES This examiatio paper cosists of TWO
SCORE. Exam 2. MA 114 Exam 2 Fall 2017
 Exam Name: Sectio ad/or TA: Do ot remove this aswer page you will retur the whole exam. You will be allowed two hours to complete this test. No books or otes may be used. You may use a graphig calculator
Exam Name: Sectio ad/or TA: Do ot remove this aswer page you will retur the whole exam. You will be allowed two hours to complete this test. No books or otes may be used. You may use a graphig calculator
Math 25 Solutions to practice problems
 Math 5: Advaced Calculus UC Davis, Sprig 0 Math 5 Solutios to practice problems Questio For = 0,,, 3,... ad 0 k defie umbers C k C k =! k!( k)! (for k = 0 ad k = we defie C 0 = C = ). by = ( )... ( k +
Math 5: Advaced Calculus UC Davis, Sprig 0 Math 5 Solutios to practice problems Questio For = 0,,, 3,... ad 0 k defie umbers C k C k =! k!( k)! (for k = 0 ad k = we defie C 0 = C = ). by = ( )... ( k +
4x 2. (n+1) x 3 n+1. = lim. 4x 2 n+1 n3 n. n 4x 2 = lim = 3
 Exam Problems (x. Give the series (, fid the values of x for which this power series coverges. Also =0 state clearly what the radius of covergece is. We start by settig up the Ratio Test: x ( x x ( x x
Exam Problems (x. Give the series (, fid the values of x for which this power series coverges. Also =0 state clearly what the radius of covergece is. We start by settig up the Ratio Test: x ( x x ( x x
Ma 530 Introduction to Power Series
 Ma 530 Itroductio to Power Series Please ote that there is material o power series at Visual Calculus. Some of this material was used as part of the presetatio of the topics that follow. What is a Power
Ma 530 Itroductio to Power Series Please ote that there is material o power series at Visual Calculus. Some of this material was used as part of the presetatio of the topics that follow. What is a Power
Math 341 Lecture #31 6.5: Power Series
 Math 341 Lecture #31 6.5: Power Series We ow tur our attetio to a particular kid of series of fuctios, amely, power series, f(x = a x = a 0 + a 1 x + a 2 x 2 + where a R for all N. I terms of a series
Math 341 Lecture #31 6.5: Power Series We ow tur our attetio to a particular kid of series of fuctios, amely, power series, f(x = a x = a 0 + a 1 x + a 2 x 2 + where a R for all N. I terms of a series
Lecture 17Section 10.1 Least Upper Bound Axiom
 Lecture 7Sectio 0. Least Upper Boud Axiom Sectio 0.2 Sequeces of Real Numbers Jiwe He Real Numbers. Review Basic Properties of R: R beig Ordered Classificatio N = {0,, 2,...} = {atural umbers} Z = {...,
Lecture 7Sectio 0. Least Upper Boud Axiom Sectio 0.2 Sequeces of Real Numbers Jiwe He Real Numbers. Review Basic Properties of R: R beig Ordered Classificatio N = {0,, 2,...} = {atural umbers} Z = {...,
ANSWERS TO MIDTERM EXAM # 2
 MATH 03, FALL 003 ANSWERS TO MIDTERM EXAM # PENN STATE UNIVERSITY Problem 1 (18 pts). State ad prove the Itermediate Value Theorem. Solutio See class otes or Theorem 5.6.1 from our textbook. Problem (18
MATH 03, FALL 003 ANSWERS TO MIDTERM EXAM # PENN STATE UNIVERSITY Problem 1 (18 pts). State ad prove the Itermediate Value Theorem. Solutio See class otes or Theorem 5.6.1 from our textbook. Problem (18
Real Analysis Fall 2004 Take Home Test 1 SOLUTIONS. < ε. Hence lim
 Real Aalysis Fall 004 Take Home Test SOLUTIONS. Use the defiitio of a limit to show that (a) lim si = 0 (b) Proof. Let ε > 0 be give. Defie N >, where N is a positive iteger. The for ε > N, si 0 < si
Real Aalysis Fall 004 Take Home Test SOLUTIONS. Use the defiitio of a limit to show that (a) lim si = 0 (b) Proof. Let ε > 0 be give. Defie N >, where N is a positive iteger. The for ε > N, si 0 < si
Sequences A sequence of numbers is a function whose domain is the positive integers. We can see that the sequence
 Sequeces A sequece of umbers is a fuctio whose domai is the positive itegers. We ca see that the sequece 1, 1, 2, 2, 3, 3,... is a fuctio from the positive itegers whe we write the first sequece elemet
Sequeces A sequece of umbers is a fuctio whose domai is the positive itegers. We ca see that the sequece 1, 1, 2, 2, 3, 3,... is a fuctio from the positive itegers whe we write the first sequece elemet
In this section, we show how to use the integral test to decide whether a series
 Itegral Test Itegral Test Example Itegral Test Example p-series Compariso Test Example Example 2 Example 3 Example 4 Example 5 Exa Itegral Test I this sectio, we show how to use the itegral test to decide
Itegral Test Itegral Test Example Itegral Test Example p-series Compariso Test Example Example 2 Example 3 Example 4 Example 5 Exa Itegral Test I this sectio, we show how to use the itegral test to decide
Quiz. Use either the RATIO or ROOT TEST to determine whether the series is convergent or not.
 Quiz. Use either the RATIO or ROOT TEST to determie whether the series is coverget or ot. e .6 POWER SERIES Defiitio. A power series i about is a series of the form c 0 c a c a... c a... a 0 c a where
Quiz. Use either the RATIO or ROOT TEST to determie whether the series is coverget or ot. e .6 POWER SERIES Defiitio. A power series i about is a series of the form c 0 c a c a... c a... a 0 c a where
It is always the case that unions, intersections, complements, and set differences are preserved by the inverse image of a function.
 MATH 532 Measurable Fuctios Dr. Neal, WKU Throughout, let ( X, F, µ) be a measure space ad let (!, F, P ) deote the special case of a probability space. We shall ow begi to study real-valued fuctios defied
MATH 532 Measurable Fuctios Dr. Neal, WKU Throughout, let ( X, F, µ) be a measure space ad let (!, F, P ) deote the special case of a probability space. We shall ow begi to study real-valued fuctios defied
Chapter 0. Review of set theory. 0.1 Sets
 Chapter 0 Review of set theory Set theory plays a cetral role i the theory of probability. Thus, we will ope this course with a quick review of those otios of set theory which will be used repeatedly.
Chapter 0 Review of set theory Set theory plays a cetral role i the theory of probability. Thus, we will ope this course with a quick review of those otios of set theory which will be used repeatedly.
Sequences I. Chapter Introduction
 Chapter 2 Sequeces I 2. Itroductio A sequece is a list of umbers i a defiite order so that we kow which umber is i the first place, which umber is i the secod place ad, for ay atural umber, we kow which
Chapter 2 Sequeces I 2. Itroductio A sequece is a list of umbers i a defiite order so that we kow which umber is i the first place, which umber is i the secod place ad, for ay atural umber, we kow which
Notice that this test does not say anything about divergence of an alternating series.
 MATH 572H Sprig 20 Worksheet 7 Topics: absolute ad coditioal covergece; power series. Defiitio. A series b is called absolutely coverget if the series b is coverget. If the series b coverges, while b diverges,
MATH 572H Sprig 20 Worksheet 7 Topics: absolute ad coditioal covergece; power series. Defiitio. A series b is called absolutely coverget if the series b is coverget. If the series b coverges, while b diverges,
MAS111 Convergence and Continuity
 MAS Covergece ad Cotiuity Key Objectives At the ed of the course, studets should kow the followig topics ad be able to apply the basic priciples ad theorems therei to solvig various problems cocerig covergece
MAS Covergece ad Cotiuity Key Objectives At the ed of the course, studets should kow the followig topics ad be able to apply the basic priciples ad theorems therei to solvig various problems cocerig covergece
Math 525: Lecture 5. January 18, 2018
 Math 525: Lecture 5 Jauary 18, 2018 1 Series (review) Defiitio 1.1. A sequece (a ) R coverges to a poit L R (writte a L or lim a = L) if for each ǫ > 0, we ca fid N such that a L < ǫ for all N. If the
Math 525: Lecture 5 Jauary 18, 2018 1 Series (review) Defiitio 1.1. A sequece (a ) R coverges to a poit L R (writte a L or lim a = L) if for each ǫ > 0, we ca fid N such that a L < ǫ for all N. If the
Not for reproduction
 STRATEGY FOR TESTING SERIES We ow have several ways of testig a series for covergece or divergece; the problem is to decide which test to use o which series. I this respect testig series is similar to
STRATEGY FOR TESTING SERIES We ow have several ways of testig a series for covergece or divergece; the problem is to decide which test to use o which series. I this respect testig series is similar to
Strategy for Testing Series
 Strategy for Testig Series We ow have several ways of testig a series for covergece or divergece; the problem is to decide which test to use o which series. I this respect testig series is similar to itegratig
Strategy for Testig Series We ow have several ways of testig a series for covergece or divergece; the problem is to decide which test to use o which series. I this respect testig series is similar to itegratig
Chapter 10: Power Series
 Chapter : Power Series 57 Chapter Overview: Power Series The reaso series are part of a Calculus course is that there are fuctios which caot be itegrated. All power series, though, ca be itegrated because
Chapter : Power Series 57 Chapter Overview: Power Series The reaso series are part of a Calculus course is that there are fuctios which caot be itegrated. All power series, though, ca be itegrated because
A sequence of numbers is a function whose domain is the positive integers. We can see that the sequence
 Sequeces A sequece of umbers is a fuctio whose domai is the positive itegers. We ca see that the sequece,, 2, 2, 3, 3,... is a fuctio from the positive itegers whe we write the first sequece elemet as
Sequeces A sequece of umbers is a fuctio whose domai is the positive itegers. We ca see that the sequece,, 2, 2, 3, 3,... is a fuctio from the positive itegers whe we write the first sequece elemet as
The Ratio Test. THEOREM 9.17 Ratio Test Let a n be a series with nonzero terms. 1. a. n converges absolutely if lim. n 1
 460_0906.qxd //04 :8 PM Page 69 SECTION 9.6 The Ratio ad Root Tests 69 Sectio 9.6 EXPLORATION Writig a Series Oe of the followig coditios guaratees that a series will diverge, two coditios guaratee that
460_0906.qxd //04 :8 PM Page 69 SECTION 9.6 The Ratio ad Root Tests 69 Sectio 9.6 EXPLORATION Writig a Series Oe of the followig coditios guaratees that a series will diverge, two coditios guaratee that
UNIVERSITY OF BRISTOL. Examination for the Degrees of B.Sc. and M.Sci. (Level C/4) ANALYSIS 1B, SOLUTIONS MATH (Paper Code MATH-10006)
 UNIVERSITY OF BRISTOL Exmitio for the Degrees of B.Sc. d M.Sci. (Level C/4) ANALYSIS B, SOLUTIONS MATH 6 (Pper Code MATH-6) My/Jue 25, hours 3 miutes This pper cotis two sectios, A d B. Plese use seprte
UNIVERSITY OF BRISTOL Exmitio for the Degrees of B.Sc. d M.Sci. (Level C/4) ANALYSIS B, SOLUTIONS MATH 6 (Pper Code MATH-6) My/Jue 25, hours 3 miutes This pper cotis two sectios, A d B. Plese use seprte
Measure and Measurable Functions
 3 Measure ad Measurable Fuctios 3.1 Measure o a Arbitrary σ-algebra Recall from Chapter 2 that the set M of all Lebesgue measurable sets has the followig properties: R M, E M implies E c M, E M for N implies
3 Measure ad Measurable Fuctios 3.1 Measure o a Arbitrary σ-algebra Recall from Chapter 2 that the set M of all Lebesgue measurable sets has the followig properties: R M, E M implies E c M, E M for N implies
