On the stability of the polynomial L 2 -projection on triangles and tetrahedra
|
|
|
- Harvey Preston
- 6 years ago
- Views:
Transcription
1 ASC Reot No. 5/0 On the stability of the olynomial L -ojection on tiangles and tetaheda J.M. Melenk und T. Wuze Institute fo Analysis and Scientific Comuting Vienna Univesity of Technology TU Wien ISBN
2 Most ecent ASC Reots 4/0 P. Amodio, Ch. Budd, O. Koch, G. Settanni, and E.B. Weinmülle Numeical Solution of a Second-Ode Initial Value Poblem Descibing Flow in Concete 3/0 D. Stüze, A. Anold Sectal analysis and long-time behaviou of a Fokke-Planck euation with a non-local etubation /0 M. Bessemoulin-Chatad and A. Jüngel A finite volume scheme fo a Kelle-Segel model with additional coss-diffusion /0 M. Bulatov, P. Lima, E. Weinmülle Existence and Uniueness of Solutions to Weakly Singula Integal-Algebaic and Intego-Diffeential Euations 0/0 M. Kakulik, G. Of, and D. Paetoius Convegence of adative 3D BEM fo weakly singula integal euations based on isotoic mesh-efinement 9/0 A. Jüngel, René Pinnau, and E. Röhig Existence analysis fo a simlified tansient enegy-tansot model fo semiconductos 8/0 I. Rachunková, A. Sielaue, S. Staněk and E.B. Weinmülle The stuctue of a set of ositive solutions to Diichlet BVPs with time and sace singulaities 7/0 J.-F. Mennemann, A. Jüngel, and H. Kosina Tansient Schödinge-Poisson simulations of a high-feuency esonant tunneling diode oscillato 6/0 N. Zamoni and A. Jüngel Two sinoial dift-diffusion models fo uantum electon tansot in gahene 5/0 M. Auada, M. Feischl, T. Fühe, M. Kakulik, D. Paetoius Efficiency and otimality of some weighted-esidual eo estimato fo adative D bounday element methods Institute fo Analysis and Scientific Comuting Vienna Univesity of Technology Wiedne Hautstaße Wien, Austia admin@asc.tuwien.ac.at WWW: htt:// FAX: ISBN c Alle Rechte vobehalten. Nachduck nu mit Genehmigung des Autos. ASC TU WIEN
3 On the stability of the olynomial L -ojection on tiangles and tetaheda J.M. Melenk T. Wuze July 3, 0 Abstact Fo the efeence tiangle o tetahedon T, we study the stability oeties of the L T )-ojection Π N onto the sace of olynomials of degee N. We show Π N u L T ) C u L T ) u H T ) and Π N u H T ) CN + ) / u H T ). This imlies otimal convegence ates fo the aoximation eo u Π N uu L T ) fo all u H k T ), k > /. Intoduction and main esults The study of olynomials and thei oeties as the olynomial degee tends to infinity has a vey long histoy in numeical mathematics. Concening aoximation and stability oeties of vaious high ode aoximation oeatos, the univaiate case is easonably well undestood in the way of examles, we mention the monogahs [6] fo othogonal olynomials and [8] fo issues concening aoximation); by tenso oduct aguments, also fo the case of olynomial aoximation on d- dimensional hye cubes a significant numbe of esults is available. The situation is less develoed fo simlices, and it is the uose of this note to contibute in the aea by studying the stability oeties of the olynomial L -ojection on tiangles o tetaheda. Ou main esults ae Theoems. and.3 below. These two theoems genealize known esults fo tenso oduct domains: Theoem. is the analog of [, Lemma 4.] and coesondingly, Co.. is the analog of [, Lemma 4.4] and [5, Lemma 3.5]) and Theoem.3 coesonds to [4, Thm..]. Indeendently, closely elated esults have ecently been obtained in [5]. The novelty of the esent wok ove [5] is twofold: Fistly, in the language of Coollay. below, we extend the aoximation esult of [5] fom s to s > /. Secondly, we study the H -stability of the L ojection. Although the esults of the esent note ae of indeendent inteest, the stability esult of Theoem. has alications in the analysis of the h-vesion of discontinuous Galekin methods h-dgfem) as demonstated in [4]. Moe geneally, simlicial elements ae, due to thei geate geometic flexibility as comaed to tenso oduct elements, commonly used in high ode finite element codes so that an undestanding of stability and aoximation oeties of olynomial oeatos defined on simlices could be useful in othe alications of high ode finite element methods h-fem) as well. We efe to [6, 7, 6,, 3] fo vaious asects of h-fem. To fix the notation, we intoduce the efeence tiangle T, the efeence tetahedon T 3 as well Institut fü Analysis und Scientific Comuting, Technische Univesität Wien, Austia melenk@tuwien.ac.at).
4 as the efeence cube by T : {x, y) R : < x <, < y < x}, T 3 : {x, y, z) R 3 : < x, y, z, x + y + z < },.a).b) S d :, ) d, d {,, 3}..c) Thoughout, we will denote by P N the sace of olynomials of total) degee N. We then have: Theoem.. Let T be the efeence tiangle o tetahedon and denote by Π N : L T ) P N the L T )-ojection onto the sace of olynomials of degee N. Then thee exists a constant C > 0 indeendent of N such that In aticula, theefoe, Π N u L T ) C u L T ) u H T ) u H T )..) Π N u L T ) C u / B, T ) u B /, T ),.3) whee the Besov sace B /, T ) is defined by B/, T ) L T ), H T )) /, and we used the eal method of inteolation see, e.g., [7, 8] fo details). Coollay.. Let T be the efeence tiangle o tetahedon. Then fo evey s > / thee exists a constant C s > 0 such that u Π N u L T ) C s N + ) s /) u H s T ) u H s T )..4) Theoem.3. Let T be the efeence tiangle o tetahedon. Then thee exists a constant C > 0 such that fo all N N Π N u H T ) CN + ) / u H T ) u H T )..5) We will only show the oofs fo the 3D case in Theoem 5.3 this theoem combines Theoems. and Coollay.) and in Theoem 6., which fomulates Theoem.3. The D case is teated with simila ideas. Details of the oof of Theoem. in D can be found in the Bachelo Thesis [9]. Numeical esults In this section, we illustate the shaness of Theoems.,.3 fo the D and the D case. esent the best constants in the following D and D situations: Π N u)) C D mult u L I) u H I), Π N u) L Γ) CD mult u L T ) u H T ), We Π N u H I) CH D N + u H I) u P N.) Π N u H T ) CH D N + u H T ) u P N,.) whee I, ) and Γ, ) { } T. The best constants C D constained maximization oblem. Fo examle, C D mult max{ Π Nu L Γ) u L T ) u H T ), mult, CD mult u P N}, ae solutions of which can be solved using the techniue of Lagange multilies. The constant CH D is moe eadily accessible as the solution of an eigenvalue oblem since C D H su u P N u L Γ) u. H T ) The esult of the D situation ae esented in Table wheeas the outcome of the D calculations ae shown in Table. The D calculations ae in ageement with the esults of Theoem.,.3 wheeas the D esults illustate [, Lemma 4.] and [4, Thm..].
5 Π N su N u)) Π u PN su N u)) u L I) u H u PN I) u H I) Π N su N u)) Π u PN su N u)) u L I) u H u PN I) u H I) Table : D maximization oblems N su u PN Π N u L Γ) Π N su u L Γ) u L T ) u H T u PN ) u H T ) su u PN Π N u H T ) u H T ) N+) Table : D maximization oblems 3
6 3 One-dimensional esults In the tenso-oduct setting of suaes and hexaheda, the aguments leading to Theoems.,.3 can be educed to a one-dimensional setting. Most of this eduction to a one-dimensional setting is also ossible in the esent case of simlices, and the esent section ovides the necessay one-dimensional esults. Ou basic tool fo this dimension eduction is the so-called Duffy tansfomation see 4.) below), which mas the simlex into a hye cube. Moe imotantly, as noted aleady by [9, 6, 7] othogonal olynomials on the simlex can be defined in the tansfomed vaiables though oducts of univaiate Jacobi olynomials, which exessed the desied eduction to one-dimensional settings. Although the situation is technically moe comlicated than the tenso-oduct setting since Jacobi olynomials aise the tenso-oduct setting of suaes and hexaheda ultimately leads to the study of the moe common Gegenbaue/ultasheical olynomials see, e.g., [, Sec. 3.3.], [,3,]) the Jacobi olynomials ae classical othogonal olynomials and one can daw on a lethoa of known oeties fo the uose of both analysis and design of algoithms. This undelies, fo examle, the woks [, 5, 6, 8] and is also at the heat of the esent analysis. We denote by P n α,β), α, β >, n N, the Jacobi olynomials, [6]. Fom [6, 4.3.3)] we have the following othogonality elation fo Jacobi olynomials and, N 0 : x) α x) β P α,β) hee, δ, eesent the Konecke symbol and γ α,β) : α+β+ + α + β + x)p α,β) x)dx γ α,β) δ, 3.) Γ + α + )Γ + β + ). 3.)!Γ + α + β + ) Futhemoe, we abbeviate factos that will aea natually in ou comutations: + ) h, α) : + α + ) + α + ), g, α) : α h, α) : + α + ) + α), g, α) : + α + α ) + α), α + α ) + α), 3.3) + α) h 3, α) : + α + ) + α), g 3, α) : + α ) + α ). By diect calculation we can establish elations between h i and g i. Lemma 3.. Let h, h, h 3 and g, g, g 3 be defined in 3.3). Then thee holds fo any and α N 0 g +, α) γ α,0) ) h 3 +, α), + h, α) + ) + Futhemoe, fo any 0 + g +, α) h, α) γ α,0), h +, α) + ) + + g 3 +, α) h, α), 3.4) h 3 +, α) ) h, α) h, α) h 3, α). 3.6) Poof. This follows diectly by simle calculation and the definition of the tems. Details can be found in Aendix B. 4
7 We will denote by P α,0) the antideivative of P α,0), i.e., x P α,0) x) : P α,0) t) dt. 3.7) The following lemma states imotant elations between Jacobi olynomials, thei deivatives, and thei antideivatives. Lemma 3.. Let α N 0 and h i, g i, i {,, 3} be given by 3.3) and γ α,β) i) fo x ii) fo iii) fo by 3.). Then we have t) α P α,0) t) dt x) α h, α)p α,0) + x) + h, α)p α,0) x) + h 3, α)p α,0) ), x) P α,0) P α,0) x) g, α)p α,0) x) + g, α)p α,0) x) + g 3, α)p α,0) x), x) h, α) P α,0) ) x) + h, α) P α,0) ) x) + h 3 +, α) + α,0)) x). P + Poof. The oof of i) elies on elations satisfied by Jacobi olynomials; see Aendix B fo details. ii) is taken fom []; iii) is obtained by diffeentiating ii) and using Lemma 3.. The next lemma will be used in the oof of the ensuing Lemma 3.5, which is the D vesion of Theoem.3. Lemma 3.3. Thee exists K > 0 such that fo all α, N 0 x) α ) P α,0) x) dx K + + α) γ α,0). Poof. The assetion in case of 0 is tivial. Fo α 0 see [, 5.3)]. A diect calculation shows I 0 0, I α + ) 4 α+ α +, I 3 + α) α + ) α + 4α + 3 α+4 ; fo suitable K, the assetion of the lemma is theefoe tue fo {0,, } and all α. Thus, we may assume α,. We abbeviate P : P α,0) and I : x)α P x) dx. Fom Lemma 3. ii) with + and thee we get P + g +, α) P g +, α) g +, α)g, α) P + ε )P ε P, 3.8) whee ε : g +, α)g 3, α) g +, α)g, α) α + + α) ) + + α) + α ) + α). We note that 0 ε. Futhemoe, we calculate ε )P ε P ) ε ) P ) + ε P ) ε ε )P P 5
8 so that by integation, Cauchy-Schwaz, and 0 ε : x) α ε )P x) ε P x) ) dx ε )I + ε I ). By the othogonality oeties of the Jacobi olynomials, we conclude in view of 3.8) I+ g +, α) + g +, α) ) γ α,0) + g +, α) g +, α)g, α) ) x) α ε )P x) ε P x) ) dx ) γ α,0) + g +, α) g +, α)g, α) ) + ε )I + ε I ). We oceed now by an induction agument. We note that fo any K the claimed fomula is monotone inceasing in. Hence, we can estimate ε )I + ε I ) K ) + α + ) ) and obtain by some tedious estimates fo the othe tems see Aendix B) : I+ g +, α) ) γ α,0) + K + ) + + α) + ) + [ K + ) + + α) + [ K + ) + + α) + ) g +, α) g +, α)g, α) + K + α ) ) [ K + ) + K + ) + + α ) α,0) ] )γ + + α) + ) + K + ) + K + ) + + α ] ) ) + α + 3) α) + ) + α ) ]. K + ) + K + ) + + ) The oof is comlete by ensuing that K so that the exession in backets is bounded by. The essential ingedient of the one-dimensional analysis in [4, Thm..], [5, Lemma 3.5], [, Lemma 4.] is the ability to elate the exansion coefficients u n ) n0 of the Legende exansion u n u np n 0,0) to the exansion coefficients b n ) n0 of the Legende exansion u n b np n 0,0). This elation genealizes to the case of exansions in Jacobi olynomials. A fist esult in this diection is see also [5, Lemma.] and [, Lemma.]): Lemma 3.4. Let α N 0. Let U C, ) and let x) α Ux) as well as x) α+ U x) be integable. Futhemoe, assume lim x) +α Ux) 0 and lim + x)ux) 0. Then the x x exansion coefficients u : b : satisfy the following connection fomula fo : x) α Ux)P α,0) x)dx, x) α U x)p α,0) x)dx. u h, α)b + + h, α)b + h 3, α)b. 6
9 Poof. Follows fom an integation by ats and the eesentation of antideivatives of Jacobi olynomials in tems of Jacobi olynomials given in Lemma 3. i). We efe to Aendix B fo details. The following esult is the genealization of [4, Thm..] on the H -stability of the L -ojection. While [4, Thm..] studied the H -stability of the tuncated Legende exansion, we study hee the effect of tuncating a Jacobi exansion. Lemma 3.5. Let α N 0. Let u and b be defined as in Lemma 3.4. Then thee exists a constant C > 0 indeendent of α and N such that fo evey N N we have x) α N ) u P α,0) x) dx CN b. 0 Poof. We abbeviate P : P α,0). We comute N+ u P N+ N b + + N+ N+ + b [ N+ 0 [h, α)b + + h, α)b + h 3, α)b ] P h 3 +, α)p + + b With Lemma 3. iii) we theefoe conclude N+ u P N+ N+ h, α)p h, α)p + b N+ h 3 N +, α)p N+b N + b P + N+ N h, α)p h, α)p + h, α)p b. N+ h 3 N +, α)p N+b N + N + h 3 +, α)p + h, α)p b. ] Inseting the esult of Lemma 3.3 gives x) α u P N+ dx N+ + CN CN N 3 N+ N b + CN h 3N +, α) N + α) b N b. N N + α) h, α) b This allows us to conclude the agument since P α,0) ) x) 0 0. Lemma 3.6. Fo β > and U C 0, ) C0, ]) thee holds ) x β Ux) dx x β+ U x) dx + 0 β + 0 β + U). 7
10 Poof. This vaiant of the Hady ineuality can be shown using [4, Thm. 330]. See Aendix B fo details. Lemma 3.7. Let U C, ) and assume Ux) x) α dx <, U x) x) α dx <. Let u and b be defined as in Lemma 3.4. Then thee exist constants C, C > 0 indeendent of α and U such that + α) u C 0 b C U x) x) α dx. Poof. The esult follows fom the elation between u and b given in Lemma 3.4 and fom bounds fo h, h, h 3. Next, we show a shot lemma that will be useful in the oof of Lemma 3.9. Lemma 3.8. Let α N 0 and. Then thee exists a constant C > 0 indeendent of and α such that N α j+α j α + α N + α. Poof. The oof follows by the standad agument of majoizing the sum by an integal. While Lemma 3.4 shows that the coefficients u can be exessed as a shot linea combination of the coefficients b a maximum of 3 coefficients suffices), the convese is not so easy. The following lemma may be egaded as a weak convese of Lemma 3.4 since it allows us to bound the coefficients b in tems of the coefficients u and weighted sums of the coefficients b. This is the main esult of this section and the key ingedient of the oof of Theoem. as it is esonsible fo the multilicative stuctue of the bound in Theoem.. Lemma 3.9. Assume the hyotheses of Lemma 3.4. Let α N 0. Let u and b be defined as in Lemma 3.4. Then fo thee exists a constant C > 0 indeendent of and α such that b + b C α+ j j u j / j j Poof. We may assume that the ight-hand side of the estimate in the lemma is finite. In view of the sign oeties of h, h, h 3 and 3.6) we have We intoduce the abbeviations h, α) + h, α) h 3, α). 3.9) α : h, α) h 3, α) α + α + ) + α + ) + α), ε : α α + ) b j α + ) + α + ) + α + 4) + + α) + α). By eaanging tems in Lemma 3.4 and using the tiangle ineuality we get h 3, α) b u + h, α) b + h, α) b +. /. 8
11 We set and by alying 3.9) we aive at Iteating 3.0) once gives z : u h 3, α) b z + α b + α ) b ) b z + α z+ + α + b + + α + ) b + ) + α ) b + Suaing and Cauchy-Schwaz yields z + α z + + α α + ) ) b + + α α + ) b + z + α z + + ε ) b + + ε b +. b z + α z + ) + z + α z + ) ε ) b + + ε b + ) If we abbeviate fo the fist two addends we obtain which we ewite as + ε ) b + + ε b + + ε ε ) b + b + z + α z + ) + z + α z + ) ε ) b + + ε b + ) + ε ) + ε ε ) ) b + + ε + ε ε ) ) b +. f : z + α z + ) + z + α z + ) ε ) b + + ε b + ) 3.) b f + ε )b + + ε b +, b b + f + ε b + b +). Next, we want to emloy a telescoing sum. Since we assume that the sums in the ight side of the statement of this lemma ae finite, i.e. u j <, b j <, 3.) j j j j and since j + α) α we have b 0 fo. Hence, we can wite j b + b b +j b +j+ + b +j b +j+ f +j + ε +j b ++j b ++j) + f++j + ε ++j b +3+j b ) ++j f +j ε +j b ++j + ε +j ε +j+ ) b ++j + ε ++j b +3+j f +j ε b + ε ++j b +3+j + ε +j ε +j+ ) b ++j + ε ++j b +3+j f +j ε b + + ε ++j ε ++j ) b +3+j + ε +j ε +j+ ) b ++j f +j ε b + + ε +j ε +j+ ) b ++j. 9
12 We conclude, noting that ε 0, b + b b + b + ε b + F + S +, 3.3) whee F : f j, j 3.4) S : ε jb j j with ε j : ε j ε j. 3.5) By ositivity of ε j and f j we have S + S as well as F + F. Theefoe, we get fom 3.3) and the definition of S Alying the notation we have Iteating 3.6) N times leads to A calculation shows S ε b + ε +b + + S + S + + max{ε, ε +}S +3 + max{ε, ε +}F + + max{ε, ε +})S + + max{ε, ε +}F. N S S +N+ + ε ε : max{ε, ε +} S + ε )S + + ε F. 3.6) +j) + N j ε +jf +j i0 + ε +i). 3.7) ε j αα + j)3 α + j) 5 α α + j). 3.8) Fom the definition of S in 3.5), 3.), and 3.8) it follows that lim S 0. Futhemoe, we can bound the oduct unifomly in N : N N N + ε +j) ex ln + ε +j) ex ε +j, 3.9) whee in the last estimate we used the fact that ln + x) x fo x 0. Fom 3.8) we get N ε +j N α N α + + j) α α + j) α α + j N, 3.0) whee we have used Lemma 3.8 in the last ste. Since α α+ <, inseting 3.0) in 3.9) gives N + ε +j) C. 3.) 0
13 Now, by assing to the limit N in 3.7), we obtain a closed fom bound fo S : S j ε +jf +j i0 + ε +i). Alying 3.0), 3.), 3.8) and the definition of F we can simlify S ε +jf +j j Inseting this estimate in 3.3) and using i j b + b F + f i α α + j) i i f i j α α++ <, we aive at α α + j) α α + F. α α + + F + F + F + F. 3.) We ae left with estimating F. By the definition of F in 3.4) and the definition of f in 3.) we have F z j + α j z j+ ) + j + α j z j+ ) j j z ε j ) b j+ + ε j b j+ ). 3.3) Now we estimate both sums seaately stating with the fist one: j + α j z j+ ) j z zj + αj zj+ zj. 3.4) }{{} j j Next, we use the elation between u and b fom Lemma 3.4. Futhemoe, we note that h 3, α) α+) γ α,0). Hence, we obtain z u h 3, α) u u α+ γ α,0) h 3, α) α+ u γ α,0) h 3, α) h, α)b + + h, α)b + h 3, α)b α+ u α γ α,0) ) b + + α b + b ). Inseting this in the bound 3.4), we get by alying the Cauchy-Schwaz ineuality fo sums j + α j z j+ ) j z α+ j α+ j j j u j α j ) b j+ + α j b j + b j ) u j / j j b j /.
14 We continue by estimating the second sum in 3.3). Using again z α+ u /γ α,0) we get z j + α j z j+ ) ε j ) b j+ + ε j b j+ ) j α+ j α+ j α+ j α+ j j j j j uj + α j u j+ ) ε j ) b j+ + ε j b j+ ) }{{}}{{}}{{} u j + u j+ ) b j+ + b j+ ) u j u j / / j j j+ In view of 3.) the last two estimates conclude the oof. 4 Exansions j b j+ b j To save sace we will sometimes denote oints in R 3 by just one lette, i.e. ξ ξ, ξ, ξ 3 ) fo oints in T 3 and η η, η, η 3 ) fo oints in S Duffy-Tansfomation We ecall the definition of the efeence tiangle, tetahedon, and the d-dimensional hye cube in.). The 3D-Duffy tansfomation D : S 3 T 3, [0], is given by + η ) η ) η 3 ) Dη, η, η 3 ) : ξ, ξ, ξ 3 ), + η ) ) η 3 ), η 3 4.) 4 / /. with invese D ξ, ξ, ξ 3 ) η, η, η 3 ) + ξ, + ξ ), ξ 3. ξ + ξ 3 ξ 3 Lemma 4.. The Duffy tansfomation is a bijection between the oen) cube S 3 and the oen) tetahedon T 3. Additionally, [ D ξi η) : η j ] 3 i,j D η) ) η ) η 3 ) 4 η ) η 3 ) η ) η 3 ) η 3) η ) η ) + η ) 4 + η ) + η ) 0 η ) η 0 0 η ) η 3 ),, ) ) det D η η3.
15 Poof. See, fo examle, [6]. Lemma 4.. Let D be the Duffy tansfomation and Γ : T { }. Then DΓ) Γ and D is an isometic isomohism with esect to the L Γ)-nom, i.e., fo sufficiently smooth functions u, we have fo ũ u D the elation u L Γ) ũ L Γ). Poof. Follows by insection. 4. Othogonal olynomials on tetaheda In tems of Jacobi olynomials P n α,β) we intoduce othogonal olynomials on the efeence tetahedon T 3 often associated with the names of Dubine o Koonwinde, [9, 6, 7]. Lemma 4.3. Let,, N 0 and set ψ,, : ψ,, D, whee ψ,, is defined by ψ,, η) : P 0,0) η )P +,0) η )P ++,0) η 3 ) ) ) η + η3. Then the functions ψ,, ae L T 3 ) othogonal and satisfy ψ,, P ++ T 3 ) and ψ,, ξ)ψ,, ξ) dξ δ, δ, δ, T δ, δ, δ, γ 0,0) γ +,0) γ ++,0) Poof. The oof can be found in Aendix B. 4.3 Exansion in tems of ψ,, Since ψ,, ),, N0 fom a set of othogonal olynomials we have that any u L T 3 ) can be exanded as whee u,,0 ψ,,, u L T 3 ) ψ,, ψ,, L T 3 ),,0 γ 0,0) + γ +,0) ++ γ ++,0) u,, ψ,,, 4.) u,, : ψ,,, u L T 3 ). 4.3) A basic ingedient of the oofs of Theoems. and.3 is the eduction of the analysis to onedimensional settings, fo which we have ovided the necessay esults in Section 3. The vaiable that will lay a secial ole is η 3 as will become aaent in Definition 4.4 below. Fo a function u defined in T 3 we intoduce the tansfomed function ũ : u D and get ) ) u,, uξ)ψ,, ξ) dξ ũη) ψ η η3,, η) dη T 3 S 3 ) + ) ũη)p 0,0) η )P +,0) η )P ++,0) η ++ η3 η 3 ) dη. 4.4) S 3 3
16 Definition 4.4. Let, N 0 and u L T 3 ). We define the functions U, : R R and Ũ, : R R as well as the coefficients ũ,, and ũ,, by ) + U, η 3 ) : ũη)p 0,0) η )P +,0) η η ) dη dη, 4.5) Ũ, η 3 ) : U,η 3 ), 4.6) η 3 ) + ũ,, : ũ,, : With this notation, we have by comaing 4.4) with 4.7) u,, ++ η 3 ) ++ Ũ, η 3 )P ++,0) η 3 ) dη 3, 4.7) η 3 ) ++ Ũ,η 3 )P ++,0) η 3 ) dη ) η 3 ) ++ Ũ, η 3 )P ++,0) η 3 ) dη 3 ++ ũ,,. 4.9) Since fo sufficiently smooth functions u the tansfomed function ũ is constant on η 3, othogonalities of the Jacobi olynomials give us U, ) 0 fo, ) 0, 0) 4.0) 4.4 Poeties of the univaiate functions U, and Ũ, We stat with some eliminay consideations egading estimates fo atial deivatives of the tansfomed function ũ. We have η ũη) η ) η 3 ) u) Dη), 4.) 4 η ũη) + η ) η 3 ) 4 η3 ũη) + η ) η ) u) Dη) + η 3) u) Dη), 4.) u) Dη) + η ) u) Dη) + 3 u) Dη), 4.3) 4 whee i is the atial deivative with esect to the i-th agument. In aticula, we get ) ) ) η ũη) dη u) Dη) η η3 dη S 3 η S 3 ξ u L T 3 ) u L T 3 ), 4.4) ) ) η ũη) η dη u) Dη) + ) ) η η η3 dη + ξ S 3 S 3 u L T 3 ) ξ u L T 3 ) + ξ u L T 3 ) u L T 3 ). 4.5) These estimates will be useful to ove the following lemmas. Lemma 4.5 oeties of U, ). Let u H T ) and U, be defined in Definition 4.4. Then thee exists a constant C > 0 indeendent of u such that ) U, η 3 ) η3 dη 3 u L T 3 ), 4.6),0,0 γ 0,0) γ 0,0), γ +,0) γ +,0) γ 0,0) γ +,0) ) U,η 3 ) η3 dη 3 C u L T 3 ), 4.7) + ) U, η 3 ) dη 3 C u L T 3 ). 4.8) 4
17 Futhemoe, we have fo Γ T { } 0 γ 0,0) γ +,0) U, ) u L Γ). 4.9) ) Poof. We fist ove 4.6) and 4.7). The fact that P 0,0) η )P +,0) η ) η ae othogonal olynomials in a weighted L -sace on S and the definition of U, imly fo fixed η 3 ) the eesentation ũη),0 γ 0,0) + γ +,0) which in tun gives ) ũη) η dη dη S ) η3 U, η 3 )P 0,0) η )P +,0) η ),0 γ 0,0) Since det D η Simila to the eesentation of ũ above, we get fo η3 ũ η3 ũη),0 γ +,0) ) η, U, η 3 ). 4.0) ), ) multilication with η3 and integation in η3 gives 4.6). γ 0,0) + γ +,0) Reasoning as in the case of 4.6) yields,0 γ 0,0) γ +,0) U,η 3 )P 0,0) η )P +,0) η ) ) η. U,η 3 ) ) η3 dη 3 u L T 3 ), which immediately leads to 4.7). We now tun to the oof of 4.8). By definition, we have U, η 3 ) + ũη)p 0,0) S We conside the integation in η. Integation by ats then yields ũη)p +,0) η ) η ) + dη ) ũη) η ) + +,0) P + η ) η )P +,0) η ) η ) + dη dη. 4.) η ũη) η ) +) P +,0) + η )dη η ũη) η ) + +,0) P + η ) + + )ũη) η ) +,0) P + η )dη. Hence, we obtain by inseting into 4.) U, η 3 ) η ũη)p 0,0) S ũη)p 0,0) S η ũη)p 0,0) S S η ũ)η) η ) η ) + P +,0) + η )dη dη η ) η ) P +,0) + η )dη dη η ) η ) + P +,0) + η )dη dη P 0,0) + η ) η ) P +,0) + η )dη dη, 5
18 whee in the last euation we used integation by ats in η and the fact that t)dt 0 fo. With the abbeviation g i : g i +, + ), i,, 3 we have by Lemma 3. ii) fo, the following elationshis: P +,0) P 0,0) η ) g P +,0) + η ) + g P +,0) η ) + g 3 P +,0) η ), 4.) ) P 0,0) + η ) P 0,0) η ). 4.3) P 0,0) η ) + Futhemoe, we intoduce two abbeviations ) + z, η 3 ) : η ũ)η)p 0,0) η η ) P +,0) η )dη dη 4.4) S ) + z, η 3 ) : u) D)η)P 0,0) η η ) P +,0) η )dη dη. 4.5) S Since we have 4.), using 4.), 4.3), 4.4) and 4.5) we get U, η 3 ) g z,+ η 3 + g z, η 3 ) + g 3 z, η 3 ) ) ) ) + η3 [ + g z+,+η 3 ) z,+η 3 ) ) + 4 We use g, g, g ) U, η 3 ) + g z+, η 3 ) z, η 3 ) ) + g 3 z+, η 3 ) z, η 3 ) )]. to aive at ) η3 z +,+ jη 3 ) + z,+ jη 3 ) ) + z,+ j η 3 ). 4.6) To estimate the tems on the ight side we note that the abbeviations z, and z, lead us to the eesentations η ũη) u) D)η),0,0 Since the olynomials P 0,0) η ) tiangle T we have γ 0,0) γ 0,0) η + γ +,0) + γ +,0) η ũη) η S ũ) D)η) η S z, η 3 )P 0,0) η ) z, η 3 )P 0,0) η ) η η ) P +,0) η ) ) P +,0) η ). ) +,0) P η ) ae othogonal olynomials on the efeence ) dη dη ) dη dη,0,0 γ 0,0) γ 0,0) γ +,0) γ +,0) Fomula 4.7) togethe with an integation in η 3 and an alication of 4.5) gives,0 γ 0,0) γ +,0) z, η 3 ) 4.7) z, η 3 ). 4.8) ) z, η 3 ) dη 3 η ũη) η dη u L S 3 T 3 ). 6
19 Fom the eesentation 4.8) we get by a multilication with use of 4.4) that,0 ) η3, an integation in η3 and the ) γ 0,0) γ +,0) z, η 3 ) η3 dη 3 ) ) u) D)η) η η3 dη u L S 3 T 3 ). The last two esults in combination with 4.6) conclude the agument. We finally ove 4.9). Fo the estimate 4.9), we use 4.0) with η 3. Noting Lemma 4. we have and theefoe the esult follows. u L Γ) ũ L Γ) S ũη, η, ) dη dη The estimate 4.8) does not ovide a bound fo the secial cases 0 o 0. The teatment of these two secial cases is the uose of the following lemma. Lemma 4.6. Assume the same hyotheses as in Lemma 4.5. Then thee exists a constant C > 0 indeendent of u such that 0 0 γ 0,0) γ 0,0) 0 γ,0) γ +,0) 0 U 0, η 3 ) dη 3 C u L T 3 ) 4.9) U,0 η 3 ) dη 3 C u L T 3 ). 4.30) Poof. The oof of 4.9) stat with the obsevation ) ) U 0, ũη)dη P,0) η η ) dη. We exand fo fixed η 3 the function η ũη, η, η 3 )dη as well as its deivative in tems of P,0). Lemma 3.7 then yields U 0, η 3 ) dη 3 + ) U 0, η 3 ) dη 3 0 γ 0,0) 0 γ,0) η ũη)dη η )dη dη 3 γ,0) η ũη) η S 3 ) dη u L T 3 ), whee we aealed to 4.5) in the last estimate. Analogously we deal with 4.30), whee we exand the ma η ) + ũη, η, η 3 ) η dη again fo fixed η 3 in tems of P 0,0) and conclude with Lemma 3.7 and 4.4). The estimates fo the functions U, imly easily coesonding bounds fo the functions Ũ,: Lemma 4.7 oeties of Ũ,). Let u H T ) and Ũ, be defined in Definition 4.4. Then thee exists a constant C > 0 indeendent of u such that η 3 ) ++ Ũ, η 3 ) dη 3 u L 4 T 3 ), 4.3) 4,0,0 γ 0,0) γ 0,0) γ +,0) γ +,0) η 3 ) ++ Ũ,η 3 ) dη 3 C u L T 3 ). 4.3) 7
20 Poof. We have Ũ,η 3 ) η 3 ) +) U, η 3 ) and theefoe Ũ,η 3 ) η 3 ) +) U,η 3 ) + + ) η 3 ) ++) U, η 3 ). Hence, 4 4 η 3 ) ++ Ũ, η 3 ) dη 3 η 3 ) ++ Ũ,η 3 ) dη 3 ) η3 U,η 3 ) dη 3 η3 Using the esults of Lemma 4.5 concludes the agument. ) U,η 3 ) dη ) U, η 3 ) dη 3. These esults allow us to get bounds fo weighted sums of the coefficients ũ,, and ũ,, given in Definition 4.4: Coollay 4.8. Assume the hyotheses of Lemma 4.7 and let ũ,,, ũ,, be given by Definition 4.4. Then thee exist constants C indeendent of u such that,,0,,0 γ 0,0) γ 0,0) γ +,0) γ +,0) ae othogonal olynomials in a weighted L -sace, exand- Poof. Since the olynomials P ++,0) ing Ũ, yields the eesentation Futhemoe, we have Ũ, η 3 ) 0 γ ++,0) γ ++,0) ũ,, C u L T 3 ), 4.33) ũ,, C u L T 3 ). 4.34) γ ++,0) η 3 ) ++ Ũ,η 3 ) dη 3 ũ,, P ++,0) η 3 ). 0 γ ++,0) ũ,,. The statement 4.33) now follows diectly fom 4.3) of Lemma 4.7. Analogously, we deal with 4.34), whee we exand Ũ, and conclude with 4.3) of Lemma Connections between ũ,, and ũ,, To obtain the multilicative stuctue in the estimation of Theoem. one key ingedient will be connections between ũ,, and ũ,,. This connection is essentially a one-dimensional effect and follows fom Lemma 3.4: Coollay 4.9. Let ũ,, and ũ,, be as in Definition 4.4 and h, h and h 3 be given by 3.3). Then fo and, 0 thee holds ũ,, h, + + )ũ,,+ + h, + + )ũ,, + h 3, + + )ũ,,. Poof. By density we may assume that u C T 3 ). Lemma 3.4 then imlies the esult. Fo a detailed vesion of this oof see Aendix B. 8
21 5 Tace stability Fist, we will establish a eesentation fo the tansfomed function ũ u D on the face Γ : T { }. Using A.4) and A.3) we get Theefoe we have fo ξ Γ P ++,0) ) ) P 0,++) ) ). ψ,, ξ) ψ,, D ξ, ξ, ) ) ) η Alying the exansion of u in 4.) we aive at ũη, η, ) uξ, ξ, ),,0 γ 0,0) + γ +,0) P 0,0) η ) η ) P 0,0) η )P +,0) η ). ) P +,0) η ) ) u,, ++ In view of Lemma 4. as well as the exansion 4.), we obtain fo the L Γ)-nom u L Γ) ũ L Γ),0 γ 0,0) γ +,0) ) u,, 0 ++ γ ++,0) γ ++,0). 5.). 5.) The next lemma will show that the infinite sum ove in 5.) can be exessed as a finite sum. Lemma 5.. Let N. Then thee holds ) N ++ γ ++,0) u,, ) N h N, + + ) + N N + γ ++,0) N ũ,,n ) + h 3 +, + + ) Poof. We abbeviate n : + +. In view of Coollay 4.9 we have ) N n γ n,0) ) N N+ + N+ 4.9) u,, + γ n,0) ) N + γ n,0) ũ,, + γ ++,0) + h, n )ũ,,+ + h, n )ũ,, + h 3, n )ũ,, ) h, n ) + ) h, n ) + N ) ũ,, + [ + ) N h N, n ) + γ n,0) γ n,0) ũ,, ũ,, + h, n ) γ n,0) γ n,0) N ũ,,n + N ) + h 3 +, n ) + + h, n ) N N γ n,0) h 3 +, n ) γ n,0) + ) + h 3 +, n ) + By 3.5), the exession in backets vanishes and that concludes the oof. 9 ) ũ,,. γ n,0) ũ,, + ] γ n,0) + ũ,,.
22 Since Lemma 5. assumes N, the tems coesonding to 0 in 5.) ae not included. We study this case now in Lemma 5.: Lemma 5.. Let u H T 3 ) and conside the eesentation of the noms in 5.). Fo 0 thee exists a constant C > 0 indeendent of, and u such that,0 γ 0,0) γ +,0) u,,0 ++ γ ++,0) 0 C u L T 3 ) u H T 3 ). Poof. We fist note that the coefficient u 0,0,0 u L T 3 ) so that we may focus on the sum with, ) 0, 0). Since γ 0,0) +, γ+,0) + ++ and γ++,0) , we get,0 γ 0,0) γ +,0) u,,0 ++ γ ++,0) ) 4 u,,0. To bound the sum on the ight-hand side, we note that an integation by ats and 4.0) give fo, ) 0, 0)) ++ u,,0,0 η 3 ) ++ U, η 3 )dη 3 5.3) U, ) + These two euations yield two estimates fo u,,0. ineuality ) η 3 ) ++3 U,η 3 )dη 3, 5.4) Fom 5.3), we get with the Cauchy-Schwaz ++ u,,0 η 3 ) ++ U, η 3 )dη 3 ) ) η 3 ) ++ 3 ) dη3 η 3 ) U, η 3 ) dη Fom 5.4), we obtain a second estimate as follows: ++ u,, ) ++6 U, ) + whee η 3 ) ++3 U,η 3 )dη 3 Inseting this in the bound befoe yields η 3 U, η 3 ) dη 3 5.5) η 3 ) u,, ) U, ) + η 3 ) ++3 U,η 3 )dη 3 ), ) ) ) dη3 η 3 ) U,η 3 ) dη 3 η 3 U,η 3 ). + + ) η 3 U,η 3 ) dη ) 0
23 Next, we abbeviate σ, : η 3 U, η 3 ) dη 3, τ, : Hence, alying 5.5) and 5.6) we have { ++ u,,0 ++4 min + + σ,, ) ) U, ) + min η 3 U,η 3 ) dη 3. U, ) + { σ,, ) U, ) ) σ,τ,, whee in the last ste we used that min{a, b } a b. This leads us to Hence, we conclude u,,0 + + ) 4 u,,0,0 )} + + τ, } ) 3 τ, + + ) U, ) ) σ,τ,. 5.7) + + ) U, ) +,0 + + ) U, ) +,0 u L Γ) + u L T 3 ) u L T 3 ) + + ) σ,,0 + + ) σ, τ,,0 / + + ) τ, whee, in the last ineuality, we aealed to Lemma 4.5. The statement of the lemma now fom the multilicative tace ineuality u L Γ) u L T 3 ) u H T 3 ) of, e.g., [3, Thm..6.6] and the tivial bound.,0 We ae now in osition to ove Theoem. as well as Coollay.: Theoem 5.3 tace stability of L -ojection, aoximation oeties). Fo N N 0 denote by Π N the L T 3 )-ojection onto P N T 3 ). Thee exists a constant C > 0 indeendent of N and u such that Futhemoe, Π N u L Γ) C u L T 3 ) u H T 3 ) u H T 3 ). 5.8) / Π N u L Γ) C u B /, T 3 ) u B /, T 3 ). 5.9) Additionally, fo each s > / thee is C s > 0 such that u Π N u L Γ) C s N + ) s /) u H s T 3 ) u H s T ). 5.0) Poof. In view of the multilicative tace ineuality u L Γ) u L T 3 ) u H T 3 ) see, e.g., [3, Thm..6.6]) we will only show the statement u Π N u L Γ) u L T 3 ) u H T 3 ). We abbeviate n : + + and c : γ 0,0) u Π N u L Γ),0 c γ +,0) max{0,n+ }. By 5.), we have to bound ) n γ n,0) u,,
24 + N N N c c N+ 0 N+ N+ ) ) c ) 0 n γ n,0) n γ n,0) n γ n,0) u,, u,, u,, N N c ) n 0 0 N+ γ n,0) u,, }{{} : S n + u,, + N+ 0 c ) γ n,0) }{{} : S 3 n c u,,0. N+ 0 γ n,0) 0 } {{ } : S 5 + N N+ 0 N+ N c ) 0 N+ 0 n γ n,0) c ) 0 c ) u,, n γ n,0) n γ n,0) u,, u,, } {{ } : S N 0 N+ c n γ n,0) 0 u,,0 } {{ } : S 4 Lemma 5. immediately gives S 4 +S 5 u L T 3 ) u H T 3 ). Fom Lemma 5. as well as the estimates and h N +, n ) + N N, + 0,..., N h 3 N +, n ), h 3 N +, n ) N + + N N, + 0,..., N γ n,0) N+ N , γ n,0) N+ N we obtain fo S S N N 0 0 Analogously, we get fo S and S 3 S S 3 N c ++3)ũ,,N ) ũ,,n ). 0 N+ N+ 0 c ++3)ũ,, + ++3) ũ,,0 ) c ++3)ũ,, + ++3) ũ,,0 ). Alying Lemma 3.9 the owes of two in the estimates above and in the lemma annihilate each othe.
25 Hence, S + S + S 3 gives S + S + S 3 N N N c 0 N+ N+ 0 N+ c c u L T 3 ) u L T 3 ), γ n,0) γ n,0) γ n,0) ũ,, ũ,, ũ,, / N / / 0 0 γ n,0) γ n,0) γ n,0) ũ,, ũ,, ũ,, whee in the last estimate, we have used the Cauchy-Schwaz ineuality fo sums and Coollay 4.8. Since u L T 3 ) u H T 3 ) this concludes the oof of 5.8). The estimate 5.9) follows diectly fom 5.8) in view of [7, Lemma 5.3]. Finally 5.0) is shown in the standad way. Fo abitay P N we have by the ojection oety of Π N as well as the continuity of the tace oeato γ 0 : B / /, T ) L T 3 ) cf., e.g., [7, Sec. 3]) u Π N u L T ) u L T ) + Π N u ) L T ) C u / B, T ). Hence, u Π N u L T ) C inf P N u B /, T ). Fix s > /. Let Π N : L T ) P N be an aoximation oeato with the oeties fo examle, one can combine the aoximation esults of [9, Aendix A] fo hye cubes with the well-known extension oeato of Stein, [5, Cha. VII]) u Π N u L T ) CN s u H s T ), u Π N u H s T ) C u H s T ) u H s T ). By inteolation theoy, we then have that Id Π N is a bounded linea oeato H s T ) B /, T ) L T ), H s T )) s /)/s, with nom Id Π N B /, T ) Hs T ) CN ss /)/s. 6 H -stability Ou ocedue to study the H -stability of the L -ojection Π N is to study the diectional deivative that coesonds to the deivative η3 in the tansfomed vaiable. The full gadient can be obtained fom this diectional deivative and aoiate affine tansfomations of the efeence tetahedon T 3. The key ste is theefoe to contol η3 ΠN u, whee we denote Π N u : Π N u) D. This is the uose of the ensuing lemma. Lemma 6.. Thee exists a constant C > 0 indeendent of N such that η ) η 3 ) η3 ΠN uη) dη CN u L T 3 ) u H T 3 ). S 3 Poof. We abbeviate n : + +. We see that Π N uη) N N 0 0 N 0 γ 0,0) + γ +,0) + γ n,0) ũ,, ψ,, η) / / / 3
26 by ecalling the elation between u,, and ũ,,. Diffeentiating with esect to η 3 shows us that we have to estimate the two tems I : η ) η 3 ) N N N + S γ 0,0) γ +,0) γ n,0) ũ,, ) P 0,0) η )P +,0) η η ) η 3 ) + P n,0) ) η3 ) dη 6.) I : η ) η 3 ) N N N + + S γ 0,0) γ +,0) γ n,0) ũ,, ) P 0,0) η )P +,0) η η ) η 3 ) + P n,0) η 3 ) dη 6.) Fist, we conside 6.). Fom Lemma 3.5 with α n we get I N N 0 0 N N 0 0 γ 0,0) γ 0,0) γ +,0) γ +,0) N η 3 ) n N ) 0 0 γ n,0) γ n,0) ũ,, P n,0) ) η3 ) ũ,, N u L T 3 ), whee in the last ste, we aealed to Coollay 4.8. Thus, we aive at the desied bound fo I. Next, we conside 6.). We have N N + ) N I η 3 ) + ũ,, P n,0) η 3 ) dη γ 0,0) γ 0,0) γ +,0) γ +,0) 0 γ n,0) Lemma 3.6 with β + and the nomalization convention fo Jacobi olynomials A.3) now yield N N + ) I N + ) η 3 ) n n ũ,, P,0) ) η3 ) dη 3 I + I N N 0 0 N I + N N 0 0 N N 0 γ 0,0) γ 0,0) N 0 0 γ n,0) + γ +,0) + γ +,0) γ 0,0) ũ,, P n,0) γ +,0) N 0 N 0 ) γ n,0) γ n,0) 0 N u L T 3 ) + N u L {η T 3 :η 3 }) γ n,0) 0 ũ,, P n,0) ũ,, ) ) ũ,, + N u L T 3 ) + N u L T 3 ) u H T 3 ) N u L T 3 ) γ n,0) ) N + ) γ n,0) whee we used the fact that I is bounded above and the multilicative tace ineuality [3, Thm..6.6] as in Theoem 5.3 but now alied to the bottom face {η T 3 : η 3 }. 4 ũ,, dη 3
27 We can now ove Theoem.3: Theoem 6. H -stability of L -ojection). Thee exists a constant C > 0 indeendent of N such that Π N u L T 3 ) C N u L T 3 ) u H T 3 ). Poof. Fo a function v and the tansfomed function ṽ v D, the fomula 4.3) ovides a elation between η3 ṽ and v. Reaanging tems yields η3 ṽ) D ξ) + ξ ξ 3 vξ) + ξ ξ 3 vξ) + 3 vξ). Theefoe, when tansfoming to T 3 in Lemma 6. we get + ξ Π N uξ) + ξ Π N uξ) + 3 Π N uξ) ξ 3 ξ 3 T 3 dξ N u L T 3 ). 6.3) By the symmety oeties of T 3, we see that also the following two othe emutations of indices ae valid estimates: + ξ Π N uξ) + ξ 3 3 Π N uξ) + Π N uξ) T 3 ξ ξ dξ N u L T 3 ), 6.4) + ξ 3 3 Π N uξ) + ξ Π N uξ) + Π N uξ) ξ ξ dξ N u L T 3 ). 6.5) T 3 We abbeviate ax, y) : +x y, a ij : aξ i, ξ j ) and + a 3 + a a 3 a 3 + a + a a 3 + a 3 + a 3 a Aξ, ξ, ξ 3 ) : sym + a 3 + a a 3 + a a 3 + a 3. sym sym + a 3 + a 3 Hence, we see that by adding 6.3), 6.4), and 6.5) we aive at T 3 Π N u) Aξ) Π N u dξ N u L T 3 ) Next, we obseve that nea the to vetex,, ), we have + ξ ξ 3 and + ξ ξ 3. This imlies that the functions a 3 and a 3 ae unifomly bounded on T 3. Analogously, we get bounds fo a, a 3 and a, a 3 by studying the vetices,, ) and,, ). Theefoe, we have su Aξ) L T 3 ) <. ξ T 3 By constuction, the matix Aξ) is ointwise) symmetic ositive semidefinite. Ou goal is to show that Aξ) is in fact ositive definite on the set that stays away fom the face F oosite the vetex,, ). This can be done with techniues as in [] by establishing lowe bounds fo the eigenvalues of Aξ). A diect calculation eveals det Aξ) 6 ξ + ξ ξ + ξ ξ 3 + ξ + ξ + + ξ 3 + ξ 3 ξ + ξ + ξ 3 + ξ ) + ξ 3 ) + ξ ) 6 ξ + ξ + ξ 3 ) + ξ + ξ + ξ 3 ) + + ξ + ξ + ξ 3 ) + ξ ) + ξ 3 ) + ξ ) 6 + ξ ) + ξ 3 ) + ξ ). 5
28 The face oosite the vetex,, ) contains the vetices, ),,, ),,, ) and is given by the euation ξ + ξ + ξ Futhemoe, we conclude that the signed distance of an abitay oint ξ fom this face F is given by distξ, F ) ξ + ξ + ξ 3 + ). 3 Let, fo abitay δ > 0, T δ : {ξ T 3 distξ, F ) < δ}. Then, since we stay away fom the face F, it is clea that thee exists C δ > 0 such that det Aξ) C δ ξ T δ. Combining the above findings, we have that on T δ the matix Aξ) is in fact symmetic ositive definite. Since the enties of Aξ) ae unifomly bounded in ξ, Geshgoin s cicle theoem ovides a constant C ue such that all eigenvalues of Aξ) ae bounded by C ue. A lowe bound fo the eigenvalues is obtained as follows: Denoting fo fixed ξ T δ the eigenvalues 0 < λ λ λ 3, we get fom det A λ λ λ 3 C δ det A λ λ λ 3 λ C ue. This ovides the desied lowe bound fo λ. Thus, we conclude that fo evey δ > 0 we can find c δ > 0 such that Aξ) c δ I on T δ. Hence, c δ Π N u T dξ Π N u) Aξ) Π N u dξ N u L T 3 ). δ T 3 Affine tansfomations allow us to get analogous estimates fo the sets that stay away fom the othe faces of T 3. We theefoe get the desied esult. A Poeties of Jacobi olynomials We have the following useful fomulas see [6,. 350 f], [6]): Recusion Relations with a np α,β) n+ x) a n + a 3 nx)p n α,β) x) a 4 np α,β) n x) a n : n + )n + α + β + )n + α + β) a n : n + α + β + )α β ) a 3 n : n + α + β)n + α + β + )n + α + β + ) a 4 n : n + α)n + β)n + α + β + ) A.) with b nx) d dx P n α,β) x) b nx)p n α,β) x) + b 3 nx)p α,β) b nx) : n + α + β) x ) b nx) : n α β n + α + β)x) b 3 nx) : n + α)n + β) n x) A.) 6
29 Secial Values P α,β) n ) ) n + α n A.3) P n α,β) x) ) n P n β,α) x) A.4) Secial Cases Fo the Legende Polynomial L n x) thee holds Miscellaneous Relations n x L n x) P 0,0) n x) A.5) d dx P n α,β) x) α+,β+) α + β + n + )P n x) A.6) t) α + t) β P n α,β) t) dt x) α+ + x) β+ P α+,β+) n x) A.7) B Selected oofs B. Selected oofs fo Section 3 Poof of Lemma 3. i). Using eaanged vesions of A.), A.6) and A.7) we obtain x t) α P α,0) t)dt A.7) + x) x)α+ P α+,) x) x ) x) α P α+,) x) x) α d x ) + α + dx P α,0) x) A.6) A.) x) α x) + α + α,0) αp α A.) allows us now to elace the tem xp α,0) Hence, we get x α + α)x)p α,0) x) + + α)p α,0) x) + α x) + + α)p α,0) + α + ) + α) x) by tems involving P α,0) + { t) α P α,0) t)dt x) α + α + ) + α) + ) + α + ) + α)p α,0) + + α + ) + α + ) x) + + α) + α + )P α,0) x) + α + )α P α,0) α,0) x) + α)xp x) α,0) x), P x) and P α,0) x). αp α,0) x) + + α)p α,0) x) ) } x) 7
30 Reaanging tems gives { x t) α P α,0) t)dt x) α + α + ) + α) + ) + α + ) + α) + α + ) + α + ) P α,0) + x) } + α + + α + α + P α,0) x) + + α) + α + + α + P α,0) x) { x) α + ) P α,0) + + α + ) + α + ) x) }{{} h, α) + α + α + ) + α) }{{} h, α) P α,0) x) + + α) + α + ) + α) } {{ } h 3, α) } P α,0) x) Poof of 3.5). By definition of γ α,β) we obtain in aticula α+ + α +, which leads in combination with the definition of h, h and h 3 to ) h, α) + ) + + h +, α) + ) + + h 3 +, α) + + α α + 3 α ) α+ + )+ + α + ) + α + ) α+ + α + 4) + α + ) + + α α + ) + ) α+ + α + 5) + α + 4) )+ + α + α α + 3)α + α + 4) + α + ) + α + ) + α + 4 ) )+ + ) + α + 4) + + α + 3)α + α + ) + α + ) α + α + 4) + α + ) Simly multilying out the numeato concludes the oof egading the fist euation. Inseting the definition of h, h and h 3 also leads in the case of the second euation to the conclusion h, α) h, α) α + α + ) + + ) + α) + α) + α + ) + α + ) α + α + 4α + α) + α + ) + α + ) + α + ) + α) + α) + α + ) + α + ) h 3, α). Lemma B. details of the oof of Lemma 3.3). Define fo α, N 0 Then, fo α, we have 0 ε. ε : g +, α)g 3, α) g +, α)g, α) α + + α) ) + + α) + α ) + α). 8
31 Poof. Clealy, ε 0. To see the estimate ε, we have to show α + + α) ) α ) + α ) + 3α ) + α ) α ) + α + ) + α)) + 3α ) }{{}? + α) + + α) + α )? + α ) + α) + α + )? 0 This last ineuality is cetainly tue if α ) + α + ) + α) + 3α ) 4α ) + α + ) + α) 4α ) + α) + α) 4α ) α α + α) α 4α α + α) 4α α) + α)? 0? 0? 0? 0? 0? 0 Lemma B. details of the oof of Lemma 3.3). Fo α N, we have g +, α) g +, α) g +, α)g, α) ) γ α,0) + ) + α + ) + + ) + ) + ) + α + ) + + ) + B.) B.) Poof. We stat by obseving that α+ + α +, 0 B.3) so that we obtain γ α,0) α α + + α α We stat with the bound B.). Then g +, α)) γα,0) γ α,0) g +, α)) α + ) + α + ) + α α + ) + α + γα,0) + + α + ) + α + 3) + + ) + α + ) + ) + γα,0) + 9
32 whee, in the last ste, we used, α. We now tun to the bound B.). Then ) g +, α) g +, α)g, α) ) α + α + ) + α + ) + α ) + α) + α) + α + ) + α + + α ) α + α + ) + α + ) + α ) + α) + α) + α + ) + α + + α + ) α + α + ) + α + ) + α ) + α) + α α) + α + ) + α + + α ) + α + )α + α + ) + α ) + α) + α α) + α + ) + α + + α + α ) + α + α + α α + 3) + α ) + α + + α + α + + α + 3) α γα,0) + Lemma B.3. Let U C, ) and let x) α Ux) as well as x) α+ U be integable. Futhemoe, let lim x x)+α Ux) 0 and lim + x)ux) 0. x Conside h, h and h 3 fom 3.3). We define u : b : x) α Ux)P α,0) x)dx, x) α U x)p α,0) x)dx. Then fo and α N 0 the following elationshi holds: Poof. Fom A.7) we have fo x and fo x u h, α)b + + h, α)b + h 3, α)b. x x t) α P α,0) t)dt O + x) t) α P α,0) t)dt O x) α+). Hence, using the stiulated behavio of U at the endoints, the following integation by ats can be justified: u x) α Ux)P α,0) x)dx Ux) x t) α P α,0) ) x) U x) 30 x t) α P α,0) t)dt dx.
33 In aticula, we note that b is well-defined. Futhemoe, u U x) x x) α U x) t) α P α,0) t)dt dx h, α)p α,0) h, α)b + + h, α)b + h 3, α)b, + x) + h, α)p α,0) whee in the second euation we aealed to Lemma 3. i). 0 x) + h 3, α)p α,0) x) ) dx Lemma B.4. Fo β > and U C 0, ) C0, ]) thee holds ) x β Ux) dx x β+ U x) dx + β + β + U). Poof. We define accoding to the notation of [4, Thm. 330] { U x) 0 < x < fx) : and F x) : ft) dt 0 x > Fo β >, [4, Thm. 330] states Hence, 0 0 x β F x) dx x β Ux) U)) dx 0 x ) x β+ fx) dx β + 0 { 0 x > ) x β+ U x) dx. β + 0 U) Ux) 0 < x <. By eaanging tems, we get ) x β Ux) dx x β+ U x) dx + U) x β dx 0 β ) x +β U x) dx + β + β + U). 0 B. Selected oofs fo Section 4 Poof of Lemma 4.3. With the definition of D and the abbeviation n : + + we get ψ,, ξ, ξ, ξ 3 ) ψ,, + ξ, + ξ ), ξ 3 ξ + ξ 3 ξ 3 P 0,0) + ξ ) P +,0) + ξ ) +ξ ) ) P n,0) ξ ξ 3 ) 3 + ξ3. ξ + ξ 3 ξ 3 Exanding P 0,0) ψ,, ξ, ξ, ξ 3 ) x )P +,0) y ) k0 l0 k0 l0 c kl k+l + ξ ξ + ξ 3 k0 l0 c klx k y l leads to ) k ) + l ξ P n,0) ξ 3 ) ξ 3 + ξ ξ 3 c kl k+l + + ξ ) k + ξ ) l ξ 3) l ξ ξ 3 ) ξ + ξ 3 ) k P n,0) ξ 3 ). 3 ) ξ3 ) +
34 Since P n,0) is a olynomial of degee, we see by the last tems in the sum above that ψ,, P ++ T 3 ). To see the othogonality oety, we tansfom to the cube S 3 and make use of 3.) thee times ψ,, ξ)ψ,, ξ)dξ T 3 ) ) ψ,, η) ψ,, η) η η3 dη P 0,0) η )P 0,0) η η ) η3 S 3 + δ +) η3 ) + + P +,0) η )P +,0) η ) ) P n,0) η 3 )P n,0) η 3 ) dη dη dη 3 η ) + P +,0) ) ++ + P n,0) η 3 )P n,0) η 3 ) dη dη 3 + δ + + δ n + δ + + δ δ. η )P +,0) η ) η 3 ) n P n,0) η 3 )P n,0) η 3 ) dη 3 Lemma B.5 details of Lemma 4.). Let D be the Duffy tansfomation and Γ : T { }. Then DΓ) Γ and D is an isometic isomohism with esect to the L Γ)-nom. Poof. Obviously D is an isomohism and by definition DΓ) Γ, so we will only show the isomety oety. Let u be a uadatic integable function on T 3 and conside the tansfomed function ũ u D. We have ũ L Γ) ũη, η, η 3 ) dη dη dη 3 Γ ) + u η ) + η ), η, dη dη uξ, ξ, ) dξ ξ u L Γ). T u Dη, η, ) ) dη dη Poof of Coollay 4.9. To ove this coollay we want to make use of Lemma 3.4. Theefoe, we have to claify that the conditions in the lemma ae satisfied. We oceed in two stes. Fist, we euie u C T 3 ) and show the statement in this case and then we ague by density to achieve esults in H T 3 ). Ste : By assuming that u C T 3 ) we get ũ C S 3 ). Hence, fo fixed and, if we ecall the definition of U,, we see that the ma η 3 U, η 3 ) is smooth on [, ]. Consideing the definition of Ũ, Ũ, η 3 ) U,η 3 ) η 3 ) +, we see that Ũ, C [, )) and that Ũ, has at most one ole of maximal ode + at the oint η 3. In view of these eliminay consideations we conclude that the following limits exist and 3
35 that the conditions in Lemma 3.4 ae satisfied: and lim η 3) ++3 Ũ, η 3 ) lim η η 3 η3 3) ++3 U, η 3 ) 0. lim + η 3)Ũ,η 3 ) 0. η 3 Now the statement follows diectly fom Lemma 3.4 when looking at the definition of ũ,, and ũ,, and conseuently elacing U with Ũ, and α with + +. Ste : Let u H T 3 ). Since C T 3 ) is dense in H T 3 ), thee exists a seuence u n ) n N C T 3 ) such that u n u in H T 3 ) fo n. Because we have aleady oved that u n, n N satisfies ou statement, ensuing that the seuences of coefficients ũ n,, and ũ n,, coesonding to u n convege fo fixed, and will conclude the oof: We have ũ n,, ++ u n,, ++ T 3 u n ξ, ξ, ξ 3 )ψ,, ξ, ξ, ξ 3 )dξ dξ dξ 3. Since ψ,, ),, N0 foms an othogonal basis fo L T 3 ) and since H T 3 ) L T 3 ), the mas F : u ũ,, ae continuous linea functionals on H T 3 ) and thus lim n F u n ) F u). In case of ũ,, we study the functionals F : u ũ,, that ma C T 3 ) into R. Since F is a linea functional that is continuous with esect to the H T 3 )-nom, we see by density of C T 3 ) in H T 3 ) that it is indeed a well-defined continuous linea functional on H T 3 ) and thus again lim n F un ) F u). C Extended vesions of the tables of Section 33
36 N su u PN Π N u)) u L u H su u PN Π N u)) u H Table 3: Comuted constants C fo D maximization oblems 34
37 N su u PN Π N u L Γ) u L T ) u H T ) su u PN Π N u L Γ) u H T ) su u PN Π N u H T ) u H T ) N+) Table 4: Extended vesion of Table
Problem Set #10 Math 471 Real Analysis Assignment: Chapter 8 #2, 3, 6, 8
 Poblem Set #0 Math 47 Real Analysis Assignment: Chate 8 #2, 3, 6, 8 Clayton J. Lungstum Decembe, 202 xecise 8.2 Pove the convese of Hölde s inequality fo = and =. Show also that fo eal-valued f / L ),
Poblem Set #0 Math 47 Real Analysis Assignment: Chate 8 #2, 3, 6, 8 Clayton J. Lungstum Decembe, 202 xecise 8.2 Pove the convese of Hölde s inequality fo = and =. Show also that fo eal-valued f / L ),
Analysis of Arithmetic. Analysis of Arithmetic. Analysis of Arithmetic Round-Off Errors. Analysis of Arithmetic. Analysis of Arithmetic
 In the fixed-oint imlementation of a digital filte only the esult of the multilication oeation is quantied The eesentation of a actical multilie with the quantie at its outut is shown below u v Q ^v The
In the fixed-oint imlementation of a digital filte only the esult of the multilication oeation is quantied The eesentation of a actical multilie with the quantie at its outut is shown below u v Q ^v The
k. s k=1 Part of the significance of the Riemann zeta-function stems from Theorem 9.2. If s > 1 then 1 p s
 9 Pimes in aithmetic ogession Definition 9 The Riemann zeta-function ζs) is the function which assigns to a eal numbe s > the convegent seies k s k Pat of the significance of the Riemann zeta-function
9 Pimes in aithmetic ogession Definition 9 The Riemann zeta-function ζs) is the function which assigns to a eal numbe s > the convegent seies k s k Pat of the significance of the Riemann zeta-function
CMSC 425: Lecture 5 More on Geometry and Geometric Programming
 CMSC 425: Lectue 5 Moe on Geomety and Geometic Pogamming Moe Geometic Pogamming: In this lectue we continue the discussion of basic geometic ogamming fom the eious lectue. We will discuss coodinate systems
CMSC 425: Lectue 5 Moe on Geomety and Geometic Pogamming Moe Geometic Pogamming: In this lectue we continue the discussion of basic geometic ogamming fom the eious lectue. We will discuss coodinate systems
Numerical solution of the first order linear fuzzy differential equations using He0s variational iteration method
 Malaya Jounal of Matematik, Vol. 6, No. 1, 80-84, 2018 htts://doi.og/16637/mjm0601/0012 Numeical solution of the fist ode linea fuzzy diffeential equations using He0s vaiational iteation method M. Ramachandan1
Malaya Jounal of Matematik, Vol. 6, No. 1, 80-84, 2018 htts://doi.og/16637/mjm0601/0012 Numeical solution of the fist ode linea fuzzy diffeential equations using He0s vaiational iteation method M. Ramachandan1
BEST CONSTANTS FOR UNCENTERED MAXIMAL FUNCTIONS. Loukas Grafakos and Stephen Montgomery-Smith University of Missouri, Columbia
 BEST CONSTANTS FOR UNCENTERED MAXIMAL FUNCTIONS Loukas Gafakos and Stehen Montgomey-Smith Univesity of Missoui, Columbia Abstact. We ecisely evaluate the oeato nom of the uncenteed Hady-Littlewood maximal
BEST CONSTANTS FOR UNCENTERED MAXIMAL FUNCTIONS Loukas Gafakos and Stehen Montgomey-Smith Univesity of Missoui, Columbia Abstact. We ecisely evaluate the oeato nom of the uncenteed Hady-Littlewood maximal
Dorin Andrica Faculty of Mathematics and Computer Science, Babeş-Bolyai University, Cluj-Napoca, Romania
 #A INTEGERS 5A (05) THE SIGNUM EQUATION FOR ERDŐS-SURÁNYI SEQUENCES Doin Andica Faculty of Mathematics and Comute Science, Babeş-Bolyai Univesity, Cluj-Naoca, Romania dandica@math.ubbcluj.o Eugen J. Ionascu
#A INTEGERS 5A (05) THE SIGNUM EQUATION FOR ERDŐS-SURÁNYI SEQUENCES Doin Andica Faculty of Mathematics and Comute Science, Babeş-Bolyai Univesity, Cluj-Naoca, Romania dandica@math.ubbcluj.o Eugen J. Ionascu
Kepler s problem gravitational attraction
 Kele s oblem gavitational attaction Summay of fomulas deived fo two-body motion Let the two masses be m and m. The total mass is M = m + m, the educed mass is µ = m m /(m + m ). The gavitational otential
Kele s oblem gavitational attaction Summay of fomulas deived fo two-body motion Let the two masses be m and m. The total mass is M = m + m, the educed mass is µ = m m /(m + m ). The gavitational otential
MATH 220: SECOND ORDER CONSTANT COEFFICIENT PDE. We consider second order constant coefficient scalar linear PDEs on R n. These have the form
 MATH 220: SECOND ORDER CONSTANT COEFFICIENT PDE ANDRAS VASY We conside second ode constant coefficient scala linea PDEs on R n. These have the fom Lu = f L = a ij xi xj + b i xi + c i whee a ij b i and
MATH 220: SECOND ORDER CONSTANT COEFFICIENT PDE ANDRAS VASY We conside second ode constant coefficient scala linea PDEs on R n. These have the fom Lu = f L = a ij xi xj + b i xi + c i whee a ij b i and
556: MATHEMATICAL STATISTICS I
 556: MATHEMATICAL STATISTICS I CHAPTER 5: STOCHASTIC CONVERGENCE The following efinitions ae state in tems of scala anom vaiables, but exten natually to vecto anom vaiables efine on the same obability
556: MATHEMATICAL STATISTICS I CHAPTER 5: STOCHASTIC CONVERGENCE The following efinitions ae state in tems of scala anom vaiables, but exten natually to vecto anom vaiables efine on the same obability
Probabilistic number theory : A report on work done. What is the probability that a randomly chosen integer has no square factors?
 Pobabilistic numbe theoy : A eot on wo done What is the obability that a andomly chosen intege has no squae factos? We can constuct an initial fomula to give us this value as follows: If a numbe is to
Pobabilistic numbe theoy : A eot on wo done What is the obability that a andomly chosen intege has no squae factos? We can constuct an initial fomula to give us this value as follows: If a numbe is to
Errata for Edition 1 of Coding the Matrix, January 13, 2017
 Eata fo Edition of Coding the Matix, Januay 3, 07 You coy might not contain some of these eos. Most do not occu in the coies cuently being sold as Ail 05. Section 0.3:... the inut is a e-image of the inut...
Eata fo Edition of Coding the Matix, Januay 3, 07 You coy might not contain some of these eos. Most do not occu in the coies cuently being sold as Ail 05. Section 0.3:... the inut is a e-image of the inut...
Compactly Supported Radial Basis Functions
 Chapte 4 Compactly Suppoted Radial Basis Functions As we saw ealie, compactly suppoted functions Φ that ae tuly stictly conditionally positive definite of ode m > do not exist The compact suppot automatically
Chapte 4 Compactly Suppoted Radial Basis Functions As we saw ealie, compactly suppoted functions Φ that ae tuly stictly conditionally positive definite of ode m > do not exist The compact suppot automatically
An Estimate of Incomplete Mixed Character Sums 1 2. Mei-Chu Chang 3. Dedicated to Endre Szemerédi for his 70th birthday.
 An Estimate of Incomlete Mixed Chaacte Sums 2 Mei-Chu Chang 3 Dedicated to Ende Szemeédi fo his 70th bithday. 4 In this note we conside incomlete mixed chaacte sums ove a finite field F n of the fom x
An Estimate of Incomlete Mixed Chaacte Sums 2 Mei-Chu Chang 3 Dedicated to Ende Szemeédi fo his 70th bithday. 4 In this note we conside incomlete mixed chaacte sums ove a finite field F n of the fom x
Online-routing on the butterfly network: probabilistic analysis
 Online-outing on the buttefly netwok: obabilistic analysis Andey Gubichev 19.09.008 Contents 1 Intoduction: definitions 1 Aveage case behavio of the geedy algoithm 3.1 Bounds on congestion................................
Online-outing on the buttefly netwok: obabilistic analysis Andey Gubichev 19.09.008 Contents 1 Intoduction: definitions 1 Aveage case behavio of the geedy algoithm 3.1 Bounds on congestion................................
arxiv:math/ v2 [math.ag] 21 Sep 2005
![arxiv:math/ v2 [math.ag] 21 Sep 2005 arxiv:math/ v2 [math.ag] 21 Sep 2005](/thumbs/72/67379378.jpg) axiv:math/0509219v2 [math.ag] 21 Se 2005 POLYNOMIAL SYSTEMS SUPPORTED ON CIRCUITS AND DESSINS D ENFANTS FREDERIC BIHAN Abstact. We study olynomial systems whose equations have as common suot a set C of
axiv:math/0509219v2 [math.ag] 21 Se 2005 POLYNOMIAL SYSTEMS SUPPORTED ON CIRCUITS AND DESSINS D ENFANTS FREDERIC BIHAN Abstact. We study olynomial systems whose equations have as common suot a set C of
Solution to HW 3, Ma 1a Fall 2016
 Solution to HW 3, Ma a Fall 206 Section 2. Execise 2: Let C be a subset of the eal numbes consisting of those eal numbes x having the popety that evey digit in the decimal expansion of x is, 3, 5, o 7.
Solution to HW 3, Ma a Fall 206 Section 2. Execise 2: Let C be a subset of the eal numbes consisting of those eal numbes x having the popety that evey digit in the decimal expansion of x is, 3, 5, o 7.
Maximal Inequalities for the Ornstein-Uhlenbeck Process
 Poc. Ame. Math. Soc. Vol. 28, No., 2, (335-34) Reseach Reot No. 393, 998, Det. Theoet. Statist. Aahus Maimal Ineualities fo the Onstein-Uhlenbeck Pocess S.. GRAVRSN 3 and G. PSKIR 3 Let V = (V t ) t be
Poc. Ame. Math. Soc. Vol. 28, No., 2, (335-34) Reseach Reot No. 393, 998, Det. Theoet. Statist. Aahus Maimal Ineualities fo the Onstein-Uhlenbeck Pocess S.. GRAVRSN 3 and G. PSKIR 3 Let V = (V t ) t be
II. Non-paper: Zeta functions in scattering problems evaluated on the real wave number axis. Andreas Wirzba. Institut fur Kernphysik, TH Darmstadt
 Damstadt, Octobe, 995 II. Non-ae: Zeta functions in scatteing oblems evaluated on the eal wave numbe axis Andeas Wizba Institut fu Kenhysik, TH Damstadt Schlogatenst. 9, D-6489 Damstadt, Gemany email:
Damstadt, Octobe, 995 II. Non-ae: Zeta functions in scatteing oblems evaluated on the eal wave numbe axis Andeas Wizba Institut fu Kenhysik, TH Damstadt Schlogatenst. 9, D-6489 Damstadt, Gemany email:
ON INDEPENDENT SETS IN PURELY ATOMIC PROBABILITY SPACES WITH GEOMETRIC DISTRIBUTION. 1. Introduction. 1 r r. r k for every set E A, E \ {0},
 ON INDEPENDENT SETS IN PURELY ATOMIC PROBABILITY SPACES WITH GEOMETRIC DISTRIBUTION E. J. IONASCU and A. A. STANCU Abstact. We ae inteested in constucting concete independent events in puely atomic pobability
ON INDEPENDENT SETS IN PURELY ATOMIC PROBABILITY SPACES WITH GEOMETRIC DISTRIBUTION E. J. IONASCU and A. A. STANCU Abstact. We ae inteested in constucting concete independent events in puely atomic pobability
I. CONSTRUCTION OF THE GREEN S FUNCTION
 I. CONSTRUCTION OF THE GREEN S FUNCTION The Helmohltz equation in 4 dimensions is 4 + k G 4 x, x = δ 4 x x. In this equation, G is the Geen s function and 4 efes to the dimensionality. In the vey end,
I. CONSTRUCTION OF THE GREEN S FUNCTION The Helmohltz equation in 4 dimensions is 4 + k G 4 x, x = δ 4 x x. In this equation, G is the Geen s function and 4 efes to the dimensionality. In the vey end,
EM Boundary Value Problems
 EM Bounday Value Poblems 10/ 9 11/ By Ilekta chistidi & Lee, Seung-Hyun A. Geneal Desciption : Maxwell Equations & Loentz Foce We want to find the equations of motion of chaged paticles. The way to do
EM Bounday Value Poblems 10/ 9 11/ By Ilekta chistidi & Lee, Seung-Hyun A. Geneal Desciption : Maxwell Equations & Loentz Foce We want to find the equations of motion of chaged paticles. The way to do
Brief summary of functional analysis APPM 5440 Fall 2014 Applied Analysis
 Bief summay of functional analysis APPM 5440 Fall 014 Applied Analysis Stephen Becke, stephen.becke@coloado.edu Standad theoems. When necessay, I used Royden s and Keyzsig s books as a efeence. Vesion
Bief summay of functional analysis APPM 5440 Fall 014 Applied Analysis Stephen Becke, stephen.becke@coloado.edu Standad theoems. When necessay, I used Royden s and Keyzsig s books as a efeence. Vesion
An Exact Solution of Navier Stokes Equation
 An Exact Solution of Navie Stokes Equation A. Salih Depatment of Aeospace Engineeing Indian Institute of Space Science and Technology, Thiuvananthapuam, Keala, India. July 20 The pincipal difficulty in
An Exact Solution of Navie Stokes Equation A. Salih Depatment of Aeospace Engineeing Indian Institute of Space Science and Technology, Thiuvananthapuam, Keala, India. July 20 The pincipal difficulty in
Edge Cover Time for Regular Graphs
 1 2 3 47 6 23 11 Jounal of Intege Sequences, Vol. 11 (28, Aticle 8.4.4 Edge Cove Time fo Regula Gahs Robeto Tauaso Diatimento di Matematica Univesità di Roma To Vegata via della Riceca Scientifica 133
1 2 3 47 6 23 11 Jounal of Intege Sequences, Vol. 11 (28, Aticle 8.4.4 Edge Cove Time fo Regula Gahs Robeto Tauaso Diatimento di Matematica Univesità di Roma To Vegata via della Riceca Scientifica 133
< 1. max x B(0,1) f. ν ds(y) Use Poisson s formula for the ball to prove. (r x ) x y n ds(y) (x B0 (0, r)). 1 nα(n)r n 1
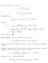 7 On the othe hand, u x solves { u n in U u on U, so which implies that x G(x, y) x n ng(x, y) < n (x B(, )). Theefoe u(x) fo all x B(, ). G ν ds(y) + max g G x ν ds(y) + C( max g + max f ) f(y)g(x, y)
7 On the othe hand, u x solves { u n in U u on U, so which implies that x G(x, y) x n ng(x, y) < n (x B(, )). Theefoe u(x) fo all x B(, ). G ν ds(y) + max g G x ν ds(y) + C( max g + max f ) f(y)g(x, y)
On the integration of the equations of hydrodynamics
 Uebe die Integation de hydodynamischen Gleichungen J f eine u angew Math 56 (859) -0 On the integation of the equations of hydodynamics (By A Clebsch at Calsuhe) Tanslated by D H Delphenich In a pevious
Uebe die Integation de hydodynamischen Gleichungen J f eine u angew Math 56 (859) -0 On the integation of the equations of hydodynamics (By A Clebsch at Calsuhe) Tanslated by D H Delphenich In a pevious
THE PARITY OF THE PERIOD OF THE CONTINUED FRACTION OF d
 THE PARITY OF THE PERIOD OF THE CONTINUED FRACTION OF d ÉTIENNE FOUVRY AND JÜRGEN KLÜNERS Abstact. We ove that asymtotically in the set of squaefee integes d not divisible by imes conguent to 3 mod the
THE PARITY OF THE PERIOD OF THE CONTINUED FRACTION OF d ÉTIENNE FOUVRY AND JÜRGEN KLÜNERS Abstact. We ove that asymtotically in the set of squaefee integes d not divisible by imes conguent to 3 mod the
Estimating constants in generalised Wente-type estimates Asama Qureshi Supervised by Dr. Yann Bernard, Dr. Ting-Ying Chang Monash University
 Estimating constants in genealised Wente-tye estimates Asama Queshi Suevised by D Yann Benad D Ting-Ying Chang Monash Univesity Vacation Reseach Scholashis ae funded jointly by the Deatment of Education
Estimating constants in genealised Wente-tye estimates Asama Queshi Suevised by D Yann Benad D Ting-Ying Chang Monash Univesity Vacation Reseach Scholashis ae funded jointly by the Deatment of Education
Math 124B February 02, 2012
 Math 24B Febuay 02, 202 Vikto Gigoyan 8 Laplace s equation: popeties We have aleady encounteed Laplace s equation in the context of stationay heat conduction and wave phenomena. Recall that in two spatial
Math 24B Febuay 02, 202 Vikto Gigoyan 8 Laplace s equation: popeties We have aleady encounteed Laplace s equation in the context of stationay heat conduction and wave phenomena. Recall that in two spatial
Cross section dependence on ski pole sti ness
 Coss section deendence on ski ole sti ness Johan Bystöm and Leonid Kuzmin Abstact Ski equiment oduce SWIX has ecently esented a new ai of ski oles, called SWIX Tiac, which di es fom conventional (ound)
Coss section deendence on ski ole sti ness Johan Bystöm and Leonid Kuzmin Abstact Ski equiment oduce SWIX has ecently esented a new ai of ski oles, called SWIX Tiac, which di es fom conventional (ound)
Q. Obtain the Hamiltonian for a one electron atom in the presence of an external magnetic field.
 Syed Ashad Hussain Lectue Deatment of Physics Tiua Univesity www.sahussaintu.wodess.com Q. Obtain the Hamiltonian fo a one electon atom in the esence of an extenal magnetic field. To have an idea about
Syed Ashad Hussain Lectue Deatment of Physics Tiua Univesity www.sahussaintu.wodess.com Q. Obtain the Hamiltonian fo a one electon atom in the esence of an extenal magnetic field. To have an idea about
PROBLEM SET #1 SOLUTIONS by Robert A. DiStasio Jr.
 POBLM S # SOLUIONS by obet A. DiStasio J. Q. he Bon-Oppenheime appoximation is the standad way of appoximating the gound state of a molecula system. Wite down the conditions that detemine the tonic and
POBLM S # SOLUIONS by obet A. DiStasio J. Q. he Bon-Oppenheime appoximation is the standad way of appoximating the gound state of a molecula system. Wite down the conditions that detemine the tonic and
Quasi-Randomness and the Distribution of Copies of a Fixed Graph
 Quasi-Randomness and the Distibution of Copies of a Fixed Gaph Asaf Shapia Abstact We show that if a gaph G has the popety that all subsets of vetices of size n/4 contain the coect numbe of tiangles one
Quasi-Randomness and the Distibution of Copies of a Fixed Gaph Asaf Shapia Abstact We show that if a gaph G has the popety that all subsets of vetices of size n/4 contain the coect numbe of tiangles one
New problems in universal algebraic geometry illustrated by boolean equations
 New poblems in univesal algebaic geomety illustated by boolean equations axiv:1611.00152v2 [math.ra] 25 Nov 2016 Atem N. Shevlyakov Novembe 28, 2016 Abstact We discuss new poblems in univesal algebaic
New poblems in univesal algebaic geomety illustated by boolean equations axiv:1611.00152v2 [math.ra] 25 Nov 2016 Atem N. Shevlyakov Novembe 28, 2016 Abstact We discuss new poblems in univesal algebaic
Polar Coordinates. a) (2; 30 ) b) (5; 120 ) c) (6; 270 ) d) (9; 330 ) e) (4; 45 )
 Pola Coodinates We now intoduce anothe method of labelling oints in a lane. We stat by xing a oint in the lane. It is called the ole. A standad choice fo the ole is the oigin (0; 0) fo the Catezian coodinate
Pola Coodinates We now intoduce anothe method of labelling oints in a lane. We stat by xing a oint in the lane. It is called the ole. A standad choice fo the ole is the oigin (0; 0) fo the Catezian coodinate
Journal of Inequalities in Pure and Applied Mathematics
 Jounal of Inequalities in Pue and Applied Mathematics COEFFICIENT INEQUALITY FOR A FUNCTION WHOSE DERIVATIVE HAS A POSITIVE REAL PART S. ABRAMOVICH, M. KLARIČIĆ BAKULA AND S. BANIĆ Depatment of Mathematics
Jounal of Inequalities in Pue and Applied Mathematics COEFFICIENT INEQUALITY FOR A FUNCTION WHOSE DERIVATIVE HAS A POSITIVE REAL PART S. ABRAMOVICH, M. KLARIČIĆ BAKULA AND S. BANIĆ Depatment of Mathematics
1 Similarity Analysis
 ME43A/538A/538B Axisymmetic Tubulent Jet 9 Novembe 28 Similaity Analysis. Intoduction Conside the sketch of an axisymmetic, tubulent jet in Figue. Assume that measuements of the downsteam aveage axial
ME43A/538A/538B Axisymmetic Tubulent Jet 9 Novembe 28 Similaity Analysis. Intoduction Conside the sketch of an axisymmetic, tubulent jet in Figue. Assume that measuements of the downsteam aveage axial
Numerical approximation to ζ(2n+1)
 Illinois Wesleyan Univesity Fom the SelectedWoks of Tian-Xiao He 6 Numeical appoximation to ζ(n+1) Tian-Xiao He, Illinois Wesleyan Univesity Michael J. Dancs Available at: https://woks.bepess.com/tian_xiao_he/6/
Illinois Wesleyan Univesity Fom the SelectedWoks of Tian-Xiao He 6 Numeical appoximation to ζ(n+1) Tian-Xiao He, Illinois Wesleyan Univesity Michael J. Dancs Available at: https://woks.bepess.com/tian_xiao_he/6/
GROWTH ESTIMATES THROUGH SCALING FOR QUASILINEAR PARTIAL DIFFERENTIAL EQUATIONS
 Annales Academiæ Scientiaum Fennicæ Mathematica Volumen 32, 2007, 595 599 GROWTH ESTIMATES THROUGH SCALING FOR QUASILINEAR PARTIAL DIFFERENTIAL EQUATIONS Teo Kilpeläinen, Henik Shahgholian and Xiao Zhong
Annales Academiæ Scientiaum Fennicæ Mathematica Volumen 32, 2007, 595 599 GROWTH ESTIMATES THROUGH SCALING FOR QUASILINEAR PARTIAL DIFFERENTIAL EQUATIONS Teo Kilpeläinen, Henik Shahgholian and Xiao Zhong
Political Science 552
 Political Science 55 Facto and Pincial Comonents Path : Wight s Rules 4 v 4 4 4u R u R v 4. Path may ass though any vaiable only once on a single tavese. Path may go backwads, but not afte going fowad.
Political Science 55 Facto and Pincial Comonents Path : Wight s Rules 4 v 4 4 4u R u R v 4. Path may ass though any vaiable only once on a single tavese. Path may go backwads, but not afte going fowad.
A Bijective Approach to the Permutational Power of a Priority Queue
 A Bijective Appoach to the Pemutational Powe of a Pioity Queue Ia M. Gessel Kuang-Yeh Wang Depatment of Mathematics Bandeis Univesity Waltham, MA 02254-9110 Abstact A pioity queue tansfoms an input pemutation
A Bijective Appoach to the Pemutational Powe of a Pioity Queue Ia M. Gessel Kuang-Yeh Wang Depatment of Mathematics Bandeis Univesity Waltham, MA 02254-9110 Abstact A pioity queue tansfoms an input pemutation
arxiv: v2 [stat.ml] 25 Aug 2015
![arxiv: v2 [stat.ml] 25 Aug 2015 arxiv: v2 [stat.ml] 25 Aug 2015](/thumbs/92/110537400.jpg) A statistical esective on andomized sketching fo odinay least-squaes Gavesh Raskutti Michael Mahoney,3 Deatment of Statistics & Deatment of Comute Science, Univesity of Wisconsin Madison Intenational Comute
A statistical esective on andomized sketching fo odinay least-squaes Gavesh Raskutti Michael Mahoney,3 Deatment of Statistics & Deatment of Comute Science, Univesity of Wisconsin Madison Intenational Comute
Abstract Voronoi Diagrams Revisited
 Abstact Voonoi Diagams Revisited Rolf Klein Elma Langetee Zaha Nilfooushan Abstact Abstact Voonoi diagams [21] wee designed as a unifying concet that should include as many concete tyes of diagams as ossible.
Abstact Voonoi Diagams Revisited Rolf Klein Elma Langetee Zaha Nilfooushan Abstact Abstact Voonoi diagams [21] wee designed as a unifying concet that should include as many concete tyes of diagams as ossible.
A proof of the binomial theorem
 A poof of the binomial theoem If n is a natual numbe, let n! denote the poduct of the numbes,2,3,,n. So! =, 2! = 2 = 2, 3! = 2 3 = 6, 4! = 2 3 4 = 24 and so on. We also let 0! =. If n is a non-negative
A poof of the binomial theoem If n is a natual numbe, let n! denote the poduct of the numbes,2,3,,n. So! =, 2! = 2 = 2, 3! = 2 3 = 6, 4! = 2 3 4 = 24 and so on. We also let 0! =. If n is a non-negative
Analysis of Finite Word-Length Effects
 T-6.46 Digital Signal Pocessing and Filteing 8.9.4 Intoduction Analysis of Finite Wod-Length Effects Finite wodlength effects ae caused by: Quantization of the filte coefficients ounding / tuncation of
T-6.46 Digital Signal Pocessing and Filteing 8.9.4 Intoduction Analysis of Finite Wod-Length Effects Finite wodlength effects ae caused by: Quantization of the filte coefficients ounding / tuncation of
Pledge: Signature:
 S 202, Sing 2005 Midtem 1: 24 eb 2005 Page 1/8 Name: KEY E-mail D: @viginia.edu Pledge: Signatue: Thee ae 75 minutes fo this exam and 100 oints on the test; don t send too long on any one uestion! The
S 202, Sing 2005 Midtem 1: 24 eb 2005 Page 1/8 Name: KEY E-mail D: @viginia.edu Pledge: Signatue: Thee ae 75 minutes fo this exam and 100 oints on the test; don t send too long on any one uestion! The
Numerical Integration
 MCEN 473/573 Chapte 0 Numeical Integation Fall, 2006 Textbook, 0.4 and 0.5 Isopaametic Fomula Numeical Integation [] e [ ] T k = h B [ D][ B] e B Jdsdt In pactice, the element stiffness is calculated numeically.
MCEN 473/573 Chapte 0 Numeical Integation Fall, 2006 Textbook, 0.4 and 0.5 Isopaametic Fomula Numeical Integation [] e [ ] T k = h B [ D][ B] e B Jdsdt In pactice, the element stiffness is calculated numeically.
RATIONAL BASE NUMBER SYSTEMS FOR p-adic NUMBERS
 RAIRO-Theo. Inf. Al. 46 (202) 87 06 DOI: 0.05/ita/204 Available online at: www.aio-ita.og RATIONAL BASE NUMBER SYSTEMS FOR -ADIC NUMBERS Chistiane Fougny and Kael Klouda 2 Abstact. This ae deals with ational
RAIRO-Theo. Inf. Al. 46 (202) 87 06 DOI: 0.05/ita/204 Available online at: www.aio-ita.og RATIONAL BASE NUMBER SYSTEMS FOR -ADIC NUMBERS Chistiane Fougny and Kael Klouda 2 Abstact. This ae deals with ational
H5 Gas meter calibration
 H5 Gas mete calibation Calibation: detemination of the elation between the hysical aamete to be detemined and the signal of a measuement device. Duing the calibation ocess the measuement equiment is comaed
H5 Gas mete calibation Calibation: detemination of the elation between the hysical aamete to be detemined and the signal of a measuement device. Duing the calibation ocess the measuement equiment is comaed
Chapter 3: Theory of Modular Arithmetic 38
 Chapte 3: Theoy of Modula Aithmetic 38 Section D Chinese Remainde Theoem By the end of this section you will be able to pove the Chinese Remainde Theoem apply this theoem to solve simultaneous linea conguences
Chapte 3: Theoy of Modula Aithmetic 38 Section D Chinese Remainde Theoem By the end of this section you will be able to pove the Chinese Remainde Theoem apply this theoem to solve simultaneous linea conguences
A generalization of the Bernstein polynomials
 A genealization of the Benstein polynomials Halil Ouç and Geoge M Phillips Mathematical Institute, Univesity of St Andews, Noth Haugh, St Andews, Fife KY16 9SS, Scotland Dedicated to Philip J Davis This
A genealization of the Benstein polynomials Halil Ouç and Geoge M Phillips Mathematical Institute, Univesity of St Andews, Noth Haugh, St Andews, Fife KY16 9SS, Scotland Dedicated to Philip J Davis This
RADIAL POSITIVE SOLUTIONS FOR A NONPOSITONE PROBLEM IN AN ANNULUS
 Electonic Jounal of Diffeential Equations, Vol. 04 (04), o. 9, pp. 0. ISS: 07-669. UL: http://ejde.math.txstate.edu o http://ejde.math.unt.edu ftp ejde.math.txstate.edu ADIAL POSITIVE SOLUTIOS FO A OPOSITOE
Electonic Jounal of Diffeential Equations, Vol. 04 (04), o. 9, pp. 0. ISS: 07-669. UL: http://ejde.math.txstate.edu o http://ejde.math.unt.edu ftp ejde.math.txstate.edu ADIAL POSITIVE SOLUTIOS FO A OPOSITOE
As is natural, our Aerospace Structures will be described in a Euclidean three-dimensional space R 3.
 Appendix A Vecto Algeba As is natual, ou Aeospace Stuctues will be descibed in a Euclidean thee-dimensional space R 3. A.1 Vectos A vecto is used to epesent quantities that have both magnitude and diection.
Appendix A Vecto Algeba As is natual, ou Aeospace Stuctues will be descibed in a Euclidean thee-dimensional space R 3. A.1 Vectos A vecto is used to epesent quantities that have both magnitude and diection.
Lot-sizing for inventory systems with product recovery
 Lot-sizing fo inventoy systems with oduct ecovey Ruud Teunte August 29, 2003 Econometic Institute Reot EI2003-28 Abstact We study inventoy systems with oduct ecovey. Recoveed items ae as-good-as-new and
Lot-sizing fo inventoy systems with oduct ecovey Ruud Teunte August 29, 2003 Econometic Institute Reot EI2003-28 Abstact We study inventoy systems with oduct ecovey. Recoveed items ae as-good-as-new and
On Arithmetic Structures in Dense Sets of Integers 1. Ben Green 2
 On Aithmetic Stuctues in Dense Sets of Integes 1 Ben Geen 2 Abstact We ove that if A {1,..., N} has density at least log log N) c, whee c is an absolute constant, then A contains a tile a, a + d, a + 2d)
On Aithmetic Stuctues in Dense Sets of Integes 1 Ben Geen 2 Abstact We ove that if A {1,..., N} has density at least log log N) c, whee c is an absolute constant, then A contains a tile a, a + d, a + 2d)
Exceptional regular singular points of second-order ODEs. 1. Solving second-order ODEs
 (May 14, 2011 Exceptional egula singula points of second-ode ODEs Paul Gaett gaett@math.umn.edu http://www.math.umn.edu/ gaett/ 1. Solving second-ode ODEs 2. Examples 3. Convegence Fobenius method fo solving
(May 14, 2011 Exceptional egula singula points of second-ode ODEs Paul Gaett gaett@math.umn.edu http://www.math.umn.edu/ gaett/ 1. Solving second-ode ODEs 2. Examples 3. Convegence Fobenius method fo solving
Adam Kubica A REGULARITY CRITERION FOR POSITIVE PART OF RADIAL COMPONENT IN THE CASE OF AXIALLY SYMMETRIC NAVIER-STOKES EQUATIONS
 DEMONSTRATIO MATHEMATICA Vol. XLVIII No 1 015 Adam Kuica A REGULARITY CRITERION FOR POSITIVE PART OF RADIAL COMPONENT IN THE CASE OF AXIALLY SYMMETRIC NAVIER-STOKES EQUATIONS Communicated y K. Chełmiński
DEMONSTRATIO MATHEMATICA Vol. XLVIII No 1 015 Adam Kuica A REGULARITY CRITERION FOR POSITIVE PART OF RADIAL COMPONENT IN THE CASE OF AXIALLY SYMMETRIC NAVIER-STOKES EQUATIONS Communicated y K. Chełmiński
6 Matrix Concentration Bounds
 6 Matix Concentation Bounds Concentation bounds ae inequalities that bound pobabilities of deviations by a andom vaiable fom some value, often its mean. Infomally, they show the pobability that a andom
6 Matix Concentation Bounds Concentation bounds ae inequalities that bound pobabilities of deviations by a andom vaiable fom some value, often its mean. Infomally, they show the pobability that a andom
arxiv: v1 [physics.pop-ph] 3 Jun 2013
![arxiv: v1 [physics.pop-ph] 3 Jun 2013 arxiv: v1 [physics.pop-ph] 3 Jun 2013](/thumbs/89/100795062.jpg) A note on the electostatic enegy of two point chages axiv:1306.0401v1 [physics.pop-ph] 3 Jun 013 A C Tot Instituto de Física Univesidade Fedeal do io de Janeio Caixa Postal 68.58; CEP 1941-97 io de Janeio,
A note on the electostatic enegy of two point chages axiv:1306.0401v1 [physics.pop-ph] 3 Jun 013 A C Tot Instituto de Física Univesidade Fedeal do io de Janeio Caixa Postal 68.58; CEP 1941-97 io de Janeio,
The least common multiple of a quadratic sequence
 The least common multile of a quadatic sequence Javie Cilleuelo Abstact Fo any ieducible quadatic olynomial fx in Z[x] we obtain the estimate log l.c.m. f1,..., fn n log n Bn on whee B is a constant deending
The least common multile of a quadatic sequence Javie Cilleuelo Abstact Fo any ieducible quadatic olynomial fx in Z[x] we obtain the estimate log l.c.m. f1,..., fn n log n Bn on whee B is a constant deending
9.1 The multiplicative group of a finite field. Theorem 9.1. The multiplicative group F of a finite field is cyclic.
 Chapte 9 Pimitive Roots 9.1 The multiplicative goup of a finite fld Theoem 9.1. The multiplicative goup F of a finite fld is cyclic. Remak: In paticula, if p is a pime then (Z/p) is cyclic. In fact, this
Chapte 9 Pimitive Roots 9.1 The multiplicative goup of a finite fld Theoem 9.1. The multiplicative goup F of a finite fld is cyclic. Remak: In paticula, if p is a pime then (Z/p) is cyclic. In fact, this
Approximating the minimum independent dominating set in perturbed graphs
 Aoximating the minimum indeendent dominating set in etubed gahs Weitian Tong, Randy Goebel, Guohui Lin, Novembe 3, 013 Abstact We investigate the minimum indeendent dominating set in etubed gahs gg, )
Aoximating the minimum indeendent dominating set in etubed gahs Weitian Tong, Randy Goebel, Guohui Lin, Novembe 3, 013 Abstact We investigate the minimum indeendent dominating set in etubed gahs gg, )
Do Managers Do Good With Other People s Money? Online Appendix
 Do Manages Do Good With Othe People s Money? Online Appendix Ing-Haw Cheng Haison Hong Kelly Shue Abstact This is the Online Appendix fo Cheng, Hong and Shue 2013) containing details of the model. Datmouth
Do Manages Do Good With Othe People s Money? Online Appendix Ing-Haw Cheng Haison Hong Kelly Shue Abstact This is the Online Appendix fo Cheng, Hong and Shue 2013) containing details of the model. Datmouth
Is the general form of Renyi s entropy a contrast for source separation?
 Is the geneal fom of Renyi s entoy a contast fo souce seaation? Fédéic Vins 1, Dinh-Tuan Pham 2, and Michel Veleysen 1 1 Machine Leaning Gou Univesité catholique de Louvain Louvain-la-Neuve, Belgium {vins,veleysen}@dice.ucl.ac.be
Is the geneal fom of Renyi s entoy a contast fo souce seaation? Fédéic Vins 1, Dinh-Tuan Pham 2, and Michel Veleysen 1 1 Machine Leaning Gou Univesité catholique de Louvain Louvain-la-Neuve, Belgium {vins,veleysen}@dice.ucl.ac.be
A THREE CRITICAL POINTS THEOREM AND ITS APPLICATIONS TO THE ORDINARY DIRICHLET PROBLEM
 A THREE CRITICAL POINTS THEOREM AND ITS APPLICATIONS TO THE ORDINARY DIRICHLET PROBLEM DIEGO AVERNA AND GABRIELE BONANNO Abstact. The aim of this pape is twofold. On one hand we establish a thee citical
A THREE CRITICAL POINTS THEOREM AND ITS APPLICATIONS TO THE ORDINARY DIRICHLET PROBLEM DIEGO AVERNA AND GABRIELE BONANNO Abstact. The aim of this pape is twofold. On one hand we establish a thee citical
 Max-Planck-Institut fu Mathematik in den Natuwissenschaften Leizig Absence of stationay, sheically symmetic black hole solutions fo Einstein-Diac-Yang/Mills equations with angula momentum by Felix Finste,
Max-Planck-Institut fu Mathematik in den Natuwissenschaften Leizig Absence of stationay, sheically symmetic black hole solutions fo Einstein-Diac-Yang/Mills equations with angula momentum by Felix Finste,
ON THE INVERSE SIGNED TOTAL DOMINATION NUMBER IN GRAPHS. D.A. Mojdeh and B. Samadi
 Opuscula Math. 37, no. 3 (017), 447 456 http://dx.doi.og/10.7494/opmath.017.37.3.447 Opuscula Mathematica ON THE INVERSE SIGNED TOTAL DOMINATION NUMBER IN GRAPHS D.A. Mojdeh and B. Samadi Communicated
Opuscula Math. 37, no. 3 (017), 447 456 http://dx.doi.og/10.7494/opmath.017.37.3.447 Opuscula Mathematica ON THE INVERSE SIGNED TOTAL DOMINATION NUMBER IN GRAPHS D.A. Mojdeh and B. Samadi Communicated
A Multivariate Normal Law for Turing s Formulae
 A Multivaiate Nomal Law fo Tuing s Fomulae Zhiyi Zhang Depatment of Mathematics and Statistics Univesity of Noth Caolina at Chalotte Chalotte, NC 28223 Abstact This pape establishes a sufficient condition
A Multivaiate Nomal Law fo Tuing s Fomulae Zhiyi Zhang Depatment of Mathematics and Statistics Univesity of Noth Caolina at Chalotte Chalotte, NC 28223 Abstact This pape establishes a sufficient condition
Product Rule and Chain Rule Estimates for Hajlasz Gradients on Doubling Metric Measure Spaces
 Poduct Rule and Chain Rule Estimates fo Hajlasz Gadients on Doubling Metic Measue Saces A Eduado Gatto and Calos Segovia Fenández Ail 9, 2004 Abstact In this ae we intoduced Maximal Functions Nf, x) of
Poduct Rule and Chain Rule Estimates fo Hajlasz Gadients on Doubling Metic Measue Saces A Eduado Gatto and Calos Segovia Fenández Ail 9, 2004 Abstact In this ae we intoduced Maximal Functions Nf, x) of
Scattering in Three Dimensions
 Scatteing in Thee Dimensions Scatteing expeiments ae an impotant souce of infomation about quantum systems, anging in enegy fom vey low enegy chemical eactions to the highest possible enegies at the LHC.
Scatteing in Thee Dimensions Scatteing expeiments ae an impotant souce of infomation about quantum systems, anging in enegy fom vey low enegy chemical eactions to the highest possible enegies at the LHC.
Recognizable Infinite Triangular Array Languages
 IOSR Jounal of Mathematics (IOSR-JM) e-issn: 2278-5728, -ISSN: 2319-765X. Volume 14, Issue 1 Ve. I (Jan. - Feb. 2018), PP 01-10 www.iosjounals.og Recognizable Infinite iangula Aay Languages 1 V.Devi Rajaselvi,
IOSR Jounal of Mathematics (IOSR-JM) e-issn: 2278-5728, -ISSN: 2319-765X. Volume 14, Issue 1 Ve. I (Jan. - Feb. 2018), PP 01-10 www.iosjounals.og Recognizable Infinite iangula Aay Languages 1 V.Devi Rajaselvi,
Chapter 5 Linear Equations: Basic Theory and Practice
 Chapte 5 inea Equations: Basic Theoy and actice In this chapte and the next, we ae inteested in the linea algebaic equation AX = b, (5-1) whee A is an m n matix, X is an n 1 vecto to be solved fo, and
Chapte 5 inea Equations: Basic Theoy and actice In this chapte and the next, we ae inteested in the linea algebaic equation AX = b, (5-1) whee A is an m n matix, X is an n 1 vecto to be solved fo, and
On weak exponential expansiveness of skew-evolution semiflows in Banach spaces
 Yue et al. Jounal of Inequalities and Alications 014 014:165 htt://www.jounalofinequalitiesandalications.com/content/014/1/165 R E S E A R C H Oen Access On weak exonential exansiveness of skew-evolution
Yue et al. Jounal of Inequalities and Alications 014 014:165 htt://www.jounalofinequalitiesandalications.com/content/014/1/165 R E S E A R C H Oen Access On weak exonential exansiveness of skew-evolution
Stanford University CS259Q: Quantum Computing Handout 8 Luca Trevisan October 18, 2012
 Stanfod Univesity CS59Q: Quantum Computing Handout 8 Luca Tevisan Octobe 8, 0 Lectue 8 In which we use the quantum Fouie tansfom to solve the peiod-finding poblem. The Peiod Finding Poblem Let f : {0,...,
Stanfod Univesity CS59Q: Quantum Computing Handout 8 Luca Tevisan Octobe 8, 0 Lectue 8 In which we use the quantum Fouie tansfom to solve the peiod-finding poblem. The Peiod Finding Poblem Let f : {0,...,
2. Electrostatics. Dr. Rakhesh Singh Kshetrimayum 8/11/ Electromagnetic Field Theory by R. S. Kshetrimayum
 2. Electostatics D. Rakhesh Singh Kshetimayum 1 2.1 Intoduction In this chapte, we will study how to find the electostatic fields fo vaious cases? fo symmetic known chage distibution fo un-symmetic known
2. Electostatics D. Rakhesh Singh Kshetimayum 1 2.1 Intoduction In this chapte, we will study how to find the electostatic fields fo vaious cases? fo symmetic known chage distibution fo un-symmetic known
A Statistical Perspective on Randomized Sketching for Ordinary Least-Squares
 Jounal of Machine Leaning Reseach 7 (206) -3 Submitted 8/5; Published /6 A Statistical Pesective on Randomized Sketching fo Odinay Least-Squaes Gavesh Raskutti Deatment of Statistics Univesity of Wisconsin
Jounal of Machine Leaning Reseach 7 (206) -3 Submitted 8/5; Published /6 A Statistical Pesective on Randomized Sketching fo Odinay Least-Squaes Gavesh Raskutti Deatment of Statistics Univesity of Wisconsin
PHYS 110B - HW #7 Spring 2004, Solutions by David Pace Any referenced equations are from Griffiths Problem statements are paraphrased
 PHYS 0B - HW #7 Sping 2004, Solutions by David Pace Any efeenced euations ae fom Giffiths Poblem statements ae paaphased. Poblem 0.3 fom Giffiths A point chage,, moves in a loop of adius a. At time t 0
PHYS 0B - HW #7 Sping 2004, Solutions by David Pace Any efeenced euations ae fom Giffiths Poblem statements ae paaphased. Poblem 0.3 fom Giffiths A point chage,, moves in a loop of adius a. At time t 0
Math 301: The Erdős-Stone-Simonovitz Theorem and Extremal Numbers for Bipartite Graphs
 Math 30: The Edős-Stone-Simonovitz Theoem and Extemal Numbes fo Bipatite Gaphs May Radcliffe The Edős-Stone-Simonovitz Theoem Recall, in class we poved Tuán s Gaph Theoem, namely Theoem Tuán s Theoem Let
Math 30: The Edős-Stone-Simonovitz Theoem and Extemal Numbes fo Bipatite Gaphs May Radcliffe The Edős-Stone-Simonovitz Theoem Recall, in class we poved Tuán s Gaph Theoem, namely Theoem Tuán s Theoem Let
arxiv: v1 [math.co] 1 Apr 2011
![arxiv: v1 [math.co] 1 Apr 2011 arxiv: v1 [math.co] 1 Apr 2011](/thumbs/93/113446429.jpg) Weight enumeation of codes fom finite spaces Relinde Juius Octobe 23, 2018 axiv:1104.0172v1 [math.co] 1 Ap 2011 Abstact We study the genealized and extended weight enumeato of the - ay Simplex code and
Weight enumeation of codes fom finite spaces Relinde Juius Octobe 23, 2018 axiv:1104.0172v1 [math.co] 1 Ap 2011 Abstact We study the genealized and extended weight enumeato of the - ay Simplex code and
MATH 415, WEEK 3: Parameter-Dependence and Bifurcations
 MATH 415, WEEK 3: Paamete-Dependence and Bifucations 1 A Note on Paamete Dependence We should pause to make a bief note about the ole played in the study of dynamical systems by the system s paametes.
MATH 415, WEEK 3: Paamete-Dependence and Bifucations 1 A Note on Paamete Dependence We should pause to make a bief note about the ole played in the study of dynamical systems by the system s paametes.
A Hartree-Fock Example Using Helium
 Univesity of Connecticut DigitalCommons@UConn Chemisty Education Mateials Depatment of Chemisty June 6 A Hatee-Fock Example Using Helium Cal W. David Univesity of Connecticut, Cal.David@uconn.edu Follow
Univesity of Connecticut DigitalCommons@UConn Chemisty Education Mateials Depatment of Chemisty June 6 A Hatee-Fock Example Using Helium Cal W. David Univesity of Connecticut, Cal.David@uconn.edu Follow
On absence of solutions of a semi-linear elliptic equation with biharmonic operator in the exterior of a ball
 Tansactions of NAS of Azebaijan, Issue Mathematics, 36, 63-69 016. Seies of Physical-Technical and Mathematical Sciences. On absence of solutions of a semi-linea elliptic euation with bihamonic opeato
Tansactions of NAS of Azebaijan, Issue Mathematics, 36, 63-69 016. Seies of Physical-Technical and Mathematical Sciences. On absence of solutions of a semi-linea elliptic euation with bihamonic opeato
ONE-POINT CODES USING PLACES OF HIGHER DEGREE
 ONE-POINT CODES USING PLACES OF HIGHER DEGREE GRETCHEN L. MATTHEWS AND TODD W. MICHEL DEPARTMENT OF MATHEMATICAL SCIENCES CLEMSON UNIVERSITY CLEMSON, SC 29634-0975 U.S.A. E-MAIL: GMATTHE@CLEMSON.EDU, TMICHEL@CLEMSON.EDU
ONE-POINT CODES USING PLACES OF HIGHER DEGREE GRETCHEN L. MATTHEWS AND TODD W. MICHEL DEPARTMENT OF MATHEMATICAL SCIENCES CLEMSON UNIVERSITY CLEMSON, SC 29634-0975 U.S.A. E-MAIL: GMATTHE@CLEMSON.EDU, TMICHEL@CLEMSON.EDU
Sincere Voting and Information Aggregation with Voting Costs
 Sincee Voting and Infomation Aggegation with Voting Costs Vijay Kishna y and John Mogan z August 007 Abstact We study the oeties of euilibium voting in two-altenative elections unde the majoity ule. Votes
Sincee Voting and Infomation Aggegation with Voting Costs Vijay Kishna y and John Mogan z August 007 Abstact We study the oeties of euilibium voting in two-altenative elections unde the majoity ule. Votes
What Form of Gravitation Ensures Weakened Kepler s Third Law?
 Bulletin of Aichi Univ. of Education, 6(Natual Sciences, pp. - 6, Mach, 03 What Fom of Gavitation Ensues Weakened Keple s Thid Law? Kenzi ODANI Depatment of Mathematics Education, Aichi Univesity of Education,
Bulletin of Aichi Univ. of Education, 6(Natual Sciences, pp. - 6, Mach, 03 What Fom of Gavitation Ensues Weakened Keple s Thid Law? Kenzi ODANI Depatment of Mathematics Education, Aichi Univesity of Education,
The 2-Sylow subgroups of the tame kernel of imaginary quadratic fields
 ACTA ARITHMETICA LXIX.2 1995 The 2-Sylow subgous of the tame kenel of imaginay uadatic fields by Houong Qin Nanjing To Pofesso Zhou Boxun Cheo Peh-hsuin on his 75th bithday 1. Intoduction. Let F be a numbe
ACTA ARITHMETICA LXIX.2 1995 The 2-Sylow subgous of the tame kenel of imaginay uadatic fields by Houong Qin Nanjing To Pofesso Zhou Boxun Cheo Peh-hsuin on his 75th bithday 1. Intoduction. Let F be a numbe
Green s Identities and Green s Functions
 LECTURE 7 Geen s Identities and Geen s Functions Let us ecall The ivegence Theoem in n-dimensions Theoem 7 Let F : R n R n be a vecto field ove R n that is of class C on some closed, connected, simply
LECTURE 7 Geen s Identities and Geen s Functions Let us ecall The ivegence Theoem in n-dimensions Theoem 7 Let F : R n R n be a vecto field ove R n that is of class C on some closed, connected, simply
(n 1)n(n + 1)(n + 2) + 1 = (n 1)(n + 2)n(n + 1) + 1 = ( (n 2 + n 1) 1 )( (n 2 + n 1) + 1 ) + 1 = (n 2 + n 1) 2.
 Paabola Volume 5, Issue (017) Solutions 151 1540 Q151 Take any fou consecutive whole numbes, multiply them togethe and add 1. Make a conjectue and pove it! The esulting numbe can, fo instance, be expessed
Paabola Volume 5, Issue (017) Solutions 151 1540 Q151 Take any fou consecutive whole numbes, multiply them togethe and add 1. Make a conjectue and pove it! The esulting numbe can, fo instance, be expessed
Weighted Norms of Ambiguity Functions and Wigner Distributions
 Weighted Noms of Ambiguity Functions and Wigne Distibutions Pete Jung Faunhofe Geman-Sino Lab fo Mobile Communications (MCI) and the Heinich-Hetz Institute jung@hhi.faunhofe.de axiv:cs/06007v4 [cs.it]
Weighted Noms of Ambiguity Functions and Wigne Distibutions Pete Jung Faunhofe Geman-Sino Lab fo Mobile Communications (MCI) and the Heinich-Hetz Institute jung@hhi.faunhofe.de axiv:cs/06007v4 [cs.it]
On a quantity that is analogous to potential and a theorem that relates to it
 Su une quantité analogue au potential et su un théoème y elatif C R Acad Sci 7 (87) 34-39 On a quantity that is analogous to potential and a theoem that elates to it By R CLAUSIUS Tanslated by D H Delphenich
Su une quantité analogue au potential et su un théoème y elatif C R Acad Sci 7 (87) 34-39 On a quantity that is analogous to potential and a theoem that elates to it By R CLAUSIUS Tanslated by D H Delphenich
AST 121S: The origin and evolution of the Universe. Introduction to Mathematical Handout 1
 Please ead this fist... AST S: The oigin and evolution of the Univese Intoduction to Mathematical Handout This is an unusually long hand-out and one which uses in places mathematics that you may not be
Please ead this fist... AST S: The oigin and evolution of the Univese Intoduction to Mathematical Handout This is an unusually long hand-out and one which uses in places mathematics that you may not be
On the ratio of maximum and minimum degree in maximal intersecting families
 On the atio of maximum and minimum degee in maximal intesecting families Zoltán Lóánt Nagy Lale Özkahya Balázs Patkós Máté Vize Mach 6, 013 Abstact To study how balanced o unbalanced a maximal intesecting
On the atio of maximum and minimum degee in maximal intesecting families Zoltán Lóánt Nagy Lale Özkahya Balázs Patkós Máté Vize Mach 6, 013 Abstact To study how balanced o unbalanced a maximal intesecting
Deterministic vs Non-deterministic Graph Property Testing
 Deteministic vs Non-deteministic Gaph Popety Testing Lio Gishboline Asaf Shapia Abstact A gaph popety P is said to be testable if one can check whethe a gaph is close o fa fom satisfying P using few andom
Deteministic vs Non-deteministic Gaph Popety Testing Lio Gishboline Asaf Shapia Abstact A gaph popety P is said to be testable if one can check whethe a gaph is close o fa fom satisfying P using few andom
CONGRUENCES INVOLVING ( )
 Jounal of Numbe Theoy 101, 157-1595 CONGRUENCES INVOLVING ZHI-Hong Sun School of Mathematical Sciences, Huaiyin Nomal Univesity, Huaian, Jiangsu 001, PR China Email: zhihongsun@yahoocom Homeage: htt://wwwhytceducn/xsjl/szh
Jounal of Numbe Theoy 101, 157-1595 CONGRUENCES INVOLVING ZHI-Hong Sun School of Mathematical Sciences, Huaiyin Nomal Univesity, Huaian, Jiangsu 001, PR China Email: zhihongsun@yahoocom Homeage: htt://wwwhytceducn/xsjl/szh
On the Efficiency of Markets with Two-sided Proportional Allocation Mechanisms
 On the Efficiency of Makets with Two-sided Pootional Allocation Mechanisms Volodymy Kuleshov and Adian Vetta Deatment of Mathematics and Statistics, and School of Comute Science, McGill Univesity volodymy.kuleshov@mail.mcgill.ca,
On the Efficiency of Makets with Two-sided Pootional Allocation Mechanisms Volodymy Kuleshov and Adian Vetta Deatment of Mathematics and Statistics, and School of Comute Science, McGill Univesity volodymy.kuleshov@mail.mcgill.ca,
Appendix A. Appendices. A.1 ɛ ijk and cross products. Vector Operations: δ ij and ɛ ijk
 Appendix A Appendices A1 ɛ and coss poducts A11 Vecto Opeations: δ ij and ɛ These ae some notes on the use of the antisymmetic symbol ɛ fo expessing coss poducts This is an extemely poweful tool fo manipulating
Appendix A Appendices A1 ɛ and coss poducts A11 Vecto Opeations: δ ij and ɛ These ae some notes on the use of the antisymmetic symbol ɛ fo expessing coss poducts This is an extemely poweful tool fo manipulating
A Relativistic Electron in a Coulomb Potential
 A Relativistic Electon in a Coulomb Potential Alfed Whitehead Physics 518, Fall 009 The Poblem Solve the Diac Equation fo an electon in a Coulomb potential. Identify the conseved quantum numbes. Specify
A Relativistic Electon in a Coulomb Potential Alfed Whitehead Physics 518, Fall 009 The Poblem Solve the Diac Equation fo an electon in a Coulomb potential. Identify the conseved quantum numbes. Specify
arxiv: v1 [math.nt] 12 May 2017
![arxiv: v1 [math.nt] 12 May 2017 arxiv: v1 [math.nt] 12 May 2017](/thumbs/93/113642317.jpg) SEQUENCES OF CONSECUTIVE HAPPY NUMBERS IN NEGATIVE BASES HELEN G. GRUNDMAN AND PAMELA E. HARRIS axiv:1705.04648v1 [math.nt] 12 May 2017 ABSTRACT. Fo b 2 and e 2, let S e,b : Z Z 0 be the function taking
SEQUENCES OF CONSECUTIVE HAPPY NUMBERS IN NEGATIVE BASES HELEN G. GRUNDMAN AND PAMELA E. HARRIS axiv:1705.04648v1 [math.nt] 12 May 2017 ABSTRACT. Fo b 2 and e 2, let S e,b : Z Z 0 be the function taking
Why Professor Richard Feynman was upset solving the Laplace equation for spherical waves? Anzor A. Khelashvili a)
 Why Pofesso Richad Feynman was upset solving the Laplace equation fo spheical waves? Anzo A. Khelashvili a) Institute of High Enegy Physics, Iv. Javakhishvili Tbilisi State Univesity, Univesity St. 9,
Why Pofesso Richad Feynman was upset solving the Laplace equation fo spheical waves? Anzo A. Khelashvili a) Institute of High Enegy Physics, Iv. Javakhishvili Tbilisi State Univesity, Univesity St. 9,
