Unit 5: Quadratic Equations & Functions
|
|
|
- Christiana Hudson
- 6 years ago
- Views:
Transcription
1 Date Perod Unt 5: Quadratc Equatons & Functons DAY TOPIC 1 Modelng Data wth Quadratc Functons Factorng Quadratc Epressons 3 Solvng Quadratc Equatons 4 Comple Numbers Smplfcaton, Addton/Subtracton & Multplcaton 5 Comple Numbers Dvson 6 Completng the Square 7 The Quadratc Formula Dscrmnant 8 QUIZ 9 Propertes of Parabolas 10 Translatng Parabolas 11 Graphs of Quadratc Inequaltes and Systems of Quadratc Inequaltes 1 Applcatons of Quadratcs (Applcatons WS) 13 REVIEW
2 Date Perod U5 D1: Modelng Date wth Quadratc Functons The study of quadratc equatons and ther graphs plays an mportant role n many applcatons. For nstance, physcsts can model the heght of an object over tme t wth quadratc equatons. Economsts can model revenue and proft functons wth quadratc equatons. Usng such models to determne mportant concepts such as mamum heght, mamum revenue, or mamum proft, depends on understandng the nature of a parabolc graph. f ( ) = a + b + c a - term b - term c - term Standard Form: f ( ) = a + b + c a postve a negatve Ma or Mn? Verte As of Symmetry y-ntercept Property Eample: y =
3 Sometmes we wll need to determne f a functon s quadratc. Remember, f there s no words, a = 0 ), then the functon wll most lkely be lnear. term (n other When a functon s a quadratc, the graph wll look lke a (sometmes upsde down. When?). We talked a lttle about an as of symmetry what does symmetry mean?! Use symmetry for the followng problems: Warmup: Quck revew of graphng calculator procedures Fnd a quadratc functon to model the values n the table below shown: Step 1: Plug all values nto Step : Solve the of 3 varables. (Favorte solvng method?) Step 3: Wrte the functon *Note: If a = 0
4 Sometmes, modelng the data s a lttle too comple to do by hand Graphng Calc! c. What s the mamum heght? d. When does t ht the ground? The graph of each functon contans the gven pont. Fnd the value of c. 1) y 5 c; (, 14) = + ) y = + c ; 3, Closure: Descrbe the dfference between a lnear and quadratc functon (both algebracally & graphcally). Lst 3 thngs that you learned today. 3
5 Date Perod U5 D: Factorng Quadratc Epresson GCF: Dfference of Squares: 49 ( + 1) Guess & Check: ( ) ( ) Brtsh Method:
6 Factor the followng. You may use the Brtsh method, guess and check method, or any other method necessary to factor completely p w + w 6. ( + 1) + 8( + 1) ( ) ( ) ( 3) 7( 3)
7 y ( ) ( ) ( ) ( 4 49) 7. ( )
8 Date Perod U5 D3: Solvng Quadratc Equatons Objectve: Be able to solve quadratc equatons usng any one of three methods. Factorng Takng Square Roots Graphng + 18 = 9 9 = = 0 Addtonal Notes: Partnered Unfar Game! 7
9 Date Perod U5 D4: Comple Numbers Intro & Operatons (not Dvson) 1. On your home screen, type 9. What answer does the calculator gve you?. Go to MODE and change your calculator from REAL to a + b form (3 rd row from the bottom) 3. On your home screen, type 9 agan. Ths tme what answer does t gve you? 4. Use the calculator to smplfy each of the followng: a. 5 b. 9 4 c. 100 Now look for the on your calculator (t s the nd. near 0), then calculate each of the followng: a. b. ( )( 5 3) + c. ( 4)( 1+ ) 5. From your nvestgaton, what does represent? What knd of number s? 6. What s the meanng of a + b? Imagnary numbers are not nvsble numbers, or made-up numbers. They are numbers that arse naturally from tryng to solve equatons such as + 1= 0 Imagnary numbers : the number whose square s -1. = = Smplfy the followng:
10 Comple number: magnary numbers and real numbers together. a and b are real numbers, ncludng 0. a + b REAL PART IMAGINARY PART Smplfy n the form a + b 5. Wrte the comple number n the form a + b You can use the comple number plane to represent a comple number geometrcally. Locate the real part of the number on the horzontal as and the magnary part on the vertcal as. You graph 3 4 the same way you would graph (3,-4) on the coordnate plane. 1 Imagnary as Real as (3-4) 6. On the graph above, plot the ponts and
11 Absolute value of a comple number s ts dstance from the orgn on the comple number plane. To fnd the absolute value, use the Pythagorean Theorem. Fnd the absolute value of the followng a + b = a + b Addtve Inverse of Comple Numbers Fnd the addtve nverse of the followng: a + b Addng/Subtractng Comple Numbers 14. ( 5+ 7) + ( + 6) 15. ( 8+ 3) ( + 4) 16. ( ) Multplyng Comple Numbers 17. Fnd ( 5)( 4) 18. ( + 3)( 3+ 6) 19. ( 1)( 7 ) 0. ( 6 5)( 4 3) 1. ( 4 9) ( 4 3) ( 3 ) Fndng Comple Solutons. Solve = = = = 0 Closure: What are two comple numbers that have a square of -1? 10
12 Date Perod Warmup: Fll n the table U5 D5: Comple Numbers & Comple Dvson Generalze ths cyclc concept to fnd the followng: 80 =, 133 =, 1044 = = 3 4 = = = Dvde the eponent by 4 and fnd the remander Match the remander the chart on the left. Use that value as your answer. The conjugate of a+b s a-b (note t s NOT the nverse), and the conjugate of a-b s a+b Eamples ; the conjugate s ; the conjugate s ; the conjugate s -5 snce the conjugate of 0+5 s ; the conjugate of 6 s 6 snce 6-0 s the conjugate of 6+0 Comple dvson To dvde comple numbers, multply the numerator and demonnator by the conjugate of the denomnator
13 Date Perod Worksheet U5 D
14 Date Perod U5 D6: Completng the Square Another solvng method for quadratcs s completng the square. The goal s to get the left sde of your equaton to be n the form of ( + #) so that you can take the of both sdes. Quck eample: = 36 Epressons lke because they factor nto ( ) # are called + # + #. + nstead of two dfferent bnomals ( )( ) Unfortunately, sometmes our epresson on the left s not a perfect square. Soluton: the square to make t perfect! Eamples: 1 1) The value that completes the square s always ) 7 + 3) + Now let s apply ths process to solvng an equaton. Eample #1: 5= 0 STEP 1: Get the equaton n the form (move the # s to the rght). STEP : Fnd the amount to be added by takng. STEP 3: Add that amount to both sdes. + = 5 + STEP 4: Factor the left sde and smplfy the rght STEP 5: Take the square root of both sdes. Eample #: = 0 13
15 Notce n the prevous eamples, a = 1. If t does not, we have to t! Eample #3: = Eample #4: = Eample #3: The equaton ht () = t + 3t+ 4models the heght, h n feet, of a ball thrown after t seconds. Complete the square to fnd how many second t wll take for the ball to ht the ground. Classwork Eamples: = 0. 4 = + 3. = The equaton ht () = t + t+ 3models the heght, h n feet, of a ball thrown after t seconds. Complete the square to fnd how many second t wll take for the ball to ht the ground = 0 6. =
16 Date Perod U5 D7: The Quadratc Formula & Dscrmnant When gven an quadratc equaton, we have learned several ways to solve Factor (f applcable), the square, takng square roots, and. Today we wll (re?)learn another method: Everyone s favorte, the formula!!!! If a b c + + = 0, then Dscrmnant Eample 1: 4+ 3= 0 ) = 0 3) 1= 5 Drectons: Just fnd the dscrmnate for each equaton 4) = 0 5) 4 5= 0 6) = 0 The determnant can tell us about the graph and the number of solutons, and even the solvng methods 15
17 On the frst day of the unt, we looked how the values of a quadratc functon effect the graph Look of Graph Dscrmnant Soluton Types Solvng Method WoRdIE: The functon ht ( ) 16t 1t = + models the heght of a bowlng ball thrown nto the ar. Use the quadratc formula to fnd the tme t wll take for the ball to ht the ground. Then, use your calculator to fnd the tme t wll take for the ball to ht the ground (check). Fnally, use your calculator to fnd the tme of the mamum heght, and what that ma heght s More classwork eamples on the net page 16
18 17
19 Date Perod U5 D9: Propertes of Parabolas Forms: ( ) y = 3 y = Quadratcs!!! General Equaton Verte As of Symmetry Intercepts Standard Form Verte Form Today we wll focus more on standard form, and tomorrow we wll cover verte form. Drectons: For each equaton, fnd (a) the verte, (b) the as of symmetry, and (c) the y-ntercept. 1. y = 6 +. y = y =
20 Now we are gong to graph the parabolas of the quadratc functons. 1. y = STEP 1: Fnd the verte. V: STEP : Fnd the as of symmetry AoS: STEP 3: Fnd the y-ntercept. & ts match STEP 4: Fnd one more pont by choosng a value for. Addtonal Informaton: Mn or Ma -ntercepts 19
21 Applcaton: Suppose you are tossng a baseball up to a frend on a thrd-story balcony. After t seconds the heght of the apple n feet s gven by the functon ht ( ) = 16t t Your frend catches the ball just as t reaches ts hghest pont. How long does the ball take to reach your frend, and at what heght does he catch t?! Convertng Forms: Verte Standard ( ) y = Standard Verte y = + 6 (You must complete the square!!!!!!!!!!!!!!!!) Closure: What are the general equatons for standard and verte form of a quadratc? Lst how you can fnd mportant nformaton from each (such as verte, as of symmetry, ntercepts, etc ) 0
22 Date Perod U5 D10: Translatng Parabolas 1. Revew the general equaton for verte form and standard form of a quadratc. Identfy the verte and the y-ntercept from the equatons below a) y = ( 4) + 3 b) y ( ) = + 5 c) y = We wll graph verte form n a smlar way that we dd standard from, ecept now the verte s easy! y = 1 ( ) + 1 STEP 1: Fnd the verte. V: STEP : Fnd the as of symmetry AoS: STEP 3: Fnd another pont. & ts match STEP 4: Repeat step 3 4. Graph each of the followng: a) y = ( + ) 3 b) y ( ) =
23 5. Sometmes we wll need to wrte the equaton of the parabola. Step 1: Locate the Verte Step : Locate another pont Step 3: Plug n to y = a( h) + k and solve for a. 3. verte s ( 3, 6 ) and y-ntercept s 4. verte s ( 3, 6) and pont s ( 1, ) Closure: the equaton of one of the parabolas n the graph at the rght s ( ) y = 4 +. Wrte the equaton of the other parabola. Then, f you have tme, wrte both equatons n standard form, and dentfy the y-ntercepts.
24 Date Perod U5 D11: Graphs of Quadratc Inequaltes & Systems Warm-up: For each nequalty, dentfy above/below and sold/dashed <, >,, Graph the followng: 1. y > 3. y y y > y <
25 Date Perod U5 D1: Applcatons of Quadratcs Worksheet 4
26 Date Perod U5 D13: Revew for Unt 5 Test Problems 1 7 should all be done by hand. The calculator can be used for Answers should be left n smplest radcal form. 1. Wrte the equaton of the parabola n standard form through the ponts (, 7), (-1, 10) and (0, 5).. Wrte the equaton of the parabola wth a verte of (3, 1), through the pont (-1, -15). 3. Wrte each of the followng equatons n verte form by completng the square (f not done already). Sketch the graph by determnng the verte, the lne of symmetry, the y-ntercept, and the -ntercept(s) f they est. a. y = b. y = 1 c. = y d. y = ( + ) Solve each quadratc equaton. Use a varety of methods. a. + 4 = 1 b. 5 5 = 0 c = 5 d. + = 10 e = 0 f. + = 5
27 5. Smplfy each epresson nto a+b form. Show all work. 4 3 a. (8+4)(1-3) b. ( 3 6 ) c. 111 (smplfy- hnt: fnd remander) d f. 5 e. 3 5( 1 + 8) 6. Evaluate the dscrmnant and determne the type and number of solutons. a = 0 b = 0 7. Wrte an equaton n whch the dscrmnant s equal to -9. What type of solutons does your equaton have? 8. Graph the system of quadratc nequaltes. Shade the regon and fnd the ntersecton ponts. y 8 y ( 4) 9. The equaton y = represents the parabolc flght of a certan cannonball shot at an angle of 6, where y s the heght of the cannonball and s the vertcal dstance traveled n meters. Try ths WINDOW [-5, 60, 5, -1, 10, 1], ths follows the order of mn, ma etc. a. What s the mamum heght of the cannonball? How do you know? Eplan your method. b. What s the total horzontal dstance traveled by the cannonball? How do you know? Eplan your method. 10. A rectangular backyard wll be fenced n on 3 sdes. If there s 00ft of fencng, a. Determne the dmensons of the fence for the mamum area. b. Determne the mamum area. 6
Section 8.3 Polar Form of Complex Numbers
 80 Chapter 8 Secton 8 Polar Form of Complex Numbers From prevous classes, you may have encountered magnary numbers the square roots of negatve numbers and, more generally, complex numbers whch are the
80 Chapter 8 Secton 8 Polar Form of Complex Numbers From prevous classes, you may have encountered magnary numbers the square roots of negatve numbers and, more generally, complex numbers whch are the
Section 3.6 Complex Zeros
 04 Chapter Secton 6 Comple Zeros When fndng the zeros of polynomals, at some pont you're faced wth the problem Whle there are clearly no real numbers that are solutons to ths equaton, leavng thngs there
04 Chapter Secton 6 Comple Zeros When fndng the zeros of polynomals, at some pont you're faced wth the problem Whle there are clearly no real numbers that are solutons to ths equaton, leavng thngs there
The Fundamental Theorem of Algebra. Objective To use the Fundamental Theorem of Algebra to solve polynomial equations with complex solutions
 5-6 The Fundamental Theorem of Algebra Content Standards N.CN.7 Solve quadratc equatons wth real coeffcents that have comple solutons. N.CN.8 Etend polnomal denttes to the comple numbers. Also N.CN.9,
5-6 The Fundamental Theorem of Algebra Content Standards N.CN.7 Solve quadratc equatons wth real coeffcents that have comple solutons. N.CN.8 Etend polnomal denttes to the comple numbers. Also N.CN.9,
Complex Numbers. x = B B 2 4AC 2A. or x = x = 2 ± 4 4 (1) (5) 2 (1)
 Complex Numbers If you have not yet encountered complex numbers, you wll soon do so n the process of solvng quadratc equatons. The general quadratc equaton Ax + Bx + C 0 has solutons x B + B 4AC A For
Complex Numbers If you have not yet encountered complex numbers, you wll soon do so n the process of solvng quadratc equatons. The general quadratc equaton Ax + Bx + C 0 has solutons x B + B 4AC A For
Pre-Calculus Summer Assignment
 Pre-Calculus Summer Assgnment Dear Future Pre-Calculus Student, Congratulatons on our successful completon of Algebra! Below ou wll fnd the summer assgnment questons. It s assumed that these concepts,
Pre-Calculus Summer Assgnment Dear Future Pre-Calculus Student, Congratulatons on our successful completon of Algebra! Below ou wll fnd the summer assgnment questons. It s assumed that these concepts,
Lectures - Week 4 Matrix norms, Conditioning, Vector Spaces, Linear Independence, Spanning sets and Basis, Null space and Range of a Matrix
 Lectures - Week 4 Matrx norms, Condtonng, Vector Spaces, Lnear Independence, Spannng sets and Bass, Null space and Range of a Matrx Matrx Norms Now we turn to assocatng a number to each matrx. We could
Lectures - Week 4 Matrx norms, Condtonng, Vector Spaces, Lnear Independence, Spannng sets and Bass, Null space and Range of a Matrx Matrx Norms Now we turn to assocatng a number to each matrx. We could
8.6 The Complex Number System
 8.6 The Complex Number System Earler n the chapter, we mentoned that we cannot have a negatve under a square root, snce the square of any postve or negatve number s always postve. In ths secton we want
8.6 The Complex Number System Earler n the chapter, we mentoned that we cannot have a negatve under a square root, snce the square of any postve or negatve number s always postve. In ths secton we want
COMPLEX NUMBERS AND QUADRATIC EQUATIONS
 COMPLEX NUMBERS AND QUADRATIC EQUATIONS INTRODUCTION We know that x 0 for all x R e the square of a real number (whether postve, negatve or ero) s non-negatve Hence the equatons x, x, x + 7 0 etc are not
COMPLEX NUMBERS AND QUADRATIC EQUATIONS INTRODUCTION We know that x 0 for all x R e the square of a real number (whether postve, negatve or ero) s non-negatve Hence the equatons x, x, x + 7 0 etc are not
UNIT 3 EXPRESSIONS AND EQUATIONS Lesson 4: Fundamental Theorem of Algebra. Instruction. Guided Practice Example 1
 Guded Practce 3.4. Example 1 Instructon For each equaton, state the number and type of solutons by frst fndng the dscrmnant. x + 3x =.4x x = 3x = x 9x + 1 = 6x 1. Fnd the dscrmnant of x + 3x =. The equaton
Guded Practce 3.4. Example 1 Instructon For each equaton, state the number and type of solutons by frst fndng the dscrmnant. x + 3x =.4x x = 3x = x 9x + 1 = 6x 1. Fnd the dscrmnant of x + 3x =. The equaton
332600_08_1.qxp 4/17/08 11:29 AM Page 481
 336_8_.qxp 4/7/8 :9 AM Page 48 8 Complex Vector Spaces 8. Complex Numbers 8. Conjugates and Dvson of Complex Numbers 8.3 Polar Form and DeMovre s Theorem 8.4 Complex Vector Spaces and Inner Products 8.5
336_8_.qxp 4/7/8 :9 AM Page 48 8 Complex Vector Spaces 8. Complex Numbers 8. Conjugates and Dvson of Complex Numbers 8.3 Polar Form and DeMovre s Theorem 8.4 Complex Vector Spaces and Inner Products 8.5
Quadratic Formula, Completing the Square, Systems Review Sheet
 Quadratc Formula Completng the Square Systems Revew Sheet 1. Factor the polynomal completely. 6. Use the graph to approxmate the real zeros of the functon. 2. Fnd the real-number solutons of the equaton.
Quadratc Formula Completng the Square Systems Revew Sheet 1. Factor the polynomal completely. 6. Use the graph to approxmate the real zeros of the functon. 2. Fnd the real-number solutons of the equaton.
9. Complex Numbers. 1. Numbers revisited. 2. Imaginary number i: General form of complex numbers. 3. Manipulation of complex numbers
 9. Comple Numbers. Numbers revsted. Imagnar number : General form of comple numbers 3. Manpulaton of comple numbers 4. The Argand dagram 5. The polar form for comple numbers 9.. Numbers revsted We saw
9. Comple Numbers. Numbers revsted. Imagnar number : General form of comple numbers 3. Manpulaton of comple numbers 4. The Argand dagram 5. The polar form for comple numbers 9.. Numbers revsted We saw
For all questions, answer choice E) NOTA" means none of the above answers is correct.
 0 MA Natonal Conventon For all questons, answer choce " means none of the above answers s correct.. In calculus, one learns of functon representatons that are nfnte seres called power 3 4 5 seres. For
0 MA Natonal Conventon For all questons, answer choce " means none of the above answers s correct.. In calculus, one learns of functon representatons that are nfnte seres called power 3 4 5 seres. For
Mathematics Intersection of Lines
 a place of mnd F A C U L T Y O F E D U C A T I O N Department of Currculum and Pedagog Mathematcs Intersecton of Lnes Scence and Mathematcs Educaton Research Group Supported b UBC Teachng and Learnng Enhancement
a place of mnd F A C U L T Y O F E D U C A T I O N Department of Currculum and Pedagog Mathematcs Intersecton of Lnes Scence and Mathematcs Educaton Research Group Supported b UBC Teachng and Learnng Enhancement
1 Matrix representations of canonical matrices
 1 Matrx representatons of canoncal matrces 2-d rotaton around the orgn: ( ) cos θ sn θ R 0 = sn θ cos θ 3-d rotaton around the x-axs: R x = 1 0 0 0 cos θ sn θ 0 sn θ cos θ 3-d rotaton around the y-axs:
1 Matrx representatons of canoncal matrces 2-d rotaton around the orgn: ( ) cos θ sn θ R 0 = sn θ cos θ 3-d rotaton around the x-axs: R x = 1 0 0 0 cos θ sn θ 0 sn θ cos θ 3-d rotaton around the y-axs:
THE CHINESE REMAINDER THEOREM. We should thank the Chinese for their wonderful remainder theorem. Glenn Stevens
 THE CHINESE REMAINDER THEOREM KEITH CONRAD We should thank the Chnese for ther wonderful remander theorem. Glenn Stevens 1. Introducton The Chnese remander theorem says we can unquely solve any par of
THE CHINESE REMAINDER THEOREM KEITH CONRAD We should thank the Chnese for ther wonderful remander theorem. Glenn Stevens 1. Introducton The Chnese remander theorem says we can unquely solve any par of
Structure and Drive Paul A. Jensen Copyright July 20, 2003
 Structure and Drve Paul A. Jensen Copyrght July 20, 2003 A system s made up of several operatons wth flow passng between them. The structure of the system descrbes the flow paths from nputs to outputs.
Structure and Drve Paul A. Jensen Copyrght July 20, 2003 A system s made up of several operatons wth flow passng between them. The structure of the system descrbes the flow paths from nputs to outputs.
Math1110 (Spring 2009) Prelim 3 - Solutions
 Math 1110 (Sprng 2009) Solutons to Prelm 3 (04/21/2009) 1 Queston 1. (16 ponts) Short answer. Math1110 (Sprng 2009) Prelm 3 - Solutons x a 1 (a) (4 ponts) Please evaluate lm, where a and b are postve numbers.
Math 1110 (Sprng 2009) Solutons to Prelm 3 (04/21/2009) 1 Queston 1. (16 ponts) Short answer. Math1110 (Sprng 2009) Prelm 3 - Solutons x a 1 (a) (4 ponts) Please evaluate lm, where a and b are postve numbers.
Digital Signal Processing
 Dgtal Sgnal Processng Dscrete-tme System Analyss Manar Mohasen Offce: F8 Emal: manar.subh@ut.ac.r School of IT Engneerng Revew of Precedent Class Contnuous Sgnal The value of the sgnal s avalable over
Dgtal Sgnal Processng Dscrete-tme System Analyss Manar Mohasen Offce: F8 Emal: manar.subh@ut.ac.r School of IT Engneerng Revew of Precedent Class Contnuous Sgnal The value of the sgnal s avalable over
Week3, Chapter 4. Position and Displacement. Motion in Two Dimensions. Instantaneous Velocity. Average Velocity
 Week3, Chapter 4 Moton n Two Dmensons Lecture Quz A partcle confned to moton along the x axs moves wth constant acceleraton from x =.0 m to x = 8.0 m durng a 1-s tme nterval. The velocty of the partcle
Week3, Chapter 4 Moton n Two Dmensons Lecture Quz A partcle confned to moton along the x axs moves wth constant acceleraton from x =.0 m to x = 8.0 m durng a 1-s tme nterval. The velocty of the partcle
Gravitational Acceleration: A case of constant acceleration (approx. 2 hr.) (6/7/11)
 Gravtatonal Acceleraton: A case of constant acceleraton (approx. hr.) (6/7/11) Introducton The gravtatonal force s one of the fundamental forces of nature. Under the nfluence of ths force all objects havng
Gravtatonal Acceleraton: A case of constant acceleraton (approx. hr.) (6/7/11) Introducton The gravtatonal force s one of the fundamental forces of nature. Under the nfluence of ths force all objects havng
APPENDIX 2 FITTING A STRAIGHT LINE TO OBSERVATIONS
 Unversty of Oulu Student Laboratory n Physcs Laboratory Exercses n Physcs 1 1 APPEDIX FITTIG A STRAIGHT LIE TO OBSERVATIOS In the physcal measurements we often make a seres of measurements of the dependent
Unversty of Oulu Student Laboratory n Physcs Laboratory Exercses n Physcs 1 1 APPEDIX FITTIG A STRAIGHT LIE TO OBSERVATIOS In the physcal measurements we often make a seres of measurements of the dependent
Physics 2A Chapter 3 HW Solutions
 Phscs A Chapter 3 HW Solutons Chapter 3 Conceptual Queston: 4, 6, 8, Problems: 5,, 8, 7, 3, 44, 46, 69, 70, 73 Q3.4. Reason: (a) C = A+ B onl A and B are n the same drecton. Sze does not matter. (b) C
Phscs A Chapter 3 HW Solutons Chapter 3 Conceptual Queston: 4, 6, 8, Problems: 5,, 8, 7, 3, 44, 46, 69, 70, 73 Q3.4. Reason: (a) C = A+ B onl A and B are n the same drecton. Sze does not matter. (b) C
of Nebraska - Lincoln
 Unversty of Nebraska - Lncoln DgtalCommons@Unversty of Nebraska - Lncoln MAT Exam Expostory Papers Math n the Mddle Insttute Partnershp 008 The Square Root of Tffany Lothrop Unversty of Nebraska-Lncoln
Unversty of Nebraska - Lncoln DgtalCommons@Unversty of Nebraska - Lncoln MAT Exam Expostory Papers Math n the Mddle Insttute Partnershp 008 The Square Root of Tffany Lothrop Unversty of Nebraska-Lncoln
UNIT 4 EXTENDING THE NUMBER SYSTEM Lesson 3: Operating with Complex Numbers Instruction
 Prerequste Sklls Ths lesson requres the use of the followng sklls: understandng that multplyng the numerator and denomnator of a fracton by the same quantty produces an equvalent fracton multplyng complex
Prerequste Sklls Ths lesson requres the use of the followng sklls: understandng that multplyng the numerator and denomnator of a fracton by the same quantty produces an equvalent fracton multplyng complex
Kernel Methods and SVMs Extension
 Kernel Methods and SVMs Extenson The purpose of ths document s to revew materal covered n Machne Learnng 1 Supervsed Learnng regardng support vector machnes (SVMs). Ths document also provdes a general
Kernel Methods and SVMs Extenson The purpose of ths document s to revew materal covered n Machne Learnng 1 Supervsed Learnng regardng support vector machnes (SVMs). Ths document also provdes a general
Chapter 8. Potential Energy and Conservation of Energy
 Chapter 8 Potental Energy and Conservaton of Energy In ths chapter we wll ntroduce the followng concepts: Potental Energy Conservatve and non-conservatve forces Mechancal Energy Conservaton of Mechancal
Chapter 8 Potental Energy and Conservaton of Energy In ths chapter we wll ntroduce the followng concepts: Potental Energy Conservatve and non-conservatve forces Mechancal Energy Conservaton of Mechancal
CHAPTER 4. Vector Spaces
 man 2007/2/16 page 234 CHAPTER 4 Vector Spaces To crtcze mathematcs for ts abstracton s to mss the pont entrel. Abstracton s what makes mathematcs work. Ian Stewart The man am of ths tet s to stud lnear
man 2007/2/16 page 234 CHAPTER 4 Vector Spaces To crtcze mathematcs for ts abstracton s to mss the pont entrel. Abstracton s what makes mathematcs work. Ian Stewart The man am of ths tet s to stud lnear
Chapter 3. r r. Position, Velocity, and Acceleration Revisited
 Chapter 3 Poston, Velocty, and Acceleraton Revsted The poston vector of a partcle s a vector drawn from the orgn to the locaton of the partcle. In two dmensons: r = x ˆ+ yj ˆ (1) The dsplacement vector
Chapter 3 Poston, Velocty, and Acceleraton Revsted The poston vector of a partcle s a vector drawn from the orgn to the locaton of the partcle. In two dmensons: r = x ˆ+ yj ˆ (1) The dsplacement vector
8.4 COMPLEX VECTOR SPACES AND INNER PRODUCTS
 SECTION 8.4 COMPLEX VECTOR SPACES AND INNER PRODUCTS 493 8.4 COMPLEX VECTOR SPACES AND INNER PRODUCTS All the vector spaces you have studed thus far n the text are real vector spaces because the scalars
SECTION 8.4 COMPLEX VECTOR SPACES AND INNER PRODUCTS 493 8.4 COMPLEX VECTOR SPACES AND INNER PRODUCTS All the vector spaces you have studed thus far n the text are real vector spaces because the scalars
Salmon: Lectures on partial differential equations. Consider the general linear, second-order PDE in the form. ,x 2
 Salmon: Lectures on partal dfferental equatons 5. Classfcaton of second-order equatons There are general methods for classfyng hgher-order partal dfferental equatons. One s very general (applyng even to
Salmon: Lectures on partal dfferental equatons 5. Classfcaton of second-order equatons There are general methods for classfyng hgher-order partal dfferental equatons. One s very general (applyng even to
= = = (a) Use the MATLAB command rref to solve the system. (b) Let A be the coefficient matrix and B be the right-hand side of the system.
 Chapter Matlab Exercses Chapter Matlab Exercses. Consder the lnear system of Example n Secton.. x x x y z y y z (a) Use the MATLAB command rref to solve the system. (b) Let A be the coeffcent matrx and
Chapter Matlab Exercses Chapter Matlab Exercses. Consder the lnear system of Example n Secton.. x x x y z y y z (a) Use the MATLAB command rref to solve the system. (b) Let A be the coeffcent matrx and
15-381: Artificial Intelligence. Regression and cross validation
 15-381: Artfcal Intellgence Regresson and cross valdaton Where e are Inputs Densty Estmator Probablty Inputs Classfer Predct category Inputs Regressor Predct real no. Today Lnear regresson Gven an nput
15-381: Artfcal Intellgence Regresson and cross valdaton Where e are Inputs Densty Estmator Probablty Inputs Classfer Predct category Inputs Regressor Predct real no. Today Lnear regresson Gven an nput
Kinematics in 2-Dimensions. Projectile Motion
 Knematcs n -Dmensons Projectle Moton A medeval trebuchet b Kolderer, c1507 http://members.net.net.au/~rmne/ht/ht0.html#5 Readng Assgnment: Chapter 4, Sectons -6 Introducton: In medeval das, people had
Knematcs n -Dmensons Projectle Moton A medeval trebuchet b Kolderer, c1507 http://members.net.net.au/~rmne/ht/ht0.html#5 Readng Assgnment: Chapter 4, Sectons -6 Introducton: In medeval das, people had
Chapter Twelve. Integration. We now turn our attention to the idea of an integral in dimensions higher than one. Consider a real-valued function f : D
 Chapter Twelve Integraton 12.1 Introducton We now turn our attenton to the dea of an ntegral n dmensons hgher than one. Consder a real-valued functon f : R, where the doman s a nce closed subset of Eucldean
Chapter Twelve Integraton 12.1 Introducton We now turn our attenton to the dea of an ntegral n dmensons hgher than one. Consder a real-valued functon f : R, where the doman s a nce closed subset of Eucldean
= z 20 z n. (k 20) + 4 z k = 4
 Problem Set #7 solutons 7.2.. (a Fnd the coeffcent of z k n (z + z 5 + z 6 + z 7 + 5, k 20. We use the known seres expanson ( n+l ( z l l z n below: (z + z 5 + z 6 + z 7 + 5 (z 5 ( + z + z 2 + z + 5 5
Problem Set #7 solutons 7.2.. (a Fnd the coeffcent of z k n (z + z 5 + z 6 + z 7 + 5, k 20. We use the known seres expanson ( n+l ( z l l z n below: (z + z 5 + z 6 + z 7 + 5 (z 5 ( + z + z 2 + z + 5 5
Difference Equations
 Dfference Equatons c Jan Vrbk 1 Bascs Suppose a sequence of numbers, say a 0,a 1,a,a 3,... s defned by a certan general relatonshp between, say, three consecutve values of the sequence, e.g. a + +3a +1
Dfference Equatons c Jan Vrbk 1 Bascs Suppose a sequence of numbers, say a 0,a 1,a,a 3,... s defned by a certan general relatonshp between, say, three consecutve values of the sequence, e.g. a + +3a +1
IMGS-261 Solutions to Homework #9
 IMGS-6 Solutons to Homework #9. For f [] SINC [] sn[π], use the modulaton theorem to evaluate and sketch π the Fourer transform of f [] f [] f [] (f []) Soluton: We know that F{RECT []} SINC [] so we use
IMGS-6 Solutons to Homework #9. For f [] SINC [] sn[π], use the modulaton theorem to evaluate and sketch π the Fourer transform of f [] f [] f [] (f []) Soluton: We know that F{RECT []} SINC [] so we use
Lecture 12: Discrete Laplacian
 Lecture 12: Dscrete Laplacan Scrbe: Tanye Lu Our goal s to come up wth a dscrete verson of Laplacan operator for trangulated surfaces, so that we can use t n practce to solve related problems We are mostly
Lecture 12: Dscrete Laplacan Scrbe: Tanye Lu Our goal s to come up wth a dscrete verson of Laplacan operator for trangulated surfaces, so that we can use t n practce to solve related problems We are mostly
12. The Hamilton-Jacobi Equation Michael Fowler
 1. The Hamlton-Jacob Equaton Mchael Fowler Back to Confguraton Space We ve establshed that the acton, regarded as a functon of ts coordnate endponts and tme, satsfes ( ) ( ) S q, t / t+ H qpt,, = 0, and
1. The Hamlton-Jacob Equaton Mchael Fowler Back to Confguraton Space We ve establshed that the acton, regarded as a functon of ts coordnate endponts and tme, satsfes ( ) ( ) S q, t / t+ H qpt,, = 0, and
Complex Numbers Alpha, Round 1 Test #123
 Complex Numbers Alpha, Round Test #3. Wrte your 6-dgt ID# n the I.D. NUMBER grd, left-justfed, and bubble. Check that each column has only one number darkened.. In the EXAM NO. grd, wrte the 3-dgt Test
Complex Numbers Alpha, Round Test #3. Wrte your 6-dgt ID# n the I.D. NUMBER grd, left-justfed, and bubble. Check that each column has only one number darkened.. In the EXAM NO. grd, wrte the 3-dgt Test
Chapter 8: Further Applications of Trigonometry
 Secton 8. Polar Form of Complex Numbers 1 Chapter 8: Further Applcatons of Trgonometry In ths chapter, we wll explore addtonal applcatons of trgonometry. We wll begn wth an extenson of the rght trangle
Secton 8. Polar Form of Complex Numbers 1 Chapter 8: Further Applcatons of Trgonometry In ths chapter, we wll explore addtonal applcatons of trgonometry. We wll begn wth an extenson of the rght trangle
The Order Relation and Trace Inequalities for. Hermitian Operators
 Internatonal Mathematcal Forum, Vol 3, 08, no, 507-57 HIKARI Ltd, wwwm-hkarcom https://doorg/0988/mf088055 The Order Relaton and Trace Inequaltes for Hermtan Operators Y Huang School of Informaton Scence
Internatonal Mathematcal Forum, Vol 3, 08, no, 507-57 HIKARI Ltd, wwwm-hkarcom https://doorg/0988/mf088055 The Order Relaton and Trace Inequaltes for Hermtan Operators Y Huang School of Informaton Scence
THE SUMMATION NOTATION Ʃ
 Sngle Subscrpt otaton THE SUMMATIO OTATIO Ʃ Most of the calculatons we perform n statstcs are repettve operatons on lsts of numbers. For example, we compute the sum of a set of numbers, or the sum of the
Sngle Subscrpt otaton THE SUMMATIO OTATIO Ʃ Most of the calculatons we perform n statstcs are repettve operatons on lsts of numbers. For example, we compute the sum of a set of numbers, or the sum of the
P A = (P P + P )A = P (I P T (P P ))A = P (A P T (P P )A) Hence if we let E = P T (P P A), We have that
 Backward Error Analyss for House holder Reectors We want to show that multplcaton by householder reectors s backward stable. In partcular we wsh to show fl(p A) = P (A) = P (A + E where P = I 2vv T s the
Backward Error Analyss for House holder Reectors We want to show that multplcaton by householder reectors s backward stable. In partcular we wsh to show fl(p A) = P (A) = P (A + E where P = I 2vv T s the
Section 8.1 Exercises
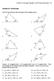 Secton 8.1 Non-rght Trangles: Law of Snes and Cosnes 519 Secton 8.1 Exercses Solve for the unknown sdes and angles of the trangles shown. 10 70 50 1.. 18 40 110 45 5 6 3. 10 4. 75 15 5 6 90 70 65 5. 6.
Secton 8.1 Non-rght Trangles: Law of Snes and Cosnes 519 Secton 8.1 Exercses Solve for the unknown sdes and angles of the trangles shown. 10 70 50 1.. 18 40 110 45 5 6 3. 10 4. 75 15 5 6 90 70 65 5. 6.
Physics 207: Lecture 20. Today s Agenda Homework for Monday
 Physcs 207: Lecture 20 Today s Agenda Homework for Monday Recap: Systems of Partcles Center of mass Velocty and acceleraton of the center of mass Dynamcs of the center of mass Lnear Momentum Example problems
Physcs 207: Lecture 20 Today s Agenda Homework for Monday Recap: Systems of Partcles Center of mass Velocty and acceleraton of the center of mass Dynamcs of the center of mass Lnear Momentum Example problems
ACTM State Calculus Competition Saturday April 30, 2011
 ACTM State Calculus Competton Saturday Aprl 30, 2011 ACTM State Calculus Competton Sprng 2011 Page 1 Instructons: For questons 1 through 25, mark the best answer choce on the answer sheet provde Afterward
ACTM State Calculus Competton Saturday Aprl 30, 2011 ACTM State Calculus Competton Sprng 2011 Page 1 Instructons: For questons 1 through 25, mark the best answer choce on the answer sheet provde Afterward
Solutions to Selected Exercises
 6 Solutons to Selected Eercses Chapter Secton.. a. f ( 0) b. Tons of garbage per week s produced by a cty wth a populaton of,000.. a. In 99 there are 0 ducks n the lake b. In 000 there are 0 ducks n the
6 Solutons to Selected Eercses Chapter Secton.. a. f ( 0) b. Tons of garbage per week s produced by a cty wth a populaton of,000.. a. In 99 there are 0 ducks n the lake b. In 000 there are 0 ducks n the
Grid Generation around a Cylinder by Complex Potential Functions
 Research Journal of Appled Scences, Engneerng and Technolog 4(): 53-535, 0 ISSN: 040-7467 Mawell Scentfc Organzaton, 0 Submtted: December 0, 0 Accepted: Januar, 0 Publshed: June 0, 0 Grd Generaton around
Research Journal of Appled Scences, Engneerng and Technolog 4(): 53-535, 0 ISSN: 040-7467 Mawell Scentfc Organzaton, 0 Submtted: December 0, 0 Accepted: Januar, 0 Publshed: June 0, 0 Grd Generaton around
e i is a random error
 Chapter - The Smple Lnear Regresson Model The lnear regresson equaton s: where + β + β e for,..., and are observable varables e s a random error How can an estmaton rule be constructed for the unknown
Chapter - The Smple Lnear Regresson Model The lnear regresson equaton s: where + β + β e for,..., and are observable varables e s a random error How can an estmaton rule be constructed for the unknown
MEM 255 Introduction to Control Systems Review: Basics of Linear Algebra
 MEM 255 Introducton to Control Systems Revew: Bascs of Lnear Algebra Harry G. Kwatny Department of Mechancal Engneerng & Mechancs Drexel Unversty Outlne Vectors Matrces MATLAB Advanced Topcs Vectors A
MEM 255 Introducton to Control Systems Revew: Bascs of Lnear Algebra Harry G. Kwatny Department of Mechancal Engneerng & Mechancs Drexel Unversty Outlne Vectors Matrces MATLAB Advanced Topcs Vectors A
8.1 Arc Length. What is the length of a curve? How can we approximate it? We could do it following the pattern we ve used before
 .1 Arc Length hat s the length of a curve? How can we approxmate t? e could do t followng the pattern we ve used before Use a sequence of ncreasngly short segments to approxmate the curve: As the segments
.1 Arc Length hat s the length of a curve? How can we approxmate t? e could do t followng the pattern we ve used before Use a sequence of ncreasngly short segments to approxmate the curve: As the segments
U.C. Berkeley CS294: Beyond Worst-Case Analysis Luca Trevisan September 5, 2017
 U.C. Berkeley CS94: Beyond Worst-Case Analyss Handout 4s Luca Trevsan September 5, 07 Summary of Lecture 4 In whch we ntroduce semdefnte programmng and apply t to Max Cut. Semdefnte Programmng Recall that
U.C. Berkeley CS94: Beyond Worst-Case Analyss Handout 4s Luca Trevsan September 5, 07 Summary of Lecture 4 In whch we ntroduce semdefnte programmng and apply t to Max Cut. Semdefnte Programmng Recall that
Lecture 10 Support Vector Machines II
 Lecture 10 Support Vector Machnes II 22 February 2016 Taylor B. Arnold Yale Statstcs STAT 365/665 1/28 Notes: Problem 3 s posted and due ths upcomng Frday There was an early bug n the fake-test data; fxed
Lecture 10 Support Vector Machnes II 22 February 2016 Taylor B. Arnold Yale Statstcs STAT 365/665 1/28 Notes: Problem 3 s posted and due ths upcomng Frday There was an early bug n the fake-test data; fxed
Inner Product. Euclidean Space. Orthonormal Basis. Orthogonal
 Inner Product Defnton 1 () A Eucldean space s a fnte-dmensonal vector space over the reals R, wth an nner product,. Defnton 2 (Inner Product) An nner product, on a real vector space X s a symmetrc, blnear,
Inner Product Defnton 1 () A Eucldean space s a fnte-dmensonal vector space over the reals R, wth an nner product,. Defnton 2 (Inner Product) An nner product, on a real vector space X s a symmetrc, blnear,
Physics 4B. A positive value is obtained, so the current is counterclockwise around the circuit.
 Physcs 4B Solutons to Chapter 7 HW Chapter 7: Questons:, 8, 0 Problems:,,, 45, 48,,, 7, 9 Queston 7- (a) no (b) yes (c) all te Queston 7-8 0 μc Queston 7-0, c;, a;, d; 4, b Problem 7- (a) Let be the current
Physcs 4B Solutons to Chapter 7 HW Chapter 7: Questons:, 8, 0 Problems:,,, 45, 48,,, 7, 9 Queston 7- (a) no (b) yes (c) all te Queston 7-8 0 μc Queston 7-0, c;, a;, d; 4, b Problem 7- (a) Let be the current
n α j x j = 0 j=1 has a nontrivial solution. Here A is the n k matrix whose jth column is the vector for all t j=0
 MODULE 2 Topcs: Lnear ndependence, bass and dmenson We have seen that f n a set of vectors one vector s a lnear combnaton of the remanng vectors n the set then the span of the set s unchanged f that vector
MODULE 2 Topcs: Lnear ndependence, bass and dmenson We have seen that f n a set of vectors one vector s a lnear combnaton of the remanng vectors n the set then the span of the set s unchanged f that vector
Advanced Circuits Topics - Part 1 by Dr. Colton (Fall 2017)
 Advanced rcuts Topcs - Part by Dr. olton (Fall 07) Part : Some thngs you should already know from Physcs 0 and 45 These are all thngs that you should have learned n Physcs 0 and/or 45. Ths secton s organzed
Advanced rcuts Topcs - Part by Dr. olton (Fall 07) Part : Some thngs you should already know from Physcs 0 and 45 These are all thngs that you should have learned n Physcs 0 and/or 45. Ths secton s organzed
Module 14: THE INTEGRAL Exploring Calculus
 Module 14: THE INTEGRAL Explorng Calculus Part I Approxmatons and the Defnte Integral It was known n the 1600s before the calculus was developed that the area of an rregularly shaped regon could be approxmated
Module 14: THE INTEGRAL Explorng Calculus Part I Approxmatons and the Defnte Integral It was known n the 1600s before the calculus was developed that the area of an rregularly shaped regon could be approxmated
Chapter 2 - The Simple Linear Regression Model S =0. e i is a random error. S β2 β. This is a minimization problem. Solution is a calculus exercise.
 Chapter - The Smple Lnear Regresson Model The lnear regresson equaton s: where y + = β + β e for =,..., y and are observable varables e s a random error How can an estmaton rule be constructed for the
Chapter - The Smple Lnear Regresson Model The lnear regresson equaton s: where y + = β + β e for =,..., y and are observable varables e s a random error How can an estmaton rule be constructed for the
Spring Force and Power
 Lecture 13 Chapter 9 Sprng Force and Power Yeah, energy s better than orces. What s net? Course webste: http://aculty.uml.edu/andry_danylov/teachng/physcsi IN THIS CHAPTER, you wll learn how to solve problems
Lecture 13 Chapter 9 Sprng Force and Power Yeah, energy s better than orces. What s net? Course webste: http://aculty.uml.edu/andry_danylov/teachng/physcsi IN THIS CHAPTER, you wll learn how to solve problems
A new Approach for Solving Linear Ordinary Differential Equations
 , ISSN 974-57X (Onlne), ISSN 974-5718 (Prnt), Vol. ; Issue No. 1; Year 14, Copyrght 13-14 by CESER PUBLICATIONS A new Approach for Solvng Lnear Ordnary Dfferental Equatons Fawz Abdelwahd Department of
, ISSN 974-57X (Onlne), ISSN 974-5718 (Prnt), Vol. ; Issue No. 1; Year 14, Copyrght 13-14 by CESER PUBLICATIONS A new Approach for Solvng Lnear Ordnary Dfferental Equatons Fawz Abdelwahd Department of
Linear Approximation with Regularization and Moving Least Squares
 Lnear Approxmaton wth Regularzaton and Movng Least Squares Igor Grešovn May 007 Revson 4.6 (Revson : March 004). 5 4 3 0.5 3 3.5 4 Contents: Lnear Fttng...4. Weghted Least Squares n Functon Approxmaton...
Lnear Approxmaton wth Regularzaton and Movng Least Squares Igor Grešovn May 007 Revson 4.6 (Revson : March 004). 5 4 3 0.5 3 3.5 4 Contents: Lnear Fttng...4. Weghted Least Squares n Functon Approxmaton...
Problem Do any of the following determine homomorphisms from GL n (C) to GL n (C)?
 Homework 8 solutons. Problem 16.1. Whch of the followng defne homomomorphsms from C\{0} to C\{0}? Answer. a) f 1 : z z Yes, f 1 s a homomorphsm. We have that z s the complex conjugate of z. If z 1,z 2
Homework 8 solutons. Problem 16.1. Whch of the followng defne homomomorphsms from C\{0} to C\{0}? Answer. a) f 1 : z z Yes, f 1 s a homomorphsm. We have that z s the complex conjugate of z. If z 1,z 2
Solution of Linear System of Equations and Matrix Inversion Gauss Seidel Iteration Method
 Soluton of Lnear System of Equatons and Matr Inverson Gauss Sedel Iteraton Method It s another well-known teratve method for solvng a system of lnear equatons of the form a + a22 + + ann = b a2 + a222
Soluton of Lnear System of Equatons and Matr Inverson Gauss Sedel Iteraton Method It s another well-known teratve method for solvng a system of lnear equatons of the form a + a22 + + ann = b a2 + a222
Physics 5153 Classical Mechanics. D Alembert s Principle and The Lagrangian-1
 P. Guterrez Physcs 5153 Classcal Mechancs D Alembert s Prncple and The Lagrangan 1 Introducton The prncple of vrtual work provdes a method of solvng problems of statc equlbrum wthout havng to consder the
P. Guterrez Physcs 5153 Classcal Mechancs D Alembert s Prncple and The Lagrangan 1 Introducton The prncple of vrtual work provdes a method of solvng problems of statc equlbrum wthout havng to consder the
Solutions to Problem Set 6
 Solutons to Problem Set 6 Problem 6. (Resdue theory) a) Problem 4.7.7 Boas. n ths problem we wll solve ths ntegral: x sn x x + 4x + 5 dx: To solve ths usng the resdue theorem, we study ths complex ntegral:
Solutons to Problem Set 6 Problem 6. (Resdue theory) a) Problem 4.7.7 Boas. n ths problem we wll solve ths ntegral: x sn x x + 4x + 5 dx: To solve ths usng the resdue theorem, we study ths complex ntegral:
(2mn, m 2 n 2, m 2 + n 2 )
 MATH 16T Homewk Solutons 1. Recall that a natural number n N s a perfect square f n = m f some m N. a) Let n = p α even f = 1,,..., k. be the prme factzaton of some n. Prove that n s a perfect square f
MATH 16T Homewk Solutons 1. Recall that a natural number n N s a perfect square f n = m f some m N. a) Let n = p α even f = 1,,..., k. be the prme factzaton of some n. Prove that n s a perfect square f
Math 261 Exercise sheet 2
 Math 261 Exercse sheet 2 http://staff.aub.edu.lb/~nm116/teachng/2017/math261/ndex.html Verson: September 25, 2017 Answers are due for Monday 25 September, 11AM. The use of calculators s allowed. Exercse
Math 261 Exercse sheet 2 http://staff.aub.edu.lb/~nm116/teachng/2017/math261/ndex.html Verson: September 25, 2017 Answers are due for Monday 25 September, 11AM. The use of calculators s allowed. Exercse
Physics 2A Chapters 6 - Work & Energy Fall 2017
 Physcs A Chapters 6 - Work & Energy Fall 017 These notes are eght pages. A quck summary: The work-energy theorem s a combnaton o Chap and Chap 4 equatons. Work s dened as the product o the orce actng on
Physcs A Chapters 6 - Work & Energy Fall 017 These notes are eght pages. A quck summary: The work-energy theorem s a combnaton o Chap and Chap 4 equatons. Work s dened as the product o the orce actng on
November 5, 2002 SE 180: Earthquake Engineering SE 180. Final Project
 SE 8 Fnal Project Story Shear Frame u m Gven: u m L L m L L EI ω ω Solve for m Story Bendng Beam u u m L m L Gven: m L L EI ω ω Solve for m 3 3 Story Shear Frame u 3 m 3 Gven: L 3 m m L L L 3 EI ω ω ω
SE 8 Fnal Project Story Shear Frame u m Gven: u m L L m L L EI ω ω Solve for m Story Bendng Beam u u m L m L Gven: m L L EI ω ω Solve for m 3 3 Story Shear Frame u 3 m 3 Gven: L 3 m m L L L 3 EI ω ω ω
Workshop: Approximating energies and wave functions Quantum aspects of physical chemistry
 Workshop: Approxmatng energes and wave functons Quantum aspects of physcal chemstry http://quantum.bu.edu/pltl/6/6.pdf Last updated Thursday, November 7, 25 7:9:5-5: Copyrght 25 Dan Dll (dan@bu.edu) Department
Workshop: Approxmatng energes and wave functons Quantum aspects of physcal chemstry http://quantum.bu.edu/pltl/6/6.pdf Last updated Thursday, November 7, 25 7:9:5-5: Copyrght 25 Dan Dll (dan@bu.edu) Department
Quantum Mechanics I - Session 4
 Quantum Mechancs I - Sesson 4 Aprl 3, 05 Contents Operators Change of Bass 4 3 Egenvectors and Egenvalues 5 3. Denton....................................... 5 3. Rotaton n D....................................
Quantum Mechancs I - Sesson 4 Aprl 3, 05 Contents Operators Change of Bass 4 3 Egenvectors and Egenvalues 5 3. Denton....................................... 5 3. Rotaton n D....................................
ˆ (0.10 m) E ( N m /C ) 36 ˆj ( j C m)
 7.. = = 3 = 4 = 5. The electrc feld s constant everywhere between the plates. Ths s ndcated by the electrc feld vectors, whch are all the same length and n the same drecton. 7.5. Model: The dstances to
7.. = = 3 = 4 = 5. The electrc feld s constant everywhere between the plates. Ths s ndcated by the electrc feld vectors, whch are all the same length and n the same drecton. 7.5. Model: The dstances to
GAUTENG DEPARTMENT OF EDUCATION SENIOR SECONDARY INTERVENTION PROGRAMME PHYSICAL SCIENCES GRADE 12 SESSION 1 (LEARNER NOTES)
 PHYSICAL SCIENCES GRADE 1 SESSION 1 (LEARNER NOTES) TOPIC 1: MECHANICS PROJECTILE MOTION Learner Note: Always draw a dagram of the stuaton and enter all the numercal alues onto your dagram. Remember to
PHYSICAL SCIENCES GRADE 1 SESSION 1 (LEARNER NOTES) TOPIC 1: MECHANICS PROJECTILE MOTION Learner Note: Always draw a dagram of the stuaton and enter all the numercal alues onto your dagram. Remember to
CS 3710: Visual Recognition Classification and Detection. Adriana Kovashka Department of Computer Science January 13, 2015
 CS 3710: Vsual Recognton Classfcaton and Detecton Adrana Kovashka Department of Computer Scence January 13, 2015 Plan for Today Vsual recognton bascs part 2: Classfcaton and detecton Adrana s research
CS 3710: Vsual Recognton Classfcaton and Detecton Adrana Kovashka Department of Computer Scence January 13, 2015 Plan for Today Vsual recognton bascs part 2: Classfcaton and detecton Adrana s research
Modeling of Dynamic Systems
 Modelng of Dynamc Systems Ref: Control System Engneerng Norman Nse : Chapters & 3 Chapter objectves : Revew the Laplace transform Learn how to fnd a mathematcal model, called a transfer functon Learn how
Modelng of Dynamc Systems Ref: Control System Engneerng Norman Nse : Chapters & 3 Chapter objectves : Revew the Laplace transform Learn how to fnd a mathematcal model, called a transfer functon Learn how
1 GSW Iterative Techniques for y = Ax
 1 for y = A I m gong to cheat here. here are a lot of teratve technques that can be used to solve the general case of a set of smultaneous equatons (wrtten n the matr form as y = A), but ths chapter sn
1 for y = A I m gong to cheat here. here are a lot of teratve technques that can be used to solve the general case of a set of smultaneous equatons (wrtten n the matr form as y = A), but ths chapter sn
2.3 Nilpotent endomorphisms
 s a block dagonal matrx, wth A Mat dm U (C) In fact, we can assume that B = B 1 B k, wth B an ordered bass of U, and that A = [f U ] B, where f U : U U s the restrcton of f to U 40 23 Nlpotent endomorphsms
s a block dagonal matrx, wth A Mat dm U (C) In fact, we can assume that B = B 1 B k, wth B an ordered bass of U, and that A = [f U ] B, where f U : U U s the restrcton of f to U 40 23 Nlpotent endomorphsms
where v means the change in velocity, and t is the
 1 PHYS:100 LECTURE 4 MECHANICS (3) Ths lecture covers the eneral case of moton wth constant acceleraton and free fall (whch s one of the more mportant examples of moton wth constant acceleraton) n a more
1 PHYS:100 LECTURE 4 MECHANICS (3) Ths lecture covers the eneral case of moton wth constant acceleraton and free fall (whch s one of the more mportant examples of moton wth constant acceleraton) n a more
Statistics MINITAB - Lab 2
 Statstcs 20080 MINITAB - Lab 2 1. Smple Lnear Regresson In smple lnear regresson we attempt to model a lnear relatonshp between two varables wth a straght lne and make statstcal nferences concernng that
Statstcs 20080 MINITAB - Lab 2 1. Smple Lnear Regresson In smple lnear regresson we attempt to model a lnear relatonshp between two varables wth a straght lne and make statstcal nferences concernng that
CSci 6974 and ECSE 6966 Math. Tech. for Vision, Graphics and Robotics Lecture 21, April 17, 2006 Estimating A Plane Homography
 CSc 6974 and ECSE 6966 Math. Tech. for Vson, Graphcs and Robotcs Lecture 21, Aprl 17, 2006 Estmatng A Plane Homography Overvew We contnue wth a dscusson of the major ssues, usng estmaton of plane projectve
CSc 6974 and ECSE 6966 Math. Tech. for Vson, Graphcs and Robotcs Lecture 21, Aprl 17, 2006 Estmatng A Plane Homography Overvew We contnue wth a dscusson of the major ssues, usng estmaton of plane projectve
CALCULUS CLASSROOM CAPSULES
 CALCULUS CLASSROOM CAPSULES SESSION S86 Dr. Sham Alfred Rartan Valley Communty College salfred@rartanval.edu 38th AMATYC Annual Conference Jacksonvlle, Florda November 8-, 202 2 Calculus Classroom Capsules
CALCULUS CLASSROOM CAPSULES SESSION S86 Dr. Sham Alfred Rartan Valley Communty College salfred@rartanval.edu 38th AMATYC Annual Conference Jacksonvlle, Florda November 8-, 202 2 Calculus Classroom Capsules
3.1 Expectation of Functions of Several Random Variables. )' be a k-dimensional discrete or continuous random vector, with joint PMF p (, E X E X1 E X
 Statstcs 1: Probablty Theory II 37 3 EPECTATION OF SEVERAL RANDOM VARIABLES As n Probablty Theory I, the nterest n most stuatons les not on the actual dstrbuton of a random vector, but rather on a number
Statstcs 1: Probablty Theory II 37 3 EPECTATION OF SEVERAL RANDOM VARIABLES As n Probablty Theory I, the nterest n most stuatons les not on the actual dstrbuton of a random vector, but rather on a number
Problem Solving in Math (Math 43900) Fall 2013
 Problem Solvng n Math (Math 43900) Fall 2013 Week four (September 17) solutons Instructor: Davd Galvn 1. Let a and b be two nteger for whch a b s dvsble by 3. Prove that a 3 b 3 s dvsble by 9. Soluton:
Problem Solvng n Math (Math 43900) Fall 2013 Week four (September 17) solutons Instructor: Davd Galvn 1. Let a and b be two nteger for whch a b s dvsble by 3. Prove that a 3 b 3 s dvsble by 9. Soluton:
APPENDIX A Some Linear Algebra
 APPENDIX A Some Lnear Algebra The collecton of m, n matrces A.1 Matrces a 1,1,..., a 1,n A = a m,1,..., a m,n wth real elements a,j s denoted by R m,n. If n = 1 then A s called a column vector. Smlarly,
APPENDIX A Some Lnear Algebra The collecton of m, n matrces A.1 Matrces a 1,1,..., a 1,n A = a m,1,..., a m,n wth real elements a,j s denoted by R m,n. If n = 1 then A s called a column vector. Smlarly,
5 The Rational Canonical Form
 5 The Ratonal Canoncal Form Here p s a monc rreducble factor of the mnmum polynomal m T and s not necessarly of degree one Let F p denote the feld constructed earler n the course, consstng of all matrces
5 The Ratonal Canoncal Form Here p s a monc rreducble factor of the mnmum polynomal m T and s not necessarly of degree one Let F p denote the feld constructed earler n the course, consstng of all matrces
Causal Diamonds. M. Aghili, L. Bombelli, B. Pilgrim
 Causal Damonds M. Aghl, L. Bombell, B. Plgrm Introducton The correcton to volume of a causal nterval due to curvature of spacetme has been done by Myrhem [] and recently by Gbbons & Solodukhn [] and later
Causal Damonds M. Aghl, L. Bombell, B. Plgrm Introducton The correcton to volume of a causal nterval due to curvature of spacetme has been done by Myrhem [] and recently by Gbbons & Solodukhn [] and later
Introduction to Vapor/Liquid Equilibrium, part 2. Raoult s Law:
 CE304, Sprng 2004 Lecture 4 Introducton to Vapor/Lqud Equlbrum, part 2 Raoult s Law: The smplest model that allows us do VLE calculatons s obtaned when we assume that the vapor phase s an deal gas, and
CE304, Sprng 2004 Lecture 4 Introducton to Vapor/Lqud Equlbrum, part 2 Raoult s Law: The smplest model that allows us do VLE calculatons s obtaned when we assume that the vapor phase s an deal gas, and
Chapter 5. Solution of System of Linear Equations. Module No. 6. Solution of Inconsistent and Ill Conditioned Systems
 Numercal Analyss by Dr. Anta Pal Assstant Professor Department of Mathematcs Natonal Insttute of Technology Durgapur Durgapur-713209 emal: anta.bue@gmal.com 1 . Chapter 5 Soluton of System of Lnear Equatons
Numercal Analyss by Dr. Anta Pal Assstant Professor Department of Mathematcs Natonal Insttute of Technology Durgapur Durgapur-713209 emal: anta.bue@gmal.com 1 . Chapter 5 Soluton of System of Lnear Equatons
ON A DETERMINATION OF THE INITIAL FUNCTIONS FROM THE OBSERVED VALUES OF THE BOUNDARY FUNCTIONS FOR THE SECOND-ORDER HYPERBOLIC EQUATION
 Advanced Mathematcal Models & Applcatons Vol.3, No.3, 2018, pp.215-222 ON A DETERMINATION OF THE INITIAL FUNCTIONS FROM THE OBSERVED VALUES OF THE BOUNDARY FUNCTIONS FOR THE SECOND-ORDER HYPERBOLIC EUATION
Advanced Mathematcal Models & Applcatons Vol.3, No.3, 2018, pp.215-222 ON A DETERMINATION OF THE INITIAL FUNCTIONS FROM THE OBSERVED VALUES OF THE BOUNDARY FUNCTIONS FOR THE SECOND-ORDER HYPERBOLIC EUATION
From Biot-Savart Law to Divergence of B (1)
 From Bot-Savart Law to Dvergence of B (1) Let s prove that Bot-Savart gves us B (r ) = 0 for an arbtrary current densty. Frst take the dvergence of both sdes of Bot-Savart. The dervatve s wth respect to
From Bot-Savart Law to Dvergence of B (1) Let s prove that Bot-Savart gves us B (r ) = 0 for an arbtrary current densty. Frst take the dvergence of both sdes of Bot-Savart. The dervatve s wth respect to
PES 1120 Spring 2014, Spendier Lecture 6/Page 1
 PES 110 Sprng 014, Spender Lecture 6/Page 1 Lecture today: Chapter 1) Electrc feld due to charge dstrbutons -> charged rod -> charged rng We ntroduced the electrc feld, E. I defned t as an nvsble aura
PES 110 Sprng 014, Spender Lecture 6/Page 1 Lecture today: Chapter 1) Electrc feld due to charge dstrbutons -> charged rod -> charged rng We ntroduced the electrc feld, E. I defned t as an nvsble aura
How Differential Equations Arise. Newton s Second Law of Motion
 page 1 CHAPTER 1 Frst-Order Dfferental Equatons Among all of the mathematcal dscplnes the theory of dfferental equatons s the most mportant. It furnshes the explanaton of all those elementary manfestatons
page 1 CHAPTER 1 Frst-Order Dfferental Equatons Among all of the mathematcal dscplnes the theory of dfferental equatons s the most mportant. It furnshes the explanaton of all those elementary manfestatons
OPTIMISATION. Introduction Single Variable Unconstrained Optimisation Multivariable Unconstrained Optimisation Linear Programming
 OPTIMIATION Introducton ngle Varable Unconstraned Optmsaton Multvarable Unconstraned Optmsaton Lnear Programmng Chapter Optmsaton /. Introducton In an engneerng analss, sometmes etremtes, ether mnmum or
OPTIMIATION Introducton ngle Varable Unconstraned Optmsaton Multvarable Unconstraned Optmsaton Lnear Programmng Chapter Optmsaton /. Introducton In an engneerng analss, sometmes etremtes, ether mnmum or
The Geometry of Logit and Probit
 The Geometry of Logt and Probt Ths short note s meant as a supplement to Chapters and 3 of Spatal Models of Parlamentary Votng and the notaton and reference to fgures n the text below s to those two chapters.
The Geometry of Logt and Probt Ths short note s meant as a supplement to Chapters and 3 of Spatal Models of Parlamentary Votng and the notaton and reference to fgures n the text below s to those two chapters.
CHAPTER-5 INFORMATION MEASURE OF FUZZY MATRIX AND FUZZY BINARY RELATION
 CAPTER- INFORMATION MEASURE OF FUZZY MATRI AN FUZZY BINARY RELATION Introducton The basc concept of the fuzz matr theor s ver smple and can be appled to socal and natural stuatons A branch of fuzz matr
CAPTER- INFORMATION MEASURE OF FUZZY MATRI AN FUZZY BINARY RELATION Introducton The basc concept of the fuzz matr theor s ver smple and can be appled to socal and natural stuatons A branch of fuzz matr
Measurement Uncertainties Reference
 Measurement Uncertantes Reference Introducton We all ntutvely now that no epermental measurement can be perfect. It s possble to mae ths dea quanttatve. It can be stated ths way: the result of an ndvdual
Measurement Uncertantes Reference Introducton We all ntutvely now that no epermental measurement can be perfect. It s possble to mae ths dea quanttatve. It can be stated ths way: the result of an ndvdual
Chapter 14 Simple Linear Regression
 Chapter 4 Smple Lnear Regresson Chapter 4 - Smple Lnear Regresson Manageral decsons often are based on the relatonshp between two or more varables. Regresson analss can be used to develop an equaton showng
Chapter 4 Smple Lnear Regresson Chapter 4 - Smple Lnear Regresson Manageral decsons often are based on the relatonshp between two or more varables. Regresson analss can be used to develop an equaton showng
