Chapter 8: Further Applications of Trigonometry
|
|
|
- Darrell O’Connor’
- 6 years ago
- Views:
Transcription
1 Secton 8. Polar Form of Complex Numbers 1 Chapter 8: Further Applcatons of Trgonometry In ths chapter, we wll explore addtonal applcatons of trgonometry. We wll begn wth an extenson of the rght trangle trgonometry we explored n Chapter 5 to stuatons nvolvng non-rght trangles. We wll explore the polar coordnate system and parametrc equatons as new ways of descrbng curves n the plane. In the process, we wll ntroduce vectors and an alternatve way of wrtng complex numbers, two mportant mathematcal tools we use when analyzng and modelng the world around us. Secton 8. Polar Form of Complex Numbers... Secton 8.4 Vectors... 1 Secton 8.5 Parametrc Equatons... 6
2 Secton 8. Polar Form of Complex Numbers From prevous classes, you may have encountered magnary numbers the square roots of negatve numbers and, more generally, complex numbers whch are the sum of a real number and an magnary number. Whle these are useful for expressng the solutons to quadratc equatons, they have much rcher applcatons n electrcal engneerng, sgnal analyss, and other felds. Most of these more advanced applcatons rely on propertes that arse from lookng at complex numbers from the perspectve of polar coordnates. We wll begn wth a revew of the defnton of complex numbers. Imagnary Number The most basc complex number s, defned to be 1, commonly called an magnary number. Any real multple of s also an magnary number. Example 1 Smplfy 9. We can separate 9 as 9 1. We can take the square root of 9, and wrte the square root of -1 as. 9 = 9 1 A complex number s the sum of a real number and an magnary number. Complex Number A complex number s a number z a b, where a and b are real numbers a s the real part of the complex number b s the magnary part of the complex number 1 Plottng a complex number We can plot real numbers on a number lne. For example, f we wanted to show the number, we plot a pont:
3 Secton 8. Polar Form of Complex Numbers To plot a complex number lke 4, we need more than just a number lne snce there are two components to the number. To plot ths number, we need two number lnes, crossed to form a complex plane. Complex Plane In the complex plane, the horzontal axs s the real axs and the vertcal axs s the magnary axs. magnary real Example Plot the number 4 on the complex plane. The real part of ths number s, and the magnary part s -4. To plot ths, we draw a pont unts to the rght of the orgn n the horzontal drecton and 4 unts down n the vertcal drecton. magnary real Because ths s analogous to the Cartesan coordnate system for plottng ponts, we can thnk about plottng our complex number z a b as f we were plottng the pont (a, b) n Cartesan coordnates. Sometmes people wrte complex numbers as z x y to hghlght ths relaton. Arthmetc on Complex Numbers Before we dve nto the more complcated uses of complex numbers, let s make sure we remember the basc arthmetc nvolved. To add or subtract complex numbers, we smply add the lke terms, combnng the real parts and combnng the magnary parts. Example Add 4 and 5. Addng ( 4) ( 5), we add the real parts and the magnary parts Try t Now 1. Subtract 5 from 4. We can also multply and dvde complex numbers.
4 Example 4 Multply: 4( 5). To multply the complex number by a real number, we smply dstrbute as we would when multplyng polynomals. 4( 5) = Example 5 Dvde ( 5 ). (4 ) To dvde two complex numbers, we have to devse a way to wrte ths as a complex number wth a real part and an magnary part. We start ths process by elmnatng the complex number n the denomnator. To do ths, we multply the numerator and denomnator by a specal complex number so that the result n the denomnator s a real number. The number we need to multply by s called the complex conjugate, n whch the sgn of the magnary part s changed. Here, 4+ s the complex conjugate of 4. Of course, obeyng our algebrac rules, we must multply by 4+ on both the top and bottom. ( 5 ) (4 ) (4 ) (4 ) To multply two complex numbers, we expand the product as we would wth polynomals (the process commonly called FOIL frst outer nner last ). In the numerator: ( 5 )(4 ) Expand Snce 1, ( 1) Smplfy Followng the same process to multply the denomnator (4 )(4 ) Expand ( ) Snce 1, 1 (16 ( 1)) =17 Combnng ths we get
5 Secton 8. Polar Form of Complex Numbers 5 Try t Now. Multply 4 and. Wth the nterpretaton of complex numbers as ponts n a plane, whch can be related to the Cartesan coordnate system, you mght be startng to guess our next step to refer to ths pont not by ts horzontal and vertcal components, but usng ts polar locaton, gven by the dstance from the orgn and an angle. Polar Form of Complex Numbers Remember, because the complex plane s analogous to the Cartesan plane that we can thnk of a complex number z x y as analogous to the Cartesan pont (x, y) and recall how we converted from (x, y) to polar (r, θ) coordnates n the last secton. Brngng n all of our old rules we remember the followng: x cos( ) r x r cos( ) y sn( ) r y r sn( ) y tan( ) x y r x magnary r θ x x + y y real Wth ths n mnd, we can wrte z x y r cos( ) r sn( ). Example 6 Express the complex number 4 usng polar coordnates. On the complex plane, the number 4 s a dstance of 4 from the orgn at an angle of, so 4 4cos 4sn Note that the real part of ths complex number s In the 18 th century, Leonhard Euler demonstrated a relatonshp between exponental and trgonometrc functons that allows the use of complex numbers to greatly smplfy some trgonometrc calculatons. Whle the proof s beyond the scope of ths class, you wll lkely see t n a later calculus class.
6 Polar Form of a Complex Number and Euler s Formula The polar form of a complex number s z re, where Euler s Formula holds: re r cos( ) r sn( ) Smlar to plottng a pont n the polar coordnate system we need r and to fnd the polar form of a complex number. Example 7 Fnd the polar form of the complex number -7. Treatng ths s a complex number, we can consder the unsmplfed verson Plotted n the complex plane, the number -7 s on the negatve horzontal axs, a dstance of 7 from the orgn at an angle of π from the postve horzontal axs. The polar form of the number -7 s 7 e. Pluggng r = 7 and θ = π back nto Euler s formula, we have: 7e 7cos( ) 7 sn( ) as desred. Example 8 Fnd the polar form of 4 4. On the complex plane, ths complex number would correspond to the pont (-4, 4) on a Cartesan plane. We can fnd the dstance r and angle θ as we dd n the last secton. r r x y ( 4) 4 r 4 To fnd θ, we can use cos( ) 4 cos( ) 4 Ths s one of known cosne values, and snce the pont s n the second quadrant, we can conclude that. 4 The polar form of ths complex number s x r 4 e
7 Secton 8. Polar Form of Complex Numbers 7 Note we could have used check the quadrant. y tan( ) nstead to fnd the angle, so long as we remember to x Try t Now. Wrte n polar form. Example 9 Wrte e 6 n complex a b form. e 6 cos sn Smplfy Evaluate the trg functons The polar form of a complex number provdes a powerful way to compute powers and roots of complex numbers by usng exponent rules you learned n algebra. To compute a power of a complex number, we: 1) Convert to polar form ) Rase to the power, usng exponent rules to smplfy ) Convert back to a + b form, f needed Example 10 Evaluate Whle we could multply ths number by tself fve tmes, that would be very tedous. To compute ths more effcently, we can utlze the polar form of the complex number. In an earler example, we found that e. Usng ths, Wrte the complex number n polar form 4 4 e 6 4 e Utlze the exponent rule ( m m ab) a m n On the second factor, use the rule ( a ) a b m mn
8 e e Smplfy At ths pont, we have found the power as a complex number n polar form. If we want the answer n standard a + b form, we can utlze Euler s formula e 9 768cos 9 768sn 9 Snce s cotermnal wth, we can use our specal angle knowledge to evaluate the sne and cosne cos 9 768sn 6 We have found that (0) 768(1) 768 The result of the process can be summarzed by DeMovre s Theorem. DeMovre s Theorem z r cos sn n n If, then for any nteger n, z r cos n sn n We omt the proof, but note we can easly verfy t holds n one case usng Example 10: ( 4 4) 4 cos 6 sn6 768 cos sn Example 11 Evaluate 9. To evaluate the square root of a complex number, we can frst note that the square root 1 s the same as havng an exponent of : 1/ 9 (9). To evaluate the power, we frst wrte the complex number n polar form. Snce 9 has no real part, we know that ths value would be plotted along the vertcal axs, a dstance of 9 from the orgn at an angle of. Ths gves the polar form: 9e 9.
9 Secton 8. Polar Form of Complex Numbers 9 9 = 9e 1/ (9 ) Use the polar form 1/ 9 9 1/ e e 1/ 1 1/ Use exponent rules to smplfy Smplfy e 4 Rewrte usng Euler s formula f desred cos sn 4 4 Evaluate the sne and cosne Usng the polar form, we were able to fnd a square root of a complex number. 9 Alternatvely, usng DeMovre s Theorem we can wrte 9e 1/ cos sn 4 4 and smplfy Try t Now 4. Wrte 6 n polar form. You may remember that equatons lke x 4 have two solutons, and - n ths case, though the square root 4 only gves one of those solutons. Lkewse, the square root we found n Example 11 s only one of two complex numbers whose square s 9. Smlarly, the equaton z 8 would have three solutons where only one s gven by the cube root. In ths case, however, only one of those solutons, z =, s a real value. To fnd the others, we can use the fact that complex numbers have multple representatons n polar form. Example 1 Fnd all complex solutons to z 8.
10 1/ Snce we are tryng to solve z 8, we can solve for x as z 8. Certanly one of these solutons s the basc cube root, gvng z =. To fnd others, we can turn to the polar representaton of 8. Snce 8 s a real number, s would st n the complex plane on the horzontal axs at an angle of 0, gvng the polar form 8 e 0. Takng the 1/ power of ths gves the real soluton: 0 8 1/ 1/ 0 0 e 8 e 1/ e cos(0) sn(0) However, snce the angle π s cotermnal wth the angle of 0, we could also represent the number 8 as 8 e. Takng the 1/ power of ths gves a frst complex soluton: 1/ 1/ 1 8e 8 1/ e e cos sn 1 To fnd the thrd root, we use the angle of 4π, whch s also cotermnal wth an angle of / 1/ e 8 1/ 4 e e cos sn 1 Altogether, we found all three complex solutons to z 8, 1 z, 1, 1 Graphed, these three numbers would be equally spaced on a crcle about the orgn at a radus of. 1 Important Topcs of Ths Secton Complex numbers Imagnary numbers Plottng ponts n the complex coordnate system Basc operatons wth complex numbers Euler s Formula DeMovre s Theorem Fndng complex solutons to equatons Try t Now Answers 1. ( 4 ) ( 5 ) 1 9. ( 4 )( ) n polar form s e
11 Secton 8. Polar Form of Complex Numbers 11 Secton 8. Exercses Smplfy each expresson to a sngle complex number Smplfy each expresson to a sngle complex number. (5 ) (6 ) (4 ) 1. ( ) 5 ( ) 1. 6 (5) (4 ) ( ) (4 ) Rewrte each complex number from polar form nto a b form. 9. e e 1. e 8e.. e e 7 4 Rewrte each complex number nto polar re form
12 Compute each of the followng, leavng the result n polar e e 5 5. e 4e re 5. form. 6e e e 55. 6e 4 e e e 58. 9e Compute each of the followng, smplfyng the result nto a b form Solve each of the followng equatons for all complex solutons z 66. z 67. z z 1
13 Secton 8.4 Vectors 1 Secton 8.4 Vectors A woman leaves home, walks mles north, then mles southeast. How far s she from home, and n whch drecton would she need to walk to return home? How far has she walked by the tme she gets home? Ths queston may seem famlar ndeed we dd a smlar problem wth a boat n the frst secton of ths chapter. In that secton, we solved the problem usng trangles. In ths secton, we wll nvestgate another way to approach the problem usng vectors, a geometrc entty that ndcates both a dstance and a drecton. We wll begn our nvestgaton usng a purely geometrc vew of vectors. A Geometrc Vew of Vectors Vector A vector s an object that has both a length and a drecton. Geometrcally, a vector can be represented by an arrow that has a fxed length and ndcates a drecton. If, startng at the pont A, a vector, whch means carrer n Latn, moves toward pont B, we wrte AB to represent the vector. A vector may also be ndcated usng a sngle letter n boldface type, lke u, or by cappng the letter representng the vector wth an arrow, lke u. Example 1 Fnd a vector that represents the movement from the pont P(-1, ) to the pont Q(,) By drawng an arrow from the frst pont to the second, we can construct a vector PQ. P Q Usng ths geometrc representaton of vectors, we can vsualze the addton and scalng of vectors. To add vectors, we envson a sum of two movements. To fnd u v, we frst draw the vector u, then from the end of u we drawn the vector v. Ths corresponds to the noton that frst we move along the frst vector, and then from that end poston we move along the second vector. The sum u v s the new vector that travels drectly from the begnnng of u to the end of v n a straght path.
14 Addng Vectors Geometrcally To add vectors geometrcally, draw v startng from the end of u. The sum u v s the vector from the begnnng of u to the end of v. u v u v Example Gven the two vectors shown below, draw u v u v v We draw v startng from the end of u, then draw n the sum u v from the begnnng of u to the end of v. u u v Notce that path of the walkng woman from the begnnng of the secton could be vsualzed as the sum of two vectors. The resultng sum vector would ndcate her end poston relatve to home. Try t Now 1. Draw a vector, v, that travels from the orgn to the pont (, 5). Note that although vectors can exst anywhere n the plane, f we put the startng pont at the orgn t s easy to understand ts sze and drecton relatve to other vectors. To scale vectors by a constant, such as u, we can magne addng u u u. The result wll be a vector three tmes as long n the same drecton as the orgnal vector. If we were to scale a vector by a negatve number, such as u, we can envson ths as the opposte of u ; the vector so that u ( u) returns us to the startng pont. Ths vector u would pont n the opposte drecton as u but have the same length. Another way to thnk about scalng a vector s to mantan ts drecton and multply ts length by a constant, so that u would pont n the same drecton but wll be tmes as long.
15 Secton 8.4 Vectors 15 Scalng a Vector Geometrcally To geometrcally scale a vector by a constant, scale the length of the vector by the constant. Scalng a vector by a negatve constant wll reverse the drecton of the vector. Example Gven the vector shown, draw u, u, and u. u The vector u wll be three tmes as long. The vector u wll have the same length but pont n the opposte drecton. The vector u wll pont n the opposte drecton and be twce as long. u u u By combnng scalng and addton, we can fnd the dfference between vectors geometrcally as well, snce u v u ( v). Example 4 Gven the vectors shown, draw u v u From the end of u we draw v v, then draw n the result. u v v u Notce that the sum and dfference of two vectors are the two dagonals of a parallelogram wth the vectors u and v as edges. u u v v u v v u Try t Now. Usng vector v from Try t Now #1, draw v.
16 u θ Component Form of Vectors Whle the geometrc nterpretaton of vectors gves us an ntutve understandng of vectors, t does not provde us a convenent way to do calculatons. For that, we need a handy way to represent vectors. Snce a vector nvolves a length and drecton, t would be logcal to want to represent a vector usng a length and an angle θ, usually measured from standard poston. Magntude and Drecton of a Vector A vector u can be descrbed by ts magntude, or length, u, and an angle θ. A vector wth length 1 s called unt vector. Whle ths s very reasonable, and a common way to descrbe vectors, t s often more convenent for calculatons to represent a vector by horzontal and vertcal components. Component Form of a Vector The component form of a vector represents the vector usng two components. u x, y ndcates the vector represents a dsplacement of x unts horzontally and y unts vertcally. u θ x y Notce how we can see the magntude of the vector as the length of the hypotenuse of a rght trangle, or n polar form as the radus, r. Alternate Notaton for Vector Components Sometmes you may see vectors wrtten as the combnaton of unt vectors and j, where ponts the rght and j ponts up. In other words, 1, 0 and j 0, 1. In ths notaton, the vector u, 4 would be wrtten as u 4 j snce both ndcate a dsplacement of unts to the rght, and 4 unts down. Whle t can be convenent to thnk of the vector u x, y as an arrow from the orgn to the pont (x, y), be sure to remember that most vectors can be stuated anywhere n the plane, and smply ndcate a dsplacement (change n poston) rather than a poston.
17 Secton 8.4 Vectors 17 It s common to need to convert from a magntude and angle to the component form of the vector and vce versa. Happly, ths process s dentcal to convertng from polar coordnates to Cartesan coordnates, or from the polar form of complex numbers to the a+b form. Example 5 Fnd the component form of a vector wth length 7 at an angle of 15 degrees. Usng the converson formulas x r cos( ) and y r sn( ), we can fnd the components 7 x 7cos(15) 7 y 7sn(15) Ths vector can be wrtten n component form as 7 7,. Example 6 Fnd the magntude and angle representng the vector u,. Frst we can fnd the magntude by rememberng the relatonshp between x, y and r: r ( ) 1 r 1 Second we can fnd the angle. Usng the tangent, tan( ) tan 1.69, or wrtten as a cotermnal postve angle, 6.1, because we know our pont les n the 4 th quadrant. Try t Now. Usng vector v from Try t Now #1, the vector that travels from the orgn to the pont (, 5), fnd the components, magntude and angle that represent ths vector.
18 In addton to representng dstance movements, vectors are commonly used n physcs and engneerng to represent any quantty that has both drecton and magntude, ncludng veloctes and forces. Example 7 An object s launched wth ntal velocty 00 meters per second at an angle of 0 degrees. Fnd the ntal horzontal and vertcal veloctes. By vewng the ntal velocty as a vector, we can resolve the vector nto horzontal and vertcal components. x 00cos(0) m/sec 00 m/s 1 y 00sn(0) m/sec 0 17 m/s 100 m/s Ths tells us that, absent wnd resstance, the object wll travel horzontally at about 17 meters each second. Gravty wll cause the vertcal velocty to change over tme we ll leave a dscusson of that to physcs or calculus classes. Addng and Scalng Vectors n Component Form To add vectors n component form, we can smply add the correspondng components. To scale a vector by a constant, we scale each component by that constant. Combnng Vectors n Component Form To add, subtract, or scale vectors n component form If u u,u 1, v v,v 1, and c s any constant, then u v u1 v1, u v u v u1 v1, u v cu cu,cu 1 Example 8 Gven u, and v 1, 4, fnd a new vector w u v Usng the vectors gven, w u v, 1,4 Scale each vector 9, 6,8 Subtract correspondng components 11, 14
19 Secton 8.4 Vectors 19 By representng vectors n component form, we can fnd the resultng dsplacement vector after a multtude of movements wthout needng to draw a lot of complcated nonrght trangles. For a smple example, we revst the problem from the openng of the secton. The general procedure we wll follow s: 1) Convert vectors to component form ) Add the components of the vectors ) Convert back to length and drecton f needed to sut the context of the queston Example 9 A woman leaves home, walks mles north, then mles southeast. How far s she from home, and what drecton would she need to walk to return home? How far has she walked by the tme she gets home? Let s begn by understandng the queston n a lttle more depth. When we use vectors to descrbe a travelng drecton, we often poston thngs so north ponts n the upward drecton, east ponts to the rght, and so on, as pctured here. NW W N NE E Consequently, travellng NW, SW, NE or SE, means we are travellng through the quadrant bordered by the gven drectons at a 45 degree angle. SW S SE Wth ths n mnd, we begn by convertng each vector to components. A walk mles north would, n components, be 0,. A walk of mles southeast would be at an angle of 45 South of East, or measurng from standard poston the angle would be 15. Convertng to components, we choose to use the standard poston angle so that we do not have to worry about whether the sgns are negatve or postve; they wll work out automatcally. cos(15 ), sn(15), 1.414, Addng these vectors gves the sum of the movements n component form 0, 1.414, ,1.586 To fnd how far she s from home and the drecton she would need to walk to return home, we could fnd the magntude and angle of ths vector. Length =
20 To fnd the angle, we can use the tangent tan( ) tan north of east Of course, ths s the angle from her startng pont to her endng pont. To return home, she would need to head the opposte drecton, whch we could ether descrbe as = 8.7 measured n standard poston, or as 48.7 south of west (or west of south). She has walked a total dstance of = 7.15 mles. Keep n mnd that total dstance travelled s not the same as the length of the resultng dsplacement vector or the return vector. Try t Now 4. In a scavenger hunt, drectons are gven to fnd a bured treasure. From a startng pont at a flag pole you must walk 0 feet east, turn 0 degrees to the north and travel 50 feet, and then turn due south and travel 75 feet. Sketch a pcture of these vectors, fnd ther components, and calculate how far and n what drecton you must travel to go drectly to the treasure from the flag pole wthout followng the map. Whle usng vectors s not much faster than usng law of cosnes wth only two movements, when combnng three or more movements, forces, or other vector quanttes, usng vectors quckly becomes much more effcent than tryng to use trangles. Example 10 Three forces are actng on an object as shown below, each measured n Newtons (N). What force must be exerted to keep the object n equlbrum (where the sum of the forces s zero)? 7 N 6 N N We start by resolvng each vector nto components.
21 Secton 8.4 Vectors 1 The frst vector wth magntude 6 Newtons at an angle of 0 degrees wll have components 1 6cos(0 ),6sn(0) 6,6, The second vector s only n the horzontal drecton, so can be wrtten as 7, 0. The thrd vector wth magntude 4 Newtons at an angle of 00 degrees wll have components 1 4cos(00 ),4sn(00) 4,4, To keep the object n equlbrum, we need to fnd a force vector the four vectors s the zero vector, 0, 0., 7, 0, x, y 0, 0 Add component-wse 7, 0 x, y 0, 0 Smplfy 5, x, y 0, 0 Solve x, y 0, 0 5, x, y 5, 0.196, x, y so the sum of Ths vector gves n components the force that would need to be appled to keep the object n equlbrum. If desred, we could fnd the magntude of ths force and drecton t would need to be appled n. Magntude = ( 0.196) N Angle: tan( ) tan Ths s n the wrong quadrant, so we adjust by fndng the next angle wth the same tangent value by addng a full perod of tangent: To keep the object n equlbrum, a force of Newtons would need to be appled at an angle of
22 Important Topcs of Ths Secton Vectors, magntude (length) & drecton Addton of vectors Scalng of vectors Components of vectors Vectors as velocty Vectors as forces Addng & Scalng vectors n component form Total dstance travelled vs. total dsplacement Try t Now Answers v v v,5 magntude 4 tan ft 50 ft 75 ft v 1 v f 0,0 v 50cos(0),50sn(0) v 0, cos(0),50sn(0) , 50 Magntude = 88.7 feet at an angle of 4. south of east.
23 Secton 8.4 Vectors Secton 8.4 Exercses Wrte the vector shown n component form. 1.. Gven the vectors shown, sketch u v, u v, and u.. 4. Wrte each vector below as a combnaton of the vectors u and v from queston # From the gven magntude and drecton n standard poston, wrte the vector n component form. 7. Magntude: 6, Drecton: Magntude: 10, Drecton: Magntude: 8, Drecton: Magntude: 7, Drecton: 05 Fnd the magntude and drecton of the vector , 4 1., , 5 14., 7 15., , 1 17., , , , 9 Usng the vectors gven, compute u v, u v, and u v. 1. u,, v 1, 5. u,4, v, 1
24 . A woman leaves home and walks mles west, then mles southwest. How far from home s she, and n what drecton must she walk to head drectly home? 4. A boat leaves the marna and sals 6 mles north, then mles northeast. How far from the marna s the boat, and n what drecton must t sal to head drectly back to the marna? 5. A person starts walkng from home and walks 4 mles east, mles southeast, 5 mles south, 4 mles southwest, and mles east. How far have they walked? If they walked straght home, how far would they have to walk? 6. A person starts walkng from home and walks 4 mles east, 7 mles southeast, 6 mles south, 5 mles southwest, and mles east. How far have they walked? If they walked straght home, how far would they have to walk? 7. Three forces act on an object: F, 5, F 0,1, F 4, 7 force actng on the object Fnd the net 8. Three forces act on an object: F,5, F 8,, F 0, 7 actng on the object. 1. Fnd the net force 9. A person starts walkng from home and walks mles at 0 north of west, then 5 mles at 10 west of south, then 4 mles at 15 north of east. If they walked straght home, how far would they have to walk, and n what drecton? 0. A person starts walkng from home and walks 6 mles at 40 north of east, then mles at 15 east of south, then 5 mles at 0 south of west. If they walked straght home, how far would they have to walk, and n what drecton? 1. An arplane s headng north at an arspeed of 600 km/hr, but there s a wnd blowng from the southwest at 80 km/hr. How many degrees off course wll the plane end up flyng, and what s the plane s speed relatve to the ground?. An arplane s headng north at an arspeed of 500 km/hr, but there s a wnd blowng from the northwest at 50 km/hr. How many degrees off course wll the plane end up flyng, and what s the plane s speed relatve to the ground?. An arplane needs to head due north, but there s a wnd blowng from the southwest at 60 km/hr. The plane fles wth an arspeed of 550 km/hr. To end up flyng due north, the plot wll need to fly the plane how many degrees west of north?
25 Secton 8.4 Vectors 5 4. An arplane needs to head due north, but there s a wnd blowng from the northwest at 80 km/hr. The plane fles wth an arspeed of 500 km/hr. To end up flyng due north, the plot wll need to fly the plane how many degrees west of north? 5. As part of a vdeo game, the pont (5, 7) s rotated counterclockwse about the orgn through an angle of 5 degrees. Fnd the new coordnates of ths pont. 6. As part of a vdeo game, the pont (7, ) s rotated counterclockwse about the orgn through an angle of 40 degrees. Fnd the new coordnates of ths pont. 7. Two chldren are throwng a ball back and forth straght across the back seat of a car. The ball s beng thrown 10 mph relatve to the car, and the car s travellng 5 mph down the road. If one chld doesn't catch the ball and t fles out the wndow, n what drecton does the ball fly (gnorng wnd resstance)? 8. Two chldren are throwng a ball back and forth straght across the back seat of a car. The ball s beng thrown 8 mph relatve to the car, and the car s travellng 45 mph down the road. If one chld doesn't catch the ball and t fles out the wndow, n what drecton does the ball fly (gnorng wnd resstance)?
26 Secton 8.5 Parametrc Equatons Many shapes, even ones as smple as crcles, cannot be represented as an equaton where y s a functon of x. Consder, for example, the path a moon follows as t orbts around a planet, whch smultaneously rotates around a sun. In some cases, polar equatons provde a way to represent such a path. In others, we need a more versatle approach that allows us to represent both the x and y coordnates n terms of a thrd varable, or parameter. Parametrc Equatons A system of parametrc equatons s a par of functons x( and y( n whch the x and y coordnates are the output, represented n terms of a thrd nput parameter, t. Example 1 Movng at a constant speed, an object moves at a steady rate along a straght path from coordnates (-5, ) to the coordnates (, -1) n 4 seconds, where the coordnates are measured n meters. Fnd parametrc equatons for the poston of the object. The x coordnate of the object starts at -5 meters, and goes to + meters, ths means the x drecton has changed by 8 meters n 4 seconds, gvng us a rate of meters per second. We can now wrte the x coordnate as a lnear functon wth respect to tme, t, x( 5 t. Smlarly, the y value starts at and goes to -1, gvng a change n y value of 4 meters, meanng the y values have decreased by 4 meters n 4 seconds, for a rate of -1 meter per second, t x y gvng equaton y( t. Together, these are the 0-5 parametrc equatons for the poston of the object: 1 - x( 5 t -1 1 y( t Usng these equatons, we can buld a table of t, x, and y values. Because of the context, we lmted ourselves to non-negatve t values for ths example, but n general you can use any values. From ths table, we could create three possble graphs: a graph of x vs. t, whch would show the horzontal poston over tme, a graph of y vs. t, whch would show the vertcal poston over tme, or a graph of y vs. x, showng the poston of the object n the plane.
27 Secton 8.5 Parametrc Equatons 7 Poston of x as a functon of tme x Poston of y as a functon of tme y t t Poston of y relatve to x y x Notce that the parameter t does not explctly show up n ths thrd graph. Sometmes, when the parameter t does represent a quantty lke tme, we mght ndcate the drecton of movement on the graph usng an arrow, as shown above. There s often no sngle parametrc representaton for a curve. In Example 1 we assumed the object was movng at a steady rate along a straght lne. If we kept the assumpton about the path (straght lne) but dd not assume the speed was constant, we mght get a system lke: x( 5 t y( x( t y( t Ths starts at (-5, ) when t = 0 and ends up at (, -1) when t =. If we graph the x( and y( functon separately, we can see that those are no longer lnear, but f we graph x vs. y we wll see that we stll get a straght-lne path. t=0 t=1 y x t=
28 Example Sketch a graph of x( t 1 y( t We can begn by creatng a table of values. From ths table, we can plot the (x, y) ponts n the plane, sketch n a rough graph of the curve, and ndcate the drecton of moton wth respect to tme by usng arrows. y t x y x Notce that here the parametrc equatons descrbe a shape for whch y s not a functon of x. Ths s an example of why usng parametrc equatons can be useful snce they can represent such a graph as a set of functons. Ths partcular graph also appears to be a parabola where x s a functon of y, whch we wll soon verfy. Whle creatng a t-x-y table, plottng ponts and connectng the dots wth a smooth curve usually works to gve us a rough dea of what the graph of a system of parametrc equatons looks lke, t's generally easer to use technology to create these tables and (smultaneously) much ncer-lookng graphs. Example Sketch a graph of x( cos(. y( sn( y Usng technology we can generate a graph of ths equaton, producng an ellpse. Smlar to graphng polar equatons, you must change the MODE on your calculator (or select parametrc equatons on your graphng technology) before graphng a system of parametrc equatons. You wll know you have successfully entered parametrc mode when the equaton nput has changed to ask for a x(= and y(= par of equatons. x
29 Secton 8.5 Parametrc Equatons 9 Try t Now 1. Sketch a graph of x( 4cos(t ). Ths s an example of a Lssajous fgure. y( sn( Example 4 The populatons of rabbts and wolves on an sland over tme are gven by the graphs below. Use these graphs to sketch a graph n the r-w plane showng the relatonshp between the number of rabbts and number of wolves. Wolves Years Rabbts Years For each nput t, we can determne the number of rabbts, r, and the number of wolves, w, from the respectve graphs, and then plot the correspondng pont n the r-w plane Rabbts Wolves Ths graph helps reveal the cyclcal nteracton between the two populatons. Convertng from Parametrc to Cartesan In some cases, t s possble to elmnate the parameter t, allowng you to wrte a par of parametrc equatons as a Cartesan equaton. It s easest to do ths f one of the x( or y( functons can easly be solved for t, allowng you to then substtute the remanng expresson nto the second part.
30 Example 6 x( t 1 Wrte y( t as a Cartesan equaton, f possble. Here, the equaton for y s lnear, so s relatvely easy to solve for t. Snce the resultng Cartesan equaton wll lkely not be a functon, and for convenence, we drop the functon notaton. y t Solve for t y t Substtute ths for t n the x equaton x ( y ) 1 Notce that ths s the equaton of a parabola wth x as a functon of y, wth vertex at (1,), openng to the rght. Comparng ths wth the graph from Example, we see (unsurprsngly) that t yelds the same graph n the x-y plane as dd the orgnal parametrc equatons. Try t Now. Wrte x( t y( t 6 as a Cartesan equaton, f possble. Example 7 x( t Wrte y( log( as a Cartesan equaton, f possble. We could solve ether the frst or second equaton for t. Solvng the frst, x t x t Square both sdes x t y x Substtute nto the y equaton log Snce the parametrc equaton s only defned for t 0, ths Cartesan equaton s equvalent to the parametrc equaton on the correspondng doman. The parametrc equatons show that when t > 0, x > and y > 0, so the doman of the Cartesan equaton should be lmted to x >. To ensure that the Cartesan equaton s as equvalent as possble to the orgnal parametrc equaton, we try to avod usng doman-restrcted nverse functons, such as the nverse trg functons, when possble. For equatons nvolvng trg functons, we often try to fnd an dentty to utlze to avod the nverse functons.
31 Secton 8.5 Parametrc Equatons 1 Example 8 x( cos( Wrte y( sn( as a Cartesan equaton, f possble. To rewrte ths, we can utlze the Pythagorean dentty cos ( t ) sn ( 1. x x cos( so cos( y y sn( so sn( Startng wth the Pythagorean Identty cos ( t ) sn ( 1 Substtute n the expressons from the parametrc form x y x y Smplfy Ths s a Cartesan equaton for the ellpse we graphed earler. Parameterzng Curves Whle convertng from parametrc form to Cartesan can be useful, t s often more useful to parameterze a Cartesan equaton convertng t nto parametrc form. If the Cartesan equaton gves one varable as a functon of the other, then parameterzaton s trval the ndependent varable n the functon can smply be defned as t. Example 9 Parameterze the equaton x y y. In ths equaton, x s expressed as a functon of y. By defnng y t we can then substtute that nto the Cartesan equaton, yeldng x t t. Together, ths produces the parametrc form: x( t t y( t Try t Now. Wrte x y n parametrc form, f possble.
32 In addton to parameterzng Cartesan equatons, we also can parameterze behavors and movements. Example 10 A robot follows the path shown. Create a table of values for the x( and y( functons, assumng the robot takes one second to make each movement. Snce we know the drecton of moton, we can ntroduce consecutve values for t along the path of the robot. Usng these values wth the x and y coordnates of the robot, we can create the tables. For example, we desgnate the startng pont, at (1, 1), as the poston at t = 0, the next pont at (, 1) as the poston at t = 1, and so on. t x t y Notce how ths also tes back to vectors. The journey of the robot as t moves through the Cartesan plane could also be dsplayed as vectors and total dstance traveled and dsplacement could be calculated. Example 11 A lght s placed on the edge of a bcycle tre as shown and the bcycle starts rollng down the street. Fnd a parametrc equaton for the poston of the lght after the wheel has rotated through an angle of θ. r θ Startng Rotated by θ Relatve to the center of the wheel, the poston of the lght can be found as the coordnates of a pont on a crcle, but snce the x coordnate begns at 0 and moves n the negatve drecton, whle the y coordnate starts at the lowest value, the coordnates of the pont wll be gven by: x r sn( ) y r cos( )
33 Secton 8.5 Parametrc Equatons The center of the wheel, meanwhle, s movng horzontally. It remans at a constant heght of r, but the horzontal poston wll move a dstance equvalent to the arclength of the crcle drawn out by the angle, s r. The poston of the center of the crcle s then x r y r Combnng the poston of the center of the wheel wth the poston of the lght on the wheel relatve to the center, we get the followng parametrc equatonw, wth θ as the parameter: x r r sn( ) r sn( ) y r r cos( ) r 1 cos( ) The result graph s called a cyclod. Example 1 A moon travels around a planet as shown, orbtng once every 10 days. The planet travels around a sun as shown, orbtng once every 100 days. Fnd a parametrc equaton for the poston of the moon, relatve to the center of the sun, after t days. For ths example, we ll assume the orbts are crcular, though n real lfe they re actually ellptcal. The coordnates of a pont on a crcle can always be wrtten n the form x r cos( ) y r sn( ) 0 6
34 Snce the orbt of the moon around the planet has a perod of 10 days, the equaton for the poston of the moon relatve to the planet wll be x( 6cos t 6cos t 10 5 y( 6sn t 6sn t 10 5 Wth a perod of 100 days, the equaton for the poston of the planet relatve to the sun wll be x( 0cos t 0cos t y( 0sn t 0sn t Combnng these together, we can fnd the poston of the moon relatve to the sun as the sum of the components. x( 6cos t 0cos t 5 50 y( 6sn t 0sn t 5 50 The resultng graph s shown here. Try t Now 4. A wheel of radus 4 s rolled around the outsde of a crcle of radus 7. Fnd a parametrc equaton for the poston of a pont on the boundary of the smaller wheel. Ths shape s called an epcyclod. Important Topcs of Ths Secton Parametrc equatons Graphng x(, y( and the correspondng x-y graph Sketchng graphs and buldng a table of values Convertng parametrc to Cartesan Convertng Cartesan to parametrc (parameterzng curves)
35 Secton 8.5 Parametrc Equatons 5 Try t Now Answers y x x( cos( y( sn( 11 x( 11cos t 4cos t 4 11 y( 11sn t 4sn t 4
36 Secton 8.5 Exercses Match each set of equatons wth one of the graphs below. xt t xt t y t t 1 y t t 4. x t y t sn( 4cos( 5. x t t y t t. 6. x t y t x t y t 4sn cos t t t t A B C D E F From each par of graphs n the t-x and t-y planes shown, sketch a graph n the x-y plane
37 Secton 8.5 Parametrc Equatons 7 From each graph n the x-y plane shown, sketch a graph of the parameter functons n the t-x and t-y planes Sketch the parametrc equatons for t. xt 1t y t t t t x t y t Elmnate the parameter t to rewrte the parametrc equaton as a Cartesan equaton xt 5 t xt 6t y t 8t y t 10 t x t t 1 y t t x t y t e t 15t y t t x t t t x t y t x t y t e e t 6t 4cos 5sn t t x t t y t t xt 4log t 18. y t t 4 xt t t 0. y t t 5 xt t. 10 y t t xt sn t 4. y t 6cos t
38 Parameterze (wrte a parametrc equaton for) each Cartesan equaton 5. yx x y x sn x x y log y y 8. x y y y 9. x y x y Parameterze the graphs shown Parameterze the lne from ( 1,5) to (,) so that the lne s at ( 1,5) at t = 0, and at (, ) at t = Parameterze the lne from (4,1) to (6, ) so that the lne s at (4,1) at t = 0, and at (6, ) at t = 1.
39 Secton 8.5 Parametrc Equatons 9 The graphs below are created by parameterc equatons of the form Fnd the values of a, b, c, and d to acheve each graph. cos sn x t a bt y t c dt An object s thrown n the ar wth vertcal velocty 0 ft/s and horzontal velocty 15 ft/s. The object s heght can be descrbed by the equaton y t 16t 0t, whle the object moves horzontally wth constant velocty 15 ft/s. Wrte parametrc equatons for the object s poston, then elmnate tme to wrte heght as a functon of horzontal poston. 4. A skateboarder rdng on a level surface at a constant speed of 9 ft/s throws a ball n the ar, the heght of whch can be descrbed by the equaton y t 16t 10t 5. Wrte parametrc equatons for the ball s poston, then elmnate tme to wrte heght as a functon of horzontal poston.
40 4. A carnval rde has a large rotatng arm wth dameter 40 feet centered 5 feet off the ground. At each end of the large arm are two smaller rotatng arms wth dameter 16 feet each. The larger arm rotates once every 5 seconds, whle the smaller arms rotate once every seconds. If you board the rde when the pont P s closest to the ground, fnd parametrc equatons for your poston over tme. P 44. A hypocyclod s a shape generated by trackng a fxed pont on a small crcle as t rolls around the nsde of a larger crcle. If the smaller crcle has radus 1 and the large crcle has radus 6, fnd parametrc equatons for the poston of the pont P as the smaller wheel rolls n the drecton ndcated. P
Section 8.3 Polar Form of Complex Numbers
 80 Chapter 8 Secton 8 Polar Form of Complex Numbers From prevous classes, you may have encountered magnary numbers the square roots of negatve numbers and, more generally, complex numbers whch are the
80 Chapter 8 Secton 8 Polar Form of Complex Numbers From prevous classes, you may have encountered magnary numbers the square roots of negatve numbers and, more generally, complex numbers whch are the
Section 8.1 Exercises
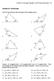 Secton 8.1 Non-rght Trangles: Law of Snes and Cosnes 519 Secton 8.1 Exercses Solve for the unknown sdes and angles of the trangles shown. 10 70 50 1.. 18 40 110 45 5 6 3. 10 4. 75 15 5 6 90 70 65 5. 6.
Secton 8.1 Non-rght Trangles: Law of Snes and Cosnes 519 Secton 8.1 Exercses Solve for the unknown sdes and angles of the trangles shown. 10 70 50 1.. 18 40 110 45 5 6 3. 10 4. 75 15 5 6 90 70 65 5. 6.
Section 3.6 Complex Zeros
 04 Chapter Secton 6 Comple Zeros When fndng the zeros of polynomals, at some pont you're faced wth the problem Whle there are clearly no real numbers that are solutons to ths equaton, leavng thngs there
04 Chapter Secton 6 Comple Zeros When fndng the zeros of polynomals, at some pont you're faced wth the problem Whle there are clearly no real numbers that are solutons to ths equaton, leavng thngs there
Unit 5: Quadratic Equations & Functions
 Date Perod Unt 5: Quadratc Equatons & Functons DAY TOPIC 1 Modelng Data wth Quadratc Functons Factorng Quadratc Epressons 3 Solvng Quadratc Equatons 4 Comple Numbers Smplfcaton, Addton/Subtracton & Multplcaton
Date Perod Unt 5: Quadratc Equatons & Functons DAY TOPIC 1 Modelng Data wth Quadratc Functons Factorng Quadratc Epressons 3 Solvng Quadratc Equatons 4 Comple Numbers Smplfcaton, Addton/Subtracton & Multplcaton
Difference Equations
 Dfference Equatons c Jan Vrbk 1 Bascs Suppose a sequence of numbers, say a 0,a 1,a,a 3,... s defned by a certan general relatonshp between, say, three consecutve values of the sequence, e.g. a + +3a +1
Dfference Equatons c Jan Vrbk 1 Bascs Suppose a sequence of numbers, say a 0,a 1,a,a 3,... s defned by a certan general relatonshp between, say, three consecutve values of the sequence, e.g. a + +3a +1
Physics 2A Chapter 3 HW Solutions
 Phscs A Chapter 3 HW Solutons Chapter 3 Conceptual Queston: 4, 6, 8, Problems: 5,, 8, 7, 3, 44, 46, 69, 70, 73 Q3.4. Reason: (a) C = A+ B onl A and B are n the same drecton. Sze does not matter. (b) C
Phscs A Chapter 3 HW Solutons Chapter 3 Conceptual Queston: 4, 6, 8, Problems: 5,, 8, 7, 3, 44, 46, 69, 70, 73 Q3.4. Reason: (a) C = A+ B onl A and B are n the same drecton. Sze does not matter. (b) C
Week3, Chapter 4. Position and Displacement. Motion in Two Dimensions. Instantaneous Velocity. Average Velocity
 Week3, Chapter 4 Moton n Two Dmensons Lecture Quz A partcle confned to moton along the x axs moves wth constant acceleraton from x =.0 m to x = 8.0 m durng a 1-s tme nterval. The velocty of the partcle
Week3, Chapter 4 Moton n Two Dmensons Lecture Quz A partcle confned to moton along the x axs moves wth constant acceleraton from x =.0 m to x = 8.0 m durng a 1-s tme nterval. The velocty of the partcle
8.6 The Complex Number System
 8.6 The Complex Number System Earler n the chapter, we mentoned that we cannot have a negatve under a square root, snce the square of any postve or negatve number s always postve. In ths secton we want
8.6 The Complex Number System Earler n the chapter, we mentoned that we cannot have a negatve under a square root, snce the square of any postve or negatve number s always postve. In ths secton we want
Advanced Circuits Topics - Part 1 by Dr. Colton (Fall 2017)
 Advanced rcuts Topcs - Part by Dr. olton (Fall 07) Part : Some thngs you should already know from Physcs 0 and 45 These are all thngs that you should have learned n Physcs 0 and/or 45. Ths secton s organzed
Advanced rcuts Topcs - Part by Dr. olton (Fall 07) Part : Some thngs you should already know from Physcs 0 and 45 These are all thngs that you should have learned n Physcs 0 and/or 45. Ths secton s organzed
Chapter 3. r r. Position, Velocity, and Acceleration Revisited
 Chapter 3 Poston, Velocty, and Acceleraton Revsted The poston vector of a partcle s a vector drawn from the orgn to the locaton of the partcle. In two dmensons: r = x ˆ+ yj ˆ (1) The dsplacement vector
Chapter 3 Poston, Velocty, and Acceleraton Revsted The poston vector of a partcle s a vector drawn from the orgn to the locaton of the partcle. In two dmensons: r = x ˆ+ yj ˆ (1) The dsplacement vector
COMPLEX NUMBERS AND QUADRATIC EQUATIONS
 COMPLEX NUMBERS AND QUADRATIC EQUATIONS INTRODUCTION We know that x 0 for all x R e the square of a real number (whether postve, negatve or ero) s non-negatve Hence the equatons x, x, x + 7 0 etc are not
COMPLEX NUMBERS AND QUADRATIC EQUATIONS INTRODUCTION We know that x 0 for all x R e the square of a real number (whether postve, negatve or ero) s non-negatve Hence the equatons x, x, x + 7 0 etc are not
C/CS/Phy191 Problem Set 3 Solutions Out: Oct 1, 2008., where ( 00. ), so the overall state of the system is ) ( ( ( ( 00 ± 11 ), Φ ± = 1
 C/CS/Phy9 Problem Set 3 Solutons Out: Oct, 8 Suppose you have two qubts n some arbtrary entangled state ψ You apply the teleportaton protocol to each of the qubts separately What s the resultng state obtaned
C/CS/Phy9 Problem Set 3 Solutons Out: Oct, 8 Suppose you have two qubts n some arbtrary entangled state ψ You apply the teleportaton protocol to each of the qubts separately What s the resultng state obtaned
THE SUMMATION NOTATION Ʃ
 Sngle Subscrpt otaton THE SUMMATIO OTATIO Ʃ Most of the calculatons we perform n statstcs are repettve operatons on lsts of numbers. For example, we compute the sum of a set of numbers, or the sum of the
Sngle Subscrpt otaton THE SUMMATIO OTATIO Ʃ Most of the calculatons we perform n statstcs are repettve operatons on lsts of numbers. For example, we compute the sum of a set of numbers, or the sum of the
Module 9. Lecture 6. Duality in Assignment Problems
 Module 9 1 Lecture 6 Dualty n Assgnment Problems In ths lecture we attempt to answer few other mportant questons posed n earler lecture for (AP) and see how some of them can be explaned through the concept
Module 9 1 Lecture 6 Dualty n Assgnment Problems In ths lecture we attempt to answer few other mportant questons posed n earler lecture for (AP) and see how some of them can be explaned through the concept
AP Physics 1 & 2 Summer Assignment
 AP Physcs 1 & 2 Summer Assgnment AP Physcs 1 requres an exceptonal profcency n algebra, trgonometry, and geometry. It was desgned by a select group of college professors and hgh school scence teachers
AP Physcs 1 & 2 Summer Assgnment AP Physcs 1 requres an exceptonal profcency n algebra, trgonometry, and geometry. It was desgned by a select group of college professors and hgh school scence teachers
Week 9 Chapter 10 Section 1-5
 Week 9 Chapter 10 Secton 1-5 Rotaton Rgd Object A rgd object s one that s nondeformable The relatve locatons of all partcles makng up the object reman constant All real objects are deformable to some extent,
Week 9 Chapter 10 Secton 1-5 Rotaton Rgd Object A rgd object s one that s nondeformable The relatve locatons of all partcles makng up the object reman constant All real objects are deformable to some extent,
Moments of Inertia. and reminds us of the analogous equation for linear momentum p= mv, which is of the form. The kinetic energy of the body is.
 Moments of Inerta Suppose a body s movng on a crcular path wth constant speed Let s consder two quanttes: the body s angular momentum L about the center of the crcle, and ts knetc energy T How are these
Moments of Inerta Suppose a body s movng on a crcular path wth constant speed Let s consder two quanttes: the body s angular momentum L about the center of the crcle, and ts knetc energy T How are these
Lectures - Week 4 Matrix norms, Conditioning, Vector Spaces, Linear Independence, Spanning sets and Basis, Null space and Range of a Matrix
 Lectures - Week 4 Matrx norms, Condtonng, Vector Spaces, Lnear Independence, Spannng sets and Bass, Null space and Range of a Matrx Matrx Norms Now we turn to assocatng a number to each matrx. We could
Lectures - Week 4 Matrx norms, Condtonng, Vector Spaces, Lnear Independence, Spannng sets and Bass, Null space and Range of a Matrx Matrx Norms Now we turn to assocatng a number to each matrx. We could
Physics 40 HW #4 Chapter 4 Key NEATNESS COUNTS! Solve but do not turn in the following problems from Chapter 4 Knight
 Physcs 40 HW #4 Chapter 4 Key NEATNESS COUNTS! Solve but do not turn n the ollowng problems rom Chapter 4 Knght Conceptual Questons: 8, 0, ; 4.8. Anta s approachng ball and movng away rom where ball was
Physcs 40 HW #4 Chapter 4 Key NEATNESS COUNTS! Solve but do not turn n the ollowng problems rom Chapter 4 Knght Conceptual Questons: 8, 0, ; 4.8. Anta s approachng ball and movng away rom where ball was
Physics 5153 Classical Mechanics. Principle of Virtual Work-1
 P. Guterrez 1 Introducton Physcs 5153 Classcal Mechancs Prncple of Vrtual Work The frst varatonal prncple we encounter n mechancs s the prncple of vrtual work. It establshes the equlbrum condton of a mechancal
P. Guterrez 1 Introducton Physcs 5153 Classcal Mechancs Prncple of Vrtual Work The frst varatonal prncple we encounter n mechancs s the prncple of vrtual work. It establshes the equlbrum condton of a mechancal
A Tale of Friction Basic Rollercoaster Physics. Fahrenheit Rollercoaster, Hershey, PA max height = 121 ft max speed = 58 mph
 A Tale o Frcton Basc Rollercoaster Physcs Fahrenhet Rollercoaster, Hershey, PA max heght = 11 t max speed = 58 mph PLAY PLAY PLAY PLAY Rotatonal Movement Knematcs Smlar to how lnear velocty s dened, angular
A Tale o Frcton Basc Rollercoaster Physcs Fahrenhet Rollercoaster, Hershey, PA max heght = 11 t max speed = 58 mph PLAY PLAY PLAY PLAY Rotatonal Movement Knematcs Smlar to how lnear velocty s dened, angular
So far: simple (planar) geometries
 Physcs 06 ecture 5 Torque and Angular Momentum as Vectors SJ 7thEd.: Chap. to 3 Rotatonal quanttes as vectors Cross product Torque epressed as a vector Angular momentum defned Angular momentum as a vector
Physcs 06 ecture 5 Torque and Angular Momentum as Vectors SJ 7thEd.: Chap. to 3 Rotatonal quanttes as vectors Cross product Torque epressed as a vector Angular momentum defned Angular momentum as a vector
Physics 2A Chapters 6 - Work & Energy Fall 2017
 Physcs A Chapters 6 - Work & Energy Fall 017 These notes are eght pages. A quck summary: The work-energy theorem s a combnaton o Chap and Chap 4 equatons. Work s dened as the product o the orce actng on
Physcs A Chapters 6 - Work & Energy Fall 017 These notes are eght pages. A quck summary: The work-energy theorem s a combnaton o Chap and Chap 4 equatons. Work s dened as the product o the orce actng on
For all questions, answer choice E) NOTA" means none of the above answers is correct.
 0 MA Natonal Conventon For all questons, answer choce " means none of the above answers s correct.. In calculus, one learns of functon representatons that are nfnte seres called power 3 4 5 seres. For
0 MA Natonal Conventon For all questons, answer choce " means none of the above answers s correct.. In calculus, one learns of functon representatons that are nfnte seres called power 3 4 5 seres. For
Physics 201, Lecture 4. Vectors and Scalars. Chapters Covered q Chapter 1: Physics and Measurement.
 Phscs 01, Lecture 4 Toda s Topcs n Vectors chap 3) n Scalars and Vectors n Vector ddton ule n Vector n a Coordnator Sstem n Decomposton of a Vector n Epected from prevew: n Scalars and Vectors, Vector
Phscs 01, Lecture 4 Toda s Topcs n Vectors chap 3) n Scalars and Vectors n Vector ddton ule n Vector n a Coordnator Sstem n Decomposton of a Vector n Epected from prevew: n Scalars and Vectors, Vector
Complex Numbers. x = B B 2 4AC 2A. or x = x = 2 ± 4 4 (1) (5) 2 (1)
 Complex Numbers If you have not yet encountered complex numbers, you wll soon do so n the process of solvng quadratc equatons. The general quadratc equaton Ax + Bx + C 0 has solutons x B + B 4AC A For
Complex Numbers If you have not yet encountered complex numbers, you wll soon do so n the process of solvng quadratc equatons. The general quadratc equaton Ax + Bx + C 0 has solutons x B + B 4AC A For
= 1.23 m/s 2 [W] Required: t. Solution:!t = = 17 m/s [W]! m/s [W] (two extra digits carried) = 2.1 m/s [W]
![= 1.23 m/s 2 [W] Required: t. Solution:!t = = 17 m/s [W]! m/s [W] (two extra digits carried) = 2.1 m/s [W] = 1.23 m/s 2 [W] Required: t. Solution:!t = = 17 m/s [W]! m/s [W] (two extra digits carried) = 2.1 m/s [W]](/thumbs/78/76802454.jpg) Secton 1.3: Acceleraton Tutoral 1 Practce, page 24 1. Gven: 0 m/s; 15.0 m/s [S]; t 12.5 s Requred: Analyss: a av v t v f v t a v av f v t 15.0 m/s [S] 0 m/s 12.5 s 15.0 m/s [S] 12.5 s 1.20 m/s 2 [S] Statement:
Secton 1.3: Acceleraton Tutoral 1 Practce, page 24 1. Gven: 0 m/s; 15.0 m/s [S]; t 12.5 s Requred: Analyss: a av v t v f v t a v av f v t 15.0 m/s [S] 0 m/s 12.5 s 15.0 m/s [S] 12.5 s 1.20 m/s 2 [S] Statement:
THE CHINESE REMAINDER THEOREM. We should thank the Chinese for their wonderful remainder theorem. Glenn Stevens
 THE CHINESE REMAINDER THEOREM KEITH CONRAD We should thank the Chnese for ther wonderful remander theorem. Glenn Stevens 1. Introducton The Chnese remander theorem says we can unquely solve any par of
THE CHINESE REMAINDER THEOREM KEITH CONRAD We should thank the Chnese for ther wonderful remander theorem. Glenn Stevens 1. Introducton The Chnese remander theorem says we can unquely solve any par of
Solutions to Problem Set 6
 Solutons to Problem Set 6 Problem 6. (Resdue theory) a) Problem 4.7.7 Boas. n ths problem we wll solve ths ntegral: x sn x x + 4x + 5 dx: To solve ths usng the resdue theorem, we study ths complex ntegral:
Solutons to Problem Set 6 Problem 6. (Resdue theory) a) Problem 4.7.7 Boas. n ths problem we wll solve ths ntegral: x sn x x + 4x + 5 dx: To solve ths usng the resdue theorem, we study ths complex ntegral:
PHYS 705: Classical Mechanics. Newtonian Mechanics
 1 PHYS 705: Classcal Mechancs Newtonan Mechancs Quck Revew of Newtonan Mechancs Basc Descrpton: -An dealzed pont partcle or a system of pont partcles n an nertal reference frame [Rgd bodes (ch. 5 later)]
1 PHYS 705: Classcal Mechancs Newtonan Mechancs Quck Revew of Newtonan Mechancs Basc Descrpton: -An dealzed pont partcle or a system of pont partcles n an nertal reference frame [Rgd bodes (ch. 5 later)]
Modeling curves. Graphs: y = ax+b, y = sin(x) Implicit ax + by + c = 0, x 2 +y 2 =r 2 Parametric:
 Modelng curves Types of Curves Graphs: y = ax+b, y = sn(x) Implct ax + by + c = 0, x 2 +y 2 =r 2 Parametrc: x = ax + bxt x = cos t y = ay + byt y = snt Parametrc are the most common mplct are also used,
Modelng curves Types of Curves Graphs: y = ax+b, y = sn(x) Implct ax + by + c = 0, x 2 +y 2 =r 2 Parametrc: x = ax + bxt x = cos t y = ay + byt y = snt Parametrc are the most common mplct are also used,
Kernel Methods and SVMs Extension
 Kernel Methods and SVMs Extenson The purpose of ths document s to revew materal covered n Machne Learnng 1 Supervsed Learnng regardng support vector machnes (SVMs). Ths document also provdes a general
Kernel Methods and SVMs Extenson The purpose of ths document s to revew materal covered n Machne Learnng 1 Supervsed Learnng regardng support vector machnes (SVMs). Ths document also provdes a general
How Differential Equations Arise. Newton s Second Law of Motion
 page 1 CHAPTER 1 Frst-Order Dfferental Equatons Among all of the mathematcal dscplnes the theory of dfferental equatons s the most mportant. It furnshes the explanaton of all those elementary manfestatons
page 1 CHAPTER 1 Frst-Order Dfferental Equatons Among all of the mathematcal dscplnes the theory of dfferental equatons s the most mportant. It furnshes the explanaton of all those elementary manfestatons
Supplemental Instruction sessions next week
 Homework #4 Wrtten homework due now Onlne homework due on Tue Mar 3 by 8 am Exam 1 Answer keys and scores wll be posted by end of the week Supplemental Instructon sessons next week Wednesday 8:45 10:00
Homework #4 Wrtten homework due now Onlne homework due on Tue Mar 3 by 8 am Exam 1 Answer keys and scores wll be posted by end of the week Supplemental Instructon sessons next week Wednesday 8:45 10:00
ELASTIC WAVE PROPAGATION IN A CONTINUOUS MEDIUM
 ELASTIC WAVE PROPAGATION IN A CONTINUOUS MEDIUM An elastc wave s a deformaton of the body that travels throughout the body n all drectons. We can examne the deformaton over a perod of tme by fxng our look
ELASTIC WAVE PROPAGATION IN A CONTINUOUS MEDIUM An elastc wave s a deformaton of the body that travels throughout the body n all drectons. We can examne the deformaton over a perod of tme by fxng our look
Spin-rotation coupling of the angularly accelerated rigid body
 Spn-rotaton couplng of the angularly accelerated rgd body Loua Hassan Elzen Basher Khartoum, Sudan. Postal code:11123 E-mal: louaelzen@gmal.com November 1, 2017 All Rghts Reserved. Abstract Ths paper s
Spn-rotaton couplng of the angularly accelerated rgd body Loua Hassan Elzen Basher Khartoum, Sudan. Postal code:11123 E-mal: louaelzen@gmal.com November 1, 2017 All Rghts Reserved. Abstract Ths paper s
10. Canonical Transformations Michael Fowler
 10. Canoncal Transformatons Mchael Fowler Pont Transformatons It s clear that Lagrange s equatons are correct for any reasonable choce of parameters labelng the system confguraton. Let s call our frst
10. Canoncal Transformatons Mchael Fowler Pont Transformatons It s clear that Lagrange s equatons are correct for any reasonable choce of parameters labelng the system confguraton. Let s call our frst
of Nebraska - Lincoln
 Unversty of Nebraska - Lncoln DgtalCommons@Unversty of Nebraska - Lncoln MAT Exam Expostory Papers Math n the Mddle Insttute Partnershp 008 The Square Root of Tffany Lothrop Unversty of Nebraska-Lncoln
Unversty of Nebraska - Lncoln DgtalCommons@Unversty of Nebraska - Lncoln MAT Exam Expostory Papers Math n the Mddle Insttute Partnershp 008 The Square Root of Tffany Lothrop Unversty of Nebraska-Lncoln
Lecture 12: Discrete Laplacian
 Lecture 12: Dscrete Laplacan Scrbe: Tanye Lu Our goal s to come up wth a dscrete verson of Laplacan operator for trangulated surfaces, so that we can use t n practce to solve related problems We are mostly
Lecture 12: Dscrete Laplacan Scrbe: Tanye Lu Our goal s to come up wth a dscrete verson of Laplacan operator for trangulated surfaces, so that we can use t n practce to solve related problems We are mostly
CHAPTER 4. Vector Spaces
 man 2007/2/16 page 234 CHAPTER 4 Vector Spaces To crtcze mathematcs for ts abstracton s to mss the pont entrel. Abstracton s what makes mathematcs work. Ian Stewart The man am of ths tet s to stud lnear
man 2007/2/16 page 234 CHAPTER 4 Vector Spaces To crtcze mathematcs for ts abstracton s to mss the pont entrel. Abstracton s what makes mathematcs work. Ian Stewart The man am of ths tet s to stud lnear
Celestial Mechanics. Basic Orbits. Why circles? Tycho Brahe. PHY celestial-mechanics - J. Hedberg
 PHY 454 - celestal-mechancs - J. Hedberg - 207 Celestal Mechancs. Basc Orbts. Why crcles? 2. Tycho Brahe 3. Kepler 4. 3 laws of orbtng bodes 2. Newtonan Mechancs 3. Newton's Laws. Law of Gravtaton 2. The
PHY 454 - celestal-mechancs - J. Hedberg - 207 Celestal Mechancs. Basc Orbts. Why crcles? 2. Tycho Brahe 3. Kepler 4. 3 laws of orbtng bodes 2. Newtonan Mechancs 3. Newton's Laws. Law of Gravtaton 2. The
332600_08_1.qxp 4/17/08 11:29 AM Page 481
 336_8_.qxp 4/7/8 :9 AM Page 48 8 Complex Vector Spaces 8. Complex Numbers 8. Conjugates and Dvson of Complex Numbers 8.3 Polar Form and DeMovre s Theorem 8.4 Complex Vector Spaces and Inner Products 8.5
336_8_.qxp 4/7/8 :9 AM Page 48 8 Complex Vector Spaces 8. Complex Numbers 8. Conjugates and Dvson of Complex Numbers 8.3 Polar Form and DeMovre s Theorem 8.4 Complex Vector Spaces and Inner Products 8.5
Formulas for the Determinant
 page 224 224 CHAPTER 3 Determnants e t te t e 2t 38 A = e t 2te t e 2t e t te t 2e 2t 39 If 123 A = 345, 456 compute the matrx product A adj(a) What can you conclude about det(a)? For Problems 40 43, use
page 224 224 CHAPTER 3 Determnants e t te t e 2t 38 A = e t 2te t e 2t e t te t 2e 2t 39 If 123 A = 345, 456 compute the matrx product A adj(a) What can you conclude about det(a)? For Problems 40 43, use
Gravitational Acceleration: A case of constant acceleration (approx. 2 hr.) (6/7/11)
 Gravtatonal Acceleraton: A case of constant acceleraton (approx. hr.) (6/7/11) Introducton The gravtatonal force s one of the fundamental forces of nature. Under the nfluence of ths force all objects havng
Gravtatonal Acceleraton: A case of constant acceleraton (approx. hr.) (6/7/11) Introducton The gravtatonal force s one of the fundamental forces of nature. Under the nfluence of ths force all objects havng
Foundations of Arithmetic
 Foundatons of Arthmetc Notaton We shall denote the sum and product of numbers n the usual notaton as a 2 + a 2 + a 3 + + a = a, a 1 a 2 a 3 a = a The notaton a b means a dvdes b,.e. ac = b where c s an
Foundatons of Arthmetc Notaton We shall denote the sum and product of numbers n the usual notaton as a 2 + a 2 + a 3 + + a = a, a 1 a 2 a 3 a = a The notaton a b means a dvdes b,.e. ac = b where c s an
Modeling of Dynamic Systems
 Modelng of Dynamc Systems Ref: Control System Engneerng Norman Nse : Chapters & 3 Chapter objectves : Revew the Laplace transform Learn how to fnd a mathematcal model, called a transfer functon Learn how
Modelng of Dynamc Systems Ref: Control System Engneerng Norman Nse : Chapters & 3 Chapter objectves : Revew the Laplace transform Learn how to fnd a mathematcal model, called a transfer functon Learn how
Physics 53. Rotational Motion 3. Sir, I have found you an argument, but I am not obliged to find you an understanding.
 Physcs 53 Rotatonal Moton 3 Sr, I have found you an argument, but I am not oblged to fnd you an understandng. Samuel Johnson Angular momentum Wth respect to rotatonal moton of a body, moment of nerta plays
Physcs 53 Rotatonal Moton 3 Sr, I have found you an argument, but I am not oblged to fnd you an understandng. Samuel Johnson Angular momentum Wth respect to rotatonal moton of a body, moment of nerta plays
ˆ (0.10 m) E ( N m /C ) 36 ˆj ( j C m)
 7.. = = 3 = 4 = 5. The electrc feld s constant everywhere between the plates. Ths s ndcated by the electrc feld vectors, whch are all the same length and n the same drecton. 7.5. Model: The dstances to
7.. = = 3 = 4 = 5. The electrc feld s constant everywhere between the plates. Ths s ndcated by the electrc feld vectors, whch are all the same length and n the same drecton. 7.5. Model: The dstances to
Inner Product. Euclidean Space. Orthonormal Basis. Orthogonal
 Inner Product Defnton 1 () A Eucldean space s a fnte-dmensonal vector space over the reals R, wth an nner product,. Defnton 2 (Inner Product) An nner product, on a real vector space X s a symmetrc, blnear,
Inner Product Defnton 1 () A Eucldean space s a fnte-dmensonal vector space over the reals R, wth an nner product,. Defnton 2 (Inner Product) An nner product, on a real vector space X s a symmetrc, blnear,
The KMO Method for Solving Non-homogenous, m th Order Differential Equations
 The KMO Method for Solvng Non-homogenous, m th Order Dfferental Equatons Davd Krohn Danel Marño-Johnson John Paul Ouyang March 14, 2013 Abstract Ths paper shows a smple tabular procedure for fndng the
The KMO Method for Solvng Non-homogenous, m th Order Dfferental Equatons Davd Krohn Danel Marño-Johnson John Paul Ouyang March 14, 2013 Abstract Ths paper shows a smple tabular procedure for fndng the
APPENDIX 2 FITTING A STRAIGHT LINE TO OBSERVATIONS
 Unversty of Oulu Student Laboratory n Physcs Laboratory Exercses n Physcs 1 1 APPEDIX FITTIG A STRAIGHT LIE TO OBSERVATIOS In the physcal measurements we often make a seres of measurements of the dependent
Unversty of Oulu Student Laboratory n Physcs Laboratory Exercses n Physcs 1 1 APPEDIX FITTIG A STRAIGHT LIE TO OBSERVATIOS In the physcal measurements we often make a seres of measurements of the dependent
Iterative General Dynamic Model for Serial-Link Manipulators
 EEL6667: Knematcs, Dynamcs and Control of Robot Manpulators 1. Introducton Iteratve General Dynamc Model for Seral-Lnk Manpulators In ths set of notes, we are gong to develop a method for computng a general
EEL6667: Knematcs, Dynamcs and Control of Robot Manpulators 1. Introducton Iteratve General Dynamc Model for Seral-Lnk Manpulators In ths set of notes, we are gong to develop a method for computng a general
Problem Solving in Math (Math 43900) Fall 2013
 Problem Solvng n Math (Math 43900) Fall 2013 Week four (September 17) solutons Instructor: Davd Galvn 1. Let a and b be two nteger for whch a b s dvsble by 3. Prove that a 3 b 3 s dvsble by 9. Soluton:
Problem Solvng n Math (Math 43900) Fall 2013 Week four (September 17) solutons Instructor: Davd Galvn 1. Let a and b be two nteger for whch a b s dvsble by 3. Prove that a 3 b 3 s dvsble by 9. Soluton:
The classical spin-rotation coupling
 LOUAI H. ELZEIN 2018 All Rghts Reserved The classcal spn-rotaton couplng Loua Hassan Elzen Basher Khartoum, Sudan. Postal code:11123 louaelzen@gmal.com Abstract Ths paper s prepared to show that a rgd
LOUAI H. ELZEIN 2018 All Rghts Reserved The classcal spn-rotaton couplng Loua Hassan Elzen Basher Khartoum, Sudan. Postal code:11123 louaelzen@gmal.com Abstract Ths paper s prepared to show that a rgd
CHAPTER 14 GENERAL PERTURBATION THEORY
 CHAPTER 4 GENERAL PERTURBATION THEORY 4 Introducton A partcle n orbt around a pont mass or a sphercally symmetrc mass dstrbuton s movng n a gravtatonal potental of the form GM / r In ths potental t moves
CHAPTER 4 GENERAL PERTURBATION THEORY 4 Introducton A partcle n orbt around a pont mass or a sphercally symmetrc mass dstrbuton s movng n a gravtatonal potental of the form GM / r In ths potental t moves
3.1 Expectation of Functions of Several Random Variables. )' be a k-dimensional discrete or continuous random vector, with joint PMF p (, E X E X1 E X
 Statstcs 1: Probablty Theory II 37 3 EPECTATION OF SEVERAL RANDOM VARIABLES As n Probablty Theory I, the nterest n most stuatons les not on the actual dstrbuton of a random vector, but rather on a number
Statstcs 1: Probablty Theory II 37 3 EPECTATION OF SEVERAL RANDOM VARIABLES As n Probablty Theory I, the nterest n most stuatons les not on the actual dstrbuton of a random vector, but rather on a number
coordinates. Then, the position vectors are described by
 Revewng, what we have dscussed so far: Generalzed coordnates Any number of varables (say, n) suffcent to specfy the confguraton of the system at each nstant to tme (need not be the mnmum number). In general,
Revewng, what we have dscussed so far: Generalzed coordnates Any number of varables (say, n) suffcent to specfy the confguraton of the system at each nstant to tme (need not be the mnmum number). In general,
From Biot-Savart Law to Divergence of B (1)
 From Bot-Savart Law to Dvergence of B (1) Let s prove that Bot-Savart gves us B (r ) = 0 for an arbtrary current densty. Frst take the dvergence of both sdes of Bot-Savart. The dervatve s wth respect to
From Bot-Savart Law to Dvergence of B (1) Let s prove that Bot-Savart gves us B (r ) = 0 for an arbtrary current densty. Frst take the dvergence of both sdes of Bot-Savart. The dervatve s wth respect to
Module 14: THE INTEGRAL Exploring Calculus
 Module 14: THE INTEGRAL Explorng Calculus Part I Approxmatons and the Defnte Integral It was known n the 1600s before the calculus was developed that the area of an rregularly shaped regon could be approxmated
Module 14: THE INTEGRAL Explorng Calculus Part I Approxmatons and the Defnte Integral It was known n the 1600s before the calculus was developed that the area of an rregularly shaped regon could be approxmated
The equation of motion of a dynamical system is given by a set of differential equations. That is (1)
 Dynamcal Systems Many engneerng and natural systems are dynamcal systems. For example a pendulum s a dynamcal system. State l The state of the dynamcal system specfes t condtons. For a pendulum n the absence
Dynamcal Systems Many engneerng and natural systems are dynamcal systems. For example a pendulum s a dynamcal system. State l The state of the dynamcal system specfes t condtons. For a pendulum n the absence
Physics 207: Lecture 20. Today s Agenda Homework for Monday
 Physcs 207: Lecture 20 Today s Agenda Homework for Monday Recap: Systems of Partcles Center of mass Velocty and acceleraton of the center of mass Dynamcs of the center of mass Lnear Momentum Example problems
Physcs 207: Lecture 20 Today s Agenda Homework for Monday Recap: Systems of Partcles Center of mass Velocty and acceleraton of the center of mass Dynamcs of the center of mass Lnear Momentum Example problems
1 Matrix representations of canonical matrices
 1 Matrx representatons of canoncal matrces 2-d rotaton around the orgn: ( ) cos θ sn θ R 0 = sn θ cos θ 3-d rotaton around the x-axs: R x = 1 0 0 0 cos θ sn θ 0 sn θ cos θ 3-d rotaton around the y-axs:
1 Matrx representatons of canoncal matrces 2-d rotaton around the orgn: ( ) cos θ sn θ R 0 = sn θ cos θ 3-d rotaton around the x-axs: R x = 1 0 0 0 cos θ sn θ 0 sn θ cos θ 3-d rotaton around the y-axs:
Fundamental loop-current method using virtual voltage sources technique for special cases
 Fundamental loop-current method usng vrtual voltage sources technque for specal cases George E. Chatzaraks, 1 Marna D. Tortorel 1 and Anastasos D. Tzolas 1 Electrcal and Electroncs Engneerng Departments,
Fundamental loop-current method usng vrtual voltage sources technque for specal cases George E. Chatzaraks, 1 Marna D. Tortorel 1 and Anastasos D. Tzolas 1 Electrcal and Electroncs Engneerng Departments,
Physics 5153 Classical Mechanics. D Alembert s Principle and The Lagrangian-1
 P. Guterrez Physcs 5153 Classcal Mechancs D Alembert s Prncple and The Lagrangan 1 Introducton The prncple of vrtual work provdes a method of solvng problems of statc equlbrum wthout havng to consder the
P. Guterrez Physcs 5153 Classcal Mechancs D Alembert s Prncple and The Lagrangan 1 Introducton The prncple of vrtual work provdes a method of solvng problems of statc equlbrum wthout havng to consder the
Spring 2002 Lecture #13
 44-50 Sprng 00 ecture # Dr. Jaehoon Yu. Rotatonal Energy. Computaton of oments of nerta. Parallel-as Theorem 4. Torque & Angular Acceleraton 5. Work, Power, & Energy of Rotatonal otons Remember the md-term
44-50 Sprng 00 ecture # Dr. Jaehoon Yu. Rotatonal Energy. Computaton of oments of nerta. Parallel-as Theorem 4. Torque & Angular Acceleraton 5. Work, Power, & Energy of Rotatonal otons Remember the md-term
Spectral Graph Theory and its Applications September 16, Lecture 5
 Spectral Graph Theory and ts Applcatons September 16, 2004 Lecturer: Danel A. Spelman Lecture 5 5.1 Introducton In ths lecture, we wll prove the followng theorem: Theorem 5.1.1. Let G be a planar graph
Spectral Graph Theory and ts Applcatons September 16, 2004 Lecturer: Danel A. Spelman Lecture 5 5.1 Introducton In ths lecture, we wll prove the followng theorem: Theorem 5.1.1. Let G be a planar graph
Exercises. 18 Algorithms
 18 Algorthms Exercses 0.1. In each of the followng stuatons, ndcate whether f = O(g), or f = Ω(g), or both (n whch case f = Θ(g)). f(n) g(n) (a) n 100 n 200 (b) n 1/2 n 2/3 (c) 100n + log n n + (log n)
18 Algorthms Exercses 0.1. In each of the followng stuatons, ndcate whether f = O(g), or f = Ω(g), or both (n whch case f = Θ(g)). f(n) g(n) (a) n 100 n 200 (b) n 1/2 n 2/3 (c) 100n + log n n + (log n)
Change. Flamenco Chuck Keyser. Updates 11/26/2017, 11/28/2017, 11/29/2017, 12/05/2017. Most Recent Update 12/22/2017
 Change Flamenco Chuck Keyser Updates /6/7, /8/7, /9/7, /5/7 Most Recent Update //7 The Relatvstc Unt Crcle (ncludng proof of Fermat s Theorem) Relatvty Page (n progress, much more to be sad, and revsons
Change Flamenco Chuck Keyser Updates /6/7, /8/7, /9/7, /5/7 Most Recent Update //7 The Relatvstc Unt Crcle (ncludng proof of Fermat s Theorem) Relatvty Page (n progress, much more to be sad, and revsons
General Tips on How to Do Well in Physics Exams. 1. Establish a good habit in keeping track of your steps. For example, when you use the equation
 General Tps on How to Do Well n Physcs Exams 1. Establsh a good habt n keepng track o your steps. For example when you use the equaton 1 1 1 + = d d to solve or d o you should rst rewrte t as 1 1 1 = d
General Tps on How to Do Well n Physcs Exams 1. Establsh a good habt n keepng track o your steps. For example when you use the equaton 1 1 1 + = d d to solve or d o you should rst rewrte t as 1 1 1 = d
LAB # 4 - Torque. d (1)
 LAB # 4 - Torque. Introducton Through the use of Newton's three laws of moton, t s possble (n prncple, f not n fact) to predct the moton of any set of partcles. That s, n order to descrbe the moton of
LAB # 4 - Torque. Introducton Through the use of Newton's three laws of moton, t s possble (n prncple, f not n fact) to predct the moton of any set of partcles. That s, n order to descrbe the moton of
SCALARS AND VECTORS All physical quantities in engineering mechanics are measured using either scalars or vectors.
 SCALARS AND ECTORS All phscal uanttes n engneerng mechancs are measured usng ether scalars or vectors. Scalar. A scalar s an postve or negatve phscal uantt that can be completel specfed b ts magntude.
SCALARS AND ECTORS All phscal uanttes n engneerng mechancs are measured usng ether scalars or vectors. Scalar. A scalar s an postve or negatve phscal uantt that can be completel specfed b ts magntude.
1. Estimation, Approximation and Errors Percentages Polynomials and Formulas Identities and Factorization 52
 ontents ommonly Used Formulas. Estmaton, pproxmaton and Errors. Percentages. Polynomals and Formulas 8. Identtes and Factorzaton. Equatons and Inequaltes 66 6. Rate and Rato 8 7. Laws of Integral Indces
ontents ommonly Used Formulas. Estmaton, pproxmaton and Errors. Percentages. Polynomals and Formulas 8. Identtes and Factorzaton. Equatons and Inequaltes 66 6. Rate and Rato 8 7. Laws of Integral Indces
An Algorithm to Solve the Inverse Kinematics Problem of a Robotic Manipulator Based on Rotation Vectors
 An Algorthm to Solve the Inverse Knematcs Problem of a Robotc Manpulator Based on Rotaton Vectors Mohamad Z. Al-az*, Mazn Z. Othman**, and Baker B. Al-Bahr* *AL-Nahran Unversty, Computer Eng. Dep., Baghdad,
An Algorthm to Solve the Inverse Knematcs Problem of a Robotc Manpulator Based on Rotaton Vectors Mohamad Z. Al-az*, Mazn Z. Othman**, and Baker B. Al-Bahr* *AL-Nahran Unversty, Computer Eng. Dep., Baghdad,
First Law: A body at rest remains at rest, a body in motion continues to move at constant velocity, unless acted upon by an external force.
 Secton 1. Dynamcs (Newton s Laws of Moton) Two approaches: 1) Gven all the forces actng on a body, predct the subsequent (changes n) moton. 2) Gven the (changes n) moton of a body, nfer what forces act
Secton 1. Dynamcs (Newton s Laws of Moton) Two approaches: 1) Gven all the forces actng on a body, predct the subsequent (changes n) moton. 2) Gven the (changes n) moton of a body, nfer what forces act
Quantum Mechanics for Scientists and Engineers. David Miller
 Quantum Mechancs for Scentsts and Engneers Davd Mller Types of lnear operators Types of lnear operators Blnear expanson of operators Blnear expanson of lnear operators We know that we can expand functons
Quantum Mechancs for Scentsts and Engneers Davd Mller Types of lnear operators Types of lnear operators Blnear expanson of operators Blnear expanson of lnear operators We know that we can expand functons
= = = (a) Use the MATLAB command rref to solve the system. (b) Let A be the coefficient matrix and B be the right-hand side of the system.
 Chapter Matlab Exercses Chapter Matlab Exercses. Consder the lnear system of Example n Secton.. x x x y z y y z (a) Use the MATLAB command rref to solve the system. (b) Let A be the coeffcent matrx and
Chapter Matlab Exercses Chapter Matlab Exercses. Consder the lnear system of Example n Secton.. x x x y z y y z (a) Use the MATLAB command rref to solve the system. (b) Let A be the coeffcent matrx and
Introduction to Vapor/Liquid Equilibrium, part 2. Raoult s Law:
 CE304, Sprng 2004 Lecture 4 Introducton to Vapor/Lqud Equlbrum, part 2 Raoult s Law: The smplest model that allows us do VLE calculatons s obtaned when we assume that the vapor phase s an deal gas, and
CE304, Sprng 2004 Lecture 4 Introducton to Vapor/Lqud Equlbrum, part 2 Raoult s Law: The smplest model that allows us do VLE calculatons s obtaned when we assume that the vapor phase s an deal gas, and
= z 20 z n. (k 20) + 4 z k = 4
 Problem Set #7 solutons 7.2.. (a Fnd the coeffcent of z k n (z + z 5 + z 6 + z 7 + 5, k 20. We use the known seres expanson ( n+l ( z l l z n below: (z + z 5 + z 6 + z 7 + 5 (z 5 ( + z + z 2 + z + 5 5
Problem Set #7 solutons 7.2.. (a Fnd the coeffcent of z k n (z + z 5 + z 6 + z 7 + 5, k 20. We use the known seres expanson ( n+l ( z l l z n below: (z + z 5 + z 6 + z 7 + 5 (z 5 ( + z + z 2 + z + 5 5
ENGN 40 Dynamics and Vibrations Homework # 7 Due: Friday, April 15
 NGN 40 ynamcs and Vbratons Homework # 7 ue: Frday, Aprl 15 1. Consder a concal hostng drum used n the mnng ndustry to host a mass up/down. A cable of dameter d has the mass connected at one end and s wound/unwound
NGN 40 ynamcs and Vbratons Homework # 7 ue: Frday, Aprl 15 1. Consder a concal hostng drum used n the mnng ndustry to host a mass up/down. A cable of dameter d has the mass connected at one end and s wound/unwound
THE VIBRATIONS OF MOLECULES II THE CARBON DIOXIDE MOLECULE Student Instructions
 THE VIBRATIONS OF MOLECULES II THE CARBON DIOXIDE MOLECULE Student Instructons by George Hardgrove Chemstry Department St. Olaf College Northfeld, MN 55057 hardgrov@lars.acc.stolaf.edu Copyrght George
THE VIBRATIONS OF MOLECULES II THE CARBON DIOXIDE MOLECULE Student Instructons by George Hardgrove Chemstry Department St. Olaf College Northfeld, MN 55057 hardgrov@lars.acc.stolaf.edu Copyrght George
APPENDIX A Some Linear Algebra
 APPENDIX A Some Lnear Algebra The collecton of m, n matrces A.1 Matrces a 1,1,..., a 1,n A = a m,1,..., a m,n wth real elements a,j s denoted by R m,n. If n = 1 then A s called a column vector. Smlarly,
APPENDIX A Some Lnear Algebra The collecton of m, n matrces A.1 Matrces a 1,1,..., a 1,n A = a m,1,..., a m,n wth real elements a,j s denoted by R m,n. If n = 1 then A s called a column vector. Smlarly,
Digital Signal Processing
 Dgtal Sgnal Processng Dscrete-tme System Analyss Manar Mohasen Offce: F8 Emal: manar.subh@ut.ac.r School of IT Engneerng Revew of Precedent Class Contnuous Sgnal The value of the sgnal s avalable over
Dgtal Sgnal Processng Dscrete-tme System Analyss Manar Mohasen Offce: F8 Emal: manar.subh@ut.ac.r School of IT Engneerng Revew of Precedent Class Contnuous Sgnal The value of the sgnal s avalable over
Work is the change in energy of a system (neglecting heat transfer). To examine what could
 Work Work s the change n energy o a system (neglectng heat transer). To eamne what could cause work, let s look at the dmensons o energy: L ML E M L F L so T T dmensonally energy s equal to a orce tmes
Work Work s the change n energy o a system (neglectng heat transer). To eamne what could cause work, let s look at the dmensons o energy: L ML E M L F L so T T dmensonally energy s equal to a orce tmes
Week 11: Chapter 11. The Vector Product. The Vector Product Defined. The Vector Product and Torque. More About the Vector Product
 The Vector Product Week 11: Chapter 11 Angular Momentum There are nstances where the product of two vectors s another vector Earler we saw where the product of two vectors was a scalar Ths was called the
The Vector Product Week 11: Chapter 11 Angular Momentum There are nstances where the product of two vectors s another vector Earler we saw where the product of two vectors was a scalar Ths was called the
Chapter Twelve. Integration. We now turn our attention to the idea of an integral in dimensions higher than one. Consider a real-valued function f : D
 Chapter Twelve Integraton 12.1 Introducton We now turn our attenton to the dea of an ntegral n dmensons hgher than one. Consder a real-valued functon f : R, where the doman s a nce closed subset of Eucldean
Chapter Twelve Integraton 12.1 Introducton We now turn our attenton to the dea of an ntegral n dmensons hgher than one. Consder a real-valued functon f : R, where the doman s a nce closed subset of Eucldean
MA 323 Geometric Modelling Course Notes: Day 13 Bezier Curves & Bernstein Polynomials
 MA 323 Geometrc Modellng Course Notes: Day 13 Bezer Curves & Bernsten Polynomals Davd L. Fnn Over the past few days, we have looked at de Casteljau s algorthm for generatng a polynomal curve, and we have
MA 323 Geometrc Modellng Course Notes: Day 13 Bezer Curves & Bernsten Polynomals Davd L. Fnn Over the past few days, we have looked at de Casteljau s algorthm for generatng a polynomal curve, and we have
9. Complex Numbers. 1. Numbers revisited. 2. Imaginary number i: General form of complex numbers. 3. Manipulation of complex numbers
 9. Comple Numbers. Numbers revsted. Imagnar number : General form of comple numbers 3. Manpulaton of comple numbers 4. The Argand dagram 5. The polar form for comple numbers 9.. Numbers revsted We saw
9. Comple Numbers. Numbers revsted. Imagnar number : General form of comple numbers 3. Manpulaton of comple numbers 4. The Argand dagram 5. The polar form for comple numbers 9.. Numbers revsted We saw
and problem sheet 2
 -8 and 5-5 problem sheet Solutons to the followng seven exercses and optonal bonus problem are to be submtted through gradescope by :0PM on Wednesday th September 08. There are also some practce problems,
-8 and 5-5 problem sheet Solutons to the followng seven exercses and optonal bonus problem are to be submtted through gradescope by :0PM on Wednesday th September 08. There are also some practce problems,
Bezier curves. Michael S. Floater. August 25, These notes provide an introduction to Bezier curves. i=0
 Bezer curves Mchael S. Floater August 25, 211 These notes provde an ntroducton to Bezer curves. 1 Bernsten polynomals Recall that a real polynomal of a real varable x R, wth degree n, s a functon of the
Bezer curves Mchael S. Floater August 25, 211 These notes provde an ntroducton to Bezer curves. 1 Bernsten polynomals Recall that a real polynomal of a real varable x R, wth degree n, s a functon of the
Physics 106a, Caltech 11 October, Lecture 4: Constraints, Virtual Work, etc. Constraints
 Physcs 106a, Caltech 11 October, 2018 Lecture 4: Constrants, Vrtual Work, etc. Many, f not all, dynamcal problems we want to solve are constraned: not all of the possble 3 coordnates for M partcles (or
Physcs 106a, Caltech 11 October, 2018 Lecture 4: Constrants, Vrtual Work, etc. Many, f not all, dynamcal problems we want to solve are constraned: not all of the possble 3 coordnates for M partcles (or
MEV442 Introduction to Robotics Module 2. Dr. Santhakumar Mohan Assistant Professor Mechanical Engineering National Institute of Technology Calicut
 MEV442 Introducton to Robotcs Module 2 Dr. Santhakumar Mohan Assstant Professor Mechancal Engneerng Natonal Insttute of Technology Calcut Jacobans: Veloctes and statc forces Introducton Notaton for tme-varyng
MEV442 Introducton to Robotcs Module 2 Dr. Santhakumar Mohan Assstant Professor Mechancal Engneerng Natonal Insttute of Technology Calcut Jacobans: Veloctes and statc forces Introducton Notaton for tme-varyng
One Dimension Again. Chapter Fourteen
 hapter Fourteen One Dmenson Agan 4 Scalar Lne Integrals Now we agan consder the dea of the ntegral n one dmenson When we were ntroduced to the ntegral back n elementary school, we consdered only functons
hapter Fourteen One Dmenson Agan 4 Scalar Lne Integrals Now we agan consder the dea of the ntegral n one dmenson When we were ntroduced to the ntegral back n elementary school, we consdered only functons
8.1 Arc Length. What is the length of a curve? How can we approximate it? We could do it following the pattern we ve used before
 .1 Arc Length hat s the length of a curve? How can we approxmate t? e could do t followng the pattern we ve used before Use a sequence of ncreasngly short segments to approxmate the curve: As the segments
.1 Arc Length hat s the length of a curve? How can we approxmate t? e could do t followng the pattern we ve used before Use a sequence of ncreasngly short segments to approxmate the curve: As the segments
Physics 4B. A positive value is obtained, so the current is counterclockwise around the circuit.
 Physcs 4B Solutons to Chapter 7 HW Chapter 7: Questons:, 8, 0 Problems:,,, 45, 48,,, 7, 9 Queston 7- (a) no (b) yes (c) all te Queston 7-8 0 μc Queston 7-0, c;, a;, d; 4, b Problem 7- (a) Let be the current
Physcs 4B Solutons to Chapter 7 HW Chapter 7: Questons:, 8, 0 Problems:,,, 45, 48,,, 7, 9 Queston 7- (a) no (b) yes (c) all te Queston 7-8 0 μc Queston 7-0, c;, a;, d; 4, b Problem 7- (a) Let be the current
Mathematics Intersection of Lines
 a place of mnd F A C U L T Y O F E D U C A T I O N Department of Currculum and Pedagog Mathematcs Intersecton of Lnes Scence and Mathematcs Educaton Research Group Supported b UBC Teachng and Learnng Enhancement
a place of mnd F A C U L T Y O F E D U C A T I O N Department of Currculum and Pedagog Mathematcs Intersecton of Lnes Scence and Mathematcs Educaton Research Group Supported b UBC Teachng and Learnng Enhancement
Physics 181. Particle Systems
 Physcs 181 Partcle Systems Overvew In these notes we dscuss the varables approprate to the descrpton of systems of partcles, ther defntons, ther relatons, and ther conservatons laws. We consder a system
Physcs 181 Partcle Systems Overvew In these notes we dscuss the varables approprate to the descrpton of systems of partcles, ther defntons, ther relatons, and ther conservatons laws. We consder a system
12. The Hamilton-Jacobi Equation Michael Fowler
 1. The Hamlton-Jacob Equaton Mchael Fowler Back to Confguraton Space We ve establshed that the acton, regarded as a functon of ts coordnate endponts and tme, satsfes ( ) ( ) S q, t / t+ H qpt,, = 0, and
1. The Hamlton-Jacob Equaton Mchael Fowler Back to Confguraton Space We ve establshed that the acton, regarded as a functon of ts coordnate endponts and tme, satsfes ( ) ( ) S q, t / t+ H qpt,, = 0, and
Conservation of Angular Momentum = "Spin"
 Page 1 of 6 Conservaton of Angular Momentum = "Spn" We can assgn a drecton to the angular velocty: drecton of = drecton of axs + rght hand rule (wth rght hand, curl fngers n drecton of rotaton, thumb ponts
Page 1 of 6 Conservaton of Angular Momentum = "Spn" We can assgn a drecton to the angular velocty: drecton of = drecton of axs + rght hand rule (wth rght hand, curl fngers n drecton of rotaton, thumb ponts
Lecture 10 Support Vector Machines II
 Lecture 10 Support Vector Machnes II 22 February 2016 Taylor B. Arnold Yale Statstcs STAT 365/665 1/28 Notes: Problem 3 s posted and due ths upcomng Frday There was an early bug n the fake-test data; fxed
Lecture 10 Support Vector Machnes II 22 February 2016 Taylor B. Arnold Yale Statstcs STAT 365/665 1/28 Notes: Problem 3 s posted and due ths upcomng Frday There was an early bug n the fake-test data; fxed
Linear Feature Engineering 11
 Lnear Feature Engneerng 11 2 Least-Squares 2.1 Smple least-squares Consder the followng dataset. We have a bunch of nputs x and correspondng outputs y. The partcular values n ths dataset are x y 0.23 0.19
Lnear Feature Engneerng 11 2 Least-Squares 2.1 Smple least-squares Consder the followng dataset. We have a bunch of nputs x and correspondng outputs y. The partcular values n ths dataset are x y 0.23 0.19
