A Curious Property of Convex Functions and Mechanism Design
|
|
|
- Martin Cole
- 6 years ago
- Views:
Transcription
1 A Curious Property of Convex Functions and Mechanism Design Sergiu Hart August 11, 217 Abstract The solution of a simple problem on convex functions that has nothing to do with mechanism design namely, the largest convex function with given values on the axes makes use of the payoff functions of mechanism design. 1 The S-Transform Let b : R d R be a a real convex function defined on the nonnegative orthant of the d-dimensional Euclidean space; without loss of generality assume that b() =. For each z R d let s(z) := b (z;z) b(z), where b (z;z) := lim δ (b(z δz) b(z))/δ is the directional derivative of b at z in the direction z (see September 212 (first version); October 213 (revised and expanded); November 216 (minor corrections). The author thanks Noam Nisan, Phil Reny, and Benji Weiss for useful discussions. Research partially supported by an ERC Advanced Investigator Grant. The Hebrew University of Jerusalem (Center for the Study of Rationality, Institute of Mathematics, and Department of Economics). hart@huji.ac.il Web site: 1
2 Rockafellar 197). The function s satisfies s() = and s(z) = z b(z) b(z) at all points z where b is differentiable (i.e., at almost every z). When d = 1, we have s (z) = zb (z) b(z), and s is a nondecreasing function (for instance, when b is C 2 we have s (z) = zb (z) ); that is however no longer true when d > 1 (cf. Hart and Reny 215). Let d = 2. For every z R 2, let β(t) := b(tz)/t, then β (t) = s(tz)/t 2, and so one can reconstruct the function b from the function 1 s: b(z) := 1 s(tz) t 2 dt. Let Sb denote the function s obtained from b; we will call it the S- transform of b. 2 A Curious Property of the s Functions Let b 1 (x) and b 2 (y) be two nondecreasing convex functions defined on R, with b 1 () = b 2 () =. Assume for simplicity that b 1 and b 2 are continuously differentiable (i.e., in C 1 ; see below for the extension to the nondifferentiable case). Let b (x,y) be the largest convex function b on R 2 such that b(x, ) = b 1 (x) and b(,y) = b 2 (y); we will refer to this as the two-axes condition. The function b is well defined since there is always a function satisfying the two-axes condition (e.g., b(x,y) = b 1 (x) b 2 (y)), and the maximum of the collection of such convex functions is a convex function. 1 Assume for instance that b(z) = for all z in a neighborhood of. 2
3 Define 2 s 1 (x) := xb 1(x) b 1 (x), s 2 (y) := yb 2(y) b 2 (y), s (x,y) := xb x(x,y) yb y(x,y) b (x,y). Thus s 1 := Sb 1, s 2 := Sb 2, and s = Sb. We write λ for 1 λ. Theorem 1 Assume that 3 sup x s 1 (x) = sup y s 2 (y) >. Then for every x,y > there is < λ < 1 such that ) ( ) b (x,y) = λb 1 λ λb ỹ 2, λ ) ( ) ỹ s (x,y) = s 1 = s 2, λ λ b x(x,y) = b 1, and ( λ) ) ỹ b y(x,y) = b 2. λ Thus, b is the envelope of the b i functions along equi-s lines. What appears curious and intriguing here is that the solution of a simple problem on convex functions that has nothing to do with mechanism design (namely, the largest convex function with given values on the axes) involves the payoff functions from mechanism design (with s the seller payoff function and b the buyer payoff function). Proof. Extend b 1 and b 2 to R 2 : put b 1 (x, ) := b 1 (x) when y = and b 1 (x,y) := otherwise; similarly, put b 2 (,y) := b 2 (y) when x = and 2 The two partial derivatives of b are denoted b x and b y. 3 See below for the extension to the general case. 3
4 b 2 (x,y) := otherwise. Then b 1 and b 2 are convex functions on R 2 ; let b := conv {b 1,b 2 } be their convex hull (see Rockafellar 197, page 37), i.e., the greatest convex function such that b (x,y) b i (x,y) for i = 1, 2. The function b is given by 4 epi b = conv (epi b 1 epi b 2 ), and satisfies (see Theorem 5.6 in Rockafellar 197) { b (x,y) = inf λb 1 (x 1,y 1 ) λb 2 (x 2,y 2 ) : λ(x 1,y 1 ) λ(x } 2,y 2 ) = (x,y). λ 1 For x,y >, the expression λb 1 (x 1,y 1 ) λb 2 (x 2,y 2 ) is finite only when < λ < 1, (x 1,y 1 ) = (x/λ, ), and (x 2,y 2 ) = (,y/ λ), and so { ) ( )} b (x,y) = inf λb 1 <λ<1 λ λb ỹ 2 ; (1) λ for y =, it is finite only when λ = 1, and so b (x, ) = b 1 (x); and for x =, only when λ =, and so b (,y) = b 2 (y). Thus b is in fact the greatest convex function satisfying the axes condition, i.e., b b. Next, the derivative of λb 1 (x/λ) λb 2 (y/ λ) with respect to λ is ) b 1 λb 1 ( λ λ) xλ ) ( ) ( ) ỹ 2 b 2 λb ỹ 2 λ λ ( ) ỹ ) = s 2 s 1. λ λ ( ) y λ 2 This is a nondecreasing function of 5 λ, and it vanishes when ) ( ) ỹ s 1 = s 2, λ λ which yields thus its minimal value. Finally, using the envelope theorem gives b x(x,y) = λb 1(x/λ) (1/λ) = 4 epi f denotes the epigraph of f, i.e., {(z,α) R 2 R : f(z) α}. 5 With s 2 (y/ λ) s 1 (x/λ) nonnegative as λ and nonpositive as λ 1 (recall that s i () = < s i (t) for t large enough). 4
5 b 1(x/λ) and b y(x,y) = λb 2(y/ λ) (1/ λ) = b y (y/ λ), and thus s (x,y) = λs 1 (x/λ) λs 2 (y/ λ) = λs 1 (x/λ) = λs 2 (y/ λ). Remarks. (a) Geometrically, the graph of the function b is obtained by connecting with straight lines all pairs of points ((x, ),b 1 (x)) and ((,y),b 2 (y)) that satisfy s 1 (x) = s 2 (y). (b) If f 1 and f 2 are the buyer payoff functions in two single-good IC and IR mechanisms thus b 1(x),b 2(y) 1 for all x,y then s 1 and s 2 are the corresponding seller payoff functions. 6 In this case the functions b and s are the payoff functions of the buyer and the seller, respectively, in a two-good IC and IR mechanism. Moreover, along each line connecting (x, ) with (,y) such that s 1 (x) = s 2 (y), the corresponding menu item (q 1,q 1,s) is constant: q 1 (x,y) = b 1(x), q 2 (x,y) = b 2(y), and s(x,y) = s 1 (x) = s 2 (y). In particular, the mechanism corresponding to b is monotonic (i.e., s is a nondecreasing function); moreover, the collection of all allocations q(x, y) = (q 1 (x,y),q 2 (x,y)) is well-ordered, i.e., for any (x,y) and (x,y ), either q(x,y) q(x,y ) or q(x,y) q(x,y ). (c) Alternative characterization: For every c, let h c (x,y) be the largest affine function with h c (, ) = c such that h c (x, ) b 1 (x) and h c (,y) b 2 (y) for all x,y. Then b (x,y) = sup c h c (x,y). (d) If, say, sup x s 1 (x) =: M 1 < M 2 := sup y s 2 (y), then let ȳ be such that s 2 (ȳ) = M 1 ; the characterization of Theorem 1 holds for all (x,y) with y < ȳ, and for y ȳ we have b (x,y) = b 2 (y) (the infimum in (1) is reached as λ ). (e) If the function f i are not C 1, then f i and s i are defined almost every- 6 A function b : R R is a buyer payoff function iff it is convex, its derivatives b (x) lie in the interval [,1], and b() =. Such a function b(x) lies in the convex hull of the functions [x p] for p and the identically function. The corresponding seller payoff function is a nondecreasing function with s() =, which lies in the convex hull of the functions p1 x p for all p and the identically function (without loss of generality we have made s continuous from the right). 5
6 where. For every t let x t := inf(x : s 1 (x) t} and y t := inf{y : s 2 (y) t} (could be ), then the graph of b (x,y) is obtained by connecting with straight lines all pairs of points ((x t, ),b 1 (x t )) and ((,y t ),b 2 (y t )). This includes the case of (d) above where sup x s 1 (x) and sup y s 2 (y) may be different (if, say, x t = and y t is finite, then the line becomes {((x,y t ),b 2 (y t )) : x }, i.e., in (x,y) space it is parallel to the x-axis). Moreover, we have s 1 (x) = s 2 (y) = s (x,y) = t 1 x x t =1 dt = t 1 y y t =1 dt = t 1 x x t y y t =1 dt = 1 x x t 1 dt, 1 y y t 1 dt, 1 x x t y y t 1 dt, and so, for random variables X and Y, E [s 1 (X)] = E [s 2 (Y )] = E [s (X,Y )] = [ X P [ Y P P ] 1 dt, x t ] 1 dt, y [ t X Y ] 1 x t y t dt. (f) In the symmetric case where b 1 (t) = b 2 (t), it is easy to see that b(x,y) = b 1 (x y) = b 2 (x y). This is used in Theorem 28 in Hart and Nisan (212). (g) When b 1(x) [, 1] for all x then b 1 lies in the closed convex hull generated by the functions [x p] for p. Similarly for b 2. However, this does not imply that b lies in the closed convex hull of the functions 6
7 [a 1 x a 2 y p] with a 1,a 2 [, 1] and p. An example: b 1 (x) = max {, 12 } x 1,x 3 b 2 (y) = max {, 25 } y 1,y 3 b(x, y) = max {, 12 x 25 } y 1,x y 3. Then b(x,y) = 1 [ x 6 ] 5 y 3 2 [ x 9 = 1 [x 45 ] 2 y ] 1 y 3 ] [ 5 6 x y 1 3 (in the first decomposition, where the weights 1/3 2/3 = 1, we have the linear coefficients 3/2, 6/5 > 1; in the second decomposition, where all linear coefficients are 1, we have 1/2 3/5 > 1). Note that b 1 (x) = 1 2 [x 2] 1 2 [x 4] b 2 (y) = 2 [ y 5 ] 3 [ y 1 ] A Two-Good Revenue Maximization Problem Theorem 2 Let F be a two-dimensional cumulative distribution function with density function f. Assume that there is a = (a 1,a 2 ) such that f(x,y) = when x < a 1 or y < a 2, and for (x,y) a the function f(x,y) is differentiable and satisfies xf x (x,y) α 1 f(x,y) and yf y (x,y) α 2 f(x,y) (2). 7
8 for some α 1,α 2 with α 1 α 2 = 3. Then, to maximize revenue, it suffices to consider functions b as obtained from Theorem 1. Proof. Let b correspond to a two-dimensional IC and IR mechanism, then R(b, F) = sup (xb x (x,y) yb y (x,y) b(x,y))f(x,y) dx dy. M>a 1,a 2 a 2 a 1 For each y we integrate by parts the xb x (x,y)f(x,y) term: a 1 b x (x,y)xf(x,y) dx = [b(x,y)xf(x,y)] M a 1 = b(a 1,y)a 1 f(a 1,y) b(m,y)mf(m,y) a 1 a 1 b(x,y) (f(x,y) xf x (x,y)) dx. b(x,y) (f(x,y) xf x (x,y)) dx Similarly for the yb y (x,y)f(x,y) term; altogether (do not forget the b(x,y)f(x,y) term) we get r M (b) = a 1 M a 2 b(a 1,y)f(a 1,y) dy a 2 a 2 a 2 a 1 a 1 a 2 b(m,y)f(m,y) dy M a 1 a 1 b(x,a 2 )f(x,a 2,y) dx b(x,m)f(x,m) dx b(x,y) ( α 1 f(x,y) xf x (x,y)) dx dy b(x,y) ( α 2 f(x,y) yf y (x,y)) dy dx (we split the 3b(x,y)f(x,y) term into two parts, α 1 b(x,y)f(x,y)α 2 b(x,y)f(x,y), which appear in the last two integrals). Fixing the functions b(,a 2 ) and b(a 1, ), and thus the first two integrals above, in order to maximize r M (b) we should take b(x,y) as large as possible (all the coefficients of b in the other integrals are nonnegative), and thus b is the maximal convex function with the given values on the axes. Finally, let 8
9 M. If F is a product distribution (i.e., the goods values are independent: F = F 1 F 2, with densities f 1 and f 2, respectively), then condition (2) becomes xf 1(x) α 1 f(x) and yf 2(y) α 2 f(y) for α 1 α 2 = 3; cf. Wang and Tang (217). If moreover F 1 = F 2 (i.e., i.i.d. goods), then b is symmetric and 7 b(x,y) = b(a,x y a) = b(x y a,a), and so b corresponds to bundling; cf. Theorem 28 in Hart and Nisan (212). Remark. The resulting function s is monotonic; cf. Hart and Reny (215). 4 Higher Dimensions 4.1 One-Dimensional Axes Conditions Let b i : R R be convex functions with b i () =, and let b : R d R be the maximal convex function such that b(xe i ) = b i (x) for every x and 1 i d, where e i is the i th unit vector in R d. Theorem 1 and its proof easily generalize to any dimension d. Theorem 3 Assume that sup x s i (x) = S > for all i. Then for every x R d there are < λ i < 1 with d i=1 λ i = 1 such that b (x) = d ( ) xi λ i b i, i=1 λ i ( ) s xi (x) = s i, and λ ( i ) b i(x) = b xi i. 7 Make the change of variables x = x a and y = y a. λ i 9
10 4.2 Higher-Dimensional Axes Conditions In general, given boundary conditions b i, the maximal convex function b is given by (cf. (1)) { b (x) = inf λ i b i (y i ) : i i λ i y i = 1, i λ i = 1, λ i The parallel of Theorems 1 and 3 is slightly more complicated. }. (3) We illustrate it with the special case where d = 3 and the given boundary conditions are b 1 (,x 2,x 3 ),b 2 (x 1,,x 3 ) and b 3 (x 1,x 2, ). If the infimum in (3) is attained at a point where all λ i >, then we have y i j R for i j with x = 3 i=1 λ iy i and (µ 1,µ 2,µ 3,ν) such that s i (y i ) = ν = s (x) b i (y i ) = µ x j = b (x) j x j b (x) = 3 ( λ i b ) i y i. (If some λ i = then the corresponding first-order conditions become inequalities.) i=1 If in addition we are in the symmetric case where b i β for all i, then b is also symmetric, and it is given by b (x) = { β ( 1 2 (x 1 x 2 x 3 ), 1 2 (x 1 x 2 x 3 ) ), if x i 1 2 (x 1 x 2 x 3 ) for all i, β(x j x k,x i ), if x i 1 2 (x 1 x 2 x 3 ) for some i. Note that x 1 (x 1 x 2 x 2 )/2 is equivalent to x 1 x 2 x 3 (and in this case we get λ 1 = in (3)). 1
11 References Hart, S. and N. Nisan (212), Approximate Revenue Maximization with Multiple Items, The Hebrew University of Jerusalem, Center for Rationality DP-66; arxiv ; revised (217). Hart, S. and P. J. Reny (215), Maximal Revenue with Multiple Goods: Nonmonotonicity and Other Observations, Theoretical Economics 1, Rockafellar, T. R. (197), Convex Analysis, Princeton University Press. Tang, P. and Z. Wang (217), Optimal Mechanisms with Simple Menus, Journal of Mathematical Economics 69,
Subgradients. subgradients. strong and weak subgradient calculus. optimality conditions via subgradients. directional derivatives
 Subgradients subgradients strong and weak subgradient calculus optimality conditions via subgradients directional derivatives Prof. S. Boyd, EE364b, Stanford University Basic inequality recall basic inequality
Subgradients subgradients strong and weak subgradient calculus optimality conditions via subgradients directional derivatives Prof. S. Boyd, EE364b, Stanford University Basic inequality recall basic inequality
Shiqian Ma, MAT-258A: Numerical Optimization 1. Chapter 4. Subgradient
 Shiqian Ma, MAT-258A: Numerical Optimization 1 Chapter 4 Subgradient Shiqian Ma, MAT-258A: Numerical Optimization 2 4.1. Subgradients definition subgradient calculus duality and optimality conditions Shiqian
Shiqian Ma, MAT-258A: Numerical Optimization 1 Chapter 4 Subgradient Shiqian Ma, MAT-258A: Numerical Optimization 2 4.1. Subgradients definition subgradient calculus duality and optimality conditions Shiqian
Convex Sets with Applications to Economics
 Convex Sets with Applications to Economics Debasis Mishra March 10, 2010 1 Convex Sets A set C R n is called convex if for all x, y C, we have λx+(1 λ)y C for all λ [0, 1]. The definition says that for
Convex Sets with Applications to Economics Debasis Mishra March 10, 2010 1 Convex Sets A set C R n is called convex if for all x, y C, we have λx+(1 λ)y C for all λ [0, 1]. The definition says that for
Convex Analysis and Economic Theory AY Elementary properties of convex functions
 Division of the Humanities and Social Sciences Ec 181 KC Border Convex Analysis and Economic Theory AY 2018 2019 Topic 6: Convex functions I 6.1 Elementary properties of convex functions We may occasionally
Division of the Humanities and Social Sciences Ec 181 KC Border Convex Analysis and Economic Theory AY 2018 2019 Topic 6: Convex functions I 6.1 Elementary properties of convex functions We may occasionally
Approximate Revenue Maximization with Multiple Items
 Approximate Revenue Maximization with Multiple Items Sergiu Hart Noam Nisan May 28, 2014 arxiv:1204.1846v2 [cs.gt] 27 May 2014 Abstract Myerson s classic result provides a full description of how a seller
Approximate Revenue Maximization with Multiple Items Sergiu Hart Noam Nisan May 28, 2014 arxiv:1204.1846v2 [cs.gt] 27 May 2014 Abstract Myerson s classic result provides a full description of how a seller
Subgradients. subgradients and quasigradients. subgradient calculus. optimality conditions via subgradients. directional derivatives
 Subgradients subgradients and quasigradients subgradient calculus optimality conditions via subgradients directional derivatives Prof. S. Boyd, EE392o, Stanford University Basic inequality recall basic
Subgradients subgradients and quasigradients subgradient calculus optimality conditions via subgradients directional derivatives Prof. S. Boyd, EE392o, Stanford University Basic inequality recall basic
17.1 Hyperplanes and Linear Forms
 This is page 530 Printer: Opaque this 17 Appendix 17.1 Hyperplanes and Linear Forms Given a vector space E over a field K, a linear map f: E K is called a linear form. The set of all linear forms f: E
This is page 530 Printer: Opaque this 17 Appendix 17.1 Hyperplanes and Linear Forms Given a vector space E over a field K, a linear map f: E K is called a linear form. The set of all linear forms f: E
Set, functions and Euclidean space. Seungjin Han
 Set, functions and Euclidean space Seungjin Han September, 2018 1 Some Basics LOGIC A is necessary for B : If B holds, then A holds. B A A B is the contraposition of B A. A is sufficient for B: If A holds,
Set, functions and Euclidean space Seungjin Han September, 2018 1 Some Basics LOGIC A is necessary for B : If B holds, then A holds. B A A B is the contraposition of B A. A is sufficient for B: If A holds,
Convex Optimization Theory. Chapter 5 Exercises and Solutions: Extended Version
 Convex Optimization Theory Chapter 5 Exercises and Solutions: Extended Version Dimitri P. Bertsekas Massachusetts Institute of Technology Athena Scientific, Belmont, Massachusetts http://www.athenasc.com
Convex Optimization Theory Chapter 5 Exercises and Solutions: Extended Version Dimitri P. Bertsekas Massachusetts Institute of Technology Athena Scientific, Belmont, Massachusetts http://www.athenasc.com
Convex Functions and Optimization
 Chapter 5 Convex Functions and Optimization 5.1 Convex Functions Our next topic is that of convex functions. Again, we will concentrate on the context of a map f : R n R although the situation can be generalized
Chapter 5 Convex Functions and Optimization 5.1 Convex Functions Our next topic is that of convex functions. Again, we will concentrate on the context of a map f : R n R although the situation can be generalized
Math 341: Convex Geometry. Xi Chen
 Math 341: Convex Geometry Xi Chen 479 Central Academic Building, University of Alberta, Edmonton, Alberta T6G 2G1, CANADA E-mail address: xichen@math.ualberta.ca CHAPTER 1 Basics 1. Euclidean Geometry
Math 341: Convex Geometry Xi Chen 479 Central Academic Building, University of Alberta, Edmonton, Alberta T6G 2G1, CANADA E-mail address: xichen@math.ualberta.ca CHAPTER 1 Basics 1. Euclidean Geometry
CHAPTER 2: CONVEX SETS AND CONCAVE FUNCTIONS. W. Erwin Diewert January 31, 2008.
 1 ECONOMICS 594: LECTURE NOTES CHAPTER 2: CONVEX SETS AND CONCAVE FUNCTIONS W. Erwin Diewert January 31, 2008. 1. Introduction Many economic problems have the following structure: (i) a linear function
1 ECONOMICS 594: LECTURE NOTES CHAPTER 2: CONVEX SETS AND CONCAVE FUNCTIONS W. Erwin Diewert January 31, 2008. 1. Introduction Many economic problems have the following structure: (i) a linear function
Only Intervals Preserve the Invertibility of Arithmetic Operations
 Only Intervals Preserve the Invertibility of Arithmetic Operations Olga Kosheleva 1 and Vladik Kreinovich 2 1 Department of Electrical and Computer Engineering 2 Department of Computer Science University
Only Intervals Preserve the Invertibility of Arithmetic Operations Olga Kosheleva 1 and Vladik Kreinovich 2 1 Department of Electrical and Computer Engineering 2 Department of Computer Science University
Optimality Conditions for Nonsmooth Convex Optimization
 Optimality Conditions for Nonsmooth Convex Optimization Sangkyun Lee Oct 22, 2014 Let us consider a convex function f : R n R, where R is the extended real field, R := R {, + }, which is proper (f never
Optimality Conditions for Nonsmooth Convex Optimization Sangkyun Lee Oct 22, 2014 Let us consider a convex function f : R n R, where R is the extended real field, R := R {, + }, which is proper (f never
Approximate Revenue Maximization with Multiple Items
 Approximate Revenue Maximization with Multiple Items Sergiu Hart Noam Nisan September 20, 2017 Abstract Maximizing the revenue from selling more than one good (or item) to a single buyer is a notoriously
Approximate Revenue Maximization with Multiple Items Sergiu Hart Noam Nisan September 20, 2017 Abstract Maximizing the revenue from selling more than one good (or item) to a single buyer is a notoriously
Continuity. Matt Rosenzweig
 Continuity Matt Rosenzweig Contents 1 Continuity 1 1.1 Rudin Chapter 4 Exercises........................................ 1 1.1.1 Exercise 1............................................. 1 1.1.2 Exercise
Continuity Matt Rosenzweig Contents 1 Continuity 1 1.1 Rudin Chapter 4 Exercises........................................ 1 1.1.1 Exercise 1............................................. 1 1.1.2 Exercise
3. Convex functions. basic properties and examples. operations that preserve convexity. the conjugate function. quasiconvex functions
 3. Convex functions Convex Optimization Boyd & Vandenberghe basic properties and examples operations that preserve convexity the conjugate function quasiconvex functions log-concave and log-convex functions
3. Convex functions Convex Optimization Boyd & Vandenberghe basic properties and examples operations that preserve convexity the conjugate function quasiconvex functions log-concave and log-convex functions
Convex analysis and profit/cost/support functions
 Division of the Humanities and Social Sciences Convex analysis and profit/cost/support functions KC Border October 2004 Revised January 2009 Let A be a subset of R m Convex analysts may give one of two
Division of the Humanities and Social Sciences Convex analysis and profit/cost/support functions KC Border October 2004 Revised January 2009 Let A be a subset of R m Convex analysts may give one of two
Convex Functions. Pontus Giselsson
 Convex Functions Pontus Giselsson 1 Today s lecture lower semicontinuity, closure, convex hull convexity preserving operations precomposition with affine mapping infimal convolution image function supremum
Convex Functions Pontus Giselsson 1 Today s lecture lower semicontinuity, closure, convex hull convexity preserving operations precomposition with affine mapping infimal convolution image function supremum
The Menu-Size Complexity of Auctions
 The Menu-Size Complexity of Auctions Sergiu Hart Noam Nisan November 6, 2017 Abstract We consider the menu size of auctions and mechanisms in general as a measure of their complexity, and study how it
The Menu-Size Complexity of Auctions Sergiu Hart Noam Nisan November 6, 2017 Abstract We consider the menu size of auctions and mechanisms in general as a measure of their complexity, and study how it
CSCI : Optimization and Control of Networks. Review on Convex Optimization
 CSCI7000-016: Optimization and Control of Networks Review on Convex Optimization 1 Convex set S R n is convex if x,y S, λ,µ 0, λ+µ = 1 λx+µy S geometrically: x,y S line segment through x,y S examples (one
CSCI7000-016: Optimization and Control of Networks Review on Convex Optimization 1 Convex set S R n is convex if x,y S, λ,µ 0, λ+µ = 1 λx+µy S geometrically: x,y S line segment through x,y S examples (one
A Brief Review on Convex Optimization
 A Brief Review on Convex Optimization 1 Convex set S R n is convex if x,y S, λ,µ 0, λ+µ = 1 λx+µy S geometrically: x,y S line segment through x,y S examples (one convex, two nonconvex sets): A Brief Review
A Brief Review on Convex Optimization 1 Convex set S R n is convex if x,y S, λ,µ 0, λ+µ = 1 λx+µy S geometrically: x,y S line segment through x,y S examples (one convex, two nonconvex sets): A Brief Review
Subgradient. Acknowledgement: this slides is based on Prof. Lieven Vandenberghes lecture notes. definition. subgradient calculus
 1/41 Subgradient Acknowledgement: this slides is based on Prof. Lieven Vandenberghes lecture notes definition subgradient calculus duality and optimality conditions directional derivative Basic inequality
1/41 Subgradient Acknowledgement: this slides is based on Prof. Lieven Vandenberghes lecture notes definition subgradient calculus duality and optimality conditions directional derivative Basic inequality
MAT 570 REAL ANALYSIS LECTURE NOTES. Contents. 1. Sets Functions Countability Axiom of choice Equivalence relations 9
 MAT 570 REAL ANALYSIS LECTURE NOTES PROFESSOR: JOHN QUIGG SEMESTER: FALL 204 Contents. Sets 2 2. Functions 5 3. Countability 7 4. Axiom of choice 8 5. Equivalence relations 9 6. Real numbers 9 7. Extended
MAT 570 REAL ANALYSIS LECTURE NOTES PROFESSOR: JOHN QUIGG SEMESTER: FALL 204 Contents. Sets 2 2. Functions 5 3. Countability 7 4. Axiom of choice 8 5. Equivalence relations 9 6. Real numbers 9 7. Extended
Division of the Humanities and Social Sciences. Supergradients. KC Border Fall 2001 v ::15.45
 Division of the Humanities and Social Sciences Supergradients KC Border Fall 2001 1 The supergradient of a concave function There is a useful way to characterize the concavity of differentiable functions.
Division of the Humanities and Social Sciences Supergradients KC Border Fall 2001 1 The supergradient of a concave function There is a useful way to characterize the concavity of differentiable functions.
Convex Optimization Boyd & Vandenberghe. 5. Duality
 5. Duality Convex Optimization Boyd & Vandenberghe Lagrange dual problem weak and strong duality geometric interpretation optimality conditions perturbation and sensitivity analysis examples generalized
5. Duality Convex Optimization Boyd & Vandenberghe Lagrange dual problem weak and strong duality geometric interpretation optimality conditions perturbation and sensitivity analysis examples generalized
Real Analysis Math 131AH Rudin, Chapter #1. Dominique Abdi
 Real Analysis Math 3AH Rudin, Chapter # Dominique Abdi.. If r is rational (r 0) and x is irrational, prove that r + x and rx are irrational. Solution. Assume the contrary, that r+x and rx are rational.
Real Analysis Math 3AH Rudin, Chapter # Dominique Abdi.. If r is rational (r 0) and x is irrational, prove that r + x and rx are irrational. Solution. Assume the contrary, that r+x and rx are rational.
Lecture 1: Background on Convex Analysis
 Lecture 1: Background on Convex Analysis John Duchi PCMI 2016 Outline I Convex sets 1.1 Definitions and examples 2.2 Basic properties 3.3 Projections onto convex sets 4.4 Separating and supporting hyperplanes
Lecture 1: Background on Convex Analysis John Duchi PCMI 2016 Outline I Convex sets 1.1 Definitions and examples 2.2 Basic properties 3.3 Projections onto convex sets 4.4 Separating and supporting hyperplanes
BASICS OF CONVEX ANALYSIS
 BASICS OF CONVEX ANALYSIS MARKUS GRASMAIR 1. Main Definitions We start with providing the central definitions of convex functions and convex sets. Definition 1. A function f : R n R + } is called convex,
BASICS OF CONVEX ANALYSIS MARKUS GRASMAIR 1. Main Definitions We start with providing the central definitions of convex functions and convex sets. Definition 1. A function f : R n R + } is called convex,
Chapter 2: Preliminaries and elements of convex analysis
 Chapter 2: Preliminaries and elements of convex analysis Edoardo Amaldi DEIB Politecnico di Milano edoardo.amaldi@polimi.it Website: http://home.deib.polimi.it/amaldi/opt-14-15.shtml Academic year 2014-15
Chapter 2: Preliminaries and elements of convex analysis Edoardo Amaldi DEIB Politecnico di Milano edoardo.amaldi@polimi.it Website: http://home.deib.polimi.it/amaldi/opt-14-15.shtml Academic year 2014-15
The general programming problem is the nonlinear programming problem where a given function is maximized subject to a set of inequality constraints.
 1 Optimization Mathematical programming refers to the basic mathematical problem of finding a maximum to a function, f, subject to some constraints. 1 In other words, the objective is to find a point,
1 Optimization Mathematical programming refers to the basic mathematical problem of finding a maximum to a function, f, subject to some constraints. 1 In other words, the objective is to find a point,
Optimality, Duality, Complementarity for Constrained Optimization
 Optimality, Duality, Complementarity for Constrained Optimization Stephen Wright University of Wisconsin-Madison May 2014 Wright (UW-Madison) Optimality, Duality, Complementarity May 2014 1 / 41 Linear
Optimality, Duality, Complementarity for Constrained Optimization Stephen Wright University of Wisconsin-Madison May 2014 Wright (UW-Madison) Optimality, Duality, Complementarity May 2014 1 / 41 Linear
Lecture 8: Basic convex analysis
 Lecture 8: Basic convex analysis 1 Convex sets Both convex sets and functions have general importance in economic theory, not only in optimization. Given two points x; y 2 R n and 2 [0; 1]; the weighted
Lecture 8: Basic convex analysis 1 Convex sets Both convex sets and functions have general importance in economic theory, not only in optimization. Given two points x; y 2 R n and 2 [0; 1]; the weighted
1 Definition of the Riemann integral
 MAT337H1, Introduction to Real Analysis: notes on Riemann integration 1 Definition of the Riemann integral Definition 1.1. Let [a, b] R be a closed interval. A partition P of [a, b] is a finite set of
MAT337H1, Introduction to Real Analysis: notes on Riemann integration 1 Definition of the Riemann integral Definition 1.1. Let [a, b] R be a closed interval. A partition P of [a, b] is a finite set of
3. Convex functions. basic properties and examples. operations that preserve convexity. the conjugate function. quasiconvex functions
 3. Convex functions Convex Optimization Boyd & Vandenberghe basic properties and examples operations that preserve convexity the conjugate function quasiconvex functions log-concave and log-convex functions
3. Convex functions Convex Optimization Boyd & Vandenberghe basic properties and examples operations that preserve convexity the conjugate function quasiconvex functions log-concave and log-convex functions
Power series solutions for 2nd order linear ODE s (not necessarily with constant coefficients) a n z n. n=0
 Lecture 22 Power series solutions for 2nd order linear ODE s (not necessarily with constant coefficients) Recall a few facts about power series: a n z n This series in z is centered at z 0. Here z can
Lecture 22 Power series solutions for 2nd order linear ODE s (not necessarily with constant coefficients) Recall a few facts about power series: a n z n This series in z is centered at z 0. Here z can
In Progress: Summary of Notation and Basic Results Convex Analysis C&O 663, Fall 2009
 In Progress: Summary of Notation and Basic Results Convex Analysis C&O 663, Fall 2009 Intructor: Henry Wolkowicz November 26, 2009 University of Waterloo Department of Combinatorics & Optimization Abstract
In Progress: Summary of Notation and Basic Results Convex Analysis C&O 663, Fall 2009 Intructor: Henry Wolkowicz November 26, 2009 University of Waterloo Department of Combinatorics & Optimization Abstract
5. Duality. Lagrangian
 5. Duality Convex Optimization Boyd & Vandenberghe Lagrange dual problem weak and strong duality geometric interpretation optimality conditions perturbation and sensitivity analysis examples generalized
5. Duality Convex Optimization Boyd & Vandenberghe Lagrange dual problem weak and strong duality geometric interpretation optimality conditions perturbation and sensitivity analysis examples generalized
Helly's Theorem and its Equivalences via Convex Analysis
 Portland State University PDXScholar University Honors Theses University Honors College 2014 Helly's Theorem and its Equivalences via Convex Analysis Adam Robinson Portland State University Let us know
Portland State University PDXScholar University Honors Theses University Honors College 2014 Helly's Theorem and its Equivalences via Convex Analysis Adam Robinson Portland State University Let us know
Real Analysis. Joe Patten August 12, 2018
 Real Analysis Joe Patten August 12, 2018 1 Relations and Functions 1.1 Relations A (binary) relation, R, from set A to set B is a subset of A B. Since R is a subset of A B, it is a set of ordered pairs.
Real Analysis Joe Patten August 12, 2018 1 Relations and Functions 1.1 Relations A (binary) relation, R, from set A to set B is a subset of A B. Since R is a subset of A B, it is a set of ordered pairs.
Convexity in R n. The following lemma will be needed in a while. Lemma 1 Let x E, u R n. If τ I(x, u), τ 0, define. f(x + τu) f(x). τ.
 Convexity in R n Let E be a convex subset of R n. A function f : E (, ] is convex iff f(tx + (1 t)y) (1 t)f(x) + tf(y) x, y E, t [0, 1]. A similar definition holds in any vector space. A topology is needed
Convexity in R n Let E be a convex subset of R n. A function f : E (, ] is convex iff f(tx + (1 t)y) (1 t)f(x) + tf(y) x, y E, t [0, 1]. A similar definition holds in any vector space. A topology is needed
ON POSITIVE, LINEAR AND QUADRATIC BOOLEAN FUNCTIONS
 Kragujevac Journal of Mathematics Volume 36 Number 2 (2012), Pages 177 187. ON POSITIVE, LINEAR AND QUADRATIC BOOLEAN FUNCTIONS SERGIU RUDEANU Abstract. In [1], [2] it was proved that a function f : {0,
Kragujevac Journal of Mathematics Volume 36 Number 2 (2012), Pages 177 187. ON POSITIVE, LINEAR AND QUADRATIC BOOLEAN FUNCTIONS SERGIU RUDEANU Abstract. In [1], [2] it was proved that a function f : {0,
Mathematical Economics: Lecture 16
 Mathematical Economics: Lecture 16 Yu Ren WISE, Xiamen University November 26, 2012 Outline 1 Chapter 21: Concave and Quasiconcave Functions New Section Chapter 21: Concave and Quasiconcave Functions Concave
Mathematical Economics: Lecture 16 Yu Ren WISE, Xiamen University November 26, 2012 Outline 1 Chapter 21: Concave and Quasiconcave Functions New Section Chapter 21: Concave and Quasiconcave Functions Concave
Chapter 2 Convex Analysis
 Chapter 2 Convex Analysis The theory of nonsmooth analysis is based on convex analysis. Thus, we start this chapter by giving basic concepts and results of convexity (for further readings see also [202,
Chapter 2 Convex Analysis The theory of nonsmooth analysis is based on convex analysis. Thus, we start this chapter by giving basic concepts and results of convexity (for further readings see also [202,
The Menu-Size Complexity of Revenue Approximation
 The Menu-Size Complexity of Revenue Approximation Moshe Babaioff Yannai A. Gonczarowski Noam Nisan March 27, 2016 Abstract We consider a monopolist that is selling n items to a single additive buyer, where
The Menu-Size Complexity of Revenue Approximation Moshe Babaioff Yannai A. Gonczarowski Noam Nisan March 27, 2016 Abstract We consider a monopolist that is selling n items to a single additive buyer, where
The Menu-Size Complexity of Revenue Approximation
 The Menu-Size Complexity of Revenue Approximation Moshe Babaioff Yannai A. Gonczarowski Noam Nisan April 9, 2017 Abstract arxiv:1604.06580v3 [cs.gt] 9 Apr 2017 We consider a monopolist that is selling
The Menu-Size Complexity of Revenue Approximation Moshe Babaioff Yannai A. Gonczarowski Noam Nisan April 9, 2017 Abstract arxiv:1604.06580v3 [cs.gt] 9 Apr 2017 We consider a monopolist that is selling
Real Analysis Problems
 Real Analysis Problems Cristian E. Gutiérrez September 14, 29 1 1 CONTINUITY 1 Continuity Problem 1.1 Let r n be the sequence of rational numbers and Prove that f(x) = 1. f is continuous on the irrationals.
Real Analysis Problems Cristian E. Gutiérrez September 14, 29 1 1 CONTINUITY 1 Continuity Problem 1.1 Let r n be the sequence of rational numbers and Prove that f(x) = 1. f is continuous on the irrationals.
EC /11. Math for Microeconomics September Course, Part II Lecture Notes. Course Outline
 LONDON SCHOOL OF ECONOMICS Professor Leonardo Felli Department of Economics S.478; x7525 EC400 20010/11 Math for Microeconomics September Course, Part II Lecture Notes Course Outline Lecture 1: Tools for
LONDON SCHOOL OF ECONOMICS Professor Leonardo Felli Department of Economics S.478; x7525 EC400 20010/11 Math for Microeconomics September Course, Part II Lecture Notes Course Outline Lecture 1: Tools for
Econ Slides from Lecture 1
 Econ 205 Sobel Econ 205 - Slides from Lecture 1 Joel Sobel August 23, 2010 Warning I can t start without assuming that something is common knowledge. You can find basic definitions of Sets and Set Operations
Econ 205 Sobel Econ 205 - Slides from Lecture 1 Joel Sobel August 23, 2010 Warning I can t start without assuming that something is common knowledge. You can find basic definitions of Sets and Set Operations
Optimization and Optimal Control in Banach Spaces
 Optimization and Optimal Control in Banach Spaces Bernhard Schmitzer October 19, 2017 1 Convex non-smooth optimization with proximal operators Remark 1.1 (Motivation). Convex optimization: easier to solve,
Optimization and Optimal Control in Banach Spaces Bernhard Schmitzer October 19, 2017 1 Convex non-smooth optimization with proximal operators Remark 1.1 (Motivation). Convex optimization: easier to solve,
Extreme Abridgment of Boyd and Vandenberghe s Convex Optimization
 Extreme Abridgment of Boyd and Vandenberghe s Convex Optimization Compiled by David Rosenberg Abstract Boyd and Vandenberghe s Convex Optimization book is very well-written and a pleasure to read. The
Extreme Abridgment of Boyd and Vandenberghe s Convex Optimization Compiled by David Rosenberg Abstract Boyd and Vandenberghe s Convex Optimization book is very well-written and a pleasure to read. The
Lecture 4: Convex Functions, Part I February 1
 IE 521: Convex Optimization Instructor: Niao He Lecture 4: Convex Functions, Part I February 1 Spring 2017, UIUC Scribe: Shuanglong Wang Courtesy warning: These notes do not necessarily cover everything
IE 521: Convex Optimization Instructor: Niao He Lecture 4: Convex Functions, Part I February 1 Spring 2017, UIUC Scribe: Shuanglong Wang Courtesy warning: These notes do not necessarily cover everything
Convex Optimization Notes
 Convex Optimization Notes Jonathan Siegel January 2017 1 Convex Analysis This section is devoted to the study of convex functions f : B R {+ } and convex sets U B, for B a Banach space. The case of B =
Convex Optimization Notes Jonathan Siegel January 2017 1 Convex Analysis This section is devoted to the study of convex functions f : B R {+ } and convex sets U B, for B a Banach space. The case of B =
Solutions Final Exam May. 14, 2014
 Solutions Final Exam May. 14, 2014 1. Determine whether the following statements are true or false. Justify your answer (i.e., prove the claim, derive a contradiction or give a counter-example). (a) (10
Solutions Final Exam May. 14, 2014 1. Determine whether the following statements are true or false. Justify your answer (i.e., prove the claim, derive a contradiction or give a counter-example). (a) (10
Convex Optimization. Newton s method. ENSAE: Optimisation 1/44
 Convex Optimization Newton s method ENSAE: Optimisation 1/44 Unconstrained minimization minimize f(x) f convex, twice continuously differentiable (hence dom f open) we assume optimal value p = inf x f(x)
Convex Optimization Newton s method ENSAE: Optimisation 1/44 Unconstrained minimization minimize f(x) f convex, twice continuously differentiable (hence dom f open) we assume optimal value p = inf x f(x)
Convex Analysis Notes. Lecturer: Adrian Lewis, Cornell ORIE Scribe: Kevin Kircher, Cornell MAE
 Convex Analysis Notes Lecturer: Adrian Lewis, Cornell ORIE Scribe: Kevin Kircher, Cornell MAE These are notes from ORIE 6328, Convex Analysis, as taught by Prof. Adrian Lewis at Cornell University in the
Convex Analysis Notes Lecturer: Adrian Lewis, Cornell ORIE Scribe: Kevin Kircher, Cornell MAE These are notes from ORIE 6328, Convex Analysis, as taught by Prof. Adrian Lewis at Cornell University in the
Strong Dual for Conic Mixed-Integer Programs
 Strong Dual for Conic Mixed-Integer Programs Diego A. Morán R. Santanu S. Dey Juan Pablo Vielma July 14, 011 Abstract Mixed-integer conic programming is a generalization of mixed-integer linear programming.
Strong Dual for Conic Mixed-Integer Programs Diego A. Morán R. Santanu S. Dey Juan Pablo Vielma July 14, 011 Abstract Mixed-integer conic programming is a generalization of mixed-integer linear programming.
Lecture 2: Convex functions
 Lecture 2: Convex functions f : R n R is convex if dom f is convex and for all x, y dom f, θ [0, 1] f is concave if f is convex f(θx + (1 θ)y) θf(x) + (1 θ)f(y) x x convex concave neither x examples (on
Lecture 2: Convex functions f : R n R is convex if dom f is convex and for all x, y dom f, θ [0, 1] f is concave if f is convex f(θx + (1 θ)y) θf(x) + (1 θ)f(y) x x convex concave neither x examples (on
Introduction and Math Preliminaries
 Introduction and Math Preliminaries Yinyu Ye Department of Management Science and Engineering Stanford University Stanford, CA 94305, U.S.A. http://www.stanford.edu/ yyye Appendices A, B, and C, Chapter
Introduction and Math Preliminaries Yinyu Ye Department of Management Science and Engineering Stanford University Stanford, CA 94305, U.S.A. http://www.stanford.edu/ yyye Appendices A, B, and C, Chapter
Real Analysis, 2nd Edition, G.B.Folland Elements of Functional Analysis
 Real Analysis, 2nd Edition, G.B.Folland Chapter 5 Elements of Functional Analysis Yung-Hsiang Huang 5.1 Normed Vector Spaces 1. Note for any x, y X and a, b K, x+y x + y and by ax b y x + b a x. 2. It
Real Analysis, 2nd Edition, G.B.Folland Chapter 5 Elements of Functional Analysis Yung-Hsiang Huang 5.1 Normed Vector Spaces 1. Note for any x, y X and a, b K, x+y x + y and by ax b y x + b a x. 2. It
8. Conjugate functions
 L. Vandenberghe EE236C (Spring 2013-14) 8. Conjugate functions closed functions conjugate function 8-1 Closed set a set C is closed if it contains its boundary: x k C, x k x = x C operations that preserve
L. Vandenberghe EE236C (Spring 2013-14) 8. Conjugate functions closed functions conjugate function 8-1 Closed set a set C is closed if it contains its boundary: x k C, x k x = x C operations that preserve
h(x) lim H(x) = lim Since h is nondecreasing then h(x) 0 for all x, and if h is discontinuous at a point x then H(x) > 0. Denote
 Real Variables, Fall 4 Problem set 4 Solution suggestions Exercise. Let f be of bounded variation on [a, b]. Show that for each c (a, b), lim x c f(x) and lim x c f(x) exist. Prove that a monotone function
Real Variables, Fall 4 Problem set 4 Solution suggestions Exercise. Let f be of bounded variation on [a, b]. Show that for each c (a, b), lim x c f(x) and lim x c f(x) exist. Prove that a monotone function
8. Geometric problems
 8. Geometric problems Convex Optimization Boyd & Vandenberghe extremal volume ellipsoids centering classification placement and facility location 8 Minimum volume ellipsoid around a set Löwner-John ellipsoid
8. Geometric problems Convex Optimization Boyd & Vandenberghe extremal volume ellipsoids centering classification placement and facility location 8 Minimum volume ellipsoid around a set Löwner-John ellipsoid
Lecture: Duality.
 Lecture: Duality http://bicmr.pku.edu.cn/~wenzw/opt-2016-fall.html Acknowledgement: this slides is based on Prof. Lieven Vandenberghe s lecture notes Introduction 2/35 Lagrange dual problem weak and strong
Lecture: Duality http://bicmr.pku.edu.cn/~wenzw/opt-2016-fall.html Acknowledgement: this slides is based on Prof. Lieven Vandenberghe s lecture notes Introduction 2/35 Lagrange dual problem weak and strong
Characterization of quadratic mappings through a functional inequality
 J. Math. Anal. Appl. 32 (2006) 52 59 www.elsevier.com/locate/jmaa Characterization of quadratic mappings through a functional inequality Włodzimierz Fechner Institute of Mathematics, Silesian University,
J. Math. Anal. Appl. 32 (2006) 52 59 www.elsevier.com/locate/jmaa Characterization of quadratic mappings through a functional inequality Włodzimierz Fechner Institute of Mathematics, Silesian University,
Mixed-integer nonlinear programming, Conic programming, Duality, Cutting
 A STRONG DUAL FOR CONIC MIXED-INTEGER PROGRAMS DIEGO A. MORÁN R., SANTANU S. DEY, AND JUAN PABLO VIELMA Abstract. Mixed-integer conic programming is a generalization of mixed-integer linear programming.
A STRONG DUAL FOR CONIC MIXED-INTEGER PROGRAMS DIEGO A. MORÁN R., SANTANU S. DEY, AND JUAN PABLO VIELMA Abstract. Mixed-integer conic programming is a generalization of mixed-integer linear programming.
4. Convex optimization problems
 Convex Optimization Boyd & Vandenberghe 4. Convex optimization problems optimization problem in standard form convex optimization problems quasiconvex optimization linear optimization quadratic optimization
Convex Optimization Boyd & Vandenberghe 4. Convex optimization problems optimization problem in standard form convex optimization problems quasiconvex optimization linear optimization quadratic optimization
Maths Class 11 Chapter 5 Part -1 Quadratic equations
 1 P a g e Maths Class 11 Chapter 5 Part -1 Quadratic equations 1. Real Polynomial: Let a 0, a 1, a 2,, a n be real numbers and x is a real variable. Then, f(x) = a 0 + a 1 x + a 2 x 2 + + a n x n is called
1 P a g e Maths Class 11 Chapter 5 Part -1 Quadratic equations 1. Real Polynomial: Let a 0, a 1, a 2,, a n be real numbers and x is a real variable. Then, f(x) = a 0 + a 1 x + a 2 x 2 + + a n x n is called
Analysis and Linear Algebra. Lectures 1-3 on the mathematical tools that will be used in C103
 Analysis and Linear Algebra Lectures 1-3 on the mathematical tools that will be used in C103 Set Notation A, B sets AcB union A1B intersection A\B the set of objects in A that are not in B N. Empty set
Analysis and Linear Algebra Lectures 1-3 on the mathematical tools that will be used in C103 Set Notation A, B sets AcB union A1B intersection A\B the set of objects in A that are not in B N. Empty set
SOLUTIONS TO ADDITIONAL EXERCISES FOR II.1 AND II.2
 SOLUTIONS TO ADDITIONAL EXERCISES FOR II.1 AND II.2 Here are the solutions to the additional exercises in betsepexercises.pdf. B1. Let y and z be distinct points of L; we claim that x, y and z are not
SOLUTIONS TO ADDITIONAL EXERCISES FOR II.1 AND II.2 Here are the solutions to the additional exercises in betsepexercises.pdf. B1. Let y and z be distinct points of L; we claim that x, y and z are not
Functions and Equations
 Canadian Mathematics Competition An activity of the Centre for Education in Mathematics and Computing, University of Waterloo, Waterloo, Ontario Euclid eworkshop # Functions and Equations c 006 CANADIAN
Canadian Mathematics Competition An activity of the Centre for Education in Mathematics and Computing, University of Waterloo, Waterloo, Ontario Euclid eworkshop # Functions and Equations c 006 CANADIAN
Economics 204 Summer/Fall 2011 Lecture 5 Friday July 29, 2011
 Economics 204 Summer/Fall 2011 Lecture 5 Friday July 29, 2011 Section 2.6 (cont.) Properties of Real Functions Here we first study properties of functions from R to R, making use of the additional structure
Economics 204 Summer/Fall 2011 Lecture 5 Friday July 29, 2011 Section 2.6 (cont.) Properties of Real Functions Here we first study properties of functions from R to R, making use of the additional structure
The proximal mapping
 The proximal mapping http://bicmr.pku.edu.cn/~wenzw/opt-2016-fall.html Acknowledgement: this slides is based on Prof. Lieven Vandenberghes lecture notes Outline 2/37 1 closed function 2 Conjugate function
The proximal mapping http://bicmr.pku.edu.cn/~wenzw/opt-2016-fall.html Acknowledgement: this slides is based on Prof. Lieven Vandenberghes lecture notes Outline 2/37 1 closed function 2 Conjugate function
11. Equality constrained minimization
 Convex Optimization Boyd & Vandenberghe 11. Equality constrained minimization equality constrained minimization eliminating equality constraints Newton s method with equality constraints infeasible start
Convex Optimization Boyd & Vandenberghe 11. Equality constrained minimization equality constrained minimization eliminating equality constraints Newton s method with equality constraints infeasible start
EC9A0: Pre-sessional Advanced Mathematics Course. Lecture Notes: Unconstrained Optimisation By Pablo F. Beker 1
 EC9A0: Pre-sessional Advanced Mathematics Course Lecture Notes: Unconstrained Optimisation By Pablo F. Beker 1 1 Infimum and Supremum Definition 1. Fix a set Y R. A number α R is an upper bound of Y if
EC9A0: Pre-sessional Advanced Mathematics Course Lecture Notes: Unconstrained Optimisation By Pablo F. Beker 1 1 Infimum and Supremum Definition 1. Fix a set Y R. A number α R is an upper bound of Y if
CVaR and Examples of Deviation Risk Measures
 CVaR and Examples of Deviation Risk Measures Jakub Černý Department of Probability and Mathematical Statistics Stochastic Modelling in Economics and Finance November 10, 2014 1 / 25 Contents CVaR - Dual
CVaR and Examples of Deviation Risk Measures Jakub Černý Department of Probability and Mathematical Statistics Stochastic Modelling in Economics and Finance November 10, 2014 1 / 25 Contents CVaR - Dual
Problem Set 5: Solutions Math 201A: Fall 2016
 Problem Set 5: s Math 21A: Fall 216 Problem 1. Define f : [1, ) [1, ) by f(x) = x + 1/x. Show that f(x) f(y) < x y for all x, y [1, ) with x y, but f has no fixed point. Why doesn t this example contradict
Problem Set 5: s Math 21A: Fall 216 Problem 1. Define f : [1, ) [1, ) by f(x) = x + 1/x. Show that f(x) f(y) < x y for all x, y [1, ) with x y, but f has no fixed point. Why doesn t this example contradict
J. Banasiak Department of Mathematics and Applied Mathematics University of Pretoria, Pretoria, South Africa BANACH LATTICES IN APPLICATIONS
 J. Banasiak Department of Mathematics and Applied Mathematics University of Pretoria, Pretoria, South Africa BANACH LATTICES IN APPLICATIONS Contents 1 Introduction.........................................................................
J. Banasiak Department of Mathematics and Applied Mathematics University of Pretoria, Pretoria, South Africa BANACH LATTICES IN APPLICATIONS Contents 1 Introduction.........................................................................
Bounds on the Menu-Size of Approximately Optimal Auctions via Optimal-Transport Duality
 Bounds on the Menu-Size of Approximately Optimal Auctions via Optimal-Transport Duality arxiv:1708.08907v1 [cs.gt] 29 Aug 2017 Yannai A. Gonczarowski August 29, 2017 Abstract The question of the minimum
Bounds on the Menu-Size of Approximately Optimal Auctions via Optimal-Transport Duality arxiv:1708.08907v1 [cs.gt] 29 Aug 2017 Yannai A. Gonczarowski August 29, 2017 Abstract The question of the minimum
Functional Analysis Exercise Class
 Functional Analysis Exercise Class Week 9 November 13 November Deadline to hand in the homeworks: your exercise class on week 16 November 20 November Exercises (1) Show that if T B(X, Y ) and S B(Y, Z)
Functional Analysis Exercise Class Week 9 November 13 November Deadline to hand in the homeworks: your exercise class on week 16 November 20 November Exercises (1) Show that if T B(X, Y ) and S B(Y, Z)
Almost Convex Functions: Conjugacy and Duality
 Almost Convex Functions: Conjugacy and Duality Radu Ioan Boţ 1, Sorin-Mihai Grad 2, and Gert Wanka 3 1 Faculty of Mathematics, Chemnitz University of Technology, D-09107 Chemnitz, Germany radu.bot@mathematik.tu-chemnitz.de
Almost Convex Functions: Conjugacy and Duality Radu Ioan Boţ 1, Sorin-Mihai Grad 2, and Gert Wanka 3 1 Faculty of Mathematics, Chemnitz University of Technology, D-09107 Chemnitz, Germany radu.bot@mathematik.tu-chemnitz.de
ECARES Université Libre de Bruxelles MATH CAMP Basic Topology
 ECARES Université Libre de Bruxelles MATH CAMP 03 Basic Topology Marjorie Gassner Contents: - Subsets, Cartesian products, de Morgan laws - Ordered sets, bounds, supremum, infimum - Functions, image, preimage,
ECARES Université Libre de Bruxelles MATH CAMP 03 Basic Topology Marjorie Gassner Contents: - Subsets, Cartesian products, de Morgan laws - Ordered sets, bounds, supremum, infimum - Functions, image, preimage,
2 (Bonus). Let A X consist of points (x, y) such that either x or y is a rational number. Is A measurable? What is its Lebesgue measure?
 MA 645-4A (Real Analysis), Dr. Chernov Homework assignment 1 (Due 9/5). Prove that every countable set A is measurable and µ(a) = 0. 2 (Bonus). Let A consist of points (x, y) such that either x or y is
MA 645-4A (Real Analysis), Dr. Chernov Homework assignment 1 (Due 9/5). Prove that every countable set A is measurable and µ(a) = 0. 2 (Bonus). Let A consist of points (x, y) such that either x or y is
Convex Optimization. Convex Analysis - Functions
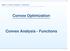 Convex Optimization Convex Analsis - Functions p. 1 A function f : K R n R is convex, if K is a convex set and x, K,x, λ (,1) we have f(λx+(1 λ)) λf(x)+(1 λ)f(). (x, f(x)) (,f()) x - strictl convex,
Convex Optimization Convex Analsis - Functions p. 1 A function f : K R n R is convex, if K is a convex set and x, K,x, λ (,1) we have f(λx+(1 λ)) λf(x)+(1 λ)f(). (x, f(x)) (,f()) x - strictl convex,
APPLICATIONS OF DIFFERENTIABILITY IN R n.
 APPLICATIONS OF DIFFERENTIABILITY IN R n. MATANIA BEN-ARTZI April 2015 Functions here are defined on a subset T R n and take values in R m, where m can be smaller, equal or greater than n. The (open) ball
APPLICATIONS OF DIFFERENTIABILITY IN R n. MATANIA BEN-ARTZI April 2015 Functions here are defined on a subset T R n and take values in R m, where m can be smaller, equal or greater than n. The (open) ball
REVIEW OF ESSENTIAL MATH 346 TOPICS
 REVIEW OF ESSENTIAL MATH 346 TOPICS 1. AXIOMATIC STRUCTURE OF R Doğan Çömez The real number system is a complete ordered field, i.e., it is a set R which is endowed with addition and multiplication operations
REVIEW OF ESSENTIAL MATH 346 TOPICS 1. AXIOMATIC STRUCTURE OF R Doğan Çömez The real number system is a complete ordered field, i.e., it is a set R which is endowed with addition and multiplication operations
PROXIMAL POINT ALGORITHMS INVOLVING FIXED POINT OF NONSPREADING-TYPE MULTIVALUED MAPPINGS IN HILBERT SPACES
 PROXIMAL POINT ALGORITHMS INVOLVING FIXED POINT OF NONSPREADING-TYPE MULTIVALUED MAPPINGS IN HILBERT SPACES Shih-sen Chang 1, Ding Ping Wu 2, Lin Wang 3,, Gang Wang 3 1 Center for General Educatin, China
PROXIMAL POINT ALGORITHMS INVOLVING FIXED POINT OF NONSPREADING-TYPE MULTIVALUED MAPPINGS IN HILBERT SPACES Shih-sen Chang 1, Ding Ping Wu 2, Lin Wang 3,, Gang Wang 3 1 Center for General Educatin, China
SOLUTIONS FOR PROBLEMS 1-30
 . Answer: 5 Evaluate x x + 9 for x SOLUTIONS FOR PROBLEMS - 0 When substituting x in x be sure to do the exponent before the multiplication by to get (). + 9 5 + When multiplying ( ) so that ( 7) ( ).
. Answer: 5 Evaluate x x + 9 for x SOLUTIONS FOR PROBLEMS - 0 When substituting x in x be sure to do the exponent before the multiplication by to get (). + 9 5 + When multiplying ( ) so that ( 7) ( ).
Convex Analysis Background
 Convex Analysis Background John C. Duchi Stanford University Park City Mathematics Institute 206 Abstract In this set of notes, we will outline several standard facts from convex analysis, the study of
Convex Analysis Background John C. Duchi Stanford University Park City Mathematics Institute 206 Abstract In this set of notes, we will outline several standard facts from convex analysis, the study of
Immerse Metric Space Homework
 Immerse Metric Space Homework (Exercises -2). In R n, define d(x, y) = x y +... + x n y n. Show that d is a metric that induces the usual topology. Sketch the basis elements when n = 2. Solution: Steps
Immerse Metric Space Homework (Exercises -2). In R n, define d(x, y) = x y +... + x n y n. Show that d is a metric that induces the usual topology. Sketch the basis elements when n = 2. Solution: Steps
Module 2: First-Order Partial Differential Equations
 Module 2: First-Order Partial Differential Equations The mathematical formulations of many problems in science and engineering reduce to study of first-order PDEs. For instance, the study of first-order
Module 2: First-Order Partial Differential Equations The mathematical formulations of many problems in science and engineering reduce to study of first-order PDEs. For instance, the study of first-order
arxiv: v1 [math.ds] 27 Jul 2017
![arxiv: v1 [math.ds] 27 Jul 2017 arxiv: v1 [math.ds] 27 Jul 2017](/thumbs/96/128497858.jpg) POLYNOMIAL VECTOR FIELDS ON THE CLIFFORD TORUS arxiv:1707.08859v1 [math.ds] 27 Jul 2017 JAUME LLIBRE AND ADRIAN C. MURZA Abstract. First we characterize all the polynomial vector fields in R 4 which have
POLYNOMIAL VECTOR FIELDS ON THE CLIFFORD TORUS arxiv:1707.08859v1 [math.ds] 27 Jul 2017 JAUME LLIBRE AND ADRIAN C. MURZA Abstract. First we characterize all the polynomial vector fields in R 4 which have
On the Complexity of Optimal Lottery Pricing and Randomized Mechanisms
 On the Complexity of Optimal Lottery Pricing and Randomized Mechanisms Xi Chen Ilias Diakonikolas Anthi Orfanou Dimitris Paparas Xiaorui Sun Mihalis Yannakakis Abstract We study the optimal lottery problem
On the Complexity of Optimal Lottery Pricing and Randomized Mechanisms Xi Chen Ilias Diakonikolas Anthi Orfanou Dimitris Paparas Xiaorui Sun Mihalis Yannakakis Abstract We study the optimal lottery problem
GEOMETRIC APPROACH TO CONVEX SUBDIFFERENTIAL CALCULUS October 10, Dedicated to Franco Giannessi and Diethard Pallaschke with great respect
 GEOMETRIC APPROACH TO CONVEX SUBDIFFERENTIAL CALCULUS October 10, 2018 BORIS S. MORDUKHOVICH 1 and NGUYEN MAU NAM 2 Dedicated to Franco Giannessi and Diethard Pallaschke with great respect Abstract. In
GEOMETRIC APPROACH TO CONVEX SUBDIFFERENTIAL CALCULUS October 10, 2018 BORIS S. MORDUKHOVICH 1 and NGUYEN MAU NAM 2 Dedicated to Franco Giannessi and Diethard Pallaschke with great respect Abstract. In
Preliminary notes on auction design
 Division of the Humanities and Social Sciences Preliminary notes on auction design kcb Revised Winter 2008 This note exposits a simplified version of Myerson s [8] paper on revenue-maximizing auction design
Division of the Humanities and Social Sciences Preliminary notes on auction design kcb Revised Winter 2008 This note exposits a simplified version of Myerson s [8] paper on revenue-maximizing auction design
Mathematics 426 Robert Gross Homework 9 Answers
 Mathematics 4 Robert Gross Homework 9 Answers. Suppose that X is a normal random variable with mean µ and standard deviation σ. Suppose that PX > 9 PX
Mathematics 4 Robert Gross Homework 9 Answers. Suppose that X is a normal random variable with mean µ and standard deviation σ. Suppose that PX > 9 PX
CHAPTER 4: HIGHER ORDER DERIVATIVES. Likewise, we may define the higher order derivatives. f(x, y, z) = xy 2 + e zx. y = 2xy.
 April 15, 2009 CHAPTER 4: HIGHER ORDER DERIVATIVES In this chapter D denotes an open subset of R n. 1. Introduction Definition 1.1. Given a function f : D R we define the second partial derivatives as
April 15, 2009 CHAPTER 4: HIGHER ORDER DERIVATIVES In this chapter D denotes an open subset of R n. 1. Introduction Definition 1.1. Given a function f : D R we define the second partial derivatives as
ECON 4117/5111 Mathematical Economics Fall 2005
 Test 1 September 30, 2005 Read Me: Please write your answers on the answer book provided. Use the rightside pages for formal answers and the left-side pages for your rough work. Do not forget to put your
Test 1 September 30, 2005 Read Me: Please write your answers on the answer book provided. Use the rightside pages for formal answers and the left-side pages for your rough work. Do not forget to put your
Formulas for probability theory and linear models SF2941
 Formulas for probability theory and linear models SF2941 These pages + Appendix 2 of Gut) are permitted as assistance at the exam. 11 maj 2008 Selected formulae of probability Bivariate probability Transforms
Formulas for probability theory and linear models SF2941 These pages + Appendix 2 of Gut) are permitted as assistance at the exam. 11 maj 2008 Selected formulae of probability Bivariate probability Transforms
EE 546, Univ of Washington, Spring Proximal mapping. introduction. review of conjugate functions. proximal mapping. Proximal mapping 6 1
 EE 546, Univ of Washington, Spring 2012 6. Proximal mapping introduction review of conjugate functions proximal mapping Proximal mapping 6 1 Proximal mapping the proximal mapping (prox-operator) of a convex
EE 546, Univ of Washington, Spring 2012 6. Proximal mapping introduction review of conjugate functions proximal mapping Proximal mapping 6 1 Proximal mapping the proximal mapping (prox-operator) of a convex
