arxiv: v1 [math.ca] 6 Nov 2015
|
|
|
- Hillary Barton
- 6 years ago
- Views:
Transcription
1 rxiv:5.0207v mh.a 6 Nov 205 uo derivives of frcionl vrile order: numericl roximions Din Tvres, dvres@ileiri. Ricrdo Almeid ricrdo.lmeid@u. Delfim F. M. Torres delfim@u. ESES, Polyechnic Insiue of Leiri, Leiri, Porugl ener for Reserch nd Develomen in Mhemics nd Alicions IDMA), Dermen of Mhemics, Universiy of Aveiro, Aveiro, Porugl Asrc We resen new numericl ool o solve ril differenil equions involving uo derivives of frcionl vrile order. Three uo-ye frcionl oerors re considered, nd for ech one of hem n roximion formul is oined in erms of sndrd inegerorder) derivives only. Esimions for he error of he roximions re lso rovided. We hen comre he numericl roximion of some es funcion wih is exc frcionl derivive. We end wih n exemlificion of how he resened mehods cn e used o solve ril frcionl differenil equions of vrile order. Keywords: frcionl clculus, frcionl vrile order, frcionl differenil equions, roximion mehods. MS 200: 33F05, 35R. PAS 200: G, Lj. Inroducion As is well nown, severl hysicl henomen re ofen eer descried y frcionl derivives, 8, 36. This is minly due o he fc h frcionl oerors e ino considerion he evoluion of he sysem, y ing he glol correlion, nd no only locl chrcerisics. Moreover, ineger-order clculus someimes conrdic he exerimenl resuls nd herefore derivives of frcionl order my e more suile 2. An ineresing recen generlizion of he heory of frcionl clculus consiss o llow he frcionl order of he derivive o e non-consn, deending on ime 5, 9, 20. Wih his roch, he non-locl roeries re more eviden nd numerous licions hve een found in hysics, conrol nd signl rocessing 7, 3, 22, 2, 26, 27, 34. One difficul issue, h usully rises when deling wih such frcionl oerors, is he exreme difficuly in solving nlyiclly such rolems 2, 37. Thus, in mos cses, we do nonow he exc soluion for he rolem nd one needs o see numericl roximion. Severl numericl mehods cn e found in he lierure, yiclly lying some discreizion over ime or relcing he frcionl oerors y roer decomosiion 2, 37. Recenly, new roximion formuls were given for frcionl consn order oerors, wih he dvnge h higher-order derivives re no required o oin good ccurcy of he Pr of firs uhor s Ph.D., which is crried ou he Universiy of Aveiro under he Docorl Progrmme Mhemics nd Alicions of Universiies of Aveiro nd Minho. Thisis rerinofer whose finl nd definie formisin ommunicions in Nonliner Science nd Numericl Simulion, ISSN: Per sumied 27/My/205; revised 06/Oc/205; cceed 30/Oc/205.
2 mehod, 23, 24. These decomosiions only deend on ineger-order derivives, nd y relcing he frcionl oerors h er in he rolem y hem, one leves he frcionl conex ending u in he resence of sndrd rolem, where numerous ools re ville o solve hem. Here we exend such decomosiions o uo frcionl rolems of vrile order. The er is orgnized s follows. To sr, in Secion 2 we formule he needed definiions. Nmely, we resen hree yes of uo derivives of vrile frcionl order. Firs, we consider one indeenden vrile only Secion 2.); hen we generlize for severl indeenden vriles Secion 2.2). Secion 3 is he min core of he er: we rove roximion formuls for he given frcionl oerors nd uer ound formuls for he errors. To es he efficiency of he roosed mehod, in Secion 4 we comre he exc frcionl derivive of some es funcion wih he numericl roximions oined from he decomosiion formuls given in Secion 3. To end, in Secion 5 we ly our mehod o roxime wo hysicl rolems involving uo frcionl oerors of vrile order ime-frcionl diffusion equion in Secion 5. nd frcionl Burgers ril differenil equion in fluid mechnics in Secion 5.2) y clssicl rolems h my e solved y well-nown sndrd echniques. 2 Frcionl clculus of vrile order In he lierure of frcionl clculus, severl differen definiions of derivives re found 28. One of hose, inroduced y uo in nd sudied indeendenly y oher uhors, lie Džršjn nd Nersesjn in nd Ronov in , hs found mny licions nd seems o e more suile o model hysic henomen 6, 8, 9, 5, 6, 3, 33, 35. Before generlizing he uo derivive for vrile order of differeniion, we recll wo yes of secil funcions: he Gmm nd Psi funcions. The Gmm funcion is n exension of he fcoril funcion o rel numers, nd is defined y Γ) = 0 τ ex τ)dτ, > 0. We menion h oher definiions exis for he Gmm funcion, nd i is ossile o define i for comlex numers, exce he non-osiive inegers. A sic u fundmenl roery h we will use ler is he following: Γ+) = Γ). The Psi funcion is he derivive of he logrihm of he Gmm funcion: Ψ) = d d lnγ)) = Γ ) Γ). Given α 0,), he lef nd righ uo frcionl derivives of order α of funcion x :, R re defined y D α D α x) x)) nd D α D α x) x)), resecively, where D αx) nd D α x) denoe he lef nd righ Riemnn Liouville frcionl derivive of order α, h is, nd D α d Γ α) d D α d Γ α) d τ) α xτ)dτ τ ) α xτ)dτ. 2
3 If x is differenile, hen, inegring y rs, one cn rove he following equivlen definiions: nd Dα Γ α) Dα Γ α) τ) α x τ)dτ τ ) α x τ)dτ. From hese definiions, i is cler h he uo frcionl derivive of consn is zero, which is flse when we consider he Riemnn Liouville frcionl derivive. Also, he oundry condiions h er in he Llce rnsform of he uo derivive deend on ineger-order derivives, nd so coincide wih he clssicl cse. 2. Vrile order uo derivives for funcions of one vrile Our gol is o consider frcionl derivives of vrile order, wih α deending on ime. In fc, some henomen in hysics re eer descried when he order of he frcionl oeror is no consn, for exmle, in he diffusion rocess in n inhomogeneous or heerogeneous medium, or rocesses where he chnges in he environmen modify he dynmic of he ricle 4, 30, 32. Moived y he ove considerions, we inroduce hree yes of uo frcionl derivives. The order of he derivive is considered s funcion α) ing vlues on he oen inervl 0, ). To sr, we define wo differeninds of Riemnn Liouville frcionl derivives. Definiion Riemnn Liouville frcionl derivives of order α) yes I nd II). Given funcion x :, R,. he ye I lef Riemnn Liouville frcionl derivive of order α) is defined y D α) d Γ α)) d τ) α) xτ)dτ; 2. he ye I righ Riemnn Liouville frcionl derivive of order α) is defined y D α) d Γ α)) d τ ) α) xτ)dτ; 3. he ye II lef Riemnn Liouville frcionl derivive of order α) is defined y D α) d d Γ α)) ) τ) α) xτ)dτ ; 4. he ye II righ Riemnn Liouville frcionl derivive of order α) is defined y D α) d ) τ ) α) xτ)dτ. d Γ α)) The uo derivives re given using he revious Riemnn Liouville frcionl derivives. Definiion 2 uo frcionl derivives of order α) yes I, II nd III). Given funcion x :, R,. he ye I lef uo derivive of order α) is defined y D α) D α) x) x)) = d Γ α)) d τ) α) xτ) x)dτ; 3
4 2. he ye I righ uo derivive of order α) is defined y Dα) D α) x) x)) = d Γ α)) d τ ) α) xτ) x)dτ; 3. he ye II lef uo derivive of order α) is defined y D α) D α) x) x)) = d d Γ α)) τ) α) xτ) x)dτ 4. he ye II righ uo derivive of order α) is defined y D α) D α) x) x)) = d ) τ ) α) xτ) x)dτ ; d Γ α)) 5. he ye III lef uo derivive of order α) is defined y D α) Γ α)) τ) α) x τ)dτ; 6. he ye III righ uo derivive of order α) is defined y Dα) Γ α)) τ ) α) x τ)dτ. In conrs wih he cse when α is consn, definiions of differen yes do no coincide. Theorem 3. The following relions eween he lef frcionl oerors hold: D α) D α) α ) x) + τ) α) x τ) Γ2 α)) α) ln τ) dτ ) nd Dα) Dα) Proof. Inegring y rs, one ges Dα) x) α )Ψ α)) Γ α)) d Γ α)) d d = Γ α)) d Differeniing he inegrl, i follows h D α) α ) Γ α)) α)) 2 + α) ) ; τ) α) xτ) x)dτ. 2) τ) α) xτ) x)dτ α) τ) α) x τ) = α ) Dα) x) + Γ2 α)) The second formul follows from direc clculions. τ) α) x τ)dτ τ) α) x τ)dτ. α )ln τ)+ α) dτ τ τ) α) x τ) α) ln τ) dτ. 4
5 Therefore, when he order α) c is consn, or for consn funcions x), we hve Dα) Similrly, we oin he nex resul. Dα) Dα) x). Theorem 4. The following relions eween he righ frcionl oerors hold: nd Dα) Dα) x) + Dα) Dα) α ) Γ2 α)) x)+ α )Ψ α)) Γ α)) Theorem 5. Le x,,r). A = = D α) Dα) D α) Dα) τ ) α) x τ) lnτ ) dτ α) τ ) α) xτ) x)dτ. D α) 0; Dα) 0. Proof. We sr roving he hird equliy he iniil ime =. We simly noe h D α) x x) Γ α)) τ) α) dτ = x Γ2 α)) ) α), which is zero =. For he firs equliy =, using equion ), nd he wo nex relions τ) α) x τ) α) dτ x α))2 α)) )2 α) nd τ) α) x τ)ln τ)dτ x 2 α) )2 α) ln ) 2 α), his ler inequliy oined from inegrion y rs, we rove h Dα) 0 =. Finlly, we rove he second equliy = y considering equion 2): erforming n inegrion y rs, we ge τ) α) xτ) x)dτ x α))2 α)) )2 α) nd so D α) 0 =. The roof h he righ frcionl oerors lso vnish he end oin = follows y similr rgumens. Wih some comuions, relionshi eween he Riemnn Liouville nd he uo frcionl derivives is esily deduced: D α) D α) x) + = Dα) x) + x) d Γ α)) d x) Γ α)) ) α) + x)α ) Γ2 α)) ) α) τ) α) dτ α) ln ) 5
6 nd D α) D α) x)+x) d d For he righ frcionl oerors, we hve Γ α)) = x) Dα) x) + Γ α)) ) α) D α) D α) x) + ) τ) α) dτ + x)α ) Γ2 α)) ) α) Ψ2 α)) ln ). x) Γ α)) ) α) x)α ) Γ2 α)) ) α) α) ln ) nd D α) D α) x) x) + Γ α)) ) α) x)α ) Γ2 α)) ) α) Ψ2 α)) ln ). Thus, i is immedie o conclude h if x) = 0, hen nd if x) = 0, hen D α) D α) D α) x) nd D α) Dα) x) nd D α) D α) x) Dα) x). Nex we oin formuls for he uo frcionl derivives of ower funcion. Lemm 6. Le ) γ wih γ > 0. Then, D α) Γγ +) Γγ α)+) )γ α) α Γγ +) ) Γγ α)+2) )γ α)+ ln ) Ψγ α)+2)+ψ α)), Γγ +) Dα) Γγ α)+) )γ α) α Γγ +) ) Γγ α)+2) )γ α)+ ln ) Ψγ α)+2), Γγ +) Dα) Γγ α)+) )γ α). Proof. The formul for D α) x) follows immediely from 29. For he second equliy, one hs D α) d ) τ) α) τ ) γ dτ d Γ α)) = d ) α) τ ) α) τ ) dτ) γ. d Γ α)) 6
7 Wih he chnge of vriles τ = s ), nd wih he hel of he Be funcion B, ), we rove h Dα) d ) α) ) s) α) s γ ) γ+ ds d Γ α)) 0 = d ) ) γ α)+ Bγ +, α)) d Γ α)) = d ) Γγ +) d Γγ α)+2) )γ α)+. We oin he desired formul y differeniing his ler exression. The ls equliy follows in similr wy. Anlogous relions o hose of Lemm 6, for he righ uo frcionl derivives of vrile order, re esily oined. Lemm 7. Le ) γ wih γ > 0. Then, Dα) Dα) D α) Γγ +) Γγ α)+) )γ α) +α Γγ +) ) Γγ α)+2) )γ α)+ ln ) Ψγ α)+2)+ψ α)), Γγ +) Γγ α)+) )γ α) +α Γγ +) ) Γγ α)+2) )γ α)+ ln ) Ψγ α)+2), Γγ +) Γγ α)+) )γ α). Wih Lemm 6 in mind, we immediely see h Dα) x) Dα) x) Dα) x). Also, lesforheowerfuncion, isuggessh Dα) x) my e more suile inverse oerion of he frcionl inegrl when he order is vrile. For exmle, consider funcions 2 nd y) = ) 2, nd he frcionl order α) = 5+ 0, 0,. Then, 0. α) 0.6 for ll. Nex we comre he frcionl derivives of x nd y of order α) wih he frcionl derivives of consn order α = 0. nd α = 0.6. By Lemm 6, we now h he lef uo frcionl derivives of order α) of x re given y 0 Dα) 0 D α) 0 D α) 2 Γ3 α)) 2 α) 3 α) Γ4 α)) ln) Ψ4 α))+ψ α)), 2 Γ3 α)) 2 α) 3 α) 2 Γ3 α)) 2 α), Γ4 α)) ln) Ψ4 α)), while y Lemm 7, he righ uo frcionl derivives of order α) of y re given y D α) y) = D α) y) = Dα) y) = 2 Γ3 α)) )2 α) + )3 α) Γ4 α)) ln ) Ψ4 α))+ψ α)), 2 Γ3 α)) )2 α) + )3 α) 2 Γ3 α)) )2 α). Γ4 α)) ln ) Ψ4 α)), 7
8 For consn order α, we hve 0 Dα 2 Γ3 α) 2 α nd Dα y) = 2 Γ3 α) )2 α. The resuls cn e seen in Figure. 2.2 Vrile order uo derivives for funcions of severl vriles Pril frcionl derivives re nurl exension nd re defined in similr wy. Le m N, m {,...,m}, nd consider funcion x : i, i R wih m vriles. For simliciy, we define he vecors nd i= τ =,...,,τ,+,..., m ) R m ) =,..., m ) R m. Definiion 8 Pril uo frcionl derivives of vrile order yes I, II nd III). Given funcion x : m i= i, i R nd frcionl orders α :, 0,), {,...,m},. he ye I ril lef uo derivive of order α ) is defined y D α ) Γ α )) τ) α ) xτ x )dτ; 2. he ye I ril righ uo derivive of order α ) is defined y D α ) Γ α )) τ ) α ) xτ x )dτ; 3. he ye II ril lef uo derivive of order α ) is defined y D α ) Γ α )) τ) α ) xτ x )dτ 4. he ye II ril righ uo derivive of order α ) is defined y D α ) ) τ ) α ) xτ x )dτ ; Γ α )) 5. he ye III ril lef uo derivive of order α ) is defined y D α ) τ) α ) x τ dτ; Γ α )) 6. he ye III ril righ uo derivive of order α ) is defined y D α ) τ ) α ) x τ dτ. Γ α )) Similrly s done efore, relions eween hese definiions cn e roven. ) ; 8
9 ) 0 Dα) x) ) 0 Dα) x) c) 0 Dα) x) d) Dα) y) e) Dα) y) f) Dα) y) Figure : omrison eween vrile order nd consn order frcionl derivives. Theorem 9. The following four formuls hold: D α ) D α ) x) + α ) Γ2 α )) τ) α ) x τ α ) ln τ) dτ, 3) 9
10 D α ) D α ) x) α )Ψ α )) τ) α ) xτ x dτ, 4) Γ α )) nd D α ) D α ) x) + α ) Γ2 α )) τ ) α ) x τ D α ) D α ) x)+ α )Ψ α )) Γ α )) α ) lnτ ) dτ τ ) α ) xτ x dτ. 3 Aroximion of vrile order uo derivives Le N. We define A = + Γ+ α )) l=n + Γα ) n+) B = Γ α ))Γα )) n)!, n x V ) = τ ) τ dτ, L ) = mx x τ. τ, Γα ) n+l), Γα ) )l n+)! Theorem 0. Le x n+ m i= i, i,r) wih n N. Then, for ll {,...,m} nd for ll N N such h N n, we hve D α ) n = A ) α ) x The roximion error E) is ounded y + B ) n α ) V )+E). exn α )) 2 +n α )) E) L n+ ) Γn+ α ))N n α ) n α )) ) n+ α ). Proof. By definiion, D α ) =n τ) α ) x τ dτ Γ α )) nd, inegring y rs wih u τ) = τ) α ) nd vτ) = x τ, we deduce h D α ) ) α ) x + Γ2 α )) Γ2 α )) τ) α ) 2 x 2 Inegring gin y rs, ing u τ) = τ) α ) nd vτ) = 2 xτ 2, we ge D α ) ) α ) x + ) 2 α) Γ2 α )) Γ3 α )) + Γ3 α )) 2 x 2 τ) 2 α ) 3 x 3 τ dτ. τ dτ. 0
11 Reeing he sme rocedure n 2 more imes, we ge he exnsion formul D α ) Using he equliies wih we rrive D α ) n = ) α ) x Γ+ α )) + Γn+ α )) τ) n α ) = ) n α ) τ = n = = ) n α ) E) = =N+ ) α ) x Γ+ α )) + ) n α ) Γn+ α )) n = N =0 n α ) τ) n α ) n+ x n+ ) n α ) n α ) ) ) τ ) ), =0 ) α ) x Γ+ α )) + ) n α ) Γn+ α )) =0 ) ) τ ) ) +E) τ dτ. n α ) ) ) τ ) n+ x ) n+ τ dτ +E) ) n α ) ) ) τ ) n+ x n+ τ dτ +E) wih E) = ) n α ) E) n+ x Γn+ α )) n+ τ dτ. Now, we sli he ls sum ino = 0 nd he remining erms =,...,N nd inegre y rs wih uτ) = τ ) nd v τ) = n+ xτ. Oserving h we oin: ) n α ) Γn+ α )) =0 ) n α ) n+ ) n α ) ) = Γα ) n+), Γα ) n)! ) ) = ) n α ) n x Γn+ α )) n n x n ) n x n τ ) n x n τ ) n+ x n+ + ) n α ) Γn+ α )) τ dτ τ dτ = Γα ) n+) Γα ) n)! )
12 = ) n α ) Γn+ α )) + ) n α ) Γn α )) Thus, we ge n D α ) n x n + ) n α ) Γn+ α )) = = n x n + = Γα ) n+) Γα ) n)! Γα ) n+) Γα )+ n) )! ) τ ) n x n τ dτ. ) α ) Γ+ α )) x + ) n α ) n x Γn+ α )) n + + ) n α ) Γn α )) τ ) n x n = = Γα ) n+) Γα ) n)! Γα ) n+) Γα )+ n) )! ) τ dτ +E). Reeing he rocess n more imes wih resec o he ls sum, h is, sliing he firs erm of he sum nd inegring y rs he oined resul, we rrive o n D α ) ) α ) x Γα ) n+l) Γ+ α )) + Γα ) )l n+)! = + =n l=n + Γα ) n+) Γ α ))Γα )) n)! ) n α ) τ ) n x τ dτ +E). We now see he uer ound formul for E). Using he wo relions τ ), if τ, nd n α ) exn α )) 2 +n α )), n+ α ) we ge Then, E) =N+ N exn α )) 2 +n α )) n+ α ) exn α )) 2 +n α )) n+ α ) d = exn α )) 2 +n α )). N n α ) n α )) exn α )) 2 +n α )) E) L n+ ) Γn+ α ))N n α ) n α )) ) n+ α ). This concludes he roof. Remr. In Theorem 0 we hve for ll m i= i, i nd n N. lim E) = 0 N 2
13 Theorem 2. Le x n+ m i= i, i,r) wih n N. Then, for ll {,...,m} nd for ll N N such h N n, we hve D α ) n A ) α ) x + B ) n α ) V ) = + α ) ) α ) Γ2 α )) =n α ) ln ) + =0 The roximion error E) is ounded y ) N =0 ) α ) ) ) V n+) α ) ) ) N r r= ) +rv n++r) exn α )) 2 +n α )) E) L n+ ) Γn+ α ))N n α ) n α )) ) n+ α ) + α ex α )) 2 + α )) ) L ) Γ2 α ))N α ) α )) α ) ln ) + ) 2 α ). N Proof. Ting ino ccoun relion 3) nd Theorem 0, we only need o exnd he erm +E). α ) τ) α ) x τ Γ2 α )) α ) ln τ) dτ. 5) Sliing he inegrl, nd using he exnsion formuls τ) α ) = ) α ) τ = ) α ) N =0 α ) ) α ) ) ) τ ) ) +E ) wih nd wih E ) = =N+ α ) ) ) τ ) ) ln τ) = ln )+ln τ ) τ ) r = ln ) r ) r E 2) E 2 ) = r=n+ r= τ ) r r ) r, 3
14 we conclude h 5) is equivlen o ) α ) Γ2 α )) α ) ln ) τ) α ) x τ dτ τ) α ) ln τ ) x τ dτ α = ) ) Γ2 α )) α ) ln ) ) α ) α ) ) ) τ ) x =0 ) τ dτ + ) α ) α ) ) ) τ ) τ ) r x =0 ) r r= ) r τ dτ α + ) ) Γ2 α )) α ) ln ) ) α ) E ) x τ dτ + ) α ) E )E 2 ) x τ dτ = α ) ) α ) ) Γ2 α )) α ) ln N ) ) α ) ) =0 ) V n+) + α ) ) ) N r =0 r= ) +rv n++r) + α ) ) α ) Γ2 α )) ) α ) ln ). E ) x τ dτ + For he error nlysis, we now from Theorem 0 h E ) ex α )) 2 + α )). N α ) α )) E )E 2 ) x τ dτ Then, ) α ) E ) x τ dτ L ) ex α )) 2 + α )) N α ) 2 α ). ) α )) 6) On he oher hnd, we hve ) α ) E )E 2 ) x τ dτ L ) ex α )) 2 + α )) N α ) α ) ) α )) r ) r τ ) r dτ = L ) ex α )) 2 + α )) N α ) α )) ) α ) L ) ex α )) 2 + α )) N 2 α ) 2 α ). ) α )) r=n+ r=n+ We ge he desired resul y comining inequliies 6) nd 7). rr +) 7) 4
15 Theorem 3. Le x n+ m i= i, i,r) wih n N. Then, for ll {,...,m} nd for ll N N such h N n, we hve D α ) n A ) α ) x + B ) n α ) V ) = + α ) ) α ) Γ2 α )) + =0 α ) ) ) N r= The roximion error E) is ounded y =n Ψ2 α )) ln )) =0 r ) +rv n++r) +E). ) α ) ) ) V n+) exn α )) 2 +n α )) E) L n+ ) Γn+ α ))N n α ) n α )) ) n+ α ) + α ex α )) 2 + α )) ) L ) Γ2 α ))N α ) α )) Ψ2 α )) ln ) + ) 2 α ). N Proof. Sring wih relion 4), nd inegring y rs he inegrl, we oin h D α ) D α ) x)+ α )Ψ α )) Γ2 α )) The res of he roof is similr o he one of Theorem 2. τ) α ) x τ dτ. Remr 4. As riculr cses of Theorems 0, 2 nd 3, we oin exnsion formuls for x), D α) x) nd D α) x). D α) Wih resec o he hree righ frcionl oerors of Definiion 8, we se, for N, ) Γα ) n+l) = +, Γ+ α )) Γα ) )l n+)! l=n + Γα ) n+) D = Γ α ))Γα )) n)!, n x W ) = τ) τ dτ, M ) = mx x τ. τ, The exnsion formuls re given in Theorems 5, 6 nd 7. We omi he roofs since hey re similr o he corresonding lef ones. Theorem 5. Le x n+ m i= i, i,r) wih n N. Then, for ll {,...,m} nd for ll N N such h N n, we hve D α ) n = ) α ) x The roximion error E) is ounded y + D ) n α ) W )+E). exn α )) 2 +n α )) E) M n+ ) Γn+ α ))N n α ) n α )) ) n+ α ). =n 5
16 Theorem 6. Le x n+ m i= i, i,r) wih n N. Then, for ll {,...,m} nd for ll N N such h N n, we hve D α ) n ) α ) x + D ) n α ) W ) = + α ) ) α ) Γ2 α )) + =0 =n α ) ln ) α ) ) ) N r r= ) +rw n++r) The roximion error E) is ounded y ) N =0 +E). ) α ) ) ) W n+) exn α )) 2 +n α )) E) M n+ ) Γn+ α ))N n α ) n α )) ) n+ α ) + α ex α )) 2 + α )) ) M ) Γ2 α ))N α ) α )) α ) ln ) + ) 2 α ). N Theorem 7. Le x n+ m i= i, i,r) wih n N. Then, for ll {,...,m} nd for ll N N such h N n, we hve D α ) n ) α ) x + D ) n α ) W ) = + α ) ) α ) Γ2 α )) + =0 α ) ) ) N r= The roximion error E) is ounded y =n Ψ2 α )) ln )) =0 r ) +rw n++r) +E). ) α ) ) ) W n+) exn α )) 2 +n α )) E) M n+ ) Γn+ α ))N n α ) n α )) ) n+ α ) + α ex α )) 2 + α )) ) M ) Γ2 α ))N α ) α )) Ψ2 α )) ln ) + ) 2 α ). N 4 An exmle To es he ccurcy of he roosed mehod, we comre he frcionl derivive of concree given funcion wih some numericl roximions of i. For 0,, le 2 e he es funcion. For he order of he frcionl derivives we consider wo cses: α) = nd β) = We consider he roximions given in Theorems 0, 2 nd 3, wih fixed n = nd N {2,4,6}. The error of roximing f) y f) is mesured y f) f). See Figures
17 ) 0 Dα) x) ) Error Figure 2: Tye III lef uo derivive of order α) for he exmle of Secion 4 nlyic versus numericl roximions oined from Theorem 0. ) 0 Dα) x) ) Error Figure 3: Tye I lef uo derivive of order α) for he exmle of Secion 4 nlyic versus numericl roximions oined from Theorem 2. 5 Alicions In his secion we ly he roosed echnique o some concree frcionl differenil equions of hysicl relevnce. 5. A ime-frcionl diffusion equion We exend he one-dimensionl ime-frcionl diffusion equion 4 o he vrile order cse. onsider u = ux,) wih domin 0, 2. The ril frcionl differenil equion of order α) is he following: 0 D α) ux,) 2 u x2x,) = fx,) for x 0,, 0,, 8) 7
18 ) 0 Dα) x) ) Error Figure 4: Tye II lef uo derivive of order α) for he exmle of Secion 4 nlyic versus numericl roximions oined from Theorem 3. ) 0 Dβ) x) ) Error Figure 5: Tye III lef uo derivive of order β) for he exmle of Secion 4 nlyic versus numericl roximions oined from Theorem 0. sujec o he oundry condiions nd ux,0) = gx), for x 0,), 9) u0,) = u,) = 0, for 0,. 0) We menion h when α), one oins he clssicl diffusion equion, nd when α) 0 one ges he clssicl Helmholz elliic equion. Using Lemm 6, i is esy o chec h ux,) = 2 sin2πx) is soluion o 8) 0) wih ) 2 fx,) = Γ3 α)) 2 α) +4π 2 2 sin2πx) 8
19 ) 0 Dβ) x) ) Error Figure 6: Tye I lef uo derivive of order β) for he exmle of Secion 4 nlyic versus numericl roximions oined from Theorem 2. ) 0 Dβ) x) ) Error Figure 7: Tye II lef uo derivive of order β) for he exmle of Secion 4 nlyic versus numericl roximions oined from Theorem 3. nd gx) = 0 comre wih Exmle in 4). The numericl rocedure is he following: relce 0 Dα) u wih he roximion given in Theorem 0, ing n = nd n rirry N, h is, 0 Dα) ux,) A α) u N x,)+ B α) V x,) = 9
20 wih A = + Γ2 α)) l= Γα) +) B = Γ α))γα)) )!, V x,) = 0 τ u x,τ)dτ. Γα) +l), Γα) )l! Then, he iniil frcionl rolem 8) 0) is roximed y he following sysem of secondorder ril differenil equions: nd A α) u x,)+ N V = B α) V x,) 2 u x2x,) = fx,) x,) = ux,), =,...,N, for x 0, nd for 0,, sujec o he oundry condiions ux,0) = 0, for x 0,), nd u0,) = u,) = 0, for 0,, V x,0) = 0, for x 0,, =,...,N. Remr 8. As ws menioned in Theorem 0, s N increses, he error of he roximion decreses nd he given roximion formul converges o he frcionl derivive. Thus, in order o hve good ccurcy for he mehod, one should e higher vlues for N. Remr 9. We re no wre of similr mehods o our, concerning vrile frcionl clculus, in order o comre he erformnce of he roosed mehod o oher numericl roximion mehods. For his reson, we decided o comre wih he exc soluion. In he ville lierure, using discreizion rocess, FDEs re solved s finie differences. Our echnique is quie differen: we rewrie he FDE s sysem of ordinry differenil equions, nd hen we cn ly ny nown echnique o solve i. Noe h he reson why we soed here wih N = 6 ws o hve n roximion h is enough close o he exc soluion u sill visully disinguishly when we increse N more, he roximion nd he exc soluion er o e he sme in he los). In erms of erformnce of he mehod, i is roughly he sme o u N = 6 or igger. 5.2 A frcionl ril differenil equion in fluid mechnics We now ly our roximion echniques o he following one-dimensionl liner inhomogeneous frcionl Burgers equion of vrile order see 7, Exmle 5.2): 0 Dα) ux,)+ u x x,) 2 u 22 α) x2x,) = +2x 2, for x 0,, 0,, ) Γ3 α)) sujec o he oundry condiion ux,0) = x 2, for x 0,). 2) Here, Fx,) = 22 α) Γ3 α)) +2x 2 20
21 is he exernl force field. Burgers equion is used o model gs dynmics, rffic flow, urulence, fluid mechnics, ec. The exc soluion is ux,) = x The frcionl rolem ) 2) cn e roximed y A α) u N x,)+ B α) V x,)+ u x x,) 2 u 22 α) x2x,) = Γ3 α)) +2x 2 = wih A, B nd V, {,...,N}, s in Secion 5.. The roximion error cn e decresed s much s desired y incresing he vlue of N. Acnowledgmens This wor ws suored y Poruguese funds hrough he ener for Reserch nd Develomen in Mhemics nd Alicions IDMA) nd The Poruguese Foundion for Science nd Technology FT), wihin rojec UID/MAT/0406/203. Tvres ws lso suored y FT hrough he Ph.D. fellowshi SFRH/BD/42557/2007; Torres y rojec PTD/EEI-AUT/450/202, co-finnced y FEDER under POF-QREN wih OMPETE reference FOMP FEDER The uhors re very greful o hree nonymous referees, for severl commens nd imrovemen suggesions. References T. M. Ancovic, M. Jnev, S. Piliovic nd D. Zoric, An exnsion formul for frcionl derivives of vrile order, en. Eur. J. Phys. 203), no. 0, A. Angn nd A. H. loo, Siliy nd convergence of he sce frcionl vrile-order Schrödinger equion, Adv. Difference Equ. 203, 203:80, 0. 3 M. uo, Liner model of dissiion whose Q is lmos frequency indeenden II, Geohys. J. R. Asr. Soc ), A. V. hechin, R. Gorenflo nd I. M. Soolov, Frcionl diffusion in inhomogeneous medi, J. Phys. A ), no. 42, L679 L S. hen, F. Liu nd K. Burrge, Numericl simulion of new wo-dimensionl vrile-order frcionl ercolion equion in non-homogeneous orous medi, omu. Mh. Al ), no. 9, F. M. oimr, Mechnics wih vrile-order differenil oerors, Ann. Phys. 8) ), no. -2, F. M. oimr,. M. Soon nd M. H. Koyshi, The vrile viscoelsiciy oeror, Annlen der Physi ), M. Dlir nd M. Bshour, Alicions of frcionl clculus, Al. Mh. Sci. Ruse) 4 200), no. 2-24, K. Diehelm, The nlysis of frcionl differenil equions, Lecure Noes in Mhemics, 2004, Sringer, Berlin, M. M. Džršjn nd A. B. Nersesjn, Frcionl derivives nd he uchy rolem for differenil equions of frcionl order, Izv. Ad. Nu Armjn. SSR Ser. M ), no., R. Herrmnn, Folded oenils in cluser hysics comrison of Yuw nd oulom oenils wih Riesz frcionl inegrls, J. Phys. A ), no. 40, , 2. 2 R. Hilfer, Alicions of frcionl clculus in hysics, World Sci. Pulishing, River Edge, NJ, D. Ingmn nd J. Suzdlnisy, onrol of dming oscillions y frcionl differenil oeror wih ime-deenden order, omu. Mehods Al. Mech. Engrg ), no. 52, Y. Lin nd. Xu, Finie difference/secrl roximions for he ime-frcionl diffusion equion, J. omu. Phys ), no. 2,
22 5 J. A. T. Mchdo, M. F. Silv, R. S. Bros, I. S. Jesus,. M. Reis, M. G. Mrcos nd A. F. Glhno, Some licions of frcionl clculus in engineering, Mh. Prol. Eng ), Ar. ID 63980, D. A. Murio nd. E. Mejí, Generlized ime frcionl IHP wih uo frcionl derivives, J. Phys. onf. Ser ), Ar. ID 02074, 8. 7 Z. Odi nd S. Momni, The vriionl ierion mehod: n efficien scheme for hndling frcionl ril differenil equions in fluid mechnics, omu. Mh. Al ), no. -2, T. Odzijewicz, A. B. Mlinows nd D. F. M. Torres, Frcionl clculus of vriions in erms of generlized frcionl inegrl wih licions o hysics, Asr. Al. Anl. 202, Ar. ID 8792, 24. rxiv: T. Odzijewicz, A. B. Mlinows nd D. F. M. Torres, Vrile order frcionl vriionl clculus for doule inegrls, Proceedings of he 5s IEEE onference on Decision nd onrol, Decemer 0 3, 202, Mui, Hwii, Ar. no ), rxiv: T. Odzijewicz, A. B. Mlinows nd D. F. M. Torres, Frcionl vriionl clculus of vrile order, in Advnces in hrmonic nlysis nd oeror heory, 29 30, Oer. Theory Adv. Al., 229, Birhäuser/Sringer Bsel AG, Bsel, 203. rxiv: T. Odzijewicz, A. B. Mlinows nd D. F. M. Torres, Noeher s heorem for frcionl vriionl rolems of vrile order, en. Eur. J. Phys. 203), no. 6, rxiv: P. W. Oslczy, P. Duch, D. W. Brzezińsi nd D. Snowsi, Order Funcions Selecion in he Vrile-, Frcionl-Order PID onroller, Advnces in Modelling nd onrol of Non-ineger-Order Sysems, Lecure Noes in Elecricl Engineering ), S. Pooseh, R. Almeid nd D. F. M. Torres, Aroximion of frcionl inegrls y mens of derivives, omu. Mh. Al ), no. 0, rxiv: S. Pooseh, R. Almeid nd D. F. M. Torres, Numericl roximions of frcionl derivives wih licions, Asin J. onrol 5 203), no. 3, rxiv: Yu. N. Ronov, ree rolems in srucurl memers, Norh-Hollnd Series in Alied Mhemics nd Mechnics, Amserdm/London, L. E. S. Rmirez nd. F. M. oimr, On he vrile order dynmics of he nonliner we cused y sedimening ricle, Phys. D ), no. 3, M. R. Rić nd A. Pisno, Vrile-order frcionl oerors for dive order nd rmeer esimion, IEEE Trns. Auom. onrol ), no. 3, S. G. Smo, A. A. Kils nd O. I. Mrichev, Frcionl inegrls nd derivives, rnsled from he 987 Russin originl, Gordon nd Brech, Yverdon, S. G. Smo nd B. Ross, Inegrion nd differeniion o vrile frcionl order, Inegrl Trnsform. Sec. Func. 993), no. 4, F. Snmri, S. Wils, E. de Schuer nd G. J. Augusine, Anomlous diffusion in Purinje cell dendries cused y sines, Neuron ), K. Singh, R. Sxen nd S. Kumr, uo-sed frcionl derivive in frcionl Fourier rnsform domin, IEEE Journl on Emerging nd Seleced Toics in ircuis nd Sysems 3 203), H. G. Sun, W. hen nd Y. Q. hen, Vrile order frcionl differenil oerors in nomlous diffusion modeling, Physic A ) N. H. Sweilm nd H. M. AL-Mrwm, On he Numericl Soluions of he Vrile Order Frcionl He Equion, Sudies in Nonliner Sciences 2 20), D. Vlério nd J. Sá d os, Vrile order frcionl conrollers, Asin J. onrol 5 203), no. 3, T. Yjim nd K. Ymsi, Geomery of surfces wih uo frcionl derivives nd licions o incomressile wo-dimensionl flows, J. Phys. A ), no. 6, 06520, B. Zheng, G /G)-exnsion mehod for solving frcionl ril differenil equions in he heory of mhemicl hysics, ommun. Theor. Phys. Beijing) ), no. 5, P. Zhung, F. Liu, V. Anh nd I. Turner, Numericl mehods for he vrile-order frcionl dvecion-diffusion equion wih nonliner source erm, SIAM J. Numer. Anl ), no. 3,
Research Article An Expansion Formula with Higher-Order Derivatives for Fractional Operators of Variable Order
 Hindwi Pulishing Corporion The Scienific World Journl Volume 23, Aricle ID 95437, pges hp://dx.doi.org/.55/23/95437 Reserch Aricle An Expnsion Formul wih Higher-Order Derivives for Frcionl Operors of Vrile
Hindwi Pulishing Corporion The Scienific World Journl Volume 23, Aricle ID 95437, pges hp://dx.doi.org/.55/23/95437 Reserch Aricle An Expnsion Formul wih Higher-Order Derivives for Frcionl Operors of Vrile
On Hadamard and Fejér-Hadamard inequalities for Caputo k-fractional derivatives
 In J Nonliner Anl Appl 9 8 No, 69-8 ISSN: 8-68 elecronic hp://dxdoiorg/75/ijn8745 On Hdmrd nd Fejér-Hdmrd inequliies for Cpuo -frcionl derivives Ghulm Frid, Anum Jved Deprmen of Mhemics, COMSATS Universiy
In J Nonliner Anl Appl 9 8 No, 69-8 ISSN: 8-68 elecronic hp://dxdoiorg/75/ijn8745 On Hdmrd nd Fejér-Hdmrd inequliies for Cpuo -frcionl derivives Ghulm Frid, Anum Jved Deprmen of Mhemics, COMSATS Universiy
On The Hermite- Hadamard-Fejér Type Integral Inequality for Convex Function
 Turkish Journl o Anlysis nd Numer Theory, 4, Vol., No. 3, 85-89 Aville online h://us.scieu.com/jn//3/6 Science nd Educion Pulishing DOI:.69/jn--3-6 On The Hermie- Hdmrd-Fejér Tye Inegrl Ineuliy or Convex
Turkish Journl o Anlysis nd Numer Theory, 4, Vol., No. 3, 85-89 Aville online h://us.scieu.com/jn//3/6 Science nd Educion Pulishing DOI:.69/jn--3-6 On The Hermie- Hdmrd-Fejér Tye Inegrl Ineuliy or Convex
Hermite-Hadamard-Fejér type inequalities for convex functions via fractional integrals
 Sud. Univ. Beş-Bolyi Mh. 6(5, No. 3, 355 366 Hermie-Hdmrd-Fejér ype inequliies for convex funcions vi frcionl inegrls İmd İşcn Asrc. In his pper, firsly we hve eslished Hermie Hdmrd-Fejér inequliy for
Sud. Univ. Beş-Bolyi Mh. 6(5, No. 3, 355 366 Hermie-Hdmrd-Fejér ype inequliies for convex funcions vi frcionl inegrls İmd İşcn Asrc. In his pper, firsly we hve eslished Hermie Hdmrd-Fejér inequliy for
Refinements to Hadamard s Inequality for Log-Convex Functions
 Alied Mhemics 899-93 doi:436/m7 Pulished Online Jul (h://wwwscirporg/journl/m) Refinemens o Hdmrd s Ineuli for Log-Convex Funcions Asrc Wdllh T Sulimn Dermen of Comuer Engineering College of Engineering
Alied Mhemics 899-93 doi:436/m7 Pulished Online Jul (h://wwwscirporg/journl/m) Refinemens o Hdmrd s Ineuli for Log-Convex Funcions Asrc Wdllh T Sulimn Dermen of Comuer Engineering College of Engineering
How to prove the Riemann Hypothesis
 Scholrs Journl of Phsics, Mhemics nd Sisics Sch. J. Phs. Mh. S. 5; (B:5-6 Scholrs Acdemic nd Scienific Publishers (SAS Publishers (An Inernionl Publisher for Acdemic nd Scienific Resources *Corresonding
Scholrs Journl of Phsics, Mhemics nd Sisics Sch. J. Phs. Mh. S. 5; (B:5-6 Scholrs Acdemic nd Scienific Publishers (SAS Publishers (An Inernionl Publisher for Acdemic nd Scienific Resources *Corresonding
How to Prove the Riemann Hypothesis Author: Fayez Fok Al Adeh.
 How o Prove he Riemnn Hohesis Auhor: Fez Fok Al Adeh. Presiden of he Srin Cosmologicl Socie P.O.Bo,387,Dmscus,Sri Tels:963--77679,735 Emil:hf@scs-ne.org Commens: 3 ges Subj-Clss: Funcionl nlsis, comle
How o Prove he Riemnn Hohesis Auhor: Fez Fok Al Adeh. Presiden of he Srin Cosmologicl Socie P.O.Bo,387,Dmscus,Sri Tels:963--77679,735 Emil:hf@scs-ne.org Commens: 3 ges Subj-Clss: Funcionl nlsis, comle
A FINITE-DIFFERENCE SCHEME FOR SOLUTION OF A FRACTIONAL HEAT DIFFUSION-WAVE EQUATION WITHOUT INITIAL CONDITIONS
 Beilev, V. D., e l.: A Finie-Difference Scheme for Soluion of... THERMAL SCIENCE: Yer 5, Vol. 9, No.,. 53-536 53 A FINITE-DIFFERENCE SCHEME FOR SOLUTION OF A FRACTIONAL HEAT DIFFUSION-WAVE EQUATION WITHOUT
Beilev, V. D., e l.: A Finie-Difference Scheme for Soluion of... THERMAL SCIENCE: Yer 5, Vol. 9, No.,. 53-536 53 A FINITE-DIFFERENCE SCHEME FOR SOLUTION OF A FRACTIONAL HEAT DIFFUSION-WAVE EQUATION WITHOUT
Positive and negative solutions of a boundary value problem for a
 Invenion Journl of Reerch Technology in Engineering & Mngemen (IJRTEM) ISSN: 2455-3689 www.ijrem.com Volume 2 Iue 9 ǁ Sepemer 28 ǁ PP 73-83 Poiive nd negive oluion of oundry vlue prolem for frcionl, -difference
Invenion Journl of Reerch Technology in Engineering & Mngemen (IJRTEM) ISSN: 2455-3689 www.ijrem.com Volume 2 Iue 9 ǁ Sepemer 28 ǁ PP 73-83 Poiive nd negive oluion of oundry vlue prolem for frcionl, -difference
A Structural Approach to the Enforcement of Language and Disjunctive Constraints
 A Srucurl Aroch o he Enforcemen of Lnguge nd Disjuncive Consrins Mrin V. Iordche School of Engineering nd Eng. Tech. LeTourneu Universiy Longview, TX 7607-700 Pnos J. Ansklis Dermen of Elecricl Engineering
A Srucurl Aroch o he Enforcemen of Lnguge nd Disjuncive Consrins Mrin V. Iordche School of Engineering nd Eng. Tech. LeTourneu Universiy Longview, TX 7607-700 Pnos J. Ansklis Dermen of Elecricl Engineering
Contraction Mapping Principle Approach to Differential Equations
 epl Journl of Science echnology 0 (009) 49-53 Conrcion pping Principle pproch o Differenil Equions Bishnu P. Dhungn Deprmen of hemics, hendr Rn Cmpus ribhuvn Universiy, Khmu epl bsrc Using n eension of
epl Journl of Science echnology 0 (009) 49-53 Conrcion pping Principle pproch o Differenil Equions Bishnu P. Dhungn Deprmen of hemics, hendr Rn Cmpus ribhuvn Universiy, Khmu epl bsrc Using n eension of
Integral Transform. Definitions. Function Space. Linear Mapping. Integral Transform
 Inegrl Trnsform Definiions Funcion Spce funcion spce A funcion spce is liner spce of funcions defined on he sme domins & rnges. Liner Mpping liner mpping Le VF, WF e liner spces over he field F. A mpping
Inegrl Trnsform Definiions Funcion Spce funcion spce A funcion spce is liner spce of funcions defined on he sme domins & rnges. Liner Mpping liner mpping Le VF, WF e liner spces over he field F. A mpping
e t dt e t dt = lim e t dt T (1 e T ) = 1
 Improper Inegrls There re wo ypes of improper inegrls - hose wih infinie limis of inegrion, nd hose wih inegrnds h pproch some poin wihin he limis of inegrion. Firs we will consider inegrls wih infinie
Improper Inegrls There re wo ypes of improper inegrls - hose wih infinie limis of inegrion, nd hose wih inegrnds h pproch some poin wihin he limis of inegrion. Firs we will consider inegrls wih infinie
Mathematics 805 Final Examination Answers
 . 5 poins Se he Weiersrss M-es. Mhemics 85 Finl Eminion Answers Answer: Suppose h A R, nd f n : A R. Suppose furher h f n M n for ll A, nd h Mn converges. Then f n converges uniformly on A.. 5 poins Se
. 5 poins Se he Weiersrss M-es. Mhemics 85 Finl Eminion Answers Answer: Suppose h A R, nd f n : A R. Suppose furher h f n M n for ll A, nd h Mn converges. Then f n converges uniformly on A.. 5 poins Se
ENGR 1990 Engineering Mathematics The Integral of a Function as a Function
 ENGR 1990 Engineering Mhemics The Inegrl of Funcion s Funcion Previously, we lerned how o esime he inegrl of funcion f( ) over some inervl y dding he res of finie se of rpezoids h represen he re under
ENGR 1990 Engineering Mhemics The Inegrl of Funcion s Funcion Previously, we lerned how o esime he inegrl of funcion f( ) over some inervl y dding he res of finie se of rpezoids h represen he re under
EXISTENCE AND UNIQUENESS OF SOLUTIONS FOR A SECOND-ORDER ITERATIVE BOUNDARY-VALUE PROBLEM
 Elecronic Journl of Differenil Equions, Vol. 208 (208), No. 50, pp. 6. ISSN: 072-669. URL: hp://ejde.mh.xse.edu or hp://ejde.mh.un.edu EXISTENCE AND UNIQUENESS OF SOLUTIONS FOR A SECOND-ORDER ITERATIVE
Elecronic Journl of Differenil Equions, Vol. 208 (208), No. 50, pp. 6. ISSN: 072-669. URL: hp://ejde.mh.xse.edu or hp://ejde.mh.un.edu EXISTENCE AND UNIQUENESS OF SOLUTIONS FOR A SECOND-ORDER ITERATIVE
MTH 146 Class 11 Notes
 8.- Are of Surfce of Revoluion MTH 6 Clss Noes Suppose we wish o revolve curve C round n is nd find he surfce re of he resuling solid. Suppose f( ) is nonnegive funcion wih coninuous firs derivive on he
8.- Are of Surfce of Revoluion MTH 6 Clss Noes Suppose we wish o revolve curve C round n is nd find he surfce re of he resuling solid. Suppose f( ) is nonnegive funcion wih coninuous firs derivive on he
1.0 Electrical Systems
 . Elecricl Sysems The ypes of dynmicl sysems we will e sudying cn e modeled in erms of lgeric equions, differenil equions, or inegrl equions. We will egin y looking fmilir mhemicl models of idel resisors,
. Elecricl Sysems The ypes of dynmicl sysems we will e sudying cn e modeled in erms of lgeric equions, differenil equions, or inegrl equions. We will egin y looking fmilir mhemicl models of idel resisors,
4.8 Improper Integrals
 4.8 Improper Inegrls Well you ve mde i hrough ll he inegrion echniques. Congrs! Unforunely for us, we sill need o cover one more inegrl. They re clled Improper Inegrls. A his poin, we ve only del wih inegrls
4.8 Improper Inegrls Well you ve mde i hrough ll he inegrion echniques. Congrs! Unforunely for us, we sill need o cover one more inegrl. They re clled Improper Inegrls. A his poin, we ve only del wih inegrls
A LIMIT-POINT CRITERION FOR A SECOND-ORDER LINEAR DIFFERENTIAL OPERATOR IAN KNOWLES
 A LIMIT-POINT CRITERION FOR A SECOND-ORDER LINEAR DIFFERENTIAL OPERATOR j IAN KNOWLES 1. Inroducion Consider he forml differenil operor T defined by el, (1) where he funcion q{) is rel-vlued nd loclly
A LIMIT-POINT CRITERION FOR A SECOND-ORDER LINEAR DIFFERENTIAL OPERATOR j IAN KNOWLES 1. Inroducion Consider he forml differenil operor T defined by el, (1) where he funcion q{) is rel-vlued nd loclly
FURTHER GENERALIZATIONS. QI Feng. The value of the integral of f(x) over [a; b] can be estimated in a variety ofways. b a. 2(M m)
![FURTHER GENERALIZATIONS. QI Feng. The value of the integral of f(x) over [a; b] can be estimated in a variety ofways. b a. 2(M m) FURTHER GENERALIZATIONS. QI Feng. The value of the integral of f(x) over [a; b] can be estimated in a variety ofways. b a. 2(M m)](/thumbs/75/72845579.jpg) Univ. Beogrd. Pul. Elekroehn. Fk. Ser. M. 8 (997), 79{83 FUTHE GENEALIZATIONS OF INEQUALITIES FO AN INTEGAL QI Feng Using he Tylor's formul we prove wo inegrl inequliies, h generlize K. S. K. Iyengr's
Univ. Beogrd. Pul. Elekroehn. Fk. Ser. M. 8 (997), 79{83 FUTHE GENEALIZATIONS OF INEQUALITIES FO AN INTEGAL QI Feng Using he Tylor's formul we prove wo inegrl inequliies, h generlize K. S. K. Iyengr's
0 for t < 0 1 for t > 0
 8.0 Sep nd del funcions Auhor: Jeremy Orloff The uni Sep Funcion We define he uni sep funcion by u() = 0 for < 0 for > 0 I is clled he uni sep funcion becuse i kes uni sep = 0. I is someimes clled he Heviside
8.0 Sep nd del funcions Auhor: Jeremy Orloff The uni Sep Funcion We define he uni sep funcion by u() = 0 for < 0 for > 0 I is clled he uni sep funcion becuse i kes uni sep = 0. I is someimes clled he Heviside
Numerical Approximations to Fractional Problems of the Calculus of Variations and Optimal Control
 Numericl Approximions o Frcionl Problems of he Clculus of Vriions nd Opiml Conrol Shkoor Pooseh, Ricrdo Almeid, Delfim F. M. Torres To cie his version: Shkoor Pooseh, Ricrdo Almeid, Delfim F. M. Torres.
Numericl Approximions o Frcionl Problems of he Clculus of Vriions nd Opiml Conrol Shkoor Pooseh, Ricrdo Almeid, Delfim F. M. Torres To cie his version: Shkoor Pooseh, Ricrdo Almeid, Delfim F. M. Torres.
September 20 Homework Solutions
 College of Engineering nd Compuer Science Mechnicl Engineering Deprmen Mechnicl Engineering A Seminr in Engineering Anlysis Fll 7 Number 66 Insrucor: Lrry Creo Sepember Homework Soluions Find he specrum
College of Engineering nd Compuer Science Mechnicl Engineering Deprmen Mechnicl Engineering A Seminr in Engineering Anlysis Fll 7 Number 66 Insrucor: Lrry Creo Sepember Homework Soluions Find he specrum
5.1-The Initial-Value Problems For Ordinary Differential Equations
 5.-The Iniil-Vlue Problems For Ordinry Differenil Equions Consider solving iniil-vlue problems for ordinry differenil equions: (*) y f, y, b, y. If we know he generl soluion y of he ordinry differenil
5.-The Iniil-Vlue Problems For Ordinry Differenil Equions Consider solving iniil-vlue problems for ordinry differenil equions: (*) y f, y, b, y. If we know he generl soluion y of he ordinry differenil
( ) ( ) ( ) ( ) ( ) ( y )
 8. Lengh of Plne Curve The mos fmous heorem in ll of mhemics is he Pyhgoren Theorem. I s formulion s he disnce formul is used o find he lenghs of line segmens in he coordine plne. In his secion you ll
8. Lengh of Plne Curve The mos fmous heorem in ll of mhemics is he Pyhgoren Theorem. I s formulion s he disnce formul is used o find he lenghs of line segmens in he coordine plne. In his secion you ll
f t f a f x dx By Lin McMullin f x dx= f b f a. 2
 Accumulion: Thoughs On () By Lin McMullin f f f d = + The gols of he AP* Clculus progrm include he semen, Sudens should undersnd he definie inegrl s he ne ccumulion of chnge. 1 The Topicl Ouline includes
Accumulion: Thoughs On () By Lin McMullin f f f d = + The gols of he AP* Clculus progrm include he semen, Sudens should undersnd he definie inegrl s he ne ccumulion of chnge. 1 The Topicl Ouline includes
LAPLACE TRANSFORM OVERCOMING PRINCIPLE DRAWBACKS IN APPLICATION OF THE VARIATIONAL ITERATION METHOD TO FRACTIONAL HEAT EQUATIONS
 Wu, G.-.: Lplce Trnsform Overcoming Principle Drwbcks in Applicion... THERMAL SIENE: Yer 22, Vol. 6, No. 4, pp. 257-26 257 Open forum LAPLAE TRANSFORM OVEROMING PRINIPLE DRAWBAKS IN APPLIATION OF THE VARIATIONAL
Wu, G.-.: Lplce Trnsform Overcoming Principle Drwbcks in Applicion... THERMAL SIENE: Yer 22, Vol. 6, No. 4, pp. 257-26 257 Open forum LAPLAE TRANSFORM OVEROMING PRINIPLE DRAWBAKS IN APPLIATION OF THE VARIATIONAL
ON NEW INEQUALITIES OF SIMPSON S TYPE FOR FUNCTIONS WHOSE SECOND DERIVATIVES ABSOLUTE VALUES ARE CONVEX.
 ON NEW INEQUALITIES OF SIMPSON S TYPE FOR FUNCTIONS WHOSE SECOND DERIVATIVES ABSOLUTE VALUES ARE CONVEX. MEHMET ZEKI SARIKAYA?, ERHAN. SET, AND M. EMIN OZDEMIR Asrc. In his noe, we oin new some ineuliies
ON NEW INEQUALITIES OF SIMPSON S TYPE FOR FUNCTIONS WHOSE SECOND DERIVATIVES ABSOLUTE VALUES ARE CONVEX. MEHMET ZEKI SARIKAYA?, ERHAN. SET, AND M. EMIN OZDEMIR Asrc. In his noe, we oin new some ineuliies
3. Renewal Limit Theorems
 Virul Lborories > 14. Renewl Processes > 1 2 3 3. Renewl Limi Theorems In he inroducion o renewl processes, we noed h he rrivl ime process nd he couning process re inverses, in sens The rrivl ime process
Virul Lborories > 14. Renewl Processes > 1 2 3 3. Renewl Limi Theorems In he inroducion o renewl processes, we noed h he rrivl ime process nd he couning process re inverses, in sens The rrivl ime process
Analytic solution of linear fractional differential equation with Jumarie derivative in term of Mittag-Leffler function
 Anlyic soluion of liner frcionl differenil equion wih Jumrie derivive in erm of Mig-Leffler funcion Um Ghosh (), Srijn Sengup (2), Susmi Srkr (2b), Shnnu Ds (3) (): Deprmen of Mhemics, Nbdwip Vidysgr College,
Anlyic soluion of liner frcionl differenil equion wih Jumrie derivive in erm of Mig-Leffler funcion Um Ghosh (), Srijn Sengup (2), Susmi Srkr (2b), Shnnu Ds (3) (): Deprmen of Mhemics, Nbdwip Vidysgr College,
Hermite-Hadamard and Simpson Type Inequalities for Differentiable Quasi-Geometrically Convex Functions
 Trkish Jornl o Anlysis nd Nmer Theory, 4, Vol, No, 4-46 Aville online h://ssciecom/jn/// Science nd Edcion Plishing DOI:69/jn--- Hermie-Hdmrd nd Simson Tye Ineliies or Dierenile Qsi-Geomericlly Convex
Trkish Jornl o Anlysis nd Nmer Theory, 4, Vol, No, 4-46 Aville online h://ssciecom/jn/// Science nd Edcion Plishing DOI:69/jn--- Hermie-Hdmrd nd Simson Tye Ineliies or Dierenile Qsi-Geomericlly Convex
Some Inequalities variations on a common theme Lecture I, UL 2007
 Some Inequliies vriions on common heme Lecure I, UL 2007 Finbrr Hollnd, Deprmen of Mhemics, Universiy College Cork, fhollnd@uccie; July 2, 2007 Three Problems Problem Assume i, b i, c i, i =, 2, 3 re rel
Some Inequliies vriions on common heme Lecure I, UL 2007 Finbrr Hollnd, Deprmen of Mhemics, Universiy College Cork, fhollnd@uccie; July 2, 2007 Three Problems Problem Assume i, b i, c i, i =, 2, 3 re rel
FM Applications of Integration 1.Centroid of Area
 FM Applicions of Inegrion.Cenroid of Are The cenroid of ody is is geomeric cenre. For n ojec mde of uniform meril, he cenroid coincides wih he poin which he ody cn e suppored in perfecly lnced se ie, is
FM Applicions of Inegrion.Cenroid of Are The cenroid of ody is is geomeric cenre. For n ojec mde of uniform meril, he cenroid coincides wih he poin which he ody cn e suppored in perfecly lnced se ie, is
A new model for solving fuzzy linear fractional programming problem with ranking function
 J. ppl. Res. Ind. Eng. Vol. 4 No. 07 89 96 Journl of pplied Reserch on Indusril Engineering www.journl-prie.com new model for solving fuzzy liner frcionl progrmming prolem wih rning funcion Spn Kumr Ds
J. ppl. Res. Ind. Eng. Vol. 4 No. 07 89 96 Journl of pplied Reserch on Indusril Engineering www.journl-prie.com new model for solving fuzzy liner frcionl progrmming prolem wih rning funcion Spn Kumr Ds
2k 1. . And when n is odd number, ) The conclusion is when n is even number, an. ( 1) ( 2 1) ( k 0,1,2 L )
 Scholrs Journl of Engineering d Technology SJET) Sch. J. Eng. Tech., ; A):8-6 Scholrs Acdemic d Scienific Publisher An Inernionl Publisher for Acdemic d Scienific Resources) www.sspublisher.com ISSN -X
Scholrs Journl of Engineering d Technology SJET) Sch. J. Eng. Tech., ; A):8-6 Scholrs Acdemic d Scienific Publisher An Inernionl Publisher for Acdemic d Scienific Resources) www.sspublisher.com ISSN -X
GENERALIZATION OF SOME INEQUALITIES VIA RIEMANN-LIOUVILLE FRACTIONAL CALCULUS
 - TAMKANG JOURNAL OF MATHEMATICS Volume 5, Number, 7-5, June doi:5556/jkjm555 Avilble online hp://journlsmhkueduw/ - - - GENERALIZATION OF SOME INEQUALITIES VIA RIEMANN-LIOUVILLE FRACTIONAL CALCULUS MARCELA
- TAMKANG JOURNAL OF MATHEMATICS Volume 5, Number, 7-5, June doi:5556/jkjm555 Avilble online hp://journlsmhkueduw/ - - - GENERALIZATION OF SOME INEQUALITIES VIA RIEMANN-LIOUVILLE FRACTIONAL CALCULUS MARCELA
C 0 Approximation on the Spatially Homogeneous Boltzmann Equation for Maxwellian Molecules*
 Alied Mhemics,,, 54-59 doi:.46/m..666 Published Online December (h://www.scip.org/journl/m) C Aroximion on he Silly Homogeneous Bolzmnn Equion or Mxwellin Molecules Absrc Minling Zheng School o Science,
Alied Mhemics,,, 54-59 doi:.46/m..666 Published Online December (h://www.scip.org/journl/m) C Aroximion on he Silly Homogeneous Bolzmnn Equion or Mxwellin Molecules Absrc Minling Zheng School o Science,
Convergence of Singular Integral Operators in Weighted Lebesgue Spaces
 EUROPEAN JOURNAL OF PURE AND APPLIED MATHEMATICS Vol. 10, No. 2, 2017, 335-347 ISSN 1307-5543 www.ejpm.com Published by New York Business Globl Convergence of Singulr Inegrl Operors in Weighed Lebesgue
EUROPEAN JOURNAL OF PURE AND APPLIED MATHEMATICS Vol. 10, No. 2, 2017, 335-347 ISSN 1307-5543 www.ejpm.com Published by New York Business Globl Convergence of Singulr Inegrl Operors in Weighed Lebesgue
Motion. Part 2: Constant Acceleration. Acceleration. October Lab Physics. Ms. Levine 1. Acceleration. Acceleration. Units for Acceleration.
 Moion Accelerion Pr : Consn Accelerion Accelerion Accelerion Accelerion is he re of chnge of velociy. = v - vo = Δv Δ ccelerion = = v - vo chnge of velociy elpsed ime Accelerion is vecor, lhough in one-dimensionl
Moion Accelerion Pr : Consn Accelerion Accelerion Accelerion Accelerion is he re of chnge of velociy. = v - vo = Δv Δ ccelerion = = v - vo chnge of velociy elpsed ime Accelerion is vecor, lhough in one-dimensionl
A Kalman filtering simulation
 A Klmn filering simulion The performnce of Klmn filering hs been esed on he bsis of wo differen dynmicl models, ssuming eiher moion wih consn elociy or wih consn ccelerion. The former is epeced o beer
A Klmn filering simulion The performnce of Klmn filering hs been esed on he bsis of wo differen dynmicl models, ssuming eiher moion wih consn elociy or wih consn ccelerion. The former is epeced o beer
Solutions for Nonlinear Partial Differential Equations By Tan-Cot Method
 IOSR Journl of Mhemics (IOSR-JM) e-issn: 78-578. Volume 5, Issue 3 (Jn. - Feb. 13), PP 6-11 Soluions for Nonliner Pril Differenil Equions By Tn-Co Mehod Mhmood Jwd Abdul Rsool Abu Al-Sheer Al -Rfidin Universiy
IOSR Journl of Mhemics (IOSR-JM) e-issn: 78-578. Volume 5, Issue 3 (Jn. - Feb. 13), PP 6-11 Soluions for Nonliner Pril Differenil Equions By Tn-Co Mehod Mhmood Jwd Abdul Rsool Abu Al-Sheer Al -Rfidin Universiy
22.615, MHD Theory of Fusion Systems Prof. Freidberg Lecture 10: The High Beta Tokamak Con d and the High Flux Conserving Tokamak.
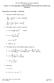 .615, MHD Theory of Fusion Sysems Prof. Freidberg Lecure 1: The High Be Tokmk Con d nd he High Flux Conserving Tokmk Proeries of he High Tokmk 1. Evlue he MHD sfey fcor: ψ B * ( ) 1 3 ρ 1+ ν ρ ρ cosθ *
.615, MHD Theory of Fusion Sysems Prof. Freidberg Lecure 1: The High Be Tokmk Con d nd he High Flux Conserving Tokmk Proeries of he High Tokmk 1. Evlue he MHD sfey fcor: ψ B * ( ) 1 3 ρ 1+ ν ρ ρ cosθ *
Fractional Calculus. Connor Wiegand. 6 th June 2017
 Frcionl Clculus Connor Wiegnd 6 h June 217 Absrc This pper ims o give he reder comforble inroducion o Frcionl Clculus. Frcionl Derivives nd Inegrls re defined in muliple wys nd hen conneced o ech oher
Frcionl Clculus Connor Wiegnd 6 h June 217 Absrc This pper ims o give he reder comforble inroducion o Frcionl Clculus. Frcionl Derivives nd Inegrls re defined in muliple wys nd hen conneced o ech oher
Honours Introductory Maths Course 2011 Integration, Differential and Difference Equations
 Honours Inroducory Mhs Course 0 Inegrion, Differenil nd Difference Equions Reding: Ching Chper 4 Noe: These noes do no fully cover he meril in Ching, u re men o supplemen your reding in Ching. Thus fr
Honours Inroducory Mhs Course 0 Inegrion, Differenil nd Difference Equions Reding: Ching Chper 4 Noe: These noes do no fully cover he meril in Ching, u re men o supplemen your reding in Ching. Thus fr
New Inequalities in Fractional Integrals
 ISSN 1749-3889 (prin), 1749-3897 (online) Inernionl Journl of Nonliner Science Vol.9(21) No.4,pp.493-497 New Inequliies in Frcionl Inegrls Zoubir Dhmni Zoubir DAHMANI Lborory of Pure nd Applied Mhemics,
ISSN 1749-3889 (prin), 1749-3897 (online) Inernionl Journl of Nonliner Science Vol.9(21) No.4,pp.493-497 New Inequliies in Frcionl Inegrls Zoubir Dhmni Zoubir DAHMANI Lborory of Pure nd Applied Mhemics,
RESPONSE UNDER A GENERAL PERIODIC FORCE. When the external force F(t) is periodic with periodτ = 2π
 RESPONSE UNDER A GENERAL PERIODIC FORCE When he exernl force F() is periodic wih periodτ / ω,i cn be expnded in Fourier series F( ) o α ω α b ω () where τ F( ) ω d, τ,,,... () nd b τ F( ) ω d, τ,,... (3)
RESPONSE UNDER A GENERAL PERIODIC FORCE When he exernl force F() is periodic wih periodτ / ω,i cn be expnded in Fourier series F( ) o α ω α b ω () where τ F( ) ω d, τ,,,... () nd b τ F( ) ω d, τ,,... (3)
Fuji Power MOSFET Power calculation method
 Fuji Power MOSFE Power clculi mehod Design ool Cher. Overview is necessry o check wheher he ower loss hs no exceeded he Asolue Mximum Rings for using MOSFE. Since he MOSFE loss cnno e mesured using ower
Fuji Power MOSFE Power clculi mehod Design ool Cher. Overview is necessry o check wheher he ower loss hs no exceeded he Asolue Mximum Rings for using MOSFE. Since he MOSFE loss cnno e mesured using ower
Abstract. W.W. Memudu 1 and O.A. Taiwo, 2
 Theoreicl Mhemics & Applicions, vol. 6, no., 06, 3-50 ISS: 79-9687 prin, 79-9709 online Scienpress d, 06 Eponenilly fied collocion pproimion mehod for he numericl soluions of Higher Order iner Fredholm
Theoreicl Mhemics & Applicions, vol. 6, no., 06, 3-50 ISS: 79-9687 prin, 79-9709 online Scienpress d, 06 Eponenilly fied collocion pproimion mehod for he numericl soluions of Higher Order iner Fredholm
INTEGRALS. Exercise 1. Let f : [a, b] R be bounded, and let P and Q be partitions of [a, b]. Prove that if P Q then U(P ) U(Q) and L(P ) L(Q).
![INTEGRALS. Exercise 1. Let f : [a, b] R be bounded, and let P and Q be partitions of [a, b]. Prove that if P Q then U(P ) U(Q) and L(P ) L(Q). INTEGRALS. Exercise 1. Let f : [a, b] R be bounded, and let P and Q be partitions of [a, b]. Prove that if P Q then U(P ) U(Q) and L(P ) L(Q).](/thumbs/78/77677920.jpg) INTEGRALS JOHN QUIGG Eercise. Le f : [, b] R be bounded, nd le P nd Q be priions of [, b]. Prove h if P Q hen U(P ) U(Q) nd L(P ) L(Q). Soluion: Le P = {,..., n }. Since Q is obined from P by dding finiely
INTEGRALS JOHN QUIGG Eercise. Le f : [, b] R be bounded, nd le P nd Q be priions of [, b]. Prove h if P Q hen U(P ) U(Q) nd L(P ) L(Q). Soluion: Le P = {,..., n }. Since Q is obined from P by dding finiely
Research Article New General Integral Inequalities for Lipschitzian Functions via Hadamard Fractional Integrals
 Hindwi Pulishing orporion Inernionl Journl of Anlysis, Aricle ID 35394, 8 pges hp://d.doi.org/0.55/04/35394 Reserch Aricle New Generl Inegrl Inequliies for Lipschizin Funcions vi Hdmrd Frcionl Inegrls
Hindwi Pulishing orporion Inernionl Journl of Anlysis, Aricle ID 35394, 8 pges hp://d.doi.org/0.55/04/35394 Reserch Aricle New Generl Inegrl Inequliies for Lipschizin Funcions vi Hdmrd Frcionl Inegrls
Green s Functions and Comparison Theorems for Differential Equations on Measure Chains
 Green s Funcions nd Comprison Theorems for Differenil Equions on Mesure Chins Lynn Erbe nd Alln Peerson Deprmen of Mhemics nd Sisics, Universiy of Nebrsk-Lincoln Lincoln,NE 68588-0323 lerbe@@mh.unl.edu
Green s Funcions nd Comprison Theorems for Differenil Equions on Mesure Chins Lynn Erbe nd Alln Peerson Deprmen of Mhemics nd Sisics, Universiy of Nebrsk-Lincoln Lincoln,NE 68588-0323 lerbe@@mh.unl.edu
ON THE OSTROWSKI-GRÜSS TYPE INEQUALITY FOR TWICE DIFFERENTIABLE FUNCTIONS
 Hceepe Journl of Mhemics nd Sisics Volume 45) 0), 65 655 ON THE OSTROWSKI-GRÜSS TYPE INEQUALITY FOR TWICE DIFFERENTIABLE FUNCTIONS M Emin Özdemir, Ahme Ock Akdemir nd Erhn Se Received 6:06:0 : Acceped
Hceepe Journl of Mhemics nd Sisics Volume 45) 0), 65 655 ON THE OSTROWSKI-GRÜSS TYPE INEQUALITY FOR TWICE DIFFERENTIABLE FUNCTIONS M Emin Özdemir, Ahme Ock Akdemir nd Erhn Se Received 6:06:0 : Acceped
Analytical Solution of Time-Fractional Advection Dispersion Equation
 Aville h://vu.edu/ Al. Al. Mh. ISSN: 93-9466 Vol. 4 Iue (June 9). 76 88 (Previoul Vol. 4 No. ) Alicion nd Alied Mheic: An Inernionl Journl (AAM) Anlicl Soluion of Tie-Frcionl Advecion Dierion Equion Triq
Aville h://vu.edu/ Al. Al. Mh. ISSN: 93-9466 Vol. 4 Iue (June 9). 76 88 (Previoul Vol. 4 No. ) Alicion nd Alied Mheic: An Inernionl Journl (AAM) Anlicl Soluion of Tie-Frcionl Advecion Dierion Equion Triq
Chapter 2. First Order Scalar Equations
 Chaper. Firs Order Scalar Equaions We sar our sudy of differenial equaions in he same way he pioneers in his field did. We show paricular echniques o solve paricular ypes of firs order differenial equaions.
Chaper. Firs Order Scalar Equaions We sar our sudy of differenial equaions in he same way he pioneers in his field did. We show paricular echniques o solve paricular ypes of firs order differenial equaions.
NEW FRACTIONAL DERIVATIVES WITH NON-LOCAL AND NON-SINGULAR KERNEL Theory and Application to Heat Transfer Model
 Angn, A., e l.: New Frcionl Derivives wih Non-Locl nd THERMAL SCIENCE, Yer 216, Vol. 2, No. 2, pp. 763-769 763 NEW FRACTIONAL DERIVATIVES WITH NON-LOCAL AND NON-SINGULAR KERNEL Theory nd Applicion o He
Angn, A., e l.: New Frcionl Derivives wih Non-Locl nd THERMAL SCIENCE, Yer 216, Vol. 2, No. 2, pp. 763-769 763 NEW FRACTIONAL DERIVATIVES WITH NON-LOCAL AND NON-SINGULAR KERNEL Theory nd Applicion o He
1. Introduction. 1 b b
 Journl of Mhemicl Inequliies Volume, Number 3 (007), 45 436 SOME IMPROVEMENTS OF GRÜSS TYPE INEQUALITY N. ELEZOVIĆ, LJ. MARANGUNIĆ AND J. PEČARIĆ (communiced b A. Čižmešij) Absrc. In his pper some inequliies
Journl of Mhemicl Inequliies Volume, Number 3 (007), 45 436 SOME IMPROVEMENTS OF GRÜSS TYPE INEQUALITY N. ELEZOVIĆ, LJ. MARANGUNIĆ AND J. PEČARIĆ (communiced b A. Čižmešij) Absrc. In his pper some inequliies
Boundary layer problem for system of first order of ordinary differential equations with linear non-local boundary conditions
 IJS 3 37A3 Secil issue-mheics: 389-396 Irnin Journl of Science & echnology h://ijssshirzucir Boundry lyer role for syse of firs order of ordinry differenil euions wih liner non-locl oundry condiions M
IJS 3 37A3 Secil issue-mheics: 389-396 Irnin Journl of Science & echnology h://ijssshirzucir Boundry lyer role for syse of firs order of ordinry differenil euions wih liner non-locl oundry condiions M
Procedia Computer Science
 Procedi Compuer Science 00 (0) 000 000 Procedi Compuer Science www.elsevier.com/loce/procedi The Third Informion Sysems Inernionl Conference The Exisence of Polynomil Soluion of he Nonliner Dynmicl Sysems
Procedi Compuer Science 00 (0) 000 000 Procedi Compuer Science www.elsevier.com/loce/procedi The Third Informion Sysems Inernionl Conference The Exisence of Polynomil Soluion of he Nonliner Dynmicl Sysems
Calculus of variations with fractional derivatives and fractional integrals
 Anis do CNMAC v.2 ISSN 1984-820X Clculus of vritions with frctionl derivtives nd frctionl integrls Ricrdo Almeid, Delfim F. M. Torres Deprtment of Mthemtics, University of Aveiro 3810-193 Aveiro, Portugl
Anis do CNMAC v.2 ISSN 1984-820X Clculus of vritions with frctionl derivtives nd frctionl integrls Ricrdo Almeid, Delfim F. M. Torres Deprtment of Mthemtics, University of Aveiro 3810-193 Aveiro, Portugl
Solutions to Problems from Chapter 2
 Soluions o Problems rom Chper Problem. The signls u() :5sgn(), u () :5sgn(), nd u h () :5sgn() re ploed respecively in Figures.,b,c. Noe h u h () :5sgn() :5; 8 including, bu u () :5sgn() is undeined..5
Soluions o Problems rom Chper Problem. The signls u() :5sgn(), u () :5sgn(), nd u h () :5sgn() re ploed respecively in Figures.,b,c. Noe h u h () :5sgn() :5; 8 including, bu u () :5sgn() is undeined..5
FRACTIONAL-order differential equations (FDEs) are
 Proceedings of he Inernionl MuliConference of Engineers nd Compuer Scieniss 218 Vol I IMECS 218 Mrch 14-16 218 Hong Kong Comprison of Anlyicl nd Numericl Soluions of Frcionl-Order Bloch Equions using Relible
Proceedings of he Inernionl MuliConference of Engineers nd Compuer Scieniss 218 Vol I IMECS 218 Mrch 14-16 218 Hong Kong Comprison of Anlyicl nd Numericl Soluions of Frcionl-Order Bloch Equions using Relible
(9) P (x)u + Q(x)u + R(x)u =0
 STURM-LIOUVILLE THEORY 7 2. Second order liner ordinry differentil equtions 2.1. Recll some sic results. A second order liner ordinry differentil eqution (ODE) hs the form (9) P (x)u + Q(x)u + R(x)u =0
STURM-LIOUVILLE THEORY 7 2. Second order liner ordinry differentil equtions 2.1. Recll some sic results. A second order liner ordinry differentil eqution (ODE) hs the form (9) P (x)u + Q(x)u + R(x)u =0
Research Article Generalized Fractional Integral Inequalities for Continuous Random Variables
 Journl of Proiliy nd Sisics Volume 2015, Aricle ID 958980, 7 pges hp://dx.doi.org/10.1155/2015/958980 Reserch Aricle Generlized Frcionl Inegrl Inequliies for Coninuous Rndom Vriles Adullh Akkur, Zeynep
Journl of Proiliy nd Sisics Volume 2015, Aricle ID 958980, 7 pges hp://dx.doi.org/10.1155/2015/958980 Reserch Aricle Generlized Frcionl Inegrl Inequliies for Coninuous Rndom Vriles Adullh Akkur, Zeynep
Solutions of half-linear differential equations in the classes Gamma and Pi
 Soluions of hlf-liner differenil equions in he clsses Gmm nd Pi Pvel Řehák Insiue of Mhemics, Acdemy of Sciences CR CZ-6662 Brno, Czech Reublic; Fculy of Educion, Msryk Universiy CZ-60300 Brno, Czech Reublic
Soluions of hlf-liner differenil equions in he clsses Gmm nd Pi Pvel Řehák Insiue of Mhemics, Acdemy of Sciences CR CZ-6662 Brno, Czech Reublic; Fculy of Educion, Msryk Universiy CZ-60300 Brno, Czech Reublic
ECE Microwave Engineering. Fall Prof. David R. Jackson Dept. of ECE. Notes 10. Waveguides Part 7: Transverse Equivalent Network (TEN)
 EE 537-635 Microwve Engineering Fll 7 Prof. Dvid R. Jcson Dep. of EE Noes Wveguides Pr 7: Trnsverse Equivlen Newor (N) Wveguide Trnsmission Line Model Our gol is o come up wih rnsmission line model for
EE 537-635 Microwve Engineering Fll 7 Prof. Dvid R. Jcson Dep. of EE Noes Wveguides Pr 7: Trnsverse Equivlen Newor (N) Wveguide Trnsmission Line Model Our gol is o come up wih rnsmission line model for
Properties of Logarithms. Solving Exponential and Logarithmic Equations. Properties of Logarithms. Properties of Logarithms. ( x)
 Properies of Logrihms Solving Eponenil nd Logrihmic Equions Properies of Logrihms Produc Rule ( ) log mn = log m + log n ( ) log = log + log Properies of Logrihms Quoien Rule log m = logm logn n log7 =
Properies of Logrihms Solving Eponenil nd Logrihmic Equions Properies of Logrihms Produc Rule ( ) log mn = log m + log n ( ) log = log + log Properies of Logrihms Quoien Rule log m = logm logn n log7 =
On the Pseudo-Spectral Method of Solving Linear Ordinary Differential Equations
 Journl of Mhemics nd Sisics 5 ():136-14, 9 ISS 1549-3644 9 Science Publicions On he Pseudo-Specrl Mehod of Solving Liner Ordinry Differenil Equions B.S. Ogundre Deprmen of Pure nd Applied Mhemics, Universiy
Journl of Mhemics nd Sisics 5 ():136-14, 9 ISS 1549-3644 9 Science Publicions On he Pseudo-Specrl Mehod of Solving Liner Ordinry Differenil Equions B.S. Ogundre Deprmen of Pure nd Applied Mhemics, Universiy
LAPLACE TRANSFORMS. 1. Basic transforms
 LAPLACE TRANSFORMS. Bic rnform In hi coure, Lplce Trnform will be inroduced nd heir properie exmined; ble of common rnform will be buil up; nd rnform will be ued o olve ome dierenil equion by rnforming
LAPLACE TRANSFORMS. Bic rnform In hi coure, Lplce Trnform will be inroduced nd heir properie exmined; ble of common rnform will be buil up; nd rnform will be ued o olve ome dierenil equion by rnforming
Average & instantaneous velocity and acceleration Motion with constant acceleration
 Physics 7: Lecure Reminders Discussion nd Lb secions sr meeing ne week Fill ou Pink dd/drop form if you need o swich o differen secion h is FULL. Do i TODAY. Homework Ch. : 5, 7,, 3,, nd 6 Ch.: 6,, 3 Submission
Physics 7: Lecure Reminders Discussion nd Lb secions sr meeing ne week Fill ou Pink dd/drop form if you need o swich o differen secion h is FULL. Do i TODAY. Homework Ch. : 5, 7,, 3,, nd 6 Ch.: 6,, 3 Submission
ON NEW INEQUALITIES OF SIMPSON S TYPE FOR FUNCTIONS WHOSE SECOND DERIVATIVES ABSOLUTE VALUES ARE CONVEX
 Journl of Applied Mhemics, Sisics nd Informics JAMSI), 9 ), No. ON NEW INEQUALITIES OF SIMPSON S TYPE FOR FUNCTIONS WHOSE SECOND DERIVATIVES ABSOLUTE VALUES ARE CONVEX MEHMET ZEKI SARIKAYA, ERHAN. SET
Journl of Applied Mhemics, Sisics nd Informics JAMSI), 9 ), No. ON NEW INEQUALITIES OF SIMPSON S TYPE FOR FUNCTIONS WHOSE SECOND DERIVATIVES ABSOLUTE VALUES ARE CONVEX MEHMET ZEKI SARIKAYA, ERHAN. SET
REAL ANALYSIS I HOMEWORK 3. Chapter 1
 REAL ANALYSIS I HOMEWORK 3 CİHAN BAHRAN The quesions re from Sein nd Shkrchi s e. Chper 1 18. Prove he following sserion: Every mesurble funcion is he limi.e. of sequence of coninuous funcions. We firs
REAL ANALYSIS I HOMEWORK 3 CİHAN BAHRAN The quesions re from Sein nd Shkrchi s e. Chper 1 18. Prove he following sserion: Every mesurble funcion is he limi.e. of sequence of coninuous funcions. We firs
Anatoly A. Kilbas. tn 1. t 1 a. dt 2. a t. log x
 J. Koren Mh. So. 38 200) No. 6. 9 204 HADAMARD-TYPE FRACTIONAL CALCULUS Anoly A. Kilbs Absr. The er is devoed o he sudy of frionl inegrion nd differeniion on finie inervl [ b] of he rel xis in he frme
J. Koren Mh. So. 38 200) No. 6. 9 204 HADAMARD-TYPE FRACTIONAL CALCULUS Anoly A. Kilbs Absr. The er is devoed o he sudy of frionl inegrion nd differeniion on finie inervl [ b] of he rel xis in he frme
Exponential Decay for Nonlinear Damped Equation of Suspended String
 9 Inernionl Symoium on Comuing, Communicion, nd Conrol (ISCCC 9) Proc of CSIT vol () () IACSIT Pre, Singore Eonenil Decy for Nonliner Dmed Equion of Suended Sring Jiong Kemuwn Dermen of Mhemic, Fculy of
9 Inernionl Symoium on Comuing, Communicion, nd Conrol (ISCCC 9) Proc of CSIT vol () () IACSIT Pre, Singore Eonenil Decy for Nonliner Dmed Equion of Suended Sring Jiong Kemuwn Dermen of Mhemic, Fculy of
Power Transformations and Unit Mean and Constant Variance Assumptions of the Multiplicative Error Model: The Generalized Gamma Distribution
 Briish Journl of Mhemics & Comuer Science (): 88-06, 0 SCIENCEDOMAIN inernionl www.sciencedomin.org Power Trnsformions nd Uni Men nd Consn Vrince Assumions of he Mulilicive Error Model: The Generlized
Briish Journl of Mhemics & Comuer Science (): 88-06, 0 SCIENCEDOMAIN inernionl www.sciencedomin.org Power Trnsformions nd Uni Men nd Consn Vrince Assumions of he Mulilicive Error Model: The Generlized
FRACTIONAL EULER-LAGRANGE EQUATION OF CALDIROLA-KANAI OSCILLATOR
 Romnin Repors in Physics, Vol. 64, Supplemen, P. 7 77, Dediced o Professor Ion-Ioviz Popescu s 8 h Anniversry FRACTIONAL EULER-LAGRANGE EQUATION OF CALDIROLA-KANAI OSCILLATOR D. BALEANU,,3, J. H. ASAD
Romnin Repors in Physics, Vol. 64, Supplemen, P. 7 77, Dediced o Professor Ion-Ioviz Popescu s 8 h Anniversry FRACTIONAL EULER-LAGRANGE EQUATION OF CALDIROLA-KANAI OSCILLATOR D. BALEANU,,3, J. H. ASAD
Some basic notation and terminology. Deterministic Finite Automata. COMP218: Decision, Computation and Language Note 1
 COMP28: Decision, Compuion nd Lnguge Noe These noes re inended minly s supplemen o he lecures nd exooks; hey will e useful for reminders ou noion nd erminology. Some sic noion nd erminology An lphe is
COMP28: Decision, Compuion nd Lnguge Noe These noes re inended minly s supplemen o he lecures nd exooks; hey will e useful for reminders ou noion nd erminology. Some sic noion nd erminology An lphe is
GENERALIZED OSTROWSKI TYPE INEQUALITIES FOR FUNCTIONS WHOSE LOCAL FRACTIONAL DERIVATIVES ARE GENERALIZED s-convex IN THE SECOND SENSE
 Journl of Alied Mthemtics nd Comuttionl Mechnics 6, 5(4), - wwwmcmczl -ISSN 99-9965 DOI: 75/jmcm64 e-issn 353-588 GENERALIZED OSTROWSKI TYPE INEQUALITIES FOR FUNCTIONS WHOSE LOCAL FRACTIONAL DERIVATIVES
Journl of Alied Mthemtics nd Comuttionl Mechnics 6, 5(4), - wwwmcmczl -ISSN 99-9965 DOI: 75/jmcm64 e-issn 353-588 GENERALIZED OSTROWSKI TYPE INEQUALITIES FOR FUNCTIONS WHOSE LOCAL FRACTIONAL DERIVATIVES
CALDERON S REPRODUCING FORMULA FOR DUNKL CONVOLUTION
 Avilble online hp://scik.org Eng. Mh. Le. 15, 15:4 ISSN: 49-9337 CALDERON S REPRODUCING FORMULA FOR DUNKL CONVOLUTION PANDEY, C. P. 1, RAKESH MOHAN AND BHAIRAW NATH TRIPATHI 3 1 Deprmen o Mhemics, Ajy
Avilble online hp://scik.org Eng. Mh. Le. 15, 15:4 ISSN: 49-9337 CALDERON S REPRODUCING FORMULA FOR DUNKL CONVOLUTION PANDEY, C. P. 1, RAKESH MOHAN AND BHAIRAW NATH TRIPATHI 3 1 Deprmen o Mhemics, Ajy
Weighted Hardy-Type Inequalities on Time Scales with Applications
 Medierr J Mh DOI 0007/s00009-04-054-y c Sringer Bsel 204 Weighed Hrdy-Tye Ineuliies on Time Scles wih Alicions S H Sker, R R Mhmoud nd A Peerson Absrc In his er, we will rove some new dynmic Hrdy-ye ineuliies
Medierr J Mh DOI 0007/s00009-04-054-y c Sringer Bsel 204 Weighed Hrdy-Tye Ineuliies on Time Scles wih Alicions S H Sker, R R Mhmoud nd A Peerson Absrc In his er, we will rove some new dynmic Hrdy-ye ineuliies
M r. d 2. R t a M. Structural Mechanics Section. Exam CT5141 Theory of Elasticity Friday 31 October 2003, 9:00 12:00 hours. Problem 1 (3 points)
 Delf Universiy of Technology Fculy of Civil Engineering nd Geosciences Srucurl echnics Secion Wrie your nme nd sudy numer he op righ-hnd of your work. Exm CT5 Theory of Elsiciy Fridy Ocoer 00, 9:00 :00
Delf Universiy of Technology Fculy of Civil Engineering nd Geosciences Srucurl echnics Secion Wrie your nme nd sudy numer he op righ-hnd of your work. Exm CT5 Theory of Elsiciy Fridy Ocoer 00, 9:00 :00
22.615, MHD Theory of Fusion Systems Prof. Freidberg Lecture 9: The High Beta Tokamak
 .65, MHD Theory of Fusion Sysems Prof. Freidberg Lecure 9: The High e Tokmk Summry of he Properies of n Ohmic Tokmk. Advnges:. good euilibrium (smll shif) b. good sbiliy ( ) c. good confinemen ( τ nr )
.65, MHD Theory of Fusion Sysems Prof. Freidberg Lecure 9: The High e Tokmk Summry of he Properies of n Ohmic Tokmk. Advnges:. good euilibrium (smll shif) b. good sbiliy ( ) c. good confinemen ( τ nr )
Fractional operators with exponential kernels and a Lyapunov type inequality
 Abdeljwd Advnces in Difference Equions (2017) 2017:313 DOI 10.1186/s13662-017-1285-0 RESEARCH Open Access Frcionl operors wih exponenil kernels nd Lypunov ype inequliy Thbe Abdeljwd* * Correspondence: bdeljwd@psu.edu.s
Abdeljwd Advnces in Difference Equions (2017) 2017:313 DOI 10.1186/s13662-017-1285-0 RESEARCH Open Access Frcionl operors wih exponenil kernels nd Lypunov ype inequliy Thbe Abdeljwd* * Correspondence: bdeljwd@psu.edu.s
P441 Analytical Mechanics - I. Coupled Oscillators. c Alex R. Dzierba
 Lecure 3 Mondy - Deceber 5, 005 Wrien or ls upded: Deceber 3, 005 P44 Anlyicl Mechnics - I oupled Oscillors c Alex R. Dzierb oupled oscillors - rix echnique In Figure we show n exple of wo coupled oscillors,
Lecure 3 Mondy - Deceber 5, 005 Wrien or ls upded: Deceber 3, 005 P44 Anlyicl Mechnics - I oupled Oscillors c Alex R. Dzierb oupled oscillors - rix echnique In Figure we show n exple of wo coupled oscillors,
Hadamard-Type Inequalities for s Convex Functions I
 Punjb University Journl of Mthemtics ISSN 6-56) Vol. ). 5-6 Hdmrd-Tye Ineulities for s Convex Functions I S. Hussin Dertment of Mthemtics Institute Of Sce Technology, Ner Rwt Toll Plz Islmbd Highwy, Islmbd
Punjb University Journl of Mthemtics ISSN 6-56) Vol. ). 5-6 Hdmrd-Tye Ineulities for s Convex Functions I S. Hussin Dertment of Mthemtics Institute Of Sce Technology, Ner Rwt Toll Plz Islmbd Highwy, Islmbd
3 Motion with constant acceleration: Linear and projectile motion
 3 Moion wih consn ccelerion: Liner nd projecile moion cons, In he precedin Lecure we he considered moion wih consn ccelerion lon he is: Noe h,, cn be posiie nd neie h leds o rie of behiors. Clerl similr
3 Moion wih consn ccelerion: Liner nd projecile moion cons, In he precedin Lecure we he considered moion wih consn ccelerion lon he is: Noe h,, cn be posiie nd neie h leds o rie of behiors. Clerl similr
Improved Approximate Solutions for Nonlinear Evolutions Equations in Mathematical Physics Using the Reduced Differential Transform Method
 Journal of Applied Mahemaics & Bioinformaics, vol., no., 01, 1-14 ISSN: 179-660 (prin), 179-699 (online) Scienpress Ld, 01 Improved Approimae Soluions for Nonlinear Evoluions Equaions in Mahemaical Physics
Journal of Applied Mahemaics & Bioinformaics, vol., no., 01, 1-14 ISSN: 179-660 (prin), 179-699 (online) Scienpress Ld, 01 Improved Approimae Soluions for Nonlinear Evoluions Equaions in Mahemaical Physics
Characteristic Function for the Truncated Triangular Distribution., Myron Katzoff and Rahul A. Parsa
 Secion on Survey Reserch Mehos JSM 009 Chrcerisic Funcion for he Trunce Tringulr Disriuion Jy J. Kim 1 1, Myron Kzoff n Rhul A. Prs 1 Nionl Cener for Helh Sisics, 11Toleo Ro, Hysville, MD. 078 College
Secion on Survey Reserch Mehos JSM 009 Chrcerisic Funcion for he Trunce Tringulr Disriuion Jy J. Kim 1 1, Myron Kzoff n Rhul A. Prs 1 Nionl Cener for Helh Sisics, 11Toleo Ro, Hysville, MD. 078 College
Inventory Management Models with Variable Holding Cost and Salvage value
 OSR Journl of Business nd Mngemen OSR-JBM e-ssn: -X p-ssn: 9-. Volume ssue Jul. - Aug. PP - www.iosrjournls.org nvenory Mngemen Models wi Vrile Holding os nd Slvge vlue R.Mon R.Venkeswrlu Memics Dep ollege
OSR Journl of Business nd Mngemen OSR-JBM e-ssn: -X p-ssn: 9-. Volume ssue Jul. - Aug. PP - www.iosrjournls.org nvenory Mngemen Models wi Vrile Holding os nd Slvge vlue R.Mon R.Venkeswrlu Memics Dep ollege
Solution of Integro-Differential Equations by Using ELzaki Transform
 Global Journal of Mahemaical Sciences: Theory and Pracical. Volume, Number (), pp. - Inernaional Research Publicaion House hp://www.irphouse.com Soluion of Inegro-Differenial Equaions by Using ELzaki Transform
Global Journal of Mahemaical Sciences: Theory and Pracical. Volume, Number (), pp. - Inernaional Research Publicaion House hp://www.irphouse.com Soluion of Inegro-Differenial Equaions by Using ELzaki Transform
Application on Inner Product Space with. Fixed Point Theorem in Probabilistic
 Journl of Applied Mhemics & Bioinformics, vol.2, no.2, 2012, 1-10 ISSN: 1792-6602 prin, 1792-6939 online Scienpress Ld, 2012 Applicion on Inner Produc Spce wih Fixed Poin Theorem in Probbilisic Rjesh Shrivsv
Journl of Applied Mhemics & Bioinformics, vol.2, no.2, 2012, 1-10 ISSN: 1792-6602 prin, 1792-6939 online Scienpress Ld, 2012 Applicion on Inner Produc Spce wih Fixed Poin Theorem in Probbilisic Rjesh Shrivsv
LAGRANGIAN AND HAMILTONIAN MECHANICS WITH FRACTIONAL DERIVATIVES
 LAGRANGIAN AND HAMILTONIAN MEHANIS WITH FRATIONAL DERIVATIVES EMIL POPESU 2,1 1 Asronomicl Insiue of Romnin Acdemy Sr uiul de Argin 5, 40557 Buchres, Romni 2 Technicl Universiy of ivil Engineering, Bd
LAGRANGIAN AND HAMILTONIAN MEHANIS WITH FRATIONAL DERIVATIVES EMIL POPESU 2,1 1 Asronomicl Insiue of Romnin Acdemy Sr uiul de Argin 5, 40557 Buchres, Romni 2 Technicl Universiy of ivil Engineering, Bd
Minimum Squared Error
 Minimum Squred Error LDF: Minimum Squred-Error Procedures Ide: conver o esier nd eer undersood prolem Percepron y i > for ll smples y i solve sysem of liner inequliies MSE procedure y i = i for ll smples
Minimum Squred Error LDF: Minimum Squred-Error Procedures Ide: conver o esier nd eer undersood prolem Percepron y i > for ll smples y i solve sysem of liner inequliies MSE procedure y i = i for ll smples
Class Meeting # 10: Introduction to the Wave Equation
 MATH 8.5 COURSE NOTES - CLASS MEETING # 0 8.5 Inroducion o PDEs, Fall 0 Professor: Jared Speck Class Meeing # 0: Inroducion o he Wave Equaion. Wha is he wave equaion? The sandard wave equaion for a funcion
MATH 8.5 COURSE NOTES - CLASS MEETING # 0 8.5 Inroducion o PDEs, Fall 0 Professor: Jared Speck Class Meeing # 0: Inroducion o he Wave Equaion. Wha is he wave equaion? The sandard wave equaion for a funcion
..,..,.,
 57.95. «..» 7, 9,,. 3 DOI:.459/mmph7..,..,., E-mil: yshr_ze@mil.ru -,,. -, -.. -. - - ( ). -., -. ( - ). - - -., - -., - -, -., -. -., - - -, -., -. : ; ; - ;., -,., - -, []., -, [].,, - [3, 4]. -. 3 (
57.95. «..» 7, 9,,. 3 DOI:.459/mmph7..,..,., E-mil: yshr_ze@mil.ru -,,. -, -.. -. - - ( ). -., -. ( - ). - - -., - -., - -, -., -. -., - - -, -., -. : ; ; - ;., -,., - -, []., -, [].,, - [3, 4]. -. 3 (
Minimum Squared Error
 Minimum Squred Error LDF: Minimum Squred-Error Procedures Ide: conver o esier nd eer undersood prolem Percepron y i > 0 for ll smples y i solve sysem of liner inequliies MSE procedure y i i for ll smples
Minimum Squred Error LDF: Minimum Squred-Error Procedures Ide: conver o esier nd eer undersood prolem Percepron y i > 0 for ll smples y i solve sysem of liner inequliies MSE procedure y i i for ll smples
6. Gas dynamics. Ideal gases Speed of infinitesimal disturbances in still gas
 6. Gs dynmics Dr. Gergely Krisóf De. of Fluid echnics, BE Februry, 009. Seed of infiniesiml disurbnces in sill gs dv d, dv d, Coninuiy: ( dv)( ) dv omenum r r heorem: ( ( dv) ) d 3443 4 q m dv d dv llievi
6. Gs dynmics Dr. Gergely Krisóf De. of Fluid echnics, BE Februry, 009. Seed of infiniesiml disurbnces in sill gs dv d, dv d, Coninuiy: ( dv)( ) dv omenum r r heorem: ( ( dv) ) d 3443 4 q m dv d dv llievi
Variational Iteration Method for Solving System of Fractional Order Ordinary Differential Equations
 IOSR Journal of Mahemaics (IOSR-JM) e-issn: 2278-5728, p-issn: 2319-765X. Volume 1, Issue 6 Ver. II (Nov - Dec. 214), PP 48-54 Variaional Ieraion Mehod for Solving Sysem of Fracional Order Ordinary Differenial
IOSR Journal of Mahemaics (IOSR-JM) e-issn: 2278-5728, p-issn: 2319-765X. Volume 1, Issue 6 Ver. II (Nov - Dec. 214), PP 48-54 Variaional Ieraion Mehod for Solving Sysem of Fracional Order Ordinary Differenial
Chapter 2. Motion along a straight line. 9/9/2015 Physics 218
 Chper Moion long srigh line 9/9/05 Physics 8 Gols for Chper How o describe srigh line moion in erms of displcemen nd erge elociy. The mening of insnneous elociy nd speed. Aerge elociy/insnneous elociy
Chper Moion long srigh line 9/9/05 Physics 8 Gols for Chper How o describe srigh line moion in erms of displcemen nd erge elociy. The mening of insnneous elociy nd speed. Aerge elociy/insnneous elociy
GRADIENTS, PREFERRED METRICS AND ASYMMETRIES
 GRADENTS, PREFERRED METRCS AND ASYMMETRES ANDERS LNNÉR ABSTRACT Assume he curves low ccording o / = Φ ( ) Evoluions h only use locl d, such s curve shorening, yield ril dierenil equions n he resen er glol
GRADENTS, PREFERRED METRCS AND ASYMMETRES ANDERS LNNÉR ABSTRACT Assume he curves low ccording o / = Φ ( ) Evoluions h only use locl d, such s curve shorening, yield ril dierenil equions n he resen er glol
