Boundary layer problem for system of first order of ordinary differential equations with linear non-local boundary conditions
|
|
|
- Reynold Warren
- 5 years ago
- Views:
Transcription
1 IJS 3 37A3 Secil issue-mheics: Irnin Journl of Science & echnology h://ijssshirzucir Boundry lyer role for syse of firs order of ordinry differenil euions wih liner non-locl oundry condiions M Jhnshhi * A R Srhsi S Ashrfi nd N Aliev Deren of Mheics Azrijn Shhid Mdni Universiy riz Irn Deren of Mheics Bu Se Universiy Bu Azerijn E-il: jhnshhi@zrunivedu Asrc In his er we sudy he oundry lyer roles in which oundry condiions re non-locl Here we ry o find he necessry condiions y he hel of fundenl soluion o he given djoin euion By geing hel fro hese condiions firs he oundry condiion is chnged fro non-locl o locl he in i of his er is o idenify he locion of he oundry lyer In oher words which oin he oundry lyer is fored Keywords: Singulr erurion roles; oundry lyer; fundenl soluion; necessry condiions Inroducion An iorn sujec in lied heics is he heory of singulr erurion roles he heicl odel for his ind of role is usully in he for of eiher ordinry differenil euions ODE or ril differenil euions PDE in which he highes derivive is ulilied y soe owers of s osiive sll reer [-3] he ojec heory of singulr erurion is o solve differenil euion wih soe iniil or oundry condiions wih sll reer hese roles re essenilly he her of oundry vlue nd iniil vlue roles [3-] hrough hese sudies we cn find ou wheher he oundry condiions ecoe locl ye Dirichle nd he soluion of he oundry lyer role is sisfied in oundry condiions hen here is no oundry lyer If he lii soluion when is no sisfied in he oundry condiion hen here will e oundry lyer In oo [4] fer he firs nd second chers he unsolved oundry lyer role is seen which shows h oundry lyer roles wih non-locl oundry condiions hve no een sudied crefully So in his er nd soe oher wors: M Jhnshhi & A R Srhsi [-4] nd N Aliev & S Ashrfi [5] [6] we sudy he oundry lyer roles in which oundry condiions re non-locl Here n e is de o find he necessry condiions wih he hel of he fundenl soluion of he given djoin *orresonding uhor Received: 8 Augus / Acceed: Ferury 3 euion By ing dvnge of hese condiions firs he oundry condiions re chnged for nonlocl o locl nd finlly s efore here will e locl cse nd he reson for he oundry lyer loc will e sudied [] Mheicl seen of role We consider he following oundry lyer role: l [ ] f where is sll reer re he sure rices of n order in which he eleens re rel coninuous funcions nd f nd re colun vecors whose funcions re rel coninuous nd f coefficiens of euion re nown funcions while is unnown vecor funcion D of oundry condiion in he role h is nd is sure rices of n order wih rel consn eleens nd of colun vecor hs n coonens wih rel consn eleens Euion esily shows h when i chnges o n lgeric syse Bsed on his fc i cn e verified wheher soluions of liner lgeric syse exis in oundry condiion or no As fr s we now if
2 IJS 3 37A3 Secil issue-mheics: he lii funcion is sisfied in oundry condiion here is no oundry lyer in ny of he nd oins If he lii funcion is no sisfied in oundry condiion hen oundry lyer exiss 3 he djoin euion of in euion o oin he djoin euion we firs eslish he following le 3 Le If re coninuous funcions hen he ssocied djoin euion of euion will e: ly y [ ] y 3 where nd rices re he rnsoses of Proof: o do his we e o ge he Lgrnge forul of syse [5]onsider he following sclr roduc of rel funcions: y l y y y [ y l d y [ ] y { y y [ ] d d d ] y } d 4 Forl soluion Now we refer o consrucing he forl soluion of he syse y [ ] y 4 wih reer A firs we verify roof of he nex le: 4 Le If in he syse 4 rix eleens of nd re infiniely differenile funcions nd he roos of he chrcerisic euion of his syse de[ E] 5 E is he ideniy rix of order n re disinc nd he rel rs of he re no zero h is: Re s s [ ] n hen he forl soluion of syse will e d y e ; [ ] 6 n where n Here is scler funcions Moreover re he colun vecors of n coonens in which he eleens re funcions h re oined fro hese syses: 7 or According o Lgrnge forul he inside of he ove inegrl er gives he ssocied djoin euion 3 If we use r of he inegrl ehod for he firs senence on he righ hnd side he Lgrnge forul leds o he resen inegrls of he le in forul 3
3 39 IJS 3 37A3 Secil issue-mheics: n n n n nn n n n n n n n n n Proof: In order o verify le we u he forl soluion 6 in syse 4 nd oi exonenil ers fro oh sides I cn e esily seen h relions 7 re he coefficiens of successive owers of sll reer According o he generl for of 7 he firs syse of euions is: [ E] 8 or n n n n nn n In order o hve non rivil soluions he deerinn of syse 8 should e zero I ens h for n re he roos of chrcerisic euion 5 In his cse for fixed he eleens of will e: j jr jr P e j n 9 where j re rirry funcions nd P includes he whole of ssocied co-fcors of r row of rix P E so i is shown s P jr e jr Here we should choose r in such wy h co-fcors of he row do no ecoe zero siulneously I should e h os one row of rix P E cn e zero s resul of hving differen roos Also e jr is del of Kroncer h is: e jr j r j r he colun vecor which consiss of he rirry funcions in 9 is resuled fro wriing insed of h is soluion of syse 8 Becuse he syse 8 is hoogeneous so funcions of j re rirry funcions By fcoring hese rirry funcions finlly we ulily he eleens of one row of rix P E o co -fcors of row r in h rix his one gin is zero sed on liner lger heores [6] So he unnown sclrs funcions of nd lso vecors of firs syse in he syse se 7 cn e oined Now in order o verify he soluion of he second syse in 7 in which we should find he resuled syse fro unnown colun vecor = o e he syse solvle i is necessry h he righ hnd side of he resuled syse fro ecoes orhogonl o he eigenvecor of djoin euions Becuse he righ hnd includes he rirry funcion so we cn ly he orhogonliy condiion ecuse he deerinn of coefficiens of he resuled syse fro is zero By following his rocess he whole soluions of he firs nd second euions of yses 7 will e clculed s he deerined funcions of Now Le us confir his forl soluion s rel nd clssic soluion For his y idenifying he
4 IJS 3 37A3 Secil issue-mheics: nd of unnown funcions in syse 7 nd ccording o forl soluion 6 he nex er h should e considerd is exonenil ers in 6 Bsed on choosing which ws discussed in he ove le when exonenil er is will led o zero Finlly ccording o infiniy series in he for of forl soluion of 6 he syoic exnsions of liner indeenden soluions of 4 cn e oined [4-6] We cn conclude his le: 4 Le On he condiion of le 4 he syoic exnsions of y for n y : leds o d M M y e O ; [ ] n M where O is error er 5 Fundenl soluion Now for clculing he fundenl soluion consider he non-hoogeneous syse reled o syse 4: [ ] g where sure rices of n order in h consis of rel funcions nd is unnown vecor Here g is he nown colun vecor of n order A firs we eslish he following le 5 Le Under he condiions of le 4 fundenl soluion of syse will e: Here is he funcion of Heviside nd is he rix soluion of syse 4 Proof: A firs we oin he generl soluion of non hoogeneous syse hrough vriion of vrile ehod: A 3 Here A is he unnown colun vecor By using 3 in we will hve: [ A ] A A g where is he rix soluion of inhoogeneous syse 4: or A A g g Here we cn find his relion for A A A g d 4 If in 4 we suose A nd u his one in he soluion of he non hoogeneous syse will e: y g d g d g d g d Here we cn see h he fundenl soluion of 4 is in he for of In fc if we u soluion in he lef side of 4 i will e:
5 393 IJS 3 37A3 Secil issue-mheics: ] [ ] [ } ]} [ { ] [ Noe h he second er of he ls relion will e zero ecuse is soluion of reled hoogenous syse 4 So his soluion is he fundenl soluion of he syse 4 h is: [ ] E 5 Where is he Dirc-del funcion nd E is he ideniy rix of n order 6 Fundenl relions nd necessry condiions A firs we verify he following le: 6 Le Under he condiions of le 4 he rirry soluion of syse is sisfied in he following relions: f d 6 In which he second cse gives us he necessry condiions Proof: Nex we ulily he wo sides of syse o rnsose fundenl soluion in he lef hnd nd hen oin he inegrl in ] [ d f d d ] [ or ] [ d f d d he relion 5 nd fro he roeries of he Dirc-del funcion [8] [9] give us relions 6 { [ ]} f d d d We use he second cse of ls relion nd ge he necessry condiion s follows: d f d f According o firs relion we will hve: f d 7
6 IJS 3 37A3 Secil issue-mheics: Noe h we show We should consider h in he second relion he ove will e s idenified s follows f d he inegrl er will e zero fro 7 Loclizion of oundry condiions In his r we conver non-locl condiions y using he ove necessry condiions for locl oundry condiions A firs we rove he following le 7 Le Under he condiions of le 4 we ssue: de[ ] 8 so for oundry vlues of unnown funcion we hve he following relions: f d [ ] [ f d] [ ] [ f d] 9 Proof: If we consider he relion 7 nd oundry condiion s n lgeric syse for he unnowns nd nd solve his syse y rer rule we will hve he relions 9 for oundry vlues of In his cse he nonlocl oundry condiions were convered o locl oundry condiions 8 Soluion of in oundry vlue role In order o give nlyicl seen o soluion of in role - we rove his heore: 8 heore Assue in he syse of in role is sll reer nd re he sure rices of n order in which he eleens re funcions of infiniely differenile f is funcion of colun vecors h in coninuous is unnown vecor of n order nd re sure rices of n order which hs consn eleens nd is consn colun vecor of n order nd non-locl oundry condiions re liner indeenden Moreover he roos of he chrcerisic euion 5 re disinc nd heir rel rs will no e zero Also we ssue condiion 8 will hold hen he soluion of he oundry lyer role - will e: f d [ f d ] [ ] [ f d] [ ] [ f d] where is he rnsose of fundenl soluion Proof: According o he disinc roos in euion 5 nd he for of forl soluion 6 in he syse 4 we cn oin norl for of i in le 5 On he oher hnd syoic exnsion of norl liner indeenden soluion 4 hs een given in le 4 nd in le 5 he fundenl soluion of syse 4 sed on he relion nd lso he sic relion nd necessry condiion y relion 7 is offered Finlly in le 7 we cn find oundry condiion in locl for In his siuion in order o verify he heore i is enough o u he oundry condiions of loclizion 9 in he lef hnd side of 6 Firs cse of relion 6 gives he soluion of role - 9 Liiing ehvior of soluion Now le us sudy he liied siuion of soluion where For his when he lii of syse is f If he deerinn of he ove syse is no zero h is:
7 395 IJS 3 37A3 Secil issue-mheics: de[ ] 3 So f 4 In he syse 5 where he fundenl soluion is usle when he soluion will e: E 5 or such s we will hve 6 [ ] Now y considering 6 he liiing relions 9 nd when will e: f f nd 7 f 8 We consider he relion 8 is he se s relion 4 which is liiing se of role - he forion of oundry lyers As enioned in he inroducion he forion or non forion of oundry lyers is iorn for consrucing roxie soluions [] [3] hey esily see he liiing siuion of soluion of he in role is djusle in liiing siuion of syse hence we hve his heore: heore Under he condiions of heore 8 nd he condiion If we hve his relion de[ ] f f 9 hen here will e no oundry lyer in ny of he oundry oin's Proof: We cn see fro 9 h he liiing siuion of soluion in role - when in re sisfied wih he liiing siuion of oundry condiion Hence in his cse ccording o oundry lyer roles we hve no oundry lyers heore Under he condiions of heore nd he condiion: de[ ] Also he condiion 9 does no hold so I if f he oundry lyer fors jus in II if f oundry lyer will e in oh nd Proof: In fc if we don hve condiion 9 here will e fored oundry lyer Bu if f we cn do he liiing siuion of soluion in firs relion 9 However does no sisfy wih second relion 9 Becuse of his oundry lyer in will e fored Referring o he fc h he lii funcion is no sisfied wih relions 9 finlly in oh nd oins we will hve oundry lyer Acnowledgeen he uhors re greful o ProfM K Mirni for ediing he er nd reviewers for heir suggesions o irove nuscri of he er References [] Prndle L 934 Uer Flussigeis-ewegung ei Kleiner Reiung Verhndlungen III IN Mh Gongress uener Leizig [] O Mlley J R E 974 Inroducion o Singulr Perurion New or Acdeic Press [3] O Mlley J R E 99 Singulr Perurion Mehods for O D E s Sringer Verlg [4] Dooln E P Miller J J & Schilders W H 98 Unifor Nuericl Mehods for Proles wih Iniil nd Boundry Lyers Boole Press Dulin [5] Birhoff G D 98 On he syeoic of he soluion of cerin liner differenil euions conining reer rns Aer Mh Soc 9-3 & [6] ohen D S 973 Mulile soluions of nonliner ril differenil euions Nonliner roles in he hysicl sciences nd iologg eds I Sgold D D Joseh D H Singer Lecure Noes in Mheics 3 Sringer Verlg Berlin 5-77 [7] Keller H B 968uulr cheicl recors wih recycles SIAM-AMS Proc 8 ed cohen [8] Nir M A 968 Liner differenil oerors r II New or Unger [9] Veldiirov V S 97 Euion of Mheicl Physics 3rd edn Nu Moscow
8 IJS 3 37A3 Secil issue-mheics: [] Jhnshhi M Invesigion of oundry lyers in singulr erurion role including 4h order ordinry differenil euions Journl of sciences Islic Reulic of Irn ehrn [] Srhsi A R & Jhnshhi M 9 Asyoic soluion of singulr erurion role for second order liner O D E wih locl oundry condiions Exended Asrcs 4h Annul Irnin Mheics onference [] Srhsi A R & Jhnshhi M Invesigion of oundry lyers in singulr erurion roles wih generl liner non-locl oundry condiions Exended Asrcs o IV ongress of he uric world heicl sociey Bu Azryjn [3] Srhsi A R & Jhnshhi M Asyoic Soluion of Prole of Singulr Perurion of Second-Order Liner wih onsn oefficiens wih Dirichle ondiion Journl of Sciences ehrn Universiy of ri Molle [4] Srhsi A R Jhnshhi M Ashrfi S Srhsi M 3 Invesigion of Boundry Lyers in Soe Singulr Perurion Proles Including Fourh Order Ordinry Differenil Euion World Alied Sciences Journl [5] Ashrfi S Medov & Aliev N Invesigion of Arising of Boundry Lyer in Boundry Vlue Prole for he Fourh Order Ordinry Differenil Euions J Bsic Al Sci Res [6] Ashrfi S & Aliev N Invesigion of Boundry Lyers for Second Order Euions under Locl nd Non- Locl Boundry ondiions J Bsic Al Sci Res
P441 Analytical Mechanics - I. Coupled Oscillators. c Alex R. Dzierba
 Lecure 3 Mondy - Deceber 5, 005 Wrien or ls upded: Deceber 3, 005 P44 Anlyicl Mechnics - I oupled Oscillors c Alex R. Dzierb oupled oscillors - rix echnique In Figure we show n exple of wo coupled oscillors,
Lecure 3 Mondy - Deceber 5, 005 Wrien or ls upded: Deceber 3, 005 P44 Anlyicl Mechnics - I oupled Oscillors c Alex R. Dzierb oupled oscillors - rix echnique In Figure we show n exple of wo coupled oscillors,
September 20 Homework Solutions
 College of Engineering nd Compuer Science Mechnicl Engineering Deprmen Mechnicl Engineering A Seminr in Engineering Anlysis Fll 7 Number 66 Insrucor: Lrry Creo Sepember Homework Soluions Find he specrum
College of Engineering nd Compuer Science Mechnicl Engineering Deprmen Mechnicl Engineering A Seminr in Engineering Anlysis Fll 7 Number 66 Insrucor: Lrry Creo Sepember Homework Soluions Find he specrum
e t dt e t dt = lim e t dt T (1 e T ) = 1
 Improper Inegrls There re wo ypes of improper inegrls - hose wih infinie limis of inegrion, nd hose wih inegrnds h pproch some poin wihin he limis of inegrion. Firs we will consider inegrls wih infinie
Improper Inegrls There re wo ypes of improper inegrls - hose wih infinie limis of inegrion, nd hose wih inegrnds h pproch some poin wihin he limis of inegrion. Firs we will consider inegrls wih infinie
Contraction Mapping Principle Approach to Differential Equations
 epl Journl of Science echnology 0 (009) 49-53 Conrcion pping Principle pproch o Differenil Equions Bishnu P. Dhungn Deprmen of hemics, hendr Rn Cmpus ribhuvn Universiy, Khmu epl bsrc Using n eension of
epl Journl of Science echnology 0 (009) 49-53 Conrcion pping Principle pproch o Differenil Equions Bishnu P. Dhungn Deprmen of hemics, hendr Rn Cmpus ribhuvn Universiy, Khmu epl bsrc Using n eension of
A LIMIT-POINT CRITERION FOR A SECOND-ORDER LINEAR DIFFERENTIAL OPERATOR IAN KNOWLES
 A LIMIT-POINT CRITERION FOR A SECOND-ORDER LINEAR DIFFERENTIAL OPERATOR j IAN KNOWLES 1. Inroducion Consider he forml differenil operor T defined by el, (1) where he funcion q{) is rel-vlued nd loclly
A LIMIT-POINT CRITERION FOR A SECOND-ORDER LINEAR DIFFERENTIAL OPERATOR j IAN KNOWLES 1. Inroducion Consider he forml differenil operor T defined by el, (1) where he funcion q{) is rel-vlued nd loclly
ENGR 1990 Engineering Mathematics The Integral of a Function as a Function
 ENGR 1990 Engineering Mhemics The Inegrl of Funcion s Funcion Previously, we lerned how o esime he inegrl of funcion f( ) over some inervl y dding he res of finie se of rpezoids h represen he re under
ENGR 1990 Engineering Mhemics The Inegrl of Funcion s Funcion Previously, we lerned how o esime he inegrl of funcion f( ) over some inervl y dding he res of finie se of rpezoids h represen he re under
5.1-The Initial-Value Problems For Ordinary Differential Equations
 5.-The Iniil-Vlue Problems For Ordinry Differenil Equions Consider solving iniil-vlue problems for ordinry differenil equions: (*) y f, y, b, y. If we know he generl soluion y of he ordinry differenil
5.-The Iniil-Vlue Problems For Ordinry Differenil Equions Consider solving iniil-vlue problems for ordinry differenil equions: (*) y f, y, b, y. If we know he generl soluion y of he ordinry differenil
1.0 Electrical Systems
 . Elecricl Sysems The ypes of dynmicl sysems we will e sudying cn e modeled in erms of lgeric equions, differenil equions, or inegrl equions. We will egin y looking fmilir mhemicl models of idel resisors,
. Elecricl Sysems The ypes of dynmicl sysems we will e sudying cn e modeled in erms of lgeric equions, differenil equions, or inegrl equions. We will egin y looking fmilir mhemicl models of idel resisors,
How to Prove the Riemann Hypothesis Author: Fayez Fok Al Adeh.
 How o Prove he Riemnn Hohesis Auhor: Fez Fok Al Adeh. Presiden of he Srin Cosmologicl Socie P.O.Bo,387,Dmscus,Sri Tels:963--77679,735 Emil:hf@scs-ne.org Commens: 3 ges Subj-Clss: Funcionl nlsis, comle
How o Prove he Riemnn Hohesis Auhor: Fez Fok Al Adeh. Presiden of he Srin Cosmologicl Socie P.O.Bo,387,Dmscus,Sri Tels:963--77679,735 Emil:hf@scs-ne.org Commens: 3 ges Subj-Clss: Funcionl nlsis, comle
0 for t < 0 1 for t > 0
 8.0 Sep nd del funcions Auhor: Jeremy Orloff The uni Sep Funcion We define he uni sep funcion by u() = 0 for < 0 for > 0 I is clled he uni sep funcion becuse i kes uni sep = 0. I is someimes clled he Heviside
8.0 Sep nd del funcions Auhor: Jeremy Orloff The uni Sep Funcion We define he uni sep funcion by u() = 0 for < 0 for > 0 I is clled he uni sep funcion becuse i kes uni sep = 0. I is someimes clled he Heviside
Improved Analysis of the Coupling of Optical Waves into Multimode Waveguides Using Overlap Integrals
 464 rogress In Elecrogneics Reserch Syosiu 5, Hngzhou, Chin, Augus -6 Iroved Anlysis of he Couling of Oicl Wves ino Muliode Wveguides Using Overl Inegrls M Sllein, C Kollec, nd G Mrozynsi Universiy of
464 rogress In Elecrogneics Reserch Syosiu 5, Hngzhou, Chin, Augus -6 Iroved Anlysis of he Couling of Oicl Wves ino Muliode Wveguides Using Overl Inegrls M Sllein, C Kollec, nd G Mrozynsi Universiy of
A note on diagonalization of integral quadratic forms modulo p m
 NNTDM 7 ( 3-36 A noe on diagonalizaion of inegral quadraic fors odulo Ali H Hakai Dearen of Maheaics King Khalid Universiy POo 94 Abha Posal Code: 643 Saudi Arabia E-ail: aalhakai@kkuedusa Absrac: Le be
NNTDM 7 ( 3-36 A noe on diagonalizaion of inegral quadraic fors odulo Ali H Hakai Dearen of Maheaics King Khalid Universiy POo 94 Abha Posal Code: 643 Saudi Arabia E-ail: aalhakai@kkuedusa Absrac: Le be
[5] Solving Multiple Linear Equations A system of m linear equations and n unknown variables:
![[5] Solving Multiple Linear Equations A system of m linear equations and n unknown variables: [5] Solving Multiple Linear Equations A system of m linear equations and n unknown variables:](/thumbs/78/77852027.jpg) [5] Solving Muliple Liner Equions A syse of liner equions nd n unknown vribles: + + + nn = b + + + = b n n : + + + nn = b n n A= b, where A =, : : : n : : : : n = : n A = = = ( ) where, n j = ( ); = :
[5] Solving Muliple Liner Equions A syse of liner equions nd n unknown vribles: + + + nn = b + + + = b n n : + + + nn = b n n A= b, where A =, : : : n : : : : n = : n A = = = ( ) where, n j = ( ); = :
INTEGRALS. Exercise 1. Let f : [a, b] R be bounded, and let P and Q be partitions of [a, b]. Prove that if P Q then U(P ) U(Q) and L(P ) L(Q).
![INTEGRALS. Exercise 1. Let f : [a, b] R be bounded, and let P and Q be partitions of [a, b]. Prove that if P Q then U(P ) U(Q) and L(P ) L(Q). INTEGRALS. Exercise 1. Let f : [a, b] R be bounded, and let P and Q be partitions of [a, b]. Prove that if P Q then U(P ) U(Q) and L(P ) L(Q).](/thumbs/78/77677920.jpg) INTEGRALS JOHN QUIGG Eercise. Le f : [, b] R be bounded, nd le P nd Q be priions of [, b]. Prove h if P Q hen U(P ) U(Q) nd L(P ) L(Q). Soluion: Le P = {,..., n }. Since Q is obined from P by dding finiely
INTEGRALS JOHN QUIGG Eercise. Le f : [, b] R be bounded, nd le P nd Q be priions of [, b]. Prove h if P Q hen U(P ) U(Q) nd L(P ) L(Q). Soluion: Le P = {,..., n }. Since Q is obined from P by dding finiely
Green s Functions and Comparison Theorems for Differential Equations on Measure Chains
 Green s Funcions nd Comprison Theorems for Differenil Equions on Mesure Chins Lynn Erbe nd Alln Peerson Deprmen of Mhemics nd Sisics, Universiy of Nebrsk-Lincoln Lincoln,NE 68588-0323 lerbe@@mh.unl.edu
Green s Funcions nd Comprison Theorems for Differenil Equions on Mesure Chins Lynn Erbe nd Alln Peerson Deprmen of Mhemics nd Sisics, Universiy of Nebrsk-Lincoln Lincoln,NE 68588-0323 lerbe@@mh.unl.edu
How to prove the Riemann Hypothesis
 Scholrs Journl of Phsics, Mhemics nd Sisics Sch. J. Phs. Mh. S. 5; (B:5-6 Scholrs Acdemic nd Scienific Publishers (SAS Publishers (An Inernionl Publisher for Acdemic nd Scienific Resources *Corresonding
Scholrs Journl of Phsics, Mhemics nd Sisics Sch. J. Phs. Mh. S. 5; (B:5-6 Scholrs Acdemic nd Scienific Publishers (SAS Publishers (An Inernionl Publisher for Acdemic nd Scienific Resources *Corresonding
Mathematics 805 Final Examination Answers
 . 5 poins Se he Weiersrss M-es. Mhemics 85 Finl Eminion Answers Answer: Suppose h A R, nd f n : A R. Suppose furher h f n M n for ll A, nd h Mn converges. Then f n converges uniformly on A.. 5 poins Se
. 5 poins Se he Weiersrss M-es. Mhemics 85 Finl Eminion Answers Answer: Suppose h A R, nd f n : A R. Suppose furher h f n M n for ll A, nd h Mn converges. Then f n converges uniformly on A.. 5 poins Se
4.8 Improper Integrals
 4.8 Improper Inegrls Well you ve mde i hrough ll he inegrion echniques. Congrs! Unforunely for us, we sill need o cover one more inegrl. They re clled Improper Inegrls. A his poin, we ve only del wih inegrls
4.8 Improper Inegrls Well you ve mde i hrough ll he inegrion echniques. Congrs! Unforunely for us, we sill need o cover one more inegrl. They re clled Improper Inegrls. A his poin, we ve only del wih inegrls
Integral Transform. Definitions. Function Space. Linear Mapping. Integral Transform
 Inegrl Trnsform Definiions Funcion Spce funcion spce A funcion spce is liner spce of funcions defined on he sme domins & rnges. Liner Mpping liner mpping Le VF, WF e liner spces over he field F. A mpping
Inegrl Trnsform Definiions Funcion Spce funcion spce A funcion spce is liner spce of funcions defined on he sme domins & rnges. Liner Mpping liner mpping Le VF, WF e liner spces over he field F. A mpping
The solution is often represented as a vector: 2xI + 4X2 + 2X3 + 4X4 + 2X5 = 4 2xI + 4X2 + 3X3 + 3X4 + 3X5 = 4. 3xI + 6X2 + 6X3 + 3X4 + 6X5 = 6.
 [~ o o :- o o ill] i 1. Mrices, Vecors, nd Guss-Jordn Eliminion 1 x y = = - z= The soluion is ofen represened s vecor: n his exmple, he process of eliminion works very smoohly. We cn elimine ll enries
[~ o o :- o o ill] i 1. Mrices, Vecors, nd Guss-Jordn Eliminion 1 x y = = - z= The soluion is ofen represened s vecor: n his exmple, he process of eliminion works very smoohly. We cn elimine ll enries
1. Find a basis for the row space of each of the following matrices. Your basis should consist of rows of the original matrix.
 Mh 7 Exm - Prcice Prolem Solions. Find sis for he row spce of ech of he following mrices. Yor sis shold consis of rows of he originl mrix. 4 () 7 7 8 () Since we wn sis for he row spce consising of rows
Mh 7 Exm - Prcice Prolem Solions. Find sis for he row spce of ech of he following mrices. Yor sis shold consis of rows of he originl mrix. 4 () 7 7 8 () Since we wn sis for he row spce consising of rows
A Structural Approach to the Enforcement of Language and Disjunctive Constraints
 A Srucurl Aroch o he Enforcemen of Lnguge nd Disjuncive Consrins Mrin V. Iordche School of Engineering nd Eng. Tech. LeTourneu Universiy Longview, TX 7607-700 Pnos J. Ansklis Dermen of Elecricl Engineering
A Srucurl Aroch o he Enforcemen of Lnguge nd Disjuncive Consrins Mrin V. Iordche School of Engineering nd Eng. Tech. LeTourneu Universiy Longview, TX 7607-700 Pnos J. Ansklis Dermen of Elecricl Engineering
EXISTENCE AND UNIQUENESS OF SOLUTIONS FOR A SECOND-ORDER ITERATIVE BOUNDARY-VALUE PROBLEM
 Elecronic Journl of Differenil Equions, Vol. 208 (208), No. 50, pp. 6. ISSN: 072-669. URL: hp://ejde.mh.xse.edu or hp://ejde.mh.un.edu EXISTENCE AND UNIQUENESS OF SOLUTIONS FOR A SECOND-ORDER ITERATIVE
Elecronic Journl of Differenil Equions, Vol. 208 (208), No. 50, pp. 6. ISSN: 072-669. URL: hp://ejde.mh.xse.edu or hp://ejde.mh.un.edu EXISTENCE AND UNIQUENESS OF SOLUTIONS FOR A SECOND-ORDER ITERATIVE
Hermite-Hadamard-Fejér type inequalities for convex functions via fractional integrals
 Sud. Univ. Beş-Bolyi Mh. 6(5, No. 3, 355 366 Hermie-Hdmrd-Fejér ype inequliies for convex funcions vi frcionl inegrls İmd İşcn Asrc. In his pper, firsly we hve eslished Hermie Hdmrd-Fejér inequliy for
Sud. Univ. Beş-Bolyi Mh. 6(5, No. 3, 355 366 Hermie-Hdmrd-Fejér ype inequliies for convex funcions vi frcionl inegrls İmd İşcn Asrc. In his pper, firsly we hve eslished Hermie Hdmrd-Fejér inequliy for
22.615, MHD Theory of Fusion Systems Prof. Freidberg Lecture 10: The High Beta Tokamak Con d and the High Flux Conserving Tokamak.
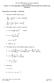 .615, MHD Theory of Fusion Sysems Prof. Freidberg Lecure 1: The High Be Tokmk Con d nd he High Flux Conserving Tokmk Proeries of he High Tokmk 1. Evlue he MHD sfey fcor: ψ B * ( ) 1 3 ρ 1+ ν ρ ρ cosθ *
.615, MHD Theory of Fusion Sysems Prof. Freidberg Lecure 1: The High Be Tokmk Con d nd he High Flux Conserving Tokmk Proeries of he High Tokmk 1. Evlue he MHD sfey fcor: ψ B * ( ) 1 3 ρ 1+ ν ρ ρ cosθ *
On The Hermite- Hadamard-Fejér Type Integral Inequality for Convex Function
 Turkish Journl o Anlysis nd Numer Theory, 4, Vol., No. 3, 85-89 Aville online h://us.scieu.com/jn//3/6 Science nd Educion Pulishing DOI:.69/jn--3-6 On The Hermie- Hdmrd-Fejér Tye Inegrl Ineuliy or Convex
Turkish Journl o Anlysis nd Numer Theory, 4, Vol., No. 3, 85-89 Aville online h://us.scieu.com/jn//3/6 Science nd Educion Pulishing DOI:.69/jn--3-6 On The Hermie- Hdmrd-Fejér Tye Inegrl Ineuliy or Convex
Conservation of Momentum. The purpose of this experiment is to verify the conservation of momentum in two dimensions.
 Conseraion of Moenu Purose The urose of his exerien is o erify he conseraion of oenu in wo diensions. Inroducion and Theory The oenu of a body ( ) is defined as he roduc of is ass () and elociy ( ): When
Conseraion of Moenu Purose The urose of his exerien is o erify he conseraion of oenu in wo diensions. Inroducion and Theory The oenu of a body ( ) is defined as he roduc of is ass () and elociy ( ): When
Riemann Hypothesis and Primorial Number. Choe Ryong Gil
 Rieann Hyohesis Priorial Nuber Choe Ryong Gil Dearen of Maheaics Universiy of Sciences Gwahak- dong Unjong Disric Pyongyang DPRKorea Eail; ryonggilchoe@sar-conek Augus 8 5 Absrac; In his aer we consider
Rieann Hyohesis Priorial Nuber Choe Ryong Gil Dearen of Maheaics Universiy of Sciences Gwahak- dong Unjong Disric Pyongyang DPRKorea Eail; ryonggilchoe@sar-conek Augus 8 5 Absrac; In his aer we consider
Positive and negative solutions of a boundary value problem for a
 Invenion Journl of Reerch Technology in Engineering & Mngemen (IJRTEM) ISSN: 2455-3689 www.ijrem.com Volume 2 Iue 9 ǁ Sepemer 28 ǁ PP 73-83 Poiive nd negive oluion of oundry vlue prolem for frcionl, -difference
Invenion Journl of Reerch Technology in Engineering & Mngemen (IJRTEM) ISSN: 2455-3689 www.ijrem.com Volume 2 Iue 9 ǁ Sepemer 28 ǁ PP 73-83 Poiive nd negive oluion of oundry vlue prolem for frcionl, -difference
On Hadamard and Fejér-Hadamard inequalities for Caputo k-fractional derivatives
 In J Nonliner Anl Appl 9 8 No, 69-8 ISSN: 8-68 elecronic hp://dxdoiorg/75/ijn8745 On Hdmrd nd Fejér-Hdmrd inequliies for Cpuo -frcionl derivives Ghulm Frid, Anum Jved Deprmen of Mhemics, COMSATS Universiy
In J Nonliner Anl Appl 9 8 No, 69-8 ISSN: 8-68 elecronic hp://dxdoiorg/75/ijn8745 On Hdmrd nd Fejér-Hdmrd inequliies for Cpuo -frcionl derivives Ghulm Frid, Anum Jved Deprmen of Mhemics, COMSATS Universiy
An integral having either an infinite limit of integration or an unbounded integrand is called improper. Here are two examples.
 Improper Inegrls To his poin we hve only considered inegrls f(x) wih he is of inegrion nd b finie nd he inegrnd f(x) bounded (nd in fc coninuous excep possibly for finiely mny jump disconinuiies) An inegrl
Improper Inegrls To his poin we hve only considered inegrls f(x) wih he is of inegrion nd b finie nd he inegrnd f(x) bounded (nd in fc coninuous excep possibly for finiely mny jump disconinuiies) An inegrl
FURTHER GENERALIZATIONS. QI Feng. The value of the integral of f(x) over [a; b] can be estimated in a variety ofways. b a. 2(M m)
![FURTHER GENERALIZATIONS. QI Feng. The value of the integral of f(x) over [a; b] can be estimated in a variety ofways. b a. 2(M m) FURTHER GENERALIZATIONS. QI Feng. The value of the integral of f(x) over [a; b] can be estimated in a variety ofways. b a. 2(M m)](/thumbs/75/72845579.jpg) Univ. Beogrd. Pul. Elekroehn. Fk. Ser. M. 8 (997), 79{83 FUTHE GENEALIZATIONS OF INEQUALITIES FO AN INTEGAL QI Feng Using he Tylor's formul we prove wo inegrl inequliies, h generlize K. S. K. Iyengr's
Univ. Beogrd. Pul. Elekroehn. Fk. Ser. M. 8 (997), 79{83 FUTHE GENEALIZATIONS OF INEQUALITIES FO AN INTEGAL QI Feng Using he Tylor's formul we prove wo inegrl inequliies, h generlize K. S. K. Iyengr's
ON NEW INEQUALITIES OF SIMPSON S TYPE FOR FUNCTIONS WHOSE SECOND DERIVATIVES ABSOLUTE VALUES ARE CONVEX.
 ON NEW INEQUALITIES OF SIMPSON S TYPE FOR FUNCTIONS WHOSE SECOND DERIVATIVES ABSOLUTE VALUES ARE CONVEX. MEHMET ZEKI SARIKAYA?, ERHAN. SET, AND M. EMIN OZDEMIR Asrc. In his noe, we oin new some ineuliies
ON NEW INEQUALITIES OF SIMPSON S TYPE FOR FUNCTIONS WHOSE SECOND DERIVATIVES ABSOLUTE VALUES ARE CONVEX. MEHMET ZEKI SARIKAYA?, ERHAN. SET, AND M. EMIN OZDEMIR Asrc. In his noe, we oin new some ineuliies
f t f a f x dx By Lin McMullin f x dx= f b f a. 2
 Accumulion: Thoughs On () By Lin McMullin f f f d = + The gols of he AP* Clculus progrm include he semen, Sudens should undersnd he definie inegrl s he ne ccumulion of chnge. 1 The Topicl Ouline includes
Accumulion: Thoughs On () By Lin McMullin f f f d = + The gols of he AP* Clculus progrm include he semen, Sudens should undersnd he definie inegrl s he ne ccumulion of chnge. 1 The Topicl Ouline includes
Minimum Squared Error
 Minimum Squred Error LDF: Minimum Squred-Error Procedures Ide: conver o esier nd eer undersood prolem Percepron y i > for ll smples y i solve sysem of liner inequliies MSE procedure y i = i for ll smples
Minimum Squred Error LDF: Minimum Squred-Error Procedures Ide: conver o esier nd eer undersood prolem Percepron y i > for ll smples y i solve sysem of liner inequliies MSE procedure y i = i for ll smples
Minimum Squared Error
 Minimum Squred Error LDF: Minimum Squred-Error Procedures Ide: conver o esier nd eer undersood prolem Percepron y i > 0 for ll smples y i solve sysem of liner inequliies MSE procedure y i i for ll smples
Minimum Squred Error LDF: Minimum Squred-Error Procedures Ide: conver o esier nd eer undersood prolem Percepron y i > 0 for ll smples y i solve sysem of liner inequliies MSE procedure y i i for ll smples
On the Pseudo-Spectral Method of Solving Linear Ordinary Differential Equations
 Journl of Mhemics nd Sisics 5 ():136-14, 9 ISS 1549-3644 9 Science Publicions On he Pseudo-Specrl Mehod of Solving Liner Ordinry Differenil Equions B.S. Ogundre Deprmen of Pure nd Applied Mhemics, Universiy
Journl of Mhemics nd Sisics 5 ():136-14, 9 ISS 1549-3644 9 Science Publicions On he Pseudo-Specrl Mehod of Solving Liner Ordinry Differenil Equions B.S. Ogundre Deprmen of Pure nd Applied Mhemics, Universiy
Solutions of half-linear differential equations in the classes Gamma and Pi
 Soluions of hlf-liner differenil equions in he clsses Gmm nd Pi Pvel Řehák Insiue of Mhemics, Acdemy of Sciences CR CZ-6662 Brno, Czech Reublic; Fculy of Educion, Msryk Universiy CZ-60300 Brno, Czech Reublic
Soluions of hlf-liner differenil equions in he clsses Gmm nd Pi Pvel Řehák Insiue of Mhemics, Acdemy of Sciences CR CZ-6662 Brno, Czech Reublic; Fculy of Educion, Msryk Universiy CZ-60300 Brno, Czech Reublic
Honours Introductory Maths Course 2011 Integration, Differential and Difference Equations
 Honours Inroducory Mhs Course 0 Inegrion, Differenil nd Difference Equions Reding: Ching Chper 4 Noe: These noes do no fully cover he meril in Ching, u re men o supplemen your reding in Ching. Thus fr
Honours Inroducory Mhs Course 0 Inegrion, Differenil nd Difference Equions Reding: Ching Chper 4 Noe: These noes do no fully cover he meril in Ching, u re men o supplemen your reding in Ching. Thus fr
M r. d 2. R t a M. Structural Mechanics Section. Exam CT5141 Theory of Elasticity Friday 31 October 2003, 9:00 12:00 hours. Problem 1 (3 points)
 Delf Universiy of Technology Fculy of Civil Engineering nd Geosciences Srucurl echnics Secion Wrie your nme nd sudy numer he op righ-hnd of your work. Exm CT5 Theory of Elsiciy Fridy Ocoer 00, 9:00 :00
Delf Universiy of Technology Fculy of Civil Engineering nd Geosciences Srucurl echnics Secion Wrie your nme nd sudy numer he op righ-hnd of your work. Exm CT5 Theory of Elsiciy Fridy Ocoer 00, 9:00 :00
Optimization and Application of initial Value of Non-equidistant New Information GM(1,1) Model
 IJCSI Inernionl Journl of Copuer Science Issues, Vol., Issue, No, Mrch 3 ISSN Prin: 694-84 ISSN Online: 694-784 www.ijcsi.org 8 Opiizion nd Applicion of iniil Vlue of Non-equidisn New Inforion GM, Model
IJCSI Inernionl Journl of Copuer Science Issues, Vol., Issue, No, Mrch 3 ISSN Prin: 694-84 ISSN Online: 694-784 www.ijcsi.org 8 Opiizion nd Applicion of iniil Vlue of Non-equidisn New Inforion GM, Model
Procedia Computer Science
 Procedi Compuer Science 00 (0) 000 000 Procedi Compuer Science www.elsevier.com/loce/procedi The Third Informion Sysems Inernionl Conference The Exisence of Polynomil Soluion of he Nonliner Dynmicl Sysems
Procedi Compuer Science 00 (0) 000 000 Procedi Compuer Science www.elsevier.com/loce/procedi The Third Informion Sysems Inernionl Conference The Exisence of Polynomil Soluion of he Nonliner Dynmicl Sysems
Chapter Direct Method of Interpolation
 Chper 5. Direc Mehod of Inerpolion Afer reding his chper, you should be ble o:. pply he direc mehod of inerpolion,. sole problems using he direc mehod of inerpolion, nd. use he direc mehod inerpolns o
Chper 5. Direc Mehod of Inerpolion Afer reding his chper, you should be ble o:. pply he direc mehod of inerpolion,. sole problems using he direc mehod of inerpolion, nd. use he direc mehod inerpolns o
Chapter 2. First Order Scalar Equations
 Chaper. Firs Order Scalar Equaions We sar our sudy of differenial equaions in he same way he pioneers in his field did. We show paricular echniques o solve paricular ypes of firs order differenial equaions.
Chaper. Firs Order Scalar Equaions We sar our sudy of differenial equaions in he same way he pioneers in his field did. We show paricular echniques o solve paricular ypes of firs order differenial equaions.
REAL ANALYSIS I HOMEWORK 3. Chapter 1
 REAL ANALYSIS I HOMEWORK 3 CİHAN BAHRAN The quesions re from Sein nd Shkrchi s e. Chper 1 18. Prove he following sserion: Every mesurble funcion is he limi.e. of sequence of coninuous funcions. We firs
REAL ANALYSIS I HOMEWORK 3 CİHAN BAHRAN The quesions re from Sein nd Shkrchi s e. Chper 1 18. Prove he following sserion: Every mesurble funcion is he limi.e. of sequence of coninuous funcions. We firs
Extension of Hardy Inequality on Weighted Sequence Spaces
 Jourl of Scieces Islic Reublic of Ir 20(2): 59-66 (2009) Uiversiy of ehr ISS 06-04 h://sciecesucir Eesio of Hrdy Iequliy o Weighed Sequece Sces R Lshriour d D Foroui 2 Dere of Mheics Fculy of Mheics Uiversiy
Jourl of Scieces Islic Reublic of Ir 20(2): 59-66 (2009) Uiversiy of ehr ISS 06-04 h://sciecesucir Eesio of Hrdy Iequliy o Weighed Sequece Sces R Lshriour d D Foroui 2 Dere of Mheics Fculy of Mheics Uiversiy
IX.1.1 The Laplace Transform Definition 700. IX.1.2 Properties 701. IX.1.3 Examples 702. IX.1.4 Solution of IVP for ODEs 704
 Chper IX The Inegrl Trnform Mehod IX. The plce Trnform November 4, 7 699 IX. THE APACE TRANSFORM IX.. The plce Trnform Definiion 7 IX.. Properie 7 IX..3 Emple 7 IX..4 Soluion of IVP for ODE 74 IX..5 Soluion
Chper IX The Inegrl Trnform Mehod IX. The plce Trnform November 4, 7 699 IX. THE APACE TRANSFORM IX.. The plce Trnform Definiion 7 IX.. Properie 7 IX..3 Emple 7 IX..4 Soluion of IVP for ODE 74 IX..5 Soluion
Some Inequalities variations on a common theme Lecture I, UL 2007
 Some Inequliies vriions on common heme Lecure I, UL 2007 Finbrr Hollnd, Deprmen of Mhemics, Universiy College Cork, fhollnd@uccie; July 2, 2007 Three Problems Problem Assume i, b i, c i, i =, 2, 3 re rel
Some Inequliies vriions on common heme Lecure I, UL 2007 Finbrr Hollnd, Deprmen of Mhemics, Universiy College Cork, fhollnd@uccie; July 2, 2007 Three Problems Problem Assume i, b i, c i, i =, 2, 3 re rel
MTH 146 Class 11 Notes
 8.- Are of Surfce of Revoluion MTH 6 Clss Noes Suppose we wish o revolve curve C round n is nd find he surfce re of he resuling solid. Suppose f( ) is nonnegive funcion wih coninuous firs derivive on he
8.- Are of Surfce of Revoluion MTH 6 Clss Noes Suppose we wish o revolve curve C round n is nd find he surfce re of he resuling solid. Suppose f( ) is nonnegive funcion wih coninuous firs derivive on he
Refinements to Hadamard s Inequality for Log-Convex Functions
 Alied Mhemics 899-93 doi:436/m7 Pulished Online Jul (h://wwwscirporg/journl/m) Refinemens o Hdmrd s Ineuli for Log-Convex Funcions Asrc Wdllh T Sulimn Dermen of Comuer Engineering College of Engineering
Alied Mhemics 899-93 doi:436/m7 Pulished Online Jul (h://wwwscirporg/journl/m) Refinemens o Hdmrd s Ineuli for Log-Convex Funcions Asrc Wdllh T Sulimn Dermen of Comuer Engineering College of Engineering
GENERALIZATION OF SOME INEQUALITIES VIA RIEMANN-LIOUVILLE FRACTIONAL CALCULUS
 - TAMKANG JOURNAL OF MATHEMATICS Volume 5, Number, 7-5, June doi:5556/jkjm555 Avilble online hp://journlsmhkueduw/ - - - GENERALIZATION OF SOME INEQUALITIES VIA RIEMANN-LIOUVILLE FRACTIONAL CALCULUS MARCELA
- TAMKANG JOURNAL OF MATHEMATICS Volume 5, Number, 7-5, June doi:5556/jkjm555 Avilble online hp://journlsmhkueduw/ - - - GENERALIZATION OF SOME INEQUALITIES VIA RIEMANN-LIOUVILLE FRACTIONAL CALCULUS MARCELA
More on Magnetically C Coupled Coils and Ideal Transformers
 Appenix ore on gneiclly C Couple Coils Iel Trnsformers C. Equivlen Circuis for gneiclly Couple Coils A imes, i is convenien o moel mgneiclly couple coils wih n equivlen circui h oes no involve mgneic coupling.
Appenix ore on gneiclly C Couple Coils Iel Trnsformers C. Equivlen Circuis for gneiclly Couple Coils A imes, i is convenien o moel mgneiclly couple coils wih n equivlen circui h oes no involve mgneic coupling.
M x t = K x F t x t = A x M 1 F t. M x t = K x cos t G 0. x t = A x cos t F 0
 Forced oscillaions (sill undaped): If he forcing is sinusoidal, M = K F = A M F M = K cos G wih F = M G = A cos F Fro he fundaenal heore for linear ransforaions we now ha he general soluion o his inhoogeneous
Forced oscillaions (sill undaped): If he forcing is sinusoidal, M = K F = A M F M = K cos G wih F = M G = A cos F Fro he fundaenal heore for linear ransforaions we now ha he general soluion o his inhoogeneous
22.615, MHD Theory of Fusion Systems Prof. Freidberg Lecture 9: The High Beta Tokamak
 .65, MHD Theory of Fusion Sysems Prof. Freidberg Lecure 9: The High e Tokmk Summry of he Properies of n Ohmic Tokmk. Advnges:. good euilibrium (smll shif) b. good sbiliy ( ) c. good confinemen ( τ nr )
.65, MHD Theory of Fusion Sysems Prof. Freidberg Lecure 9: The High e Tokmk Summry of he Properies of n Ohmic Tokmk. Advnges:. good euilibrium (smll shif) b. good sbiliy ( ) c. good confinemen ( τ nr )
1 jordan.mcd Eigenvalue-eigenvector approach to solving first order ODEs. -- Jordan normal (canonical) form. Instructor: Nam Sun Wang
 jordnmcd Eigenvlue-eigenvecor pproch o solving firs order ODEs -- ordn norml (cnonicl) form Insrucor: Nm Sun Wng Consider he following se of coupled firs order ODEs d d x x 5 x x d d x d d x x x 5 x x
jordnmcd Eigenvlue-eigenvecor pproch o solving firs order ODEs -- ordn norml (cnonicl) form Insrucor: Nm Sun Wng Consider he following se of coupled firs order ODEs d d x x 5 x x d d x d d x x x 5 x x
Motion. Part 2: Constant Acceleration. Acceleration. October Lab Physics. Ms. Levine 1. Acceleration. Acceleration. Units for Acceleration.
 Moion Accelerion Pr : Consn Accelerion Accelerion Accelerion Accelerion is he re of chnge of velociy. = v - vo = Δv Δ ccelerion = = v - vo chnge of velociy elpsed ime Accelerion is vecor, lhough in one-dimensionl
Moion Accelerion Pr : Consn Accelerion Accelerion Accelerion Accelerion is he re of chnge of velociy. = v - vo = Δv Δ ccelerion = = v - vo chnge of velociy elpsed ime Accelerion is vecor, lhough in one-dimensionl
Application on Inner Product Space with. Fixed Point Theorem in Probabilistic
 Journl of Applied Mhemics & Bioinformics, vol.2, no.2, 2012, 1-10 ISSN: 1792-6602 prin, 1792-6939 online Scienpress Ld, 2012 Applicion on Inner Produc Spce wih Fixed Poin Theorem in Probbilisic Rjesh Shrivsv
Journl of Applied Mhemics & Bioinformics, vol.2, no.2, 2012, 1-10 ISSN: 1792-6602 prin, 1792-6939 online Scienpress Ld, 2012 Applicion on Inner Produc Spce wih Fixed Poin Theorem in Probbilisic Rjesh Shrivsv
Analytical Solution of Time-Fractional Advection Dispersion Equation
 Aville h://vu.edu/ Al. Al. Mh. ISSN: 93-9466 Vol. 4 Iue (June 9). 76 88 (Previoul Vol. 4 No. ) Alicion nd Alied Mheic: An Inernionl Journl (AAM) Anlicl Soluion of Tie-Frcionl Advecion Dierion Equion Triq
Aville h://vu.edu/ Al. Al. Mh. ISSN: 93-9466 Vol. 4 Iue (June 9). 76 88 (Previoul Vol. 4 No. ) Alicion nd Alied Mheic: An Inernionl Journl (AAM) Anlicl Soluion of Tie-Frcionl Advecion Dierion Equion Triq
Magnetostatics Bar Magnet. Magnetostatics Oersted s Experiment
 Mgneosics Br Mgne As fr bck s 4500 yers go, he Chinese discovered h cerin ypes of iron ore could rc ech oher nd cerin mels. Iron filings "mp" of br mgne s field Crefully suspended slivers of his mel were
Mgneosics Br Mgne As fr bck s 4500 yers go, he Chinese discovered h cerin ypes of iron ore could rc ech oher nd cerin mels. Iron filings "mp" of br mgne s field Crefully suspended slivers of his mel were
Characteristic Function for the Truncated Triangular Distribution., Myron Katzoff and Rahul A. Parsa
 Secion on Survey Reserch Mehos JSM 009 Chrcerisic Funcion for he Trunce Tringulr Disriuion Jy J. Kim 1 1, Myron Kzoff n Rhul A. Prs 1 Nionl Cener for Helh Sisics, 11Toleo Ro, Hysville, MD. 078 College
Secion on Survey Reserch Mehos JSM 009 Chrcerisic Funcion for he Trunce Tringulr Disriuion Jy J. Kim 1 1, Myron Kzoff n Rhul A. Prs 1 Nionl Cener for Helh Sisics, 11Toleo Ro, Hysville, MD. 078 College
On Absolute Indexed Riesz Summability of Orthogonal Series
 Ieriol Jourl of Couiol d Alied Mheics. ISSN 89-4966 Volue 3 Nuer (8). 55-6 eserch Idi Pulicios h:www.riulicio.co O Asolue Ideed iesz Suiliy of Orhogol Series L. D. Je S. K. Piry *. K. Ji 3 d. Sl 4 eserch
Ieriol Jourl of Couiol d Alied Mheics. ISSN 89-4966 Volue 3 Nuer (8). 55-6 eserch Idi Pulicios h:www.riulicio.co O Asolue Ideed iesz Suiliy of Orhogol Series L. D. Je S. K. Piry *. K. Ji 3 d. Sl 4 eserch
3. Renewal Limit Theorems
 Virul Lborories > 14. Renewl Processes > 1 2 3 3. Renewl Limi Theorems In he inroducion o renewl processes, we noed h he rrivl ime process nd he couning process re inverses, in sens The rrivl ime process
Virul Lborories > 14. Renewl Processes > 1 2 3 3. Renewl Limi Theorems In he inroducion o renewl processes, we noed h he rrivl ime process nd he couning process re inverses, in sens The rrivl ime process
Weighted Hardy-Type Inequalities on Time Scales with Applications
 Medierr J Mh DOI 0007/s00009-04-054-y c Sringer Bsel 204 Weighed Hrdy-Tye Ineuliies on Time Scles wih Alicions S H Sker, R R Mhmoud nd A Peerson Absrc In his er, we will rove some new dynmic Hrdy-ye ineuliies
Medierr J Mh DOI 0007/s00009-04-054-y c Sringer Bsel 204 Weighed Hrdy-Tye Ineuliies on Time Scles wih Alicions S H Sker, R R Mhmoud nd A Peerson Absrc In his er, we will rove some new dynmic Hrdy-ye ineuliies
Section 3.5 Nonhomogeneous Equations; Method of Undetermined Coefficients
 Secion 3.5 Nonhomogeneous Equaions; Mehod of Undeermined Coefficiens Key Terms/Ideas: Linear Differenial operaor Nonlinear operaor Second order homogeneous DE Second order nonhomogeneous DE Soluion o homogeneous
Secion 3.5 Nonhomogeneous Equaions; Mehod of Undeermined Coefficiens Key Terms/Ideas: Linear Differenial operaor Nonlinear operaor Second order homogeneous DE Second order nonhomogeneous DE Soluion o homogeneous
Convergence of Singular Integral Operators in Weighted Lebesgue Spaces
 EUROPEAN JOURNAL OF PURE AND APPLIED MATHEMATICS Vol. 10, No. 2, 2017, 335-347 ISSN 1307-5543 www.ejpm.com Published by New York Business Globl Convergence of Singulr Inegrl Operors in Weighed Lebesgue
EUROPEAN JOURNAL OF PURE AND APPLIED MATHEMATICS Vol. 10, No. 2, 2017, 335-347 ISSN 1307-5543 www.ejpm.com Published by New York Business Globl Convergence of Singulr Inegrl Operors in Weighed Lebesgue
Some basic notation and terminology. Deterministic Finite Automata. COMP218: Decision, Computation and Language Note 1
 COMP28: Decision, Compuion nd Lnguge Noe These noes re inended minly s supplemen o he lecures nd exooks; hey will e useful for reminders ou noion nd erminology. Some sic noion nd erminology An lphe is
COMP28: Decision, Compuion nd Lnguge Noe These noes re inended minly s supplemen o he lecures nd exooks; hey will e useful for reminders ou noion nd erminology. Some sic noion nd erminology An lphe is
ASYMPTOTIC BEHAVIOR OF INTERMEDIATE SOLUTIONS OF FOURTH-ORDER NONLINEAR DIFFERENTIAL EQUATIONS WITH REGULARLY VARYING COEFFICIENTS
 Elecronic Journl of Differenil Equions, Vol. 06 06), No. 9, pp. 3. ISSN: 07-669. URL: hp://ejde.mh.xse.edu or hp://ejde.mh.un.edu ASYMPTOTIC BEHAVIOR OF INTERMEDIATE SOLUTIONS OF FOURTH-ORDER NONLINEAR
Elecronic Journl of Differenil Equions, Vol. 06 06), No. 9, pp. 3. ISSN: 07-669. URL: hp://ejde.mh.xse.edu or hp://ejde.mh.un.edu ASYMPTOTIC BEHAVIOR OF INTERMEDIATE SOLUTIONS OF FOURTH-ORDER NONLINEAR
Solutions to Problems from Chapter 2
 Soluions o Problems rom Chper Problem. The signls u() :5sgn(), u () :5sgn(), nd u h () :5sgn() re ploed respecively in Figures.,b,c. Noe h u h () :5sgn() :5; 8 including, bu u () :5sgn() is undeined..5
Soluions o Problems rom Chper Problem. The signls u() :5sgn(), u () :5sgn(), nd u h () :5sgn() re ploed respecively in Figures.,b,c. Noe h u h () :5sgn() :5; 8 including, bu u () :5sgn() is undeined..5
A new model for solving fuzzy linear fractional programming problem with ranking function
 J. ppl. Res. Ind. Eng. Vol. 4 No. 07 89 96 Journl of pplied Reserch on Indusril Engineering www.journl-prie.com new model for solving fuzzy liner frcionl progrmming prolem wih rning funcion Spn Kumr Ds
J. ppl. Res. Ind. Eng. Vol. 4 No. 07 89 96 Journl of pplied Reserch on Indusril Engineering www.journl-prie.com new model for solving fuzzy liner frcionl progrmming prolem wih rning funcion Spn Kumr Ds
IX.1.1 The Laplace Transform Definition 700. IX.1.2 Properties 701. IX.1.3 Examples 702. IX.1.4 Solution of IVP for ODEs 704
 Chper IX The Inegrl Trnform Mehod IX. The plce Trnform November 6, 8 699 IX. THE APACE TRANSFORM IX.. The plce Trnform Definiion 7 IX.. Properie 7 IX..3 Emple 7 IX..4 Soluion of IVP for ODE 74 IX..5 Soluion
Chper IX The Inegrl Trnform Mehod IX. The plce Trnform November 6, 8 699 IX. THE APACE TRANSFORM IX.. The plce Trnform Definiion 7 IX.. Properie 7 IX..3 Emple 7 IX..4 Soluion of IVP for ODE 74 IX..5 Soluion
Fractional Fourier Series with Applications
 Aeric Jourl o Couiol d Alied Mheics 4, 4(6): 87-9 DOI: 593/jjc446 Frciol Fourier Series wih Alicios Abu Hd I, Khlil R * Uiversiy o Jord, Jord Absrc I his er, we iroduce coorble rciol Fourier series We
Aeric Jourl o Couiol d Alied Mheics 4, 4(6): 87-9 DOI: 593/jjc446 Frciol Fourier Series wih Alicios Abu Hd I, Khlil R * Uiversiy o Jord, Jord Absrc I his er, we iroduce coorble rciol Fourier series We
Inventory Management Models with Variable Holding Cost and Salvage value
 OSR Journl of Business nd Mngemen OSR-JBM e-ssn: -X p-ssn: 9-. Volume ssue Jul. - Aug. PP - www.iosrjournls.org nvenory Mngemen Models wi Vrile Holding os nd Slvge vlue R.Mon R.Venkeswrlu Memics Dep ollege
OSR Journl of Business nd Mngemen OSR-JBM e-ssn: -X p-ssn: 9-. Volume ssue Jul. - Aug. PP - www.iosrjournls.org nvenory Mngemen Models wi Vrile Holding os nd Slvge vlue R.Mon R.Venkeswrlu Memics Dep ollege
Forms of Energy. Mass = Energy. Page 1. SPH4U: Introduction to Work. Work & Energy. Particle Physics:
 SPH4U: Inroducion o ork ork & Energy ork & Energy Discussion Definiion Do Produc ork of consn force ork/kineic energy heore ork of uliple consn forces Coens One of he os iporn conceps in physics Alernive
SPH4U: Inroducion o ork ork & Energy ork & Energy Discussion Definiion Do Produc ork of consn force ork/kineic energy heore ork of uliple consn forces Coens One of he os iporn conceps in physics Alernive
( ) ( ) ( ) ( ) ( ) ( y )
 8. Lengh of Plne Curve The mos fmous heorem in ll of mhemics is he Pyhgoren Theorem. I s formulion s he disnce formul is used o find he lenghs of line segmens in he coordine plne. In his secion you ll
8. Lengh of Plne Curve The mos fmous heorem in ll of mhemics is he Pyhgoren Theorem. I s formulion s he disnce formul is used o find he lenghs of line segmens in he coordine plne. In his secion you ll
ODEs II, Lecture 1: Homogeneous Linear Systems - I. Mike Raugh 1. March 8, 2004
 ODEs II, Lecure : Homogeneous Linear Sysems - I Mike Raugh March 8, 4 Inroducion. In he firs lecure we discussed a sysem of linear ODEs for modeling he excreion of lead from he human body, saw how o ransform
ODEs II, Lecure : Homogeneous Linear Sysems - I Mike Raugh March 8, 4 Inroducion. In he firs lecure we discussed a sysem of linear ODEs for modeling he excreion of lead from he human body, saw how o ransform
(b) 10 yr. (b) 13 m. 1.6 m s, m s m s (c) 13.1 s. 32. (a) 20.0 s (b) No, the minimum distance to stop = 1.00 km. 1.
 Answers o Een Numbered Problems Chper. () 7 m s, 6 m s (b) 8 5 yr 4.. m ih 6. () 5. m s (b).5 m s (c).5 m s (d) 3.33 m s (e) 8. ().3 min (b) 64 mi..3 h. ().3 s (b) 3 m 4..8 mi wes of he flgpole 6. (b)
Answers o Een Numbered Problems Chper. () 7 m s, 6 m s (b) 8 5 yr 4.. m ih 6. () 5. m s (b).5 m s (c).5 m s (d) 3.33 m s (e) 8. ().3 min (b) 64 mi..3 h. ().3 s (b) 3 m 4..8 mi wes of he flgpole 6. (b)
Viscous Damping Summary Sheet No Damping Case: Damped behaviour depends on the relative size of ω o and b/2m 3 Cases: 1.
 Viscous Daping: && + & + ω Viscous Daping Suary Shee No Daping Case: & + ω solve A ( ω + α ) Daped ehaviour depends on he relaive size of ω o and / 3 Cases:. Criical Daping Wee 5 Lecure solve sae BC s
Viscous Daping: && + & + ω Viscous Daping Suary Shee No Daping Case: & + ω solve A ( ω + α ) Daped ehaviour depends on he relaive size of ω o and / 3 Cases:. Criical Daping Wee 5 Lecure solve sae BC s
t is a basis for the solution space to this system, then the matrix having these solutions as columns, t x 1 t, x 2 t,... x n t x 2 t...
 Mah 228- Fri Mar 24 5.6 Marix exponenials and linear sysems: The analogy beween firs order sysems of linear differenial equaions (Chaper 5) and scalar linear differenial equaions (Chaper ) is much sronger
Mah 228- Fri Mar 24 5.6 Marix exponenials and linear sysems: The analogy beween firs order sysems of linear differenial equaions (Chaper 5) and scalar linear differenial equaions (Chaper ) is much sronger
A Kalman filtering simulation
 A Klmn filering simulion The performnce of Klmn filering hs been esed on he bsis of wo differen dynmicl models, ssuming eiher moion wih consn elociy or wih consn ccelerion. The former is epeced o beer
A Klmn filering simulion The performnce of Klmn filering hs been esed on he bsis of wo differen dynmicl models, ssuming eiher moion wih consn elociy or wih consn ccelerion. The former is epeced o beer
Fuji Power MOSFET Power calculation method
 Fuji Power MOSFE Power clculi mehod Design ool Cher. Overview is necessry o check wheher he ower loss hs no exceeded he Asolue Mximum Rings for using MOSFE. Since he MOSFE loss cnno e mesured using ower
Fuji Power MOSFE Power clculi mehod Design ool Cher. Overview is necessry o check wheher he ower loss hs no exceeded he Asolue Mximum Rings for using MOSFE. Since he MOSFE loss cnno e mesured using ower
Mathematical Modeling
 ME pplie Engineering nlsis Chper Mhemicl Moeling Professor Ti-Rn Hsu, Ph.D. Deprmen of Mechnicl n erospce Engineering Sn Jose Se Universi Sn Jose, Cliforni, US Jnur Chper Lerning Ojecives Mhemicl moeling
ME pplie Engineering nlsis Chper Mhemicl Moeling Professor Ti-Rn Hsu, Ph.D. Deprmen of Mechnicl n erospce Engineering Sn Jose Se Universi Sn Jose, Cliforni, US Jnur Chper Lerning Ojecives Mhemicl moeling
Math 2142 Exam 1 Review Problems. x 2 + f (0) 3! for the 3rd Taylor polynomial at x = 0. To calculate the various quantities:
 Mah 4 Eam Review Problems Problem. Calculae he 3rd Taylor polynomial for arcsin a =. Soluion. Le f() = arcsin. For his problem, we use he formula f() + f () + f ()! + f () 3! for he 3rd Taylor polynomial
Mah 4 Eam Review Problems Problem. Calculae he 3rd Taylor polynomial for arcsin a =. Soluion. Le f() = arcsin. For his problem, we use he formula f() + f () + f ()! + f () 3! for he 3rd Taylor polynomial
φ p ( B) AR polynomial of B of order p, p Non-seasonal differencing operator = 1 B
 ARIMA Noion The ARIMA roceure coues he reer esies for given sesonl or non-sesonl univrie ARIMA oel. I lso coues he fie vlues, forecsing vlues, n oher rele vribles for he oel. The following noion is use
ARIMA Noion The ARIMA roceure coues he reer esies for given sesonl or non-sesonl univrie ARIMA oel. I lso coues he fie vlues, forecsing vlues, n oher rele vribles for he oel. The following noion is use
Existence and Uniqueness of Solution for a Fractional Order Integro-Differential Equation with Non-Local and Global Boundary Conditions
 Applied Mthetic 0 9-96 doi:0.436/.0.079 Pulihed Online Octoer 0 (http://www.scirp.org/journl/) Eitence nd Uniquene of Solution for Frctionl Order Integro-Differentil Eqution with Non-Locl nd Glol Boundry
Applied Mthetic 0 9-96 doi:0.436/.0.079 Pulihed Online Octoer 0 (http://www.scirp.org/journl/) Eitence nd Uniquene of Solution for Frctionl Order Integro-Differentil Eqution with Non-Locl nd Glol Boundry
Abstract. W.W. Memudu 1 and O.A. Taiwo, 2
 Theoreicl Mhemics & Applicions, vol. 6, no., 06, 3-50 ISS: 79-9687 prin, 79-9709 online Scienpress d, 06 Eponenilly fied collocion pproimion mehod for he numericl soluions of Higher Order iner Fredholm
Theoreicl Mhemics & Applicions, vol. 6, no., 06, 3-50 ISS: 79-9687 prin, 79-9709 online Scienpress d, 06 Eponenilly fied collocion pproimion mehod for he numericl soluions of Higher Order iner Fredholm
FM Applications of Integration 1.Centroid of Area
 FM Applicions of Inegrion.Cenroid of Are The cenroid of ody is is geomeric cenre. For n ojec mde of uniform meril, he cenroid coincides wih he poin which he ody cn e suppored in perfecly lnced se ie, is
FM Applicions of Inegrion.Cenroid of Are The cenroid of ody is is geomeric cenre. For n ojec mde of uniform meril, he cenroid coincides wih he poin which he ody cn e suppored in perfecly lnced se ie, is
dt = C exp (3 ln t 4 ). t 4 W = C exp ( ln(4 t) 3) = C(4 t) 3.
 Mah Rahman Exam Review Soluions () Consider he IVP: ( 4)y 3y + 4y = ; y(3) = 0, y (3) =. (a) Please deermine he longes inerval for which he IVP is guaraneed o have a unique soluion. Soluion: The disconinuiies
Mah Rahman Exam Review Soluions () Consider he IVP: ( 4)y 3y + 4y = ; y(3) = 0, y (3) =. (a) Please deermine he longes inerval for which he IVP is guaraneed o have a unique soluion. Soluion: The disconinuiies
Exercises: Similarity Transformation
 Exercises: Similariy Transformaion Problem. Diagonalize he following marix: A [ 2 4 Soluion. Marix A has wo eigenvalues λ 3 and λ 2 2. Since (i) A is a 2 2 marix and (ii) i has 2 disinc eigenvalues, we
Exercises: Similariy Transformaion Problem. Diagonalize he following marix: A [ 2 4 Soluion. Marix A has wo eigenvalues λ 3 and λ 2 2. Since (i) A is a 2 2 marix and (ii) i has 2 disinc eigenvalues, we
Physics 2A HW #3 Solutions
 Chper 3 Focus on Conceps: 3, 4, 6, 9 Problems: 9, 9, 3, 41, 66, 7, 75, 77 Phsics A HW #3 Soluions Focus On Conceps 3-3 (c) The ccelerion due o grvi is he sme for boh blls, despie he fc h he hve differen
Chper 3 Focus on Conceps: 3, 4, 6, 9 Problems: 9, 9, 3, 41, 66, 7, 75, 77 Phsics A HW #3 Soluions Focus On Conceps 3-3 (c) The ccelerion due o grvi is he sme for boh blls, despie he fc h he hve differen
Analytic solution of linear fractional differential equation with Jumarie derivative in term of Mittag-Leffler function
 Anlyic soluion of liner frcionl differenil equion wih Jumrie derivive in erm of Mig-Leffler funcion Um Ghosh (), Srijn Sengup (2), Susmi Srkr (2b), Shnnu Ds (3) (): Deprmen of Mhemics, Nbdwip Vidysgr College,
Anlyic soluion of liner frcionl differenil equion wih Jumrie derivive in erm of Mig-Leffler funcion Um Ghosh (), Srijn Sengup (2), Susmi Srkr (2b), Shnnu Ds (3) (): Deprmen of Mhemics, Nbdwip Vidysgr College,
PHYSICS 1210 Exam 1 University of Wyoming 14 February points
 PHYSICS 1210 Em 1 Uniersiy of Wyoming 14 Februry 2013 150 poins This es is open-noe nd closed-book. Clculors re permied bu compuers re no. No collborion, consulion, or communicion wih oher people (oher
PHYSICS 1210 Em 1 Uniersiy of Wyoming 14 Februry 2013 150 poins This es is open-noe nd closed-book. Clculors re permied bu compuers re no. No collborion, consulion, or communicion wih oher people (oher
rank Additionally system of equation only independent atfect Gawp (A) possible ( Alb ) easily process form rang A. Proposition with Definition
 Defiion nexivnol numer ler dependen rows mrix sid row Gwp elimion mehod does no fec h numer end process i possile esily red rng fc for mrix form der zz rn rnk wih m dcussion i holds rr o Proposiion ler
Defiion nexivnol numer ler dependen rows mrix sid row Gwp elimion mehod does no fec h numer end process i possile esily red rng fc for mrix form der zz rn rnk wih m dcussion i holds rr o Proposiion ler
Chapter 3 Common Families of Distributions
 Chaer 3 Common Families of Disribuions Secion 31 - Inroducion Purose of his Chaer: Caalog many of common saisical disribuions (families of disribuions ha are indeed by one or more arameers) Wha we should
Chaer 3 Common Families of Disribuions Secion 31 - Inroducion Purose of his Chaer: Caalog many of common saisical disribuions (families of disribuions ha are indeed by one or more arameers) Wha we should
2k 1. . And when n is odd number, ) The conclusion is when n is even number, an. ( 1) ( 2 1) ( k 0,1,2 L )
 Scholrs Journl of Engineering d Technology SJET) Sch. J. Eng. Tech., ; A):8-6 Scholrs Acdemic d Scienific Publisher An Inernionl Publisher for Acdemic d Scienific Resources) www.sspublisher.com ISSN -X
Scholrs Journl of Engineering d Technology SJET) Sch. J. Eng. Tech., ; A):8-6 Scholrs Acdemic d Scienific Publisher An Inernionl Publisher for Acdemic d Scienific Resources) www.sspublisher.com ISSN -X
Probability, Estimators, and Stationarity
 Chper Probbiliy, Esimors, nd Sionriy Consider signl genered by dynmicl process, R, R. Considering s funcion of ime, we re opering in he ime domin. A fundmenl wy o chrcerize he dynmics using he ime domin
Chper Probbiliy, Esimors, nd Sionriy Consider signl genered by dynmicl process, R, R. Considering s funcion of ime, we re opering in he ime domin. A fundmenl wy o chrcerize he dynmics using he ime domin
THE GENERALIZED PASCAL MATRIX VIA THE GENERALIZED FIBONACCI MATRIX AND THE GENERALIZED PELL MATRIX
 J Korean Mah Soc 45 008, No, pp 479 49 THE GENERALIZED PASCAL MATRIX VIA THE GENERALIZED FIBONACCI MATRIX AND THE GENERALIZED PELL MATRIX Gwang-yeon Lee and Seong-Hoon Cho Reprined from he Journal of he
J Korean Mah Soc 45 008, No, pp 479 49 THE GENERALIZED PASCAL MATRIX VIA THE GENERALIZED FIBONACCI MATRIX AND THE GENERALIZED PELL MATRIX Gwang-yeon Lee and Seong-Hoon Cho Reprined from he Journal of he
ECE Microwave Engineering. Fall Prof. David R. Jackson Dept. of ECE. Notes 10. Waveguides Part 7: Transverse Equivalent Network (TEN)
 EE 537-635 Microwve Engineering Fll 7 Prof. Dvid R. Jcson Dep. of EE Noes Wveguides Pr 7: Trnsverse Equivlen Newor (N) Wveguide Trnsmission Line Model Our gol is o come up wih rnsmission line model for
EE 537-635 Microwve Engineering Fll 7 Prof. Dvid R. Jcson Dep. of EE Noes Wveguides Pr 7: Trnsverse Equivlen Newor (N) Wveguide Trnsmission Line Model Our gol is o come up wih rnsmission line model for
LAPLACE TRANSFORM OVERCOMING PRINCIPLE DRAWBACKS IN APPLICATION OF THE VARIATIONAL ITERATION METHOD TO FRACTIONAL HEAT EQUATIONS
 Wu, G.-.: Lplce Trnsform Overcoming Principle Drwbcks in Applicion... THERMAL SIENE: Yer 22, Vol. 6, No. 4, pp. 257-26 257 Open forum LAPLAE TRANSFORM OVEROMING PRINIPLE DRAWBAKS IN APPLIATION OF THE VARIATIONAL
Wu, G.-.: Lplce Trnsform Overcoming Principle Drwbcks in Applicion... THERMAL SIENE: Yer 22, Vol. 6, No. 4, pp. 257-26 257 Open forum LAPLAE TRANSFORM OVEROMING PRINIPLE DRAWBAKS IN APPLIATION OF THE VARIATIONAL
..,..,.,
 57.95. «..» 7, 9,,. 3 DOI:.459/mmph7..,..,., E-mil: yshr_ze@mil.ru -,,. -, -.. -. - - ( ). -., -. ( - ). - - -., - -., - -, -., -. -., - - -, -., -. : ; ; - ;., -,., - -, []., -, [].,, - [3, 4]. -. 3 (
57.95. «..» 7, 9,,. 3 DOI:.459/mmph7..,..,., E-mil: yshr_ze@mil.ru -,,. -, -.. -. - - ( ). -., -. ( - ). - - -., - -., - -, -., -. -., - - -, -., -. : ; ; - ;., -,., - -, []., -, [].,, - [3, 4]. -. 3 (
Properties of Logarithms. Solving Exponential and Logarithmic Equations. Properties of Logarithms. Properties of Logarithms. ( x)
 Properies of Logrihms Solving Eponenil nd Logrihmic Equions Properies of Logrihms Produc Rule ( ) log mn = log m + log n ( ) log = log + log Properies of Logrihms Quoien Rule log m = logm logn n log7 =
Properies of Logrihms Solving Eponenil nd Logrihmic Equions Properies of Logrihms Produc Rule ( ) log mn = log m + log n ( ) log = log + log Properies of Logrihms Quoien Rule log m = logm logn n log7 =
